Chủ đề phương trình quy về phương trình bậc hai Toán 10 KNTTVCS

Tài liệu gồm 28 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tuyển tập một số dạng phương trình cơ bản và bài tập trắc nghiệm chủ đề phương trình quy về phương trình bậc hai Toán 10 Kết Nối Tri Thức Với Cuộc Sống, có đáp án và lời giải chi tiết.

83 42 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT)

Môn: Toán 10

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề 4: PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
I. MỘT SỐ DẠNG PHƯƠNG TRÌNH CƠ BẢN
1. Phương trình dạng:
22
ax bx c dx ex f
Để giải phương trình:
Ta làm như sau:
22
ax bx c dx ex f
Bước 1: Bình phương hai vế, rút gọn rồi giải phương trình bậc 2 hoặc bậc nhất.
Bước 2: Thử lại các giá trị
x
tìm được có thỏa phương trình ban đầu hay không? Sau đó
kết luận nghiệm
Hoặc
hoÆc chän
22
22
22
00ax bx c dx ex f
ax bx c dx ex f
ax bx c dx ex f
Câu 1:
Giải phương trình
22
2 4 2 2. x x x x
Câu 2: Giải các phương trình sau:
a)
22
3 6 1 2 9 1; x x x x
b)
22
2 3 5 7. x x x
2. Phương trình dạng:
2
ax bx c dx e
Để giải phương trình:
Ta làm như sau:
Bước 1: Bình phương hai vế, rút gọn rồi giải phương trình bậc 2 hoặc bậc nhất.
Bước 2: Thử lại các giá trị
x
tìm được có thỏa phương trình ban đầu hay không? Sau đó
kết luận nghiệm
Hoặc
2
2
2
0dx e
ax bx c dx e
ax bx c dx e

Câu 3:
Giải phương trình
2
2 5 9 1x x x
Câu 4: Giải các phương trình sau:
b)
2
2 3 1x x x
b)
2
3 13 14 3x x x
Câu 5: Giải các phương trình sau:
a)
22
3 4 1 2 4 3; x x x x
b)
22
2 3 2 5; x x x
c)
22
2 3 3 1; x x x x
d)
22
5 4 2 4 2. x x x x
Câu 6: Giải các phương trình sau:
a)
2
6 13 13 2 4; x x x
b)
2
2 5 3 3 ; x x x
c)
2
3 17 23 3; x x x
d)
2
2 4 2. x x x
Câu 7: Giải các phương trình sau:
a)
1 3; xx
b)
2
9 5 ; x x x
c)
2
3 6 3 2 1;x x x
d)
2
2 3 1 1; x x x
e)
2
3 3 ; x x x
f)
2
3 4 4 3 2. x x x
Câu 8: Giải các phương trình sau:
a)
2
4 3 2 0; x x x
b)
2
( 3 2) 3 0. x x x
Câu 9: Giải các phương trình sau:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
a)
22
3 10 12; x x x x
b)
2
1 5 1 1. x x x
Câu 10: Giải các phương trình sau:
a)
22
2 8 8 3; x x x x
b)
2
1 3 3 4 5 2 0; x x x x
c)
2
4 1 3 5 2 6; x x x x
d)
2
2 8 4 4 2 ; x x x x
e)
3
2
5 2 5 2 2. x x x x
Câu 11: Tìm m để phương trình
2
4 3 0x x x m
có đúng hai nghiệm phân biệt.
Câu 12: Tìm tham số
m
để phương trình
2
0x x x m
chỉ có một nghiệm.
Câu 13: Tìm
m
để phương trình
2
1x x m x
có duy nhất một nghiệm.
Câu 14: Tìm
m
để phương trình
2
2 2 1x x m x
có hai nghiệm phân biệt.
Câu 15: Cho tứ giác
ABCD
có
;AB CD
2;AB
13;BC
8;CD
5.DA
Gọi
H
là giao điểm của
AB
và
CD
và đặt
x AH
. Hãy thiết lập một phuơng trình để tính độ dài
x
, từ đó tính diện
tích tứ giác
.ABCD
Câu 16: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường.
Minh đứng tại vị trí
A
cách lề đường một khoảng
50m
để chờ Hùng. Khi nhìn thấy Hùng
đạp xe đến địa điểm
B
, cách mình một đoạn
200m
thì Minh bắt đầu đi bộ ra lề đường để bắt
kịp xe. Vận tốc đi bộ của Minh là
5/km h
, vận tốc xe đạp của Hùng là
15 /km h
. Hãy xác định
vị trí
C
trên lề đường (Hình vẽ) để hai bạn gặp nhau mà không bạn nào phải chờ người kia
(làm tròn kết quả đến hàng phần mười).
II. BÀI TẬP TRẮC NGHIỆM
Câu 17: Nghiệm của phương trình
2 1 3xx
là
A.
3
4
x
. B.
2
3
x
. C.
4
3
x
. D.
3
2
x
.
Câu 18: Tập nghiệm của phương trình
2 3 3xx
là
A.
2;6T
. B.
T 
. C.
6T
. D.
2;6T
.
Câu 19: Tổng tất cả các nghiệm của phương trình và
2
3 2 2x x x
là
A.
3
. B.
4
. C.
1
. D.
3
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 20: Tập nghiệm của phương trình
32xx
là
A.
S 
. B.
1
2;
2
S




. C.
1
2
S



. D.
1
2
S




.
Câu 21: Số nghiệm của phương trình
2
4 1 3x x x
là
A. Vô số. B.
0.
C.
1.
D.
2.
Câu 22: Nghiệm của phương trình
2
7 10 4 x x x
thuộc tập nào dưới đây?
A.
4;5
. B.
5;6
. C.
5;6
. D.
5;6
.
Câu 23: Số nghiệm của phương trình
2
2 14 3x x x
là
A. Vô số. B.
0.
C.
1.
D.
2.
Câu 24: Tập nghiệm của phương trình
2
2 4 3 0x x x
là
A.
2;3S
. B.
2S
. C.
1;3S
. D.
1;2;3S
.
Câu 25: Phương trình
2
1 1 0x x x
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 26: Số nghiệm của phương trình
2
3 2 3
0
1
x x x
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 27: Số nghiệm của phương trình
2
4 2 3 0x x x
là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 28: Số nghiệm của phương trình
2
2 3 2 0x x x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 29: Số nghiệm của phương trình
2
16 3 0xx
là
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 30: Tổng các nghiệm của phương trình
2
3 2 6 9x x x
bằng
A.
2
. B.
3
. C.
1
. D.
7
.
Câu 31: Phương trình
2
1 2 1 0x x x
có tất cả bao nhiêu nghiệm?
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 32: Phương trình
2 2 2
6 17 6x x x x x
có bao nhiêu nghiệm phân biệt?
A. 2. B. 1. C. 3. D. 4.
Câu 33: Tìm tập hợp nghiệm của phương trình
3 2 1xx
.
A.
2
. B.
1; 2
. C.
1;2
. D.
1
.
Câu 34: Số nghiệm nguyên của phương trình sau
3 2 1 1xx
là:
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 35: Số nghiệm của phương trình
3 1 2 1xx
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 36: Số nghiệm của phương trình
2
2 2 3 6 1 7x x x x x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 37: Tổng các nghiệm của phương trình
22
1 10 3 2x x x x
bằng
A.
4.
B.
1.
C.
2.
D.
3.
Câu 38: Biết phương trình
22
2 2 2 2 10 x x x x x
có
2
nghiệm phân biệt
2x
và
3
; , .
3

ab
x a b
Tính
22
.S a b
A. 81. B. 90. C. 85. D. 91.
Câu 39: Nếu đặt
1tx
thì phương trình
2 1 0xx
trở thành phương trình nào trong các
phương trình sau?
A.
2
10tt
. B.
2
0tt
. C.
2
20tt
. D.
2
20tt
.
Câu 40: Cho phương trình
22
3 5 2 6 5 0x x x x
. Nếu đặt
2
35t xx 
thì phương trình đã
cho trở thành phương trình nào dưới đây?
A.
2
02 15tt
. B.
2
02 15tt
. C.
2
50t t
. D.
2
50tt
.
Câu 41: Tổng các nghiệm của phương trình
22
4 3 27 3 22x x x x
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 42: Số nghiệm của phương trình
22
2 5 2 3x x x x
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 43: Số nghiệm của phương trình
22
3 86 19 3 16 0x x x x
là.
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 44: Tích của các nghiệm của phương trình
22
3 9 5 2 3 3 1x x x x
bằng
A.
2
. B.
2
. C.
3
. D.
3
.
Câu 45: Cho phương trình:
22
5 2 2 5 10 0x x x x
. Đặt
2
5 10t x x
thì phương trình trở
thành phương trình nào sau đây?
A.
2
2 10 0tt
. B.
2
2 2 0tt
. C.
2
2 8 0tt
. D.
2
2 8 0tt
.
Câu 46: Phương trình:
23
2 5 1 7 1x x x
có nghiệm là
ab
thì
2ab
bằng
A.
2.
B.
1.
C.
.
3.
D.
4.
Câu 47: Số nghiệm của phương trình
22
3 86 19 3 16 0x x x x
là.
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 48: Tổng bình phương các nghiệm của phương trình
22
5 2 2 5 10 0x x x x
là
A.
5
. B.
13
. C.
10
. D.
25
.
Câu 49: Tổng các bình phương các nghiệm của phương trình
2
1 3 3 4 5 2 0x x x x
là:
A.
17
. B.
4
. C.
16
. D.
8
.
Câu 50: Biết phương trình
2
4 3 1 8 5 6 2x x x x x
có một nghiệm dạng
x a b
với
,0ab
. Tính
.ab
A. 7. B. 5. C. 4. D. 6.
Câu 51: Tìm tất cả các giá trị của tham số
m
để phương trình
10x x m
có hai nghiệm phân
biệt.
A.
;1 m
. B.
1; m
. C.
1; m
. D.
;1 . m
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 52: Tìm tất cả các giá trị của tham số
m
để phương trình
2
0
3
x m x m
x
có nghiệm.
A.
;1m 
. B.
1;m 
. C.
1;m 
. D.
m
.
Câu 53: Tìm tất cả các giá trị của tham số
m
để phương trình
2
40x x x m
có ba nghiệm phân
biệt.
A.
;0 m
. B.
0; m
. C.
0; m
. D.
;0 . m
Câu 54: Số giá trị nguyên của tham số
m
để phương trình
2
1x x m x
có hai nghiệm phân
biệt là
A.
4
. B.
0
. C. Vô số. D.
3
.
Câu 55: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
21x m x
có 2 nghiệm phân
biệt?
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 56: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 2 2x x m x
có nghiệm.
A.
1m
. B.
1;m 
. C.
2m
. D.
2m
.
Câu 57: Giá trị của tham số
m
để phương trình
2
2 2 2x x m x
có 2 nghiệm phân biệt là
;m a b
với
,ab
. Tính
S a b
.
A.
1
.
8
S 
B.
81
.
8
S
C.
5.S
D.
41
.
8
S
Câu 58: Tìm tất cả các giá trị
m
để phương trình
2
2 3 2 2x x m x
có nghiệm.
A.
2m 
. B.
2m 
. C.
2m
. D.
2m
.
Câu 59: Có bao nhiêu giá trị nguyên của tham số m để phương trình
22
4 1 ( 1) 0x x m
có
nghiệm thuộc khoảng
0; 15 ?
A.
1
. B.
4
. C.
3
. D.
0.
Câu 60: Có bao nhiêu giá trị m nguyên để phương trình
2
4 3 3 2 9 1 0x x x m
có
nghiệm?
A. 9. B. 11. C. 5. D. 10.
Câu 61: Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 2 2 4 0x x x m
có
nghiệm?
A.
4
. B.
5
. C. Vô số. D.
10
.
LỜI GIẢI CHI TIẾT
I. MỘT SỐ DẠNG PHƯƠNG TRÌNH CƠ BẢN
Câu 1:
Giải phương trình
22
2 4 2 2. x x x x
Lời giải:
Bình phương hai vế của phương trình ta được:
22
2 4 2 2x x x x
Sau khi thu gọn ta được
2
30xx
Từ đó tìm được
0x
hoặc
3x
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy chỉ có
3x
thỏa mãn.
Vậy nghiệm của phương trình đã cho là
3x
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 2: Giải các phương trình sau:
c)
22
3 6 1 2 9 1x x x x
b)
22
2 3 5 7x x x
Lời giải:
a)
22
3 6 1 2 9 1x x x x
Bình phương hai vế của phương trình ta được
22
3 6 1 2 9 1x x x x
.
Sau khi thu gọn ta được
2
5 3 0xx
.
Từ đó tìm được
0x
hoặc
3
5
x 
.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy
0x
và
3
5
x 
thỏa
mãn.
Vậy tập nghiệm của phương trình đã cho là
3
0;
5
S




b)
22
2 3 5 7x x x
Bình phương hai vế của phương trình ta được
22
2 3 5 7x x x
.
Sau khi thu gọn ta được
2
3 2 0xx
.
Từ đó tìm được
1x
hoặc
2x
.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy không có giá trị nào thỏa
mãn.
Vậy tập nghiệm của phương trình đã cho là
S 
.
2. Phương trình dạng:
2
ax bx c dx e
Để giải phương trình:
Ta làm như sau:
2
ax bx c dx e
Bước 1: Bình phương hai vế, rút gọn rồi giải phương trình bậc 2 hoặc bậc nhất.
Bước 2: Thử lại các giá trị
x
tìm được có thỏa phương trình ban đầu hay không? Sau đó
kết luận nghiệm
Hoặc
2
2
2
0dx e
ax bx c dx e
ax bx c dx e

Câu 3:
Giải phương trình
2
2 5 9 1x x x
Lời giải:
Bình phương hai vế của phương trình ta được:
22
2 5 9 2 1x x x x
.
Sau khi thu gọn ta được
2
3 10 0xx
.
Từ đó tìm được
2x 
hoặc
5x
.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy chỉ có
5x
thỏa mãn.
Vậy nghiệm của phương trình đã cho là
5x
.
Câu 4: Giải các phương trình sau:
d)
2
2 3 1x x x
b)
2
3 13 14 3x x x
Lời giải:
c) Bình phương hai vế của phương trình ta được
22
2 3 1 2x x x x
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Sau khi thu gọn ta được
2
3 2 0xx
Từ đó tìm được
1x 
hoặc
2x 
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy
1x 
hoặc
2x 
thỏa
mãn.
Vậy tập nghiệm của phương trình đã cho là
1; 2S
.
d) Bình phương hai vế của phương trình ta được
22
3 13 14 6 9x x x x
.
Sau khi thu gọn ta được
2
2 7 5 0xx
.
Từ đó tìm được
1x
hoặc
5
2
x
.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy không có giá trị nào thỏa
mãn.
Vậy tập nghiệm của phương trình đã cho là
S 
.
*Chú ý: Một số dạng phương trình chứa ẩn dưới dấu căn khác
1) Dạng:
2
0
BA
B
BA
2) Dạng:
0; 0
2
AB
A B C
A B AB C

3) Dạng:
DCBA
.
* Nếu A+B = C+D (hoặc A.B = C.D) thì bình phương 2 vế ta được phương trình tương
đương.
* Nếu A+C = B+D (hoặc A.C = B.D) thì phải đưa phương trình về dạng:
BDCA
sau đó bình phương hai vế, tìm nghiệm sau đó thử lại để chọn nghiệm.
4) Dạng:
3
33
CBA
* Lập phương hai vế ta được:
3 3 3
3.A B AB A B C
.
Sau đó thay thế:
3
33
CBA
vào phương trình, ta được:
CABCBA
3
.3
Chú ý: Sự thay thế này có thể dẫn đến nghiệm ngoại lai, vì vậy phải thử lại nghiệm.
Câu 5: Giải các phương trình sau:
a)
22
3 4 1 2 4 3; x x x x
b)
22
2 3 2 5; x x x
c)
22
2 3 3 1; x x x x
d)
22
5 4 2 4 2. x x x x
Lời giải:
a)
22
3 4 1 2 4 3x x x x
22
3 4 1 2 4 3x x x x
2
4x
2
2
x
x

.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy cả hai đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
2;2S 
.
b)
22
2 3 2 5x x x
22
2 3 2 5x x x
2
3 2 8 0xx
4
3
2
x
x

Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy
4
3
x
thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
4
3
S



.
c)
22
2 3 3 1x x x x
22
2 3 3 1x x x x
2
3 4 4 0xx
2
3
2
x
x

.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy cả hai giá trị này không
thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
S 
.
d)
22
5 4 2 4 2x x x x
22
5 4 2 4 2x x x x
2
60xx
3
2
x
x

.
Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy
2x
thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
2S
.
Câu 6: Giải các phương trình sau:
a)
2
6 13 13 2 4; x x x
b)
2
2 5 3 3 ; x x x
c)
2
3 17 23 3; x x x
d)
2
2 4 2. x x x
Lời giải:
a)
2
6 13 13 2 4x x x
22
6 13 13 4 16 16x x x x
2
2 3 3 0xx
3 33
4
3 33
4
x
x
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
3 34
4
S





b)
2
2 5 3 3x x x
22
2 5 3 9 6x x x x
2
60xx
3
2
x
x

Thay lần lượt hai giá trị này của
x
vào phương trình đã cho, ta thấy cả hai giá trị này không
thỏa mãn.
Vậy tập nghiệm của phương trình là
S 
c)
2
3 17 23 3x x x
22
3 17 23 6 9x x x x
2
2 11 14 0xx
2
7
2
x
x
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy
7
2
x
thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
7
2
S



d)
2
2 4 2x x x
22
2 4 4 4x x x x
2
2 6 0xx
0
3
x
x
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy
3x
thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là
3S
.
Câu 7: Giải các phương trình sau:
a)
1 3; xx
b)
2
9 5 ; x x x
c)
2
3 6 3 2 1;x x x
d)
2
2 3 1 1; x x x
e)
2
3 3 ; x x x
f)
2
3 4 4 3 2. x x x
Lời giải:
a)
2
2
3
30
3
1 3 5
5
7 10 0
13
2


x
x
x
x x x
x
xx
xx
x
Vậy phương trình có nghiệm
5x
.
b) Ta có
2
2 2 2
00
9 41
95
4
9 5 2 9 5 0
xx
x x x x
x x x x x




.
Vậy phương trình trên có
2
nghiệm.
c) Ta có:
2
22
2 1 0
3 6 3 2 1
3 6 3 4 4 1
x
x x x
x x x x

2
1
1
2
2
13
2 2 0
13
x
x
xl
xx
xn








.
d)
2
2 3 1 1x x x
2
2
10
2 3 1 1
x
x x x

2
1
0
x
xx

1
0
1
x
x
x
1x
.
e) Ta có
2
2 2 2
00
3 33
33
4
3 3 2 3 3 0
xx
x x x x
x x x x x





Vậy phương trình trên chỉ có
1
nghiệm.
f) Ta có:
2
2
2
2
2
3 2 0
3 4 4 3 2
3
3 4 4 3 2
6 16 0
x
x
x x x
x x x
xx





Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2
3
0
8
0,
3
x
x
xx

.
Vậy tập nghiệm của phương trình là
0
.
Câu 8: Giải các phương trình sau:
a)
2
4 3 2 0; x x x
b)
2
( 3 2) 3 0. x x x
Lời giải:
a) ĐK:
2x
.
2
1 ( )
4 3 0
3 ( )
20
2 ( )
xl
xx
pt x tm
x
x tm

.
b) ĐK:
3x
.
Ta có:
2
( 3 2) 3 0x x x
2
1
3 2 0
2
30
3

x
xx
x
x
x
3x
.
Câu 9: Giải các phương trình sau:
a)
22
3 10 12; x x x x
b)
2
1 5 1 1. x x x
Lời giải:
a) Điều kiện:
2
10 0 10 10 xx
.
Khi đó:
22
3 10 12 x x x x
22
3 10 3 4 3 10 4 0 x x x x x x x
2
3
10 4

x
xx
.
Vì phương trình
2
10 4 xx
vô nghiệm với mọi
x
thoả
10 10 x
.
Vậy
3x 
là nghiệm duy nhất của phương trình đã cho.
b) ĐK:
1
.
5
x 
Phương trình
2
1 5 1 1 1 5 1 1 0x x x x x x
1
5 1 1 *
x
xx
Phương trình
22
1
11
0
*
0
3
5 1 2 1 3 0
3
x
xx
x
x
x
x x x x x
x



Vậy phương trình đã cho có các nghiệm là:
0; 1; 3x x x
.
Câu 10: Giải các phương trình sau:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
a)
22
2 8 8 3; x x x x
b)
2
1 3 3 4 5 2 0; x x x x
c)
2
4 1 3 5 2 6; x x x x
d)
2
2 8 4 4 2 ; x x x x
e)
3
2
5 2 5 2 2. x x x x
Lời giải:
a) Đặt
2
8t x x
,
0t
. Pt:
22
1
2 3 2 3 0
3
tL
t t t t
tN

.
Với
22
9
3 8 3 8 9 0
1
x
t x x x x
x

.
Vậy tổng các nghiệm của phương trình bằng
8
.
b)
2 2 2
1 3 3 4 5 2 0 4 3 3 4 5 2 0 x x x x x x x x
Đặt
2
4 5 0x x t t
ta được phương trình:
22
1(TM)
2 3 2 0 3 4 0
4 (L)

t
t t t t
t
Với
1,t
ta được
2 2 2
4 5 1 4 5 1 4 4 0 2. x x x x x x x
Vậy tổng bình phương nghiệm của phương trình trên là 4.
c) Ta có
2
4 1 3 5 2 6x x x x
22
5 2 3 5 2 0x x x x
.
Đặt
2
5 2 0t x x t
. Khi đó, phương trình trở thành:
2
4 3 0tt
1
4
tl
tn

.
+) Với
2
4: 5 2 4 t x x
2
5 2 16xx
2
5 14 0xx
2
7
x
x

.
d) Đặt
2
2 8 0t x x t
, khi đó phương trình trở thành:
2
0
4
4
t
tt
tL

.
Với
2
4
0: 2 8 0
2

x
t x x
x
.
e) Đặt
3
2
52t x x
ta được phương trình:
33
2 2 2 2 4 0 2t t t t t
Với
3
22
2
2: 5 2 2 5 6 0 .
3


x
t x x x x
x
Câu 11: Tìm m để phương trình
2
4 3 0x x x m
có đúng hai nghiệm phân biệt.
Lời giải:
Phương trình tương đương:
2
1
4 3 0
3
xm
xm
xm
xm
x
xx
x




.
Phương trình có đúng hai nghiệm phân biệt khi và chỉ khi
31m
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 12: Tìm tham số
m
để phương trình
2
0x x x m
chỉ có một nghiệm.
Lời giải:
Điều kiện
1xm
.
2
0x x x m
2
0
0
xx
xm


0
1
1
x
x
x m tm

.
Phương trình luôn có nghiệm
xm
. Để phương trình có nghiệm duy nhất thì
1.xm
Câu 13: Tìm
m
để phương trình
2
1x x m x
có duy nhất một nghiệm.
Lời giải:
Ta có:
2
22
1 0 1
1.
1 2 1
xx
x x m x
x x m x m x x





Bảng biến thiên
2
21y x x
trên
1; :

x
1
1

y
2
2

Dựa vào bảng biến thiên, yêu cầu bài toán
; 2 2 .m 
Câu 14: Tìm
m
để phương trình
2
2 2 1x x m x
có hai nghiệm phân biệt.
Lời giải:
Ta có:
2
2
2
2
10
1
2 2 1 .
41
2 2 1
x
x
x x m x
m x x
x x m x




Bảng biến thiên
2
41y x x
trên
1; :

x
1
2

y
4
5

Dựa vào bảng biến thiên, yêu cầu bài toán
4;5 .m
Câu 15: Cho tứ giác
ABCD
có
;AB CD
2;AB
13;BC
8;CD
5.DA
Gọi
H
là giao điểm của
AB
và
CD
và đặt
x AH
. Hãy thiết lập một phuơng trình để tính độ dài
x
, từ đó tính diện
tích tứ giác
.ABCD
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
+) Sử dụng định lí Pytago để tìm
x
.
Ta có:
2
25HD x
. Điều kiện:
2
0
0 5 *
25 0
x
x
x

Xét tam giác vuông
BHC
, ta có
222
HB HC BC
2
2
2 2 2 2 2
22
2 25 8 13 4 4 25 16 25 64 169 0
16 25 76 4 4 25 19 1
x x x x x x
x x x x
Bình phương hai vế của phương trình ta được
22
16 25 361 38x x x
Sau khi thu gọn ta được
2
3
17 38 39 0
13
17
x
xx
x
Thay lần lượt hai giá trị này của
x
vào phương trình
1
và kết hợp với điều kiện
*
, ta thấy
3x
thỏa mãn.
+) Để tính diện tích tứ giác
ABCD
, ta áp dụng công thức tính diện tích tam giác cho
,BHC AHD
.
Ta có
5, 12, 3, 4.HB HC HA HD
1 1 1
. . . . 5.12 3.4 24
2 2 2
ABCD BHC AHD
S S S HB HC HA HD
.
Câu 16: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường.
Minh đứng tại vị trí
A
cách lề đường một khoảng
50m
để chờ Hùng. Khi nhìn thấy Hùng
đạp xe đến địa điểm
B
, cách mình một đoạn
200m
thì Minh bắt đầu đi bộ ra lề đường để bắt
kịp xe. Vận tốc đi bộ của Minh là
5/km h
, vận tốc xe đạp của Hùng là
15 /km h
. Hãy xác định
vị trí
C
trên lề đường (Hình vẽ) để hai bạn gặp nhau mà không bạn nào phải chờ người kia
(làm tròn kết quả đến hàng phần mười).
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Vận tốc của bạn Minh:
1
5/v km h
.
Vận tốc của bạn Hùng:
2
15 /v km h
.
Áp dụng định lý Pithago vào tam giác vuông
AHB
:
22
15
0,2 0,05
20
BH km
Gọi
,0BC x km x
.
Suy ra:
15
20
CH x
,
15
20
x
.
Ta cần xác định vị trí điểm
C
để Minh và Hùng gặp nhau mà không bạn nào phải chờ người
kia
Nghĩa là: ta cần tìm
x
để thời gian hai bạn di chuyển đến
C
là bằng nhau.
Thời gian Hùng đi từ
B
đến
C
là:
2
2
15
BC
S
x
th
v

.
Quãng đường
AC
mà Minh đã đi là:
2
2
22
15
0,05
20
AC CH AH x




Thời gian Minh đã đi từ
A
đến
C
là:
2
2
1
1
15
0,05
20
5
AC
x
S
th
v





.
Theo yêu cầu bài toán:
2
2
15
0.05
20
5 15
x
x




Bình phương 2 vế:
2
2
2
15
0.05
20
25 225
x
x




2 2 2
0,3
3 15 9 9 15 9
9 8 0
0,1
80 10 400 10 25




x
x x x x x
x
Vì
15
0 0.19
20
x
nên
0,1x
thỏa mãn.
Vậy hai bạn Minh và Hùng di chuyển đến vị trí
C
cách điểm
B
một đoạn
0,1 100 .x km m
II. BÀI TẬP TRẮC NGHIỆM
Câu 17: Nghiệm của phương trình
2 1 3xx
là
A.
3
4
x
. B.
2
3
x
. C.
4
3
x
. D.
3
2
x
.
Lời giải:
Thay các nghiệm
x
vào phương trình thấy
4
3
x
là nghiệm.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 18: Tập nghiệm của phương trình
2 3 3xx
là
A.
2;6T
. B.
T 
. C.
6T
. D.
2;6T
.
Lời giải:
Ta có
2
30
2 3 3
2 3 3
x
xx
xx

2
3
3
6
2
8 12 0
6
x
x
x
x
xx
x


.
Vậy phương trình có tập nghiệm
6T
.
Câu 19: Tổng tất cả các nghiệm của phương trình và
2
3 2 2x x x
là
A.
3
. B.
4
. C.
1
. D.
3
.
Lời giải:
Ta có
2
22
2
22
3 2 2
0
3 2 2 4 0
4
x
xx
x x x
x
x x x x x
x



.
Vậy tập nghiệm của phương trình
0;4S
nên tổng các nghiệm là
4
.
Câu 20: Tập nghiệm của phương trình
32xx
là
A.
S 
. B.
1
2;
2
S




. C.
1
2
S



. D.
1
2
S




.
Lời giải:
Ta có:
20
1
32
1
2
2
2
2
3
x
x
x
x
xx
x
x



.
Vậy tập nghiệm của phương trình là
1
2
S



.
Câu 21: Số nghiệm của phương trình
2
4 1 3x x x
là
A. Vô số. B.
0.
C.
1.
D.
2.
Lời giải:
Ta có:
2
4 1 3x x x
22
30
4 1 6 9
x
x x x x

3
1
x
x
(vô nghiệm).
Câu 22: Nghiệm của phương trình
2
7 10 4 x x x
thuộc tập nào dưới đây?
A.
4;5
. B.
5;6
. C.
5;6
. D.
5;6
.
Lời giải:
Ta có:
2
7 10 4 x x x
2
2
40
7 10 4

x
x x x
4
6 5;6 .
6
x
x
x
Câu 23: Số nghiệm của phương trình
2
2 14 3x x x
là
A. Vô số. B.
0.
C.
1.
D.
2.
Lời giải:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
22
2
2
30
2 14 3 2 14 3
2 14 3
x
x x x x x x
x x x

2 2 2
33
2 14 9 6 8 9 0
xx
x x x x x x





3
9
1
x
x
x

(loaïi)
(nhaän)
1x
.
Vậy phương trình đã cho có nghiệm là
1x 
.
Câu 24: Tập nghiệm của phương trình
2
2 4 3 0x x x
là
A.
2;3S
. B.
2S
. C.
1;3S
. D.
1;2;3S
.
Lời giải:
Điều kiện:
2 0 2xx
(*).
Với điều kiện (*), phương trình đã cho tương đương với
2
2
20
1
4 3 0
3
x
x
x
xx
x


.
So với điều kiện (*) chỉ có
2x
,
3x
thỏa mãn.
Vậy tập nghiệm của phương trình là
2;3S
.
Câu 25: Phương trình
2
1 1 0x x x
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải:
Điều kiện
1 0 1xx
.
Ta có
2
1 1 0x x x
2
0
0
1 0 1
1 0 1
x
x
xx
xx
1x
Vậy
1S
.
Câu 26: Số nghiệm của phương trình
2
3 2 3
0
1
x x x
x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải:
Điều kiện
3x
.
Khi đó pt
2
1
3 2 0
2
30
3
x
xx
x
x
x

. Kết hợp với điều kiện suy ra phương trình có nghiệm
duy nhất
3x
.
Câu 27: Số nghiệm của phương trình
2
4 2 3 0x x x
là
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có
2
4 2 3 0x x x
3
2
0
2
3
2
x
x
x
x

3
2
2
x
x
.
Vậy phương trình có
2
nghiệm phân biệt.
Câu 28: Số nghiệm của phương trình
2
2 3 2 0x x x
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải:
Điều kiện xác định:
2x
(*)
Ta có:
2
2
2 /
20
2 3 2 0 2
1
3 2 0
2 /
x T M
x
x x x x
x KTM
xx
x T M


Vậy phương trình
1
có một nghiệm
2x
.
Câu 29: Số nghiệm của phương trình
2
16 3 0xx
là
A.
1
. B.
3
. C.
0
. D.
2
.
Lời giải:
+ Điều kiện
3*x
.
Phương trình
2
2
16 0
16 3 0
30
x
xx
x


.
+
2
4
16 0
4
x
x
x

so sánh điều kiện (*) suy ra
4x 
là một nghiệm của phương trình
đã cho.
+
3 0 3xx
thỏa mản điều kiện (*) suy ra
3x
là một nghiệm của phương trình đã
cho.
Vậy phương trình đã cho có
2
nghiệm.
Câu 30: Tổng các nghiệm của phương trình
2
3 2 6 9x x x
bằng
A.
2
. B.
3
. C.
1
. D.
7
.
Lời giải:
Điều kiện xác định của phương trình:
2 6 0 3xx
Ta có
2
3
3 2 6 9 3 2 6 3 0
2 6 3
x
x x x x x x
xx
Giải phương trình
2
2
30
3
2 6 3
4 3 0
2 6 3
x
x
xx
xx
xx



.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
3
1
1
3
3
x
x
x
x
x






Vậy phương trình đã cho có ba nghiệm là
1, 3, 3x x x
.
Tổng các nghiệm của phương trình là
1 3 3 1
.
Câu 31: Phương trình
2
1 2 1 0x x x
có tất cả bao nhiêu nghiệm?
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải:
+) Điều kiện
2
10
1
2 1 0
x
x
x



.
+)
2
2
2
1 0 1
10
1 2 1 0
2 1 2
2 1 0
x
x
x x x
xx
xx


Giải
1
:
2
1
10
1
xn
x
xl

Giải
2
:
22
12
2 1 2 1 1 2 1 0
12
xn
x x x x do x x x
xl


Vậy số nghiệm của phương trình là
2.
Câu 32: Phương trình
2 2 2
6 17 6x x x x x
có bao nhiêu nghiệm phân biệt?
A. 2. B. 1. C. 3. D. 4.
Lời giải:
2 2 2 2 2
2
2
2
2
6 17 6 6 17 1 0
0( )
60
6( )
0
17 0
4
17
17 1
17 1






x x x x x x x x
x TM
xx
xL
x
x
x
x
x
x
Vậy phương trình có 3 nghiệm phân biệt.
Câu 33: Tìm tập hợp nghiệm của phương trình
3 2 1xx
.
A.
2
. B.
1; 2
. C.
1;2
. D.
1
.
Lời giải:
Đk:
23x
3 2 1 3 3 2 2 3 3 2 2 2 2 2 x x x x x x x x x x
2
0
0
1
2
2




x
x
x
xx
x
.
Câu 34: Số nghiệm nguyên của phương trình sau
3 2 1 1xx
là:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải:
3 2 1 1xx
Điều kiện
30
1
2 1 0
2
x
x
x



.
Khi đó phương trình
3 1 2 1xx
3 1 2 2 1 2 1x x x
2 2 1 3xx
2
30
4 2 1 3
x
xx
2
3
14 13 0
x
xx
1x
.
Câu 35: Số nghiệm của phương trình
3 1 2 1xx
là
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải:
- Điều kiện:
1
3 1 0
1
2.
3
20
3
2
x
x
x
x
x




- PT
3 1 1 2xx
22
3 1 1 2xx
3 1 1 2 2 2x x x
2 2 4 2xx
2 2 1xx
2
2 1 0
2 2 1

x
xx
2
1
2
2 4 4 1
x
x x x
2
1
2
4 3 1 0
x
xx
1
2
1
1
4

x
x
x
1x
(thỏa mãn điều kiện).
Vậy phương trình đã cho có một nghiệm
1x
.
Câu 36: Số nghiệm của phương trình
2
2 2 3 6 1 7x x x x x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải:
Điều kiện
31x
.
Phương trình
2
2 2 3 6 1 7x x x x x
22
3 3 1x x x
3 3 1
3 3 1
x x x
x x x VN
1 1 2 3x x x
1
1 1 1 0
23
x
xx
x





10x
(do
1
1 1 0, 3;1
23
x
xx
x

)
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
1x
(thỏa mãn)
Câu 37: Tổng các nghiệm của phương trình
22
1 10 3 2x x x x
bằng
A.
4.
B.
1.
C.
2.
D.
3.
Lời giải:
Điều kiện xác định
10 10x
22
2
2
1 10 3 2
1( )
1 10 2 1
10 2(*)
x x x x
x TM
x x x x
xx
Giải (*):
2
2
2
2
2
10 2
3( )
10 2
1( )
x
x
xx
x TM
xx
xL

Vậy tổng các nghiệm của phương trình bằng 4.
Câu 38: Biết phương trình
22
2 2 2 2 10 x x x x x
có
2
nghiệm phân biệt
2x
và
3
; , .
3

ab
x a b
Tính
22
.S a b
A. 81. B. 90. C. 85. D. 91.
Lời giải:
Điều kiện của phương trình
2
2 2 0 . x x x
Phương trình đã cho tương đương
2
2
2
2 2 2 2 2 5 .
2 2 2 5 *
x
x x x x x
x x x
Ta có:
22
2
5
2 5 0
*
2
2 2 4 20 25
3 18 23 0




x
x
x x x x
xx
5
9 2 3
2
.
3
9 2 3
3



x
x
x
Suy ra
9; 2 85. a b S
Câu 39: Nếu đặt
1tx
thì phương trình
2 1 0xx
trở thành phương trình nào trong các
phương trình sau?
A.
2
10tt
. B.
2
0tt
. C.
2
20tt
. D.
2
20tt
.
Lời giải:
Ta có:
2 1 0 1 1 1 0.x x x x
Đặt
2
1 1.t x t x
Vậy pt trở thành:
2
1 0.tt
Câu 40: Cho phương trình
22
3 5 2 6 5 0x x x x
. Nếu đặt
2
35t xx 
thì phương trình đã
cho trở thành phương trình nào dưới đây?
A.
2
02 15tt
. B.
2
02 15tt
. C.
2
50t t
. D.
2
50tt
.
Lời giải:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2 2 2 2
3 5 2 6 5 0 3 5 2 3 5 0x x x x x x x x
Đặt
2
3 5 0. t x x
Suy ra
2 2 2 2
3 5 3 5t x x x x t
Phương trình đã cho trở thành:
22
2 5 05 2 15 0t tt t 
.
Câu 41: Tổng các nghiệm của phương trình
22
4 3 27 3 22x x x x
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Điều kiện xác định:
2
2
3 99
3 27 0 0
24
x x x



(luôn đúng).
Khi đó, ta có:
22
4 3 27 3 22x x x x
22
3 22 4 3 27 0x x x x
22
3 27 4 3 27 5 0x x x x
(1)
Đặt
2
3 27x x t
3 11
2
t




.
Phương trình (1) trở thành:
2
3 11
1
2
4 5 0
3 11
5
2
khoâng tm
tm
tt
tt
tt









.
Với
5t
ta có:
2 2 2
1
3 27 5 3 27 25 3 2 0
2
x
x x x x x x
x
.
Vậy tổng các nghiệm của phương trình đã cho là
3
.
Câu 42: Số nghiệm của phương trình
22
2 5 2 3x x x x
là
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải:
Ta có:
2
2 5 0, x x x
Đặt
2
25t x x
, ta có phương trình trở thành
2tt
2
2
2
2
2
24
1
5 4 0
2
4
t
t
t
t t t
t
tt
tt
t


.
Khi đó
2
2
4 2 5 1 0 1x x x x
. Thử lại ta thấy
1x
thỏa mãn.
Suy ra phương trình đã cho có một nghiệm.
Câu 43: Số nghiệm của phương trình
22
3 86 19 3 16 0x x x x
là.
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải:
Phương trình
2 2 2 2
3 86 19 3 16 0 3 16 19 3 16 70 0 *x x x x x x x x
Đặt
2
3 16t x x
,
0t
. Khi đó
2
14
* 19 70 0
5
tn
tt
tn
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Với
22
15
14 : 3 16 14 3 180 0
12
x
t x x x x
x

.
Với
22
3 3 5
2
5 : 3 16 5 3 9 0
3 3 5
2
x
t x x x x
x
.
Vậy phương trình đã cho có 4 nghiệm.
Câu 44: Tích của các nghiệm của phương trình
22
3 9 5 2 3 3 1x x x x
bằng
A.
2
. B.
2
. C.
3
. D.
3
.
Lời giải:
Ta có:
2 2 2 2
3 9 5 2 3 3 1 3 3 3 2 3 3 5 0x x x x x x x x
.
Đặt
2
33x x t
;
0t
.
Khi đó phương trình trở thành :
2
1
3 2 5 0
5
()
3
t
tt
tL

.
Với
2 2 2
1
1 3 3 1 3 3 1 3 2 0
2
x
t x x x x x x
x


.
Vậy tích các nghiệm là
12
. ( 1).( 2) 2xx
.
Câu 45: Cho phương trình:
22
5 2 2 5 10 0x x x x
. Đặt
2
5 10t x x
thì phương trình trở
thành phương trình nào sau đây?
A.
2
2 10 0tt
. B.
2
2 2 0tt
. C.
2
2 8 0tt
. D.
2
2 8 0tt
.
Lời giải:
Ta có
2
5 10 0x x x
.
Đặt
2
5 10t x x
0t
.
22
5 10t x x
phương trình đã cho trở thành
2
2 8 0tt
.
Câu 46: Phương trình:
23
2 5 1 7 1x x x
có nghiệm là
ab
thì
2ab
bằng
A.
2.
B.
1.
C.
.
3.
D.
4.
Lời giải:
Điều kiện:
1x
.
Ta có
2 3 2 2
2 5 1 7 1 1 3 1 72 111x x x x x x x x x
Với
1x
ta thấy không thỏa mãn
1
nên không phải là nghiệm.
Với
1x
ta có:
22
22
1 2 2 7 3 0
11
13
1
1 7 1 1
1
xx
x
xx
x x x
x
x x x


Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2
2
2
22
2
1
1
4 3 5
1
1
12
14
9
3
0
46
1 8 10 0
1
1
1
xx
xx
xx
x
x x x
x
x
x
x
x
xx




.
Suy ra
4a
và
6b
. Do đó,
2 2.4 6 2ab
.
Câu 47: Số nghiệm của phương trình
22
3 86 19 3 16 0x x x x
là.
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải:
Phương trình
2 2 2 2
3 86 19 3 16 0 3 16 19 3 16 70 0 *x x x x x x x x
Đặt
2
3 16t x x
,
0t
. Khi đó
2
14
* 19 70 0
5
tn
tt
tn
Với
22
15
14 3 16 14 3 180 0
12
x
t x x x x
x

.
Với
22
3 3 5
2
5 3 16 5 3 9 0
3 3 5
2
x
t x x x x
x
.
Vậy phương trình đã cho có 4 nghiệm.
Câu 48: Tổng bình phương các nghiệm của phương trình
22
5 2 2 5 10 0x x x x
là
A.
5
. B.
13
. C.
10
. D.
25
.
Lời giải:
Điều kiện xác định
2
5 10 0x x x
.
Khi đó phương trình
22
5 10 2 5 10 8 0x x x x
2
2
5 10 2
5 10 4
xx
xx
1
22
2
3
5 10 2 5 6 0
2
x
x x x x
x


.
Vậy
2 2 2 2
12
2 3 13xx
.
Câu 49: Tổng các bình phương các nghiệm của phương trình
2
1 3 3 4 5 2 0x x x x
là:
A.
17
. B.
4
. C.
16
. D.
8
.
Lời giải:
Ta có
2
1 3 3 4 5 2 0x x x x
22
4 5 3 4 5 4 0x x x x
2
4 5 1xx
2
4 5 1xx
2
4 4 0 2x x x
.
Câu 50: Biết phương trình
2
4 3 1 8 5 6 2x x x x x
có một nghiệm dạng
x a b
với
,0ab
. Tính
.ab
A. 7. B. 5. C. 4. D. 6.
Lời giải:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2
4 3 1 8 5 6 2x x x x x
( điều kiện:
1
3
x 
)
1 8 5 2 6 2 ( 1)x x x x x


22
1 4 1 4 1
0
8 5 2 6 2 1
x x x x x
x x x x
2
11
4 1 0
8 5 2 6 2 1
x
xx
x x x x



2
4 1 0
25
11
0
25
8 5 2 6 2 1
Vo ânghieäm
xx
x
x
x
x x x x




.
Câu 51: Tìm tất cả các giá trị của tham số
m
để phương trình
10x x m
có hai nghiệm phân
biệt.
A.
;1 m
. B.
1; m
. C.
1; m
. D.
;1 . m
Lời giải:
Điều kiện:
0.x m x m
Phương trình
1
.
x
xm
Yêu cầu bài toán
1.m
Câu 52: Tìm tất cả các giá trị của tham số
m
để phương trình
2
0
3
x m x m
x
có nghiệm.
A.
;1m 
. B.
1;m 
. C.
1;m 
. D.
m
.
Lời giải:
Điều kiện:
3x 
.
Với
3x 
;phương trình
2
0
3
x m x m
x
20x m x m
3xm
.
Để phương trình có nghiệm thì
3 3 1mm
1;m 
.
Câu 53: Tìm tất cả các giá trị của tham số
m
để phương trình
2
40x x x m
có ba nghiệm phân
biệt.
A.
;0 m
. B.
0; m
. C.
0; m
. D.
;0 . m
Lời giải:
Điều kiện:
0.x m x m
Phương trình
2
0
40
4.
0
x
xx
x
xm
xm


Yêu cầu bài toán
0.m
Câu 54: Số giá trị nguyên của tham số
m
để phương trình
2
1x x m x
có hai nghiệm phân
biệt là
A.
4
. B.
0
. C. Vô số. D.
3
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Ta có:
2
22
1 0 1
1.
1 2 1
xx
x x m x
x x m x m x x





Bảng biến thiên
2
21y x x
trên
1; :

x
1
1

y
2
2

Dựa vào bảng biến thiên, yêu cầu bài toán
2;2 2; 1;0;1 .
m
mm

Câu 55: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
21x m x
có 2 nghiệm phân
biệt?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải:
Ta có
21x m x
2
2
10
1
41
21
x
x
m x x
x m x




Xét hàm số
2
41y x x
trên nửa khoảng
1;

ta được bảng biến thiên như sau
Từ bảng biến thiên ta thấy để phương trình có 2 nghiệm phân biệt thì
3 2.m
Do
m
suy ra
2m 
.
Câu 56: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 2 2x x m x
có nghiệm.
A.
1m
. B.
1;m 
. C.
2m
. D.
2m
.
Lời giải:
Ta có:
2
2
2
2
20
2
2 2 2 2
2 4 2 *
2 2 2 2
x
x
x x m x
x x m
x x m x



.
Xét hàm số
2
24f x x x
,
2x
BBT:
Phương trình đã cho có nghiệm
*
có nghiệm
2 2 4 2x m m
.
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 57: Giá trị của tham số
m
để phương trình
2
2 2 2x x m x
có 2 nghiệm phân biệt là
;m a b
với
,ab
. Tính
S a b
.
A.
1
.
8
S 
B.
81
.
8
S
C.
5.S
D.
41
.
8
S
Lời giải:
Ta có
2
2 2 2x x m x
2
2
2
2 2 2
x
x x m x

2
2
2 5 4

x
m x x
.
Bảng biến thiên
2
54y xx 
trên
2; :

x
2
5
2

y
10
41
4

Dựa vào bảng biến thiên, yêu cầu bài toán
41 41
2 10 5.
48
mm
Suy ra
41
,5
8
ab
. Vậy
1
8
ab
.
Câu 58: Tìm tất cả các giá trị
m
để phương trình
2
2 3 2 2x x m x
có nghiệm.
A.
2m 
. B.
2m 
. C.
2m
. D.
2m
.
Lời giải:
Ta có
2
2
2
20
2 2 4
2 3 2 2
6 3 6 2 2
2 3 2 2
x
xx
x x m x
x m x m
x x m x



Phương trình đã cho có nghiệm khi chỉ khi
2 4 2mm
.
Câu 59: Có bao nhiêu giá trị nguyên của tham số m để phương trình
22
4 1 ( 1) 0x x m
có
nghiệm thuộc khoảng
0; 15 ?
A.
1
. B.
4
. C.
3
. D.
0.
Lời giải:
Ta có:
22
4 1 ( 1) 0x x m
22
1 4 1 0x x m
.
Đặt
2
1tx
.
Với
0; 15x
thì
1;4t
.
Phương trình trở thành:
2
40t t m
2
4*m t t
.
Xét hàm số
2
( ) 4f t t t
với
1;4t
.
Ta có BBT:
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Dựa vào BBT, suy ra phương trình đã cho có nghiệm thuộc khoảng
0; 15
.
Phương trình (*) có nghiệm thuộc khoảng
1;4t
40m
.
Vậy các giá trị nguyên
m
thỏa là
4; 3; 2; 1 m
.
Câu 60: Có bao nhiêu giá trị m nguyên để phương trình
2
4 3 3 2 9 1 0x x x m
có
nghiệm?
A. 9. B. 11. C. 5. D. 10.
Lời giải:
Điều kiện:
33x
.
Đặt
33t x x
22
6 2 9tx
2
2
6
9
2
t
x
. Điều kiện:
6 2 3t
.
Phương trình trở thành:
2
6
4 2 1 0
2
t
tm
2
4 7 0 (*)t t m
.
Xét hàm số
2
47f t t t
, có bảng biến thiên
Phương trình (*) có nghiệm thỏa
6 2 3t
1 4 6 5 8 3m
5 8 3 1 4 6m
.
Vậy có 10 giá trị nguyên của m là
18; 17;...; 10; 9
.
Câu 61: Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 2 2 4 0x x x m
có
nghiệm?
A.
4
. B.
5
. C. Vô số. D.
10
.
Lời giải:
Điều kiện:
22x
Đặt
22t x x
2
4 2 2 2 4 2t x x t
Lại có:
2 2 2 2 2 4 2 2 2 x x x x x x
2
4 2 2 2 8 2 2 2 2.  t x x t
Suy ra
2;2 2 .t


Phương trình trở thành:
2
40t t m
2
41t t m
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Yêu cầu bài toán
tìm
m
để phương trình (1) có nghiệm
2;2 2t


đồ thị hàm số
2
4f t t t
cắt đường thẳng
ym
trong đoạn
2;2 2


(*)
Bảng biến thiên của
2
4f t t t
trên
2;2 2


Từ BBT ta có (*)
2 4 2 2. m
Do
2;3;4;5;6 . mm
____________________ HẾT ____________________
Huế, 15h Ngày 30 tháng 01 năm 2023
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

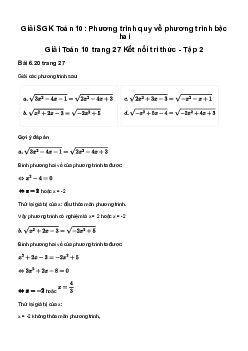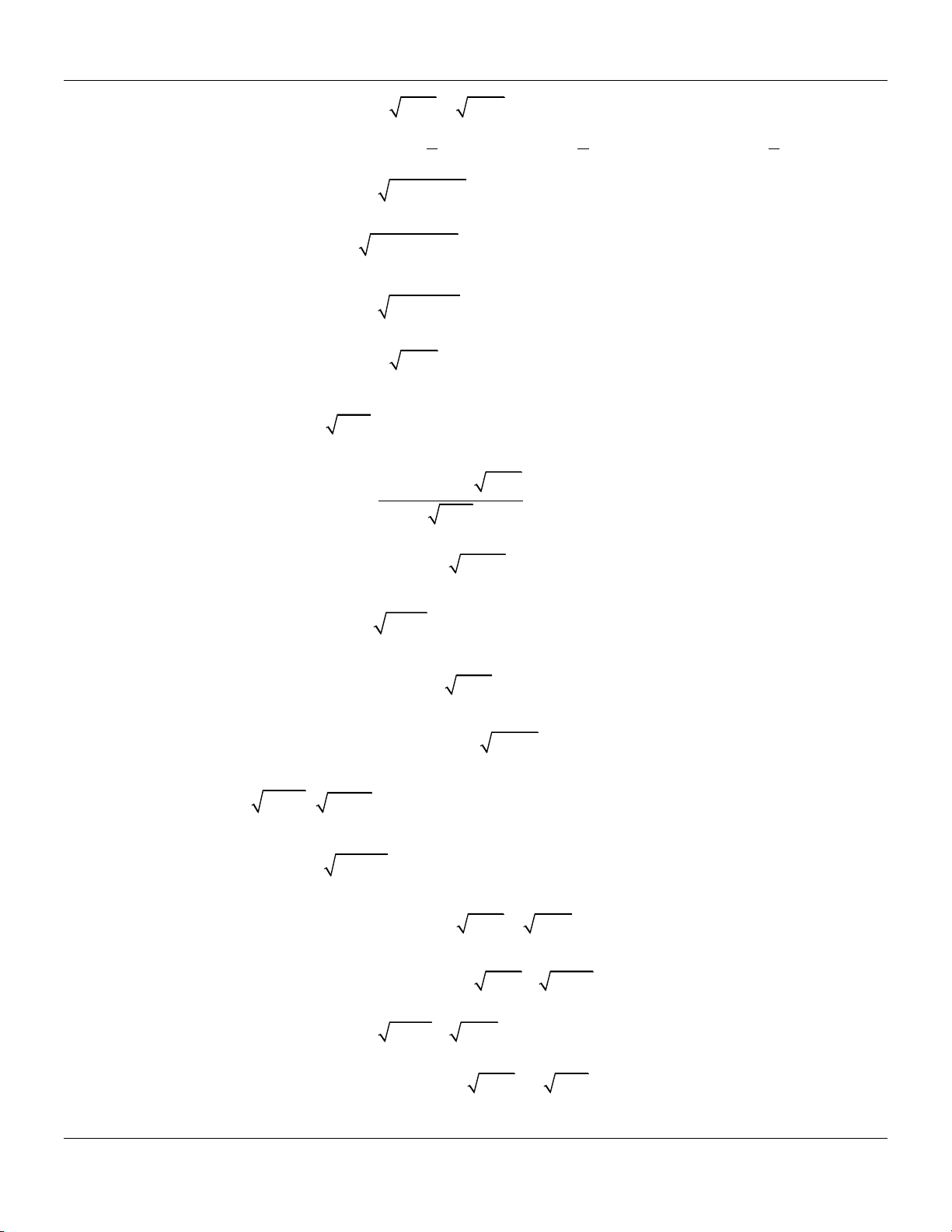
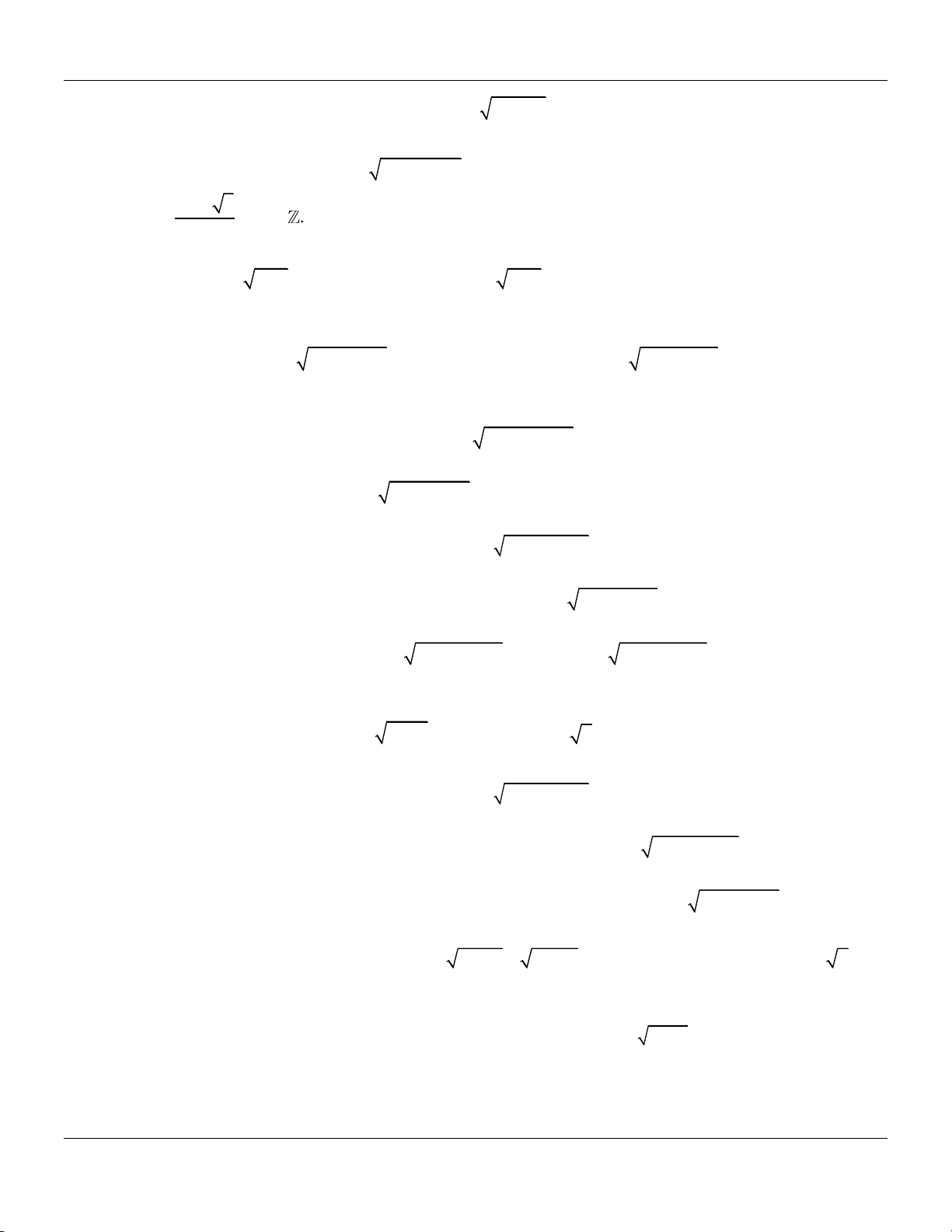
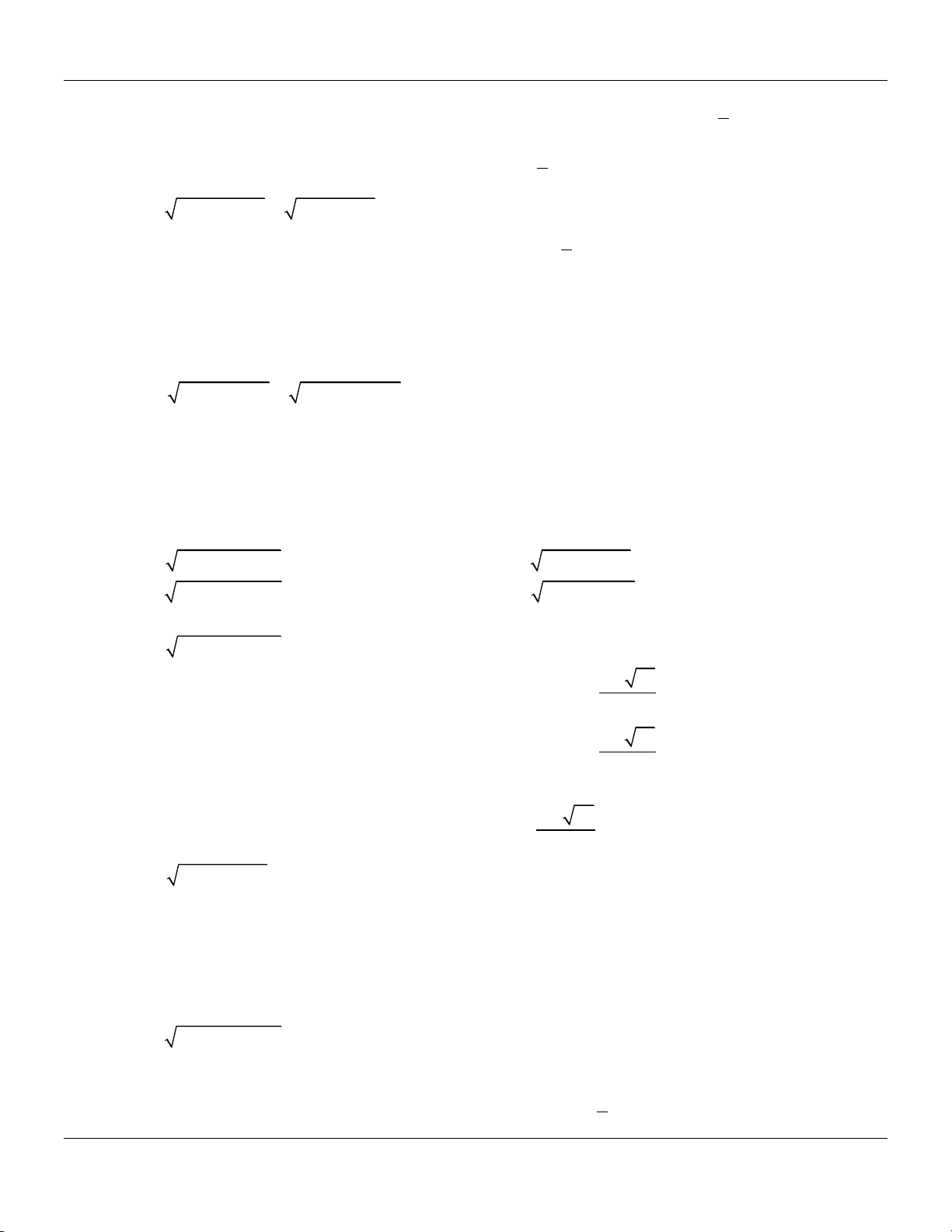
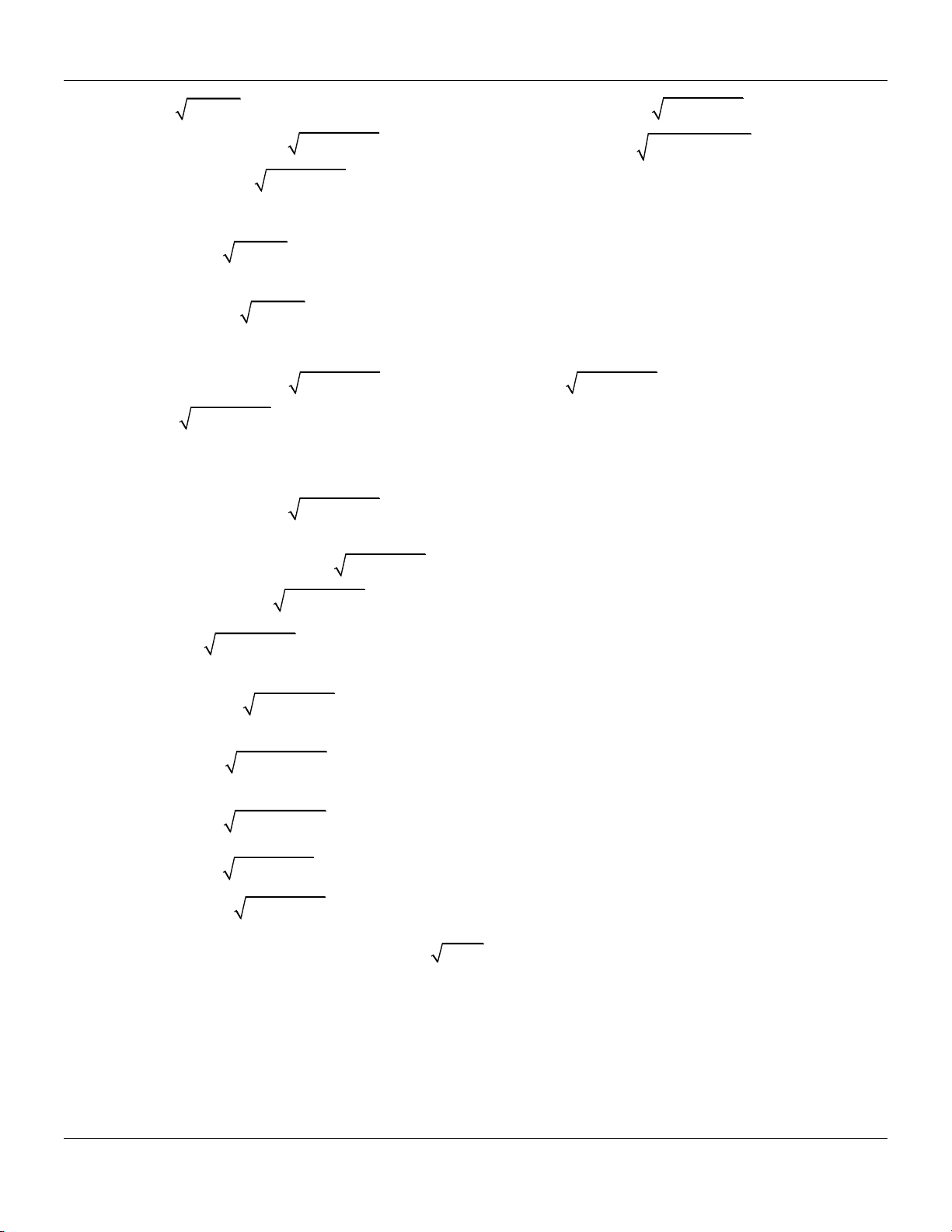
Preview text:

Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT Chủ đề 4:
PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
I. MỘT SỐ DẠNG PHƯƠNG TRÌNH CƠ BẢN
1. Phương trình dạng: 2 2
ax bx c
dx ex f
Để giải phương trình: Ta làm như sau: 2 2
ax bx c
dx ex f
Bước 1: Bình phương hai vế, rút gọn rồi giải phương trình bậc 2 hoặc bậc nhất.
Bước 2: Thử lại các giá trị x tìm được có thỏa phương trình ban đầu hay không? Sau đó kết luận nghiệm 2
ax bx c  0hoÆc chän 2
dx ex f  0 Hoặc 2 2
ax bx c dx ex f   2 2
ax bx c dx ex f Câu 1: Giải phương trình 2 2
2x  4x  2 
x x  2. Câu 2:
Giải các phương trình sau: a) 2 2
3x  6x 1  2
x  9x 1; b) 2 2
2x  3x  5  x  7.
2. Phương trình dạng: 2
ax bx c dx e
Để giải phương trình: Ta làm như sau: 2
ax bx c dx e
Bước 1: Bình phương hai vế, rút gọn rồi giải phương trình bậc 2 hoặc bậc nhất.
Bước 2: Thử lại các giá trị x tìm được có thỏa phương trình ban đầu hay không? Sau đó kết luận nghiệm
dx e  0  Hoặc 2
ax bx c dx e  
ax bx c   dx  e2 2 Câu 3: Giải phương trình 2
2x  5x  9  x 1 Câu 4:
Giải các phương trình sau: b) 2
2x x  3  1 x b) 2
3x 13x 14  x  3 Câu 5:
Giải các phương trình sau: a) 2 2
3x  4x 1 
2x  4x  3; b) 2 2
x  2x  3  2  x  5; c) 2 2
2x  3x  3 
x x 1; d) 2 2
x  5x  4  2
x  4x  2. Câu 6:
Giải các phương trình sau: a) 2
6x 13x 13  2x  4; b) 2
2x  5x  3  3   ; x c) 2
3x 17x  23  x  3; d) 2
x  2x  4  x  2. Câu 7:
Giải các phương trình sau:
a) x 1  x  3; b) 2
x  9x  5  ; x c) 2 3x 6x 3 2x 1; d) 2
2x  3x 1  x 1; e) 2
3  3x x  ; x f) 2
3x  4x  4  3x  2. Câu 8:
Giải các phương trình sau: a)  2
x  4x  3 x  2  0; b) 2
(x  3x  2) x  3  0. Câu 9:
Giải các phương trình sau:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT a)  x   2 2 3
10  x x x 12; b)  x   2 1
5x 1  x 1.
Câu 10: Giải các phương trình sau: a) 2 2
2 x  8x x  8x  3;
b)  x   x   2 1
3  3 x  4x  5  2  0;
c)  x   x   2 4
1  3 x  5x  2  6; d) 2
x  2x  8  4 4  x x  2;
e) x x   3 2
5  2 x  5x  2  2.
Câu 11: Tìm m để phương trình  2
x  4x  3 x m  0 có đúng hai nghiệm phân biệt.
Câu 12: Tìm tham số m để phương trình  2
x xx m  0 chỉ có một nghiệm.
Câu 13: Tìm m để phương trình 2
x x m x  1 có duy nhất một nghiệm.
Câu 14: Tìm m để phương trình 2
2x  2x m x  1 có hai nghiệm phân biệt.
Câu 15: Cho tứ giác ABCD có AB CD; AB  2; BC  13; CD  8; DA  5. Gọi H là giao điểm của
AB và CD và đặt x AH . Hãy thiết lập một phuơng trình để tính độ dài x , từ đó tính diện tích tứ giác ABC . D
Câu 16: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường.
Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng
đạp xe đến địa điểm B , cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt
kịp xe. Vận tốc đi bộ của Minh là 5 km / h , vận tốc xe đạp của Hùng là 15 km / h . Hãy xác định
vị trí C trên lề đường (Hình vẽ) để hai bạn gặp nhau mà không bạn nào phải chờ người kia
(làm tròn kết quả đến hàng phần mười).
II. BÀI TẬP TRẮC NGHIỆM
Câu 17: Nghiệm của phương trình 2x 1  3  x là 3 2 4 3 A. x  . B. x  . C. x  . D. x  . 4 3 3 2
Câu 18: Tập nghiệm của phương trình 2x  3  x  3 là
A. T  2;6 .
B. T   . C. T    6 .
D. T  2;  6 .
Câu 19: Tổng tất cả các nghiệm của phương trình và 2
x  3x  2  x  2 là A. 3 . B. 4 . C. 1  . D. 3  .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Câu 20: Tập nghiệm của phương trình 3  x x  2 là  1  1   1
A. S   . B. S   2;  .
C. S   .
D. S    .  2  2  2
Câu 21: Số nghiệm của phương trình 2
x  4x 1  x  3 là A. Vô số. B. 0. C. 1. D. 2.
Câu 22: Nghiệm của phương trình 2
x  7x 10  x  4 thuộc tập nào dưới đây? A. 4;5 . B. 5;6 . C. 5;6 . D. 5;6 .
Câu 23: Số nghiệm của phương trình 2
2x 14x x  3 là A. Vô số. B. 0. C. 1. D. 2.
Câu 24: Tập nghiệm của phương trình x   2
2 x  4x  3  0 là
A. S  2;  3 . B. S    2 .
C. S  1;  3 .
D. S  1; 2;  3 .
Câu 25: Phương trình x  2 x   1
x 1  0 có bao nhiêu nghiệm? A. 2 . B. 1. C. 0 . D. 3 .
 2x 3x2 x3
Câu 26: Số nghiệm của phương trình  0 là x 1 A. 1. B. 2 . C. 3 . D. 0 .
Câu 27: Số nghiệm của phương trình x  2
x  4 2x  3  0 là A. 2 . B. 0 . C. 1. D. 3 .
Câu 28: Số nghiệm của phương trình x   2
2 x  3x  2  0 là A. 1 . B. 2 . C. 3 . D. 0 .
Câu 29: Số nghiệm của phương trình  2
x 16 3  x  0 là A. 1. B. 3 . C. 0 . D. 2 .
Câu 30: Tổng các nghiệm của phương trình  x   2 3
2x  6  x  9 bằng A. 2 . B. 3 . C. 1. D. 7 .
Câu 31: Phương trình 2
x 1  2x 1  x  0 có tất cả bao nhiêu nghiệm? A. 1. B. 4 . C. 3 . D. 2 .
Câu 32: Phương trình  2 x x 2 2 6
17  x x  6x có bao nhiêu nghiệm phân biệt? A. 2. B. 1. C. 3. D. 4.
Câu 33: Tìm tập hợp nghiệm của phương trình 3  x x  2 1 . A.  2 . B. 1;   2 . C. 1;  2 . D.   1  .
Câu 34: Số nghiệm nguyên của phương trình sau x  3  2x 1  1 là: A. 0 . B. 2 . C. 1. D. 3 .
Câu 35: Số nghiệm của phương trình 3x 1  2  x  1 là A. 3 . B. 0 . C. 1. D. 2 .
Câu 36: Số nghiệm của phương trình 2
x  2x  2x x  3  6 1 x  7 là A. 0 . B. 1. C. 2 . D. 3 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Câu 37: Tổng các nghiệm của phương trình x   2 2 1
10  x x  3x  2 bằng A. 4. B. 1. C. 2. D. 3.
Câu 38: Biết phương trình  x   2 2 2
x  2x  2  2x x 10 có 2 nghiệm phân biệt x  2 và a b 3 x
; a, b  . Tính 2 2
S a b . 3 A. 81. B. 90. C. 85. D. 91.
Câu 39: Nếu đặt t x 1 thì phương trình x  2  x 1  0 trở thành phương trình nào trong các phương trình sau? A. 2
t t 1  0 . B. 2 t t  0 . C. 2
t t  2  0 . D. 2
t  2t  0 .
Câu 40: Cho phương trình 2 2
x  3x  5  2x  6x  5  0 . Nếu đặt 2
t x  3x  5 thì phương trình đã
cho trở thành phương trình nào dưới đây? A. 2 2
t t 15  0 . B. 2
2t t 15  0 . C. 2
t t  5  0 . D. 2
t t  5  0 .
Câu 41: Tổng các nghiệm của phương trình 2 2
x  4 x  3x  27  3x  22 bằng A. 1. B. 2 . C. 3 . D. 4 .
Câu 42: Số nghiệm của phương trình 2 2
x  2x  5  x  2x  3 là A. 2 . B. 3 . C. 1. D. 0 .
Câu 43: Số nghiệm của phương trình 2 2
x  3x  86  19 x  3x  16  0 là. A. 4 . B. 1 . C. 3 . D. 2 .
Câu 44: Tích của các nghiệm của phương trình 2 2
3x  9x  5  2 x  3x  3  1 bằng A. 2  . B. 2 . C. 3  . D. 3 .
Câu 45: Cho phương trình: 2 2
x  5x  2  2 x  5x 10  0 . Đặt 2 t
x  5x 10 thì phương trình trở
thành phương trình nào sau đây? A. 2
t  2t 10  0 . B. 2
t  2t  2  0 . C. 2
t  2t  8  0 . D. 2
t  2t  8  0 .
Câu 46: Phương trình: 2 3
2x  5x 1  7 x 1 có nghiệm là a b thì 2a b bằng A. 2. B. 1. C.. 3. D. 4.
Câu 47: Số nghiệm của phương trình 2 2
x  3x  86  19 x  3x  16  0 là. A. 4 . B. 1 . C. 3 . D. 2 .
Câu 48: Tổng bình phương các nghiệm của phương trình 2 2
x  5x  2  2 x  5x 10  0 là A. 5 . B. 13 . C. 10 . D. 25 .
Câu 49: Tổng các bình phương các nghiệm của phương trình  x   x   2 1
3  3 x  4x  5  2  0 là: A. 17 . B. 4 . C. 16 . D. 8 .
Câu 50: Biết phương trình 2
x  4x  3   x   1
8x  5  6x  2 có một nghiệm dạng x a b với
a, b  0 . Tính a  . b A. 7. B. 5. C. 4. D. 6.
Câu 51: Tìm tất cả các giá trị của tham số m để phương trình x   1
x m  0 có hai nghiệm phân biệt.
A. m    ;1 .
B. m  1;  .
C. m 1;  .
D. m   ;1 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
2 x m  x m
Câu 52: Tìm tất cả các giá trị của tham số m để phương trình  0 có nghiệm. x  3 A. m  ;    1 . B. m  1  ;. C. m  1  ; . D. m  .
Câu 53: Tìm tất cả các giá trị của tham số m để phương trình  2
x  4xx m  0 có ba nghiệm phân biệt. A. m  ;  0 .
B. m 0;  .
C. m 0;  .
D. m   ;  0.
Câu 54: Số giá trị nguyên của tham số m để phương trình 2
x x m x  1 có hai nghiệm phân biệt là A. 4 . B. 0 . C. Vô số. D. 3 .
Câu 55: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2x m x  1 có 2 nghiệm phân biệt? A. 1 . B. 0 . C. 2 . D. 3 .
Câu 56: Tìm tất cả các giá trị của tham số m để phương trình 2
2x  2x  2m x  2 có nghiệm.
A. m  1.
B. m 1;  .
C. m  2 .
D. m  2 .
Câu 57: Giá trị của tham số m để phương trình 2
2x x  2m x  2 có 2 nghiệm phân biệt là m   ;
a b với a,b
. Tính S a b . 1 81 41
A. S   . B. S  .
C. S  5. D. S  . 8 8 8
Câu 58: Tìm tất cả các giá trị m để phương trình 2
x  2x  3m  2  x  2 có nghiệm.
A. m  2 .
B. m  2 .
C. m  2 . D. m  2 .
Câu 59: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
x  4 x 1  (m 1)  0 có
nghiệm thuộc khoảng 0; 15? A. 1. B. 4 . C. 3 . D. 0.
Câu 60: Có bao nhiêu giá trị m nguyên để phương trình  x    x  2 4 3 3
 2 x  9  m 1  0 có nghiệm? A. 9. B. 11. C. 5. D. 10.
Câu 61: Có bao nhiêu giá trị nguyên của m để phương trình 2
2  x  2  x  2 4  x m  0 có nghiệm? A. 4 . B. 5 . C. Vô số. D. 10 .
LỜI GIẢI CHI TIẾT
I. MỘT SỐ DẠNG PHƯƠNG TRÌNH CƠ BẢN Câu 1: Giải phương trình 2 2
2x  4x  2 
x x  2. Lời giải:
Bình phương hai vế của phương trình ta được: 2 2
2x  4x  2  x x  2
Sau khi thu gọn ta được 2 x  3x  0
Từ đó tìm được x  0 hoặc x  3
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x  3 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x  3 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT Câu 2:
Giải các phương trình sau: c) 2 2
3x  6x 1  2
x  9x 1 b) 2 2
2x  3x  5  x  7 Lời giải: a) 2 2
3x  6x 1  2
x  9x 1
Bình phương hai vế của phương trình ta được 2 2
3x  6x 1  2
x  9x 1 . Sau khi thu gọn ta được 2
5x  3x  0 . 3
Từ đó tìm được x  0 hoặc x   . 5 3
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x  0 và x   thỏa 5 mãn.  3
Vậy tập nghiệm của phương trình đã cho là S  0;    5  b) 2 2
2x  3x  5  x  7
Bình phương hai vế của phương trình ta được 2 2
2x  3x  5  x  7 .
Sau khi thu gọn ta được 2
x  3x  2  0 .
Từ đó tìm được x  1 hoặc x  2 .
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy không có giá trị nào thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S   .
2. Phương trình dạng: 2
ax bx c dx e
Để giải phương trình: Ta làm như sau: 2
ax bx c dx e
Bước 1: Bình phương hai vế, rút gọn rồi giải phương trình bậc 2 hoặc bậc nhất.
Bước 2: Thử lại các giá trị x tìm được có thỏa phương trình ban đầu hay không? Sau đó kết luận nghiệm
dx e  0  Hoặc 2
ax bx c dx e  
ax bx c   dx e2 2 Câu 3: Giải phương trình 2
2x  5x  9  x 1 Lời giải:
Bình phương hai vế của phương trình ta được: 2 2
2x  5x  9  x  2x 1.
Sau khi thu gọn ta được 2
x  3x 10  0 .
Từ đó tìm được x  2 hoặc x  5 .
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x  5 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x  5 . Câu 4:
Giải các phương trình sau: d) 2
2x x  3  1 x b) 2
3x 13x 14  x  3 Lời giải:
c) Bình phương hai vế của phương trình ta được 2 2
2x x  3  1 2x x
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Sau khi thu gọn ta được 2
x  3x  2  0
Từ đó tìm được x  1 hoặc x  2
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x  1 hoặc x  2 thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S   1  ;  2 .
d) Bình phương hai vế của phương trình ta được 2 2
3x 13x 14  x  6x  9 . Sau khi thu gọn ta được 2
2x  7x  5  0 . 5
Từ đó tìm được x  1 hoặc x  . 2
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy không có giá trị nào thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S   .
*Chú ý: Một số dạng phương trình chứa ẩn dưới dấu căn khác B  0
A  0;B  0 
1) Dạng: A B   2) Dạng: A B C   A  2 B
A B  2 AB C
3) Dạng: A B C D .
* Nếu A+B = C+D (hoặc A.B = C.D) thì bình phương 2 vế ta được phương trình tương đương.
* Nếu A+C = B+D (hoặc A.C = B.D) thì phải đưa phương trình về dạng: A C D B
sau đó bình phương hai vế, tìm nghiệm sau đó thử lại để chọn nghiệm. 4) Dạng: 3 3 3 A B C
* Lập phương hai vế ta được: 3 A B AB  3 3 3.
A B   C . Sau đó thay thế: 3 3 3 A B
C vào phương trình, ta được: A B  3 3. ABC C
Chú ý: Sự thay thế này có thể dẫn đến nghiệm ngoại lai, vì vậy phải thử lại nghiệm. Câu 5:
Giải các phương trình sau: a) 2 2
3x  4x 1 
2x  4x  3; b) 2 2
x  2x  3  2  x  5; c) 2 2
2x  3x  3 
x x 1; d) 2 2
x  5x  4  2
x  4x  2. Lời giải: a) 2 2
3x  4x 1  2x  4x  3 x  2 2 2
 3x  4x 1  2x  4x  3 2  x  4   . x  2 
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S   2  ;  2 . b) 2 2
x  2x  3  2  x  5  4 x  2 2  
x  2x  3  2  x  5 2
 3x  2x 8  0  3  x  2 
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT 4
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x  thỏa mãn. 3 4
Vậy tập nghiệm của phương trình đã cho là S   . 3 c) 2 2
2x  3x  3  x x 1  2 x  2 2  
2x  3x  3  x x 1 2
 3x  4x  4  0  3  . x  2 
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị này không thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S   . d) 2 2
x  5x  4  2
x  4x  2 x  3  2 2
 x  5x  4  2
x  4x  2 2
x x  6  0   . x  2
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x  2 thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S    2 . Câu 6:
Giải các phương trình sau: a) 2
6x 13x 13  2x  4; b) 2
2x  5x  3  3   ; x c) 2
3x 17x  23  x  3; d) 2
x  2x  4  x  2. Lời giải: a) 2
6x 13x 13  2x  4  3  33 x  2 2  4
6x 13x 13  4x 16x 16 2
 2x  3x  3  0    3  33 x   4
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai đều thỏa mãn. 3 34 
Vậy tập nghiệm của phương trình đã cho là S     4   b) 2
2x  5x  3  3   x x  3 2 2
 2x  5x  3  9  6x x 2
x x  6  0   x  2 
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị này không thỏa mãn.
Vậy tập nghiệm của phương trình là S   c) 2
3x 17x  23  x  3 x  2 2 2  
3x 17x  23  x  6x  9 2
 2x 11x 14  0   7 . x   2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT 7
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x  thỏa mãn. 2 7 
Vậy tập nghiệm của phương trình đã cho là S    2 d) 2
x  2x  4  x  2 x  0 2 2
 x  2x  4  x  4x  4 2
 2x  6x  0   x  3
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy x  3 thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là S    3 . Câu 7:
Giải các phương trình sau:
a) x 1  x  3; b) 2
x  9x  5  ; x c) 2 3x 6x 3 2x 1; d) 2
2x  3x 1  x 1; e) 2
3  3x x  ; x f) 2
3x  4x  4  3x  2. Lời giải: x  3 x  3  0  x  3 
a) x 1  x  3      x   x  x 1   x 3 5 5 2 2
x  7x 10  0  x  2
Vậy phương trình có nghiệm x  5 . x  0 x  0 9  41 b) Ta có 2
x  9x  5  x      x  . 2 2 2
x  9x  5  x
2x  9x  5  0 4
Vậy phương trình trên có 2 nghiệm.  1 x      1 2x  1  0 2 x    c) Ta có: 2
3x  6x  3  2x  1     2   . 2 2
x  1  3 l
3x  6x  3  4x  4x  1  2
x  2x  2   0  x  1 3  n    x 1 x 1  0  x 1  d) 2
2x  3x 1  x 1    
 x  0  x  1.
2x  3x 1   x  2 2 1 2 x x  0  x 1 x  0 x  0 3   33 e) Ta có 2
3  3x x x      x  2 2 2 3
  3x x x
2x  3x  3  0 4
Vậy phương trình trên chỉ có 1nghiệm.  2 3x  2  0  x   f) Ta có: 2
3x  4x  4  3x  2    
3x  4x  4   3x  2 3 2 2 2
6x 16x  0
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT  2 x    3    x  0 . 8
x  0, x    3
Vậy tập nghiệm của phương trình là   0 . Câu 8:
Giải các phương trình sau: a)  2
x  4x  3 x  2  0; b) 2
(x  3x  2) x  3  0. Lời giải: a) ĐK: x  2 .  x 1 (l) 2
x  4x  3  0  pt    x  3 (tm)  . x  2  0 x  2 (tm)  b) ĐK: x  3 . x 1 2
x  3x  2  0  Ta có: 2
(x  3x  2) x  3  0    x  2   x  3 . x  3  0 x  3  Câu 9:
Giải các phương trình sau: a)  x   2 2 3
10  x x x 12; b)  x   2 1
5x 1  x 1. Lời giải: a) Điều kiện: 2
10  x  0   10  x  10 . Khi đó:  x   2 2 3
10  x x x 12  x   2
x  x  x    x   2 3 10 3 4 3
10  x x  4  0 x  3    . 2
 10  x x  4 Vì phương trình 2
10  x x  4 vô nghiệm với mọi x thoả  10  x  10 .
Vậy x  3 là nghiệm duy nhất của phương trình đã cho. 1 b) ĐK: x   . 5
Phương trình  x   2 1
5x 1  x 1   x  
1  5x 1  x   1  0 x 1  
 5x 1  x 1  * x  1  x  1  x  1   x  0
Phương trình *    
 x  0   2 2 5
x 1  x  2x 1
x  3x  0  x  3 x  3
Vậy phương trình đã cho có các nghiệm là: x  0; x  1; x  3 .
Câu 10: Giải các phương trình sau:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT a) 2 2
2 x  8x x  8x  3;
b)  x   x   2 1
3  3 x  4x  5  2  0;
c)  x   x   2 4
1  3 x  5x  2  6; d) 2
x  2x  8  4 4  x x  2;
e) x x   3 2
5  2 x  5x  2  2. Lời giải:
t  1 L a) Đặt 2 t
x  8x , t  0 . Pt: 2 2
2t t  3  t  2t  3  0   . t  3  N  x  9 Với 2 2 t  3 
x  8x  3  x  8x  9  0   . x  1 
Vậy tổng các nghiệm của phương trình bằng 8 .
b)  x   x   2 2 2 1
3  3 x  4x  5  2  0  x  4x  3  3 x  4x  5  2  0 Đặt 2
x  4x  5  t t  0 ta được phương trình: t 1(TM) 2 2
t  2  3t  2  0  t  3t  4  0   t  4  (L)
Với t  1, ta được 2 2 2
x  4x  5  1  x  4x  5  1  x  4x  4  0  x  2.
Vậy tổng bình phương nghiệm của phương trình trên là 4.
c) Ta có  x   x   2 4
1  3 x  5x  2  6 2 2
x  5x  2  3 x  5x  2  0 .
t  1 l Đặt 2 t
x  5x  2 t  0 . Khi đó, phương trình trở thành: 2
t  4  3t  0   . t  4  n x  +) Với 2
t  4 : x  5x  2  4 2
x  5x  2  16 2
x  5x 14  2 0   . x  7  t  0 d) Đặt 2 t
x  2x 8 t  0 , khi đó phương trình trở thành: 2t   4t   . t  4   L x  4 Với 2
t  0 : x  2x  8  0   . x  2  e) Đặt 3 2 t
x  5x  2 ta được phương trình: 3 3
t  2  2t  2  t  2t  4  0  t  2  x  2  Với 3 2 2 t  2
 : x  5x  2  2
  x  5x  6  0  .  x  3 
Câu 11: Tìm m để phương trình  2
x  4x  3 x m  0 có đúng hai nghiệm phân biệt. Lời giải: x mx m   x m
Phương trình tương đương: x m   .  x  1  2 
x  4x  3  0 x  3 
Phương trình có đúng hai nghiệm phân biệt khi và chỉ khi 3  m  1.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Câu 12: Tìm tham số m để phương trình  2
x xx m  0 chỉ có một nghiệm. Lời giải:
Điều kiện x m   1 . x  0  2 x x  0  2
x xx m  0    x 1 . x m  0 x m  tm 1
Phương trình luôn có nghiệm x m . Để phương trình có nghiệm duy nhất thì x m  1.
Câu 13: Tìm m để phương trình 2
x x m x  1 có duy nhất một nghiệm. Lời giải: x  1 0 x  1  Ta có: 2
x x m x  1     . 2 2
x x m x  1
m  x  2x  1 Bảng biến thiên 2
y  x  2x  1 trên 1;   : x 1  1  2 y 2  
Dựa vào bảng biến thiên, yêu cầu bài toán  m; 2     2 .
Câu 14: Tìm m để phương trình 2
2x  2x m x  1 có hai nghiệm phân biệt. Lời giải: x  1  0  x  1  Ta có: 2
2x  2x m x  1     . 2
2x  2x m   x 12 2
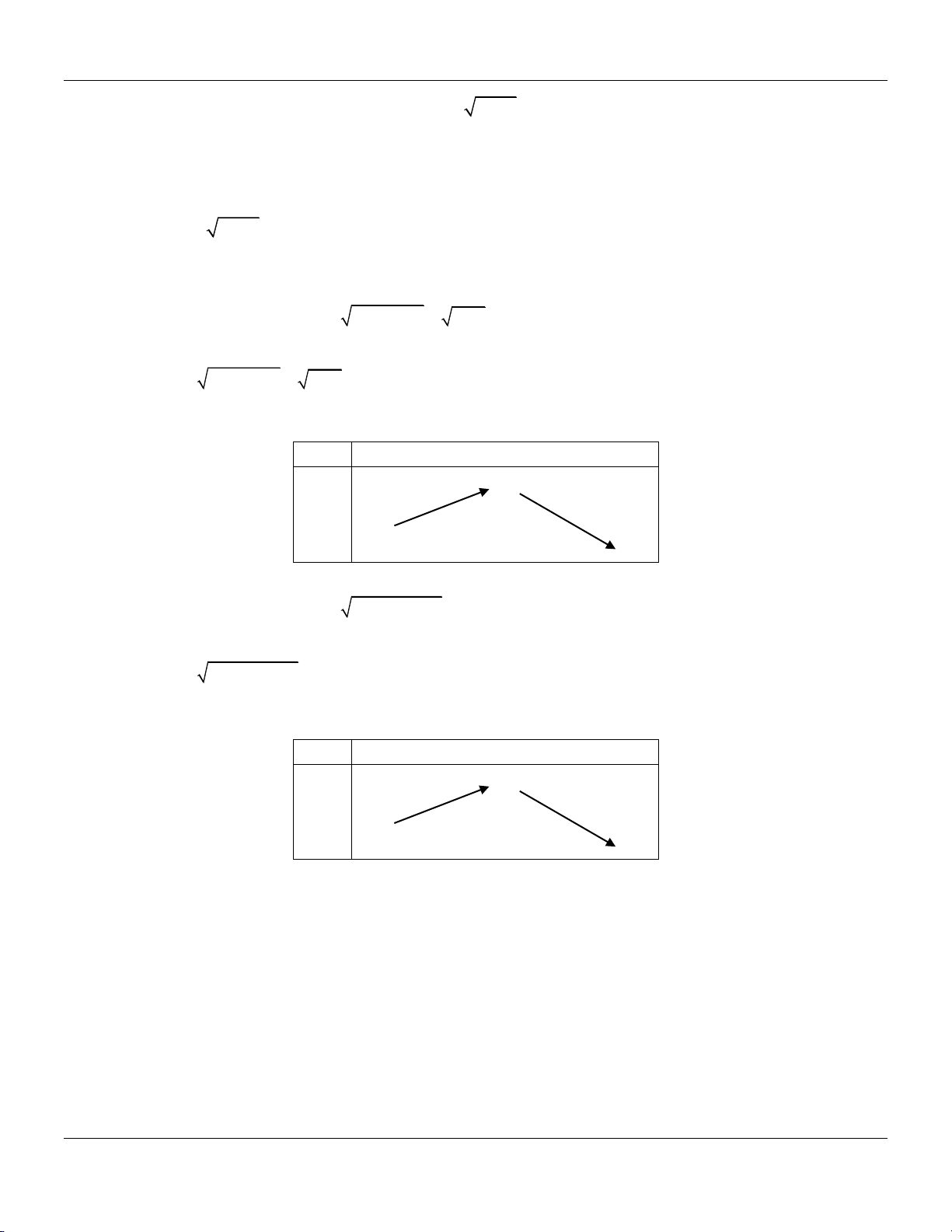
m  x  4x  1 Bảng biến thiên 2
y  x  4x  1 trên 1;   : x 1  2  5 y 4  
Dựa vào bảng biến thiên, yêu cầu bài toán  m 4; 5  .
Câu 15: Cho tứ giác ABCD có AB CD; AB  2; BC  13; CD  8; DA  5. Gọi H là giao điểm của
AB và CD và đặt x AH . Hãy thiết lập một phuơng trình để tính độ dài x , từ đó tính diện tích tứ giác ABC . D
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT Lời giải:
+) Sử dụng định lí Pytago để tìm x . x  0  Ta có: 2 HD
25  x . Điều kiện: 
 0  x  5 * 2 25  x  0
Xét tam giác vuông BHC , ta có 2 2 2
HB HC BC
 x  2   25 x 82 2 2 2 2 2 2
13  x  4x  4  25  x 16 25  x  64 169  0 2 2
 16 25  x  76  4x  4 25  x 19  x   1
Bình phương hai vế của phương trình ta được  2  x  2 16 25
 361 38x x x  3  Sau khi thu gọn ta được 2
17x  38x  39  0   13  x   17
Thay lần lượt hai giá trị này của x vào phương trình  
1 và kết hợp với điều kiện * , ta thấy x  3 thỏa mãn.
+) Để tính diện tích tứ giác ABCD , ta áp dụng công thức tính diện tích tam giác cho
BHC ,  AHD .
Ta có HB  5, HC  12, HA  3, HD  4. 1 1 1 SSS  .H . B HC  .H . A HD    . ABCD BHC AHD 5.12 3.4 24 2 2 2
Câu 16: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường.
Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng
đạp xe đến địa điểm B , cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt
kịp xe. Vận tốc đi bộ của Minh là 5 km / h , vận tốc xe đạp của Hùng là 15 km / h . Hãy xác định
vị trí C trên lề đường (Hình vẽ) để hai bạn gặp nhau mà không bạn nào phải chờ người kia
(làm tròn kết quả đến hàng phần mười).
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT Lời giải:
Vận tốc của bạn Minh: v  5 km / h . 1  
Vận tốc của bạn Hùng: v  15 km / h . 2   2 2 15
Áp dụng định lý Pithago vào tam giác vuông AHB : BH  0, 2  0,05  km 20
Gọi BC x km, x  0 . 15 15 Suy ra: CH   x , x  . 20 20
Ta cần xác định vị trí điểm C để Minh và Hùng gặp nhau mà không bạn nào phải chờ người kia
Nghĩa là: ta cần tìm x để thời gian hai bạn di chuyển đến C là bằng nhau. S x
Thời gian Hùng đi từ B đến C là: BC t   h . 2   v 15 2 2  15  2
Quãng đường AC mà Minh đã đi là: 2 2
AC CH AH  
x   0,05   20   2  15  
x  0,052 20 S  
Thời gian Minh đã đi từ A đến C là: AC t   h . 1   v 5 1 2  15  
x   0.052 20   x Theo yêu cầu bài toán:  5 15 2  15  
x   0.052 2 20   x Bình phương 2 vế:  25 225  3 15  9 9 15 9 x  0,3 2 2 2  9  x x    x  8x x   0     80 10 400 10 25   x  0,1 15 Vì 0  x
 0.19 nên x  0,1 thỏa mãn. 20
Vậy hai bạn Minh và Hùng di chuyển đến vị trí C cách điểm B một đoạn
x  0,1km 100 m.
II. BÀI TẬP TRẮC NGHIỆM
Câu 17: Nghiệm của phương trình 2x 1  3  x là 3 2 4 3 A. x  . B. x  . C. x  . D. x  . 4 3 3 2 Lời giải: 4
Thay các nghiệm x vào phương trình thấy x  là nghiệm. 3
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Câu 18: Tập nghiệm của phương trình 2x  3  x  3 là
A. T  2;6 .
B. T   . C. T    6 .
D. T  2;  6 . Lời giải:    x 3 x  3  0  x  3 
Ta có 2x  3  x  3    
 x  2  x  6. 2x  3   x 32 2
x 8x 12  0  x  6
Vậy phương trình có tập nghiệm T    6 .
Câu 19: Tổng tất cả các nghiệm của phương trình và 2
x  3x  2  x  2 là A. 3 . B. 4 . C. 1  . D. 3  . Lời giải: x  2   x  2   x  2   Ta có 2
x  3x  2  x  2      x  0 . 2 2
x  3x  2  x  2
x  4x  0  x  4
Vậy tập nghiệm của phương trình S  0; 
4 nên tổng các nghiệm là 4 .
Câu 20: Tập nghiệm của phương trình 3  x x  2 là  1  1   1
A. S   . B. S   2;  .
C. S   .
D. S    .  2  2  2 Lời giải: x  2  x  2  0  1
Ta có: 3  x x  2     1  x  . 3
  x x  2 x  2  2 1 
Vậy tập nghiệm của phương trình là S   . 2
Câu 21: Số nghiệm của phương trình 2
x  4x 1  x  3 là A. Vô số. B. 0. C. 1. D. 2. Lời giải: x  3  0 x  3 Ta có: 2
x  4x 1  x  3     2 2  (vô nghiệm).
x  4x 1  x  6x  9 x 1
Câu 22: Nghiệm của phương trình 2
x  7x 10  x  4 thuộc tập nào dưới đây? A. 4;5 . B. 5;6 . C. 5;6 . D. 5;6 . Lời giải: x  4  0  x  4 Ta có: 2
x  7x 10  x  4    
x  65;6.
x  7x 10   x  42 2 x 6
Câu 23: Số nghiệm của phương trình 2
2x 14x x  3 là A. Vô số. B. 0. C. 1. D. 2. Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT 3   x  0  2 2
2x 14x x  3  2x 14x  3  x   2x 14x   3 x2 2    x 3 x  3 x  3     
 x  9 (loaïi)  x  1. 2 2 2
2x 14x  9  6x x
x 8x 9  0  x  1  (nhaän)
Vậy phương trình đã cho có nghiệm là x  1 .
Câu 24: Tập nghiệm của phương trình x   2
2 x  4x  3  0 là
A. S  2;  3 . B. S    2 .
C. S  1;  3 .
D. S  1; 2;  3 . Lời giải:
Điều kiện: x  2  0  x  2 (*).
Với điều kiện (*), phương trình đã cho tương đương với x  2 x  2  0    x  1 . 2 
x  4x  3  0 x  3 
So với điều kiện (*) chỉ có x  2 , x  3 thỏa mãn.
Vậy tập nghiệm của phương trình là S  2;  3 .
Câu 25: Phương trình x  2 x   1
x 1  0 có bao nhiêu nghiệm? A. 2 . B. 1. C. 0 . D. 3 . Lời giải:
Điều kiện x 1  0  x  1 . x  0 x  0   Ta có x  2 x   1 x 1  0 2
x 1  0  x  1     x  1 x 1 0 x 1   Vậy S    1 .
 2x 3x2 x3
Câu 26: Số nghiệm của phương trình  0 là x 1 A. 1. B. 2 . C. 3 . D. 0 . Lời giải:
Điều kiện x  3 . x 1 2
x  3x  2  0  Khi đó pt    x  2 
. Kết hợp với điều kiện suy ra phương trình có nghiệm  x 3  0 x  3  duy nhất x  3 .
Câu 27: Số nghiệm của phương trình x  2
x  4 2x  3  0 là A. 2 . B. 0 . C. 1. D. 3 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT  3 x   2     3  x   Ta có x  2
x  4 2x  3  0  x  0    2 .   x  2      x 2   3 x   2
Vậy phương trình có 2 nghiệm phân biệt.
Câu 28: Số nghiệm của phương trình x   2
2 x  3x  2  0 là A. 1 . B. 2 . C. 3 . D. 0 . Lời giải:
Điều kiện xác định: x  2 (*)
x  2 T / M  x  2  0  Ta có: x  2  2
x  3x  2  0     x 1 
KTM   x  2 2
x  3x  2  0   x  2  T / M  Vậy phương trình  
1 có một nghiệm x  2 .
Câu 29: Số nghiệm của phương trình  2
x 16 3  x  0 là A. 1. B. 3 . C. 0 . D. 2 . Lời giải:
+ Điều kiện x  3 * . x 16  0
Phương trình  x 16 2 2 3  x  0   .  3 x  0 x  4 + 2 x 16  0  
so sánh điều kiện (*) suy ra x  4 là một nghiệm của phương trình x  4  đã cho.
+ 3  x  0  x  3 thỏa mản điều kiện (*) suy ra x  3 là một nghiệm của phương trình đã cho.
Vậy phương trình đã cho có 2 nghiệm.
Câu 30: Tổng các nghiệm của phương trình  x   2 3
2x  6  x  9 bằng A. 2 . B. 3 . C. 1. D. 7 . Lời giải:
Điều kiện xác định của phương trình: 2x  6  0  x  3 x  3
Ta có x  3 2
2x  6  x  9   x  3 2x  6  x 3  0 
 2x  6  x  3 x  3  0  x  3
Giải phương trình 2x  6  x  3    . 2x  6   x 32 2
x  4x  3  0
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTTx  3   x  1   x  1     x  3  x  3 
Vậy phương trình đã cho có ba nghiệm là x  1, x  3, x  3  .
Tổng các nghiệm của phương trình là 1 3  3  1 .
Câu 31: Phương trình 2
x 1  2x 1  x  0 có tất cả bao nhiêu nghiệm? A. 1. B. 4 . C. 3 . D. 2 . Lời giải: 2 x 1  0 +) Điều kiện   x  1. 2x 1  0 2 2  x 1  0 1 x 1  0 +) 2
x 1  2x 1  x    0    
 2x 1  x  0
 2x 1  x  2
x  1n Giải   1 : 2 x 1  0   x  1  l
x 1 2 n Giải 2 : 2
2x 1  x  2x 1  x do x   2
1  x  2x 1  0   x  1 2  l
Vậy số nghiệm của phương trình là 2.
Câu 32: Phương trình  2 x x 2 2 6
17  x x  6x có bao nhiêu nghiệm phân biệt? A. 2. B. 1. C. 3. D. 4. Lời giải:  2x 6x 2 2
17  x x  6x   2 x  6x 2 17  x   1  0
x  0(TM ) 2
x  6x  0  
x  6(L) x  0 2   17   x  0     x  17   x  4  2  17  x 1  2 17   x 1
Vậy phương trình có 3 nghiệm phân biệt.
Câu 33: Tìm tập hợp nghiệm của phương trình 3  x x  2 1 . A.  2 . B. 1;   2 . C. 1;  2 . D.   1  . Lời giải: Đk: 2   x  3 3  x
x  2 1  3  x x  3  2 x  2  3  x x  3  2 x  2  2x  2 x  2 x  0 x  0     x  1  . 2 x x  2  x  2
Câu 34: Số nghiệm nguyên của phương trình sau x  3  2x 1  1 là:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT A. 0 . B. 2 . C. 1. D. 3 . Lời giải:
x  3  2x 1  1 x  3  0 1 Điều kiện   x  . 2x 1 0 2
Khi đó phương trình  x  3  1 2x 1 x  3  0  
x  3  1 2 2x 1  2x 1  2 2x 1  x  3   4  2x   1  x  32 x  3    x  1. 2
x 14x 13  0
Câu 35: Số nghiệm của phương trình 3x 1  2  x  1 là A. 3 . B. 0 . C. 1. D. 2 . Lời giải:  1 3  x 1 0 x   1 - Điều kiện:    3    x  2.  2  x  0 3  x  2
- PT  3x 1  1 2  2 2
x   3x 1  1   2  x   
  3x 1  1 2 2  x  2  x   1 2x 1  0 x   
2 2  x  4x  2 
2  x  2x 1     2  2  x   2x  2 1 2
2 x  4x 4x 1  1 x   1   2 x     2 x 1
x  1 (thỏa mãn điều kiện). 2  
4x  3x 1  0 1 x    4
Vậy phương trình đã cho có một nghiệm x  1 .
Câu 36: Số nghiệm của phương trình 2
x  2x  2x x  3  6 1 x  7 là A. 0 . B. 1. C. 2 . D. 3 . Lời giải: Điều kiện 3   x  1. Phương trình       2 2 x x 3 3 1 x 2
x  2x  2x x  3  6 1 x  7   x x  3  3 1 x   x x 3   
3 1 xVN     x
1 x  1 x  2  x  1
3  1 x  1 x 1   0   2  x  3     1 x
1 x  0 (do 1 x 1  0, x   3   ;1 ) 2  x  3
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
x  1 (thỏa mãn)
Câu 37: Tổng các nghiệm của phương trình x   2 2 1
10  x x  3x  2 bằng A. 4. B. 1. C. 2. D. 3. Lời giải:
Điều kiện xác định  10  x  10 x  2 2 1
10  x x  3x  2   x TM x  1 1( ) 2
10  x  x  2x  1   2
 10  x x  2(*) x  2 x  2  Giải (*): 2
10  x x  2    x TM  10   x   x  22 3( ) 2   x  1   (L)
Vậy tổng các nghiệm của phương trình bằng 4.
Câu 38: Biết phương trình  x   2 2 2
x  2x  2  2x x 10 có 2 nghiệm phân biệt x  2 và a b 3 x
; a, b  . Tính 2 2
S a b . 3 A. 81. B. 90. C. 85. D. 91. Lời giải:
Điều kiện của phương trình 2
x  2x  2  0  x  .
Phương trình đã cho tương đương x  x  2 2 2
x  2x  2   x  22x  5   . 2
x  2x  2  2x  5  *  5 2x  5  0 x   Ta có: *     2 2 2
x  2x  2  4x  20x  25 2 3
 x 18x  23  0  5 x    2 9  2 3    x  . Suy ra a  9
 ;b  2  S  85. 9  2 3 3 x   3
Câu 39: Nếu đặt t x 1 thì phương trình x  2  x 1  0 trở thành phương trình nào trong các phương trình sau? A. 2
t t 1  0 . B. 2 t t  0 . C. 2
t t  2  0 . D. 2
t  2t  0 . Lời giải:
Ta có: x  2  x 1  0   x   1 
x 1 1  0. Đặt 2 t
x 1  t x 1. Vậy pt trở thành: 2
t t 1  0.
Câu 40: Cho phương trình 2 2
x  3x  5  2x  6x  5  0 . Nếu đặt 2
t x  3x  5 thì phương trình đã
cho trở thành phương trình nào dưới đây? A. 2 2
t t 15  0 . B. 2
2t t 15  0 . C. 2
t t  5  0 . D. 2
t t  5  0 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT 2 2 2
x x   x x  
x x    2 3 5 2 6 5 0 3 5
2 x  3x  5  0 Đặt 2 t
x  3x  5  0. Suy ra 2 2 2 2
t x  3x  5  x  3x t  5
Phương trình đã cho trở thành: t   2 t  5 2 2
 5  0  2t t 15  0 .
Câu 41: Tổng các nghiệm của phương trình 2 2
x  4 x  3x  27  3x  22 bằng A. 1. B. 2 . C. 3 . D. 4 . Lời giải: 2  3  99 Điều kiện xác định: 2
x  3x  27  0  x    0   (luôn đúng).  2  4 Khi đó, ta có: 2 2
x  4 x  3x  27  3x  22 2 2
x  3x  22  4 x  3x  27  0 2 2
x  3x  27  4 x  3x  27  5  0 (1)  3 11  Đặt 2
x  3x  27  t t     . 2     3 11  t  1
  khoâng tm t     2   
Phương trình (1) trở thành: 2
t  4t  5  0   .  3 11 
t  5 tmt      2    x 1 Với t  5 ta có: 2 2 2
x  3x  27  5  x  3x  27  25  x  3x  2  0   . x  2
Vậy tổng các nghiệm của phương trình đã cho là 3 .
Câu 42: Số nghiệm của phương trình 2 2
x  2x  5  x  2x  3 là A. 2 . B. 3 . C. 1. D. 0 . Lời giải: Ta có: 2
x  2x  5  0, x   Đặt 2
t x  2x  5 , ta có phương trình trở thành t t  2  t  2  t  2   t  2 
t t  2          . t     t t t  2 1 4 2 2 t   5t  4  0  t  4
Khi đó  x x    x  2 2 4 2 5 1
 0  x 1. Thử lại ta thấy x  1 thỏa mãn.
Suy ra phương trình đã cho có một nghiệm.
Câu 43: Số nghiệm của phương trình 2 2
x  3x  86  19 x  3x  16  0 là. A. 4 . B. 1 . C. 3 . D. 2 . Lời giải: Phương trình 2 2 2 2
x  3x  86  19 x  3x  16  0  x  3x  16  19 x  3x  16  70  0 * t  14 n Đặt 2
t x  3x  16 , t  0 . Khi đó *   2
t  19t  70  0   t  5  n
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTTx  15 Với 2 2
t  14 : x  3x  16  14  x  3x  180  0   . x  12    3  3 5 x  Với 2 2           2 t 5 : x 3x 16 5 x 3x 9 0 .  3  3 5 x   2
Vậy phương trình đã cho có 4 nghiệm.
Câu 44: Tích của các nghiệm của phương trình 2 2
3x  9x  5  2 x  3x  3  1 bằng A. 2  . B. 2 . C. 3  . D. 3 . Lời giải: Ta có: 2 2 x x   x x     2 x x   2 3 9 5 2 3 3 1 3 3
3  2 x  3x  3  5  0 . Đặt 2
x  3x  3  t ; t  0 . t  1
Khi đó phương trình trở thành : 2 
3t  2t  5  0  5  . t   (L)  3 x  1  Với 2 2 2 t  1 
x  3x  3  1  x  3x  3  1  x  3x  2  0   . x  2 
Vậy tích các nghiệm là x .x  ( 1  ).( 2)   2 . 1 2
Câu 45: Cho phương trình: 2 2
x  5x  2  2 x  5x 10  0 . Đặt 2 t
x  5x 10 thì phương trình trở
thành phương trình nào sau đây? A. 2
t  2t 10  0 . B. 2
t  2t  2  0 . C. 2
t  2t  8  0 . D. 2
t  2t  8  0 . Lời giải: Ta có 2
x  5x 10  0 x   . Đặt 2 t
x  5x 10 t  0 . 2 2
t x  5x 10 phương trình đã cho trở thành 2
t  2t  8  0 .
Câu 46: Phương trình: 2 3
2x  5x 1  7 x 1 có nghiệm là a b thì 2a b bằng A. 2. B. 1. C.. 3. D. 4. Lời giải:
Điều kiện: x  1. Ta có 2 3
2x  5x 1  7 x 1  2 2 x x   1  3 x   1  7  x   1  2 x x   1   1
Với x  1 ta thấy không thỏa mãn  
1 nên không phải là nghiệm. Với x  1 ta có:            x x x x x
x 1  3x   1  7 x  
1 x x  1 2 2 2 2 1 1 1 2  2  7  3  0 x  1 x  1
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT 2  2 x x 1 1
x x 1 1    2   x 1 2   4x  3x  5 x 1 4  0       x  4  6 . 2 2  2    x x 1
x  8x 10  0 x x 1    9 3     x 1 x 1
Suy ra a  4 và b  6 . Do đó, 2a b  2.4  6  2 .
Câu 47: Số nghiệm của phương trình 2 2
x  3x  86  19 x  3x  16  0 là. A. 4 . B. 1 . C. 3 . D. 2 . Lời giải: Phương trình 2 2 2 2
x  3x  86  19 x  3x  16  0  x  3x  16  19 x  3x  16  70  0* t  14 n Đặt 2
t x  3x  16 , t  0 . Khi đó *   2
t  19t  70  0   t  5  n x  15 Với 2 2
t  14  x  3x  16  14  x  3x  180  0   . x  12    3  3 5 x  Với 2 2            2 t 5 x 3x 16 5 x 3x 9 0 .  3  3 5 x   2
Vậy phương trình đã cho có 4 nghiệm.
Câu 48: Tổng bình phương các nghiệm của phương trình 2 2
x  5x  2  2 x  5x 10  0 là A. 5 . B. 13 . C. 10 . D. 25 . Lời giải:
Điều kiện xác định 2
x  5x 10  0  x  . Khi đó phương trình 2 2
x  5x 10  2 x  5x 10  8  0 2
x  5x 10  2      x 3 2 2 1
x  5x 10  2  x  5x  6  0   . 2   
x  5x 10  4  x 2  2 Vậy 2 2 2 2
x x  2  3  13. 1 2
Câu 49: Tổng các bình phương các nghiệm của phương trình  x   x   2 1
3  3 x  4x  5  2  0 là: A. 17 . B. 4 . C. 16 . D. 8 . Lời giải:
Ta có  x   x   2 1
3  3 x  4x  5  2  0 2 2
x  4x  5  3 x  4x  5  4  0  2
x  4x  5  1  2
x  4x  5  1  2
x  4x  4  0  x  2 .
Câu 50: Biết phương trình 2
x  4x  3   x   1
8x  5  6x  2 có một nghiệm dạng x a b với
a, b  0 . Tính a  . b A. 7. B. 5. C. 4. D. 6. Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT 2 1
x  4x  3   x   1
8x  5  6x  2 ( điều kiện: x   ) 3   x  
1  8x  5   x  2   6x  2  (x 1) x   2
x x   2 1 4 1 x  4x 1   
x    x   0 8 5 2
6x  2  x 1    x 1 1  2
x  4x   1     
x    x   0 8 5 2
6x  2  x 1  2
x  4x 1  0 x  2  5   x 1 1     . 0 Vo ânghieäm     
x    x   x 2 5 8 5 2
6x  2  x 1
Câu 51: Tìm tất cả các giá trị của tham số m để phương trình x   1
x m  0 có hai nghiệm phân biệt.
A. m    ;1 .
B. m  1;  .
C. m 1;  .
D. m   ;1 . Lời giải:
Điều kiện: x m  0  x  . m x  1 Phương trình   . x   m
Yêu cầu bài toán  m  1.
2 x m  x m
Câu 52: Tìm tất cả các giá trị của tham số m để phương trình  0 có nghiệm. x  3 A. m  ;    1 . B. m  1  ;. C. m  1  ; . D. m  . Lời giải:
Điều kiện: x  3 .
2 x m  x m
Với x  3 ;phương trình
 0  2x m  x m  0  x  3m . x  3
Để phương trình có nghiệm thì 3m  3  m  1  m  1  ; .
Câu 53: Tìm tất cả các giá trị của tham số m để phương trình  2
x  4xx m  0 có ba nghiệm phân biệt. A. m  ;  0 .
B. m 0;  .
C. m 0;  .
D. m   ;  0. Lời giải:
Điều kiện: x m  0  x  . m x  0 2
x  4x  0  Phương trình    x  4 .  x m   0 x m
Yêu cầu bài toán  m  0.
Câu 54: Số giá trị nguyên của tham số m để phương trình 2
x x m x  1 có hai nghiệm phân biệt là A. 4 . B. 0 . C. Vô số. D. 3 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT Lời giải: x  1 0 x  1  Ta có: 2
x x m x  1     . 2 2
x x m x  1
m  x  2x  1 Bảng biến thiên 2
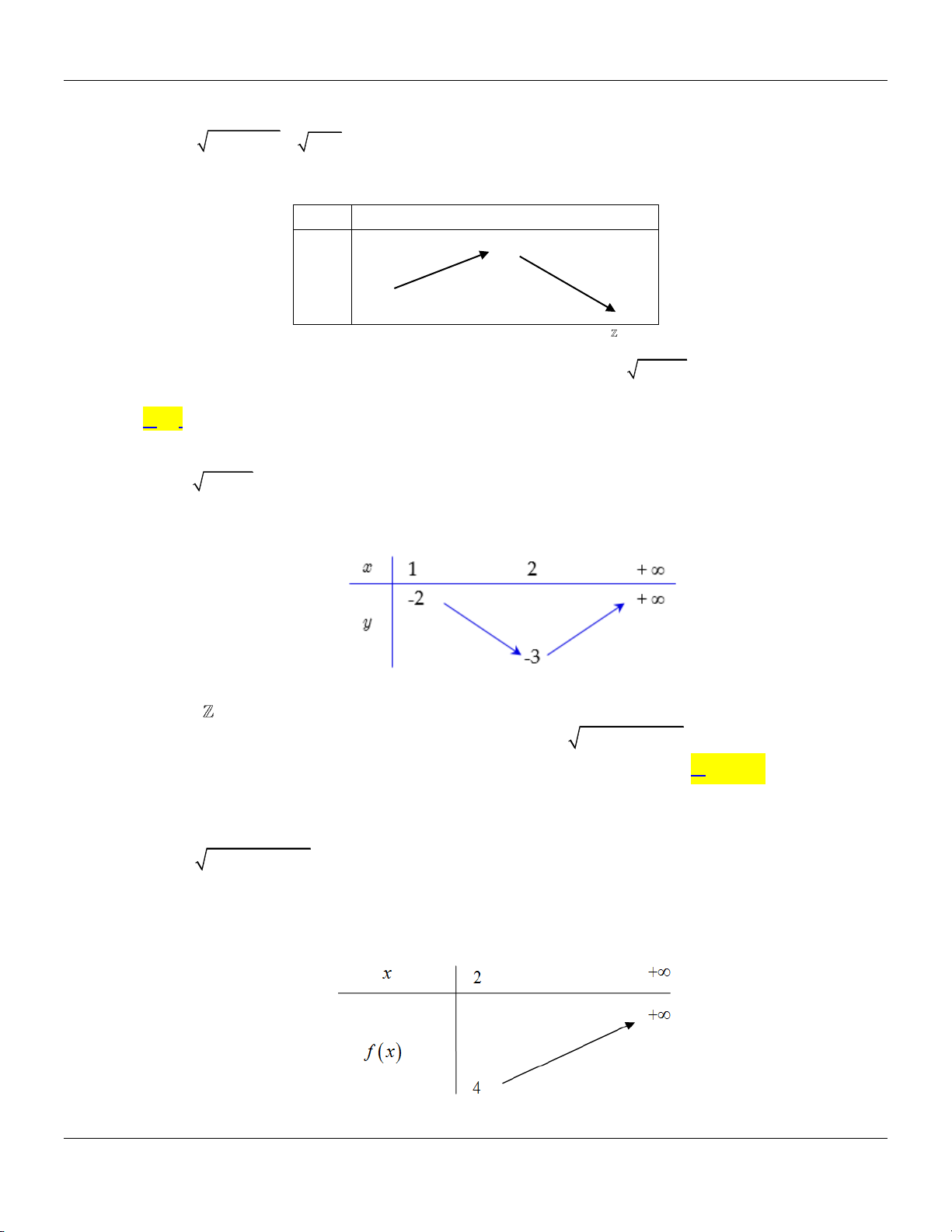
y  x  2x  1 trên 1;   : x 1  1  2 y 2  
Dựa vào bảng biến thiên, yêu cầu bài toán   2  ;2   m m    m 2  ; 1  ;0;  1 .
Câu 55: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2x m x  1 có 2 nghiệm phân biệt? A. 1 . B. 0 . C. 2 . D. 3 . Lời giải: x  1  0  x  1
Ta có 2x m x  1     2x m   x 12 2
m x  4x  1 Xét hàm số 2
y x  4x  1 trên nửa khoảng 1;  
 ta được bảng biến thiên như sau
Từ bảng biến thiên ta thấy để phương trình có 2 nghiệm phân biệt thì 3  m  2.
Do m  suy ra m  2 .
Câu 56: Tìm tất cả các giá trị của tham số m để phương trình 2
2x  2x  2m x  2 có nghiệm.
A. m  1.
B. m 1;  .
C. m  2 .
D. m  2 . Lời giải: x  2  0  x  2  Ta có: 2
2x  2x  2m x  2     . 2
2x  2x  2m   x  22 2
x  2x  4  2m  *
Xét hàm số f x 2
x  2x  4 , x  2 BBT:
Phương trình đã cho có nghiệm  * có nghiệm x  2  2m  4  m  2 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Câu 57: Giá trị của tham số m để phương trình 2
2x x  2m x  2 có 2 nghiệm phân biệt là m   ;
a b với a,b
. Tính S a b . 1 81 41
A. S   . B. S  .
C. S  5. D. S  . 8 8 8 Lời giải: x  2   x  2  Ta có 2
2x x  2m x  2     .
2x x  2m   x  22 2 2
2m x  5x  4 Bảng biến thiên 2
y x  5x  4 trên  2  ;  : x 2  5  2  y 10 41  4 41 41
Dựa vào bảng biến thiên, yêu cầu bài toán    2m  10    m  5. 4 8 41 1 Suy ra a  
, b  5 . Vậy a b   . 8 8
Câu 58: Tìm tất cả các giá trị m để phương trình 2
x  2x  3m  2  x  2 có nghiệm.
A. m  2 .
B. m  2 .
C. m  2 . D. m  2 . Lời giải: x  2  0  x  2 2x  4 Ta có 2
x  2x  3m  2  x  2      
x  2x  3m  2   x  22 2
6x  3m  6
2x m  2
Phương trình đã cho có nghiệm khi chỉ khi m  2  4  m  2 .
Câu 59: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
x  4 x 1  (m 1)  0 có
nghiệm thuộc khoảng 0; 15? A. 1. B. 4 . C. 3 . D. 0. Lời giải: Ta có: 2 2
x  4 x 1  (m 1)  0 2 2
x 1 4 x 1  m  0 . Đặt 2 t x 1 .
Với x 0; 15thì t 1;4 .
Phương trình trở thành: 2
t  4t m  0 2
m t  4t * . Xét hàm số 2
f (t)  t  4t với t  1; 4 . Ta có BBT:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Dựa vào BBT, suy ra phương trình đã cho có nghiệm thuộc khoảng 0; 15 .
 Phương trình (*) có nghiệm thuộc khoảng t 1;4  4  m  0 .
Vậy các giá trị nguyên m thỏa là m  4  ; 3  ; 2  ;  1 .
Câu 60: Có bao nhiêu giá trị m nguyên để phương trình  x    x  2 4 3 3
 2 x  9  m 1  0 có nghiệm? A. 9. B. 11. C. 5. D. 10. Lời giải: Điều kiện: 3   x  3 . 2 t  6
Đặt t x  3  3  x 2 2
t  6  2 9  x 2  9  x
. Điều kiện: 6  t  2 3 . 2 2 t  6
Phương trình trở thành: 4t  2  m 1  0 2
t  4t m  7  0 (*) . 2
Xét hàm số f t  2
t  4t  7 , có bảng biến thiên
Phương trình (*) có nghiệm thỏa 6  t  2 3
 1 4 6  m  5  8 3  5
 8 3  m  1 4 6 .
Vậy có 10 giá trị nguyên của m là  18  ; 17  ;...; 10  ;  9 .
Câu 61: Có bao nhiêu giá trị nguyên của m để phương trình 2
2  x  2  x  2 4  x m  0 có nghiệm? A. 4 . B. 5 . C. Vô số. D. 10 . Lời giải: Điều kiện: 2   x  2
Đặt t  2  x  2  x 2
t  4  2 2  x2  x  4  t  2
Lại có: 2 2  x2  x  2  x  2  x  4  2  x2  x  2 2
t  4  2 2  x2  x  8   2  2  t  2 2.
Suy ra t  2; 2 2  .   Phương trình trở thành: 2
t t  4  m  0 2
t t  4  m  1
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI Đại số 10 KNTT
Yêu cầu bài toán  tìm m để phương trình (1) có nghiệm t  2; 2 2   
 đồ thị hàm số f t 2
t t  4 cắt đường thẳng y  m trong đoạn 2;2 2   (*)
Bảng biến thiên của f t  2
t t  4 trên 2;2 2  
Từ BBT ta có (*)  2  m  4  2 2. Do m   m2;3;4;5;  6 .
____________________ HẾT ____________________
Huế, 15h Ngày 30 tháng 01 năm 2023
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115