Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên môn Xác suất thống kê| Trường Đại học Ngoại Thương

09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu
Phần I: Lý thuyết xác suất
Chương 1: Biến cố ngẫu nhiên và xác suất 1 Định nghĩa
•Việc thực hiện 1 nhóm các điều kiện để quan sát
sự vật hay hiện tượng được gọi là thực hiện một phép thử. Ký hiệu : T
•Kết quả của phép thử được gọi là biến cố Ký hiệu: A, B, C,… 2 1 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24 Ví dụ
•Ví dụ 1. Tung một đồng tiền cân
đối đồng chất trên mặt phẳng là
thực hiện một phép thử. Các biến
cố của phép thử là S = “mặt sấp
xuất hiện’, N = “mặt ngửa xuất hiện”. 3 •Ví dụ 2.
Bắn một phát súng vào
một tấm bia là thực hiện
một phép thử. Các biến cố
là “đạn trúng bia”, “đạn không trúng bia”,… 4 2 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
Định nghĩa các loại biến cố
•Biến cố sơ cấp (𝜔) là kết quả cụ thể nhỏ nhất của phép thử
•Không gian mẫu là không gian các biến cố sơ cấp:
Ω = { 𝜔 ∶ biến cố sơ cấp }
•Biến cố chắc chắn là biến cố nhất định xảy ra khi thực hiện phép thử. •Ký hiệu: 𝑈
•Biến cố không : là biến cố không thể xảy ra khi thực hiện phép thử •Ký hiệu: 𝑉 5 •Ví dụ:
•1. Tung đồng tiền trên mặt phẳng : T (phép thử)
•Các biến cố sơ cấp là 𝑆, 𝑁
•không gian mẫu là: Ω = {𝑆, 𝑁}
•A: Biến cố số mặt sấp xuất hiện lớn hơn 2 A là V – biến cố không 6 3 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24 Ví dụ •Ví dụ 2:
•Tung con xúc sắc trên mặt phẳng : T
•Gọi 𝐴 là mặt 𝑖chấm xuất hiện (𝑖 = 1,6)
Ω = {𝐴, 𝐴, 𝐴, 𝐴, 𝐴, 𝐴}
A: Biến cố số mặt chẵn xuất hiện ⇔
𝐴 ℎ𝑜ặ𝑐 𝐴 ℎ𝑜ặ𝑐 𝐴xuất hiện 7
Quan hệ giữa các biến cố
•A kéo theo B 𝐴 ⊂ 𝐵 : Khi A xảy ra thì B xảy ra
• 𝐴 = 𝐵 xảy ra khi và chỉ khi 󰇫𝐴 ⊂ 𝐵 𝐵 ⊂ 𝐴
•𝐴 ∪ 𝐵 xảy ra khi và chỉ khi hoặc A xảy ra hoặc 𝐵xảy ra •Ký hiệu: A+B
•𝐴 ∩ 𝐵 xảy ra khi và chỉ khi 󰇫𝐴 𝑥ả𝑦 𝑟𝑎 𝐵 𝑥ả𝑦 𝑟𝑎 •Ký hiệu: AB
•𝐴 \B xảy ra khi và chỉ khi 󰇫𝐴 𝑥ả𝑦 𝑟𝑎
𝐵 𝑘ℎô𝑛𝑔 𝑥ả𝑦 𝑟𝑎
•A và B xung khắc khi và chỉ khi 𝐴 ∩ 𝐵 = 𝑉 8 4 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
•Ví dụ: 𝐴 và 𝐴 là 2 biến cố xung khắc
•A và B là 2 biến cố đối lập nếu 󰇫𝐴 ∪ 𝐵 = Ω 𝐴 ∩ 𝐵 = 𝑉 –ký hiệu: 𝐵 = 𝐴ha  y 𝐴 = 𝐵
•𝐴và 𝐵độc lập nhau khi và chỉ khi xảy ra biến
cố này không ảnh hướng tới việc xảy ra biến cố kia.
–VD: A = Tung xúc xắc ra mặt sấp
B = Trúng giải vietlott 100 tỷ 9 Tính chất
•Giao hoán: 𝐴 + 𝐵 = 𝐵 + 𝐴 và 𝐴𝐵 = 𝐵𝐴
•Kết hợp: 𝐴 + 𝐵 + 𝐶 = 𝐴 + (𝐵 + 𝐶)
•Phân phối: 𝐴 𝐵 + 𝐶 = 𝐴𝐵 + 𝐴𝐶
•Một số tính chất khác:
𝐴 + 𝐴 = 𝐴 , 𝐴𝐴 = 𝐴
𝐴𝑈 = 𝐴; 𝐴𝑉 = 𝑉
𝐴 + 𝐵 = 𝐴 𝐵; 𝐴𝐵 = 𝐴+ 𝐵 10 5 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
•Ví dụ: 3 xạ thủ bắn mỗi người 1 viên đạn vào 1 tấm bia.
Gọi 𝐴là biến cố “xạ thủ thứ i bắn trúng bia” (𝑖 = 1,2,3)
Hãy biểu diễn Các biến cố sau theo 𝐴
•a. Bia bị trúng đạn : A
•𝐴 = 𝐴+ 𝐴+ 𝐴
•b. Bia bị trúng 3 viên đạn : B
•𝐵 = 𝐴𝐴𝐴
•c. Bia bị trúng 1 viên đạn : C
•𝐶 = 𝐴 𝐴 𝐴+ 𝐴 𝐴 𝐴+ 𝐴 𝐴 𝐴 11 Định nghĩa
•Xác suất xuất hiện biến cố A trong 1 phép
thử là tỉ số giữa kết cục thuận lợi cho A
và tổng số các kết cục duy nhất đồng khả
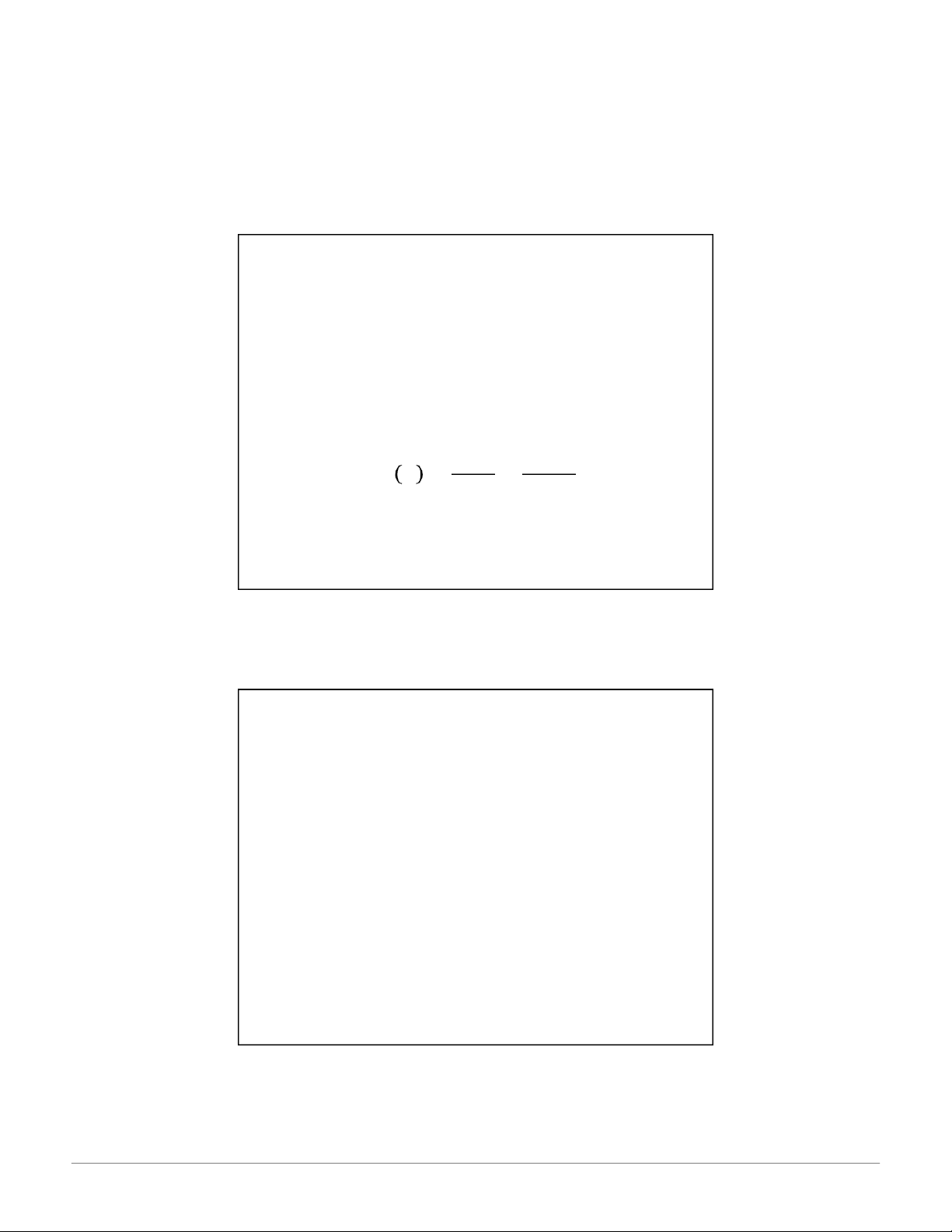
năng có thể xảy ra khi thực hiện phép thử đó. •Ký hiệu: 𝑃 𝐴 = 𝑚𝑛=|Ω| |Ω| 12 6 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
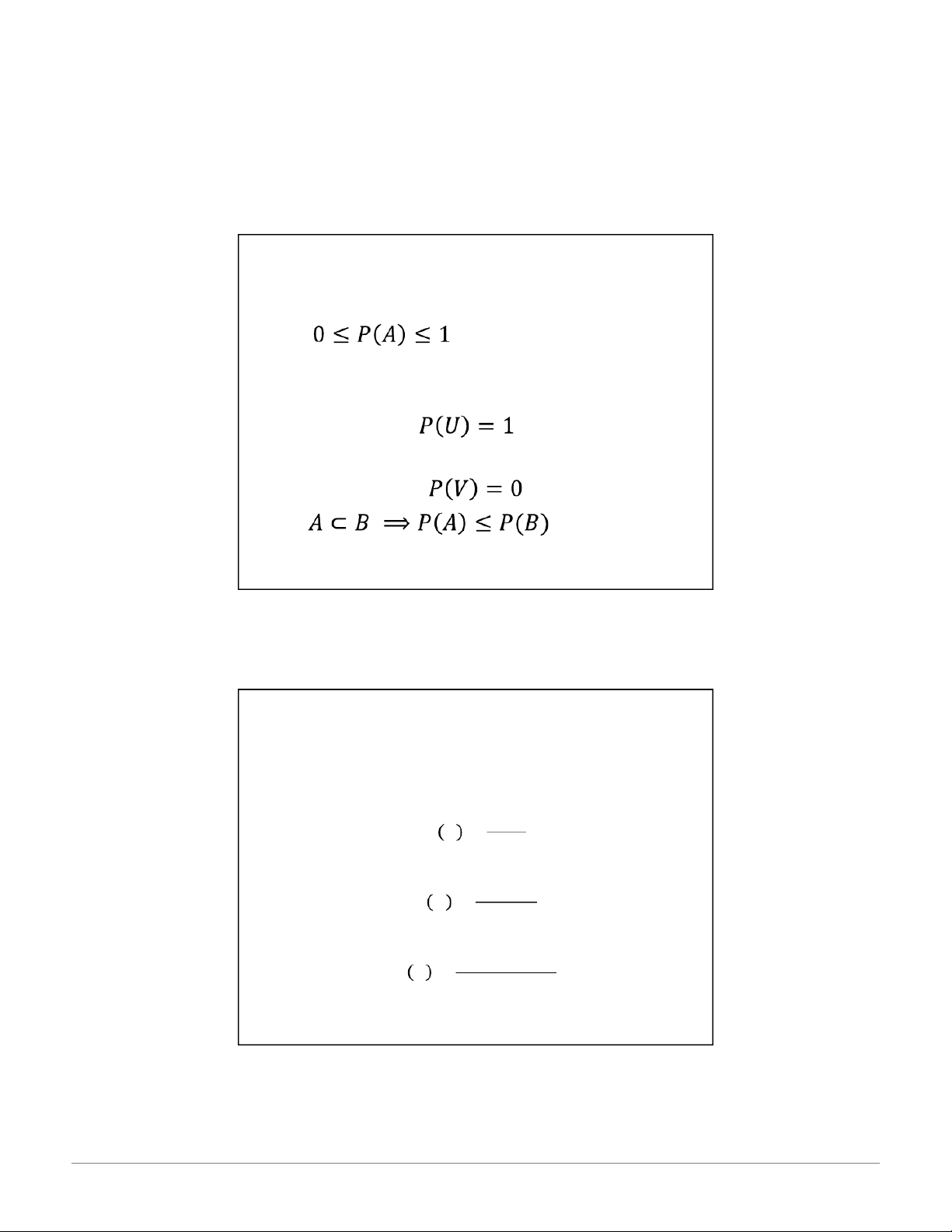
Các tính chất của xác suất •a.
•b. Xác suất của một biến cố chắc chắn bằng 1
•c. Xác suất biến cố không thể bằng 0 •d. 13 Ví dụ:
Một hộp có 4 bi đỏ và 6 bi xanh. lấy từ hộp đó 2 viên bi. Tính xác suất của: a. A = 2 viên bi khác màu
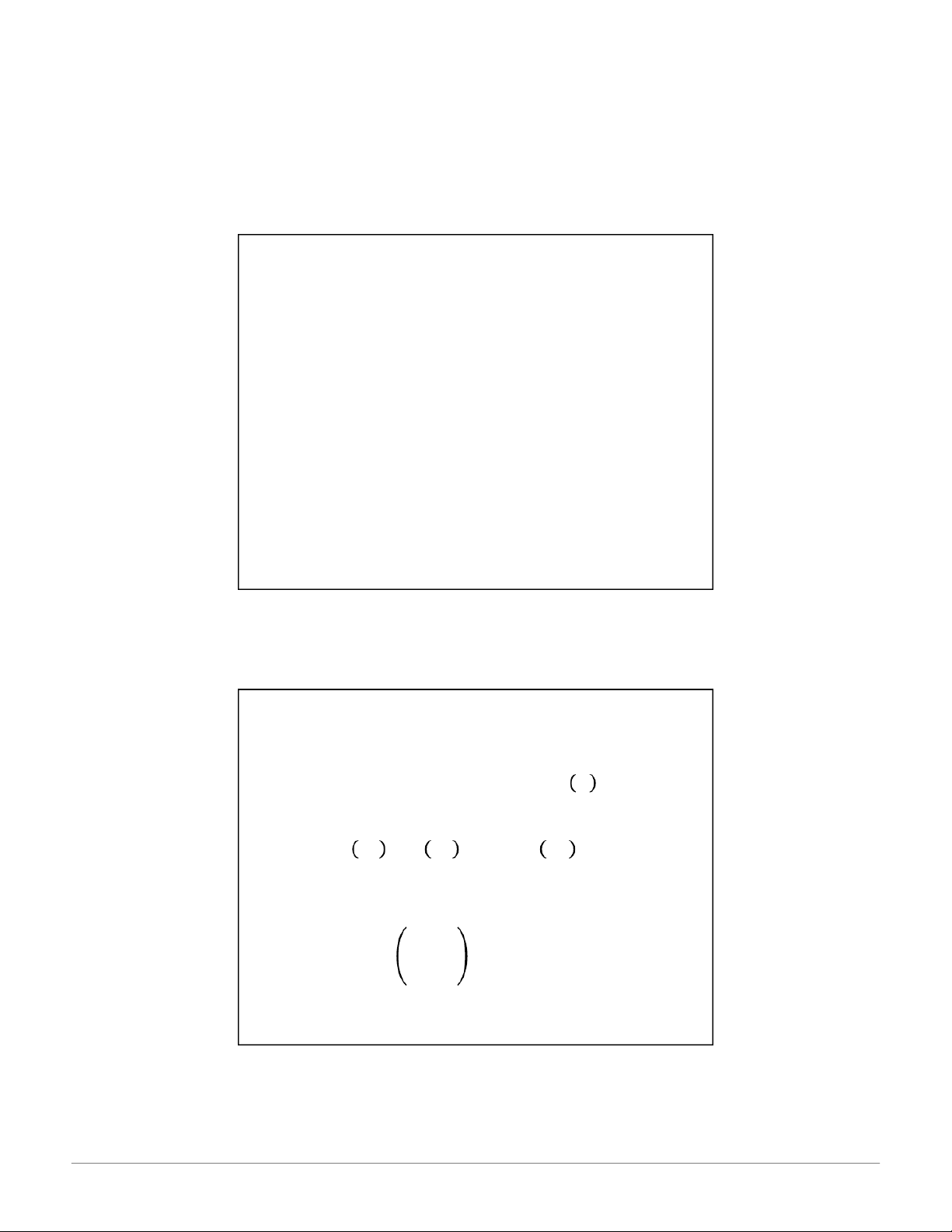
𝑃 𝐴 = 𝐶𝐶 𝐶 b. B = 2 viên bi cùng màu
𝑃 𝐵 = 𝐶+ 𝐶 𝐶
c. C = có ít nhất 1 viên bi màu đỏ
𝑃 𝐶 = 𝐶𝐶+ 𝐶𝐶 𝐶 14 7 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
Định nghĩa thống kê về xác suất
•Giả sử tiến hành n phép thử cùng loại, trong
mỗi phép thử có thể xuất hiện hoặc không xuất
hiện biến cố A, gọi k là số phép thử xuất hiện
biến cố A trong n phép thử.
•Ký hiệu 𝑓𝐴 =   với số lần xuất hiện biến cố
A là k và n là số phép thử
•Với n đủ lớn thì 𝑃 𝐴 = lim
→𝑓(𝐴) ≈ 𝑓𝐴 15
•Ví dụ: 1 học sinh đi thi ielts 10 lần thì có 7 lần điểm trên 8.0
•A = “học sinh đạt điểm trên 8.0”
•𝑃 𝐴 ≈ 𝑓𝐴 =   = 0.7
•Chú ý: định nghĩa xác suất bằng thống kê
thường được sử dụng nhiều trong thực tiễn 16 8 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
Định nghĩa hình học của xác suất
•Cho miền G trong mặt phẳng (đường thẳng,
không gian 3 chiều, …) và một miền con đo
được g của G. Gọi A là biến cố lấy ngẫu nhiên
một điểm thì điểm đó thuộc g. Khi đó, xác suất của A xác định bởi 𝑃 𝐴 = 𝑆(𝑔 (G) =𝑆(Ω) 𝑆(Ω) 17
•Ví dụ: 2 người hẹn gặp nhau tại FTU từ 20h –
21h. Biết rằng người đến trước chỉ chờ không
quá 20p. Hãy tính xác suất 2 người đó gặp nhau. •Giải:
•Hãy mô hình hóa thời gian gặp của 2 bạn đến FTU 18 9 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24
Định nghĩa tiên đề về xác suất
Hệ tiên đề được xây dựng trên cơ sở khái niệm
về không gian các biến sơ cấp 𝐸, 𝐸, … , 𝐸, thực
tế là tập hợp mọi kết cục có thể có của phép
thử. Lúc đó mỗi biến cố A có thể quan niệm như
1 tập hợp con của không gian đó. Từ đó ta có các tiên đề sau: 19 Hệ tiên đề
Tiên đề 1: Với mọi biến cố A đều có 𝑃 𝐴 ≥ 0
Tiên đề 2: Nếu 𝐸, 𝐸, … , 𝐸tạo nên không gian các biến cố sơ cấp thì :
𝑃 𝐸+ 𝑃 𝐸+ … + 𝑃 𝐸= 1
Tiên đề 3: Nếu các biến cố 𝐴, 𝐴, … , 𝐴, … là các
tập hợp con không giao nhau của các biến cố sơ cấp thì   𝑃󰇌𝐴    =  𝑃(𝐴)  20 10 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu 21-Oct-24 21 11 09:14, 28/01/2026
Chương 1 - Lý thuyết Xác suất và Biến cố Ngẫu nhiên - Studocu