






























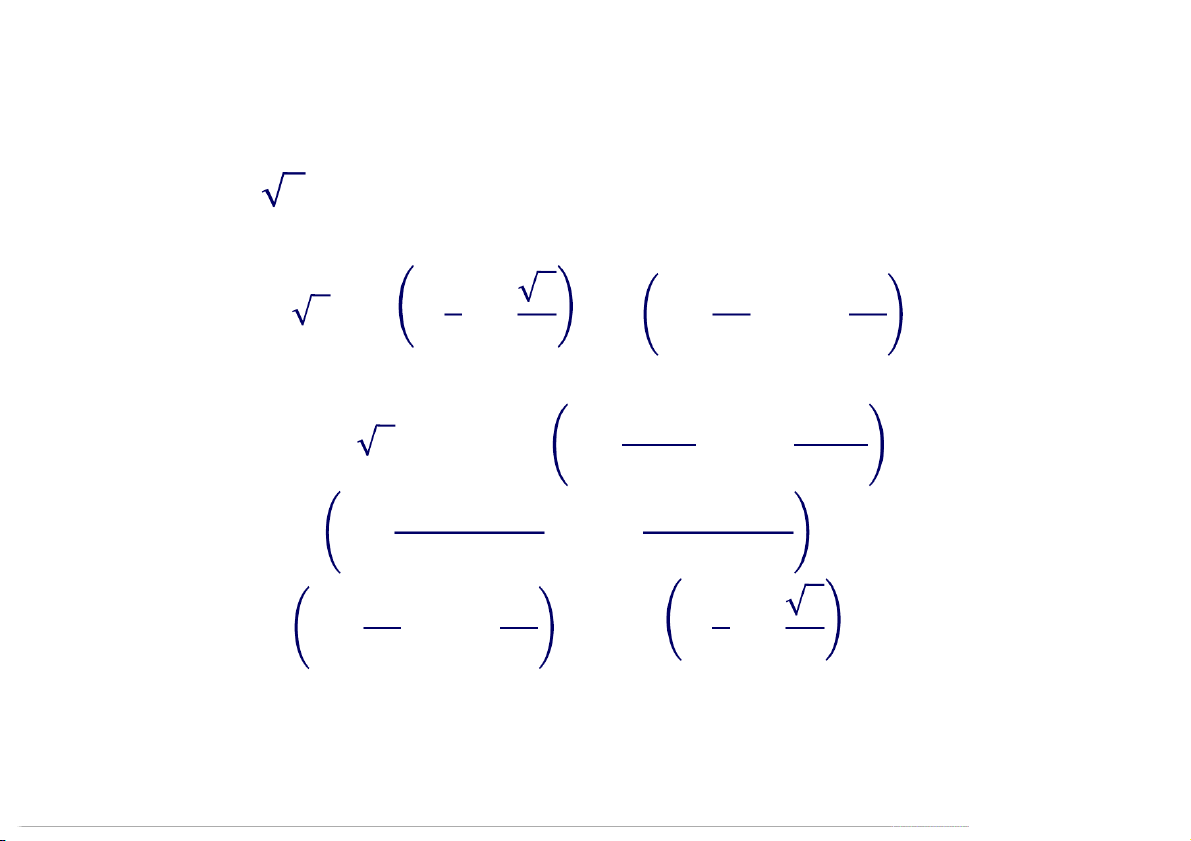
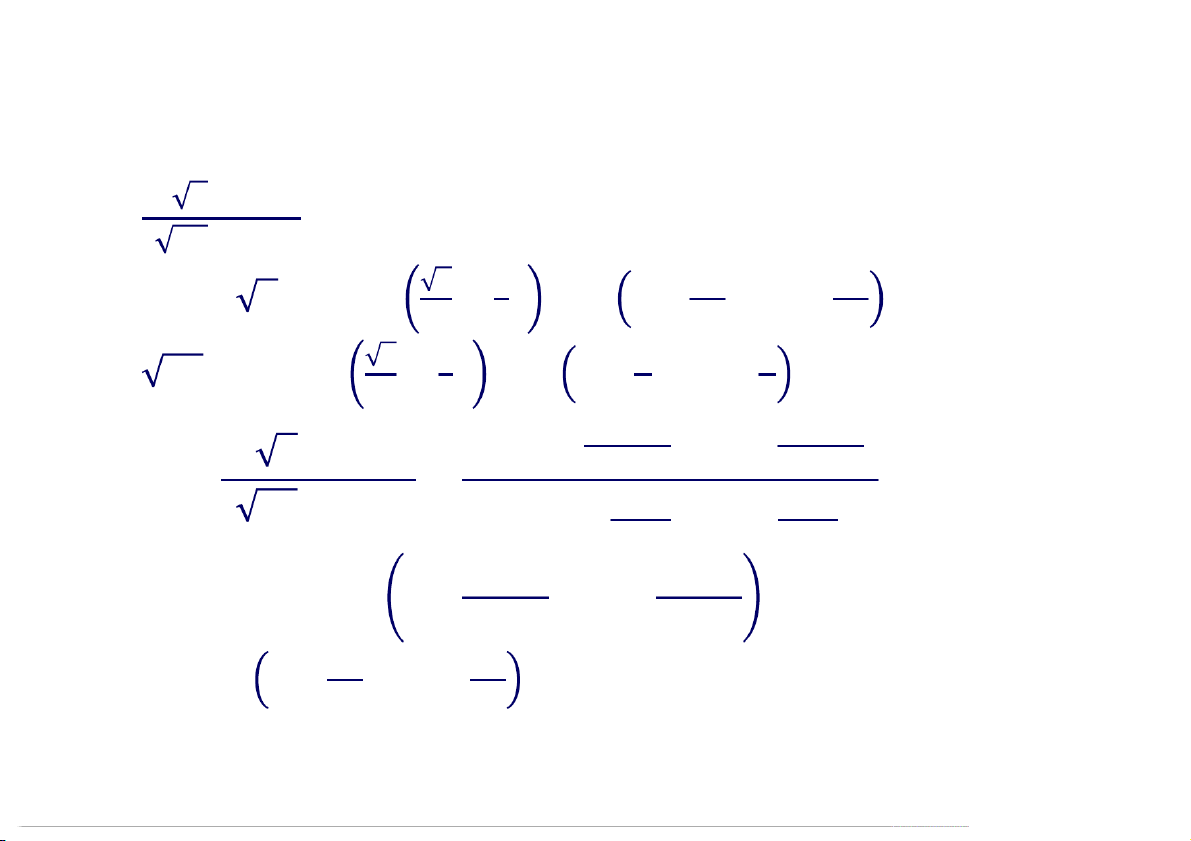
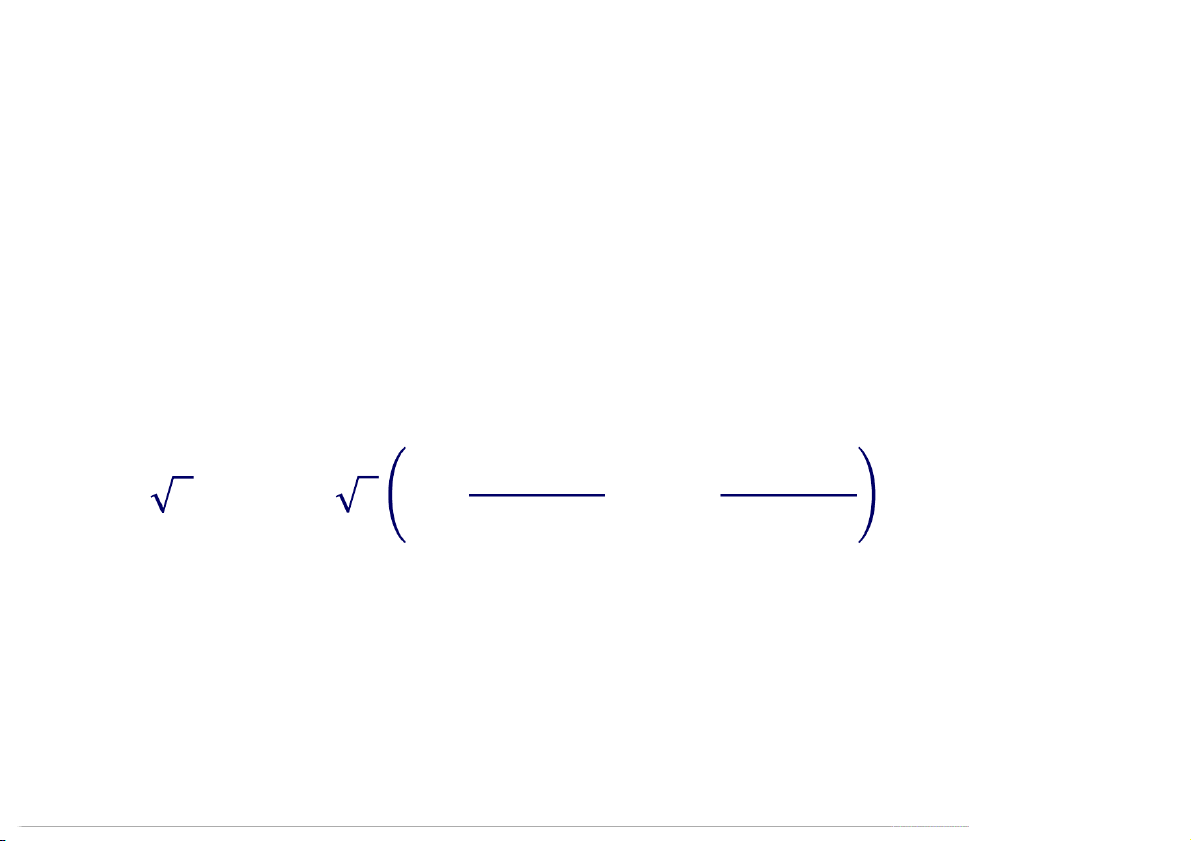








Preview text:
Đại số Tuyến tính Giảng viên: Đào Như Mai 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 1 Chương 1 Số phức Ánh xạ Cấu trúc Đại số Số phức Dạng đại số Dạng lượng giác Dạng số mũ
Định lý cơ bản của đại số 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 2 1. Ánh xạ
Một số tập thường gặp:
Số tự nhiên: = {0,1,2,3 … }.
Số nguyên: = {0, ±1, ±2, … }.
Số hữu tỷ: = { : ≠ 0, , ∈ , , = 1}:
số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Số vô tỷ: số thập phân vô hạn không tuần hoàn.
Số thực: tập hợp các số vô tỷ và hữu tỷ, ký hiệu 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 3
1. Ánh xạ, cấu trúc Đại số Ánh xạ
Định nghĩa. Ánh xạ từ tập X vào tập Y là 1 quy
luật liên hệ giữa X và Y sao cho khi tác động vào
1 phần tử ∈ sẽ tạo ra duy nhất 1 phần tử ∈ . Ký hiệu
: → , = ()
gọi là ảnh của , gọi là nghịch ảnh của
Ánh xạ : → , ⊂ , ảnh của tập qua ánh xạ :
= : = , ∈ = {: ∃ ∈ , = ()}
⊂ thì = { ∈ : = ∈ } gọi là
nghịch ảnh của qua ánh xạ . 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 4 1. Ánh xạ Định nghĩa
Ánh xạ : → gọi là đơn ánh nếu:
≠ → ≠ .
Ánh xạ : → gọi là toàn ánh nếu: = .
Ánh xạ : → là song ánh nếu đơn ánh, toàn ánh.
Ví dụ : → , = là song ánh. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 5 1. Ánh xạ Định nghĩa
Xét song ánh : → , khi đó ứng với mỗi ∈
có duy nhất ∈ sao cho = (), ngược lại
với mỗi ∈ có duy nhất ∈ sao cho = f()
Ánh xạ từ → cũng là 1 song ánh và được gọi
là ánh xạ ngược của ánh xạ : → , ký hiệu .
Do đó: : → , = (). 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 6 2 1. Ánh xạ 1.5 Ví dụ 1
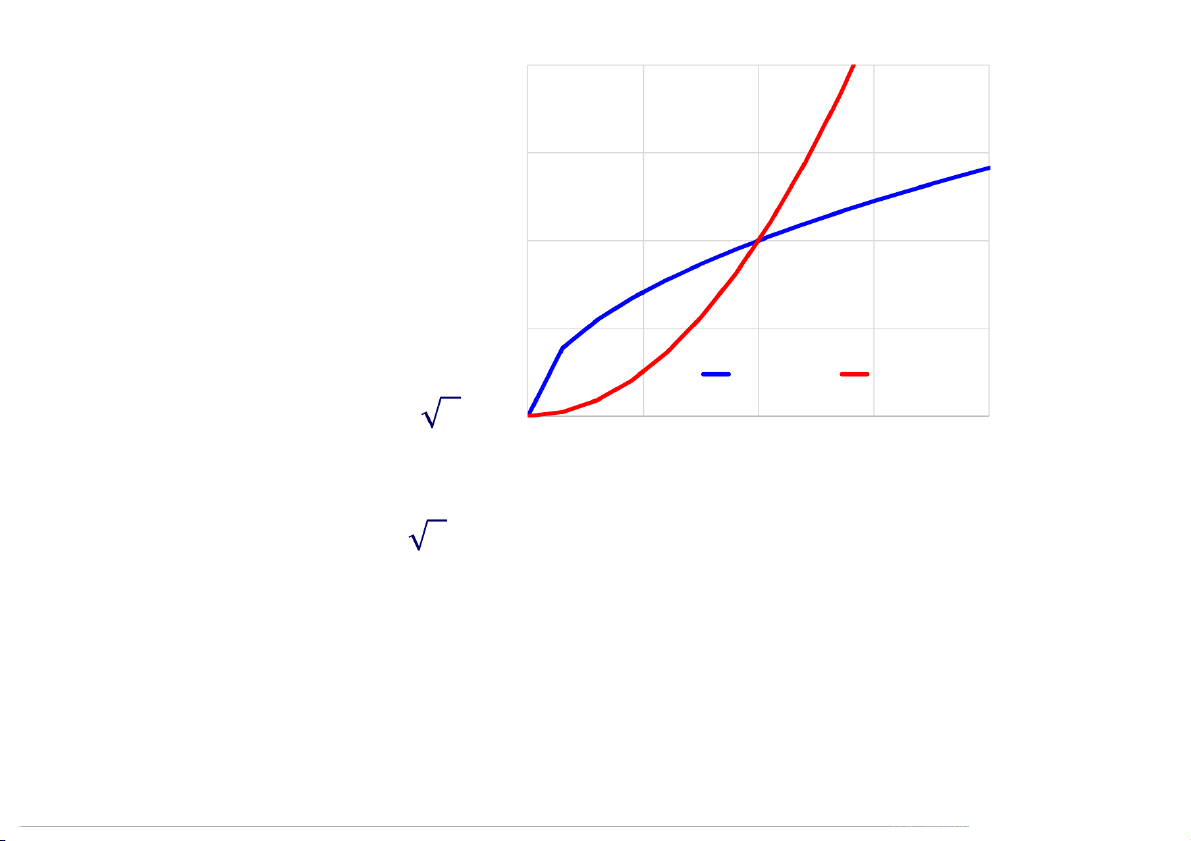
: → , = là song ánh. Ánh xạ ngược: 0.5 y=sqrt(x) y=x^2
: → , = . 0 0 0.5 1 1.5 2
Đồ thị 2 ánh xạ này trùng nhau.
Đổi lại biến: = .
Đồ thị của ánh xạ ngược và ánh xạ ban đầu đối xứng với
nhau qua đường phân giác của góc phần tư thứ nhất 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 7 2. Cấu trúc Đại số
Định nghĩa Phép toán 2 ngôi
Ánh xạ : x → gọi là 1 phép toán 2 ngôi trên tập .
Có 2 cách ký hiệu phần tử (, )
Lối cộng: , = +
Lối nhân: , = (hoặc . ; ∗ ; x ) 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 8 2. Cấu trúc Đại số
Phép toán 2 ngôi trên tập , theo lối nhân.
Khi đó có một số tính chất sau:
Kết hợp: = , ∀, , ∈ .
Giao hoán: = , ∀, ∈ .
Phần tử trung hòa: nếu ∃ ∈ : = = , ∀ ∈ .
Phần tử khả nghịch: ∈ gọi là khả nghịch nếu
∃ ∈ : = = .
là phần tử trung hòa của phép toán 2 ngôi .
gọi là phần tử nghịch đảo (hoặc phần tử đối) của . 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 9 2. Cấu trúc Đại số Ví dụ
(, +): phép toán kết hợp, giao hoán, có phần tử trung hòa là số 0.
(, . ): phép toán kết hợp, giao hoán, có phần tử trung hòa là số 1.
(, +): mọi phần tử đều khả nghịch, nghịch đảo của là −.
(, . ): có 2 phần tử khả nghịch là số 1 và -1. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 10 2. Cấu trúc Đại số Tính chất
Phép toán 2 ngôi có phần tử trung hòa , thì là duy nhất.
Thật vậy, giả sử tồn tại phần tử trung hòa , khi đó: = . =
Phép toán 2 ngôi có tính kết hợp, thì mỗi phần
tử khả nghịch có duy nhất 1 phần tử nghịch đảo, ký hiệu .
Thật vậy, giả sử có nghịch đảo , , ta có:
= = . Do đó:
= = = = = 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 11 2. Cấu trúc Đại số Tính chất
Chú ý. Trong trường hợp phép toán 2 ngôi ký
hiệu theo lối cộng, thì phần tử trung hòa thường
gọi là phần tử 0, phần tử nghịch đảo của ký
hiệu là −, và gọi là phần tử đối của .
Định nghĩa: Một tập hợp có trang bị một hay
nhiều phép toán 2 ngôi với những tính chất
xác định, sẽ tạo nên một cấu trúc Đại số.
Cấu trúc đại số thông dụng: nhóm, vành, trường. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 12 2. Cấu trúc Đại số Nhóm
Định nghĩa: Nhóm là 1 tập hợp khác rỗng, được
trang bị 1 phép toán 2 ngôi có tính chất kết hợp,
có phần tử trung hòa, mọi phần tử đều có khả nghịch.
(, . ) là nhóm nếu thỏa mãn:
= ; , , ∈ .
∃ ∈ : = = ; ∈ .
∀ ∈ , ∃ ∈ : = = .
Nếu phép toán 2 ngôi có tính giao hoán, thì
nhóm (, . ) gọi là nhóm Abel. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 13 2. Cấu trúc Đại số Nhóm Ví dụ
, + , (, +) là các nhóm Abel.
(, . ) không phải là nhóm, vì số 0 không khả nghịch
đối với phép toán nhân. Tính chất
Phần tử trung hòa là duy nhất.
Phần tử khả nghịch là duy nhất.
Quy tắc giản ước: = → = .
Phương trình: = có nghiệm duy nhất: = . 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 14 2. Cấu trúc Đại số Vành
Định nghĩa: Vành là một tập ≠ {∅} trang bị 2
phép toán 2 ngôi, 1 phép toán ký hiệu theo lối
cộng, 1 phép toán ký hiệu theo lối nhân, thỏa mãn: (, +) là nhóm Abel.
Phép nhân có tính kết hợp:
= ; ∀, , ∈ .
Phép nhân phân phối đối với phép cộng:
+ = + .
+ = + . 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 15 2. Cấu trúc Đại số Vành
Trong nhóm Abel (, +) phần tử trung hòa thường
ký hiệu là số 0, gọi là phần tử 0 của vành. Phần tử
nghịch đảo của ký hiệu là −, và gọi là phần tử đối
của . Tổng + (−) thường viết là − , và gọi là hiệu của , .
Nếu phép nhân có tính giao hoán: = , thì vành
(, +, . ) gọi là vành giao hoán.
Nếu phép nhân có phần tử trung hòa, thì phần tử
trung hòa đó gọi là đơn vị của vành (, +, . ), thường
ký hiệu là số 1, và vành (, +, . ) gọi là vành có đơn vị.
Ví dụ: , +, . , , +, . , , +, . : các vành có đơn vị là số 1. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 16 2. Cấu trúc Đại số
Giả sử là vành, khi đó: 0 = 0 = 0 , ∈
Thật vậy: vì 0 = 0 + 0 nên 0 = 0 + 0 = 0 + 0 → 0 = 0. Tương tự: 0 = 0.
− = − = − , , ∈ .
Thật vậy: + − = + − = 0 = 0, nên − = − .
Tương tự: − = −().
− (−) = , , ∈ .
Thật vậy: áp dụng liên tiếp 2 lần tính chất trên ta có:
− − = − − = − − = vì + [− ] = 0.
− = − ; − = − .
Thật vậy, − = + − = + − = − .
Nhóm nguyên: là 1 vành (, +, . ) thỏa mãn:
x = 0 → = 0 hoặc = 0 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 17
Số phức – dạng lượng giác
Định nghĩa. Cho số phức = +
Môđun của z một số thực dương, ký hiệu , xác định: = +
Góc là argument của số phức và được ký hiệu
là arg(z). 0 ≤ < 2 hoặc − < ≤ . = =
hoặc = = =
Dạng lượng giác của số phức 2 2 a b z a b i r(cos i sin) 2 2 2 2 a b a b 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 31
Số phức – dạng lượng giác Ví dụ
Tìm tất cả các số phức thỏa mãn: 1. − 2 + 3 = 5
2. − + + = 4 3. − 2 = + 2 Giải
1. − 2 + 3 = 5 ↔ − (2 − 3) = 5
Đường tròn tâm (2, −3), bán kính 5
2. − + + = 4
Tập hợp các điểm trong mặt phẳng sao cho tổng khoảng cách từ
đó đến hai điểm cho trước (0,1) và (0,-1) không thay đổi bằng 4 – Ellipse 1. − 2 = + 2
Tập hợp tất cả các điểm trong mặt phẳng sao cho khoảng cách từ
đó đến hai điểm cho trước (2,0) và (-2,0) bằng nhau - trục tung 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 32
Số phức – dạng lượng giác
Tính chất môđun của số phức = . = || ; ≠ 0. || = ||. + ≤ + ||. = ||. = || . 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 33/
Số phức – dạng lượng giác Ví dụ
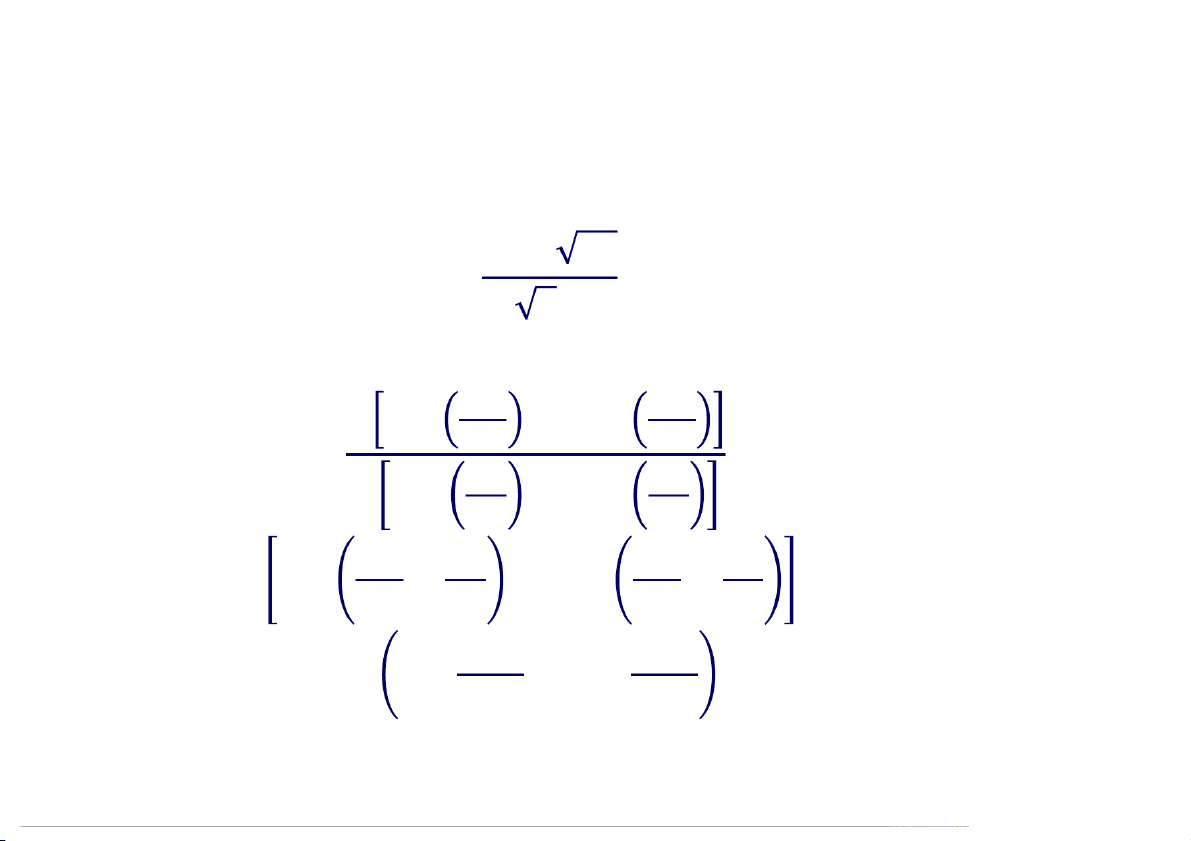
Tìm dạng lượng giác của số phức = −1 + 3 Giải = −1, = 3,
môđun: = = + = 2. Argument: 1 1 3 3 = = − = − = 3 + 1 2 , = = 3 + 1 2 . Suy ra: = 2/3. Dạng lượng giác: 2 2
= −1 + 3 = 2 3 + 3 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 34
Số phức – dạng lượng giác Các phép tính
Cho hai số phức dưới dạng lượng giác:
z r (cos i sin ) 1 z 1 r (cos 1 isin 1 ); 2 2 2 2 r r Bằng nhau 1 2 z z 1 2 k 1 2 2 Phép nhân 1 z z2 1 r 2 r [ cos( 1 2) isin( 1 2)]
Nhân 2 số phức: môđun nhân với nhau, argument cộng lại. z r Phép chia 1 1 [cos( i 1 2 ) sin( 1 2 )] 2 z 2 r
Chia 2 số phức: thương của hai môđun, hiệu của hai argument 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 35
Số phức – dạng lượng giác
Ví dụ Tìm dạng lượng giác của số phức: = 1 + 1 − 3 Giải = 1 + 1 − 3 − −
= 2 4 + 4 .2 3 + 3 = − −
= 2 2 4 + 3 + 4 + 3 = − −
= 2 2 12 + 12 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 36
Số phức – dạng lượng giác
Ví dụ Tìm dạng lượng giác của số phức: 2 − 12 = − 3+ Giải 4 − = 3 + − 3 2 5 6 + 5 6 − 5 − 5
= 2 3 − 6 + 3 − 6 = −7 −7
= 2 6 + 6 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 37 Số phức – dạng mũ
Định lý Euler (1707-1783) ie cos isin
Dạng đại số z a bi
Dạng lượng giác z r(cos isin ) Dạng mũ i z re 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 38 Số phức – dạng mũ Ví dụ
Tìm dạng mũ của z 3 i 5 5
Dạng lượng giác z 2 cos isin 5 i 6 6 Dạng mũ 6 z 2e
Biểu diễn trên mặt phẳng phức = , ∈ Dạng lượng giác 2
z e cos i sin
Trên mf phức là đường tròn bán kính 2 r e const 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 39
Số phức – lũy thừa cấp n
Cho = + . Khi đó:
= . = + + = − + 2
= . = + 3 + 3()+()=
= + 3 − 3 −
= − 3 + 3 − ⋯ ⋯ = ( + )= =
+ + ()+ ⋯ + = = + 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 40
Số phức – lũy thừa cấp n
Lũy thừa bậc của số phức 1 i i 5 3 2 i i i i 2 i 1 6 4 2 i i i 1 3 2 i i i i 7 5 2 i i i i 4 2 2 i i i 1 8 4 4 i i i 1
Giả sử ∈ ∗, khi đó = , với là phần dư của chia cho 4 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 41
Số phức – lũy thừa cấp n Ví dụ
Cho = 2 + . Tính . 5 z 2 i 0 5 1 4 2 3 2 3 2 3 4 4 5 5
C 2 C 2 i C 2 i C 2 i C 2i C i 5 5 5 5 5 5
32 516i 10 8 1 10 4 i 5 21 i 38 41i
Tính = . Ta có: 1987 = 4 × 496 + 3.
Do đó: = × = = − 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 42
Số phức – lũy thừa cấp n Công thức Moivre
Cho số phức biểu diễn dưới dạng = ( + )
với > 0, ∈ , khi đó: = ( + ) Ví dụ (1 + )
Ta có: = 1 + = 2 + = 2 + 25
= (1 + )= ( 2) 25 4 + 4 = 1 1
= 2 2 4 + 4 = 2 2 + 2 2 = 2 + 2 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 43
Số phức – lũy thừa cấp n b. (−1 + 3) Ta có: 1 3 2 2
= −1 + 3 = 2 − 2 + 2 = 2 3 + 3
Theo công thức Moivre ta có: 400
= (−1 + 3)= 2 400 3 + 3 396 + 4 = 2 396 + 4 3 + 3 4 1 3 = 2 4
3 + 3 = 2 −2 − 2 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 44
Số phức – lũy thừa cấp n c. ( ) ( )
Ta có: 3 − = 2 − = 2 +
12 + 2 = 4 + = 4 + ( 3 − ) 2( −17 = = 6 + −17 6 ) ( 12 + 2) 4( 20 6 + 20 6 ) −37 = 2 −37 6 + 6
= 2 + 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 45 Số phức – căn bậc n
Căn bậc ∈ của số phức là số phức , sao cho =
Cho số phức dưới dạng lượng giác:
= ( + ) Khi đó: + 2 + 2 = = + , = 0. . − 1.
Chú ý: Căn bậc của số phức có đúng nghiệm phân biệt 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 46 Số phức – căn bậc n
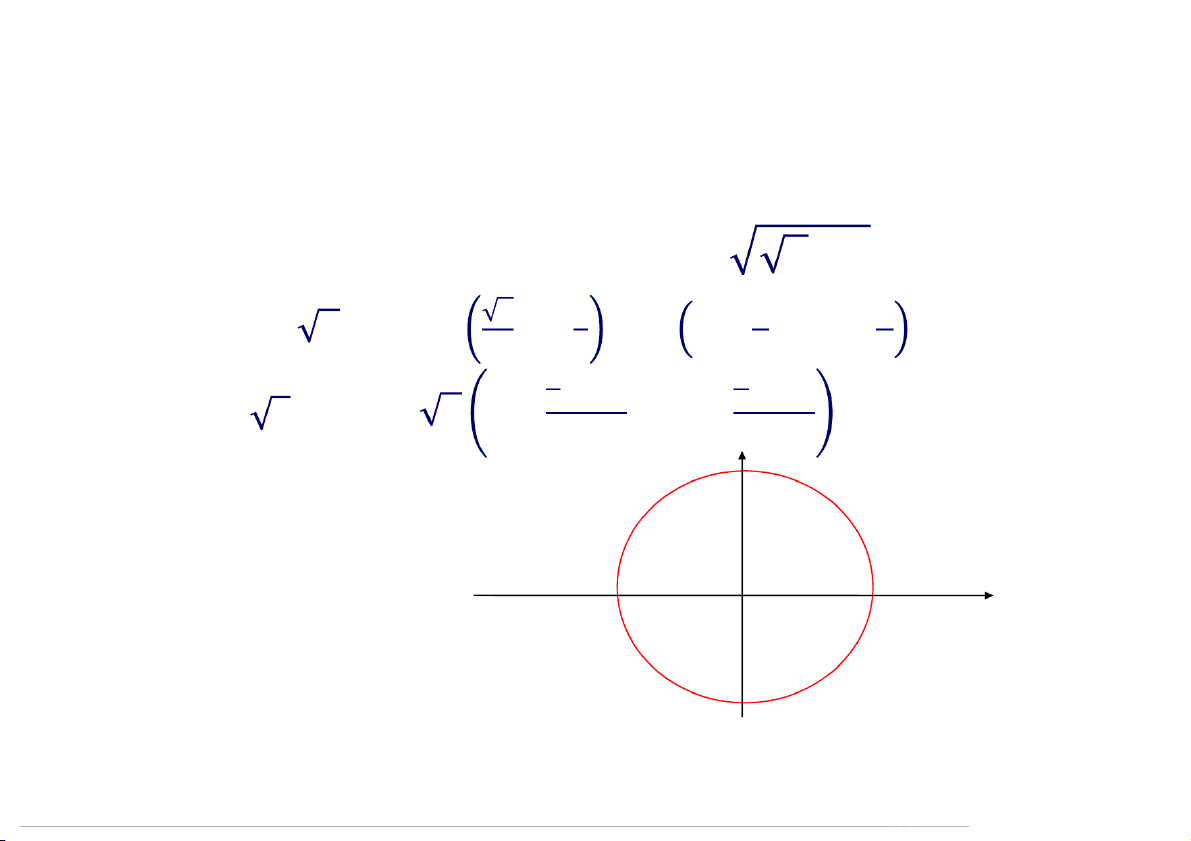
Ví dụ. Tìm căn bậc của số phức sau, biểu diễn
các nghiệm trên mặt phẳng phức: 3 +
Ta có: z = 3 + = 2 + = 2 + Do đó: = = 2 + , = 0,1,2,3. 1 z z0 z2 z3 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 47
Định lý cơ bản của Đại số
ĐN. Đa thức là các hàm số có dạng:
= + + + ⋯ + , ∈ , ∈ ∗
≠ 0: () có bậc . Thuật toán chia Euclid
Chia đa thức = − 7 + − 6
cho đa thức: = + − − 1
Định lý cơ bản. Đa thức () bậc có đúng
nghiệm thực, phức kể cả nghiệm bội.
Chú ý: Định lý cơ bản của Đại Số cho biết được số
nghiệm của phương trình mà không đưa ra cách tìm nghiệm đó như thế nào. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 48
Định lý cơ bản của Đại số
Hệ quả: Nếu z = + là một nghiệm phức của đa
thức () với hệ số thực, thì = − cũng là
một nghiệm phức của đa thức ().
Chứng minh: xét đa thức với hệ số thực:
= + + + ⋯ + , ∈ , ≠ 0, ∈ ∗
Ta có: = + + + ⋯ + =
= + + + ⋯ + = + + + ⋯ + = ()
= 0 → = () = 0 = 0
Do đó cũng là nghiệm của đa thức () 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 49
Định lý cơ bản của Đại số
Hệ quả: Nếu z = + là một nghiệm phức của
đa thức () với hệ số thực, thì = − cũng
là một nghiệm phức của đa thức ().
Định lý: Đa thức () với hệ số thực
= + + + ⋯ + , ∈ , ≠ 0, ∈ ∗
đều có thể phân tích được dưới dạng:
= − … − + + … ( + + ) trong đó:
, , ∈ và − 4 < 0. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 50
Định lý cơ bản của Đại số Ví dụ
Tìm đa thức bậc 3 với hệ số thực, biết đa thức đó có
2 nghiệm là: = 3 và = 2 + .
Tìm đa thức bậc 4 với hệ số thực, biết đa thức đó có
2 nghiệm là: = 3 và = 2 + . Giải
Bài 1 Không tồn tại đa thức thỏa mãn yêu cầu.
Bài 2. Đa thức cần tìm:
= − − − −
= − 3 + 3 − 2 + − 2 −
= ( + 9)( − 4 + 5)
= − 4 + 14 − 36 + 45 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 51
Định lý cơ bản của Đại số
Ví dụ. Giải các phương trình sau trong trường số phức : + 1 − = 0 + + 1 = 0 + + 2 = 0 + 2 + 1 − = 0
Giải phương trình: + + = 0
Bước 1: Tính ∆= − 4
Bước 2: Tính ∆= ∆,
Bước 3: = ∆ ; = ∆ 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 52
Định lý cơ bản của Đại số
Ví dụ Tìm tất cả các nghiệm của đa thức:
= − 4 + 14 − 36 + 45, biết đa thức đó có 1 nghiệm là 2 + . Giải
() với hệ số thực, nên () cũng có 1 nghiệm là 2 − .
Mà: − (2 + ) − (2 − ) = − 4 + 5.
Dùng phép chia đa thức có thể phân tích được như sau:
= ( − 4 + 5)( + 9)
+ 9 có 2 nghiệm là 3 và −3.
Vậy ta tìm được cả 4 nghiệm của () là:
2 + , 2 − , 3, −3 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 53
Định lý cơ bản của Đại số
Ví dụ: Giải phương trình sau trong : + = 0 Giải
+ = 0 ↔ = − ↔ = − .
Có: − = 0 − 1. = + . Do đó: − − 2 + 2 2 + 2 = − = 9 + 9 , = 0. . 8 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 54
Định lý cơ bản của Đại số Các định nghĩa
Phân thức là tỉ số của 2 đa thức: () . ()
() không là đa thức đồng nhất 0.
, () là các đa thức với hệ số thực.
Bậc của tử nhỏ hơn bậc của mẫu thì phân thức goi là phân thức thực sự.
() ; , ∈ : gọi là phân thức đơn giản loại 1.
() ; , , , ∈ ; − 4 < 0: gọi là
phân thức đơn giản loại 2. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 55
Định lý cơ bản của Đại số
Định lý. Mọi phân thức thực sự có dạng: () ()
() = ( − )… − + + … ( + + )
đều có thể phân tích được dưới dạng sau: () () = − + ⋯ + + ⋯ + + ⋯ + + − − − + + + + + ⋯ + + ⋯ + +
+ + + + + + + ⋯ + +
+ +
trong đó: , , , ∈ được xác định bằng pp đồng nhất thức. 12:29
Trường Đại học Công nghệ, ĐHQG Hà Nội 56




