Chương 10: Cây nhiều nhánh - Cấu trúc dữ liệu và giải thuật | Trường Đại học CNTT Thành Phố Hồ Chí Minh

Chöông 10 – Caây nhieàu nhaùnh
Chöông 10 – CAÂY NHIEÀU NHAÙNH
Chöông naøy tieáp tuïc nghieân cöùu veà caùc caáu truùc döõ lieäu caây, taäp trung vaøo caùc
caây maø soá nhaùnh taïi moãi nuùt nhieàu hôn hai. Chuùng ta baét ñaàu töø vieäc trình baøy
caùc moái noái trong caây nhò phaân. Keá tieáp chuùng ta tìm hieåu veà moät lôùp cuûa caây goïi
laø trie ñöôïc xem nhö töø ñieån chöùa caùc töø. Sau ñoù chuùng ta tìm hieåu ñeán caây B-tree
coù yù nghóa raát lôùn trong vieäc truy xuaát thoâng tin trong caùc taäp tin. Moãi phaàn
trong soá naøy ñoäc laäp vôùi caùc phaàn coøn laïi. Cuoái cuøng, chuùng ta aùp duïng yù töôûng
cuûa B-tree ñeå coù ñöôïc moät lôùp khaùc cuûa caây nhò phaân tìm kieám goïi laø caây ñoû-ñen (red-black tree).
Vöôøn caây, caây, vaø caây nhò phaân
Nhö chuùng ta ñaõ thaáy, caây nhò phaân laø moät daïng caáu truùc döõ lieäu ñôn giaûn vaø
hieäu quaû. Tuy nhieân, vôùi moät soá öùng duïng caàn söû duïng caáu truùc döõ lieäu caây maø
trong ñoù soá con cuûa moãi nuùt chöa bieát tröôùc, caây nhò phaân vôùi haïn cheá moãi nuùt chæ
coù toái ña hai con khoâng ñaùp öùng ñöôïc. Phaàn naøy laøm saùng toû moät ñieàu ngaïc nhieân
thuù vò vaø höõu ích: caây nhò phaân cung caáp moät khaû naêng bieåu dieãn nhöõng caây khaùc bao quaùt hôn.
Caùc teân goïi cho caây
Tröôùc khi môû roäng veà caùc loaïi caây, chuùng ta xeùt ñeán caùc ñònh nghóa. Trong
toaùn hoïc, khaùi nieäm caây coù moät yù nghóa roäng: ñoù laø moät taäp baát kyø caùc ñieåm (goïi
laø ñænh), vaø taäp baát kyø caùc caëp noái hai ñænh khaùc nhau (goïi laø caïnh hoaëc nhaùnh)
sao cho luoân coù moät daõy lieân tuïc caùc caïnh (ñöôøng ñi) töø moät ñænh baát kyø ñeán moät
ñænh baát kyø khaùc, vaø khoâng coù chu trình, nghóa laø khoâng coù ñöôøng ñi naøo baét ñaàu
töø moät ñænh naøo ñoù laïi quay veà chính noù.
Ñoái vôùi caùc öùng duïng trong maùy tính, chuùng ta thöôøng khoâng caàn nghieân cöùu
caây moät caùch toång quaùt nhö vaäy, vaø khi caàn laøm vieäc vôùi nhöõng caây naøy, ñeå nhaán
maïnh, chuùng ta thöôøng goïi chuùng laø caùc caây töï do (free tree). Caùc caây cuûa chuùng
ta phaàn lôùn luoân coù moät ñænh ñaëc bieät, goïi laø goác cuûa caây, vaø caùc caây daïng naøy
chuùng ta seõ goïi laø caùc caây coù goá
c (rooted tree).
Moät caây coù goác coù theå ñöôïc veõ theo caùch thoâng thöôøng cuûa chuùng ta laø goác naèm
treân, caùc nuùt vaø nhaùnh khaùc quay xuoáng döôùi, vôùi caùc nuùt laù naèm döôùi cuøng. Maëc
duø vaäy, caùc caây coù goác vaãn chöa phaûi laø taát caû caùc daïng caây maø chuùng ta thöôøng
duøng. Trong moät caây coù goác, thöôøng khoâng phaân bieät traùi hoaëc phaûi, hoaëc khi moät
nuùt coù nhieàu nuùt con, khoâng theå noùi raèng nuùt naøo laø nuùt con thöù nhaát, thöù hai,
v.v...Neáu khoâng vì moät lyù do naøo khaùc, söï thi haønh tuaàn töï caùc leänh thöôøng buoäc
chaët moät thöù töï leân caùc nuùt con cuûa moät nuùt. Chuùng ta ñònh nghóa moät caây coù thöù
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh
töï (ordered tree) laø moät caây coù goác trong ñoù caùc con cuûa moät nuùt ñöôïc gaùn cho moät thöù töï.
Löu yù raèng caùc caây coù thöù töï maø trong ñoù moãi nuùt coù khoâng quaù hai con vaãn
chöa phaûi cuøng moät lôùp vôùi caây nhò phaân. Neáu moät nuùt trong caây nhò phaân chæ coù
moät con, noù coù theå naèm beân traùi hoaëc beân phaûi, luùc ñoù ta coù hai caây nhò phaân
khaùc nhau, nhöng chuùng cuøng laø moät caây coù thöù töï.
Nhö moät nhaän xeùt cuoái cuøng lieân quan ñeán caùc ñònh nghóa, chuùng ta haõy löu yù raèng caây 2-tre
e maø chuùng ta ñaõ nghieân cöùu khi phaân tích caùc giaûi thuaät ôû nhöõng
chöông tröôùc laø moät caây coù goác (nhöng khoâng nhaát thieát phaûi laø caây coù thöù töï) vôùi
ñaëc tính laø moãi nuùt trong caây coù 0 hoaëc 2 nuùt con.
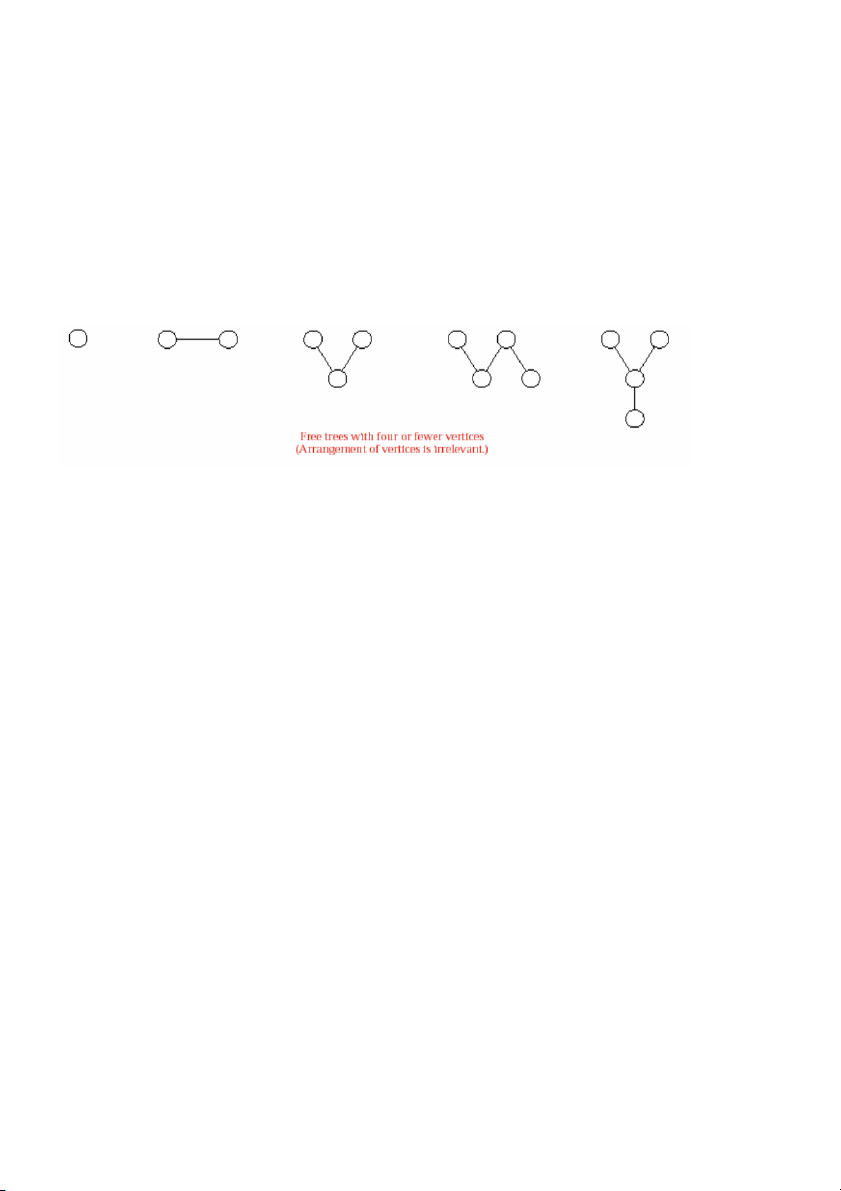
Hình 10.1 - Caùc daïng khaùc nhau cuûa caây.
Hình 10.1 cho thaáy raát nhieàu daïng caây khaùc nhau vôùi soá nuùt nhoû. Moãi lôùp caây
keå töø caây ñaàu tieân coù ñöôïc baèng caùch keát hôïp caùc caây töø caùc lôùp coù tröôùc theo
nhieàu caùch khaùc nhau. Caùc caây nhò phaân coù theå coù ñöôïc töø caùc caây coù thöù töï töông
öùng, baèng caùch phaân bieät caùc nhaùnh traùi vaø phaûi.
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh
Caây coù thöù töï
Hieän thöïc trong maùy tính
Neáu chuùng ta muoán söû duïng moät caây coù thöù töï nhö moät caáu truùc döõ lieäu, moät
caùch hieån nhieân ñeå hieän thöïc trong boä nhôù maùy tính laø môû roäng caùch hieän thöïc
chuaån cuûa moät caây nhò phaân, vôùi soá con troû thaønh vieân trong moãi nuùt töông öùng
soá caây con coù theå coù, thay vì chæ coù hai nhö ñoái vôùi caây nhò phaân. Chaúng haïn,
trong moät caây coù moät vaøi nuùt coù ñeán möôøi caây con, chuùng ta caàn phaûi giöõ ñeán
möôøi con troû thaønh vieân trong moät nuùt. Nhöng nhö vaäy seõ daãn ñeán vieäc caây phaûi
chöùa moät soá raát lôùn caùc con troû chöùa trò
. Chuùng ta coù theå tính ñöôïc chính
xaùc con soá naøy. Neáu caây coù n nuùt, moãi nuùt coù k con troû thaønh vieân, thì seõ coù taát caû
laø n x k con troû. Moãi nuùt coù chính xaùc laø moät con troû tham chieáu ñeán noù, ngoaïi tröø
nuùt goác. Nhö vaäy coù n-1 con troû khaùc . Tæ leä caùc con troû seõ laø: (n x k) – (n – 1) 1 ⎯⎯⎯⎯⎯⎯⎯ > 1 - ⎯ n x k k
Neáu moät nuùt coù theå coù möôøi caây con, thì coù hôn 90% con troû laø . Roõ raøng
laø phöông phaùp bieåu dieãn caây coù thöù töï naøy hao toán raát nhieàu vuøng nhôù. Lyù do laø
vì, trong moãi nuùt, chuùng ta ñaõ giöõ moät danh saùch lieân tuïc caùc con troû ñeán taát caû
caùc con cuûa noù, vaø caùc danh saùch lieân tuïc naøy chöùa quaù nhieàu vuøng nhôù chöa ñöôïc
söû duïng. Chuùng ta caàn tìm caùch thay theá caùc danh saùch lieân tuïc naøy bôûi caùc danh saùch lieân keát.
Hieän thöïc lieân keát
Ñeå naém caùc con cuûa moät nuùt trong moät danh saùch lieân keát, chuùng ta caàn hai
loaïi tham chieáu. Thöù nhaát laø tham chieáu töø nuùt cha ñeán nuùt con ñaàu tieân beân traùi
cuûa noù, chuùng ta seõ goïi laø
. Thöù hai, moãi nuùt, ngoaïi tröø nuùt goác, seõ
xuaát hieän nhö moät phaàn töû trong danh saùch lieân keát naøy, do ñoù noù caàn theâm moät
tham chieáu ñeán nuùt keá trong danh saùch, nghóa laø tham chieáu ñeán nuùt con keá tieáp
cuøng cha. Tham chieáu thöù hai naøy ñöôïc goïi laø
. Hieän thöïc naøy ñöôïc minh hoïa trong hình 10.2.
Hình 10.2 – Hieän thöïc lieân keát cuûa caây coù thöù töï
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh
Söï töông öùng töï nhieân
Ñoái vôùi moãi nuùt cuûa caây coù thöù töï chuùng ta ñaõ ñònh nghóa hai tham chieáu vaø
. Baèng caùch söû duïng hai tham chieáu naøy chuùng ta
coù ñöôïc caáu truùc cuûa moät caây nhò phaân, nghóa laø, hieän thöïc lieân keát cuûa moät caây coù
thöù töï laø moät caây nhò phaân lieân keát. Neáu muoán, chuùng ta coù theå coù ñöôïc moät hình
aûnh deã nhìn hôn cho caây nhò phaân baèng caùch söû duïng hieän thöïc lieân keát cuûa caây
coù thöù töï vaø quay theo chieàu kim ñoàng hoà moät goùc nhoû, sao cho caùc tham chieáu höôùng xuoáng (
) höôùng sang traùi, vaø caùc tham chieáu naèm ngang (
) höôùng sang phaûi. Ñoái vôùi hình 10.2, chuùng ta coù ñöôïc caây nhò phaân ôû hình 10.3.
Hình 10.3 – Hình ñaõ ñöôïc quay cuûa hieän thöïc lieân keát
Söï töông öùng ngöôïc laïi
Giaû söû nhö chuùng ta laøm ngöôïc laïi caùc böôùc cuûa quaù trình treân, baét ñaàu töø moät
caây nhò phaân vaø coá gaéng khoâi phuïc laïi moät caây coù thöù töï. Ñieàu quan saùt ñaàu tieân
chuùng ta caàn nhaän thaáy laø khoâng phaûi moïi caây nhò phaân ñeàu coù theå coù ñöôïc töø
moät caây coù thöù töï bôûi quaù trình treân: do tham chieáu cuûa nuùt goác
cuûa caây coù thöù töï luoân baèng
neân goác cuûa caây nhò phaân töông öùng luoân coù caây
con beân phaûi roãng. Ñeå tìm hieåu söï töông öùng ngöôïc laïi naøy moät caùch caån thaän,
chuùng ta caàn phaûi xem xeùt moät lôùp caáu truùc döõ lieäu khaùc qua moät soá ñònh nghóa môùi döôùi ñaây.
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh Röøng vaø vöôøn
Trong quaù trình tìm hieåu veà caây nhò phaân chuùng ta ñaõ coù kinh nghieäm veà caùch
söû duïng ñeä quy, ñoái vôùi caùc lôùp khaùc cuûa caây chuùng ta cuõng seõ tieáp tuïc laøm nhö
vaäy. Söû duïng ñeä quy coù nghóa laø thu heïp vaán ñeà thaønh vaán ñeà nhoû hôn. Do ñoù
chuùng ta neân xem thöû ñieàu gì seõ xaûy ra neáu chuùng ta laáy moät caây coù goác hoaëc
moät caây coù thöù töï vaø caét boû ñi nuùt goác. Nhöõng phaàn coøn laïi, neáu khoâng roãng, seõ
laø moät taäp caùc caây coù goác hoaëc moät taäp coù thöù töï caùc caây coù thöù töï töông öùng.
Thuaät ngöõ chuaån ñeå goïi moät taäp tröøu töôïng caùc caây ñoù laø röøng (forest), nhöng
khi chuùng ta duøng thuaät ngöõ naøy, noùi chung chuùng ta thöôøng hình dung ñoù laø caùc
caây coù goác. Cuïm töø “röøng coù thöù töï” (ordered forest) ñoâi khi coøn ñöôïc söû duïng ñeå
goïi taäp coù thöù töï caùc caây coù thöù töï, do ñoù chuùng ta seõ ñeà cöû moät thuaät ngöõ coù
tính ñaëc taû töông töï cho lôùp caùc caây coù thöù töï, ñoù laø thuaät ngöõ vöôøn (orchard).
Löu yù raèng chuùng ta khoâng chæ coù ñöôïc moät röøng hoaëc moät vöôøn nhôø vaøo
caùch loaïi boû ñi nuùt goác cuûa moät caây coù goác hoaëc moät caây coù thöù töï, chuùng ta
coøn coù theå taïo neân moät caây coù goác hoaëc moät caây coù thöù töï baèng caùch baét ñaàu töø
moät röøng hoaëc moät vöôøn, theâm moät nuùt môùi taïi ñænh, vaø noái caùc nhaùnh töø nuùt
môùi naøy ñeán goác cuûa taát caû caùc caây trong röøng hoaëc vöôøn ñoù. Caùch naøy ñöôïc minh hoïa trong hình 10.4.
Hình 10.4 – Loaïi boû vaø theâm nuùt goác.
Chuùng ta seõ söû duïng quaù trình naøy ñeå ñöa ra moät ñònh nghóa ñeä quy môùi cho
caùc caây coù thöù töï vaø caùc vöôøn. Tröôùc heát, chuùng ta haõy xem thöû neân baét ñaàu nhö
theá naøo. Chuùng ta nhôù raèng moät caây nhò phaân coù theå roãng. Moät röøng hay moät
vöôøn cuõng coù theå roãng. Tuy nhieân moät caây coù goác hay moät caây coù thöù töï khoâng theå
laø caây roãng, vì noù phaûi chöùa ít nhaát laø moät nuùt goác. Neáu chuùng ta muoán baét ñaàu
xaây döïng caây vaø röøng, chuùng ta coù theå löu yù raèng moät caây vôùi chæ moät nuùt coù theå
coù ñöôïc baèng caùch theâm moät goác môùi vaøo moät röøng ñang roãng. Moät khi chuùng ta
ñaõ coù caây naøy roài thì chuùng ta coù theå taïo ñöôïc moät röøng goàm bao nhieâu caây moät
nuùt cuõng ñöôïc. Sau ñoù chuùng ta coù theå theâm goác môùi ñeå taïo caùc caây coù goác chieàu
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh
cao laø 1. Baèng caùch naøy chuùng ta coù theå tieáp tuïc taïo neân caùc caây coù goác phuø hôïp
vôùi ñònh nghóa ñeä quy sau:
Ñònh nghóa: Moät caây coù goác (rooted tree) bao goàm moät nuùt ñôn ν, goïi laø goác
(root) cuûa caây, vaø moät röøng F (forest) goàm caùc caây goïi laø caùc caây con cuûa nuùt goác.
Moät röøng F laø moät taäp (coù theå roãng) caùc caây coù goác.
Moät quaù trình taïo töông töï cho caùc caây coù thöù töï vaø vöôøn.
Ñònh nghóa: Moät caây coù thöù töï T (ordered tree) bao goàm moät nuùt ñôn ν, goïi laø
goác (root) cuûa caây,vaø moät vöôøn O (orchard) goàm caùc caây ñöôïc goïi laø caùc caây con cuûa goác ν.
Chuùng ta coù theå bieåu dieãn caây coù thöù töï baèng moät caëp coù thöù töï T = {ν, O}.
Moät vöôøn O hoaëc laø moät taäp roãng, hoaëc goàm moät caây coù thöù töï T, goïi laø caây thöù
nhaát (first tree) cuûa vöôøn, vaø moät vöôøn khaùc O’ (chöùa caùc caây coøn laïi cuûa vöôøn).
Chuùng ta coù theå bieåu dieãn vöôøn baèng moät caëp coù thöù töï
O = (T, O’).
Löu yù raèng thöù töï cuûa caùc caây aån chöùa trong ñònh nghóa cuûa vöôøn. Moät vöôøn
khoâng roãng chöùa caây thöù nhaát vaø caùc caây coøn laïi taïo neân moät vöôøn khaùc, vöôøn
naøy laïi coù moät caây thöù nhaát vaø laø caây thöù hai cuûa vöôøn ban ñaàu. Tieáp tuïc ñoái vôùi
caùc vöôøn coøn laïi chuùng ta coù caây thöù ba, thöù tö, v.v...cho ñeán khi vöôøn cuoái cuøng laø
moät vöôøn roãng. Xem hình 10.5.
Hình 10.5 – Caáu truùc ñeä quy cuûa caùc caây coù thöù töï vaø vöôøn.
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh
Söï töông öùng hình thöùc
Baây giôø chuùng ta coù theå coù moät keát quaû mang tính nguyeân taéc cho phaàn naøy.
Ñònh lyù: Cho S laø moät taäp höõu haïn baát kyø goàm caùc nuùt. Coù moät aùnh xaï moät-moät f
töø taäp caùc vöôøn coù taäp nuùt laø S ñeán taäp caùc caây nhò phaân coù taäp nuùt laø S.
Chöùng minh ñònh lyù:
Chuùng ta seõ duøng nhöõng kyù hieäu trong caùc ñònh nghóa ñeå chöùng minh ñònh lyù
treân. Tröôùc heát chuùng ta caàn moät kyù hieäu töông töï cho caây nhò phaân. Moät caây nhò
phaân B hoaëc laø moät taäp roãng ∅ hoaëc goàm moät nuùt goác ν vaø hai caây nhò phaân B1
vaø B2. Kyù hieäu cho moät caây nhò phaân khoâng roãng laø moät boä ba B = [ν, B1, B2].
Chuùng ta seõ chöùng minh ñònh lyù baèng phöông phaùp quy naïp toaùn hoïc treân soá
nuùt trong S. Tröôøng hôïp thöù nhaát ñöôïc xeùt laø moät vöôøn roãng ∅, töông öùng vôùi
moät caây nhò phaân roãng. f(∅) = ∅.
Neáu vöôøn O khoâng roãng, noù ñöôïc kyù hieäu baèng moät boä hai
O = (T, O2)
vôùi T laø moät caây coù thöù töï vaø O2 laø moät vöôøn khaùc. Caây thöù töï T ñöôïc kyù hieäu bôûi moät caëp T ={ν, O1}
vôùi ν laø moät nuùt vaø O1 laø moät vöôøn khaùc. Thay bieåu thöùc T vaøo bieåu thöùc O ta coù
O = ({ν, O1}, O2).
Theo giaû thieát quy naïp, f laø moät aùnh xaï moät-moät töø caùc vöôøn coù ít nuùt hôn S ñeán
caùc caây nhò phaân, vôùi O1 vaø O2 nhoû hôn O, neân caùc caây nhò phaân f(O1) vaø f(O2)
ñöôïc xaùc ñònh bôûi giaû thieát quy naïp. Neáu chuùng ta ñònh nghóa aùnh xaï f töø moät
vöôøn ñeán moät caây nhò phaân bôûi
f({ν, O1}, O2) = [ν, f(O1), f(O2)].
thì f laø moät söï töông öùng moät-moät giöõa caùc vöôøn vaø caùc caây nhò phaân coù cuøng soá
nuùt. Vôùi baát kyø caùch thay theá naøo cho caùc kyù töï ν, O1, vaø O2 ôû veá traùi ñeàu coù chính
xaùc moät caùch ñeå thay theá cho chuùng ôû veá phaûi, vaø ngöôïc laïi.
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh Pheùp quay
Chuùng ta coù theå söû duïng daïng kyù hieäu cuûa söï töông öùng ñeå hình dung pheùp
bieán ñoåi töø vöôøn sang caây nhò phaân. Trong caây nhò phaân [ν, f(O1), f(O2)] tham
chieáu traùi töø ν ñeán nuùt goác cuûa caây nhò phaân f (O1), ñoù laø nuùt con thöù nhaát cuûa ν
trong caây coù thöù töï {ν, O1}. Tham chieáu phaûi töø ν ñeán nuùt voán laø goác cuûa caây coù
thöù töï keá tieáp veà beân phaûi trong vöôøn. Coù nghóa laø, “tham chieáu traùi” trong caây
nhò phaân töông öùng vôùi “con thöù nhaát” trong caây coù thöù töï, vaø “tham chieáu phaûi”
töông öùng “em keá”. Caùc quy taéc bieán ñoåi trong hình nhö sau:
1. Veõ vöôøn sao cho con thöù nhaát cuûa moãi nuùt naèm ngay döôùi noù, thay vì canh
khoaûng caùch cho taát caû caùc con naèm ñeàu beân döôùi nuùt naøy.
2. Veõ moät tham chieáu thaúng ñöùng töø moãi nuùt ñeán nuùt con thöù nhaát cuûa noù, vaø
veõ moät tham chieáu naèm ngang töø moãi nuùt ñeán em keá cuûa noù.
3. Loaïi boû taát caû caùc tham chieáu khaùc coøn laïi.
4. Quay sô ñoà 45 ñoä theo chieàu kim ñoàng hoà, sao cho caùc tham chieáu thaúng
ñöùng trôû thaønh caùc tham chieáu traùi vaø caùc tham chieáu naèm ngang trôû thaønh caùc tham chieáu phaûi.
5. Quaù trình naøy ñöôïc minh hoïa trong hình 10.6
Hình 10.6 – Chuyeån ñoåi töø vöôøn sang caây nhò phaân. Toång keát
Chuùng ta ñaõ xem xeùt ba caùch bieåu dieãn söï töông öùng giöõa caùc vöôøn vaø caùc caây nhò phaân:
• Caùc tham chieáu first_child vaø next_sibling.
• Pheùp quay caùc sô ñoà.
• Söï töông ñöông kyù hieäu moät caùch hình thöùc.
Nhieàu ngöôøi cho raèng caùch thöù hai, quay caùc sô ñoà, laø caùch deã nhôù vaø deã hình
dung nhaát. Caùch thöù nhaát, taïo caùc tham chieáu, thöôøng ñöôïc duøng ñeå vieát caùc
chöông trình thöïc söï. Cuoái cuøng, caùch thöù ba, söï töông ñöông kyù hieäu moät caùch
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh
hình thöùc, thöôøng raát coù ích trong vieäc chöùng minh raát nhieàu ñaëc tính cuûa caây nhò phaân vaø vöôøn.
Caây töø ñieån tìm kieám: Trie
Trong caùc chöông tröôùc chuùng ta ñaõ thaáy söï khaùc nhau trong vieäc tìm kieám
trong moät danh saùch vaø vieäc tra cöùu trong moät baûng. Chuùng ta coù theå aùp duïng yù
töôûng trong vieäc tra cöùu baûng vaøo vieäc truy xuaát thoâng tin trong moät caây baèng
caùch söû duïng moät khoùa hoaëc moät phaàn cuûa khoùa. Thay vì tìm kieám baèng caùch so
saùnh caùc khoùa, chuùng ta coù theå xem khoùa nhö laø moät chuoãi caùc kyù töï (chöõ caùi hoaëc
kyù soá), vaø söû duïng caùc kyù töï naøy ñeå xaùc ñònh ñöôøng ñi taïi moãi böôùc. Neáu caùc khoùa
cuûa chuùng ta chöùa caùc chöõ caùi, chuùng ta seõ taïo moät caây coù 26 nhaùnh töông öùng 26
chöõ caùi laø kyù töï ñaàu tieân cuûa caùc khoùa. Moãi caây con beân döôùi laïi coù 26 nhaùnh
töông öùng vôùi kyù töï thöù hai, vaø cöù theá tieáp tuïc ôû caùc möùc cao hôn. Tuy nhieân
chuùng ta cuõng coù theå tieán haønh phaân thaønh nhieàu nhaùnh ôû moät soá möùc ban ñaàu,
sau ñoù neáu caây trôû neân quaù lôùn, chuùng ta coù theå duøng moät vaøi caùch thöùc khaùc naøo
ñoù ñeå saép thöù töï cho nhöõng möùc coøn laïi. Tries
Coù moät phöông phaùp laø caét tæa bôùt caùc nhaùnh khoâng caàn thieát trong caây. Ñoù laø
caùc nhaùnh khoâng daãn ñeán moät khoùa naøo. Laáy ví duï, trong tieáng Anh, khoâng coù
caùc töø baét ñaàu bôûi ‘bb’, ‘bc’, ‘bf’, ‘bg’, ..., nhöng coù caùc töø baét ñaàu bôûi ‘ba’, ‘bd’, ‘be’.
Do ñoù, moïi nhaùnh vaø nuùt cho caùc töø khoâng toàn taïi coù theå ñöôïc loaïi khoûi caây. Caây
keát quaû naøy ñöôïc goïi laø
. Töø naøy nguyeân thuûy ñöôïc laáy töø retrieval, nhöng
thöôøng ñöôïc ñoïc laø “try”.
Ñònh nghóa: Moät caây
baäc m coù theå ñöôïc ñònh nghóa moät caùch hình thöùc laø
moät caây roãng hoaëc goàm moät chuoãi noái tieáp coù thöù töï cuûa m caây baäc m.
Tìm kieám moät khoùa
Giaû söû caùc töø coù 3 kyù töï coù nghóa goàm caùc töø ñöôïc löu trong caây ôû hình
10.7. Vieäc tìm kieám moät khoùa ñöôïc baét ñaàu töø nuùt goác. Kyù töï ñaàu tieân cuûa khoùa
ñöôïc duøng ñeå xaùc ñònh nhaùnh naøo caàn ñi xuoáng. Nhaùnh caàn ñi roãng coù nghóa laø
khoùa caàn tìm chöa coù trong caây. Ngöôïc laïi, treân nhaùnh ñöôïc choïn naøy, kyù töï thöù
hai laïi ñöôïc duøng ñeå xaùc ñònh nhaùnh naøo trong möùc keá tieáp caàn ñi xuoáng, vaø cöù
theá tieáp tuïc. Khi chuùng ta xeùt ñeán cuoái töø, laø chuùng ta ñaõ ñeán ñöôïc nuùt coù con troû
tham chieáu ñeán thoâng tin caàn tìm. Ñoái vôùi nuùt töông öùng moät töø khoâng coù nghóa
seõ coù con troû tham chieáu ñeán thoâng tin laø
. Chaúng haïn, töø a laø phaàn ñaàu cuûa
töø aba, töø naøy laïi laø phaàn ñaàu cuûa töø abaca, nhöng chuoãi kyù töï abac khoâng phaûi
laø moät töø coù nghóa, do ñoù nuùt bieåu dieãn abac coù con troû tham chieáu thoâng tin laø .
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät
Chöông 10 – Caây nhieàu nhaùnh Giaûi thuaät C++
Chuùng ta seõ chuyeån quaù trình tìm kieám vöøa ñöôïc moâ taû treân thaønh moät
phöông thöùc tìm kieám caùc baûn ghi coù khoùa laø caùc chuoãi kyù töï. Chuùng ta seõ söû duïng phöông thöùc
traû veà kyù töï taïi vò trí
trong khoùa hoaëc kyù töï roãng neáu khoùa coù chieàu daøi ngaén hôn ,
Hình 10.7 – Trie chöùa caùc töø ñöôïc caáu taïo töø a, b, c. vaø haøm phuï trôï
traû veà thöù töï cuûa
trong baûng chöõ caùi. Haøm naøy traû veà 0 cho kyù töï roãng, 27 cho caùc kyù töï
khoâng phaûi chöõ caùi. Trong hieän thöïc lieân keát, caây
chöùa moät con troû ñeán nuùt goác cuûa noù.
aùc phöông thöùc caäp nhaät, tìm kieám, truy xuaát.
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät