Tài liệu sưu tầm. Chuong 2. Các khái niệm cơ bản về logic mở

Chương 2: Các khái niệm cơ bản về Logic mờ
2.1. Giới thiệu Logic Mờ Mục tiêu
Chương này giới thiệu về sự cần thiết của logic mờ như một công cụ toán học
để mô hình hóa sự không chắc chắn và mơ hồ vốn có trong ngôn ngữ tự nhiên và
các hệ thống trong thế giới thực. Logic cổ điển, với tính nhị phân đúng/sai tuyệt đối,
tỏ ra không đủ khả năng để nắm bắt các khái niệm định tính như "cao", "nóng",
"nhanh" mà con người sử dụng một cách hiệu quả trong tư duy và ra quyết định hàng ngày. Nội dung chi tiết
Cần phải phân biệt rõ ràng giữa hai loại không chắc chắn. Lý thuyết xác suất
xử lý sự không chắc chắn liên quan đến tính ngẫu nhiên của một sự kiện (ví dụ: "xác
suất tung được mặt ngửa là 50%"). Sự kiện "mặt ngửa" là một khái niệm rõ ràng, sự
không chắc chắn nằm ở việc nó có xảy ra hay không. Ngược lại, logic mờ xử lý sự
không chắc chắn về mặt ngữ nghĩa, hay còn gọi là sự mơ hồ (vagueness). Khi ta nói
"nhiệt độ phòng này ấm", khái niệm "ấm" không có một ranh giới rõ ràng. Một nhiệt
độ có thể vừa "hơi ấm" vừa "hơi mát".
Để giải quyết vấn đề này, Giáo sư Lotfi Zadeh tại Đại học California,
Berkeley, đã đề xuất Lý thuyết Tập mờ vào năm 1965. Đây là một sự mở rộng của
lý thuyết tập hợp cổ điển, cho phép một phần tử có thể "thuộc về một phần" (partially
belong) vào một tập hợp, thay vì chỉ có hai lựa chọn thuộc về hoặc không thuộc về.
2.2. Tập mờ và Hàm thuộc Mục tiêu
Phần này định nghĩa các khái niệm cốt lõi của lý thuyết tập mờ, là nền tảng cho tất
cả các kỹ thuật và ứng dụng sẽ được thảo luận sau này. Nội dung chi tiết
● Tập mờ (Fuzzy Set): Trong khi một tập hợp rõ (crisp set) trên một không
gian nền (universe of discourse) X có thể được định nghĩa bởi một hàm đặc
trưng ánh xạ mỗi phần tử của X tới tập {0, 1}, một tập mờ A trên X được định
nghĩa bởi một hàm thuộc (membership function) μA(x) ánh xạ mỗi phần tử
x∈X tới một giá trị trong đoạn liên tục. Giá trị μA(x) biểu thị "mức độ thuộc
về" của x trong tập mờ A. 𝜇 (𝑥): 𝐴 → [ 0 1]
○ μA(x) = 1 có nghĩa là x hoàn toàn thuộc về A.
○ μA(x) = 0 có nghĩa là x hoàn toàn không thuộc về A.
○ 0 < μA(x) < 1 có nghĩa là x thuộc về A một phần.
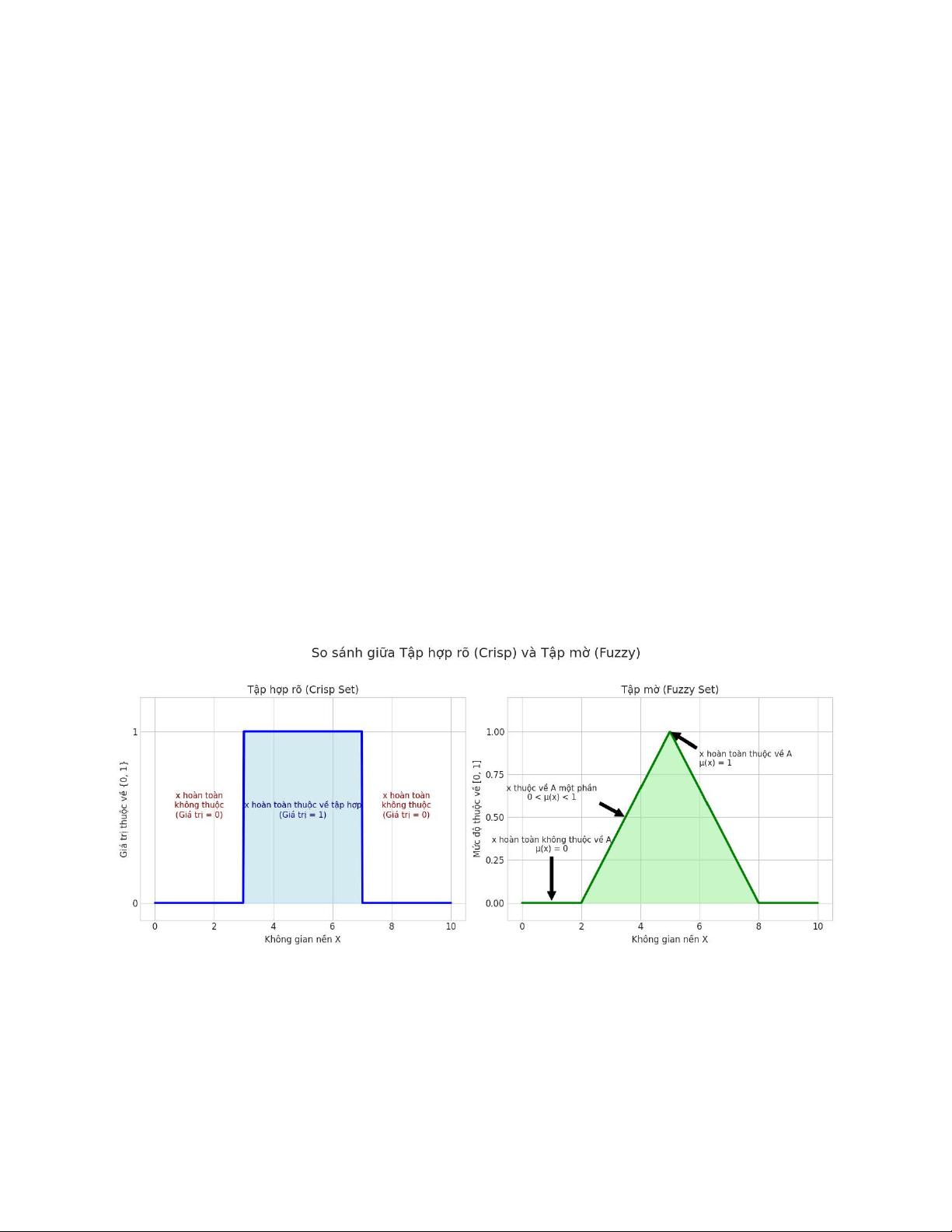
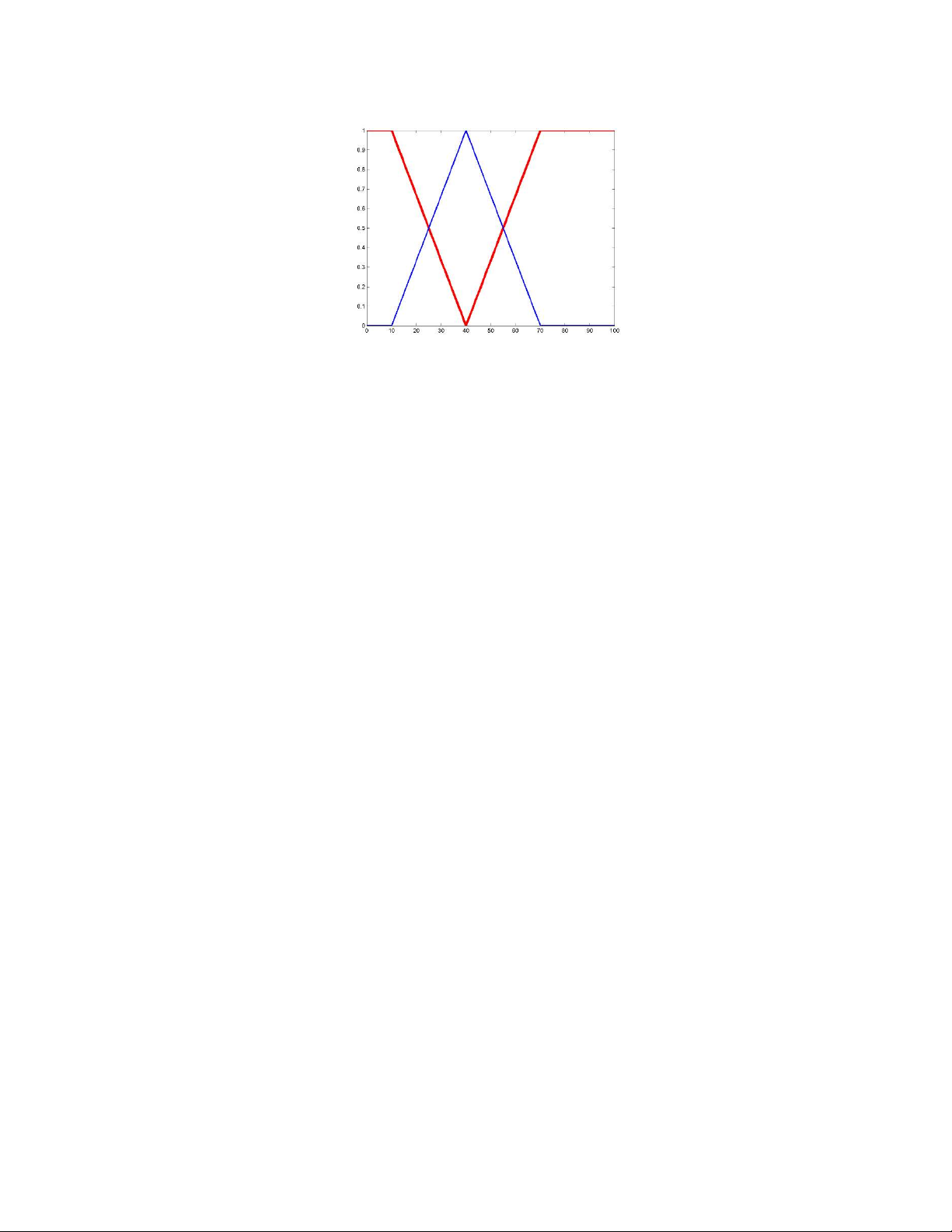
Hình 2-1. So sánh giữa tập rõ (Crisp) và tập mờ (Fuzzy)
Ví dụ: So sánh giữa tập mờ và tập hợp rõ trong không gian từ số 3 đến số 7. Với
tập hợp rõ, số 5 chắc chắn thuộc về, còn số 8 thì chắc chắn không. Không có trạng
thái "hơi thuộc về" hay "gần thuộc về". Với tập mờ, tập "Số gần bằng 5". Số 5,1
vẫn được xem là "gần bằng 5" nhưng với mức độ thấp hơn một chút so với chính số 5. Ví dụ:
Hãy xét tập hợp mờ A = "Nhiệt độ ấm áp".
Chúng ta muốn đánh giá các giá trị nhiệt độ x khác nhau:
 Với nhiệt độ x=25°C, đây là một nhiệt độ rất lý tưởng, dễ chịu. Ta có thể xác
định nó hoàn toàn thuộc vào tập "Nhiệt độ ấm áp". 𝜇 (25 𝐶) = 1 Ấ á
Ngược lại, với nhiệt độ x=5°C, trời rất lạnh. Nó hoàn toàn không thuộc vào
tập "Nhiệt độ ấm áp". 𝜇 (5 𝐶) = 0 Ấ á
 Với nhiệt độ x=20°C, trời khá mát mẻ, có thể xem là "hơi ấm". Nó thuộc một
phần vào tập "Nhiệt độ ấm áp". 𝜇 (20 𝐶) = 0.7 Ấ á
Như vậy, khi bạn thấy μA(x)=1, nó thể hiện một sự chắc chắn tuyệt đối rằng phần
tử đó thỏa mãn hoàn toàn định nghĩa của tập hợp mờ.
● Biến ngôn ngữ (Linguistic Variable): Đây là khái niệm then chốt kết nối
giữa lý thuyết toán học trừu tượng của tập mờ và tri thức chuyên gia trong
thực tế. Một biến ngôn ngữ là một biến mà các giá trị của nó không phải là số
mà là các từ hoặc cụm từ trong ngôn ngữ tự nhiên.
Ví dụ: Biến "Nhiệt độ" có thể có các giá trị ngôn ngữ là {"Rất Lạnh",
"Lạnh", "Mát", "Ấm", "Nóng", "Rất Nóng"}. Mỗi giá trị ngôn ngữ này được
định nghĩa bởi một tập mờ tương ứng trên không gian nền của nhiệt độ (ví dụ,
từ -10°C đến 40°C). Chính biến ngôn ngữ cho phép chúng ta chuyển đổi tri
thức định tính, mơ hồ của con người ("nếu nhiệt độ hơi cao thì...") thành một
cấu trúc hình thức, có thể tính toán được.
● Các dạng hàm thuộc phổ biến: Việc lựa chọn hình dạng của hàm thuộc là
một bước quan trọng trong thiết kế hệ mờ. Các dạng phổ biến bao gồm :
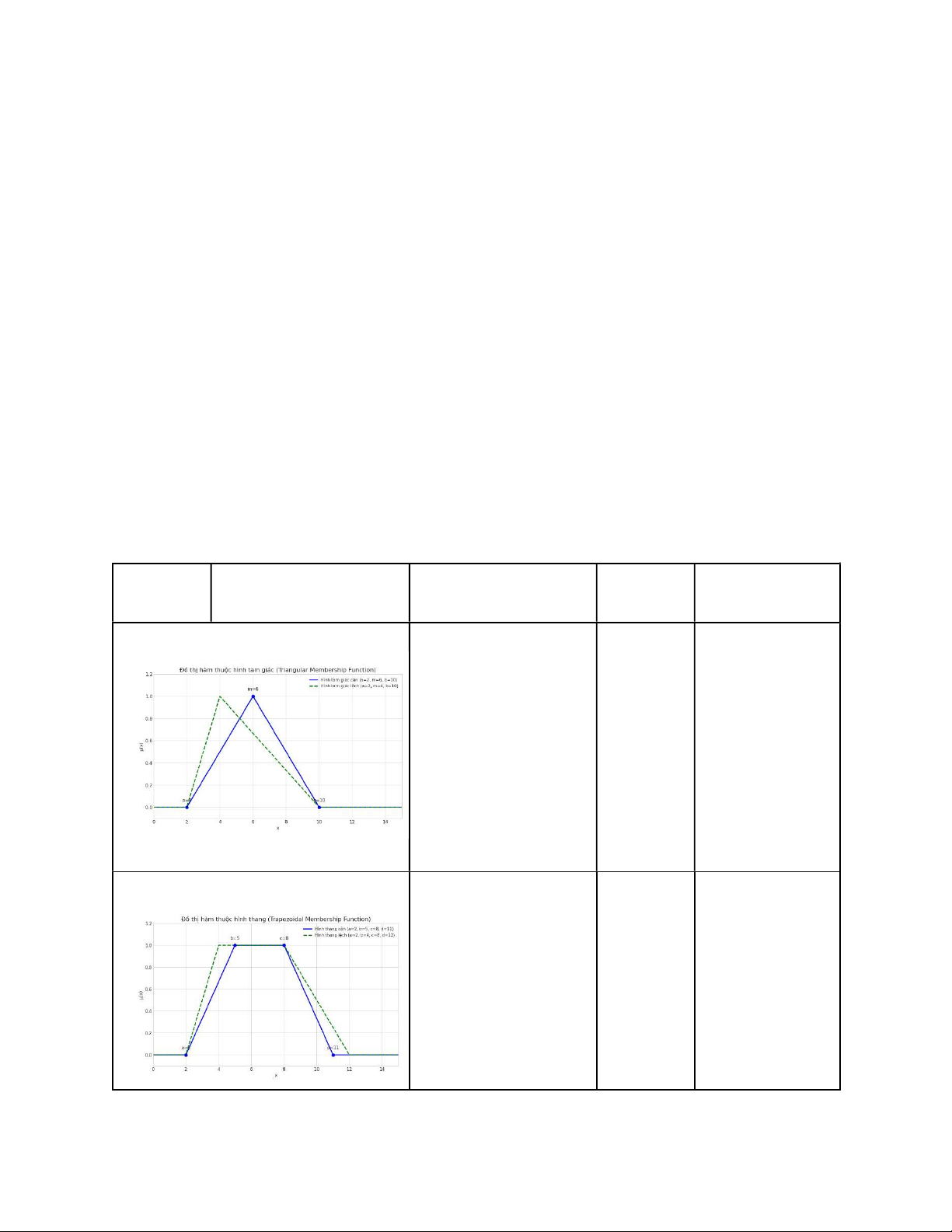
○ Hàm tam giác: Được định nghĩa bởi ba điểm, tạo thành một hình tam
giác. Đơn giản để tính toán.
○ Hàm hình thang: Một sự tổng quát hóa của hàm tam giác, được định
nghĩa bởi bốn điểm. Nó cho phép một khoảng giá trị có độ thuộc bằng 1.
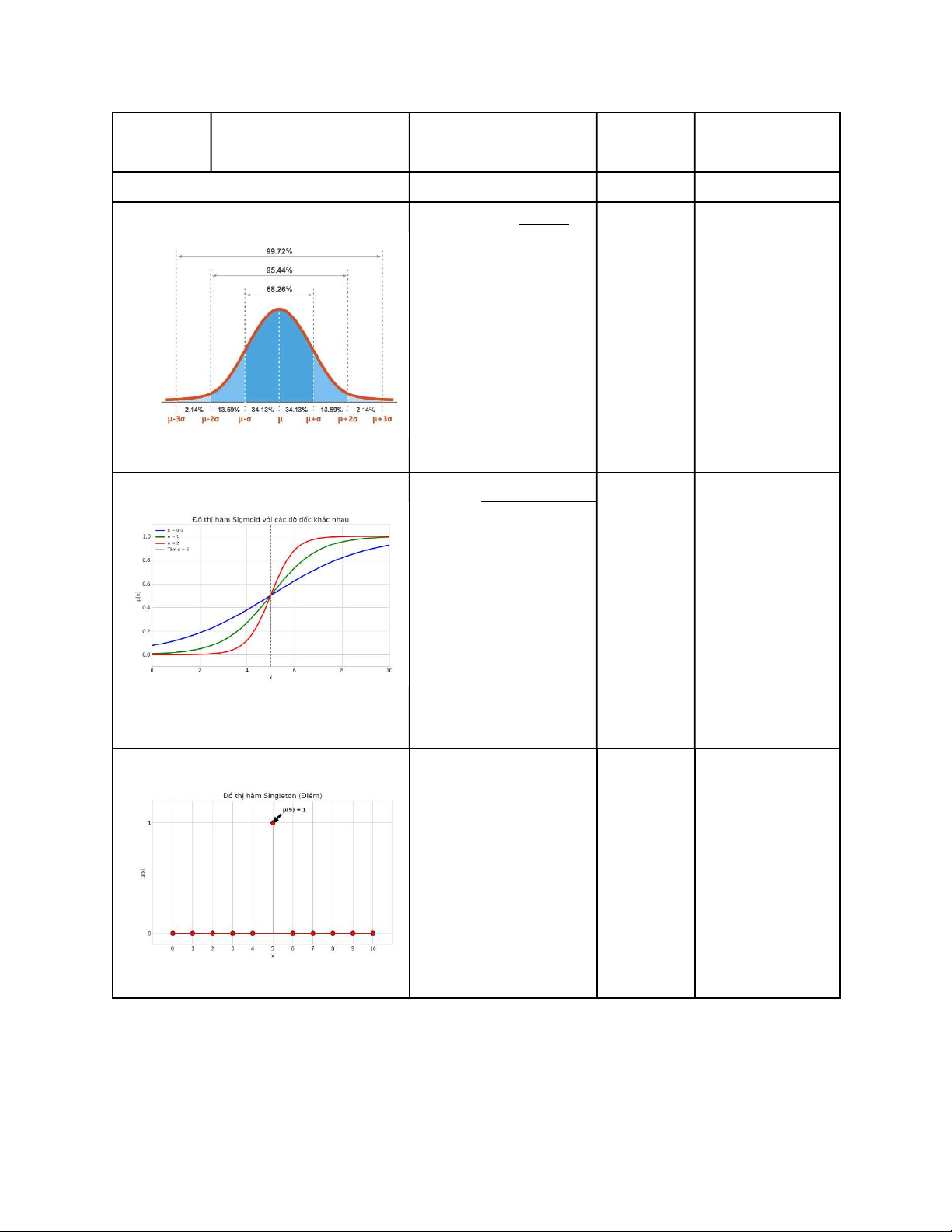
○ Hàm Gaussian (dạng chuông): Mượt mà và có đạo hàm tại mọi điểm,
hữu ích trong các thuật toán học dựa trên gradient.
○ Hàm Sigmoid: Có hình dạng chữ S, thường được sử dụng để biểu diễn
các khái niệm như "lớn" hoặc "nhỏ" ở các rìa của không gian nền.
Bảng 2.1: Các dạng hàm thuộc phổ biến và công thức toán học
Tên hàm Hình dạng đồ thị Công thức toán học Số tham Đặc điểm (minh họa) (dạng đơn giản) số Tam giác Tuyến tính từng 3 Đơn giản, tính đoạn, xác định bởi 3 toán nhanh. điểm (a, m, b)
Hình tam giác cân hoặc lệch Hình thang Tuyến tính từng 4 Cho phép một đoạn, xác định bởi 4 khoảng giá trị điểm (a, b, c, d) có độ thuộc tối đa.
Tên hàm Hình dạng đồ thị Công thức toán học Số tham Đặc điểm (minh họa) (dạng đơn giản) số
Hình thang cân hoặc lệch Gaussian ( ) 2 Mượt mà, có 𝜇(𝑥) = 𝑒
(tâm c, độ đạo hàm liên
rộng σ) tục, biểu diễn tự nhiên cho các giá trị trung tâm. Hình chuông đối xứng Sigmoid 1 2 Phù hợp để biểu 𝜇(𝑥) = 1 + 𝑒 (
) (độ dốc a, diễn các khái
điểm uốn niệm không có c) giới hạn rõ ràng (ví dụ: "rất lớn"). Hình chữ S Singleton 𝜇(𝑥) = 1 tại x=c, và 1 Thường dùng 0 tại các điểm khác
(vị trí c) để biểu diễn giá trị đầu ra trong một số mô hình suy diễn mờ.
Một đường thẳng đứng
2.3. Các phép toán trên Tập mờ
Để xây dựng các quy tắc logic, chúng ta cần định nghĩa các phép toán tương ứng
với AND, OR, và NOT trên các tập mờ. Các phép toán chuẩn của các tập cùng cơ
sở được định nghĩa như sau :
● Phép hợp (Union - OR): Hàm thuộc của A ∪ B được định nghĩa bằng toán tử max.
𝜇 ∪ (𝑥) = max (𝜇 (𝑥), 𝜇 (𝑥))
● Phép giao (Intersection - AND): Hàm thuộc của A ∩ B được định nghĩa bằng toán tử min.
𝜇 ∩ (𝑥) = min (𝜇 (𝑥), 𝜇 (𝑥))
● Phép bù (Complement - NOT): Hàm thuộc của 𝐴 được định nghĩa là:
𝜇 (𝑥) = 1 − 𝜇 (𝑥)
2.4. Luật hợp thành mờ (Fuzzy Composition)
Luật hợp thành mờ là cách biểu diễn các quy tắc suy luận "IF-THEN" (Nếu-Thì),
vốn là xương sống của các hệ thống dựa trên tri thức mờ.
● Cấu trúc luật mờ: Một luật mờ có dạng: IF x is A THEN y is B, trong đó x,
y là các biến ngôn ngữ, và A, B là các giá trị ngôn ngữ (tập mờ) tương ứng.
Ví dụ: "IF Nhiệt độ IS Nóng THEN Tốc độ quạt IS Cao".
● Suy diễn mờ: Quá trình suy diễn mờ (fuzzy inference) xác định kết quả đầu
ra (một tập mờ) dựa trên một đầu vào (có thể là một giá trị rõ hoặc một tập
mờ) và một tập các luật mờ. Phương pháp suy diễn phổ biến nhất là của
Mamdani, sử dụng phép toán min để đánh giá phần tiền đề (IF) của luật và
sau đó "cắt" (clip) hoặc "co giãn" (scale) hàm thuộc của phần kết luận (THEN).
● Luật hợp thành là tên chung gọi mô hình R biểu diễn một hay nhiều hàm liên
thuộc 𝜇  (𝑥) cho một hay nhiều mệnh đề hợp thành A=>B.
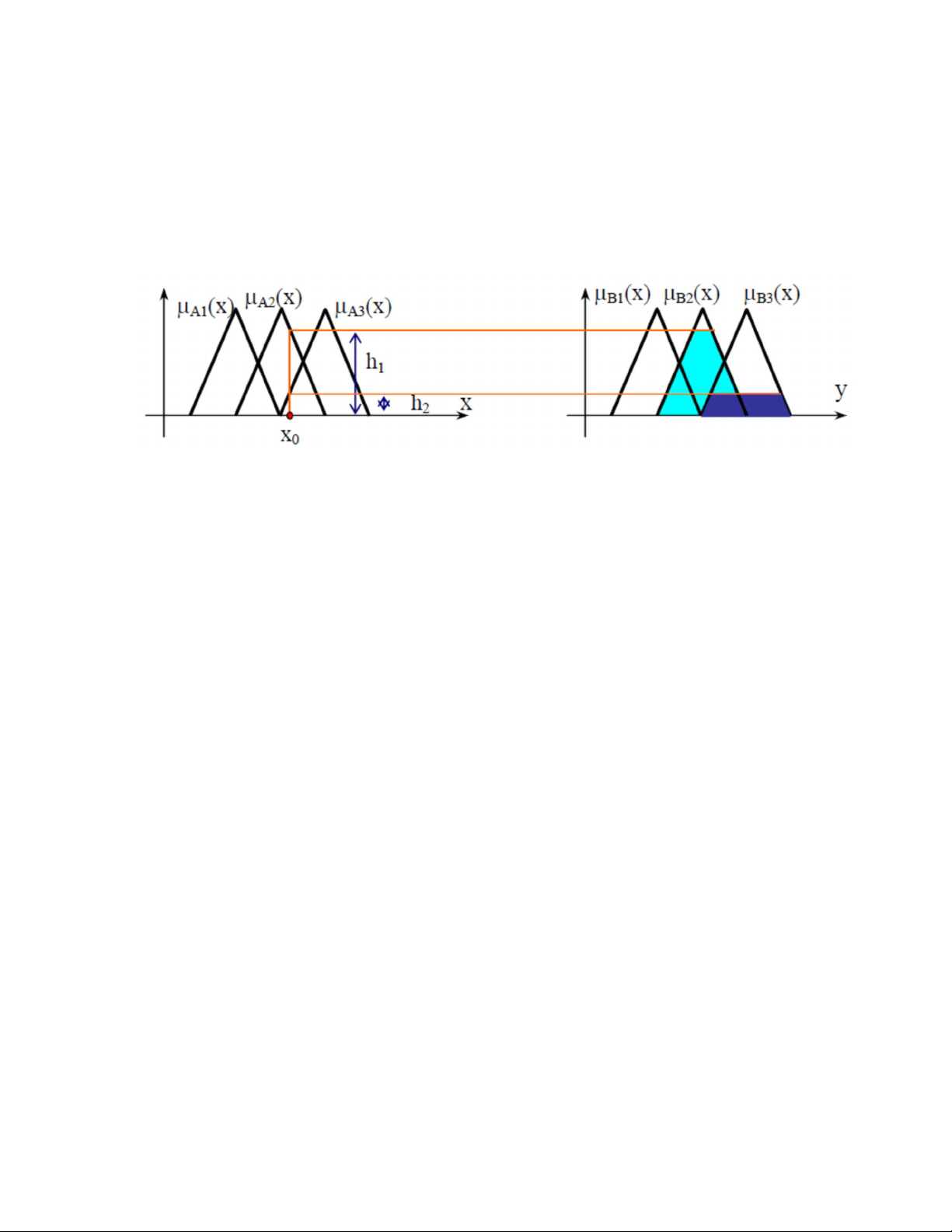
Xét luật hợp thành R gồm 3 mệnh đề hợp thành:
R1: Nếu x = A1 Thì y = B1 hoặc
R2: Nếu x = A2 Thì y = B2 hoặc
R1: Nếu x = A3 Thì y = B3 hoặc
Với mỗi giá trị rõ x0 của biến ngôn ngữ đầu vào, ta có 3 tập mờ ứng với 3
mệnh đề hợp thành R1, R2, R3 của luật hợp thành R. Gọi hàm liên thuộc của
các tập mờ đầu ra là 𝜇 (𝑦); 𝜇 (𝑦); 𝜇 (𝑦) thì giá trị của luật hợp thành R
ứng với x0 là tập mờ B’ thu được qua phép hợp 3 tập mờ: 𝐵 = 𝐵 ∪ 𝐵 ∪ 𝐵 .
2.5. Giải mờ (Defuzzification)
Kết quả của quá trình suy diễn mờ là một tập mờ tổng hợp, biểu thị đầu ra
điều khiển. Tuy nhiên, các thiết bị chấp hành trong thế giới thực (như động cơ, van)
yêu cầu một tín hiệu điều khiển rõ ràng, là một con số cụ thể. Quá trình chuyển đổi
từ tập mờ kết quả sang một giá trị số rõ ràng được gọi là giải mờ.
Ví dụ: Các quy tắc được thiết kế để quyết định mức độ áp suất cần áp dụng có
thể dẫn đến "Giảm áp suất (15%), Duy trì áp suất (34%), Tăng áp suất (72%)". Giải
mờ là việc diễn giải các mức độ thành viên của các tập mờ thành một quyết định cụ
thể hoặc giá trị thực.
Phương pháp giải mờ đơn giản nhất nhưng ít hữu ích nhất là chọn tập hợp có
độ thành viên cao nhất, trong trường hợp này là "Tăng Áp suất" vì nó có độ thành
viên 72%, và bỏ qua các tập hợp khác, rồi chuyển đổi 72% này thành một số nào đó.
Vấn đề với cách tiếp cận này là nó làm mất thông tin. Các quy tắc yêu cầu giảm hoặc
duy trì áp suất có thể cũng không tồn tại trong trường hợp này.
Một kỹ thuật giải mờ phổ biến và hữu ích là trọng tâm. Đầu tiên, kết quả của các
quy tắc phải được cộng lại với nhau theo một cách nào đó. Hàm thành viên tập mờ
điển hình nhất có đồ thị hình tam giác. Bây giờ, nếu tam giác này được cắt theo một
đường thẳng nằm ngang ở đâu đó giữa đỉnh và đáy, và phần trên cùng bị loại bỏ,
phần còn lại sẽ tạo thành hình thang . Bước đầu tiên của quá trình giải mờ thường là
"cắt bỏ" các phần của đồ thị để tạo thành hình thang (hoặc các hình dạng khác nếu
hình dạng ban đầu không phải là hình tam giác). Ví dụ: nếu đầu ra có "Giảm áp suất
(15%)", thì tam giác này sẽ được cắt 15% từ đáy lên. Trong kỹ thuật phổ biến nhất,
tất cả các hình thang này sau đó được chồng lên nhau, tạo thành một hình dạng hình
học duy nhất . Sau đó, trọng tâm của hình này, được gọi là trọng tâm mờ , được tính
toán. Tọa độ x của trọng tâm là giá trị đã được giải mờ.
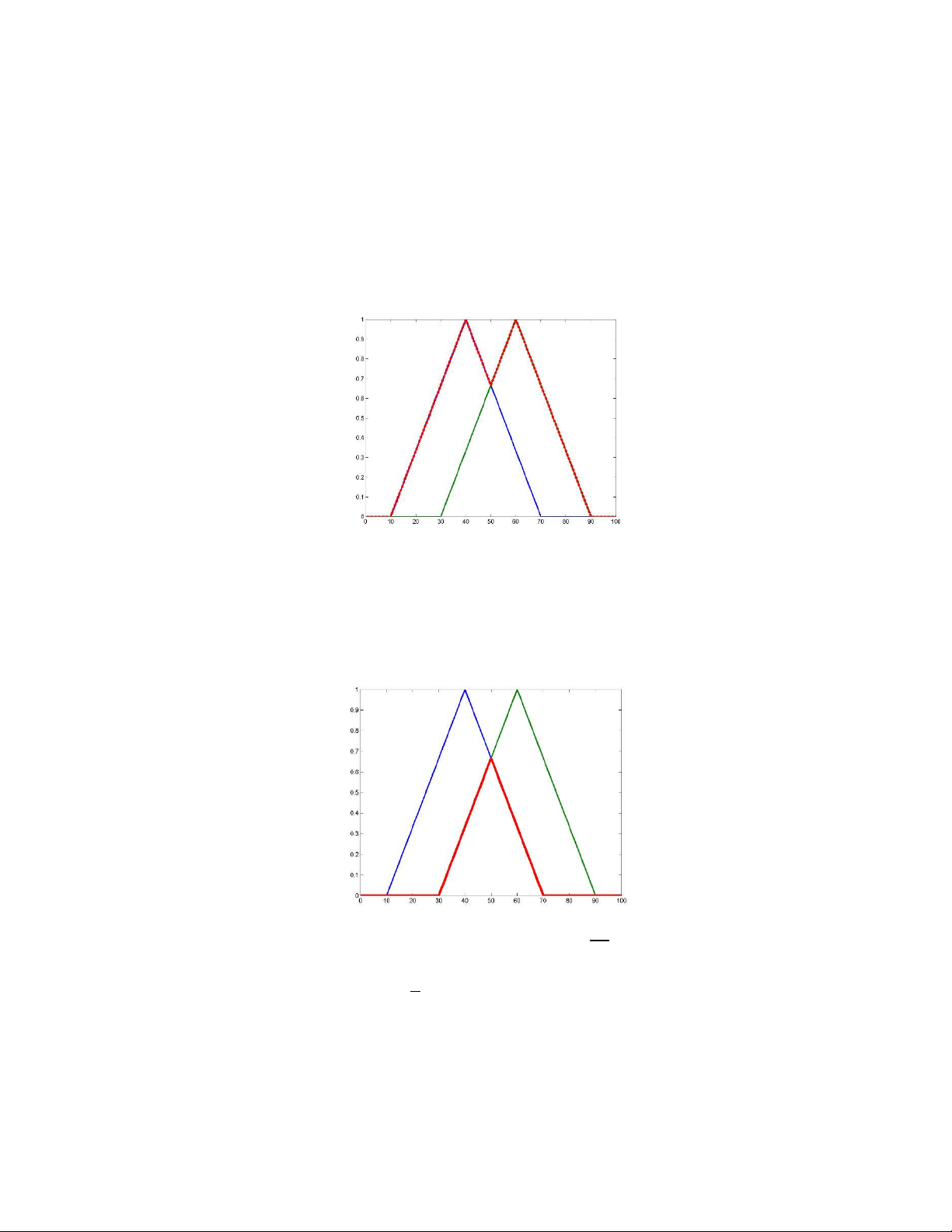
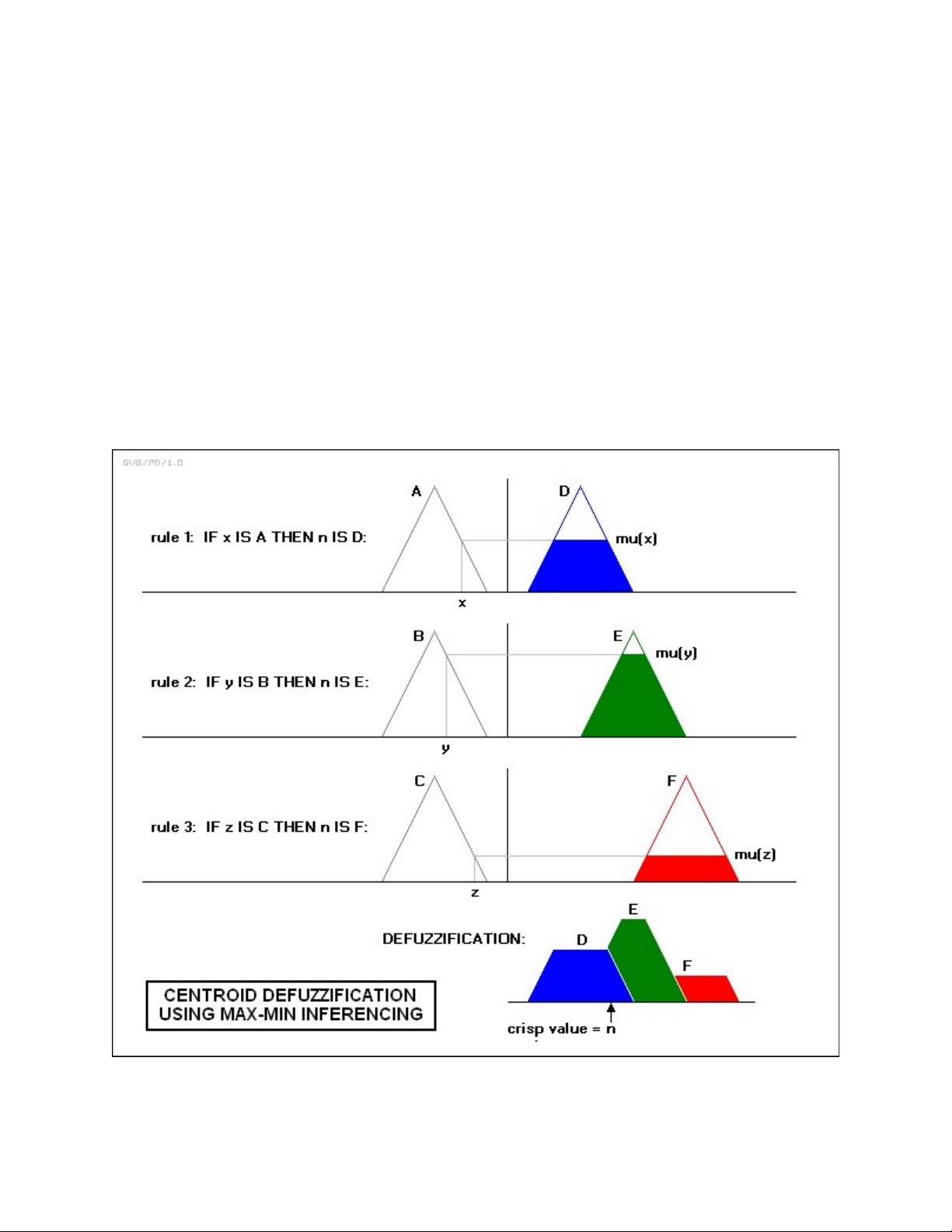
Hình 2-2. Một số phương pháp khử mờ đặc biệt
Các phương pháp giải mờ phổ biến bao gồm :
● Phương pháp Trọng tâm (Centroid of Area - COA): Đây là phương pháp
được sử dụng rộng rãi nhất. Nó tính toán hoành độ của trọng tâm của diện
tích được giới hạn bởi hàm thuộc của tập mờ kết quả. Phương pháp này cho
kết quả điều khiển mượt mà và tính đến tất cả các thông tin trong tập mờ đầu ra.
● Phương pháp Cực đại (Maximum Methods): Các phương pháp này chọn
một giá trị rõ ràng dựa trên điểm có độ thuộc cao nhất trong tập mờ kết quả. Có các biến thể như:
○ Trung bình của các cực đại (Middle of Maximum- MOM): Lấy giá
trị trung bình của tất cả các điểm có độ thuộc cao nhất.
○ Cực đại nhỏ nhất (First of Maximum - FOM): Lấy giá trị nhỏ nhất
trong số các điểm có độ thuộc cao nhất.
○ Cực đại lớn nhất (Last of Maximum - LOM): Lấy giá trị lớn nhất
trong số các điểm có độ thuộc cao nhất. Phương pháp trọng tâm thường
được ưa chuộng hơn vì nó ổn định và ít bị ảnh hưởng bởi sự thay đổi
nhỏ trong hình dạng của tập mờ đầu ra.