Chương 2 ĐỘNG HỌC CHẤT ĐIỂM MỤC TIÊU
Sau bài học này, sinh viên phải :
• Nêu được các khái niệm: vận tốc, gia tốc và
các công thức xác định vectơ vận tốc, gia
tốc trong chuyển động cong, thẳng, tròn.
• Nêu được tính chất của chuyển động dựa
trên quan hệ giữa vectơ vận tốc và gia tốc.
• Viết được phương trình chuyển động,
đường đi, vận tốc, gia tốc của các chuyển động đơn giản.
• Vận dụng giải các bài toán cơ bản về chuyển động. NỘI DUNG:
§1.1 – CÁC KHÁI NIỆM CƠ BẢN VỀ CHUYỂN ĐỘNG
§1.2 – TỐC ĐỘ VÀ VẬN TỐC §1.3 – GIA TỐC
§1.4 – VẬN TỐC, GIA TỐC TRONG CHUYỂN ĐỘNG TRÒN
§1.5 – MỘT SỐ CHUYỂN ĐỘNG ĐƠN GIẢN
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ 1) Cơ học, động học:
• Cơ học: ngành vật lý nghiên cứu về
chuyển động của các vật thể.
• Động học: ngành vật lý nghiên cứu các
tính chất, qui luật chuyển động mà không
tính tới nguyên nhân của chuyển động đó.
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ
2) Chuyển động, chất điểm:
• Chuyển động cơ học (chuyển động): là sự
thay đổi vị trí của các vật thể.
• Chất điểm: là vật thể có kích thước không
đáng kể so với những kích thước, khoảng cách mà ta xét.
Lưu ý: khái niệm chuyển động, chất điểm có tính tương đối.
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ
2) Chuyển động, chất điểm:
Ví dụ về tính tương đối của chất điểm
Ví dụ về tính tương đối của chuyển động
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ
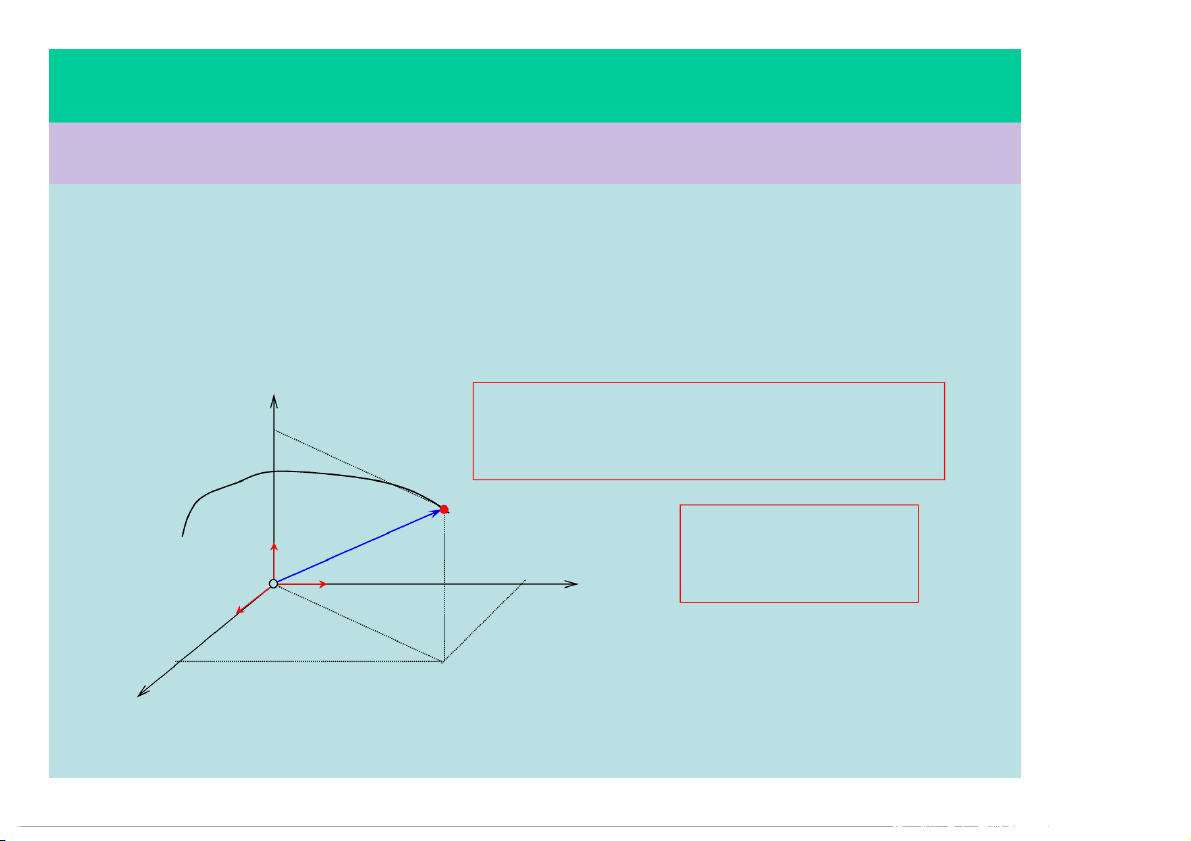
3) Quĩ đạo, quãng đường và độ dời:
• Quĩ đạo: là tập hợp các vị trí của Quãng đường
chất điểm trong quá trình chuyển động. s  M M  r
• Quãng đường: là độ dài của vết mà o
chất điểm vạch ra trong thời gian khảo sát chuyển động. Độ dời
• Độ dời: là vectơ nối từ vị trí đầu đến vị trí cuối. Qũi đạo
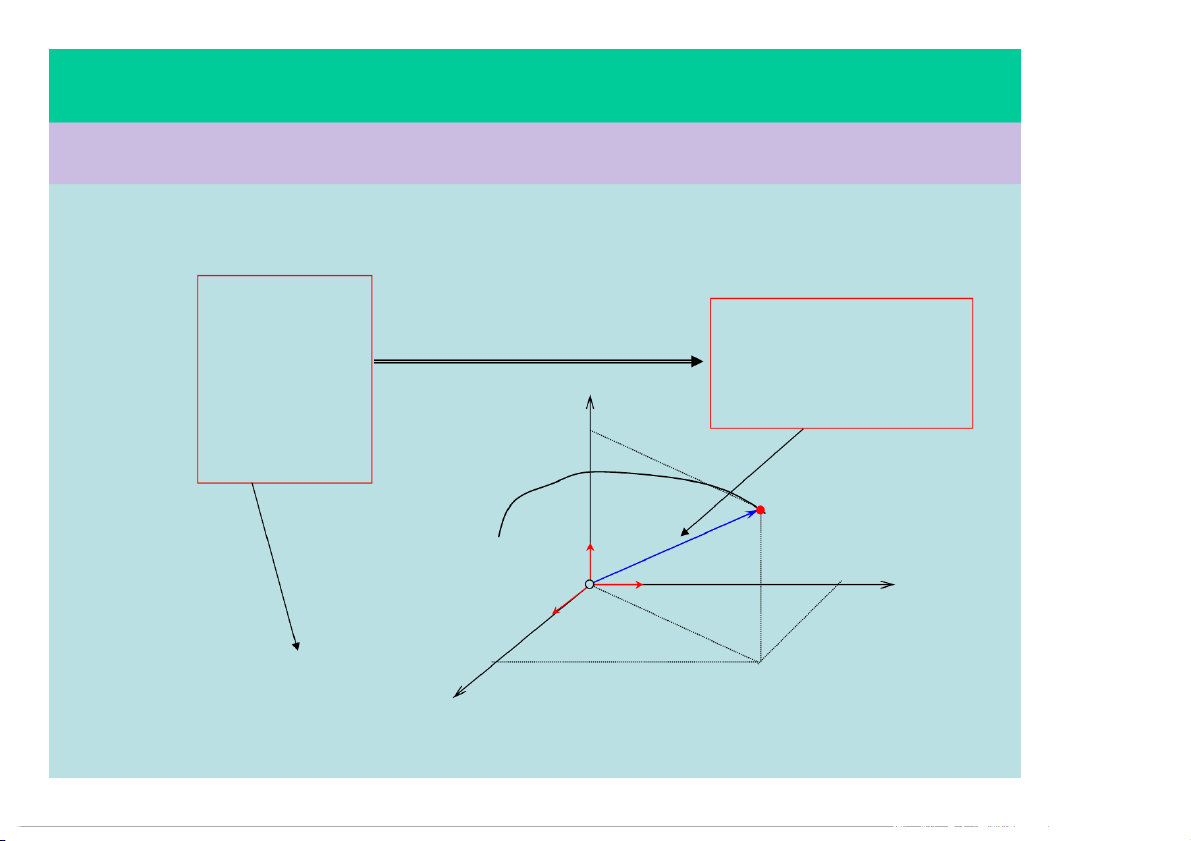
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ 4) Hệ qui chiếu:
Là hệ thống gồm một vật mốc, hệ tọa độ gắn với
vật mốc đó và đồng hồ đo thời gian, dùng để xác
định vị trí của các vật khác. z      z
r  OM  x i  y j  z k  M  r  k  y r  (x, y, z) y i  O j x Hay: M(x,y,z) x Hệ tọa độ Descartes
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ
5) Ph/trình chuyển động, ph/trình quĩ đạo: PTCĐ PTQĐ x  f (t)  Khử t  ( F x, , y z)  0 y  g(t) z G(x, ,yz)  0   z z  h(t)  M  Chko biết hình dạn  y g qũi điạo y  O j x
Cho biết vị trí ở thời điểm t x
§1.1 . CÁC K/N CƠ BẢN VỀ CĐ
Ví dụ: Xác định qũi đạo biết PTCĐ có dạng: x  5t  3 3  x 15t 9 a)     y  3x  13 y 15t   4 y 15t  4 
Vậy, quĩ đạo là đường thẳng (d): y  3x  13 b) x  5t 1 2  x 1   y  4  50  2  2x  4x  6 2 y   4  50t  5 
Vậy, quĩ đạo là parabol (P): 2 y  2x  4x  6 More example
§1.2 TỐC ĐỘ VÀ VẬN TỐC
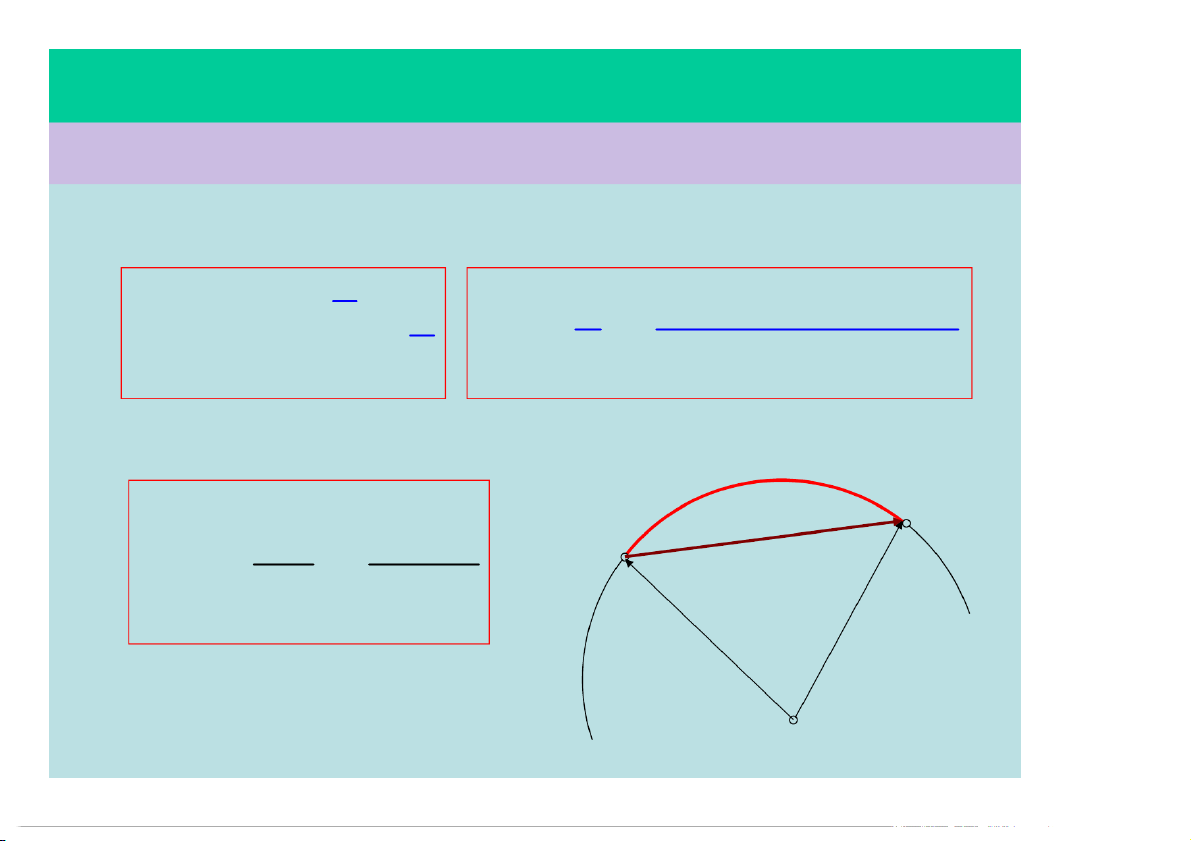
1 – Tốc độ trung bình và vận tốc trung bình: Tốc độ trung bình: s s s  s  ...  s v  v  v  1 2 n v   s tb s t t t  t  ...  t 1 2 n Vận tốc trung bình: s     M  M r r  r  r o 0 v   tb t  t  t0   r r 0 O
§1.2 TỐC ĐỘ VÀ VẬN TỐC Ví dụ:
Một canô xuôi dòng từ bến A đến bến B với tốc
độ v1 = 30km/h; rồi ngược dòng từ B về A với
tốc độ v = 20km/h. Tính tốc độ trung bình trên 2
lộ trình đi – về của canô. Giải: s AB  BA AB  AB 2 v v v    1 2  s t t  t AB AB v  v 1 2  1 2 v v 1 2 2.30.20   24km / h 30  20 More example
§1.2 TỐC ĐỘ VÀ VẬN TỐC
2 – Tốc độ tức thời và vận tốc tức thời:  Tốc độ tt: v s ds v  lim   s ' s s t 0  t dt  M M  r o Vận tốc tt:   r r   0  r dr  O v  lim   ( r ) ' t0 t  dt
§1.2 TỐC ĐỘ VÀ VẬN TỐC
2 – Tốc độ tức thời và vận tốc tức thời:
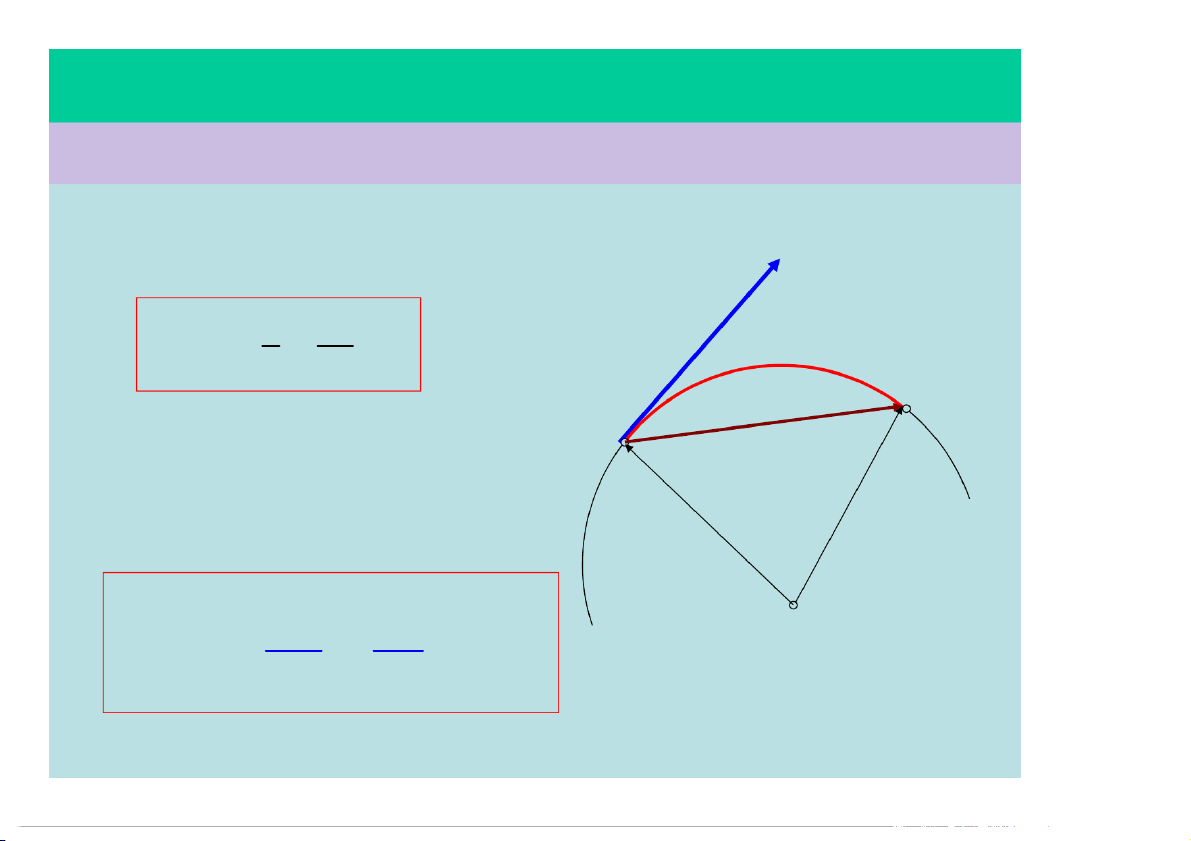
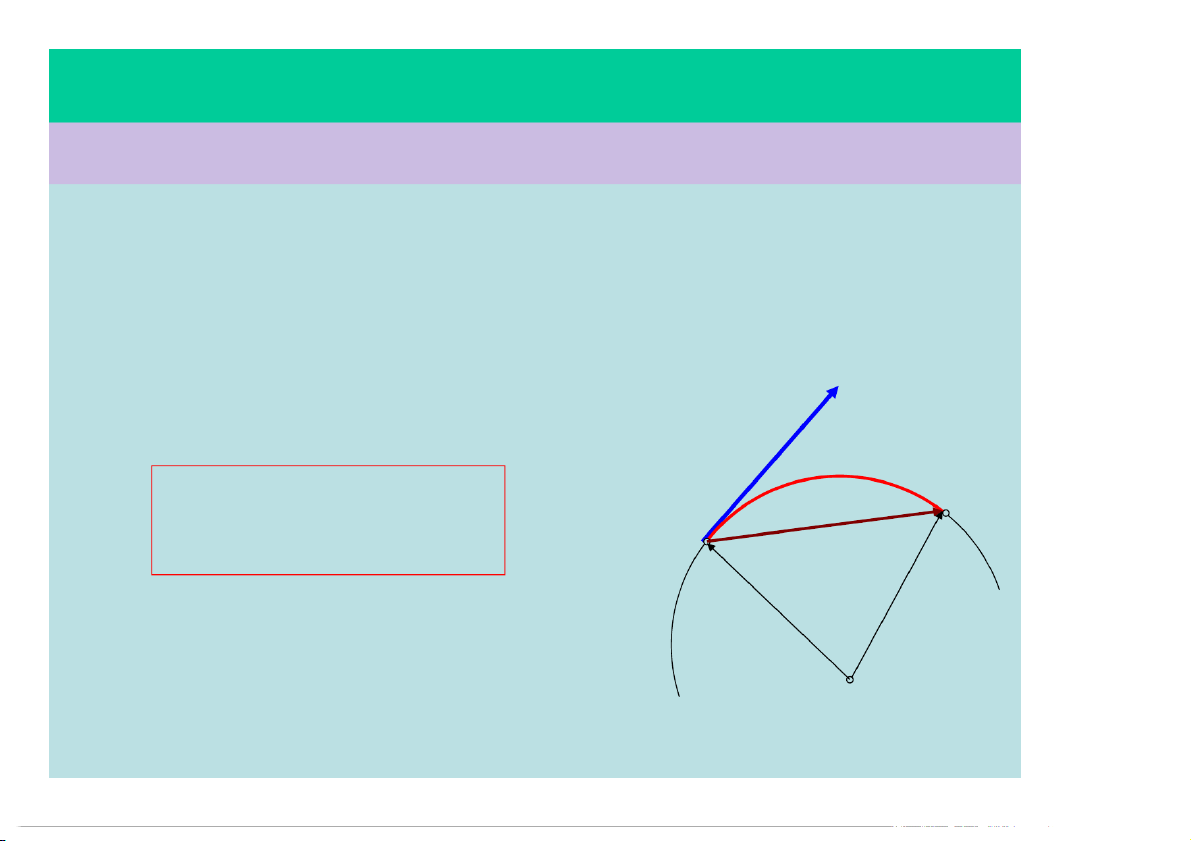
Đặc điểm của vectơ vận tốc tức thời:
• Phương: tiếp tuyến với quĩ đạo 
• Chiều: theo chiều chuyển động v
• Độ lớn: đạo hàm của quãng đường s   M M  r o v |  v | v  s ' s   r r 0
• Điểm đặt: tại điểm khảo sát O
§1.2 TỐC ĐỘ VÀ VẬN TỐC
3 – Ý nghĩa của tốc độ và vận tốc:
• Tốc độ là đại lượng vô hướng, không âm, đặc trưng
cho tính nhanh, chậm của chuyển động.
• Vận tốc là đại lượng vectơ. Vận tốc tức thời đặc trưng
cho phương, chiều và độ nhanh chậm của chuyển động.
• Độ lớn của vận tốc tức thời chính là tốc độ tức thời.
§1.2 TỐC ĐỘ VÀ VẬN TỐC
4 – Biểu thức giải tích của vectơ vận tốc:     
Trong hệ tọa độ Descartes: r  OM  x i  y j z k   dr    2 2 2 v 
 v . i  v . j v .k  (v , v , v ) v  v  v  v X y z x y z x y z dt dx dy dz v   x '; v   y '; v   z '; x y z dt dt dt
§1.2 TỐC ĐỘ VÀ VẬN TỐC 5. Tính quãng đường: Tổng quát: t2  với: s  vdt  v |  v | t1 Nếu v = const thì: s = v.(t ) = v.t 2 – t1
Ví dụ: trong mp (Oxy), chất x   5 10sin 2 t 
điểm chuyển động với pt:  S ( I) y  4 10sin 2 t 
a) Xác định vị trí của chất điểm lúc t = 5s. b) Xác định quĩ đạo.
c) Xác định vận tốc lúc t = 5s.
d) Tính quãng đường vật đi từ lúc t = 0 đến t = 5s.
Suy ra tốc độ TB trên quãng đường này. §1.3 – GIA TỐC
Ví dụ: Chất điểm chuyển động với phương trình: x  15t  S ( I) y  5t 2 
a) Xác định vectơ vận tốc, gia tốc lúc t = 2s.
b) Xác định a , a , R lúc t = 2s. t n
c) Tính s,v , trong thời gian 2s kể từ lúc t = 0. tb Giải Ta có: v  x ' 15   a  x '  0 x  x v  (SI) ; a  (SI) v  y '  10t  a  y '  10 y  y 2 2  2 v  v  v  2 10 2, 25  t ; a  10m / s  const x y §1.3 – GIA TỐC
Ví dụ: Chất điểm chuyển động với phương trình: x  15t  S ( I) y  5t 2 
a) Xác định vectơ vận tốc, gia tốc lúc t = 2s.
b) Xác định a , a , R lúc t = 2s. t n
c) Tính s,v , trong thời gian 2s kể từ lúc t = 0. tb Giải Ta có: v  x ' 15   a  x '  0 x  x v  (SI) ; a  (SI) v  y '  10t  a  y '  10 y  y 2 2  2 v  v  v  2 10 2, 25  t ; a  10m / s  const x y §1.3 – GIA TỐC a) Lúc t = 2s thì: v = 25m/s 2 a  10m / s
b) Gia tốc tt, pt, bán kính quĩ đạo lúc t = 2s: t
Gia tốc tiếp tuyến: a  (v)'  10.  2 8m / s t 2 2, 25  t 2 2
Gia tốc pháp tuyến: a  a  a  2 6m / s n t
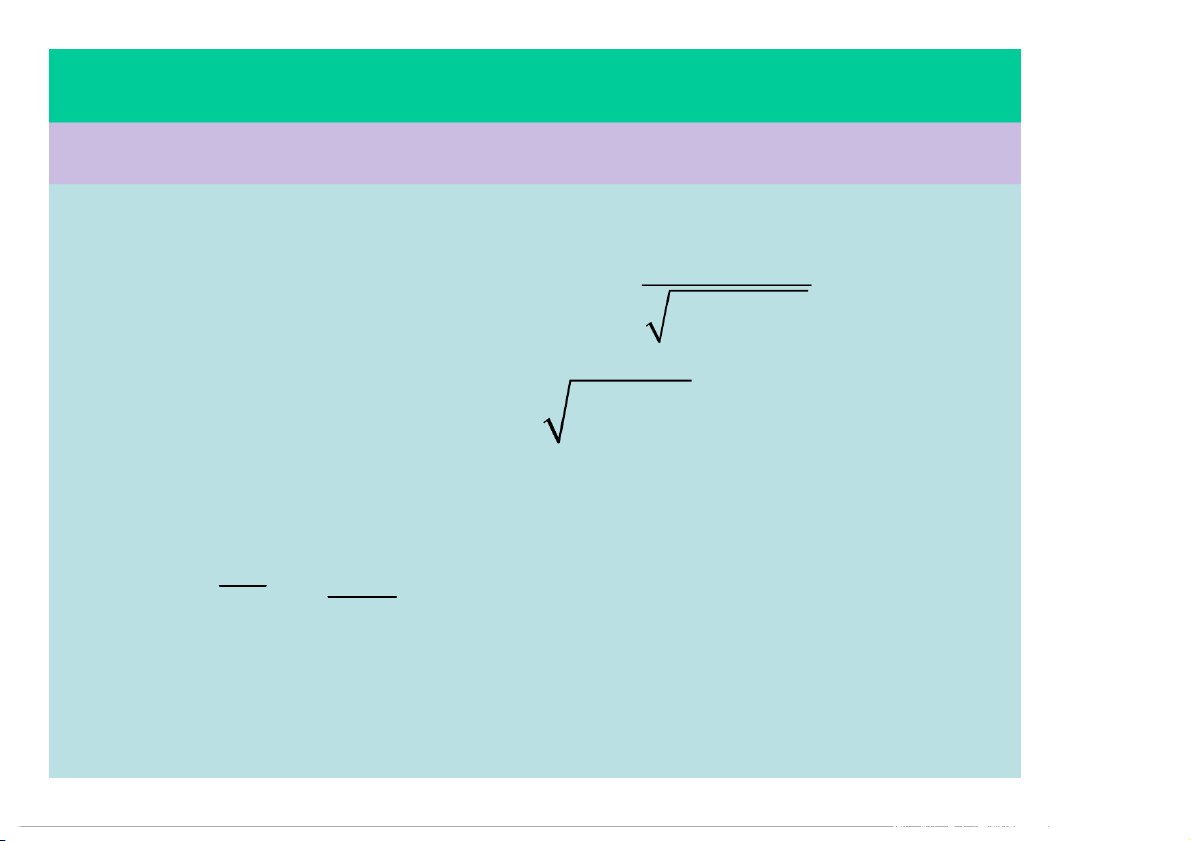
Bán kính chính khúc của quĩ đạo: 2 v R   625 104m an 6 §1.3 – GIA TỐC
c) Tính s, v trong thời gian 2s kể từ t = 0: tb 2 2 s  vdt   2 10 2, 25  t dt  0 0 t 2, 25 2 2 2 s  10[ 2, 25  t 
ln | t  2, 25  t |]  37, 4m 0 2 2 s 37, 4 v    18,7m / s tb t 2 §1.3 – GIA TỐC
Ví dụ 2: Chất điểm chuyển động với phương trình:  4 2 3 x  3t  t  3 (SI) y   8t
Xác định vận tốc, gia tốc a, a , a , R lúc t = 2s. t n Giải Ta có: 2  v   x '  6t  4t x v  (SI) 2 2 2 2
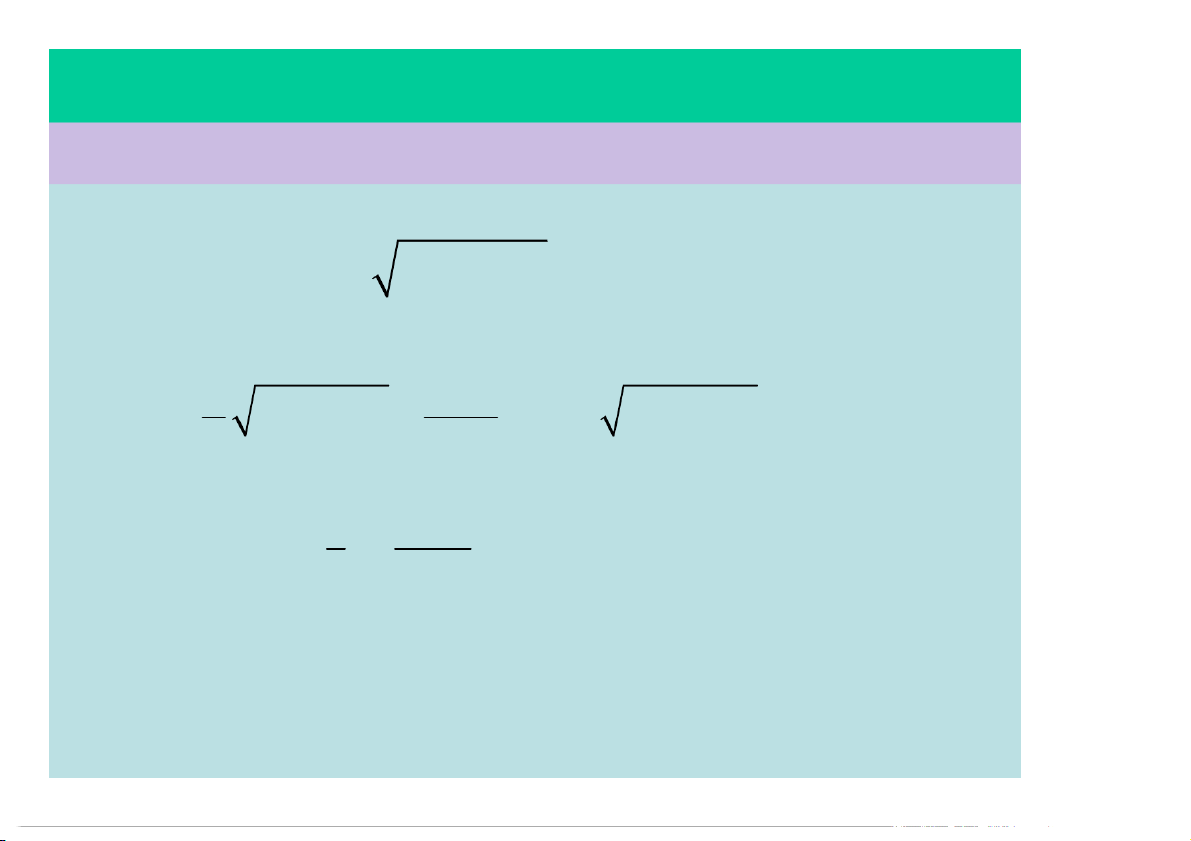
 v  v  v  (6t  4t )  64 v  y '  8  x y  y  a   x '  6  8t  x 2 2 a  (SI)  a  a  a |  6  8t | x y a  y '  0  y  §1.3 – GIA TỐC Lúc t = 2s thì: 2
v  (12 16)  64  4 5  8, 94m / s 2 a |  6  8.2 | 10m / s Gia tốc tiếp tuyến: 2 (6t  4t )(6  8t) a  (v) '   2 2 (6t  4t )  64 '  t  2 2 (6t  4t )  64 2  2 5  4, 47m / s Gia tốc pháp tuyến: 2 2 a  a  a 2   n t 4 5 8, 94m / s
Bán kính chính khúc của quĩ đạo: 2 v 2 8, 94 R    8,94m a 8, 94 n
Bài tập trên lớp và về nhà
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT
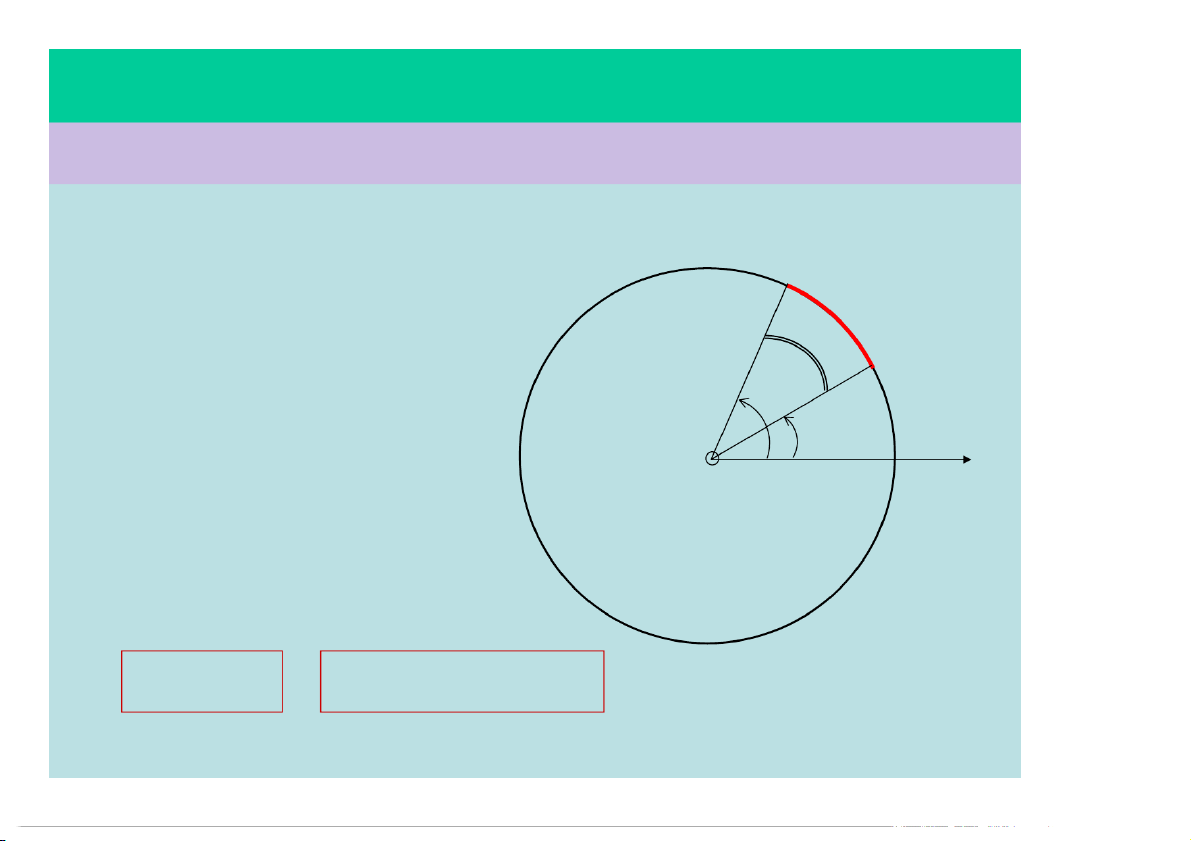
1) Chuyển động tròn - các biến số góc: Chuyển động tròn: Là
chuyển động có qũi đạo tròn M s Các biến số góc: Mo : toạ độ góc    : góc quay o : vận tốc góc O  : gia tốc góc Ta có: s = .R  =  - 0
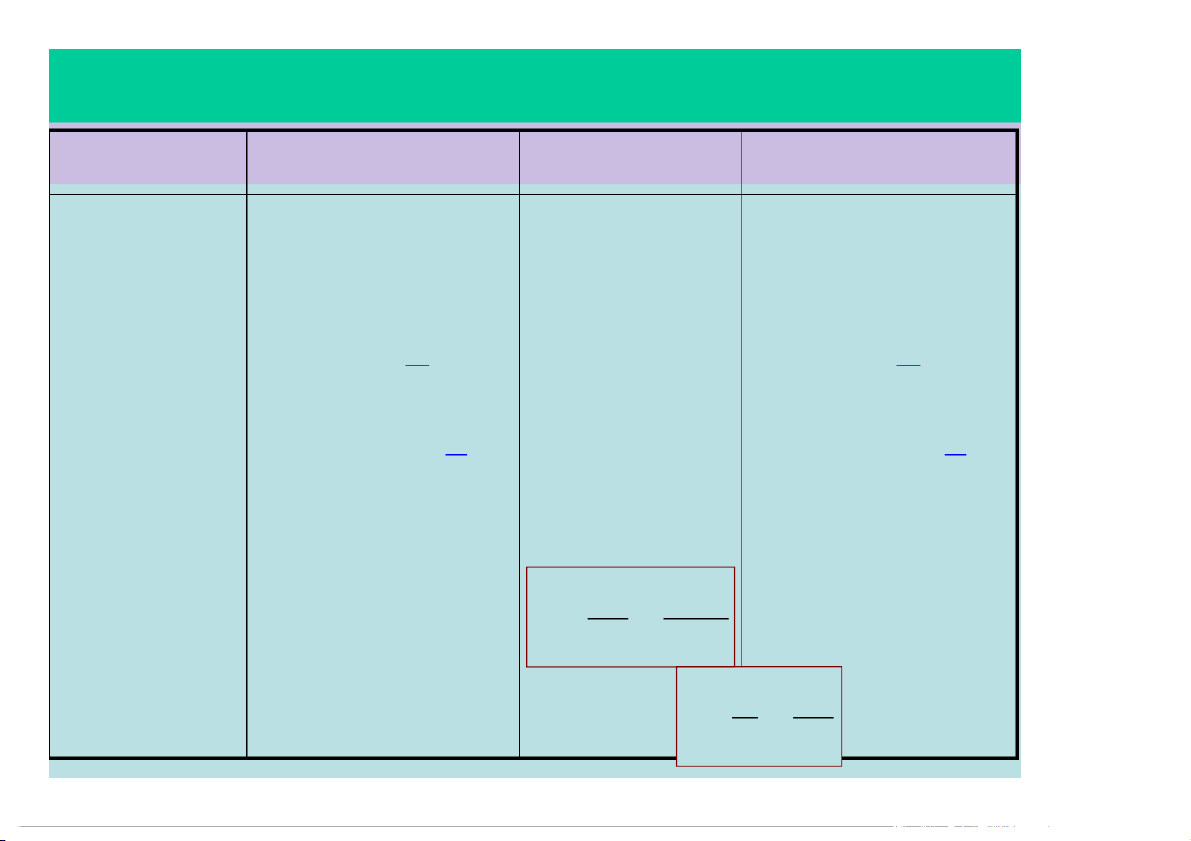
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT
So sánh các biến số giữa cđ thẳng & tròn: Chuyển động thẳng Chuyển động tròn Toạ độ : x Toạ độ góc:  Quãng đường: s Góc quay:  Vận tốc: v Vận tốc góc:  Gia tốc: a Gia tốc góc: 
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT
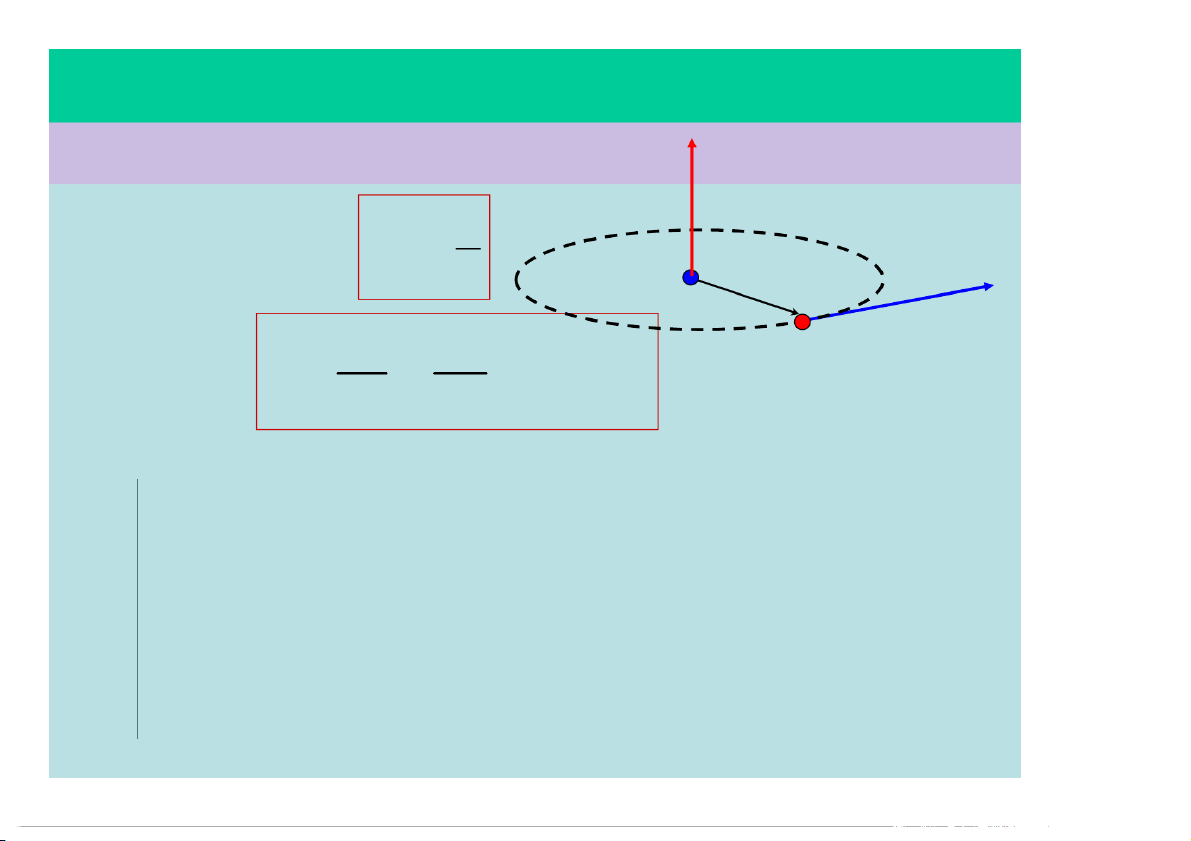
2) Tốc độ góc, vận tốc góc:   T/đ góc tr/bình:     tb  t v R T/đ góc tt: d d     '  ' dt dt Vectơ vận tốc góc tt:
Phương: vuông góc mặt phẳng qũi đạo. 
 Chiều:theo qui tắc đinh ốc hoặc nắm tay phải.
Độ lớn: đạo hàm của góc quay:   '
Điểm đặt: tâm của qũi đạo.
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT 2) Vận tốc góc:
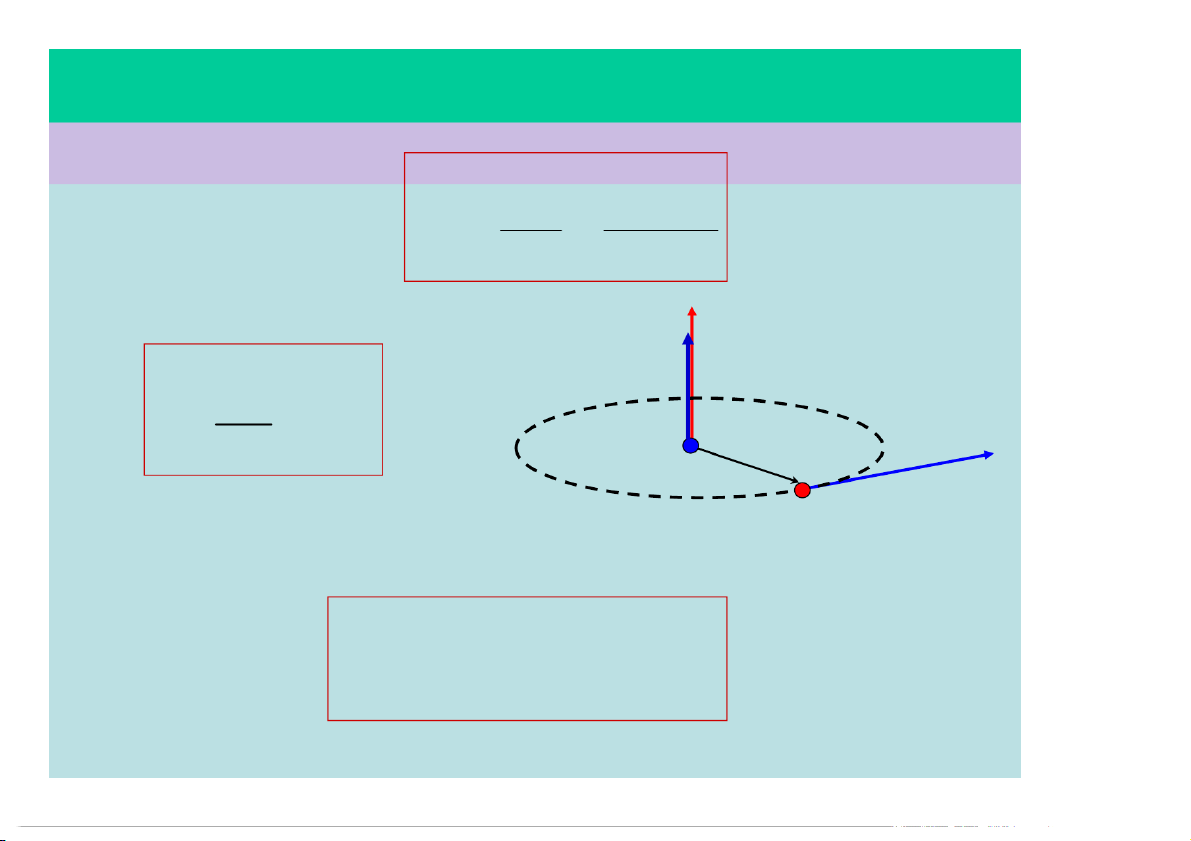
Quan hệ giữa vận tốc góc và vận tốc dài:    v  ,  R  v  R       
Quan hệ giữa vận tốc góc  và gia tốc pháp tuyến:  v R v2 a 2    R n R Tính góc quay:
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT 3) Gia tốc góc:     Gia tốc góc TB:     o    tb t t  Gia tốc góc tức thời:      d         ( ) ' v dt R
Q/hệ giữa gt góc và gt tiếp tuyến:    a     t ,R a R t    
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT Ví dụ 1:
Chất điểm chuyển động tròn với phương trình:  = 6t – 2t3 (SI)
a) Xác định vận tốc góc, gia tốc góc lúc t = 0
và lúc chất điểm dừng.
b) Xác định góc mà chất điểm đã quay trong thời gian trên.
c) Tính tốc độ góc trung bình, gia tốc góc
trung bình trong thời gian trên.
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT Giải: Ta có:  = 6t – 2t3 2    '  6 6t    '  12  t a) Lúc t = 0 thì: 2
  6(rad / s);   0(rad / s ) o 0 Lúc dừng thì: 2
  0  t 1s    1  2(rad / s )
§1.4 – VẬN TỐC, GIA TỐC TRONG CĐT Giải: 1 1
b) Góc quay:   dt   2 (6  6t )dt  4(rad)  0 0
c) Tốc độ góc trung bình:     4(rad / s) tb t Gia tốc góc trung bình:   0 2    6  (rad / s ) tb t
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
1. Chuyển động thẳng đều.
2. Chuyển động thẳng biến đổi đều. 3. Rơi tự do.
4. Chuyển động tròn đều.
5. Chuyển động tròn biến đổi đều.
6. Chuyển động ném xiên, đứng, ngang.
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN TĐ TBĐĐ TRÒN ĐỀU TRÒN BĐĐ a = 0 a = const  = 0  = const v = const v = v + at  = const  =   0 0 + t  1 1 2 s = vt s  v t  at 2  = t    t  t 0 0 2 2 1 1 2 x  x  vt 0 x  x  v t  at 2     t  0      t  t 0 0 0 0 2 2 2 2 v  v   Chu kì: 0 2a(x x0) 2 2    2  0 2as 2 2 R  T   Rơi tự do:  v v  0 = 0; a = g Tần số: 1 f   T 2
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
1) Chuyển động thẳng đều:   Gia tốc : a  0   Vận tốc : v  const
Pt c/động : x = x + v(t – t o o) = xo + vt Quãng đường : s = vt
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
Ví dụ về chuyển động thẳng đều:
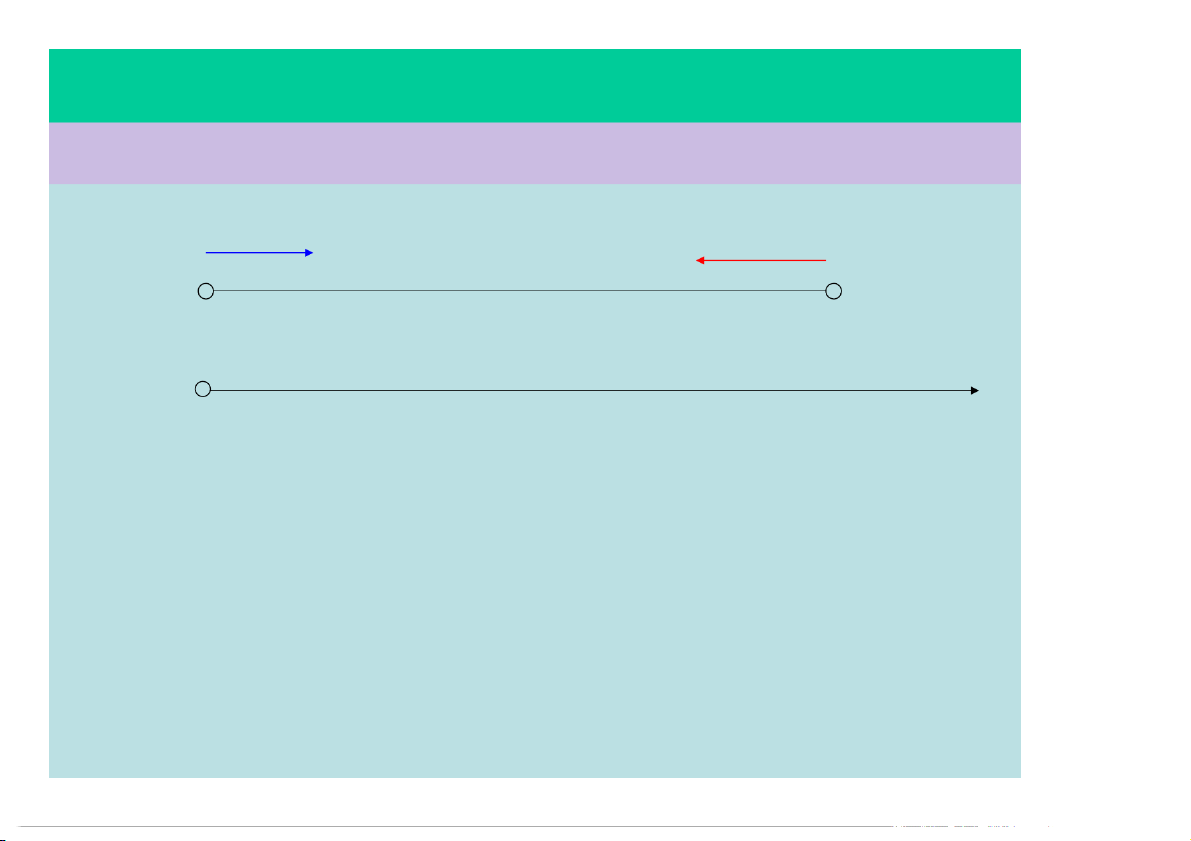
Lúc 6h , một ôtô khởi hành từ A, cđ đều
về B với vận tốc 40km/h. Lúc 7h, một
môtô cđ từ B về A với vận tốc 50km/h. Biết AB = 220km.
a) Viết phương trình cđ của 2 xe.
b) Xác định vị trí và thời điểm 2 xe gặp nhau.
c) Xác định các thời điểm 2 xe cách nhau 60km.
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Giải v = 40km/h v = 50km/h 1 2 6 h 7 h A 220km B 0 X (km)
a)Chọn trục Ox như hình vẽ, gốc thời gian là lúc 6 giờ.
Phương trình chuyển động của xe 1: x1 = x + v (t – t ) = 01 1 01
0 + 40(t – 0) = 40t (t: h; x: km)
Phương trình chuyển động của xe 2: x 220 - 50(t – 1)= 270 - 50t 2 = x + v (t – t ) = 02 2 02 (t:h; x:km)
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Giải b) Khi gặp nhau: x = x  1 2 40t = 270 – 50t  t = 3h
Vậy thời điểm hai xe gặp nhau là lúc 6 + 3 = 9 giờ.
Chỗ gặp nhau cách A một khoảng x = 40.3 = 120km
c) Hai xe cách nhau 60km  |x1 – x2| = 60
 |90t – 270| = 60 t = 2 h 20’ hoặc t = 3 h 40’
Vậy, hai xe cách nhau 60km vào các thời điểm 8h 20’ và 9h 40’
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
2) Chuyển động thẳng biến đổi đều:   Gia tốc : a  const Vận tốc: v  v  at o 1 PT chuyển động : 2 x  x  v t  at o o 2 1 Quãng đường : 2 s  v t  at o 2
Công thức độc lập thời gian : v2  v2  2as o
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
Ví dụ về chuyển động thẳng biến đổi đều:
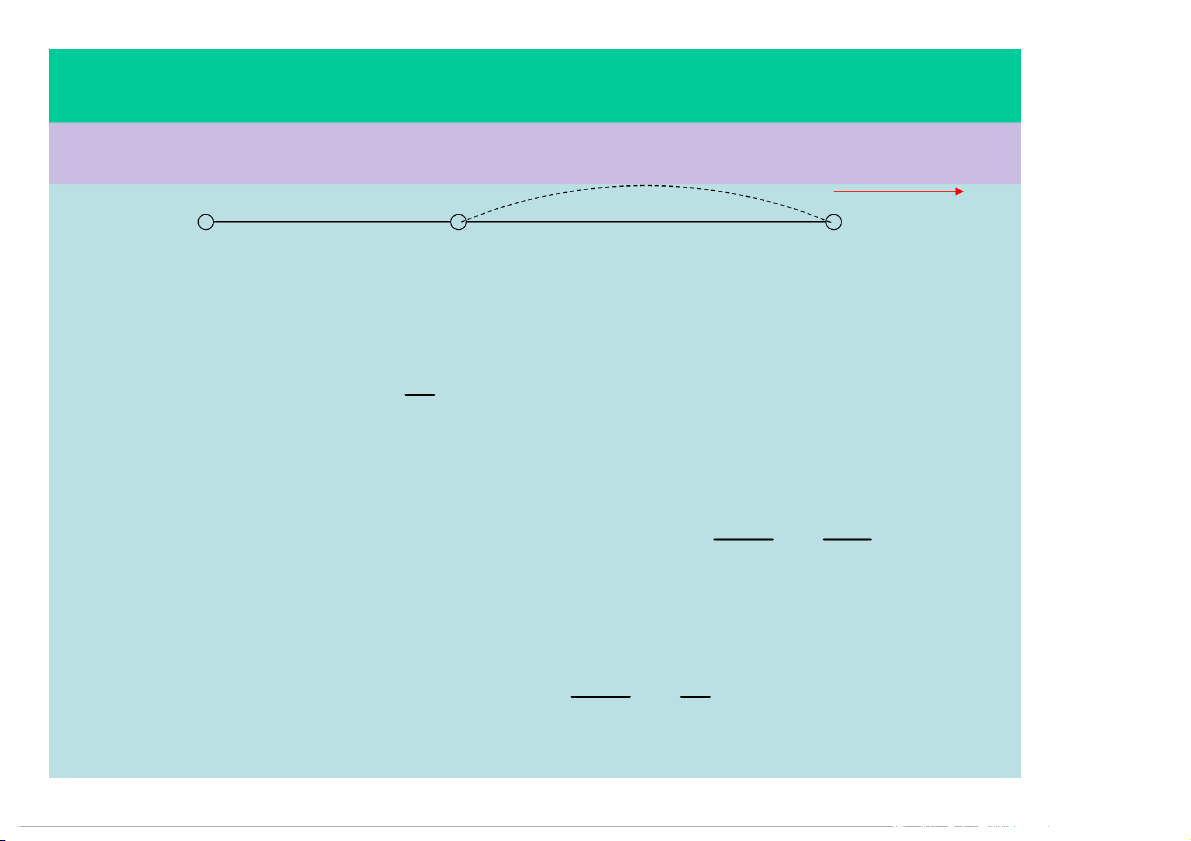
Một ôtô bắt đầu chuyển động nhanh dần
đều từ O, lần lượt qua A và B. Biết AB =
20m, thời gian xe đi từ A đến B là 2 giây,
vận tốc khi qua B là 12m/s.
a) Tính vận tốc khi qua A và quãng đường OA.
b) Tính thời gian đi từ O đến A.
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Giải v = 12m/s B 20m O A 2s B a) Ta có: v
 v  at  12  v  2a (1) B A A 1 2 s  AB  v t  at  20  2 v  2a (2) A A 2
Giải (1) và (2), ta được: vA = 8m/s; a = 2m/s2 2 2 Mà: 2 2 v 8 v  v  2as A      A 0 s OA 16m 2a 4
b) Thời gian đi từ O đến A: v 8 A v  v  at  A O OA t    4s OA a 2
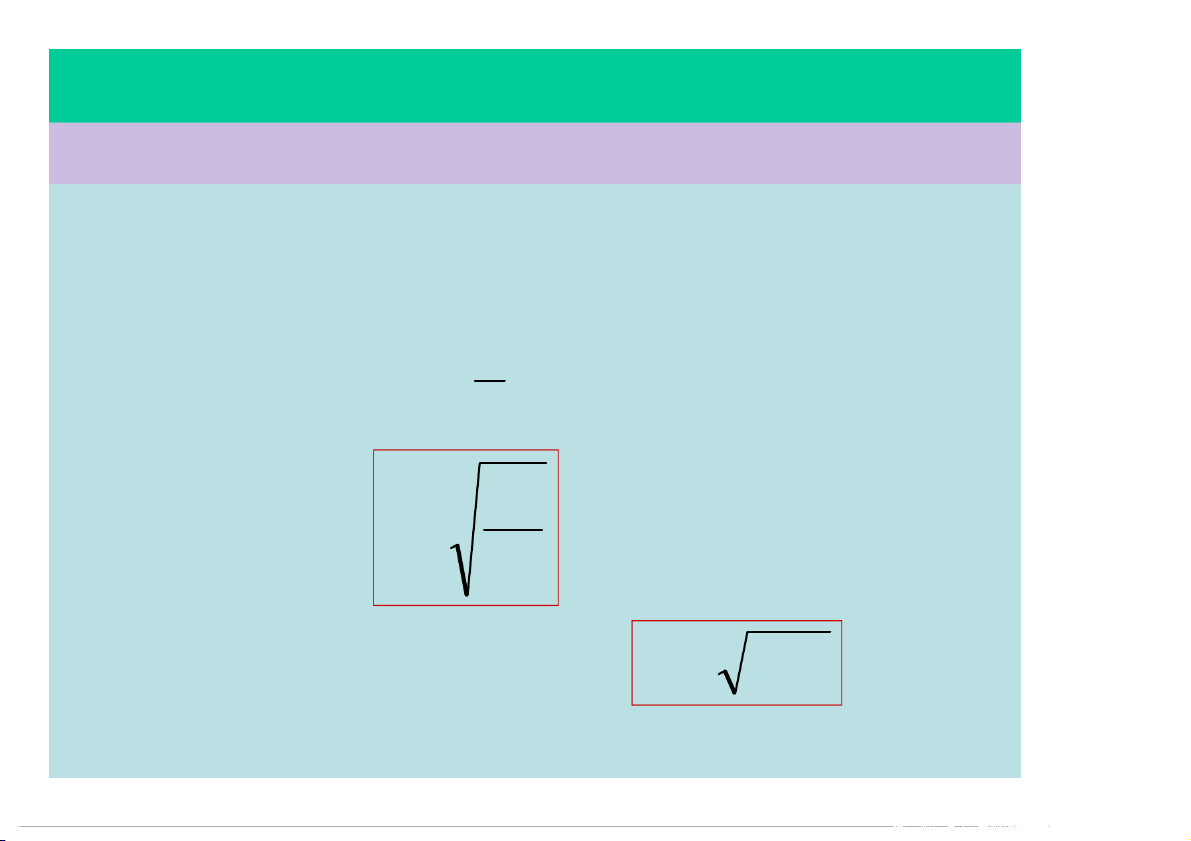
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN 3) Rơi tự do:    Gia tốc: 2
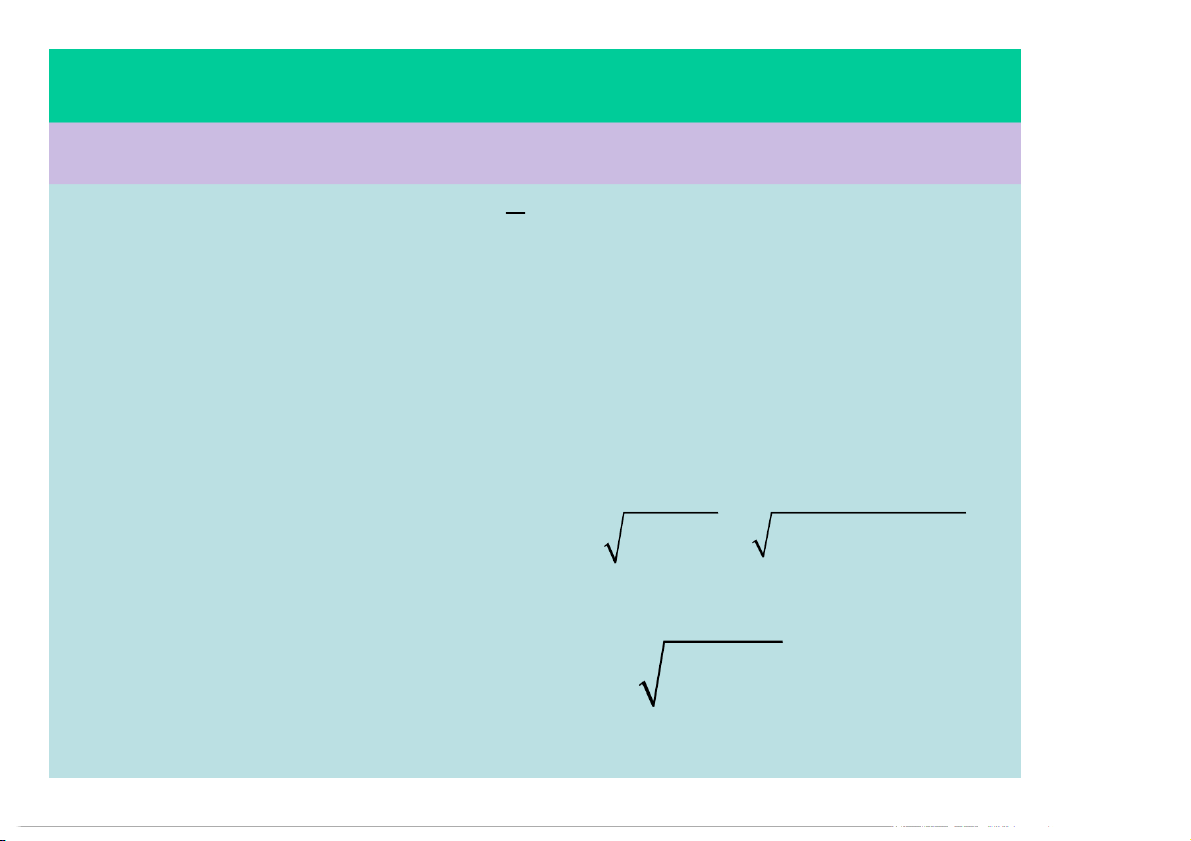
a  g  const; g  10m / s Vận tốc: v = gt; vo = 0 1 Quãng đường: 2 s  gt 2 Thời gian rơi: 2h t  g
Vận tốc ngay khi chạm đất: v  g 2 h
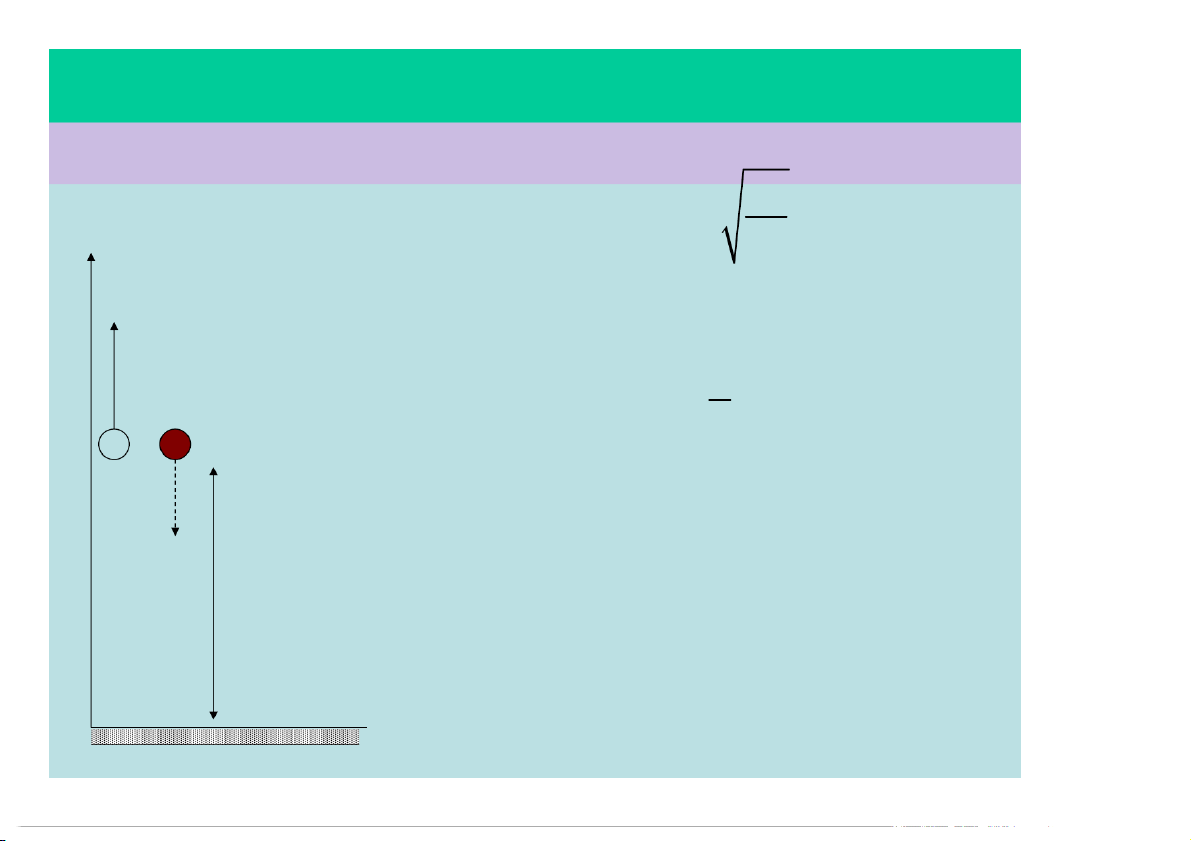
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Ví dụ: y
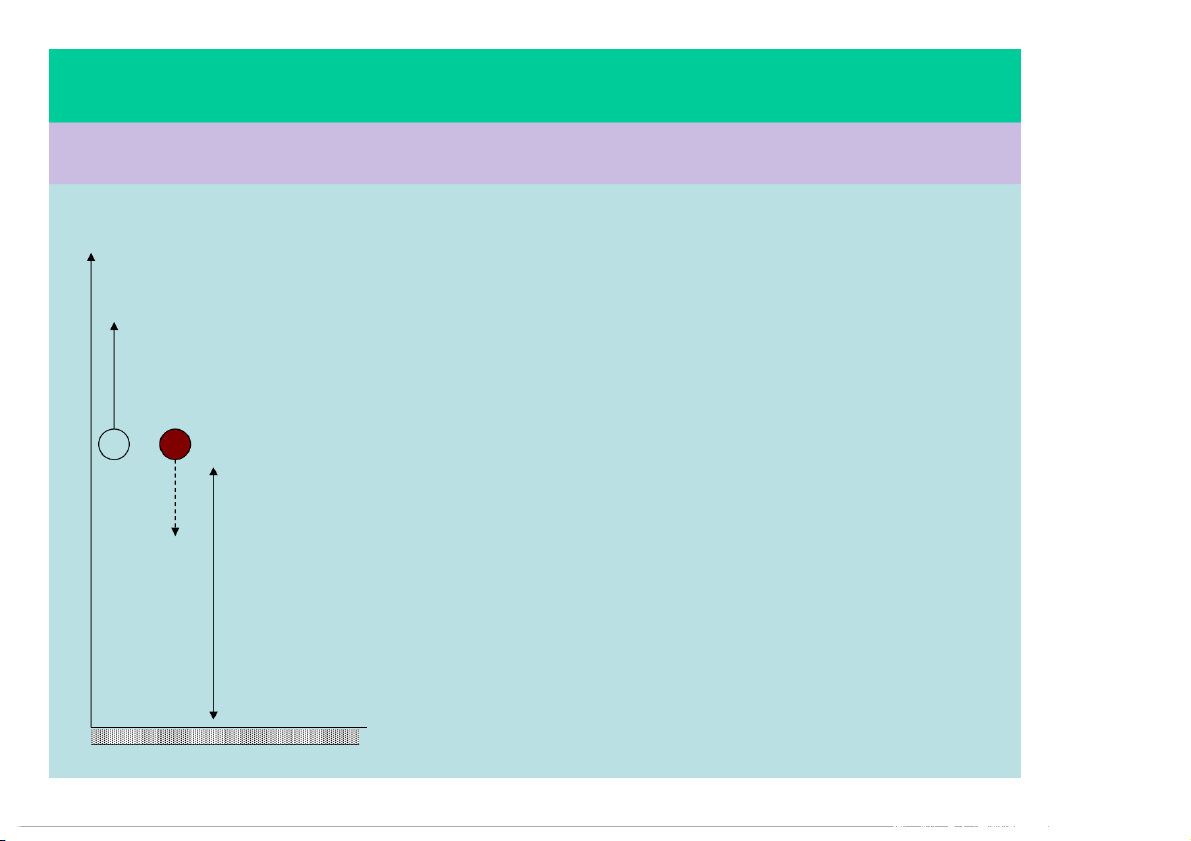
Từ độ cao 20m, người ta ném
đứng vật A với vận tốc v , đồng  0 v
thời thả rơi vật B. Bỏ qua sức 0
cản không khí, hãy xác định: B
a) v để A rơi xuống đất chậm 0 hơn B 1s. A
b) Khoảng cách lớn nhất giữa A
và B trong quá trình chuyển động (ứng với v h = 20m 0). O
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Giải: Thời gian rơi của B: 2h t   2s y B g  v Thời gian cđ của A:    0 t t 1 3s A B Ptcđ của A: 1 2 2       B y y v t gt 20 v t 5t A 0 0 0 2 A
Khi A chạm đất thì t = 3s và yA = 0. Suy ra: 2
0  20  v .3 5.3  v  8, 3m / s 0 0 h = 20m K/c giữa hai vật: d |  y  y | = v t A B 0  d  v t  8,3.2  16,6m max 0 B O
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
4) Chuyển động tròn đều: •Gia tốc góc:  = 0 •Vận tốc góc:  = const •Toạ độ góc:  =  +  o t •Góc quay:  = t •Quãng đường: s = R  = vt
•Chu kì quay: T = 2/ = 2R/v •Tần số (vòng): f = 1/T
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Ví dụ:
Chất điểm chuyển động với phương trình: x  10sin 5 t   (cm;s) y 10(1cos5 t  )
a) Chứng tỏ vật chuyển động tròn đều. Tính
chu kì và bán kính qũi đạo.
b) Tính quãng đường và góc mà chất điểm đã quay trong thời gian 5s.
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Giải
a) Phương trình quĩ đạo: x2 + (y – 10)2 = 100
Vậy chất điểm chuyển động trên đường tròn
tâm I(0;10)cm, bán kính R = 10cm. Ta có: v  x '   50 cos 5 t  x  2 2  v  v  v
 50  157cm / s  const v  y '   50sin 5 t  x y y  CĐ đều Chu kì: 2R T   0, 4s v
b) Quãng đường đi trong 5s: s = vt = 785cm = 7,85m Góc quay: s 785     78,5rad R 10
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
5) Chuyển động tròn biến đổi đều: Gia tốc góc:  = const
Vận tốc góc:  =  +  o t 1 Toạ độ góc: 2      t  t  o o 2 Góc quay: 1 2    t  t  o 2 Công thức độc lập 2  2   2  o t/gian:    1 2
Vận tốc góc trung bình:   tb 2
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Ví dụ :
Bánh mài của máy mài đang quay với vận tốc
300 vòng/phút thì bị ngắt điện. Nó quay chậm
dần đều, sau đó 1 phút, vận tốc còn 180 vòng/phút.
a) Tính gia tốc góc và số vòng quay của bánh mài trong 1 phút đó.
b) Sau bao lâu kể từ khi ngắt điện, bánh
mài sẽ dừng? Khi đó nó đã quay được
bao nhiêu vòng? Tính vận tốc góc trung bình trong thời gian đó.
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Giải        a) Gia tốc góc: 6 10 0     2  (rad / s ) t 60 15 2 2    2 2 (6)  (10) 0 Góc quay:     480(rad) 1 2 2 /15 Số vòng quay: 1 N   240 1 2 b) Khi dừng:      t   0  0 t    150s 0  2 Góc quay: 2 2 0     2  0 2    750 (  rad) 2 2 Số vòng quay: 2 N   375 2 2 Vận tốc góc trung bình:  750 2     5(rad / s) tb t 150
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
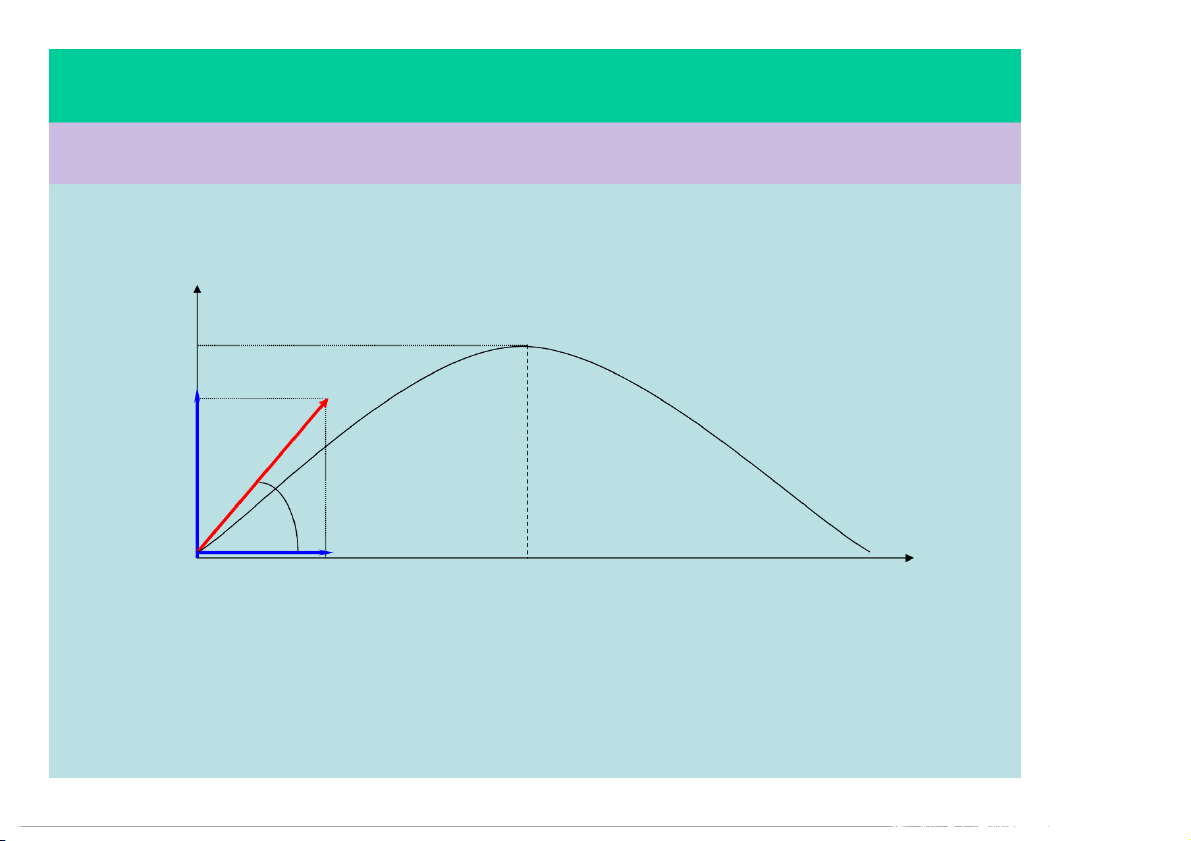
6) Chuyển động ném xiên: y ymax   vo v oy  x O  xmax v ox
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
Các phương trình của chuyển động ném xiên:  a  Gia tốc:  0 a  x (1) a  g y
Vận tốc: v  v  v cos   x ox o v  (2)
v  v  a t  v sin   gt  y oy y o x  v t  v cos.t (3) PTCĐ:  ox o  1 y  y  v sin.t  2 gt (4)  o o 2
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN
Các phương trình của chuyển động ném xiên: PTQĐ: g y  t . x g  x . 2  Parabol (5) 2v2 cos2  o 2  Độ cao cực đại: v sin2 h  y o  max o (6) 2g 2  Tầm xa: v sin 2 o L  x  max (7) Ném tại mặt đất g
Lưu ý: Ném tại độ cao thì xác định L bằng cách
cho y = 0 (vật chạm đất).
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Nhận xét:
• Tầm xa lớn nhất khi góc ném  = 45o.
• Có 2 góc ném:  và (900 - )  cho cùng một tầm xa.
• Khi  = 0, ta có cđ ném ngang.
• Khi  = 90o, ta có cđ ném đứng.
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Ví dụ 1:
Tàu cướp biển đang neo ở ngoài khơi cách bờ biển
2000m, nơi có đặt pháo đài bảo vệ. Súng đại bác đặt
ngang mặt biển, bắn đạn với vận tốc đầu nòng
200m/s. Hỏi tàu cướp có nằm trong tầm bắn của súng
không? Nếu có thì phải đặt nghiêng nòng súng một
góc bao nhiêu để bắn trúng tàu? Giải 2 2 Tầm bắn của v 200 o L    4000m  2000m súng: g 10
Vậy tàu cướp nằm trong tầm bắn của súng. 2 Để bắn trúng: v s in2 o 0 0 x   2000m    15 ; 75 max g
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Ví dụ 2:
Hai vật được ném cùng lúc tại cùng một điểm trên
mặt đất với cùng vận tốc v = 25m/s. Vật A ném o
đứng lên cao; vật B, ném xiên góc 60o so với
phương ngang. Bỏ qua sức cản không khí; lấy g = 10m/s2.
a) Tính khoảng cách giữa 2 vật sau khi ném 1,7s. b) Tính tầm xa của B.
c) Hai vật có rơi xuống đất cùng lúc không? Nếu
không, vật nào chạm đất trước? Trước vật kia bao lâu?
ĐS: a) 22m; b) 54m; c) B trước 0,7s
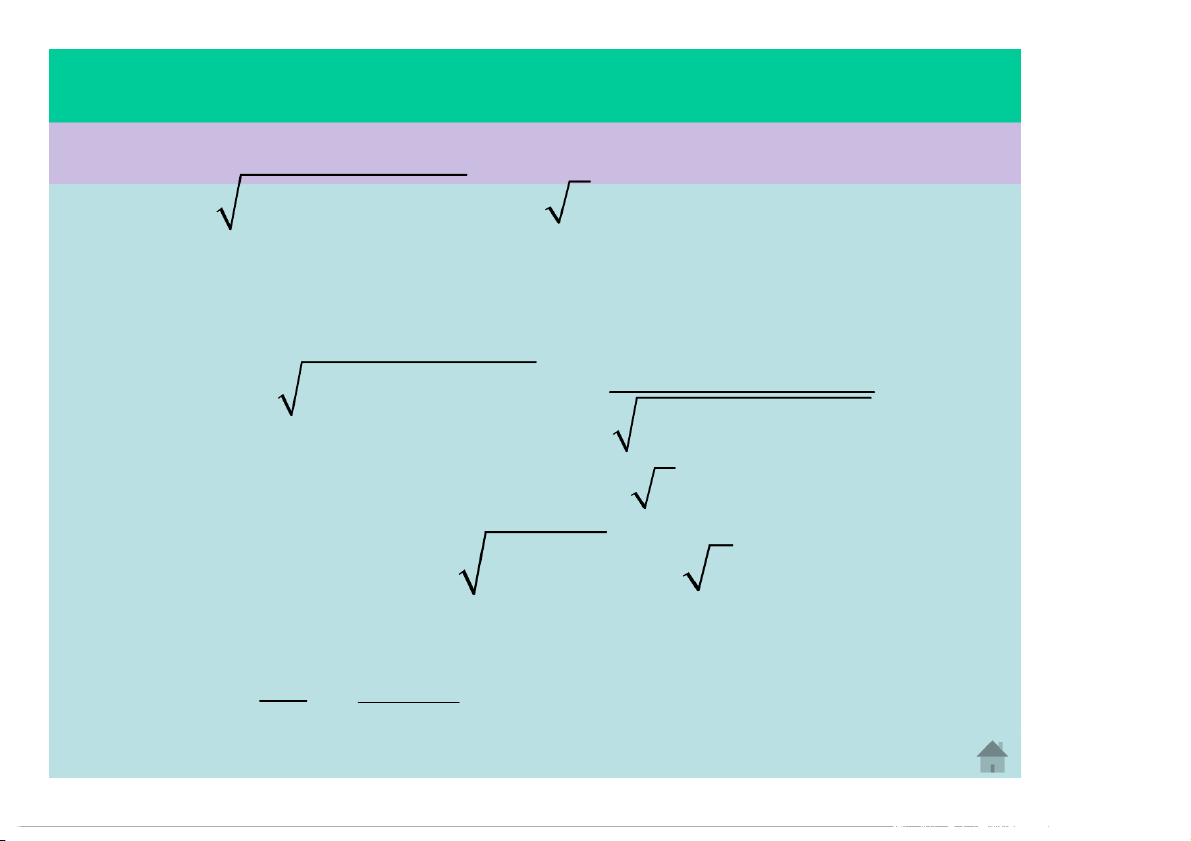
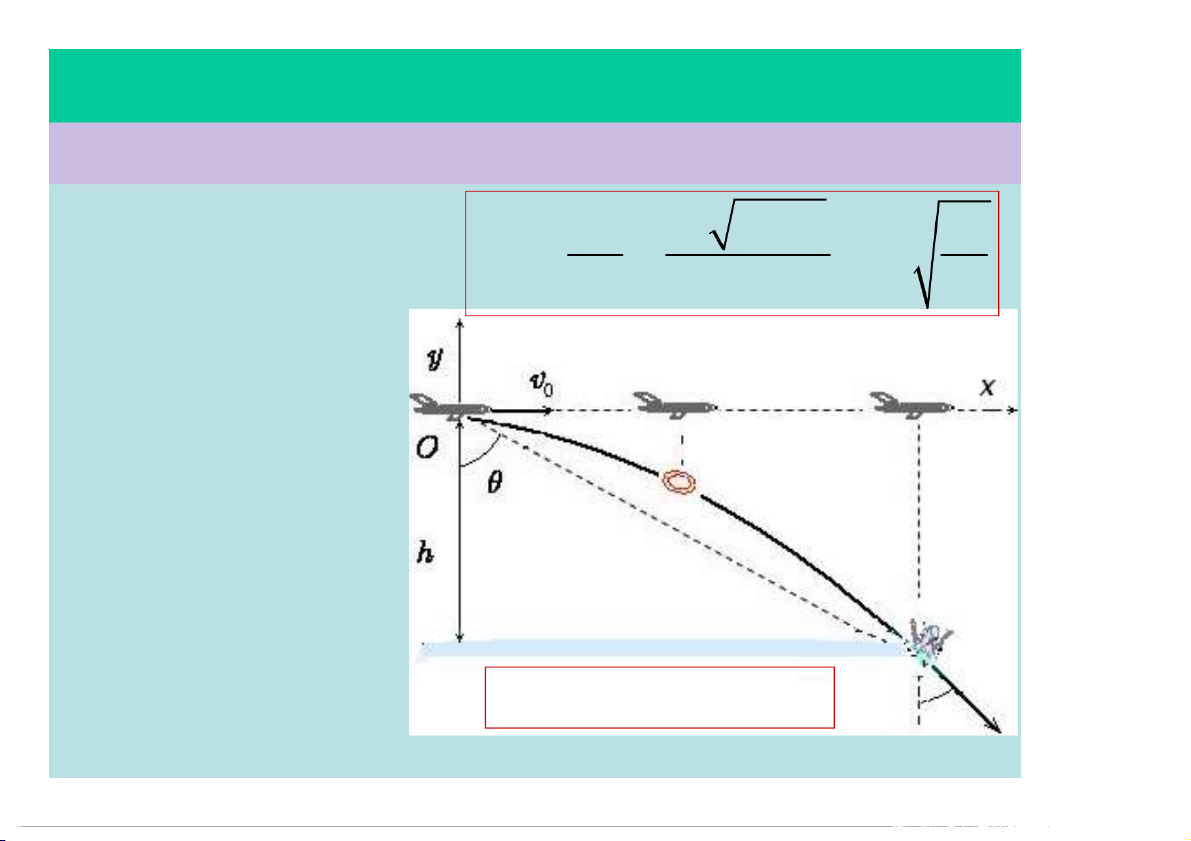
§1.5 – CÁC CHUYỂN ĐỘNG ĐƠN GIẢN Ví dụ 3: Một máy bay cứu v t v 2h / g nạn bay ở độ cao 2 0 0 tg    v0 h=1200m với tốc độ h h gh v0=430km/h đến cứu một người đang ngấp ngoái trên biển. Hỏi nhân viên cứu hộ phải thả phao cứu nạn dưới góc ngắm bao nhiêu để phao rơi trúng (rất gần) người bi 0 tg  1, 54    57 nạn? REVIEW
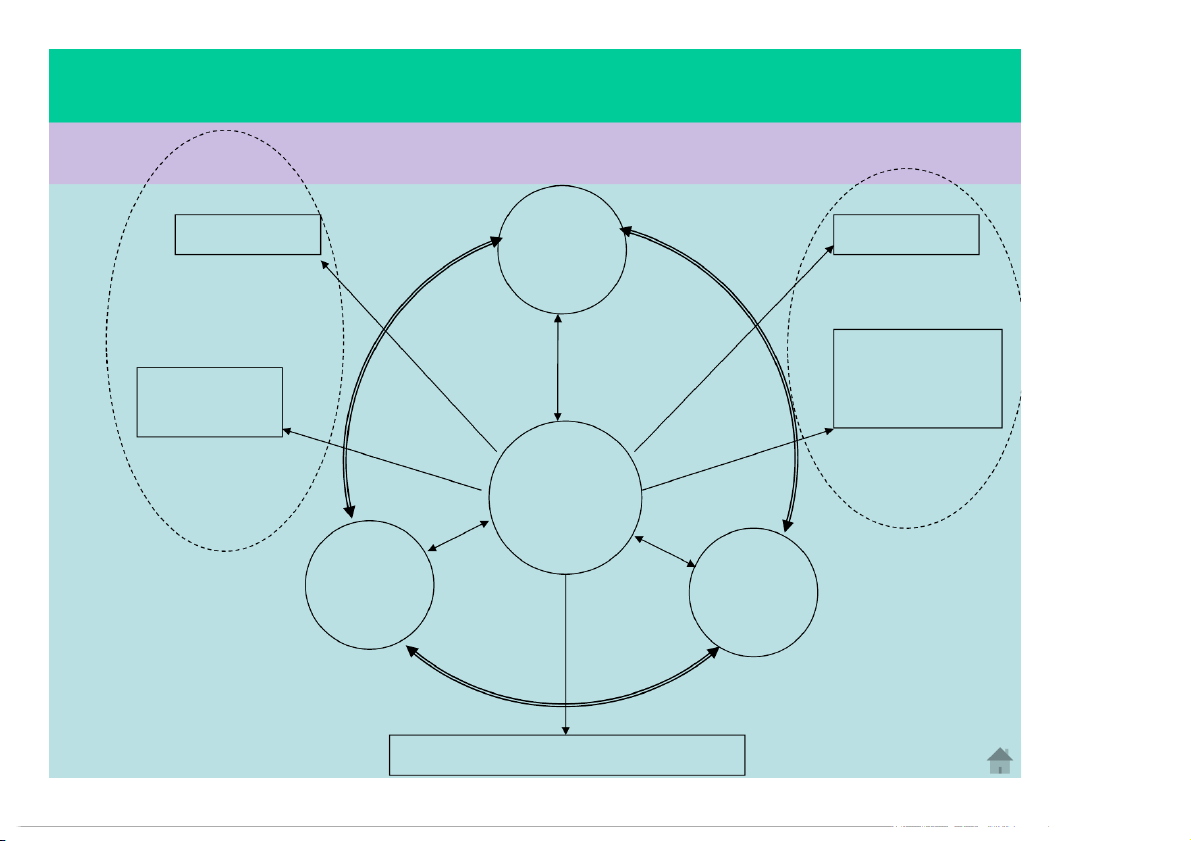
Nội dung của động học chất điểm: Troøn ñeàu ÑÖÔØNG ÑI Thaúng ñeàu ĐỘ DỜI Thaúng bieán ñoåi ñeàu, rôi Troøn bieán töï do ñoåi ñeàu CHUYEÅN ÑOÄNG TỐC ĐỘ GIA TOÁC VAÄN TOÁC a, a , t, an  Neùm xieân, ñöùng, ngang BÀI TẬP CUỐI CHƯƠNG
Chương: Động học chất điểm
Bài tập bắt buộc: 1.1; 1.4; 1.5; 1.7; 1.8; 1.12
– 1.15; 1.20 – 1.23; 1.25; 1.27 – 1.29;
Bài tập làm thêm: Các bài còn lại.
Từ một đỉnh tháp cao h = 25m ta ném một hòn đá theo phương nằm
ngang với vận tốc ban đầu vo = 15m/s. Bỏ qua
sức cản của không khí. Lấy g = 9,8m/s2.
a. Thiết lập phương trình chuyển động của hòn đá.
b. Tìm quĩ đạo của hòn đá.
c. Tính tầm bay xa (theo phương ngang) của nó.
d. Tính thời gian hòn đá rơi từ đỉnh tháp xuống mặt đất.
e. Tính vận tốc, gia tốc tiếp tuyến và pháp tuyến của nó lúc chạm đất.
Từ độ cao h =2,1m, người ta ném một hòn đá lên cao với vận tốc ban
đầu v nghiêng một góc α = 45o so với phương o
ngang. Hòn đá đạt được tầm bay xa l = 42m. Tính:
a. Vận tốc ban đầu của hòn đá,
b. Thời gian hòn đá chuyển động trong không gian,
c. Độ cao cực đại mà hòn đá đạt được.
Một vật rơi tự do từ điểm A ở độ cao H = 20m xuống mặt đất theo
phương thẳng đứng AB (điểm B ở mặt đất).
Cùng lúc đó, một vật thứ 2 được
ném lên theo phương thẳng đứng từ điểm B với vận tốc ban đầu vo.
Xác định thời gian chuyển động và vận tốc ban
đầu vo để hai vật gặp nhau
ở độ cao h=17,5m. Bỏ qua sức cản của không khí. Lấy g =9,8m/s2.