Chương 2: Hướng dẫn bài tập Động học – Bài tập và momen quán tính | Đại học Kiến trúc Thành phố Hồ Chí Minh

lOMoARcP SD| 59256 994 HƯỚNG DẪN BÀI TẬP Chương 2: ĐỘNG HỌC
Bài 1: Cho hệ thống gồm 2 vật: Đĩa tròn đồng chất bán kính R=20cm, khối lượng
M=2kg gắn chặt vào đầu một thanh dài đồng chất L=1m, khối lượng m=1kg. Hãy xác định: A a) Khối tâm của hệ.
b) Momen quán tính của hệ thống đối với trục quay đi qua A vuông góc với đĩa tròn.
a) Để tính vị trí khối tâm, ta coi:
- Đĩa tròn như một hạt có khối lượng M=2kg đặt tại O, với O là khối tâm của đĩa tròn.
- Thanh dài như một hạt có khối lượng m=1kg đặt tại O’, với O’ là khối tâm của
thanh. Bài toán trở thành tính khối tâm của 2 hạt đặt tại O và O’. Ta làm như sau:
Chọn hệ trục tọa độ như hình vẽ, xác định tọa độ O, O’ : O  (x y1, 1)  (0,0)
O '  (x y2, 2)  L2 ,0 (50,0)
 Vị trí khối tâm: G  (x yG, G ) x O A
G  m x1. 1 m x2. 2  M x. 1 m x. 2  50 O’ m1 m2 M m 3
m y1. 1 m y2. 2 M y. 1 m y. 2 0 yG    m1 m2 M m
b) Momen quán tính của hệ: I  I1 I2 . Với I1, I2: Momen quán tính của đĩa và thanh đối với
trục quay đi qua A, tính được bằng công thức chuyển trục I  I md. 2 như sau: 1 2 A G
M OA( )2  1 .2.0,22  2.12  2,04kg m. 2 I1  MR  2 2 12 m O A(
' )2  1 .1.12 1.0,52  0,33kg m. 2 I2  mL  12 12
Vậy: I   I1 I2 2,040,33  2,37kg m. 2 1 lOMoARcP SD| 59256 994
Bài 2: Cho hệ như hình vẽ gồm: Thanh AB đồng chất khối lượng m1  4kg D
dài L1  40cm ;Thanh CD đồng chất khối lượng m2  2kg dài L2  20cm
; Vành tròn đồng chất khối lượng m 1kg bán kính A O B C
R  10cm có tâm O nằm tại trung điểm AB.
a) Xác định khối tâm G của hệ.
b) Tính mômen quán tính đi qua A và vuông góc với mặt phẳng chứa hệ.
a) Để tính vị trí khối tâm, ta coi:
- Thanh dài AB như một hạt có khối lượng m1  4kg đặt tại O, với O là khối tâm của thanh AB.
- Thanh dài CD như một hạt có khối lượng m2  2kg đặt tại B, với B là khối tâm của thanh CD.
- Vành tròn như một hạt có khối lượng m3 1kg đặt tại O, với O là khối tâm của vành tròn.
Bài toán trở thành tính khối tâm của 3 hạt đặt tại O và B. Chọn hệ trục tọa độ như hình vẽ, xác định tọa độ O, B: 
O  (x y1,1)  (x y3,3 )  (0,0) ; B  (x y2, 2)  AB2 ,0  (20,0)
Vị trí khối tâm: G  (x yG, G )
xG  m x1. 1 m x2. 2 m x3. 3 m D 1  m2 m3  m x B
1. 1 m x2. 2 m x. 3  4.0 2.201.0  A O 5,7cm C m1  m2 m 4 2 1
yG  m y1. 1 m y2. 2 m y3. 3  m1.0m2.0m3.0  0 m1 m2 m3 m1 m2 m3 2 lOMoARcP SD| 59256 994
b) Momen quán tính của hệ: I   I1 I2 I3 . Với I1, I2 , I3: Lần lượt là momen quán tính của
thanh AB, thanh CD và vành tròn đối với trục quay đi qua A, tính được bằng công thức
chuyển trục I  I md. 2 như sau: A G 1 2 m L.
I1  12 1 1 m OA1.2  121 m L1 1. 2 m1. L21 2  13 m L1 1. 2  1 2 m AB2.( )2  1 m L2 2. 2
m L2.( 1)2 I2  m L2 2.  12 12 2 m OA.( )2 I3 m R3.  3
m R3. 2 m3. L21 2  Vậy: I  I1 I2 I3
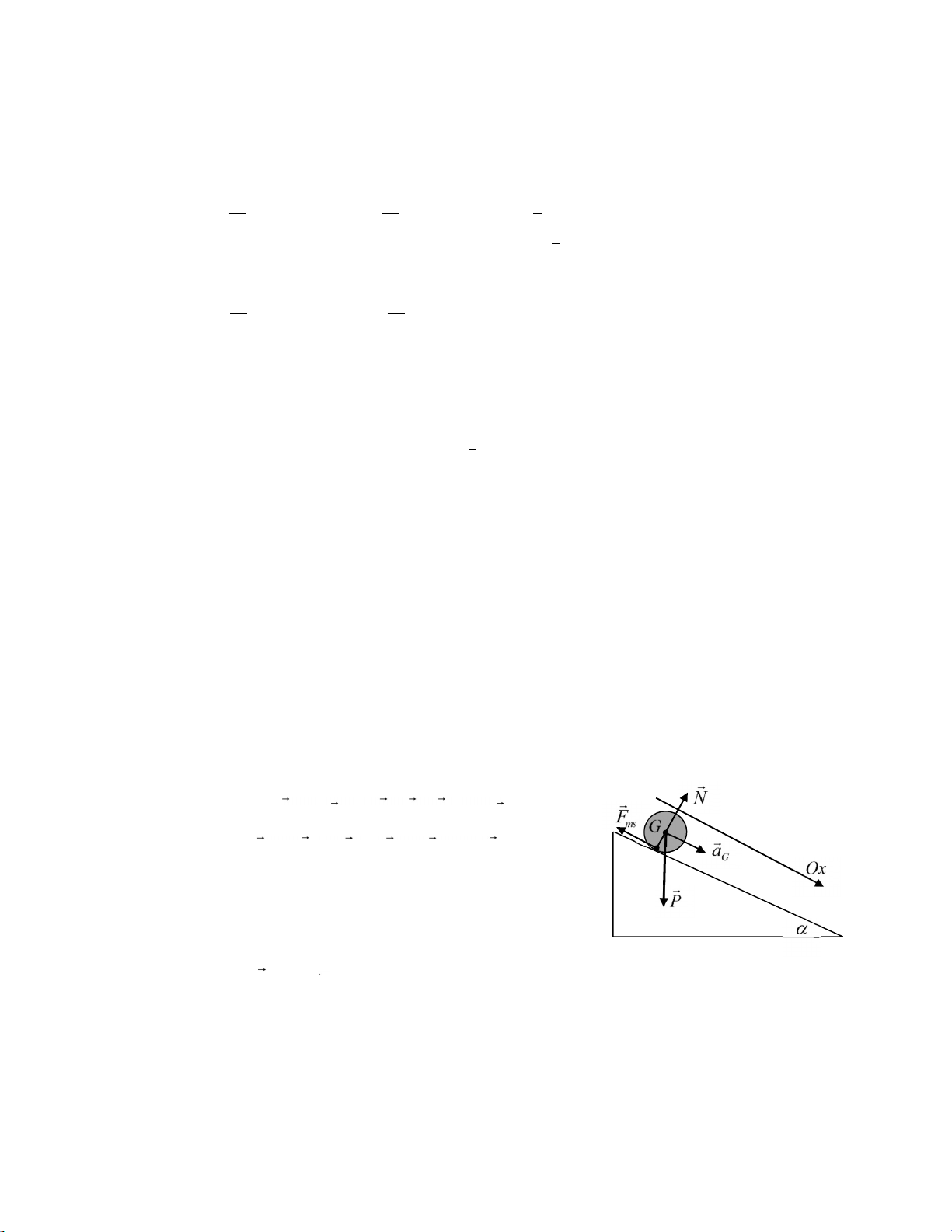
Bài 3: Quả cầu đồng chất được đặt trên đỉnh mặt phẳng nghiêng α sau đó thả cho lăn không trượt, tìm gia tốc khối tâm.
Các lực tác dụng lên quả cầu như hình vẽ, lưu ý lực ma sát là ma sát lăn, vì lăn không
trượt nên bản chất ma sát bề mặt tác dụng lên quả cầu là lực ma sát nghỉ.
Xét chuyển động của quả cầu, ta thấy nó vừa quay và vừa di chuyển theo đường thẳng.
Do đó ta xem quả cầu đang thực hiện đồng thời hai chuyển động: (1) quay quanh trục quay đi
qua khối tâm G vuông góc với mặt phẳng hình vẽ và (2) chuyển động tịnh tiến đi xuống.
Phương trình Newton viết cho 2 chuyển động:
Tịnh tiến: F M a . G   P N Fms M a. G Quay:
M  I. MP MN MF  I. ms 
Xét độ lớn các moment lực đối với trục quay đi qua khối
tâm: MP  Pd.  P.0  0 , MN  N d.  N.0  0 . Nên pt quay trở thành MF  ms I.
Chiếu: P.sin 0 Fms  M a. G (1) MF  I. F ms ms.R  I. (2)
Phương trình bổ sung: aG .R (3) 3 lOMoARcP SD| 59256 994 
Từ (1), (2), (3) ta giải ra được: a 5 G  MP.sin R I2  7 g.sin
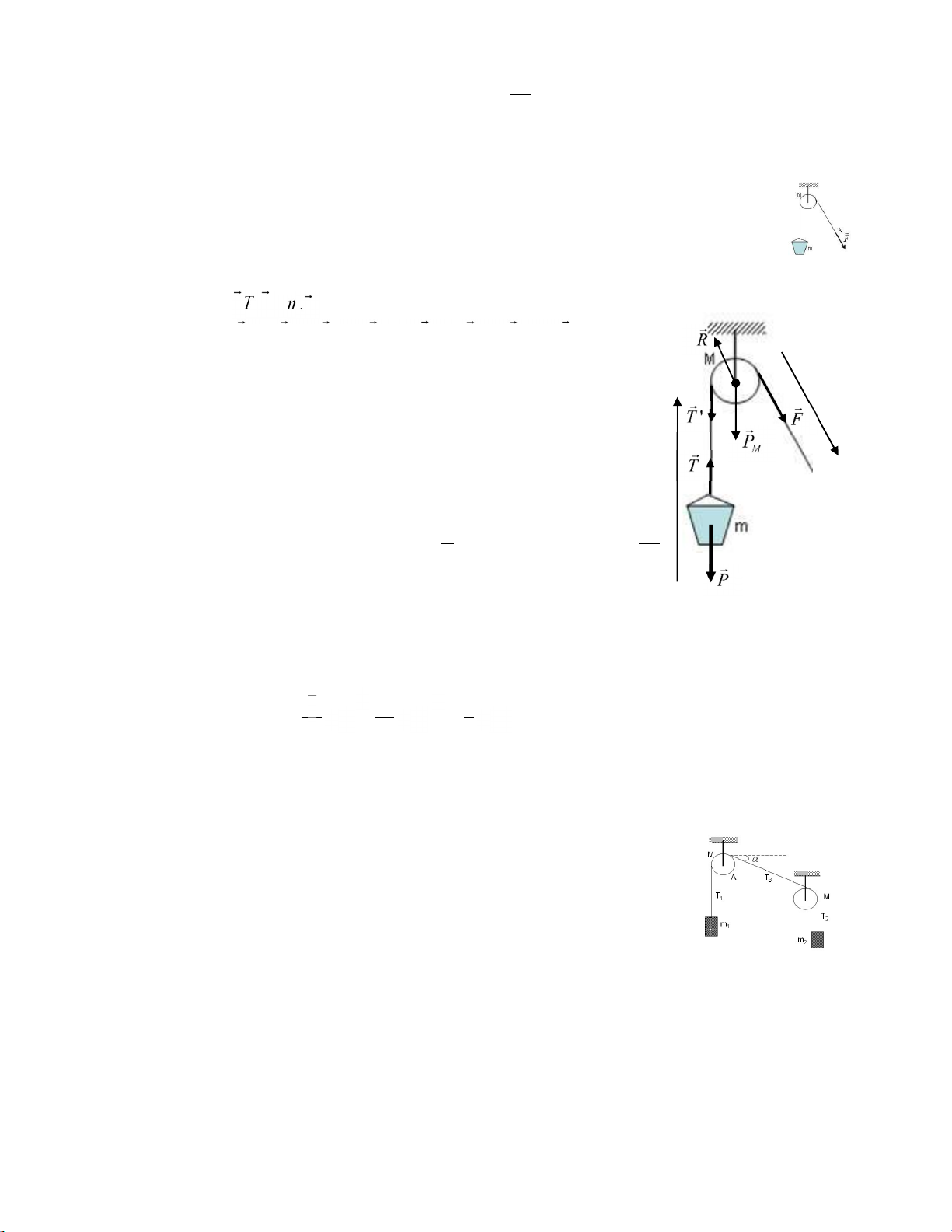
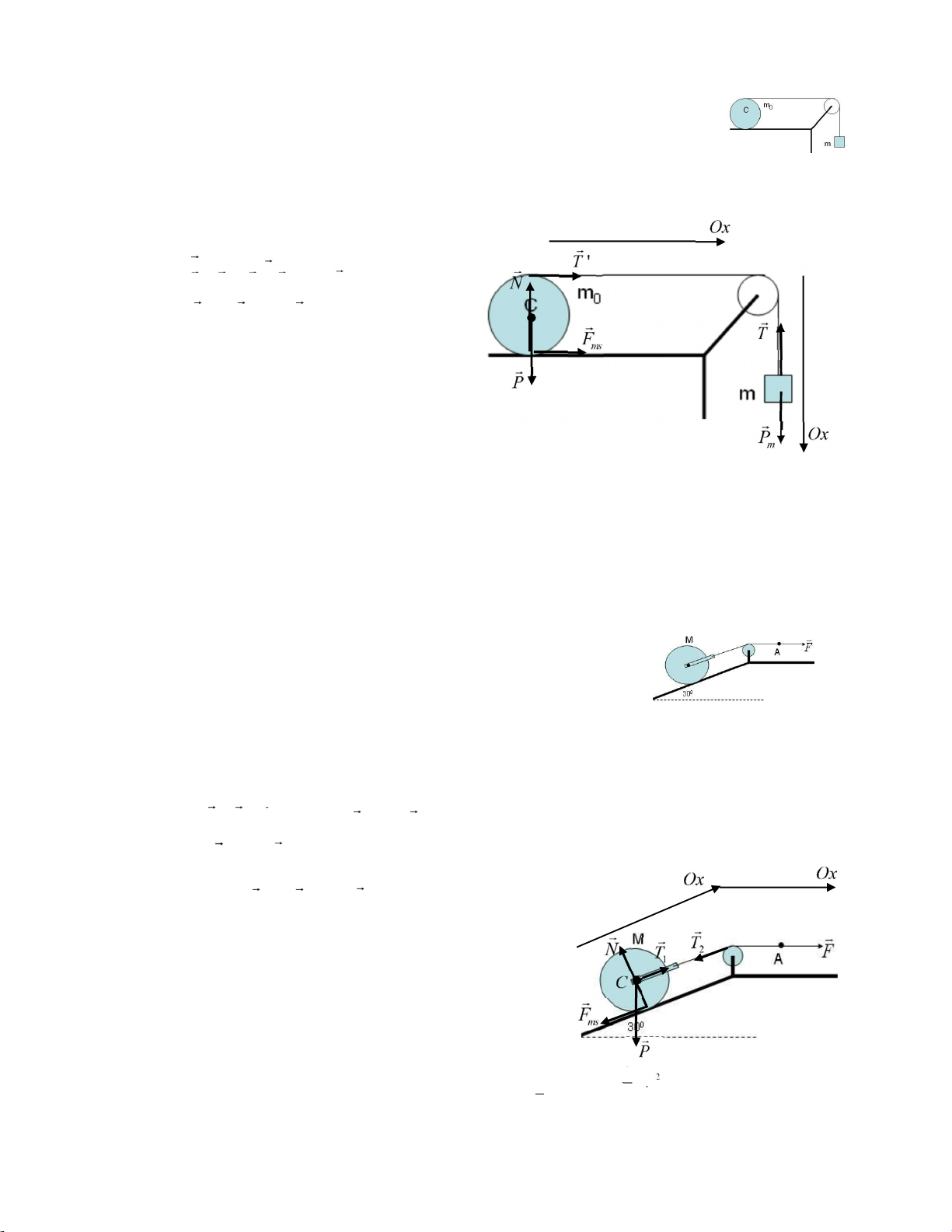
Bài 4: Ta dùng một lực F=121N tác dụng lên đầu dây A để kéo một xô vữa lên cao. Xô vữa có khối
lượng m=10kg. Ròng rọc là đĩa tròn đặc, đồng chất có khối lượng M=1kg. Cho rằng sợi dây không
co dãn, khối lượng không đáng kể. Tính gia tốc của xô vữa và lực căng dây. Lấy g=10m/s2
Vẽ tất cả các lực lên hệ gồm vật m và ròng rọc M, chọn trục tọa độ, Pt Newton: PT . m a  M T ' MF MP M M
R  I. MT ' MF  I. Chiếu:   P T ma. (1) 
MT ' MF  I.T R F R'.  .  I. (2)
Phương trình bổ sung: T T a ', .R (3) Giải hệ (1), (2), và (3) tìm a như sau:
• Thay (3) vào (2) :   a
T R F R. .  I. R   T F I. a R 2 (4)
• Cộng (4) với (1):       a T F  P T I. R 2 ma.
 a I F P  F m g . 121 10.10  2m s/ 2 m m 10    M 1 R2 2 2
Lực căng dây: T  T ' ma P.  10.2 10.10 120N
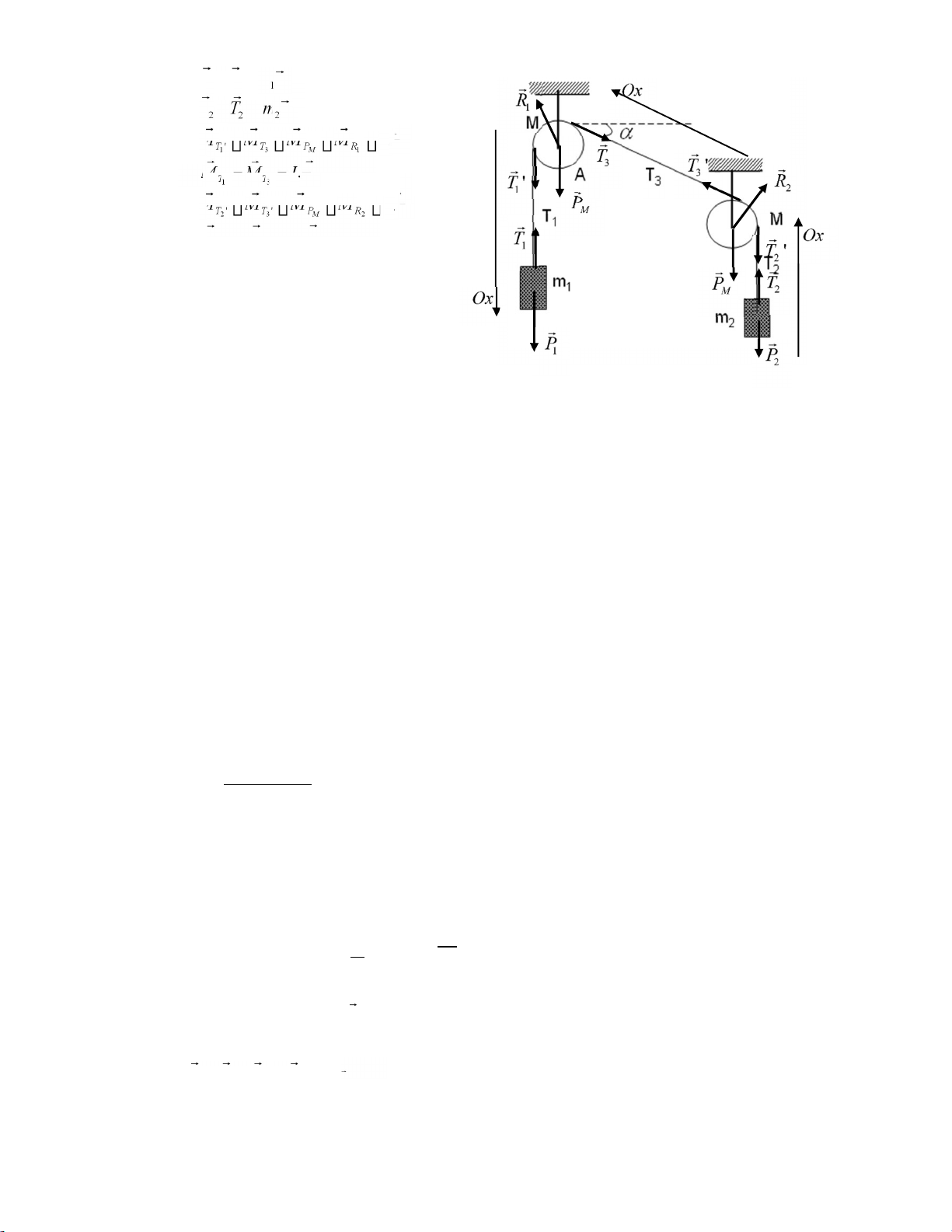
Bài 5: Cho cơ hệ như hình vẽ, các vật m1=2kg, m2=1kg. Các ròng rọc là các đĩa tròn
đặc, đồng chất có khối lượng M=2kg. Hệ bắt đầu chuyển động từ trạng thái đứng
yên. Dây nối không co dãn, khối lượng không đáng kể.
a) Tính gia tốc của các vật m1 và các lực căng dây.
b) Tính phản lực tác dụng lên ròng rọc A, biết  300.
a) Vẽ tất cả các lực lên hệ gồm 2 vật và hai ròng rọc, chọn trục tọa độ như hình vẽ. Phương trình Newton: 4 lOMoARcP SD| 59256 994 ma 1 1 1 P T ma 2  2  2 M M M M I. T  T  P  R   1 ' 3 M 1 A M M I.  T  T   1 ' 3 M M M M I. T  T  P  R   2 ' 3 ' M 2 P  T  MT2 ' MT3 '  I. Chiếu: P T1  1 ma1 (1)   P2 T2m a2 (2) MT  I. 1' MT3
T R T R1 '.  3.  I. (3) MT2 ' MT3 '  I.
T R T R2 '.  3 '.  I. (4)
Phương trình bổ sung: a .R T; 1 T1 '; T2 T2 '; T3 T3 ' (5)
Từ (1), (2), (3), (4) và (5), giải hệ ta được gia tốc: m g m g1  2 a  m1 m2 M * Các lực căng dây:
Từ (1)    T1 ' T1P1 ma1 ; Từ (2)    T2 ' T2P2 m a2 
Từ (3)    T3 ' T3T1 ' I. T R1 '.  M a R 2
b) Phản lực trục quay R1: 5 lOMoARcP SD| 59256 994
Phương trình Newton tịnh tiến viết cho ròng rọc:
R T1    1 ' PM T3 M a. G  0 Chiếu lên hai trục: Ox R:
1x   00 T3.cos 0 
Oy R:1y  T1 ' PM T3.sin 0  R1x T3.cos
R1y T1 'PM T3.sin
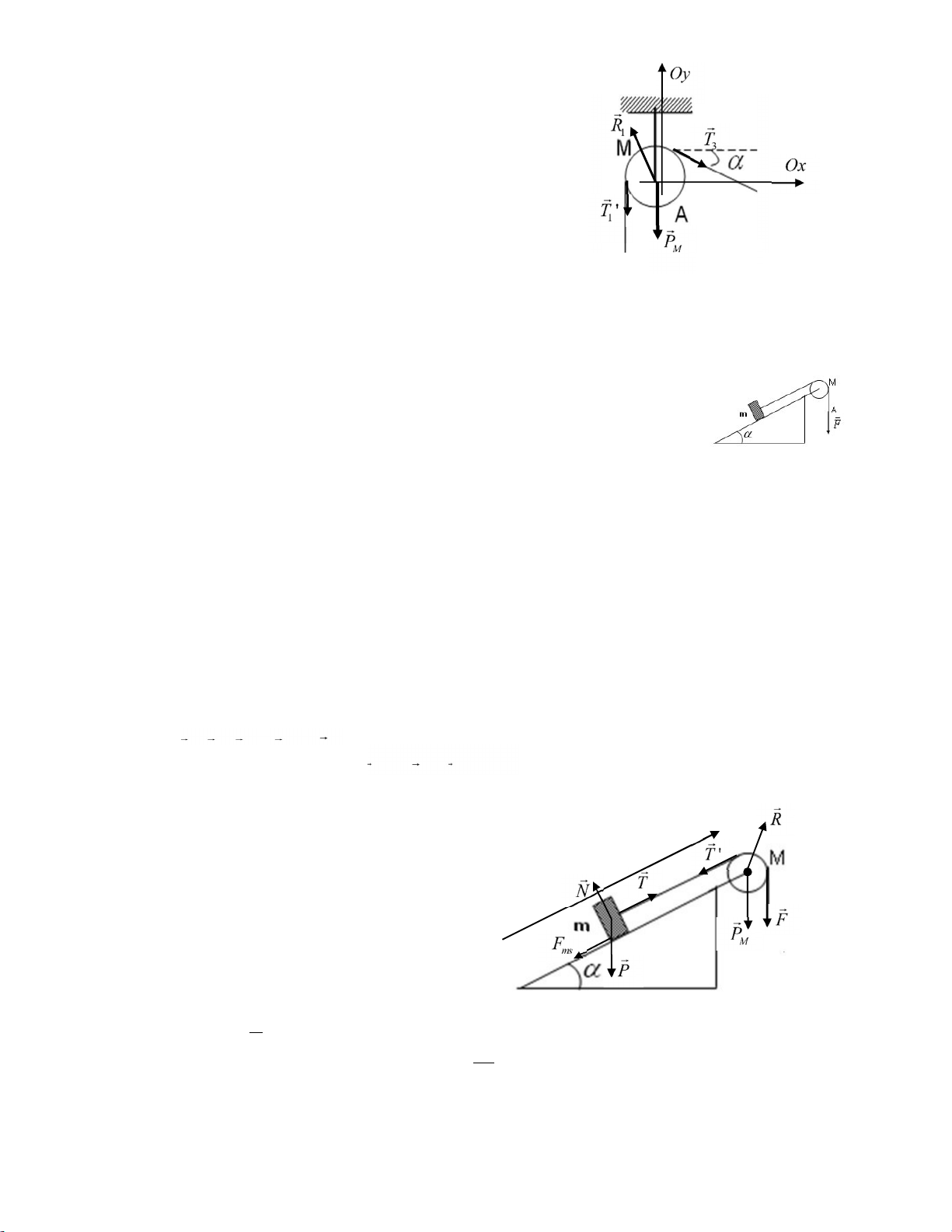
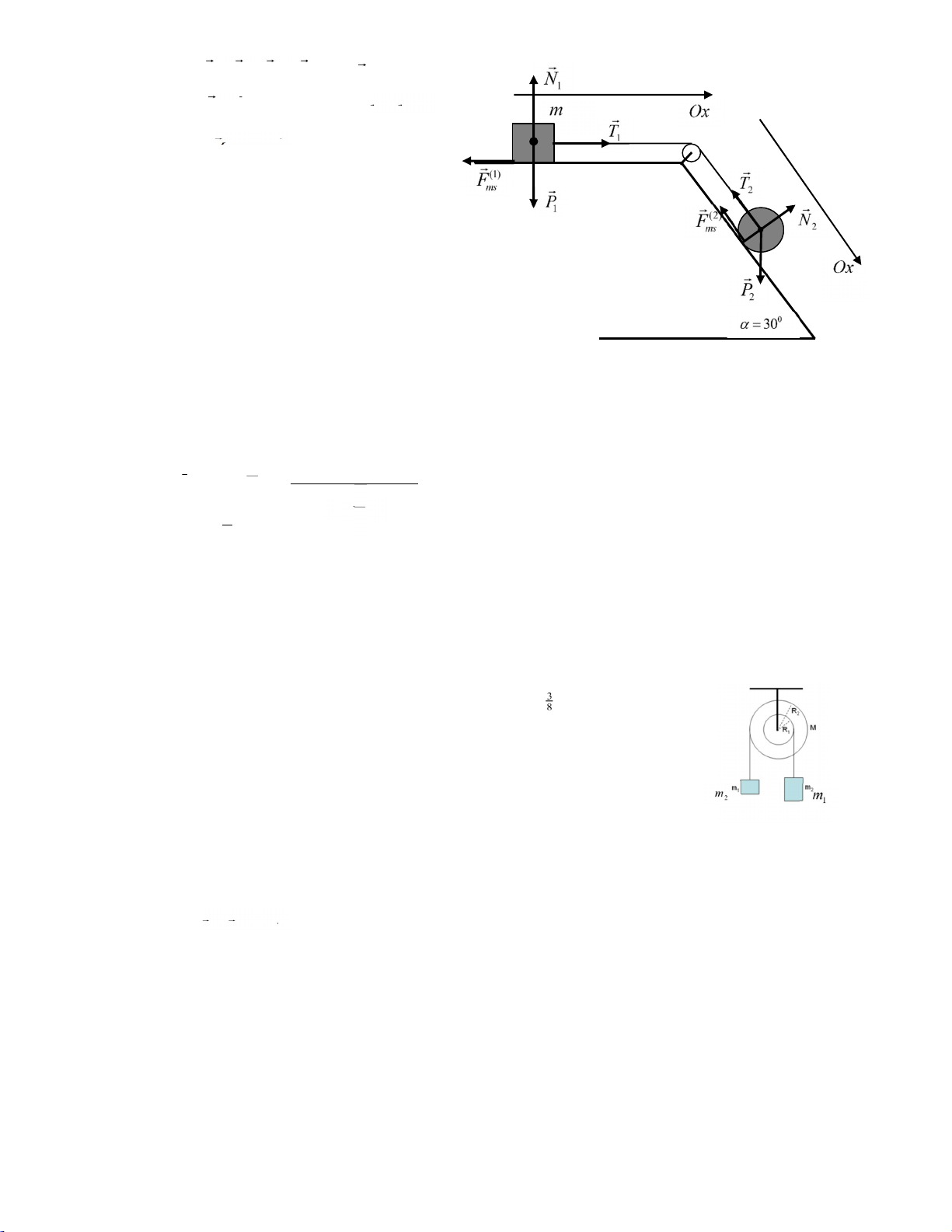
Bài 6: Cho cơ hệ như hình vẽ, vật m=2kg. Ròng rọc là đĩa tròn đặc, đồng chất có khối
lượng M=2kg. Tác dụng lên đầu dây A một lực F=16N. Dây nối không co dãn, khối
lượng không đáng kể. Chiều dài của mặt phẳng nghiêng là 50cm. Cho  300. Hệ số
ma sát giữa vật và mặt nghiêng là 0,2. Tính:
a) Gia tốc của các vật m và lực căng dây.
b) Phản lực tác dụng lên ròng rọc.
a) Vẽ tất cả các lực lên hệ gồm vật m và ròng rọc M, chọn trục tọa độ như hình vẽ.
Khi vẽ lực ma sát ta cần đánh giá xu hướng chuyển động của vật m như sau: giả sử không có ma sát,
thành phần lực lôi vật đi xuống là hình chiếu trọng lực lên phương chuyển động, thành phần này có
độ lớn P.sinmg. .sin 2.10.sin 300 10N . Thành phần lực lôi vật đi lên là T , lực T có giá trị lớn
nhất là T  F 16N . Khi giá trị lực T lớn nhất cao hơn 10N thì ta kết luận vật có xu hướng bị kéo đi
lên, và lực ma sát tác dụng lên vật có chiều ngược lại như hình vẽ. Phương trình Newton: P T Fms  N ma. MT ' MF MP M M
R  I. MT ' MF  I. Chiếu:
P.sin T Fms ma. (1)
MT ' MF  I.T R F R'.  .  I. (2) Phương trình bổ sung: T T a ', .R (3)
Giải hệ (1), (2), và (3) tìm a như sau: a
• Thay (3) vào (2) :  T R F R. .  I. R a    . T F I R2 (4) a 6 lOMoARcP SD| 59256 994
• Cộng (4) với (1):    T F  P.sin T F  ms  I. R2 ma.
a  F P.sinFms  F mg .sink mg. . .cos m m I   M R2 2
Lực căng dây: T T '  ma F ms P.sin ma k mg . cosmg sin
b) Vận tốc tại đỉnh mặt phẳng nghiêng: v2  v 2 2 as v 2 as 0 2as   v2 0
c) Phản lực trục quay R tác dụng lên ròng rọc:
Phương trình Newton tịnh tiến viết cho ròng rọc:
R T   ' PM F M a. G M.0  0 Chiếu lên hai trục:
Ox R: x T '.cos  0 0 0  Rx T '.cos   Oy R:
y T '.sinPM  F 0
Ry T '.sinPM F  Bài 7: Tương tự bài 6 Bài 8: Tương tự bài
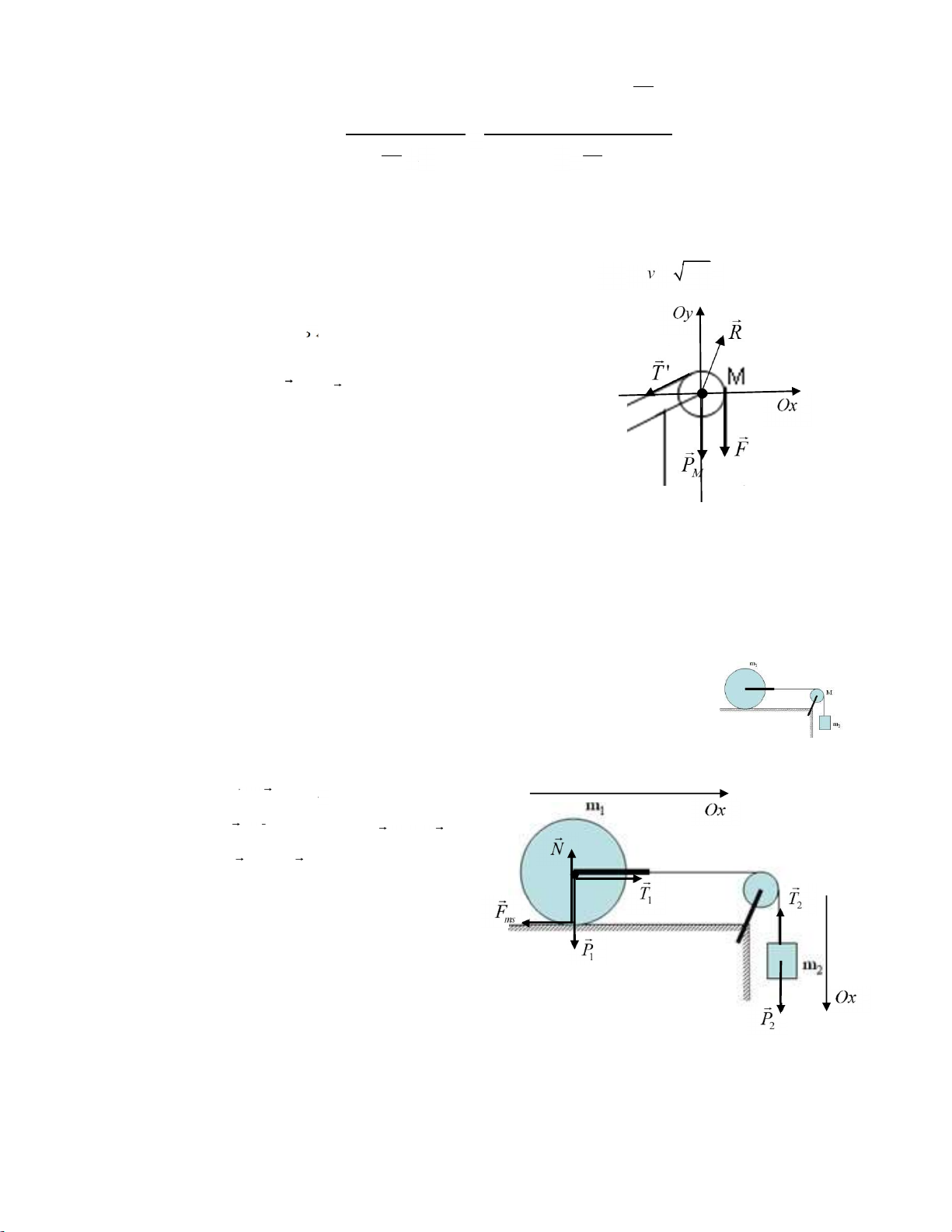
Bài 9: Cho cơ hệ như hình vẽ. Trong đó vật m1 là khối trụ đặc khối lượng 5kg, m2= 2kg.
Thả cho cơ hệ chuyển động từ trạng thái nghỉ, khối trụ lăn không trượt trên mặt sàn.
Cho rằng dây không co dãn, dây và ròng rọc có khối lượng không đáng kể. Tính gia tốc
của vật m2 và lực căng dây a) Phương trình Newton Vật m2: P T2  2 m a2.
Vật m1: P T N F1   1ms m a1. C m a1. MF  I. Chiếu: ms P2 T2  m a2. (1)
0   T1 0 Fms m a1. (2) MF  ms I.  F R ms.  I. (3) Phương trình bổ sung: T1 T2; a .R (4)
Từ (1), (2), (3) và (4) giải ta thu được a và T T1, 2 7 lOMoARcP SD| 59256 994
Bài 10: Cho cơ hệ như hình vẽ. Vật m0 là một khối trụ đặc, đồng chất, được quấn vào
cuộn dây. Thả cho hệ chuyển động từ trạng thái nghỉ, vật m0 chuyển động lăn không trượt
trên mặt ngang. Biết m0=2m. Dây không co dãn, khối lượng dây và ròng rọc không đáng kể.
a. Tính gia tốc của m và khối tâm C của vật m0. b. Tính lực căng dây.
b) Phương trình Newton Pm  T ma
P T  ' N Fms m a0 C MT ' MF  ms I. Chiếu: Pm  T ma (1) 0   T ' 0 F ms m a0 C (2) M T ' MF  ms I.
T R F R'.  ms.  I. (3) Phương trình bổ sung:
T T a';  2aC; aC .R (4)
Từ (1), (2), (3) và (4) giải ta thu được a a, C
c) Lực căng dây: T   T ' Pm ma  mg ma
Bài 11: Cho cơ hệ như hình vẽ. Trong đó, vật M là khối trụ đặc đồng
chất khối lượng 40kg, ròng rọc là đĩa tròn đặc đồng chất có khối lượng
là m= 2kg. Tác dụng vào A một lực F=215,5N kéo khối trụ lăn không
trượt lên dốc nghiêng. Cho rằng dây không co dãn, có khối lượng không đáng kể.
Tính gia tốc của điểm C và lực căng dây. Phương trình Newton
Vật M: P T N F  1ms M a. C M a. MF  ms I. Ròng rọc m: MT M 2 F  Im.m Chiếu: P.sin T 1 Fms  M a. (1) MF  ms
I.  F Rms.  I. (2) MT  M 2
F  Im.m T r2.  F r.  Im.m (3) 2 1 2
Lưu ý:R, r lần lượt là bán kính khối trụ và ròng rọc; I  1 ; . m r  2 M R I. 8 lOMoARcP SD| 59256 994 2 m Phương trình bổ sung:
T1 T2; a .R a; m.r (4)
Giải hệ (1), (2), (3) và (4):
- Thay (4)vào (3) và (2) ta được: a a
(2)  F Rms.  I. R  Fms  I. R2 (5) a a a . .
(3)  T r F r2..  Im. r   T1 F Im r2   T1F Im r2(6) - Thay (5) và (6) vào (1):    
P.sin FIm.ra2 I. Ra2  M a.  a MP .sinIrm2 RIF2 32P..sinM  12 .mF  0,25m s/ 2 Lực căng dây: a 1 . (6)    T2 T1 F Im r2  F 2 ma.
Bài 12: Cho cơ hệ như hình vẽ. Trong đó, vật m=20kg có thể trượt trên sàn
với hệ số ma sát 0,1. Ròng rọc hai bán kính R2  2R1 , có khối lượng là
M= 4kg, momen quán tính đối trục quay là MR 2
2 . Tác dụng lực F lên điểm
A, F  20N . Biết dây nhẹ và không co gãn. Tính: a) Gia tốc của m b) Lực căng dây.
c) Phản lực trục quay tác dụng lên ròng rọc.
Bài 13: Hệ cơ học như hình vẽ, trong đó vật M là một khối trụ đặc, đồng
chất, M= 5kg lăn không trượt trên mặt phẳng nghiêng. Vật m=2kg là một
khối hộp trượt trên sàn nằm ngang với hệ số ma sát 0,1. Cho rằng dây
không dãn, khối lượng dây và ròng rọc không đáng kể.
Tính gia tốc vật m và lực căng dây. Phương trình Newton 9 lOMoARcP SD| 59256 994 Vật m: P T N (1) 1   11 Fms ma. Vật M: P T (2) 2   2 N2 Fms M a. C M a. MF  ms(2) I. Chiếu: T (1) 1 Fms ma. (1) P (2) 2.sin T2Fms  M a. (2) M F  ms(2) I.  F (2) ms .R  I. (3) Phương trình bổ sung: T1 T2; a .R (4)
Từ (1), (2), (3) và (4) giải ta thu được a P (1) 2.sinFms M g. .sinkmg. . a  3 3 m M m M  2 2 Lực căng dây: T T (1) 1  2 ma F.  ms ma kmg.  . .
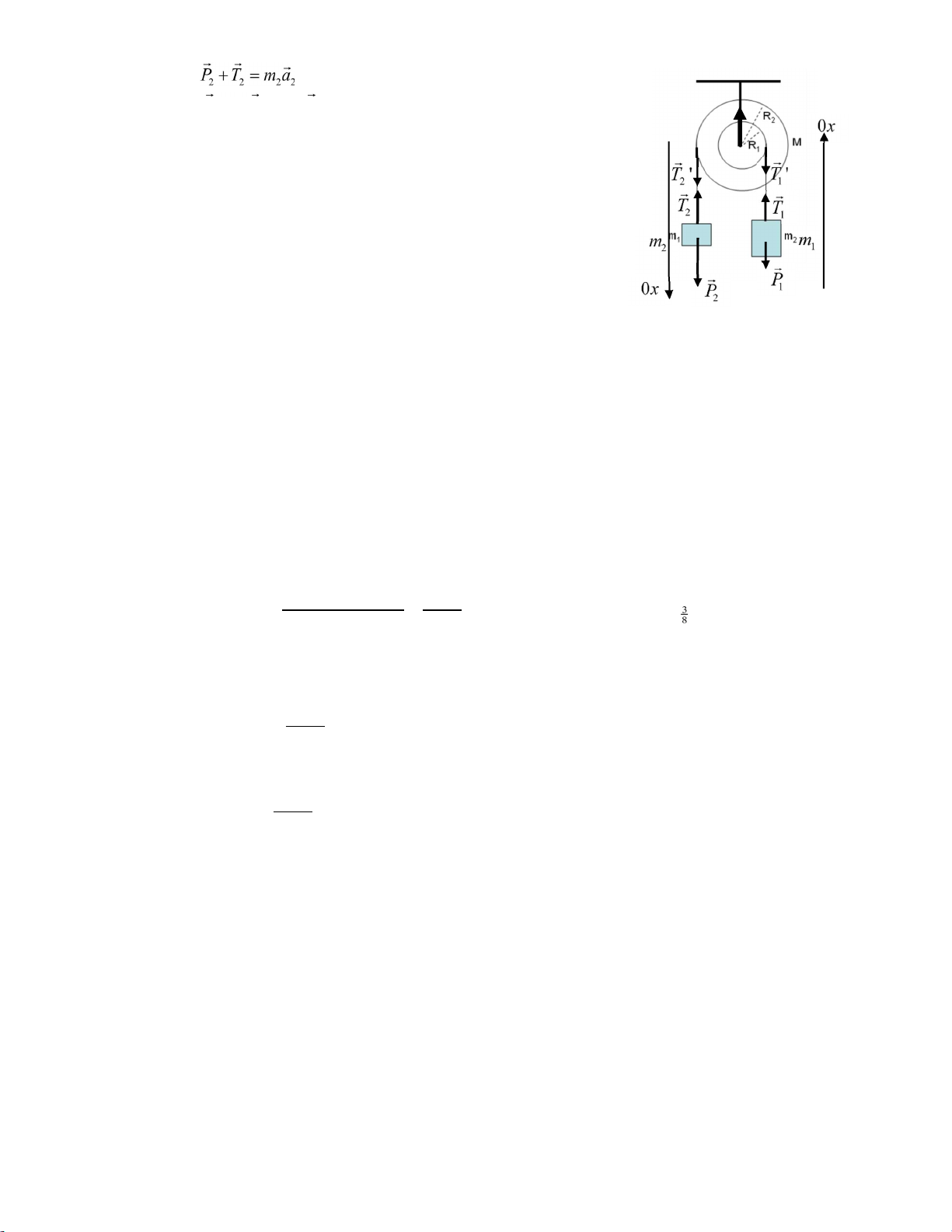
Bài 14: Cho hệ cơ học như hình vẽ, m1=2kg, m2=3kg. Ròng rọc 2 bán kính R2=2R1,
M=1kg. Momen qun tính của ròng rọc so với trục đối xứng là MR 2 2 . Tính gia tốc
các vật và các lực căng dây.
Vẽ tất cả các lực lên hệ gồm 2 vật và ròng rọc, chọn trục tọa độ như hình vẽ. Lưu ý hai vật chuyển
động khác nhau nên gia tốc không như nhau. Phương trình Newton: P T1  1 ma1 1 10 lOMoARcP SD| 59256 994
MT1 ' MT2 '  I. Chiếu:   P T1 1 ma1 1 (1) P 2 T2 m a2 2 (2) M T
1 ' MT2 '  I.T R1 '. 1 T R2 '. 2  I. (3) Phương trình bổ sung: T 1 T1 ' ; T2 T2 '; (4) a1 .R1; a2 .R2 (5)
Giải hệ (1), (2), (3), (4), (5) như sau:  Thay (5) vào (1) và (2)   P T1 1 m1.(.R1) (6) P2  T2 m2.(.R2) (7)  Thay (4) vào (3):
T R1 1. T R2. 2  I. (8) 
Rút T1 từ (6) và T2 từ (7) thay vào (8):
 (P1 m1. .R R1). 1  (P2 m2. .R R2). 2  I.
 I m RPR2 . 2 2PR1 1m R2. 22  31.80R1 rad s/ 2 , thay I  MR22; R2  2R1 1 1 Gia tốc các vật: 80 2 a1 .R1  .R1  2,6m s/ 31.R1 a2 .R2  80.2R1  5, 2m s/2 31.R1
Dựa vào (1) và (2) tính các lực căng dây.
T1 T1 ' ma1 1 P1  2.2,6  2.10  25,2N
T2 T2 '  P2 m a2 2  3.10  3.5,2 14,4N 11