Chương 2: Mạng Tinh Thể và Tính Chất của Vật Liệu | Mạng máy tính | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Vật liệu cơ khí là các chất được con người sử dụng trong sản xuất cơ khí để tạo dựng nên sản phẩm cho cuộc sống như: máy móc, thiết bị, xây dựng công trình, nhà cửa, … Các nhóm vật liệu phổ biến dùng trong công nghiệp là: vật liệu kim loại, vật liệu vô cơ- ceramic, vật liệu hữu cơ-polyme, vật liệu kết hợp- compozit. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Mạng máy tính (HUS) 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 687 tài liệu
Tác giả:
Preview text:
Phần 2: VẬT LIỆU CHẾ TẠO
CHƯƠNG 1: CẤU TRÚC VẬT LIỆU
1.1. Khái quát về kim loại và hợp kim của kim loại
1.1.1. Sơ lược về vật liệu cơ khí
Vật liệu cơ khí là các chất được con người sử dụng trong sản xuất
cơ khí để tạo dựng nên sản phẩm cho cuộc sống như: máy móc, thiết bị,
xây dựng công trình, nhà cửa, …
Các nhóm vật liệu phổ biến dùng trong công nghiệp là: vật liệu kim
loại, vật liệu vô cơ- ceramic, vật liệu hữu cơ-polyme, vật liệu kết hợp- compozit.
Vật liệu kim loại là những vật thể dẫn điện tốt, có ánh kim, có khả
năng biến dạng tốt ngay cả ở nhiệt độ thường, kém bền vững hóa học.
Vật liệu kim loại thông dụng là thép, gang, đồng, nhôm, ...và các hợp
kim của chúng, đây cũng là nhóm vật liệu được dùng chủ yếu trong sản
xuất cơ khí và là đối tượng chính của môn học.
1.1.2. Tầm quan trọng của kim loại và hợp kim
Vật liệu kim loại có vai trò quyết định đến sự phát triển của xã hội
và kỹ thuật. Đó là vật liệu cơ bản để chế tạo ra những máy móc và những
công trình xây dựng. Sự phát triển không ngừng của máy động lực, máy
công cụ gắn liền với sự phát triển của các vật liệu kim loại với tính năng ngày càng cao.
1.2. Cấu tạo của kim loại 1.2.1. Định nghĩa
Kim loại có các tính chất đặc trưng như sau: có ánh kim, khối
lượng riêng tương đối lớn, dễ kéo dài và dát mỏng, thông thường có điểm
nóng chảy cao, cứng, có khả năng dẫn điện dẫn nhiệt tốt. 1.2.2. Phân loại
Kim loại cơ bản: là kim loại thông dụng như sắt, niken, đồng, chì và kẽm.
Kim loại đen: bao gồm gang và thép, sắt, titan, crôm, và nhiều kim
loại đen khác. Kim loại đen là kim loại có bề mặt màu đen do lớp oxy
hóa, đây là những hợp kim trên cơ sở sắt và cacbon.
Kim loại màu (kim loại không chứa sắt): bạc, vàng, đồng, kẽm, và
nhiều kim loại màu khác. Kim loại màu là kim loại có các màu như màu
vàng, màu ghi (bạc), đồng, ... Mạng tinh thể kim loại 1 1.2.3. Các khái niệm
a. Vật tinh thể và vật vô định hình
Theo quan điểm của vật lý chất rắn, các vật rắn được gọi là vật tinh
thể khi chúng đồng thời thỏa các điều kiện sau:
- Là những vật luôn tồn tại với hình dáng xác định trong không
gian, hình dáng bên ngoài của chúng mô tả một phần các tính chất bên
trong. - Vật tinh thể luôn luôn tồn tại một nhiệt độ nóng chảy (hoặc kết
tinh) xác định. Có nghĩa là khi nung nóng vật tinh thể luôn có một nhiệt
độ chuyển biến từ trạng thái rắn sang trạng thái lỏng xác định. Điều này
cũng đúng khi làm nguội vật tinh thể từ trạng thái lỏng.
- Vật tinh thể khi bị đập gãy (phá hủy), sẽ bị gãy theo các mặt xác
định và bề mặt vết gãy không nhẵn bóng. Tính chất này thể hiện rõ rệt sự
khác biệt về tính chất của vật tinh thể với vật vô định hình.
- Vật đa tinh thể luôn có tính dị hướng
Ngược lại với vật tinh thể là các vật vô định hình. Vật vô định hình
là những vật không tồn tại một hình dạng xác định trong không gian (có
hình dáng là của vật chứa nó). Không có nhiệt độ nóng chảy hoặc kết
tinh xác định, không thể hiện tính dị hướng, gia công áp lực khi đang
chảy dẻo ... Một số vật vô định hình tiêu biểu như nhựa đường, parafin, thủy tinh... b. Mạng tinh thể
Là sự sắp xếp các nguyên tử trong không một cách trật tự tuân theo
quy luật hình học xác định.
Mạng tinh thể lý tưởng là mạng đáp ứng hoàn hảo các quy luật xắp
xếp của chất điểm tại các vị trí: mọi nút mạng đều ở vị trí cân bằng, mọi
nút mạng đều chứa nguyên tử (ion dương) và không chứa các nguyên tử tạp chất. c. Mặt tinh thể
Là mặt phẳng bất kỳ có:
- Chứa ba nút mạng không thẳng hàng.
- Hai phương tinh thể không trùng nhau, không chéo nhau.
- Một phương tinh thể và một nút mạng nằm ngoài phương tinh thể d. Ô cơ sở 2
Hình 2.1. Ô cơ sở và hệ tọa độ
Ô cơ sở được xây dựng trên ba vectơ đơn vị , tương ứng với
ba trục tọa độ Ox, Oy, Oz đặt trên ba cạnh của ô (hình 2.1). Môđun của
ba vec tơ đó a, b, c là kích thước của ô cơ sở còn gọi là hằng số mạng hay
thông số mạng, vì chúng đặc trưng cho từng nguyên tố hóa học hay đơn
chất, Các góc , , hợp bởi các vec tơ đơn vị.
Tùy thuộc vào tương quan giữa các cạnh và góc của ô cơ sở có bảy
hệ tinh thể khác nhau là:
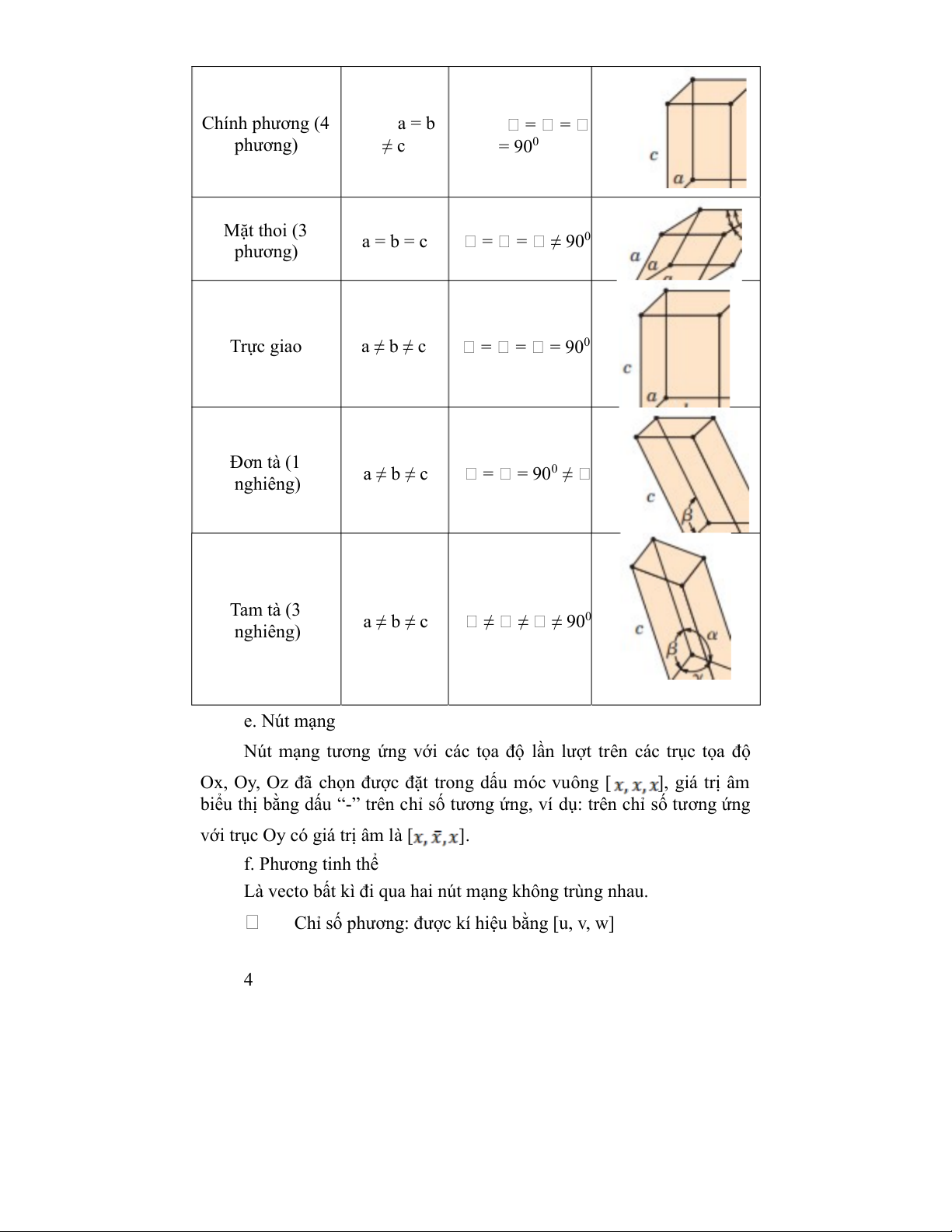
Bảng 2.1. Mối quan hệ tham số mạng và số liệu hiển thị hình học ô đơn
vị cho bảy hệ tinh thể Hệ thống tinh Mối quan Mỗi quan hệ hệ giữa các Dạng hình học thể giữa các góc cạnh Lập phương a = b = c = = = 900 Lục giác (6 = = 900, = phương) a = b ≠ c 1200 3 Chính phương (4 a = b = = phương) ≠ c = 900 Mặt thoi (3 a = b = c 0 phương) = = ≠ 90 Trực giao a ≠ b ≠ c = = = 900 Đơn tà (1 a ≠ b ≠ c 0 nghiêng) = = 90 ≠ Tam tà (3 a ≠ b ≠ c 0 nghiêng) ≠ ≠ ≠ 90 e. Nút mạng
Nút mạng tương ứng với các tọa độ lần lượt trên các trục tọa độ
Ox, Oy, Oz đã chọn được đặt trong dấu móc vuông [ ], giá trị âm
biểu thị bằng dấu “-” trên chỉ số tương ứng, ví dụ: trên chỉ số tương ứng
với trục Oy có giá trị âm là [ ]. f. Phương tinh thể
Là vecto bất kì đi qua hai nút mạng không trùng nhau.
Chỉ số phương: được kí hiệu bằng [u, v, w] 4
Ba chỉ số u, v, w là ba số nguyên tỷ lệ thuận với tọa độ của nút
mạng nằm trên phương đó ở gần gốc tọa độ nhất. Chú ý: Phương và mặt
tinh thể có kích thước vô hạn.
Hình 2.2: Các phương điển hình của hệ lập phương
Hình 2.2 giới thiệu ba phương điển hình trong mạng tinh thể của hệ lập phương:
- Đường chéo khối [111], đường chéo mặt [110], đường chéo cạnh [100].
- Các phương có các giá trị tuyệt đối u, v, w giống nhau, tạo nên họ phương.
Ví dụ: họ gồm các phương sau đây chúng có cùng quy luật sắp xếp
nguyên tử: [110], [011], [101], [110], [011], [101], [110], [011], [101],
[110], [011], [101] (các đường chéo).
Chỉ số Miller của mặt tinh thể:
Mặt tinh thể là tập hợp các mặt có cách sắp xếp nguyên tử giống
hệt nhau, song song và cách đều nhau, chúng có cùng một ký hiệu.
Người ta ký hiệu mặt bằng chỉ số Miller (h k l).
Hình 2.3. Sơ đồ ký hiệu mặt tinh thể theo chỉ số Miller 5
Các chỉ số h, k, l được xác định theo các bước như sau:
- Tìm giao điểm của mặt phẳng trên ba trục theo thứ tự Ox, Oy, Oz.
- Xác định tọa độ các giao điểm, rồi lấy các giá trị nghịch đảo,
- Quy đồng mẫu số, lấy các giá trị của tử số, đó chính là các chỉ số
h, k, l. Ví dụ, xác định các chỉ số Miller cho các mặt:
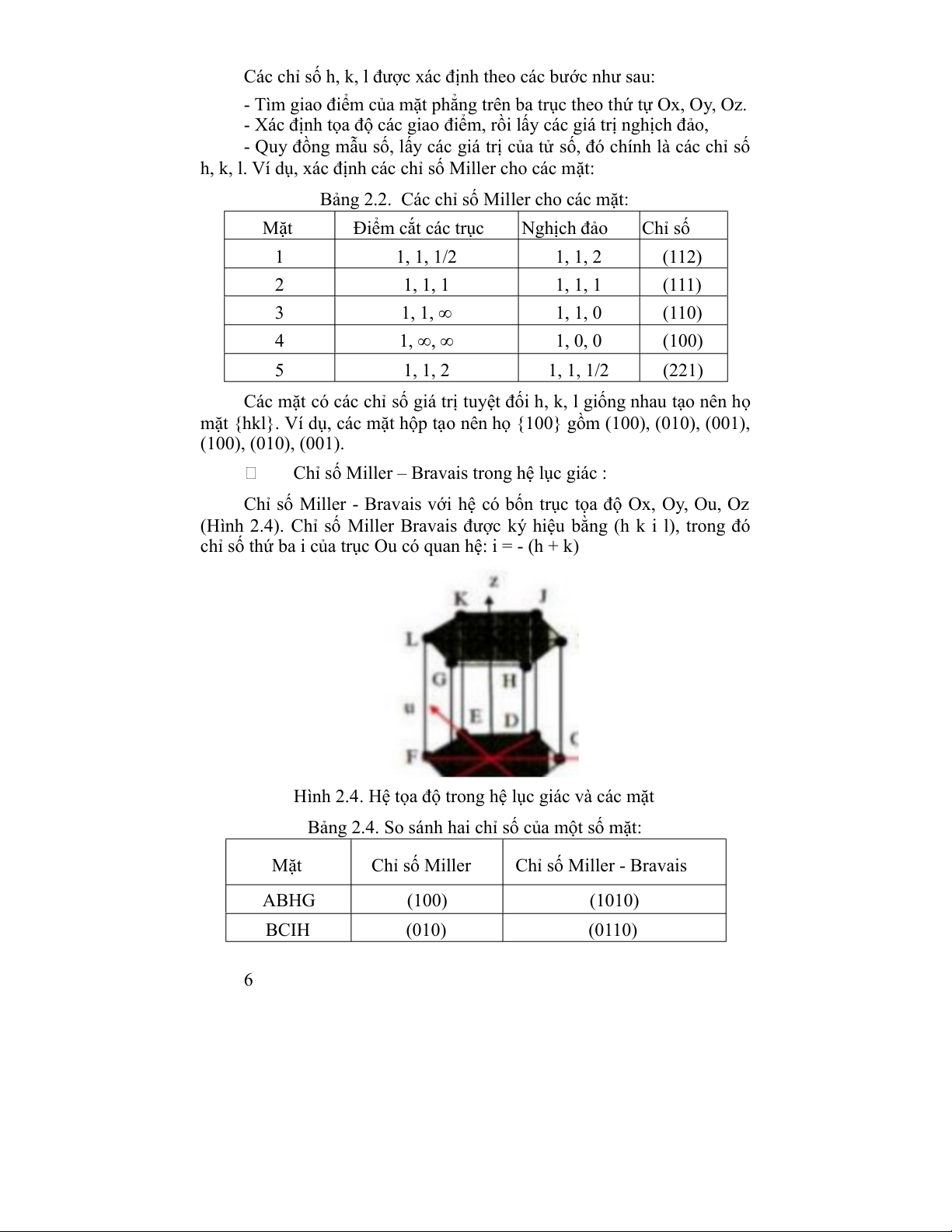
Bảng 2.2. Các chỉ số Miller cho các mặt: Mặt Điểm cắt các trục Nghịch đảo Chỉ số 1 1, 1, 1/2 1, 1, 2 (112) 2 1, 1, 1 1, 1, 1 (111) 3 1, 1, ∞ 1, 1, 0 (110) 4 1, ∞, ∞ 1, 0, 0 (100) 5 1, 1, 2 1, 1, 1/2 (221)
Các mặt có các chỉ số giá trị tuyệt đối h, k, l giống nhau tạo nên họ
mặt {hkl}. Ví dụ, các mặt hộp tạo nên họ {100} gồm (100), (010), (001), (100), (010), (001).
Chỉ số Miller – Bravais trong hệ lục giác :
Chỉ số Miller - Bravais với hệ có bốn trục tọa độ Ox, Oy, Ou, Oz
(Hình 2.4). Chỉ số Miller Bravais được ký hiệu bằng (h k i l), trong đó
chỉ số thứ ba i của trục Ou có quan hệ: i = - (h + k)
Hình 2.4. Hệ tọa độ trong hệ lục giác và các mặt
Bảng 2.4. So sánh hai chỉ số của một số mặt: Mặt Chỉ số Miller Chỉ số Miller - Bravais ABHG (100) (1010) BCIH (010) (0110) 6 AGLF (110) (1100) ABCDEF (001) (001) ACIG (1120) g. Khối cơ bản
Là phần thể tích nhỏ nhất của mạng tinh thể còn duy trì quy luật
sắp xếp của các nguyên tử trong không gian.
Hình 2.5. Khối cơ bản (cơ sở) h. Thông số mạng
Hằng số mạng, hoặc tham số mạng, đề cập đến kích thước vật lý
của các ô đơn vị trong mạng tinh thể. Mạng trong ba chiều thường có:
- Ba hằng số mạng về hình dáng hay còn gọi là góc mạng: là góc
giữa các cạnh của khối cơ bản, được ký hiệu bằng các chữ cái Hy Lạp
viết thường α, β, γ…., có đơn vị là độ (o), radian (rad). Trong trường hợp
đặc biệt của cấu trúc tinh thể lập phương, ta có α = β = γ = 90o.
- Ba hằng số mạng về kích thước: là khoảng cách ngắn nhất giữa
các nút mạng trên các cạnh của khối cơ bản, được gọi là a, b và c.
Tuy nhiên, trong trường hợp đặc biệt của cấu trúc tinh thể lập
phương, tất cả các hằng số đều bằng nhau và được gọi là a. Tương tự,
trong các cấu trúc tinh thể lục giác, hằng số a và b bằng nhau và chúng ta
chỉ đề cập đến hằng số a và c. Ba hằng số này có đơn vị có đơn vị là Angstrom (𝐴°).
Tập hợp đầy đủ các thông số mạng bao gồm ba hằng số mạng về
hình dáng và ba hằng số mạng về kích thước đặc trưng cho quy luật sắp
xếp của các nguyên tử trong không gian.
Đơn vị đo thông số mạng là kx (nanomét) hay ăngstrông, 1kx =
1,00202, A0=1,00202.10-8 cm. Theo thông số mạng ta có thể tính được
đường kính nguyên tử kim loại. Thông số mạng thường ký hiệu a i. Nút mạng 7
Là vị trí cân bằng (trung tâm) mà các nguyên tử hoặc ion dao động xung quanh. j. Nút trống
Trong mạng tinh thể các nguyên tử (ion) luôn luôn dao động quanh
vị trí cân bằng của chúng nhờ năng lượng dao động. Một số nguyên tử
nào đó có năng lượng đủ lớn với biên độ dao động lớn, chúng có khả
năng bứt khỏi vị trí cân bằng của mình, để lại ở đó vị trí không có nguyên
tử chiếm chỗ gọi là nút trống. k. Lỗ trống
Trong mạng tinh thể các nguyên tử (ion) luôn luôn dao động quanh
vị trí cân bằng của chúng nhờ năng lượng dao động. Một số nguyên tử
nào đó có năng lượng đủ lớn với biên độ dao động lớn, chúng có khả
năng bứt khỏi vị trí cân bằng của mình, để lại ở đó vị trí không có nguyên
tử chiếm chỗ gọi là nút trống. l. Sai lệch mạng
Trong thực tế không phải mọi nguyên tử hoặc ion đều nằm đúng vị
trí quy định mà ở một vài bộ phận còn có những nguyên tử nằm lệch ra
khỏi vị trí của nó gây nên sai lệch mạng
Ảnh hưởng của sai lệch mạng: làm thay đổi tính chất của tinh thể,
dẫn đến thay đổi tính chất của vật liệu.
1.3. Các kiểu mạng tinh thể thường gặp
1.3.1. Lập phương thể tâm
Tên gọi: Lập phương thể tâm (BCC, body – centered cubic), (a = b = c, = = = 900)
Hình dáng: 8 nguyên tử nằm ở 8 đỉnh và 1 nguyên tử nằm ở tâm của khối cơ bản
Hình 2.6. Kiểu mạng lập phương tâm khối (BCC) 8
Số thể tích nguyên tử trong khối cơ bản:
Các nguyên tố có kiểu mạng này: Fe , Cr, W, V, Mo, … Mật độ khối:
- Bán kính nguyên tử: rnt = 4r = a
- Thể tích của một nguyên tử: r3
- Thể tích của một ô cơ bản: V = a3 Mật độ khối Mv = = 68%
Còn 32% thể tích là trống, không có nguyên tử chiếm chỗ (4 mặt, 8 mặt)
Hình 2.7: Mặt cắt mặt nguyên tử dày đặc nhất của mạng Nút trống khối 4 mặt:
Hình 2.8. Nút trống khối 4 mặt của kiểu mạng BCC
Vị trí: nằm ở đường thẳng nối điểm giữa hai cạnh bên đối diện trên cùng một mặt bên.
Số lượng: n = 4 (mặt) = x.y.z. Trong đó: 9
x = phần điểm trống thuộc khối cơ bản
y = 4 số vị trí trên một mặt bên z = 6 số mặt bên
n = x 4 x 6 = 12 nút trống
Đường kính nút trống khối 4 mặt:
= 0.0221d với d là đường kính biểu kiến của nguyên tử kim loại Nút trống khối 8 mặt:
Hình 2.9. Nút trống khối 8 mặt của kiểu mạng BCC
Vị trí: ở tâm các mặt bên và điểm giữa các cạnh bên Số lượng:
Đường kính nút trống khối 8 mặt:
với d là đường kính nguyên tử kim loại
Ví dụ: ở nhiệt độ thường, sắt (Fe ), Cr, Mo, W có kiểu mạng lập
phương thể tâm với thông số mạng a = 2.9 A0, 2.884 A0, 3.174 A0, 3.165 A0
1.3.2. Lập phương đơn giản
Tên gọi: Lập phương đơn giản (SC Simple Cubic), (a = b = c, = = = 900).
Hình dáng: các nguyên tử, ion nằm ở 8 đỉnh của khối cơ bản.
Số thể tích nguyên tử trong khối cơ bản: 10
Hình 2.10. Kiểu mạng lập phương đơn giản (SC)
1.3.3. Lục giác xếp chặt
Tên gọi: Lục giác xếp chặt (HCP Hexagonal close – packed), (a = b < c, = = 900, = 1200)
Hình dáng: Các nguyên tử nằm ở các đỉnh, ở giữa hai mặt đáy
hình lăng trụ lục giác và ở tâm ba khối lăng trụ tam giác cách đều.
Hình 2.11. Mặt đáy của mạng lục giác xếp chặt
Liên kết theo từng lớp chặt hơn so với liên kết giữa các lớp, thông số mạng a, c: : độ chính phương
Cấu trúc lục giác xếp chặt
Các lớp dễ dàng trượt lên nhau Tỷ số
là trường hợp lý tưởng Số thể tích nguyên tử trong khối cơ bản:
Nguyên tố thường gặp: Zn, Cd, Mg, Ti, … 11
Hình 2.11. Kiểu mạng lục giác xếp chặt (HCP)
1.3.4. Chính phương thể tâm
Tên gọi: chính phương thể tâm (a = b < c, = = = 900)
Hình dáng: có thể coi mạng chính phương thể tâm là mạng lập
phương thể tâm bị kéo dài theo một trục. Thông số mạng a, c: khi : độ chính phương thành mạng lập phương
Nguyên tố thường gặp: tổ chức Martensite 1.3.5. Tính thù hình
Mỗi kim loại có kiểu mạng đặc trưng. Tuy nhiên có một số kim loại
có nhiều mạng tinh thể khác nhau ở trong khoảng nhiệt độ và áp suất
khác nhau, tính chất đó gọi là tính đa hình. Mỗi kiểu mạng ổn định trong
khoảng nhiệt độ xác định, gọi là kiểu thù hình (đa hình). Ví dụ: Fe, Co,
Mn, Sn, Te, Ce, …Các dạng thì hình khác nhau của cùng một nguyên tố
được ký hiệu bằng chữ cái Hy Lạp: , , , ,… trong đó chỉ dạng tồn
tại ở nhiệt độ thấp nhất còn , , ,… lần lượt ở các nhiệt độ cao hơn. Ví
dụ: Fe , Fe , Fe ,… (Hình 2.13). Quá trình thay đổi cấu trúc mạng từ
dạng thù hình này sang dạng thù hình khác được gọi là chuyển biến thù hình. 12
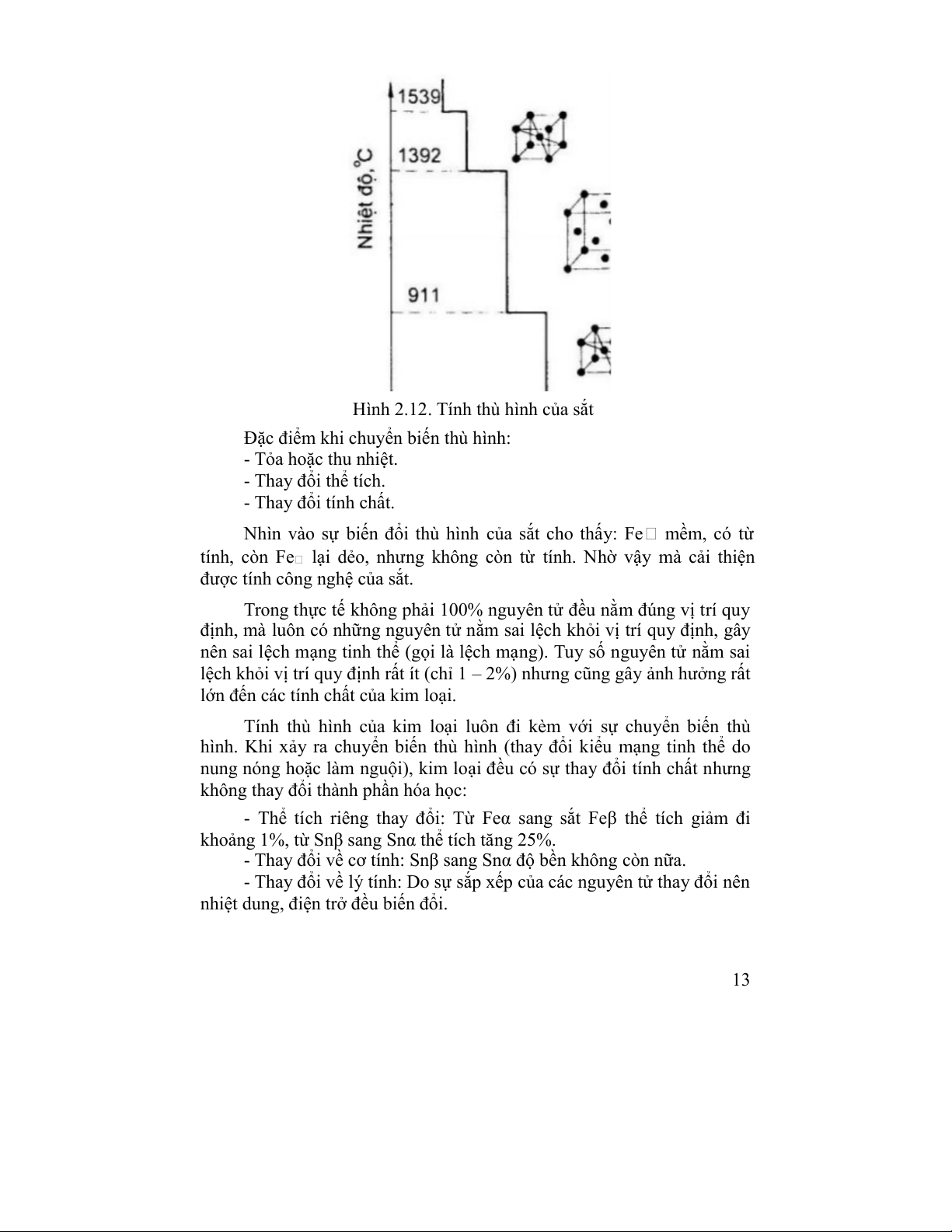
Hình 2.12. Tính thù hình của sắt
Đặc điểm khi chuyển biến thù hình: - Tỏa hoặc thu nhiệt. - Thay đổi thể tích. - Thay đổi tính chất.
Nhìn vào sự biến đổi thù hình của sắt cho thấy: Fe mềm, có từ
tính, còn Fe lại dẻo, nhưng không còn từ tính. Nhờ vậy mà cải thiện
được tính công nghệ của sắt.
Trong thực tế không phải 100% nguyên tử đều nằm đúng vị trí quy
định, mà luôn có những nguyên tử nằm sai lệch khỏi vị trí quy định, gây
nên sai lệch mạng tinh thể (gọi là lệch mạng). Tuy số nguyên tử nằm sai
lệch khỏi vị trí quy định rất ít (chỉ 1 – 2%) nhưng cũng gây ảnh hưởng rất
lớn đến các tính chất của kim loại.
Tính thù hình của kim loại luôn đi kèm với sự chuyển biến thù
hình. Khi xảy ra chuyển biến thù hình (thay đổi kiểu mạng tinh thể do
nung nóng hoặc làm nguội), kim loại đều có sự thay đổi tính chất nhưng
không thay đổi thành phần hóa học:
- Thể tích riêng thay đổi: Từ Feα sang sắt Feβ thể tích giảm đi
khoảng 1%, từ Snβ sang Snα thể tích tăng 25%.
- Thay đổi về cơ tính: Snβ sang Snα độ bền không còn nữa.
- Thay đổi về lý tính: Do sự sắp xếp của các nguyên tử thay đổi nên
nhiệt dung, điện trở đều biến đổi. 13
Sự thay đổi của tính chất kim loại khi chuyển biến đa hình được
nghiên cứu sâu để tận dụng các tính chất có lợi và ngăn ngừa các tính
chất bất lợi. Tính đa hình của sắt sử dụng nhiều trong nhiệt luyện.
1.4. Cấu trúc của kim loại
1.4.1. Các sai hỏng trong mạng tinh thể
Các cấu trúc tinh thể trình bày ở trên là cấu trúc của tinh thể lý
tưởng vì khi xét đã bỏ qua dao động nhiệt và các sai hỏng (lệch lạc) trong
trật tự sắp xếp của các nguyên tử (ion, phân tử). Trong thực tế không phải
100% nguyên tử đều nằm đúng vị trí quy định, gây nên những sai hỏng
được gọi là sai lệch mạng tinh thể hay khuyết tật mạng. Tuy số nguyên tử
nằm lệch vị trí quy định chiếm tỷ lệ rất thấp (chỉ 1 - 2%) song gây ra các
ảnh hưởng rất xấu đến các hành vi của tinh thể dưới tác dụng của ngoại
lực (biến dạng dẻo, biến cứng...) tức đến độ bền - chỉ tiêu cơ tính hàng
đầu, nên việc khảo sát các sai lệch này có ý nghĩa lý thuyết và thực tế lớn lao, không thể bỏ qua.
Khuyết tật trong mang tinh thể là các dạng sai lệch, làm thay đổi
quy luật, vị trí, kích thước của mang tinh thể, trong đó:
- Quy luật: là quy luật sắp xếp chất điểm và các mặt tinh thể
- Vị trí: là sự xuất hiện hoặc thiếu hụt các chất điểm và các vùng
tinh thể không theo quy luật ban đầu
- Kích thước: là sự tăng hay giảm của thông sô mạng.
Từ các kết quả nghiên cứu mới nhất về cấu trúc vật liệu có thể đưa
ra các loại khuyết tật mang tinh thể chủ yếu là: a. Sai lệch điểm Sai lệch bên trong
Sai lệch nút trống và sai lệch tự xen kẽ:
Trong mạng tinh thể của chất rắn luôn luôn tồn tại các nút trống và
nguyên tử xen kẽ nằm giữa các nút mạng gọi tắt là nguyên tử tự xen kẽ.
Trong tinh thể, nguyên tử luôn bị dao động nhiệt quanh vị trí quy định
gọi là vị trí cân bằng.
Do ba động nhiệt (biến thiên năng lượng xung quanh giá trị cân
bằng) một số nguyên tử có năng lượng cao, biên độ dao động lớn có khả
năng bứt khỏi nút mạng để lại nút không có nguyên tử gọi là nút trống.
Sau khi rời khỏi nút mạng, nguyên tử có thể chuyển sang vị trí xen kẽ
giữa các nút mạng trở thành nguyên tử tự xen kẽ (hoặc đi đến vị trí trên bề mặt). 14 Sai lệch nút trống Sai lệch tự xen kẽ Hình 2.13. Sai lệch
Nguyên tử xen kẽ có r ≤ 0,59rnguyên tử
Ảnh hưởng: tạo ra một vùng xô lệch trong mạng tinh thể và gây
ứng suất dư trong mạng.
Số lượng sai lệch điểm tăng:
- Độ bền, độ cứng tăng
- Độ dẻo, độ dai giảm - Điện trở tăng
- Dễ bị oxy hóa, ăn mòn hóa học.
Chú ý: các nút trống không đứng yên mà luôn luôn đổi chỗ bằng
cách trao đổi vị trí với các nguyên tử bên cạnh.
Bảng 2.5. Sai lệch Schottky và Sai lệch Frenkel: Sai lệch Schottky Sai hỏng Frenkel
Là nút khuyết (haycặp nút
Là cặp lỗ trống và nguyên tử xen Khái khuyết) trong chất ion.
kẽ được tạo ra khi ion di chuyển niệm
vào vị trí xen kẽ để lại nút khuyết. Phân loại Sai hỏng Sai lệch Anti- Sai hỏng Anti- Anti-Frenkel: Frenkel: Sai hỏng
nguyên tử xen nguyên tử xen Frenkel: Frenkel:nguyên kẽ là ion âm. kẽ là ion âm. nguyêntử xen tử xen kẽ là ion kẽ là ion âm. dương. Sai lệch do tạp chất 15
Trong thực tế không thể có vật liệu hoặc kim loại sạch tuyệt đối.
Phụ thuộc vào kích thước, nguyên tử lẫn vào (thường gọi là tạp chất hay
nguyên tử lạ) có thể thay thế các nguyên tử nền ở nút mạng hoặc xen giữa các nút.
Do sự sai khác về đường kính nguyên tử giữa các nguyên tố nền và
tạp chất nên khi thay thế cho nhau bao giờ cũng làm cho mạng của nền
giãn nở ra hay co lại gây nên sai lệch có dạng bao quanh một điểm. Còn
khi xen kẽ (hay tự xen kẽ) bao giờ cũng làm mạng nền giãn ra vì kích
thước lỗ hổng luôn nhỏ hơn đường kính nguyên tử. Các nguyên tử nền
xung quanh lỗ hổng có khuynh hướng xích lại gần nhau. Trong nhiều
trường hợp có thể chủ động tạo ra dạng sai lệch này bằng cách đưa thêm
một lượng đáng kể nguyên tố (cấu tử) thứ hai vào nền.
Số lượng nút trống các nguyên tử có xu hướng phụ thuộc vào nhiệt
độ, nhiệt độ càng tăng thì số lượng chúng càng nhiều, tuy nhiên không
vượt quá 1÷2%. Kim loại càng bẩn thì khả năng nguyên tử lạ chui vào
mạng tinh thể càng nhiều và do đó số lượng sai lêch điểm càng tăng.
Ví dụ: sắt chứa một lượng nhỏ carbon đưa vào sẽ trở nên cứng hơn.
Khi pha các nguyên tử B hoặc P vào Silic sẽ làm cho Silic trở thành loại p hoặc loại n. b. Sai lệch đường
Sai lệch đường là loại sai lệch mạng có kích thước nhỏ theo hai
chiều đo và lớn theo chiều đo còn lại, tức là có dạng đường (thẳng hoặc cong).
Cũng có thể coi sai lệch đường là tập hợp các sai lệch điểm xếp
liên tiếp, gồm lệch thẳng (lệch biên), lệch xoắn và lệch hỗn hợp (lệch biên + lệch xoắn)
Lệch thẳng (lệch biên):
Nguyên nhân: Do phần của mặt tinh thể bị thiếu trong các mặt tinh
thể song song dẫn đến tạo ra các trục có năng lượng cao hơn, do đó kém
ổn định hơn từ đó tạo ra trục lệch Để đánh giá cường độ lệch có thể dùng véc tơ Burgers: b 16
Hình 2.14. Mô hình lệch thẳng (lệch biên)
Lệch thẳng có thể hình dung bằng cách sau: Giả sử có mạng tinh thể
hoàn chỉnh gồm những mặt nguyên tử song song và cách đều nhau. Nếu
chèn thêm nửa mặt phẳng ABCD vào nửa phần trên của tinh thể thì các
mặt nguyên tử thẳng đứng nằm về hai phía mặt ABCD sẽ không còn
hoàn toàn song song nhau nữa, chúng bị cong đi ở vùng gần đường AD.
Các nguyên tử nằm trong vùng này bị xê dịch khỏi vị trí cân bằng cũ của
mình: Các nguyên tử ở vùng phía dưới đường AD bị đẩy xa ra một ít
(vùng có ứng suất kéo) còn các nguyên tử ở phía trên đường AD bị ép lại
một ít (vùng có ứng suất nén). Như vậy vùng có sai lệch nằm xung quanh
đường thẳng AD và vì vậy người ta gọi là lệch thẳng. Đường AD được
gọi là trục của lệch thẳng.
Nếu bán mặt được gài từ trên xuống, sẽ tạo thành lệch
dương (ký hiệu ┴), gài từ dưới lên gọi là lệch đường âm (ký hiệu T). Lệch xoắn:
Nguyên nhân: Do sự dịch chuyển của các mặt tinh thể không hoàn
chỉnh tạo ra các bề mặt nhấp nhô tế vi trong mạng tinh thể.
Lệch xoắn có thể hình dung bằng cách sau: Cắt tinh thể hoàn chỉnh
bằng nửa mặt phẳng ABCD xong xê dịch hai mép ngoài ngược chiều
nhau làm thế nào để mặt nguyên tử nằm ngang thứ nhất bên phải trùng
với mặt nguyên tử thứ hai bên trái. Kết quả làm cho các nguyên tử nằm
gần đường AB bị xê dịch khỏi vị trí cân bằng cũ của mình. Xem như
được hình thành từ ứng suất tiếp gây ra vặn xoắn. Sở dĩ có danh từ lệch
xoắn vì các lớp nguyên tử trong vùng sai lệch mạng đi theo hình xoắn ốc. 17
Hình 2.15. Mô hình sai lệch xoắn
Mặt phẳng PMNO gọi là mặt trượt của lệch. Các nguyên tử nằm
trong vùng dọc theo trục L. Trục L gọi là trục của lệch xoắn. Các nguyên
tử xung quanh trục sắp xếp theo đường xoắn.
Véc tơ Burgers của lệch xoắn luôn luôn song song với trục lệch. Lệch hỗn hợp
Lệch hỗn hợp là lệch trung gian giữa thẳng và xoắn, mang các đặc
điểm của cả hai loại lệch đã nêu, có dạng hình học rất phức tạp
Hình 2.16. Cách xác định vecto trượt (Burgers)
a: Trong tinh thể hoàn chỉnh; b: Trong lệch đường; c; Trong lệch xoắn. c. Sai lệch mặt
Sai lệch mặt là sai lệch mạng có kích thước nhỏ theo một chiều đo
và lớn theo hai chiều đo còn lại. Bao gồm: Biên giới hạt
Do sự phân chia mạng tinh thể thành các vùng, các vùng khác nhau
có định hướng tinh thể khác nhau (thường gọi là hạt). Biên giới hạt
thường xuất hiện trong vật liệu đa tinh thể. 18
Hình 2.17. Mô hình biên hạt
- Biên hạt nghiêng: biên giữa hai hạt lệch nhau ít – gần tương tự như lệch mạng biên.
- Biên hạt sinh đôi: Xuất hiện khi những tinh thể ở 2 phía của 1 mặt
giống nhau. Mặt biên giữa những tinh thể sinh đôi là mặt đơn nguyên tử
không có sai hỏng. Những nguyên tử biên thuộc về cả hai mặt sinh đôi. a b
Hình 2.18. Hình ảnh biên hạt nghiêng (a) và biên hạt sinh đôi (b) Biên giới siêu hạt:
Nếu đi sâu nghiên cứu, trong mỗi hạt phương mạng cũng không
tuyệt đối ổn định. Hạt còn gồm nhiều bộ phận nhỏ hơn với kích thước 10-6
÷10-4cm , phương mạng giữa chúng lệch nhau một góc rất nhỏ khoảng vài
phút đến 10, được gọi là siêu hạt hay block. Như vậy mạng tinh thể giữa
các block cũng bị xô lệch nhưng với mức độ thấp hơn so với biên giới hạt.
Mặt ngoài của tinh thể:
Mặt ngoài của tinh thể có trạng thái sắp xếp nguyên tử khác với
những vùng phía trong. Trên bề mặt mỗi nguyên tử chỉ được liên kết với
một số nguyên tử nằm ở phía trong số sắp xếp bé hơn trị số quy định và do
đó lực liên kết không cân bằng. Đó là nguyên nhân làm cho các nguyên tử
ở mặt ngoài sắp xếp không có trật tự, tạo nên sai lệch mặt. 19
Do mạng tinh thể bị xô lệch nên mặt ngoài có năng lượng tự do cao
hơn. Phần năng lượng tự do được tăng thêm trên một đơn vị diện tích bề
mặt gọi là năng lượng bề mặt hoặc sức căng bề mặt.
Hình 2.19. Mô hình sắp xếp nguyên tử của mặt ngoài tinh thể. Vết nứt gãy:
Xuất hiện khi có những liên kết bị đứt gãy trong quá trình hình
thành những mặt mới. Xuất hiện khi có sự trầy xước do phân tử bụi. Sai
hỏng thường xuất hiện trên bề mặt vật rắn hơn bên trong khối. Sai hỏng
này giúp xác định được chất rắn sẽ bị đứt gãy như thế nào và ở vị trí nào.
Hình 2.20. Hình ảnh vết nứt d. Sai lệch khối
Sai lệch khối trong mạng tinh thể của vật liệu là các dạng sai lệch
có kích thước lớn theo cả ba chiều đo.
Trong các sai lệch khối chúng ta có thể chia làm hai loại cơ bản
như sau, theo ảnh hưởng của chúng đến tính chất của vật liệu:
- Loại xuất hiện ngẫu nhiên trong quá trình sản xuất vật liệu (luyện,
đúc kim loại, hợp kim ...).
- Loại xuất hiện do sự cố ý của người sản xuất, thực chất đó là sự
tiết pha thứ hai do phân hủy dung dịch rắn quá bão hòa.
Đặc trưng về hình thái của lệch và tác dụng của lệch:
Mật độ lệch (kí hiệu là ρ) là tổng chiều dài trục lệch trong một đơn
vị thể tích của tinh thể, có thứ nguyên là cm/cm3. Mật độ lệch phụ thuộc
rất mạnh vào độ “sạch“ và trạng thái gia công. 20