










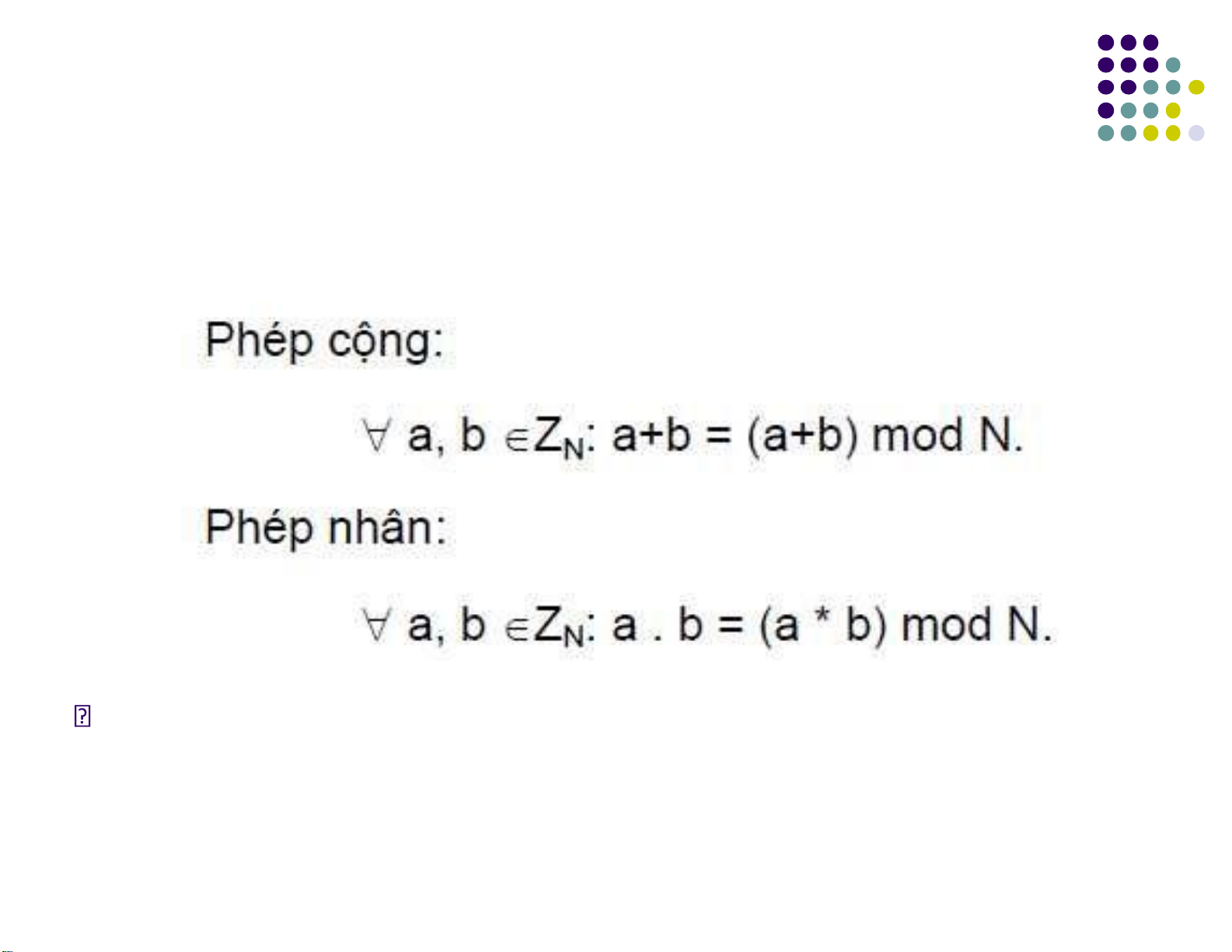































































Preview text:
lOMoARcPSD| 40651217 lOMoAR cPSD| 40651217 lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 1. Modulo số học
Hai số nguyên a và b ược gọi là ồng dư modulo n, tức
a ≡ b(mod n) nếu a – b = kn, hay: a = kn + b (k là một sô ́ nguyên, n > 1).
Nếu a>0, b>0, acho n.
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217
Cách gọi khác: b là thặng dư của a theo modulo n,
hoặc a là ồng dư của b theo modulo n lOMoARcPSD| 40651217 1. Modulo số học Ví dụ 1:
4 ≡ 1 (mod 3), vì: 4 – 1 = 1.3, hay 4 = 1.3 + 1 Ví dụ 2: 5 ≡ 2 (mod 3) 5 ≡ 0 (mod 5) 38 ≡ 14 (mod 2)
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 1. Modulo số học Ví dụ 3: 2 ≡ -3 (mod 5) -3 ≡ 7 (mod 5) -3 ≡ -8 (mod 5)
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 1. Modulo số học Câu hỏi 1: 28 ≡ ? (mod 3) 28 ≡ ? (mod 35) 28 ≡ -1 (mod ?) Câu hỏi 2:
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 28 ≡ 17 (mod 11) ? 1. Modulo số học Quan hệ
ồng dư là quan hệ tương ương:
Tính phản xạ: a ≡ a (mod n)
Tính ối xứng: a ≡ b (mod n) b ≡ a (mod n) a, b
Tính bắc cầu: nếu a ≡ b (mod n) và b ≡ c (mod n) thì a ≡ c (mod n)
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 1. Modulo số học
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 1. Modulo số học Các phép tính Modulo n
(a + b) mod n = ((a mod n) + (b mod n)) mod n
(a - b) mod n = ((a mod n) - (b mod n)) mod n
(a × b) mod n = ((a mod n) × (b mod n)) mod n
(a × (b + c)) mod n = (((a × b) mod n) + ((a × c) mod n)) mod n
Các phép tính trong các hệ mã mật hầu hết ều thực
hiện ối với một modulo N nào ó.
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 2. Vành ZN
Tập các sô ́ nguyên ZN = {0, 1, …, N-1} tron g ó N
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 2. Vành ZN
là một số tự nhiên dương với hai phép toán cộng (+) và
nhân (.) ược ịnh nghĩa như sau:
Hầu hết các tính toán trong các hệ mã mật ều ược thực
hiện trên một vành ZN nào ó. lOMoARcPSD| 40651217 2. Vành ZN Trên vành ZN
số 0 là phần tử trung hòa vì
số 1 ược gọi là phần tử ơn vị vì Ví dụ N=9
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217 2. Vành ZN Câu hỏi: cho N=6 Z6 = ? 3 + 4 = 7 ? (mod 6) 4 5 = 20 ? (mod 6) 2 + 3 = ? 2 3 = ? lOMoARcPSD| 40651217
3. Phần tử nghịch ảo trên vành Z N
Khái niệm về số nghịch ảo của một số trên một vành số nguyên ZN:
Gỉa sử a ZN và tồn tại b ZN sao cho: a.b = (a b) mod N = 1
Khi ó, b ược gọi là phần tử nghịch ảo của a trên ZN , ký hiệu: a-1 = b. lOMoARcPSD| 40651217
3. Phần tử nghịch ảo trên vành
Hầu hết các tính toán trong các hệ mã mật ều ược thực
hiện trên một vành ZN nào ó. Z N
Tìm phần tử nghịch ảo của một số a ZN cho trước tìm 2 số b và k sao cho: a.b = k.N + 1, với b, k ZN hay: a-1 b (mod N). lOMoARcPSD| 40651217
3. Phần tử nghịch ảo trên vành Ví dụ: 30-1 64 (mod 101)
Câu hỏi: Tìm phần tử nghịch ảo trên Z9 của a) a = 4 b) a = 6 Z N
Định lý về sự tồn tại của phần tử nghịch ảo: lOMoARcPSD| 40651217
3. Phần tử nghịch ảo trên vành
Nếu ước số chung lớn nhất (GCD-Greatest Common Divisor) GCD(a, N) = 1,
Thì tồn tại duy nhất 1 số
là phần tử nghịch ảo của a, nghĩa là thỏa mãn lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
mã dịch vòng (shift cipher) Shift Cipher:
Một trong những phương pháp lâu ời nhất ược sử dụng ể mã hóa.
Thông iệp ược mã hóa bằng cách dịch chuyển xoay
vòng từng ký tự i k vị trí trong bảng chữ cái
Trường hợp với k=3 gọi là phương pháp mã hóa Caesar. Phương pháp ơn giản, lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
Thao tác xử lý mã hóa và giải mã ược thực hiện nhanh chóng
Không gian khóa K = {0, 1, 2, …, n-1} = Zn
Dễ bị phá vỡ bằng cách thử mọi khả năng khóa k lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
mã dịch vòng ( shift cipher) Ví dụ:
Mã hóa một thông iệp ược biểu diễn bằng các chữ cái từ
A ến Z (26 chữ cái), ta sử dụng Z26.
Thông iệp ược mã hóa sẽ không an toàn và có thể dễ dàng
bị giải mã bằng cách thử lần lượt 26 giá trị khóa k. lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
Tính trung bình, thông iệp ã ược mã hóa có thể bị giải mã
sau khoảng 26/2 = 13 lần thử khóa lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ Ta có sơ ồ mã như sau: lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
Giả sử P = C = K = Z26 với 0 k 25
Mã hóa: ek(x) = (x + k) mod 26
Giải mã: dk(x) = (y – k) mod 26 (x,y Z26)
mã dịch vòng ( shift cipher)
Ví dụ: Cho bản rõ (K=17)
X = x1; x2; : : : ; x6 = A T T A C K .
X = x1; x2; : : : ; x6 = 0; 19; 19; 0; 2; 10. lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ Mã hóa
y1 = (x1 + k) mod 26 = (0 + 17) mod 26 = 17 = R. y2 = y3 = (19 + 17) mod 26 = 10 = K. y4 = 17 = R.
y5 = (2 + 17) mod 26 = 19 = T. y6 = (10 + 17) mod 26 = 1 = B. Bản mã: R K K R T B lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
mã dịch vòng ( shift cipher) Giải mã
Y = y1; y2; : : : ; y6 = R K K R T B . Y = y1; y2; : : : ; y6 =
17; 10; 10; 17; 19; 1 x1 = (y1 - k) mod 26 = (17 - 17) mod 26 = 0 = A.
x2 = x3 = (10 - 17) mod 26 = 19 = T. x4 =
0 = A. x5 = (19 - 17) mod 26 = 2 = C. x6 = (1 - 17) mod 26 = 10 = K. lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ Bản rõ: ATTACK
mã dịch vòng ( shift cipher)
Bài tập 1: Cho bản rõ (thông iệp) sau X = A N TOAN VA BAO MAT THONG TIN.
Hãy mã hóa và giải mã nó bằng hệ mã dịch vòng, với khóa K = 6
Bài tập 2: Cho bản mã sau lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ
X = G T Z U G T B G H G U S G Z Z N U T M Z O T Hãy giải
mã nó bằng hệ mã dịch vòng, với khóa K là (3 số cuối Mã số sv) mod 15.
mã dịch vòng ( shift cipher)
Bài tập 3: Cho bản rõ (thông iệp) sau X = 63CNTT1.
Hãy mã hóa và giải mã nó bằng hệ mã dịch vòng, với khóa
K = 15, sử dụng vành Z36 dưới ây: lOMoARcPSD| 40651217
4. Các hệ mật mã cổ iển – Hệ 0 1 2 3 4 5 6 7 8 9 26 27 28 29 30 31 32 33 34 35 lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher) Substitution Cipher:
Phương pháp mã hóa nổi tiếng
Được sử dụng phổ biến hàng trăm năm nay
Ý tưởng: thay mỗi ký tự trong P bằng một ký tự khác.
Quy tắc thay thế chính là khóa, trong ó mỗi khóa là một
hoán vị của bảng chữ cái. Mã hóa thông iệp hoán vị
các phần tử trong bảng chữ cái (tổng quát hơn là hoán vị
các phần tử trong tập nguồn P) lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher)
1. Thay thế ơn (A simple substitution cipher):
là hệ mã trong ó một ký tự của bản rõ ược thay bằng môt ̣
ký tự tương ứng trong bản mã.
Một ánh xạ 1-1 từ bản rõ tới bản mã ược sử dụng ể mã hoá toàn bộ thông iệp. lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher)
2. Thay thế ồng âm (A homophonic substitution cipher):
một ký tự của bản rõ có thể ược ánh xạ tới một trong số
một và i ký tự của bản mã
Sơ ồ ánh xạ 1-n (one-to-many): ví dụ, “A” có thể tương ứng
với 5, 13, 25, hoăc̣ 56, “B” có thể tương ứng với 7, 19, 31, hoăc ̣ 42, v.v. lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher)
3. Thay thế a mẫu tự (A polyalphbetic substitution cipher):
ược tạo nên từ nhiều thuật toán mã hoá thay thế ơn. Ánh xạ 1-1.
Ví dụ, có thể có năm thuật toán mã hoá ơn khác nhau ược sử
dụng; ăc ̣ biêṭ thuật toán mã hoá ơn ược sử dụng thay ổi theo
vị trí của mỗi ký tự trong bản rõ. lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher) 4.
Thay thế a sơ ồ (A polygram substitution cipher):
các khối ký tự ược mã hoá theo nhóm.
là thuật toán tổng quát nhất, cho phép thay thế các nhóm
ký tự của văn bản gốc.
Ví dụ, “ABA” có thể tương ứng với “RTQ”, “ABB” có thể
tương ứng với “SLL”, v.v. lOMoARcPSD| 40651217 5.
Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher) Tổng quát: Cho P = C = Zn
K là tập hợp tất cả các hoán vị của n phần tử 0, 1, …, n- 1. mỗi khóa
là một hoán vị của n phần tử 0, 1, …, n-1. lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher) Ưu iểm:
Đơn giản, thao tác mã hóa và giải mã ược thực hiện nhanh chóng
Không gian khóa K gồm n! phần tử
Khắc phục hạn chế của phương pháp Shift Cipher: việc tấn
công bằng cách vét cạn các giá trị khóa k K là không khả thi Thật sự an toàn??? lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher) AO VCO JO IBU RIBU
AO VCO JO IBU RITấn công BU dựa trên tần số xuất hiện
?A H?A ?A ?NG tron??của ký tự g ngôn NG ngữ lOMoARcPSD| 40651217 MA HOA VA UNG DUNG
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher)
L FDPH L VDZ L FRQTXHUHG L FDPH
L VDZ L FRQTXHUHG i ?a?e i ?a? i
?????e?e? i came i saw i conquered lOMoARcPSD| 40651217
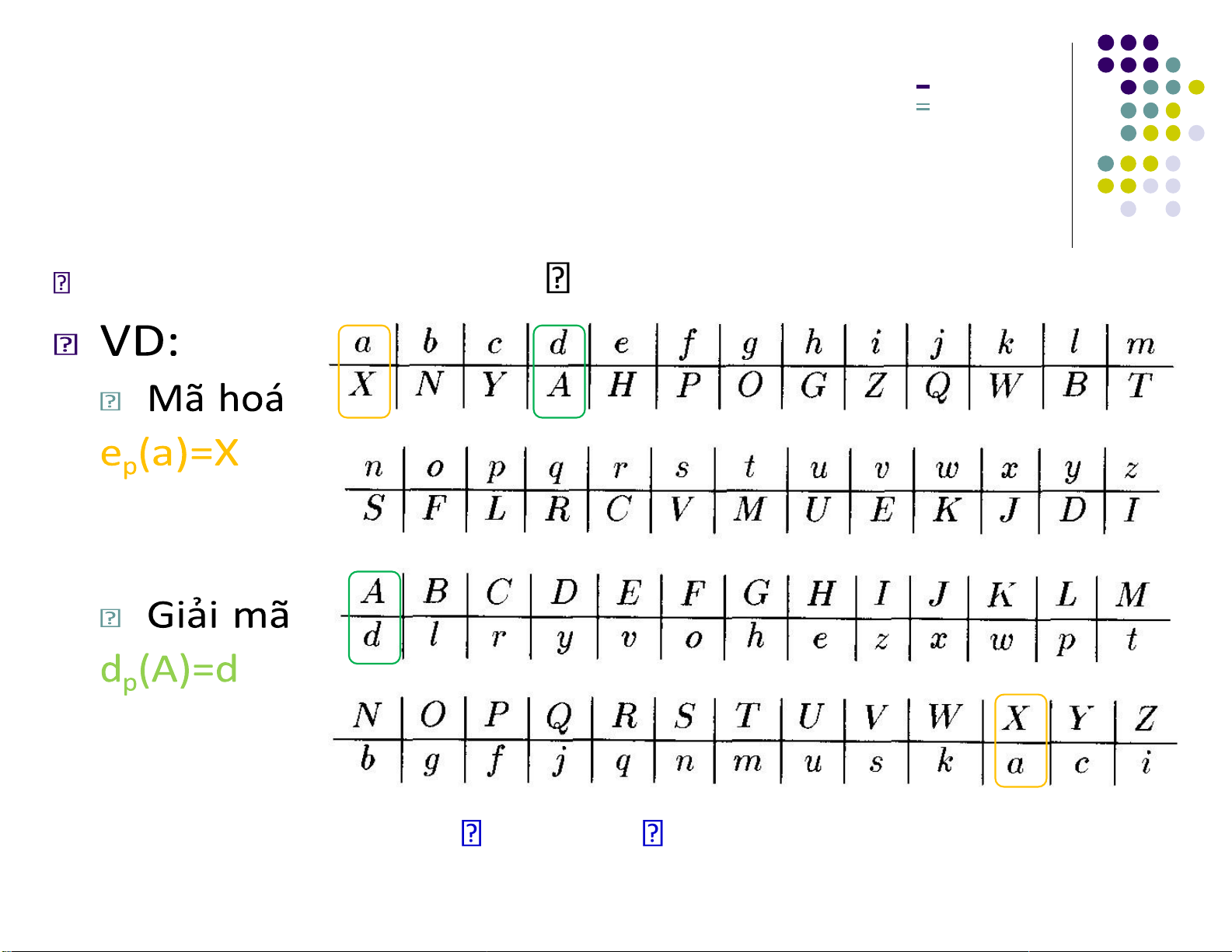
5. Các hệ mật mã cổ iển- Hệ mã hóa thay thế(Substitution Cipher)
Chọn một hoán vị p: Z26 Z26 làm khoá.
“happy” “GXLLD” “happy” lOMoARcPSD| 40651217
Độ an toàn của mã thay thế
Một khoá là một hoán vị của 26 chữ cái.
Có 26! (≈ 4.1026) hoán vị (khoá) Phá mã:
Không thể duyệt từng khoá một. Cách khác? lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa
thay thế(Substitution Cipher)
Phân tích tần số (tần suất):
Tính tần suất các ký tự hoặc nhóm ký tự trong bản mã so
sánh với tần suất thực tế trong các văn bản thường.
Ký tự: E > T > A > O >… > X > Q > Z
Nhóm 2 ký tự (digraph): TH > HE > IN > ER > RE
> ON > AN > EN > …
Nhóm 3 ký tự (Trigraph): THE > AND > TIO > ATI > FOR > THA > TER > RES >… lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa
thay thế(Substitution Cipher) ồ tần suất các ký tự (trong tiếng Anh) lOMoARcPSD| 40651217
5. Các hệ mật mã cổ iển- Hệ mã hóa
thay thế(Substitution Cipher)
Trong phân tích mật mã, phép phân tích tần suất là phương pháp thường dùng
ể phân tích mật mã cổ iển, bằng cách tính tần suất các ký tự hoặc nhóm ký tự
trong bản mã và so sánh với tần suất thực tế trong các văn bản thường.
Nguyên lý của phân tích tần suất dựa trên một thực tế là trong mỗi ngôn ngữ,
mỗi ký tự trong bảng chữ cái có một tần suất xuất hiện nhất ịnh. Tần suất này
càng rõ ràng khi văn bản phân tích càng dài. Ví dụ trong tiếng Anh, E, T, A và
O là những chữ cái xuất hiện nhiều nhất, trong khi Z, Q và X lại rất hiếm hoi.
Tương tự, ta có TH, ER, ON, và AN là các nhóm ký tự phổ thông nhất, còn SS,
EE, TT, và FF là các bộ ôi ký tự lặp xuất hiện nhiều nhất[1]. "ETAOIN SHRDLU"
là 12 ký tự có tần suất cao nhất trong một văn bản tiếng Anh thông thường.
Trong một số bản mã, khi một vài ặc trưng ngôn ngữ ược tìm thấy, rất có thể
nó có thể bị phá vỡ bằng tấn công chỉ từ bản mã. lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã Affine lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã Affine lOMoARcPSD| 40651217 VD và bài tập a = 7, b = 13: y = (7x + 13) (mod 26). Mã hóa: BAOMATTHONGTIN ? lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã Affine Vấn
ề: giải mã chính xác thông tin ??? • ek phải là song ánh
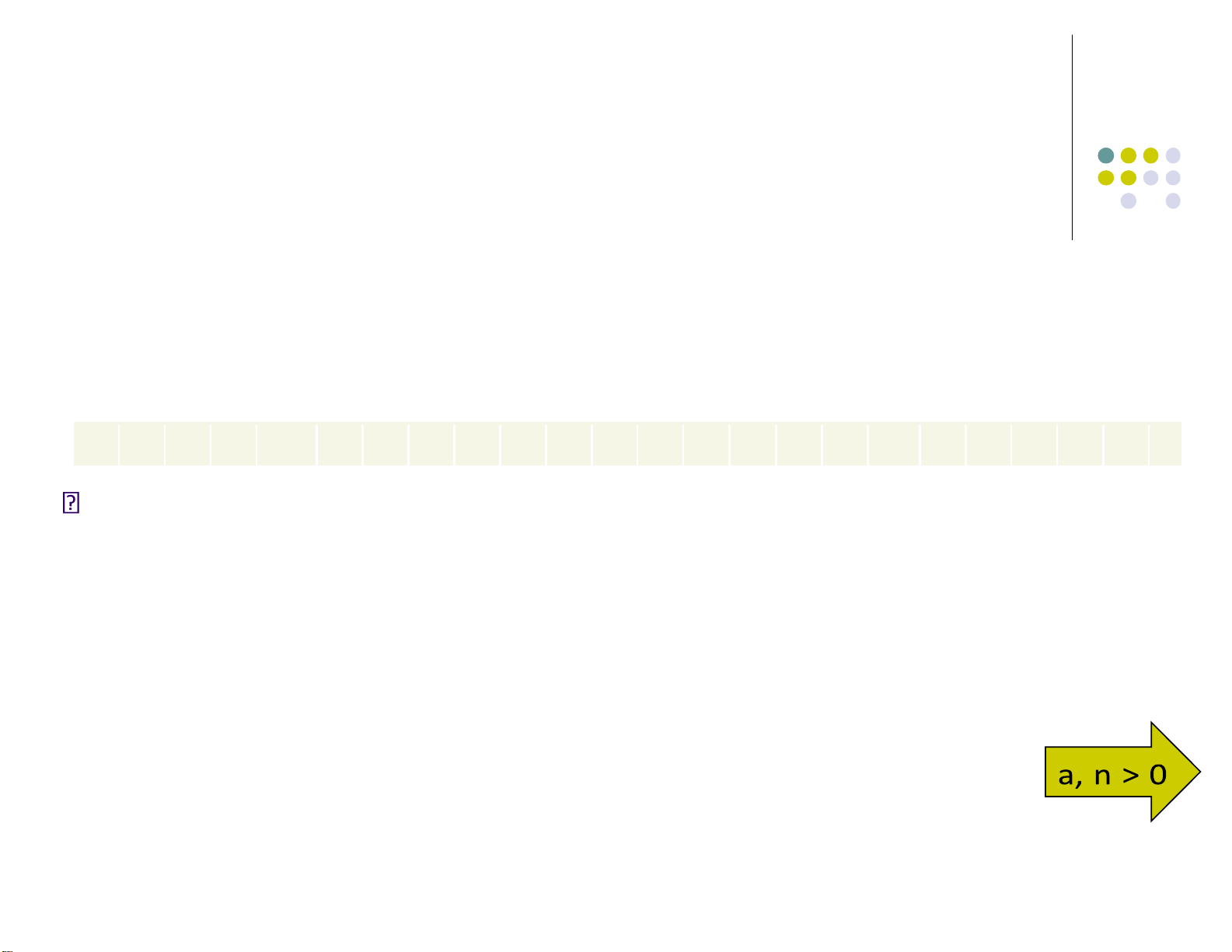
• a và n nguyên tố cùng nhau: GCD(a, n)=1
6. Các hệ mật mã cổ iển - Hệ mã Affine
Ví dụ: Giả sử P = C = Z26. Thuật toán: lOMoARcPSD| 40651217 mã hóa: khóa: giải mã:
. iều kiện: a và 26 nguyên tố cùng nhau: GCD(a, n)=1 lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã Affine Ví dụ Khóa
• Plain(a): abcdefghijklmnopqrstuvwxyz • Cipher(b): DKVQFIBJWPESCXHTMYAUOLRGZN Mã hóa: lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã
• Plaintext: ifwewishtoreplaceletters • Ciphertext: WIRFRWAJUHYFTSDVFSFUUFYA Affine
Nhận xét: ek(x) = (ax + b) mod 26, trong ó a, b Z26.
Trường hợp a = 1: mã dịch vòng (shift cipher). lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã
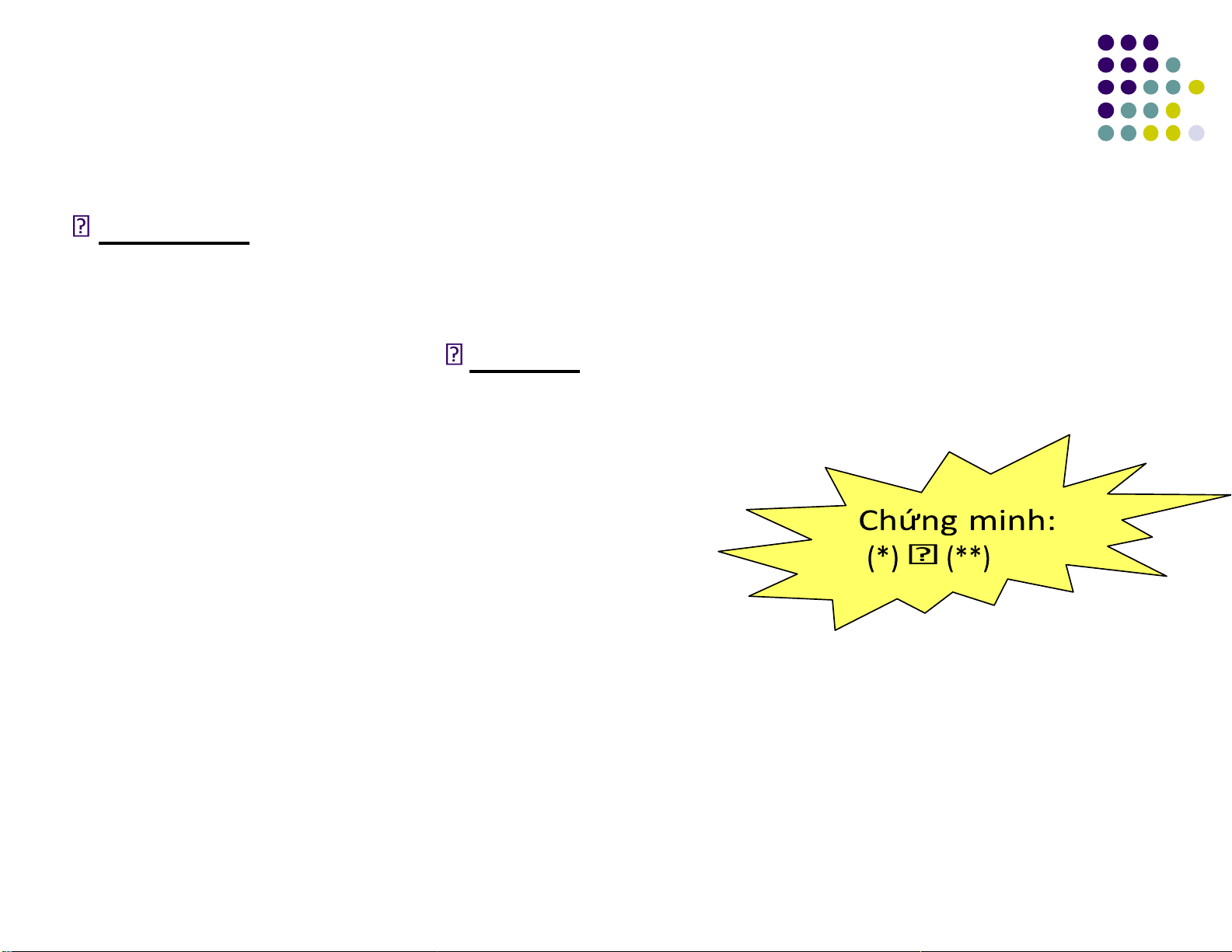
Giải mã: Tìm x? y = (ax + b) (mod
26) (*) ax = (y – b) (mod 26) x = a-1(y
– b) (mod 26). (**) Vấn ề: Tính a-1.
Để có a-1, cần GCD (a, 26)=1.
Tính a-1: Thuật toán Euclide mở rộng. lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã Affine Chứng minh: y = (ax + b) mod 26
y = (ax mod 26 + b mod 26) mod 26
y mod 26 = ax mod 26 + b mod 26
ax mod 26 = y mod 26 – b mod 26 lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã
ax = (y mod 26 – b mod 26) mod 26 ax = (y-b) mod 26 x = a-1 ((y-b) mod 26) lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã lOMoARcPSD| 40651217
6. Các hệ mật mã cổ iển - Hệ mã
(n) khả năng chọn giá trị a n
(n) khả năng chọn lựa khóa k = (a, b) lOMoARcPSD| 40651217
7. Thuật toán Euclide mở rộng Giải pt nx + ay = 1.
• Nếu d = UCLN(n, a) thì tồn tại các số nguyên x, y sao cho nx + ay = d • Đặt r0 = n, r1 = a.
• Chia r0 cho r1 ược số dư r2 và thương số nguyên q1.
• Nếu r2 = 0 thì dừng, nếu r2 khác 0 thì tiếp tục chia r1 cho r2 ược số dư r3, …
• Vì dãy ri là giảm thực sự nên sau hữu hạn bước thì ta ược
số dư r(m+2) = 0., trong ó số dư cuối cùng khác 0 là r(m+1) = d. lOMoARcPSD| 40651217
7. Thuật toán Euclide mở rộng
• Tìm x, y theo công thức truy hồi:
n.xi + a.yi = ri với i = 0,1,… • Như vậy từ ri = q(i+1) .r(i+1) + r(i+2)
suy ra công thức mà có thể chọn: x(i+2) = xi –
q(i+1).x(i+1) (1) y(i+2) = yi – q(i+1).y(i+1) (2) lOMoARcPSD| 40651217 lOMoARcPSD| 40651217
7. Thuật toán Euclide mở rộng Xây dựng dãy số: Nhận xét: lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 lOMoARcPSD| 40651217
Ví dụ: Tìm số nghịch ảo (nếu có) của 30 (a) theo modulo 101 (n) Bước i n a r q y0 y1 y 0 101 30 11 3 0 1 -3 1 30 11 8 2 1 -3 7 2 11 8 3 1 -3 7 -10 3 8 3 2 2 7 -10 27 4 3 2 1 1 -10 27 -37 5 2 1 0 . . . .
-37 mod 101 = 64 hay 30-1 = 64 (mod 101). lOMoARcPSD| 40651217 Bài tập 1.
Tìm số nghịch ảo (nếu có) của 26 (a) theo modulo 101 (n) 2.
Viết chương trình mã hóa ANBMTT với K = (a, b) = (7,3) trên Z26 3.
Viết chương trình giải mã chuỗi AXG với K = (a, b) = (7,3) trên Z26 lOMoARcPSD| 40651217 Bài tập 4. Cho chuỗi mã trong Z26: J T N Z Q
A H Q Y L S L U D X P U D S T N Z D J
Giải mã chuỗi trên, biết:
A = 17597, B = 1229; y = Ax +B lOMoARcPSD| 40651217
Giải thuật function ModuloInverse(a , n); (a, n>0): begin y0:= 1; y1:= 0; while n ≠ 0 do begin q:= a div n; y:= y0 - q * y1; y0:= y1; y1:= y; r:= a mod n; a:= n; n:= r; end; Result:= y0; end; lOMoARcPSD| 40651217
Gợi ý: Tìm số nghịch modulo ảo của 17597 (a) theo 26 (n) Bước i n a r q y0 y1 y 0 26 17597 21 676 1 0 1 1 21 26 5 1 0 1 -1 2 5 21 1 4 1 -1 5 3 1 5 0 5 -1 5 -26 4 0 1 . . 5 -26 . 17597-1 = 5 (mod 26).
=> Giải mã: x = (A-1(y-B)) mod 26 lOMoARcPSD| 40651217 Bài tập 6.
Mã hóa chuỗi HAPPYNEWYEAR với K = (a, b) trên Z26 (a
là phần dư khi chia 2 số cuối mã số sinh viên của 1
người trong nhóm (≤2) cho 26, b = (a + 2) mod 26)
Ghi chuỗi ã mã hóa ra 1 tờ giấy và bổ sung thêm vào cuối
chuỗi này chuỗi mã hóa của 1 từ tùy ý nào ó, kèm khóa
K và họ tên, mã số sinh viên của nhóm mình. 7.
Giải mã chuỗi mã của nhóm khác cùng bàn ở trên (nếu
số nhóm là lẻ, thì nhóm dư lại kết hợp cùng nhóm ở bàn dưới). lOMoARcPSD| 40651217 8. Phương pháp Vigenere
Trong phương pháp mã hóa bằng thay thế: với một khóa k
ược chọn, mỗi phần tử x P ược ánh xạ vào duy nhất một phần tử y C.
Phương pháp Vigenere sử dụng khóa có ộ dài m.
Được ặt tên theo nhà khoa học Blaise de Vigenere (thế kỷ 16)
Có thể xem phương pháp mã hóa Vigenere bao gồm m phép
mã hóa bằng dịch chuyển ược áp dụng
luân phiên nhau theo chu kỳ
Không gian khóa K của phương pháp Vigenere có số phần tử là nm
Ví dụ: n=26, m=5 thì không gian khóa ~1.1 x 107 lOMoARcPSD| 40651217 . Phương pháp Vigenere lOMoARcPSD| 40651217 8
Chọn số nguyên dương m. Định nghĩa P = C = K = (Zn)m lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 Bài tập Cho chuỗi mã trong Z26:
9 8 22 10 15 15 13 9 14 25 15 12 21
Giải mã chuỗi trên, biết m = 5, keyword là LUCKY Bổ
sung thêm vào cuối chuỗi mã trên 5 cặp số là các cặp số lOMoARcPSD| 40651217
trong mã sinh viên mod 26, giải mã nó với keyword LUCKY.
(Ví dụ: 2154027079 => 21 2 2 18 1) Đáp án: Y O U A R E T H E B E S T lOMoARcPSD| 40651217 Bài tập 1.
Mã hóa họ và tên ầy ủ của bạn trong Z26 với keyword do bạn chọn. 2.
Ghi chuỗi mã hóa ra 1 tờ giấy trắng, kèm theo keyword
và mã số sinh viên của bạn (trong ngoặc) 3.
Sinh viên mỗi dãy giải mã chuỗi mã hóa của sinh viên
ở dãy bên cạnh (vị trí ngồi ối xứng qua ường phân
cách). Nộp lại kết quả quá trình giải mã.
9. Phương pháp mã hóa Hill Mật mã Hill (1929) lOMoARcPSD| 40651217
Tác giả: Lester S. Hill (1891–1961) Ý tưởng chính:
Sử dụng m tổ hợp tuyến tính của m ký tự trong
plaintext ể tạo ra m ký tự trong ciphertext Ví dụ:
9. Phương pháp mã hóa Hill
Chọn số nguyên dương m. Định nghĩa P = C = (Zn)m
là tập hợp các ma trận khả nghịch.
Lưu ý: mọi phép toán số học dưới ây ều ược thực hiện trên Zn lOMoARcPSD| 40651217 lOMoARcPSD| 40651217
9. Phương pháp mã hóa Hill
Ví dụ: cho hệ mã Hill có M = 2 (khóa là các ma trận vuông
cấp 2) và bảng chữ cái là bảng chữ cái tiếng Anh (N = 26). Cho khóa:
Hãy mã hóa xâu P = “HELP” và giải mã ngược lại bản mã thu ược.
9. Phương pháp mã hóa Hill Mã hóa: lOMoARcPSD| 40651217
Chia xâu bản rõ thành 2 vecto 2 chiều “H E” (7, 4) và “L P” (11, 15).
Tiến hành mã hóa lần lượt: Với P1 = (7, 4) ta có:
C1 = P1*K = (7, 4) = (3, 15) = (D, P) Với P2 = (11, 15) ta có: C2 = P2*K = (11, 15) = (11, 4) = (L, E) Vậy bản mã thu ược là C = “DPLE” lOMoARcPSD| 40651217 Giải mã:
9Tính khóa giải mã: . Phương pháp mã hóa
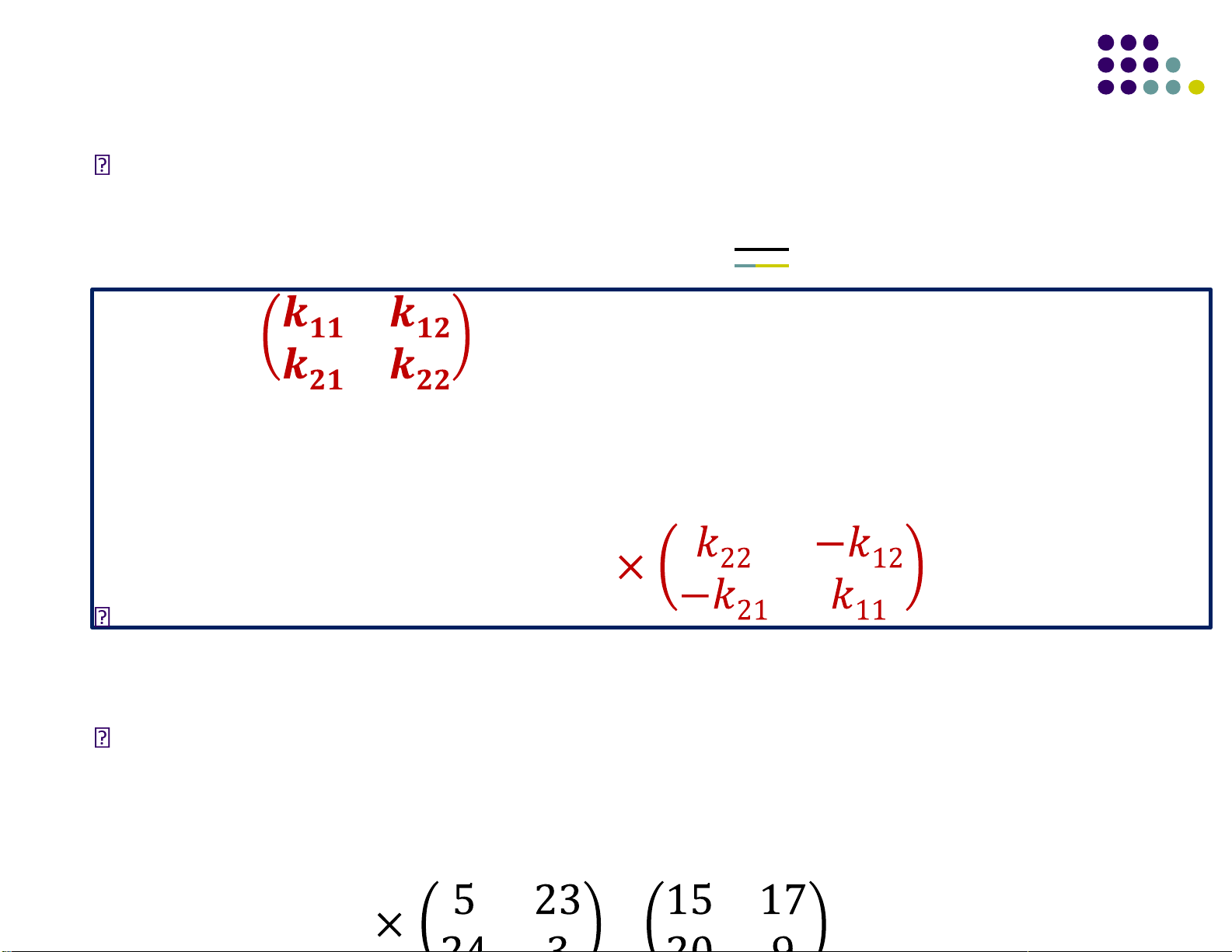
Hillma trận nghịch ảo của ma trận khóa trên Z26
Với K = và det(K) = (k11*k22-k21*k12) mod N là một phần tử có
phần tử nghịch ảo det(K)-1 trên ZN thì khóa giải mã sẽ là K-1 = det(K)-1
Áp dụng vào trường hợp trên, ta có det(K) = (15-6) mod 26 = 9.
GCD(9, 26) = 1 nên áp dụng thuật toán Euclid mở rộng tìm ược det(K)-1 = 3. lOMoARcPSD| 40651217 Vậy K-1 = 3 =
9. Phương pháp mã hóa Hill Giải mã: C = “D P” = (3, 15) P = C*K-1 = (3, 15) = (3, 15) = “H E”.
Tương tự, kết quả giải mã xâu C = “L E” là bản rõ P = “L P”.
Lưu ý: trong ví dụ trên sử dụng khóa K có kích thước nhỏ nên
không khó ể tìm ược khóa giải mã. Trong trường hợp tổng
quát, iều này là không dễ dàng.
Downloaded by Phuong Le (lephuong0301@gmail.com) lOMoARcPSD| 40651217
9. Phương pháp mã hóa Hill
Bài tập: cho hệ mã Hill có M = 2 (khóa là các ma trận vuông
cấp 2) và bảng chữ cái là bảng chữ cái tiếng Anh (N = 26). Cho khóa:
Gỉa sử Mã số SV là ABCDEFGHIJ
Hãy mã hóa xâu P = “GODNESS” và giải mã ngược lại bản mã thu ược với
a11 = IJ mod 26, a12 = GH mod 26, a21 = EF mod 26, a22 = CD mod 26




