


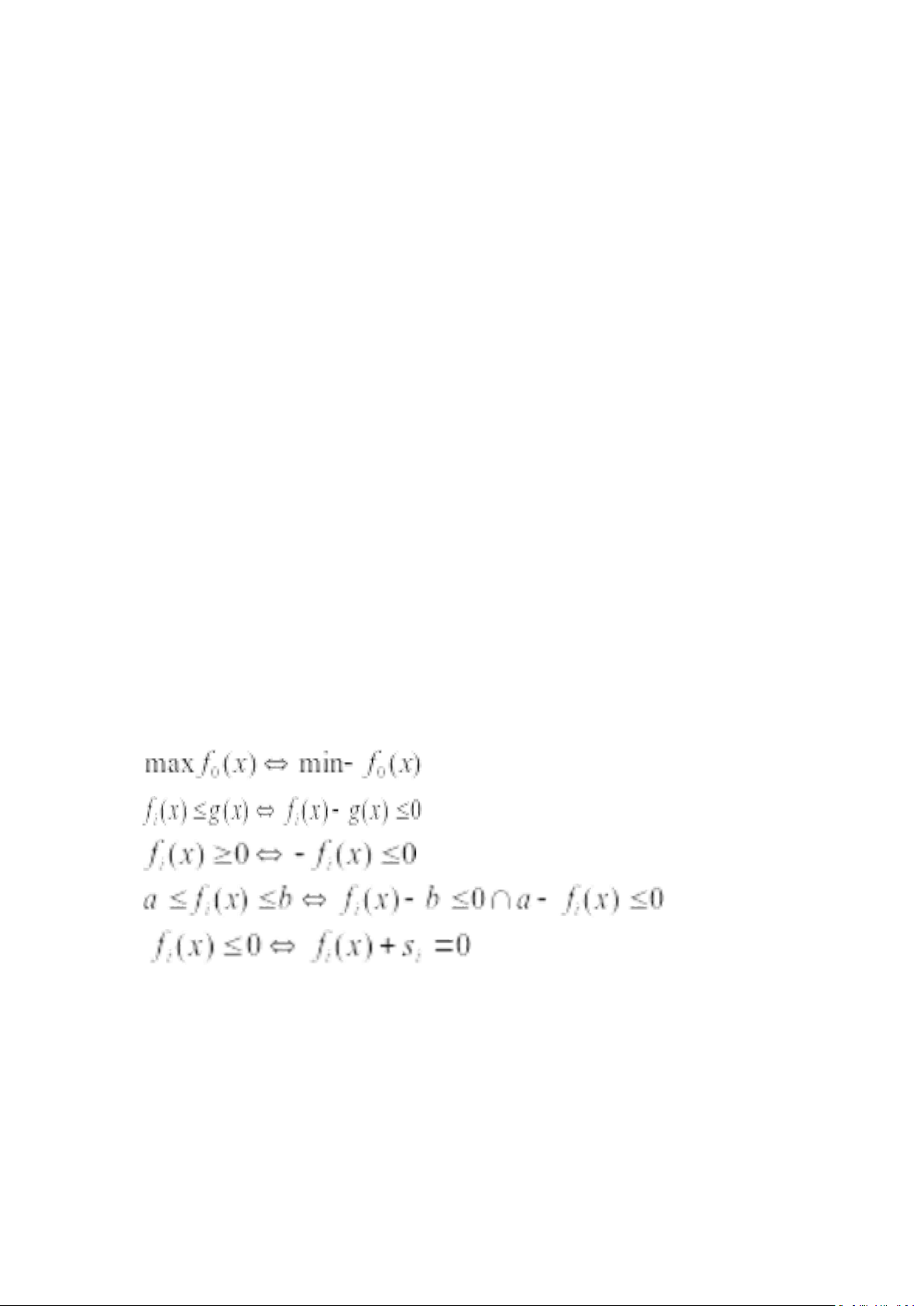


Preview text:
CHƯƠNG 2: LINEAR PROGRAMMING
1. Khái niệm về quy hoạch tuyến tính (Linear programming)
1.1 Quy hoạch tuyến tính là gì ?
- Quy hoạch tuyến tính (Linear programming) là một trong những dạng bài
toán tối ưu cơ bản nhất, sử dụng thuật toán nhằm tim ra một kế hoạch hay
phương án tốt nhất từ vô số những lựa chọn khác nhau. Hiểu một cách đơn
giản hơn, quy hoạch tuyến tính chính là chọn ra phương án tối ưu dựa trên
những ràng buộc, hạn chế, điều kiện đặt ra.
- Dạng bài toán này yêu cầu chúng ta phải tối ưu hóa một hàm mục tiêu
tuyến tính và phải thỏa mãn một số ràng buộc tuyến tính.
1.2 Các thành phần của quy hoạch tuyến tính
- Mô hình Quy hoạch tuyến tính được chia làm 2 phần là hàm mục tiêu và các điều kiện.
- Trong đó: hàm mục tiêu thể hiện chính xác và cụ thể mục tiêu phải đạt
được. Các điều kiện là hạn chế mà nguồn lực phải tuân theo.
- Trong quy hoạch tuyến tính, hai khái niệm này luôn song hành cùng nhau,
ràng buộc với nhau và không tách rời nhau. Nếu thiếu đi một trong hai yếu
tố thì không phải quy hoạch tuyến tính. 1.3 Đặc điểm
Phân tích đặc điểm
*Hàm mục tiêu tuyến tính
Mục tiêu của LP là tối ưu hóa hoặc tối thiếu hóa một hàm tuyến tính. Điều
này có thể là lợi nhuận tối đa, chi phí tối thiểu hoặc một mục tiêu khác dựa
trên các biến quyết định *Biến quyết định
Đây là các yếu tố mà chúng ta muốn tối ưu hóa hoặc điều chỉnh. Chúng
thường được biểu diễn bằng các ký hiệu và thuồng là các biến liên tục.
*Ràng buộc tuyến tính
LP đi kèm với một tập hợp các ràng buộc tuyến, những điều kiện mà các
biến phải tuân theo. Các ràng buộc này thường được biểu diễn bằng các
phương trình hoặc bất phương trình tuyến tính. Khả năng tim giải pháp
LP có khả năng tim ra giải pháp tối ưu toàn cục(nếu tồn tại) cho bài toán.
Nếu có lời giải, LP có thể xác định xem đâu là giá trị tối ưu cho hàm mục tiêu.
*Phương pháp giải quyết
Có nhiều phương pháp để giải quyết mô hình LP, phổ biến nhất là Simplex
Method. Các phương pháp khác bao gồm Interior Point Method, Branch
and Bound, và các thuật toán tối ưu hóa khác. *Áp dụng rộng rãi
LP được áp dụng rộng rãi trong nhiều lĩnh vực từ kinh doanh, quản lý, tài
chính đến công nghiệp, logistics,vận tải và nhiều lĩnh vực khác.
Giới hạn về dạng tuyến tính
LP chỉ có thể giải quyết các bài toán mà hàm mục tiêu và ràng buộc có dạng tuyến tính. Ưu điểm ✓ Tính toán hiệu quả
✓ LP có thể được giải quyết bằng nhiều phương pháp hiệu quả, bao gồm
Simplex Method và các thuật toán nâng cao khác. Điều này giúp tim ra
lời giải tối ưu trong thời gian tương đối ngắn. ✓ Áp dụng rộng rãi
✓ LP được sử dụng rộng rãi trong lĩnh vực như quản lý tài nguyên, sản
xuất, vận chuyển, kế hoạch, tài chính và nhiều lĩnh vực khác.
✓ Giải quyết được các vấn đề tối ưu hóa lớn
✓ LP có khả năng giải các bài toán lớn với hàng trăm, thậm chí hàng hàng
nghìn biến và ràng buộc.
✓ Hiệu quả trong việc tim giải pháp tối ưu
✓ Đối với bài toán tuyến tính, LP đảm bảo tim được giải pháp tối ưu hóa
toàn cục(nếu tồn tại), không chỉ pháp cục bộ. Nhược điểm
✓ Giới hạn về dạng tuyến tính
✓ LP chỉ áp dụng cho các bài toán có thể biểu diễn tuyến tính. Các bài toán
phi tuyến tính sẽ không thể giải quyết trực tiếp bằng LP.
✓ Khả năng thất bại khi không có giải quyết tuyệt đối
✓ Nếu không tồn tại giải pháp tối ưu(ví dụ: do ràng buộc không thể đạt
được), LP có thể không cung cấp thông tin hữu ích hoặc chỉ ra rằng vấn đề không có giải pháp.
✓ Nhạy cảm với dữ liệu không chính xác
✓ Khi dữ liệu đầu vào không chính xác hoặc thay đổi, kết quả của LP có
thể bị ảnh hưởng mạnh mẽ.
✓ Khó khăn khi giải quyết các bài toàn lớn không còn tuyến tính rõ ràng
✓ Đôi khi, trong việc giải quyết các bài toán lớn với nhiều ràng buộc phức
tạp, việc mô hình hóa tuyến tính không còn phản ánh đầy đủ hiệu suất
của hệ thống thực tế.
Đánh giá hiệu suất
-Hiệu suất của mô hình LP vẫn còn phụ thuộc vào các công cụ và những
thuật toán được sử dụng.Những thuật toán hiện đại như Simplex, Interior
Point Method(IMP), hoặc các biến thể của chúng có thể cái thiện hiệu suất của mô hình LP
2. Ứng dụng quy hoạch tuyến tính vào các bài toán thực tế
● Bài toán ngân sách tối ưu
● Phân bổ nguồn vốn dựa trên danh mục đầu tư
● Giải bài toán chi phí thấp mà vẫn bảo đảm sản xuất tối ưu
● Lựa chọn hợp lý nhất cho sản xuất sản phẩm đầu ra
● Đưa ra kế hoạch sử dụng máy móc, lựa chọn kênh vận chuyển thấp nhất
● Đặt ra nhiều kế hoạch bay khác nhau trong các chuyến bay
● Lựa chọn vị trí đặt nhà xưởng phù hợp nhất
● Bài toán vận chuyển hàng hóa, tối ưu chi phí sản xuất, canh tác
3. Bài toán quy hoạch tuyến tính
*Dạng tiêu chuẩn của bài toán vận chuyển là bài toán qui hoạch tuyến
tính có dạng như sau:
x∗=arg minf 0(x )
f i( x) ≤0 ,i=1,2 , . . ,m
ℎ j( x)=0 , j=1,2 , . ., p
Phát biểu bằng lời: Tìm giá trị của biến x để tối thiểu hàm f 0(x) trong số các
giá trị của x thoả mãn các điều kiện ràng buộc. - Trong đó: Kí hiệu Giải thích x∈ Rn Biến tối ưu f 0( x) Hàm mục tiêu n
f i(x)≤0 , f i: R →R
Ràng buộc dạng bất đẳng thức n
ℎj(x)=0 ,ℎj : R → R
Ràng buộc dạng đẳng thức
Tập xác định ( tập hợp các điểm
thỏa hàm mục tiêu và các ràng buộc)
- Một điểm x∗ được gọi là một điểm optimal point (điểm tối ưu), hoặc là
nghiệm của bài toán nếu x∗ là và f 0¿)= p∗. Tập hợp tất cả các điểm tối
ưu được gọi là tập tối ưu
- Nếu tập tối ưu là một tập không rỗng, ta nói bài toán là solvable (giải
được). Ngược lại, nếu tập tối ưu là một tập rỗng, ta nói giá trị tối
ưu là không thể đạt được
Ví dụ: xét hàm mục tiêu f(x)=1/x với ràng buộc x>0. Giá trị tối ưu của bài
toán này là x∗= 0 nhưng tập tối ưu là một tập rỗng vì không có giá trị nào
của x để hàm mục tiêu đạt giá trị 0. Lúc này ta nói giá trị tối ưu là không đạt được. Một vài lưu ý
- Muốn giải bất kỳ bài toán quy hoạch tuyến tính nào bằng thuật toán đơn
hình, trước tiên phải đổi bài toán ra dạng chuẩn (standard form). Dạng
chuẩn của bài toán có những yêu cầu sau:
● Tất cả các biến phải không âm.
● Yêu cầu bài toán là tối thiểu hóa (minimization)
● Hệ số vế phải không âm.
● Tất cả các ràng buộc phải là đẳng thức (trừ ràng buộc không âm)
- Mặc dù trong định nghĩa bài toán tối ưu là cho bài toán tối thiểu hàm mục
tiêu với các ràng buộc thoả mãn các điều kiện nhỏ hơn hoặc bằng 0, các bài
toán tối ưu với tối đa hàm mục tiêu và điều kiện ràng buộc ở dạng khác đều
có thể đưa về được dạng này: vàs ≥ 0 i
(si được gọi là biến phụ)
*Dạng tổng quát của bài toán vận chuyển là bài toán qui hoạch tuyến tính có dạng như sau:
x=arg mincT x+ d Với :
Ở điều kiện ràng buộc thì G ∈ Rm x n, A ∈ Rp x n, h ∈ Rm, b ∈ Rp. Dòng thứ của ma
trận G là gi được xem như hệ số của điều kiện ràng buộc dạng bất đẳng
thức gi ( x )=gi x ≤ℎi . ℎi là giá trị phần tử thứ của véc tơ h . Tương tự dòng
thứ của ma trận A cũng là hệ số của hệ điều kiện ràng buộc dạng đẳng
thức. Một điều kiện đẳng thức cũng có thể được chuyển hoá sang điều kiện
bất đẳng thức nếu như chúng ta thay chúng bằng hai điều kiện: a x≤b i i và a x≥b i
i. Do đó một số tài liệu người ta chỉ có điều kiện bất đẳng thức.
Một số bài toán thực tế sẽ xuất hiện thêm điều kiện x ≥ 0 ij . Khi đó chúng ta
có thể đổi dấu của x ≤ 0
ij để chuyển về điều kiện −xij
Đối với hàm mục tiêu thì véc tơ c được xem như véc tơ trọng số của biến
mục tiêu x. d là một đại lượng vô hướng và không ảnh hưởng tới nghiệm.
Minh hoạ bằng hình học của bài toán LP
Các bài toán LP có thể được minh hoạ như hình dưới đây:
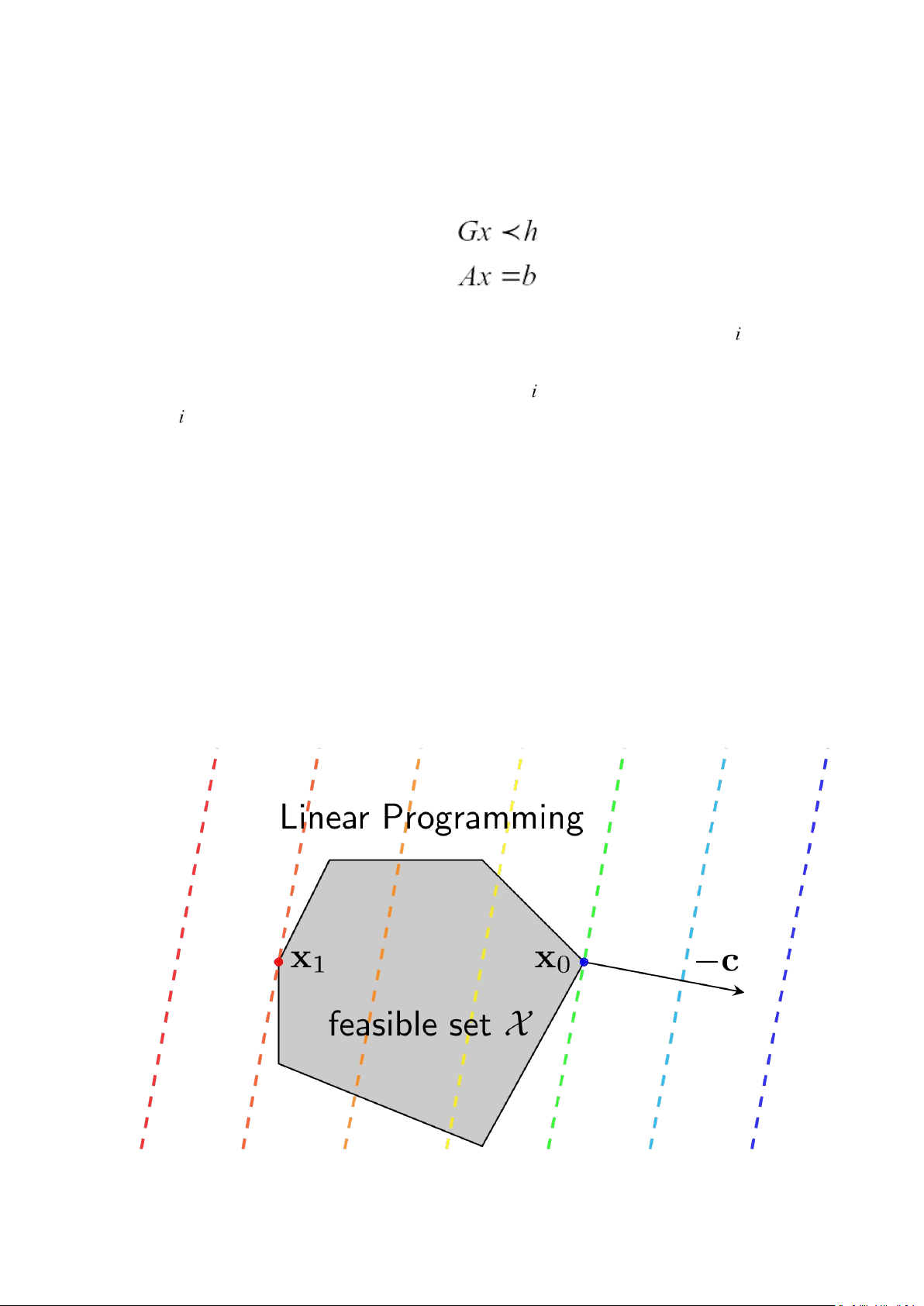
Hình Biểu diễn hình học của Linear Programming.
Điểm x0 chính là điểm làm cho hàm mục tiêu đạt giá trị nhỏ nhất, điểm x1
chính là điểm làm cho hàm mục tiêu đạt giá trị lớn nhất. Với các bài toán LP,
nghiệm, nếu có, thường là một điểm ở đỉnh của đa giác hoặc là một
mặt của đa giác đó (trong trường hợp các đường level sets của hàm mục
tiêu song song với mặt đó, và trên mặt đó, hàm mục tiêu đạt giá trị tối ưu).
Một bên của đường thẳng sẽ tương ứng với dấu lớn hơn và bên còn lại sẽ là
nhỏ hơn. Trong hình, bên tô màu tương ứng với bên nhỏ hơn (thỏa ràng
buộc). Giao của 3 phần tô màu và giới hạn x , y ≥ 0 tại trục tọa độ sẽ tạo nên
miền khả thi hay miền xác định (feasible region) của bài toán, được mô tả
với các đường đứt đoạn trên hình. Điểm nằm trong miền khả thi được gọi
là một nghiệm (feasible solution). Các điểm khác ở ngoài miền này sẽ không
thỏa một trong các ràng buộc của bài toán, do đó sẽ không khả thi
(infeasible). Sau đó, chúng ta vẽ các đường thể hiện hàm mục tiêu với các giá tr x,y thay đổi. XÉT BÀI TOÁN
Một nhà hàng có 30 con hào, 24 con tôm và 18 con nhím biển. Tuy nhiên,
các loại hải sản này phải được chế biến theo món:
Món A giá 8 đồng cần 5 con hào, 2 con tôm và 1 con nhím biển.
Món B giá 6 đồng cần 3 con hào, 3 con tôm và 3 con nhím biển.
Hãy xác định số lượng của từng món để mang về nhiều lợi nhuận nhất.
Từ dữ kiện đề bài cho lập hàm mục tiêu và các điều kiện ràng buộc: max Sao cho
Giải bằng đồ thị tuy chỉ có thể áp dụng với các bài toán có 2 hoặc 3 biến,
nhưng có thể cho các bạn thấy phần nào hướng giải của bài toán này.
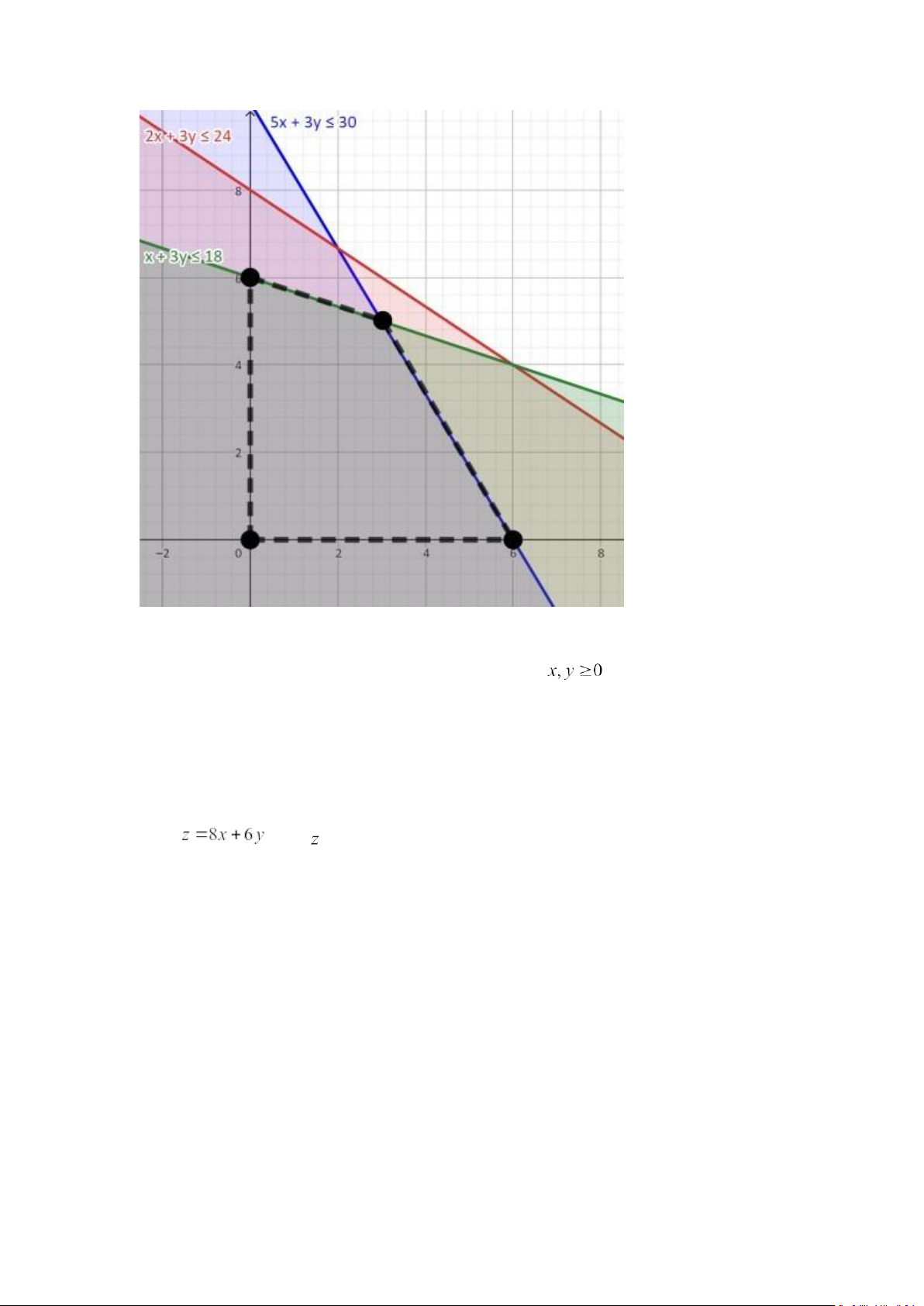
Chúng ta sẽ có một hệ tọa độ tương ứng với 2 biến và của bài
toán. Trong hệ tọa độ này, chúng ta sẽ lần lượt vẽ các đường (xanh dương), (đỏ), (xanh lá):
Một bên của đường thẳng sẽ tương ứng với dấu lớn hơn và bên còn lại sẽ là
nhỏ hơn. Trong hình, bên tô màu tương ứng với bên nhỏ hơn (thỏa ràng
buộc). Giao của 3 phần tô màu và giới hạn
tại trục tọa độ sẽ tạo
nên miền khả thi hay miền xác định (feasible region) của bài toán, được mô
tả với các đường đứt đoạn trên hình. Điểm nằm trong miền khả thi được
gọi là một nghiệm (feasible solution). Các điểm khác ở ngoài miền này sẽ
không thỏa một trong các ràng buộc của bài toán, do đó sẽ không khả thi
(infeasible). Sau đó, chúng ta vẽ các đường thể hiện hàm mục tiêu với thay đổi.
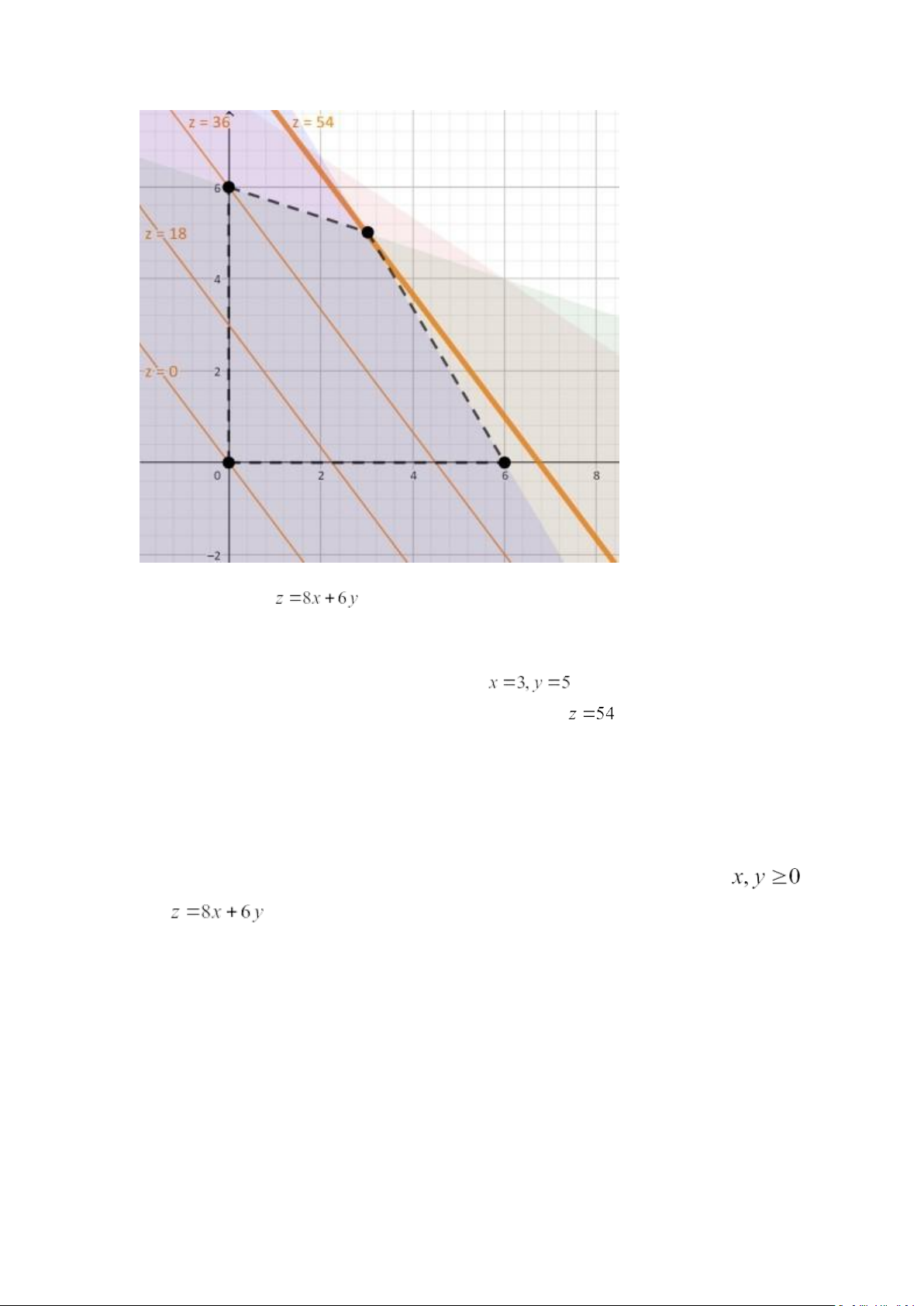
Chúng ta có thể thấy, khi tăng dần hàm mục tiêu của chúng ta, chúng ta di chuyển đường
từ góc dưới trái lên góc trên phải. Điểm cuối cùng
mà đường thẳng này chạm vào miền khả thi chính là điểm mà chúng ta cần
tim. Điểm đó được gọi là nghiệm tối ưu (optimal solution) của bài toán.
Trong ví dụ này, điểm này có tọa độ là , tức 3 món A và 5 món B.
Tại điểm này, lợi nhuận là cực đại và có giá trị là .
Không phải bài toán quy hoạch tuyến tính nào cũng có nghiệm tối ưu. Bài
toán mà miền xác định là rỗng được gọi là vô nghiệm (infeasible). Nếu bài
toán không đủ ràng buộc, hàm mục tiêu có thể tăng (khi tối đa hóa) hoặc
giảm (khi tối thiểu hóa) thoải mái không có giới hạn, thì bài toán đó được
gọi là không có cận (unbounded).
Ví dụ, nếu trong bài toán ví dụ trên không có ràng buộc nào ngoài thì
có thể tăng thoải mái và do đó, bài toán không có cận và
không có nghiệm tối ưu. Sẽ luôn luôn có một nghiệm tối ưu là đỉnh của hình
đa giác tạo nên bởi miền tối ưu.
XÉT BÀI TOÁN CHI PHÍ SẢN XUẤT
Một nhà máy sản xuất ra 4 loại sản phẩm là:
● Đũa tre (5 triệu/tấn) ● Tăm tre (6 triệu/tấn)
● Chân hương (4.5 triệu/tấn)
● Xiên thịt (5.5 triệu/tấn)
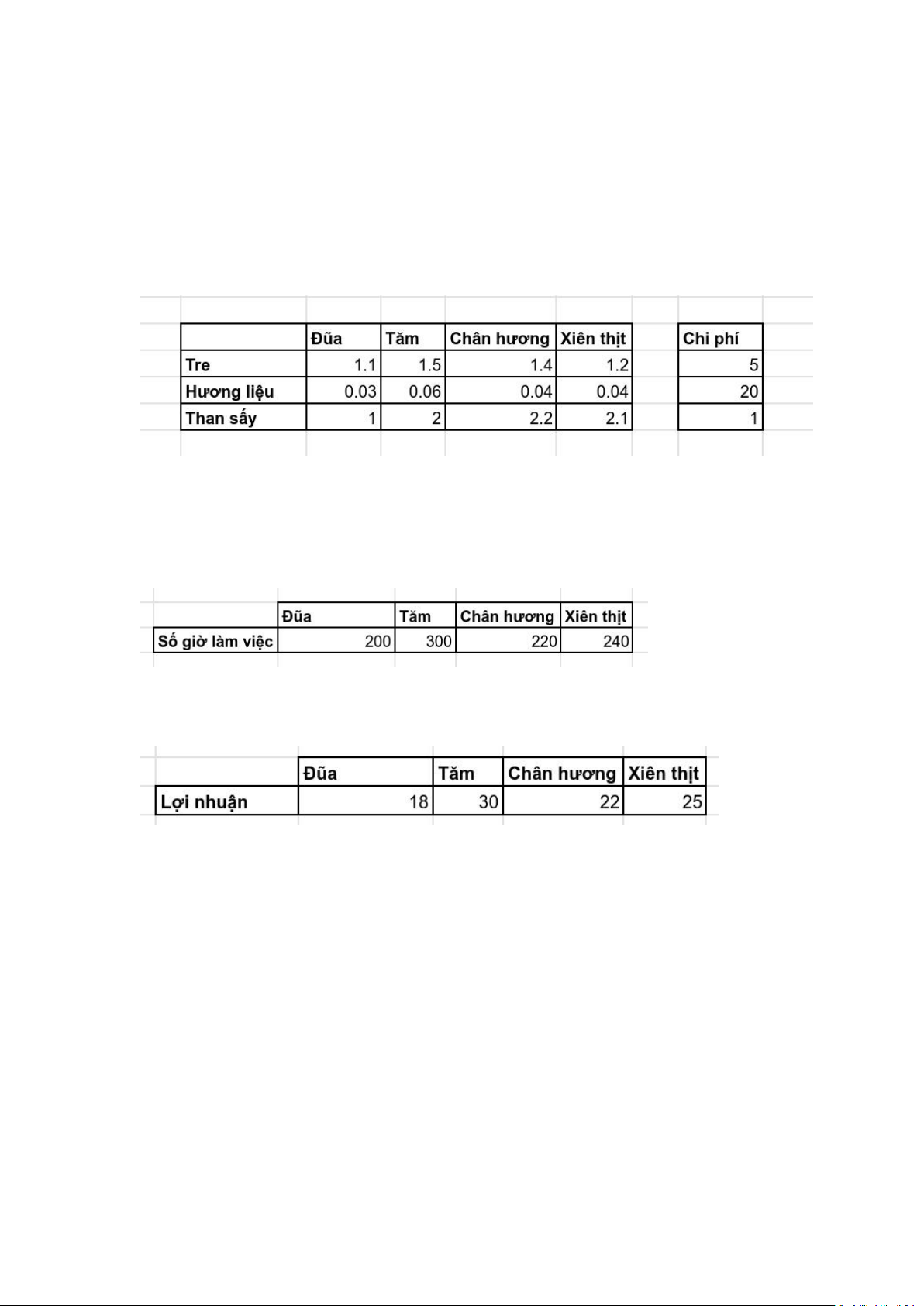
Biết rằng để sản xuất được 1 tấn của lần lượt các loại sản phẩm trên thì nhà
máy cần tiêu tốn nguyên liệu và nhân công như sau:
Nguyên liệu và chi phí nguyên liệu:
Số giờ làm việc của nhân công:
Lợi nhuận bán ra của từng loại:
Kế hoạch trong tháng tới nhà máy có 1000 giờ làm việc và tối đa 5 tấn tre,
0.2 tấn hương liệu và 10 tấn than sấy. Hỏi nhà máy cần lập kết hoạch sản
xuất như thế nào để tối đa lợi nhuận. Lời giải
Giả định sản lượng sản xuất của mỗi loại lần lượt là . Bài toán tối ưu lợi
nhuận: x=arg max f ( x)=18 x1+30 x2+22 x3+ 25 x4
Tương đương với bài toán: x=arg minf (x)=− 18 x1 −30 x2− 22x3− 25x4
Ràng buộc về nguyên liệu:
Đối với Tre: 1.1 x1+1.5 x2+1.4 x3+1.2 x4≤ 5
Đối với Hương liệu: 0.03 x1+0.06x2+0.04 x3+0.04 x4 ≤0.2
Đối với than sấy: x ≤ 10
1+ 2 x2 +2.2 x3 +2.1 x4
Ràng buộc về số giờ làm việc: 200 x ≤1000
1+300 x2 +220 x3 +240 x4
Ràng buộc về số lượng: x , x , x x ≥0 1 2 3 , 4
GIẢI BẰNG CODE PYTHON Từ đề bài ta có
x=arg max f ( x)=18 x1+30 x2+22 x3+ 25 x4
1.1 x1+1.5 x2+1.4 x3+1.2 x4≤ 5
0.03 x1+ 0.06 x2+0.04 x3+0.04 x4 ≤ 0.2
x1+ 2 x2+2.2 x3+2.1 x4≤ 10
200 x1+300 x2+220 x3+240 x4 ≤1000
x1, x2, x3, x4 ≥0
Từ dạng tổng quát ta có c=[−18,−30,−22,−25]T G = 1.1 1.5 1.4 1.2 0.03 0.06 0.04 0.04 1 2 2.2 2.1 -1 0 0 0 0 -1 0 0 0 0 -1 0 0 0 0 -1
h=[ 5,0.2,10,0,0,0,0]T
- Ma trận G có 3 dòng đầu là hệ số của điều kiện ràng buộc, 4 dòng sau là
điều kiện không âm của 4 biến.
- Vecto h là hệ số không âm của vế phải HÌNH CODE PỴTHON HÌNH XUẤT KẾT QUẢ
Document Outline
- 1.2Các thành phần của quy hoạch tuyến tính
- *Biến quyết định
- *Ràng buộc tuyến tính
- *Phương pháp giải quyết
- *Áp dụng rộng rãi
- Ưu điểm
- Nhược điểm
- Đánh giá hiệu suất
- 2.Ứng dụng quy hoạch tuyến tính vào các bài toán thự
- 3.Bài toán quy hoạch tuyến tính
- Một vài lưu ý
- *Dạng tổng quát của bài toán vận chuyển là bài toá
- Với :
- Minh hoạ bằng hình học của bài toán LP
- XÉT BÀI TOÁN
- XÉT BÀI TOÁN CHI PHÍ SẢN XUẤT
- Lời giải
- Ràng buộc về nguyên liệu:
- GIẢI BẰNG CODE PYTHON



