Chương 3: Lý thuyết mã hóa và các khái niệm cơ bản môn Lý thuyết thông tin | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58736390 Lý thuyết thông tin
Chương 3: Lý thuyết mã hóa
Các định nghĩa và khái niệm cơ bản:
Mã hóa: là một ánh xạ 1:1 đi từ tập các tin rời rạc ai lên tập các từ mã αini
Mã (bộ mã) là sản phẩm của phép mã hóa, là tập hợp các từ mã lập nên theo một luật định trước
Các yếu tố của từ mã
Từ mã là chuỗi các ký hiện mã biểu diễn cho tin của nguồn
Độ dài từ mã l,n: là số các dấu mã cần thiết để biểu diễn cho tin ai
Nếu ni=const với mọi i => Bộ mã đều
Nếu ni khác nj => Bộ mã không đều
Cơ số mã m: số các dấu mã khác nhau(về giá trị) được dùng trong bộ mã m=2 là
mã nhị phân được lấy từ trường GF(2) Độ thừa của bộ mã đều D: ( D=1−H A) (%)
H (V ) H ( A )=logs H (V )=nlogm
Các từ mã không được sử dụng gọi là từ mã cấm
Khoảng cách mã d: khoảng cách mã giữa 2 từ mã bất kỳ là số các dấu mã khác nhau khi tính
cùng một vị trí giữa hai từ mã.
d (αi¿,αjnj) Tính chất:
d (αi¿ ,αjnj)=d (α jn j ,αini)
0≤d(αi¿,αjnj)≤n Tc tam giác:
d (αi¿ ,αjnj)+d (α jn j ,αknk)≥d(αi¿,αknk)
Khoảng cách hamming(khoảng cách tối thiểu d0): dùng để đánh định lượng khả năng khống chế
sai(phát hiện + sửa sai) của một bộ mã. lOMoAR cPSD| 58736390
d 0=mind(αi¿,αjnj)
Trọng số của từ mã (w): là số các dấu mã khác 0 trong từ mã
VD: α7=0110101→W (α7)=4 Tính chất:
0≤W (αin)≤n
d (αi¿,αjnj)=W (αi¿+αjnj) (phép cộng trọng số 2 từ mã theo XOR) Khả năng
khống chế sai của bộ mã đều nhị phân:
Khả năng phát hiện sai (t):
Một bộ mã đều nhị phân có độ thừa do>=3 có khả năng phát hiện t lỗi t=do−1
Khả năng sửa sai (e): Một bộ mã đều nhị phân có độ thừa do>=3 có khả năng sửa e lỗi e
Mã non-singular: khi tất cả các từ mã trong bộ mã đều khác nhau
Mã prefix: khi không có bất kỳ từ mã nào là phần đầu của từ mã khác trong bộ mã Các phương pháp biểu diễn mã:
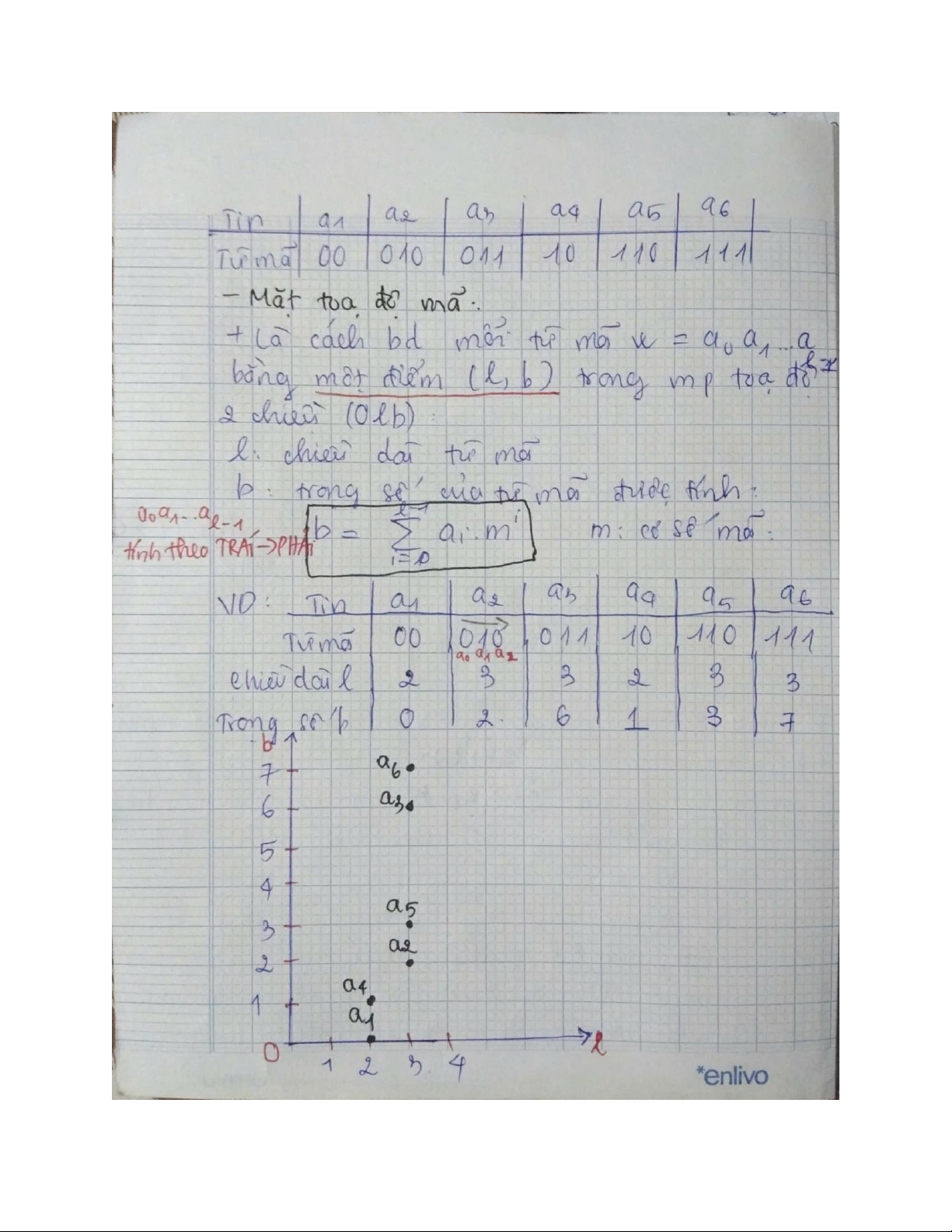
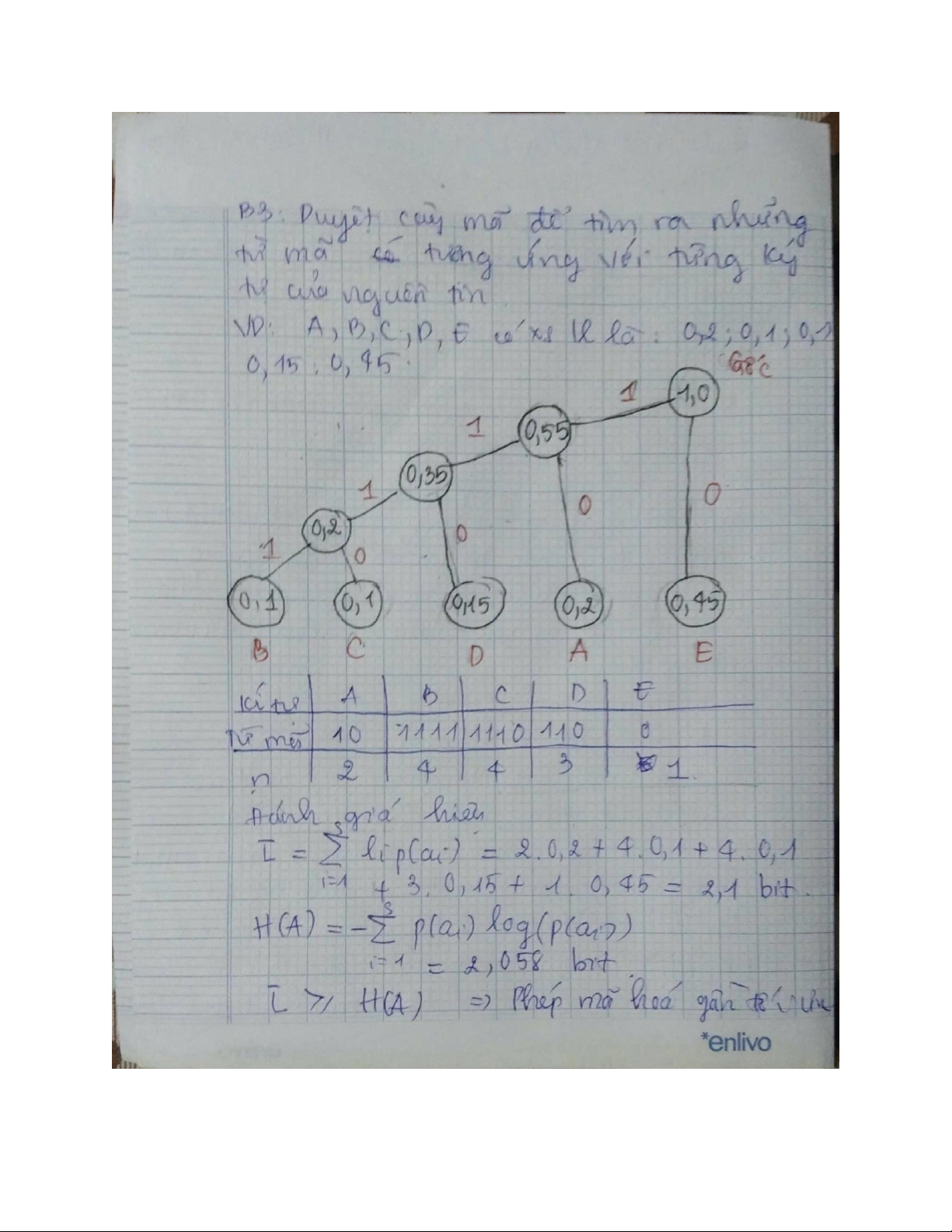
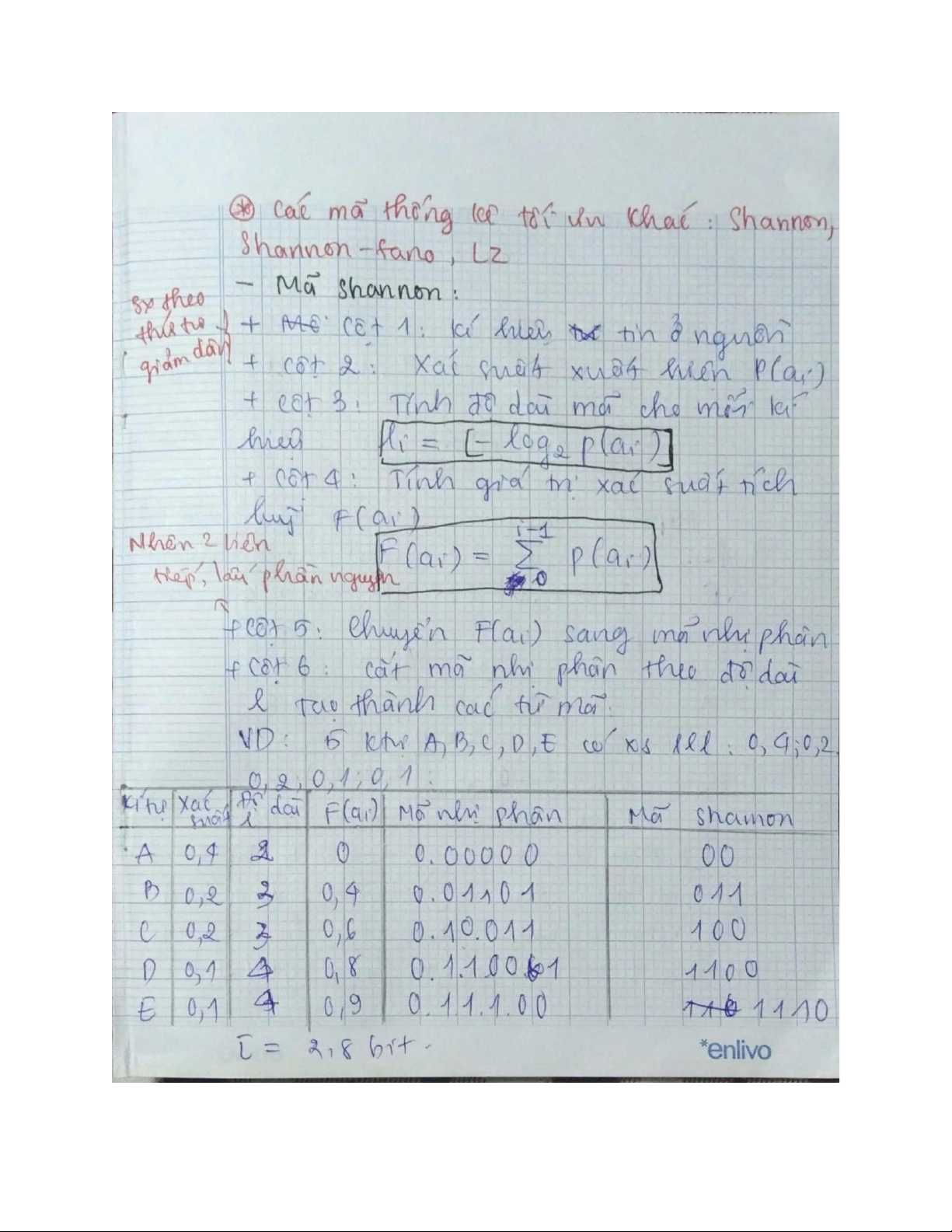
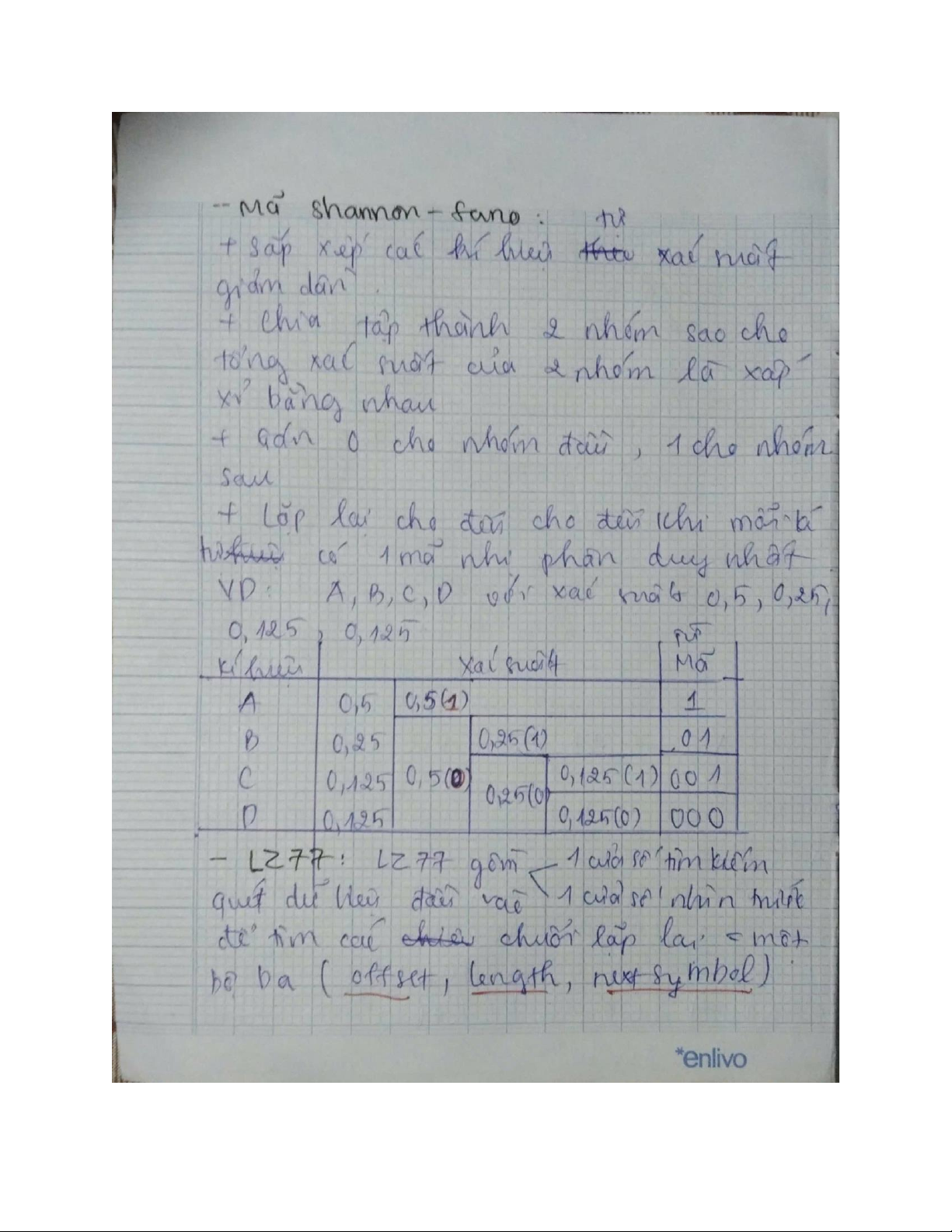
Bảng đối chiếu mã: là cách đối chiếu và từ mã tương ứng trong một bảng Cây mã Đồ hình kết cấu mã Mặt tọa độ mã Hàm cấu trúc mã lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390