










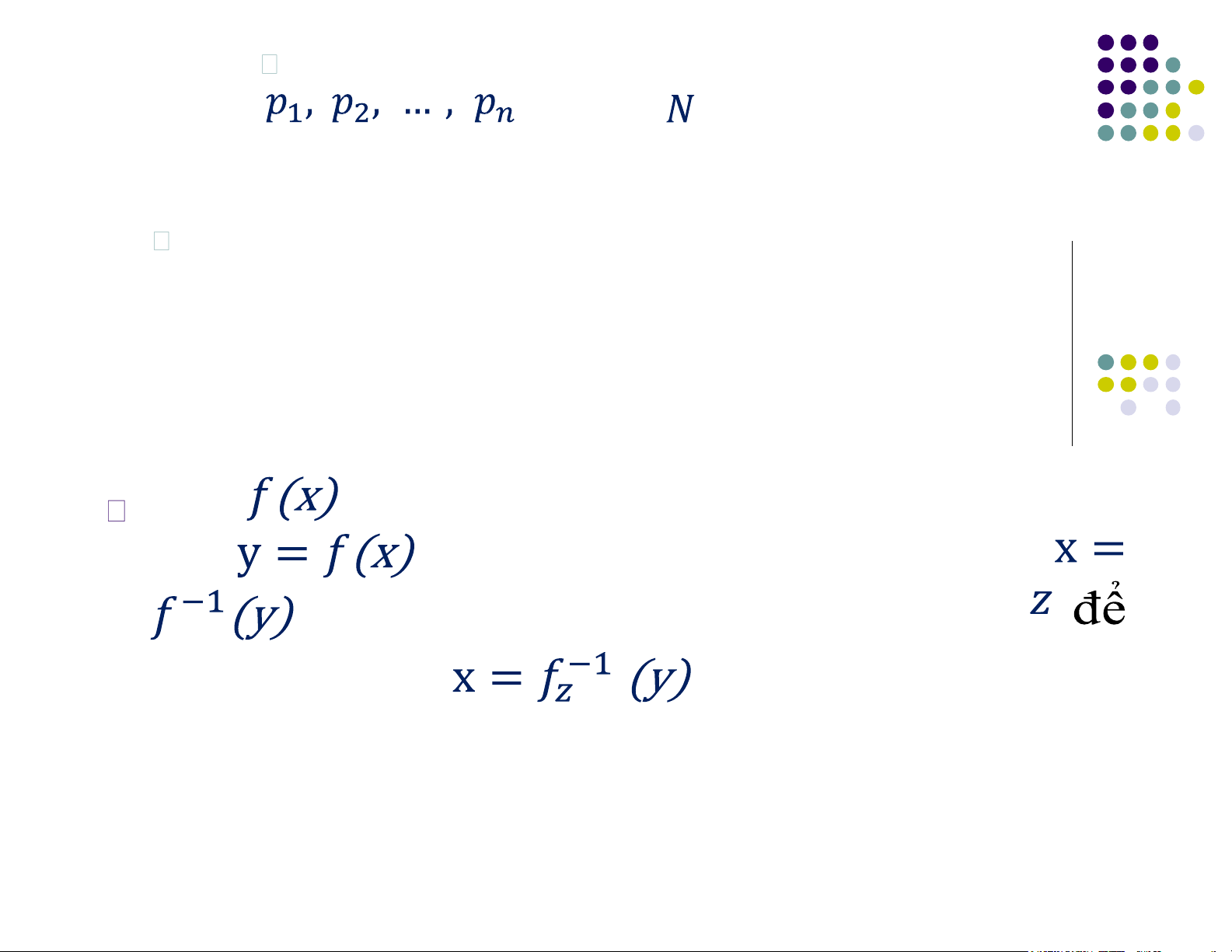



Preview text:
lOMoAR cPSD| 58412604 lOMoAR cPSD| 58412604 Nội dung Giới thiệu chung Thuật toán mã hoá RSA Các hàm Hash và MAC
Chữ ký số và chứng thực lOMoAR cPSD| 58412604 lOMoAR cPSD| 58412604 1. Mật mã khóa công khai
Ý tưởng về khoá công khai được Diffie và Hellman đưa ra vào năm 1976.
Sự phát triển của hệ thống mã hoá khoá công khai
đã tạo ra một cuộc cách mạng trong lịch sử ngành mật mã. lOMoAR cPSD| 58412604
. Mật mã khóa công khai (tt) lOMoAR cPSD| 58412604
Các mật mã đối xứng dùng chung một khoá cho quá
trình mã hoá và giải mã. Chúng đều dựa trên nền
tảng của phép thay thế và hoán vị. Nhưng các thuật 1
toán mã hoá công khai dựa trên các hàm toán học là chủ yếu.
Hệ mật mã khoá công khai là bất đối xứng, cho phép
sử dụng hai khoá riêng biệt cho các quá trình mã hoá và giải mã. lOMoAR cPSD| 58412604
1. Mật mã khóa công khai (tt)
Đặc điểm của hệ mật mã khoá công khai:
Không thể suy ra khóa bí mật dù biết trước thuật toán và khóa công khai.
Một trong hai khóa đều có thể dùng để mã hóa và khóa còn lại dùng đề giải mã.
1. Mật mã khóa công khai (tt)
Các thành phần của hệ mã khoá công khai: lOMoAR cPSD| 58412604
Bản rõ: thông điệp có thể đọc, đầu vào của giải thuật Giải thuật mã hóa
Khóa công khai và bí mật: một cặp khóa được chọn sao cho 1
khóa dùng để mã hóa và 1 khóa dùng để giải mã.
Bản mã: thông điệp đầu ra ở dạng không đọc được, phụ thuộc vào
bản rõ và khóa. Nghĩa là với cùng một thông điệp, 2 khóa khác
nhau sinh ra 2 bảng mã khác nhau. Giải thuật giải mã 2. Một vài ứng dụng
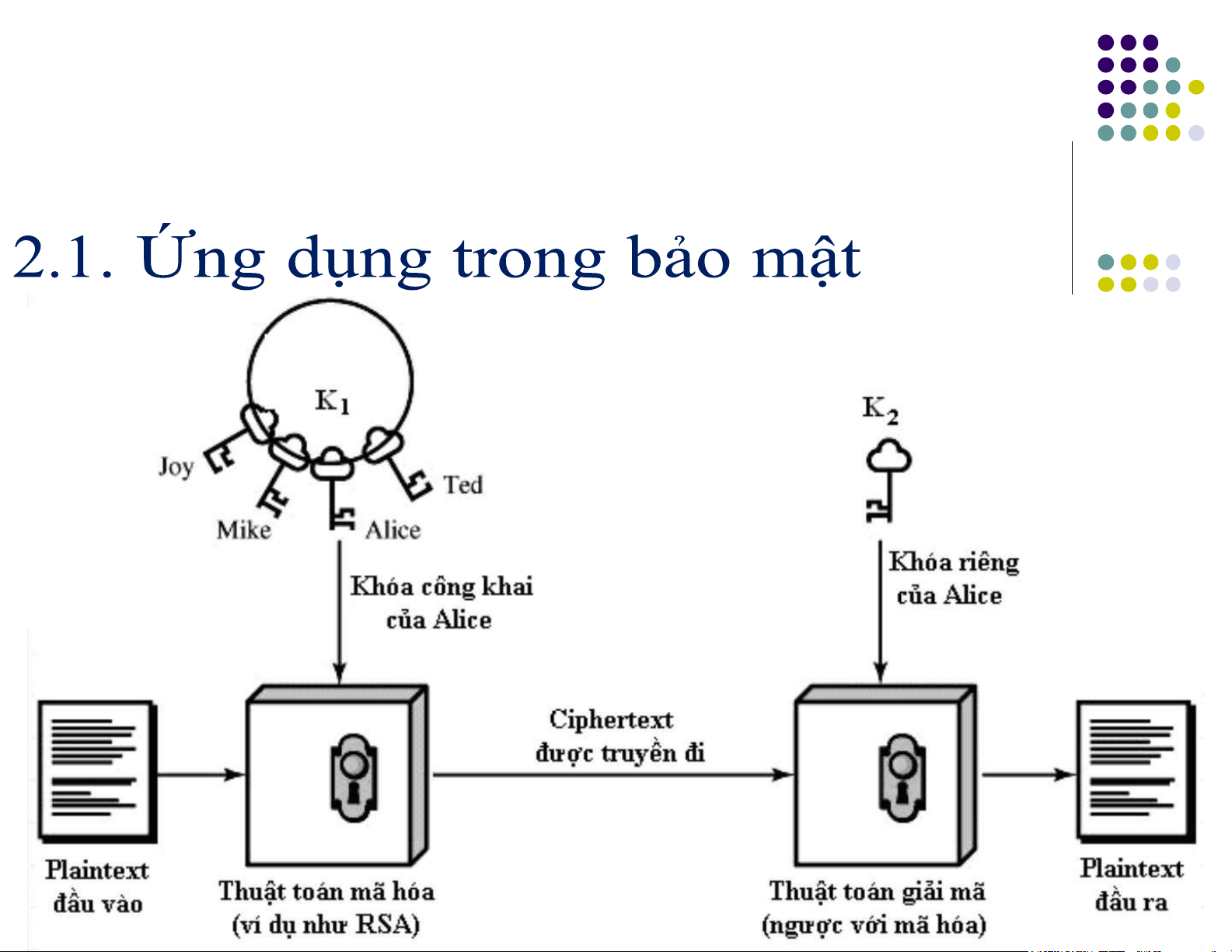
2.1. Ứng dụng trong bảo mật lOMoAR cPSD| 58412604
Giả sử mỗi người dùng sử dụng hai khoá (K1, K2),
trong đó K1 dùng để mã hoá, K2 dùng để giải mã.
Người đó có thể công bố công khai khoá K1 (trong
“danh bạ”) để người gửi tin mã hoá thông điệp, và
giữ bí mật K2 (dùng riêng cho mình) để giải mã khi
nhận được thông điệp. lOMoAR cPSD| 58412604 lOMoAR cPSD| 58412604
2. Một vài ứng dụng (tt)
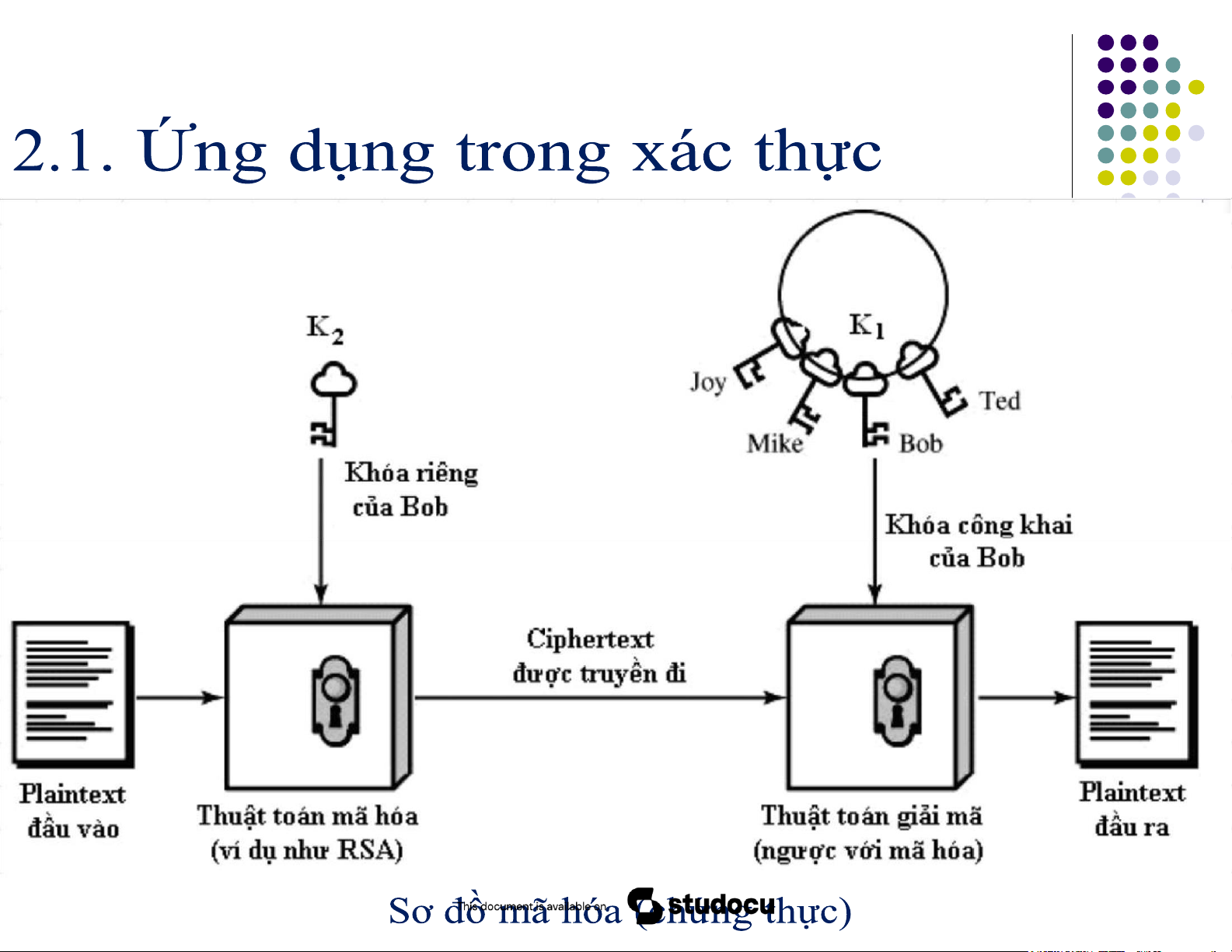
2.1. Ứng dụng trong xác thực
Nếu người gửi muốn khẳng định thông điệp là của
mình, không phải do kẻ khác làm giả, anh ta có thể
mã hoá thông điệp bằng khoá bí mật K2 của mình trước khi gửi đi.
Người nhận sẽ dùng khoá công khai K1 của người
gửi để giải mã. Nếu giải mã thành công thì chứng
tỏ thông điệp đó đúng là của người gửi. lOMoAR cPSD| 58412604
Downloaded by LU MY (mymycv.hr@gmail.com) lOMoAR cPSD| 58412604
3. Hàm một chiều (One-way function)
Nhắc lại: không thể suy ra khoá bí mật dù biết thuật toán và khoá công khai.
Có thể đạt được điều đó nhờ các hàm toán học đặc
biệt gọi là hàm một chiều. 3. Hàm một chiều (tt) Hàm
được gọi là hàm một chiều nếu: lOMoAR cPSD| 58412604 Đối với mọi tính ra là dễ dàng
Khi biết rất khó để tính ngược .
Nói cách khác, thời gian tiêu tốn để tính hàm ngược
là vô cùng lớn, và được coi là không giải được! 3. Hàm một chiều (tt) Ví dụ: Cho số nguyên tố . Dễ dàng tính được: N = lOMoAR cPSD| 58412604
Tuy nhiên rất khó để tính được các số nguyên tố
nếu biết , nhất là khi các thừa số
này là các số nguyên tố lớn.
Số nguyên tố lớn: dài tới hàng trăm chữ số thập phân
4. Hàm cửa lật một chiều (Trapdoor one-way function) Hàm
được gọi là hàm cửa lật một chiều nếu tính là dễ, tính
là không thể, nhưng có cửa lật dễ dàng tính được . lOMoAR cPSD| 58412604
Tạo PKC (public key cryptosystem) bằng hàm
cửa lật: giữ bí mật cửa bẫy.
Ví dụ: trong ví dụ hàm một chiều, dãy là cửa lật.
4. Hàm cửa lật một chiều (Trapdoor one-way function)
Tạo hệ mã PKC sử dụng hàm lật một chiều:
Lấy (hàm sinh mã) là hàm lật một chiều.
Khóa bí mật chính là bí mật cửa bẫy.
Nếu biết khóa bí mật thì có thể dễ dàng tính được nghịch
đảo của , tức là (hàm giải mã), còn không thì rất khó. lOMoAR cPSD| 58412604
Khả năng bị phá: thử vét cạn. Tuy nhiên phương pháp
này bất khả thi vì khối lượng tính toán quá lớn. Ứng dụng: hệ mã RSA. lOMoAR cPSD| 58412604 lOMoAR cPSD| 58412604 1. Giới thiệu
Phát minh bởi R. Rivest, A. Shamir & L. Adleman (1977)
Là hệ mật mã khóa công khai phổ biến và đa năng nhất trong thực tế
RSA là một thuật toán mã hoá khối, mỗi khối là một
dãy bít nhị phân ứng với một số nguyên trong
khoảng từ 0 đến n – 1.
Kích thước điển hình của n là 1024 bit, hay 309 chữ số thập phân. Tức là lOMoAR cPSD| 58412604
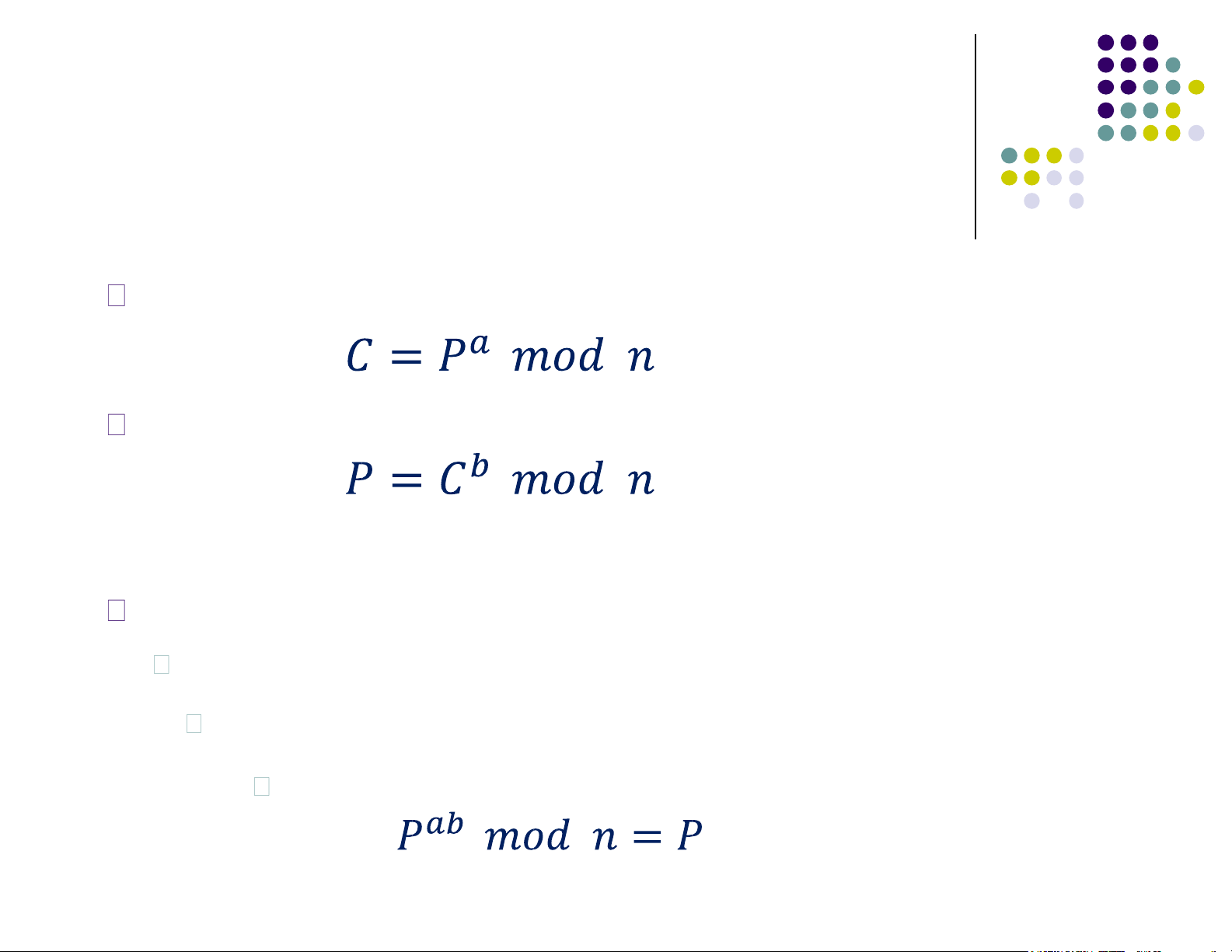
2. Công thức mã hóa – giải mã Công thức mã hoá: (1) Công thức giải mã: (2) Trong đó:
n = p.q là tích của hai số nguyên tố lớn
P (plaintext), C (ciphertext) thuộc Zn
a và b là các số nguyên thoả mãn điều kiện: (3)




