
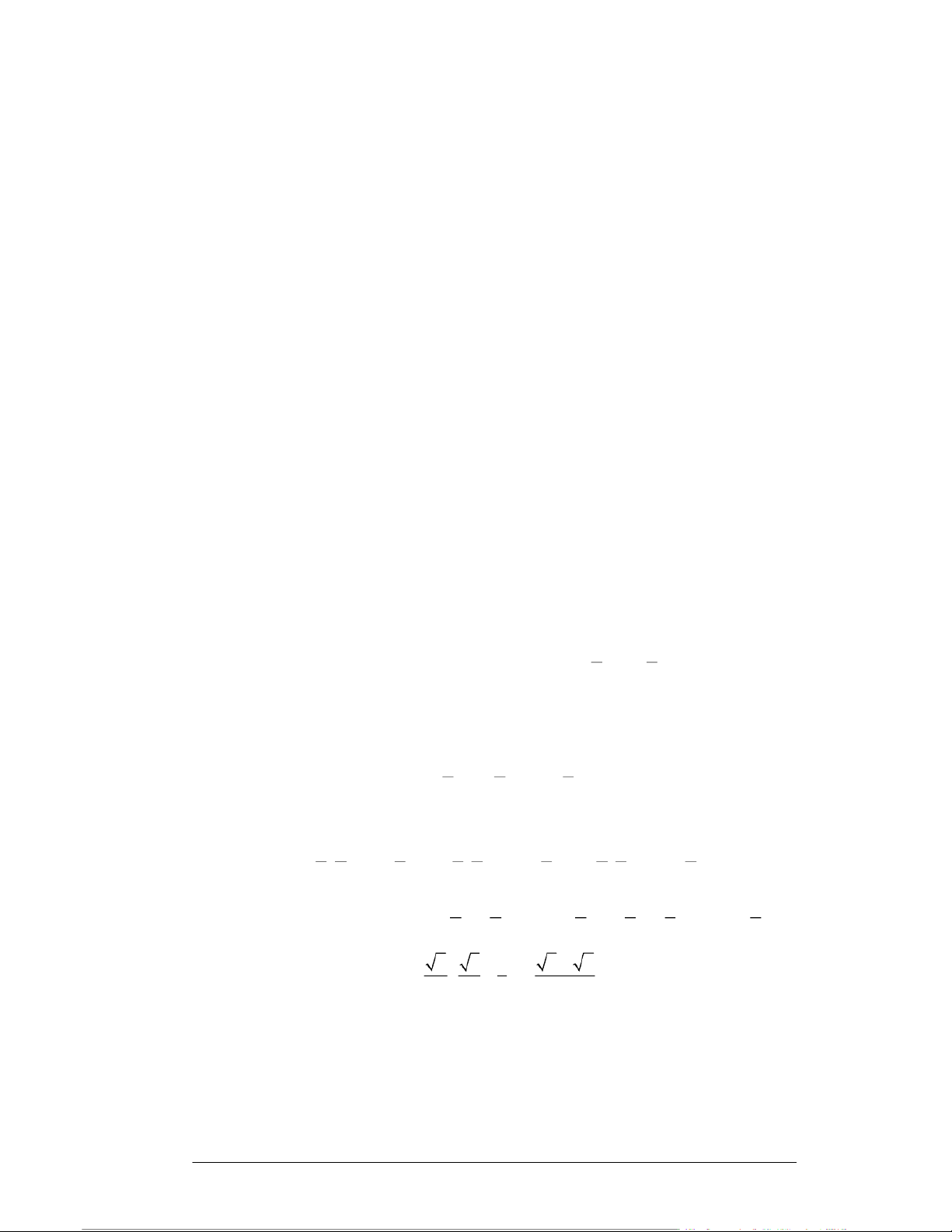

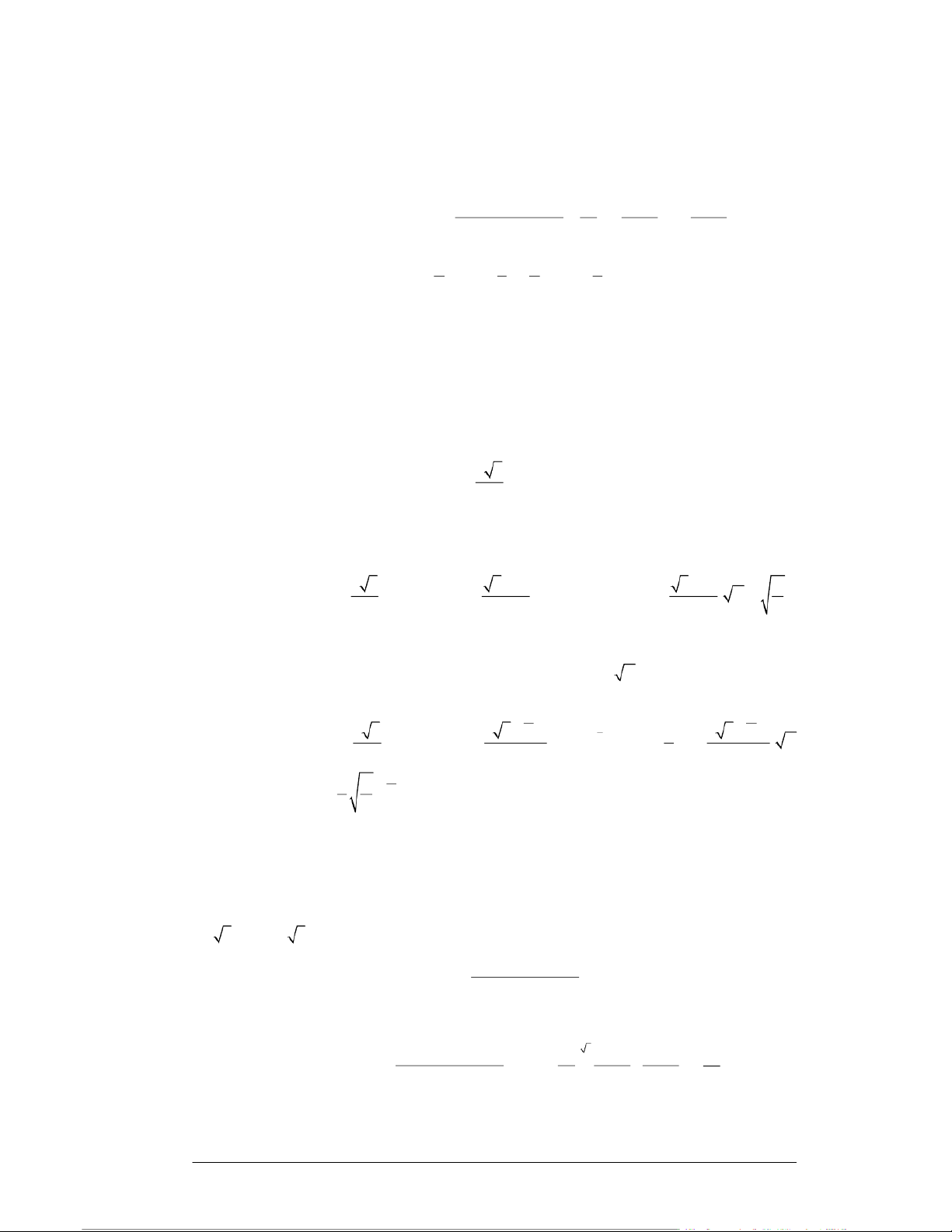

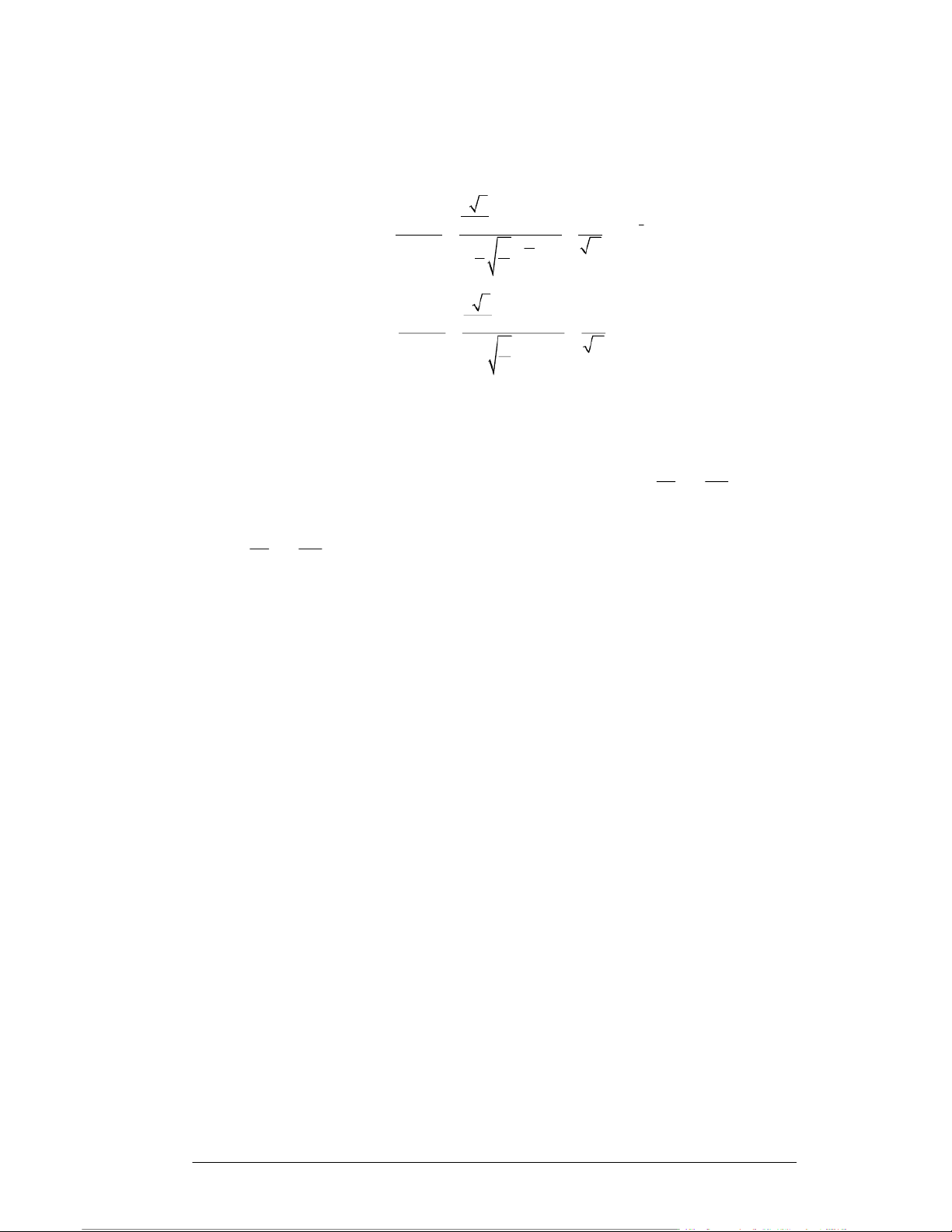








Preview text:
20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
Chương 4. Biến ngẫu nhiên hai chiều 4.1 Khái niệm
Biến ngẫu nhiên hai chiều là cặp (X, Y), trong đó X, Y là các biến ngẫu nhiên.
Nếu X và Y là các biến ngẫu nhiên rời rạc thì (X, Y) được gọi là các biến ngẫu
nhiên hai chiều rời rạc.
Nếu X và Y là các biến ngẫu nhiên liên tục thì (X, Y) được gọi là các biến ngẫu
nhiên hai chiều liên tục.
4.2 Quy luật phân phối xác suất của biến ngẫu nhiên hai chiều
4.2.1 Bảng phân phối xác suất của biến ngẫu nhiên hai chiều rời rạc
Cho (X, Y) là biến ngẫu nhiên hai chiều rời rạc. Tập giá trị mà X có thể nhận là
{x1, x2, …, xn}. Tập giá trị mà Y có thể nhận là {y1, y2, …, ym}. Ký hiệu
P(xi, yj) = P(X=xi, Y=yj), i 1,n; j 1,m
Ta có bảng phân phối xác suất của biến ngẫu nhiên hai chiều rời rạc (X, Y) như
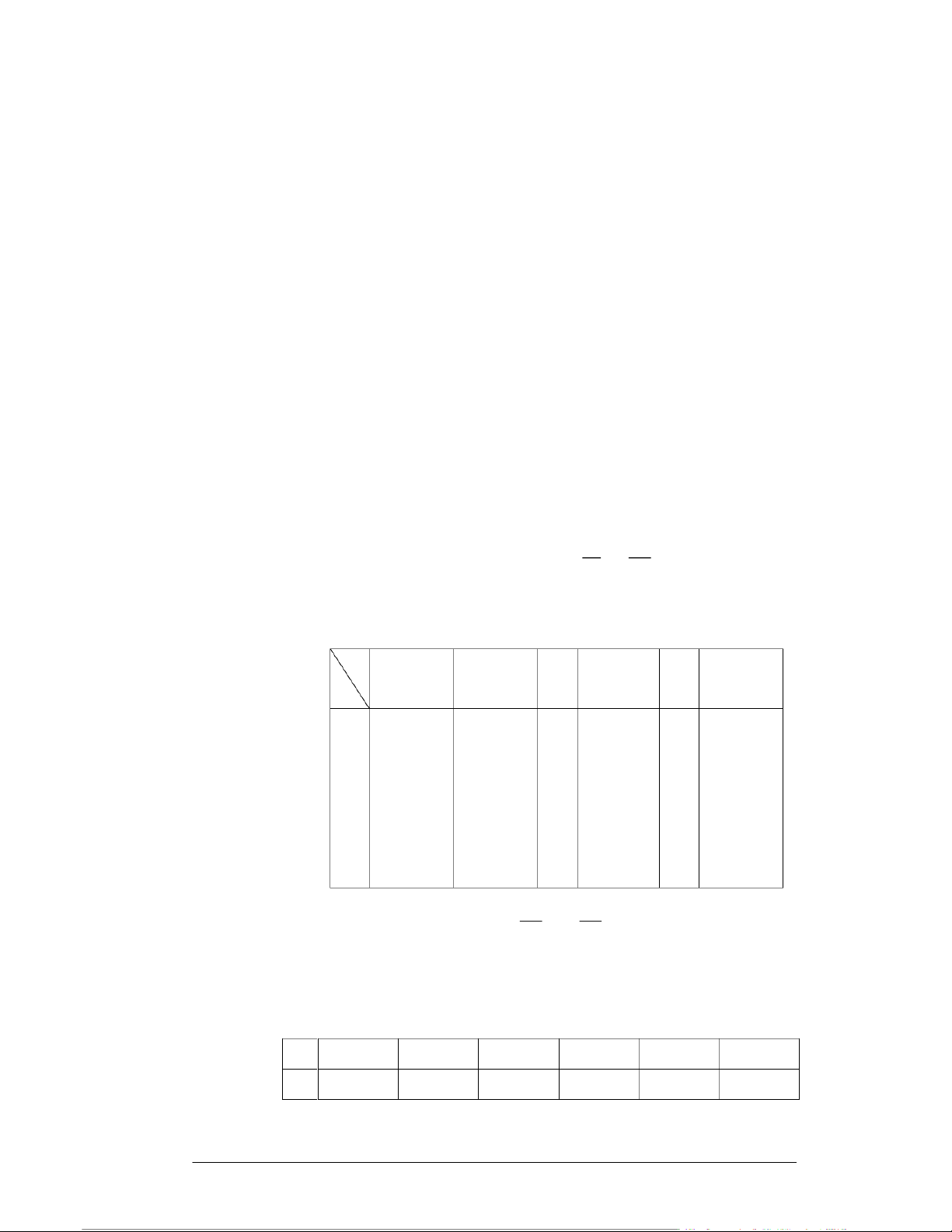
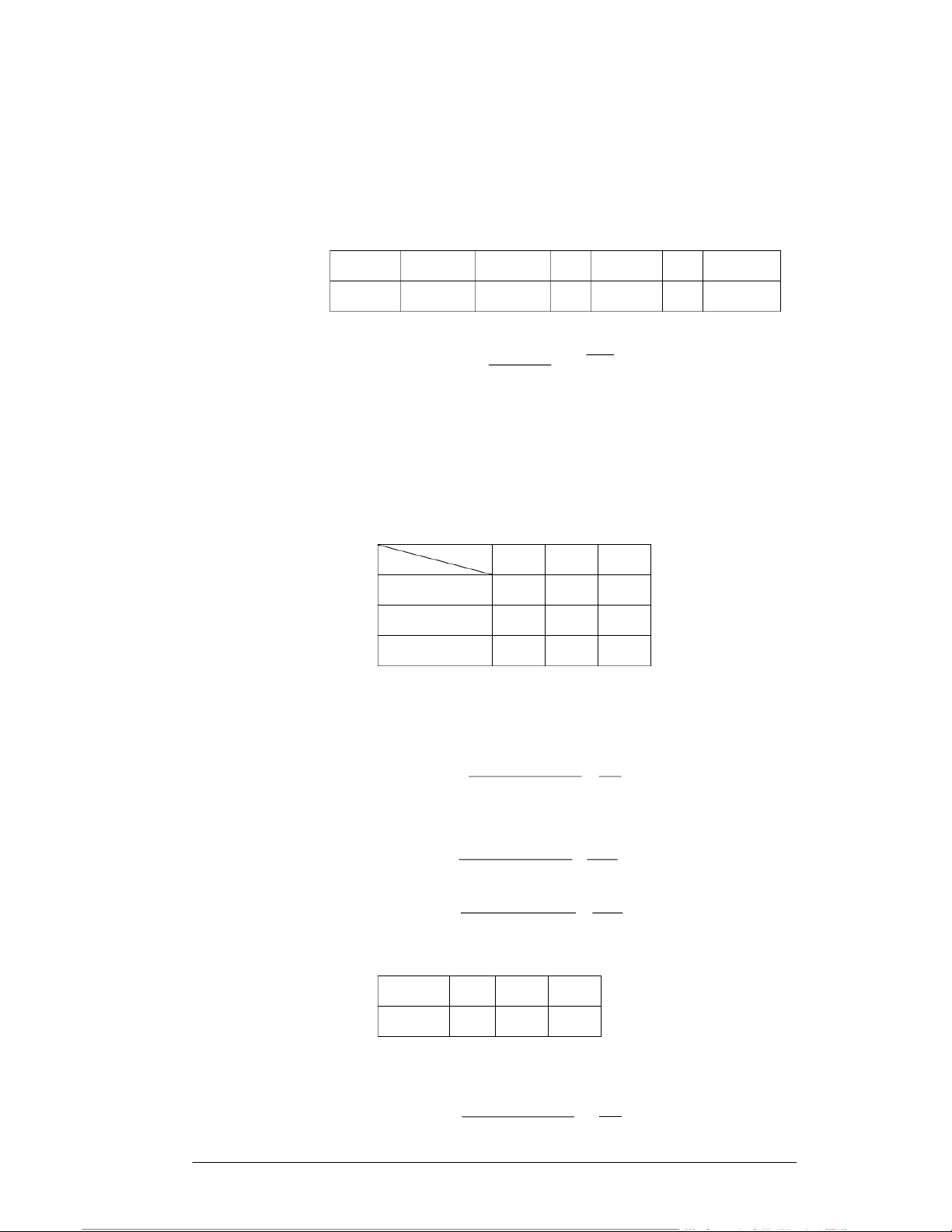
sau (còn gọi là bảng phân phối xác suất đồng thời của X và Y): X x1 x2 … xi … xn Y y1
P(x1, y1) P(x2, y1) … P(xi, y1) … P(xn, y1) y2
P(x1, y2) P(x2, y2) … P(xi, y2) … P(xn, y2) … … … … … … … yj P(x1, yj)
P(x2, yj) … P(xi, yj) … P(xn, yj) … … … … … … … ym P(x1, ym) P(x2, ym) P(xi, ym) P(xn, ym) Chú ý.
0 ≤ P(xi, yj) ≤ 1, i = 1, , j = n 1,m ; P(x ,y ) 1 n m i j i1 j 1
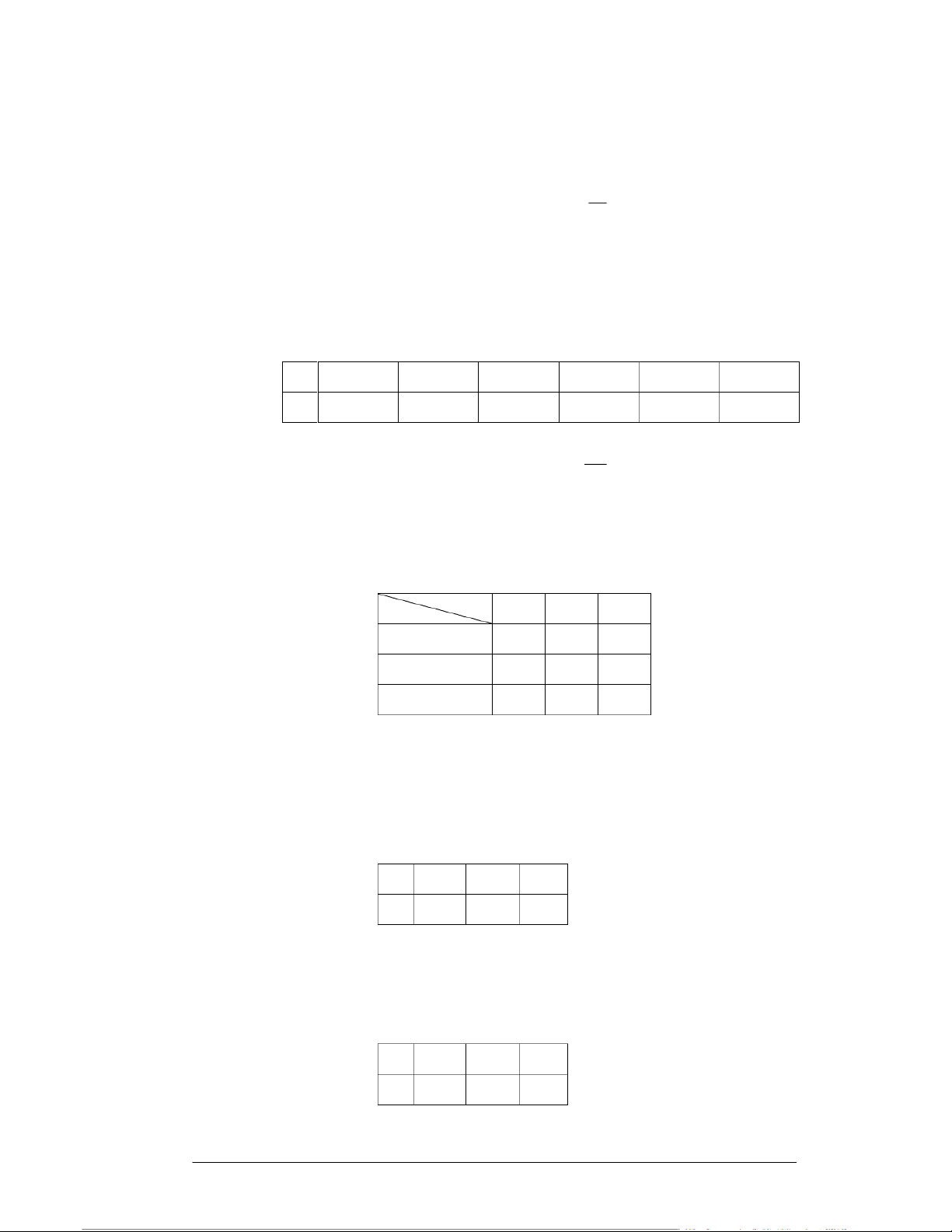
Khi đó, bảng phân phối xác suất biên của thành phần X là: X x1 x2 . . xi . . xn P P(x1) P(x2) . . P(xi) . . P(xn) trong đó
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu m P(xi) = P(x , i = i , y 1,n j ) j 1
được gọi là xác suất biên của thành phần X. n
Chú ý. P(x ) 1 i i 1
Bảng phân phối xác suất biên của thành phần Y là: Y y1 y2 . . yi . . ym P P(y1) P(y2) . . P(yi) . . P(ym) trong đó n P(yj) = P y , j = 1, m . j (x , ) i i 1 m Chú ý. P(y ) 1 j j 1
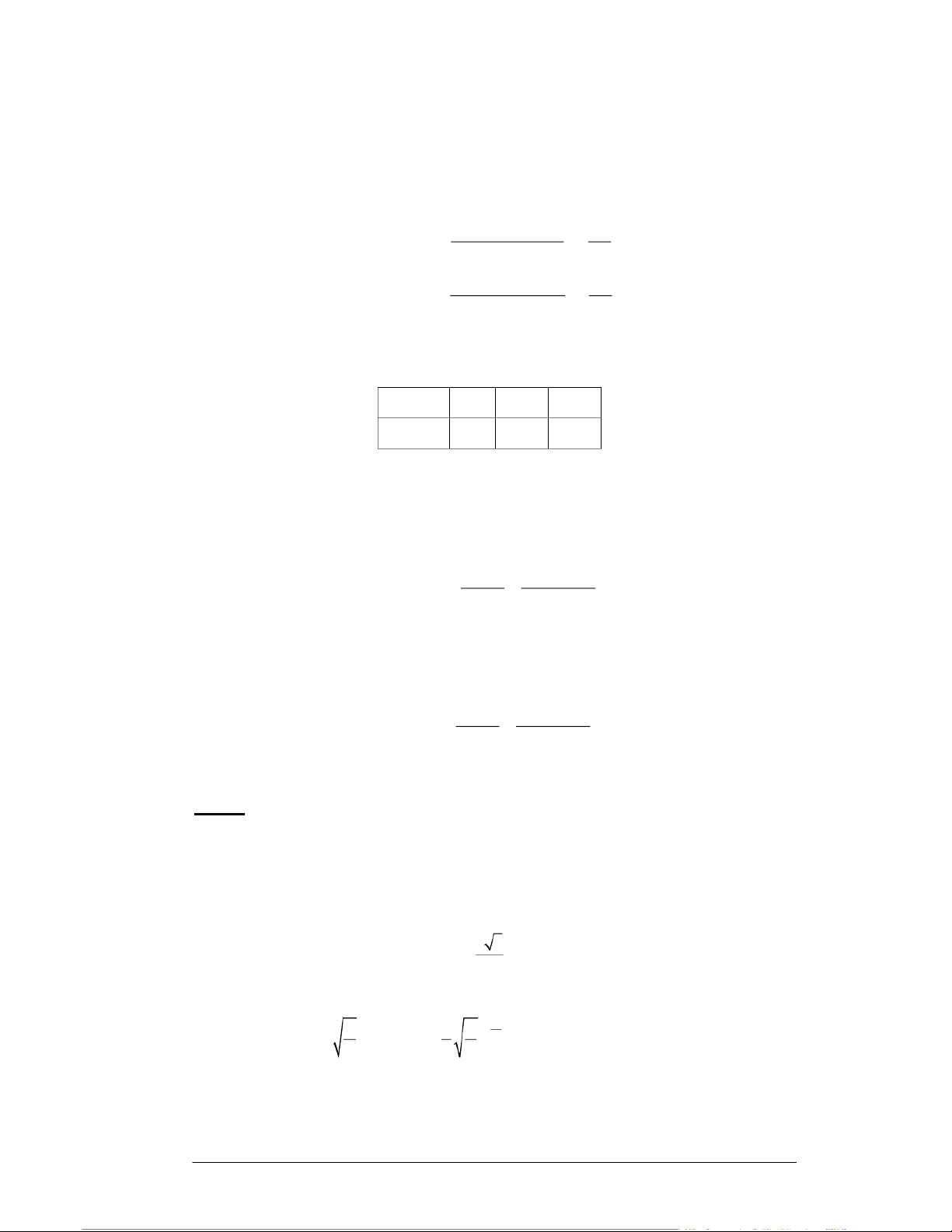
Ví dụ. Cho biết bảng phân phối xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau: Y X 100 150 200 0 0,1 0,05 0,05 1 0,05 0,2 0,15 2 0 0,1 0,3
Tìm phân phối biên của mỗi thành phần.
Giải. Ta có: P(X = 100) = 0,1 + 0,05 + 0 = 0,15
P(X = 150) = 0,05 + 0,2 + 0,1 = 0,35
P(X = 200) = 0,05 + 0,15 + 0,3 = 0,5
Ta có bảng phân phối xác suất của X như sau: X 100 150 200 P 0,15 0,35 0,5
P(Y=0) = 0,1 + 0,05 + 0,05 = 0,2
P(Y=1)= 0,05 + 0,2 + 0,15 = 0,4 P(Y=2)= 0 + 0,1 + 0,3 = 0,4
Ta có bảng phân phối xác suất của Y như sau: Y 0 1 2 P 0,2 0,4 0,4
4.2.2 Hàm phân bố xác suất của biến ngẫu nhiên hai chiều
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
1) Định nghĩa. Hàm phân bố xác suất của biến ngẫu nhiên hai chiều (X, Y), hay hàm
phân bố xác suất đồng thời của X và Y, kí hiệu là F(x, y) được xác định như sau:
F(x, y) = P(X < x, Y < y).
Ví dụ. Tìm xác suất để trong kết quả của phép thử thành phần X của biến ngẫu nhiên hai chi 1 1
ều (X, Y) nhận giá trị X2 và thành phần Y nhận giá trị Y3 nếu biết hàm
phân bố xác suất của nó có dạng: 1 1 1 1 F(x, y) 2 2 arctg2x ar ctg3y
Giải. Theo định nghĩa của hàm phân bố xác suất của biến ngẫu nhiên hai chiều, ta có 1 1 1 1 1 1 1 1 P X , Y = 1 1 F ; = arctg2. a rct g3. 2 3 2 3 2 3 2 2 = 1 1 1 1 arctg1 2 ar 2 ctg1 1 1 1 1 1 1 1 1 9 = . . = 4 4 2 2 4 2 4 2 16 = 0,5625 2) Tính chất
Tính chất 1. 0 F(x, y) 1
Tính chất 2. Hàm phân phối đồng thời F(x, y) là hàm không giảm theo từng đối số
hay theo cả hai đối số, nghĩa là
F(x1, y) F(x2, y) khi x1 < x2
F(x, y1) F(x, y2) khi y1 < y2
F(x1, y1) F(x2, y2) khi x1 < x2, y1 < y2.
Tính chất 3. Nếu ít nhất một đối số dần tới thì F(x, y) dần tới không, nghĩa là F( , y) lim F(x, y) 0 x F(x, ) lim F(x, y) 0 y F( , ) lim F(x, y) 0 x y
Tính chất 4. Nếu một đối số dần tới thì F(x, y) dần tới hàm phân bố xác suất của biến số kia, nghĩa là F( ,
y) lim F(x, y) F (y) Y x
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu F(x, ) lim F(x, y) F X(x) y
Tính chất 5. Nếu cả hai đối số dần tới thì F(x, y) dần tới 1, nghĩa là F( , ) lim F(x, y) 1 . x y
Chú ý. Từ các tính chất trên, ta có thể suy ra:
- Xác suất để biến ngẫu nhiên (X, Y) nhận giá trị trong hình chữ nhật
( x1 < X < x2, y1 < Y < y2) bằng
P(x1 < X < x2, y1 < Y < y2) = F(x1, y1) + F(x2, y2) – F(x1, y2) – F(x2, y1)
- Xác suất để biến ngẫu nhiên (X, Y) nhận giá trị trong hình chữ nhật
( x1 < X < x2, Y < y) bằng
P(x1 < X < x2, Y < y) = F(x2, y) – F(x1, y)
- Xác suất để biến ngẫu nhiên (X, Y) nhận giá trị trong hình chữ nhật
( X < x, y1 < Y < y2) bằng
P( X < x, y1 < Y < y2) = F(x, y2) – F(x, y1)
Ví dụ. Cho hàm phân bố xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau: s inx sin y, nÕu (x,y)D 0 , 0 ,
F(x,y) 2 2 0 , nÕu (x, y) D
Tìm xác xuất để biến ngẫu nhiên (X, Y) nhận giá trị trong hình chữ nhật giới
hạn bởi các đường thẳng x = 0, x4 , y6 và y3 . Giải. Ta có P(0 X ; Y ) = F , F 0, F , F 0, 4 6 3 4 3 3 4 6 6 = sin .sin si n0.s in sin .s in sin0.sin 4 3 3 4 6 6 2 3 1 6 2 = 2 2 2 = 4
4.2.3 Hàm mật độ xác suất của biến ngẫu nhiên hai chiều liên tục
Đối với biến ngẫu nhiên liên tục (X, Y) ngoài hàm phân bố xác suất, ta còn có
thể dùng hàm mật độ xác suất để biểu diễn quy luật phân phối xác suất của nó.
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
1) Định nghĩa. Hàm mật độ xác suất của biến ngẫu nhiên hai chiều liên tục (X, Y),
hay còn gọi là hàm mật độ xác suất đồng thời của hai biến ngẫu nhiên liên tục X và Y,
ký hiệu là f(x, y), là đạo hàm riêng hỗn hợp cấp 2 của hàm phân bố xác suất đồng thời: f(x, y) = x F y(x, y)
Ví dụ. Tìm hàm mật độ xác suất của biến ngẫu nhiên hai chiều (X, Y) nếu biết hàm
phân bố xác suất của nó: F(x, y) = sinx.siny (0 x ,0 y ) . 2 2 Giải. Ta có Fc x osx.siny
Vậy hàm mật độ xác suất đồng thời của biến ngẫu nhiên hai chiều (X, Y) là: f(x, y) = Fc osx.cosy , với 0 x ,0 y . xy 2 2 2) Tính chất
Tính chất 1. f(x, y) 0. Tính chất 2. f (x, y) dxdy 1 .
Ví dụ. Cho hàm mật độ xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau: C(2x y),n
f(x,y) Õu 2 < x < 6, 0 < y < 5
0, víi c¸c gi¸ trÞ kh¸c cña x, y Xác định tham số C. Giải. Ta có 6 5 6 5 6 1 = 25 f (x, y)dxdy C(2x y) dxdy C ( 2 x y)dy dx C(10x ) dx 210C 2 2 0 2 0 2 1 C210 . x y
Tính chất 3. F(x, y) f (u, v) dudv -
VÍ dụ. Tìm hàm phân bố xác suất đồng thời của biến ngẫu nhiên (X, Y) theo hàm mật
độ xác suất đồng thời sau đây: 1 f(x,y) (1 x )(1 y ) 2 2 2
Giải. Theo tính chất của hàm mật độ xác suất đồng thời, ta có
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu x x y y x y dudv 1 du dv F(x, y) f ( u,v) dudv (1 u )(1 v ) 1 u 1 v 2 2 2 2 2 2 - - 1 1 1 .1 arctgx+ arctgy+ 2 2
Tính chất 4. Gọi f1, f2 lần lượt là hàm mật độ xác suất biên của thành phần X và Y. Khi đó f 1(x) f (x, y)dy ; f 2(y) f (x, y)dx
Ví dụ. Hàm mật độ xác suất của biến ngẫu nhiên hai chiều (X,Y) có dạng: 3 3 2 2 4 6 9 f ( ,x y) e x xy y
Tìm hàm mật độ xác suất của các thành phần. Giải. Ta có 2 2 3 3 x x 13 3 3 2 2 x xy y
e e 3 2 y x 3 2 4 6 9 (3 ) 3 f ( )x
f( ,x )y dy e dy e
(d3 y )x . x e
(Ở đây ta áp dụng tích phân 2 u e du ) 27 2 2 2 7 y y 3 4 4 2 2 2 e e (2 ) 3 3 4 6 9 3 3 2x y x xy y 3 3 3 f (y)
f ( ,x )ydx e dx e d(2 x ) y . 2 2 2 2 27 2 3 3 y 4 e 2 Tính chất 5. P [ X, Y D
] f(x, y)dxdy D
Ví dụ 1. Tìm xác suất để (X, Y) nhận giá trị trong hình chữ nhật với các đỉnh K(1; 1),
L( 3 ; 1), N( 3; 0), M(1; 0) nếu biến ngẫu nhiên (X, Y) có hàm mật độ sau: f(x, y) = 1 2 2 2 (1 x )(1 y ) Giải. Ta có 3 1 P[(X, Y) D] = 1 1 = dx dy . 2 2(1 x )2(1 y ) dxdy 2 = 1 2 2 1 x 1 y 48 D 1 0
Ví dụ 2. Cho hàm mật độ xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau:
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu 1(2x y),n f (x,y) 210
Õu 2 < x < 6, 0 < y < 5 0
, víi c¸c gi¸ trÞ kh¸c cña x, y
Tìm xác suất P(3 < X < 4, Y > 2). Giải. Ta có 4 5 4 5 4 P 1 1 1 21 3
3 X 4,Y 2
(2 )xy dxdy (2 )
x y dy dx 6 x dx . 210 210 210 2 20 3 2 3 2 3
Ví dụ 3. Cho hàm mật độ phân bố xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau: 8 xy,n
f(x,y) Õu 0 < x < 1, 0 < y < x 0
, víi c¸c gi¸ trÞ kh¸c cña x, y 1
Tìm xác suất P(0 < X < , 0 < Y < x). 2 Giải. Ta có 1 1 1 x x 2 2 2 3
P(0 < X < 1 , 0 < Y < x) = f(x,y)dxdy 8xydxdy 4 x dx 0,0625 2 . 0 0 0 0 0
4.3 Quy luật phân phối xác suất có điều kiện của các biến ngẫu nhiên thành phần
4.3.1 Bảng phân phối xác suất có điều kiện
Xét biến ngẫu nhiên hai chiều rời rạc (X, Y), trong đó tập các giá trị mà X có
thể nhận là {x1, x2, …, xn}, còn tập các giá trị mà Y có thể nhận là {y1, y2, …, ym}.
Bảng phân phối xác suất có điều kiện của thành phần X với điều kiện Y = yj có dạng X/Y=yj x1 x2 . . xi . . xn P
P(x1/yj) P(x2/yj) … P(xi/yj) … P(xn/yj)
trong đó : P(xi/yj) = P(X = xi/Y = yj) (i 1,
n; j 1,m) là xác suất có điều kiện của thành
phần X nhận giá trị bằng xi với điều kiện thành phần Y nhận giá trị bằng yj được tính bằng công thức: P(x P(x , y ) ;(i 1,n) i/yj) = i j P(Y y ) j n Chú ý. P(x / y ) 1 i j i 1
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
Tương tự, bảng phân phối xác suất có điều kiện của thành phần Y với điều kiện
X = xi có dạng Y/X=xi y1 y2 … yj … ym P
P(y1/xi) P(y2/xi) … P(yj/xi) … P(ym/xi)
trong đó các xác suất có điều kiện được tính bằng công thức P(y P(x , y ) ;(j 1, m) j/xi) = i j P(X x ) i m Chú ý. P(y / x ) 1 j i j 1
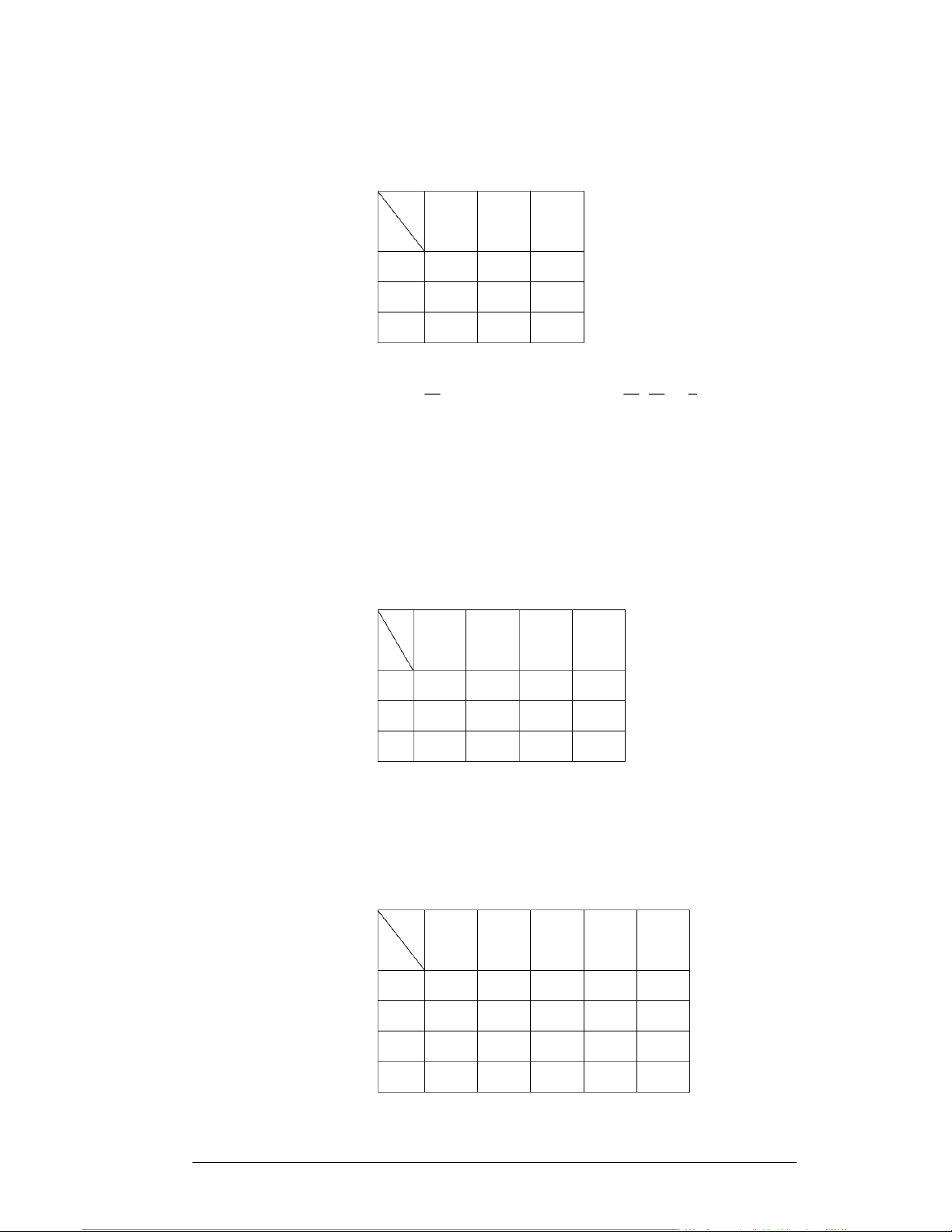
Ví dụ. Cho biết bảng phân phối xác suất của biến ngẫu nhiên hai chiều (X, Y), trong
đó X = "Doanh thu", Y = "Chi phí quảng cáo" như sau: (Đơn vị tính: Triệu đồng) Y X 100 150 200 0 0,1 0,05 0,05 1 0,05 0,2 0,15 2 0 0,1 0,3
Tìm phân phối xác suất của doanh thu khi không có quảng cáo và khi chi phí
quảng cáo là 2 triệu đồng.
Giải. +) Ta có: P(Y = 0) = 0, 1 + 0,05 + 0,05 = 0,2 P 0)X 0,1 0, 100 / 5. Y 0 P(X 100, Y P(Y 0) 0,2 P X P(X 150,Y 0) 0,05 150 / Y 0 ) 0,2 0,25. P(Y 0 P X P(X 200,Y 0) 0,05 200 / Y 0 0) 0, 2 . 0,25 P(Y
Vậy bảng phân phối xác suất của doanh thu khi không có quảng cáo là X/Y =0 100 150 200 P 0,5 0,25 0,25
+) Ta có: P(Y = 2) = 0 + 0,1 + 0,3 = 0,4 P(X=100/Y=2) = P(X 100, Y 2) = 0 = 0 P(Y 2) 0,4
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu P(X=150/Y=2) = P(X 150, Y 2) = 0,1 = 0,25 P(Y 2) 0,4 P(X=200/Y=2) = P(X 200 ,Y 2) = 0,3 = 0,75 P(Y 2) 0,4
Vậy bảng phân phối xác suất của doanh thu khi chi phí quảng cáo là 2 triệu đồng là X/Y =2 100 150 200 P 0 0,25 0,75
4.3.2 Hàm mật độ xác suất có điều kiện
Giả sử (X, Y) là biến ngẫu nhiên hai chiều liên tục. Hàm mật độ xác suất có
điều kiện của thành phần X với Y = y, ký hiệu là f(x/y) là biểu thức: f x f (x, y) f (x, y) / y . 2 f (y) f (x, y)d x
Tương tự, hàm mật độ xác suất có điều kiện của thành phần Y với X = x, ký
hiệu là f(y/x) là biểu thức: f(y/x) = f(x, y) f(x,y) f (x) f (x, y)dy 1
Chú ý: f(x/y) 0 và f(x / y)dx 1
f(y/x) 0 và f(y/ x)dy 1.
Ví dụ. Hàm mật độ xác suất của biến ngẫu nhiên hai chiều có dạng: 3 3 2 2 4 6 9 f ( ,x y) e x xy y
Tìm hàm mật độ xác suất có điều kiện của các thành phần. 227 2 Giải. Ta có: 3 34x 3 3 f (x ) e ,f (y ) 2 y 1 2 e
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu 2 2 3 3 4 x 6 9xy y 3 e 2 (2 ) f ( ,x ) y 2 x y 2 f (x/ ) y ( ) 3 3 e 27 2 f 24 y e y 2 3 3 2 2 4 x 6 9xy y e f x y 2 ( , ) 3 (x y3 )
f (y /x ) ( ) 3 e f x e 2 1 3 x
Trên cơ sở các phân phối xác suất có điều kiện, ta có các công thức sau:
+) Nếu (X, Y) là biến ngẫu nhiên hai chiều rời rạc, trong đó tập các giá trị mà X có thể
nhận là {x1, x2, …, xn}, còn tập các giá trị mà Y có thể nhận là {y1, y2, …, ym} thì P(x ,y ) P ( X x )P(y / x ) = P(Y= ) y P(x / y ) ; vớii1,n; j 1,m i j i j i j i j
Đặc biệt: X và Y độc lập với nhau khi và chỉ khi P(xi, yj) = P(X = xi).P(Y = yj), với mọi i1,n; j 1,m
+) Nếu (X, Y) là biến ngẫu nhiên hai chiều liên tục thì
f(x, y) = f1(x)f(y/x) = f2(y)f(x/y)
Đặc biệt: X và Y độc lập với nhau khi và chỉ khi f(x, y) = f1(x)f2(y).
4.4 Tham số đặc trưng của biến ngẫu nhiên hai chiều:
4.4.1 Kỳ vọng và phương sai của biến ngẫu nhiên thành phần.
1) Nếu (X, Y) là biến ngẫu nhiên 2 chiều rời rạc, trong đó tập các giá trị mà X có thể
nhận là {x1, x2, …, xn}, còn tập các giá trị mà Y có thể nhận là {y1, y2, …, ym} thì: n n m E X i x P(X ix ) i x P( ix j, y ) i 1 i 1 j 1 n n m V X E X – E X 22 2 2 2 2 x P(X x ) X
x P(x , y ) E X i i E i i j i 1 i 1 j 1 m m n E Y y j P(Y yj) yjP(xi j, y ) j 1 j 1 i 1 m m n V Y E Y – E Y 2 2 2 2 2 2 y P(Y y ) Y y P(x , y) E Y j j E j i j j 1 j 1 i 1
Ví dụ. Cho (X, Y) là biến ngẫu nhiên hai chiều có bảng phân phối xác suất đồng thời như sau:
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu Y X 100 150 200 0 0,1 0,05 0,05 1 0,05 0,2 0,15 2 0 0,1 0,3 Tìm E(X), V(X), E(Y), V(Y). Giải. Y X 100 150 200 P(yj) 0 0,1 0,05 0,05 0,2 1 0,05 0,2 0,15 0,4 2 0 0,1 0,3 0,4 P(xi) 0,15 0,35 0,5
E(X) = 100.P(X = 100) + 150.P(X = 150) + 200.P(X = 200) = 100.0,15 + 150.0,35 + 200.0,5 = 167,5
V(X) = (1002.P(X = 100) + 1502.P(X = 150) + 2002.P(X = 200)) – [E(X)]2
= (1002.0,15 + 1502.0,35 + 2002.0,5) ( – 167,5)2 = 29375 28056,25 = – 1318,75
E(Y) = 0.P(Y = 0) + 1.P(Y = 1) + 2.P(Y = 2) = 0.0,2 + 1.0,4 + 2.0,4 = 1,2
V(Y) = (02.P(Y = 0) + 12.P(Y = 1) + 22.P(Y = 2)) – [E(Y)]2
= (02.0,2 + 12.0,4 + 22.0,4) – (1,2)2 = 2 – 1,44 = 0,56
b) Nếu (X, Y) là biến ngẫu nhiên 2 chiều liên tục thì: E X xf (x)dx xf (x, y) ; 1 dxdy V X 2 2 2 2 x f 1(x)dx E X x f(x,y) E dxdy X .
E Y yf (y)dy yf(x,y) ; 2 dxdy V 2 2 2 2 Y y f 2 (y)dy E Y y f(x,y) E dxdy Y .
Ví dụ. Cho hàm mật độ phân bố xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau: 1 (2x y),n f (x,y) 210
Õu 2 < x < 6, 0 < y < 5 0
, víi c¸c gi¸ trÞ kh¸c cña x, y
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu Tìm E(X), V(X), E(Y), V(Y). Giải. Ta có 6 5 6 E(X) = 1x(2x y) 1 2144 268 xf (x, y)dxdy = 21 0 dxdy = x(4x 5) dx 84 504 63 2 0 2 6 5 2 2 V(X) = 2 1x (2x y) 2 68 x f (x, y) dxdy [ E(X)] = - 2 21 0 dxdy 63 2 0 62 1x (4x 5) 2 1220 2 5036 = 2 68 2 68 84 dx - = = 63 63 - 63 3969 . 2 6 5 1y(2x y) 5 1y(2y 16)dy
E(Y) = yf(x,y)dxdy = 21 0 dxdy = 105 = 170 63 2 0 0 6 5 2 V(Y) = 2 y f (x, y) 1y (2x y) dxdy - [E(Y)]2 = 21 0 dxdy - [E(Y)]2 2 0 52 1y (2y 16)dy 2 170 2 1175 170 = 105 - = = 16225 63 126 63 7938 0
4.4.2 Hiệp phương sai và hệ số tương quan
Hiệp phương sai và hệ số tương quan là các số đặc trưng cho mức độ chặt chẽ
của sự phụ thuộc giữa các biến ngẫu nhiên.
1) Hiệp phương sai
a) Định nghĩa. Hiệp phương sai của các biến ngẫu nhiên X và Y, ký hiệu Cov(X, Y),
là kỳ vọng của tích các sai lệch của các biến ngẫu nhiên đó với kỳ vọng của chúng:
CovX , Y E X
– E X Y – E Y E XY –
E X E Y Đặc biệt: n m
i) Nếu (X, Y) là biến ngẫu nhiên rời rạc thì Cov X, Y x i jy P(ix , jy ) E(X)E(Y) i 1 j 1
ii) Nếu (X, Y) là biến ngẫu nhiên liên tục thì CovX, Y
xyf(x,y)dxdy E(X)E(Y) b) Tính chất
i) Nếu X, Y độc lập thì Cov(X, Y) = 0.
Điều ngược lại chưa chắc đã đúng, tức là nếu Cov(X, Y) = 0 thì X và Y có thể độc lập, có thể phụ thuộc.
Ví dụ 1. Cho hai biến ngẫu nhiên X và Y có bảng phân phối xác suất đồng thời như sau:
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu Y -1 0 1 X -1 4/15 1/15 4/15 0 1/15 2/15 1/15 1 0 2/15 0
Cov(X, Y) = 0 nhưng X và Y không độc lập vì
P(X = -1, Y = -1) = 4 P(X = -1).P(Y = -1) = 9 . 5 = 1 . 15 15 15 5
ii) Nếu X và Y là hai biến ngẫu nhiên phụ thuộc thì 2 2 V aX ( b Y ) a V X ( ) b V Y ( )a 2 bCov X (Y , )
Đặc biệt: Nếu a = b = 1 thì V X (
Y )V X ( V)Y ( )C 2 ov X (Y , )
Ví dụ 2. Có hai loại cổ phiếu A, B được bán trên thị trường chứng khoán và lãi suất
của chúng là 2 biến ngẫu nhiên X, Y tương ứng (Đơn vị tính là %). Giả sử (X, Y) có
bảng phân bố xác suất như sau: Y -2 0 5 10 X 0 0 0,05 0,05 0,1 4 0,05 0,1 0,25 0,15 6 0,1 0,05 0,1 0
a) Nếu mục tiêu là nhằm đạt được lãi suất kỳ vọng là lớn nhất thì nên đầu tư vào cả hai
loại cổ phiếu trên theo tỷ lệ nào?
b) Muốn hạn chế rủi ro về lãi suất đến mức thấp nhất thì nên đầu tư vào hai loại cổ
phiếu trên theo tỷ lệ nào? Giải. Y -2 0 5 10 P(xi) X 0 0 0,05 0,05 0,1 0,2 4 0,05 0,1 0,25 0,15 0,55 6 0,1 0,05 0,1 0 0,25 P(yj) 0,15 0,2 0,4 0,25
E(X) = 0.0,2 + 4.0,55 + 6.0,25 = 3,7%; V(X) = (02.0,2 + 42.0,55 + 62.0,25) – 3,72 = 4,11
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu E(Y) = 4,2%; V(Y) = 17,96
a) Nếu ký hiệu là tỷ lệ đầu tư vào cổ phiếu A thì ta có tỷ lệ đầu tư vào cổ phiếu B là
(1 - ). Vậy ta phải tìm sao cho E(X + (1 - )Y) max
Ta có E(X + (1 - )Y) = E(X) + (1 - )E(Y) = .3,7 + (1 - )4,2 = 4,2 – 0,5
E(X + (1 - )Y) max khi = 0. Tức là muốn đạt được lãi suất kỳ vọng là lớn
nhất thì phải đầu tư vào mua toàn bộ cổ phiếu B.
b) Xác định sao cho V(X + (1 - )Y) min
Ta có: P(X = 0, Y = -2) P(X = 0).P(Y = -2) = 0,2.0,15 = 0,03 X, Y là hai biến phụ thuộc.
Do đó V(X + (1 - )Y) = 2V(X) + (1 - )2V(Y) + 2(1 - )Cov(X, Y)
Cov(X, Y) = x y p(x , y ) - E(X)E(Y) = 12,4 – 3,7.4,2 = -3,14 i j i j
V(X + (1 - )Y)=4,112 +17,96(1 - )2 + 2(1 - )(-3,14) = 28,352 – 42,2 + 17,96 = f()
f'() = 56,7 - 42,2 = 0 = 0,7443. 'f( ) 56,7 0
Vậy, V(X + (1 - )Y) min khi = 0,7443.
Kết luận: Nếu đầu tư vào cổ phiếu A và B theo tỷ lệ 74,43% và 25,57% sẽ có mức
độ rủi ro là thấp nhất.
Từ định nghĩa trên ta thấy, hiệp phương sai có đơn vị đo lường bằng tích đơn vị
đo lường của biến ngẫu nhiên X và Y. Do đó, hiệp phương sai sẽ có các giá trị khác
nhau tùy thuộc vào đơn vị đo lường của các biến đó. Vì vậy, hiệp phương sai thường
không có ý nghĩa và cũng không phản ánh chính xác mức độ chặt chẽ của sự phụ
thuộc giữa các biến ngẫu nhiên X và Y. Để khắc phục hạn chế này người ta đưa ra một
tham số là hệ số tương quan.
2) Hệ số tương quan
a) Định nghĩa. Hệ số tương quan của hai biến ngẫu nhiên X và Y, ký hiệu là , là tỷ XY
số giữa hiệp phương sai và tích các độ lệch chuẩn của biến ngẫu nhiên đó: Cov(X,Y) XY . X Y b) Tính chất
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu i) . XY YX i i) 1 1 . XY
iii) Nếu X và Y độc lập với nhau th ì XY 0 .
Điều ngược lại chưa chắc đã đúng, tức là nếu XY 0
thì X và Y có thể độc lập, có thể phụ thuộc.
c) Ý nghĩa. Hệ số tương quan được dùng để đo mức độ phụ thuộc tuyến tính giữa XY
hai biến ngẫu nhiên X và Y. Nếu | |
càng gần gần 1 thì mức độ phụ thuộc tuyến XY
tính giữa X và Y càng chặt. Đặc biệt nế u X Y 1
thì a, b R sao cho Y = aX + b. Nếu | |
càng gần gần 0 thì mức độ phụ thuộc tuyến tính giữa X và Y càng yếu. Đặc XY
biệt, nếu = 0 thì 2 biến X và Y không có mối quan hệ tuyến tính. XY
Định nghĩa. Hai biến ngẫu nhiên X và Y được gọi là tương quan với nhau nếu XY 0
. Trường hợp ngược lại, nếu
XY 0 thì ta nói X và Y không tương quan. Chú ý.
i) Nếu hai biến ngẫu nhiên tương quan với nhau thì cũng phụ thuộc nhau. Song điều
ngược lại chưa chắc đã đúng, tức là nếu các biến ngẫu nhiên phụ thuộc thì chúng có
thể tương quan nhưng cũng có thể không tương quan với nhau.
Ví dụ 3. Hai biến ngẫu nhiên X và Y trong vídụ 1 phụ thuộc nhau nhưng chúng không tương quan với nhau.
ii) Nếu hai biến ngẫu nhiên X và Y độc lập với nhau thì chúng không tương quan với nhau.
Ví dụ 4. Cho biết bảng phân phối xác suất của biến ngẫu nhiên hai chiều (X, Y), trong đó
X = "Doanh thu", Y = "Chi phí quảng cáo" như sau: (Đơn vị tính: Triệu đồng) Y X 100 150 200 0 0,1 0,05 0,05 1 0,05 0,2 0,15 2 0 0,1 0,3
Doanh thu và chi phí quảng cáo có tương quan với nhau không? Giải. Cov(X, Y) = x y P(x , y ) E(X)E(Y) i j i j
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
= (100.0.0,1 + 100.1.0,05 + 100.2.0 + 150.0.0,05 + 150.1.0,2 +
150.2.0,1 + 200.0.0,05 + 200.1.0,15 + 200.2.0,3) – 167,5.1,2 = 215 – 201 = 14 Cov(X,Y) 14 0,5152 0. XY V(X).V(Y) 1318,75.0,56
Vậy, doanh thu và chi phí quảng cáo có tương quan với nhau
Ví dụ 5. Cho hàm mật độ phân bố xác suất của biến ngẫu nhiên hai chiều (X, Y) như sau: 1 (2x y),n f (x,y) 210
Õu 2 < x < 6, 0 < y < 5 0
, víi c¸c gi¸ trÞ kh¸c cña x, y
X và Y có tương quan với nhau không? Giải. Ta có 6 5 Cov(X, Y) = x 1 yf(x,y)dxdy - E(X)E(Y) = xy 210 (2 x y)dxdy - E(X)E(Y) 2 0 = 80 268 170 200 . 7 63 63 3969 Cov(X,Y) 2 00/3969 0,03129 XY V(X).V(Y) 5036/3969 16225/7938
Vậy, X và Y có tương quan với nhau.
4.5 Kỳ vọng có điều kiện, hàm hồi quy
4.5.1 Kỳ vọng có điều kiện:
1) Nếu (X, Y) là biến ngẫu nhiên rời rạc, trong đó tập các giá trị mà X có thể nhận là
{x1, x2, …, xn}, còn tập các giá trị mà Y có thể nhận là {y1, y2, …, ym}, thì kỳ vọng
toán có điều kiện của biến ngẫu nhiên Y với X = xi được xác định như sau: m E
Y / X x y P(Y y / X x ) . i1 j j i j
Tương tự, kỳ vọng toán có điều kiện của X khi Y = yj: EX n
/ Y y x P(X x / Y y ). j1 i i j i
2) Nếu (X, Y) là biến ngẫu nhiên liên tục thì kỳ vọng toán có điều kiện của biến ngẫu
nhiên Y với X = x được xác định như sau: EY/ X x , yf(y/x)dy
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
trong đó f(y/x) là hàm mật độ xác suất có điều kiện của Y với X = x.
Tương tự, kỳ vọng toán có điều kiện của X khi Y = y: EX/ Y y , xf(x/y)dx
trong đó f(x/y) là hàm mật độ xác suất có điều kiện của X với Y = y. 4.5.2 Hàm hồi quy
Định nghĩa. Hàm hồi quy của Y đối với X là kỳ vọng toán có điều kiện của Y đối với X: f(x) = E(Y/X=x)
Tương tự, hàm hồi quy của X đối với Y là kỳ vọng toán có điều kiện của X đối với Y: f(y) = E(X/Y=y)
Ý nghĩa. Các hàm hồi quy cho biết giá trị trung bình của biến ngẫu nhiên này phụ
thuộc vào biến kia như thế nào.
Ví dụ 1. Cho biết bảng phân phối xác suất của biến ngẫu nhiên hai chiều (X, Y), trong
đó X = "Doanh thu", Y = "Chi phí quảng cáo" như sau: (Đơn vị tính: Triệu đồng) Y X 100 150 200 0 0,1 0,05 0,05 1 0,05 0,2 0,15 2 0 0,1 0,3
Xác định doanh thu trung bình theo chi phí quảng cáo.
Giải. Doanh thu trung bình theo chi phí quảng cáo là kỳ vọng có điều kiện của X theo Y.
Ta có bảng phân phối xác suất của doanh thu khi không có quảng cáo là X/Y =0 100 150 200 P 0,5 0,25 0,25
E(X/Y=0) = 100.0,5 + 150.0,25 + 200.0,25 = 137,5
Bảng phân phối xác suất của doanh thu khi chi phí quảng cáo là 1 triệu đồng là X/Y =1 100 150 200 P 0,05 0,125 0,4 0,2 0,5 0,4 0,15 0,375 0,4
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu
E(X/Y=1) = 100.0,125 + 150.0,5 + 200.0,375 = 162,5
Bảng phân phối xác suất của doanh thu khi chi phí quảng cáo là 2 triệu đồng là X/Y =2 100 150 200 P 0 0,25 0,75
E(X/Y=2) = 100.0 + 150.0,25 + 200.0,75 = 187,5
Ví dụ 2. Biến ngẫu nhiên (X, Y) có hàm mật độ phân bố xác suất như sau: 8 xy,n f(x,y) Õu 0
0, víi c¸c gi¸ trÞ kh¸c cña x, y
Tìm kỳ vọng có điều kiện E(X/Y=y), E(Y/X=x). Giải. Ta có x3 8xydy,n 4 Õ x u , 0 < xn (x) f ( x,y)dy < 1 Õu 0 < x < 1 f0, nÕu x (0;1) 1 0 0 , nÕu x (0;1) 1 2 8xydx,n 4 Õ y u (1 0 < y y ) <, n 1 Õu 0 < y < 1 f0, nÕu y (0 ; 1) 2 ( y) f ( x, y)dx y 0, nÕu y (0;1) 2x ,n f(x,y) Õu y 2 f(x/y)= f0, v 1 íi y (y) c¸c gi¸ trÞ kh¸c cña x 2 2y ,n f(x,y) 2 f(y/x)= f0, víi c x Õu 0 (x) ¸c gi¸ trÞ kh¸c cña y 1 13 2 Ta có: 2x 2(1 y ) 2(1 y y ) E(X/Y y) xf(x/ y)dx x dx 2 2 1 y 3(1 y ) 3(1 y) y x 2y 2x E(Y/ X x) yf (y / x)dy y dy . 2 x 3 0
GV: Nguyễn Dương Nguyễn, BM Toán, Khoa Cơ bản, FTU 20:33, 27/01/2026
Chương 4: Biến Ngẫu Nhiên Hai Chiều và Phân Phối Xác Suất XSTK - Studocu




