
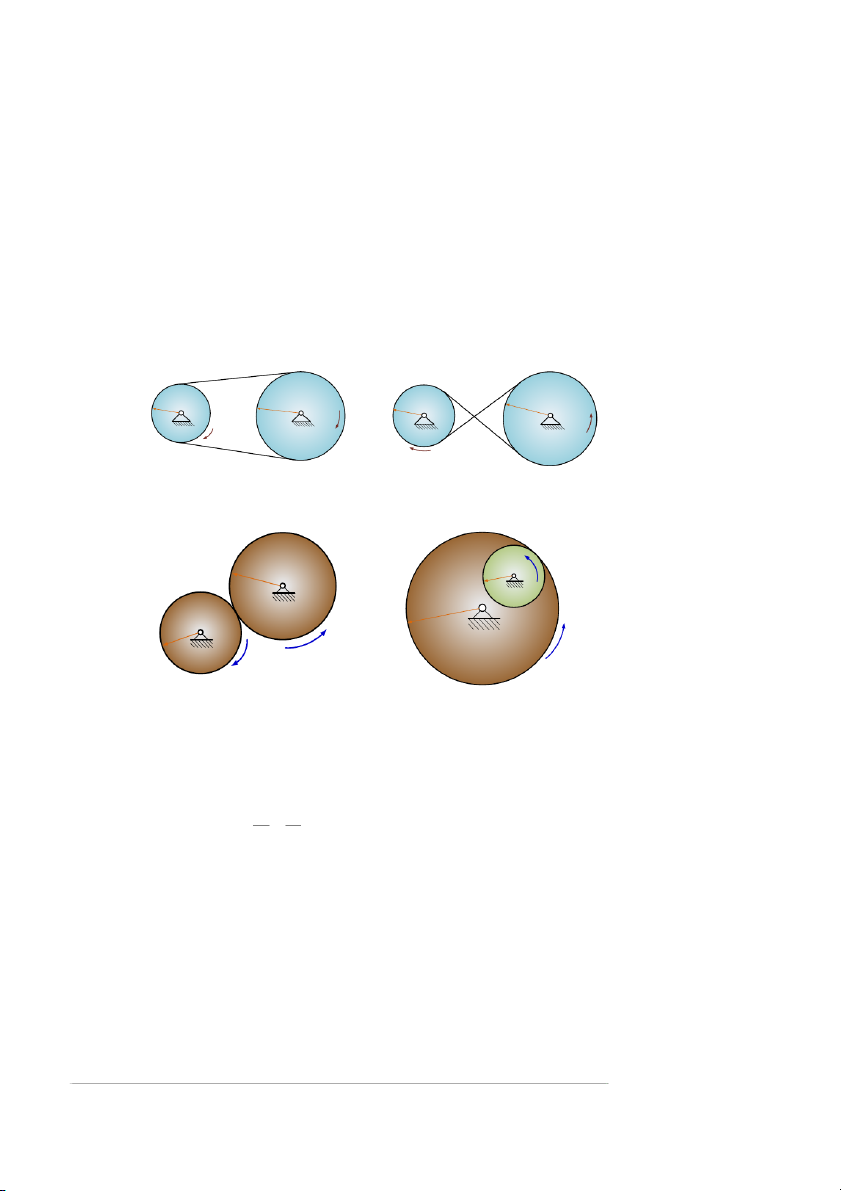
Preview text:
Cơ học kỹ thuật Nguyễn Hoàng Châu Chương 4
CHUYỂN ĐỘNG CƠ BẢN CỦA VẬT RẮN
1. MỤC TIÊU CỦA CHƯƠNG
- Nắm vững các định nghĩa chuyển động cơ bản của vật rắn
- Nắm vững cách xác đinh phương trình chuyển động, xác định á
c c thông số cơ bản của vật
rắn quay quanh trục cố định.
- Hiểu các biểu thức tính vận tốc, gia tốc trong các trường hợp chuyển động.
- Phân tích các chuyển động của hệ vật rắn, tìm quan hệ động học của các vật.
- Vận dụng các quan hệ động học, xác định ứng xử của từng vât trong cơ hệ.
- Vận dụng các loại truyền động, tìm ứng xử khi hệ vật rắn có thêm nhiều bộ truyền động đơn giản.
- Đánh giá các ứng xử tìm được trong bài toán cơ hệ thực tế.
2. CHUYỂN ĐỘNG TỊNH TIẾN 2.1. Định nghĩa
Vật rắn chuyển động tịnh tiến khi bất kỳ đường thẳng nào thuộc vật cũng song song chính nó
trong quá trình chuyển động.
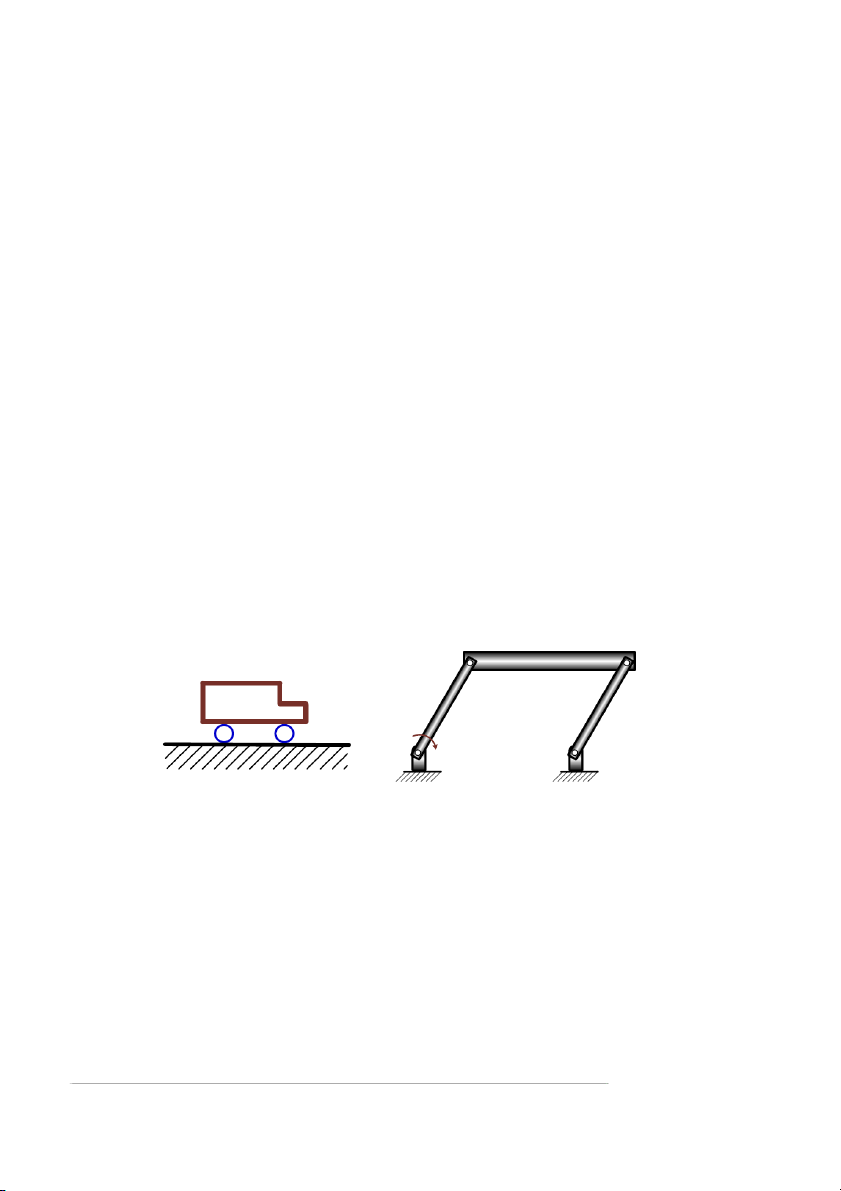
Ví dụ: Xe chuyển động trên đường thẳng (hình 4.1), thanh truyền BC trong cơ cấu hình bình hành ABCD (hình 4.2). B C A ω D hình 4.1 hình 4.2
2.2. Tính chất chuyển động
Định lý: tất cả các điểm thuộc vật chuyển động tịnh tiến đều có có cùng quĩ đạo, mỗi thời điểm
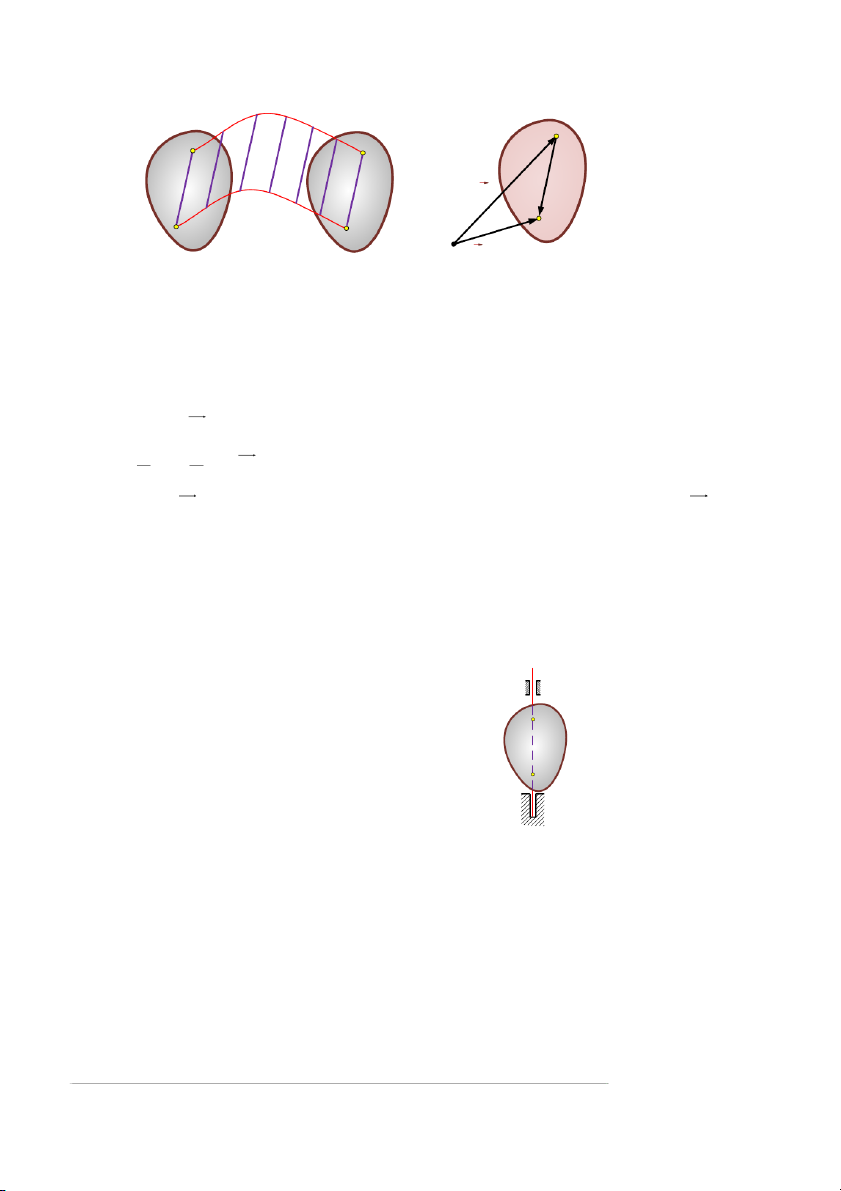
chúng có cùng vận tốc và gia tốc. 20 B B B1 rB A A A 1 r O A hình 4.3 hình 4.4 Chứng minh:
- Các đoạn cong nhỏ song song. Quĩ đạo là tập hợp vô số đoạn cong nhỏ nên quĩ đạo của A song
song với B chúng song song (hình 4.3).
- Lấy hai điểm A, B thuộc vật (hình 4.4), ta có :
r = r + BA A B d d (r ) = (r + B ) A (a) dt A dt B
Vectơ BA có phương chiều không đổi, độ dài đoạn BA không đổi vì thuộc vật rắn nên BA là vectơ hằng. Vậy từ (a) : v = v A B Từ đó a = a A B
3. CHUYỂN ĐỘNG QUAY CỦA VẬT RẮN QUANH TRỤC CỐ ĐỊNH 3.1. Định nghĩa
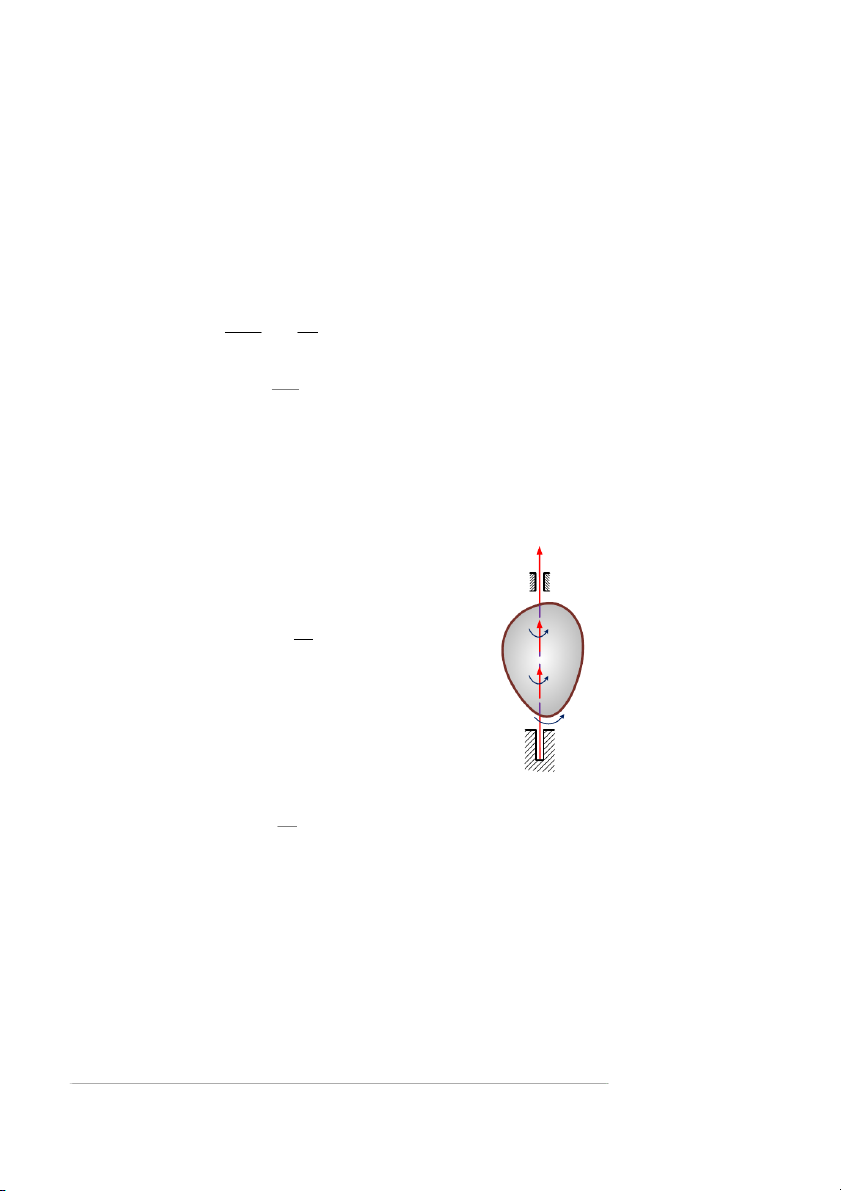
Vật rắn chuyển động mà có ít nhất 2 điểm thuộc Z
vật cố đinh gọi là vật quay quanh trục, đường B
thẳng đi qua hai điểm đó gọi là trục quay.
Hình (4.5) là mô hình không gian của vật rắn A
quay quanh trục cố định. Hai điểm A, B cố định
z là trục quay của vật rắn hình 4.5
3.2. Phương trình chuyển động
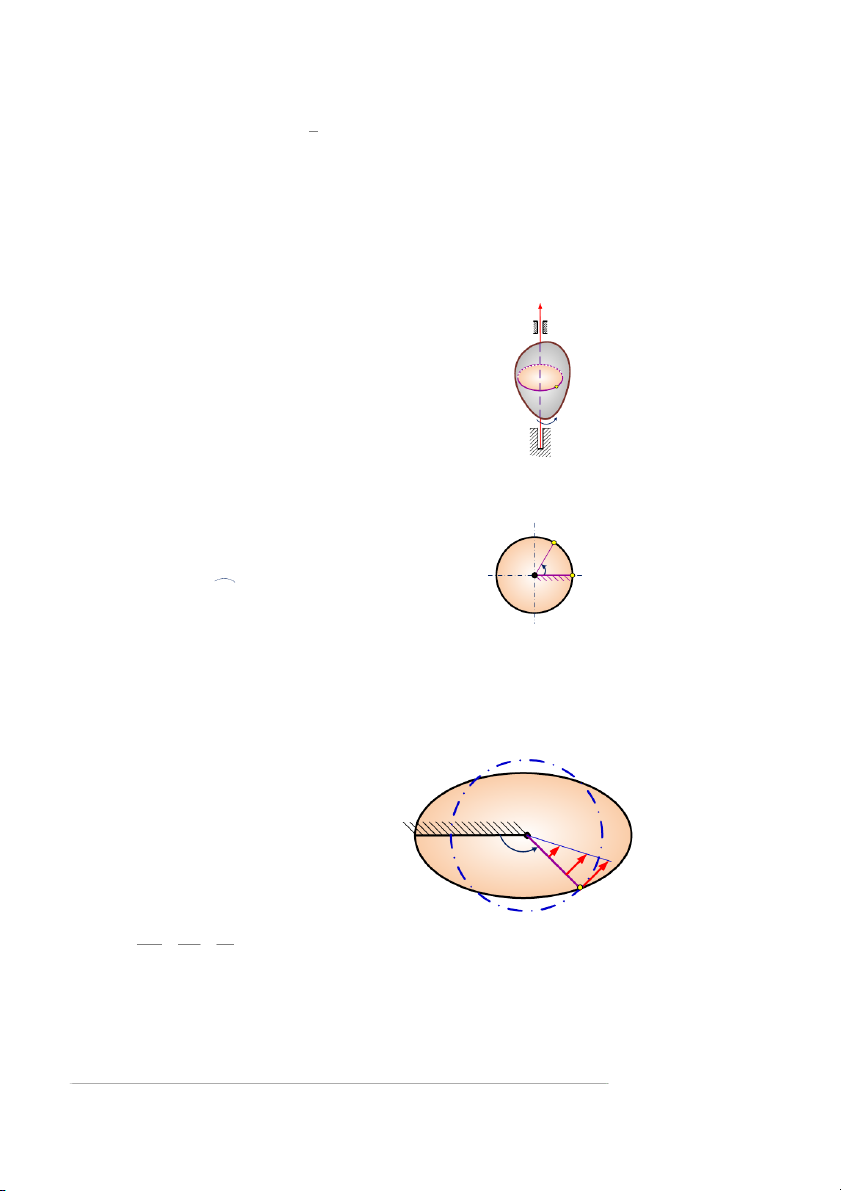
Dựng mặt phẳng P cố định và chứa trục quay. Dựng mặt phẳng Q chứa trục quay và gắn liền
với vật rắn (hình 4.6). Vị trí của vật rắn xác định khi xác định được vị trí mặt phẳng Q nghĩa là
xác định góc nhị diện φ. Vật quay nên φ thay đổi theo thời gian. φ = φ(t) (4.1)
Là phương trình chuyển động của vật. 21 Z φ C M1 φ M2 P hình 4.7 Q hình 4.6
Mô hình phẳng: Giao của mặt phẳng R vuông góc với trục quay và cắt vật cho ta mô hình
phẳng để khảo sát vật rắn quay (hình 4.7). Góc φ tạo bỡi hai tia CM1 và CM2 là g a i o tuyến của R với P và Q.
Chiều quay dương thường được chọn là ngược chiều kim đồng hồ.
Quan hệ giữa góc quay (rad) và số vòng quay N(vòng): = 2 N
3.3. Vận tốc góc - Gia tốc góc
Vận tốc góc và gia tốc góc là hai đại lượng cơ bản của chuyển động quay.
3.3.1. Vận tốc góc
Vận tốc góc của vật đặc trưng cho tốc độ thay đổi của góc quay, là đạo hàm góc quay theo thời gian. d = = (4.2) dt
Đơn vị của vận tốc góc là rad/s hay 1/s.
Dấu của vận tốc góc cho biết chiều quay của vật 0 thì vật quay theo chiều dương và 0 vật quay theo chiều âm.
Quan hệ giữa vận tốc góc ω(rad/s) và số vòng quay n(v/ph): n = (4.3) 30
3.3.2. Gia tốc góc
Gia tốc góc của vật đặc trưng cho sự thay đổi vận tốc góc, là đạo hàm vận tốc góc theo thời gian. d d 2 = = = (4.4) 2 dt dt
Đơn vị của gia tốc góc là rad/s2 hay 1/s2. 22
3.3.3. Chuyển động quay đều - biến đổi đều
Gia tốc góc của vật đặc trưng cho sự thay đổi vận tốc góc nên:
• Khi = 0 → = const : vật quay đều.
• Khi = const : chuyển động quay biến đổi đều. • Khi .
0 : chuyển động quay nhanh dần. Chứng minh: d( )2 d Ta có: = 2 = 2 . dt dt 2 d > 0 thì 0 2 dt
Hàm (t) hay (2 (t)) đồng biến nên chuyển động quay nhanh dần.
3.4. Vectơ vận tốc góc - Vectơ gia tốc góc
Để mô tả vật rắn quay một cách đầy đủ về trục quay, chiều quay, tính chất chuyển động người
ta đưa ra đại lượng vectơ vận tốc góc, vectơ gia tốc góc (hình 4.8) Vectơ vận tốc góc có: Z
• Phương nằm trên trục quay.
• Chiều theo qui tắc bàn tay phải. d
• Cường độ: | |= = . dt ω
Vectơ gia tốc góc có: ε
• Phương nằm trên trục quay. φ
• Cùng chiều vectơ vận tốc góc khi chuyển
động nhanh dần, ngược chiều vectơ vận tốc
góc khi chuyển động chậm dần. hình 4.8 d
• Cường độ: | | = | |. dt
Gọi k là vectơ đơn vị chỉ phương trên trục quay, ta c ó : = k và = k
3.5. Chuyển động quay đều - biến đổi đều
3.5.1. Chuyển động quay biến đổi đều: = const
Vận tốc góc : = t 0 23 1 Góc quay : 2
= + t t 0 0 2
Các công thức trên lấy dấu + khi chuyển động nhanh dần, dấu – khi chuyển động chậm dần.
3.5.2. Chuyển động quay đều
= const → = t
4. KHẢO SÁT CHUYỂN ĐỘNG CỦA ĐIỂM THUỘC VẬT QUAY
4.1. Quĩ đạo
Quĩ đạo của điểm M thuộc vật rắn quay quanh Z
trục là đường tròn nằm trong mặt phẳng vuông
góc với trục quay (hình 4.9).
Vì quĩ đạo của điểm đã xác định nên ta khảo sát M
chuyển động của điểm theo phương pháp tọa độ tự φ nhiên. hình 4.9
4.2. Phương trình chuyển động
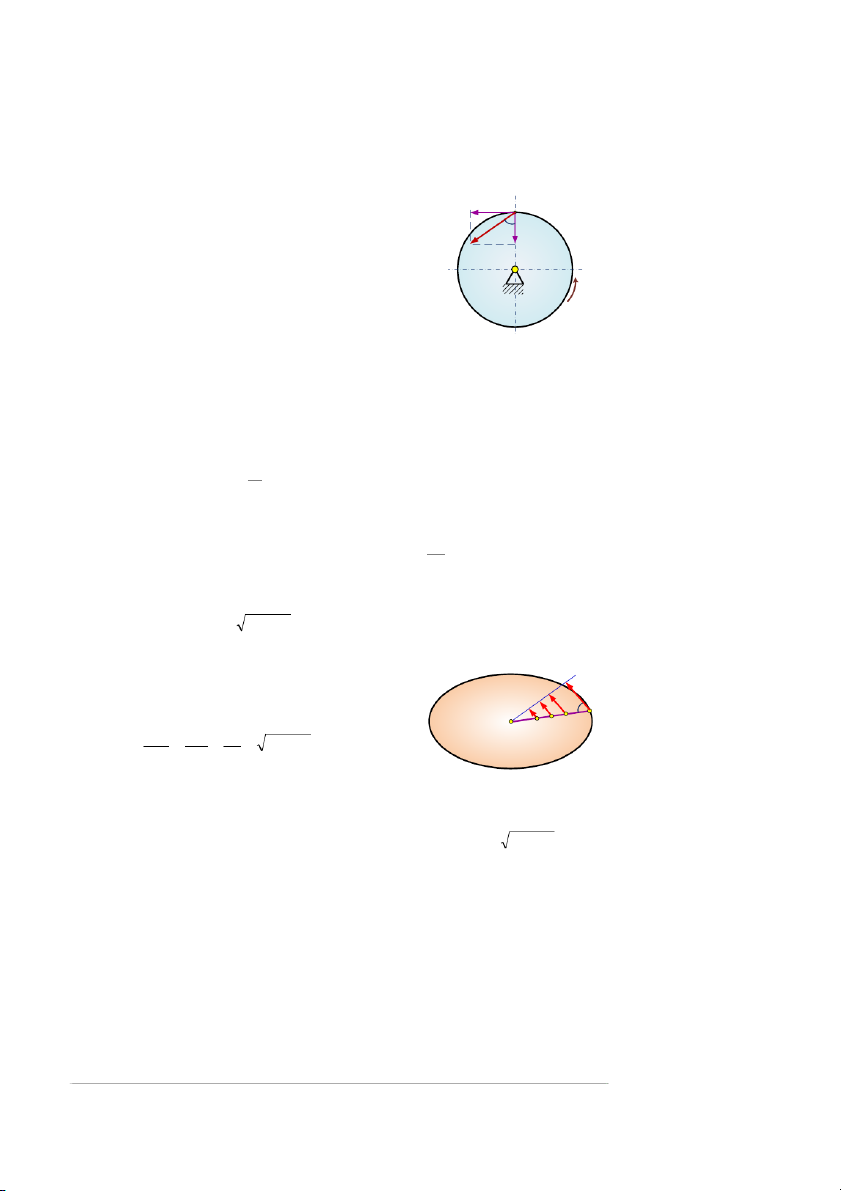
Chọn điểm gốc M0 trên quĩ đạo (hình 4.10). Vị trí M
của điểm M được xác định bằng độ dài cung: φ M s = M M C 0 0
Vậy phương trình chuyển động của điểm: s = R (t) hình 4.10
4.3. Vận tốc của điểm thuộc vật quay quanh trục cố định
Trong hệ tọa độ tự nhiên vận tốc điểm M nằm trên trục tiếp tuyến, cùng chiều chuyển động. v = v = s → v = = Rω R (4.5) t
Vectơ vận tốc của điểm có:
• Phương: vuông góc bán kính.
• Chiều: cùng chiều vận tốc góc. C vI v
• Cường độ: bằng tích trị số vận tốc N φ v I M góc và bán kính. N Các điểm M, N M , I thuộc vật, ta có: v v v hình 4.11 M = N = I = CM CN CI
Vậy: vận tốc các điểm phân bố theo qui luật tam giác vuông đồng dạng (hình 4.11).
4.4. Gia tốc của điểm 24
Điểm thuộc vật quay chuyển động trên quĩ đạo cong nên gia tốc có hai thành phần là gia tốc tiếp
và gia tốc pháp (hình 4.12).
4.4.1. Gia tốc tiếp Gia tốc tiếp có: a A t
• Phương vuông góc bán kính. α a a n
• Chiều cùng chiều gia tốc góc. ε • Có giá trị : a = v = = Rε s . (4.6) t t hình 4.12
4.4.2. Gia tốc pháp • Phương trùngbán kính
• Chiều hướng về tâm. 2 v • Có giá trị: 2 a = = R (4.7) n R Gia tốc toàn phần có:
• Phương: tạo với bán kính một góc α, tg = 2
• Cùng chiều vectơ gia tốc góc • Trị số : 4 2
a = R + .
Các điểm M, N, I thuộc vật (hình 4.13), a a M N aI α ta có: M C N I a a a M N I 4 2 = = = + CM CN CI
Vậy: gia tốc các điểm thuộc vật rắn hình 4.13
chuyển động quay phân bố
theo qui luật tam giác thường đồng dạng, tỉ đồng dạng là 4 2 + .
4.5. Vận tốc và gia tốc của điểm theo công thức Euler
Biểu thức vectơ của vận tốc dài:
v = r (4.8)
Vectơ định vị r có gốc là điểm bất kỳ nằm trên trục quay, ngọn là điểm đang xét.
Biểu thức vectơ của gia tốc dài ε ω a = r + v (4.9) 25 • Gia tốc tiếp: ε a = r t • Gia tốc pháp = ω a v n
5. TRUYỀN ĐỘNG ĐƠN GIẢN
5.1. Các loại truyền động
Truyền động đơn giản dùng để truyền chuyển động quay giữa các trục song song.
Các loại bộ truyền thường gặp:
• Bộ truyền đai thẳng (hình 4.14), bộ truyền đai chéo (hình 4.15).
• Bộ truyền bánh răng ăn khớp ngoài (hình 4.16), bộ truyền bánh răng ăn khớp trong (hình 4.17). R R R 2 1 2 1 R ω1 ω2 ω2 ω1 hình 4.14 hình 4.15 2 1 ω 2 1 O R R 2 A 1 1 A R2 ω O 2 1 R ω2 ω1 hình 4.16 hình 4.17
5.2. Tỉ số truyền
Các bánh đai, bánh răng trong bộ truyền có thể quay cùng chiều hoặc ngược chiều nhau. ω R Tỉ số truyền: 1 2 u = = (4.10) 12 ω R 2 1 26




