79 trang 5 lượt tải

Chương 4: Tích phân bất đinh | Bài tập ôn tập môn giải tích

9

Chương 4: Tích phân bất đinh | Bài tập ôn tập môn giải tích

Môn: Giải tích 1 90 tài liệu

Trường: Đại học Bách Khoa Hà Nội 4.8 K tài liệu

Tác giả:

Profile

Xuân Lộc Nguyễn

3 ngày trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/79
Toaùn cao caáp : Giaûi tích 101
Chöông VI TÍCH PHAÂN BAÁT ÑÒNH
I. Nguyeân haøm - tích phaân baát ñònh:
1. Ñònh nghóa: Cho caùc haøm soá f, F xaùc ñònh treân [a, b].
F ñöôïc goïi laø nguyeân haøm cuûa f treân (a, b) neáu
F’(x) = f(x), ∀x ∈ (a, b).
F goïi laø nguyeân haøm cuûa f treân [a, b] neáu:
F’(x) = f(x), ∀x ∈ (a, b)
vaø F’(a
+
) = f(a), F’(b
-
) = f(b)
Ví duï:
• (- cosx) laø nguyeân haøm cuûa sinx vì (-cosx)’ = sinx
• (- cosx + 7) cuõng laø nguyeân haøm cuûa sinx.
•
3
3
x
,
3
−
5
3
x
,
3
−
x
C
laø nhöõng nguyeân haøm cuûa x
2
vì:
/ / /
3
5
3 3 3
= − = −
3 3
x x x
C = x
2
2. Ñònh lyù:
Neáu haøm soá f lieân tuïc treân [a, b] thì f coù nguyeân
haøm treân [a, b].
3. Ñònh lyù:
Giaû söû F laø nguyeân haøm cuûa f treân (a, b). Khi ñoù:
i)
F + C (C laø haèng soá) cuõng laø moät nguyeân haøm cuûa f treân
(a, b).
ii)
Neáu G laø moät nguyeân haøm cuûa f treân (a, b) thì
G(x) = F (x) + C, ∀x ∈ (a, b).
Chöùng minh
:
i) (F(x) + C)’ = F’(x) = f(x), ∀x ∈ (a, b)
⇒
F + C laø moät nguyeân haøm cuûa f treân (a, b)
ii) [G(x) - F(x)]’ = G’(x) - F’(x) = f(x) - f(x) = 0, ∀x ∈ (a, b)
Toaùn cao caáp : Giaûi tích
102
⇒ G(x) - F(x) = C (haèng soá), ∀x ∈ (a, b)
⇒ G(x) = F(x) + C, ∀x ∈ (a, b)
Ghi chuù:
• Ñònh lyù treân vaãn ñuùng neáu thay (a, b) baèng [a, b].
• Neáu f coù moät nguyeân haøm thì f coù voâ soá nguyeân haøm vaø 2
nguyeân haøm baát kyø cuûa cuøng moät haøm thì sai khaùc nhau moät
haèng soá.
4. Ñònh nghóa: Taäp hôïp taát caû nhöõng nguyeân haøm cuûa f treân [a, b]
ñöôïc goïi laø tích phaân baát ñònh cuûa f treân [a, b], kyù hieäu:
∫
( )
f x dx
.
Neáu F laø moät nguyeân haøm cuûa f thì
(
)
( ) =F x
f x dx C
+
∫
.
II. Tính chaát cuûa tích phaân baát ñònh:
Cho f, g laø caùc haøm soá coù nguyeân haøm treân (a, b). Khi ñoù:
i)
( )
( ) ( ( ) )' =f x
=
∫ ∫
d
f x dx f x dx
dx
ii)
(
)
( ) =f x
∫
d f x dx dx
iii)
(
)
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx
± = ±
∫ ∫ ∫
iv)
(
)
( ) =k f x ,kf x dx dx k
∈
∫ ∫
ℝ
Heä quaû:
1 1
( ) ( )
n n
i i i i
i i
k f x dx k f x dx
= =
=
∑ ∑
∫ ∫
v)
Neáu F’(x) = f(x) thì
(
)
(
)
'( ) ( ) =F x
F x dx dF x C f x dx
= + =
∫ ∫ ∫
vaø
(
)
(
)
(
)
, ( ) ,...
f y dy F y C f t dt F t C
= + = +
∫ ∫
Chöùng minh
: Daønh cho ñoäc giaû (suy ra töø tính chaát ñaïo haøm).
III. Caùc coâng thöùc tích phaân baát ñònh cô baûn:
Toaùn cao caáp : Giaûi tích 103
1.
∫
0 =C
dx
2.
= ax+ C
∫
adx
3.
( )
1
= + C n -1
1
+
≠
+
∫
n
n
x
x dx
n
4.
= ln x
+
∫
dx
C
x
( vì (ln|x| + C)’ = (ln|x|)’ =
(ln )' , 0
ln( )' , 0
>
− <
x x
x x
=
1
, 0
1 1
, 0
>
− = <
−
x
x
x
x x
=
1
x
, x ≠ 0)
5.
x
= e
+
∫
x
e dx C
6.
= +C
ln
∫
x
x
a
a dx
a
(vì
/
ln
x
a
a
= a
x
)
7.
sin = - cosx + C
∫
xdx
8.
cos = sinx+ C
∫
xdx
9.
2
1
cos
dx
x
∫
=
2
(1 )
tg x dx tgx C
+ = +
∫
10.
2
1
sin
dx
x
∫
=
2
(1 cot ) cot
g x dx gx C
+ = − +
∫
11.
+
∫
2
= arctgx+ C
1
dx
x
12.
−
∫
2
= arcsinx+ C
1
dx
x
13.
n
dx
x
∫
=
n
x dx
−
∫
=
1
+ C
1
− +
− +
n
x
n
=
−
−
−
1
1
( 1)
n
n x
+ C (
1
n
≠
)
Toaùn cao caáp : Giaûi tích
104
2
dx
x
∫
=
x
+ C
14.
tgxdx
∫
=
sin
cos
x
dx
x
∫
=
(cos )
=-ln cosx
cos
d x
C
x
−
+
∫
15.
cot
gxdx
∫
=
cos
sin
x
dx
x
∫
=
(sin )
=ln sinx
sin
d x
C
x
+
∫
16.
2 2
arcsin
dx x
C
a
a x
= +
−
∫
17.
2 2
1
dx x
arctg C
a x a a
= +
+
∫
18.
2
2
ln
dx
x x b C
x b
= + + +
+
∫
19.
2 2
1
ln
2
dx x a
C
x a a x a
−
= +
− +
∫
(a
≠
0)
20.
1
ln
( )( )
dx x b
C
x a x b b a x a
−
= +
− − − −
∫
(a
≠
b)
21.
2
2 2 2 2
sin
2 2
x a x
a x dx a x arc C
a
− = − + +
∫
(a ≠ 0)
22.
2
2 2 2 2 2 2
ln
2 2
x a
a x dx a x x a x C
+ = + + + + +
∫
IV. Vaøi ví duï:
a.
4 3 2
2
5 3 7
1
x x x x
dx
x
− − + +
+
∫
=
2
2
8 9
5 2
1
x
x x dx
x
+
− − +
+
∫
Toaùn cao caáp : Giaûi tích 105
=
3 2
2
5 8 9
2
3 2 1
x x x
x dx
x
+
− − +
+
∫
=
3 2
2 2
5 4.2
2 9
3 2 1 1
x x xdx dx
x
x x
− − + +
+ +
∫ ∫
=
+
− − + +
+
∫
3 2 2
2
5 ( 1)
2 4 9
3 2
1
x x d x
x arctgx
x
+ C
=
3 2
2
5
2 4ln( 1) 9
3 2
x x
x x arctgx
− − + + + + C
b.
2
( )
x x x x dx
+
∫
=
1 1
2
2 4
( )
x x x x dx
+
∫
=
3 3
(2 ) (1 )
4 4
x x dx
+ +
+
∫
=
11 7
4 4
x x dx
+
∫
=
15 11
4 4
4 4
15 11
x x C
+ +
c.
3
7
x x
e dx
∫
=
3
( 7)
x
e dx
∫
=
3
3
( 7)
ln 7
x
e
e
=
3
7
3 ln7
x x
e
+
+ C
d.
dx
x a
+
∫
=
( )
=ln x+a
d x a
C
x a
+
+
+
∫
e.
3
sin
cos
xdx
x
∫
=
2
cos
tgxdx
x
∫
=
( )
tgxd tgx
∫
=
2
2
tg x
+ C
Caùch khaùc:
3
sin
cos
xdx
x
∫
=
3
(cos )
cos
d x
x
−
∫
=
2
1
2cos
x
+ C
=
2
1
(1 )
2
tg x
+ + C =
2
2
tg x
+ K
f.
2 2
2
2 2
2 2
( 1)
( 1)
( 1)
+ +
− +
− +
∫ ∫
dx x x
dx
x x
x x
=
2 2 2
( 2 1 1)
+ + + +
∫
x x x x dx
Toaùn cao caáp : Giaûi tích
106
=
1
3
2
2
3
+ +
∫
x
x u du
(u = x
2
+ 1
⇒
du = 2xdx)
=
1
1
3
2
2
1
3
1
2
+
+ +
+
x u
x
+ C =
3
3 2
2
2 2
( 1)
3 3
+ + +
x x x + C
g.
2 2
dx
x a
−
∫
=
( )( )
dx
x a x a
− +
∫
1 ( ) ( )
2 ( )( )
x a x a
dx
a x a x a
+ − −
=
− +
∫
=
1 1 1
2
dx
a x a x a
−
− +
∫
=
1
2
a
[
ln
|
x - a
|
- ln
|
x + a
|]
+ C
=
1
ln
2
x a
a x a
−
+
+ C (
0
a
≠
)
h.
2
tg xdx
∫
=
2
( 1 1)
tg x dx
+ −
∫
= tgx - x + C
i.
5
tg xdx
∫
=
5 3 3
( )
tg x tg x tg x tgx tgx dx
+ − + −
∫
=
3 2 2
( 1) ( 1)
tg x tg x dx tgx tg x dx tgxdx
+ − + +
∫ ∫ ∫
=
4 2
ln cos +C
4 2
tg x tg x
x− −
V. Phöông phaùp tính tích phaân baát ñònh:
1. Phöông phaùp ñoåi bieán:
a.
Giaû söû f laø haøm soá coù nguyeân haøm treân mieàn D.
Ñaët x = ϕ(t), vôùi ϕ laø haøm khaû vi ñôn ñieäu ñoái vôùi bieán t vaø
mieàn giaù trò cuûa ϕ(t) chöùa trong D. Khi ñoù:
( ) ( ( )) '( )
f x dx f t t dt
ϕ ϕ
=
∫ ∫
Ví duï:
1)
3
3 2
sin
x
dx
x
∫
Ñaët: x = t
3
⇒
dx = 3t
2
dt ,
3
2
x
= t
2
,
3
x
= t
Toaùn cao caáp : Giaûi tích 107
⇒ I=
2
2
(sin )3
t t dt
t
∫
=
3sin
tdt
∫
= -3cost + C = -3cos
3
x
+ C
2) I =
2 2
a x dx
−
∫
(a > 0) , a
2
- x
2
≥
0
⇔
- a
≤
x
≤
a
Ñaët : x = asint vôùi
2 2
t
π π
− ≤ ≤
⇒
dx = acostdt
⇒
sint=
x
a
⇒
I =
2 2
a x dx
−
∫
=
2 2 2
sin
a a t
−
∫
acostdt
=
2
cos cos
a ta tdt
∫
=
2
cos cos
a t tdt
∫
=
2 2
cos
a tdt
∫
(vì t ∈
,
2 2
π π
−
⇒ cost ≥ 0 ⇒ |cost| = cost )
=
2
(1 cos2 )
2
a t
dt
+
∫
=
2 2
sin2
2 4
a a
t t
+ + C
=
2 2
arcsin 2sin cos
2 4
a x a
t t
a
+ +C
=
2 2 2
2
arcsin 1
2 2
a x a x x
a a a
+ − + C
=
2
2 2
arcsin
2 2
a x x
a x
a
+ − + C
b.
Ñaët u = h(x) vôùi h khaû vi lieân tuïc. Ta coù:
( ( )) '( ) ( )
g h x h x dx g u du
=
∫ ∫
Ví duï : 1)
( )
18
7 8
3
3 5 5
8
x x x dx
+ +
∫
Ñaët : u =
8
3
5
8
x
x
+ ⇒ du = (3x
7
+ 5)dx
( u = h(x) ⇒ du = h’(x)dx)
⇒ I=
18
u du
∫
=
19
19
u
+ C =
19
8
1 3
5
19 8
x x
+
+ C
Toaùn cao caáp : Giaûi tích
108
2)
4 2
3
6 15
xdx
x x+ +
∫
=
2 2
3
( 3) 6
xdx
x
+ +
∫
Ñaët : u = x
2
+ 3
⇒
du = 2xdx
⇒
I=
2 2
3 2
2 ( 3) 6
xdx
x
+ +
∫
=
2
3
2 6
du
u
+
∫
=
6
4
arctg
6
u
+ C =
6
4
arctg
2
3
6
x
+
+ C
3) I =
3
2
1
x
x
e dx
e
+
∫
Ñaët : u = e
x
⇒
du = e
x
dx
I =
3
2
1
x
x
e dx
e
+
∫
=
2
2
1
x x
x
e e dx
e
+
∫
=
2
2
1
u du
u
+
∫
=
2
2
1 1
1
u
du
u
+ −
+
∫
=
2
1
− = − + = − +
+
∫ ∫
x x
du
du u arctgu C e arctge C
u
4)
2
2 2 2
1
1
dx dx
x a a
x
a
=
+
+
∫ ∫
=
2
1
1
1
dx
a
a
x
a
+
∫
=
2
1
( )
1
du x
u
a u a
=
+
∫
1 1
arctan arctan
x
u C C
a a a
= + = +
5)
2 2
dx
a x
−
∫
=
2
2
1
dx
x
a
a
−
∫
=
2
1
dx
x
a
a
−
∫
=
2
arcsin arcsin
1
= = + = +
−
∫
du x x
u u C C
a a
u
(a>0)
6)
2
dx
x b
+
∫
= ln
2
x x b
+ + + C
Ñaët u = x +
2
x b
+
⇒
du =
2
2
x b x
dx
x b
+ +
+
Toaùn cao caáp : Giaûi tích 109
⇒
2
dx
x b
+
=
2
du
x b x
+ +
=
du
u
⇒
2
dx
x b
+
∫
=
du
u
∫
= ln
|
u
|
+ C = ln
2
x x b
+ + + C
2. Phöông phaùp tích phaân töøng phaàn:
Cho
(
)
(
)
,
u u x v v x
= = laø caùc haøm khaû vi vaø coù ñaïo haøm lieân
tuïc. Khi ño
ù:
udv uv vdu
= −
∫ ∫
Chöùng minh:
Ta coù: d(uv) = vdu + udv
⇒
( )
d uv udv vdu
= +
∫ ∫ ∫
Suy ra
udv uv vdu
= −
∫ ∫
Thoâng thöôøng ñeå tính :
( )
f x dx
∫
, ta phaân tích : f(x)dx = udv
sao cho tính ñöôïc caùc tích phaân
vdu
∫
vaø dv
∫
.
Nhaän xeùt:
•
Daïng:
∫
( ) cos
sin
x
e
p x x dx
x
. Ñaët u = p(x) vaø dv =
cos
sin
x
e
x dx
x
•
Daïng:
∫
ln
( )
arcsin
x
p x arctgx dx
x
.
Ñaët u=
ln
arcsin
x
arctgx
x
vaø dv =p(x)dx
Ví duï:
a)
2
x
x e dx
∫
Toaùn cao caáp : Giaûi tích
110
Ñaët: u = x
2
⇒ du = 2xdx
dv = e
x
dx, choïn v = e
x
(dv = e
x
dx ⇒ v = e
x
+ C, choïn C = 0)
Do ñoù :
2
x
x e dx
∫
= uv -
vdu
∫
= x
2
e
x
-
2
x
xe dx
∫
Ñaët: u = 2x
⇒
du = 2dx; dv = e
x
dx, choïn v = e
x
⇒
2
x
x e dx
∫
= x
2
e
x
-
[
2xe
x
-
2
x
e dx
∫
]
= x
2
e
x
- 2xe
x
+ 2e
x
+ C
Toång quaùt :
n x
x e dx
∫
= x
n
e
x
- nx
n - 1
e
x
+ n(n - 1)x
n - 2
e
x
+ ... + (-1)
n - 1
n! xe
x
+ (-1)
n
n! e
x
+ C
b)
ln
xdx
∫
Ñaët :u = lnx
⇒
du =
dx
x
;
dv = dx, choïn v = x
ln
xdx
∫
= xlnx -
xdx
x
∫
= xlnx - x + C
c)
ln
n
x xdx
∫
, n
≠
-1
Ñaët : u = lnx
⇒
du =
1
x
dx; dv = x
n
dx, choïn v =
1
1
n
x
n
+
+
ln
n
x xdx
∫
=
1 1
ln
1 ( 1)
n n
x x
x dx
n n x
+ +
−
+ +
∫
=
1 1
2
ln
1 ( 1)
n n
x x
x
n n
+ +
−
+ +
+ C
d) I=
3
sin
x xdx
∫
Ñaët: u = x
3
⇒
du = 3x
2
dx
dv = sinxdx, choïn v = -cosx
⇒
I = -x
3
cosx +
2
3 cos
x xdx
∫
= -x
3
cosx + 3x
2
sinx -
6 sin
x xdx
∫
= -x
3
cosx + 3x
2
sinx + 6xcosx -
6cos
xdx
∫
Toaùn cao caáp : Giaûi tích 111
= -x
3
cosx + 3x
2
sinx + 6xcosx - 6sinx + C
e) I =
xarctgxdx
∫
Ñaët: u = arctgx ⇒ du =
2
1
dx
x
+
dv = xdx, v =
1
2
(x
2
+ 1) (Choïn C =
1
2
)
⇒
I=
1
2
(x
2
+ 1)arctgx -
2
2
1 1
( 1)
2 1
x dx
x
+
+
∫
=
1
2
(x
2
+ 1) arctgx -
1
2
x +C
f)
2 2
a x dx
−
∫
Ñaët: u =
2 2
a x
−
⇒
du =
2 2 2 2
2
2
xdx xdx
a x a x
−
= −
− −
dv = dx, choïn v = x
⇒
I= x
2 2
a x
−
2
2 2
− −
−
∫
x dx
a x
= x
2 2
a x
−
2 2 2
2 2
− + −
−
−
∫
x a a
dx
a x
= x
2 2
a x
−
-
2 2
a x dx
−
∫
+ a
2
2 2
dx
a x
−
∫
⇒
2I = x
2 2
a x
−
+ a
2
2 2
dx
a x
−
∫
⇒
I =
−
2 2
a
2
x
x
+
2
2
a
arcsin
x
a
+ C
Töông töï:
J =
2 2
a x dx
+
∫
Ñaët: u =
2 2
a x
+
⇒
du =
2 2
xdx
a x
+
, dv = dx, choïn v = x
Ta coù:
Toaùn cao caáp : Giaûi tích
112
J = x
2 2
a x
+
-
2
2 2
x dx
a x
+
∫
=
2 2
x a x
+
-
2 2 2
2 2
x a a dx
a x
+ −
+
∫
⇒
2J=
2 2 2
2 2
dx
x a x a
a x
+ +
+
∫
⇒
J=
+ +
+
∫
2
2 2
2 2
2 2
x a dx
a x
a x
= +
2 2
2
x
a x
+
2
2
a
ln(x +
2 2
a x
+
) + C
VI. Tích phaân caùc haøm höõu tæ :
Nhaéc laïi :
dx
x a
+
∫
= ln|x + a| + C
( )
k
dx
x a
+
∫
=
1
1
( 1)( )
k
k x a
−
−
− +
+ C
2 2
dx
x a
−
∫
=
1
2
a
ln
x a
x a
−
+
+ C
1 2
1 2 2 1 1 2
( ) ( )
1
( )( ) ( )( )
x x x x
dx
dx
x x x x x x x x x x
− − −
=
− − − − −
∫ ∫
=
2 1 2 1
1 1 1
dx
x x x x x x
−
− − −
∫
=
2
1 2
2 1 1
1
ln ( x x )
x x
C
x x x x
−
+ ≠
− −
1. Tích phaân daïng:
I=
2
( )
Ax B dx
ax bx c
+
+ +
∫
( a
≠
0)
I =
2
2
2
A ax b
dx
a ax bx c
+
+ +
∫
+
2
2
Ab dx
B
a ax bx c
−
+ +
∫
Toaùn cao caáp : Giaûi tích 113
=
2
A
a
ln|
ax
2
+ bx + c
|
+
2
2
Ab dx
B
a ax bx c
−
+ +
∫
Tính: I
1
=
2
dx
ax bx c
+ +
∫
(a
≠
0)
I
1
=
2
1
dx
b c
a
x x
a a
+ +
∫
=
1
a
2
2
2
2 4
dx
b c b
x
a a a
+ + −
∫
=
1
a
2
2
2 4
dx
b
x
a a
∆
+ −
∫
i) Neáu ∆ < 0:
I
1
=
2 2
1
du
a u
α
+
∫
vôùi α
2
=
2
4
a
−∆
, u = x +
2
b
a
=
1
a
α
arctg
u
α
+ C
ii) Neáu ∆ = 0:
I
1
=
1
a
2
1
du
u au
= −
∫
+ C
iii) Neáu ∆ > 0:
ax
2
+ bx + c = a(x - x
1
)(x - x
2
)
vôùi x
1
, x
2
laø nghieäm cuûa ax
2
+ bx + c = 0
2. Phaân tích moät ña thöùc thaønh tích cuûa nhöõng nhò thöùc vaø
tam thöùc:
(Ñöa moät phaân thöùc veà toång cuûa nhöõng phaân
thöùc ñôn giaûn)
Ghi chuù: Ta chæ xeùt caùc ña thöùc coù theå vieát döôùi daïng tích cuûa
nhöõng nhò thöùc baäc nhaát vaø nhöõng tam thöùc baäc hai.
Ví duï:
Toaùn cao caáp : Giaûi tích
114
Tính :
(3 5)
( 3)( 2)( 1)
x dx
x x x
−
− + −
∫
Ta coù
3 5
( 3)( 2)( 1)
x
x x x
−
− + −
=
3 2 1
A B C
x x x
+ +
− + −
=
( 2)( 1) ( 3)( 1) ( 3)( 2)
( 3)( 2)( 1)
A x x B x x C x x
x x x
+ − + − − + − +
− + −
Cho : x = 3
⇒
10A = 4
⇒
A =
2
5
;
x = -2
⇒
15B = -11
⇒
B =
11
15
−
x = 1
⇒
-6C = -2
⇒
C =
1
3
⇒
3 5
( 3)( 2)( 1)
x
x x x
−
− + −
=
2 11 1
5( 3) 15( 2) 3( 1)
x x x
− +
− + −
(3 5)
( 3)( 2)( 1)
x
dx
x x x
−
− + −
∫
=
2
5
ln|x - 3| -
11
15
ln|x + 2| +
1
3
ln|x - 1| + C
Ghi chuù: Ta coù theå tính A, B theo caùch khaùc :
−
− + −
3 5
( 3)( 2)( 1)
x
x x x
≡
2
( ) ( 4 ) 2 3 6
( 3)( 2)( 1)
A B C x A B C x A B C
x x x
+ + + − − − + −
− + −
Ñoàng nhaát 2 veá
⇒
0
4 3
2 3 6 5
A B C
A B C
A B C
+ + =
− − =
− + − = −
Ghi chuù: Neáu a
n
x
n
+ a
n -1
x
n - 1
... + a
1
x + a
0
= 0 coù nhieàu hôn
n nghieäm thöïc
⇒
a
n
= a
n - 1
= ... = a
0
= 0
Toaùn cao caáp : Giaûi tích 115
Ví duï: ax
2
+ bx + c = 0 coù 3 nghieäm phaân bieät ⇒ a = b = c = 0
Ví duï 1:
2 2 3
5 2
( 1) (3 2)
x
x x
+
+ −
=
2 2 2 2 3
1 ( 1) 3 2 (3 2) (3 2)
Ax B Cx D E F G
x x x x x
+ +
+ + + +
+ + − − −
Ví duï 2:
2
2 4
6 7 2
( 1)( 2)
x x
x x x
− +
− + +
=
2 2 3 4
1 2 ( 2) ( 2) ( 2)
Ax B C D E F
x x x x x x
+
+ + + +
− + + + + +
Ví duï 3:
4
1
1
x
+
=
2 2 2
2 2
1 1
( 1) 2
( 2 1)( 2 1)
x x
x x x x
=
+ −
− + + +
=
2 2
2 1 2 1
Ax B Cx D
x x x x
+ +
+
− + + +
Ví duï 4: Tính
3
1
dx
x
+
∫
=
2
( 1)( 1)
+ − +
∫
dx
x x x
3
1
1
x
+
=
2
1 1
A Bx C
x x x
+
+
+ + +
=
2
3
( 1) ( )( 1)
1
A x x Bx C x
x
− + + + +
+
Cho : x = -1
⇒
3A = 1
⇒
A =
1
3
x = 0
⇒
A + C = 1
⇒
C =
2
3
x = 1
⇒
A + 2(B + C) = 1
⇒
B + C =
1
3
⇒
B = -
1
3
3
1
dx
x
+
∫
=
1
3 1
dx
x
+
∫
+
2
1 2
3 3
1
x dx
x x
− +
− +
∫
Toaùn cao caáp : Giaûi tích
116
=
1
3
ln|
x + 1
|
-
2
1 2 1
3.2 1
x
dx
x x
−
− +
∫
+
2
2 1
3 6 1
dx
x x
−
− +
∫
=
1
3
ln|x + 1| -
1
6
ln(x
2
- x + 1) +
2
1
2
1 3
2 4
dx
x
− +
∫
=
2
1
2( )
1
1 1 2
2
ln
3 2
3 3
1
−
+
+
− +
x
x
arctg
x x
+ C
5. Tích phaân bieåu thöùc löôïng giaùc:
Baèng caùc pheùp ñoåi bieán thích hôïp, ta coù theå ñöa tích phaân
bieåu thöùc löôïng giaùc
(
)
sin ,cos
R x x dx
∫
, trong ñoù R laø haøm höõu
tyû, veà tích phaân bieåu thöùc höõu tyû.
1. Tröôøng hôïp toång quaùt:
ta duøng coâng thöùc ñoåi bieán
=
⇒
=
2 tg
2
x
t tg x arc t
vaø aùp duïng coâng thöùc
2
2 2 2
2 1 2
sin , cos ,
1 1 1
t t dt
x x dx
t t t
−
= = =
+ + +
Ví duï:
4sin 3cos 5
dx
I
x x
=
+ +
∫
Ñaët
2
2
x
t tg x arctgt
=
⇒
=
ta co
ù:
( )
2 2
2 2
2 2
1 2
2 1
1 4 4
2
4 3 5
1 1
1 1
2
2
2
= = =
−
+ + +
+
+ +
+ +
−
= + = − +
+
+
∫ ∫ ∫
dt dt dt
I
t t
t t t
t
t t
C C
x
t
tg
2. Daïng ñaëc bieät:
i. Neáu
(
)
(
)
sin ,cos sin ,cos
R x x R x x
− = −
thì ñaët
cos
t x
=
Toaùn cao caáp : Giaûi tích 117
ii. Neáu
(
)
(
)
sin , cos sin ,cos
R x x R x x
− = −
thì ñaët
sin
t x
=
iii.
Neáu
(
)
(
)
sin , cos sin ,cos
− − =
R x x R x x
thì ñaët
t tgx
=
,
hay
cotg
t x
=
Ví duï 1:
(
)
(
)
2 3 2 2
sin cos 2cos sin cos 2 cos
I x x x dx x x xdx
= + = +
∫ ∫
Ñaët
sin cos
t x dt xdx
=
⇒
=
;
(
)
2 2 2 2 4 2
sin cos 2 1 2 2
x x t t t t
+ = − + = − + +
ta coù:
( )
5 3
4 2
5 3
2 2
5 3
sin sin
2sin
5 3
= − + + = − + + +
−
= + + +
∫
t t
I t t dt t C
x x
x C
Ví duï 2:
2 2
sin sin2 3cos
dx
I
x x x
=
+ −
∫
Ñaët
2
1
cos
t tgx dt dx
x
= ⇒ = ta coù:
( )
( )( )
2
2 2
2 3 1 3
cos 2 3
1 1 1 1 1 1 1
ln ln
4 1 3 4 3 4 3
= = =
+ − − +
+ −
− −
= − = + = +
− + + +
∫ ∫ ∫
∫
dx dt dt
I
t t t t
x tg x tgx
t tgx
dt C C
t t t tgx
3.
Daïng
sin cos
m n
x xdx
∫
i.
Neáu m ( hoaëc n) laø soá nguyeân leû thì ñoåi bieán
cos
t x
=
(hoaëc
sin
t x
=
).
ii.
Neáu m vaø n laø soá nguyeân döông chaün thì duøng coâng thöùc
haï baäc.
iii.
Neáu m vaø n nguyeân chaün vaø coù moät soá aâm thì ñoåi bieán
t tgx
=
(hoaëc
cotgx
t
=
)
Toaùn cao caáp : Giaûi tích
118
Ví duï: Tính ( daønh cho ñoäc giaû )
2 4
sin cos
K x xdx
=
∫
3 2
sin cos
L x xdx
=
∫
2
4
sin
cos
x
M dx
x
=
∫
2
4
cos
sin
=
∫
x
N dx
x
VI. Tích phaân bieåu thöùc coù chöùa caên:
Vôùi caùc pheùp ñoåi
bieán thích hôïp, ta coù theå ñöa tích phaân cuûa bieåu thöùc coù caên
soá veà tích phaân cuûa bieåu thöùc höõu tyû.
1.
Caùc tích phaân sau coù theå ñöa veà tích phaân haøm löôïng
giaùc:
i. Daïng
2 2
,
R x A x dx
−
∫
ñaët
π π
= ∈ −
sin , ,
2 2
x A t t
ii. Daïng
2 2
,
R x A x dx
+
∫
ñaët
π π
= ∈ −
, ,
2 2
x Atgt t
iii. Daïng
2 2
,
R x x A dx
−
∫
ñaët
( )
π
π
= ∈
, 0, \
cos 2
A
x t
t
2. Daïng
, ,
+ +
+ +
∫
m r
n s
dx
ax b ax b
R x
cx d cx d
Ñaët
k
ax b
t
cx d
+
=
+
vôùi k laø boäi soá chung nhoû nhaát cuûa n vaø s.
Khi ñoù
( )
1
2
k
k
k
k
dt b ad bc
x dx kt
ct a
ct a
−
− + −
=
⇒
=
−
−
thay vaøo bieåu
thöùc tích phaân ta coù tích phaân cuûa haøm höõu tyû.
Ví duï 1:
3 6
1 1
dx
I
x x
=
− − −
∫
Toaùn cao caáp : Giaûi tích 119
k = 6, ñaët
6 5
1 6
t x dx t dt
= − ⇒ = . Suy ra
( )
( ) ( )
= = = + + + +
− −
−
= + + + + − +
−
= + − + −
+ − + − − +
∫ ∫ ∫
5 4
3 2
2
4 3 2
2/3
1/2 1/3
6 6
6 6 1
6 1
1 1
6 ln 1
4 3 2
3 1
2 1 3 1
2
6 1 6ln 1 1
t dt t dt
I t t t dt
t t
t t
t t t
t t C
x
x x
x x C
Ví duï 2:
1 1
1
x
I dx
x x
−
=
+
∫
Ñaët
( )
2
2
2
2
1 1 4
;
1 1
1
x t t
t x dx dt
x t
t
− − + −
= ⇒ = =
+ +
+
( )
( )( )
2 2
2
2
2 2
2
2 2
1 4
4
1
1 1
1
1 1 1
2 2 ln
1 1 1
1
1
1
1
2 ln
1
1
1
1
t t t
I t dt dt
t
t t
t
t
arctgt C
t t t
x
x
x
arctg C
x
x
x
+ −
= =
− +
− +
+
−
= + = + +
+ − +
−
−
−
+
= + +
+
−
+
+
∫ ∫
∫
3. Daïng vi phaân nhò thöùc
(
)
p
m n
x a bx dx
+
∫
vôùi m, n, p laø
caùc soá höõu tyû.
- Neáu p laø soá nguyeân, ta ñaët
k
t x
=
, trong ñoù k laø boäi soá
chung nhoû nhaát cuûa maãu soá cuûa m vaø maãu soá cuûa n.
Toaùn cao caáp : Giaûi tích
120
- Neáu
1
m
n
+
laø soá nguyeân, ñaët
k n
t a bx
= +
vôùi k laø maãu soá
cuûa p.
- Neáu
1
m
p
n
+
+
laø soá nguyeân thì ñaët
k n
t ax b
−
= +
vôùi k laø
maãu soá cuûa p.
Ví duï:
a)
( )
8
3 6
1
dx
I
x x
=
+
∫
( p= -8 laø soá nguyeân)
Ñaët
6 5
6
x t dx t dt
= ⇒ =
( ) ( )
5 3
8 8
2
6
6
1 1
t dt t dt
I
t t t
= =
+ +
∫ ∫
b)
5
4
1
x
I dx
x
+
=
∫
1
( 1/ 2; 1/ 4; 1/ 5 2 )
m
m n p
n
+
= − = =
⇒
= ∈
Ñaët
(
)
(
)
4 3
5 5 5 4
4
1 1 20 1
t x x t dx t t dt
= + ⇒ = − ⇒ = −
(
)
( )
( )
3
5 4
5 5
2
5
.20 1
20 1
1
t t t dt
I t t dt
t
−
= = −
−
∫ ∫
c)
(
)
3
1 x
I dx
x
+
=
∫
1
1/ 2; 1/ 3; 1/ 2 2
m
m n p p
n
+
= − = = ⇒ + = ∈
ℤ

Tài liệu khác của Đại học Bách Khoa Hà Nội

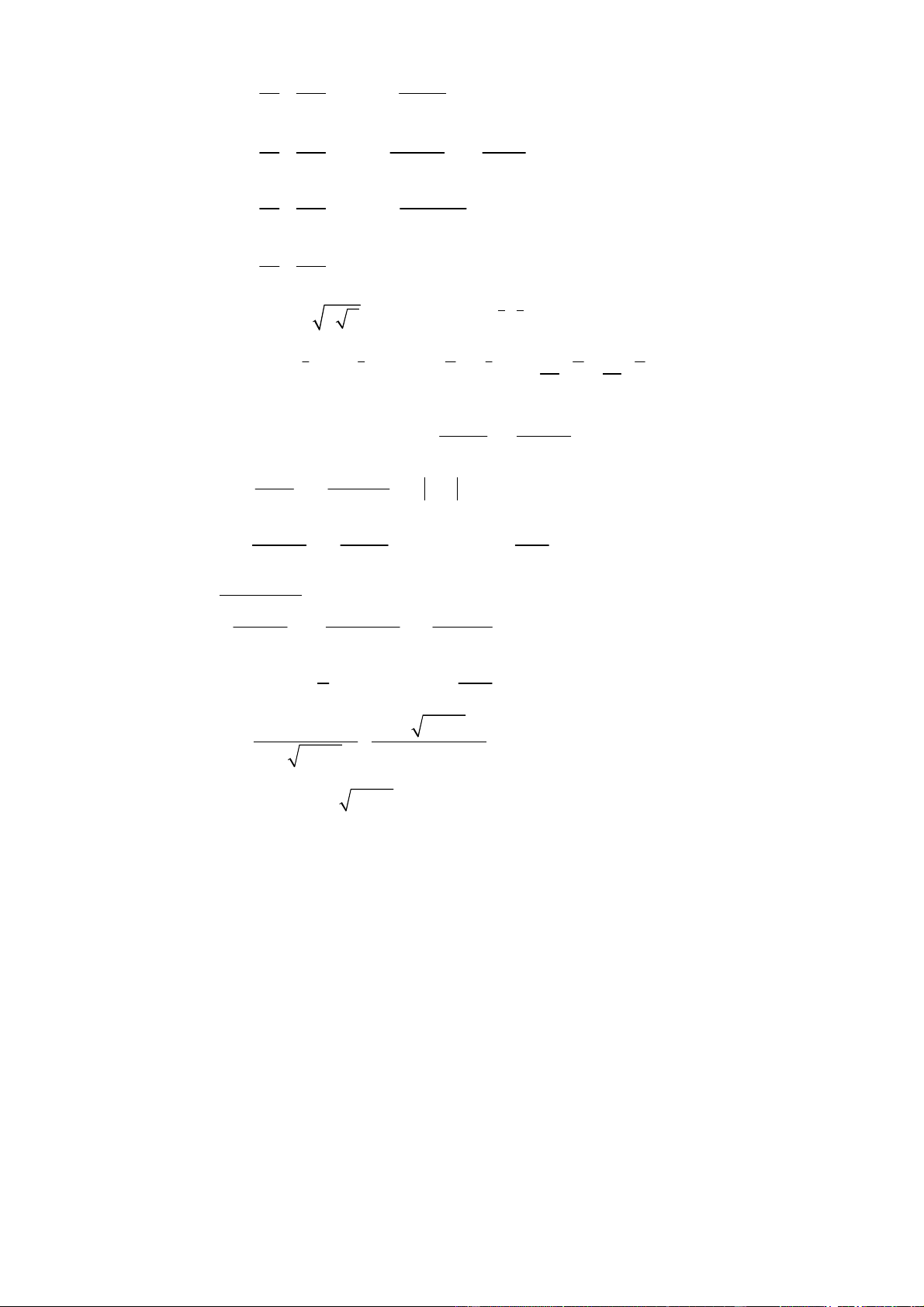
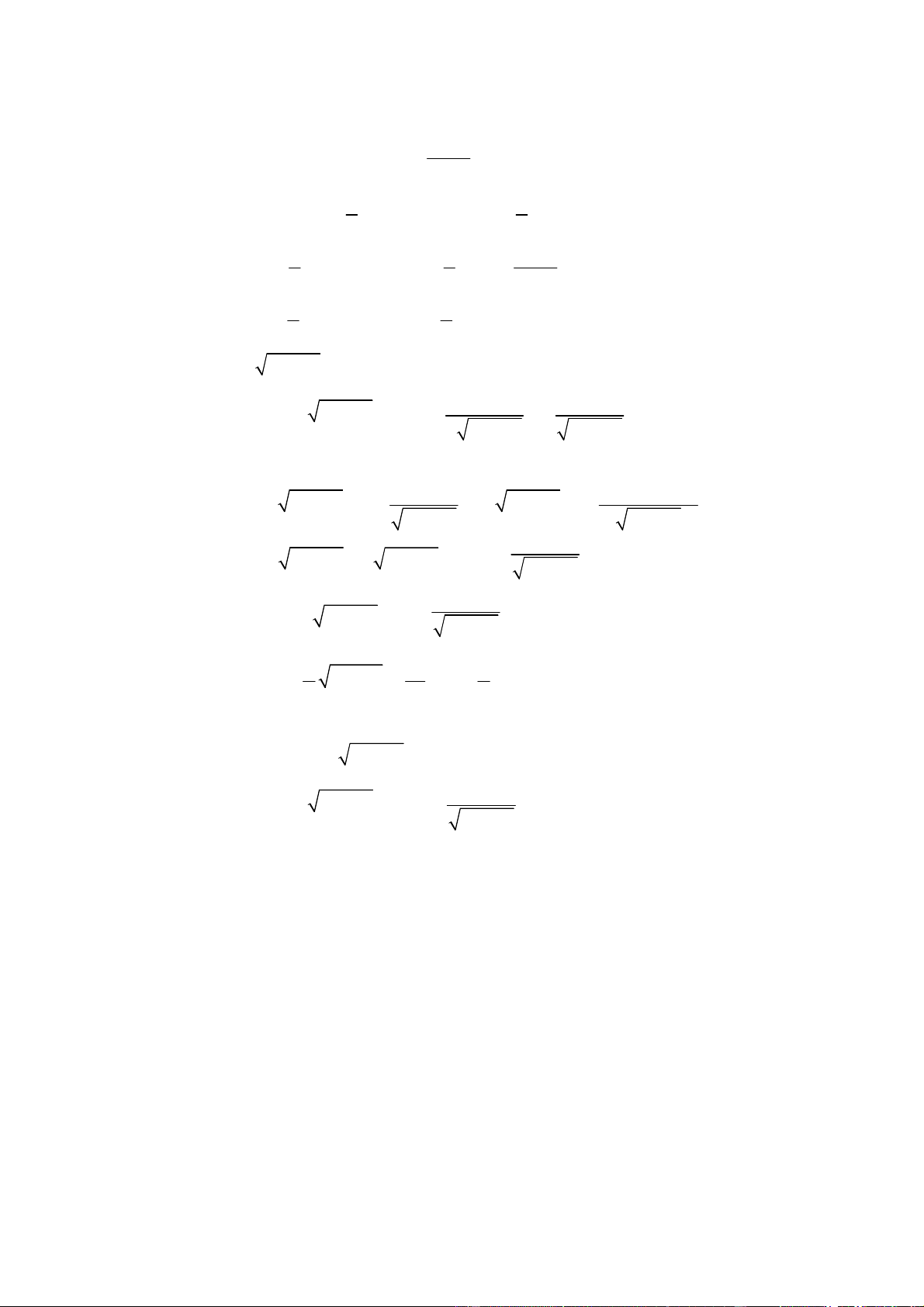
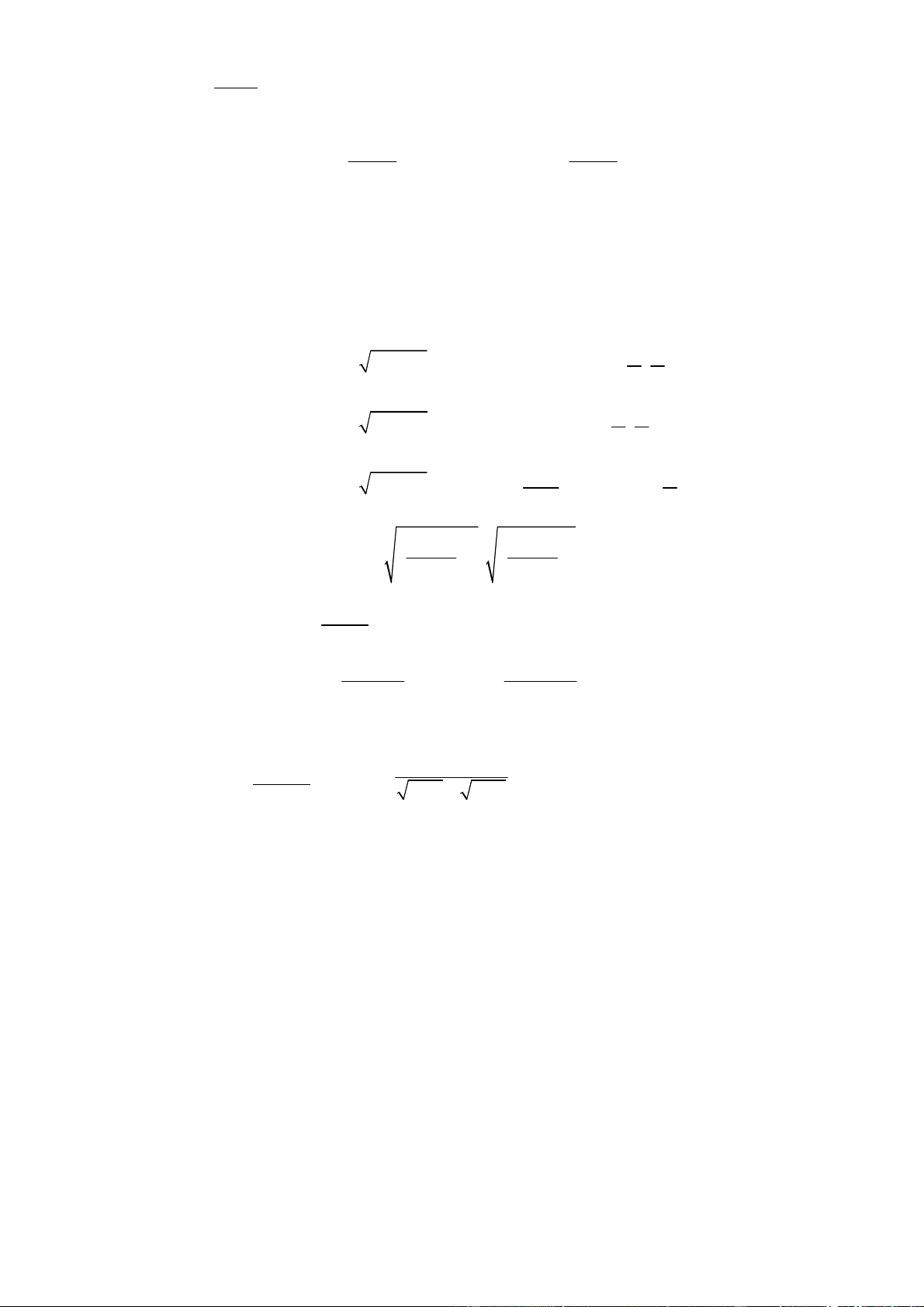
Preview text:

Toaùn cao caáp : Giaûi tích 101
Chöông VI TÍCH PHAÂN BAÁT ÑÒNH I.
Nguyeân haøm - tích phaân baát ñònh: 1.
Ñònh nghóa: Cho caùc haøm soá f, F xaùc ñònh treân [a, b].
F ñöôïc goïi laø nguyeân haøm cuûa f treân (a, b) neáu
F’(x) = f(x), ∀x ∈ (a, b).
F goïi laø nguyeân haøm cuûa f treân [a, b] neáu:
F’(x) = f(x), ∀x ∈ (a, b)
vaø F’(a+) = f(a), F’(b-) = f(b) Ví duï:
• (- cosx) laø nguyeân haøm cuûa sinx vì (-cosx)’ = sinx
• (- cosx + 7) cuõng laø nguyeân haøm cuûa sinx. 3 3 3 • x x x , − 5 ,
− C laø nhöõng nguyeân haøm cuûa x2 vì: 3 3 3 / / / 3    3   3 x x x    =  − 5 =  −C  = x2  3   3   3  2.
Ñònh lyù: Neáu haøm soá f lieân tuïc treân [a, b] thì f coù nguyeân haøm treân [a, b]. 3.
Ñònh lyù: Giaû söû F laø nguyeân haøm cuûa f treân (a, b). Khi ñoù:
i) F + C (C laø haèng soá) cuõng laø moät nguyeân haøm cuûa f treân (a, b).
ii) Neáu G laø moät nguyeân haøm cuûa f treân (a, b) thì
G(x) = F (x) + C, ∀x ∈ (a, b). Chöùng minh: i)
(F(x) + C)’ = F’(x) = f(x), ∀x ∈ (a, b)
⇒ F + C laø moät nguyeân haøm cuûa f treân (a, b)
ii) [G(x) - F(x)]’ = G’(x) - F’(x) = f(x) - f(x) = 0, ∀x ∈ (a, b)
Toaùn cao caáp : Giaûi tích 102
⇒ G(x) - F(x) = C (haèng soá), ∀x ∈ (a, b)
⇒ G(x) = F(x) + C, ∀x ∈ (a, b) Ghi chuù:
• Ñònh lyù treân vaãn ñuùng neáu thay (a, b) baèng [a, b].
• Neáu f coù moät nguyeân haøm thì f coù voâ soá nguyeân haøm vaø 2
nguyeân haøm baát kyø cuûa cuøng moät haøm thì sai khaùc nhau moät haèng soá.
4. Ñònh nghóa: Taäp hôïp taát caû nhöõng nguyeân haøm cuûa f treân [a, b]
ñöôïc goïi laø tích phaân baát ñònh cuûa f treân [a, b], kyù hieäu:
∫ f (x)dx .
Neáu F laø moät nguyeân haøm cuûa f thì f
∫ (x)dx =F(x)+C . II.
Tính chaát cuûa tích phaân baát ñònh:
Cho f, g laø caùc haøm soá coù nguyeân haøm treân (a, b). Khi ñoù: i) d
∫ f (x)dx = (∫ f (x)dx)' =f (x) dx
ii) d∫ f (x)dx =f (x)dx
iii) ∫( f (x)± (
g x)) dx = f
∫ (x)dx ± ∫ ( g x)dx iv) kf
∫ (x)dx =k∫ f (x)dx,k ∈ℝ n n
Heä quaû: ∫ ∑ k f (x)dx = ∑ k f ∫ (x)dx i i i i i 1 = i 1 = v) Neáu F’(x) = f(x) thì F
∫ '(x)dx = dF
∫ (x) =F(x) +C = f ∫ (x)dx
vaø ∫ f (y)dy = F(y) +C, ∫ f (t)dt = F (t) +C,...
Chöùng minh: Daønh cho ñoäc giaû (suy ra töø tính chaát ñaïo haøm). III.
Caùc coâng thöùc tích phaân baát ñònh cô baûn:
Toaùn cao caáp : Giaûi tích 103 1. ∫ 0dx =C 2. ∫ adx = ax+ C n 1 + 3. ∫ x n x dx = + C (n ≠ - ) 1 n +1 (
 ln x)' , x > 0
4. ∫ dx = ln x +C ( vì (ln|x| + C)’ = (ln|x|)’ = x
ln(−x)' , x < 0  1 , x > 0  =  x  = 1 , x ≠ 0) 1 1 − = , x x < 0  −x x 5. x
∫ xedx = e +C / xx a  6. ∫ a x a dx = + C (vì   = ax) ln a  ln a
7. ∫sin xdx = - cosx + C
8. ∫ cos xdx = sinx+ C 9. 1 dx ∫ = 2
∫(1+ tg x)dx = tgx +C 2 cos x 10. 1 dx ∫ = 2
∫(1+ cot g x)dx = −cot gx +C 2 sin x
11. ∫ dx = arctgx+ C 1+ 2 x
12. ∫ dx = arcsinx+ C 1− 2 x −n 1 + 13. dx 1 ∫ = − x − n x dx ∫ = + C = + C ( n ≠ 1) n x −n +1 − ( − 1 1) n n x
Toaùn cao caáp : Giaûi tích 104 dx ∫ = x + C 2 x 14. x −d x tgxdx ∫ = sin dx ∫ = (cos ) ∫ =-ln cosx + C cos x cos x 15. cot x d x gxdx ∫ = cos dx ∫ = (sin ) ∫ =ln sinx + C sin x sin x 16. dx x ∫ = arcsin + C 2 2 a − x a 17. dx 1 x ∫ = arctg + C 2 2 a + x a a 18. dx 2 ∫
= ln x + x + b + C 2 x + b 19. dx 1 x − a ∫ = ln + C (a ≠ 0) 2 2 x − a 2a x + a 20. dx 1 x − b ∫ = ln + C (a ≠ b)
(x − a)(x − b) b − a x − a 2 21. x a x 2 2 2 2 a ∫ − x dx = a − x + arc sin + C (a ≠ 0) 2 2 a 2 22. x a 2 2 2 2 2 2 a ∫ + x dx = a + x +
ln x + a + x + C 2 2 IV. Vaøi ví duï: 4 3 2 a.
x − 5x − x + 3x + 7 dx ∫ 2 x +1 =  2 8x + 9 
∫ x −5x − 2 +  dx 2  x +1 
Toaùn cao caáp : Giaûi tích 105 3 2 = x 5x  8x + 9 2  − − x + ∫  dx 2 3 2  x +1  3 2 = x 5x 4.2 − − 2 xdx + ∫ + 9 dx x ∫ 2 2 3 2 x +1 x +1 3 2 2 = x 5x d(x +1) − − 2x + 4∫ + 9arctgx + C 2 3 2 x +1 3 2 = x 5x 2 −
− 2x + 4 ln(x +1) + 9arctgx + C 3 2 1 1 b. 2
∫(x + x) x xdx = 2 2 4
∫(x + x)x x dx 3 3   11 7 15 11 = (2+ ) (1+ ) 4 4 4 4 ∫ x + xdx = 4 4 x ∫ + x dx = 4 4 x + x + C   15 11 3 x 3x x c. (e 7) e 7 3x 7x e dx ∫ = 3 ( 7)x e dx ∫ = = + C 3 ln e 7 3 + ln 7 d. dx d x + a ∫ = ( ) ∫ =ln x+a + C x + a x + a 2 e. sin xdx ∫ = tgxdx ∫ = tg x tgxd(tgx ∫ ) = + C 3 cos x 2 cos x 2 Caùch khaùc: sin xdx −d(cos x) 1 ∫ = ∫ = + C 3 cos x 3 cos x 2 2 cos x 2 = 1 2 (1+ tg x tg x) + C = + K 2 2 2 2 f. dx (x + x +1) ∫ ∫ dx 2 2 2 2 2
(x − x +1) x −(x +1) = 2 2 2
∫(x + 2x x +1 + x +1)dx
Toaùn cao caáp : Giaûi tích 106 3 1 = x 2 2
+ x + ∫u du (u = x2 + 1 ⇒ du = 2xdx) 3 1 1 3 + 2 3 = 2 x 2 2 + + u x + C = 3 2 2
x + x + (x +1) + C 3 1 +1 3 3 2 g. dx
1 (x + a) − (x − a) ∫ = dx = dx 2 2 ∫ ∫ x − a
(x − a)(x + a) 2a (x − a)(x + a) = 1  1 1  ∫ −
dx = 1 [ln|x - a| - ln|x + a|] + C
2a x − a x + a  2a
= 1 ln x − a + C ( a ≠ 0 ) 2a x + a h. 2 tg xdx ∫ = 2
∫(tg x +1−1)dx = tgx - x + C i. 5 tg xdx ∫ = 5 3 3
∫(tg x + tg x − tg x + tgx −tgx)dx = 3 2 2 tg x ∫
(tg x +1)dx − tgx
∫ (tg x +1)dx + tgxdx ∫ 4 2 = tg x tg x − − ln cos x +C 4 2
V. Phöông phaùp tính tích phaân baát ñònh:
1. Phöông phaùp ñoåi bieán:
a. Giaû söû f laø haøm soá coù nguyeân haøm treân mieàn D.
Ñaët x = ϕ(t), vôùi ϕ laø haøm khaû vi ñôn ñieäu ñoái vôùi bieán t vaø
mieàn giaù trò cuûa ϕ(t) chöùa trong D. Khi ñoù: f
∫ (x)dx = f
∫ (ϕ(t))ϕ '(t)dt Ví duï: 3 1) sin x dx ∫
Ñaët: x = t3 ⇒ dx = 3t2dt , 3 2 x = t2, 3 x = t 3 2 x
Toaùn cao caáp : Giaûi tích 107 2 (sin t)3t dt ⇒ I= ∫ = 3sin tdt ∫
= -3cost + C = -3cos 3 x + C 2 t 2) I = 2 2 a ∫
− x dx (a > 0) , a2 - x2 ≥ 0 ⇔ - a ≤ x ≤ a Ñaët : x = asint vôùi π π − ≤ x t ≤ ⇒ dx = acostdt ⇒ sint= 2 2 a ⇒ I = 2 2 a ∫ − x dx = 2 2 2 a ∫
− a sin t acostdt = 2
a cos ta cos tdt ∫ = 2
a cos t cos tdt ∫ = 2 2 a cos tdt ∫ (vì t ∈  π ,π  − 
⇒ cost ≥ 0 ⇒ |cost| = cost ) 2 2    2 2 2 = a (1+ cos2t) a a dt ∫ = t + sin 2t + C 2 2 4 2 2 = a arcsin x a + 2sin t cost +C 2 a 4 2 2 2 = a arcsin x a x + 1 x − + C 2 2 a 2 a a 2 = a x x 2 2 arcsin + a − x + C 2 a 2
b. Ñaët u = h(x) vôùi h khaû vi lieân tuïc. Ta coù: ∫ ( g (
h x))h '(x)dx = ∫ ( g u)du 18 Ví duï : 1) ∫( 7 3   x + 5) 3 8
x + 5x dx  8  8
Ñaët : u = 3x + 5x ⇒ du = (3x7 + 5)dx 8
( u = h(x) ⇒ du = h’(x)dx) 19 19 u 1  3  ⇒ I= 18 u du ∫ = + C = 8
x + 5x  + C 19 19  8 
Toaùn cao caáp : Giaûi tích 108 2) 3xdx 3 ∫ = xdx ∫ 4 2 x + 6x +15 2 2 (x + 3) + 6
Ñaët : u = x2 + 3 ⇒ du = 2xdx 3 2xdx 3 du ⇒ I= ∫ = ∫ 2 2 2 (x + 3) + 6 2 2 u + 6 2  x + 3 
= 6 arctg u + C = 6 arctg   + C 4 6 4  6  3x 3) I = e dx ∫
Ñaët : u = ex ⇒ du = exdx 2x e +1 3x 2x x 2 2 I = e dx u +1−1 ∫ = e e dx ∫ = u du ∫ = du ∫ 2x e +1 2x e +1 2 u +1 2 u +1 = ∫ − ∫ du du
= u − arctgu + C = x e − x arctge +C 2 u +1 1 dx 4) dx 1 dx 1 1 ∫ = ∫ = a ∫ = du ∫ ( x u = ) 2 2 2 2 x + a a  2 2 x a x a u +1 a   +1   +1  a   a  1 1 x
= arctan u + C = arctan + C a a a 5) dx ∫ = dx ∫ = dx ∫ 2 2 a − x 2   2 2  x  1  x a −    a 1−    a       a  =   ∫ du x xu =
 = arcsin u + C = arcsin + C (a>0) 2 1 u a  − a 6) dx ∫ = ln 2
x + x + b + C 2 x + b 2 Ñaët u = x + 2 x + b + x x + b ⇒ du = dx 2 x + b
Toaùn cao caáp : Giaûi tích 109 dx du du ⇒ = = 2 x + b 2 x + b + x u dx du ⇒ ∫ = ∫ = ln|u| + C = ln 2
x + x + b + C 2 x + b u 2.
Phöông phaùp tích phaân töøng phaàn:
Cho u = u(x),v = v(x) laø caùc haøm khaû vi vaø coù ñaïo haøm lieân
tuïc. Khi ñoù: udv ∫ = uv − vdu ∫ Chöùng minh:
Ta coù: d(uv) = vdu + udv ⇒ d ∫ (uv) = udv ∫ + vdu ∫ Suy ra udv ∫ = uv − vdu ∫
Thoâng thöôøng ñeå tính : f (x)dx ∫
, ta phaân tích : f(x)dx = udv
sao cho tính ñöôïc caùc tích phaân vdu ∫ vaø dv ∫ . Nhaän xeùt: xe xe    •   Daïng: ∫ (
p x) cos xdx . Ñaët u = p(x) vaø dv = cos x dx       sin x  sin x   ln x  •   Daïng: ∫ (
p x) arctgx dx .   arcsin x ln x  Ñaët u=  
arctgx  vaø dv =p(x)dx   arcsin x Ví duï: a) 2 x x e dx ∫
Toaùn cao caáp : Giaûi tích 110 Ñaët: u = x2 ⇒ du = 2xdx dv = exdx, choïn v = ex
(dv = exdx ⇒ v = ex + C, choïn C = 0) Do ñoù : 2 x x e dx ∫ = uv - vdu ∫ = x2ex - 2 x xe dx ∫
Ñaët: u = 2x ⇒ du = 2dx; dv = exdx, choïn v = ex ⇒ 2 x x e dx ∫ = x2ex - [2xex - 2 x e dx ∫ ] = x2ex - 2xex + 2ex + C Toång quaùt : n x x e dx ∫
= xnex - nxn - 1ex + n(n - 1)xn - 2ex + ... + (-1)n - 1n! xex + (-1)nn! ex + C b) ln dx xdx ∫ Ñaët :u = lnx ⇒ du = ; x dv = dx, choïn v = x ln xdx xdx ∫ = xlnx - ∫ = xlnx - x + C x c) n x ln xdx ∫ , n ≠ -1 n 1 +
Ñaët : u = lnx ⇒ du = 1 dx; dv = xndx, choïn v = x x n +1 n 1 + n 1 x x + n 1 + n 1 x x + n x ln xdx ∫ = ln x − dx ∫ = ln x − + C n +1 (n +1)x 2 n +1 (n +1) d) I= 3 x sin xdx ∫ Ñaët: u = x3 ⇒ du = 3x2dx dv = sinxdx, choïn v = -cosx ⇒ I = -x3cosx + 2 3x cos xdx ∫
= -x3cosx + 3x2sinx - 6x sin xdx ∫
= -x3cosx + 3x2sinx + 6xcosx - 6 cos xdx ∫
Toaùn cao caáp : Giaûi tích 111
= -x3cosx + 3x2sinx + 6xcosx - 6sinx + C e) I = xarctgxdx ∫ Ñaët: u = arctgx dx ⇒ du = 2 1+ x
dv = xdx, v = 1 (x2 + 1) (Choïn C = 1 ) 2 2 1 1 ⇒ I= 1 (x2 + 1)arctgx - 2 ∫ (x +1) dx 2 2 2 1+ x = 1 (x2 + 1) arctgx - 1 x +C 2 2 f) 2 2 a ∫ − x dx Ñaët: u = 2 2 −2xdx xdx
a − x ⇒ du = = − 2 2 2 2 2 a − x a − x dv = dx, choïn v = x 2 2 2 2 x dx − + − ⇒ I= x 2 2
a − x −∫ − = x 2 2
a − x −∫ x a a dx 2 2 a − x 2 2 a − x dx = x 2 2 ∫ a − x - 2 2 a ∫ − x dx + a2 2 2 a − x dx ⇒ 2I = x 2 2 ∫ a − x + a2 2 2 a − x x 2 a x ⇒ I = 2 − 2 a x + arcsin + C 2 2 a Töông töï: J = 2 2 a ∫ + x dx Ñaët: u = 2 2 xdx a + x ⇒ du = , dv = dx, choïn v = x 2 2 a + x Ta coù:
Toaùn cao caáp : Giaûi tích 112 2 2 2 2 J = x 2 2 x dx
x + a − a dx a + x - ∫ = 2 2 x a + x - ∫ 2 2 a + x 2 2 a + x dx ⇒2J= 2 2 2
x a + x + a ∫ 2 2 a + x 2 x a dx ⇒J= 2 a + 2 x + ∫ 2 a + 2 2 2 x 2 = x 2 a a + 2 x + ln(x + 2 2 a + x ) + C 2 2
VI. Tích phaân caùc haøm höõu tæ : Nhaéc laïi : dx ∫ = ln|x + a| + C x + a dx 1 ∫ = − + C (x + a)k 1 ( −1)( + )k k x a − dx ∫
= 1 ln x − a + C 2 2 x − a 2a x + a dx 1
(x − x ) − (x − x ) 1 2 ∫ = dx ∫
(x − x )(x − x ) x − x
(x − x )(x − x ) 1 2 2 1 1 2 1  1 1  = ∫ −  dx x −  − − 2 1 x x x2 x 1 x  1 = x − x2 ln + C ( x ≠ x ) 1 2 x − − 2 1 x x 1 x 1.
Tích phaân daïng: I= (Ax + B)dx ∫ ( a≠ 0) 2
ax + bx + c I = A 2ax + bAb dx dx ∫ +  B −  ∫ 2
2a ax + bx + c 2 
2a ax + bx + c
Toaùn cao caáp : Giaûi tích 113
= A ln|ax2 + bx + c| +  Ab dxB −  ∫ 2a 2 
2a ax + bx + c Tính: I dx 1 = ∫ (a ≠ 0) 2
ax + bx + c I 1 dx dx 1 = ∫ = 1 ∫ a 2 b c x + x + a 2 2  b c b  +  + − a a x 2  2a a 4a = 1 dx ∫ a 2  b  ∆  x +  − 2  2a  4a i) Neáu ∆ < 0: I 1 du −∆ b 1 = ∫ vôùi α2 = , u = x + 2 2 a u +α 2 4a 2a = 1 arctg u + C aα α ii) Neáu ∆ = 0: I du 1 1 = 1 ∫ = − + C a 2 u au iii) Neáu ∆ > 0:
ax2 + bx + c = a(x - x1)(x - x2)
vôùi x1, x2 laø nghieäm cuûa ax2 + bx + c = 0
2. Phaân tích moät ña thöùc thaønh tích cuûa nhöõng nhò thöùc vaø tam thöùc:
(Ñöa moät phaân thöùc veà toång cuûa nhöõng phaân thöùc ñôn giaûn)
Ghi chuù: Ta chæ xeùt caùc ña thöùc coù theå vieát döôùi daïng tích cuûa
nhöõng nhò thöùc baäc nhaát vaø nhöõng tam thöùc baäc hai. Ví duï:
Toaùn cao caáp : Giaûi tích 114 Tính : (3x − 5)dx ∫
(x −3)(x + 2)(x −1) Ta coù 3x − 5 = A B C + +
(x − 3)(x + 2)(x −1)
x − 3 x + 2 x −1
= A(x + 2)(x −1) + B(x − 3)(x −1) + C(x − 3)(x + 2)
(x − 3)(x + 2)(x −1)
Cho : x = 3 ⇒ 10A = 4 ⇒ A = 2 ; 5
x = -2 ⇒ 15B = -11 ⇒ B = 11 − 15 x = 1 ⇒ -6C = -2 ⇒ C = 1 3 x − ⇒ 3 5 = 2 11 1 − +
(x − 3)(x + 2)(x −1)
5(x −3) 15(x + 2) 3(x −1) (3x − 5) dx ∫
(x −3)(x + 2)(x −1)
= 2 ln|x - 3| - 11 ln|x + 2| + 1 ln|x - 1| + C 5 15 3
Ghi chuù: Ta coù theå tính A, B theo caùch khaùc : 3x − 5 ≡
(x − 3)(x + 2)(x −1) 2
(A + B + C)x + (A − 4B −C)x − 2A + 3B − 6C
(x − 3)(x + 2)(x −1)
A + B + C = 0 Ñoàng nhaát 2 veá 
⇒ A − 4B − C = 3 
−2A + 3B − 6C = −5
Ghi chuù: Neáu anxn + an -1xn - 1 ... + a1x + a0 = 0 coù nhieàu hôn
n nghieäm thöïc ⇒ an = an - 1 = ... = a0 = 0
Toaùn cao caáp : Giaûi tích 115
Ví duï: ax2 + bx + c = 0 coù 3 nghieäm phaân bieät ⇒ a = b = c = 0 Ví duï 1: 5x + 2 = 2 2 3
(x +1) (3x − 2) Ax + B Cx + D E F G + + + + 2 2 2 2 3 x +1 (x +1)
3x − 2 (3x − 2) (3x − 2) Ví duï 2: 2 6x − 7x + 2 = 2 4
(x − x +1)(x + 2) Ax + B C D E F + + + + 2 2 3 4
x − x +1 x + 2 (x + 2) (x + 2) (x + 2) Ví duï 3: 1 = 1 1 = 4 x +1 2 2 2 2 2 (x +1) − 2x
(x − 2x +1)(x + 2x +1) = Ax + B Cx + D + 2 2
x − 2x +1 x + 2x +1 Ví duï 4: Tính dx ∫ = ∫ dx 3 x +1 2
(x +1)(x − x +1) 2 1 = A Bx + C
A(x − x +1) + (Bx + C)(x +1) + = 3 x +1 2
x +1 x + x +1 3 x +1
Cho : x = -1 ⇒ 3A = 1 ⇒ A = 1 3
x = 0 ⇒ A + C = 1 ⇒ C = 2 3
x = 1 ⇒ A + 2(B + C) = 1 ⇒ B + C = 1 ⇒ B = - 1 3 3  1 2 
 − x +  dx dx ∫ = 1 dx ∫ +  3 3  ∫ 3 x +1 3 x +1 2 x − x +1
Toaùn cao caáp : Giaûi tích 116 = 1 ln 1 2x −1  2 1 |x + 1| -  dx dx ∫ +  −  ∫ 3 2 3.2 x − x +1 2
 3 6  x − x +1 = 1 ln 1 |x + 1| - 1 ln(x2 - x + 1) + dx ∫ 3 6 2 2  1  3  x −  +  2  4 1 2(x − ) 1 x +1 = 1 2 2 ln + arctg + C 2 3 x − x +1 2 3 3
5. Tích phaân bieåu thöùc löôïng giaùc:
Baèng caùc pheùp ñoåi bieán thích hôïp, ta coù theå ñöa tích phaân
bieåu thöùc löôïng giaùc R(sin x,cos x)dx ∫
, trong ñoù R laø haøm höõu
tyû, veà tích phaân bieåu thöùc höõu tyû.
1. Tröôøng hôïp toång quaùt: ta duøng coâng thöùc ñoåi bieán = x
t tg ⇒ x = 2arc tgt 2 2
vaø aùp duïng coâng thöùc 2t 1− t 2 sin = , cos = , dt x x dx = 2 2 2 1+ t 1+ t 1+ t Ví duï: dx I = ∫
4sin x + 3cos x + 5 Ñaët x
t = tg ⇒ x = 2arctgt ta coù: 2 1 2 = ∫
dt = ∫ dt = dt I 2 2 2 2t 1 ∫ − t 1+ t t + 4t + 4 (t + 2 4 + 3 + 5 )2 2 2 1+ t 1+ t −1 1 = + C = − + C t + 2 x tg + 2 2
2. Daïng ñaëc bieät:
i. Neáu R(−sin x,cos x) = −R(sin x,cos x) thì ñaët t = cos x
Toaùn cao caáp : Giaûi tích 117
ii. Neáu R(sin x,−cos x) = −R(sin x,cos x) thì ñaët t = sin x
iii. Neáu R(−sin x,−cos x) = R(sin x,cos x) thì ñaët t = tgx , hay t = cotgx Ví duï 1: I = ∫( 2 3 x x + x)dx = ∫( 2 2 sin cos 2 cos
sin x cos x + 2)cosxdx
Ñaët t = sin x ⇒ dt = cos xdx ; 2 2 2 x x + = t ( 2 − t ) 4 2 sin cos 2 1
+ 2 = −t + t + 2 ta coù: = ∫(− + + 2) 5 3 4 2 = − t + t I t t dt + 2t + C 5 3 5 3 −sin x sin = +
x +2sin x +C 5 3 Ví duï 2: dx I = ∫ 2 2
sin x + sin2x − 3cos x Ñaët 1
t = tgx ⇒ dt = dx ta coù: 2 cos x = ∫ dx = ∫ dt = ∫ dt I 2 cos x ( 2
tg x + 2tgx − 3) 2 t + 2t − 3 (t − )1(t +3) 1  1 1  1 t −1 1 tgx −1 = ∫ −  dt = ln + C = ln + C
4  t −1 t + 3  4 t + 3 4 tgx + 3
3. Daïng sinm cosn x xdx ∫
i. Neáu m ( hoaëc n) laø soá nguyeân leû thì ñoåi bieán
t = cos x (hoaëc t = sin x ).
ii. Neáu m vaø n laø soá nguyeân döông chaün thì duøng coâng thöùc haï baäc.
iii. Neáu m vaø n nguyeân chaün vaø coù moät soá aâm thì ñoåi bieán
t = tgx (hoaëc t = co tgx )
Toaùn cao caáp : Giaûi tích 118
Ví duï: Tính ( daønh cho ñoäc giaû ) 2 4
K = ∫sin x cos xdx 3 2
L = ∫sin x cos xdx 2 sin x 2 cos M = dx ∫ = 4 cos ∫ x N dx x 4 sin x
VI. Tích phaân bieåu thöùc coù chöùa caên: Vôùi caùc pheùp ñoåi
bieán thích hôïp, ta coù theå ñöa tích phaân cuûa bieåu thöùc coù caên
soá veà tích phaân cuûa bieåu thöùc höõu tyû.
1. Caùc tích phaân sau coù theå ñöa veà tích phaân haøm löôïng giaùc:   i. Daïng  2 2 R x ∫ , A x d  − x ñaët π π
x = Asin t, t ∈ − ,     2 2    ii. Daïng  2 2 R x ∫ , A x d  + x ñaët π π
x = Atgt, t ∈ − ,     2 2  A   iii. Daïng  2 2 R x ∫ , x A d  −
x ñaët x = , t ∈(0, ) π π \     cost  2   m r
2. Daïng ∫ R x,  ax + b ax b n ,  +   s      dx   cx + d
cx + d     Ñaët ax + b k t =
vôùi k laø boäi soá chung nhoû nhaát cuûa n vaø s. cx + d k Khi ñoù −dt + b − ad − bc k 1 x = ⇒ dx = kt thay vaøo bieåu k ct − a ( k ct − a)2
thöùc tích phaân ta coù tích phaân cuûa haøm höõu tyû. Ví duï 1: dx I = ∫ 3 6
x −1 − x −1
Toaùn cao caáp : Giaûi tích 119 k = 6, ñaët 6 5
t = x −1⇒ dx = 6t dt . Suy ra 5 4 6t dt 6t dt  1  I = ∫ = ∫ = 6∫ 3 2 t t t 1 dt 2  + + + +  t − t t −1  t −1  4 3 2  =6 t t t
+ + + t + ln t −1  +C  4 3 2  3(x − )2/3 1 = + 2(x − )1/2 1 + 3(x − )1/3 1 2 + 6 6 x −1 + 6
6 ln x −1 −1 + C 1 1 Ví duï 2: − x I = dx ∫ x 1+ x 2 Ñaët 1− x −t +1 4 = ⇒ = ; − t t x dx = dt 2 1+ x t +1 ( 2t + )2 1 2 2 t +1 −4t = ∫ = 4 t I t dt dt 2 ∫ −t +1 (t + )2 1 ( 2t − )1( 2 2 t + ) 1  1 1  t −1 = 2∫ + = 2arctgt + ln + C 2 2  t 1 t 1 + −  t +1 1− x −1 1− x 1 = 2 + ln + x arctg + C 1+ x 1− x +1 1+ x
3. Daïng vi phaân nhò thöùc ∫ ( + )p m n x a bx
dx vôùi m, n, p laø caùc soá höõu tyû.
- Neáu p laø soá nguyeân, ta ñaët kt = x , trong ñoù k laø boäi soá
chung nhoû nhaát cuûa maãu soá cuûa m vaø maãu soá cuûa n.
Toaùn cao caáp : Giaûi tích 120
- Neáu m +1 laø soá nguyeân, ñaët k n
t = a + bx vôùi k laø maãu soá n cuûa p.
- Neáu m +1 + p laø soá nguyeân thì ñaët k −n
t = ax + b vôùi k laø n maãu soá cuûa p. Ví duï: a) dx I = ∫
( p= -8 laø soá nguyeân) x ( + x )8 3 6 1 Ñaët 6 5
x = t ⇒ dx = 6t dt 5 3 6t dt = ∫ = 6 t dt I ∫ t (1+ t)8 (1+ t)8 2 5 4 b) 1+ x I = dx ∫ x m +1
(m = −1/ 2;n = 1/ 4; p = 1/ 5 ⇒ = 2∈ℤ) n Ñaët 4
t = 1+ x ⇒ x = (t − )4
1 ⇒ dx = 20(t − )3 5 5 5 4 1 t dt t.20(t − )3 5 4 1 t dt 5 I = ∫ = 20 t
∫ ( 5t −1 dt 2 5 ) (t − )1 ( 3 1+ x ) c) I = dx ∫ x m +1
m = −1/ 2;n = 1/ 3; p = 1/ 2⇒ + p = 2∈ℤ n

Tài liệu liên quan: