Đại số Tuyến tính Giảng viên: Đào Như Mai 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 1
Chương 6: Ánh xạ tuyến tính  Định nghĩa, ví dụ
 Nhân, ảnh của ánh xạ tuyến tính
 Ma trận của ánh xạ tuyến tính
 Ma trận chuyển cơ sở, đồng dạng 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 2 Định nghĩa
 Ánh xạ tuyến tính. Cho tập  và  là các không gian véc tơ
trên trường , ánh xạ tuyến tính :  →  giữa 2 không
gian véc tơ  và  là một ánh xạ thỏa mãn:
  +  =   +   , ∀,  ∈ .
  =   , ∀ ∈ ,  ∈ . 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 3 Định nghĩa
 Ví dụ. Chứng tỏ ánh xạ :  →  xác định như sau:
 , ,  = ( + 2 − 3, 2 + )
là ánh xạ tuyến tính (axtt).
∀ = , ,  ;∀ = , ,  ∈ ;  ∈ , ta có:
  +  =   + ,  + ,  +  =
=  +  + 2 + 2 − 3 − 3, 2 + 2 +  + 
=  + 2 − 3,2 +  + ( + 2 − 3,2 + ) =   + ().
  =   ,,  =  ,,  =
=  + 2 − 3, 2 +  =
=   + 2 − 3, 2 +  = (). Vậy  là axtt. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 4 Định nghĩa
 Chú ý. Cho :  →  là axtt.
Xét  = {, , … , } là tập sinh của .
Giả sử biết:   ,   , … , (). Khi đó:
∀ ∈  ↔  =  +  + ⋯+  Suy ra:
  =   +  + ⋯ +  =
=   +   + ⋯ +   =
=   +   + ⋯ +  
Ánh xạ tuyến tính  được hoàn toàn xác định nếu biết được
ảnh của một tập sinh của  08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 5 Định nghĩa
 Ví dụ. Cho :  →  là axtt, biết:
 1,1,0 = 2, −1 ,  1,1,1 = 1,2 ,  1,0,1 = −1,1 . a. Tìm (3,1,5). b. Tìm ().
a. Ta có: 3,1,5 =  1,1,0 +  1,1,1 +  1,0,1 .  +  +  = 3
↔   +  = 1 ↔  = −2,  = 3,  = 2 .  +  = 5 Do đó:
 3,1,5 =   1,1,0 +  1,1,1 +  1,0,1 =
=  1,1,0 +  1,1,1 +  1,0,1 =
= −2 2, −1 + 3 1,2 + 2 −1,1 = (−3,10) 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 6 Định nghĩa  Ví dụ (tiếp)
b. Ta có:  = , ,  =  1,1,0 +  1,1,1 + (1,0,1).  +  +  =   =  − 
↔   +  =  ↔  = − +  +  .  +  =   =  −  Do đó:
  = (, , ) =   1,1,0 +  1,1,1 +  1,0,1 =
=  1,1,0 +  1,1,1 +  1,0,1 =
=  −  2, −1 + − +  +  1,2 +
+( − ) −1,1 = (2 − , −2 +  + 3)
Vậy   = (2 − , −2 +  + 3). 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 7 Định nghĩa
 Ánh xạ nào sau đây là ánh xạ tuyến tính?
1. :  → ; , = 2 + 3,
2. :  → ; , =  + 2,0
3. :  → ;  ,  = 2 − ,  + 1
4. :  → ;  ,  = 1,  −  5. :  
 → ;  ,  =  + , 
6. :  → ; , = , 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 8
Nhân, ảnh của ánh xạ tuyến tính
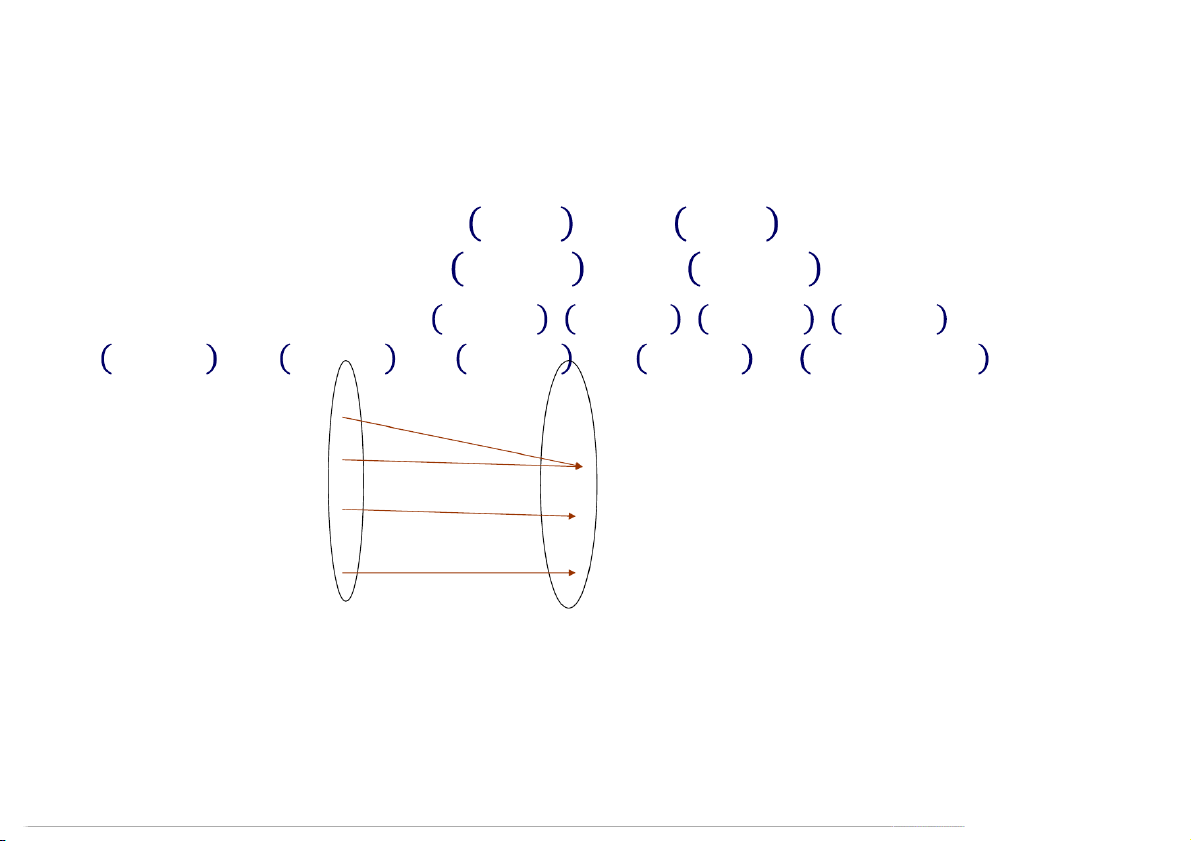
 Nhân của ánh xạ tuyến tính
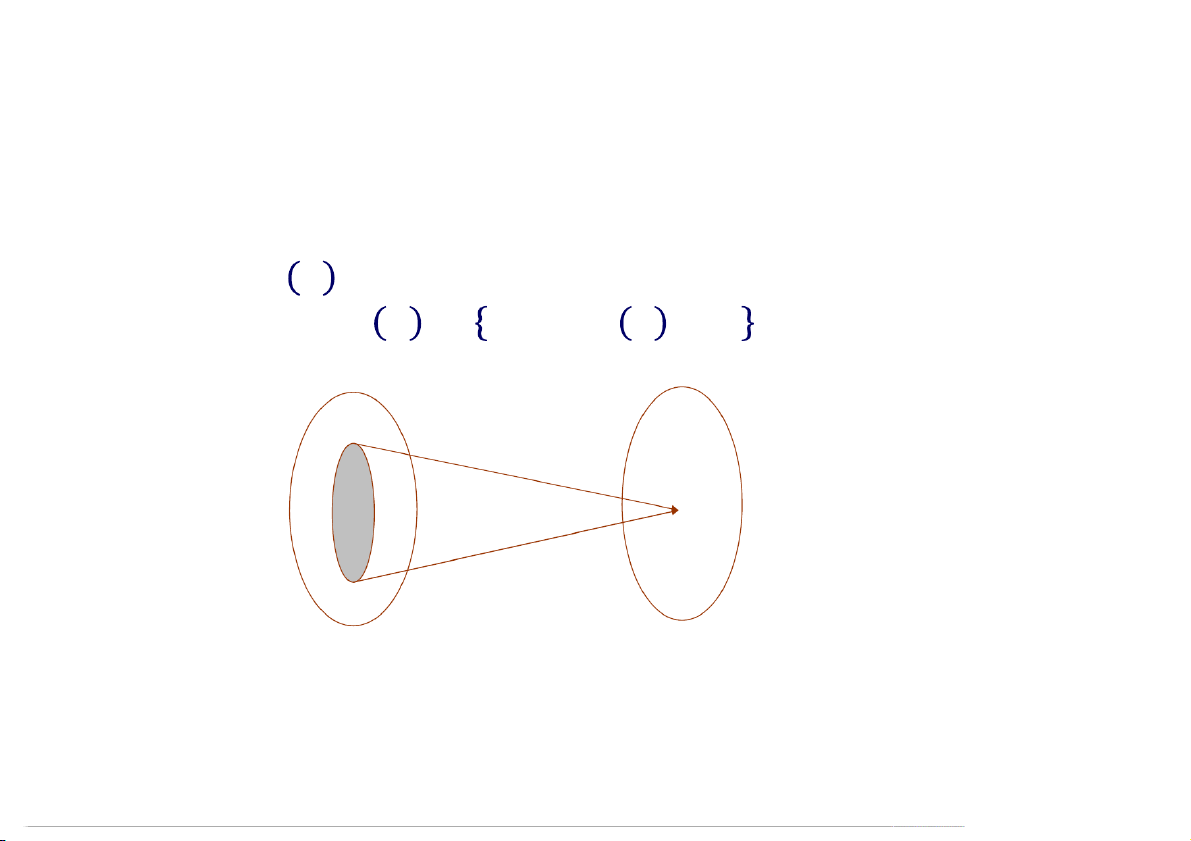
Cho axtt: :  → , nhân của axtt  là tập hợp tất cả các véc tơ
 ∈  sao cho   = .
  =  ∈ :   =  . V W Kerf  08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 9
Nhân, ảnh của ánh xạ tuyến tính
 Ảnh của ánh xạ tuyến tính
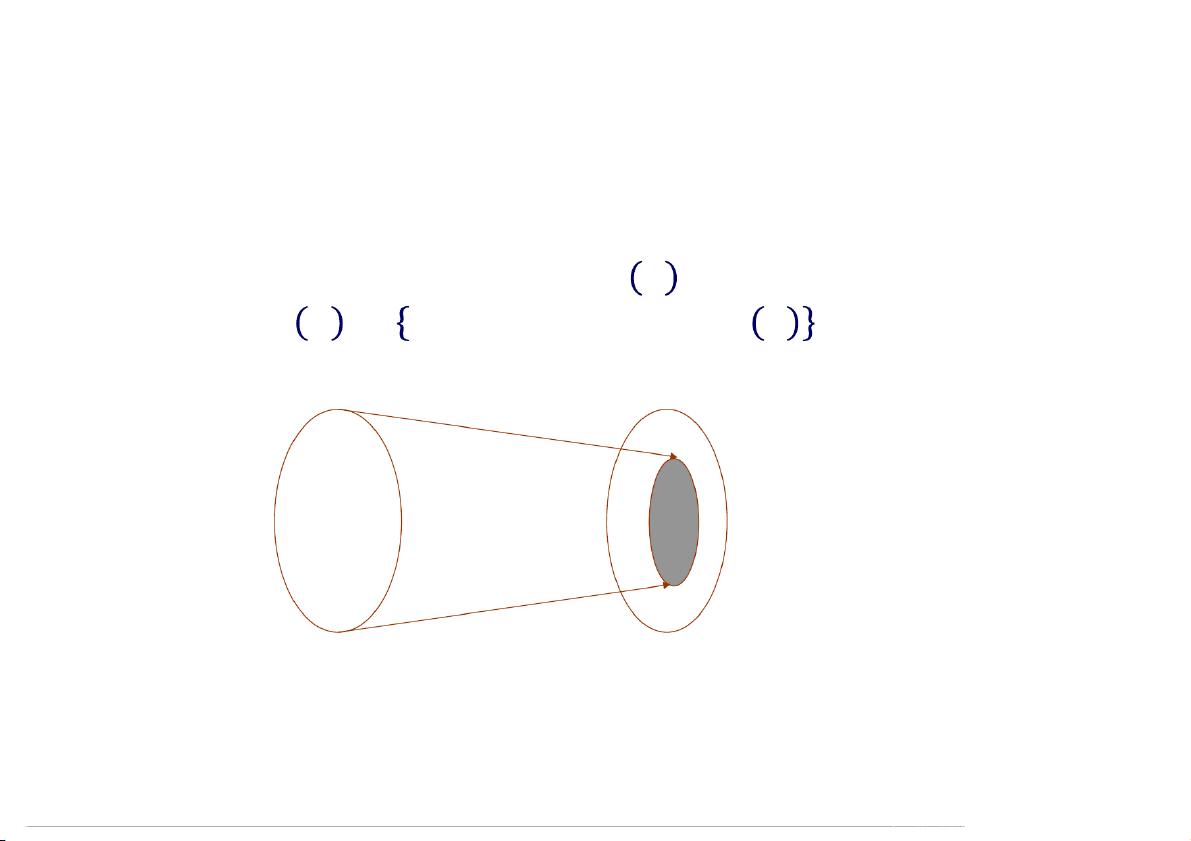
Cho axtt: :  → , ảnh của axtt  là tập hợp tất cả các véc tơ
 ∈  sao cho tồn tại  ∈  để  =   .
  =  ∈ : ∃ ∈ ,  =   . V W Imf 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 10
Nhân, ảnh của ánh xạ tuyến tính
 Tính chất Cho axtt: :  →     = .
  − = −  , ∀ ∈ .
   −  =   −   , ∀,  ∈ .
 Định lý Cho axtt: :  → 
 1. Nhân của axtt  là không gian con của .
 2. Ảnh của axtt  là không gian con của .
 3. dim  = dim  + dim  .
 Định nghĩa. Cho axtt: :  → , khi đó dim() được gọi
là hạng của axtt , ký hiệu: (). 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 11
Nhân, ảnh của ánh xạ tuyến tính  Tính chất
 Mệnh đề. Cho axtt: :  → , ảnh của axtt  là không gian
con được sinh ra bởi ảnh của một tập sinh của .
Chứng minh: Giả sử tập sinh của  là  = {, , … , }.
∀ ∈  ↔ ∃ ∈ :  =   .
Mặt khác:  =  +  + ⋯ + , do đó:
 =   =   +  + ⋯+  =
=   +   + ⋯ + ()
→  = {  ,  , … ,   } sinh ra .
Hay  =   ,   , … ,   . 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 12
Nhân, ảnh của ánh xạ tuyến tính
 Chú ý. Các bước tìm ảnh của ánh xạ tuyến tính  Cho axtt: :  → 
 1. Chọn một cơ sở của  là  = {, , … , }.
 2. Xác định   ,   , … ,   .
 3.  =   ,   , … ,   .
 Còn có các cách giải khác.
 Tùy theo bài toán mà ta chọn cơ sở (ở bước 1) phù hợp, để
việc tìm ảnh của cơ sở đó thuận tiện. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 13
Nhân, ảnh của ánh xạ tuyến tính
 Ví dụ. Cho axtt: :  → , biết:
 , ,  =  +  − , 2 + 3 − , 3 + 5 −  .
Tìm cơ sở, số chiều của  Giải
∀ = , ,  ∈  ↔   = .
↔  +  − , 2 + 3 − , 3 + 5 −  = (0,0,0).  +  −  = 0
↔ 2 + 3 −  = 0 ↔  = 2,  = −,  tùy ý.
3 + 5 −  = 0
→  = 2, −,  = (2, −1,1). Do đó:  = {(2, −1,1)} là tập
sinh và cơ sở của  → dim  = 1. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 14
Nhân, ảnh của ánh xạ tuyến tính
 Ví dụ. Cho axtt: :  → , biết:
 , ,  =  +  − , 2 + 3 − , 3 + 5 −  .
Tìm cơ sở, số chiều của Im  Giải
Chọn cơ sở chính tắc của :  = 1,0,0 , 0,1,0 , 0,0,1 . Do đó:
 =  1,0,0 ,  0,1,0 ,  0,0,1 =
= 1,2,3 , 1,3,5 , −1, −1, −1
Lập ma trận , dùng phép bđsc hàng đưa ma trận  về dạng bậc
thang → dim  = 2, cơ sở  = { 1,1,1 , 0,1,2 }. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 15
Nhân, ảnh của ánh xạ tuyến tính
 Ví dụ. Cho axtt: :  → , biết:
 1,1,1 = 1,2,1 ;  1,1,2 = 2,1, −1 ;  1,2,1 = 5,4, −1
Tìm cơ sở, số chiều của .
 Cách 1: Hệ cơ sở của :  = { 1,1,1 , 1,1,2 , 1,2,1 }.
∀ = , ,  ∈ , ta có:
 = , , =  1,1,1 +  1,1,2 + (1,2,1).  +  +  = 
 = 3 −  − 
↔  +  + 2 =  ↔   =  −  .  + 2 +  =   =  −  08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 16
Nhân, ảnh của ánh xạ tuyến tính  Ví dụ (tiếp)
  = 3 −  −  1,2,1 +  −  (2,1, −1) +( − )(5,4,1)
→   = −4 + 4 + , + 2 − ,5 − 2 − 2 .
∀ = , ,  ∈  ↔   = .
−4 + 4 +  = 0
↔   + 2 −  = 0 ↔  = 2,  = 4, tùy ý.
5 − 2 − 2 = 0
→  = 2, ,4 = (2,1,4). Do đó:  = {(2,1,4)} là tập
sinh và cơ sở của  → dim  = 1. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 17
Nhân, ảnh của ánh xạ tuyến tính  Ví dụ (tiếp). Cách 2
Chọn cơ sở của :  = 1,1,1 , 1,1,2 , 1,2,1 .
∀ ∈  ↔   = .
Giả sử []= [, , ], khi đó:
 =  1,1,1 +  1,1,2 +  1,2,1 .
Do đó:   =  1,1,1 +  1,1,2 +  1,2,1 .
↔   = ( + 2 + 5, 2 +  + 4,  −  − ).
Từ   =  ↔  = −,  = −2,  tùy ý.
Do đó []= [−, −2, ].
Nên  = − 1,1,1 − 2 1,1,2 +  1,2,1 = −(2,1,4).
Cơ sở của  là  = {(2,1,4)}, dim() = 1. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 18
Nhân, ảnh của ánh xạ tuyến tính
 Ví dụ. Cho axtt: :  → , biết:
 1,1,1 = 1,2,1 ;  1,1,2 = 2,1, −1 ;  1,2,1 = 5,4, −1
Tìm cơ sở, số chiều của .  Giải:
Hệ cơ sở của :  = { 1,1,1 , 1,1,2 , 1,2,1 }.
Do đó:  =  1,1,1 ,  1,1,2 ,  1,2,1 =
= 1,2,1 , 2,1, −1 , 5,4, −1 .
Lập ma trận , dùng phép bđsc hàng đưa  về dạng bậc thang.
dim() = 2, cơ sở  = { 1,2,1 , 0,1,1 }. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 19
Nhân, ảnh của ánh xạ tuyến tính
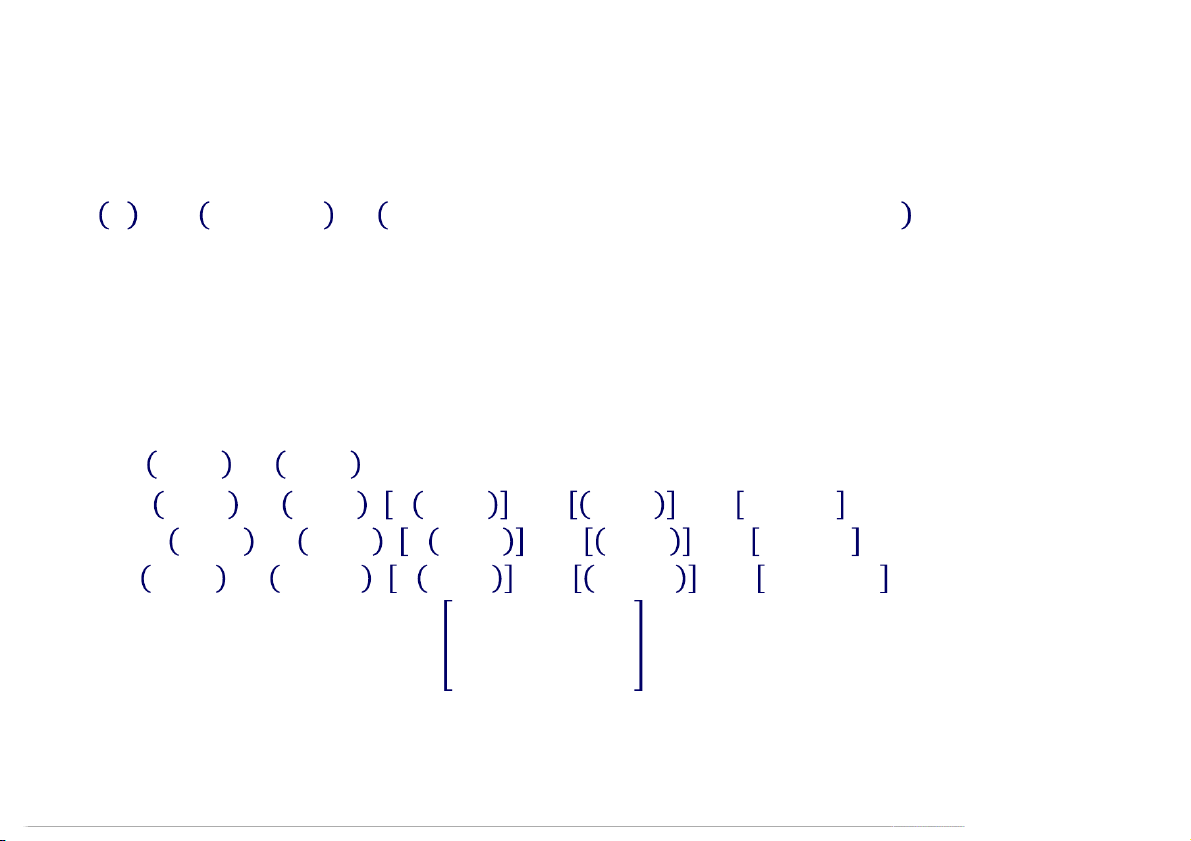
 Ví dụ Tìm một ánh xạ tuyến tính :  →  , biết:
Im =<  = 1,1,1 ,  = 1,2,1 >,
Ker =<  = 1,1,1,0 , = 2,1,0,1 >
Chọn cơ sở của :  = { 1,1,1,0 , 2,1,0,1 , 0,0,1,1 , 0,0,0,1 }.
 1,1,1,0 +  2,1,0,1 +  0,0,1,1 +  0,0,0,1 = , , ,  1 e (1,1,1,0)  2 e (2,1,0,1)  (  0,0,0) 3 e (0,0,1,1)   f (1,1,1) 1 4 e (0,0,0,1)   f (1, 2,1) 2 f (  
f (e )  (1,1,1), f (e )  (1, 2,1) 1 e ) f ( 2 e ) 0 3 4  f (x)
Chú ý: lời giải không duy nhất! 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 20
Nhân, ảnh của ánh xạ tuyến tính  Ví dụ (tiếp)
Chọn cơ sở của :  = { 1,1,1,0 , 2,1,0,1 , 0,0,1,1 , 0,0,0,1 }.
 1,1,1,0 =  2,1,0,1 = 0,  0,0,1,1 = 1,1,1 ,  0,0,0,1 = (1,2,1)
∀ = , , ,  ∈ 
 1,1,1,0 +  2,1,0,1 +  0,0,1,1 +  0,0,0,1 = , , ,   + 2 =   = 2 −   +  =   =  −   + c =  → 
c =  − 2 +   +  +  = 
 = −2 + 3 −  + 
  =  0,0,0 +  0,0,0 +  1,1,1 +  1,2,1
  = (− +  + ,−3 + 4 −  + 2, − +  + )
Nếu chọn  = { 1,1,1,0 , 2,1,0,1 , 0,0,1,0 , 0,0,0,1 }.
  = (− +  + , − +  + 2, − +  + ) 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 21
Ma trận của ánh xạ tuyến tính
 Ma trận của ánh xạ tuyến tính Cho axtt :  → 
 = {, , … , } là cơ sở của .
 = {, , … , } là cơ sở của .
Ma trận  cấp mxn với cột thứ  là tọa độ của véc tơ () trên hệ
cơ sở  được gọi là ma trận của axtt  trên cặp cơ sở , .
 = [()] [()] … [()]  . 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 22
Ma trận của ánh xạ tuyến tính
 Ví dụ Cho axtt :  → , biết:
  = ( + 2 − 3,2 + )
 Tìm ma trận của axtt  trên cặp cơ sở:
 = 1,1,1 , 1,0,1 , 1,1,0 ;  = { 1,1 , 1,2 }
 1,1,1 = 0,3 →  1,1,1  = −3,3 
 1,0,1 = −2,3 →  1,0,1  = −7,5 
 1,1,0 = 3,2 →  1,1,0  = 4, −1 
Vậy ma trận của axtt  là:  = −3 −7 4 3 5 −1 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 23
Ma trận của ánh xạ tuyến tính
Định lý. 1. Cho axtt :  → , giả sử:
 = {, , … , } là cơ sở của ,  = {, , … , } là cơ sở của , khi
đó tồn tại duy nhất một ma trận của axtt f là  sao cho: ()  =    .
2. Cho ma trận  = ()
, khi đó tồn tại duy nhất
 trên trường số 
một axtt :  →  sao cho: ()  =    .
Chú ý 1. Mỗi axtt tương ứng duy nhất một ma trận và ngược lại.
2. Ta coi axtt là ma trận, thông thường không phân biệt 2 khái niệm này.
Định lý. Cho axtt :  → , khi đó () bằng hạng của ma trận của
 đối với cặp cơ sở bất kỳ nào đó. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 24
Ma trận của ánh xạ tuyến tính
 Ví dụ. Cho axtt :  → , biết ma trận của  trên cặp cơ sở
B1.  = 1,1,1 , 1,0,1 , 1,1,0 ;  = { 1,1 , 2,1 } là:  = 2 1 −3 0 3 4 . Tìm (3,1,5).
Tìm tọa độ của (3,1,5) trong cơ sở : (3,1,5)   = 3,2, −2 .
B2: Sử dụng công thức: ()  =   3 (3,1,5)  = 2 1 −3 0 3 4 2 = 14 −2 −2 .
B3: Đổi tọa độ của ảnh cần tìm:
 3,1,5 = 14. 1,1 − 2. 2,1 = 10,12 . 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 25
Ma trận của ánh xạ tuyến tính
Ví dụ. Cho axtt :  → , biết ma trận của  trên cặp cơ sở
 = 1,1,1 , 1,0,1 , 1,1,0 ;  = { 1,1 , 2,1 } là:  = 2 1 −3 0 3 4 . Tìm ().
Giải. ∀ = , ,  =  1,1,1 +  1,0,1 +  1,1,0 .
 = − +  +  − +  +  ↔   =  −  ↔   =  −  .  =  −   − 
Theo công thức ta có: ()  =   . − +  +  ↔ ()  = 2 1 −3  0 3 4  − 
= −4 +  + 5 .  7 − 3 − 4  −  
↔   = −4 +  + 5 . 1,1 + 7 − 3 − 4 . 2,1 .
↔   = 10 − 5 − 3, 3 − 2 +  . 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 26
Ma trận của ánh xạ tuyến tính
Ví dụ. Cho axtt :  → , biết ma trận của  trên cơ sở
 = 1,1,1 , 1,0,1 , 1,1,0 là: 1 1 −1  = 2 3 3 1 2 4 1. Tìm (2,3, −1)
2. Tìm cơ sở, số chiều của .
Cách 1: tìm  có thể tìm thông qua ().
 ∈  ↔   = . ↔ ()  = 0,0,0  ↔    = 0,0,0 . Giả sử  
 = , ,  , khi đó: 1 1 −1  0 6
↔ 2 3 3  = 0 ↔   = −5 1 2 4  0 
→  =  +  +  = 6 1,1,1 − 5 1,0,1 +  1,1,0 = (2,7,1).
Vậy  = {(2,7,1)} là tập sinh, cơ sở của . → dim  = 1. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 27
Ma trận chuyển cơ sở, đồng dạng
 Nhắc lại. Ma trận chuyển cơ sở
Xét hai cơ sở của kgvt :  =    
, , … ,  ;  = {, , … , }
∀ ∈ :  =  + .+ ⋯ + . (1)  =      
 +  + ⋯ + . (2) Mặt khác:
 =  +  + ⋯ + .
 =  +  + ⋯+ . .......
 =  +  + ⋯ + . 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 28
Ma trận chuyển cơ sở, đồng dạng  Lập ma trận a a ... a  11 12 1n   a a ... a 21 22 2n P     ... ... ... ...    a a ... a  n1 n 2 nn
 được gọi là ma trận chuyển cơ sở từ cơ sở  sang cơ sở . Hơn nữa ta có:
 =   +  + ⋯+  +
+  +  + ⋯ +  + ⋯+
+( +  + ⋯ + ) 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 29
Ma trận chuyển cơ sở, đồng dạng
 So sánh đẳng thức này với (1), và viết lại dưới dạng ma trận ta có: '  x  a a ... a   x  1 11 12 1n 1       ' x a a ... a x 2 21 22 2n      2   ...  ... ... ... ...   ...       ' x  a a ... a  x  n n1 n 2 nn n
 Hay: []= . [] .
 Chú ý: cấu trúc ma trận : chuyển cơ sở từ  → :   =   
    …   08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 30
Ma trận chuyển cơ sở, đồng dạng
 Ví dụ. Trong  cho cặp cơ sở:
 = 1,1,1 , 1,0,1 , 1,1,0 ,  = 1,1,2 , 1,2,1 , 1,1,1 .
Tìm ma trận chuyển cơ sở từ  → .
Giải Tìm tọa độ của  = (1,1,2) trên cơ sở : []= [2,0, −1] Tương tự:  
 = (1,2,1): []= [2, −1,0].  
 = 1,1,1 : []= [1,0,0] 2 2 1
Do đó ma trận chuyển cơ sở từ  → :  = 0 −1 0 −1 0 0 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 31
Ma trận chuyển cơ sở, đồng dạng  Định lý
Cho axtt :  → , trên  cho 2 cơ sở:  =    
, , … ,  ,  = {, , … , }
Gọi  là ma trận chuyển cơ sở từ  → .
 là ma trận của axtt  trên cơ sở .  là ma trận của axtt 
trên cơ sở . Khi đó:  = . E A E P P E’ P-1AP E’ 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 32
Ma trận chuyển cơ sở, đồng dạng
 Ví dụ. Cho axtt :  → , biết ma trận của axtt  trên cơ sở
 = { 1,2,1 , 1,1,2 , 1,1,1 } là: 1 0 1  = 2 1 4 .
Tìm ma trận của  trên cơ sở chính tắc. 1 1 3
 Cơ sở chính tắc:  = { 1,0,0 , 0,1,0 , 0,0,1 }.
 Gọi ma trận chuyển cơ sở từ  →  là .  là ma trận của axtt
 trên cơ sở chính tắc . Khi đó:  = . −1 1 0 1 1 1 18 −4 −6  = −1 0
1 ;  = 2 1 1 →  = 20 −4 −7 . 3 −1 −1 1 2 1 27 −6 −9 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 33
Ma trận chuyển cơ sở, đồng dạng
 Định nghĩa. Ma trận đồng dạng
Cho 2 ma trận vuông ,  cấp nxn trên cùng trường .
 và  được gọi là đồng dạng nếu tồn tại một ma trận khả
nghịch  sao cho:  = .
 Cho axtt :  → , giả sử:
 là ma trận của axtt  trên cơ sở .  là ma trận của axtt 
trên cơ sở . Khi đó  và  là hai ma trận đồng dạng.
(tồn tại ma trận P khả nghịch, P là ma trận chuyển cơ sở từ  → ). 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 34 Ví dụ - Tổng quan
Bài 1. Cho :  → , là ánh xạ tuyến tính. Với
  =  , ,  =  +  + ,  +  + ,  +  +  1. Tính f(2,1,5)
2. Tìm ma trận của ánh xạ tuyến tính f trên cơ sở
E ={(1,1,1); (1,1,2); (1,2,1)}
3. Tính f(2,1,5) sử dụng 2), so sánh với 1). Giải 1.  2,1,5 = 8,0,5 ;
2.  1,1,1 = 3,2,6 ;  1,1,1  = 3,2,6  = 1,3, −1 
 1,1,2 = 4,1,5 ;  1,1,2  = 4,1,5  = 6,1, −3 
 1,2,1 = 4,3,10 ;  1,2,1  = 4,3,10  = −1,6, −1  1 6 −1  = 3 1 6 −1 −3 −1 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 35 Ví dụ - Tổng quan Bài 1 (tiếp)
3. 2,1,5  = 0,3, −1 ;  2,1,5  =    = 19, −3, −8 
 2,1,5 = 19 1,1,1 − 3 1,1,2 − 8 1,2,1 = (8,0,5)
Biểu diễn tọa độ các vec tơ qua cơ sở E, giải hệ ptr với các vế phải khác nhau
        () 1 1 1 2 3 4 4 1 1 2 1 2 1 3  → 1 2 1 5 6 5 10 1 1 1 2 3 4 4 0 1 6 −1
0 0 1 −1 −1 −3 −1 → 3 3 1 6 0 1 0 3 3 1 6 −1 −1 −3 −1 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 36 Ví dụ - Tổng quan
Bài 2 Cho :  →  là ánh xạ tuyến tính, biết ma trận của f trên
cơ sở E = {(1,1,1); (1,1,0); (1,0,0)} là: 1 0 1  = 2 1 4 1 1 3 1. Tính f (4,3, 5).
2. Tìm cơ sở và số chiều của Imf.
3. Tìm cơ sở và số chiều của Kerf. 1 0 1 5 6
4,3,5  = 5, −2,1 ;  4,3,5  = 2 1 4 −2 = 12 1 1 3 1  6 
 4,3,5 = 6 1,1,1 + 12 1,1,0 + 6 1,0,0 = (24,12,6) 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 37 Ví dụ - Tổng quan  Bài 2 (tiếp) 1
 1,1,1  = 2  1,1,1 = 1 1,1,1 + 2 1,1,0 + 1 1,0,0 = (4,3,1) 1  0
 1,1,0  = 1  1,1,0 = 0 1,1,1 + 1 1,1,0 + 1 1,0,0 = (2,1,0) 1  1
 1,0,0  = 4  1,1,0 = 1 1,1,1 + 4 1,1,0 + 3 1,0,0 = (8,5,1) 3 
 =  1,1,1 ,  1,1,0 ,  1,0,0 = 4,3,1 , 2,1,0 , 8,5,1 .
Lập ma trận , dùng phép bđsc hàng đưa  về dạng bậc thang.
dim() = 2, cơ sở  = { 2,1,0 , 0,1,1 }. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 38 Ví dụ - Tổng quan Bài 2(tiếp).
∀ ∈  ↔   = .
Giả sử []= [, , ], khi đó:
 =  1,1,1 +  1,1,0 +  1,0,0
  =  1,1,1 +  1,1,0 +  1,0,0
  =  4,3,1 +  2,1,0 +  8,5,1
↔   = (4 + 2 + 8,3 +  + 5,  + ).
Từ   =  ↔  = −,  = −2,  tùy ý.
Do đó []= [−, −2, ].
Nên  = − 1,1,1 − 2 1,1,2 +  1,2,1 = −(2,1,4).
Cơ sở của  là  = {(2,1,4)}, dim() = 1. 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 39 Ví dụ - Tổng quan
Bài 3. Cho :  →  là ánh xạ tuyến tính, biết ma trận của f trên
cơ sở  =  +  + ,  + 2 + , 2 +  +  là 2 1 3  = 1 2 0 1 1 −1
Tìm ma trận của f trên cơ sở F=  +  + ,  + ,  +  1 −2 2 1 4 −2  = 0 1 0  0 1 0 0 1 −1 0 −1 1 A =  = 1 4 −2 2 1 3 1 −2 2 4 4 13 0 1 0 1 2 0 0 1 0 = 1 0 2 0 −1 1 1 1 −1 0 1 −1 0 −2 1 08:49
Trường Đại học Công nghệ, ĐHQG Hà Nội 40