14 trang 228 lượt tải

Chương 6_ Phương Pháp dây cung | Bài giảng môn Phương pháp tính | Đại học Bách khoa Hà Nội

455

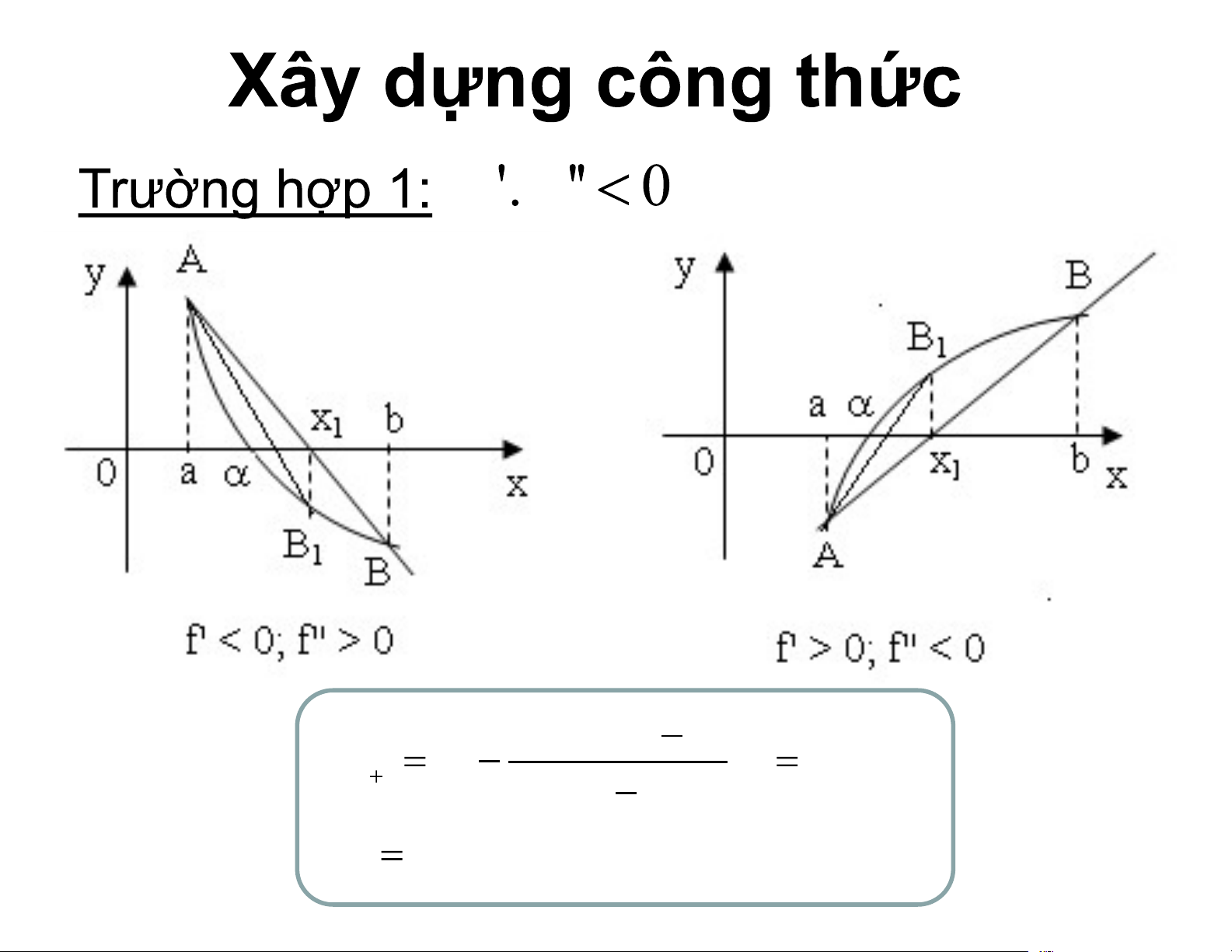
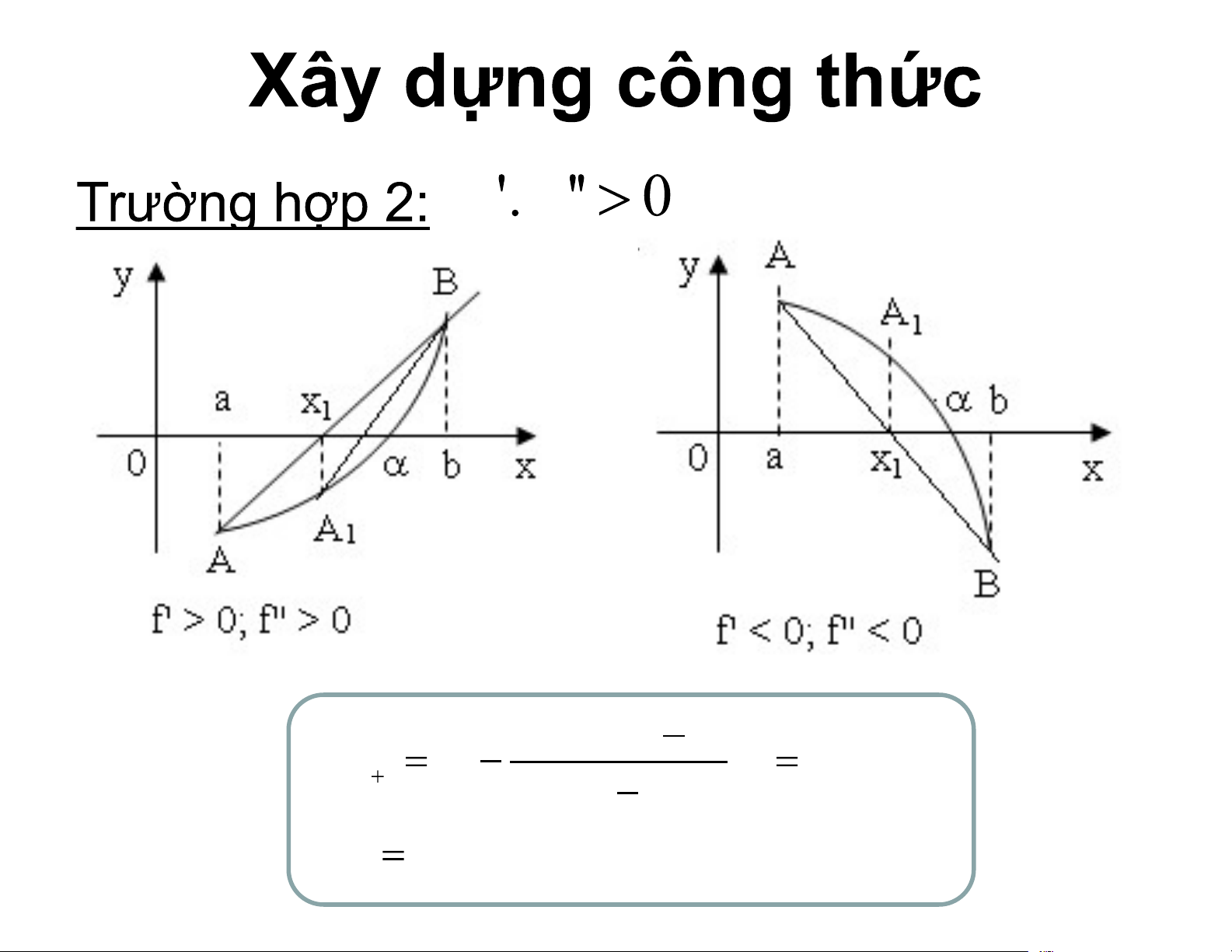
Thay thế đường cong y = f(x) trên [a,b] bằng dây cung nối hai đầu mút. Tìm giao điểm của dây cung với trục hoành thay cho giao điểm đường cong với trục hoành. Tài liệu được Sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Môn: Phương pháp tính (BK) 44 tài liệu

Trường: Đại học Bách Khoa Hà Nội 5.2 K tài liệu

Tác giả:

Profile

VietJack

1 năm trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/14
y f x
1
x
M
0
M
1
M
f f
1
0
( )( )
, 0,1,2,...
( ) ( )
n n
n n
n
f x x a
x x n
f x f a
x b
f f
1
0
( )( )
, 0,1,2,...
( ) ( )
n n
n n
n
f x x b
x x n
f x f b
x a
sao cho
Tính theo công
trong và
,...2,1,0,
)()(
))((
1
n
dfxf
dxxf
xx
n
nn
nn
0
x a
0
x b
0
f x f
0
x a
d b
d a
0
x b
là phân ly
trình
và liên trên
và không trên
f x
a b
a b
a b
ff
f
f
0
x d
0 0 0
x f x f x
1
n
n
f x
x x
m
1 1
1
1
n n n
M m
x x x x
m
tính theo tính giá
hàm là
( 1: )
1n
x
n
x
n
f x
f
1n n
x x
Cho ph
1.
2. x
5
f x x
1.
2.
pháp dây cung.
3.
4.
không quá 0,5.10
3
4 2
x x x
2
x
2
x

Tài liệu khác của Đại học Bách Khoa Hà Nội

Preview text:

y f x M 1 x M M1 0 f f f (x )(x a) n n x x ,n 0,1,2,... n 1 n f (x ) f (a) n x b 0 f f f (x )(x b) n n x x ,n 0,1,2,... n 1 n f (x ) f (b) n x a 0 0 x a 0 x b sao cho f 0 x f Tính theo công f (xn )(xn d) xn 1 xn , n , 1 , 0 , 2 ... f (xn ) f (d) trong d a và 0 x b d b 0 x a a b là phân ly trình f x f và f liên trên a b f và f không trên a b 0 x d 0 x f 0 x f 0 x f n x n x x 1 m M1 1 m n x x n x n x 1 1 m tính n x 1theo n x tính giá hàm f là f n x ( 1: x x ) n 1 n Cho ph f x x 1. 2. x5 4 2 x x x 1. 2. 2 x pháp dây cung. 3. 2 x 4. không quá 0,5.10 3

Tài liệu liên quan: