Chương 7: Phương pháp tiếp tuyến | Bài giảng môn Phương pháp tính | Đại học Bách khoa Hà Nội

Thay thế đường cong trên bằng TIẾP TUYẾN Tìm giao điểm của tiếp tuyến với trục hoành thay cho giao điểm đường cong với trục hoành.

Tài liệu được Sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính (BK)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

13 trang 3 tháng trước

Tác giả:

Profile Lân Nguyễn
PHƯƠNG PHÁP TIẾP TUYẾN
GIẢI PT f(x) = 0
Ý tưởng phương pháp
• Thay thế đường cong trên
bằng TIẾP TUYẾN
• Tìm giao điểm của tiếp tuyến với trục
hoành thay cho giao điểm đường cong với
trục hoành.
( )
y f x=
[a,b]
Ý tưởng phương pháp
Phương pháp tiếp tuyến
• Chọn xấp xỉ đầu hoặc sao cho
• Tính theo công thức
( )
00
"( ) 0f x f x
0
xa=
0
xb=
1
()
, 0,1,2,...
'( )
n
nn
n
fx
x x n
fx
+
= − =
Điều kiện hội tụ
• (a,b) là khoảng cách ly nghiệm
• liên tục trên
• xác định dấu không đổi trên
• Chọn đúng
,'ff
( ) ( )
0 0 0
: " 0.x f x f x
[a,b]
[a,b]
Tại sao
x
y
'0f
x
1
x
0
d
1
d
Tại sao
"0f
Đánh giá sai số
( )
( )
1
*1
n
n
fx
xx
m
−
( )
2
2
1
1
*2
2
n n n
M
x x x x
m
−
− −
( )
( )
12
,,
min ' ; max "
x a b x a b
m f x M f x

==
Nhận xét
• Để tính theo cần tính hai giá trị của
hàm là và
• Tốc độ hội tụ nhanh (bậc 2: )
1n
x
+
n
x
()
n
fx
2
1
O( )
nn
xx
+
−
'( )
n
fx
Bài tập
Dùng phương pháp tiếp tuyến tính với
6 chữ số đáng tin sau dấu phẩy trên khoảng .
5
17
( )
1;2
• là nghiệm của phương trình
• Kiểm tra các điều kiện hội tụ của phương pháp
tiếp tuyến
5
17
5
17 0.x −=
5
10
44
17
4 17
;2
5
55
n
n n n
nn
x
x x x x
xx
+
−
= − = − =
• Cách 1: Dùng công thức sai số mục tiêu, ta có
0 2
1 1.8125 2.560956001
2 1.765040839 0.1306480311
3 1.762348599 3.9797x10^(-4)
4 1.762340348 8.0875x10^(-9)
n
x
( )
n
fx
( )
6
1
2.5 10
n
f x m
−
=
n
• Cách 2: Dùng CT sai số theo 2 xấp xỉ liên tiếp
• trùng 3 chữ số sau dấu phẩy là đủ
2
6
2
1
1
6
3
1
* 0.5 10
2
0.5 10
0.177 10
16
n n n
nn
M
x x x x
m
xx
−
−
−
−
−
− −
− =
1
,
nn
xx
−
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

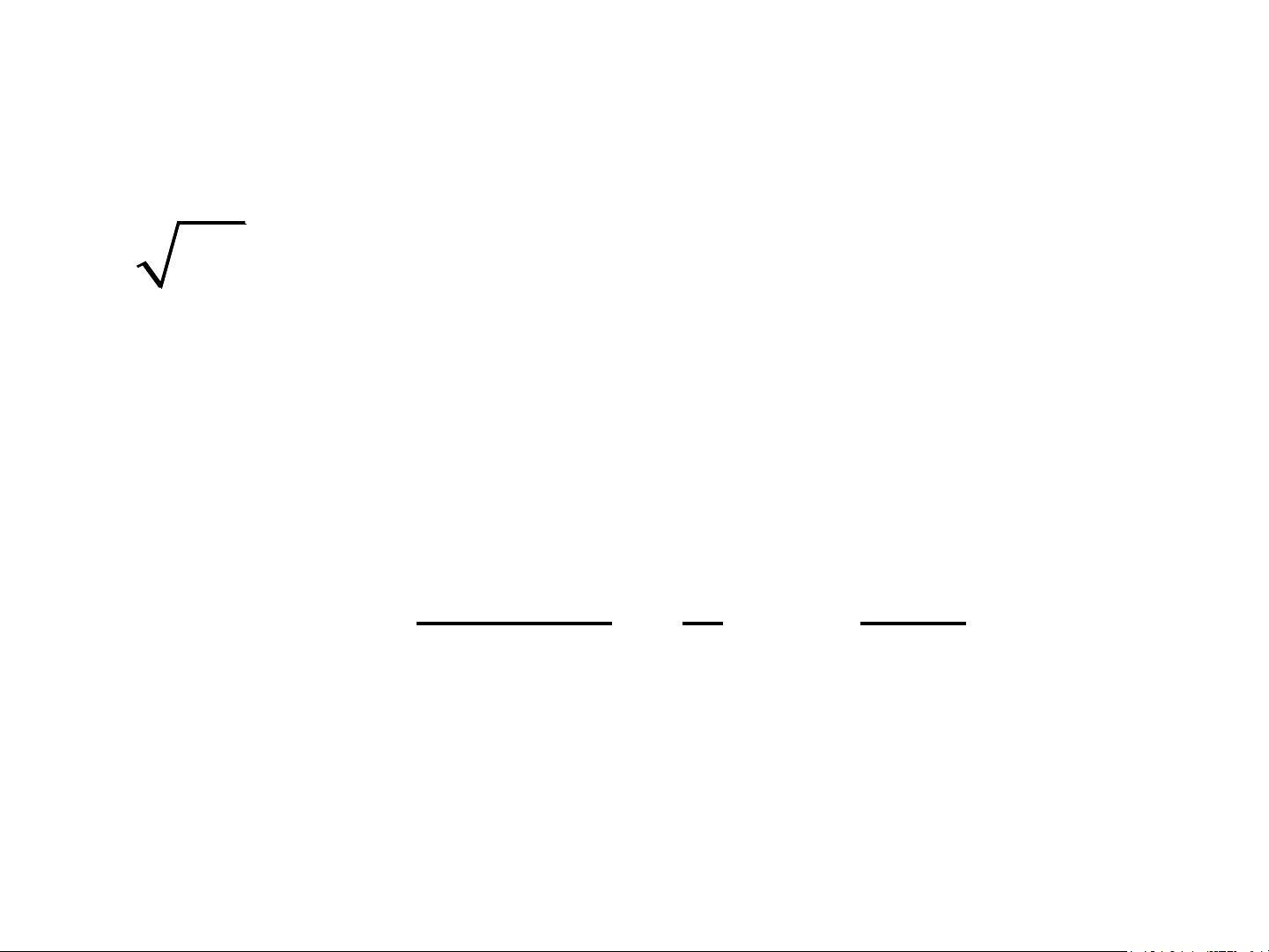
Preview text:

PHƯƠNG PHÁP TIẾP TUYẾN GIẢI PT f(x) = 0
Ý tưởng phương pháp
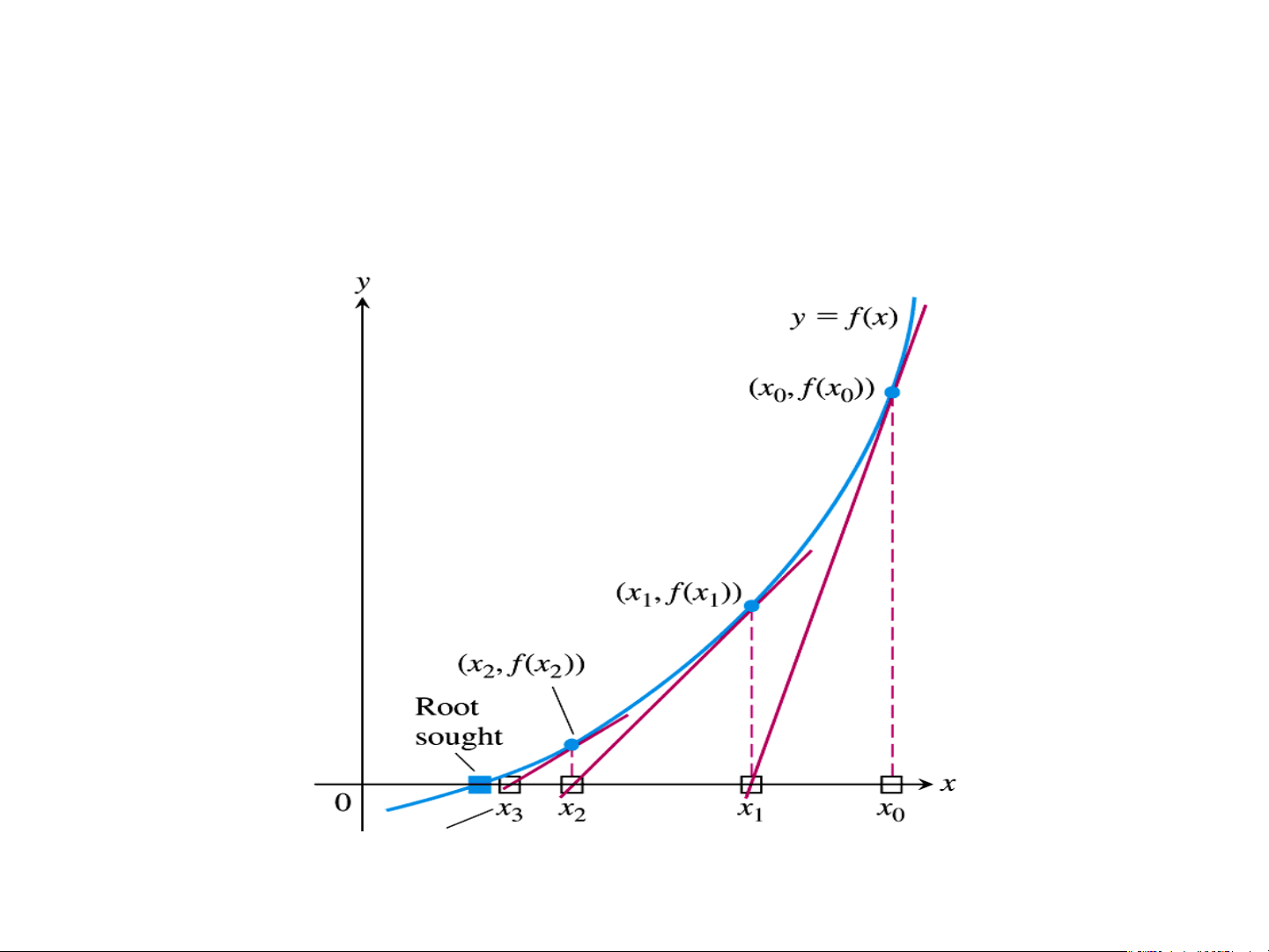
• Thay thế đường cong y = f ( x) trên
[a, b] bằng TIẾP TUYẾN
• Tìm giao điểm của tiếp tuyến với trục
hoành thay cho giao điểm đường cong với trục hoành.
Ý tưởng phương pháp
Phương pháp tiếp tuyến
• Chọn xấp xỉ đầu x = a hoặc x = b sao cho 0 0 f ( x f "(x )  0 0 ) 0 • Tính theo công thức f (x ) n x = x − , n = 0,1, 2,... n 1 + n f '(x ) n
Điều kiện hội tụ
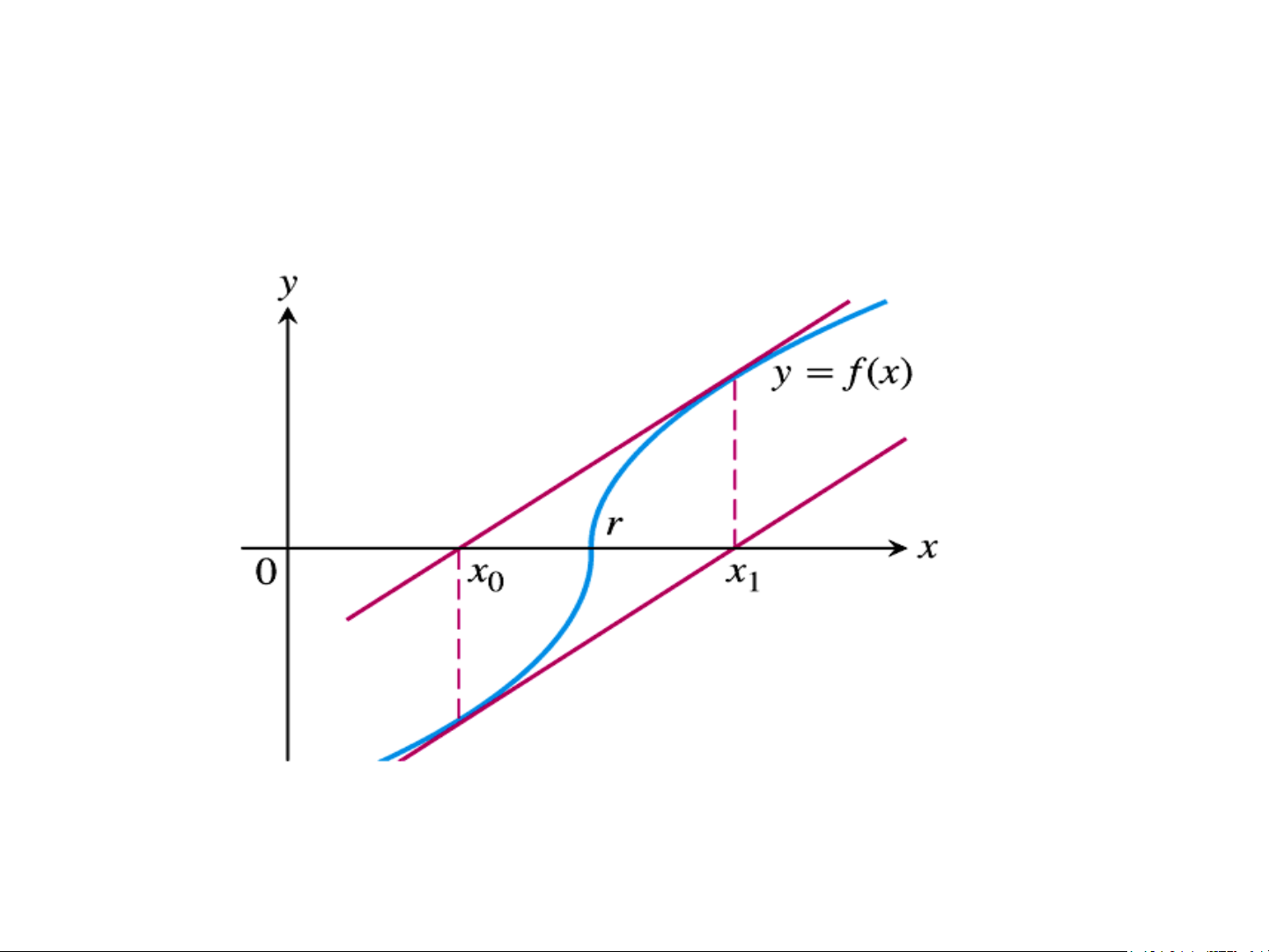
• (a,b) là khoảng cách ly nghiệm •
f , f ' liên tục trên [a, b]
• f ', f ' xác định dấu không đổi trên[a,b]
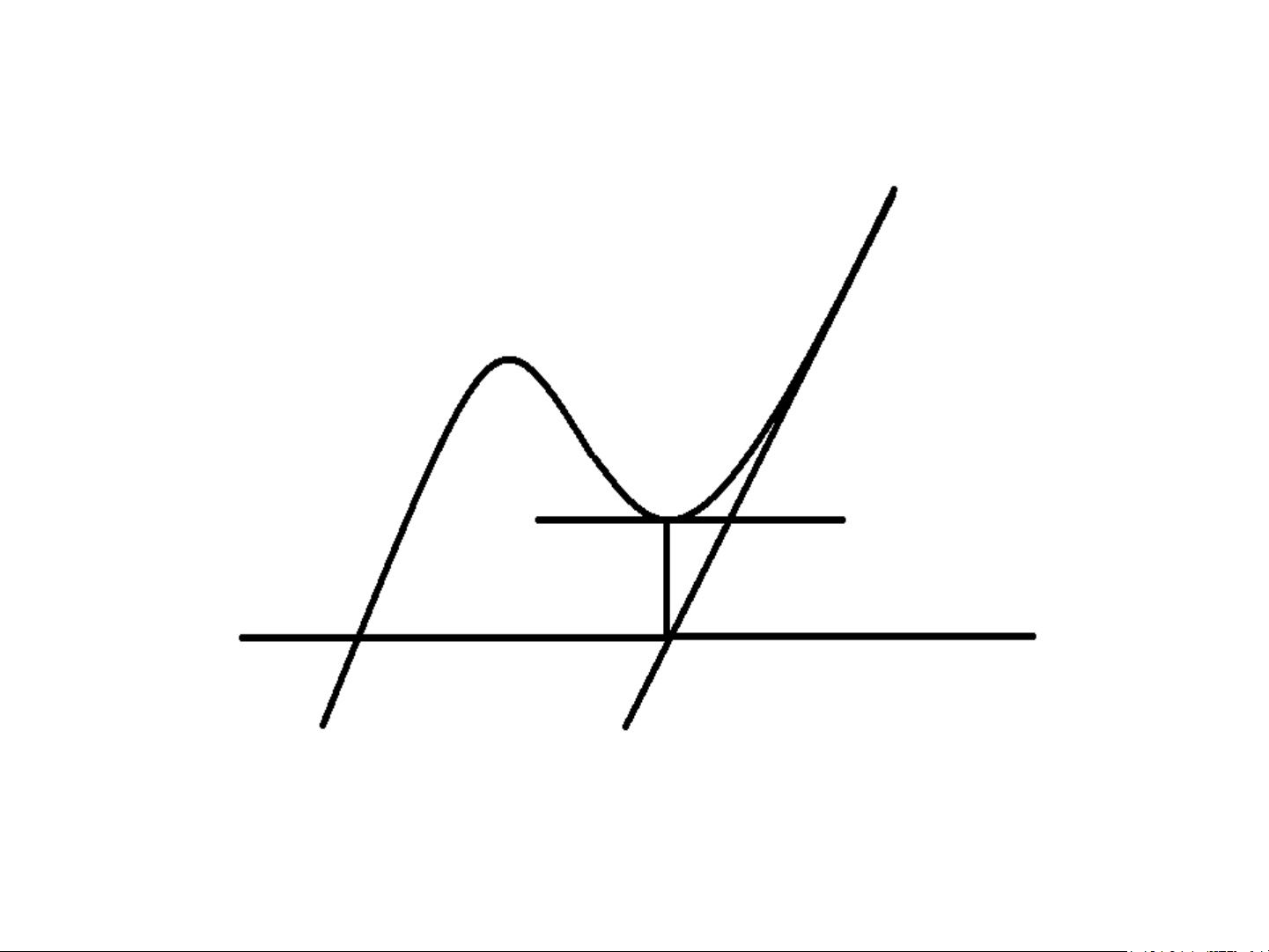
• Chọn đúng x : f x f " x  0. 0 ( 0) ( 0) Tại sao f '  0 d0 y d1 x x 1 x Tại sao f "  0 Đánh giá sai số f ( xn ) x − x *  n ( ) 1 m1 M 2 2 x − x *  x − x 2 n n n 1 − ( ) 2m1 m = min
f ' x ; M = max f " x 1 x   a,b ( ) 2 x   a,b ( ) Nhận xét
• Để tính x + theo x cần tính hai giá trị của n 1 n
hàm là f (x ) và n f '(x ) n • Tốc độ hội tụ 2 nhanh (bậc 2: O(x + − x ) n 1 n ) Bài tập
Dùng phương pháp tiếp tuyến tính 5 17 với
6 chữ số đáng tin sau dấu phẩy trên khoảng (1;2 . )
• 5 17 là nghiệm của phương trình 5 x −17 = 0.
• Kiểm tra các điều kiện hội tụ của phương pháp tiếp tuyến 5 x −17 4 17 n x = x − = x − ; x = 2 n 1 + n n 0 4 4 5x 5 5x n n
• Cách 1: Dùng công thức sai số mục tiêu, ta có f ( x ) 6 m  −  = 2.510 n 1 n x f ( xn ) n 0 2 1 1.8125 2.560956001 2 1.765040839 0.1306480311 3 1.762348599 3.9797x10^(-4) 4 1.762340348 8.0875x10^(-9)
• Cách 2: Dùng CT sai số theo 2 xấp xỉ liên tiếp M 2 2 6 − x − x *  x − x  0.510 n n n 1 − 2m1 6 − 0.5 10 3 −  x − x  = 0.177 10 n n 1 − 16
• x , x − trùng 3 chữ số sau dấu phẩy là đủ n n 1