Chương 7: Trị riêng – vector riêng - Đại số tuyến tính | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Chương 7: Trị riêng – vector riêng - Đại số tuyến tính | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Đại số (MAT1093)
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Tác giả:
Tài liệu liên quan:
Preview text:
Đại số Tuyến tính Giảng viên: Đào Như Mai 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 1
Chương 7: Trị riêng – vector riêng
Trị riêng, vector riêng của ma trận Chéo hóa ma trận
Chéo hóa ma trận đối xứng
Trị riêng, vector riêng của ánh xạ tuyến tính 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 2
Trị riêng, vector riêng của ma trận Ví dụ
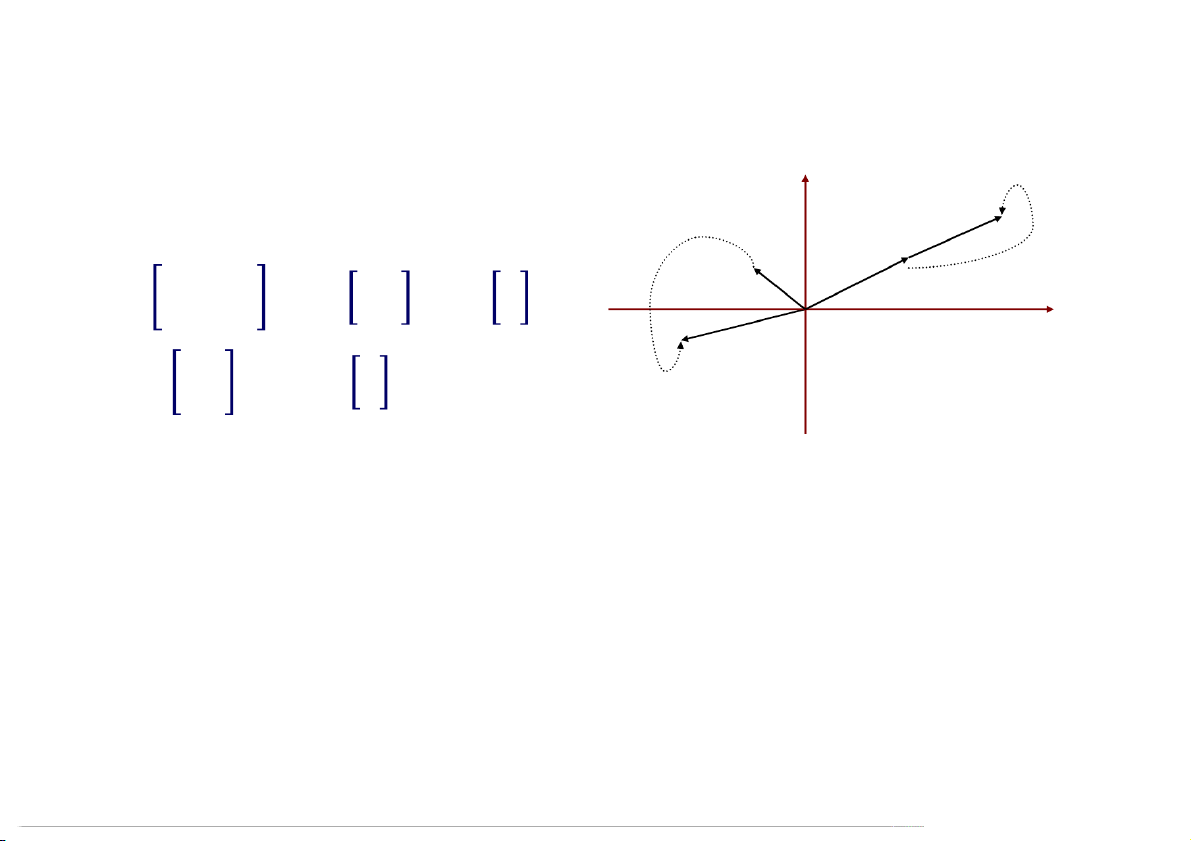
Tính và . Hãy cho biết nhận xét. Av u = 3 −2 v 1 0 = −1 1 = 21 Au = −5 −1 = 42 = 2 Định nghĩa
được gọi là trị riêng của ma trận vuông , nếu tồn tại vector ≠ sao cho: = .
Khi đó, vector được gọi là vector riêng của ma trận vuông ứng với trị riêng . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 3
Trị riêng, vector riêng của ma trận Ví dụ
vector nào là vector riêng của ma trận sau: = 1 6 5 2 = 6 −5 = 3 −2 6 Ta có: = 1 6 5 2 −5 = −24 20 = −4 6 −5 = −4.
→ là vector riêng của . = 1 6 3 5 2 −2 = −9 11 .
→ ∄ để = → không là vector riêng của . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 4
Trị riêng, vector riêng của ma trận Ví dụ
Số nào là trị riêng của ma trận : = 3 4 6 5 = −1 = 3. Xét = : ↔ 3 4 6 5 = −1 ↔ 4 + 4 = 0 6 + 6 = 0
Hệ này có vô số nghiệm, nên tồn tại 1 nghiệm khác θ = (0,0), ví
dụ = (1, −1) thỏa mãn = .
Do đó là trị riêng của ma trận .
Tương tự không là trị riêng của ma trận . 4 = 0 6 + 2 = 0 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 5
Trị riêng, vector riêng của ma trận Định nghĩa
Giả sử là trị riêng của ma trận vuông : ↔ ∃ ≠
= ↔ − = 0 ↔ − = 0.
Đây là hệ phương trình thuần nhất có nghiệm khác không. ↔ det − = 0.
được gọi là phương trình đặc trưng của ma trận .
Đa thức det − được gọi là đa thức đặc trưng của ma trận .
Do đó: là trị riêng của ma trận vuông khi và chỉ khi là
nghiệm của phương trình đặc trưng. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 6
Trị riêng, vector riêng của ma trận
Tìm trị riêng, vector riêng của ma trận vuông A cấp nxn
Bước 1: lập phương trình đặc trưng: det − = 0
(phương trình bậc theo ).
Bước 2: giải phương trình đặc trưng, tất cả các nghiệm của
phương trình đặc trưng là trị riêng của ma trận , và ngược lại.
Bước 3: tìm vector riêng của tương ứng với trị riêng vừa tìm được: − = 0.
Tất cả các nghiệm ≠ của pt trên là vector riêng của ứng với trị riêng . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 7
Trị riêng, vector riêng của ma trận Không gian riêng
Không gian nghiệm của pt: − = 0 được gọi là không gian
con riêng ứng với trị riêng . Định lý
Các vector riêng ứng với các trị riêng khác nhau thì độc lập tuyến tính. Chứng minh:
= , , ⋯ , là các véc tơ riêng ứng với các trị riêng.
l, l, ⋯ , l là các trị riêng tương ứng.
Giả sử hạng của bằng . Có thể giả sử , , ⋯ , là hệ véctơ độc
lập tuyến tính cực đại của E 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 8
Trị riêng, vector riêng của ma trận
Định lý. Các vector riêng ứng với các trị riêng khác nhau thì độc lập tuyến tính.
Khi đó là tổ hợp tuyến tính của , , ⋯ ,
= ∑ Þ − l = − l ∑
0 = l − l
vì , , ⋯ , độc lập tuyến tính nên: ∀, = 0Þ = 0 vô lý vì là véc tơ riêng.
Định lý Ma trận đối xứng cấp n có n trị riêng thực và n
vector riêng trực chuẩn tương ứng. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 9
Trị riêng, vector riêng của ma trận Ví dụ. Cho ma trận: 3 1 1 = 2 4 2 1 1 3
Tìm trị riêng, cơ sở, chiều của các không gian con riêng. Giải
Phương trình đặc trưng: det − = 0. 3 − 1 1 ↔ 2 4 − 2
= 0 ↔ ( − 2) − 6 = 0. 1 1 3 −
Trị riêng: = 2 (bội 2), = 6 (bội 1). 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 10
Trị riêng, vector riêng của ma trận
Ví dụ. Cơ sở, chiều của các không gian con riêng ứng với = 2:
Giải phương trình: − = 0. 1 1 1 0 0 0 0 0
2 2 2 = 0 ⇒ 0 0 0 = 0 ⇒ 1 1 1 0 1 1 1 0 − −
Giải hệ này bằng cách biến đổi ma trận hệ số, ta thu được nghiệm tổng
quát có dạng: ,, = 1,0,−1 + 0,1,−1 .
Do đó: 1,0, −1 , 0,1, −1 là cơ sở của k/g con riêng ứng với = 2,
và số chiều của k/g con riêng đó là 2.
Tương tự ta tìm được cơ sở, số chiều của k/g con riêng ứng với = 6.: 1,2,1 −3 1 1 0 0 0 0 0 2 −2 2 = 0 ⇒ 0 −1 2 = 0 ⇒ 2 1 1 −3 0 1 1 −3 0 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 11
Trị riêng, vector riêng của ma trận
Ví dụ. Cho là trị riêng của ma trận vuông . Chứng minh: a.
là trị riêng của ma trận . b. Nếu khả nghịch, thì
là trị riêng của . Giải
a. là trị riêng của ↔ ∃ ≠ : = .
Ta có: = . … . = . … = ⋯ = . Do đó
là trị riêng của ma trận .
b. Vì khả nghịch, nên ∃ vì: là trị riêng của
↔ ∃ ≠ : = . ↔
= ↔ =
↔ = - Suy ra đpcm. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 12
Trị riêng, vector riêng của ma trận
Định lý. Hai ma trận đồng dạng có cùng đa thức đặc trưng
(tức là cùng chung trị riêng).
Chứng minh: giả sử hai ma trận vuông , đồng dạng tức là tồn tại
khả nghịch sao cho = .
Xét: det − = det − =
= det − = det − =
= det det − det = det − .
Vậy và có cùng đa thức đặc trưng.
Chú ý: 2 ma trận đồng dạng có cùng trị riêng, nhưng các vector riêng thì khác nhau. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 13 Chéo hóa ma trận Định nghĩa
Ma trận vuông chéo hóa được nếu đồng dạng với ma trận chéo .
Có nghĩa tồn tại ma trận khả nghịch mà = , là ma trận chéo. Chú ý.
Không phải ma trận vuông nào cũng chéo hóa được.
Chéo hóa ma trận vuông có nghĩa tìm ma trận khả nghịch và ma trận chéo . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 14 Chéo hóa ma trận
Phân tích cấu trúc của ma trận và
Giả sử ma trận vuông chéo hóa được bởi ma trận và . … … 0 …
= … … … , = … … … , = … … … … 0 … …
= ∗ ∗ … ∗
trong đó ∗, ∗,. ., ∗ là các cột thứ 1, 2, . ., n tương ứng của .
Có = = . Xét cột thứ nhất của và
… … … … … … … … = ∗
… …
… … 0 … … … … … … = ∗ … 0 … 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 15 Chéo hóa ma trận
Vậy ∗ = ∗, hay là trị riêng của ma trận .
Và ∗ là vector riêng của ứng với trị riêng .
Tương tự ta thấy: tất cả các cột của ma trận là các vector riêng của .
Các phần tử nằm trên đường chéo của là các trị riêng của ma trận .
Vì là ma trận khả nghịch nên tất cả các cột (các vector riêng của
) độc lập tuyến tính.
Định lý. Ma trận vuông cấp nxn chéo hóa được khi và chỉ
khi tồn tại vector riêng độc lập tuyến tính.
Hệ quả. Nếu ma trận vuông cấp nxn có đúng trị riêng
phân biệt thì chéo hóa được. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 16 Chéo hóa ma trận
Các bước chéo hóa ma trận vuông A cấp nxn
Bước 1: lập phương trình đặc trưng. Giải tìm trị riêng.
Bước 2: giải các hệ phương trình tương ứng với từng trị riêng. Tìm
cơ sở của các không gian con riêng. Tìm vector riêng tương ứng.
Bước 3: nếu có đủ vector riêng ĐLTT thì chéo hóa được,
ngược lại không chéo hóa được.
Giả sử chéo hóa được, khi đó ma trận có các cột là các
cơ sở của những không gian con riêng (vector riêng tương
ứng). Các phần tử trên đường chéo chính của là các trị riêng của ma trận . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 17 Chéo hóa ma trận
Ví dụ. Chéo hóa ma trận sau (nếu được): 1 3 3 = −3 −5 −3 . 3 3 1
Giải. Tìm trị riêng của :.
det − = 0 ↔ − − 3 + 4 = − + 2 − − 4 = + 2 1 − = 0
→ = 1 bội 1 ; = −2 bội 2
Tìm vector riêng của : giải hệ pt tuyến tính thuần nhất − = 0 0 3 3 0 1
= 1 → −3 −6 −3 = 0 → = − = −1 3 3 0 0 1 Cơ sở = 1, −1,1 . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 18 Chéo hóa ma trận Ví dụ (tiếp) 3 3 3 0 −1 −1
= −2 → −3 −3 −3 = 0 → = 1 + 0 , 3 3 3 0 0 1 cơ sở { .
= −1,1,0 , = −1,0,1 }
Hệ vector {, , } ĐLTT (SV tự kiểm tra).
Do đó chéo hóa được (có 3 vector riêng ĐLTT).
Thiết lập ma trận , : 1 −1 −1 1 −1 −1 1 0 0 = −1 1
0 ; = 0 0 −1 = 0 −2 0 1 0 1 0 1 2 0 0 −2
Chú ý: các cột của có thể đổi chỗ cho nhau, miễn sao trị riêng và
vector riêng tương ứng nằm trên cùng một cột. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 19 Chéo hóa ma trận
Ví dụ. Chéo hóa ma trận sau, tính : 5 0 0 0 = 0 5 0 0 1 4 −3 0 −1 −2 0 −3
Giải Tìm trị riêng của :
det − = 0 ↔ ( − 5)( + 3)= 0.
= 5(bội 2); = −3(bội 2).
Tìm vector riêng của :
= 5: vector riêng = −8,4,1,0 ; = (−16,4,0,1).
= −3: vector riêng = 0,0,1,0 ; = 0,0,0,1 .
Hệ vector riêng , , , ĐLTT, nên chéo hóa được. 09:52
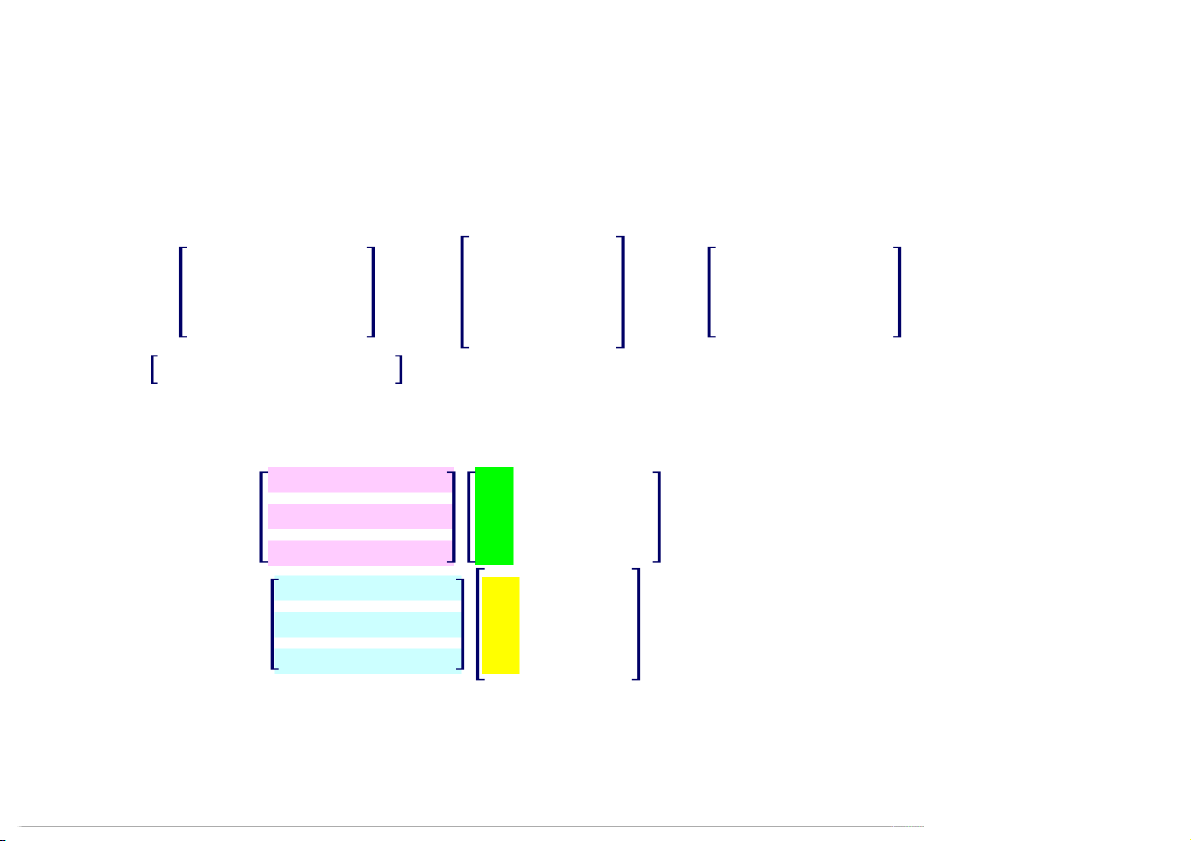
Trường Đại học Công nghệ, ĐHQG Hà Nội 20 Khi = 5 0 0 0 0 0 0 0 0 −8 −16 0 0 0 0 0 0 0 0 4 4 +
1 4 −8 0 ⇒ 1 4 −8 0 ⇒ 1 0 −1 −2 0 −8 0 2 −8 −8 0 1 Khi = −3 8 0 0 0 1 0 0 0 0 0 0 0 8 0 0 0 1 0 0 ⇒ 0 0 0 1 4 0 0 ⇒ 1 4 0 0 = + 1 0 −1 −2 0 0 −1 −2 0 0 0 1 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 21 Chéo hóa ma trận
Ví dụ (tiếp)−8 −16 0 0 5 0 0 0 = 4 4 0 0 0 5 0 0 1 0 1 0 = 0 0 −3 0 0 1 0 1 0 0 0 −3
Có: = ↔ = .
→ = . … . =
= … = . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 22 Chéo hóa ma trận
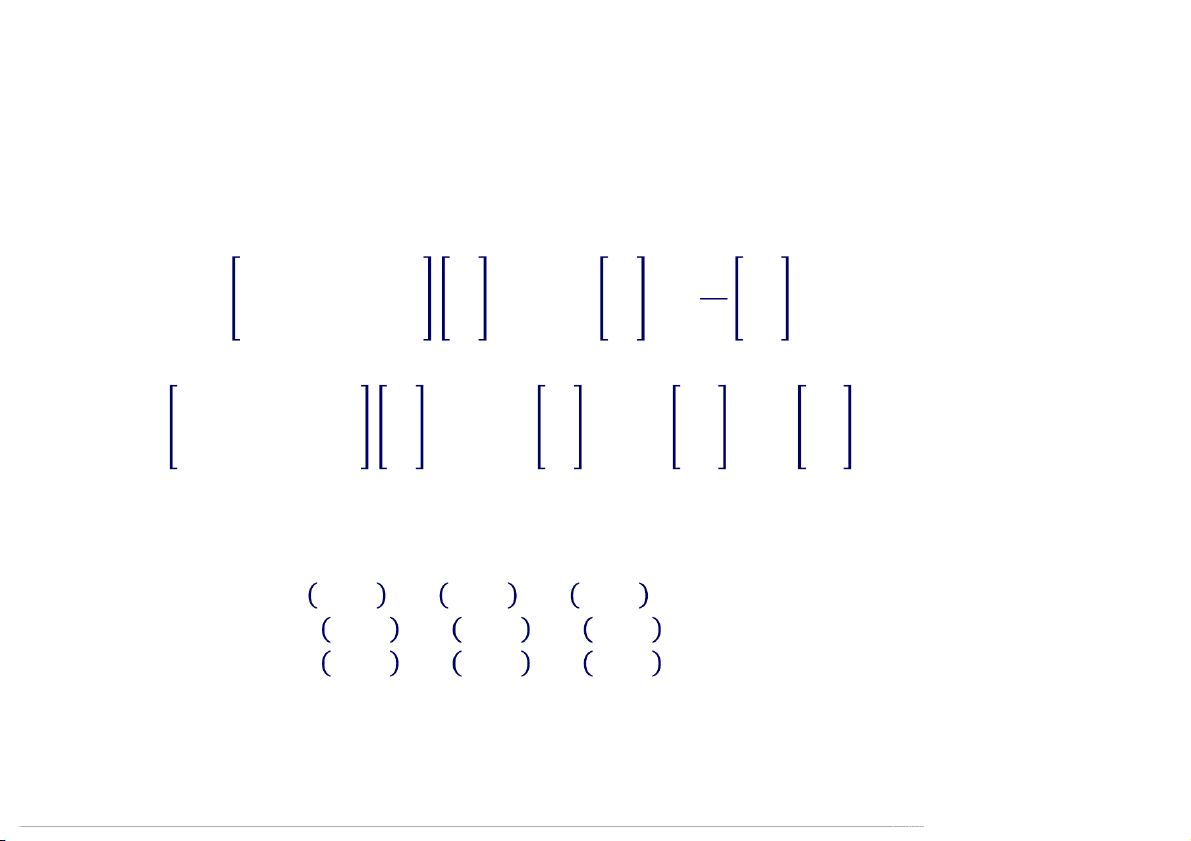
Ví dụ. Tìm ma trận vuông thực cấp 3 có các trị riêng là 2, -3, 1 và
các vector riêng tương ứng là = [2,1,1], = [1,2,1], = [1,1,1].
chéo hóa được bởi ma trận và như sau: 2 1 1 2 0 0 = 1 2 1 ; = 0 −3 0 . 1 1 1 0 0 1
Do đó ma trận vuông cần tìm: 2 1 1 2 0 0 1 0 −1 3 −4 2
= = 1 2 1 0 −3 0 0 1 −1 = 1 −7 7 1 1 1 0 0 1 −1 −1 3 1 −4 4 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 23
Chéo hóa ma trận đối xứng Ma trận đối xứng.
Ma trận vuông = ( thỏa mãn: )
= , = 1, ; = 1, thì
được gọi là ma trận đối xứng ( = ). Ma trận trực giao
Ma trận vuông được gọi là ma trận trực giao nếu: = =
Ma trận vuông là ma trận trực giao ↔ = .
Định lý. Ma trận vuông = (
là ma trận trực giao nếu )
các cột của tạo thành hệ trực chuẩn.
Định nghĩa. Ma trận vuông = () được gọi là chéo hóa
trực giao được nếu tồn tại ma trận trực giao và ma trận chéo sao cho: = . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 24
Chéo hóa ma trận đối xứng Định lý. Ma trận vuông = (
là ma trận đối xứng thực. Khi đó các ) mệnh đề sau đúng:
Trị riêng của là thực.
Ma trận chéo hóa trực giao được.
Các vector riêng ứng với các trị riêng khác nhau thì trực giao với nhau. Chú ý.
Ma trận vuông tùy ý chưa chắc chéo hóa được.
Ma trận đối xứng thực luôn chéo hóa được bởi ma trận trực giao . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 25
Chéo hóa ma trận đối xứng Chứng minh
1. Xét đại lượng =
Khi đó ta có: = = = = = Vậy là số thực
Giả sử l là trị riêng và là véctơ riêng đơn vị tương ứng. Khi đó
= l = l =
= l = l ∈
Vậy trị riêng là số thực.
2. Giả sử l, l, …, l là n trị riêng của ma trận tuỳ ý A.
Giả sử l, là một cặp trị riêng, véctơ riêng đơn vị.
Giả sử {, , …, } là cơ sở trực chuẩn của không gian 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 26
Chéo hóa ma trận đối xứng Chứng minh (tiếp)
Xét ma trận trực giao = |, |, ⋯ |, , có l ⋯ ∗ ∗
= 0⋮ khi đó
có các trị riêng là l, l, …, l 0
Tương tự, ta phân tích ma trận thành dạng l ⋯ ∗ ∗ 0 = ⋮ khi đó có các trị riêng là l, l, …, l 0
Tiếp tục quá trình, có: = , là ma trận tam giác trên, là
ma trận vuông tùy ý. Quá trình phân tích này là Schur factorization. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 27
Chéo hóa ma trận đối xứng Chứng minh (tiếp)
A là ma trận đối xứng nên = =
= = = = đối xứng,
và = vậy A chéo hóa trực giao được
3. GT(l,)(l,) là 2 cặp trị riêng, véctơ riêng khác biệt
Có = l và = l
= (l) = l = l ,
= = = l = l ,
l , = l , (l − l) , = 0 , = 0
Vậy hai véctơ riêng này vuông góc với nhau 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 28
Chéo hóa ma trận đối xứng
Các bước chéo hóa trực giao ma trận đối xứng thực
Lập phương trình đặc trưng, giải tìm trị riêng.
Giải các hệ phương trình tương ứng với từng trị riêng. Tìm cơ sở
trực chuẩn của các không gian con riêng.
Ma trận có các cột là các cơ sở trực chuẩn của những không
gian con riêng. Các phần tử trên đường chéo chính của là các trị riêng.
Chú ý. Để tìm cơ sở trực chuẩn của một không gian con
riêng nào đó ta chọn một cơ sở tùy ý rồi dùng quá trình Gram-Schmidt (nếu cần). 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 29
Chéo hóa ma trận đối xứng
Ví dụ. Chéo hóa trực giao ma trận sau: 3 −2 4 = −2 6 2 4 2 3
Giải. Phương trình đặc trưng:
det − = − − 7 + 2 = 0 → = 7, = −2 2 1 −2 − −4 −2 4
−2 −1 2 ⇒ 0 0 0 ⇒ 2 4 2 −4 0 0 0
Cơ sở của các không gian con riêng: 2 + − 2 = 0
= 7; = [1,0,1], = [−1,2,0]
Dùng quá trình Gram-Schmidt, tìm cơ sở trực giao = , của
không gian con riêng ứng với = 7: < , >
= = [1,0,1]; = −
+ = −1,4,1 . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 30
Chéo hóa ma trận đối xứng
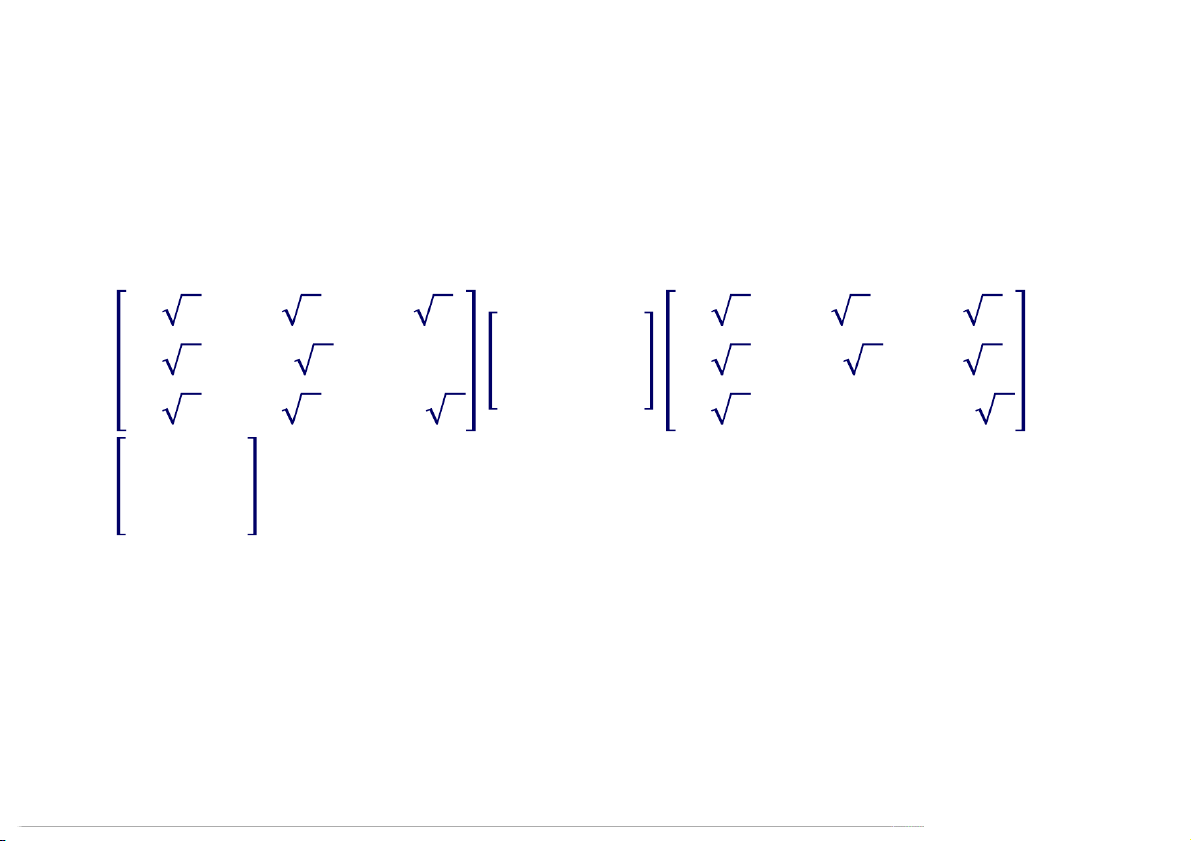
Ví dụ (tiếp) Trực chuẩn hóa, tìm cơ sở trực chuẩn: 1/ 2 −1/ 18 = 0 , 4/ 18 . 1/ 2 1/ 18
Cơ sở của không gian con riêng ứng với
= −2: = [2,1, −2] Cơ sở trực chuẩn: 0 0 0 2 5 −2 4 2 1 2
−2 8 2 ⇒ −1 4 1 ⇒ 1 ⇒ = 4 2 5 0 18 9 −2 3 ,3 , − 3
Vậy ma trận trực giao và ma trận chéo có dạng: 1/ 2 −1/ 18 2/3 7 0 0 = 0 4/ 18 1/3 = 0 7 0 . 1/ 2 1/ 18 −2/3 0 0 −2 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 31
Chéo hóa ma trận đối xứng
Ví dụ. Tìm một ma trận đối xứng thực cấp 3 (khác ma trận
chéo) sao cho có 3 trị riêng là 2, -1, 1. Giải
là ma trận đối xứng thực nên chéo hóa được bởi ma trận trực
giao và ma trận chéo .
Theo đề bài ta có ma trận chéo: 2 0 0 = 0 −1 0 0 0 1
Tìm một ma trận trực giao ?
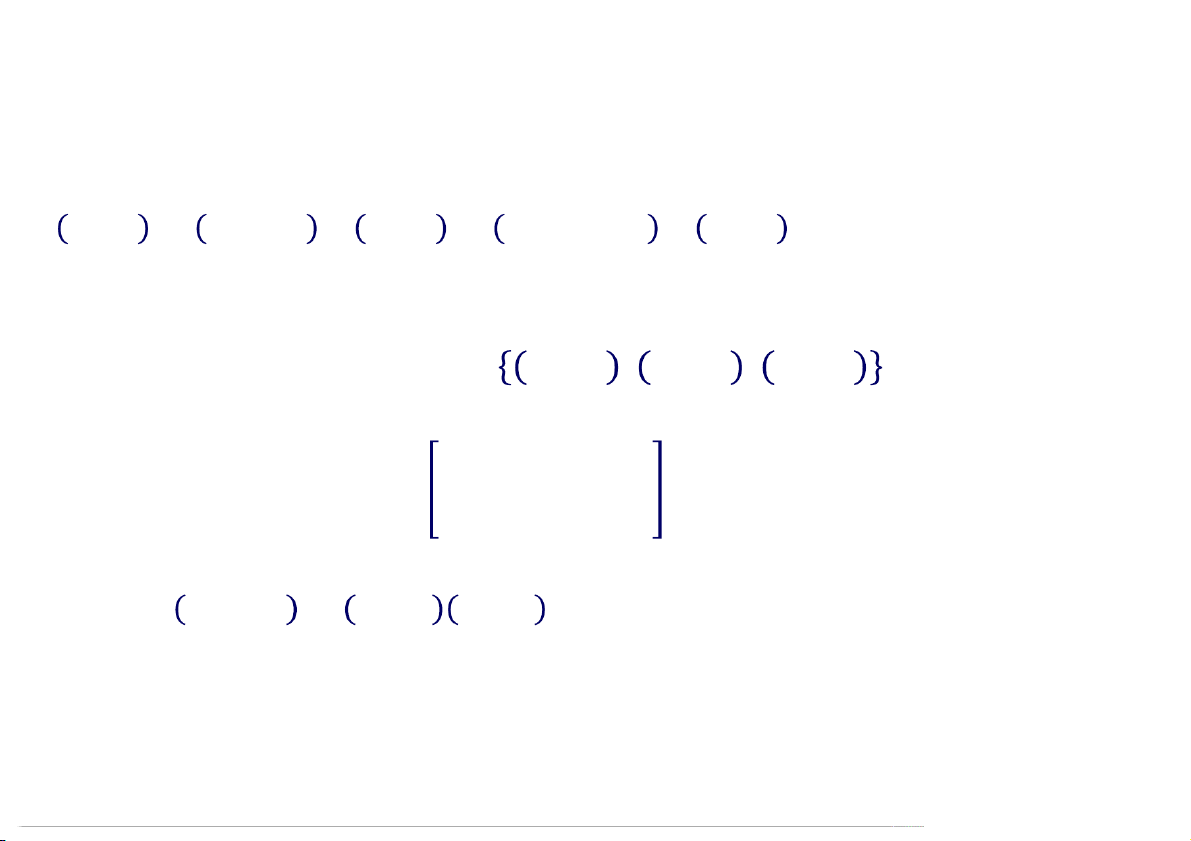
Chọn một cơ sở tùy ý (khác với cơ sở chính tắc) của . = 1,1,1 , 1,0,1 , 1,1,0 . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 32 1,1,1 , 1,0,1 , 1,1,0 , , , = − − − ⋯ − , , , = 1,1,1 1,0,1 1,1,1 1 2 1 = 1,0,1 − 3 1,1,1 = 3,−3,3 1,1,0 1,1,1 1,1,0 1, −2,1 = 1,1,0 − 3 1,1,1 − 6 1, −2,1 1 1 = 2,0,−2 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 33
Chéo hóa ma trận đối xứng Ví dụ (tiếp)
Dùng quá trình Gram-Schmidt đưa về cơ sở trực giao, sau đó
trực chuẩn hóa, ta được hệ cơ sở trực chuẩn: 1/ 3 1/ 6 1/ 2
= 1/ 3 ; = −2/ 6 ; = 0 . 1/ 3 1/ 6 −1/ 2
Các cột của ma trận trực giao là hệ cơ sở trực chuẩn này. 1/ 3 1/ 6 1/ 2 → = 1/ 3 −2/ 6 0 . 1/ 3 1/ 6 −1/ 2 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 34
Chéo hóa ma trận đối xứng Ví dụ (tiếp)
Do đó, ma trận đối xứng thực cần tìm:
= = = 1/ 3 1/ 6 1/ 2 2 0 0 1/ 3 1/ 3 1/ 3 = 1/ 3 −2/ 6 0 0 −1 0 1/ 6 −2/ 6 1/ 6 1/ 3 1/ 6 −1/ 2 0 0 1 1/ 2 0 −1/ 2 1 1 0 = 1 0 1 . 0 1 1 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 35
Trị riêng, vector riêng của ánh xạ tuyến tính
Trong chương ánh xạ tuyến tính ta biết: có thể coi ánh xạ
tuyến tính là ma trận, cho nên tìm trị riêng, vector riêng của
ánh xạ tuyến tính là tìm trị riêng, vector riêng của ma trận.
Cho -kgvt, axtt : → .
∈ được gọi là trị riêng của axtt , nếu ∃ ≠ : = .
Khi đó, vector được gọi là vector riêng của axtt tương ứng với trị riêng . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 36
Trị riêng, vector riêng của ánh xạ tuyến tính Nhận xét
Cho -kgvt, axtt : → . là một cơ sở của .
là ma trận của axtt trên hệ cơ sở .
Giả sử là trị riêng của axtt ↔ ∃ ≠ , ∈ : = .
[]= [()]= []= [].
Do đó: là trị riêng của ma trận .
[] là vector riêng của ma trận ứng với trị riêng . Kết luận
Trị riêng của ma trận là trị riêng của axtt và ngược lại.
Nếu vector là vector riêng của ma trận ứng với trị riêng ,
thì vector sao cho []= là vector riêng của axtt ứng với trị riêng . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 37
Trị riêng, vector riêng của ánh xạ tuyến tính
Tìm trị riêng, vector riêng của ánh xạ tuyến tính : →
1. Chọn một cơ sở tùy ý của kgvt , tìm ma trận của axtt trên hệ cơ sở .
2. Tìm trị riêng, vector riêng của ma trận . 3. Kết luận:
Trị riêng của ma trận là trị riêng của axtt và ngược lại.
Nếu vector là vector riêng của ma trận ứng với trị riêng ,
thì vector sao cho []= là vector riêng của axtt ứng với trị riêng . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 38
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Cho axtt : → , biết:
= , , =
= (5 − 10 − 5, 2 + 14 + 2, −4 − 8 + 6)
Tìm trị riêng, vector riêng của axtt .
Giải : Chọn hệ cơ sở chính tắc của : = 1,0,0 , 0,1,0 , 0,0,1 .
Ma trận của axtt trên hệ cơ sở : 5 −10 −5 = 2 14 2 −4 −8 6
Tìm trị riêng của ma trận : det − = 0 → = 5, = 10.
Đây cũng là trị riêng của axtt 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 39
Trị riêng, vector riêng của ánh xạ tuyến tính Ví dụ (tiếp)
Tìm vector riêng của ma trận :
Với = 5 và = 10 (bội 2), giải hệ phương trình: 0 −10 −5 5 2 9 2 = 0 ⇒ = −2 −4 −8 1 4 4 −5 −10 −5 −2 −1 2 4
2 = 0 ⇒ = 1 + 0 −4 −8 −4 0 1
suy ra các vector riêng của : []
= [5, −2,4] ; []= [−1,0,1] , []= [−2,1,0]
Do là hệ cơ sở chính tắc suy ra vector riêng của axtt là:
= 5 1,0,0 − 2 0,1,0 + 4 0,0,1 = (5, −2,4)
= −1 1,0,0 + 0 0,1,0 + 1 0,0,1 = (−1,0,1)
= −2 1,0,0 + 1 0,1,0 + 0 0,0,1 = (−2,1,0) 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 40
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Cho axtt : → , biết:
1,1,1 = 2,1,3 ; 1,0,1 = 6,3,5 ; 1,1,0 = −2, −1, −3 .
Tìm trị riêng, vector riêng của axtt . 1 1 1 + − 1 0 1 ⇒ −
Chọn hệ cơ sở của : 1 1 0 − = 1,1,1 , 1,0,1 , 1,1,0 .
Ma trận của axtt trên hệ cơ sở : []= [()] 2 2 −2 = 1 3 −1 . −1 1 1
Tìm trị riêng của ma trận :
det − = 0 → = 0, = 2, = 4.
Đây cũng là trị riêng của axtt . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 41
Trị riêng, vector riêng của ánh xạ tuyến tính
Tìm vector riêng của ma trận : − []= 0 2 2 −2 0 2 −2
1 3 −1 = 0; 1 1 −1 = 0 và −1 1 1 −1 1 −1 −2 2 −2 1 −1 −1 = 0 −1 1 −3
Nhận được các vector riêng của :
[]= [1,0,1], []= 0,1,1 , []= [1,1,0].
vector riêng của axtt là:
= 0 → () = 1 1,1,1 + 0 1,0,1 + 1 1,1,0 = 2,2,1
= 2 → () = 0 1,1,1 + 1 1,0,1 + 1 1,1,0 = (2,1,1)
= 4 → () = 1 1,1,1 + 1 1,0,1 + 0 1,1,0 = (2,1,2) 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 42
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Cho axtt : → , biết ma trận của axtt trên hệ
cơ sở = { 1,1,1 , 1,2,1 , 1,1,2 } là 2 −2 −1 = −2 −1 −2 . 14 25 14
Tìm trị riêng, vector riêng của axtt .
Giải. Chọn hệ cơ sở của : = 1,1,1 , 1,2,1 , 1,1,2 .
Tìm trị riêng của ma trận :
det − = 0 → = 3, = 6(bội 2)
Đây cũng là trị riêng của axtt . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 43
Trị riêng, vector riêng của ánh xạ tuyến tính
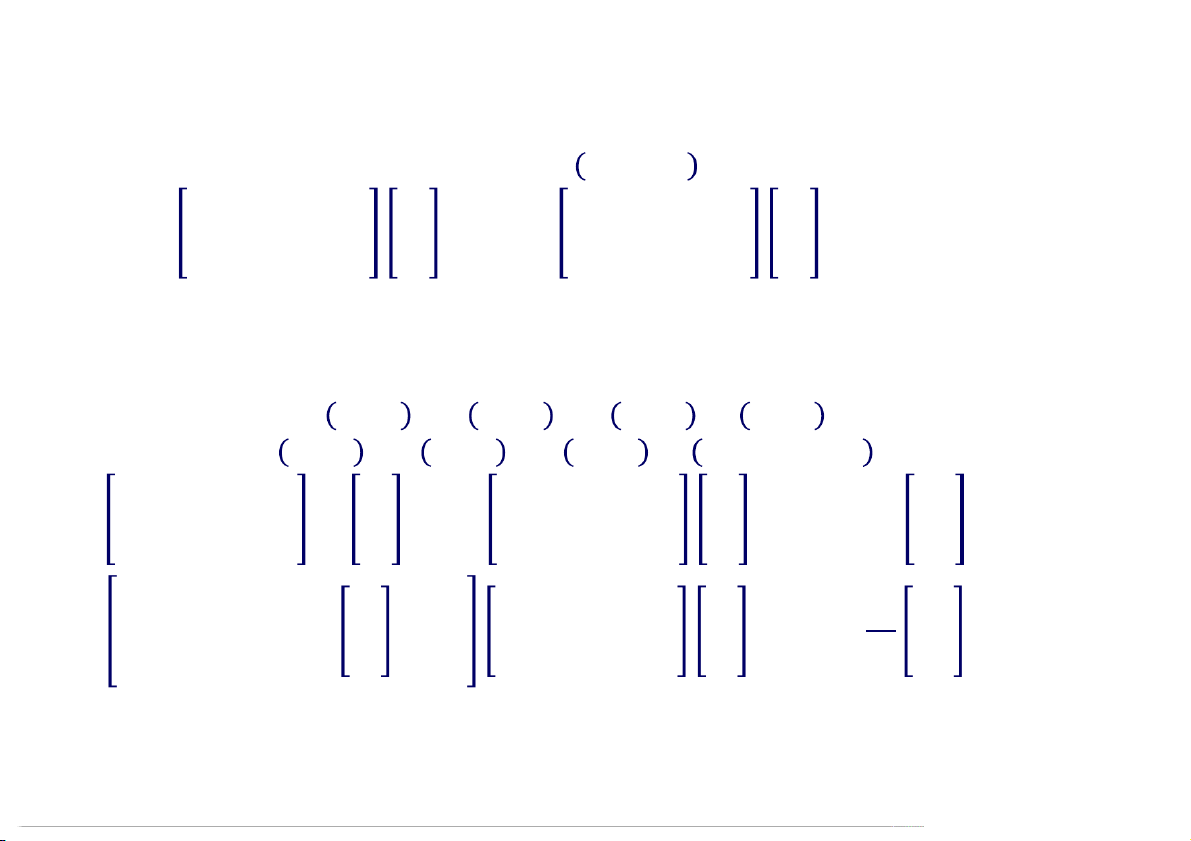
Tìm vector riêng của ma trận từ hệ: − , []= 0 −1 −2 −1 −4 −2 −1
−2 −4 −2 = 0 và −2 −7 −2 = 0 14 25 11 14 25 8
Nhận được các vector riêng của :
[]= [1, −1,1], []= [1,2, −8]
Do đó vector riêng của axtt là:
= 1 1,1,1 − 1 1,2,1 + 1 1,1,2 = 1,0,2 .
= 1 1,1,1 + 2 1,2,1 − 8 1,1,2 = −5, −3, −13 . −1 −2 −1 −1 −2 −1 1
−2 −4 −2 = 0 ⇒ 0 0 0 = 0 ⇒ −1 14 25 11 0 −1 −1 1 −4 −2 −1 −4 −2 −1 1 −2 −7 −2 = 0 ⇒ 0 4 1 = 0 ⇒ 2 14 25 8 8 0 0 0 −8 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 44
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Cho axtt : → , biết ma trận của axtt trên hệ
cơ sở = { 1,1,1 , 1,2,1 , 1,1,2 } là: 2 −2 −1 = −2 −1 −2 . 14 25 14 Tính 2,4,3 , (2,0,4).
Giải: theo ví dụ trước ta thấy vector (2,0,4) là vector riêng
của axtt ứng với trị riêng = 3, nên: 2,0,4 = 3 2,0,4 = 6,0,12 . Tọa độ của 2,4,3 = −1,2,1 [()]
= []= −7, −2,50
2,4,3 = −7 1,1,1 − 2 1,2,1 + 50 1,1,2 = 41,39,91 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 45
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Tìm axtt : → , biết axtt có 3 trị riêng: 2, 1, 0 và 3
vector riêng tương ứng: 1,1,1 , 1,2,1 , 1,1,2 .
Giải Theo định nghĩa trị riêng, vector riêng của axtt : 1,1,1 = 2 1,1,1 = (2,2,2). 1,2,1 = 1 1,2,1 = (1,2,1). 1,1,2 = 0 1,1,2 = (0,0,0).
Chọn hệ cơ sở của là: = 1,1,1 , 1,2,1 , 1,1,2 . 1 1 1 3 − −
∀(, , ) → 1 2 1 = → = − 1 1 2 −
= 1,1,1 + 1,2,1 + 1,1,2
= 3 − − 2,2,2 + − 1,2,1 + − 0,0,0
= 5 − − 2, 4 − 2, 5 − − 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 46
Trị riêng, vector riêng của ánh xạ tuyến tính
Nhận xét. Cho axtt : → .
Trong chương trước ta biết axtt luôn xác định bởi một ma trận trên một hệ cơ sở nào đó.
Khi làm việc với axtt ta làm việc với ma trận này.
Trong kgvt có vô số cơ sở , , … khác nhau. Tương ứng với các cơ sở đó
sẽ có vô số ma trận của axtt trên các cơ sở khác nhau đó.
Mỗi ma trận đều đại diện (thay thế) cho axtt . Khi làm việc với axtt , ta
làm việc với một trong các ma trận này.
Chọn một ma trận có cấu trúc đơn giản nhất, nếu có thể ta chọn ma trận chéo .
Bài toán đặt ra: cho axtt : → , tìm một cơ sở (nếu có) của kgvt sao
cho trên cơ sở đó, ma trận của axtt là ma trận chéo. Chú ý
Ma trận của axtt trong các cơ sở khác nhau thì đồng dạng, do đó các ma
trận này có cùng đa thức đặc trưng, cùng tập trị riêng.
Nếu ma trận của axtt trên hệ cơ sở chéo hóa được, thì ma trận của axtt
trên hệ cơ sở khác cũng chéo hóa được. 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 47
Trị riêng, vector riêng của ánh xạ tuyến tính
Tìm một cơ sở trên đó ma trận của axtt : → có dạng chéo
Chọn một cơ sở của kgvt , xác định ma trận của axtt trên hệ cơ sở . Chéo hóa ma trận .
Nếu không chéo hóa được, thì không tồn tại một hệ cơ sở mà
trên đó ma trận của axtt có dạng chéo.
Nếu chéo hóa được bởi ma trận và ma trận chéo , chuyển sang bước tiếp theo.
Khi đó cơ sở cần tìm có: tọa độ mỗi vector của trên hệ cơ sở
là một cột của ma trận .
Khi đó ma trận của axtt trên hệ cơ sở là ma trận chéo . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 48
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Cho axtt : → , biết:
= , ,
= (2 − 2 − , −2 − − 2, 14 + 25 + 14)
Tìm một cơ sở của sao cho ma trận của axtt trên hệ cơ sở đó có dạng chéo.
Chọn hệ cơ sở chính tắc của : = 1,0,0 , 0,1,0 , 0,0,1 .
Ma trận của axtt trên hệ cơ sở : 2 −2 −1 = −2 −1 −2 . 14 25 14
Ma trận không chéo hóa được.
Do đó không tồn một cơ sở nào sao cho ma trận của axtt có dạng chéo 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 49
Trị riêng, vector riêng của ánh xạ tuyến tính
Ví dụ. Cho axtt : → , biết:
1,1,1 = 1, −7,9 ; 1,0,1 = −7,4, −15 ; 1,1,0 = (−7,1, −12).
Tìm một cơ sở của sao cho ma trận của axtt trên hệ cơ sở đó có dạng chéo.
Chọn hệ cơ sở của : = 1,1,1 , 1,0,1 , 1,1,0 .
Ma trận của axtt trên hệ cơ sở : 1 −4 −4 = 8 −11 −8 −8 8 5 Chéo hóa ma trận :
det − = − 1 + 3 = 0 → = 1, = −3
Đây cũng là trị riêng của axtt . 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 50
Trị riêng, vector riêng của ánh xạ tuyến tính
giải hệ phương trình − []= 0 0 −4 −4 4 −4 −4
8 −12 −8 = 0 và 8 −8 −8 = 0 −8 8 4 −8 8 8
Các vector riêng của :
= [1,2, −2] , []= [1,1,0] , []= [1,0,1]
Do đó các vector riêng của axtt là:
= 1 1,1,1 + 2 1,0,1 − 2 1,1,0 = (1, −1,3).
= 1 1,1,1 + 1 1,0,1 + 0 1,1,0 = (2,1,2).
= 1 1,1,1 + 0 1,0,1 + 1 1,1,0 = (2,2,1). 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 51
Trị riêng, vector riêng của ánh xạ tuyến tính
hệ cơ sở cần tìm là
= (1, −1,3), (2,1,2), (2,2,1) .
Ma trận của axtt trên hệ cơ sở có dạng: 1 0 0 = 0 −3 0 0 0 −3 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 52 Tổng kết – Ví dụ
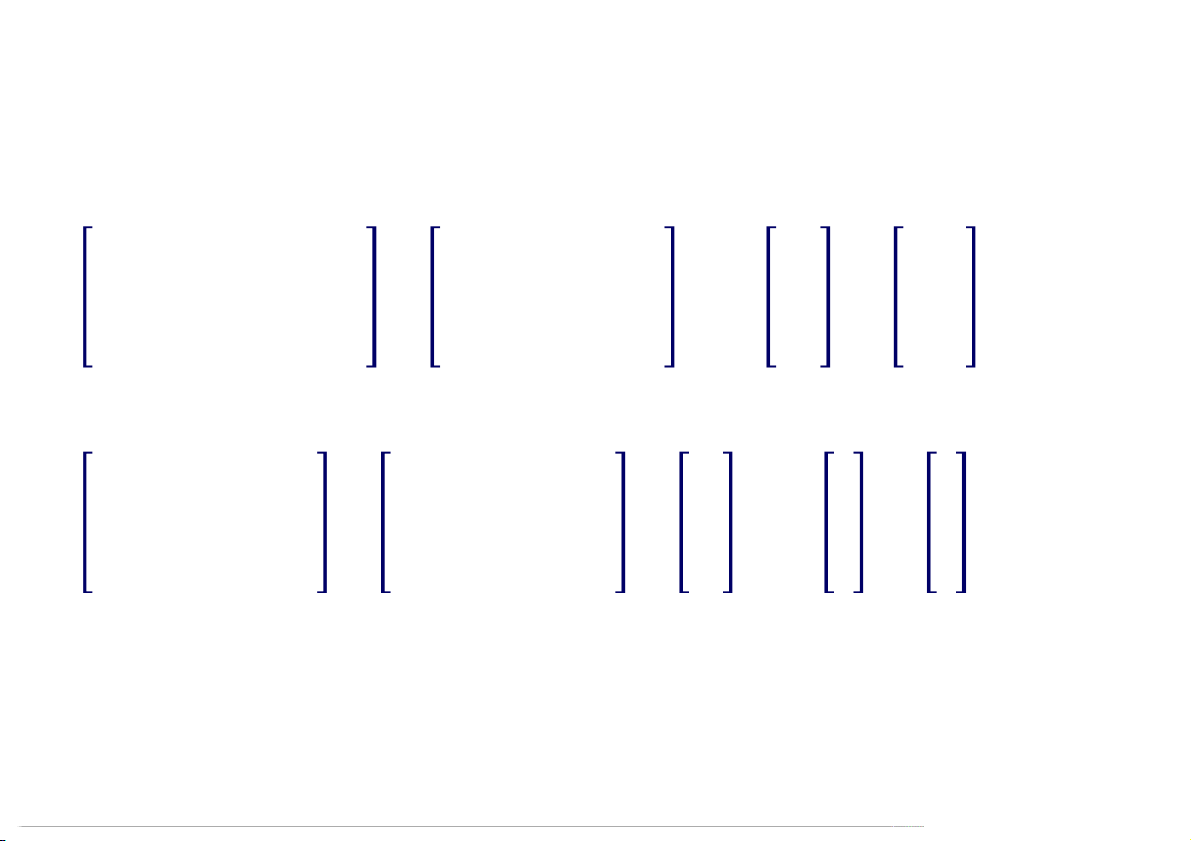
Chéo hóa các ma trận sau (nếu được): −1 4 −2 1 0 0 1 2 1
1. = −3 4 0 → D = 0 2 0 ; = 1 3 3 −3 1 3 0 0 3 1 3 4 4 2 2 2 0 0 −1 −1 1
2. = 2 4 2 → D = 0 2 0 ; = 1 0 1 2 2 4 0 0 8 0 1 1 2 2 −1 0 0 0 1 1 1
3. = 1 3 −1 → D = 0 1 0 ; = 1 0 1 1 −1 0 0 0 4 4 1 0 4 0 −2 4 0 0 1 −2 −2
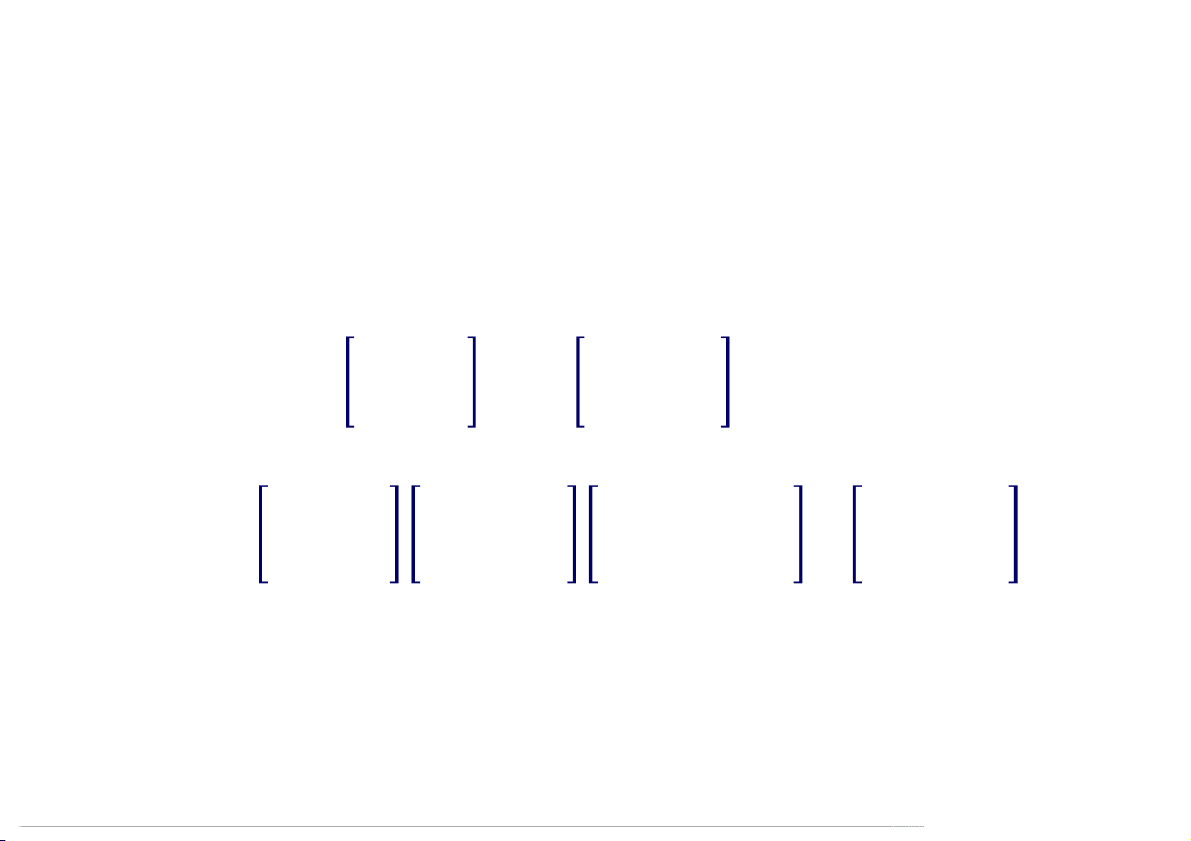
4. = 2 5 4 → D = 0 5 0 ; = −2 1 0 0 0 5 0 0 5 0 1 1 7 4 16 1 0 0 −2 −4 −1 5. = 2 5 8 → D = 0 3 0 ; = −1 0 1 −2 −2 −5 0 0 3 1 1 0 0 −4 −6 1 0 0 −2 −3 −2
6. = −1 0 −3 → D = 0 2 0 ; = −1 0 1 1 2 5 0 0 2 1 1 0 09:52
Trường Đại học Công nghệ, ĐHQG Hà Nội 53