






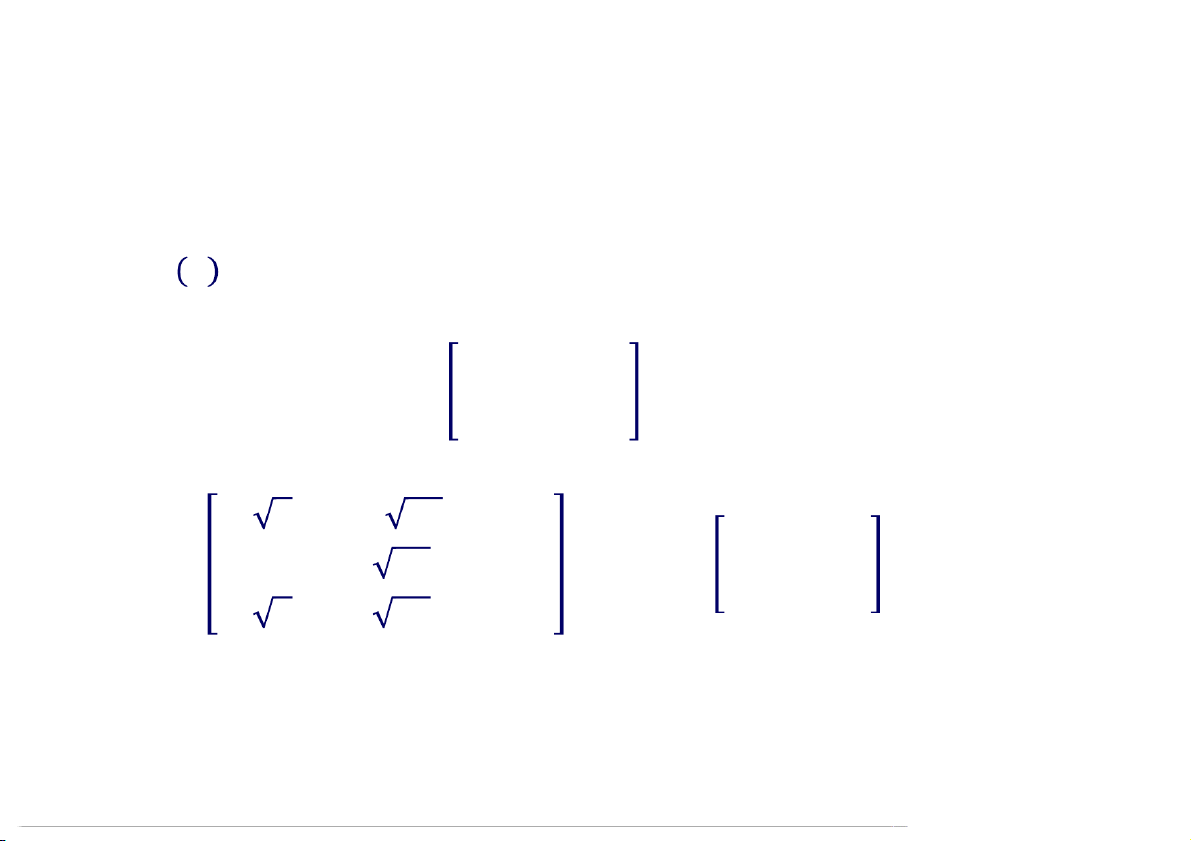





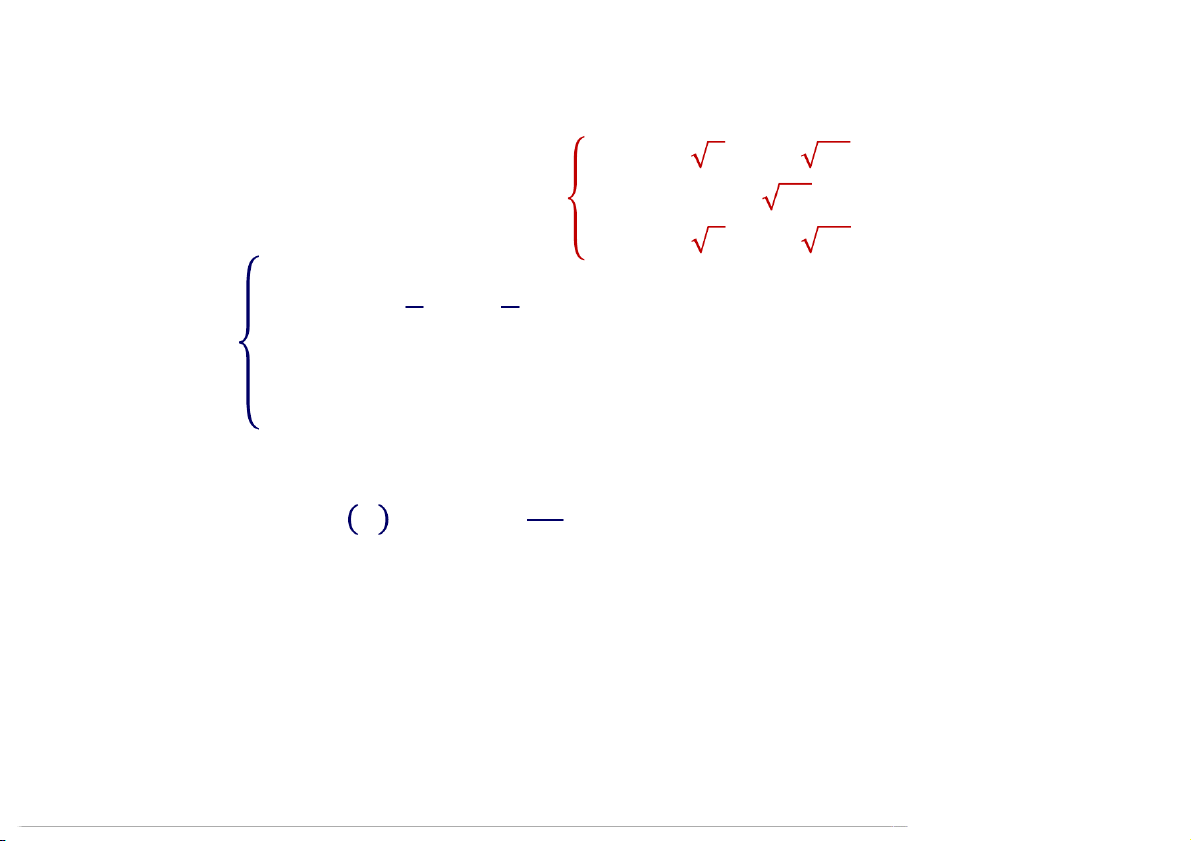












Preview text:
Đại số Tuyến tính Giảng viên: Đào Như Mai 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 1
Chương 9: Dạng toàn phương Dạng toàn phương
Đưa dạng toàn phương về dạng chính tắc
Dạng toàn phương xác định dương
Nhận dạng đường cong, mặt cong 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 2 Dạng toàn phương
Dạng toàn phương trong là một hàm số thực: : → ∀ = , , … ,
∈ : = .
trong đó là ma trận đối xứng thực, và được gọi là ma trận của
dạng toàn phương (trong cơ sở chính tắc).
Ví dụ. Cho = và = 2 −3 −3 4
Khi đó dạng toàn phương trong có dạng: = 2 −3 −3 4 = 2
− 3 −3 + 4 = 2
− 3 − 3 + 4 = 2 − 6 + 4 = 2
− 6 + 4 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 3 Dạng toàn phương
Dạng toàn phương trong có dạng:
= , , = =
+ + C + 2 + 2 + 2
Ma trận của dạng toàn phương lúc này là ma trận đối xứng: =
Khi đó () có thể viết lại: =
, , = = 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 4 Dạng toàn phương Ví dụ. ∀ = , , ∈ : = 3
+ 2 − 4 + 4 + 2 − 6
Viết ma trận của dạng toàn phương. Giải 3 2 −3 = 2 2 1 −3 1 −43 2 −3
Þ = = 2 2 1 −3 1 −4 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 5 Dạng toàn phương Cho dạng toàn phương .
= với =
Vì A là ma trận đối xứng thực nên A chéo hóa được bởi ma trận trực
giao P và ma trận chéo D: =
Khi đó: = =
Đặt = Û = , vậy có l 0 0
= Û 0 l 0 0 0 l Û =
, , = l + l + l
Dạng toàn phương = được gọi là dạng chính tắc của
dạng toàn phương = . 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 6 Dạng toàn phương
Dạng chính tắc của dạng toàn phương là dạng toàn phương
có các số hạng là các bình phương.
Ma trận là ma trận của dạng toàn phương =
trong hệ cơ sở chính tắc.
Ma trận cũng là ma trận của dạng toàn phương =
trong cơ sở tạo nên từ các cột của ma trận trực giao .
Khi làm việc với dạng toàn phương, ta có thể làm việc trên
ma trận , hoặc . Tất nhiên ma trận có cấu trúc đơn giản hơn. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 7
Đưa dạng toàn phương về dạng chính tắc
Phép biến đổi trực giao
Viết ma trận của dạng toàn phương (trong hệ cơ sở chính tắc).
Chéo hóa bởi ma trận trực giao và ma trận chéo . Kết luận:
Dạng chính tắc cần tìm: = .
là ma trận của dạng toàn phương ban đầu trong hệ cơ sở trực
chuẩn từ các cột của ma trận trực giao .
Phép biến đổi cần tìm (phép đổi biến): = . 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 8
Đưa dạng toàn phương về dạng chính tắc
Ví dụ. Đưa dạng toàn phương sau về dạng chính tắc bằng
phép biến đổi trực giao, nêu rõ phép đổi biến. = 3
+ 6 + 3 − 4 + 4 + 8
1. Ma trận của dạng toàn phương: 3 −2 4 = −2 6 2 4 2 3
2. Chéo hóa bởi ma trận trực giao : 1/ 2 −1/ 18 2/3 7 0 0 = 0 4/ 18 1/3 = 0 7 0 1/ 2 1/ 18 −2/3 0 0 −2 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 9
Đưa dạng toàn phương về dạng chính tắc Ví dụ (tiếp)
Dạng chính tắc cần tìm:
, , = 7 + 7 − 2 Phép đổi biến:
= / 2 − / 18 + 2/3
= ↔ = ↔ = 4 / 18 + /3
= / 2 + / 18 − 2/3 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 10
Đưa dạng toàn phương về dạng chính tắc
Phép biến đổi Lagrange
Phép đổi biến = được gọi là phép biến đổi không suy biến
nếu ma trận là ma trận không suy biến.
Nội dung của phương pháp Lagrange là sử dụng các phép biến
đổi không suy biến đưa dạng toàn phương về dạng chính tắc.
Phép biến đổi này rất dễ thực hiện vì chỉ dùng các phép biến đổi
sơ cấp, không phải tìm trị riêng, véc tơ riêng của ma trận.
Nhược điểm của của phép biến đổi này là làm việc với dạng chính
tắc trên một cơ sở thường là không trực chuẩn. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 11
Đưa dạng toàn phương về dạng chính tắc
Phép biến đổi Lagrange
1. Chọn một hệ số khác 0 của số hạng .
Lập thành 2 nhóm: một nhóm chứa , nhóm còn lại không chứa .
2. Trong nhóm đầu tiên: lập thành tổng bình phương.
Ta có một tổng bình phương và một dạng toàn phương không chứa .
3. Sử dụng bước 1, 2 cho dạng toàn phương không chứa số hạng .
Chú ý: nếu trong dạng toàn phương ban đầu tất cả các hệ số của
đều bằng 0, thì ta chọn một hệ số khác 0 của số hạng . Dùng phép đổi biến:
= , = − , = + , ∀ ≠ , . 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 12
Đưa dạng toàn phương về dạng chính tắc
Ví dụ. Đưa dạng toàn phương sau về dạng chính tắc bằng phép
biến đổi Lagrange, nêu rõ phép đổi biến. = 3
+ 6 + 3 − 4 + 4 + 8
1. Chọn thừa số 3 , lập thành 2 nhóm: = 3
− 4 + 8 + (6 + 3 + 4) 4 8 = 3
− 3 + 3 + (6 + 3 + 4)
2. Lập thành tổng bình phương đủ ở nhóm 1: 2 4 16 4 16 = 3(
− 3 +3)+ 3 − 3 − 3 + +(6 + 3 + 4) 2 4 14 7 28 = 3
− 3 +3 + ( 3 − 3 + 3 ) 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 13
Đưa dạng toàn phương về dạng chính tắc Ví dụ (tiếp)
3. Lặp lại bước 1, 2 cho dạng toàn phương: 14 7 28
3 − 3 + 3 Chọn thừa số , lập thành 2 nhóm: 14 28 7 14 7
3 + 3 − 3 = 3 + 2 − 3
Lập thành tổng bình phương đủ ở nhóm đầu: 14 14 7 14
3 ( + )− 3 − 3 = 3 ( + )−7 2 4 14 = 3
− 3 + 3 + 3 ( + )−7 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 14
Đưa dạng toàn phương về dạng chính tắc
= / 2 − / 18 + 2/3 Ví dụ (tiếp)
= 4/ 18 + /3 Đặt
= / 2 + / 18 − 2/3 2 4
= − 3 + 3 (∗) = + =
Vậy dạng chính tắc cần tìm là:14 = 3 + 3 − 7
(*) là phép biến đổi cần tìm. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 15
Đưa dạng toàn phương về dạng chính tắc
Ví dụ. Đưa dạng toàn phương sau về dạng chính tắc bằng
phép biến đổi Lagrange, nêu rõ phép đổi biến.
= 4 + 4 + 4
Trong dạng toàn phương không có hệ số của .
Chọn một hệ số tùy ý chứa , ví dụ: 4.
Thực hiện phép đổi biến: = − = + = = 4
− 4 + 4 + + 4( − ) 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 16
Đưa dạng toàn phương về dạng chính tắc Ví dụ (tiếp) = 4
− 4 + 4 + + 4( − ) = 4
+ 8 − 4 = (4 + 8) − 4 = 4
+ 2 − 4 = 4 + − 4 − 4
Thực hiện phép đổi biến: = + = =
Dạng chính tắc là: = 4 − 4 − 4
= − −
Phép đổi biến: = + − = 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 17
Dạng toàn phương xác định dương
Dạng toàn phương = được gọi là:
Xác định dương, nếu ∀ ≠ : > 0.
Xác định âm, nếu ∀ ≠ : < 0.
Nửa xác định dương, nếu:
≥ 0 và ∃ ≠ : = 0.
Nửa xác định âm, nếu:
≤ 0 và ∃ ≠ : = 0.
Không xác định dấu, nếu:
∃, : < 0 và > 0. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 18
Dạng toàn phương xác định dương
Giả sử dạng toàn phương đưa về dạng chính tắc được: =
+ + ⋯ +
1. Nếu > 0, ∀, thì dạng toàn phương là xác định dương.
2. Nếu < 0, ∀, thì dạng toàn phương là xác định âm.
3. Nếu ≥ 0, ∀ và ∃ = 0 thì dạng toàn phương là nửa xđ dương.
4. Nếu ≤ 0, ∀ và ∃ = 0 thì dạng toàn phương là nửa xđ âm.
5. Nếu ∃ < 0, > 0 thì dạng toàn phương không xác định dấu. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 19
Dạng toàn phương xác định dương
Giả sử dạng toàn phương đưa về dạng chính tắc được: =
+ + ⋯ +
Số các hệ số dương được gọi là chỉ số dương quán tính.
Số các hệ số âm được gọi là chỉ số âm quán tính.
Tồn tại rất nhiều phương pháp đưa dạng toàn phương về dạng
chính tắc. Các phương pháp này thường khác nhau.
Tuy nhiên, các phương pháp này có điểm chung của các dạng
chính tắc như sau: số lượng các hệ số dương và số lượng các hệ
số âm là không thay đổi. Định lý quán tính
Chỉ số dương quán tính, chỉ số âm quán tính của dạng toàn phương
là những đại lượng bất biến, không phụ thuộc vào cách đưa dạng
toàn phương về dạng chính tắc. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 20
Dạng toàn phương xác định dương
Cho ma trận vuông, thực cấp nxn.
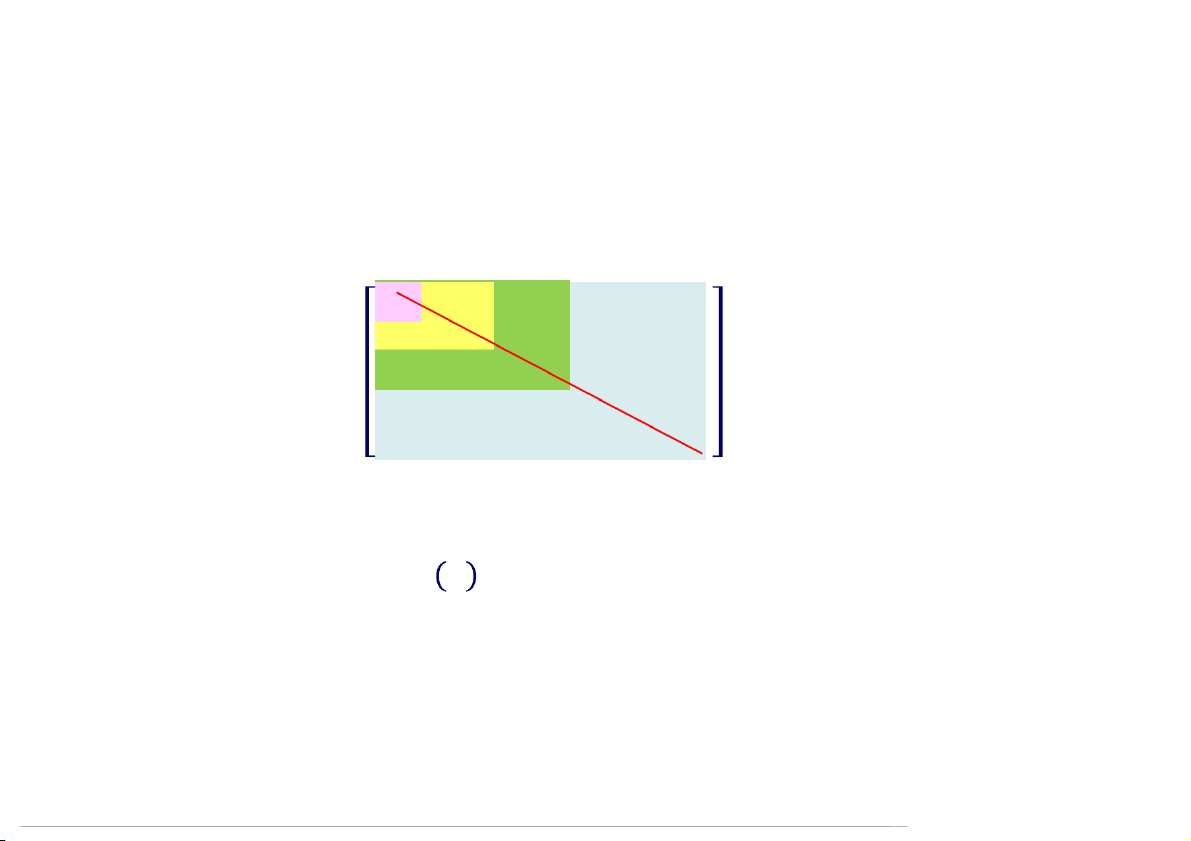
Tất cả các định thức con tạo nên dọc theo đường chéo chính
được gọi là định thức con chính cấp 1, 2,…, n.
⋮
⋮
= ⋮ ⋯ ⋯ ⋯ ⋯ ⋯
⋮
∆ ∆ ∆ ⋯ ∆ Định lý (Sylvester)
Cho dạng toàn phương =
1. () xác định dương ↔ ∆> 0, ∀ = 1. .
2. () xác định âm ↔ (−1)∆> 0, ∀ = 1. . 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 21
Dạng toàn phương xác định dương
Ví dụ. Với giá trị nào của thì dạng toàn phương sau xác định dương: =
+ 4 + − 2 + 4 + 8
Ma trận của dạng toàn phương là: 1 −1 4 = −1 4 2 4 2
Dạng toàn phương xác định dương khi và chỉ khi các định thức con chính đều dương.
∆= = 1 > 0 ∆ = 1 −1 −1 4 = 3 > 0 1 −1 4
∆= −1 4 2 = 3 − 84 > 0 → > 28 4 2 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 22
Dạng toàn phương xác định dương
Ví dụ. Tìm để dạng toàn phương sau không xác định dấu: =
+ 5 + − 4 + 2 + 6
Đưa dạng toàn phương về dạng chính tắc bằng phép biến đổi Lagrange: = (
− 4 + 6) + (5 + + 2) = (
− 2 + 3)+ + 14 + ( − 9) = (
− 2 + 3)+( + 7)+( − 58)
Dạng toàn phương không xác định dấu khi và chỉ khi có ít nhất một
hệ số âm và một hệ số dương: ↔ < 58. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 23
Nhận dạng đường cong, mặt cong
Công thức tịnh tiến, quay trục tọa độ
Công thức tịnh tiến hệ trục tọa độ tới điểm (, ): Từ Oxy sang Ouv = + = +
Công thức quay hệ trục tọa độ một góc : Từ Oxy sang Ouv
= −
= + 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 24
Nhận dạng đường cong, mặt cong
Ví dụ. Trong hệ trục tọa độ Oxy cho đường cong có phương trình: y
3 + 2 + 3 − 4 2 − 2 = 0
Nhận dạng và vẽ đường cong này. x o
Xét dạng toàn phương , = 3 + 2 + 3
Vẽ đường cong trong hệ trục Oxy là làm việc với hệ cơ sở chính tắc trong R2.
Đưa dạng toàn phương này về dạng chính tắc để khử đi hệ số 2xy.
Nếu đưa dạng toàn phương về chính tắc bằng biến đổi Lagrange thì ta
chỉ có thể nhận dạng được đường cong này, còn khó vẽ hình được vì lúc
đó ta sẽ làm việc với hệ cơ sở (thường là) không trực chuẩn
Tức là vẽ hình trong hệ trục tọa độ không vuông góc
Do đó, ta cần phép biến đổi trực giao để có hệ cơ sở trực chuẩn. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 25
Nhận dạng đường cong, mặt cong
Ma trận của dạng toàn phương: = 3 1 1 3
Phương trình đặc trưng:
det − = 0 ↔ − 6 + 8 = 0 → = 2, = 4.
Cơ sở trực chuẩn của các không gian con riêng: 1 1 1 1 = 2: = − , ; , ) 2 2 = 4: = ( 2 2 Phép đổi biến:
= = 1/ 2 −1/ 2 1/ 2 1/ 2 Hay: = − ; = + 2 2 2 2 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 26
Nhận dạng đường cong, mặt cong
Hay = . − . ; = . + v.cos
Phép quay hệ trục Oxy sang hệ trục Ouv một góc = /4
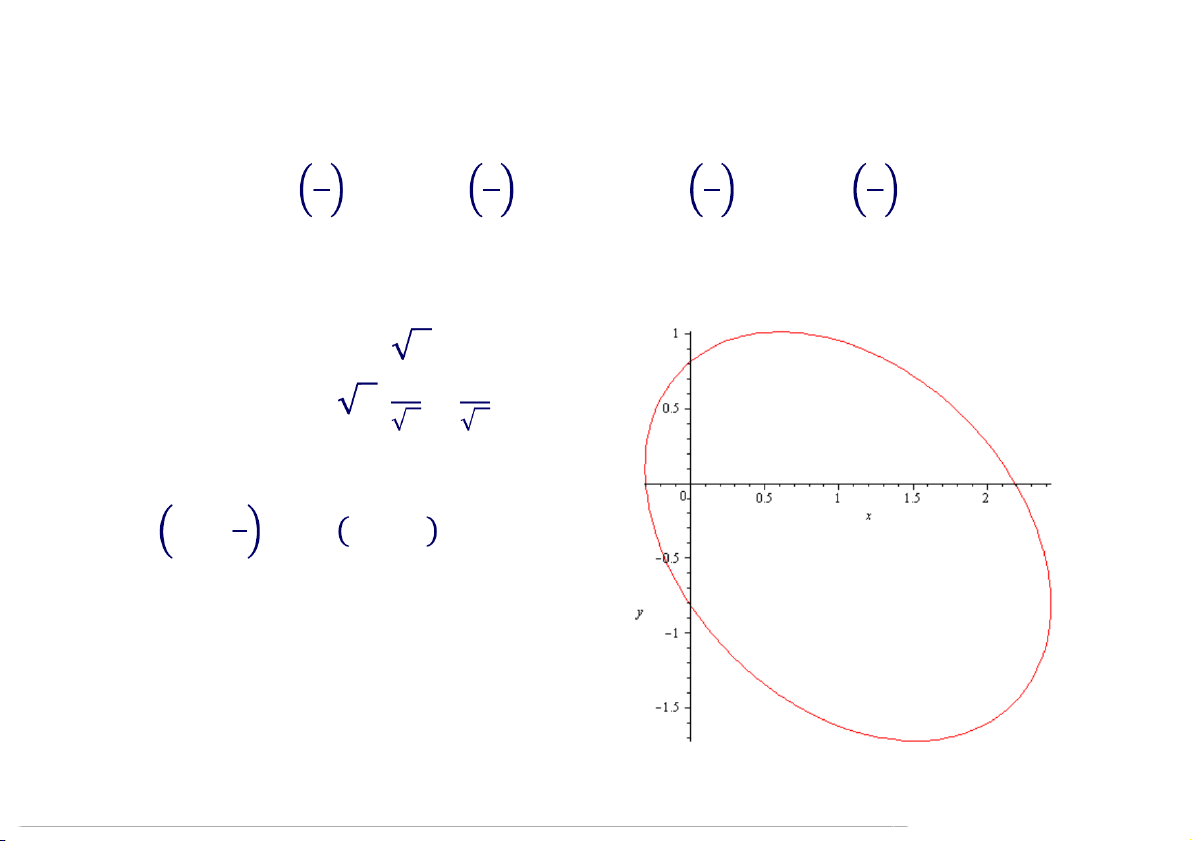
Đường cong đã cho có phương trình trong hệ trục tọa độ Ouv là:
3 + 2 + 3 − 4 2 − 2 = 0
↔ 4 + 2 − 4 2( − ) − 2 = 0
↔ 4 − 4 + 2( + 2) − 2 = 0
↔ 4 − + 2 + 1 = 5 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 27
Nhận dạng đường cong, mặt cong
Ví dụ. Nhận dạng mặt bậc hai:
2 + 2 + 3 − 2 − 2 − 16 = 0
Ma trận của dạng toàn phương: 2 0 −1 0 2 −1 −1 −1 3
Phương trình đặc trưng:
det − = 0 ↔ = 1, = 2, = 4.
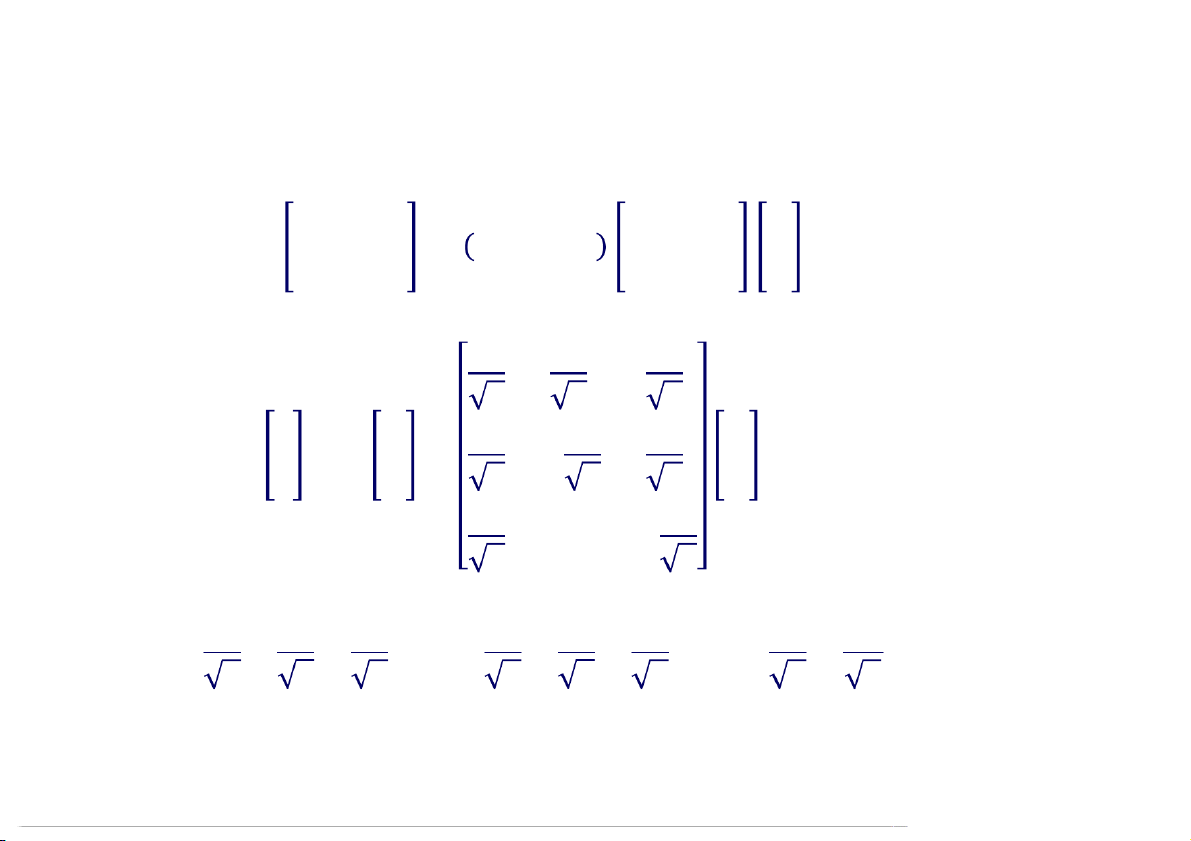
Cơ sở trực chuẩn của các không gian con riêng: 1 1 1 1 1 = 1: = , , ; , − , 0 ; 3 3 3 = 2: = 2 2 1 1 2
= 4: = ( , , − ) 6 6 6 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 28 1 0 −1 0 0 0 0 1 0 1 −1 → 0
1 −1 = 0 → = 1 −1 −1 2 −1 −1 2 0 1 0 0 −1 0 0 0 0 1 0 0 −1 → 0
0 −1 = 0 → = −1 −1 −1 1 −1 −1 1 0 0 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 29
Nhận dạng đường cong, mặt cong Ví dụ (tiếp) 1 0 0 1 0 0
= 0 2 0 ⇒ 0 2 0 0 0 4 0 0 4 Phép đổi biến: 1 1 1 3 2 6 1 1 1 = = − 3 2 6 1 2 0 − 3 6 Hay: 2 = + + ; = − + ; = − 3 2 6 3 2 6 3 6 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 30
Nhận dạng đường cong, mặt cong Ví dụ (tiếp)
Mặt cong đã cho có phương trình trong hệ trục tọa độ Ouvw là:
+ 2 + 4 − 16 = 0. Hay: 16 + 8 + 4 = 1.
Phương trình của mặt Ellipsoid có các bán trục lần lượt là: 4, 8, 2. 17:40
Trường Đại học Công nghệ, ĐHQG Hà Nội 31




