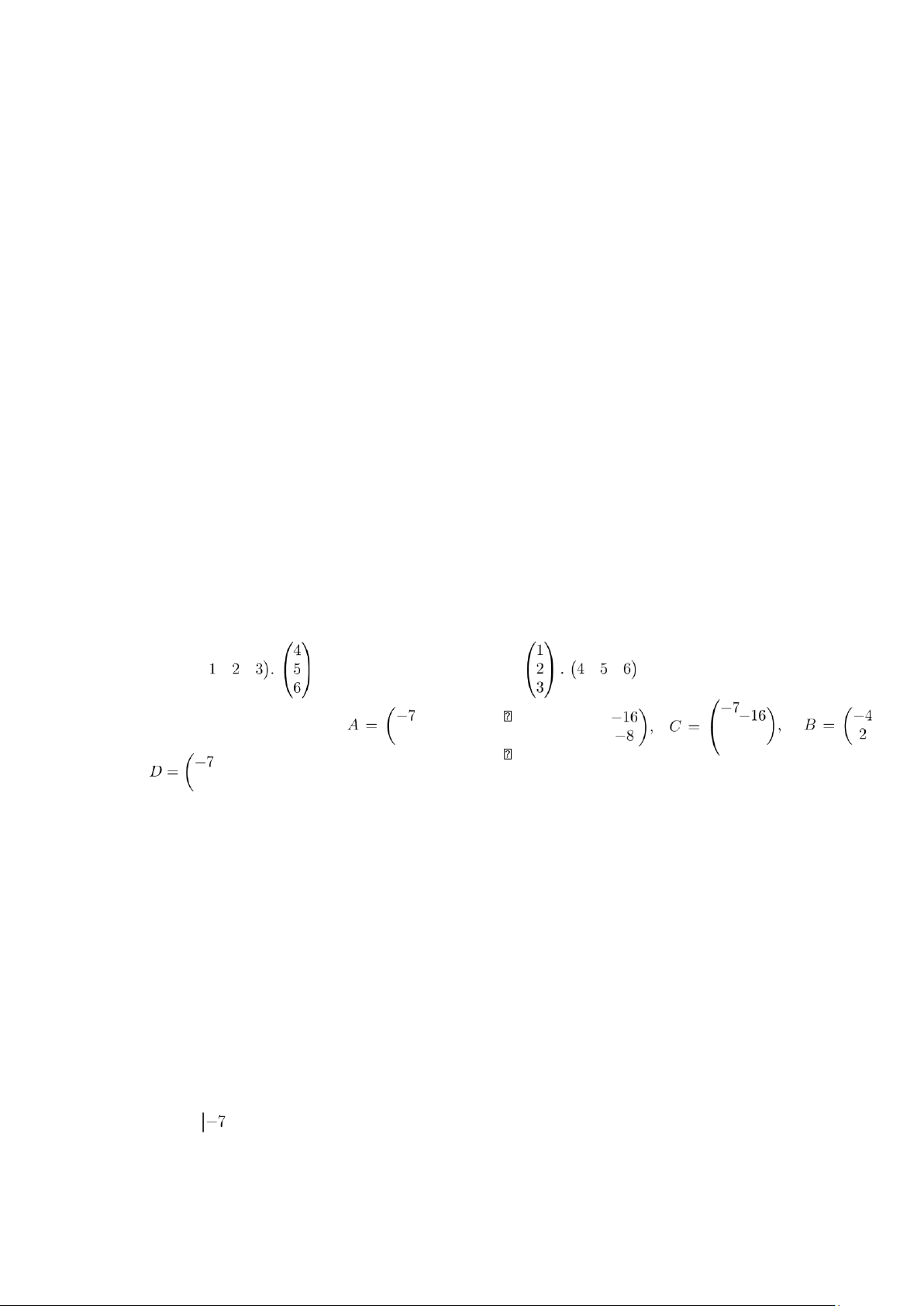













Preview text:
lOMoAR cPSD| 58970315
CHƯƠNG I : MA TRẬN - ĐỊNH THỨC VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
BUỔI 1-2. MA TRẬN - ĐỊNH THỨC - MA TRẬN NGHỊCH ĐẢO Nội dung lý thuyết:
• Khái niệm ma trận, các dạng ma trận: ma trận cỡ m × n, ma trận vuông cấp n, ma trận tam giác, ma
trận đối xứng, ma trận đường chéo, ma trận đơn vị, ma trận không.
• Các phép toán trên ma trận: cộng hai ma trận, trừ hai ma trận, nhân một số với ma trận, chuyển vị ma
trận, nhân hai ma trận.
• Định nghĩa định thức và ví dụ.
• Các tính chất cơ bản của định thức.
• Phương pháp tính định thức.
• Định nghĩa ma trận nghịch đảo - Điều kiện khả nghịch. Bài tập về nhà: Bài 1.
a. Viết ma trận đơn vị cấp 2, cấp 3.
b. Viết ma trận không cỡ 2 × 3, 3 × 4. Bài 2.Thực hiện phép nhân ma trận. a. b. −16 Bài 3. Cho các ma trận3 8 và 3 8 4 2 −16 1 . 3 8 5
a. Thực hiện chuyển vị các ma trận trên.
b. Tìm M biết M = A2 + 2A − 3I với I là ma trận đơn vị cấp 2.
c. Tìm N biết N = 2A − 5BT.
d. Thực hiện các phép nhân ma trận: A.B; B.A; A.D; C.BT; DT.A;
e. Tìm thêm các phép nhân ma trận trên các ma trận đã cho.
Bài 4.Tính định thức bằng định nghĩa: −16 4 1 2 3 lOMoAR cPSD| 58970315 a.b.3 8 4c.4 5 6 3 8 4 2 17 8 9
Bài 5.Tính các định thức (nhờ tính chất định thức): −16 4 1 2 1 a.3 8 4 b.2 1 3 4 2 1 3 5 7 8 1 3 c. 2 4 5 28 41 53 Bài 6.Tính
các định thức (nhờ tính chất định thức) Cho Tính.
Bài 7.Xác định giá trị tham số a để ma trận sau khả nghịch. −7 −16 4 B = 3 8 4 a 2 1 1 2 1 1 −2 2 1 3 D = 1 2 −1 . 3 5 7 1 2 a lOMoAR cPSD| 58970315
BUỔI 3-4. MA TRẬN NGHỊCH ĐẢO - HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Nội dung lý thuyết:
• Các tính chất của ma trận khả nghịch.
• Tìm ma trận nghịch đảo bằng phương pháp phần phụ đại số.
• Hệ phương trình tuyến tính - Phương pháp Gauss để giải hệ phương trình tuyến tính Bài tập về nhà:
Bài 1.Tìm ma trận nghịch đảo của các ma trận sau (phương pháp phần phụ đại số). −7 −16 4 1 2 1 lOMoAR cPSD| 58970315 B = 3 8 4 C = 2 1 3 3 8 4 2 1 −3 5 7 1 1 −2
Bài 2. Cho ma trận A = 1 2 −1 . 1 2 a
a. Xác định giá trị tham số a để ma trận A khả nghịch.
b. Khi a = 1 hãy tìm ma trận nghịch đảo của A.
Bài 3.Giải các hệ phương trình đại số tuyến tính. lOMoAR cPSD| 58970315 (
x − y + 2z = 0 x − 2y = 1 a.
b. 3x + 4y + z = 0 −3x + 6y = −3
5x + 2y + 5z = 0
x + 2y + 3z = −1 (
2x + y + z = 3
c. −2x + y + 3z = 1 d.
2x + y − z = 4
x + 7y + 12z = −2
2x + y − z − t = 0
x + 3y + 5z − 2t = 1 e.
x + y − z + 2t = 0 f.
2x + 7y + 3z + t = 1 lOMoAR cPSD| 58970315
2x + 3y + z − 2t = 0
x + 5y − 9z + 8t = −1
Bài 4.Giải các hệ phương trình đại số tuyến tính. (
x − 3y + 2z = 0 3x − 2y = 1 a.
b. x + 4y + z = 0 −x + 4y = −3
5x − 2y + 5z = 0
( x + 2y + 3z = 0 c.
−2x + y + 3z = 0 (
2x + y + z = 1 d. lOMoAR cPSD| 58970315
x + y − 2z = 0
CHƯƠNG II: KHÔNG GIAN VÉC TƠ- ÁNH XẠ TUYẾN TÍNH
BUỔI 5-6 KHÔNG GIAN TUYẾN TÍNH - KHÔNG GIAN CON
• Định nghĩa không gian tuyến tính thực và các ví dụ về không gian tuyến tính thực.
• Tính chất cơ bản của không gian tuyến tính thực.
• Không gian con và các ví dụ về không gian con .
• Tổ hợp tuyến tính, hệ sinh.
• Hệ phụ thuộc tuyến tính - hệ độc lập tuyến tính, ví dụ.
• Cơ sở và số chiều của không gian tuyến tính, tính chất và các ví dụ.
• Tọa độ véc tơ trong một cơ sở. Bài tập về nhà:
Bài 1.Chứng minh rằng mỗi tập A sau là không gian con của không gian tuyến tính V .
a. A = {(x,y) ∈R2/2x − 3y = 0} là không gian con của R2.
b. A = {(x,y,z) ∈R3/2x − y − z = 0} là không gian con của R3.
c. A = {(x,y,z) ∈R3/x − 3y = 0, y − 4z = 0} là không gian con của R3.
Bài 2.Xét tính độc lập tuyến tính, phụ thuộc tuyến tính của hệ véc tơ sau:
a. A = {a = (1;0);b = (1;2);c = (4;5)} trong R2.
b. B = {a = (−1;1;0);b = (2;−2;0);c = (4,5,6);d = (1;2;4)} trong R3.
c. C = {a = (1;1;1);b = (1;2;3);c = (−1;4;1)} trong R3.
d. D = {a = (1;1;1;0);b = (1;−1;2;0);c = (4;1;1;4)} trongR4.
Bài 3.Cho hệ vectơ {a;b;c} độc lập tuyến tính trong không gian R3. Hãy xét tính độc lập, phụ thuộc tuyến tính của các hệ vectơ sau:
a. A = {a + b;a − c;c}.
b. B = {a + b;a − c;b + c}.
Bài 4.Tìm hệ sinh của mỗi không gian con A
a. A = {(x,y) ∈R2/2x − 3y = 0} là không gian con của R2.
b. A = {(x,y,z) ∈R3/2x − y − z = 0} là không gian con của R3.
c. A = {(x,y,z) ∈R3/x − 3y = 0, y − 4z = 0} là không gian con của R3.
( x + 2y + z = 0
Bài 5.Cho hệ phương trình . 3x − y − 5z = 0 lOMoAR cPSD| 58970315
a. Viết công thức nghiệm của hệ phương trình.
b. Từ đó suy ra hệ sinh của không gian con A = {(x,y,z) ∈R3/x + 2y + z = 0,3x − y − 5z = 0}.
Bài 6.Chứng minh hệ véc tơ A là cơ sở của không gian tuyến tính V .
a. A = {a = (1;−1);b = (2;3)}, V = R2.
b. A = {a = (1;−1;0);b = (2;1;0);c = (0;1;2)}, V = R3.
c. A = {a = (1;2;0);b = (1;0;2);c = (0;1;2)}, V = R3.
d. A = {a = (2;−1);b = (0;3)}, V = R2.
e. A = {a = (2;−1;0);b = (2;−1;1);c = (3;1;2)}, V = R3.
f. A = {a = (1;2;2);b = (1;0;−2);c = (3;1;−2)}, V = R3.
Bài 7.Xác định một cơ sở và số chiều của các không gian sau.
a. A = {(x,y) ∈R2/x − 2y = 0}.
b. B = {(x,y,z) ∈R3/x − 2y + z = 0}.
c. C = {(x,y,z) ∈R3/x + 2y = 0, y − z = 0}.
Bài 8.Cho hệ véc tơ A là cơ sở của không gian tuyến tính V , tìm tọa độ của véc tơ u trong cơ sở A.
a. A = {a = (1;−1);b = (2;3)}, V = R2, u = (4,6).
b. A = {a = (1;−1;0);b = (2;1;0);c = (0;1;2)}, V = R3, u = (1;3;4).
c. A = {a = (1;2;0);b = (1;0;2);c = (0;1;2)}, V = R3, u = (−1;−3;4).
d. A = {a = (1;−1);b = (2;−3)}, V = R2, u = (−2,2).
e. A = {a = (1;−1;0);b = (2;1;1);c = (0;−1;2)}, V = R3, u = (1;3;−4).
f. A = {a = (1;2;3);b = (1;3;2);c = (3;1;2)}, V = R3, u = (1;3;4).
BUỔI 7-8. ÁNH XẠ TUYẾN TÍNH Nội dung lí thuyết:
• Định nghĩa ánh xạ tuyến tính.
• Khái niệm hạt nhân, ảnh (Kerf, Imf).
• Ma trận của ánh xạ tuyến tính
• Giá trị riêng, véc tơ riêng của phép biến đổi tuyến tính. Bài tập về nhà:
Bài 1. Cho f : R2 →R2,f(x,y) = (x + y,2x + 3y).
a. Chứng minh f là ánh xạ tuyến tính (phép biến đổi tuyến tính). lOMoAR cPSD| 58970315
b. Tìm không gian ảnh Imf, không gian nhân Kerf?
Bài 2. Xác định một cơ sở và số chiều của không gian nhân Kerf và không gian ảnh Imf cho các ánh xạ tuyến tính sau:
a. Cho f : R3 →R2,f(x,y,z) = (x − y,y − 2z).
b. Cho f : R3 →R3,f(x,y,z) = (x + y − 2z,x + 2y − z,x + 4y + z).
Bài 3. Cho ánh xạ tuyến tính f : R2 →R3,
f(x,y) = (x + y,x − 2y,−2x + 5y).
a. Viết ma trận của f trong cặp cơ sở chính tắc của R2,R3
b. Tìm chiều và một cơ sở của không gian Imf, Kerf.
Bài 4. Cho f(x,y) = (2x + 2x,2x + 5y) là phép biến đổi tuyến tính trên R2. Véc tơ nào sau đây là véc tơ riêng
của f? Và véc tơ riêng đó ứng với giá trị riêng nào? a. u = (1;2). b. v = (2;−1). c. s = (−1;2). d. r = (1;1).
Bài 5. Trên R2 cho phép biến đổi tuyến tính f(x,y) = (5x − 2y;−2x + 8y).
a. Tìm ma trận biểu diễn A của f trong cơ sở chính tắc E của R2.
b. Tìm trị riêng, véc tơ riêng của f.
c. Viết ma trận biểu diễn của f trong cơ sở véc tơ riêng.
Bài 6. Trên R3 cho phép biến đổi tuyến tính f(x,y,z) = (−x + y;x − y,2z).
a. Tìm ma trận biểu diễn A của f trong cơ sở chính tắc E của R3.
b. Tìm trị riêng, véc tơ riêng của f.
c. Viết ma trận biểu diễn của f trong cơ sở véc tơ riêng.
Bài 7. Tìm giá trị riêng và véc tơ riêng của ma trận. −2 0 1 1 a. 2 4 b. 2 3 0 0 0 5
CHƯƠNG III : ĐẠO HÀM VÀ VI PHÂN
BUỔI 9. GIỚI HẠN HÀM SỐ- HÀM SỐ LIÊN TỤC Nội dung lí thuyết:
• Định nghĩa giới hạn hàm số lOMoAR cPSD| 58970315 • Vô cùng bé
• Hàm liên tục và một vài tính chất Bài tập về nhà:
Bài 1 Tính giới hạn các hàm số sau : 4 a)b)c) d) m) n) e) f) g) h)
Bài 2 (3 điểm ) Tìm a,b để hàm số sau liên tục trên R
khi x > 0khi x > 0 a)b)
khi x ≤ 0khi x ≤ 0
khi x > 0khi x > 0
c)d) khi x ≤ 0khi x ≤ 0.
BUỔI 10-11. ĐẠO HÀM - VI PHÂN VÀ CÁC ỨNG DỤNG Nội dung lí thuyết:
• Định nghĩa hàm khả vi- Ý nghĩa cơ học của hàm khả vi.
• Vi phân và ứng dụng vi phân tính gần đúng
• Đạo hàm và vi phân cấp cao
• Công thức Taylor và khai triển Taylor một số hàm sơ cấp
• Quy tắc L’ Hospital và các ứng dụng quy tắc L’ Hospital trong việc tìm giới hạn. Bài tập về nhà:
Bài 1. Viết khai triển Maclaurin của hàm f(x) đến cấp n
a. f(x) = sin2x, n = 4
b. f(x) = cos3x, n = 5
c. f(x) = e3x, n = 4
d.f(x) = ln(1 − 2x), n = 3 e.
Bài 2. Cho hàm số f(x) = xe2x
a. Viết khai triển Maclaurin của hàm f(x) đến cấp 6.
b. Tính f(5)(0).
Bài 3. Cho hàm số f(x) = (x + 1)ln(1 + 2x),
a. Viết khai triển Maclaurin của hàm f(x) đến cấp 5,
b. Tính f(4)(0).
Bài 4.Viết công thức khai triển Maclaurin của hàm f(x) đến xn, tính f(n)(0) lOMoAR cPSD| 58970315
a) f(x) = x2.sin2x, n = 7
b) f(x) = (x2 + 1).sin2x, n = 7
c)f(x) = x3.cosx, n = 9
d) f(x) = (x3 + x).cos3x, n = 9
e) f(x) = x3.ln(1 − 2x), n = 6
f) f(x) = (x2 + x + 1).ln(1 + 2x), n = 6
Bài 5. Tính giới hạn các hàm số bằng quy tắc L’Hospital a. b.
Bài 6. Tính giới hạn các hàm số a) , b) c) d) e) f) , g)
BUỔI 12-13 . HÀM NHIỀU BIẾN - ĐẠO HÀM RIÊNG CỦA HÀM NHIỀU BIẾNCỰC TRỊ CỦA HÀM HAI BIẾN Nội dung lí thuyết:
• Định nghĩa hàm nhiều biến
• Đạo hàm riêng cấp 1, cấp 2 của hàm nhiều biến
• Cực trị của hàm 2 biến Bài tập về nhà:
Bài 1.Tính tất cả các đạo hàm riêng đạo hàm riêng cấp 1 của hàm số sau
a) f(x,y) = x2 + y3x tại (1,2)
b) f(x,y,z) = x2z + y2x + xyz2 tại (1,2,3) xy
khi (x,y) 6= (0,0) x 2 + y 2 c) f(x,y) = 0
khi (x,y) = (0,0)
d) f(x,y) = p3 x3 + y3 x3y
khi (x,y) 6= (0,0) e) f(x,y) = x6 + y2 0
khi (x,y) = (0,0)
Bài 2. Tính các đạo hàm riêng cấp 2 của các hàm số sau
a) f(x,y) = x2 + y3x − xcos(x2 + y)
b) f(x,y,z) = x2z + ln(x + y + z) + xyz2 lOMoAR cPSD| 58970315
c) f(x,y) = x3y + 2xy2 − sin(x + 2y)
d) f(x,y,z) = (x2 + y + z)e2x+y−3z
Bài 3. Tìm cực trị các hàm số dưới đây
a) f(x,y) = x2 − 2xy + 4y3
b) f(x,y) = x3 − 4xy + y2
c) f(x,y) = x3 − 3x + 6y − 4y3
d) f(x,y) = −3x3 + 12x − 9y + y3
e) f(x,y) = x2 + xy2 − 2x + 1
f) f(x,y) = x3 + 2xy + 4y2 + 2y CHƯƠNG IV : TÍCH PHÂN
BUỔI 14-15 .TÍCH PHÂN XÁC ĐỊNH- TÍCH PHÂN KÉP- ỨNG DỤNG CỦA TÍCH PHÂN Nội dung lí thuyết:
• Nguyên hàm và bảng nguyên hàm
• Định nghĩa tích phân xác định- Công thức Newton-Leibnitz
• Định nghĩa tích phân kép- Định lý Fubini
• Ứng dụng tích phân tính diện tích miền phẳng Bài tập về nhà:
BÀI 1: Tính các nguyên hàm sau R R
a) (x2 − 3x + 2cosx)dx b) sin4xdx R c) xexdx d)
Bài 2: Tính nguyên hàm các hàm hữu tỉ a) b) c) d) e)
Bài 3: Tính các tích phân xác định sau a) b) c)
Bài 4: Tính tích phân xác định bằng đổi biến a) b) c) lOMoAR cPSD| 58970315
Bài 5: Tính tích phân bằng tích phân từng phần a) b) c)
Bài 6: Tính tích phân hàm hữu tỉ a) b) c)
Bài 7. Sử dụng Định lý Fubini tính các tích phân kép RR a)
D(x2 + xy)dxdy;
D = {(x,y) : 1 ≤ x ≤ 2,−1 ≤ y ≤ 1 b)
Bài 8. Chọn thứ tự thích hợp để tính các tích phân kép a) RRD ycosxydxdy;
D = {(x,y) : 0 ≤ x ≤ 1,0 ≤ y ≤ π/3
b) RRD(y + 1)ex(y+1)dxdy;
D = {(x,y) : 0 ≤ x ≤ 1,−1 ≤ y ≤ 1 c)
Bài 9.Tính các tích phân kép a) b) c) d)
Bài 10 : Vẽ miền D rồi tính các tích phân kép
a) RRD xydxdy, D là miền giới hạn bởi x = 0,y = 2x + 1,y = −2x + 5
b) RRD(x + y)dxdy , D nằm trong góc phần tư thứ nhất, giới hạn bởi x = 0,y = x2,y = 8 − x2. RR c)
D y2dxdy, D là miền giới hạn bới x = 1,y = 2x + 2,y = −x − 1 √ RR d)
D 12ydxdy, D là miền giới hạn bởi y = 2 − x,y = x,y = 0.
Bài 11: Tính diện tích miền phẳng
a) D = {y = x2,y = 2x} b)
c) D = {(x,y) : y2 = x,x = 1} lOMoAR cPSD| 58970315
Bài 12 : Vẽ miền D rồi tính diện tích các miền bằng tích phân kép
a) D giới hạn bởi x = 0,y = 2x + 1,y = −2x + 5
b) D nằm trong góc phần tư thứ nhất, giới hạn bởi x = 0,y = x2,y = 8 − x2.
c) D là miền giới hạn bới x = 1,y = 2x + 2,y = −x − 1 √
d) D là miền giới hạn bởi y = 2 − x,y = x,y = 0.
BUỔI 16-17. ÔN TẬP VÀ KIỂM TRA



