Giới hạn Hàm 1 Biến: Hàm Lượng Giác và Dãy Số | Môn Toán cao cấp 1 - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58970315 1
I. Các hàm lượng giác ngược 1. Hàm Arcsin
Ánh xạ [ / 2; / 2] [ 1;1] là một song ánh, do đó có ánh xạ ngược. x sin x
Ánh xạ này gọi là hàm Arcsin. Như vậy, có thể nói Arcsin là hàm ngược
của hàm sin thu hẹp vào [ ; ]. 2 2
Chú ý rằng, từ định nghĩa, ta có sin x t Ar sinc x t [ t / 2; / 2].
Chẳng hạn, để tìm Arcsin(-1/2), có thể lập luận như sau: Đặt t=Arcsin(-1/2), ta có sint [t
1/ 2;/ 2 / 2]. Do đó có t / 6. Vậy Ar sin( 1/ 2)c / 6.
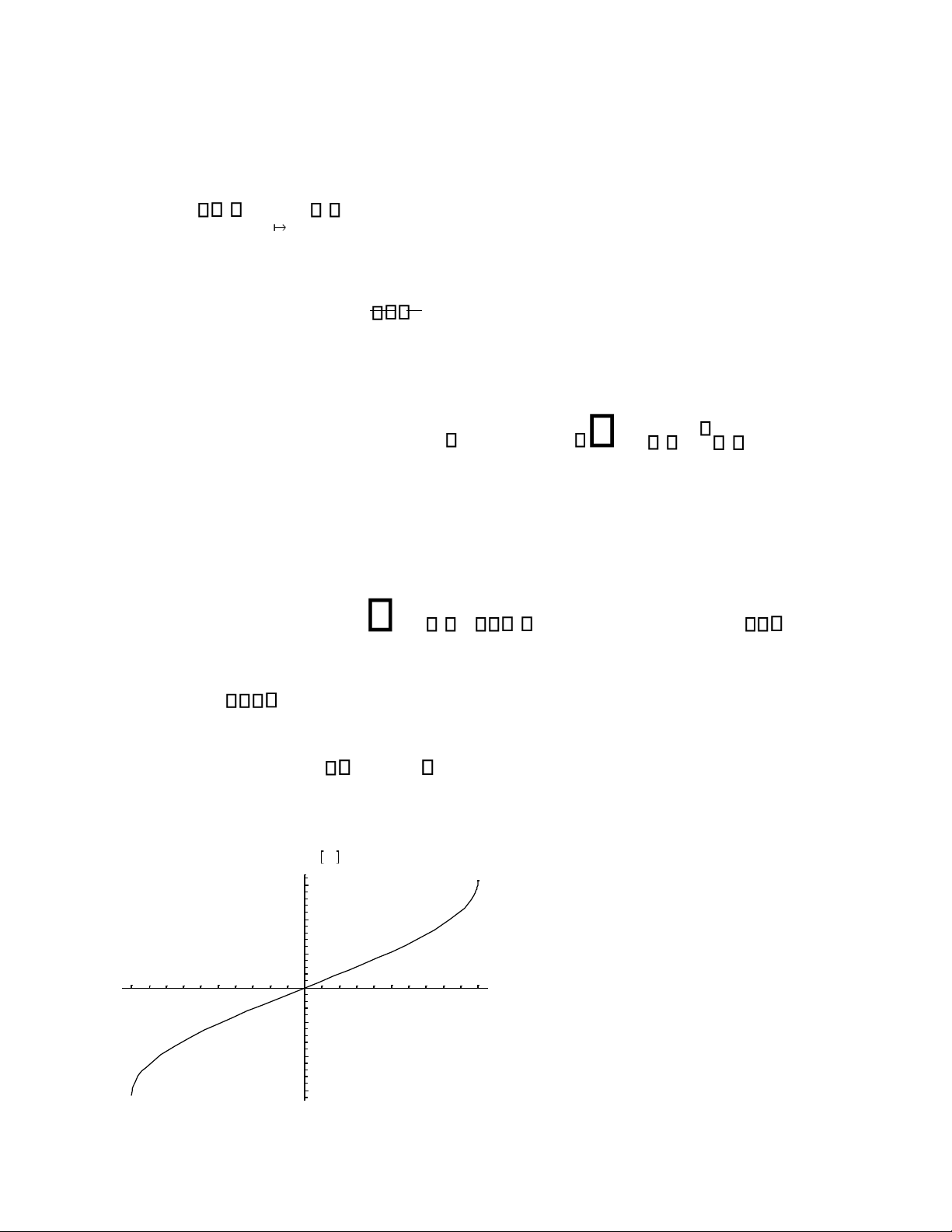
Hàm Arcsin là hàm lẻ ( hàm ngược của hàm lẻ là hàm lẻ), tăng trên
tập xác định[-1;1] từ / 2 đến / 2 Đồ thị hàm y=Arcsinx ArcSin x 1.5 1 0.5 -1 -0.5 0.5 1 x -0.5 -1 -1.5 lOMoAR cPSD| 58970315 2 2. Hàm Arccos
Ánh xạ [0; ] [ 1;1] là một song ánh, do đó có ánh xạ ngược. Ánh xạ x c xos
này gọi là hàm Arccos. Như vậy, có thể nói Arccos là hàm ngược của
hàm cos thu hẹp vào [0; ].
Chú ý rằng, từ định nghĩa, ta có cos t x
t Arccosx t [0 ; ]. Chẳng hạn,
để tìm Arccos(-1/2), có thể lập luận như sau: Đặt t=Arccos(-1/2), ta có cos t 1/ 2 t [0 ; ]
. Do đó có t 2 /3. Vậy Arccos( 1/ 2) 2 /3.
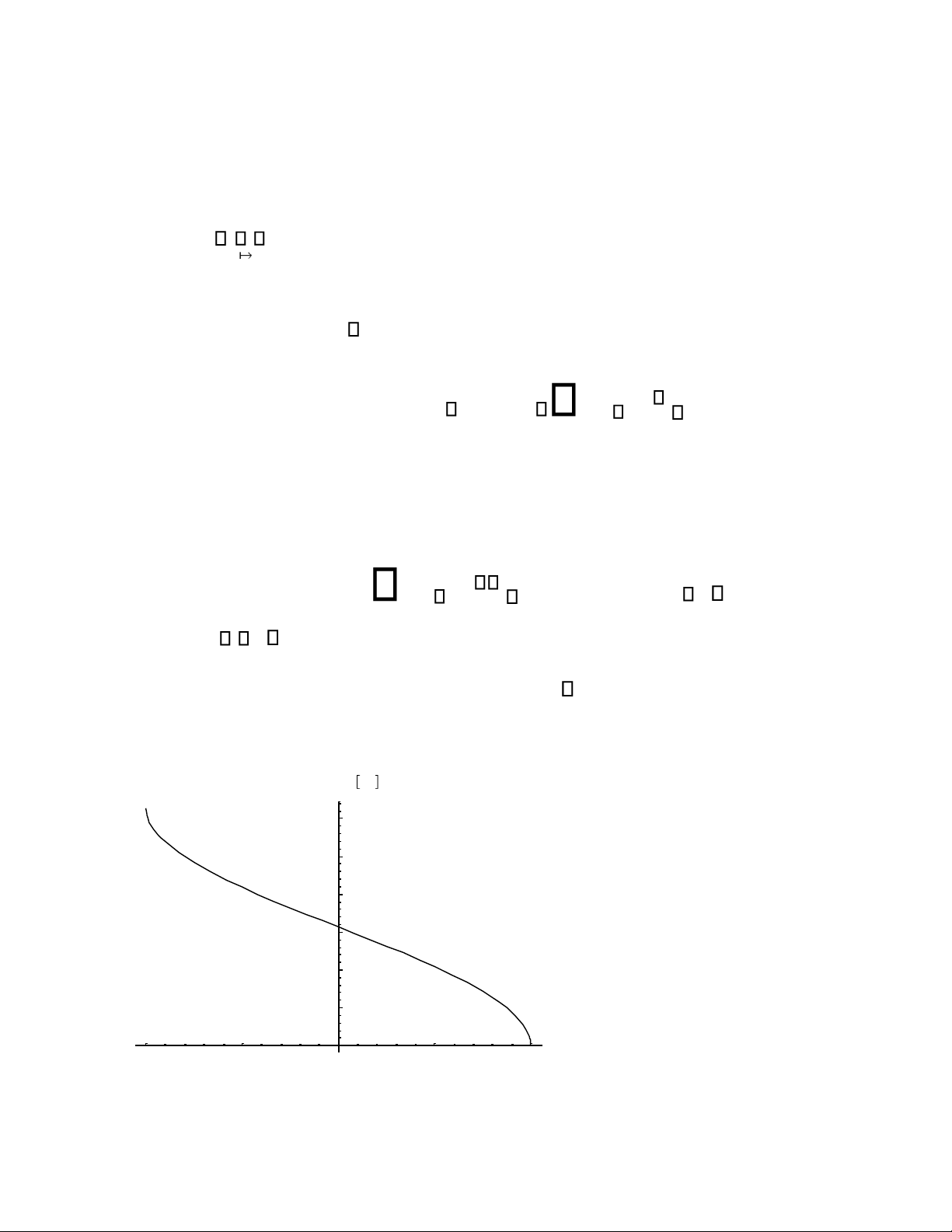
Hàm Arccos giảm trên tập xác định[-1;1] từ đến 0. Đồ thị hàm y=Arccosx ArcCos x 3 2.5 2 1.5 1 0.5 -1 -0.5 0.5 1 x lOMoAR cPSD| 58970315 3 Chú ý
Có thể chứng minh được hằng đẳng thức
x [ 1;1], Arcsinx Arccosx / 2. 3. Hàm Arctan
Ánh xạ ( / 2; / 2) là một song ánh, do đó có ánh xạ ngược. Ánh xạ x tan x
này gọi là hàm Arctan. Như vậy, có thể nói Arctan là hàm ngược của hàm tan thu hẹp vào ( ; ). 2 2
Chú ý rằng, từ định nghĩa, ta có tan t t Ar tanc x t ( x/ 2; / 2).
Chẳng hạn, để tìm Arcsin(-1), có thể lập luận như sau: Đặt t=Arctan(-1), ta có ttan (t
/ 2;1 / 2) . Do đó có t / 4. Vậy Ar tan( 1)c / 4.
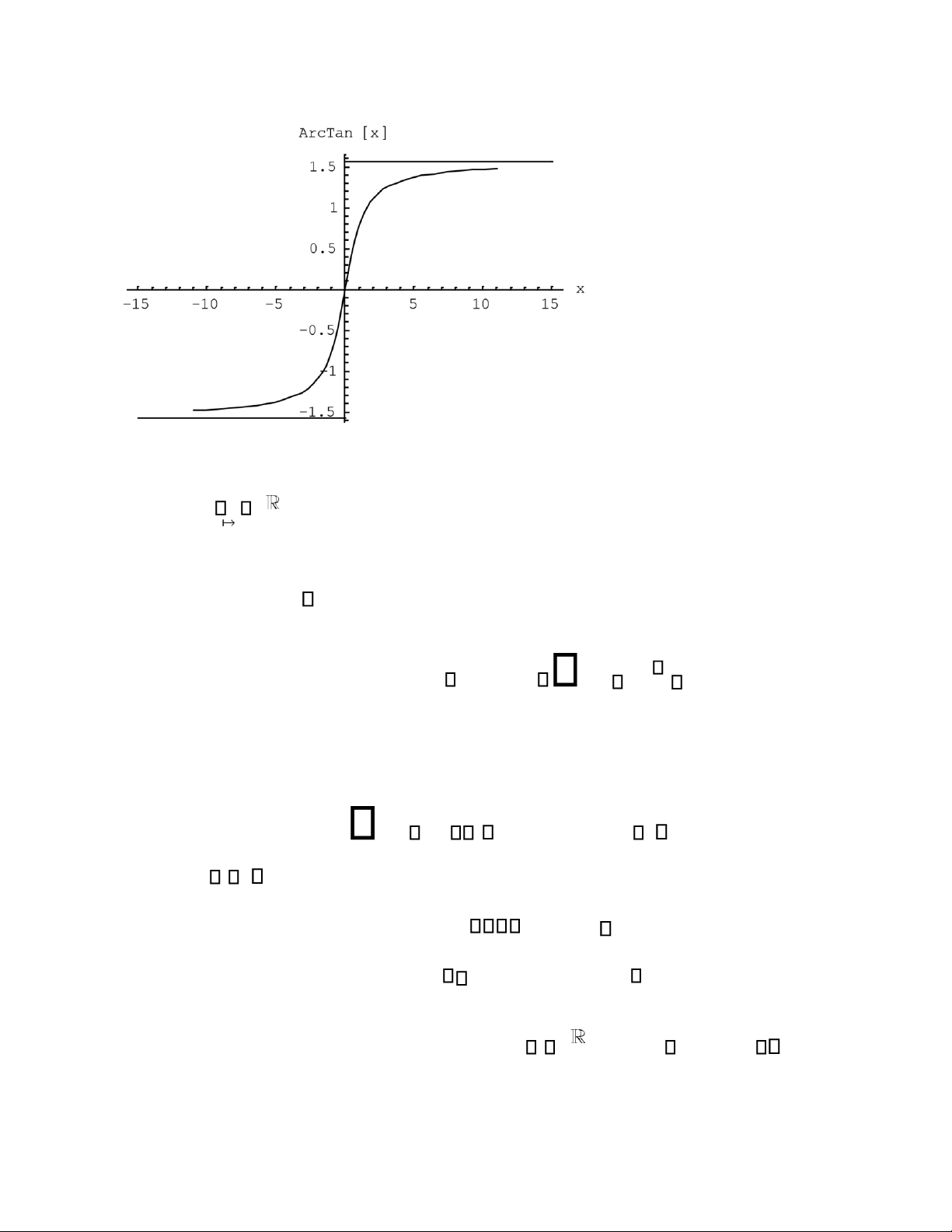
Hàm Arcsin là hàm lẻ ( hàm ngược của hàm lẻ là hàm lẻ), tăng trên tập xác định( ; ) từ
/ 2 đến / 2. Đồ thị y=Arctanx có 2 tiệm cận ngang y
/ 2 ( phía trái) và y / 2 (phía phải) lOMoAR cPSD| 58970315 4 4. Hàm Arccot
Ánh xạ (0; ) là một song ánh, do đó có ánh xạ ngược. Ánh xạ này x cot x
gọi là hàm Arccot. Như vậy, có thể nói Arccot là hàm ngược của hàm cot thu hẹp vào (0; ) .
Chú ý rằng, từ định nghĩa, ta có cot t x t Ar cotcx t (0 ; ). Chẳng hạn, để tìm
Arcot(-1), có thể lập luận như sau: Đặt t=Arccot(-1), ta có tcot (0t
; )1. Do đó có t 3 / 4. Vậy Ar cot( 1)c 3 / 4.
Hàm Arccot giảm trên tập xác định( ; ) từ đến 0. Đồ thị
y=Arccotx có 2 tiệm cận ngang y ( phía trái) và y 0 (phía phải) Chú ý
Có thể chứng minh được hằng đẳng thức x ,Arctanx Arccot x / 2. lOMoAR cPSD| 58970315 5
II. Các hàm sơ cấp cơ bản và các hàm sơ cấp
1. Danh sách các hàm sơ cấp cơ bản 1. Hàm hằng a 2. Hàm lũy thừa x
x với a là số thực cho trước. Lưu ý rằng, khi a là *
số vô tỷ, tập xác định của hs này là . 3. Hàm mũ x ax với 0 a 1
4. Hàm logarit x loga x với 0 a 1. Chú ý rằng hàm x loga x là hàm ngược của hàm x ax
5. Các hàm lượng giác và lượng giác ngược: sin, cos, tan, cot, Arcsin, Arccos, Arctan và Arccot.
2. Khái niệm hàm sơ cấp
Các hàm lập nên từ các hàm sơ cấp bởi các phép toán số học ( cộng,
trừ, nhân, chia) và phép lấy hàm hợp gọi là các hàm sơ cấp ( hoặc các
hàm thông dụng (tiếng Pháp: fonctions usuelles). Chú ý rằng các hàm
sơ cấp thường được cho bằng biểu thức giải tích, khi không nói gì về
tập xác định, thì qui ước tập xác định là tập các giá trị của biến số sao
cho biểu thức có nghĩa. Chẳng hạn, để tìm txđ của hàm 1 log2 x , ta cần
giải bpt 1 log2 x 0. Kết quả được txđ là (0;2]. III. Dãy số 1. Định nghĩa dãy
Dãy các số thực (phức) là ánh xạ : ( tương ứng ).
Chú ý rằng, nếu kí hiệu ánh xạ trên là u, thì đôi khi, thay vì nói dãy u:
hoặc dãy u: , người ta còn viết dãy ( )u n , hoặc đơn giản
là dãy ( )u n , thậm chí, một cách lạm dụng ký hiệu, người ta còn viết dãy
u un , trong đó un là ảnh của n. Chẳng hạn, với dãy u: *
n 1 /n , người ta
có thể nói: 1/n là dãy đơn điệu giảm và có giới hạn bằng 0.
2. Định nghĩa giới hạn của dãy số thực ; Dãy hội tụ a)Xét dãy u :
Phần tử a gọi là giới hạn của u khi và chỉ khi : lOMoAR cPSD| 58970315 6 0, N( ) , n
,(n N( ) |un
a| ). Để dễ nhớ, có thể nói
đơn giản là, un có thể “gần” a một cách tùy ý, miễn là n đủ lớn. Để chỉ
rằng a là giới hạn của u, người ta viết limun a hoặc un a khi n . Nếu tồn tại a n
sao cho u có giới hạn bằng a ( u có giới hạn hữu hạn), thì nói u là dãy
hội tụ. Một dãy không hội tụ gọi là phân kỳ.
Chú ý: Với dãy số phức z: , ta xét đồng thời 2 dãy số thực x:
; y: , khi đó có zn xn iyn . n Re(zn) n Im(zn)
Ngoài ra, dễ chứng minh được lim zn a bi limlimnnxy nn ab n VD
Dùng định nghĩa, dễ chứng minh được lim1/ n 0. n
b) Dãy số thực u gọi là có giới hạn khi và chỉ khi
M0, N M(), n ,(n N M( ) un M)
c) Dãy số thực u gọi là có giới hạn khi và chỉ khi
M0, N M(), n ,(n N M( ) un M)
3. Tính duy nhất của giới hạn
Giả sử a, b cùng là giới hạn của dãy (un). Khi đó a=b. 4. Dãy bị chặn a) Dãy bị chặn trên
Dãy ( )u n gọi là bị chặn trên, nếu tồn tai số thưc A sao cho n ,un
A b) Dãy bị chặn dưới lOMoAR cPSD| 58970315 7
Dãy ( )u n gọi là bị chặn dưới, nếu tồn tai số thưc A sao cho n ,un A c) Dãy bị chặn
Dãy ( )u n gọi là bị chặn, nếu tồn tai số thưc A>0 sao cho n ,|un | A Nói
cách khác: dãy vừa bị chặn trên, vừa bị chặn dưới gọi là dãy bị chặn. Nhận xét
Mọi dãy thực có giới hạn đều bị chặn dưới và không bị chặn trên.
Mọi dãy thực có giới hạn đều bị chặn trên và không bị chặn dưới.
Mọi dãy số thực hoặc phức hội tụ đều bị chăn.
5. Các tính chất đại số của dãy hội tụ. Mệnh đề
( về giới hạn của tổng, tích, thương của hai dãy hội tụ và của tích của 1
dãy hội tụ với một số)
Cho hai dãy ( )u n và ( )v n là hai dãy số phức. và các số phức , ,a b. Khi
đó 1*) Nếu un a, thì | un | | a | 2*)
Nếu un a và vn b, thì un vn
a b và u vn n ab 3*)
Nếu un a, thì un a
4*) Nếu un 0 và ( )v n bị chặn, thì u vn n 0 5*) Nếu , thì u u n
n a và vn b
0, ngoài ra khi n đủ lớn, vn 0 a vn b 5)
Với những dãy không hội tụ, nhưng có giới hạn , có thể chứng minh các mệnh đề sau
Cho hai dãy số thực ( )u n và ( )v n lOMoAR cPSD| 58970315 8 1*) Nếu un và vn , thì un vn 2*) Nếu un
và (vn) bị chặn dưới, thì un vn 3*) Nếu un
và (vn) thỏa mãn điều kiện: khi n đủ lớn, vn C const>0, thì un vn
6) Một số tiêu chuẩn tồn tại giới hạn a) Tiêu chuẩn bị kẹp
Cho ba dãy(un), (vn) và (wn) sao cho khi n đủ lớn, un wn vn . Khi đó, nếu
(un)và (vn) hội tụ và có cùng giới hạn bằng a, thì (wn) hội tụ về a. VD
Dùng tiêu chuẩn bị kẹp, chứng minh rằng lim n n 1 n Hướng dẫn
Đặt n n 1 un . Cần chứng minh un 0 n n 1 u n
n n 1 un (1 un)n n (1) Mặt khác: (1 u 2
n)n 1 nun
n n( 1)un ...(2) 2 Từ (1), (2) suy ra 1) 1 n n( u 2 2 n
n, từ đó un 2 . Vì un 0, nên 2 n 2 * 0 un n.
Từ đó, theo tiêu chuẩn bị kẹp, suy ra đpcm. n
b) Tiêu chuẩn tăng và bị chặn trên hoặc giảm và bị chặn dưới ĐN lOMoAR cPSD| 58970315 9
Dãy (un) gọi là tăng,( tương ứng: tăng nghiêm ngặt), nếu n ,un un 1
(tương ứng: nếu n ,un un 1 )
Dãy (un) gọi là giảm ,( tương ứng: giảm nghiêm ngặt), nếu n ,un un 1
(tương ứng: nếu n ,un un 1 )
Dãy đơn điệu là dãy tăng hoặc giảm. Định lý
1) Một dãy số thực tăng và bị chặn trên thì hội tụ.
2) Một dãy số thực giảm và bị chặn dưới thì hội tụ.
*)Ví dụ dẫn tới định nghĩa số e
Có thể chứng minh được dãy (un) xác định bởi : n *, un (1
1)n 1 là n dãy giảm. Mặt khác, dãy này bị chặn dưới bởi số 0. Suy ra ( )u n hội tụ.
Mặt khác (1 1)n (1 1)n 1 :(1 1). Do đó, dãy (1 1)n là dãy hội tụ. Giới n n n n
hạn của dãy này gọi là số e.
Người ta chứng minh được e là số vô tỉ và có thể biểu diễn e bằng số
thập phân với hàng nghìn chữ số sau dấu phẩy
(e=2.718281828459045235360287471352662497757247…) Ví dụ 2
Tìm giới hạn của dãy un 2n n! 2n 1 2n 2 Ta có un 1
. un khi n>1. Suy ra dãy đơn điêụ giảm. Mặt (n 1)! n! n 1
khác. dãy bị chặn dưới bởi 0. Vậy dãy hội tụ. Gọi giới hạn là a, ta có 2n 1 2n 2 a limun 1 lim lim( . ) a.0 0 n (n 1)! n n! 1 lOMoAR cPSD| 58970315 10 n n 2n Vậy lim 0 n! n c) Tiêu chuẩn Cauchy
Xét dãy số thực hoặc phức(un). Dãy (un) gọi là dãy Cauchy, nếu thỏa mãn điều kiện :
0, N( ) , ( , m n) 2,(n N( ) &m N( ) |um un | )
Đôi khi, đk trên viết dưới dạng khác: 0, N( ) , p
N, n ,(n N( ) | un un p | ) 7) Dãy con ĐN
Mọi ánh xạ tăng nghiêm ngặt : gọi là một hàm trích. Với dãy
(un), một dãy (u ( )n ) với là một hàm trích, gọi là một dãy con của dãy (un)
Chẳng hạn (u2n),(u2n 1),(un2 ) là những dãy con của (un) Mệnh đề
Nếu dãy (un) hội tụ đến a, thì mọi dãy con của (un) hội tụ đến a.
Dùng mệnh đề này, để chứng minh một dãy không hội tụ, ta có thể chỉ
ra hai dãy con của dãy có giới hạn khác nhau. VD
Không tồn tại giới hạn của dãy un ( 1)n
Chọn 2 dãy con: u2n ( 1)2n và u2n 1 ( 1)2n 1. Hiển nhiên u2n 1;u2n 1 1 Suy ra đpcm. Mệnh đề
Để dãy (un) hội tụ đến a, đk là 2 dãy (u2n),(u2n 1) cùng hội tụ đến a. lOMoAR cPSD| 58970315 11
8) Về các phương pháp tìm giới hạn của dãy.
Để tìm giới hạn của dãy, tùy trường hợp, có thể áp dụng các mệnh đề đã
nêu ở các mục trên. Ngoài ra, khi đã thành thạo tìm giới hạn của hàm số
( xem các phần tiếp theo), có thể thông qua giới hạn của hàm số.
Chẳng hạn, có thể tìm lim n n như sau n
Giới hạn cần tìm bằng limx1/x x Ta có ln x
x1/x e1/ lnx x. Mặt khác lim
0. Vậy limx1/x e01. x x x
IV. Giới hạn của hàm số
Trong các phần tiếp theo, ký hiệu chỉ tập hợp số thực bổ sung thêm 2
phần tử . Như vậy, khi viếta , thì điều này nghĩa là a có thể là số thực, hoặc a
1. Khái niệm lân cận, điểm tụ ĐN 1) Cho a
. Lân cận của a với bán kính r, ký hiệu U ar ( ) là khoảng mở
(r;r). Khi không cần nêu rõ bán kính, người ta nói gọn là “ lân cận điểm
a”. Chẳng hạn, khi nói “ hàm f bị chặn trong lân cận điểm a”, thì điều
này nghĩa là: tồn tại r>0 sao cho f bị chặn trong U ar ( ) ( f bị chặn trên X
nghĩa là M 0, x X,| f x( ) | M ) ĐN 2)
Lân cận với bk r (r>0) của a= (a= ) là khoảng (1/r; ) ( tương ứng khoảng ( ; 1/ r)). lOMoAR cPSD| 58970315 12 ĐN 3) Phần tử a
gọi là điểm tụ của tập A , nếu với mọi r>0, U ar ( )
X ( điều này nghĩa là trong lân cận của a có vô số phần tử của A)
2. Các định nghĩa giới hạn. ĐN 1)
Cho hàm f : X ;a và a là điểm tụ của X. Số thực b gọi là giới hạn của f tại a khi và chỉ khi 0, ( ), x X,(0 | x a| | f x( )
b| ) Điều này nghĩa là: f(x) có thể “gần” b tùy ý khi x đủ “gần” a. Để
chỉ rằng b là giới hạn của f tại a, người ta viết lim f x( ) b hoặc x a
lim f b hoặc f x( ) b a x a ĐN 2a)
Cho hàm f : X ;a và a là điểm tụ của X. Phần tử gọi là giới hạn của
f tại a khi và chỉ khi M 0, (M), x X,(0 | x
a | f x( ) M) ĐN 2b)
Cho hàm f : X ;a và a là điểm tụ của X. Phần tử gọi là giới hạn của
f tại a khi và chỉ khi M 0, (M), x X,(0 | x
a | f x( ) M) ĐN 3)
Cho hàm f : X ; là điểm tụ của X. Số thực b gọi là giới hạn của f
tại khi và chỉ khi 0, M( ) , x
X,(x M | f x( ) b | ) ĐN 3b) lOMoAR cPSD| 58970315 13
Cho hàm f : X ; là điểm tụ của X. Số thực b gọi là giới hạn của f
tại khi và chỉ khi 0, M( ) , x
X,(x M | f x( ) b| ) ĐN 4)
Cho hàm f : X ; là điểm tụ của X. Phần tử gọi là giới hạn của f
tại khi và chỉ khi M 0, (M), x X,(x f x( ) M)
Tương tự, có thể nêu đn hàm f có giới hạn bằng tại , có gh bằng tại
Để chỉ rằng b là giới hạn của f tại a ( (a b, ) ( )2 ), người ta viết lim f
x( ) b hoặc lim f b. Chẳng hạn x a
a lim ex 0; lim ex ; limex 1; lim 1 , v.v. x x x 0 0 x2
3) Giới hạn phải, giới hạn trái
Cho hàm f : X ;a và a là điểm tụ của X.
Số thực b gọi là giới hạn phải của f tại a khi và chỉ khi
0,( ), x X,(0 xa | f x( ) b | )
Số thực c gọi là giới hạn trái của f tại a khi và chỉ khi 0, ( ), xX,( x a 0 | f x( ) c| )
Giới hạn phải của f tại a ký hiệu là lim f x( ) hoặc f a( ). Ký hiệu tương tự x a cho giới hạn trái.
Tương tự ĐN 2a) và 2b), có thể ĐN trường hợp f có giới hạn phải hoặc trái bằng VD 1 1
lim e1/x 0; lim e1/x ; lim ;lim x 0 x 0 0 x 0 x lOMoAR cPSD| 58970315 14 Định lý
Cần và đủ để tồn tại giới hạn của f tại a là tồn tại f a( ), f a( ) và f a( ) f a( ) VD Hàm x
e1/x không có giới hạn tại 0 vì gh phải và gh trái không bằng nhau.
4) Các phép toán đại số với hàm có giới hạn hữu hạn Mệnh đề 1) f x( ) b | f x( )| |b| x a x a f x( ) b 2) ) g x( )x ax a b'
f x( ) g x( )x a b b' (
3) Nếu f x( ) 0 và hàm g bị chặn trong lân cận của a, thì f x g x( ) ( ) 0 x a x a 4)
g xf x( )( )x ax a
bb' f x g x( ) ( )x a bb' f x( ) b 5)
g x( )x a x a b'
0 f x( ) / g x( )x a b b/ '
5) Trường hợp giới hạn vô hạn Mệnh đề 1) Nếu f x( )
và g bị chặn dưới trong lân cận của a, thì lOMoAR cPSD| 58970315 15 x a f x( ) g x( ) x a 2) Nếu f x( )
và g bị chặn dưới trong lân cận của a bởi số dương, x a thì f x g x( ) ( ) x a Nói riêng
g xf x( )( )x a
x a b' 0 f x g x( ) ( )x a
Phát biểu tương tự cho trường hợp f x( ) x a
6) Giới hạn của hàm hợp
Mệnh đề về giới hạn hàm hợp có thể viết ngắn gọn như sau ( bỏ qua
những giả thiết chặt chẽ cần có)
Giả sử f x( ) b và g t( ) c. Khi đó g f x( ( )) c x a t b x a VD 1 lim(Ar tanc x ) limAr tanc t
;lime1 cosx
lime1 t e0 1 x t 1 4 x 0 t 1 x
7) Một số tiêu chuẩn tồn tại giới hạn Mệnh đề 1)
Cần và đủ để lim f x( ) b là: với mọi dãy (un) có giới hạn là a, dãy giá trị x a
tương ứng của f ( dãy ( f u( n)) có giới hạn là b. VD lOMoAR cPSD| 58970315 16
Chứng minh rằng hàm sin không có giới hạn tại
Chọn 2 dãy u:n / 2 2n và v:n n . Ta có sin(un) 1 1 và sin(vn) 0
0. Suy ra không tồn tại giới hạn tại
của hàm sin. Dùng định lý
trên , trong một số trường hợp, có thể tìm được giới hạn của dãy (un)
cho trước nào đó. Cách làm là tìm hàm f sao cho f n( ) un sau đó tìm lim
f x( ) . Giới hạn tìm được chính là giới hạn của dãy đã cho x ( xem VD mục II.8) Mệnh đề 2) Cho f : X
là hàm sơ cấp và a là điểm tụ của X. Nếu f tăng và bị chặn trên trên ( ; )a
X hoặc giảm và bị chặn dưới trên ( ; )a X ,
thì tồn tại giới hạn trái f a( )
. Phát biểu tương tự cho trường hợp tồn tại f a( ) .
8) Định lý về tính liên tục của hàm sơ cấp Định lý Cho f : X
là hàm sơ cấp và a là điểm tụ của X và a thuộc X. Khi đó lim
f x( ) f a( ) x a VD Cho hàm f : x x xtan3 x
Áp dụng định lý trên, ta có xlim /4 f x( ) f ( / 4) ( / 4 1/ 4) 3
Tuy nhiên, đl không áp dụng được cho trường hợp lim f x( ) vì 0 không 0x lOMoAR cPSD| 58970315 17
thuộc tập xác đinh của f; ngoài ra, các định lý nêu ở các mục trước
cũng không áp dụng được ( đây là dạng vô định sẽ xét sau, để tìm tan x limx 0 x x
3 cần biết cách khử các dạng vô định ).
9) Giới thiệu 7 dạng vô định
Trong thực hành, ta có thể gặp các bài toán tìm giới hạn mà các định lý
thông dụng không áp dụng được, như ví dụ đã nêu ở mục 8). 0 0;00 hiểu theo nghĩa sau
Có 7 dạng vô định là ; ;0. ; ;1 ; 0 *) Nếu f x( )
lim f x( ) lim g x( ) 0 , thì giới hạn lim gọi là dạng vô định 0/0 x a x a g x( )
x a *) Nếu lim | f x( ) | lim | g x( ) f x( ) | , thì giới hạn lim
gọi là dạng vô định x a x a g x( ) x a
*) Nếu lim f x( ) 0;lim | g x( ) |
, thì giới hạn lim( ( ) ( ))f x g x gọi là dạng vô x a x a x a định 0. *) Xét hàm x
u x( )v x( ) , với u, v là hai hàm sơ cấp cho trước ( chú ý:
những hàm dạng này chỉ xác định khi u(x)> 0 và x thuộc txđ của v).
Trong trường hợp limu x( ) A ;lim g x( ) B , ta có ngay x a x a
limu x( )v x( ) AB x a lOMoAR cPSD| 58970315 18
Tuy nhiên, nếu xảy ra các trường hợp sau, thì ta có các trường hợp vô định “ dạng mũ”:
1) u x( ) 1;v x( ) : dạng vô định 1 x a x a 2) u x( )
; ( )v x 0: dạng vô định 0 x a x a
3) u x( ) 0;v x( ) 0: dạng vô định 00 x a x a
V. Phương pháp khử các dạng vô định 1.
Qui tắc thay hàm tương đương
a) Định nghĩa tính trội
Cho các hàm f, g xác định trong lân cận U a( ) của a sao cho
xU a( ) \{ },a g x( ) 0, g x( ) 0. Nếu tồn tại hàm sao cho
x U a( )\{ },af x( )
( ) ( )x g x và ( )x 0, thì nói f không đáng kể so với g x a
hoặc g trội hơn f trong lân cận a và viết f o g( ) hoặc viết a
f x( ) o g x( ( )) khi x a VD Trong lân cận 0: x2 o x( ) ;
trong lân cận : x o x( 2) Chú ý f x( ) ,
thì f o g( ) 1)Nếu có lim 0 x a g x( ) a
2) Ký hiệu f o(1) nghĩa là lim f x( ) 0 a x a
3) Người ta chứng minh được: khi x
, loga x o x( k) ; xk o a( x) (a 1;k
0). Do đó, các giới hạn sau không thuộc dạng vô định: lOMoAR cPSD| 58970315 19 log x lim x a x k k 0; limx log a x 0 (a 1;k 0) x
b) Định nghĩa hàm tương đương
Nói rằng f tương đương với g ( ký hiệu : f ~ g hoặc f x( ) ~ g x( )) trong a x a f x( ) thì g
~ f lân cận của a, nếu lim 1. Dễ thấy, nếu f ~ g x a g x( ) a a
( do đó có thể nói f và g là 2 hàm tương đương với nhau trong lân cận
của a). Cũng dễ thấy là nếu f ~ g và g ~ h, thì f ~ h a a a
c) Qui tắc ngắt bỏ hàm không đáng kể
Nếu f o g( ), thì f g ~ g a a Thật vậy, lim
f x( ) g x( ) lim( f x( ) 1) 0 1 1 x a g x( ) x a g x( ) VD
Arctanx x
x2 ~ x2 ; x2 ex ~ ex x x
d) Qui tắc thay hàm tương đương Nếu f x( ) f
f ~ f g1; ~ g1, thì lim lim
x1( ) (1). a x a g x( ) x a g x1( )
Tương tự , nếu f ~ f g1; ~ g1, thì lim( f x g x( )( )) lim( f x g x1( ) 1( )) (2). a x a x a
Đẳng thức (1) và (2) hiểu theo nghĩa sau:nếu giới hạn ở một trong 2 vế
tồn tại ( giới hạn hữu hạn hoặc vô hạn) , thì giới hạn ở vế còn lại cũng
tồn tại và hai giới hạn bằng nhau. lOMoAR cPSD| 58970315 20
Nói một cách đơn giản, ta có qui tắc sau: khi tìm giới hạn của một tích hoặc
một thương, có thể thay một thừa số bởi một hàm tương đương với nó. VD xlim
logsin2x x- x 23xx22 xlim 23xx22 32; limx
x22e x 5 e1x xlim
52eexx 52 x
e) Các hàm thông dụng tương đương trong lân cận điểm 0 Trong lân
cận điểm 0, ta có: x ~ sinx ~ tanx ~ Arcsin x ~ Arctan x ~ ln(1 x) ~ (ex 1);(1
x) ~ x ( 0) Bảng trên còn gọi là bảng vô cùng bé tương đương (
hàm có giới hạn bằng 0 khi x a gọi là vô cùng bé khi x a) VD limx 0 sin3sin2xx
2xx23 limx 0 sin2sin3xx 23; limx 0 ln(1e2x 51x)
limx 0 52xx 52;limx 0 tan4sin3xx
sinx32 x limx 0 43xx 43 2) Qui tắc L’Hospital
Định lý sau gọi là qui tắc L’Hospital
lim f x( ) lim g x( ) 0 x a x a 1) Giả sử f '( )x lim g x'( ) b x a f x( ) và giới
hạn này cũng bằng b. Khi đó lim g x( ) x a
lim f x( ) lim ( )g x x a x a 2) Giả sử f '( )x lim g x'( ) b x a