

















Preview text:
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12
Chuyên đề HỆ TRỤC TOẠ ĐỘ OXYZ BIỂU THỨC TOẠ ĐỘ
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Chủ đề 3: BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ I. LÝ THUYẾT
1. Biểu thức tọa độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
Trong không gian Oxyz, cho hai vectơ a x; y; z và b x ; y ; z. Ta có:
a b x x ; y y ; z z;
a b x x ; y y ; z z;
k.a kx; ky; kz; k .
Nhận xét. Vectơ a x; y; z cùng phương với vectơ b x ; y ; z 0 khi và chỉ khi tồn tại số x kx
thực k sao cho y ky. z kz
2. Tọa độ trung điểm, tọa độ trọng tâm
Trong không gian Oxyz, cho ba điểm không thẳng hàng Ax ; y ; z ,Bx ; y ; z và A A A B B B
C x ; y ; z . Khi đó: C C C
x x y y z z
- Tọa độ trung điểm của đoạn thẳng AB là A B ; A B ; A B ; 2 2 2
x x x y y y z z z
- Tọa độ trọng tâm của tam giác ABC là A B C ; A B C ; A B C . 3 3 3
3. Biểu thức tọa độ của tích vô hướng
Trong không gian Oxyz, tích vô hướng của hai vectơ a x; y; z và b x ; y ; z được xác
định bởi công thức: a.b xx yy zz . Nhận xét.
- Hai vectơ a và b vuông góc với nhau nếu và chỉ nếu a.b 0 xx yy zz 0.
- Nếu a x; y; z thì 2 2 2
a x y z .
- Nếu a x; y; z và b x ; y ; z là hai vectơ khác 0 thì a b a.b xx yy zz cos , 2 2 2 2 2 2 a . b
x y z . x y z
II. BÀI TẬP TỰ LUẬN Câu 1:
Trong không gian Oxyz , cho 2 vectơ a 2;3; 5 ,b 0; 3 ;4,c 1; 2
;3 . Tìm tọa độ của
vectơ n 3a 2b c . Câu 2:
Trong không gian Oxyz, cho hai vec tơ u 1;1;0 và v 2;0;
1 . Tính u 2v . Câu 3:
Trong không gian Oxyz, tìm x; y để ba điểm A 1
;2; 3 , B1;0;2 , Cx; y;13 thẳng hàng. Câu 4:
Trong không gian Oxyz, tính góc giữa hai vectơ a 1; 2; 2 và b 1; 1;0. Câu 5:
Trong không gian Oxyz, cho vectơ u (2;0; 1
) . Tìm vectơ v biết v cùng phương với u và u.v 20 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025 Câu 6:
Trong không gian Oxyz, cho tam giác ABC có A0; 2;
1 và B 2;0;3 . Tìm tọa độ điểm C sao
cho G 1; 2; 2 là trọng tâm tam giác ABC. Câu 7:
Trong không gian Oxyz, cho hai điểm A1; 2;
1 , B 2;1; 2. Tìm điểm M trên trục Ox và cách đều hai điểm , A . B Câu 8:
Trong không gian Oxyz , cho ba điểm M 2;3; 1 , N 1 ;1
;1 , P 1; m 1;3 . Tìm m để tam
giác MNP vuông tại N. Câu 9:
Trong không gian Oxyz, cho hai điểm A1; 2 ;1 , B 3; 4
;1 . Đường thẳng AB cắt mặt MB
phẳng Oxz tại M . Tính tỉ số . MA
Câu 10: Trong không gian Oxyz, cho ba điểm A1; 1 ;
1 , B 3;2;2 ,C 3;1; 5 . Tìm tọa độ điểm
M x; y; z thỏa mãn MA 2 AB 4CM .
Câu 11: Trong không gian Oxyz , cho hai điểm B(0;3;1) , C( 3;6; 4) . Gọi M là điểm nằm trên đoạn BC sao cho MC
2MB . Tìm tọa độ điểm M .
Câu 12: Trong không gian Oxyz, cho ba điểm A 2 ;3
;1 , B 2;1;0 , C 3 ; 1
;1 . Tìm tọa độ điểm D
là điểm sao cho ABCD là hình thang có cạnh đáy AD và diện tích hình thang ABCD bằng 4
lần diện tích tam giác ABC .
Câu 13: Trong không gian Oxyz, cho tam giác OAB có A2;2; 1 và B 0; 4
;3. Tính độ dài đường phân giác trong góc . AOB 8 4 8
Câu 14: Trong không gian Oxyz , cho hai điểm M (2; 2;1) , N ; ;
. Tìm tọa độ tâm đường tròn 3 3 3
nội tiếp tam giác OMN .
Câu 15: Trong không gian Oxyz, một hình chữ nhật có hai đỉnh không liên tiếp có tọa độ là
3;2;2 3, 3;2;2 3; hai đỉnh còn lại nằm trên mặt phẳng Oxy có hoành độ và tung
độ độ đều là số nguyên. Có bao nhiêu hình chữ nhật như thế?
Câu 16: Trong không gian Oxyz , cho hai điểm A1; 2; 2 , B2; 1
;2 . Tìm tọa độ điểm M trên mặt
phẳng Oxyz cho MA MB đạt giá trị nhỏ nhất.
Câu 17: Trong không gian Oxyz , cho A1; 2
;3; B2;2;4;C 3; 3
;2. Tìm tọa độ điểm M trên mặt
phẳng (Oxy) sao cho: MA MB MC ngắn nhất.
Câu 18: Trong không gian Oxyz , cho hai điểm A 3 ;3;
1 , B 2; 2; 4 . Tìm tọa độ điểm M thuộc
mặt phẳng Oyz sao cho biểu thức 2 2
T 3MA 2MB đạt giá trị nhỏ nhất.
Câu 19: Trong không gian Oxyz, cho hai điểm A 1
;2;2 , B3;2;6 . Xét hai điểm M , N thay đổi
thuộc mặt phẳng Oxy sao cho MN
16 . Tính giá trị nhỏ nhất của AM BN.
Câu 20: Trong không gian Oxyz, cho hai điểm A1; 3 ; 4
và điểm B 2
;1;2. Xét hai điểm M và
N thay đổi thuộc mặt phẳng Oxy sao cho MN 2 . Tính giá trị lớn nhất của AM BN .
III. BÀI TẬP TRẮC NGHIỆM
Câu 21: Trong không gian Oxyz, cho hai điểm A2;1; 1
, B1;2;3. Độ dài đoạn thẳng AB bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025 A. 18 . B. 3 2 . C. 3 . D. 22 .
Câu 22: Trong không gian Oxyz, cho vectơ a 2i j 2k . Tính độ dài của vectơ a . A. 1. B. 4. C. 5. D. 3.
Câu 23: Trong không gian Oxyz, cho a 2; 1
;3 . Tọa độ của vectơ 2a là
A. 4; 2;3 .
B. 4; 1;3 .
C. 4; 2;6 . D. 4; 2;5 .
Câu 24: Trong không gian Oxyz, cho 2 véc tơ a 2 ;2; 4 và b 3 ;3; 6
. Khẳng định nào sau đây đúng?
A. 2b 3a .
B. 2a 3b . C. 2 a 3b . D. 2 b 3a .
Câu 25: Trong không gian Oxyz, cho hai vectơ a 4 ;5; 3 , b 2; 2
;1 . Tìm tọa độ của vectơ
x a 2b . A. x 0; 1 ;1 .
B. x 0;1; 1 . C. x 8 ;9; 5 .
D. x 2;3; 2 .
Câu 26: Trong không gian Oxyz, cho hai vectơ u 1;1; 3 và v 2
;1; 3 . Tính 2u 3v . A. 242 . B. 216 . C. 152 . D. 322 .
Câu 27: Trong không gian Oxyz, cho a 2 j 3k , b 4i j k . Tính độ dài của v 2a b A. 74 . B. 3 6 . C. 5 2 . D. 42 .
Câu 28: Trong không gian Oxyz, cho hai điểm A1; 2; 3 và B 3
;4;5 . Tìm tọa độ trung điểm I
của đoạn thẳng AB . A. I 1 ;3 ;1 .
B. I 1 ; 3 ;1 .
C. I 2 ;1;4 .
D. I 2; 1 ; 4 .
Câu 29: Trong không gian Oxyz, cho đoạn thẳng AB có trung điểm I . Biết A2;1;
1 , I 1; 2;0 . Khi
đó, điểm B có tọa độ là A. 1; 1 ; 1 . B. 3;0; 2 .
C. 0; 3;1 .
D. 1;1;1 .
Câu 30: Trong không gian Oxyz, cho tam giác ABC với A1;3; 4, B 2; 1
;0,C 3;1;2 . Tọa độ trọng
tâm G của tam giác ABC là 2 A. G 3; ;3 .
B. G 2; 1 ;2.
C. G 2;1; 2 .
D. G 6;3;6 . 3
Câu 31: Trong không gian Oxyz, cho hai điểm M 1 ;2;3 và N 2
;1; 3 . Tọa độ trọng tâm của tam giác OMN là 3 3
A. 1;1;0 . B. ; ;0 . C. 1 ;1; 6 . D. 1;1;3 . 2 2
Câu 32: Trong không gian Oxyz, cho tam giác ABC có trọng tâm G 2;1;0 và A1;1;0, B 2;3;5.
Tọa độ điểm C là A. 4; 2; 1 . B. 6 ; 2 ;0. C. 3; 1 ; 5 . D. 12 ;0;8 .
Câu 33: Trong không gian Oxyz, cho các điểm A1; 2 ;3, B0;1; 2
, E 3;2;2 . Gọi C ; m ; n p là
điểm thỏa mãn E là trọng tâm của tam giác ABC . Tổng m n p bằng 10 A. 13 . B. 15 . C. . D. 20 . 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 34: Trong không gian Oxyz, cho tam giác ABC có A1; 1 ; 2
và trọng tâm G2;1; 3 . Tọa độ
của vectơ u AB AC là A. 3;6;3 .
B. 3;6; 3 .
C. 3; 3;6 . D. 3; 2; 1 .
Câu 35: Trong không gian Oxyz , cho tam giác ABC biết A1;3; 3 ,B 2;4;
5 ,C a;2;b và G2;c; 3 là
trọng tâm. Tổng a b c bằng A. 5 . B. 3 . C. 1. D. 1.
Câu 36: Trong không gian Oxyz, cho ABC có A2;1; 2 , B 1 ;1;2, C 7; 1
;2 . Độ dài trung tuyến AM bằng A. 5 3 . B. 2 3 . C. 3 2 . D. 4 2 .
Câu 37: Trong không gian Oxyz, cho tứ diện ABCD có (
A 1;0;0), B(0;2;0),C(0;0;3), D(1;2;3). Tìm tọa
độ trọng tâm G của tứ diện ABC . D 1 1 3 1 3 2 4 A. G ; ; . B. G ;1; . C. G ; ; 2 .
D. G 2; 4;6 . 4 2 4 2 2 3 3
Câu 38: Trong không gian Oxyz, cho tứ diện ABCD với A1;0; 2 , B 2
;1;3 , C 3;2;4 , D6;9;5 .
Tìm tọa độ trọng tâm của tứ diện ABC . D A. 2;3; 1 . B. 2; 3; 1 . C. 2;3; 1 . D. 2;3; 1 .
Câu 39: Trong không gian Oxyz, cho tam giác ABC với A1;1; 1 , B 1
;1; 0, C 4;1; 2. Chu vi của tam giác ABC bằng A. 29 2 5 .
B. 29 5 10 .
C. 13 5 10 . D. 2 2 5 .
Câu 40: Trong không gian Oxyz, cho tam giác ABC với A1;1; 1 , B 1
;1; 0, C 4;1; 2. Chu vi của
tam giác GBC với G là trọng tâm tam giác, bằng 29 58 73 58 A. 73 . B. 29 . 3 3 73 29 29 55 C. 58 . D. 58 . 3 3
Câu 41: Trong không gian Oxyz, cho tam giác ABC với A7;1; 1 , B 1
; 3; 0, C 2; 3; 2 . Biết điểm
D là điểm sao cho tứ giác ABCD là hình bình hành. Chu vi tam giác DBC bằng
A. 69 134 13 .
B. 69 13 13 .
C. 69 134 134 .
D. 139 134 13 .
Câu 42: Trong không gian Oxyz, cho ba vectơ a 1
;1;0,b 1;1;0,c 1;1
;1 . Vectơ u a b c có tọa độ là A. u 1 ;1 ;1 . B. u 1 ; 1 ;1 .
C. u 1; 1 ; 1 . D. u 1 ;1; 1 .
Câu 43: Trong không gian Oxyz, cho ba vectơ a 5;7; 2,b 3;0 ;1 , c 6 ;1; 1 . Tìm tọa độ của
vectơ m 3a 2b c . A. m 3; 22 ;3.
B. m 3; 22; 3 . C. m 3 ;22; 3
. D. m 3;22;3 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 44: Trong không gian Oxyz, cho a 2; 3
;3 , b 0;2; 1 , c 3; 1
;5 . Tìm tọa độ của vectơ
u 2a 3b 2c . A. 10; 2 ;13 . B. 2 ;2; 7 . C. 2 ; 2 ;7 . D. 2; 2;7 .
Câu 45: Trong không gian Oxyz, cho hai vectơ a 1;
3; 3 và b 2;1; 2. Tọa độ của vectơ b a là A. 3; 2; 1 .
B. 1;4; 5 .
C. 1; 2;3 . D. 3; 2 ;1 .
Câu 46: Trong không gian Oxyz, cho hai vectơ u 1;3; 2 và v 2;1;
1 . Tọa độ của vetơ u v là
A. 3; 4; 3 . B. 1; 2; 3 . C. 1; 2; 1 . D. 1; 2; 1 .
Câu 47: Trong không gian Oxyz, cho ba vectơ a 1; 1
;2 , b 3;0; 1 và c 2 ;5 ;1 . Vectơ
d a b c có tọa độ là
A. 6;0; 6 . B. 0;6; 6 .
C. 6; 6;0 . D. 6;6;0 .
Câu 48: Trong không gian Oxyz, cho các véc tơ u 2i 2 j k , v ; m 2; m
1 với m là tham số thực.
Có bao nhiêu giá trị của m để u v ? A. 0 . B. 1. C. 2 . D. 3 .
Câu 49: Trong không gian Oxyz, cho a 1
;2;3, b 2; 3
;4, c 3;4; 5 , d 4 ;5; 1 . Hãy
phân tích vectơ d theo 3 vectơ a, b, c . 97 59 17 97 59 17 A. d a b c .
B. d a b c . 96 48 96 96 48 96 59 97 17 97 17 59
C. d a b c .
D. d a b c . 48 96 96 96 96 48
Câu 50: Trong không gian Oxyz, cho tọa độ điểm A3; 2
;1 . Gọi H là hình chiếu của điểm A trên
trục Ox . Độ dài đoạn thẳng AH bằng A. 3 . B. 10 . C. 1. D. 5 .
Câu 51: Trong không gian Oxyz, cho hai vectơ a 3 j k và b 1; ;
m 6. Giá trị của tham số m để a
vuông góc với b là
A. m 3.
B. m 2.
C. m 3. D. m 2.
Câu 52: Trong không gian Oxyz, cho ba điểm A1; 2 ;1; B 3
;1;0 và C 2; ; m 5
. Tìm m biết tam giác
ABC vuông tại A . 8 4 4 8 A. m . B. m .
C. m .
D. m . 3 3 3 3
Câu 53: Trong không gian Oxyz, cho ba điểm M 2;3; 1 , N 1 ;1
;1 và P 1; m 1; 2 . Biết tam giác
MNP vuông tại N . Khẳng định nào sau đây đúng?
A. m 2 .
B. m 2 .
C. m 4 . D. m 4 .
Câu 54: Trong không gian Oxyz, cho tam giác ABC có tọa độ các đỉnh A2; 1 ;4 , B0; 1 ;0 , C 3; 2
;m 2. Tìm m để tam giác ABC vuông tại . A 5 3 A. . B. . C. 6. D. 2 . 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 55: Trong không gian Oxyz , cho hai điểm A1; 2;0 , B 2; 1
;1 . Tìm điểm C có hoành độ dương
trên trục Ox sao cho tam giác ABC vuông tại C .
A. C 3;0;0 .
B. C 2;0;0 .
C. C 1;0;0 .
D. C 5;0;0 .
Câu 56: Trong không gian Oxyz, cho hai điểm A1; 2; 1 , B 2; 1
;3 . Tìm tọa độ điểm I thỏa mãn
IA 2IB 0 . 5 5 5 5 5 5 5 5 A. I ;0; . B. I ; ; 0 . C. I ; 0; .
D. I 0; ; . 3 3 3 3 3 3 3 3
Câu 57: Trong không gian Oxyz , cho 2 điểm B1; 2; 3 và C7;4; 2
. Nếu điểm E thỏa mãn đẳng
thức CE 2EB thì tọa độ điểm E là 8 8 8 8 8 1 A. 3; ; . B. ; 3; . C. 3; 3; D. 1;2; 3 3 3 3 3 3
Câu 58: Trong không gian Oxyz, cho hai vectơ PQ 0;1; 2 , PR 2
;1;0 và điểm M 1; 2;2
trung điểm của đoạn QR. Tọa độ điểm Q là A. 1 ;1; 2 . B. 2 ;2; 3 .
C. 0;1;3 . D. 2; 1; 1 .
Câu 59: Trong không gian Oxyz, cho bốn điểm A2;0;0, B 0; 2;0 , C 0;0; 2 và D 2; 2; 2 . Gọi M
và N lần lượt là trung điểm của AB và CD . Tọa độ trung điểm I của đoạn thẳng MN là 1 1
A. I 1;1;0 . B. I ; ;1 . C. I 1;1; 1 . D. I 1; 1 ;2 2 2
Câu 60: Trong không gian Oxyz, cho hai vectơ a 2; 1 ;4; b 3
;0;2 . Khi đó, cosa;b bằng 2 1 1 2 A. . B. . C. . D. . 273 273 273 273
Câu 61: Trong không gian Oxyz, cho u 1;
3;2 , v 3 ;1;2. Khi đó, . u v bằng A. 3. B. 2. C. 4. D. 10.
Câu 62: Trong không gian Oxyz, cho hai véctơ u 1; 2
;3 và v 2; 2 ;1 . Tích vô hướng . u v bằng A. 9 . B. 1. C. 3 . D. 1 .
Câu 63: Trong không gian Oxyz, cho các vectơ a 1;0;3 và b 2
;2;5. Tích vô hướng .
a a b bằng A. 25 B. 23 . C. 27 . D. 29 .
Câu 64: Trong không gian Oxyz, cho ba véctơ a 1
;1;0,b 1;1;0,c 1;1 ;1 . Trong các mệnh đề
sau, mệnh đề nào sai? A. b . c
B. a 2
C. a b
D. c 3
Câu 65: Trong không gian Oxyz, cho ba điểm A3; 2
;1 , B 1;3; 2 ,C 2; 4; 3 . Tính tích vô hướng A . B AC. A. 6 . B. 10 . C. 2 . D. 2 .
Câu 66: Trong không gian Oxyz, cho hai vectơ a (2;1; ) 1 ; b ; (1 3; ) m . Tìm m để ; a b 90 . A. m 5 .
B. m 5 .
C. m 1.
D. m 2 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 67: Trong không gian Oxyz, cho hai vectơ a 1; 2;0 và b 1
;3;0 . Tính góc giữa hai vectơ đó. A. 45 . B. 135 . C. 30 . D. 60 .
Câu 68: Trong không gian Oxyz, góc giữa hai vectơ a 1; 2; 2 và b 1; 1;0 bằng A. 60 . B. 135 . C. 30 . D. 45 .
Câu 69: Trong không gian Oxyz, cho hai vectơ u (0; 1
;0) và v ( 3;1;0). Góc giữa u và v bằng A. 30 . B. 120 . C. 60 . D. 90 .
Câu 70: Trong không gian Oxyz, cho hai vectơ u 1
;3;2 và v 2 ;0;
1 . Khẳng định nào dưới đây đúng?
A. u v . B. u v 4 cos ;
. C. u, v cùng phương. D. u,v 30 . 70
Câu 71: Trong không gian Oxyz, cho hai vectơ a 2;1; 2
, b 0; 2; 2. Tất cả giá trị của m để hai
véc tơ u 2a 3mb và v ma b vuông góc với nhau là 11 2 26 26 2 2 6 2 26 2 A. . B. . C. . D. . 18 6 6 6
Câu 72: Trong không gian Oxyz, góc giữa hai vectơ j và u 0; 3; 1 là A. 30 . B. 120 . C. 150 . D. 60 .
Câu 73: Trong không gian Oxyz, cho u ; x 0
;1 , v 2; 2;0 . Tìm x để góc giữa u và v bằng o 60 .
A. x 1 .
B. x 0 .
C. x 1 .
D. x 1 .
Câu 74: Trong không gian Oxyz, cho ba điểm A1;1;0 , B 1; 2; 1 ,C 0;1
;1 . Tính góc giữa hai vectơ AB và AC . A. 60 . B. 120 . C. 30 . D. 150 .
Câu 75: Trong không gian Oxyz, cho hai điểm A1;0;0 và B 3;1;0 . Số đo góc AOB của tam giác OAB bằng A. 30 . B. 120 . C. 150 . D. 60 .
Câu 76: Trong không gian Oxyz, cho vectơ a ;
m 2; m và b ;1
m ; 0 với m . Gọi S là tập hợp
tất cả các giá trị thực của m để góc giữa hai vectơ a,b có số đo bằng 90 . Tích các phần tử của S bằng A. 2 . B. 2 . C. 2 . D. 2 .
Câu 77: Trong không gian Oxyz, cho vec tơ u 1;1; 2
, v 1;0;m. Tìm tất cả giá trị của m để góc
giữa u, v bằng 45 .
A. m 2 6 .
B. m 2 6 .
C. m 2 6 . D. m 2 .
Câu 78: Trong không gian Oxyz, cho điểm (
A 0; 2; 1) và B(1; 1
;2) . Tìm tọa độ điểm M sao cho MA 2M . B 2 4 1 3 1 A. M ; ;1 . B. M ; ; .
C. M (2;0;5) .
D. M (1; 3; 4) . 3 3 2 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 79: Trong không gian Oxyz, cho hai điểm A4; 2;
1 , B 2; 1; 4 . Điểm M a; ; b c thỏa mãn
AM 3BM 0 . Khi đó, 2a b c bằng 5 A. 2 . B. 3 . C. . D. 6 . 2
Câu 80: Trong không gian Oxyz, cho hai điểm A1; 0; 1 , B 1;
1;2 . Điểm M nằm trên trục
Ox và cách đều hai điểm ,
A B có tọa độ là
A. 0; 2; 0 .
B. 1;0;0 . C. 0;1; 1 . D. 1 ;0;0 .
Câu 81: Trong không gian Oxyz, cho hai điểm A1;3; 4 và B 1;0;
1 . Điểm M nằm trên trục Oz và cách đều hai điểm ,
A B có tọa độ là
A. 0;0; 4 .
B. 2;0;0 .
C. 0;0; 2 . D. 0; 4;0 .
Câu 82: Trong không gian Oxyz, cho hai điểm B(0;3;1) , C( 3;6; 4) . Gọi M là điểm nằm trên đoạn BC sao cho MC
2MB . Tính tọa độ điểm M . A. ( 1; 4; 2) . B. ( 1; 4; 2) . C. (1; 4; 2) . D. ( 1; 4; 2) .
Câu 83: Trong không gian Oxyz, cho hai điểm A1; 2;3, B 2;4;9 . Điểm M thuộc đoạn AB sao
cho MA 2MB . Độ dài đoạn thẳng OM là A. 5 . B. 3 . C. 54 . D. 17 .
Câu 84: Trong không gian Oxyz, cho ba điểm A1;1;1 , B2;3; 2 , C 3; 1
;3 . Tìm toạ độ điểm D sao
cho bốn điểm A , B , C , D lập thành một hình chữ nhật.
A. D 4;3; 4 . B. D 4; 1 ;4 . C. D 2; 3 ;2 .
D. D 4;1; 4 . Câu 85: Trong không gian Oxyz, cho hình chữ nhật ABCD trong đó A 1
;1;2, B2;0;3, C O , x D ; a ;
b c . Tính giá trị biểu thức P a b c . A. 1 . B. 1. C. 2 . D. 0 .
Câu 86: Trong không gian Oxyz, cho ba điểm A2; 1;5 , B 5; 5;7 ; M x; y ;1 . Khi , A B, M thẳng hàng thì giá trị của ; x y là
A. x 4; y 7 .
B. x 4; y 7 .
C. x 4; y 7 .
D. x 4; y 7 .
Câu 87: Trong không gian Oxyz, cho ba điểm A0;1;
1 , B 1; 2;0 ; C ; m ;
n 0 . Tìm m, n sao cho ba điểm ,
A B, C thẳng hàng.
A. m 1; n 1 .
B. m 1; n 2 .
C. m 2; n 1 .
D. m 2; n 2 .
Câu 88: Trong không gian Oxyz, cho ba điểm A 1 ;2; 3
,B1;0;2 ,C ;x ;y 2
thẳng hàng. Tính tổng
x y. 11 11
A. x y 17 .
B. x y .
C. x y 1.
D. x y . 5 5
Câu 89: Trong không gian Oxyz, cho hai điểm A 2 ;2;
1 , B 0; 1; 2 . Tọa độ điểm M thuộc mặt
phẳng Oxy sao cho ba điểm A, B , M thẳng hàng là
A. M 4; 5;0 .
B. M 4 ;5;0 .
C. M 4;5;0 .
D. M 4 ; 5;0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 90: Trong không gian Oxyz, cho hai điểm A 2 ;2;
1 , B 0; 1; 2 . Đường thẳng AB cắt mặt
phẳng Oxy tại điểm M . Tìm tọa độ điểm M .
A. M 4; 5;0 .
B. M 4 ;5;0 .
C. M 4;5;0 .
D. M 4 ; 5;0
Câu 91: Trong không gian Oxyz, cho hai điểm A 2 ;3
;1 và B 5; 6; 2 . Đường thẳng AB cắt mặt AM
phẳng Oxz tại điểm M . Tính tỉ số . BM AM 1 AM AM 1 AM A. . B. 2 . C. . D. 3. BM 2 BM BM 3 BM
Câu 92: Trong không gian Oxyz, cho hai điểm A 4
;1;5;B1;5;3. Gọi C là giao điểm của đường
thẳng AB và mặt phẳng Oyz . Trong các khẳng định sau, khẳng định nào đúng? 1 A. AC AB .
B. AB 5BC .
C. AC 4BC .
D. AC 4 BC 4
Câu 93: Trong không gian Oxyz, cho ba điểm A1; 2; 1 , B 2; 1 ;3 , C 4
;7;5 . Tọa độ chân đường
phân giác trong góc B của tam giác ABC là 2 11 2 11 1 11 A. 2 ;11 ;1 . B. ; ;1 . C. ; ; . D. ; 2 ;1 . 3 3 3 3 3 3
Câu 94: Trong không gian Oxyz, cho tam giác ABC , có A1;3; 1 ; B 1 ;1; 1 , C 3; 3 ; 1 . Tọa độ
chân đường phân giác trong của góc B là 5 5 A. ;1; 1 . B. 1; ; 1 . C. 2; 1 ; 1 . D. 3; 1 ; 1 . 3 3
Câu 95: Trong không gian Oxyz, cho tam giác ABC , có A0; 4 ;0 ; B 5
;6;0 , C 3;2;0 . Tọa độ
chân đường phân giác ngoài của góc A là A. 15; 4 ;0.
B. 12;1;0 . C. 3 ;12;0 . D. 3;1; 1 .
Câu 96: Trong không gian Oxyz, cho tam giác OAB , có O là gốc tọa độ, A0; 2 ;1 ; B 0; 4; 2 . Tọa độ
chân đường phân giác ngoài của góc O là A. 0;0; 4 .
B. 2;1;0 .
C. 0;1; 2 . D. 3;0; 1 .
Câu 97: Trong không gian Oxyz, cho ba điểm A1;2;3, B 0;1;1, C 1;0; 2
. Tìm tọa độ điểm M nằm
trên mặt phẳng Oxz sao cho 2 2 2 MA 2MB
3MC đạt giá trị nhỏ nhất. 2 1 1 2 2 1 2 1 A. M ; 0; . B. M ;0; . C. M ;0; . D. M 0; ; . 3 6 3 3 3 6 3 6
Câu 98: Trong không gian Oxyz, cho hai điểm A6; 3
;4, Ba; ;
b c . Gọi M , N, P lần lượt là giao
điểm của đường thẳng AB với các mặt phẳng tọa độ Oxy, Oxz và Oyz . Biết rằng
M , N , P nằm trên đoạn AB sao cho AM MN NP PB . Giá trị của tổng a b c là A. 17 . B. 17 . C. 11. D. 11.
Câu 99: Trong không gian Oxyz, cho ba điểm A1; 2;
1 , B 2;3; 4 và C 3;5; 2
. Gọi I a; ; b c là tâm
đường tròn ngoại tiếp tam giác ABC . Giá trị của 2 2 2
T a b c bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025 93 15 93 A. T . B. T .
C. T 15 . D. T . 4 2 2
Câu 100: Trong không gian Oxyz, cho tam giác ABC với tọa độ các đỉnh A1;1 ;1 , B 4;1 ;1 ,C 1;1;5 .
Tìm tọa độ điểm I là tâm đường tròn nội tiếp tam giác ABC . A. I 2 ;1;3.
B. I 2; 1 ;3.
C. I 2;1; 2. D. I 2; 2 ;1 . 8 4 8
Câu 101: Trong không gian Oxyz, cho hai điểm A2; 2 ;1 , B ; ;
. Biết I a; ;
b c là tâm đường 3 3 3
tròn nội tiếp của tam giác OAB . Tính S a b . c
A. S 0 .
B. S 1 .
C. S 2 .
D. S 1 .
Câu 102: Trong không gian Oxyz, cho ba điểm A1; 2 ;2 , B 5
;6;4 và C 0;1; 2
. Độ dài đường
phân giác trong của góc A của ABC bằng 3 2 2 74 3 74 A. . B. . C. . D. . 2 74 3 74 3 2
Câu 103: Trong không gian Oxyz, cho tam giác ABC có A1; 2;
1 , B 2; 1; 3 , C 4 ; 7; 5 . Tọa độ
chân đường phân giác trong góc B của tam giác ABC là 2 11 1 2 11 11 A. ; ; . B. ; ; 1 . C. ; 2; 1 . D. 2 ;11; 1 . 3 3 3 3 3 3
Câu 104: Trong không gian Oxyz, cho ba điểm A 2
;3;1 , B2;1;0 , C 3 ;1
;1 . Tìm tất cả các điểm
D sao cho ABCD là hình thang có đáy AD và S 3S ABCD ABC D 8; 7; 1 D 8;7; 1
A. D 8;7; 1 . B. . C. .
D. D 12 ;1;3 . D 12;1; 3 D 12;1;3
Câu 105: Trong không gian Oxyz, cho A 1
;4;2, B3;2 ;1 , C 2
;0;2. Tìm tất cả các điểm D sao cho
ABCD là hình thang có đáy AD và diện tích hình thang ABCD gấp ba lần diện tích tam giác ABC .
A. D 9;8;0 . B. D 11
;0;4 và D9;8;0 .
C. D 11 ;0;4 . D. D 11;0; 4 và D 9 ; 8 ;0 .
Câu 106: Trong không gian Oxyz, cho tam giác ABC với A0; 0; 3 , B 0; 0; 1 , C 1; 0; 1 . Tìm tọa
độ tâm I của đường tròn ngoại tiếp tam giác ABC . 1 1
A. I 1;0; 2 . B. I ; 0;1 .
C. I 0;0; 1 . D. I ; 0; 0 . 2 2
Câu 107: Trong không gian Oxyz, cho hai điểm E 1; 2 ;4 , F 1; 2 ; 3
. Gọi M là điểm thuộc mặt
phẳng Oxy sao cho tổng ME MF có giá trị nhỏ nhất. Tìm tọa độ của điểm M . A. M 1 ;2;0 . B. M 1 ; 2 ;0 . C. M 1; 2 ;0 .
D. M 1; 2;0 .
Câu 108: Trong không gian Oxyz, cho hai điểm A 3 ; 2; 1 , B 1 ; 0; 1 . Điểm M ; a ; b 0 thỏa mãn M .
A MB nhỏ nhất. Tính a 2 . b A. 0 . B. 1. C. 1 . D. 3 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 109: Trong không gian Oxyz, cho hai điểm A1; 2
;1 ; B 2;1;3 và điểm M ; a ; b 0 sao cho 2 2
MA MB nhỏ nhất. Giá trị của a b là: A. 2 . B. 2 . C. 1. D. 3 .
IV. LỜI GIẢI CHI TIẾT Câu 1:
Trong không gian Oxyz , cho 2 vectơ a 2;3; 5 ,b 0; 3 ;4,c 1; 2
;3 . Tìm tọa độ của
vectơ n 3a 2b c . Lời giải: Ta có a 2;3; 5 3a 6;9; 1 5 . b 0; 3 ;4 2b 0; 6 ;8 ; c 1; 2 ;3
n 3a 2b c 5;5;10 . Câu 2:
Trong không gian Oxyz, cho hai vec tơ u 1;1;0 và v 2;0;
1 . Tính u 2v . Lời giải:
Ta có u 2; v 5 ; uv 1.2 1.0 0. 1 2 . 2 2 2
Suy ra u 2v u 4uv 4 v 2 4.2 4.5 30 .
Vậy u 2v 30 . Câu 3:
Trong không gian Oxyz, tìm x; y để ba điểm A 1
;2; 3 , B1;0;2 , Cx; y;13 thẳng hàng. Lời giải:
Ta có AB2; 2; 5 , AC x 1; y 2; 10 . Ba điểm A 1
;2; 3 , B1;0;2 , Cx; y;13 thẳng hàng khi AB,AC cùng phương x 1 y 2 1 0 x 5 . 2 2 5 y 6 Câu 4:
Trong không gian Oxyz, tính góc giữa hai vectơ a 1; 2; 2 và b 1; 1;0. Lời giải: . a b 1. 1 2. 1 2 .0 1
Ta có cos a , b
a , b 135 . a . b 1 2 2 2 . 2 1 2 2 2 2 2 1 0 Câu 5:
Trong không gian Oxyz, cho vectơ u (2;0; 1) . Tìm vectơ v biết v cùng phương với u và u.v 20 . Lời giải:
Vì v cùng phương với u nên v k.u (2k;0; k) , với k 0. Ta có .
u v 4k k 5k 20 k 4 . Vậy v (8;0; 4 ) . Câu 6:
Trong không gian Oxyz, cho tam giác ABC có A0; 2;
1 và B 2;0;3 . Tìm tọa độ điểm C sao
cho G 1; 2; 2 là trọng tâm tam giác ABC. Lời giải:
Gọi điểm C ; a ; b c .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025 0 2 a 1 3 a 1 2 0 b
Vì G 1; 2; 2 là trọng tâm ABC 2 b
4 C 1;4;4 . 3 c 4
1 3 c 2 3 Câu 7:
Trong không gian Oxyz, cho hai điểm A1; 2;
1 , B 2;1; 2. Tìm điểm M trên trục Ox và cách đều hai điểm , A . B Lời giải:
Điểm M trên trục Ox M ; m 0; 0.
AM m AM m 2 2 1; 2; 1. 1 4 1 m 2m 6 BM m
BM m 2 2 2;1; 2. 2
1 4 m 4m 9. 3
M cách đều hai điểm 2 2 ,
A B AM BM m 2m 6 m 4m 9 m . 2 3 Vậy M ;0;0 . 2 Câu 8:
Trong không gian Oxyz , cho ba điểm M 2;3; 1 , N 1 ;1
;1 , P 1; m 1;3 . Tìm m để tam
giác MNP vuông tại N. Lời giải:
Ta có NM 3; 2; 2 , NP 2; m 2; 2
Tam giác MNP vuông tại N khi NM .NP 0 2.3 2(m 2) 4 0 m 1. Câu 9:
Trong không gian Oxyz, cho hai điểm A1; 2 ;1 , B 3; 4
;1 . Đường thẳng AB cắt mặt MB
phẳng Oxz tại M . Tính tỉ số . MA Lời giải: MB
d B,Oxz y 4
Đường thẳng AB cắt mặt phẳng Oxz tại M B . MA d , A Oxz 2 y 2 A
Câu 10: Trong không gian Oxyz, cho ba điểm A1; 1 ;
1 , B 3;2;2 ,C 3;1; 5 . Tìm tọa độ điểm
M x; y; z thỏa mãn MA 2 AB 4CM . Lời giải: x x x 3 1 2.2 4 3 3 3 27
Ta có: MA 2AB 4CM 1 y 2.3 4 y 1 y M 3; ; .
z z 5 5 5 1 2. 3 4 5 27 z 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
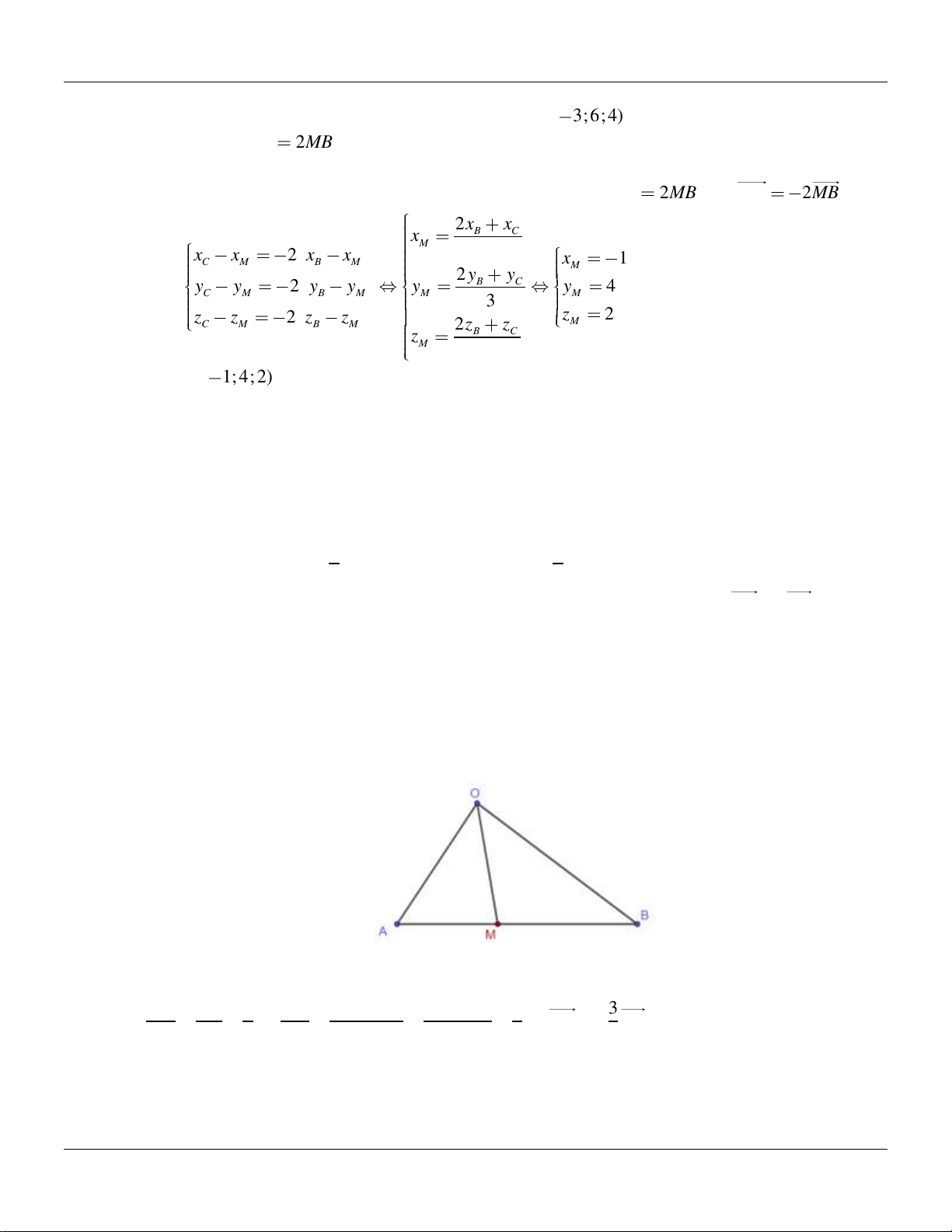
Câu 11: Trong không gian Oxyz , cho hai điểm B(0;3;1) , C( 3;6; 4) . Gọi M là điểm nằm trên đoạn BC sao cho MC
2MB . Tìm tọa độ điểm M . Lời giải:
Giả sử M x ; y ; z . Vì M là điểm nằm trên đoạn BC thỏa MC 2MB nên MC 2MB . 2x x B C xM 3 x x 2 x x C M B M x 1 M 2 y y Hay y y 2 B C y y y y 4 . C M B M M 3 M z z 2 z z z 2 2 M C M B M z z B C zM 3
Vậy M ( 1; 4; 2) .
Câu 12: Trong không gian Oxyz, cho ba điểm A 2 ;3
;1 , B 2;1;0 , C 3 ; 1
;1 . Tìm tọa độ điểm D
là điểm sao cho ABCD là hình thang có cạnh đáy AD và diện tích hình thang ABCD bằng 4
lần diện tích tam giác ABC . Lời giải: Gọi D ; a ; b c. 1 1 Ta có S 4S
d BC AD BC AD d BC AD BC ABCD ABC , 4. , 2 2
BC AD 4BC AD 3BC . Do ABCD là hình thang có đáy AD AD 3BC a 2 15 a 17 b 3 6 b 3
D17;3;4. c 1 3 c 4
Câu 13: Trong không gian Oxyz, cho tam giác OAB có A2;2; 1 và B 0; 4
;3. Tính độ dài đường phân giác trong góc . AOB Lời giải:
Gọi M là chân đường phân giác trong góc AOB .
Ta có: OA 3,OB 5 , theo tính chất đường phân giác trong: MA OA 3 MA MA OA 3 3
MA AB MB OB 5 AB MA MB OA OB 8 8
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025 3 x x M 5 2 0 2 8 M 4 3 1 5 1 1 30
Nên: 2 y
y M OM M 4 2 ; ; . 8 M 4 4 4 2 4 3 1 z z M 3 1 1 M 8 2 8 4 8
Câu 14: Trong không gian Oxyz , cho hai điểm M (2; 2;1) , N ; ;
. Tìm tọa độ tâm đường tròn 3 3 3
nội tiếp tam giác OMN . Lời giải:
Ta có bài toán bài toán sau
Trong tam giác ABC , I là tâm đường tròn nột tiếp ABC ta có: a .IA . b IB . c IC 0 . với BC ; a AC ; b AB c . Thật vậy: A I B C A'
Gọi A là chân đường phân giác trong kẻ từ A . c BA A C bBA cCA 0 1 b c c b c IA A I A I A I aIA b c IA 0 A ' B ac a b c aIA bIB cIC bBA cCA 0 aIA bIB cIC 0 do 1 .
Áp dụng công thức trong tam giác OMN , ta được: OM .IN ON.IM MN.IO 0 OM .x ON.x MN.x N M O x 0 I OM ON MN OM . y ON. y MN. y N M O y 1. I OM ON MN OM .z ON.z MN.z N M O z 1 I OM ON MN
Vậy điểm I (0;1;1) là điểm cần tìm.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 15: Trong không gian Oxyz, một hình chữ nhật có hai đỉnh không liên tiếp có tọa độ là
3;2;2 3, 3;2;2 3; hai đỉnh còn lại nằm trên mặt phẳng Oxy có hoành độ và tung
độ độ đều là số nguyên. Có bao nhiêu hình chữ nhật như thế? Lời giải:
Giả sử: B 3; 2;2 3 và D 3 ;2; 2 3 .
Ta có: gốc tọa độ O 0;0;0 là trung điểm của . BD
Tứ giác ABCD là hình chữ nhật O là trung điểm của AC ( thỏa điều kiện đồng phẳng). Gọi A ; a ;
b 0 C ; a ; b 0 . Ta có: 2 2
BD 10 AC 10 a b 25 và 2 2 .
AB AD 0 a b 25 . a 4 Vì a;b có 2 hình chữ nhật. b 3 a 3 a;b có 2 hình chữ nhật. b 4
Câu 16: Trong không gian Oxyz , cho hai điểm A1; 2; 2 , B2; 1
;2 . Tìm tọa độ điểm M trên mặt
phẳng Oxyz cho MA MB đạt giá trị nhỏ nhất. Lời giải:
Ta có: AB 1; 3
;4, AM x 1; y 2; z 2 .
Ta có: MA MB AB , dấu bằng xảy ra khi M nằm giữa A và B AM k AB . 3 x 2 x 1 k x k 1 1 1
y 2 3k y 3k 2 z 0 k y . 2 2 z 2 4k z 4k 2 z 0 3 1 Vậy M ; ; 0 . 2 2
Câu 17: Trong không gian với hệ tọa độ Oxyz, cho A1; 2
;3; B2;2;4;C 3; 3
;2 . Tìm tọa độ điểm
M trên mặt phẳng (Oxy) sao cho: MA MB MC ngắn nhất. Lời giải:
Gọi G là trọng tâm tam giác ABC suy ra G(2; 1 ;3) .
Gọi H là hình chiếu vuông góc của G lên mp(Oxy) suy ra H (2; 1 ;0),GH 3
MA MB MC 3MG 3MG 3HG 9
Vậy MA MB MC ngắn nhất bằng 9 khi M trùng H, khi đó M 2; 1 ;0.
Câu 18: Trong không gian Oxyz , cho hai điểm A 3 ;3;
1 , B 2; 2; 4 . Tìm tọa độ điểm M thuộc
mặt phẳng Oyz sao cho biểu thức 2 2
T 3MA 2MB đạt giá trị nhỏ nhất. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025 2 2 2 2
Xét T MA MB MI IA MI IB 2 2 2 3 2 3 2
5MI 5IA 2IB 2MI 3IA 2IB 2 IA 12
Gọi I là điểm thỏa mãn 3IA 2IB 0 I 1 ;1; 1 2 IB 27 Khi đó: 2 2 2 2
T 5MI 3IA 2IB 5MI 90 . Do đó T MI . min min
Gọi H là hình chiếu vuông góc của I lên mặt phẳng Oyz H 0;1; 1 Dễ thấy 2
IM IH T 5IH 90 95 min
Dấu “=” xảy ra M H 0;1 ;1 .
Câu 19: Trong không gian Oxyz, cho hai điểm A
1; 2; 2 , B 3; 2;6 . Xét hai điểm M , N thay đổi
thuộc mặt phẳng Oxy sao cho MN
16 . Tính giá trị nhỏ nhất của AM BN. Lời giải: Gọi A'
1; 2; 0 , B ' 3; 2;0 lần lượt là hình chiếu của A , B trên Oxy , khi đó: 2 2 2 2 2 2 AM BN AA' A' M BB ' B ' N AA' BB ' A' M B ' N .
Ta có MA' A' B ' B ' N MN A ' M NB ' MN A ' B ' A ' M NB ' 12 . 2 2 Nên 2 2 AM BN AA' BB ' A' M B ' N 8 12 4 13 . AA' A' M Đẳng thức xảy ra
M , A' , B ' , N theo thứ tự thẳng hàng và 3 . BB ' B ' N
Câu 20: Trong không gian Oxyz, cho hai điểm A1; 3 ; 4
và điểm B 2
;1;2. Xét hai điểm M và
N thay đổi thuộc mặt phẳng Oxy sao cho MN 2 . Tính giá trị lớn nhất của AM BN . Lời giải:
Gọi A' đối xứng với A qua mặt phẳng Oxy . Suy ra A'1; 3 ;4 .
Dựng BB ' NM . Khi đó B ' thuộc mặt phẳng Q qua B và song song Oxy .
Phương trình Q : z 2 . Và BB ' 2 .
Suy ra B ' thuộc đường tròn tâm B , bán kính R 2 trong Q .
Ta có: AM BN A' M MB ' A' B '. Trong đó A '; B ' cùng phía so với Oxy .
Gọi H là hình chiếu của A ' trên Q . Suy ra H 1; 3 ;2 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Suy ra A' H 2; HB ' HB BB ' 5 2 7 . Khi đó 2 2 A' B '
A' H HB ' 4 49 53 .
Dấu bằng xảy ra khi B nằm giữa B ' và H và M A' B ' Oxy và BB ' NM .
Câu 21: Trong không gian Oxyz, cho hai điểm A2;1;
1 , B 1; 2;3 . Độ dài đoạn thẳng AB bằng A. 18 . B. 3 2 . C. 3 . D. 22 . Lời giải: 2 2 2
Ta có AB 1 2 2 1 3 1 3 2 .
Câu 22: Trong không gian Oxyz, cho vectơ a 2i j 2k . Tính độ dài của vectơ a . A. 1. B. 4. C. 5. D. 3. Lời giải:
Ta có a i j k a a 2 2 2 2 2 2;1; 2 2 1 2 3.
Câu 23: Trong không gian Oxyz, cho a 2; 1
;3 . Tọa độ của vectơ 2a là
A. 4; 2;3 .
B. 4; 1;3 .
C. 4; 2;6 . D. 4; 2;5 . Lời giải:
Ta có a 2; 1
;3 suy ra 2a 4; 2 ;6 .
Câu 24: Trong không gian Oxyz, cho 2 véc tơ a 2 ;2; 4 và b 3 ;3; 6
. Khẳng định nào sau đây đúng?
A. 2b 3a .
B. 2a 3b . C. 2 a 3b . D. 2 b 3a . Lời giải:
Dễ thấy 2b 6 ;6; 1 2, 3a 6 ;6; 1
2 2b 3a .
Câu 25: Trong không gian Oxyz, cho hai vectơ a 4 ;5; 3 , b 2; 2
;1 . Tìm tọa độ của vectơ
x a 2b . A. x 0; 1 ;1 .
B. x 0;1; 1 . C. x 8 ;9; 5 .
D. x 2;3; 2 . Lời giải:
Ta có x a 2b 4 2.2;5 2. 2 ; 3 2 .1 0;1; 1 .
Câu 26: Trong không gian Oxyz, cho hai vectơ u 1;1; 3 và v 2
;1; 3 . Tính 2u 3v . A. 242 . B. 216 . C. 152 . D. 322 .
Lời giải: Ta có: u 2 v 3 = ; 4 15 ; 1
. Suy ra 2u 3v 242 .
Câu 27: Trong không gian Oxyz, cho a 2 j 3k , b 4i j k . Tính độ dài của v 2a . b A. 74 . B. 3 6 . C. 5 2 . D. 42 . Lời giải:
v 2a b 22 j 3k 4i j k 4 j 6k 4i j k 4
i 3 j 7k 2 2 v 4
;3; 7 v 2 4 3 7 74 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 28: Trong không gian Oxyz, cho hai điểm A1; 2; 3 và B 3
;4;5 . Tìm tọa độ trung điểm I
của đoạn thẳng AB . A. I 1 ;3 ;1 .
B. I 1 ; 3 ;1 .
C. I 2 ;1;4 .
D. I 2; 1 ; 4 . Lời giải: x x x A B 1 I 2 y y
Tọa độ trung điểm I của đoạn thẳng AB là y A B 3 I . I 1;3; 1 2 z z z A B 1 I 2
Câu 29: Trong không gian Oxyz, cho đoạn thẳng AB có trung điểm I . Biết A2;1;
1 , I 1; 2;0 . Khi
đó, điểm B có tọa độ là A. 1; 1 ; 1 . B. 3;0; 2 .
C. 0; 3;1 .
D. 1;1;1 .
Câu 30: Trong không gian Oxyz, cho tam giác ABC với A1;3; 4, B 2; 1
;0,C 3;1;2 . Tọa độ trọng
tâm G của tam giác ABC là 2 A. G 3; ;3 .
B. G 2; 1 ;2.
C. G 2;1; 2 .
D. G 6;3;6 . 3 Lời giải:
Theo công thức trọng tâm của tam giác, ta có: G 2;1; 2 .
Câu 31: Trong không gian Oxyz, cho hai điểm M 1 ;2;3 và N 2
;1; 3 . Tọa độ trọng tâm của tam giác OMN là 3 3
A. 1;1;0 . B. ; ;0 . C. 1 ;1; 6 . D. 1;1;3 . 2 2 Lời giải:
x x x O M N x G 3
y y y
Gọi G là trọng tâm O M N OM N y G . G 1;1;0 3
z z z O M N z G 3
Câu 32: Trong không gian Oxyz, cho tam giác ABC có trọng tâm G 2;1;0 và A1;1;0, B 2;3;5.
Tọa độ điểm C là A. 4; 2; 1 . B. 6 ; 2 ;0. C. 3; 1 ; 5 . D. 12 ;0;8 . Lời giải:
x 3x x x
x 3.2 1 2 3 C G A B C
Vì G là trọng tâm ABC nên y 3y y y y 3.11 3 1 C G A B C
z 3z z z
z 3.0 0 5 5 C G A B C Do đó: C 3; 1 ; 5 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
Chuyên đề VECTO TRONG KHÔNG GIAN Luyện thi THPT 2025
Câu 33: Trong không gian Oxyz, cho các điểm A1; 2 ;3, B0;1; 2
, E 3;2;2 . Gọi C ; m ; n p là
điểm thỏa mãn E là trọng tâm của tam giác ABC . Tổng m n p bằng 10 A. 13 . B. 15 . C. . D. 20 . 3 Lời giải:
x x x A B C x E 3
y y y
Vì E là trọng tâm của tam giác ABC nên A B C y . E 3
z z z A B C z E 3 1 0 m 3 3 m 8 2 1 n Thay số được 2
n 7 m n p 20 3 p 5 3 2 p 2 3
Câu 34: Trong không gian Oxyz, cho tam giác ABC có A1; 1 ; 2
và trọng tâm G2;1; 3 . Tọa độ
của vectơ u AB AC là A. 3;6;3 .
B. 3;6; 3 .
C. 3; 3;6 . D. 3; 2; 1 . Lời giải:
Gọi M là trung điểm cạnh BC. 3
Ta có: u AB AC 2.AM 2. .AG 3AG 3;6; 3 . 2
Câu 35: Trong không gian Oxyz , cho tam giác ABC biết A1;3; 3 ,B 2;4;
5 ,C a;2;b và G2;c; 3 là
trọng tâm. Tổng a b c bằng A. 5 . B. 3 . C. 1. D. 1. Lời giải:
Vì G là trọng tâm của tam giác ABC nên ta có: 3x x x x 6 1 2 a a 3 G A B C 3y y y y 3c 3 4 2 c 3 G A B C 3z z z z 9 3 5 b b 1 G A B C Vậy a b c 1.
Câu 36: Trong không gian Oxyz, cho ABC có A2;1; 2 , B 1 ;1;2, C 7; 1
;2 . Độ dài trung tuyến AM là A. 5 3 . B. 2 3 . C. 3 2 . D. 4 2 . Lời giải:
Gọi M là trung điểm BC suy ra M 3;0; 2. 2 2 2
Vậy AM 3 2 0 1 2 2 3 2 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115
