
















Preview text:
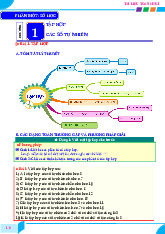
CHUYÊN ĐỀ 1. ÔN TẬP VÀ BỔ TÚC VỀ SỐ TỰ NHIÊN
BÀI 4. CÁC PHÉP TÍNH VỀ SỐ TỰ NHIÊN Mục tiêu Kiến thức
+ Nhận biết được điều kiện để có phép trừ trong tập số tự nhiên và điều kiện để thực hiện được phép chia.
+ Biết các tính chất của phép cộng và phép nhân.
+ Nắm được quan hệ giữa các số trong các phép cộng, phép trừ, phép nhân, phép chia hết và phép chia có dư. Kĩ năng
+ Xác định được vai trò của các số trong các phép tính, từ đó tìm được số chưa biết trong một phép tính.
+ Biết cách vận dụng các tính chất giao hoán, kết hợp, tính chất phân phối của phép nhân đối với
phép cộng… vào tính nhẩm, tính nhanh một cách hợp lí.
+ Biết cách vận dụng kiến thức về các phép toán để giải các bài toán thực tế. Trang 1 I. LÍ THUYẾT TRỌNG TÂM
1. Phép cộng và phép nhân
Tổng và tích của hai số tự nhiên a + b = c
(Số hạng) + (Số hạng) = (Tổng) a . b = d
(Thừa số) . (Thừa số) = (Tích)
Chú ý. Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một Ví dụ. . a b a ; b
thừa số bằng số, ta có thể không cần viết dấu nhân giữa các số. 4.x.y 4xy. Nhận xét:
+ Tích của một số với số 0 thì bằng 0.
+ Nếu tích của hai thừa số mà bằng 0 thì có ít nhất một thừa số bằng 0. Tính chất Phép tính Cộng Nhân Tính chất Giao hoán a b b a . a b . b a
abc abc .ab.c .a .bc Kết hợp Cộng với số 0 a 0 0 a a Nhân với số 1 . a 1 1.a a Phân phối của phép nhân đối với ab c ab ac phép cộng
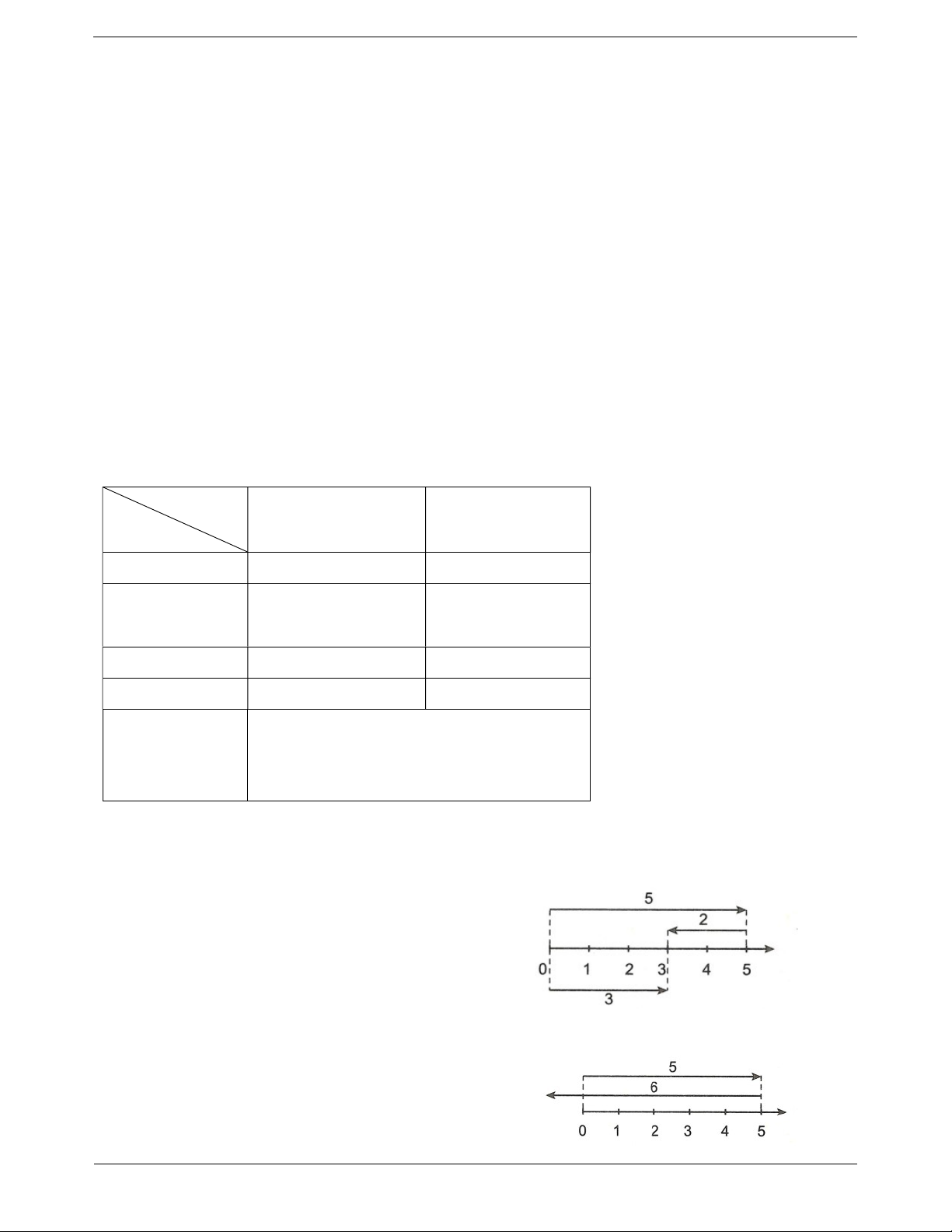
2. Phép trừ hai số tự nhiên Ví dụ.
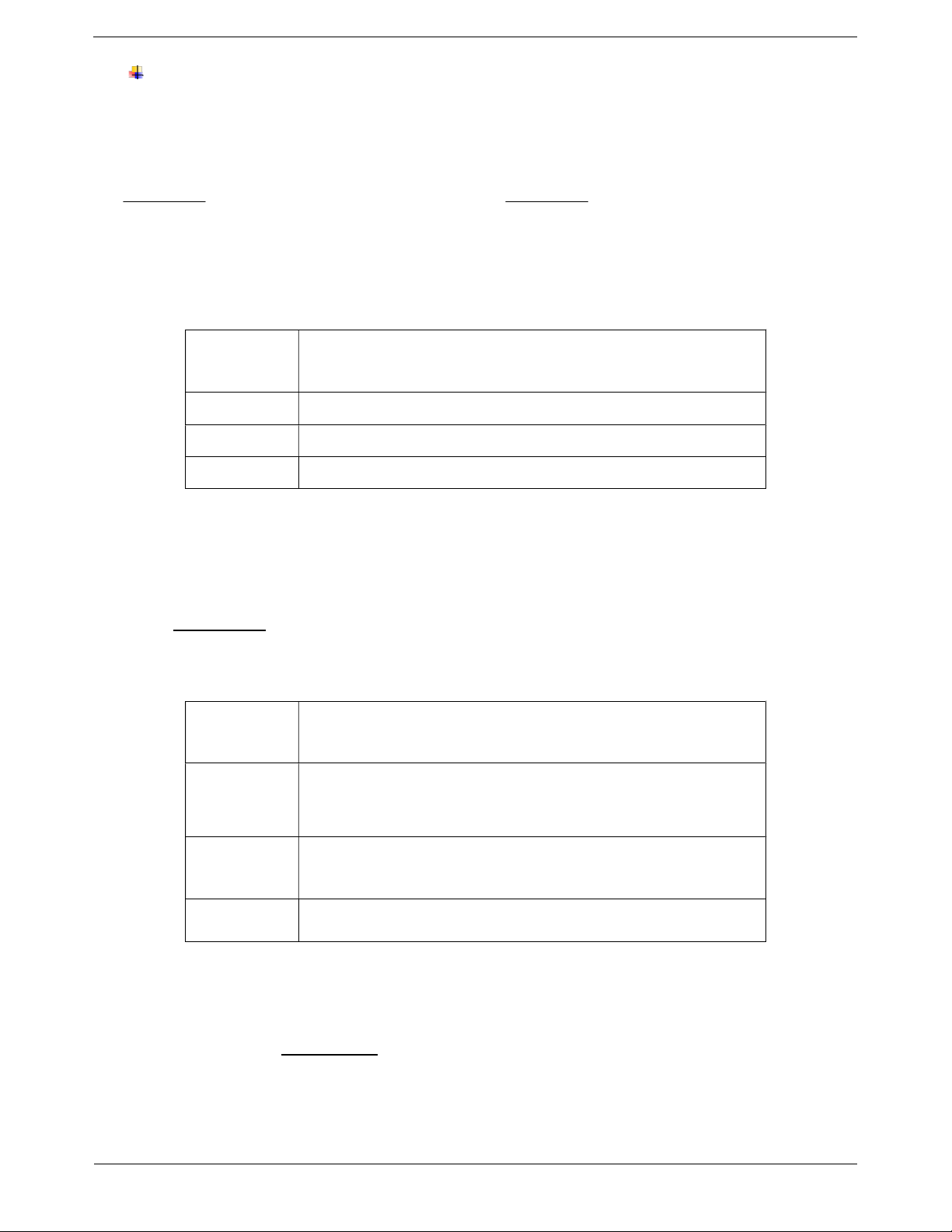
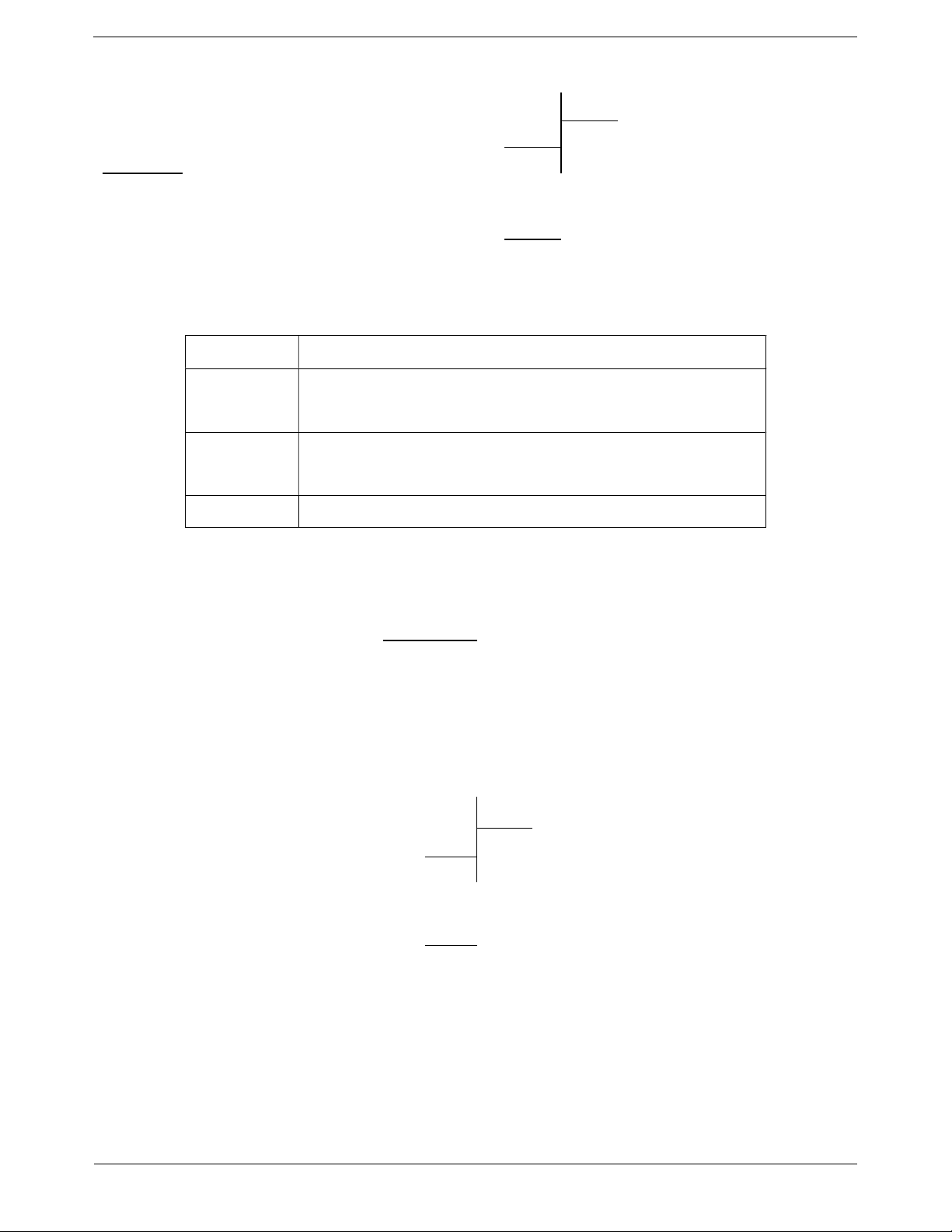
Cho hai số tự nhiên a và b, nếu có số tự nhiên x sao
cho b x a thì ta có phép trừ: a b = c
(Số bị trừ) (Số trừ) = (Hiệu) Nhận xét:
Hình vẽ trên thể hiện phép trừ 5 2 3. + a a 0. + a 0 . a
+ Điều kiện để có hiệu a b trong tập số tự Trang 2 nhiên là a . b
Hình vẽ trên cho thấy không có hiệu 5 6 trong phạm vi số tự nhiên. 3. Phép chia
Phép chia hai số tự nhiên
Cho hai số tự nhiên a và b, trong đó b 0, nếu có số tự nhiên x sao cho .
b x a thì ta có phép chia: a : b = x
(Số bị chia) : (Số chia) = (Thương) Nhận xét: + 0 : a 0,a 0. + a : a 1,a 0. + a :1 . a
+ Điều kiện để có thể thực hiện được phép chia là số chia khác 0. Phép chia hết
Số tự nhiên a chia hết cho số tự nhiên b khác 0 nếu có số tự nhiên q sao cho: a . b q Phép chia có dư a .
b q r (trong đó 0 r b ).
Số bị chia = Số chia Thương + Số dư
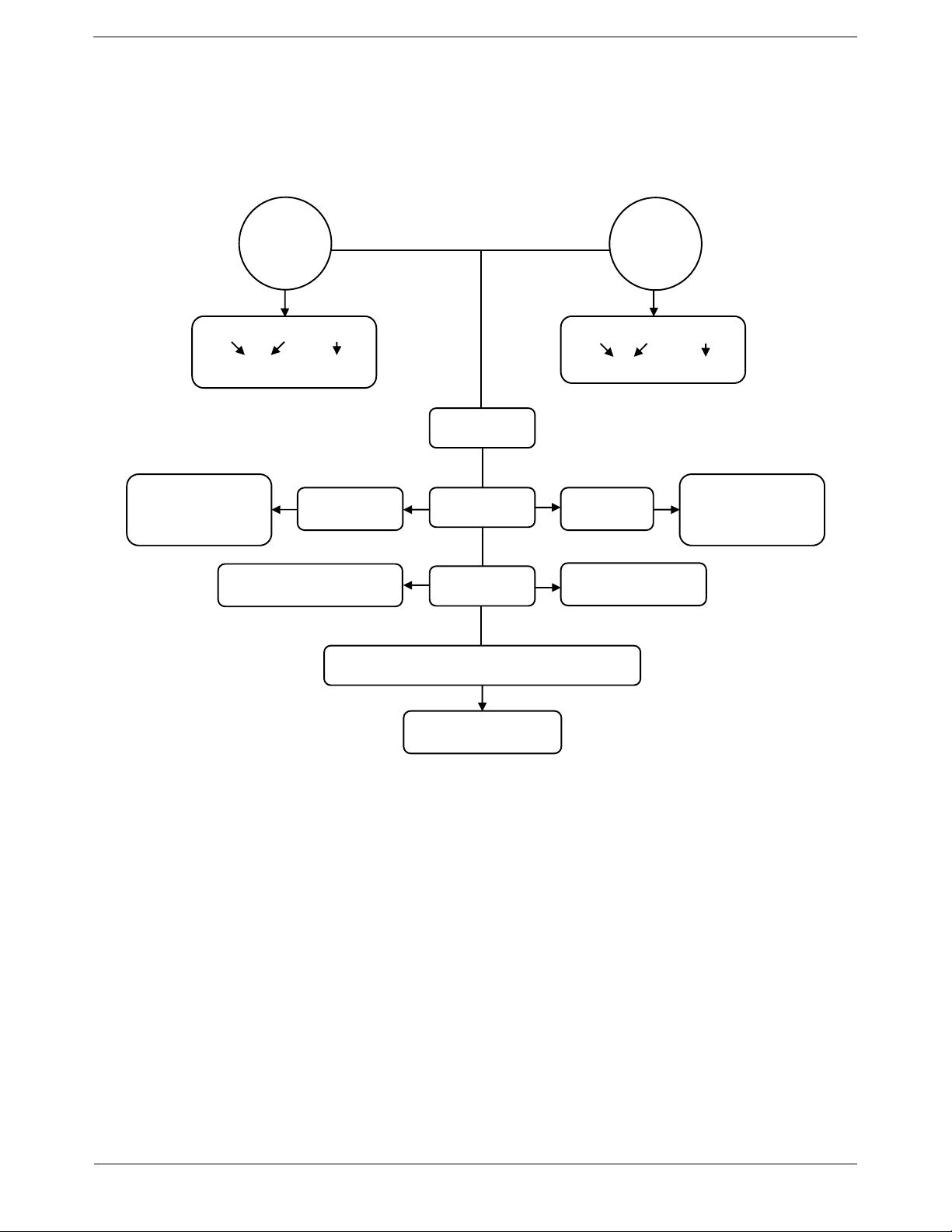
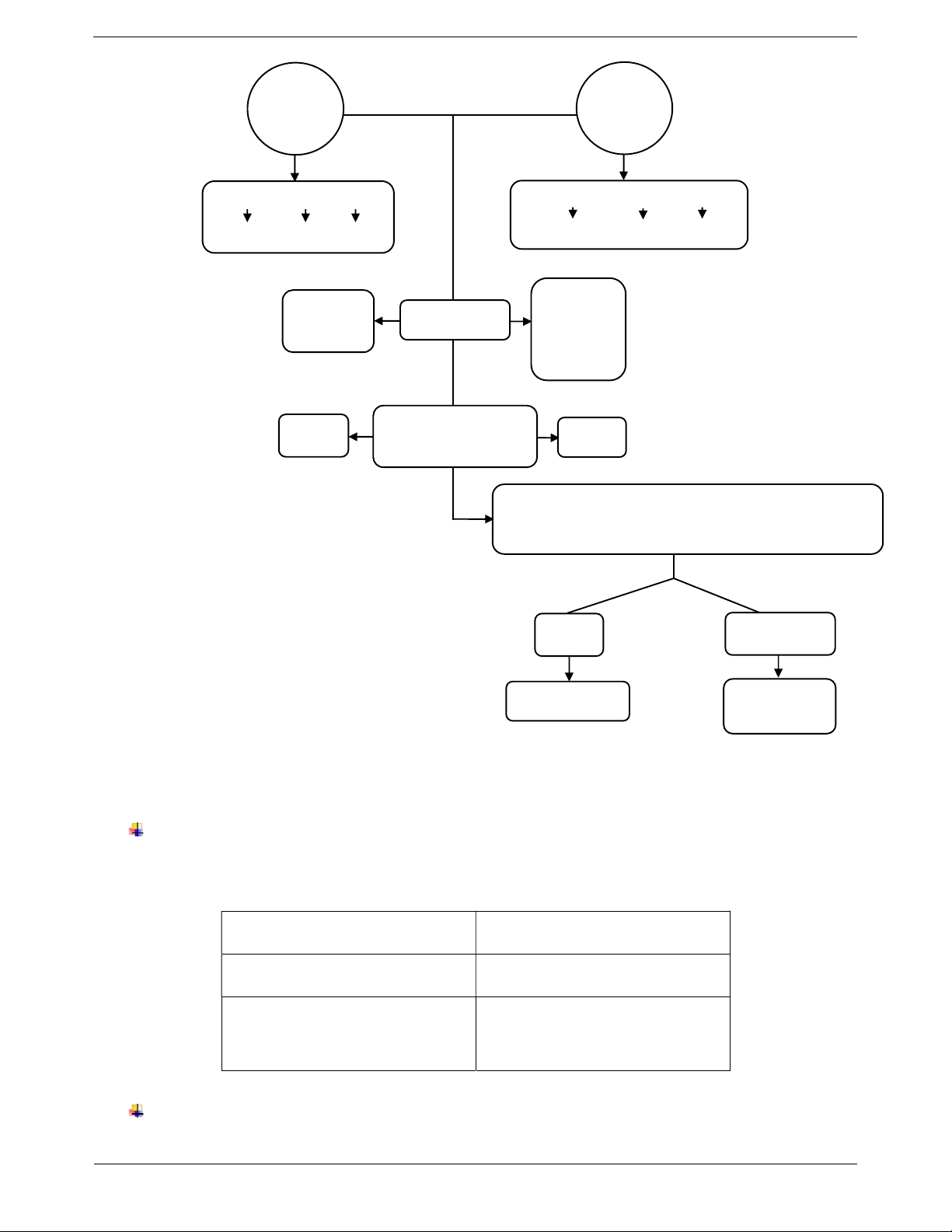
Nhận xét: Số dư bao giờ cũng nhỏ hơn số chia. Trang 3 SƠ ĐỒ HỆ THỐNG HÓA
CÁC PHÉP TÍNH VỀ SỐ TỰ NHIÊN Phép Phép cộng nhân a + b = x a . b = x Thừa số Tích Số hạng Tổng Tính chất Cộng với 0: a Nhân với 1: b b a Giao hoán . a b . b a a 0 0 a a . a 1 1.a a
a bc abc Kết hợp . a .bc .ab.c
Phân phối của phép nhân đối với phép .
a b c .ab .ac Trang 4 Phép Phép trừ chia a b = x a : b = x
Số bị trừ Số trừ Hiệu
Số bị chia Số chia Thương 0 : a 0 a a 0 Nhận xét a a : a 1 0 a a :1 a
Điều kiện để thực hiện a b b 0 phép tính
Với hai số tự nhiên a, b (b khác 0) luôn tìm được hai số tự nhiên q, r sao cho a . b q r 0 r b r 0 0 r b Phép chia hết Phép chia có dư II. CÁC DẠNG BÀI TẬP
Dạng 1: Thực hiện phép tính Phương pháp giải
Để thực hiện phép tính bằng cách hợp lí nhất (tính nhanh), ta cần đưa về tổng, hiệu, tích, thương của số
tròn chục, tròn trăm, tròn nghìn,… và áp dụng các tính chất:
Tính chất kết hợp của phép cộng
abc abc;
Tính chất kết hợp của phép nhân
.ab.c .a .bc; ab:c a:cb:c
Chia một tổng cho một số
(trong trường hợp chia hết) Ví dụ mẫu
Ví dụ 1. Thực hiện các phép tính sau bằng cách hợp lí nhất: Trang 5 a) 81 243 19;
b) 12.53 53.172 53.84.
c) 36.28 36.82 64.69 64.41;
d) 2.31.12 4.6.42 8.27.3; e) 5.25.2.16.4; f) 1.2.3.4.5.6. Hướng dẫn giải a) Ta có b) Ta có: 81 243 19 12.53 53.172 53.84 8119 243 53.12 172 84 100 243 53.100 343. 5300. c) Ta có: d) Ta có
36.28 36.82 64.69 64.41 2.31.12 4.6.42 8.27.3
36.28 82 64.69 4 1 31.24 24.42 27.24 36.110 64.110 24.31 42 27 110.36 64 24.100 2400. 110.100
Ta kí hiệu: 1.2.3....n n! f) Ta có: 11000.
là tích các số tự nhiên liên 1.2.3.4.5.6 e) Ta có:
tiếp từ 1 đến n, đọc là n 5.25.2.16.4 2.5.3.4.6 giai thừa. 5.2.25.4.16 10.3.24 10.72 10.100.16 720. 16000. Ví dụ 2. Tính nhẩm: Để tính nhẩm nhanh, ta a) 997 37; b) 123 98; thường làm như sau: c) 25.32; d) 72 : 6;
- Thêm vào số hạng này, bớt e) 49.101; f) 98.36;
đi số hạng kia cùng một số. g) 72.125.6; h) 999.202.
- Thêm vào số bị trừ và số trừ Hướng dẫn giải cùng một số.
- Nhân vào thừa số này, chia
a) Ta có: 997 37 997 3 37 3 1000 34 1034;
đi thừa số kia với cùng một số.
b) Ta có: 123 98 123 2 98 2 125 100 25;
- Đưa về số tròn trăm, tròn Trang 6
c) Ta có: 25.32 25.4.32 : 4 100.8 800; nghìn,…
- Nhân vào thừa số này, chia
d) Ta có: 72 : 6 60 12 : 6 60 : 6 12 : 6 10 2 12;
đi ở thừa số kia với cùng một
e) Ta có: 49.101 49.100
1 49.100 49.1 4900 49 4949; số.
- Đưa về số tròn trăm, tròn
f) Ta có: 98.36 100 2.36 100.36 2.36 3600 72 3528; nghìn,… g) Ta có:
72.125.6 72 :8.125.8.6 8.125.9.6 1000.54 54000; h) Ta có: 999.202 1000 1 .202 1000.202 1.202
202000 202 201798.
Ví dụ 3. Thực hiện phép tính:
100 95 90 85 80 75 70 65 60 55 50 45. Hướng dẫn giải
Vận dụng tính chất kết hợp, ta có:
100 95 90 85 80 75 70 65 60 55 50 45
100 95 90 85 80 75 70 65 60 55 50 45
5 5 5 5 5 5 5.6 30.
Ví dụ 4. So sánh A và B mà không cần tính giá trị của chúng, biết: A 234.234; B 233.235. Hướng dẫn giải
Ta có: A 234.234 234.233 1 234.233 234;
B 233.235 233.234 1 233.234 233. Vì 234 233 nên A B. Vậy A . B
Ví dụ 5. Tính tổng: S 1 2 3 ... . n Hướng dẫn giải
Tổng S có số số hạng là: n 1 :11 n (số hạng). Xét 2S n
1 n 1 2 n 2 3 ... n 1 .n nn 1
n caëp Trang 7 nn 1 Vậy: S . 2 Nhận xét:
Để tính tổng của dãy các số tự nhiên cách đều, ta dùng công thức: Soá soá haïng Soá ñaàu + Soá cuoái 2
Bài tập tự luyện dạng 1 Bài tập cơ bản
Câu 1: Thực hiện phép tính: a) 936 54; b) 331 29 69; c) 875 : 25; d) 29.8 50.2 31.8;
e) 185 434 515 266 155.
Câu 2: Trong các tích sau, hãy tìm các tích bằng nhau mà không cần tính kết quả của chúng:
13.18; 20.45; 13.2.9; 3.15.20; 3.6.13; 2.10.5.9.
Câu 3: Tính bằng cách hợp lí nhất. a) 135 360 65 40; b) 38.63 37.38; c) 277 113 323 87;
d) 63.28 63.82 37.69 37.41;
e) 35.34 35.38 65.75 65.45; f) 39.8 60.2 21.8.
Câu 4: Thực hiện các phép tính: a) 6!; b) 2! 3! 5!; c) 7! 3.4!; d) 3.3! 2.5! 7!.
Câu 5: Xác định dạng của các tích sau: a) a0.111; b) a . b 101; c) ab . c 1001;
Câu 6: Xác định dạng của các thương sau: a) aaa : ; a b) abcabc : ab . c Câu 7: Tính nhẩm: a) 9996 45; b) 50.12; c) 58.102; d) 97.32; e) 12.125.6; f) 998.102. Câu 8:
a) Cho 1538 3425 S. Không làm phép tính, hãy tìm giá trị của: S 1538; S 3425;
b) Cho 9142 2451 D. Không làm phép tính, hãy tìm giá trị của: D 2451; 9142 D. Câu 9:
a) Cho biết 37.3 111. Hãy tính nhanh: 37.12.
b) Cho biết 15 873.7 111111. Hãy tính nhanh 15 873.21. Trang 8 Bài tập nâng cao
Câu 10: Thực hiện các phép tính:
a) 102 96 90 84 78 72 66 60 54 48.
b) 99 97 95 93 91 89 ... 7 5 3 1.
Câu 11. So sánh A và B mà không cần tính giá trị của chúng, biết:
a) A 2002.2002; B 2001.2004.
b) A 123.123; B 120.124. Câu 12. Tính tổng:
a) 1 2 3 ... 1000;
b) 2 4 6 ... 1024;
c) 1 3 5 ... 567;
d) 13 15 17 ... 1051. Dạng 2: Tìm x Phương pháp giải
Xác định vai trò của số đã biết và số chưa biết trong phép tính, sau đó áp dụng: Phép toán Tìm số chưa biết Phép cộng
Số hạng chưa biết = Tổng – Số hạng đã biết
Số trừ = Số bị trừ – Hiệu Phép trừ
Số bị trừ = Hiệu + Số trừ Phép nhân
Thừa số chưa biết = Tích : Thừa số đã biết
Số chia = Số bị chia : Thương Phép chia hết
Số bị chia = Số chia . Thương Ví dụ mẫu
Ví dụ 1. Tìm số tự nhiên x, biết: a) x 45.36 0. b) 32 x 16 32. c) 3456 : x 2.
d) x 105 : 21 15. Hướng dẫn giải
a) Ta có: x 45.36 0
b) Ta có: 32x 16 32 x 45 0 : 36 x 16 32 : 32 x 45 0 x 16 1 x 0 45 x 116 x 45. x 17. Vậy x 45. Vậy x 17. c) Ta có: 3456 : x 2
d) Ta có: x 105 : 21 15 x 3456 : 2 x 105 15.21 Trang 9 x 1728. x 105 315 Vậy x 1728. x 315 105 x 420 Vậy x 420.
Ví dụ 2. Tìm số tự nhiên x, biết 558 15 : x 29.17 14. Hướng dẫn giải
Ta có: 558 15 : x 29.17 14
15: x 29.17 55814 15: x 29.17 544 15 : x 29 544 :17 15 : x 29 32 15 : x 32 29 15 : x 3 x 15 : 3 x 5. Vậy x 5.
Ví dụ 3. Tìm số các tự nhiên x, biết: 2x 4x 3 0. Hướng dẫn giải
Vì tích số bằng 0 khi có ít nhất một trong hai số bằng 0 nên
2x 4x 3 0suy ra 2x 4 0 hoặc x 3 0
+ Nếu 2x 4 0 thì x 2.
+ Nếu x 3 0 thì không tồn tại số tự nhiên x thỏa mãn. Vậy x 2.
Bài tập tự luyện dạng 2 Bài tập cơ bản
Câu 1: Trong tập số tự nhiên, tìm x biết: a) x 50 : 25 8;
b) x 40.15 75.24
c) x 32 15 0; d) 1234 : x 2.
Câu 2: Tìm số tự nhiên x, biết: a) x 34.26 0; b) 152 x 23 1 : 2 358.
Câu 3: Trong tập hợp số tự nhiên, tìm x biết: Trang 10
a) 45.2.x 4.13 0;
b) x 50 : 25 8; c) 5.x 38 :19 13;
d) 100 3.8 x 1;
e) x 12 17 : 5 4; f) 84 4.2.x 1 48.
Câu 4: Tìm số tự nhiên x, biết: a) 17x 33x 100;
b) 23x 15x 7 105; c) 32x 1 1 4x 152;
d) 513x 5 406 223x 5. Bài tập nâng cao
Câu 5: Tìm số tự nhiên x, biết: 1 2 3 ... x 55.
Dạng 3. Bài toán có lời văn Ví dụ mẫu
Ví dụ 1. Tìm hai số tự nhiên có tổng bằng 148, biết rằng số lớn gấp 3 lần số bé. Hướng dẫn giải
Gọi số bé là x, khi đó số lớn là 3x x .
Theo đề bài, ta có: x 3x 148 4x 148 x 148 : 4 x 37
Vậy số bé là 37, số lớn là 111.
Ví dụ 2. Trong tập hợp các số tự nhiên, một phép chia hết có thương bằng 7, số bị chia lớn hơn số chia 84
đơn vị. Tìm số bị chia và số chia. Hướng dẫn giải Thương = 7 Đề cho
Số bị chia – Số chia = 84. Cần tìm Số bị chia và số chia. Gọi số chia là x. Hướng giải
Biểu diễn số bị chia theo x.
Gọi số chia là x, khi đó số bị chia là: x 84.
Vì số bị chia = (số chia) . (thương) nên ta có: x 84 7.x 84 7.x x 84 x 7 1 84 6.x x 84 : 6 x 14 Trang 11
Vậy số chia là 14 và số bị chia là 98.
Ví dụ 3. Bạn Lan dùng 50 000 đồng để mua bút và vở. Biết rằng mỗi cái bút Tóm tắt:
có giá 3000 đồng và mỗi quyển vở có giá là 7000 đồng. Hỏi: Có: 50 000 đồng.
a) Nếu chỉ mua bút thì bạn Lan mua được nhiều nhất bao nhiêu cái? Bút: 3000 đồng/cái.
b) Nếu chỉ mua vở thì bạn Lan mua được nhiều nhất bao nhiêu quyển? Vở: 7000 đồng/cái
c) Bạn Lan mua được nhiều nhất bao nhiêu cái bút và bao nhiêu quyển vở
với số lượng bằng nhau? Hướng dẫn giải Hướng giải:
a) Ta có: 50 000 chia cho 3000 được 16 và dư 2000 đồng.
a) Số bút nhiều nhất mua
Vậy nếu chỉ mua bút thì bạn Lan mua được nhiều nhất 16 cái.
được = Số tiền : giá một
b) Ta có 50 000 chia cho 7000 được 7 và dư 1000 đồng. cái bút.
Vậy nếu chỉ mua vở thì bạn Lan mua được nhiều nhất 7 quyển. b) Tương tự a).
c) Giá của một cái bút và một quyển vở là: 3000 7000 10000 (đồng). c) Cần tính xem giá của Ta có: 50000 :10000 5.
một cái bút và một quyển
Vậy nếu mua bút và vở với số lượng bằng nhau thì bạn Lan mua được nhiều vở. Làm tương tự a) và b).
nhất 5 cái bút và 5 quyển vở.
Ví dụ 4. Một tàu hỏa cần chở 950 hành khách đi du lịch. Biết rằng mỗi toa
có 10 khoang, mỗi khoang có 6 chỗ ngồi. Hỏi cần ít nhất bao nhiêu toa để
chở hết số hành khách đi du lịch. Tóm tắt: Hướng dẫn giải Có: 950 hành khách.
Mỗi toa chở được số người là 6.10 60 (người). 1 toa: 10 khoang
Ta có: 950 chia cho 60 được 15 và dư 50. 1 khoang: 6 chỗ ngồi.
Vậy cần ít nhất 16 toa để chở hết số hành khách đi du lịch. ? toa.
Bài tập tự luyện dạng 3 Bài tập cơ bản
Câu 1. Bạn Trang dùng 40 000 đồng để mua bút. Biết rằng có hai loại bút: mỗi cái loại I có giá 3000
đồng và mỗi cái bút loại II có giá 3500 đồng. Hỏi bạn Trang mua được nhiều nhất bao nhiêu cái bút nếu a) chỉ mua bút loại I. b) chỉ mua bút loại II.
c) mua cả hai loại bút với số lượng bằng nhau.
Câu 2. Một tàu hỏa cần chở 700 hành khách đi tham quan. Biết rằng mỗi toa có 12 khoang, mỗi khoang
có 4 chỗ ngồi. Hỏi cần ít nhất bao nhiêu toa để chở hết số hành khách đi tham quan.
Câu 3. Để vận chuyển hết 250 tấn lương thực, người ta dùng hai loại xe. Biết xe loại I chở được tối đa 3
tấn, xe loại II chở được tối đa 4 tấn. Hỏi cần ít nhất bao nhiêu xe, nếu: a) chỉ dùng xe loại I. Trang 12 b) chỉ dùng xe loại II.
Câu 4. Một chiếc đồng hồ treo tường có đặc điểm như sau: Khi kim phút chỉ đúng số 12 thì đồng hồ đánh
số chuông tương ứng với số kim giờ chỉ. Hỏi một ngày đồng hồ phải đánh bao nhiêu tiếng chuông? Bài tập nâng cao
Câu 5. Một phép trừ có tổng của số bị trừ, số trừ và hiệu bằng 1062. Số trừ lớn hơn hiệu là 279. Tìm số bị trừ và số trừ.
Câu 6. Tìm hai số tự nhiên biết hiệu của chúng bằng 68. Nếu gạch bỏ chữ số 5 ở hàng đơn vị của số lớn thì được số nhỏ.
Câu 7. Viết một số A bất kì cho ba chữ số, viết tiếp ba chữ số đó một lần nữa, được số B có sáu chữ số.
Chia số B cho 7, rồi chia thương tìm được cho 11, sau đó lại chia thương tìm được cho 13. Kết quả được
số A, hãy giải thích vì sao?
Dạng 4. Toán về phép chia có dư Phương pháp giải Trong phép chia có dư:
Số bị chia = Số chia Thương + Số dư (0 < Số dư < Số chia).
Số chia = (Số bị chia – Số dư) : Thương.
Thương = (Số bị chia – Số dư) : Số chia. Số dư
= Số bị chia – Số chia Thương. Ví dụ mẫu
Ví dụ 1. Tìm số dư và thương trong phép chia: a) 507 chia cho 14. b) 243 chia cho 11. Hướng dẫn giải
a) Ta có: 507 14.36 3 nên phép chia 507 cho 14 được thương là 36 và số dư là 3.
b) Ta có: 243 11.22 1 nên phép chia 243 cho 11 được thương là 22 và số dư là 1. Ví dụ 2.
a) Trong phép chia một số tự nhiên cho 5, số dư có thể bằng bao nhiêu?
b) Viết dạng tổng quát của một số tự nhiên chia cho 4 và có số dư lần lượt là 0; 1; 2; 3. Hướng dẫn giải
a) Vì số dư bao giờ cũng nhỏ hơn số chia nên số dư của phép chia một số tự nhiên cho 5 có thể bằng 0; 1; 2; 3; 4.
b) Số tự nhiên chia cho 4, dư 0 (chia hết cho 4) có dạng tổng quát là: 4k với k
Số tự nhiên chia cho 4, dư 1 có dạng tổng quát là: 4k 1, với k .
Số tự nhiên chia cho 4, dư 2 có dạng tổng quát là: 4k 2, với k .
Số tự nhiên chia cho 4, dư 3 có dạng tổng quát là: 4k 3, với k . Trang 13
Ví dụ 3. Tìm số bị chia trong phép chia có số chia bằng 8, thương bằng 35, số dư là số lớn nhất có thể có trong phép chia đó. Hướng dẫn giải
Vì số chia bằng 8 và số dư không vượt quá số chia nên số dư lớn nhất có thể có là 7.
Do vậy ta có: số chia =8, thương =35, số dư =7.
Vậy số bị chia là: 35.8 7 287.
Ví dụ 4. Ngày 1 tháng 5 năm 2018 là thứ ba. Hỏi ngày 1 tháng 5 năm + Cứ sau 7 ngày (1 tuần): thứ 2019 là thứ mấy? sẽ lặp lại. Hướng dẫn giải
+ Từ ngày 1/5/2018 đến ngày
Ta thấy từ ngày 1/5/2018 đến ngày 1/5/2019 là 1 năm (tức 365 ngày).
1/5/2019 là 1 năm (365 ngày).
Lại có: 365 chia cho 7 được 52 và dư 1.
+ Cần tính xem: 365 chia cho
Vậy ngày 1/5/2019 là thứ tư. 7 dư mấy?
Bài tập tự luyện dạng 4 Bài tập cơ bản
Câu 1. Trong tập hợp các số tự nhiên, phép chia cho 2, cho 3, cho 4 có thể có số dư bằng bao nhiêu?
Câu 2. Viết dạng tổng quát của số tự nhiên chia hết cho 5, chia cho 5 dư 1 và chia cho 5 dư 3.
Câu 3. Năm nhuận có 366 ngày. Hỏi năm nhuận gồm bao nhiêu tuần và còn dư mấy ngày?
Câu 4. Ngày 20 tháng 11 năm 2017 là thứ hai. Hỏi ngày 20 tháng 11 năm 2019 là thứ mấy?
Câu 5. Tìm số chia trong phép chia có số bị chia là số lớn nhất có ba chữ số, thương bằng 5 và số dư kém thương 1 đơn vị.
Câu 6. Tìm hai số, biết:
a) Tổng của hai số là 361, số lớn chia số nhỏ được thương là 9 và dư 11.
b) Hiệu của hai số là 578, số lớn chia số nhỏ được thương là 8 và dư 53. Bài tập nâng cao
Câu 7. Tổng của số bị chia và số chia bằng 22. Thương bằng 3 và số dư bằng 2. Tìm số bị chia và số chia.
Câu 8. Một phép chia có thương bằng 82, số dư bằng 47, số bị chia nhỏ hơn 4000. Tìm số chia.
Dạng 5. Tìm số chưa biết trong một phép tính Phương pháp giải Phép toán Cách làm Phép cộng và phép trừ
Tính lần lượt theo cột từ phải sang trái. Chú ý những trường hợp có “nhớ”. Phép nhân
Thực hiện phép nhân từ phải sang trái, suy luận từng bước để tìm ra những số chưa biết. Phép chia
Đặt tính và lần lượt thực hiện phép chia từ hàng lớn nhất. Trang 14 Ví dụ mẫu
Ví dụ 1. Thay dấu * bằng những chữ số thích hợp. * * 4 * 6 * 6 * 1 7 6 * * 8 * 4 a) b) * * 9 0 0 2 8 5 6 Hướng dẫn giải a) Hàng đơn vị
Ta thấy *+* được số tận cùng bằng 0 mà ở hàng chục, 4 6 có
tận cùng bằng 0, do đó * * 0. Hàng chục
Có 4 6 10, viết 0 nhớ 1 sang cột hàng trăm. Hàng trăm
Có * 7 +1 (do có nhớ) = 9, suy ra * 1. Hàng nghìn
Có * 1 được một số có hai chữ số nên * 9.
Vậy ta có phép cộng sau: 9 1 4 0 + 1 7 6 0 1 0 9 0 0 b)
Hàng đơn vị Có * 4 ta được chữ số 6 thì * chỉ có thể bằng 0 (vì 10 4 6 )
và có mượn 1 đơn vị của hàng chục. Hàng chục Có 6 –*
1 (do có nhớ) được chữ số 5, suy ra * 0. Hàng trăm
Có * –8 được chữ số 8 thì * chỉ có thể bằng 6 (vì16 –8 8) và
có mượn 1 đơn vị ở hàng nghìn Hàng nghìn Có 6 –*
1 (do có nhớ) được chữ số 2, suy ra * 3. Vậy ta có phép trừ: 6 6 6 0 - 3 8 0 4 2 8 5 6 Trang 15
Ví dụ 2. Thay dấu * bằng những chữ số thích hợp. a) * 8 * 3 b) 1 0 * * * * * 2 * 7 9 * * 7 0 * 7 * - * * 0 Hướng dẫn giải a) Hàng đơn vị
Có 3.9 27, viết 7 nhớ 2 đơn vị sang hàng chục. Suy ra * 7. Hàng chục
Có *.9 7 2 5 (do nhớ 2 đơn vị), suy ra * chỉ có thể bằng 5.
Ta có: 5.9 45, viết 5 nhớ 4 sang hàng trăm. Hàng trăm
Có 8.9 72 4 76 (do có nhớ 4 đơn vị), suy ra * 6, viết 6 nhớ 7. Hàng nghìn
Có *.9 70 7 63 (do có nhớ 7 đơn vị), suy ra * 7. Vậy ta có phép nhân: 7 8 5 3 9 7 0 6 7 7
b) Ta có: 10 : 2 5 nên số chia là 5.
Chữ số hàng chục của thương là 0 (vì phải hạ * ở hàng đơn vị).
Cuối cùng 7.5 35 nên ** 35. Vậy ta có phép chia: 1 0 3 5 5 3 5 2 0 7 3 5 - 3 5 0 Trang 16
Bài tập tự luyện dạng 5 Bài tập nâng cao
Câu 1. Thay dấu * và các chữ cái bởi các chữ số thích hợp. a) * 1 * 2 b) a a a 9 a 1 0 * 3 * 3 * * a
Câu 2. Thay dấu * bởi những chữ số thích hợp * * * * * 97.
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN
Dạng 1. Thực hiện phép tính Bài tập cơ bản Câu 1. a) 936 54 882.
b) 331 29 69 331 69 29 400 29 429. c) 875 : 25 35.
d) 29.8 50.2 31.8 8.29 3
1 50.2 8.60 100 580.
e) Ta có: 185 434 515 266 155
185 515 434 266 155 700 700 155 1400 155 1555. Câu 2.
Ta có: 13.18 13.2.9 13.3.6;
20.45 20.3.15 2.10.3.3.5 2.10.9.5.
Vậy các tích bằng nhau là: 13.18 13.2.9 3.6.13;
20.45 3.15.20 2.10.5.9. Câu 3. a) Ta có: b) Ta có: 135 360 65 40 38.63 37.38
135 65 360 40 38.63 37 200 400 38.100 600. 3800. Trang 17 c) Ta có: d) Ta có: 277 113 323 87
63.28 63.82 37.69 37.41
277 323 113 87
63.28 82 37.69 4 1 600 200 63.110 37.110 800. 110.63 37 110.100 11000. e) Ta có: f) Ta có:
35.34 35.38 65.75 65.45 39.8 60.2 21.8
35.34 38 65.75 45 8.39 2 1 60.2 35.72 65.120 8.60 60.2
35.2.36 65.2.60 60.8 2 70.36 130.60 600. 2520 7800 10320. Câu 4. a) Ta có: b) Ta có: 6! 1.2.3.4.5.6 2! 3! 5! 2.5.3.4.6 1.2 1.2.3 1.2.3.4.5 10.3.24 1.2.13 3.4.5 10.72 2.4 60 720. 2.64 128. c) Ta có: d) Ta có: 7! 3.4! 3.3! 2.5! 7!
1.2.3.4.5.6.7 3.1.2.3.4
3.1.2.3 2.1.2.3.4.5 1.2.3.4.5.6.7 1.2.3.4.5.6.7 3
1.2.3.3 2.4.5 4.5.6.7 24.30.7 3
6.3 2.20 20.42 24.213 6.3 40 840 5112. 6.883 5298. Câu 5. Trang 18 a) a0.111 . a 10.111 b) a . b 101 a . b 100 1 . a 11 1 .10 a . b 100 a . b 1 aa . a10 ab00 ab aaa0. aba . b c) abc.1001 ab . c 1000 1 ab . c 1000 ab . c 1 abc000 abc abcab . c Câu 6. Ta có: aaa : a . a 11 1 : a 111.
Ta có: abcabc : abc abc.1000 abc: abc ab . c 1000 : abc abc : abc 1000 1 1001. Câu 7. a) Ta có: b) Ta có: 9996 45 50.12
9996 4 45 4 50.2.12 : 2 10000 41 100.6 10041. 600. c) Ta có: d) Ta có: 58.102 97.32 58.100 2 100 3.32 58.100 58.2 100.32 3.32 5800 116 3200 96 5916. 3104. e) Ta có: f) Ta có: 12.125.6 998.102 3.4.125.6 1000 2.102 3.6.4.125 1000.102 2.102 18.500 102000 204 9000. 101796. Trang 19 Câu 8.
a) S 1538 3425; S 3425 1538.
b) D 2451 9142; 9142 D 2451. Câu 9.
a) 37.12 37.3.4 37.3.4 111.4 444.
b) 15 873.21 15 873.7.3 15 873.7.3 111 111.3 333 333. Bài tập nâng cao Câu 10.
Ta có: 102 96 90 84 78 72 66 60 54 48
102 96 90 84 78 72 66 60 54 48 6 6 6 6 6 6.5 30.
Ta có: 99 97 95 93 91 89 ... 7 5 3 1
99 97 95 93 9189 ... 7 5 3 1
2 2 2 ... 2 2 25 soá 2.25 50. Câu 11.
a) Ta có: A 2002.2002 2002.2001 1 2002.2001 2002;
B 2001.2004 2001.2002 2 2001.2002 2001.2 2001.2002 4002.
Vì 2002 4002 nên A B.
b) Ta có: A 123.123 123.120 3 123.120 123.3 123.120 369;
B 120.124 120.123
1 120.123 120.1 120.123 120 Vậy A . B Câu 12.
a) Số số hạng: 1000 1 :11 1000;
Số cặp số: 1000 : 2 500.
Tổng 1 2 3 ... 1000 1000
1 .500 1001.500 500500.
b) Số số hạng: 1024 2 : 2 1 512;
Số cặp số: 512 : 2 256. Trang 20
Tổng: 2 4 6 ... 1024 1024 2.256 262656.
c) Số số hạng: 567 1 : 2 1 284;
Số cặp số: 284 : 2 142.
Tổng 1 3 5 ... 567 567 1 .142 80656.
d) Số số hạng: 105113 : 2 1 520;
Số cặp số: 520 : 2 260.
Tổng 13 15 17 ... 1051 105113.260 276640. Dạng 2. Tìm x Bài tập cơ bản Câu 1. a) x 50 : 25 8
b) x 40.15 75.24 x 2 8 x 40 75.24 :15 x 8 2 x 40 120 x 10 x 120 40 x 80. c) x 32 15 0 d) 1234 : x 2 x 32 15 x 1234 : 2 x 15 32 x 617. x 47. Câu 2.
a) Ta có: x 34.26 0
b) Ta có: 152 x 23 1 : 2 358 x 34 0 : 26
x 23 1:2 358152 x 34 0 x 23 1:2 206 x 0 34 x 34 x 231 206.2 Vậy x 34. x 231 412 x 412 231 x 181 Vậy x 181. Câu 3.
a) 45.2.x 4.13 0 b) x 50 : 25 8 45.2.x 4 0 x 50 8.25 x 50 200 Trang 21 2x 4 0 x 200 50 2.x 4 x 250. x 2. c) 5.x 38 :19 13
d) 100 3.8 x 1 5.x 2 13 3.8 x 100 1 5.x 13 2 5.x 15 3.8 x 99 x 15 : 5 8 x 99 : 3 x 3. 8 x 33
e) x 12 17 :5 4 x 33 8 x 25. x 1217 4.5 f) 84 4.2.x 1 48 x 1217 20 4.2.x 1 84 48 x 12 20 17 x 12 37 4.2.x 1 36 x 37 12 2.x 1 36 : 4 x 25. 2.x 1 9 2.x 9 1 2.x 8 x 8 : 2 x 4. Câu 4. a) Ta có: b) Ta có: 17x 33x 100 23x 15x 7 105 x.1733 100 23x 15x 15.7 105 x.50 100 23x 15x 0 x 100 : 50 38x 0 x 2. x 0. Vậy x 2. Vậy x 0. c) Ta có: d) Ta có: 32x 1 1 4x 152
513x 5 406 223x 5 32x 32.11 4x 152
51.3x 51.5 406 22.3x 22.5 32x 4x 152 32.11
153x 66x 22.5 406 51.5 36x 504 87x 261 Trang 22 x 14. x 3. Vậy x 14. Vậy x 3. Bài tập nâng cao Câu 5.
Ta có: 1 2 3 ... x 55 x.x 1 : 2 55 x.x 1 55.2 x.x 1 110
Với x là số tự nhiên thì x và x
1 là hai số tự nhiên liên tiếp.
Mà 110 10.11 nên x 10.
Dạng 3. Bài toán có lời văn Bài tập cơ bản Câu 1.
a) Ta có: 40 000 chia cho 3000 được 13 và dư 1000 đồng.
Vậy nếu chỉ mua bút loại I thì bạn Trang mua được nhiều nhất 13 cái.
b) Ta có: 40 000 chia cho 3500 được 11 và dư 1500 đồng.
Vậy nếu chỉ mua bút loại II thì bạn Trang mua được nhiều nhất 11 cái.
c) Giá của một cái bút loại I và một cái bút loại II là: 3000 3500 6500 (đồng).
Ta có: 40 000 chia cho 6500 được 6 và dư 1000 đồng.
Vậy nếu mua cả hai loại bút với số lượng bằng nhau thì bạn Trang mua được nhiều nhất 6 cái bút mỗi loại.
Câu 2. Mỗi toa chở được số người là: 12.4 48 (người).
Ta có: 700 chia cho 48 được 14 và dư 28.
Vậy cần ít nhất 15 toa để chở hết số hành khách đi tham quan. Câu 3.
a) Ta có: 250 chia cho 3 được 83 và dư 1.
Vậy nếu chỉ dùng xe loại I thì cần ít nhất 84 xe loại I.
b) Ta có: 250 chia 4 được 62 và dư 2.
Vậy nếu chỉ dùng xe loại II thì cần ít nhất 63 xe loại II. Câu 4.
Khi kim giờ chỉ số 1 và kim phút chỉ số 12 thì đồng hồ phải đánh 1 tiếng chuông.
Khi kim giờ chỉ số 2 và kim phút chỉ số 12 thì đồng hồ phải đánh 2 tiếng chuông.
.......................................................................
Khi kim giờ chỉ số 12 và kim phút chỉ số 12 thì đồng hồ phải đánh 12 tiếng chuông. Trang 23
Do đó, từ 1 giờ đến 12 giờ, số chuông mà đồng hồ đánh là: 12.12 1
1 2 3 ...1112 78 (tiếng). 2
Mỗi ngày kim giờ phải quay hai vòng, nên số chuông đồng hồ đánh mỗi ngày là: 2.78 156 (tiếng). Bài tập nâng cao Câu 5.
Số bị trừ + số trừ + hiệu = 1062.
Do số trừ + hiệu = số bị trừ nên: 2 lần số bị trừ = 1062.
Suy ra số bị trừ 1062 : 2 531.
Ta có: số trừ - hiệu = 279; số trừ + hiệu = 531.
Do đó: số trừ 531 279 : 2 405.
Câu 6. Vì nếu gạch bỏ chữ số 5 ở hàng đơn vị của số lớn thì ta được số nhỏ nên số lớn chia cho số nhỏ
được thương là 10 và số dư là 5.
Gọi số nhỏ là x x . Vì số dư là 5 nên x 5.
Suy ra số lớn là: x.10 5.
Hiệu hai số đó là: x.10 5 x 68 x.10 x 685 9.x 63 x 63 : 9 x 7.
Vậy hai số cần tìm là 7 và 75. Câu 7. A ab , c B abc ab . c Ta có:
abc abc : 7 :11:13 abc suy ra abc abc abc.13.11.7. Vì abc.13.11.7. ab .
c 13.11.7 ab .c1001 abc abc
Dạng 4. Toán về phép chia có dư Bài tập cơ bản Câu 1.
Vì số dư phải nhỏ hơn số chia nên:
- Phép chia cho 2, số dư có thể là: 0; 1.
- Phép chia cho 3, số dư có thể là: 0; 1; 2.
- Phép chia cho 4, số dư có thể là: 0; 1; 2; 3. Câu 2. Trang 24
Số tự nhiên chia hết cho 5 có dạng là 5k k .
Số tự nhiên chia cho 5 dư 1 có dạng là 5k 1 k .
Số tự nhiên chia cho 5 dư 3 có dạng là 5k 3 k . Câu 3.
Ta có 366 chia cho 7 được 52 và dư 2. Vậy năm nhuận gồm 52 tuần và còn dư 2 ngày. Câu 4.
Từ ngày 20/11/2017 đến ngày 20/11/2019 là 2 năm. Mà trong hai năm này không có năm nhuận nên có 730 ngày.
Ta có 730 chia cho 7 được 104 và dư 2.
Vậy ngày 20 tháng 11 năm 2019 là thứ tư. Câu 5.
Số lớn nhất có ba chữ số là 999. Do đó, số bị chia là 999. Số dư là: 5 1 4.
Vậy số chia của phép chia đó là: 999 4 : 5 199. Câu 6.
a) Gọi số nhỏ là x x , vì số dư là 11 nên x 11.
Do số lớn chia số nhỏ được thương là 9 và dư 11 nên số lớn là: x.9 11.
Tổng của hai số là: x.9 1 1 x 361 x.9 x 36111 x.9 1 350 x.10 350 x 35
Do đó số nhỏ là 35, suy ra số lớn là: 35.9 11 326.
Vậy hai số cần tìm là 326 và 35.
b) Gọi số nhỏ là x x , vì số dư là 53 nên x 53.
Suy ra số lớn là: x.8 53.
Hiệu của hai số là: x.8 53 x 578 x.8 x 578 53 7.x 525 x 75
Do đó số nhỏ là 75, suy ra số lớn là: 75.8 53 653.
Vậy hai số cần tìm là 653 và 75. Trang 25 Bài tập nâng cao Câu 7.
Làm tương tự Câu 30, với số bị chia đóng vai trò là số lớn, số chia là số bé.
Đáp số: Số bị chia bằng 17 và số chia bằng 5. Câu 8.
Gọi số bị chia là a, số chia là b. Số chia phải lớn hơn số dư nên b 47.
Nếu b 48 thì a 48.82 47 3983 4000, chọn.
Nếu b 49 thì a 49.82 47 4065 4000, loại. Vậy số chia bằng 48.
Dạng 5. Tìm số chưa biết trong một phép tính Câu 1.
a) Hàng đơn vị: Có 2.9 18, viết 8 nhớ 1 đơn vị sang hàng chục. Suy ra * 8.
Hàng chục: Có *.9 3 1 2 (do nhớ 1 đơn vị), suy ra * chỉ có thể bằng 8.
Ta có: 8.9 72, viết 2 nhớ 7 sang hàng trăm.
Hàng trăm: Có 1.9 7 16 (do có nhớ), viết 6 nhớ 1. Suy ra * 6.
Hàng nghìn: *.9 1 10 (do có nhớ), suy ra * 1.
Vậy ta có phép nhân: 1182.9 10638.
b) Hàng đơn vị: Có a.a có tận cùng là a nên a 0;1;5; 6 .
Dễ thấy a 0 và a 1.
Thử: 555.5 2775 (loại) 666.6 3996 (đúng).
Vậy ta có phép nhân: 666.6 3996. Câu 2.
Xét hàng chục: có * * *9, mà hàng chục lớn nhất là 9 9 18 *9, suy ra ở hàng chục có * * 9
và được nhớ một đơn vị từ hàng đơn vị. Tức là 9 9 18 1 19 (do có nhớ).
Xét hàng đơn vị: Vì có nhớ 1 đơn vị sang hàng chục nên ta có: * * 17.
Vậy ta có phép tính: 99 98 197 hoặc 98 99 197. Trang 26