Chuyên Đề Căn Bậc Hai Ôn Thi Vào 10 Giải Chi Tiết

CHUYÊN ĐỀ 2: CĂN BẬC HAI.
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. [NB]Cho số thực a  0 . Số nào sau dây là căn bậc hai số học của a? D. 2 a . A. 2a . B.  a . C. a . Lời giải
Với số dương a, số a được gọi là căn bậc hai số học của a
Đáp án cần chọn là C.
Câu 2. [NB]Cho số thực a  0 . Căn bậc hai số học của a là x khi và chỉ khi? A. x  a . B. a  x . C. 2
a  x, x  0 . D. 2
a  x, x  0 . Lời giải
Với số dương a, số x được gọi là căn bậc hai số học của a khi và chỉ khi ìï x ³ 0 ï a = x Û í 2 ï x = a ïî
Đáp án cần chọn là: D
Câu 3. [NB]Số bào sau đây là căn bậc hai số học của số a  0,36 ? A. 0  ,6 . B. 0,9 . C. 0,18 . D. 0, 6 . Lời giải
Căn bậc hai số học của a  0,36 là 0,36 = 0,6 Đáp án cần chọn là: B
Câu 4. [NB]Khẳng định nào sau đây là đúng? A B. C. D. A 
B  0  A  B 2 2 . A  B  A  B A  , A A  0 . A  , A A  0 Lời giải
Với A, B không âm ta có A  B  0  A  B nên A đúng,D sai. Trang 1 ìï A khi A ³ 0 Ta có hằng đẳng thức 2 ï A = A = í nên A, B sai ï - A khi A < 0 ïî
Đáp án cần chọn là: A
Câu 5. [TH] So sánh hai số 2 và 1 + 2 : D. Không thể so A. 2 ³ 1 + 2 . B. 2 = 1 + 2 . C. 2 < 1 + 2 . sánh. Lời giải Tách 2 = 1 + 1 = 1 + 1 Vì 1 < 2 Û 1 < 2 Û 1< 2 Û 1+ 1< 1+ 2 Û 2 < 1+ 2
Đáp án cần chọn là: C
Câu 6. [TH] Biểu thức x - 3 có nghĩa khi : D. . A. x ³ 3 x < 3 .
B. x < 0 .
C. x ³ 0 . Lời giải
Ta có x - 3 có nghĩa khi x - 3 ³ 0 Û x ³ 3
Đáp án cần chọn là: D 2 9 16
Câu 7. [TH] Rút gọn biểu thức 25 - +
169 ta được kết quả là: 5 2 81 A.13 . B. 12 . D. 14 . D. 15 . Lời giải Ta có 2 25 = 5 = 5 = 5 2 16 4 æ ö 4 4 = ç ÷ ç ÷ = = , 2 169 = 13 = 13 = 13 81 çè9÷ø 9 9 2 9 16 2 9 4 Nên 25 - + 169 = .5- . + 13 = 2- 2+ 13 = 13 5 2 81 5 2 9 Trang 2
Đáp án cần chọn là: A
Câu 8. [TH]: Tìm các số x không âm thỏa mãn x ³ 3 D. . A. x £ 9 x < 9 .
B. x > 9 .
C. x ³ 9 . Lời giải Vì 3 =
9 nên x ³ 3 được viết là x ³ 9. Vì x không âm nên x ³ 9 Û x ³ 9
Đáp án cần chọn là: C
Câu 9. [VD]: Với giá trị nào của x để 4 + x - 1 = 2 ? A. 22 . B. 2 . C. 1 . D.17 . Lời giải
ĐKXĐ: x ³ 1 4 + x - 1 = 2 Þ 4 + x - 1 = 4 Þ
x - 1 = 0 Þ x - 1 = 0 Þ x = 1(t / m )
Vậy đáp án cần chọn : C
Câu 10. [VD] Tính giá trị biểu thức: ( - )2 2 3 + ( - )2 1 3 A. 3 . B. 12 . C. 1 . D. 2 3 . Lời giải Ta có: ( - )2 2 3 = 2 - 3 mà 2 = 4 > 3 (vì 4 > 3) nên 2 - 3 > 0 . Từ đó ( - )2 2 3 = 2 - 3 = 2 - 3 Ta có ( - )2 1 3 = 1- 3 mà 1= 1 < 3 (vì 1 < 3) nên 1- 3 < 0 . Từ đó ( - )2 1 3 = 1- 3 = 3 - 1 Nên ( - )2 2 3 + ( - )2 1 3 = 2 - 3 + 3 - 1 = 1
Đáp án cần chọn là: C Trang 3 P -
Câu 11. [VD]: Cho P = 6 + 4 2 . Khi đó 4 Q =
= a + b 2 thì ab bằng P - 2 A. - 2 B.- 1 . C. 1 . D. 2 .
Câu 12. [VDC] : Cho biểu thức 1 1 1 1 A = + + + ..... + 1.199 2.198 3.197 199.1
.Khẳng định nào sau đây là đúng?
A. A = 1, 99 .
B. A ³ 1, 99.
C. A > 1, 99.
D. A < 1, 99.
2. TRẮC NGHIỆM ĐÚNG SAI
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Trong các nhận xét sau, câu nào đúng, câu nào sai ?
A. Căn bậc hai số học của 36 là 6 và
B. 25 có hai căn bậc hai là 5 và - 5 . - 6 .
C. Số 0 có đúng một căn bậc hai là
D. Số - 7 không có căn bậc hai. chính nó. Lời giải
Đáp án B, C, D đúng. Căn bậc hai số học của 36 là 6. Vậy đáp án A sai.
Câu 2.Hãy chọn hệ thức đúng A. 9  3  B. 1, 44  1  ,2 16 4 D. 2 2 5  4  5  4 C.  9 3 Lời giải
A. Sai, sửa lại là: 9  3
B. Sai, sửa lại là: 1, 44  1, 2 C.Đúng D. Sai, sửa lại là: 2 2 2
5  4  25 16  3  3 .
Câu 3. Trong các hệ thức sau, hệ thức nào đúng, hệ thức nào sai với mọi số , a b  0 A.
a  b  a  b
B. a  b  a  b
D.Cả 3 hệ thức đều sai C.
a  b  a  b Lời giải Trang 4  ab2 Ta có
 a  b  1 2 2 2
Lại có:  a  b   a    b  2 a b  a  b  2 a b 2
Từ (1)(2) suy ra đáp án A và B đều sai
- Do a  b  a  b  2 a b  0  2 a b , do vậy C là hệ thức đúng.
Câu 4.Cho số dương a. Khẳng định nào sau đây là đúng, khẳng định nào là sai:
A. Nếu a 1 thì a  1 B.
Nếu a 1 thì a  a C.A) đúng; B) sai D. A,B đều sai Lời giải Xét đáp án A
Do a 1 và 1  0 nên a và 1 đều xác định và đều là số dương 2
Ta có: a  1  a 1  0, ta có: a    a  2 1 1   a   1  a   1 Vì a 1  0 và a 1  0
 nên a 1  0  a  1
Xét đap án B : Từ đáp án A, ta có a  1, nhân cả hai vế của bất đẳng thức với
a  a  0 , ta được: 2
a. a  a  a  a  a  a
Vậy ta chọn đáp án C đúng, D sai
3. TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. [NB] Điều kiện của x để biểu thức 4x 12 có nghĩa: 1 1  C. x  3 
D. x  3 A. x  B. x  3 3 Lời giải
4x 12 có nghĩa khi 4x 12  0  4x 12  x  3 Chọn D
Câu 2. [NB] Giá trị của x thỏa mãn 8  4x  2 là: A. x  1  3 B. x 
C. x 1 3 2 D. x   2 Lời giải:
ĐKXĐ: 8 4x  0  x  2 Trang 5
Ta có: 8  4x  4  4x  8  4  4  x 1(T/M)
Vậy x 1 Chọn C
Câu 3. [TH]Với giá trị nào của x để căn thức x 1  1 x có nghĩa? A. 1   x 1 B. x  1 
C. x 1
D. 0  x 1 Lời giải: x 1 0 x  1 
x 1  1 x có nghĩa khi     1   x 1 1   x  0  x  1 Chọn A x  2
Câu 4. [TH] Khi x  49 , biểu thức
có giá trị bằng: 1  x A. 2 B. 2 3 3 C. D. 2 2 Lời giải: ĐKXĐ: x  0
Với x  49 thỏa mãn điều kiện x  0 ta có: 49  2 7  2 9 3     1 49 1 7 6  2 Chọn D
Câu 5. [VD] Giá trị rút gọn biểu thức P  2 27  300  3 75 bằng A. 31 3 B. 3 C. 8 3 D. 3 3 Lời giải:
P  2 27  300  3 75
 2. 9.3  100.3  3 25.3  2.3 3 10 3  3.5 3   6 3 10 3 15 3  3 Chọn B 2 2
Câu 6. [VDC] Biểu thức  11  3  3  11 có giá trị bằng: Trang 6 A. 2 11  6 B. 0 C. 6  D. 2 11 Lời giải   2    2 11 3 3 11  11  3  3  11
 11  3  11  3  2 11  6 Chọn A
PHẦN II. BÀI TẬP TỰ LUẬN
DẠNG 1: TÍNH TOÁN, THU GỌN BIỂU THỨC CHỨA CĂN BẬC HAI ĐƠN GIẢN Phương pháp giải
☑️Bước 1: Vận dụng thích hợp các phép tính và các phép biến đổi đã biết làm
xuất hiện căn thức cùng loại; + Đưa thừa số 2
A ra ngoài dấu căn: 2 A B  A B với B ≥ 0; 2
 A B; A  0
+ Đưa thừa số vào tròn dấu căn: A B   2
 A B; A  0 A A AB 1 + Khử căn ở mẫu:   
AB; B  0, AB  0 2 B AB B B
m A  B A A B m 
+ Trục căn thức ở mẫu:  ;  . B B  A  B A  B
☑️Bước 2: Cộng, trừ, các căc thức bậc hai cùng loại. BÀI TẬP MẪU
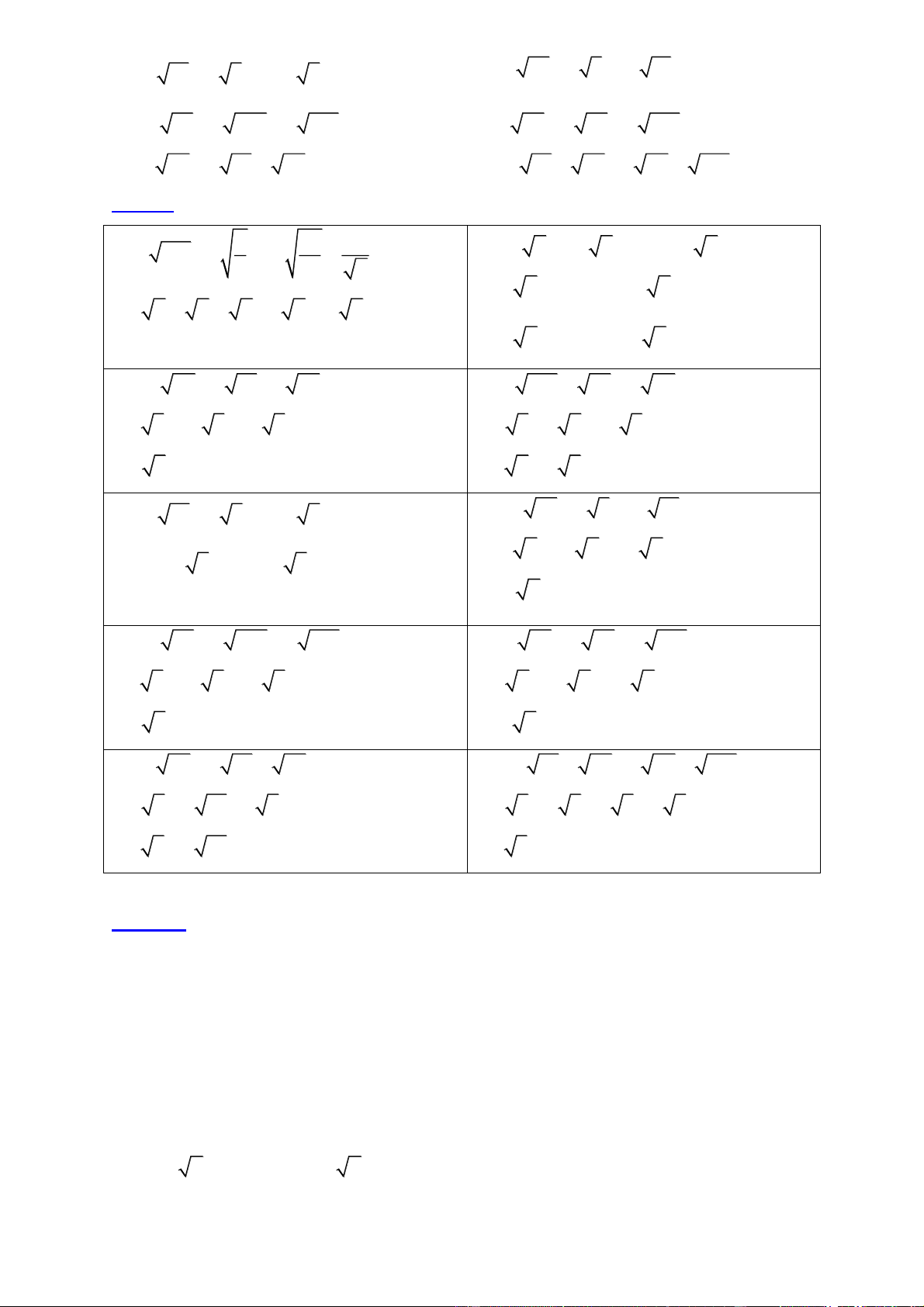
Ví dụ 1 [NB]: Tính 4 3 a) 2 5  125  80  605 b) 2 27  6  75 3 5
c) 15  216  33 12 6 d) 8 3  2 25 12  4 196 Lời giải Trang 7
a) 2 5  125  80  605 4 3 b) 2 27  6  75  3 5 2 5  5 5  4 5 11 5 2 3  10 5  6 3  6. 3  .5 3 3 5  6 3  4 3  3 3  5 3 c) 15  216  33 12 6 d) 8 3  2 25 12  4 196  15 6 6  3312 6
 8 3  2 25.2 3  4 8 6
 9  2.3 6  6  24  2.3.2 6  9  8 3 5 8 3  4 8 3    0
3  6   2 6  3
 3 62 6 3  6 Ví dụ 2 [TH]: Tính 3  5 3  5  5 22 2  3 2  3 10  2 10 8  8 5 a)  b) c)  d) 2  3 2  3 10  2 5  2 1 5 2 5  4 Lời giải 2  3 2  3 3  5 3  5 a)  b) 2  3 2  3 10  2  2  32  3 2 32 3
3  5 3  5 10  2    1 1 8
   2    2 3  5 2 10  2 2  2 3 2 3  8  2  3  2  3 3  5  10  2   4  4 10  2 10 8  5 22  c)  8 5 5  2 1 5 d) 2 5  4 Trang 8
102 10 5 2 81 5 5  4 5  4  8 5    2 5  4 3 4  9  4 5  10 5 10 2 10 2  4 5    2  2 5 2 5 4 3 94 52 5 4  
5  2  2 5   5  2 4 18 5  36  40 16 5  4 2 5  4  4 5  2  2
Ví dụ 3 [TH]: Tính giá trị của biểu thức B  4  10  2 5  4  10  2 5 Lời giải c) Ta có: B 
4  10  2 5  4  10  2 5 2   2  B 
4  10  2 5  4  10  2 5     2
 B  4  10  2 5  4  10  2 5  2 4 10 2 5 4 10 2 5  2
 B  8 2 6  2 5 2
 B  8 2 5 2 5 1  B     2 2 8 2 5 1 ; B  0
 B  8  2 5   1  B  6  2 5
 B  5 2 5 1  B    2 5 1  B  5 1 Trang 9 Vậy B  5 1
Ví dụ 4 [VD]: Chứng minh rằng: 5  2 649  20 6 5  2 6  9 3 11 2 Lời giải
Ta có: VT  5  2 6 49  20 6  5  2 6
 5 2 625 2.5.2 6  24 3 2 6  2      2   2 5 2 6 5 2 6 3 2
 52 6 3  2
 5 3  5 2  6 2  4 3  9 3 11 2
Mà: VP  9 3 11 2 VT VP
Vậy 5  2 649  20 6 5  2 6  9 3 11 2 (đpcm)
Ví dụ 5 [VD]: Tính giá trị của biểu thức: 1 1 1 1 A     ....... 3  5 5  7 7  9 97  99 Lời giải 1 1 1 1 A     ....... 3  5 5  7 7  9 97  99 1
 . 5  3  7  5  9  7 ....... 97  99 2 1  . 99  3 2
BÀI TẬP TỰ LUYỆN
Dạng 1: Biểu thức số trong căn có dạng hằng đẳngthức: Phương pháp:
Chú ý các hằng đẳng thức: Trang 10
a  a b  b  a  b 2 2 2
với b  0 a 
ab  b   a  b 2 2
với a  0,b  0 2
a  b  (a  b).(a  b) với b  0
a  b  ( a  b).( a  b) với a  0, b  0
Sau khi nhận dạng, tách số hạng và viết được dưới dạng hằng đẳng thức trên thì áp dụng: 2
 A  A (A 0) 2 A  A   2
 A  A (A  0)
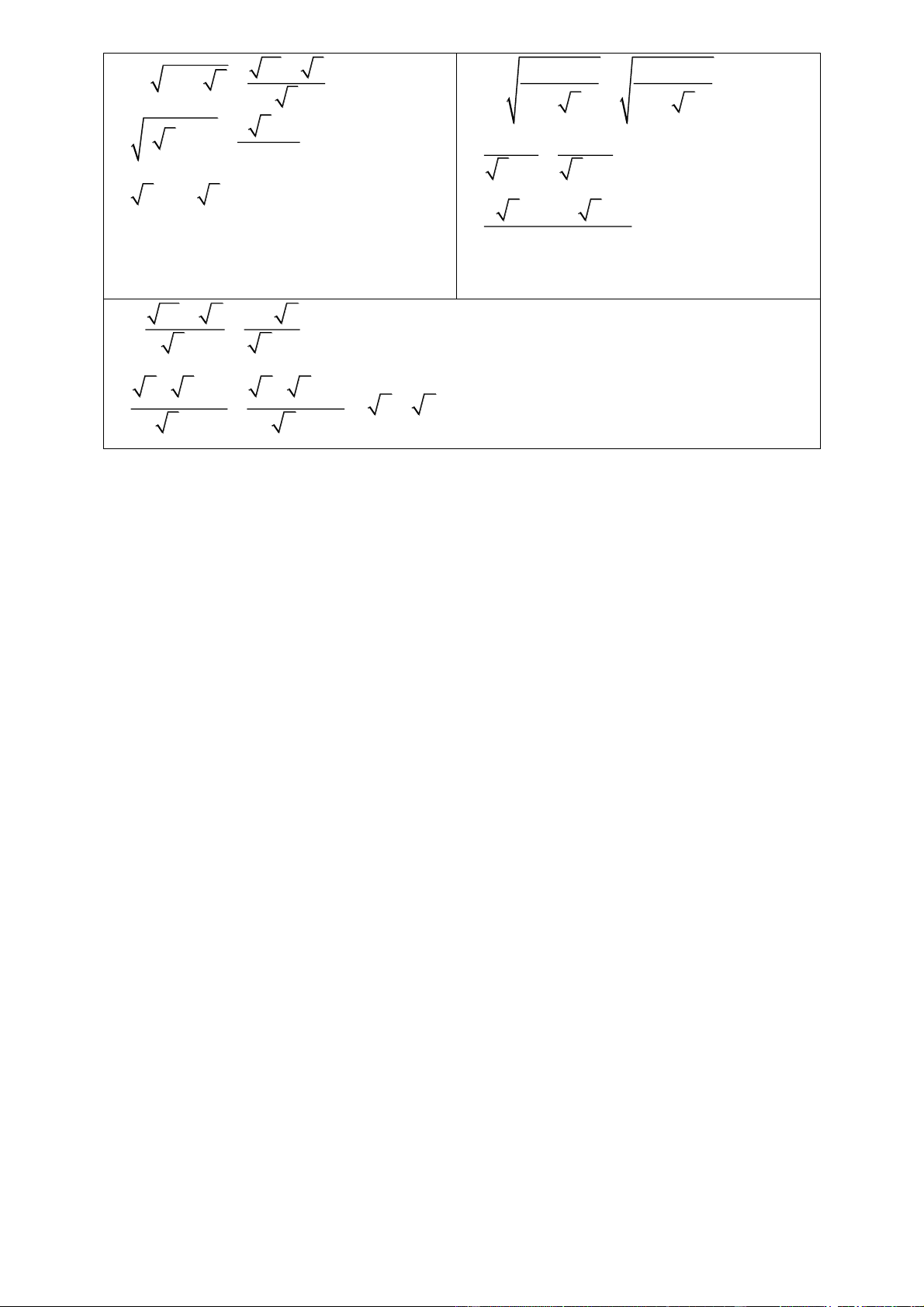
Bài 1. [NB] Tính giá trị các biểu thức: a) 8  2 15 b) 3  8 c) 11 4 6 d) 14  6 5 e) 22  8 6 f) 16  6 7 9 g)  2 4 Hướng dẫn: a     2 ) 8 2 15 5 3 b     2 ) 3 8 2 1
 2 1c) 11 4 6  11 2 24  5  3    2 8 3  8  3
d) 14  6 5  9  2 45  5 ) e
22  8 6  16  2 96  6 f ) 16  6 7  9  2 63  7
 9  5  3  5    2 16 6  4  6    2 9 7  3  7 9 1 1 2 g)  2   2. . 2  2   1  1 2     2  4 4 2  2  2
Bài 2. [TH] Tính giá trị các biểu thức: 289  4 72 b) 2. 7  3 5 59 6 a) c)  2 16 25 5 Trang 11 d) 2  3. 6  2 
e)  21  7. 10  2 21 Đáp án 289  4 72
b) 2. 7  3 5  14  2.3 5 59 6 a) c)  2 16 25 5
 9  2. 45  5   9  52 288  2 288 1 288 1 9 3     2. . 2  2   4 4 3 5 25 5 2  3  3   2   2    5  5
d ) 2  3 . 6  2 
e) 21  7. 10  2 21       2 2 3 . 6 2
  21  7.  7  32
 2 3.6 12  2
  217. 7  3
 2 3.8 4 3
 7 3  3 7  7 7  7 3  4 7
 16  8 3 8 3 12  2
Dạng II: Biến đổi biểu thức bằng cách đưa thừa số ra ngoài hoặc vào trong dấu căn: Phương pháp
Đưa thừa số ra ngoài dấu căn: 2
A .B  A . B với B  0 Nếu A  0 thì 2
A .B  A B Nếu A  0 thì 2
A .B  A B
Đưa thừa số vào trong dấu căn:
Nếu A  0, B  0 thì 2 A B  A .B
Nếu A  0, B  0 thì 2
A B   A .B
Bài 3. [VD] Tính giá trị biểu thức: 1 1 21
B  3 2.4  2  31 2 22 A  112  7 14  7 28 7
C  2 27  5 12  3 48
D  147  54  4 27 Trang 12   E    2 15 2 3 12 5 F  3 50 7 8 12 18
G  2 80  2 245  2 180 H  28  4 63  7 112 M  20  2 10  45
N  2 12  48  3 27  108 Đáp án 1 1 21
B  3 2.4  2  31 2 22 A  112  7 14  7 28 7
12 2  6  3.9 4 2
 4 7  7  7  3 7   7
 12 2  6  27 12 2  21
C  2 27  5 12  3 48   D  147 54 4 27  6 3 10 3 12 3    7 3 3 6 12 3  4 3   3 6 5 3   E    2 15 2 3 12 5 F  3 50 7 8 12 18     15 2 14 2 36 2 15 12 5 12 12 5   37 2 27
G  2 80  2 245  2 180 H  28  4 63  7 112  8 5 14 5 12 5    2 7 12 7 28 7  6 5  18 7 M  20  2 10  45
N  2 12  48  3 27  108  2 5  2 10  3 5     4 3 4 3 9 3 6 3  5 5  2 10  3 3
Dạng III: Rút gọn biểu thức số dạng phân số. Phương pháp:
-Rút gọn thừa số chung của tử và mẫu nếu có.
-Sử dụng hằng đẳng thức để đưa biểu thức số ra khỏi dấu căn
-Nếu mẫu số chứa căn thì nhân cả tử và mẫu với biểu thức liên hợp mẫu để triệt tiêu căn ở mẫu
- Quy đồng mẫu nếu cần để rút gọn.
Chú ý: a  b liên hợp với a  b Trang 13
a  b liên hợp với a  b
Bài 4[VD] Rút gọn biểu thức 1 1 1 1 A   B   5  2 6 5  2 6 3  2 3  2 3 2 3 15  12 1 C   D   3 3 1 5  2 2  3 3  5 5  3 5  2 5 3  3 E   F     5  3 3  5 5  3 5 3 15  3 4 4 G  6  2 5  H   2 2 3 2 5 2 5 10  2 2  2 I   5 1 2 1 Đáp án 1 1 1 1 A   B   5  2 6 5  2 6 3  2 3  2 5  2 6  5  2 6     3 2 3 2  25  24 3  4  4 6  4 3 2 3 15  12 1 C   D   3 3 1 5  2 2  3 15  2 3 2  3 2 3.( 3 1)    3  5  2 4  3 3 1   3  2  3  2  3  3  3  3 3  5 5  3 5  2 5 3  3 E   F     5  3 3  5 5  3 5 3   2   2 3 5 5 3 5 5 10 3 3  3       5  3 3  5 5  3 5 3
 5  2  3 1 5  3 3
  2 15  5  5  2 15  3   3 2  2  15 Trang 14 15  3 4 4 G  6  2 5  H   2 2 3 2 5 2 5    2 3 5 3 5 1  2 2 3   5  2 5  2  5 1 5 1 2 5  4  2 5  4   2 5  4  8 10  2 2  2 I   5 1 2 1 2. 5   1 2. 2   1    2  2  0 5 1 2 1 Trang 15