67 trang 5 lượt tải

Chuyên đề cấp số nhân môn Toán 11 định hướng cấu trúc mới

10

Tài liệu gồm 67 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, bao gồm lý thuyết và bài tập chuyên đề cấp số nhân môn Toán 11 định hướng cấu trúc mới.

Chủ đề: Tài liệu chung Toán 11 83 tài liệu

Môn: Toán 11 3.5 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/67
CẤP SỐ NHÂN
TOÁN 11
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề DÃY SỐ - CẤP SỐ
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
.q
q
( )
n
u
q
1
,2
nn
u u q n
−
=
( )
n
u
1
u
q
n
u
1
1
,2
n
n
u u q n
−
=
12
,,
k k k
u u u
++
( )
n
u
( )
2
21k k k
u u u
++
=
n
( )
n
u
.q
1 2 3
... .
nn
S u u u u= + + +
( )
1
1
1
n
n
uq
S
q
−
=
−
( )
n
u
( )
21
5;
+
=−
n
n
u
( )
31
1 .3 ;
+
=−
n
n
n
u
1
2
1
2
.
+
=
=
nn
u
uu
( )
n
u
q
16
2, 486 uu==
;q
4
28
,
3 21
qu==
1
;u
1
3, 2 uq= = −
15
26
51
102
uu
uu
+=
+=
2 4 5
3 5 6
10
20
u u u
u u u
− + =
− + =
42
53
72
144
uu
uu
−=
−=
1 3 5
17
65
325
u u u
uu
− + =
+=
35
26
90
240
uu
uu
+=
−=
1 2 3
1 2 3
14
. . 64
u u u
u u u
+ + =
=
1 2 3
1 2 3
21
1 1 1 7
12
u u u
u u u
+ + =
+ + =
1 2 3 4
2222
1 2 3 4
30
340
u u u u
uuuu
+ + + =
+ + + =
148
9
a
b
, 2 , 2 a a b a b++
( ) ( )
22
1 , 5, 1 b ab a+ + +
2 1 2
,,
y x y y z−−
,, x y z
,, a b c
( )
log log log
, , 1, 0 1
log log log
a a b
c b c
N N N
a b c N
N N N
−
=
−
, 3; 2xx+
5 10 15
2 3; 3; 5 3u x u x u x= − = + = −
.x
5 , 5 2 , 8 x y x y x y+ + +
( ) ( )
22
1 , 1, 2 y xy x− − +
x
y
2
2 2 2
7
10 10 ... 10 9 99 ... 999..9
1 1 1
7 77 777 ... 777...7 2 4 ... 2
2 4 2
n sè 9
sè
a) b)
c) d)
= + + + = + + +
= + + + + = + + + + + +
n
n
n
n
AB
CD
2 99 2
12
1 2.2 3.2 ... 100.2 1. 2. ... .. b) = + + + + = + + +
n
P P x x nx
( )
( )
n sè 5
a) b)
c) d)
e)
n
n
n
n
AB
C D x x x x
x
xx
En
= + + + = + + +
= + + + + = + + + + + +
= + + + + −
2
2 2 2
2 2009 2
2
2
5 5 ... 5 15 155 ... 1555...5
1 1 1
1 2.3 3.3 .. 2010.3 ... 0
1 4.5 7.5 ... 3 2 5 f)
n
n
F
−
= + + +
2
1 3 2 1
...
2
22
( )
n
u
, mk
mk
.
k k m k m
u u u
−+
=
0
90A =
6
,,
3
a b c
q
( )
( )
12
11
1, 2
:
3 2 2
n
n n n
uu
u
u u u n
+−
==
= −
( )
n
v
( )
1
1
n n n
v u u n
+
= −
( )
n
v
( )
n
u
( )
( )
n
n
n
u
u
u
un
+
=
+
=
1
2
1
2
:
4
1
4
( )
n
u
( )
( )
1
1
4
:
12 1
n
nn
u
u
u u n
+
=
= +
( )
n
u
1; 1; 1; 1−−
1; 3; 9;10−
1; 0; 0;0
32; 16; 8;4
1; 3;9; 27;54−−
1;2; 4;8;16
1; 1;1; 1;1−−
1; 2; 4; 8;16−−
( )
n
u
n
un= 3
n
n
u = 2
n
u
n
=
1
n
n
u =+21
( )
n
u
1*
3
.2 ,
5
n
n
un
−
=
1
6
,2
5
uq==
1
3
,2
5
uq= = −
1
6
,2
5
uq= = −
2
3
,2
5
uq==
( )
n
u
1
u
0q
( )
n
u
*
1
.
n
n
u q u n=
*
1n
u u q n=
1*
1
.
n
n
u q u n
−
=
1*
1
n
n
u u q n
−
=
( )
n
u
1
2u =
2
6u =
3
4−
1
3
4
( )
n
u
4
9u =
5
81u =
3
72
18
9
( )
n
u
2
6u =
5
162u =
3
3−
2
1
3
1
2
3,
3
uq= − =
96
243
−
( )
n
u
1
3u =−
2q =−
192−
( )
?
n
u
6
7
5
8
2−
1024−
11
10
9
8
( )
n
u
1
2u =−
3q =
2
u
2
6.u =−
2
1u =
2
18.u =−
2
6.u =
( )
n
u
1
1
1
8
5
n
n
u
u
u
+
=
+
=
( )
n
v
2
nn
vu=−
( )
n
v
q
2
5
q =
5q =
8
5
q =
1
5
q =
( )
n
u
25
8; 64uu= − =
6
u
512
256
128−
1024−
( )
n
u
2
8u =−
5
64u =
3
u
16−
32
32−
16
( )
n
u
24
35
60
180
uu
uu
+=
+=
1
u
3
6
2
5
( )
n
u
27
38
198
396
uu
uu
+=
+=
( )
n
u
2
3
4
1
u
( )
n
u
10 1
7 4 1
511
73
uu
u u u
−=
+ + =
1
1u =
1
2u =
1
1u =−
1
2u =−
.
n
u
2018 2020
2019
2
uu
u
2019 2018 2020
.u u u
2
2019 2018 2019
.u u u
2019 2018 2020
.u u u
2 1, , 2 1x x x−+
.x
1
3
1.=x
3
3
3
x
2 3; ; 2 3x x x−+
3x =
3x =
3x =
5=x
x
1; ; 2xx+
2
3
1
0
2−
256
8
15
32768−
16384
16384−
32768
2
; 8;xx
x
4.x
5.x
2.x
1.x
x
2 , 3 3, 5 5x x x++
250
3
−
250
3
250
250−
( )
n
u
1
1u =
2q =
( )
n
u
3
7
9
5
( )
n
u
1
2u =
3q =−
4
( )
n
u
162
160−
40−
1
2
( )
n
u
3
9u =
3q =−
3
S
3
( )
n
u
7.
36.
14.−
1
( )
n
u
2
6u =−
5
48u =
5
S
33
31−
93
11
1
3u =
2q =
5
5
S
5
93S =
5
45S =−
5
93S =−
5
45S =
( )
n
u
23
4, 13SS==
2
0u
5
S
11
2
35
16
181
16
( )
n
u
1 2 3
41
13
26
u u u
uu
+ + =
−=
( )
n
u
8
1093S =
8
9841S =
8
3280S =
8
3820S =
( )
n
u
nn
S u u u= + + +
12
...
u S S+ = =
2 4 3
43, 13
S
6
182
728
364
121
( )
n
u
1
*
1
2020
1
,
3
+
=
=
nn
u
u u n
1 2 3
...= + + + +
nn
S u u u u
n
lim
n
S
2020
1
3
3030
0
3
3
x
y
3
x
y
9
xy+
5−
7
0
11
( )
n
u
1
2
1
1
3 2 ; 1
nn
u
u u n
+
=
= +
2 2 2 2
1 2 3 2011
...S u u u u= + + + +
2011
3 2012S =−
2011
3 2011S =−
2011
31S =−
2011
3S =
( )
n
u
2
2u =−
5
54u =
1000
1000
1000
31
.
2
S
−
=
1000
1000
13
.
4
S
−
=
1000
1000
13
.
6
S
−
=
1000
1000
31
.
6
S
−
=
1
3u =
2q =
n
21
n
10n =
3n =
7n =
n
1
u
( )
n
u
1 2 3
21u u u+ + =
4 5 6
567u u u+ + =
3
21
13
9
13
21
( )
n
u
1
2u =
1 2 3
20 10u u u−+
( )
n
u
6250
31250
136250
39062
( )
n
u
1
*
1
3
,
3
+
=

=
nn
u
n
uu
( )
n
u
3=
n
n
u
1+
=
n
n
un
1
3
+
=
n
n
u
1
3
−
=
n
n
u
()
n
u
1
1
1
8
5
n
n
u
u
u
+
=
+
=
()
n
v
2
nn
vu=−
()
n
v
2
5
5q =
8
5
q =
1
5
q =
( )
n
u
( )
3 4 5 6 7 8
2 u u u u u u+ + = + +
8 9 10
2 3 4
uuu
u u u
++
++
4
1
8
2
( )
n
u
1 1 2 2
*
1
3 3 6
2,
nn
u u u u
u u n
+
= − + +
=
n
2021
2
n
u
2021
1012
2022
1011
10
2
12288 m
2
6 m
2
12 m
2
24 m
2
3m
3240
1
81
82
80
79
20. 000
9
10.
20. 000
20. 000
40. 000
1n +
n
X
X
32767
31797
12060
35067
50000
7%
( )
50 m
20326446
21326446
23326446
22326446
18895000
1422851
18892000
18892200
A
120
6% /
10
A
A
214,90
224,10
234,90
215,10
44mm
2
1m
60. 000
575000
387500
465000
232500
( )
15 m
( )
35 m
( )
50 m
( )
30 m
( )
25 m
1 1 1 1
A B C D
1k
A
+
1k
B
+
1k
C
+
1k
D
+
kk
AB
kk
BC
kk
CD
kk
DA
1,2,...).k =
2018 2018 2018 2018
A B C D
2019
2
.
2
1006
2
.
2
2018
2
.
2
1007
2
.
2
m
( )
3 2 2
7 2 6 8 0x x m m x− + + − =
342−
216−
344
216
( )
n
u
( )
21
5;
+
=−
n
n
u
( )
31
1 .3 ;
+
=−
n
n
n
u
1
2
1
2
.
+
=
=
nn
u
uu
( )
( )
( )
21
2
*
1
23
1
5
5 25, .
5
+
+
+
+
=−
⎯⎯→ = − =
=−
n
n
n
n
n
n
u
u
n
u
u
( )
n
u
( )
3
1
5 125= − = −u
25.q =
( )
( )
31
3*
1
1
34
1
1 .3
3 27, .
1 .3 ;
+
+
+
+
+
=−
⎯⎯→ = − = −
=−
n
n
n
n
n
n
n
n
u
u
n
u
u
( )
n
u
1
81=−u
27.q =−
1
1 2 3
2
1
2
2; 4; 16.
+
=
⎯⎯→ = = =
=
nn
u
u u u
uu
3
2
12
u
u
uu
( )
n
u
( )
n
u
q
16
2, 486 uu==
;q
4
28
,
3 21
qu==
1
;u
1
3, 2 uq= = −
55
61
486 243 9 3.= = = =u u q q q
3
4 1 1
89
.
21 7
= = =u u q u
( )
1
1
1
192 192 3. 2 7.
n
n
n
u u q n
−
−
= = = − =
192
15
26
51
102
uu
uu
+=
+=
2 4 5
3 5 6
10
20
u u u
u u u
− + =
− + =
42
53
72
144
uu
uu
−=
−=
1 3 5
17
65
325
u u u
uu
− + =
+=
35
26
90
240
uu
uu
+=
−=
1 2 3
1 2 3
14
. . 64
u u u
u u u
+ + =
=
1 2 3
1 2 3
21
1 1 1 7
12
u u u
u u u
+ + =
+ + =
1 2 3 4
2222
1 2 3 4
30
340
u u u u
uuuu
+ + + =
+ + + =
( )
4
4
11
15
11
4
5
26
11
11
51
51
51
102
102
102
(1)
(2)
u u q
uu
u u q
uu
q u u q
u q u q
+=
+=
+=


+=
+=
+=
51 102 2qq= =
1
3u =
( )
( )
23
34
1
2 4 5
1 1 1
2 4 5
2 2 3
3 5 6
1 1 1
1
1 10
10
10
20
20
1 20
(1)
(2)
u q q q
u u u
u q u q u q
u u u
u q u q u q
u q q q
− + =
− + =
− + =


− + =
− + =
− + =
2q =
1
1u =
( )
2
2
1
1 2 3
1 1 1
2
2
1 2 3
1 1 1
1
1 21
21
21
1 1 1 7
1 1 1 7
1 1 1 7
1
12
12
12
u q q
u u u
u u q u q
u u u
u u q u q
u q q
+ + =
+ + =
+ + =



+ + =
+ + =
+ + =


( )
2
1
2
2
1
1 21
1 1 7
.
12
(1)
(2)
u q q
qq
uq
+ + =
++
=
1
0u =
0q =
( )
2
1
21
11qq
u
+ + =
1
22
1
22
1
1
6
21 7
36
6
12
uq
uq
uq
uq
=
= =
=−
11
6
6u q u
q
= =
2
23
6 15 6 0
1
12
2
qu
qq
qu
= =
− + =
= =
11
6
6u q u
q
= − = −
1
2
1
9 65 27 3 65
42
6 27 6 0
9 65 27 3 65
42
qu
qq
qu
− + +
= =
+ + =
− − −
= =
( )
( )
( )
( )
( )
2
2
2
1
1 1 1
1 2 3
1
2
3
1 2 3
1 1 1
1
1
1 14
14
14
1 14
. . 64
. . 64
4
64
u q q
u u q u q
u u u
u q q
u u u
u u q u q
uq
uq
+ + =
+ + =
+ + =
+ + =
=
=
=
=

0q =
11
4
4u q u
q
= =
1
2
1
22
4 10 4 0
1
8
2
qu
qq
qu
= =
− + =
= =
148
9
1 2 3 4
, , , a a a a
( )
( )
( )
( )
( ) ( )
2
2
2 1 2
2
1 1 2
2 1 3
21
12
3 2 4
2
1
14
2
11
23
22
2
*
21
2 14
2 14 2
2
12
14
12 3
12
12 4
12 2
a a a d
a q a q a d
a a a
a d a
a a d
a a a
a
aa
a q a q
qq
aa
aad
da
=+
= + +
=
+ = −
+ + =
=+

=
+=
+=
+
+=
+ + =
=−
( )
25 15 9 3
2,4,8,12 , , , ,
2 2 2 2



( )
n
a
24
, aa
2
6
30 144 0
24
t
tt
t
=
− + =
=
1
1
2
2
3
41
1
1
2
2
3
4
1
6
6
6
4
24 24
24
24
24
61
6
6
24 4
aq
aq
a
q
a a q
aq
aq
a
a
q
aq
=
=
=
=
==

=
=
=

=
==
=
1q
1
3, 2aq==
( )
10
10 1
21
3. 1024 1 3069
21
Su
−
= = − =
−
a
b
, 2 , 2 a a b a b++
( ) ( )
22
1 , 5, 1 b ab a+ + +
, 2 , 2 a a b a b++
( ) ( )
2 2 2 3 (1)a a b a b a b + + = + =
( ) ( )
22
1 , 5, 1 b ab a+ + +
( ) ( ) ( )
2 2 2
1 1 5b a ab + + = +
( )( ) ( )
( )( )
( )( )
2
2
1 1 5
1 1 5
1 1 5
b a ab
b a ab
b a ab
+ + = +
+ + = +


+ + = − −
( )( )
1 1 5b a ab+ + = +
3ab=
( )( )
2
1 3 1 3 5 1 3b b b b a+ + = + = =
( )( )
1 1 5b a ab+ + = − −
3ab=
( )( )
2
1 3 1 3 5 2 4 2b b b b b+ − + = − + − = = −
2 1 2
,,
y x y y z−−
,, x y z
2 1 2
,,
y x y y z−−
( ) ( )
( )( )
2 2 2 1
y z y x
y x y z y y x y z y
− + −
+ = =
− − − −
( ) ( )( )
2y y x z y x y z − − = − −
2
xz y=
,, x y z
,, a b c
( )
log log log
, , 1, 0 1
log log log
a a b
c b c
N N N
a b c N
N N N
−
=
−
( )
2
1ac b=
( ) ( )
2
log log log log 2log 2
N N N N N
ac b a C b = + =
1 1 2 1 1 1 1
log log log log log log log
a C b a b b C
N N N N N N N
+ = − = −
log log log log log log log
log .log log .log log log log
log log log
log log log
− − −
= =
−
−
=
−
b a c b b a a
a b c b c b c
a b a
b c c
N N N N N N N
N N N N N N N
N N N
N N N
, 3; 2xx+
5 10 15
2 3; 3; 5 3u x u x u x= − = + = −
.x
5 , 5 2 , 8 x y x y x y+ + +
( ) ( )
22
1 , 1, 2 y xy x− − +
x
y
2
2 2 2
7
10 10 ... 10 9 99 ... 999..9
1 1 1
7 77 777 ... 777...7 2 4 ... 2
2 4 2
n sè 9
sè
a) b)
c) d)
= + + + = + + +
= + + + + = + + + + + +
n
n
n
n
AB
CD
2
10 10 ... 10
n
A = + + +
A
n
( )
n
u
1
10, 10 uq==
( )
2
1 10 10
10 10 ... 10 10. 10 1
1 10 9
n
nn
A
−
= + + + = = −
−
( )
( ) ( )
22
9 99 ... 999..9 10 1 10 1 ... 10 1 10 10 ... 10
n sè 9
nn
Bn= + + + = − + − + + − = + + + −
( )
10
9 99 ... 999..9 10 1
9
n sè 9
n
Bn= + + + = − −
7
7 77 777 ... 777...7 9 99 999 ... 99...9
9
n sè 9
n sè 7
C

= + + + + = + + + +

( )
7 10
7 77 777 ... 777...7 10 1
99
n sè 7
n
Cn

= + + + + = − −

2
2
1 1 1
4 2 16 2 ... 2 2
4 16 2
= + + + + + + + + +
n
n
S
( )
2
2
1 1 1
4 16 .. 2 2 ..
4 16 2

= + + + + + + + +


n
n
n
( )( )
1
12
2
2
1
4 1 2 1 4 1 1 2 1
4. 2 . 4. 2 .
1
3 4 3 3 2
1
4
4 1 4 1
4 1 4.4 1
2 . 2
3 4 3.4
n n n
n
n
nn
nn
nn
S n n
nn
−
+
− − −
= + + = + +
−
−+
−+
= + = +
2 99 2
12
1 2.2 3.2 ... 100.2 1. 2. ... .. b) = + + + + = + + +
n
P P x x nx
2 99
1
1 2.2 3.2 ... 100.2 (1) P = + + + +
2 3 4 99 100
1
2 2 2.2 3.2 4.2 ... 99.2 100.2 (2)P = + + + + + +
( )
2 3 99 100
1
100
100 2 3 99 100 100
1
1 2 2 2 ... 2 100.2
21
100.2 1 2 2 2 ... 2 100.2 99.2 1
21
P
P
− = + + + + + −
−
= − + + + + + = − = +
−
2 1 2
0 2 0
1 2. 3. ... 1. 2. ... .
nn
P x x nx P xP x x nx
−
= + + + + = = + + +
2
00xP= =
( )
2
1
1 1 2 ...
2
nn
x P n
+
= = + + + =
1x
2 1 2
0 2 0
1 2. 3. ... 1. 2. ... .
nn
P x x nx P xP x x nx
−
= + + + + = = + + +
( )
( )
2 3 1
2 0 2 2
22
1 ...
1 1 1
1
1 1 1
nn
nn
nn
P P P xP x x x x nx
xx
P x nx P nx
x x x
−
− = − = + + + + + −

−−
− = − = −

− − −

( )
( )
n sè 5
a) b)
c) d)
e)
n
n
n
n
AB
C D x x x x
x
xx
En
= + + + = + + +
= + + + + = + + + + + +
= + + + + −
2
2 2 2
2 2009 2
2
2
5 5 ... 5 15 155 ... 1555...5
1 1 1
1 2.3 3.3 .. 2010.3 ... 0
1 4.5 7.5 ... 3 2 5 f)
n
n
F
−
= + + +
2
1 3 2 1
...
2
22
( )
n
u
, mk
mk
.
k k m k m
u u u
−+
=
0
90A =
6
,,
3
a b c
2 2 2
22
23
32
a b c
b ac b ac
=+
= =
( )( ) ( )
2 2 2 2
3
2 3 2 2 2 0 2 2 0
2
a ac c a ac c a c a c a c a c= + = + + − = = +
00
1
cos 60 , 30
2
c
B B C
a
= = = =
q
AB AC=
,, B C AH AB
12
2cot
2cot sin
1
sin
BC HC
C
q AH AH
CC
AH
B
q AB
= = =
=
==
22
2cos sin 1 cosC C C= = −
( )
20
cos 2cos 1 0 cos 1 2 0 90 C C C C + − = = − +
( )
sin 2 2 1C =−
( )
( )
1 1 1
2 2 1
sin 2
2 2 1
q
C
= = = +
−
( )
( )
12
11
1, 2
:
3 2 2
n
n n n
uu
u
u u u n
+−
==
= −
( )
n
v
( )
1
1
n n n
v u u n
+
= −
( )
n
v
( )
n
u
( )
1 1 1
2 : 2 2
n n n n n n
n u u u u v v
+ − −
− = − =
( )
n
v
2.q =
( ) ( )
( )
1 1 2 2 1 1 1 2 1
... ... 1
n n n n n n n
u u u u u u u u v v v
− − − − −
= − + − + + − + = + + + +
1
1
1 2 1 1
1. 1 2
... 2 1
12
n
n
n n n
v v v S
−
−
− − −

−

+ + + = = = −
−
( )
n
u
1
2
n
n
u
−
=
( )
( )
n
n
n
u
u
u
un
+
=
+
=
1
2
1
2
:
4
1
4
( )
n
u
1 2 3
2, 2, 2 u u u= = =
( )
21
n
un=
1
1: 2 nu==
nk=
( )
21
k
uk=
1nk=+
( )
1
21
k
uk
+
=
2
1
4
44
2
44
k
k
u
u
+
+
+
= = =
( )
21
n
un=
( )
n
u
( )
( )
1
1
4
:
12 1
n
nn
u
u
u u n
+
=
= +
( )
n
u
1; 1; 1; 1−−
1; 3; 9;10−
1; 0; 0;0
32; 16; 8;4
( )
n
u
q
1
1
.
n
nn
n
u
u u q q
u
+
+
= =
1; 1;1; 1−−
1q =−
1;3;9;10−
1;0;0;0
0q =
32;16;8; 4
1
2
q =
1; 3;9; 27;54−−
1;2; 4;8;16
1; 1;1; 1;1−−
1; 2; 4; 8;16−−
1;2; 4;8;16
2q =
1; 1;1; 1;1−−
1q =−
1; 2;4; 8;16−−
2q =−
1; 3;9; 27;54−−
3 1.( 3);( 27).( 3) 81 54− = − − − =
( )
n
u
n
un= 3
n
n
u = 2
n
u
n
=
1
n
n
u =+21
2,nn
( )
2
n
n
u =
1
1
2
2
2
n
n
n
n
u
u
−
−
==
qu==
1
2, 2
( )
n
u
1*
3
.2 ,
5
n
n
un
−
=
1
6
,2
5
uq==
1
3
,2
5
uq= = −
1
6
,2
5
uq= = −
2
3
,2
5
uq==
11
1
33
.2
55
u
−
==
21
2
2
1
36
.2 2
55
u
uq
u
−
= = = =
1
3
5
u =
2q =
( )
n
u
1
u
0q
( )
n
u
*
1
.
n
n
u q u n=
*
1n
u u q n=
1*
1
.
n
n
u q u n
−
=
1*
1
n
n
u u q n
−
=
1*
1
n
n
u u q n
−
=
( )
n
u
1
2u =
2
6u =
3
4−
1
3
4
q
( )
n
u
2
21
1
6
.3
2
u
u u q q
u
= = = =
3q =
( )
n
u
4
9u =
5
81u =
3
72
18
9
4
4
5
4
9
9
9
81
. 81
u
u
q
u
uq
=
=
=

=
=
( )
n
u
2
6u =
5
162u =
3
3−
2
1
3
4
51
21
.
.
u u q
u u q
=
=
33
5
52
2
162
. 27 3
6
u
u u q q q
u
= = = = =
1
2
3,
3
uq= − =
96
243
−
1
1
1
96 96 2 96
. 3. 5.
243 243 3 243
n
n
n
u u q n
−
−
− − −

= = − = =


96
243
−
( )
n
u
1
3u =−
2q =−
192−
( )
?
n
u
6
7
5
8
192−
n
( )
n
u
*
n
1
1
192 .
n
uq
−
−=
( ) ( )
1
192 3 . 2
n−
− = − −
( )
1
64 2
n−
= −
( ) ( )
61
22
n−
− = −
61n = −
7 n=
192−
7
( )
n
u
2−
1024−
11
10
9
8
2
3 1 1 1
. 4 2u u q u u= = =
( ) ( )
1
1
1
. 2. 2 2 1024 10
nn
n
n
u u q n
−
−
= = − = − − = − =
( )
n
u
1
2u =−
3q =
2
u
2
6.u =−
2
1u =
2
18.u =−
2
6.u =
21
.u u q=
2.3 6= − = −
( )
n
u
1
1
1
8
5
n
n
u
u
u
+
=
+
=
( )
n
v
2
nn
vu=−
( )
n
v
q
2
5
q =
5q =
8
5
q =
1
5
q =
11
2 2 1
nn
v u v u= − = − = −
11
22
n n n n
u v u v
++
= + = +
1
1 1 1
28
1 1 1
2 2 2
5 5 5 5
nn
n n n n n
n
vv
v v v v v
v
+
+ + +
++
+ = + = + = =
( )
n
v
1
5
q =
( )
n
u
25
8; 64uu= − =
6
u
512
256
128−
1024−
1
u
( )
n
u
1
1
2
1
5
1
4
3
.8
.8
8
4
64
2
. 64
8
uq
uq
u
u
u
q
uq
q
=−
=−
=−
=

=
=−
=
=−

( )
5
61
5
. 4. 2 128u u q= = − = −
( )
n
u
2
8u =−
5
64u =
3
u
16−
32
32−
16
3
52
.2u u q q= = −
32
. 16u u q==
( )
n
u
24
35
60
180
uu
uu
+=
+=
1
u
3
6
2
5
( )
( )
2
3
1
11
1
24
22
11
1
. 1 60
. . 60
2
3
. . 180
. 1 180
u q q
u q u q
u
q
u q u q
u q q
+=
+=
=


=
+=
+=
1
2u =
( )
n
u
27
38
198
396
uu
uu
+=
+=
( )
n
u
2
3
4
q
( )
n
u
( )
( )
5
6
1
27
11
27
25
38
11
1
1 198
198
198
2
396
396
1 396
u q q
uu
u q u q
q
uu
u q u q
u q q
+=
+=
+=
=
+=
+=
+=
1
u
( )
n
u
10 1
7 4 1
511
73
uu
u u u
−=
+ + =
1
1u =
1
2u =
1
1u =−
1
2u =−
10 1
7 4 1
511
73
uu
u u u
−=
+ + =
9
11
63
1 1 1
. 511
. . 73
u q u
u q u q u
−=
+ + =
( )
( )
9
1
63
1
. 1 511
. 1 73
uq
u q q
−=
+ + =
( ) ( )
( )
3 6 3
1
63
1
. 1 . 1 511
. 1 73
u q q q
u q q
− + + =
+ + =
( )
3
63
1
17
. 1 73
q
u q q
−=
+ + =
1
2
1
q
u
=
=
.
n
u
2018 2020
2019
2
uu
u
2019 2018 2020
.u u u
2
2019 2018 2019
.u u u
2019 2018 2020
.u u u
n
u
2
1 1 1 1
. . .
n n n n n n
u u u u u u
2019n
2019 2018 2020
..u u u
2 1, , 2 1x x x−+
.x
1
3
1.=x
3
3
3
2 1, , 2 1x x x−+
( ) ( )
2 2 2 2
13
2 1 2 1 4 1
33
x x x x x x x− + = − = = =
x
2 3; ; 2 3x x x−+
3x =
3x =
3x =
5=x
2 3; ; 2 3x x x−+
0x
( )( )
2
2 3 2 3x x x= − +
2 2 2
4 9 3 3x x x x = − = =
x
1; ; 2xx+
2
3
1
0
1; ; 2xx+
( )
22
13
1 2 2 2 0
13
x
x x x x
x
=+
+ = − − =
=−
2−
256
8
15
32768−
16384
16384−
32768
1
1
1
7
8
1
2
2
2
256
2
. 256
u
u
u
u
q
uq
=−
=−
=−

=
=−
=
14 14
15 1
. 2.( 2) 32768u u q = = − − = −
2
; 8;xx
x
4.x
5.x
2.x
1.x
2
; 8;xx
23
. 8 8 2x x x x
x
2 , 3 3, 5 5x x x++
250
3
−
250
3
250
250−
2 , 3 3, 5 5x x x++

Tài liệu khác của Toán 11

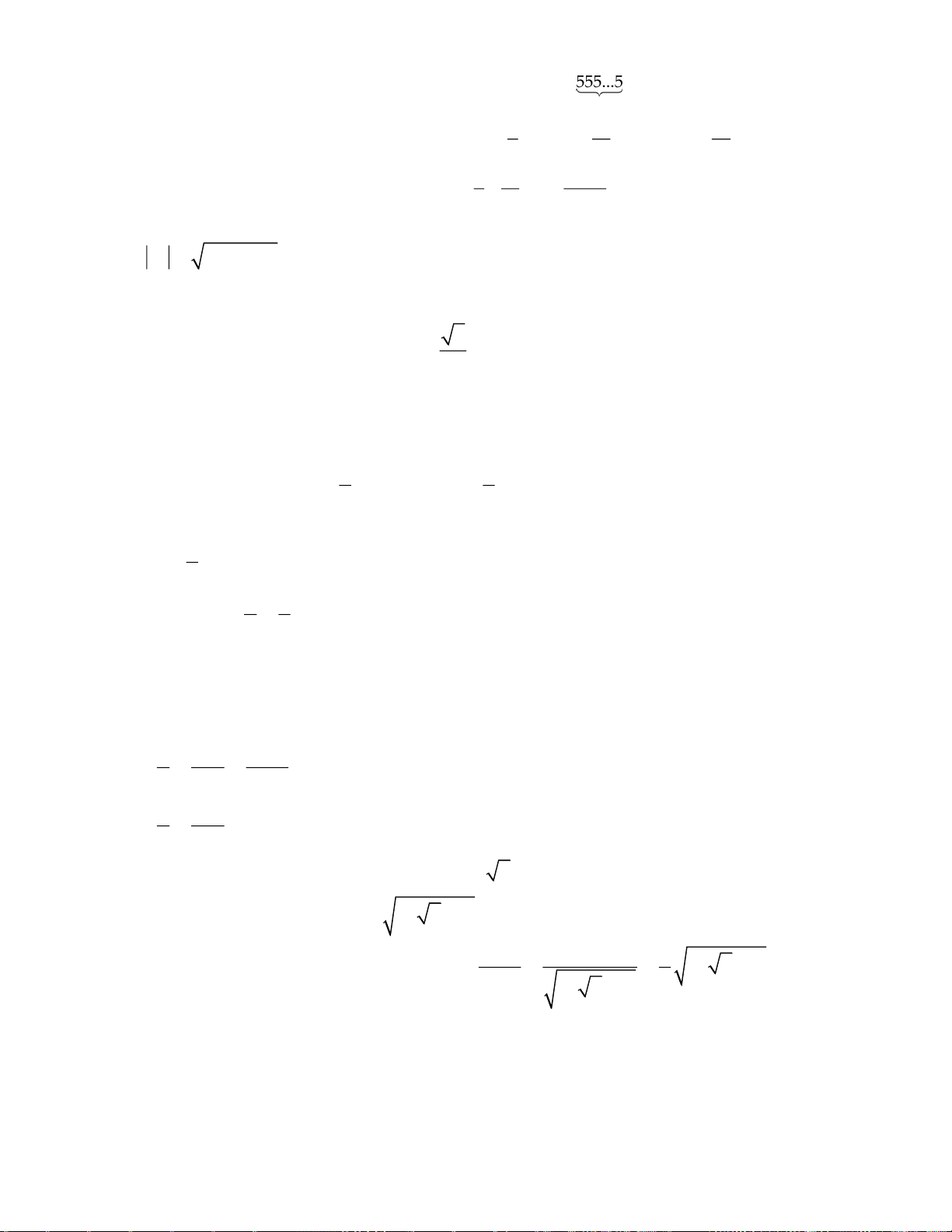
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 11
Chuyên đề DÃY SỐ - CẤP SỐ CẤP SỐ NHÂN
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT CHƯƠNG II
DÃY SỐ. CẤP SỐ CỘNG. CẤP SỐ NHÂN Chủ đề 2: CẤP SỐ NHÂN I. TÓM TẮT LÝ THUYẾT 1. ĐỊNH NGHĨA
Cấp số nhân là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng
đều bằng số hạng đứng ngay trước nó nhân với một số không đổi q. Số q được gọi là công
bội của cấp số nhân.
Cấp số nhân (u với công bội q được cho bởi hệ thức truy hồi: u = u q, n   2 n ) n n−1
2. SỐ HẠNG TỔNG QUÁT
Nếu cấp số nhân (u có số hạng đầu u và công bội q thì số hạng tổng quát u của nó được n ) 1 n
xác định theo công thức: n−1 u = u q ,n  2 n 1 Chú ý:
Nếu u ,u ,u u thì u u = u k k+2 ( k+1)2 k k+1
k+ là ba số hạng liên tiếp của cấp số nhân ( n ) 2
3. TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ NHÂN
Cho cấp số nhân (u với công bội q. Đặt S = u + u + u + ...u . n ) n 1 2 3 n u 1 n − q 1 ( ) Khi đó: S = n 1 − q II. BÀI TẬP TỰ LUẬN
Câu 1: Các dãy số (un ) sau đây, dãy số nào là cấp số nhân, trong trường hợp là cấp số nhân, hãy xác
định số hạng đầu và công bội tương ứng? u = 2 n+ +  1 a) u = u = − n n  . n (− )2 1 5 ; b) n ( ) 3 1 1 .3 ; c) 2 u =  u n 1 + n
Câu 2: Cho các cấp số nhân (un ) với công bội q .
a) Biết u = 2, u = 486 q 1 6 . Tìm ; 2 8 b) Biết q = , u = u ; 4 . Tìm 3 21 1
c) Biết u = 3, q = 2 − 1
. Hỏi số 192 là số hạng thứ mấy?
Câu 3: Tìm số hạng đầu và công bội của cấp số nhân, biết: u  + u = 51 u
 − u + u =10 1 5 2 4 5 a)  b)  u + u = 102 
u − u + u = 20 2 6  3 5 6 u − u = 72 u
 − u + u = 65 4 2 1 3 5 c)  d)  u − u = 144  u + u = 325 5 3  1 7 u  + u = 90 u  + u + u =14 3 5 1 2 3 e)  g)  u − u = 240 
u .u .u = 64 2 6  1 2 3 u  + u + u = 21 1 2 3  u
 + u + u + u = 30  1 2 3 4 h)  1 1 1 7 + + = k)   2 2 2 2 u
 + u + u + u = 340 u u u 12   1 2 3 4 1 2 3
Câu 4: a) Giữa các số 160 và 5, hãy chèn vào 4 số nữa để tạo thành một cấp số nhân.
b) Giữa các số 243 và 1, hãy đặt thêm 4 số nữa để tạo thành một cấp số nhân.
Câu 5: Tìm 3 số hạng liên tiếp của một cấp số nhân biết tổng của chúng là 19 và tích là 216.
Câu 6: a) Tìm số hạng đầu của một cấp số nhân, biết rằng công bội là 3, tổng số các số hạng là 728 và số hạng cuối là 486.
b) Tìm công bội của một cấp số nhân có số hạng đầu là 7, số hạng cuối là 448 và tổng số các số hạng là 889.
Câu 7: a) Tìm 4 góc của một tứ giác, biết rằng các góc đó lập thành một cấp số nhân và góc cuối gấp 9 lần góc thứ hai.
b) Độ dài các cạnh của ABC lập thành một cấp số nhân. Chứng minh rằng: ABC có hai góc không quá 600.
Câu 8: Tìm bốn số hạng liên tiếp của một cấp số nhân, trong đó số hạng thứ hai nhỏ hơn số hạng thứ
nhất 35, còn số hạng thứ ba lớn hơn số hạng thứ tư 560.
Câu 9: Số số hạng của một cấp số nhân là một số chẵn. Tổng tất cả các số hạng của nó lớn gấp 3 lần
tổng các số hạng có chỉ số lẻ. Xác định công bội của cấp số đó. 148
Câu 10: Tìm 4 số hạng đầu của một cấp số nhân, biết rằng tổng 3 số hạng đầu là , đồng thời, theo 9
thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.
Câu 11: Tìm 3 số hạng đầu của một cấp số nhân, biết rằng khi tăng số thứ hai thêm 2 thì các số đó tạo
thành một cấp số cộng, còn nếu sau đó tăng số cuối thêm 9 thì chúng lại lập thành một cấp số nhân.
Câu 12: Tìm 4 số trong đó ba số đầu là ba số hạng kế tiếp của một cấp số nhân, còn ba số sau là ba số
hạng kế tiếp của một cấp số cộng; tổng hai số đầu và cuối bằng 32, tổng hai số giữa bằng 24.
Câu 13: Tìm bốn số biết rằng ba số hạng đầu lập thành một cấp số nhân, ba số hạng sau lập thành
một cấp số cộng. Tổng của hai số hạng đầu và cuối bằng 14, còn tổng của hai số ở giữa là 12?
Câu 14: Tổng của số hạng thứ hai và thứ tư của một cấp số nhân (tăng nghiêm ngặt) là 30, và tích của
chúng bằng 144. Tìm tổng mười số hạng đầu tiên của dãy số đó ?
Câu 15: Tìm các số dương a và b sao cho a, a + 2b, 2a + b lập thành một cấp số cộng và
(b + )2 ab + (a + )2 1 , 5,
1 lập thành một cấp số nhân. 2 1 2
Câu 16: Chứng minh rằng nếu 3 số , ,
x y z lập
y − x y y − lập thành một cấp số cộng thì 3 số , , z
thành một cấp số nhân.
Câu 17: Chứng minh rằng nếu 3 số dương a, b, c theo thứ tự tạo thành một cấp số nhân thì: log N log N − log N a a b =
(a, ,b c 1, 0  N  ) 1 log N log N − log N c b c
Câu 18: a) Tìm x để ba số x, 3; x + 2 lập thành cấp số nhân
b) Cho cấp số nhân u = 2x − 3;u = x + 3; u = 5x − 3 5 10 15 . Tìm . x
Câu 19: Biết các số x + 5 y, 5x + 2 y, 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các 2 2 số ( y − )
1 , xy −1, ( x + 2) theo thứ tự đó lập thành một cấp số nhân. Hãy tìm x và y .
Câu 20: Tính các tổng sau: 2
a) A = 10 + 10 + ... + 10n b) B = 9 + 99 + ... + 999..9 n sè 9 2 2 2  1   1   n 1 
c) C = 7 + 77 + 777 + ... + 777...7 d) D = 2 + + 4 + + ... + 2 +      n n       sè 7 2 4 2
Câu 21: Tính các tổng sau: a) 2 99 2
= 1+ 2.2 + 3.2 + ...+100.2 . b) = 1. + 2. + ...+ n P P x x nx . 1 2
Câu 22: Tính các tổng sau: a) 2 n
A = 5 + 5 + ... + 5 b) B = 15 + 155 + ... + 1555...5 n sè 5  1 2  1 2  1 2 c) C = 1 + 2.3 + 2 3.3 + .. + 2009 2010.3 d) 2 n D = x + + x + + ... + x + x     0 2    n ( )  x   x   x  1 3 2n − 1 e) E = 1 + 4.5 + 2 7.5 + ... + ( n 3 − 2) n 5 f) F = + + ... + 2 n 2 2 2
Câu 23: Cho cấp số nhân (u m k
n ) và cho các số nguyên dương
, với m k . Chứng minh rằng: u = u .u k k −m k +m
Áp dụng: Hãy tìm một cấp số nhân với công bội âm, có 7 số hạng, số hạng thứ 3 bằng 2 và tích
số hạng đầu và cuối bằng 18. 0 6
Câu 24: Cho tam giác ABC có A = 90 và a, ,
b c theo thứ tự đó lập thành một cấp số nhân. Tính 3
góc B, C của tam giác ABC.
Câu 25: Cho tam giác ABC cân tại A. Cạnh BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành
một cấp số nhân . Hãy tính công bội q của cấp số nhân đó. u  = 1, u = 2  1 2
Câu 26: Cho dãy số (u v v = u − u n  1 n ) : 
. Xét dãy ( n ) biết n n 1 + n ( ) u
= 3u − 2u n  2  n 1+ n n 1 − ( )
a) Chứng minh dãy (vn ) là một cấp số nhân.
b) Tìm số hạng tổng quát của dãy số (un ) . u  = 2  1
Câu 27: Cho dãy số (u :  2 +
. Chứng minh: (un ) vừa là cấp số cộng vừa là cấp số n ) u 4 n u  = n  1 n+1 ( )  4 nhân. u  = 4  1
Câu 28: Cho dãy số (u u n ) : 
. Chứng minh: ( n ) vừa là cấp số cộng vừa là cấp u  = u +12 n  1  n 1+ n ( ) số nhân.
III. BÀI TẬP TRẮC NGHIỆM
Câu 29: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; −1; 1; −1 .
B. 1; − 3; 9;10 . C. 1; 0; 0; 0 . D. 32; 16; 8; 4 .
Câu 30: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; − 3;9; − 27;54 .
B. 1; 2; 4;8;16 .
C. 1; −1;1; −1;1.
D. 1; − 2; 4; − 8;16 .
Câu 31: Trong các dãy số (u sau đây, dãy số nào là cấp số nhân? n )
A. u = 3n . B. n u = 2 . C. u = 1 . D. n u = 2 + 1. n n n n n 3
Câu 32: Cấp số nhân (u u .2n− = , n
n ) có số hạng tổng quát là 1 * n
. Số hạng đầu tiên và công bội của 5 cấp số nhân đó là 6 3 6 3
A. u = , q = 2 u = , q = 2 − u = , q = 2 − u = , q = 2 1 . B. . C. D. . 5 1 5 1 5 2 5
Câu 33: Cho cấp số nhân (u u q
n ) có số hạng đầu 1 và công bội
0 . Công thức xác định số hạng tổng
quát của cấp số nhân (un ) là A. * u = . n q u n   u = u q n   n 1 . B. * n 1 . C. 1 − * u = . n q u n   n u u q − = n   n 1 . D. 1 * n 1 .
Câu 34: Cho cấp số nhân (u u = 2 u = 6 n ) với 1 và 2
. Công bội của cấp số nhân đã cho bằng 1 A. 3 . B. −4 . C. . D. 4 . 3
Câu 35: Cấp số nhân (u u = 9 u = 81 n ) có 4 , 5 có công bội là A. 3 . B. 72 . C. 18 . D. 9 .
Câu 36: Cho cấp số nhân (u u = 6 u = 162 n ) với 2 và 5
. Công bội của cấp số nhân đã cho bằng 1 A. 3 . B. 3 − . C. 2 . D. . 3 2 96 −
Câu 37: Cho cấp số nhân có u = 3, − q = . Số
là số hạng thứ mấy của cấp số này? 1 3 243 A. Thứ 6. B. Thứ 8. C. Thứ 5. D. Thứ 7.
Câu 38: Cho cấp số nhân (u có u = −3 , công bội q = −2 . Hỏi −192 là số hạng thứ mấy của (u n ) ? n ) 1 A. Số hạng thứ 6 B. Số hạng thứ 7 C. Số hạng thứ 5 D. Số hạng thứ 8
Câu 39: Một cấp số nhân với công bội bằng 2
− có số hạng thứ ba bằng 8 và số hạng cuối bằng −1024 .
Hỏi cấp số nhân đó có bao nhiêu số hạng? A. 11 B. 10 C. 9 D. 8
Câu 40: Cho cấp số nhân (u u = −2 q = u n ) có 1 và công bội 3 . Số hạng 2 là A. u = −6. u = 1 u = −18. u = 6. 2 B. 2 . C. 2 D. 2 u  = 1 1 
Câu 41: Cho dãy số (u v v = u − v
n ) xác định bởi 
u + 8 và dãy số ( n ) xác định bởi 2 . Biết ( n ) n u = n nn 1+  5
là một cấp số nhân có công bội q . Khi đó 2 8 1 A. q = .
B. q = 5 .
C. q = .
D. q = . 5 5 5
Câu 42: Cho cấp số nhân (un ) biết u = − = 2 8; 5 u
64 . Giá trị của u6 bằng A. 512 . B. 256 . C. −128 . D. −1024 .
Câu 43: Cho cấp số nhân (u u = −8 u = 64 u n ) biết 2 ; 5 . Giá trị của 3 bằng A. −16 . B. 32 . C. −32 . D. 16 . u  + u = 60 2 4
Câu 44: Cho cấp số nhân (u u n ) có  . Tìm . u + u = 180  1 3 5 A. 3 . B. 6 . C. 2 . D. 5 . u + u =198
Câu 45: Cho cấp số nhân (u u n ) có 2 7 
. Khi đó công bội của cấp số nhân ( n ) là u + u = 396  3 8 A. 2 . B. 3 . C. 4 . D. 1. u  − u = 511
Câu 46: Tìm số hạng đầu u u
1 của cấp số nhân ( n ) biết rằng: 10 1  .
u + u + u = 73  7 4 1 A. u = 1 u = 2 u = −1 u = −2 1 . B. 1 . C. 1 . D. 1 .
Câu 47: Cho cấp số nhân u . n
Khi đó đẳng thức nào sau đây là đúng? u u A. 2018 2020 u u u .u 2019 . B. . 2 2019 2018 2020 C. 2 u u .u u u .u 2019 2018 2019 . D. 2019 2018 2020 .
Câu 48: Ba số 2x −1, x, 2x +1 theo thứ tự lập thành một cấp số nhân. Hãy tìm . x 1 3 A.  .
B. x = 1. C.  . D.  3 . 3 3
Câu 49: Xác định x là số thực dương để 2x − 3; ;
x 2x + 3 lập thành một cấp số nhân.
A. x = 3 .
B. x = 3 .
C. x =  3 . D. x = 5 .
Câu 50: Có bao nhiêu giá trị nguyên dương của x để ba số 1; x ; x + 2 theo thứ tự lập thành một cấp số nhân? A. 2 . B. 3 . C. 1. D. 0 .
Câu 51: Viết thêm sáu số xen giữa hai số 2
− và 256 để được một cấp số nhân có 8 số hạng. Nếu
viết tiếp thì số hạng thứ 15 là bao nhiêu? A. −32768 . B. 16384 . C. −16384 . D. 32768 .
Câu 52: Biết ba số 2
x ; 8;x theo thứ tự lập thành cấp số nhân. Giá trị của x bằng A. x 4. B. x 5. C. x 2. D. x 1.
Câu 53: Với x là số nguyên dương, ba số 2x, 3x + 3, 5x + 5 theo thứ tự là ba số hạng liên tiếp của
một cấp số nhân. Số hạng tiếp theo của cấp số nhân đó là 250 250 A. − . B. . C. 250 . D. −250 . 3 3
Câu 54: Cho dãy số (u u = 1 q =
n ) là cấp số nhân có số hạng đầu 1 , công bội
2 . Tổng ba số hạng đầu
của cấp số nhân (un ) là A. 3 . B. 7 . C. 9 . D. 5 .
Câu 55: Cho cấp số nhân (u u = 2 q = − u n ) có 1 và công bội
3 . Tổng 4 số hạng đầu của cấp số nhân ( n ) bằng 1 A. 162 . B. −160 . C. −40 . D. . 2
Câu 56: Cho cấp số nhân (u u = 9 q = − S n ) biết 3 và công bội
3 . Tính tổng 3 của 3 số hạng đầu của
cấp số nhân (un ) . A. 7. B. 36. C. −14. D. 1.
Câu 57: Cho cấp số nhân (u u = −6 u = 48 S n ) có 2 , 5 . Tính 5 . A. 33 . B. −31. C. 93 . D. 11.
Câu 58: Cho cấp số nhân có số hạng đầu u = 3 S 1
, công bội q = 2 . Tính tổng 5 số hạng đầu tiên 5 của cấp số nhân. A. S = 93 S = −45 S = −93 S = 45 5 . B. 5 . C. 5 . D. 5 .
Câu 59: Cho cấp số nhân (u S = 4, S = 13 u  0 S n ) có 2 3 . Biết 2
, giá trị của 5 bằng 35 181 A. 11. B. 2 . C. . D. . 16 16 u  + u + u =13
Câu 60: Cho cấp số nhân (u u n ) thỏa mãn 1 2 3 
. Tổng 8 số hạng đầu của cấp số nhân ( n ) là u − u = 26  4 1 A. S = 1093 S = 9841 S = 3280 S = 3820 8 . B. 8 . C. 8 . D. 8 .
Câu 61: Cho (u là cấp số nhân, đặt S = u + u + ... + u . Biết u + S = 43, S = 13 . Tính S . n ) n 1 2 n 2 4 3 6 A. 182 . B. 728 . C. 364 . D. 121. u = 2020 1 
Câu 62: Cho dãy số (u
S = u + u + u + ...+ u
n ) thỏa mãn điều kiện 1 . Gọi là tổng * u = u ,n n 1 2 3 n  1+  n 3 n
của n số hạng đầu tiên của dãy số đã cho. Khi đó lim Sn bằng 1 A. 2020 . B. . C. 3030 . D. 0 . 3
Câu 63: Biết 3 số nguyên 3 , x , y theo thứ tự đó lập thành một cấp số nhân và 3 số x , y , 9 theo thứ
tự đó lập thành một cấp số cộng. Khi đó x + y bằng A. 5 − . B. 7 . C. 0 . D. 11. u = 1  1
Câu 64: Cho dãy số (u
S = u + u + u + ...+ u
n ) xác định bởi  . Tính tổng 2 2 2 2 : 2 1 2 3 2011 u
= 3u + 2 ;n  1  n 1+ n A. 2011 S = 3 − 2012 . B. 2011 S = 3 − 2011. C. 2011 S = 3 −1 . D. 2011 S = 3 .
Câu 65: Cho cấp số nhân (u có u = −2 và u = 54 . Tính tổng 1000 số hạng đầu tiên của cấp số nhân n ) 2 5 đã cho. 1000 3 − 1 1000 1 − 3 1000 1 − 3 1000 3 − 1 A. S = . B. S = . C. S = . D. S = . 1000 2 1000 4 1000 6 1000 6
Câu 66: Một cấp số nhân có số hạng đầu u = 3 q = 1 , công bội
2 . Biết rằng tổng n số hạng đầu tiên bằng 21 . Tìm n . A. n = 10 .
B. n = 3 .
C. n = 7 .
D. Không có giá trị n .
Câu 67: Tìm số hạng đầu u u
u + u + u = 21
u + u + u = 567
1 của cấp số nhân ( n ) biết rằng: 1 2 3 và 4 5 6 . 21 13 A. 3 . B. . C. 9 D. . 13 21
Câu 68: Cho cấp số nhân (u u = 2
20u −10u + u n ) có 1 và biểu thức 1 2
3 đạt giá trị nhỏ nhất. Số hạng thứ
bảy của cấp số nhân (un ) có giá trị bằng A. 6250 . B. 31250 . C. 136250 . D. 39062 u = 3
Câu 69: Cho dãy số (u  ,n u n ) biết 1
* . Tìm số hạng tổng quát của dãy số ( n ) . u = 3  u n 1 + n A. u = 3n u n u u n . B. 1 + = n n . C. 1 3 + = n n . D. 1 3 − = n n . u  = 1 1 
Câu 70: Cho dãy số (u ) v v = u − n xác định bởi 
u + 8 và dãy số ( ) xác định bởi công thức 2 . n u = n n nn 1+  5 Biết (v ) n
là cấp số nhân có công bội q. Khi đó 2 8 1 A. q= .
B. q = 5 . C. q = . D. q = . 5 5 5 u + u + u
Câu 71: Cho cấp số nhân (u thỏa mãn 2(u + u + u = u + u + u . Tính 8 9 10 3 4 5 ) n ) 6 7 8 u + u + u 2 3 4 A. 4 . B. 1. C. 8 . D. 2 . 3
 u = 3u −u + u + 6
Câu 72: Cho dãy số (u u n ) thỏa mãn 1 1 2 2 
. Tìm giá trị nhỏ nhất của n để 2021 2 . * n u  = 2u , n    n 1+ n A. 2021 . B. 1012 . C. 2022 . D. 1011.
Câu 73: Nguời ta thiết kế một cái tháp gồm 10 tầng theo cách: Diện tích bề mặt trên của mỗi tầng
bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng 1 bằng
nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là 2
12288 m , diện tích bề mặt trên cùng của tháp bằng A. 2 6 m . B. 2 12 m . C. 2 24 m . D. 2 3m .
Câu 74: Người ta trồng 3240 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ
hàng thứ hai trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có
tất cả bao nhiêu hàng cây? A. 81. B. 82 . C. 80 . D. 79 .
Câu 75: Một du khách vào trường đua ngựa đặt cược, lần đầu đặt 20.000 đồng, mỗi lần sau đặt gấp
đôi lần tiền đặt cọc trước. Người đó thắng 9 lần liên tiếp và thua ở lần thứ 10. Hỏi vị khách
trên thắng hay thua bao nhiêu? A. Hòa vốn.
B. Thắng 20.000 đồng.
C. Thua 20.000 đồng.
D. Thắng 40.000 đồng
Câu 76: Sắp đến ngày sinh nhật của mẹ, Lan quyết định tiết kiệm tiền để mua quà tặng mẹ theo cách
sau: ngày thứ nhất Lan bỏ ống tiết kiệm 1 nghìn đồng, ngày thứ hai Lan bỏ ống tiết kiệm 2
nghìn đồng, ngày thứ ba Lan bỏ ống tiết kiệm 4 nghìn đồng,…, số tiền bỏ ống tiết kiệm của
ngày thứ n +1 gấp đôi số tiền bỏ ống tiết kiệm của ngày thứ n . Số tiền Lan tiết kiệm được sau
khi bỏ ống được 15 ngày là X nghìn đồng, hỏi X bằng bao nhiêu?
A. 32767 nghìn đồng.
B. 31797 nghìn đồng.
C. 12060 nghìn đồng.
D. 35067 nghìn đồng.
Câu 77: Một cơ sở khoan giếng có đơn giá như sau: giá của mét khoan đầu tiên là 50000 đồng và kể
từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 7% so với giá của mét khoan
ngay trước đó. Tính số tiền mà chủ nhà phải trả cho cơ sở khoan giếng để khoan được 50(m)
giếng gần bằng số nào sau đây? A. 20326446 . B. 21326446 . C. 23326446 . D. 22326446 .
Câu 78: Nhà bạn Minh cần khoan một cái giếng nước. Biết rằng giá tiền của mét khoan đầu tiên là
200.000đ và kể từ mét khoan thứ hai, giá tiền của mỗi mét sau tăng thêm 7% so với giá tiền
của mét khoan ngay trước nó. Hỏi nếu nhà bạn An khoan cái giếng sâu 30m thì hết bao nhiêu
tiền (làm tròn đến hàng nghìn)? A. 18895000 đ. B. 1422851đ. C. 18892000 đ. D. 18892200 đ.
Câu 79: Ông A gửi 120 triệu đồng tiền vào ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau 10 năm, tổng số tiền mà ông A nhận được là bao nhiêu, giả định
trong khoảng thời gian này lãi suất không thay đổi và ông A không rút tiền ra? (Lấy kết quả
gần đúng đến hàng phần trăm)
A. 214,90 triệu đồng. B. 224,10 triệu đồng. C. 234,90 triệu đồng. D. 215,10 triệu đồng.
Câu 80: Một thợ thủ công muốn vẽ trang trí một hình vuông kích thước 4m  4m bằng cách vẽ một
hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu, và tô kín màu
lên hai tam giác đối diện (như hình vẽ). Quá trình vẽ và tô theo quy luật đó được lặp lại 5
lần. Tính số tiền nước sơn để người thợ đó hoàn thành trang trí hình vuông như trên? Biết tiền nước sơn 2 1m là 60.000 đ. A. 575000 đ. B. 387500 đ. C. 465000 đ. D. 232500 đ.
Câu 81: Một quả bóng cao su từ độ cao 15 (m) so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên
một độ cao bằng hai phần năm độ cao lần rơi ngay trước đó. Biết rằng quả bóng luôn chuyển
động vuông góc với mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến
lúc bóng không nảy nữa) khoảng: A. 35 (m) . B. 50 (m) . C. 30 (m) . D. 25 (m) .
Câu 82: Cho hình vuông A B C D có cạnh bằng 1. Gọi A B C D 1 1 1 1 k+ , 1 k+ , 1 k+ , 1
k+ thứ tự là trung điểm các 1
cạnh A B , B C , C D , D A (với k = 1, 2,...). Chu vi của hình vuông A B C D bằng k k k k k k k k 2018 2018 2018 2018 2 2 2 2 A. . B. . C. . D. . 2019 2 1006 2 2018 2 1007 2
Câu 83: Biết rằng tồn tại đúng hai giá trị của tham số
m để phương trình 3 2 x − x + ( 2 7
2 m + 6m) x −8 = 0 có ba nghiệm phân biệt lập thành một cấp số nhân. Tính tổng
lập phương của hai giá trị đó. A. −342 . B. −216 . C. 344 . D. 216 .
IV. LỜI GIẢI CHI TIẾT
Câu 1: Các dãy số (un ) sau đây, dãy số nào là cấp số nhân, trong trường hợp là cấp số nhân, hãy xác
định số hạng đầu và công bội tương ứng? u = 2 n+ +  1 a) u = u = − n n  . n (− )2 1 5 ; b) n ( ) 3 1 1 .3 ; c) 2 u =  u n 1 + n Lời giải: u = n ( 5 − n  )2 1+ u 2 a) Ta có: n 1 +  ⎯⎯ → = ( 5 − ) * = 25,n  .  = − nu u + ( 5)2 +3 1 n n Vậy (u u = 5 − = 1 − 25
n ) cấp số nhân với ( )3 1
và công bội q = 25. u = n (− n  ) 3n 1 1 .3 + un 1+ 3 * b) Ta có:  ⎯⎯ → = 3 − = 27, − n  .  = − nn u u + ( ) 1+ 3 +4 1 .3 ; 1 n n Vậy (u u = −81 −
n ) cấp số nhân với 1
và công bội q = 27. u = 2  1 c)  ⎯⎯
→u = 2;u = 4;u = 16. 2 1 2 3 u =  u n 1 + n u u Do 2 3 
nên (un ) không phải là cấp số nhân. u u 1 2
Câu 2: Cho các cấp số nhân (un ) với công bội q .
a) Biết u = 2, u = 486 q 1 6 . Tìm ; 2 8 b) Biết q = , u = u ; 4 . Tìm 3 21 1
c) Biết u = 3, q = 2 − 1
. Hỏi số 192 là số hạng thứ mấy? Lời giải: a) Ta có: 5 5
u = u q = 486  q = 243  q = 9 3. 6 1 8 9 b) Ta có: 3 u = u q =  u = . 4 1 1 21 7 n− c) Ta có: u 192 n u q − = =  192 = 3. −  n = n ( 2) 1 1 7. 1
Vậy 192 là số hạng thứ 7 của khai triển.
Câu 3: Tìm số hạng đầu và công bội của cấp số nhân, biết: u  + u = 51 u
 − u + u =10 1 5 2 4 5 a)  b)  u + u = 102 
u − u + u = 20 2 6  3 5 6 u − u = 72 u
 − u + u = 65 4 2 1 3 5 c)  d)  u − u = 144  u + u = 325 5 3  1 7 u  + u = 90 u  + u + u =14 3 5 1 2 3 e)  g)  u − u = 240 
u .u .u = 64 2 6  1 2 3 u  + u + u = 21 1 2 3  u
 + u + u + u = 30  1 2 3 4 h)  1 1 1 7 + + = k)   2 2 2 2 u
 + u + u + u = 340 u u u 12   1 2 3 4 1 2 3 Lời giải: 4 4 u  + u = 51 u  + u q = 51 u  + u q = 51  1 1 (1) 1 5 1 1 a)      5 u + u = 102  u
q + u q = 102 q u + u q = 102 2 6 (2)  1 1  ( 4 1 1 )
Thay (1) vào (2) ta có: 51q = 102  q = 2 thay vào (1), ta được: u = 3 1 . u
 − u + u = 10 u
 q − u q + u q =10 uq  ( 2 3 3 4 1− q + q = 10 1 (1) 2 4 5 1 1 1 ) b)      2 4 5 2
u − u + u = 20  u
q − u q + u q = 20  uq  ( 2 3 3 5 6 1− q + q = 20 1 1 1 1 ) (2)
Thay (1) vào (2) ta có: q = 2 thay vào (1), ta được: u = 1 1 . u  + u + u = 21 u
 + u q + u q = 21 u
 1+ q + q = 21 1 2 3 1 1 1 ( 2 2 1 )    h)  1 1 1 7   1 1 1 7   1  1 1  7 + + = + + =   2  1+ + =  2 u u u 12 u u q u q 12   1 2 3  1 1 1 u   q q  12 1 u  ( 2 1+ q + q = 21 1 ) (1)   2  1 1+ q + q 7  . = (2) 2 u q 12  1 21 Xét u = 0 q = 1  1+ q + q = 1 và 0 không thỏa hệ, nên ( ) 2
(*) thay vào (2) ta có phương u1 21 7 u q = 6 2 2 1 trình: =  u q = 36  2 2 1  u q 12 u q = 6 − 1  1
q = 2  u = 3 6 
TH 1: u q = 6  u =
6q −15q + 6 = 0  1 1 thay vào (*) ta có: 2 1 qq =  u =12  2 6 TH 2: u q = 6 −  u = − 1 1 thay vào (*) ta có: q  9 − + 65 27 + 3 65 q =  u = 1 4 2 2
6q + 27q + 6 = 0    9 − − 65 27 − 3 65 q =  u = 1  4 2 2 u  + u + u = 14
u + u q + u q = 14 u  1+ q + q =14   1 1 1  u
 1+ q + q = 14 1 2 3 ( 2 ) 1 ( 2 1 ) g)       
u .u .u = 64  u .  (u q).  ( 2 u q ) = 64 (  u q = 64 uq = 4  1 )3 1 2 3 1 1 1  1 4
Dễ thấy q = 0 không thỏa hệ, ta có u q = 4  u = 1 1
thay vào phương trình trên ta có: q
q = 2  u = 2 1 2 4q 10q 4 0  − + =  1  q =  u = 8 1  2
Câu 4: a) Giữa các số 160 và 5, hãy chèn vào 4 số nữa để tạo thành một cấp số nhân.
b) Giữa các số 243 và 1, hãy đặt thêm 4 số nữa để tạo thành một cấp số nhân.
Câu 5: Tìm 3 số hạng liên tiếp của một cấp số nhân biết tổng của chúng là 19 và tích là 216.
Câu 6: a) Tìm số hạng đầu của một cấp số nhân, biết rằng công bội là 3, tổng số các số hạng là 728 và số hạng cuối là 486.
b) Tìm công bội của một cấp số nhân có số hạng đầu là 7, số hạng cuối là 448 và tổng số các số hạng là 889.
Câu 7: a) Tìm 4 góc của một tứ giác, biết rằng các góc đó lập thành một cấp số nhân và góc cuối gấp 9 lần góc thứ hai.
b) Độ dài các cạnh của ABC lập thành một cấp số nhân. Chứng minh rằng: ABC có hai góc không quá 600.
Câu 8: Tìm bốn số hạng liên tiếp của một cấp số nhân, trong đó số hạng thứ hai nhỏ hơn số hạng thứ
nhất 35, còn số hạng thứ ba lớn hơn số hạng thứ tư 560.
Câu 9: Số số hạng của một cấp số nhân là một số chẵn. Tổng tất cả các số hạng của nó lớn gấp 3 lần
tổng các số hạng có chỉ số lẻ. Xác định công bội của cấp số đó. 148
Câu 10: Tìm 4 số hạng đầu của một cấp số nhân, biết rằng tổng 3 số hạng đầu là , đồng thời, theo 9
thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.
Câu 11: Tìm 3 số hạng đầu của một cấp số nhân, biết rằng khi tăng số thứ hai thêm 2 thì các số đó tạo
thành một cấp số cộng, còn nếu sau đó tăng số cuối thêm 9 thì chúng lại lập thành một cấp số nhân.
Câu 12: Tìm 4 số trong đó ba số đầu là ba số hạng kế tiếp của một cấp số nhân, còn ba số sau là ba số
hạng kế tiếp của một cấp số cộng; tổng hai số đầu và cuối bằng 32, tổng hai số giữa bằng 24.
Câu 13: Tìm bốn số biết rằng ba số hạng đầu lập thành một cấp số nhân, ba số hạng sau lập thành
một cấp số cộng. Tổng của hai số hạng đầu và cuối bằng 14, còn tổng của hai số ở giữa là 12? Lời giải:
Gọi 4 số phải tìm là a , a , a , a 1 2
3 4 . Theo đầu bài ta có hệ:
a = a a + d * 2  
2a q = a q + a + d 1 a = a a 1 1 2 ( ) 2 2 2 1 ( 2 ) ( ) 2 1 3    a + d = − a
2a = a + a
a + a + 2d = 14 (2) 2 14  2 1 1 2  3 2 4       12 2 a + a = 14 
a q + a q = 12 3 a = 1 4 1 1 ( )  1 2 q + qa a 12   + =  2 3
a + a + d = 12 4  2 2 ( ) d = 12 − 2a  2  
Giải hệ phương trình ta có kết quả: ( ) 25 15 9 3 2,4,8,12 , , , ,    2 2 2 2 
Câu 14: Tổng của số hạng thứ hai và thứ tư của một cấp số nhân (tăng nghiêm ngặt) là 30, và tích của
chúng bằng 144. Tìm tổng mười số hạng đầu tiên của dãy số đó ? Lời giải:
Gọi cấp số nhân tăng nghiêm ngặt là (a a , a
n ) . Theo đầu bài ta có 2 4 là hai nghiệm của phương trình: a q = 6 1 a = 6 a q = 6 1 2  2   = = q = 4 t = 6 3 a 24 a q 24   2
t − 30t +144 = 0  4 1        a q = 24 t = 24 1 a = 24 a q = 24  2 1       6 1 3 2  a = 6   = = = 4 a q 6 q  1   24 4
Do cấp số nhân tăng nghiêm ngặt, cho nên q  1 , do vậy ta chọn a = 3, q = 2 1 10 2 −1 Cho nên : S = u = 3. 1024 −1 = 3069 10 1 ( ) 2 − 1
Câu 15: Tìm các số dương a và b sao cho a, a + 2b, 2a + b lập thành một cấp số cộng và
(b + )2 ab + (a + )2 1 , 5,
1 lập thành một cấp số nhân. Lời giải:
Ta có: a, a + 2b, 2a + b lập thành một cấp số cộng  a + (2a + b) = 2(a + 2b)  a = 3b (1) Mặt khác: (b + )2 2 2 2 ab + (a + )2 1 , 5,
1 lập thành một cấp số nhân  (b + ) 1 (a + ) 1 = (ab + 5)  + + = + 2 b 1 a 1 ab 5 2 ( )( )  (b + ) 1 (a + ) 1  =  (ab + 5)   (b + ) 1 (a + ) 1 = −ab − 5 TH 1: (b + ) 1 (a + )
1 = ab + 5 , thay a = 3b ta được phương trình: (b + )( b + ) 2 1 3
1 = 3b + 5  b = 1  a = 3 TH 2: (b + ) 1 (a + )
1 = −ab − 5 , thay a = 3b ta được phương trình: (b + )(− b + ) 2 1 3 1 = 3 − b + 5  2
− b = 4  b = 2 − (loại) 2 1 2
Câu 16: Chứng minh rằng nếu 3 số , ,
x y z lập
y − x y y − lập thành một cấp số cộng thì 3 số , , z
thành một cấp số nhân. Lời giải: 2 1 2 Ta có: , ,
y − x y y − lập thành một cấp số cộng z 2 2 2
( y − z) + ( y − x) 1  + =  = y − x y − z y
( y − x)( y − z) y
y(2y − x − z) = ( y − x)( y − z) 2  xz = y
x, y, z lập thành một cấp số nhân (đ.p.c.m)
Câu 17: Chứng minh rằng nếu 3 số dương a, b, c theo thứ tự tạo thành một cấp số nhân thì: log N log N − log N a a b =
(a, ,b c 1, 0  N  ) 1 log N log N − log N c b c Lời giải: 2
Theo giả thiết , nếu ba số a,b,c lập thành cấp số nhân thì : ac = b ( ) 1
Lấy logarit cơ số N hai vế của (1) ta có :  (ac) 2 log
= log b  log a + log C = 2log b (2 N N N N N )
Sử dụng công thức đổi cơ số : 1 1 2 1 1 1 1 (2)  + =  − = − log N log N log N log N log N log N log N a C b a b b C log N − log N log N − log N log N − log N log  N b a = c bb a = a log N.log N log N.log N log N − log N log N a b c b c b c log N − log N log  N a b = a log N − log N log N b c c
Câu 18: a) Tìm x để ba số x, 3; x + 2 lập thành cấp số nhân
b) Cho cấp số nhân u = 2x − 3;u = x + 3; u = 5x − 3 5 10 15 . Tìm . x
Câu 19: Biết các số x + 5 y, 5x + 2 y, 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các 2 2 số ( y − )
1 , xy −1, ( x + 2) theo thứ tự đó lập thành một cấp số nhân. Hãy tìm x và y .
Câu 20: Tính các tổng sau: 2
a) A = 10 + 10 + ... + 10n b) B = 9 + 99 + ... + 999..9 n sè 9 2 2 2  1   1   n 1 
c) C = 7 + 77 + 777 + ... + 777...7 d) D = 2 + + 4 + + ... + 2 +      n n       sè 7 2 4 2 Lời giải: 2 a) 10 10 ... 10n A = + + +
Xem A là tổng của n số hạng của 1 cấp số nhân (u u = 10, q = 10 n ) với 1 n − Suy ra: 2 n 1 10 10 =10 +10 + ...+10 =10. = (10n A − ) 1 1− 10 9 b) = + + +
= ( − ) + ( 2 − ) + + ( n − ) 2 9 99 ... 999..9 10 1 10 1 ... 10 1 = 10 +10 + ... +10n B − n n sè 9 10 Theo câu trên, suy ra: = 9 + 99 + ...+ 999..9 = (10n B − ) 1 − n n sè 9 9 7  
c) C = 7 + 77 + 777 + ... + 777...7 = 9 + 99 + 999 + ...+ 99...9     n sè 7 9 n sè 9 7 10  Theo câu trên, suy ra:
= 7 + 77 + 777 + ...+ 777...7 =  (10n C − ) 1 − n   n sè 7 9 9  1   1   n 1  d) Ta có : 2 S = 4 + 2 + + 16 + 2 + + ...+ 2 + 2 +      2n   4   16   2  ( n  1 1 1 2 
= 4 +16 + ..+ 2 ) + 2n + + + ..+  2n   4 16 2  1 n 1 − n 2 2 4 1 2 −1 4 −1 1 2 n n −1  S = 4. + 2n + . = 4. + 2n + . 2 3 4 1 3 3 2 n −1 4 4n −1 4.4n +1 (4n − )1( n 1 4 + + ) 1 = 2n + . = 2n + 3 4n 3.4n
Câu 21: Tính các tổng sau: 2 99 2 a)
= 1+ 2.2 + 3.2 + ...+100.2 . b) = 1. + 2. + ...+ n P P x x nx . 1 2 Lời giải: 2 99
a) P = 1+ 2.2 + 3.2 + ... +100.2 (1) 1 2 3 4 99 100
 2P = 2 + 2.2 + 3.2 + 4.2 + ...+ 99.2 +100.2 1 (2)
Lấy (1) trừ (2), ta được: 2 3 99 100
−P = 1+ 2 + 2 + 2 + ...+ 2 −100.2 1 −
P = 100.2 − (1+ 2 + 2 + 2 +...+ 2 ) 100 100 2 3 99 100 2 1 100 = 100.2 − = 99.2 +1 1 2 −1 2 n 1 − 2 n
b) Đặt P = 1+ 2.x + 3.x + ... + nx
P = xP = 1.x + 2.x + ...+ nx . 0 2 0
TH 1: Xét x = 0  P = 0 2 . n(n + ) 1
TH 2: Xét x = 1  P = 1+ 2 + ... + n = 2 2 2 n 1 − 2 n
TH 3: Xét x  1. Xét P = 1+ 2.x + 3.x + ... + nx
P = xP = 1.x + 2.x + ...+ nx . 0 2 0
P − P = P − xP = ( 2 3 n 1
1+ x + x + x + ... − n + x − nx 2 0 2 2 ) n x −1 1 n  −  n x 1  P 1 n − x = − nx P = − nx 2 ( ) 2   x −1
x −1  x −1 
Bài tập tương tự:
Câu 22: Tính các tổng sau: a) 2 n
A = 5 + 5 + ... + 5 b) B = 15 + 155 + ... + 1555...5 n sè 5  1 2  1 2  1 2 c) C = 1 + 2.3 + 2 3.3 + .. + 2009 2010.3 d) 2 n D = x + + x + + ... + x + x     0 2    n ( )  x   x   x  1 3 2n − 1 e) E = 1 + 4.5 + 2 7.5 + ... + ( n 3 − 2) n 5 f) F = + + ... + 2 n 2 2 2
Câu 23: Cho cấp số nhân (u m k
n ) và cho các số nguyên dương
, với m k . Chứng minh rằng: u = u .u k k −m k +m
Áp dụng: Hãy tìm một cấp số nhân với công bội âm, có 7 số hạng, số hạng thứ 3 bằng 2 và tích
số hạng đầu và cuối bằng 18. 6
Câu 24: Cho tam giác ABC có 0 A = 90 và a, ,
b c theo thứ tự đó lập thành một cấp số nhân. Tính 3
góc B, C của tam giác ABC. Lời giải: 2 2 2
a = b + c
Theo giả thiết ta có hệ : 2 2 2 3
b = ac b = ac 3 2 Từ đó suy ra: 2 3 2 2 2
a = ac + c  2a = 3ac + 2c  (2a + c)(a − 2c) = 0  a = 2c(2a + c  0) 2 c 1 Mà: 0 0 cos B =
=  B = 60 , C = 30 . a 2
Câu 25: Cho tam giác ABC cân tại A. Cạnh BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành
một cấp số nhân . Hãy tính công bội q của cấp số nhân đó. Lời giải:
Theo giả thiết: AB = AC và BC, AH , AB lập thành cấp số cộng nên ta có hệ: 1 BC 2HC = = = 2cot C q AH AH
 2cot C = sin C  2 2
2cosC = sin C = 1− cos C 1 AH  = = sin B q AB 2  C + C − =  C = − + ( 0 cos 2cos 1 0 cos 1 2 0  C  90 )
Do C là nhọn cho nên sin C = 2( 2 − ) 1 1 1 1
Cho nên công bội của cấp số nhân là : q = = = 2( 2 + ) C ( − ) 1 sin 2 2 2 1 u  = 1, u = 2  1 2
Câu 26: Cho dãy số (u v v = u − u n  1 n ) : 
. Xét dãy ( n ) biết n n 1 + n ( ) u
= 3u − 2u n  2  n 1+ n n 1 − ( )
a) Chứng minh dãy (vn ) là một cấp số nhân.
b) Tìm số hạng tổng quát của dãy số (un ) . Lời giải: a) Ta có: n
  2 : u − u = 2 u − uv = 2v n 1 + n ( n n 1−) n n 1 − Suy ra: (v q =
n ) là cấp số nhân với công bội 2.
b) Do u = (u − u + u − u
+ ...+ u − u + u = v + v + ...+ v +1 n n n 1 − ) ( n 1− n−2)
( 2 1) 1 n 1− n−2 1 n 1 1. 1  − 2 −    − Mặt khác: n 1 v + v + ...+ v = S = = 2 −1 n 1 − n−2 1 n 1 − 1− . 2
Do đó, số hạng tổng quát của dãy (u u − = n ) là: 1 2n n . u  = 2  1
Câu 27: Cho dãy số (u :  2 +
. Chứng minh: (un ) vừa là cấp số cộng vừa là cấp số n ) u 4 n u  = n  1 n+1 ( )  4 nhân. Lời giải:
Ta có: u = 2, u = 2, u = 2 1 2 3 …
Dự đoán: u = 2 n n ( )
1 (*). Ta chứng minh (*) bằng qui nạp toán học:
* Với n = 1: u = 2 1 (Đúng)
* Giả sử (*) đúng với n = k tức là: u = 2 k n = k + k ( )
1 . Ta cần chứng minh (*) đúng với 1 tức là: u = 2 k  1 k 1 + ( ) . 2 u + 4 4 + 4 * Thật vậy: Xét k u = = = 2 k 1 + 4 4
Vậy u = 2 n u n ( )
1 , nên ( n ) vừa là cấp số cộng, vừa là cấp số nhân. (đ.p.c.m)
Bài tập tương tự: u  = 4  1
Câu 28: Cho dãy số (u u n ) : 
. Chứng minh: ( n ) vừa là cấp số cộng vừa là cấp u  = u +12 n  1  n 1+ n ( ) số nhân.
III. BÀI TẬP TRẮC NGHIỆM
Câu 29: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; −1; 1; −1 .
B. 1; − 3; 9;10 . C. 1; 0; 0; 0 . D. 32; 16; 8; 4 . Lời giải: u Nếu (u u = u . n q q + =
n ) là cấp số nhân với công bội q ta có: 1 n 1 + n . un 1; 1 − ;1; 1
− là cấp số nhân với q = −1. 1
− ;3;9;10 không là cấp số nhân.
1;0;0;0 là cấp số nhân với q = 0 . 1
32;16;8; 4 là cấp số nhân với q = . 2
Câu 30: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; − 3;9; − 27;54 .
B. 1; 2; 4;8;16 .
C. 1; −1;1; −1;1.
D. 1; − 2; 4; − 8;16 . Lời giải:
Dãy 1; 2; 4;8;16 là cấp số nhân với công bội q = 2 .
Dãy 1; −1;1; −1;1 là cấp số nhân với công bội q = −1 .
Dãy 1; − 2; 4; − 8;16 là cấp số nhân với công bội q = −2 .
Dãy 1; − 3;9; − 27;54 không phải là cấp số nhân vì 3 − =1.( 3 − );( 27 − ).( 3 − ) = 81  54 .
Câu 31: Trong các dãy số (u sau đây, dãy số nào là cấp số nhân? n )
A. u = 3n . B. n u = 2 . C. u = 1 . D. n u = 2 + 1. n n n n n Lời giải: un 2n Ta thấy, với n
  2,n  dãy số(u ) = 2n có tính chất: =
= 2 nên là cấp số nhân với n n 1 u − n− 2 1
công bội q = 2, u = 2 . 1 3
Câu 32: Cấp số nhân (u u .2n− = , n
n ) có số hạng tổng quát là 1 * n
. Số hạng đầu tiên và công bội của 5 cấp số nhân đó là 6 3 6 3
A. u = , q = 2 u = , q = 2 − u = , q = 2 − u = , q = 2 1 . B. . C. D. . 5 1 5 1 5 2 5 Lời giải: 3 − 3 3 − 6 u Ta có 1 1 u = .2 = u = .2 =  q = = 2 1 và 2 1 2 . 5 5 2 5 5 u1 3 Vậy u = q = 1 và 2 . 5
Câu 33: Cho cấp số nhân (u u q
n ) có số hạng đầu 1 và công bội
0 . Công thức xác định số hạng tổng
quát của cấp số nhân (un ) là A. * u = . n q u n   u = u q n   n 1 . B. * n 1 . C. 1 − * u = . n q u n   n u u q − = n   n 1 . D. 1 * n 1 . Lời giải:
Công thức tổng quát của cấp số nhân n 1 − * u = u q n   n 1 .
Câu 34: Cho cấp số nhân (u u = 2 u = 6 n ) với 1 và 2
. Công bội của cấp số nhân đã cho bằng 1 A. 3 . B. −4 . C. . D. 4 . 3 Lời giải:
Gọi q là công bội của cấp số nhân (un ) . u 6 Ta có: 2
u = u .q q = = = 3 2 1 . u 2 1 Vậy q = 3 .
Câu 35: Cấp số nhân (u u = 9 u = 81 n ) có 4 , 5 có công bội là A. 3 . B. 72 . C. 18 . D. 9 . Lời giải: u = 9  u = 9 Ta có 4 4     q = 9 . u = 81 u .q = 81  5  4
Câu 36: Cho cấp số nhân (u u = 6 u = 162 n ) với 2 và 5
. Công bội của cấp số nhân đã cho bằng 1 A. 3 . B. 3 − . C. 2 . D. . 3 Lời giải: 4 u  = u .q u 162 Ta có: 5 1  . Do đó: 3 3 5
u = u .q q = = = 27  q = 3. u = u .q 5 2  u 6 2 1 2 2 96 −
Câu 37: Cho cấp số nhân có u = 3, − q = . Số
là số hạng thứ mấy của cấp số này? 1 3 243 A. Thứ 6. B. Thứ 8. C. Thứ 5. D. Thứ 7. Lời giải: n 1 9 − 6 − −   − n− 96 2 96 Ta có: 1 u =  u .q =  3 − . =  n = 5. n 1   243 243  3  243 96 − Vậy số
là số hạng thứ 5 của cấp số. 243
Câu 38: Cho cấp số nhân (u có u = −3 , công bội q = −2 . Hỏi −192 là số hạng thứ mấy của (u n ) ? n ) 1 A. Số hạng thứ 6 B. Số hạng thứ 7 C. Số hạng thứ 5 D. Số hạng thứ 8 Lời giải:
Giả sử −192 là số hạng thứ n của (u với * n .Ta có n ) 1 n− n− 6 n−1 192 . n u q − − =  − = (− ) (− ) 1 192 3 . 2  = (− ) 1 64 2  ( 2 − ) = ( 2
− )  6 = n − 1  7 = n . 1
Do đó −192 là số hạng thứ 7 của (u . n )
Câu 39: Một cấp số nhân với công bội bằng 2
− có số hạng thứ ba bằng 8 và số hạng cuối bằng −1024 .
Hỏi cấp số nhân đó có bao nhiêu số hạng? A. 11 B. 10 C. 9 D. 8 Lời giải: Ta có 2
u = u .q = 4u u = 2 3 1 1 1 . n 1 − n − Ta lại có n 1 u = u .q = 2. 2 − = − 2 − = 1 − 024  n =10 n 1 ( ) ( )
. Vậy cấp số nhân có 10 số hạng.
Câu 40: Cho cấp số nhân (u u = −2 q = u n ) có 1 và công bội 3 . Số hạng 2 là A. u = −6. u = 1 u = −18. u = 6. 2 B. 2 . C. 2 D. 2 Lời giải:
Ta có u = u .q = −2.3 = −6 2 1 . u  = 1 1 
Câu 41: Cho dãy số (u v v = u − v
n ) xác định bởi 
u + 8 và dãy số ( n ) xác định bởi 2 . Biết ( n ) n u = n nn 1+  5
là một cấp số nhân có công bội q . Khi đó 2 8 1 A. q = .
B. q = 5 .
C. q = .
D. q = . 5 5 5 Lời giải:
Ta có v = u − 2  v = u − 2 = −1
u = v + 2  u = v + 2 n n 1 1 và n n n 1 + n 1 + . v + 2 + 8 1 1 v 1 Suy ra n n 1 v + 2 =
v + 2 = v + 2  v = v +  = n 1 + n 1 + n n 1 . 5 5 + 5 n v 5 n 1 Vậy (v q =
n ) là một cấp số nhân có công bội . 5
Câu 42: Cho cấp số nhân (un ) biết u = − = 2 8; 5 u
64 . Giá trị của u6 bằng A. 512 . B. 256 . C. −128 . D. −1024 . Lời giải: Gọi 1
u và q lần lượt là số hạng đầu và công bội của cấp số nhân (un ) u  = 8 − u  .q = 8 − u   .q = 8 −   = 2 1 1 u 4 Ta có 1       4 3  =   =   = −  = − 5 u 64 u .q 64 q 8 q 2 1 5 Vậy: 5 = = − = − 6 u 1 u .q 4.( 2) 128 .
Câu 43: Cho cấp số nhân (u u = −8 u = 64 u n ) biết 2 ; 5 . Giá trị của 3 bằng A. −16 . B. 32 . C. −32 . D. 16 . Lời giải: Ta có 3
u = u .q q = −2 5 2 .
Vậy u = u .q = 16 3 2 . u  + u = 60
Câu 44: Cho cấp số nhân (u u n ) có 2 4  . Tìm . u + u = 180  1 3 5 A. 3 . B. 6 . C. 2 . D. 5 . Lời giải: u
 .q + u .q = 60 u  .q  ( 2 3 1+ q = 60 1 ) u  = 2 1 1 1 Ta có      . 2 4 2 u
 .q + u .q =180  u  .q  ( 2 1+ q = 180 q = 3 1 1 1 ) Vậy u = 2 1 . u + u =198
Câu 45: Cho cấp số nhân (u u n ) có 2 7 
. Khi đó công bội của cấp số nhân ( n ) là u + u = 396  3 8 A. 2 . B. 3 . C. 4 . D. 1. Lời giải:
Gọi q là công bội của cấp số nhân (un ) . Khi đó: u + u = 198
u q + u q =198  u q  ( 5 6 1+ q = 198 1 ) 2 7 1 1       q = 2 . 2 7 2 u + u = 396  u q + u q = 396  uq  ( 5 3 8 1 1 1+ q = 396 1 ) u  − u = 511 10 1
Câu 46: Tìm số hạng đầu u u
1 của cấp số nhân ( n ) biết rằng:  .
u + u + u = 73  7 4 1 A. u = 1 u = 2 u = −1 u = −2 1 . B. 1 . C. 1 . D. 1 . Lời giải: u  − u = 511 9 u  9
 .q − u = 511 u  . q −1 = 511  1 ( ) 10 1 Ta có:  1 1    
u + u + u = 73  6 3  + + = u  .  ( 6 3 q + q +1 = 73 1 ) 7 4 1 u .q u .q u 73  1 1 1 u  .  ( 3 q − ) 1 .( 6 3 q + q +1 = 511 3 q −1 = 7 1 ) q = 2        . u  . u .  ( 6 3 q + q +1 = 73 u =1 1 )  ( 6 3 q + q +1 = 73  1 ) 1
Câu 47: Cho cấp số nhân u . n
Khi đó đẳng thức nào sau đây là đúng? u u A. 2018 2020 u u u .u 2019 . B. . 2 2019 2018 2020 C. 2 u u .u u u .u 2019 2018 2019 . D. 2019 2018 2020 . Lời giải: Vì u u u .u u u .u .
n là một cấp số nhân nên 2 n n 1 n 1 n n 1 n 1 Khi đó, với n 2019 ta được u u .u . 2019 2018 2020
Câu 48: Ba số 2x −1, x, 2x +1 theo thứ tự lập thành một cấp số nhân. Hãy tìm . x 1 3 A.  .
B. x = 1. C.  . D.  3 . 3 3 Lời giải:
Ba số 2x −1, x, 2x +1 theo thứ tự lập thành một cấp số nhân nên: (2x − ) 1 (2x + ) 1 3 2 2 2 2
1 = x  4x −1 = x x =  x =  3 3
Câu 49: Xác định x là số thực dương để 2x − 3; ;
x 2x + 3 lập thành một cấp số nhân.
A. x = 3 .
B. x = 3 .
C. x =  3 . D. x = 5 . Lời giải: Vì 2x − 3; ;
x 2x + 3 ( x  0 ) theo thứ tự lập thành một cấp số nhân nên 2
x = (2x − 3)(2x + 3) 2 2 2
x = 4x − 9  x = 3  x = 3 .
Câu 50: Có bao nhiêu giá trị nguyên dương của x để ba số 1; x ; x + 2 theo thứ tự lập thành một cấp số nhân? A. 2 . B. 3 . C. 1. D. 0 . Lời giải:
Để ba số 1; x ; x + 2 theo thứ tự lập thành một cấp số x =1+ 3 nhân  1( x + 2) 2 2
= x x − 2x − 2 = 0   . x =1− 3
Vậy không có số nguyên dương nào thỏa mãn yêu cầu bài toán.
Câu 51: Viết thêm sáu số xen giữa hai số 2
− và 256 để được một cấp số nhân có 8 số hạng. Nếu
viết tiếp thì số hạng thứ 15 là bao nhiêu? A. −32768 . B. 16384 . C. −16384 . D. 32768 . Lời giải: u  = 2 − u  = 2 − u  = 2 − Theo đề bài ta có: 1 1 1      . 7 u = 256  u .q = 256  q = 2 − 8 1 14 14
u = u .q = 2.( − 2) − = 32 − 768 15 1 .
Câu 52: Biết ba số 2
x ; 8;x theo thứ tự lập thành cấp số nhân. Giá trị của x bằng A. x 4. B. x 5. C. x 2. D. x 1. Lời giải: Do ba số 2
x ; 8;x theo thứ tự lập thành cấp số nhân nên theo tính chất cấp số nhân ta được 2 3 x .x 8 x 8 x 2 .
Câu 53: Với x là số nguyên dương, ba số 2x, 3x + 3, 5x + 5 theo thứ tự là ba số hạng liên tiếp của
một cấp số nhân. Số hạng tiếp theo của cấp số nhân đó là 250 250 A. − . B. . C. 250 . D. −250 . 3 3 Lời giải:
Ba số 2x, 3x + 3, 5x + 5 theo thứ tự là ba số hạng liên tiếp của một cấp số nhân nên

Tài liệu liên quan: