






























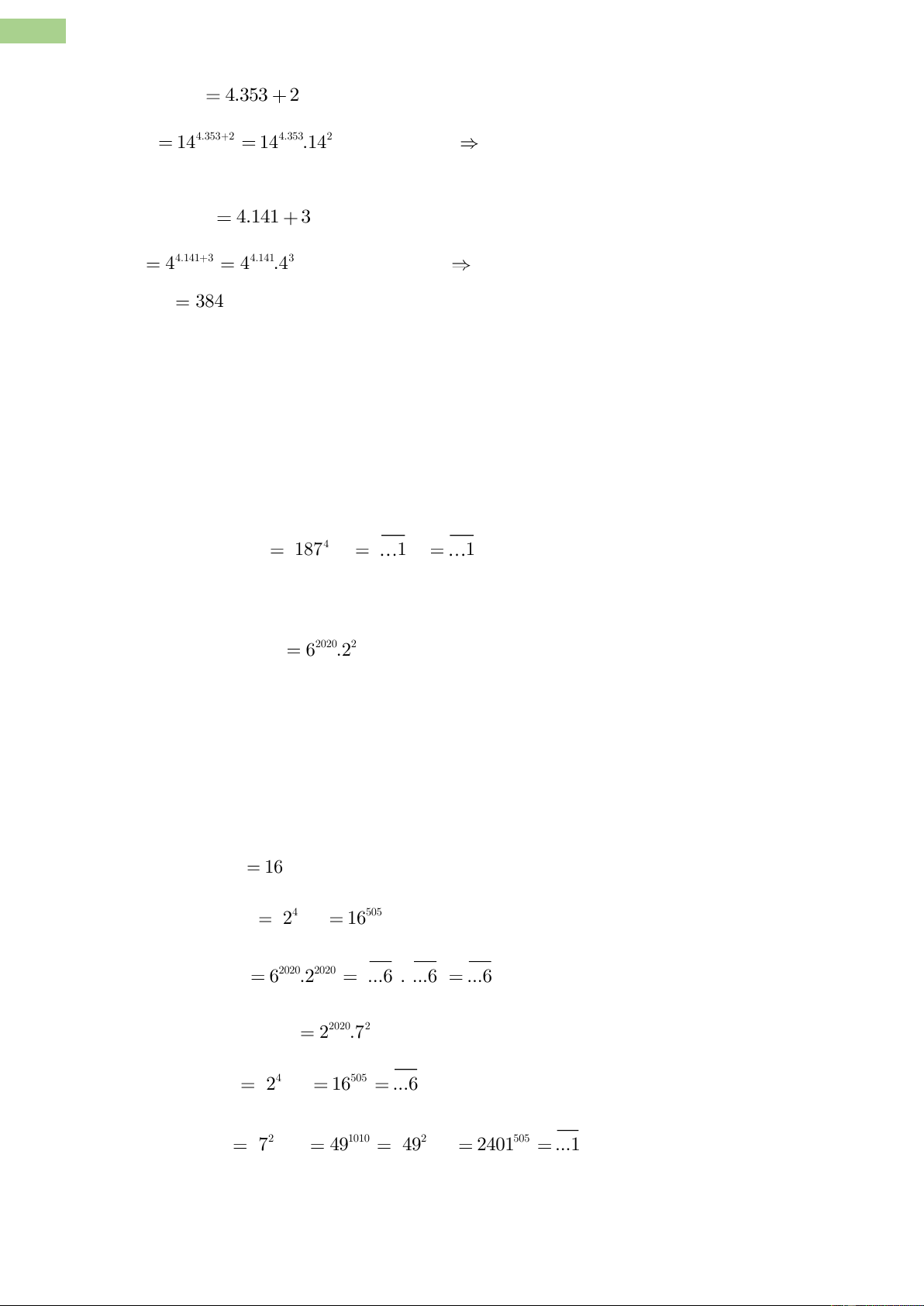













Preview text:
1
CHUYÊN ĐỀ .CHỮ SỐ TẬN CÙNG
A.TRỌNG TÂM CẦN ĐẠT
I. TÓM TẮT LÝ THUYẾT
1. Tìm 1 chữ số tận cùng Tính chất 1:
a) Các số có chữ số tận cùng là 0, 1, 5, 6 khi nâng lên lũy thừa bậc bất kì thì chữ số tận cùng vẫn không thay đổi.
b) Các số có chữ số tận cùng là 4, 9 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng vẫn không thay đổi.
c) Các số có chữ số tận cùng là 3, 7, 9 khi nâng lên lũy thừa bậc 4n n thì chữ số tận cùng là1 .
d) Các số có chữ số tận cùng là 2, 4, 8 khi nâng lên lũy thừa bậc 4n n thì chữ số tận cùng là 6 .
Chú ý: Muốn tìm chữ số tận cùng của số tự nhiên m x
a , trước hết ta xác định chữ số tận
cùng của a :
- Nếu chữ số tận cùng của a là 0, 1, 5, 6 thì x cũng có chữ số tận cùng là 0, 1, 5, 6 .
- Nếu chữ số tận cùng của a là 3, 7, 9 : Phân tích: m 4n r 4n . r a a a a với r 0, 1, 2, 3 Từ tính chất 1c
chữ số tận cùng của x chính là chữ số tận cùng của r a .
- Nếu chữ số tận cùng của a là 2, 4, 8 : cũng như trường hợp trên Từ tính chất 1d
chữ số tận cùng của x chính là chữ số tận cùng của 6 r a . Tính chất 2:
Một số tự nhiên bất kì, khi nâng lên lũy thừa bậc 4n 1 n
thì chữ số tận cùng vẫn không thay đổi.
Chữ số tận cùng của một tổng các lũy thừa được xác định bằng cách tính tổng các chữ số tận cùng
của từng lũy thừa trong tổng. 2 Tính chất 3:
a) Số có chữ số tận cùng là 3 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 7; số có chữ
số tận cùng là 7 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 3.
b) Số có chữ số tận cùng là 2 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 8; số có chữ
số tận cùng là 8 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 2.
c) Các số có chữ số tận cùng là 0, 1, 4, 5, 6, 9 khi nâng lên lũy thừa bậc 4n 3 sẽ không thay
đổi chữ số tận cùng. Tính chất 4: Nếu a và a , 5 1 thì 100 a 1 chia hết cho 125. Chứng minh: Do 20 a 1 chia hết cho 25 nên 20 40 60 80
a , a , a , a khi chia cho 25 có cùng số dư là 1 20 40 60 80 a a a a 1 chia hết cho 5. Vậy 100 20 80 60 40 20 a 1 a 1 a a a a 1 chia hết cho 125.
* Phương pháp dùng cấu tạo số để tìm chữ số tận cùng của số k A n với , n k N . k
- Giả sử A 10q r . Khi đó, k 10 10t k A q r p r với r ; 0 r 9
Suy ra, chữ số cuối cùng của A chính là chữ số cuối cùng của số k r . - Nếu A 100a bc
abc thì bc là hai chữ số cuối cùng của A . - Nếu A 1000a bcd
abcd thì bcd là ba chữ số cuối cùng của A . - Nếu A 10m.a a a
a ...a a thì a
a là m chữ số cuối cùng của A . m m 1... 0 m 1 0 m 1... 0
2. Tìm hai chữ số tận cùng
Việc tìm hai chữ số tận cùng của số tự nhiên x chính là việc tìm số dư của phép chia x cho 100.
Phương pháp tìm hai chữ số tận cùng của số tự nhiên n x a :
Trước hết, ta có nhận xét sau: 20 2 76 mod 100 20 3 01 mod 100 3 5 6 76 mod 100 4 7 01 mod 100 Mà: 76n 76 mod 100 với n 1 , 5n 25 mod 100 với n 2 . Suy ra kết quả sau với * k : 20k a 00 mod 100 nếu a 0 mod 10 , 20k a 01 mod 100 nếu a 1; 3; 7; 9 mod 10 , 20k a 25 mod 100 nếu a 5 mod 10 , 20k a 76 mod 100 nếu a 2; 4; 6; 8 mod 100 .
Vậy để tìm hai chữ số tận cùng của n
a ta lấy số mũ n chia cho 20 . Dạng 1.
- Các số có tận cùng bằng 01; 25; 76 nâng lên luỹ thừa nào (khác 0) cũng tận cùng bằng 01; 25; 76 - Các số 20 3 (hoặc 5 81 ); 4 2 2
7 ; 51 ; 99 có tận cùng bằng 01. - Các số 20 5 4 2 4 2 2 ; 6 ; 18 ; 24 ; 8
6 ; 74 có tận cùng bằng 76 . - Số 26n n 1 có tận cùng bằng 76 .
- Các số có chữ số tận cùng là 01;25;76 khi nâng lên lũy thừa bậc bất kì khác 0 thì hai chữ số tận
cùng vẫn không thay đổi. (1) - Các số 20 4 10 2 5 2
3 ;7 ;9 ;51 ;81 ;99 có chữ số tận cùng là 01. (2) - Các số 10 5 4 2 4 2
4 ;6 ;18 ;24 ;68 ;74 có chữ số tận cùng là 76. (3) n - Số 26 (n
1) có chữ số tận cùng là 76. (4)
Như vậy, muốn tìm chữ số tận cùng của số tự nhiên m x
a , trước hết ta xác định chữ số tận cùng của a. Dạng 2. CHÚ Ý: - 10
4 có 2 chữ số tận cùng là 76. - 2
5 có 2 chữ số tận cùng là 25. 4 - 20
8 có 2 chữ số tận cùng là 76. - 10
9 có 2 chữ số tận cùng là 01.
3. Tìm ba chữ số tận cùng trở lên
Việc tìm ba chữ số tận cùng của số tự nhiên x chính là việc tìm số dư của phép chia x cho 1000. k Giả sử n 100k r với 0 r 100 , khi đó: n 100k r 100 . r a a a a . Giả sử: a x mod 10 , x 0, 1, 2, ..., 9 100 Ta có: 100 100 a 10k x x mod 1000
Vậy 3 chữ số tận cùng của 100
a cũng chính là 3 chữ số tận cùng của 100 x .
Dùng quy nạp với mọi n 1 , ta có: 625n 625 mod 1000 , 376n 376 mod 1000 . - Nếu x 0 thì 100 x 000 mod 1000 25 - Nếu x 5 thì 4 4 x 5 625 100 4 3 x 5 625 mod 10 - Nếu x
1; 3; 7; 9 ta có tương ứng: 25 4 x 1;81; 2401; 6561 1 mod 40 100 3 x 40k 1 1 mod 10 - Nếu x 2;4; 6;8 thì 100 100 x 2 8 . Ta có: x , 125 1 nên 100 x
1 mod 125 (Định lí Euler).
Giả sử 3 chữ số tận cùng của 100
x là abc ta có: 100 x 1000k abc abc 8 và abc 1 mod 125
Trong các số 1; 126; 376; 501; 626; 751; 876 (các số có 3 chữ số chia cho 125 dư 1) chỉ có duy nhất
một số chia hết cho 8 là 376. Vậy 100 x 376 mod 1000 .
Do đó ta có kết quả sau: 100k 3 a 000 mod 10 nếu a 0 mod 10 100k 3 a 001 mod 10 nếu a 1; 3; 7; 9 mod 10 5 100k 3 a 625 mod 10 nếu a 5 mod 10 100k 3 a 376 mod 10 nếu a 2; 4; 6; 8 mod 10
Vậy để tìm ba chữ số tận cùng của n
a ta tìm 2 chữ số tận cùng của số mũ n .
Dạng 3. Một số trường hợp cụ thể về 3 chữ số tận cùng
Các số có tận cùng bằng 001; 376; 625 nâng lên luỹ thừa nào (khác 0) cũng tận cùng bằng 001; 376; 625.
Các số có tận cùng bằng 0625 nâng lên luỹ thừa nào (khác 0) cũng tận cùng bằng 0625. II. CÁC DẠNG TOÁN
Dạng 1: Tìm 1 chữ số tận cùng
Ví dụ 1.1: Tìm chữ số tận cùng của các số sau: 40 2019 50 2020 a)32 b) 2018 c)27 d) 2019 Phân tích:
- Ta biết rằng các số tận cùng là 2; 4;6; 8 khi nâng lên lũy thừa 4n đều cho tận cùng là 6 .
Còn các số tận cùng là 1;3;7;9 khi nâng lên lũy thừa 4n đều cho tận cùng là 1.
- Để đưa về lũy thừa 4n thì em cần viết số mũ dưới dạng công thức của phép chia có dư với số chia là 4 .
- Để tìm chữ số tận cùng của mỗi lũy thừa trên ta chỉ cần tìm chữ số tận cùng của hàng đơn vị. Lời giải
a) Để tìm chữ số tận cùng của 40
32 ta tìm chữ số tận cùng của 40 2 Ta xét 40 2 , ta có 40 4.10 2 2 ...6 Vậy 40
32 có chữ số tận cùng là 6 .
b) Để tìm chữ số tận cùng của 2019 2018
ta tìm chữ số tận cùng của 2019 8 Ta xét, ta có 2019 4.502 8 8 8 ...6 8 ...8 Vậy 2019 2018 có tận cùng là 8 .
c) Chữ số tận cùng của 50
27 cũng là chữ số tận cùng của 50 7 Ta có 50 4.12 2 7 7 7 ...1 49 ...9 6
Vậy chữ số tận cùng của 50 27 là 9 .
d) Chữ số tận cùng của 2020 2019
cũng là chữ số tận cùng của 2020 9 Ta có 2020 4.505 9 9 ...1
Vậy chữ số tận cùng của 2020 2019 là 1 . Bình luận:
Với phần d) ta có thể giải như sau:
Vì chữ số tận cùng là 9 mà khi nâng lên lũy thừa chẵn sẽ ra tận cùng là 1, do vậy 2020 2019 có tận cùng là 1 .
Với cách giải này ta hoàn toàn có thể mở rộng số cho phần d), chẳng hạn số 2021 2020 2019 , 2050 .... 2020 2019 ,…
Ví dụ 1.2: Tìm chữ số tận cùng của 2020 3 Phân tích:
Để tìm được chữ số tận cùng của số trên ta phải đưa về số có tận cùng là 1 hoặc 6 . Lời giải Ta thấy 4 3
81 , số tận cùng bằng 1 nâng lên bậc lũy thừa nào cũng có chữ số tận cùng bằng 1 nên ta phân tích 2020 4.505 505 3 3 81 . Vậy số 2020 3
có chữ số tận cùng bằng 1 .
Ví dụ 1.3: Tìm chữ số tận cùng của các số sau 52 24 2015 51 25 2014 50 a)26 b)2013 c)78 Phân tích:
Trong bài này ta không thể viết ngay số mũ ở dạng 4n , để cho dễ biểu diễn ta dùng đồng dư thức
để tìm dư của phép chia số mũ cho 4 . Lời giải
a) Trước hết ta tìm số dư của phép chia 24 25 khi chia cho 4 . Ta có 24 24 * 25 1 mod 4 25 1 mod 4 25 4k 1 k N 7 24 Suy ra, 25 4k 1 4 26 26 26 k 26 ...6 26 ...6 Vậy 24 25 26 có tận cùng là 6 .
Nhận xét: Trong phần này rõ ràng dựa vào nhận xét ‘Số có tận cùng là 6 khi nâng lên lũy thừa bất
kỳ luôn có tận cùng là 6 ’ thì lời giải rất đơn giản.
b) Tương tự, ta tìm số dư khi chia số mũ của 2013 cho 4 . 2015 2015 2014 2 mod 4 2014 2 mod 4 2015 2014 0 mod 4 Ta có 2015 2.1002 1002 2 2 2 4 2 2015 2014 4k k N * Do đó 2015 2014 4k 4 2013 2013 2013 k ...1 Vậy 2015 2014 2013 có tận cùng là 1 .
c) Trước hết ta tìm số dư trong phép chia 52 51 50 khi chia cho 4 . Ta có 2 50 2 mod 4 ; 50 0 mod 4 ; 50k 0 mod 4 k 2 52 Suy ra 51 50 0 mod 4 n N Mà 52 51 là số lẻ nên 52 52 51 51 50 0 mod 4 50 4m(m N) 52 Từ đó ta có 51 50 4m 4 78 78 78 m ...6 52 Vậy 51 50 78 có tận cùng là 6 . Bình luận:
Với bài toán ở dạng lũy thừa tầng thì ta luôn chú ý tìm cách viết số mũ dưới dạng công thức của
phép chia có dư với số chia là 4 . Tuy nhiên, nếu tận cùng là một trong các số đặc biệt như:
0;1;5;6 thì ta nhận xét ngay mà không cần quan tâm đến giá trị của số mũ. Còn nếu tận cùng là 4
hoặc 9 thì ta có thể xem xét tính chẵn lẻ của số mũ để suy ra kết quả.
Ví dụ 1.4: Tìm chữ số tận cùng của 89 81 a)7 4 2014 1955 b)2 .9 Lời giải 8 a) Ta có: 89 4.21 21 7 7 .7
7.2401 nên số này có số tận cùng bằng 7 . 81 2.40 40 4 4 .4
16 .4 nên số này có số tận cùng bằng 4 . Vậy số 89 81 7
4 có chữ số tận cùng bằng 3 b) Ta có: 2014 4.506 2 506 2 2 .2
16 .4 nên số này có số tận cùng bằng 4 . 1955 2.977 977 9 9 .9
81 .9 nên số này có số tận cùng bằng 9 . Vậy số 2014 1955 2 .9
có chữ số tận cùng bằng 6 .
Ví dụ 1.5: Tìm chữ số tận cùng của các tích sau: 2020 27 28 a)26 .27 b) 1.3.5....2019 202 200 100 c) 8.18.28.38...198
d) 1.3.9.11.13.17....2019 Phân tích:
Để tìm chữ số tận cùng của tích ta có thể tìm chữ số tận cùng của từng thừa số hoặc nhóm các thừa số. Lời giải
a) Ta thấy 26 có tận cùng là 6 , mà số tận cùng là 6 nâng lên lũy thừa bao nhiêu vẫn tận cùng là 6 . Do đó, 27 26 có tận cùng là 6 . 5Có 28 4.7 27 27 ...1 Suy ra 27 28 26 27 ...6 ...1 ...6
Vậy tích có tận cùng là 6 .
Khai thác: - Vì tích có tận cùng là 6 nên ta có thể yêu cầu khác như sau: 27 28 26 27 4 Chứng minh rằng số là số tự nhiên. 10
- Nếu để ý đến công thức lũy thừa của một tích ta có thể làm như sau: 4 6 3 27 27 28 27 27 26 27 26 27 27 26 27 27 ...2 27 4 6 3 ...2 ...2 27 ...6 ...8 27 ...6 9
) Ta biết rằng tích của 5 với bất kỳ số lẻ nào cũng có tận cùng là 5, do đó tích 1 3 5 ... 2019
sẽ có tận cùng là 5. Mặt khác, số có tận cùng là 5 khi nâng lên lũy thừa bất kỳ vẫn tận cùng là 5. 2020 Vậy 1 3 5 ... 2019 có tận cùng là 5.
Khai thác: Ta biết rằng tích của hai số tự nhiên liên tiếp sẽ có tận cùng là 1 trong các số sau:
0;2;6 do đó, ta có thể ra bài toán như sau:
Tìm tất cả các số tự nhiên n sao cho: 2020 2020 2 a)n n 1 3 5 ... 2019 ; b) 2n 1 2n 2 1 3 5 ... 2019
c) Đặt A
8 18 28 38 ... 198 . Số thừa số của tích này là: 198 8 : 10 1 20 (số hạng) (1)
Ta thấy tích 4 thừa số có tận cùng là 8 sẽ có tận cùng là 6 . Vì có 20 thừa số ta kết hợp được 5
nhóm mỗi nhóm có 4 thừa số, tích mỗi nhóm này có chữ số tận cùng là 6 . Do đó kết quả của tích A
có chữ số tận cùng là 6 . Mà số có tận cùng là 6 nâng lên lũy thừa bất kỳ sẽ có tận cùng là 6 , suy ra 202 200 A sẽ có tận cùng là 6 .
Vậy lũy thừa của tích có tận cùng là 6 .
Khai thác: - Ta để ý, chữ số tận cùng của A cũng là chữ số tận cùng của 8 8 8 ... 8 (20 thừa 202
số), do đó ta có thể quy về việc tìm chữ số tận cùng của 200 20 8
- Ta có mở rộng bài toán bằng cách cho tăng số lượng các thừa số của tích.
- Hoàn toàn tương tự, ta cũng có thể thay đổi chữ số tận cùng của mỗi thừa số trong tích bởi một chữ số khác.
Chẳng hạn, tìm chữ số tận cùng của các số sau: 2020 A 2 12 22 ... 2022 200 100 B 7 17 27 ... 2017
d) Ta để ý rằng các nhóm 1 3 7 9;11 13 17 19;...;2011 2013 2017 2019 đều có tận
cùng giống nhau, nên ta đi tìm chữ số tận cùng của 1 nhóm. Ta có 1 3 7 9 ...9 Có số nhóm là: (2011 ) 1 : 10 1 202 (nhóm) 10 Suy ra 202 4 50 2 4 50 2 1 3 7 9 11 13 17 ... 2019 ...9 ...9 ...9 ...9 ...1 ...1 ...1 100 100
Vậy 1 3 7 9 11 13 17 ... 2019 ...1
...1 nên có tận cùng là 1.
Khai thác: Ta thấy tất cả các thừa số của tích đều không chia hết cho 5 , nên ta có thể thay đổi cách
phát biểu bài toán như sau: Cho số A
1 3 5 7 9 11 13 15 ... 2019 , sau khi gạch bỏ tất cả các số chia hết cho
5 của A, ta được số B. Tìm chữ số tận cùng của 100 B .
- Bài toán trên có thể thay đổi các thừa số lẻ bằng các thừa số chẵn, chẳng hạn: Tìm chữ số tận cùng 2019 của số B 2 4 6 8 12 14 16 ... 2018
Ví dụ 1.6: Tìm chữ số tận cùng của các tổng sau: 1 5 9 8009 S 2 3 4 2004 . Phân tích:
Trong dạng bài này ta phải tìm được quy luật của tổng, quy luật ở đây chính là số mũ của các số
hạng trong S, các số mũ này đều chia 4 dư 1. Mà ta biết các số khi nâng lên lũy thừa dạng 4n 1
sẽ có tận cùng không đổi. Lời giải:
Nhận xét: Mọi lũy thừa trong S đều có số mũ khi chia cho 4 thì dư 1(các lũy thừa đều có dạng 4 n – 2 1 n
, n thuộc 2; 3; 4...;2004 )
Theo tính chất, suy ra mọi lũy thừa trong S và các cơ số tương ứng đều có chữ số tận cùng giống
nhau, bằng chữ số tận cùng của tổng: 2 3 9 199. 1 2 9 1 2 3 4 200 1 2 9 9 9009 .
Vậy chữ số tận cùng của tổng S là 9 . Tổng quát hóa:
Tìm chữ số tận cùng của tổng sau: 4 2 1 1 5 9 2 3 4 n n S
Ví dụ 1.7: Tìm chữ số tận cùng của tổng 3 7 11 8011 T 2 3 4 ... 2004 . Lời giải: 11
Nhận xét: Mọi lũy thừa trong T đều có số mũ khi chia cho 4 thì dư 3 (các lũy thừa đều có dạng 4(n 2) 3 n
, n thuộc 2; 3; 4...;2004 ) Theo quy tắc 3 thì 3
2 có chữ số tận cùng là 8 ; 7
3 có chữ số tận cùng là 7 ; 11 4 có chữ số tận cùng là 4 ;
Như vậy, tổng T có chữ số tận cùng bằng chữ số tận cùng của tổng: (8 7 4 5 6 3 2 9) 199.(1 8 7 4 5 6 3 2 9) 1 8 7 4 200.(1 8 7 4 5 6 3 2 9 8 7 4 9019
Vậy chữ số tận cùng của tổng T là 9 Tương tự hóa:
Tìm chữ số tận cùng của 4 2 3 3 7 11 2 3 4 n n S
Ví dụ 1.8: Tìm số dư của phép chia: a) 1 5 9 8005 Q 2 3 4 ... 2003 cho 5 b) 3 7 11 8007 R 2 3 4 ...2003 cho 5 Lời giải:
a) Nhận xét: Mọi lũy thừa trong S đều có số mũ khi chia cho 4 thì dư 1 (các lũy thừa đều có dạng 4(n 2) 1 n
, n thuộc 2; 3; 4...;2003 )
Theo quy tắc 2, Chữ số tận cùng của tổng Q các lũy thừa bằng cách tính tổng các chữ số tận cùng
của từng lũy thừa trong tổng S.
Mọi lũy thừa trong Q và các cơ số tương ứng đều có chữ số tận cùng giống nhau, bằng chữ số tận cùng của tổng: (2 3 ... 9) 199.(1 2 ... 9) 1 2 3 200(1 2 ... 9) 5 9005
Vậy chữ số tận cùng của tổng Q là 5 nên chia 5 không có dư.
b) Nhận xét: Mọi lũy thừa trong R đều có số mũ khi chia cho 4 thì dư 3 (các lũy thừa đều có dạng 4(n 2) 3 n
, n thuộc 2; 3; 4...;2003 ) Theo quy tắc 3 thì 3
2 có chữ số tận cùng là 8 ; 7
3 có chữ số tận cùng là 7 ; 11 4 có chữ số tận cùng là 4 12
Như vậy, tổng R có chữ số tận cùng bằng chữ số tận cùng của tổng: (8 7 4 5 6 3 2 9) 199.(1 8 7 4 5 6 3 2 9) 1 8 7 200.(1 8 7 4 5 6 3 2 9 8 7 9015
Vậy chữ số tận cùng của tổng R là 5 nên chia 5 không có dư.
Ví dụ 1.9: Cho H 1234567891011121314151617
.được viết bởi các số tự nhiên liên tiếp và có 121 chữ số. Số 2019 H
có chữ số tận cùng là chữ số nào? Phân tích:
Trước hết ta phải tìm được chữ số tận cùng của H, muốn vậy ta phải tính xem với 121 chữ số thì
chữ số cuối cùng được viết là chữ số nào. Ta dựa vào bài toán ngược của bài toán “Đánh số trang sách”. Lời giải:
Ta có từ 1 đến 9 có 9 số, mỗi số gồm 1 chữ số.
Từ 10 đến 99 có 90 số, mỗi số gồm 2 chữ số nên khi viết chúng liên tiếp ta có 90.2 180 (chữ số). Mà 9 121
180nên chữ số tận cùng của H phải ở số có hai chữ số.
Số chữ số của các số có 2 chữ số viết ở H là: 121 9 112 (chữ số)
Số các số có 2 chữ số viết viết ở H là 112 : 2 56
Số thứ 56 kể từ 10 có 2 chữ số là: 10 56 1 65
suy ra chữ số tận cùng của H là chữ số 5 (là chữ số hàng đơn vị của số 65). Mặt khác, 2019 5
có tận cùng là 5 . Vậy chữ số tận cùng của 2019 H là chữ số 5. Tổng quát hóa:
Bài toán có thể mở rộng cho số các chữ số của số đã cho. Cho H 1234567891011121314151617
.được viết bởi các số tự nhiên liên tiếp và có n chữ số (n N *). Số 2019 H
có chữ số tận cùng là chữ số nào?
Với mỗi giá trị của n ta được một bài toán mới. 2
Ví dụ 1.10: Tìm số tự nhiên x thỏa mãn 14 9 4 14 9 3 10 A x 14 9
2 với A là số tự nhiên khác 0 . Phân tích: 13
Rõ ràng ta không thể tính được giá trị vế phải, để ý rằng x chính là chữ số tận cùng của biểu thức 10 A
x nên ta suy nghĩ theo hướng tìm chữ số tận cùng của vế phải. Lời giải
Ta biết rằng, số có tận cùng là 4 (hoặc 9 ) khi nâng lên lũy thừa chẵn cho tận cùng là 6 (hoặc 1),
còn khi nâng lên lũy thừa lẻ sẽ tận cùng không đổi.
Do đó, chữ số tận cùng của 14 14
14 là 6 , chữ số tận cùng của 99 9 là 9 Mặt khác, 43 81 4 20 1 4 20 2 2 2 2 2 ...6 2 ...2
suy ra chữ số tận cùng của 43 2 là 2 .
Do vậy, chữ số tận cùng của vế phải giống chữ số tận cùng của 6 9 2 17 , tức là 7 . 2 Ta thấy 10 A
x có tận cùng là x nên 10 A x có tận cùng bằng tận cùng của 2 x
Vì không có số nào lũy thừa bậc 2 lên để có tận cùng là 7 , nên không tìm được x thỏa mãn.
Vậy không có x thỏa mãn. Bình luận:
Việc phát hiện ra x là chữ số tận cùng của biểu thức trong ngoặc là mấu chốt để giải bài toán. Tổng quát hóa:
Vì không có số nào lũy thừa với số mũ khác 4n 1 hoặc 4n
3 lại có tận cùng là 7 , nên ta có thể
tổng quát bài toán như sau:
Với mỗi số tự nhiên n , hãy tìm số tự nhiên x thỏa mãn: 4n 2 14 9 4 a) 14 9 3 10 A x 14 9
2 với A là số tự nhiên khác 0 . 4n 14 9 4 b) 14 9 3 10 A x 14 9
2 với A là số tự nhiên khác 0 .
Ví dụ 1.11: Chứng minh 4n 4n 4n 4 2012 2013 2014 2015 n N
không phải là số chính
phương với mọi n là số nguyên dương. Lời giải Ta có 4 2012 n
(...6)n nên số này có số tận cùng bằng 6 4 2013 n
(...1)n nên số này có số tận cùng bằng 1 4 2014 n
(...6)n nên số này có số tận cùng bằng 6 14 4
2015 n số này có số tận cùng bằng 5
Suy ra số N có chữ số tận cùng bằng 8 , mà số chính phương không có chữ số tận cùng bằng 8 .
Vậy số N không là số chính phương.
Ví dụ 1.12: Tồn tại hay không số tự nhiên n sao cho 2 n n 1 chia hết cho 2000 1995 Lời giải: 2000 1995
tận cùng bởi chữ số 5 nên chia hết cho 5 . Vì vậy, ta đặt vấn đề là liệu 2 n n 1 có chia hết cho 5 không? Ta có 2 n n n n
1 là tích của hai số tự nhiên liên tiếp nên chữ số tận cùng của 2 n n chỉ có thể là 0;2;6 2 n n
1 chỉ có thể tận cùng là 1; 3;7 2 n n 1 không chia hết cho 5.
Vậy không tồn tại số tự nhiên n sao cho 2 n n 1 chia hết cho 2000 1995
Sử dụng tính chất: “ một số chính phương chỉ có thể tận cùng bởi các chữ số 0;1;5;6;9 ”, ta có thể
giải được bài toán sau:
Ví dụ 1.13: Cho p là số nguyên tố lớn hơn 5. Chứng minh rằng 8n 4 3. n p p 4 chia hết cho 5. Lời giải:
Theo tính chất trên, ta có p là số nguyên tố lớn hơn 5 vậy chữ số tận cùng của p là các chữ số
1;3;7;9 , các lũy thừa của p có dạng 4n Chữ số tận cùng của 8n 4 ; n p p là 1.
Vậy chữ số tận cùng của 8n 4 3. n p p
4là 0 nên chia hết cho 5 (dpcm).
Dạng 2: Tìm hai chữ số tận cùng
Ví dụ 2.1: Tìm hai số tận cùng của 100 2 Lời giải Chú ý rằng: 10 2
1024 bình phương của số có tận cùng bằng 24 thì tận cùng bằng 76, số có tận
cùng bằng 76 thì nâng lên lũy thừa nào (khác 0) cũng tận cùng bằng 76. 10 5 5 Do đó 100 10 10 2 2 2 1024 1024 ...76 ...76
Vậy hai chữ số tận cùng của 100 2 là 76.
Ví dụ 2.2: Tìm hai chữ số tận cùng của 1991 7 Lời giải 15 Ta thấy: 4 7
2401, số có tận cùng bằng 01 nâng lên lũy thừa nào cũng tận cùng bằng 01. 497 497 Do đó: 1991 1988 3 4 7 7 .7 7 .343 ...01 .343 ...01 .343 ...43. Vậy 1991 7
có hai chữ số tận cùng là 43.
Bài toán tương tự
Tìm hai chữ số tận cùng của: 99 a) 51 51 ; b) 99 99 ; c) 666 6 ; d) 101 101 14 .16 Hướng dẫn: 25 25 a) 51 2 51 51 .51 01 .51 51. k k 99 b) 99 2k 1 2 99 99 99 .99 01 .99 99 . 133 c) 666 5 6 6 .6 76 .6 56 . 101 50 50 d) 101 101 101 2 14 .16 14.16 224 224 .224 76 .224 76 .224 24 .
Ví dụ 2.3: Tìm 2 chữ số tận cùng của 56 77 1976 .2015 Lời giải Ta thấy: Chữ số tận cùng của 56
1976 cũng là chữ số tận cùng của 56 76 mà 56 76 ...76 Chữ số tận cùng của 77
2015 cũng là chữ số tận cùng 77 của 77 15 mà 77 77 77 20.3 17 77 17 15 3.5 3 .5 3 .5 3 ...01 . ...25 ...63 ...25 ...75. Suy ra: 56 77 1976 .2015 ...76 . ...75 ...00. Vậy 56 77
1976 .2015 có 2 chữ số tận cùng là 00.
Ví dụ 2.4: Tìm hai chữ số tận cùng của số 999 C 2 Lời giải 16 Ta có: 10 2 1 1024 1 1025 25 suy ra 20 10 10 2 – 1 2 1 2 – 1 25 50 Ta lại có 1000 20 20 2 – 1 2 – 1 2 – 1 suy ra 1000 2 – 1 25 Do đó 1000 2
chữ số tận cùng là 26;51;76 nhưng 1000 2 4 Suy ra 1000 2 tận cùng là 76 999
2 tận cùng là 38 hoặc 88 vì 999 2 4 Vậy 999 2 tận cùng là 88 Vậy 999 C
2 có hai chữ số tận cùng là 88.
Ví dụ 2.5: Tìm hai chữ số tận cùng của các tổng a) 2002 2002 2002 2002 S 1 2 3 2004 1 b) 2003 2003 2003 2003 S 1 2 3 2004 2 Phân tích:
Trong bài tập này ta sử dụng tính chất sau: Nếu a N và , a 5 1 thì 20 a 1 25 . (*) Lời giải
a) Dễ thấy, nếu a chẵn thì 2
a chia hết cho 4 ; nếu a lẻ thì 100 a
1 chia hết cho 4 ; nếu a chia hết cho 5 thì 2 a chia hết cho 25.
Mặt khác, từ tính chất (*) ta suy ra với mọi a N và a ,5 1 ta có 100 a 1 25. Vậy với mọi a N ta có 2 100 a a 1 100 . Do đó 2002 2 2000 2 2000 2 2 2 S 1 2 2 1 ... 2004 2004 1 2 3 ... 2004 . 1
Nên hai chữ số tận cùng của tổng S1 cũng chính là hai chữ số tận cùng của tổng 2 2 2 2 1 2 3 ... 2004 . n n 1 2n 1 Ta có: 2 2 2 2 1 2 3 ... n 6 2 2 2 1 2 ... 2004 2005.4009.334
2684707030 , tận cùng là 30. 17
Vậy hai chữ số tận cùng của tổng S1 là 30.
b) Hoàn toàn tương tự như câu a, 2003 3 2000 3 2000 3 3 3 S 1 2 2 1 ... 2004 2004 1 2 3 2004 . 2
Nên hai chữ số tận cùng của tổng S2 cũng chính là hai chữ số tận cùng của tổng 3 3 3 3 1 2 3 ... 2004 . 2 2 n n 1 Áp dụng công thức: 3 3 3 1 2 ... n 1 2 ... n 2 2 3 3 3 1 2 ... 2004 2005.1002
4036121180100, tận cùng là 00.
Vậy hai chữ số tận cùng của tổng S2 là 00.
Ví dụ 2.6: Tìm 2 chữ số tận cùng của 2004 4 Lời giải
Do 4 là số chẵn nên ta tìm số n nhỏ nhất để 4n
1 25 . Ta tìm được n 10 thỏa mãn. Mặt khác 2004 10.200 4. Nên 2004 10.200 4 4 10 200 4 4 4 4 (4 ) 1 4 100k 256
Vậy chữ số tận cùng của 2004 4 là 56.
Ví dụ 2.7: Tìm 2 chữ số tận cùng của 2020 51 Lời giải Ta có 2020 2.1010nên 2020 2 1010 1010 51 (51 ) 2601
. Khi đó theo quy tắc (1) chữ số tận cùng của 2020 51 là 01.
Ví dụ 2.8: Tìm 2 chữ số tận cùng của a) 2015 7 b) 66 57 Lời giải a) Ta có: 4 7 2401 nên 2015 4.503 3 4 503 3 503 7 7 (7 ) .7 2401 .343 (...01).343 ...43 2015 Chữ số tận cùng của 7 là 43. b) ta có 66 4 16 2 16 57 (57 ) .57 (...01) .3249 ...49 18 Bình luận:
Ở ví dụ này ta đã áp dụng tính chất:
Nếu A có 2 chữ số tận cùng là ab và B có 2 chữ số tận cùng làcd thì 2 chữ số tận cùng của A.B là 2
chữ số tận cùng của tích ab và cd
Ví dụ 2.9: Tìm 2 chữ số tận cùng của 2 a) 123 2098 b) 19 1996 Phân tích:
+ Ta thấy 2 chữ số tận cùng của 123
2098 cũng là 2 chữ số tận cùng của 123 98
+ tương tự ta thấy 2 chữ số tận cùng của 2 19
1996 cũng là 2 chữ số tận cùng của 2 19 96 . Lời giải a)Ta có: 123 123 123 123 98 (49.2) 49 .2 mà: 123 2.61 1 61 49 49 2401 .49 (...01).49 .....49 123 20.6 3 20 6 3 6 2 2 (2 ) .2 (....76) .8 ......08 123 123 123 123 98 (49.2) 49 .2 (.....49).(....08) .....92
Vậy 2 chữ số tận cùng của 123 2098 là 92. 2 b) ta có: 19 361 361 361 361 5 361 361 1805 361 96 96 (32.3) 32 .3 (2 ) .3 2 .3 . Mà 1805 20.90 5 20 90 5 90 2 2 (2 ) .2 (...76) .32 ....32 361 20.18 1 20 18 18 3 3 (3 ) .3 (....01) .3 ....03 2 19 361 361 361 361 5 361 361 1805 361 96 96 (32.3) 32 .3 (2 ) .3 2 .3 (....32).(....03) ....96
Vậy 2 chữ số tận cùng của 2 19 1996 là 96.
Dạng 3: Tìm ba chữ số tận cùng
Ví dụ 3.1: Tìm 3 chữ số tận cùng của 101 123 Phân tích:
Nhận thấy rằng (123,5) =1 nên ta sẽ áp dụng tính chất 4, khi đó chia hết cho 125. 19 Lời giải:
+ Vì (123,5) =1nên áp dụng tính chất ta có 101 123 −1 chia hết cho 125. (1)
+ Ta lại có chia hết cho 8 (2)
Vì (8;125)=1 và kết hợp (1),(2) ta có chia hết cho 1000 Khi đó
Vậy 3 chữ số tận cùng của là 123
Ví dụ 3.2: Tìm 3 chữ số tận cùng của 200 2004 Phân tích:
Cách 1: Ta dễ dàng chứng minh được chia hết cho 8, khi đó ta sẽ tìm 3 chữ số tận cùng bằng cách
gián tiếp: tìm dư phép chia số đó cho 125 từ đó suy ra các khả năng 3 chữ số tận cùng , cuối cùng
kiểm tra điều kiện chia hết cho 8
+ Ta có nên suy ra chia hết cho 8
+ Ta lại có (2014,5) = 1 nên 100 2004 1 mod 125 => 200 2004 1 mod 125 Hay ( 200 2004
1) chia hết cho 125 khi đó số 200
2004 có các khả năng 3 chữ số tận cùng là 126;251;376;501;626;751;876 Vì 200
2004 chia hết cho 8 nên số đó có chữ số tận cùng là 376 Cách 2. Ta thấy đ 200 2.100 2004 4 mod1 0 khi ó 2004 2004 376 mod1 000
Vậy số đó có chữ số tận cùng là 376
Từ bài toán trên ta có bài toán tổng quát:
Cho A là một số chẵn không chia hết cho 10. Tìm 3 chữ số tận cùng của 200 A Phân tích:
Vì A là một số chẵn không chia hết cho 10 nên (A,5)=1. Khi đó ta áp dụng tính chất ta có 100 A 1 chia hết cho 125. Lời giải: 200
+ Do A là một số chẵn nên 200 200 200 A 2n 2 .n
0 mod 8 (với n N và (n;5)=1) 20 Suy ra 200 A chia hết cho 8 (1)
+ Vì A là một số chẵn không chia hết cho 10 nên (A,5)=1. Khi đó áp dụng tính chất ta có 100 A 1 mod 125 => 200 A 1 mod 125 Hay ( 200 A
1) chia hết cho 125 khi đó số 200
A có các khả năng 3 chữ số tận cùng là 126;251;376;501;626;751;876 Vì 200
A chia hết cho 8 nên số đó có chữ số tận cùng là 376 Bình luận:
Bài toán tổng quát này cũng có thể coi là phần chứng minh ý (4) trong phần chú ý Ví dụ 3.3: 2003
Tìm 3 chữ số tận cùng của 9 2 Lời giải
- Tìm 2 chữ số tận cùng của 2003 9 Ta có 2003 3 2000 3 20 50 9 9 .9 9 .(3 ) 29 mod1 00 - Khi đó ta có 2003 9 100k 29 29 100k 2 2 2 .2 912.376 912 mod 1000
Vậy 3 chữ số tận cùng là 912 Ví dụ 3.4: 213
Tìm 3 chữ số tận cùng của 7 3 Lời giải 26 Ta có 213 26.8 5 8 5 26 5 5 7 7 7 .7 1 .7 7 7 mod 100 Khi đó 213 7 100k 7 100k 7 3 3 3 .3 1. 7 3 187 mod 1000
Vậy 3 chữ số tận cùng của 213 7 3 là 187
Ví dụ 3.5: Cho (a, 10) = 1. Chứng minh rằng ba chữ số tận cùng của a101 cũng bằng ba chữ số tận cùng của a. Phân tích:
Để chứng minh ba chữ số tận cùng của a101 cũng bằng ba chữ số tận cùng của a thì ta cần đưa ra dạng a101 = 100k + a.
Ta thấy (a,10)=1 thì a chỉ có thể là các số lẻ tận cùng khác 5 21 Lời giải.
+ Do (a,10)=1 nên khi đó ta có a 1;3;7;9 mod 10
Áp dụng chú ý phần (2) ta có 100 a 1 mod 1000 Ta xét 101 100 a a .a 1.a mod1 000 a mod1 000 => 101 a 1000k a (với k * N )
Điều này có nghĩa ba chữ số tận cùng của a101 cũng bằng ba chữ số tận cùng của a. (đpcm)
Ví dụ 3.6: Tìm ba chữ số tận cùng của 1992 5 Lời giải 498 1992 4 498 498 5 5 625 0625 0625
Vậy bốn chữ số tận cùng của 1992 5 là 0625
Ví dụ 3.7: Tìm ba chữ số tận cùng của số 946 T 5 Lời giải Ta có 3
5 có ba chữ số tận cùng là 125
Suy ra T = 5946 = (53)315.5=( 125 n )315.5= 125 m .5=t625 (Với , n , m t ) Vậy 946 T
5 có ba chữ số tận cùng là125 .
Ví dụ 3.8: Tìm ba chữ số tận cùng của số: 1994 P 5 Lời giải Ta có: 4 5 0625 tận cùng là 0625 ; 5 5 tận cùng là 3125 ; 6 5 tận cùng là 5625 7 5 tận cùng là 8125 ; 8 5 tận cùng là 0625 ; 9 5 tận cùng là 3125 ; 10 5 tận cùng là 5625; 11 5 tận cùng là 8125 ; 12 5 tận cùng là 0625 Chu kỳ lặp là 4. Suy ra: 4
5 m tận cùng là 0625 ; 4 1
5 m tận cùng là 3125 4 2
5 m tận cùng là 5625; 4 3
5 m tận cùng là 8125 Mà 1994 có dạng 4m 2 , do đó 1994 M 5
có 4 chữ số tận cùng là 5625.
Ví dụ 3.9: Tìm ba chữ số tận cùng của số: 101 R 123 Lời giải 22 Do 100 123,5 1 123 1 chia hết cho 125 (1). Mặt khác: 100 25 25 50 100 123 1 123 1 123 1 123 1 123 1 chia hết cho 8 (2). Vì 8,125 1 , từ (1) và (2) suy ra 100 : 123 1 chi hết cho 1000 101 100 123 123 123 1 123 1000k 123 k N . Vậy 101
123 có ba chữ số tận cùng là123 .
Ví dụ 3.10: Tìm ba chữ số tận cùng của 399...98 3 Lời giải Do 100 9,5 1 9 1 chi hết cho 125 (1). Ta có 100 9 1 chia hết cho 8 (2). Vì 8,125
1 , từ (1) và (2) suy ra: 100 9 1 chia hết cho 1000 399...98 199...9 100p 99 99 100p 99 99 3 9 9 9 9 1 9 1000q 9 , p q .
Vậy ba chữ số tận cùng của 399...98 3
cũng chính là ba chữ số tận cùng của 99 9 . Lại vì 100 9 1 chia hết cho 1000
ba chữ số tận cùng của 100 9 là 001 mà 99 100 9 9 : 9
ba chữ số tận cùng của 999 là 889 (dễ kiểm tra chữ số tận cùng của 999 là 9, sau đó dựa vào phép nhân ??9 9 ...001 để xác định ??9 889 ).
Vậy ba chữ số tận cùng của 3399...98 là 889.
Ví dụ 3.11: Tìm ba chữ số tận cùng của 200 2004 Lời giải Do 2004, 5 1 100 2004 chia cho 125 dư 1 2 200 100 2004 2004 chia cho 125 dư 1 200
2004 chỉ có thể tận cùng là126,251, 376,501,626,751, 876 . Do 200
2004 chia hết cho 8 nên chỉ có thể tận cùng là 376.
Ví dụ 3.12: Tìm ba chữ số tận cùng của tổng 1 5 9 8009 S 2 3 4 2004 . Lời giải
Nhận thấy: lũy thừa trong S đều có số mũ khi chia cho 4 thì dư 1
(các lũy thừa đều có dạn 4 k 2 1 gn , k thuộc 2, 3, ,2004 ). 23
Mọi lũy thừa trong S đều có chữ số tận cùng là chữ số tận cùng của cơ số tương ứng:
Chữ số tận cùng của tổng S là chữ số tận cùng của tổng: 2 3 9 199. 0 1 2 9 1 2 3 4 200 1 2 9 9 9009 .
Vậy ba chữ số tận cùng sẽ là 009
Ví dụ 3.13: Tìm ba chữ số tận cùng của tổng 3 7 11 8011 T 2 3 4 2004 . Lời giải
Mọi lũy thừa trong T đều có số mũ khi chia cho 4 thì dư 3 (các lũy thừa đều có dạng 4 n 2 3 n , n thuộc 2, 3, ,2004 ). 3
2 có chữ số tận cùng là 7
8;3 có chữ số tận cùng là 7 ; 11
4 có chữ số tận cùng là 4 ; …
Như vậy, tổng T có chữ số tận cùng bằng chữ số tận cùng của tổng: 8 7 4 5 6 3 2 9 199. 1 8 7 4 5 6 3 2 9 1 8 7 4 Vậy 200 1 8 7 4 5 6 3 2 9 8 7 4 9019.
ba chữ số tận cùng của tổng T là 019.
Dạng 4: Vận dụng chứng minh chia hết, chia có dư
Ví dụ 4.1: Chứng minh rằng 8102 - 2102 chia hêt cho 10 Lời giải
Ta thấy các số có tận cùng bằng 2 hoặc 8 nâng lên luỹ thừa 4 thì được số có tân cùng là 6.Một số có
tận cùng bằng 6 nâng lên luỹ thừa nào (khác 0) cũng tận cùng bằng 6.
Do đó ta biến đổi như sau:
8102 =(84)25.82 = (….6)25.64=(….6).64 = …4
2102 =( 24)25.22 =1625.4 =(…6).4 = …4
Vậy 8102 -2102 tận cùng bằng 0 nên chia hết cho 10
Ví dụ 4.2: Tồn tại hay không số tự nhiên n sao cho n2 + n + 1 chia hết cho 19952000. Lời giải
Theo tính chất 1a => 19952000 tận cùng bởi chữ số 5 nên chia hết cho 5.
Vì vậy, ta đặt vấn đề là liệu n2 + n + 1 có chia hết cho 5 không ?
Ta có n2 + n = n(n + 1), là tích của hai số tự nhiên liên tiếp
=> Chữ số tận cùng của n2 + n chỉ có thể là 0 ; 2 ; 6
=> n2 + n + 1 chỉ có thể tận cùng là 1 ; 3 ; 7
=> n2 + n + 1 không chia hết cho 5.
Vậy không tồn tại số tự nhiên n sao cho n2 + n + 1 chia hết cho 19952000. 24
Ví dụ 4.3: Chứng minh rằng 261570 chia hết cho 8 Lời giải
Ta thấy:265= 11881376 ,số có tận cùng bằng 376 nâng lên luỹ thừa nào(khác 0) cũng có tận cùng bằng 376.Do đó:
261570=(265)314=(…376)314=(…376) Mà 376 chia hết cho 8
Một số có ba chữ số tận cùng chia hết cho 8 thì chia hết cho 8 Vậy 261570 chia hết cho 8
Ví dụ 4.4: Chứng minh rằng với mọi số tự nhiên n. a) 4 7 n 1 chia hết cho 5; b) 4n 1 3 2 chia hết cho 5; c) 4n 1 2 3 chia hết cho 5; d) 4n 2 2 1 chia hết cho 5; e) 2n 1 9 1 chia hết cho 10. Lời giải a) 4n 4 7 1 (7 )n 1 2401n 1 ... ...1 1, tận cùng bằng 0. Vậy 4 7 n 1 5 . b) 4n 1 3 2 (3n)n.3 2 81 . n 3 2 ...1.3 2 , tận cùng bằng 5. Vậy 4n 1 3 2 5 . c) 4n 1 4 2 3 (2 )n.2 3 16 . n 2 3 ...6.2 3 , tận cùng bằng 5. Vậy 4n 1 2 3 5 . d) 4n 2 2
1 tận cùng bằng 5 nên chia hết cho 5. e) 2n 1 2 9 1 (9 )n.9 1 81 . n 9 1 ...1.9 1 , tận cùng bằng 0. Vậy 2n 1 9 1 chia hết cho 10.
Ví dụ 4.5: Chứng minh răng 261570 chia hết cho 8 Lời giải
Ta thấy:265 = 11881376, số có tận cùng bằng 376 nâng lên lũy thừa
Nào (khác 0) cũng có tận cùng bằng 376. Do đó:
261570 = (265)314 = (…376)314 = (…376) Mà 376 chia hết cho 8
Một số có ba chữ số tận cùng chia hết cho 8 thì chia hết cho 8 25 Vậy 261570 chia hết cho 8
Ví dụ 4.6: Tồn tại hay không số tự nhiên n sao cho số n2 + n + 1 chia hết cho 20052005 Lời giải
Số 20052005 có tận cùng là 5. nên nó chia hết cho 5
Ta có n2 + n + 1 = n(n+1) +1 chỉ có thể có các chữ số tận cùng là 1, 3, 7. nên nó không chia hết cho 5 Vậy không tồn tại n.
Ví dụ 4.7: Cho P là số nguyên tố lớn hơn 5. chứng minh rằng ( P8n + 3p4n - 4 )⋮5. Lời giải
Vì P là số nguyên tố lớn hơn 5 nên tận cùng của p chỉ có thể là các chữ số: 1; 3; 7; 9
Nếu P có tận cùng là 1 thì P8n + 3p4n – 4 có tận cùng là 0 nên nó chia hết cho 5
Nếu P có tận cùng là 3 thì p4n = 10k+ 34n = 10k + 81n có tận cùng là 1. p8n có tận cùng là 1. nên: P8n
+ 3p4n – 4 có tận cùng là 0. nên nó chia hết cho 5
Nếu p có tận cùng là 7 thì tương tự. tận cùng của p4n và p8n cũng có tận cùng là 1. nên tổng chia hết cho 5
Nếu p có tận cùng là 9 thì:p4n = 10k + 94n = 10k + 812n có tận cùng là 1và p8n = 4n 2 (p ) có tận cùng là 1
Nên tổng trên cũng chia hết cho 5.
Tóm lại với p nguyên tố lớn hơn 5 thì tổng luôn chia hết cho 5
Nhận xét chung về phương pháp:
1. Tách an dưới dạng (10k + a1)n với a1 = {0, 1,.....9}
2. Viết n dưới dạng n = 4q + r ( r = 0, 1, 2, 3)
3. Sử dụng nhận xét 1, 2, 3 đã chứng minh ở trên.
Ví dụ 4.8: Chứng minh rằng n5 và n có chữ số tận cung giống nhau Lời giải
Để chứng minh n5 và n có cùng chữ số tận cùng là đi chứng minh n5 – n 10
Ta có: A =n5 – n = n(n4-1).(n2+1) = (n-1).n(n+1).(n2+1) Ta có 10 =2.5 và (2.5)=1
(n-1), n, n+1 là các số tự nhiên liên tiếp Suy ra A 2
Chứng minh A 5 nếu n 5 thì Ạ 5 Nếu n 5 dư 1 suy ra n-1 5 A 5
n: 5 dư 2 suy ra n2+1 = (5k+2)2+1 = (5k)2+20k+4+1 5 A 5
n: 5 dư 3 suy ra n2 +1 =(5k+3)2+1 = (5k)2+30k+9+1 5 A 5 26 n: 5 dư 4 suy ra n+1 5 A 5 Vậy A 2 và A 5 A 10
Vậy n5 và n có cùng chữ số tận cùng.
Dạng 5: Vận dụng chữ số tận cùng vào bài toán chính phương Ví dụ 5.1: Cho 2 2 2 2 n 2016 2017 2018
2019 . Chứng minh n không là số chính phương. Phân tích:
Để chứng minh n không là số chính phương ta chỉ ra số này có chữ số tận cùng là 2, 3, 7, 8. Lời giải Ta có 2
2016 có chữ số tận cùng là 6 2
2017 có chữ số tận cùng là 9 2
2018 có chữ số tận cùng là 4 2
2019 có chữ số tận cùng là 1 2 2 2 2 2016 2017 2018
2019 có chữ số tận cùng giống với chữ số tận cùng của 6 9 4 1 18 . 2 2 2 2 2016 2017 2018
2019 có chữ số tận cùng là 8. 2 2 2 2 2016 2017 2018
2019 không phải là số chính phương. Bình luận:
Bài toán này giáo viên có thể thay đổi các cơ số tùy thích sao cho tổng hiệu các chữ số tận cùng
của các số trong tổng hiệu là một số có chữ số tận cùng là 2, 3, 7, 8.
Việc chứng một số n không là số chính phương còn có một số cách khác:
Chứng minh n không viết được dưới dạng 2 k (k ).
Dựa vào phép chia cho 3, 4, 5, 8 . 2
Chỉ ra n nằm giữa hai số chính phương liên tiếp, tức là 2 k n k 1 , k .
Ví dụ 5.2: Cho n 1.3.5.7
2021. Chứng minh rằng n
3 không là số chính phương. Phân tích 27
Để ý ta thấy rằng n là tích của các số tự nhiên lẻ từ 1 đến 2021 nên n là số lẻ, mà n chia hết cho
5 do đón có chữ số tận cùng là 5. Vì thế bài toán này có thể vận dụng chữ số tận cùng để chứng minh n
3 không là số chính phương. Lời giải n 5, n lẻ
chữ số tận cùng của n là 5. n
3có chữ số tận cùng là 8. n
3không là số chính phương. Bình luận:
Bài toán này có thể sử dụng tính chất một số chia hết cho 3 mà không chia hết cho 9 thì số đó không
phải là số chính phương.
Thật vậy, n 3 và n 9 n 3 3 nhưng n 3 9 n
3 không là số chính phương.
Ví dụ 5.3: Biết a và a 2. Tìm a sao cho ( a a 1). ( a a 1) (a 2)a ( a a 1). Lời giải 2
Đẳng thức đã cho được viết lại như sau: a(a 1) (a 2)aa(a 1) .
Do vế trái là một số chính phương nên vế phải cũng là một số chính phương.
Một số chính phương chỉ có thể tận cùng bởi một trong các chữ số 0,1, 4,5,6,9 nên a chỉ có thể tận
cùng bởi một trong các chữ số 1,2,5,6,7, 0 (1)
Do a là chữ số nên a
9 , kết hợp với điều kiện đề bài ta có a và 2 a 9 (2)
Từ (1) và (2) suy ra a có thể nhận được một trong các giá trị 5, 6, 7 .
Thử trực tiếp với a 5,6,7 chỉ có với a 7 thì 2 (a 2)a ( a a 1) 5776 76 .
Ví dụ 5.4: Tìm số chính phương có 4 chữ số, biết rằng chữ số hàng nghìn bằng chữ số hàng đơn vị
và số chính phương đó viết dưới dạng 2 (5n 4) với n . Lời giải Số 5n
4 tận cùng bằng 4 hoặc 9. Xét hai trường hợp: 28 Trường hợp 5n 4 tận cùng bằng 4 thì 2 (5n
4) tận cùng bằng 6. Cần tìm số có dạng
6 * *6 là bình phương của một số tận cùng bằng 4. Không có số nào thỏa mãn điều kiện trên vì 2 2 74 5476 6 * *6 7056 84 . Trường hợp 5n 4 tận cùng bằng 9 thì 2 (5n
4) tận cùng bằng 1. Cần tìm số có dạng
1 * *1 là bình phương của một số tận cùng bằng 9. Ta thấy 2 2 29 841 1 * *1 2401 49 , còn 2 39 1521.
Vậy số chính phương phải tìm là 1521.
Ví dụ 5.5: Tìm tất cả các số nguyên dương n sao cho n !
2019 là một số chính phương. (Ở đây n ! 1.2.3 n )
(Đề thi IMSO 2019) Phân tích:
Bài toán yêu cầu tìm tất cả các số nguyên dương n sao cho n !
2019 là một số chính phương nên
các sốn là hữu hạn. Do đó ta có thể tìm tất cả các các số nguyên dương n sao cho n ! 2019
không là số chính phương, sau đó thử trực tiếp các giá trị n còn lại vào n ! 2019 để tìm ra n
thỏa mãn yêu cầu bài toán. Lời giải
Dựa vào nhận xét một số có 2 chữ số lẻ tận cùng không là số chính phương. Nếu n 5 thì n !
1.2.3.4.5 n có hai chữ số tận cùng là y0 trong đó y là chữ số chẳn nên n !
2019có hai chữ số lẻ tận cùng nên không là số chính phương.
Thử trực tiếp với n
1,2, 3, 4 chỉ có với n 3 thì 2 n ! 2019 2025 45 . Bình luận:
Bài toán này có thể sử dụng tính chất chia hết và chia có dư.
Dựa vào nhận xét một số chia hết cho 3 nhưng không chia hết cho 9 thì không là số chính phương. Nếu n 6 thì n !
1.2.3.4.5.6 nchia hết cho 9. Do 2019 3 nhưng 2019 9 29 Nên với n 6 thì n !
2019 chia hết cho 3 nhưng không chia hết cho 9 nên không là số chính phương.
Thử trực tiếp với n
1,2, 3, 4,5 chỉ có với n 3 thì 2 n ! 2019 2025 45 .
Dựa vào nhận xét một số chia hết cho 4 dư 3 không là số chính phương.
Do 2019chia hết cho 4 dư 3 nên với n 4 thì n !
1.2.3.4 n chia hết cho 4 và n ! 2019chia
cho 4 dư 3 nên không là số chính phương.
Thử trực tiếp với n
1,2, 3 chỉ có với n 3 thì 2 n ! 2019 2025 45 .
1. Định nghĩa số chính phương:
Số chính phương là số bằng bình phương đúng của một số nguyên
2. Tính chất số chính phương (tính chất liên quan đến chữ số tận cùng)
- Số chính phương chỉ có thể có chữ số tận cùng bằng 0; 1; 4; 5; 6; 9 không thể có chữ số tận cùng bằng 2; 3; 7; 8.
- Số chính phương có chữ số tận cùng bằng 1; 4 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
- Số chính phương có chữ số tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
- Số chính phương có chữ số tận cùng bằng 5 thì chữ số hàng chục là 2.
Ví dụ 5.6: Tìm số chính phương có 4 chữ số gồm các chữ số 0; 2; 3; 5 Lời giải
Một số chính phương có chữ số tận cùng không thể là 2 hoặc 3.
Nếu số chính phương có chữ số tận cùng là 0 thì chữ số hang chục cũng là 0 .
Do đó số chính phương cần tìm có chữ số tận cùng là 5.
Mà số chính phương có chữ số tận cùng bằng 5 thì chữ số hàng chục là 2
Nên số chính phương cần tìm chỉ có thể là 3025 Thử lại: 2 3025 55
Vậy chính phương cần tìm là 3025
Ví dụ 5.7: Tìm số tự nhiên có hai chữ số biết rằng khi nhân số đó với 135 ta được một số chính phương. Lời giải 30
Gọi số tự nhiên cần tìm là ab 9 ab 100;a;b 10
Theo đề bài ta có ab.135 là số chính phương Có 9.135 . ab 135 100.135 1215 . ab 135 13500 Có .
ab 135 là số chính phương chia hết cho 135 nên .
ab 135 là số có chữ số tận cùng là 0 hoặc 5 x x 1 .x x 1 x 2 xx x 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . ab 135
35 ;40 ;45 ;50 ;55 ;60 ;65 ;70 ;75 ;80 ;85 ; 90 ;95 ;100 ;105 ; 110 ;115 Mà .
ab 135 là số chính phương chia hết cho 135 nên 2 2 . ab 135 45 ;90 ab 15;60
Vậy số phải tìm là 15;60
Ví dụ 5.8: Tìm số tự nhiên n 1sao cho A 1! 2! 3! .... n ! là một số chinh phương. Lời giải Với n 1 thì 2
A 1! 1 1 là số chính phương
+) Với n 2 thì A 1! 2!
3 không là số chính phương +) Với n 3 thì 2 A 1! 2! 3! 9 3 là số chính phương
+) Với n 4 ta có 1! 2! 3! 4! 33
Mà 5!;6!;7 !;...;n ! đều có tận cùng là 0 do đó A là số có chữ số tận cùng là 3 nên A không là số chính phương. Vậy n 1;n 3 31
Ví dụ 5.9: Cho 5 số chinh phương bất kỳ có chữ số hàng chục khác nhau còn chữ số hang đơn vị
đều là 6. Chứng minh rằng tổng các chữ số hàng chục của 5 số chính phương đó là một số chính phương. Lời giải
Số chính phương có chữ số hang đơn vị à 6 thì chữ số hàng chục của số đó là số lẻ.
Mà chữ số hàng chục của 5 số chính phương đã cho khác nhau
Vì vậy chữ số hàng chục của 5 số chính phương đã cho là 1; 3; 5; 7; 9 do đó tổng của chúng là: 2
1 3 5 7 9 25 5 là số chính phương.
Ví dụ 5.10: Chứng minh rằng 4n 4n 4n 4 2012 2013 2014 2015 n N
không phải là số chính phương Lời giải Ta có 4
2012 có chữ số tận cùng bằng 6 nên 4
2012 n có chữ số tận cùng bằng 6 Có 4
2013 có chữ số tận cùng bằng 1 nên 4
2013 n có chữ số tận cùng bằng 1 Có 4
2014 có chữ số tận cùng bằng 6 nên 4
2014 n có chữ số tận cùng bằng 6 Mà 4
2015 n có chữ số tận cùng bằng 5 Do đó 4n 4n 4n 4 2012 2013 2014 2015 n N
có chữ số tận cùng bằng 8
Mặt khác, không có số chính phương nào có chữ số tận cùng bằng 8.
Vậy N không là số chính phương. III. BÀI TẬP
Bài 1: Tìm chữ số tận cùng của các số: 99 1414 567 a ) 7 b ) 14 ) c 4 Lời giải:
a) Trước hết, ta tìm số dư của phép chia 99cho 4 : 99 96 3 4.24 3 4.24 3 99 4.24 3 7 7 7 7 .7 Từ kết luận (II)
chữ số tận cùng của 99
7 chính là chữ số tận cùng của 3 7 343 là 3 .
b) Chữ số tận cùng của 14 là 4 32 Ta có: 1414 4.353 2 1414 4.353 2 4.353 2 14 14 14 .14 từ kết luận (III)
Chữ số tận cùng của 1414 14
là chữ số tận cùng của là 6 . c) Ta có: 567 4.141 3 567 4.141 3 4.141 3 4 4 4 .4 từ kết luận (III)
Chữ số tận cùng của 567 4 là chữ số tận cùng của 3 6.4 384 là 4 .
Bài 2: Tìm chữ số tận cùng của các số: a) 324 187 . b) 2020 12 . c) 2020 14 . Lời giải
a) Ta thấy các số có tận cùng bằng 7 nâng lên luỹ thừa bậc 4 thì được số có tận cùng bằng
1. Các số có tận cùng bằng 1 nâng lên luỹ thừa nào (khác 0 ) cũng tận cùng bằng 1. 81 81 Do đó 324 4 187 187 1 1
Vậy chữ số tận cùng của 324 187 là 1 . b) Ta có: 2020 2020 2020 12 6 .2 Nhận thấy: 1 6 có tận cùng là 6 ; 2 6 có tận cùng là 6 ; 3 6 có tận cùng là 6 ;
Vậy 6n có tận cùng là 6 suy ra 2020 6 có tận cùng là 6 . Lại có: 4 2 16 có tận cùng là 6 ; 505 Suy ra 2020 4 5 5 0 2 2 16 có tận cùng là 6 Vậy 2020 2020 2020 12 6 .2 ...6 . ...6 ...6 có tận cùng là 6 . c) Ta thấy: 2020 2020 2020 14 2 .7 . 505 Mà: 2020 4 505 2 2 16 ...6 có tận cùng là 6 . 1010 505 Và 2020 2 1010 2 505 7 7 49 49 2401 ...1 có tận cùng là 1. 33 Vậy 2020 14
...6 . ...1 có tận cùng là 6 .
Bài 3: Tìm chữ số tận cùng của các số: 9 14 7 6 a/ 9 7 ; b/ 14 14 ; c/ 5 3 Lời giải 9 a/ Có: 9 9 8 1 4k 1, với k 9 9 4k 1 4k 2 7 7 7.7
7.49 k có chữ số tận cùng là 7.1 7 . 7 b/ Ta có 14 7 14 196 49.4 4k với k 14 4 1 4k 4 14 2 .7 k
16k.2401k nên có chữ số tận cùng là 6 . 7 7 6 c/ Có 6 5 4 1 4k 1 với k 7 6 5 4k 1 4 3 3 3.3 k
3.81k có tận cùng là 3.1 3.
Bài 4: Chứng minh rằng: a/ 102 102 8 2 chia hêt cho 10 . b/ 2 n n 1 không chia hết cho 2020 2015 với mọi n . c/ 8n 4 p 3 n p
4 chia hết cho 5 với p là số nguyên tố lớn hơn 5 và n . Lời giải
a/ Ta thấy các số có tận cùng bằng 2 hoặc 8 nâng lên luỹ thừa 4 thì được số có tân cùng là 6 .
Một số có tận cùng bằng 6 nâng lên luỹ thừa nào (khác 0 ) cũng có tận cùng bằng 6 .
Do đó ta biến đổi như sau: 25 25 102 4 2 8 8 .8 ...6 .64 ...6 .64 4 có tận cùng là 4 . 25 102 4 2 25 2 2 .2 16 .4 6 .4 4 có tận cùng là 4 . Vậy 102 102 8
2 có tận cùng bằng 0 nên chia hết cho 10 . b/ Ta thấy so 2020 2015
có chữ số tận cùng là 5 , nên nó chia hết cho 5 Ta có 2 n n 1 n n 1
1 chỉ có thể có các chữ số tận cùng là 1, 3, 7 (vì n n 1
có tận cùng là 0,2, 6 ), nên nó không chia hết cho 5 34 Vậy 2 n n
1 không chia hết cho 5 với mọi n .
c/ Vì p là số nguyên tố lớn hơn 5 nên tận cùng của p chỉ có thể là các chữ số: 1; 3; 7; 9 .
- Nếu p có tận cùng là 1 thì 8n 4 p 3 n
p – 4 có tận cùng là 0 nên nó chia hết cho 5 ;
- Nếu p có tận cùng là 3 thì 4n 4 10 3 n 10 81n p k k có tận cùng là 1 ; 8n
p có tận cùng là 1, nên: 8n 4 p 3 n
p – 4 có tận cùng là 0 , nên nó chia hết cho 5.
- Nếu p có tận cùng là 7 thì tương tự: tận cùng của 4n p và 8n
p cũng có tận cùng là 1, nên tổng đó chia hết cho 5.
- Nếu p có tận cùng là 9 thì: 4n 4n 2 10 9 10 81 n p k k có tận cùng là 1 và 4n 8n 2 p p
có tận cùng là 1 , nên tổng trên cũng chia hết cho 5 .
Tóm lại với p là số nguyên tố lớn hơn 5thì 8n 4 p 3 n
p – 4 luôn chia hết cho 5 , với n .
Bài 5: Tìm hai chữ số tận cùng của 1991 5 Lời giải
Vì 25 lũy thừa bao nhiêu lên cũng có tận cùng là 25 nên ta tìm cách tách 1991 5 thành tích của lũy
thừa có cơ số 25 và một bộ phận còn lại: 1991 1990 2 995 995 5 5 .5 (5 ) .5 25 .5 Vì 995
25 có hai số tận cùng là 25 mà 25.5 = 125 nên 995
25 .5 có hai số tận cùng là 25 24
Bài 6: Tìm hai chữ số tận cùng của 24 24 Lời giả Vì 24
24 là một số tự nhiên chẵn nên đặt 2424 = 2k ( k là số tự nhiên đủ lớn), từ đó 24 24 2k 2 24 24 (24 )k 576k
Vì những số tự nhiên có tận cùng bằng 76 thì lũy thừa lên bao nhiêu cũng là số có tận cùng bằng 76 24 24
nên hai chữ số tận cùng của 24 là 76
Bài 7: Tìm hai chữ số tận cùng của 236 45 11 Lời giải Ta có 35 118 236 2 118 45 45 2025 ....25 236 45 11 .........36
Hai chữ số tận cùng của 236 45 11 là 36 Bài 8: Cho 2 3 39 A 2 2 2 ..... 2
Tìm hai chữ số tận cùng của A Lời giải 2 3 39 A 2 2 2 ..... 2 2 3 40 2.A 2 2 .......... 2 40 A 2 2 2 Có 40 20 2 2 2
1048576 , mà những số có hai số tận cùng là 76 nâng lên lũy thừa khác 0 đều
bằng số tự nhiên có hai số tận cùng là 76 nên 40
2 có hai số tận cùng là 76. Từ đó 40 A 2 2 có hai số tận cùng là 74
Bài 9: Tìm hai chữ số tận cùng của 71991 Lời giải 1991 1988 3 4 497 497 7 7 .7 (7 ) .343 (2401) .343 .....01.343 .....43
Vậy hai chữ số tận cùng của 71991 là 43
Bài 10: Tìm hai chữ số tận cùng của 51 51 Lời giải 51 50 2 25 25 51 51 .51 (51 ) .51 (.....01) .51 .......01.51 .....51
Vậy hai chữ số tận cùng của 51 51 là 51
Bài 11: Tìm hai chữ số tận cùng của 99 99 99 Lời giải Vì 99
99 là số lẻ nên đặt 99 99 2k 1 . Ta có 99 k 99 2k 1 2k 2 99 99 99 .99 (99 )k.99 .9801 .99 ......01.99 ....99
Vậy hai chữ số tận cùng của 99 99 99 là 99 36
Bài 12: Chứng minh rằng 236 45 11 chia hết cho 4 Lời giải Ta có 118 236 2 118 45 45 2025 ....25 236 45 11 .........36
Vì có hai chữ số tận cùng là 36 mà 36 chia hết cho 4 nên 236 45 11 chia hết cho 4
Bài 13: Tìm hai chữ số tận cùng của các số: 2003 a) 2 9 9 b) 7 Phân tích: a) Do 2003 2
là số chẵn, ta tìm số tự nhiên n nhỏ nhất sao cho n 1 2 25 . Viết n m p q ; p q
, trong đó q là số nhỏ nhất để aq ∶ 4 ta có: 2003 2 2q(2pn 1) 2q x
trong đó 2q(2pn 1) 100 b) Nếu 99
7 lẻ , gọi n là số tự nhiên sao cho n 1 7 100 . Viết n m u v ; u v , 0 v n ta có 99 7 7v(7un 1) 7v x .
Trong đó 7v(7un 1) 100 Lời giải: a) Ta có 10 10 20 10 10 2 1024 2 1 1025 25 2 1 2 1 2 1 25 3 20 2 2 1 100 Mặt khác: 2003 3 2000 3 3 20 100 3 2 2 (2 1) 2 2 [(2 ) 1] 2 100k 8 (k ).
Vậy hai chữ số tận cùng của 2003 2 là 08.
b) Cách 1: Ta có 4 4 7 2401 7 1 2400 100 Mặt khác: 9 9 9 – 1∶ 4 9 4k 1 (k ) Vậy 99 4k 1 4 7 7 7(7 k 1) 7 100q 7 (q
). Vậy hai chữ số tận cùng của 99 7 là 07. 37
Cách 2: Ta có 4 7
2401 , số có tận cùng bằng 01 nâng lên lũy thừa nào cũng có tận cùng bằng 01. Do đó 9 k 9 4k 1 4 k 7 7 7 .7 2401 .7 ...01 .7 ...07 9
Vậy hai chữ số tận cùng của 9 7 là 07.
Bài toán tương tự:
Tìm hai chữ số tận cùng của các số: a) 517 3 b) 1991 7
Bài 14: Tìm hai chữ số tận cùng của các số: 999 a) 2 999 b) 3 Lời giải:
a) Cách 1: Ta thấy rằng 999 1000 2 2 : 2 . Mặt khác ta có: +) 1000 2
chia 25 dư 1, do đó hai chữ số tận cùng của 1000 2 có thể là 01;26; 51; 76 +) 1000 2 là bội của 4 Suy ra 1000 2
có hai chữ số tận cùng phải là 76.
Như vậy hai chữ số tận cùng của 999 2 có thể là 38 (
76 : 2 ) hoặc 88 ( 176 : 2 ). Nhưng do 999 2
cũng là bội của 4 nên hai chữ số tận cùng của nó là 88.
Cách 2: Ta có 10 2
1024 , bình phương của hai số có tận cùng bằng 24 thì tận cùng bằng 76, số có
tận cùng bằng 76 thì nâng lên lũy thừa nào (khác 0) cũng có tận cùng là 76. Do đó 100 100 50 50 1000 10 2 2 2 1024 1024 ...76 ...76
Làm tiếp tục làm như Cách 1 b) Ta có 4 3 81 19(mod100); 8 2 3 19 61(mod100) 10 3 61.9 49(mod100) 100 10 3 49 01(mod100) 38
Nghĩa là hai chữ số tận cùng của 1000 3 là 01. Vì 1000 3
là bội của 3, nên chữ số hàng trăm của nó khi
chia cho 3 phải cho số dư là 2 (chia tiếp thì số 201 chia hết cho 3, nếu số dư là 0 hay 1 thì số 001,
101 không chia hết cho 3). Vậy số 999 1000 3 3
: 3có hai chữ số lận cùng là 76 (=201:3).
Bài 15: Tìm hai chữ số tận cùng của tổng: 2002 2002 2002 2002 S 1 2 3 2004 Lời giải:
Dễ thấy, nếu a chẵn thì 2
a chia hết cho 4 ; nếu a lẻ thì 100 a
1 chia hết cho 4 ; nếu a chia hết cho 5 thì 2 a chia hết cho 25.
Mặt khác, với mọi a và ( , a 1) 1(a, 5) = 1 ta có 20 100 a 1 25 a 1 25 . Vậy với mọi a ta có 2 100 a (a 1) 100. Do đó 2002 2 2000 2 2000 2 2 2 S 1 2 (2 1) ... 2004 (2004 1) 2 3 ... 2004 .
Vì thế hai chữ số tận cùng của tổng S cũng chính là hai chữ số tận cùng của tổng 2 2 2 2 1 2 3 ...
2004 . áp dụng công thức: n n 1 2n 1 2 2 2 2 1 2 3 ... 2004 6 2 2 2 2 1 2 3 ... 2004 26847 7 0 0 0 3
Vậy hai chữ số tận cùng của tổng S là 30.
Bài toán tương tự:
Tìm hai chữ số tận cùng của tổng: 2003 2003 2003 2003 S 1 2 3 ... 2004
Tìm hai chữ số tận cùng của 2015 2016 2017 2 2 2 . Lời giải: Ta có 2015 2016 2017 2000 15 16 17 2 2 2 2 (2 2 2 ). Ta lại có 2000 20 100 2 (2 ) . 100 Vì 20 2 76 mod100 nên 20 2 76(mod100) hay 2000 2
có hai chữ số tận cùng là 76 . Từ đó
suy ra hai chữ số tận cùng của tổng trên là hai chữ số tận cùng của tích 76.76 là
Bài 16: Tìm ba chữ số tận cùng của 399 98 3 . Lời giải: 39 Do 100 9,5 1 9 – 1 125 (1) Mà 100 9 – 1 8 2 . Lại có 8, 125 1, từ (1) và (2) suy ra: 100 399 98 199 9 100p 99 99 100p 99 9 – 1 1000 3 9 9 9 (9 – 1 ) 9 99 1000q 9 , p q N .
Vậy ba chữ số tận cùng của 399 98 3
. cũng chính là ba chữ số tận cùng của 99 9 . Lại vì 100
9 – 1 1000 => ba chữ số tận cùng của 100 9 là 001 mà 99 100 9 9 : 9 ba chữ số tận cùng của 399 98 3
là 889 (dễ kiểm tra chữ số tận cùng của 99
9 là 9, sau đó dựa vào phép
nhân ¯¯¯¯¯¯¯¯??9.9=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯...001??9¯.9=...001¯ để xác định ¯¯¯¯¯¯¯¯??9=889??9¯=889 ).
Vậy ba chữ số tận cùng của 399 98 3 là 889 .
Tìm 3 chữ số tận cùng của A 3.7.11 2011 Lời giải:
Gọi x là 3 chữ số tận cùng của A , ta có A
x(mod1000) và x lẻ.
Vì trong A chứa 15, 35, 55 nên A 125 x 125 x 125;375;625;875 Ta có: A 3.7.11...2011 3.(4.1 3)(4.2 3)...(4.502 3) 3.7 3.7 ... 3.7 .3 5.5...5.3 1.1...1.5.3 7(mod 8) 251 251 x 7(mod 8) x 375
Vậy 3 chữ số tận cùng của A là 375
Bài 17: Tìm 3 chữ số tận cùng là tích A của 11 số nguyên dương đầu tiên. Lời giải: Ta có: A 1.2.3.4 11
Trong biểu thức A c
ó thừa số 2; 5; 10 nên A chia hết cho 100
Vậy 2 chữ số tận cùng của A là 00. A Ta có: 1.3.4.6.7.8.9.11 2.6.7.8.9.11 100 2.7.8.9.11 4.8.9.11 2.9.11 8.11 8(mod10)
Vậy 3 chữ số tận cùng của A là 800.
Bài 18: Chứng minh rằng 8102 - 2102 chia hêt cho 10 40 Lời giải
Ta thấy các số có tận cùng bằng 2 hoặc 8 nâng lên luỹ thừa 4 thì được số có tân cùng là
6.Một số có tận cùng bằng 6 nâng lên luỹ thừa nào (khác 0) cũng tận cùng bằng 6.
Do đó ta biến đổi như sau:
8102 =(84)25.82 = (….6)25.64=(….6).64 = …4
2102 =( 24)25.22 =1625.4 =(…6).4 = …4
Vậy 8102 -2102 tận cùng bằng 0 nên chia hết cho 10
Bài 19: Tồn tại hay không số tự nhiên n sao cho n2 + n + 1 chia hết cho 19952000. Lời giải
Theo tính chất 1a => 19952000 tận cùng bởi chữ số 5 nên chia hết cho 5.
Vì vậy, ta đặt vấn đề là liệu n2 + n + 1 có chia hết cho 5 không ?
Ta có n2 + n = n(n + 1), là tích của hai số tự nhiên liên tiếp
=> Chữ số tận cùng của n2 + n chỉ có thể là 0 ; 2 ; 6
=> n2 + n + 1 chỉ có thể tận cùng là 1 ; 3 ; 7
=> n2 + n + 1 không chia hết cho 5.
Vậy không tồn tại số tự nhiên n sao cho n2 + n + 1 chia hết cho 19952000.
Bài 20: Chứng minh rằng 261570 chia hết cho 8 Lời giải
Ta thấy:265= 11881376 , số có tận cùng bằng 376 nâng lên luỹ thừa nào(khác 0) cũng có tận cùng bằng 376.Do đó:
261570=(265)314=(…376)314=(…376) Mà 376 chia hết cho 8
Một số có ba chữ số tận cùng chia hết cho 8 thì chia hết cho 8 Vậy 261570 chia hết cho 8
Bài 21: Chứng minh số 2 2 2 2 n 2004 2003 2002
2001 không phải là số chính phương. Phân tích:
Số chính phương chỉ có chữ số tận cùng là 0,1, 4,5,6,9 nếu các số tận cùng là 2, 3,7, 8 thì không
phải là số chính phương. Lời giải
Ta thấy chữ số tận cùng của các số 2 2 2 2
2004 ,2003 ,2002 ,2001 lần lượt là 6,9, 4,1 . Do đó số n có
chữ số tận cùng là 8 , 8 nên n không phải là số chính phương.
Bài 22: Chứng tỏ rằng 14 9 4 14 9 3 A 14 9
2 không phải là số chính phương. 41 Phân tích:
- Số có chữ số tận cùng là 3 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 7 ; số có
chữ số tận cùng là 7 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 3 .
- Số có chữ số tận cùng là 2 khi nâng lên lũy thừa bậc 4n
3sẽ có chữ số tận cùng là 8 ; số có
chữ số tận cùng là 8 khi nâng lên lũy thừa bậc 4n
3 sẽ có chữ số tận cùng là 2 .
- Các số có chữ số tận cùng là 0,1, 4, 5, 6, 9 , khi nâng lên lũy thừa bậc 4n
3 sẽ không thay đổi
chữ số tận cùng. Lời giải 14 9 4 14 9 3 A 14 9 2 14 Ta có: 14 14
có chữ số tận cùng là 6 9 9
9 có chữ số tận cùng là 9 4 3
2 có chữ số tận cùng là 2
Suy ra A có chữ số tận cùng là 6 9 2 7 ..
Vậy A không phải là số chính phương.
Bài 23: Chứng tỏ rằng 2 3 4 2020 C 5 5 5 5 ... 5
không phải là số chính phương. Lời giải 2 3 4 2020 C 5 5 5 5 ... 5 Ta có: 2 3 4 2020 5 5 5 5 ... 5 5 2 3 4 2020 5 5 5 ... 5 25 2 3 4 2020 C 5 5 5 5 ... 5 không chia hết cho 25
Vậy C không phải là số chính phương. 42
Bài 24: Chứng minh 1234567890 không phải là số chính phươngLời giải
Ta thấy số chia hết cho vì chữ số tận cùng là nhưng lại không chia hết cho vì hai chữ số tận cùng
là . Vì vậy, số không phải là số chính phương. Lời giải
Ta thấy số 1234567890 chia hết cho 5 vì chữ số tận cùng là 0 nhưng lại không chia hết cho 25 vì
hai chữ số tận cùng là 90. Vì vậy, số 1234567890 không phải là số chính phương. Bài 25: Cho B 1 3 5 7
... 2021 chứng tỏ B là số chính phương. Lời giải B 1 3 5 7 ... 2021 2021 1 2021 1 Số số hạng: 1 2 2 2 2021 1 2021 1 2021 1 Tổng 2 B . 1011 2 2 2
Vậy B là số chính phương. Bài 26: Cho 2013 2012 2011 2 A 200. 9 9 9 .......... 9 9
1 . Chứng minh rằng A 25 là số chính phương. Lời giải Đặt 2013 2012 2011 2 B 9 9 9 ......... 9 9 1 3 2014 2013 2 9B 9 9 ................. 9 9 9 2014 9 1 2014 8B 9 1 B 8 2014 9 1 2014 A 200.B 200. 25. 9 1 8 2 2014 1007 A 25 25.9 5.9
Vậy A+ 25 là số chính phương. 43
B.BÀI TOÁN TRONG ĐỀ THI HSG VÀ CHUYÊN TOÁN 6 Bài 1.
a) Tìm hai chữ số tận cùng của các số sau: 100 1991 2 ;7
b) Tìm 4 chữ số tận cùng của số sau: 1992 5
Bài 2. Tìm chữ số tận cùng của các số sau: a) 1999 57 b) 1999 93 Bài 3. Cho 2 3 48 49
S =1+ 3 + 3 + 3 +..... + 3 + 3
Tìm chữ số tận cùng của S
Bài 4. (Đề HSG 6 trường Lê Quý Đôn năm 2014-2015)
Tìm hai chữ số tận cùng của 100 2 ?
Bài 5. (Đề HSG 6 trường Võ Thị Sáu năm 2014-2015)
Cho A = 2 + 22 + 23 + 24 + . . . + 220. Tìm chữ số tận cùng của A. Bài 6.
Tìm chữ số tận cùng của các số sau: a) 572011 b) 931999
Bài 7. (Đề HSG 2019-2020)
Tìm chữ số tận cùng của các số sau: a) 1999 57 b) 1999 93
Bài 8. (Đề HSG 2017-2018) Cho 2 96
A = 5 + 5 + ...... + 5 . Tìm chữ số tận cùng của A HƯỚNG DẪN Bài 1.
a) Tìm hai chữ số tận cùng của các số sau: 100 1991 2 ;7
b) Tìm 4 chữ số tận cùng của số sau: 1992 5 Lời giải
a) *Tìm hai số tận cùng của 100 2 10
2 = 1024 , bình phương của hai số có tận cùng là 24 thì tận cùng bằng 76, có số tận cùng bằng 76
nên nâng lên lũy thừa nào cũng bằng 76. Do đó: = ( )10 = ( )5 = ( )5 100 10 2 2 2 1024 ....76 = .....76
Vậy hai số tận cùng của 100 2 là 76.
*Tìm hai chữ số tận cùng của 1991 7 44 Ta thấy 4
7 = 2401, số có tận cùng bằng 01 nâng lên lũy thừa nào cũng bằng 01. Do đó: = = ( )497 = ( )497 1991 1988 3 4 7 7 .7 7 .343 ...01 .343 = (...0 ) 1 .343 = .......43 Vậy 1991 7
có hai số tận cùng bằng 43.
b) Tìm 4 số tận cùng của 1992 5 Ta có: = ( )498 1992 4 498 5 5 = 0625 = ....0625
Bài 2. Tìm chữ số tận cùng của các số sau: a) 1999 57 b) 1999 93 Lời giải a) Ta có: = ( )499 1999 4 3 499 7 7
.7 = 2401 .343 nên chữ số tận cùng là 3 Vậy số 1999 57
có chữ số tận cùng là 3 b) = ( )499 1999 4 3 499 3 3
.3 = 81 .27 nên có chữ số tận cùng là 7 Bài 3. Cho 2 3 48 49
S =1+ 3 + 3 + 3 +..... + 3 + 3
Tìm chữ số tận cùng của S Lời giải S = ( 2 3 + + + ) + ( 4 5 6 7 + + + ) + + ( 44 45 46 47 + + + ) 48 49 1 3 3 3 3 3 3 3 ..... 3 3 3 3 + 3 + 3
Các tổng 4 số hạng đều chia hết cho 10, do đó tận cùng bằng 0 Mặt khác: 48 49 4.12 48 3 + 3 = 3 +3 .3=....1+....1.3=....4
Vậy S có tận cùng bằng 4
Bài 4.(Đề HSG trường Lê Quý Đôn năm 2014-2015)
Tìm hai chữ số tận cùng của 100 2 ? Lời giải 10 5 Ta có: 10 100 = = ( 10 ) 10 = = ( 2 2 1024; 2 2 1024 1024 )
Mà 1024 2 có hai chữ số tận cùng là 76
=>( 1024 2 ) 5 có hai chữ số tận cùng là 76 Vậy 100 2
có hai chữ số tận cùng là 76
Bài 5.(Đề HSG 6 trường Võ Thị Sáu năm 2014-2015)
Cho A = 2 + 22 + 23 + 24 + . . . + 220. Tìm chữ số tận cùng của A. Lời giải
A. 2 = (2 + 22 + 23 + 24 + . . . + 220.). 2 = 22 + 23 + 24 + 25 + . . . + 221. 45 Nên A.2 - A = 221 -2 A = 221 - 2
Ta có : 221 = 24.5+1 = (24)5 . 2 = 165 .2
... 165 có tận cùng là 6 . Nên 165 . 2 có tận cùng là 6. 2 có tận cùng là 2.
Vậy A có tận cùng là 2. Bài 6.
Tìm chữ số tận cùng của các số sau: a) 572011 b) 931999 Lời giải
a) Tìm chữ số tận cùng của số 572011
Xét 72011; ta có: 72011 = (74)502.73 = 2401502. 343
Suy ra chữ số tận cùng bằng 3
Vậy số 572011 có chữ số tận cùng là 3.
b) Tìm chữ số tận cùng của số 931999
Xét 31999; ta có: 31999 = (34)499. 33 = 81499.27
Suy ra chữ số tận cùng bằng 7
Vậy số 31999 có chữ số tận cùng là 7.
Bài 7. (Đề HSG 2019-2020)
Tìm chữ số tận cùng của các số sau: b) 1999 57 b) 1999 93 Lời giải a) Ta có: = ( )499 1999 4 3 499 7 7
.7 = 2401 .343 nên chữ số tận cùng là 3 Vậy số 1999 57
có chữ số tận cùng là 3 b) = ( )499 1999 4 3 499 3 3
.3 = 81 .27 nên có chữ số tận cùng là 7
Bài 8. (Đề HSG 2017-2018) Cho 2 96
A = 5 + 5 + ...... + 5 . Tìm chữ số tận cùng của A Lời giải 2 96 2 3 96 97 A = 5 + 5 + ...... + 5
5A = 5 + 5 + ...... + 5 + 5 97 5 − 5 97 5A − A = 5 − 5 A = 4 Ta có: 97
5 có chữ số tận cùng là 5 97
5 − 5 có chữ số tận cùng là 0
Vậy chữ số tận cùng của A là 0.




