

Preview text:
CHUYÊN ĐỀ:
KHẢO SÁT CHUYỂN ĐỘNG CỦA CÁC VẬT BẰNG CÁC PHƯƠNG TRÌNH
CƠ BẢN CỦA ĐỘNG LỰC HỌC. I. CƠ SỞ LÝ THUYẾT:
1. PHƯƠNG TRÌNH CHUYỂN ĐỘNG CỦA CHẤT ĐIỂM:
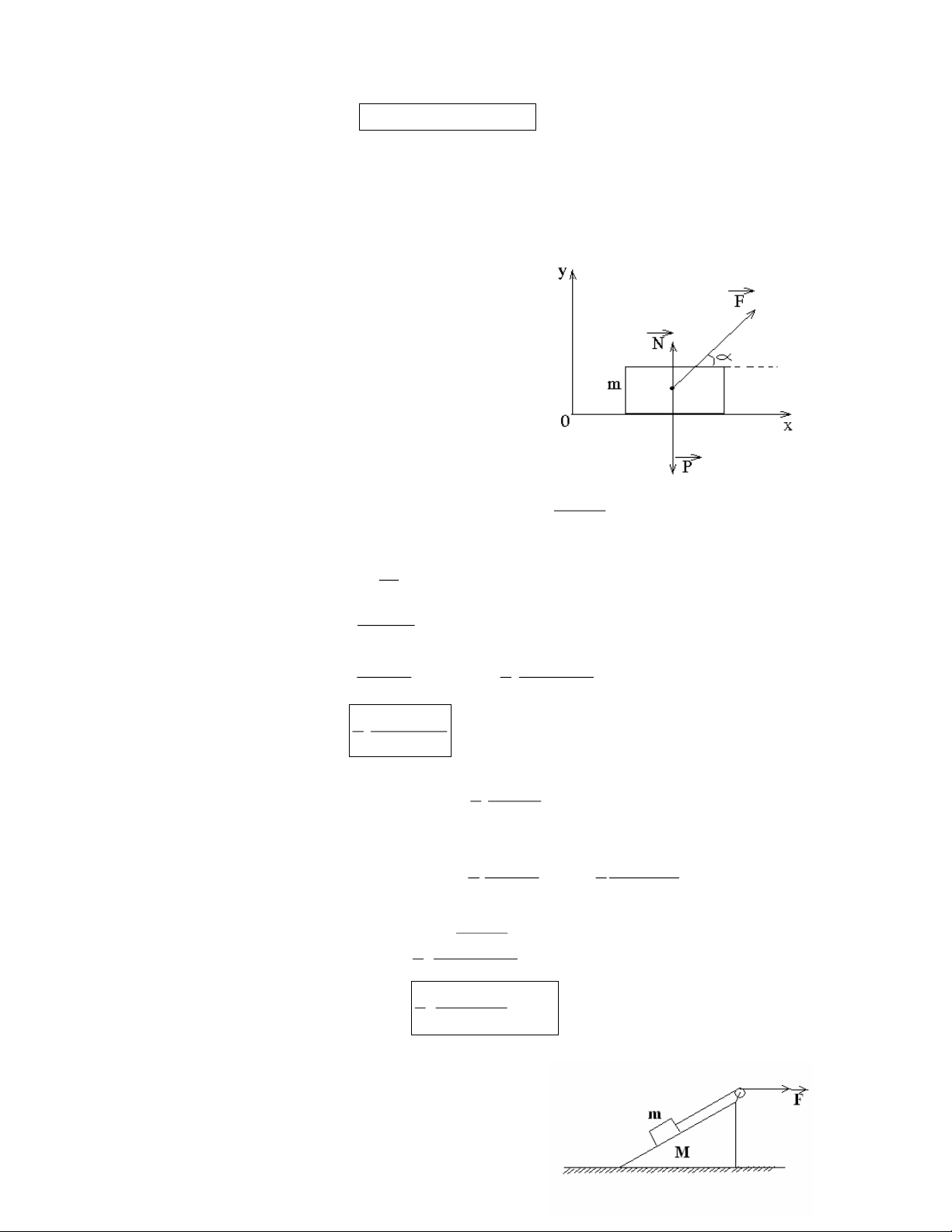
Chất điểm M có khối lượng m, chịu tác dụng của lực F , chuyển động trong hệ quy
chiếu quán tính với gia tốc a , thỏa mãn phương trình sau: ma F
được gọi là phương trình cơ bản của động lực học.
Trong trường hợp chất điểm chịu tác dụng của nhiều lực, thì lực F là lực tổng hợp của
các lực đó, tức là F F . k
2. PHƯƠNG TRÌNH CHUYỂN ĐỘNG TỊNH TIẾN CỦA VẬT RẮN:
Khi một vật rắn chuyển động tịnh tiến bất kỳ thì khối tâm của vật rắn chuyển động như
một chất điểm có khối lượng bằng khối lượng của cả vật, dưới tác dụng của một lực
bằng tổng các ngoại lực đặt vào vật rắn. ma F F c k k
Xét phương trình trên trong hệ tọa độ cố định oxy ta có: ma F xc
x với F F i F j x y ma F yc y
* Trường hợp bảo toàn chuyển động khối tâm của cơ hệ:
Nếu tổng hình học của các ngoại lực tác dụng lên hệ luôn bằng không thì khối tâm của
cơ hệ đứng yên hoặc chuyển động thẳng đều.
F 0 a 0 v const. k c c k
3. PHƯƠNG TRÌNH CHUYỂN ĐỘNG QUAY CỦA VẬT RẮN:
Vật rắn chuyển động quay quanh một trục dưới tác dụng của momen ngoại lực M
được mô tả bởi phương trình sau: I M
I là momen quán tính của vật đối với trục quay. II. BÀI TẬP ÁP DỤNG:
Câu 1: Một vật được truyền vận tốc ban đầu v0 và chỉ chịu lực cản tỉ lệ với độ lớn vận tốc v, F = kv.
1. Tính vận tốc v theo quãng đường đi được x, tính quãng đường X đi được cho tới lúc dừng.
2. Tính vận tốc theo thời gian đi được, tính thời gian để v = v0/2. Giải: dv
1. Ta viết định luật II Niutơn dưới dạng: F m dt dv
Ta có: kv m
hay –kdx = mdv. Lấy tích phân ta có: dt
-kx = mv + C. Ban đầu x = 0, v = v0, => C = -mv0. k Vậy v x v0 m m
Cho v = 0, ta được: X v0 k Nguyễn Anh Văn. - 1 - 2. Ta có: dv dv k kv m
dt .Lấy tích phân với điều kiện đầu v = v dt v m 0 ta được: k t m v v e 0 cho v 1 ta được: m T ln 2 . v 2 k 0
Câu 2: Viết phương trình chuyển động của một vật rơi tự do theo thời gian nếu kể đến lực cản của không khí F v
k , k là một hằng số dương. c 2 k t Đáp số: mg m g x t 1 ( m e ) 2 k k
Câu 3: Một chất điểm có khối lượng m chịu tác dụng của một lực theo phương ngang
x là F = psinkt, trong p, k là những hằng số đã biết. Tìm chuyển động của chất diểm
biết rằng lúc ban đầu t = 0, thì chất điểm ở vị trí x0, và có vận tốc v0. p p
Đáp số: x x v t sin kt . 0 0 km k 2m
Câu 4: Một tàu thủy có khối lượng là m mở máy chuyển động từ trạng thái đứng yên
trên mặt nước yên tĩnh. Cho biết lực tổng hợp bao gồm lực phát động và lực cản tác
dụng vào tàu, có cường độ là F = A – Bv, trong đó A, B là các hằng số dương đã biết,
v là tốc độ chuyển động của tàu.
1. Xác định vận tốc giới hạn của tàu.
2. Xác định phương trình chuyển động củ tàu. A B t v 1 A m e v gh B B Đáp số: A mA B t x t 1 m e 2 B B
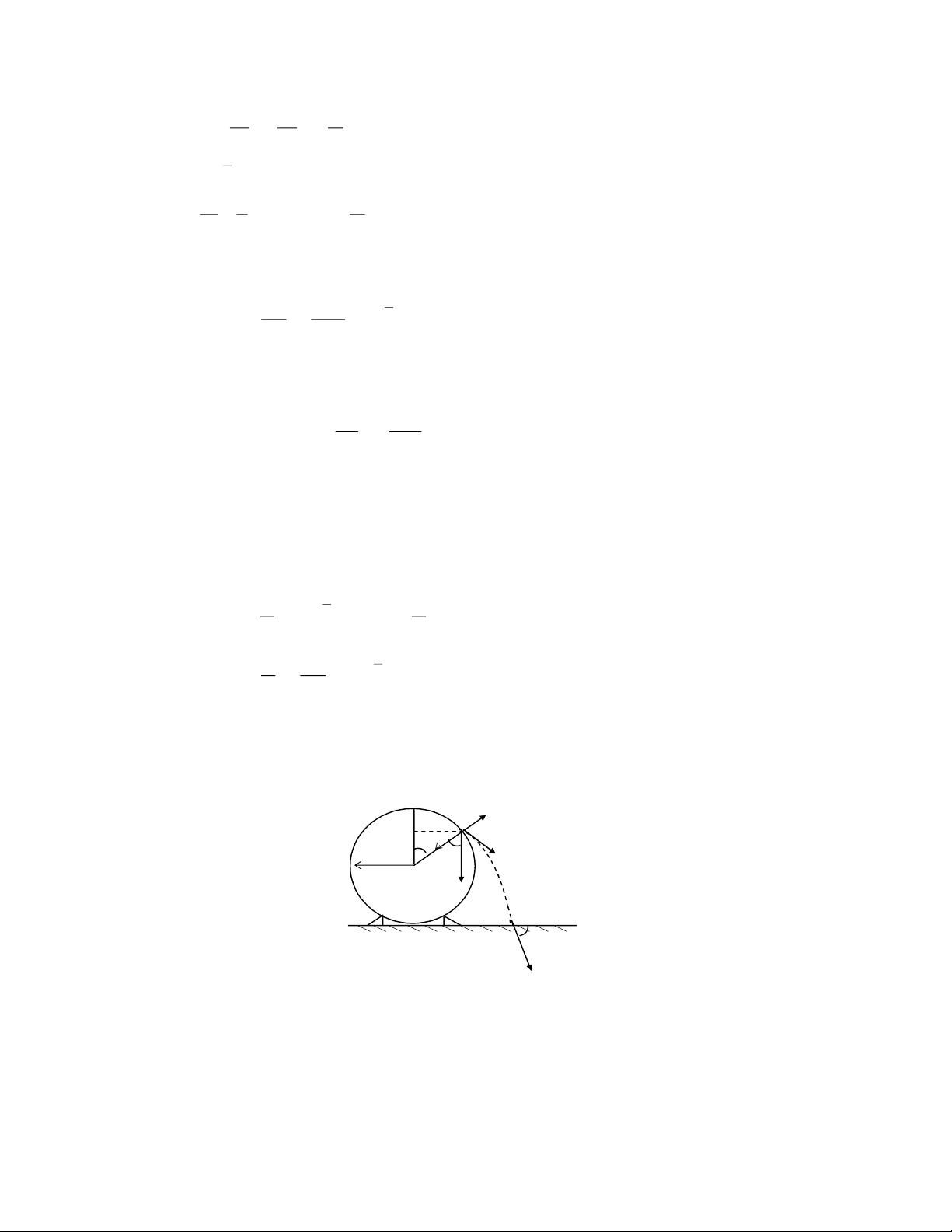
Câu 5: Mét qu¶ cÇu ®-îc g¾n cè ®Þnh trªn m¨t bµn n»m ngang. Tõ ®Ønh A cña qu¶
cÇu mét vËt nhá b¾t ®Çu tr-ît kh«ng ma s¸t víi vËn tèc ban ®Çu b»ng 0. Hái vËt sÏ
ch¹m vµo mÆt bµn d-íi mét gãc b»ng bao nhiªu? A N V R X O mg V1 Giải:
Gi¶ sö b¸n kÝnh qu¶ cÇu b»ng R. ChuyÓn ®éng cña vËt trªn mÆt qu¶ cÇu cho ®Õn
khi rêi khái nã lµ chuyÓn ®éng trßn kh«ng ®Òu víi b¸n kÝnh quü ®¹o b»ng R. Tr-íc hÕt
chóng ta t×m gãc vµ vËn tèc V cña vËt khi rêi khái mÆt qu¶ cÇu. VËt chÞu t¸c dông cña träng lùc g
m vµ ph¶n lùc ph¸p tuyÕn N cña qu¶ cÇu. Ph-¬ng tr×nh chuyÓn ®éng cña
vËt chiÕu lªn trôc X cã d¹ng:
mgcos N ma , n Nguyễn Anh Văn. - 2 - 2 ë ®©y V a
lµ gia tèc ph¸p tuyÕn. Vµo thêi ®iÓm vËt rêi khái mÆt qu¶ cÇu th× N=0, n R v× vËy ta ®-îc: V2 gR cos .
§Ó t×m V vµ cÇn cã thªm mét ph-¬ng tr×nh n÷a. Sö dông ®Þnh luËt b¶o toµn c¬ n¨ng: mV2 (
mg R R cos) V2 gR 2
(1 cos ) 2
Gi¶i hÖ hai ph-¬ng tr×nh víi c¸c Èn lµ V vµ ta t×m ®-îc : cos 2 / ; 3 V gR 2 / 3 .
B©y giê chóng ta t×m vËn tèc V cña vËt khi ch¹m vµo mÆt bµn. Dïng ®Þnh luËt 1
b¶o toµn c¬ n¨ng: c¬ n¨ng cña vËt t¹i ®Ønh h×nh cÇu b»ng c¬ n¨ng khi vËt ch¹m bµn. mV 2 2mgR 1 , 2
tõ ®ã tÝnh ®-îc V 2 gR. Trong kho¶ng thêi gian tõ lóc rêi mÆt qu¶ cÇu ®Õn khi 1
ch¹m mÆt bµn thµnh phÇn vËn tèc theo ph-¬ng ngang cña vËt kh«ng thay ®æi. V× vËy
nÕu gäi gãc r¬i cña vËt khi ch¹m bµn lµ th× ta cã:
Vcos V cos . 1
Thay c¸c biÓu thøc cña V, V vµ cos ®· t×m ®-îc ë trªn vµo sÏ tÝnh ®-îc: 1 6 0 arcos 74 . 9
Câu 6: Cho hÖ c¬ nh- h×nh vÏ. Ban ®Çu hÖ ë tr¹ng th¸i c©n b»ng sau ®ã ng-êi ta ®èt
d©y n»m ngang gi÷ m . X¸c ®Þnh gia tèc cña m ngay sau khi ®èt d©y. BiÕt gãc vµ 1 2
c¸c khèi l-îng m , m . 1 2 Giải:
Ngay t¹i thêi ®iÓm ban ®Çu c¸c lùc t¸c dông lªn qu¶ cÇu 1 gåm : träng lùc m g , lùc 1
c¨ng c¸c d©y T vµ T . Lùc t¸c dông lªn qu¶ cÇu 2 1 2
gåm: träng lùc m g , lùc c¨ng d©y T (ta kh«ng 2 2
biÓu diÔn träng lùc trªn h×nh)
Khi Êy qu¶ cÇu 2 sÏ chØ cã thµnh phÇn gia tèc theo
ph-¬ng th¼ng ®øng a . Do d©y kh«ng gi·n nªn 2
thµnh phÇn gia tèc theo ph-¬ng th¼ng ®øng cña qu¶ 1 còng lµ a . 2
C¸c ph-¬ng tr×nh Newton theo ph-¬ng Y:
m g T T cos m a ) 1 ( 1 2 1 1 2
m g T m a ( ) 2 2 2 2 2
Ngay t¹i thêi ®iÓm ban ®Çu vËn tèc cña m1 b»ng 0: nªn thµnh phÇn gia tèc cña m theo 1 2 v
ph-¬ng h-íng t©m b»ng kh«ng: a 0 ht R
T T cos m g cos m a 0 T T cos m g cos ) 3 ( 1 2 1 1 ht 1 2 1 Nguyễn Anh Văn. - 3 -
Tõ (1), (2), (3) ta dÔ dµng thu ®-îc: m m a 1 2 g 2 m1 m 2 2 sin
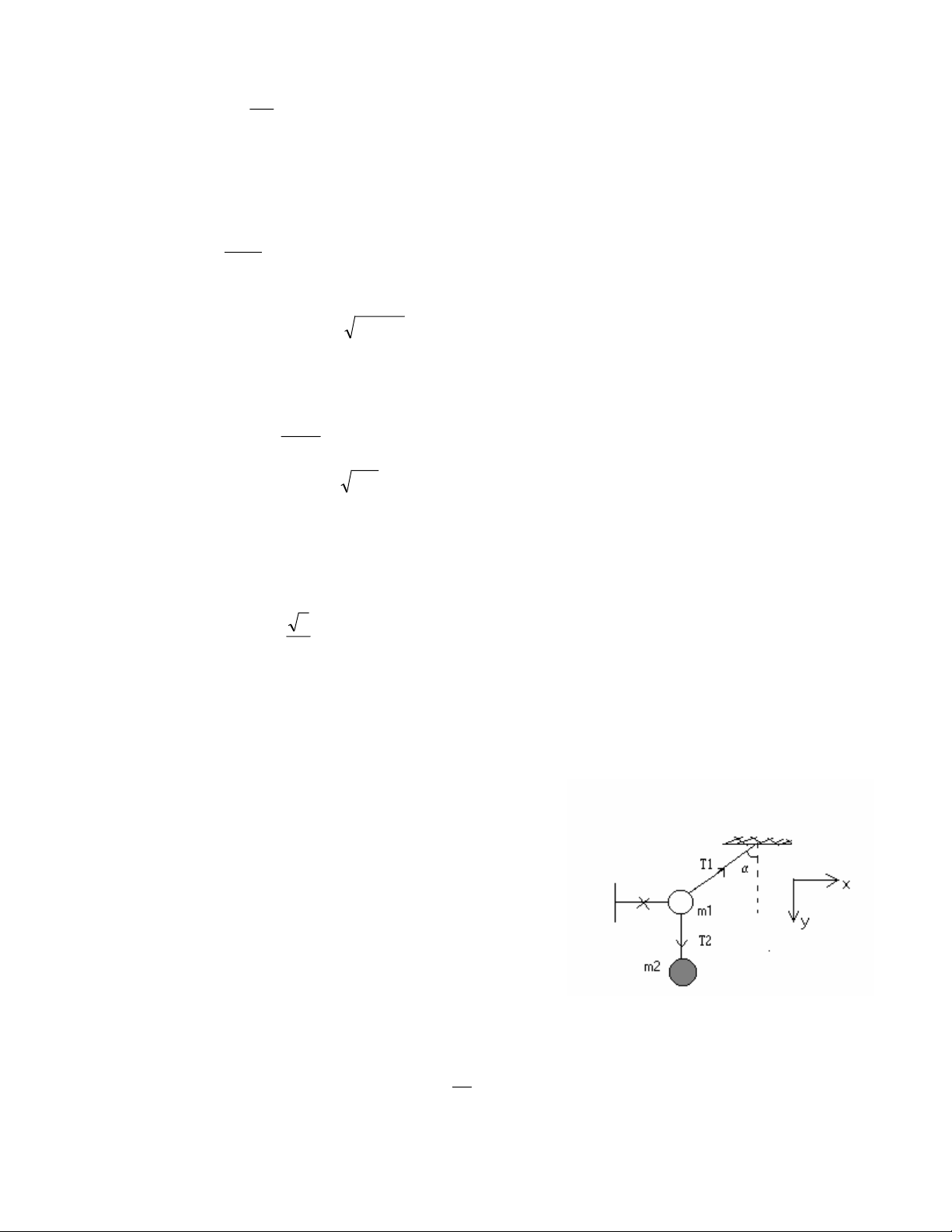
Câu 7: Mét thanh nh½n ®-îc cè ®Þnh vµo t-êng vµ lµm víi ®-êng n»m ngang gãc
. X©u chiÕc nhÉn khèi l-îng m1 vµo thanh. Sîi d©y m¶nh kh«ng gi·n khèi l-îng
kh«ng ®¸ng kÓ ®-îc buéc mét ®Çu vµo nhÉn cßn ®Çu kia buéc mét qu¶ cÇu khèi l-îng
m2. Gi÷ nhÉn cè ®Þnh sao cho d©y ë vÞ trÝ th¼ng ®øng. TÝnh lùc c¨ng d©y ngay sau khi th¶ nhÉn ra. Giải:
Ngay sau khi th¶ nhÉn ra ta cã thÓ kh¼ng ®Þnh r»ng
gia tèc cña m h-íng theo thanh cßn gia tèc cña m 1 2
h-íng theo ph-¬ng ®øng. ¸p dông ®Þnh luËt hai Newton cho vËt 1, ta cã T m g m a 1 .sin ) 1 ( 1 1
Trong hÖ quy chiÕu g¾n víi vßng nhÉn qu¶ cÇu chÞu lùc qu¸n tÝnh: f m a qt 2 1
Áp dông ®Þnh luËt hai Newton cho qu¶ cÇu 2 theo ph-¬ng d©y:
T f sin m g m a qt 2 2 ht 2 mv
Tại t = 0 vËn tèc qu¶ cầu b»ng kh«ng nªn F ma 0 ht ht l
T m a sin m g 0 ( ) 2 2 1 2
Tõ (1) vµ (2) ta dÔ dµng thu ®-îc: 1 T m g m 2 2 1 1 ( tg 2 ) m1
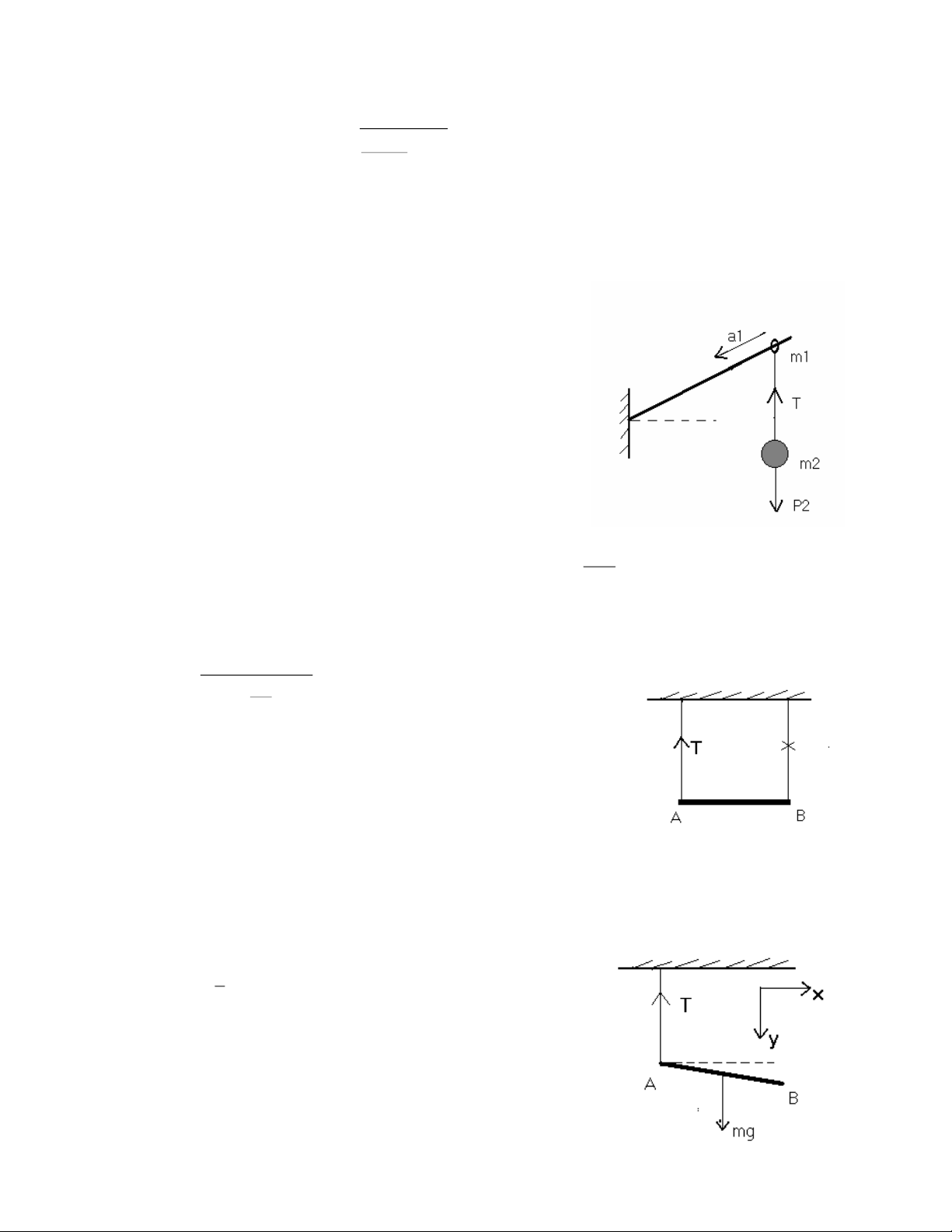
Câu 8: Mét thanh AB ®ång chÊt chiÒu dµi 2l khèi l-îng
m ®-îc gi÷ n»m ngang bëi hai d©y treo th¼ng ®øng nh-
h×nh vÏ. X¸c ®Þnh lùc c¨ng d©y tr¸i ngay sau khi ®èt d©y ph¶i. Giải:
Ngay sau khi ®èt d©y c¸c lùc t¸c dông lªn thanh gåm:
lùc c¨ng d©y T, träng lùc mg. §Þnh luËt 2 Newton theo trôc y: mg T . m a ) 1 ( y
§Þnh luËt hai Newton cho chuyÓn ®éng quay cña thanh quanh khèi t©m: 1 T. 2 l ml (2) 3
Ta cÇn t×m mèi liªn hÖ gi÷a a vµ gia tèc gãc . y
XÐt sau mét kho¶ng thêi gian t rÊt nhá sau khi ®èt
d©y, d©y vÉn cßn th¼ng ®øng, thanh th× bÞ lÖch khái
ph-¬ng ngang mét gãc nhá. Trong kho¶ng thêi gian
rÊt nhá ®ã, ta coi nh- gia tèc khèi t©m vµ gia tèc gãc Nguyễn Anh Văn. - 4 -
cña thanh lµ kh«ng ®æi. Khi ®ã ®é dÞch chuyÓn cña khèi t©m lµ: y l .
§¹o hµm hai lÇn hai vÕ cña ph-¬ng tr×nh trªn theo t, ta ®-îc: a l. ) 3 ( y
Tõ c¸c ph-¬ng tr×nh (1), (2) ,(3) ta thu ®-îc: 1 T mg 4
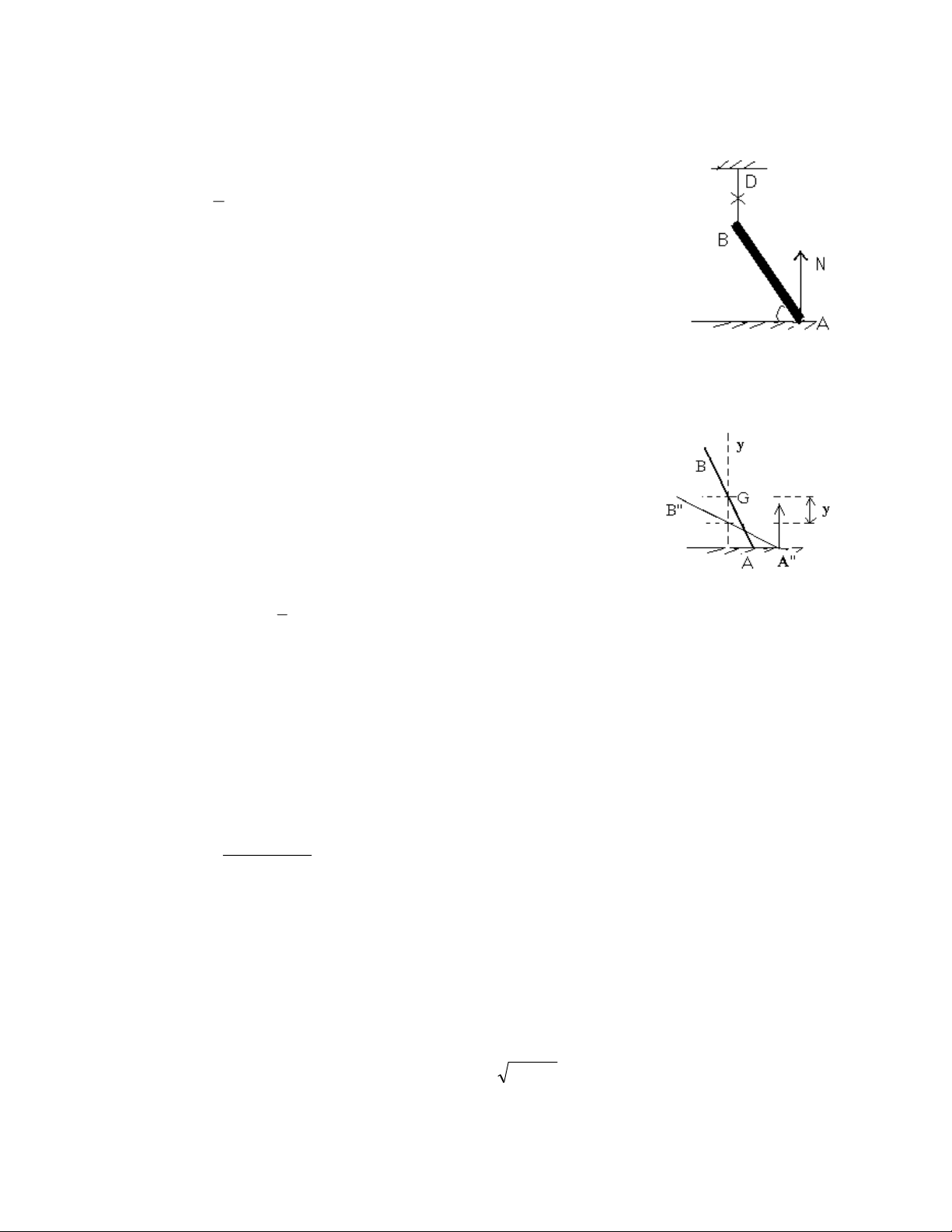
Câu 9 : Mét thanh ®ång chÊt AB dµi 2l, träng l-îng P, ®Çu
A tùa trªn sµn ngang nh½n vµ lËp víi sµn mét gãc 0, ®Çu B
®-îc treo b»ng d©y DB th¼ng ®øng, kh«ng gi·n, kh«ng 0
träng l-îng. T¹i mét thêi ®iÓm nµo ®ã d©y bÞ ®øt vµ thanh
b¾t ®Çu chuyÓn ®éng. X¸c ®Þnh ¸p lùc cña thanh lªn sµn
ngay t¹i thêi ®iÓm thanh b¾t ®Çu chuyÓn ®éng. Giải :
Do kh«ng cã ngo¹i lùc t¸c dông lªn thanh theo ph-¬ng
ngang nªn khèi t©m thanh chØ chuyÓn ®éng theo ®-êng
th¼ng ®øng xuèng d-íi. Ngay sau khi thanh b¾t ®Çu
chuyÓn ®éng c¸c lùc t¸c dông lªn thanh lµ: träng lùc mg, ph¶n lùc N cña sµn.
§Þnh luËt 2 Newton theo trôc y: mg N . m a ) 1 ( y
§Þnh luËt 2 Newton cho chuyÓn ®éng quay cña thanh quanh khèi t©m: 1 N.l.cos 2 ml (2) 0 3
Ta cÇn t×m mèi liªn hÖ gi÷a ay vµ dùa trªn c¸c ®iÒu kiÖn ban ®Çu cña chuyÓn ®éng.
XÐt khi thanh hîp víi ph-¬ng ngang mét gãc = 0 - d . Qu·ng ®-êng mµ khèi t©m ®· dÞch chuyÓn lµ:
y l sin l sin l.(sin sin( d )) 0 0 0
lsin sin cos d cos sin d 0 0 0
y l.cos . d 0
§¹o hµm hai vÕ cña ph-¬ng tr×nh trªn ta cã : a l.cos . ) 3 ( y 0
Tõ (1), (2), (3) ta thu ®-îc: 1 N mg . . 3 cos2 1 0
Câu 10: Qu¶ cÇu M khèi l-îng m ®-îc nèi víi mét trôc th¼ng ®øng t¹i hai ®iÓm A,
B b»ng hai thanh chiÒu dµi l, khèi l-îng kh«ng ®¸ng kÓ (kho¶ng c¸ch AB = 2a). C¸c
chç nèi ®Òu lµ c¸c chèt nªn hai thanh chØ bÞ kÐo hoÆc nÐn. C¶ hÖ quay kh«ng ma s¸t
quanh trôc th¼ng ®øng víi vËn tèc gãc kh«ng ®æi (xem h×nh vÏ).
TÝnh c¸c lùc T vµ T’ mµ vËt m t¸c dông lªn c¸c thanh AM vµ BM t-¬ng øng. C¸c thanh bÞ kÐo hay bÞ nÐn? Giải: Gäi TM, '
T lµ c¸c lùc do c¸c thanh t¸c dông lªn vËt M. VËt M chÞu c¸c lùc: mg, T M M, ' T vµ lùc hướng t©m: F = 2 2 2 2 m R m l a M Nguyễn Anh Văn. - 5 - Gi¶ thiÕt TM vµ '
T cã chiÒu nh- h×nh vÏ. Gäi M y gãc AMH = BMH = ; sin a
; cos =R/l. ChiÕu A l TM xuèng H l X vµ HY cã: M T T' M M cos m 2R x H T T' ' M M sin mg B TM m g a
Nhân pt đầu với sin , pt thứ hai với cos =R/l, l
sau đó cộng và trừ các pt ta được: ml 2 g T M 2 a ' ml 2 g T M 2 a
TM >0, chiÒu gi¶ thiÕt lµ ®óng. TM lµ chiÒu do thanh t¸c dông lªn M. Ng-îc l¹i, M
t¸c dông lªn thanh lùc trùc ®èi T. VËy thanh AM bÞ kÐo. g T' o nÕu
(quay ®ñ nhanh), thanh BM bÞ kÐo M a g T' 0 nÕu thanh BM bÞ nÐn M a g T' 0 nÕu
thanh BM kh«ng chÞu lùc nµo M l
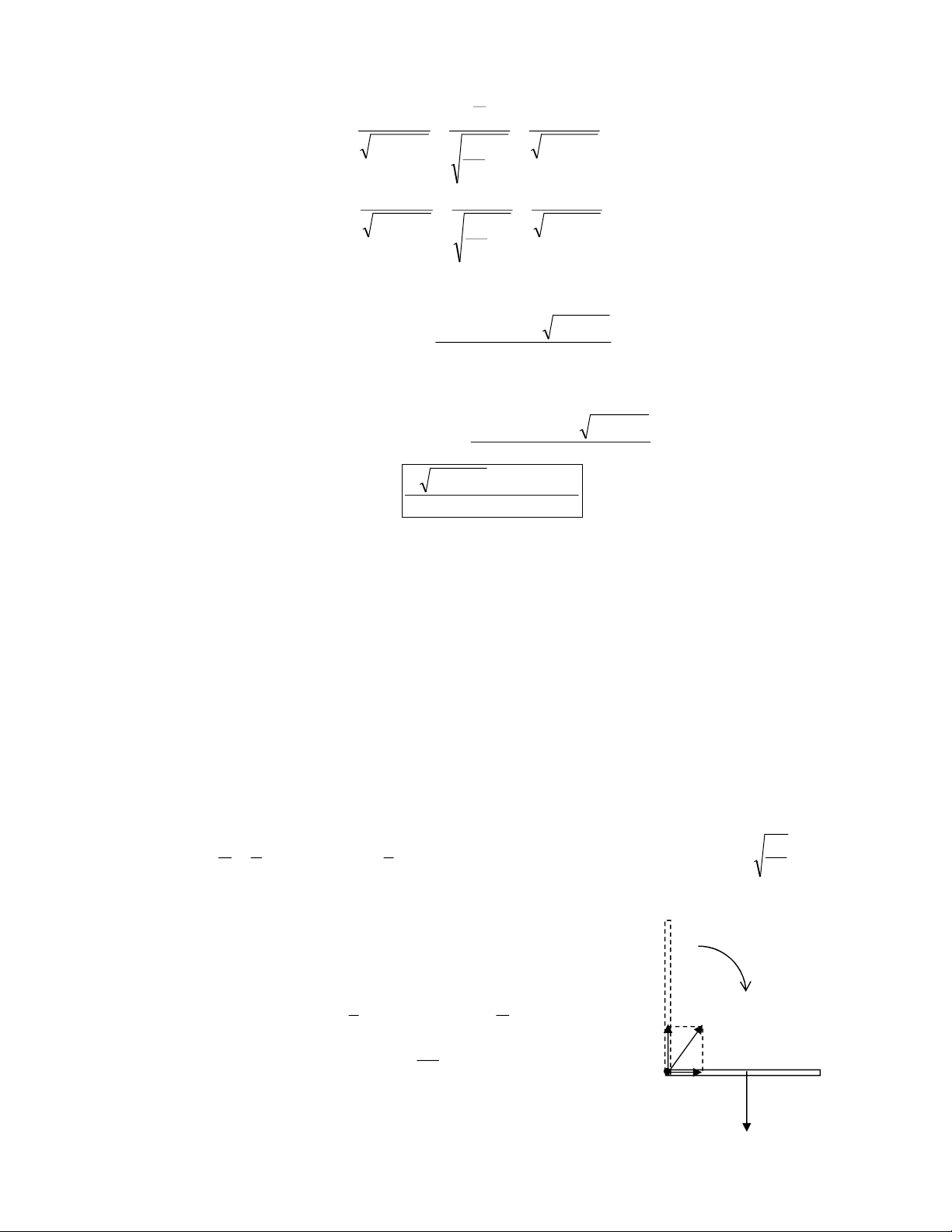
Câu 11: Cho c¬ hÖ nh- h×nh vÏ. Lóc ®Çu hÖ c©n b»ng, bµn nhËn ®-îc
gia tèc a theo ph-¬ng ngang nh- h×nh vÏ. TÝnh gia tèc
cña M ®èi víi mÆt ®Êt, biÕt hÖ sè ma s¸t tr-ît gi÷a M vµ sµn lµ . Giải:
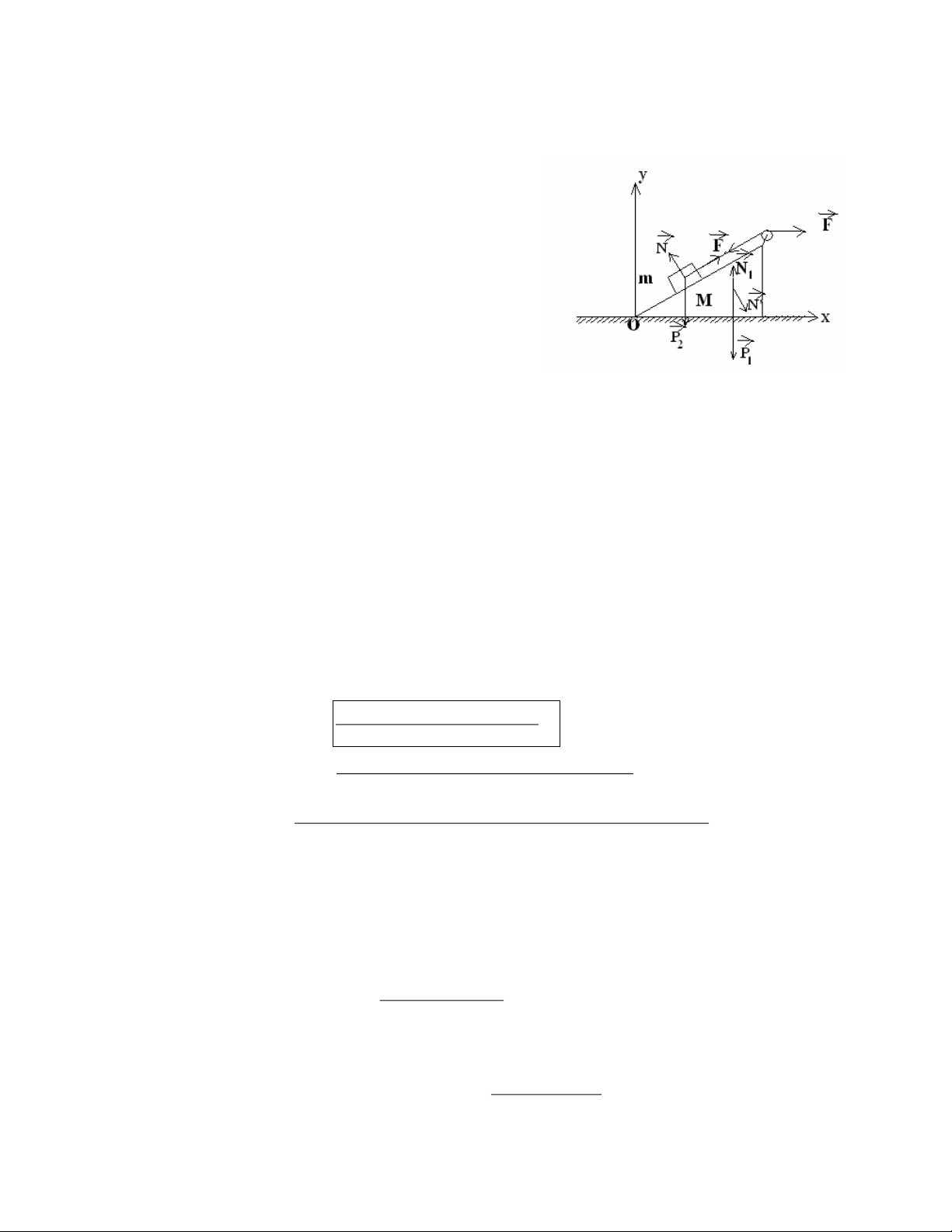
Chän hÖ quy chiÕu oxy g¾n vµo bµn nh- h×nh vÏ. Trong hÖ quy chiÕu oxy:
• Ph-¬ng tr×nh chuyÓn ®éng cña vËt M
T F F Ma qt ms 0 Hay:
T Ma N Ma ) 1 ( , 1 0 trong ®ã:
a lµ gia tèc cña M ®èi víi bµn 0
a lµ gia tèc cña bµn ®èi víi ®Êt.
• Ph-¬ng tr×nh chuyÓn ®éng cña vËt m: Fqt ma a tg 2 ( ) 2 P mg g 2
F sin mg cos T ma ) 3 ( qt 2 0 Tõ (3) suy ra:
ma sin mg cos T ma (4) 0 Tõ (1) vµ (4) suy ra: Ma N
masin mg cos 1 a ) 5 ( 0 m M Tõ (2) suy ra: Nguyễn Anh Văn. - 6 - a tg g a sin ( ) 6 2 tg 1 2 2 2 a a g 1 2 g 1 1 g cos (7) 2 tg 1 2 2 2 a a g 1 2 g Vµ N Mg ) 8 ( 1
ThÕ (6), (7), (8) vµo (5) ta rót ra: Ma Mg m a2 g 2 a 0 m M
Gia tèc cña M ®èi víi ®Êt:
a a a M 0 Ma Mg m a2 g 2
a a a a M 0 m M
m a2 g 2 Mg mg a M m M C©u12:
Mét thanh ®ång chÊt cã khèi l-îng m cã thÓ quay tù do xung quanh mét
trôc n»m ngang ®i qua mét ®Çu cña thanh. N©ng thanh ®Ó nã cã ph-¬ng th¼ng
®øng råi th¶ nhÑ th× thanh ®æ xuèng vµ quay quanh trôc. Cho momen qu¸n tÝnh
cña thanh ®ång chÊt cã khèi l-îng m, chiÒu dµi L ®èi víi mét trôc ®i qua mét ®Çu
cña thanh vµ vu«ng gãc víi thanh lµ I = mL2/3. T¹i thêi ®iÓm khi thanh cã ph-¬ng ngang, h·y t×m:
1) Tèc ®é gãc vµ gia tèc gãc cña thanh.
2) C¸c thµnh phÇn lùc theo ph-¬ng ngang vµ theo ph-¬ng th¼ng ®øng mµ
trôc quay t¸c dông lªn thanh. Giải:
1) Theo ®Þnh luËt b¶o toµn c¬ n¨ng: L 1 3g 2 1 mg I . Thay 2
I mL ta thu ®-îc tèc ®é gãc cña thanh: . 2 2 3 L
C¸c lùc t¸c dông lªn thanh gåm träng lùc P vµ lùc N mµ lùc mµ trôc
quay t¸c dông lªn thanh. M«men cña lùc N ®èi
víi trôc quay b»ng 0 nªn ®Þnh luËt II Niut¬n
cho chuyÓn ®éng quay cña thanh quanh trôc O cã d¹ng: 1 L M I . Thay 2
I mL vµ M mg ta ®-îc P 3 P 2 N N y gia tèc gãc cña thanh: 3g . 2L
2) Theo ®Þnh II Niut¬n cho chuyÓn ®éng tÞnh O Nx tiÕn: P Nguyễn Anh Văn. - 7 -
P N a m (1)
ChiÕu ph-¬ng tr×nh (1) lªn ph-¬ng ngang: 2 L
N ma ma m x x n 2
Thay gi¸ trÞ tèc ®é gãc t×m ®-îc ë phÇn 1 vµo ta t×m ®-îc thµnh phÇn
n»m ngang cña lùc mµ trôc quay t¸c dông lªn thanh: N 3mg / 2 . x
ChiÕu ph-¬ng tr×nh (1) lªn ph-¬ng th¼ng ®øng: L
P N ma ma m y y t 2
Thay gi¸ trÞ gia tèc gãc t×m ®-îc ë phÇn 1 vµo ta t×m ®-îc thµnh phÇn
th¼ng ®øng cña lùc mµ trôc quay t¸c dông lªn thanh: N mg / 4 . y
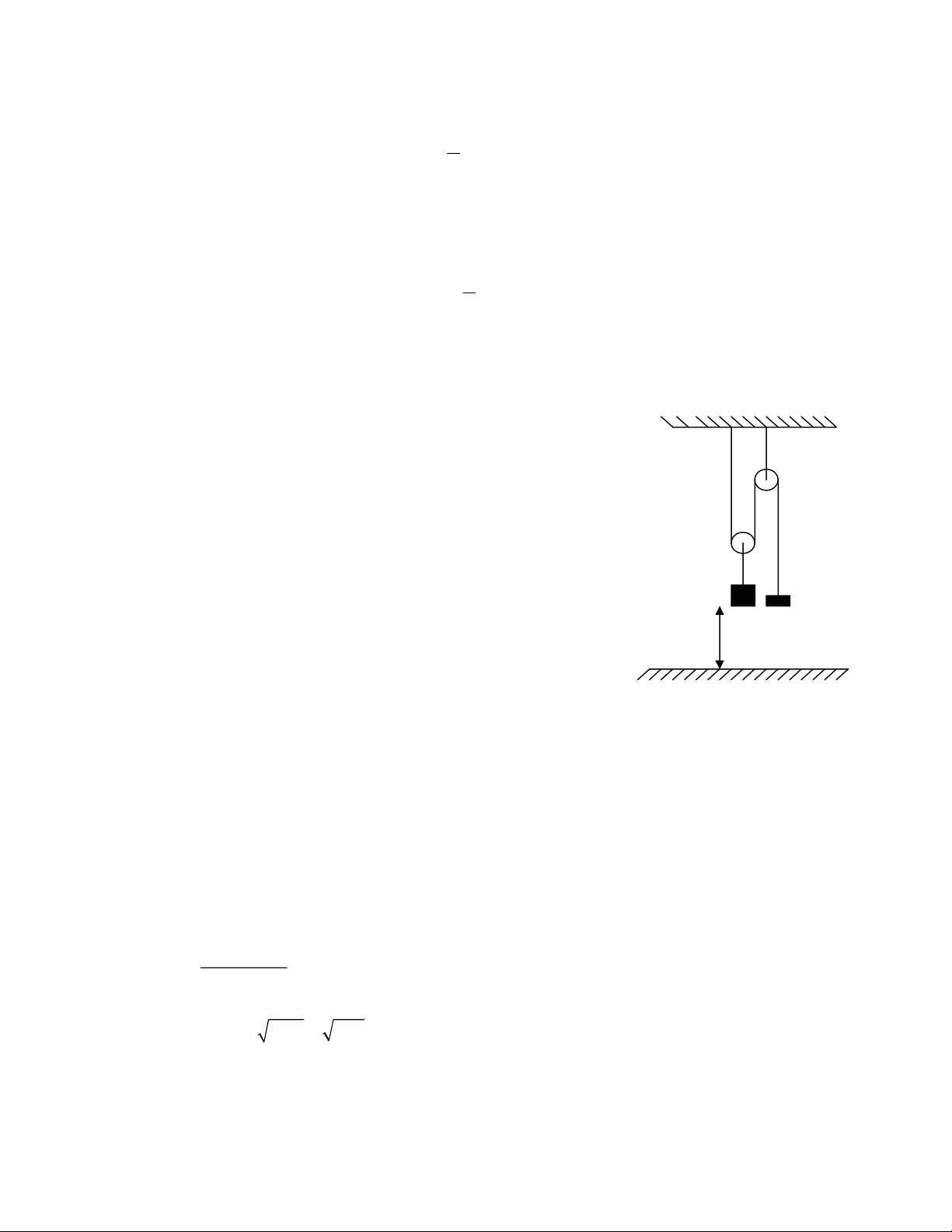
Câu 13: Cho cơ hệ như hình vẽ:
Vật 1 có khối lượng m1 , vật 2 có khối lượng m2 = 6 m1 = 6 kg,
ban đầu hệ được giữ đứng yên và hai vật cách mặt đất một đoạn
là h = 40cm. Thả cho hai vật bắt đầu chuyển động. Khối lượng
ròng rọc, các dây nối và ma sát đều không đáng kể. Xem sợi dây
không co, giãn trong quá trình chuyển động. Lấy g = 10m/s2.
a, Tính gia tốc của mỗi vật trong quá trình chuyển động.
b, Tính giá trị cực đại mà vật 1 đạt được trong quá trình chuyển động.
c, Trong khi 2 vật đang chuyển động người ta cho giá đỡ chuyển động
hướng thẳng đứng lên trên với gia tốc a = 2 m/s2. m1
Tính lực căng dây khi m2 đang chuyển động. Giải: h m2
a. PTĐL II newtơn cho mỗi vật: Vật 1:
p T m a (1) 1 1 1 1 Vật 2:
p T m a (2) 2 2 2 2
Chiếu (1) và (2) lên hướng chuyển động của mỗi vật ta đc:
(1) T p m a (3) 1 1 1 1
(2) p T m a (4) 2 2 2 2
Từ h v ta thấy khi vật 2 đi đc quãng đường S
Thì vật 1 đi đc 2S => a 2a và T 1 2
2 = 2T1 thay vào (3),(4) đồng thời khử T ta đc:
(m 2m )g 2 1 a = 4 (m/s2) và a 2 4m m 1 = 8 (m/s2) 1 2
b. Khi vật 2 chạm đất thì vật 1 đi đc đoạn đường là S1 = 2h = 0,8m. Khi đó vật 1 đạt đc
vân tốc v 2a s 12,8 (m/s) 1 1 1
và thực hiện chuyển động ném đứng với vận tốc ban đầu v1. Quãng đường vật 1 đi
được đến khi đạt độ cao cực đại là: S 2 1max= v1 /2g = 0,64 m
Vậy độ cao cực đại cần tìm là: hmax = S1 + S1max = 1,44m Nguyễn Anh Văn. - 8 -
c. Xét trong hệ quy chiếu gắn với giá đỡ m2 . Các vật chịu thêm lực quán tính F ma ,
p T m a m a đặt 2 p
p m a m g g 12m / s 2 2 2 2 2 2hd 2 2 2 hd hd (m 2m ) Tương tự câu a suy ra , 2 1 a g 4,8 (m/s2) 2 4 hd m m 1 2 , 2 ,
a 9,6m / s T m (g a ) 21,6N 1 1 1 hd 1 Câu 14 :
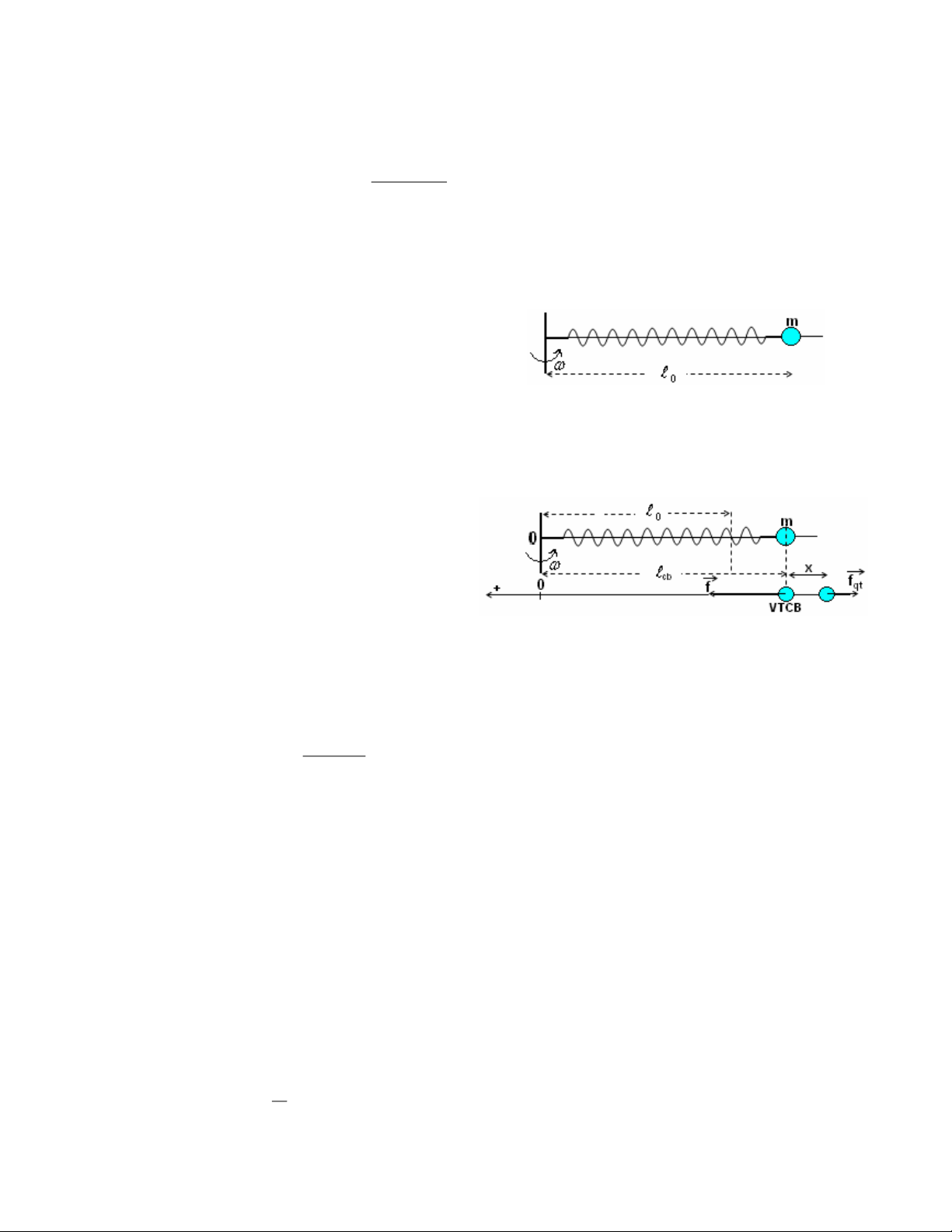
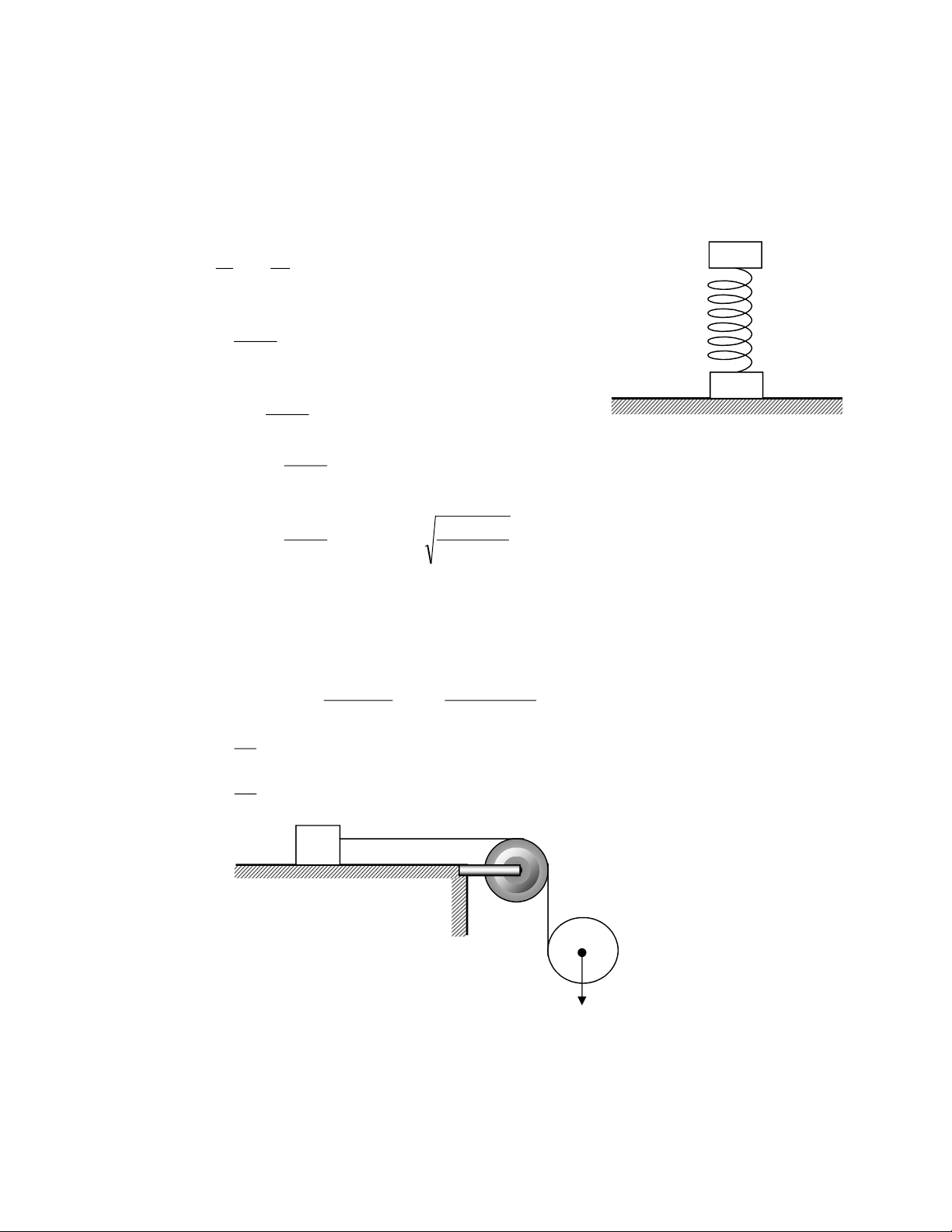
Một vật khối lượng m được gắn vào đầu một lò xo có độ cứng k và chiều dài tự nhiên như 0
hình vẽ. Vật có thể trượt không ma sát trên một thanh ngang. Cho thanh ngang quay quanh
một trục thẳng đứng đi qua đầu còn lại của lò xo
với vận tốc không đổi.
a. Tính chiều dài của lò xo.
b. Đưa vật ra khỏi vị trí cân bằng mới một
đoạn x rồi buông nhẹ. Chứng tỏ vật dao động 0
điều hòa và lập biểu thức li độ. Giải:
a. Tính chiều dài của lò xo.
- Chọn O là hệ qui chiếu (qui chiếu không quán tính). Trong hệ qui chiếu này m ở vị trí cân bằng nên : f + f = 0 (1) 0 qt
Với : f là lực đàn hồi f = k( ) 0 0 cb 0
f là lực quán tính f = - m a với qt qt ht a = . 2 ht cb
Chiếu phương trình (1) lên trục hướng tâm, ta được : f - f = 0 0 qt
k( ) - m. . 2 = 0 (2) cb 0 cb
k. - k. - m. . 2 = 0 cb 0 cb k = 0 cb 2 k m
b. Tại vị trí bất kỳ có li độ x so với vị trí cân bằng mới (như hình vẽ)
- Theo định luật 2 Newtơn ta có :
f + f = m a (3) qt
- Chiếu phương trình (3) lên trục hướng tâm, ta có : f - ma = ma ht k( ) - m. . 2 = mx // (4) 0
Trừ phương trình (4) cho phương trình (2) vế theo vế ta được : k( ) - m. . 2
- k( ) + m. . 2 = mx // 0 cb 0 cb k - m. . 2 -k - m. . 2 = mx // cb cb k( - ) - m 2 ( - ) = mx // cb cb Trong đó : x = ( - ) cb x(k - m 2 ) = mx // k x // - 2 x = 0 (*) m
Phương trình (*) có nghiệm tổng quát : Nguyễn Anh Văn. - 9 - x = Asin( t + ) k Với tần số góc : = 2 m k
Vậy m dao động điều hòa với tần số góc = 2 m
Theo điều kiện ban đầu : + t = 0, x = x 0 + t = 0, v = 0
Giả sử x > 0 ta có : A = x ; = 0 0 2 k
Biểu thức li độ có dạng : x = x sin 2 .t 0 m 2
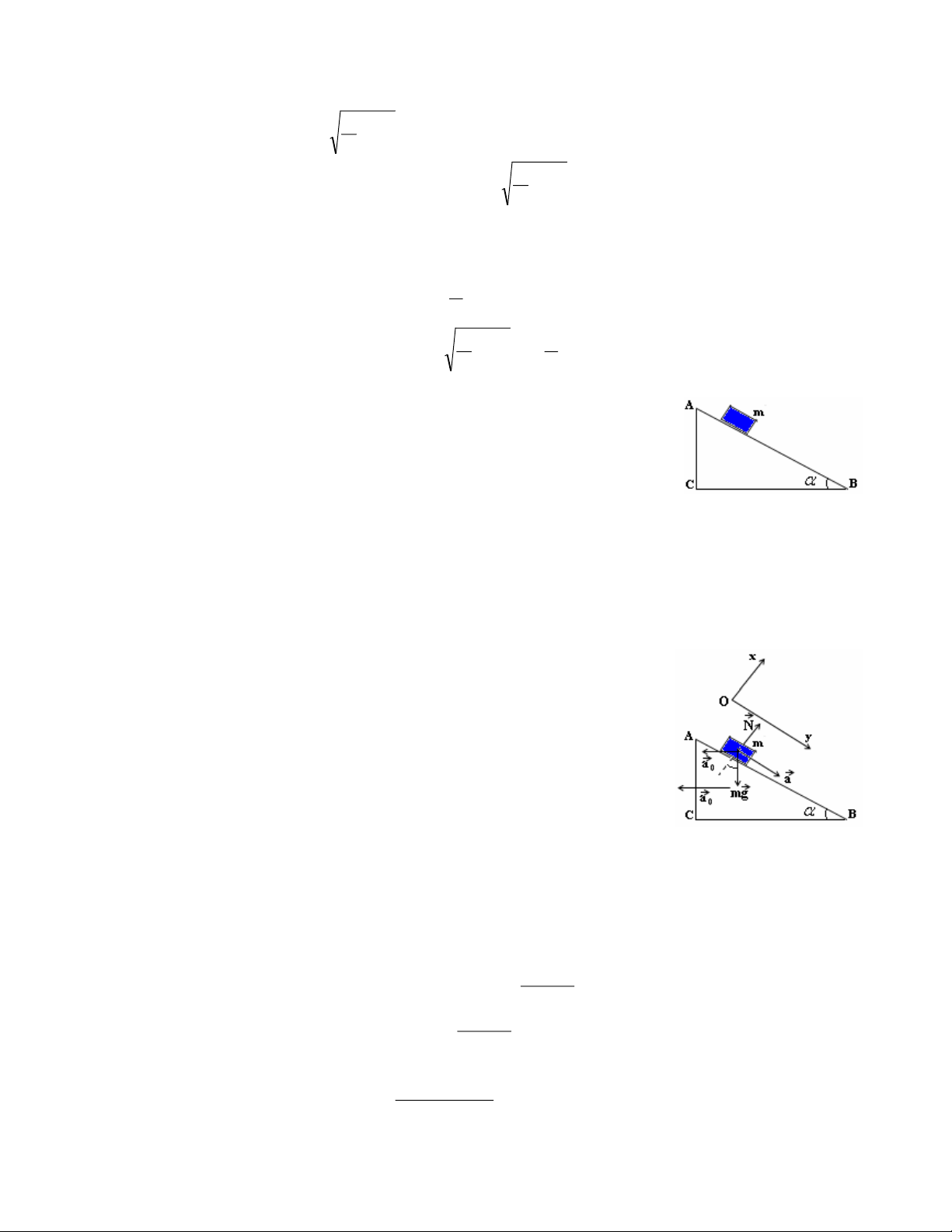
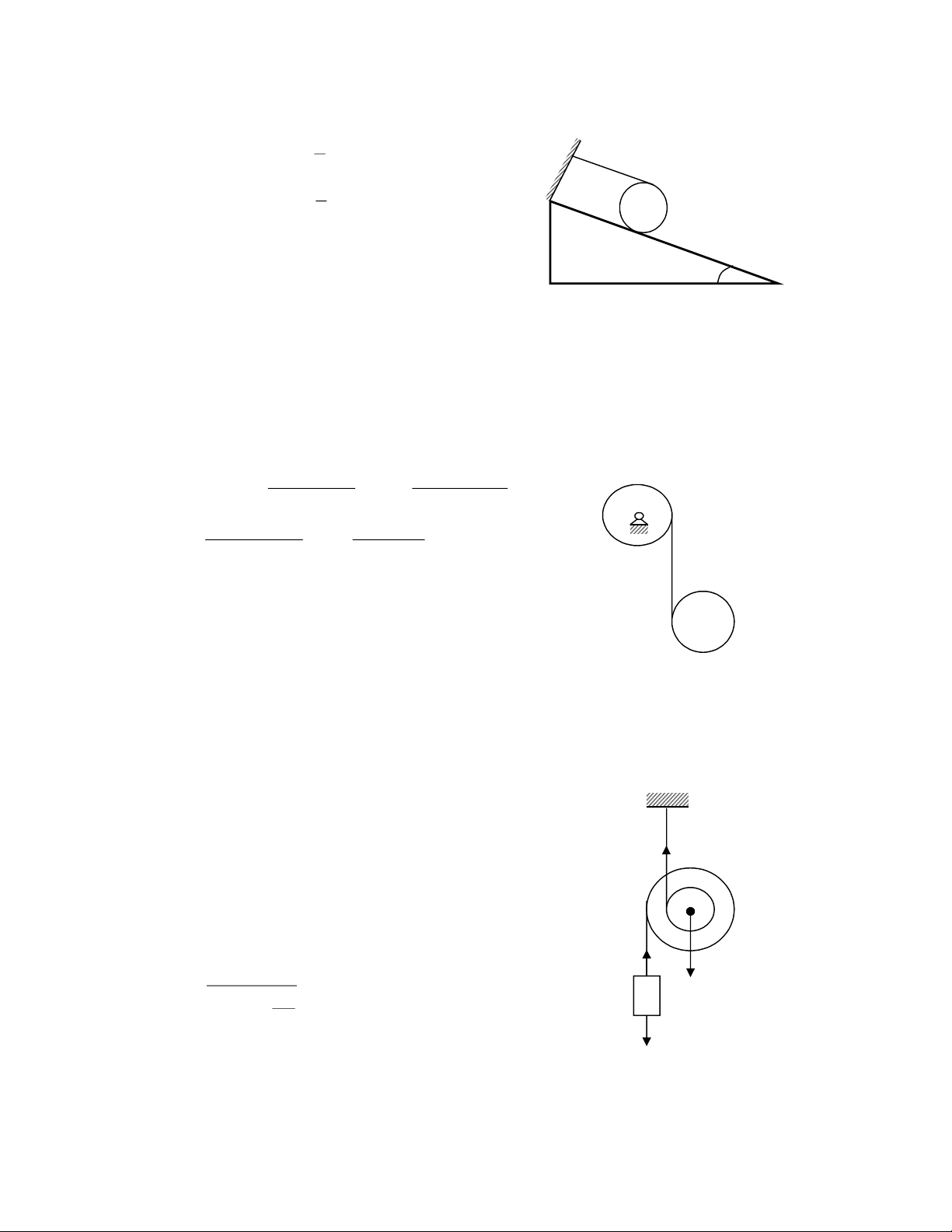
Câu 15 : Một vật có khối lượng m có thể trượt không ma sát trên một
cái nêm ABC ; AB = , Cˆ = 90 0 , Bˆ = . Nêm ban đầu đứng yên,
có khối lượng M và có thể trượt không ma sát trên mặt sàn nằm ngang. ( như hình vẽ )
Cho vật m trượt từ đỉnh A của nêm không vận tốc đầu.
a. Thiết lập biểu thức tính gia tốc a của vật đối với nêm và gia tốc
a của nêm đối với sàn. 0
b. Lấy hệ tọa độ xOy gắn với sàn, ban đầu trùng với BCA. Tính hoành độ của vật m và
của đỉnh C khi vật trượt tới đỉnh B. Quỹ đạo của vật là đường gì ? Cho m = 0,1 (kg), M =
2m, = 30 0 , = 1 (m), g = 10 (m/s 2 ). Giải :
a. Tính gia tốc a của vật đối với nêm và gia tốc a của nêm đối với sàn. 0
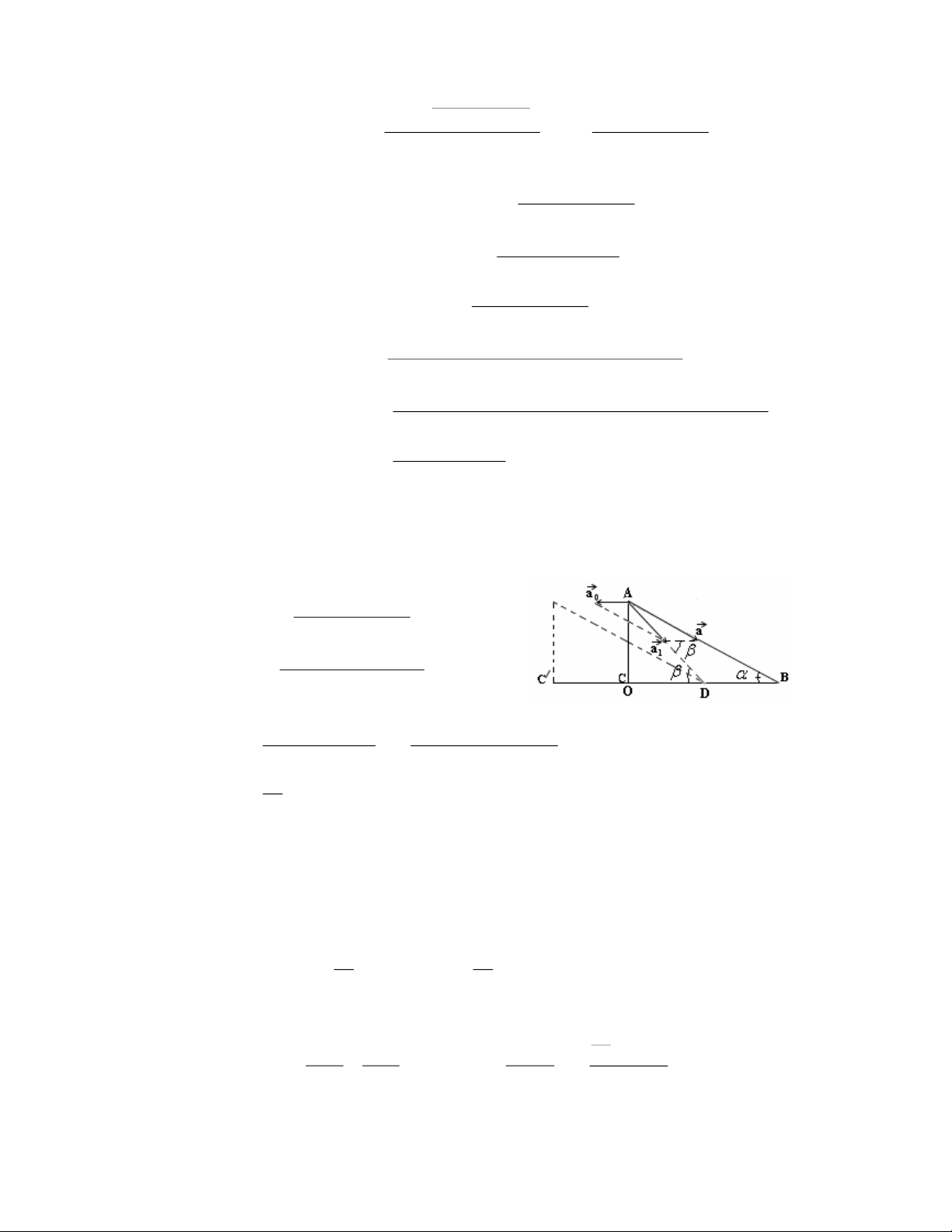
- Chọn hệ tục tọa độ xOy như hình vẽ
- Động lượng của hệ bằng 0 Vật đi xuống sang phải thi
nêm phải sang trái giá trị đại số gia tốc của nêm là a < 0. 0
+ Vật m chịu tác dụng của 2 lực : trọng lực m g , phản lực
N của nêm vuông góc với AB ( như hình vẽ bên )
+ Gia tốc của vật đối với sàn :
a = a + a 1 0
+ Phương trình chuyển động của vật :
Theo phương AB : mgsin = m(a + a .cos ) (1) 0
Theo phương vông góc với AB : N - mgcos = m a sin (2) 0
+ Phương trình chuyển động của nêm chịu thành phần nằm ngang của - N :
Chọn trục Ox trùng với hướng chuyển động của nêm - N sin = M a (3) 0 N sin
Từ (2) và (3) ta có : N mg cos .( m ) sin M N sin N + m.sin = mgcos M
N(M + m.sin 2 ) = M mgcos M .mg.cos N = 2 M . m sin
Thế vào phương trình (3) ta được : Nguyễn Anh Văn. - 10 - M mg . .cos sin . 2 .sin mg a = - M m = - .sin 2 0 M (
2 M msin 2 )
Thế vào phương trình (1) ta được : mg mgsin = m(a + (- .sin 2 ).cos ) (
2 M msin 2 ) 2 m g .sin 2 .soc
mgsin = m.a - (2M msin2) mg a = gsin + sin 2 .cos (
2 M msin 2 )
2Mg sin 2mg sin3 mg sin 2.cos = (
2 M msin 2 ) 2 2 Mg mg mg 2 sin 2 sin 1 ( cos ) 2 sin .cos a = (
2 M msin 2 )
(M m)g.sin a = 2 M msin
b. Lấy hệ tọa độ xOy gắn với sàn, O trùng với đỉnh C. Tính hoành độ của vật m
và của đỉnh C khi vật trượt tới đỉnh B. Quỹ đạo của vật là đường gì ?
Cho m = 0,1 kg, M = 2m, = 30 0 , = 1 m, g = 10 m/s 2 . Thay số ta tính được : mg a = - .sin 2 0 (
2 M msin 2 ) . 1 , 0 . 10 sin 600 = - ( 2 , 0 2 . 1 , 0 sin 2 300 ) = - 1,92 m/s 2 .
(M m)g.sin 0 a = = ( , 0 2 . 10 ). 1 , 0 sin 30 2 M msin 2 0 , 0 2 . 1 , 0 sin 30 20 a = m/s 2 . 3 Ta nhận thấy rằng :
a có hướng cố định , a có hướng cố định song song với 0 AB nên :
a = a + a cũng có hướng cố định hợp với phương ngang một góc 1 0 ( như hình vẽ )
Ta có : a 2 = a 2 + a 2 - 2.a.a .cos 1 0 0 2 20 20 = 2 0 ) 92 , 1 ( . 2 ). 92 , 1 .( cos30 3 3 a = 5,1 m/s 2 . 1 20 .sin300 sin sin a sin Mặt khác : sin = = 3 = 0,6536 a a a 1 , 5 1 1
= 40,8 0 Quỹ đạo vật m là đường thẳng AD nghiêng góc 40,8 0 so với phương ngang. Nguyễn Anh Văn. - 11 - AC
Xét tam giác ACD với AC = 0,5 m ta có : tan = OD AC 5 , 0 x = OD = = = 0,58 (m) 1 tan 0 tan 8 , 40
Vậy hoành độ của vật m là 0,58 (m)
Trong thời gian vật đi xuống thì nêm trượt sang trái và khi B trùng với D thì C
ở vị trí C / với hoành độ : x = - ( CB - OD ) = - ( AB.cos - OD) 2
= - ( 1.cos30 0 - 0,58) = - 0,29 (m)
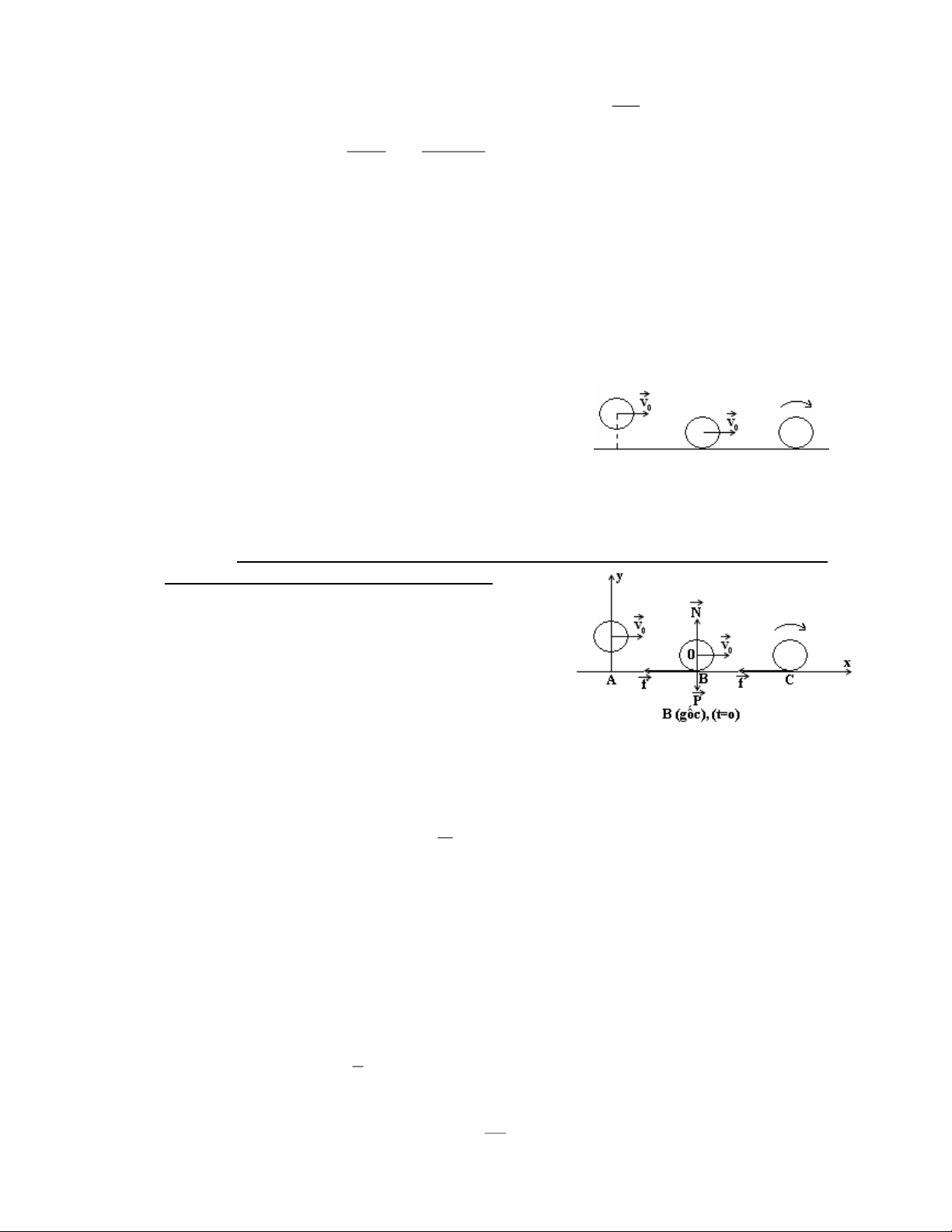
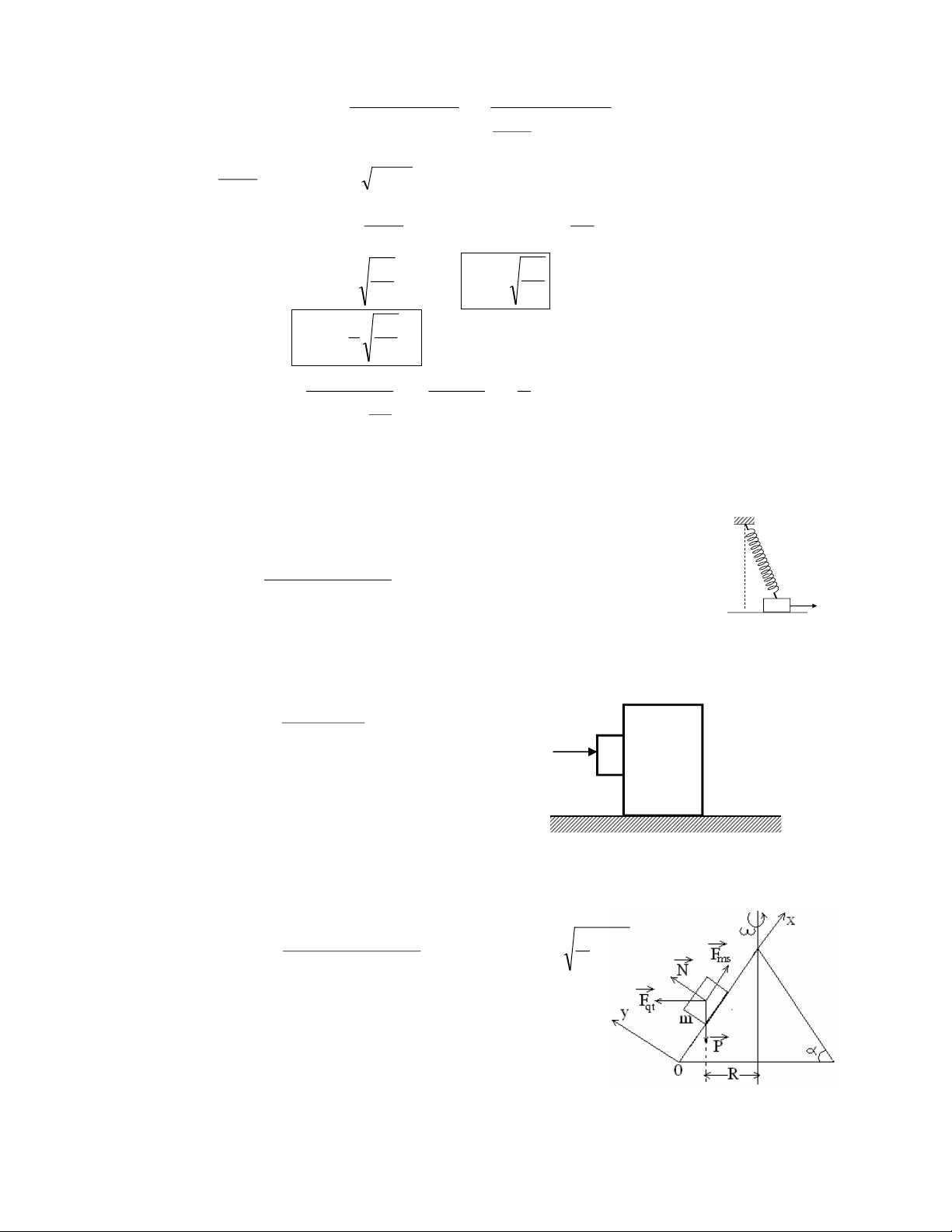
Câu 16: Một quả bóng bowling hình cầu, đồng chất có bán
kính R, khối lượng m, được ném theo phương ngang dọc
theo rãnh chạy nằm ngang ở trạng thái ban đầu không quay.
a. Tính đoạn đường bóng chuyển động dọc theo rãnh
trước khi nó bắt đầu lăn không trượt. Giả sử bóng không bị nảy lên. Cho biết :
Vận tốc ném là v có phương ngang. 0
Hệ số ma sát giữa bóng và rãnh là k.
Gia tốc trọng trường là g.
b. Áp dụng bằng số : v = 4 (m/s) ; k = 0,2 ; g = 10 (m/s 2 ) 0 Giải:
a. Tính đoạn đường bóng chuyển động dọc theo rãnh trước khi nó bắt đầu lăn
không trượt. Giả sử bóng không bị nảy lên. Gọi : + A là vị trí ném
+ B là vị trí chạm đường rãnh chạy
+ C là vị trí bóng lăn không trượt
Chọn vị trí B làm gốc, chiều dương trùng với Ox
Gốc thời gian lúc bóng chạm rãnh (t = 0 ) 0 Ta có :
- Phương trình động lực học cho gia tốc thẳng a :
P N f ma (1)
Chiếu phương trình (1) lên 0x : - f = ma a = - f (2) m
Chiếu phương tình (1) lên 0y : N = mg (3)
Với : f là lực ma sát trượt : f = k.N
- Phương trình động lực học cho gia tốc gốc : M = I. (4)
M là mômen của f đối với trục quay 0 : M = f.R (5)
I là mômen quán tính của bóng : I = 2 2 mR (6) 5
Thay (5) vào (4) ta được :
f.R = I. = fR (7) I Nguyễn Anh Văn. - 12 -
- Các phương trình động học : Chuyển động thẳng : v = v + at = v - f .t (8) 0 0 m
x = x + v t + 1 a.t 2 = = x + v t - f 2 t (9) 0 0 2 0 0 2m
- Chuyển động quay ( phương trình vận tốc góc ) fR t. = + .t (10) 0 0 I
* Trong giai đoạn bóng chuyển động vừa lăn vừa trượt, các phương trình (8) và
(10) hoàn toàn độc lập với nhau. Khi bóng bắt đầu lăn không trượt thì các đại lượng v
và liên hệ với nhau bằng công thức : v = .R (11)
* Thay (8) và (10) vào phương trình (11) ta được : fR2 v - f .t / = .R + .t / 0 m 0 I
* Tại thời điểm t = 0 thì = 0, giải phương trình trên ta được : 0 v t / = 0 (12) f fR2 m I
* Tại thời điểm t = t / bóng chuyển động lăn không trượt, thay (12)
vào (9) với x = 0 ta được : 0 2 2 f v x = v0 - 0 (13) 1 R2 2 2m f fR f m I m I v 12 2 Thay f = kmg ; I = 2 2
mR vào (13) ta được : x = 0 5 k . 49 .g
Đoạn đường bóng chuyển động dọc theo rãnh trước khi nó bắt đầu lăn không v 12 2 trượt : x = 0 k . 49 .g
b. Áp dụng bằng số : v = 4 (m/s) ; k = 0,2 ; g = 10 (m/s 2 ) 0 v 12 2 4 . 12 2 x = 0 = 96 , 1 (m) k . 49 .g , 0 . 49 10 . 2
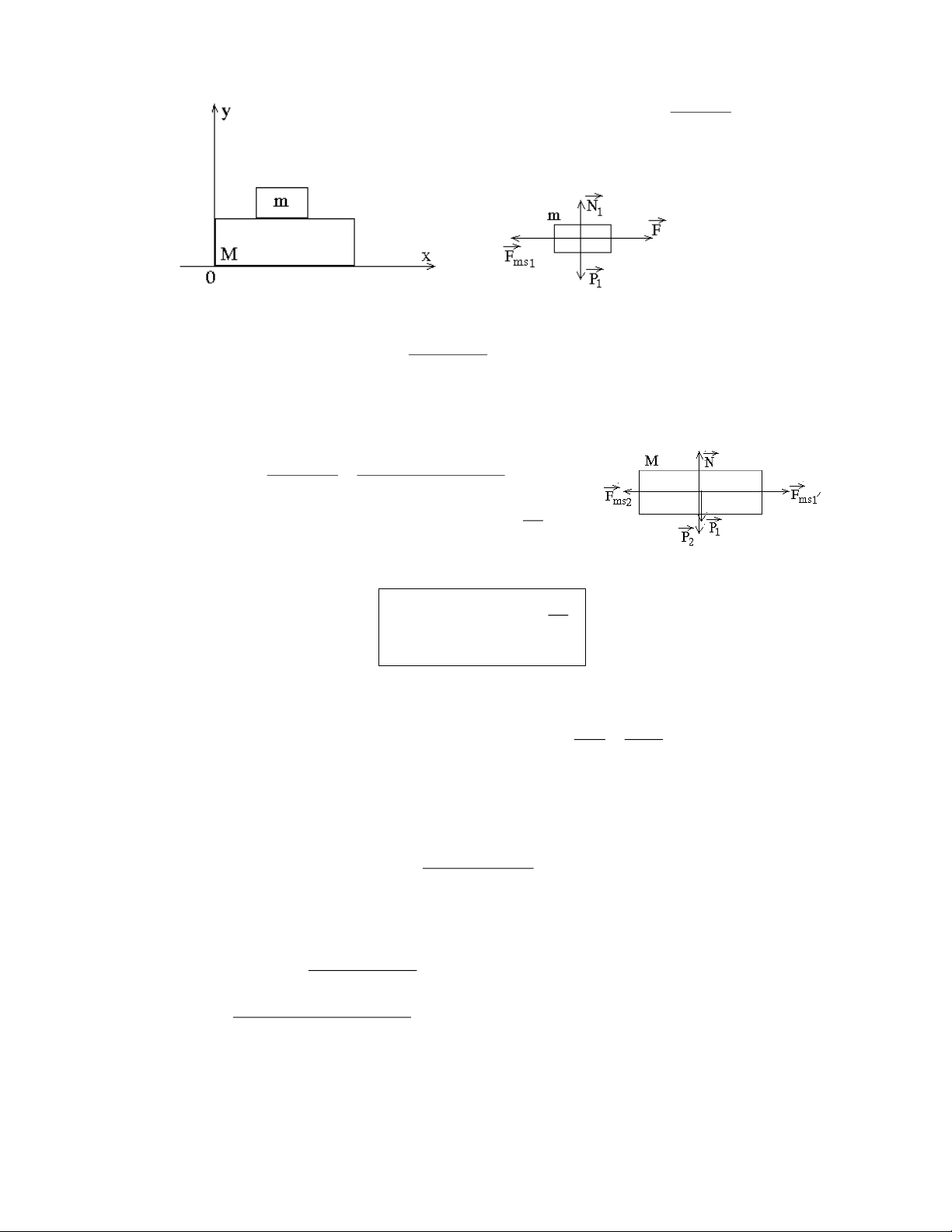
Câu 17: Cho c¬ hÖ nh- h×nh vÏ. HÖ sè ma s¸t gi÷a M vµ m lµ , 1
gi÷a M vµ sµn lµ . T×m ®é lín cña lùc F n»m ngang: 2
a. §Æt lªn m ®Ó m tr-ît trªn M.
b. §Æt lªn M ®Ó M tr-ît khái m. Gi¶i:
a. Khi t¸c dông lùc F lªn m.
Ph-¬ng tr×nh chuyÓn ®éng cña m tr-ît trªn M: Nguyễn Anh Văn. - 13 - F F ma ms1 1 F F a ms1 N P 1 1 1 m
Ph-¬ng tr×nh chuyÓn ®éng cña M: F' F Ma ms1 ms2 2 F' F a ms1 ms2
N P P (m M )g 2 M 1 2 §Ó m tr-ît trªn M th×:
a a ; F ' = F ; F = (m+M)g. 1 2 ms1 ms1= mg 1 ms2 2 hay: F mg
mg (m M )g 1 1 2 m M m
F ( )(m M ) g 1 2 M
Víi ®iÒu kiÖn: a 0 F mg. 1 1
VËy ®¸p sè cña bµi to¸n nµy: m F 1
2 m M g M
F mg 1
b. Khi t¸c dông lùc F lªn M :
Ph-¬ng tr×nh chuyÓn ®éng cña m: F ma F N ms1 1 a ms1 1 1 g
N P mg 1 m m 1 1 1
Ph-¬ng tr×nh chuyÓn ®éng cña vËt M: F F F Ma ms1 ms2 2
N N N P P (m M )g 1 2 1 2 F F F a ms1 ms2 2 M F F mg
§Ó M tr-ît khái m th×: a a (chó ý: ms1 ms ' 1 1 ) 2 1 F ms2
2 M mg
F F' F hay ms1 ms 2 g M 1
F mg (m M )g 1 2 g M 1
Cuèi cïng: F ( )(m M )g ) 1 ( 1 2 §iÒu kiÖn a 0 2
hay F mg (m M )g ( ) 2 1 2
§iÒu kiÖn (2) bao hµm trong ®iÒu kiÖn (1). Nguyễn Anh Văn. - 14 -
Do vËy kÕt qu¶ bµi to¸n :
F ( )(m M )g . 1 2
Câu 18: Mét vËt nhá ®ang n»m yªn trªn mÆt ph¼ng n»m ngang nh¼n, lóc t 0 vËt ®ã
chÞu t¸ dông cña mét lùc phô thuéc thêi gian F t ( lµ h»ng sè). Lùc hîp víi mÆt nghang gãc kh«ng ®æi .
a. TÝnh vËn tèc cña vËt lóc rêi mÆt ph¼ng ngang.
b. Qu¶ng ®-êng vËt ®i ®-îc trong kho¶ng thêi gian ®ã. Gi¶i:
a. XÐt c¸c lùc t¸c dông vµo vËt:
F p N ma ChiÕu lªn 0x:
F cos ma (1) ChiÕu lªn 0y:
N F sin p 0 (2)
N p F sin mg t.sin
VËt rêi khái mÆt ngang khi : N 0 Hay
mg t.sin 0 mg
Thêi gian ®Ó nã rêi khái mÆt ph¼ng ngang: t 0 sin
Tõ (1): F cos ma Hay: dv
t.cos m dt .cos dv t. dt . m v t0 cos 1 t. 2.cos dv t dt . v . 0 m 2 m 0 0 2 1 mg .cos v . 2 2 .sin a. Ph-¬ng tr×nh vËn tèc : 1 cos 2 v . .t 2 m
Qu¶ng ®-êng vËt ®i ®-îc tõ 0 t : 0 t0 1 cos t 2 1 3.cos S ds . 0 t dt 2 m 6 m 0 mA 1 sin S cos 6 m 1 2 3 m S g cos . 6 2.sin3
Câu 19: Cho c¬ hÖ nh- h×nh vÏ. Nªm cã khèi l-îng M, gãc gi÷a mÆt nªm vµ ph-¬ng
ngang lµ . CÇn ph¶i kÐo d©y theo ph-¬ng ngang mét lùc F lµ bao nhiªu ®Ó vËt cã
khèi l-îng m chuyÓn ®éng lªn trªn theo
mÆt nªm ? T×m gia tèc cña m vµ M ®èi víi mÆt ®Êt? Nguyễn Anh Văn. - 15 -
Bá qua mäi ma s¸t, khèi l-îng d©y nèi vµ rßng räc. Gi¶i:
Gäi gia tèc cña nªm vµ vËt ®èi víi mÆt ®Êt lÇn
l-ît lµ lµ a vµ a . 1 2
Ph-¬ng tr×nh ®éng lùc häc cho m:
F P N ma 2 2 chiÕu lªn ox:
F cos N sin ma ) 1 ( 2 x chiÕu lªn oy:
F sin N sin mg ma ( ) 2 2 y
Nªm chÞu t¸c dông cña P , N , hai lùc F vµ 1 1
F' ®Ì lªn rßng räc vµ lùc nÐn N' cã ®é lín b»ng N.
Ph-¬ng tr×nh chuyÓn ®éng cña M:
P N N 'F F' a M 1 1 1 ChiÕu lªn ox:
N sin F F cos Ma ) 3 ( 1
Gäi a lµ gia tèc cña m ®èi víi nªm M. 21
Theo c«ng thøc céng gia tèc:
a a a (4) 2 21 1
ChiÕu (4) lªn 0x: a a a cos 2 x 1 21
0y: a a sin 2 y 21 Tõ ®ã suy ra:
a (a a ) tan ) 5 ( 2 y 2 x 1
Tõ (1), (2), (3) vµ(5) suy ra: F 1
( cos ) mg sin cos a (6) 1 2 M msin
F(m sin 2 M cos ) Mmg sin cos a 2 x
m(M m sin 2 )
F cosM m 1( cos) mg(M m)sin costan a 2 y
m(M m sin 2 )
§Ó m dÞch chuyÓn lªn trªn nªm th×: a 0 (I ) 2y N 0 (II) Gi¶i (I):
a 0 F cosM m 1
( cos ) mg(M m)sin cos 0 2 y
mg(M m) sin F (7) M m 1 ( cos ) Gi¶i (II):
Thay (6) vµo (3) rót ra N vµ tõ ®iÒu kiÖn N > 0 ta suy ra: cos Mg F ) 8 ( 1 ( cos )sin Nguyễn Anh Văn. - 16 -
Tõ (7) vµ (8) ta suy ra ®Ó m leo lªn ®-îc mÆt nªm M th× lùc F ph¶i tho¶ m·n ®iÒu kiÖn
mg(M m)sin Mg cos F M m 1 ( cos ) 1 ( cos )sin
Lóc ®ã gia tèc cña nªm ®èi víi mÆt ®Êt lµ a1 ë (6). Gia tèc cña vËt ®èi víi mÆt ®Êt sÏ lµ : a a2 2
2x a 2 y . 2
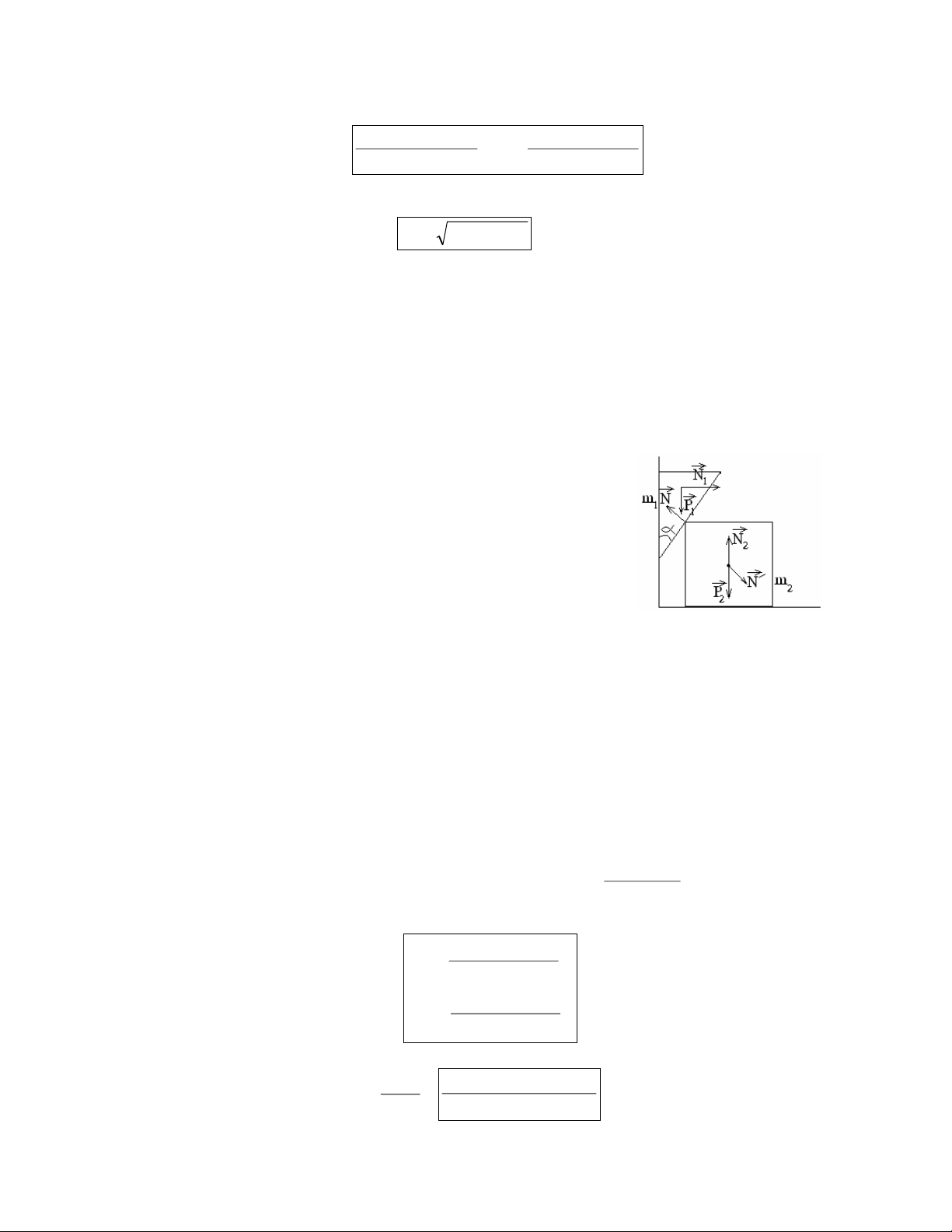
Câu 20: Khèi l¨ng trô tam gi¸c cã khèi l-îng m1, víi gãc nh- h×nh vÏ cã thÓ
tr-ît theo ®-êng th¼ng ®øng vµ tùa lªn khèi lËp ph-¬ng khèi l-îng m2 cßn khèi lËp
ph-¬ng cã thÓ tr-ît trªn mÆt ph¼ng ngang. Bá qua mäi ma s¸t.
a. TÝnh gia tèc gi÷a mçi khèi vµ ¸p lùc gi÷a hai khèi ?
b. X¸c ®Þnh sao cho gia tốc vật 2 lµ lín nhÊt. TÝnh gi¸ trÞ gia tèc cña mçi khèi trong tr-êng hîp ®ã ? Gi¶i: a. VËt 1:
C¸c lùc t¸c dông vµo m1: P , ph¶n lùc N do bê t-êng t¸c dông lªn m 1 1 1, ph¶n lùc do m2 t¸c dông N . Theo ®Þnh luËt II Newton:
P N N m a 1 1 1 1 ChiÕu lªn ox:
N cos N 0 1 ChiÕu lªn oy:
P N sin m a (1) 1 1 1
VËt 2: Cã 3 lùc t¸c dông lªn m2: P , ph¶n lùc N do sµn t¸c dông lªn khèi lËp 2 2
ph-¬ng, ph¶n lùc N' do m1 t¸c dông lªn khèi lËp ph-¬ng.
Theo ®Þnh luËt II Newton:
P N N ' m a 1 2 2 2 chiÕu lªn ox:
N cos m a (do N' N ) (2) 2 2
MÆt kh¸c khi m2 dêi ®-îc mét ®o¹n x th× m1 dêi ®-îc mét ®o¹n y vµ ta lu«n
cã: x y tan
Hay: a a tan 2 1 Tõ (1) vµ (2) suy ra:
N sin m g m a 1 1 1 m g a 1 1 tan (3) N cos m a m a 2 2 2 2
Thay a a tan vµo (3) ta suy ra: 2 1 m a 1 g 1 m m 2 tan 1 2 m tan a 1 g 2 m m 2 tan 1 2 ¸p lùc gi÷a m1 vµ m2: m a m m tan N 2 2 1 2 cos
m m tan2 1 2 cos b. Ta cã : Nguyễn Anh Văn. - 17 - m tan m a 1 g 1 g 2
m m tan 2 m 1 2 1 m tan tan 2 m Do 1
m tan 2 m m 2 1 2 tan m m DÊu b»ng x¶y ra khi : 1 2 1
m tan tan 2 tan m2 m m 1 tan 1 arctan m m 2 2 1 m Lóc ®ã : a 1 .g 2 min 2 m2 m m g 1 a . 1 g g 1 m 1 m m 2 m m . 1 1 1 2 m2
Câu 21: Một vật có khối lượng m nằm trên mặt bàn nằm ngang, gắn vào đầu một lò
xo thẳng đứng có độ cứng K. Ban đầu lò xo không biến dạng và chiều dài l0. Bàn
chuyển động đều theo phương ngang, lò xo nghiêng góc so với phương thẳng đứng.
Tìm hệ số ma sát giữa vật và bàn.
Áp dụng: K = 10 N/m, l0 = 0,1 m, 0 60 , m = 0,5 kg. Kl 1 ( cos).tan Đáp số: 0 , 0,2 . P Kl 1 ( cos ) 0 v
Câu 22: Hai vật có khối lượng lần lượt là m = 16kg, M = 88kg, không gắn với nhau,
hệ số ma sát tĩnh giữa chúng là 38 , 0
, còn mặt ở dưới M không có ma sát. Hỏi độ
lớn tối thiểu của lực nằm ngang F phải bằng bao nhiêu để giữ m đứng yên đối với M.
mgM m Đáp số: F . min M F m M
Câu 23: Trªn mét mÆt nãn trßn xoay víi gãc nghiªng cã thÓ quay quanh trôc th¼ng
®øng. Mét vËt cã khèi l-îng m ®Æt trªn mÆt nãn c¸ch trôc quay mét kho¶ng R. MÆt
nãn quay ®Òu víi vËn tèc gãc . TÝnh gi¸ trÞ nhá nhÊt cña hÖ sè ma s¸t tr-ît ( ) gi÷a
vËt vµ mÆt nãn ®Ó vËt vÉn ®øng yªn trªn mÆt nãn.
g sin 2 R cos g Đáp số: víi ®iÒu kiÖn cot . min
g cos 2 R sin R Hướng dẫn:
§iÒu kiÖn ®Ó m ®øng yªn trªn mÆt nãn: N 0 F N ms
Câu 24: Hai vật A, B có trọng lượng tương ứng bằng P1, P2 được nối với nhau bằng lò
xo thẳng đứng và đặt trên mặt phẳng ngang cố định. Vật A dao động theo phương Nguyễn Anh Văn. - 18 -
thẳng đứng quanh tâm O theo quy luật z a sin kt , với a, k = const > 0. Bỏ qua trọng A
lượng của lò xo, tìm áp lực của vật B lên mặt ngang. Tần số k phải thỏa mãn điều kiện
gì để vật B không bị nảy lên khỏi mặt phẳng ngang. Giải:
Áp dụng định luật II Newton ta có:
Ma P P N (1) zc 1 2
trong đó zc là tọa độ khối tâm của hệ, được xác định theo công thức: P P A Mz 1 z 2 z với z c A B g g B = const.
Đạo hàm hai lần biểu thức này ta tìm được gia tốc khối tâm: P ak 2 Ma 1 sin kt . zc g
Thay biểu thức này vào (1) ta được: B P ak 2
N P P 1 sin kt 1 2 g P ak 2 N P P 1 min 1 2 g
Để vật B không bị nảy lên khỏi mặt phẳng ngang, tần số k phải thỏa mãn điều kiện: 2 P ak
gP P 1 2 1 N P P 0 hay k min 1 2 g aP1
Câu 25 :Một vật A trọng lượng P được buộc vào đầu một sợi dây không giãn, không
trọng lượng, dây vắt qua ròng rọc cố định O ; đầu kia của dây cuốn vào khối trụ có
trọng lượng Q, bán kính R. Vật A có thể trượt trên mặt phẳng ngang, hệ số ma sát giữa
vật A và mặt phẳng ngang là f. Tìm gia tốc vật A và gia tốc tâm C của khối trụ khi hệ
chuyển động, bỏ qua khối lượng ròng rọc. Q 3 fP
Q 2 f P
Đáp số : a g;a g. A Q 3P C Q 3P Nếu Q f
thì vật sẽ chuyển động với gia tốc a 3P A. Q Nếu f
thì vật A sẽ đứng yên, khối trụ chuyển động với gia tốc a 3P C = (2/3)g. A O C
Câu 26 : quấn hai sợi dây mềm không dãn vào vật khối trụ tròn xoay đồng chất một
cách đối xứng qua mặt phẳng trung bình song song với hai đáy. Khối trụ khối lượng m
đặt trên mặt phẳng nghiêng góc đối với mặt phẳng nằm ngang sao cho đường sinh
của nó vuông góc với đường dốc chính, rồi buộc hai đầu dây tự do vào hai điểm cố
định. Hai sợi dây song song với đường dốc chính AB, hệ số ma sát trượt giữa mặt trụ Nguyễn Anh Văn. - 19 -
và mặt nghiêng là . Khối trụ trượt xuống không vận tốc đầu. tìm quy luật chuyển
động của trục khối trụ khi dây quấn mở ra chưa hết và lực căng mỗi dây. 2
a gsin 2 cos Đáp số : 3 1
T mgsin cos 6 α
Câu 27 : Hai trụ tròn xoay đồng chất A và B có trọng lượng lần lượt là P1 và P2 và bán
kính lần lượt là R1 và R2 . Quấn hai sợi dây mềm vào hai đầu của hai khối trụ một cách
đối xứng đối với mặt phẳng trung bình song song với đáy của hai khối trụ. Khối trụ A
quay quanh một trục cố định trùng với đường trục tâm của các khối trụ. Khối trụ B rơi
tự do không vận tốc đầu, làm dây quấn nhả ra và quay khối trụ A. Bỏ qua ma sát và
các lực cản. Xác định sức căng của mỗi dây quấn, vận tốc góc của hai khối trụ,
phương trình chuyển động của khối trụ B. P P 2gP A Đáp số : 1 2 T ; 2 ; 23P 2P 1 R 3 2 1 P1 2 t P 1 2 2gP
gP P 1 2 1 ; 2 s t 2 R 3 2 3P 2P 2 P1 2 t P 1 2 B
Câu 28 : Cho cơ hệ như hình vẽ, quả nặng A có khối lượng m, ròng rọc B có khối
lượng M có mo men quán tính là I đối với trục quay và các bán kính là R và 2R. khối
lượng không đáng kể. Tìm gia tốc của quả nặng sau khi được buông rơi. Giải :
Khi quả nặng A đi xuống, ròng rọc B quay làm dây trên quấn vào ròng rọc, B đi lên.
Vì không có sự trượt nên : a 2R ; a R 12 23
a a a a a a R a 13 12 23 13 12 23 23
Các phương trình chuyển động : T2
ma mg T 13 1
Ma T T Mg 23 2 1 B
I T 2R T R 1 2
Giải các phương trình trên ta được : T 1
m M g Mg a 13 I A m M 2 R
Nếu M = m thì không có chuyển động khi buông A ra. mg
Câu 29 : Trong hình vẽ bên , thanh mãnh đồng chất AB chiều dài d, khối lượng M
nằm trên đĩa ED quay quanh trục thẳng đứng với tốc độ góc không đổi. Trục của Ab
trùng với phương của bán kính đĩa, trọng vật P có khối lượng m được treo bằng một
đoạn chỉ vắt qua ròng rọc rồi buộc vào đầu A của thanh, phương thẳng đứng của sợi Nguyễn Anh Văn. - 20 -



