Chuyên đề hàm số bậc hai Toán 10 Kết Nối Tri Thức Với Cuộc Sống

Tài liệu gồm 59 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tổng hợp tóm tắt lý thuyết, bài tập tự luận và bài tập trắc nghiệm chuyên đề Hàm Số Bậc Hai trong chương trình môn Toán 10 Kết Nối Tri Thức Với Cuộc Sống, có đáp án và lời giải chi tiết.

105 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT)

Môn: Toán 10

Thông tin:

59 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chủ đề 2: HÀM SỐ BẬC HAI
I. TÓM TẮT LÝ THUYẾT
1) Hàm số bậc hai có dạng
2
; ; ; ; 0 .y ax bx c a b c a
2) Khảo sát sự biến thiên của hàm số bậc hai
Xét hàm số
2
; ; ; ; 0 .y ax bx c a b c a
+) TXĐ:
.D
+) Đồ thị hàm số bậc hai có dạng parabol
P
với bề lõm hướng lên trên với
0,a
bề lõm hướng
xuống dưới với
0.a
- Trục đối xứng của
P
là
.
2
b
x
a

- Đỉnh của
P
là
;.
24
b
I
aa




0a
0a
x
y
-
Δ
__
4a
2a
__
-b
O
1
x
y
-
Δ
__
4a
2a
__
-b
O
1
- Để vẽ đường parabol
2
y ax bx c
ta tiến hành theo các bước sau:
1. Xác định toạ độ đỉnh
;
24




b
I
aa
;
2. Vẽ trục đối xứng
2

b
x
a
;
3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài
điểm đặc biệt trên parabol;
4. Vẽ parabol.
+) Sự biến thiên của hàm số
0a
0a
Bảng biến thiên:
x

2
b
a

y

4a

+) Hàm số đồng biến (tăng) trên
;.
2
b
a




+) Hàm số nghịch biến (giảm) trên
;.
2
b
a




Bảng biến thiên:
x

2
b
a

y

4a

+) Hàm số đồng biến (tăng) trên
;.
2
b
a




+) Hàm số nghịch biến (giảm) trên
;.
2
b
a




Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Nhận xét:
+) Khi
0:a
Hàm số có giá trị nhỏ nhất bằng
4a
đạt được tại
.
2
b
x
a

+) Khi
0:a
Hàm số có giá trị lớn nhất bằng
4a
đạt được tại
.
2
b
x
a

II. BÀI TẬP TỰ LUẬN
Câu 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a)
2
3 2;y x x
b)
2
2 5 2;y x x
c)
2
2 1;y x x
d)
2
2 3;y x x
e)
2
2;yx
f)
2
2 1.y x x
Câu 2: Xác định hàm số bậc hai
2
2,y x bx c
biết đồ thị của nó:
a) Có trục đối xứng là
1x
và cắt trục tung tại điểm có tung độ là 4.
b) Có đỉnh là
1; 2I 
.
c) Có hoành độ đỉnh là 2 và đi qua điểm
1; 2A
.
Câu 3: Xác định parabol
2
: ; ; ; , 0 .P y ax bx c a b c a
Biết
P
đi qua các điểm
1;6 , 3;2AB
và
2;0 .C
Câu 4: Xác địnhparabol
2
: ; ; ; , 0 .P y ax bx c a b c a
Biết
P
đi qua điểm
1;8A
và có
đỉnh
2; 1 .I
Câu 5: Xác định hàm số
2
0y ax bx c a
biết hàm số đạt giá trị nhỏ nhất bằng
4
tại
2x
và
đồ thị hàm số đi qua điểm
0;6A
.
Câu 6: Xác định parapol
P
:
2
2y x bx c
, biết
P
:
a) Có trục đối xứng
1x
vá cắt trục tung tại điểm
0;4
;
b) Có đỉnh
1; 2I 
;
c) Đi qua hai điểm
0; 1A
và
4;0B
;
d) Có hoành độ đỉnh là 2 và đi qua điểm
1; 2M
.
Câu 7: Xác định parapol
P
:
2
4y ax x c
, biết
P
:
a) Đi qua hai điểm
1; 2A
và
2;3B
;
b) Có đỉnh
2; 1I 
;
c) Có hoành độ đỉnh là
3
và đi qua điểm
2;1P
;
d) Có trục đối xứng là đường thẳng
2x
vá cắt trục hoành tại điểm
3;0M
.
Câu 8: Tìm parapol
P
:
2
2y ax bx
, biết
P
:
a) Đi qua hai điểm
1;5M
và
2;8N
;
b) Đi qua điểm
3; 4A
và có trục đối xứng
3
4
x 
;
c) Có đỉnh
2; 2I
;
d) Đi qua điểm
1;6B
, đỉnh có tung độ
1
4
Câu 9: Xác định parapol
P
:
2
y ax bx c
, biết
P
:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
a) Đi qua ba điểm
0; 1 , 1; 1 , 1;1A B C
;
b) Đi qua điểm
3;0D
và có đỉnh là
1;4I
;
c) Đi qua
8;0A
và có đỉnh
6;12I
;
d) Đạt GTNN bằng 4 tại
2x 
và đi qua
0;6A
;
Câu 10: Cho hàm số
2
23y x x
có đồ thị
.P
a) Lập bảng biến thiên và vẽ đồ thị
.P
b) Dựa vào đồ thị
,P
biện luận số nghiệm của phương trình
2
2 2 0.x x m
c) Tìm
m
để phương trình
2
2 3 1x x m
có 4 nghiệm phân biệt.
d) Tìm
m
để phương trình
2
2 2 0x x m
có 4 nghiệm phân biệt.
e) Tìm
m
để phương trình
2
10f x m f x m


có 8 nghiệm phân biệt.
Câu 11: Tìm
m
để parabol
2
2y x x
cắt đường thẳng
ym
tại
2
điểm phân biệt.
Câu 12: Cho parabol
2
: 2 1P y x x m
. Tìm tất cả các giá trị thực của
m
để parabol cắt
Ox
tại
hai điểm phân biệt có hoành độ dương.
Câu 13: Tìm tất cả các giá trị thực của tham số
m
sao cho parabol
2
:4P y x x m
cắt
Ox
tại hai
điểm phân biệt
, AB
thỏa mãn
3.OA OB
Câu 14: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
:d y mx
cắt đồ thị hàm số
32
: 6 9P y x x x
tại ba điểm phân biệt.
Câu 15: Cho parabol
2
: 4 3P y x x
và đường thẳng
:3d y mx
. Tìm giá trị thực của tham số
m
để
d
cắt
P
tại hai điểm phân biệt
,AB
có hoành độ
12
,xx
thỏa mãn
33
12
8xx
.
Câu 16: Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
5 7 2 0x x m
có nghiệm
thuộc đoạn
1;5
.
III. BÀI TẬP TRẮC NGHIỆM
Câu 17: Trong các hàm số sau hàm số nào là hàm số bậc hai?
A.
2
2 3 5y x x
B.
3
2 3 5xx
y
x

. C.
23
2 3 5y x x
. D.
32yx
.
Câu 18: Điểm nào sau đây không thuộc đồ thị hàm số
2
2yx
?
A.
2;2P
. B.
3;3 .Q
C.
2;2 .N
D.
1; 1 .M
Câu 19: Đồ thị hàm số
2
y x x
đi qua điểm nào dưới đây?
A.
2;6N
. B.
1;1M
. C.
2;3P
. D.
1;1Q
.
Câu 20: Cho hàm số
2
3 4 3y x x
có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương
trình:
A.
2
3
x
. B.
2
3
x 
. C.
4
3
x
. D.
4
3
x 
Câu 21: Đỉnh của parabol
2
45 y x x
có toạ độ là
A.
0;2
. B.
1;2
. C.
2;0
. D.
2;1
.
Câu 22: Tìm
m
để parabol
2
( ): 2 3P y mx x
có trục đối xứng là đường thẳng
2x
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A.
2m
. B.
1m 
. C.
1m
. D.
1
2
m
.
Câu 23: Hàm số nào dưới đây có đồ thị nhận đường thẳng
2x 
làm trục đối xứng?
A.
2
2 4 3y x x
. B.
2
2 4 3y x x
. C.
2
43y x x
. D.
2
43y x x
.
Câu 24: Hàm số nào có đồ thị là đường Parabol có đỉnh là
1;3 ?I
A.
2
2 4 3y x x
. B.
2
2 2 1y x x
. C.
2
2 4 5y x x
. D.
2
22y x x
.
Câu 25: Giá trị nhỏ nhất của hàm số
2
45y x x
là
A.
min
0y
. B.
min
2y 
. C.
min
2y
. D.
min
1y
.
Câu 26: Hàm số
2
5 6 7 y x x
đạt giá trị nhỏ nhất khi
A.
26
.
5
x
B.
3
5
x
. C.
3
5
x
. D.
6
5
x
.
Câu 27: Giá trị lớn nhất của hàm số
2
24y x x
bằng
A.
5.
B.
5
. C.
1
. D.
1
.
Câu 28: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
2
42y x x
trên đoạn
0;3
.
Tính giá trị biểu thức
Mm
.
A.
1
. B.
4
. C.
0
. D.
1
.
Câu 29: Tìm giá trị nhỏ nhất của hàm số
22
5 4 1y x x
.
A.
5
. B.
5
. C.
1
. D.
1
.
Câu 30: Cho hàm số
2
y ax bx c
,với
0a
. Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng
;
2
b
a




.
B. Hàm số nghịch biến trên khoảng
;
2
b
a




.
C. Hàm số nghịch biến trên khoảng
;
2
b
a




.
D. Đồ thị hàm số có trục đối xứng là đường thẳng
2
b
x
a

Câu 31: Cho hàm số
2
y ax bx c
có đồ thị là parabol trong hình sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;
. B.
1; 
. C.
;1
. D.
;2
.
Câu 32: Cho hàm số bậc hai có bảng biến thiên như sau:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;
. B.
;2
. C.
3
. D.
1;
.
Câu 33: Cho hàm số
2
2 4 1y x x
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
;2
. B. Hàm số nghịch biến trên khoảng
; 
.
C. Hàm số đồng biến trên khoảng
2;
. D. Hàm số nghịch biến trên khoảng
2;
.
Câu 34: Cho hàm số
2
35y x x
. Hàm số đã cho đồng biến trên khoảng nào?
A.
;3
. B.
3
;
2



. C.
3
;
2




. D.
3
;
2




.
Câu 35: Hàm số nào sau đây đồng biến trên ?
A.
2
1yx
. B.
2
y x x
. C.
1yx
. D.
1yx
.
Câu 36: Cho hàm số
2
2y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên khoảng
1; .
B. Hàm số đã cho nghịch biến trên khoảng
1; . 
C. Hàm số đã cho đồng biến trên khoảng
1; . 
D. Hàm số đã cho nghịch biến trên khoảng
1; .
Câu 37: Cho hàm số
2
2018 2020.f x x x
Khẳng định nào sau đây đúng?
A.
2019 2018
11
22
ff
. B.
2019 2018
11
22
ff
.
C.
1009 1008
22ff
. D.
1008 1007
22ff
.
Câu 38: Tìm tất cả giá trị tham số
m
để hàm số
2
12y x m x m
đồng biến trên
1; 
.
A.
3m 
. B.
3m 
. C.
3m 
. D.
3m 
.
Câu 39: Tìm tất cả các giá trị của tham số
m
để hàm số
2
2 1 2y x m x m
nghịch biến trên
khoảng
1;2
.
A.
1m
. B.
1m
. C.
0m
. D.
0m
.
Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
( ) 2 2 2021 y f x m x mx m
nghịch biến trên khoảng
;3 ?
A.
2.
B.
1.
C.
3.
D.
4.
Câu 41: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2 1 3y x m x
nghịch biến trên
2; ?
A.
3
. B.
6
. C.
5
. D.
4
.
Câu 42: Cho hàm số bậc hai
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Tìm tất cả các giá trị của
x
để
0.y
A.
;0
. B.
3; 
. C.
0;3
. D.
0;3
.
Câu 43: Hàm số
2 2 2
2 2 2 1f x x m m x m m
. Mệnh đề nào sau đây sai?
A. Hàm số đạt giá trị lớn nhất trên đoạn
1;0
bằng
0f
.
B. Hàm số nghịch biến trên khoảng
0;
.
C. Hàm số đặt giá trị lớn nhất trên đoạn
1;0
bằng
1f
.
D. Hàm số nghịch biến trên khoảng
;0
.
Câu 44: Hàm số nào dưới đây có bảng biến thiên như sau?
A.
2
1.yx
B.
2
3 1.y x x
C.
2
1.y x x
D.
2
3 1.yx
Câu 45: Bảng biến thiên dưới đây là của hàm số nào?
A.
2
5
.
4
y x x
B.
2
3
.
2
y x x
C.
2
3
.
2
y x x
D.
2
2 1. y x x
Câu 46: Bảng biến thiên của hàm số
2
21y x x
là
A. . B. .
C. . D. .
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 47: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào?
A.
2
2.y x x
. B.
2
2.y x x
C.
2
2 1.y x x
D.
2
2.y x x
Câu 48: Đồ thị sau là đồ thị của hàm số nào?
A.
2
23y x x
. B.
2
21y x x
. C.
2
22y x x
. D.
2
21y x x
.
Câu 49: Hình bên là đồ thị của hàm số nào sau đây?
A.
2
23y x x
. B.
2
23y x x
. C.
2
23y x x
. D.
2
23y x x
.
Câu 50: Hàm số
2
4 3 1y x x
có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào?
A. . B. . C. . D. .
Câu 51: Đồ thị hàm số
2
2y x x
thể hiện bởi hình vẽ nào dưới đây?
A.
x
y
2
-1
O
1
B.
x
y
2
O
1
C.
x
y
1
2
-1
O
1
D.
x
y
-1
2
-1
O
1
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 52: Cho hàm số
2
()y f x x bx c
có đồ thị như hình vẽ bên dưới:
Nhận định nào sau đây đúng về dấu hệ số
b
và
?c
A.
0b
;
0c
. B.
0b
;
0c
. C.
0b
;
0c
. D.
0b
;
0c
.
Câu 53: Đồ thị hàm số:
2
y ax bx c
như hình vẽ bên dưới:
Trong các hệ số
,,abc
có bao nhiêu giá trị dương?
A.
1
.
B.
0
. C.
2
. D.
3
.
Câu 54: Cho hàm số
2
y f x ax bx c
có bảng biến thiên như sau :
Khẳng định nào sau đây sai ?
A.
0a
. B.
0b
. C.
0c
. D. TXĐ
D
.
Câu 55: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên dưới:
Khẳng định nào dưới đây đúng?
A.
0, 0, 0abc
. B.
0, 0, 0a b c
.
C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 56: Cho hàm số
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Tích
abc
bằng
A.
12
B.
12.
C.
3.
D.
0.
Câu 57: Cho hàm số
2
f x ax bx c
có đồ thị như hình bên dưới:
Giá trị của biểu thức:
2T a b c
bằng
A.
1.
B.
1.
C.
0.
D.
2.
Câu 58: Cho hàm số
2
y f x ax bx c
có đồ thị như hình vẽ bên dưới:
Giá trị của biểu thức
42T a b c
bằng
A.
8
. B.
6
. C.
3
. D.
4
.
Câu 59: Cho parabol
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Khẳng định nào dưới đây đúng?
A.
0; 0; 0a b c
. B.
0; 0; 0a b c
. C.
0; 0; 0a b c
. D.
0; 0; 0a b c
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 60: Tọa độ giao điểm của đường thẳng
:4d y x
và parabol
2
7 12y x x
là
A.
(2;2)
và
(4;0)
. B.
(2;2)
và
(4;8)
.
C.
(2; 2)
và
(4;0)
. D.
( 2;6)
và
(4;8)
.
Câu 61: Hai đồ thị hàm số
2
23y x x
và
21yx
có bao nhiêu điểm chung?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 62: Toạ độ giao điểm của đồ thị hàm số
2
2y x x
với trục tung là
A.
0; 2 .
B.
2;0 .
C.
0;2 .
D.
1;0
.
Câu 63: Số giao điểm của Parabol
2
: 4 4P y x x
với trục hoành là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 64: Đồ thị hàm số nào sau đây tiếp xúc trục hoành?
A.
2
1
2y x x
. B.
2
2
32y x x
. C.
2
3
2 2 1y x x
. D.
2
4
44y x x
.
Câu 65: Toạ độ giao điểm của parabol
2
1
( ): 2 2 3P y x x
với parabol
2
2
( ): 6P y x x
là
A.
1;7
và
3;27
. B.
7;1
và
27;3
. C.
1;3
và
3;15
. D.
3; 1
và
15; 3
.
Câu 66: Cho hàm số
2
f x ax bx c
có đồ thị như hình vẽ bên dưới:
Phương trình
2fx
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 67: Cho hàm số
2
f x ax bx c
có đồ thị như hình vẽ bên dưới:
Phương trình
2fx
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 68: Cho hàm số
2
0y f x ax bx c a
có bảng biến thiên như sau:
Tìm tất cả các giá trị của
m
để phương trình
2
| | 1f x m
có 4 nghiệm phân biệt.
A.
21
12
m
m

. B.
12m
. C.
12m
. D.
01m
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 69: Cho hàm số
2
f x ax bx c
có đồ thị như hình bên dưới:
Số nghiệm của phương trình
2
2 1 1f f x x
là
A.
1.
B.
2.
C.
3.
D.
4.
Câu 70: Cho hàm số bậc hai
fx
có đồ thị hàm số như hình bên dưới:
Hỏi
m
thuộc tập hợp nào dưới đây thì phương trình
2
fx mm
có 4 nghiệm thực phân
biệt?
A.
;.; 21 
B.
1;0 1;2 .

C.
;1;0 12
D.
;0 1; . 
Câu 71: Cho hàm số
2
y f x ax bx c
có đồ thị như hình vẽ.
Số giá trị nguyên của
m
để phương trình
2
f x m
có đúng 4 nghiệm phân biệt là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 72: Cho Parabol (P):
2
23 y x x
. Số giá trị nguyên âm của tham số
m
để Parabol (P) cắt
đường thẳng d:
y x m
tại hai điểm phân biệt là
A.
4
. B.
5
. C.
7
. D.
6
.
Câu 73: Cho đường thẳng
: 2 5 1d y m x m
và parabol
22
:3P y x mx m
(
m
là tham số).
Có tất cả bao nhiêu giá trị nguyên của
m
nhỏ hơn 5 để đường thẳng
d
cắt parabol
P
tại
hai điểm phân biệt?
A.
4
. B.
5
. C.
7
. D.
6
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 74: Đồ thị hàm số
2
2y x x
cắt đường thẳng
2
2y m x
tại hai điểm phân biệt có hoành độ lần
lượt là
12
;xx
. Giá trị của
12
T x x
bằng
A.
2.
B.
2.
C.
4.
D.
2
4.m
Câu 75: Tìm tập hợp tất cả các giá trị của
a
để đường thẳng
d
:
21y a x a
cắt parabol
P
:
2
1y x x
tại hai điểm phân biệt nằm về hai phía đối với trục tung.
A.
;3 .
B.
;1 .
C.
1; .
D.
.
Câu 76: Cho đồ thị hàm số
22
2 2 1y x mx m
cắt đồ thị hàm số
2yx
tại các điểm có hoành
độ lần lượt là
12
;xx
. Gọi
,Mm
là giá trị lớn nhất, nhỏ nhất của
22
1 2 1 2
H x x x x
. Đặt
.T M m
Khẳng định nào sau đây đúng?
A.
10T
. B.
10,20T
. C.
20,30T
. D.
30T
.
Câu 77: Tìm tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số
2y m x
cắt parabol
2
2y x x
tại hai điểm phân biệt cùng có hoành độ nhỏ hơn 1.
A.
7
. B.
8
. C.
9
. D.
10
.
Câu 78: Gọi
S
là tập hợp các giá trị thực của tham số
m
sao cho Parabol
2
:3P y x x m
cắt trục
Ox
tại hai điểm phân biệt
,AB
thoả mãn
2OA OB
. Tổng các phần tử của tập hợp
S
bằng
A.
2
. B.
3
. C.
18
. D.
16
.
Câu 79: Có bao nhiêu giá trị của tham sô
m
để đường thẳng
: ( 1) 2d y m x
cắt Parabol
2
: 2 2P y x m x m
tại hai điểm phân biệt
,AB
sao cho
42AB
?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 80: Gọi
,AB
là hai giao điểm của đường thẳng
:1y x k
và parabol
2
:.P y x x
Tìm tập
hợp tất cả các giá trị của tham số
k
để trung điểm
I
của đoạn thẳng
AB
nằm trên đường
thẳng
: 2.d y x
A.
2; 1 .
B.
2; 1 .
C.
2.
D.
1.
Câu 81: Cho hàm số
2
22y x x
có đồ thị là parabol
P
và đường thẳng
d
có phương trình
y x m
. Giá trị của
m
để đường thẳng
d
cắt parabol
P
tại hai điểm phân biệt
,AB
sao
cho
22
OA OB
đạt giá trị nhỏ nhất là
A.
1
2
m 
. B.
5
2
m 
. C.
1
2
m
. D.
5
2
m
.
Câu 82: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng
3y mx
cắt parabol
2
:2P y x x
tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB
thuộc đường thẳng
6.yx
Tính tổng tất cả các phần tử của S.
A.
5
. B.
1
. C.
3
. D.
3
.
Câu 83: Biết Parabol
P
:
2
4y ax x c
có đỉnh
1; 6I 
. Tính
S a c
A.
6
. B.
6
. C.
2
. D.
2
.
Câu 84: Cho hàm số
2
y f x x bx c
có đồ thị là một Parabol
P
có đỉnh
1; 4I
. Tính
bc
.
A.
12
. B.
8
. C.
10
. D.
5
.
Câu 85: Tìm parabol
2
: 3 2,P y ax x
biết rằng parabol có trục đối xứng
3x 
?
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A.
2
3 2.y x x
B.
2
1
2.
2
y x x
C.
2
1
3 3.
2
y x x
D.
2
1
3 2.
2
y x x
Câu 86: Đồ thị của hàm số
2
3y ax x c
đi qua hai điểm
2;3A
và
1;6B
. Giá trị biểu thức
36T a c
bằng
A.
17
. B.
38
. C.
72
. D.
73
.
Câu 87: Cho đồ thị hàm số
2
4y ax bx
có đỉnh là điểm
1; 2I
. Tính
3ab
.
A.
20
. B.
18
. C.
30
. D.
25
Câu 88: Xác định
2
:P y ax bx c
, biết
P
có đỉnh là
(1;3)I
và đi qua
(0;1)A
A.
2
: 2 3 1P y x x
. B.
2
: 2 4 1P y x x
.
C.
2
: 2 4 1P y x x
. D.
2
: 2 4 1P y x x
.
Câu 89: Cho parabol
2
:P y ax bx c
, , ; 0a b c a
có hoành độ đỉnh bằng 1 và đi qua hai
điểm
0 ; 1M
,
1 ; 3N
. Khi đó parabol
P
là đồ thị của hàm số nào?
A.
2
2 4 1y x x
. B.
2
41y x x
. C.
2
2 4 1y x x
. D.
2
2 4 1y x x
.
Câu 90: Biết Parabol
2
y ax bx c
đi qua điểm
8;0A
và có đỉnh
6; 12I
, khi đó
abc
là:
A. 85 B. 63. C. 36. D. 96.
Câu 91: Biết đồ thị hàm số
2
0y ax bx c a
biết đồ thị hàm số đi qua ba điểm
0;4 ; 1;3 ; 1;9 .A B C
Tính
.ab c
A.
1.
B.
2.
C.
1.
D.
2.
Câu 92: Xác định hàm số bậc hai
2
y ax bx c
biết đồ thị của nó có đỉnh
(1, 1)I
và đi qua
(2,0)A
.
A.
2
32y x x
. B.
2
2y x x
. C.
2
2 4 3y x x
. D.
2
2y x x
.
Câu 93: Biết rằng hàm số
2
y ax bx c
đạt giá trị nhỏ nhất bằng 1 và đồ thị hàm số cắt đường thẳng
2022 2yx
tại một điểm trên trục
Oy
. Tính
2 2 2
. S a b c
A.
10
. B.
9
. C.
50
. D.
4
.
Câu 94: Cho parabol
2
:P y ax bx c
, biết hàm số
2
y ax bx c
đạt giá trị nhỏ nhất là
4
tại
2x
và đồ thị của nó cắt trục tung tại điểm có tung độ là 6. Tính
2.a b c
A.
6
. B.
5
. C.
4
. D.
2
.
Câu 95: Cho hàm số
2
y ax b x c
với
a
,
b
,
c
, hệ số
0.a
Biết rằng hàm số đạt giá trị nhỏ
nhất bằng
1
tại
2x
và đồ thị hàm số đi qua điểm
1;0M
. Tính
.T abc
A.
6T
. B.
5T
. C.
4T
. D.
12T
.
Câu 96: Gọi
T
là tổng tất cả các giá trị của tham số
m
để parabol
2
:5P y x x m
cắt trục
Ox
tại
hai điểm phân biệt
,AB
thỏa mãn
4OA OB
. Tính
T
.
A.
64
9
T 
. B.
64
9
T
. C.
2T
. D.
2T 
.
Câu 97: Cho parabol
P
:
2
y ax bx c
,
0a
biết
P
đi qua
(4;3)M
cắt
Ox
tại
(3;0)N
và
Q
sao
cho
INQ
có diện tích bằng
1
biết hoành độ điểm
Q
nhỏ hơn
3
với
I
là đỉnh của
P
. Tính
abc
.
A.
1
. B.
1
. C.
0
. D.
2
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 98: Có tất cả bao nhiêu giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
21f x x x m
trên
1;2
bằng 5?
A. 3. B. 1. C. 2. D. 4.
Câu 99: Cho hình chữ nhật
, 10, 6ABCD AB AD
. Trên các cạnh
,,AB BC CD
lấy các điểm
,,P Q R
sao cho
AP BQ CR x
. Giá trị của
x
trong khoảng nào để diện tích tam giác
PQR
đạt giá
trị nhỏ nhất?
R
C
A
B
D
P
Q
A.
3;5
. B.
6;8
. C.
8;10
. D.
4;8
.
Câu 100: Biết có 2 giá trị thực của tham số
m
là
12
,mm
để giá trị nhỏ nhất của hàm số
22
( ) 4 4 2y f x x mx m m
trên đoạn [-2; 0] bằng 3. Tổng
12
mm
bằng
A.
3
.
2
B.
1
.
2
C.
1
.
2
D.
3
.
2
Câu 101: Gọi
S
là tập hợp các giá trị thực của tham số
m
để giá trị nhỏ nhất của hàm số
22
4 4 2y f x x mx m m
trên đoạn
2; 0
bằng 3. Tính tổng
T
các phần tử của
S
.
A.
3
2
T
. B.
9
2
T
. C.
1
2
T
. D.
3
2
T 
.
Câu 102: Tìm tập hợp tất cả các giá trị của tham số
k
để đường thẳng
:3y kx
cắt parabol
2
: 4 3P y x x
tại hai điểm phân biệt
,AB
sao cho diện tích tam giác
OAB
bằng
3
.
2
A.
5; 3 .
B.
3;3 .
C.
5;5 .
D.
5; 3 .
Câu 103: Cho parabol
22
( ): 2 x 3 4 3P y x m m m
(
m
là tham số) có đỉnh
I
. Gọi
, AB
là hai
điểm thuộc
Ox
sao cho
2022AB
. Khi đó
IAB
có diện tích nhỏ nhất bằng:
A.
1011
. B.
2022
. C.
4044
. D.
1010.
Câu 104: Cho Parabol
2
: 4 3P y x x
và đường thẳng
: 2 1d y m x
. Tính tổng các giá trị
của tham số
m
để đường thẳng
d
cắt Parabol
P
tại hai điểm phân biệt
,AB
sao cho diện
tích tam giác
IAB
bằng
10
với điểm
2;3I
.
A.
6
. B.
0
. C.
2
. D.
4
.
Câu 105: Một vật chuyển động với vận tốc theo quy luật của hàm số bậc hai
2
12v t t t
với
ts
là
quãng thời gian tính từ khi vật bắt đầu chuyển động và
v
(m/s) là vận tốc của vật. Trong
9
giây đầu tiên kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu?
A.
144 / .ms
B.
243 / .ms
C.
27 / .ms
D.
36 / .ms
Câu 106: Một chiếc cổng hình parabol dạng
2
1
2
yx
có chiều rộng
8dm
. Hãy tính chiều cao
h
của
cổng. (Xem hình minh họa)
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A.
9hm
. B.
8hm
. C.
7hm
. D.
5hm
.
Câu 107: Một của hàng buôn giày nhập một đôi với giá là
40
đôla. Cửa hàng ước tính rằng nếu đôi
giày được bán với giá
x
đôla thì mỗi tháng khách hàng sẽ mua
120 x
đôi. Hỏi của hàng
bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
A.
80
USD. B.
160
USD. C.
40
USD. D.
240
USD.
Câu 108: Cổng Ac-xơ tại thành phố Xanh Lu-i (Mĩ) có hình dạng là một parabol hướng bề lõm xuống
dưới (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có
độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo
phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn
10 m. Giả sử các số liệu trên là chính xác. Hãy tính chiều cao của cổng Ac-xơ (tính từ điểm cao
nhất trên cổng xuống mặt đất).
A. 197,5 m. B. 275,6 m. C. 185,6 m. D. 348,3 m
Câu 109: Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả
bóng được sút lên từ độ cao
1m
sau đó
1
giây nó đạt độ cao
10 m
và
3,5
giây nó ở độ cao
6,25 m
. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?
A.
11m
. B.
12 m
. C.
13 m
. D.
14 m
.
Câu 110: Một chiếc cổng hình parabol có chiều rộng
12 m
và chiều cao
8 m
như hình vẽ. Giả sử một
chiếc xe tải có chiều ngang
6 m
đi vào vị trí chính giữa cổng . Hỏi chiều cao
h
của xe tải thỏa
mãn điều kiện gì để có thể đi vào cổng mà không chạm tường?
A.
06h
. B.
06h
. C.
07h
. D.
07h
.
Câu 111: Trong số các hình chữ nhật có cùng chu vi bằng
16
, hình chữ nhật có diện tích lớn nhất bằng bao
nhiêu?
A.
64.
B.
4.
C.
16.
D.
8.
Câu 112: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa
phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x
4m. Hãy tính khoảng cách giữa hai điểm
A
và
B
. (xem hình vẽ bên dưới)
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A. 5m. B. 8,5m. C. 7,5m. D. 8m.
Câu 113: Một tấm tôn có bề rộng
AB
là
100cm
. Người ta chọn 2 điểm
M
và
N
trên đoạn
AB
sao cho
có thể làm được một máng nước như hình vẽ. (
AMNB
là hình chữ nhật). Tính
MN
để máng
nước có diện tích
AMNB
lớn nhất.
A.
50 .MN cm
B.
60 .MN cm
C.
45 .MN cm
D.
55 .MN cm
Câu 114: Một người ném một quả bóng từ độ cao cách mặt đất 80m, tại thời điểm 1 giây sau khi ném,
người ta đo được độ cao của quả bóng so với mặt đất là 128m. Biết rằng quỹ đạo bay của quả
bóng là một đường Parabol (như hình vẽ). Tính độ cao tối đa mà quả bóng đạt được.
A.
143m
. B.
144m
. C.
144,5m
. D.
145m
.
Câu 115: Cô Tình có
60m
lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một
cạnh là tường, cô Tình chỉ cần rào
3
cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính
hộ diện tích lớn nhất mà cô Tình có thể rào được?
A.
2
400m
. B.
2
450m
. C.
2
350m
. D.
2
425m
.
Câu 116: Dây truyền đỡ nền cầu treo có dạng Parabol
ACB
như hình vẽ. Đầu cuối của dây được gắn
chặt vào điểm
A
và
B
trên trụ cốt thép bê tông
AA
và
BB
với độ cao
30(m)
so với nền cầu.
Chiều dài nhịp
200(m)AB

. Độ cao ngắn nhất của dây truyền trên nền cầu là
5(m)OC
.
Người ta nối dây đỡ với nền bằng
7
sợi cáp song song cách đều hai trụ
AA
và
BB
.
Xác định
tổng các chiều dài
7
các dây cáp treo đó.
A.
78,15(m)
. B.
78,75(m)
. C.
72,75(m)
. D.
80,70(m)
.
_________________HẾT_________________
Huế, 10h20’ Ngày 03 tháng 01 năm 2023
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
LỜI GIẢI CHI TIẾT
II. BÀI TẬP TỰ LUẬN
Câu 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a)
2
3 2;y x x
b)
2
2 5 2;y x x
c)
2
2 1;y x x
d)
2
2 3;y x x
e)
2
2;yx
f)
2
2 1.y x x
Câu 2: Xác định hàm số bậc hai
2
2,y x bx c
biết đồ thị của nó:
a) Có trục đối xứng là
1x
và cắt trục tung tại điểm có tung độ là 4.
b) Có đỉnh là
1; 2I 
.
c) Có hoành độ đỉnh là 2 và đi qua điểm
1; 2A
.
Lời giải:
a) Trục đối xứng
14
24
bb
xb
a

.
Theo giả thiết, (P) cắt trục tung tại
0;4
4 (0)yc
.
Vậy
2
2 4 4.y x x
b) Đỉnh của (P) là
1; 2I
2
14
24
4 16 8
20
48
bb
xb
a
b ac c
yc
a


Vậy
2
2 4 .y x x
c) Hoành độ đỉnh:
28
24
bb
xb
a

.
Đồ thị qua điểm
1; 2A
2 (1) 6 4y c c
.
Vậy
2
2 8 4.y x x
Câu 3: Xác định parabol
2
: ; ; ; , 0 .P y ax bx c a b c a
Biết
P
đi qua các điểm
1;6 , 3;2AB
và
2;0 .C
Lời giải:
Do
1;6 , 3;2 , 2;0A P B P C P
nên ta có hệ:
61
9 3 2 3.
4 2 0 2
a b c a
a b c b
a b c c





Vậy
2
: 3 2.P y x x
Câu 4: Xác địnhparabol
2
: ; ; ; , 0 .P y ax bx c a b c a
Biết
P
đi qua điểm
1;8A
và có
đỉnh
2; 1 .I
Lời giải:
Trục đối xứng của
P
là
:.
2
b
x
a
Do
2; 1I
là đỉnh của
P
và
1;8AP
nên ta có hệ:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
4 2 1
4 2 1 1
2 4 0 4.
2
83
8
a b c
IP
a b c a
b
I a b b
a
a b c c
AP
a b c



Vậy
2
: 4 3.P y x x
Câu 5: Xác định hàm số
2
0y ax bx c a
biết hàm số đạt giá trị nhỏ nhất bằng
4
tại
2x
và
đồ thị hàm số đi qua điểm
0;6A
.
Lời giải:
Hàm số đạt cực tiểu bằng
4
tại
2x
nên
2
2
.
4
4
b
a
a


Đồ thị hàm số đi qua điểm
0;6A
nên ta có
6.c
Từ đó ta có hệ
22
2
1
2
44
2
4 4 16 16 8 0 2.
4
6 6 6
6





b
a
a
b a b a
b ac a a a b
a
c c c
c
Vậy
2
1
2 6.
2
y x x
Câu 6: Xác định parapol
P
:
2
2y x bx c
, biết
P
:
a) Có trục đối xứng
1x
vá cắt trục tung tại điểm
0;4
;
Đáp số: b=
4, c= 4
b) Có đỉnh
1; 2I 
;
Đáp số: b= 4, c= 0
c) Đi qua hai điểm
0; 1A
và
4;0B
;
Đáp số: b=
31/4, c=
1
d) Có hoành độ đỉnh là 2 và đi qua điểm
1; 2M
.
Đáp số: b=
8, c= 4
Câu 7: Xác định parapol
P
:
2
4y ax x c
, biết
P
:
a) Đi qua hai điểm
1; 2A
và
2;3B
;
Đáp số: a= 3, c=
1
b) Có đỉnh
2; 1I 
;
Đáp số: a=
1, c=
5
c) Có hoành độ đỉnh là
3
và đi qua điểm
2;1P
;
Đáp số: a=
2/3, c=
13/3
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
d) Có trục đối xứng là đường thẳng
2x
vá cắt trục hoành tại điểm
3;0M
.
Đáp số: a=1, c= 3
Câu 8: Tìm parapol
P
:
2
2y ax bx
, biết
P
:
a) Đi qua hai điểm
1;5M
và
2;8N
;
Đáp số: a=2, b=1
b) Đi qua điểm
3; 4A
và có trục đối xứng
3
4
x 
;
Đáp số: a=
4
9
, b=
2
3
c) Có đỉnh
2; 2I
;
Đáp số: a=1, b=4
d) Đi qua điểm
1;6B
, đỉnh có tung độ
1
4
Đáp số: a=16, b=12 hoặc a=1, b=
3
Câu 9: Xác định parapol
P
:
2
y ax bx c
, biết
P
:
a) Đi qua ba điểm
0; 1 , 1; 1 , 1;1A B C
;
Đáp số: a=1, b=
1, c=
1
b) Đi qua điểm
3;0D
và có đỉnh là
1;4I
;
Đáp số: a=
1, b=2, c=3
c) Đi qua
8;0A
và có đỉnh
6;12I
;
Đáp số: a=
3, b=36, c=
96
d) Đạt GTNN bằng 4 tại
2x 
và đi qua
0;6A
;
Đáp số: a=1/2, b=2, c=6
Câu 10: Cho hàm số
2
23y x x
có đồ thị
.P
a) Lập bảng biến thiên và vẽ đồ thị
.P
b) Dựa vào đồ thị
,P
biện luận số nghiệm của phương trình
2
2 2 0.x x m
c) Tìm
m
để phương trình
2
2 3 1x x m
có 4 nghiệm phân biệt.
d) Tìm
m
để phương trình
2
2 2 0x x m
có 4 nghiệm phân biệt.
e) Tìm
m
để phương trình
2
10f x m f x m


có 8 nghiệm phân biệt.
Lời giải:
a) TXĐ:
.D
+) Trục đối xứng của
:P
1.x
+) Đỉnh của
: 1; 4 .PI
Bảng biến thiên:
x

1

y


Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
4
Hàm số đồng biến trên
1; ;
nghịch biến trên
;1 .
Vẽ đồ thị:
x
y
-3
-4
O
1
b) Điều kiện:
.x
Ta có:
22
2 2 0 2 3 2 3x x m x x m
Số nghiệm của phương trình bằng số giao điểm của
P
và đường thẳng
: 2 3.d y m
x
y
2m-3
-3
-4
O
1
Biện luận:
+) Với
1
2 3 4 :
2
mm
d
và
P
không có điểm chung
Phương trình vô nghiệm.
+) Với
1
2 3 4 :
2
mm
d
và
P
có một điểm chung
Phương trình có duy nhất
nghiệm.
+) Với
1
2 3 4 :
2
mm
d
và
P
có hai điểm chung
Phương trình có hai nghiệm.
c) Đặt
2
2 3.f x x x
Ta có:
khi
khi
2
0
2 3 .
0
f x y
x x f x
f x y

Cách vẽ đồ thị
:P y f x
suy ra từ
::P y f x
+) Giữ nguyên phần đồ thị
P
phía trên
,Ox
bỏ phần đồ thị
P
phía dưới
.Ox
+) Lấy đối xứng phần đồ thị bị bỏ của
P
qua trục
.Ox
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
x
y
m-1
4
-3
O
1
Số nghiệm của phương trình bằng số giao điểm của
P
và đường thẳng
: 1.d y m
Dựa vào đồ thị, yêu cầu bài toán
0 1 4 1 5.mm
d) Điều kiện:
.x
Ta có:
22
2 2 0 2 3 5x x m x x m
Đặt
2
2 3.f x x x
Ta có:
khi
khi
2
0
2 3 .
0
f x x
x x f x
f x x

Cách vẽ đồ thị
:P y f x
suy ra từ
::P y f x
+) Giữ nguyên phần đồ thị
P
phía bên phải
,Oy
bỏ phần đồ thị
P
phía bên trái
.Oy
+) Lấy đối xứng phần đồ thị được giữ của
P
qua trục
.Oy
x
y
m-5
-1
-3
-4
O
1
Số nghiệm của phương trình bằng số giao điểm của
P
và đường thẳng
: 5.d y m
Dựa vào đồ thị, yêu cầu bài toán
4 5 3 1 2.mm
e) Điều kiện:
.x
Đánh giá: Phương trình
2
10f x m f x m


có dạng
2
10t m t m
với
.t f x
Cách vẽ đồ thị
:P y f x
suy ra từ
::P y f x
+) Giữ nguyên phần đồ thị
P
phía trên
,Ox
bỏ phần đồ thị
P
phía dưới
.Ox
+) Lấy đối xứng phần đồ thị bị bỏ của
P
qua trục
.Ox
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
x
y
m-1
4
-3
O
1
Ta có:
2
1
10
fx
f x m f x m
f x m


Dựa vào đồ thị
1fx
có 4 nghiệm phân biệt.
Phương trình đã cho có 8 nghiệm phân biệt
Phương trình
f x m
có 4 nghiệm phân biệt
khác các nghiệm của phương trình
1.fx
Yêu cầu bài toán
04
.
1
m
m

Câu 11: Tìm
m
để parabol
2
2y x x
cắt đường thẳng
ym
tại
2
điểm phân biệt.
Lời giải:
Ta có
22
2 2 0x x m x x m
(1).
Yêu cầu bài toán
(1) có 2 nghiệm phân biệt
' 1 0 1mm
.
Câu 12: Cho parabol
2
: 2 1P y x x m
. Tìm tất cả các giá trị thực của
m
để parabol cắt
Ox
tại
hai điểm phân biệt có hoành độ dương.
Lời giải:
Phương trình hoành độ giao điểm của
P
và trục
Ox
là
2
2 1 0.x x m
1
Để parabol cắt
Ox
tại hai điểm phân biệt có hoành độ dương khi và chỉ khi
1
có hai
nghiệm dương
20
2
2 0 1 2
1
10
m
m
Sm
m
Pm

.
Câu 13: Tìm tất cả các giá trị thực của tham số
m
sao cho parabol
2
:4P y x x m
cắt
Ox
tại hai
điểm phân biệt
, AB
thỏa mãn
3.OA OB
Lời giải:
Phương trình hoành độ giao điểm:
2
4 0.x x m
1
Để
P
cắt
Ox
tại hai điểm phân biệt
, AB
thì
1
có hai nghiệm phân biệt
4 0 4 mm
*
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Theo giả thiết
3
3 3 .
3
AB
AB
AB
xx
OA OB x x
xx


+) TH1:
Viet
3
3 4 . 3.
.
AB
A B A B A B
AB
xx
x x x x m x x
x x m

+) TH2:
Viet
3
3 4 . 12
.
AB
A B A B A B
AB
xx
x x x x m x x
x x m

 
: không thỏa mãn
*
.
Câu 14: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
:d y mx
cắt đồ thị hàm số
32
: 6 9P y x x x
tại ba điểm phân biệt.
Lời giải:
Phương trình hoành độ giao điểm của
P
với
d
là
32
69x x x mx
2
2
0
6 9 0
6 9 0. 1
x
x x x m
x x m
Để
P
cắt
d
tại ba điểm phân biệt khi và chỉ
1
có hai nghiệm phân biệt khác
0
2
0
00
9 0 9
0 6.0 9 0
mm
mm
m




.
Câu 15: Cho parabol
2
: 4 3P y x x
và đường thẳng
:3d y mx
. Tìm giá trị thực của tham số
m
để
d
cắt
P
tại hai điểm phân biệt
,AB
có hoành độ
12
,xx
thỏa mãn
33
12
8xx
.
Lời giải:
Phương trình hoành độ giao điểm của
P
và
d
là
2
4 3 3x x mx
0
40
4
x
x x m
xm

.
Để
d
cắt
P
tại hai điểm phân biệt
,AB
khi và chỉ khi
4 0 4mm
.
Khi đó, ta có
3
33
12
8 0 4 8 4 2 2x x m m m
.
Câu 16: Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
5 7 2 0x x m
có nghiệm
thuộc đoạn
1;5
.
Lời giải:
Ta có
22
5 7 2 0 5 7 2 .x x m x x m
*
Phương trình
*
là phương trình hoành độ giao điểm của parabol
2
: 5 7P x x
và đường
thẳng
2ym
(song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số
2
57y x x
trên
1;5
như sau:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Dựa vào bảng biến ta thấy
1;5x
thì
3
;7
4
y



.
Do đo để phương trình
*
có nghiệm
3 3 7
1;5 2 7 .
4 8 2
x m m
III. BÀI TẬP TRẮC NGHIỆM
Câu 17: Trong các hàm số sau hàm số nào là hàm số bậc hai?
A.
2
2 3 5y x x
B.
3
2 3 5xx
y
x

. C.
23
2 3 5y x x
. D.
32yx
.
Câu 18: Điểm nào sau đây không thuộc đồ thị hàm số
2
2yx
?
A.
2;2P
. B.
3;3 .Q
C.
2;2 .N
D.
1; 1 .M
Lời giải:
Với
2x
2
2 2 2 y
2;2N
thuộc đồ thị hàm số.
Câu 19: Đồ thị hàm số
2
y x x
đi qua điểm nào dưới đây?
A.
2;6N
. B.
1;1M
. C.
2;3P
. D.
1;1Q
.
Lời giải:
Đồ thị hàm số
2
y x x
đi qua điểm
2;6N
.
Câu 20: Cho hàm số
2
3 4 3y x x
có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương
trình:
A.
2
3
x
. B.
2
3
x 
. C.
4
3
x
. D.
4
3
x 
Lời giải:
Trục đối xứng của (P) là
42
2 6 3
b
x
a
.
Câu 21: Đỉnh của parabol
2
45 y x x
có toạ độ là
A.
0;2
. B.
1;2
. C.
2;0
. D.
2;1
.
Lời giải:
Đỉnh của parabol
2
45 y x x
.có toạ độ là
2;1
.
Câu 22: Tìm
m
để parabol
2
( ): 2 3P y mx x
có trục đối xứng là đường thẳng
2x
.
A.
2m
. B.
1m 
. C.
1m
. D.
1
2
m
.
7
3
5
1
x
y
5
2
3
4
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Lời giải:
Vì
P
là Parabol nên
0m
. Khi đó Parabol
P
có trục đối xứng
21
2
xx
mm
Theo bài ra trục đối xứng
2x
nên
11
2
2
m
m
.
Câu 23: Hàm số nào dưới đây có đồ thị nhận đường thẳng
2x 
làm trục đối xứng?
A.
2
2 4 3y x x
. B.
2
2 4 3y x x
. C.
2
43y x x
. D.
2
43y x x
.
Lời giải:
Đồ thị hàm số
2
,0y ax bx c a
nhận đường thẳng
2
b
x
a

làm trục đối xứng.
Đồ thị hàm số
2
2 4 3y x x
nhận đường thẳng
1x
làm trục đối xứng.
Đồ thị hàm số
2
2 4 3y x x
nhận đường thẳng
1x 
làm trục đối xứng.
Đồ thị hàm số
2
43y x x
nhận đường thẳng
2x
làm trục đối xứng.
Đồ thị hàm số
2
43y x x
nhận đường
2x 
làm trục đối xứng.
Câu 24: Hàm số nào có đồ thị là đường Parabol có đỉnh là
1;3 ?I
A.
2
2 4 3y x x
. B.
2
2 2 1y x x
. C.
2
2 4 5y x x
. D.
2
22y x x
.
Câu 25: Giá trị nhỏ nhất của hàm số
2
45y x x
là
A.
min
0y
. B.
min
2y 
. C.
min
2y
. D.
min
1y
.
Lời giải:
Hàm số
2
45y x x
có
10a 
, do đó hàm số đạt giá trị nhỏ nhất tại
2
2
b
x
a

và
min
21yy
.
Câu 26: Hàm số
2
5 6 7 y x x
đạt giá trị nhỏ nhất khi
A.
26
.
5
x
B.
3
5
x
. C.
3
5
x
. D.
6
5
x
.
Lời giải:
Hàm số
2
5 6 7 y x x
có
50a 
nên đạt giá trị nhỏ nhất tại hoành độ đỉnh của
.P
Câu 27: Giá trị lớn nhất của hàm số
2
24y x x
bằng
A.
5
. B.
5
. C.
1
. D.
1
.
Lời giải:
Tập xác định:
D
.
Tọa độ đỉnh:
1;5I
.
Bảng biến thiên:
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số
2
24y x x
bằng 5.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 28: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
2
42y x x
trên đoạn
0;3
.
Tính giá trị biểu thức
Mm
.
A.
1
. B.
4
. C.
0
. D.
1
.
Lời giải:
Ta có bảng biến thiên của hàm số
2
42y x x
trên đoạn
0;3
:
Từ bảng biến thiên ta có:
2; 2Mm
nên
0Mm
.
Câu 29: Tìm giá trị nhỏ nhất của hàm số
22
5 4 1y x x
.
A.
5
. B.
5
. C.
1
. D.
1
.
Lời giải:
Đặt
2
11t x t
Suy ra:
22
1xt
Từ đó,
22
1 5 4 4 6y t t t t
trên
1; 
.
Ta có hàm số trên có đồ thị là 1 parabol đỉnh
2; 10I 
Bảng biến thiên trên
1; 
:
Vậy
10Miny x
Hàm số không có giá trị lớn nhất.
Câu 30: Cho hàm số
2
y ax bx c
,với
0a
. Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng
;
2
b
a




.
B. Hàm số nghịch biến trên khoảng
;
2
b
a




.
C. Hàm số nghịch biến trên khoảng
;
2
b
a




.
D. Đồ thị hàm số có trục đối xứng là đường thẳng
2
b
x
a

Câu 31: Cho hàm số
2
y ax bx c
có đồ thị là parabol trong hình sau:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;
. B.
1; 
. C.
;1
. D.
;2
.
Lời giải:
Dựa vào đồ thị, ta có hàm số đã cho đồng biến trên khoảng
1; 
.
Câu 32: Cho hàm số bậc hai có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;
. B.
;2
. C.
3
. D.
1;
.
Lời giải:
Dựa vào bảng biến thiên ta có hàm số đồng biến trên
1;
.
Câu 33: Cho hàm số
2
2 4 1y x x
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
;2
. B. Hàm số nghịch biến trên khoảng
; 
.
C. Hàm số đồng biến trên khoảng
2;
. D. Hàm số nghịch biến trên khoảng
2;
.
Lời giải:
Theo định lý về chiều biến thiên của hàm số bậc hai ta có hàm số
2
2 4 1y x x
đồng biến
trên khoảng
1;
nên đồng biến trên khoảng
2;
.
Câu 34: Cho hàm số
2
35y x x
. Hàm số đã cho đồng biến trên khoảng nào?
A.
;3
. B.
3
;
2



. C.
3
;
2




. D.
3
;
2




.
Lời giải:
Hàm số
2
y ax bx c
với
0a
đồng biến trên khoảng
;
2
b
a




và nghịch biến trên
khoảng
;
2
b
a



. Suy ra hàm số
2
35y x x
đồng biến trên khoảng
3
;
2




.
Câu 35: Hàm số nào sau đây đồng biến trên ?
A.
2
1yx
. B.
2
y x x
. C.
1yx
. D.
1yx
.
Lời giải:
Hàm số
1yx
đồng biến trên vì
10a 
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 36: Cho hàm số
2
2y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên khoảng
1; .
B. Hàm số đã cho nghịch biến trên khoảng
1; . 
C. Hàm số đã cho đồng biến trên khoảng
1; . 
D. Hàm số đã cho nghịch biến trên khoảng
1; .
Lời giải:
Với
0a
thì hàm số
2
y ax bx c
nghịch biến trên khoảng
;
2
b
a




và đồng biến trên
khoảng
;
2
b
a




.
Hàm số
2
2y x x
có
2
1 0, 1
2 2.1
b
a
a
nên hàm số
2
2y x x
đồng biến trên
khoảng
1; .
Câu 37: Cho hàm số
2
2018 2020.f x x x
Khẳng định nào sau đây đúng?
A.
2019 2018
11
22
ff
. B.
2019 2018
11
22
ff
.
C.
1009 1008
22ff
. D.
1008 1007
22ff
.
Lời giải:
Hàm số
2
2018 2020 f x x x
có hoành độ đỉnh là
1009
và hệ số
10a 
nên
đồng biến
trên khoảng
1009;
và nghịch biến trên khoảng
;1009
.
Vì
2019 2018
2019 2018 2019 2018
1 1 1 1
2 2 1009
2 2 2 2
ff
.
Câu 38: Tìm tất cả giá trị tham số
m
để hàm số
2
12y x m x m
đồng biến trên
1; 
.
A.
3m 
. B.
3m 
. C.
3m 
. D.
3m 
.
Lời giải:
Hàm số đã cho xác định với mọi
x
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có hàm số đã cho đồng biến trên khoảng
1; 
khi
1
13
2
m
m
.
Câu 39: Tìm tất cả các giá trị của tham số
m
để hàm số
2
2 1 2y x m x m
nghịch biến trên
khoảng
1;2
.
A.
1m
. B.
1m
. C.
0m
. D.
0m
.
Lời giải:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Hàm số đã cho xác định với mọi
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên khoảng
1;2
khi
12m 
1m
.
Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
( ) 2 2 2021 y f x m x mx m
nghịch biến trên khoảng
;3 ?
A.
2.
B.
1.
C.
3.
D.
4.
Lời giải:
+ Trường hợp
2 4 2021 m y x
, nghịch biến trên
;3
. Tức
2m
thỏa mãn yêu cầu
bài toán.
+ Trường hợp
2m
: Dựa vào sự biến thiên hàm bậc hai ta thấy
fx
nghịch biến trên
khoảng
;3
20
23
3
2
m
m
m
m

.
Từ các trường hợp trên, suy ra:
23m
mà
2
3
m
m
m
.
Vậy có 2 giá trị nguyên của tham số
m
.
Câu 41: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2 1 3y x m x
nghịch biến trên
2; ?
A.
3
. B.
6
. C.
5
. D.
4
.
Lời giải:
Ta có trục đối xứng là đường thẳng
1xm
.
Hàm số bậc hai nghịch biến trên
1;m
.
Để hàm số nghịch biến trên
2;
thì
2;
1;m
1 2 1 3mm
Suy ra
1; 0 ;1; 2 ; 3m
.
Câu 42: Cho hàm số bậc hai
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Tìm tất cả các giá trị của
x
để
0.y
A.
;0
. B.
3; 
. C.
0;3
. D.
0;3
.
Lời giải:
Dựa vào đồ thị ta có
0 ;0 3;yx  
.
0 0;3yx
.
Câu 43: Hàm số
2 2 2
2 2 2 1f x x m m x m m
. Mệnh đề nào sau đây sai?
A. Hàm số đạt giá trị lớn nhất trên đoạn
1;0
bằng
0f
.
B. Hàm số nghịch biến trên khoảng
0;
.
C. Hàm số đặt giá trị lớn nhất trên đoạn
1;0
bằng
1f
.
D. Hàm số nghịch biến trên khoảng
;0
.
Lời giải:
Ta có
2
2
17
2
24
0
2 2 2
m
b m m
a





Và
0a
nên hàm số đồng biến trên khoảng
2
2
;
2
mm





nghịch biến trên khoảng
2
2
; 0;
2
mm


 


.
Câu 44: Hàm số nào dưới đây có bảng biến thiên như sau?
A.
2
1.yx
B.
2
3 1.y x x
C.
2
1.y x x
D.
2
3 1.yx
Lời giải:
Từ bảng biến thiên ta suy ra đồ thị hàm số
2
y ax bx c
có
0a
và tọa độ đỉnh
0;1I
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Suy ra
0
0
00
2
1
1
a
a
b
b
a
c
c



. Chọn đáp án
2
1.yx
Câu 45: Bảng biến thiên dưới đây là của hàm số nào?
A.
2
5
.
4
y x x
B.
2
3
.
2
y x x
C.
2
3
.
2
y x x
D.
2
2 1. y x x
Câu 46: Bảng biến thiên của hàm số
2
21y x x
là
A. . B. .
C. . D. .
Lời giải:
Ta có:
2
21y x x
nên đỉnh của Parabol là
1;2I
.
Do
10a
nên Parabol có bề lõm xuống dưới.
Câu 47: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào?
A.
2
2.y x x
. B.
2
2.y x x
C.
2
2 1.y x x
D.
2
2.y x x
Lời giải:
Từ đồ thị ta có hệ số
0a
; hoành độ đỉnh bằng -1; tung độ đỉnh bẳng 1.
Nên hàm số là
2
2.y x x
Câu 48: Đồ thị sau là đồ thị của hàm số nào?
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A.
2
23y x x
. B.
2
21y x x
. C.
2
22y x x
. D.
2
21y x x
.
Lời giải:
Đồ thị đã cho là đồ thị của hàm số bậc hai, giả sử
2
,0y ax bx c a
Vì bề lõm của parabol hướng xuống nên
0a
.
Dựa vào các đáp án, ta có
1a 
.
Đỉnh của parabol là
1;2
nên
1 2 2
2
b
ba
a
2
1 2 1.1 2.1 2 1y c c
. Vậy
2
21y x x
.
Câu 49: Hình bên là đồ thị của hàm số nào sau đây?
A.
2
23y x x
. B.
2
23y x x
. C.
2
23y x x
. D.
2
23y x x
.
Lời giải:
Dựa vào hình bên ta có
+ Tọa độ đỉnh
(1;4)I
.
+) Đồ thị hàm số cắt trục tung tại điểm có tung độ
3y
.
+) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
1x 
và
3x
.
Do đó hình bên là đồ thị hàm số của hàm số
2
23y x x
.
Câu 50: Hàm số
2
4 3 1y x x
có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào?
A. . B. . C. . D. .
Lời giải:
Từ hàm số
2
4 3 1y x x
ta có hệ số
1c
tọa độ giao điểm với trục
Oy
tại
0; 1
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Nên ta loại
A, C
và B, D thỏa mãn.
Hoành độ đỉnh của Parabol là
3
0
28
b
x
a
loại
D
và B thỏa mãn.
Câu 51: Đồ thị hàm số
2
2y x x
thể hiện bởi hình vẽ nào dưới đây?
A.
x
y
2
-1
O
1
B.
x
y
2
O
1
C.
x
y
1
2
-1
O
1
D.
x
y
-1
2
-1
O
1
Lời giải:
Cách 1: Vẽ
22
: 2 2P y x x y x x
bằng cách giữ phần đồ thị của
P
phía trên trục
Ox
và lấy đối xứng phần
P
phía dưới trục
Ox
qua trục
.Ox
Kiểm tra đỉnh parabol
2;2
ta thấy đồ thị ở đáp án D là phù hợp.
Cách 2: Kiểm tra điểm
1;1
thuộc đồ thị và xác định giao điểm với
,Ox
ta thấy đồ thị ở đáp
án B là phù hợp.
Câu 52: Cho hàm số
2
()y f x x bx c
có đồ thị như hình vẽ bên dưới:
Nhận định nào sau đây đúng về dấu hệ số
b
và
?c
A.
0b
;
0c
. B.
0b
;
0c
. C.
0b
;
0c
. D.
0b
;
0c
.
Lời giải:
Bề lõm của đồ thị hướng xuống nên
0a
.
Hoành độ đỉnh của đồ thị có giá trị dương nên
0 0 0
2
b
bb
a
.
Đồ thị cắt trục tung tại điểm mà tung độ mang giá trị âm nên
0c
.
Câu 53: Đồ thị hàm số:
2
y ax bx c
như hình vẽ bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Trong các hệ số
,,abc
có bao nhiêu giá trị dương?
A.
1
.
B.
0
. C.
2
. D.
3
.
Lời giải:
Từ đồ thị hàm số ta có
0a
, hoành độ đỉnh của đồ thị hàm số là:
1 0, 0 0
2
b
x a b
a
.
Giao điểm với trục tung có tung độ bằng
3 3 0c
.
Vậy các giá trị dương là
,bc
.
Câu 54: Cho hàm số
2
y f x ax bx c
có bảng biến thiên như sau :
Khẳng định nào sau đây sai ?
A.
0a
. B.
0b
. C.
0c
. D. TXĐ
D
.
Lời giải:
Từ bảng biến thiên của hàm số ta có
0, 1ac
và hàm số luôn xác định trên , đồng thời
hoành độ đỉnh parapol là
0
2
b
x
a
nên
0.b
Câu 55: Cho hàm số
2
y f x ax bx c
có đồ thị như hình bên dưới:
Khẳng định nào dưới đây đúng?
A.
0, 0, 0abc
. B.
0, 0, 0a b c
.
C.
0, 0, 0abc
. D.
0, 0, 0a b c
.
Lời giải:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Đồ thị là parabol có bề lõm quay xuống nên
0a
.
Đồ thị cắt trục trung tại điểm phía dưới trục hoành nên
0c
.
Hoành độ đỉnh dương nên
,ab
trái dấu, mà
0a
nên
0b
.
Câu 56: Cho hàm số
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Tích
abc
bằng
A.
12
B.
12.
C.
3.
D.
0.
Lời giải:
Đồ thị hàm số
2
y ax bx c
đi qua
0;3 3Ac
Đồ thị hàm số
2
y a x bx c
đi qua
1;0 0 B a b c
Đồ thị hàm số
2
y a x bx c
đi qua
3;0 0 9 3C a b c
Ta có:
31
04
9 3 0 3
ca
a b c b
a b c c






Vậy ta có:
. . 1. 4 .3 12.abc
Câu 57: Cho hàm số
2
f x ax bx c
có đồ thị như hình bên dưới:
Giá trị của biểu thức:
2T a b c
bằng
A.
1.
B.
1.
C.
0.
D.
2.
Lời giải:
Đồ thị cắt trục tung tại điểm có tung độ bằng
1
nên
1c 
. Suy ra
2
1y ax bx
Trục đối xứng
1 1 2 0
2
b
x a b
a
.
Khi đó
2 0 ( 1) 1.T a b c
Câu 58: Cho hàm số
2
y f x ax bx c
có đồ thị như hình vẽ bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Giá trị của biểu thức
42T a b c
bằng
A.
8
. B.
6
. C.
3
. D.
4
.
Lời giải:
Từ giả thiết ta có:
03
43
f
f
3
16 4 3
c
a b c
3
4
c
ba

.
Do đó
4 2 6T a b c
.
Câu 59: Cho parabol
2
y ax bx c
có đồ thị như hình vẽ bên dưới:
Khẳng định nào dưới đây đúng?
A.
0; 0; 0a b c
. B.
0; 0; 0a b c
. C.
0; 0; 0a b c
. D.
0; 0; 0a b c
.
Lời giải:
+ Parabol có bề lõm hướng xuống nên
0a
.
+ Parabol cắt trục
Oy
tại điểm có tọa độ là
0;3
nên
30c 
.
+ Parabol có hoành độ đỉnh
11
2
I
b
x
a
mà
0a
nên
0b
.
Câu 60: Tọa độ giao điểm của đường thẳng
:4d y x
và parabol
2
7 12y x x
là
A.
(2;2)
và
(4;0)
. B.
(2;2)
và
(4;8)
.
C.
(2; 2)
và
(4;0)
. D.
( 2;6)
và
(4;8)
.
Lời giải:
Phương trình hoành độ giao điểm
2
4 7 12x x x
2
6 8 0xx
2
4
x
x
.
Với
2x
suy ra
2y 
.
Với
4x
suy ra
0y
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Vậy tọa độ giao điểm cần tìm là
(2; 2)
và
(4;0)
.
Câu 61: Hai đồ thị hàm số
2
23y x x
và
21yx
có bao nhiêu điểm chung?
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải:
Xét phương trình:
22
2 3 2 1 4 4 0 2x x x x x x
.
Vì phương trình có một nghiệm nên hai đồ thị hàm số cắt nhau tại 1 điểm.
Câu 62: Toạ độ giao điểm của đồ thị hàm số
2
2y x x
với trục tung là
A.
0; 2 .
B.
2;0 .
C.
0;2 .
D.
1;0
.
Lời giải:
Gọi M là giao điểm của trục tung và đồ thị của hàm số
2
2y x x
. Khi đó tọa độ của M có
dạng
0;
M
My
.
Do M thuộc đồ thị của hàm số
22
2 0 0 2 2
M
y x x y
.
Vậy
0;2M
.
Câu 63: Số giao điểm của Parabol
2
: 4 4P y x x
với trục hoành là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải:
Xét
2
2
0 4 4 0 2 0 2y x x x x
.
Vậy Parabol
2
: 4 4P y x x
giao với trục hoành tại một điểm
2;0
.
Câu 64: Đồ thị hàm số nào sau đây tiếp xúc trục hoành?
A.
2
1
2y x x
. B.
2
2
32y x x
. C.
2
3
2 2 1y x x
. D.
2
4
44y x x
.
Lời giải:
Xét hàm số
2
4
44y x x
Ta có:
2
4 4 0 2x x x
(nghiệm kép) nên đồ thị hàm số
4
y
tiếp xúc cắt trục hoành.
Câu 65: Toạ độ giao điểm của parabol
2
1
( ): 2 2 3P y x x
với parabol
2
2
( ): 6P y x x
là
A.
1;7
và
3;27
. B.
7;1
và
27;3
. C.
1;3
và
3;15
. D.
3; 1
và
15; 3
.
Lời giải:
Phương trình hoành độ giao điểm:
2 2 2
1
2 2 3 6 4 3 0
3
x
x x x x x x
x
Vậy có hai giao điểm cần tìm:
1;7
và
3;27
.
Câu 66: Cho hàm số
2
f x ax bx c
có đồ thị như hình vẽ bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Phương trình
2fx
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 67: Cho hàm số
2
f x ax bx c
có đồ thị như hình vẽ bên dưới:
Phương trình
2fx
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải:
Ta có
2
2
2
fx
fx
fx


. Dường thẳng
2y
cắt đồ thị
y f x
tại 2 điểm phân biệt
nên
2fx
có 2 nghiệm phân biệt. Đường thẳng
2y 
không cắt đồ thị
y f x
nên
phương trình
2fx
vô nghiệm. Vậy phương trình đã cho có 2 nghiệm phân biệt.
Câu 68: Cho hàm số
2
0y f x ax bx c a
có bảng biến thiên như sau:
Tìm tất cả các giá trị của
m
để phương trình
2
| | 1f x m
có 4 nghiệm phân biệt.
A.
21
12
m
m

. B.
12m
. C.
12m
. D.
01m
.
Lời giải:
Dựa vào BBT của hàm số
y f x
, ta suy ra bảng biến thiên của hàm số
||y f x
Để phương trình có 4 nghiệm phân biệt thì
2
21
0 1 1
12
m
m
m

.
Câu 69: Cho hàm số
2
f x ax bx c
có đồ thị như hình bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Số nghiệm của phương trình
2
2 1 1f f x x
là
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Đặt
2
2 1 ,u f x x
phương trình đã cho trở thành
1 (*) fu
Phương trình
(*)
chính là phương trình hoành độ giao điểm của đồ thị đồ thị
fu
và
đường
thẳng
1y 
Dựa vào đồ thị, ta có
0
0
(*)
1
u
uu

Với
2
1
2
2
2
2 1 0 (1)
0 2 1 0
2 1 1 (2)
x x x
u f x x
x x x
Vì
1
0x
nên phương trình
(1)
vô nghiệm
Vì
2
1x
nên phương trình
(2)
luôn có hai nghiệm trái dấu.
Với
2
3
2
00
2
4
2 1 0 (3)
1 2 1
2 1 1 (4)
x x x
u u f x x u
x x x
Vì
3
0x
nên phương trình
(3)
vô nghiệm
Vì
4
1x
nên phương trình
(4)
luôn có hai nghiệm trái dấu.
Vậy phương trình đã cho có
4
nghiệm.
Câu 70: Cho hàm số bậc hai
fx
có đồ thị hàm số như hình bên dưới:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Hỏi
m
thuộc tập hợp nào dưới đây thì phương trình
2
fx mm
có 4 nghiệm thực phân
biệt?
A.
;.; 21 
B.
1;0 1;2 .

C.
;1;0 12
D.
;0 1; . 
Lời giải:
Dựa vào đồ thị, ta thấy phương trình
fx t
có 4 nghiệm thực phân biệt khi và chỉ khi
02t
. Do đó, phương trình
2
fx mm
có 4 nghiệm thực phân biệt khi và chỉ khi
2
1
10
10
02
0
12
1 2 0
12
m
mm
m
mm
m
m
mm
m





Vậy
21;0 1;m 
.
Câu 71: Cho hàm số
2
y f x ax bx c
có đồ thị như hình vẽ.
Số giá trị nguyên của
m
để phương trình
2
f x m
có đúng 4 nghiệm phân biệt là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Đặt
2
0xX
, ta có phương trình
f X m
(*). Để phương trình
2
f x m
có đúng 4
nghiệm phân biệt thì điều kiện là phương trình (*) có đúng 2 nghiệm dương phân biệt.
Đồ thị hàm số
y f X
có dạng như hình vẽ:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Do đó, để phương trình (*) có đúng 2 nghiệm dương phân biệt thì
0m
hoặc
13m
.
Mà
m
nên
0;2m
có hai giá trị nguyên của
m
.
Câu 72: Cho Parabol (P):
2
23 y x x
. Số giá trị nguyên âm của tham số
m
để Parabol (P) cắt
đường thẳng d:
y x m
tại hai điểm phân biệt là
A.
4
. B.
5
. C.
7
. D.
6
.
Lời giải:
Phương trình hoành độ giao điểm:
22
2 3 3 3 0 x x x m x x m
(P) cắt d tại hai điểm phân biệt
Phương trình (1) có hai nghiệm phân biệt
21
0 9 12 4 0 .
4
mm
Vậy các giá trị
m
thỏa mãn yêu cầu đề bài là
5; 4; 3; 2; 1 .m
Câu 73: Cho đường thẳng
: 2 5 1d y m x m
và parabol
22
:3P y x mx m
(
m
là tham số).
Có tất cả bao nhiêu giá trị nguyên của
m
nhỏ hơn 5 để đường thẳng
d
cắt parabol
P
tại
hai điểm phân biệt?
A.
4
. B.
5
. C.
7
. D.
6
.
Lời giải:
PTHĐGĐ:
2 2 2 2
2 5 1 3 2 1 5 2 0 1m x m x mx m x m x m m
.
Đường thẳng
d
cắt parabol
P
tại hại điểm phân biệt khi và chỉ khi PT (1) có hai nghiệm
phân biệt.
Khi đó:
2
2
0 1 5 2 0 3 3 0 1m m m m m
.
Với
m
nguyên và nhỏ hơn 5 ta có
0,1,2,3,4m
. Vậy có 5 giá trị
m
thỏa mãn ycbt.
Câu 74: Đồ thị hàm số
2
2y x x
cắt đường thẳng
2
2y m x
tại hai điểm phân biệt có hoành độ lần
lượt là
12
;xx
. Giá trị của
12
T x x
bằng
A.
2.
B.
2.
C.
4.
D.
2
4.m
Lời giải:
Phương trình hoành độ giao điểm của đường thẳng và Parabol đã cho là
2 2 2 2
2 2 4 0 (1).x x m x x x m
Yêu cầu bài toán tương đương với phương trình
(1)
có 2 nghiệm phân biệt
12
;xx
.
Ta có
'2
4 0, .mm
Do đó phương trình
(1)
luôn có 2 nghiệm phân biệt
12
;xx
.
Theo định lý Viet thì
12
4
4
1
b
xx
a

.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 75: Tìm tập hợp tất cả các giá trị của
a
để đường thẳng
d
:
21y a x a
cắt parabol
P
:
2
1y x x
tại hai điểm phân biệt nằm về hai phía đối với trục tung.
A.
;3 .
B.
;1 .
C.
1; .
D.
.
Lời giải:
Xét phương trình:
22
1 2 1 2 1 0x x a x a x ax a
(1).
Yêu cầu bài toán
Phương trình (1) có hai nghiệm trái dấu
1 0 1.aa
Câu 76: Cho đồ thị hàm số
22
2 2 1y x mx m
cắt đồ thị hàm số
2yx
tại các điểm có hoành
độ lần lượt là
12
;xx
. Gọi
,Mm
là giá trị lớn nhất, nhỏ nhất của
22
1 2 1 2
H x x x x
. Đặt
.T M m
Khẳng định nào sau đây đúng?
A.
10T
. B.
10,20T
. C.
20,30T
. D.
30T
.
Lời giải:
Xét phương trình hoành độ giao điểm của 2 đồ thị
22
2 2 2 1x x mx m
22
2 1 2 1 0 *x m x m
2 đồ thị cắt nhau tại các điểm có hoành độ lần lượt là
12
;xx
phương trình
*
có 2
nghiệm
12
;xx
2
2
1 2 1 0mm
2
20mm
02m
.
Theo Vi-et ta có
12
2
12
22
21
x x m
x x m

22
1 2 1 2
H x x x x
2
1 2 1 2
x x x x
2
2
2 2 2 1mm
2
2 8 3mm
BBT
Từ BBT suy ra
27, 3Mm
.Vậy
30T
.
Câu 77: Tìm tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số
2y m x
cắt parabol
2
2y x x
tại hai điểm phân biệt cùng có hoành độ nhỏ hơn 1.
A.
7
. B.
8
. C.
9
. D.
10
.
Lời giải:
Phương trình tương giao
22
2 2 4x x m x x x m
(*).
Xét hàm số
2
4f x x x
với
1x
, có bảng biến thiên như sau:
Để thỏa mãn bài ra thì phương trình (*) phải có 2 nghiệm phân biệt nhỏ hơn 1. Do đó đường
thẳng
ym
phải cắt đồ thị hàm số
y f x
tại hai điểm phân biệt nên
45m
.
Mà
m
nên
3; 2; 1;0;1;2;3;4m
có 8 giá trị nguyên của
m
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 78: Gọi
S
là tập hợp các giá trị thực của tham số
m
sao cho Parabol
2
:3P y x x m
cắt trục
Ox
tại hai điểm phân biệt
,AB
thoả mãn
2OA OB
. Tổng các phần tử của tập hợp
S
bằng
A.
2
. B.
3
. C.
18
. D.
16
.
Lời giải:
Phương trình hoành độ giao điểm của parabol
2
:3P y x x m
và trục
Ox
là
2
3 0 1x x m
.
Parabol
P
cắt trục
Ox
tại hai điểm phân biệt
,1AB
có hai nghiệm phân biệt
9
0 9 4 0
4
mm
.
Giả sử
,
AB
xx
là hoành độ hai điểm
,AB
. Ta có
3
.
AB
AB
xx
x x m

.
Ta có
2 2 2 2
2
2 4 4
2
AB
AB
AB
xx
OA OB OA OB x x
xx

.
Với
2
AB
xx
ta được
32
. 1 2
2.
A B A
A B B
A B A B
x x x
x x m x m
x x x x m






(thoả mãn điều kiện
9
4
m
).
Với
2
AB
xx
ta được
36
. 3 18
2.
A B A
A B B
A B A B
x x x
x x m x m
x x x x m





(thoả mãn điều kiện
9
4
m
).
Vậy tổng các giá trị của
m
là
2 18 16
.
Câu 79: Có bao nhiêu giá trị của tham sô
m
để đường thẳng
: ( 1) 2d y m x
cắt Parabol
2
: 2 2P y x m x m
tại hai điểm phân biệt
,AB
sao cho
42AB
?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải:
Xét phương trình tìm hoành độ giao điểm của
P
và
d
:
22
2 2 1 2 2 2 0x m x m m x x x m
Để đường thẳng
d
cắt Parabol
P
tại hai điểm phân biệt
,AB
thì
0 3 0 3mm
Gọi
11
; 1 2A x m x 
và
22
; 1 2B x m x 
.
Khi đó:
2
2
2
2 1 2 1
11AB x x m x m x


2
2 2 2
22
2 1 2 1 2 1 1 2 1 2
1 1 4x x m x x x x m m x x x x




2 2 3 2
1 4 4 2 1 4 12 4 12 4 12m m m m m m m


.
Theo giả thiết:
32
4 2 4 12 4 12 32 1AB m m m m
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Câu 80: Gọi
,AB
là hai giao điểm của đường thẳng
:1y x k
và parabol
2
:.P y x x
Tìm tập
hợp tất cả các giá trị của tham số
k
để trung điểm
I
của đoạn thẳng
AB
nằm trên đường
thẳng
: 2.d y x
A.
2; 1 .
B.
2; 1 .
C.
2.
D.
1.
Lời giải:
Xét phương trình:
22
1 2 1 0x x x k x x k
(1)
Để
cắt
P
tại hai điểm phân biệt
Phương trình (1) có hai nghiệm phân biệt
4 4 1 4 0 0k k k
(*).
Lúc đó, hai giao điểm tương ứng là
1 1 2 2
; 1 , ; 1 .A x x k B x x k
Do
I
là trung điểm của
AB
nên
12
12
1
2
1; .
22
2
I
I
xx
x
Ik
x x k
xk


Yêu cầu bài toán
1; 1 2 1.I k d k k
Câu 81: Cho hàm số
2
22y x x
có đồ thị là parabol
P
và đường thẳng
d
có phương trình
y x m
. Giá trị của
m
để đường thẳng
d
cắt parabol
P
tại hai điểm phân biệt
,AB
sao
cho
22
OA OB
đạt giá trị nhỏ nhất là
A.
1
2
m 
. B.
5
2
m 
. C.
1
2
m
. D.
5
2
m
.
Lời giải:
Phương trình hoành độ giao điểm của đường thẳng
d
cắt parabol
P
là
22
2 2 3 2 0 1x x x m x x m
.
Để đường thẳng
d
cắt parabol
P
tại hai điểm phân biệt thì phương trình
1
có 2 nghiệm
phân biệt
17
9 4 8 17 4 0
4
m m m
.
Khi đó, phương trình
1
có 2 nghiệm
12
,xx
thỏa mãn
12
12
3
.2
xx
x x m


.
Giả sử
1 1 2 2
, , ;A x x m B x x m
, ta có:
22
2 2 2 2
1 1 2 2
OA OB x x m x x m
2
2 2 2 2
1 2 1 2 1 2 1 2 1 2
2
22
2 2 2 2 2 2 2
5 27 27
2 9 2 4 6 2 2 10 26 2
2 2 2





x x m x x m x x x x m x x m
m m m m m m
Vậy
22
OA OB
đạt giá trị nhỏ nhất khi
5
2
m
.
Câu 82: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng
3y mx
cắt parabol
2
:2P y x x
tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB
thuộc đường thẳng
6.yx
Tính tổng tất cả các phần tử của S.
A.
5
. B.
1
. C.
3
. D.
3
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Lời giải:
Phương trình hoành độ giao điểm:
22
2 3 2 3 0.x x mx x m x
Để đường thẳng cắt parabol tại hai điểm phân biệt thì
2
0 2 12 0, .mm
Giả sử
12
,xx
là hai nghiệm, khi đó
1 2 1 2
1 1 2 2
; 3 , ; 3 ; 3
22
x x x x
A x mx B x mx I m




Theo Viet
2
12
2 2 2 2 6
2 ; 3 ;
2 2 2 2






m m m m m
x x m I m I
2
2
1
2 6 2
: 6 6 3 4 0 3.
4
22

m
m m m
I d y x m m S
m
Câu 83: Biết Parabol
P
:
2
4y ax x c
có đỉnh
1; 6I 
. Tính
S a c
A.
6
. B.
6
. C.
2
. D.
2
.
Lời giải:
Cách 1:
Áp dụng công thức đỉnh của Parabol ta có:
1
2
b
a
4
1
2a
2a
.
6
4a
2
4
6
4
b ac
a
2
4 4.2.
6
4.2
c

4c
.
Vậy
S a c
24
2
.
Cách 2:
14f a c
64ac
2ac
.
Câu 84: Cho hàm số
2
y f x x bx c
có đồ thị là một Parabol
P
có đỉnh
1; 4I
. Tính
bc
.
A.
12
. B.
8
. C.
10
. D.
5
.
Lời giải:
Ta có:
2
1
5
2
3
14
b
b
bc
c
bc




.
Câu 85: Tìm parabol
2
: 3 2,P y ax x
biết rằng parabol có trục đối xứng
3x 
?
A.
2
3 2.y x x
B.
2
1
2.
2
y x x
C.
2
1
3 3.
2
y x x
D.
2
1
3 2.
2
y x x
Lời giải:
Ta có trục đối xứng của
2
: 3 2P y ax x
là
31
3
22
xa
a
Vậy
2
1
: 3 2.
2
P y x x
Câu 86: Đồ thị của hàm số
2
3y ax x c
đi qua hai điểm
2;3A
và
1;6B
. Giá trị biểu thức
36T a c
bằng
A.
17
. B.
38
. C.
72
. D.
73
.
Lời giải:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Đồ thị của hàm số
2
3y ax x c
đi qua hai điểm
2;3A
và
1;6B
nên ta có:
4 6 3 4 9 2
3 6 3 1
a c a c a
a c a c c

Suy ra
36 36.2 1 73T a c
Câu 87: Cho đồ thị hàm số
2
4y ax bx
có đỉnh là điểm
1; 2I
. Tính
3ab
.
A.
20
. B.
18
. C.
30
. D.
25
Lời giải:
Do đồ thị hàm số
2
4y ax bx
có đỉnh là điểm
1; 2I
1
2
12
b
a
y

20
42
ab
ab

6
12
a
b

3 30ab
.
Câu 88: Xác định
2
:P y ax bx c
, biết
P
có đỉnh là
(1;3)I
và đi qua
(0;1)A
A.
2
: 2 3 1P y x x
. B.
2
: 2 4 1P y x x
.
C.
2
: 2 4 1P y x x
. D.
2
: 2 4 1P y x x
.
Lời giải:
Ta có tọa độ đỉnh
( ; )
24
b
I
aa

3
1
2
abc
b
a

(1)
()P
đi qua điểm
(0;1)A
nên
1c
thay vào (1) ta được
2; 4ab
Câu 89: Cho parabol
2
:P y ax bx c
, , ; 0a b c a
có hoành độ đỉnh bằng 1 và đi qua hai
điểm
0 ; 1M
,
1 ; 3N
. Khi đó parabol
P
là đồ thị của hàm số nào?
A.
2
2 4 1y x x
. B.
2
41y x x
. C.
2
2 4 1y x x
. D.
2
2 4 1y x x
.
Lời giải:
+) Hoành độ của đỉnh Parabol bằng
1 1 2
2
b
ba
a
.
+) Đồ thị hàm số đi qua các điểm
0; 1
và
1; 3
. Như vậy ta có hệ phương trình:
2
2
2
2 1 2
.0 .0 1 1 2 4
3 2 1
.1 .1 3
ba
b a c a
a b c c b a b
a b c a b c
a b c

.
Vậy parabol
P
là đồ thị của hàm số
2
2 4 1y x x
.
Câu 90: Biết Parabol
2
y ax bx c
đi qua điểm
8;0A
và có đỉnh
6; 12I
, khi đó
abc
là:
A. 85 B. 63. C. 36. D. 96.
Lời giải:
Ta có:
8;0
64 8 0
6; 12
36 6 12
AP
a b c
I
IP
a b c


Hoành độ đỉnh:
6
2
b
x
a

12 0a b II
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Từ
I ; II
được hệ:
64 8 0
36 6 12
12 0
a b c
a b c
ab

3
36
96
a
b
c
. Vậy
3 36 96 63abc
.
Câu 91: Biết đồ thị hàm số
2
0y ax bx c a
biết đồ thị hàm số đi qua ba điểm
0;4 ; 1;3 ; 1;9 .A B C
Tính
.ab c
A.
1.
B.
2.
C.
1.
D.
2.
Lời giải:
Hàm số
2
0y ax bx c a
có đồ thị là Parabol
P
.
P
đi qua điểm
0;4A
nên
4c
. Suy ra:
2
: 4 0P y ax bx a
.
P
đi qua điểm
1;3B
nên
2
3 .1 .1 4 1a b a b
.
P
đi qua điểm
1;9C
nên
2
9 . 1 . 1 4 5a b a b
.
Ta có hệ:
2 : 0
1 2 4
51
3
a tmdk a
a b a
a b b a
b





Vậy
6 4 2.ab c
Câu 92: Xác định hàm số bậc hai
2
y ax bx c
biết đồ thị của nó có đỉnh
(1, 1)I
và đi qua
(2,0)A
.
A.
2
32y x x
. B.
2
2y x x
. C.
2
2 4 3y x x
. D.
2
2y x x
.
Lời giải:
Vì
()P
có đỉnh
(1, 1)I
và đi qua
(2,0)A
nên ta có hệ phương trình
1
2 0 1
2
1 1 2
4 2 0 4 2 0 0
b
a b a
a
a b c a b c b
a b c a b c c





. Vậy hàm số cần tìm là
2
2y x x
.
Câu 93: Biết rằng hàm số
2
y ax bx c
đạt giá trị nhỏ nhất bằng 1 và đồ thị hàm số cắt đường thẳng
2022 2yx
tại một điểm trên trục
Oy
. Tính
2 2 2
. S a b c
A.
10
. B.
9
. C.
50
. D.
4
.
Lời giải:
Vi hàm số đạt giá trị nhỏ nhất bằng 1 khi
1x
nên ta có
1
2
1
b
a
abc
.
Giao điểm của đường thẳng
2022 2yx
với trục
Oy
là điểm
0;2A
.
Từ giả thiết ta suy ra đồ thị hàm số đã cho đi qua
0;2A
.
Suy ra
2 .0 .0 2a b c c
Ta có hệ
20
1
ab
ab

1
2
a
b

. Vậy
9S
.
Câu 94: Cho parabol
2
:P y ax bx c
, biết hàm số
2
y ax bx c
đạt giá trị nhỏ nhất là
4
tại
2x
và đồ thị của nó cắt trục tung tại điểm có tung độ là 6. Tính
2.a b c
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A.
6
. B.
5
. C.
4
. D.
2
.
Lời giải:
Do hàm số đạt giá trị nhỏ nhất nên
0a
.
Ta có:
1
2
4
2
2
4 2 4 4 2 2 2
6 6 6



b
a
ba
a
a b c a b b
c c c
(nhận).
Vậy hàm số cần tìm là
2
1
26
2
y x x
.
Vậy
2 1 2 6 5.a b c
Câu 95: Cho hàm số
2
y ax bx c
với
a
,
b
,
c
, hệ số
0.a
Biết rằng hàm số đạt giá trị nhỏ
nhất bằng
1
tại
2x
và đồ thị hàm số đi qua điểm
1;0M
. Tính
.T abc
A.
6T
. B.
5T
. C.
4T
. D.
12T
.
Lời giải:
Tập xác định
D
.
Do đồ thị hàm số đã cho đi qua điểm
1;0M
nên có:
0abc
1
.
Trên , hàm số
2
y ax bx c
đạt giá trị nhỏ nhất bằng
1
tại
2x
, ta có:
0
2
2
4 2 1
a
b
a
a b c

0
40
4 2 1
a
ab
a b c

2
.
Kết hợp
1
và
2
ta có:
0
40
4 2 1
0
a
ab
a b c
abc

1
4 12.
3
a
b T abc
c
Câu 96: Gọi
T
là tổng tất cả các giá trị của tham số
m
để parabol
2
:5P y x x m
cắt trục
Ox
tại
hai điểm phân biệt
,AB
thỏa mãn
4OA OB
. Tính
T
.
A.
64
9
T 
. B.
64
9
T
. C.
2T
. D.
2T 
.
Lời giải:
Phương trình hoành độ giao điểm của
()P
và trục
Ox
là:
2
5 0 (1)x x m
.
()P
cắt trục
Ox
tại hai điểm phân biệt
,AB
thỏa mãn
4OA OB
phương trình
(1)
có hai
nghiệm phân biệt
1
x
,
2
x
thỏa mãn
12
4xx
12
12
0
4
4
xx
xx


12
12
25 4 0
4
4
m
xx
xx


12
12
25
2
4
43
44
m
xx
xx

.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Mặt khác, theo định lý Viet cho phương trình
(1)
thì:
12
12
5
5
.
xx
x x m

.
Với
12
4xx
, thì
11
1
11
45
1
5
.4
4
xx
x
x x m
m



.
Với
12
4xx
, thì
1
11
11
5
45
3
5
.4
100
9
x
xx
x x m
m







.
Vậy có hai giá trị của
m
là
4m
và
100
9
m 
.
Vậy
64
9
T 
.
Câu 97: Cho parabol
P
:
2
y ax bx c
,
0a
biết
P
đi qua
(4;3)M
cắt
Ox
tại
(3;0)N
và
Q
sao
cho
INQ
có diện tích bằng
1
biết hoành độ điểm
Q
nhỏ hơn
3
với
I
là đỉnh của
P
. Tính
abc
.
A.
1
. B.
1
. C.
0
. D.
2
.
Lời giải:
Vì
P
đi qua
(4;3)M
nên
3 16 4a b c
.
1
Mặt khác
P
cắt
Ox
tại
(3;0)N
suy ra
0 9 3a b c
2
,
P
cắt
Ox
tại
Q
nên
;0 , 3Q t t
.
Theo định lý Viét ta có
3
3
b
t
a
c
t
a
Ta có
1
.
2
INQ
S IH NQ
với
H
là hình chiếu của
;
24
b
I
aa




lên trục hoành
Do
4
IH
a

,
33NQ t t
nên
1
1 . 3 1
24
INQ
St
a
2
2
3
3
2 2 8
3 3 3 3
24
t
bc
t t t t
a a a a a



3
.
Từ
1
và
2
ta có
7 3 3 7a b b a
suy ra
3 7 1 4
3
3
at
t
aa

Thay vào
3
ta có
3
32
84
3 3 27 73 49 0 1
3
t
t t t t t
Suy ra
1 4 3a b c
.
Vậy
P
cần tìm là
2
43y x x
.
Câu 98: Có tất cả bao nhiêu giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
21f x x x m
trên
1;2
bằng 5?
A. 3. B. 1. C. 2. D. 4.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Lời giải:
Đặt
2
21g x x x m
. Đồ thị hàm số
gx
là parabol có đỉnh
1;Im
.
Ta có:
14
1
21
gm
gm
gm

, suy ra
1;2
1;2
min
max 4
g x m
g x m

.
Ta xét các trường hợp sau:
Trường hợp 1:
0m
.
1;2
min f x m
5m
.
Trường hợp 2:
4 0 4mm
.
1;2
min 4f x m
4 5 9mm
.
Trường hợp 3:
0 4 4 0m m m
.
1;2
min 0fx
mà theo bài
1;2
min 5fx
nên không có
m
thỏa mãn.
Vậy có hai giá trị của tham số
m
thỏa mãn yêu cầu bài toán là
9m 
và
5m
.
Câu 99: Cho hình chữ nhật
, 10, 6ABCD AB AD
. Trên các cạnh
,,AB BC CD
lấy các điểm
,,P Q R
sao cho
AP BQ CR x
. Giá trị của
x
trong khoảng nào để diện tích tam giác
PQR
đạt giá
trị nhỏ nhất.
R
C
A
B
D
P
Q
A.
3;5
. B.
6;8
. C.
8;10
. D.
4;8
.
Lời giải:
Ta có:
2
1 1 1
10.6 . 10 .6 . . 10 . . 6
2 2 2
8 30.
PQR ABCD ADRP PBQ QCR
S S S S S x x x x x x
xx


Diện tích của tam giác
PQR
là một hàm số bậc hai do đó diện tích của tam giác
PQR
đạt giá
trị nhỏ nhất khi
4
2
b
x
a
.
Vậy
min
14 4
PQR
Sx
.
Câu 100: Biết có 2 giá trị thực của tham số
m
là
12
,mm
để giá trị nhỏ nhất của hàm số
22
( ) 4 4 2y f x x mx m m
trên đoạn [-2; 0] bằng 3. Tổng
12
mm
bằng
A.
3
.
2
B.
1
.
2
C.
1
.
2
D.
3
.
2
Lời giải:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Đồ thị hàm số
y f x
là parabol có hệ số bậc hai là
40
nên bề lõm hướng lên. Hoành độ
TH1: Nếu
24
2
m
m
thì
20
I
x
. Suy ra
fx
đồng biến trên đoạn [-2; 0].
Do đó
2
2;0
min 2 6 16f x f m m
.
Theo yêu cầu bài toán:
2
6 16 3mm
(vô nghiệm).
TH2: Nếu
2 0 4 0
2
m
m
thì
I
x
[-2; 0]. Suy ra
fx
đạt giá trị nhỏ nhất tại đỉnh.
Do đó đỉnh
2
I
m
x
.
2;0
min 2
2
m
mf x f


.
Theo yêu cầu bài toán
3
23
2
mm
(thỏa mãn
40m
).
TH3: Nếu
00
2
m
m
thì
02
I
x
. Suy ra
fx
nghịch biến trên đoạn [-2; 0].
Do đó
2;0
2
in 0 2.m f x f m m
Theo yêu cầu bài toán:
2
2 3 1mmm
(loại) hoặc
3m
(thỏa mãn).
Kết luận:
3
2
m 
hoặc
3m
.
Câu 101: Gọi
S
là tập hợp các giá trị thực của tham số
m
để giá trị nhỏ nhất của hàm số
22
4 4 2y f x x mx m m
trên đoạn
2; 0
bằng 3. Tính tổng
T
các phần tử của
S
.
A.
3
2
T
. B.
9
2
T
. C.
1
2
T
. D.
3
2
T 
.
Lời giải:
Ta có:
4
2 2.4 2
b m m
x
a
Trường hợp 1:
2
4
2
2;0 ; 4 (0; )
0
2
0
2
m
m
m
m
mm


Khi đó, giá trị nhỏ nhất của hàm số là
2
2 6 16f m m
hoặc
2
02f m m
.
*Nếu
22
2 0 6 16 2 8 16 2f f m m m m m m
Thì giá trị nhỏ nhất của hàm số là
22
2 3 6 16 3 6 13 0f m m m m m
.
*Nếu
22
2 0 6 16 2 8 16 2f f m m m m m m
Thì giá trị nhỏ nhất của hàm số là
22
1( )
0 3 2 3 2 3 0
3
m loai
f m m m m
m

.
Trường hợp 2:
2;0 2 0 4 0
22
mm
m
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Khi đó, giá trị nhỏ nhất của hàm số là
2
m
f



Suy ra:
2
2
3
4. 4 . 2 3 2 3
4 2 2
mm
m m m m m
(nhận)
Vậy,
3 3 3
;3 3
2 2 2
ST



.
Câu 102: Tìm tập hợp tất cả các giá trị của tham số
k
để đường thẳng
:3y kx
cắt parabol
2
: 4 3P y x x
tại hai điểm phân biệt
,AB
sao cho diện tích tam giác
OAB
bằng
3
.
2
A.
5; 3 .
B.
3;3 .
C.
5;5 .
D.
5; 3 .
Lời giải:
Xét phương trình:
2
0
4 3 3 4 0 .
4
x
x x kx x x k
xk



Để
cắt
P
tại hai điểm phân biệt
4 0 4kk
(*).
Lúc đó, hai giao điểm tương ứng là
2
0;3 , 4; 4 3 .A Oy B k k k
Gọi
H
là hình chiếu vuông góc của
B
trên
4.
B
OA BH x k
x
y
3
H
B
A
O
1
Theo giả thiết:
3
3 1 3
.3. 4 4 1 .
5
2 2 2
OAB
k
S k k
k


Câu 103: Cho parabol
22
( ): 2 x 3 4 3P y x m m m
(
m
là tham số) có đỉnh
I
. Gọi
, AB
là hai
điểm thuộc
Ox
sao cho
2022AB
. Khi đó
IAB
có diện tích nhỏ nhất bằng:
A.
1011
. B.
2022
. C.
4044
. D.
1010.
Lời giải:
Ta có
P
có đỉnh
2
( ; 2 4 3)I m m m
. Diện tích tam giác
IAB
bằng:
2 2 2
2
11
. ; . . 2 4 3 .2022 1011. 2 4 3 1011. 2 4 3
22
1011. 2 1 1 1011.1 1011.
IAB
S d I AB AB m m m m m m
m
Dấu “=” xảy ra khi
1m
.
Câu 104: Cho Parabol
2
: 4 3P y x x
và đường thẳng
: 2 1d y m x
. Tính tổng các giá trị
của tham số
m
để đường thẳng
d
cắt Parabol
P
tại hai điểm phân biệt
,AB
sao cho diện
tích tam giác
IAB
bằng
10
với điểm
2;3I
.
A.
6
. B.
0
. C.
2
. D.
4
.
Lời giải:
Xét phương trình tìm hoành độ giao điểm của
P
và
d
:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
22
2
4 3 2 1 4 2 4 0
2
x
x x m x x m x m
xm

Để đường thẳng
d
cắt Parabol
P
tại hai điểm phân biệt
,AB
thì
2 2 0mm
.
Gọi
2; 1A
và
2
2; 1B m m
. Ta thấy điểm
A
và điểm
I
nằm trên đường thẳng
2x
và
đoạn thẳng
4IA
. Suy ra:
1
.4. 2 2 10 5 5
2
IAB
S m m m
.
Câu 105: Một vật chuyển động với vận tốc theo quy luật của hàm số bậc hai
2
12v t t t
với
ts
là
quãng thời gian tính từ khi vật bắt đầu chuyển động và
v
(m/s) là vận tốc của vật. Trong
9
giây đầu tiên kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu?
A.
144 / .ms
B.
243 / .ms
C.
27 / .ms
D.
36 / .ms
Lời giải:
Ta có BBT:
t
0
6
9
vt
36
Dựa vào BBT, ta thấy
0;9
max 6 36 / .
t
v t v m s



Câu 106: Một chiếc cổng hình parabol dạng
2
1
2
yx
có chiều rộng
8dm
. Hãy tính chiều cao
h
của
cổng. (Xem hình minh họa)
A.
9hm
. B.
8hm
. C.
7hm
. D.
5hm
.
Lời giải:
HD: Đường thẳng chứa chiều rộng
8dm
cắt
P
tại
4;Ah
.
Điểm
2
1
.4 8
2
A P h h m
.
Câu 107: Một của hàng buôn giày nhập một đôi với giá là
40
đôla. Cửa hàng ước tính rằng nếu đôi
giày được bán với giá
x
đôla thì mỗi tháng khách hàng sẽ mua
120 x
đôi. Hỏi của hàng
bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
A.
80
USD. B.
160
USD. C.
40
USD. D.
240
USD.
Lời giải:
Gọi
y
là số tiền lãi của cửa hàng bán giày.
Ta có
120 40y x x
2
160 4800xx
2
80 1600 1600x
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Dấu
""
xảy ra
80x
.
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá
80
USD.
Câu 108: Cổng Ac-xơ tại thành phố Xanh Lu-i (Mĩ) có hình dạng là một parabol hướng bề lõm xuống
dưới (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có
độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo
phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn
10 m. Giả sử các số liệu trên là chính xác. Hãy tính chiều cao của cổng Ac-xơ (tính từ điểm cao
nhất trên cổng xuống mặt đất).
A. 197,5 m. B. 275,6 m. C. 185,6 m. D. 348,3 m
Lời giải:
Chọn hệ trục
Oxy
như hình vẽ.
Khi đó Parabol có phương trình dạng:
2
0y ax c a
.
Parabol đi qua điểm
81;0B
và
71;43M
nên
2
2
43
0 .81
1520
282123
43 . 71
1520
a
ac
ac
c




.
Chiều cao của cổng Ac-xơ là:
282123
0 185,6072368
1520
h y c
(m).
Câu 109: Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả
bóng được sút lên từ độ cao
1m
sau đó
1
giây nó đạt độ cao
10 m
và
3,5
giây nó ở độ cao
6,25 m
. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét?
A.
11m
. B.
12 m
. C.
13 m
. D.
14 m
.
Lời giải:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
12
10
8
6
4
2
5
y
x
O
A
B
C
Biết rằng quỹ đạo của quả bóng là một cung parabol nên phương trình có dạng
2
y ax bx c
Theo bài ra gắn vào hệ tọa độ và sẽ tương ứng các điểm
A
,
B
,
C
nên ta có
1
10
12,25 3,5 6,25
c
abc
a b c
3
12
1
a
b
c


.
Suy ra phương trình parabol là
2
3 12 1y x x
.
Parabol có đỉnh
(2;13)I
. Khi đó quả bóng đạt vị trí cao nhất tại đỉnh tức
13 mh
.
Câu 110: Một chiếc cổng hình parabol có chiều rộng
12 m
và chiều cao
8 m
như hình vẽ. Giả sử một
chiếc xe tải có chiều ngang
6 m
đi vào vị trí chính giữa cổng . Hỏi chiều cao
h
của xe tải thỏa
mãn điều kiện gì để có thể đi vào cổng mà không chạm tường?
A.
06h
. B.
06h
. C.
07h
. D.
07h
.
Lời giải:
Chọn hệ trục tọa độ như hình vẽ . Parabol có phương trình dạng
2
y ax bx
.
Vì chiếc cổng hình parabol có chiều rộng
12 m
và chiều cao, theo hình vẽ ta có parabol đi qua
các điểm
12;0
và
6;8
, suy ra:
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
2
144 12 0
9
36 6 8 8
3
a
ab
ab
b




.
Suy ra parabol có phương trình
2
28
93
yx
.
Do chiếc xe tải có chiều ngang
6 m
đi vào vị trí chính giữa cổng nên xe sẽ chạm tường tại
điểm
3; 6A
khi đó chiều cao của xe là 6.
Vậy điều kiện để xe tải có thể đi vào cổng mà không chạm tường là
06h
.
Câu 111: Trong số các hình chữ nhật có cùng chu vi bằng
16
, hình chữ nhật có diện tích lớn nhất bằng bao
nhiêu?
A.
64.
B.
4.
C.
16.
D.
8.
Lời giải:
Gọi
x
là chiều dài của hình chữ nhật.
Khi đó chiều rộng là
8 x
.
Diện tích hình chữ nhật là
8xx
.
Lập bảng biến thiên của hàm số bậc hai
2
8f x x x
trên khoảng
0;8
ta được
0;8
max 4 16f x f
.
Vậy hình chữ nhật có diện tích lớn nhất bằng
16
khi chiều dài bằng chiều rộng bằng
4
.
Câu 112: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa
phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x
4m. Hãy tính khoảng cách giữa hai điểm
A
và
B
. (xem hình vẽ bên dưới)
A. 5m. B. 8,5m. C. 7,5m. D. 8m.
Lời giải:
Gắn hệ trục tọa độ
Oxy
như hình vẽ, chiếc cổng là 1 phần của parabol
P
:
2
y ax bx c
với
0a
.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Do parabol
P
đối xứng qua trục tung nên có trục đối xứng
0 0 0
2
b
xb
a
.
Chiều cao của cổng parabol là 4m nên
0;4G
4c
.
P
:
2
4y ax
Lại có, kích thước cửa ở giữa là 3m x 4m nên
2;3 , 2;3EF
1
3 4 4
4
aa
.
Vậy
P
:
2
1
4
4
yx
.
Ta có
2
4
1
40
4
4
x
x
x

nên
4;0A
,
4;0B
hay
8AB
(m).
Câu 113: Một tấm tôn có bề rộng
AB
là
100cm
. Người ta chọn 2 điểm
M
và
N
trên đoạn
AB
sao cho
có thể làm được một máng nước như hình vẽ. (
AMNB
là hình chữ nhật). Tính
MN
để máng
nước có diện tích
AMNB
lớn nhất.
A.
50 .MN cm
B.
60 .MN cm
C.
45 .MN cm
D.
55 .MN cm
Lời giải:
2 0 50, 50MN x x x cm AM NB x
.
Khi đó diện tích bề mặt ngang là
2
2 50 2 100S x x x x
.
Vậy
50MN cm
thì
2
max 1250S cm
.
Câu 114: Một người ném một quả bóng từ độ cao cách mặt đất 80m, tại thời điểm 1 giây sau khi ném,
người ta đo được độ cao của quả bóng so với mặt đất là 128m. Biết rằng quỹ đạo bay của quả
bóng là một đường Parabol (như hình vẽ). Tính độ cao tối đa mà quả bóng đạt được.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
A.
143m
. B.
144m
. C.
144,5m
. D.
145m
.
Lời giải:
Gọi
2
()h t at bt c
.
Từ giả thiết bài toán, Parabol qua các điểm
0;80 , 5;0 , 1;128A B C
.
Nên ta có hệ phương trình
80 80 16
25 5 0 25 5 80 64
128 48 80
c c a
a b c a b b
a b c a b c
.
2
( ) 16 64 80h t t t
Tọa độ đỉnh của Parabol là
2;144S
.
Vậy quả bóng đạt độ cao tối đa là 144m.
Câu 115: Cô Tình có
60m
lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một
cạnh là tường, cô Tình chỉ cần rào
3
cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính
hộ diện tích lớn nhất mà cô Tình có thể rào được?
A.
2
400m
. B.
2
450m
. C.
2
350m
. D.
2
425m
.
Lời giải:
y
x
x
Gọi hai cạnh của hình chữ nhật có độ dài là
,xy
(như hình vẽ);
0 , 60xy
.
Ta có
2 60 60 2x y y x
.
Diện tích hình chữ nhật là
1 1 2 60 2
60 2 .2 60 2 450
22
xx
S xy x x x x
x




.
Vậy diện tích hình chữ nhật lớn nhất là
2
450 m
, đạt được khi
15, 30xy
.
Câu 116: Dây truyền đỡ nền cầu treo có dạng Parabol
ACB
như hình vẽ. Đầu cuối của dây được gắn
chặt vào điểm
A
và
B
trên trụ cốt thép bê tông
AA
và
BB
với độ cao
30(m)
so với nền cầu.
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chiều dài nhịp
200(m)AB

. Độ cao ngắn nhất của dây truyền trên nền cầu là
5(m)OC
.
Người ta nối dây đỡ với nền bằng
7
sợi cáp song song cách đều hai trụ
AA
và
BB
.
Xác định
tổng các chiều dài
7
các dây cáp treo đó.
A.
78,15(m)
. B.
78,75(m)
. C.
72,75(m)
. D.
80,70(m)
.
Lời giải:
Chọn trục
Oy
trùng với trục đối xứng của Parabol, trục
Ox
nằm trên nền cầu như hình vẽ.
Khi đó ta có
(100;30), (0;5)AC
, ta tìm phương trình của Parabol có dạng
2
y ax bx c
.
Parabol có đỉnh là
C
và đi qua
A
nên ta có hệ phương trình:
2
1
0
2 400
.0 .0 5 0
.100 .100 30 5
b
a
a
a b c b
a b c c







. Suy ra Parabol có phương trình
2
1
5
400
yx
.
Bài toán đưa việc xác định chiều dài các dây cáp treo sẽ là tính tung độ những điểm
1 2 3
,,M M M
của Parabol. Ta dễ dàng tính được tung độ các điểm có các hoành độ
1 2 3
25, 50, 75x x x
lần lượt là
12
6,5625(m), 11,25(m)yy
3
19,0625(m)y
.
Do đó tổng độ dài các dây cáp treo cần tính là:
6,5625 11,25 19,0625 .2 5 78,75(m)
.
_________________HẾT_________________
Huế, 10h20’ Ngày 03 tháng 01 năm 2023
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Chủ đề 2: HÀM SỐ BẬC HAI I. TÓM TẮT LÝ THUYẾT
1) Hàm số bậc hai có dạng 2
y ax bx c;a;b;c  ;a  0.
2) Khảo sát sự biến thiên của hàm số bậc hai Xét hàm số 2
y ax bx c;a;b;c  ;a  0. +) TXĐ: D  .
+) Đồ thị hàm số bậc hai có dạng parabol P với bề lõm hướng lên trên với a  0, bề lõm hướng
xuống dưới với a  0. b
- Trục đối xứng của P là x   . 2ab  
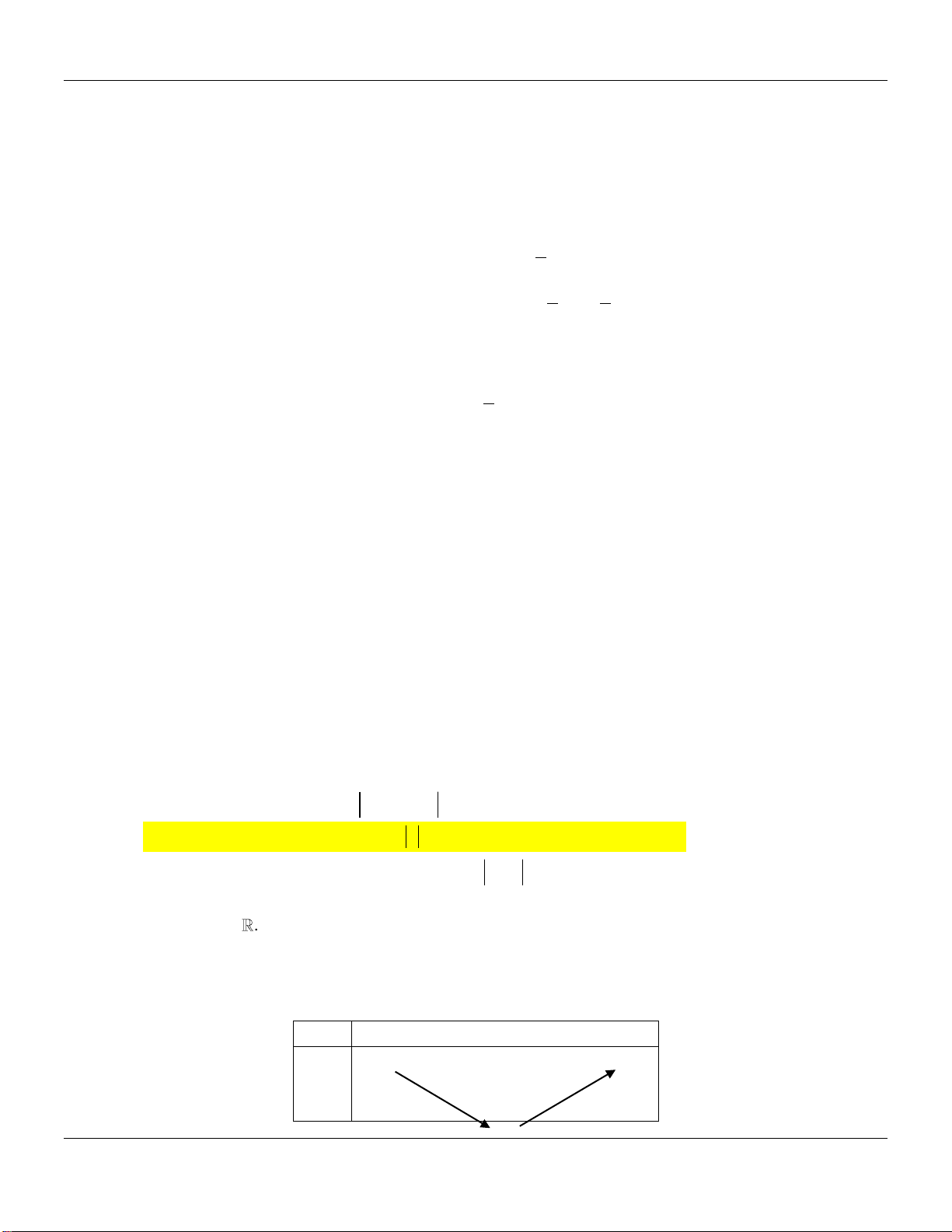
- Đỉnh của P là I  ;   .  2a 4a a  0 a  0 y y -Δ __ 4a __ -b 2a x O x 1 O 1 __ -b 2a -Δ __ 4a
- Để vẽ đường parabol 2
y ax bx c ta tiến hành theo các bước sau: b  
1. Xác định toạ độ đỉnh I  ;    ;  2a 4a
2. Vẽ trục đối xứng   b x ; 2a
3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài
điểm đặc biệt trên parabol; 4. Vẽ parabol.
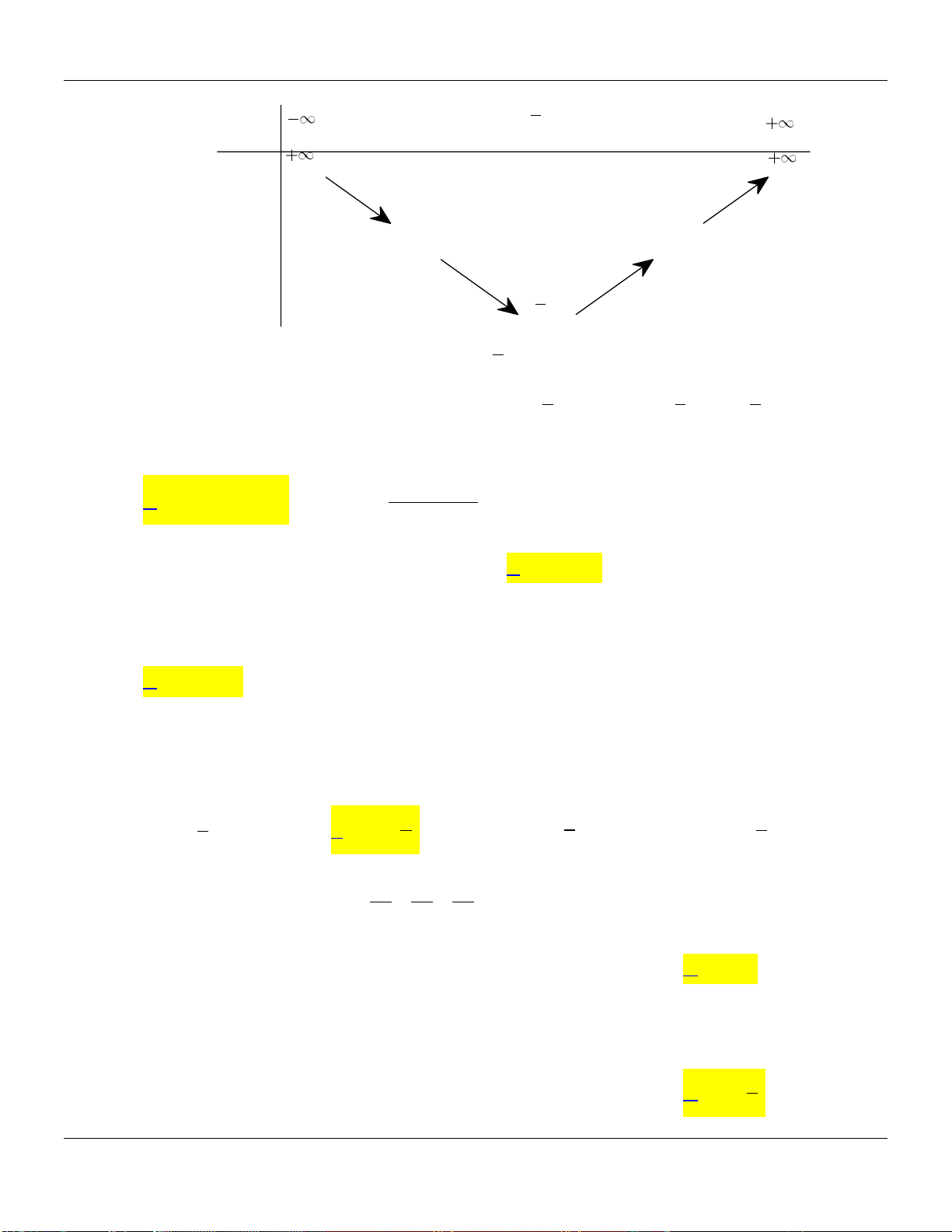
+) Sự biến thiên của hàm số a  0 a  0 Bảng biến thiên: Bảng biến thiên: x  b   x  b   2a 2a     y y 4a   4a    b   b
+) Hàm số đồng biến (tăng) trên  ;   .
+) Hàm số đồng biến (tăng) trên ;   .  2a   2a   b   b
+) Hàm số nghịch biến (giảm) trên ;  
. +) Hàm số nghịch biến (giảm) trên  ;   .  2a   2a
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Nhận xét: b
+) Khi a  0 : Hàm số có giá trị nhỏ nhất bằng
đạt được tại x   . 4a 2ab
+) Khi a  0 : Hàm số có giá trị lớn nhất bằng
đạt được tại x   . 4a 2a II. BÀI TẬP TỰ LUẬN Câu 1:
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) 2
y x  3x  2; b) 2 y  2
x  5x  2; c) 2
y  x  2x  1; d) 2 y  2
x x  3; e) 2 y x  2; f) 2
y x  2x  1. Câu 2:
Xác định hàm số bậc hai 2
y  2x bx c, biết đồ thị của nó:
a) Có trục đối xứng là x  1 và cắt trục tung tại điểm có tung độ là 4.
b) Có đỉnh là I 1; 2 .
c) Có hoành độ đỉnh là 2 và đi qua điểm A1; 2 . Câu 3:
Xác định parabol P 2
: y ax bx c; a;b;c  , a  0. Biết P đi qua các điểm A 1  ;6 , B3;  2 và C 2;0. Câu 4:
Xác địnhparabol P 2
: y ax bx c; a;b;c  , a  0. Biết P đi qua điểm A1;8 và có
đỉnh I 2; 1. Câu 5: Xác định hàm số 2
y ax bx ca  0 biết hàm số đạt giá trị nhỏ nhất bằng 4 tại x  2 và
đồ thị hàm số đi qua điểm A0;6 . Câu 6:
Xác định parapol P : 2
y  2x bx c , biết P :
a) Có trục đối xứng x  1 vá cắt trục tung tại điểm 0; 4 ;
b) Có đỉnh I 1; 2 ;
c) Đi qua hai điểm A0; 1 và B4;0 ;
d) Có hoành độ đỉnh là 2 và đi qua điểm M 1; 2 . Câu 7:
Xác định parapol P : 2
y ax  4x c , biết P :
a) Đi qua hai điểm A1; 2 và B2; 3 ;
b) Có đỉnh I 2; 1 ;
c) Có hoành độ đỉnh là 3
 và đi qua điểm P2;1 ;
d) Có trục đối xứng là đường thẳng x  2 vá cắt trục hoành tại điểm M 3;0 . Câu 8: Tìm parapol P : 2
y ax bx  2 , biết P :
a) Đi qua hai điểm M 1; 5 và N 2;8 ; 3
b) Đi qua điểm A3; 4 và có trục đối xứng x   ; 4
c) Có đỉnh I 2; 2 ;
d) Đi qua điểm B1;6 , đỉnh có tung độ  1 4 Câu 9:
Xác định parapol P : 2
y ax bx c , biết P :
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
a) Đi qua ba điểm A0; 1  , B1; 1  , C 1  ;1 ;
b) Đi qua điểm D3;0 và có đỉnh là I 1; 4 ;
c) Đi qua A8;0 và có đỉnh I 6;12 ;
d) Đạt GTNN bằng 4 tại x  2 và đi qua A0;6 ; Câu 10: Cho hàm số 2
y x  2x  3 có đồ thị P.
a) Lập bảng biến thiên và vẽ đồ thị P.
b) Dựa vào đồ thị P , biện luận số nghiệm của phương trình 2
x  2x  2m  0.
c) Tìm m để phương trình 2
x  2x  3  m  1 có 4 nghiệm phân biệt.
d) Tìm m để phương trình 2
x  2 x  2  m  0 có 4 nghiệm phân biệt. 2
e) Tìm m để phương trình  f  x  
m 1 f x  m  0 có 8 nghiệm phân biệt.
Câu 11: Tìm m để parabol 2
y x  2x cắt đường thẳng y m tại 2 điểm phân biệt.
Câu 12: Cho parabol  P 2
: y x  2x m 1 . Tìm tất cả các giá trị thực của m để parabol cắt Ox tại
hai điểm phân biệt có hoành độ dương.
Câu 13: Tìm tất cả các giá trị thực của tham số m sao cho parabol  P 2
: y x  4x m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA  3 . OB
Câu 14: Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y mx cắt đồ thị hàm số P 3 2
: y x  6x  9x tại ba điểm phân biệt.
Câu 15: Cho parabol  P 2
: y x  4x  3 và đường thẳng d : y mx  3 . Tìm giá trị thực của tham số
m để d cắt  P tại hai điểm phân biệt ,
A B có hoành độ x , x thỏa mãn 3 3 x x  8 . 1 2 1 2
Câu 16: Tìm tất cả các giá trị thực của tham số m để phương trình 2
x  5x  7  2m  0 có nghiệm thuộc đoạn 1;5 .
III. BÀI TẬP TRẮC NGHIỆM
Câu 17: Trong các hàm số sau hàm số nào là hàm số bậc hai? 3 2x  3x  5 A. 2
y  2x  3x  5 B. y  . C. 2 3
y  2x  3x  5 . D. y  3x  2 . x
Câu 18: Điểm nào sau đây không thuộc đồ thị hàm số 2
y x  2 ?
A. P 2; 2 .
B. Q 3;3.
C. N 2; 2.
D. M 1;   1 .
Câu 19: Đồ thị hàm số 2
y x x đi qua điểm nào dưới đây? A. N  2  ;6 .
B. M 1;  1 .
C. P 2;3 .
D. Q 1;  1 . Câu 20: Cho hàm số 2 y  3
x  4x  3 có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương trình: 2 2 4 4 A. x  .
B. x   . C. x  .
D. x   3 3 3 3
Câu 21: Đỉnh của parabol 2
y x  4x  5 có toạ độ là A. 0; 2 . B. 1; 2 . C. 2;0 . D. 2;  1 .
Câu 22: Tìm m để parabol 2
(P) : y mx  2x  3 có trục đối xứng là đường thẳng x  2 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 1 A. m  2 .
B. m  1.
C. m  1. D. m  . 2
Câu 23: Hàm số nào dưới đây có đồ thị nhận đường thẳng x  2 làm trục đối xứng? A. 2
y  2x  4x  3 . B. 2 y  2
x  4x  3 . C. 2
y x  4x  3 . D. 2
y  x  4x  3 .
Câu 24: Hàm số nào có đồ thị là đường Parabol có đỉnh là I  1  ;3? A. 2 y  2
x  4x  3. B. 2
y  2x  2x 1. C. 2
y  2x  4x  5 . D. 2
y  2x x  2 .
Câu 25: Giá trị nhỏ nhất của hàm số 2
y x  4x  5 là A. y  0. B. y  2 . C. y  2 . D. y  1. min min min min Câu 26: Hàm số 2
y  5x  6x  7 đạt giá trị nhỏ nhất khi 26 3 3 6 A. x  . B. x  .
C. x   . D. x  . 5 5 5 5
Câu 27: Giá trị lớn nhất của hàm số 2
y  x  2x  4 bằng A. 5. B. 5  . C. 1. D. 1  .
Câu 28: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 2
y  x  4x  2 trên đoạn 0;  3 .
Tính giá trị biểu thức M m . A. 1. B. 4  . C. 0 . D. 1  .
Câu 29: Tìm giá trị nhỏ nhất của hàm số 2 2
y x  5  4 x  1 . A. 5 . B. 5  . C. 1. D. 1  . Câu 30: Cho hàm số 2
y ax bx c ,với a  0 . Khẳng định nào sau đây sai? b
A. Hàm số đồng biến trên khoảng  ;    .  2a   b
B. Hàm số nghịch biến trên khoảng  ;     .  2a   b
C. Hàm số nghịch biến trên khoảng ;    .  2a b
D. Đồ thị hàm số có trục đối xứng là đường thẳng x   2a Câu 31: Cho hàm số 2
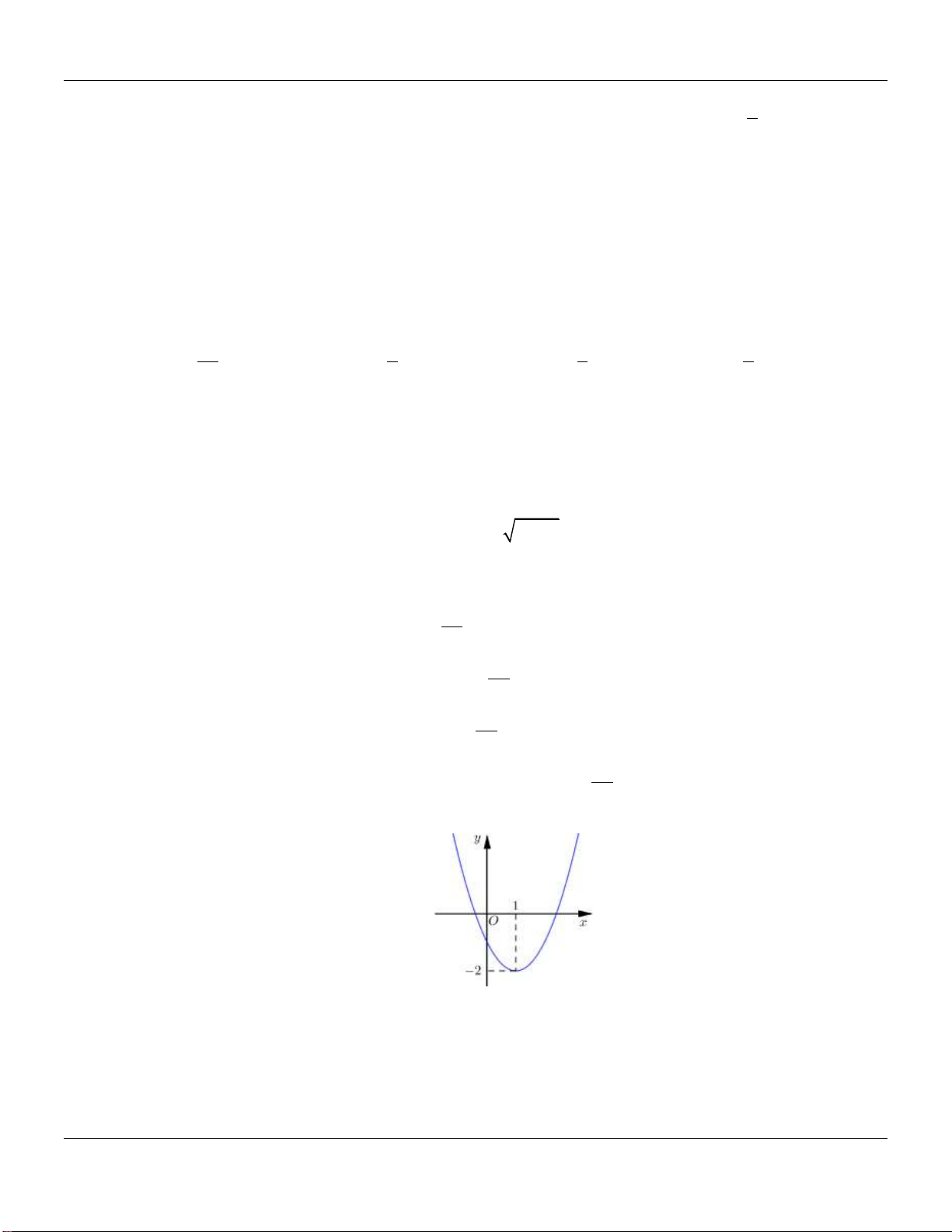
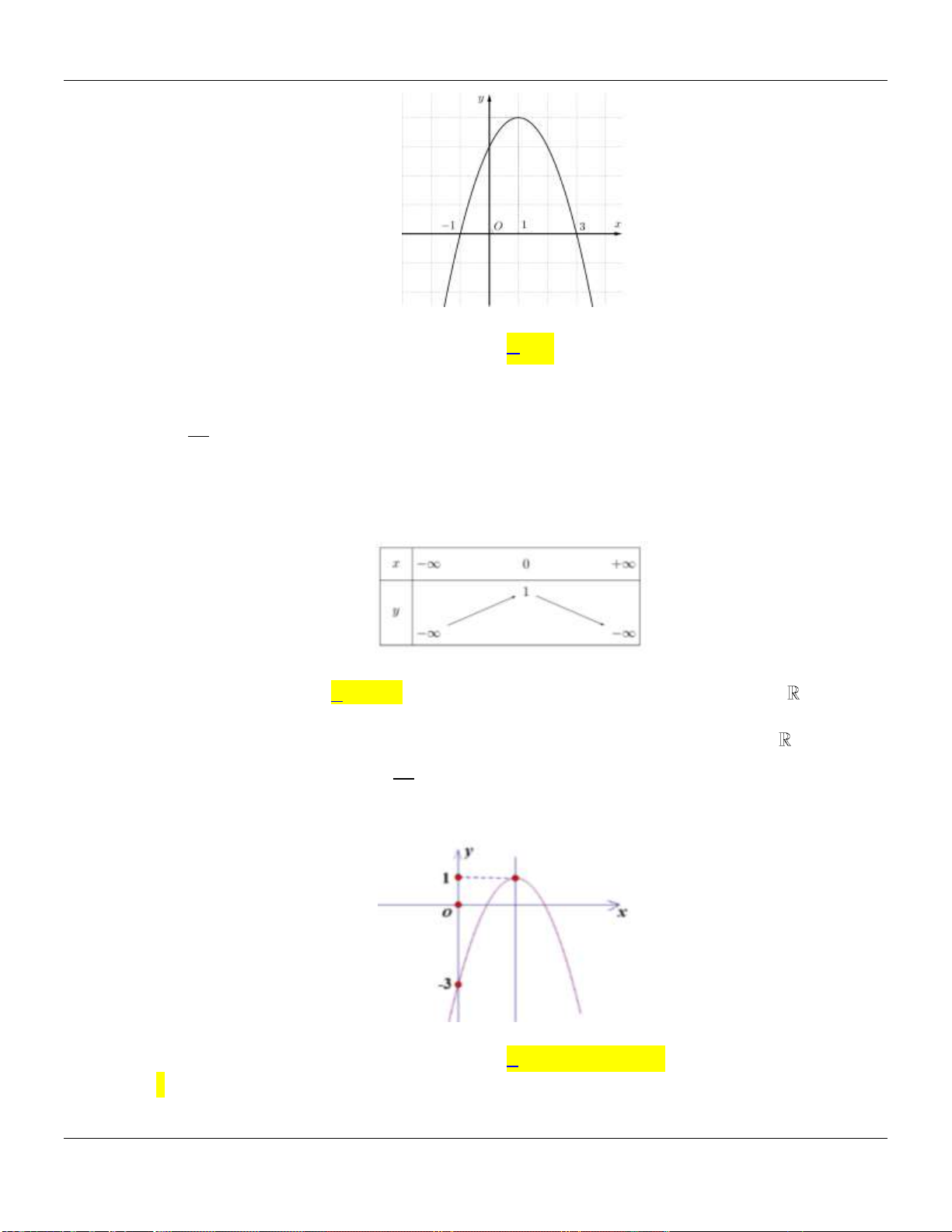
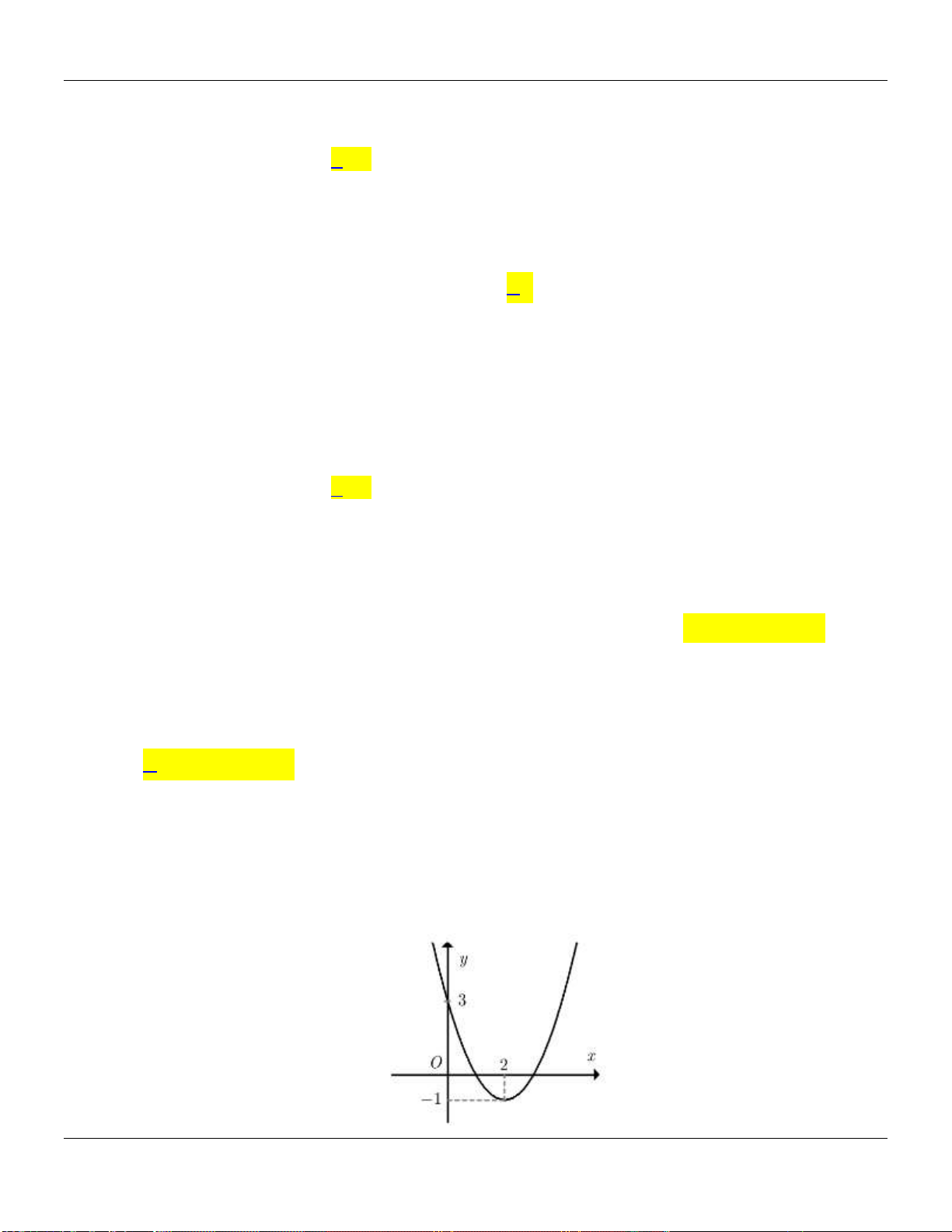
y ax bx c có đồ thị là parabol trong hình sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  2;    . B. 1;   . C.  ;   1 . D.  ;   2 .
Câu 32: Cho hàm số bậc hai có bảng biến thiên như sau:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  2;    .
B.  ; 2 . C. 3 . D.  1;    . Câu 33: Cho hàm số 2
y  2x  4x 1. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng  ; 2 . B. Hàm số nghịch biến trên khoảng ;  .
C. Hàm số đồng biến trên khoảng 2;  . D. Hàm số nghịch biến trên khoảng 2;  . Câu 34: Cho hàm số 2
y  x  3x  5 . Hàm số đã cho đồng biến trên khoảng nào?  3   3   3  A.  ;3 .
B.  ;     . C.  ;   . D. ;    .  2   2   2 
Câu 35: Hàm số nào sau đây đồng biến trên ? A. 2
y x 1. B. 2
y  x x .
C. y  x 1.
D. y x 1. Câu 36: Cho hàm số 2
y x  2x . Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên khoảng 1; .
B. Hàm số đã cho nghịch biến trên khoảng  1  ;.
C. Hàm số đã cho đồng biến trên khoảng  1  ;.
D. Hàm số đã cho nghịch biến trên khoảng 1; .
Câu 37: Cho hàm số f x 2
x  2018x  2020. Khẳng định nào sau đây đúng?  1   1   1   1  A. ff     . B. ff     . 2019 2018  2   2  2019 2018  2   2  1009 1008 1008 1007
C. f 2   f 2 .
D. f 2  f 2 .
Câu 38: Tìm tất cả giá trị tham số m để hàm số 2
y x  m  
1 x m  2 đồng biến trên 1;  .
A. m  3 .
B. m  3 .
C. m  3 . D. m  3 .
Câu 39: Tìm tất cả các giá trị của tham số m để hàm số 2
y x  2 m  
1 x m  2 nghịch biến trên khoảng 1; 2 .
A. m  1.
B. m  1.
C. m  0 . D. m  0 . Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
y f x  m   2 ( )
2 x  2mx m  2021 nghịch biến trên khoảng ;3? A. 2. B. 1. C. 3. D. 4.
Câu 41: Có bao nhiêu giá trị nguyên của tham số m để hàm số 2
y  x  2 m 1 x  3 nghịch biến trên 2 ;  ? A. 3 . B. 6 . C. 5 . D. 4 .
Câu 42: Cho hàm số bậc hai 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Tìm tất cả các giá trị của x để y  0. A.  ;  0.
B. 3;  . C. 0;  3 . D. 0;3 .
Câu 43: Hàm số f x 2  x   2 m m   2
2 x  2m  2m 1. Mệnh đề nào sau đây sai?
A. Hàm số đạt giá trị lớn nhất trên đoạn 1;0 bằng f 0 .
B. Hàm số nghịch biến trên khoảng 0;  .
C. Hàm số đặt giá trị lớn nhất trên đoạn 1;0 bằng f   1 .
D. Hàm số nghịch biến trên khoảng  ;  0.
Câu 44: Hàm số nào dưới đây có bảng biến thiên như sau? A. 2
y  x 1. B. 2
y x  3x 1. C. 2
y  x x 1. D. 2
y  3x 1.
Câu 45: Bảng biến thiên dưới đây là của hàm số nào? 5 3 3 A. 2
y  x x  . B. 2
y x x  . C. 2
y  x x  . D. 2
y  2x x 1. 4 2 2
Câu 46: Bảng biến thiên của hàm số 2
y  x  2x 1 là A. . B. . C. . D. .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
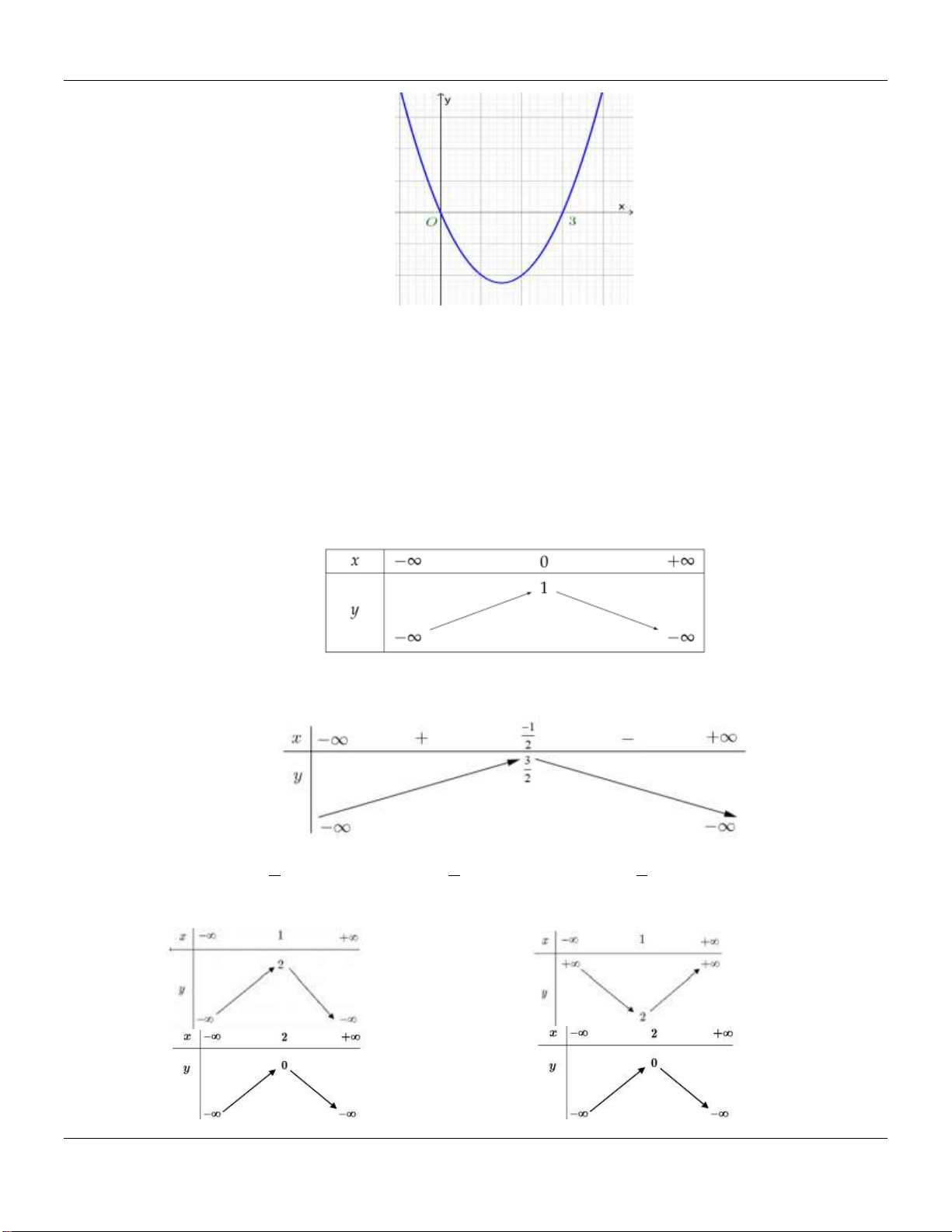
Câu 47: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào? A. 2
y  x  2 . x . B. 2 y x  2 . x C. 2
y  x  2x 1. D. 2
y  x  2 . x
Câu 48: Đồ thị sau là đồ thị của hàm số nào? A. 2
y x  2x  3 . B. 2
y  x  2x 1. C. 2
y  x  2x  2 . D. 2
y  x  2x 1.
Câu 49: Hình bên là đồ thị của hàm số nào sau đây? A. 2
y  x  2x  3 . B. 2
y  x  2x  3 . C. 2
y x  2x  3 . D. 2
y  x  2x  3 . Câu 50: Hàm số 2
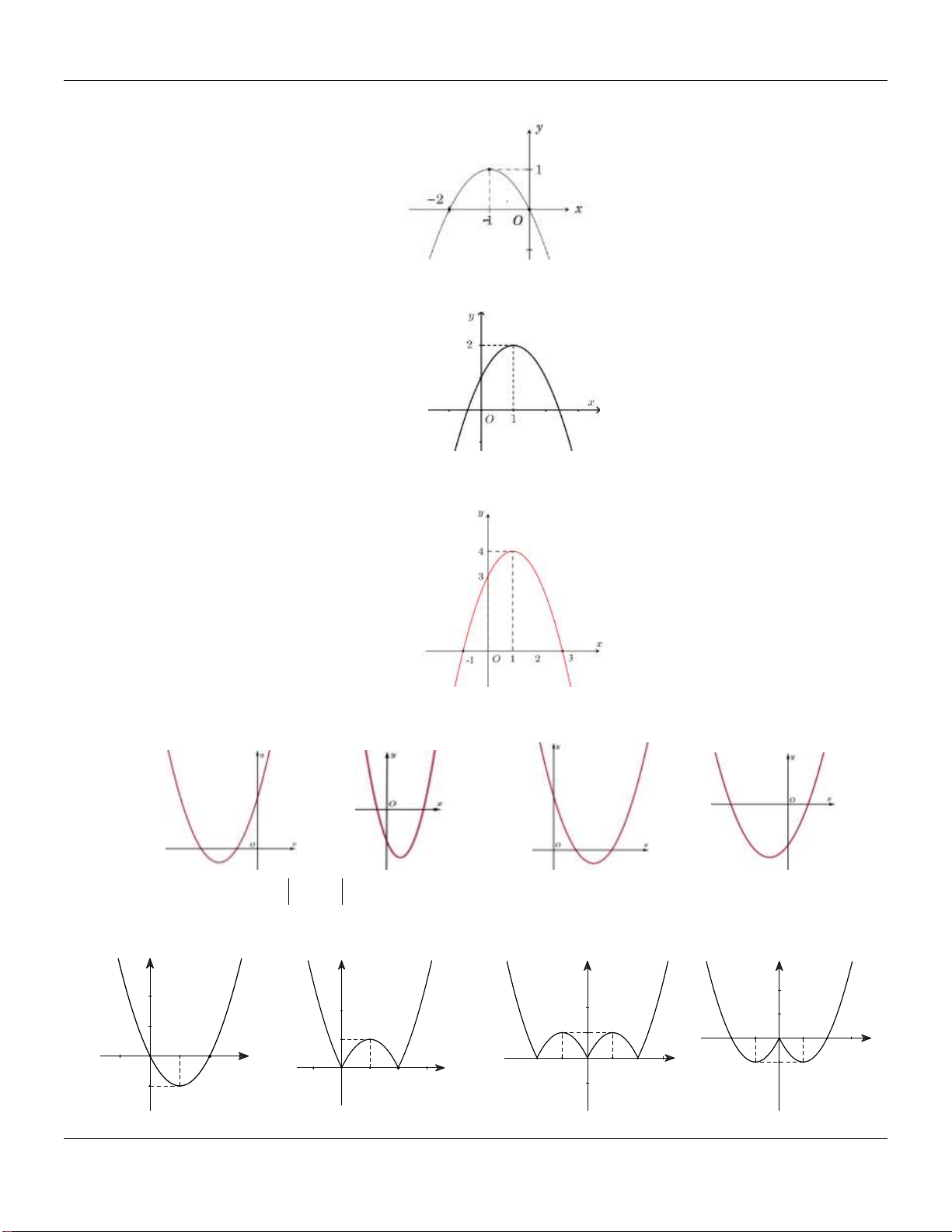
y  4x  3x 1 có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào? A. . B. . C. . D. .
Câu 51: Đồ thị hàm số 2
y x  2x thể hiện bởi hình vẽ nào dưới đây? A. B. C. D. y y y y 1 -1 O 1 1 2 x 2 O x -1 2 O 1 x 2 -1 O 1 x -1
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Câu 52: Cho hàm số 2
y f (x)  x bx c có đồ thị như hình vẽ bên dưới:
Nhận định nào sau đây đúng về dấu hệ số b và c ?
A. b  0 ; c  0 .
B. b  0 ; c  0 .
C. b  0 ; c  0 .
D. b  0 ; c  0 .
Câu 53: Đồ thị hàm số: 2
y ax bx c như hình vẽ bên dưới:
Trong các hệ số a, b, c có bao nhiêu giá trị dương? A. 1. B. 0 . C. 2 . D. 3 .
Câu 54: Cho hàm số    2 y
f x ax bx c có bảng biến thiên như sau :
Khẳng định nào sau đây sai ? A. a  0 .
B. b  0 .
C. c  0 . D. TXĐ D  .
Câu 55: Cho hàm số    2 y
f x ax bx c có đồ thị như hình bên dưới:
Khẳng định nào dưới đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  0, c  0 .
D. a  0,b  0, c  0 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Câu 56: Cho hàm số 2
y ax bx c có đồ thị như hình vẽ bên dưới: Tích abc bằng A. 12 B. 12. C. 3. D. 0.
Câu 57: Cho hàm số   2
f x ax bx c có đồ thị như hình bên dưới:
Giá trị của biểu thức: T  2a b c bằng A. 1. B. 1. C. 0. D. 2.
Câu 58: Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ bên dưới:
Giá trị của biểu thức T  4a b  2c bằng A. 8 . B. 6 . C. 3 . D. 4 . Câu 59: Cho parabol 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Khẳng định nào dưới đây đúng?
A. a  0; b  0; c  0 .
B. a  0;b  0; c  0 . C. a  0; b  0; c  0 . D. a  0; b  0; c  0 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 60: Tọa độ giao điểm của đường thẳng d : y  x  4 và parabol 2
y x  7x  12 là
A. (2; 2) và (4; 0) .
B. (2; 2) và (4;8) .
C. (2; 2) và (4; 0) .
D. (2; 6) và (4;8) .
Câu 61: Hai đồ thị hàm số 2
y x  2x  3 và y  2x 1 có bao nhiêu điểm chung? A. 2 . B. 1. C. 0 . D. 3 .
Câu 62: Toạ độ giao điểm của đồ thị hàm số 2
y x x  2 với trục tung là
A. 0; 2.
B. 2;0. C. 0; 2. D.  1  ;0 .
Câu 63: Số giao điểm của Parabol  P 2
: y x  4x  4 với trục hoành là A. 0 . B. 1. C. 2 . D. 3 .
Câu 64: Đồ thị hàm số nào sau đây tiếp xúc trục hoành? A. 2
y x x  2 . B. 2
y  x  3x  2 . C. 2
y  2x  2x  1 . D. 2
y x  4x  4 . 1 2 3 4
Câu 65: Toạ độ giao điểm của parabol 2
(P ) : y  2x  2x  3 với parabol 2
(P ) : y x  6x là 1 2
A. 1;7 và 3;27 . B. 7;  1 và 27;3 .
C. 1;3 và 3;15 . D. 3;  1 và 15;3 .
Câu 66: Cho hàm số   2
f x ax bx c có đồ thị như hình vẽ bên dưới:
Phương trình f x  2 có bao nhiêu nghiệm? A. 2 . B. 1. C. 3 . D. 4 .
Câu 67: Cho hàm số   2
f x ax bx c có đồ thị như hình vẽ bên dưới:
Phương trình f x  2 có bao nhiêu nghiệm? A. 2 . B. 1. C. 3 . D. 4 . 2
Câu 68: Cho hàm số y f x  ax bx c a  0 có bảng biến thiên như sau:
Tìm tất cả các giá trị của m để phương trình f x 2 |
| m 1 có 4 nghiệm phân biệt.  2  m  1 A.  .
B. 1  m  2 .
C. 1  m  2 .
D. 0  m  1 . 1   m  2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 69: Cho hàm số   2
f x ax bx c có đồ thị như hình bên dưới:
Số nghiệm của phương trình f f  2 x  2x   1  1  là A. 1. B. 2. C. 3. D. 4.
Câu 70: Cho hàm số bậc hai f x có đồ thị hàm số như hình bên dưới:
Hỏi m thuộc tập hợp nào dưới đây thì phương trình   2
f x m m có 4 nghiệm thực phân biệt? A. ; 1
  2;. B.  1  ;0  1  ;2.     C.  1
 ;0   ;12 D.    ;0 1;.
Câu 71: Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ.
Số giá trị nguyên của m để phương trình  2
f x   m có đúng 4 nghiệm phân biệt là A. 1. B. 2 . C. 3 . D. 4 .
Câu 72: Cho Parabol (P): 2
y x  2x  3 . Số giá trị nguyên âm của tham số m để Parabol (P) cắt
đường thẳng d: y x m tại hai điểm phân biệt là A. 4 . B. 5 . C. 7 . D. 6 .
Câu 73: Cho đường thẳng d : y  2  mx  5m 1 và parabol  P 2 2
: y x mx m  3 ( m là tham số).
Có tất cả bao nhiêu giá trị nguyên của m nhỏ hơn 5 để đường thẳng d cắt parabol  P tại hai điểm phân biệt? A. 4 . B. 5 . C. 7 . D. 6 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 74: Đồ thị hàm số 2
y x  2x cắt đường thẳng 2
y m  2x tại hai điểm phân biệt có hoành độ lần
lượt là x ; x . Giá trị của T x x bằng 1 2 1 2 A. 2. B. 2. C. 4. D. 2 m  4.
Câu 75: Tìm tập hợp tất cả các giá trị của a để đường thẳng d : y  2a  1 x a cắt parabol P : 2
y x x  1 tại hai điểm phân biệt nằm về hai phía đối với trục tung.
A. ; 3.
B. ;1.
C. 1; . D. . 
Câu 76: Cho đồ thị hàm số 2 2 y x 2mx 2m
1 cắt đồ thị hàm số y  2x tại các điểm có hoành
độ lần lượt là x ; x . Gọi M , m là giá trị lớn nhất, nhỏ nhất của 2 2
H x x x x . Đặt 1 2 1 2 1 2 T M  .
m Khẳng định nào sau đây đúng?
A. T  10 .
B. T  10, 20 .
C. T  20,30 . D. T  30 .
Câu 77: Tìm tất cả các giá trị nguyên của tham số m để đồ thị hàm số y m  2x cắt parabol 2
y x  2x tại hai điểm phân biệt cùng có hoành độ nhỏ hơn 1. A. 7 . B. 8 . C. 9 . D. 10 .
Câu 78: Gọi S là tập hợp các giá trị thực của tham số m sao cho Parabol  P 2
: y x  3x m cắt trục
Ox tại hai điểm phân biệt ,
A B thoả mãn OA  2OB . Tổng các phần tử của tập hợp S bằng A. 2 . B. 3 . C. 18 . D. 16 .
Câu 79: Có bao nhiêu giá trị của tham sô m để đường thẳng d  : y m(x 1)  2 cắt Parabol P 2
: y x  m  2 x  2m tại hai điểm phân biệt ,
A B sao cho AB  4 2 ? A. 2 . B. 1. C. 3 . D. 4 .
Câu 80: Gọi A, B là hai giao điểm của đường thẳng  : y  x k  1 và parabol P 2 : y x  . x Tìm tập
hợp tất cả các giá trị của tham số k để trung điểm I của đoạn thẳng AB nằm trên đường
thẳng d :y x  2. A. 2;   1 . B. 2;   1 . C.   2 . D.   1 . Câu 81: Cho hàm số 2
y x  2x  2 có đồ thị là parabol  P và đường thẳng d có phương trình
y x m . Giá trị của m để đường thẳng d cắt parabol  P tại hai điểm phân biệt , A B sao cho 2 2
OA OB đạt giá trị nhỏ nhất là 1 5 1 5 A. m   .
B. m   . C. m  . D. m  . 2 2 2 2
Câu 82: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y mx  3 cắt parabol P 2
: y  x  2x tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB
thuộc đường thẳng y x  6. Tính tổng tất cả các phần tử của S. A. 5 . B. 1  . C. 3 . D. 3  .
Câu 83: Biết Parabol  P : 2
y ax  4x c có đỉnh I  1
 ; 6 . Tính S a c A. 6  . B. 6 . C. 2 . D. 2  .
Câu 84: Cho hàm số    2 y
f x x bx c có đồ thị là một Parabol  P có đỉnh I 1;  4 . Tính b c . A. 12 . B. 8  . C. 10 . D. 5  .
Câu 85: Tìm parabol  P 2
: y ax  3x  2, biết rằng parabol có trục đối xứng x  3 ?
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 1 1 1 A. 2
y x  3x  2. B. 2 y x x  2. C. 2 y
x  3x  3. D. 2 y x  3x  2. 2 2 2
Câu 86: Đồ thị của hàm số 2
y ax  3x c đi qua hai điểm A2;3 và B 1;6 . Giá trị biểu thức
T  36a c bằng A. 17 . B. 38 . C. 72 . D. 73 .
Câu 87: Cho đồ thị hàm số 2
y ax bx  4 có đỉnh là điểm I 1; 2 . Tính a  3b . A. 20 . B. 18 . C. 30 . D. 25
Câu 88: Xác định  P 2
: y ax bx c , biết  P có đỉnh là I (1;3) và đi qua ( A 0;1) A. P 2 : y  2
x  3x 1. B. P 2 : y  2
x  4x 1. C. P 2 : y  2
x  4x 1. D. P 2 : y  2
x  4x 1.
Câu 89: Cho parabol  P 2
: y ax bx c a, , b c
;a  0 có hoành độ đỉnh bằng 1 và đi qua hai
điểm M 0 ;  
1 , N 1 ;  3 . Khi đó parabol  P là đồ thị của hàm số nào? A. 2
y  2x  4x 1 . B. 2
y x  4x  1 . C. 2
y  2x  4x  1 . D. 2 y  2
x  4x 1.
Câu 90: Biết Parabol 2
y ax bx c đi qua điểm A8;0 và có đỉnh I 6; 1
 2 , khi đó a b c là: A. 85 B. 63. C. 36. D. 96.
Câu 91: Biết đồ thị hàm số 2
y ax bx ca  0 biết đồ thị hàm số đi qua ba điểm
A0; 4; B 1;3; C 1;9. Tính ab c. A. 1. B. 2. C. 1. D. 2.
Câu 92: Xác định hàm số bậc hai 2
y ax bx c biết đồ thị của nó có đỉnh I (1, 1) và đi qua ( A 2, 0) . A. 2
y x  3x  2 . B. 2
y x  2x . C. 2
y  2x  4x  3 . D. 2
y x  2x .
Câu 93: Biết rằng hàm số 2
y ax bx c đạt giá trị nhỏ nhất bằng 1 và đồ thị hàm số cắt đường thẳng
y  2022x  2 tại một điểm trên trục Oy . Tính 2 2 2
S a b c . A. 10 . B. 9 . C. 50 . D. 4 .
Câu 94: Cho parabol  P 2
: y ax bx c , biết hàm số 2
y ax bx c đạt giá trị nhỏ nhất là 4 tại
x  2 và đồ thị của nó cắt trục tung tại điểm có tung độ là 6. Tính 2a b c. A. 6 . B. 5 . C. 4 . D. 2 . Câu 95: Cho hàm số 2
y ax bx c với a , b , c
, hệ số a  0. Biết rằng hàm số đạt giá trị nhỏ nhất bằng 1
 tại x  2 và đồ thị hàm số đi qua điểm M 1;0 . Tính T abc. A. T  6 .
B. T  5 .
C. T  4 .
D. T  12 .
Câu 96: Gọi T là tổng tất cả các giá trị của tham số m để parabol  P 2
: y x  5x m cắt trục Ox tại hai điểm phân biệt ,
A B thỏa mãn OA  4OB . Tính T . 64 64 A. T   . B. T  .
C. T  2 .
D. T  2 . 9 9
Câu 97: Cho parabol  P : 2
y ax bx c , a  0 biết  P đi qua M (4;3) cắt Ox tại N (3;0) và Q sao
cho INQ có diện tích bằng 1 biết hoành độ điểm Q nhỏ hơn 3 với I là đỉnh của  P . Tính
a b c . A. 1  . B. 1. C. 0 . D. 2 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 98: Có tất cả bao nhiêu giá trị của tham số m để giá trị nhỏ nhất của hàm số f x 2
x  2x m 1 trên 1;2 bằng 5? A. 3. B. 1. C. 2. D. 4.
Câu 99: Cho hình chữ nhật ABC ,
D AB  10, AD  6 . Trên các cạnh AB, BC,CD lấy các điểm P, Q, R
sao cho AP BQ CR x . Giá trị của x trong khoảng nào để diện tích tam giác PQR đạt giá trị nhỏ nhất? A P B Q D R C A. 3;5 . B. 6;8 . C. 8;10 . D. 4;8 .
Câu 100: Biết có 2 giá trị thực của tham số m là m , m 1
2 để giá trị nhỏ nhất của hàm số 2 2
y f (x)  4x  4mx m  2m trên đoạn [-2; 0] bằng 3. Tổng m m 1 2 bằng 3 1 1 3 A.  . .  . . 2 B. 2 C. 2 D. 2
Câu 101: Gọi S là tập hợp các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số
y f x 2 2
 4x  4mx m  2m trên đoạn 2; 0 bằng 3. Tính tổng T các phần tử của S . 3 9 1 3 A. T  . B. T  . C. T  . D. T   . 2 2 2 2
Câu 102: Tìm tập hợp tất cả các giá trị của tham số k để đường thẳng  : y kx  3 cắt parabol  3 P 2
: y x  4x  3 tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng . 2 A. 5;   3 . B. 3;  3 . C. 5;  5 . D. 5;   3 . Câu 103: Cho parabol 2 2
(P) : y  x  2 x
m  3m  4m  3 ( m là tham số) có đỉnh I . Gọi , A B là hai
điểm thuộc Ox sao cho AB  2022 . Khi đó IAB có diện tích nhỏ nhất bằng: A. 1011. B. 2022 . C. 4044 . D. 1010.
Câu 104: Cho Parabol  P 2
: y x  4x  3 và đường thẳng d  : y mx  2 1 . Tính tổng các giá trị
của tham số m để đường thẳng d  cắt Parabol  P tại hai điểm phân biệt , A B sao cho diện
tích tam giác IAB bằng 10 với điểm I 2;3 . A. 6 . B. 0 . C. 2 . D. 4 .
Câu 105: Một vật chuyển động với vận tốc theo quy luật của hàm số bậc hai vt 2  t
  12t với ts là
quãng thời gian tính từ khi vật bắt đầu chuyển động và v (m/s) là vận tốc của vật. Trong 9
giây đầu tiên kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu?
A. 144 m / s.
B. 243 m / s.
C. 27 m / s.
D. 36 m / s. 1
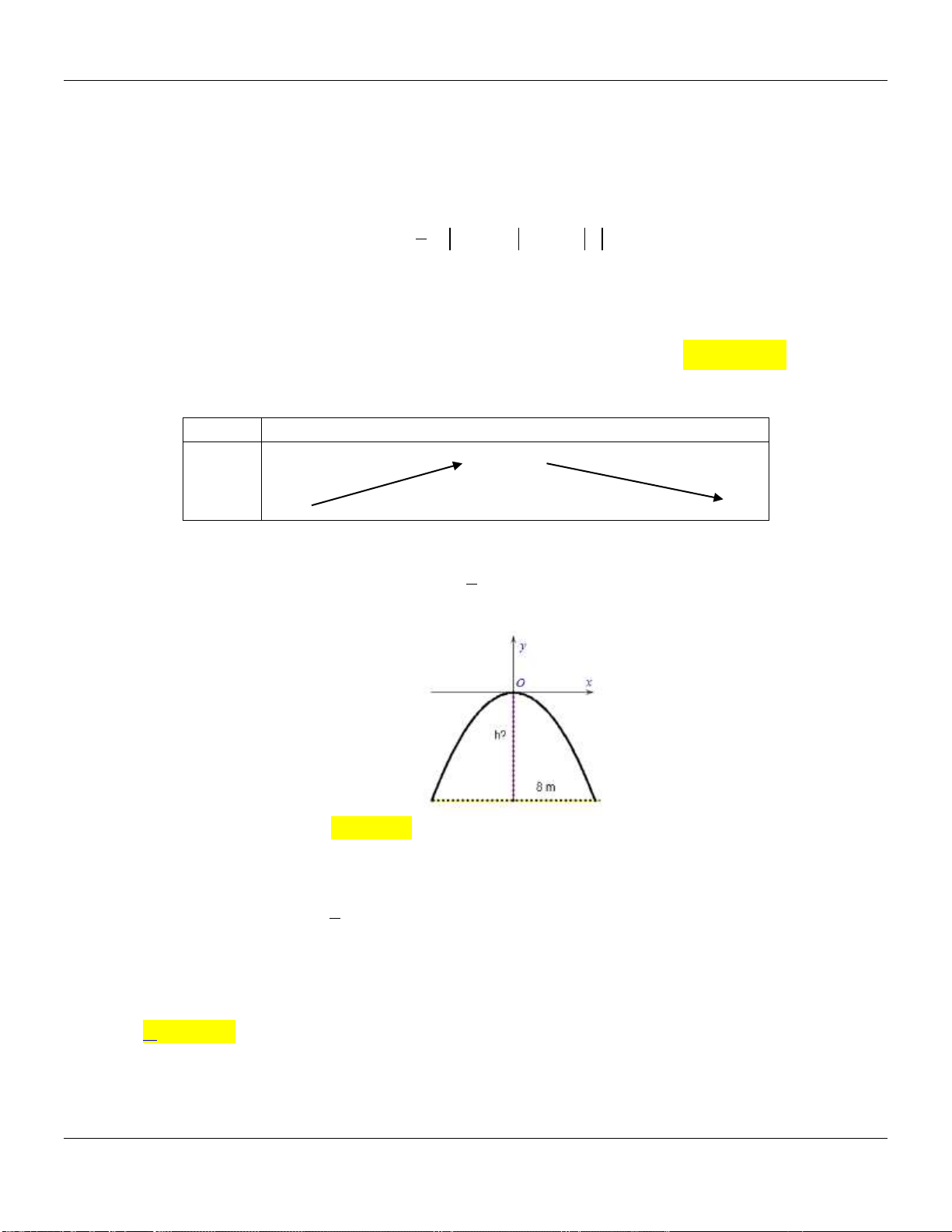
Câu 106: Một chiếc cổng hình parabol dạng 2 y  
x có chiều rộng d  8m . Hãy tính chiều cao h của 2
cổng. (Xem hình minh họa)
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
A. h  9m .
B. h  8m .
C. h  7m .
D. h  5m .
Câu 107: Một của hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu đôi
giày được bán với giá x đôla thì mỗi tháng khách hàng sẽ mua 120  x đôi. Hỏi của hàng
bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất? A. 80 USD. B. 160 USD. C. 40 USD. D. 240 USD.
Câu 108: Cổng Ac-xơ tại thành phố Xanh Lu-i (Mĩ) có hình dạng là một parabol hướng bề lõm xuống
dưới (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có
độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo
phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn
10 m. Giả sử các số liệu trên là chính xác. Hãy tính chiều cao của cổng Ac-xơ (tính từ điểm cao
nhất trên cổng xuống mặt đất). A. 197,5 m. B. 275,6 m. C. 185,6 m. D. 348,3 m
Câu 109: Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả
bóng được sút lên từ độ cao 1 m sau đó 1 giây nó đạt độ cao 10 m và 3,5 giây nó ở độ cao
6, 25 m . Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11 m . B. 12 m . C. 13 m . D. 14 m .
Câu 110: Một chiếc cổng hình parabol có chiều rộng 12 m và chiều cao 8 m như hình vẽ. Giả sử một
chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa cổng . Hỏi chiều cao h của xe tải thỏa
mãn điều kiện gì để có thể đi vào cổng mà không chạm tường?
A. 0  h  6 .
B. 0  h  6 .
C. 0  h  7 .
D. 0  h  7 .
Câu 111: Trong số các hình chữ nhật có cùng chu vi bằng 16 , hình chữ nhật có diện tích lớn nhất bằng bao nhiêu? A. 64. B. 4. C. 16. D. 8.
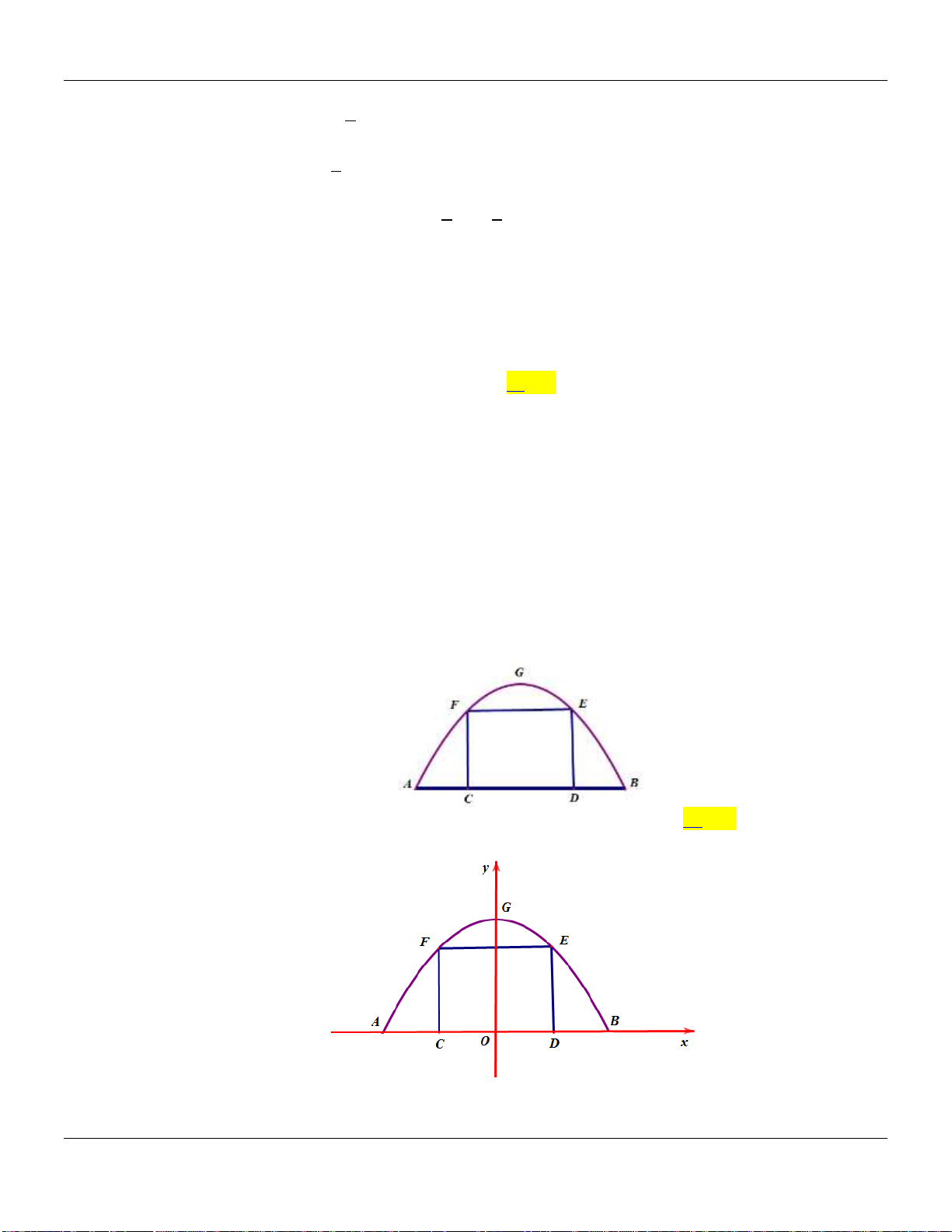
Câu 112: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa
phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x
4m. Hãy tính khoảng cách giữa hai điểm A và B . (xem hình vẽ bên dưới)
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống A. 5m. B. 8,5m. C. 7,5m. D. 8m.
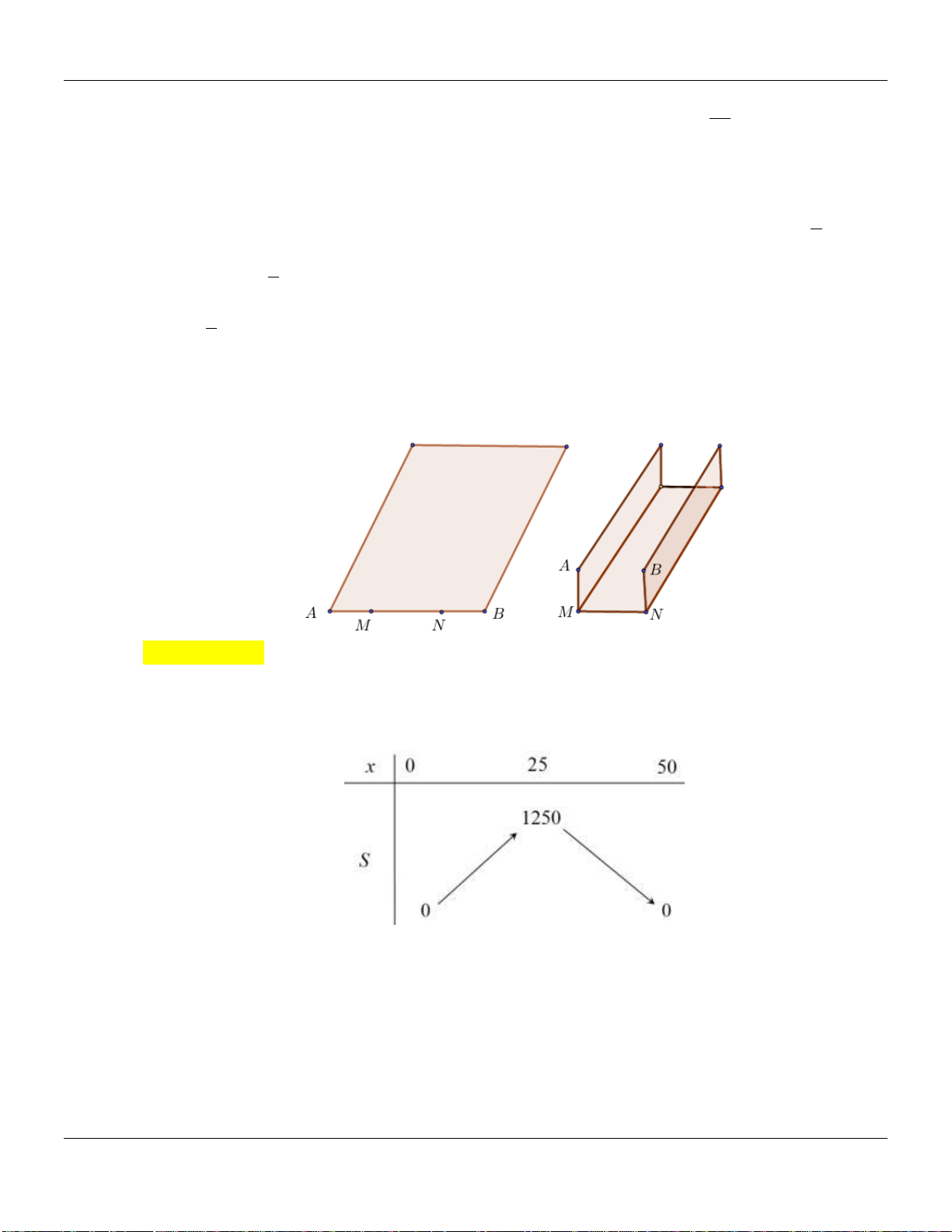
Câu 113: Một tấm tôn có bề rộng AB là 100cm . Người ta chọn 2 điểm M và N trên đoạn AB sao cho
có thể làm được một máng nước như hình vẽ. ( AMNB là hình chữ nhật). Tính MN để máng
nước có diện tích AMNB lớn nhất. A. MN  50 . cm B. MN  60 . cm C. MN  45 . cm D. MN  55 . cm
Câu 114: Một người ném một quả bóng từ độ cao cách mặt đất 80m, tại thời điểm 1 giây sau khi ném,
người ta đo được độ cao của quả bóng so với mặt đất là 128m. Biết rằng quỹ đạo bay của quả
bóng là một đường Parabol (như hình vẽ). Tính độ cao tối đa mà quả bóng đạt được. A. 143m .
B. 144m .
C. 144,5m .
D. 145m .
Câu 115: Cô Tình có 60m lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một
cạnh là tường, cô Tình chỉ cần rào 3 cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính
hộ diện tích lớn nhất mà cô Tình có thể rào được? A. 2 400m . B. 2 450m . C. 2 350m . D. 2 425m .
Câu 116: Dây truyền đỡ nền cầu treo có dạng Parabol ACB như hình vẽ. Đầu cuối của dây được gắn
chặt vào điểm A và B trên trụ cốt thép bê tông AA và BB với độ cao 30(m) so với nền cầu.
Chiều dài nhịp AB  200(m) . Độ cao ngắn nhất của dây truyền trên nền cầu là OC  5(m) .
Người ta nối dây đỡ với nền bằng 7 sợi cáp song song cách đều hai trụ AA và BB . Xác định
tổng các chiều dài 7 các dây cáp treo đó. A. 78,15(m) . B. 78, 75(m) . C. 72, 75(m) . D. 80, 70(m) .
_________________HẾT_________________
Huế, 10h20’ Ngày 03 tháng 01 năm 2023
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
LỜI GIẢI CHI TIẾT II. BÀI TẬP TỰ LUẬN Câu 1:
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) 2
y x  3x  2; b) 2 y  2
x  5x  2; c) 2
y  x  2x  1; d) 2 y  2
x x  3; e) 2 y x  2; f) 2
y x  2x  1. Câu 2:
Xác định hàm số bậc hai 2
y  2x bx c, biết đồ thị của nó:
a) Có trục đối xứng là x  1 và cắt trục tung tại điểm có tung độ là 4.
b) Có đỉnh là I 1; 2 .
c) Có hoành độ đỉnh là 2 và đi qua điểm A1; 2 . Lời giải: bb
a) Trục đối xứng x 1    b  4  . 2a 4
Theo giả thiết, (P) cắt trục tung tại 0; 4  4  y(0)  c . Vậy 2
y  2x  4x  4.  bbx    1  b  4  2a 4
b) Đỉnh của (P) là I  1  ; 2     2 b  4ac 16  8cy      2  c  0  4a 8 Vậy 2 y  2x  4 . x bb
c) Hoành độ đỉnh: x    2  b  8  . 2a 4
Đồ thị qua điểm A1; 2  2
  y(1)  6  c c  4. Vậy 2
y  2x  8x  4. Câu 3:
Xác định parabol P 2
: y ax bx c; a;b;c  , a  0. Biết P đi qua các điểm A 1  ;6 , B3;  2 và C 2;0. Lời giải:
a b c  6 a  1   Do A 1
 ;6P, B3;2P, C2;0P nên ta có hệ: 9a  3b c  2  b  3  .  
4a  2b c  0 c  2   Vậy P 2
: y x  3x  2. Câu 4:
Xác địnhparabol P 2
: y ax bx c; a;b;c  , a  0. Biết P đi qua điểm A1;8 và có
đỉnh I 2; 1. Lời giải: b
Trục đối xứng của P là  :x   . 2a Do I 2; 1
  là đỉnh của P và A 1
 ;8P nên ta có hệ:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống      I P 4a 2b c 1
4a  2b c  1  a  1    b   I     2
 4a b  0  b  4  .     A P 2a
a b c  8 c  3 
a b c  8    Vậy P 2
: y x  4x  3. Câu 5: Xác định hàm số 2
y ax bx ca  0 biết hàm số đạt giá trị nhỏ nhất bằng 4 tại x  2 và
đồ thị hàm số đi qua điểm A0;6 . Lời giải: b   2  2a
Hàm số đạt cực tiểu bằng 4 tại x  2 nên  .    4  4a
Đồ thị hàm số đi qua điểm A0;6 nên ta có c  6.  b  2  1  2a a   b  4  ab  4a  2      Từ đó ta có hệ 2 2 
 4  b  4ac  16a  1
 6a  8a  0  b  2. 4  a    c  6 c  6 c  6 c  6       1 Vậy 2 y x  2x  6. 2 Câu 6:
Xác định parapol P : 2
y  2x bx c , biết P :
a) Có trục đối xứng x  1 vá cắt trục tung tại điểm 0; 4 ;
Đáp số: b= 4, c= 4
b) Có đỉnh I 1; 2 ; Đáp số: b= 4, c= 0
c) Đi qua hai điểm A0; 1 và B4;0 ;
Đáp số: b= 31/4, c=1
d) Có hoành độ đỉnh là 2 và đi qua điểm M 1; 2 .
Đáp số: b= 8, c= 4 Câu 7:
Xác định parapol P : 2
y ax  4x c , biết P :
a) Đi qua hai điểm A1; 2 và B2; 3 ;
Đáp số: a= 3, c= 1
b) Có đỉnh I 2; 1 ;
Đáp số: a= 1, c= 5
c) Có hoành độ đỉnh là 3
 và đi qua điểm P2;1 ;
Đáp số: a= 2/3, c= 13/3
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
d) Có trục đối xứng là đường thẳng x  2 vá cắt trục hoành tại điểm M 3;0 . Đáp số: a=1, c= 3 Câu 8: Tìm parapol P : 2
y ax bx  2 , biết P :
a) Đi qua hai điểm M 1; 5 và N 2;8 ; Đáp số: a=2, b=1 3
b) Đi qua điểm A3; 4 và có trục đối xứng x   ; 4
Đáp số: a= 4 , b= 2 9 3
c) Có đỉnh I 2; 2 ; Đáp số: a=1, b=4
d) Đi qua điểm B1;6 , đỉnh có tung độ  1 4
Đáp số: a=16, b=12 hoặc a=1, b=3 Câu 9:
Xác định parapol P : 2
y ax bx c , biết P :
a) Đi qua ba điểm A0; 1  , B1; 1  , C 1  ;1 ;
Đáp số: a=1, b=1, c= 1
b) Đi qua điểm D3;0 và có đỉnh là I 1; 4 ;
Đáp số: a=1, b=2, c=3
c) Đi qua A8;0 và có đỉnh I 6;12 ;
Đáp số: a=3, b=36, c=96
d) Đạt GTNN bằng 4 tại x  2 và đi qua A0;6 ;
Đáp số: a=1/2, b=2, c=6 Câu 10: Cho hàm số 2
y x  2x  3 có đồ thị P.
a) Lập bảng biến thiên và vẽ đồ thị P.
b) Dựa vào đồ thị P , biện luận số nghiệm của phương trình 2
x  2x  2m  0.
c) Tìm m để phương trình 2
x  2x  3  m  1 có 4 nghiệm phân biệt.
d) Tìm m để phương trình 2
x  2 x  2  m  0 có 4 nghiệm phân biệt. 2
e) Tìm m để phương trình  f  x  
m 1 f x  m  0 có 8 nghiệm phân biệt. Lời giải:
a) TXĐ: D  .
+) Trục đối xứng của P : x  1.
+) Đỉnh của P : I 1; 4  . Bảng biến thiên: x  1    y
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 4
Hàm số đồng biến trên 1; ; nghịch biến trên ;1. Vẽ đồ thị: y 1 x O -3 -4
b) Điều kiện: x  . Ta có: 2 2
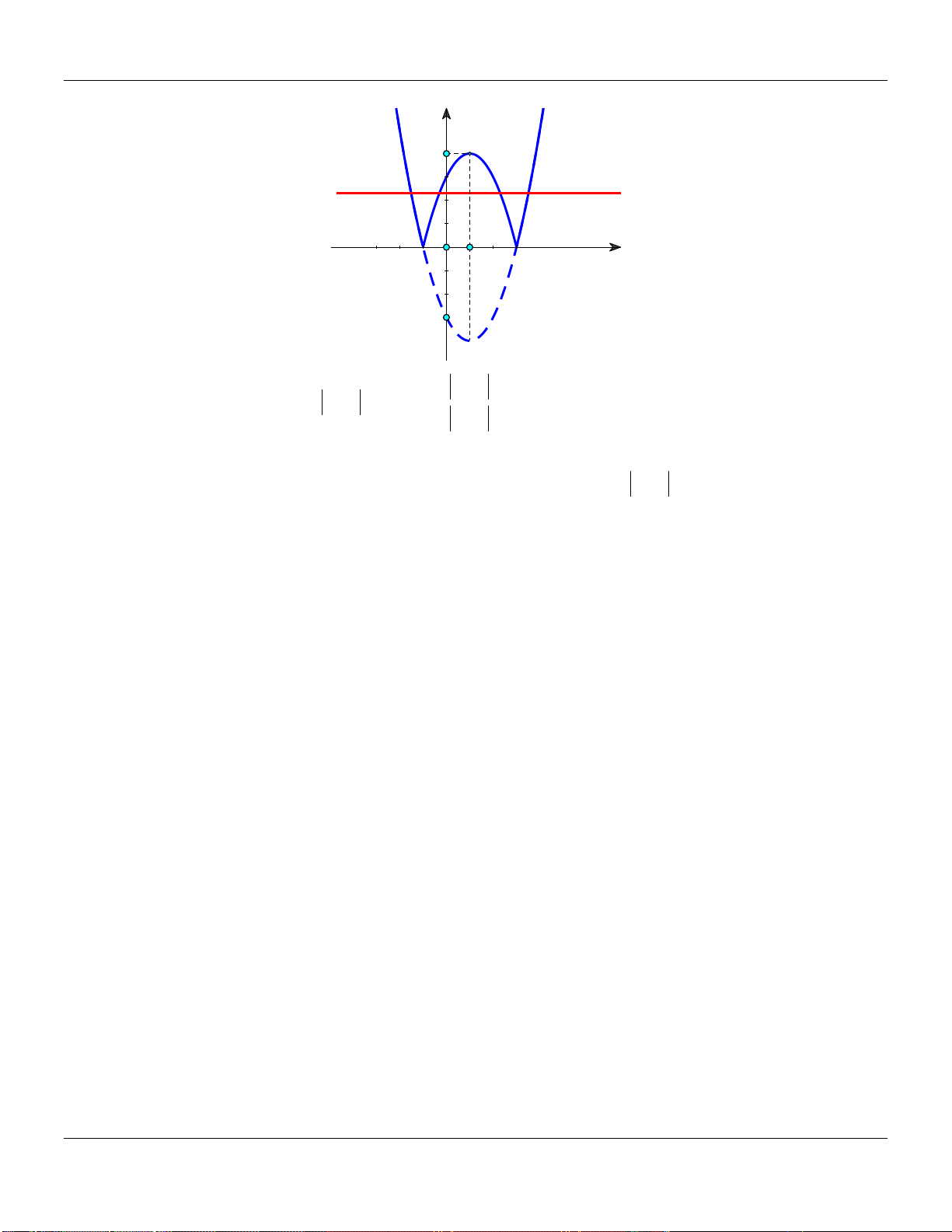
x  2x  2m  0  x  2x  3  2m  3
Số nghiệm của phương trình bằng số giao điểm của P và đường thẳng d : y  2m  3. y 1 x O 2m-3 -3 -4 Biện luận: 1 +) Với 2m  3  4
  m   : d và P không có điểm chung  Phương trình vô nghiệm. 2 1 +) Với 2m  3  4
  m   : d và P có một điểm chung  Phương trình có duy nhất 2 nghiệm. 1 +) Với 2m  3  4
  m   : d và P có hai điểm chung  Phương trình có hai nghiệm. 2
c) Đặt f x 2
x  2x  3.
f x khi y   0 Ta có: 2
x  2x  3  f x      f  x . khi y   0
Cách vẽ đồ thị P : y f x suy ra từ P : y f x :
+) Giữ nguyên phần đồ thị P phía trên Ox, bỏ phần đồ thị P phía dưới . Ox
+) Lấy đối xứng phần đồ thị bị bỏ của P qua trục . Ox
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống y 4 m-1 1 x O -3
Số nghiệm của phương trình bằng số giao điểm của P và đường thẳng d : y m  1.
Dựa vào đồ thị, yêu cầu bài toán  0  m  1  4  1  m  5.
d) Điều kiện: x  . Ta có: 2 2
x  2 x  2  m  0  x  2 x  3  m  5 Đặt f x 2
x  2x  3.
f x khi x   0 Ta có: 2
x  2 x  3  f x      f  x . khi x   0
Cách vẽ đồ thị P : y f x  suy ra từ P : y f x :
+) Giữ nguyên phần đồ thị P phía bên phải Oy, bỏ phần đồ thị P phía bên trái Oy.
+) Lấy đối xứng phần đồ thị được giữ của P qua trục Oy. y x -1 O 1 -3 m-5 -4
Số nghiệm của phương trình bằng số giao điểm của P và đường thẳng d : y m  5.
Dựa vào đồ thị, yêu cầu bài toán  4
  m  5  3  1  m  2.
e) Điều kiện: x  . 2
Đánh giá: Phương trình f 2  x  
m 1 f x  m  0 có dạng t m1t m  0 với t f x .
Cách vẽ đồ thị P : y f x suy ra từ P : y f x :
+) Giữ nguyên phần đồ thị P phía trên Ox, bỏ phần đồ thị P phía dưới . Ox
+) Lấy đối xứng phần đồ thị bị bỏ của P qua trục . Ox
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống y 4 m-1 1 x O -3   2 f x 1 Ta có:  f  x  
m1 f x  m  0  
f x  m
Dựa vào đồ thị f x  1 có 4 nghiệm phân biệt.
Phương trình đã cho có 8 nghiệm phân biệt  Phương trình f x  m có 4 nghiệm phân biệt
khác các nghiệm của phương trình f x  1. 0  m  4 Yêu cầu bài toán   . m   1
Câu 11: Tìm m để parabol 2
y x  2x cắt đường thẳng y m tại 2 điểm phân biệt. Lời giải: Ta có 2 2
x  2x m x  2x m  0 (1).
Yêu cầu bài toán  (1) có 2 nghiệm phân biệt   '  1 m  0  m  1.
Câu 12: Cho parabol  P 2
: y x  2x m 1 . Tìm tất cả các giá trị thực của m để parabol cắt Ox tại
hai điểm phân biệt có hoành độ dương. Lời giải:
Phương trình hoành độ giao điểm của  P và trục Ox là 2
x  2x m 1  0.   1
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương khi và chỉ khi   1 có hai
  2  m  0  m  2
nghiệm dương  S  2  0    1  m  2.  m 1
P m 1  0 
Câu 13: Tìm tất cả các giá trị thực của tham số m sao cho parabol  P 2
: y x  4x m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA  3 . OB Lời giải:
Phương trình hoành độ giao điểm: 2
x  4x m  0.   1
Để  P cắt Ox tại hai điểm phân biệt ,
A B thì  
1 có hai nghiệm phân biệt
   4  m  0  m  4 *
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống x  3x
Theo giả thiết OA  3OB   x  3 A B x  . A Bx  3  xA Bx  3x A B  +) TH1: Viet
x  3x 
x x  4 
m x .x  3. A B A B A B
x .x mA Bx  3  x A B  +) TH2: Viet x  3  x 
x x  4 
m x .x  12 : không thỏa mãn * . A B A B A B
x .x mA B
Câu 14: Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y mx cắt đồ thị hàm số P 3 2
: y x  6x  9x tại ba điểm phân biệt. Lời giải:
Phương trình hoành độ giao điểm của  P với d là 3 2
x  6x  9x mx    xx 0 2
x  6x  9  m  0   2
x  6x  9  m  0.    1
Để  P cắt d tại ba điểm phân biệt khi và chỉ  
1 có hai nghiệm phân biệt khác 0   0 m  0 m  0       . 2
0  6.0  9  m  0 9   m  0 m  9
Câu 15: Cho parabol  P 2
: y x  4x  3 và đường thẳng d : y mx  3 . Tìm giá trị thực của tham số
m để d cắt  P tại hai điểm phân biệt ,
A B có hoành độ x , x thỏa mãn 3 3 x x  8 . 1 2 1 2 Lời giải:
Phương trình hoành độ giao điểm của  P và d là 2
x  4x  3  mx  3  
xx m   x 0 4  0   . x m  4
Để d cắt  P tại hai điểm phân biệt ,
A B khi và chỉ khi 4  m  0  m  4 .
Khi đó, ta có x x  8  0  4  m3 3 3
 8  4  m  2  m  2  . 1 2
Câu 16: Tìm tất cả các giá trị thực của tham số m để phương trình 2
x  5x  7  2m  0 có nghiệm thuộc đoạn 1;5 . Lời giải: Ta có 2 2
x  5x  7  2m  0  x  5x  7  2 . m *
Phương trình * là phương trình hoành độ giao điểm của parabol  P 2
: x  5x  7 và đường
thẳng y  2m (song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số 2
y x  5x  7 trên 1;5 như sau:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống 5 1 5 x 2 y 7 3 3 4 3 
Dựa vào bảng biến ta thấy x 1;5 thì y  ; 7   . 4 
Do đo để phương trình * có nghiệm x   3 3 7 1;5   2
m  7    m   . 4 8 2
III. BÀI TẬP TRẮC NGHIỆM
Câu 17: Trong các hàm số sau hàm số nào là hàm số bậc hai? 3 2x  3x  5 A. 2
y  2x  3x  5 B. y  . C. 2 3
y  2x  3x  5 . D. y  3x  2 . x
Câu 18: Điểm nào sau đây không thuộc đồ thị hàm số 2
y x  2 ?
A. P 2; 2 .
B. Q 3;3.
C. N 2; 2.
D. M 1;   1 . Lời giải: Với x  2 2
 2  2  2  y N 2;2 thuộc đồ thị hàm số.
Câu 19: Đồ thị hàm số 2
y x x đi qua điểm nào dưới đây? A. N  2  ;6 .
B. M 1;  1 .
C. P 2;3 .
D. Q 1;  1 . Lời giải: Đồ thị hàm số 2
y x x đi qua điểm N  2  ;6 . Câu 20: Cho hàm số 2 y  3
x  4x  3 có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương trình: 2 2 4 4 A. x  .
B. x   . C. x  .
D. x   3 3 3 3 Lời giải: b  4  2 
Trục đối xứng của (P) là x    . 2a 6 3
Câu 21: Đỉnh của parabol 2
y x  4x  5 có toạ độ là A. 0; 2 . B. 1; 2 . C. 2;0 . D. 2;  1 . Lời giải: Đỉnh của parabol 2
y x  4x  5 .có toạ độ là 2;  1 .
Câu 22: Tìm m để parabol 2
(P) : y mx  2x  3 có trục đối xứng là đường thẳng x  2 . 1 A. m  2 .
B. m  1.
C. m  1. D. m  . 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Lời giải: 2  1
Vì  P là Parabol nên m  0 . Khi đó Parabol  P có trục đối xứng x    x  2m m 1 1
Theo bài ra trục đối xứng x  2 nên  2  m  . m 2
Câu 23: Hàm số nào dưới đây có đồ thị nhận đường thẳng x  2 làm trục đối xứng? A. 2
y  2x  4x  3 . B. 2 y  2
x  4x  3 . C. 2
y x  4x  3 . D. 2
y  x  4x  3 . Lời giải: b Đồ thị hàm số 2
y ax bx c, a  0 nhận đường thẳng x   làm trục đối xứng. 2a Đồ thị hàm số 2
y  2x  4x  3 nhận đường thẳng x  1 làm trục đối xứng. Đồ thị hàm số 2 y  2
x  4x  3 nhận đường thẳng x  1 làm trục đối xứng. Đồ thị hàm số 2
y x  4x  3 nhận đường thẳng x  2 làm trục đối xứng. Đồ thị hàm số 2
y  x  4x  3 nhận đường x  2 làm trục đối xứng.
Câu 24: Hàm số nào có đồ thị là đường Parabol có đỉnh là I  1  ;3? A. 2 y  2
x  4x  3. B. 2
y  2x  2x 1. C. 2
y  2x  4x  5 . D. 2
y  2x x  2 .
Câu 25: Giá trị nhỏ nhất của hàm số 2
y x  4x  5 là A. y  0. B. y  2 . C. y  2 . D. y  1. min min min min Lời giải: b  Hàm số 2
y x  4x  5 có a  1  0 , do đó hàm số đạt giá trị nhỏ nhất tại x   2 và 2a yy 2  1. min   Câu 26: Hàm số 2
y  5x  6x  7 đạt giá trị nhỏ nhất khi 26 3 3 6 A. x  . B. x  .
C. x   . D. x  . 5 5 5 5 Lời giải: Hàm số 2
y  5x  6x  7 có a  5  0 nên đạt giá trị nhỏ nhất tại hoành độ đỉnh của P.
Câu 27: Giá trị lớn nhất của hàm số 2
y  x  2x  4 bằng A. 5 . B. 5  . C. 1. D. 1  . Lời giải:
Tập xác định: D  .
Tọa độ đỉnh: I 1;5 . Bảng biến thiên:
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số 2
y  x  2x  4 bằng 5.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 28: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số 2
y  x  4x  2 trên đoạn 0;  3 .
Tính giá trị biểu thức M m . A. 1. B. 4  . C. 0 . D. 1  . Lời giải:
Ta có bảng biến thiên của hàm số 2
y  x  4x  2 trên đoạn 0;  3 :
Từ bảng biến thiên ta có: M  2; m  2 nên M m  0 .
Câu 29: Tìm giá trị nhỏ nhất của hàm số 2 2
y x  5  4 x  1 . A. 5 . B. 5  . C. 1. D. 1  . Lời giải: Đặt 2
t x  1 t   1 Suy ra: 2 2 x t  1 Từ đó, 2 2
y t  1  5  4t t  4t  6 trên 1;    .
Ta có hàm số trên có đồ thị là 1 parabol đỉnh I  2  ; 1  0
Bảng biến thiên trên 1;    : Vậy Miny  1   x  0
Hàm số không có giá trị lớn nhất. Câu 30: Cho hàm số 2
y ax bx c ,với a  0 . Khẳng định nào sau đây sai? b
A. Hàm số đồng biến trên khoảng  ;    .  2a   b
B. Hàm số nghịch biến trên khoảng  ;     .  2a   b
C. Hàm số nghịch biến trên khoảng ;    .  2a b
D. Đồ thị hàm số có trục đối xứng là đường thẳng x   2a Câu 31: Cho hàm số 2
y ax bx c có đồ thị là parabol trong hình sau:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  2;    . B. 1;   . C.  ;   1 . D.  ;   2 . Lời giải:
Dựa vào đồ thị, ta có hàm số đã cho đồng biến trên khoảng 1;   .
Câu 32: Cho hàm số bậc hai có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  2;    .
B.  ; 2 . C. 3 . D.  1;    . Lời giải:
Dựa vào bảng biến thiên ta có hàm số đồng biến trên  1;    . Câu 33: Cho hàm số 2
y  2x  4x 1. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng  ; 2 . B. Hàm số nghịch biến trên khoảng ;  .
C. Hàm số đồng biến trên khoảng 2;  . D. Hàm số nghịch biến trên khoảng 2;  . Lời giải:
Theo định lý về chiều biến thiên của hàm số bậc hai ta có hàm số 2
y  2x  4x 1 đồng biến
trên khoảng 1;  nên đồng biến trên khoảng 2;  . Câu 34: Cho hàm số 2
y  x  3x  5 . Hàm số đã cho đồng biến trên khoảng nào?  3   3   3  A.  ;3 .
B.  ;     . C.  ;   . D. ;    .  2   2   2  Lời giải: b  Hàm số 2
y ax bx c với a  0 đồng biến trên khoảng ;    và nghịch biến trên  2a   b   3  khoảng  ;     . Suy ra hàm số 2
y  x  3x  5 đồng biến trên khoảng ;    .  2a   2 
Câu 35: Hàm số nào sau đây đồng biến trên ? A. 2
y x 1. B. 2
y  x x .
C. y  x 1.
D. y x 1. Lời giải:
Hàm số y x 1 đồng biến trên vì a  1  0 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Câu 36: Cho hàm số 2
y x  2x . Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên khoảng 1; .
B. Hàm số đã cho nghịch biến trên khoảng  1  ;.
C. Hàm số đã cho đồng biến trên khoảng  1  ;.
D. Hàm số đã cho nghịch biến trên khoảng 1; . Lời giải: b
Với a  0 thì hàm số 2
y ax bx c nghịch biến trên khoảng  ;     và đồng biến trên  2a   b  khoảng  ;    .  2ab 2  Hàm số 2
y x  2x có a  1  0,    1 nên hàm số 2
y x  2x đồng biến trên 2a 2.1
khoảng 1; .
Câu 37: Cho hàm số f x 2
x  2018x  2020. Khẳng định nào sau đây đúng?  1   1   1   1  A. ff     . B. ff     . 2019 2018  2   2  2019 2018  2   2  1009 1008 1008 1007
C. f 2   f 2 .
D. f 2  f 2 . Lời giải:
Hàm số f x 2
x  2018x  2020 có hoành độ đỉnh là 1009 và hệ số a  1  0 nên đồng biến
trên khoảng 1009;  và nghịch biến trên khoảng  ;10  09 . 1 1  1   1  Vì 2019 2018 2  2   1009  ff     . 2019 2018 2019 2018 2 2  2   2 
Câu 38: Tìm tất cả giá trị tham số m để hàm số 2
y x  m  
1 x m  2 đồng biến trên 1;  .
A. m  3 .
B. m  3 .
C. m  3 . D. m  3 . Lời giải:
Hàm số đã cho xác định với mọi x  . Bảng biến thiên
Dựa vào bảng biến thiên ta có hàm số đã cho đồng biến trên khoảng 1;  khi m 1  1  m  3  . 2
Câu 39: Tìm tất cả các giá trị của tham số m để hàm số 2
y x  2 m  
1 x m  2 nghịch biến trên khoảng 1; 2 .
A. m  1.
B. m  1.
C. m  0 . D. m  0 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Hàm số đã cho xác định với mọi x  . Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên khoảng 1; 2 khi
m  1  2  m  1 . Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
y f x  m   2 ( )
2 x  2mx m  2021 nghịch biến trên khoảng ;3? A. 2. B. 1. C. 3. D. 4. Lời giải:
+ Trường hợp m  2  y  4
x  2021, nghịch biến trên  ;3
  . Tức m  2 thỏa mãn yêu cầu bài toán.
+ Trường hợp m  2 : Dựa vào sự biến thiên hàm bậc hai ta thấy f x nghịch biến trên m  2  0  khoảng  ;3     m  2  m  3 .  3 m2 m  2
Từ các trường hợp trên, suy ra: 2  m  3 mà m    . m  3
Vậy có 2 giá trị nguyên của tham số m .
Câu 41: Có bao nhiêu giá trị nguyên của tham số m để hàm số 2
y  x  2 m 1 x  3 nghịch biến trên 2 ;  ? A. 3 . B. 6 . C. 5 . D. 4 . Lời giải:
Ta có trục đối xứng là đường thẳng x m 1 .
Hàm số bậc hai nghịch biến trên  m 1 ;   .
Để hàm số nghịch biến trên 2 ;   thì 2 ;     m 1 ;    m 1  2  1   m  3 Suy ra m  1  ; 0 ;1; 2 ;  3 .
Câu 42: Cho hàm số bậc hai 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Tìm tất cả các giá trị của x để y  0. A.  ;  0.
B. 3;  . C. 0;  3 . D. 0;3 . Lời giải:
Dựa vào đồ thị ta có
y  0  x   ;  0 3; .
y  0  x  0;3 .
Câu 43: Hàm số f x 2  x   2 m m   2
2 x  2m  2m 1. Mệnh đề nào sau đây sai?
A. Hàm số đạt giá trị lớn nhất trên đoạn 1;0 bằng f 0 .
B. Hàm số nghịch biến trên khoảng 0;  .
C. Hàm số đặt giá trị lớn nhất trên đoạn 1;0 bằng f   1 .
D. Hàm số nghịch biến trên khoảng  ;  0. Lời giải: 2  1  7 m     2 b m m  2  2  4 Ta có     0 2a 2 2 2 
m m  2 
Và a  0 nên hàm số đồng biến trên khoảng  ; 
 nghịch biến trên khoảng  2  2
m m  2  
;    0; .  2 
Câu 44: Hàm số nào dưới đây có bảng biến thiên như sau? A. 2
y  x 1. B. 2
y x  3x 1. C. 2
y  x x 1. D. 2
y  3x 1. Lời giải:
Từ bảng biến thiên ta suy ra đồ thị hàm số 2
y ax bx c có a  0 và tọa độ đỉnh I 0;  1 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống a  0 a  0  b  Suy ra 
 0  b  0 . Chọn đáp án 2
y  x 1. 2a   c 1   c  1 
Câu 45: Bảng biến thiên dưới đây là của hàm số nào? 5 3 3 A. 2
y  x x  . B. 2
y x x  . C. 2
y  x x  . D. 2
y  2x x 1. 4 2 2
Câu 46: Bảng biến thiên của hàm số 2
y  x  2x 1 là A. . B. . C. . D. . Lời giải: Ta có: 2
y  x  2x 1 nên đỉnh của Parabol là I 1; 2 .
Do a  1  0 nên Parabol có bề lõm xuống dưới.
Câu 47: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào? A. 2
y  x  2 . x . B. 2 y x  2 . x C. 2
y  x  2x 1. D. 2
y  x  2 . x Lời giải:
Từ đồ thị ta có hệ số a  0 ; hoành độ đỉnh bằng -1; tung độ đỉnh bẳng 1. Nên hàm số là 2
y  x  2 . x
Câu 48: Đồ thị sau là đồ thị của hàm số nào?
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống A. 2
y x  2x  3 . B. 2
y  x  2x 1. C. 2
y  x  2x  2 . D. 2
y  x  2x 1. Lời giải:
Đồ thị đã cho là đồ thị của hàm số bậc hai, giả sử 2
y ax bx c, a  0
Vì bề lõm của parabol hướng xuống nên a  0 .
Dựa vào các đáp án, ta có a  1 . b
Đỉnh của parabol là 1; 2 nên 1 b  2  a  2 2a y   2 1  2  1
 .1  2.1 c  2  c 1. Vậy 2
y  x  2x 1.
Câu 49: Hình bên là đồ thị của hàm số nào sau đây? A. 2
y  x  2x  3 . B. 2
y  x  2x  3 . C. 2
y x  2x  3 . D. 2
y  x  2x  3 . Lời giải:
Dựa vào hình bên ta có
+ Tọa độ đỉnh I (1; 4) .
+) Đồ thị hàm số cắt trục tung tại điểm có tung độ y  3 .
+) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ x  1 và x  3 .
Do đó hình bên là đồ thị hàm số của hàm số 2
y  x  2x  3 . Câu 50: Hàm số 2
y  4x  3x 1 có đồ thị là một trong bốn hình vẽ dưới đây. Đồ thị đó là đồ thị nào? A. . B. . C. . D. . Lời giải: Từ hàm số 2
y  4x  3x 1 ta có hệ số c  1  tọa độ giao điểm với trục Oy tại 0;   1 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Nên ta loại A, C và B, D thỏa mãn. b 3
Hoành độ đỉnh của Parabol là x  
  0  loại D và B thỏa mãn. 2a 8
Câu 51: Đồ thị hàm số 2
y x  2x thể hiện bởi hình vẽ nào dưới đây? A. B. C. D. y y y y 1 -1 O 1 1 2 x 2 O x -1 2 O 1 x -1 2 O 1 -1 x Lời giải:
Cách 1: Vẽ P 2 2
: y x  2x y x  2x bằng cách giữ phần đồ thị của P phía trên trục Ox
và lấy đối xứng phần P phía dưới trục Ox qua trục . Ox
Kiểm tra đỉnh parabol 2; 2 ta thấy đồ thị ở đáp án D là phù hợp.
Cách 2: Kiểm tra điểm 1;1 thuộc đồ thị và xác định giao điểm với Ox, ta thấy đồ thị ở đáp án B là phù hợp. Câu 52: Cho hàm số 2
y f (x)  x bx c có đồ thị như hình vẽ bên dưới:
Nhận định nào sau đây đúng về dấu hệ số b và c ?
A. b  0 ; c  0 .
B. b  0 ; c  0 .
C. b  0 ; c  0 .
D. b  0 ; c  0 . Lời giải:
Bề lõm của đồ thị hướng xuống nên a  0 . b
Hoành độ đỉnh của đồ thị có giá trị dương nên  0  b
  0  b  0 . 2a
Đồ thị cắt trục tung tại điểm mà tung độ mang giá trị âm nên c  0 .
Câu 53: Đồ thị hàm số: 2
y ax bx c như hình vẽ bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Trong các hệ số a, b, c có bao nhiêu giá trị dương? A. 1. B. 0 . C. 2 . D. 3 . Lời giải:
Từ đồ thị hàm số ta có a  0 , hoành độ đỉnh của đồ thị hàm số là: b x  
1  0,a  0  b  0 . 2a
Giao điểm với trục tung có tung độ bằng 3  c  3  0 .
Vậy các giá trị dương là b, c .
Câu 54: Cho hàm số    2 y
f x ax bx c có bảng biến thiên như sau :
Khẳng định nào sau đây sai ? A. a  0 .
B. b  0 .
C. c  0 . D. TXĐ D  . Lời giải:
Từ bảng biến thiên của hàm số ta có a  0, c  1 và hàm số luôn xác định trên , đồng thời b
hoành độ đỉnh parapol là x    0 nên b  0. 2a
Câu 55: Cho hàm số    2 y
f x ax bx c có đồ thị như hình bên dưới:
Khẳng định nào dưới đây đúng?
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  0, c  0 .
D. a  0,b  0, c  0 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Đồ thị là parabol có bề lõm quay xuống nên a  0 .
Đồ thị cắt trục trung tại điểm phía dưới trục hoành nên c  0 .
Hoành độ đỉnh dương nên a,b trái dấu, mà a  0 nên b  0 . Câu 56: Cho hàm số 2
y ax bx c có đồ thị như hình vẽ bên dưới: Tích abc bằng A. 12 B. 12. C. 3. D. 0. Lời giải: Đồ thị hàm số 2
y ax bx c đi qua A0;3  3  c Đồ thị hàm số 2
y ax bx c đi qua B 1;0  0  a b c Đồ thị hàm số 2
y ax bx c đi qua C 3;0  0  9a  3b c c  3 a  1  
a b c  0  b   4  Ta có:  
9a  3b c  0 c  3   Vậy ta có: . a . b c  1. 4  .3  12. 
Câu 57: Cho hàm số   2
f x ax bx c có đồ thị như hình bên dưới:
Giá trị của biểu thức: T  2a b c bằng A. 1. B. 1. C. 0. D. 2. Lời giải:
Đồ thị cắt trục tung tại điểm có tung độ bằng 1
 nên c  1. Suy ra 2
y ax bx 1 b
Trục đối xứng x  1  
1  2a b  0 . 2a
Khi đó T  2a b c  0  (1)  1.
Câu 58: Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Giá trị của biểu thức T  4a b  2c bằng A. 8 . B. 6 . C. 3 . D. 4 . Lời giải: f  0  3 c  c  Từ giả thiết ta có:   3   3  .  f  4  3 1
 6a  4b c  3 b   4  a
Do đó T  4a b  2c  6 . Câu 59: Cho parabol 2
y ax bx c có đồ thị như hình vẽ bên dưới:
Khẳng định nào dưới đây đúng?
A. a  0; b  0; c  0 .
B. a  0;b  0; c  0 . C. a  0; b  0; c  0 . D. a  0; b  0; c  0 . Lời giải:
+ Parabol có bề lõm hướng xuống nên a  0 .
+ Parabol cắt trục Oy tại điểm có tọa độ là 0;3 nên c  3  0 . b
+ Parabol có hoành độ đỉnh x  1 
1 mà a  0 nên b  0 . I 2a
Câu 60: Tọa độ giao điểm của đường thẳng d : y  x  4 và parabol 2
y x  7x  12 là
A. (2; 2) và (4; 0) .
B. (2; 2) và (4;8) .
C. (2; 2) và (4; 0) .
D. (2; 6) và (4;8) . Lời giải: x  2
Phương trình hoành độ giao điểm 2
x  4  x  7x 12 2
x  6x  8  0   . x  4
Với x  2 suy ra y  2 .
Với x  4 suy ra y  0 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Vậy tọa độ giao điểm cần tìm là (2; 2) và (4; 0) .
Câu 61: Hai đồ thị hàm số 2
y x  2x  3 và y  2x 1 có bao nhiêu điểm chung? A. 2 . B. 1. C. 0 . D. 3 . Lời giải:
Xét phương trình: 2 2
x  2x  3  2x 1  x  4x  4  0  x  2 .
Vì phương trình có một nghiệm nên hai đồ thị hàm số cắt nhau tại 1 điểm.
Câu 62: Toạ độ giao điểm của đồ thị hàm số 2
y x x  2 với trục tung là
A. 0; 2.
B. 2;0. C. 0; 2. D.  1  ;0 . Lời giải:
Gọi M là giao điểm của trục tung và đồ thị của hàm số 2
y x x  2 . Khi đó tọa độ của M có dạng M 0; y . M
Do M thuộc đồ thị của hàm số 2 2
y x x  2  y  0  0  2  2 . M Vậy M 0; 2 .
Câu 63: Số giao điểm của Parabol  P 2
: y x  4x  4 với trục hoành là A. 0 . B. 1. C. 2 . D. 3 . Lời giải:
Xét y   x x     x  2 2 0 4 4 0 2  0  x  2 . Vậy Parabol  P 2
: y x  4x  4 giao với trục hoành tại một điểm 2; 0 .
Câu 64: Đồ thị hàm số nào sau đây tiếp xúc trục hoành? A. 2
y x x  2 . B. 2
y  x  3x  2 . C. 2
y  2x  2x  1 . D. 2
y x  4x  4 . 1 2 3 4 Lời giải: Xét hàm số 2
y x  4x  4 Ta có: 2
x  4x  4  0  x  2 (nghiệm kép) nên đồ thị hàm số y 4 4
tiếp xúc cắt trục hoành.
Câu 65: Toạ độ giao điểm của parabol 2
(P ) : y  2x  2x  3 với parabol 2
(P ) : y x  6x là 1 2
A. 1;7 và 3;27 . B. 7;  1 và 27;3 .
C. 1;3 và 3;15 . D. 3;  1 và 15;3 . Lời giải: x 1
Phương trình hoành độ giao điểm: 2 2 2
2x  2x  3  x  6x x  4x  3  0   x  3
Vậy có hai giao điểm cần tìm: 1;7 và 3; 27 .
Câu 66: Cho hàm số   2
f x ax bx c có đồ thị như hình vẽ bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Phương trình f x  2 có bao nhiêu nghiệm? A. 2 . B. 1. C. 3 . D. 4 .
Câu 67: Cho hàm số   2
f x ax bx c có đồ thị như hình vẽ bên dưới:
Phương trình f x  2 có bao nhiêu nghiệm? A. 2 . B. 1. C. 3 . D. 4 . Lời giải:
f x  2
Ta có f x  2  
. Dường thẳng y  2 cắt đồ thị y f x tại 2 điểm phân biệt  f   x  2 
nên f x  2 có 2 nghiệm phân biệt. Đường thẳng y  2 không cắt đồ thị y f x nên
phương trình f x  2
 vô nghiệm. Vậy phương trình đã cho có 2 nghiệm phân biệt. 2
Câu 68: Cho hàm số y f x  ax bx c a  0 có bảng biến thiên như sau:
Tìm tất cả các giá trị của m để phương trình f x 2 |
| m 1 có 4 nghiệm phân biệt.  2  m  1 A.  .
B. 1  m  2 .
C. 1  m  2 .
D. 0  m  1 . 1   m  2 Lời giải:
Dựa vào BBT của hàm số y f x , ta suy ra bảng biến thiên của hàm số y |  f x|  2  m  1 2
Để phương trình có 4 nghiệm phân biệt thì 0  m 1  1   . 1   m  2
Câu 69: Cho hàm số   2
f x ax bx c có đồ thị như hình bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Số nghiệm của phương trình f f  2 x  2x   1  1  là A. 1. B. 2. C. 3. D. 4. Lời giải:
Đặt u f  2 x  2x  
1 , phương trình đã cho trở thành f u   1  (*)
Phương trình (*) chính là phương trình hoành độ giao điểm của đồ thị đồ thị f u và đường thẳng y  1 u  0
Dựa vào đồ thị, ta có (*)   u u  1  0
x  2x 1  x  0 (1)
 Với u  0  f  2 x  2x   2 1 1  0   2
x  2x 1  x 1 (2)  2
 Vì x  0 nên phương trình (1) vô nghiệm 1
 Vì x  1 nên phương trình (2) luôn có hai nghiệm trái dấu. 2
x  2x 1  x  0 (3)
 Với u u 1  f  2
x  2x 1  u   0  2 3 0 2
x  2x 1  x 1 (4)  4
 Vì x  0 nên phương trình (3) vô nghiệm 3
 Vì x  1 nên phương trình (4) luôn có hai nghiệm trái dấu. 4
Vậy phương trình đã cho có 4 nghiệm.
Câu 70: Cho hàm số bậc hai f x có đồ thị hàm số như hình bên dưới:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Hỏi m thuộc tập hợp nào dưới đây thì phương trình   2
f x m m có 4 nghiệm thực phân biệt? A. ; 1
  2;. B.  1  ;0  1  ;2.     C.  1
 ;0   ;12 D.    ;0 1;. Lời giải:
Dựa vào đồ thị, ta thấy phương trình f x  t có 4 nghiệm thực phân biệt khi và chỉ khi
0  t  2 . Do đó, phương trình   2
f x m m có 4 nghiệm thực phân biệt khi và chỉ khi     m    m 1 1 m  0   1   m  0 2
0  m m  2         m    m 1 m  2 0  0 1    m  2  1   m  2 Vậy m  1  ;0 1;2 .
Câu 71: Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ.
Số giá trị nguyên của m để phương trình  2
f x   m có đúng 4 nghiệm phân biệt là A. 1. B. 2 . C. 3 . D. 4 . Lời giải: Đặt 2
x X  0 , ta có phương trình f X   m (*). Để phương trình  2
f x   m có đúng 4
nghiệm phân biệt thì điều kiện là phương trình (*) có đúng 2 nghiệm dương phân biệt.
Đồ thị hàm số y f X  có dạng như hình vẽ:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Do đó, để phương trình (*) có đúng 2 nghiệm dương phân biệt thì m  0 hoặc 1  m  3 .
Mà m  nên m 0; 
2  có hai giá trị nguyên của m .
Câu 72: Cho Parabol (P): 2
y x  2x  3 . Số giá trị nguyên âm của tham số m để Parabol (P) cắt
đường thẳng d: y x m tại hai điểm phân biệt là A. 4 . B. 5 . C. 7 . D. 6 . Lời giải:
Phương trình hoành độ giao điểm: 2 2
x  2x  3  x m x  3x  3  m  0
(P) cắt d tại hai điểm phân biệt  Phương trình (1) có hai nghiệm phân biệt 21
   0  9 12  4m  0  m   . 4
Vậy các giá trị m thỏa mãn yêu cầu đề bài là m 5;  4  ; 3;  2  ;  1 .
Câu 73: Cho đường thẳng d : y  2  mx  5m 1 và parabol  P 2 2
: y x mx m  3 ( m là tham số).
Có tất cả bao nhiêu giá trị nguyên của m nhỏ hơn 5 để đường thẳng d cắt parabol  P tại hai điểm phân biệt? A. 4 . B. 5 . C. 7 . D. 6 . Lời giải:
PTHĐGĐ:   m 2 2 2
x m   x mx m   x  m   2 2 5 1 3 2
1 x m  5m  2  0   1 .
Đường thẳng d cắt parabol  P tại hại điểm phân biệt khi và chỉ khi PT (1) có hai nghiệm phân biệt.
Khi đó:    m  2   2 0 1
m  5m  2  0  3m  3  0  m  1  .
Với m nguyên và nhỏ hơn 5 ta có m 0,1, 2,3, 
4 . Vậy có 5 giá trị m thỏa mãn ycbt.
Câu 74: Đồ thị hàm số 2
y x  2x cắt đường thẳng 2
y m  2x tại hai điểm phân biệt có hoành độ lần
lượt là x ; x . Giá trị của T x x bằng 1 2 1 2 A. 2. B. 2. C. 4. D. 2 m  4. Lời giải:
Phương trình hoành độ giao điểm của đường thẳng và Parabol đã cho là 2 2 2 2
x  2x m  2x x  4x m  0 (1).
Yêu cầu bài toán tương đương với phương trình (1) có 2 nghiệm phân biệt x ; x . 1 2 Ta có ' 2
  4  m  0, m
  . Do đó phương trình (1) luôn có 2 nghiệm phân biệt x ; x . 1 2 b  4 
Theo định lý Viet thì x x    4  . 1 2 a 1
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 75: Tìm tập hợp tất cả các giá trị của a để đường thẳng d : y  2a  1 x a cắt parabol P : 2
y x x  1 tại hai điểm phân biệt nằm về hai phía đối với trục tung.
A. ; 3.
B. ;1.
C. 1; . D. .  Lời giải:
Xét phương trình: 2
x x    a   2 1 2
1 x a x  2ax a  1  0 (1).
Yêu cầu bài toán  Phương trình (1) có hai nghiệm trái dấu  a  1  0  a  1.
Câu 76: Cho đồ thị hàm số 2 2 y x 2mx 2m
1 cắt đồ thị hàm số y  2x tại các điểm có hoành
độ lần lượt là x ; x . Gọi M , m là giá trị lớn nhất, nhỏ nhất của 2 2
H x x x x . Đặt 1 2 1 2 1 2 T M  .
m Khẳng định nào sau đây đúng?
A. T  10 .
B. T  10, 20 .
C. T  20,30 . D. T  30 . Lời giải:
Xét phương trình hoành độ giao điểm của 2 đồ thị 2 2 2x x 2mx 2m 1 2 2 x 2 m 1 x 2m 1 0 *
2 đồ thị cắt nhau tại các điểm có hoành độ lần lượt là x ; x  phương trình * có 2 1 2 2
nghiệm x ; x    m     2 1 2m   1  0 2
 2m m  0  0  m  2 . 1 2 x x  2  m  2 Theo Vi-et ta có 1 2  2 x x  2m 1  1 2 2 2 2
H x x x x   x x
x x   m    2 2 2 2m   1 2
 2m  8m  3 1 2 2 1 2 1 2 1 2 BBT
Từ BBT suy ra M  27, m  3.Vậy T  30 .
Câu 77: Tìm tất cả các giá trị nguyên của tham số m để đồ thị hàm số y m  2x cắt parabol 2
y x  2x tại hai điểm phân biệt cùng có hoành độ nhỏ hơn 1. A. 7 . B. 8 . C. 9 . D. 10 . Lời giải: Phương trình tương giao 2 2
x  2x m  2x x  4x m (*).
Xét hàm số f x 2
x  4x với x  1, có bảng biến thiên như sau:
Để thỏa mãn bài ra thì phương trình (*) phải có 2 nghiệm phân biệt nhỏ hơn 1. Do đó đường
thẳng y m phải cắt đồ thị hàm số y f x tại hai điểm phân biệt nên 4  m  5 .
Mà m  nên m  3  ; 2  ; 1  ;0;1;2;3; 
4  có 8 giá trị nguyên của m .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 78: Gọi S là tập hợp các giá trị thực của tham số m sao cho Parabol  P 2
: y x  3x m cắt trục
Ox tại hai điểm phân biệt ,
A B thoả mãn OA  2OB . Tổng các phần tử của tập hợp S bằng A. 2 . B. 3 . C. 18 . D. 16 . Lời giải:
Phương trình hoành độ giao điểm của parabol  P 2
: y x  3x m và trục Ox là 2
x  3x m  0   1 .
Parabol  P cắt trục Ox tại hai điểm phân biệt , A B   
1 có hai nghiệm phân biệt 9
   0  9  4m  0  m  . 4 x x  3
Giả sử x , x là hoành độ hai điểm , A B . Ta có A B  . A B
x .x mA Bx  2x Ta có 2 2 2 2
OA  2OB OA  4OB x  4 A B x  . A Bx  2  xA Bx x  3 x  2 A B A   9
Với x  2x ta được x .x m  x  1
m  2 (thoả mãn điều kiện m  ). A B A B B   4 x  2x
x .x mA BA Bx x  3 x  6 A B A   9 Với x  2
x ta được x .x m  x  3   m  18
 (thoả mãn điều kiện m  ). A B A B B   4 x  2  x
x .x mA BA B
Vậy tổng các giá trị của m là 2   1  8  1  6 .
Câu 79: Có bao nhiêu giá trị của tham sô m để đường thẳng d  : y m(x 1)  2 cắt Parabol P 2
: y x  m  2 x  2m tại hai điểm phân biệt ,
A B sao cho AB  4 2 ? A. 2 . B. 1. C. 3 . D. 4 . Lời giải:
Xét phương trình tìm hoành độ giao điểm của  P và d  : 2
x  m   x m mx   2 2 2
1  2  x  2x m  2  0
Để đường thẳng d  cắt Parabol  P tại hai điểm phân biệt , A B thì
  0  m  3  0  m  3
Gọi Ax ;m x 1  2 và B x ; m x 1  2 . 2  2   1  1   2 Khi đó: 2
AB   x x
 m x 1  m x 1  2 1    2   1  2
 x x 2  m
  x x  2   
x x 2 m  1  m  1x x 2 2 2  4x x  2 1 2 1 2 1 1 2 1 2     2 m      m     2
m   m   3 2 1 4 4 2 1 4
12  4m 12m  4m 12 . Theo giả thiết: 3 2
AB  4 2  4m 12m  4m 12  32  m  1 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Câu 80: Gọi A, B là hai giao điểm của đường thẳng  : y  x k  1 và parabol P 2 : y x  . x Tìm tập
hợp tất cả các giá trị của tham số k để trung điểm I của đoạn thẳng AB nằm trên đường
thẳng d :y x  2. A. 2;   1 . B. 2;   1 . C.   2 . D.   1 . Lời giải:
Xét phương trình: 2 2
x x  x k  1  x  2x  1  k  0 (1)
Để  cắt P tại hai điểm phân biệt  Phương trình (1) có hai nghiệm phân biệt
   4  41  k  4k  0  k  0 (*).
Lúc đó, hai giao điểm tương ứng là Ax ; x k  1 ,B x ; x k  1 . 1 1   2 2   x x 1 2 x   1   I
Do I là trung điểm của AB nên 2   I  1  ; k.
x x  2k  2  1 2 x   k I  2
Yêu cầu bài toán  I  1
 ; kd k  1 2  k  1. Câu 81: Cho hàm số 2
y x  2x  2 có đồ thị là parabol  P và đường thẳng d có phương trình
y x m . Giá trị của m để đường thẳng d cắt parabol  P tại hai điểm phân biệt , A B sao cho 2 2
OA OB đạt giá trị nhỏ nhất là 1 5 1 5 A. m   .
B. m   . C. m  . D. m  . 2 2 2 2 Lời giải:
Phương trình hoành độ giao điểm của đường thẳng d cắt parabol  P là 2 2
x  2x  2  x m x  3x m  2  0   1 .
Để đường thẳng d cắt parabol  P tại hai điểm phân biệt thì phương trình   1 có 2 nghiệm 17
phân biệt    9  4m  8  17  4m  0  m  . 4 x x  3
Khi đó, phương trình  
1 có 2 nghiệm x , x thỏa mãn 1 2  . 1 2
x .x m  2  1 2 2 2
Giả sử Ax , x m , B x ; x m , ta có: 2 2 2
OA OB x   x m 2
x x m 1 1 2  2  1 1   2 2 
 2x x   2mx x   2m  2x x 2 2 2 2  2  x x
 2mx x  2  2m 1 2 1 2 1 2 1 2 1 2   2  
 29  2m  4 5 27 27 2 2
 6m  2m  2m 10m  26  2 m       2  2 2 5 Vậy 2 2
OA OB đạt giá trị nhỏ nhất khi m  . 2
Câu 82: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y mx  3 cắt parabol P 2
: y  x  2x tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB
thuộc đường thẳng y x  6. Tính tổng tất cả các phần tử của S. A. 5 . B. 1  . C. 3 . D. 3  .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Lời giải:
Phương trình hoành độ giao điểm: 2 2
x  2x mx  3  x  m  2 x  3  0.
Để đường thẳng cắt parabol tại hai điểm phân biệt thì    m  2 0 2 12  0, m   .  x x x x
Giả sử x , x là hai nghiệm, khi đó Ax ;mx  3 , B x ; mx  3  I ; m 3 1 1   2 2  1 2 1 2   1 2  2 2  2  2  m 2  m
 2  m m  2m  6 
Theo Viet x x  2  m I ; m  3    I  ;  1 2  2 2   2 2  2
m  2m  6 2  mm  1  2
I d : y x  6  
 6  m  3m  4  0   S  3.  2 2 m  4
Câu 83: Biết Parabol  P : 2
y ax  4x c có đỉnh I  1
 ; 6 . Tính S a c A. 6  . B. 6 . C. 2 . D. 2  . Lời giải: Cách 1:
Áp dụng công thức đỉnh của Parabol ta có: b   1  4    1   a  2 . 2a 2a  2  2    b 4ac 4 4.2.c 6     6    6  c  4 . 4a 4a 4.2
Vậy S a c  2   4    2 . Cách 2: f  1
   a  4  c  6  a  4  c a c  2.
Câu 84: Cho hàm số    2 y
f x x bx c có đồ thị là một Parabol  P có đỉnh I 1;  4 . Tính b c . A. 12 . B. 8  . C. 10 . D. 5  . Lời giải: Ta có:  b  1 b   2   2  
b c  5 .  c  3  1
  b c  4
Câu 85: Tìm parabol  P 2
: y ax  3x  2, biết rằng parabol có trục đối xứng x  3 ? 1 1 1 A. 2
y x  3x  2. B. 2 y x x  2. C. 2 y
x  3x  3. D. 2 y x  3x  2. 2 2 2 Lời giải: 3  1
Ta có trục đối xứng của  P 2
: y ax  3x  2 là x   3   a  2a 2 1 Vậy  P 2 : y x  3x  2. 2
Câu 86: Đồ thị của hàm số 2
y ax  3x c đi qua hai điểm A2;3 và B 1;6 . Giá trị biểu thức
T  36a c bằng A. 17 . B. 38 . C. 72 . D. 73 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Đồ thị của hàm số 2
y ax  3x c đi qua hai điểm A2;3 và B 1;6 nên ta có:
4a  6  c  3
4a c  9 a  2     
a  3 c  6 a c  3 c  1
Suy ra T  36a c  36.2 1  73
Câu 87: Cho đồ thị hàm số 2
y ax bx  4 có đỉnh là điểm I 1; 2 . Tính a  3b . A. 20 . B. 18 . C. 30 . D. 25 Lời giải:
Do đồ thị hàm số 2
y ax bx  4 có đỉnh là điểm I 1; 2  b   1
 2a b  0  a  6   2a    
a  3b  30 . 
a b  4  2  b   12  y    1  2
Câu 88: Xác định  P 2
: y ax bx c , biết  P có đỉnh là I (1;3) và đi qua ( A 0;1) A. P 2 : y  2
x  3x 1. B. P 2 : y  2
x  4x 1. C. P 2 : y  2
x  4x 1. D. P 2 : y  2
x  4x 1. Lời giải:
a b c  3 b   
Ta có tọa độ đỉnh I ( ; )   b (1) 2a 4a   1  2a (P) đi qua điểm (
A 0;1) nên c  1 thay vào (1) ta được a  2;b  4
Câu 89: Cho parabol  P 2
: y ax bx c a, , b c
;a  0 có hoành độ đỉnh bằng 1 và đi qua hai
điểm M 0 ;  
1 , N 1 ;  3 . Khi đó parabol  P là đồ thị của hàm số nào? A. 2
y  2x  4x 1 . B. 2
y x  4x  1 . C. 2
y  2x  4x  1 . D. 2 y  2
x  4x 1. Lời giải: b
+) Hoành độ của đỉnh Parabol bằng 1    1  b  2  a . 2a
+) Đồ thị hàm số đi qua các điểm 0; 
1 và 1;3 . Như vậy ta có hệ phương trình: b   2  a b   2  ac  1  a  2     2  .0 a  .0 b c  1   c  1   b   2  a b   4 .     2 .1 a  .1 b c  3 
a b c  3  a b  2  c  1     
Vậy parabol  P là đồ thị của hàm số 2
y  2x  4x 1 .
Câu 90: Biết Parabol 2
y ax bx c đi qua điểm A8;0 và có đỉnh I 6; 1
 2 , khi đó a b c là: A. 85 B. 63. C. 36. D. 96. Lời giải:
 A8;0P
 64a  8b c  0 Ta có:      I I 6; 1  2P   3
 6a  6b c  1  2 b
Hoành độ đỉnh: x
 6  12a b  0II  2a
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
 64a  8b c  0  a  3  
Từ  I ;II  được hệ: 36
a  6b c  12   b
  36 . Vậy a b c  3  36  96  63 .   12a b  0  c  96 
Câu 91: Biết đồ thị hàm số 2
y ax bx ca  0 biết đồ thị hàm số đi qua ba điểm
A0; 4; B 1;3; C 1;9. Tính ab c. A. 1. B. 2. C. 1. D. 2. Lời giải: Hàm số 2
y ax bx ca  0 có đồ thị là Parabol  P .
P đi qua điểm A0;4 nên c  4. Suy ra: P 2
: y ax bx  4 a  0 .
P đi qua điểm B1;3 nên 2 3  .1 a  .1
b  4  a b  1  .  2
P đi qua điểm C 1;9 nên 9  . a   1  . b  
1  4  a b  5 . a b  1  2a  4
a  2tmdk :a  0 Ta có hệ:      a b  5 b   1   a b   3 
Vậy ab c  6  4  2.
Câu 92: Xác định hàm số bậc hai 2
y ax bx c biết đồ thị của nó có đỉnh I (1, 1) và đi qua ( A 2, 0) . A. 2
y x  3x  2 . B. 2
y x  2x . C. 2
y  2x  4x  3 . D. 2
y x  2x . Lời giải:
Vì (P) có đỉnh I (1, 1) và đi qua (
A 2, 0) nên ta có hệ phương trình  b  1 
2a b  0 a 1 2a   
a b c  1  a b c  1  b
  2 . Vậy hàm số cần tìm là 2
y x  2x .   
4a  2b c  0
4a  2b c  0 c  0    
Câu 93: Biết rằng hàm số 2
y ax bx c đạt giá trị nhỏ nhất bằng 1 và đồ thị hàm số cắt đường thẳng
y  2022x  2 tại một điểm trên trục Oy . Tính 2 2 2
S a b c . A. 10 . B. 9 . C. 50 . D. 4 . Lời giải: b   1
Vi hàm số đạt giá trị nhỏ nhất bằng 1 khi x  1 nên ta có  2a .
a b c 1
Giao điểm của đường thẳng y  2022x  2 với trục Oy là điểm A0; 2 .
Từ giả thiết ta suy ra đồ thị hàm số đã cho đi qua A0; 2 . Suy ra 2  .0 a  .0
b c c  2
2a b  0 a 1 Ta có hệ    . Vậy S  9 . a b  1  b   2 
Câu 94: Cho parabol  P 2
: y ax bx c , biết hàm số 2
y ax bx c đạt giá trị nhỏ nhất là 4 tại
x  2 và đồ thị của nó cắt trục tung tại điểm có tung độ là 6. Tính 2a b c.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống A. 6 . B. 5 . C. 4 . D. 2 . Lời giải:
Do hàm số đạt giá trị nhỏ nhất nên a  0 .  b  1   2 a   ab  4  a  2 2   
Ta có: 4a  2b c  4  4a  2b  2   b  2  (nhận).    c  6 c  6 c  6      1
Vậy hàm số cần tìm là 2 y
x  2x  6 . 2
Vậy 2a b c  1  2  6  5. Câu 95: Cho hàm số 2
y ax bx c với a , b , c
, hệ số a  0. Biết rằng hàm số đạt giá trị nhỏ nhất bằng 1
 tại x  2 và đồ thị hàm số đi qua điểm M 1;0 . Tính T abc. A. T  6 .
B. T  5 .
C. T  4 .
D. T  12 . Lời giải:
Tập xác định D  .
Do đồ thị hàm số đã cho đi qua điểm M 1;0 nên có: a b c  0   1 . Trên , hàm số 2
y ax bx c đạt giá trị nhỏ nhất bằng 1
 tại x  2 , ta có: a  0  a  0  b    2
 4a b  0 2 . 2a   
4a  2b c  1 
4a  2b c  1   a  0  a 1
4a b  0  Kết hợp   1 và 2 ta có:   b  4
  T abc  12  .
4a  2b c  1    c  3 
a b c  0
Câu 96: Gọi T là tổng tất cả các giá trị của tham số m để parabol  P 2
: y x  5x m cắt trục Ox tại hai điểm phân biệt ,
A B thỏa mãn OA  4OB . Tính T . 64 64 A. T   . B. T  .
C. T  2 .
D. T  2 . 9 9 Lời giải:
Phương trình hoành độ giao điểm của (P) và trục Ox là: 2
x  5x m  0 (1) .
(P) cắt trục Ox tại hai điểm phân biệt ,
A B thỏa mãn OA  4OB  phương trình (1) có hai
nghiệm phân biệt x , x thỏa mãn x  4 x 1 2 1 2  25   0 25  4m  0 m  2  4     x  4x
 x  4x   . 1 2 1 2 x  4x 3 1 2      x  4  x  x  4  x  1 2  1 2 x  4  x 4  1 2  
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống x x  5
Mặt khác, theo định lý Viet cho phương trình (1) thì: 1 2  5 .
x .x m  1 2
x  4x  5 x 1
Với x  4x , thì 5 1 1 1     . 1 2
x .4x m  m  4 1 1  5 x       1 x 4x 5  
Với x  4x , thì   1 1 3 5     . 1 2 x . 4  x m 100  1  1  m    9 100
Vậy có hai giá trị của m là m  4 và m   . 9 64 Vậy T   . 9
Câu 97: Cho parabol  P : 2
y ax bx c , a  0 biết  P đi qua M (4;3) cắt Ox tại N (3;0) và Q sao
cho INQ có diện tích bằng 1 biết hoành độ điểm Q nhỏ hơn 3 với I là đỉnh của  P . Tính
a b c . A. 1  . B. 1. C. 0 . D. 2 . Lời giải:
Vì  P đi qua M (4;3) nên 3  16a  4b c .   1
Mặt khác  P cắt Ox tại N (3;0) suy ra 0  9a  3b c 2 ,  P cắt Ox tại Q nên
Q t;0, t  3 .  b t  3    a
Theo định lý Viét ta có  c  3t   a 1  b   Ta có S
IH.NQ với H là hình chiếu của I  ;    lên trục hoành INQ 2  2a 4a   1  Do IH  
, NQ  3  t  3  t nên S 1   .  t INQ 3  1 4a 2 4a 2 2       tb c 2  
   t t 3 2  t     t3 8 3 3 3 3    3 .  2a a a 4 a a 3  7a 1 4  t Từ  
1 và 2 ta có 7a b  3  b  3  7a suy ra t  3     a a 3  3 8 4 t
Thay vào 3 ta có 3  t    3 2 
 3t  27t  73t  49  0  t 1 3
Suy ra a  1  b  4  c  3 .
Vậy  P cần tìm là 2
y x  4x  3 .
Câu 98: Có tất cả bao nhiêu giá trị của tham số m để giá trị nhỏ nhất của hàm số f x 2
x  2x m 1 trên 1;2 bằng 5? A. 3. B. 1. C. 2. D. 4.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống Lời giải:
Đặt g x 2
x  2x m 1. Đồ thị hàm số gx là parabol có đỉnh I 1;m. g   1  m  4 
min g x  m  1;2 Ta có: g   1  m , suy ra  .  max g
x  m  4 g  2  m 1   1;2
Ta xét các trường hợp sau:
Trường hợp 1: m  0 .
min f x  m m  5 .  1  ;2
Trường hợp 2: m  4  0  m  4 .
min f x  m  4  m  4  5  m  9 .  1  ;2
Trường hợp 3: m  0  m  4  4  m  0 .
min f x  0 mà theo bài min f x  5 nên không có m thỏa mãn.  1  ;2  1  ;2
Vậy có hai giá trị của tham số m thỏa mãn yêu cầu bài toán là m  9 và m  5 .
Câu 99: Cho hình chữ nhật ABC ,
D AB  10, AD  6 . Trên các cạnh AB, BC,CD lấy các điểm P, Q, R
sao cho AP BQ CR x . Giá trị của x trong khoảng nào để diện tích tam giác PQR đạt giá trị nhỏ nhất. A P B Q D R C A. 3;5 . B. 6;8 . C. 8;10 . D. 4;8 . Lời giải: Ta có: 1 SSSSS   x   x   xx xx PQR ABCD ADRP PBQ QCR    1    1 10.6 . 10 .6 . . 10 . .6  2 2 2 2
x  8x  30.
Diện tích của tam giác PQR là một hàm số bậc hai do đó diện tích của tam giác PQR đạt giá b
trị nhỏ nhất khi x    4 . 2a Vậy S      14 x 4. PQR min
Câu 100: Biết có 2 giá trị thực của tham số m là m , m 1
2 để giá trị nhỏ nhất của hàm số 2 2
y f (x)  4x  4mx m  2m trên đoạn [-2; 0] bằng 3. Tổng m m 1 2 bằng 3 1 1 3 A.  . .  . . 2 B. 2 C. 2 D. 2 Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Đồ thị hàm số y f x là parabol có hệ số bậc hai là 4  0 nên bề lõm hướng lên. Hoành độ m TH1: Nếu  2   m  4  thì x  2
  0 . Suy ra f x đồng biến trên đoạn [-2; 0]. 2 I
Do đó min f x  f  2   2
m  6m 16 .  2  ;0 Theo yêu cầu bài toán: 2
m  6m 16  3 (vô nghiệm). m TH2: Nếu 2    0  4
  m  0 thì x [-2; 0]. Suy ra f x đạt giá trị nhỏ nhất tại đỉnh. 2 I m Do đó đỉnh x  . I 2  m
min f x  f  2  m .    2  ;0  2  3 Theo yêu cầu bài toán 2
m  3  m   (thỏa mãn 4  m  0 ). 2 m TH3: Nếu
 0  m  0 thì x  0  2
 . Suy ra f x nghịch biến trên đoạn [-2; 0]. 2 I Do đó m
f x  f   2 in 0  m  2 . m  2  ;0 Theo yêu cầu bài toán: 2
m  2m  3  m  1 (loại) hoặc m  3 (thỏa mãn). 3 Kết luận: m   hoặc m  3 . 2
Câu 101: Gọi S là tập hợp các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số
y f x 2 2
 4x  4mx m  2m trên đoạn 2; 0 bằng 3. Tính tổng T các phần tử của S . 3 9 1 3 A. T  . B. T  . C. T  . D. T   . 2 2 2 2 Lời giải: b 4  m m Ta có: x      2a 2.4 2 m  2  m  m  4 2 
Trường hợp 1:  2  ;0     m   ;   4 (0;  ) 2 m  m  0  0  2
Khi đó, giá trị nhỏ nhất của hàm số là f   2
2  m  6m 16 hoặc f   2
0  m  2m .
*Nếu f    f   2 2 2
0  m  6m 16  m  2m  8m  1  6  m  2 
Thì giá trị nhỏ nhất của hàm số là f   2 2
2  3  m  6m 16  3  m  6m 13  0  m   .
*Nếu f    f   2 2 2
0  m  6m 16  m  2m  8m  1  6  m  2  m  1  (loai)
Thì giá trị nhỏ nhất của hàm số là f 0 2 2
 3  m  2m  3  m  2m  3  0   . m  3 m m
Trường hợp 2:  2  ;0  2    0  4   m  0 2 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống m
Khi đó, giá trị nhỏ nhất của hàm số là f    2  2 m m 3 Suy ra: 2 4.  4 . m
m  2m  3  2
m  3  m   (nhận) 4 2 2  3  3 3
Vậy, S   ; 3  T    3  .  2  2 2
Câu 102: Tìm tập hợp tất cả các giá trị của tham số k để đường thẳng  : y kx  3 cắt parabol  3 P 2
: y x  4x  3 tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng . 2 A. 5;   3 . B. 3;  3 . C. 5;  5 . D. 5;   3 . Lời giải: Xét phương trình: yx  0 2
x  4x  3  kx  3  x x  
k  4  0    . x k   4 A
Để  cắt P tại hai điểm phân biệt  k  4  0  k  4 (*). 3 Lúc đó, hai giao điểm tương ứng là A Oy B 2 0; 3 ,
k  4; k  4k  3. H B Gọi
H là hình chiếu vuông góc của B trên x
OA BH x k  4 . O 1 B 3 1 3 k  3  Theo giả thiết: S
  .3. k  4   k  4  1   . OAB 2 2 2 k  5   Câu 103: Cho parabol 2 2
(P) : y  x  2 x
m  3m  4m  3 ( m là tham số) có đỉnh I . Gọi , A B là hai
điểm thuộc Ox sao cho AB  2022 . Khi đó IAB có diện tích nhỏ nhất bằng: A. 1011. B. 2022 . C. 4044 . D. 1010. Lời giải:
Ta có  P có đỉnh 2 I ( ; m 2
m  4m  3) . Diện tích tam giác IAB bằng: 1 S  .d I AB AB   m m  
m m   m m IAB  ;  1 2 2 2 . . 2 4 3 .2022 1011. 2 4 3 1011. 2 4 3 2 2 1011. 2m  2 1 1  1011.1  1011.
Dấu “=” xảy ra khi m  1.
Câu 104: Cho Parabol  P 2
: y x  4x  3 và đường thẳng d  : y mx  2 1 . Tính tổng các giá trị
của tham số m để đường thẳng d  cắt Parabol  P tại hai điểm phân biệt , A B sao cho diện
tích tam giác IAB bằng 10 với điểm I 2;3 . A. 6 . B. 0 . C. 2 . D. 4 . Lời giải:
Xét phương trình tìm hoành độ giao điểm của  P và d  :
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống x  2 2
x  4x  3  m x  2 2
1  x  4  mx  2m  4  0   x m  2
Để đường thẳng d  cắt Parabol  P tại hai điểm phân biệt ,
A B thì m  2  2  m  0 . Gọi A2;   1 và B  2
m  2; m  
1 . Ta thấy điểm A và điểm I nằm trên đường thẳng x  2 và 1
đoạn thẳng IA  4 . Suy ra: S
 .4. m  2  2 10  m  5  m  5  . IAB 2
Câu 105: Một vật chuyển động với vận tốc theo quy luật của hàm số bậc hai vt 2  t
  12t với ts là
quãng thời gian tính từ khi vật bắt đầu chuyển động và v (m/s) là vận tốc của vật. Trong 9
giây đầu tiên kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu?
A. 144 m / s.
B. 243 m / s.
C. 27 m / s.
D. 36 m / s. Lời giải: Ta có BBT: t 0 6 9 36 vt
Dựa vào BBT, ta thấy max vt  v6  36m / s. t0;9   1
Câu 106: Một chiếc cổng hình parabol dạng 2 y  
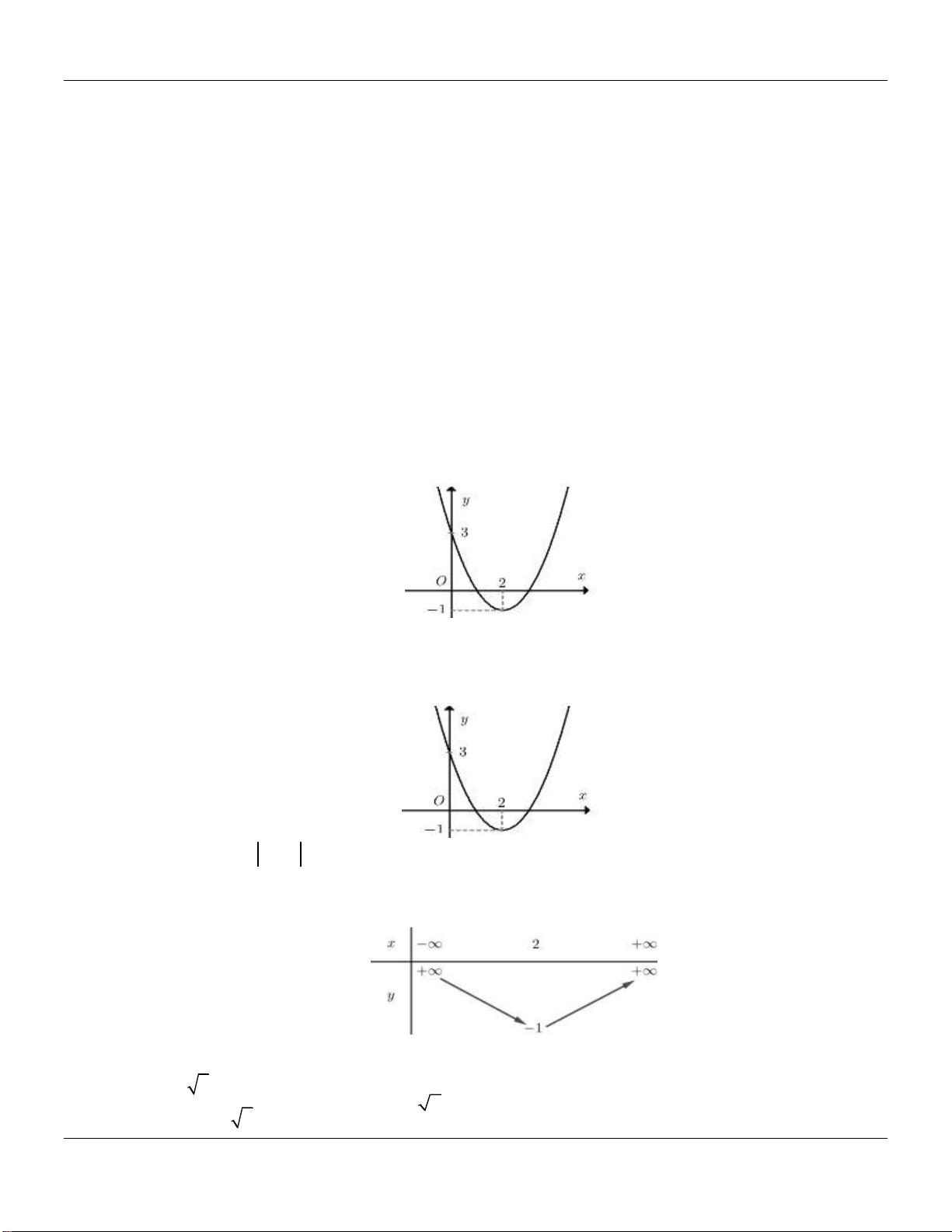
x có chiều rộng d  8m . Hãy tính chiều cao h của 2
cổng. (Xem hình minh họa)
A. h  9m .
B. h  8m .
C. h  7m .
D. h  5m . Lời giải:
HD: Đường thẳng chứa chiều rộng d  8m cắt  P tại A4; h . 1
Điểm A P 2
 h   .4  h  8m . 2
Câu 107: Một của hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu đôi
giày được bán với giá x đôla thì mỗi tháng khách hàng sẽ mua 120  x đôi. Hỏi của hàng
bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất? A. 80 USD. B. 160 USD. C. 40 USD. D. 240 USD. Lời giải:
Gọi y là số tiền lãi của cửa hàng bán giày.
Ta có y  120  x x  40 2
 x 160x  4800  x  2 80 1600 1600 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Dấu "  " xảy ra  x  80 .
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá 80 USD.
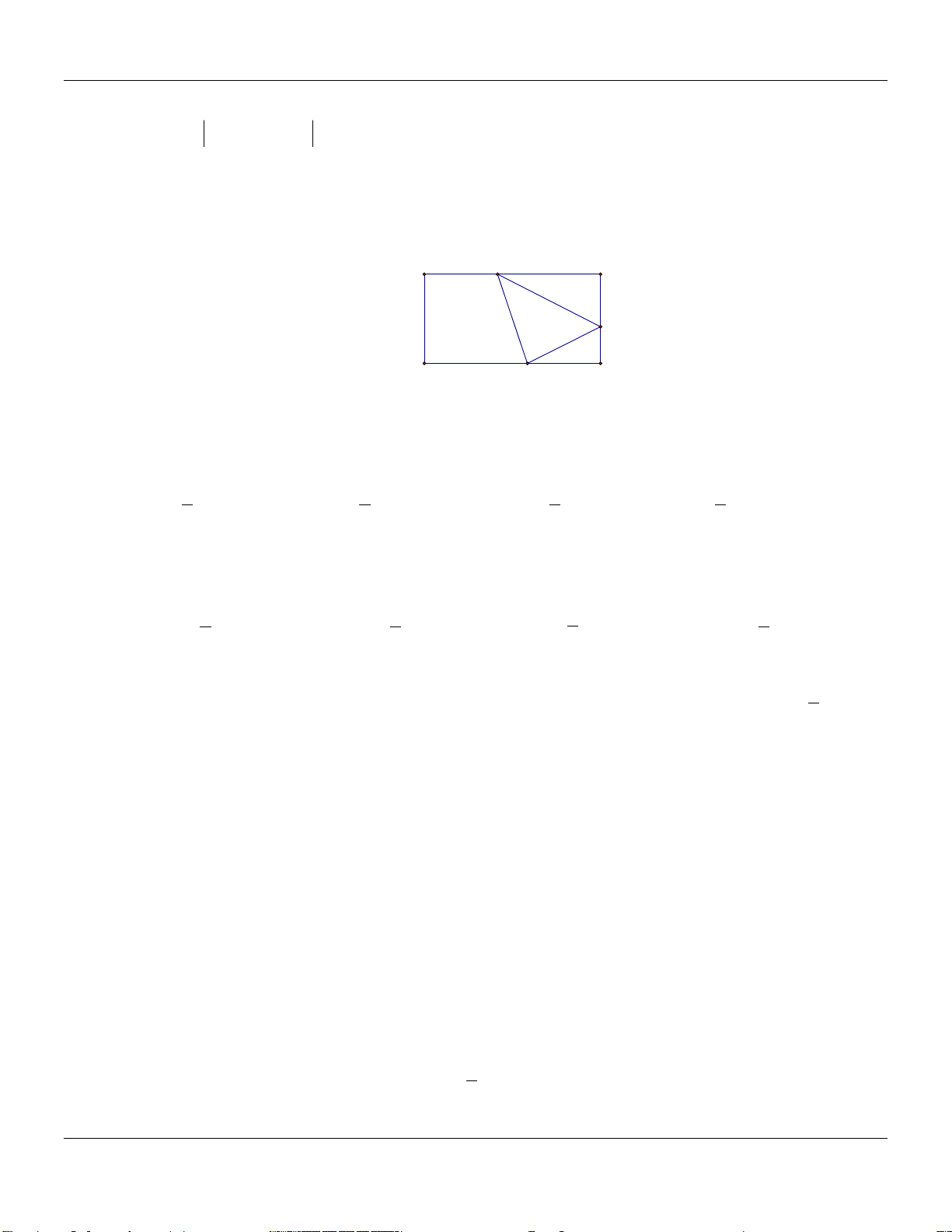
Câu 108: Cổng Ac-xơ tại thành phố Xanh Lu-i (Mĩ) có hình dạng là một parabol hướng bề lõm xuống
dưới (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có
độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo
phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn
10 m. Giả sử các số liệu trên là chính xác. Hãy tính chiều cao của cổng Ac-xơ (tính từ điểm cao
nhất trên cổng xuống mặt đất). A. 197,5 m. B. 275,6 m. C. 185,6 m. D. 348,3 m Lời giải:
Chọn hệ trục Oxy như hình vẽ.
Khi đó Parabol có phương trình dạng: 2
y ax c a  0 .  43 2   0  .81 a ac    1520
Parabol đi qua điểm B 81;0 và M  71  ;43 nên    . 43  . a   7  2 1  c 282123 c   1520
Chiều cao của cổng Ac-xơ là: h y   282123 0  c   185,6072368 (m). 1520
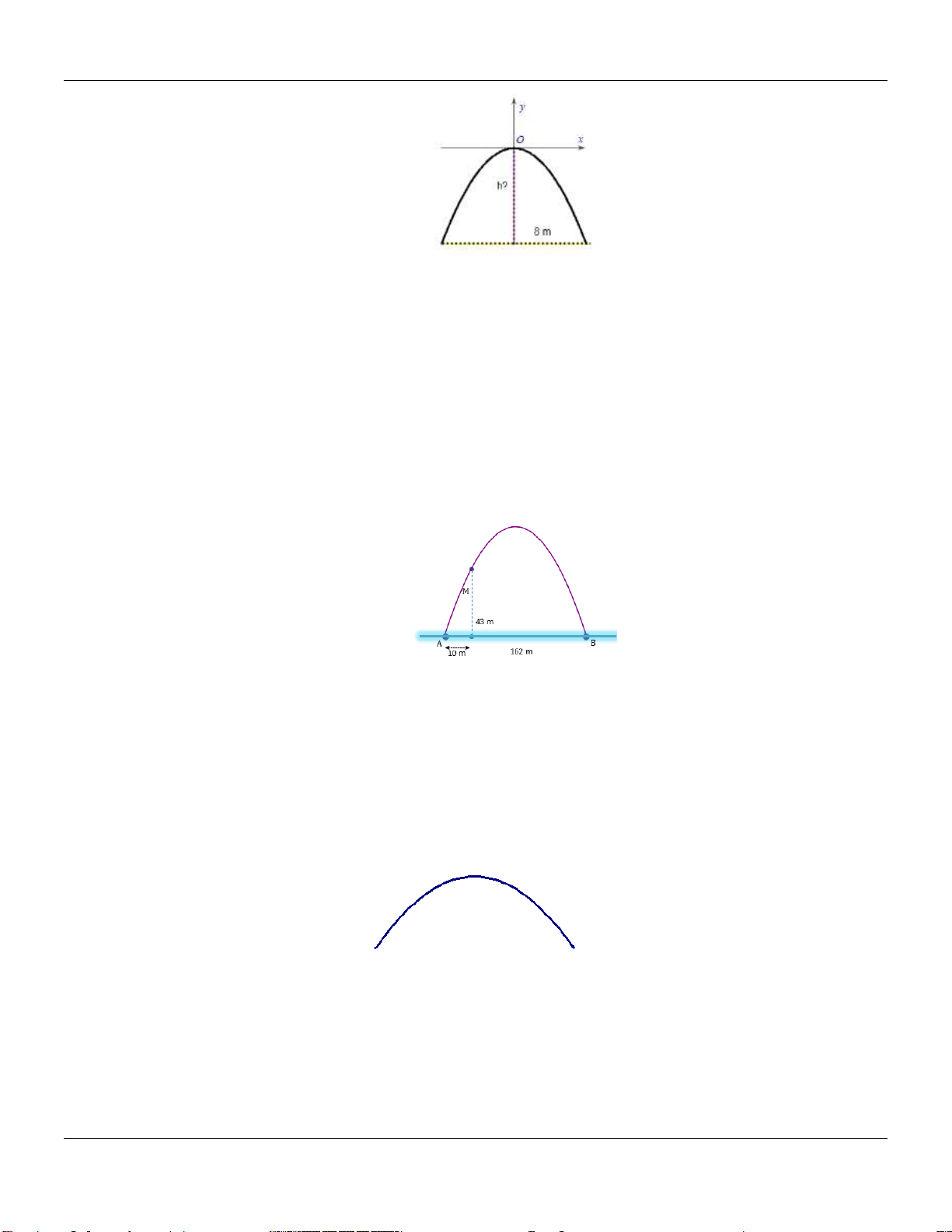
Câu 109: Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả
bóng được sút lên từ độ cao 1 m sau đó 1 giây nó đạt độ cao 10 m và 3,5 giây nó ở độ cao
6, 25 m . Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11 m . B. 12 m . C. 13 m . D. 14 m . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống y 12 B 10 8 C 6 4 2 A x O 5
Biết rằng quỹ đạo của quả bóng là một cung parabol nên phương trình có dạng 2
y ax bx c
Theo bài ra gắn vào hệ tọa độ và sẽ tương ứng các điểm A , B , C nên ta có c 1 a  3   
a b c  10  b   12 .  
12, 25a  3, 5b c  6, 25  c  1 
Suy ra phương trình parabol là 2 y  3
x 12x 1 .
Parabol có đỉnh I (2;13) . Khi đó quả bóng đạt vị trí cao nhất tại đỉnh tức h  13 m .
Câu 110: Một chiếc cổng hình parabol có chiều rộng 12 m và chiều cao 8 m như hình vẽ. Giả sử một
chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa cổng . Hỏi chiều cao h của xe tải thỏa
mãn điều kiện gì để có thể đi vào cổng mà không chạm tường?
A. 0  h  6 .
B. 0  h  6 .
C. 0  h  7 .
D. 0  h  7 . Lời giải:
Chọn hệ trục tọa độ như hình vẽ . Parabol có phương trình dạng 2
y ax bx .
Vì chiếc cổng hình parabol có chiều rộng 12 m và chiều cao, theo hình vẽ ta có parabol đi qua
các điểm 12;0 và 6;8 , suy ra:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống  2 a   14
 4a 12b  0  9    . 36
a  6b  8 8 b    3 2 8
Suy ra parabol có phương trình 2 y   x  . 9 3
Do chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa cổng nên xe sẽ chạm tường tại
điểm A3; 6 khi đó chiều cao của xe là 6.
Vậy điều kiện để xe tải có thể đi vào cổng mà không chạm tường là 0  h  6 .
Câu 111: Trong số các hình chữ nhật có cùng chu vi bằng 16 , hình chữ nhật có diện tích lớn nhất bằng bao nhiêu? A. 64. B. 4. C. 16. D. 8. Lời giải:
Gọi x là chiều dài của hình chữ nhật.
Khi đó chiều rộng là 8  x .
Diện tích hình chữ nhật là x 8  x .
Lập bảng biến thiên của hàm số bậc hai f x 2
 x  8x trên khoảng 0;8 ta được
max f x  f 4  16 . 0;8
Vậy hình chữ nhật có diện tích lớn nhất bằng 16 khi chiều dài bằng chiều rộng bằng 4 .
Câu 112: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa
phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x
4m. Hãy tính khoảng cách giữa hai điểm A và B . (xem hình vẽ bên dưới) A. 5m. B. 8,5m. C. 7,5m. D. 8m. Lời giải:
Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol  P : 2
y ax bx c với a  0 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống b
Do parabol  P đối xứng qua trục tung nên có trục đối xứng x  0    0  b  0 . 2a
Chiều cao của cổng parabol là 4m nên G 0; 4  c  4 .  P: 2 y ax  4 1
Lại có, kích thước cửa ở giữa là 3m x 4m nên E 2;3, F  2
 ;3  3  4a  4  a   . 4 1 Vậy  P : 2 y   x  4 . 4 1 x  4 Ta có 2
x  4  0  
nên A4;0 , B 4;0 hay AB  8 (m). 4 x  4 
Câu 113: Một tấm tôn có bề rộng AB là 100cm . Người ta chọn 2 điểm M và N trên đoạn AB sao cho
có thể làm được một máng nước như hình vẽ. ( AMNB là hình chữ nhật). Tính MN để máng
nước có diện tích AMNB lớn nhất. A. MN  50 . cm B. MN  60 . cm C. MN  45 . cm D. MN  55 . cm Lời giải:
MN  2x 0  x  50, x cm  AM NB  50  x .
Khi đó diện tích bề mặt ngang là S x   x 2 2 50  2  x 100x .
Vậy MN  50cm thì 2
S max  1250cm .
Câu 114: Một người ném một quả bóng từ độ cao cách mặt đất 80m, tại thời điểm 1 giây sau khi ném,
người ta đo được độ cao của quả bóng so với mặt đất là 128m. Biết rằng quỹ đạo bay của quả
bóng là một đường Parabol (như hình vẽ). Tính độ cao tối đa mà quả bóng đạt được.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống A. 143m .
B. 144m .
C. 144,5m .
D. 145m . Lời giải: Gọi 2
h(t)  at bt c .
Từ giả thiết bài toán, Parabol qua các điểm A0;80, B 5;0,C 1;128 . c  80 c  80 a  1  6   
Nên ta có hệ phương trình 25a  5b c  0  25a  5b  8  0  b   64 .   
a b c  128 a b  48 c  80    2  h(t)  16
t  64t  80
Tọa độ đỉnh của Parabol là S 2;144 .
Vậy quả bóng đạt độ cao tối đa là 144m.
Câu 115: Cô Tình có 60m lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một
cạnh là tường, cô Tình chỉ cần rào 3 cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính
hộ diện tích lớn nhất mà cô Tình có thể rào được? A. 2 400m . B. 2 450m . C. 2 350m . D. 2 425m . Lời giải: y x x
Gọi hai cạnh của hình chữ nhật có độ dài là x, y (như hình vẽ); 0  x, y  60 .
Ta có 2x y  60  y  60  2x . 1
1  2x  60  2x
Diện tích hình chữ nhật là S xy x 60  2x  .2x 60  2x   450   . 2 2  x
Vậy diện tích hình chữ nhật lớn nhất là  2
450 m  , đạt được khi x  15, y  30 .
Câu 116: Dây truyền đỡ nền cầu treo có dạng Parabol ACB như hình vẽ. Đầu cuối của dây được gắn
chặt vào điểm A và B trên trụ cốt thép bê tông AA và BB với độ cao 30(m) so với nền cầu.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề HÀM SỐ Toán 10 Kết nối tri thức với cuộc sống
Chiều dài nhịp AB  200(m) . Độ cao ngắn nhất của dây truyền trên nền cầu là OC  5(m) .
Người ta nối dây đỡ với nền bằng 7 sợi cáp song song cách đều hai trụ AA và BB . Xác định
tổng các chiều dài 7 các dây cáp treo đó. A. 78,15(m) . B. 78, 75(m) . C. 72, 75(m) . D. 80, 70(m) . Lời giải:
Chọn trục Oy trùng với trục đối xứng của Parabol, trục Ox nằm trên nền cầu như hình vẽ. 2 Khi đó ta có (
A 100;30), C(0;5) , ta tìm phương trình của Parabol có dạng y ax bx c . Parabol có đỉnh là C và đi qua
A nên ta có hệ phương trình:  b  1   0 a    2a 400   1  .0 a  .0 b c  5  b   0
. Suy ra Parabol có phương trình 2 y x  5 .  400 2  .1 a 00  .1
b 00  c  30 c  5    
Bài toán đưa việc xác định chiều dài các dây cáp treo sẽ là tính tung độ những điểm M , M , M 1 2
3 của Parabol. Ta dễ dàng tính được tung độ các điểm có các hoành độ
x  25, x  50, x  75   y  19, 0625(m) 1 2 3 lần lượt là y 6, 5625(m), y 11, 25(m) . 1 2 3
Do đó tổng độ dài các dây cáp treo cần tính là:
6,562511,2519,0625.25  78,75(m) .
_________________HẾT_________________
Huế, 10h20’ Ngày 03 tháng 01 năm 2023
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935785115