-
Thông tin
-
Hỏi đáp
Chuyên đề hệ thức lượng trong tam giác vuông Toán 9 Chân Trời Sáng Tạo
Tài liệu gồm 58 trang, bao gồm trọng tâm kiến thức, các dạng bài tập và bài tập vận dụng (có đáp án và lời giải chi tiết) chuyên đề hệ thức lượng trong tam giác vuông môn Toán 9 bộ sách Chân Trời Sáng Tạo (CTST).Mời bạn đọc đón xem!
Chủ đề: Chương 4: Hệ thức lượng trong tam giác vuông (CTST) 2 tài liệu
Môn: Toán 9 2.5 K tài liệu
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
301
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Chûúng 4
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Baâi 1
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN A
TRỌNG TÂM KIẾN THỨC
1 Khái niệm tỉ số lượng giác của góc nhọn
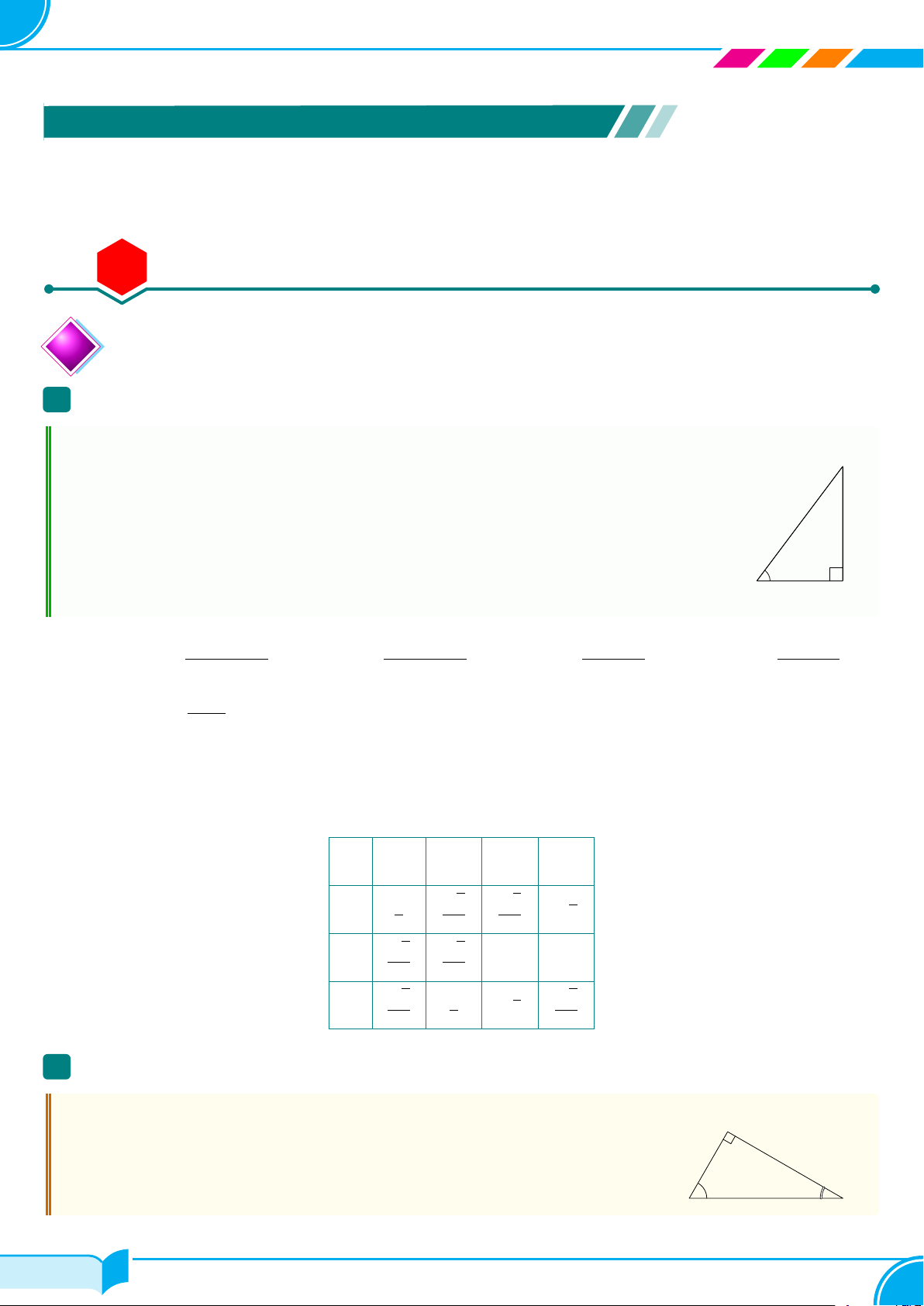
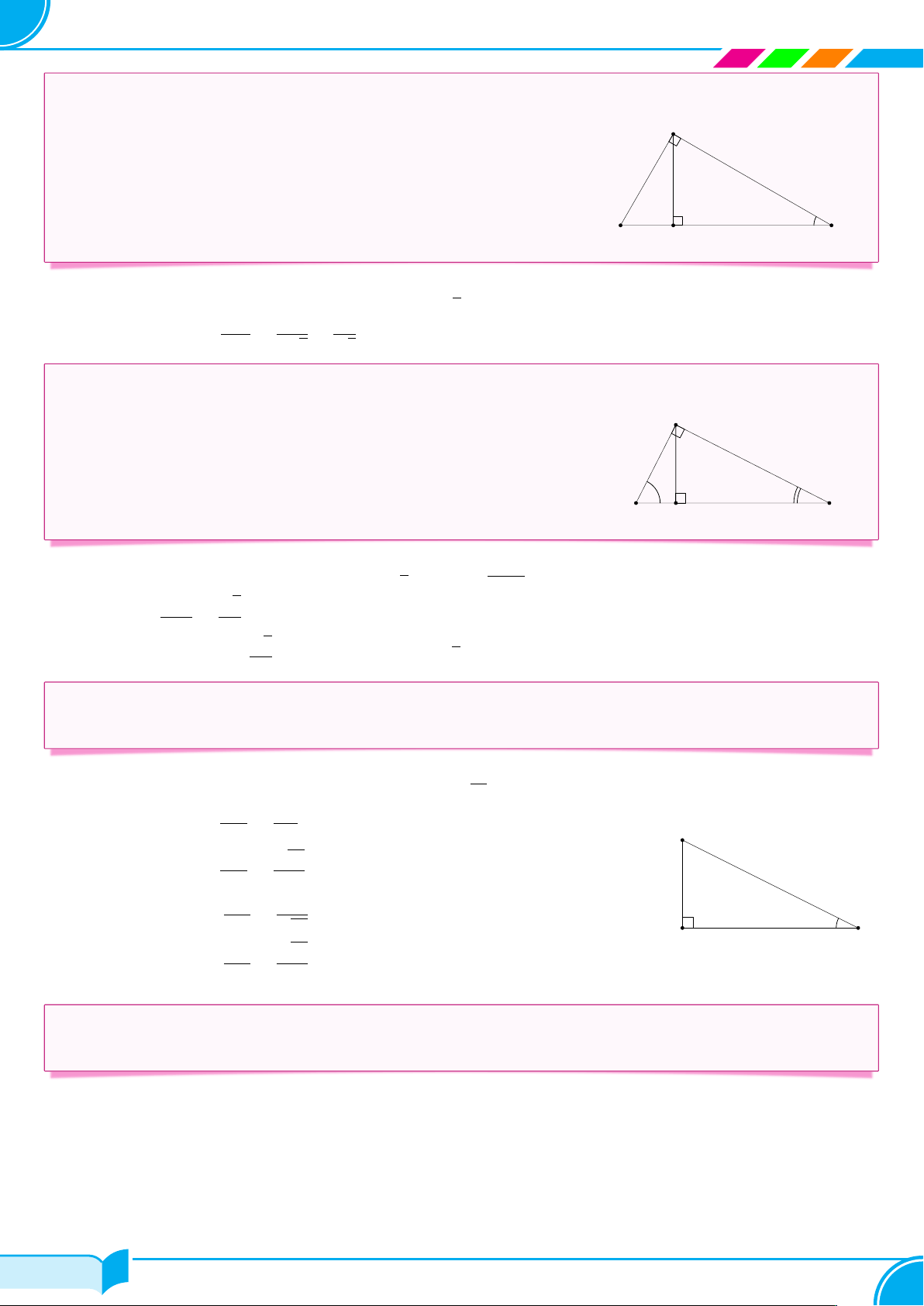
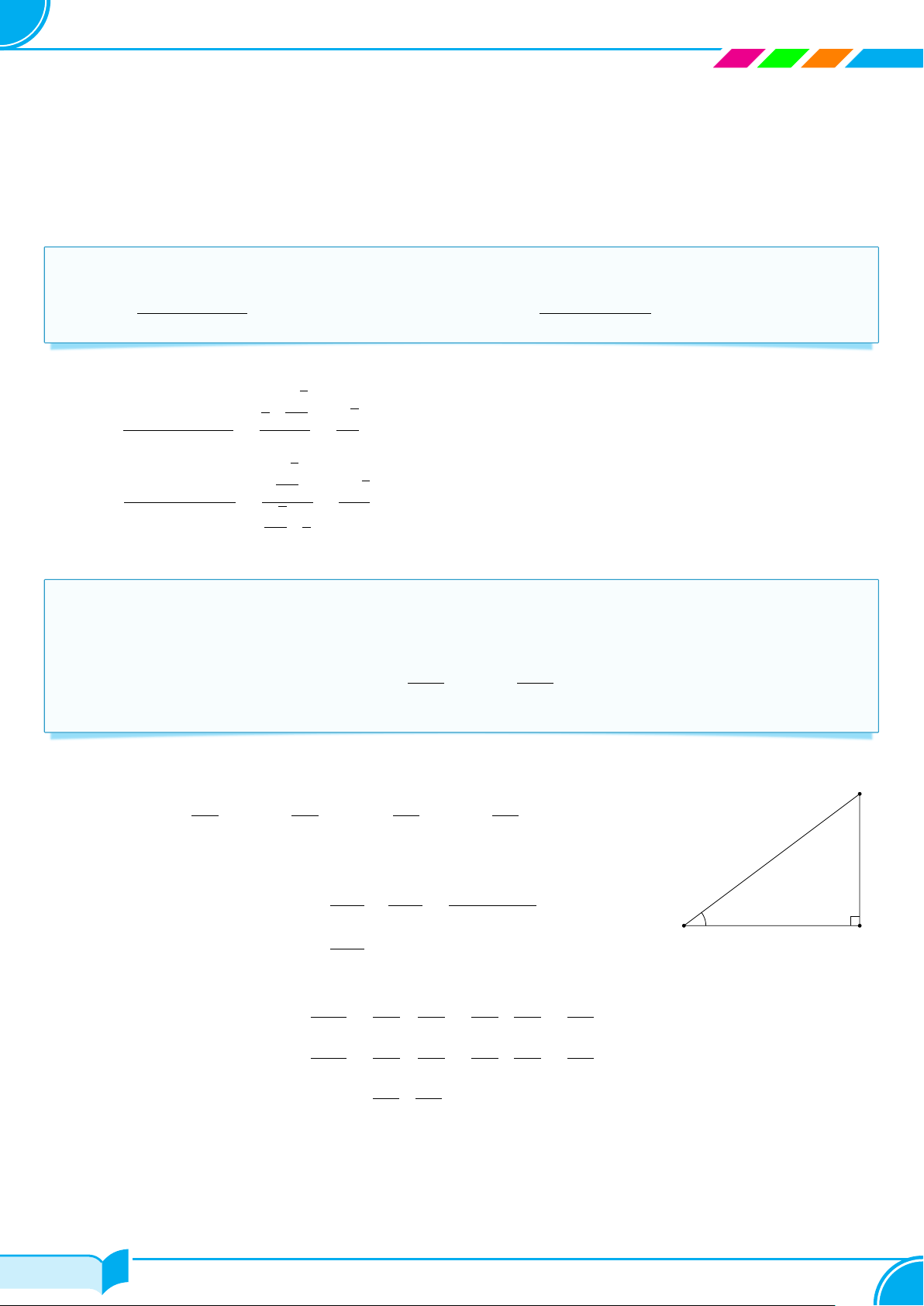
Cho góc nhọn α. Xét tam giác ABC vuông tại A có góc nhọn B bằng α. Ta có: C
○ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của α, kí hiệu sin α. ền ○ đối
Tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của α, kí hiệu cos α. huy
○ Tỉ số giữa cạnh đối và cạnh kề của góc α gọi là tang của α, kí hiệu tan α. cạnh cạnh α
○ Tỉ số giữa cạnh kề và cạnh đối của góc α gọi là côtang của α, kí hiệu cot α. B A cạnh kề cạnh đối cạnh kề cạnh đối cạnh kề ○ sin α = ; ○ cos α = ; ○ tan α = ; ○ cot α = ; cạnh huyền cạnh huyền cạnh kề cạnh đối 1 ○ cot α = ; tan α
○ sin α, cos α, tan α, cot α gọi là các tỉ số lượng giác của góc nhọn α.
sin, côsin của góc nhọn luôn dương và bé hơn 1 vì trong tam giác vuông, cạnh huyền dài nhất.
Ta có bảng các giá trị lượng giác đặc biệt: α sin α cos α tan α cot α √ √ 1 3 3 √ 30◦ 3 2 2 3 √ √ 2 2 45◦ 1 1 2 2 √ √ 3 1 √ 3 60◦ 3 2 2 3
2 Tỉ số lượng giác của hai góc phụ nhau
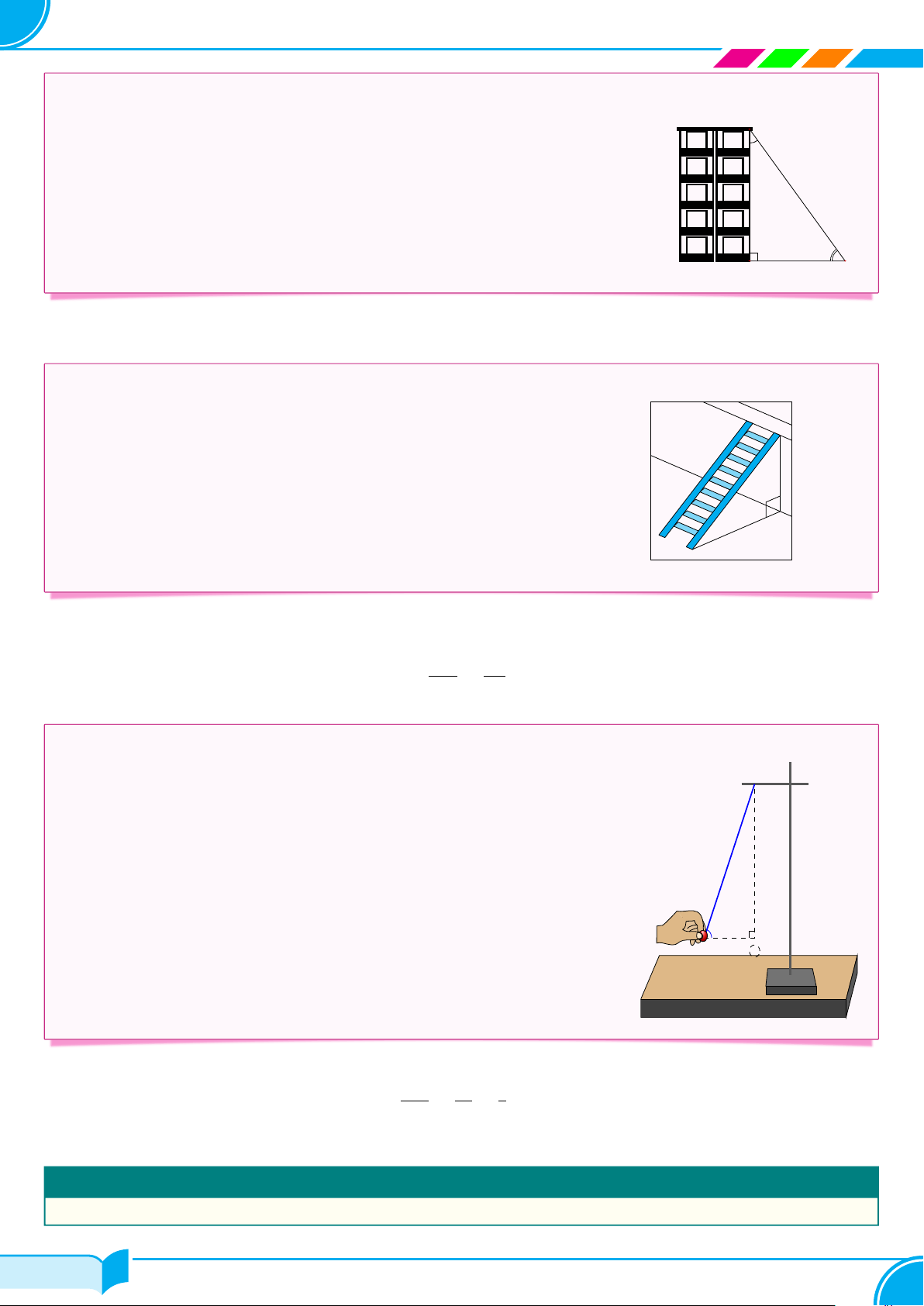
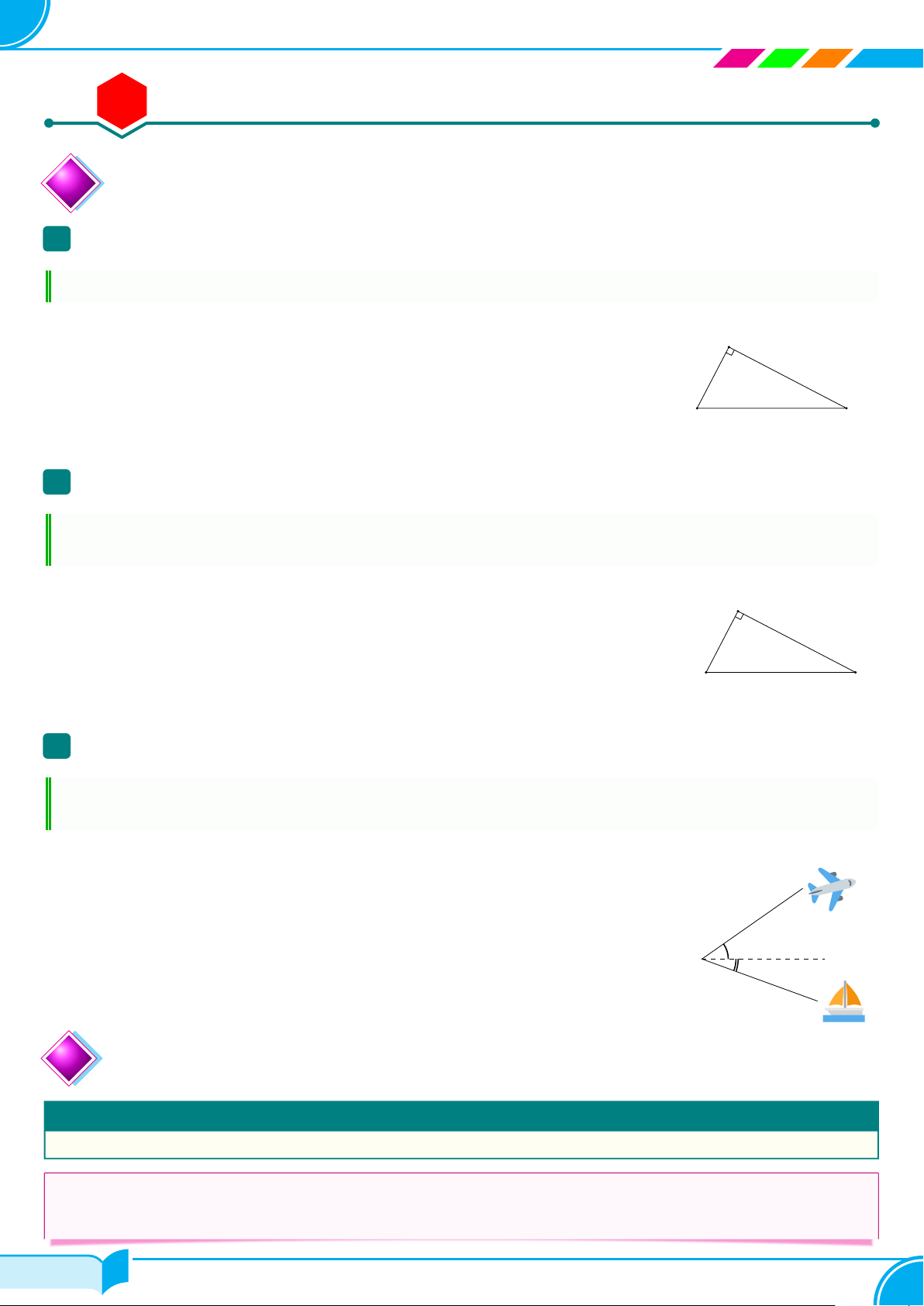
Nếu hai gọc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng C côtang góc kia.
Cho α và β là hai góc phụ nhau, khi đó
sin α = cos β, cos α = sin β, tan α = cot β, cot α = tan β. α β A B
Tổng quát, với góc nhọn α ta có: 301/476 301/476 302
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
○ sin(90◦ − α) = cos α;
○ cos(90◦ − α) = sin α;
○ tan(90◦ − α) = cot α;
○ cot(90◦ − α) = tan α.
3 Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn
Bảng tóm tắt cách tính tỉ số lượng giác của góc nhọn Để tính Thứ tự các nút sin α jα )= cos α kα )= tan α lα )= cot α 1Plα )=
Để tìm góc α khi biết cot α, ta có thể tìm tan của góc (90◦ − α) (vì tan(90◦ − α) = cot α) rồi suy ra α. A B CÁC DẠNG BÀI TẬP
Dạng 1. Sử dụng MTCT tính tỉ số lượng giác, tính góc
c Ví dụ 1. Sử dụng MTCT tính các tỉ số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:
a) sin 27◦, cos 32◦15′, tan 52◦12′ và cot 35◦23′.
b) sin 40◦54′, cos 52◦15′, tan 69◦36′ và cot 25◦18′. Lời giải. Để tính Bấm phím Kết quả sin 27◦ j2 7 x = 0,4539904997 a) cos 32◦15′ k3 2 x 1 5 x = 0,8457278217 tan 52◦12′ l5 2 x 1 2 x = 1,289192232 cot 35◦23′ l3 5 x 2 3 x = u = 1,408003909
Làm tròn đến chữ số thập phân thứ ba ta được sin 27◦ ≈ 0,454; cos 32◦15′ ≈ 0,846; tan 52◦12′ ≈ 1,289; cot 35◦23′ ≈ 1,408. 1 Lưu ý, cot 35◦23′ = . tan 35◦23′ Để tính Bấm phím Kết quả sin 40◦54′ j4 0 x 5 4 x = 0,6547408137 b) cos 52◦15′ k5 2 x 1 5 x = 0,61221728 tan 69◦36′ l6 9 x 3 6 x = 2,688918967 cot 25◦18′ l2 5 x 1 8 x = u = 2,115516356
Làm tròn đến chữ số thập phân thứ ba ta được sin 40◦54′ ≈ 0,655; cos cos 52◦15′ ≈ 0,612; tan 69◦36′ ≈ 2,689; cot 25◦18′ ≈ 2,116. □
c Ví dụ 2. Dùng MTCT, tìm các góc (làm tròn đến phút) biết
a) sin α1 = 0,3214, cos α2 = 0,4321, tan α3 = 1,2742 và cot α4 = 1,5384.
b) sin α1 = 0,3782, cos α1 = 0,6251, tan α1 = 2,154 và cot α1 = 3,253. Lời giải. 302/476 302/476 303
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Biết Bấm phím Kết quả Bấm tiếp x sin α1 = 0,3214 q j0 . 3 2 1 4 = 18,74761209 18◦44′51,4” a) cos α2 = 0,4321 q k0 . 4 3 2 1 = 64,39909458 64◦23′56,74” tan α3 = 1,2742 q l1 . 2 7 4 2 = 51,87495892 51◦52′29,85” cot α4 = 1,5384
q l1 . 6 3 8 4 u = 33,02491482 33◦1′29,69”
Làm tròn đến phút ta được: α1 ≈ 18◦45′, α2 ≈ 64◦24′, α3 ≈ 51◦52′, α4 ≈ 33◦1′. Biết Bấm phím Kết quả Bấm tiếp x sin α = 0,3782 q j0 . 3 7 8 2 = 22,222231 22◦13′20,03” b) cos α = 0,6251
q k0 . 6 2 5 1 = 51,31047244 51◦18′37,7” tan α = 2,154 q l2 . 1 5 4 = 65,09679426 65◦5′48,46” cot α = 3,253
q l3 . 2 5 3 u = 17,08787556 17◦5′16,35”
Làm tròn đến phút ta được: α1 ≈ 22◦13′, α2 ≈ 51◦19′, α3 ≈ 65◦6′, α4 ≈ 17◦5′. □
Dạng 2. Tính tỉ số lượng giác của góc nhọn trong một tam giác vuông c Ví dụ 3.
Cho hình thoi ABCD có hai đường chéo cắt nhau tại điểm O. B OB OB a) Tỉ số
là sin của góc nhọn nào? Tỉ số là côsin của góc nhọn AB BC O nào? A C
b) Viết tỉ số lượng giác của mỗi góc nhọn sau: tan ’ OCD, cot ’ OAD. D Lời giải.
Hình thoi ABCD có hai đường chéo cắt nhau tại điểm O nên AC vuông góc với BD tại O. OB OD
a) Tam giác OAB vuông tại O nên = sin ’ OAB.
b) Tam giác OCD vuông tại O nên tan ’ OCD = . AB OC OB OA
Tam giác OBC vuông tại O nên = cos ’ OBC.
Tam giác OAD vuông tại O nên cot ’ OAD = . BC OD □ c Ví dụ 4.
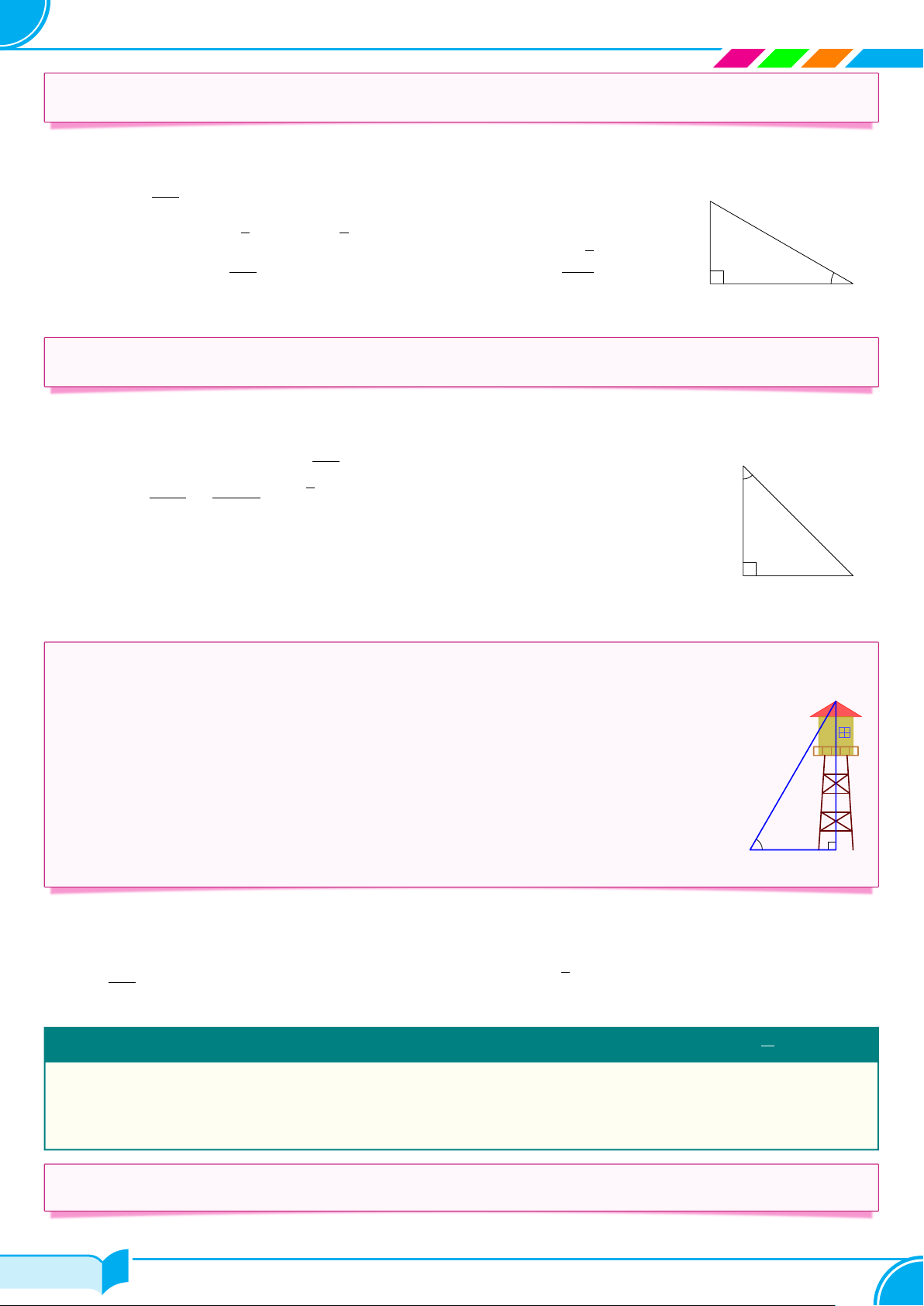
Tính các tỉ số lượng giác của góc α trong tam giác ABC ở hình vẽ bên. A 12 9 α B C 15 Lời giải.
Xét tam giác ABC vuông tại A, “ B = α, ta có AC 9 AB 12 sin α = = = 0,6; cos α = = = 0,8; BC 15 BC 15 AC 9 AB 12 4 tan α = = = 0,75; cot α = = = . □ AB 12 AC 9 3
c Ví dụ 5. Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có “ B = 90◦ ở hình sau. 303/476 303/476 304
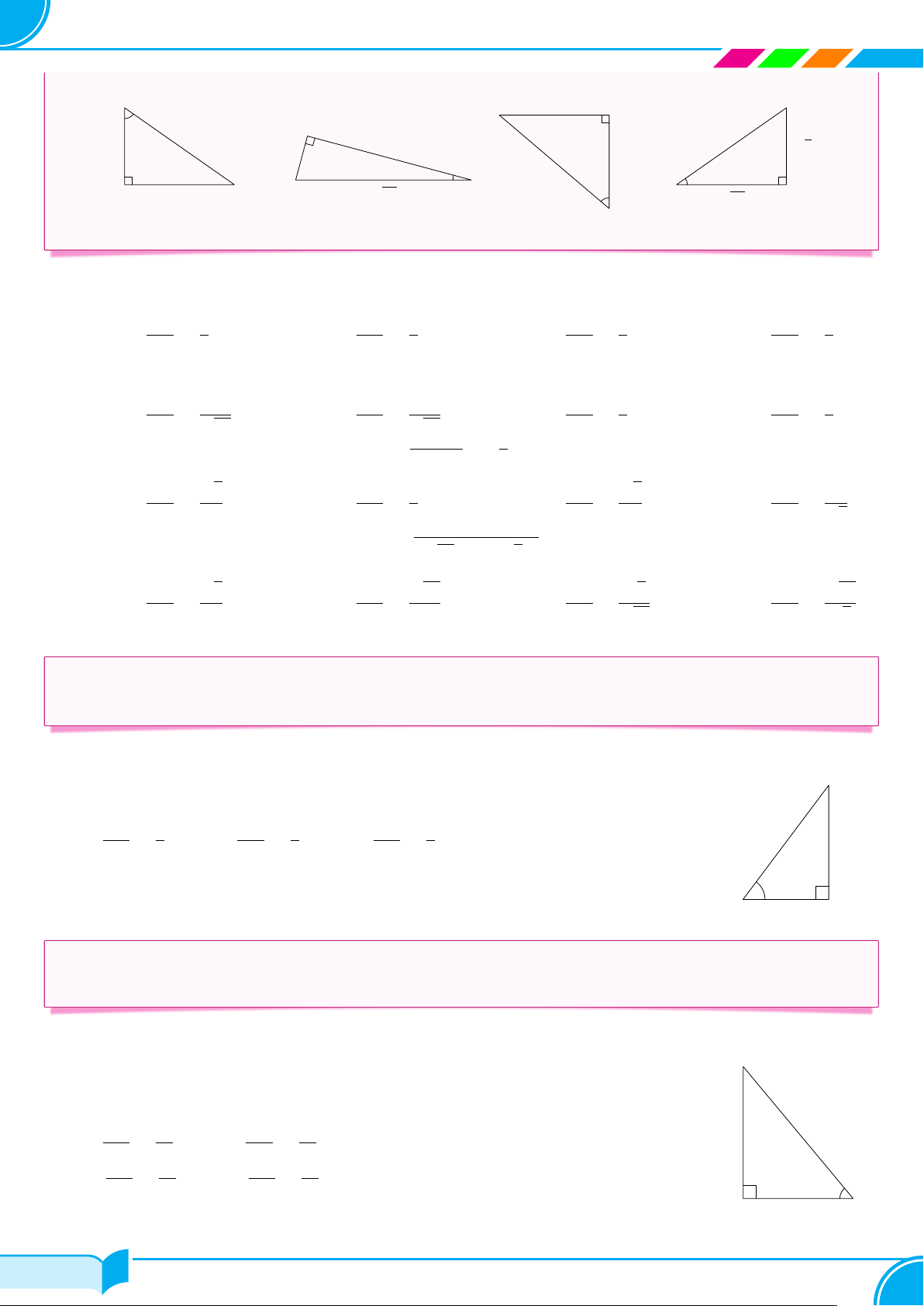
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN A C C B B √ 3 5 4 6 1 2 3 √ √ B 4 C C 17 A A 10 B a) b) c) A d) Lời giải.
Xét △ABC vuông tại B (Hình a), ta có BC 4 AB 3 BC 4 AB 3 ○ sin A = = ; ○ cos A = = ; ○ tan A = = ; ○ cot A = = . AC 5 AC 5 AB 3 BC 4
Xét △ABC vuông tại B (Hình b), ta có BC 1 AB 4 BC 1 AB 4 ○ sin A = = √ ; ○ cos A = = √ ; ○ tan A = = ; ○ cot A = = . AC 17 AC 17 AB 4 BC 1 √ √
Xét △ABC vuông tại B (Hình c), ta có BC = 32 − 22 = 5; √ √ BC 5 AB 2 BC 5 AB 2 ○ sin A = = ; ○ cos A = = ; ○ tan A = = ; ○ cot A = = √ . AC 3 AC 3 AB 2 BC 5 q √ √ Ä ä2 Ä ä2
Xét △ABC vuông tại B (Hình d), ta có AC = 10 − 6 = 2; √ √ √ √ BC 6 AB 10 BC 6 AB 10 ○ sin A = = ; ○ cos A = = ; ○ tan A = = √ ; ○ cot A = = √ . AC 2 AC 2 AB 10 BC 6 □
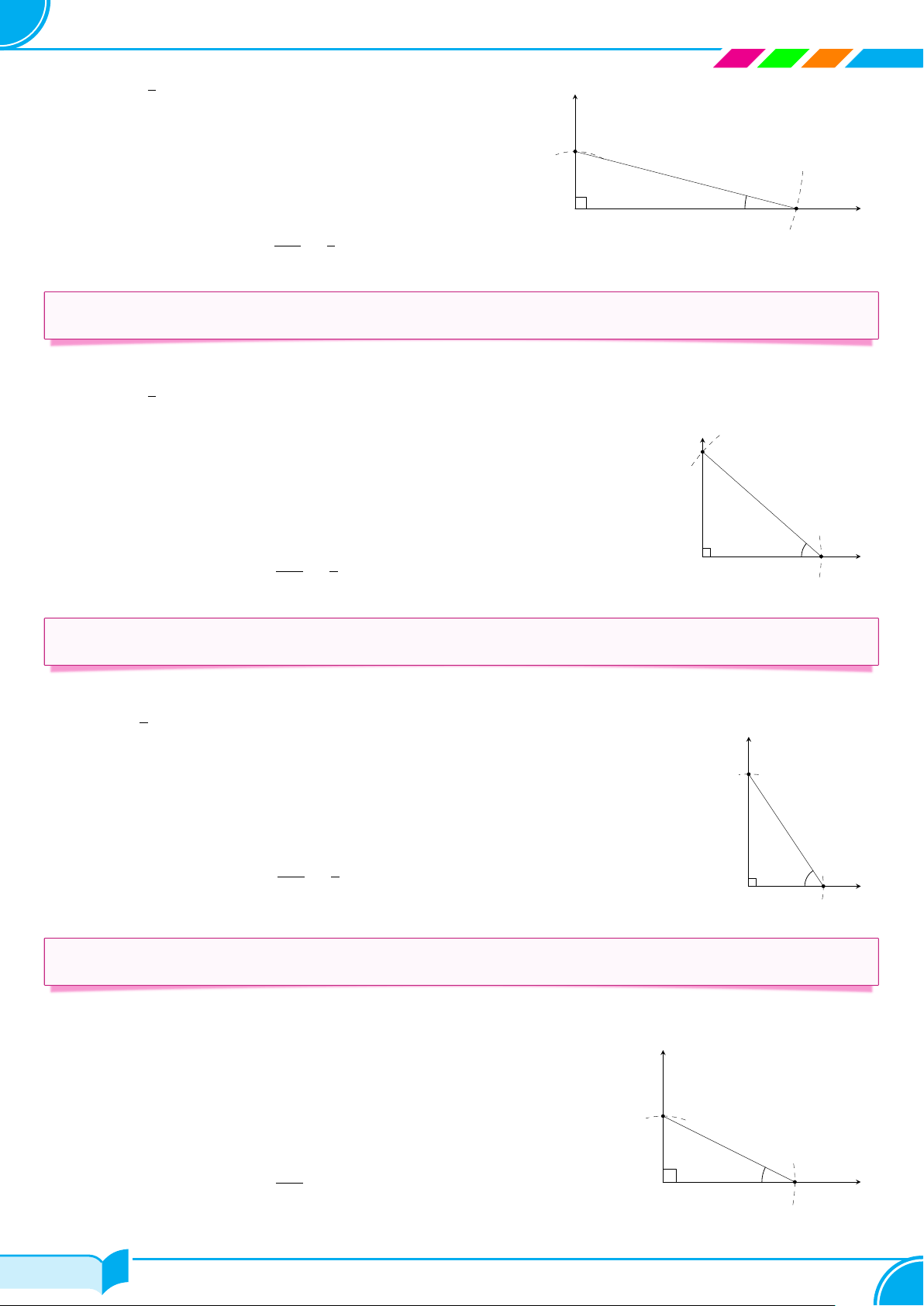
c Ví dụ 6. Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Hãy tính các tỉ số lượng giác sin α, cos α, tan α với α = “ B. Lời giải.
Xét △ABC vuông tại A, “ B = α. C
Theo định lí Pythagore, ta có: BC2 = AC2 + AB2 = 42 + 32 = 25 nên BC = 5 (cm).
Theo định nghĩa của tỉ số lượng giác sin, côsin , tang, ta có AC 4 AB 3 AC 4 sin α = = , cos α = = , tan α = = . 4 cm BC 5 BC 5 AB 3 α B A 3 cm □
c Ví dụ 7. Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B. Lời giải. Xét △ABC vuông tại A C
Theo định lí Pythagore, ta có
BC2 = AC2 + AB2 = 122 + 52 = 169 nên BC = 13 (cm).
Theo định nghĩa của tỉ số lượng giác sin, côsin , tang, côtang ta có AC 12 AB 5 12 cm sin α = = , cos α = = , BC 13 BC 13 AC 12 AB 5 tan α = = , cot α = = . AB 5 AC 12 A B 5 cm □ 304/476 304/476 305
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG c Ví dụ 8.
Tính tỉ số lượng giác của góc B trong hình bên. B 5 12 A C Lời giải.
Ta có BC2 = AB2 + AC2 = 52 + 122 = 169 ⇒ BC = 13. AC 12 AB 5 AC 12 AB 5 Do đó sin B = = ; cos B = = ; tan B = = ; cot B = = . □ BC 13 BC 13 AB 5 AC 12
c Ví dụ 9. Cho tam giác M N P vuông tại M , M N = 3 cm, M P = 4 cm. Tính các tỉ số lượng giác của góc P . Lời giải. √ √
Trong tam giác M N P vuông tại M , ta có N P = M N 2 + M P 2 = 32 + 42 = √ M 25 = 5.
Xét tam giác M N P vuông tại M , ta có M N 3 M P 4 sin P = = ; cos P = = N P 5 N P 5 M N 3 M P 4 tan P = = ; cot P = = . N P M P 4 M N 3 □
c Ví dụ 10. △ABC vuông tại A có BC = 2AB. Tính các tỉ số lượng giác của góc C. Lời giải. √
Ta đặt AB = m thì BC = 2m, suy ra AC2 = BC2 − AB2 = 4m2 − m2 = 3m2 ⇒ AC = m 3. AB m 1 Ta có sin C = = = ; BC 2m 2 B √ √ AC m 3 3 cos C = = = ; BC 2m 2 AB m 1 tan C = = √ = √ ; AC m 3 3 √ AC m 3 √ cot C = = = 3. A C AB m □
c Ví dụ 11. Tam giác ABC cân tại A, có BC = 6, đường cao AH = 4. Tính các tỉ số lượng giác của góc B. Lời giải. √ Ta có BH = 6 : 2 = 3; AB = 42 + 32 = 5. AH 4 Do đó sin B = = = 0, 8; AB 5 A BH 3 cos B = = = 0, 6; AB 5 AH 4 tan B = = ; 4 AB 3 BH 3 cot B = = = 0, 75. H AH 4 B C 6 □ 305/476 305/476 306
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN c Ví dụ 12.
Tính tan C trong hình bên. A 6 B C 3 H Lời giải. √
Ta có AH2 = AB2 − BH2 = 62 − 32 = 27 ⇒ AH = 3 3. BH 3 1 Do đó tan C = cot B = = √ = √ . □ AH 3 3 3 c Ví dụ 13.
Tính sin M + cos N trong hình bên. O M N 1 H 3 Lời giải. √ √
Ta có OH2 = HM · HN = 1 · 3 = 3 ⇒ OH = 3; OM = 1 + 3 = 2. √ OH 3 Do đó sin M = = . OM 2 √3 √ Mặt khác cos N = sin M = nên sin M + cos N = 3. □ 2
c Ví dụ 14. Tam giác ABC vuông tại A, AB = 1, 5; BC = 3, 5. Tính tỉ số lượng giác của góc C rồi suy ra
các tỉ số lượng giác của góc B. Lời giải. √
Ta có AC2 = BC2 − AB2 = 3, 52 − 1, 52 = 10 ⇒ AC = 10. AB 1, 5 Do đó cos B = sin C = = ≈ 0, 4286; BC 3, 5 B √ AC 10 sin B = cos C = = ≈ 0, 9035; 3, 5 BC 3, 5 1, 5 AB 1, 5 cot B = tan C = = √ ≈ 0, 4743; AC 10 √ A C AC 10 tan B = cot C = = ≈ 2, 1082. AB 1, 5 □
c Ví dụ 15. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45◦:
sin 60◦, cos 75◦, sin 52◦30′, tan 80◦, cot 82◦. Lời giải. Ta có:
sin 60◦ = cos(90◦ − 60◦) = cos 30◦;
cos 75◦ = sin(90◦ − 75◦) = sin 15◦;
sin 52◦30′ = cos(90◦ − 52◦30′) = cos 37◦30′;
tan 80◦ = cot(90◦ − 80◦) = cot 10◦;
cot 82◦ = tan(90◦ − 82◦) = tan 8◦. □ 306/476 306/476 307
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG c Ví dụ 16.
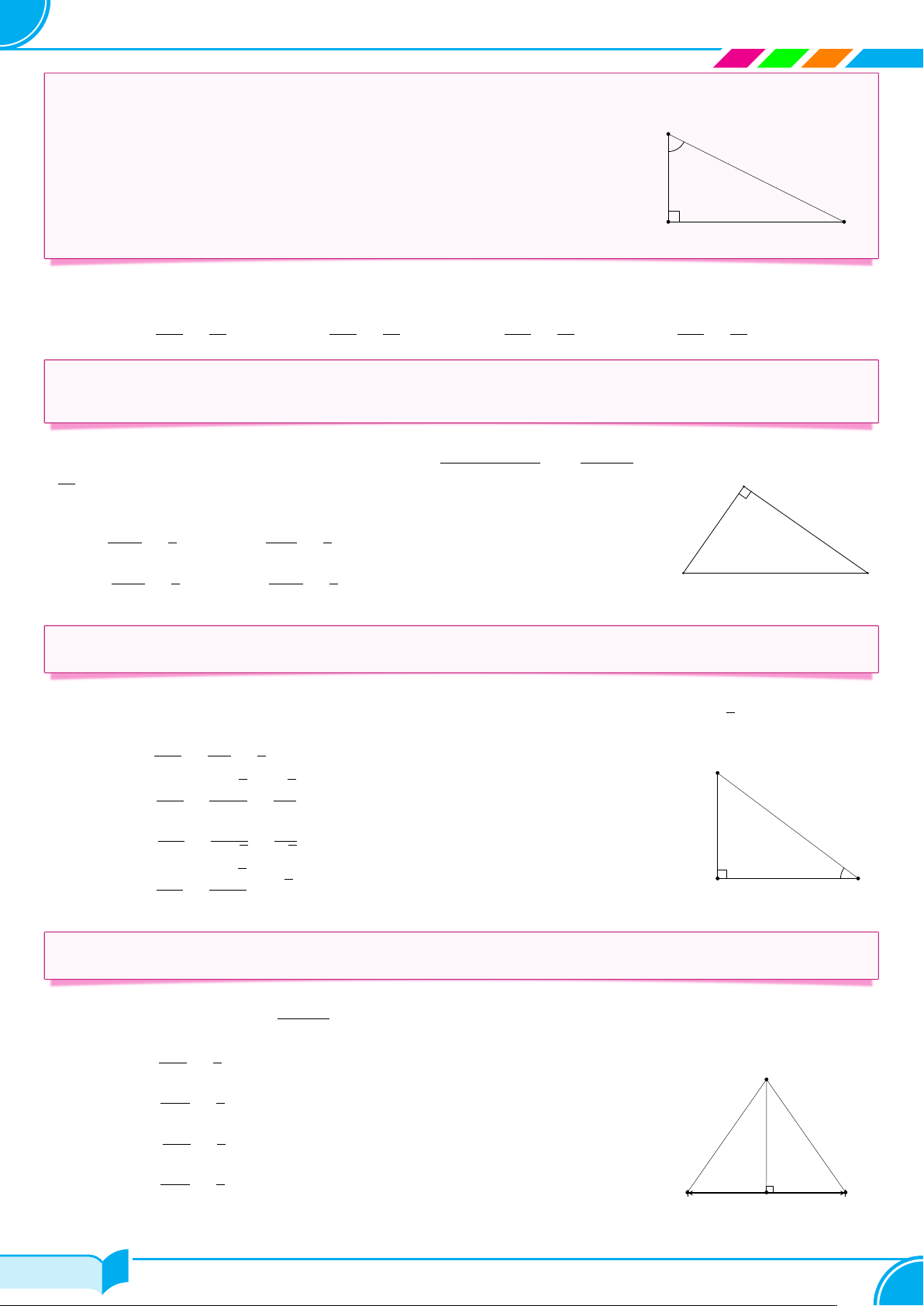
Tia nắng chiếu qua điểm B của nó tòa nhà tạo với mặt đất một góc x và tạo với B
cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x ≈ 0,78 và cot x ≈ 1,25.
Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm). y x A C Lời giải.
Do góc x và góc y là hai góc phụ nhau nên sin y = cos x ≈ 0,78 và tan y = cot x ≈ 1,25. □ c Ví dụ 17.
Hình bên mô tả một chiếc thang có chiều dài AB = 4 m được
đặt dựa vào tường, khoảng cách từ chân thang đến chân tường là A
BH = 1,5 m. Tính góc tạo bởi cạnh AB và phương nằm ngang
trên mặt đất (làm tròn kết quả đến hàng đơn vị của độ). H B Lời giải.
Ta có, góc tạo bởi cạnh AB và phương nằm ngang trên mặt đất là ’ ABH. BH 1,5
Xét tam giác ABH vuông tại H, ta có cos ’ ABH = = = 0,375. AB 4 Vậy ’ ABH ≈ 68◦. □ c Ví dụ 18.
Treo quả cầu kim loại nhỏ vào giá thí nghiệm bằng sợi dây mảnh nhẹ không
dãn. Khi quả cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng B
đứng. Kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông ra thì quả
cầu sẽ chuyển động qua lại quanh vị trí cân bằng. Khi kéo quả cầu khỏi vị
trí cân bằng, giả sử tâm A của quả cầu cách B một khoảng AB = 60 cm và bằng
cách vị trí cân bằng một khoảng AH = 20 cm (Hình 9). Tính số đo góc α 60 cm cân
tạo bởi sợi dây BA và vị trí cân bằng (làm tròn kết quả đến hàng đơn vị của trí độ). Vị α H A 20 cm Lời giải. AH 20 1
Xét tam giác ABH vuông tại H, ta có: sin α = = = . AB 60 3 Do đó α ≈ 19◦.
Vậy góc α tạo bởi sợi dây BA và vị trí cân bằng có số đo khoảng 19◦. □
Dạng 3. Tính các cạnh trong một tam giác vuông sử dụng tỉ số lượng giác của góc nhọn 307/476 307/476 308
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
c Ví dụ 19. Cho tam giác ABC vuông tại A có “
C = 30◦ và BC = a. Tính các cạnh AB, AC theo a. Lời giải. AB Ta có sin C =
, suy ra AB = BC · sin C = a · sin 30◦. BC C 1 a Theo bảng trên, sin 30◦ = nên AB = . 2 2 √ AC a 3 Tương tự, ta có cos C =
, suy ra AC = BC · cosC = a · cos 30◦ = . 30◦ BC 2 A B □
c Ví dụ 20. Cho tam giác ABC vuông tại A có “
C = 45◦ và AB = c. Tính BC và AC theo c. Lời giải. AB
Xét ∆ABC vuông tại A có sin C = BC C AB c √ Suy ra BC = = = c 2. 45◦ sin C sin 45◦
Xét ∆ABC vuông tại A có “ B + “ C = 90◦. Do đó “ B = “ C = 45◦.
Suy ra ∆ABC vuông cân tại A. A B Suy ra AC = AB = c. □ c Ví dụ 21.
Tìm chiều cao của tháp canh trong hình bên (kết quả là tròn đến hàng phần trăm). A 60◦ C 5,8 m B Lời giải.
Xét △ABC vuông tại B, ta có AB √ tan C =
, suy ra AB = CB tan C hay AB = 5,8 · tan 60◦ = 5,8 · 3 ≈ 10,05 (m). CB
Vậy chiều cao của tháp canh gần bằng 10,05 mét. □
Dạng 4. Dựng góc nhọn α biết một tỉ số lượng giác của góc đó bằng mn
Dựng một tam giác vuông có cạnh là m và n (m và n tương ứng là cạnh góc vuông và cạnh huyền nếu tỉ số
lượng giác đã cho là sin hoặc cos; m và n là hai cạnh góc vuông nếu tỉ số lượng giác đã cho là tan hoặc cot)
rồi vận dụng định nghĩa để nhận ra góc α.
c Ví dụ 22. Dựng góc α, biết sin α = 0, 25. Lời giải. 308/476 308/476 309
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 1 Ta có 0, 25 = . y 4 ○ Dựng góc vuông xOy; A
○ Trên cạnh Ox đặt OA = 1; 4 1
○ Dựng đường tròn (A; 4) cắt cạnh Oy tại B. α O B Å OA 1 ã x Khi đó ’ ABO = α vì sin α = = . AB 4 □
c Ví dụ 23. Dựng góc α, biết cos α = 0, 75. Lời giải. 3 Ta có 0, 75 = . 4 y A ○ Dựng góc vuông xOy;
○ Trên cạnh Oy đặt OB = 3; 4
○ Dựng đường tròn (B; 4) cắt cạnh Ox tại A. α Å OB 3 ã Khi đó O 3 B ’ ABO = α vì cos α = = . x AB 4 □
c Ví dụ 24. Dựng góc α, biết tan α = 1, 5. Lời giải. 3 Ta có 1, 5 = . y 2 ○ Dựng góc vuông xOy; A
○ Trên cạnh Ox đặt OA = 3; 4
○ Trên cạnh Oy đặt OB = 2. Å OA 3 ã Khi đó α ’ ABO = α vì tan α = = . OB 2 O 3 B x □
c Ví dụ 25. Dựng góc α, biết cot α = 2. Lời giải. y ○ Dựng góc vuông xOy;
○ Trên cạnh Ox đặt OA = 1; A
○ Trên cạnh Oy đặt OB = 2. 1 Å OB ã α Khi đó ’ ABO = α vì cot α = = 2 . OA O 2 B x □ 309/476 309/476 310
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
Dạng 5. Tính giá trị của biểu thức lượng giác với các góc đặc biệt
○ Sử dụng bảng giá trị các tỉ số lượng giác của các góc 30◦; 45◦; 60◦.
○ Sử dụng tỉ số lượng giác của hai góc phụ nhau.
c Ví dụ 26. Tính giá trị của mỗi biểu thức sau: sin 30◦ · cos 60◦ a) sin2 45◦ + cos2 45◦; b) tan 30◦ · cot 30◦; c) tan 45◦ Lời giải. √ √ Ç å2 Ç å2 2 2 1 1 a) sin2 45◦ + cos2 45◦ = + = + = 1. 2 2 2 2 √3 √ b) tan 30◦ · cot 30◦ = · 3 = 1. 3 1 1 sin 30◦ · cos 60◦ · 1 c) = 2 2 = . tan 45◦ 1 4 □
c Ví dụ 27. Tính giá trị của các biểu thức sau 2 cos 45◦ √ 2 sin 60◦ a) A = √ + 3 tan 30◦; b) B = √ − cot 45◦. 2 3 Lời giải. √2 √ 2 cos 45◦ √ 2 · √ 3 a) Ta có A = √ + 3 tan 30◦ = 2 √ + 3 · = 1 + 1 = 2; 2 2 3 √3 2 sin 60◦ 2 · b) Ta có B = √ − cot 45◦ = 2 √ − 1 = 1 − 1 = 0. 3 3 □
c Ví dụ 28. Tính giá trị của biểu thức √ 2 sin 30◦ − sin 60◦ a) M = 4 cos2 45◦ + 3 cot 30◦ − 16 cos3 60◦; b) N = . cos2 30◦ − cos 60◦ Lời giải. √ 2 sin 30◦ − sin 60◦ a) M = 4 cos2 45◦ + 3 cot 30◦ − 16 cos3 60◦ b) N = √ cos2 30◦ − cos 60◦ Ç å2 √ √ 2 √ √ Å 1 ã3 1 3 3 = 4 · + 3 · 3 − 16 · 2 · − 1 − 2 2 √ = 2 2 2 √ = = 4 − 2 3. Ç å2 3 1 = 2 + 3 − 2 = 3. 3 1 − − 4 2 2 2 □ 310/476 310/476 311
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG c Ví dụ 29. Tính: a) sin 61◦ − cos 29◦; b) cos 15◦ − sin 75◦; c) tan 28◦ − cot 62◦; d) cot 47◦ − tan 43◦. Lời giải.
a) sin 61◦ − cos 29◦ = sin 61◦ − sin 61◦ = 0;
b) cos 15◦ − sin 75◦ = cos 15◦ − cos 15◦ = 0;
c) tan 28◦ − cot 62◦ = tan 28◦ − tan 28◦ = 0;
d) cot 47◦ − tan 43◦ = cot 47◦ − cot 47◦ = 0. □
c Ví dụ 30. Tính giá trị của biểu thức
a) P = sin2 30◦ − sin2 40◦ − sin2 50◦ + sin2 60◦;
b) Q = cos2 25◦ − cos2 35◦ + cos2 45◦ − cos2 55◦ + cos2 65◦. Lời giải.
a) P = sin2 30◦ − sin2 40◦ − sin2 50◦ + sin2 60◦
= sin2 30◦ + sin2 60◦ − sin2 40◦ + sin2 50◦
= sin2 30◦ + cos2 30◦ − sin2 40◦ + cos2 40◦ = 1 − 1 = 0.
b) Q = cos2 25◦ − cos2 35◦ + cos2 45◦ − cos2 55◦ + cos2 65◦
= cos2 25◦ + cos2 65◦ − cos2 35◦ + cos2 55◦ + cos2 45◦ √ Ç å2 2
= cos2 25◦ + sin2 25◦ − cos2 35◦ + sin2 35◦ + 2 1 1 = 1 − 1 + = . 2 2 □
Dạng 6. So sánh các tỉ số lượng giác mà không dùng máy tính hoặc bảng số
Dùng định lí tỉ số lượng giác của hai góc phụ nhau (nếu cần) và căn cứ vào những tính chất sau:
○ Khi góc nhọn α tăng từ 0◦ đến 90◦ thì
— sin α tăng và tan α tăng;
— cos α giảm và cot α giảm.
○ sin α < tan α; cos α < cot α. c Ví dụ 31. So sánh a) sin 25◦ và cos 65◦; b) cos 25◦ và sin 65◦; c) tan 25◦ và cot 65◦; d) cot 25◦ và tan 65◦. Lời giải. Ta có
a) sin 25◦ = cos(90◦ − 25◦) = cos 65◦;
b) cos 25◦ = sin(90◦ − 25◦) = sin 65◦;
c) tan 25◦ = cot(90◦ − 25◦) = cot 65◦;
d) cot 25◦ = tan(90◦ − 25◦) = tan 65◦. □ 311/476 311/476 312
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN c Ví dụ 32.
a) So sánh sin 72◦ và cos 18◦; cos 72◦ và sin 18◦; tan 72◦ và cot 18◦.
b) Cho biết sin 18◦ ≈ 0,31; tan 18◦ ≈ 0,32. Tính cos 72◦ và cot 72◦. Lời giải.
a) sin 72◦ = cos(90◦ − 72◦) = cos 18◦;
cos 72◦ = sin(90◦ − 72◦) = sin 18◦;
tan 72◦ = cot(90◦ − 72◦) = cot 18◦.
b) sin 18◦ = cos 72◦ ≈ 0,31;
tan 18◦ = cot 72◦ ≈ 0,32. □ sin 50◦ cot 70◦
c Ví dụ 33. So sánh hai số m và n, biết m = ; n = . cos 65◦ tan 35◦ Lời giải. sin 50◦ sin 50◦ sin 25◦ Ta có m = = > = 1; (1) cos 65◦ sin 25◦ sin 25◦ cot 70◦ tan 20◦ tan 35◦ n = = < = 1. (2) tan 35◦ tan 35◦ tan 35◦
Từ (1) và (2) suy ra m > n. □
c Ví dụ 34. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
a) sin 70◦, cos 30◦, cos 40◦, sin 51◦;
b) cos 34◦, sin 57◦, cot 32◦. Lời giải.
a) Ta có cos 30◦ = sin 60◦; cos 40◦ = sin 50◦.
Vì sin 50◦ < sin 51◦ < sin 60◦ < sin 70◦ nên cos 40◦ < sin 51◦ < cos 30◦ < sin 70◦.
b) Ta có cos 34◦ = sin 56◦; cot 32◦ = tan 58◦.
Vì sin 56◦ < sin 57◦ < sin 58◦ < tan 58◦ nên cos 34◦ < sin 57◦ < cot 32◦. □
c Ví dụ 35. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
a) cot 40◦, sin 40◦, cot 43◦, tan 42◦;
b) tan 52◦, cot 63◦, tan 72◦, cot 31◦, sin 27◦. Lời giải.
a) Ta có cot 40◦ = tan 50◦; cot 43◦ = tan 47◦.
Vì sin 40◦ < tan 40◦ < tan 42◦ < tan 47◦ < tan 50◦ nên sin 40◦ < tan 42◦ < cot 43◦ < cot 40◦.
b) Ta có cot 63◦ = tan 27◦; cot 31◦ = tan 59◦.
Vì sin 27◦ < tan 27◦ < tan 52◦ < tan 59◦ < tan 72◦ nên sin 27◦ < cot 63◦ < tan 52◦ < cot 31◦ < tan 72◦. □
c Ví dụ 36. Cho 25◦ < α < 50◦, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần:
sin α; cos (α + 40◦) ; tan (α + 10◦). Lời giải.
Vì 25◦ < α < 50◦ nên α + 10◦ > α > 50◦ − α.
Mặt khác góc 50◦ − α phụ với góc a + 40◦.
Ta có tan (α + 10◦) > sin (α + 10◦) > sin α > sin (50◦ − α), do đó tan (α + 10◦) > sin α > cos (α + 40◦). □ 312/476 312/476 313
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG A C BÀI TẬP VẬN DỤNG
c Bài 1. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau a) BC = 5 cm; AB = 3 cm; b) BC = 13 cm; AC = 12 cm; √ √ c) BC = 5 2 cm; AB = 5 cm; d) AB = a 3; AC = a. Lời giải. √
a) Áp dụng định lí Pythagore ta được AC =
52 − 32 = 4 cm. Tỉ số lượng giác của “ B là AC 4 AB 3 AC 4 AB 3 sin B = = ; cos B = = ; tan B = = ; cot B = = . BC 5 BC 5 AB 3 AC 4 √
b) Áp dụng định lí Pythagore ta được AB =
132 − 122 = 5 cm. Tỉ số lượng giác của “ B là AC 12 AB 5 AC 12 AB 5 sin B = = ; cos B = = ; tan B = = ; cot B = = . BC 13 BC 13 AB 5 AC 12 q √ Ä ä2
c) Áp dụng định lí Pythagore ta được AC = 5 2
− 52 = 5 cm. Ta có tam giác ABC là tam giác vuông
cân nên tỉ số lượng giác của “ B là AB 5 AB 5 sin B = cos B = = √ ≈ 0,71; tan B = cot B = = = 1. BC 5 2 AC 5 √ AB a 3 √ d) Ta có cot B = = = 3 nên “ B = 30◦. Do đó AC a √ √ 1 3 3 sin B = sin 30◦ = ; cos B = cos 30◦ = ; tan B = tan 30◦ = . 2 2 3 □
c Bài 2. Cho tam giác ABC vuông tại A có AC = 4 cm, BC = 6 cm. Tính các tỉ số lượng giác của góc B. Lời giải.
Xét tam giác ABC vuông tại A, ta có A √ p AB = BC2 − AC2 = 2 5. √ √ AC 4 2 AB 2 5 5 sin “ B = = = ; cos “ B = = = ; BC 6 3 BC 6 3 √ √ C B AC 4 2 AB 2 5 5 tan √ √ “ B = = = ; cot “ B = = = . AB 2 5 5 AC 4 2 □
c Bài 3. Cho tam giác ABC vuông tại A có AB = 2 cm, AC = 3 cm. Tính các tỉ số lượng giác của góc C. Lời giải.
Xét tam giác ABC vuông tại A, ta có A √ p BC = AB2 + AC2 = 13. AB 2 AC 3 sin √ √ “ C = = ; cos “ C = = ; BC 13 BC 13 AB 2 AC 3 B C tan “ C = = ; cot “ C = = . AC 3 AB 2 □
c Bài 4. Cho tam giác M N P có M N = 5 cm, M P = 12 cm, N P = 13 cm. Chứng minh tam giác M N P
vuông tại M . Từ đó, tính các tỉ số lượng giác của góc N . 313/476 313/476 314
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN Lời giải. ®N P 2 = 169 Ta có ⇒ N P 2 = M N 2 + M P 2. M M N 2 + M P 2 = 169
Vậy tam giác M N P vuông tại M .
Xét tam giác M N P vuông tại M , ta có M P 12 M N 5 sin “ N = = ; cos “ N = = ; N P 13 N P 13 N P M P 12 N M 5 tan “ N = = ; cot “ N = = . M N 5 M P 12 □
c Bài 5. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết: a) AB = 8 cm, BC = 17 cm; b) AC = 0,9 cm, AB = 1,2 cm. Lời giải. a) Xét △ABC vuông tại A.
Theo định lí Pythagore, ta có: BC2 = AB2 + AC2
AC2 = BC2 − AB2 = 172 − 82 = 225 AC = 15 (cm).
Theo định nghĩa tỉ số lượng giác, ta có: AC 15 AB 8 AC 15 AB 8 sin B = = , cos B = = , tan B = = , cot B = = . BC 17 BC 17 AB 8 AC 15 AB 8 AC 15 AB 8 AC 15 sin C = = , cos C = = , tan C = = , cot C = = . BC 17 BC 17 AC 15 AB 8 b) Xét △ABC vuông tại A.
Theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 1,22 + 0,92 = 2,25 BC = 1,5 (cm).
Theo định nghĩa tỉ số lượng giác, ta có: AC 0,9 3 AB 1,2 4 AC 0,9 3 AB 1,2 4 sin B = = = , cos B = = = , tan B = = = , cot B = = = . BC 1,5 5 BC 1,5 5 AB 1,2 4 AC 0,9 3 AB 1,2 4 AC 0,9 3 AB 1,2 4 AC 0,9 3 sin C = = = , cos C = = = , tan C = = = , cot C = = = . BC 1,5 5 BC 1,5 5 AC 0,9 3 AB 1,2 4 □ c Bài 6.
Hình bên mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm A
ngang trên mặt đất một góc α = ’
ABH. Sử dụng máy tính cầm tay, tính
số đo góc α (làm tròn kết quả đến hàng đơn vị của độ), biết AH = 2m, BH = 5m. 2m α 5m B H Lời giải. AH 2
Xét tam giác vuông ABH, ta có: tan α = = . BH 5 Do đó α = 21,8◦. □ c Bài 7. 314/476 314/476 315
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc α. Cho B
biết tòa nhà cao 21 m và bóng của nó trên mặt đất dài 15 m. Tính góc
α.(kết quả làm tròn đến độ). 21 m α 15 m C A Lời giải. 21 Ta có tan α =
, sử dụng máy tính ta tính được α ≈ 54◦28′. 15 Vậy α ≈ 54◦28′. □ c Bài 8.
Một cái thang dài 12 m được đặt dựa vào một bức tường sao cho chân thang cách tường 7 C
m. Tính góc α tạo bởi thang và tường. α m 12 7 m B A Lời giải. 7 Ta có sin α =
, sử dụng máy tính ta tính được α ≈ 35◦41′. 12
Vậy góc tạo bởi thang và tường gần bằng 35◦41′. □ √
c Bài 9. Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và
3. Tính góc giữa đường chéo và
cạnh ngắn hơn của hình chữ nhật (Sử dụng bảng giá trị lượng giác). Lời giải. √
Hình chữ nhật ABCD có AB = 3, AD = 3. D C Xét ∆ABD vuông tại A. √ AB 3 √ 3 Ta có tan √ ’ ADB = = = 3. cm AD 3 Khi đó ’ ADB = 60◦.
Vậy góc giữa đường chéo và cạnh ngắn hơn bằng 60◦. A B 3 cm □
c Bài 10. Cho tam giác vuông có một góc nhọn 60◦ và cạnh kề với góc 60◦ bằng 3 cm. Hãy tính cạnh đối của góc này. Lời giải.
Xét △ABC vuông tại A, có “ B = 60◦, AB = 3 cm. A AC Khi đó tan B = . AB √
AC = AB · tan B = 3 · tan 60◦ = 3 3 (cm). cm √ 3
Vậy cạnh đối của góc 60◦ bằng 3 3 cm. 60◦ B C □
c Bài 11. Cho tam giác vuông có một góc nhọn 30◦ và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác. 315/476 315/476 316
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN Lời giải.
Xét △ABC vuông tại A, có “ C = 30◦, AB = 5 cm. A AB Khi đó sin C = . BC
BC = AB : sin C = 5 · sin 30◦ = 10 (cm). cm 5
Vậy cạnh huyền của tam giác bằng 10 cm. 30◦ B C □
c Bài 12. Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau a) 26◦; b) 72◦; 81◦27′ c) Lời giải. a) sin 26◦ ≈ 0,44; cos 26◦ ≈ 0,9; tan 26◦ ≈ 0,49; cot 26◦ ≈ 2,05. b) sin 72◦ ≈ 0,95; cos 72◦ ≈ 0,31; tan 72◦ ≈ 3,08; cot 72◦ ≈ 0,32. c) sin 81◦27′ ≈ 0,99; cos 81◦27′ ≈ 0,15; tan 81◦27′ ≈ 6,65; cot 81◦27′ ≈ 0,15. □
c Bài 13. Sử dụng máy tính cầm tay, tìm góc nhọn α trong mỗi trường hợp sau đây 3 a) cos α = 0,6; b) tan α = . 4 Lời giải.
a) Ta có cos α = 0,6 sử dụng máy tính ta tìm được α ≈ 53◦8′; 3 b) Ta có tan α =
sử dụng máy tính ta tìm được α ≈ 36◦52′; 4 □
c Bài 14. Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba): a) sin 40◦12′; b) cos 52◦54′; c) tan 63◦36′; d) cot 25◦18′. Lời giải. Để tính Bấm phím Kết quả sin 40◦12′ j4 0 x 1 2 x = 0,6454576877 cos cos 52◦54′ k5 2 x 5 4 x = 0,6032079877 tan 63◦36′ l6 3 x 3 6 x = 2,014486937 cot 25◦18′ l2 5 x 1 8 x = u = 2,115516356
Làm tròn đến chữ số thập phân thứ ba ta được: a) sin 40◦12′ ≈ 0,645. b) cos 52◦54′ ≈ 0,603. c) tan 69◦36′ ≈ 2,014. d) cot 25◦18′ ≈ 2,116. □
c Bài 15. Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng: a) sin x = 0,2368; b) cos x = 0,6224; c) tan x = 1,236; d) cot x = 2,154. Lời giải. 316/476 316/476 317
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Biết Bấm phím Kết quả Bấm tiếp x sin x = 0,2368 q j0 . 2 3 6 8 = 13,6977504 13◦41′51,9” cos x = 0,6224
q k0 . 6 2 2 4 = 51,50839221 51◦30′30,21” tan x = 1,236 q l1 . 2 3 6 = 51,02501186 51◦1′30,04” cot x = 2,154
q l2 . 1 5 4 u = 24,90320574 24◦54′11,54”
Làm tròn đến phút ta được: a) x ≈ 13◦42′; b) x ≈ 51◦31′; c) x ≈ 51◦2′; d) x ≈ 24◦54′. □ c Bài 16.
a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45◦.
sin 55◦, cos 62◦, tan 57◦, cot 64◦. tan 25◦ b) Tính , tan 34◦ − cot 56◦. cot 65◦ Lời giải.
a) sin 55◦ = cos(90◦ − 55◦) = cos 35◦.
cos 62◦ = sin(90◦ − 62◦) = sin 28◦.
tan 57◦ = cot(90◦ − 57◦) = cot 33◦.
cot 64◦ = tan(90◦ − 64◦) = tan 26◦. tan 25◦ cot(90◦ − 25◦) cot 65◦ b) = = = 1. cot 65◦ cot 65◦ cot 65◦
tan 34◦ − cot 56◦ = tan 34◦ − tan(90◦ − 56◦) = tan 34◦ − tan 34◦ = 0. □
c Bài 17. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45◦ a) sin 60◦; b) cos 75◦; c) tan 80◦. Lời giải. a) sin 60◦ = cos 30◦; b) cos 75◦ = sin 15◦; c) tan 80◦ = cot 10◦. □
c Bài 18. Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63◦? Vì sao? a) sin 27◦; b) cos 27◦; c) tan 27◦; d) cot 27◦. Lời giải.
Ta thấy 27◦ + 63◦ nên theo định lí về hai góc phụ nhau ta có a) sin 27◦ = cos 63◦; c) tan 27◦ = cot 63◦; b) cos 27◦ = sin 63◦; d) cot 27◦ = tan 63◦. □
c Bài 19. Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị biểu thức
A = sin 25◦ + cos 25◦ − sin 65◦ − cos 65◦. 317/476 317/476 318
1. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN Lời giải.
Vì 25◦ + 65◦ = 90◦ nên ta có
A = sin 25◦ + cos 25◦ − sin 65◦ − cos 65◦
= sin 25◦ + cos 25◦ − cos 25◦ − sin 25◦ = 0. □
c Bài 20. Tính giá trị của các biểu thức sau sin 30◦ · cos 30◦ tan 30◦ a) A = ; b) B = . cot 45◦ cos 45◦ · cos 60◦ Lời giải. √ 1 3 √ sin 30◦ · cos 30◦ · 3 a) A = = 2 2 = ; cot 45◦ 1 4 √3 √ tan 30◦ 2 6 b) B = = 3 √ = . cos 45◦ · cos 60◦ 2 1 3 · 2 2 □
c Bài 21. Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho “ B = α.
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA. sin α cos α
b) Chứng minh sin2 α + cos2 α = 1; tan α = ; cot α = ; tan α · cot tan α = 1. cos α sin α
Từ đó tính giá trị biểu thức S = sin2 35◦ + cos2 35◦; T = tan 61◦ · cot 61◦. Lời giải. C AC AB AC AB a) Ta có sin α = , cos α = , tan α = , cot α = . BC BC AB AC
b) Ta có (sử dụng thêm định lí Pythagore) AC2 AB2 AC2 + AB2 sin2 α + cos2 α = + = BC2 BC2 BC2 α BC2 B A = = 1. BC2 Ta có sin α AC AB AC BC AC = : = · = = tan α. cos α BC BC BC AB AB cos α AB AC AB BC AB = : = · = = cot α. sin α BC BC BC AC AC AC AB tan α · cot α = · = 1. AB AC
Áp dụng các kết quả trên, ta có ngay S = 1 và T = 1. □ 318/476 318/476 319
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Baâi 2
HỆ THỨC GIỮA CẠNH VÀ GÓC CỦA TAM GIÁC VUÔNG A
TRỌNG TÂM KIẾN THỨC
1 Hệ thức giữa cạnh huyền và cạnh góc vuông
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Trong tam giác ABC vuông tại A, ta có A b = a · sin B = a · cos C; b c c = a · sin C = a · cos B. B a C
2 Hệ thức giữa hai cạnh góc vuông
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Trong tam giác ABC vuông tại A, ta có A b = c · tan B = c · cot C; b c c = b · tan C = b · cot B. B a C
3 Giải tam giác vuông
Trong một tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được
tất cả các cạnh và các góc còn lại của tam giác vuông đó. Bài toán này gọi là bài toán Giải tam giác vuông.
Trong đo đạc, khi người quan sát có hướng nhìn ngang theo tia Ox (Hình bên) A thì ○ Góc ’
xOA gọi là góc nghiêng lên hay góc nâng; x ○ O Góc ’
xOB gọi là góc nghiêng xuống hay góc hạ. B A B CÁC DẠNG BÀI TẬP
Dạng 1. Giải tam giác vuông
c Ví dụ 1. Giải các tam giác vuông ở hình sau. Làm tròn kết quả độ dài đến hàng đơn vị và số đo góc đến độ. 319/476 319/476 320
2. HỆ THỨC GIỮA CẠNH VÀ GÓC CỦA TAM GIÁC VUÔNG B R D B 5 9 13 9 6 11 32◦ A 6 C A C E F Q P a) b) c) d) Lời giải.
a) Xét △ABC vuông tại A, theo định lí Pythagore, ta có √ √ BC = AB2 + AC2 = 52 + 82 ≈ 9,4. AB 5 Ta có tan C = = = 0,625. AC 8 Từ đó tìm được “ C ≈ 32◦, suy ra “ B = 90◦ − “ C ≈ 90◦ − 32◦ = 58◦.
b) Xét tam giác ABC vuông tại A, ta có: AB 6 sin C = = suy ra “ C ≈ 33◦, “ B ≈ 90◦ − 33◦ = 57◦. BC 11
Theo định lí Pythagore, ta có √ √ √ AC = BC2 − AB2 = 112 − 62 = 121 − 36 ≈ 9.
c) Xét tam giác DEF vuông tại D, ta có: “ F = 90◦ − 32◦ = 58◦.
DE = DF · cot E = 9 · cot 32◦ ≈ 14. DF DF 9 sin E = nên EF = = ≈ 17. EF sin E sin 32◦
d) Xét tam giác P QR vuông tại P , ta có: P R 9 cos R = = , suy ra b R ≈ 46◦, “ Q ≈ 90◦ − 46◦ = 44◦. QR 13
Theo định lí Pythagore, ta có: √ √ p QP = QR2 − RP 2 = 132 − 92 = 169 − 81 ≈ 9. □
c Ví dụ 2. Giải tam giác ABC vuông tại A biết: a) AB = 4, AC = 6; b) AB = 4, BC = 8; c) AB = 3, “ B = 42◦; d) BC = 9, “ C = 53◦; Lời giải.
a) Xét tam giác ABC vuông tại A., ta có √ B
BC2 = AB2 + AC2 = 42 + 62 = 52 hay BC = 52 ≈ 7,2 (cm); AC 6 3 tan B = = = , suy ra “ B ≈ 56◦; AB 4 2 4 “ B + “
C = 90◦ (tổng hai góc nhọn của tam giác vuông), suy ra “ C = 90◦ − “ B = 90◦ − 56◦ = 34◦. A C 6
b) Xét tam giác ABC vuông tại A, ta có √ √ √ C AC = BC2 − AC2 = 82 − 42 = 4 3 ≈ 6,928. AB 4 1 cos B = = = BC 8 2 8 ⇒ “ B = 60◦. “ C = 90◦ − 60◦ = 30◦. A B 4 320/476 320/476