17 trang 14 lượt tải

Chuyên Đề Nguyên Hàm Tích Phân Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

28

Cho khối tròn xoay như Hình 7. Tính thể tích của khối tròn xoay được tạo thành bởi hình phẳng cho ở Hình 7 khi quay quanh trục Ox(viết kết quả dưới dạng số  thập phân và làm tròn đến hàng phần mười). Chủ một trung tâm thương mại muốn cho thuê một số gian hàng như nhau. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Chủ đề: Tài liệu ôn thi THPTQG môn Toán 278 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Mỹ Châu

3 ngày trước
Danh sách Quiz
/17
Trang 1
CHUYÊN ĐỀ: NGUYÊN HÀM VÀ TÍCH PHÂN
A. TÓM TẮT LÝ THUYẾT
I. NGUYÊN HÀM
1. Định nghĩa
Cho
K
là một khoảng, đoạn hoặc nửa khoảng của tập số thực .
• Cho hàm số
fx
xác định trên
K
. Hàm số
Fx
được gọi là nguyên hàm của hàm số
fx
trên
K
nếu
'F x f x
với mọi
thuộc
K
.
• Nếu
Fx
là một nguyên hàm của hàm số
fx
trên
K
thì mọi nguyên hàm của hàm số
fx
trên
K
đều
có dạng
F x C
với
C
là một hằng số. Vì vậy,
df x x F x C
• Mọi hàm số liên tục trên
K
đều có nguyên hàm trên
K
. Ta có:
' dF x x F x C
2. Tính chất
Cho
,fxgx
là hai hàm số liên tục trên
K
.
•
d dkf x x k f x x

với
k
là hằng số khác 0;
•
d d df x g x x f x x g x x


•
d d df x g x x f x x g x x


3. Nguyên hàm một số hàm số sơ cấp cơ bản
• Với
1
ta có
1
d
1
x
x x C

•
1
d lnx x C
x

•
sin d cos .x x x C
•
2
1
d cot .
sin
x x C
x
•
cos d sin .x x x C
•
2
1
d tan .
cos
x x C
x

• Với
0; 1aa
ta có
d.
ln
x
x
a
a x C
a

II. TÍCH PHÂN
1. Định nghĩa
Cho
fx
là hàm số liên tục trên
; ab
. Giả sử
Fx
là một nguyên hàm của
fx
trên đoạn
; ab
. Khi đó
d
b
a
f x x F b F a
2. Tính chất
Cho các hàm số
, y f x y g x
liên tục trên đoạn
; ab
. Ta có:
•
d d
bb
aa
kf x x k f x x

(
k
là hằng số).
•
d d d
b b b
a a a
f x g x x f x x g x x


;
•
d d d
b b b
a a a
f x g x x f x x g x x


Trang 2
• Giả sử
, , m n c
là ba số thực tuỳ ý thuộc đoạn
; ab
, ta có:
d d d
n c n
m m c
f x x f x x f x x
.
3. Tích phân một số hàm số sơ cấp cơ bản
• Với
1
, ta có:
1 1 1
d
11
b
b
a
a
x b a
xx



• Với hàm số
1
fx
x
liên tục trên đoạn
; ab
, ta có:
1
d ln ln ln
b
b
a
a
x x b a
x
•
sin d cos cos cos
b
b
a
a
x x x a b
•
cos d sin sin sin
b
b
a
a
x x x b a
• Với hàm số
2
1
sin
fx
x
liên tục trên
; ab
, ta có:
2
1
d cot cot cot
sin
b
b
a
a
x x a b
x
.
• Với hàm số
2
1
()
cos
fx
x
liên tục trên
;ab
, ta có:
2
1
d tan tan tan ;
cos
b
b
a
a
x x b a
x
• Với
0a
,
1a
, ta có
d
ln ln
x
x
a a a
ax
aa


.
4. Úng dụng
• Cho hàm số
y f x
liên tục trên đoạn
;ab
. Khi đó, diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm
số
y f x
, trục hoành và hai đường thẳng
,x a x b
là
( ) d
b
a
S f x x
.
• Cho các hàm số
,y f x y g x
liên tục trên đoạn
;ab
. Khi đó, diện tích hình phẳng giới hạn bởi đồ thị
của các hàm số
,y f x y g x
và hai đường thẳng
,x a x b
là
d
b
a
S f x g x x
.
• Cắt một vật thể bởi hai mặt phẳng vuông góc với trục
Ox
tại
xa
và
xb
()ab
. Một mặt phẳng tuỳ ý
vuông góc với
Ox
tại
()a x b
cắt vật thể đó theo hình phẳng có diện tích là
()Sx
. Giả sử hàm số
()Sx
liên tục trên
;ab
. Khi đó, thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng trên được tính bởi công
thức
d.
b
a
V S x x
• Cho hàm số
y f x
liên tục, không âm trên đoạn
;ab
. Hình phẳng
()H
giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường thẳng
,x a x b
quay quanh trục
Ox
tạo thành một khối tròn xoay có
thể tích bằng
Trang 3
2
b
a
V f x dx


.
B . MỘT SỐ VÍ DỤ
Dạng 1. Câu trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.
Ví dụ 1. [MĐ1] Hàm số
3
( ) 2 2 1F x x x
là nguyên hàm của hàm số nào sau đây?
A.
2
62f x x
B.
42
1
2
f x x x x
C.
42
1
2
f x x x x C
. D.
2
62f x x C
.
Lời giải
Chọn A
Ta có:
32
( ) ( ) 2 2 1 6 2f x F x x x x
.
Ví dụ 2. [MĐ1] Diện tích hình phẳng giới hạn bởi hai đường thẳng
0,xx

, đồ thị hàm số
cosyx
và
trục
Ox
là:
A.
0
cos dS x x
B.
2
0
cos dS x x
.
C.
0
cos dS x x
. D.
0
cos dS x x
.
Lời giải
Chọn C
Diện tích hình phẳng giới hạn bởi hai đường thẳng
,x a x b
và các đồ thị hàm số
( ), ( )y f x y g x
là
| ( ) ( ) | d
b
a
S f x g x x
. Khi đó, theo đề bài ta có
0
cos dS x x
.
Ví dụ 3. [MĐ1] Gọi
V
là thể tích khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường
, 0, 0, 2
x
y e y x x
quay quanh
Ox
. Phát biểu nào sau đây là đúng?
A.
2
2
0
d
x
V e x
. B.
2
0
d
x
V e x
.
C.
2
0
d
x
V e x
. D.
2
2
0
d
x
V e x
.
Lời giải
Chọn A
Hình phẳng giới hạn bởi các đường
, 0, 0, 2
x
y e y x x
quay quanh
Ox
sẽ tạo thành một khối
tròn xoay có thể tích bằng
2
2
2
0
d
a
x
b
exV f x dx

.
Ví dụ 4. [MĐ1] Một vật chuyển động với vận tốc
( ) 1 2sin 2 ( m/s)v t t
. Quãng đường vật di chuyển trong
khoảng thời gian từ
0t
(giây) đến thời điểm
3
4
t
(giây) được tính theo công thức:
Trang 4
A.
3
4
0
1 2sin2 ds t t t

. B.
2
3
4
0
1 2sin 2 ds t t t

.
C.
3
4
0
( ) (1 2sin2 )d
π
s t t t
. D.
3
( ) (0)
4
π
s t v v




.
Lời giải
Chọn A
Gọi
()st
là quãng đường mà vật di chuyển trong khoảng thời gian từ
0t
(giây) đến
3
4
π
t
(giây). Mà
'( ) ( )s t v t
nên ta có
3
4
0
( ) (1 2sin2 )d
π
s t t t
.
Dạng 2: Trắc nghiệm đúng -sai
Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.
Ví dụ 5: [MĐ1] Giả sử
()st
là phương trình quãng đường chuyển động của một vật theo thời gian
t
(giây) và
()vt
là phương trình vận tốc của chuyển động đó theo thời gian
t
(giây).
a)
( )dt ( )s t v t C
.
b)
( )dt ( )v t s t C
.
c)
t'( )d ( )s t v t C
.
d)
'( )dt ( )s t s t C
.
Lời giải
Ý
a)
b)
c)
d)
Kết quả
S
Đ
S
Đ
Vì
()st
,
()vt
lần lượt là phương trình quãng đường và phương trình vận tốc của chuyển động đó theo thời gian
t
(giây) nên ta có
'( ) ( )s t v t
và
( )dt ( ) Cv t s t
.
a)
( )dt ( )s t v t C
. Suy ra Sai.
b)
( )dt ( )v t s t C
. Suy ra Đúng.
c)
t'( )d ( )s t v t C
. Suy ra Sai.
d)
'( )dt ( )s t s t C
. Suy ra Đúng.
Ví dụ 6: [MĐ2] Cho hàm số
3
( ) 2 1F x x x
,
¡x
là một nguyên hàm của hàm số
()fx
.
a) Nếu hàm số
()Gx
cũng là một nguyên hàm của hàm số
()fx
và
( 1) 3G 
thì
1G x F x
,
¡x
.
b) Nếu hàm số
()Hx
cũng là một nguyên hàm của hàm số
()fx
và
(1) 3H 
thì
3H x F x
,
¡x
.
c) Nếu hàm số
()Kx
cũng là một nguyên hàm của hàm số
()fx
và
(0) 0K
thì
1K x F x
,
¡x
.
d) Nếu hàm số
()Mx
cũng là một nguyên hàm của hàm số
()fx
và
(2) 4M
thì
1M x F x
,
¡x
.
Lời giải
Ý
a)
b)
c)
d)
Kết quả
S
Đ
S
Đ
a) Vì
()Gx
là một nguyên hàm của hàm số
()fx
trên
¡
nên
( ) ( )G x F x C
, với
C
1à một hằng số.
Mà
( 1) 3G 
nên ta có
( 1) ( 1) 3 2 1G F C C C
.
Trang 5
Vậy
1G x F x
,
¡x
.
Suy ra Sai.
b) Vì
()Hx
là một nguyên hàm của hàm số
()fx
trên
¡
nên
( ) ( )H x F x C
, với
C
1à một hằng số.
Mà
(1) 3H 
nên ta có
(1) (1) 3 0 3H F C C C
.
Vậy
3H x F x
,
¡x
.
Suy ra đúng.
c) Vì
()Kx
là một nguyên hàm của hàm số
()fx
trên
¡
nên
( ) ( )K x F x C
, với
C
1à một hằng số. Mà
(0) 0K
nên ta có
(0) (0) 0 1 1K F C C C
. Vậy
1K x F x
,
¡x
.
Suy ra Sai.
d) Vì
()Mx
là một nguyên hàm của hàm số
()fx
trên
¡
nên
( ) ( )M x F x C
, với
C
1à một hằng số. Mà
(2) 4M
nên ta có
(2) (2) 4 5 1M F C C C
. Vậy
1M x F x
,
¡x
.
Suy ra Đúng.
Ví dụ 7: [MĐ2] Một vật chuyển động với gia tốc
2
( ) 2cos m / sa t t
.
a) Tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng
0
. Khi đó, vận tốc của vật được biểu diễn bởi hàm
số
( ) 2sin ( m / s)v t t
.
b) Vận tốc của vật tại thời điềm
2
π
t
là
1 m/s
.
c) Quãng đường vật đi được từ thời điểm
0 ( s)t
đến thời điểm
(s)t π
là
4 m
.
d) Quãng đường vật đi được từ thời điểm
2
π
t
(s) đến thời điểm
3
4
π
t
(s) là
2m
.
Lời giải
Ý
a)
b)
c)
d)
Kết quả
Đ
S
Đ
S
a) Ta có
( ) ( )d 2cos d 2sinv t a t t t t t C

.
Mà tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng 0 nên ta có
(0) 0v
hay
0C
. Vậy
( ) 2sinv t t
.
Suy ra đúng.
b) Vận tốc của vật tại thời điểm
2
π
t
là
2sin 2( m / s)
22
ππ
v




.
Suy ra sai.
c) Quãng đường vật đi được từ thời điểm
0 ( s)t
đến thời điểm
(s)t π
là
0
00
( )d 2sin d 2cos 2cos ( 2cos0) 4( m).
ππ
π
v t t t t t π

Suy ra đúng.
d) Quãng đường vật đi được từ thời điểm
2
π
t
(s) đến thời điểm
3
4
π
t
(s) là
33
3
44
4
2
22
3
( )d 2sin d 2cos 2cos 2cos 2 ( m).
42
ππ
π
π
ππ
ππ
v t t t t t




Suy ra Sai.
Dạng 3: Câu trắc nghiệm trả lời ngắn
Trang 6
Ví dụ 8: [MĐ2] Cho hàm số
Fx
là một nguyên hàm của hàm số
2
3 4 1f x x x
và
22F
. Tính
3F
.
Lời giải
Ta có
2 3 2
3 4 1 2F x f x dx x x dx x x x C

. Mà
22F
nên suy ra
0C
Vậy
hàm số
32
2F x x x x
. Suy ra
3 12F
.
Ví dụ 9: [MĐ2] Cho đồ thị hàm số
2
2
x
y
và hình phẳng được tô màu như Hình 1. Hình phẳng đó được giới
hạn bởi các đường nào? Tính diện tích hình phẳng đó (viết kết quả dưới dạng số thập phân và làm tròn đến
hàng phần trăm).
Lời giải
Hình phẳng đã cho ở Hình 1 được giới hạn bởi đồ thị hàm số
2
2y
, trục hoành và hai đường thẳng
0x
,
2x
. Khi đó, diện tích hình phẳng là
1
2
22
1
22
1
00
2
2
2
2 2 2,89
ln2
ln2
x
x
x
S dx dx







.
Ví dụ 9: [MĐ2] Một vật chuyển động với gia tốc được cho bởi hàm số
2
5cos /a t t m s
. Lúc bắt đầu
chuyển động vật có vận tốc
2,5 /ms
. Tính gia tốc của vật tại thời điểm vận tốc đạt giá trị lớn nhất trong
s
đầu tiên.
Lời giải
Vận tốc của vật được biểu diễn bởi hàm số
5cos 5sinv t a t dt tdt t C

.
Khi bắt đầu chuyển động, vật có vận tốc
2,5 /ms
nên ta có:
0 2,5 5sin0 2,5 C 2,5vC
.
Suy ra
5sin 2,5v t t
. Mà
5sin 2,5 7,5t 
. Vậy vận tốc đạt giá trị lớn nhất tại
2
t
. Khi đó, gia
tốc của vật tại thời điểm
2
t
là
5.cos 0
22
a


2
/ms
.
C. BÀI TẬP LUYỆN TẬP
Dạng 1: Câu trắc nghiệm nhiều phương án lựa chọn
Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1. [MĐ1] Phát biểu nào sau đây là đúng?
Trang 7
A.
F x dx F x C

. B.
F x dx F x C

.
C.
F x dx F x C
. D.
F x dx F x C


.
Lời giải
Chọn A
Câu 2. [MĐ1] Phát biểu nào sau đây là đúng?
A.
33xx
e dx e C


. B.
33
1
3
xx
e dx e C

.
C.
33
1
3
xx
e dx e C


. D.
33
1
3
xx
e dx e


.
Lời giải
Chọn B
Câu 3. [MĐ1] Cho hàm số
y f x
liên tục trên đoạn
;ab
. Gọi
D
là hình phẳng giới hạn vởi đồ thị
hàm số
y f x
, trục hoành và hai đường thẳng
xa
,
xb
ab
. Tính thể tích khối tròn xoay
được tạo thành khi quay
D
quanh trục hoành là
A.
2
b
a
V f x dx


. B.
2
2
b
a
V f x dx


.
C.
2
2
b
a
V f x dx


. D.
2
b
a
V f x dx
.
Lời giải
Chọn A
Câu 4. [MĐ2] Cho hàm số
y f x
có đồ thị như Hình 2. Gọi
S
là phần diện tích hình phẳng được tô
màu. Phát biểu nào sau đây là đúng?
A.
0,5
1
S f x dx
. B.
0
1
S f x dx
.
C.
0,5
1
S f x dx

. D.
0,5
1
S f x dx

.
Lời giải
Chọn D
Ta có
0,5 0,5
11
0S f x dx f x dx



.
Trang 8
Câu 5. [MĐ1] Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
1
y
x
, trục hoành và hai đường thẳng
1x
,
4x
. Thể tích
V
của khối tròn xoay tạo thành khi cho hình phẳng
H
quay quanh trục
Ox
là
A.
4
1
1
dV πx
x
. B.
4
2
1
1
dVx
x
.
C.
4
2
1
1
dV πx
x
. D.
4
2
2
1
1
dV πx
x
.
Lời giải
Chọn C
Thể tích
V
của khối tròn xoay tạo thành khi cho hình phẳng
H
giới hạn bởi đồ thị hàm số
1
y
x
,
trục hoành và hai đường thẳng
1x
,
4x
quay quanh trục
Ox
là
4
2
1
1
dV πx
x
.
Câu 6. [MĐ1] Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
sinyx
, trục hoành và hai đường thẳng
0x
,
x
. Thể tích
V
của khối tròn xoay tạo thành khi cho hình phẳng
D
quay xung quanh trục
Ox
là
A.
0
sin d
π
V π x x
. B.
2
0
sin d
π
V π x x
.
C.
0
sin d
π
V π x x
. D.
22
0
sin d
π
V π x x
.
Lời giải
Chọn B
Thể tích
V
của khối tròn xoay tạo thành khi cho hình phẳng
D
giới hạn bởi đồ thị hàm số
sinyx
, trục hoành và hai đường thẳng
0x
,
x
quay quanh trục
Ox
là
2
1
sin d
π
V π x x
.
Câu 7. [MĐ1] Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
yx
, trục hoành và hai đường thẳng
1x
,
2x
. Thể tích
V
của khối tròn xoay tạo thành khi cho hình phẳng
H
quay xung quanh trục
Ox
là
A.
2
1
dV π x x
. B.
2
0
d
π
V π x x
.
C.
2
2
1
dV π x x
. D.
2
1
dV π x x
.
Lời giải
Chọn D
Thể tích
V
của khối tròn xoay tạo thành khi cho hình phẳng
H
giới hạn bởi đồ thị hàm số
yx
,
trục hoành và hai đường thẳng
1x
,
2x
quay quanh trục
Ox
là
2
1
dV π x x
.
Câu 8. [MĐ1] Gọi
S
là diện tích hình phẳng được tô đậm trong Hình 3. Công thức tính
S
là
Trang 9
A.
12
11
ddS f x x f x x


. B.
12
11
ddS f x x f x x


.
C.
2
1
dS f x x
. D.
2
1
dS f x x

.
Lời giải
Chọn B
Dựa vào đồ thị, suy ra diện tích hình phẳng là
12
11
ddS f x x f x x


.
Câu 9. [MĐTH]
2
2dxx
bằng:
A.
21
2
21
x
C
. B.
2 2 1
2
21
x
C
. C.
2
2
ln 2
x
C
x
. D.
2
2xC
.
Lời giải
Chọn B
Đặt
1
2 d 2d d d
2
t x t x x t
.
Ta có
21
2
2
11
2d
22
21
t
x x t dt C

.
Thay
2tx
ta có
21
2
2
1
2d
2
21
x
x x C

2 2 1
2
21
x
C

.
Câu 10. [MĐTH]
2
sin cos d
22
xx
x



bằng:
A.
cosx x C
. B.
2
cos sin
22
xx
C



.
C.
3
1
sin cos
3 2 2
xx
C




. D.
cosx x C
.
Lời giải
Chọn A
Ta có:
2
sin cos
22
xx



22
sin 2sin .cos cos
2 2 2 2
x x x x
1 sinx
.
Trang 10
Khi đó
2
sin cos d 1 sin d
22
xx
x x x




d sin d cosx x x x x C

.
Câu 11. [MĐTH]
2
d
xx
e e x
bằng:
A.
2
2
xx
e e C

. B.
2xx
e e C

. C.
2
1
2
xx
e e C

. D.
1 2 1
1 2 1
xx
ee
C
xx

.
Lời giải
Chọn C
Ta có:
22
d d d
x x x x
e e x e x e x

2
1
d d 2
2
xx
e x e x

2
1
2
xx
e e C
.
Câu 12. [MĐTH]
2
cos d
2
x
x



bằng:
A.
sinx x C
. B.
3
1
cos
32
x
C



. C.
2
sin
2
x
C



. D.
11
sin
22
x x C
.
Lời giải
Chọn D
Ta có:
2
1 cos
cos d d
22
xx
xx




11
d cos d
22
x x x

11
sin
22
x x C
.
Câu 13. [MĐTH]
2
2
5 6 d
x
x
ex



bằng:
A.
2
1
2
xx
e e C

. B.
2
25
12
2ln5
x
x
eC

. C.
2
2
xx
e e C

. D.
1 2 1
1 2 1
xx
ee
C
xx

.
Lời giải
Chọn B
Ta có
2
22
5 6e d 25 d 12 e
2
xx
xx
x
x x d







22
25 25
12e 12e
ln25 2ln5
xx
xx
CC

.
Câu 14. [MĐVD] Cho hàm số
y f x
có đồ thị
y f x
cắt trục
Ox
tại ba điểm có hoành độ
abc
như Hình 4. Mệnh đề nào sau đây là đúng?
Trang 11
A.
f c f a f b
. B.
f c f b f a
.
C.
f a f b f c
. D.
f b f a f c
.
Lời giải
Chọn A
Dựa vào đồ thị hàm số
y f x
ta có bảng biến thiên sau
Dựa vào bảng biến thiên ta có:
f a f b
;
f c f b
1
.
Gọi
1
S
là diện tích giới hạn bởi đồ thị hàm số
y f x
, trục hoành và các đường thẳng
;x a x b
.
Gọi
2
S
là diện tích giới hạn bởi đồ thị hàm số
y f x
, trục hoành và các đường thẳng
;x b x c
.
Ta có:
1
b
a
S f x dx

a
b
f x dx f a f b
;
2
c
b
S f x dx f c f b
.
Quan sat hình vẽ ta thấy
21
SS
f c f b f a f b
2f c f a
.
Từ
1
và
2
ta có
f c f a f b
.
Câu 15. [MĐTH] Vi khuẩn E.coli sống chủ yếu ở đường ruột và có số lượng lớn nhất trong hệ vi sinh vật của
cơ thể . Một quần thể vi khuẩn E. coli được quan sát trong điều kiện thích hợp, có tốc độ sinh trưởng được cho
bởi hàm số
480.2 ln2.
t
ft
Trong đó
t
tính bằng giờ
0t
,
ft
tính bằng cá thể/giờ (Nguồn: R
Larson and B.Edwards,Calculus 10e, Cengage). Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước
tính một cách chính xác khoảng 480 cá thể. Hàm số biểu thị số lượng cá thể theo thời gian
t
là:
A.
480.2 ln2
t
Ft
B.
480.2
t
Ft
C.
2
480.
ln2
t
Ft
D.
2
480.
ln2
t
F t C
Trang 12
Lời giải
Chọn B
Do
2
480.2 ln2 480.ln2. 480.2 ( )
ln2
t
tt
f t dt dt C C F t

Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước tính một cách chính xác khoảng 480 cá thể nên
0
(0) 480.2 480 0F C C
Dạng 2: Trắc nghiệm đúng -sai
Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.
Câu 16. [MĐNB] Cho
fx
là hàm số liên tục trên R
a)
'.f x dx f x C
b)
'.f x dx f x C
c)
'.f x dx f x
d)
'' ' .f x dx f x C
Lời giải
Ý
a)
b)
c)
d)
Kết quả
sai
đúng
sai
đúng
Do định nghĩa của nguyên hàm ta có kết quả trên.
Câu 17. [MĐTH] Giả sử
vt
là phương trình vận tốc của một vật chuyển động theo thời gian
t
(giây),
()at
là phương trình gia tốc của vật đó chuyển động theo thời gian
t
(giây).
a)
.a t dt v t C
b)
.v t dt a t C
c)
'.v t dt a t C
d)
'.v t dt v t C
Lời giải
Ý
a)
b)
c)
d)
Kết quả
đúng
sai
sai
đúng
a) Do nguyên hàm của hàm gia tốc là hàm vận tốc. Suy ra đúng.
b) Do nguyên hàm của hàm vận tốc là hàm quãng đường. Suy ra sai.
c) Do
'.v t dt v t C
Suy ra sai
d) Do định nghĩa nguyên hàm. Suy ra đúng.
Câu 18. [MĐTH] Giả sử
vt
là phương trình vận tốc của một vật chuyển động theo thời gian
t
(giây),
()at
là phương trình gia tốc của vật đó chuyển động theo thời gian
t
(giây). Xét chuyển động trong khoảng
thời gian từ
c
(giây) đến
(giây).
Trang 13
a)
.
b
c
a t dt v b v c
b)
.
b
c
v t dt a b a c
c)
.
b
c
v t dt v c v b

d)
.
b
c
v t dt v b v c

Lời giải
Ý
a)
b)
c)
d)
Kết quả
Đúng
Sai
Sai
Đúng
Do
a t v t
Suy ra a), d) đúng.
Câu 19. Cho vật thể tròn xoay như Hình 5.
a) Vật thể được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số
y f x
và hai đường thẳng
,x a x b
quay quanh trục
Ox
.
b) Vậy thể được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường
thẳng
,x a x b
quay quanh trục
Ox
.
c) Thể tích của vật thể được tính theo công thức
dx
b
a
V f x
.
d) Thể tích của vật thể được tính theo công thức
2
dx
b
a
V f x


.
Lời giải
Ý
a)
b)
c)
d)
Kết quả
Sai
Đúng
Sai
Đúng
Theo lý thuyết về thể tích vật tròn xoay thì b, d đúng.
Câu 20. Tại một khu di tích vào ngày lễ hội hằng năm, tốc độ thay đổi lượng khách tham quan được biểu diễn
bằng hàm số
32
4 72 288Q t t t t
, trong đó t tính bằng giờ
Trang 14
(
0 13t
) ,
Qt
tính bằng khách/giờ . Nguồn: R.Larson and B. Eawads, Calculus 10e, Cengage). Sau 2 giờ
đã có 500 người có mặt.
a) Lượng khách tham quan được biểu diễn bởi hàm số
4 3 2
24 144Q t t t t
.
b) Sau 5 giờ lượng khách tham quan là 1325 người.
c) Lượng khách tham quan lớn nhất là 1296 người.
d) Tốc độ thay đổi lượng khách tham quan lớn nhất tại thời điểm
6t
.
Lời giải
Ý
a)
b)
c)
d)
Kết quả
Sai
Đúng
Sai
Đúng
Ta có
43
. 24 144 2 500 100.Q t Q t dt t t t C Q C
Suy ra
43
24 144 100Q t t t t
a) sai.
Sau 5 giờ lượng khách tham quan là
5 1325Q
. Do đó b) đúng.
Ta có
0;13
max 6 1396.Q t Q
Do đó d) đúng, c) Sai
Dạng 3. Câu trắc nghiệm trả lời ngắn
Câu 21.
1
2
2
0
3
d
2
x
x
x
có giá trị bằng bao nhiêu? (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần
mười).
Lời giải
Trả lời:
0,1
Ta có:
1
11
2
2
00
0
3
3 1 3
4
dd
3
2 9 4
9ln
4
x
x
x
x
xx








1
0,1
3
36ln
4
.
Câu 22. Cho hàm số
Fx
là một nguyên hàm của hàm số
2
2 2 1f x x x
và
1
1
6
F 
. Tính
1
2
F



(viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm).
Lời giải
Trả lời:
0,49
Ta có:
2
2 2 1f x x x
32
2 4 2x x x
.
Suy ra
32
d 2 4 2 dF x f x x x x x x

32
2 d d 4 d 2dx x x x x x x
4 3 2
11
2 2 ,
23
x x x x C C
Mà
1
1
6
F 
nên suy ra
0C
.
Trang 15
Vậy hàm số
4 3 2
1 1 1 47
2 2 0,49
2 3 2 96
F x x x x x F




Câu 23. Cho đồ thị hàm số
cosyx
và hình phẳng được tô màu như Hình 6. Tính diện tích hình phẳng đó
(viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần mười).
Lời giải
Trả lời:
4,7
Hình phẳng đã cho được giới hạn bởi các đồ thị hàm số
cos ,y x y x
và hai đường thẳng
1, 3xx
. Khi đó diện tích hình phẳng được tính theo công thức
3
1
cos dS x x x
. Vì
cos , 1;3x x x
nên ta có:
3
3
2
1
1
cos d sin 4 sin3 sin1 4,7
2
x
S x x x x



.
Câu 24. Cho khối tròn xoay như Hình 7. Tính thể tích của khối tròn xoay được tạo thành bởi hình phẳng cho
ở Hình 7 khi quay quanh trục
Ox
(viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần
mười).
Lời giải
Trả lời:
1,57
Hình phẳng đã cho giới hạn bởi đồ thị hàm số
yx
, trục hoành và các đường thẳng
0, 1xx
,
khi quay hình phẳng đó quanh trục
Ox
ta được khối tròn xoay như Hình 7. Thể tích của khối tròn
xoay đó là:
1
11
2
2
00
0
d d . 1,57
22
x
V x x x x

Trang 16
Câu 25. Cho
0
d , 0 7
x
g x f t t x
trong đó
ft
là hàm số có đồ thị như Hình 8. Tính
3g
.
Lời giải
Trả lời: 7
Ta có:
3 1 2 3
0 0 1 2
3 d d d dg f t t f t t f t t f t t
1 2 3
0 1 2
2d 2 d 12 4 dt t t t t
3
2
1
22
0
1
2
2 12 2 7t t t t
.
Câu 26. Một vật được ném lên từ độ cao 300 m với vận tốc được cho bởi công thức
9,81 29,43 m/sv t t
(Nguồn: R.Larson anh B. Edwards, Calculus 10e, Cengage). Gọi
mht
là độ cao của vật tại thời điểm
st
. Sau bao lâu kể từ khi bắt đầu được ném lên thì vật đó
chạm đất (làm tròn kết quả đến hàng đơn vị của mét)?
Lời giải
Trả lời: 11
Ta có:
2
9,81
d 9,81 29,43 d 29,43
2
h t v t t t t t t C

.
Vì vật được ném lên từ độ cao 300 m nên
0 300 300hC
.
Vậy
2
9,81
29,43 300
2
h t t t
. Khi vật bắt đầu chạm đất ứng với
0ht
.
Nên ta có:
2
9,81
29,43 300 0 11
2
t t t
hoặc
5t 
.
Do
0t
nên
11 st
.
Câu 27. Chủ một trung tâm thương mại muốn cho thuê một số gian hàng như nhau. Người đó muốn tăng giá
cho thuê của mỗi gian hàng thêm
x
(triệu đồng)
0x
. Tốc độ thay đổi doanh thu từ các gian hàng
đó được biểu diễn bởi hàm số
20 300T x x
, trong đó
Tx
tính bằng triệu đồng (Nguồn:
R.Larson anh B. Edwards, Calculus 10e, Cengage). Biết rằng nếu người đó tăng giá thuê cho mỗi
gian hàng thêm 10 triệu đồng thì doanh thu là 12 000 triệu đồng. Tìm giá trị của
để người đó có
doanh thu là cao nhất?
Trang 17
Lời giải
Trả lời: 15
Ta có:
d 20 300 dT x T x x x x

2
10 300 ,x x C C
.
Khi người đó tăng giá cho thuê mỗi gian hàng thêm 10 triệu đồng thì doanh thu là 12 000 triệu đồng.
Nên ứng với
10x
ta có
10 12000T
suy ra
2
12000 10.10 300.10 10000CC
.
Vậy
2
10 300 10000T x x x
. Ta có
Tx
là một hàm bậc hai với hệ số
0a
và đồ thị hàm số
có đỉnh là
15;12250I
.
Vậy doanh thu cao nhất mà người đó có thể thu về là 12 250 triệu đồng và khi đó mỗi gian hàng đã
tăng giá cho thuê thêm 15 triệu đồng.

Tài liệu khác của Toán

Preview text:

CHUYÊN ĐỀ: NGUYÊN HÀM VÀ TÍCH PHÂN A. TÓM TẮT LÝ THUYẾT I. NGUYÊN HÀM 1. Định nghĩa
Cho K là một khoảng, đoạn hoặc nửa khoảng của tập số thực .
• Cho hàm số f xxác định trên K . Hàm số F x được gọi là nguyên hàm của hàm số f x trên K nếu
F ' x  f x với mọi x thuộc K .
• Nếu F x là một nguyên hàm của hàm số f xtrên K thì mọi nguyên hàm của hàm số f x trên K đều
có dạng F x C với C là một hằng số. Vì vậy, f
 x dx F xC
• Mọi hàm số liên tục trên K đều có nguyên hàm trên K . Ta có: F '
 x dx F xC 2. Tính chất
Cho f x, g x là hai hàm số liên tục trên K . • kf
 x dx k f
 x dx với k là hằng số khác 0; •  f
 x gx dx f
 x dx g  x dx •  f
 x gx dx f
 x dx g  x dx
3. Nguyên hàm một số hàm số sơ cấp cơ bản  1  • Với    x
1ta có x dx   C     • 1  dx ln x C  1 x • 1
sin xdx   cos x C.  •
dx   cot x C.  2 sin x • 1
cos xdx  sin x C.  •
dx  tan x C.  2 cos x x a
• Với a  0;a  1 ta có x a dx   C.  ln a II. TÍCH PHÂN 1. Định nghĩa
Cho f x là hàm số liên tục trên ;
a b. Giả sử F x là một nguyên hàm của f x trên đoạn  ;
a b. Khi đó b f
 xdx F b F aa 2. Tính chất
Cho các hàm số y f x, y g x liên tục trên đoạn  ;
a b. Ta có: b b • kf
 x dx k f
 x dx (k là hằng số). a a b b b •  f
 x gx dx f
 x dx g  x dx; a a a b b b •  f
 x gx dx f
 x dx g  x dx a a a Trang 1 n c n • Giả sử , m ,
n c là ba số thực tuỳ ý thuộc đoạn  ;
a b, ta có: f
 x dx f
 x dx f  x dx. m m c
3. Tích phân một số hàm số sơ cấp cơ bản b b  1   1   1   • Với   x b a
1, ta có: x dx     1  1 a a b • Với hàm số   1 b f x
liên tục trên đoạn  ;
a b, ta có: 1 dx  ln x  ln b  ln ax a x a b • b
sin x dx   cos x  cos a  cos ba a b • b
cos x dx  sin x  sin b  sin aa a b • Với hàm số 1 b f x 1  liên tục trên  ;
a b, ta có:
dx   cot x  cot a  cot b  . 2 sin x 2 sin a x a • Với hàm số 1 f (x)  liên tục trên  ; a b , ta có: 2 cos x b 1 b
dx  tan x  tan b  tan ; a  2 cos a x a   x   a a a
• Với a  0 , a  1, ta có x a dx    . ln a ln a   4. Úng dụng
• Cho hàm số y f x liên tục trên đoạn  ;
a b . Khi đó, diện tích S của hình phẳng giới hạn bởi đồ thị hàm
số y f x , trục hoành và hai đường thẳng x a, x b là b S f (x) dx  . a
• Cho các hàm số y f x, y g x liên tục trên đoạn  ;
a b . Khi đó, diện tích hình phẳng giới hạn bởi đồ thị
của các hàm số y f x, y g x và hai đường thẳng x a, x b là b S f
 x gxdx . a
• Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x a và x b (a b) . Một mặt phẳng tuỳ ý
vuông góc với Ox tại x (a x b) cắt vật thể đó theo hình phẳng có diện tích là S (x) . Giả sử hàm số S (x) liên tục trên  ;
a b . Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng trên được tính bởi công thức b V S  xd .x a
• Cho hàm số y f x liên tục, không âm trên đoạn  ;
a b . Hình phẳng (H ) giới hạn bởi đồ thị hàm số
y f x , trục hoành và hai đường thẳng x a, x b quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng Trang 2 b V    f
 x 2 dx  . a
B . MỘT SỐ VÍ DỤ
Dạng 1. Câu trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.
Ví dụ 1. [MĐ1] Hàm số 3
F(x)  2x  2x 1 là nguyên hàm của hàm số nào sau đây? A. 1 f x 2  6x  2
B. f x 4 2
x x x 2
C. f x 1 4 2
x x x C .
D. f x 2
 6x  2C . 2 Lời giải Chọn A
Ta có: f x Fx   3 x x   2 ( ) ( ) 2 2 1  6x  2 .
Ví dụ 2. [MĐ1] Diện tích hình phẳng giới hạn bởi hai đường thẳng x  0, x   , đồ thị hàm số y  cos x và trục Ox là:  
A. S  cos x dxB. 2
S  cos x dx  . 0 0  
C. S  cos x dx  .
D. S   cos x dx  . 0 0 Lời giải Chọn C
Diện tích hình phẳng giới hạn bởi hai đường thẳng x a, x b và các đồ thị hàm số  b
y f (x), y g(x) là S
|f (x)  g(x) | dx
. Khi đó, theo đề bài ta có S  cos x dx  . a 0
Ví dụ 3. [MĐ1] Gọi V là thể tích khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường x
y e , y  0, x  0, x  2 quay quanh Ox . Phát biểu nào sau đây là đúng? 2 2 A. 2 x
V   e dx  . B. x
V e dx  . 0 0 2 2 C. x
V   e dx  . D. 2 x
V e dx  . 0 0 Lời giải Chọn A
Hình phẳng giới hạn bởi các đường x
y e , y  0, x  0, x  2 quay quanh Ox sẽ tạo thành một khối b 2
tròn xoay có thể tích bằng V    f  x 2 2 x
dx   e dx   . a 0
Ví dụ 4. [MĐ1] Một vật chuyển động với vận tốc v(t)  1 2sin 2t ( m/s) . Quãng đường vật di chuyển trong 
khoảng thời gian từ t  0 (giây) đến thời điểm 3 t
(giây) được tính theo công thức: 4 Trang 3 3 3 4 4
A. s t   1 2sin 2tdt .
B. s t   1 2sin 2t2dt . 0 0 3π  3π C. 4 s(t)  (1 2sin 2t)dt  .
D. s(t)  vv(0)   . 0  4  Lời giải Chọn A π
Gọi s(t) là quãng đường mà vật di chuyển trong khoảng thời gian từ t  0 (giây) đến 3 t  (giây). Mà 4 3π
s '(t)  v(t) nên ta có 4 s(t)  (1 2sin 2t)dt  . 0
Dạng 2: Trắc nghiệm đúng -sai
Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.
Ví dụ 5: [MĐ1] Giả sử s(t) là phương trình quãng đường chuyển động của một vật theo thời gian t (giây) và
v(t) là phương trình vận tốc của chuyển động đó theo thời gian t (giây).
a) s(t)dt  v(t)  C  .
b) v(t)dt  s(t)  C  .
c) s '(t)dt  v(t)  C  .
d) s '(t)dt  s(t)  C  . Lời giải Ý a) b) c) d) Kết quả S Đ S Đ
Vì s(t) , v(t) lần lượt là phương trình quãng đường và phương trình vận tốc của chuyển động đó theo thời gian
t (giây) nên ta có s '(t)  v(t) và v(t)dt  s(t)  C  .
a) s(t)dt  v(t)  C  . Suy ra Sai.
b) v(t)dt  s(t)  C  . Suy ra Đúng.
c) s '(t)dt  v(t)  C  . Suy ra Sai.
d) s '(t)dt  s(t)  C  . Suy ra Đúng.
Ví dụ 6: [MĐ2] Cho hàm số 3
F(x)  x  2x 1 , x ¡ là một nguyên hàm của hàm số f (x) .
a) Nếu hàm số G(x) cũng là một nguyên hàm của hàm số f (x) và G(1)  3 thì G x  F x 1, x¡ .
b) Nếu hàm số H (x) cũng là một nguyên hàm của hàm số f (x) và H (1)  3    thì H x
F x 3 , x¡ .
c) Nếu hàm số K (x) cũng là một nguyên hàm của hàm số f (x) và K (0)  0 thì K x  F x 1 , x¡ .
d) Nếu hàm số M (x) cũng là một nguyên hàm của hàm số f (x) và M (2)  4 thì M x  F x 1, x¡ . Lời giải Ý a) b) c) d) Kết quả S Đ S Đ
a) Vì G(x) là một nguyên hàm của hàm số f (x) trên ¡ nên G(x)  F (x)  C , với C 1à một hằng số.
Mà G(1)  3 nên ta có G( 1  )  F( 1
 )  C  3  2  C C 1. Trang 4
Vậy G x  F x 1, x¡ . Suy ra Sai.
b) Vì H (x) là một nguyên hàm của hàm số f (x) trên ¡ nên H (x)  F (x)  C , với C 1à một hằng số. Mà H (1)  3
 nên ta có H (1)  F(1)  C  3
  0  C C  3  .
Vậy H x  F x 3 , x¡ . Suy ra đúng.
c) Vì K (x) là một nguyên hàm của hàm số f (x) trên ¡ nên K (x)  F (x)  C , với C 1à một hằng số. Mà
K (0)  0 nên ta có K (0)  F (0)  C  0  1 C C  1
 . Vậy K x  F x 1, x¡ . Suy ra Sai.
d) Vì M (x) là một nguyên hàm của hàm số f (x) trên ¡ nên M (x)  F (x)  C , với C 1à một hằng số. Mà
M (2)  4 nên ta có M (2)  F (2)  C  4  5  C C  1
 . Vậy M x  F x 1, x¡ . Suy ra Đúng.
Ví dụ 7: [MĐ2] Một vật chuyển động với gia tốc a t t  2 ( ) 2 cos m / s  .
a) Tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng 0 . Khi đó, vận tốc của vật được biểu diễn bởi hàm
số v(t)  2 sin t ( m / s) . π
b) Vận tốc của vật tại thời điềm t  là 1 m / s . 2
c) Quãng đường vật đi được từ thời điểm t  0 ( s) đến thời điểm t π (s) là 4 m . π π d) Quãng đườ 3
ng vật đi được từ thời điểm t
(s) đến thời điểm t  (s) là 2 m . 2 4 Lời giải Ý a) b) c) d) Kết quả Đ S Đ S
a) Ta có v(t)  a(t)dt  2 cos t dt  2 sin t C   .
Mà tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng 0 nên ta có v(0)  0 hay C  0 . Vậy v(t)  2sin t . Suy ra đúng. ππ π
b) Vận tốc của vật tại thời điểm t  là v  2sin  2( m / s)   . 2  2  2 Suy ra sai.
c) Quãng đường vật đi được từ thời điểm t  0 ( s) đến thời điểm t π (s) là π π π
v(t)dt
2sin t dt   2cost  2  cosπ  ( 2  cos0)  4( m).   0 0 0 Suy ra đúng. π π d) Quãng đườ 3
ng vật đi được từ thời điểm t
(s) đến thời điểm t  (s) là 2 4 3π 3π 4 4 3π 3ππ  4
v(t)dt  2sin d
t t   2 cos t  2  cos  2  cos  2 ( m).   π   4  2 π π  2 2 2 Suy ra Sai.
Dạng 3: Câu trắc nghiệm trả lời ngắn Trang 5
Ví dụ 8: [MĐ2] Cho hàm số F x là một nguyên hàm của hàm số f x 2
 3x  4x 1 và F 2  2. Tính F 3 . Lời giải
Ta có F x  f
 xdx  2x x   3 2 3 4
1 dx x  2x x C . Mà F 2  2 nên suy ra C  0 Vậy
hàm số F x 3 2
x  2x x . Suy ra F   3  12 . x
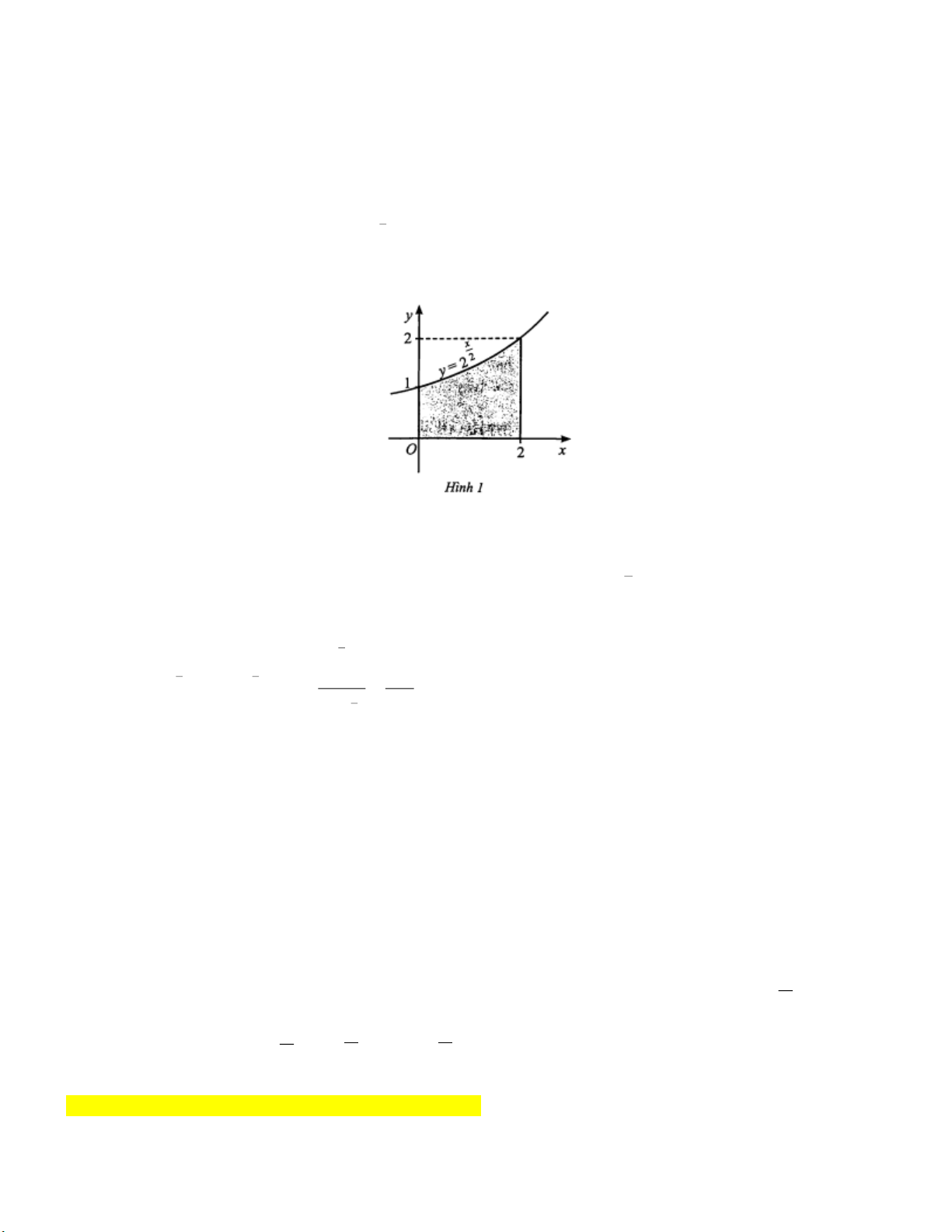
Ví dụ 9: [MĐ2] Cho đồ thị hàm số 2
y  2 và hình phẳng được tô màu như Hình 1. Hình phẳng đó được giới
hạn bởi các đường nào? Tính diện tích hình phẳng đó (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm). Lời giải
Hình phẳng đã cho ở Hình 1 được giới hạn bởi đồ thị hàm số 2
y  2 , trục hoành và hai đường thẳng
x  0 , x  2 . Khi đó, diện tích hình phẳng là x 1   2 x  2  2 x 2 1     2 2 2 S  2 dx   2  dx    2,89 . 1 ln 2   0 0 2 ln 2
Ví dụ 9: [MĐ2] Một vật chuyển động với gia tốc được cho bởi hàm số a t   t  2 5 cos
m / s  . Lúc bắt đầu
chuyển động vật có vận tốc 2,5 m / s . Tính gia tốc của vật tại thời điểm vận tốc đạt giá trị lớn nhất trong
 s đầu tiên. Lời giải
Vận tốc của vật được biểu diễn bởi hàm số v t   a
 tdt  5costdt  5sint C  .
Khi bắt đầu chuyển động, vật có vận tốc 2, 5 m / s nên ta có:
v0  2,5  5sin 0  C  2,5  C  2,5 . 
Suy ra v t  5sin t  2,5. Mà 5sin t  2,5  7,5 . Vậy vận tốc đạt giá trị lớn nhất tại t  . Khi đó, gia 2       
tốc của vật tại thời điểm t  là a  5.cos  0      2 m / s  . 2  2   2 
C. BÀI TẬP LUYỆN TẬP
Dạng 1: Câu trắc nghiệm nhiều phương án lựa chọn
Mỗi câu thí sinh chỉ chọn một phương án. Câu 1.
[MĐ1] Phát biểu nào sau đây là đúng? Trang 6 A. F
 xdx F xC . B. F
 xdx FxC . C. F
 xdx F xC . D. F
 xdx FxC . Lời giải Chọn A Câu 2.
[MĐ1] Phát biểu nào sau đây là đúng?  x 1 A. 3  x 3  x e dx eC  . B. 3 3  x e dx   eC  . 3   x 1 x 1 C. 3 3  x e dx eC  . D. 3 3  x e dx   e  . 3 3 Lời giải Chọn B Câu 3.
[MĐ1] Cho hàm số y f x liên tục trên đoạn  ;
a b. Gọi D là hình phẳng giới hạn vởi đồ thị
hàm số y f x , trục hoành và hai đường thẳng x a , x b a b . Tính thể tích khối tròn xoay
được tạo thành khi quay D quanh trục hoành là b b
A. V    f
  x 2 dx  .
B. V    f   x 2 2  dx  . a a b b C. V    f  x 2 2  dx  . D. 2 V   f  xdx. a a Lời giải Chọn A Câu 4.
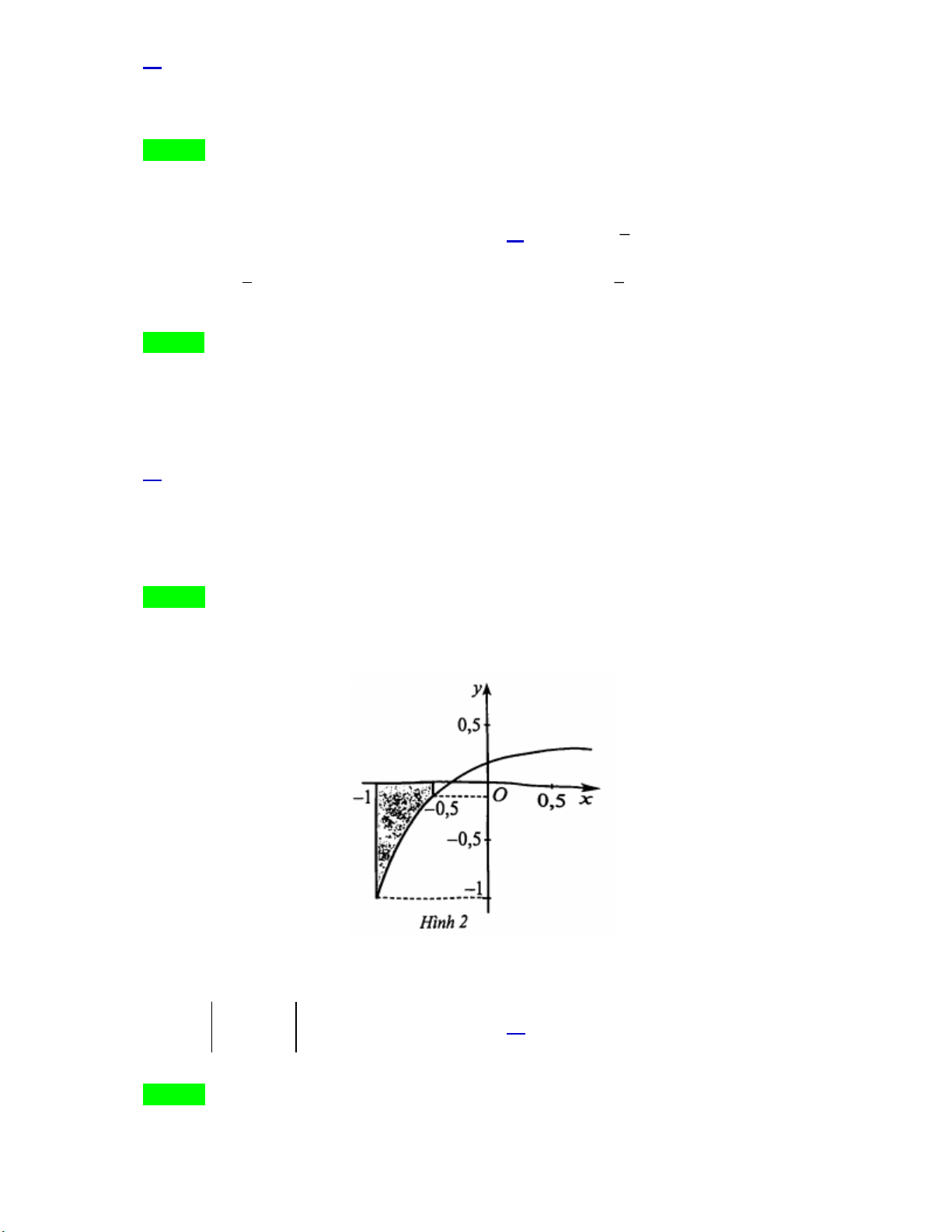
[MĐ2] Cho hàm số y f x có đồ thị như Hình 2. Gọi S là phần diện tích hình phẳng được tô
màu. Phát biểu nào sau đây là đúng? 0  ,5 0 A. S f  xdx . B. S f  xdx . 1  1  0  ,5 0,5 C. S   f  xdx . D. S   f  xdx . 1 1  Lời giải Chọn D 0,5 0,5 Ta có S   0  f  
x dx   f   xdx. 1  1  Trang 7 Câu 5.
[MĐ1] Gọi H là hình phẳng giới hạn bởi đồ thị hàm số 1 y
, trục hoành và hai đường thẳng x 1 x
, x  4 . Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng H quay quanh trục Ox là 4 1 4 1
A. V π dx  . B. V  dx  . x 2 x 1 1 4 1 4 1
C. V π dx  . D. 2 V π dx  . 2 x 2 x 1 1 Lời giải Chọn C
Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng H giới hạn bởi đồ thị hàm số 1 y  , x 4
trục hoành và hai đường thẳng 1
x  1, x  4 quay quanh trục Ox là V π dx  . 2 x 1 Câu 6.
[MĐ1] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y  sin x , trục hoành và hai đường thẳng
x  0 , x   . Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng D quay xung quanh trục Ox là π π
A. V π sin x dx  . B. 2 V π sin d x x  . 0 0 π π
C. V π sin xdx . D. 2 2 V π sin d x x  . 0 0 Lời giải Chọn B
Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng D giới hạn bởi đồ thị hàm số π
y   sin x , trục hoành và hai đường thẳng x  0 , x   quay quanh trục Ox là 2 V π sin d x x  . 1 Câu 7.
[MĐ1] Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y x , trục hoành và hai đường thẳng
x  1, x  2 . Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng H quay xung quanh trục Ox là 2 π
A. V π xdx  . B. 2 V π d x x  . 1 0 2 2 C. 2 V π xdx  .
D. V π d x x  . 1 1 Lời giải Chọn D
Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng H giới hạn bởi đồ thị hàm số y x , 2
trục hoành và hai đường thẳng x 1, x  2 quay quanh trục Ox là V π d x x  . 1 Câu 8.
[MĐ1] Gọi S là diện tích hình phẳng được tô đậm trong Hình 3. Công thức tính S là Trang 8 1 2 1 2 A. S f
 xdxf  xdx . B. S f
 xdxf  xdx. 1  1 1  1 2 2 C. S f  xdx . D. S   f  xdx . 1  1  Lời giải Chọn B 1 2
Dựa vào đồ thị, suy ra diện tích hình phẳng là S f
 xdxf  xdx. 1  1 Câu 9.
[MĐTH] x 2 2 dx  bằng:   2 x 2 1 2 2 2 1 2 x  2xA.C . B.C . C.C . D.   2 2xC . 2 1 2 1 ln 2xLời giải Chọn B 1
Đặt t  2x  dt  2dx  dx  dt . 2 1 1 t  Ta có 2x 2 1 2 2 dx t dt   C  . 2 2 2 1  1 x 2 2 1 2 x
Thay t  2x ta có 2x   2 1 2 2 dx   C   C . 2 2 1 2 1 2  x x Câu 10. [MĐTH] sin  cos dx   bằng:  2 2  2  x x
A. x  cos x C . B.  cos  sin  C   .  2 2  3 1  x x C. sin  cos  C   .
D. x  cos x C . 3  2 2  Lời giải Chọn A 2  x x x x x x Ta có: sin  cos   2 2  sin  2sin .cos  cos  2 2  2 2 2 2 1sin x. Trang 9 2   Khi đó x x sin  cos dx   
1sin xdx  2 2   dx  sin d
x x x  cos x C   .
Câu 11. [MĐTH]  x 2  x e e dx bằng: x 1  2  x 1    x 1  e e A. x 2  2 x e eC . B. x 2 x e eC . C. 2 x e eC . D.   C . 2 x 1 2  x 1 Lời giải Chọn C Ta có:  x 2  x   x 2 d  d  x e e x e x e dx   x 1 x 1 2  d  x e x e d    2  x 2  xe eC . 2 2 2  x Câu 12. [MĐTH] cos dx   bằng:  2  3 2 1  x   x  1 1
A. x  sin x C . B. cos  C   . C. sin  C   . D. x  sin x C . 3  2   2  2 2 Lời giải Chọn D 2  x  1 cos x Ta có: cos dx  dx     2  2 1 1  dx  cos d x x   1 1
x  sin x C . 2 2 2 2 x    Câu 13. [MĐTH] 2 x 2
5 6e dx bằng:   x xx 1  2  x 1  x 1  25  e e A. 2 x e eC . B. 2
12e C . C. x 2  2 x e eC . D.   C . 2 2 ln 5 x 1 2  x 1 Lời giải Chọn B x x      x  Ta có 2 x 2 x 2
5 6e dx  25 dx12 e d         2  25x x  25x x  2 2  12e  C  12e  C . ln 25 2 ln 5
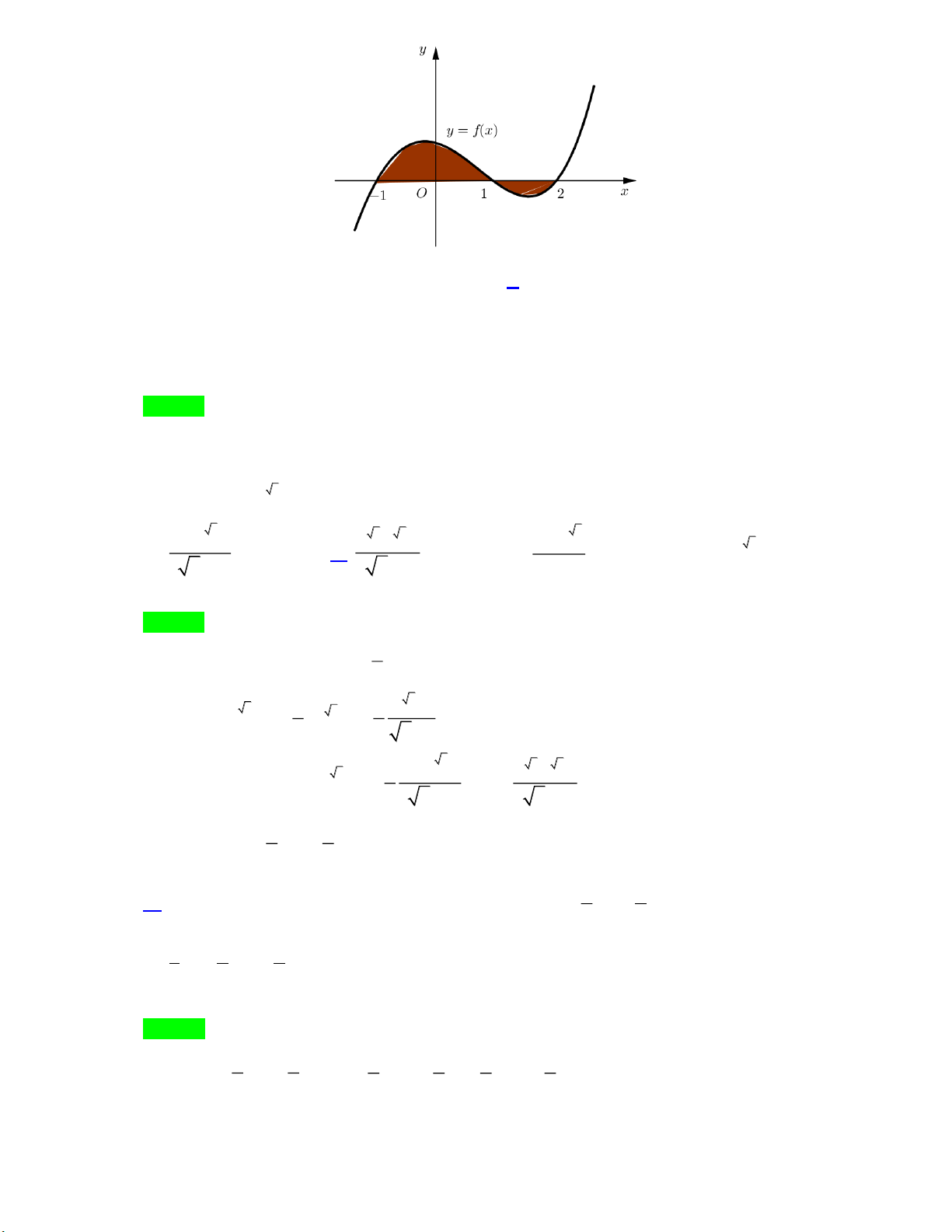
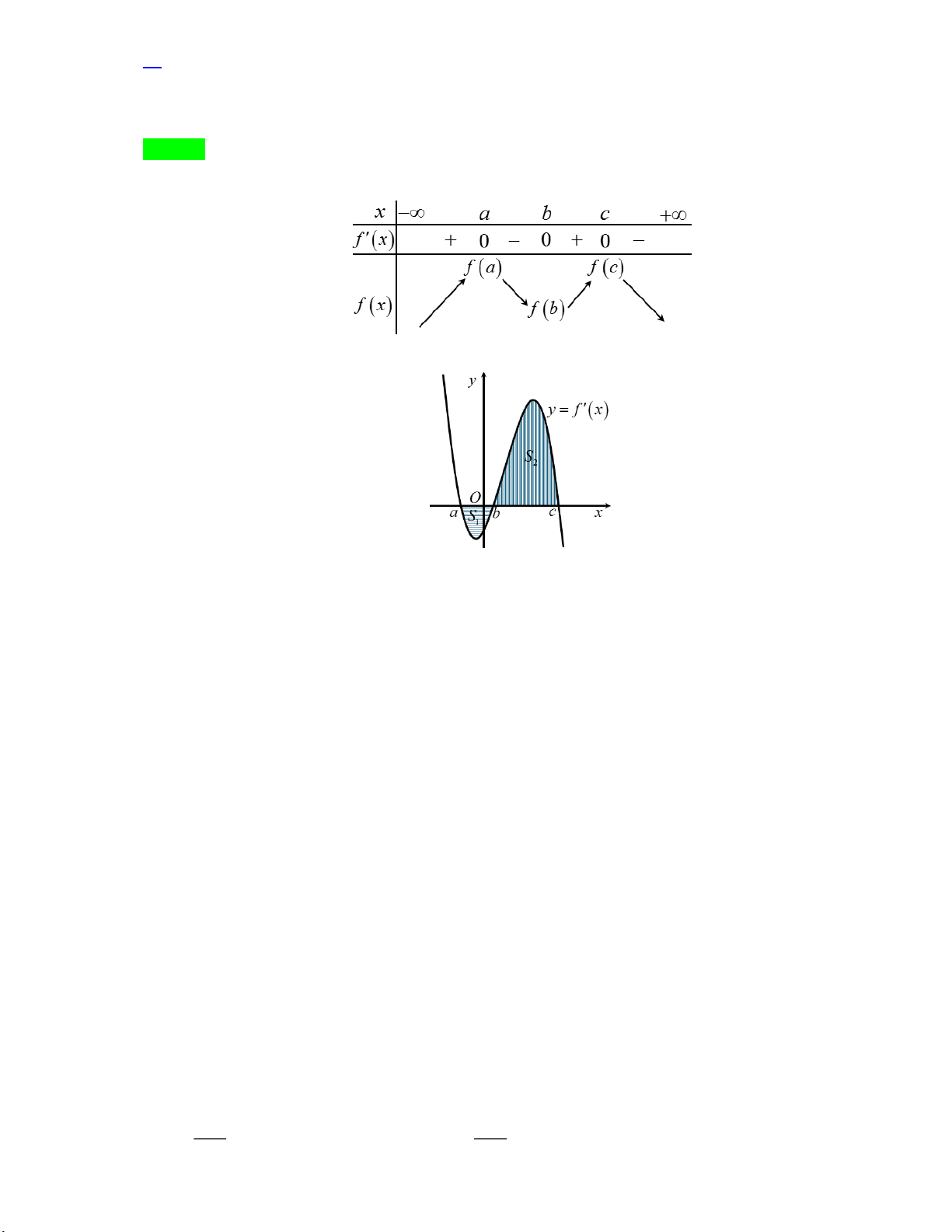
Câu 14. [MĐVD] Cho hàm số y f x có đồ thị y f  x cắt trục Ox tại ba điểm có hoành độ a b c
như Hình 4. Mệnh đề nào sau đây là đúng? Trang 10
A. f c  f a  f b .
B. f c  f b  f a .
C. f a  f b  f c .
D. f b  f a  f c . Lời giải Chọn A
Dựa vào đồ thị hàm số y f x ta có bảng biến thiên sau
Dựa vào bảng biến thiên ta có: f a  f b; f c  f b   1 .
Gọi S là diện tích giới hạn bởi đồ thị hàm số y f x , trục hoành và các đường thẳng 1
x a; x b .
Gọi S là diện tích giới hạn bởi đồ thị hàm số y f x , trục hoành và các đường thẳng 2 x  ; b x c . b a Ta có: S   f x dx   f
 xdx f a f b; 1    a b c S
f x dx f c f b  . 2       b
Quan sat hình vẽ ta thấy S S f c  f b  f a  f b 2 1
f c  f a 2. Từ  
1 và 2 ta có f c  f a  f b .
Câu 15. [MĐTH] Vi khuẩn E.coli sống chủ yếu ở đường ruột và có số lượng lớn nhất trong hệ vi sinh vật của
cơ thể . Một quần thể vi khuẩn E. coli được quan sát trong điều kiện thích hợp, có tốc độ sinh trưởng được cho
bởi hàm số   480.2t f t
ln 2. Trong đó t tính bằng giờ t  0 , f t  tính bằng cá thể/giờ (Nguồn: R
Larson and B.Edwards,Calculus 10e, Cengage). Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước
tính một cách chính xác khoảng 480 cá thể. Hàm số biểu thị số lượng cá thể theo thời gian t là: A.   480.2t F t   ln 2 B.   480.2t F t t t
C. F t  2  480.
D. F t  2  480.  C ln 2 ln 2 Trang 11 Lời giải Chọn B t Do    t 2  480.2 ln 2  480.ln 2.   480.2t f t dt dt C
C F(t)  ln 2
Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước tính một cách chính xác khoảng 480 cá thể nên 0
F(0)  480.2  C  480  C  0
Dạng 2: Trắc nghiệm đúng -sai
Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.
Câu 16. [MĐNB] Cho f x là hàm số liên tục trên R a) f
 xdx f 'xC. b) f '
 xdx f xC. c) f '
 xdx f x. d) f '
 xdx f 'x C. Lời giải Ý a) b) c) d)
Kết quả sai đúng sai đúng
Do định nghĩa của nguyên hàm ta có kết quả trên.
Câu 17. [MĐTH] Giả sử v t  là phương trình vận tốc của một vật chuyển động theo thời gian t (giây),
a(t) là phương trình gia tốc của vật đó chuyển động theo thời gian t (giây). a) a
 tdt vtC. b) v
 tdt atC. c) v '
 tdt atC. d) v '
 tdt vtC. Lời giải Ý a) b) c) d)
Kết quả đúng sai sai đúng
a) Do nguyên hàm của hàm gia tốc là hàm vận tốc. Suy ra đúng.
b) Do nguyên hàm của hàm vận tốc là hàm quãng đường. Suy ra sai. c) Do v '
 tdt vtC. Suy ra sai
d) Do định nghĩa nguyên hàm. Suy ra đúng.
Câu 18. [MĐTH] Giả sử v t  là phương trình vận tốc của một vật chuyển động theo thời gian t (giây),
a(t) là phương trình gia tốc của vật đó chuyển động theo thời gian t (giây). Xét chuyển động trong khoảng
thời gian từ c (giây) đến b (giây). Trang 12 b a) a
 tdt vb vc. c b b) v
 tdt ab ac. c b c) v
 tdt vcvb. c b d) v
 tdt vbvc. c Lời giải Ý a) b) c) d)
Kết quả Đúng Sai Sai Đúng
Do a t   vt  Suy ra a), d) đúng.
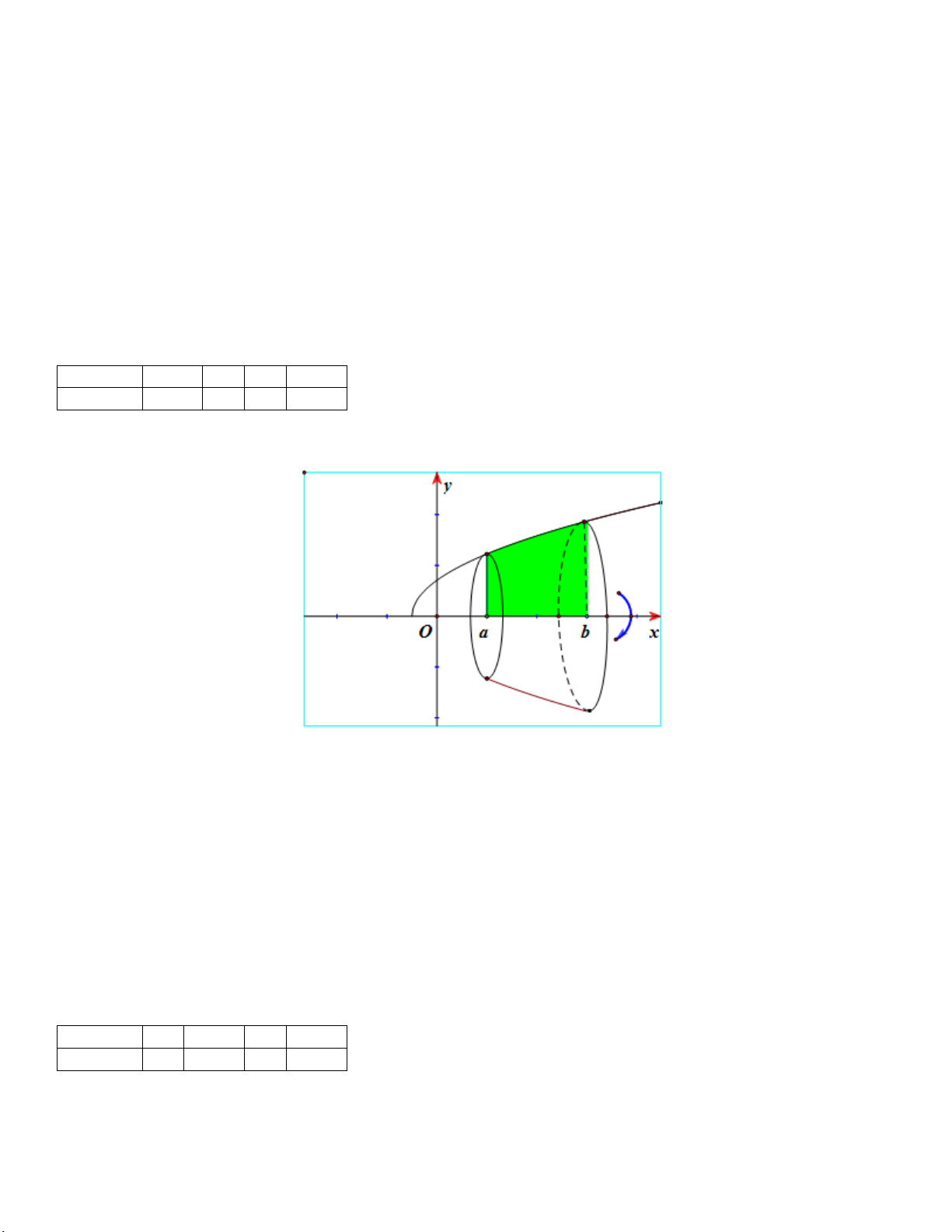
Câu 19. Cho vật thể tròn xoay như Hình 5.
a) Vật thể được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số y f x và hai đường thẳng
x a, x b quay quanh trục Ox .
b) Vậy thể được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường
thẳng x a, x b quay quanh trục Ox . b
c) Thể tích của vật thể được tính theo công thức V   f  xdx . a 2 b
d) Thể tích của vật thể được tính theo công thức V    f  x dx  . a Lời giải Ý a) b) c) d)
Kết quả Sai Đúng Sai Đúng
Theo lý thuyết về thể tích vật tròn xoay thì b, d đúng.
Câu 20. Tại một khu di tích vào ngày lễ hội hằng năm, tốc độ thay đổi lượng khách tham quan được biểu diễn
bằng hàm số Qt 3 2
 4t 72t  288t , trong đó t tính bằng giờ Trang 13
( 0  t 13) , Qt tính bằng khách/giờ . Nguồn: R.Larson and B. Eawads, Calculus 10e, Cengage). Sau 2 giờ
đã có 500 người có mặt.
a) Lượng khách tham quan được biểu diễn bởi hàm số Qt 4 3 2
t  24t 144t .
b) Sau 5 giờ lượng khách tham quan là 1325 người.
c) Lượng khách tham quan lớn nhất là 1296 người.
d) Tốc độ thay đổi lượng khách tham quan lớn nhất tại thời điểm t  6 . Lời giải Ý a) b) c) d)
Kết quả Sai Đúng Sai Đúng
Ta có Q t   Q  t 4 3
.dt t  24t 144t C Q 2  500  C  100. Suy ra Qt 4 3
t  24t 144t 100  a) sai.
Sau 5 giờ lượng khách tham quan là Q5 1325 . Do đó b) đúng.
Ta có max Q t   Q 6  1396. Do đó d) đúng, c) Sai 0;1  3
Dạng 3. Câu trắc nghiệm trả lời ngắn 1 x2 3 Câu 21. dx
có giá trị bằng bao nhiêu? (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần 2 2 x 0 mười). Lời giải Trả lời: 0,1 1 x  3  1 x2 1 x   3 1  3   4  Ta có: dx  dx     2 2 x 9  4 3  0 0 9 ln 4 0 1    0,1. 3 36 ln 4
Câu 22. Cho hàm số F x là một nguyên hàm của hàm số f x   2
x  22x   1 và F   1 1  . Tính 6  1  F  
 (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm).  2  Lời giải Trả lời: 0, 49
Ta có: f x   2
x  22x   1 3 2
 2x x  4x  2 .
Suy ra F x  f
 xx   3 2 d
2x x  4x  2dx 3 2
 2x dx x dx  4 d x x  2dx     1 1 4 3 2
x x  2x  2x C,C  2 3 Mà F   1 1  nên suy ra C  0 . 6 Trang 14  
Vậy hàm số F x 1 1 1 47 4 3 2
 x x  2x  2x F    0, 49   2 3  2  96
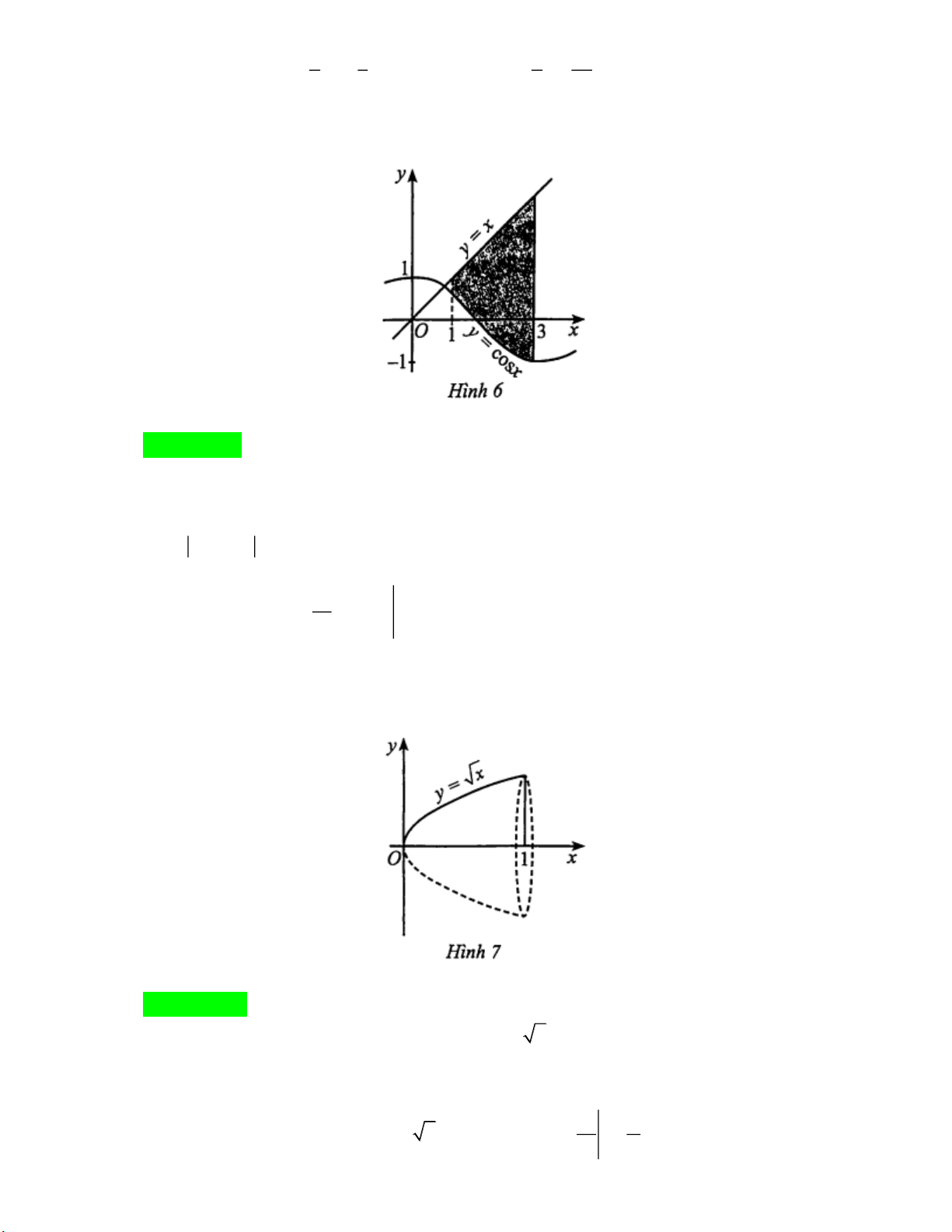
Câu 23. Cho đồ thị hàm số y  cos x và hình phẳng được tô màu như Hình 6. Tính diện tích hình phẳng đó
(viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần mười). Lời giải Trả lời: 4, 7
Hình phẳng đã cho được giới hạn bởi các đồ thị hàm số y  cos x, y x và hai đường thẳng
x  1, x  3 . Khi đó diện tích hình phẳng được tính theo công thức 3 S
cos x x dx  . Vì x  cos , x x  1;  3 nên ta có: 1 3 3    xS x  cos x 2 dx  
 sin x  4sin3 sin1 4,7 .  2  1 1
Câu 24. Cho khối tròn xoay như Hình 7. Tính thể tích của khối tròn xoay được tạo thành bởi hình phẳng cho
ở Hình 7 khi quay quanh trục Ox (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần mười). Lời giải Trả lời: 1,57
Hình phẳng đã cho giới hạn bởi đồ thị hàm số y x , trục hoành và các đường thẳng x  0, x  1,
khi quay hình phẳng đó quanh trục Ox ta được khối tròn xoay như Hình 7. Thể tích của khối tròn xoay đó là:     1 1 1 2 2 xV x dx   d x x   .  1,57  2 2 0 0 0 Trang 15 x
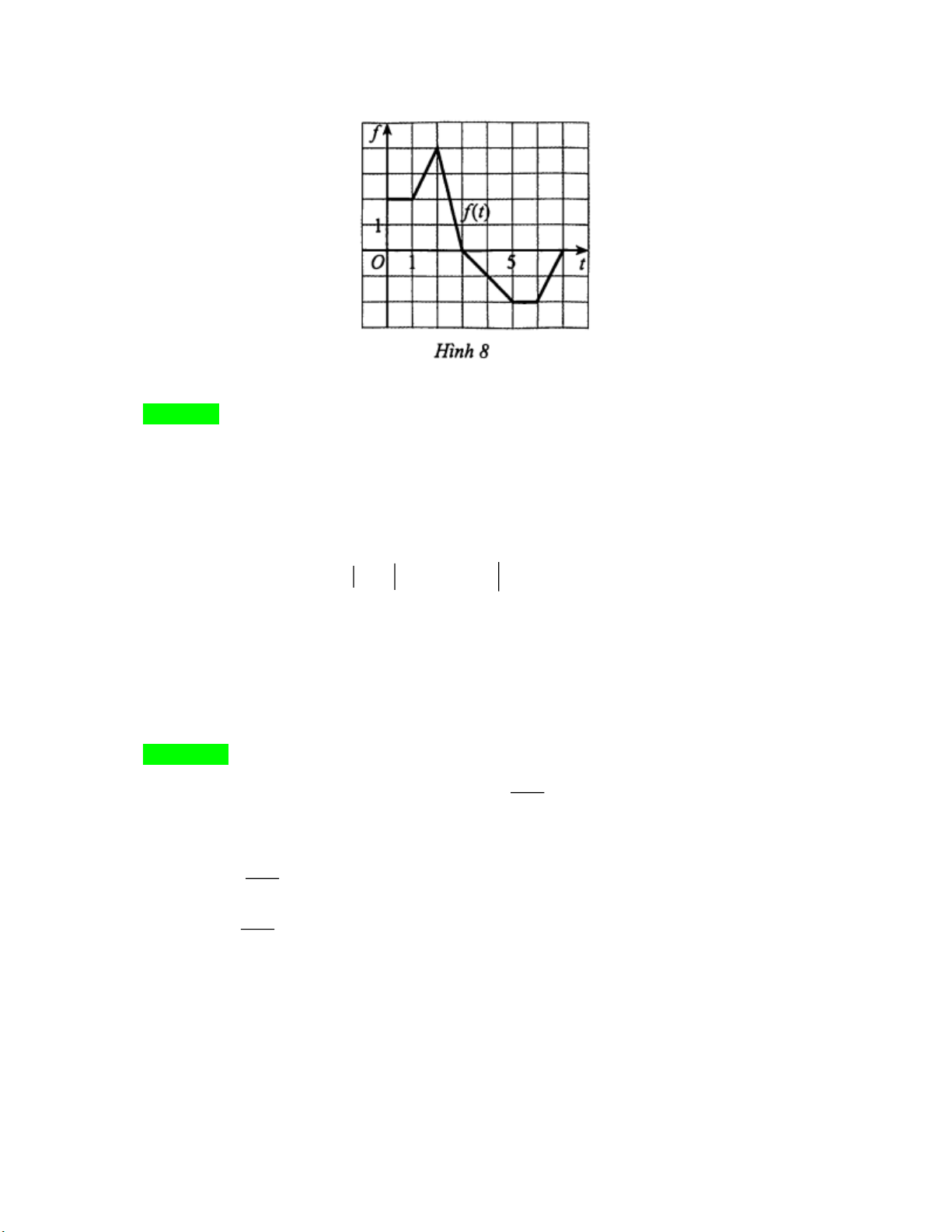
Câu 25. Cho g x  f
 tdt,0  x  7 trong đó f t là hàm số có đồ thị như Hình 8. Tính g3. 0 Lời giải Trả lời: 7 3 1 2 3
Ta có: g 3  f
 tdt f
 tdt f
 tdt f  tdt 0 0 1 2 1 2 3  2dt  2 d t t   
124tdt 0 1 2 2 1 2  2t t   2 12t  2t  7 . 0 3 1 2
Câu 26. Một vật được ném lên từ độ cao 300 m với vận tốc được cho bởi công thức vt  9
 ,81t  29,43m/s (Nguồn: R.Larson anh B. Edwards, Calculus 10e, Cengage). Gọi
htm là độ cao của vật tại thời điểm t s . Sau bao lâu kể từ khi bắt đầu được ném lên thì vật đó
chạm đất (làm tròn kết quả đến hàng đơn vị của mét)? Lời giải Trả lời: 11 9,81
Ta có: h t   v
 tdt   9  ,81t  29, 43 2 dt  
t  29, 43t C . 2
Vì vật được ném lên từ độ cao 300 m nên h0  300  C  300. Vậy ht 9,81 2  
t  29, 43t  300 . Khi vật bắt đầu chạm đất ứng với h t   0 . 2 9,81 Nên ta có: 2 
t  29, 43t  300  0  t  11 hoặc t  5  . 2
Do t  0 nên t  11s.
Câu 27. Chủ một trung tâm thương mại muốn cho thuê một số gian hàng như nhau. Người đó muốn tăng giá
cho thuê của mỗi gian hàng thêm x (triệu đồng) x  0 . Tốc độ thay đổi doanh thu từ các gian hàng
đó được biểu diễn bởi hàm số Tx  2
 0x  300, trong đó Tx tính bằng triệu đồng (Nguồn:
R.Larson anh B. Edwards, Calculus 10e, Cengage). Biết rằng nếu người đó tăng giá thuê cho mỗi
gian hàng thêm 10 triệu đồng thì doanh thu là 12 000 triệu đồng. Tìm giá trị của x để người đó có
doanh thu là cao nhất? Trang 16 Lời giải Trả lời: 15
Ta có: T x  T
 xdx   20
x  300dx 2  1
 0x  300x C,C  .
Khi người đó tăng giá cho thuê mỗi gian hàng thêm 10 triệu đồng thì doanh thu là 12 000 triệu đồng.
Nên ứng với x 10 ta có T 10 12000 suy ra 2 12000  1
 0.10  300.10  C C 10000 . Vậy T x 2  1
 0x 300x 10000. Ta có T x là một hàm bậc hai với hệ số a  0 và đồ thị hàm số
có đỉnh là I 15;12250 .
Vậy doanh thu cao nhất mà người đó có thể thu về là 12 250 triệu đồng và khi đó mỗi gian hàng đã
tăng giá cho thuê thêm 15 triệu đồng. Trang 17
Document Outline

  • Dạng 2: Trắc nghiệm đúng -sai
  • Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.
  • C. BÀI TẬP LUYỆN TẬP
  • Dạng 1: Câu trắc nghiệm nhiều phương án lựa chọn
    • Mỗi câu thí sinh chỉ chọn một phương án.
    • Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.
  • Dạng 3. Câu trắc nghiệm trả lời ngắn

Tài liệu liên quan: