45 trang 31 lượt tải

Chuyên Đề Nguyên Hàm Và Tích Phân Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1 m . Một ô tô A đang chạy với vận tốc 15 m/s bỗng gặp ô tô B đang đứng chờ đèn đỏ nên ô tô A hãm phanh và chuyển động chậm dần đều bởi vận tốc được biểu thị bởi công thức. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Chủ đề: Tài liệu ôn thi THPTQG môn Toán 278 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Mỹ Châu

1 tuần trước

Danh sách Quiz

Trang 1

CHUYÊN ĐỀ: NGUYÊN HÀM VÀ TÍCH PHÂN

I. NGUYÊN HÀM

A. TÓM TẮT LÝ THUYẾT

1. Định nghĩa

Cho

 .



 





 



 

trên



   

'F x f x







 



 

trên



 

trên



 

F x C





   

df x x F x C







. Ta có:

   

' dF x x F x C



2. Tính chất

Cho

   

,fxgx





   

d dkf x x k f x x





0k 



       

d d df x g x x f x x g x x  





  



       

d d df x g x x f x x g x x  





  

3. Nguyên hàm một số hàm số sơ cấp cơ bản







ta có

x x C











. 

d lnx x C







sin d cos .x x x C  





d cot .

sin

x x C

  





cos d sin .x x x C





d tan .

cos

x x C







0; 1aa

ta có

a x C





B. BÀI TẬP TỰ LUẬN

Dạng 1. Nguyên hàm hàm lũy thừa

Ví dụ 1: Tìm ncác :

 

2f x x x

 

3 2 2025f x x x   

Lời giải

 

3 4 2

d 2 d

f x x x x x x x C    



 

2 3 2

d 3 2 2025 d 2025 .f x x x x x x x x C        



Dạng 2. Nguyên hàm hàm số lượng giác

Ví dụ 2: Tìm ncác :

 

1 sinf x x

 

2cos 3f x x x

 

cos



Lời giải

   

d 1 sin d 1d sin d cosf x x x x x x x x x C      

   

   

d 2cos 3 d 2sin

f x x x x x x x C    



 

d 1 d tan

cos

f x x x x x C



    







Dạng 3. Nguyên hàm hàm số mũ

Ví dụ 3: Tìm ncác :

Trang 2

 

fx

 

fx

 

7 .2





Lời giải

 

d e d e

f x x x C  



 

d 3 d

ln3

f x x x C  



 

   

 

d d 42 d 4 14d 7 .2 7 . . d42 .

xx x x x

x x x x Cf x x



    

 

Dạng 4. Nguyên hàm có điều kiện

Bài toán: Tìm nguyên hàm

 



 

mãn

 

F a b

» Bước 1: D

» Bước 2: D

 

F a b



» Bước 3: K

Ví dụ 4: Tìm nguyên hàm

 



 

sin cosf x x x













Lời giải

Ta có:

     

d sin cos d cos sin .F x f x x x x x x x C      



Theo :

cos sin 2 1 2 1

2 2 2

F C C C

  



         





 

cos sin 1F x x x    

Ví dụ 5: Cho

 



 

f x x



 

F 

. Tìm

 

Lời giải

Ta có:

 

e 2 d e

F x x x x C    



Theo :

   

3 1 1

0 1 e

2 2 2

F C C F x x        

Ví dụ 6: 

 

3.f x x





Tìm nguyên hàm

 



 



mãn

 

0 1.f 

Lời giải

Ta có:

   

d 3 df x f x x x x x C



   



Mà

 

0 1 0 1 1f C C     

. 

 

.f x x C

Ví dụ 7: 

 

y f x



 

0;



 

2f x x







 

0;x 

và

 

11f 



 

Lời giải



 

0;x 

, ta có:

   

d 2 df x f x x x x x C





     







Vì

     

1 1 67

1 1 1 1 4 16 1

f C f x x f

           

Ví dụ 8:   

 

y f x

  

 

12 2f x x





 

x

và

 

13f 

 

 

là



 



 

02F 



 

Lời giải



x

, ta có:

   

 

d 12 2 d 4 2f x f x x x x x x C



     



Vì

   

1 3 3 4 2 3f C f x x x       

Trang 3



   

 

3 4 2

d 4 2 3 d 3F x f x x x x x x x x C       



     

0 2 2 3 2 1 1F C F x x x x F         

Dạng 5. Bài toán thực tế (liên quan đến vận tốc, gia tốc, quãng đường,…)

» Bước 1: X

 

 



 



o hàm cng là vn tc:

   

s t v t





+ Nguyên hàm ca vn tng:

   

ds t v t t



 

 



 



o hàm ca vn tc là gia tc:

   

v t a t





+ Nguyên hàm ca gia tc là vn tc:

   

dv t a t t



» Bước 2: D.

» Bước 3: K

Ví dụ 9:        

19 m/s

          

   

19 2 m/s .v t t



Lời giải

Ta có

     

19 2 19s t v t dt t dt t t C     



Vì

 

0 0 19.0 0 0 0s C C      

. Suy ra

 

19s t t t



5,t 



 

5 19.5 5 70 .sm  

Ví dụ 10: 

giây (coi

0t 





   

160 9,8 /v t t m s

. 



a) sau

5t 

giây.

b) klàm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải



 







     

d 160 9,8 d 160 4,9h t v t t t t t t C     



 

00h 

nên

0C 

   

4,9 160h t t t m   

a) Sau

5t 

giây.



giây là

   

5 4,9.5 160.5 677,5hm   

b) làm tròn kết quả đến chữ số thập phân thứ nhất).



 

64000

1306,1

4 49



   

khi

800

2 49

  

giây.

C. BÀI TẬP TRẮC NGHIỆM

Phần 1. Trắc nghiệm nhiều phương án lựa chọn

Câu 1. 

 

y f x

và

 

y g x

 . sai?

       

d d df x g x x f x x g x x  





  

. B.

       

d d df x g x x f x x g x x  





  

   

ddkf x x k f x x





 

\0k 

. D.

       

. d d . df x g x x f x x g x x

  

Câu 2. 

   

df x x F x C



. K

   

f x F x





. B.

   

f x F x C





. C.

   

F x f x C





. D.

   

F x f x





Câu 3. Cho hàm s

 

32f x x x

. Trong các hàm s  nào là mt nguyên hàm ca

 

trên

Trang 4

 

. 4F x x x  

. B

 

Fx

. C

 

. 1F x x x  

. D

 

. 3F x x x

Câu 4. Cho hàm s

 

f x x x

. Trong các hàm s  nào là mt nguyên hàm ca

 

trên

 

. 4F x x x  

. B

 

Fx

. C

 

F x x  

. D

 

. 2 1F x x

Câu 5. H tt c các nguyên hàm ca hàm s

 

24f x x

là

. 2 4x x C

. B

. 4x x C

. C

. xC

. D

. 2xC

Câu 6. H tt c các nguyên hàm ca hàm s

 

2f x x

là

 

. d 2f x x x C  

. B

 

. d 2

f x x x C   

 

. d 2f x x x x C   

. D

 

. d 2f x x x x C   

Câu 7. Mt nguyên hàm ca hàm s

 

2025

fx

là

 

. .2025

F x x





. B

 

. 2025.2024

Fx

 

. 2025 ln2025

Fx

. D

 

2025

ln2025

Fx

Câu 8. H tt c nguyên hàm ca hàm s

 

44f x x

là

. 2 4x x C

. B

. 4x x C

. C

. xC

. D

. 2xC

Câu 9. Bit

 

1F x x

  

là mt nguyên hàm ca hàm s

 

trên khong

 





. M 

 

. ln

f x x x

. B

 

. 3f x x



. C

 

. 3f x x



. D

 

. ln

f x x x x C   

Câu 10. H nguyên hàm ca hàm s

    

12f x x x  

là

. 2 3xC

. B

. 2

x x C  

. C

. 2

x x C  

. D

. 2

x x C  

Câu 11. Tìm h nguyên hàm ca hàm s

 

52x





 

. d

f x x C

   

. B

 

. d

f x x C

   

 

. d 5ln

f x x x C   

. D

 

. d 2f x x x C

   

Câu 12. Nguyên hàm ca hàm s

 

3cos 4sinf x x x

là

. 3sin 4cosxx

. B

. 3sin 4cosxx

. C

. 3sin 4cosx x C

. D

. 3sin 4cosx x C  

Câu 13. Nguyên hàm ca hàm s

 

2sin

sin

f x x



là

. 2cos 3cotx x C

. B

. 2cos 3tanx x C

. C

. 2cos 3cotx x C  

. D

. 2cos 3cotx x C

Câu 14. Mt nguyên hàm ca hàm s

 

2f x x x

có dng

 

F x ax bx

. Tính

4T a b

. 0T 

. B

. 1T 

. C

. 2T 

. D

. 3T 

Câu 15. Cho hàm s

 

y F x

là mt nguyên hàm ca hàm s

yx

. Tính

 

25F



A. 25. B. 125. C. 5. D. 625.

Câu 16. Cho

 

l



m



t nguyên h



m c



 



. Bi



 

10F 

. T



 

2 2ln2 1F 

. B.

 

2 ln2F 

. C.

 

2 2ln3 2F 

. D.

 

2 2ln2F 

Trang 5

Câu 17. Nguyên hàm

 

ca hàm s

 

2sin cosf x x x

tha mãn











là

 

. 2cos sin 1F x x x  

. B

 

. 2cos sin 1 3F x x x   

 

. 2cos sin 1F x x x   

. D

 

. 2cos sin 1F x x x   

Câu 18. Cho hàm s

 

tha mãn

 

3 5cosf x x



và

 

05f 

. M 

 

. 3 5sin 5f x x x  

. B

 

. 3 5sin 5f x x x  

. C

 

. 3 5sin 2f x x x  

. D

 

. 3 5sin 5f x x x  

Câu 19. Bit

 

là mt nguyên hàm ca ca hàm s

 

sinf x x

 th hàm s

 

y F x

m

 

0;1M

. Tính









. 2











. B

. 1











. C

. 0











. D

. 1











Câu 20. Cho hàm s

 

y f x

o hàm là

 

e 2 1,

f x x x



    R

và

 

01f 

. Bit

 

là nguyên

hàm ca

 

tha mãn

 

1eF 

. Tính

 

. B



. C

. D



Phần 2. Trắc nghiệm đúng – sai

Câu 1. Cho hàm s

( ) 2 1F x x x  

là mt nguyên hàm ca hàm s

()fx

a) Nu hàm s

()Gx

là mt nguyên hàm ca hàm s

()fx

và

( 1) 3G 

thì

   

1G x F x

x

b) Nu hàm s

()Hx

là mt nguyên hàm ca hàm s

()fx

và

(1) 3H 

thì

   

3H x F x

x

c) Nu hàm s

()Kx

là mt nguyên hàm ca hàm s

()fx

và

(0) 0K 

thì

   

1K x F x

x

d) Nu hàm s

()Mx

là mt nguyên hàm ca hàm s

()fx

và

(2) 4M 

thì

   

1M x F x

x

Câu 2. Cho

 

 .

   

d ' .f x x f x C



   

' d .f x x f x C



   

' d .f x x f x



   

'' d ' .f x x f x C



Câu 3. 

 



(giây),

()at





(giây).

   

d.a t t v t C



   

d.v t t a t C



   

' d .v t t a t C



   

' d .v t t v t C



Câu 4. Cho hàm s

 

f x x

. Gi

 

là 1 nguyên hàm ca

 

f x x C  

. b) Bit

 

31F 

thì

 

F 

 

2 3 2

2 1 d (2 1) d 2

f x x x x x x x C        

. d)

 

. 2 d 2

x f x x x C     





Câu 5. Cho

 

34f x x x

và

 

là nguyên hàm ca

 

trên

   

F x f x





 

2F x x x C  

 

21F x x x  

vi

 

01F 

. d) Cho

 

01F 



3 27













Phần 3. Trả lời ngắn

Câu 1. 

 



 

3 4 1f x x x  

và

 

22F 

. Tính

 

Trang 6

Câu 2.   

 

      

 

2 2 1f x x x  

và

 

F 

. Tính









(viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm).

Câu 3. Cho hàm s

 

y f x

o hàm là

 

12 2,f x x x



   R

và

 

13f 

. Bit

 

là nguyên

hàm ca

 

tha mãn

 

02F 

. Tính

 

Câu 4. Cho hàm s

 

tha mãn

 

3 5sinf x x



và

 

0 10f 

.    

 

có dng

 

3 cosf x x b x c  

vi

,bc

là các s nguyên. Tính

bc

Câu 5. Bit

(2sin cos ) d sin2 cos2x x x a x x bx C     

, vi

,abQ

. Tính

ab

. (kết quả làm tròn đến

hàng phần mười).

Câu 6.  :

) trong mt dây dn ti thm

giây là

   

3 6 5I t Q t t t



   

vi

 

: C) truyn trong dây dn ti thm

. Bit khi

1t 

ng

truyn trong dây dn là

 

14Q 

. Tính ding truyn trong dây dn khi

3t 

Câu 7. i ta truyn nhit cho mt bình nuôi cy vi sinh vt t

1 C.

T  ca bình ti thi

m

phút

 

05t

c cho bi hàm s

 



3 C/f t t

phút

)

. Bit rng nhi ci thi

m

là mt nguyên hàm ca hàm s

 

. Tìm nhi ca bình ti thm 3 phút k t khi truyn

nhit.

II. TÍCH PHÂN

A. TÓM TẮT LÝ THUYẾT

1. Định nghĩa

Cho



[ ; ].ab





trên 

[ ; ].ab



( ) ( )F b F a

a b 

( ),fx



 

f x x





     

F x F b F a



( ) ( )F b F a



       

f x x F x F b F a  



2. Tính chất của tích phân

 

. ( )d . ( )d

k f x x k f x x k



 

( ) ( ) d ( )d ( )d

b b b

a a a

f x g x x f x x g x x  

  

 

( ) ( ) d ( )d ( )d

b b b

a a a

f x g x x f x x g x x  

  

( )d ( )d ( )d

b c b

a a c

f x x f x x f x x

  

(

a c b

)

B. BÀI TẬP TỰ LUẬN

Dạng 1. Tính tích phân theo định nghĩa – tính chất

Ví dụ 1: Cho

 

d5f x x 



và

 

d2g x x 



. Tính:

   

df x g x x







. b)

   

df x g x x







 

3df x x



. d)

   

2 3 df x g x x







Lời giải

   

df x g x x







   

d d 5 2 7f x x g x x    



Trang 7

   

df x g x x







   

d d 5 2 3f x x g x x    



   

3 d 3 d 3.5 15f x x f x x  



       

3 3 3

0 0 0

2 3 d 2 d 3 d 2.5 3.2 4f x g x x f x x g x x     





  

Ví dụ 2: Cho

 

d1f x x







 

d4f t t







. Tính

 

df y y



Lời giải

Ta có:

   

ddf t t f x x







   

ddf y y f x x





     

2 4 4

2 2 2

d d df x x f x x f x x





  

     

4 4 2

2 2 2

d d d 4 1 5f x x f x x f x x



       

  



 

d5f y y 



Ví dụ 3: Cho

      

 

1;3

 mãn

   

3 d 10f x g x x







   

2 d 6f x g x x







. Tính

   

df x g x x







Lời giải

         

3 3 3

1 1 1

3 d 10 d 3 d 10 1f x g x x f x x g x x    





  

         

3 3 3

1 1 1

2 d 6 2 d d 6 2f x g x x f x x g x x    





  



 

dX f x x



 

dY g x x





 

và

 



3 10 4

2 6 2

X Y X

X Y Y

  







  





 

d4f x x 



và

 

d2g x x 





   

d 4 2 6f x g x x   







Dạng 2. Tích phân hàm số chứa dấu trị tuyệt đối

Tính tích phân:

 

I f x x



Phương pháp:

Bước 1

 



 

;ab

Bước 2

 

;ab



 



 tính

 

I f x x



Ví dụ 3: Tính các tích phân sau:

1dA x x







. b)

2dB x x x x



  



Lời giải

Trang 8

1dA x x







Xét

 

1f x x



 

2;2

Cho

 

 

2;2

1 2

f x x





    

















     

2 1 1 2

2 2 1

1 d 1 d 1 d 1 dA x x x x x x x x



  

       

   

3 3 3

1 1 2

2 1 1

2 2 2 2 2 2

3 3 3 3 3 3 3 3 3

x x x





     

     

     

               

     

     

     

     

     

2dB x x x x



  



Xét

 

2f x x x x  

trên

 

2;1

Cho

 

 

2 ;

0 2 0 0

2;1

f x x x x x







      

















   

1 0 1

3 2 2 3 2

2 d 2 d 2 dB x x x x x x x x x x x x



        

  

2 4 2

1 1 1 1 8 5 37

4 3 4 3 3 12 12

x x x x x x



       

           

       

       

Dạng 3. Tích phân hàm số cho bởi nhiều công thức

Ví dụ 4: 

 

21 khi

2 3 khi 2x











  







. Tính

 

dI f x x



Lời giải

Ta có:

 

   

3 2 3

d 2 3 d 1 d 3

3 3 3

I f x x x x x x x x x x

   

           

   

   

  

Ví dụ 5: 

 

3 khi 0 1

4 khi 1 2









  



. Tính

 

df x x



Lời giải



   

3 d 4 d 4 1 8 2 4

2 2 2

x x x x x xf x x



           





 

Dạng 4. Bài toán thực tế

Ví dụ 6: 

10 /ms



 

3a t t t

. Tính 



Lời giải

Trang 9



   

 

d 3 d

v t a t t t t t C     





 

0t 



 

0 10 10vC   



 

vt   

Sa

3 2 4

3 4300

10 d 10

3 2 12 2 3

t t t t

s x t m

   

      

   

   



Ví dụ 7: 

(giây) là

 

32v t t t  

(m/s). T

13t

a) 

b) 

Lời giải

a) 



13t

là

 

3 2 3 2

3 3 3 3 1 3 2

d 3 2 d 2 2 3 2

3 2 3 2 3 2 3

v t t t t t t

   





             

   





   



b) 



13t

là

 

   

3 3 2 3

2 2 2

1 1 1 2

d 3 2 d 3 2 d 3 2 d 1

v t t t t t t t t t t t            

   

C. BÀI TẬP TRẮC NGHIỆM

Phần 1. Trắc nghiệm nhiều phương án lựa chọn

Câu 1. Nu

 

d2f x x





và

 

d3g x x







   

df x g x x









bng

A. 5. B. 6. C. 1. D. -1.

Câu 2. Cho hàm s

 

y f x

liên tn

 

6;11

và tha mãn

 

d8f x x





 

d3f x x

. Giá tr

ca biu thc

   

2 11

ddP f x x f x x



   

bng

. 4P 

. B

. 11P 

. C

. 5P 

. D

. 2P 

Câu 3. Cho

   

d 3; d 1f x x g x x



    



   

2 3 dI x f x g x x



   





bng

A. 10. B

. C

. D

Câu 4. Bit

 

F x x

là mt nguyên hàm ca hàm s

 

trên

. Giá tr ca

 

2df x x

là

A. 7. B. 9. C

. D

Câu 5. Cho hàm s

 

liên tc trên

. Gi

 

là mt nguyên hàm ca

 

trên

tha mãn

   

2 0 5FF



 

3df x x

bng

A. 6. B. 15. C. 10. D. 5.

Câu 6. Nu

 

2 d 6f x x

thì

 

f x x x









bng

A. 4. B. 7. C. 3. D. 2.

Câu 7. Tính

2 1dxx





. B. 2. C

. D

Trang 10

Câu 8. Cho hàm s

 

y f x

 nh và liên tc trên

, tha mãn

 

sin d 10f x x x



  





. Tính

 

dI f x x





. 4I 

. B

. 8I 

. C

. 12I 

. D

. 6I 

Câu 9. Cho bit

 

4 sin dx x a b



   

, vi

,ab

là các s nguyên. Tính

ab

A. 1. B. -4. C. 6. D. 3.

Câu 10. Cho hàm s

 

3 khi 0 1

4 khi 1 2

y f x









  



. Tính tích phân

 

df x x

. B. 1. C

. D

Câu 11. Tính tích phân

2dI x x



2I 

. B.

4I 

. C.

2I 

. D.

0I 

Câu 12. Cho hàm s

 

2 khi 3 1

k hi 1

    











thì

 

df x x





bng

. B

. C

. D

Câu 13. Cho hàm s

 

3 2 khi 1

3 2 4 khi 1

x x x









  



. Gi s

 

là nguyên hàm ca

 

trên

tha

mãn

 

24F 

. Giá tr ca

   

2 4 3FF

bng

A. 16. B. 8. C. 18. D. 2.

Câu 14. Mt vt chuyng vi gia tc

 

2cos m /sa t t

, bit rng ti thm bu chuyng,

vt có vn tc bng vc t thm

 

0 ts

n thm

 





 

. 5 m

. B

 

. 3 m

. C

 

. 2 m

. D

 

. 4 m

Câu 15.  m bng, các xe ô tô khi d phi cách nhau ti thiu

 

1 m

. Mt ô tô

y vi vn tc

15 m/s

bng gp ô tô

ng ch  nên ô tô

hãm

phanh và chuyng chm du bi vn tc biu th bi công thc

   

15 5 m/s

v t t

 hai ô

tô

và

t khong cách an toàn khi dng li thì ô tô

phi hãm phanh khi cách ô tô

mt khong ít

nht là

mét. Giá tr ca

bng

A. 23,5. B. 21. C. 22,9. D. 21,6.

Phần 2. Trắc nghiệm đúng – sai

Câu 1. Cho

   

d 3; d 5f x x f x x   

 

d3f x x

. b)

 

d2f x x

 

2 d 1f x x x   

. d)

 

2 d 2f x x x  

Câu 2. Cho hàm s

23 khi 2

()

khi 2















 

( )d 1 df x x x x



. b)

 

( )d 2 3 df x x x x x  



 

1 41

2 12

f x x 



. d)

 

( )d 2 3 df x x x x x  



Trang 11

Câu 3. 



 

2 khi 0

khi 0

a x x x

















 

d 2 df x x x x







. b)

 

f x x 



c) Khi

2a 

 

f x dx







. d) 

 

d3f x x







là

6a 

Câu 4. Cho hàm s

   

,f x g x

liên tc trên

a) Nu

 

d5f x x

và

 

g x x  

thì

   

f x g x x  





b) Nu

 

2 3 d 10g x x x   





thì

 

d4g x x

c) Nu

   

f x e F

thì









d) Nu

   

2 1; 2f x x g x x   

thì

 

d ln

x a b c

  

, , , 4a b c c



7abc  

Phần 3. Trả lời ngắn

Câu 1. 

d ln2

x a b







. Tính

ab

Câu 2. 

3 2 4

d ln3

x a b







. Tính

ab

Câu 3. Nu

 





và

 

11F 

thì giá tr ca

 

bng bao nhiêu? (làm tròn kết quả đến chữ số thập

phân thứ 2)

Câu 4. Cho hàm s

 

 o hàm liên tc trên

có

 

25f 

và

 

42f x x





. Tích phân

 

f x x





(vi

ti gin và



,abZ

. Tính

ab

Câu 5. Bit

ln2

2 2 d

ln2



  



vi

,ab

là các s nguyên. Tính giá tr ca biu thc

T a b

Câu 6. Cho

 

1 khi 1

2 1 khi 1













. Tính

 

dJ f x x







Câu 7. Cho

 

4 2 dI x m x



. Có bao nhiêu giá tr nguyên ca



60I 

Câu 8. Cho

     

d , 0 7

g x f t t x  





 

. Tính

 

III. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN

A. TÓM TẮT LÝ THUYẾT

1) Tính diện tích hình phẳng:

Trang 12

a) H

 

y f x



 

;ab

 



;x a x b

b) H        

   

;y f x y g x

  

 

;ab

  



;x a x b

()

( ) d

y f x

S f x x

























 

: ( )

( ) ( )d

C y f x

C y g x

S f x g x x























2) Tính thể tích vật thể:

+ 





và

 





 

a x b



 



 

;ab





 

V S x x



+ 

 

y f x



, x a x b



:Ox

 

()

( ) d

y f x

V f x x



























B. BÀI TẬP TỰ LUẬN

Dạng 1. Xây dựng công thức tính diện tích theo hình vẽ

Phương pháp

▪ Xác định công thức diện tích hình phẳng:

» Bước 1: 

» Bước 2: 

Trang 13

» Bước 3: 

   

S f x g x x



» Bước 4: 



▪ Xác định công thức thể tích khối tròn xoay:

» Bước 1: 

» Bước 2: 

» Bước 3: 

 





V f x xp

Ví dụ 1: S là  . cS.

Lời giải



 

y f x





1 1 2   ;;x x x



         

2 1 2 1 2

1 1 1 1 1  



     



    

d d d d dS f x x f x x f x x f x x f x x

Ví dụ 2: 

 

y f x

bên. bên.

Lời giải

Ta có:

 

;

H y x x



  



  





  



Ta có:

   

3 2 1 dS x x x x



     



 

2 2 4 dx x x



   



(dn

12;







ph th

3yx  

n th

21y x x  

Ví dụ 3: 

 

y f x















 gì?

Lời giải

Trang 14

T



 

dV f x xp









Dạng 2. Diện tích hình phẳng giới hạn bởi y = f(x), Ox và x = a, x = b

Phương pháp

Diện tích hình phẳng giới hạn:

 



















;

y f x

Ox S f x x

x a x b



» Bước 1: 

 

0fx



 

, ,..., ;

x x x a b

 

...

a x x x b    

» Bước 2: Tính

     

d d ... d

a x x

S f x x f x x f x x   

  

     

d d ... d

a x x

f x x f x x f x x   

  

Chú ý: 

Ví dụ 4: Tính d



yx





1x 

2x 

Lời giải



dS x x



dxx









Ví dụ 5: Tính d

 

21yx  



12,xx

Lời giải



 

2 1 0





   







Ta có:

 

2 2 2

1 1 1

2 1 4 3 4 3

         

  

d d d .S x x x x x x x x

Ví dụ 6: 



2y x x

0y 

4x 

1x 

Lời giải

Xét p





  









   

1 0 1

2 2 2

4 4 0

2 2 2d d dS x x x x x x x x x



     

  



   

   

   

   

38

Ví dụ 7: 

    

1yx





2x 

Lời giải



1 0 1xx   

Trang 15

2 1 2

3 3 3

0 0 1

1 1 1d d dS x x x x x x     

  

   

11ddx x x x   



4 4 2

   

    

   

   

Dạng 3. Diện tích hình phẳng giới hạn bởi y = f(x), y = g(x) và x = a, x = b

Phương pháp

Diện tích hình phẳng giới hạn:

 

     







   













;

y f x

y g x S f x g x x

x a x b



» Bước 1: 

   

f x g x



 

, ,..., ;

x x x a b

 

...

a x x x b    

» Bước 2: Tính

           

d d ... d

a x x

S f x g x x f x g x x f x g x x      

  

   

 

   

 

   

 

d d ... d

a x x

f x g x x f x g x x f x g x x      

  

Ví dụ 8: 

 

1y x x

và

y x x

 bao nhiêu?

Lời giải

Ta có:

 

3 3 2

1 2 0 2

x x x x x x x x







         











 

1y x x

và

y x x



1 0 1

3 2 3 2 3 2

2 2 0

2 2 2d d dS x x x x x x x x x x x x



        

  

   

3 2 3 2

8 5 37

3 12 12

ddx x x x x x x x



        





Dạng 4. Thể tích vật thể tính theo mặt cắt vuông góc trục hoành

Ví dụ 9: Tính th tích

ca phn vt th gii hn bi hai mt phng

1x 

và

3,x 

bit rng khi ct vt th

bi mt phng tùy ý vuông góc vi trc

t

13()x

c thit din là mt hình

ch nht có hai cnh là

và

Lời giải

Ta có d

 

33.S x x x x



3 60

  



dV x x x

Ví dụ 10: 



0x 

và

x p







 

0 x p



2 sin x

Lời giải

Ta có d

 

2sin si. nxxSx

Trang 16

 

3 233

   



ds ond ci sV S x x x x x

Dạng 5. Thể tích khối tròn xoay

Ví dụ 11: 

yx





1x 

;

4x 



Lời giải



yx



1x 

và

4x 



 

ddV x x x xpp



Ví dụ 12: Tính th tích khi tròn xoay sinh ra khi quay hình phng gii hn bng sau xung quanh

trc

2 0 0 2    , , ,y x x y x x

Lời giải

Th tích khi tròn xoay

 

2



dV x x xp



C. BÀI TẬP TRẮC NGHIỆM

Phần 1. Trắc nghiệm nhiều phương án lựa chọn

Câu 1. 

0,xx







cosyx



là

cos dS x x







cos dS x x







. C.

cos dS x x







. D.

cos dS x x







Câu 2. 

                 

, 0, 0, 2

y e y x x   

quay quanh



V e x







. B.

V e x



. C.

V e x







. D.

V e x



Câu 3. Cho hàm s

 

liên tc trên

. Gi

là din tích hình phng gii hn b  ng

 

, 0, 1, 2y f x y x x    

). M 

   

. d dS f x x f x x



   

. B

   

. d dS f x x f x x



   

   

. d dS f x x f x x



   

. D

   

. d dS f x x f x x



   

Câu 4. Gi S là din tích hình phng gii hn b  ng

 

y f x

, tr    ng thng

3, 2xx  

t

   

d , da f x x b f x x



   

. M 

Trang 17

. S a b  

. B

. S a b

. C

. S a b

. D

. S b a

Câu 5. Din tích hình phng phn gch chéo trong hình v c tính theo công th

 

3 3 2

. 2 5 6 dS x x x x



    

. B

 

3 3 2

. 2 10 dS x x x x



    

 

3 3 2

. 2 10 dS x x x x



    

. D

 

3 3 2

. 2 5 6 dS x x x x



     

Câu 6. Tính din tích

hình phng

 

gii hn bng cong

12y x x  

và

yx

937

S 

. B

343

S 

. C

397

S 

. D

793

S 

Câu 7. Din tích hình phng gii hn b th hàm s

yx

và

8yx

là

A. 12. B. 32. C

. D

Câu 8. Din tích phn sch sc trong hình v bng

. 2 3 dx x x



   

. B

 

. 2 3 dx x x



  

. C

 

. 2 3 dx x x



  

. D

 

. 2 3 dx x x



   

Câu 9. Din tích ca phn hình phng gch chéo trong hình bên bng

Trang 18

. B

. C

. D

Câu 10. Cho hình

 

là hình phng gii hn b ng cong

yx

 ng thng

23yx  

và trc

hoành (phn gch chéo trong hình v). Din tích hình phng

 

là

S 

. B

S 

. C

S 

. D

. 2S 

Câu 11. Tính th tích

ca phn vt th gii hn bi hai mt phng

0, 1xx

, có thit din b ct bi mt

phng vuông góc vi trc

t

 

0 1xx

là mu có cnh bng





. B

V 

. C





. D

V 

Câu 12. Tính th tích

ca phn vt th gii hn bi hai mt phng

0x 

và

3x 

, bit rng khi ct vt th

bi mt phng tùy ý vuông góc vi trc

t

(

03x

c thit din là mt

hì dài cnh bng

29 x

A. 90. B

. 72



. C

. 78



. D. 72.

Câu 13. Cho hình phng

 

gii hn b th hàm s

ye

 ng thng

0, ln3xx

và trc

hoành. Th tích khi tròn xoay sinh bi

 

khi quay quanh trc hoành là

. 2



. B

. 4



. C. 4. D



Câu 14. Th tích kh  c khi quay hình phng gii hn b ng

43y x x  

và

0y 

quanh trc

bng

. B



. C



. D

Câu 15. Th tích vt th tròn xoay khi cho hình phng gii hn b th hàm s

4y x x

và trc hoành

quay quanh

là

. B

512

. C



. D

512



Câu 16. Cho hình phng

gii hn bng

1yx

, trc hoành và

5x 

. Th tích khi tròn xoay

to thành khi quay

quanh trc

bng



. B

. C

. 8



. D. 8.

Trang 19

Câu 17. Cho hình phng

 

c gii hn b th ca hàm s

yx

 th ca hàm s

yx

(tham

kho hình v). Th tích ca khc khi quay

 

quanh trc

bng





. B





. C





. D





Câu 18. Th tích khi tròn xoay gii hn bng

2 , 0y x x y  

khi quay quanh trc

là



. B



. C



. D



Câu 19. Cho hình phng gii hn b th hàm s

yx

ng thng

4y 

quay quanh trc

. Th

tích khi tròn xoay sinh ra bng



. B

128



. C

256



. D

152



Câu 20. Tính th tích chc ca mt cái chén, bit phn trong ca nó có dng khc to

thành khi quay quanh trc

hình phng gii hn bng

22yx

và trc

), bát có

  trên tr).

. 78 cm

. B

. 274 cm

. C

. 87 cm

. D

. 247 cm

Phần 2. Trắc nghiệm đúng – sai

Câu 1. 

 



 

4 4 y x x C  

 

4 12 y x C



a) 

 

là

8 16 dxxS x



b) 

 

4 4 d 4 12 d

V x x x x x



    



c) 

 

và

 



 

4;4M

d) 









32ab

Câu 2. 

Trang 20

a) Hình phc gii h th

;y x y x

b) Th tích ca vt tròn xoay to thành khi quay hình phng trên quanh trc

là

 

dx x x







c) 



 



 

:P y x

;

 

:C y x







d) Din tích hình phng tô màu trong hình v là

Câu 3. 

; ( 2)y x y x  







yx



0; 1xx



 

1yx



1; 2xx

dS x x



. b)

ddS x x x x



 

2dS x x  



. d) 

Câu 4. 

ABCD à



I 



mét. xy AB, A, B và I 



a) 

 

;0 , ;0 , 0;3

A B I



   

   

   

. b) P là

yx  

c) Din tích thm làm nn là

18m

. d)  

36Vm

Bấm Tải xuống để xem toàn bộ.

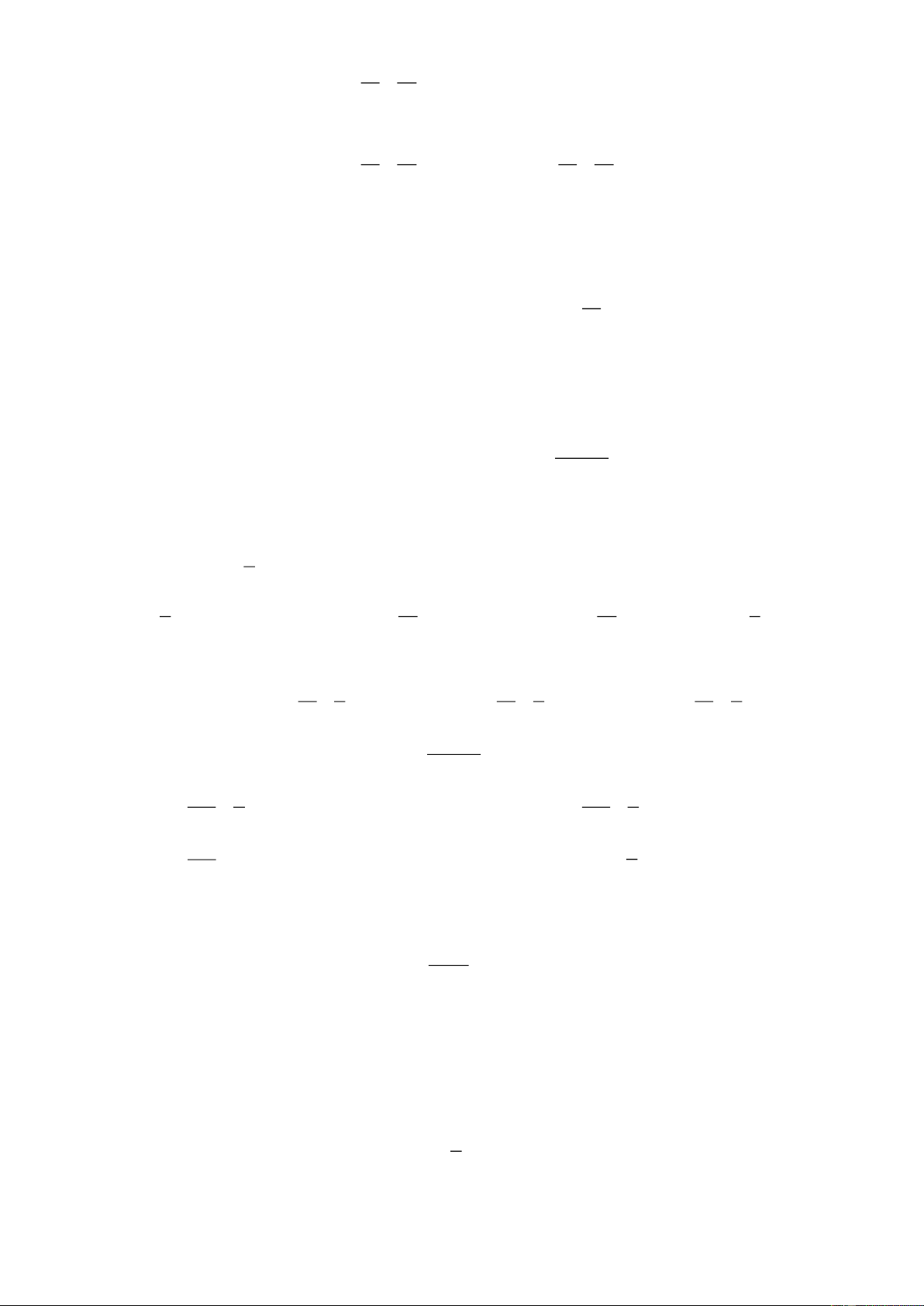
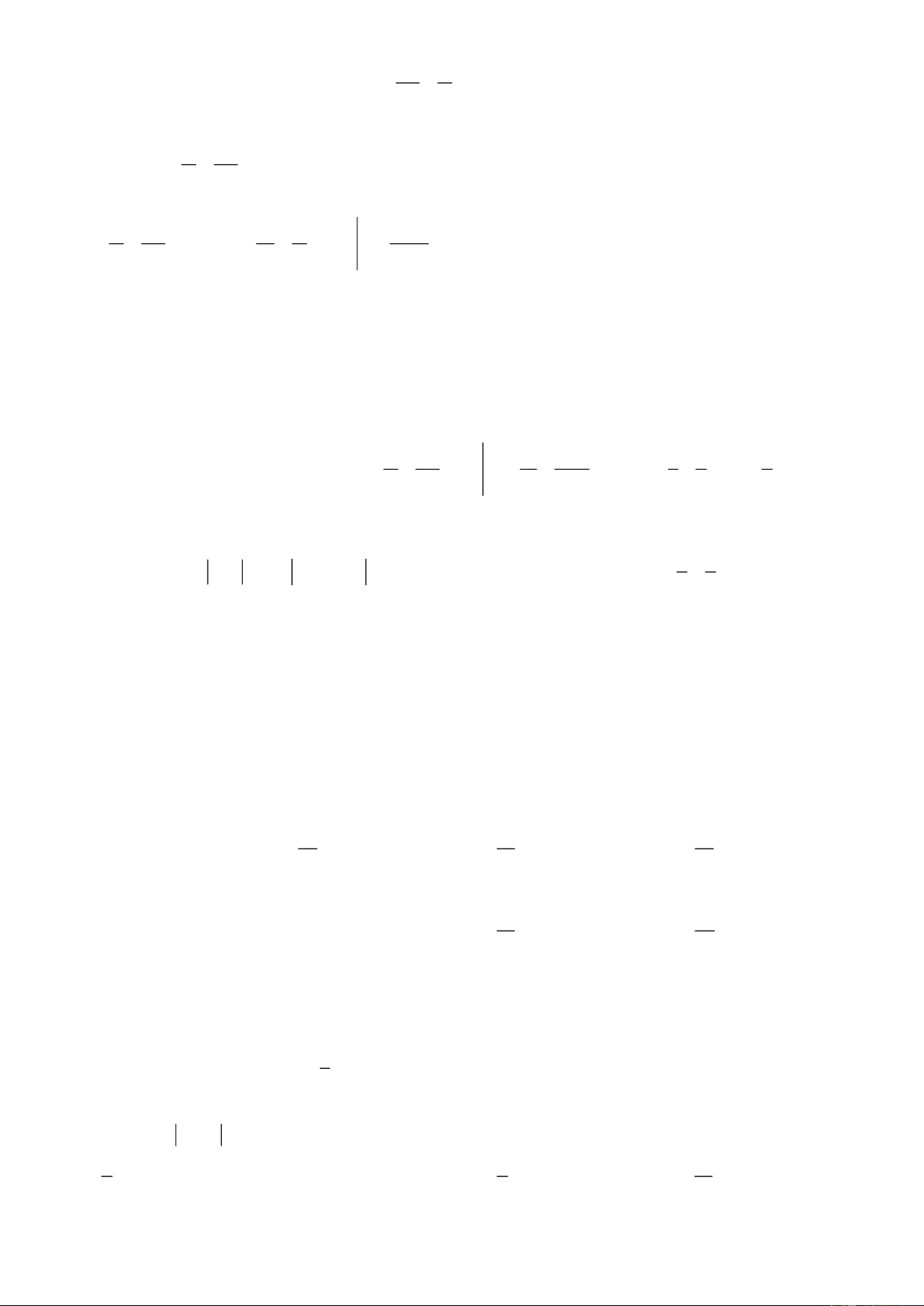
Preview text:

CHUYÊN ĐỀ: NGUYÊN HÀM VÀ TÍCH PHÂN I. NGUYÊN HÀM A. TÓM TẮT LÝ THUYẾT 1. Định nghĩa
Cho K là tập con của tập số thực .
• Cho hàm số f x xác định trên K . Hàm số F x được gọi là nguyên hàm của hàm số f x trên K
nếu F 'x  f x với mọi x thuộc K .
• Nếu F x là một nguyên hàm của hàm số f x trên K thì mọi nguyên hàm của hàm số f x trên
K đều có dạng F  x  C với C là một hằng số. Vì vậy, f
 x dx  F xC .
• Mọi hàm số liên tục trên K đều có nguyên hàm trên K . Ta có: F '
 x dx  F xC . 2. Tính chất
Cho f  x, g  x là hai hàm số liên tục trên K . • kf
 x dx  k f
 x dx với k  0. •  f
 x gx dx  f 
 x dx  g  x dx. •  f
 x gx dx  f 
 x dx  g
 x dx .
3. Nguyên hàm một số hàm số sơ cấp cơ bản  1  • Với    x
1 ta có x dx   C     . • 1 dx ln x C  . 1 x • 1
sin xdx   cos x  C.  •
dx   cot x  C.  2 sin x • 1
cos xdx  sin x  C.  •
dx  tan x  C.  2 cos x x a
• Với a  0;a  1 ta có x a dx   C.  ln a B. BÀI TẬP TỰ LUẬN
Dạng 1. Nguyên hàm hàm lũy thừa
Ví dụ 1: Tìm nguyên hàm của các hàm số:
a) f  x 3  x  2x
b) f  x 2  3
 x  2x  2025 . Lời giải 1 a) f
 xdx   3x  2x 4 2 dx 
x  x  C . 4 b) f
 x x   2  x  x   3 2 d 3 2
2025 dx   x  x  2025x  C.
Dạng 2. Nguyên hàm hàm số lượng giác
Ví dụ 2: Tìm nguyên hàm của các hàm số: 1
a) f  x 1 sin x
b) f  x  2cos x  3x
c) f  x  1 . 2 cos x Lời giải a) f
 xdx  1sin xdx  1dx  sin d
x x  x  cos x  C   . 3 b) f
 xdx  2cos x3x 2
dx  2sin x  x  C . 2  1  c) f
 xdx  1
dx  x  tan x  C   . 2  cos x 
Dạng 3. Nguyên hàm hàm số mũ
Ví dụ 3: Tìm nguyên hàm của các hàm số: Trang 1 a)   ex f x  b)   3x f x 
c) f  x x x2  7 .2 . Lời giải
a)   d  exd  ex f x x x  C  . x b) f  x x 3 dx  3 dx   C  . ln 3 x x x x x 14x x c) f
 xdx   2 7 .2 dx   2 7 2
. .2 dx  47 2
.  dx  4 14 dx  4.  C  . n l 4 1
Dạng 4. Nguyên hàm có điều kiện
Bài toán: Tìm nguyên hàm F  x của f  x thỏa mãn F a  b .
» Bước 1: Dựa vào bảng nguyên hàm, tính chất nguyên hàm, các phương pháp biến đổi.
» Bước 2: Dựa vào điều kiện của giả thiết F a  b để tìm C .
» Bước 3: Kết luận.   
Ví dụ 4: Tìm nguyên hàm F x của hàm số f x  sin x  cos x thoả mãn F  2   .  2  Lời giải
Ta có: F  x  f
 xdx  sin x cos xdx  cos x sin x C.      Theo đề: F
 cos  sin  C  2  1 C  2  C 1  
 F x  cos x sin x 1.  2  2 2
Ví dụ 5: Cho F x là một nguyên hàm của    ex f x
 2x thỏa mãn F   3 0 
. Tìm F  x . 2 Lời giải
Ta có: F  x   x  x x 2 e 2
dx  e  x  C . 3 1 x 1
Theo đề: F 0  1 C 
 C   F x 2
 e  x  . 2 2 2
Ví dụ 6: Cho hàm số f x 2
 3x . Tìm nguyên hàm f x của f x thỏa mãn f 0 1. Lời giải
Ta có: f  x  f   x 2 3
dx  3x dx  x  C  . Mà f   3
0 1 0  C 1  C 1. Vậy f  x 3  x  . C Ví dụ 1
7: Cho hàm số y  f  x xác định trên khoảng 0; . Biết rằng f  x  2x 
với mọi x 0; 2 x và f  
1  1. Tính giá trị f 4 . Lời giải  1  1
Với mọi x0; , ta có: f  x  f   x 2 dx  2x  dx  x   C   . 2  x  x 1 1 67 Vì f  
1  1  C  1  f  x 2
 x  1 f 4 16  1 . x 4 4
Ví dụ 8: Cho hàm số y  f x có đạo hàm f x 12x  2 với mọi x và f  
1  3 . Biết F  x là
nguyên hàm của f  x thoả mãn F 0  2. Tính giá trị F   1 . Lời giải
Với mọi x , ta có: f  x  f 
 xdx   2 12x  2 3
dx  4x  2x  C . 1 Vì f   1  3  C  3
  f x 3
 4x  2x 3. 1 Trang 2
Lại có: F  x  f
 xdx   3
4x  2x  3 4 2
dx  x  x  3x  C 2
F 0  2  C  2  F  x 4 2
 x  x 3x  2  F 1 1. 2  
Dạng 5. Bài toán thực tế (liên quan đến vận tốc, gia tốc, quãng đường,…)
» Bước 1: Xét mối liên hệ giữa các đại lượng
▪ Xét mối quan hệ giữa các đại lượng vận tốc vt , quãng đường st và thời gian t .
+ Đạo hàm của quãng đường là vận tốc: st  vt .
+ Nguyên hàm của vận tốc là quãng đường: s t   v  tdt .
▪ Xét mối quan hệ giữa các đại lượng vận tốc vt , gia tốc at và thời gian t .
+ Đạo hàm của vận tốc là gia tốc: vt  at .
+ Nguyên hàm của gia tốc là vận tốc: v t   a  tdt .
» Bước 2: Dựa vào điều kiện của giả thiết để tìm đại lượng yêu cầu.
» Bước 3: Kết luận.
Ví dụ 9: Một ô tô đang chạy với vận tốc 19 m/s thì hãm phanh và chuyển động chậm dần với tốc độ
v t 19  2t m/s. Kể từ khi hãm phanh, quãng đường ô tô đi được sau 5 giây là bao nhiêu? Lời giải
Ta có s t   v
 tdt    t 2
19 2 dt  19t  t  C . Vì s   2
0  0 19.0  0  C  0  C  0 . Suy ra s t 2 19t t .
Vậy sau 5 giây thì t  5, quãng đường ô tô đi được là s  2 5 19.5  5  70 . m
Ví dụ 10: Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi t  0 là thời
điểm viên đạn được bắn lên), vận tốc của nó được cho bởi vt 160 9,8t  /
m s . Tìm độ cao của viên đạn (tính từ mặt đất)
a) sau t  5 giây.
b) khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất). Lời giải
Gọi ht là độ cao của viên đạn bắn lên từ mặt đất sau t giây kể từ thời điểm đạn được bắn lên.
Khi đó ht  v
 t t    t 2 d
160 9,8 dt  160t  4, 9t  C .
Do h 0  0 nên C  0  ht 2  4
 ,9t 160t m.
a) Sau t  5 giây.
Độ cao của viên đạn sau 5 giây là h  2 5  4
 ,9.5 160.5  677,5 m.
b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất). 
Viên đạn đạt độ cao lớn nhất là 64000 b 800 h   
 1306,1 m khi t    giây. 4a 49 2a 49
C. BÀI TẬP TRẮC NGHIỆM
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Cho hai hàm số y  f  x và y  g  x liên tục trên . Mệnh đề nào sau đây là sai? A.  f
 x gxdx  f 
 xdx  g  xdx . B.  f
 x gxdx  f 
 xdx  g
 xdx. C. kf
 xdx  k f
 xdx với k \  0 . D. f
 x.gxdx  f
 xd .x g  xdx. Câu 2. Biết f
 xdx  F xC . Khẳng định nào sau đây đúng?
A. f  x  F  x .
B. f  x  F  x  C .
C. F x  f  x C .
D. F x  f  x .
Câu 3. Cho hàm số f  x 2
 3x  2x . Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của f x trên R ? Trang 3 x x
A . F  x 3 2
 x  x  4. B. F x   .
C. F x  x  x 1.
D. F x  3x  x . 4   3 2 3   3 2 2   3 2 1 3 2
Câu 4. Cho hàm số   2
f x  x  x . Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của f  x trên R?? x x x x
A . F  x 3 2
 x  x  4. B. F x   . C. F x  
 x . D. F x  2x 1. 4   3   3 2 2   3 2 1 3 2 3 2
Câu 5. Họ tất cả các nguyên hàm của hàm số f  x  2x  4 là A 2
. 2x  4x  C . B 2
. x  4x  C . C 2 . x  C . D 2 . 2x  C .
Câu 6. Họ tất cả các nguyên hàm của hàm số f  x 2  x  2 là x
A .  f  xdx  2x  C .
B  f  x 3 . dx   2x  C . 3
C  f  x 2 .
dx  x  2x  C .
D  f  x 3 .
dx  x  2x  C .
Câu 7. Một nguyên hàm của hàm số   2025x f x  là A   1 . .2025x F x x   .
B.   2025.2024x F x  . x
C .   2025x F x  ln2025.
D F  x 2025 .  . ln2025
Câu 8. Họ tất cả nguyên hàm của hàm số f  x  4x  4 là A 2
. 2x  4x  C . B 2
. x  4x  C . C 2 . x  C . D 2 . 2x  C . 1
Câu 9. Biết F  x 3
 x  1 là một nguyên hàm của hàm số f x trên khoảng 0; 
 . Mệnh đề nào đúng? x 1 1 1 1
A . f  x 4  x  lnx .
B. f  x 2  3x  .
C. f  x 2  3x  .
D. f  x 4
 x  lnx  x  C . 4 2 x 2 x 4
Câu 10. Họ nguyên hàm của hàm số f  x   x   1  x  2 là 3 x 2 3 x 2 3 x 3
A . 2x  3 C . B 2 .
 x  2x  C . C 2 .
 x  2x  C . D 2 .
 x  2x  C . 3 3 3 3 3 2 5  2x
Câu 11. Tìm họ nguyên hàm của hàm số f  x 4  . 2 x x x
A  f  x 3 2 5 . dx    C .
B  f  x 3 2 5 . dx    C . 3 x 3 x 2x 5
C .  f  x 3 2 dx 
 5lnx  C .
D.  f  x 3 dx  2x   C . 3 x
Câu 12. Nguyên hàm của hàm số f  x  3cosx  4sinx là
A . 3sinx  4cosx . B. 3
 sinx  4cosx .
C. 3sinx  4cosx  C . D. 3
 sinx  4cosx C . 3
Câu 13. Nguyên hàm của hàm số f  x  2sinx  là 2 sin x A . 2
 cosx 3cotx C .
B. 2cosx  3tanx  C . C. 2
 cosx 3cotx C .
D. 2cosx  3cotx  C .
Câu 14. Một nguyên hàm của hàm số f  x 3
 x  2x có dạng   4 2
F x  ax  bx . Tính T  4a  b . A . T  0. B. T 1. C. T  2. D. T  3 .
Câu 15. Cho hàm số y  F  x là một nguyên hàm của hàm số 2
y  x . Tính F25 . A. 25. B. 125. C. 5. D. 625.
Câu 16. Cho F  x là mô ̣t nguyên hàm của   2 f x  . Biết F  
1  0 . Tính F 2. x
A. F 2  2ln 2 1.
B. F 2  ln 2 .
C. F 2  2ln 3 2 .
D. F 2  2ln 2 . Trang 4    3
Câu 17. Nguyên hàm F  x của hàm số f  x  2sinx  cosx thỏa mãn F     là  3  2
A . F  x  2cosx sinx 1.
B. F  x  2cosx  sinx 1 3 .
C . F  x  2
 cosx sinx 1.
D. F  x  2
 cosx sinx 1.
Câu 18. Cho hàm số f  x thỏa mãn f  x  35cosx và f 0  5 . Mệnh đề nào dưới đây đúng?
A . f  x  3x 5sinx 5 . B. f  x  3x  5sinx  5 . C. f  x  3x  5sinx  2 . D. f  x  3x 5sinx  5 .
Câu 19. Biết F  x là một nguyên hàm của của hàm số f  x  sinx và đồ thị hàm số y  F  x đi qua điểm    M 0;  1 . Tính F   .  2              A . F  2   . B. F  1   . C. F  0   . D. F  1   .  2   2   2   2 
Câu 20. Cho hàm số y  f  x có đạo hàm là    ex f x  2x 1, x
 R và f 0 1. Biết F x là nguyên
hàm của f  x thỏa mãn F  
1  e. Tính F 0 . 5 1 1 5 A . . B.  . C. . D.  . 6 6 6 6
Phần 2. Trắc nghiệm đúng – sai Câu 1. Cho hàm số 3
F(x)  x  2x 1 là một nguyên hàm của hàm số f (x) .
a) Nếu hàm số G(x) là một nguyên hàm của hàm số f (x) và G(1)  3 thì G  x  F  x 1, x  .
b) Nếu hàm số H (x) là một nguyên hàm của hàm số f (x) và H (1)  3    thì H  x
F  x 3 , x  .
c) Nếu hàm số K (x) là một nguyên hàm của hàm số f (x) và K (0)  0 thì K  x  F  x 1 , x  .
d) Nếu hàm số M (x) là một nguyên hàm của hàm số f (x) và M (2)  4 thì M  x  F  x 1, x  .
Câu 2. Cho f  x là hàm số liên tục trên . a) f
 xdx  f 'xC. b) f '
 xdx  f xC. c) f '
 xdx  f x. d) f '
 xdx  f 'xC.
Câu 3. Giả sử v t  là phương trình vận tốc của một vật chuyển động theo thời gian t (giây), a(t) là phương
trình gia tốc của vật đó chuyển động theo thời gian t (giây). a) a
 tdt  vtC. b) v
 tdt  atC. c) v '
 tdt  atC. d) v '
 tdt  vtC. Câu 4. Cho hàm số   2
f x  x . Gọi F  x là 1 nguyên hàm của f  x . x
a)  f  x 3 dx   C .
b) Biết F 3  1 thì F   4 4  . 3 3 4 x x
c)  f 2x   2 3 2
1 dx  (2x 1) dx 
x  2x  x  C . d)  x f  x   4 3 2 . 2  dx    2x  C  . 3 4 3
Câu 5. Cho f  x 2
 3x  4x và F x là nguyên hàm của f x trên R .
a) F x  f  x
b) F  x 3 2
 x  2x C .  1 23
c) F  x 3 2
 x  2x 1 với F 0 1.
d) Cho F 0 1, khi đó F      .  3  27
Phần 3. Trả lời ngắn
Câu 1. Cho hàm số F  x là một nguyên hàm của hàm số f  x 2
 3x 4x 1 và F 2  2. Tính F 3 . Trang 5
Câu 2. Cho hàm số F  x là một nguyên hàm của hàm số f  x   2
x  22x   1 và F   1 1  . Tính 6  1  F  . 
 (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm).  2 
Câu 3. Cho hàm số y  f  x có đạo hàm là f  x 2 12x  2, x  R và f  
1  3 . Biết F  x là nguyên
hàm của f  x thỏa mãn F 0  2. Tính F   1 .
Câu 4. Cho hàm số f  x thỏa mãn f  x  3 5sinx và f 0 10. Khi đó hàm số f  x có dạng
f  x  3x  c
b osx  c với ,
b c là các số nguyên. Tính b  c . Câu 5. Biết 2
(2sinx  cosx) dx  s
a in2x  cos2x  bx  C , với a, b  Q . Tính 2 2
a  b . (kết quả làm tròn đến hàng phần mười).
Câu 6. Cường độ dòng điện (đơn vị: A ) trong một dây dẫn tại thời điểm t giây là I t  Qt 2
 3t  6t  5
với Q t  là điện lượng (đơn vị: C) truyền trong dây dẫn tại thời điểm t . Biết khi t  1 giây thì điện lượng
truyền trong dây dẫn là Q 
1  4 . Tính diện lượng truyền trong dây dẫn khi t  3 .
Câu 7. Người ta truyền nhiệt cho một bình nuôi cấy vi sinh vật từ 1 C. Tốc độ tăng nhiệt độ của bình tại thời
điểm t phút 0  t  5 được cho bởi hàm số f t 2
 3t  C / phút ) . Biết rằng nhiệt độ của bình đó tại thời
điểm t là một nguyên hàm của hàm số f t . Tìm nhiệt độ của bình tại thời điểm 3 phút kể từ khi truyền nhiệt. II. TÍCH PHÂN A. TÓM TẮT LÝ THUYẾT 1. Định nghĩa
Cho f là hàm số liên tục trên đoạn [ ;
a b]. Giả sử F là một nguyên hàm của f trên đoạn [ ; a b]. b Hiệu số F( )
b  F(a) được gọi là tích phân từ a đến b của hàm số f (x), kí hiệu là f  x d . x  a
Ta dùng kí hiệu F x b  F b  F a để chỉ hiệu số F( )
b  F(a) . a b Vậy f  x b
dx  F  x  F b  F a . a a
2. Tính chất của tích phân b b b b b
a) k. f (x)dx  k. f (x)dx k    
b)  f (x)  g(x)dx  f (x)dx  g(x)dx   a a a a a b b b b c b
c)  f (x)  g(x)dx  f (x)dx  g(x)dx   d)
f (x)dx 
f (x)dx  f (x)dx   
( a  c  b ) a a a a a c B. BÀI TẬP TỰ LUẬN
Dạng 1. Tính tích phân theo định nghĩa – tính chất 3 3
Ví dụ 1: Cho f
 xdx  5 và g
 xdx  2. Tính: 0 0 3 3 a)  f
 x gxdx  . b)  f
 x gxdx  . 0 0 3 3
c) 3 f  x dx  . d) 2 f
 x3gxdx  0 0 Lời giải 3 3 3 a)  f
 x gxdx   f
 xdx g
 xdx  5 2  7 . 0 0 0 Trang 6 3 3 3 b)  f
 x gxdx   f
 xdx g
 xdx  52  3. 0 0 0 3 3 c) 3 f
 xdx  3 f
 xdx  3.5 15. 0 0 3 3 3 d) 2 f
 x3gxdx  2 f 
 xdx 3 g
 xdx  2.53.2  4 . 0 0 0 2 4 4
Ví dụ 2: Cho f
 xdx 1, f tdt  4   . Tính
f  y dy  . 2  2  2 Lời giải 4 4 4 4 Ta có: f
 tdt  f
 xdx, f
 ydy  f  xdx . 2  2  2 2 2 4 4 Khi đó: f
 xdx f
 xdx  f  xdx. 2  2 2  4 4 2 4
 f xdx  f xdx  f xdx  4  1  5    
. Vậy f  ydy  5   . 2 2  2  2 3
Ví dụ 3: Cho f , g là hai hàm liên tục trên đoạn 1;  3 thoả mãn  f
 x3gx dx 10  , 1 3 3 2 f
 x gx dx  6  . Tính  f
 x gx dx  . 1 1 Lời giải 3 3 3  f
 x3gxdx 10  f 
 xdx3 g
 xdx 10  1. 1 1 1 3 3 3 2 f
 x gxdx  6  2 f 
 xdx g
 xdx  6 2 . 1 1 1 3 3 Đặt X  f
 xdx, Y  g  xdx. 1 1
X  3Y 10 X  4 Từ  
1 và 2 ta có hệ phương trình:    . 2X Y  6 Y   2 3 3 3 Do đó ta được: f
 xdx  4 và g
 xdx  2. Vậy  f
 x gx dx  42  6  . 1 1 1
Dạng 2. Tích phân hàm số chứa dấu trị tuyệt đối b
Tính tích phân: I  f  x dx a Phương pháp:
Bước 1. Xét dấu f x trên đoạn  ; a b .
Bước 2. Dựa vào bảng xét dấu trên đoạn  ;
a b để khử f  x . Sau đó sử dụng các phương pháp tính tích phân b
đã học để tính I  f
 x dx . a
Ví dụ 3: Tính các tích phân sau: 2 1 a) 2 A  x 1 dx  . b) 3 2 B 
x  x  2x dx  . 2  2  Lời giải Trang 7 2 a) 2 A  x 1 dx  . 2  Xét f  x 2
 x 1 trên đoạn  2  ;  2 . x  1   2  ;2 Cho f  x 2
 0  x 1  0   . x 1   2;  2 Bảng xét dấu: 2 1  1 2 Do đó: 2 A  x  x   2 1 d x   1 dx   2
1 x dx   2 x      1dx 2  2  1  1 1  1 2 3 3 3  x   x   x 
2  2  2  2  2  2 
   x  x      x           4.           3   3   3 
3  3  3  3  3  3  2  1  1 1 b) 3 2 B 
x  x  2x dx  . 2  Xét f  x 3 2
 x  x  2x trên  2  ;  1 . x  2   ; 2  1  Cho f  x 3 2
 0  x  x  2x  0  x  0 2   ;1 . x 1 2    ;1 Bảng xét dấu: Do đó: 1 0 3 2 B 
x  x  2x dx     1 3 2
x  x  2xdx   3 2
x  x  2xdx 2  2  0 0 1  1 1   1 1   8   5  37 4 3 2 4 3 2  x  x  x  x  x  x       .          4 3   4 3   3   12  12 2  0
Dạng 3. Tích phân hàm số cho bởi nhiều công thức 2 x 1 khi x  2 3
Ví dụ 4: Cho hàm số f  x   . Tính I  f  xdx . 2
x  2x  3 khi x  2 1 Lời giải 2 3 3 2 3 3 3  x   x  23 Ta có: I  f
 xdx   2x 2x3dx  2x   2 1 dx  
 x  3x     x  .  3   3  3 1 1 2 1 2 2 3  x khi 0  x  1 2
Ví dụ 5: Cho hàm số f x   . Tính
f  x dx  .
4  x khi 1 x  2 0 Lời giải 2 1 2 1 2 2     Khi đó f  x x 1 7 2
dx  3x dx   4 x 3 dx  x
 4x   1 8 2 4    .  2   2  2 0 0 1 0 1
Dạng 4. Bài toán thực tế
Ví dụ 6: Một vật chuyển động với vận tốc 10 m / s thì tăng tốc với gia tốc at 2
 3t t . Tính quãng đường
vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. Lời giải Trang 8
Hàm vận tốc       t t v t
a t dt  3t t  2 3 3 2 dt    C . 2 3
Lấy mốc thời gian t  0 lúc tăng tốc v0 10  C 10 . Ta được:   3 2 t 3t v t   10 . 3 2
Sau 10 giây kể từ lúc tăng tốc, quãng đường vật đi được là 0 1 10 3 2 4 3  t 3t   t t  4300 s    
10dx    10t   m .  3 2  12 2  3 0 0
Ví dụ 7: Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là v t  2
 t 3t  2 (m/s). Trong khoảng thời gian 1 t  3,
a) Tìm độ dịch chuyển của vật.
b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này. Lời giải
a) Tìm độ dịch chuyển của vật.
Độ dịch chuyển của vật trong khoảng thời gian 1 t  3 là 3 3 3     t t      
v t dt  t 3t  2 3 2 3 2 3 3 3 3 1 3 2 2 dt     2t      23   2    .  3 2   3 2   3 2  3 1 1 1
b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này.
Tổng quãng đường vật đi được trong khoảng thời gian 1 t  3 là 3 3 2 3 v  t 5 1 2 dt 
t  3t  2 dt    2t
  3t  2dt   2t 3t  2dt   1. 6 6 1 1 1 2
C. BÀI TẬP TRẮC NGHIỆM
Phần 1. Trắc nghiệm nhiều phương án lựa chọn Câu 1. Nếu 4
 f x dx  2 và 4
 g x dx  3. Khi đó 4
  f x  g x  dx 1       1    1     bằng A. 5. B. 6. C. 1. D. -1.
Câu 2. Cho hàm số y  f  x liên tục trên đoạn  6  ;1  1 và thỏa mãn 11
 f x dx  8 , 6
 f x dx  3 . Giá trị 2   6    của biểu thức 2 P   f    x 11 dx f x dx bằng 6 6   A . P  4 . B. P 11. C. P  5. D. P  2 . Câu 3. Cho 2  f     . Khi đó 2
I   x  2 f x  3g x  dx 1        x 2 dx 3; g x dx 1 1 1     bằng 21 19 17 A. 10. B. . C. . D. . 2 2 2 Câu 4. Biết   3
F x  x là một nguyên hàm của hàm số f  x trên R . Giá trị của 2
 2  f x dx là 1    15 23 A. 7. B. 9. C. . D. . 4 4
Câu 5. Cho hàm số f  x liên tục trên R . Gọi F  x là một nguyên hàm của f  x trên R thỏa mãn
F 2  F 0  5 . Khi đó 2
 3 f x dx bằng 0   A. 6. B. 15. C. 10. D. 5. 1  Câu 6. Nếu 1
 2 f x dx  6 thì 1
f x  2x dx bằng 0   0     3  A. 4. B. 7. C. 3. D. 2. Câu 7. Tính 2
 2x 1 dx . 1  1 5 13 A . . B. 2. C. . D. . 2 2 2 Trang 9 Câu 8. Cho hàm số 
y  f  x xác định và liên tục trên R , thỏa mãn   f x  sinx dx  10 0     . Tính 
I   f x dx . 0   A . I  4 . B. I  8 . C. I  12. D. I  6 .  Câu 9. Cho biết 2
 4  sinx dx  a  b , với a,b là các số nguyên. Tính a b . 0   A. 1. B. -4. C. 6. D. 3. 2 3  x khi 0  x  1
Câu 10. Cho hàm số y  f  x   . Tính tích phân 2  f x dx . 0  
4  x khi 1 x  2 7 5 3 A . . B. 1. C. . D. . 2 2 2 2
Câu 11. Tính tích phân I  x  2 dx  . 0 A. I  2  . B. I  4 . C. I  2 . D. I  0 .
x  2 khi  3  x  1 
Câu 12. Cho hàm số f  x   thì 3
 f x dx bằng 3    2 x k hi x  1  31 28 22 26 A . . B. . C. . D. . 3 3 3 3 3   2x khi x  1
Câu 13. Cho hàm số f  x  
. Giả sử F  x là nguyên hàm của f  x trên R thỏa 2 3
 x  2x  4 khi x 1
mãn F 2  4. Giá trị của F  2    4F   3 bằng A. 16. B. 8. C. 18. D. 2.
Câu 14. Một vật chuyển động với gia tốc a t   t  2
2cos m / s  , biết rằng tại thời điểm bắt đầu chuyển động,
vật có vận tốc bằng 0. Tính quãng đường vật đi được từ thời điểm t  0 s đến thời điểm t   s . A . 5m . B. 3 m . C. 2m. D. 4m.
Câu 15. Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu
1 m . Một ô tô A đang chạy với vận tốc 15 m / s bỗng gặp ô tô B đang đứng chờ đèn đỏ nên ô tô A hãm
phanh và chuyển động chậm dần đều bởi vận tốc được biểu thị bởi công thức v t 15  5t m / s . Để hai ô A 
tô A và B đạt khoảng cách an toàn khi dừng lại thì ô tô A phải hãm phanh khi cách ô tô B một khoảng ít
nhất là s mét. Giá trị của s bằng A. 23,5. B. 21. C. 22,9. D. 21,6.
Phần 2. Trắc nghiệm đúng – sai Câu 1. Cho 2  f x 3
dx  3;  f x dx  5. 0 0   a) 0
 f x dx  3 . b) 3
 f x dx  2 . 2   2   c) 2
 f x  2x dx  1  . d) 3
 f x  2x dx  2 . 0    0    2
x  2x  3 khi x  2
Câu 2. Cho hàm số f (x)   . x 1 khi x  2 2 2 3 3 a)
f (x)dx   x     1 dx . b)
f (x)dx  
 2x 2x3dx . 1 1 2 2 3 1 41 2 2 c)
f  x dx   . d)
f (x)dx  
 2x 2x3dx . 2 12 1 1 1 Trang 10 2x khi x  0 
Câu 3. Cho số thực a và hàm số f  x   . a   2
x  x  khi x  0 0 0 1 a a) f
 xdx  2 dxx  . b)
f  xdx    . 6 1  1  0 1 2 2
c) Khi a  2 ,
f  x dx    .
d) Điều kiện cần và đủ để f
 xdx 3 là a  6  . 1  3 1 
Câu 4. Cho hàm số f  x, g  x liên tục trên R . 1 11 a) Nếu 2
 f x dx  5 và 2
 g x dx   thì 2
  f x  g x  dx  1      1   1    . 2 2 b) Nếu 3
 g x  2x  3 dx  10 3
 g x dx  4. 1     thì 1    1  x 1
c) Nếu f  x 3
 e , F 0  thì F  e   . 3  3  f x 5  
d) Nếu f  x  2x 1; g  x  x  2 thì 
dx  a  blnc , a, ,
b c  , c  4 . Khi đó a  b  c  7 . 3 g  x
Phần 3. Trả lời ngắn 2 3x  4 Câu 1. Biết
dx  a  b ln 2 
. Tính a  b . x 1 3 2 3x  2x  4 Câu 2. Biết
dx  a  b ln 3 
. Tính a  b . x 1
Câu 3. Nếu F  x 1  và F  
1  1 thì giá trị của F 4 bằng bao nhiêu? (làm tròn kết quả đến chữ số thập 2x phân thứ 2)
Câu 4. Cho hàm số f  x có đạo hàm liên tục trên R có f 2  5 và f  x  4x  2 . Tích phân 4    a a f x dx  (với
tối giản và a,b  Z . Tính a  b . 2 b b 2 a  b x ln2
Câu 5. Biết I  2  2 dx  
với a, b là các số nguyên. Tính giá trị của biểu thức T  a  b . 0 ln2  x  2
Câu 6. Cho f  x 1 khi 1   . Tính J  f  xdx.
2x 1 khi x 1 1  1
Câu 7. Cho I    2
4x  2m dx . Có bao nhiêu giá trị nguyên của m để I  6  0 ? 0 x
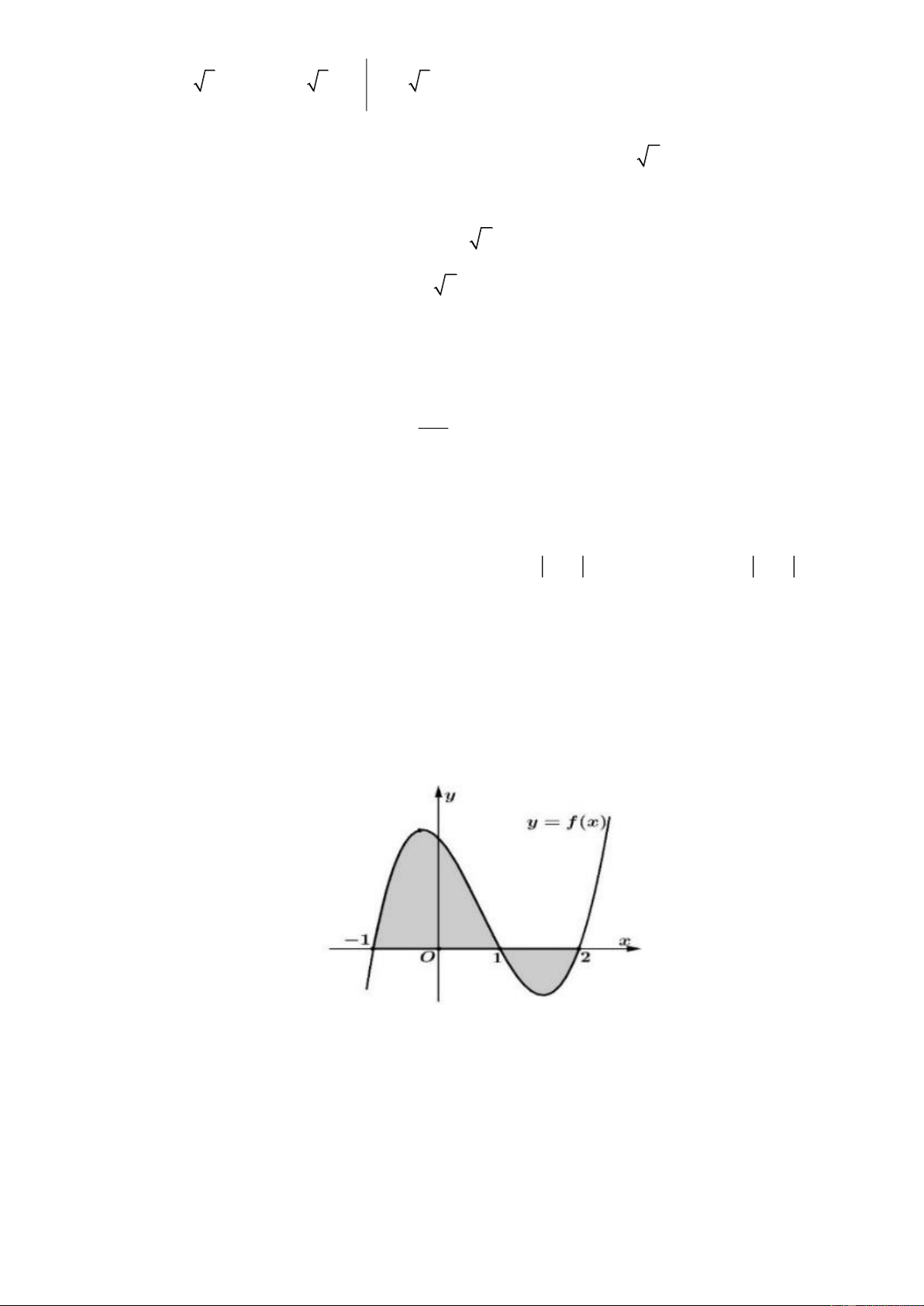
Câu 8. Cho g  x  f
 tdt,0  x  7 trong đó f t là hàm số có đồ thị như Hình vẽ. Tính g3. 0
III. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN A. TÓM TẮT LÝ THUYẾT
1) Tính diện tích hình phẳng: Trang 11
a) Hình phẳng giới hạn bởi đồ thị hàm số y  f  x b) Hình phẳng giới hạn bởi đồ thị hàm số liên tục trên đoạn 
y  f  x; y  g  x
a;b , trục hoành và hai đường
liên tục trên a;b và hai đường thẳng thẳng   x  ;
a x  b . x ; a x b .
y  f (x)  
 C : y  f (x) 1  y  0 b   S  f (x) dx  
 C : y  g(x) b 2  a x  a   S 
f (x)  g(x) dx   a x  a   x  b x  b
2) Tính thể tích vật thể:
+ Định nghĩa: Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b,
S  x là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, a  x  b
Giả sử S x là hàm số liên tục trên đoạn  ; a b b
Khi đó, thể tích của vật thể B được xác định: V  S  xdx . a
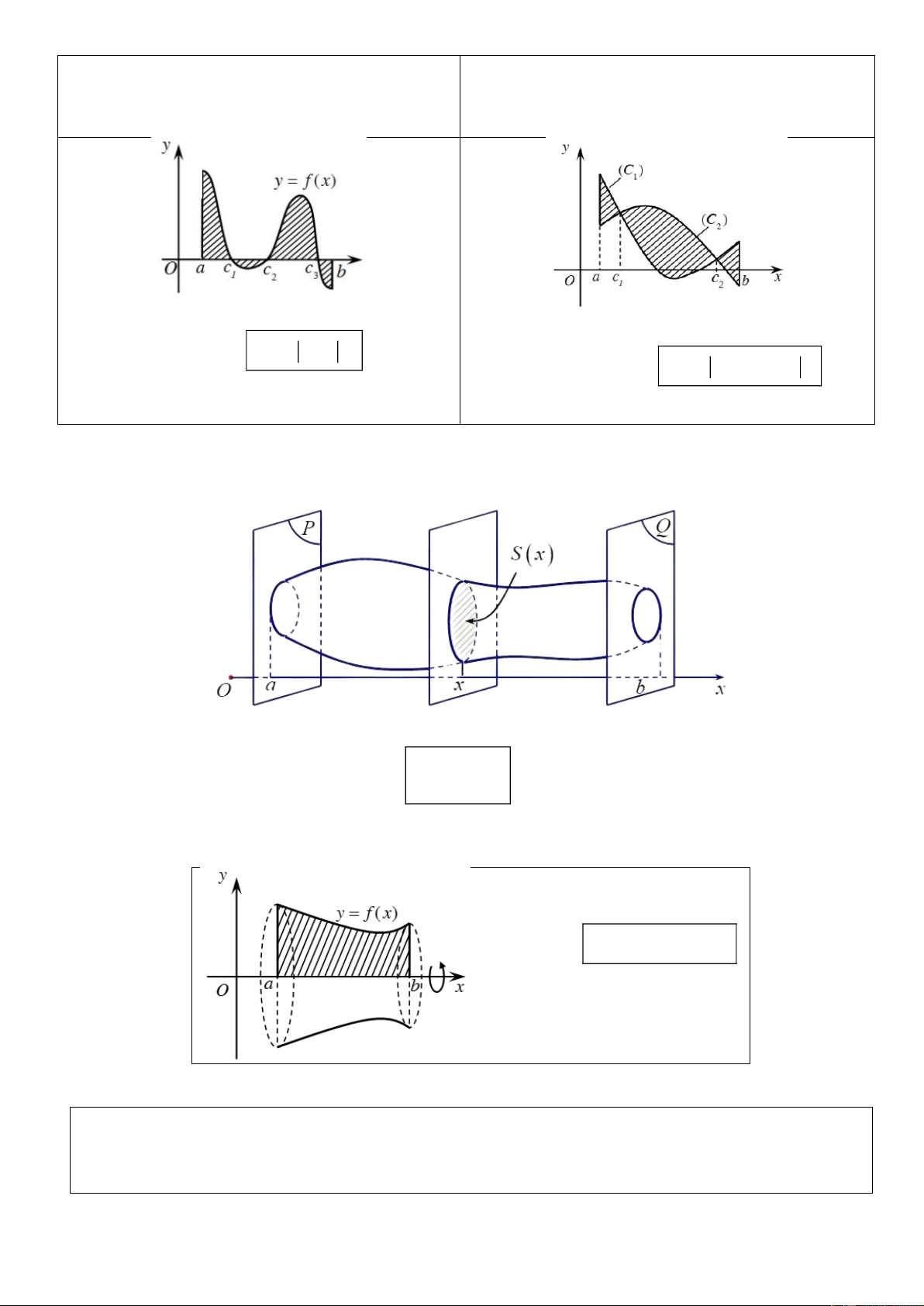
+ Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi y  f  x , Ox và hai đường thẳng
x  a, x  b quanh trục Ox :
y  f (x)  y  0 b  V   f x x  Ox  ( )2 d a x  a  x  b B. BÀI TẬP TỰ LUẬN
Dạng 1. Xây dựng công thức tính diện tích theo hình vẽ Phương pháp
▪ Xác định công thức diện tích hình phẳng:
» Bước 1: Xác định đồ thị của các hàm số được cho trên hình vẽ.
» Bước 2: Xác định các vị trí tương giao giữa các đồ thị. Trang 12 b
» Bước 3: Áp dụng công thức tính diện tích S  f
 xgx dx. a
» Bước 4: Phá trị tuyệt đối: Lấy công thức hàm số của đồ thị nằm trên trừ công thức hàm số của đồ thị nằm dưới
▪ Xác định công thức thể tích khối tròn xoay:
» Bước 1: Xác định đồ thị của các hàm số được cho trên hình vẽ.
» Bước 2: Xác định các vị trí tương giao giữa các đồ thị. b
» Bước 3: Áp dụng công thức tính diện tích 2
V  p  f xdx . a
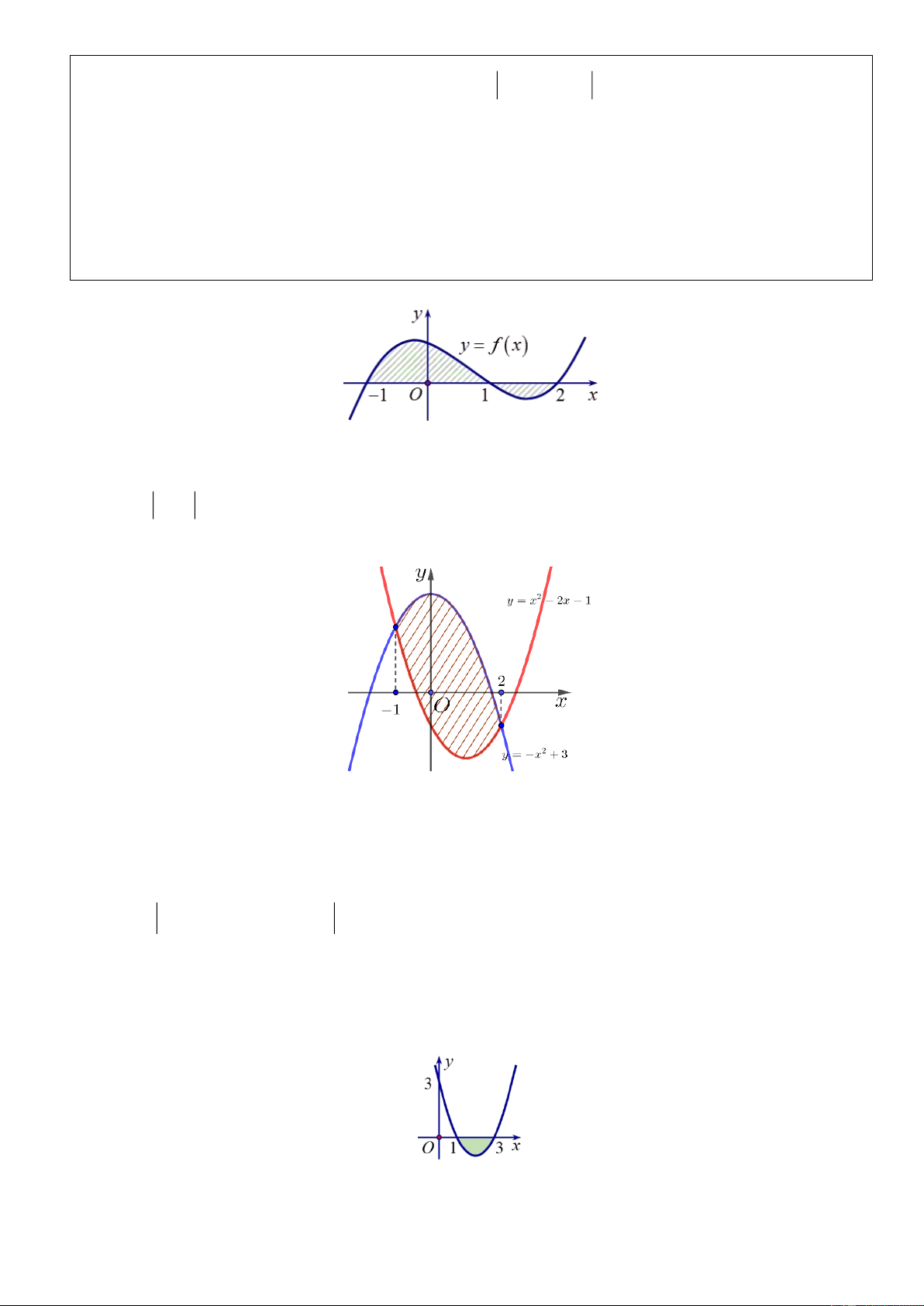
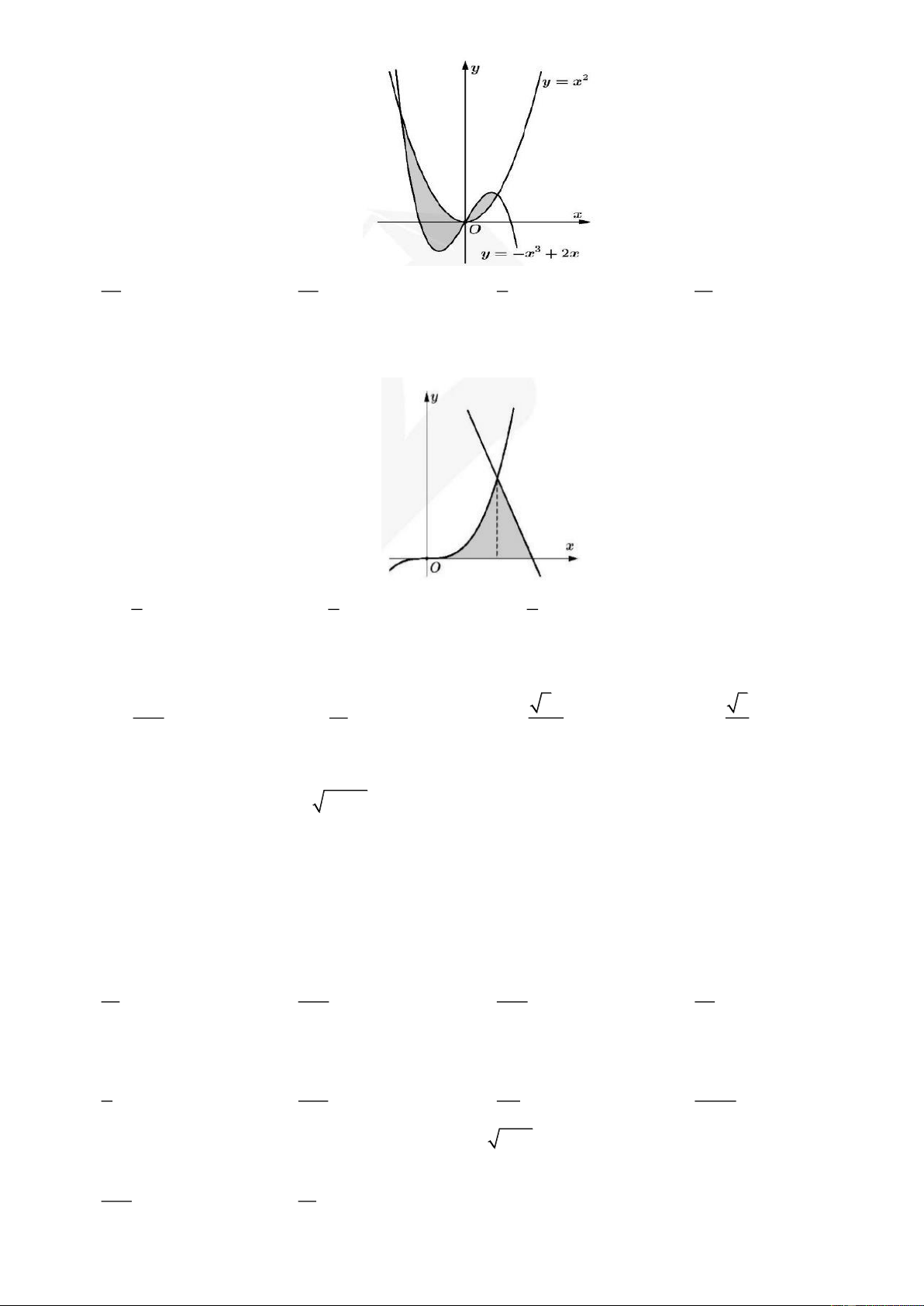
Ví dụ 1: Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên dưới. Xây dựng công thức tính S. Lời giải
Thấy rằng đồ thị hàm số y  f x cắt trục Ox tại ba điểm x  1
 ; x 1; x  2 . 2 1 2 1 2
Do đó S   f x dx   f xdx  
 f xdx   f xdx  
 f xdx . 1  1  1 1  1
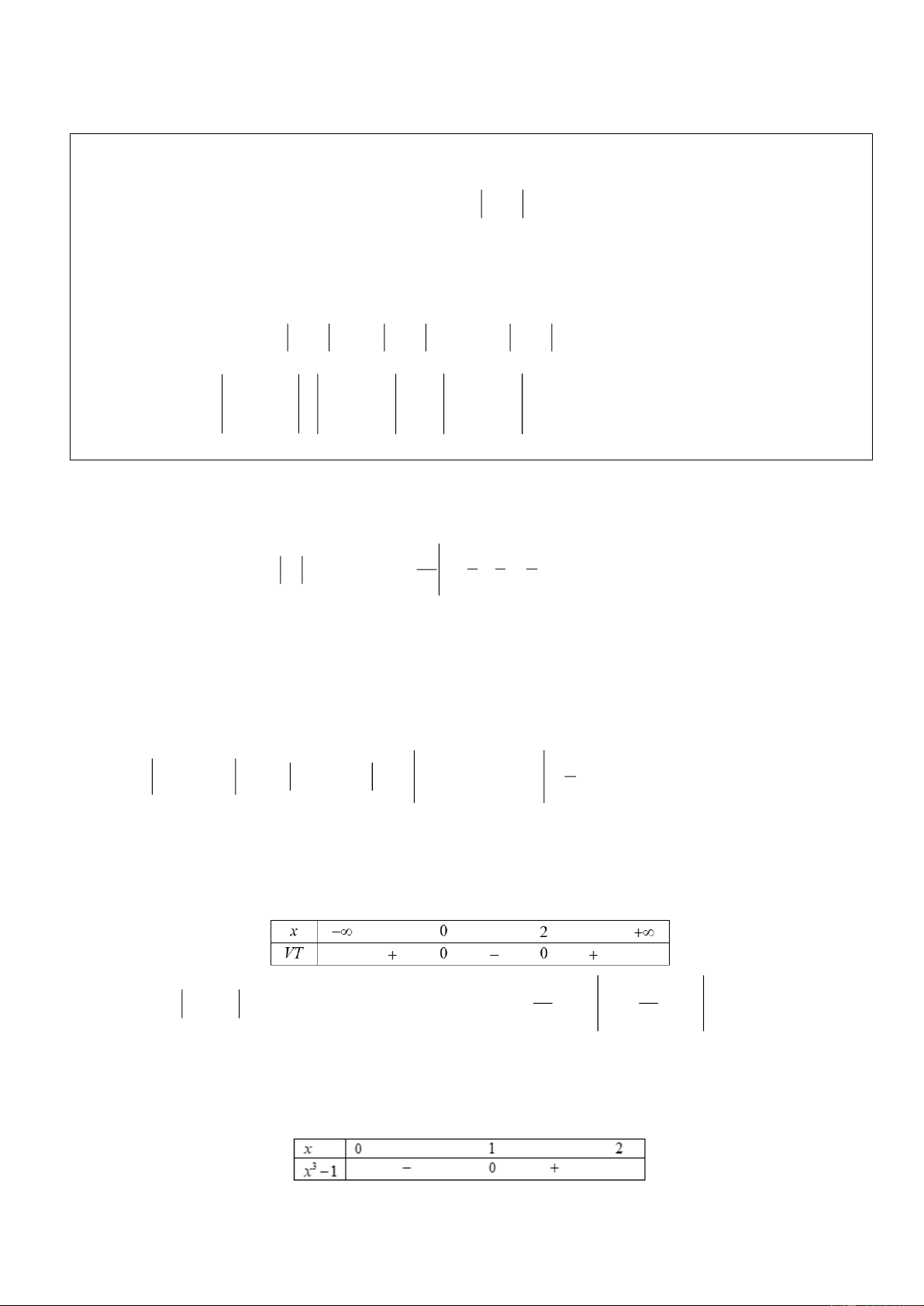
Ví dụ 2: Cho đồ thị y  f x như hình vẽ bên. Xác định công thức diện tích miền được gạch sọc ở hình bên. Lời giải 2
y  x  3  Ta có: H 2
: y  x  2x 1. x  1  ; x  2  2 2 Ta có: S   2 x  3  2 x  2x   1dx   2 2
 x  2x  4dx (do trên đoạn  1  ; 2   phần đồ thị 2
y  x  3 1  1  nằm trên đồ thị 2
y  x  2x 1).
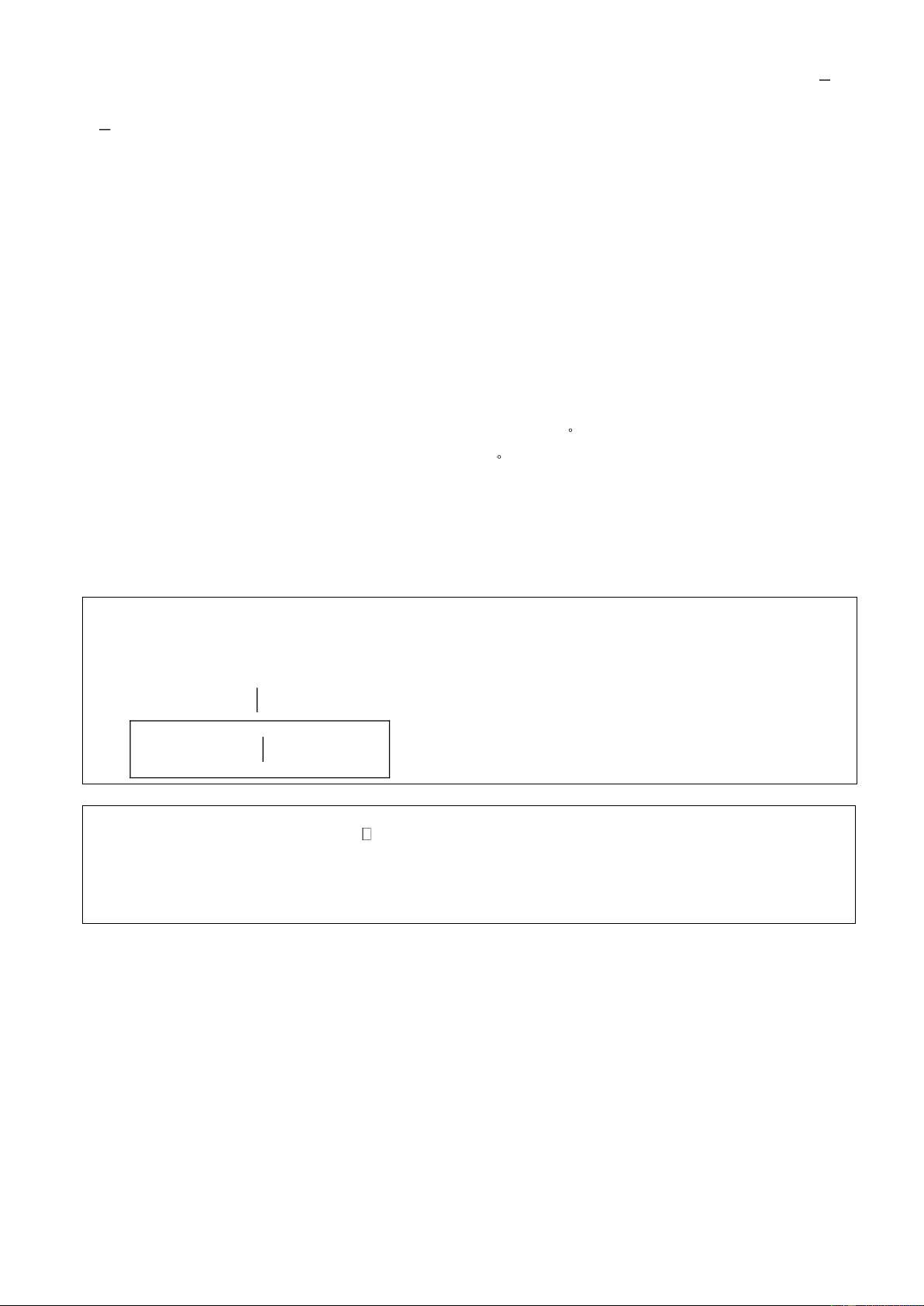
Ví dụ 3: Cho hàm số y  f x liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị
hàm số đã cho và trục Ox . Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được
xác định theo công thức gì? Lời giải Trang 13 3 2
Thể tích khối tròn xoay khi quay hình phẳng D quanh trục Ox : V  p  f
 x dx  . 1
Dạng 2. Diện tích hình phẳng giới hạn bởi y = f(x), Ox và x = a, x = b Phương pháp
y  f x  b
Diện tích hình phẳng giới hạn: Ox
 S   f x dx.
x  a;x  a  b
Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau:
» Bước 1: Giải f x  0 tìm nghiệm x , x ,..., x  a; b a  x  x  ...  x  b . 1 2 n  1 2 n   x x 1 2 b
» Bước 2: Tính S  f
 x dx f
 x dx... f  x dx a x x 1 n x x 1  f  x 2 b dx  f
 xdx ... f  xdx a x x 1 n
Chú ý: Ngoài cách trên, ta có thể dựa vào đồ thị để bỏ dấu giá trị tuyệt đối.
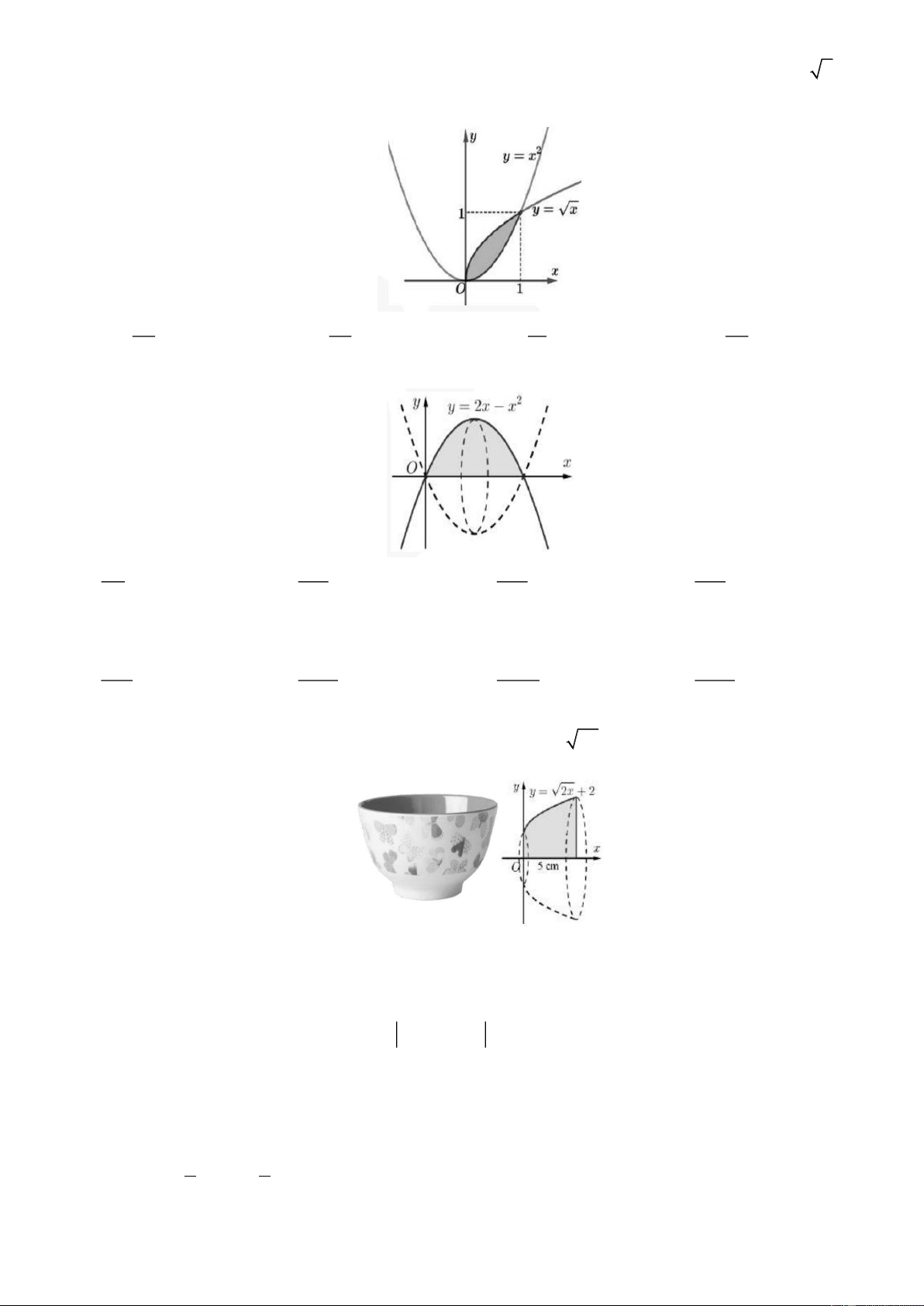
Ví dụ 4: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y  x , trục hoành Ox , các đường thẳng
x 1, x  2 . Lời giải 2 2 2 3
Diện tích hình phẳng là x 2 S  x dx  2  x dx   8 1   7  . 3 3 3 3 1 1 1
Ví dụ 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  x  2 2
1, trục hoành và hai đường thẳng
x 1,x  2 . Lời giải x 
Xét phương trình x  2 1 2 1  0   . x  3 2 2 2 2 2
Ta có: S  x  2 2
1 dx  x  4x  3 dx   2
x  4x  3dx     . 3 1 1 1
Ví dụ 6: Tính diện tích S của hình phẳng giới hạn bởi 2
y  x  2x , y  0 , x  4  , x 1. Lời giải x  0
Xét phương trình hoành độ giao điểm: 2
x  2x  0   . x  2 0 1 1 0 1 3 3     Diện tích: x x 2 S 
x  2x dx  
  2x 2xdx 2x 2xdx 2 2
   x    x   38 . 3 3     4  4  0 4  0
Ví dụ 7: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 3
y  x 1, trục hoành, trục tung và
đường thẳng x  2. Lời giải
Phương trình hoành độ giao điểm 3
x 1 0  x 1. Trang 14 1 2 2 1 2 1 2 4 4  x   x  7 3 3 3
S  x 1 dx  x 1dx  x 1dx      3
1 x dx   3 x   
1dx x   x  . 4 4 2     0 0 1 0 1 0 1
Dạng 3. Diện tích hình phẳng giới hạn bởi y = f(x), y = g(x) và x = a, x = b Phương pháp
y  f x  b
Diện tích hình phẳng giới hạn: y  gx  S   f x gx dx .
x  a;x  a  b
Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau:
» Bước 1: Giải f x  g x tìm nghiệm x , x ,..., x  a; b a  x  x  ...  x  b . 1 2 n  1 2 n   x x 1 2 b
» Bước 2: Tính S  f
 x gx dx f
 xgx dx... f
 xgx dx a x x 1 n x x 1
  f x gx 2 b
dx    f x gxdx ...   f x gxdx a x x 1 n
Chú ý: Ngoài cách trên, ta có thể dựa vào đồ thị để bỏ dấu giá trị tuyệt đối.
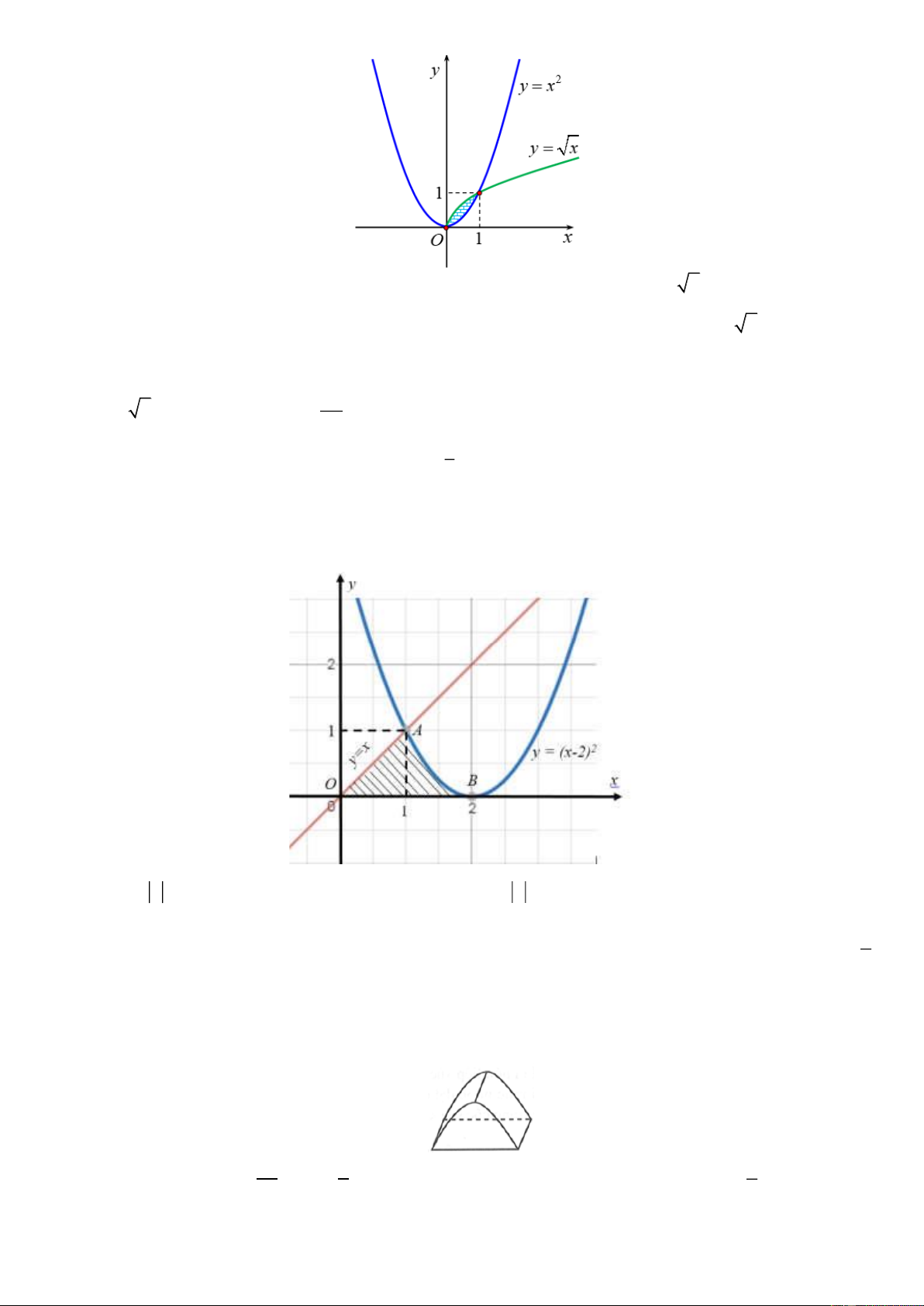
Ví dụ 8: Hình phẳng giới hạn bởi các đường cong y  x1 x và 3
y  x  x có diện tích bằng bao nhiêu? Lời giải x  0 
Ta có: x 1 x 3 3 2
 x  x  x  x  2x  0  x  2   x 1 
Gọi S là diện tích hình phẳng giới hạn bởi các đường cong y  x1 x và 3
y  x  x . 1 0 1 Khi đó 3 2 3 2 3 2 S 
x  x  2x dx 
x  x  2x dx  x  x  2x dx    2  2  0 0
 x  x  2x 1 8 5 37 3 2 dx   3 2
x  x  2xdx      ( đvdt). 3 12 12 2  0
Dạng 4. Thể tích vật thể tính theo mặt cắt vuông góc trục hoành
Ví dụ 9: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x 1 và x  3, biết rằng khi cắt vật thể
bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x 1
(  x  3) thì được thiết diện là một hình
chữ nhật có hai cạnh là 3x và 2 x . Lời giải
Ta có diện tích thiết diện: Sx 2 3  3 . x x  3x . 3 3 3 Khi đó 3 4 V  3x x  x  60  d . 4 1 1
Ví dụ 10: Tính thể tích V của vật thể nằm giữa hai mặt phẳng x  0 và x  p , biết rằng thiết diện của vật thể
bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x  p  là một tam giác đều cạnh 2 sin x . Lời giải
Ta có diện tích thiết diện: Sx  2 sin x 2 3 .  3 sin x . 4 Trang 15 p p p
V  Sxdx  3 s n
i xdx   3 o c sx  2 3  . 0 0 0
Dạng 5. Thể tích khối tròn xoay
Ví dụ 11: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y  x , trục Ox và hai đường thẳng
x 1; x  4 khi quay quanh trục hoành được tính bởi công thức nào? Lời giải
Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y  x , trục Ox , x 1 và x  4 được tính bởi công thức 4
V  p  x  4 2
dx  p xdx  . 1 1
Ví dụ 12: Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox : 2
y  2x  x , y  0, x  0, x  2. Lời giải 2 2 16
Thể tích khối tròn xoay V  p  2 2x  
x  dx  p . 15 0
C. BÀI TẬP TRẮC NGHIỆM
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Diện tích hình phẳng giới hạn bởi hai đường thẳng x  0, x   , đồ thị hàm số y  cos x và trục Ox là    
A. S  cos x dx  B. 2
S  cos x dx  . C. S  cos x dx  .
D. S   cos x dx  . 0 0 0 0
Câu 2. Gọi V là thể tích khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường x
y  e , y  0, x  0, x  2 quay quanh Ox . Phát biểu nào sau đây là đúng? 2 2 2 2 A. 2 x
V   e dx  . B. x
V  e dx  . C. x
V   e dx  . D. 2 x
V  e dx  . 0 0 0 0
Câu 3. Cho hàm số f  x liên tục trên R . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y  f  x, y  0, x  1
 , x  2 (như hình vẽ). Mệnh đề nào dưới đây đúng? A 1 . S   f   1 2      x 2 dx f x dx . B. S f x dx f x dx . 1    1   1 1   C 1
. S    f   1 2      x 2 dx f x dx . D. S f x dx f x dx . 1    1   1 1  
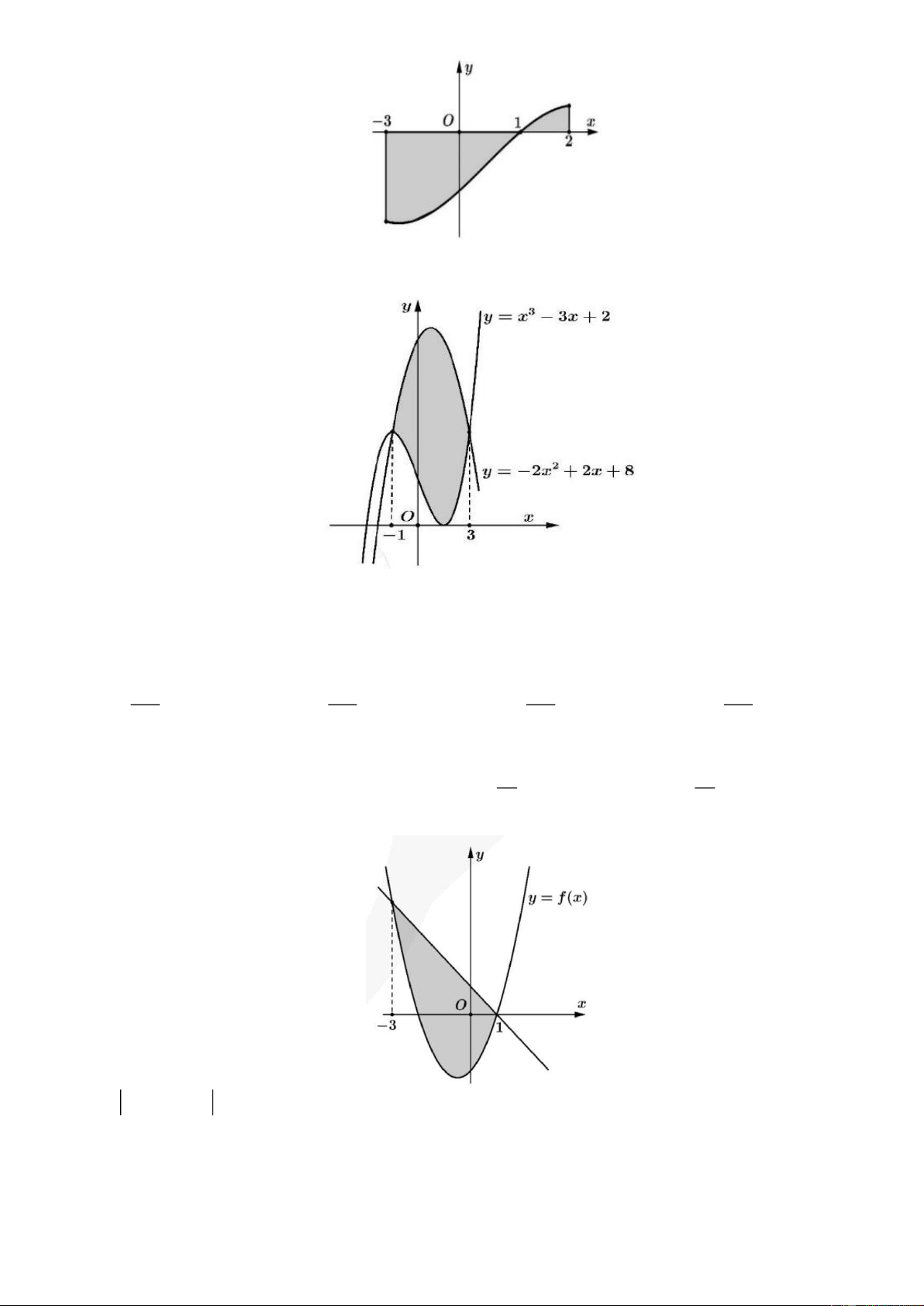
Câu 4. Gọi S là diện tích hình phẳng giới hạn bởi các đường y  f  x , trục hoành và hai đường thẳng x  3
 , x  2 (như hình vẽ). Đặt 1 a   f    x 2 d , x b
f x dx . Mệnh đề nào sau đây là đúng? 3 1   Trang 16
A . S  a  b .
B. S  a  b .
C. S  a b .
D. S  b  a .
Câu 5. Diện tích hình phẳng phần gạch chéo trong hình vẽ bên được tính theo công thức nào sau đây? A 3 . S      3 3 2        3 2 x 2x 5x 6 dx . B. S x 2x x 10 dx . 1    1  C 3 . S      3 3 2         3 2 x 2x x 10 dx . D. S x 2x 5x 6 dx . 1    1 
Câu 6. Tính diện tích S hình phẳng H  giới hạn bởi đường cong 3
y  x 12x và 2 y  x . 937 343 397 793 A . S  . B. S  . C. S  . D. S  . 12 12 4 4
Câu 7. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 y  x và 2
y  8  x là 3 64 A. 12. B. 32. C. . D. . 64 3
Câu 8. Diện tích phần sạch sọc trong hình vẽ bằng A 1 2 . 
x  2x  3 dx . B 1 .    1 2    1 2       2 x 2x 3 dx . C. x 2x 3 dx . D. x 2x 3 dx . 3    3    3  3 
Câu 9. Diện tích của phần hình phẳng gạch chéo trong hình bên bằng Trang 17 55 37 9 15 A . . B. . C. . D. . 12 12 4 4
Câu 10. Cho hình H  là hình phẳng giới hạn bởi đường cong 3
y  x , đường thẳng y  2  x  3 và trục
hoành (phần gạch chéo trong hình vẽ). Diện tích hình phẳng H  là 1 1 5 A . S  . B. S  . C. S  . D. S  2. 4 2 4
Câu 11. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  0, x  1, có thiết diện bị cắt bởi mặt
phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x  
1 là một tam giác đều có cạnh bằng x . 12 12 3 3 A . V  . B. V  . C. V  . D. V  . 5 5 12 12
Câu 12. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  0 và x  3, biết rằng khi cắt vật thể
bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x ( 0  x  3 ) thì được thiết diện là một
hình vuông có độ dài cạnh bằng 2 2 9  x . A. 90. B. 72 . C. 78 . D. 72.
Câu 13. Cho hình phẳng H  giới hạn bởi đồ thị hàm số x
y  e , các đường thẳng x  0, x  ln3 và trục
hoành. Thế tích khối tròn xoay sinh bởi H  khi quay quanh trục hoành là A . 2 . B. 4 . C. 4. D.  .
Câu 14. Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y  x  4x  3 và
y  0 quanh trục Ox bằng 16 16 31 31 A . . B. . C. . D. . 15 15 30 30
Câu 15. Thể tích vất thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  4x và trục hoành quay quanh Ox là 4 512 4 512 A . . B. . C. . D. . 3 15 3 15
Câu 16. Cho hình phẳng D giới hạn bởi các đường y 
x 1 , trục hoành và x  5. Thể tích khối tròn xoay
tạo thành khi quay D quanh trục Ox bằng 15 15 A . . B. . C. 8 . D. 8. 2 2 Trang 18
Câu 17. Cho hình phẳng H  được giới hạn bởi đồ thị của hàm số 2
y  x và đồ thị của hàm số y  x (tham
khảo hình vẽ). Thể tích của khối tròn xoay thu được khi quay H  quanh trục Ox bằng 9 3  7 A . V  . B. V  . C. V  . D. V  . 10 10 10 10
Câu 18. Thể tích khối tròn xoay giới hạn bởi các đường 2
y  2x  x , y  0 khi quay quanh trục Ox là 4 13 14 16 A . . B. . C. . D. . 3 15 15 15
Câu 19. Cho hình phẳng giới hạn bởi đồ thị hàm số 2
y  x và đường thẳng y  4 quay quanh trục Ox . Thể
tích khối tròn xoay sinh ra bằng 64 128 256 152 A . . B. . C. . D. . 5 5 5 5
Câu 20. Tính thể tích chứa được của một cái chén, biết phần trong của nó có dạng khối tròn xoay được tạo
thành khi quay quanh trục Ox hình phẳng giới hạn bởi đường y  2x  2 và trục Ox (như hình vẽ), bát có
độ sâu 5 cm, đơn vị trên trục là centimet (làm tròn đến hàng đơn vị). A 3 . 78 cm . B 3 . 274 cm . C 3 . 87 cm . D 3 . 247 cm .
Phần 2. Trắc nghiệm đúng – sai
Câu 1. Cho hình phẳng H  giới hạn bởi các đường 2
y  x  4x  4 C , y  4x 12 C và trục Ox . 2  1  4
a) Diện tích của hình phẳng H  là 2 S 
x  8x 16 dx  . 3 4 4 2 2
b) Thể tích của vật tròn xoay là V
   2x  4x  4 dx  4x 12 dx . Ox 2 3
c) Các đường C và C đều đi qua điểm M 4;4 . 2  1  a d) Nếu V
 . (với a là phân số tối giản) thì a b  32. Ox b b
Câu 2. Cho hình phẳng được tô trong hình bên dưới. Trang 19
a) Hình phẳng được tô màu trong hình trên được giới hạn các đồ thị 2
y  x ; y  x . 1
b) Thể tích của vật tròn xoay tạo thành khi quay hình phẳng trên quanh trục Ox là   2
x  x dx . 0
c) Thể tích V của vật tròn xoay tạo thành khi quay hình phẳng H  giới hạn bởi các đường P 2 : y  x ;  
C  : y  x quanh trục Ox bằng 3 . 10 1
d) Diện tích hình phẳng tô màu trong hình vẽ là . 3
Câu 3. Đồ thị các đường 2 y  ;
x y  (x  2) cho bởi hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi 1
đường y  x , trục hoành, x  0; x  1. S diện tích hình phẳng giới hạn bởi đường y   x  2 1 , trục hoành, 2
x  1; x  2 . 1 1 1 a) S  x dx  . b) S  x dx  d x x   . 1 1 0 0 0 2 2 c) S   x  2 dx  .
d) Diện tích hình phẳng phần gạch chéo trên hình bằng 1 . 2   6 1
Câu 4. Để tham dự hội chợ xuân người ta dự định dựng một lều trại có dạng parabol, với kích thước: nền trại
là hình chữ nhật ABCD có chiều rộng là 3 mét, chiều sâu là 6 mét và trải thảm, đỉnh I của parabol cách mặt
đất là 3 mét. Chọn hệ trục tọa độ Oxy sao cho: O là trung điểm của cạnh AB, A, B thuộc trục hoành và I thuộc trục tung.  3    3  4
a) Tọa độ các điểm A ; 0 , B ; 0 , I   
 0;3 . b) Phương trình của parabol là 2 y   x  6 .  2   2  3
c) Diện tích thảm làm nền là 2 18m .
d) Thể tích phần không gian phía trong trại là 3 V  36m . Trang 20

Chuyên Đề Nguyên Hàm Và Tích Phân Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Tài liệu liên quan:

Chuyên Đề Cấp Số Cộng Cấp Số Nhân Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên Đề Nguyên Hàm Tích Phân Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên Đề Hình Học Không Gian Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên Đề Vectơ Và Phương Pháp Tọa Độ Trong Không Gian Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên Đề Một Số Yếu Tố Thống Kê Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết