






Preview text:
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN MỤC LỤC Trang
ĐỀ MINH HỌA BGD KỲ THI THPT QUỐC GIA NĂM 2025 .................... 1
Kiến thức cần nhớ về ứng dụng đạo hàm ................................................................................ 5
Dạng toán 1. Câu 13. Trả lời đúng sai liên quan đến ứng dụng đạo hàm (60 Câu BTRL) ... 15
Dạng toán 2. Câu 14. Trả lời đúng sai liên quan đến toán chuyển động (60 Câu BTRL) .... 29
Dạng toán 3. Câu 15. Trả lời đúng sai liên quan đến xác suất, thống kê (60 Câu BTRL) ... 49
Dạng toán 4. Câu 16. Trả lời đúng sai liên quan đến hình học Oxyz (50 Câu BTRL) ......... 82
Dạng toán 5. Câu 17. Trả lời ngắn: Bài toán khoảng cách (90 Câu BTRL)........................ 97
Dạng toán 6. Câu 18. Trả lời: Bài toán đường đi ngắn nhất (28 Câu BTRL) ..................... 118
Dạng toán 7. Câu 19. Trả lời ngắn: Bài toán hình học Oxyz (65 câu BTRL) ..................... 128
Dạng toán 8. Câu 20. Trả lời ngắn: Bài toán ứng dụng tích phân (74 Câu BTRL) ............. 146
Dạng toán 9. Câu 21. Trả lời ngắn: Bài toán thực tế ứng dụng đạo hàm (60 Câu BTRL)... 184
Dạng toán 10. Câu 22. Trả lời ngắn: Bài toán xác suất (80 Câu BTRL) ............................ 196
100 ĐỀ TRẮC NGHIỆM 4 PHƯƠNG ÁN ............................................................... 196
Đề số 01-25. ....................................................................................................................... 196
Đề số 26-50. ...................................................................................................................... 242
Đề số 51-75. ...................................................................................................................... 277
Đề số 76-100. .................................................................................................................... 314
Phụ lục. ............................................................................................................................. 351
https://www.facebook.com/ToanThayTienHa/
https://www.facebook.com/ThayHaPowerMath/
ĐT: 0949.888.993 – Zalo Thầy Nguyễn Tiến Hà
Quý thầy cô cần file dạy xin liên hệ tác giả (phí coffee ạ), file GV và file HS.
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
ĐỀ MINH HỌA KỲ THI THPT QUỐC GIA NĂM 2025
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Nguyên hàm của hàm số x
f x e là x 1 e x e A. C . B. x
e C . C. C . D. 1 . x x e C . x 1 x NGUY
Câu 2: Cho hàm số y f x liên tục, nhận giá trị dương trên đoạn a ;b
. Xét hình phẳng H giới
hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x a ,x b . Khối tròn ỄN TI
xoay được tạo thành khi quay hình phẳng H quanh trục Ox có thể tích là b b Ế A. V π f
x dx . B. V π2 f xdx . N H a a b b À 2 2 2 C. V π f
x dx . D. V π f
x dx . a a
Câu 3: Hai mẫu số liệu ghép nhóm M , M có bảng tần số ghép nhóm như sau: 1 2 Nhóm 8;10 10;12 12;14 14;16 16;18 M 1 Tần số 3 4 8 6 4 Nhóm 8;10 10;12 12;14 14;16 16;18 M 2 Tần số 6 8 16 12 8
Gọi s , s lần lượt là độ lệch chuẩn của mẫu số liệu ghép nhóm M , M . Phát biểu nào sau 1 2 1 2 đây là đúng?
A. s s .
B. s 2s .
C. 2s s .
D. 4s s . 1 2 1 2 1 2 1 2 NGUY
Câu 4: Trong không gian với hệ trục tọa độ Oxyz , phương trình của đường thẳng đi qua điểm
M 1;3;5 và có một vectơ chỉ phương u 2;1; 1 là Ễ x 1 y 3 z 5 x 1 y 3 z 5 N TI A. . B. . 2 1 1 2 1 1 x 1 y 3 z 5 x 1 y 3 z 5 Ế C. . D. . N H 2 1 1 2 1 1 ax b À
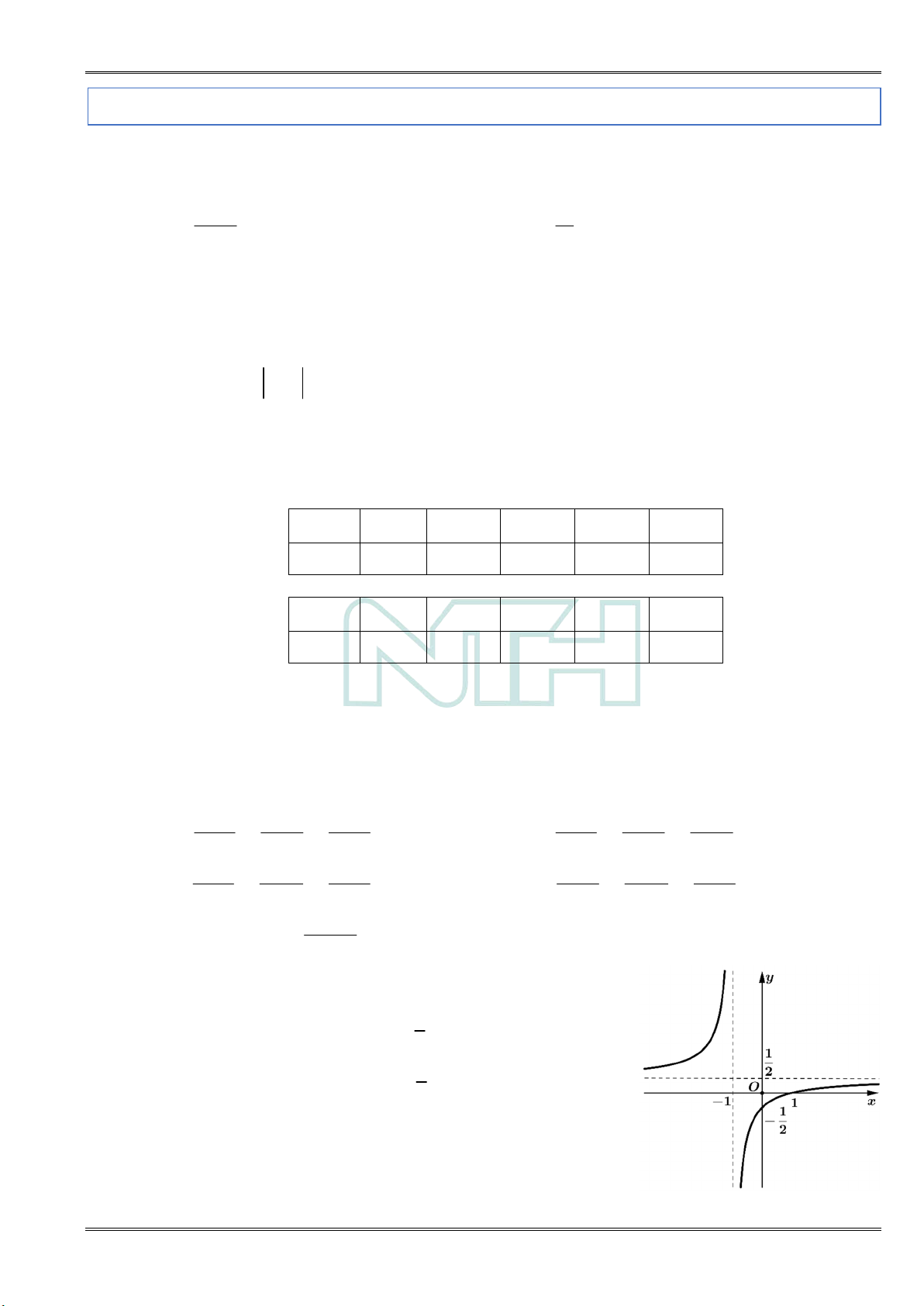
Câu 5: Cho hàm số y
c 0,ad bc 0 có đồ thị như hình vẽ bên. Tiệm cận ngang cx d
của đồ thị hàm số là 1 A. x 1 . B. y . 2 1
C. y 1 . D. x . 2
Câu 6: Tập nghiệm của bất phương trình log x 1 3 là 2 A. 1;9. B. ;9. C. 9; . D. 1;7.
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 1
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
Câu 7: Trong không gian với hệ trục Oxyz , cho mặt phẳng P có phương trình x 3y z 8 0
. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng P ?
A. n 1;3;1 .
B. n 1;3;1 .
C. n 1;3; 8 . D. n 1; 3; 8 . 4 3 2 1
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ABCD. Mặt phẳng
nào sau đây vuông góc với mặt phẳng ABCD? NGUY
A. SAB.
B. SBC .
C. SCD. D. SBD.
Câu 9: Nghiệm của phương trình 2x 6 là x log 2 x x x log 6 Ễ A. . B. 3 . C. 4 . D. . 6 2 N TI
Câu 10: Cấp số cộng u có u 1 và u 3 . Số hạng u của cấp số cộng là n 1 2 5 Ế A. 5. B. 7. C. 9. D. 11. N H
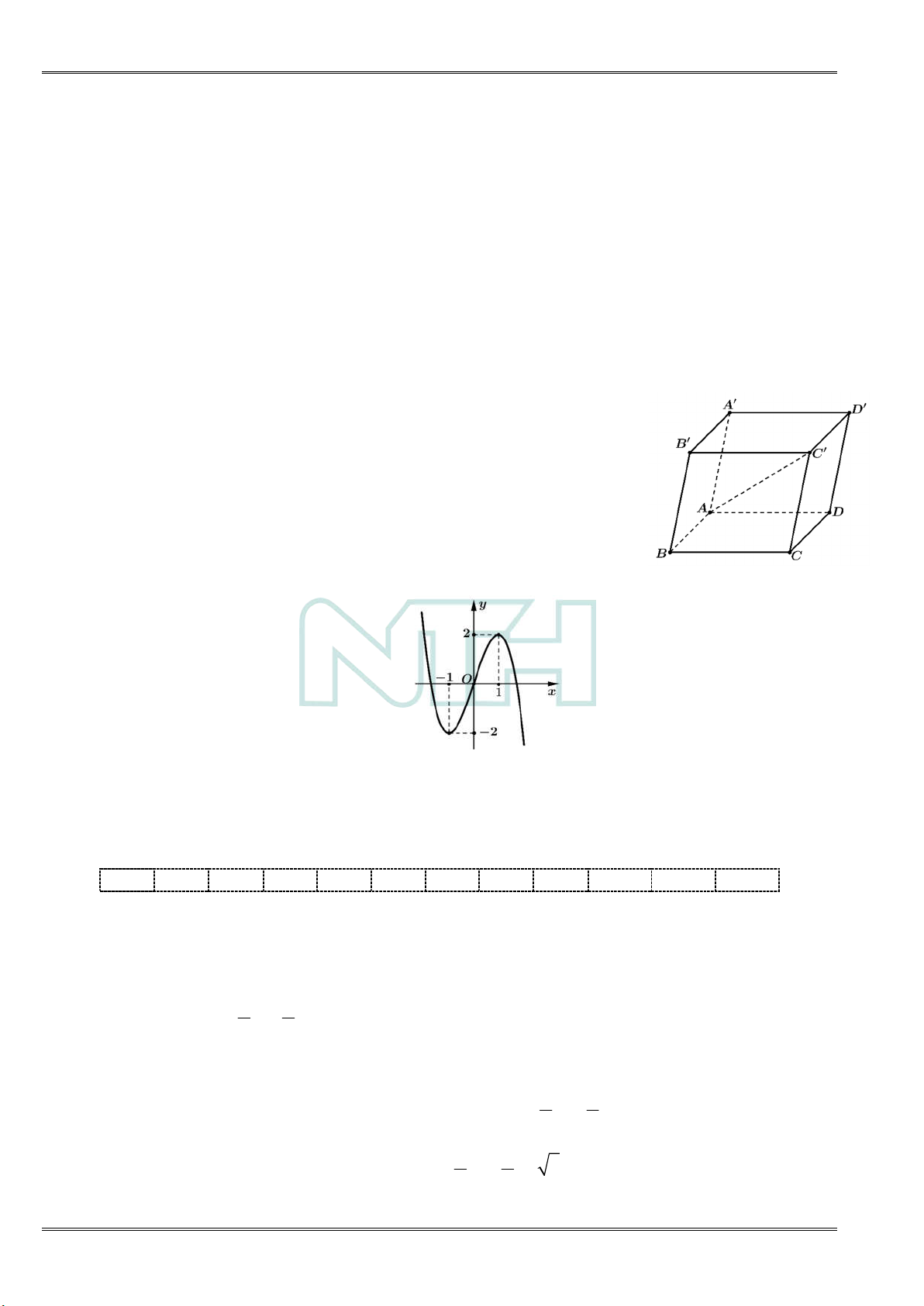
Câu 11: Cho hình hộp ABCD.AB C D
(minh họa như hình bên).
Phát biểu nào sau đây là đúng? À
A. AB BB B A
AC .
B. AB BC C D
AC .
C. AB AC AA AC .
D. AB AA AD AC .
Câu 12: Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến
trên khoảng nào sau đây? NGUY A. ; 1 . B. ; 1 . C. 1; 1 . D. 1;. ----------------- Ễ N TI BẢNG ĐÁP ÁN Ế 1.B 2.D 3.A 4.C 5.B 6.A 7.B 8.A 9.D 10.C 11.D 12.C N H
PHẦN II. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn À đúng hoặc sai.
Câu 13: Cho hàm số f x 2 cos x x . a) f π π 0 2; f . 2 2
b) Đạo hàm của hàm số đã cho là f x 2 sin x 1 . π π
c) Nghiệm của phương trình f x 0 trên đoạn 0; là . 2 6 π π
d) Giá trị lớn nhất của f x trên đoạn 0; là 3 . 2 6
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 2
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
Câu 14: Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô
cách điểm nhập làn 200 m, tốc độ của ô tô là 36 km/h. Hai giây sau đó, ô tô bắt đầu tăng
tốc với tốc độ v t at b (a,b ,a
0 ), trong đó t là thời gian tính bằng giây kể từ
khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 12 giây và duy trì sự tăng tốc
trong 24 giây kể từ khi bắt đầu tăng tốc.
a) Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 180m.
b) Giá trị của b là 10. NGUY
c) Quãng đường S t (đơn vị: mét) mà ô tô đi được trong thời gian t giây ( 0 t 24 ) kể 24
từ khi tăng tốc được tính theo công thức: S t v tdt . Ễ 0 N TI
d) Sau 24 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho phép là 100 km/h. Ế
Câu 15: Trước khi đưa một loại sản phẩm ra thị trường, người ta đã phỏng vấn ngẫu nhiên 200 N H
khách hàng về sản phẩm đó. Kết quả thống kê như sau: có 105 người trả lời “sẽ mua”; có À
95 người trả lời “không mua”. Kinh nghiệm cho thấy tỉ lệ khách hàng thực sự sẽ mua sản
phẩm tương ứng với những cách trả lời “sẽ mua” và “không mua” lần lượt là 70% và 30%.
Gọi A là biến cố “Người được phỏng vấn thực sự sẽ mua sản phẩm”.
Gọi B là biến cố “Người được phỏng vấn trả lời sẽ mua sản phẩm”.
a) Xác suất P B 21 và P B 19 . 40 40
b) Xác suất có điều kiện P | A B 0, 3 .
c) Xác suất P A 0, 51 .
d) Trong số những người được phỏng vấn thực sự sẽ mua sản phẩm có 70% người đã trả lời
“sẽ mua” khi được phỏng vấn (kết quả tính theo phần trăm được làm tròn đến hàng đơn vị).
Câu 16: Các thiên thạch có đường kính lớn hơn 140 m và có thể lại gần Trái Đất ở khoảng cách nhỏ
hơn 7 500 000 km được coi là những vật thể có khả
năng va chạm gây nguy hiểm cho Trái Đất. Để NGUY
theo dõi những thiên thạch này, người ta đã thiết
lập các trạm quan sát các vật thể bay gần Trái Đất.
Giả sử có một hệ thống quan sát có khả năng theo Ễ
dõi các vật thể ở độ cao không vượt quá 6 600 km N TI
so với mực nước biển. Coi Trái Đất là khối cầu có
bán kính 6 400 km. Chọn hệ trục tọa độ Oxyz Ế N H
trong không gian có gốc O tại tâm Trái Đất và đơn
vị độ dài trên mỗi trục tọa độ là 1000 km. Một thiên À
thạch (coi như một hạt) chuyển động với tốc độ
không đổi theo một đường thẳng từ điểm
M 6;20;0 đến điểm N 6;12;16.
x 6 3t
a) Đường thẳng MN có phương trình tham số là y 20 8t (t ).
z 4t
b) Vị trí đầu tiên thiên thạch di chuyển vào phạm vi theo dõi của hệ thống quan sát là điểm A3;4;12.
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 3
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
c) Khoảng cách giữa vị trí đầu tiên và vị trí cuối cùng mà thiên thạch di chuyển trong phạm
vi theo dõi của hệ thống quan sát là 18 900 km (kết quả làm tròn đến hàng trăm theo đơn vị km).
d) Nếu thời gian di chuyển của thiên thạch trong phạm vi theo dõi của hệ thống quan sát
là 3 phút thì thời gian nó di chuyển từ M đến N là 6 phút.
PHẦN III. Thí sinh trả lời từ câu 17 đến câu 22 NGUY
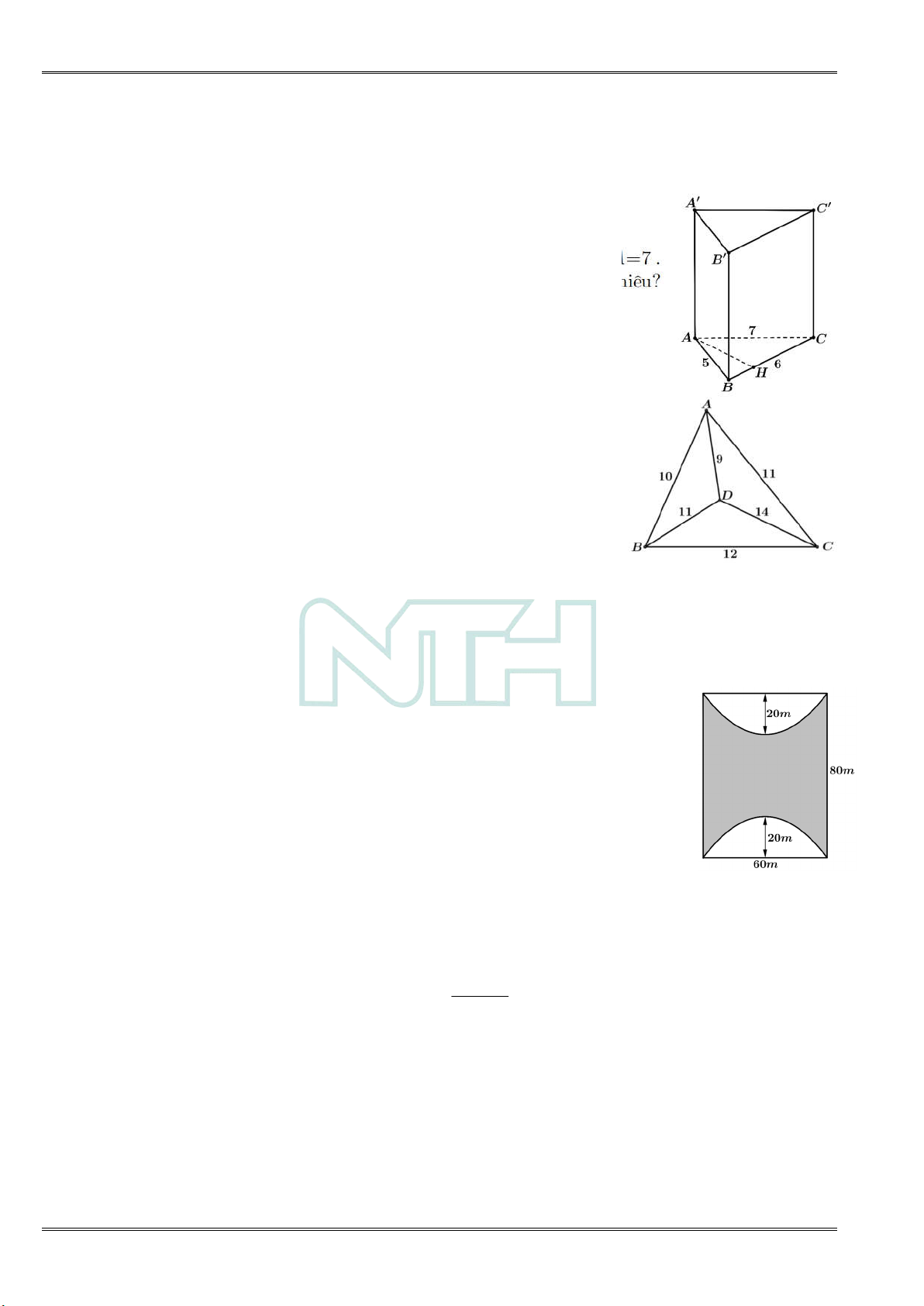
Câu 17: Cho hình lăng trụ đứng ABC .AB C
có AB 5 , BC 6 , CA 7 .
Khoảng cách giữa hai đường thẳng AA và BC bằng bao nhiêu?
(làm tròn kết quả đến hàng phần mười). Ễ N TI Ế
Câu 18: Một trò chơi điện tử quy định như sau: Có 4 trụ , A , B C,D với N H
số lượng các thử thách trên đường đi giữa các cặp trụ được mô À
tả trong hình bên. Người chơi xuất phát từ một trụ nào đó, đi
qua tất cả các trụ còn lại, mỗi khi đi qua một trụ thì trụ đó sẽ
bị phá hủy và không thể quay trở lại trụ đó được nữa, nhưng
người chơi vẫn phải trở về trụ ban đầu. Tổng số thử thách của
đường đi thoả mãn điều kiện trên nhận giá trị nhỏ nhất là bao nhiêu?
Câu 19: Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác
định vị trí của một vật thể trong không gian. Trong cùng một thời điểm, vị trí của một
điểm M trong không gian sẽ được xác định bởi bốn vệ tinh cho trước nhờ các bộ thu phát
tín hiệu đặt trên các vệ tinh. Giả sử trong không gian với hệ tọa độ Oxyz , có bốn vệ tinh
lần lượt đặt tại các điểm A3;1; 0, B 3;6;6 , C 4;6;2 , D 6;2;14 ; vị trí M a;b;c thỏa
mãn MA 3 , MB 6 , MC 5 , MD 1
3 . Khoảng cách từ điểm M đến
điểm O bằng bao nhiêu? NGUY
Câu 20: Kiến trúc sư thiết kế một khu sinh hoạt cộng đồng có dạng hình chữ
nhật với chiều rộng và chiều dài lần lượt là 60m và 80m. Trong đó, phần
được tô màu đậm là sân chơi, phần còn lại để trồng hoa. Mỗi phần trồng Ễ
hoa có đường biên cong là một phần của parabol với đỉnh thuộc một N TI
trục đối xứng của hình chữ nhật và khoảng cách từ đỉnh đó đến trung
điểm cạnh tương ứng của hình chữ nhật bằng 20m (xem hình minh họa). Ế
Diện tích của phần sân chơi là bao nhiêu mét vuông? N H
Câu 21: Một doanh nghiệp dự định sản xuất không quá 500 sản phẩm. Nếu doanh nghiệp sản xuất
x sản phẩm (1 x 500 ) thì doanh thu nhận được khi bán hết số sản phẩm đó là À F x 3 2
x 1999x 1001000x 250000 (đồng), trong khi chi phí sản xuất bình quân
cho một sản phẩm là G x 250000 x 1000
(đồng). Doanh nghiệp cần sản xuất bao x
nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
Câu 22: Có hai chiếc hộp, hộp I có 6 quả bóng màu đỏ và 4 quả bóng màu vàng, hộp II có 7 quả
bóng màu đỏ và 3 quả bóng màu vàng, các quả bóng có cùng kích thước và khối lượng. Lấy
ngẫu nhiên một quả bóng từ hộp I bỏ vào hộp II. Sau đó, lấy ra ngẫu nhiên một quả bóng
từ hộp II. Tính xác suất để quả bóng được lấy ra từ hộp II là quả bóng được chuyển từ hộp
I sang, biết rằng quả bóng đó có màu đỏ (làm tròn kết quả đến hàng phần trăm).
-----------------HẾT-----------------
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 4
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
§ CHỦ ĐỀ 1. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dạng toán 1. Câu 13. Ứng dụng đạo hàm
KIẾN THỨC CẦN NHỚ
1. Caùc quy taéc tính ñaïo haøm u u v v u NGUY ( . u v) u v v . u ( . k ) u . k u , (k ) . 2 v v
2. Baûng ñaïo haøm cuûa Ễ N TI o (C ) 0 C . o x 1. Ế n n n n o x n x n u n u u n N H 1 . ( ). o 1 . . ( ). u À o x 1 (x 0). o u (u 0). 2 x 2 u 1 1 1 u o (x 0). o (u 0). 2 x x 2 u u o Công thức tính nhanh ax b 2 ad bc 2
a x b x c
abx 2acx bc 1) 1 1 1 2) (tích huyền trừ 2
cx d (cx d) 2 2 2
a x b x c
(a x b x c ) 2 2 2 2 2 2 tích sắc)
3. Baûng ñaïo haøm cuûa haøm soá löôïng giaùc
o (sin x) cos x.
o (sin u) u . cos . u
o (cos x) sin x. o (cos u) u .sin . u NGUY 1 u o 2
(tan x) 1 tan x o 2
(tan u) u .(1 tan u) 2 cos x 2 cos u Ễ 1 u N TI o 2 (cotx) (
1 cot x) o 2 (cotu) u
.(1 cot u) 2 sin x 2 sin u Ế
4. Baûng ñaïo haøm cuûa haøm soá muõ - logarit N H 1 u x x u u (log x) (lnu) À (a ) a .lna (e ) u .e a x lna u . ( u
a ) u . u a .lna
(ex ) ex u 1 (log u) (ln x) a u lna x
5. Caùc coâng thöùc löôïng giaùc quan troïng
5.1. Ñöôøng troøn löôïng giaùc vaø daáu cuûa caùc giaù trò löôïng giaùc Cung I II III IV phần tư
0 90 90 180 180 270 270 360 Giá trị LG sin + + – – cos + – – + tan + – + – cot + – + –
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 5
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
5.2. Coâng thöùc löôïng giaùc cô baûn 1 1 2 2
sin cos 1 2 2 1 tan 1 cot tan .
cot 1 2 cos 2 sin
5.3. Cung goùc lieân keát Cung đối nhau Cung bù nhau Cung phụ nhau
Cung hơn kém NGUY cos( a ) cosa
sin( a) sina
sin a cosa a a sin( ) sin 2 sin( a ) sina
cos( a) cosa
cos a sina a a cos( ) cos Ễ 2 N TI tan( a ) tana
tan( a) tana a a
tan a cota tan( ) tan 2 Ế N H cot( a ) cota
cot( a) cota
cot a tana cot( a) cota 2 À
5.4. Coâng thöùc coäng cung
sin(a b) sina cosb cosa sin . b
cos(a b) cosa cosb sina sin . b tana tanb tana tanb tan(a b) tan(a b)
1 tana tanb
1 tana tanb
5.5. Coâng thöùc nhaân ñoâi vaø haï baäc Nhân đôi Hạ bậc
sin2 2 sin cos 1 cos 2 2 sin 2 2 2
cos sin 1 cos 2 2 cos 2 cos 2 2
2 cos 1 1 2 sin 2 NGUY
5.6. Coâng thöùc bieán ñoåi toång thaønh tích Ễ a b a b a b a b N TI
cosa cosb 2 cos cos
cosa cosb 2 sin sin 2 2 2 2 Ế a b a b a b a b N H
sina sinb 2 sin cos
sina sinb 2 cos sin 2 2 2 2 À Đặc biệt
sin x cos x 2 sin x 2 cos x 4 4
sin x cos x 2 sin x
2 cos x 4 4
5.7. Coâng thöùc bieán ñoåi tích thaønh toång 1 1 cosa cosb
cos(a b) cos(a b) sina sinb
cos(a b) cos(a b) 2 2 1 sina cosb
sin(a b) sin(a b) 2
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 6
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
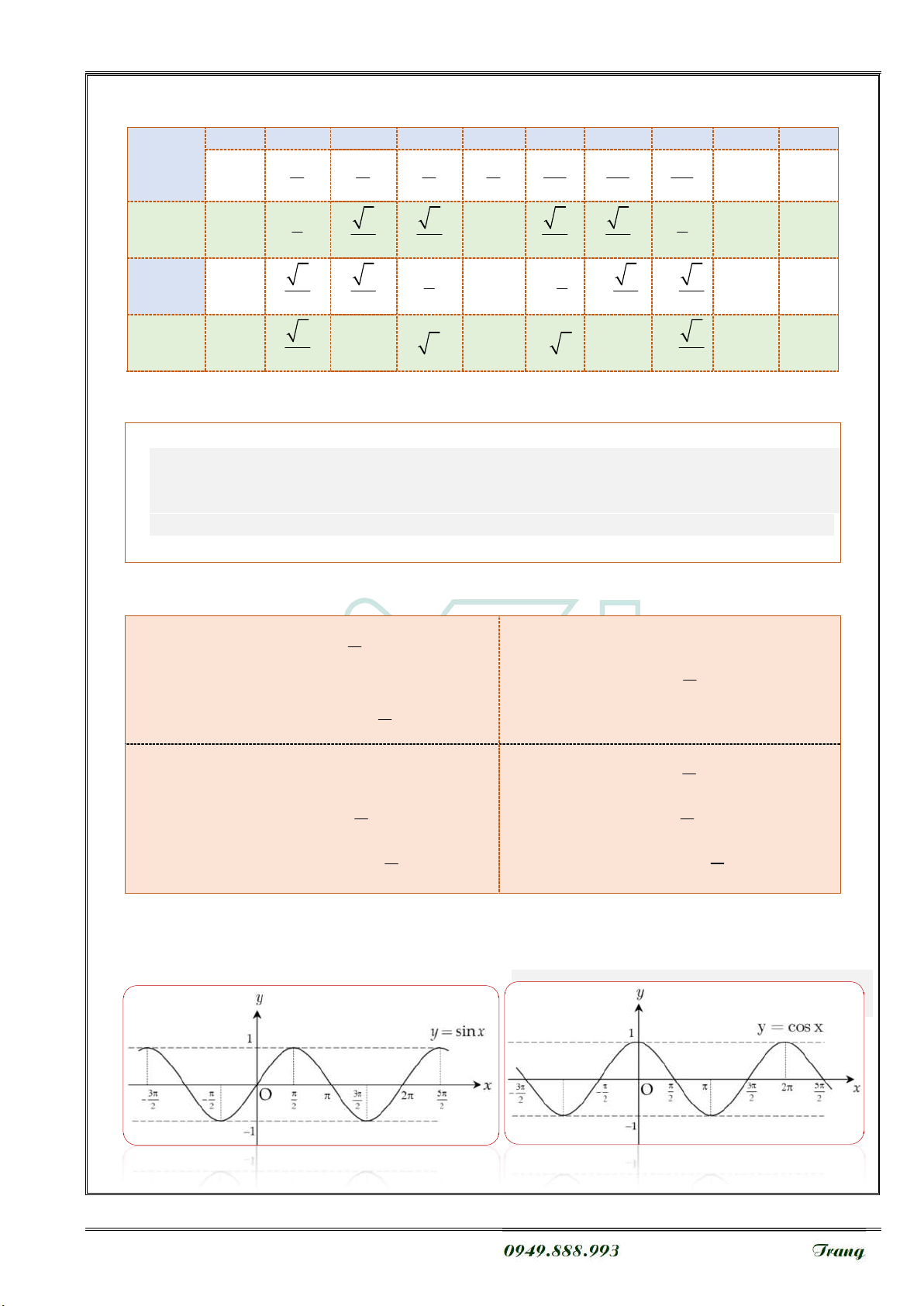
5.8. Baûng giaù trò löôïng giaùc moät soá goùc ñaëc bieät 00 300 450 600 900 1200 1350 1500 1800 3600 2 3 5 0 2 6 4 3 2 3 4 6 sin 1 2 3 3 2 1 0 1 0 0 2 2 2 2 2 2 NGUY cos 3 2 1 1 2 3 1 0 1 1 2 2 2 2 2 2 Ễ tan N TI 3 3 0 1 3 kxđ 3 1 0 0 3 3 Ế N H
5.9. Coâng thöùc nghieäm cuûa caùc phöông trình löôïng giaùc cô baûn À Với k ,
ta có các phương trình lượng giác cơ bản sau: a
b k2 a
b k2 sina sinb
cosa cosb a
b k2 a b k2
tana tanb a b k .
cota cotb a b k .
Nếu đề bài cho dạng độ ( )
thì ta sẽ chuyển k2 k360 ,
k k180 , với 180 . 5.10. Vôùi k ,
ta caàn nhôù nhöõng tröôøng hôïp nghieäm ñaëc bieät:
sin x 1 x k2
cos x 1 x k2 2
sin x 0 x k
cos x 0 x k 2
sin x 1 x k2
cos x 1 x k2 2 NGUY
tan x 0 x k
cotx 0 x k 2 Ễ
tan x 1 x k
cotx 1 x k N TI 4 4 tanx 1
x k
cotx 1 x k Ế 4 4 N H À
5.11. Ñoà thò haøm soá löôïng giaùc
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 7
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
6. ÖÙng duïng ñaïo haøm ñeå khaûo saùt haøm soá
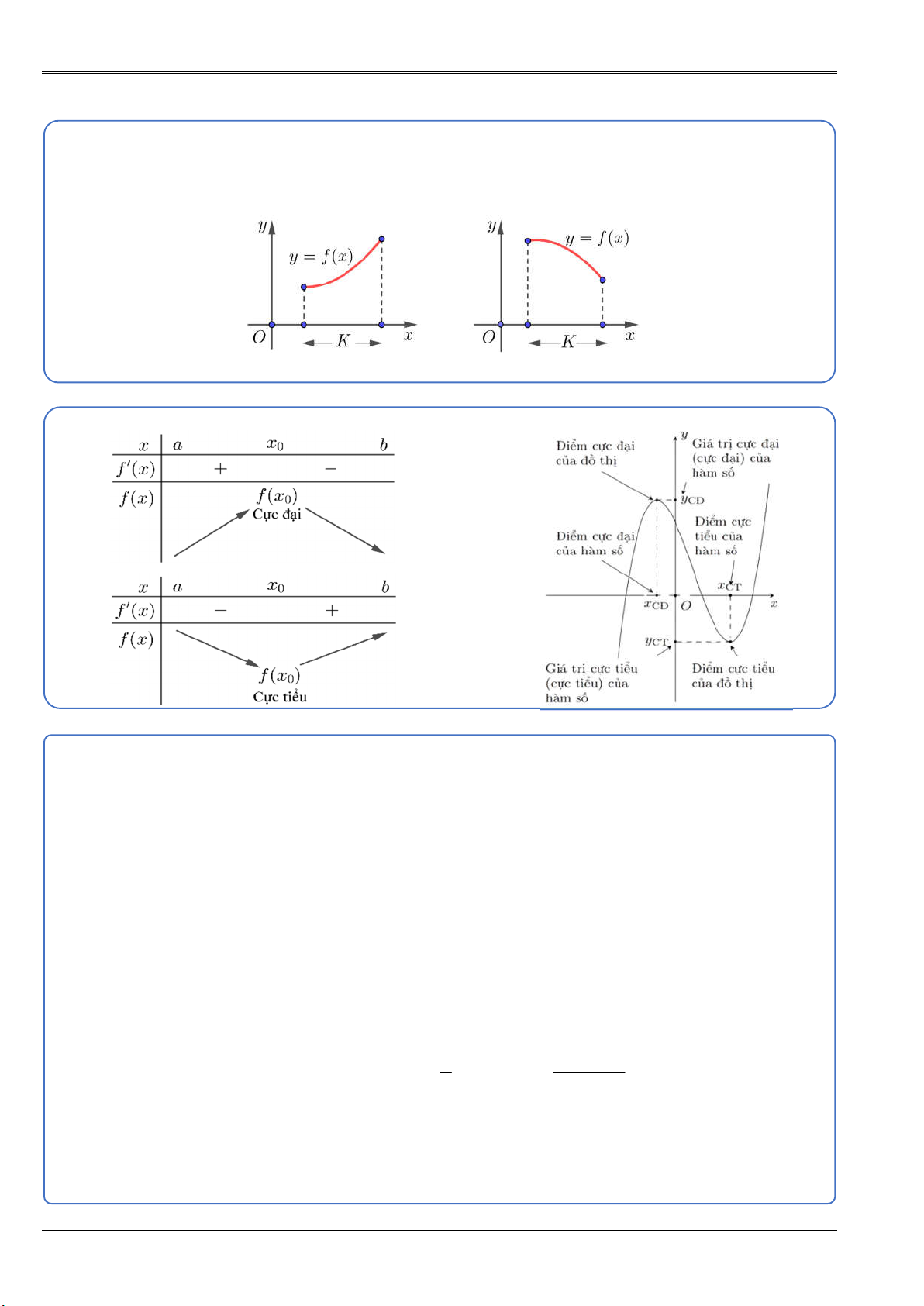
1. Tính đồng biến, nghịch biến của hàm số
Hàm số y f x đồng biến trên K thì đồ thị đi lên từ trái sang phải (Hình 1a).
Hàm số y f x nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (Hình 1b). NGUY Ễ N TI Hình 1a Hình 1b Ế N H
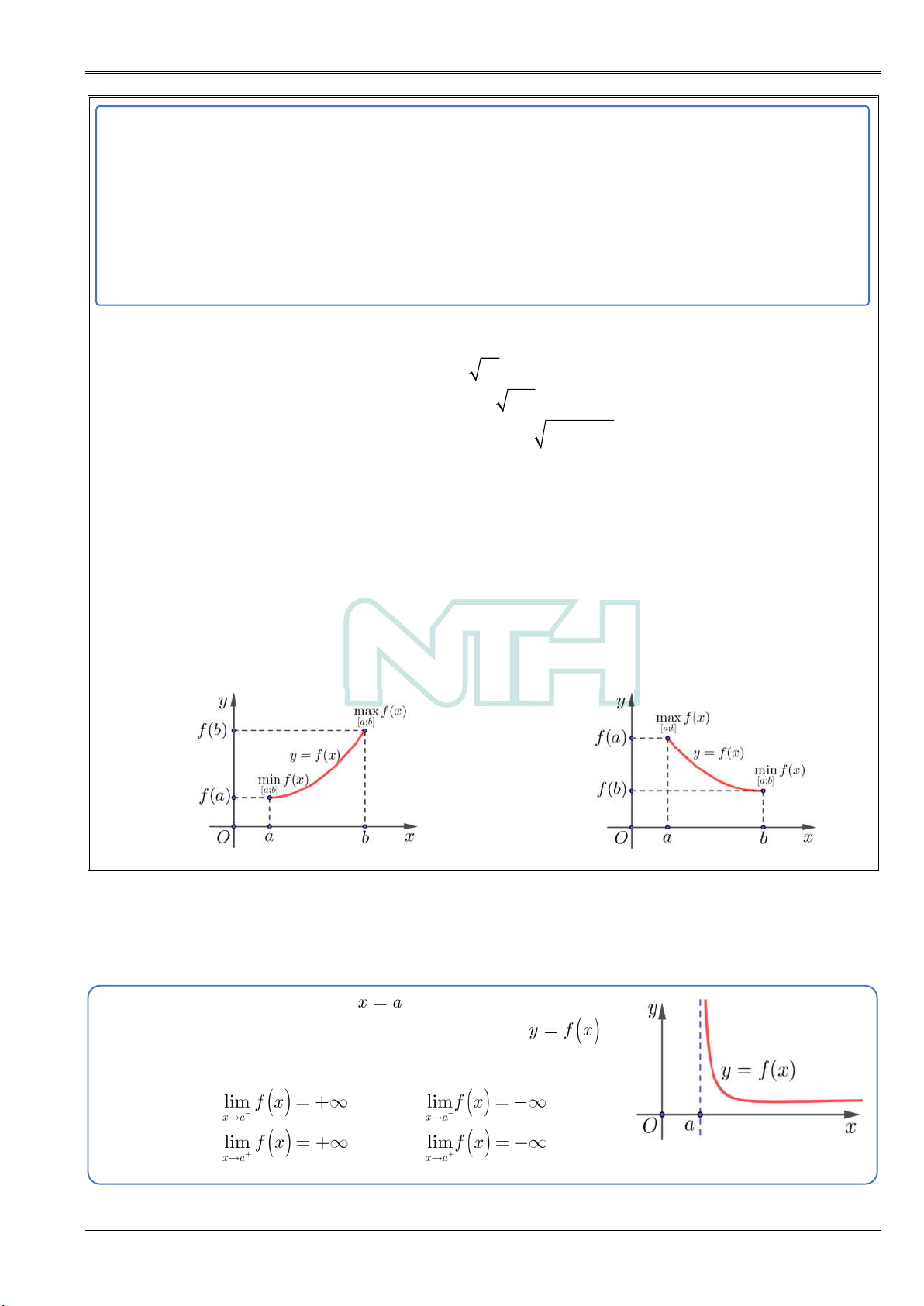
2. Cực trị của hàm số À
3. Bài toán liên quan tính đơn điệu có chứa tham số NGUY
⑴ Tìm tham số m để hàm số bậc ba 3 2
y ax bx cx d đơn điệu trên tập xác định Ễ Bước 1:
Tập xác định: D Tính đạo hàm 2
y 3ax 2bx c N TI Bước 2:
Điều kiện để hàm đơn điệu: Ế a 0 N H
Để y đồng biến trên y 0 x 0 y À a 0
Để y nghịch biến trên y 0 x 0 y ax b
⑵ Tìm tham số m để hàm số y
đơn điệu trên từng khoảng xác định cx d d ad cb Bước 1:
Tập xác định: D \ y Tính c cx d2 Bước 2:
Điều kiện để hàm đơn điệu:
Để y đồng biến trên từng khoảng xác định y 0 ad bc 0
Để y nghịch biến trên từng khoảng xác định y 0 ad bc 0 .
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 8
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
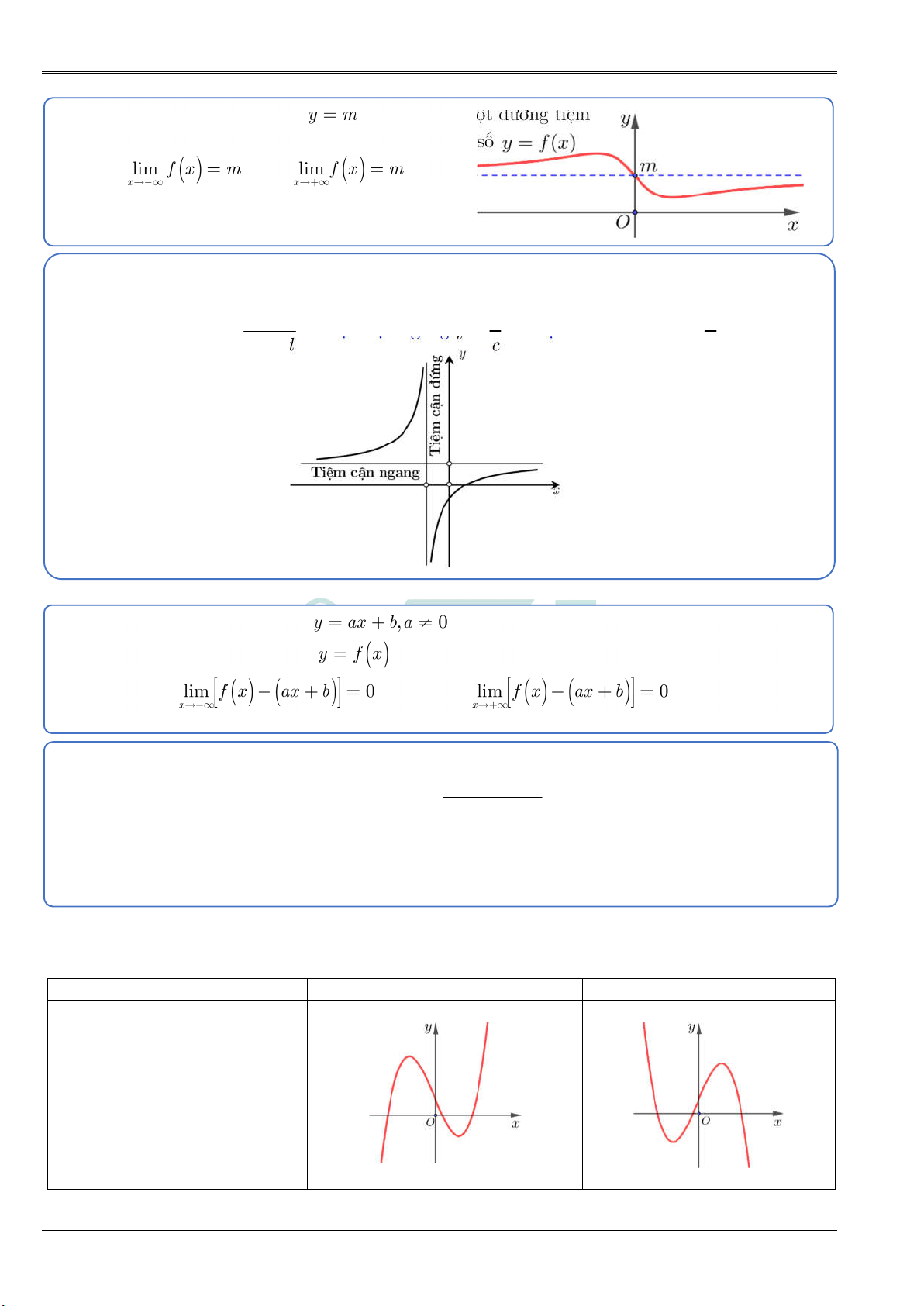
4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x liên tục trên đoạn a;b :
Bước 1: Tìm các điểm x ;x ;...;x thuộc a;b sao cho f x 0 . 1 2 n
Bước 2: Tính f a; f x ; f x ;...; f x ; f b 1 2 n
Bước 3: Gọi M là số lớn nhất và m là số nhỏ nhất trong các giá trị ở Bước 2. NGUY
Khi đó M max f x và m min f x. a ;b a;b Ễ
Sử dụng bất đẳng thức thường gặp: N TI
Bất đẳng thức Cô-si:
▪ Với hai số thực không âm: a b 2 ab . Dấu bằng xảy ra a b . Ế N H
▪ Với ba số thực không âm: 3
a b c 3 abc . Dấu bằng xảy ra a b c . À
▪ Với n thực không âm: n
a a a n a a a . 1 2 n 1 2 n
Dấu bằng xảy ra a a a . 1 2 n
Sử dụng “Tập giá trị” của hàm số lượng giác: 2 1 sin x 1 0 sin x 1
▪ Dựa vào tập giá trị của hàm số lượng giác: 2 1 cos x 1 0 cos x 1
Chú ý: Nếu y f x : mi n f
x f a mi n f
x f b a;b a;b
đồng biến trên a ;b thì .
nghịch biến trên a;b ma x f thì
x f b ma x f
x f a a;b a;b NGUY Ễ N TI Ế N H
5. Đường tiệm cận của đồ thị hàm số À
a) Đường tiệm cận đứng:
Định nghĩa: Đường thẳng
được gọi là một đuờng tiệm
cận đứng (hay tiệm cận đúng) của đồ thị hàm số
nếu ít nhất một trong các điều kiện sau thoả mãn:
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 9
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
b) Đường tiệm cận ngang:
Định nghĩa: Đường thẳng
được gọi là một đường tiệm
cận ngang (hay tiệm cận ngang) của đồ thị hàm số nếu: hoặc NGUY Đặc biệt: Ễ ax b a d N TI
Đối với hàm số y
có tiệm cận ngang y
và tiệm cận đứng x cx d c c Ế N H À
c) Đường tiệm cận xiên:
Định nghĩa: Đường thẳng
, được gọi là đuờng tiệm cận xiên (hay tiệm
cận xiên) của đồ thị hàm số nếu hoặc NGUY
Chú ý: Đối với hàm số phân thức 2 ax bx c f x
ta có thể chia đa thức để biến đổi mx n Ễ N TI về dạng e f x a x b với e 0 . mx n Ế Suy ra y a x
b là đường tiệm cận xiên của đồ thị hàm số N H À
6. Đồ thị hàm số a) Hàm số bậc ba 3 2
y ax bx cx d a 0 Trường hợp a 0 a 0
Phương trình y 0
có 2 nghiệm phân biệt
2b 3ac 0
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 10
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ Trường hợp a 0 a 0
Phương trình y 0
có 2 nghiệm phân biệt
2b 3ac 0 NGUY Ễ N TI Ế N H
Phương trình y 0 À có nghiệm kép
2b 3ac 0
Phương trình y 0 vô nghiệm
2b 3ac 0 ax b NGUY
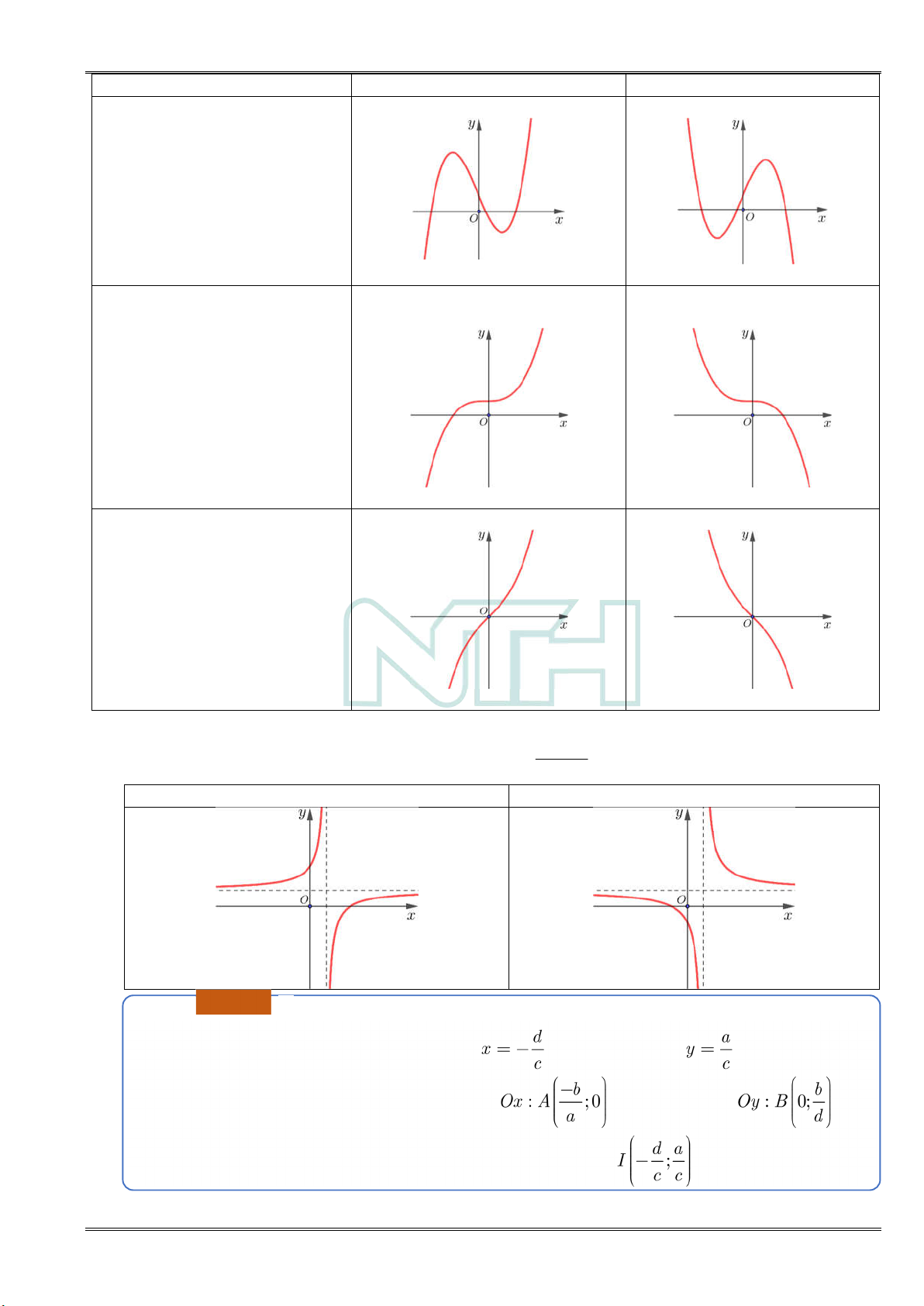
b) Hàm số phân thức bậc nhất trên bậc nhất y
c 0, ad bc 0 cx d
D ad bc 0
D ad bc 0 Ễ N TI Ế N H À Chú ý
Đồ thị hàm số có tiệm cận đứng , tiệm cận ngang .
Các điểm đặc biệt: Giao điểm với , Giao điểm với .
Giao của hai đường tiệm cận là tâm đối xứng.
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 11
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ 2
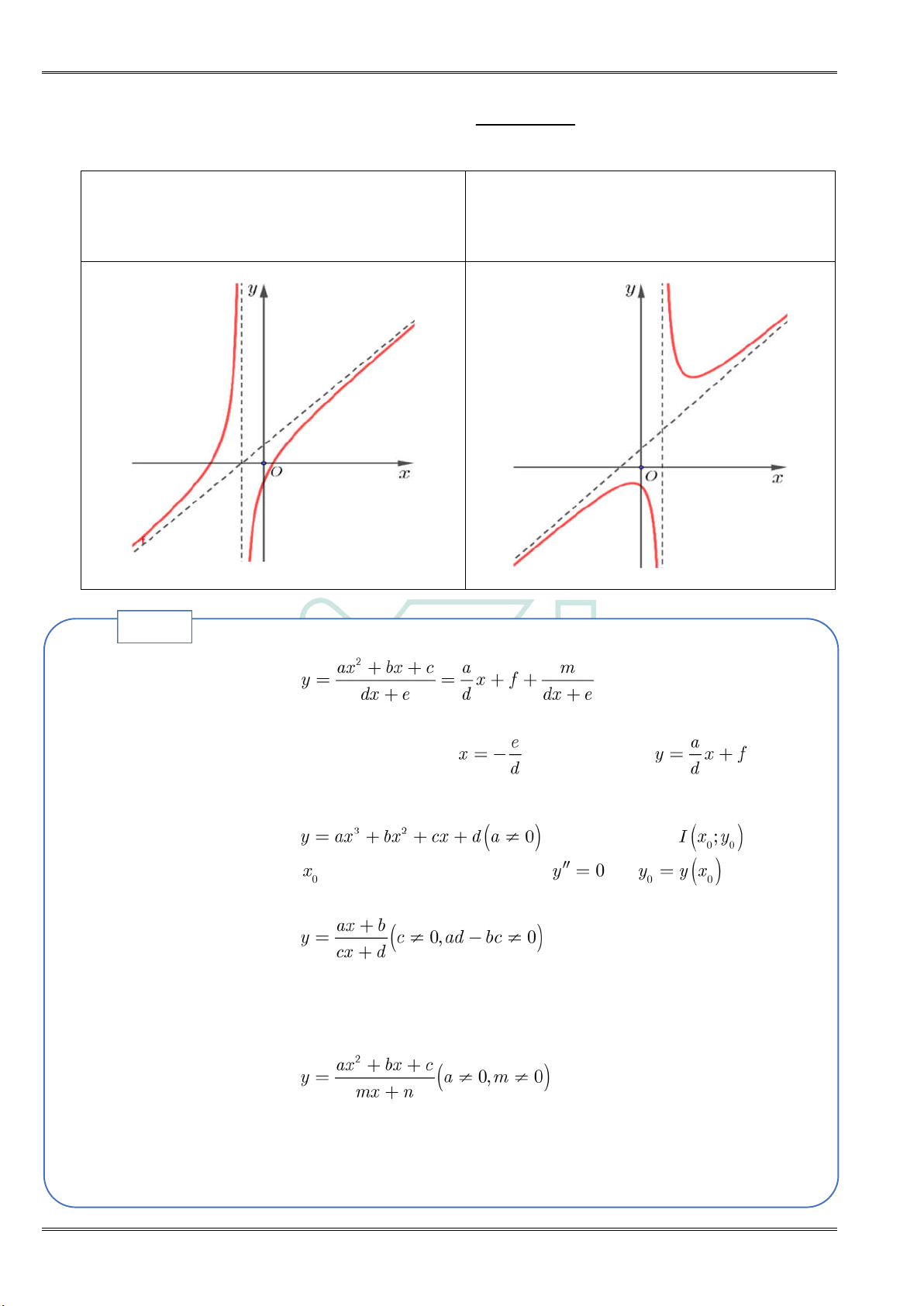
ax bx c
c) Hàm số phân thức bậc hai trên bậc nhất y a 0 dx e
y 0 vô nghiệm hoặc
y 0 có hai nghiệm phân biệ có nghiệm kép NGUY Ễ N TI Ế N H À Chú ý
Ta luôn tách được . NGUY
Khi đó đồ thị hàm số có tiện cận đứng , Tiệm cận xiên . Ễ N TI
Đồ thị của hàm số luôn nhận điểm làm tâm đối xứng, trong đó
là nghiệm của phương trình và . Ế N H À
Đồ thị của hàm số :
(a) Nhận giao điểm của tiệm cận đứng và tiệm cận ngang làm tâm đối xứng;
(b) Nhận hai đường phân giác của các góc tạo bởi tiệm cận đứng và tiệm cận ngang làm trục đối xứng.
Đồ thị của hàm số :
(a) Nhận giao điểm của tiệm cận đứng và tiệm cận xiên làm tâm đối xứng;
(b) Nhận hai đường phân giác của các góc tạo bởi tiệm cận đứng và tiệm cận xiên làm trục đối xứng.
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 12
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ
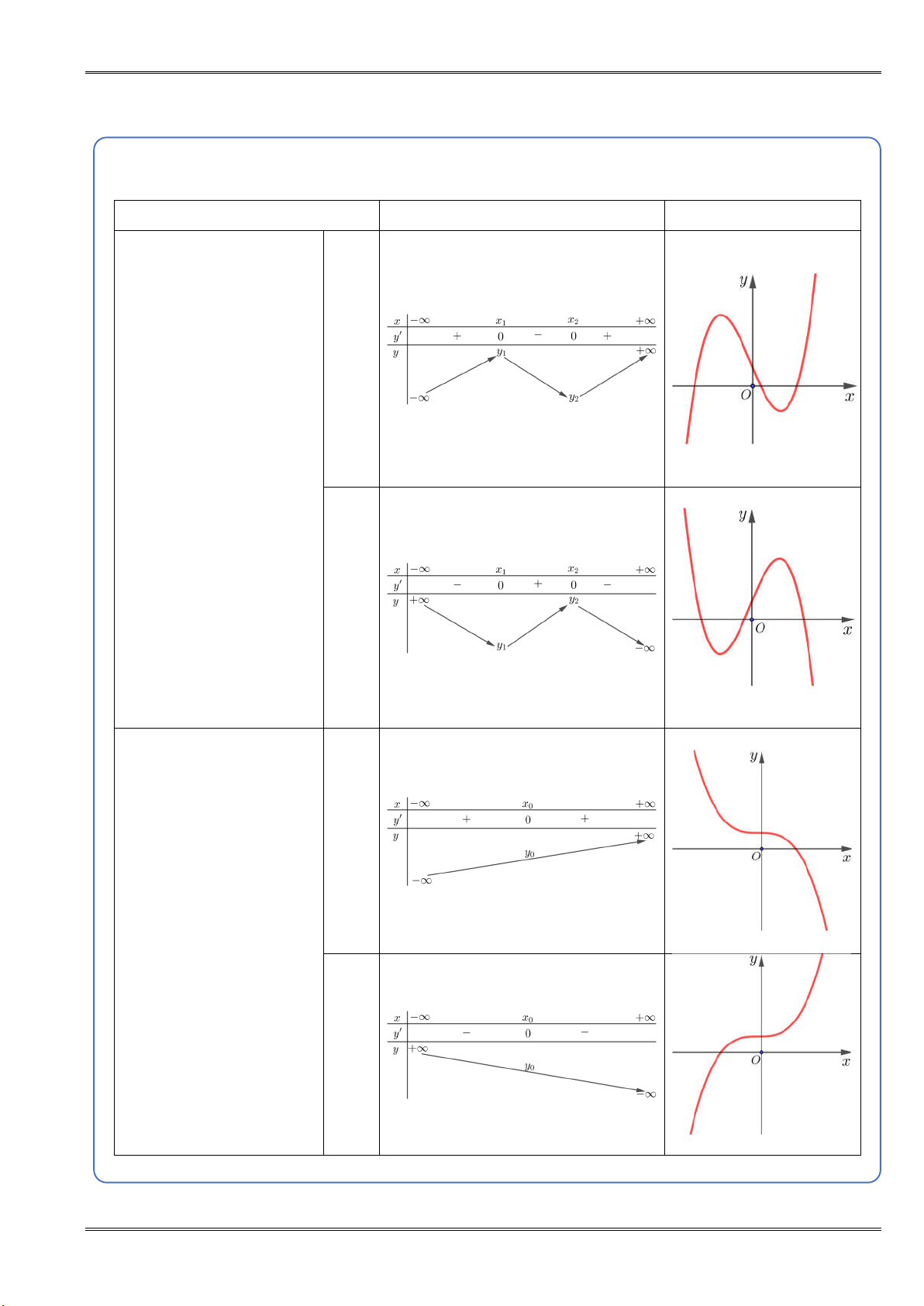
d) Nhận dạng hàm số khi biết đồ thị - bảng biến thiên (a) Hàm số 3 2
y ax bx cx d, a 0 Ta có 2
y 3ax 2bx c Bảng biến thiên Đồ thị NGUY Ễ N TI a 0 Ế N H À
TH1: y có 2 nghiệm phân biệt x ,x x x 1 2 1 2 a 0 NGUY Ễ N TI a 0 Ế N H À
TH2: y có 1 nghiệm x 0 a 0
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 13
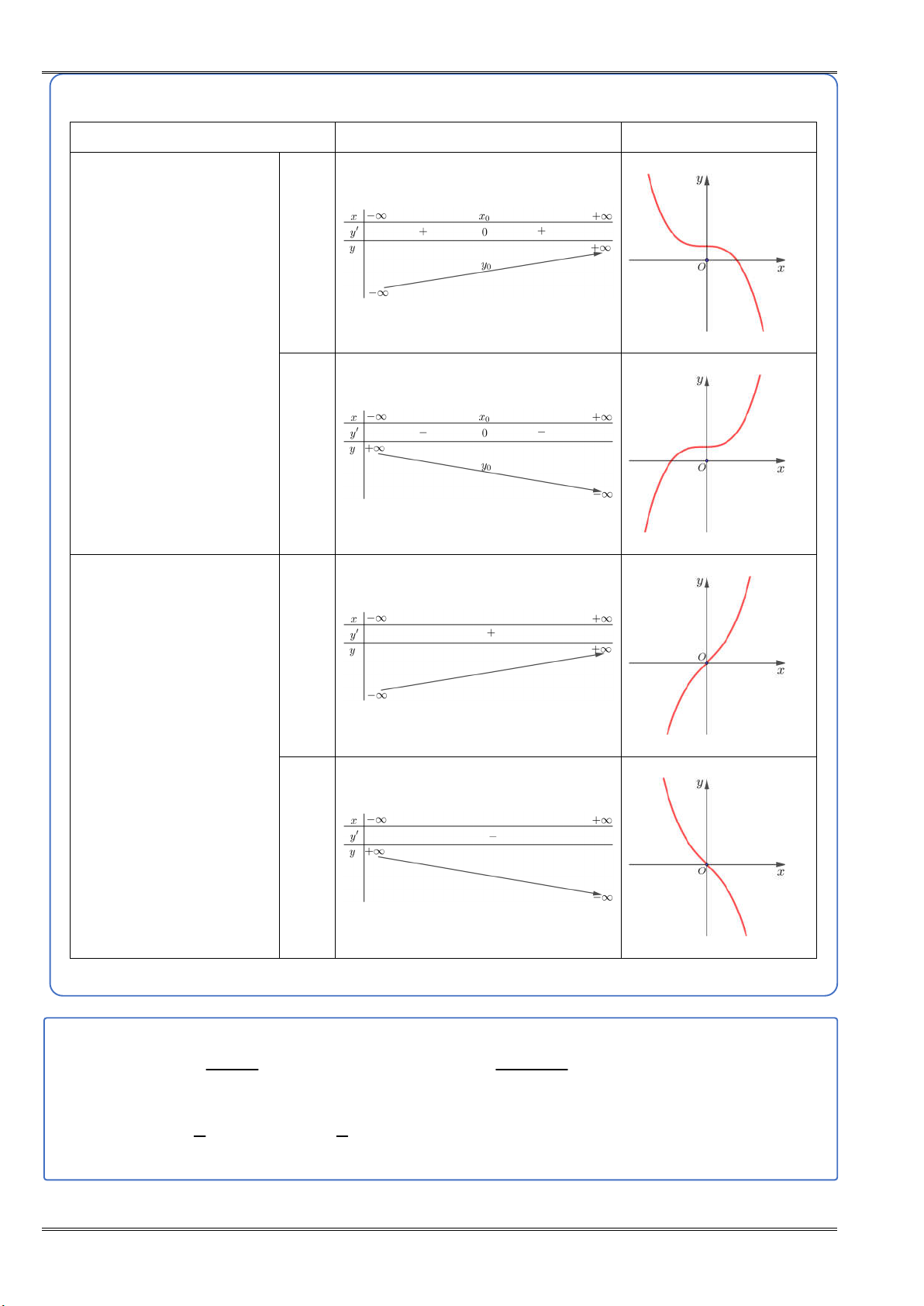
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ Ta có 2
y 3ax 2bx c Bảng biến thiên Đồ thị NGUY a 0 Ễ N TI
TH2: y có 1 nghiệm x 0 Ế N H À a 0 a 0 NGUY
TH3: y vô nghiệm Ễ N TI a 0 Ế N H À ax b ad bc
(b) Hàm số y
c 0,ad bc 0 có y cx d cx d2 d a
và TCĐ: x và TCN: y c c
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 14
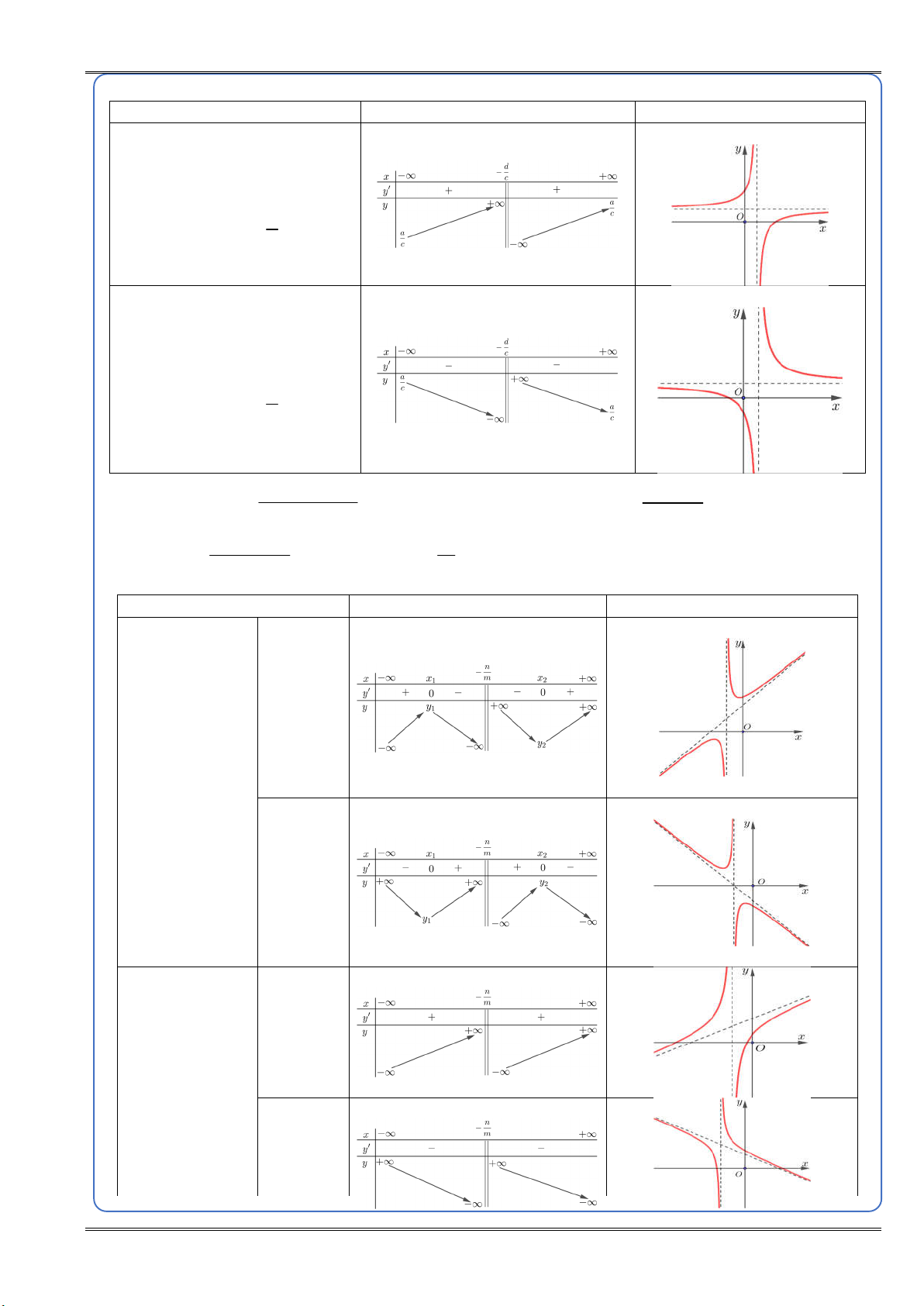
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN KIẾN THỨC CẦN NHỚ Bảng biến thiên Đồ thị TH1: ad bc 0 d
y 0 x c NGUY Ễ N TI TH2: ad bc 0 Ế N H d
y 0 x c À 2
ax bx c C
(c) Hàm số y
a 0,m 0 có y Ax B mx n mx n C n
y A
và TCĐ: x
và TCX: y Ax B mx n2 m Bảng biến thiên Đồ thị A 0 NGUY TH1:
y có 2 nghiệm Ễ phân biệt N TI Ế A 0 N H À A 0 TH2:
y có 1 nghiệm hoặc vô nghiệm A 0
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 15
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN DẠNG CÂU 13 ĐMH
DẠNG TOÁN ÔN TẬP KÌ THI TN.THPT NĂM 2025
DẠNG CÂU 13. BÀI TẬP RÈN LUYỆN (60 CÂU)
(Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.) Câu 13.1.
(ĐTK2025) Cho hàm số f x 2 cos x x . Xét tính đúng sai của các mệnh đề sau: NGUY a) f π π 0 2; f . 2 2
b) Đạo hàm của hàm số đã cho là f x 2 sin x 1 . Ễ N TI π π
c) Nghiệm của phương trình f x 0 trên đoạn 0; là . 2 6 Ế N H π π
d) Giá trị lớn nhất của f x trên đoạn 0; là 3 . 2 6 À Câu 13.2.
Cho hàm số f (x) cos2x x . Xét tính đúng sai của các mệnh đề sau:
а) f (0) 1; f 1 . 2 2
b) Đạo hàm của hàm số đã cho là f 'x 2sin2x 1 .
c) Nghiệm của phương trình f 'x 0 trên đoạn 0; là . 4 6
d) Giá trị nhỏ nhất của f (x) trên đoạn 0; là . 4 4 Câu 13.3.
Cho hàm số f (x) 4 sin x 2x . Xét tính đúng sai của các mệnh đề sau:
а) f (0) 0; f 4 . 2 NGUY
b) Đạo hàm của hàm số đã cho là f 'x 4cosx 2 . 2
c) Nghiệm của phương trình f 'x 0 trên đoạn 0; . Ễ là 3 N TI
d) Giá trị lớn nhất của f (x) trên đoạn 0; là 2 1. x Ế Câu 13.4.
Cho hàm số f x sin e
2 sin x . Xét tính đúng sai của các mệnh đề sau: N H
a) f 0 1; f 0 . À x
b) Đạo hàm của hàm số đã cho là f x sin cos x.e 2 cos x .
c) Nghiệm của phương trình f x 0 trên đoạn 0; là . 3
d) Giá trị lớn nhất của f x trên đoạn 0; là e 2 . Câu 13.5.
Cho hàm số f (x) sin 2x 2x . Xét tính đúng sai của các mệnh đề sau:
а) f (0) 0; f 2 .
b) Đạo hàm của hàm số đã cho là f '(x) 2cos2x 2 .
c) Nghiệm của phương trình f 'x 0 trên đoạn 0; là 0 và .
d) Giá trị lớn nhất của f (x) trên đoạn 0; là .
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 16
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN DẠNG CÂU 13 ĐMH Câu 13.6.
Cho hàm số f x sinx 2x . Xét tính đúng sai của các mệnh đề sau: a) f
0 0; f 1 . 2
b) Đạo hàm của hàm số đã cho là f x cos x 2 .
c) Nghiệm của phương trình f x 0 trên đoạn 0; là . 2 6 NGUY
d) Giá trị nhỏ nhất của f x trên đoạn 0; là 1 . 2 Ễ N TI Câu 13.7.
Cho hàm số f (x) x sin 2x . Xét tính đúng sai của các mệnh đề sau: a) f (
x) 1 2 cos 2x . Ế 1 N H b) Khi f (
x) 0 cos 2x . 2 À
c) Trên đoạn 0;
f x có tổng các nghiệm bằng . phương trình ( ) 0 3 5
d) Giá trị lớn nhất của f (x) trên đoạn 0; là . 2 6 Câu 13.8.
Cho hàm số ex f x
x . Xét tính đúng sai của các mệnh đề sau:
a) Tập xác định của hàm số f x là 0;
b) Đạo hàm của hàm số f x là ex f x 1
c) Giá trị lớn nhất của hàm số f x trên tập xác định là 1.
d) Phương trình ex x 42 0 có đúng hai nghiệm phân biệt thuộc khoảng 6; 4. Câu 13.9.
Cho hàm số f (x) 4 sin x 2x 1.
Xét tính đúng sai của các mệnh đề sau: NGUY
а) f (0) 1; f 3 . 2
b) Đạo hàm của hàm số đã cho là f 'x 4cosx 2 . Ễ N TI 2
c) Nghiệm của phương trình f 'x 0 trên đoạn 0; là . 3 Ế
d) Giá trị lớn nhất của f (x) trên đoạn 0; . N H là 2 1
Câu 13.10. Cho hàm số f x 2 sin x x 2 . Xét tính đúng sai của các mệnh đề sau: À
a) f 0 2; f 4 . 2 2
b) Đạo hàm của hàm số đã cho là f 'x 2 cos x 1. 2
c) Nghiệm của phương trình f 'x 0 trên đoạn ; là . 2 3
d) Giá trị nhỏ nhất của hàm số f x trên đoạn ; là 2 . 2 2
Câu 13.11. Cho hàm số f x cos 2x 3x . Xét tính đúng sai của các mệnh đề sau:
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 17
ÔN THI TN.THPT NĂM 2025 THEO DẠNG TOÁN DẠNG CÂU 13 ĐMH
a) Đạo hàm của hàm số đã cho là f x 2 sin 2x 3 . 2
b) Phương trình f x 0 có 2 trên đoạn 0; là và . 3 3
c) Hàm số f x nghịch biến trên ; . 6 3 f x ; NGUY
d) Giá trị lớn nhất của trên đoạn là 1 3 . 6
Câu 13.12. Cho hàm số f (x) 2 sin x . Xét tính đúng sai của các mệnh đề sau: Ễ a)
f (x)dx c
os2x C . N TI b) f ( ) 0 . Ế N H
x k2
c) Ngiệm của phương trình f (x) 1 là 6 k Z. À 5 x k2 6
d) Giá trị lớn nhất của hàm số đã cho trên 0; là 2.
Câu 13.13. Cho hàm số f (x) sin 2x 3x . Xét tính đúng sai của các mệnh đề sau: 3
a) f (0) 0; f 1 . 4 4
b) Đạo hàm của hàm số đã cho là f (
x) cos 2x 3 .
c) Số nghiệm của phương trình f (
x) 0 trên đoạn 0; là 2 2 6 3
d) Giá trị lớn nhất của f (x) trên đoạn 0; là . 2 12 NGUY
Câu 13.14. Cho hàm số f (x) sin 2x x . Xét tính đúng sai của các mệnh đề sau:
a) f (0) 0; f . Ễ 2 2 N TI
b) Đạo hàm của hàm số đã cho là f (
x) cos 2x 1 . Ế
c) Nghiệm của phương trình f (
x) 0 trên đoạn 0; là N H 2 3 À 3
d) Giá trị lớn nhất của f (x) trên đoạn 0; là . 2 2 3 2 x x
Câu 13.15. Cho hàm số f (x) sin cos .
Xét tính đúng sai của các mệnh đề sau: 2 2 a) f 0 1 .
b) f x 0 sin x 0 .
c) Trên đoạn 0;2
phương trình f x 0 có đúng một nghiệm . 2
d) Giá trị lớn nhất của hàm số đã cho trên đoạn 0; là 2 .
Bieân soaïn & giaûng daïy: ThS. Nguyeãn Tieán Haø – 0949.888.993 Trang 18




