Chuyên đề phân số bồi dưỡng học sinh giỏi Toán 6 – 7

CHUYÊN ĐỀ PHÂN SỐ
DẠNG 1: Tìm n để phân số tối giản:
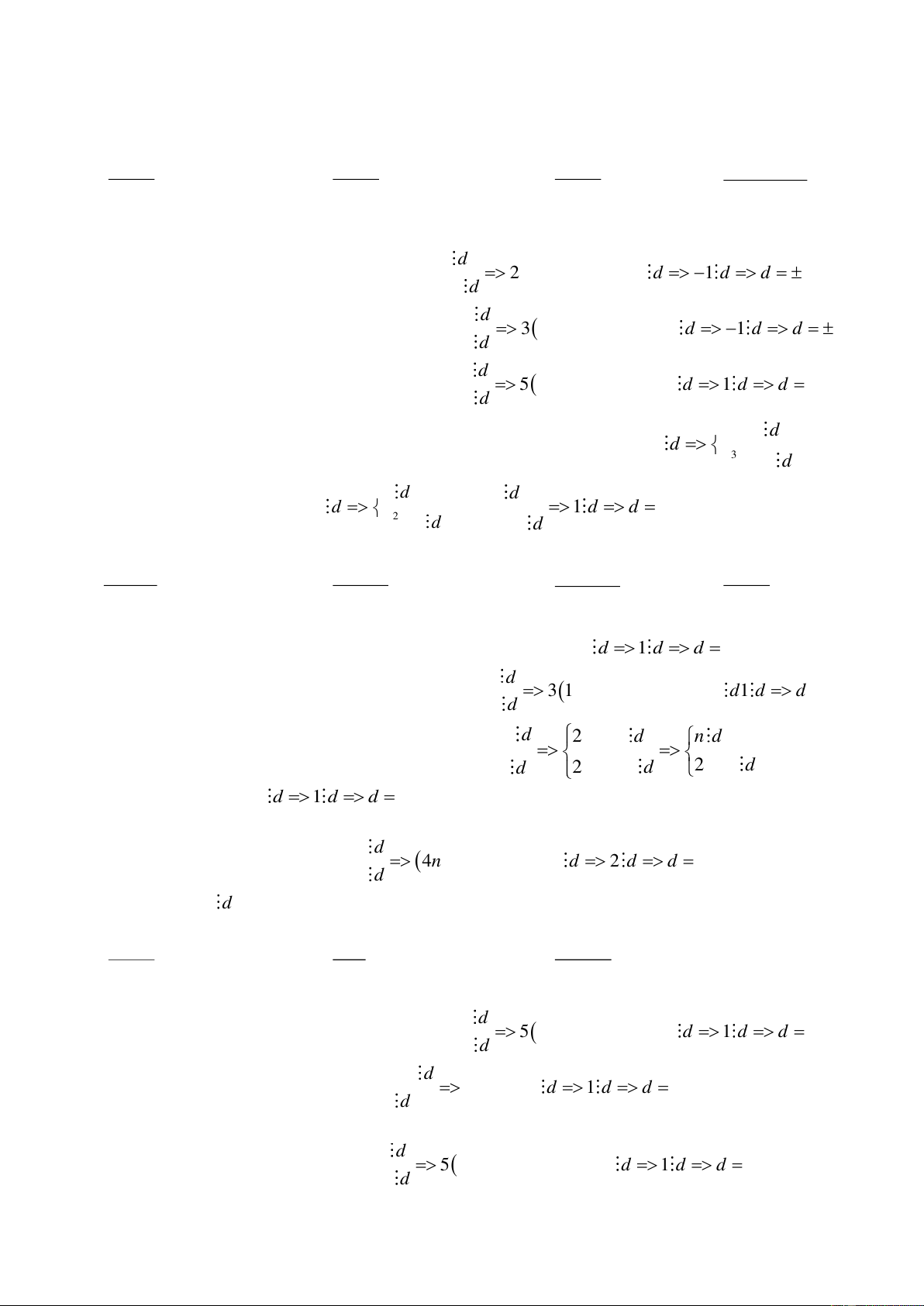
Bài 1: Tìm n  N để các phân số tối giản: n + 7 n +13 2n + 3 3n + 2 a, A = B = C = A = n − b, 2 n − c, 2 4n + d, 1 7n + 1 HD: n − 2 + 9 9 a, A = =1+ n − 2 n − 2 9 Để A tối giản thì
n −  k = n  k + k  N n − tối giản hay 2 3 3 2( ) 2 n − 2 +15 15 b, A = =1+ n − 2 n − 2 15 Để A tối giản thì
n −  k = n  k + k  N và n − tối giản hay 2 3 3 2( ) 2
n − 2  5h = n  5h + 2(h  N )
c, Gọi d =UCLN( 2n+3; 4n+1) => 2( 2n+3) - (4n +1) d=> 5 d,
Để C tối giản thì d # 5 hay 2n+3 # 5k => 2n+8 # 5k=>n # 5k – 4 (k  N)
d, Gọi d=UCLN (3n+2; 7n+1) => 7(3n+2) - 3(7n+1) d => 11 d,
Để A tối giản thì d # 11 hay 3n+2 # 11k=> n # 11k+3 (k  N)
Bài 2: Tìm n  N để các phân số tối giản: 2n + 7 8n +193 18n + 3 21n + 3 a, A = C = A = A = 5n + b, 2 4n + c, 3 21n + d, 7 6n + 4 HD:
a, Gọi d = UCLN (3n + 2;2n + 7) = 5(2n + 7) − 2(5n + 2) d = 31 d
Để A tối giản thì d  31 = 2n + 7  31 = 2n + 7 + 31 31 = 2(n +19) 31 = n # 31k – 19 (k N)
b, Gọi d = UCLN (8n +193;4n + ) 3 = (8n +19 ) 3 − 2(4n + ) 3 d = 187 d
Mà 187 = 11.17 , Nên để C tối giản thì: d  11, d  17
TH1: d  11 = 4n + 311 = 4n + 3 −1111 = 4n − 811 = n − 2 11k = n  11k + 2(k  N ) TH2: d  = n +  = n + + 
= (n + ) = n  h − ( * 17 4 3 17 4 3 17 17 4 5 17 17 5 h  N )
c, Gọi d = UCLN (18n + 3;21n + 7) = 7(18n + )
3 − 6(21n + 7) d = 21 d
Mà 21 = 3.7 , Nên để A tối giản thì d  3,7
Thấy hiển nhiên d  3,(21n + 7  ) 3
Với d  7 = 18n + 3 7 = 18n + 3 = 3(6n + )
1  7 = 6n +1− 7  7 = n  7k +1
d, Gọi d = UCLN (21n + 3;6n + 4) = 2(21n + )
3 − 7(6n + 4) d = 22 d
Mà 22 = 2.11, Nên để A tối giản thì: d  2,d  11
TH1: d  2 = 21n + 3  2k = n là số chẵn
TH2: d  11 = 6n + 4 11 = 6n + 4 − 22 11 = n − 311 = n  11k + 3 n + 3
Bài 3: Tìm n  N để các phân số tối giản: B = n − 12
GV: Ngô Thế Hoàng _ THCS Hợp Đức 1 21n + 3
Bài 4: Tìm n để A = 6n + rút gọn được 4 HD:
Giả sử tử và mẫu cùng chia hết cho số nguyên tố d => 22 d=> d=2 hoặc d=11
TH1: d=1=> 6n+4 2 với mọi n và 21n +3 2 khi n lẻ
TH2: d=11=> 21n +3 11=> n – 3 11=> n = 11k +3 => Với n= 11k+3 => 6n+4 11 2 7n +1 n n
Bài 5: CMR nếu phân số :
là số tự nhiên với n N thì các phân số và là các phân số tối 6 2 3 giản ? HD : 2 7n +1 Vì phân số
là số tự nhiên với mọi n nên 2
7n +1 6 => n lẻ và n không chia hết cho 3 6 n n Vậy ;
là các phân số tối giản 2 3 3 2 a + 2a −1
Bài 6: Cho biểu thức A = 3 2
a + 2a + 2a +1 a/ Rút gọn biểu thức
b/ CMR nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a là 1 phân số tối giản n + 3
Bài 7: Tìm tất cả các số tự nhiên n để n − là phân số tối giản 12 3n − 1
Bài 8: Tìm các giá trị nguyên của n để phân số M = n − có giá trị là số nguyên 1 HD: 3n − 1 M =
 Z = 3n −1 n −1 = 3(n − )
1 + 2 n − 2 = 2 n − 1 n − 1
GV: Ngô Thế Hoàng _ THCS Hợp Đức 2
DẠNG 2: Chứng minh các phân số sau tối giản:
Bài 1: Chứng minh các phân số sau tối giản: n +1 2n + 3 5n + 3 3 n + 2n a, 2n + b, 3 3n + c, 5 3n + d, 2 4 2 n + 3n −1 HD: n +1 d
a, Gọi d = UCLN (n +1;2n + ) 3 =  = 2(n + ) 1 − (2n + ) 3 d = 1 − d = d = 1  2n + 3 d 2n + 3 d
b, Gọi d = UCLN (2n + 3;3n + 5) = 
= 3(2n + 3) − 2(3n + 5) d = 1 − d = d = 1  3n + 5 d 5  n + 3 d
c, Gọi d = UCLN (5n + 3;3n + 2) = 
= 5(3n + 2) − 3(5n + 3) d = 1 d = d = 1  3n + 2 d n +1 d
d, Gọi d = UCLN (n + 2 ; n n + 3n − )
1 = n (n + 2n) − (n + 3n − ) 2 3 4 2 3 4 2 1 d =  3 n + 2n d n d 2 n d = ( 3
n + 2n) − n ( 2 n + ) 1 d =  = 
= 1 d = d = 1  2 n +1 d 2 n +1 d
Bài 2: Chứng minh các phân số sau tối giản: 16n + 5 14n + 3 2n +1 2n + 3 a, d, 6n + b, 2 21n + c, 4 2 ( n n +1) 4n + 8 HD:
a, Gọi d = UCLN (16n + 5;6n + 2) = 8(6n + 2) − 3(16n + )
5 d = 1 d = d = 1  1  4n + 3 d
b, Gọi d = UCLN (14n + 3;21n + 4) =  = 3(14n + )
3 − 2 (21n + 4) d1 d = d = 1  21n + 4 d
n 2n +1 d 2n + n d n d
c, Gọi d = UCLN (2n +1;2n + 2n) ( ) 2 2 =  =  =  2 2 2n + 2n d 2n + 2n d 2n +1 d = (2n + )
1 − 2n d = 1 d = d = 1  d, Gọi = (  + n + n + ) 2n 3 d d UCLN 2 3;4 8 = 
= (4n + 8) − 2(2n + )
3 d = 2 d = d = 1  ,d = 2  4n + 8 d
Vì 2n + 3 d mà 2n+3 là số lẻ nên d lẻ, vậy d = 2  loại
Bài 3: Chứng minh các phân số sau tối giản: 3n + 2 n 12n +1 a, 5n+ b, 3 n + c, 1 30n + 2 HD: 5  n + 3 d
a, Gọi d = UCLN (5n + 3;3n + 2) = 
= 5(3n + 2) − 3(5n + 3) d = 1 d = d = 1  3n + 2 d n +1 d
b, Gọi d = UCLN ( ; n n + ) 1 =  = (n + )
1 − n d = 1 d = d = 1  n d c, Gọi = (  + n + n + ) 12n 1 d d UCLN 12 1;30 2 =  = 5(12n + )
1 − 2 (30n + 2) d = 1 d = d = 1  , 30n + 2 d
GV: Ngô Thế Hoàng _ THCS Hợp Đức 3
Bài 4: Tìm n Z để các phân số sau là số nguyên: 6 n 2n + 7 12 a, n − b, 3 n − c, 4 n + d, 3 3n −1 HD: 6 a, Để A =
 Z = n − 3U (6) = 1;2;3;  6 = n = ..  . n − 3 n n − 4 + 4 4 b, Để B = = = 1+
 Z = n − 4U (4) = 1; 2  ;  4 n − 4 n − 4 n − 4 2n + 7 2n + 6 + 1 1 c, Để C = = = 2 +
 Z = n + 3U ( ) 1 =   1 = n ..  . n + 3 n + 3 n + 3 12 d, Để D =
 Z = 3n −1U (12) =  1  ; 2  ;  4 n −  3n − , Vì 3 1 3 1
Bài 5: Tìm n Z để các phân số sau là số nguyên: 3n + 2 6n − 4 3n + 4 6n − 3 a, n− b, 1 2n + c, 3 n − d, 1 3n + 1 HD: 3n + 2 3n − 3 + 5 5 a, Để A = = = 3+
 Z = n −1U (5) =  1  ;  5 n − 1 n − 1 n − 1 6n − 4 6n + 9 −13 13 b, Để B = = = 3−
 Z = 2n + 3U (13) =  1  ; 1  3 2n + 3 2n + 3 2n + 3 3n + 4 3n − 3 + 7 7 c, Để C = = = 3+
 Z = n −1U (7) =  1  ;  7 n −1 n −1 n − 1 6n − 3 6n + 2 − 5 5 d, Để D = = = 2 −
 Z = 3n +1U (5) =  1  ;  5 3n + 1 3n + 1 3n + 1 63
Bài 6: Cho phân số A = 3n + với n N, tìm n để A là số tự nhiên 1
Bài 7: Tìm n Z để các phân số sau là số nguyên: n +10 n + 3 2n + 3 2 n + 3 a, d, 2n − b, 8 2n − c, 2 7 n + 2 HD :
a, Ta có : 2n – 8 =2(n-4) => n+10 2 và n+10 n – 4 hay n là số chẵn và n + 10 n − 4
b, Ta có : 2n – 2 =2(n – 1)=> n+3 2 và n+3 n – 1 hay n là số lẻ và n + 3 n −1
c, Ta có : 2n+3 7 => 2n+10 7= >n+5 7 => n= 7k – 5 (k  N ) d, Ta có : 2
n + 2n − 2n + 3 n + 2 = (
n n + 2) − 2n − 4 + 7 n + 2 = (
n n + 2) − 2(n + 2) + 7 n + 2 =>7 n+2 8n +193
Bài 8: Tìm n  N để A = 4n+ sao cho: 3
a, Có giá trị là số tự nhiên
b, Là phân số tối giản
c, Với n từ 150-170 thì A rút gọn được HD : 187 a, A = 2 + 1  ; 1  1; 1  7; 1  87
4n + để A là số tự nhiên thì 4n+3  U(187) =  3 187
b, Để A tối giản thì 4n+ tối giản hay 187 không chia hết cho 4n+3 hay 4n+3 # 11k và 4n+3 3 # 17
GV: Ngô Thế Hoàng _ THCS Hợp Đức 4 1
 00 11k + 2 170
c, Để A rút gọn được thì n = 11k + 2 hoặc n = 17h – 5=>  1
 00 17h − 5 170 3a + 5b + 2
Bài 9: CMR nếu (a – 1; b+1) thì A = 5a +8b + là phân số tối giản 3 HD:
Gọi d=UCLN(3a+5b+2; 5a+8b+3) => 5(3a+5b+2) – 3(5a+8b+3) d=> b+1 d
Và 8(3a+5b+2) – 5(5a+8b+3) d=> a – 1 d => d UC( a – 1; b+1)
Mà UCLN( a – 1; b+1) =1 => d =1; - 1 2 n + 4
Bài 10: Tìm n Z sao cho cả A = B = n − và 1
n + là các số nguyên 1 n + 9
Bài 11: Cho phân số A = n − (n Z, n > 6), Tìm n để phân số có giá trị nguyên dương 6 75
Bài 12: Cho phân số A = 5n − (n N*). Tìm n để 2
a, Phân số A là số tự nhiên b, A rút gọn được 2n + 7
Bài 13: Tìm n  N để n + là số nguyên 1 Bài 14: Tìm số tự nhiên n nhỏ nhất
để các phân số sau tối giản: 1 2 3 2001 2002 ; ; ;...; ;
n + 3 n + 4 n + 5 n + 2003 n + 2004 HD: a
Các phân số đã cho có dạng: n + 2+ với a=1; 2; 3; ...; 2001; 2002 a a
Để n+ 2+ tối giản thì UCLN(n+2+a;a) =1, => UCLN(n+2; a)=1=> n+2 và a là nguyên tố a cùng nhau
Với mỗi số 1,2,3,..., 2002 và n+2 nhỏ nhất thì n+2=2003( Vì 2003 là số nguyên tố) 19 n
Bài 15: Tìm n để tích hai phân số có giá trị ngyên n − và 1 9 2 3x − 2
Bài 16: Tìm x để giá trị của biểu thức: P = là số nguyên 2 3x +1 2017 − x
Bài 17: Cho T = 10− , tìm các giá trị nguyên của x để: T có giá trị nguyên, T có giá trị lớn nhất x x + 2
Bài 19: Cho M = x − , biết x là số hữu tỉ âm, và M là số nguyên, Tìm x 1
GV: Ngô Thế Hoàng _ THCS Hợp Đức 5
DẠNG 3: Tìm n để phân số có GTLN hoặc GTNN
Bài 1: Tìm n  Z để các phân số sau có GTNN: 6n − 4 6n −1 x −13 2x + 4 a, A = B = A = B = 2n + b, 3 3n + c, 2 x + d, 3 x + 1 HD: 13 13
a, Do n  Z nên 2n+3 Z , Để A = 3 − 2n + nhỏ nhất thì 3
2n + số dương lớn nhất 3
khi 2n+3 là số nguyên dương nhỏ nhất=> 2n+3 =1=> n = -1 5 5
b, Do n Z nên 3n+2 Z , Để B = 2 − 3n+ nhỏ nhất thì 2 3n + là số dương lớn nhất 2
hay 3n+2 là số nguyên dương bé nhất => 3n+2 =1 =>n = -1/3( loại) nên 3m+2 =2=> n=0 16 16
c, Do x Z nên x+3 Z Để A = 1− x + nhỏ nhất thì 3
x + là số dương lớn nhất 3
hay x+3 là số nguyên dương nhỏ nhất hay x+3 =1=> x = - 2 2 2
d, Do x Z nên x+1 Z để B = 2 + x + nhỏ nhất thì 1
x + là số âm nhỏ nhất 1
hay x+1 là số nguyên âm lớn nhất hay x+1 = - 1 => x = - 2
Bài 2: Tìm n  Z để các phân số sau có GTNN: 10x + 25 3x + 7 20a +13 a, E = A = B = 2x + b, 4 x − c, 1 4a + d, 3 3 − D = 2x − 5 HD: 5 5
a, Do x  Z nên 2x+4 Z Để E = 5 + 2x + nhỏ nhất thì 4 2x + là số âm nhỏ nhất 4
hay 2x+4 là số nguyên âm lớn nhất hay 2x+4 = - 1 => x= - 5/2 (loại) khi đó 2x+4 = - 2 => x= - 3 10 10
b, Do x Z nên x-1  Z Để A = 3 + x − nhỏ nhất thì 1
x − là số âm nhỏ nhất 1
hay x -1 là số nguyên âm lớn nhất hay x - 1 = - 1=> x=0 2 2
c, Do a Z nên 4a+3 Z Để B = 5 − 4a + nhỏ nhất thì 3
4a + là số dương lớn nhất 3
hay 4a+3 là số nguyên dương nhỏ nhất hay 4a+3 =1=> a =-1/2(loại)
hay 4a+3 =2 => a = -1/4(loại) hay 4a+3=3=> a=0 3 −
d, Do x Z nên 2x-5  Z , Đề D = 2x − nhỏ nhất thì 2x – 5 là số nguyên dương bé nhất 5 hay 2x – 5 =1=> x =3
Bài 3: Tìm n  Z để các phân số sau có GTNN: 4n +1 2n − 3 8 − x 3 − a, A = B = C = E = 2n + b, 3 n + c, 2 x − d, 3 2n − 5 HD: 5 5
a, Do n Z nên 2n+3  Z , Để A = 2 − 2n + nhỏ nhất thì 3
2n + là số dương lớn nhất 3
=> 2n+3 là số nguyên dương nhỏ nhất => 2n+3=1=> n= - 1 7 7
b, Do n Z nên n+2  Z , Để B = 2 − n + nhỏ nhất thì 2 n +
là số dương lớn nhất 2
=> n+2 là số nguyên dương nhỏ nhất=> n+2 =1=> n= - 1
GV: Ngô Thế Hoàng _ THCS Hợp Đức 6 5 5
c, Do x  Z nên x-3 Z , Để C = 1
− + x− nhỏ nhất thì 5
x − là số âm nhỏ nhất 5
=> x – 5 là số nguyên âm lớn nhất => x – 5 = - 1 => x= 4 3 − 3
d, Do n Z nên 2n-5  Z , Để E = 2n − nhỏ nhất thì 5
2n − là số dương lớn nhất 5
=> 2n-5 là số nguyên dương nhỏ nhất => 2n-5 =1=>n=3 x
Bài 4: Tìm x  Z để các phân số sau có GTNN: A = 5x − 2 HD : 1  5x  1  2  2
Do x Z nên 5x-2 Z , Để A = = 1+     nhỏ nhất thì
5  5x − 2  5  5x − 2  5x − là số âm nhỏ 2 nhất 1
=> 5x - 2 là số nguyên âm lớn nhất => 5x - 2= -1 = x =
(loại) khi đó 5x - 2= - 2 => x = 0 5
Bài 5: Tìm n, x Z để các phân số sau có GTLN n +1 14 − n 7 − x 1 a, C = D = E = C = n − b, 2 4 − c, n x − d, 5 4 + x HD: 3 3
a, Do n  Z nên n-2  Z , Để C = 1+ n − lớn nhất thì 2
n − là số dương lớn nhất 2
khi đó n – 2 là số nguyên dương nhỏ nhất => n - 2 = 1=> n = 3 10 10
b, Do n Z nên 4 – n  Z , Để D = 1+ 4− lớn nhất thì n 4 − là số dương lớn nhất n
hay 4 – n là số nguyên dương nhỏ nhất => 4 – n = 1 => n = 3 2 2
c, Do x Z nên x-5 Z , Để E = 1
− + x− lớn nhất thì 5
x − là số dương lớn nhất 5
hay x – 5 là số nguyên dương nhỏ nhất => x – 5 = 1=> x = 6 1 1
d, Do x Z nên 4+x  Z , Để C = 4+ lớn nhất thì x 4 + là số dương lớn nhất x
hay 4+x là số nguyên dương nhỏ nhất => 4 + x = 1 => x = 3
Bài 6: Tìm n, x  Z để các phân số sau có GTLN 5x −19 3 − 3n −1 a, D = D = C = x − b, 9 2x − c, 5 2 − n + 3 HD: 26 26
a, Do x Z nên x-9  Z , Để D = 5 + x − lớn nhất thì 9
x − là số dương lớn nhất 9
hay x – 9 là số nguyên dương nhỏ nhất => x – 9 =1=> x = 10 3 − 3
b, Do x Z nên 2x-5 Z ,Để D = 2x − lớn nhất thì 5
2x − là số ấm nhỏ nhất 5
hay 2x -5 là số nguyên âm lớn nhất => 2 x – 5= - 1=> x = 2 1  6n − 2  1  7 
c, Do n Z nên -2n + 3 Z , Để C = = 3 − +     lớn nhất 2  2 − n + 3  2  2 − n + 3  7 hay 2
− n + là số dương lớn nhất, hay -2n + 3 là số nguyên dương bé nhất => -2n+3 =1 => n 3 =1
GV: Ngô Thế Hoàng _ THCS Hợp Đức 7
Bài 7: Tìm n  Z để các phân số sau có GTNN: 7n − 8 2n − 3 1 8 − x a, A = B = D = A = 2n − b, 3 n − c, 2 n + d, 3 x − 3
Bài 8: Tìm n  Z để các phân số sau có GTNN: x − 3 14 − x 1 a, B = C = D = x + b, 2 4 − c, x x + 5
Bài 9: Tìm n  Z để các phân số sau có GTLN 1 n +1 6n − 3 a, C = E = D = x + b, 5 n − c, 5 3n + d, 1 2n − 3 E = n − 2
Bài 10: Tìm n  Z để các phân số sau có GTLN n +1 4n +1 2n − 3 6n − 3 a, A = B = C = E = n − b, 5 2n + c, 3 n + d, 2 3n +1
Bài 11: Tìm n  Z để các phân số sau có GTLN 7n − 8 2n − 3 3n −1 6n − 3 a, F = G = I = d, K = 2n − b, 3 n − c, 2 −2n + 3 3n + 1 10n − 3
Bài 12: Tìm số tự nhiên n để B = 4n − Đạt giá trị lớn nhất, Tìm GTLN đó 10 HD : 5(2n − 5) + 22 5 11 B = = + 2(2n − 5) 2 2n − 5 1− 6n
Bài 13: Tìm số nguyên n sao cho A = 3x − đạt giá trị nhỏ nhất 2
Bài 14: Tìm các giá trị nguyên của x để: 2 8 − x a, A = B = 6 − có giá trị lớn nhất b, x x − có GTNN 3 ab
Bài 15: Tìm GTNN của phân số : A = a + b 5x −19
Bài 16: Tìm GTNN của mỗi biểu thức: A = = + nếu x+y=1 x − , 2 2 C x y 4
Bài 17: Tìm các số tự nhiên a, b nhỏ nhất sao cho 7 8 a = b (1) HD: 7  a  Từ 7 8
a = b => b =   vì b N nên a b => a=b.k (k  N)  b  a Và vì a > b =>
1 = k  2 , thay a = b.k vào (1) ta được 7 7 8 7
b .k = b = k = b b Mà k  2 => 7 7 7
k  2 = b  2 mà b nhỏ nhất nên 7
b = 2 , khi đó k = 2 => 7 8 a = 2 .2 = 2 n
Bài 18: Cho số tự nhiên n có hai chữ số, chữ số hàng chục là x, hàng đơn vị là y, Gọi M = x + y a, Tìm n để M=2
b, Tìm n để M nhỏ nhất HD: 10x + y a, Ta có:
= 2 = y = 8x , Mà x,y là các chữ số nên x=1 và y=8 x + y
GV: Ngô Thế Hoàng _ THCS Hợp Đức 8
x + y + 9x 9x 9 y b, M = =1+ = 1+ để M nhỏ nhất thì 1 +
lớn nhất hay y lớn nhất và x x + y x + y y x 1+ x nhỏ nhât
GV: Ngô Thế Hoàng _ THCS Hợp Đức 9
DẠNG 4: Các bài toán liên qua đến phân số 30 1
Bài 1: Tìm a, b, c, d  N* , biết : = 43 1 a + 1 b + 1 c + d 17 11
Bài 2: Cộng cả tử và mẫu của phân số
với cùng 1 số nguyên rồi rút gọn ta được phân số . 21 13 Hãy tìm số nguyên đó ? 3
Bài 3: Khi cộng cả tử và mẫu của phân số
với cùng 1 số nguyên x thì được 1 phân số có giá trị bằng 7 1 . Tìm số nguyên x? 3
Bài 4: Tìm 1 phân số tối giản, Biết rằng khi cộng cả tử và mẫu của phân số ấy với mẫu của số đó thì
được 1 số mới lớn giấp hai lần phân số ban đầu ? HD: a
Gọi phân số tối giản lúc đầu là
, nếu chỉ cộng mẫu số vào mẫu số ta được phân số : b a a = a là 2 lần, b +
phân số này nhỏ hơn phân số b 2b b a + b Để
gấp hai lần phân số ban đầu thì a+b giấp 4 lần a 2b 1
=> Mẫu số b phải giấp 3 lần tử số a, phân số tối giản thỏa mãn điều kiện trên là 3 a a 9 21
Bài 5: Tìm phân số tối giản
nhỏ nhât khác 0 sao cho khi chia cho mỗi phân số và ta được b b 14 35
kết quả là 1 số tự nhiên
Bài 6: Tìm số tự nhiên n nhỏ nhất để các phân số sau tối giản: 1 2 3 2001 2002 ; ; ;...; ;
n + 3 n + 4 n + 5 n + 2003 n + 2004 HD : a a
Các phân số trên có dạng , a  =1,2,3,...,2002, để n + 2 + a n + 2 + tối giản thì : a UCLN ( ;
a n + a + 2) = 1 = UCLN (n + 2; a) = 1 = n+2 và a là hai số nguyên tố cùng nhau
Với mỗi số : 1,2,3,...,2002 và n+2 nhỏ nhất =>n+2=2003 là số nguyên tố=> n=2001 1 1 1 1 51
Bài 7: Cho 50 số tự nhiên: a ,a ,a ,...,a , t/ m : + + +...+ = , Chứng minh rằng trong 1 2 3 50 a a a a 2 1 2 3 50
50 số đó có ít nhất hai số bằng nhau
GV: Ngô Thế Hoàng _ THCS Hợp Đức 10