Thông tin
Quiz

Chuyên đề phép chia phân số Toán 6

Tài liệu gồm 25 trang, trình bày lý thuyết trọng tâm, các dạng toán và bài tập chuyên đề phép chia phân số, có đáp án và lời giải chi tiết, hỗ trợ học sinh lớp 6 trong quá trình học tập chương trình Toán 6 phần Số học chương 3: Phân số.

Chủ đề:

Chương 6: Phân số (KNTT) 32 tài liệu

Môn:

Toán 6 2.4 K tài liệu

Thông tin:

25 trang 1 năm trước

Tác giả:

Nguyễn Vân

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề phép chia phân số Toán 6

162 81 lượt tải Tải xuống

Trang 1

CHƯƠNG 3

BÀI 9. PHÉP CHIA PHÂN SỐ

Mục tiêu

 Kiến thức

+ Học sinh phát biểu được khái niệm số nghịch đảo và biết cách tìm số nghịch đảo của một số

khác 0.

+ Phát biểu và vận dụng được quy tắc chia hai phân số.

 Kĩ năng

+ Thực hiện được phép chia phân số.

Trang 2

I. LÍ THUYẾT TRỌNG TÂM

Số nghịch đảo

– Hai số được gọi là nghịch đảo của nhau nếu tích của

chúng bằng 1.

– Mỗi số khác 0 có duy nhất một số nghịch đảo với số đó.

Quy tắc chia phân số

– Muốn chia một phân số hoặc một số nguyên cho một

phân số, ta nhân số bị chia với số nghịch đảo của số chia.

 

. .

: . ; : . 0 .

a c a d a d c d a d

a a c

b d b c b c d c c

    

Ví dụ: 2 và

là hai số nghịch đảo

Ví dụ:

2 4 2 9 2.9 3

: . ;

3 9 3 4 3.4 2

  

3 5

3: 3. 5.

5 3

 

SƠ ĐỒ HỆ THỐNG HÓA

Trang 3

II. CÁC DẠNG BÀI TẬP

Dạng 1: Tìm số nghịch đảo của một số cho trước

Phương pháp giải

Hai số gọi là nghịch đảo của nhau nếu tích của

chúng bằng 1.

Nhận xét:

 Với

a b





và

0, 0

a b

 

thì

và

là hai

số nghịch đảo.

 Với

, 0

a a

 



thì

và

là hai số nghịch đảo.

 Số 1 (hoặc



) có nghịch đảo là chính nó.

 Số 0 không có số nghịch đảo.

 Mỗi số khác 0 chỉ có duy nhất một số nghịch đảo.

Ví dụ:



và

là hai số nghịch đảo.





và



là hai số nghịch đảo.

 1 và 1 là hai số nghịch đảo.

Ví dụ mẫu

Ví dụ 1. Tìm số nghịch đảo của các số sau:

2 11 1

4; ; 1; ; .

5 13 7



 

Hướng dẫn giải

Số nghịch đảo của

2 11 1

4; ; 1; ;

5 13 7



 

lần lượt là

1 5 13

; ; 1; ; 7.

4 2 11



 

Ví dụ 2. Tìm các cặp số nghịch đảo của nhau trong các cặp số sau:



0,5 và 2;



0,3 và 3;



0,25 và 4;



3,5 và 5,3.

Hướng dẫn giải



Vì

0,5.2 1



nên 0,5 và 2 là hai số nghịch đảo của nhau.



Vì

0,3.3



0,9 1



nên 0,3 và 3 không là hai số nghịch đảo của nhau.



Vì

0,25.4 1



nên 0,25 và 4 là hai số nghịch đảo của nhau.



Vì

3,5.5,3 18,55 1

 

nên 3,5 và 5,3 không là hai số nghịch đảo của nhau.

Ví dụ 3. Tính giá trị của a, b, c, d rồi tìm số nghịch đảo của chúng.



2 1

3 7

 

;



1 5 3

12 2 10

b  

;

Trang 4



 

2 9

. . 5

3 6

 

;



1 3 1 1

. .

2 4 2 4

d  

Hướng dẫn giải



Ta có

2 1 14 3 17

3 7 21 21 21

a     

. Suy ra số nghịch đảo của a là



Ta có

1 5 3 1 5.3 1 3 1 9 8 2

. .

12 2 10 12 2.10 12 4 12 12 12 3

 

         

Suy ra số nghịch đảo của b là





Ta có

 









2.9. 5 2.3.3. 5

2 9

. . 5 5

3 6 3.6 3.2.3

 

     

Suy ra số nghịch đảo của c là





Ta có

1 3 1 1 1 3 1 1 4 1 1

. . . . .1

2 4 2 4 2 4 4 2 4 2 2

 

      

 

 

Suy ra số nghịch đảo của d là 2.

Ví dụ 4. Cho

1 1 1 1 1 1 1 1 1

90 72 56 42 30 20 12 6 2

        

Tìm A rồi tìm số nghịch đảo của nó.

Hướng dẫn giải

Ta có

1 1 1 1 1 1 1 1 1

90 72 56 42 30 20 12 6 2

        

1 1 1 1 1 1 1 1 1

10.9 9.8 8.7 7.6 6.5 5.4 4.3 3.2 2.1

        

10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1

10.9 9.8 8.7 7.6 6.5 5.4 4.3 3.2 2.1

        

        

1 1 1 1 1 1 1 1 1

... 1

9 10 8 9 7 8 2 3 2

         

          

         

         



 

1 10

10 10



 



Vậy số nghịch đảo của A là

Trang 5

Bài tập tự luyện dạng 1

Bài tập cơ bản

Câu 1: Tìm số nghịch đảo của các số sau :

1 7

5; ; ; 1.

3 4



Câu 2: Tìm các cặp số nghịch đảo trong các cặp số sau :



và 3,5



0,5 và 5



2,4 và



3,1 và 1,3

Câu 3: Tính giá trị của biểu thức

1 5 3 1 7

7 14 2 6 12

 

  

 

 

rồi tìm số nghịch đảo của nó.

Bài tập nâng cao

Câu 4: Tính giá trị của các biểu thức sau rồi tìm số nghịch đảo của chúng :



1 1 1 1

1 . 1 . 1 ... 1

2 3 4 10

       

    

       

       

;



2 2 2 2 2

1 1 1 1 1

1 . 1 . 1 . 1 . 1

2 3 4 5 6

         

     

         

         

Câu 5: Cho

8 15 24 35 48 63

. . . . .

9 16 25 36 49 64

A  ;

1 1 1 1 1 1

1 . 1 . 1 . 1 . 1 . 1

3 6 10 15 21 28

           

      

           

           



Tính A, B rồi tìm số nghịch đảo của chúng.



Tìm tổng của các số nghịch đảo của A và B.

ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN

Câu 1:

Số nghịch đảo của các số

1 7

5; ; ; 1

3 4



lần lượt là

1 4

; 3; ; 1.

5 7

 

Câu 2:

Xét tích của các cặp số đã cho. Ta thấy chỉ có



2,4. 1

nên 2,4 và

là hai số nghịch đảo của nhau.

Câu 3:

Ta có:

1 5 3 1 7

7 14 2 6 12

 

  

 

 

1 14 3 2 7

7 5 2 12 12

 

  

 

 

Trang 6

2 3 5

5 2 12



 

2 5

5 8



 

16 25

40 40

 



Vậy số nghịch đảo của A là

Câu 4:



Ta có:

1 1 1 1

1 . 1 . 1 ... 1

2 3 4 10

       

    

       

       

1 2 3 9

. . ...

2 3 4 10



1.2.3...9

2.3.4...10



Vậy số nghịch đảo của A là 10.



Ta có:

2 2 2 2 2

1 1 1 1 1

1 . 1 . 1 . 1 . 1

2 3 4 5 6

         

     

         

         

1 1 1 1 1

1 . 1 . 1 . 1 . 1

4 9 16 25 36

         

     

         

         

3 8 15 24 35

. . . .

4 9 16 25 36



1.3 2.4 3.5 4.6 5.7

. . . .

2.2 3.3 4.4 5.5 6.6



1.2.3.4.5 3.4.5.6.7

2.3.4.5.6 2.3.4.5.6



1 7

6 2



Vậy số nghịch đảo của B là

Trang 7

Câu 5:



Tính tượng tự câu 4, ta được



1 1 1 1 1 1

1 . 1 . 1 . 1 . 1 . 1

3 6 10 15 21 28

           

      

           

           

2 5 9 14 20 27

. . . . .

3 6 10 15 21 28



2 2 3

2 5 3 2.7 2 .5 3

. . . . .

3 2.3 2.5 3.5 3.7

2 .7



4 5 2

4 4 2 2

2 .3 .5 .7



Số nghịch đảo của A và B lần lượt là

và



Tổng của các số nghịch đảo của A và B là

4 7 11

3 3 3

 

Dạng 2: Thực hiện phép chia phân số

Phương pháp giải

Muốn chia một phân số hay một số nguyên cho

một phân số, ta nhân số bị chia với số nghịch

đảo của số chia.

 

. .

: . ; : .

, , , ; , , 0 .

a c a d a d c d a d

a a

b d b c b c d c c

a b c d b c d

   

 

Muốn chia một phân số cho một số nguyên ta

giữ nguyên tử của phân số và nhân mẫu với số nguyên.

 

, , ; a, 0 .

c c

d d a

a c d d



 

Ví dụ 1:





2 .3

2 4 2 3 3

: . ;

5 3 5 4 5.4 10



  

  

   





3 .7

6 7 7

3 : 3 . .

7 6 6 2



    

Ví dụ 2:

3 3 3

: 2 .

5 5.2 10

 

Ví dụ mẫu

Ví dụ 1. Thực hiện các phép chia



4 1

5 11



;



3 3

7 11



;

Trang 8



0 :

;





Hướng dẫn giải



4 1 4 4.11 44

: .11 .

5 11 5 5 5

   

  



 

3 3 3 11 11 11 11

: . .

7 11 7 3 7 7

7. 1

 

   

 





0 : 0.





9 9 1 3

:3 . .

4 4 3 4

  

 

Ví dụ 2.



Tính giá trị của mỗi biểu thức sau:

;

3 2

7 5

;

3 5

7 4



So sánh số chia với 1 trong mỗi trường hợp trên.



So sánh giá trị tìm được với số bị chia rồi rút ra kết luận.

Hướng dẫn giải

Trường hợp 1.

3 3

7 7



. Số chia bằng 1. Thương bằng số bị chia.

Trường hợp 2.

3 2 3 5 15

: .

7 5 7 2 14

 

. Số chia

nhỏ hơn 1.

Ta thấy



và



nên thương lớn hơn số bị chia.

Trường hợp 3.

3 5 3 4 12

: .

7 4 7 5 35

  . Số chia

lớn hơn 1.

Ta thấy

3 15 12

7 35 35

 

nên thương nhỏ hơn số bị chia.

Bình luận: Trong phép chia có

tử và mẫu là các số nguyên

dương:

– Nếu số chia bằng 1 thì thương

bằng số bị chia.

– Nếu số chia nhỏ hơn 1 thì

thương lớn hơn số bị chia.

– Nếu số chia lớn hơn 1 thì

thương nhỏ hơn số bị chia.

Ví dụ 3. Cho hai phân số

và

. Tìm số lớn nhất sao cho khi chia mỗi phân số này cho số đó ta được

kết quả là số nguyên.

Hướng dẫn giải

Giả sử số lớn nhất phải tìm là

với

, , b 0

a b

 



và





ÖCLN , 1

a b



Để

lớn nhất thì a phải lớn nhất và b phải nhỏ nhất.





Trang 9

Ta có

8 8 8

: .

15 15 15

a b b

b a a

 

là số nguyên thì

8 15 .

b a



Mà





ÖCLN 8,15 1



nên



và

15.







Lại có

18 18 18

: .

35 35 35

a b b

b a a

 

là số nguyên thì

18 35 .

b a



Mà





ÖCLN 18,35 1



nên



và

35.







Từ









và





suy ra





 

ÖCLN 8,18 2.





BCNN 15,35 105.

b  

Vậy phân số cần tìm là

105

Thử lại

8 2 8 105

: . 4.7 28.

15 105 15 2

  

18 2 18 105

: . 9.3 27.

35 105 35 2

  

Bài tập tự luyện dạng 2

Câu 1: Thực hiện các phép tính



4 2

27 9



;



4 2 8

: .

7 3 7

 

 

 

Câu 2: Thực hiện các phép chia



39 26

25 5

;



85 17

54 63



;



3 15

4 8



;



 

: 15

 .

LỜI GIẢI BÀI TẬP TỰ LUYỆN

Câu 1:











 

  

  



2 . 1

4 2 4 9 2

: . .

27 9 27 2 3 3



4 2 8 4 16 4 21 3

: . : . .

7 3 7 7 21 7 16 4

 

  

 

 

Câu 2:



39 26 39 5 39.5 3

: . .

25 5 25 26 25.26 10

  



85 17 85 63 85.63 35

: . .

54 63 64 17 64.17 6

   

  



3 15 3 8 3.8 2

: . .

4 8 4 15 4.15 5

   

  



 

5 5 1 1

: 15 . .

9 9 15 27

  

 

Dạng 3: Viết một phân số dưới dạng thương của hai phân số

Phương pháp giải

Trang 10

Ta thực hiện theo các bước sau:

Bước 1. Viết tử và mẫu dưới dạng tích của hai

số nguyên.

Bước 2. Lập tích các phân số có tử và mẫu được

chọn trong các số nguyên đó.

Bước 3. Chuyển phép nhân phân số thành phép chia

cho số nghịch đảo.

Ví dụ: Viết phân số

dưới dạng thương

của hai phân số có tử và mẫu là các số

nguyên dương khác nhau.

Hướng dẫn giải

Ta có

2 1.2 1.2

9 3.3 3.9

 

1 2 2 1 1 2 2 1

. . . .

3 3 3 3 9 1 1 9

   

1 3 2 1 1 2

: :3 : : 9.

3 2 3 9 2 1

   

Vậy phân số

có thể viết dưới dạng

thương của hai phân số có tử và mẫu là các

số nguyên dương khác nhau.

Ví dụ mẫu

Ví dụ 1. Viết phân số

dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một

chữ số

Hướng dẫn giải

Ta có

8 2.4 1.8

15 3.5 3.5

 

. Suy ra

   

8 2 4 2 5 8 5 2 5 3

. : ; . : ;

15 3 5 3 4 15 4 3 4 2

   

8 2 4 2 3 8 4 2 4 5

. : ; . : ;

15 5 3 5 4 15 3 5 3 2

   

8 1 8 1 5 8 8 1 8

. : ; . : 3;

15 3 5 3 8 15 5 3 5

   

8 1 8 1 3 8 8 1 8

. : ; . : 5.

15 5 3 5 8 15 3 5 3

Ví dụ 2. Viết phân số

143

530

dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có

hai chữ số.

Hướng dẫn giải

Ta có

143 11.13

530 10.53

 . Suy ra

Trang 11

143 11 13 11 53

. : ;

530 10 53 10 13

 

143 13 11 13 10

. : ;

530 53 10 53 11

 

143 11 13 11 10

. : ;

530 53 10 53 13

 

143 13 11 13 53

. : .

530 10 53 10 11

 

Bài tập tự luyện dạng 3

Câu 1: Viết phân số

dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một

chữ số.

Câu 2: Viết phân số

221

209

dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có hai

chữ số.

LỜI GIẢI BÀI TẬP TỰ LUYỆN

Câu 1:

Ta có

6 2.3 1.6

35 5.7 5.7

 

, suy ra

6 2 3 2 7

. : ;

35 5 7 5 3

 

6 3 2 3 5

. : ;

35 7 5 7 2

 

6 2 3 2 5

. : ;

35 7 5 7 3

 

6 3 2 3 7

. : ;

35 5 7 5 2

 

6 1 6 1 7

. : ;

35 5 7 5 6

 

6 6 1 6

. : 5;

35 7 5 7

 

6 1 6 1 5

. : ;

35 7 5 7 6

 

6 6 1 6

. : 7.

35 5 7 5

 

Câu 2:

Ta có

221 13.17

209 11.19



. Suy ra

221 13 17 13 19

. : ;

209 11 19 11 17

 

221 17 13 17 11

. : ;

209 19 11 19 13

 

221 13 17 13 11

. : ;

209 19 11 19 17

 

221 17 13 17 19

. : .

209 11 19 11 13

 

Dạng 4: Tìm x

Ví dụ mẫu

Ví dụ 1. Tìm x biết:



2 3

7 5



;



4 2 1

7 3 5

 

;



1 6 4

. :

3 5 15







;



5 3 1

12 4 3

 

Trang 12

Hướng dẫn giải



Ta có

2 3

7 5



3 2

5 7

x 

3 7

5 2

x 

Vậy

x 



Ta có

4 2 1

7 3 5

 

4 1 2

7 5 3

 

4 3 10

7 15 15

x  

4 13

7 15

x 

13 4

15 7

x 

13 7

15 4

x 

Vậy

x 



Ta có

1 6 4

. :

3 5 15







1 6 15

. .

3 5 4

x 

 

1 9

3 2



9 1

2 3

x 

x  

Vậy

 

hoặc

x 



Ta có

5 3 1

12 4 3

 

3 5 1

4 12 3

 

3 5 4

4 12 12

 

3 1

4 12

x 

1 3

12 4

x 

1 4

12 3

x 



Vậy



Trang 13

Ví dụ 2. Tìm x biết:



1 1 28 1 1

. .

7 3 3 4 7

   

  

   

   

;



x x

 

Hướng dẫn giải



Ta có

1 1 28 1 1

. .

7 3 3 4 7

   

  

   

   

3 7 28 7 4

. .

21 21 3 28 28

   

  

   

   

4 28 3

. .

21 3 28





. 1













Vậy







Ta có

x x

 

. 1 74

 

 

 

 

25 12

. 74

25 25

 

 

 

 

. 74



74 :

x 

74.

x 

50.



Vậy

50.



Ví dụ 3. Tìm số nguyên x biết :



4 3 8 2 2

7 5 15 21

 

  ;



2 5 1 5 49

9 3 18 54

x 

  .

Hướng dẫn giải



Ta có

4 3 8 2 2

7 5 15 21

 

 

4 3 8 2 2

7 5 21 15

x  

 

4 3 8 8

7 5 35

 



3 8 8 4

5 35 7

x  



3 8 8 7

5 35 4

x  



3 8 2

5 5

 





Ta có

2 5 1 5 49

9 3 18 54

x 

 

2 5 1 49 5

9 3 54 18

x 

 

2 5 1 32

9 3 27

x 



5 1 32 2

3 27 9

x 



5 1 32 9

3 27 2

x 



5 1 16

3 3

x 



Trang 14

3 8 2

   

3 2 8

  

3 6



6 :3



Vậy



5 1 16

  

5 16 1

 

5 15



15: 3



Vậy



Bài tập tự luyện dạng 4

Câu 1: Tìm x biết :



7 21

6 4





;



1 3 7

2 4 24



 

;



2 2 5

5 3 7







;



7 5 1

9 3 6



 

Câu 2: Tìm x biết:



1 3 3

7 4 5

 

;



1 7 5

4 5 3

 

  ;



3 5 3

2 6 4

x x

  

Câu 3: Tìm số nguyên x biết:



2 3 6 21

4 5 10

x 



;





 

9 5 3 1 7

8 7 2 14

LỜI GIẢI BÀI TẬP TỰ LUYỆN

Câu 1:



Ta có

7 21

6 4





21 7

4 6





21 6

4 7









Vậy







Ta có

1 3 7

2 4 24



 

3 7 1

4 24 2



 

3 19

4 24

x 

19 3

24 4

x 

19 4

24 3

x 

Vậy

x 

Trang 15



Ta có

2 2 5

5 3 7







2 2 7

5 3 5

x 

 

2 14

5 15

x 

14 2

15 5

x 

14 5

15 2

x 



  

Vậy





hoặc





Ta có

7 5 1

9 3 6



 

5 7 1

3 9 6



 

5 28 6

3 36 36

x  

5 17

3 18



17 5

18 3

x 

17 3

18 5

x 

Vậy

x 

Câu 2:



Ta có

1 3 3

7 4 5

 

3 1 3

4 7 5

 

3 16

4 35





16 3

35 4





105





Vậy

105







Ta có

1 7 5

4 5 3

 

 

1 7 5

4 5 3



 

1 5 7

4 3 5



 

1 4

4 15





4 1

15 4









Vậy





Trang 16



Ta có

3 5 3

2 6 4

x x

  

3 3 5

2 4 6

x x



  

3 19

. 1

2 12

 



 

 

 

1 19

2 12





19 1

12 2









Vậy





Câu 3:



Ta có

2 3 6 21

4 5 10

x 







2 3 21 6

4 10 5

2 3 21 5

4 10 6

x 



2 3 7

4 4

x 



2 3 7

  

2 7 3

 

2 10



10 : 2



Vậy





Ta có

9 5 3 1 1

8 7 2 7

 

 

9 5 3 1 1

8 7 7 2

x 

 

9 5 3 9

8 7 14

 



5 3 9 9

7 14 8

x 



5 3 9 8

7 14 9

x 



5 3 4

7 7

 



5 3 4

   





3 5 4

  

3 9



9 :3



Vậy



Trang 17

Dạng 5: Bài toán có lời văn

Ví dụ mẫu

Ví dụ 1. Một tấm bìa hình chữ nhật có diện tích

. Biết chiều dài là

, tính chiều rộng của tấm

bìa đó.

Hướng dẫn giải

Chiều rộng của tấm bìa là

2 2 2 5 1

: . m.

15 5 15 2 3

 

Ví dụ 2. An đi xe đạp từ nhà đến trường với vận tốc 12km/h hết

giờ. Khi về, An đạp xe với vận tốc

15km/h. Tính thời gian An đi từ trường về nhà.

Hướng dẫn giải

Quãng đường từ nhà An đến trường là

2 24

12. km

5 5



Thời gian An đi từ trường về nhà là

24 24 1 24 8

:15 .

5 5 15 75 25

  

(giờ)

Ví dụ 3. Hai người đang cùng thực hiện một công việc. Sau khi hoàn thành được

công việc thì người

thứ nhất nghỉ. Người thứ hai phải một mình hoàn thành nốt công việc còn lại và mỗi giờ người đó làm

được

công việc. Hỏi sau bao lâu người thứ hai hoàn thành được công việc?

Hướng dẫn giải

Coi khối lượng công việc mà cả hai người đang thực hiện là 1 đơn vị.

Người thứ hai phải hoàn thành nốt số phần công việc là:

3 2

5 5

 

(công việc)

Thời gian để người thứ hai hoàn thành công việc là:

2 1 2

: .10 4

5 10 5

 

(giờ)

Vậy sau 4 giờ thì người thứ hai hoàn thành được công việc.

Ví dụ 4. Một người đi xe máy từ A đến B với vận tốc 40km/h. Khi đi đến B người đó nghỉ 1 giờ rồi quay

trở về A với vận tốc 50km/h. Thời gian cả đi và về (kể cả thời gian nghỉ) 5 giờ 30 phút. Hỏi:



Thời gian người đó đi 1km lúc đi và thời gian người đó đi 1km lúc về?

Trang 18



Quãng đường AB dài bao nhiêu kilômét?

Hướng dẫn giải



Lúc đi người đó đi với vận tốc 40km/h, tức là người đó đi 40km trong 1 giờ.

Suy ra, 1 (km) lúc đi người đó đi trong

(giờ).

Tương tự, vận tốc lúc về của người đó là 50km/h.

Suy ra, 1 (km) lúc về người đó đi trong

(giờ).



Giả sử quãng đường AB là a (km)







Vì 1 (km) lúc đi người đó đi trong

(giờ) nên a (km) người đó đi trong

(giờ).

Tương tự, thời gian người đó đi lúc về là

(giờ).

Đổi 5 giờ 30 phút

  (giờ)

 

(giờ)



(giờ).

Vì thời gian cả đi và về (tính cả thời gian nghỉ) là

giờ nên ta có

40 50 2

a a

  

40 50 12

a a

  

9 9

200 2



9 900

200 200



9 900



900 : 9



100.



Vậy quãng đường AB dài 100km.

Ví dụ 5. Tìm hai số, biết rằng

của số này bằng

của số kia và tổng của hai số đó là 258.

Hướng dẫn giải

Gọi hai số cần tìm là a và b.

Theo đề bài ta có

9 6

. .

11 7

a b



. Suy ra

6 9 6 11 22

: . .

7 11 7 9 21

   

Khi đó bài toán trở thành:

Trang 19

“Tìm hai số biết tổng là 258 và tỉ số của chúng là

”.

Suy ra





258: 22 21 .22 132.

a   





258: 22 21 .21 126.

b   

Vậy hai số cần tìm là 132 và 126.

Bài tập tự luyện dạng 5

Câu 1: Người ta cần đong một thùng nước nắm 210 lít vào các chai loại

lít. Hỏi đóng được tất cả bao

nhiêu chai nước mắm ?

Câu 2: Một mảnh vườn hình chữ nhật có diện tích

. Biết chiều rộng là

, tính chu vi của mảnh

vườn đó.

Câu 3: Một người đi xe máy từ A đến B với vận tốc 40km/h thì mất 3 giờ. Nếu người đó đi ô tô thì chỉ

mất

giờ đã tới nơi. Hỏi người đó đi ô tô với vận tốc bằng bao nhiêu ?

Câu 4: Có hai vòi cùng chảy vào một bể đã chứa

bể nước. Nếu vòi thứ nhất chảy tiếp một mình thì sau

2 giờ đầy bể. Nếu vòi thứ hai chảy tiếp một mình thì sau 3 giờ đầy bể. Hỏi :



Trong 1 giờ mỗi vòi đã chảy được một lượng nước bằng bao nhiêu phần bể ?



Trong 1 giờ cả hai vòi đã chảy được một lượng nước bằng bao nhiêu phần bể ?

Câu 5: Một người đi ô tô từ A đến B với vận tốc 80km/h. Khi đi đến B người đó nghỉ 30 phút rồi quay

trở về A với vận tốc 70km/h. Thời gian cả đi và về (kể cả thời gian nghỉ) là 4 giờ 15 phút. Hỏi :



Thời gian ô tô đi 1km lúc đi và thời gian ô tô đi 1km lúc về là bao nhiêu ?



Quãng đường AB dài bao nhiêu kilômét ?

Câu 6: Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho

và chia a cho

ta đều được kết quả là một

số tự nhiên.

Câu 7: Tích của hai phân số là

, nếu thêm vào thừa số thứ nhất 2 đơn vị thì tích là

. Tìm hai phân số

đó.

Câu 8: Tìm hai số biết rằng

của số này bằng

của số kia và hiệu của hai số đó bằng 9.

LỜI GIẢI BÀI TẬP TỰ LUYỆN

Trang 20

Câu 1:

Đóng được số chai nước mắm là

3 4

210 : 210. 280

4 3

 

(chai).

Câu 2:

Chiều dài của mảnh vườn là

 

35 15 35 4 14

: . m .

2 4 2 15 3

 

Chu vi của mảnh vườn là

 

14 15 101

.2 m

5 4 6

 

 

 

 

Câu 3:

Quãng đường AB là





4.30 120 km



Vận tốc của người đó khi đi ô tô là

 

5 3

120 : 120. 72 km/h .

3 5

 

Câu 4:



Phần bể còn lại chưa có nước là

1 3

4 4

 

bể.

Như vậy, vòi thứ nhất chảy trong 2 giờ được

bể. Do đó trong 1 giờ, vòi thứ nhất chảy được số phần

bể là

3 3 3

: 2

4 4.2 8

 

bể.

Tương tự, trong 1 giờ vòi thứ hai chảy được số phần bể là

3 1

4 4



bể.



Trong 1 giờ, cả hai vòi chảy được số phần bể là

3 1 3 2 5

8 4 8 8 8

   

bể.

Câu 5:



Lúc đi ô tô đi với vận tốc 80km/h, tức là ô tô đi 80km trong 1 giờ.

Suy ra, 1 km lúc đi người đó đi trong

giờ.

Tương tự, vận tốc lúc về của người đó là 70km/h.

Suy ra, 1 km lúc về người đó đi trong

giờ.



Giả sử quãng đường AB là a (km)







Vì 1 km lúc đi người đó đi trong

(giờ) nên a (km) người đó đi trong

giờ.

Tương tự, thời gian người đó đi lúc về là

giờ.

Trang 21

Đổi 30 phút



giờ



giờ.

4 giờ 15 phút = 4 giờ +

giờ

 

giờ

 (giờ)

Vì thời gian cả đi và về (tính cả thời gian nghỉ) là

giờ nên ta có

1 17

80 70 2 4

a a

  

17 1

80 70 4 2

a a

  

3 15

112 4



3 420

112 112



3 420



420 : 3



140.



Vậy quãng đường AB dài 140km.

Câu 6:

Ta có

6 7 7

: . .

7 6 6

a a 

là một số tự nhiên thì

7 6



, suy ra



(vì 6 và 7 là hai số nguyên tố cùng nhau).





Tương tự,

10 11 11

: .

11 10 10

a a 

là số tự nhiên thì







Từ





và





suy ra





6,10

a BC

Để a nhỏ nhất thì





BCNN 6,10 30

 

Thử lại

6 7

30 : 30. 5.7 35;

7 6

  

10 11

30 : 30. 3.11 33.

11 10

  

Vậy số phải tìm là 30.

Câu 7:

Gọi hai phân số cần tìm là a và b. Theo đề bài ta có



a b

và

 

 

2 . .

a b

Ta có

Trang 22

 

 

2 .

a b

 

. 2.

a b b

 

3 13

7 21

  

13 3

21 7



: 2



Suy ra

   

3 3 2 3 21 9

: : . .

7 7 21 7 2 2

a b

Vậy hai phân số cần tìm là

và

Câu 8:

Gọi hai số cần tìm là a và b.

Theo bài ra ta có :



7 28

. .

9 33

a b

suy ra

   

28 7 28 9 4.3 12

: . .

33 9 33 7 11 11

Bài toán trở thành: “Tìm hai số biết hiệu bằng 9 và tỉ số của hai số đó bằng

”

Suy ra





  

9 : 12 11 .12 108;





  

9 : 12 11 .11 99.

Dạng 6: Tính giá trị của một biểu thức

Ví dụ mẫu

Ví dụ 1. Thực hiện các phép tính sau một cách hợp lí



 

 

 

5 11 5

: .

9 13 9

;





1 4 4 8

. : .

2 5 7 9

;



 

5 17 5 9 5 1

: : :

6 25 6 25 6 25

Hướng dẫn giải



     

   

     

     

5 11 5 5 5 11 5 5 11 11 13

: . : . : : 1: .

9 13 9 9 9 13 9 9 13 13 11

Trang 23



   

 

  

    

 



 

 

1 4 4 8 1 4 4 8 2 7 8 2.7.8 4.7 28

. : . . : . . . .

2 5 7 9 2 5 7 9 5 4 9 45

5. 4 .9 5. 1 .9



 

       

 

 

5 17 5 9 5 1 5 17 9 1 5 25 5 5

: : : : : :1 .

6 25 6 25 6 25 6 25 25 25 6 25 6 6

Ví dụ 2. Tính giá trị của các biểu thức



 

 



 

 

 

 

1 8 16 81

: : .

9 27 48 128

A ;



     

    

     

     

4 8 7 6 6 12 1

. :

3 3 4 4 5 5 5

Hướng dẫn giải



Ta có

 

 



 

 

 

 

1 8 16 81

: : .

9 27 48 128

 

 



 

 

 

 

1 27 16 81

. : .

9 8 48 128

 



 

 

3 16 81

: .

8 48 128



3 48 81

. .

8 16 128



3.48.81

8.16.128



3.3.16.81

8.16.128



3.3.81

8.128



729

1024



Ta có

     

    

     

     

4 8 7 6 6 12 1

. :

3 3 4 4 5 5 5



12 1 19

. :

3 4 5



Ví dụ 3. Tính nhanh giá trị của các biểu thức sau



 



 

2 2 2

3 5 9

4 4 4

3 5 9

M ;



   



   

2 2 2 1 1 1

5 9 11 3 4 5

7 7 7 7 7 7

5 9 11 6 8 10

N .

Hướng dẫn giải



Ta có

 

 

 

 

 

   

 

 

 

 

1 1 1

2 2 2

3 5 9

2 1

3 5 9

4 4 4

4 2

1 1 1

3 5 9

Trang 24



Ta có

 

 

 

     

 

    

   

   

   

   

1 1 1

2 2 2 1 1 1 1 1 1

5 9 11

2 1 2 2

5 9 11 3 4 5 3 4 5

: : : : 1.

7 7 7 7 7 7 7

7 7 7

1 1 1 7 1 1 1

7. .

5 9 11 6 8 10 2

5 9 11 2 3 4 5

Bài tập tự luyện dạng 6

Câu 1: Tính giá trị của các biểu thức sau





1 2 4

. ;

2 3 5





3 1 1

3: . ;

4 4 3





3 5 18 14

. : . ;

15 9 17 17



 

 

5 2 5 11

. . 1.

8 13 8 13

Câu 2: Tính giá trị của các biểu thức sau



 



 

 

4 7 4

: ;

9 11 9



   



   

   

4 4 5 16 1

: . : ;

5 5 4 25 5



   



  

   

   

11 7 1 2 5

: ;

12 9 3 3 15



 



  

 

 

2 9 16 3 9

. .

5 8 32 4 10

Câu 3: Tính



 

 

1 1

2 2

;



 

 

1 1

3 3

Câu 4: Tính nhanh giá trị của các biểu thức sau



 



 

3 3 3

4 7 11

6 6 6

4 7 11

P ;



   



   

4 4 4 1 1 1

3 9 13 2 3 7

5 5 5 5 5 5

3 9 13 8 12 28

ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN

Câu 1:



;



;





;



Câu 2:





;





;



;





Câu 3:



Ta có

Trang 25



         



    

 

1 1 1 1 1 1 3 2

1 .

1 1 1 1 2

1 2 5 5

1 1 1 1 1

1 1 1 3

1 1

2 2 2 2



Ta có



           



     

 

1 1 1 1 1 1 1 1 4 10

2 .

1 1 1 1 3 3 1 7

7 7

1 1 1 1 1 1

1 1 2 4

2 4 2 4

1 1

3 3 3 3

Câu 4:



 

 

 

 

 

   

 

 

 

 

1 1 1

3 3 3

4 7 11

3 1

4 7 11

6 6 6

6 2

1 1 1

4 7 11



 

 

 

     

 

    

   

   

   

   

1 1 1

4 4 4 1 1 1 1 1 1

3 9 13

4 1 4 4

3 9 13 2 3 7 2 3 7

: : : : 1.

5 5 5 5 5 5 5

5 5 5

1 1 1 5 1 1 1

5. .

3 9 13 8 12 28 4

3 9 13 4 2 3 7

Bấm Tải xuống để xem toàn bộ.

| 1/25

| | Tải xuống

Preview text:

CHƯƠNG 3 BÀI 9. PHÉP CHIA PHÂN SỐ Mục tiêu  Kiến thức
+ Học sinh phát biểu được khái niệm số nghịch đảo và biết cách tìm số nghịch đảo của một số khác 0.
+ Phát biểu và vận dụng được quy tắc chia hai phân số.  Kĩ năng
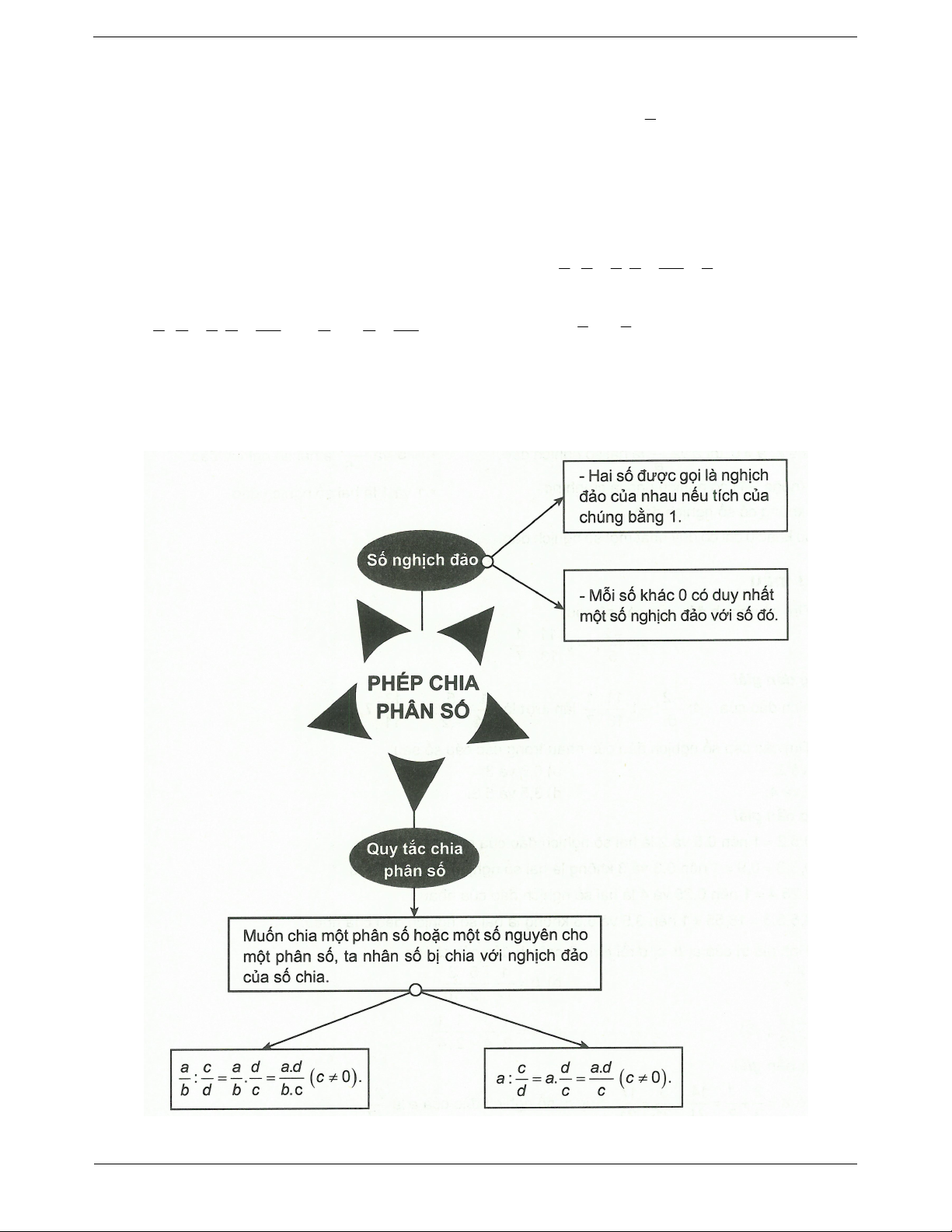
+ Thực hiện được phép chia phân số. Trang 1 I. LÍ THUYẾT TRỌNG TÂM Số nghịch đảo 1
Ví dụ: 2 và là hai số nghịch đảo
– Hai số được gọi là nghịch đảo của nhau nếu tích của 2 chúng bằng 1.
– Mỗi số khác 0 có duy nhất một số nghịch đảo với số đó. Quy tắc chia phân số Ví dụ:
– Muốn chia một phân số hoặc một số nguyên cho một 2 4 2 9 2.9 3 :  .   ;
phân số, ta nhân số bị chia với số nghịch đảo của số chia. 3 9 3 4 3.4 2 a c a d . a d c d . a d 3 5 :  .  ; a :  . a  c  0. 3 :  3.  5. b d b c . b c d c c 5 3 SƠ ĐỒ HỆ THỐNG HÓA Trang 2 II. CÁC DẠNG BÀI TẬP
Dạng 1: Tìm số nghịch đảo của một số cho trước Phương pháp giải
Hai số gọi là nghịch đảo của nhau nếu tích của chúng bằng 1. Ví dụ: Nhận xét: 2 3 
và là hai số nghịch đảo. a b 3 2  Với ,
a b và a  0,b  0 thì và là hai b a 1  5 và
là hai số nghịch đảo. số nghịch đảo. 5  1
 1 và 1 là hai số nghịch đảo.
 Với a ,a  0 thì a và là hai số nghịch đảo. a  Số 1 (hoặc 1
 ) có nghịch đảo là chính nó.
 Số 0 không có số nghịch đảo.
 Mỗi số khác 0 chỉ có duy nhất một số nghịch đảo. Ví dụ mẫu
Ví dụ 1. Tìm số nghịch đảo của các số sau: 2 11 1 4; ; 1; ; . 5 13 7 Hướng dẫn giải 2  11 1 1 5 13
Số nghịch đảo của 4; ; 1; ; lần lượt là ; ; 1; ; 7. 5 13 7 4  2 11
Ví dụ 2. Tìm các cặp số nghịch đảo của nhau trong các cặp số sau: a 0,5 và 2; b 0,3 và 3; c 0,25 và 4; d 3,5 và 5,3. Hướng dẫn giải
a Vì 0,5.2 1nên 0,5 và 2 là hai số nghịch đảo của nhau.
b Vì 0,3.3  0,9 1nên 0,3 và 3 không là hai số nghịch đảo của nhau.
c Vì 0,25.4 1nên 0,25 và 4 là hai số nghịch đảo của nhau.
d Vì 3,5.5,3 18,55  1nên 3,5 và 5,3 không là hai số nghịch đảo của nhau.
Ví dụ 3. Tính giá trị của a, b, c, d rồi tìm số nghịch đảo của chúng. a 2 1 1 5 3 a   ; b b   . ; 3 7 12 2 10 Trang 3 c 2 9 1 3 1 1 c  . . 5   ; d d  .  . . 3 6 2 4 2 4 Hướng dẫn giải 2 1 14 3 17 21
a Ta có a      . Suy ra số nghịch đảo của a là . 3 7 21 21 21 17 1 5 3 1 5.3 1 3 1 9 8 2
b Ta có b   .         . 12 2 10 12 2.10 12 4 12 12 12 3 3 
Suy ra số nghịch đảo của b là . 2 2 9 2.9. 5  2.3.3. 5 
c Ta có c  . .5        5 3 6 3.6 3.2.3 1 
Suy ra số nghịch đảo của c là . 5   d 1 3 1 1 1 3 1 1 4 1 1 Ta có d  .  .  .     .  .1  2 4 2 4 2  4 4  2 4 2 2
Suy ra số nghịch đảo của d là 2. 1 1 1 1 1 1 1 1 1 Ví dụ 4. Cho A          90 72 56 42 30 20 12 6 2
Tìm A rồi tìm số nghịch đảo của nó. Hướng dẫn giải Ta có 1 1 1 1 1 1 1 1 1 A          90 72 56 42 30 20 12 6 2 1 1 1 1 1 1 1 1 1         
10.9 9.8 8.7 7.6 6.5 5.4 4.3 3.2 2.1
10  9 9  8 8  7 7  6 6  5 5  4 4  3 3 2 2 1          10.9 9.8 8.7 7.6 6.5 5.4 4.3 3.2 2.1
 1 1   1 1   1 1   1 1   1              ...      1  9 10 8 9 7 8 2 3 2            1   1 10 1  10   10 10 9  . 10 10
Vậy số nghịch đảo của A là . 9 Trang 4
Bài tập tự luyện dạng 1 Bài tập cơ bản 1 7
Câu 1: Tìm số nghịch đảo của các số sau : 5; ; ; 1. 3 4
Câu 2: Tìm các cặp số nghịch đảo trong các cặp số sau : a 5 5 và 3,5 b 0,5 và 5 c 2,4 và d 3,1 và 1,3 3 12 1 5 3  1 7 
Câu 3: Tính giá trị của biểu thức A  :  
rồi tìm số nghịch đảo của nó. 7 14 2  6 12    Bài tập nâng cao
Câu 4: Tính giá trị của các biểu thức sau rồi tìm số nghịch đảo của chúng :         a 1 1 1 1
A  1 .1 .1 ...1  ; 2 3 4 10                    b 1 1 1 1 1 B  1 .1 .1 .1 .1  . 2 2 2 2 2 2 3 4 5 6            8 15 24 35 48 63  1   1   1   1   1   1  Câu 5: Cho A  . . . . .
; B  1 .1 .1 .1 .1 .1 . 9 16 25 36 49 64 3 6 10 15 21 28             
a Tính A, B rồi tìm số nghịch đảo của chúng.
b Tìm tổng của các số nghịch đảo của A và B.
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN Câu 1: 1 7 1 4
Số nghịch đảo của các số 5; ; ; 1 lần lượt là ; 3; ; 1. 3 4 5  7 Câu 2: 5 5
Xét tích của các cặp số đã cho. Ta thấy chỉ có 2,4.  1 nên 2,4 và
là hai số nghịch đảo của nhau. 12 12 Câu 3: Ta có: 1 5 3  1 7  A  :   7 14 2  6 12    1 14 3  2 7   .   7 5 2 12 12    Trang 5 2 3 5 .    5 2 12 2 5   5 8 16 25   40 40 41  . 40 40
Vậy số nghịch đảo của A là . 41 Câu 4:         a 1 1 1 1
Ta có: A  1 .1 .1 ...1  2 3 4 10          1 2 3 9  . . ... 2 3 4 10 1.2.3...9  2.3.4...10 1  . 10
Vậy số nghịch đảo của A là 10.           b 1 1 1 1 1 Ta có: B  1 .1 .1 .1 .1  2 2 2 2 2 2 3 4 5 6             1   1   1   1   1 
 1 .1 .1 .1 .1  4 9 16 25 36            3 8 15 24 35  . . . . 4 9 16 25 36 1.3 2.4 3.5 4.6 5.7  . . . . 2.2 3.3 4.4 5.5 6.6 1.2.3.4.5 3.4.5.6.7  . 2.3.4.5.6 2.3.4.5.6 1 7  . 6 2 7  . 12 12
Vậy số nghịch đảo của B là . 7 Trang 6 Câu 5: a 3
Tính tượng tự câu 4, ta được A  . 4  1   1   1   1   1   1 
B  1 .1 .1 .1 .1 .1  3 6 10 15 21 28              2 5 9 14 20 27  . . . . . 3 6 10 15 21 28 2 2 3 2 5 3 2.7 2 .5 3  . . . . . 2 3 2.3 2.5 3.5 3.7 2 .7 4 5 2 2 .3 .5 .7  4 4 2 2 2 .3 .5 .7 3  . 7 4 7
Số nghịch đảo của A và B lần lượt là và . 3 3 4 7 11
b Tổng của các số nghịch đảo của A và B là   . 3 3 3
Dạng 2: Thực hiện phép chia phân số Phương pháp giải
Muốn chia một phân số hay một số nguyên cho Ví dụ 1:
một phân số, ta nhân số bị chia với số nghịch 2  4 2 3 2.3 3 :  .   ; đảo của số chia. 5 3 5 4 5.4 10 a c a d . a d c d . 6 7 3  .7 :  .  ; :  . a d a a  3:  3   7  b d b c . b c d c c .   . 7 6 6 2  ,a ,bc,d  ;  , b , c d  0.
Muốn chia một phân số cho một số nguyên ta Ví dụ 2:
giữ nguyên tử của phân số và nhân mẫu với số nguyên. 3 3 3 : 2   . 5 5.2 10 c : c a  d d.a
 ,ac,d ; a,d  0. Ví dụ mẫu
Ví dụ 1. Thực hiện các phép chia a 4  1 3 3  : ; b : ; 5 11 7 11 Trang 7 c 23 9  0 : ; d :3 . 20 4 Hướng dẫn giải 4  1 4 4.11 4  4 a :  .11   . 5 11 5 5 5 b 3 3  3 11 11 11 1  1 :  .     7.  . 7 11 7 3 1 7  7 23 c 0 :  0. 20 9  9  1 3 d  : 3  .  . 4 4 3 4 Ví dụ 2.
a Tính giá trị của mỗi biểu thức sau: 3 :1 3 2 3 5 ; : ; : . 7 7 5 7 4
b So sánh số chia với 1 trong mỗi trường hợp trên.
c So sánh giá trị tìm được với số bị chia rồi rút ra kết luận. Hướng dẫn giải
Bình luận: Trong phép chia có
tử và mẫu là các số nguyên 3 3
Trường hợp 1. :1  . Số chia bằng 1. Thương bằng số bị chia. dương: 7 7
– Nếu số chia bằng 1 thì thương 3 2 3 5 15 2 bằng số bị chia. Trường hợp 2. :  .  . Số chia nhỏ hơn 1. 7 5 7 2 14 5
– Nếu số chia nhỏ hơn 1 thì 15 3
thương lớn hơn số bị chia. Ta thấy
 1 và  1 nên thương lớn hơn số bị chia. 14 7 3 5 3 4 12 5 Trường hợp 3. :  .  . Số chia lớn hơn 1. 7 4 7 5 35 4
– Nếu số chia lớn hơn 1 thì
thương nhỏ hơn số bị chia. 3 15 12 Ta thấy  
nên thương nhỏ hơn số bị chia. 7 35 35 8 18
Ví dụ 3. Cho hai phân số và
. Tìm số lớn nhất sao cho khi chia mỗi phân số này cho số đó ta được 15 35 kết quả là số nguyên. Hướng dẫn giải a
Giả sử số lớn nhất phải tìm là với a,b  , b  0 và ÖCLN , a b 1. b a
Để lớn nhất thì a phải lớn nhất và b phải nhỏ nhất.   1 b Trang 8 8 a 8 b 8b Ta có :  . 
là số nguyên thì 8b  15 . a 15 b 15 a 15a
Mà ÖCLN 8,15 1 nên 8  a và b  15. 2 18 a 18 b 18b Lại có :  . 
là số nguyên thì 18b  35 . a 35 b 35 a 35a
Mà ÖCLN 18,35  1 nên 18  a và b  35. 3 Từ  
1 , 2 và 3 suy ra a  ÖCLN8,18  2.
b  BCNN 15,35  105. 2
Vậy phân số cần tìm là . 105 8 2 8 105 Thử lại :  .  4.7  28. 15 105 15 2 18 2 18 105 :  .  9.3  27. 35 105 35 2
Bài tập tự luyện dạng 2
Câu 1: Thực hiện các phép tính   a 4  2 : 4 2 8 ; b : . . 27 9  7 3 7   
Câu 2: Thực hiện các phép chia 39 26 8  5 17 3  15 5 a : ; b : ; c : ; d : 15 . 25 5 54 63 4 8 9
LỜI GIẢI BÀI TẬP TỰ LUYỆN Câu 1: 4 2
4 9 2.  1   a 2 : 4 2 8 4 16 4 21 3  .   . b : .  :  .    . 27 9 27 2 3 3 7  3 7  7 21 7 16 4 Câu 2: a 39 26 39 5 39.5 3 : 8  5 17 85 63 8  5.63 3  5  .   . b :  .   . 25 5 25 26 25.26 10 54 63 64 17 64.17 6 3  15 3  8 3  .8 2 5 5 1 1 c :  .   . d :15  .  . 4 8 4 15 4.15 5 9 9 15 2  7
Dạng 3: Viết một phân số dưới dạng thương của hai phân số Phương pháp giải Trang 9
Ta thực hiện theo các bước sau: 2
Ví dụ: Viết phân số dưới dạng thương 9
của hai phân số có tử và mẫu là các số nguyên dương khác nhau. Hướng dẫn giải
Bước 1. Viết tử và mẫu dưới dạng tích của hai 2 1.2 1.2 Ta có   số nguyên. 9 3.3 3.9
Bước 2. Lập tích các phân số có tử và mẫu được 1 2 2 1 1 2 2 1  .  .  .  .
chọn trong các số nguyên đó. 3 3 3 3 9 1 1 9
Bước 3. Chuyển phép nhân phân số thành phép chia 1 3 2 1 1 2  :  : 3  :  : 9. 3 2 3 9 2 1 cho số nghịch đảo. 2 Vậy phân số
có thể viết dưới dạng 9
thương của hai phân số có tử và mẫu là các
số nguyên dương khác nhau. Ví dụ mẫu 8 Ví dụ 1. Viết phân số
dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một 15 chữ số Hướng dẫn giải 8 2.4 1.8 Ta có   . Suy ra 15 3.5 3.5 8 2 4 2 5 8 5 2 5 3  .  : ;  .  : ; 15 3 5 3 4 15 4 3 4 2 8 2 4 2 3 8 4 2 4 5  .  : ;  .  : ; 15 5 3 5 4 15 3 5 3 2 8 1 8 1 5 8 8 1 8  .  : ;  .  : 3; 15 3 5 3 8 15 5 3 5 8 1 8 1 3 8 8 1 8  .  : ;  .  : 5. 15 5 3 5 8 15 3 5 3 143 Ví dụ 2. Viết phân số
dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có 530 hai chữ số. Hướng dẫn giải 143 11.13 Ta có  . Suy ra 530 10.53 Trang 10 143 11 13 11 53 143 13 11 13 10  .  : ;  .  : ; 530 10 53 10 13 530 53 10 53 11 143 11 13 11 10 143 13 11 13 53  .  : ;  .  : . 530 53 10 53 13 530 10 53 10 11
Bài tập tự luyện dạng 3 6 Câu 1: Viết phân số
dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một 35 chữ số. 221 Câu 2: Viết phân số
dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có hai 209 chữ số.
LỜI GIẢI BÀI TẬP TỰ LUYỆN Câu 1: 6 2.3 1.6 Ta có   , suy ra 35 5.7 5.7 6 2 3 2 7 6 3 2 3 5 6 2 3 2 5 6 3 2 3 7  .  : ;  .  : ;  .  : ;  .  : ; 35 5 7 5 3 35 7 5 7 2 35 7 5 7 3 35 5 7 5 2 6 1 6 1 7 6 6 1 6 6 1 6 1 5 6 6 1 6  .  : ;  .  : 5;  .  : ;  .  : 7. 35 5 7 5 6 35 7 5 7 35 7 5 7 6 35 5 7 5 Câu 2: 221 13.17 Ta có  . Suy ra 209 11.19 221 13 17 13 19 221 17 13 17 11  .  : ;  .  : ; 209 11 19 11 17 209 19 11 19 13 221 13 17 13 11 221 17 13 17 19  .  : ;  .  : . 209 19 11 19 17 209 11 19 11 13 Dạng 4: Tìm x Ví dụ mẫu Ví dụ 1. Tìm x biết: 2 3 4 2 1 a .x  ; b .x   ; 7 5 7 3 5 c 1 6 4 x . 5 3 1  : ; d  .x  . 3 5 15 12 4 3 Trang 11 Hướng dẫn giải a Ta có b Ta có 2 3 .x 4 2 1  .x   7 5 7 3 5 3 2 x 4 1 2  : .x   5 7 7 5 3 3 7 x 4 3 10  . .x   5 2 7 15 15 21 x 4 13  . .x  10 7 15 21 13 4 Vậy x  . x  : 10 15 7 13 7 x  . 15 4 91 x  . 60 91 Vậy x  . 60 c Ta có d Ta có 1 6 4 x . 5 3 1  :  .x  3 5 15 12 4 3 1 6 15 x . 3 5 1  . .x   3 5  4 4 12 3 1 9 x . 3 5 4  .x   3 2 4 12 12 9 1 x 3 1  : .x  2 3 4 12 9 x 1 3  .3 x  : 2 12 4 27 x 1 4  x  . 2 12 3 27 x 1   . x  . 2 9 27 27 1 Vậy x   hoặc x  . Vậy x  . 2 2 9 Trang 12 Ví dụ 2. Tìm x biết:     12 a 1 1 28 1 1  .x  .   ; b x  x  74 . 7 3 3  4 7      25 Hướng dẫn giải a Ta có b Ta có  1 1  28  1 1  12  .x  .   x  x  74 7 3 3  4 7      25  3 7  28  7 4   12   .x  .   x. 1    74 21 21 3  28 28       25  4  28 3  25 12  .x  . x.     74 21 3 28  25 25  4  .x 37  1 x.  74 21 25 4 x 37  1: x  74 : 21 25 21 x  25  . x  74. 4 37 21 x  50. Vậy x   . 4 Vậy x  50.
Ví dụ 3. Tìm số nguyên x biết : 4 3x  8 2 2 2 5x 1 5 49 a .    ; b .   . 7 5 15 21 9 3 18 54 Hướng dẫn giải a Ta có b Ta có 4 3x  8 2 2 x .  2 5 1 5 49   .   7 5 15 21 9 3 18 54 4 3x  8 2 2 x . 2 5 1 49 5   .   7 5 21 15 9 3 54 18 4 3x  8 8 x . 2 5 1 32  .  7 5 35 9 3 27 3x  8 8  4 5x 1 32 2  :  : 5 35 7 3 27 9 3x  8 8  7 5x 1 32 9  .  . 5 35 4 3 27 2 3x  8 2 5x 1 16   5 5 3 3 Trang 13  3x  8  2  5x 1  16 3x  2  8 5x  16 1 3x  6 5x  15 x  6 : 3 x  15 : 3 x  2. x  5. Vậy x  2. Vậy x  5.
Bài tập tự luyện dạng 4 Câu 1: Tìm x biết : 7 21 1  3 7 2 2 5 7 5 1 a .x   ; b  .x  ; c x  : ; d .x    . 6 4 2 4 24 5 3 7 9 3 6 Câu 2: Tìm x biết: 1 3 3 3 5 3 a 1 7 5  x  ; b x     ; c x   x  . 7 4 5 4 5 3 2 6 4
Câu 3: Tìm số nguyên x biết: 2x  3 6 21 9 5 3x 1 7 a .   ; b .   . 4 5 10 8 7 2 14
LỜI GIẢI BÀI TẬP TỰ LUYỆN Câu 1: a Ta có b Ta có 7 21 .x  1  3 7   .x  6 4 2 4 24 21 7 x  3 7 1  : .x    4 6 4 24 2 21 6 x  3 19  . .x  4 7 4 24 9 x  19 3  . x  : 2 24 4 9 19 4 Vậy x   . x  . 2 24 3 19 x  . 18 19 Vậy x  . 18 Trang 14 c Ta có d Ta có 2 2 5 x 7 5 1  : .x    5 3 7 9 3 6 2 2 7 x 5 7 1  . .x    5 3  5 3 9 6 2 14 x 5 28 6  .x   5 15 3 36 36 14 2 x 5 17  : .x  15 5 3 18 14 5 x 17 5  . x  : 15 2 18 3 7 x 17 3  x  . 3 18 5 7 17  x   x  . 3 30 7 7 17 Vậy x   hoặc x  . Vậy x  . 3 3 30 Câu 2: a Ta có b Ta có 1 3 3 1 7 5  x  x     7 4 5 4 5 3 3 1 3 x   1 7 5 4 7 5 x    4 5 3 3 16 x   1 5 7 4 35 x    4 3 5 16 3 x   : 1 4 35 4 x   4 15 64 x   . 4 1 105 x   : 15 4 64 Vậy x   . 16 105 x   . 15 16 Vậy x   . 15 Trang 15 c Ta có 3 5 3 x   x  2 6 4 3 3 5 x x     2 4 6  3  1  9 x. 1   2    12 1 1  9 x.  2 12 19 1 x   : 12 2 19 x   . 6 19 Vậy x   . 6 Câu 3: a Ta có b Ta có 2x  3 6 21  x . 9 5 3 1 1   .   4 5 10 8 7 2 7 2x  3 21 6 9 5 3x 1 1  : .   4 10 5 8 7 7 2 2x  3 21 5 9 5 3x 9  . .  4 10 6 8 7 14 2x  3 7 5  3x 9 9   : 4 4 7 14 8  2x  3  7 5 3x 9  8  . 2x  7  3 7 14 9 2x  10 5  3x 4   x  10 : 2 7 7 x  5.  5  3x  4 Vậy x  5. 3x  5  4 3x  9 x  9 : 3 x  3. Vậy x  3. Trang 16
Dạng 5: Bài toán có lời văn Ví dụ mẫu 2 2
Ví dụ 1. Một tấm bìa hình chữ nhật có diện tích 2
m . Biết chiều dài là m , tính chiều rộng của tấm 15 5 bìa đó. Hướng dẫn giải
Chiều rộng của tấm bìa là 2 2 2 5 1 :  .  m. 15 5 15 2 3 2
Ví dụ 2. An đi xe đạp từ nhà đến trường với vận tốc 12km/h hết giờ. Khi về, An đạp xe với vận tốc 5
15km/h. Tính thời gian An đi từ trường về nhà. Hướng dẫn giải
Quãng đường từ nhà An đến trường là 2 24 12.  km 5 5
Thời gian An đi từ trường về nhà là 24 24 1 24 8 :15  .   (giờ) 5 5 15 75 25 3
Ví dụ 3. Hai người đang cùng thực hiện một công việc. Sau khi hoàn thành được công việc thì người 5
thứ nhất nghỉ. Người thứ hai phải một mình hoàn thành nốt công việc còn lại và mỗi giờ người đó làm 1 được
công việc. Hỏi sau bao lâu người thứ hai hoàn thành được công việc? 10 Hướng dẫn giải
Coi khối lượng công việc mà cả hai người đang thực hiện là 1 đơn vị.
Người thứ hai phải hoàn thành nốt số phần công việc là: 3 2 1  (công việc) 5 5
Thời gian để người thứ hai hoàn thành công việc là: 2 1 2 :  .10  4 (giờ) 5 10 5
Vậy sau 4 giờ thì người thứ hai hoàn thành được công việc.
Ví dụ 4. Một người đi xe máy từ A đến B với vận tốc 40km/h. Khi đi đến B người đó nghỉ 1 giờ rồi quay
trở về A với vận tốc 50km/h. Thời gian cả đi và về (kể cả thời gian nghỉ) 5 giờ 30 phút. Hỏi:
a Thời gian người đó đi 1km lúc đi và thời gian người đó đi 1km lúc về? Trang 17
b Quãng đường AB dài bao nhiêu kilômét? Hướng dẫn giải
a Lúc đi người đó đi với vận tốc 40km/h, tức là người đó đi 40km trong 1 giờ. 1
Suy ra, 1 (km) lúc đi người đó đi trong (giờ). 40
Tương tự, vận tốc lúc về của người đó là 50km/h. 1
Suy ra, 1 (km) lúc về người đó đi trong (giờ). 50
b Giả sử quãng đường AB là a (km) a  0. 1 a
Vì 1 (km) lúc đi người đó đi trong
(giờ) nên a (km) người đó đi trong (giờ). 40 40 a
Tương tự, thời gian người đó đi lúc về là (giờ). 50 30 1 11
Đổi 5 giờ 30 phút  5  (giờ)  5  (giờ)  (giờ). 60 2 2 11
Vì thời gian cả đi và về (tính cả thời gian nghỉ) là giờ nên ta có 2 a a 11  1  40 50 2 a a 11   1 40 50 12 9a 9  200 2 9a 900  200 200 9a  900 a  900 : 9 a  100.
Vậy quãng đường AB dài 100km. 9 6
Ví dụ 5. Tìm hai số, biết rằng
của số này bằng của số kia và tổng của hai số đó là 258. 11 7 Hướng dẫn giải
Gọi hai số cần tìm là a và b. 6 9 6 a 7 6 9 6 11 22 Theo đề bài ta có .a  .b . Suy ra   :  .  . 11 7 b 9 7 11 7 9 21 11
Khi đó bài toán trở thành: Trang 18 22
“Tìm hai số biết tổng là 258 và tỉ số của chúng là ”. 21
Suy ra a  258 : 22  2  1 .22  132. b  258 : 22  2  1 .21  126.
Vậy hai số cần tìm là 132 và 126.
Bài tập tự luyện dạng 5 3
Câu 1: Người ta cần đong một thùng nước nắm 210 lít vào các chai loại lít. Hỏi đóng được tất cả bao 4 nhiêu chai nước mắm ? 35 15
Câu 2: Một mảnh vườn hình chữ nhật có diện tích 2 m . Biết chiều rộng là m , tính chu vi của mảnh 2 4 vườn đó.
Câu 3: Một người đi xe máy từ A đến B với vận tốc 40km/h thì mất 3 giờ. Nếu người đó đi ô tô thì chỉ 5
mất giờ đã tới nơi. Hỏi người đó đi ô tô với vận tốc bằng bao nhiêu ? 3 1
Câu 4: Có hai vòi cùng chảy vào một bể đã chứa bể nước. Nếu vòi thứ nhất chảy tiếp một mình thì sau 4
2 giờ đầy bể. Nếu vòi thứ hai chảy tiếp một mình thì sau 3 giờ đầy bể. Hỏi :
a Trong 1 giờ mỗi vòi đã chảy được một lượng nước bằng bao nhiêu phần bể ?
b Trong 1 giờ cả hai vòi đã chảy được một lượng nước bằng bao nhiêu phần bể ?
Câu 5: Một người đi ô tô từ A đến B với vận tốc 80km/h. Khi đi đến B người đó nghỉ 30 phút rồi quay
trở về A với vận tốc 70km/h. Thời gian cả đi và về (kể cả thời gian nghỉ) là 4 giờ 15 phút. Hỏi :
a Thời gian ô tô đi 1km lúc đi và thời gian ô tô đi 1km lúc về là bao nhiêu ?
b Quãng đường AB dài bao nhiêu kilômét ? 6 10
Câu 6: Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho và chia a cho
ta đều được kết quả là một 7 11 số tự nhiên. 3 13
Câu 7: Tích của hai phân số là , nếu thêm vào thừa số thứ nhất 2 đơn vị thì tích là . Tìm hai phân số 7 21 đó. 7 28
Câu 8: Tìm hai số biết rằng của số này bằng
của số kia và hiệu của hai số đó bằng 9. 9 33
LỜI GIẢI BÀI TẬP TỰ LUYỆN Trang 19 Câu 1: 3 4
Đóng được số chai nước mắm là 210 :  210.  280 (chai). 4 3 Câu 2: 35 15 35 4 14
Chiều dài của mảnh vườn là :  .  m. 2 4 2 15 3  14 15  101
Chu vi của mảnh vườn là  .2    m  5 4  6 Câu 3:
Quãng đường AB là 4.30  120km 5 3
Vận tốc của người đó khi đi ô tô là 120 :  120.  72km/h. 3 5 Câu 4: 1 3
a Phần bể còn lại chưa có nước là 1  bể. 4 4 3
Như vậy, vòi thứ nhất chảy trong 2 giờ được bể. Do đó trong 1 giờ, vòi thứ nhất chảy được số phần 4 bể là 3 3 3 : 2   bể. 4 4.2 8 3 1
Tương tự, trong 1 giờ vòi thứ hai chảy được số phần bể là : 3  bể. 4 4 3 1 3 2 5
b Trong 1 giờ, cả hai vòi chảy được số phần bể là     bể. 8 4 8 8 8 Câu 5:
a Lúc đi ô tô đi với vận tốc 80km/h, tức là ô tô đi 80km trong 1 giờ. 1
Suy ra, 1 km lúc đi người đó đi trong giờ. 80
Tương tự, vận tốc lúc về của người đó là 70km/h. 1
Suy ra, 1 km lúc về người đó đi trong giờ. 70
b Giả sử quãng đường AB là a (km) a  0. 1 a
Vì 1 km lúc đi người đó đi trong
(giờ) nên a (km) người đó đi trong giờ. 80 80 a
Tương tự, thời gian người đó đi lúc về là giờ. 70 Trang 20 30 1 Đổi 30 phút  giờ  giờ. 60 2 15 1 17 4 giờ 15 phút = 4 giờ + giờ  4  giờ  (giờ) 60 4 4 17
Vì thời gian cả đi và về (tính cả thời gian nghỉ) là giờ nên ta có 4 a a 1 17    80 70 2 4 a a 17 1    80 70 4 2 3a 15  112 4 3a 420  112 112 3a  420 a  420 : 3 a  140.
Vậy quãng đường AB dài 140km. Câu 6: 6 7 7a Ta có a :  . a  . 7 6 6
7a là một số tự nhiên thì 7a  6, suy ra a  6 (vì 6 và 7 là hai số nguyên tố cùng nhau).  1 6 10 11 11a Tương tự, a :  . a 
là số tự nhiên thì a  10. 2 11 10 10 Từ  
1 và 2 suy ra aBC 6,10 .
Để a nhỏ nhất thì a  BCNN 6,10  30 . 6 7
Thử lại 30 :  30.  5.7  35; 7 6 10 11 30 :  30.  3.11  33. 11 10
Vậy số phải tìm là 30. Câu 7: 3 13
Gọi hai phân số cần tìm là a và b. Theo đề bài ta có .
a b  và a  2.b  . 7 21 Ta có Trang 21 13 a2.b  21 13 . a b  2.b  21 3 13  2.b  7 21 13 3  2.b   21 7 4 2.b  21 4 b  : 2 21 2 b  . 21 3 3 2 3 21 9 Suy ra a  : b  :  .  . 7 7 21 7 2 2 9 2
Vậy hai phân số cần tìm là và . 2 21 Câu 8:
Gọi hai số cần tìm là a và b. 7 28 a 28 7 28 9 4.3 12 Theo bài ra ta có : .a  .b suy ra  :  .   . 9 33 b 33 9 33 7 11 11 12
Bài toán trở thành: “Tìm hai số biết hiệu bằng 9 và tỉ số của hai số đó bằng ” 11
Suy ra a  9 : 12 1  1 .12  108; b  9 : 12 1  1 .11  99.
Dạng 6: Tính giá trị của một biểu thức Ví dụ mẫu
Ví dụ 1. Thực hiện các phép tính sau một cách hợp lí 5  11 5  a : 1 4 4 8 5 17 5 9 5 1  . ; b . : . ; c :  :  : . 9 13 9  2 5 7 9 6 25 6 25 6 25 Hướng dẫn giải
5  11 5  5  5 11   5 5  a 11 11 13 : .  : .  : :  1:        .
9 13 9  9  9 13   9 9  13 13 11 Trang 22 1 4 4 8  1 4  b 4 8 2 7 8 2.7.8 4.7 28 . : .  . : .  . .  .
2 5 7 9  2 5  7 9 5 4 9 5.4  .9 5.     1 .9 45 5 17 5 9 5 1 5  17 9 1  c 5 25 5 5 :  :  :  :    :  :1    .
6 25 6 25 6 25 6  25 25 25  6 25 6 6
Ví dụ 2. Tính giá trị của các biểu thức  1 8  16  a 81 A   :  : . ;  9 27  48 128
 4 8   7 6   6 12 1  b B   .  :         .  3 3   4 4   5 5 5  Hướng dẫn giải a Ta có b Ta có  1 8  16  81
 4 8   7 6   6 12 1  A   :  : . B   .  :          9 27  48 128  3 3   4 4   5 5 5   1 27  16  81 12 1 19   .  : .  . :  9 8  48 128 3 4 5  3 16  81 19   1:  : . 5  8 48  128 5 3 48 81  .  . . 19 8 16 128 3.48.81  8.16.128 3.3.16.81  8.16.128 3.3.81  8.128 729  . 1024
Ví dụ 3. Tính nhanh giá trị của các biểu thức sau 2 2 2 2 2 2 1 1 1       a M  3 5 9 ; b N  5 9 11 3 4 5 : . 4 4 4 7 7 7 7 7 7       3 5 9 5 9 11 6 8 10 Hướng dẫn giải  1 1 1  2 2 2 2.       3 5 9 a 3 5 9 2 1 Ta có   M     . 4 4 4  1 1 1    4 2 4.     3 5 9  3 5 9  Trang 23 b Ta có  1 1 1  2 2 2 1 1 1 2.   1 1 1         5 9 11 3 4 5  5 9 11 3 4 5 2 1 2 2 N  :  :  :  :  1. 7 7 7 7 7 7
 1 1 1  7  1 1 1  7 7     7 7 7.   .       5 9 11 6 8 10  5 9 11 2  3 4 5  2
Bài tập tự luyện dạng 6
Câu 1: Tính giá trị của các biểu thức sau a 1 2 4 3 1 1 3 5 18 14 5 2 5 11  . ; b 3:  . ; c . : . ; d .  . 1. 2 3 5 4 4 3 15 9 17 17 8 13 8 13
Câu 2: Tính giá trị của các biểu thức sau  4 7  4  4 5   16 1  a 4    : ; b : . :     ;  9 11 9 5  5 4   25 5  11  7 1  2 5  2  9 16 3  c 9 :       ; d .    . 12    9 3   3 15  5  8 32 4  10 Câu 3: Tính a 1 1 1 1 A   ; b B   . 1 1 1 1 1  1 1 1 1 1 1 1 1  1 1 1 2 2 3 3
Câu 4: Tính nhanh giá trị của các biểu thức sau 3 3 3 4 4 4 1 1 1       a P  4 7 11 ; b Q  3 9 13 2 3 7 : 6 6 6 5 5 5 5 5 5       4 7 11 3 9 13 8 12 28
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN Câu 1: 31 47 3 a 7 ; b ; c ; d . 30 12 81 8 Câu 2: 83 a 19 20 5 ; b ; c ; d . 44 11 48 4 Câu 3: a Ta có Trang 24 1 1 1 1 1 1 3 2 A        1  . 1 1 1 1 1 2 2      5 5 1 1 1 1 1 1 1 1 3   3 1 1 2 2 2 2 b Ta có 1 1 1 1 1 1 1 1 4 10 B          2   . 1 1 1 1 3 3 1 7       7 7 1 1 1 1 1 1 1 1 2 4   2 4 2 4 1 1 3 3 3 3 Câu 4:  1 1 1  3 3 3 3.       4 7 11 a 4 7 11 3 1   P     . 6 6 6  1 1 1    6 2 6.     4 7 11  4 7 11  1 1 1  4 4 4 1 1 1 4.   1 1 1         3 9 13 b 3 9 13 2 3 7 2 3 7 4 1 4 4   Q  :  :  :  :  1. 5 5 5 5 5 5
 1 1 1  5  1 1 1  5 5     5 5 5.   .       3 9 13 8 12 28  3 9 13  4  2 3 7  4 Trang 25