















Preview text:
BÀI 5. PHÉP NHÂN VÀ PHÉP CHIA HAI LŨY THỪA CÙNG CƠ SỐ Mục tiêu Kiến thức
+ Hiểu định nghĩa lũy thừa, phân biệt được cơ số và số mũ.
+ Hiểu được quy tắc nhân và chia hai lũy thừa cùng cơ số.
+ Hiểu được khái niệm số chính phương. Kĩ năng
+ Thực hiện được các phép tính lũy thừa.
+ Biết cách viết gọn một biểu thức dưới dạng lũy thừa.
+ So sánh được các lũy thừa.
+ Biết biểu diễn một số tự nhiên bất kì dưới dạng tổng các lũy thừa của 10. Trang 1 I. LÍ THUYẾT TRỌNG TÂM
1. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng
nhau, mỗi thừa số bằng a: n a a.a. . a ... .a (n 0) Ví dụ. 4 2.2.2.2 2 ; n thõa sè 3
Trong đó a gọi là cơ số, n gọi là số mũ. . x . x x x .
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa. Quy ước 1 a a ; 0 a 1 a 0 . Chú ý: + 0 0 không có nghĩa. + 2
a còn được gọi là a bình phương (hay bình phương của a). + 3
a còn được gọi là a lập phương (hay lập phương của a).
2. Nhân hai lũy thừa có cùng cơ số Ví dụ. 2 5 25 7 3 .3 3 3 ;
Khi nhân hai lũy thừa có cùng cơ số, ta giữ 4 14 5 . a a a a .
nguyên cơ số và cộng các số mũ: m . n m n a a a
3. Chia hai lũy thừa cùng cơ số Ví dụ. 12 8 128 4 5 : 5 5 5 ;
Khi chia hai lũy thừa có cùng cơ số (khác 0), ta 7 3 73 4 x : x x x x 0 .
giữ nguyên cơ số và trừ các số mũ: m : n mn a a a a 0; m n 4. Chú ý Ví dụ.
Mọi số tự nhiên đều viết được dưới dạng tổng 2345 2.1000 3.100 4.10 5 các lũy thừa của 10. 3 2 1 0
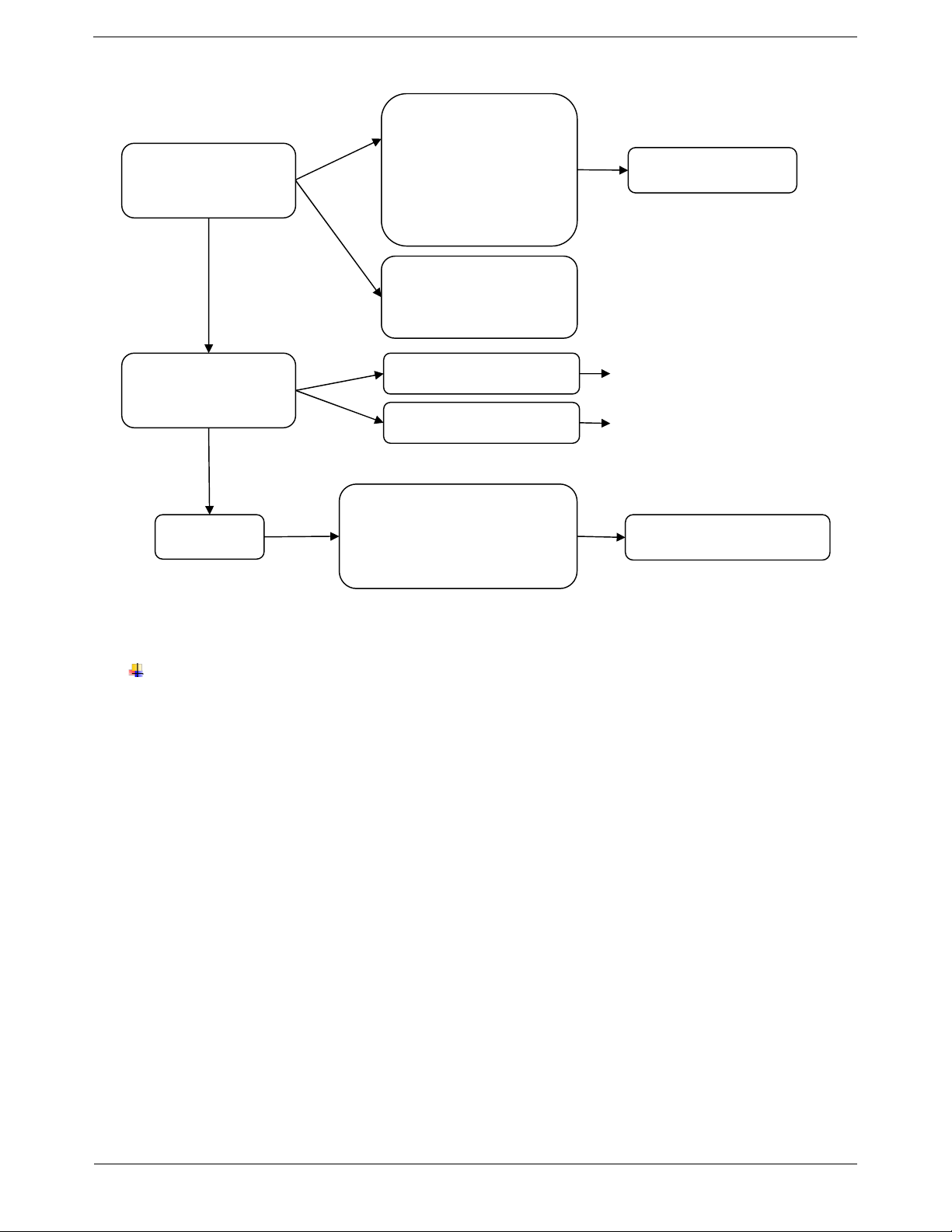
2.10 3.10 4.10 5.10 . Trang 2 SƠ ĐỒ HỆ THỐNG HÓA n a a.a. . a ... .a (n 0) n thõa sè Lũy thừa với số 0 0 không có nghĩa a là cơ số, a 0 mũ tự nhiên n là số mũ 0 a 1; 1 a a a 0 Giữ nguyên cơ số Các phép toán lũy m . n m n a a a Cộng số mũ thừa m : n m n a a a Trừ số mũ
Mọi số tự nhiên đều viết Chú ý
được dưới dạng tổng các lũy 2 0 251 2.10 5.10 1.10 thừa của 10. II. CÁC DẠNG BÀI TẬP
Dạng 1: Viêt gọn một biểu thức dưới dạng lũy thừa Ví dụ mẫu
Ví dụ 1. Viết gọn các tích sau dưới dạng lũy thừa:
a) 5.5.5.5.5.5.5; b) 3.5.15.15.45; c) 3.3.3.4.4.4.4; d) . a . a . b . b . b . b b . Hướng dẫn giải
a) Ta có: 5.5.5.5.5.5.5 = 57. b) Ta có: 3.5.15.15.45 = 5 4
3.5. 3.5 . 3.5 . 3.3.5 3 .5 .
c) Ta có: 3.3.3.4.4.4.4 = 3 2 2 2 2 3 2222 3 8 3 .2 .2 .2 .2 3 .2 3 .2 . d) Ta có: 2 5 . a . a . b . b . b . b b a .b .
Ví dụ 2. Viết gọn các kết quả sau dưới dạng lũy thừa: a) 10 4 2 : 2 ; b) 2 4 5 .5 ; c) 5 14 4 2 .3 : 6 ; d) ab7 5 : b với b 0 . Hướng dẫn giải a) Ta có: 10 4 104 6 2 : 2 2 2 . b) Ta có: 2 4 24 6 5 .5 5 5 . Trang 3 c) Ta có: 4 5 14 4 5 14 5 14
4 4 5 4 14 4 10 2 .3 : 6 2 .3 : 2.3 2 .3 : 2 .3 2 : 2 : 3 : 3 2.3 . d) Ta có: ab7 5 7 7 5 7 75 7 2 : b a .b : b a .b a .b .
Ví dụ 3. Viết mỗi số sau dưới dạng lũy thừa của 10: a) 1000; b) 1 000 000; c) 1 tỉ; d) 1 00...0 ; 12 ch÷ sè 0 Hướng dẫn giải a) Ta có: 3 1000 10 . Tổng quát: b) Ta có: 6 1000 000 10 . 1 00...0 10n n ch÷ sè 0 c) Ta có: 1 tỉ 9 1000000000 10 . d) Ta có: 12 1 00...0 10 . 12 ch÷ sè 0
Ví dụ 4. Viết các số sau dưới dạng tổng các lũy thừa của 10: a) ab ; b) abc ; c) abcd . Hướng dẫn giải a) Ta có: 1 0 ab . a 10 b . a 10 . b 10 . b) Ta có: 2 1 0 abc . a 100 . b 10 c . a 10 . b 10 . c 10 . c) Ta có: 3 2 1 0 abcd . a 1000 . b 100 . c 10 . a 10 . b 10 . c 10 d.10 .
Ví dụ 5. Mỗi tổng sau có phải là số chính phương hay không? a) 3 3 3 3 1 2 3 4 ; b) 3 3 3 3 3 1 2 3 4 5 . Hướng dẫn giải a) Ta có: 3 3 3 3 2
1 2 3 4 1 8 27 64 100 10 . Tổng quát: Vậy 3 3 3 3
1 2 3 4 là một số chính phương. 3 3 3 3 3
1 2 3 4 ... n 2 b) Ta có: 3 3 3 3 3 3 2
1 2 3 4 5 100 5 100 125 225 15 .
1 2 3... n Vậy 3 3 3 3 3
1 2 3 4 5 là một số chính phương.
Bài tập tự luyện dạng 1 Bài tập cơ bản
Câu 1. Viết gọn các biểu thức sau bằng cách dùng lũy thừa
a) 2.2.2.2.3.3.3.3.3; b) 2.4.5.10.20.25; c) 3.3.7.9.21.49 d) . m . m . m m . n n .
Câu 2. Viết gọn các kết quả sau bằng cách dùng lũy thừa: Trang 4
a) 7.7.7.7.7; b) 2.2.3.3.3; c) 5.5.5 – 3.3.3.3; d) 4.4.4.8 : 2.2.2; e) 2.2.5.10; f) . x y.y. . y x .
Câu 3. Viết kết quả của các phép tính sau dưới dạng lũy thừa: a) 5 4 2 2 . ; b) 10 10 4.3 5.3 ; c) 15 7 5 : 5 ; d) 6 3 x . . x x
Câu 4. Viết các số sau dưới dạng tổng các lũy thừa của 10: a) 567; b) 1024; c) abcde ;
Câu 5. Dùng lũy thừa để viết các số sau:
a) Khối lượng Trái Đất bằng 6 00...0 tấn. 21 ch÷ sè 0
b) Khối lượng khí quyển Trái Đất bằng 5 00...0 tấn. 15 ch÷ sè 0 Bài tập nâng cao
Câu 6. Viết gọn các tích sau bằng cách dùng lũy thừa: a) 2 3 99 . x x .x ...x ; b) 3 5 99 . x x .x ...x ; c) 2 4 6 100 x .x .x ...x . Câu 1. a) Ta có: 4 5 2.2.2.2.3.3.3.3.3 2 .3 . b) Ta có: 2 2 6 5
2.4.5.10.20.25 2.2 .5. 2.5 . 2.2.5 .5 2 .5 . c) Ta có: 2 2 5 4
3.3.7.9.21.49 3.3.7.3 . 3.7 .7 3 .7 . d) Ta có: 4 2 . m . m . m m . n n m n . Câu 2. a) 5 7.7.7.7.7 7 . b) 2 3 2.2.3.3.3 2 .3 . c) 3 4
5.5.5 3.3.3.3 5 3 . d) 2 2 2 3 9 8 10
4.4.4.8 : 2.2.2 2 .2 .2 .2 : 2.2.2 2 : 2.2.2 2 .2.2 2 . e) 3 2
2.2.5.10 2.2.5.2.5 2 .5 . f) 2 3 . x . y . y . y x x .y . Câu 3. Ta có: 5 4 54 9 2 .2 2 2 . Ta có: 10 10 10 10 10 2 102 12 4.3 5.3
3 . 4 5 3 .9 3 .3 3 3 . Ta có: 15 7 157 8 5 : 5 5 5 . Ta có: 6 3 6 1 3 10 x . . x x x x . Câu 4. Ta có: 2 1 0
567 5.100 6.10 7 5.10 6.10 7.10 . Trang 5 Ta có: 3 1 0
1024 1000 24 1000 2.10 4 10 2.10 4.10 . Ta có: abcde . a 10000 . b 1000 . c 100 d.10 e 4 3 2 1 0 . a 10 . b 10 . c 10 d.10 . e 10 . Câu 5. a) 21 6 00...0 6.10 . 21 ch÷ sè 0 b) 15 5 00...0 5.10 . 15 ch÷ sè 0 Câu 6. a) Ta có: 2 3 99 1 2 3 ... 99 . x x .x ...x x .
Xét tổng: 1 2 3 ... 99
+ Số số hạng: 99 1 1 99 .
+ Tổng: 1 2 3 ... 99 99
1 .99 : 2 100.99 : 2 4950 . Vậy 2 3 99 4950 . x x .x ...x x . b) Ta có: 3 5 99 135...99 199.50:2 2500 . x x .x ...x x x x . c) Ta có: 2 4 6 100 246 . .. 1 00 1002.50:2 2550 x .x .x ...x x x x .
Dạng 2: Tính giá trị của biểu thức Ví dụ mẫu
Ví dụ 1. Tính giá trị của các biểu thức: a) 6 2 4 3 : 3 3 ; b) 2 2 2 2 5 . 3 . 81: 3 . Hướng dẫn giải a) Ta có: 6 2 4 62 4 4 4 3 : 3 3 3 3 3 3 0 . b) Ta có: . . : . 2 2 2 2 4 2 2 5 3 81 3 2 5 3 . 3 : 3 2 2 10 .3 3 100 3 . 9 300 9 291.
Ví dụ 2. Tính giá trị của các biểu thức: a) 2 2 4.6 2 6 . ; b) 2 4 5 2 8 4 9 5 . .9 3 . 9 .5 ; c) 2018 2019 2017 2 2 : 2 ; d) 101 100 99 4 4 : 4 . Hướng dẫn giải a) Ta có: b) Ta có: Trang 6 2 2 4.6 2.6 2 4 5 2 8 4 9 5 . .9 .3 9 .5 2 6 .4 2 2 4 5 8 4 9 .5 .9 .9 9 5 . 2 6 .6 8 4 8 4 9 .5 9 .5 36.6 0. 216. c) Ta có: d) Ta có: 2018 2019 2 2 2017 : 2 101 100 4 4 99 : 4 2018 2017 2019 2017 2 : 2 2 : 2 101 99 100 99 4 : 4 4 : 4 20182017 20192017 2 2 10199 10099 4 4 2 2 2 2 4 4 2 4 16 4 6. 12. Ví dụ 3. Tính nhẩm: 2 2 2 2 2 2 15 ;25 ;35 ;45 ;75 1 ; 25 . Hướng dẫn giải Ta có: Tương tự, ta có: 2 2 2
35 1225;45 2025;75 5625.
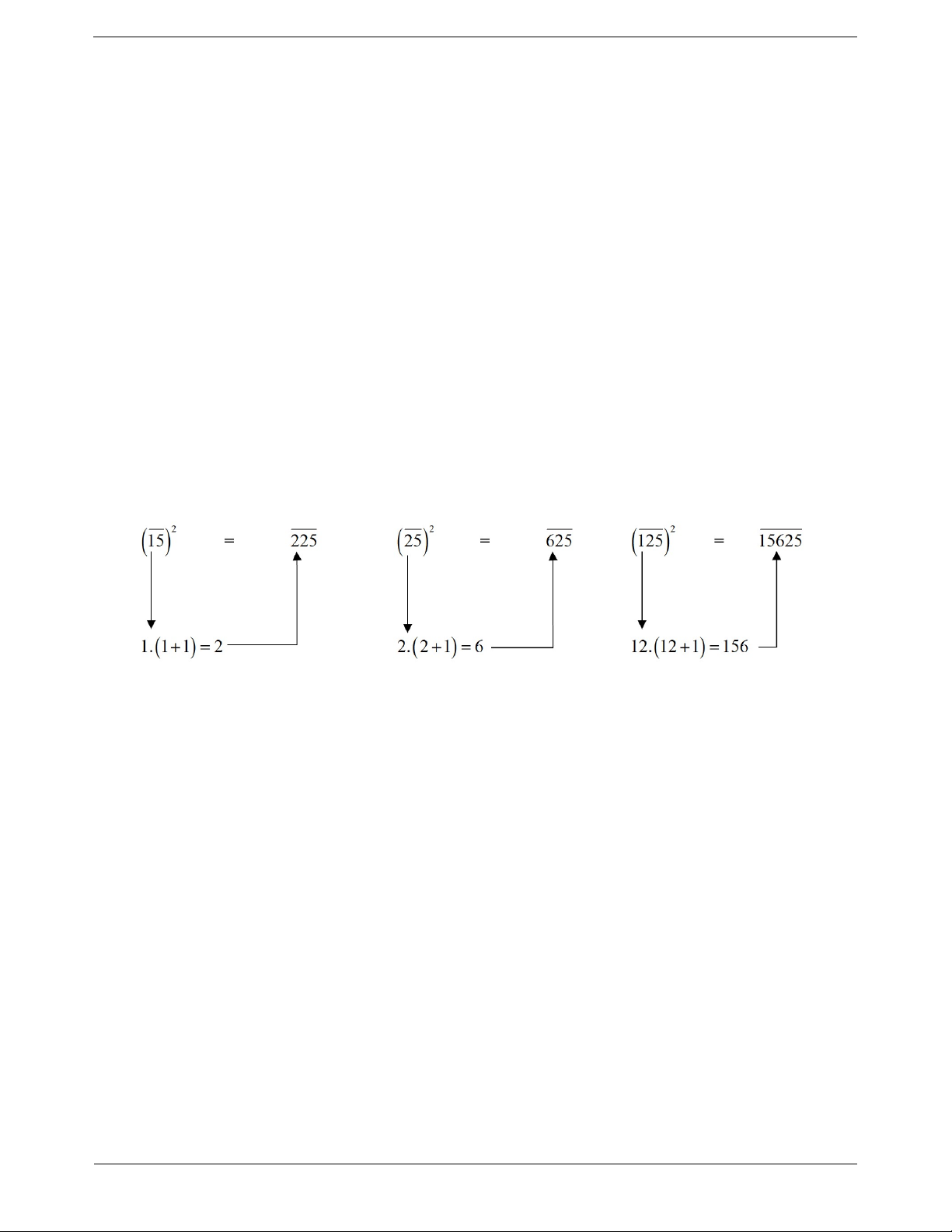
Muốn bình phương một số có tận cùng bằng
5, ta lấy số chục nhân với số chục cộng 1,
rồi viết thêm số 25 ở bên phải của tích vừa nhận được. Ví dụ 4. Tính tổng 2 3 99 100
S 1 2 2 2 ... 2 2 . Hướng dẫn giải
Để tính tổng S có dạng Ta có: 2 3 99 100
S 1 2 2 2 ... 2 2 . (1) 2 3 1 ... n S a a a a (1)
Nhân cả 2 vế với 2, ta được: Ta làm như sau: 2 3 4 100 101
2S 2 2 2 2 ... 2 2 . (2)
Nhân cả 2 vế của S với a ta được:
Trừ theo từng vế của (2) cho (1) ta được: 2 3 4 1 . ... n a S a a a a a . (2) 2S S 2 3 4 100 101
2 2 2 2 ... 2 2
Trừ theo vế của (2) cho (1) ta 2 3 99 100
1 2 2 2 ... 2 2 được: 101 S 2 1. Vậy 101 S 2 1. Trang 7 n 1 . a S S a 1 a n 1 1 S a 1 n 1 a 1 S . a 1 n 1 a 1 Vậy S . a 1
Bài tập tự luyện dạng 2 Bài tập cơ bản
Câu 1. Điền vào các bảng sau: a 1 2 3 4 5 6 7 8 9 10 a2 a3 a 11 12 13 14 15 16 17 18 19 20 a2 Câu 2. Tính nhẩm: a) 2 55 ; b) 2 65 ; c) 2 105 ; d) 2 145 .
Câu 3. Thực hiện các phép tính: a) 5 7 3 .3 ; b) 10 3 2 : 2 ; c) 2 3 2 .5 1 . 0 ; d) 5 2 3 3 7 . .49 : 21 .
Câu 4. Mỗi biểu thức sau có phải là một số chính phương hay không? a) 2 2 3 4 ; b) 3 3 8 : 2 ; c) 2 2 5 12 ; d) 3 3 3 3 3 3
1 2 3 4 5 6 .
Câu 5. Thực hiện các phép tính: a) : 2 125 25 ; b) 9 9 . . 10 2 16 2 34 : 2 ; c) 4 2 . . 5 3 57 9 21 : 3 ; d) 8 4 2 3 3 : 3 2 .2 .
Câu 6. Thực hiện các phép tính: a) 8 3 : 5 3 2 8 2 .2 ; b) 1997 1995 : 1994 7 7 7 .7 ; Bài tập nâng cao Câu 7. Tính tổng: a) 2 3 50
1 2 2 2 ... 2 ; b) 2 3 1999 2000
1 3 3 3 ... 3 3 ; Đáp án Câu 1. Trang 8 a 1 2 3 4 5 6 7 8 9 10 a2 1 4 9 16 25 36 49 64 81 100 a3 1 8 27 64 125 216 343 512 729 1000 a 11 12 13 14 15 16 17 18 19 20 a2 121 144 169 196 225 256 289 324 361 400 Câu 2. a) 2 55 3025 . b) 2 65 4225 . c) 2 105 11025 . d) 2 145 21025 . Câu 3. a) 5 7 12 3 .3 3 . b) 10 3 7 2 : 2 2 . c) 2 3 2 3 3 4
2 .5 .10 2 .5 .2.5 2 .5 . d) 3 5 2 3 5 2 2 3 .7 .49 : 21 3 .7 .7 : 3.7 5 4 3 .7 : 3 3 3 .7 2 3 .7. Câu 4. a) Ta có: 2 2 2
3 4 9 16 25 5 . Vậy 2 2
3 4 là một số chính phương. 3 2 b) Ta có: 3 3 3 3 3.3 3 93 6 3 8 : 2 2 : 2 2 : 2 2 2 2 . Vậy 3 3
8 : 2 là một số chính phương. c) Ta có: 2 2 2
5 12 25 144 169 13 . Vậy 2 2
5 12 là một số chính phương. d) Ta có: 3 3 3 3 3 3 2
1 2 3 4 5 6 225 216 9 3 . Vậy 3 3 3 3 3 3
1 2 3 4 5 6 là một số chính phương. Câu 5. a) Ta có: 2 2 125 : 25 5 25 . b) Ta có: 9 9 10 9 10 2 .16 2 .34 : 2 2 . 16 34 : 2 Trang 9 9 2 .50 10 : 2 9 2 .2.25 10 : 2 10 2 .25 10 : 2 25. 10 10 2 : 2 25. c) Ta có: 4 2 5 4 4 5
3 .57 9 .21 : 3 3 .57 3 .21 : 3 4 3 .57 2 5 1 : 3 4 3 .36 5 : 3 4 3 .3.12 5 : 3 5 3 .12 5 : 3 12. 5 5 3 : 3 12. d) Ta có: 8 4 2 3 84 23 3 : 3 2 .2 3 2 4 5 3 2 81 32 113. Câu 6. 3 a) Ta có: 8
3 5 3 8 3 5 3 2 8 : 2 .2 2 2 : 2 8 9 2 2 8 : 2 8 8 2 : 2 9 8 2 : 2 1 2 3. b) Ta có: 1997 1995
1994 1997 1995 1995 7 7 : 7 .7 7 7 : 7 1997 1995 7 : 7 1995 1995 7 : 7 2 7 1 48. Bài tập nâng cao Câu 7. a) Đặt 2 3 50
A 1 2 2 2 ... 2 (1)
Nhân cả hai vế của A với 2 ta được: 2 3 4 51
2.A 2 2 2 2 ... 2 (2)
Trừ từng vế của (2) cho (1) ta được: Trang 10 2.A A 2 3 4 51
2 2 2 2 ... 2 2 3 50
1 2 2 2 ... 2 51 A 2 1. Vậy 51 A 2 1. 2001 3 1
b) Tương tự câu a) ta có: 2 3 1999 2000
1 3 3 3 ... 3 3 . 2
Dạng 3: Tìm cơ số hoặc số mũ của một lũy thừa Phương pháp giải + Đưa về cùng cơ số: m n a a suy ra m n . Ví dụ. 2x 8 x 3 2 2 x 3 + Đưa về cùng số mũ: m m a b suy ra a b Ví dụ. 2 x 9 2 2 x 3 x 3 Ví dụ mẫu
Ví dụ 1. Tìm số tự nhiên n sao cho: a) 2n 32 ; b) 4n 64 ;
c) 5n 625 ; d) 15n 225 ; Hướng dẫn giải Vì 5 32 2 nên n 5 2 2 suy ra n 5 . Vì 3 64 4 nên n 3 4 4 suy ra n 3. Vì 4 625 5 nên n 4 5 5 suy ra n 4 . Vì 2 225 15 nên n 2 15 15 suy ra n 2 .
Ví dụ 2. Tìm số tự nhiên x sao cho: a) 2 x 25 ; b) 3 x 64 ; c) n
x 1 với n ; d) 100 x x ; Hướng dẫn giải a) Vì 2 25 5 nên 2 2 2
x 25 x 5 suy ra x 5 . b) Vì 3 64 4 nên 3 3 3
x 64 x 4 suy ra x 4 .
c) Vì 1n 1 với mọi số tự nhiên n nên n x 1 suy ra x 1. d) Ta có: 100 x x Nhận xét: m n x x với x, m, n là Trang 11 100 x x 0
các số tự nhiên thì x 0 . x 99 x 1 0. hoặc x 1. Suy ra x 0 hoặc 99 x 1 0 . Với 99 x 1 0 suy ra 99 x 1, do đó x 1.
Ví dụ 3. Tìm số tự nhiên x, biết: a) x 2 4 1 25 9 . ; b) x x3 2 2 144 ; c) x 12 4
2.3 10.3 8.27 ; d) x 3 2 1 12 15 . Hướng dẫn giải a) Ta có: x 2 4 1 25.9 b) Ta có: x x3 2 2 144 x. 3 2 1 2 144 4x 2 1 25 9 . x 2 .9 144 4x 2 2 2 1 5 .3 2x 144 : 9 4x 2 2 1 15 2x 16. 4x 1 15 Vì 4 16 2 nên x 4 . 4x 15 1 4x 16 Vậy x 4 . x 4. Vậy x 4 . c) Ta có: x 12 4 2.3 10.3 8.27 d) Ta có: x 3 2 1 12 15 3x 12 4 10.3 8 2 . 7 : 2 2x 3 1 15 12 x 12 4 3 10 3 . : 2 8 2 . 7 : 2 2x 3 1 27 x 12 4 3 5 3 . 4.27 2x 3 3 1 3 x 12 12 3 5 3 . 4.3 2x 1 3 x 12 3 3 5 4 2x 3 1 x 12 3 3 .9 2x 2 x 12 2 3 3 .3 x 1. x 14 3 3 Vậy x 1. x 14. Vậy x 14 .
Bài tập tự luyện dạng 3 Bài tập cơ bản
Câu 1. Tìm số tự nhiên x, biết rằng: a) 2x 16 b) 3x 81; c) 3 x 64 ; d) 2 x 81 .
Câu 2. Tìm số tự nhiên x, biết rằng: Trang 12 a) 2x.8 512 ; b) 20 x x ; c) x 3 2 1 125 ; d) x 10 3 0 .
Câu 3. Tìm số tự nhiên x, biết rằng: a) x x2 3 3 90 ; b) x 2 2 1 625 ; c) 2 5 3 x : 4 5 : 5 29 ; d) 9. x 10 2019 16 2019 . Bài tập nâng cao Câu 4. Cho 2 3 2008
A 3 3 3 ... 3
. Tìm số tự nhiên n, biết rằng 2 3 3n A . Đáp án Câu 1. a) Ta có: 2x 16 b) Ta có: 3x 81 x 4 2 2 x 4 3 3 x 4. x 4. Vậy x 4. Vậy x 4. c) Ta có: 3 x 64 d) Ta có: 2 x 81 3 3 x 4 2 2 x 9 x 4. x 9. Vậy x 4. Vậy x 9. Câu 2. a) Ta có: 2 .x8 512 b) Ta có: 20 x x 2x 512 : 8 20 x x 0 2x 64 . x 19 x 1 0. x 6 2 2 Suy ra x 0 hoặc 19 x 1 0 . x 6. Vậy x 6. Với 19
x 1 0 ta được x 1. Vậy x 0 hoặc x 1. c) Ta có: x 3 2 1 125 d) Ta có: x 10 3 0 x 3 3 2 1 5 x 3 0 2x 1 5 x 3. 2x 5 1 Vậy x 3. 2x 4 x 4 : 2 x 2. Vậy x 2. Câu 3. Trang 13 a) Ta có: x x2 3 3 90 b) Ta có: x 2 2 1 625 3x. 2 1 3 90 x 2 2 2 1 25 3x.10 90 2x 1 25 3x 90 :10 2x 25 1 3x 9 2x 24 x 2 3 3 x 24 : 2 x 2. x 12. Vậy x 2. Vậy x 12. c) Ta có: 2 5 3 x : 4 5 : 5 29 d) Ta có: 9 x 10 2019 . 16 2019 2 2 x : 4 5 29 10 9 x 16 2019 : 2019 2 x : 4 25 29 x 16 2019 2 x : 4 29 25 x 2019 16 2 x : 4 4 x 2035. 2 x 4.4 Vậy x 2035. 2 2 x 4 x 4. Vậy x 4. Câu 4. Xét tổng 2 3 2008
A 3 3 3 ... 3 . (1)
Nhân cả hai vế của A với 3, ta được: 2 3 4 2009
3A 3 3 3 ... 3 . (2)
Trừ theo từng vế của (2) cho (1), ta được: 3.A A 2 3 4 2009 3 3 3 ... 3 2 3 2008 3 3 3 ... 3 2009 2.A 3 3 A 2009 3 3 : 2. Khi đó: 2 3 3n A 2. 2009 3 3 : 2 3 3n 2009 3 3 3 3n 2009 3 3n n 2009. Vậy n 2009.
Dạng 4: So sánh các số viết dưới dạng lũy thừa Phương pháp giải
Để so sánh các số viết dưới dạng lũy thừa, ta có Ví dụ. So sánh: Trang 14
thể làm theo một trong ba cách sau: a) 3 2 và 2 3 :
Cách 1. Tính cụ thể rồi so sánh. 3 2 2 8; 3 9 . Suy ra 3 2 2 3 .
Cách 2. Đưa về cùng cơ số là số tự nhiên, rồi b) 4 9 và 2 27 : so sánh hai số mũ: 4 4 2 2 4 . 8 9 3 3 3 ; Nếu m n thì m n a a . 2 2 3 3 2 . 6 27 3 3 3 . Suy ra 4 2 9 27 .
Cách 3. Đưa về cùng số mũ, rồi so sánh hai cơ c) 30 3 và 20 5 : số: . 10 30 3 10 3 10 3 3 3 27 ; Nếu a b thì m m a b . . 10 20 2 10 2 10 5 5 5 25 . Suy ra 30 20 3 5 . Ví dụ mẫu Ví dụ 1. Hãy so sánh: a) 3 5 và 5 3 ; b) 5 2 và 4 3 ; c) 4 3 và 2 8 . Hướng dẫn giải Ta có: 3 5 5 125; 3 243, suy ra 3 5 5 3 . Ta có: 5 4 2 32; 3 81, suy ra 5 4 2 3 . Ta có: 4 2 3 81; 8 64 , suy ra 4 2 3 8 . Ví dụ 2. Hãy so sánh: a) 19 16 và 25 8 ; b) 11 27 và 8 81 ; c) 5 625 và 7 125 . Hướng dẫn giải a) Ta có: 19 19 4 4.19 76 16 2 2 2 ; a) Các cơ số 16 và 8 tuy
khác nhau, nhưng đều là lũy 25 25 3 3 2 . 5 75 8 2 2 2 .
thừa của 2 nên ta có thể đưa Vì 76 75 nên 76 75 2 2 , suy ra 19 25 16 8 . chúng về cùng cơ số 2. b) Ta có: 11 11 3 3.11 33 27 3 3 3 ;
b) Đưa về cùng cơ số 3. 8 8 4 4.8 32 81 3 3 3 . Vì 33 32 nên 33 32 3 3 , suy ra 11 8 27 81 . Trang 15 c) Ta có: 5 5 4 4 5 . 20 625 5 5 5 ;
c) Đưa về cùng cơ số 5. 7 7 3 3 7 . 21 125 5 5 5 . Vì 20 21 nên 20 21 5 5 , suy ra 5 7 625 125 . Ví dụ 3. Hãy so sánh: a) 300 2 và 200 3 ; b) 36 5 và 24 11 ; c) 2 3 n và 3 2 n với n . Hướng dẫn giải a) Ta có: . 100 300 3 100 3 100 2 2 2 8 ;
a) Hai số mũ 300 và 200 đều
chia hết cho 100 nên ta nghĩ . 100 200 2 100 2 100 100 3 3 3 9 8 .
đến việc đưa chúng về lũy Vậy 300 200 2 3 .
thừa có cùng số mũ là 100. b) Ta có: . 12 36 3 12 3 12 5 5 5 125 ;
b) 36 và 24 đều là bội của 12
nên đưa về cùng số mũ là 12. . 12 24 2 12 2 12 12 11 11 11 121 125 . Vậy 36 24 5 11 . n c) Ta có: 2n 2.n 2 3 3 3 9n ;
c) Đưa về cùng số mũ là n. n 3n 3.n 3 2 2 2 8n 9n . Vậy 2n 3 3 2 n . Ví dụ 4. So sánh: a) 23 5 và 22 6 5 . ; b) 333 222 và 222 333 ; c) 11 31 và 14 17 . Hướng dẫn giải a) Ta có: 23 22 5 5 5 . .
a) Đưa hai số về dạng một tích, Vì 22 22 5.5 6 5 . nên 23 22 5 6 5 . .
trong đó có chung thừa số 22 5 . b) Ta có: . 111 333 3 111 3 222 222 222 ;
b) Ta thấy hai cơ số 222 và 333
đều chia hết cho 111 nên ta sẽ . 111 222 2 111 2 333 333 333 . phân tích 222 2 1 . 11; 333 3 1 . 11 Vì 111 3 222 và 111 2 333
có cùng số mũ là 111 nên ta sẽ so sánh 3 222 và 2 333 . Lại có: . 3 3 3 3 2 2 222 111 2 111 .2 111 1 . 11.8 111 8 . 88 ; . 2 2 2 333 111 3 111 9 . Trang 16 Ta thấy 2 2 111 .888 111 9 . suy ra 3 2 222 333 . c) Ta có: 11 11 11 5 5.11 55 31 32 2 2 2 .
c) Ta thấy 31 là số liền trước của
32 và 17 là số liền sau của 16. 14 14 14 4 4 1 . 4 56 17 16 2 2 2 .
Mà 32 và 16 có thể đưa về cùng Vì 55 56 2 2 , suy ra 11 14 31 17 . cơ số 2. Do vậy để so sánh 11 31 và 14 17
ta sử dụng tính chất bắc cầu.
Bài tập tự luyện dạng 4 Bài tập cơ bản Câu 1. Hãy so sánh: a) 2 5 và 5 2 ; b) 30 9 và 20 27 ; c) 210 2 và 140 5 ; d) 13 7 2 . và 16 2 ; e) 15 21 và 5 8 27 .49 ; f) 91 2 và 35 5 . Câu 2. So sánh: a) 45 25 và 30 125 ; b) 300 2 và 200 3 ; c) 5 8 và 7 3 4 . ; d) 303 202 và 202 303 ; e) 444 333 và 333 444 . Bài tập nâng cao Câu 3. So sánh: 50 107 và 75 73 ,
Câu 4. Tìm số tự nhiên n, biết: a) 9 3n 81; b) 25 5n 125 . Đáp án Câu 1. a) Ta có: 2 5 25 và 5 2 32 , suy ra 2 5 5 2 . b) Ta có: 30 30 2 2.30 60 9 3 3 3 ; 20 20 3 3.20 60 27 3 3 3 . Vậy 30 20 9 27 . c) Ta có: 70 210 3.70 3 70 2 2 2 8 ; 70 140 2.70 2 70 5 5 5 25 . Vậy 210 140 2 5 . d) Ta có: 16 3 1 3 3 13 13 13 2 2 2 .2 8.2 7.2 . Trang 17 Vậy 13 16 7.2 2 . e) Ta có: 15 15 15 15 21 3.7 3 .7 ; 5 8 5 8 3 2 3.5 2.8 15 16 27 .49 3 . 7 3 .7 3 .7 . Vậy 15 5 8 21 27 .49 . f) Ta có: 18 91 90 5.18 5 18 2 2 2 2 32 ; 18 35 36 2.18 2 18 5 5 5 5 25 . Vậy 91 35 2 5 . Câu 2. a) Ta có: 45 45 2 2.45 90 25 5 5 5 ; 30 30 3 3.30 90 125 5 5 5 . Vậy 45 30 25 125 . b) Ta có: 100 300 3.100 3 100 2 2 2 8 ; 100 200 2.100 2 100 3 3 3 9 . Vậy 300 200 2 3 . c) Ta có: 5 5 3 3.5 15 8 2 2 2 ; 7 7 2 2.7 14 15 3.4 3. 2 3.2 3.2 2 . Vậy 5 7 8 3.4 . d) Ta có: 101 303 3.101 3 202 202 202 ; 101 202 2.101 2 303 303 303 . Ta so sánh: 3 202 và 2 303 . Lại có: 3 3 3 3 2 2 202
2.101 2 .101 8.101.101 808.101 ; 2 2 2 2 2 2 303
3.101 3 .101 9.101 808.101 . Suy ra 3 2 202 303 . Vậy 303 202 202 303 .
e) Tương tự câu d) ta có: 444 333 333 444 Bài tập nâng cao Câu 3. Ta có: 50 50 50 2 3 50 100 150 107 108 4.27 2 .3 2 .3 Trang 18 75 75 75 3 2 75 225 150 100 150 73 72 8.9 2 .3 2 .3 2 .3 Vậy 50 75 107 73 . Câu 4. a) n 2 n 4
9 3 81 3 3 3 . Vì n là số tự nhiên nên n 3 . b) n 2 n 3
25 5 125 5 5 5 . Vì n là số tự nhiên nên n 2 hoặc n 3 .
Dạng 5: Tìm chữ số tận cùng của số có dạng lũy thừa Phương pháp giải Chữ số tận cùng của n
a chính là chữ số tận Ví dụ. cùng của n
x (với x là chữ số tận cùng của a).
- Chữ số tận cùng của 5
2019 bằng chữ số tận cùng
Các số có tận cùng là 0; 1; 5; 6 khi nâng lên lũy của 5 9 .
thừa bất kì (khác 0) cũng có chữ số tận cùng là 0; - 3 10 100 ...0;5 .. 5 . 1; 5; 6. 50 80 11 .. 1 . ;6 ...6 .
Các số có tận cùng là 4; 9 khi nâng lên lũy thừa - 20 4 .. 6 . (số mũ chẵn); 21 4 .. 4 . (số mũ lẻ).
lẻ thì chữ số tận cùng không thay đổi, khi nâng lên 2
lũy thừa chẵn thì có chữ số tận cùng lần lượt là 6; 9 ...1 (số mũ chẵn); 3 9 .. 9 . (số mũ lẻ). 1. Ví dụ mẫu
Ví dụ 1. Tìm chữ số tận cùng của: a) 1000 10 ; b) 2011 2011 ; c) 100 5 ; d) 2020 6 ; e) 50 4 ; f) 120 9 . Hướng dẫn giải a) 1000 10 .. 0 . . b) 2011 2011 ...1. c) 100 5 .. 5 . . d) 2020 6 .. 6 . . e) 50
4 ...6 (vì số mũ chẵn). f) 120 9 .. 1 . (vì số mũ chẵn).
Ví dụ 2. Tìm chữ số tận cùng của các số sau: a) 2018 2000 ; b) 2019 1111 ; c) 4321 12345 ; d) 1000 2016 . Hướng dẫn giải a) 2018 2000
có chữ số tận cùng là 0.
Ta thấy các số trên có tận cùng b) 2019 1111
có chữ số tận cùng là 1.
lần lượt là 0; 1; 5; 6 nên khi
nâng lên lũy thừa bất kì cũng Trang 19 c) 4321 12345
có chữ số tận cùng là 5.
có chữ số tận cùng là 0; 1; 5; d) 1000 2016
có chữ số tận cùng là 6. 6.
Ví dụ 3. Tìm chữ số tận cùng của các số sau: a) 210 55 5 4 ; b) 2010 10 1; c) 30 56 2016 9 ; d) 70 26 2021 .14 . Hướng dẫn giải a) Ta có: 210 5 .. 5 . 55 4 .. 4 . (vì số mũ lẻ). Suy ra 210 55 5
4 ...5 .. 4. ...1.
Vậy chữ số tận cùng của 210 55 5 4 là 1. b) Ta có: 2010 10 .. 0 . . Suy ra: 2010 10
1 .. 0.1...1,
Vậy chữ số tận cùng của 2010 10 1 là 1. c) Ta có: 30 2016 .. 6 . ; 56 9 .. 1 . (do số mũ chẵn). Suy ra: 30 56
2016 9 ...6 ... 1 ...7 .
Vậy chữ số tận cùng của 30 56 2016 9 là 7. d) Ta có: 70 2021 ...1 26
14 ...6 (do số mũ chẵn). Suy ra: 70 26 2021 .14 ... 1 .. 6 . .. 6 . .
Vậy chữ số tận cùng của 70 26 2021 1 . 4 là 6.
Ví dụ 4. Tìm chữ số hàng đơn vị của: 2019 2020 2021 2016 2015 2014 . Hướng dẫn giải Ta có: 2019 2016 ...6; 2020 2015 .. 5 . ; 2021 2014 .. 4 . (vì số mũ lẻ). Suy ra 2019 2020 2021 2016 2015 2014
.. 6. .. 5... 4. .. 7. .
Vậy số đã cho có chữ số hàng đơn vị là 7.
Bài tập tự luyện dạng 5 Bài tập cơ bản
Câu 1. Tìm chữ số tận cùng của các lũy thừa sau: Trang 20 a) 2019 16 ; b) 2010 4 ; c) 999 9 ; d) 101 5 . Bài tập nâng cao
Câu 2. Tìm chữ số tận cùng của các lũy thừa: a) 234 135 ; b) 9 15 211 1 . 26 ; c) 100 100 1000 109 ; d) 18 36 95 51 .
Câu 3. Tìm chữ số hàng đơn vị của: a) 10 101 51 P 1005 .11 24 ; b) 87 120 30 Q 216 9 100 . Đáp án Bài tập cơ bản Câu 1. a) Ta có: 2019 16 .. 6 . . b) Ta có: 2010 4
...6 (vì số mũ chẵn). c) Ta có: 999 9 ...9 (vì số mũ lẻ). d) Ta có: 101 5 ...5. Bài tập nâng cao Câu 2.
a) Vì 135 có chữ số tận cùng là 5 nên 234
135 cũng có chữ số tận cùng là 5. b) Ta thấy 9
211 có chữ số tận cùng là 1 và 15
126 có chữ số tận cùng là 6. Suy ra 9 15 211 1 . 26 ... 1 ... 6 . ...6 . c) Vì 100 1000 .. 0
. nên chữ số tận cùng của 100 100
1000 109 chính là chữ số tận cùng của 100 9 . Ta có: 100 9
...1 (vì số mũ chẵn).
Vậy chữ só tận cùng của 100 100 1000 109 là 1. d) Ta có: 18 36
95 51 ...5 ... 1 .. 4 . . Câu 3. a) Ta có: 10 1005 .. 5 . ; 101 11 ...1; 51 24 .. 4 . . Suy ra: P .. 5 . .... 1 ...4 ...1.
Vậy P có chữ số hàng đơn vị là 1. b) Ta có: 87 216 ...6; 120 9 ...1; Trang 21 30 100 ...0 .
Suy ra: Q ...6 ... 1 ...0 ...7 .
Vậy Q có chữ số hàng đơn vị là 7.
THAM KHẢO ĐỀ KIỂM TRA 15 PHÚT SỐ 1 Trang 22