Chuyên đề: Phương pháp cộng vận tốc trong bài toán cực trị của chuyển động môn Vật lí lớp 9

CHUYÊN ĐỀ:
PHƯƠNG PHÁP CỘNG VẬN TỐC
TRONG BÀI TOÁN CỰC TRỊ CỦA CHUYỂN ĐỘNG – VẬT LÍ THCS
1.2. Tính tương đối của vận tốc: Vận tốc của cùng một vật trong các hệ quy chiếu khác nhau thì khác nhau.
- Công thức cộng vận tốc    v  v  v 13 12 23 
v13 : vận tốc vật 1 đối với vật 3( vận tốc tuyệt đối) 
v12 : vận tốc vật 1 đối với vật 2(vận tốc tương đối) 
v23 : vận tốc vật 2 đối với vật 3(vận tốc kéo theo)   v  v 13 31   v  v 12 21   v  v 23 32 1.3. Hệ quả:   - Nếu v , v v v v 12
13 cùng phương ,cùng chiều thì độ lớn: 13 12 23   - Nếu v , v v v v 12
13 cùng phương, ngược chiều thì độ lớn: 13 12 23   - Nếu v , v 2 v  v v 12
13 vuông góc với nhau thì độ lớn: 2 13 12 23 - Nếu   2 2
v ,v tạo với nhau một góc  thì độ lớn: v  v v 2v v co  s 12 13 13 12 23 12 23 2. Kiến thức toán học: B 2.1. Định lí Pitago:
Cho ∆ABC vuông tại A. Ta có: 2 2 2 BC  AB  AC
2.2. Hàm số lượng giác của góc nhọn: A C Theo (H-1): (H-1) AC AB AC AB SinB  ;CosB  ;tgB  ;CotgB  BC BC AB AC (1) AB AC AB AC SinC  ;CosC  ;tgC  ;CotgC  BC BC AC AB 2.3. Định lý hàm Sin: B
Cho ∆ ABC bất kỳ ta có: (H-2) a b c   (2) S in A SinB SinC 2.4. Định lý hàm Cos : A C Cho ABC bất kỳ ta có: 2 2 2 a  b c 2b . c cos A 2 2 2 b  c  a 2a . c cos B (3) 2 2 2 c  a b 2a . b cosC
2.5. Công thức cộng góc: Co ( s   )  Cos .  Cos sin .  sin Si ( n   )  Sin C  os Cos .  Sin
2.6. Hàm số lượng giác của các góc có liên quan đặc biệt: Ví dụ: Sin 9
( 00   )  Cos với 0     90 II. Nội dung bài tập:
1.1. Các bài tập ví dụ:
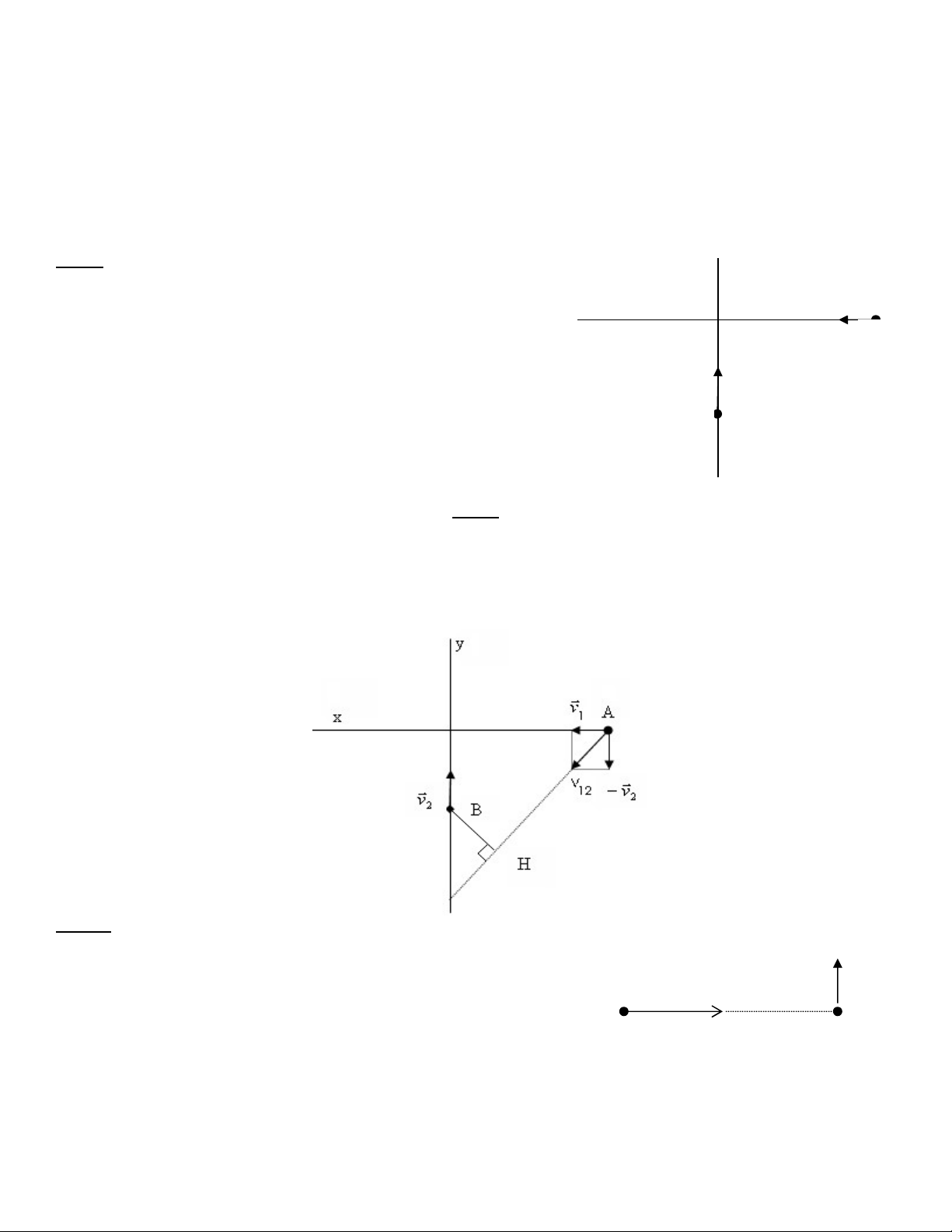
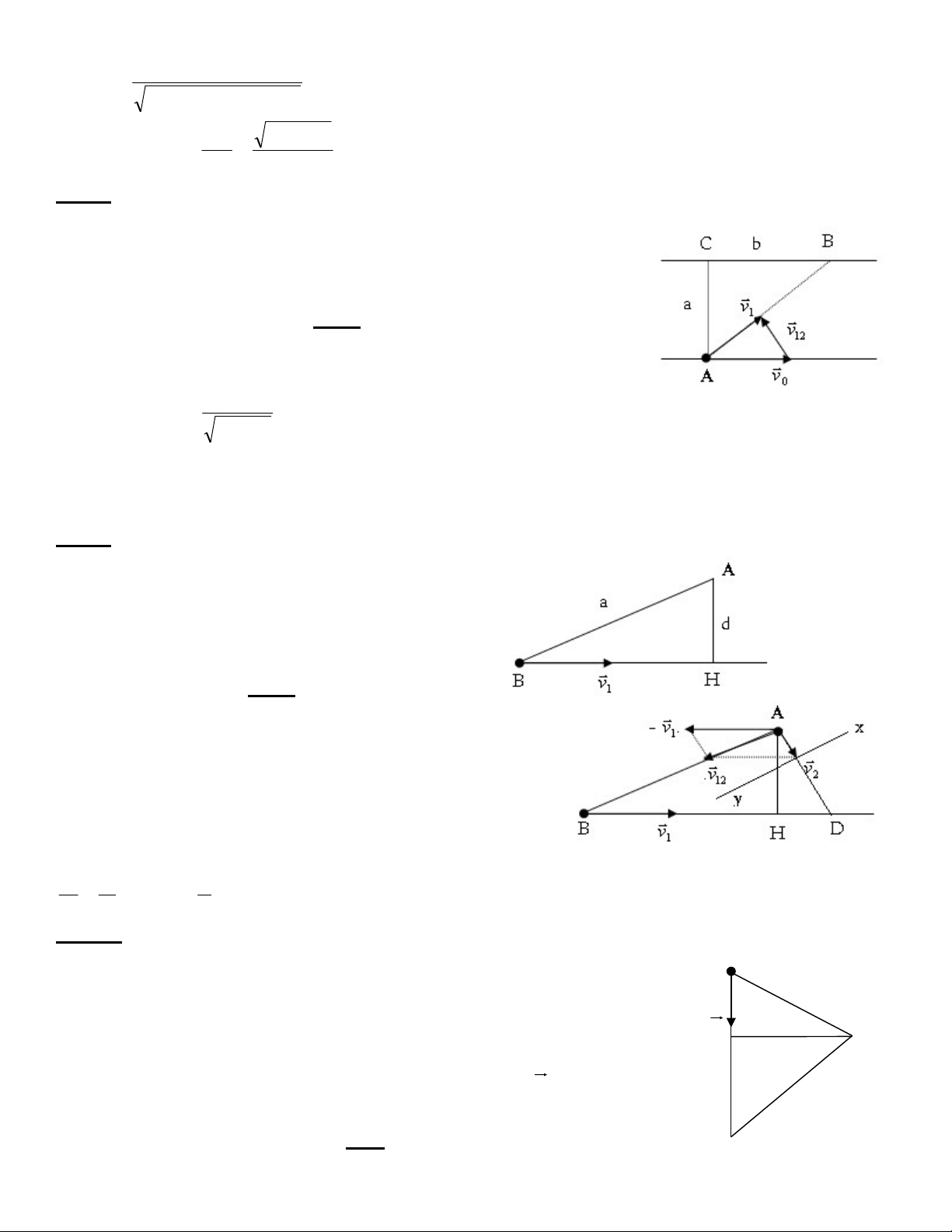
Bài 1:(Bài tập lí thuyết) y
Hai chất điểm chuyển động trên hai đường thẳng Ax và x v
By vuông góc với nhau, tốc độ lần lượt là v 1 1 và v2( Hình vẽ) A
a. Vẽ vẽ véc tơ vận tốc của chất điểm 1 so với chất điểm 2 
b. Biểu diễn trên cùng một hình vẽ khoảng cách ngắn v 2 B
nhất giữa hai chất điểm trong quá trình chuyển động. Giải:
Xét chuyển động tương đối của vật 1 so với vật 2, ta có:     
v  v  (v )  v  v 12 1 2 1 2
Đoạn BH vuông góc với đường thẳng chứa véc tơ vận tốc v chính là khoảng cách ngắn 12
nhất giữa hai chất điểm. Bài 2:
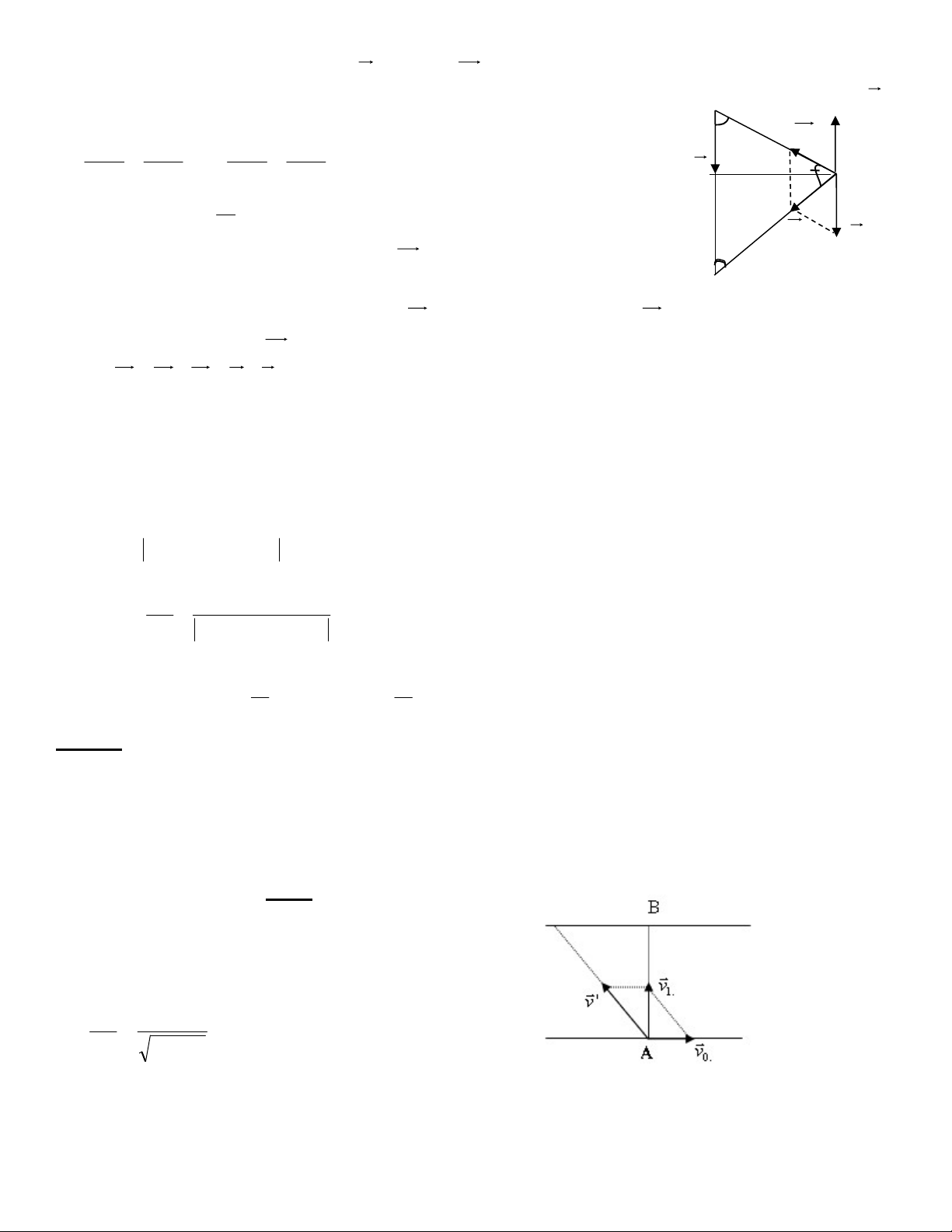
Từ hai bến A, B trên cùng 1 bờ sông có hai ca nô V2
cùng khởi hành. Khi nước sông không chảy do sức đẩy V
của động cơ chiếc ca nô từ A chạy song song với bờ theo 1 A B
chiều từ A B có V1 = 24km/h. Còn chiếc ca nô chạy từ
B vuông góc với bờ có vận tốc 18km/h. Quãng đường AB là 1km. Hỏi khoảng cách nhỏ nhất
giữa hai ca nô trong quá trình chuyển động là bao nhiêu nếu nước chảy từ A  B với V3 =
6km/h (sức đẩy của các động cơ không đổi) (Trích đề thi chuyên lý vào). Giải
Theo đề bài ta có hình vẽ.
Do dòng nước chảy từ từ A B với
vận tốc là 6km/h nên khi canô 1 chuyển động H
xuôi dòng vận tốc của nó là : V21 V2 V’2
Vx = V1 + V3 = 24 + 6 = 30km/h
- Canô 1 xuất phát từ B nhưng do bị nước 
đẩy ta có hướng của vận tốc ' V như hình vẽ. 2 A A V’x V1 B V3
Áp dụng định lý Pitago trong tam giác vuông B ' V V 2 3 ta được : '2 V = 2 2
V  V = 182 + 62 = 6 10 km/h 2 2 3
Ta áp dụng tính tương đối của vận tốc cho bài toán này. Canô 1 đi từ AB với vận tốc Vx
nhưng ta tưởng tượng rằng coi như canô 1 đứng yên và điểm B chuyển động với vận tốc V ' X với V ' = V ngược chiều với V X x còn hướng của V 'X
x. Do đó canô 2 mặc dù chuyển động theo hướng '
V nhưng khi chọn mốc là canô1 thì hướng chuyển động của canô lúc này là V 2 21 hợp với
AB góc . Từ đây dễ dàng suy ra khoảng cách nhỏ nhất giữa 2 canô có độ lớn bằng độ dài của đoạn AH V21
Ta sẽ tính AH trong tam giác vuông AHB
Có Sin = AH  AH = AB Sin (1) AB
Mặt khác xét trong tam giácvuông BV2V21 Có :V 2 = V 2( '
V V ) 2 = 182 + (30 – 6)2 = 900 21 2 X 3  V 21 = 30km/h Và Sin V 18 2   =  , 0 6 (2) V 30 21
Thế (2) vào (1) ta được AH = AB.sin = 1.0,6 = 0,6(km)
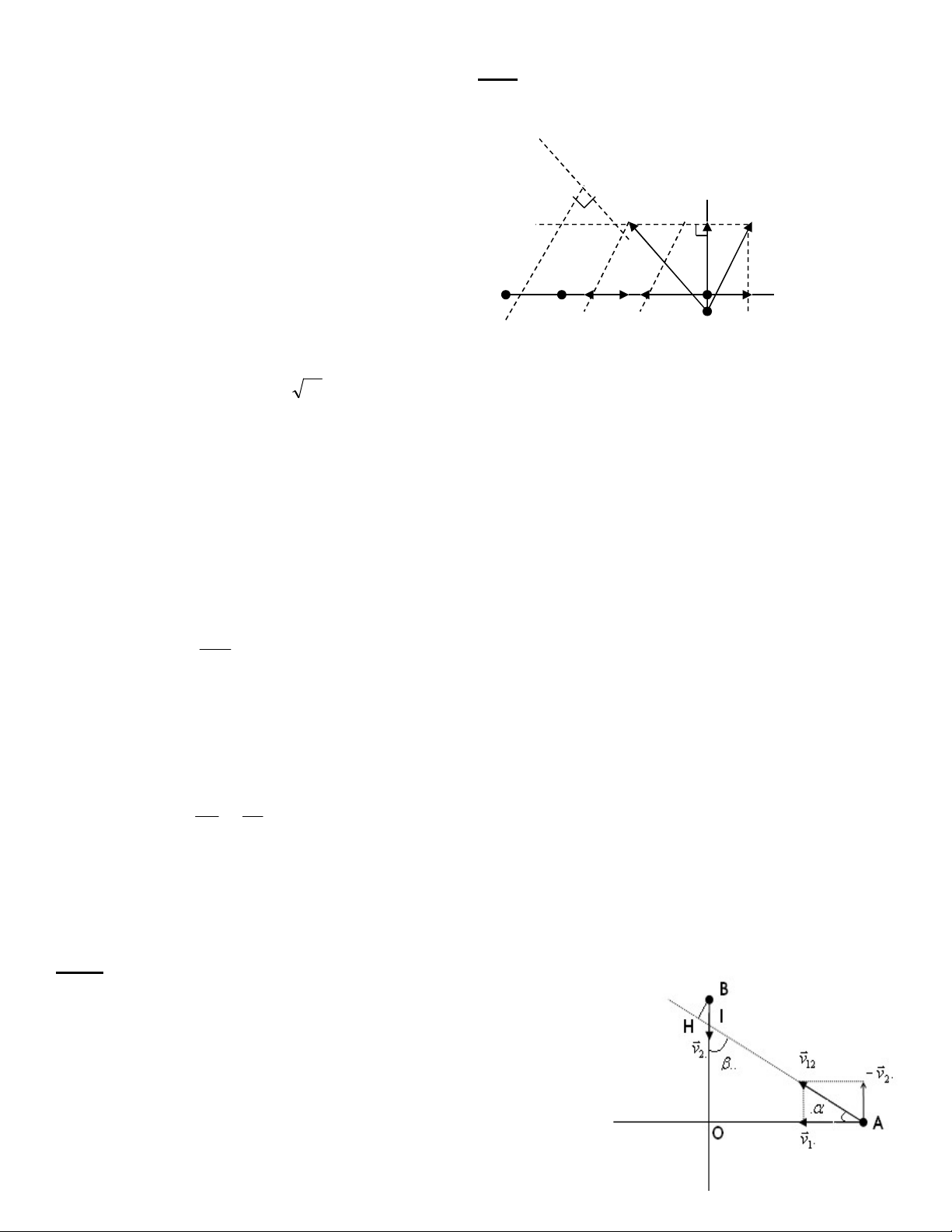
Vậy khoảng cách nhỏ nhất của 2 canô trong quá trình chuyển động trên là 0,6km. Bài 3:
Hai xe chuyển động trên hai đường vuông góc với
nhau, xe A đi về hướng tây với tốc độ 50km/h, xe B đi về
hướng Nam với tốc độ 30km/h. Vào một thời điểm nào đó xe
A và B còn cách giao điểm của hai đường lần lượt 4,4km và
4km và đang tiến về phía giao điểm. Tìm khoảng cách ngắn nhất giũa hai xe. Giải
Xét chuyển động tương đối của vật 1 so với vật 2, ta có:     
v  v  (v )  v  v 12 1 2 1 2
Đoạn BH vuông góc với đường thẳng chứa véc tơ vận tốc v chính là khoảng cách ngắn nhất 12 giữa hai xe  dmin= BH tan v 3 2    0 0    59 ,   31 v 5 1
dmin= BH = BI. sin  = (BO - OI) sin  = (BO - OA.tan ).sin  = 1,166(km)
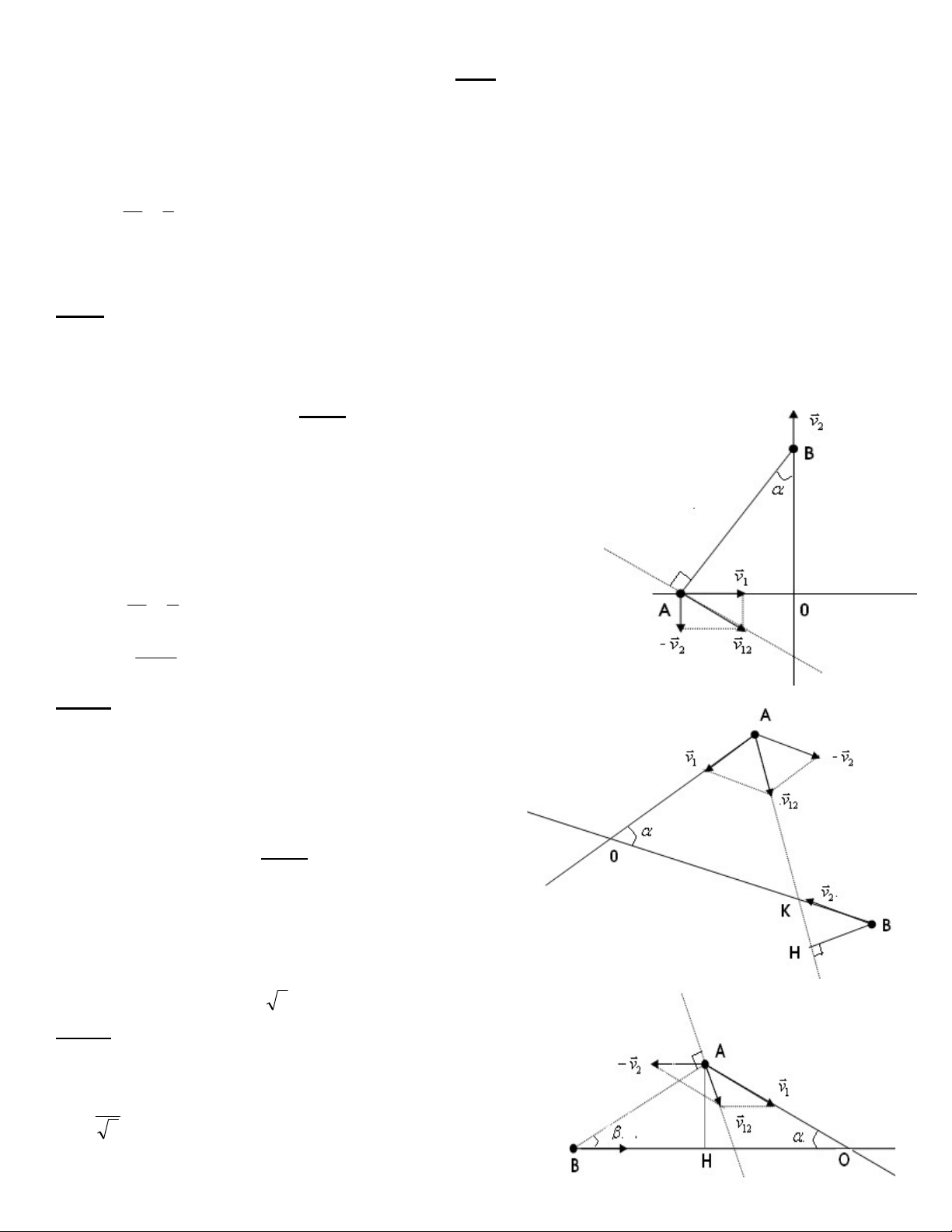
Bài 4.( đề thi HSG Nghệ An 2005-2006, bảng B )
Hai vật chuyển động trên hai đường đường thẳng vuông góc với nhau với tốc độ không
đổi có giá trị lần lượt v1= 30km/h, v2= 20km/h. Tại thời điểm khoàng cách giữa hai vật nhỏ nhất
thì vật 1 cách giao điểm s1=500m. Hỏi lúc đó vật 2 cách giao điểm trên đoạn s2 bằng bao nhiêu. Giải:
Xét chuyển động tương đối của vật 1 so với vật 2, ta có:     
v  v  (v )  v  v 12 1 2 1 2 -Tại A cách O đoạn s  
1=500m dựng véc tơ v và véc tơ - v , và 1 2
v . Kẻ đường AB vuông góc với đường thẳng chứa véc tơ 12
v ( Theo đề bài đây là khoảng cách ngắn nhất d 12 min= AB) tan = v 2 1  v 3 2  BO = 0A  750(m) tan Bài 5:
Hai tàu chuyển động đều với tốc độ như nhau
trên hai đường hợp với nhau một góc 0   60 và
đang tiến về phía giao điểm O. Xác định khoảng
cách nhỏ nhất giữa hai tàu. Cho biết lúc đầu hai tàu
cách giao điểm O những khoảng l1=20km, l2=30km. Giải:
Xét chuyển động tương đối của vật 1 so 2 ta có:     
v  v  (v )  v  v 12 1 2 1 2
dmin= BH, OAK là tam giác đều (vì tốc độ hai tàu như nhau)  dmin=KB.sin
KB = l2 - l1  dmin= 5 3 (km) Bài 6:
Hai vật chuyển động thẳng đều trên hai đường
thẳng tạo với nhau một góc  =300 với tốc độ v1 v 
và đang hướng về phía giao điểm, tại thời điểm 2 3
khoảng cách giữa hai vật nhỏ nhất thì vật 1 cách giao
điểm một đoạn d1= 30 3 m. Hỏi vật 2 cách giao điểm một đoạn bao nhiêu? Giải:
Xét chuyển động tương đối của vật 1 so 2 ta có     
v  v  (v )  v  v 12 1 2 1 2 BA   v , d 12 min = AB Vì v1 v  nên chứng minh được 0     30 2 3 Hạ đường AH  BO
AH = AO.sin300 = d1.sin300 =15 3 (m) HO = d1.cos300 = 45 (m)
BH = AH  45m  BO=d2= 90(m) tan 300 Bài 7:
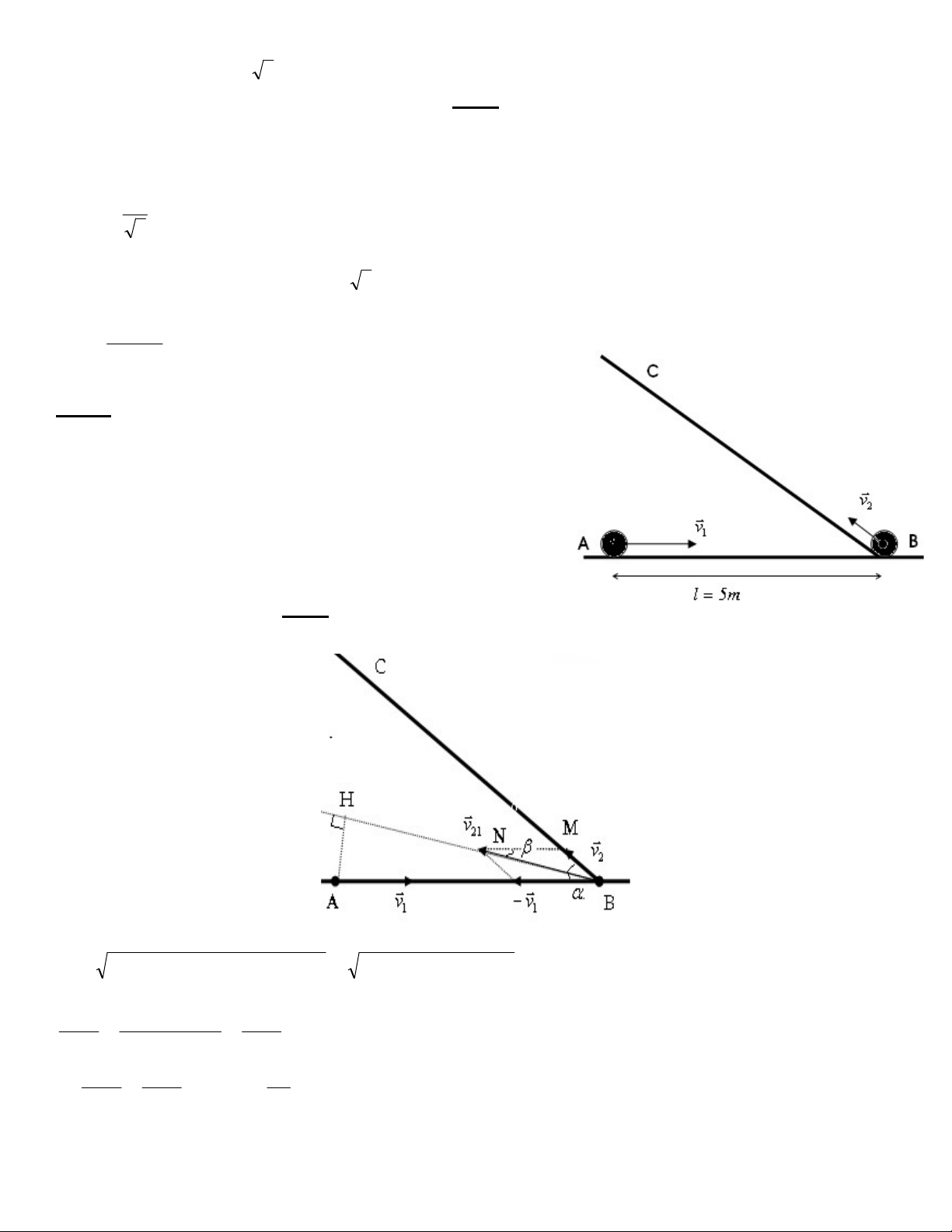
Có hai vật M1 và M2 lúc đầu cách nhau một
khoảng l =2m (Hình vẽ), cùng lúc hai vật chuyển động
thẳng đều M1 chạy về B với tốc độ
v1=10m/s, M2 chạy về C với tốc độ v2=5m/s . Tính
khoảng cách ngắn nhất giữa hai vật và thời gian để đạt
được khoảng cách này. Biết góc tạo bởi hai đường 0   45 . Giải:
Xét chuyển động tương đối của vật 1 so vật 2, ta có:     
v  v  (v )  v  v 12 1 2 1 2 d min = AH = AB.sin  v 2 2 0 2 2 21= v  v  2v v cos 1
( 80   )  v  v  2v v cos 1 2 1 2 1 2 1 2
- Áp dụng định lí hàm sin, ta có: BM BN BN   sin  sin 1 ( 800   ) sin v v v 2 12 2    sin   sin  sin v12 lv sin  d  2  0,5( m) min 2 v  2 v  2v v cos 1 2 1 2 2 BH l  2 d BH= v t.  t   min  0,138(s) 12 v v 12 12 Bài 8:
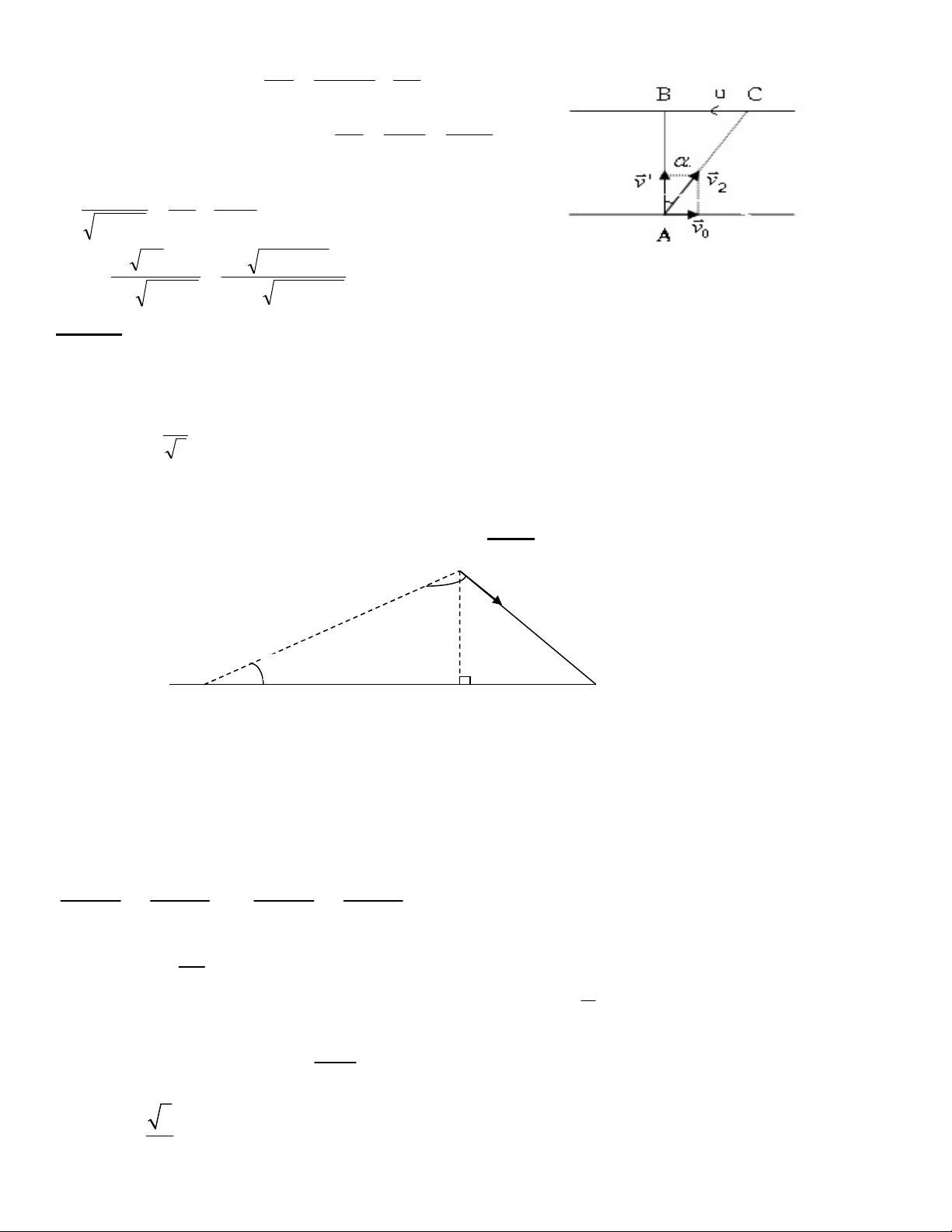
Ở một đoạn sông thẳng có dòng nước chãy với vận tốc vo,
một người từ vị trí A ở bờ sông bên này muốn chèo thuyền tới
B ở bờ sông bên kia. Cho AC; CB = a. Tính vận tốc nhỏ nhất
của thuyền so với nước mà người này phải chèo để có thể tới B. Giải: Ta có   
v  v  v . Ta biểu diễn các véc tơ vận tốc trên hình vẽ 1 o 12 Vì v  
o không đổi nên v12 nhỏ nhất khi v  v  12 1 V v b 0 12= vo.sin = 2 a  b2 */ Nhận xét:
Các bài toán trên hoàn toàn có thể giải theo cách thiết lập phương trình, rồi sau đó lí
luận theo hàm bậc hai về mặt toán học, tuy nhiên lời giải khá dài hơn! Bài 9:
Một ô tô chuyển động thẳng đều với vận tốc v1 =
54km/h. Một hành khách cách ô tô đoạn a = 400m và
cách đường đoạn d = 80m, muốn đón ô tô. Hỏi người ấy
phải chạy theo hướng nào, với vận tốc nhỏ nhất là bao nhiêu để đón được ô tô? Giải:
Xét chuyển động tương đối của vật 2 so vật 1, ta có:     
v  v  (v )  v  v 21 2 1 2 1
Để 2 gặp được 1 thì v phải luôn có hướng AB. 21
Véc tơ vận tốc v có ngọn luôn nằm trên đường 2 Xy // AB.   
v khi v  xy , tức là v  AB. 2 2 2
Tính chất đồng dạng của tam giác: DAB và AHD , ta có: v v d 2 1   v  v  10 8 , km / h d a 2 1 a Bài 10:
Hai tàu A và B ban đầu cách nhau một khoảng l. Chúng chuyển A
động cùng một lúc với các vận tốc có độ lớn lần lượt là v1, v2. Tàu A
chuyển động theo hướng AC tạo với AB góc  (hình vẽ).
a. Hỏi tàu B phải đi theo hướng nào để có thể gặp tàu A. Sau bao v 1 B
lâu kể từ lúc chúng ở các vị trí A và B thì hai tàu gặp nhau? H
b. Muốn hai tàu gặp nhau ở H (BH vuông góc với v ) thì các độ lớn 1
vận tốc v1, v2 phải thỏa mản điều kiện gì? Giải: C
a. Tàu B chuyển động với vận tốc v hợp với BA góc  . 2
- Hai tàu gặp nhau tại M. Ta có AM = v A 1.t, BM = v2.t - v 1 - Trong tam giác ABM:  v 21 + AM BM   v t v t 1 2  sin  sin sin  sin v 1 B H   sin  = v1 sin (1) v2 v  2 v 1
- Tàu B phải chạy theo hướng hợp với
BA một góc  thỏa mãn (1)
- Cos = cos[1800 – (   ) ] = - cos(   ) = sin.sin   cos.cos  M
- Gọi vận tốc của tàu B đối với tàu A là v . Tại thời điểm ban đầu v 21 21
cùng phương chiều với BA. Theo công thức cộng vận tốc: v  v  v  v  v 21 23 13 2 1 => 2 2 2 v  v  v  2v v cos 21 2 1 2 1 => 2 2
v  v (sin 2   cos2  ) 2
 v (sin 2   cos2 )  2v v (sin.sin   cos.cos  ) 21 2 1 1 2 =( 2 2 2 2
sin .v  2sin sin .v v  sin .v )+( 2 2 2 2
cos .v  2cos cos .v v  cos .v ) 2 1 2 1 2 1 2 1 =( 2 sin .v  sin.v ) +( 2 cos .v  cos.v ) 2 1 2 1 = ( 2
cos .v  cos.v ) ( theo (1) ) 2 1
=> v21 = v .cos  v cos  1 2
Vậy thời gian để tàu B chuyển động đến gặp tàu A là: t = AB l  v v cos  v cos  21 1 2
b. Để 2 tàu gặp nhau ở H thì:     900    900   sin   sin(900 )  cos Theo (1) ta có: v v 1 2 cos  sin  tan  v v 2 1 Bài 11:
Hai người bơi xuất phát từ A trên bờ một cón sông và phải đạt tới điểm B ở bờ bên kia
nằm đối diện với điểm A. Muốn vậy, người thứ nhất bơi để chuyển động được theo đúng đường
thẳng AB, còn người thứ hai luôn bơi theo hướng vuông góc với với dòng chảy, rồi đến bờ bên
kia tại C, sau đó chạy ngược tới A với vận tốc u. Tính giá trị u để hai người tới A cùng lúc. Biết
vận tốc nước chảy vo=2km/h, vận tốc của mỗi người bơi đối với nước là v’=2,5km/h Giải: *Xét người thứ nhất:
-Vận tốc của người đối với bờ:     v  v' v , do 2 '2 2 v  v  v  v  v 1 0 1 0 1 0
Thời gian người thứ nhất đến B là: t AB AB 1=  2 2 v1 v  v 1 0 *Xét người thứ hai:
Vận tốc của người thứ hai đối với bờ     v  v' v , do 2 2 2 v'  v  v  v' v 2 0 0 2 0 Thời gian đến C là t AC AB AB 20=  = v v cos v' 2 2
Thời gian chạy trên bờ: t’ BC v t. v .AB 0 20 0 20=   u u v' u .
Theo đề bài t1= t20+t’20 AB AB v AB 0    v'2 v2 v' v' u . 0 v v'2  v2 2 5 , 2 2  22  u 0 0    k 3 m / h v' v'2 v2 5 , 2  5 , 2 2  22 0 Bài 12:
Một người đứng ở A cách đường quốc lộ h=100m nhìn thấy một xe ô tô vừa đến B cách
mình d=500m đang chạy trên đường với vận tốc v1=50km/h (hình vẽ). Đúng lúc nhìn thấy xe
thì người ấy chạy theo hướng AC ( B
 AC   ) với vận tốc v2. a. Biết 20 v  km/h. Tính  2 3
b.  bằng bao nhiêu thì v cực tiểu? Tính vận tốc cực tiểu đó. 2 Giải: A  v d ∝ 2 h B β  C H v1
Gọi t là thời gian để ô tô và người đi đến C. Ta có: AC  v . t ; BC = v . t 2 1
Theo định lý hàm sin có: A C B C v .t v .t 2 1    sin  sin  sin  sin  v1  sin   .sin  (1) v2 h Mặt khác: sin  (2) d v .h 1
Từ (1) và (2) suy ra: sin   v .d (3) 2 3 0 0 => sin    60 ; 120 2 v .h 1 b. Từ (3) => v  (*) 2 sin 1  d.sin
Ta thấy v1, h, d không đổi nên v2 min khi 0 90 . hv1 Lúc đó: v  10km/ h 2(min) h 1.2. Bài tập vận dụng: Bài 1:
Một người A đi xe đạp trên đường thẳng Ox N O
theo chiều từ trái sang phải, xuất phát từ M cách O là
OM=800m, với vận tốc không đổi V=4,2m/s. Một M ∝
người B đi bộ trên cánh đồng xuất phát từ điểm H
cách O là OH=173,2m ( 100 3m) vận tốc không đổi
v=1,2m/s theo một đường thẳng HN để gặp được A H
tại N. Hãy xác định vị trí của N nếu 2 người đến cùng một lúc.
Đáp số: N cách O là 242,2m Bài 2:
Một người đứng cách con đường thẳng một khoảng h. Trên đường một ô tô đang chạy
với vận tốc v1. Khi người ấy thấy xe cách mình một khoảng a thì bắt đầu chạy ra đường để đón ô tô.
a. Nếu vận tốc chạy của của người ấy là v2 thì người ấy phải chạy theo hướng nào để gặp được ô tô.
b. Tính vận tốc tối thiểu và hướng chạy của người để gặp được ô tô.
Áp dụng: v1=10m/s; h=50m; a=200m; v2=3m/s
Đáp số: a. Vậy người chạy theo hướng vuông góc với AB h b. v  v  2,5m / s 2min 1 a Bài 3:
Trong hệ trục toạ độ xOy (như hình vẽ), có hai vật nhỏ y
A và B chuyển động thẳng đều. Lúc bắt đầu chuyển động,
vật A cách vật B một đoạn L=100m. Biết vận tốc của vật A  A v1
là v1=10m/s theo hướng Ox, vận tốc của vật B là v2=15m/s theo hướng Oy. O  x v
a. Sau thời gian bao lâu kể từ lúc bắt đầu chuyển động, hai 2
vật A và B lại cách nhau 100m.
b. Xác định khoảng cách nhỏ nhất giữa hai vật A và B.
Đáp số: a. Sau 9,23 giây kể từ lúc bắt đầu chuyển động B b. S  55,47(m) min Bài 4:
Từ điểm O trên bờ một con sông rộng OA=0,5km, một người
muốn đi tới điểm A đối diện bên kia sông bằng cách đi thuyền từ O đến B A B
rồi đi bộ từ B về A (Hình 1). Vận tốc của thuyền đối với nước là v v
1=3km/h, vận tốc của nước đối với bờ sông là v2=2km/h, vận tốc đi bộ 1 v2
trên bờ là v=5km/h. Tìm độ dài BA để thời gian chuyển động là ngắn
nhất và tính thời gian ngắn nhất đó. O Hình 1 Đáp số: 10 125 10 t  (h) và AB   132(m) min 15 min 3
Bài 5: ( Kỳ thi chọn HS giỏi NH 06-07, vật lí 9)
Một ghe máy có vận tốc khi nước yên lặng là 6km/h đi xuôi dòng từ bến A đến bến B
cách nhau 12km. Cùng lúc đó có một thuyền máy ngược dòng từ B đến A, vận tốc thuyền máy
khi nước yên lặng là 10km/h, sau khi gặp nhau chúng quay lại và trở về bến xuất phát của mình.
Hỏi rằng vận tốc của dòng chảy ít nhất là bao nhiêu để cho ghe máy về lại bến A không sớm
hơn một giờ sau khi thuyền máy về đến bến B.