Chuyên Đề Phương Pháp Tọa Độ Trong Không Gian Ôn Thi Tốt Nghiệp Giải Chi Tiết
Trong không gian Oxyz, phương trình nào sau đây là phương trình tổng quát của mặt phẳng? Trong không gian Oxyz, phương trình nào sau đây là phương trình tổng quát của mặt phẳng? Trong không gian với hệ tọa độ Oxyz, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Tài liệu ôn thi THPTQG môn Toán 278 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
I. Phương trình mặt phẳng:
1.1. Dạng 1: Nhận biết được phương trình tổng quát của mặt phẳng.
Phương trình tổng quát của mặt phẳng
Trong không gian Oxyz , mỗi mặt phẳng đều có dạng phương trình: Ax By Cz D 0 với 2 2 2
A B C 0 , được gọi là phương trình tổng quát của mặt phẳng. Nhận xét:
Nếu mặt phẳng ( ) có phương trình Ax By Cz D 0 (với 2 2 2
A B C 0 ) thì vectơ n ( ; A ;
B C) là một vectơ pháp tuyến của mặt phẳng ( ) . Bài tập:
Câu 1. Trong không gian Oxyz , phương trình nào sau đây là phương trình tổng quát của mặt phẳng? A. 2
x 3y z 1 0 . B. 2
x 2 y 4z 2 0 .
C. 2x 3y 4z 2024 0 . D. 2
2x 3y 4z 2025 0 . Lời giải Chọn C
Phương trình tổng quát của mặt phẳng là: 2x 3y 4z 2024 0 .
Câu 2. Trong không gian Oxyz , phương trình nào sau đây là phương trình tổng quát của mặt phẳng? 3 A. x z 1 0 .
B. x 2xy 4z 2 0 . y C. 2
2x 3y 2025z 0 .
D. 2x 4z 2025 0 . Lời giải Chọn D
Phương trình tổng quát của mặt phẳng là: 2x 4z 2025 0 .
Câu 3. Trong không gian Oxyz , cho mặt phẳng (P) : 3x y 2z 1 0 . Vectơ nào dưới đây không phải là
một vectơ pháp tuyến của (P) ? A. n ( 3 ;1; 2) .
B. n (3;1; 2)
C. n (3; 1; 2) D. n (6; 2 ;4) Trang 1 Lời giải Chọn B
Véc tơ pháp tuyến của (P) là: n (3; 1; 2) . n ( 3 ;1; 2 ) 1 (3; 1
;2) là một vec tơ pháp tuyến của (P) n (6; 2 ;4) 2(3; 1
;2) là một vec tơ pháp tuyến của (P)
Câu 4. Trong không gian với hệ tọa độ Oxyz , vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng Oxy? r ur r r
A. i 1; 0; 0
B. m 1;1; 1
C. j 0;1; 0
D. k 0; 0; 1 Lời giải Chọn D r
Do mặt phẳng Oxy vuông góc với trục Oz nên nhận véctơ k 0;0;
1 làm một véc tơ pháp tuyến
Câu 5. Trong không gian Oxyz , vectơ nào dưới đây có giá vuông góc với mặt phẳng : 2x 3y 1 0?
A. a 2; 3; 1
B. b 2;1; 3
C. c 2; 3; 0
D. d 3; 2; 0 Lời giải Chọn C
Mặt phẳng có một VTPT là n 2; 3; 0 c .
1.2. Dạng 2: Thiết lập được phương trình tổng quát của mặt phẳng qua một điểm và biết vectơ pháp tuyến
trong hệ trục toạ độ Oxyz (mức độ: Thông hiểu). Phương pháp:
Trong không gian Oxyz , phương trình tổng quát của mặt phẳng đi qua điểm M (x ; y ; z ) và có vectơ pháp 0 0 0 0 tuyến n ( ; A ; B C) là: (
A x x ) B( y y ) C(z z ) 0 0 0 0
hay Ax By Cz D 0 với D Ax By Cz 0 0 0 Trang 2
Chú ý: Phải nắm vững khái niệm vectơ pháp tuyến của mặt phẳng.
Vectơ pháp tuyến của mặt phẳng là vectơ có giá vuông góc với mặt phẳng đó. Nếu n là một vectơ pháp
tuyến của mặt phẳng thì kn (k 0) cũng là một vectơ pháp tuyến của mặt phẳng đó. Bài tập minh họa:
Câu 1. Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt phẳng đi qua
điểm M 1;2;
3 và có một vectơ pháp tuyến n 1; 2 ;3 .
A. x 2 y 3z 12 0
B. x 2 y 3z 6 0
C. x 2 y 3z 12 0
D. x 2 y 3z 6 0 Lời giải Chọn A
Phương trình mặt phẳng đi qua điểm M 1;2;
3 và có một vectơ pháp tuyến n 1; 2 ;3 là 1 x
1 2 y 2 3 z
3 0 x 2 y 3z 12 0 .
Câu 2. Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A1;2; 3 có véc
tơ pháp tuyến n 2;1;3 là
A. 2x y 3z 9 0 .
B. 2x y 3z 4 0 .
C. x 2 y 4 0 .
D. 2x y 3z 4 0 . Lời giải Chọn A
Phương trình mặt phẳng đi qua điểm A1;2;3có véc tơ pháp tuyến n 2;1;3 là 2. x
1 1. y 2 3. z 3 0
2x 2 y 2 3z 9 0
2x y 3z 9 0. Trang 3
Câu 3. Trong không gian Oxyz , phương trình của mặt phẳng đi qua điểm A3;0; 1 và có véctơ pháp tuyến n 4; 2 ; 3 là
A. 4x 2 y 3z 9 0 .
B. 4x 2 y 3z 15 0 .
C. 3x z 15 0.
D. 4x 2 y 3z 15 0 . Lời giải Chọn B
Mặt phẳng đi qua điểm A3;0;
1 và có véctơ pháp tuyến n 4; 2 ; 3 có phương trình: 4 x
3 2 y 0 3 z
1 0 4x 2y 3z 15 0 .
Câu 4. Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng qua A 1 ;1; 2 và có vectơ pháp tuyến n 1; 2 ; 2 là
A. x 2 y 2z 1 0 .
B. x y 2z 1 0 .
C. x 2 y 2z 7 0 .
D. x y 2z 1 0 . Lời giải Chọn A
Mặt phẳng P đi qua A 1 ;1; 2
và có vectơ pháp tuyến n 1; 2 ; 2
nên có phương trình x 1 2 y
1 2 z 2 0 x 2y 2z 1 0 .
Vậy mặt phẳng cần tìm có phương trình: x 2y 2z 1 0 .
Câu 5. Trong không gian Oxyz , phương trình mặt phẳng Oyz là A. z 0. B. x 0 .
C. x y z 0 .
D. y 0 . Lời giải Chọn B.
Mặt phẳng Oyz nhận i 1;0;0 làm vectơ pháp tuyến và đi qua gốc tọa độ O0;0;0 có phương trình là x 0 .
Câu 6. Trong không gian Oxyz , phương trình của mặt phẳng Oxy là: A. z 0 . B. x 0 . C. y 0 .
D. x y 0 . Lời giải Trang 4 Chọn A.
phương trình của mặt phẳng Oxy là: z 0
Câu 7. Trong không gian với hệ toạ độ Oxyz , phương trình nào dưới đây là phương trình của mặt phẳng Oyz ?
A. y 0
B. x 0
C. y z 0
D. z 0 Lời giải Chọn B
Mặt phẳng Oyz đi qua điểm O0;0;0 và có vectơ pháp tuyến là i 1;0;0 nên ta có phương trình mặt
phẳng Oyz là :
1 x 0 0 y 0 0z 0 0 x 0 .
Câu 8. Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình của mặt phẳng Ozx ?
A. x 0.
B. y 1 0.
C. y 0.
D. z 0. Lời giải
Ta có mặt phẳng Ozx đi qua điểm O0;0;0 và vuông góc với trục Oy nên có VTPT n 0;1;0 .
Do đó phương trình của mặt phẳng Ozx là y 0.
Câu 9. Trong không gian Oxyz , cho điểm A (1; 2;3) và hai vectơ v ( 1 ;2;3) . Mệnh đề , u 2;0; 1
nào sau đây đúng và mệnh đề nào sai?
A. v i
2 j 3k .
B. u v .
C. Phương trình mặt phẳng đi qua điểm A (1; 2;3) v ( 1 ;2;3)
và vuông góc với giá của véctơ là:
x 2 y 3z 4 0.
D. Phương trình mặt phẳng đi qua điểm A (1; 2;3) u 2 ;0;1
và vuông góc với giá của véctơ là:
2x y 1 0 . Lời giải A. v ( 1 ;2;3) v i 2 j 3k ĐÚNG Trang 5
B. u v 1 2
2.0 3.1 0 SAI
C. Phương trình mặt phẳng đi qua điểm A (1; 2;3) và vuông góc với giá của véctơ v ( 1 ;2;3) là: 1
(x 1) 2(y 2) 3(z 3) 0 x 2y 3z 4 0 x 2y 3z 4 0. C ĐÚNG
D. Phương trình mặt phẳng đi qua điểm A (1; 2;3)
và vuông góc với giá của véctơ u 2;0; 1 là:
2x y 1 0 . Do đó D SAI
1.3. Dạng 3: Thiết lập được phương trình tổng quát của mặt phẳng qua một điểm và biết cặp vectơ chỉ
phương (suy ra vectơ pháp tuyến nhờ vào việc tìm vectơ vuông góc với cặp vectơ chỉ phương) trong hệ trục
toạ độ Oxyz (mức độ: Thông hiểu). Phương pháp:
Khi bài toán cho biết mặt phẳng ( ) đi qua điểm M (x ; y ; z ) và có cặp vectơ chỉ phương , a b : 0 0 0 0
+ Vectơ pháp tuyến của mặt phẳng: n a,b ; A ; B C
+ Mặt phẳng viết dưới dạng sau: ( ) : (
A x x ) B( y y ) C(z z ) 0 0 0 0
Chú ý: Phải nắm vững khái niệm vectơ chỉ phương của mặt phẳng.
Vectơ vectơ chỉ phương của mặt phẳng là vectơ có giá song song với mặt phẳng đó. Nếu a là một vectơ
chỉ phương của mặt phẳng thì ka (k 0) cũng là một vectơ chỉ phương của mặt phẳng đó. Bài tập:
Câu 1. Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng P qua M 0; 2 ; 1 và có cặp
vectơ chỉ phương a 1;1; 2
,b 1;0;3 là
A. 3x 5y z 6 0 .
B. 3x 5y z 6 0 .
C. 3x 5y z 6 0 .
D. 3x 5y z 6 0 . Lời giải Chọn A
Ta có n a,b 3; 5 ; 1 .
Mặt phẳng P đi qua M 0; 2 ;
1 và có vectơ pháp tuyến n 3; 5 ; 1 nên có phương trình
3 x 0 5 y 2 z
1 0 3x 5y z 6 0 . Trang 6
Vậy mặt phẳng cần tìm có phương trình: 3x 5y z 6 0 .
Câu 2. Trong không gian với hệ tọa độ Oxyz , cặp vectơ a 2;1; 2
,b 1;0;2 có giá song song với mặt
phẳng P . Phương trình mặt phẳng P qua C 1;1;3 là
A. 2x 6 y z 7 0 .
B. 2x 6 y z 5 0 .
C. 2x 6 y z 5 0 .
D. 2x 6 y z 7 0 . Lời giải Chọn D
Ta có n a,b 2; 6 ; 1 .
Mặt phẳng P đi qua C 1;1;3 và có vectơ pháp tuyến n 2; 6 ; 1 nên có phương trình 2 x 1 6 y 1 z
3 0 2x 6y z 7 0 .
Vậy mặt phẳng cần tìm có phương trình: 2x 6y z 7 0 .
1.4. Dạng 4: Thiết lập được phương trình tổng quát của mặt phẳng qua ba điểm không thẳng hàng trong hệ
trục toạ độ Oxyz (mức độ: Thông hiểu). Phương pháp:
Khi bài toán cho biết mặt phẳng ( ) đi qua ba điểm ,
A B, C không thẳng hàng thì có cặp vectơ chỉ phương AB, AC .
+ Vectơ pháp tuyến của mặt phẳng ( ) : n A , B AC ; a ; b c
+ Mặt phẳng ( ) viết dưới dạng sau:
( ) : a(x x ) b( y y ) c(z z ) 0 0 0 0 Bài tập:
Câu 1. Trong không gian Oxyz , cho ba điểm A3; 2 ; 2
, B3;2;0,C 0;2;
1 . Viết phương trình mặt
phẳng ABC . Lời giải
Đáp án: 2x 3y 6z 0 Ta có:
AB 0;4;2 , AC 3
;4;3 , n A ;
B AC 4; 6;12 .
Ta có n 4; 6;12 cùng phương n 2; 3;6 1 Trang 7
Mặt phẳng ABC đi qua điểm C 0;2;
1 và có một vectơ pháp tuyến n 2; 3;6 ABC 1 nên có phương trình là:
2 x 0 3 y 2 6 z
1 0 2x 3y 6z 0 .
Vậy phương trình mặt phẳng cần tìm là: 2x 3y 6z 0 .
Câu 2: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A0;1;2, B2; 2 ; 1 ,C 2
;1;0. Khi đó, phương
trình mặt phẳng ABC là ax y z d 0 . Hãy xác định a và d .
A. a 1, d 1 .
B. a 6, d 6 .
C. a 1, d 6 .
D. a 6, d 6 . Lời giải Chọn A Ta có: AB 2; 3 ; 1 ; AC 2 ;0; 2 . 3 1 1 2 2 3 A , B AC ; ; 6;6; 6 . 0 2 2 2 2 0 1 Chọn n ;
AB AC 1;1;
1 là một VTPT của mp ABC . Ta có pt mp ABC là: 6
x y 1 z 2 0 x y z 1 0 . Vậy a 1, d 1 .
Câu 3: Trong không gian Oxyz , gọi M , N , P lần lượt là hình chiếu vuông góc của A2; 3 ; 1 lên các mặt
phẳng tọa độ. Viết phương trình mặt phẳng MNP . Lời giải
Đáp án: 3x 2y 6z 12 0
Không mất tính tổng quát, ta giả sử M , N , P lần lượt là hình chiếu vuông góc của A2; 3 ; 1 lên các mặt
phẳng tọa độ Oxy , Oxz , Oyz . Khi đó, M 2; 3
;0, N 2;0; 1 và P 0; 3 ; 1 MN 0;3; 1 và MP 2 ;0; 1 .
Ta có, MN và MP là cặp vectơ không cùng phương và có giá nằm trong MNP Trang 8
Do đó, MNP có một vectơ pháp tuyến là n MN, MP 3; 2 ;6 .
Mặt khác, MNP đi qua M 2; 3
;0 nên có phương trình là:
3 x 2 2 y
3 6 z 0 0 3x 2y 6z 12 0.
Câu 4: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;1;4 , B2;7;9 , C 0;9;13. Mệnh đề nào
sau đây đúng và mệnh đề nào sai?
A. AB i 6 j 5k .
B. AB AC .
C. Phương trình mặt phẳng đi qua ba điểm ,
A B, C là x y z 4 0 .
D. Phương trình mặt phẳng đi qua ba điểm ,
A B, C là 2x y z 2 0 . Lời giải
A. AB i 6 j 5k . ĐÚNG
B. AB AC . SAI
C. Phương trình mặt phẳng đi qua ba điểm ,
A B, C là x y z 4 0 . ĐÚNG
D. Phương trình mặt phẳng đi qua ba điểm ,
A B, C là 2x y z 2 0 . SAI
Ta có AB 1;6;5 , AC 1 ;8;9 ,
AB 1;6;5 AB i 6 j 5k
AB AC 1.
1 6.8 5.9 0 vô lí
ABC đi qua A1;1;4 có vtpt n A , B AC 14; 1 4;14 141; 1 ;
1 có dạng x y z 4 0 .
1.5. Dạng 5: Thiết lập được điều kiện để hai mặt phẳng song song, vuông góc với nhau. (mức độ: Thông hiểu).
Phương pháp:
a. Điều kiện để hai mặt phẳng song song Trang 9
Trong không gian Oxyz , cho 2 mặt phẳng ( ) : A x B y C z D 0 và ( ) : A x B y C z D 0 1 1 1 1 1 2 2 2 2 2
có vectơ pháp tuyến lần lượt là n (A ; B ;C ), n (A ; B ;C ) . 1 1 1 1 2 2 2 2 n kn Khi đó: 1 2 ( ) // ( ) k 1 2 D kD 1 2 Chú ý: n kn 1 2 ( ) ( ) k 1 2 D kD 1 2
( ) cắt ( ) n và n không cùng phương. 1 2 1 2
b. Điều kiện để hai mặt phẳng vuông góc
Trong không gian Oxyz , cho 2 mặt phẳng ( ) : A x B y C z D 0 và ( ) : A x B y C z D 0 1 1 1 1 1 2 2 2 2 2
có vectơ pháp tuyến lần lượt là n (A ; B ;C ), n (A ; B ;C ) . 1 1 1 1 2 2 2 2
Khi đó: ( ) ( ) n .n 0 A A B B C C 0 1 2 1 2 1 2 1 2 1 2 Bài tập:
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng P : 2x my 3z 5 0 và
Q:nx8y 6z 2 0, với , m n
. Xác định m, n để P song song với Q .
A. m n 4 .
B. m 4; n 4 .
C. m 4; n 4 .
D. m n 4 . Trang 10 Lời giải Chọn B
Mặt phẳng P có véc tơ pháp tuyến n 2; ; m 3 1
Mặt phẳng Q có véc tơ pháp tuyến n ; n 8; 6 2 1 k 2 kn 2
Mặt phẳng P / / Q n k n (k ) m 8k m 4 1 2 3 6k n 4
Câu 2. Trong không gian Oxyz, cho hai mặt phẳng P : x – 2y 2z – 3 0 và Q : mx y – 2z 1 0 . Với
giá trị nào của m thì hai mặt phẳng đó vuông góc với nhau? A. m 1 B. m 1 C. m 6 D. m 6 Lời giải Chọn D
Hai mặt phẳng P,Q vuông góc với nhau khi và chỉ khi 1.m 2.1 2. 2
0 m 6 Câu 3. Trong không gian Oxyz , cho mặt phẳng ba mặt phẳng
P: x y z 1 0,
Q:2xmy 2z 3 0 và R:x2y nz 0. Tính tổng m2n , biết rằng P R và P/ /Q A. 6 . B.1. C. 0. D. 6. Lời giải Chọn C
P: x y z 1 0 có VTPT a 1;1 ;1
Q:2xmy 2z 3 0 có VTPT b 2; ; m 2
R:x2y nz 0 có VTPT c 1 ;2;n
P R .ac 0 n 1 Trang 11 P Q 2 m 2 / / m 2 1 1 1
Vậy m 2n 2 2 1 0
Câu 4. Trong không gian Oxyz , cho P : x y 2z 5 0 và Q : 4x 2 m y mz 3 0 , m là tham
số thực. Tìm tham số m sao cho mặt phẳng Q vuông góc với mặt phẳng P . A. m 3 . B. m 2 .
C. m 3 .
D. m 2 . Lời giải Chọn D
Mặt phẳng P có véctơ pháp tuyến là n 1;1; 2 . P
Mặt phẳng Q có véctơ pháp tuyến là n 4;2 ; m m . Q
Ta có: P Q n n n .
n 0 4.1 2 m 2m 0 m 2 . P Q P Q Nên m 2 .
Câu 5. Trong không gian Oxyz cho hai mặt phẳng : x 2y z 1 0 và : 2x 4y mz 2 0.
Tìm m để hai mặt phẳng và song song với nhau. A. m 1.
B. Không tồn tại m . C. m 2 . D. m 2 . Lời giải Chọn B
Ta có vec tơ pháp tuyến của là n 1;2; 1
, vec tơ pháp tuyến của là n 2;4;m . 2 1 2 4 m 2
Hai mặt phẳng và song song khi 1 2 1 1
Vậy không có giá trị nào của m thỏa mãn điều kiện trên.
Câu 6. Trong không gian Oxyz , mặt phẳng P : 2x y z 2 0 vuông góc với mặt phẳng nào dưới đây?
A. 2x y z 2 0 .
B. x y z 2 0 .
C. x y z 2 0 .
D. 2x y z 2 0 . Lời giải Chọn B
Mặt phẳng P có một vectơ pháp tuyến n 2;1 ;1 . P
Mặt phẳng Q : x y z 2 0 có một vectơ pháp tuyến n 1; 1 ; 1 . Q Trang 12
Mà n .n 2 11 0 n n P Q . P Q P Q
Vậy mặt phẳng x y z 2 0 là mặt phẳng cần tìm.
Câu 7. Trong không gian Oxyz , Cho ba mặt phẳng ( ) : x y 2z 1 0 ; ( ) : x y z 2 0 ;
( ) : x y 5 0 . Các mệnh đề sau đây đúng hay sai? A. ( ) / /( ) . B. ( ) ( ) . C. ( ) ( ) . D. ( ) ( ) . Lời giải
A. ( ) / /( ) . SAI
B. ( ) ( ) . ĐÚNG
C. ( ) ( ) . ĐÚNG
D. ( ) ( ) . ĐÚNG
( ) : x y 2z 1 0 có VTPT a 1;1;2
( ) : x y z 2 0 có VTPT b 1;1; 1
( ) : x y 5 0 có VTPT c 1; 1 ;0 Ta có ; a c 2;2; 2 0
và không song song nhau Ta có .
a b 0 Ta có .
a c 0 Ta có .
b c 0
1.6. Dạng 6: Tính được khoảng cách từ một điểm đến một mặt phẳng bằng phương pháp toạ độ. (mức độ: vận dụng): Trang 13
Trong không gian Oxyz , cho điểm M (x ; y ; z ) và mặt phẳng ( ) : Ax By Cz D 0 . Khi đó khoảng 0 0 0 0 | Ax By Cz D |
cách từ điểm M đến mặt phẳng ( ) được tính: 0 0 0 d (M , ( )) 0 0 2 2 2
A B C Bài tập:
Câu 1. Khoảng cách từ điểm M 3; 2;
1 đến mă ̣t phẳng (P): Ax Cz D 0 , . A .
C D 0 . Cho ̣n khẳng
đi ̣nh đúng trong các khẳng đi ̣nh sau:
3A C D
A 2B 3C D
A. d (M , (P))
B. d (M , (P)) . 2 2 A C 2 2 2
A B C 3A C
3A C D
C. d (M , (P)) .
D. d (M , (P)) . 2 2 A C 2 2 3 1 Lời giải Chọn A | Ax By Cz D | Áp dung công thức 0 0 0 d (M , ( )) 0 2 2 2
A B C
3A C D
Ta được: d(M ,(P)) 2 2 A C
Câu 2. Trong không gian với hê ̣ to ̣a đô ̣ Oxyz , cho mă ̣t phẳng P có phương trình: 3x 4y 2z 4 0 và điểm A1; 2
;3 . Tính khoảng cách d từ A đến P . 5 5 5 5 A. d . B. d . C. d . D. d . 9 29 29 3 Lời giải Chọn C
3x 4 y 2z 4 3 8 6 4
Khoảng cách d từ A đến P là d( , A (P)) A A A 2 2 2 3 4 2 29 5 d( , A (P)) 29
Câu 3. Trong không gian Oxyz , cho mặt phẳng P : 2x 2y z 1 0. Khoảng cách từ điểm M 1 ;2;0
đến mặt phẳng P bằng Trang 14 5 4 A. 5 . B. 2 . C. . D. . 3 3 Lời giải Chọn C 2. 1 2.2 0 1 5
Ta có d M ,P . 2 2 2 3 2 2 1
Câu 4. Trong không gian Oxyz , tính khoảng cách từ M 1;2;
3 đến mặt phẳng P :x 2y 2z 10 0. 11 7 4 A. . B. 3 . C. . D. . 3 3 3 Lời giải Chọn A
d M P 1 2 2 . 2. 3 10 11 11 ; . 2 2 2 3 3 1 2 2
Câu 5. Tính khoảng cách từ điểm Bx ; y ; z đến mă ̣t phẳng (P): y + 1 = 0. Cho ̣n khẳng đi ̣nh đúng trong 0 0 0 các khẳng đi ̣nh sau: y 1 A. y . B. y . C. 0 . D. y 1 . 0 0 0 2 Lời giải Chọn D
Câu 6. Khoảng cách từ điểm C 2
; 0; 0 đến mă ̣t phẳng (Oxy) bằng: A. 0. B. 2. C. 1. D. 2. Lời giải Chọn A
Điểm C thuô ̣c mă ̣t phẳng (Oxy) nên d C,(Oxy) 0
Câu 7. Khoảng cách từ điểm A2; 4;
3 đến mă ̣t phẳng ( ) : 2x y 2z 1 0 và ( ) : x 0 lần lươ ̣t là d ( ,
A ( )) , d ( ,
A ( )) . Các mệnh đề sau đây đúng hay sai? Trang 15 A. d ,
A ( ) 3. d , A ( ). B. d ,
A ( ) d , A ( ). C. d ,
A ( ) = d , A ( ). D. 2. d ,
A ( ) = d , A ( ). Lời giải A. d ,
A ( ) 3. d ,
A ( ). SAI B. d ,
A ( ) d ,
A ( ). SAI C. d ,
A ( ) = d ,
A ( ). SAI D. 2. d ,
A ( ) = d ,
A ( ). ĐÚNG x d A 2.x y 2.z 1 , ( ) A A A 1 ; d , A ( ) A 2. 2 2 2 2 1 2 2 1
Kết luâ ̣n: d ,
A ( ) 2.d , A () .
1.7. Dạng 7: Vận dụng được kiến thức về phương trình mặt phẳng để giải một số bài toán liên quan đến thực
tiễn. (mức độ: vận dụng) Câu 1.
Trên bản thiết kế đồ hoạ 3D của một cánh đồng điện mặt trời trong không gian Oxyz , một tấm pin
nằm trên mặt phẳng (P) : 6x 5y z 2 0 ; một tấm pin khác nằm trên mặt phẳng (Q) đi qua điểm
M (1;1;1) và song song với (P) . Phương trình mặt phẳng (Q) có dạng ax by cz 12 0 . Tính a b c Lời giải Trả lời: 12
Vì (Q) / /(P) nên (Q) có vectơ pháp tuyến là n (6;5;1) .
Phương trình mặt phẳng (Q) là 6(x 1) 5( y 1) 1(z 1) 0 6x 5y z 12 0.
Vậy a b c 12 Trang 16 Câu 2.
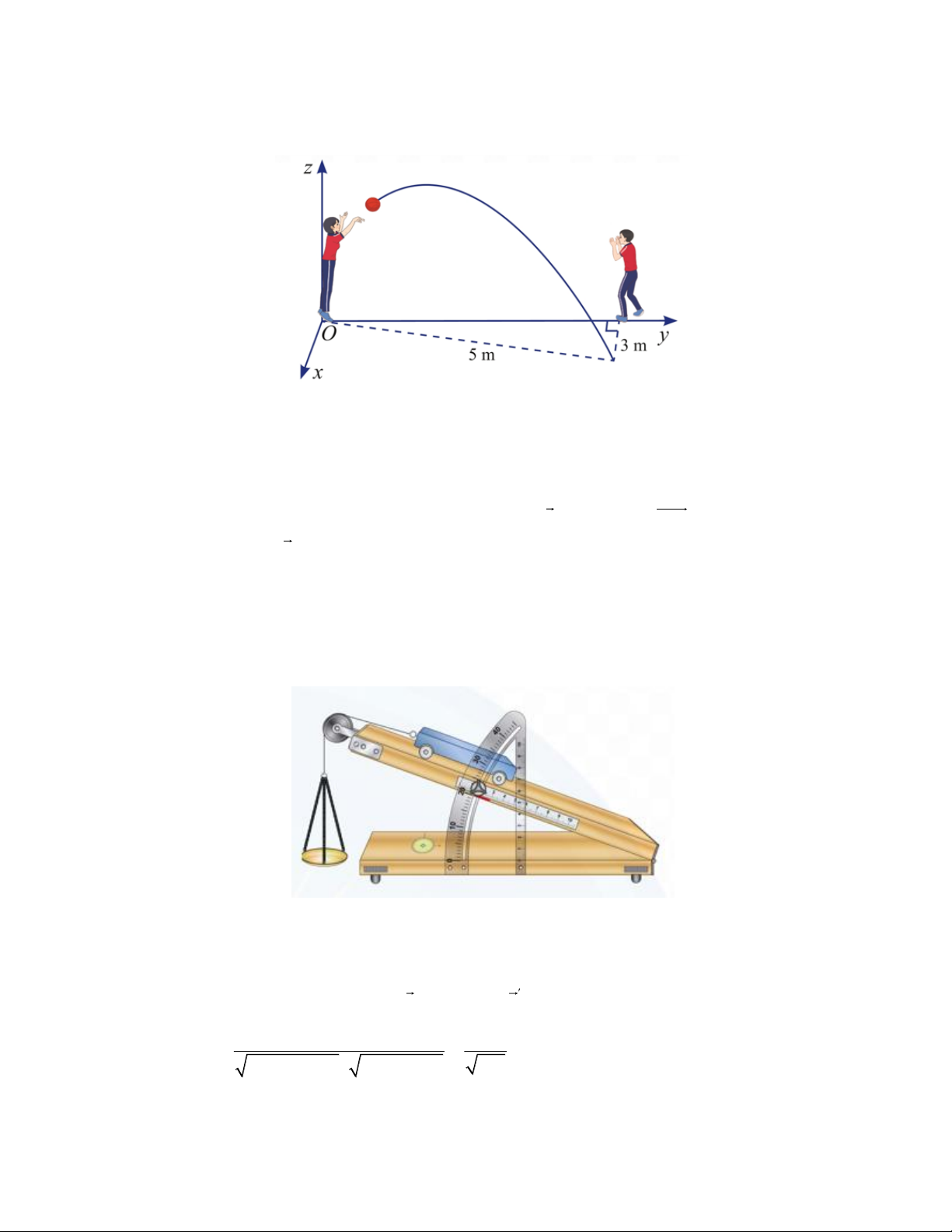
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch
sang phải và rơi xuống tại vị trí cách bạn nam 3 m , cách bạn nữ 5 m (Hình). Cho biết quỹ đạo của quả bóng
nằm trong mặt phẳng (P) vuông góc với mặt đất. Phương trình của (P) trong không gian Oxyz được mô tả
như trong hình vẽ có dạng ax 3y 0 . Tìm a Lời giải Trả lời: 4
Gọi M là điểm mà quả bóng rơi trên mặt đất.
Khi đó M (3; 4;0) . Mặt phẳng (P) có cặp vectơ chỉ phương là k (0;0;1) và OM (3;4;0) nên mặt phẳng
(P) có vectơ pháp tuyến là n ( 4 ;3;0) .
Phương trình mặt phẳng (P) là 4
x 3y 0 . Câu 3.
Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn
một hệ toạ độ Oxyz . Tính góc giữa mặt phẳng nghiêng (P) : 4x 11z 5 0 và mặt sàn (Q) : z 1 0 (làm
tròn kết quả đến hàng đơn vị của độ). Lời giải Trả lời: 20
(P) và (Q) có vectơ pháp tuyến lần lượt là n (4; 0;11) , n (0;0;1) . | 4.0 0.0 11.1| 11 Ta có cos((P), ( ) Q )
. Suy ra ((P), (Q)) 20 . 2 2 2 2 2 2 4 0 11 0 0 1 137
Bài tập tự luyện phương trình mặt phẳng:
Phần 1: Câu hỏi trắc nghiệm. Trang 17
Câu 1. Trong không gian Oxyz , mặt phẳng P : 2x 3y 4z 1 0 có một vectơ pháp tuyến là: A. n 1 ;2; 3 . B. n 3
;4;1 . C. n 2;3;4 .
D. n 2;3; 4 . 1 2 3 4
Câu 2. Trong không gian Oxyz , cho mặt phẳng P : 2x 3y z 2 0. Véctơ nào dưới đây là một véctơ
pháp tuyến của P ?
A. n 2;3; 2 .
B. n 2;3;0 .
C. n 2;3;1 .
D. n 2;0;3 . 4 2 1 3
Câu 3. Trong không gian với hệ tọa độ Oxyz , vectơ nào dưới đây là một véctơ pháp tuyến của mặt phẳng Oxy? r ur r r
A. i 1; 0; 0
B. m 1;1; 1
C. j 0;1; 0
D. k 0; 0; 1
Câu 4. Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A1;2; 3 có véc tơ
pháp tuyến n 2;1;3 là
A. 2x y 3z 9 0 . B. 2x y 3z 4 0 . C. x 2 y 4 0 .
D. 2x y 3z 4 0 .
Câu 5.Trong không gian Oxyz phương trình mặt phẳng đi qua điểm A (1; 2;3) và vuông góc với giá của véctơ v ( 1 ;2;3) là
A. x 2 y 3z 4 0.
B. x 2 y 3z 4 0. C. x 2 y 3z 4 0.
D. x 2 y 3z 4 0.
Câu 6.Trong không gian Oxyz , cho điểm A0; 3
;2 và mặt phẳng P: 2x y 3z 5 0 . Mặt phẳng đi
qua A và song song với P có phương trình là
A. 2x y 3z 9 0 . B. 2x y 3z 3 0 . C. 2x y 3z 3 0 . D. 2x y 3z 9 0 .
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A0;1; 1 ) và B1;2;
3 . Viết phương trình của
mặt phẳng P đi qua A và vuông góc với đường thẳng AB .
A. x y 2z 3 0
B. x y 2z 6 0
C. x 3y 4z 7 0 D. x 3y 4z 26 0
Câu 8. Trong không gian Oxyz, cho điểm M (8; 2 ;4) . Gọi ,
A B, C lần lượt là hình chiếu của M trên các
trục Ox, Oy, Oz . Phương trình mặt phẳng đi qua ba điểm ,
A B và C là
A. x 4 y 2z 8 0
B. x 4 y 2z 18 0 C. x 4 y 2z 8 0 D. x 4 y 2z 8 0
Câu 9. Trong không gian với hệ tọa độ Oxyz , mặt phẳng đi qua ba điểm A2; 3; 5 , B3; 2; 4 và
C 4; 1; 2 có phương trình là
A. x y 5 0 .
B. x y 5 0 .
C. y z 2 0 .
D. 2x y 7 0 .
Câu 10. Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi qua ba điểm A1;1;4 ,
B2;7;9 , C 0;9;13.
A. 2x y z 1 0 .
B. x y z 4 0 .
C. 7x 2 y z 9 0 . D. 2x y z 2 0 .
Câu 11. Trong không gian Oxyz , tính khoảng cách từ M 1;2;
3 đến mặt phẳng P :x 2y 2z 10 0. Trang 18 11 7 4 A. . B. 3 . C. . D. . 3 3 3
Câu 12. Trong không gian Oxyz , cho mặt phẳng P : 2x 2y z 1 0. Khoảng cách từ điểm M 1 ;2;0
đến mặt phẳng P bằng 5 4 A. 5 . B. 2 . C. . D. . 3 3
Câu 13. Trong không gian Oxyz khoảng cách giữa hai mặt phẳng P : x 2y 3z 1 0 và
Q: x2y 3z 6 0 là 7 8 5 A. B. C. 14 D. 14 14 14
Câu 14. Trong không gian Oxyz , cho mặt phẳng (P) qua hai điểm ( A 0; 0;3), B( 3
;0;0) và vuông góc với
mặt phẳng ( ) : 2x y z 1 0 . Khoảng cách từ gốc tọa độ O đến (P) bằng 4 3 3 1 A. . B. . C. . D. . 3 5 11 3
Câu 15. Trong không gian Oxyz , mặt phẳng P : 2x y z 2 0 vuông góc với mặt phẳng nào dưới đây?
A. 2x y z 2 0 .
B. x y z 2 0 .
C. x y z 2 0 .
D. 2x y z 2 0 .
Câu 16. Trong không gian Oxyz, mặt phẳng nào dưới đây song song với mặt phẳng (Oxy)?
A. (a ): z + 1= 0.
B. (j ):x + 1= 0 . C. ( )
b : x + z + 1= 0 . D. (g): y + 1= 0 .
Câu 17. Trong không gian Oxyz , cho mặt phẳng : x y 2z 1 0. Mặt phẳng song song với mặt
phẳng nào sau đây?
A. Q : 3x 3y 6z 1 0 .
B. P : 2x 2y 4z 2 0 .
C. R : x y z 1 0 .
D. S : x y 2z 1 0.
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng :x y z 6 0 . Điểm nào dưới đây
không thuộc ?
A. Q 3;3;0
B. N 2;2;2 C. P1;2; 3 D. M 1; 1 ; 1
Câu 19. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x 2y z 5 0. Điểm nào dưới đây
thuộc P ? A. P 0;0; 5
B. M 1;1;6 C. Q2; 1 ;5 D. N 5 ;0;0
Câu 20. Trong không gian Oxyz , mặt phẳng P : x y z 3 0 đi qua điểm nào dưới đây? A. M 1 ; 1 ; 1 B. N 1;1; 1 C. P 3 ;0;0
D. Q0;0; 3
Phần 2: Câu hỏi đúng sai Trang 19 Câu 1.
Trong không gian với hệ tọa độ Oxyz , cho ba điểm (
A 0;3;1), B(1;0; 1 ),C( 2
;1;1) .Gọi (P) là mặt phẳng đi qua ba điểm ,
A B,C . Xét tính đúng sai của các mệnh đề sau: 1 4 1
a) Toạ độ trọng tâm tam giác ABC là G ; ; . 3 3 3
b) Phương trình mặt phẳng qua A và vuông góc với BC là (Q) : 3x y 2z 5 0 .
c) Một vectơ pháp tuyến của mặt phẳng (P) là n (1; 2 ;2) . ( P)
d) Mặt phẳng (P) đi qua điểm M ( 2 ;5;3) . Câu 2.
Trong không gian Oxyz , cho hai điểm A1; 0; 0; B4;1; 2 . uuur
a) AB 3;1; 2
b) Mặt phẳng đi qua A và vuông góc với AB có phương trình là 3x y 2z 3 0 . 5 1
c) Nếu I là trung điểm đoạn thẳng AB thì I ; ;1 . 2 2
d)Mặt phẳng trung trực đoạn thẳng AB có phương trình là 3x y 2z 12 0 . Câu 3.
Trong không gian Oxyz , gọi là mặt phẳng đi qua hai điểm (
A 1;3; 4), B(2; 1 ;5) và vuông góc với
mặt phẳng (Q) : 2x 3y z 1 0 . Xét tính đúng sai của các mệnh đề sau:
a) Một vectơ pháp tuyến của mặt phẳng (Q) là n ( 4 ;6; 2 ) . 3 9
b) Trung điểm của đoạn thẳng AB là I ;1; . 2 2
c) Mặt phẳng qua A và song song với (Q) có phương trình là 2
x 3y z 3 0 .
d) Phương trình mặt phẳng (P) là x y 5z 22 0 .
Phần 3: Câu trả lời ngắn
Câu 1. Khi gắn hệ toạ độ Oxyz (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng (Oxy)
trùng với mặt sân bay. Một máy bay ở vị trí ( A 3; 2
;3) sẽ hạ cánh tới vị trí B(8;8;0) . Góc giữa đường bay
(một phần của đường thẳng AB ) và sân bay (một phần của mặt phẳng (Oxy) ) bằng bao nhiêu độ (làm tròn
kết quả đến hàng đơn vị)?
Câu 2. Khi gắn hệ trục toạ độ Oxyz (đơn vị trên mỗi trục toạ độ là decimét) vào một ngôi nhà 1 tầng, người
ta thấy rằng mặt trên và mặt dưới của mái nhà thuộc các mặt phẳng vuông góc với trục Oz . Biết rằng các vị trí (
A 3; 4;33), D(9;8;35) lần lượt thuộc mặt dưới, mặt trên của mái nhà. Độ dày của mái nhà được tính bằng
khoảng cách giữa mặt trên và mặt dưới của mái nhà đó. Hãy cho biết độ dày của mái nhà đó là bao nhiêu decimét?
Câu 3. Trong một khung lưới ô vuông gồm các hình lập phương, người ta đưa ra một cách kiểm tra bốn nút
lưới (đỉnh hình lập phương) bất kì có đồng phẳng hay không bằng cách gắn hệ trục tọ ̣ độ Oxyz vào khung
lưới ô vuông và lập phương trình mặt phẳng đi qua ba nút lưới trong bốn nút lưới đã cho. Giả sử có ba nút Trang 20