471 trang 4 lượt tải

Chuyên đề phương pháp tọa độ trong không gian từ cơ bản đến nâng cao

8

Tài liệu gồm 471 trang, bao gồm lý thuyết, các dạng toán và bài tập chuyên đề phương pháp tọa độ trong không gian từ cơ bản đến nâng cao, giúp học sinh tham khảo khi học chương trình môn Toán 12 chương trình mới.

Chủ đề: Tài liệu chung 172 tài liệu

Môn: Toán 12 4.3 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/471
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 1
Sưu tầm và biên soạn
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG
I. VECTƠ PHÁP TUYẾN VÀ CẶP VEC-TƠ CHỈ PHƯƠNG CỦA MẶT PHẲNG.
1. Định nghĩa.
Cho mặt phẳng
( )
α
.
Nếu vec-tơ
n
khác
0
và có giá vuông góc với
( )
α
thì
n
được gọi là vec-tơ pháp tuyến của
(
)
α
.
Nếu hai vec-tơ
a
và
b
không cùng phương, có giá song song hoặc nằm trong
( )
α
thì
a
,
b
được gọi là cặp vec-tơ chỉ phương của
( )
α
.
2. Chú ý.
Nếu
n
là một vec-tơ pháp tuyến của mặt phẳng
( )
α
thì
( )
0k ≠
cũng là một vec-tơ pháp tuyến của mặt phẳng
( )
α
.
Một mặt phẳng hoàn toàn được xác định khi biết một điểm
và một vec-tơ pháp tuyến hoặc một điểm và một cặp vec-tơ
chỉ phương của mặt phẳng đó.
II. XÁC ĐỊNH VEC-TƠ PHÁP TUYẾN CỦA MẶT PHẲNG KHI BIẾT MỘT CẶP VEC-TƠ CHỈ
PHƯƠNG
1. Định lý.
Trong không gian
Oxyz
, nếu mặt phẳng
(
)
α
nhận hai vec-tơ
( )
123
;;a aaa=
,
( )
123
;;b bbb
=
làm
cặp vec-tơ chỉ phương thì
( )
α
nhận vec-tơ
(
)
23 32 31 13 12 21
;;
n ab ab ab ab ab ab=−−−
làm vec-tơ
pháp tuyến.
CHƯƠNG
V
PHƯƠNG PHÁP TỌA ĐỘ
TRONG KHÔNG GIAN
LÝ THUYẾT.
I
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 2
Sưu tầm và biện soạn
2. Chú ý.
Vec-tơ
( )
23 32 31 13 12 21
;;n ab ab ab ab ab ab
=−−−
được gọi là tích có hướng của hai vec-tơ
( )
123
;;a aaa=
,
(
)
123
;;
b bbb=
. Tích có hướng của hai vec-tơ
a
và
b
, kí hiệu
,ab


.
Biểu thức
12 21
ab a b−
thường được kí hiệu
12
12
aa
bb
. Tương tự,
3
2
23 32
23
a
a
ab ab
bb
= −
và
3
1
31 13
31
a
a
ab ab
bb
= −
. Như vậy:
33
2 1 12
23 31 12
, ;;
aa
a a aa
ab
bb bb bb


=



.
Hai vec-tơ
a
và
b
cùng phương
,0
ab

⇔=

.
III. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG
1. Định nghĩa.
Trong không gian
Oxyz
, phương trình có dạng
0Ax By Cz D+ + +=
, trong đó
A
,
B
,
C
không
đồng thời bằng
0
, được gọi là phương trình tổng quát của mặt phẳng.
2. Nhận xét.
Cho mặt phẳng
( )
α
có phương trình tổng quát là
0Ax By Cz D+ + +=
. Khi đó:
Mặt phẳng
(
)
α
có một vec-tơ pháp tuyến là
(
)
;;n ABC
=
.
(
) ( )
0 00 0 0 0
;; 0
N x y z Ax By Cz D
α
∈⇔ +++=
.
Mỗi phương trình
0Ax By Cz D+ + +=
(trong đó
A
,
B
,
C
không đồng thời bằng 0) đều là
phương trình của một mặt phẳng xác định.
3. Một số dạng toán viết phương trình mặt phẳng cơ bản
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một vec-tơ pháp tuyến
Trong không gian
Oxyz
, phương trình mặt phẳng đi qua điểm
( )
0 0 00
;;M xyz
và có vec-tơ pháp
tuyến
( )
;;n ABC=
là:
( ) ( ) ( )
0 00
0Ax x B y y Cz z−+ −+ −=
hay
0Ax By Cz D+ + +=
với
000
D Ax By Cz=−−−
.
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một cặp vec-tơ chỉ
phương
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 3
Sưu tầm và biên soạn
Để lập phương trình tổng quát của mặt phẳng
( )
α
đi qua điểm
( )
0 0 00
;;M xyz
và có cặp vec-tơ
chỉ phương
a
,
b
, ta thực hiện như sau:
Tìm một vec-tơ pháp tuyến
,n ab

=


.
Viết phương trình mặt phẳng
( )
α
đi qua điểm
( )
0 0 00
;;M xyz
và có vec-tơ pháp tuyến
n
.
Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng
Để lập phương trình tổng quát của mặt phẳng
( )
α
đi qua ba điểm
A
,
B
,
C
không thẳng hàng,
ta thực hiện như sau:
Tìm cặp vec-tơ chỉ phương, chẳng hạn
AB

,
AC

.
Tìm một vec-tơ pháp tuyến
,n AB AC

=

 
.
Viết phương trình mặt phẳng
( )
α
đi qua
A
và có vec-tơ pháp tuyến
n
.
Lập phương trình tổng quát của mặt phẳng theo đoạn chắn
Phương trình tổng quát của mặt phẳng
( )
α
đi qua ba điểm
( )
;0;0Aa
,
( )
0; ;0Bb
,
( )
0;0;Cc
là:
1
xyz
abc
++=
.
4. Điều kiện để hai mặt phẳng song song, vuông góc
Điều kiện để hai mặt phẳng vuông góc
Trong không gian
Oxyz
, cho hai mặt phẳng
( )
11 1 1 1
:0Ax By Cz D
α
+ + +=
và
( )
22 2 2 2
:0Ax By Cz D
α
+ + +=
có vec-tơ pháp tuyến lần lượt là
( )
1 111
;;n ABC=
,
( )
2 222
;;n ABC=
. Khi đó:
( ) ( )
1 2 1 2 12 12 12
00n n AA BB CC
αα
⊥ ⇔⋅=⇔ + + =

.
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 4
Sưu tầm và biện soạn
Điều kiện để hai mặt phẳng song song
Trong không gian
Oxyz
, cho hai mặt phẳng
( )
11 1 1 1
:0Ax By Cz D
α
+ + +=
và
( )
22 2 2 2
:0Ax By Cz D
α
+ + +=
có vec-tơ pháp tuyến lần lượt là
( )
1 111
;;
n ABC
=
,
( )
2 222
;;n ABC=
. Khi đó:
( ) ( ) ( )
12
12
12
n kn
k
D kD
αα
=
⇔∈
≠


.
Chú ý.
( ) ( ) (
)
12
12
12
n kn
k
D kD
αα
=
≡⇔ ∈
=

.
( )
1
α
cắt
( )
21
n
α
⇔
và
2
n
không cùng phương.
5. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian
Oxyz
, mặt phẳng
( )
α
có phương trình
0Ax By Cz D+ + +=
và điểm
( )
0 0 00
;;M xyz
. Khoảng cách từ điểm
0
M
đến mặt phẳng
( )
α
được tính theo công thức:
(
)
( )
000
0
222
d,
Ax By Cz D
M
ABC
α
+++
=
++
.
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 5
Sưu tầm và biên soạn
DẠNG 1: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG KHI BIẾT MỘT ĐIỂM VÀ VECTƠ PHÁP
TUYẾN CỦA NÓ.
Câu 1: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
đi qua điểm
(1;0; 2)A −
và có vectơ
pháp tuyến
(1; 1; 2)n −
.
Câu 2: Trong không gian với hệ trục tọa độ
Oxyz
, viết phương trình mặt phẳng đi qua điểm
( )
0;1; 2A
và có vectơ pháp tuyến
( )
2;1; 0 .n = −
Câu 3: Trong không gian
Oxyz
, viết phương trình mặt phẳng đi qua
( )
1;1;1A −
và có vectơ pháp tuyến
( )
1; 2; 2n =−−
Câu 4: Trong không gian với hệ trục tọa độ
Oxyz
, cho các điểm
( )
0;1; 2A
,
( )
2; 2;1B −
,
( )
2;0;1
C −
.
Phương trình mặt phẳng đi qua
A
và vuông góc với
BC
là?
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
Phương trình tổng quát của mặt phẳng đi qua điểm và có véctơ pháp
tuyến là có dạng:
(với
).
Nếu mặt phẳng có cặp véctơ chỉ phương là thì có véctơ pháp tuyến là
Phương pháp
Trong không gian , viết phương trình mặt phẳng trung trực đoạn thẳng
Bước 1: Véctơ pháp tuyến của mặt là: .
Bước 2: Tìm tọa độ trung điểm của đoạn .
Bước 3: Viết phương trình mặt phẳng đi qua điểm và có vectơ pháp tuyến
.
Phương pháp
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 6
Sưu tầm và biện soạn
Câu 5: Trong không gian
Oxyz
, cho ba điểm
( )
1;1;1A −
,
( )
2;1; 0B
và
(
)
1; 1; 2
C
−
. Mặt phẳng đi qua
A
và vuông góc với đường thẳng
BC
có phương trình là?
Câu 6: Trong không gian
Oxyz
, cho
(
)
1; 1;1
A −−
,
( )
3;1;1B
. Phương trình mặt phẳng trung trực của
đoạn
AB
là.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1; 6; 7A −
và
( )
3; 2;1B
. Phương trình mặt
phẳng trung trực đoạn
AB
là.
Câu 8: Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
P
chứa điểm
( )
13 2
;;
M −
, cắt các tia
Ox
,
Oy
,
Oz
lần lượt tại
A
,
B
,
C
sao cho
124
OA OB OC
= =
.
Câu 9: Trong không gian
Oxyz
, cho hình hộp
.ABCD A B C D
′′′ ′
, biết rằng
( )
300;;A −
,
( )
020;;B
,
( )
001;;D
,
( )
123
;;
A
′
. Viết phương trình mặt phẳng trung trực của
CD
′
.
DẠNG 2: Viết phương trình mặt phẳng
( )
α
đi qua 1 điểm
( )
0 0 00
;;Mxyz
và song song với 1 mặt phẳng
( )
:0
Ax By Cz D
β
+ + +=
cho trước.
Câu 10: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()
P
đi qua điểm
(0; 1; 3)
M
và song song
với mặt phẳng
( ):2 3 1 0Qxz− +=
.
Câu 11: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
đi qua điểm
−( 2; 3; 1)M
và song song
với mặt phẳng
+ − +=( ): 3 2 2 0Qxyz
.
Trong không gian , viết phương trình mặt phẳng
Loại Phương pháp
⑴
Qua và song song
.
⌘ Cách 1:
≫ Véctơ pháp tuyến là: .
≫ Mặt phẳng qua điểm .
⌘ Cách 2:
≫ Do
≫ Thay điểm vào .
⑵
Song song và
cách một khoảng bằng .
≫ Vì .
≫ Vì cách một khoảng bằng
≫ Có phương trình mặt hoàn chỉnh.
Phương pháp
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 7
Sưu tầm và biên soạn
Câu 12: Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng đi điểm
( )
3;1;2M −−
và
song song với mặt phẳng
(
)
:3 2 4 0P xy z−+ +=
.
DẠNG 3: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG
( )
α
ĐI QUA 3 ĐIỂM
A
,
B
,
C
KHÔNG THẲNG
HÀNG.
Câu 13: Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
ABC
a) Với ba điểm
( )
103;; ,A −
(
)
2 11
; ;,B
−
( )
1 10;;C
−
.
b) Với ba điểm
( ) ( ) ( )
102 231 321−;; , ;; , ;;AB C
.
Câu 14: Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
ABC
a) Với ba điểm
( )
2;0;0
M
,
( )
0; 1;0N −
,
(
)
0;0;2
P
.
b) Với ba điểm
( )
( ) ( )
0; 2;0 , 3;0;0 , 0;0; 3M NP−−
.
Câu 15: Trong không gian
Oxyz
, viết phương trình mặt phẳng đi qua ba điểm
(1;0; 2),A −
(1; 1; 1),B
(0; 1; 2)C −
.
Câu 16: Trong không gian
Oxyz
, cho ba điểm
( )
1;0;0A
,
( )
0;1;1B −−
,
( )
5; 1;1C −
. Viết phương trình
mặt phẳng
(
)
ABC
.
Câu 17: Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng đi qua ba điểm
(
)
2; 3; 5A
,
( )
3; 2; 4B
và
( )
4; 1; 2C
.
Câu 18: Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng đi qua ba điểm
( )
1;1; 4A
,
( )
2;7;9B
,
( )
0;9;13C
.
Phương trình mặt phẳng di qua không thẳng hàng.
Bước 1: Tìm cặp vectơ chỉ phương .
Bước 2: Tìm một vectơ pháp tuyến .
Bước 3: Viết phương trình mặt phẳng đi qua điểm (hoặc điểm hoặc điểm
) và có vectơ pháp tuyến .
Phương trình mặt phẳng là phương trình mặt chắn, tức mặt phẳng đi qua
có dạng: .
Phương pháp
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 8
Sưu tầm và biện soạn
DẠNG 4: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG
( )
α
QUA HAI DIỂM
A
,
B
VA VUÔNG GÓC
VỚI MẶT PHẲNG
(
)
.
β
VIẾT PHƯƠNG TRÌNH MẶT PHẲNG
(
)
α
QUA DIỂM
A
VA
VUÔNG GÓC VỚI HAI MẶT PHẲNG
( ) ( )
αβ
,.
Câu 19: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()
α
đi qua điểm
(1; 2; 2), (2; 1; 4)AB−−
và vuông góc với
( )
: 2 1 0.x yz
β
− −+=
Câu 20: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
2; 4;1A
,
( )
1;1; 3B −
và mặt phẳng
( )
: 3 2 50Px y z− + −=
. Viết phương trình mặt phẳng
( )
Q
đi qua hai điểm
A
,
B
và vuông góc
với mặt phẳng
( )
P
.
Câu 21: Trong không gian hệ tọa độ
,Oxyz
cho
( ) ( )
2;1; 1 ; 1; 0;1AB−
và mặt phẳng
( )
: 2 1 0.Px yz+ −+=
Viết phương trình mặt phẳng
( )
Q
qua
;AB
và vuông góc với
( )
P
.
Trong không gian , viết phương trình mặt phẳng
Loại Phương pháp
Qua và 2 mặt
,
.
≫ Tìm cặp véctơ và .
≫ Véctơ pháp tuyến là: .
≫ Mặt phẳng qua điểm .
Hoặc bài toán sẽ gặp:
“Qua và vuông góc với giao tuyến của
; ”
Loại Phương pháp
Qua điểm và vuông góc
.
≫ Tìm cặp véctơ và .
≫ Véctơ pháp tuyến là: .
≫ Mặt phẳng qua điểm .
Phương pháp
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 9
Sưu tầm và biên soạn
Câu 22: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
đi qua điểm
( 1; 2; 5)M −−
và vuông
góc với hai mặt phẳng
( ): 2 3 1 0Qx y z+ − +=
và
( ):2 3 1 0R x yz− ++=
.
Câu 23: Trong không gian
Oxyz
, cho hai mặt phẳng
(
)
:32270
xyz
α
− + +=
và
( )
: 5 4 3 1 0.xyz− + +=
β
Phương trình mặt phẳng qua
O
, đồng thời vuông góc với cả
( )
α
và
( )
β
có phương trình là
Câu 24: Cho hai mặt phẳng
(
) (
)
:3 2 2 7 0, :5 4 3 1 0
xyz xyz
αβ
−++= −++=
. Phương trình mặt phẳng
đi qua gốc tọa độ
O
đồng thời vuông góc với cả
( )
α
và
( )
β
là:
Câu 25: Trong không gian
,Oxyz
cho hai mặt phẳng
( )
: 3 2 1 0,Px y z− + −=
( )
: 20Qxz−+=
. Mặt
phẳng
( )
α
vuông góc với cả
( )
P
và
( )
Q
đồng thời cắt trục
Ox
tại điểm có hoành độ bằng
3.
Phương trình của mp
( )
α
là
Câu 26: Trong không gian với hệ tọa độ
Oxyz
cho hai mặt phẳng
( )
:3 2 2 7 0xyz
α
− + +=
và
( )
:5 4 3 1 0xyz
β
− + +=
. Phương trình mặt phẳng đi qua
O
đồng thời vuông góc với cả
( )
α
và
( )
β
có phương trình là
Dạng 6: Viết phương trình mặt phẳng
( )
α
song song với mặt phẳng
( )
β
và cách
( )
:0Ax By Cz D
β
+ + +=
một khoảng
k
cho trước.
Phương pháp :
1. Trên mặt phẳng
( )
β
chọn 1 điểm
.M
2. Do
( )
α
//
( )
β
nên
( )
α
có phương trình
0
Ax By Cz D
′
+++=
(
DD
′
≠
).
3. Sử dụng công thức khoảng cách
( )
( )
( )
(
)
(
)
,,d dM k
αβ β
= =
để tìm
D
′
.
Câu 27: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
song song với mặt phẳng
( ): 2 2 1 0Qx y z+ − +=
và cách
()Q
một khoảng bằng 3.
Câu 28: Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng
(
)
P
song song và cách mặt
phẳng
( )
:3 2 3 0
α
−+ −=xy z
một khoảng bằng
14
.
Câu 29: Trong không gian
Oxyz
, cho mặt phẳng
: 2 2 10 0Px y z 
. Phương trình mặt phẳng
Q
với
Q
song song với
P
và khoảng cách giữa hai mặt phẳng
P
và
Q
bằng
7
3
là.
Câu 30: Trong không gian hệ toạ độ
Oxyz
, lập phương trình các mặt phẳng song song với mặt phẳng
( )
: 30xyz
β
+−+=
và cách
( )
β
một khoảng bằng
3
.
Câu 31: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
song song với mặt phẳng
( ): 2 2 1 0Qx y z+ − +=
và
()P
cách điểm
(1; 2; 1)M −
một khoảng bằng 3.
Câu 32: Trong không gian với hệ trục tọa độ
,Oxyz
viết phương trình mặt phẳng
( )
P
song song với mặt
phẳng
( )
: 2 4 10Qx y z− + −=
và cách điểm
( )
1; 3;1M −
là một khoảng bằng 2.
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 10
Sưu tầm và biện soạn
Câu 33: Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
:2 2 3 0−+ −=Q xy z
và điểm
( )
1; 2; 3A
. Viết phương trình mặt phẳng
(
)
P
song song với
( )
Q
và cách
A
một khoảng bằng
4.
DẠNG 7. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
Câu 34: Cho hình lập phương
.ABCD EFGH
cạnh
1
. Điểm
M
được cho thỏa mãn hệ thức
3AM AE CD
 
+=
. Tính khoảng cách từ điểm
M
đến mặt phẳng
( )
EBD
.
Câu 35: Cho hình lăng trụ tam giác đều
.ABC DEF
,
6AB =
,
2AD =
. Gọi
M
,
N
,
P
lần lượt là trung
điểm
DE
,
DF
,
BC
. Lập hệ trục tọa độ
Oxyz
như hình bên. Gọi điểm
S
thỏa mãn hệ thức
20+ +=SA SB SC
  
. Tính khoảng cách từ điểm
S
đến mặt phẳng
(
)
MNP
.
Tính khoảng cách từ điểm đến mặt phẳng như
sau
Bước 1: Tìm ; viết phương trình mặt phẳng
.
Bước 2: Tính khoảng cách từ điểm đến mặt phẳng
theo công thức
Lưu ý:
Phương pháp
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 11
Sưu tầm và biên soạn
DẠNG 8. VỊ TRÍ TƯƠNG ĐỐI HAI MẶT PHẲNG
Câu 36: Cho ba mặt phẳng
( )
1
:2 2 1 0P xy z− − +=
,
( )
2
:4 2 4 4 0P xyz− − +=
,
( )
3
: 4 10P x yz+ −+=
.
Chứng minh
( ) ( )
12
//PP
và
(
) (
)
13
PP⊥
.
Câu 37: Trong không gian
Oxyz
, cho hai mặt phẳng
( )
( )
22
2 20:mx y m z −+ − +=
và
( )
2
2 2 10: x my z + − +=
. Hai mặt phẳng
( )
và
( )
vuông góc với nhau khi nào?
Câu 38: Trong không gian
Oxyz
cho
(
) ( )
( )
(
)
200 040 006 246
;;, ;;, ;;, ;;ABCD
. Gọi
( )
P
là mặt phẳng
song song với
( )
mp ABC
,
( )
P
cách đều
D
và mặt phẳng
( )
ABC
. Phương trình của
( )
P
là?
Xét điểm mặt phẳng có vecto pháp tuyến , với:
Mặt phẳng có vecto pháp tuyến ,
Ta có các vị trí tương đối sau:
Mặt phẳng
Mặt phẳng
Mặt cắt mặt
Mặt song song mặt
Mặt trùng mặt
Mặt vuông góc mặt
Phương pháp
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 1
Sưu tầm và biên soạn
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG
I. VECTƠ PHÁP TUYẾN VÀ CẶP VEC-TƠ CHỈ PHƯƠNG CỦA MẶT PHẲNG.
1. Định nghĩa.
Cho mặt phẳng
( )
α
.
Nếu vec-tơ
n
khác
0
và có giá vuông góc với
( )
α
thì
n
được gọi là vec-tơ pháp tuyến của
(
)
α
.
Nếu hai vec-tơ
a
và
b
không cùng phương, có giá song song hoặc nằm trong
( )
α
thì
a
,
b
được gọi là cặp vec-tơ chỉ phương của
( )
α
.
2. Chú ý.
Nếu
n
là một vec-tơ pháp tuyến của mặt phẳng
( )
α
thì
( )
0
k ≠
cũng là một vec-tơ pháp
tuyến của mặt phẳng
( )
α
.
Một mặt phẳng hoàn toàn được xác định khi biết một điểm và một vec-tơ pháp tuyến hoặc một
điểm và một cặp vec-tơ chỉ phương của mặt phẳng đó.
II. XÁC ĐỊNH VEC-TƠ PHÁP TUYẾN CỦA MẶT PHẲNG KHI BIẾT MỘT CẶP VEC-TƠ CHỈ
PHƯƠNG
1. Định lý.
Trong không gian
Oxyz
, nếu mặt phẳng
( )
α
nhận hai vec-tơ
( )
123
;;a aa a=
,
( )
123
;;b bbb=
làm
cặp vec-tơ chỉ phương thì
( )
α
nhận vec-tơ
( )
23 32 31 13 12 21
;;n ab ab ab ab ab a b=−−−
làm vec-tơ
pháp tuyến.
CHƯƠNG
V
PHƯƠNG PHÁP TỌA ĐỘ
TRONG KHÔNG GIAN
LÝ THUYẾT.
I
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 2
Sưu tầm và biện soạn
2. Chú ý.
Vec-tơ
( )
23 32 31 13 12 21
;;n ab ab ab ab ab a b=−−−
được gọi là tích có hướng của hai vec-tơ
( )
123
;;a aa a
=
,
(
)
123
;;
b bbb=
. Tích có hướng của hai vec-tơ
a
và
b
, kí hiệu
,
ab


.
Biểu thức
12 21
ab a b
−
thường được kí hiệu
12
12
aa
bb
. Tương tự,
3
2
23 32
23
a
a
ab ab
bb
= −
và
3
1
31 13
31
a
a
ab ab
bb
= −
. Như vậy:
33
2 1 12
23 31 12
, ;;
aa
a a aa
ab
bb bb bb


=



.
Hai vec-tơ
a
và
b
cùng phương
,0ab

⇔=

.
III. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG
1. Định nghĩa.
Trong không gian
Oxyz
, phương trình có dạng
0Ax By Cz D+ + +=
, trong đó
A
,
B
,
C
không
đồng thời bằng
0
, được gọi là phương trình tổng quát của mặt phẳng.
2. Nhận xét.
Cho mặt phẳng
( )
α
có phương trình tổng quát là
0Ax By Cz D+ + +=
. Khi đó:
o Mặt phẳng
(
)
α
có một vec-tơ pháp tuyến là
( )
;;n ABC=
.
o
( ) ( )
0 00 0 0 0
;; 0N x y z Ax By Cz D
α
∈ ⇔ + + +=
.
Mỗi phương trình
0Ax By Cz D+ + +=
(trong đó
A
,
B
,
C
không đồng thời bằng 0) đều là
phương trình của một mặt phẳng xác định.
3. Một số dạng toán viết phương trình mặt phẳng cơ bản
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một vec-tơ pháp tuyến
Trong không gian
Oxyz
, phương trình mặt phẳng đi qua điểm
( )
0 0 00
;;M xyz
và có vec-tơ pháp
tuyến
( )
;;n ABC=
là:
( ) ( ) ( )
0 00
0Ax x By y Cz z−+ −+ −=
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 3
Sưu tầm và biên soạn
hay
0Ax By Cz D
+ + +=
với
000
D Ax By Cz=−−−
.
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một cặp vec-tơ chỉ
phương
Để lập phương trình tổng quát của mặt phẳng
( )
α
đi qua điểm
( )
0 0 00
;;M xyz
và có cặp vec-tơ
chỉ phương
a
,
b
, ta thực hiện như sau:
Tìm một vec-tơ pháp tuyến
,n ab

=


.
Viết phương trình mặt phẳng
( )
α
đi qua điểm
( )
0 0 00
;;M xyz
và có vec-tơ pháp tuyến
n
.
Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng
Để lập phương trình tổng quát của mặt phẳng
( )
α
đi qua ba điểm
A
,
B
,
C
không thẳng hàng,
ta thực hiện như sau:
Tìm cặp vec-tơ chỉ phương, chẳng hạn
AB

,
AC

.
Tìm một vec-tơ pháp tuyến
,n AB AC

=

 
.
Viết phương trình mặt phẳng
( )
α
đi qua
A
và có vec-tơ pháp tuyến
n
.
Lập phương trình tổng quát của mặt phẳng theo đoạn chắn
Phương trình tổng quát của mặt phẳng
( )
α
đi qua ba điểm
( )
;0;0Aa
,
( )
0; ;0Bb
,
( )
0;0;Cc
là:
1
xyz
abc
++=
.
4. Điều kiện để hai mặt phẳng song song, vuông góc
Điều kiện để hai mặt phẳng vuông góc
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 4
Sưu tầm và biện soạn
Trong không gian
Oxyz
, cho hai mặt phẳng
( )
11 1 1 1
:0Ax By Cz D
α
+ + +=
và
( )
22 2 2 2
:0Ax By Cz D
α
+ + +=
có vec-tơ pháp tuyến lần lượt là
(
)
1 111
;;
n ABC
=
,
( )
2 222
;;n ABC=
. Khi đó:
( ) ( )
1 2 1 2 12 12 12
00n n AA BB CC
αα
⊥ ⇔⋅=⇔ + + =

.
Điều kiện để hai mặt phẳng song song
Trong không gian
Oxyz
, cho hai mặt phẳng
(
)
11 1 1 1
:0
Ax By Cz D
α
+ + +=
và
( )
22 2 2 2
:0Ax By Cz D
α
+ + +=
có vec-tơ pháp tuyến lần lượt là
( )
1 111
;;n ABC=
,
( )
2 222
;;
n ABC
=
. Khi đó:
( ) ( ) ( )
12
12
12
n kn
k
D kD
αα
=
⇔∈
≠


.
Chú ý.
( ) ( ) (
)
12
12
12
n kn
k
D kD
αα
=
≡⇔ ∈
=

.
( )
1
α
cắt
(
)
21
n
α
⇔
và
2
n
không cùng phương.
5. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian
Oxyz
, mặt phẳng
( )
α
có phương trình
0Ax By Cz D+ + +=
và điểm
( )
0 0 00
;;M xyz
. Khoảng cách từ điểm
0
M
đến mặt phẳng
( )
α
được tính theo công thức:
(
)
( )
000
0
222
d,
Ax By Cz D
M
ABC
α
+++
=
++
.
DẠNG 1: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG KHI BIẾT MỘT ĐIỂM VÀ VECTƠ PHÁP
TUYẾN CỦA NÓ.
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
Phương trình tổng quát của mặt phẳng đi qua điểm và có véctơ pháp
tuyến là có dạng:
(với
).
Nếu mặt phẳng có cặp véctơ chỉ phương là thì có véctơ pháp tuyến là
Phương pháp
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 5
Sưu tầm và biên soạn
Câu 1: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
đi qua điểm
(1; 0; 2)A −
và có vectơ
pháp tuyến
(1; 1; 2)n −
.
Lời giải
Mặt phẳng
()P
đi qua điểm
(1; 0; 2)
A −
và có vectơ pháp tuyến
(1; 1; 2)n −
có phương trình là:
1( 1) 1( 0) 2( 2) 0
xy z−− −+ + =
2 30xy z⇔ −+ +=
.
Vậy phương trình mặt phẳng
()P
là:
2 30xy z−+ +=
.
Câu 2: Trong không gian với hệ trục tọa độ
Oxyz
, viết phương trình mặt phẳng đi qua điểm
( )
0;1; 2A
và có vectơ pháp tuyến
( )
2;1; 0 .n = −
Lời giải
Vậy phương trình mặt phẳng đi qua điểm
( )
0;1; 2A
và có vectơ pháp tuyến
( )
2;1; 0
n = −
có dạng:
( ) ( )
2 01 1 0xy− −+ −=
2 10xy⇔− + − =
2 10xy
⇔ − +=
.
Câu 3: Trong không gian
Oxyz
, viết phương trình mặt phẳng đi qua
( )
1;1;1A
−
và có vectơ pháp tuyến
( )
1; 2; 2n =−−
Lời giải
Mặt phẳng đi qua
( )
1;1;1A −
, có vtpt
( )
1; 2; 2n −
, suy ra phương trình mặt phẳng cần tìm là
( ) ( ) ( )
1 1 2 1 2 1 0 2 2 10x y z xyz− + − − + − = ⇔−− + −=
.
Câu 4: Trong không gian với hệ trục tọa độ
Oxyz
, cho các điểm
( )
0;1; 2A
,
( )
2; 2;1
B −
,
( )
2;0;1C
−
.
Phương trình mặt phẳng đi qua
A
và vuông góc với
BC
là?
Lời giải
Ta có:
( )
2;1; 0n BC= = −

.
Vậy phương trình mặt phẳng đi qua
A
và vuông góc với
BC
có dạng:
( ) ( )
2 01 1 0xy
− −+ −=
2 10xy⇔− + − =
2 10xy⇔ − +=
.
Câu 5: Trong không gian
Oxyz
, cho ba điểm
( )
1;1;1A −
,
( )
2;1; 0B
và
( )
1; 1; 2C −
. Mặt phẳng đi qua
A
và vuông góc với đường thẳng
BC
có phương trình là?
Trong không gian , viết phương trình mặt phẳng trung trực đoạn thẳng
Bước 1: Véctơ pháp tuyến của mặt là: .
Bước 2: Tìm tọa độ trung điểm của đoạn .
Bước 3: Viết phương trình mặt phẳng đi qua điểm và có vectơ pháp tuyến
.
Phương pháp
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 6
Sưu tầm và biện soạn
Lời giải
Ta có:
( )
1; 2; 2BC −−

.
Do mặt phẳng vuông góc với đường thẳng
BC
nên mặt phẳng có một vtpt
(
)
1; 2; 2
n −
.
Mặt phẳng đi qua
( )
1;1;1A −
, có vtpt
( )
1; 2; 2n −
, suy ra phương trình mặt phẳng cần tìm là
2 2 10xyz+ − +=
.
Câu 6: Trong không gian
Oxyz
, cho
( )
1; 1;1A −−
,
(
)
3;1;1
B
. Phương trình mặt phẳng trung trực của
đoạn
AB
là.
Lời giải
Gọi
I
là trung điểm của
AB
nên
(
)
1; 0;1
I
.
Mặt phẳng trung trực của đoạn
AB
có vtpt là
n
AB=

( )
4; 2;0
=
(
)
2 2;1; 0=
.
Phương trình mặt phẳng cần tìm là:
(
) (
)
2 11 0 0
xy−+ − =
2 20
xy⇔ +−=
.
Câu 7: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1; 6; 7A −
và
( )
3; 2;1B
. Phương trình mặt
phẳng trung trực đoạn
AB
là.
Lời giải
Mặt phẳng trung trực đoạn
AB
đi qua trung điểm
(
)
2; 4; 3I −
của đoạn
AB
và nhân
( )
2; 4;8AB = −

làm vectơ pháp tuyến có phương trình:
( ) (
) ( )
2 24 48 30xyz−− −+ +=
2 4 18 0⇔− + + =xyz
Câu 8: Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
P
chứa điểm
( )
13 2;;M
−
, cắt các tia
Ox
,
Oy
,
Oz
lần lượt tại
A
,
B
,
C
sao cho
124
OA OB OC
= =
.
Lời giải
Phương trình mặt chắn cắt tia
Ox
tại
(
)
00;;
Aa
, cắt tia
Oy
tại
( )
00;;Bb
, cắt tia
Oz
tại
( )
00;;
Cc
có dạng là
( )
P
:
1++=
y
xz
abc
(với
0>a
,
0>b
,
0>c
).
Theo đề:
124
= =
OA OB OC
124
⇔==
abc
2
2
=
⇒
=
b
a
cb
.
Vì
( )
13 2
−;;M
nằm trên mặt phẳng
( )
P
nên ta có:
13 2
1
2
2
−
++ =
b
bb
4
1⇔=
b
4⇔=b
.
Khi đó
2=a
,
8=c
.
Vậy phương trình mặt phẳng
( )
P
là:
1
248
++=
y
xz
4 2 80⇔ + +−=x yz
.
Câu 9: Trong không gian
Oxyz
, cho hình hộp
.ABCD A B C D
′′′ ′
, biết rằng
( )
300;;
A −
,
( )
020;;B
,
( )
001;;D
,
( )
123;;A
′
. Viết phương trình mặt phẳng trung trực của
CD
′
.
Lời giải
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 7
Sưu tầm và biên soạn
Gọi
( )
′
;;
C xyz
. Ta có
( )
320= ;;AB

;
( )
301
=
;;AD

;
( )
423
′
= ;;AA

.
Mà
′′
=++AC AB AD AA
   
(
)
1044
′
⇒=;;
AC

10 3
40
40
= +
⇒=−
= −
x
y
z
( )
13 4 4
′
⇒ ;;C
.
Khi đó mặt phẳng trung trực của
′
CD
:
(
)
13 5
2
22
1343



′
= =
qua ; ;
;;
I
n CD

có phương trình là
(
)
13 5
13 4 2 3 0
22

− + −+ − =


x yz
13 4 3 100 0⇔ ++− =xyz
.
DẠNG 2: Viết phương trình mặt phẳng
( )
α
đi qua 1 điểm
( )
0 0 00
;;M xyz
và song song với 1
mặt phẳng
( )
:0Ax By Cz D
β
+ + +=
cho trước.
C
B
A
C'
A'
B'
D'
D
Trong không gian , viết phương trình mặt phẳng
Loại Phương pháp
⑴
Qua và song song
.
⌘ Cách 1:
≫ Véctơ pháp tuyến là: .
≫ Mặt phẳng qua điểm .
⌘ Cách 2:
≫ Do
≫ Thay điểm vào .
⑵
Song song và
cách một khoảng bằng .
≫ Vì .
≫ Vì cách một khoảng bằng
≫ Có phương trình mặt hoàn chỉnh.
Phương pháp
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 8
Sưu tầm và biện soạn
Câu 10: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
đi qua điểm
(0; 1; 3)M
và song song
với mặt phẳng
( ):2 3 1 0Qxz− +=
.
Lời giải:
Mặt phẳng
()P
song song với mặt phẳng
( ):2 3 1 0Qxz− +=
nên mặt phẳng
()P
có phương trình
dạng:
2 3 0 ( 1)x zD D−+= ≠
.
Mặt phẳng
()P
đi qua điểm
(0; 1; 3)M
nên thay tọa độ điểm
M
vào phương trình mặt phẳng phải
thỏa mãn. Ta được:
2.0 3.3 0 9DD− +=⇔=
(thỏa mãn
1D
≠
).
Vậy phương trình mặt phẳng
()P
là:
2 3 90xz− +=
.
Câu 11: Trong không gian
Oxyz
, viết phương trình mặt phẳng
()P
đi qua điểm
−( 2; 3; 1)M
và song song
với mặt phẳng
+ − +=( ): 3 2 2 0Qxyz
.
Lời giải:
Mặt phẳng
()P
song song với mặt phẳng
+ − +=( ): 3 2 2 0Qxyz
nên mặt phẳng
()P
có phương
trình dạng:
+ −+= ≠
( ) : 3 2 0 ( 2)QxyzD D
.
Mặt phẳng
()P
đi qua điểm
−( 2; 3; 1)M
nên thay tọa độ điểm
M
vào phương trình mặt phẳng
phải thỏa mãn. Ta được:
−+ − + = ⇔ =−
2 3.3 2.1 0 5
DD
(thỏa mãn).
Vậy phương trình mặt phẳng
()P
là:
+ − −=( ): 3 2 5 0Qxyz
.
Câu 12: Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt phẳng đi điểm
( )
3;1;2M −−
và
song song với mặt phẳng
( )
:3 2 4 0P xy z−+ +=
.
Lời giải
Vì
( ) ( )
//
QP
nên
( )
:3 2 0 Q xy zm−+ + =
( )
m4≠
.
Mà
( ) ( )
3;1;2MP−− ∈
6
m
⇒=−
(thỏa mãn).
Vậy
( )
:3 2 6 0Q xy z−+ −=
.
DẠNG 3: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG
( )
α
ĐI QUA 3 ĐIỂM
A
,
B
,
C
KHÔNG THẲNG
HÀNG.
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Page 9
Sưu tầm và biên soạn
Câu 13: Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
ABC
a) Với ba điểm
( )
103;; ,A −
( )
2 11; ;,
B −
( )
1 10;;C −
.
b) Với ba điểm
( ) ( ) ( )
102 231 321−
;; , ;; , ;;AB C
.
Lời giải
a) Với ba điểm
(
)
1; 0; 3 ,
A −
( )
2; 1;1 ,
B −
( )
1; 1; 0C
−
.
Ta có
(
) ( )
312 213= −− = −−
;; ; ;;AB AC
 
Mặt phẳng
( )
ABC
có vec tơ pháp tuyến
( )
1 51

= =−−

; ;;n AC AB
 
.
Phương trình mặt phẳng
( )
ABC
là
1 5 30 5 40− + − +−=⇔−− +−=
()
x yz x yz
b) Với ba điểm
( ) ( ) ( )
1;0; 2 , 2;3;1 , 3;2;1AB C−
.
Ta có:
( ) (
)
33 1 22 1=−− = −;; , ;;AB AC
 
.
Mặt phẳng
( )
P
có một véctơ pháp tuyến là
( )
1 5 12

= =−− −

, ;;n AB AC
 
.
Phương trình mặt phẳng
( )
ABC
là
5 12 25 0 5 12 25 0−−− +=⇔++ −=
xy z xy z
Câu 14: Trong không gian
Oxyz
, viết phương trình mặt phẳng
( )
ABC
a) Với ba điểm
( )
2;0;0M
,
( )
0; 1;0N −
,
( )
0;0;2P
.
b) Với ba điểm
( )
( ) ( )
0; 2;0 , 3;0;0 , 0;0; 3M NP−−
.
Lời giải
a) Với ba điểm
( )
2;0;0M
,
( )
0; 1;0N −
,
( )
0;0;2P
.
Phương trình mặt phẳng di qua không thẳng hàng.
Bước 1: Tìm cặp vectơ chỉ phương .
Bước 2: Tìm một vectơ pháp tuyến .
Bước 3: Viết phương trình mặt phẳng đi qua điểm (hoặc điểm hoặc điểm
) và có vectơ pháp tuyến .
Phương trình mặt phẳng là phương trình mặt chắn, tức mặt phẳng đi qua
có dạng: .
Phương pháp

Tài liệu khác của Toán 12

Preview text:

CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN NG ƯƠ
V PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN CH
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG I LÝ THUYẾT.
I. VECTƠ PHÁP TUYẾN VÀ CẶP VEC-TƠ CHỈ PHƯƠNG CỦA MẶT PHẲNG. 1. Định nghĩa. Cho mặt phẳng (α ) . 
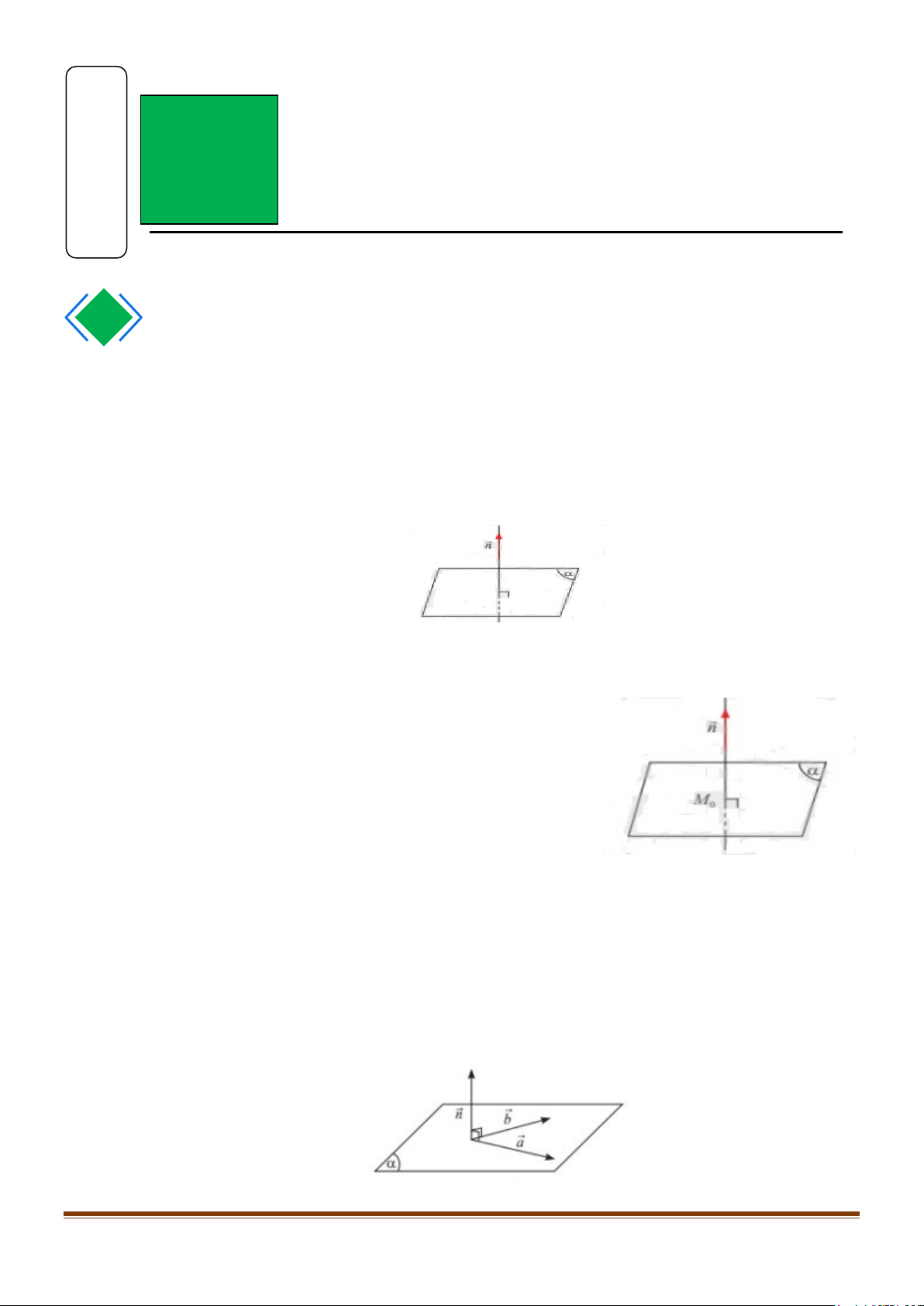
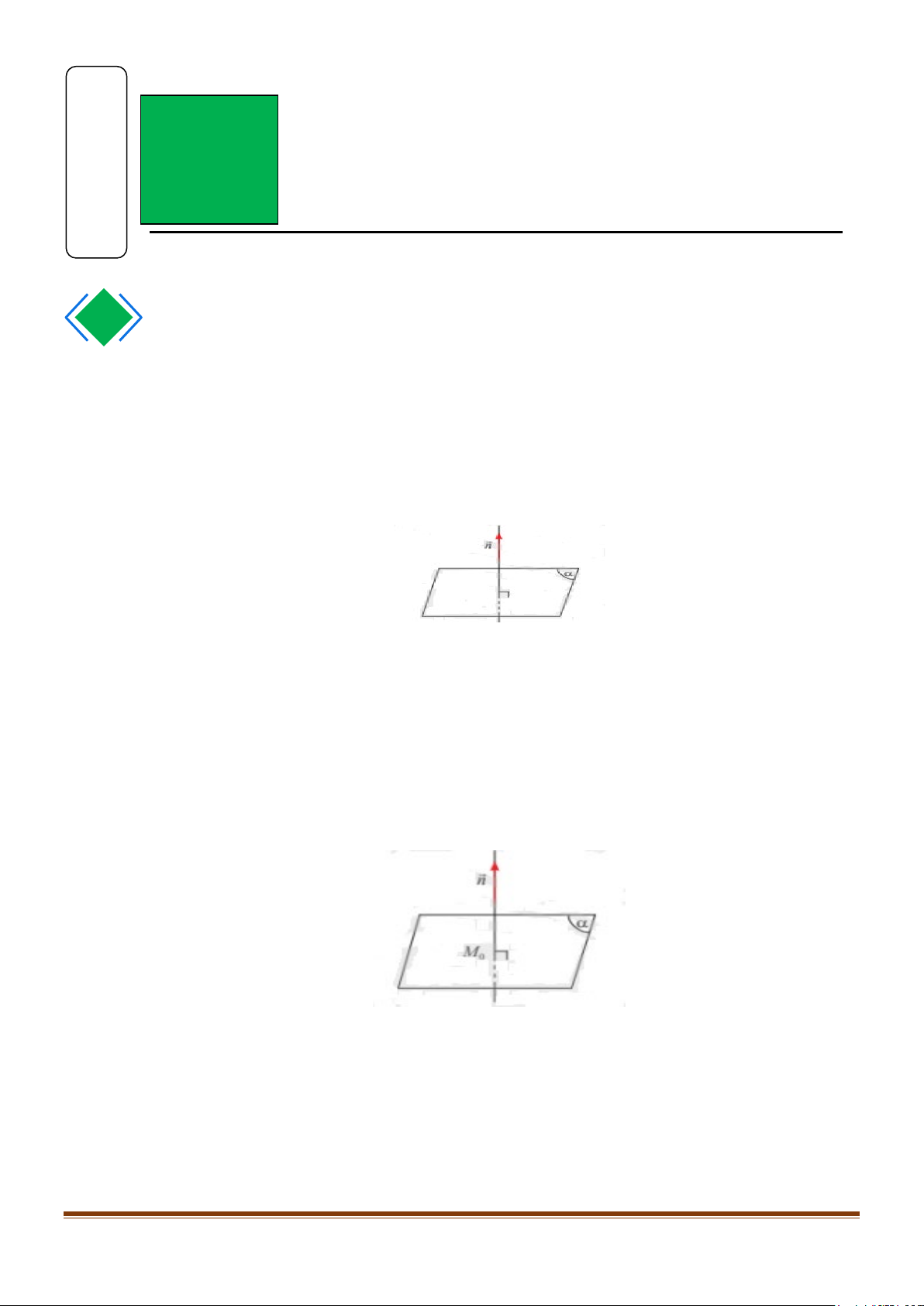
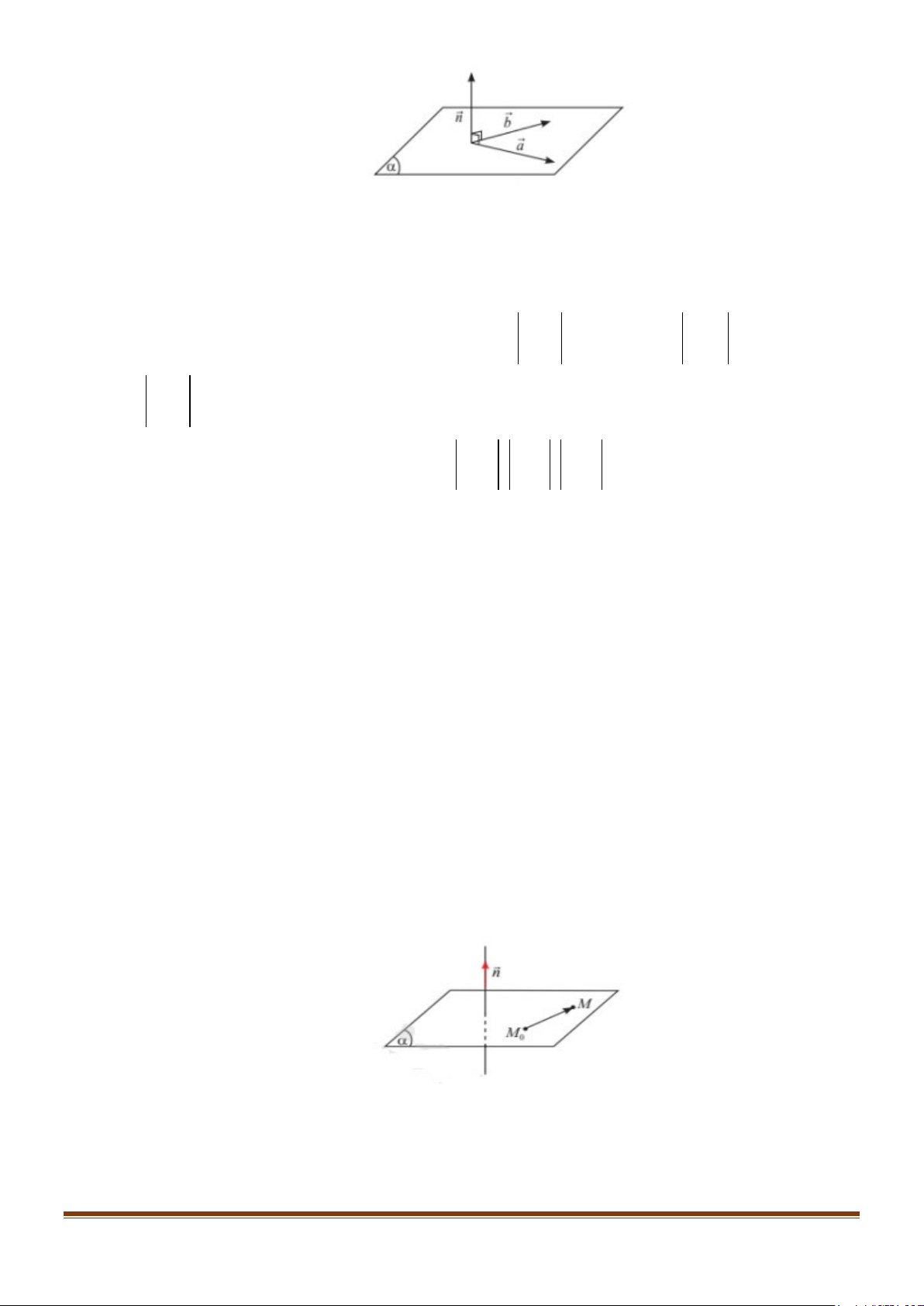
Nếu vec-tơ n khác 0 và có giá vuông góc với (α ) thì n được gọi là vec-tơ pháp tuyến của (α ).  
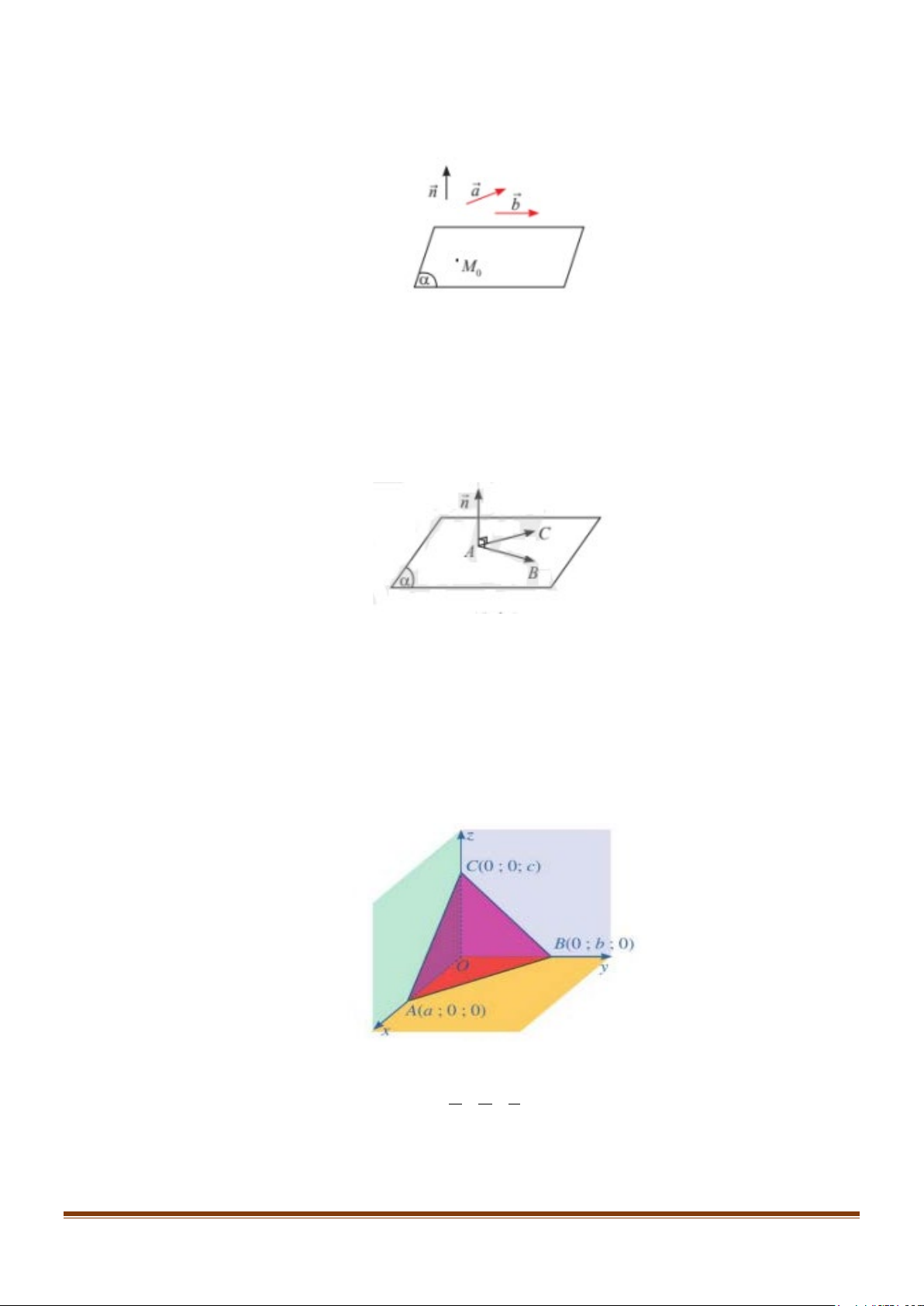
Nếu hai vec-tơ a và b không cùng phương, có giá song song hoặc nằm trong (α ) thì a , b
được gọi là cặp vec-tơ chỉ phương của (α ) . 2. Chú ý.
Nếu n là một vec-tơ pháp tuyến của mặt phẳng (α ) thì kn
(k ≠ 0) cũng là một vec-tơ pháp tuyến của mặt phẳng (α ).
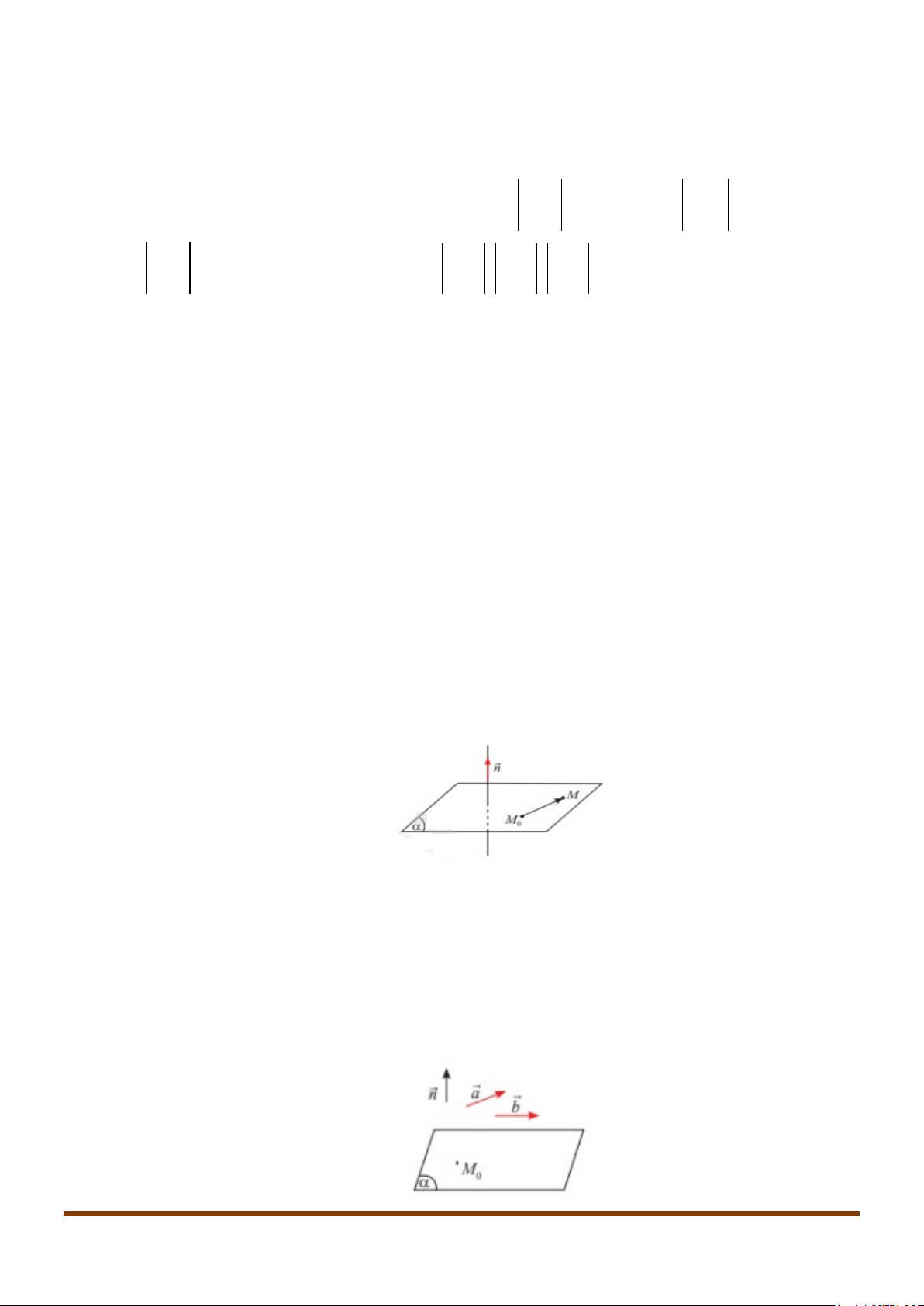
Một mặt phẳng hoàn toàn được xác định khi biết một điểm
và một vec-tơ pháp tuyến hoặc một điểm và một cặp vec-tơ
chỉ phương của mặt phẳng đó.
II. XÁC ĐỊNH VEC-TƠ PHÁP TUYẾN CỦA MẶT PHẲNG KHI BIẾT MỘT CẶP VEC-TƠ CHỈ PHƯƠNG 1. Định lý.
Trong không gian Oxyz , nếu mặt phẳng (α ) nhận hai vec-tơ a = (a ;a ;a , b = (b ;b ;b làm 1 2 3 ) 1 2 3 )
cặp vec-tơ chỉ phương thì (α ) nhận vec-tơ n = (a b − a b ;a b − a b ;a b − a b làm vec-tơ 2 3 3 2 3 1 1 3 1 2 2 1 ) pháp tuyến. Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN 2. Chú ý.
Vec-tơ n = (a b − a b ;a b − a b ;a b − a b được gọi là tích có hướng của hai vec-tơ 2 3 3 2 3 1 1 3 1 2 2 1 )    
a = (a ;a ;a , b = (b ;b ;b . Tích có hướng của hai vec-tơ a và b , kí hiệu a,b . 1 2 3 ) 1 2 3 )   a a a a
Biểu thức a b − a b thường được kí hiệu 1 2 . Tương tự, 2 3 = a b − a b và 1 2 2 1 b b 2 3 3 2 b b 1 2 2 3 a a 3   1  a a a a a a
= a b − a b . Như vậy: 2 3 3 1 1 2   = . 3 1 1 3 a,b  ; ; b b    3 1 b b b b b b  2 3 3 1 1 2     
Hai vec-tơ a và b cùng phương ⇔ a,b = 0   .
III. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG 1. Định nghĩa.
Trong không gian Oxyz , phương trình có dạng Ax + By + Cz + D = 0, trong đó A , B , C không
đồng thời bằng 0 , được gọi là phương trình tổng quát của mặt phẳng. 2. Nhận xét.
Cho mặt phẳng (α ) có phương trình tổng quát là Ax + By + Cz + D = 0. Khi đó:
Mặt phẳng (α ) có một vec-tơ pháp tuyến là n = ( ; A ; B C) .
N (x ;y ;z ∈ α ⇔ Ax + By + Cz + D = 0 . 0 0 0 ) ( ) 0 0 0
Mỗi phương trình Ax + By + Cz + D = 0 (trong đó A , B , C không đồng thời bằng 0) đều là
phương trình của một mặt phẳng xác định.
3. Một số dạng toán viết phương trình mặt phẳng cơ bản
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một vec-tơ pháp tuyến
Trong không gian Oxyz , phương trình mặt phẳng đi qua điểm M x ; y ; z và có vec-tơ pháp 0 ( 0 0 0 ) tuyến n = ( ; A ; B C) là:
A(x − x + B y − y + C z − z = 0 0 ) ( 0 ) ( 0 )
hay Ax + By + Cz + D = 0 với D = −Ax − By − Cz . 0 0 0
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một cặp vec-tơ chỉ phương Page 2
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Để lập phương trình tổng quát của mặt phẳng (α ) đi qua điểm M x ; y ; z và có cặp vec-tơ 0 ( 0 0 0 ) 
chỉ phương a , b , ta thực hiện như sau:   
Tìm một vec-tơ pháp tuyến n = a,b   .
Viết phương trình mặt phẳng (α ) đi qua điểm M x ; y ; z và có vec-tơ pháp tuyến n . 0 ( 0 0 0 )
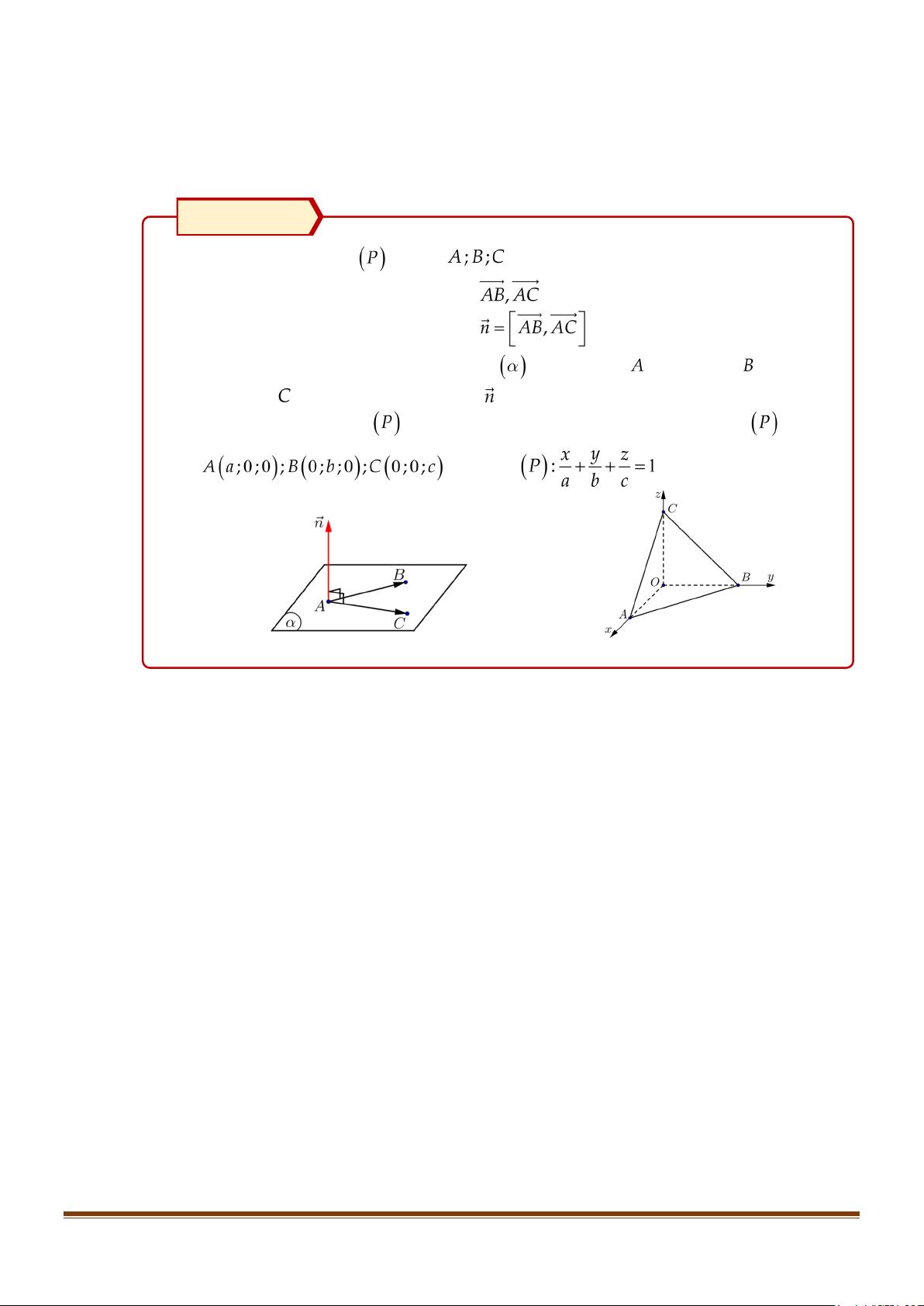
Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng
Để lập phương trình tổng quát của mặt phẳng (α ) đi qua ba điểm A , B , C không thẳng hàng, ta thực hiện như sau:  
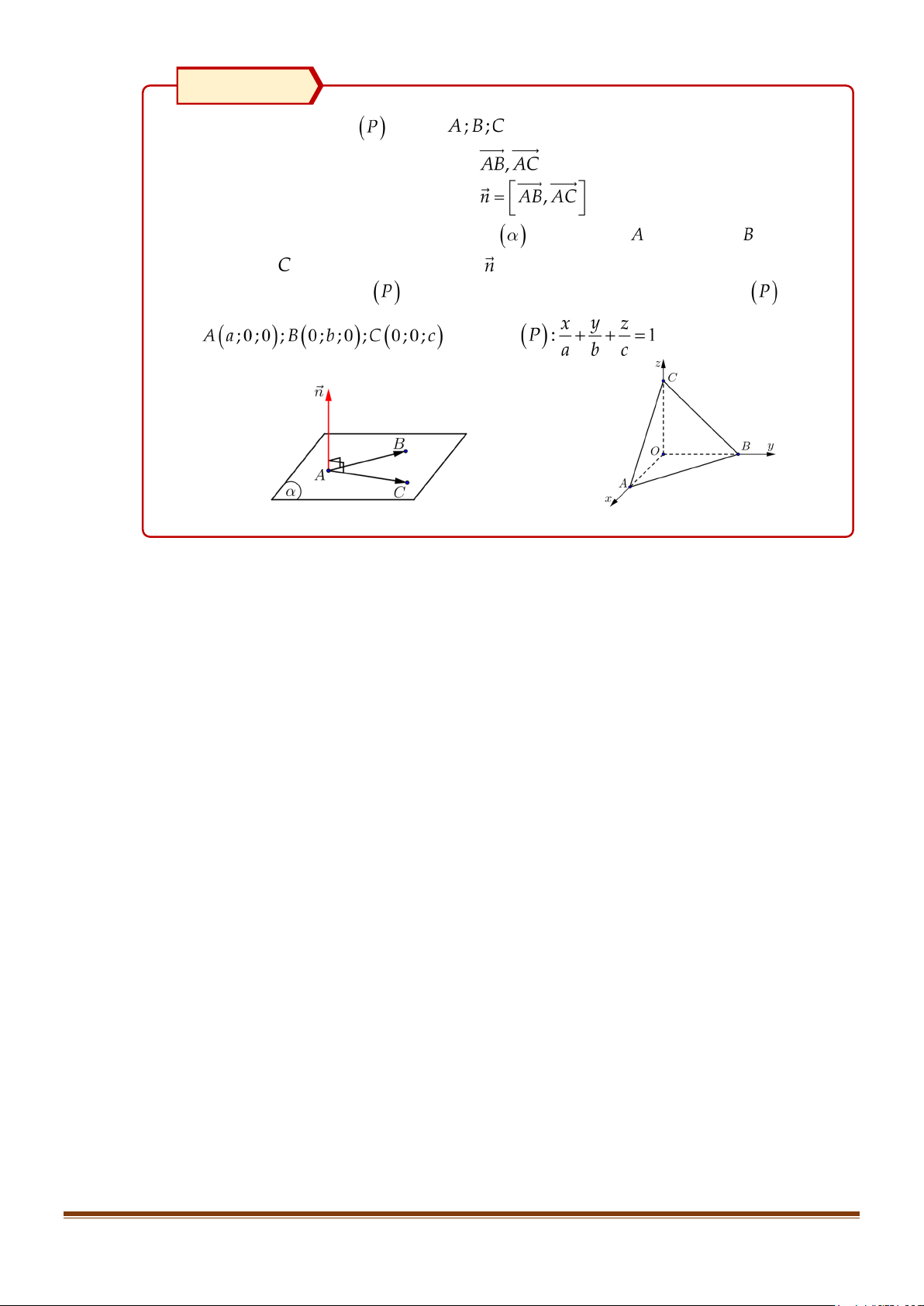
Tìm cặp vec-tơ chỉ phương, chẳng hạn AB , AC .   
Tìm một vec-tơ pháp tuyến n = AB, AC   .
Viết phương trình mặt phẳng (α ) đi qua A và có vec-tơ pháp tuyến n .
Lập phương trình tổng quát của mặt phẳng theo đoạn chắn
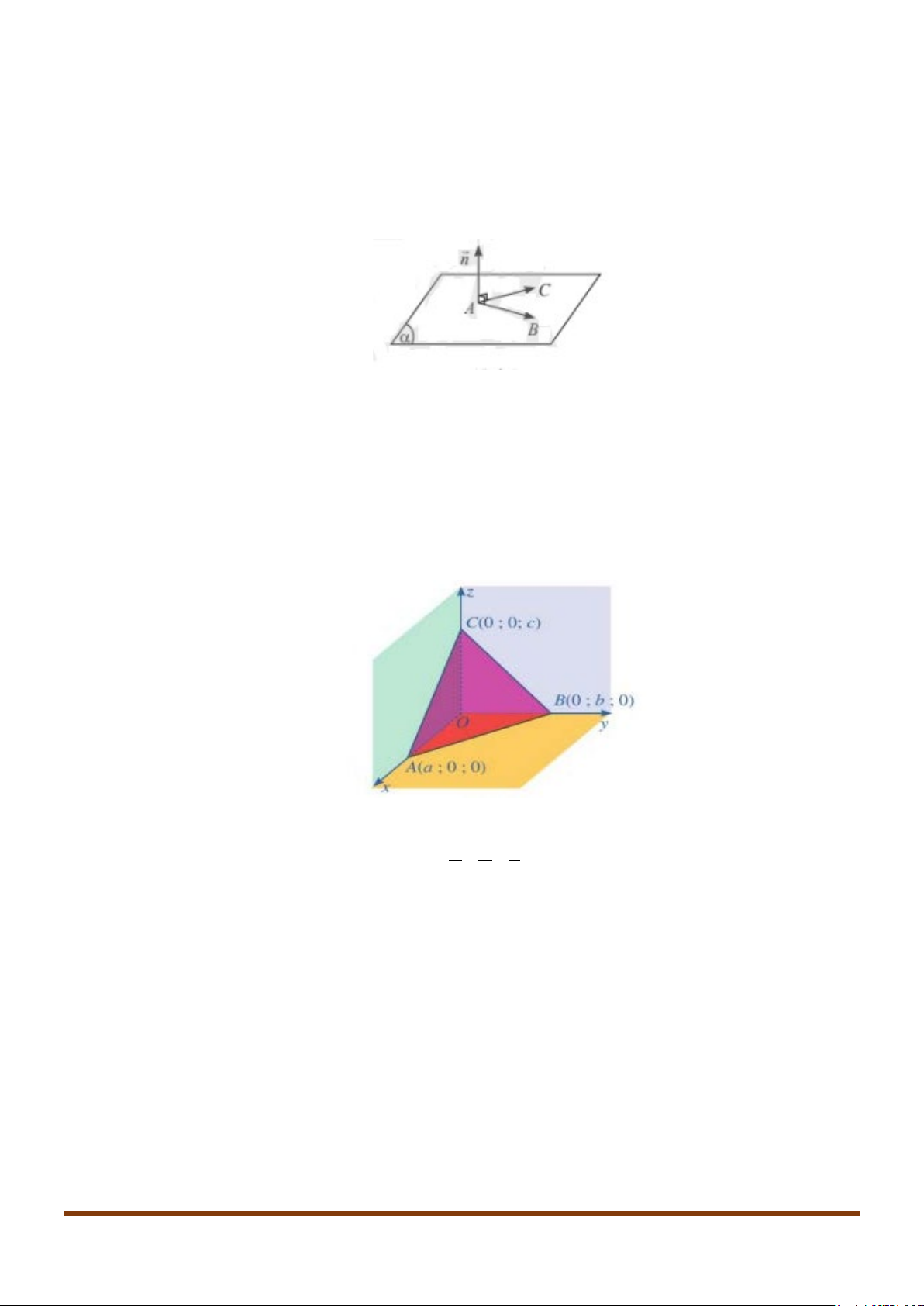
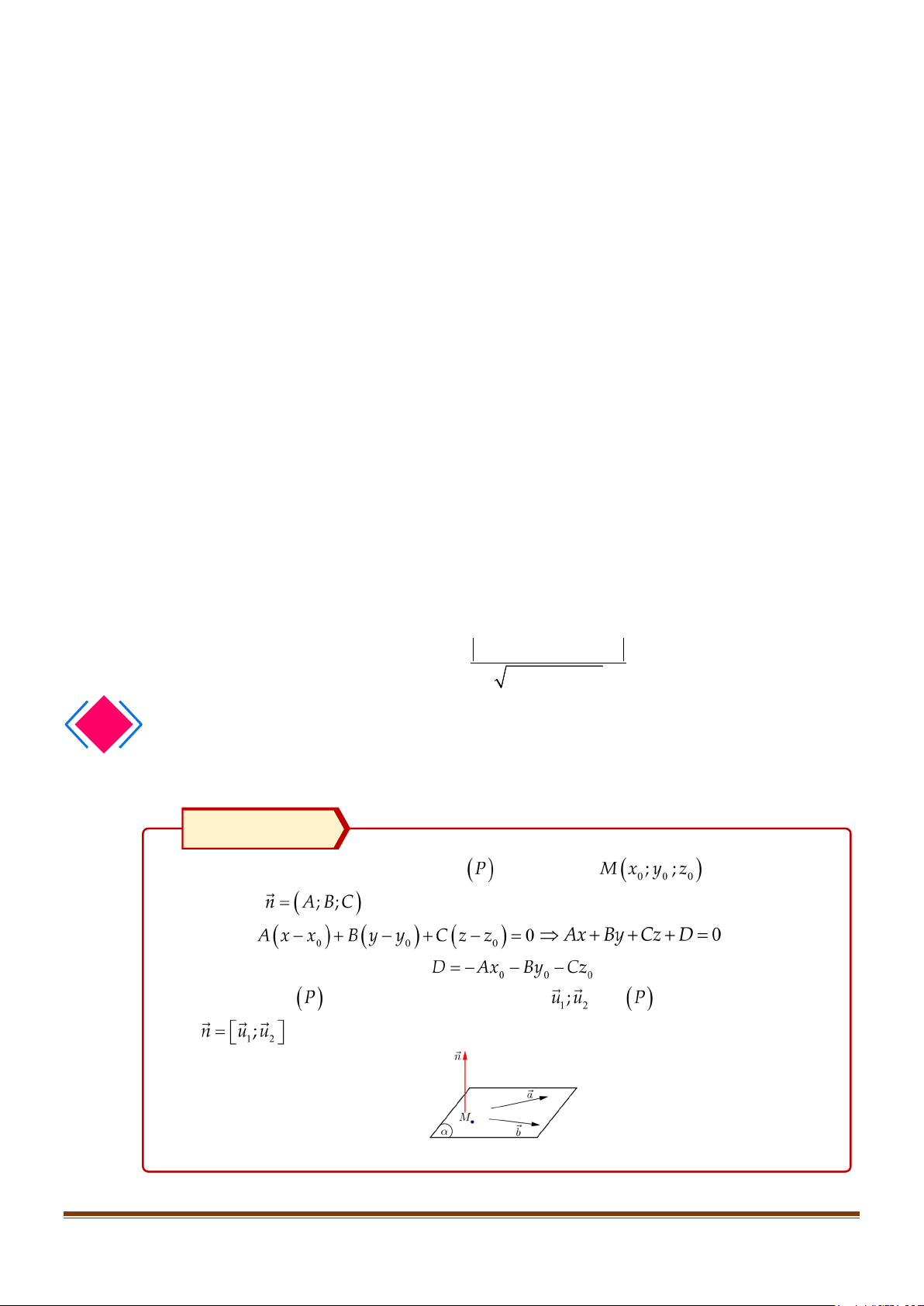
Phương trình tổng quát của mặt phẳng (α ) đi qua ba điểm A( ;0 a ;0) , B(0; ;
b 0) , C (0;0;c) là: x y z + + = 1. a b c
4. Điều kiện để hai mặt phẳng song song, vuông góc
Điều kiện để hai mặt phẳng vuông góc
Trong không gian Oxyz , cho hai mặt phẳng (α : A x + B y + C z + D = 0 và 1 ) 1 1 1 1
(α : A x + B y +C z + D = 0 có vec-tơ pháp tuyến lần lượt là n = A ;B ;C , 1 ( 1 1 1) 2 ) 2 2 2 2
n = A ; B ;C . Khi đó: 2 ( 2 2 2)
(α ⊥ α ⇔ n ⋅n = 0 ⇔ A A + B B +C C = 0. 1 ) ( 2) 1 2 1 2 1 2 1 2 Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Điều kiện để hai mặt phẳng song song
Trong không gian Oxyz , cho hai mặt phẳng (α : A x + B y + C z + D = 0 và 1 ) 1 1 1 1
(α : A x + B y +C z + D = 0 có vec-tơ pháp tuyến lần lượt là n = A ;B ;C , 1 ( 1 1 1) 2 ) 2 2 2 2
n = A ; B ;C . Khi đó: 2 ( 2 2 2)   (  = α )  (α ) n kn 1 2 ⇔  k ∈ . 1 2 ( ) D ≠  kD 1 2 Chú ý.   (  = α ) ≡ (α ) n kn 1 2 ⇔  k ∈ . 1 2 ( ) D =  kD 1 2
(α cắt (α ⇔ n và n không cùng phương. 2 ) 1 ) 1 2
5. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian Oxyz , mặt phẳng (α ) có phương trình Ax + By + Cz + D = 0 và điểm
M x ; y ; z . Khoảng cách từ điểm M đến mặt phẳng (α ) được tính theo công thức: 0 ( 0 0 0 ) 0
Ax + By + Cz + D d(M ,(α )) 0 0 0 = . 0 2 2 2 A + B + C Page 4
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
HỆ THỐNG BÀI TẬP TỰ LUẬN. II
DẠNG 1: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG KHI BIẾT MỘT ĐIỂM VÀ VECTƠ PHÁP TUYẾN CỦA NÓ. Phương pháp
Phương trình tổng quát của mặt phẳng đi qua điểm và có véctơ pháp tuyến là có dạng: (với ). Nếu mặt phẳng
có cặp véctơ chỉ phương là thì
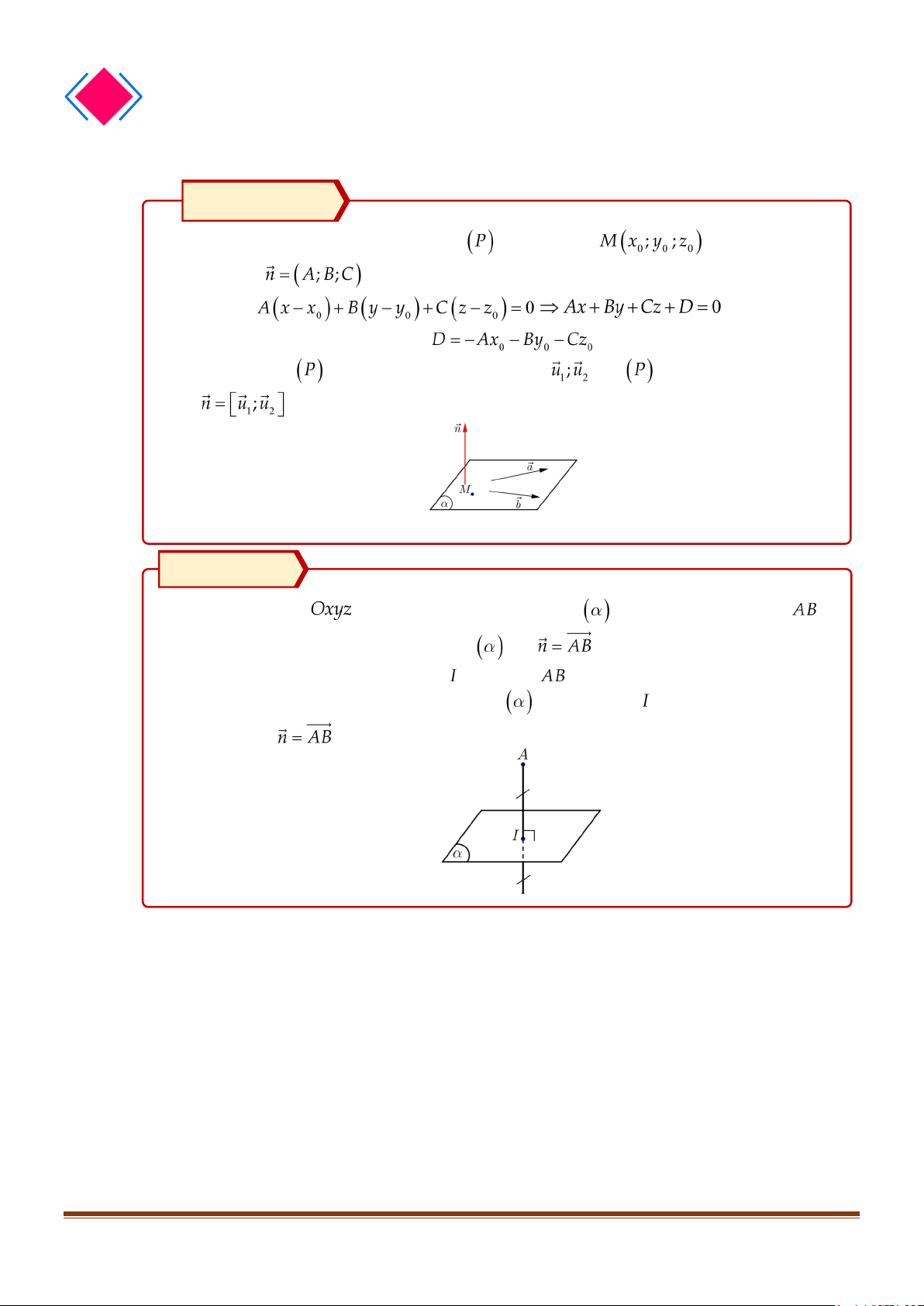
có véctơ pháp tuyến là Phương pháp Trong không gian
, viết phương trình mặt phẳng
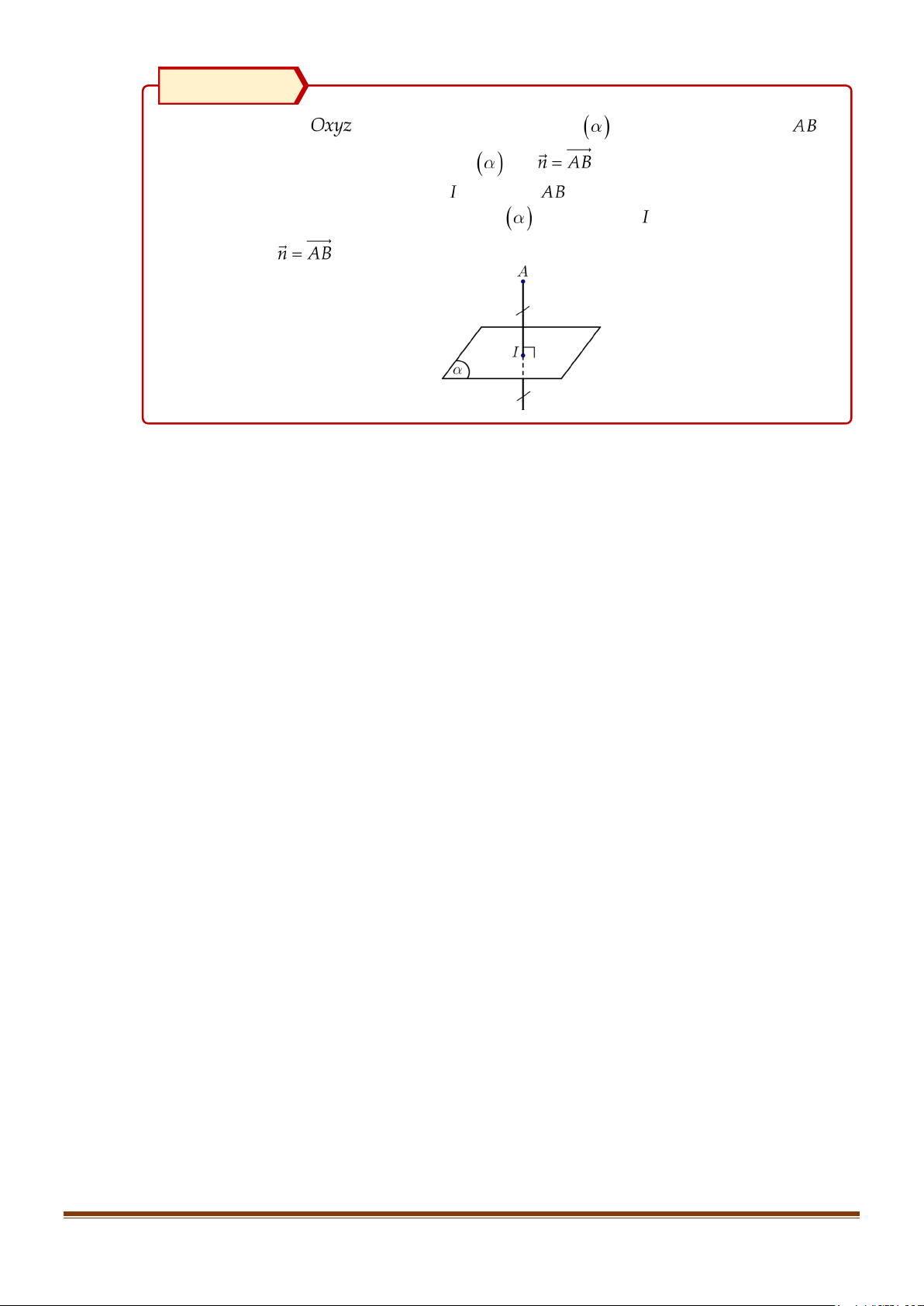
trung trực đoạn thẳng
Bước 1: Véctơ pháp tuyến của mặt là: .
Bước 2: Tìm tọa độ trung điểm của đoạn .
Bước 3: Viết phương trình mặt phẳng
đi qua điểm và có vectơ pháp tuyến .
Câu 1: Trong không gian Oxyz , viết phương trình mặt phẳng (P) đi qua điểm ( A 1;0; 2) − và có vectơ  pháp tuyến ( n 1; 1; − 2) .
Câu 2: Trong không gian với hệ trục tọa độ Oxyz , viết phương trình mặt phẳng đi qua điểm A(0;1;2) 
và có vectơ pháp tuyến n = ( 2 − ;1;0).
Câu 3: Trong không gian Oxyz , viết phương trình mặt phẳng đi qua A( 1; − 1; )
1 và có vectơ pháp tuyến n =( 1; − 2 − ;2)
Câu 4: Trong không gian với hệ trục tọa độ Oxyz , cho các điểm A(0;1;2) , B(2;− 2; ) 1 , C ( 2; − 0; ) 1 .
Phương trình mặt phẳng đi qua A và vuông góc với BC là? Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 5: Trong không gian Oxyz , cho ba điểm A( 1; − 1; )
1 , B(2;1;0) và C (1; 1;
− 2) . Mặt phẳng đi qua A
và vuông góc với đường thẳng BC có phương trình là?
Câu 6: Trong không gian Oxyz , cho A( 1; − 1; − ) 1 , B(3;1 )
;1 . Phương trình mặt phẳng trung trực của đoạn AB là.
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1;6; 7 − ) và B(3;2; ) 1 . Phương trình mặt
phẳng trung trực đoạn AB là.
Câu 8: Trong không gian Oxyz , viết phương trình mặt phẳng (P) chứa điểm M (1;3;− 2), cắt các tia
Ox , Oy , Oz lần lượt tại OA OB OC
A , B , C sao cho = = . 1 2 4
Câu 9: Trong không gian Oxyz , cho hình hộp ABC . D A B ′ C ′ D
′ ′ , biết rằng A( 3 − ;0;0) , B(0;2;0) , D(0;0; )
1 , A′(1;2;3) . Viết phương trình mặt phẳng trung trực của C D ′ .
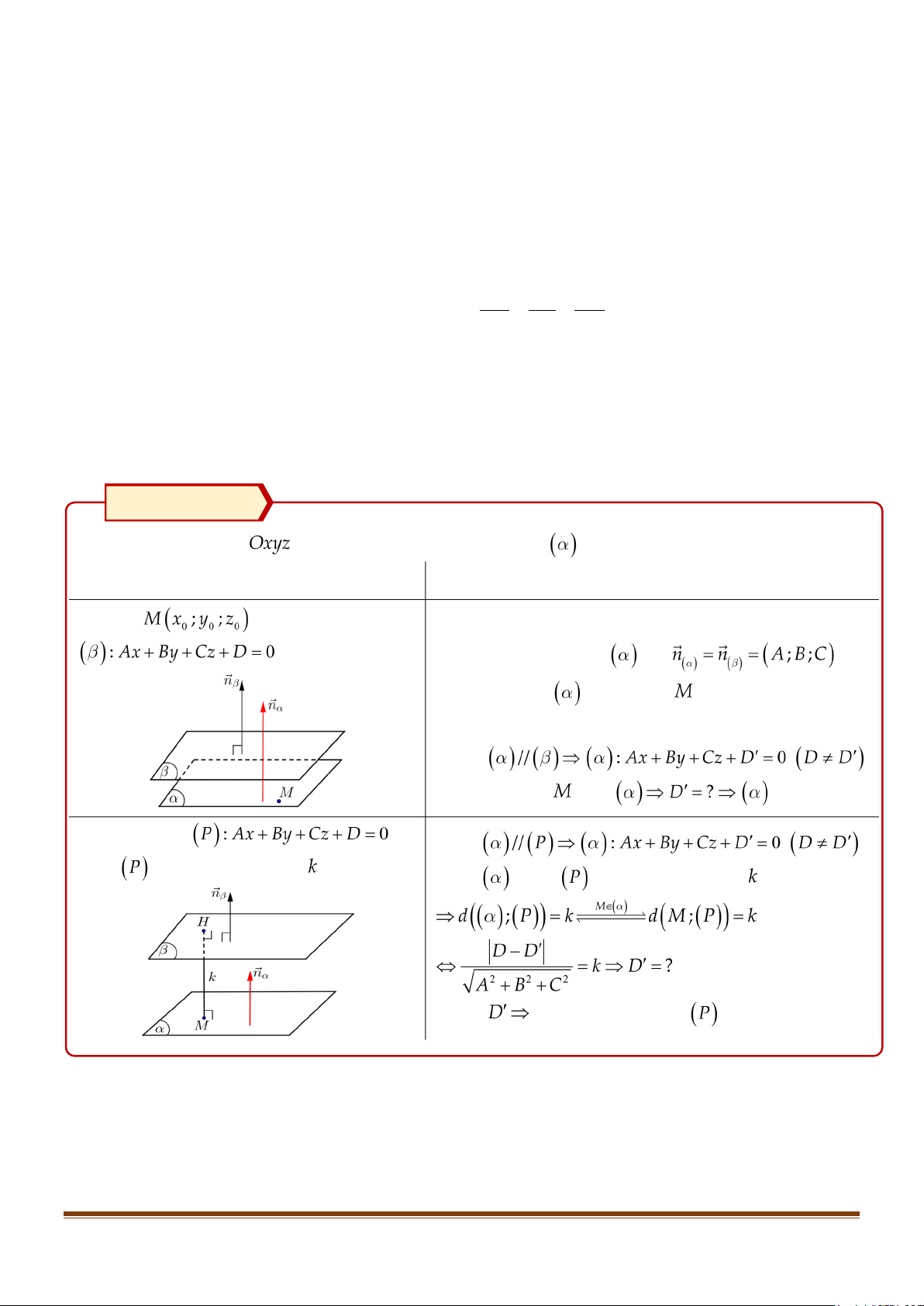
DẠNG 2: Viết phương trình mặt phẳng (α ) đi qua 1 điểm M x ; y ; z và song song với 1 mặt phẳng 0 ( 0 0 0 )
(β ): Ax+ By +Cz + D = 0 cho trước. Phương pháp Trong không gian
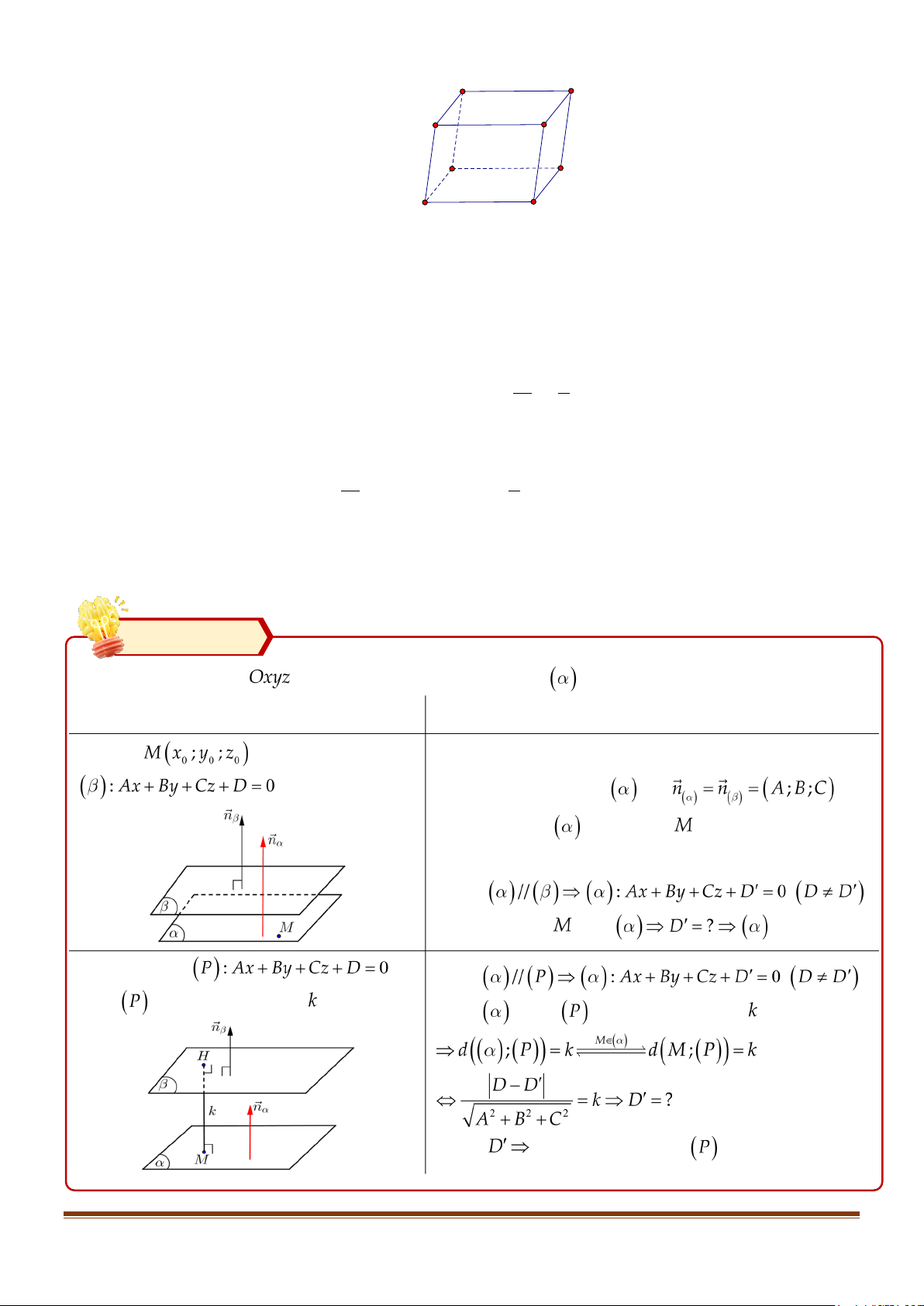
, viết phương trình mặt phẳng Loại Phương pháp ⑴ Qua và song song ⌘ Cách 1: . ≫ Véctơ pháp tuyến là: . ≫ Mặt phẳng qua điểm . ⌘ Cách 2: ≫ Do ≫ Thay điểm vào . ⑵ Song song và ≫ Vì . cách một khoảng bằng . ≫ Vì cách một khoảng bằng ≫ Có phương trình mặt hoàn chỉnh.
Câu 10: Trong không gian Oxyz , viết phương trình mặt phẳng(P) đi qua điểm M(0;1;3)và song song
với mặt phẳng(Q) : 2x − 3z + 1 = 0 .
Câu 11: Trong không gian Oxyz , viết phương trình mặt phẳng(P) đi qua điểm M(−2;3;1) và song song
với mặt phẳng(Q) : x + 3y − 2z + 2 = 0. Page 6
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 12: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi điểm M (3; 1 − ; 2 − ) và
song song với mặt phẳng (P) :3x − y + 2z + 4 = 0 .
DẠNG 3: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG (α ) ĐI QUA 3 ĐIỂM A , B, C KHÔNG THẲNG HÀNG. Phương pháp Phương trình mặt phẳng di qua không thẳng hàng.
Bước 1: Tìm cặp vectơ chỉ phương .
Bước 2: Tìm một vectơ pháp tuyến .
Bước 3: Viết phương trình mặt phẳng
đi qua điểm (hoặc điểm hoặc điểm
) và có vectơ pháp tuyến . Phương trình mặt phẳng
là phương trình mặt chắn, tức mặt phẳng đi qua có dạng: .
Câu 13: Trong không gian Oxyz , viết phương trình mặt phẳng (ABC)
a) Với ba điểm A( 1 − ;0;3) , B(2; 1 − ; ) 1 , C (1; 1 − ;0) .
b) Với ba điểm A(1;0;2),B( 2 − ;3; ) 1 ,C (3;2; ) 1 .
Câu 14: Trong không gian Oxyz , viết phương trình mặt phẳng (ABC)
a) Với ba điểm M (2;0;0) , N (0;−1;0) , P(0;0;2).
b) Với ba điểm M (0; 2;
− 0), N (3;0;0), P(0;0; 3 − ) .
Câu 15: Trong không gian Oxyz , viết phương trình mặt phẳng đi qua ba điểm (1 A ;0; 2 − ), ( B 1;1;1), C(0; 1 − ; 2).
Câu 16: Trong không gian Oxyz , cho ba điểm A(1;0;0), B(0; 1 − ;− ) 1 , C (5; 1; − ) 1 . Viết phương trình mặt phẳng ( ABC) .
Câu 17: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi qua ba điểm A(2; 3; 5) ,
B(3; 2; 4) và C (4; 1; 2) .
Câu 18: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi qua ba điểm A(1;1;4) ,
B(2;7;9) , C (0;9;13) . Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
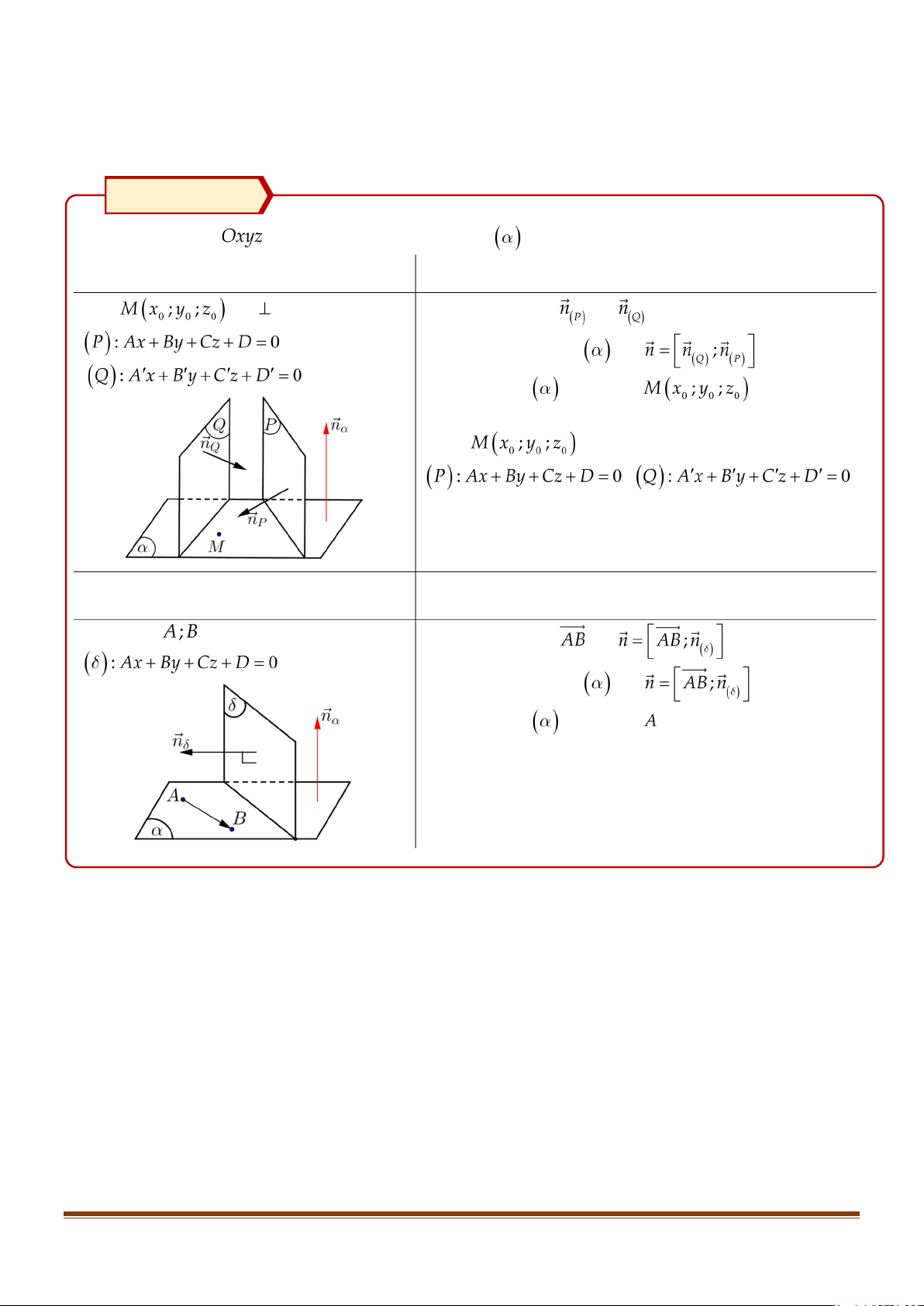
DẠNG 4: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG (α ) QUA HAI DIỂM A , B VA VUÔNG GÓC
VỚI MẶT PHẲNG (β ). VIẾT PHƯƠNG TRÌNH MẶT PHẲNG (α ) QUA DIỂM A VA
VUÔNG GÓC VỚI HAI MẶT PHẲNG (α ),(β ). Phương pháp Trong không gian
, viết phương trình mặt phẳng Loại Phương pháp Qua và 2 mặt ≫ Tìm cặp véctơ và . , ≫ Véctơ pháp tuyến là: . . ≫ Mặt phẳng qua điểm .
Hoặc bài toán sẽ gặp: “Qua
và vuông góc với giao tuyến của ; ” Loại Phương pháp Qua điểm và vuông góc ≫ Tìm cặp véctơ và . . ≫ Véctơ pháp tuyến là: . ≫ Mặt phẳng qua điểm .
Câu 19: Trong không gian Oxyz , viết phương trình mặt phẳng (α) đi qua điểm ( A 1; 2; 2) − , ( B 2; 1 − ; 4)
và vuông góc với (β ) : x − 2y − z +1 = 0.
Câu 20: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(2;4; ) 1 , B( 1; − 1;3) và mặt phẳng
(P): x −3y + 2z −5 = 0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc
với mặt phẳng (P) .
Câu 21: Trong không gian hệ tọa độ Oxyz, cho A(2;1;− ) 1 ; B(1;0; )
1 và mặt phẳng (P):x + 2y − z +1= 0.
Viết phương trình mặt phẳng (Q) qua ;
A B và vuông góc với (P) . Page 8
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 22: Trong không gian Oxyz , viết phương trình mặt phẳng (P)đi qua điểm M( 1; − 2 − ; 5) và vuông
góc với hai mặt phẳng (Q) : x + 2y − 3z + 1 = 0 và (R) : 2x − 3y + z + 1 = 0 .
Câu 23: Trong không gian Oxyz , cho hai mặt phẳng (α ) : 3x − 2y + 2z + 7 = 0 và
(β ): 5x − 4y +3z +1= 0. Phương trình mặt phẳng qua O, đồng thời vuông góc với cả (α ) và (β ) có phương trình là
Câu 24: Cho hai mặt phẳng (α ):3x − 2y + 2z + 7 = 0,(β ):5x − 4y + 3z +1= 0 . Phương trình mặt phẳng
đi qua gốc tọa độ O đồng thời vuông góc với cả(α ) và (β ) là:
Câu 25: Trong không gian Oxyz, cho hai mặt phẳng (P): x −3y + 2z −1= 0, (Q) : x − z + 2 = 0. Mặt
phẳng (α ) vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm có hoành độ bằng 3.
Phương trình của mp (α ) là
Câu 26: Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng (α ) : 3x − 2y + 2z + 7 = 0 và
(β ) :5x − 4y + 3z +1= 0. Phương trình mặt phẳng đi qua O đồng thời vuông góc với cả (α) và (β ) có phương trình là
Dạng 6: Viết phương trình mặt phẳng (α ) song song với mặt phẳng (β ) và cách
(β ): Ax+ By +Cz + D = 0 một khoảng k cho trước.
Phương pháp :
1. Trên mặt phẳng (β ) chọn 1 điểm M.
2. Do (α ) //(β ) nên (α ) có phương trình Ax + By +Cz + D′ = 0 ( D′ ≠ D ).
3. Sử dụng công thức khoảng cách d( α ),(β )) = d(M,(β )) = k để tìm D′.
Câu 27: Trong không gian Oxyz , viết phương trình mặt phẳng (P) song song với mặt phẳng
(Q) : x + 2y − 2z + 1 = 0 và cách (Q) một khoảng bằng 3.
Câu 28: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng (P) song song và cách mặt
phẳng (α ) :3x − y + 2z − 3 = 0 một khoảng bằng 14 .
Câu 29: Trong không gian Oxyz , cho mặt phẳng P: x  2y  2z 10  0. Phương trình mặt phẳng Q
với Q song song với P và khoảng cách giữa hai mặt phẳng P và Q bằng 7 là. 3
Câu 30: Trong không gian hệ toạ độ Oxyz , lập phương trình các mặt phẳng song song với mặt phẳng
(β ): x + y − z +3 = 0 và cách (β ) một khoảng bằng 3 .
Câu 31: Trong không gian Oxyz , viết phương trình mặt phẳng (P) song song với mặt phẳng
(Q) : x + 2y − 2z +1 = 0 và (P) cách điểm M(1; 2
− ;1) một khoảng bằng 3.
Câu 32: Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt
phẳng(Q) : x − 2y + 4z −1 = 0 và cách điểm M ( 1; − 3; )
1 là một khoảng bằng 2. Page 9
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 33: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (Q): 2x − y + 2z −3 = 0 và điểm A(1;2;3)
. Viết phương trình mặt phẳng (P) song song với (Q) và cách A một khoảng bằng 4.
DẠNG 7. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG Phương pháp
Tính khoảng cách từ điểm đến mặt phẳng như sau Bước 1: Tìm ; viết phương trình mặt phẳng .
Bước 2: Tính khoảng cách từ điểm đến mặt phẳng theo công thức Lưu ý:
Câu 34: Cho hình lập phương ABC .
D EFGH cạnh 1. Điểm M được cho thỏa mãn hệ thức   
AM + AE = 3CD . Tính khoảng cách từ điểm M đến mặt phẳng (EBD).
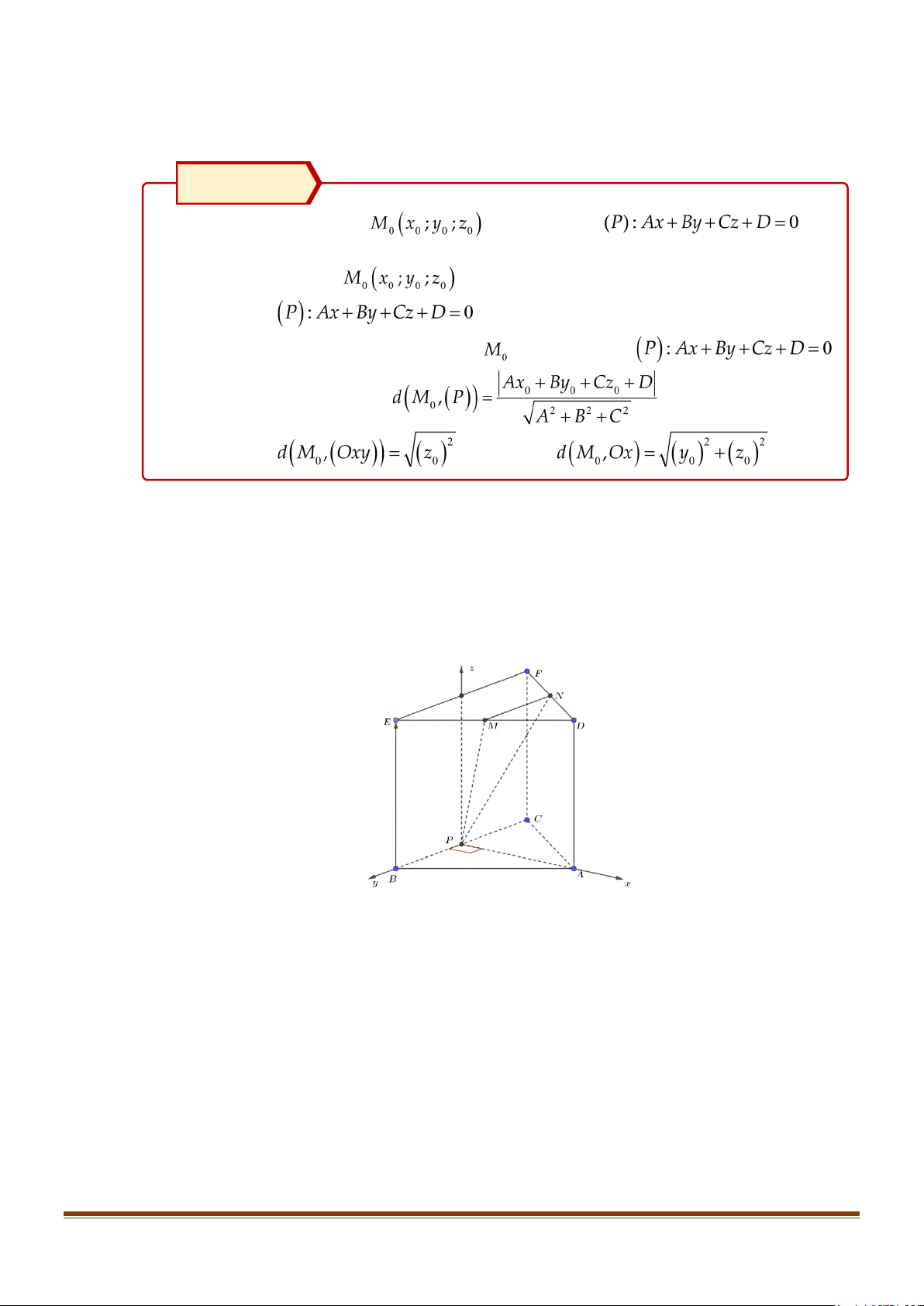
Câu 35: Cho hình lăng trụ tam giác đều ABC.DEF , AB = 6 , AD = 2. Gọi M , N , P lần lượt là trung
điểm DE , DF , BC . Lập hệ trục tọa độ Oxyz như hình bên. Gọi điểm S thỏa mãn hệ thức    
SA + 2SB + SC = 0 . Tính khoảng cách từ điểm S đến mặt phẳng (MNP) . Page 10
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
DẠNG 8. VỊ TRÍ TƯƠNG ĐỐI HAI MẶT PHẲNG Phương pháp Xét điểm mặt phẳng
có vecto pháp tuyến , với: Mặt phẳng có vecto pháp tuyến ,
Ta có các vị trí tương đối sau: Mặt phẳng Mặt cắt mặt Mặt
song song mặt Mặt phẳng Mặt trùng mặt Mặt
vuông góc mặt
Câu 36: Cho ba mặt phẳng (P : 2x − y − 2z +1= 0 , (P : 4x − 2y − 4z + 4 = 0, (P : x + 4y − z +1= 0 . 3 ) 2 ) 1 )
Chứng minh (P // P và (P ⊥ P . 1 ) ( 3) 1 ) ( 2 )
Câu 37: Trong không gian Oxyz , cho hai mặt phẳng () 2 :m x − y + ( 2
m − 2)z + 2 = 0 và () 2
:2x + m y − 2z +1 = 0 . Hai mặt phẳng () và () vuông góc với nhau khi nào?
Câu 38: Trong không gian Oxyz cho A(2;0;0),B(0;4;0),C(0;0;6),D(2;4;6) . Gọi (P) là mặt phẳng
song song với mp(ABC) , (P) cách đều D và mặt phẳng (ABC) . Phương trình của (P) là? Page 11
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN NG ƯƠ
V PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN CH
BÀI: PHƯƠNG TRÌNH MẶT PHẲNG LÝ THUYẾT. I
I. VECTƠ PHÁP TUYẾN VÀ CẶP VEC-TƠ CHỈ PHƯƠNG CỦA MẶT PHẲNG. 1. Định nghĩa. Cho mặt phẳng (α ) . 
Nếu vec-tơ n khác 0 và có giá vuông góc với (α ) thì n được gọi là vec-tơ pháp tuyến của (α ).  
Nếu hai vec-tơ a và b không cùng phương, có giá song song hoặc nằm trong (α ) thì a , b
được gọi là cặp vec-tơ chỉ phương của (α ) . 2. Chú ý.
Nếu n là một vec-tơ pháp tuyến của mặt phẳng (α ) thì kn (k ≠ 0) cũng là một vec-tơ pháp
tuyến của mặt phẳng (α ) .
Một mặt phẳng hoàn toàn được xác định khi biết một điểm và một vec-tơ pháp tuyến hoặc một
điểm và một cặp vec-tơ chỉ phương của mặt phẳng đó.
II. XÁC ĐỊNH VEC-TƠ PHÁP TUYẾN CỦA MẶT PHẲNG KHI BIẾT MỘT CẶP VEC-TƠ CHỈ PHƯƠNG 1. Định lý.
Trong không gian Oxyz , nếu mặt phẳng (α ) nhận hai vec-tơ a = (a ;a ;a , b = (b ;b ;b làm 1 2 3 ) 1 2 3 )
cặp vec-tơ chỉ phương thì (α ) nhận vec-tơ n = (a b − a b ;a b − a b ;a b − a b làm vec-tơ 2 3 3 2 3 1 1 3 1 2 2 1 ) pháp tuyến. Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN 2. Chú ý.
Vec-tơ n = (a b − a b ;a b − a b ;a b − a b được gọi là tích có hướng của hai vec-tơ 2 3 3 2 3 1 1 3 1 2 2 1 )    
a = (a ;a ;a , b = (b ;b ;b . Tích có hướng của hai vec-tơ a và b , kí hiệu a,b . 1 2 3 ) 1 2 3 )   a a a a
Biểu thức a b − a b thường được kí hiệu 1 2 . Tương tự, 2 3 = a b − a b và 1 2 2 1 b b 2 3 3 2 b b 1 2 2 3 a a 3
1 = a b − a b . Như vậy: 3 1 1 3 b b 3 1    a a a a a a  2 3 3 1 1 2 a,b =  ; ; . b b b b b b     2 3 3 1 1 2     
Hai vec-tơ a và b cùng phương ⇔ a,b = 0   .
III. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG 1. Định nghĩa.
Trong không gian Oxyz , phương trình có dạng Ax + By + Cz + D = 0, trong đó A , B , C không
đồng thời bằng 0 , được gọi là phương trình tổng quát của mặt phẳng. 2. Nhận xét.
 Cho mặt phẳng (α ) có phương trình tổng quát là Ax + By + Cz + D = 0. Khi đó:
o Mặt phẳng (α ) có một vec-tơ pháp tuyến là n = ( ; A ; B C) .
o N (x ; y ; z ∈ α ⇔ Ax + By + Cz + D = 0 0 0 0 ) ( ) 0 0 0 .
 Mỗi phương trình Ax + By + Cz + D = 0 (trong đó A , B , C không đồng thời bằng 0) đều là
phương trình của một mặt phẳng xác định.
3. Một số dạng toán viết phương trình mặt phẳng cơ bản
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một vec-tơ pháp tuyến
Trong không gian Oxyz , phương trình mặt phẳng đi qua điểm M x ; y ; z và có vec-tơ pháp 0 ( 0 0 0 ) tuyến n = ( ; A ; B C) là:
A(x − x + B y − y + C z − z = 0 0 ) ( 0 ) ( 0 ) Page 2
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
hay Ax + By + Cz + D = 0 với D = −Ax − By − Cz . 0 0 0
Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một cặp vec-tơ chỉ phương
Để lập phương trình tổng quát của mặt phẳng (α ) đi qua điểm M x ; y ; z và có cặp vec-tơ 0 ( 0 0 0 ) 
chỉ phương a , b , ta thực hiện như sau:   
Tìm một vec-tơ pháp tuyến n = a,b   .
Viết phương trình mặt phẳng (α ) đi qua điểm M x ; y ; z và có vec-tơ pháp tuyến n . 0 ( 0 0 0 )
Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng
Để lập phương trình tổng quát của mặt phẳng (α ) đi qua ba điểm A , B , C không thẳng hàng, ta thực hiện như sau:  
Tìm cặp vec-tơ chỉ phương, chẳng hạn AB , AC .   
Tìm một vec-tơ pháp tuyến n = AB, AC   .
Viết phương trình mặt phẳng (α ) đi qua A và có vec-tơ pháp tuyến n .
Lập phương trình tổng quát của mặt phẳng theo đoạn chắn
Phương trình tổng quát của mặt phẳng (α ) đi qua ba điểm A( ;0 a ;0) , B(0; ;
b 0) , C (0;0;c) là: x y z + + = 1. a b c
4. Điều kiện để hai mặt phẳng song song, vuông góc
Điều kiện để hai mặt phẳng vuông góc Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Trong không gian Oxyz , cho hai mặt phẳng (α : A x + B y + C z + D = 0 và 1 ) 1 1 1 1
(α : A x + B y +C z + D = 0 có vec-tơ pháp tuyến lần lượt là n = A ;B ;C , 1 ( 1 1 1) 2 ) 2 2 2 2
n = A ; B ;C . Khi đó: 2 ( 2 2 2)
(α ⊥ α ⇔ n ⋅n = 0 ⇔ A A + B B +C C = 0. 1 ) ( 2) 1 2 1 2 1 2 1 2
Điều kiện để hai mặt phẳng song song
Trong không gian Oxyz , cho hai mặt phẳng (α : A x + B y + C z + D = 0 và 1 ) 1 1 1 1
(α : A x + B y +C z + D = 0 có vec-tơ pháp tuyến lần lượt là n = A ;B ;C , 1 ( 1 1 1) 2 ) 2 2 2 2
n = A ; B ;C . Khi đó: 2 ( 2 2 2)   (  = α )  (α ) n kn 1 2 ⇔  k ∈ . 1 2 ( ) D ≠  kD 1 2 Chú ý.   (  = α ) ≡ (α ) n kn 1 2 ⇔  k ∈ . 1 2 ( ) D =  kD 1 2
(α cắt (α ⇔ n và n không cùng phương. 2 ) 1 ) 1 2
5. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian Oxyz , mặt phẳng (α ) có phương trình Ax + By + Cz + D = 0 và điểm
M x ; y ; z . Khoảng cách từ điểm M đến mặt phẳng (α ) được tính theo công thức: 0 ( 0 0 0 ) 0
Ax + By + Cz + D d(M ,(α )) 0 0 0 = . 0 2 2 2 A + B + C
HỆ THỐNG BÀI TẬP TỰ LUẬN. II
DẠNG 1: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG KHI BIẾT MỘT ĐIỂM VÀ VECTƠ PHÁP TUYẾN CỦA NÓ. Phương pháp
Phương trình tổng quát của mặt phẳng đi qua điểm và có véctơ pháp tuyến là có dạng: (với ). Nếu mặt phẳng
có cặp véctơ chỉ phương là thì
có véctơ pháp tuyến là Page 4
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN Phương pháp Trong không gian
, viết phương trình mặt phẳng
trung trực đoạn thẳng
Bước 1: Véctơ pháp tuyến của mặt là: .
Bước 2: Tìm tọa độ trung điểm của đoạn .
Bước 3: Viết phương trình mặt phẳng
đi qua điểm và có vectơ pháp tuyến .
Câu 1: Trong không gian Oxyz , viết phương trình mặt phẳng (P) đi qua điểm ( A 1;0; 2) − và có vectơ  pháp tuyến ( n 1; 1; − 2) . Lời giải
Mặt phẳng (P) đi qua điểm ( A 1;0; 2)
− và có vectơ pháp tuyến ( n 1; 1;
− 2) có phương trình là:
1(x −1) −1(y − 0) + 2(z + 2) = 0 ⇔ x − y + 2z + 3 = 0 .
Vậy phương trình mặt phẳng (P)là: x − y + 2z + 3 = 0 .
Câu 2: Trong không gian với hệ trục tọa độ Oxyz , viết phương trình mặt phẳng đi qua điểm A(0;1;2) 
và có vectơ pháp tuyến n = ( 2 − ;1;0). Lời giải
Vậy phương trình mặt phẳng đi qua điểm A(0;1;2) và có vectơ pháp tuyến n = ( 2 − ;1;0) có dạng: 2
− (x − 0) +1( y − ) 1 = 0 ⇔ 2
− x + y −1 = 0 ⇔ 2x − y +1 = 0.
Câu 3: Trong không gian Oxyz , viết phương trình mặt phẳng đi qua A( 1; − 1; )
1 và có vectơ pháp tuyến n =( 1; − 2 − ;2) Lời giải
Mặt phẳng đi qua A( 1; − 1; ) 1 , có vtpt n(1;2; 2
− ) , suy ra phương trình mặt phẳng cần tìm là 1 − (x + ) 1 − 2( y − ) 1 + 2(z − )
1 = 0 ⇔ −x − 2y + 2z −1 = 0 .
Câu 4: Trong không gian với hệ trục tọa độ Oxyz , cho các điểm A(0;1;2) , B(2;− 2; ) 1 , C ( 2; − 0; ) 1 .
Phương trình mặt phẳng đi qua A và vuông góc với BC là? Lời giải  
Ta có: n = BC = ( 2 − ;1;0).
Vậy phương trình mặt phẳng đi qua A và vuông góc với BC có dạng: 2
− (x − 0) +1( y − ) 1 = 0 ⇔ 2
− x + y −1 = 0 ⇔ 2x − y +1 = 0.
Câu 5: Trong không gian Oxyz , cho ba điểm A( 1; − 1; )
1 , B(2;1;0) và C (1; 1;
− 2) . Mặt phẳng đi qua A
và vuông góc với đường thẳng BC có phương trình là? Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN Lời giải  Ta có: BC ( 1; − 2 − ;2) . 
Do mặt phẳng vuông góc với đường thẳng BC nên mặt phẳng có một vtpt n(1;2; 2 − ) . 
Mặt phẳng đi qua A( 1; − 1; ) 1 , có vtpt n(1;2; 2
− ) , suy ra phương trình mặt phẳng cần tìm là
x + 2y − 2z +1 = 0.
Câu 6: Trong không gian Oxyz , cho A( 1; − 1; − ) 1 , B(3;1 )
;1 . Phương trình mặt phẳng trung trực của đoạn AB là. Lời giải
Gọi I là trung điểm của AB nên I (1;0; ) 1 . 
Mặt phẳng trung trực của đoạn 
AB có vtpt là n = AB = (4;2;0) = 2(2;1;0) .
Phương trình mặt phẳng cần tìm là: 2(x − )
1 +1( y − 0) = 0 ⇔ 2x + y − 2 = 0 .
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1;6; 7 − ) và B(3;2; ) 1 . Phương trình mặt
phẳng trung trực đoạn AB là. Lời giải
Mặt phẳng trung trực đoạn AB đi qua trung điểm I (2;4; 3
− ) của đoạn AB và nhân  AB = (2; 4;
− 8) làm vectơ pháp tuyến có phương trình:
2(x − 2) − 4( y − 4) +8(z + 3) = 0 ⇔ x − 2y + 4z +18 = 0
Câu 8: Trong không gian Oxyz , viết phương trình mặt phẳng (P) chứa điểm M (1;3;− 2), cắt các tia Ox OA OB OC
, Oy , Oz lần lượt tại A , B , C sao cho = = . 1 2 4 Lời giải
Phương trình mặt chắn cắt tia Ox tại A(a;0;0) , cắt tia Oy tại B(0;b;0) , cắt tia Oz tại x y z
C (0;0;c) có dạng là (P) : + + =1 (với a > 0 , b > 0 ,c > 0 ). a b cb Theo đề: OA OB OC a b c = = ⇔ = = a = ⇒ . 1 2 4 1 2 4  2 c =  2b Vì − 4
M (1;3;− 2) nằm trên mặt phẳng (P) nên ta có: 1 3 2 + + =1 ⇔ =1 ⇔ b = 4 . b b 2b b 2
Khi đó a = 2 , c = 8 . x y z
Vậy phương trình mặt phẳng (P) là: + + =1 ⇔ 4x + 2y + z −8 = 0 . 2 4 8
Câu 9: Trong không gian Oxyz , cho hình hộp ABC . D A B ′ C ′ D
′ ′ , biết rằng A( 3 − ;0;0) , B(0;2;0) , D(0;0; )
1 , A′(1;2;3) . Viết phương trình mặt phẳng trung trực của C D ′ . Lời giải Page 6
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN A' B' D' C' A B D C   
Gọi C′(x; y; z). Ta có AB = (3;2;0) ; AD = (3;0; ) 1 ; ′ AA = (4;2;3) .
     x =10 + 3
Mà AC′ = AB + AD + ′
AA ⇒ AC′ = (10;4;4) 
⇒ y = 4 − 0 ⇒ C′(13;4;4) . z = 4−0   13 5 qua I ; 2    ; 
Khi đó mặt phẳng trung trực của C′D :   2 2   
n = C′D =  (13;4;3) có phương trình là  13  x (y )  5 13 4 2 3  − + − + z − =   
 0 ⇔ 13x + 4y + 3z −100 = 0 .  2   2 
DẠNG 2: Viết phương trình mặt phẳng (α ) đi qua 1 điểm M x ; y ; z và song song với 1 0 ( 0 0 0 )
mặt phẳng (β ) : Ax + By +Cz + D = 0 cho trước. Phương pháp Trong không gian
, viết phương trình mặt phẳng Loại Phương pháp ⑴ Qua và song song ⌘ Cách 1: . ≫ Véctơ pháp tuyến là: . ≫ Mặt phẳng qua điểm . ⌘ Cách 2: ≫ Do ≫ Thay điểm vào . ⑵ Song song và ≫ Vì . cách một khoảng bằng . ≫ Vì cách một khoảng bằng ≫ Có phương trình mặt hoàn chỉnh. Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ V – HÌNH HỌC 12 – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Câu 10: Trong không gian Oxyz , viết phương trình mặt phẳng(P) đi qua điểm M(0;1;3)và song song
với mặt phẳng(Q) : 2x − 3z + 1 = 0 . Lời giải:
Mặt phẳng (P) song song với mặt phẳng(Q) : 2x − 3z + 1 = 0 nên mặt phẳng(P) có phương trình
dạng: 2x − 3z + D = 0 (D ≠ 1) .
Mặt phẳng (P) đi qua điểm M(0;1; 3) nên thay tọa độ điểm M vào phương trình mặt phẳng phải
thỏa mãn. Ta được: 2.0 − 3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1 ).
Vậy phương trình mặt phẳng (P)là: 2x − 3z + 9 = 0 .
Câu 11: Trong không gian Oxyz , viết phương trình mặt phẳng(P) đi qua điểm M(−2;3;1) và song song
với mặt phẳng(Q) : x + 3y − 2z + 2 = 0. Lời giải:
Mặt phẳng (P) song song với mặt phẳng(Q) : x + 3y − 2z + 2 = 0nên mặt phẳng(P) có phương
trình dạng: (Q) : x + 3y − 2z + D = 0 (D ≠ 2) .
Mặt phẳng (P) đi qua điểm M(−2; 3;1) nên thay tọa độ điểm M vào phương trình mặt phẳng
phải thỏa mãn. Ta được: −2 + 3.3 − 2.1+ D = 0 ⇔ D = −5 (thỏa mãn).
Vậy phương trình mặt phẳng (P)là: (Q) : x + 3y − 2z − 5 = 0 .
Câu 12: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi điểm M (3; 1 − ; 2 − ) và
song song với mặt phẳng (P) :3x − y + 2z + 4 = 0 . Lời giải
Vì (Q) // (P) nên (Q) :3x − y + 2z + m = 0 (m ≠ 4) . Mà M (3; 1 − ; 2
− )∈(P) ⇒ m = 6 − (thỏa mãn).
Vậy (Q) :3x − y + 2z − 6 = 0.
DẠNG 3: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG (α ) ĐI QUA 3 ĐIỂM A , B, C KHÔNG THẲNG HÀNG. Page 8
Sưu tầm và biện soạn
CHUYÊN ĐỀ V – PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN Phương pháp Phương trình mặt phẳng di qua không thẳng hàng.
Bước 1: Tìm cặp vectơ chỉ phương .
Bước 2: Tìm một vectơ pháp tuyến .
Bước 3: Viết phương trình mặt phẳng
đi qua điểm (hoặc điểm hoặc điểm
) và có vectơ pháp tuyến . Phương trình mặt phẳng
là phương trình mặt chắn, tức mặt phẳng đi qua có dạng: .
Câu 13: Trong không gian Oxyz , viết phương trình mặt phẳng (ABC)
a) Với ba điểm A( 1 − ;0;3) , B(2; 1 − ; ) 1 , C (1; 1 − ;0) .
b) Với ba điểm A(1;0;2),B( 2 − ;3; ) 1 ,C (3;2; ) 1 . Lời giải
a) Với ba điểm A( 1; − 0;3), B(2; 1; − ) 1 , C (1; 1; − 0) .   Ta có AB = (3; 1 − ; 2 − ); AC = (2; 1 − ; 3
− )   
Mặt phẳng (ABC) có vec tơ pháp tuyến  
n = AC; AB = ( 1 − ; 5 − ; ) 1 .  
Phương trình mặt phẳng (ABC) là −(x +1) −5y + z −3 = 0 ⇔ −x −5y + z − 4 = 0
b) Với ba điểm A(1;0;2), B( 2; − 3; ) 1 ,C (3;2; ) 1 .   Ta có: AB = ( 3 − ;3; − ) 1 , AC = (2;2;− ) 1 .  
Mặt phẳng (P) có một véctơ pháp tuyến là   
n = AB, AC = ( 1 − ; − 5; −12).  
Phương trình mặt phẳng (ABC) là −x −5y −12z + 25 = 0 ⇔ x + 5y +12z − 25 = 0
Câu 14: Trong không gian Oxyz , viết phương trình mặt phẳng (ABC)
a) Với ba điểm M (2;0;0) , N (0;−1;0) , P(0;0;2).
b) Với ba điểm M (0; 2;
− 0), N (3;0;0), P(0;0; 3 − ) . Lời giải
a) Với ba điểm M (2;0;0) , N (0;−1;0) , P(0;0;2). Page 9
Sưu tầm và biên soạn

Tài liệu liên quan: