Chuyên đề phương pháp tọa độ trong mặt phẳng Toán 10 KNTTvCS

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 301

BÀI 19. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

I. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG

1. Vectơ pháp tuyến của đường thẳng

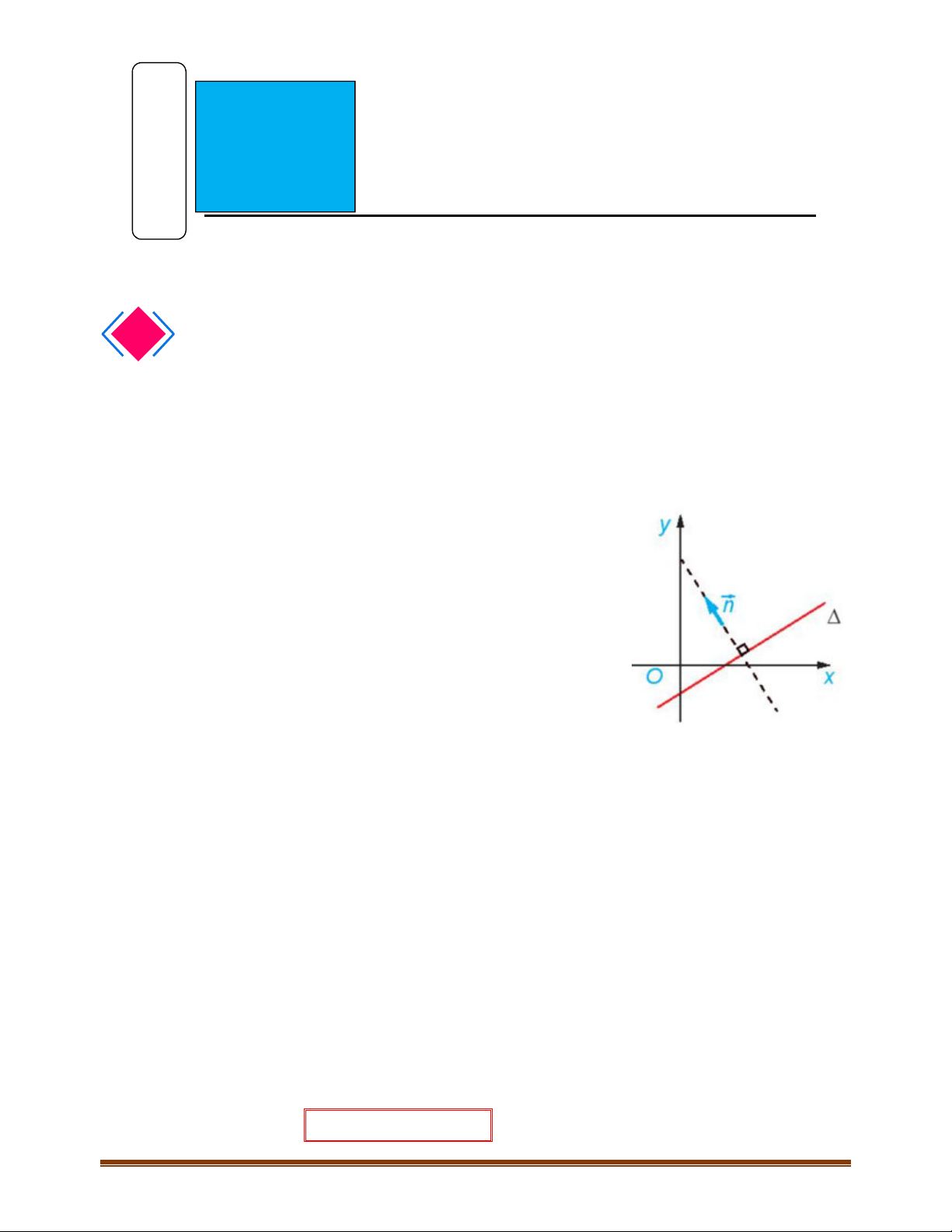
1.1. Định nghĩa: Vectơ

0n ¹



gọi là vectơ pháp tuyến (VTPT) của D nếu giá của nó

vuông góc với

D

.

1.2. Nhận xét:

a) Nếu

n



là một vtpt của đường thẳng

d

thì





., 0kn k



cũng là một vtpt của

d

.

b) Nếu

n



là một VTPT của đường thẳng

d

và

u



là một VTCP của đường thẳng

d

thì

.0nu



.

c) Một đường thẳng xác định khi biết một VTPT và mộ điểm nó đi qua.

2. Phương trình tổng quát (PTTQ) của đường thẳng

Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát dạng

0ax by c

, với

a

và

b

không đồng thời bằng

0

. Ngược lại, mỗi phương trình dạng

0ax by c

, với

a

và

b

không đồng thời bằng

0

, đều là phương trình của một đường

thẳng, nhận





;nab



là một vectơ pháp tuyến.

2.1. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có VTPT





A; Bn 



thì có phương trình

tổng quát là









00

0Ax x By y 

.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 302

2.2.

Ngược lại, trong mặt phẳng với hệ tọa độ

Oxy

mọi phương trình dạng





22

00Ax By C A B 

đều là phương trình tổng quát của đường thẳng d có

VTPT





A; Bn 



.

2.3. Một số trường hợp đặc biệt của PTTQ





22

00Ax By C A B 

.

a) Nếu

0A 

phương trình trở thành

0

C

By C y

B



đường thẳng song

song với trục hoành

Ox và cắt trục tung

Oy

tại điểm

0;

C

M

B









.

b) Nếu

0B 

phương trình trở thành

0

C

Ax C x

A



đường thẳng song

song với trục tung

Oy

và cắt trục hoành

Ox

tại

;0

C

M

A









.

c) Nếu

0C 

phương trình trở thành

0Ax By

đường thẳng đi qua gốc tọa độ



0;0O

.

d) Đường thẳng có dạng

yaxb

, (trong đó

a

được gọi là hệ số góc của đường

thẳng ) có VTPT là





;1na



. Ngược lại đường thẳng có VTPT





;nAB



thì có

hệ số góc là

A

B



.

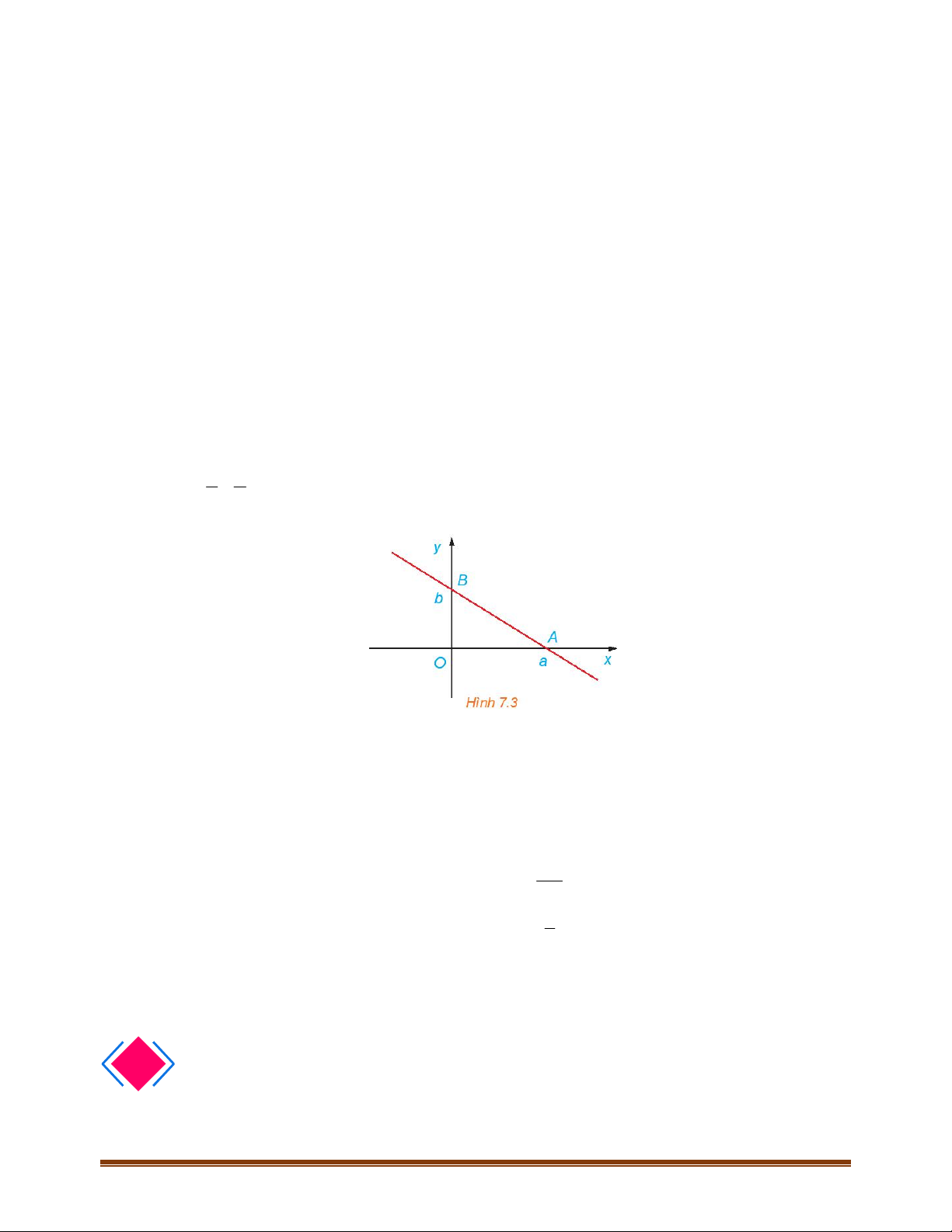
e) Đường thẳng

d

đi qua điểm





;0

A

a

và





0;Bb

có phương trình là 1.

xy

ab



II. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG

1. Véc tơ chỉ phương của đường thẳng

1.1. Định nghĩa

Vectơ 0u ¹



được gọi là vectơ chỉ phương (VTCP) của đường thẳng D

nếu giá của nó song song hoặc trùng với

D .

1.2. Nhận xét:

a) Nếu

u



là một vtcp của đường thẳng

d

thì





., 0ku k



cũng là một véc tơ chỉ

phương của

d

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 303

b) Một đường thẳng xác định khi biết một vtcp và một điểm mà nó đi qua.

2. Phương trình tham số của đường thẳng

Cho đường thẳng



đi qua điểm



00

;

A

xy

và có vectơ chỉ phương





;uab



. Khi đó

điểm





;

M

xy

thuộc đường thẳng



khi và chỉ khi tồn tại số thực t sao cho

A

Mtu



,

hay

0

x

xat

yy bt











(2)

Hệ (2) được gọi là phương trình tham số của đường thẳng

 (t là tham số).

2.1. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có vtcp



;uab



thì có phương trình

tham số là

0

x

xat

yy bt











. ( Mỗi điểm

M

bất kỳ thuộc đường thẳng



d

tương ứng với

duy nhất một số thực

t 

và ngược lại).

Nhận xét

:



00

(;),tAAxatybtÎD + + Î

2.2. Trong mặt phẳng với hệ tọa độ

Oxy

, mọi phương trình dạng

0

x

xat

yy bt











với

22

0ab

đều là phương trình của đường thẳng

d

có một vtcp là





;uab



.

3. Phương trình chính tắc của đường thẳng

Đường thẳng

d

đi qua điểm





00

;

M

xy

và có vtcp





;uab



với

0, 0ab

có

phương trình chính tắc là:

00

x

xyy

ab





III. LIÊN HỆ GIỮA VTCP VÀ VTPT

1.

Từ nhận xét “Nếu

n



là một VTPT của đường thẳng

d

và

u



là một VTCP của đường thẳng

d

thì

.0nu



” ta rút ra được: nếu





;nAB



là một VTPT của đường thẳng

d

thì một VTCP

của

d

là





;uBA



( hoặc





;uBA



).

2. Từ nhận xét “Nếu

n



là một VTPT của đường thẳng

d

và

u



là một VTCP của đường thẳng

d

thì

.0nu



” ta rút ra được: nếu





;uab



là một VTCP của đường thẳng

d

thì một VTPT

của

d

là





;nba



(hoặc





;nba



).

Hai nhận xét trên giúp ích rất nhiều trong việc chuyển đổi qua lại giữa các dạng phương trình

đường thẳng. Từ PTTQ ta có thể chuyển sang PTTS và ngược lại.

7.1.

Trong mặt phẳng tọa độ, cho

  

2;1 , 3;2 , 1;3 , 2;1 .nv AB 



BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 304

a) Lập phương trình tổng quát của đường thẳng

1

 đi qua

A

và có vectơ pháp tuyến

.n



b) Lập phương trình tham số của đường thẳng

2

 đi qua

B

và có vectơ chỉ phương

.v



c) Lập phương trình tham số của đường thẳng

.

A

B

7.2. Lập phương trình tổng quát của các trục tọa độ.

7.3. Cho hai đường thẳng

1

12

:

35

x

t

yt













và

2

:2x 3y 5 0.

a) Lập phương trình tổng quát của

1

. b) Lập phương trình tham số của

2

.

7.4. Trong mặt phẳng tọa độ, cho tam giác

A

BC

có









1; 2 , 3; 0AB và





2; 1 .C 

a) Lập phương trình đường cao kẻ từ

.

A

b) Lập phương trình đường trung tuyến kẻ từ

B.

7.5. (Phương trình đọan chắn của đường thẳng )

Chứng minh rằng, đường thẳng đi qua hai điểm



a;0 , 0;bAB

với





0.7.3ab H

có phương

trình là:

1.

xy

ab

7.6. Theo Google Maps, sân bay Nội Bài có vĩ độ là

0

21,2 Bắc, kinh độ

0

105,8 Đông, sân bay Đà

Nẵng có vĩ độ là

0

16,1 Bắc, kinh độ

0

108,2 Đông. Một máy bay, bay từ Nội Bài đến sân bay

Đà Nẵng. Tại thời điểm

t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ

0

x

Bắc, kinh độ

0

y Đông được tính theo công thức

153

21,2

40

9

105,8

5

x

t

yt

















a) Hỏi chuyến từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm

1

giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến

17

(

0

17

Bắc) chưa?

HỆ THỐNG BÀI TẬP.

II

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 305

DẠNG 1: XÁC ĐNNH VTCP, VTPT CỦA ĐƯỜNG THẲNG

{ Tích vô hướng hai vt, góc giữa hai vt, độ dài vt, độ dài đường trung tuyến, phân giác,đường cao, diện

tích tam giác, chu vi tam giác…}

1.

Trong mặt phẳng với hệ tọa độ

Oxy

phương trình dạng





22

00Ax By C A B 

có VTPT





A;Bn 



.

2. Trong mặt phẳng với hệ tọa độ

Oxy

, mọi phương trình dạng

0

x

xat

yy bt











với

22

0ab

đều là phương trình của đường thẳng

d

có một vtcp là





;uab



.

3. Nếu đường thẳng

d

có





;nAB



là một VTPT thì một VTCP của d là



;uBA



(hoặc





;uBA



).

4. Nếu đường thẳng

d

có





;uab



là một VTCP thì một VTPT của

d

là





;nba



(hoặc





;nba



).

5. Đường thẳng đi qua 2 điểm

,

A

B

thì nhận

A

B



làm VTCP.

Câu 1:

Một vectơ chỉ phương của đường thẳng

23

3

x

t

yt







 



là:

A.





1

2; –3 .u 



B.





2

3; –1 .u 



C.





3

3; 1 .u 



D.





4

3; –3u 



Câu 2: Một vectơ pháp tuyến của đường thẳng

2360xy

là :

A.





4

2; 3n 



B.





2

2;3n 



C.





3

3; 2n 



D.



1

3; 2n 



Câu 3: Vectơ chỉ phương của đường thẳng

1

32

xy



là:

A.





4

2;3u 



B.



2

3; 2u 



C.



3

3; 2u 



D.





1

2;3u 



Câu 4: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm





3; 2A 

và





?1; 4B

A.





1

1; 2 .u 



B.





2

2.;1u 



C.





3

2;6 .u 



D.





4

1; 1 .u 



Câu 5: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm





2;3A

và





4;1 ?B

A.





1

22.;n 



B.





2

2; 1 .n 



C.





3

1.;1n 



D.





4

1; 2 .n 



PHƯƠNG PHÁP.

1

BÀI TẬP TRẮC NGHIỆM.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 306

Câu 6:

Cho phương trình:





01ax by c

với

22

0ab

. Mệnh đề nào sau đây sai?

A.



1 là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là



;



nab

.

B.

0a



1

là phương trình đường thẳng song song hoặc trùng với trục

ox

.

C.

0b



1

là phương trình đường thẳng song song hoặc trùng với trục

oy

.

D.

Điểm





000

;

M

xy

thuộc đường thẳng



1

khi và chỉ khi

00

0ax by c

.

Câu 7:

Mệnh đề nào sau đây sai? Đường thẳng



d

được xác định khi biết.

A.

Một vecto pháp tuyến hoặc một vec tơ chỉ phương.

B.

Hệ số góc và một điểm thuộc đường thẳng.

C.

Một điểm thuộc



d

và biết



d

song song với một đường thẳng cho trước.

D.

Hai điểm phân biệt thuộc



d

.

Câu 8:

Đường thẳng



d

có vecto pháp tuyến





;



nab. Mệnh đề nào sau đây sai?

A.





1

;



uba

là vecto chỉ phương của



d .

B.





2

;



uba là vecto chỉ phương của



d

.

C.



;







nkakbkR là vecto pháp tuyến của



d

.

D.



d có hệ số góc



0





b

kb

a

.

Câu 9: Cho đường thẳng (d):

2340xy

. Vecto nào sau đây là vecto pháp tuyến của (d)?

A.





1

3; 2



n . B.





2

4; 6 



n . C.





3

2; 3



n . D.





4

2;3



n .

Câu 10:

Cho đường thẳng



:3 7 15 0dxy

. Mệnh đề nào sau đây sai?

A.





7;3



u là vecto chỉ phương của



d

.

B.



d

có hệ số góc

3

7

k

.

C.



d

không đi qua góc tọa độ.

D.



d

đi qua hai điểm

1

;2

3









M

và





5; 0N

.

Câu 11: Cho đường thẳng



23

:

12







 



x

t

d

yt

và điểm

7

;2.

2









A

Điểm







A

d

ứng với giá trị nào của

t?

A.

3

.

2

t

B.

1

.

2

t

C.

1

.

2

t

D.

2t 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 307

Câu 12:

Cho



23

:

54











x

t

d

yt

. Điểm nào sau đây không thuộc





?d

A.





5;3 .A B.





2;5 .B C.





1; 9 .C D.





8; 3 .D

Câu 13: Một đường thẳng có bao nhiêu vectơ chỉ phương?

A. 1. B. 2. C. 3. D. Vô số.

Câu 14: Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 1 B. 2 C. 3 D. Vô số.

Câu 15: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng

2

:

16

x

d

yt







 



?

A.





1

6;0u 



. B.





2

6;0u 



. C.





3

2;6u 



. D.





4

0;1u 



.

Câu 16: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng

1

5

:

2

33

x

t

y

t













 



?

A.





1

1; 3u 



B.

2

1

;3

2

u











C.

2

23

xy



D.

6280xy

Câu 17:

Cho đường thẳng  có phương trình tổng quát: . Vectơ nào sau đây là vectơ chỉ

phương của đường thẳng .

A. B. C. D.

Câu 18: Cho đường thẳng có phương trình tổng quát: . Vectơ nào sau đây không là

vectơ chỉ phương của

A. B. C. D.

Câu 19: Đường thẳng

:5 3 15xy

tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu?

A.

7,5

. B.

5

. C.

15

. D.

3

.

–2 3 –1 0xy







3; 2 .





2;3 .





–3;2 .





2; –3 .



–2 3 –1 0xy



2

1;

3

.











3; 2 .





2;3 .





–3; –2 .

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 308

DẠNG 2: VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN MỘT SỐ TÍNH CHẤT CHO

TRƯỚC

{ Tính chất cho trước giúp tìm được: một điểm thuộc đường thẳng và một VTCP (hay VTPT);

tìm được các hệ số A, B, C trong phương trình tổng quát; …}

1.

Đường thẳng d đi qua điểm





00

;

M

xy và có vtcp



;uab



thì có phương trình tham

số là

0

x

xat

yy bt











. ( Mỗi điểm

M

bất kỳ thuộc đường thẳng



d tương ứng với duy nhất

một số thực t  và ngược lại).

2. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có vtcp





;uab



với

0, 0ab

có

phương trình chính tắc là:

00

x

xyy

ab





3. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có VTPT





A;Bn 



thì có phương trình

tổng quát là









00

0Ax x By y 

.

2.1. Viết PTTS của đường thẳng.

Câu 1:

Viết phương trình tham số của đường thẳng  qua





3; 1A 

và có VTCP





2;3u 



.

Câu 2: Viết PTTS của đường thẳng

AB

biết









3;1 , 1; 3AB

.

Câu 3: Viết PTTS của đường thẳng  qua





1; 7M 

và song song với trục

.Ox

Câu 4: Cho đường thẳng

2

:

35

x

y

d







. Viết PTTS của đường thẳng qua và song

song với đường thẳng .

Câu 5: Cho và . Viết PTTS của đường thẳng là trung trực của đoạn thẳng .

2.2. Viết PTTQ của đường thẳng

Câu 1:

Viết PTTQ của đường thẳng

d

đi qua



1; 5K 

và có VTPT





2;1n 



.

Câu 2: Viết PTTQ của đường thẳng  đi qua





3; 2K 

và song song với đường thẳng

: 5 2017 0dx y 

.

Câu 3: Viết PTTQ của  là đường trung trực của đoạn thẳng

A

B với



4; 1 , 2;3AB

.

Câu 4: Viết PTTQ của đường thẳng qua hai điểm





5; 0A

và





0; 2B 

.

Câu 5: Cho tam giác

A

BC

có













2; 1 ; 4;5 ; 3; 2ABC

. Viết phương trình tổng quát của đường cao

A

H của tam giác

A

BC

.

2.3. Bài toán chuyển đổi qua lại giữa các dạng phương trình.





2017;2018I

d





3;1A





3; 5B 



A

B

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 309

Câu 1:

Cho đường thẳng

12

3

x

t

yt













. Viết PTTQ của đường thẳng.

Câu 2: Cho đường thẳng

:2 3 3 0xy

. Viết PTTS của đường thẳng.

2.4. Bài tập tổng hợp về viết phương trình đường thẳng

Câu 1:

Cho tam giác

A

BC

với

  

2;3 ; 4;5 ; 6; 5AB C

.

,

M

N

lần lượt là trung điểm của

A

B và

A

C

. Phương trình tham số của đường trung bình

M

N

là:

Câu 2:

Phương trình đường thẳng đi qua điểm





5; 3M

và cắt hai trục tọa độ tại hai điểm A và B sao

cho M là trung điểm của AB là:

Câu 3:

Cho ba điểm













1;1 ; 2; 0 ; 3; 4AB C

. Viết phương trình đường thẳng đi qua

A

và cách đều hai

điểm

,

B

C

.

Câu 4:

Đường thẳng

:1

x

y

d

ab



, với

0a 

,

0b 

, đi qua điểm





1; 6M  và tạo với các tia

Ox

,

Oy

một tam giác có diện tích bằng

4

. Tính

2Sa b

.

Câu 5: Cho tam giác

A

BC

biết trực tâm





1; 1H và phương trình cạnh

:5 2 6 0AB x y

, phương

trình cạnh

:4 7 21 0AC x y

. Phương trình cạnh

B

C

là

Câu 6: Gọi

H

là trực tâm của tam giác

A

BC

. Phương trình các cạnh và đường cao của tam giác là

A

B

:

740xy

;

B

H

:

240xy

;

A

H

:

20xy

. Phương trình đường cao

CH

của tam giác

A

BC

là

Câu 7: Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai đường thẳng

1

:10,xy

2

:2 1 0xy

và điểm





2;1P

.Viết phương trình đường thẳng đi qua điểm P và cắt hai

đường thẳng

1



,

2



lần lượt tại hai điểm

A

,

B

sao cho P là trung điểm

A

B .

Câu 8: Trong mặt phẳng tọa độ vuông góc

Oxy

, cho hai đường thẳng

1

d

và

2

d

lần lượt có phương

trình:

12

:1, :330dxy dx y  . Hãy viết phương trình đường thẳng

d

đối xứng với

2

d

qua đường thẳng

1

d .

Câu 9:

Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho

Δ

A

BC

có đỉnh





3; 0A

và phương trình hai

đường cao



':2 2 9 0BB x y

và



':3 12 1 0CC x y

. Viết phương trình cạnh

BC

.

Câu 10: Cho tam giác

A

BC

, đỉnh





2; 1B 

, đường cao

:3 4 27 0AA x y





và đường phân giác trong

của góc

C

là

:250CD x y

. Khi đó phương trình cạnh

A

B

là

Câu 11: Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc

Oxy

, cho

A

BC

có điểm





2; 1A 

và hai đường phân giác trong của hai góc

,

B

C

lần lượt có phương trình





:210,

B

xy





:30

C

xy

. Viết phương trình cạnh

BC

.

Câu 12:

Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc

Oxy

, cho

A

BC

vuông cân tại





4;1A và cạnh huyền BC có phương trình:

350xy

. Viết phương trình hai cạnh góc

vuông

A

C

và

.

A

B

Câu 13: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

A

BC

vuông tại A , có đỉnh





4;1C 

, phân giác

trong góc

A

có phương trình

50xy

. Viết phương trình đường thẳng

BC

, biết diện tích

tam giác

A

BC

bằng 24 và đỉnh A có hoành độ dương.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 310

Câu 14:

Cho

A

BC

có





4; 2A 

. Đường cao

:2 4 0BH x y

và đường cao

:30CK x y

. Viết

phương trình đường cao kẻ từ đỉnh A

Câu 15:

Viết Phương trình đường thẳng đi qua điểm





2; 3M và cắt hai trục tọa độ tại hai điểm A và

B sao cho tam giác OAB vuông cân.

Câu 16:

Gọi H là trực tâm của tam giác

A

BC . Phương trình các cạnh và đường cao của tam giác là:

:7 4 0; :2 4 0; : 2 0  AB x y BH x y AH x y

. Phương trình đường cao CH của tam

giác ABC là:

Câu 17:

Cho tam giác

A

BC

biết trực tâm

(1;1)H

và phương trình cạnh

:5 2 6 0AB x y

, phương

trình cạnh

:4 7 21 0AC x y

. Phương trình cạnh

BC

là

Câu 18:

Viết phương trình tham số của đường thẳng đi qua





3; 4A và có vectơ chỉ phương





3; 2u 



A.

33

24

x

t

yt







 



.

B.

36

24

x

t

yt







 



.

C.

32

43

x

t

yt











.

D.

33

42

x

t

yt











.

Câu 19: Phương trình tham số của đường thẳng qua



1; 1M 

,



4;3N

là

A.

3

4

x

t

yt











.

B.

13

14

x

t

yt











.

C.

33

43

x

t

yt











.

D.

13

14

x

t

yt







 



.

Câu 20: Phương trình tổng quát của đường thẳng đi qua



1; 2A

và nhận





1; 2



n làm véc-tơ pháp

tuyến có phương trình là

A.

20 xy

. B.

240xy

. C.

250xy

. D.

240xy

.

Câu 21: Đường thẳng đi qua điểm



1; 2A 

và nhận





2; 4n 



làm véctơ pháp tuyến có phương trình

là

A.

240xy

. B.

240xy

. C.

250xy

. D.

24 0xy 

.

Câu 22: Đường thẳng

d

qua





1; 1A và có véctơ chỉ phương





2;3u 



có phương trình tham số là

A.

1

3

x

t

yt











.

B.

12

13

x

t

yt











.

C.

2

3

x

t

yt











.

D.

2

3

x

t

yt











.

Câu 23: Phương trình đường thẳng đi qua hai điểm





2; 4A 

,



6;1B 

là

A.

34100xy

. B.

34220xy

. C.

3480xy

. D.

34220xy

.

Câu 24: Đường thẳng đi qua





1; 2A 

, nhận





2; 4n 



làm vectơ pháp tuyến có phương trình là

A.

240xy

. B.

40xy

. C.

250xy

. D.

240xy  

.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 311

Câu 25:

Phương trình tham số của đường thẳng đi qua điểm





2; 1A và nhận





3; 2



u

làm vectơ chỉ

phương là

A.

32

2

 









x

t

yt

. B.

23

12







 



x

t

yt

. C.

23

12

 









x

t

yt

. D.

23

12

 









x

t

yt

.

Câu 26: Đường thẳng đi qua





1; 2A  , nhận





2; 4n 



làm véc tơ pháo tuyến có phương trình là:

A.

240xy

B.

40xy

C.

240xy  

D.

250xy

Câu 27: Cho hai điểm





1; 2A  ,





1; 2B  . Đường trung trực của đoạn thẳng

A

B

có phương trình là

A.

20xy

. B.

20xy

. C.

20xy

. D.

210xy

.

Câu 28: Lập phương trình tổng quát đường thẳng đi qua điểm





2;1A và song song với đường thẳng

2320xy

.

A.

3280xy

. B.

2370xy

. C.

3240xy

. D.

2370xy

.

Câu 29: Cho đường thẳng

23

:

1

x

t

yt









 







t 

và điểm





1; 6M 

. Phương trình đường thẳng đi qua

M

và vuông góc với



là

A.

390xy

. B.

3170xy

. C.

330xy

. D.

3190xy

.

Câu 30: Trong mặt phẳng

Oxy

, cho đường thẳng

:210dx y

. Nếu đường thẳng



qua điểm





1; 1M 

và



song song với

d

thì



có phương trình

A.

230xy

. B.

230xy

. C.

250xy

. D.

210xy

.

Câu 31: Viết phương trình tổng quát của đường thẳng đi qua

2

điểm





0; 5A  và





3; 0B

A.

1

53

xy



. B.

1

35

xy

 

. C.

1

35

xy



. D.

1

53

xy



.

Câu 32: Trong mặt phẳng

Oxy

cho hai điểm



1; 3A 

,





2;5B 

. Viết phương trình tổng quát của

đường thẳng đi qua hai điểm

,

A

B

.

A.

8310xy

. B.

8310xy

. C.

38300xy  

. D.

38300xy  

.

Câu 33: Cho





2;3A 

,





4; 1B 

. Viết phương trình đường trung trục của đoạn

A

B

.

A.

10xy

. B.

2350xy

. C.

3210xy

. D.

2310xy

.

Câu 34: Trong mặt phẳng với hệ tọa độ

Oxy

cho đường thẳng

:210dx y

và điểm





2;3M

.

Phương trình đường thẳng



đi qua điểm

M

và vuông góc với đường thẳng

d

là

A.

280xy

. B.

240xy

. C.

210xy

. D.

270xy

.

Câu 35: Trong mặt phẳng với hệ tọa độ

Oxy

cho hai điểm





0; 1A 

,





3; 0B

. Phương trình đường

thẳng

A

B

là

A.

310xy

. B.

330xy

. C.

330xy

. D.

310xy

.

Câu 36: Phương trình đường thẳng đi qua hai điểm









2; 4 ; 6;1AB

là:

A.

3 4 10 0.xy

B.

34220.xy

C.

3480.xy

D.

34220xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 312

Câu 37:

Cho đường thẳng





:3 5 15 0dxy

. Phương trình nào sau đây không phải là một dạng khác

của (d).

A.

1

53



xy

. B.

3

5

 yx

C.



5













xt

tR

y

D.



5

3

















xt

tR

yt

.

Câu 38: Cho đường thẳng





:210dx y. Nếu đường thẳng





 đi qua





1; 1M và song song với



d

thì







có phương trình

A.

230xy

B.

250xy

C.

230xy

D.

210xy

Câu 39: Cho ba điểm

 

1; 2 , 5; 4 , 1; 4AB C

. Đường cao



A

A của tam giác ABC có phương trình

A.

3480xy

B.

34110xy

C.

68110 xy

D.

86130xy

Câu 40: Cho hai điểm









4;0 , 0;5AB. Phương trình nào sau đây không phải là phương trình của

đường thẳng AB?

A.



44

5













xt

tR

yt

B.

1

45



xy

C.

4

45







x

y

D.

5

15

4



yx

Câu 41: Cho đường thẳng





:4 3 5 0dxy

. Nếu đường thẳng







đi qua gốc tọa độ và vuông góc

với



d

thì







có phương trình:

A.

43 0xy

B.

34 0xy

C.

34 0xy

D.

43 0xy

Câu 42: Viết phương trình tổng quát của đường thẳng đi qua điểm





1; 2I 

và vuông góc với đường

thẳng có phương trình

240xy

A.

250xy  

B.

230xy

C.

20xy

D.

250xy

Câu 43: Phương trình tham số của đường thẳng (d) đi qua điểm



2;3M

và vuông góc với đường

thẳng





:3410



dxy

là

A.

24

33

 









x

t

yt

B.

23

34

 









x

t

yt

C.

23

34

 









x

t

yt

D.

54

63











x

t

yt

Câu 44: Cho

A

BC

có



2; 1 ; 4;5 ; 3;2ABC

. Viết phương trình tổng quát của đường cao

A

H .

A.

3710xy

B.

73130xy

C.

37130xy 

D.

73110xy

Câu 45: Viết phương trình tổng quát của đường thẳng đi qua điểm





2;1M và vuông góc với đường

thẳng có phương trình









21 21 0xy .

A.



12 21 1220xy B.





322 3 2 0xy   

C.









12 21 10xy D.





322 2 0xy   

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 313

Câu 46:

Cho đường thẳng



d đi qua điểm





1; 3M và có vecto chỉ phương





1; 2



a

. Phương trình

nào sau đây không phải là phương trình của



d

?

A.

1

32.











x

t

yt

B.

13

.

12







xy

C.

250.xy

D.

25. yx

Câu 47: Cho tam giác ABC có



2;3, 1; 2, 5;4.ABC

Đường trung trực trung tuyến AM có

phương trình tham số

A.

2

32.











x

t

B.

24

32.

 









x

t

yt

C.

2

23.







 



xt

yt

D.

2

32.











x

yt

Câu 48: Cho hai điểm



2;3 ; 4; 1 .AB viết phương trình trung trực đoạn AB.

A.

10.xy

B.

2310.xy

C.

2350.xy

D.

3210.xy

Câu 49: Đường thẳng đi qua cắt ; tại

M

,

N

sao cho

I

là trung điểm của

M

N

.

Khi đó độ dài

M

N

bằng

A.

52

. B. 13 . C. 10 . D. 213.

Câu 50: Cho tam giác

A

BC

với





2; 4A

; ; . Trung tuyến đi qua điểm nào dưới

đây?

A. . B. . C. . D. .

Câu 51: Cho đường thẳng : , : ,





3

d

:

3410xy

. Viết

phương trình đường thẳng



d

đi qua giao điểm của



1

d

,





2

d

và song song với





3

d

.

A.

24 32 53 0xy

. B.

24 32 53 0xy

.

C.

24 32 53 0xy

. D.

24 32 53 0xy

.

Câu 52: Cho tam giác

A

BC

có













1; 2; 0;2; 2;1ABC 

. Đường trung tuyến

B

M có phương trình

là:

A.

5360xy

B.

35100xy

C.

360xy

D.

320xy

Câu 53: Cho tam giác

A

BC

với



2; 1 ; 4;5 ; 3;2ABC

. Phương trình tổng quát của đường cao đi

qua

A

của tam giác là

A.

3710xy

B.

73130xy

C.

37130xy 

D.

73110xy



d





3; 2I

Ox

Oy





2;1B





5; 0C

CM

9

14;

2







5

10;

2













7; 6





1; 5

3





1

d

3250xy



2

d

2470xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 19. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

I. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG

1. Vectơ pháp tuyến của đường thẳng

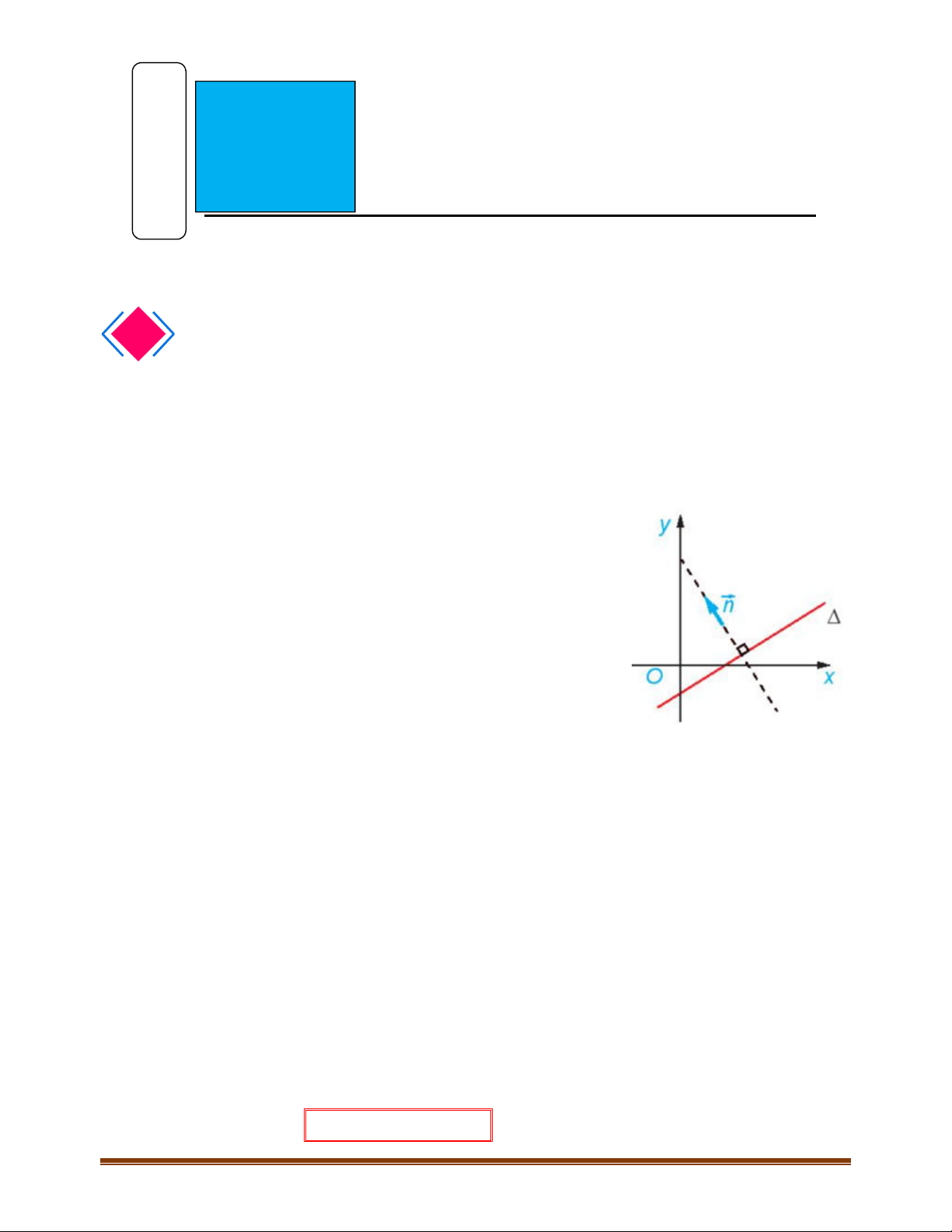
1.1. Định nghĩa: Vectơ

0n ¹



gọi là vectơ pháp tuyến (VTPT) của D nếu giá của nó

vuông góc với

D

.

1.2. Nhận xét:

a) Nếu

n



là một vtpt của đường thẳng

d

thì





., 0kn k



cũng là một vtpt của

d

.

b) Nếu

n



là một VTPT của đường thẳng

d

và

u



là một VTCP của đường thẳng

d

thì

.0nu



.

c) Một đường thẳng xác định khi biết một VTPT và mộ điểm nó đi qua.

2. Phương trình tổng quát (PTTQ) của đường thẳng

Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát dạng

0ax by c

, với

a

và

b

không đồng thời bằng

0

. Ngược lại, mỗi phương trình dạng

0ax by c

, với

a

và

b

không đồng thời bằng

0

, đều là phương trình của một đường

thẳng, nhận





;nab



là một vectơ pháp tuyến.

2.1. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có VTPT





A; Bn 



thì có phương trình

tổng quát là









00

0Ax x By y 

.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

2.2.

Ngược lại, trong mặt phẳng với hệ tọa độ

Oxy

mọi phương trình dạng





22

00Ax By C A B 

đều là phương trình tổng quát của đường thẳng d có

VTPT





A; Bn 



.

2.3. Một số trường hợp đặc biệt của PTTQ





22

00Ax By C A B 

.

a) Nếu

0A 

phương trình trở thành

0

C

By C y

B



đường thẳng song

song với trục hoành

Ox và cắt trục tung

Oy

tại điểm

0;

C

M

B









.

b) Nếu

0B 

phương trình trở thành

0

C

Ax C x

A



đường thẳng song

song với trục tung

Oy

và cắt trục hoành

Ox

tại

;0

C

M

A









.

c) Nếu

0C 

phương trình trở thành

0Ax By

đường thẳng đi qua gốc tọa độ



0;0O

.

d) Đường thẳng có dạng

yaxb

, (trong đó

a

được gọi là hệ số góc của đường

thẳng ) có VTPT là





;1na



. Ngược lại đường thẳng có VTPT





;nAB



thì có

hệ số góc là

A

B



.

e) Đường thẳng

d

đi qua điểm





;0

A

a

và





0;Bb

có phương trình là 1.

xy

ab



II. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG

1. Véc tơ chỉ phương của đường thẳng

1.1. Định nghĩa

Vectơ 0u ¹



được gọi là vectơ chỉ phương (VTCP) của đường thẳng D

nếu giá của nó song song hoặc trùng với

D .

1.2. Nhận xét:

a) Nếu

u



là một vtcp của đường thẳng

d

thì





., 0ku k



cũng là một véc tơ chỉ

phương của

d

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

b) Một đường thẳng xác định khi biết một vtcp và một điểm mà nó đi qua.

2. Phương trình tham số của đường thẳng

Cho đường thẳng



đi qua điểm



00

;

A

xy

và có vectơ chỉ phương





;uab



. Khi đó

điểm





;

M

xy

thuộc đường thẳng



khi và chỉ khi tồn tại số thực t sao cho

A

Mtu



,

hay

0

x

xat

yy bt











(2)

Hệ (2) được gọi là phương trình tham số của đường thẳng

 (t là tham số).

2.1. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có vtcp



;uab



thì có phương trình

tham số là

0

x

xat

yy bt











. ( Mỗi điểm

M

bất kỳ thuộc đường thẳng



d

tương ứng với

duy nhất một số thực

t 

và ngược lại).

Nhận xét

:



00

(;),tAAxatybtÎD + + Î

2.2. Trong mặt phẳng với hệ tọa độ

Oxy

, mọi phương trình dạng

0

x

xat

yy bt











với

22

0ab

đều là phương trình của đường thẳng

d

có một vtcp là





;uab



.

3. Phương trình chính tắc của đường thẳng

Đường thẳng

d

đi qua điểm





00

;

M

xy

và có vtcp





;uab



với

0, 0ab

có

phương trình chính tắc là:

00

x

xyy

ab





III. LIÊN HỆ GIỮA VTCP VÀ VTPT

1.

Từ nhận xét “Nếu

n



là một VTPT của đường thẳng

d

và

u



là một VTCP của đường thẳng

d

thì

.0nu



” ta rút ra được: nếu





;nAB



là một VTPT của đường thẳng

d

thì một VTCP

của

d

là





;uBA



( hoặc





;uBA



).

2. Từ nhận xét “Nếu

n



là một VTPT của đường thẳng

d

và

u



là một VTCP của đường thẳng

d

thì

.0nu



” ta rút ra được: nếu





;uab



là một VTCP của đường thẳng

d

thì một VTPT

của

d

là





;nba



(hoặc





;nba



).

Hai nhận xét trên giúp ích rất nhiều trong việc chuyển đổi qua lại giữa các dạng phương trình

đường thẳng. Từ PTTQ ta có thể chuyển sang PTTS và ngược lại.

7.1.

Trong mặt phẳng tọa độ, cho

  

2;1 , 3;2 , 1;3 , 2;1 .nv AB 



BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

a) Lập phương trình tổng quát của đường thẳng

1

 đi qua

A

và có vectơ pháp tuyến

.n



b) Lập phương trình tham số của đường thẳng

2

 đi qua

B

và có vectơ chỉ phương

.v



c) Lập phương trình tham số của đường thẳng

.

A

B

Lời giải

a) Phương trình tổng quát của đường thẳng

1



đi qua

A

và có vectơ pháp tuyến n



là

2( 1) ( 3) 0 2 5 0.   xy xy

b) Phương trình tham số của đường thẳng

2

 đi qua

B

và có vectơ chỉ phương

v



là

2

23

:

12.

 











x

t

yt

c) Lập phương trình tham số của đường thẳng

.

A

B

Đường thẳng

A

B

đi qua điểm

A

và có vectơ chỉ phương





3; 2AB  



là

13

32.











x

t

yt

7.2. Lập phương trình tổng quát của các trục tọa độ.

Lời giải

- Phương trình trục

Ox

đi qua điểm





0;0O

và nhận (0;1)j 



làm vectơ pháp tuyến có

phương trình là

0.y

- Phương trình trục

Oy

đi qua điểm





0;0O và nhận

(1; 0)i 



làm vectơ pháp tuyến có phương

trình là

0.x

7.3. Cho hai đường thẳng

1

12

:

35

x

t

yt













và

2

:2x 3y 5 0.

a) Lập phương trình tổng quát của

1

.

b) Lập phương trình tham số của

2

.

Lời giải

a) Lập phương trình tổng quát của

1

.

Đường thẳng

1

 đi qua điểm



1; 3M

, có vectơ chỉ phương





2,5u 



nên

1

 có vectơ pháp

tuyến là

(5; 2).n



Khi đó phương trình tổng quát của

1

 là:

5210.xy

b) Lập phương trình tham số của

2

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

Đường thẳng

2



đi qua điểm





1; 1N , có vectơ pháp tuyến là

(2;3)n 



nên

2



có vectơ chỉ

phương





3; 2 .u



Khi đó phương trình tham số của

2

 là:

13

12.











x

t

yt

7.4. Trong mặt phẳng tọa độ, cho tam giác

A

BC

có









1; 2 , 3; 0AB

và





2; 1 .C 

a) Lập phương trình đường cao kẻ từ

.

A

b) Lập phương trình đường trung tuyến kẻ từ

B.

Lời giải

a) Lập phương trình đường cao kẻ từ

.

A

Đường cao kẻ từ

A

đi qua





1; 2A và nhận





5;1CB 



là vectơ pháp tuyến có phương trình là

570.xy

b) Lập phương trình đường trung tuyến kẻ từ

B.

Gọi

M

là trung điểm của

A

C

thì

11

;

22

M









.

Đường trung tuyến kẻ từ

B

nhận

71

;

22

MB











là vectơ chỉ phương nên có vectơ pháp

tuyến là

(1; 7)n 



và đi qua





3; 0B

nên có phương trình là:

730xy

.

7.5. (Phương trình đọan chắn của đường thẳng )

Chứng minh rằng, đường thẳng đi qua hai điểm



a;0 , 0;bAB

với





0.7.3ab H

có phương

trình là

1.

xy

ab

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

Lời giải

Đường thẳng đi qua hai điểm



a;0 , 0;bAB

nhận





;

A

Bab



làm vectơ chỉ phương thì có

vectơ pháp tuyến là





;.nba



Khi đó phương trình đường thẳng là:

0.bx ay ab

Vì

0ab 

nên chia cả hai vế của phương trình cho

ab

ta được phương trình là

1

xy

ab



.

7.6. Theo Google Maps, sân bay Nội Bài có vĩ độ là

0

21,2

Bắc, kinh độ

0

105,8

Đông, sân bay Đà

Nẵng có vĩ độ là

0

16,1 Bắc, kinh độ

0

108,2 Đông. Một máy bay, bay từ Nội Bài đến sân bay

Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ

0

x

Bắc, kinh độ

0

y Đông được tính theo công thức

153

21,2

40

9

105,8

5

x

t

yt

















a) Hỏi chuyến từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm

1

giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến

17

(

0

17

Bắc) chưa?

Lời giải

a) Hỏi chuyến từ Hà Nội đến Đà Nẵng mất mấy giờ?

Thay

0

16,1x  ,

0

108,2y  vào công thức trên ta có

153

16,1 21, 2

4

40

9

3

108,2 105,8

5

t



















Vậy chuyến bay từ Hà Nội đến Đà Nẵng mất

4

3

giờ.

b) Tại thời điểm

1

giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến

17

(

0

17

Bắc) chưa?

Tại thời điểm 1 giờ kể từ lúc cất cánh thì máy bay đã bay đến

0

17,375 Bắc nên máy bay đã bay

qua vĩ tuyến

17

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7

DẠNG 1: XÁC ĐNNH VTCP, VTPT CỦA ĐƯỜNG THẲNG

{ Tích vô hướng hai vt, góc giữa hai vt, độ dài vt, độ dài đường trung tuyến, phân giác,đường cao, diện

tích tam giác, chu vi tam giác…}

1.

Trong mặt phẳng với hệ tọa độ

Ox

y

phương trình dạng





22

00Ax By C A B 

có VTPT





A;Bn 



.

2. Trong mặt phẳng với hệ tọa độ

Ox

y

, mọi phương trình dạng

0

x

xat

yy bt











với

22

0ab

đều là phương trình của đường thẳng

d

có một vtcp là





;uab



.

3. Nếu đường thẳng

d

có





;nAB



là một VTPT thì một VTCP của d là



;uBA



(hoặc





;uBA



).

4. Nếu đường thẳng

d

có





;uab



là một VTCP thì một VTPT của

d

là





;nba



(hoặc





;nba



).

5. Đường thẳng đi qua 2 điểm

,

A

B

thì nhận

A

B



làm VTCP.

Câu 1:

Một vectơ chỉ phương của đường thẳng

23

3

x

t

yt







 



là:

A.





1

2; –3 .u 



B.





2

3; –1 .u 



C.





3

3; 1 .u 



D.





4

3; –3u 



Lời giải

Chọn B

Từ phương trình tham số của đường thẳng ta có một VTCP của đường thẳng là





2

3; –1 .u 



Câu 2: Một vectơ pháp tuyến của đường thẳng

2360xy

là :

A.





4

2; 3n 



B.





2

2;3n 



C.





3

3; 2n 



D.





1

3; 2n 



Lời giải

Chọn A

HỆ THỐNG BÀI TẬP.

II

PHƯƠNG PHÁP.

1

BÀI TẬP TRẮC NGHIỆM.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

Từ PTTQ ta thấy một VTPT của đường thẳng là





4

2; 3n 



Câu 3: Vectơ chỉ phương của đường thẳng

1

32

xy



là:

A.





4

2;3u 



B.





2

3; 2u 



C.





3

3; 2u 



D.





1

2;3u 



Lời giải

Chọn B

12360

32

xy

xy  

nên đường thẳng có VTPT là





2;3n 



.

Suy ra VTCP là





3; 2u 



.

Câu 4:

Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm





3; 2A 

và





?1; 4B

A.





1

1; 2 .u 



B.





2

2.;1u 



C.



3

2;6 .u 



D.



4

1; 1 .u 



Lời giải

Chọn B

Ta có





4; 2AB 



một VTCP của đường thẳng

A

B

cùng phương với





4; 2AB 



.

Ta thấy



2

1

2

2;1uAB

 

vậy





2

2;1u 



là một VTCP của

A

B

Câu 5: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm





2;3A và





4;1 ?B

A.





1

22.;n 



B.





2

2; 1 .n 



C.





3

1.;1n 



D.





4

1; 2 .n 



Lời giải

Chọn C

Ta có



2; 2AB 



một VTPT

n



của đường thẳng

A

B thì vuông góc với

A

B

Suy ra



.0.2.20nAB x y   



chọn



1, 1 1;1xy n



Chú ý: Ta hoàn toàn có thể dùng nhận xét nêu ở mục 2.3.2 để giải quyết nhanh bài toán này.

Câu 6: Cho phương trình:





01ax by c

với

22

0ab

. Mệnh đề nào sau đây sai?

A.



1

là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là



;



nab.

B.

0a



1

là phương trình đường thẳng song song hoặc trùng với trục

ox

.

C.

0b



1

là phương trình đường thẳng song song hoặc trùng với trục

o

y

.

D.

Điểm





000

;

M

xy

thuộc đường thẳng



1

khi và chỉ khi

00

0ax by c

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9

Chọn D

Ta có điểm





000

;

M

xy thuộc đường thẳng



1 khi và chỉ khi

00

0ax by c

.

Câu 7: Mệnh đề nào sau đây sai? Đường thẳng



d được xác định khi biết.

A.

Một vecto pháp tuyến hoặc một vec tơ chỉ phương.

B. Hệ số góc và một điểm thuộc đường thẳng.

C.

Một điểm thuộc



d

và biết



d

song song với một đường thẳng cho trước.

D.

Hai điểm phân biệt thuộc



d

.

Lời giải

Chọn A.

Nếu chỉ có vecto pháp tuyến hoặc một vecto chỉ phương thì thiếu điểm đi qua để viết đường

thẳng.

Câu 8: Đường thẳng



d

có vecto pháp tuyến



;



nab. Mệnh đề nào sau đây sai?

A.





1

;



uba là vecto chỉ phương của



d

.

B.



2

;



uba là vecto chỉ phương của



d

.

C.



;







nkakbkR

là vecto pháp tuyến của



d .

D.



d

có hệ số góc



0





b

kb

a

.

Lời giải

Chọn D.

Phương trình đường thẳng có vecto pháp tuyến



;



nab là



00

ac

ax by c y x b

bb

  

Suy ra hệ số góc

a

k

b



.

Câu 9: Cho đường thẳng (d):

2340xy

. Vecto nào sau đây là vecto pháp tuyến của (d)?

A.





1

3; 2



n

.

B.





2

4; 6 



n

.

C.



3

2; 3



n

.

D.



4

2;3



n

.

Lời giải

Chọn B.

Ta có

    

:2 3 4 0 2;3 4; 6dxy VTPTn  



Câu 10: Cho đường thẳng



:3 7 15 0dxy. Mệnh đề nào sau đây sai?

A.





7;3



u là vecto chỉ phương của



d

.

B.



d

có hệ số góc

3

7

k

.

C.



d

không đi qua góc tọa độ.

D.



d

đi qua hai điểm

1

;2

3









M

và





5; 0N

.

Lời giải

Chọn D.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

Giả sử









5;0 :3 7 15 0 3.5 7.0 15 0Ndxy vl   

.

Câu 11: Cho đường thẳng



23

:

12







 



x

t

d

yt

và điểm

7

;2.

2









A

Điểm







A

d ứng với giá trị nào của

t?

A.

3

.

2

t

B.

1

.

2

t

C.

1

.

2

t

D. 2t 

Lời giải

Chọn C

Ta có



1

7

23

71

2

;2

2

1

22

212

2

t

Ad t

t















   



















Câu 12: Cho



23

:

54











x

t

d

yt

. Điểm nào sau đây không thuộc





?d

A.





5;3 .A B.





2;5 .B C.





1; 9 .C D.





8; 3 .D

Lời giải

Chọn B.

Thay



223 0

2;5 0

554 0

tt

B

t

tt

 







 



Câu 13: Một đường thẳng có bao nhiêu vectơ chỉ phương?

A. 1. B. 2. C. 3. D. Vô số.

Lời giải

Chọn D

Câu 14: Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 1 B. 2 C. 3 D. Vô số.

Lời giải

Chọn D

Câu 15: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng

2

:

16

x

d

yt







 



?

A.





1

6;0u 



. B.





2

6;0u 



. C.





3

2;6u 



. D.





4

0;1u 



.

Lời giải

Chọn D

Từ PTTS ta thấy một VTCP của

d

là









0;6 6 0;1u 



nên ta có thể chọn một VTCP là

()

4

0;1u =





Câu 16: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng

1

5

:

2

33

x

t

y

t













 



?

A.





1

1; 3u 



B.

2

1

;3

2

u











C.

2

23

xy



D.

6280xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11

Lời giải

Chọn D

Từ PTTS ta thấy một VTCP của



là



1

;3 2 1; 6

2

uu



   







nên ta có thể chọn một

VTCP là

()

4

1; 6u =-





Câu 17: Cho đường thẳng



có phương trình tổng quát: . Vectơ nào sau đây là vectơ chỉ

phương của đường thẳng .

A. B. C. D.

Lời giải

Chọn A

Từ PTTQ ta thấy một VTPT của là suy ra một VTCP là

Câu 18: Cho đường thẳng có phương trình tổng quát: . Vectơ nào sau đây không là

vectơ chỉ phương của

A. B. C. D.

Lời giải

Chọn C

Từ PTTQ của đường thẳng ta thấy một VTPT là suy ra một VTCP của đường thẳng

là vậy vec tơ có tọa độ không phải là VTCP của .

Câu 19: Đường thẳng

:5 3 15xy

tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu?

A.

7,5

. B.

5

. C.

15

. D.

3

.

Lời giải

Chọn A





3; 0Ox A 

,



0;5Oy B 

.

Vậy

115

7,5

22

OAB

SOAOB





.

DẠNG 2: VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG THỎA MÃN MỘT SỐ TÍNH CHẤT CHO

TRƯỚC

{ Tính chất cho trước giúp tìm được: một điểm thuộc đường thẳng và một VTCP (hay VTPT);

tìm được các hệ số A, B, C trong phương trình tổng quát; …}

–2 3 –1 0xy







3; 2 .





2;3 .





–3;2 .





2; –3 .







2;3n 







3; 2u 





–2 3 –1 0xy



2

1;

3

.











3; 2 .





2;3 .





–3; –2 .





2;3n 



  

2

3; 2 1 3; 2 3 1;

3

u















2;3



PHƯƠNG PHÁP.

1

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

1.

Đường thẳng d đi qua điểm





00

;

M

xy và có vtcp





;uab



thì có phương trình tham

số là

0

x

xat

yy bt











. ( Mỗi điểm

M

bất kỳ thuộc đường thẳng



d tương ứng với duy nhất

một số thực

t  và ngược lại).

2. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có vtcp





;uab



với

0, 0ab

có

phương trình chính tắc là:

00

x

xyy

ab





3. Đường thẳng

d

đi qua điểm





00

;

M

xy

và có VTPT





A;Bn 



thì có phương trình

tổng quát là









00

0Ax x By y 

.

2.1. Viết PTTS của đường thẳng.

Câu 1:

Viết phương trình tham số của đường thẳng  qua





3; 1A 

và có VTCP





2;3u 



.

Lời giải

Đường thẳng

 qua





3; 1A 

và có VTCP





2;3u 



có PTTS là





32

13

xt

x

t

yt















 





Câu 2: Viết PTTS của đường thẳng

A

B biết









3;1 , 1; 3AB

.

Lời giải

Ta có

  

4; 2 2 2; 1 2; 1AB u     



là một VTCP của đường thẳng

A

B

.

Vậy

AB

đi qua





3;1A

và có VTCP





2; 1u 



nên có PTTS

32

1

x

t

yt











.

Lưu ý. Ta hoàn toàn có thể dùng



4; 2AB 



làm VTCP của đường thẳng

A

B

.

Câu 3: Viết PTTS của đường thẳng



qua





1; 7M  và song song với trục .Ox

Lời giải

Ta thấy trục hoành

Ox

có VTCP chính là vec tơ đơn vị





1; 0i 



. Vì đường thẳng  song song

với trục hoành

Ox nên cũng nhận





1; 0i 



làm VTCP. Suy ra phương trình tham số của



là

1

7

x

t

y

 









Nhận xét. Hai đường thẳng song song có cùng VTCP.

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

Câu 4:

Cho đường thẳng

2

:

35

x

y

d







. Viết PTTS của đường thẳng qua và song

song với đường thẳng .

Lời giải

Ta thấy đường thẳng có một VTCP là , vì đường thẳng nên cũng nhận

làm VTCP. Vậy PTTS của là .

Câu 5: Cho và . Viết PTTS của đường thẳng là trung trực của đoạn thẳng .

Lời giải

Gọi là trung điểm của đoạn thẳng suy ra . Đường trung trực của đoạn thẳng

đi qua





0;3I và có một VTPT là



6; 4AB 



nên có một VTCP là





2;3u 



. Vậy PTTS của

A

B là

2

33

x

t

yt











.

2.2. Viết PTTQ của đường thẳng

Câu 1:

Viết PTTQ của đường thẳng

d

đi qua



1; 5K  và có VTPT





2;1n 



.

Lời giải

d

đi qua



1; 5K  và có VTPT





2;1n 



có PTTQ là









21150xy  

230xy

Câu 2: Viết PTTQ của đường thẳng



đi qua





3; 2K  và song song với đường thẳng

: 5 2017 0dx y 

.

Lời giải

Đường thẳng

d

có một VTPT là





1; 5n 



, vì

//d

nên  cũng nhận





1; 5n 



làm một

VTPT vậy PTTS của



là









135 20 5130xy xy  

Lưu ý.

Ta hoàn toàn có thể giải theo cách khác như sau.

Vì

//d

nên

, d

có cùng VTCP, PTTQ của  có dạng





5 0 2017xyC C 

, mà  đi

qua





3; 2K 

nên ta có



35 2 0 13CC

Câu 3: Viết PTTQ của  là đường trung trực của đoạn thẳng

A

B với



4; 1 , 2;3AB

.

Lời giải

Gọi I là trung điểm của đoạn thẳng



1; 1AB I

,









6; 4 2 3; 2AB 



vì

A

B nên 

có một VTPT là





3; 2n 



vậy PTTQ của  là



312103210xy xy   





2017;2018I

d





3; 5u 



//d







3; 5u 





2017 3

2018 5

x

t

yt













3;1A





3; 5B 



A

B

IAB



0;3I

AB

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

Câu 4:

Viết PTTQ của đường thẳng qua hai điểm





5; 0A

và



0; 2B 

.

Lời giải

Phương trình đường thẳng

A

B là

1251025100

52

xy

xy xy



.

Câu 5: Cho tam giác

A

BC

có













2; 1 ; 4;5 ; 3; 2ABC

. Viết phương trình tổng quát của đường cao

AH

của tam giác

A

BC

.

Lời giải

Gọi

A

H

là đường cao của tam giác.

A

H

đi qua





2; 1A  và nhận









7; 3 7;3BC   



làm VTPT









:7 2 3 1 0 7 3 11 0AH x y x y

2.3. Bài toán chuyển đổi qua lại giữa các dạng phương trình.

Câu 1:

Cho đường thẳng

12

3

x

t

yt













. Viết PTTQ của đường thẳng.

Lời giải

Cách 1.

Từ phương trình tham số ta thấy



đi qua





1; 3M

và có





2;1u 



suy ra VTPT là





1; 2n 



,

PTTQ là









112 30 270xy xy   

.

Cách 2.

12 12

27 270

3262

xtxt

xy xy

yt y t

 



 



 



.

Câu 2: Cho đường thẳng

:2 3 3 0xy

. Viết PTTS của đường thẳng.

Lời giải

Cách 1.

Để tìm một điểm mà ĐT đi qua ta cho

x

một giá trị bất kỳ tính y hoặc ngược lại.

Cho

0x 

thế vào PT đt  ta được.

330 1yy

vậy đt  đi qua điểm





0; 1A 

. Và

có VTPT





2; 3n 



suy ra VTCP





3; 2u 



. Vậy PTTS của  là

3

12

xt

yt







 



.

Cách 2.

Từ PTTQ

2

:2 3 3 0 3 2 3 1

3

xy y

x

y

x

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15

Đặt

x

t ta thu được PTTS là

2

1

3

xt

yt















2.4. Bài tập tổng hợp về viết phương trình đường thẳng

Câu 1: Cho tam giác

A

BC với

  

2;3 ; 4;5 ; 6; 5AB C.

,

M

N

lần lượt là trung điểm của

A

B

và

A

C . Phương trình tham số của đường trung bình

M

N là:

Lời giải

Ta có:









1; 4 ; 4; 1MN

.

M

N

đi qua





1; 4M 

và nhận





5; 5MN 



làm

VTCP

15

:

45

x

t

MN

yt

 











Câu 2: Phương trình đường thẳng đi qua điểm





5; 3M và cắt hai trục tọa độ tại hai điểm A và B sao

cho M là trung điểm của AB là:

Lời giải

Gọi









;0 ; 0;

A

B

A

Ox A x B Oy B y 

Ta có

M

là trung điểm

A

B

210

26

AB M A

AB M B

xx x x

yy y y

 







 



Suy ra



:135300

10 6

xy

AB x y



.

Câu 3: Cho ba điểm













1;1 ; 2; 0 ; 3; 4AB C

. Viết phương trình đường thẳng đi qua

A

và cách đều

hai điểm

,

B

C

.

Lời giải

Gọi



d là đường thẳng đi qua

A

và cách đều

,

B

C

. Khi đó ta có các trường hợp sau

TH1:

d

đi qua trung điểm của

BC

.

5

;2

2

I







là trung điểm của

BC

.

3

;1

2

AM











là VTCP

của đường thẳng

d

. Khi đó

    

:2 1 3 1 0dx y 

2310xy   

.

TH2:

d

song song với

BC

, khi đó

d

nhận





1; 4BC 



làm VTCP, phương trình đường thẳng

  

:4 1 1 0dxy

430xy   

.

Câu 4: Đường thẳng

:1

xy

d

ab



, với

0a 

,

0b 

, đi qua điểm





1; 6M 

và tạo với các tia

Ox

,

Oy

một tam giác có diện tích bằng

4

. Tính

2Sa b

.

Lời giải

:1

x

y

d

ab



đi qua điểm





1; 6M 



16

11

ab





.

Đường thẳng

:1

x

y

d

ab



tạo với các tia

Ox

;

Oy

tam giác có diện tích bằng

4



82ab

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

Từ



1

;



2

16

1

8

ab



















16

1

8

ab



















6

1

8

b

ab



















4

2

b

a













(nhận) hoặc

12

3

2

b

a















(Loại)

210ab 

.

Câu 5: Cho tam giác

ABC

biết trực tâm



1; 1H

và phương trình cạnh

:5 2 6 0AB x y

, phương

trình cạnh

:4 7 21 0AC x y

. Phương trình cạnh

BC

là

Lời giải

Phương trình

:5 2 6 0AB x y



5; 2

AB

n



.

Phương trình

:4 7 21 0AC x y



4; 7

AC

n



.

Ta có

BH AC



.0 7;4

BH AC BH

nn n

  

.

Suy ra phương trình đường thẳng

BH

có



VTPT 7; 4

qua 1;1

BH

n

H















.



:7 1 4 1 0 7 4 3 0BH x y x y   

.

Ta có điểm

B

là giao điểm của hai đường thẳng

AB

và

BH

, suy ra tọa độ điểm

B

là nghiệm

của hệ phương trình

5

5260

19

7430

2

x

xy

y

























19

5;

2

B









.

Ta lại có



.0 2;5

CH AB CH

CH AB n n n  

  

.

Suy ra phương trình đường thẳng

CH

có



VTPT 2; 5

qua 1;1

CH

n

H















.



:2 1 5 1 0 2 5 7 0CH x y x y   

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17

Ta có điểm

C

là giao điểm của hai đường thẳng

A

C

và

CH

, suy ra tọa độ điểm

C

là nghiệm

của hệ phương trình

28

47210

3

2570 7

3

x

xy

y





























28 7

;

33

C









.

Ta có

43 43

;

36

BC















1; 2

BC

n



.

Phương trình cạnh

B

C

có



VTPT 1; 2

28 7

qua ;

33

BC

n

C























.

28 7

:2 02140

33

BC x y x y



 





.

Vậy

:2140BC x y

.

Câu 6: Gọi

H

là trực tâm của tam giác

A

BC

. Phương trình các cạnh và đường cao của tam giác là

A

B

:

740xy

;

B

H

:

240xy

;

A

H

:

20xy

. Phương trình đường cao

CH

của tam giác

A

BC

là

Lời giải

Gọi



;

H

xy

.

Ta có

H

AH BH

.

Nên tọa độ điểm

H

là nghiệm của hệ phương trình:

24

2

xy











2

0

x

y













, suy ra





2;0H .

Đường thẳng

A

B

có vectơ chỉ phương là





1; 7u 



.

Đường cao

CH

vuông góc với cạnh

A

B

nên nhận

u



làm vectơ pháp tuyến.

Vậy phương trình tổng quát của đường cao

CH

là



27 00xy 

720xy 

.

H

A

C

B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18

Câu 7:

Trong mặt phẳng với hệ trục tọa độ

Ox

y

, cho hai đường thẳng

1

:10,xy

2

:2 1 0xy

và điểm





2;1P .Viết phương trình đường thẳng đi qua điểm

P

và cắt hai

đường thẳng

1



,

2



lần lượt tại hai điểm

A

,

B

sao cho P là trung điểm

A

B .

Lời giải

Ta có





12

0;1I  .

Vì





1

;1AAaa   . Vì





2;1P là trung điểm của đoạn

A

B





4;1Baa.

Mặt khác

2

8811

;

333

BaA



   





28

;

33

AP











Đường thẳng

:2 5 0AP x y

có pt là:

470xy

.

Câu 8: Trong mặt phẳng tọa độ vuông góc

Oxy

, cho hai đường thẳng

1

d và

2

d lần lượt có phương

trình:

12

:1, :330dxy dx y  

. Hãy viết phương trình đường thẳng d đối xứng với

2

d

qua đường thẳng

1

d .

Lời giải

Gọi





12

;

I

xy d d

. Khi đó tọa độ điểm I là nghiệm của hệ phương trình



10

0;1 .

330 1

xy x

I

xy y

 







 



Chọn





2

3; 0

M

d

. Gọi



đi qua

M

và vuông góc với

1

d .

Suy ra



có dạng

0xyc

.

Vì





3; 0 3Mc

:30xy   

Gọi



1

;Hxy d

. Khi đó tọa độ điểm H là nghiệm của hệ phương trình

30

1

xy











1

2

x

y















1; 2 .H

Gọi

N

là điểm đối xứng của

M

qua

1

d . Khi đó H là trung điểm của

.

M

N

21

24

NHM

xxx

yyy

















1; 4 .N

Vậy đường thẳng

d

chính là đường thẳng

IN

, ta có

01

310

13

xy





.

Câu 9: Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho

Δ

A

BC

có đỉnh





3; 0A

và phương trình hai

đường cao



':2 2 9 0BB x y

và



':3 12 1 0CC x y

. Viết phương trình cạnh

BC

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19

Gọi





;

H

xy

là trực tâm của tam giác

Δ

A

BC

. Khi đó tọa độ điểm





;

H

xy

là nghiệm của hệ

phương trình

2290

31210

xy











11

3

5

6

x

y



















11 5

;.

36

H









Phương trình cạnh

A

C

đi qua





3; 0A

và vuông góc với

B



nên





A

C

có dạng

22 0xyc

.

Vì









3; 0

A

AC

nên

60 6.cc

Do đó





:2 2 6 0 3 0AC x y x y

.

Ta có

CACCC





nên tọa độ điểm





;Cxy

là nghiệm của hệ phương trình

31210

30

xy











35

9

8

9

x

y



















35 8

;.

99

C









Phương trình cạnh

BC

đi qua điểm

35 8

;

99

C







nhận



25 1

;4;5.

36 6

AH











làm véctơ pháp

tuyến





:4 5 20 0.BC x y

Câu 10: Cho tam giác

A

BC

, đỉnh





2; 1B 

, đường cao

:3 4 27 0AA x y





và đường phân giác trong

của góc

C

là

:250CD x y

. Khi đó phương trình cạnh AB là

Lời giải

Phương trình cạnh BC đi qua





2; 1B  và vuông góc với

A



là

4350.xy

Gọi





;Cxy

, tọa độ điểm





;Cxy

thỏa mãn

250

4350

xy











1

3

x

y















1; 3C

Gọi

M

là điểm đối xứng của

B

qua

CD

. Khi đó tọa độ điểm





;

M

xy

thỏa mãn



22 10

21

250

22

xy





















250

2100

xy

















4;3 .M

Phương trình cạnh

A

C chính là

M

C , ta có

:3.AC y 

Gọi





;

A

xy

, tọa độ điểm





;

A

xy

thỏa mãn

34270

3

xy

y











5

3

x

y

















5;3 .A

Phương trình cạnh

A

B là

53

4710.

74

xy







Câu 11: Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc

Ox

y

, cho

A

BC có điểm





2; 1A 

và hai đường phân giác trong của hai góc

,

B

C

lần lượt có phương trình





:210,

B

xy





:30

C

xy

. Viết phương trình cạnh

BC

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

+) Gọi





;

H

Hx

y

là hình chiếu của điểm

A

lên

B



.0.

BB

AH u AH u



 

   

Ta có



21; ;

HHB

Hy y









23;1; 2;1.

B

HH

AH y y u



 

 

.0

B

AH u





 









22 3 1 0

HH

yy





11;1.

H

yH

Gọi

M

là điểm đối xứng của A qua

B

 .

Khi đó

H là trung điểm của

A

M

20

23

MHA

xxx

yyy

















0;3 .M

+) Gọi



;

K

xy

là hình chiếu của điểm

A

lên

C

 .0.

CC

AK u AK u



 

   

Ta có





;3;

KK C

Kx x









2; 2 ; 1; 1 .

C

KK

AK x x u



 

 

.0

C

ADK u





 

220 0

KK K

xx x





0; 3 .K

Gọi

N

là điểm đối xứng của

A

qua

C

 .

Khi đó

K là trung điểm của

A

N

22

25

NKA

MKA

xxx

yyy















2; 5 .N

Phương trình đường thẳng

BC

chính là phương trình đường thẳng

M

N

.

 đường thẳng

BC

:

03

430

28

xy







Câu 12: Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc

Oxy

, cho

A

BC

vuông cân tại





4;1A

và cạnh huyền

BC

có phương trình:

350xy

. Viết phương trình hai cạnh góc

vuông

A

C

và

.

A

B

Lời giải

Cách 1:

Viết phương trình đường thẳng đi qua A tạo với đường thẳng

BC

một góc

45 .

Cách 2:

C'

B

'

K

H

N

M

A

B

C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

Gọi





;

H

xy

là hình chiếu của





4;1A

lên

BC

.

d

đi qua





4;1A

và vuông góc với

BC

nên

d

có dạng

30.xyc

Vì





4;1 7 0 7Adcc

nên

:370.dx y

Khi đó tọa độ điểm





;

H

xy là nghiệm của hệ phương trình

350

370

xy











4

5

13

5

x

y



















413

;.

55

H









Vì

A

BC vuông cân tại

A

nên

,,

A

BC

thuộc đường tròn





C ngoại tiếp

A

BC có tâm

413

;

55

H









và bán kính

810

.

5

RAH

Phương trình đường tròn





C

:

22

4 13 128

.

555

xy

 

 

 

 

Tọa độ điểm

,

B

C

là nghiệm của hệ phương trình

22

350

4 13 128

555

xy









 

 

 



 



22

35

4 13 128

35

555

yx

xx











 

 

 



 



2

35

25 40 48 0

yx

xx













437

55

12 11

55

xy











  





Suy ra 2 điểm

437 12 11

;; ;

55 5 5

BC

 



 

 

hoặc

437 12 11

;; ; .

55 5 5

CB

 



 

 

Vậy phương trình hai cạnh

AB

và

A

C

là



41

:

437

41

55

xy

AB







290xy

;



41

:

12 11

41

55

xy

AC





 

220xy 

.

Hoặc



41

:

437

41

55

xy

AC







290xy

;



41

:

12 11

41

55

xy

AB





 

220xy 

.

Câu 13: Trong mặt phẳng tọa độ

Ox

y

, cho tam giác

A

BC

vuông tại

A

, có đỉnh





4;1C 

, phân giác

trong góc

A

có phương trình

50xy

. Viết phương trình đường thẳng

BC

, biết diện tích

tam giác

A

BC

bằng 24 và đỉnh

A

có hoành độ dương.

Lời giải

Cách 1:

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 22

Gọi

D

là điểm đối xứng của





4;1C  qua đường thẳng

50xy

suy ra tọa độ điểm





;Dxy là nghiệm của

hệ phương trình









410

41

50

22

xy





















4;9 .D

Điểm

A

thuộc đường tròn đường kính

CD

nên tọa độ điểm





;

A

xy

thỏa mãn



2

50

532

xy









 





với

0,x 

suy ra điểm





4;1 .A

Ta có

1

.24

2

ABC

SABAC

2

6

ABC

S

AB

AC

 

B

thuộc đường thẳng

:4,AD x 

suy ra tọa độ





4;By thỏa mãn



2

136y 





4;7B hoặc





4; 5 .B 

Do

d

là phân giác trong góc

A

, nên

A

B



và

A

D



cùng hướng, suy ra





4;7 .B

Do đó, đường thẳng

BC

có phương trình:

3 4 16 0.xy

Cách 2:

Gọi đường thẳng

A

C

đi qua điểm





4;1C 

có véctơ pháp tuyến





22

;, 0.nabab



Vì



,45AC d 



2

cos ,

2

AC d

nn



22

2

ab







0; 1

ab

ba













Với

0; 1ba

suy đường thẳng





:40 4;9AC x A AC d A   

( loại vì 0

A

x  )

Với

0; 1ab

suy đường thẳng



:10 4;1AC y A AC d A    

.

nên tọa độ điểm





;

A

xy

thỏa mãn



2

50

532

xy









 





với

0,x 

suy ra điểm





4;1 .A

Gọi điểm





;Bxy.

Ta có

A

BC

vuông tại A nên

.0AB AC 





44;.

x

By

Lại có

1

.24

2

ABC

SABAC

2

6

ABC

S

AB

AC

 



2

136y

.

B

A

C

D

d

B

A

C

d

45

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 23





4;7B

hoặc





4; 5 .B 

Do

d

là phân giác trong góc A , nên hai điểm A và

B

nằm khác phía đối với đường thẳng

d

,

suy ra



4;7 .B

Do đó, đường thẳng

BC

có phương trình:

3 4 16 0.xy

Câu 14: Cho

A

BC

có



4; 2A 

. Đường cao

:2 4 0BH x y

và đường cao

:30CK x y

. Viết

phương trình đường cao kẻ từ đỉnh A

Lời giải

Gọi

A

I

là đường cao kẻ từ đỉnh

A

. Gọi

1

H

là trực tâm của

A

BC , khi đó tọa độ điểm

H

thỏa mãn hệ phương trình

7

240

3

30 2

3

x

xy

y





























.

1

54

;

33

AH











A

I qua

1

72

;

33

H









và nhận





4;5n 



làm VTPT

72

:4 5 0 4 5 6 0

33

AI x y x y









Câu 15: Viết Phương trình đường thẳng đi qua điểm



2; 3M

và cắt hai trục tọa độ tại hai điểm A và

B sao cho tam giác OAB vuông cân.

Lời giải

Phương trình đoạn chắn



:1

xy

AB

ab



Do

OAB

vuông cân tại

O

ba

ab

ba













TH1:

ba

1

xy

x

ya

aa



mà









2; 3 2 3 1 1MAB aab 

Vậy





:10AB x y

TH2:

ba

1

xy

x

ya

aa



mà



2; 3 2 3 5 5MAB aab 

Vậy



:50AB x y

Câu 16: Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là:

:7 4 0; :2 4 0; : 2 0  AB x y BH x y AH x y

. Phương trình đường cao CH của tam

giác ABC là:

Lời giải

Ta có

H

BH AH H

là nghiệm của hệ phương trình



240 2

2;0

20 0

xy x

H

xy y

 







 



Ta có

:7 0CH AB CH x y c 

mà



2;0 2 7.0 0 2HCH cc

Suy ra

:720CH x y

.

Câu 17: Cho tam giác

A

BC

biết trực tâm

(1;1)H

và phương trình cạnh

:5 2 6 0AB x y

, phương

trình cạnh

:4 7 21 0AC x y

. Phương trình cạnh

BC

là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 24

Lời giải

Ta có



0;3AAB AC A





1; 2AH



Ta có





:7 4 0BH AC BH x y d 

Mà

 

1; 1 3HBHd suy ra



:7 4 3 0BH x y

Có

19

5;

2

BABBH B



 





Phương trình





BC

nhận





1; 2AH 



là VTPT và qua

19

5;

2

B









Suy ra

 

19

:52 0 2140

2

BC x y x y



   





Câu 18:

Viết phương trình tham số của đường thẳng đi qua





3; 4A và có vectơ chỉ phương





3; 2u 



A.

33

24

x

t

yt







 



.

B.

36

24

x

t

yt







 



.

C.

32

43

x

t

yt











.

D.

33

42

x

t

yt











.

Lời giải

Chọn D

Phương trình tham số của đường thẳng đi qua





3; 4A

và có vectơ chỉ phương





3; 2u 



có dạng:

33

42

x

t

yt











.

Câu 19: Phương trình tham số của đường thẳng qua



1; 1M 

,



4;3N

là

A.

3

4

x

t

yt











.

B.

13

14

x

t

yt











.

C.

33

43

x

t

yt











.

D.

13

14

x

t

yt







 



.

Lời giải

Chọn D

Đường thẳng đi qua hai điểm



1; 1M 

,



4;3N

có một véctơ chỉ phương





3; 4MN 



.

Phương trình tham số của đường thẳng qua



1; 1M 

,



4;3N

là

13

14

x

t

yt







 



.

Câu 20: Phương trình tổng quát của đường thẳng đi qua



1; 2A

và nhận





1; 2



n làm véc-tơ pháp

tuyến có phương trình là

A.

20 xy

. B.

240xy

. C.

250xy

. D.

240xy

.

Lời giải

Chọn C

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 25

Phương trình đường thẳng là









112 20 xy

hay

250xy

.

Câu 21: Đường thẳng đi qua điểm



1; 2A  và nhận





2; 4n 



làm véctơ pháp tuyến có phương trình

là

A.

240xy

. B.

240xy

. C.

250xy

. D.

24 0xy 

.

Lời giải

Chọn C

Đường thẳng đi qua điểm



1; 2A  và nhận





2; 4n 



làm véctơ pháp tuyến có phương trình

là

 

214 20xy 

24100xy   

250xy 

.

Câu 22: Đường thẳng

d

qua





1; 1A

và có véctơ chỉ phương





2;3u 



có phương trình tham số là

A.

1

3

x

t

yt











.

B.

12

13

x

t

yt











.

C.

2

3

x

t

yt











.

D.

2

3

x

t

yt











.

Lời giải

Chọn B

Đường thẳng

d

qua





1; 1A

và có véctơ chỉ phương





2;3u 



có phương trình tham số là

12

13

x

t

yt











.

Câu 23: Phương trình đường thẳng đi qua hai điểm



2; 4A 

,



6;1B 

là

A.

34100xy

. B.

34220xy

. C.

3480xy

. D.

34220xy

.

Lời giải

Chọn B

Ta có





4; 3AB  



.

Đường thẳng

A

B

qua điểm



2; 4A  và nhận

1

VTPT là





3; 4n 



nên có phương trình:









32440xy 

34220xy

.

Câu 24: Đường thẳng đi qua





1; 2A 

, nhận





2; 4n 



làm vectơ pháp tuyến có phương trình là

A.

240xy

. B.

40xy

. C.

250xy

. D.

240xy  

.

Lời giải

Chọn C

Phương trình đường thẳng cần tìm:









214 20 250xy xy   

.

Câu 25: Phương trình tham số của đường thẳng đi qua điểm





2; 1A

và nhận





3; 2



u làm vectơ

chỉ phương là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 26

A.

32

2

 









x

t

yt

.

B.

23

12







 



x

t

yt

.

C.

23

12

 









x

t

yt

.

D.

23

12

 









x

t

yt

.

Lời giải

Chọn B

Phương trình tham số của đường thẳng đi qua điểm





2; 1A

và nhận





3; 2



u làm vectơ chỉ

phương có dạng:

23

12







 



x

t

yt

.

Câu 26: Đường thẳng đi qua





1; 2A  , nhận





2; 4n 



làm véc tơ pháo tuyến có phương trình là:

A.

240xy

B.

40xy

C.

240xy  

D.

250xy

Lời giải

Chọn D.

Gọi



d là đường thẳng đi qua và nhận





2; 4n 



làm VTPT









:12 20 250dx y x y

Câu 27: Cho hai điểm





1; 2A 

,





1; 2B 

. Đường trung trực của đoạn thẳng

A

B có phương trình là

A.

20xy

. B.

20xy

. C.

20xy

. D.

210xy

.

Lời giải

Chọn C.

Gọi là

M

trung điểm của đoạn

A

B





0;0M

.

Đường trung trực của đoạn thẳng

AB đi qua điểm

M

và có vtpt





2; 4AB 



nên có phương

trình là:

20xy

Câu 28:

Lập phương trình tổng quát đường thẳng đi qua điểm





2;1A

và song song với đường thẳng

2320xy

.

A.

3280xy

. B.

2370xy

. C.

3240xy

. D.

2370xy

.

Lời giải

Chọn B

Gọi



là đường thẳng cần tìm.

*



song song với đường thẳng

2320xy

nên



có dạng:





23 0 2xym m .

*



đi qua điểm





2;1A

nên ta có

2.2 3.1 0m 7m

:2 3 7 0xy

.

Câu 29: Cho đường thẳng

23

:

1

x

t

yt









 







t 

và điểm





1; 6M 

. Phương trình đường thẳng đi qua

M

và vuông góc với



là

A.

390xy

. B.

3170xy

. C.

330xy

. D.

3190xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 27

Lời

giải

Chọn C



có một vectơ chỉ phương





3;1u 



.

Vì đường thẳng

d

vuông góc với



nên

d

có véctơ pháp tuyến





3;1nu



.

Phương trình tổng quát của đường thẳng

d

là









31 603 30xy xy   .

Câu 30: Trong mặt phẳng

Oxy

, cho đường thẳng

:210dx y

. Nếu đường thẳng



qua điểm





1; 1M  và



song song với

d

thì



có phương trình

A.

230xy

. B.

230xy

. C.

250xy

. D.

210xy

.

Lời giải

Chọn B

Đường thẳng

d

có

1

vectơ pháp tuyến là





1; 2n 



.

Đường thẳng



đi qua điểm





1; 1M  và



song song với

d

nên



nhận





1; 2n 



làm vectơ

pháp tuyến.

Phương trình tổng quát của đường thẳng



là









12 10xy 

230xy 

.

Câu 31: Viết phương trình tổng quát của đường thẳng đi qua

2

điểm





0; 5A 

và





3; 0B

A.

1

53

xy



. B.

1

35

xy

 

. C.

1

35

xy



. D.

1

53

xy



.

Lời giải

Chọn C

Phương trình tổng quát của đường thẳng đi qua hai điểm





0; 5A 

và





3; 0B

1

35

xy





1

35

xy



.

Câu 32: Trong mặt phẳng

Oxy

cho hai điểm



1; 3A  ,





2;5B  . Viết phương trình tổng quát của

đường thẳng đi qua hai điểm

,

A

B

.

A.

8310xy

. B.

8310xy

.

C.

38300xy  

. D.

38300xy

.

Lời giải

Chọn A

Ta có





3;8AB 



là vectơ chỉ phương của đường thẳng đi qua hai điểm

A

,

B

.





8;3n



là vectơ pháp tuyến của đường thẳng đi qua hai điểm

A

,

B

.

Phương trình tổng quát đường thẳng cần tìm là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 28









813 30xy  

8310xy

.

Câu 33: Cho





2;3A 

,





4; 1B 

. Viết phương trình đường trung trục của đoạn

A

B

.

A.

10xy

. B.

2350xy

. C.

3210xy

. D.

2310xy

.

Lời giải

Chọn C

Gọi

M

là trung điểm

A

B





1;1M

.

Phương trình đường trung trực của đoạn

A

B

qua





1;1M

nhận





6; 4AB 



là vectơ pháp

tuyến có dạng:









61410xy 

3210xy

.

Câu 34: Trong mặt phẳng với hệ tọa độ

Oxy

cho đường thẳng

:210dx y

và điểm





2;3M

.

Phương trình đường thẳng



đi qua điểm

M

và vuông góc với đường thẳng

d

là

A.

280xy

. B.

240xy

. C.

210xy

. D.

270xy

.

Lời giải

Chọn D



vuông góc

:210dx y



có VTPT là





2;1n 



.



qua





2;3M

nên có phương trình là



22 30xy

270xy

.

Câu 35: Trong mặt phẳng với hệ tọa độ

Oxy

cho hai điểm





0; 1A 

,





3; 0B

. Phương trình đường

thẳng

A

B

là

A.

310xy

. B.

330xy

. C.

330xy

. D.

310xy

.

Lời giải

Chọn C

Ta có





3;1AB 



là véctơ chỉ phương của đường thẳng

A

B

. Nên





1; 3n 



là véctơ pháp

tuyến của đường thẳng

A

B

.

Khi đó phươn trình đường thẳng

A

B

là



310xy

330xy 

.

Câu 36: Phương trình đường thẳng đi qua hai điểm









2; 4 ; 6;1AB

là:

A.

3 4 10 0.xy

B.

34220.xy

C.

3480.xy

D.

34220xy

Lời giải

Chọn B.

Ta có



24

:34220

43

AA

BA B A

xx yy

xy

AB x y

xx yy









Câu 37: Cho đường thẳng





:3 5 15 0dxy

. Phương trình nào sau đây không phải là một dạng khác

của (d).

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 29

A.

1

53



xy

. B.

3

5

 

yx

C.



5













xt

tR

y

D.



5

3

















xt

tR

yt

.

Lời giải

Chọn C.

Ta có đường thẳng





:3 5 15 0dxy

có VTPT







3;5

5;0

n

qua A

















5

;1

5

3

:

3

5;0

VTCP u

x

t

d

yt

qua A



























Suy ra D đúng.



:3 5 15 0 3 5 15 1

53

xy

dxy xy



Suy ra A đúng.



3

:3 5 15 0 5 3 15 1

5

dxy yx y x

Suy ra B đúng.

Câu 38: Cho đường thẳng





:210dx y

. Nếu đường thẳng







đi qua





1; 1M

và song song với



d

thì







có phương trình

A.

230xy

B.

250xy

C.

230xy

D.

210xy

Lời giải

Chọn A.

Ta có

















// 2 1 0 : 2 0 1dx y x y c c

Ta lại có













1; 1 1 2 1 0 3Mcc 

Vậy



:230xy

Câu 39: Cho ba điểm

 

1; 2 , 5; 4 , 1; 4AB C. Đường cao



A

của tam giác ABC có phương trình

A.

3480xy

B.

34110xy

C.

68110 xy

D.

86130xy

Lời giải

Chọn B.

Ta có



6;8BC 



Gọi

'AA

là đường cao của tam giác

A

BC

'

A

A

nhận



6;8

1; 2

VTPT n BC

qua A

















Suy ra









': 6 1 8 2 0 6 8 22 0 3 4 11 0AA x y x y x y 

.

Câu 40: Cho hai điểm









4;0 , 0;5AB

. Phương trình nào sau đây không phải là phương trình của

đường thẳng AB?

A.



44

5













xt

tR

yt

B. 1

45



xy

C.

4

45







x

y

D.

5

15

4





yx

Lời giải

Chọn D.

Phương trình đoạn chắn



:1

45

xy

AB



loại B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 30













5; 4 4; 5

:154200

45

4;0

VTPT n VTCP u

xy

AB x y

qua A



 



   









  

44

:

5

xt

AB t

yt













 loại A



4

:11

45 5 4 5 4

xy y x yx

AB







loại C



5

:11 5

45 5 4 4

xy y x

A

Byx 

chọn D

Câu 41: Cho đường thẳng





:4 3 5 0dxy

. Nếu đường thẳng







đi qua gốc tọa độ và vuông góc

với



d

thì







có phương trình:

A.

43 0xy

B.

34 0xy

C.

34 0xy

D.

43 0xy

Lời giải

Chọn C.

Ta có

  

:4 3 5 0 :3 4 0dxy xyc       

Ta lại có









0;0 0Oc 

Vậy





:3 4 0xy

Câu 42: Viết phương trình tổng quát của đường thẳng đi qua điểm





1; 2I 

và vuông góc với đường

thẳng có phương trình

240xy

A.

250xy  

B.

230xy

C.

20xy

D.

250xy

Lời giải

Chọn B.

Gọi



d là đường thẳng đi qua





1; 2I  và vuông góc với đường thẳng



1

:2 4 0dxy

Ta có









  





1

1; 2

dd

dd nu

 









:12 20 230dx y x y

Câu 43: Phương trình tham số của đường thẳng (d) đi qua điểm



2;3M

và vuông góc với đường

thẳng





:3410



dxy

là

A.

24

33

 









x

t

yt

B.

23

34

 









x

t

yt

C.

23

34

 









x

t

yt

D.

54

63











x

t

yt

Lời giải

Chọn B.

Ta có









:3410ddxy







3; 4

d

VTCP u



và qua



2;3M 

Suy ra

  

23

:

34

xt

dt

yt

 













Câu 44: Cho

A

BC

có



2; 1 ; 4;5 ; 3;2ABC

. Viết phương trình tổng quát của đường cao

A

H .

A.

3710xy

B.

73130xy

C.

37130xy 

D.

73110xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 31

Lời giải

Chọn C.

Ta có:





7; 3BC  



. Vì

A

HBC

nên







2; 1

:

3; 7 lam VTPT

qua A

AH

n























:3 2 7 1 0 3 7 13 0AH x y x y

Câu 45: Viết phương trình tổng quát của đường thẳng đi qua điểm





2;1M và vuông góc với đường

thẳng có phương trình









21 21 0xy 

.

A.



12 21 1220xy

B.





322 3 2 0xy   

C.









12 21 10xy D.





322 2 0xy   

Lời giải

Chọn A.

Ta có đường thẳng vuông góc đường thẳng với đường thẳng đã cho

Suy ra











:1 2 2 1 0dxyc

Mà







2,1 1 2 2Mdc

Vậy



12 21 1220xy

Câu 46: Cho đường thẳng



d

đi qua điểm





1; 3M

và có vecto chỉ phương





1; 2



a . Phương trình

nào sau đây không phải là phương trình của



d

?

A.

1

32.











x

t

yt

B.

13

.

12







xy

C.

250.xy

D.

25. yx

Lời giải

Chọn D.

Ta có



     

1; 2

11

:::

32 32

1; 3

VTCP a

xt xt

ddtdt

yt yt

qua M





 









 











loại A

Ta có

  

1

13

:

32

12

xt

xy

dt

yt







 









 loại B

Có









1; 2 2; 1VTCP a VTPT n 



suy ra

    

:2 1 1 3 0 2 3 5 0dx x xy    

loại

C

Câu 47: Cho tam giác ABC có



2;3, 1; 2, 5;4.ABC

Đường trung trực trung tuyến AM có

phương trình tham số

A.

2

32.











x

t

B.

24

32.

 









x

t

yt

C.

2

23.







 



xt

yt

D.

2

32.











x

yt

Lời giải

Chọn D.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 32

Gọi

M

trung điểm BC



2;1M



2

0; 2 :

32

x

AM AM

yt















Câu 48: Cho hai điểm



2;3 ; 4; 1 .AB viết phương trình trung trực đoạn AB.

A.

10.xy

B.

2310.xy

C.

2350.xy

D.

3210.xy

Lời giải

Chọn D.

Gọi

M

trung điểm

Ta có

Gọi là đường thẳng trung trực của .

Phương trình nhận và qua

Suy ra

Câu 49: Đường thẳng đi qua cắt ; tại

M

,

N

sao cho

I

là trung điểm của

M

N

.

Khi đó độ dài

M

N

bằng

A.

52

. B. 13 . C. 10 . D. 213.

Lời giải

Chọn D

Dễ thấy tam giác

OMN

vuông tại

O

suy ra

22

2232213MN OI 

.

Câu 50: Cho tam giác

A

BC

với





2; 4A

; ; . Trung tuyến đi qua điểm nào dưới

đây?

A. . B. . C. . D. .

Lời giải

Chọn D

là trung điểm của nên ; .

Phương trình tham số của đường thẳng là .

Với thì .

A

B





1;1M





6; 4AB 



d

A

B

d





6; 4VTPT n 







1;1M

    

:6 1 4 1 0 6 4 2 0 3 2 1 0dx y xy xy     



d



3; 2I

Ox

Oy





2;1B





5; 0C

CM

9

14;

2







5

10;

2













7; 6





1; 5

M

A

B

5

2;

2

M







5

3;

2

CM











CM

53

5

2

x

t

yt















2t 

1

5

x

y











O

N

I

M

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 33

Câu 51:

Cho đường thẳng : , : ,



3

d :

3410xy

. Viết

phương trình đường thẳng



d

đi qua giao điểm của



1

d

,



2

d

và song song với



3

d

.

A.

24 32 53 0xy

. B.

24 32 53 0xy

.

C.

24 32 53 0xy

. D.

24 32 53 0xy

.

Lời giải

Chọn A

Tọa độ giao điểm

M

của



1

d và



2

d là nghiệm của hệ

32 5

24 7

xy











3

8

31

16

x

y



















331

;

816

M









.

Phương trình đường thẳng





song song với



3

d

qua

331

;

816

M









có dạng





:

331

34 0

816

xy

 

  

 

 

53

34 0

8

xy

24 32 53 0xy

.

Câu 52: Cho tam giác

A

BC

có













1; 2; 0;2; 2;1ABC 

. Đường trung tuyến

B

M có phương trình

là:

A.

5360xy

B.

35100xy

C.

360xy

D.

320xy

Lời giải

Chọn A.

Gọi

M

là trung điểm

A

C

31

;

22

M









.

35

;

22

BM



 







B

M qua





0;2B

và nhận





5; 3n 



làm VTPT





:5 3 2 0 5 3 6 0BM x y x y

Câu 53: Cho tam giác

A

BC

với



2; 1 ; 4;5 ; 3;2ABC. Phương trình tổng quát của đường cao đi

qua

A

của tam giác là

A.

3710xy

B.

73130xy

C.

37130xy 

D.

73110xy

Lời giải

Chọn C.

Gọi

A

H là đường cao của tam giác.



7; 3BC  



.

AH đi qua





2; 1A 

và nhận





3; 7n 



làm VTPT









:3 2 7 1 0 3 7 13 0AH x y x y

3





1

d

3250xy



2

d

2470xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 314

BÀI 19. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

DẠNG 1. XÁC ĐNNH VÉCTƠ CHỈ PHƯƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG,

HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG

Câu 1: Trong mặt phẳng

Oxy

, đường thẳng









22

:0,0daxbyc a b 

. Vectơ nào sau đây là

một vectơ pháp tuyến của đường thẳng



d

?

A.





;nab



.

B.





;nba



.

C.





;nba



.

D.



;nab



.

Câu 2: Cho đường thẳng

d

có một vectơ pháp tuyến là





;nab



,

,ab 

. Xét các khẳng định sau:

1. Nếu

0b 

thì đường thẳng

d

không có hệ số góc.

2. Nếu

0b 

thì hệ số góc của đường thẳng

d

là

a

b

.

3. Đường thẳng

d có một vectơ chỉ phương là





;uba



.

4. Vectơ

kn



, k  là vectơ pháp tuyến của d .

Có bao nhiêu khẳng định

sai?

A.

3

. B.

2

. C.

1

. D.

4

.

Câu 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng

:230dx y

. Vectơ pháp tuyến của đường

thẳng

d

là

A.





1; 2n 



B.





2;1n 



C.





2;3n 



D.





1; 3n 



Câu 4:

Cho đường thẳng





:3 2 10 0dxy

. Véc tơ nào sau đây là véctơ chỉ phương của



d

?

A.



3;2u 



. B.



3; 2u 



. C.



2; 3u 



. D.



2; 3u  



.

Câu 5:

Cho đường thẳng

1

5

:

2

33

x

t

yt













 



một vectơ pháp tuyến của đường thẳng  có tọa độ

A.





5; 3

. B.



6;1

. C.

1

;3

2







. D.





5;3

.

Câu 6: Trong hệ trục tọa độ

Oxy

, Véctơ nào là một véctơ pháp tuyến của đường thẳng

2

:

12

x

t

d

yt

 





 



?

A.



2; 1n 



. B.



2; 1n 



. C.



1; 2n 



. D.



1; 2n



.

Câu 7: Vectơ chỉ phương của đường thẳng

d

:

14

23

x

t

yt







 



là:

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.

III

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 315

A.





4;3u 



. B.





4;3u 



. C.





3; 4u 



. D.





1; 2u 



.

Câu 8: Vector nào dưới đây là 1 vector chỉ phương của đường thẳng song song với trục

Ox

:

A.



1; 0u 



. B.

(1; 1)u 



. C.

(1;1)u 



. D.

(0;1)u 



.

Câu 9: Cho đường thẳng

:7 3 1 0dx y

. Vectơ nào sau đây là Vectơ chỉ phương của d?

A.





7;3u 



. B.





3; 7u 



. C.





3; 7u 



. D.





2;3u 



.

Câu 10: Cho đường thẳng

:2 3 4 0dx y

. Véctơ nào sau đây là véctơ pháp tuyến của đường thẳng

d ?

A.



1

3;2n 



. B.



1

4; 6n  



. C.





1

2; 3n 



. D.





1

2;3n 



.

Câu 11: Cho đường thẳng

: 5 3 7 0.dxy

Vectơ nào sau đây là một vec tơ chỉ phương của đường

thẳng

?d

A.





1

3; 5n 



. B.





2

3; 5n 



. C.





3

5;3n 



. D.





4

5; 3n  



.

Câu 12: Cho đường thẳng

:230xy 

. Véc tơ nào sau đây không là véc tơ chỉ phương của  ?

A.





4; 2u 



. B.





2; 1v  



. C.





2;1m 



. D.





4;2q 



.

Câu 13: Cho hai điểm





1; 2A  và





5; 4B  . Vectơ pháp tuyến của đường thẳng

A

B

là

A.





1; 2 . B.



1; 2 . C.





2;1 . D.





1; 2 .

Câu 14: Cho đường thẳng

:7 3 1 0dx y

. Vectơ nào sau đây là Vectơ chỉ phương của đường thẳng

d?

A.





7;3u 



. B.





3; 7u 



. C.





3; 7u 



. D.





2;3u 



.

Câu 15: Vectơ nào dưới đây là một vectơ pháp tuyến của : 2 2018 0dx y ?

A.





1

0; 2n 



. B.





3

2;0n 



. C.





4

2;1n



. D.





2

1; 2n 



.

Câu 16: Vectơ nào trong các vectơ dưới đây là vectơ pháp tuyến của đường thẳng

210

y

x

?

A.



2; 1

. B.



1; 2

. C.





2;1

. D.



2; 1

.

Câu 17: Trong mặt phẳng

Oxy

, cho đường thẳng

:2 1 0dxy

, một véctơ pháp tuyến của

d

là

A.





2; 1

. B.





2; 1

. C.





1; 2

. D.





1; 2

.

Câu 18: Trong mặt phẳng với hệ tọa độ

Oxy

cho đường thẳng

:2 3 4 0dx y

. Vectơ nào sau đây là

một vectơ chỉ phương của

d.

A.





4

3; 2u 



. B.





2

2;3u 



. C.





1

2; 3u 



. D.





3

3; 2u 



Câu 19: Vectơ nào sau đây là một Vectơ chỉ phương của đường thẳng

:6 2 3 0xy

?

A.





1; 3



u . B.





6; 2



u . C.





1; 3



u . D.



3; 1



u .

Câu 20: Cho hai điểm





2;3M

và





2;5N 

. Đường thẳng

M

N

có một vectơ chỉ phương là:

A.





4; 2u 



. B.



4; 2u 



. C.





4; 2u  



. D.



2; 4u 



.

Câu 21: Trong mặt phẳng với hệ tọa độ

,Ox

y

cho đường thẳng

:210.dx y

Một vectơ chỉ phương

của đường thẳng

d

là

A.





1; 2u 



. B.





2; 1u 



. C.





2; 1u 



. D.





1; 2u 



.

Câu 22: Đường thẳng

d

có một vectơ chỉ phương là





2; 1u 



. Trong các vectơ sau, vectơ nào là một

vectơ pháp tuyến của

d

?

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 316

A.





1

.1; 2n 



B.





2

1; 2 .n 



C.



3

.3; 6n 



D.



4

3; 6 .n 



Câu 23: Đường thẳng d có một vectơ pháp tuyến là



4; 2n 



. Trong các vectơ sau, vectơ nào là một

vectơ chỉ phương của

d ?

A.





1

.2; 4u 



B.





2

2; 4 .u 



C.





3

.1; 2u 



D.





4

2;1 .u 



Câu 24: Đường thẳng d có một vectơ chỉ phương là





3; 4u 



. Đường thẳng



vuông góc với d có

một vectơ pháp tuyến là:

A.





1

.4;3n 



B.





2

4; 3 .n  



C.





3

.3; 4n 



D.





4

3; 4 .n 



Câu 25: Đường thẳng d có một vectơ pháp tuyến là





2; 5n  



. Đường thẳng



vuông góc với d có

một vectơ chỉ phương là:

A.





1

.5; 2u 



B.





2

5; 2 .u 



C.





3

.2; 5u 



D.





4

2; 5 .u 



Câu 26: Đường thẳng

d

có một vectơ chỉ phương là





3; 4u 



. Đường thẳng  song song với

d

có

một vectơ pháp tuyến là:

A.





1

.4;3n 



B.





2

4;3 .n 



C.





3

.3; 4n 



D.





4

3; 4 .n 



Câu 27: Đường thẳng

d

có một vectơ pháp tuyến là





2; 5n  



. Đường thẳng  song song với

d

có

một vectơ chỉ phương là:

A.





1

.5; 2u 



B.





2

5; 2 .u  



C.





3

.2; 5u 



D.





4

2; 5 .u 



DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN

Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua

Câu 28:

Trên mặt phẳng tọa độ

Ox

y

, cho hai điểm





2;3A 

và





4; 1B 

. Phương trình nào sau đây là

phương trình đường thẳng

A

B ?

A.

30xy

. B.

21

y

x

. C.

41

64

x

y





. D.

13

12

x

t

y

t











.

Câu 29: Phương trình tham số của đường thẳng đi qua hai điểm





2; 1A 

và





2;5B

là

A.

2

6

x

t

yt











.

B.

2

56

x

t

yt











.

C.

1

26

x

yt











.

D.

2

16

x

yt







 



.

Câu 30: Trong mặt phẳng toạ độ

Oxy

, cho hai điểm



3; 1A 

và





6;2B 

. Phương trình nào dưới đây

không phải là phương trình tham số của đường thẳng

AB ?

A.

33

1

x

t

yt







 



.

B.

33

1

x

t

yt







 



.

C.

3

x

t

yt











.

D.

63

2

x

t

yt

 









.

Câu 31: Phương trình tham số của đường thẳng qua





1; 2M 

,





4;3N

là

A.

4

32

x

t

yt











.

B.

15

23

x

t

yt







 



.

C.

33

45

x

t

yt











.

D.

13

25

x

t

yt







 



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 317

Câu 32:

Phương trình tham số của đường thẳng đi qua hai điểm

 

3; 1 , 6; 2AB

là

A.

13

2

x

t

yt

 









. B.

33

1

x

t

y

t







 



. C.

33

6

x

t

y

t







 



. D.

33

1

x

t

y

t







 



.

Câu 33: Trong mặt phẳng tọa độ, cho hai điểm









3; 0 , 0; 2AB và đường thẳng

:0dx y

. Lập

phương trình tham số của đường thẳng



qua

A

và song song với d .

A.

3

x

t

yt











.

B.

3

x

t

yt











.

C.

3

x

t

yt











.

D.

3

x

t

yt











.

Câu 34: Cho đường thẳng d có phương trình tham số

5

92

x

t

yt







 



.

Phương trình tổng quát của đường

thẳng

d là

A.

210xy

. B.

210xy

. C.

210xy

. D.

2310xy

.

Câu 35: Trong mặt phẳng

Ox

y

cho điểm

(1; 2)M

. Gọi

,

A

B

là hình chiếu của

M

lên

,Ox O

y

. Viết

phương trình đường thẳng

AB

.

A.

210xy

. B.

220xy

. C.

220xy

. D.

30xy

.

Câu 36: Trong mặt phẳng tọa độ Oxy, cho đường thẳng

35

:()

14

xt

dt

yt













 . Phương trình tổng quát

của đường thẳng

d là

A.

4570.xy

. B.

4 5 17 0.xy

. C.

4 5 17 0.xy

. D.

4 5 17 0.xy

Câu 37: Trong mặt phẳng với hệ trục tọa độ

Ox

y

, cho đường thẳng d cắt hai trục

Ox

và

O

y

lần lượt

tại hai điểm





;0

A

a

và





0;Bb



0; 0ab

. Viết phương trình đường thẳng d.

A.

:0

xy

d

ab



. B.

:1.

xy

d

ab



C.

:1.

xy

d

ab



D.

:1.

xy

d

ba



.

Câu 38: Phương trình đường thẳng đi qua hai điểm









0; 4 , 6; 0AB

là:

A.

1

64

xy



. B.

1

46

xy





. C.

1

46

xy





. D.

1

64

xy



.

Dạng 2.2 Viết phương trình đường thẳng đi qua một điểm vuông góc hoặc với đường thẳng cho trước

Câu 39:

Phương trình đường thẳng

d

đi qua





1; 2A 

và vuông góc với đường thẳng

:3210xy

là:

A.

3270xy

. B.

2340xy

. C.

350xy

. D.

2330xy

.

Câu 40: Cho đường thẳng

:8 6 7 0dx y

. Nếu đường thẳng  đi qua gốc tọa độ và vuông góc với

đường thẳng

d thì  có phương trình là

A.

43 0xy

. B.

43 0xy

. C.

34 0xy

. D.

34 0xy

.

Câu 41: Đường thẳng đi qua điểm





1;1 1A

và song song với đường thẳng

35yx

có phương trình là

A.

311yx

. B.





314yx 

. C.

38yx

. D.

10yx

.

Câu 42:

Lập phương trình đường đi qua





2;5A

và song song với đường thẳng





:34?dy x

A.





:32yx

. B.





:31yx

. C.



1

:1

3

yx

. D.



:31yx

.

Câu 43:

Trong hệ trục Oxy , đường thẳng

d

qua





1;1M

và song song với đường thẳng ': 1 0dxy

có phương trình là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 318

A.

10xy

. B.

0xy

. C.

10xy 

. D.

20xy

.

Câu 44: Viết phương trình tổng quát của đường thẳng đi qua điểm





1; 2I 

và vuông góc với đường

thẳng có phương trình

240xy

.

A.

20xy

. B.

230xy

. C.

230xy

. D.

250xy

.

Câu 45: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho ba điểm





2;0A ¸





0;3B và





3; 1C  . Đường

thẳng đi qua điểm

B

và song song với

A

C

có phương trình tham số là:

A.

5

.

3

x

t

yt











B.

5

.

13

x

yt











C.

.

35

xt

yt











D.

35

.

x

t

yt











Câu 46: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho ba điểm





3; 2A ¸





4;0P và





0; 2Q  . Đường thẳng

đi qua điểm

A

và song song với

PQ

có phương trình tham số là:

A.

34

.

22

x

t

yt











B.

32

.

2

x

t

yt











C.

12

.

x

t

yt

 









D.

12

.

2

x

t

yt

 





 



Câu 47: Trong mặt phẳng với hệ tọa độ

Oxy

, cho hình bình hành

A

BCD

có đỉnh





–2;1A

và phương

trình đường thẳng chứa cạnh

CD

là

14

3

x

t

yt











. Viết phương trình tham số của đường thẳng

chứa cạnh

A

B

.

A.

23

22

x

t

yt

 





 



.

B.

24

13

x

t

yt

 









.

C.

23

14

x

t

yt

 









.

D.

23

14

x

t

yt

 









.

Câu 48: Viết phương trình tham số của đường thẳng

d

đi qua điểm





3; 5M 

và song song với đường

phân giác của góc phần tư thứ nhất.

A.

3

5

x

t

yt

 









.

B.

3

5

x

t

yt

 









.

C.

3

5

x

t

yt







 



.

D.

5

3

x

t

yt







 



.

Câu 49: Viết phương trình tham số của đường thẳng

d

đi qua điểm





4; 7M 

và song song với trục

Ox

.

A.

14

7

x

t

yt











.

B.

4

7

x

yt







 



.

C.

7

4

x

t

y

 









.

D.

7

x

t

y











.

Câu 50: Đường thẳng

d

đi qua điểm





1; 2M

và song song với đường thẳng

:2 3 12 0xy

có

phương trình tổng quát là:

A.

2380xy

. B.

2380xy

. C.

4610xy

. D.

4380xy

.

Câu 51: Phương trình tổng quát của đường thẳng d đi qua O và song song với đường thẳng

:6 4 1 0xx

là:

A.

32 0.xy

B.

46 0.xy

C.

31210.xy

D.

6410.xy

Câu 52: Đường thẳng

d

đi qua điểm



1; 2M 

và vuông góc với đường thẳng

:2 3 0xy

có phương trình tổng quát là:

A.

20xy

. B.

230xy

. C.

10xy

. D.

250xy

.

Câu 53: Viết phương trình đường thẳng  đi qua điểm





4; 3A 

và song song với đường thẳng

32

:

13

x

t

d

yt











.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 319

A.

3260xy

. B.

23170xy 

. C.

3260xy

. D.

3260xy

.

Câu 54: Cho tam giác

A

BC

có

 

2;0 , 0;3 , –3;1ABC

. Đường thẳng

d

đi qua

B

và song song với

A

C

có phương trình tổng quát là:

A.

5– 3 0xy

. B.

5–30xy

. C.

5–15 0xy

. D.

–15 15 0xy

.

Câu 55: Viết phương trình tổng quát của đường thẳng

d

đi qua điểm





1; 0M 

và vuông góc với

đường thẳng : .

2

x

t

yt













A.

220xy

. B.

220xy

. C.

210xy

. D.

210xy

.

Câu 56: Đường thẳng d đi qua điểm





2;1M  và vuông góc với đường thẳng

13

:

25

x

t

yt









 



có

phương trình tham số là:

A.

23

.

15

x

t

yt

 









B.

25

.

13

x

t

yt

 









C.

13

.

25

x

t

yt











D.

15

.

23

x

t

yt











Câu 57: Viết phương trình tham số của đường thẳng d đi qua điểm





1; 2A  và song song với đường

thẳng

:3 13 1 0xy

.

A.

113

23

x

t

yt

 









.

B.

113

23

x

t

yt







 



.

C.

113

23

x

t

yt

 









.

D.

13

213

x

t

yt











.

Câu 58: Viết phương trình tham số của đường thẳng

d

qua điểm





1; 2A 

và vuông góc với đường

thẳng

:2 4 0xy 

.

A.

12

2

x

t

yt

 









.

B.

42

xt

yt











.

C.

12

2

x

t

yt

 









.

D.

12

2

x

t

yt











.

Câu 59: Viết phương trình tổng quát của đường thẳng

d

đi qua điểm





2; 5M 

và song song với

đường phân giác góc phần tư thứ nhất.

A.

30xy

. B.

30xy

. C.

30xy

. D.

210xy

.

Câu 60: Viết phương trình tổng quát của đường thẳng d đi qua điểm





3; 1M  và vuông góc với

đường phân giác góc phần tư thứ hai.

A.

40xy

. B.

40xy

. C.

40xy

. D.

40xy

.

Câu 61: Viết phương trình tham số của đường thẳng

d

đi qua điểm





4; 0M 

và vuông góc với đường

phân giác góc phần tư thứ hai.

A.

4

xt

yt







 



.

B.

4

x

t

yt

 









.

C.

4

x

t

yt











.

D.

4

x

t

yt











.

Câu 62: Viết phương trình tổng quát của đường thẳng

d

đi qua điểm



1; 2M 

và song song với trục

Ox

.

A.

20y 

. B.

10x 

. C.

10x 

. D.

20y 

.

Câu 63: Viết phương trình tham số của đường thẳng

d

đi qua điểm





6; 10M 

và vuông góc với trục

O

y

.

A.

10

6

x

t

y











.

B.

2

:

10

x

t

d

y











.

C.

6

:

10

x

d

yt







 



.

D.

6

:

10

x

d

yt







 



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 320

Dạng 2.3 Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác

Dạng 2.3.1 Phương trình đường cao của tam giác

Câu 64:

Trên mặt phẳng tọa độ

Ox

y

, cho tam giác

A

BC có



1; 2 , 3; 1 , 5; 4ABC. Phương trình nào

sau đây là phương trình đường cao kẻ từ

A

của tam giác

A

BC ?

A.

2380xy

. B.

2380xy

. C.

3210xy

. D.

2320xy

.

Câu 65: Cho

A

BC

có













2; 1 , 4;5 , 3;2ABC. Đường cao

A

H

của

A

BC

có phương trình là

A.

73110xy

. B.

37130xy 

. C.

37170xy

. D.

73100xy

.

Câu 66: Trên mặt phẳng tọa độ

Oxy

, cho tam giác

A

BC

có

 

1; 2 , 3;1 , 5; 4ABC

. Phương trình

nào sau đây là phương trình đường cao kẻ từ

A

của tam giác

A

BC

?

A.

2380xy

. B.

2380xy

.

C.

3210xy

. D.

2320xy

.

Câu 67:

Trong mặt phẳng cho tam giác

A

BC

cân tại

C

có





2; 1B 

,





4;3A

. Phương trình đường cao

CH

là

A.

210xy

. B.

210xy

. C.

220xy

. D.

250xy

.

Câu 68: Cho

A

BC

có













2; 1 , 4;5 , 3;2ABC

. Phương trình tổng quát của đường cao

B

H là

A.

35370xy

. B.

5350xy

. C.

35130xy

. D.

35200xy

.

Câu 69: Đường trung trực của đoạn thẳng

A

B với





3; 2A 

,





3; 3B 

có một vectơ pháp tuyến là:

A.





1

6;5n 



. B.





2

0;1n 



. C.





3

3; 5n 



. D.





4

1; 0n 



.

Câu 70: Cho tam giác

A

BC

có









1;1 , 0; 2 , 4 .() ;2AB C

Lập phương trình đường trung tuyến của tam

giác

A

BC

kẻ từ

.

A

A.

20.xy

B.

230.xy

C.

230.xy

D.

0.xy

Câu 71:

Đường trung trực của đoạn AB với





1; 4A 

và





5; 2B

có phương trình là:

A.

2330.xy

B.

3210.xy

C.

340.xy

D.

10.xy

Câu 72: Đường trung trực của đoạn

A

B với





4; 1A 

và





1; 4B 

có phương trình là:

A.

1.xy

B.

0.xy

C.

0.yx

D.

1.xy

Câu 73: Đường trung trực của đoạn

A

B với





1; 4A 

và





1; 2B

có phương trình là:

A.

10.y 

B.

10.x 

C.

10.y 

D.

40.xy

Câu 74: Đường trung trực của đoạn

AB

với





1; 4A 

và





3; 4B 

có phương trình là :

A.

40.y 

B.

20.xy

C.

20.x 

D.

40.y 

Câu 75: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có









2; 1 , 4;5AB

và





3; 2C 

.

Lập phương trình đường cao của tam giác

A

BC

kẻ từ

.

A

A.

73110.xy

B.

3 7 13 0.xy 

C.

3710.xy

D.

7 3 13 0.xy

Câu 76: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có









2; 1 , 4;5AB

và



3; 2 .C 

Lập phương trình đường cao của tam giác

A

BC kẻ từ .B

A.

35130.xy

B.

3 5 20 0.xy

C.

3 5 37 0.xy

D.

5350.xy

Câu 77:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có









2; 1 , 4;5AB

và



3; 2 .C 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 321

Lập phương trình đường cao của tam giác

A

BC

kẻ từ

.C

A.

10.xy

B.

330.xy

C.

3110.xy 

D.

3110.xy 

Dạng 2.3.2 Phương trình đường trung tuyến của tam giác

Câu 78:

Cho tam giác

A

BC

với





1;1A

,





0; 2B 

,





4; 2C

. Phương trình tổng quát của đường trung

tuyến đi qua điểm

B

của tam giác

A

BC

là

A.

77140xy

. B.

5310xy

. C.

320xy

. D.

75100xy 

.

Câu 79: Trong hệ tọa độ

Oxy

, cho tam giác

A

BC có













2; 3 , 1; 0 , 1; 2ABC

. Phương trình đường

trung tuyến kẻ từ đỉnh

A của tam giác

A

BC

là:

A.

210xy

. B.

240xy

. C.

280xy

. D.

270xy

.

Câu 80: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có





1; 4A

,





3; 2B

và





7;3 .C

Viết

phương trình tham số của đường trung tuyến

CM

của tam giác.

A.

7

.

35

x

yt











B.

35

.

7

x

t

y











C.

7

.

3

x

t

y











D.

2

.

3

x

yt











Câu 81: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có





2; 4A

,





5; 0B

và





.2;1C

Trung tuyến

B

M của tam giác đi qua điểm

N

có hoành độ bằng

20

thì tung độ bằng:

A. 12. B.

25

.

2



C. 13. D.

27

.

2



Dạng 2.3.3 Phương trình cạnh của tam giác

Câu 82:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có



2; 0M

là trung điểm của cạnh

A

B . Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là

7230xy

và

640xy

. Phương trình đường thẳng

A

C

là

A.

3450xy

. B.

3450xy

. C.

3450xy

. D.

3450xy

.

Câu 83: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có phương trình cạnh

A

B là

20,xy

phương trình cạnh

A

C

là

250xy

. Biết trọng tâm của tam giác là điểm



3; 2G

và phương trình đường thẳng

BC

có dạng 0.xmyn Tìm .mn

A.

3

. B. 2 . C.

5

. D. 4 .

Dạng 2.3.4 Phương trình đường phân giác của tam giác

Câu 84:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho đường thẳng

:0ax by c

và hai điểm



;

mm

M

x

y

,



;

nn

Nx y

không thuộc  . Chọn khẳng định đúng trong các khẳng định sau:

A.

,

M

N

khác phía so với  khi









.0.

mm nn

ax by c ax by c 

B.

,

M

N

cùng phía so với  khi









.0.

mm nn

ax by c ax by c 

C.

,

M

N

khác phía so với



khi









.0.

mm nn

ax by c ax by c 

D.

,

M

N

cùng phía so với  khi



.0.

mm nn

ax by c ax by c 

Câu 85: Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:3 4 5 0dx y

và hai điểm



1; 3A

,



2;Bm

. Tìm tất cả các giá trị của tham số

m

để

A

và

B

nằm cùng phía đối với

d

.

A.

0m 

. B.

1

4

m



. C.

1m 

. D.

1

4

m



.

Câu 86: Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

2

:

13

x

t

d

yt











và hai điểm





1; 2A

,

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 322



2;Bm

. Tìm tất cả các giá trị của tham số

m

để

A

và

B

nằm cùng phía đối với

d

.

A.

13.m 

B.

13m 

. C.

13.m 

D.

13m 

.

Câu 87: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi hai đường thẳng

1

:230xy

và

2

:2 3 0xy

.

A.

30xy

và

30xy

. B.

30xy

và

360xy

.

C.

30xy

và

360xy  

. D.

360xy

và

360xy

.

Câu 88: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường thẳng

:0xy

và

trục hoành.

A.





12 0xy;





12 0xy . B.





12 0xy;





12 0xy .

C.





12 0xy

;





12 0xy 

.

D.





12 0xy 

;





12 0xy 

.

Câu 89: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có

7

;3

4

A







,



1; 2B

và





4;3C 

.

Phương trình đường phân giác trong của góc

A

là:

A.

4 2 13 0.xy

B.

48170.xy

C.

4210.xy

D.

4 8 31 0.xy

Câu 90: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có



1; 5A

,





4; 5B 

và





4; 1C 

.

Phương trình đường phân giác ngoài của góc

A

là:

A.

50.y 

B.

50.y 

C.

10.x 

D.

10.x 

Câu 91: Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

1

:3 4 3 0dxy và

2

:12 5 12 0dxy. Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng

1

d và

2

d là:

A.

31130.xy

B.

11 3 11 0.xy

C.

31130.xy

D.

11 3 11 0.xy

Câu 92: Cho tam giác ABC có phương trình cạnh

:3 4 9 0AB x y

, cạnh

:8610AC x y

, cạnh

:50BC x y

. Phương trình đường phân giác trong của góc

A

là:

A.

14 14 17 0xy

. B.

22190xy

. C.

22190xy

. D.

14 14 17 0xy

.

Câu 93: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

A

BC

với





1; 2 ,A 





2; 3 ,B 





3; 0C

. Phương

trình đường phân giác ngoài góc

A

của tam giác

A

BC là

A.

1

x



. B.

2y 

. C.

20xy

. D.

420xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 19. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

DẠNG 1. XÁC ĐNNH VÉCTƠ CHỈ PHƯƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG,

HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG

Câu 1: Trong mặt phẳng

Oxy , đường thẳng









22

:0,0daxbyc a b . Vectơ nào sau đây là

một vectơ pháp tuyến của đường thẳng



d

?

A.





;nab



.

B.





;nba



.

C.





;nba



.

D.



;nab



.

Lời giải

Chọn D

Ta có một vectơ pháp tuyến của đường thẳng



d là



;nab



.

Do đó chọn đáp án

D.





1

;.nab



Câu 2: Cho đường thẳng

d

có một vectơ pháp tuyến là





;nab



,

,ab 

. Xét các khẳng định sau:

1. Nếu

0b 

thì đường thẳng

d

không có hệ số góc.

2. Nếu

0b 

thì hệ số góc của đường thẳng

d

là

a

b

.

3. Đường thẳng

d

có một vectơ chỉ phương là





;uba



.

4. Vectơ

kn



,

k 

là vectơ pháp tuyến của

d

.

Có bao nhiêu khẳng định

sai?

A.

3

. B. 2 . C. 1. D. 4 .

Lời giải

Chọn B

d

có một vectơ pháp tuyến là





;nab



 phương trình

:0dax by c

.

Nếu

0b 

thì đường thẳng

:0dax c

không có hệ số góc khẳng định 1 đúng.

Nếu

0b  thì đường thẳng

:

ac

dy x

bb

 

có hệ số góc là

a

b





khẳng định 2 sai.

Với





;.0uba un un 



u



là một vectơ chỉ phương của

d

khẳng định 3 đúng.

Chọn



00;0kkn  



 không phải là vectơ pháp tuyến của

d

khẳng định 4 sai.

Vậy có 2 mệnh đề sai.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.

III

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

Câu 3:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng

:230dx y

. Vectơ pháp tuyến của đường

thẳng

d

là

A.





1; 2n 



B.





2;1n 



C.





2;3n 



D.





1; 3n 



Lời giải

Chọn A

Câu 4:

Cho đường thẳng





:3 2 10 0dxy

. Véc tơ nào sau đây là véctơ chỉ phương của



d

?

A.



3;2u 



. B.



3; 2u 



. C.



2; 3u 



. D.



2; 3u  



.

Lời giải

Chọn C

Đường thẳng



d có một véctơ pháp tuyến là





3;2n 



nên



d có một véctơ chỉ phương là



2; 3u 



.

Câu 5: Cho đường thẳng

1

5

:

2

33

x

t

yt













 



một vectơ pháp tuyến của đường thẳng  có tọa độ

A.





5; 3

. B.



6;1

. C.

1

;3

2







. D.





5;3

.

Lời giải

Chọn B

1

5

:

2

33

x

t

yt













 



có một vectơ chỉ phương là

1

;3

2

u











suy ra có một vectơ pháp tuyến là

1

3;

2

n











. Do đó đường thẳng  cũng có một vectơ pháp tuyến có tọa độ





6;1

.

Câu 6: Trong hệ trục tọa độ

Oxy

, Véctơ nào là một véctơ pháp tuyến của đường thẳng

2

:

12

x

t

d

yt

 





 



?

A.



2; 1n 



. B.



2; 1n 



. C.



1; 2n 



. D.



1; 2n



.

Lời giải

Chọn A

Một VTCP của đường thẳng

d

là



1; 2u 



một VTPT của

d

là



2; 1n 



.

Câu 7: Vectơ chỉ phương của đường thẳng d :

14

23

x

t

yt







 



là:

A.





4;3u 



. B.





4;3u 



. C.





3; 4u 



. D.





1; 2u 



.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

Đường thẳng d :

14

23

x

t

yt







 



có vectơ chỉ phương là





4;3u 



.

Câu 8:

Vector nào dưới đây là 1 vector chỉ phương của đường thẳng song song với trục

Ox

:

A.



1; 0u 



. B.

(1; 1)u 



. C.

(1;1)u 



. D.

(0;1)u 



.

Lời giải

Chọn A

Vector

(1; 0)i 



là một vector chỉ phương của trục

Ox

Các đường thẳng song song với trục

Ox

có 1 vector chỉ phương là

(1; 0)ui



Câu 9: Cho đường thẳng

:7 3 1 0dx y

. Vectơ nào sau đây là Vectơ chỉ phương của d?

A.





7;3u 



. B.





3; 7u 



. C.





3; 7u 



. D.





2;3u 



.

Lời giải

Chọn C

Đường thẳng d có 1 VTPT là





7;3n 



nên d có 1 VTCP là



3; 7u 



.

Câu 10: Cho đường thẳng

:2 3 4 0dx y

. Véctơ nào sau đây là véctơ pháp tuyến của đường thẳng

d ?

A.



1

3;2n 



. B.



1

4; 6n  



. C.





1

2; 3n 



. D.





1

2;3n 



.

Lời giải

Chọn B

Véctơ pháp tuyến của đường thẳng

d

:



1

4; 6n  



.

Câu 11: Cho đường thẳng

: 5 3 7 0.dxy

Vectơ nào sau đây là một vec tơ chỉ phương của đường

thẳng

?d

A.





1

3; 5n 



. B.





2

3; 5n 



. C.





3

5;3n 



. D.





4

5; 3n  



.

Lời giải

Chọn D

Đường thẳng

: 5 3 7 0dxy

có vec tơ pháp tuyến là:





5;3 .n 



Ta có:

2

.0.nn 



d

có một vec tơ chỉ phương là





2

3; 5 .n 



Câu 12: Cho đường thẳng :230xy . Véc tơ nào sau đây không là véc tơ chỉ phương của



?

A.



4; 2u 



. B.





2; 1v  



. C.





2;1m 



. D.





4;2q 



.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

Nếu

u



là một véc tơ chỉ phương của đường thẳng



thì

., 0ku k



cũng là véc tơ chỉ phương

của đường thẳng

.

Từ phương trình đường thẳng



ta thấy đường thẳng



có một véc tơ chỉ phương có toạ độ là





2;1

. Do đó véc tơ



4; 2u 



không phải là véc tơ chỉ phương của .

Câu 13: Cho hai điểm





1; 2A  và





5; 4B  . Vectơ pháp tuyến của đường thẳng

A

B

là

A.





1; 2 . B.





1; 2 . C.





2;1 . D.





1; 2 .

Lời giải

Chọn D

Ta có



4; 2 2 2;1AB 



suy ra vectơ pháp tuyến của đường thẳng

A

B là





1; 2

AB

n 



.

Câu 14: Cho đường thẳng

:7 3 1 0dx y

. Vectơ nào sau đây là Vectơ chỉ phương của đường thẳng

d?

A.





7;3u 



. B.





3; 7u 



. C.





3; 7u 



. D.





2;3u 



.

Lời giải

Chọn C

Đường thẳng d có 1 VTPT là





7;3n 



nên d có 1 VTCP là



3; 7u 



Câu 15:

Vectơ nào dưới đây là một vectơ pháp tuyến của

: 2 2018 0dx y 

?

A.





1

0; 2n 



. B.





3

2;0n 



. C.





4

2;1n



. D.





2

1; 2n 



.

Lời giải

Chọn D

Đường thẳng

: 2 2018 0dx y 

có vectơ pháp tuyến là





2

1; 2n 



.

Câu 16: Vectơ nào trong các vectơ dưới đây là vectơ pháp tuyến của đường thẳng

210

y

x

?

A.



2; 1

. B.



1; 2

. C.





2;1

. D.



2; 1

.

Lời giải

Chọn D





:210dy x

210

x

y

;



d

có VTPT là





2;1n 



hay



/

2; 1n  



Câu 17:

Trong mặt phẳng

Oxy

, cho đường thẳng

:2 1 0dxy

, một véctơ pháp tuyến của

d

là

A.





2; 1

. B.





2; 1

. C.





1; 2

. D.





1; 2

.

Lời giải

Chọn B

Một véctơ pháp tuyến của đường thẳng

d

là





2; 1n 



.

Câu 18: Trong mặt phẳng với hệ tọa độ

Oxy

cho đường thẳng

:2 3 4 0dx y

. Vectơ nào sau đây là

một vectơ chỉ phương của

d.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

A.





4

3; 2u 



. B.





2

2;3u 



.

C.





1

2; 3u 



. D.





3

3; 2u 



Lời giải

Chọn D

Ta thấy đường thẳng

d

có một vectơ pháp tuyến là





2; 3 . Do đó





3

3; 2u 



là một vectơ chỉ

phương của

d.

Câu 19: Vectơ nào sau đây là một Vectơ chỉ phương của đường thẳng

:6 2 3 0xy

?

A.





1; 3



u . B.





6; 2



u . C.





1; 3



u . D.





3; 1



u .

Lời giải

Chọn A

+) Một véctơ pháp tuyến của đường thẳng  là





6; 2n 



nên véctơ chỉ phương của đường

thẳng



là





1; 3



u

.

Câu 20: Cho hai điểm





2;3M và





2;5N  . Đường thẳng

M

N

có một vectơ chỉ phương là:

A.





4; 2u 



. B.



4; 2u 



. C.





4; 2u  



. D.



2; 4u 



.

Lời giải

Chọn B



4; 2MN 



. Do đó vectơ chỉ phương của

M

N

là



4; 2u 



.

Câu 21: Trong mặt phẳng với hệ tọa độ

,Ox

y

cho đường thẳng

:210.dx y

Một vectơ chỉ phương

của đường thẳng

d là

A.





1; 2u 



. B.





2; 1u 



. C.





2; 1u 



. D.





1; 2u 



.

Lời giải

Chọn B

Đường thẳng

:210.dx y

có vectơ pháp tuyến là (1; 2)n 



Vectơ chỉ phương của

d

là

(2;1)u 



.

Câu 22: Đường thẳng

d

có một vectơ chỉ phương là





2; 1u 



. Trong các vectơ sau, vectơ nào là một

vectơ pháp tuyến của

d

?

A.





1

.1; 2n 



B.





2

1; 2 .n 



C.





3

.3; 6n 



D.





4

3; 6 .n 



Lời giải

Đường thẳng d có VTCP:





2; 1u 



VTPT





1; 2n



hoặc





33;6.n 



Chọn D

Câu 23:

Đường thẳng

d

có một vectơ pháp tuyến là





4; 2n 



. Trong các vectơ sau, vectơ nào là một

vectơ chỉ phương của

d

?

A.





1

.2; 4u 



B.





2

2; 4 .u 



C.





3

.1; 2u 



D.





4

2;1 .u 



CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

Lời giải

Đường thẳng d có VTPT:



4; 2n 



VTCP





2; 4u



hoặc



.

1

;2

2

1u 



Chọn C

Câu 24:

Đường thẳng

d

có một vectơ chỉ phương là





3; 4u 



. Đường thẳng  vuông góc với

d

có

một vectơ pháp tuyến là:

A.





1

.4;3n 



B.





2

4; 3 .n  



C.





3

.3; 4n 



D.





4

3; 4 .n 



Lời giải







3; 4

3; 4 .

d

u

nu

d



























Chọn D

Câu 25:

Đường thẳng

d

có một vectơ pháp tuyến là





2; 5n  



. Đường thẳng  vuông góc với

d

có

một vectơ chỉ phương là:

A.





1

.5; 2u 



B.





2

5; 2 .u 



C.





3

.2; 5u 



D.





4

2; 5 .u 



Lời giải



2; 5

d

n

un

d













 











hay chọn





2;5 .n







Chọn C

Câu 26:

Đường thẳng d có một vectơ chỉ phương là





3; 4u 



. Đường thẳng



song song với d có

một vectơ pháp tuyến là:

A.





1

.4;3n 



B.





2

4;3 .n 



C.





3

.3; 4n 



D.





4

3; 4 .n 



Lời giải





 

3; 4

3; 4 4; 3 .

||

d

u

uu n

d

























 

Chọn A

Câu 27:

Đường thẳng

d

có một vectơ pháp tuyến là





2; 5n  



. Đường thẳng  song song với

d

có

một vectơ chỉ phương là:

A.





1

.5; 2u 



B.





2

5; 2 .u  



C.





3

.2; 5u 



D.





4

2; 5 .u 



Lời giải





 

2; 5

2; 5 5; 2 .

||

d

n

nu u

d









 















 

Chọn A

DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN

Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua

Câu 28:

Trên mặt phẳng tọa độ

Oxy

, cho hai điểm





2;3A 

và





4; 1B 

. Phương trình nào sau đây là

phương trình đường thẳng

A

B ?

A.

30xy

. B.

21yx

. C.

41

64

xy







. D.

13

12

x

t

y

t











.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7

Lời giải

Chọn D

Bốn phương trình đã cho trong bốn phương án đều là phương trình của đường thẳng.

Thay lần lượt tọa độ của

A , B vào từng phương án ta thấy tọa độ của cà A và B đều thỏa

phương án

D .

Câu 29: Phương trình tham số của đường thẳng đi qua hai điểm





2; 1A 

và





2;5B

là

A.

2

6

x

t

yt











.

B.

2

56

x

t

yt











.

C.

1

26

x

yt











.

D.

2

16

x

yt







 



.

Lời giải

Chọn D

Vectơ chỉ phương





0;6AB 



.

Phương trình đường thẳng

A

B đi qua

A

và có vecto chỉ phương





0;6AB 



là

2

16

x

yt







 



Câu 30:

Trong mặt phẳng toạ độ

Oxy

, cho hai điểm



3; 1A 

và





6;2B 

. Phương trình nào dưới đây

không phải là phương trình tham số của đường thẳng

A

B ?

A.

33

1

x

t

yt







 



.

B.

33

1

x

t

yt







 



.

C.

3

x

t

yt











.

D.

63

2

x

t

yt

 









.

Lời giải

Chọn B



Cách 1: Thay tọa độ các điểm

A

,

B

lần lượt vào các phương trình trong các phương án trên thì

thấy phương án B không thỏa mãn.

 Cách 2: Nhận thấy rằng các phương trình ở các phương án A, C, D thì vectơ chỉ phương của các

đường thẳng đó cùng phương, riêng chỉ có phương án B thì không. Do đó lựa Chọn B

Câu 31:

Phương trình tham số của đường thẳng qua





1; 2M  ,





4;3N là

A.

4

32

x

t

yt











. B.

15

23

x

t

yt







 



. C.

33

45

x

t

yt











. D.

13

25

x

t

yt







 



.

Lời giải

Chọn D

Đường thẳng có véctơ chỉ phương là





3; 5MN 



và đi qua





1; 2M 

nên có phương trình

tham số là

13

25

x

t

yt







 



.

Câu 32: Phương trình tham số của đường thẳng đi qua hai điểm

 

3; 1 , 6; 2AB

là

A.

13

2

x

t

yt

 









. B.

33

1

x

t

y

t







 



. C.

33

6

x

t

y

t







 



. D.

33

1

x

t

y

t







 



.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

Chọn B

Ta có

 

9;3 3; 1 .

AB

AB u   



Suy ra phương trình tham số của đường thẳng

A

B

là

33

1

x

t

y

t







 



.

Câu 33: Trong mặt phẳng tọa độ, cho hai điểm









3; 0 , 0; 2AB và đường thẳng

:0dx y

. Lập

phương trình tham số của đường thẳng

 qua

A

và song song với d .

A.

3

x

t

yt











. B.

3

x

t

yt











. C.

3

x

t

yt











. D.

3

x

t

yt











.

Lời giải

Chọn A

Ta có



song song với

d

nên





:00xyC C 

.

 qua





3; 0A

, suy ra

30 0 3CC  

Như vậy

:30xy

Vậy



có phương trình tham số:

3

x

t

yt











.

Câu 34: Cho đường thẳng

d

có phương trình tham số

5

92

x

t

yt







 



.

Phương trình tổng quát của đường

thẳng

d

là

A.

210xy

. B.

210xy

. C.

210xy

. D.

2310xy

.

Lời giải

Chọn A

Đường thẳng



5

:

92

x

t

d

yt







 



5

92

tx

yt









 







92 5yx 

210xy

.

Câu 35: Trong mặt phẳng

Ox

y

cho điểm

(1; 2)M

. Gọi

,

A

B

là hình chiếu của

M

lên

,Ox O

y

. Viết

phương trình đường thẳng

A

B .

A.

210xy

. B.

220xy

. C.

220xy

. D.

30xy

.

Lời giải:

Chọn C

Ta có hình chiếu của điểm

(1; 2)M

lên

,Ox Oy

lần lượt là A và B. Do đó phương

trình đường thẳng AB là

12 20

12

xy

xy 

.

Câu 36: Trong mặt phẳng tọa độ Oxy, cho đường thẳng

35

:()

14

xt

dt

yt















. Phương trình tổng quát

của đường thẳng

d là

A. 4570.xy. B. 4 5 17 0.xy. C. 4 5 17 0.xy. D. 4 5 17 0.xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9

Lời giải

Chọn.B.

3

35

31

5

:() 45170

14

1

54

4

x

t

xt

xy

dt xy

yt

y

t

















   



















Đáp án

B.

Câu 37: Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho đường thẳng d cắt hai trục

Ox

và

Oy

lần lượt

tại hai điểm





;0

A

a

và





0;Bb



0; 0ab

. Viết phương trình đường thẳng d.

A.

:0

xy

d

ab



. B.

:1.

xy

d

ab



C.

:1.

xy

d

ab



D.

:1.

xy

d

ba



.

Lời giải

Phương trình đoạn chắn của đường thẳng

:1.

xy

d

ab



Câu 38: Phương trình đường thẳng đi qua hai điểm









0; 4 , 6; 0AB

là:

A.

1

64

xy



. B.

1

46

xy





. C.

1

46

xy





. D.

1

64

xy



.

Lời giải

Chọn D

Phương trình đường thẳng đi qua hai điểm









;0 , 0;

M

aNb

với

,0ab

là

1

xy

ab



.

Áp dụng phương trình trên ta chọn phương án D .

Dạng 2.2 Viết phương trình đường thẳng đi qua một điểm vuông góc hoặc với đường thẳng cho trước

Câu 39:

Phương trình đường thẳng

d

đi qua





1; 2A 

và vuông góc với đường thẳng

:3210xy

là:

A.

3270xy

. B.

2340xy

. C.

350xy

. D.

2330xy

.

Lời giải

Chọn B

Do





2;3

d

dn



Mà đường thẳng

d

đi qua





1; 2A 

nên ta có phương trình:









213 202340xy xy    

.

Vậy phương trình đường thẳng

:2 3 4 0dx y

.

Câu 40: Cho đường thẳng

:8 6 7 0dx y

. Nếu đường thẳng  đi qua gốc tọa độ và vuông góc với

đường thẳng d thì

 có phương trình là

A.

43 0xy

. B.

43 0xy

. C.

34 0xy

. D.

34 0xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

Lời giải

Chọn C

Vì  vuông góc với đường thẳng

:8 6 7 0dx y

nên phương trình

:6 8 0xyC

Mà

 đi qua gốc tọa độ nên ta có:

6.0 8.0 0 0CC

.

Vậy phương trình

:6 8 0xy hay :3 4 0xy

Câu 41: Đường thẳng đi qua điểm





1;1 1A

và song song với đường thẳng

35yx

có phương trình là

A.

311yx

. B.





314yx 

. C.

38yx

. D.

10yx

.

Lời giải

Chọn C

Gọi





d

là đường thẳng cần tìm. Vì





d

song song với đường thẳng

35yx

nên





d

có

phương trình

3yxa

,

5a 

.

Vì





d

đi qua điểm





1;1 1A

nên ta có

11 3 1 8aa 

.

Vậy phương trình đường thẳng



d

cần tìm là

38yx

.

Câu 42:

Lập phương trình đường đi qua





2;5A và song song với đường thẳng





:34?dy x

A.





:32yx

. B.





:31yx

. C.



1

:1

3

yx

. D.



:31yx

.

Lời giải

Chọn B

Gọi







là đường thẳng cần tìm.

+)









// : 3 4dy x

. Suy ra phương trình







có dạng 3yxb,

4b 

.

Có



2;5 5 6

A

b   1b

Vậy





:31

y

x

.

Câu 43: Trong hệ trục

Ox

y

, đường thẳng d qua





1;1M và song song với đường thẳng

': 1 0dxy

có phương trình là

A.

10xy

. B.

0xy

. C.

10xy 

. D.

20xy

.

Lời giải

Chọn D

Do đường thẳng

d

song song với đường thẳng

': 1 0dxy

nên đường thẳng

d

nhận véc

tơ





1; 1n 



làm véc tơ pháp tuyến.

Khi đó đường thẳng

d

qua





1;1M

và nhận véc tơ





1; 1n 



làm véc tơ pháp tuyến có phương

trình là

20xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11

Câu 44:

Viết phương trình tổng quát của đường thẳng đi qua điểm





1; 2I 

và vuông góc với đường

thẳng có phương trình

240xy

.

A.

20xy

. B.

230xy

. C.

230xy

. D.

250xy

.

Lời giải

Chọn B

Ta có đường thẳng vuông góc với

240xy

có phương trình

20xym

, mà đường

thẳng này đi qua điểm





1; 2I 

, suy ra

12.2 0 3mm    

.

Vậy đường thẳng cần tìm có phương trình

230xy

.

Câu 45: Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba điểm





2;0A

¸





0;3B

và





3; 1C 

. Đường

thẳng đi qua điểm

B

và song song với

A

C

có phương trình tham số là:

A.

5

.

3

x

t

yt











B.

5

.

13

x

yt











C. .

35

xt

yt











D.

35

.

x

t

yt











Lời giải

Gọi d là đường thẳng qua B và song song với AC. Ta có







5; 1 1. 5;1

0;3

5

:

3

d

B

d

C

xt

t

A

yt

u



































Chọn A

Câu 46:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba điểm





3; 2A

¸





4;0P

và





0; 2Q 

. Đường thẳng

đi qua điểm

A

và song song với

PQ

có phương trình tham số là:

A.

34

.

22

x

t

yt











B.

32

.

2

x

t

yt











C.

12

.

x

t

yt

 









D.

12

.

2

x

t

yt

 





 



Lời giải

Gọi d là đường thẳng qua A và song song với PQ.

Ta có:







4; 2 2 2;

3; 2

32

:

1

2

d

Ad

uP

x

t

d

yt

Q

































  

2

12

:.1; 0

t

xt

dd t

y

M

t









 





 





Chọn C

Câu 47:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hình bình hành

A

BCD

có đỉnh





–2;1A

và phương

trình đường thẳng chứa cạnh

CD là

14

3

x

t

yt











. Viết phương trình tham số của đường thẳng

chứa cạnh

A

B .

A.

23

22

x

t

yt

 





 



.

B.

24

13

x

t

yt

 









.

C.

23

14

x

t

yt

 









.

D.

23

14

x

t

yt

 









.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

 



,4;3

|| 4; 3

2;1

24

:.

13

CD

AB CD

AABu

AB CD u

A

xt

Bt

yt

u









































Chọn B

Câu 48:

Viết phương trình tham số của đường thẳng d đi qua điểm





3; 5M  và song song với đường

phân giác của góc phần tư thứ nhất.

A.

3

5

x

t

yt

 









.

B.

3

5

x

t

yt

 









.

C.

3

5

x

t

yt







 



.

D.

5

3

x

t

yt







 



.

Lời giải

Góc phần tư:

  

:

3

1;1 : .

5

0

d

x

xt

uud t

yt

yVTCP

























Chọn B

Câu 49:

Viết phương trình tham số của đường thẳng

d

đi qua điểm





4; 7M 

và song song với trục

Ox

.

A.

14

7

x

t

yt











.

B.

4

7

x

yt







 



.

C.

7

4

x

t

y

 









.

D.

7

x

t

y











.

Lời giải

   

4

:.:

7

1; 0 1; 0 0; 7

7

t

Ox d

x

t

uu dd

y

xt

A

y

d







 























Chọn D

Câu 50:

Đường thẳng

d

đi qua điểm





1; 2M

và song song với đường thẳng

:2 3 12 0xy

có

phương trình tổng quát là:

A.

2380xy

. B.

2380xy

. C.

4610xy

. D.

4380xy

.

Lời giải









1; 2

:2 3 0

:2 3 12 0

12

||

M

xyc c

xy

d





























2.1 3.2 0 8.cc

Vậy

:2 3 8 0.dx y

Chọn A

Câu 51:

Phương trình tổng quát của đường thẳng

d

đi qua

O

và song song với đường thẳng

:6 4 1 0xx

là:

A.

32 0.xy

B.

46 0.xy

C.

31210.xy

D.

6410.xy

Lời giải



0;0

6.0 4.0 0 0.

:6 4 0 1

|| : 6 4 1 0

d

dx

x

O

c

d

cc

xc

x













 









Vậy

:640 :320.dx y dx y 

Chọn A

Câu 52:

Đường thẳng

d

đi qua điểm



1; 2M 

và vuông góc với đường thẳng

:2 3 0xy

có phương trình tổng quát là:

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

A.

20xy

. B.

230xy

. C.

10xy

. D.

250xy

.

Lời giải









1; 2 1; 2

12.2 0 5.

:2 3 0 : 2 0

ddMM

cc

xy dx ycd









     



 











Vậy

:250.dx y

Chọn D

Câu 53:

Viết phương trình đường thẳng



đi qua điểm





4; 3A  và song song với đường thẳng

32

:

13

x

t

d

yt











.

A.

3260xy

. B.

23170xy 

. C.

3260xy

. D.

3260xy

.

Lời giải

Ta có:







 



2;3

2;3 3;2

||

:3 4 2 3 0 :3 2 6 0.

4; 3

d

Ad

d

u

un

d

xy xy

A







 



























Câu 54: Cho tam giác

A

BC

có

 

2;0 , 0;3 , –3;1ABC

. Đường thẳng

d

đi qua

B

và song song với

A

C có phương trình tổng quát là:

A.

5– 3 0xy

. B.

5–30xy

. C.

5–15 0xy

. D.

–15 15 0xy

.

Lời giải









0;3

:1 0 .

5;1

530

|

:51

1; 5

5

|

0

AC

d

B

dd

uAC

n

xy xy

dAC



































Câu 55: Viết phương trình tổng quát của đường thẳng

d

đi qua điểm





1; 0M 

và vuông góc với

đường thẳng

:.

2

x

t

yt













A.

220xy

. B.

220xy

. C.

210xy

. D.

210xy

.

Lời giải



 

.1; 2

1

1; 0

:1 1

;2

200 :210

d

M

y

d

u

n

M

dx x

d

dy







































Chọn C

Câu 56:

Đường thẳng

d

đi qua điểm





2;1M 

và vuông góc với đường thẳng

13

:

25

x

t

yt









 



có

phương trình tham số là:

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

A.

23

.

15

x

t

yt

 









B.

25

.

13

x

t

yt

 









C.

13

.

25

x

t

yt











D.

15

.

23

x

t

yt











Lời giải



 



.3; 5

3;

2

55;

2;1

;1

25

1

3

:

3

dd

dM

t

d

u

M

x

d

n

t

d

yt





 









 











 

  













Chọn B

Câu 57:

Viết phương trình tham số của đường thẳng d đi qua điểm





1; 2A  và song song với đường

thẳng

:3 13 1 0xy

.

A.

113

23

x

t

yt

 









.

B.

113

23

x

t

yt







 



.

C.

113

23

x

t

yt

 









.

D.

13

213

x

t

yt











.

Lời giải







 



.3; 13

3; 1

2

313;3

1; 2

1;

113

:

2

|

3

|

dd

d

n

A

xt

d

nu

t

d

y











 









 















 

 









Chọn A

Câu 58:

Viết phương trình tham số của đường thẳng

d

qua điểm





1; 2A 

và vuông góc với đường

thẳng

:2 4 0xy 

.

A.

12

2

x

t

yt

 









.

B.

42

xt

yt











.

C.

12

2

x

t

yt

 









.

D.

12

2

x

t

yt











.

Lời giải







1

2; 1

2;

1; 2

;2

12

.

2

1

:

d

A

x

n

t

d

t

d

t

y

d

u

d











 









 











 















Chọn A

Câu 59:

Viết phương trình tổng quát của đường thẳng d đi qua điểm





2; 5M  và song song với

đường phân giác góc phần tư thứ nhất.

A.

30xy

. B.

30xy

. C.

30xy

. D.

210xy

.

Lời giải







2; 5

2; 5 0

25 0 3.:

:

(I) 0

0

||

0

d

x

M

cc

dx y c c

y

d



 







 























Vậy

:30.dx y

Chọn B

Câu 60:

Viết phương trình tổng quát của đường thẳng

d

đi qua điểm





3; 1M 

và vuông góc với

đường phân giác góc phần tư thứ hai.

A.

40xy

. B.

40xy

. C.

40xy

. D.

40xy

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15





 



3; 1

:0

31 0 4 .

II : 0

:40

M

dx y c

c

d

x

dx y

y

c

d























 



  









Câu 61: Viết phương trình tham số của đường thẳng d đi qua điểm





4; 0M  và vuông góc với đường

phân giác góc phần tư thứ hai.

A.

4

xt

yt







 



.

B.

4

x

t

yt

 









.

C.

4

x

t

yt











.

D.

4

x

t

yt











.

Lời giải



   



4

II : 0 1;1

.

4

4;0 0; 4

1;1

:

4

t

d

x

Md d

xy n

d

t

u

xt

dt

A

yt



















































Câu 62: Viết phương trình tổng quát của đường thẳng

d

đi qua điểm



1; 2M 

và song song với trục

Ox

.

A.

20y 

. B.

10x 

. C.

10x 

. D.

20y 

.

Lời giải





.

|| : 0

1; 2

:2

Md

dOxy

dy





















Chọn D

Câu 63:

Viết phương trình tham số của đường thẳng

d

đi qua điểm





6; 10M 

và vuông góc với trục

Oy

.

A.

10

6

x

t

y











.

B.

2

:

10

x

t

d

y











.

C.

6

:

10

x

d

yt







 



.

D.

6

:

10

x

d

yt







 



.

Lời giải







4

6; 10

6

:2

.

;10

10

:0 1;0

2

:

10

d

t

M

A

d

dOyx u

xt

d

y

xt

d

y

















































Dạng 2.3 Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác

Dạng 2.3.1 Phương trình đường cao của tam giác

Câu 64:

Trên mặt phẳng tọa độ

Oxy

, cho tam giác

A

BC có



1; 2 , 3; 1 , 5; 4ABC. Phương trình nào

sau đây là phương trình đường cao kẻ từ

A của tam giác

A

BC

?

A.

2380xy

. B.

2380xy

. C.

3210xy

. D.

2320xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

Lời giải

Chọn A

Gọi

A

H

là đường cao kẻ từ

A

của

A

BC . Ta có:

A

HBC vtptAH

là





2;3BC 



.

Phương trình









:2 1 3 2 0 2 3 8 0.AH x y x y    .

Câu 65: Cho

A

BC

có













2; 1 , 4;5 , 3;2ABC. Đường cao

A

H

của

A

BC

có phương trình là

A.

73110xy

. B.

37130xy 

. C.

37170xy

. D.

73100xy

.

Lời giải

Đường cao

AH

đi qua điểm





2; 1A 

và có VTPT là



7; 3BC  



.

Vậy phương trình

A

H

là









7231073110xy xy .

Câu 66: Trên mặt phẳng tọa độ

Oxy

, cho tam giác

A

BC

có

 

1; 2 , 3;1 , 5; 4ABC. Phương trình

nào sau đây là phương trình đường cao kẻ từ

A

của tam giác

A

BC

?

A.

2380xy

. B.

2380xy

.

C.

3210xy

. D.

2320xy

.

Lời giải

Chọn A

Ta có:



2;3BC 



Đường cao kẻ từ

A

của tam giác

A

BC

nhận



2;3BC 



làm vectơ pháp tuyến và đi qua

điểm

A

nên có phương trình:

 

213202380xy xy    .

Câu 67: Trong mặt phẳng cho tam giác

A

BC

cân tại

C

có





2; 1B 

,





4;3A

. Phương trình đường cao

CH là

A.

210xy

. B.

210xy

. C.

220xy

. D.

250xy

.

Lời giải

Chọn D

Tam giác

A

BC

cân tại

C

nên H là trung điểm của

A

B và

CH AB

.

Có





3;1H

và









2; 4 2 1; 2AB   



.

Vậy phương trình đường cao

CH

là



13210xy 

250xy 

.

Câu 68: Cho

A

BC

có













2; 1 , 4;5 , 3;2ABC

. Phương trình tổng quát của đường cao

B

H là

A.

35370xy

. B.

5350xy

. C.

35130xy

. D.

35200xy

.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17

Do

BH AC

Chọn VTPT của

B

H

là





5; 3 .

BH

nCA

 

Phương trình tổng quát của









:5 4 3 5 0 5 3 5 0.BH x y x y  

Câu 69: Đường trung trực của đoạn thẳng

A

B với





3; 2A 

,





3; 3B 

có một vectơ pháp tuyến là:

A.





1

6;5n 



.

B.



2

0;1n 



.

C.





3

3; 5n 



.

D.





4

1; 0n 



.

Lời giải

Gọi d là trung trực đoạn AB, ta có:



0;1

0;1 .

d

AB

nAB

dAB





















Chọn B

Câu 70:

Cho tam giác

A

BC

có









1;1 , 0; 2 , 4 .() ;2AB C

Lập phương trình đường trung tuyến của tam

giác

A

BC kẻ từ .

A

A.

20.xy

B.

230.xy

C.

230.xy

D.

0.xy

Lời giải

Gọi M là trung điểm của BC. Ta cần viết phương trình đường thẳng AM.

Ta có :







   

1; 1 1;1 : 2 0 .

0; 2

2;0

4; 2

AMAM

B

uAM n AMxyM

C













    









Chọn A

Câu 71:

Đường trung trực của đoạn

A

B

với





1; 4A  và





5; 2B có phương trình là:

A.

2330.xy

B.

3210.xy

C.

340.xy

D.

10.xy

Lời giải

Gọi I là trung điểm của AB và

d

là trung trực đoạn AB. Ta có















1; 4 , 5; 2 3; 1

:2 3 3 0.

4;6 2 2;3

d

A

x

d

AB n

BI

dy

dAB

 















 









Chọn A

Câu 72:

Đường trung trực của đoạn

A

B

với





4; 1A  và





1; 4B  có phương trình là:

A.

1.xy

B.

0.xy

C.

0.yx

D.

1.xy

Lời giải

Gọi I là trung điểm của AB và

d

là trung trực đoạn AB. Ta có



55

4; 1 , 1; 4 ;

22

:0.

13; 3 3 ;1

d

A

B

d

n

I

xy

dAB A



















 















Chọn B

Câu 73:

Đường trung trực của đoạn AB với





1; 4A 

và





1; 2B

có phương trình là:

A.

10.y 

B.

10.x 

C.

10.y 

D.

40.xy

Lời giải

Gọi I là trung điểm của AB và

d

là trung trực đoạn AB. Ta có

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18





1; 4 , 1; 2 1; 1

:10.

10; 6 6 0;

d

A

d

dBI

dy

AB n AB

 















 





Chọn A

Câu 74:

Đường trung trực của đoạn

A

B

với





1; 4A  và





3; 4B  có phương trình là :

A.

40.y 

B.

20.xy

C. 20.x  D.

40.y 

Lời giải

Gọi I là trung điểm của AB và

d

là trung trực đoạn AB. Ta có















1; 4 , 3; 4 2; 4

:20.

2;0 2 1;0

d

AB n AB

AB I

dx

d

  

























Chọn C

Câu 75:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC có









2; 1 , 4;5AB và





3; 2C  .

Lập phương trình đường cao của tam giác

A

BC kẻ từ .

A

A.

73110.xy

B.

3 7 13 0.xy 

C.

3710.xy

D.

7 3 13 0.xy

Lời giải

Gọi

A

h là đường cao kẻ từ A của tam giác ABC. Ta có







.

7;

2; 1

:7 3 11

37;

0

3

A

Ah

A

h

hBCn BC

xy























Chọn A

Câu 76:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có









2; 1 , 4;5AB

và



3; 2 .C 

Lập phương trình đường cao của tam giác

A

BC kẻ từ .B

A.

35130.xy

B.

3 5 20 0.xy

C.

3 5 37 0.xy

D.

5350.xy

Lời giải

Gọi

B

h là đường cao kẻ từ B của tam giác ABC. Ta có





.

5;3

4;5

;

:

5

5350

3

B

Bh

B

h

B

AC n C

y

A

hx

















 





Chọn D

Câu 77:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có









2; 1 , 4;5AB

và



3; 2 .C 

Lập phương trình đường cao của tam giác

A

BC kẻ từ .C

A.

10.xy

B.

330.xy

C.

3110.xy 

D.

3110.xy 

Lời giải

Gọi

C

h là đường cao kẻ từ C của tam giác ABC. Ta có







.

2;

3

6

;2

:

21

330

;3

C

Ch

C

h

hAB

xy

nAB

























Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19

Dạng 2.3.2 Phương trình đường trung tuyến của tam giác

Câu 78:

Cho tam giác

A

BC

với





1;1A ,





0; 2B  ,





4; 2C . Phương trình tổng quát của đường trung

tuyến đi qua điểm

B

của tam giác

A

BC là

A.

77140xy

. B.

5310xy

. C.

320xy

. D.

75100xy 

.

Lời giải

Chọn D

Gọi

M

là trung điểm của cạnh

53 57

;;

22 22

AC M BM

 



 

 



.

Đường trung tuyến

B

M nhận





7;5n 



làm một véctơ pháp tuyến. Vậy phương trình tổng

quát của đường trung tuyến qua điểm

B

của tam giác

A

BC

là:

75(2)0 75100xy xy  .

Câu 79: Trong hệ tọa độ

Oxy

, cho tam giác

A

BC

có













2; 3 , 1; 0 , 1; 2ABC

. Phương trình đường

trung tuyến kẻ từ đỉnh

A

của tam giác

A

BC

là:

A.

210xy

. B.

240xy

. C.

280xy

. D.

270xy

.

Lời giải

Chọn A

Gọi I là trung điểm của





0; 1BC I

Ta có

 

2; 4 2; 1AI n    

 

là vectơ pháp tuyến của đường thẳng

A

I .

Phương trình đường thẳng

AI là:









22 302 10xy xy 

Câu 80: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có





1; 4A

,





3; 2B

và





7;3 .C

Viết

phương trình tham số của đường trung tuyến

CM

của tam giác.

A.

7

.

35

x

yt











B.

35

.

7

x

t

y











C.

7

.

3

x

t

y











D.

2

.

3

x

yt











Lời giải







   

1; 4

7

5; 0 5 1; 0 : .

3

2

2;3

3;

A

C

x

MM

t

y

B

MC











  

















Chọn C

Câu 81:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có





2; 4A ,





5; 0B và





.2;1C

Trung tuyến

B

M của tam giác đi qua điểm

N

có hoành độ bằng

20

thì tung độ bằng:

A.

12.

B.

25

.

2



C.

13.

D.

27

.

2



Lời giải







56

51

3; 6; 5 : .

5

2

2; 4

5

2;

2

2;1

2

A

x

t

MB MB

y

M

C

t









































CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

Ta có:



5

20 5 6

2

5

25

2

20;

N

t

BM

yt

y





























Chọn B

Dạng 2.3.3 Phương trình cạnh của tam giác

Câu 82:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC có



2; 0M là trung điểm của cạnh

A

B

. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là

7230xy

và

640xy

. Phương trình đường thẳng

A

C

là

A.

3450xy

. B.

3450xy

. C.

3450xy

. D.

3450xy

.

Lời giải

Chọn C

+) Gọi

A

H và

A

D lần lượt là các đường cao và trung tuyến kẻ từ

A

của tam giác

A

BC

.

+) Tọa độ

A

là nghiệm của hệ



7230 1

1; 2

640 2

xy x

A

xy y

 







 



.

+)

M

là trung điểm của

A

B nên



23

3; 2

22

BMA

xxx

B

yyy













.

+) Đường thẳng

BC

đi qua





3; 2B 

và vuông góc với đường thẳng

A

H :

640xy

nên

có phương trình





–3 6 2 0 6 9 0xy xy

.

+)

D là giao điểm của

BC

và

A

N

nên tọa độ D là nghiệm của hệ

0

7230

3

0;

3

690

2

x

xy

D

xy

y































mà D là trung điểm của BC suy ra





3; 1C 

+) Đường thẳng

A

C

đi qua





1; 2A

và





3; 1C 

có phương trình là

3450xy

.

Câu 83: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có phương trình cạnh

A

B là

20,xy

phương trình cạnh

A

C

là

250xy

. Biết trọng tâm của tam giác là điểm



3; 2G

và phương trình đường thẳng

BC

có dạng

0.xmyn

Tìm .mn

A.

3

. B. 2 . C.

5

. D. 4 .

Lời giải

E

D

M

C

B

A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

Chọn A

Tọa độ điểm

A

là nghiệm của hệ

20 3

250 1

xy x

xy y

 







 



nên



3;1A

Gọi



;2Bbb

và



52;Ccc

,

G

là trọng tâm tam giác

A

BC

nên

,bc

là nghiệm của hệ

52 39 5

216 2

cb b

cb c

 







 



.

Vậy

(5;3); (1;2)BC





4; 1BC



chọn một véctơ pháp tuyến của đường thẳng

BC

là





1; 4

BC

n 



suy ra phương trình đường thẳng









:1 1 4 2 0 : 4 7 0.BC x y BC x y    

Dạng 2.3.4 Phương trình đường phân giác của tam giác

Câu 84:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:0ax by c

và hai điểm





;

mm

M

xy

,





;

nn

Nx

y

không thuộc  . Chọn khẳng định đúng trong các khẳng định sau:

A.

,

M

N

khác phía so với  khi









.0.

mm nn

ax by c ax by c 

B.

,

M

N

cùng phía so với  khi









.0.

mm nn

ax by c ax by c 

C.

,

M

N

khác phía so với  khi









.0.

mm nn

ax by c ax by c 

D.

,

M

N

cùng phía so với  khi



.0.

mm nn

ax by c ax by c 

Lời giải

Chọn D

Câu 85:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:3 4 5 0dx y

và hai điểm



1; 3A

,



2;Bm

. Tìm tất cả các giá trị của tham số

m

để

A

và

B

nằm cùng phía đối với

d

.

A. 0m  . B.

1

4

m 

. C. 1m  . D.

1

4

m 

.

Lời giải



1; 3A

,



2;Bm

nằm cùng phía với

:3 4 5 0dx y

khi và chỉ khi



1

34534501014 0 .

4

AA BB

xy xy m m  

Chọn B

Câu 86:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

2

:

13

x

t

d

yt











và hai điểm





1; 2A

,



2;Bm

. Tìm tất cả các giá trị của tham số

m

để

A

và

B

nằm cùng phía đối với

d

.

A.

13.m 

B.

13m 

. C.

13.m 

D.

13m 

.

Lời giải

2

::370.

13

xt

ddxy

yt















Khi đó điều kiện bài toán trở thành

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 22



3 7 3 7 0 2 13 0 13.

AA BB

xy xy m m   

Chọn C

Câu 87:

Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi hai đường thẳng

1

:230xy

và

2

:2 3 0xy

.

A.

30xy

và

30xy

. B.

30xy

và

360xy

.

C.

30xy

và

360xy  

. D.

360xy

và

360xy

.

Lời giải

Điểm





;

M

xy

thuộc đường phân giác của các góc tạo bởi

12

; khi và chỉ khi



12

30

232 3

;; .

360

55

xy

xy xy

dM dM

xy



 



  











Chọn C

Câu 88:

Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường thẳng

:0xy

và

trục hoành.

A.





12 0xy;





12 0xy . B.





12 0xy;





12 0xy .

C.





12 0xy;





12 0xy . D.





12 0xy ;





12 0xy .

Lời giải

Điểm





;

M

xy

thuộc đường phân giác của các góc tạo bởi

;:0Ox y

khi và chỉ khi

 







12 0

;; .

21

12 0

xy

xy y

dM dMOx

xy



 









 







Chọn D

Câu 89:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có

7

;3

4

A







,



1; 2B

và





4;3C 

.

Phương trình đường phân giác trong của góc

A

là:

A.

4 2 13 0.xy

B.

48170.xy

C.

4210.xy

D.

4 8 31 0.xy

Lời giải



7

;3 , 1;2 :4 3 2 0

4

.

7

;3 , 4;3 : 3 0

4

AB ABxy

AC ACy











 







 









Suy ra các đường phân giác góc

A

là:



42130 ; 4213

432 3

51

48170

1; 2 5 0

4;3 23 0

xy fxy xy

xy y

xy

fB

fC

 

 











 













suy ra đường phân giác trong góc

A

là

48170.xy

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 23

Câu 90:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có



1; 5A

,





4; 5B 

và



4; 1C 

.

Phương trình đường phân giác ngoài của góc

A

là:

A.

50.y 

B.

50.y 

C.

10.x 

D.

10.x 

Lời giải









 

1; 5 , 4; 5 : 2 3 0

.

1; 5 , 4; 1 : 2 7 0

AB ABxy

AC ACxy

  







 





Suy ra các đường phân giác góc

A

là:













4; 5 5 0

10 ; 1

2327

5055

4; 1 3 0

fB

xfxyx

xy xy

y

fC



 

   



 



 















suy ra đường phân giác trong góc

A

là

50.y 

Chọn B

Câu 91:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai đường thẳng

1

:3 4 3 0dxy và

2

:12 5 12 0dxy. Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng

1

d và

2

d là:

A.

31130.xy

B.

11 3 11 0.xy

C.

31130.xy

D.

11 3 11 0.xy

Lời giải

Các đường phân giác của các góc tạo bởi

1

:3 4 3 0dxy và

2

:12 5 12 0dxy là:

31130

34312512

.

11 3 11 0

513

xy

xy xy

xy



 











Gọi

  

12

31131; 0 ; : ,010;3Id x y MdI d d

Gọi

H

là hình chiếu của

M

lên

1

.d

Ta có:

30 12 3

130, 9,

5

IM MH



  suy ra

 

9

sin 52 2 90 .

130

MH

MIH MIH MIH

IM

   



Suy ra

:3 11 3 0dx y

là đường phân giác góc tù, suy ra đường phân giác góc nhọn là

11 3 11 0xy

. Chọn B

Câu 92:

Cho tam giác ABC có phương trình cạnh

:3 4 9 0AB x y

, cạnh

:8610AC x y

, cạnh

:50BC x y

. Phương trình đường phân giác trong của góc

A

là:

A.

14 14 17 0xy

. B.

22190xy

. C.

22190xy

. D.

14 14 17 0xy

.

Lời giải

Chọn D

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 24

:3 4 9 0AB x y

:8 6 1 0AC x y

Phương trình các đường phân giác của góc

A

của

ABC

là:

349 861

510

 



xy xy



23 4 9 8 6 1xy xy



1

2

22190

14 14 17 0















xy

Có



BABBC

. Suy ra

29 6

;

77







B

.

Có



CACBC

. Suy ra

29 41

;

14 14







C

.

Xét



1

:2 2 19 0xy

có

29 6 29 41

. 2. 2 19 2. 2 19 0

7 7 14 14

 

 

 

 

Bc

tt

.

Suy ra

,BC

nằm về cùng một phía đối với



1



, nên



1



là đường phân giác ngoài của góc

A

.

Vậy đường phân giác trong của góc

A

là



2

:14 14 17 0xy

.

Câu 93: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

với



1; 2 ,A 



2; 3 ,B 



3; 0C

. Phương

trình đường phân giác ngoài góc

A

của tam giác

ABC

là

A.

1x 

. B.

2y 

. C.

20xy

. D.

420xy

.

Lời giải

Chọn A

Bài toán tổng quát:

Gọi

d

là phân giác ngoài góc

A

của tam giác

ABC

.

Đặt

1

.AE AB

AB



 

,

1

.AF AC

AC



 

và

AD AE AF

 

.

Khi đó tứ giác

AEDF

là hình thoi.

.

Suy ra tia

AD

là tia phân giác trong góc

EAF

.

Do đó:

AD d

. Nên

AD



là vectơ pháp tuyến của đường thẳng

d

.

Áp dụng:



1; 1 , 2

2;2 , 2 2

AB AB

AC AC



 















2;0 2 1;0AD 



.

Xem đáp án chỉ có đáp án A có vectơ pháp tuyến là



1; 0

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 25

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 323

BÀI 20. VN TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG

THẲNG, GÓC VÀ KHOẢNG CÁCH

I. VN TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc. Để xét vị trí tương đối của hai đường thẳng này ta xét số nghiệm của hệ

phương trình

111

222

0

ax by c











(0.1)

+ Nếu hệ





1.1

có duy nhất 1 nghiệm ta nói hai đường thẳng trên cắt nhau tọa độ giao điểm

chính là nghiệm của hệ phương trình nói trên.

+ Nếu hệ





1.1

vô nghiệm ta nói hai đường thẳng nói trên song song với nhau.

+ Nếu hệ





1.1

nghiệm đúng với mọi

x 

thì hai đường thẳng trên trùng nhau.

+ Tuy nhiên để thuận tiện cho việc xét nhanh vị trí tương đối của hai đường thẳng ta chú ý nhận

xét sau

Nhận xét. Nếu

222

0abc 

ta có

a)



11

12

22

ab

dd I

ab



b)

111

12

222

//

abc

dd

abc



c)

111

12

222

abc

dd

abc



II. GÓC GIỮA HAI ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc. Khi đó góc giữa hai đường thẳng được tính theo công thức.



12

12 12

12

2222

12

1122

.

cos ;

.

nn

aa bb

dd

nn

abab







 

III. KHOẢNG CÁCH

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:0ax by c

và điểm





000

;

M

xy

.

Khi đó khoảng cách từ điểm

0

M

đến đường thẳng  được tính theo công thức:

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 324



00

0

22

;

ax by c

dM

ab







7.7

Xét vị trí tương đối giữa các cặp đường thẳng sau:

a)



1

:3 2 2 3 0xy

và 

2

:6 2 6 0xy .

b)



1

:320dx y

và 

2

:3 3 2 0dxy .

c)



1

:210mx y

và



2

:3 2 0mxy

.

7.8 Tính góc giữa các cặp đường thẳng sau:

a)



1

:3 4 0xy

và

 

2

:330xy

.

b)



 







1

12

:

34

x

t

d

y

t

và











2

3

:

13s

x

s

d

y

(

, ts

là các tham số).

7.9 Trong mặt phẳng toạ độ Oxy , cho điểm





A 0; 2

và đường thẳng

:40

x

y

.

a) Tính khoảng cách từ điểm

A

đến đường thẳng



.

b) Viết phương trình đường thẳng

a

đi qua điểm





M 1; 0

và song song với



.

c) Viết phương trình đường thẳng

b

đi qua điểm





N 0;3

và vuông góc với



.

7.10 Trong mặt phẳng toạ độ, cho tam giác

A

BC

có









A 1; 0 , B 3; 2

và





 C2;1

.

a) Tính độ dài đường cao kẻ từ đỉnh

A của tam giác

A

BC

.

b) Tính diện tích tam giác

A

BC

.

7.11 Chứng minh rằng hai đường thẳng





 : 0dy ax ba

và





 : 0

dyaxb a

vuông góc

với nhau khi và chỉ khi



1aa

.

7.12 Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín

hiệu đặt tại ba vị trí













O,A0; 0 1; 0 , B 1;3 nhận được cùng một thời điểm. Hãy xác định vị

trí phát tín hiệu âm thanh.

BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 325

DẠNG 1: XÉT VN TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

{các bài toán xét vị trí tương đối của hai đường thẳng, tìm điều kiện (có chứa tham số m) để hai đường

thẳng song song, cắt, trùng,….}

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc

. Để xét vị trí tương đối của hai đường thẳng này ta xét số nghiệm của hệ

phương trình

111

222

0

ax by c











(0.2)

Nếu hệ





1.1 có duy nhất 1 nghiệm ta nói hai đường thẳng trên cắt nhau tọa độ giao điểm chính

là nghiệm của hệ phương trình nói trên. Nếu hệ





1.1 vô nghiệm ta nói hai đường thẳng nói

trên song song với nhau. Nếu hệ





1.1 nghiệm đúng với mọi x  thì hai đường thẳng trên

trùng nhau. Tuy nhiên để thuận tiện cho việc xét nhanh vị trí tương đối của hai đường thẳng ta

chú ý nhận xét sau

Nhận xét. Nếu

222

0abc 

ta có

a)



11

12

22

ab

dd I

ab



b)

111

12

222

//

abc

dd

abc



c)

111

12

222

abc

dd

abc



Câu 1:

Xét vị trí tương đối của hai đường thẳng lần lượt có phương trình

2

23

xy



và

6280xy

Câu 2: Xét vị trí tương đối của hai đường thẳng

1

:2 15 0dxy  và

2

:230dx y. 

Câu 3: Tìm tọa độ giao điểm của hai đường thẳng

43260xy

và

3470xy

.

Câu 4: Cho hai đường thẳng



1

:120dmx m y m  

và

2

:2 1 0dxy. Tìm

m

để

12

//dd.

Câu 5: Cho ba đường thẳng



12

:120,:43260dmx m y m d x y   

và

3

:3 4 7 0dxy Tìm

m

để ba đường thẳng trên đồng quy.

Câu 1:

Xét vị trí tương đối của hai đường thẳng

1

:210dx y

và

2

:3 6 10 0dxy 

.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Câu 2: Xét vị trí tương đối của hai đường thẳng

1

:3 2 6 0dxy và

2

:6 2 8 0dxy.

HỆ THỐNG BÀI TẬP.

II

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 326

A.

Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Câu 3: Xét vị trí tương đối của hai đường thẳng

1

:1

34

xy

d 

và

2

:3 4 10 0dxy.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Câu 4: Xét vị trí tương đối của hai đường thẳng

1

34

:

26

x

t

d

yt

 









và

2

22

:

84

x

t

d

yt











 



.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Câu 5: Cho hai đường thẳng









12

:1,:2  dmxym d xmy

cắt nhau khi và chỉ khi :

A.

2.m

B.

1.m

C.

1.m

D.

1.m

Câu 6: Đường thẳng







:

3270xy

cắt đường thẳng nào sau đây?

A.





1

:3 2 0dxy

B.





2

:3 2 0dxy

C.





3

:3 2 7 0. dxy

D.





4

:6 4 14 0.dxy

Câu 7: Giao điểm

M

của



12

:

35







 



x

t

d

yt

và





:3 2 1 0



dxy

. Toạ độ của

M

là

A.

11

2; .

2









M

B.

1

0; .

2







M

C.

1

0; .

2









M

D.

1

;0 .

2

M









Câu 8: Phương trình nào sau đây biểu diển đường thẳng không song song với đường thẳng





:21dy x

?

A.

250.xy

B.

250.xy

C.

20.xy

D.

250.xy

Câu 9: Hai đường thẳng



1

25

:

2

 









x

t

d

yt

và





2

:4 3 18 0dxy

. Cắt nhau tại điểm có tọa độ:

A.



2;3 .

B.



3; 2 .

C.





1; 2 .

D.



2;1 .

Câu 10: Cho hai đường thẳng









12

:1,:2  dmxym d xmy

song song nhau khi và chỉ khi

A.

2.m

B.

1.m

C.

1.m

D.

1.m

Câu 11: Cho 4 điểm

   

1;2, 4;0, 1; 3, 7; 7AB C D

. Xác định vị trí tương đối của hai đường thẳng

A

B

và CD .

A.

Song song. B. Cắt nhau nhưng không vuông góc.

C.

Trùng nhau. D. Vuông góc nhau.

Câu 12: Với giá trị nào của

m

thì hai đường thẳng





1

:3 4 1 0xy

và









2

:2 1 1 0mxmy

trùng nhau.

A.

2m 

B. mọi

m

C. không có

m

D.

1m 

Câu 13: Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba đường thẳng lần lượt có phương trình

1

:34150dxy,

2

:5 2 1 0dxy và





3

:219130dmx m y m

. Tìm tất cả các giá

trị của tham số

m

để ba đường thẳng đã cho cùng đi qua một điểm.

A.

1

.

5

m 

B.

5.m 

C.

1

.

5

m 

D.

5.m 

Câu 14: Nếu ba đường thẳng

1

: 2 –4 0dxy,

2

:5 –2 3 0dxy và

3

:3–20dmx y

đồng quy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 327

thì

m

nhận giá trị nào sau đây?

A.

12

.

5

B.

12

.

5



C. 12. D. 12.

Câu 15: Với giá trị nào của

m

thì ba đường thẳng

1

:3 –4 15 0dx y,

2

:5 2 –1 0dxy và

3

:–4150dmx y đồng quy?

A.

5m 

. B.

5m 

. C.

3m 

. D.

3m 

.

Câu 16: Với giá trị nào của

m

thì ba đường thẳng

1

:2 –1 0dxy,

2

:210dx y và

3

:––70dmxy 

đồng quy?

A.

6m 

. B.

6m 

. C.

5m 

. D.

5m 

.

Câu 17: Cho

A

BC

với





1; 3 , 2; 4 , 1; 5()()AB C

và đường thẳng

:2 3 6 0dx y

. Đường thẳng

d

cắt cạnh nào của

A

BC

?

A. Cạnh

A

C

. B. Không cạnh nào. C. Cạnh

A

B . D. Cạnh

BC

.

Câu 18: Với giá trị nào của

m

thì hai đường thẳng sau đây vuông góc



2

1

11

:

2

x

mt

ymt



 













và



2

23'

:

14 '

x

t

ymt













A. 3m  B. 3m  C. 3m  D. không có

m

Câu 19: Cho 4 điểm

















3;1 , 9; 3 , 6; 0 , 2; 4AB C D 

. Tìm tọa độ giao điểm của 2 đường thẳng

AB

và

CD

.

A.





6; 1

B.





9; 3

C.





9;3

D.





0; 4

DẠNG 2: TÍNH GÓC, KHOẢNG CÁCH

{Xác định và tính góc giữa hai đường thẳng, khoảng cách từ điểm đến đường thẳng,…}

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc

. Khi đó góc giữa hai đường thẳng được tính theo công thức.



12

12 12

12

2222

12

1122

.

cos ;

.

nn

aa bb

dd

nn

abab







 

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:0ax by c

và điểm





000

;

M

xy

.

Khi đó khoảng cách từ điểm

0

M

đến đường thẳng  được tính theo công thức:



00

0

22

;

ax by c

dM

ab







Câu 1:

Tính khoảng cách từ điểm



1; 1M 

đến đường thẳng

:3 4 17 0xy

Câu 2: Cho hai đường thẳng

1

:2 4 3 0dxy và

2

:3 17 0dxy . Tính số đo góc giữa

1

d và

2

d .

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 328

Câu 3:

Cho hai đường thẳng song

1

:5 7 4 0dxyvà

2

:5 7 6 0.dxyPhương trình đường

thẳng song song và cách đều

1

d

và

2

d

là

Câu 4: Tính diện tích tam giác

A

BC với





3; 4A  ,





1; 5B ,





3;1C là

Câu 5: Cho đường thẳng đi qua hai điểm





3, 0A ,





0; 4B . Tìm tọa độ điểm

M

nằm trên

Oy

sao cho

diện tích tam giác

M

AB

bằng

6

Câu 6: Xác định tất cả các giá trị của a để góc tạo bởi đường thẳng

9

72

x

at

y

t















t  và đường

thẳng

3420xy

bằng 45.

Câu 7:

Đường thẳng



đi qua giao điểm của hai đường thẳng

1

:2 3 0dxy và

2

:210dx y

đồng thời tạo với đường thẳng

3

:10dy

một góc

0

45

có phương trình:

Câu 8: Trong mặt phẳng tọa độ

Ox

y

, cho điểm



1; 1M  và hai đường thẳng có phương trình

 

12

:10,:250dxy d xy . Gọi

A

là giao điểm của hai đường thẳng trên. Biết rằng

có hai đường thẳng



d đi qua

M

cắt hai đường thẳng trên lần lượt tại hai điểm

,

B

C

sao cho

A

BC là tam giác có 3BC AB có dạng:

0ax y b

và

0cx y d

, giá trị của

Tabcdlà

Câu 9:

Trong mặt phẳng Oxy, cho hai đường thẳng

(

)

1

:2 5 0dxy-+= và

()

2

:30dxy+-= cắt

nhau tại

I

. Phương trình đường thẳng đi qua

()

2;0M -

cắt

()()

12

,dd

tại

A

và

B

sao cho tam

giác

I

AB

cân tại

A

có phương trình dạng 20ax by++=. Tính

5Ta b=-

.

Câu 10:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





,1;1A



2; 4B 

và đường thẳng

:30mx y

. Tìm tất cả các giá trị của tham số

m

để



cách đều hai điểm

,

A

B

.

Câu 11:

Trong mặt phẳng tọa độ

Oxy

, gọi d là đường thảng đi qua

(4;2)M

và cách điểm

(1; 0)A

khoảng cách

310

10

. Biết rằng phương trình đường thẳng

d

có dạng 0xbyc với ,bc là

hai số nguyên. Tính

.bc

Câu 12: Trong mặt phẳng tọa độ

Oxy

cho

:10xy

và hai điểm









2; 1 , 9; 6 .AB

Điểm





;

M

ab

nằm trên đường  sao cho

M

AMB nhỏ nhất. Tính

.ab

Câu 13:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:4150dx y

và điểm





2;0A

.

Tìm tọa độ điểm

M

thuộc

d

để đoạn

AM

có độ dài nhỏ nhất.

Câu 14: Cho 3 điểm

(6;3); (0;1); (3;2)ABC

. Tìm

M

trên đường thẳng

:2 3 0dxy

mà

M

AMBMC

  

nhỏ nhất là

Câu 15:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có đỉnh





2; 2A

,



1; 3B 

,



2; 2C 

.

Điểm

M

thuộc trục tung sao cho

M

AMBMC

  

nhỏ nhất có tung độ là?

Câu 16:

Trong mặt phẳng tọa độ Oxy cho

:x y 1 0

và hai điểm

(2;1)A

,

(9;6)B

. Điểm

(;)

M

ab

nằm trên đường



sao cho



M

AMB

nhỏ nhất. Tính

ab

ta được kết quả là:

Câu 17: Trong mặt phẳng với hệ tọa độ

Oxy

,cho tam giác

A

BC

có đỉnh





2; 2A

và trung điểm của

BC

là





1; 2I 

. Điểm





;

M

ab

thỏa mãn

20MA MB MC

  

. Tính

Sab

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 329

Câu 18:

Trên mặt phẳng

Oxy

, cho hình vuông

A

BCD

. Gọi

M

là trung điểm của cạnh

BC

,

N

là điểm

trên cạnh

CD sao cho 2CN ND . Giả sử

11 1

;

22

M







và đường thẳng

A

N có phương trình

230xy

. Gọi





;

P

ab là giao điểm của

A

N và

B

D

. Giá trị 2ab bằng:

Câu 19: Trong mặt phẳng tọa độ

Oxy

, cho tứ giác

A

BCD

nội tiếp đường tròn đường kính

B

D

. Gọi

M

,

N

lần lượt là hình chiếu vuông góc của

A

lên

BC

và

B

D

; gọi

P

là giao điểm của

M

N

và

A

C

. Biết đường thẳng

A

C

có phương trình

10xy

,



0; 4M

,





2; 2N

và hoành độ điểm

A

nhỏ hơn

2

. Tìm tọa độ các điểm

P

,

A

,

B

.

Câu 20: Đường thẳng



: 1 , 0; 0

xy

dab

ab

  

đi qua





1; 6M  tạo với tia

,Ox Oy

một tam giác có

diện tích bằng 4. Tính

2.Sa b

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 20. VN TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG

THẲNG, GÓC VÀ KHOẢNG CÁCH

I. VN TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc

và

22 2 2

:0daxbyc

. Để xét vị trí tương đối của hai đường thẳng này ta xét số nghiệm của hệ

phương trình

111

222

0

ax by c











(0.1)

+ Nếu hệ





1.1

có duy nhất 1 nghiệm ta nói hai đường thẳng trên cắt nhau tọa độ giao điểm

chính là nghiệm của hệ phương trình nói trên.

+ Nếu hệ





1.1

vô nghiệm ta nói hai đường thẳng nói trên song song với nhau.

+ Nếu hệ





1.1

nghiệm đúng với mọi

x 

thì hai đường thẳng trên trùng nhau.

+ Tuy nhiên để thuận tiện cho việc xét nhanh vị trí tương đối của hai đường thẳng ta chú ý nhận

xét sau

Nhận xét. Nếu

222

0abc  ta có

a)



11

12

22

ab

dd I

ab



b)

111

12

222

//

abc

dd

abc



c)

111

12

222

abc

dd

abc



II. GÓC GIỮA HAI ĐƯỜNG THẲNG

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc. Khi đó góc giữa hai đường thẳng được tính theo công thức.



12

12 12

12

2222

12

1122

.

cos ;

.

nn

aa bb

dd

nn

abab







 

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

III. KHOẢNG CÁCH

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:0ax by c

và điểm





000

;

M

xy .

Khi đó khoảng cách từ điểm

0

M

đến đường thẳng



được tính theo công thức:



00

0

22

;

ax by c

dM

ab







7.7

Xét vị trí tương đối giữa các cặp đường thẳng sau:

a)



1

:3 2 2 3 0xy

và



2

:6 2 6 0xy

.

b)



1

:320dx y

và



2

:3 3 2 0dxy

.

c)



1

:210mx y

và



2

:3 2 0mxy

.

Giải:

a) Xét hệ phương trình









 





32 2 3 0

62 60

xy

có vô số nghiệm

Vậy



1

và



2

trùng nhau.

b) Xét hệ phương trình















320

3320

xy

vô nghiệm

Vậy

1

d

và

2

d

song song.

c) Xét hệ phương trình











210

320

xy



















3

7

5

7

x

y

. Hệ phương trình có nghiệm duy nhất.

Vậy

1

m

và

2

m

cắt nhau tại







35

;

77

A

.

7.8 Tính góc giữa các cặp đường thẳng sau:

a)



1

:3 4 0xy

và

 

2

:330xy

.

b)



 







1

12

:

34

x

t

d

y

t

và











2

3

:

13s

x

s

d

y

(

, ts

là các tham số).

Giải:

a)

Đường thẳng



1

có vectơ pháp tuyến







1

3;1n

.

Đường thẳng



2

có vectơ pháp tuyến





2

1; 3n

.

BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

Gọi



là góc giữa 2 đường thẳng



1

và



2

. Ta có



 





 





12

22

12

3.1 1. 3

.

3

,

2

.

31.1 3

nn

cos cos n n

nn

.

Do đó, góc giữa 2 đường thẳng



1

và



2

là





0

30

.

b) Đường thẳng

1

d

có vectơ chỉ phương







1

2; 4u

nên có vectơ pháp tuyến









1

2; 1n

.

Đường thẳng

2

d

có vectơ chỉ phương









2

1; 3u

nên có vectơ pháp tuyến





2

3;1n

.

Gọi



là góc giữa 2 đường thẳng

1

d

và

2

d

. Ta có







 

 



12

2

222

12

.

2.3 1 .1

2

,

2

.

21.31

nn

cos cos n n

nn

.

Do đó, góc giữa 2 đường thẳng

1

d

và

2

d

là





0

45

.

7.9 Trong mặt phẳng toạ độ Oxy , cho điểm





A 0; 2 và đường thẳng

:40

x

y

.

a) Tính khoảng cách từ điểm

A đến đường thẳng



.

b) Viết phương trình đường thẳng

a

đi qua điểm





M 1; 0

và song song với



.

c) Viết phương trình đường thẳng

b

đi qua điểm





N 0;3

và vuông góc với



.

Giải:

a) Áp dụng công thức tính khoảng cách từ điểm A đến đường thẳng



, ta có:





 



22

024

,32

11

dA

.

Vậy khoảng cách từ điểm

A

đến đường thẳng



là

32

.

b) Đường thẳng

:40

x

y

có vectơ pháp tuyến









1; 1n

.

Vì đường thẳng

a

song song với



nên





1; 1

a

nn







là vectơ pháp tuyến của

a

.

Lại có

a

đi qua điểm





M 1; 0

nên phương trình tổng quát của đường thẳng

a

là









  1. 1 1. 0 0xy

hay

10xy

.

c) Đường thẳng

:40

x

y

có vectơ pháp tuyến









1; 1n

.

Vì đường thẳng

b

vuông góc với



nên









1; 1

b

n

là vectơ pháp tuyến của

b

.

Lại có

b

đi qua điểm





N 0;3

nên phương trình tổng quát của đường thẳng

b

là









 1. 0 1. 3 0xy

hay

30xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

7.10 Trong mặt phẳng toạ độ, cho tam giác

ABC

có



A 1; 0 , B 3; 2

và



 C2;1

.

a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác

ABC

.

b) Tính diện tích tam giác

ABC

.

Giải:

a) Ta có:







5; 3BC

.

BC

có vectơ chỉ phương



 



5; 3BC

nên có vectơ

pháp tuyến







3; 5n

và đi qua điểm



B 3; 2

nên

phương trình tổng quát của

BC

là



 33520xy

hay

3510xy

.

Gọi H là hình chiếu của A lên

BC

. Khi đó độ dài đường cao kẻ từ đỉnh A của tam giác

ABC

chính là độ dài AH .





 



2

3.1 5.0 1

234

,

17

35

AH d A BC

.

b) Ta có:



  

22

5334BC

.

Diện tích tam giác

ABC

là:

 

11234

.. . .342

2217

ABC

SAHBC

.

7.11 Chứng minh rằng hai đường thẳng



 : 0dy ax b a

và





 : 0dyaxb a

vuông góc

với nhau khi và chỉ khi



1aa

.

Giải:

Ta có: +)



 : 0 0d y ax b a ax y b

nên đường thẳng

d

có vectơ pháp tuyến







1

;1na

.

+)



  

 : 0 0d y ax b a ax y b

nên đường thẳng



d

có vectơ pháp tuyến









2

;1na

.

Ta lại có:



   



12

.0 10 1.dd nn aa aa

7.12 Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín

hiệu đặt tại ba vị trí













O,A0;0 1;0 , B 1;3

nhận được cùng một thời điểm. Hãy xác định vị

trí phát tín hiệu âm thanh.

Giải:

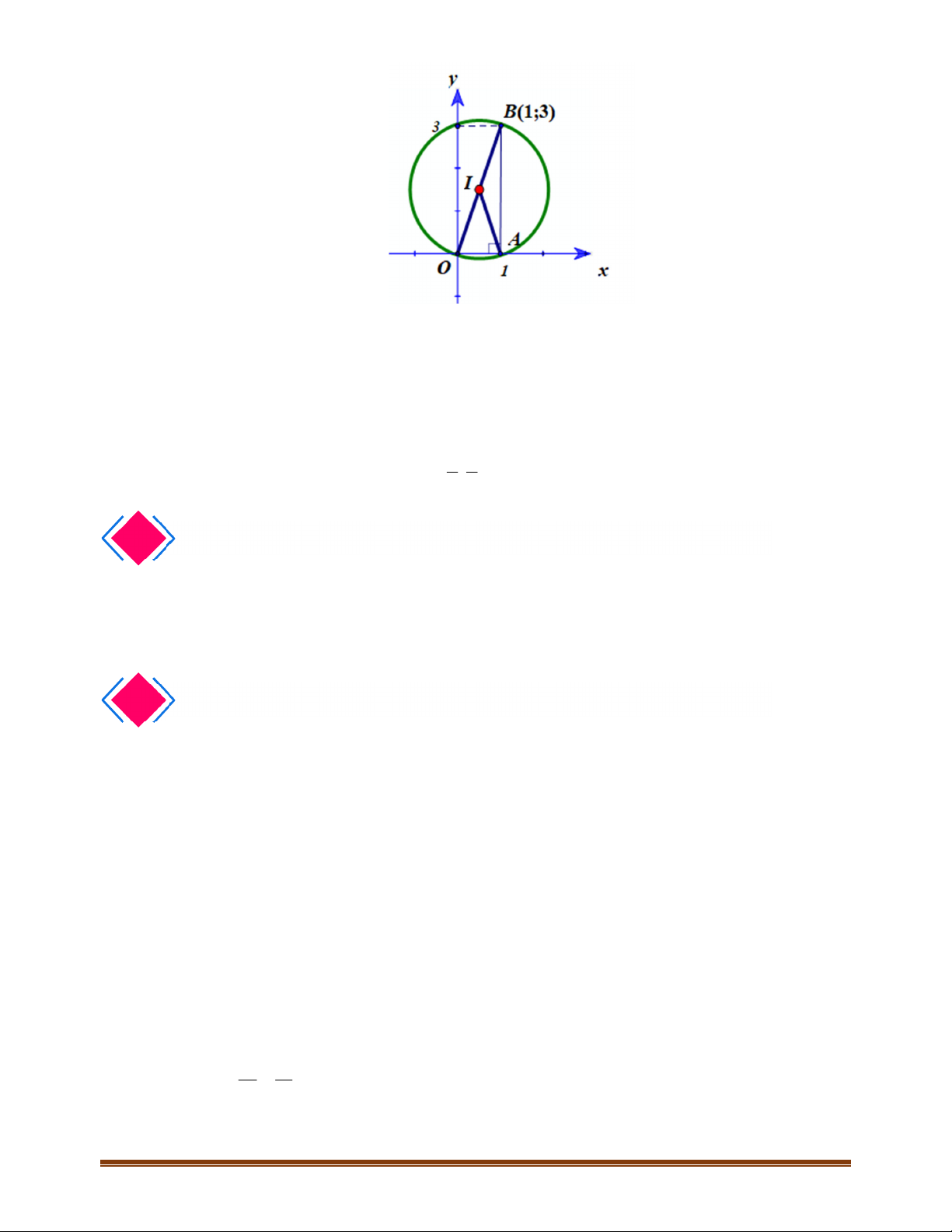
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

Vị trí phát tín hiệu âm thanh mà ba thiết bị ghi tín hiệu đặt tại ba vị trí













O,A0;0 1; 0 , B 1;3

nhận được cùng một thời điểm thì vị trí đó phải cách đều 3 điểm

,,OAB

.

Gọi I là vị trí phát tín hiệu âm thanh, khi đó I là tâm đường tròn ngoại tiếp tam giác

OAB

.

Nhận xét:

OAB

vuông tại I (biểu diễn lên hệ tục toạ độ), nên I là trung điểm của

OB

.

Vậy vị trí phát tín hiệu âm thanh là







13

;

22

I

.

DẠNG 1: XÉT VN TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

{các bài toán xét vị trí tương đối của hai đường thẳng, tìm điều kiện (có chứa tham số m) để hai đường

thẳng song song, cắt, trùng,….}

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc. Để xét vị trí tương đối của hai đường thẳng này ta xét số nghiệm của hệ

phương trình

111

222

0

ax by c











(0.2)

Nếu hệ



1.1

có duy nhất 1 nghiệm ta nói hai đường thẳng trên cắt nhau tọa độ giao điểm chính

là nghiệm của hệ phương trình nói trên. Nếu hệ



1.1

vô nghiệm ta nói hai đường thẳng nói

trên song song với nhau. Nếu hệ



1.1

nghiệm đúng với mọi

x 

thì hai đường thẳng trên

trùng nhau. Tuy nhiên để thuận tiện cho việc xét nhanh vị trí tương đối của hai đường thẳng ta

chú ý nhận xét sau

Nhận xét. Nếu

222

0abc  ta có

a)



11

12

22

ab

dd I

ab



HỆ THỐNG BÀI TẬP.

II

PHƯƠNG PHÁP.

1

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

b)

111

12

222

//

abc

dd

abc



c)

111

12

222

abc

dd

abc



Câu 1:

Xét vị trí tương đối của hai đường thẳng lần lượt có phương trình

2

23

xy



và

6280xy

Lời giải

Ta có

2

23

xy



3260xy

. Do

62

32







nên hai đường thẳng cắt nhau.

Mặt khác









6.3 2 . 2 0  

nên hai đường thẳng không vuông góc

Câu 2: Xét vị trí tương đối của hai đường thẳng

1

:2 15 0dxy  và

2

:230dx y. 

Lời giải

1

d

có vectơ pháp tuyến



1

2;1n 



.

2

d

có vectơ pháp tuyến



2

1; 2n 



.

Ta có



12

.2.11.20nn 



.

Vậy

1

d

và

2

d

vuông góc với nhau.

Câu 3: Tìm tọa độ giao điểm của hai đường thẳng

43260xy

và

3470xy

.

Lời giải

Toạ độ giao điểm của hai đường thẳng là nghiệm hệ phương trình:

43260 5

3470 2

xy x

xy y

 







 



. Vậy toạ độ giao điểm là



5; 2

.

Câu 4: Cho hai đường thẳng



1

:120dmx m y m  

và

2

:2 1 0dxy. Tìm

m

để

12

//dd.

Lời giải

Ta có

12

//dd

12

21 1

mm m

 



2m

.

Câu 5: Cho ba đường thẳng



12

:120,:43260dmx m y m d x y   

và

3

:3 4 7 0dxy

Tìm

m

để ba đường thẳng trên đồng quy.

Lời giải

giao điểm của hai đường thẳng là nghiệm hệ phương trình:

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7

43260 5

3470 2

xy x

xy y

 







 



. Vậy toạ độ giao điểm là



5; 2I 

.

Để ba đường thẳng đồng quy thì

1

d

phải đi qua



5; 2I 

suy ra



2

.5 1 2 2 0

5

mm m m 

Câu 1:

Xét vị trí tương đối của hai đường thẳng

1

:210dx y

và

2

:3 6 10 0dxy 

.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

Chọn B

1

2

12

1

|| .

:210

12

:3 6 10

10

0

36

dx y

dxy

dd











 











Câu 2: Xét vị trí tương đối của hai đường thẳng

1

:3 2 6 0dxy

và

2

:6 2 8 0dxy

.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

Chọn D



1

11

2

12

2

3

:3 2 6 0 3; 2

6

:6 2 8 0 6;

2

0

2

,

dxy n

dd

n

x

n

dy



































cắt nhau nhưng không vuông góc.

Câu 3: Xét vị trí tương đối của hai đường thẳng

1

:1

34

xy

d 

và

2

:3 4 10 0dxy.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

Lời giải

Chọn C



11

1

2

212

2

11

:1 ;

34 3 4

:3

0.

4100 3;4

xy

d

dx ny

n

nn d d





 



























Câu 4:

Xét vị trí tương đối của hai đường thẳng

1

34

:

26

x

t

d

yt

 









và

2

22

:

84

x

t

d

yt











 



.

A. Trùng nhau. B. Song song.

C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

Lời giải

Chọn B

 



111

12

2

34

:3;2,2;3

23

26

|| .

23

12

:2;3

43

xt

dA

yt

d

x

u

t

d

y

d

u

t

A

  



 



















































Câu 5: Cho hai đường thẳng









12

:1,:2  dmxym d xmy

cắt nhau khi và chỉ khi :

A.

2.m

B.

1.m

C.

1.m

D.

1.m

Lời giải

Chọn C









12

dd



11

22

mx y m

xmy

















có một nghiệm

Thay





2

vào



1













2

2111*mmyym my m 

Hệ phương trình có một nghiệm





*

có một nghiệm

2

10

1

10

m













.

Câu 6: Đường thẳng







:

3270xy

cắt đường thẳng nào sau đây?

A.





1

:3 2 0dxy

B.





2

:3 2 0dxy

C.





3

:3 2 7 0. dxy

D.





4

:6 4 14 0.dxy

Lời giải

Chọn A

Ta nhận thấy





song song với các đường



234

;;ddd

Câu 7: Giao điểm

M

của



12

:

35







 



x

t

d

yt

và





:3 2 1 0



dxy

. Toạ độ của

M

là

A.

11

2; .

2









M

B.

1

0; .

2







M

C.

1

0; .

2









M

D.

1

;0 .

2

M









Lời giải

Chọn C

Ta có

 

12

::5210

35

xt

ddxy

yt









 



Ta có

  

'

M

dd M 

là nghiệm của hệ phương trình

0

3210

1

5210

2

x

xy

y

























Câu 8: Phương trình nào sau đây biểu diển đường thẳng không song song với đường thẳng





:21dy x

?

A.

250.xy

B.

250.xy

C.

20.xy

D.

250.xy

Lời giải

Chọn D

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9

Ta có









:21 :2 10dy x d xy 

chọn D

Câu 9: Hai đường thẳng



1

25

:

2

 









x

t

d

yt

và





2

:4 3 18 0dxy . Cắt nhau tại điểm có tọa độ:

A.



2;3 . B.



3; 2 . C.





1; 2 . D.





2;1 .

Lời giải

Chọn A

Ta có

 

11

25

::2540

2

xt

ddxy

yt

 











Gọi









12

M

dd

M



là nghiệm của hệ phương trình

2540 2

43180 3

xy x

xy y

 







 



Câu 10: Cho hai đường thẳng









12

:1,:2  dmxym d xmy

song song nhau khi và chỉ khi

A.

2.m

B.

1.m

C.

1.m

D.

1.m

Lời giải

Chọn D.









12

;dd

song song nhau

2

1

2

m

mm

m









































Câu 11: Cho 4 điểm

















1;2, 4;0, 1; 3, 7; 7AB C D

. Xác định vị trí tương đối của hai đường thẳng

A

B và

CD

.

A.

Song song. B. Cắt nhau nhưng không vuông góc.

C. Trùng nhau. D. Vuông góc nhau.

Lời giải

Chọn A

Ta có









3; 2 , 6; 4AB CD 



Ta có

32

64







Suy ra

//

A

BCD

Câu 12: Với giá trị nào của

m

thì hai đường thẳng





1

:3 4 1 0xy và









2

:2 1 1 0mxmy trùng nhau.

A.

2m 

B. mọi

m

C. không có

m

D.

1m 

Lời giải

Chọn C





2

12

32 1

4

11







 









m

VL

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

Câu 13:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba đường thẳng lần lượt có phương trình

1

:34150dxy,

2

:5 2 1 0dxy và





3

:219130dmx m y m

. Tìm tất cả các giá

trị của tham số

m

để ba đường thẳng đã cho cùng đi qua một điểm.

A.

1

.

5

m 

. B. 5.m  . C.

1

.

5

m 

. D. 5.m 

Lời giải

Chọn.D

Ta có:



23

1

2

:3 4 15 0

1

:5 2 1 0

1; 3

3

dxy

x

d

dxy y

dA d











 



 

639130 5.mm m m

.

Câu 14: Nếu ba đường thẳng

1

: 2 –4 0dxy,

2

:5 –2 3 0dxy và

3

:3–20dmx y

đồng quy

thì

m

nhận giá trị nào sau đây?

A.

12

.

5

B.

12

.

5



C. 12. D. 12.

Lời giải

Chọn.D

.

2

1

13

2

5

: 2 –4 0

9

:5 –2 3 0

5

2

26

9

6

;

9

x

dxy

d

dxy

dA d

y



























 









526

2 0 12.

93

m

m

.

Câu 15: Với giá trị nào của m thì ba đường thẳng

1

:3 –4 15 0dx y

,

2

:5 2 –1 0dxy

và

3

:–4150dmx y đồng quy?

A.

5m 

. B.

5m 

. C.

3m 

. D.

3m 

.

Lời giải

Chọn.C



1

12

2

:3 –4 15 0

1

1; 3

:5 2 –1 0 3

dxy

x

dd A d

dxy y











 



12 15 0 3mm     

.

Câu 16: Với giá trị nào của

m

thì ba đường thẳng

1

:2 –1 0dxy,

2

:210dx y và

3

:––70dmxy  đồng quy?

A.

6m 

. B.

6m 

. C.

5m 

. D.

5m 

.

Lời giải

Chọn.B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11



1

12 3

2

:2 –1 0

1

1; 1 1 7 0 6 .

:210 1

dxy

x

dd A d m m

dx y y











 



Câu 17: Cho

A

BC

với





1; 3 , 2; 4 , 1; 5()()AB C và đường thẳng

:2 3 6 0dx y

. Đường thẳng

d

cắt cạnh nào của

A

BC

?

A. Cạnh

A

C

. B. Không cạnh nào. C. Cạnh

A

B . D. Cạnh

BC

.

Lời giải

Chọn B

Thay điểm

A

vào phương trình đường thẳng

d

ta được

1

Thay điểm

B

vào phương trình đường thẳng

d

ta được

10

Thay điểm

C

vào phương trình đường thẳng

d

ta được 11

Suy ra điểm

A

và

B

nằm cùng phía đối với

d

nên

d

không cắt cạnh

.

A

B

điểm

A

và

C

nằm cùng phía đối với

d

nên

d

không cắt cạnh

A

C

điểm

C

và

B

nằm cùng phía đối với

d

nên

d

không cắt cạnh

.BC

Câu 18: Với giá trị nào của m thì hai đường thẳng sau đây vuông góc



2

1

11

:

2

x

mt

ymt



 













và



2

23'

:

14 '

x

t

ymt













A. 3m  B. 3m  C. 3m  D. không có

m

Lời giải

Chọn A





1

 có



2

1

1;um m



;





2

 có



2

3; 4um 







222

1212

3140 3 3uu m m m m      

 

Câu 19: Cho 4 điểm

















3;1 , 9; 3 , 6; 0 , 2; 4AB C D 

. Tìm tọa độ giao điểm của 2 đường thẳng

A

B và

CD

.

A.





6; 1

B.





9; 3

C.





9;3

D.





0; 4

Lời giải

Chọn B.

Ta có

 

6; 4 2; 3 : 2 3 9

AB

AB VTPT n AB x y       



Ta có













4; 4 1; 1 : 6

CD

CD VTPT n CD x y  

 

Gọi

NABCD

Suy ra

N

là nghiệm của hệ



23 9 9

9; 3

63

xy x

N

xy y

 







 



CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

DẠNG 2: TÍNH GÓC, KHOẢNG CÁCH

{Xác định và tính góc giữa hai đường thẳng, khoảng cách từ điểm đến đường thẳng,…}

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

11 1 1

:0daxbyc và

22 2 2

:0daxbyc. Khi đó góc giữa hai đường thẳng được tính theo công thức.



12

12 12

12

2222

12

1122

.

cos ;

.

nn

aa bb

dd

nn

abab







 

Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:0ax by c

và điểm





000

;

M

xy .

Khi đó khoảng cách từ điểm

0

M

đến đường thẳng  được tính theo công thức:



00

0

22

;

ax by c

dM

ab







Câu 1:

Tính khoảng cách từ điểm



1; 1M 

đến đường thẳng

:3 4 17 0xy

Lời giải

Áp dụng công thức tính khoảng cách ta có



2

3

3.1 4 1 17

,

34

dM







10

5



2

.

Câu 2: Cho hai đường thẳng

1

:2 4 3 0dxy và

2

:3 17 0dxy . Tính số đo góc giữa

1

d và

2

d .

Lời giải

Ta có











 

12

22

23

2.3 4 . 1

cos ,

24.31

dd

 



 

10 2

2

10 2



Suy ra số đo góc giữa

1

d và

2

d là

0

45

.

Câu 3: Cho hai đường thẳng song

1

:5 7 4 0dxyvà

2

:5 7 6 0.dxyPhương trình đường

thẳng song song và cách đều

1

d và

2

d là

Lời giải

Cách 1: Tự luận.

Gọi là

d

đường thẳng song song và cách đều

1

d và

2

d .

Suy ra phương trình

d

có dạng:





57 0 4, 6xyc c c  

Mặt khác:









12

;;ddd ddd

 

22

46

57 57

cc



 

46

cc













5c

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

Cách 2: Trắc nghiệm.

Phương trình đường thẳng song song và cách đều

1

d

và

2

d

là

64

57 05750

2

xy xy



 

Câu 4: Tính diện tích tam giác

A

BC với





3; 4A  ,





1; 5B ,





3;1C là

Lời giải

Ta có





2;9AB 



85AB



.

Phương trình đường thẳng

A

B

là

34

29

xy





92190xy

.

Khoảng cách từ điểm

C

đến đường thẳng

A

B

là



22

9.3 2.1 19

,

92

dCAB







10

85



.

Diện tích tam giác

A

BC

là

110

85.

2

85

ABC

S 

5

.

Câu 5: Cho đường thẳng đi qua hai điểm





3, 0A ,





0; 4B . Tìm tọa độ điểm

M

nằm trên

Oy

sao cho

diện tích tam giác

M

AB

bằng

6

Lời giải

Ta có



3; 4AB 



5AB



.

Phương trình đường thẳng

A

B

là

1

34

xy



43120xy

.

Gọi





0;

M

mOy



22

312

,

34

m

dMAB







312

5

m 



.

Diện tích tam giác

M

AB

bằng

6

nên

312

1

.5 6

25

m 



31212m

30

324

m



















00;0

80;8

mM













.

Câu 6: Xác định tất cả các giá trị của

a

để góc tạo bởi đường thẳng

9

72

x

at

y

t















t 

và đường

thẳng

3420xy

bằng

45

.

Lời

giải

Gọi



là góc giữa hai đường thẳng đã cho.

Đường thẳng

9

72

x

at

y

t















t 

có vectơ chỉ phương là





;2ua



.

Đường thẳng

3420xy

có vectơ chỉ phương là



4; 3v 



.

Ta có



cos cos ,uv







.

cos 45

.

uv





2

46

1

2

54

a







2

54246aa 

22

25 100 32 96 72aaa

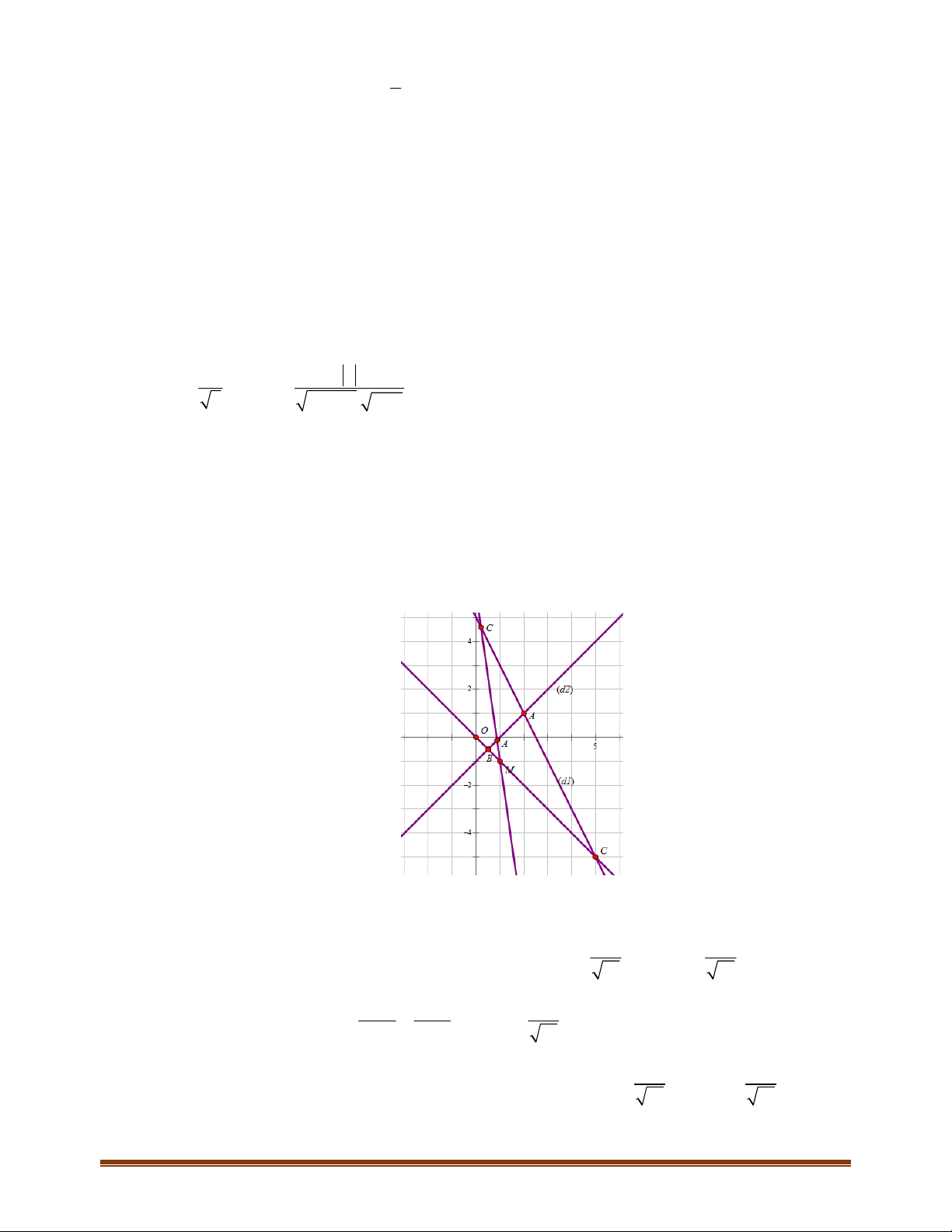
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

2

796280aa

2

7

14

a















.

Câu 7: Đường thẳng



đi qua giao điểm của hai đường thẳng

1

:2 3 0dxy và

2

:210dx y

đồng thời tạo với đường thẳng

3

:10dy một góc

0

45

có phương trình:

Lời giải



1

2

:2 3 0

1

:21 1

1;1 .

0

dxy

x

d

dx y y

dA











 



 



Ta có





33

:10 0;1,dny   



gọi









3

;, ;adbn









. Khi đó

22 2

22

.

1

1: 20

2

1, 1 : 0

1

2

0

o

.

cs

ab ab xy

b

ab b

abab xy

ab



 







      







Câu 8: Trong mặt phẳng tọa độ

Ox

y

, cho điểm



1; 1M 

và hai đường thẳng có phương trình

 

12

:10,:250dxy d xy 

. Gọi

A

là giao điểm của hai đường thẳng trên. Biết rằng

có hai đường thẳng



d

đi qua

M

cắt hai đường thẳng trên lần lượt tại hai điểm ,

B

C sao cho

A

BC

là tam giác có

3BC AB

có dạng:

0ax y b

và

0cx y d

, giá trị của

Tabcd

là

Lời

giải

Tọa độ





2;1A

Gọi



là góc giữa hai đường thẳng





1

d

và



2

d

,

1

cos

10





3

sin

10





Xét tam giác

A

BC ta có:

1

sin

sin sin

10

AB BC

C

CA



Gọi



là góc giữa hai đường thẳng



d

và



1

d

, suy ra:

13

sin cos

10 10



 



1

Giả sử



d có vec tơ pháp tuyến là





;nab



CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15

Từ



1

ta có:

22

2

33

cos 8 0

10 10

5

ab

aabb

ab





 



7

ab













Với

ab

một vec tơ pháp tuyến



1;1 : 0ndxy



Với

7ab

một vec tơ pháp tuyến



7;1 : 7 6 0ndxy



Vậy:

10762T  

Câu 9: Trong mặt phẳng Oxy, cho hai đường thẳng

()

1

:2 5 0dxy-+=

và

()

2

:30dxy+-=

cắt

nhau tại

I

. Phương trình đường thẳng đi qua

()

2;0M -

cắt

()()

12

,dd

tại

A

và

B

sao cho tam

giác

IAB

cân tại

A

có phương trình dạng

20ax by++=

. Tính

5Ta b=-

.

Lời giải

Đường thẳng

()()

12

,dd

có véc tơ pháp tuyến lần lượt là

() ()

12

2; 1 , 1;1nn=- =

 

.

Gọi

()

D

là đường thẳng cần tìm có véc tơ pháp tuyến là

()

;nab=



.

Góc giữa 2 đường thẳng

()()

12

,dd

và

()( )

2

, dD

xác định bởi:

()

12

2

222

12

.

2.1 1.1

1

,

10

.

21.11

nn

cos d d

nn

-

== =

+- +

 

.

()

2

2222 22

2

.

,

.

.1 1 2.

nn

ab ab

cos d

nn

ab ab

++

D= = =

++ +



.

Vì

()

D

cắt

()()

12

,dd

tại

A

và

B

tạo thành tam giác

IAB

cân tại

A

nên

() ()

22

12 2

22

1

,, 5

10

2.

ab

cos d d cos d a b a b

ab

+

=D =  +=+

+

()

2

22 2 2

2

5250

1

2

ab

ab a b a abb

ab

é

=-

ê

+=+++=ê

ê

=-

ê

ë

.

+

2ab=-

: chọn

21ab==-

: phương trình đường thẳng là:

() ()

22 02 40xy xy L+ -= -+=

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

+

1

2

ab=-

: chọn

12ab= =-

: phương trình đường thẳng là:

() ()

22 0 2 20 /

x

yxy Tm+- =- +=

. Do đó

(

)

515211Ta b=- =-- =

.

Câu 10: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





,1;1A



2; 4B 

và đường thẳng

:30mx y

. Tìm tất cả các giá trị của tham số

m

để



cách đều hai điểm

,

A

B

.

Lời giải

Gọi

I

là trung điểm đoạn

 

15

;

22

.

3; 3 1;1

AB

I

AB

AB n



















  







Khi đó:









:30;1nmx y m



 



cách đều

,

A

B

5

1

30

.

2

1

2

1

Im

m

































Câu 11:

Trong mặt phẳng tọa độ

Ox

y

, gọi

d

là đường thảng đi qua

(4;2)M

và cách điểm

(1; 0)A

khoảng cách

310

10

. Biết rằng phương trình đường thẳng

d

có dạng

0xbyc

với

,bc

là

hai số nguyên. Tính

.bc

Lời giải

Ta có:

(4;2) 4 2 0 4 2 .

M

dbccb 

(1)

22

2

1

310

( , ) 10(1 ) 9(1 ).

10

1

c

dAd c b

b







(2)

Thay

42cb 

vào PT

(2)

ta được PT:

2

3( )

31 120 81 0

27

()

31

btmdk

bb

bktmdk















3, 2 1.bc bc 

.

Câu 12: Trong mặt phẳng tọa độ

Ox

y

cho

:10xy

và hai điểm



2; 1 , 9; 6 .AB Điểm



;

M

ab nằm trên đường  sao cho

M

AMB nhỏ nhất. Tính .ab

Lời

giải

Gọi

A



đối xứng

A

qua

d

ta có

'(0;3)A

khi đó điểm

M

AB d





Tìm được

(3;4)M .

Câu 13: Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:4150dx y

và điểm





2;0A

.

Tìm tọa độ điểm

M

thuộc

d

để đoạn

AM

có độ dài nhỏ nhất.

Lời giải

Điểm



4 15;Md Mt t 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17

Ta có:



22

4 17 17 8 17 17 4 1 17AM t t t t t



  





,

t

.

min AM

17

, đạt được tại

4t 

. Khi đó



1; 4M

.

Câu 14: Cho 3 điểm

(6;3); (0;1); (3;2)ABC

. Tìm

M

trên đường thẳng

:2 3 0dxy

mà

M

AMBMC

  

nhỏ nhất là

Lời

giải

Cách 1:

Tìm tọa độ điểm





;

I

xy sao cho 0IA IB IC 

 

. Suy ra

4

1;

3

I









Ta có:

3

M

AMBMC MI IAIBIC 

  

3

M

AMBMC MI 

  

. Vậy

M

AMBMC

  

nhỏ nhất khí

M

I



nhỏ nhất.

M

I



nhỏ nhất khi

M

là hình chiếu vuông góc của I xuống đường thẳng

d

.

Đường thẳng

d



đi qua

I

và vuông góc với

d

có phương trình:

5

2

3

xy

M

là giao điểm của

d

và

d



nên

M

là nghiệm của hệ:

23

13 19

;

5

15 15

2

3

xy

M

xy

























Cách 2:

M

thuộc

d

suy ra



;2 3Mt t

(3 3;6 5)MA MB MC t t 

  



22

33 65

M

AMBMC t t



  

  

2

13 1

45 78 34 45

15 5

MA MB MC t t t



    





  

M

AMBMC

  

nhỏ nhất khi

13

15

t 

. Suy ra

13 19

;

15 15

M









.

Câu 15:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có đỉnh





2; 2A

,



1; 3B 

,



2; 2C 

.

Điểm

M

thuộc trục tung sao cho

M

AMBMC

  

nhỏ nhất có tung độ là?

Lời

giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18

Gọi



;Gab

là trọng tâm tam giác

ABC

. Suy ra

212 1

11

333

;

232 1

33

3

ABC

xxx

aaa

G

yyy

bb

b

























 

















.

Ta có:

33MA MB MC MG GA MG GB MG GC MG MG   

      

.

Suy ra

MA MB MC

  

nhỏ nhất khi

MG

nhỏ nhất.

Mặt khác

M

thuộc trục tung nên

MG

nhỏ nhất khi

M

là hình chiếu của

G

lên trục tung.

Vậy

1

0;

3

M







.

Câu 16: Trong mặt phẳng tọa độ Oxy cho

:x y 1 0



và hai điểm

(2;1)A

,

(9;6)B

. Điểm

(;)Mab

nằm trên đường



sao cho

MA MB

nhỏ nhất. Tính

ab

ta được kết quả là:

Lời giải

Gọi A’ là điểm đối xứng của A qua đường thẳng



Ta có:

''MA MB MA MB A B

Đẳng thức xảy ra  M trùng với M

0

(M

0

là giao điểm của



và A’B)

Ta có:

AA ' 

nên



AA '

na1;1









AA ' : x y 3 0

Gọi



H=AA' H 1;2

Vì A’ đối xứng với A qua



nên H là trung điểm AA’



A' 0;3

Đường thẳng A’B qua B có VTCP

  

A'B

A'B 9;3 3 3;1 n 1; 3 

 

A'B:x 3y 9 0



Tọa độ M

0

thỏa hệ:



0

xy10

M3;4

x3y90















M3;4

. Vậy

7



ab

Câu 17: Trong mặt phẳng với hệ tọa độ

Oxy

,cho tam giác

ABC

có đỉnh



2; 2A

và trung điểm của

BC

là



1; 2I 

. Điểm



;Mab

thỏa mãn

20MA MB MC

  

. Tính

Sab

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19

Gọi

K

trung điểm

1

;0

2

AI K









.

Ta có

2022040    

       

MA MB MC MA MI MK M K

11

0

22

ab

.

Câu 18: Trên mặt phẳng

Oxy

, cho hình vuông

ABCD

. Gọi

M

là trung điểm của cạnh

BC

,

N

là

điểm trên cạnh

CD

sao cho

2CN ND

. Giả sử

11 1

;

22

M







và đường thẳng

AN

có phương

trình

230

xy



. Gọi



;Pab

là giao điểm của

AN

và

BD

. Giá trị

2ab

bằng:

Lời giải

Ta chứng minh được

MP AN

, nên

P

là hình chiếu của

M

trên

AN

.

(Thật vậy gắn hệ trục toạ độ

Dxy

,

 

0;0, 1;0, 1;1, 0;1DCBA

. Khi đó

11

1; ; ; 0

23

MN

 

 

 

.

Phương trình đường thẳng

:BD y x

. Phương trình đường thẳng

:3 1AN x y

.

Điểm

11

;

44

P







. Khi đó

31 1

;; ;1 . 0

44 3

MP AN MP AN MP AN











   

(đpcm).

Phương trình đường thẳng

MP

qua

M

và vuông góc với

AN

là

13

20

2

xy

.

P

là giao điểm

MP

và

AN

nên toạ độ

P

là nghiệm hệ

23 5

2

13

2

xy

x

xy

y





















.

Từ đó:

5

2

a 

,

22 7bab

 

.

Câu 19: Trong mặt phẳng tọa độ

Oxy

, cho tứ giác

ABCD

nội tiếp đường tròn đường kính

BD

. Gọi

M

,

N

lần lượt là hình chiếu vuông góc của

A

lên

BC

và

BD

; gọi

P

là giao điểm của

MN

và

AC

. Biết đường thẳng

AC

có phương trình

10xy

,



0; 4M

,



2; 2N

và hoành độ điểm

A

nhỏ hơn

2

. Tìm tọa độ các điểm

P

,

A

,

B

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

* Ta chứng minh

P

là trung điểm của

A

C

.

Thật vậy: do các tứ giác

A

BMN

,

A

BCD

là các tứ giác nội tiếp nên



A

MP ABN ACD

Lại do :

//

A

MCD

(cùng vuông góc với BC ) nên



A

CD CAM PAM PMA

P

AM

cân tại

P

APM

. Đồng thời

P

CM

cân tại

P

nên

P

CPM

P

APC

hay

P

là trung điểm của

A

C

.

- Ta có :



2; 2MN 



đường thẳng

M

N

có phương trình:

40xy

Điểm

P

có tọa độ là nghiệm của hệ

5

10

53

2

;

40 3

22

2

x

xy

P

xy

y



































- Do



:10 ;1AACxy A aa

(với

2a 

)

- Do

22 2

5525525

22224

PA PM a a a

 



 

 

 

55

5

22

00;1 5;4

55 0

22

a

aA C

a



























- Do

BC

đi qua



0; 4M

và





5; 4C

nên

BC

có phương trình:

40y 

.

- Lại có:



2;3AN 



là vectơ pháp tuyến của

B

D

nên phương trình

B

D

là:

23100xy

.

Tọa độ điểm

B

là nghiệm của hệ phương trình:



40 1

1;4

23100 4

yx

B

xy y

 







 



.

Vậy



53

;,0;1, 1;4

22

PAB









.

Câu 20: Đường thẳng



: 1 , 0; 0

xy

dab

ab

  

đi qua





1; 6M 

tạo với tia

,Ox Oy

một tam giác

có diện tích bằng 4. Tính

2.Sa b

Lời giải

P

N

M

B

D

A

C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

d

đi qua



1; 6M 

16

1 (1).

ab





Đường thẳng cắt tia

Ox tại

(;0), 0 .

A

aa OAa 

Đường thẳng cắt tia

Oy tại (0; ), 0 .

B

bb OBb 

OAB vuông tại O nên có diện tích là

11

..

22

OA OB ab

Theo đề

1

48 (2).

2

ab ab 

Từ









1,2

suy ra:

2; 4 2 10ab Sab

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 330

BÀI 20. VN TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG,

GÓC VÀ KHOẢNG CÁCH

DẠNG 1. VN TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

Câu 1: Có bao nhiêu cặp đường thẳng song song trong các đường thẳng sau?



1

:2;

2

dy x 



2

1

:3;

2

dy x 



3

1

:3;

2

dy x



4

2

:2

2

dy x 

A. 3. B.

2

. C.

1

. D. 0 .

Câu 2: Phương trình nào sau đây là phương trình đường thẳng không song song với đường thẳng

:32dy x

A.

30

x

y

. B.

360

x

y

. C.

360

x

y

. D.

360

x

y

.

Câu 3: Trong mặt phẳng

Oxy

, đường thẳng

:210dx y

song song với đường thẳng có phương

trình nào sau đây?

A.

210xy

. B.

20xy

. C.

210xy 

. D.

2410xy 

.

Câu 4: Cho các đường thẳng sau.

1

3

:2

3

dy x

2

1

:1

3

dy x

3

:1 2

3

dy x



  





4

3

:1

3

d

y

x

Khẳng định nào đúng trong các khẳng định sau?

A.

234

,,ddd

song song với nhau. B.

2

d

và

4

d

song song với nhau.

C.

1

d

và

4

d

vuông góc với nhau. D.

2

d

và

3

d

song song với nhau.

Câu 5: Tìm các giá trị thực của tham số

m

để đường thẳng



2

331ym xm

song song với

đường thẳng

5yx

.

A.

2m 

. B.

2m 

. C.

2m 

. D.

2m 

.

Câu 6: Tọa độ giao điểm của hai đường thẳng

360xy

và

3410xy

là

A.

27 17

;

13 13









. B.





27;17

. C.

27 17

;

13 13









. D.



27; 17

.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.

III

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 331

Câu 7:

Cho đường thẳng

1

:2 3 15 0dxy và

2

:230dx y. Khẳng định nào sau đây đúng?

A.

1

d

và

2

d

cắt nhau và không vuông góc với nhau.

B.

1

d

và

2

d

song song với nhau.

C.

1

d

và

2

d trùng nhau.

D.

1

d

và

2

d vuông góc với nhau.

Câu 8: Hai đường thẳng

12

:5,:9dmx y m d xmy   

cắt nhau khi và chỉ khi

A.

1m 

. B.

1m 

. C.

1m 

. D.

2m 

.

Câu 9: Với giá trị nào của

m

thì hai đường thẳng

1

:3 4 10 0dx y

và





2

:2 1 10 0dmxmy 

trùng nhau?

A.

2m 

. B.

1m 

. C.

2m 

. D.

2m 

.

Câu 10: Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng có phương trình





1

:120dmx m y m  

và

2

:2 1 0dxy. Nếu

1

d song song

2

d thì:

A.

2.m 

B.

1.m 

C.

2.m 

D.

1.m 

Câu 11: Tìm

m

để hai đường thẳng

1

:2 3 4 0dxy và

2

23

:

14

x

t

d

ymt











cắt nhau.

A.

1

.

2

m 

B.

2.m 

C.

1

.

2

m 

D.

1

.

2

m 

Câu 12: Với giá trị nào của

a

thì hai đường thẳng

1

:2 –4 1 0dxy và



2

1

:

31

xat

d

yat

 







 





vuông góc với nhau?

A.

2.a 

B.

2.a 

C.

1.a 

D.

1a 

.

Câu 13: Với giá trị nào của

m

thì hai đường thẳng

1

22

:

3

x

t

d

yt

 









và



2

:

612

xmt

d

ymt









  





trùng nhau?

A.

1

2

m 

. B.

2m 

. C.

2m 

. D.

2m 

.

Câu 14: Tìm tất cả các giá trị của

m

để hai đường thẳng

1

22

:

1

x

t

d

ymt











và

2

:4 3 0dxym trùng nhau.

A.

3m 

. B.

1m 

. C.

4

3

m 

. D.

m 

.

Câu 15: Với giá trị nào của

m

thì hai đường thẳng

1

:2 4 0dxy m  và





2

:3 210dm xym

song song?

A.

1.m 

B.

1.m 

C.

2.m 

D.

3.m 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 332

Câu 16:

Tìm tất cả các giá trị của

m

để hai đường thẳng

1

:2 3 10 0xmy

và

2

:410mx y

cắt nhau.

A.

110m

. B.

1m 

. C. Không có

m

. D. Với mọi

m

.

Câu 17: Với giá trị nào của

m

thì hai đường thẳng

1

:190mx y

và



2

:1 1200mxmy

vuông góc?

A. Với mọi

m

. B.

2m 

. C. Không có

m

. D.

1m 

.

Câu 18: Với giá trị nào của

m

thì hai đường thẳng

1

:3 2 6 0dmx y và





2

:2260dm xmy 

cắt nhau?

A.

1m 

. B.

1m 

. C.

m  

. D.

1 và 1mm

.

Câu 19: Với giá trị nào của

m

thì hai đường thẳng

1

:2 3 10 0dxy và

2

23

:

14

x

t

d

ymt











vuông góc?

A.

1

2

m 

. B.

9

8

m 

. C.

9

8

m 

. D.

5

4

m 

.

Câu 20: Với giá trị nào của

m

thì hai đường thẳng

1

:4 3 3 0dxym 

và

2

12

:

4

x

t

d

ymt











trùng nhau?

A.

8

3

m 

. B.

8

3

m 

. C.

4

3

m 

. D.

4

3

m 

.

Câu 21: Với giá trị nào của

m

thì hai đường thẳng

1

:3 2 6 0dmx y và



2

:2230dm xmy 

song song?

A.

1; 1 .mm

B.

m 

. C.

2m 

. D.

1m 

.

Câu 22: Với giá trị nào của

m

thì hai đường thẳng





1

81

:

10

x

mt

d

yt

 













và

2

:2140dmx y song song?

A.

1

2

m











.

B.

1m 

. C.

2m 

. D.

m 

.

Câu 23: Với giá trị nào của

m

thì hai đường thẳng



2

1

:32 10dm x ym

và

2

:210dxmym m   

cắt nhau?

A.

1m 

. B.

1

2

m











.

C.

2m 

. D.

1

2

m











.

Câu 24: Với giá trị nào của

m

thì hai đường thẳng



1

2

:

11

xm t

ymt











 





và

2

1

:

x

mt

ymt













trùng nhau?

A. Không có

m

. B.

4

3

m 

. C.

1m 

. D.

3m 

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 333

Câu 25:

Tìm tọa độ giao điểm của hai đường thẳng

73160xy

và

10 0x 

.

A.





10; 18

. B.





10;18

. C.



10;18

. D.



10; 18

.

Câu 26: Tìm toạ độ giao điểm của hai đường thẳng

1

34

:

25

x

t

d

yt

 









và

2

14

:.

75

x

t

d

yt















A.





1; 7 .

B.



3; 2 .

C.





2; 3 .

D.





5;1 .

Câu 27: Cho hai đường thẳng

1

:2 3 19 0dxy

và

2

22 2

:

55 5

x

t

d

yt











. Tìm toạ độ giao điểm của hai

đường thẳng đã cho.

A.





2;5 .

B.



10;25 .

C.





1; 7 .

D.





5; 2 .

Câu 28: Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm



–2;0 , 1;4AB

và đường thẳng

:

2

x

t

d

yt











. Tìm tọa độ giao điểm của đường thẳng

A

B

và

d

.

A.





2;0

. B.



–2;0

. C.





0;2

. D.





0;–2

.

Câu 29: Xác định

a

để hai đường thẳng

1

:3–40dax y và

2

1

:

33

x

t

d

yt

 









cắt nhau tại một điểm

nằm trên trục hoành.

A.

1.a 

B.

1.a 

C.

2.a 

D.

2.a 

Câu 30: Tìm tất cả các giá trị của tham số

m

để hai đường thẳng

2

1

:4 3 – 0dxmym

và

2

:

62

x

t

d

yt











cắt nhau tại một điểm thuộc trục tung.

A.

0m 

hoặc

6m 

. B.

0m 

hoặc

2m 

.

C.

0m 

hoặc

2m 

. D.

0m 

hoặc

6m 

.

Câu 31: Cho ba đường thẳng

1

:3 –2 5 0dx y

,

2

:2 4 –7 0dxy

,

3

:3 4 –1 0dxy

. Phương trình

đường thẳng

d

đi qua giao điểm của

1

d và

2

d , và song song với

3

d là:

A.

24 32 – 53 0xy

. B.

24 32 53 0xy

. C.

24 – 32 53 0xy

. D.

24 – 32 – 53 0xy 

.

Câu 32: Lập phương trình của đường thẳng



đi qua giao điểm của hai đường thẳng

1

:310dx y,

2

:350dx y và vuông góc với đường thẳng

3

:2 7 0dxy.

A.

3650xy

. B.

61250xy

. C.

612100xy

. D.

2100xy

.

Câu 33: Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba đường thẳng lần lượt có phương trình

1

:34150dxy,

2

:5 2 1 0dxy và





3

:219130dmx m y m

. Tìm tất cả các giá

trị của tham số

m

để ba đường thẳng đã cho cùng đi qua một điểm.

A.

1

.

5

m 

B.

5.m 

C.

1

.

5

m 

D.

5.m 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 334

Câu 34:

Nếu ba đường thẳng:

1

: 2 –4 0dxy,

2

:5 –2 3 0dxy và

3

:3–20dmx y

đồng quy thì

m

nhận giá trị nào sau đây?

A.

12

.

5

B.

12

.

5



C.

12.

D.

12.

Câu 35: Với giá trị nào của

m

thì ba đường thẳng

1

:3 –4 15 0dx y

,

2

:5 2 –1 0dxy

và

3

:–4150dmx y

đồng quy?

A.

5m 

. B.

5m 

. C.

3m 

. D.

3m 

.

Câu 36: Với giá trị nào của

m

thì ba đường thẳng

1

:2 –1 0dxy,

2

:210dx y và

3

:––70dmxy  đồng quy?

A.

6m 

. B.

6m 

. C.

5m 

. D.

5m 

.

Câu 37: Đường thẳng

:51 30 11 0dx y

đi qua điểm nào sau đây?

A.

4

1; .

3

M









B.

4

1; .

3

N









C.

3

1; .

4

P







D.

3

1; .

4

Q









DẠNG 2. GÓC CỦA HAI ĐƯỜNG THẲNG

Dạng 2.1 Tính góc của hai đường thẳng cho trước

Câu 38:

Tính góc giữa hai đường thẳng

:320xy 

và

:310xy



 

.

A.

90



. B.

120



. C.

60



. D.

30



.

Câu 39:

Góc giữa hai đường thẳng

:3 7 0axy

và

:310bx y

là:

A.

30

. B.

90

. C.

60

. D.

45

.

Câu 40: Cho hai đường thẳng

1

:2 5 2 0dxy

và

2

:3 7 3 0dxy

. Góc tạo bởi đường thẳng

1

d

và

2

d

bằng

A.

0

30

. B.

0

135

. C.

0

45

. D.

0

60

.

Câu 41: Tìm côsin góc giữa hai đường thẳng

1

:2 1 0xy

và

2

:

1

x

t

yt













A.

10

. B.

3

10

. C.

3

5

. D.

310

10

.

Câu 42: Tìm góc giữa hai đường thẳng

1

:2150xy và



2

:.

42













xt

t

yt



A.

5



. B.

60



. C.

0



. D.

90



.

Câu 43: Tìm cosin góc giữa 2 đường thẳng

12

:270,:2490dx y d x y .

A.

3

5

.

B.

2

5

.

C.

1

5

. D.

3

5

.

Câu 44: Tính góc giữa hai đường thẳng

:320 ':310 xy vàxy    

?

A. 90

o

. B. 120

o

. C. 60

o

. D. 30

o

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 335

Câu 45:

Tính góc tạo bởi giữa hai đường thẳng:

1

:2 10 0dxy  và

2

:390.dx y

A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

135 .

Câu 46: Tính góc tạo bởi giữa hai đường thẳng

1

:7 3 6 0dxy

và

2

:2 5 4 0.dxy

A.

4



. B.

3



. C.

2

3



. D.

3

4



.

Câu 47: Tính góc tạo bởi giữa hai đường thẳng

1

:2 2 3 5 0dx y

và

2

:60.dy

A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

90 .

Câu 48: Tính góc tạo bởi giữa hai đường thẳng

1

:30dx y

và

2

.10 0: xd 

A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

90 .

Câu 49: Tính góc tạo bởi giữa hai đường thẳng

1

:6 5 15 0dxy và

2

10 6

:.

15

x

t

d

yt











A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

90 .

Câu 50: Cho đường thẳng

1

:270dx y và

2

:2 4 9 0dxy. Tính cosin của góc tạo bởi giữa hai

đường thẳng đã cho.

A.

3

5



. B.

2

5

.

C.

3

5

. D.

3

5

.

Câu 51: Cho đường thẳng

1

220: xyd  và

2

0:dxy. Tính cosin của góc tạo bởi giữa hai

đường thẳng đã cho.

A.

10

. B.

2

3

. C.

3

. D. 3.

Câu 52: Cho đường thẳng

1

0:10 5 1dxy

và

2

:

1

x

t

d

yt











. Tính cosin của góc tạo bởi giữa hai

đường thẳng đã cho.

A.

310

10

. B.

3

5

. C.

10

. D.

3

10

.

Câu 53: Cho đường thẳng

1

:3 4 1 0dxy và

2

15 12

:

15

x

t

d

yt











.

Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho.

A.

56

65

. B.

33

65



. C.

6

65

. D.

33

65

.

Dạng 2.2 Viết phương trình đường thẳng liên quan đến góc

Câu 54:

Xác định tất cả các giá trị của

a

để góc tạo bởi đường thẳng

9

72

x

at

y

t















t 

và đường

thẳng

3420xy

bằng

45

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 336

A.

1a  , 14a  . B.

2

7

a 

, 14a  . C. 2a  , 14a  . D.

2

7

a 

, 14a  .

Câu 55: Đường thẳng



đi qua giao điểm của hai đường thẳng

1

:2 3 0dxy

và

2

:210dx y

đồng thời tạo với đường thẳng

3

:10dy

một góc

0

45

có phương trình:

A.

(1 2 ) 0xy 

hoặc

:10xy

. B.

:20xy 

hoặc

:40xy 

.

C.

:0xy

hoặc

:20xy

. D.

:2 1 0x

hoặc

50.y 

.

Câu 56: Trong mặt phẳng với hệ tọa độ

Oxy

, có bao nhiêu đường thẳng đi qua điểm



2;0A

và tạo với

trục hoành một góc

45 ?

A. Có duy nhất. B.

2

. C. Vô số. D. Không tồn tại.

Câu 57: Đường thẳng



tạo với đường thẳng

:260dx y

một góc

0

45

. Tìm hệ số góc

k

của

đường thẳng



.

A.

1

3

k 

hoặc

3.k 

B.

1

3

k 

hoặc

3.k 

C.

1

3

k 

hoặc

3.k 

D.

1

3

k 

hoặc

3.k 

Câu 58: Biết rằng có đúng hai giá trị của tham số

k

để đường thẳng

:dy kx

tạo với đường thẳng

: yx

một góc

0

60

. Tổng hai giá trị của

k

bằng:

A.

8.

B.

4.

C.

1.

D.

1.

Câu 59: Trong mặt phẳng tọa độ

Oxy

, cho điểm





1; 1M  và hai đường thẳng có phương trình

 

12

:10,:250dxy d xy . Gọi

A

là giao điểm của hai đường thẳng trên. Biết rằng

có hai đường thẳng



d đi qua

M

cắt hai đường thẳng trên lần lượt tại hai điểm

,

B

C

sao cho

A

BC là tam giác có 3BC AB có dạng:

0ax y b

và

0cx y d

, giá trị của

T abcd

là

A.

5T 

. B.

6T 

. C.

2T 

. D.

0T 

.

Câu 60: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác cân

ABC

có cạnh đáy :310

B

Cx y,

cạnh bên

:50AB x y. Đường thẳng

A

C

đi qua

(4;1)

M



. Giả sử toạ độ đỉnh

()

,Cmn

.Tính

Tmn=+

.

A.

5

9

T 

. B. 3T  . C.

9

5

T 

. D.

9

5

T 

.

Câu 61: Trong mặt phẳng Oxy, cho hai đường thẳng

(

)

1

:2 5 0dxy-+=

và

()

2

:30dxy+-=

cắt

nhau tại

I

. Phương trình đường thẳng đi qua

()

2;0M -

cắt

()()

12

,dd

tại

A

và

B

sao cho tam

giác

I

AB

cân tại

A

có phương trình dạng 20ax by++=. Tính

5Ta b=-

.

A.

1T =-

. B. 9T = . C. 9T =- . D.

11T =

.

DẠNG 3. KHOẢNG CÁCH

Dạng 3.1 Tính khoảng cách từ 1 điểm đến đường thẳng cho trước

Câu 62:

Khoảng cách từ điểm





1;1A

đến đường thẳng

512 60xy

là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 337

A.

13

. B.

13

. C.

1

. D.

1

.

Câu 63:

Khoảng cách từ điểm

(

)

5; 1M -

đến đường thẳng

32130xy++=

là:

A. 213. B.

28

13

.

C.

26

. D.

13

2

.

Câu 64: Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 0xy

là

A.

1

. B.

310

5

. C.

5

2

. D.

210

.

Câu 65:

Trong mặt phẳng

Ox

y

, khoảng cách từ điểm



3; 4M 

đến đường thẳng

:3 4 1 0xy

.

A.

8

5

. B.

24

5

. C.

12

5

. D.

24

5



.

Câu 66: Khoảng cách từ điểm

(3;2)A 

đến đường thẳng

:3 1 0xy

bằng:

A.

10.

B.

11 5

.

5

C.

10 5

.

5

D.

11

.

10

Câu 67: Trong mặt phẳng

Oxy

, khoảng cách từ gốc tọa độ

O

đến đường thẳng

:4 3 1 0dx y

bằng

A.

3

. B.

4

. C.

1

. D.

1

5

.

Câu 68: Một đường tròn có tâm





3; 2I 

tiếp xúc với đường thẳng

:510.xy 

Hỏi bán kính

đường tròn bằng bao nhiêu?

A.

14

.

26

B.

7

.

13

C. 26. D.

6.

Câu 69: Trong mặt phẳng

Oxy

, khoảng cách từđiểm



0; 4M

đến đường thẳng





:420xcos ysin sin

 



bằng

A.

8. B.

4

s

in

. C.

4

cos sin 

. D.

8

.

Câu 70: Khoảng cách từ

(1; 2)I -

đến đường thẳng

:3 4 26 0xyD--=

bằng

A.

3

. B.

12

. C.

5

. D.

5

3

.

Câu 71: Khoảng cách từ giao điểm của hai đường thẳng

340xy

và

2310xy

đến đường

thẳng

:3 4 0xy

bằng:

A. 210. B.

310

5

. C.

10

5

. D.

2

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 338

Câu 72:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có





,1; 2A





0;3B

và





4;0C

.

Chiều cao của tam giác kẻ từ đỉnh

A

bằng:

A.

1

5

. B.

3

. C.

1

25

. D.

3

5

.

Câu 73: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có



3; 4 ,A 





1; 5B

và





3;1C

. Tính

diện tích tam giác

A

BC

.

A.

10.

B.

5.

C.

26.

D.

25.

Câu 74: Khoảng cách từ điểm





0;3M

đến đường thẳng



:cos sin 32sin 0xy

 



bằng:

A. 6. B. 6. C.

3sin .



D.

3

.

cos sin





Câu 75: Khoảng cách từ điểm



2;0M

đến đường thẳng

13

:

24

x

t

yt













bằng:

A.

2.

B.

2

.

5

C.

10

.

5

D.

5

.

2

Câu 76: Khoảng cách nhỏ nhất từ điểm



15;1M

đến một điểm bất kì thuộc đường thẳng

23

:

x

t

yt













bằng:

A. 10. B.

1

.

10

C.

16

.

5

D. 5.

Câu 77: Tìm tất cả các giá trị của tham số

m

để khoảng cách từ điểm





1; 2A 

đến đường thẳng

:40mx y m

bằng 25.

A.

2.m 

B.

2

1

2

m











. C.

1

2

m 

. D. Không tồn tại

m

.

Câu 78: Tìm tất cả các giá trị của tham số

m

để khoảng cách từ giao điểm của hai đường thẳng

1

:

2

x

t

d

yt











và

2

:2 0dx ym

đến gốc toạ độ bằng

2

.

A.

4

.

2

m











B.

4

.

2

m











C.

4

.

2

m











D.

4

.

2

m











Câu 79: Đường tròn





C

có tâm là gốc tọa độ





0;0O

và tiếp xúc với đường thẳng

:8 6 100 0xy

. Bán kính

R

của đường tròn





C

bằng:

A.

4

R



. B.

6R 

. C.

8R 

. D.

10R 

.

Câu 80: Đường tròn





C

có tâm





2; 2I 

và tiếp xúc với đường thẳng

:5 12 10 0xy

. Bán kính

R

của đường tròn





C

bằng:

A.

44

13

R 

. B.

24

13

R 

. C.

44

R



. D.

7

13

R 

.

Câu 81: Cho đường thẳng

:21 11 10 0.dx y

Trong các điểm



21; 3M 

,



0;4N

,





19;5P 

và

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 339



1; 5Q

điểm nào gần đường thẳng

d

nhất?

A.

M

. B.

N

. C.

P

. D.

Q

.

Câu 82: Cho đường thẳng

: 7 10 15 0.dx y

Trong các điểm





1; 3M 

,



0;4N

,





19;5P 

và



1; 5Q

điểm nào cách xa đường thẳng

d

nhất?

A.

M

. B.

N

. C.

P

. D.

Q

.

Câu 83: Khoảng cách giữa hai đường thẳng song song

1

:6 –8 3 0xy và

2

:3 –4 –6 0xy bằng:

A.

1

2

. B.

3

2

. C.

2

. D.

5

2

.

Câu 84: Tính khoảng cách giữa hai đường thẳng

:7 3 0dxy

và

2

:

27

x

t

yt

 











.

A.

32

2

. B.

15

. C.

9

. D.

9

50

.

Câu 85: Khoảng cách giữa hai đường thẳng song song

1

:6 –8 101 0dxy và

2

:3 –4 0dxy bằng:

A.

10,1

. B.

1, 01

. C.

101

. D. 101 .

Dạng 3.2 Phương trình đường thẳng liên quan đến khoảng cách

Câu 86: Cho hai điểm









3;1 , 4; 0AB

. Đường thẳng nào sau đây cách đều

A

và

B

?

A.

2230.xy 

B.

2230.xy

C.

230.xy

D.

2230.xy

Câu 87: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





2;3A

và



1; 4B

. Đường thẳng nào sau

đây cách đều hai điểm

A

và

B

?

A.

20.xy

B.

20.xy

C.

22100.xy

D.

100 0.xy 

Câu 88: Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba điểm



,0;1A



12;5B

và





3; 0 .C 

Đường thẳng

nào sau đây cách đều ba điểm

,

A

B

và

C

.

A.

340xy

. B.

10 0xy  

. C.

0xy

. D.

510xy

.

Câu 89: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





,1;1A





2; 4B 

và đường thẳng

:30mx y

. Tìm tất cả các giá trị của tham số

m

để



cách đều hai điểm

,

A

B

.

A.

1

.

2

m











B.

1

.

2

m











C.

1

.

1

m











D.

2

.

2

m











Câu 90: Đường thẳng



song song với đường thẳng

:3 4 1 0dx y

và cách

d

một khoảng bằng

1

có phương trình:

A.

3460xy

hoặc

3440xy

. B.

3460xy

hoặc

3440xy

.

C.

3460xy

hoặc

3440xy

. D.

3460xy

hoặc

3440xy

.

Câu 91: Tập hợp các điểm cách đường thẳng

:3 4 2 0xy

một khoảng bằng

2

là hai đường thẳng

có phương trình nào sau đây?

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 340

A.

3480xy

hoặc

34120xy

. B.

3480xy

hoặc

34120xy

.

C.

3480xy

hoặc

34120xy

. D.

3480xy

hoặc

34120xy

.

Câu 92: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai đường thẳng

1

:5 3 3 0dxy

và

2

:5 3 7 0dxy song song nhau. Đường thẳng vừa song song và cách đều với

12

, dd là:

A.

5320.xy

B.

5340.xy

C.

5320.xy

D.

5340.xy

Câu 93: Trên hệ trục tọa độ

Ox

y

, cho hình vuông

A

BCD

. Điểm

M

thuộc cạnh

CD

sao cho





2

M

CDM

,





0;2019N

là trung điểm của cạnh

B

C

,

K

là giao điểm của hai đường thẳng

A

M

và

B

D

. Biết đường thẳng

A

M

có phương trình

 10 2018 0

x

y

. Khoảng cách từ gốc

tọa độ

O

đến đường thẳng

N

K

bằng

A.

2019

. B. 2019 101 . C.

2018

11

. D.

2019 101

101

.

Câu 94:

Trong mặt phẳng tọa độ

Ox

y

, gọi d là đường thảng đi qua

(4;2)M

và cách điểm

(1; 0)A

khoảng cách

310

10

. Biết rằng phương trình đường thẳng

d

có dạng

0xbyc

với

,bc

là

hai số nguyên. Tính

.bc

A.

4

. B.

5

. C.

1.-

D.

5-

.

Câu 95: Trong mặt phẳng với hệ tọa độ

,Ox

y

cho đường thẳng





:1 0xm ym  

(

m

là tham số

bất kì) và điểm





5;1A

. Khoảng cách lớn nhất từ điểm

A

đến  bằng

A.

210

. B.

10

. C.

410

. D.

310

.

Câu 96: Đường thẳng

12 5 60xy

tạo với hai trục toạ độ một tam giác. Tổng độ dài các đường cao

của tam giác đó là

A.

60

13

. B.

281

13

. C.

360

17

. D.

20

.

Câu 97: Trên mặt phẳng tọa độ

Oxy

, cho các điểm



1; 1A  và



3; 4B . Gọi



d là một đường thẳng bất

kì luôn đi qua

B. Khi khoảng cách từ A đến đường thẳng



d đạt giá trị lớn nhất, đường

thẳng



d

có phương trình nào dưới đây?

A.

10xy

. B.

34 25xy

. C. 5270xy. D.

25260xy

.

DẠNG 4. XÁC ĐNNH ĐIỂM

Câu 98:

Cho đường thẳng :3 5 15 0dx y. Trong các điểm sau đây, điểm nào không thuộc đường

thẳng

d

A.





1

5; 0M

. B.





4

5; 6M 

. C.





2

0;3M

. D.



3

5;3M

.

Dạng 4.1 Xác định tọa hình chiếu, điểm đối xứng

Câu 99:

Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho tam giác

A

BC

có





4;3A

,



2;7B

,



3; 8C 

.

Tọa độ chân đường cao kẻ từ đỉnh

A

xuống cạnh

B

C

là:

A.





1; 4

. B.



1; 4

. C.





1; 4

. D.





4;1

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 341

Câu 100:

Cho đường thẳng

:3 5 0dxy

và điểm





2;1M 

. Tọa độ hình chiếu vuông góc của

M

trên

d

là

A.

74

;

55









. B.

74

;

55









. C.

74

;

55









. D.

54

;

75









.

Câu 101: Tọa độ hình chiếu vuông góc của điểm





1; 2M

lên đường thẳng

:0xy

là

A.

33

;

22







. B.





1;1 . C.





2; 2 . D.

33

;

22









.

Câu 102: Trong mặt phẳng tọa độ

Ox

y

, cho tam giác

A

BC với đỉnh

(

)

2;4A , trọng tâm

2

2;

3

G

æö

÷

ç

÷

ç

÷

ç

èø

. Biết

rằng đỉnh

B

nằm trên đường thẳng

(

)

d có phương trình

20xy++=

và đỉnh C có hình

chiếu vuông góc trên

(

)

d là điểm

(

)

2; 4H - . Giả sử

()

;Bab, khi đó 3Ta b=- bằng

A.

4T =

. B.

2T =-

. C.

2T =

. D. 0T = .

Câu 103:

Trong mặt phẳng tọa độ

Oxy

, cho hình chữ nhật

A

BCD

có điểm

C

thuộc đường thẳng d:

250xy

và điểm

(4;8)A 

. Gọi

M

đối xứng với

B

qua

C

, điểm

(5; 4)N 

là hình chiếu

vuông góc của

B

lên đường thẳng

M

D

. Biết tọa độ

(;)Cmn

, giá trị của

mn

là

A.

6

. B.

6

. C.

8

. D.

7

Dạng 4.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc

Câu 104:

Cho hai điểm









3; 1 , 0; 3AB

. Tìm tọa độ điểm

M

thuộc

Ox

sao khoảng cách từ

M

đến

đường thẳng

A

B bằng 1.

A.

7

;0

2

M







và



1; 0M

. B.





13;0M

.

C.





4;0M

. D.



2;0M

.

Câu 105: Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm



1;1A

,





4; 3B 

và đường thẳng

:210dx y

. Tìm điểm

M

thuộc

d

có tọa độ nguyên và thỏa mãn khoảng cách từ

M

đến

đường thẳng

A

B

bằng

6

.

A.





3; 7 .M

B.





7;3 .M

C.



43; 27 .M 

D.

.

27

11

3;M









CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 342

Câu 106:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho điểm





0;1A

và đường thẳng

2

:

2

3y

d

x

t











. Tìm

điểm

M

thuộc

d

và cách

A

một khoảng bằng

5

, biết

M

có hoành độ âm.

A.



4;4 .M

B.





4; 4

.

24 2

;

55

M



















C.

24 2

;.

55

M









D.





4; 4 .M 

Câu 107: Biết rằng có đúng hai điểm thuộc trục hoành và cách đường thẳng

:2 5 0xy

một

khoảng bằng

2 5 . Tích hoành độ của hai điểm đó bằng:

A.

75

.

4



B.

25

.

4



C.

225

.

4



D. Đáp số khác.

Câu 108: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





3; 1A 

và





0;3B

. Tìm điểm

M

thuộc

trục hoành sao cho khoảng cách từ

M

đến đường thẳng

A

B

bằng

1

.

A.



7

;0

2

.

1; 0

M















B.

14

;0

3

.

4

;0

3

M























C.



7

;0

2

.

1; 0

M



















D.

14

;0

3

.

4

;0

3

M



























Câu 109: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





3; 0A

và





0; 4B 

. Tìm điểm

M

thuộc

trục tung sao cho diện tích tam giác

M

AB

bằng

6.

A.







0;0

.

0; 8

M











B.





0; 8 .M 

C.



6;0 .M

D.



0;0

.

0;6

M







CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 20. VN TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG,

GÓC VÀ KHOẢNG CÁCH

DẠNG 1. VN TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

Câu 1: Có bao nhiêu cặp đường thẳng song song trong các đường thẳng sau?



1

:2;

2

dy x 



2

1

:3;

2

dy x 



3

1

:3;

2

dy x



4

2

:2

2

dy x 

A.

3

. B.

2

. C.

1

. D.

0

.

Lời giải

Chọn D

Hai đường thẳng

11

yaxb và

22

yaxb song song với nhau khi và chỉ khi

12

.

aa

bb











Trong các đường thẳng trên không có đường nào thỏa mãn. Vậy không có cặp đường thẳng nào

song song.

Câu 2: Phương trình nào sau đây là phương trình đường thẳng không song song với đường thẳng

:32dy x

A.

30

x

y

. B.

360

x

y

. C.

360

x

y

. D.

360

x

y

.

Lời giải

Chọn D

:323 20dy x x y

.





d

có VTPT





3; 1n 



.

Đường thẳng

360

x

y

có VTPT





1

3;1nkn



nên

n



và

1

n



không cùng phương. Do đó

đường thẳng

360

x

y

không song song với đường thẳng



d

.

Câu 3: Trong mặt phẳng

Oxy

, đường thẳng

:210dx y

song song với đường thẳng có phương

trình nào sau đây?

A.

210xy

. B.

20xy

. C.

210xy 

. D.

2410xy 

.

Lời giải

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.

III

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

Chọn D

Ta kiểm tra lần lượt các đường thẳng

.+) Với

1

:210dx y có

12

d



cắt

1

d .

.+) Với

2

:2 0dxy có

21

12

d







cắt

2

d .

.+) Với

3

:210dxy  có

12 1

121

d







trùng

3

d .

.+) Với

4

:2 4 1 0dxy  có

121

24 1

d







song song

4

d .

Câu 4: Cho các đường thẳng sau.

1

3

:2

3

dy x

2

1

:1

3

dy x

3

:1 2

3

dy x



  





4

3

:1

3

dy x

Khẳng định nào đúng trong các khẳng định sau?

A.

234

,,ddd

song song với nhau. B.

2

d

và

4

d

song song với nhau.

C.

1

d

và

4

d

vuông góc với nhau. D.

2

d

và

3

d

song song với nhau.

Lời giải

Chọn B

Vì

332

31

:1 2 1

3

dy x x d d



      





. Đường thẳng

2

d

và

4

d

có hệ số góc bằng

nhau;hệ số tự do khác nhau nên chúng song song.

Câu 5: Tìm các giá trị thực của tham số

m

để đường thẳng



2

331ym xm

song song với

đường thẳng

5yx

.

A.

2m 

. B. 2m  . C.

2m 

. D.

2m 

.

Lời giải

Chọn D

Để đường thẳng



2

331ym xm

song song với đường thẳng

5yx

thì điều kiện là

2

31

2

315

m



















.

Câu 6: Tọa độ giao điểm của hai đường thẳng

360xy

và

3410xy

là

A.

27 17

;

13 13









. B.





27;17

. C.

27 17

;

13 13









. D.



27; 17

.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

Ta có tọa độ giao điểm của hai đường thẳng

360xy

và

3410xy

là nghiệm của hệ

phương trình

360

3410

xy











27

13

17

3

x

y



















.

Câu 7: Cho đường thẳng

1

:2 3 15 0dxy và

2

:230dx y. Khẳng định nào sau đây đúng?

A.

1

d

và

2

d cắt nhau và không vuông góc với nhau.

B.

1

d

và

2

d song song với nhau.

C.

1

d

và

2

d

trùng nhau.

D.

1

d

và

2

d

vuông góc với nhau.

Lời giải

Chọn A

Đường thẳng

1

:2 3 15 0dxy có một vectơ pháp tuyến là





1

2;3n 



và đường thẳng

2

:230dx y

có một vectơ pháp tuyến là





2

1; 2n 



.

Ta thấy

23

12





và

12

.2.13.(2)40nn 

 

.

Vậy

1

d

và

2

d cắt nhau và không vuông góc với nhau.

Câu 8: Hai đường thẳng

12

:5,:9dmx y m d x my   cắt nhau khi và chỉ khi

A.

1m 

. B.

1m 

. C.

1m 

. D.

2m 

.

Lời giải

Chọn C

CÁCH

1

-Xét

0m 

thì

12

5 9d:y ,d :x  . Rõ ràng hai đường thẳng này cắt nhau nên

0m 

thỏa

mãn .

-Xét

0m 

thì

1

:5dy mxm   và

2

:9

x

dy

m

 

Hai đường thẳng

1

d

và

2

d

cắt nhaut

0

1

(2)

1

m





  







.

Từ và ta có

1m 

.

CÁCH 2

1

d và

2

d theo thứ tự nhận các vectơ

12

1 1n(m;),n (;m)



làm vec tơ pháp tuyến.

1

d và

2

d cắt nhau

1

n



và

2

n



không cùng phương 

11 1m.m . m .

Câu 9: Với giá trị nào của

m

thì hai đường thẳng

1

:3 4 10 0dx y và





2

:2 1 10 0dmxmy 

trùng nhau?

A.

2m 

. B.

1m 

. C.

2m 

. D.

2m 

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

Lời giải





12

2

1

2

:2 1 10 0

21 10

3410

:3 4 10 0

213

2.

4

dd

dmxmy

mm

dxy

m





 





























Câu 10: Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng có phương trình





1

:120dmx m y m  

và

2

:2 1 0dxy

. Nếu

1

d

song song

2

d

thì:

A.

2.m 

B.

1.m 

C.

2.m 

D.

1.m 

Lời giải





12

1

||

2

1

12

2

0

.

:12

1

2

21

:2 1 0

2

dd

dm

m

mx y m

mm

dx

m

y

m









































Câu 11: Tìm

m

để hai đường thẳng

1

:2 3 4 0dxy

và

2

23

:

14

x

t

d

ymt











cắt nhau.

A.

1

.

2

m 

B.

2.m 

C.

1

.

2

m 

D.

1

.

2

m 

Lời giải



21

1

2

:2 3 4 0

2;

.

3

4

23

:

2

4;

3

14

1

32

ddM

dxy

m

xt

d

n

m

nm

ymt













 































Chọn C

Câu 12:

Với giá trị nào của

a

thì hai đường thẳng

1

:2 –4 1 0dxy

và



2

1

:

31

xat

d

yat

 







 





vuông góc với nhau?

A.

2.a 

B.

2.a 

C.

1.a 

D.

1a 

.

Lời giải



12

2

1

12

2

:2 –4 1 0

1; 2

01201.

:

1;

1

31

dd

dxy

n

nn a a a

naa

xat

d

yat

















 





 





















Chọn D

Câu 13:

Với giá trị nào của

m

thì hai đường thẳng

1

22

:

3

x

t

d

yt

 









và



2

:

612

xmt

d

ymt









  





trùng nhau?

A.

1

2

m 

. B.

2m 

. C.

2m 

. D.

2m 

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

Lời giải



  

12

1

22

11

2

2.

6

1

22

:2;

;

12

,

2

3

2

:26

1

;2

2

3

dd

xt

d

m

yt

xmt

dA

ym

u

Ad

m

mm

t

du m















 



 

















  





























Chọn C

Câu 14:

Tìm tất cả các giá trị của

m

để hai đường thẳng

1

22

:

1

x

t

d

ymt











và

2

:4 3 0dxym trùng nhau.

A.

3m 

. B.

1m 

. C.

4

3

m 

. D.

m 

.

Lời giải

  



12

2

111

2

22

50

:2;1

1

8

:4 3 0 3

.

;

,2;

2

34

4

3

dd

xt

A

m

dA

y

d

mt

m

d

um

m

uxym



 

















 



 



 



















Chọn D

Câu 15:

Với giá trị nào của

m

thì hai đường thẳng

1

:2 4 0dxy m 

và





2

:3 210dm xym

song song?

A.

1.m 

B.

1.m 

C.

2.m 

D.

3.m 

Lời giải

Với

2

1

:2 0

4

:7 7 0

dxy

md

dxy

d























loại

4.m 

Với 4m 



thì



12

1

||

2

:2 4 0

31

:3 210

1

21

1.

5

421

dd

dxy m

m

dm y

m

xm

 





















 

















Chọn B

Câu 16:

Tìm tất cả các giá trị của

m

để hai đường thẳng

1

:2 3 10 0xmy và

2

:410mx y cắt nhau.

A.

110m

. B.

1m 

. C. Không có

m

. D. Với mọi

m

.

Lời giải

12

1

2

:50

00(

:2 3 10 0

:4 1 0

)

.

:

23

0

00

41

4

M

m

mm

m

x

mm

xmy

y

mx y

 





  









 



 



























thoaû maõn

Chọn D

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

Câu 17:

Với giá trị nào của

m

thì hai đường thẳng

1

:190mx y

và



2

:1 1200mxmy

vuông góc?

A. Với mọi

m

. B.

2m 

. C. Không có

m

. D.

1m 

.

Lời giải

Ta có :





  



11

22

1

.

:190 ;1

:1 200 1;1

11 1 0

n

mx y m

mxmy mm

mm m m





















Câu 18: Với giá trị nào của

m

thì hai đường thẳng

1

:3 2 6 0dmx y và





2

:2260dm xmy 

cắt nhau?

A.

1m 

. B.

1m 

. C.

m  

. D.

1 và 1mm

.

Ta có:





  

11

22

:3 2 6 0 3 ;2

:2260 2;2

dmx y m

dm xm

y

mm

n









 









12

1

2

:30

00

:30

.

22

01

32

ddM

dy

mm

dxy

m

mm

m





 









 





















thoaû maõn

Chọn D

Câu 19:

Với giá trị nào của

m

thì hai đường thẳng

1

:2 3 10 0dxy và

2

23

:

14

x

t

d

ymt











vuông góc?

A.

1

2

m 

. B.

9

8

m 

. C.

9

8

m 

. D.

5

4

m 

.

Lời giải







11

22

:2 3 10 0 2; 3

23

:4;3

14

dxy

xt

t

n

ndm

ym











 













21

9

2.4 3 . 3 0 .

8

dd

mm







Chọn C

Câu 20:

Với giá trị nào của

m

thì hai đường thẳng

1

:4 3 3 0dxym  và

2

12

:

4

x

t

d

ymt











trùng nhau?

A.

8

3

m 

. B.

8

3

m 

. C.

4

3

m 

. D.

4

3

m 

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7





  

2

11

22

:4 3 3 0 4; 3

12

:1;4,2

4

;

dxym

xt

dA

y

dn m

mt

n 

























12

1

4

380

8

.

8

3

2

dd

A

m

d

m











 

















Chọn B

Câu 21:

Với giá trị nào của

m

thì hai đường thẳng

1

:3 2 6 0dmx y và



2

:2230dm xmy 

song song?

A.

1; 1 .mm

B.

m 

. C.

2m 

. D.

1m 

.

Lời giải

Ta có





  



12

1

2

|

1

22

1

2

|

:3 2 6 0 3 ;2

:2230 2;2

:30

0

3

2

0

23

01

3

0

:2 2

2

.

6

dd

d

m

n

mx y m

dm x y m m

dy

mm

dx

m

mm

m

y











 











  

























Choïn A.

khoâng thoaû maõn

Câu 22: Với giá trị nào của

m

thì hai đường thẳng





1

81

:

10

x

mt

d

yt

 













và

2

:2140dmx y

song song?

A.

1

2

m











.

B.

1m 

. C.

2m 

. D.

m 

.

Lời giải

Ta có:



  



111

22

81

:8;10,1;1

10

:2140 ;2

n

xmt

d

y

dAm

yt

dmx mn



 





























12

2

||

2

1

0

1;1

0

0; 2

1

11

.

0

2

86

1

2

dd

A

m

d

n

m

n

m











 







































































khoâng thoaû maõn

Chọn A

Câu 23:

Với giá trị nào của

m

thì hai đường thẳng



2

1

:32 10dm x ym

và

2

:210dxmym m   

cắt nhau?

A.

1m 

. B.

1

2

m











.

C.

2m 

. D.

1

2

m











.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

Lời giải





2

1

2

:32 10

:210

dm x ym

dxmym m









   





21

1

2

:3 2 1 0

0

:10

.

1

32

0

2

1

ddM

m

dx

x

m

y

m

d









  









 



























thoaû maõn

Chọn B

Câu 24:

Với giá trị nào của

m

thì hai đường thẳng



1

2

:

11

xm t

ymt











 





và

2

1

:

x

mt

ymt













trùng nhau?

A. Không có

m

. B.

4

3

m 

. C.

1m 

. D.

3m 

.

Lời giải



12

1

2

22

2

3

2

11

2

:;1

11

1

21

:;1

1

11

10

11.

10

120

2

,2;1

0

dd

du m

d

xm t

Am

A

ymt

m

xmt

m

ymt

mmt

mmm

m

mt m

m

mmm

m

u

m

















 



































 







   

 

























. Chọn C

Câu 25:

Tìm tọa độ giao điểm của hai đường thẳng

73160xy

và

10 0x 

.

A.





10; 18

. B.





10;18

. C.



10;18

. D.



10; 18

.

Lời giải

1

2

:7 3 16 0

10

.

:100 18

dxy

x

dx y











 



Chọn A

Câu 26:

Tìm toạ độ giao điểm của hai đường thẳng

1

34

:

25

x

t

d

yt

 









và

2

14

:.

75

x

t

d

yt















A.





1; 7 .

B.



3; 2 .

C.





2; 3 .

D.





5;1 .

Lời giải

1

2

34

:

1

25

1

34 14 1

.

7

25 75 1

14

:

0

75

d

xt

d

x

yt

t

tttt

y

tttt

xt

d

t

yt



















   



  











 



























Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9

Câu 27:

Cho hai đường thẳng

1

:2 3 19 0dxy

và

2

22 2

:

55 5

x

t

d

yt











. Tìm toạ độ giao điểm của hai

đường thẳng đã cho.

A.





2;5 .

B.



10;25 .

C.





1; 7 .

D.





5; 2 .

Lời giải



12

1

2

:2 3 19 0

2

222 2 355 5 19 0 10 .

22 2

:5

55 5

dd

dxy

x

tt t

xt

dy

yt

































Chọn A

Câu 28:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm



–2;0 , 1;4AB

và đường thẳng

:

2

x

t

d

yt











. Tìm tọa độ giao điểm của đường thẳng

A

B

và

d

.

A.





2;0

. B.



–2;0

. C.





0;2

. D.





0;–2

.

Lời giải



–2;0 , 1; 4 : 4 3 8 0

4380 2

.

20 0

::20

2

AB d

ABABxy

xy x

xt

xy y

ddxy

yt





 













 

 











Chọn B

Câu 29:

Xác định

a

để hai đường thẳng

1

:3–40dax y và

2

1

:

33

x

t

d

yt

 









cắt nhau tại một điểm

nằm trên trục hoành.

A.

1.a 

B.

1.a 

C.

2.a 

D.

2.a 

Lời giải



212

12

30

2;0

30

xt x

dOdxd Ox

yt

A

y

  







  









240 2.aa    

Chọn D

Câu 30:

Tìm tất cả các giá trị của tham số

m

để hai đường thẳng

2

1

:4 3 – 0dxmym

và

2

:

62

x

t

d

yt











cắt nhau tại một điểm thuộc trục tung.

A.

0m 

hoặc

6m 

. B.

0m 

hoặc

2m 

.

C.

0m 

hoặc

2m 

. D.

0m 

hoặc

6m 

.

Lời giải



122

20 0

6

0; 2

22

xt x

dOy d Oy

y

A

ty

d

 

























2

0

60 .

6

m

mm

m













Chọn D

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

Câu 31:

Cho ba đường thẳng

1

:3 –2 5 0dx y,

2

:2 4 –7 0dxy,

3

:3 4 –1 0dxy. Phương trình

đường thẳng

d

đi qua giao điểm của

1

d

và

2

d

, và song song với

3

d

là:

A.

24 32 – 53 0xy

. B.

24 32 53 0xy

.

C.

24 – 32 53 0xy

. D.

24 – 32 – 53 0xy

.

Lời giải

1

2

331

;.

3

8

:3 –2 5 0

8

:2 4 –7 0 31

1

16

6

x

dxy

d

dx

d

y

A



























 











Ta có



3

931 53

0.

4:3 4 –1

8

|| :3 00

84

1

d

ddxyc

A

cc

dxy c

















 





Vậy

3

53

:3 4 – 0 : 24 32 53 0.

8

dx y d x y

Chọn A

Câu 32:

Lập phương trình của đường thẳng



đi qua giao điểm của hai đường thẳng

1

:310dx y

,

2

:350dx y và vuông góc với đường thẳng

3

:2 7 0dxy.

A.

3650xy

. B.

61250xy

.

C.

612100xy

. D.

2100xy

.

Lời giải

2

1

2

3

:310

2

:350

3

2

3; .

3

x

dx y

d

dx y

y

dA

































Ta có

3

25

32. 0 .

0

:2

:

70

33

2

d

dx y c

A

cc

dxy

























Vậy

5

:2 0 :3650.

3

dx y d x y 

Chọn A

Câu 33:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba đường thẳng lần lượt có phương trình

1

:34150dxy,

2

:5 2 1 0dxy và





3

:219130dmx m y m

. Tìm tất cả các giá

trị của tham số

m

để ba đường thẳng đã cho cùng đi qua một điểm.

A.

1

.

5

m 

B.

5.m 

C.

1

.

5

m 

D.

5.m 

Lời giải

Ta có:



12 3

1

2

:3 4 15 0

1

:5 2 1

3

1;

0

dxy

x

d

dxy y

dA d











 



 



639130 5.mm m m

Chọn D

Câu 34:

Nếu ba đường thẳng

1

: 2 –4 0dxy,

2

:5 –2 3 0dxy và

3

:3–20dmx y

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11

đồng quy thì

m

nhận giá trị nào sau đây?

A.

12

.

5

B.

12

.

5



C.

12.

D.

12.

Lời giải

23

1

2

5

: 2 –4 0

9

:5 –2 3 0 26

9

;

526

99

x

dxy

d

dx

d

y

dA























 

















526

2 0 12.

93

m

m

Chọn D

Câu 35:

Với giá trị nào của

m

thì ba đường thẳng

1

:3 –4 15 0dx y

,

2

:5 2 –1 0dxy

và

3

:–4150dmx y đồng quy?

A.

5m 

. B.

5m 

. C.

3m 

. D.

3m 

.

Lời giải



1

12

2

:3 –4 15 0

1

1; 3

:5 2 –1 0 3

dxy

x

dd A d

dxy y











 



12 15 0 3.mm     

Chọn C

Câu 36:

Với giá trị nào của

m

thì ba đường thẳng

1

:2 –1 0dxy

,

2

:210dx y

và

3

:––70dmxy  đồng quy?

A.

6m 

. B.

6m 

. C.

5m 

. D.

5m 

.

Lời giải



1

12 3

2

:2 –1 0

1

1; 1 1 7 0 6.

:210 1

dxy

x

dd A d m m

dx y y











 



Chọn B

Câu 37:

Đường thẳng

:51 30 11 0dx y

đi qua điểm nào sau đây?

A.

4

1; .

3

M









B.

4

1; .

3

N









C.

3

1; .

4

P







D.

3

1; .

4

Q









Lời giải

Đặt



4

1; 0

3

4

1; 80 0

;513011 .

3

0

fM f M d

f

Nf Nd

fxy x y

fP

fQ



















 



























Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

DẠNG 2. GÓC CỦA HAI ĐƯỜNG THẲNG

Dạng 2.1 Tính góc của hai đường thẳng cho trước

Câu 38:

Tính góc giữa hai đường thẳng

:320xy 

và

:310xy



 

.

A. 90



. B. 120



. C. 60



. D. 30



.

Lời giải

Chọn C

Đường thẳng  có vectơ pháp tuyến





1; 3n 



, đường thẳng





có vectơ pháp tuyến





1; 3n







.

Gọi



là góc giữa hai đường thẳng

,.







13

1

cos cos , 60

2

13.13

nn







 







.

Câu 39: Góc giữa hai đường thẳng

:3 7 0axy

và

:310bx y

là:

A.

30

. B.

90

. C.

60

. D.

45

.

Lời giải

Chọn A

Đường thẳng

a

có vectơ pháp tuyến là:





1

3; 1n 



;

Đường thẳng

b

có vectơ pháp tuyến là:





2

1; 3n 



.

Áp dụng công thức tính góc giữa hai đường thẳng có:







12

1. 3 1 3

.

3

cos ,

2.2 2

.

nn

ab

nn

 

 

 

. Suy ra góc giữa hai đường thẳng bằng

30

.

Câu 40: Cho hai đường thẳng

1

:2 5 2 0dxy

và

2

:3 7 3 0dxy

. Góc tạo bởi đường thẳng

1

d

và

2

d

bằng

A.

0

30

. B.

0

135

. C.

0

45

. D.

0

60

.

Lời giải

Chọn C

Đường thẳng

1

:2 5 2 0dxy có vectơ pháp tuyến





1

2;5n 



.

Đường thẳng

2

:3 7 3 0dxy có vectơ pháp tuyến





2

3; 7n 



.

Góc giữa hai đường thẳng được tính bằng công thức



12

2

222

.

2.3 5.( 7)

29 1

cos , cos ,

29 2 2

.

25.3 7

nn

dd nn

nn



 









0

12

;45dd

Vậy góc tạo bởi đường thẳng

1

d và

2

d bằng

0

45

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

Câu 41:

Tìm côsin góc giữa hai đường thẳng

1

:2 1 0xy

và

2

:

1

x

t

yt













A.

10

. B.

3

10

. C.

3

5

. D.

310

10

.

Lời giải

Chọn D

Véctơ pháp tuyến của đường thẳng

1

 là





2;1n 



nên véctơ chỉ phương





1; 2u 



Véctơ chỉ phương của đường thẳng

2



là





1; 1u







Khi đó



12

.

3310

cos ; cos ;

10

5. 2

.

uu



    





Câu 42: Tìm góc giữa hai đường thẳng

1

:2150xy và



2

:.

42













xt

t

yt



A.

5



. B.

60



. C.

0



. D.

90



.

Lời giải

Chọn D

Đường thẳng

1

 có VTPT là

 

1

1; 2 1 2;1nVTCP



Đường thẳng

2

 có



11;2VTCP

.

Nhận xét:





12 1 2 1 2 1 2

.0 , 90



   uu u u

 

.

Câu 43: Tìm cosin góc giữa 2 đường thẳng

12

:270,:2490dx y d x y 

.

A.

3

5

.

B.

2

5

.

C.

1

5

. D.

3

5

.

Lời giải

Chọn D

Ta có

  

12

1; 2 ; 2; 4

dd

vtptn vtptn





12

.

1.2 2.4

3

;.

5

5.2 5

.

dd

nn

cos d d

nn









Câu 44:

Tính góc giữa hai đường thẳng

:320 ':310 xy vàxy    

?

A. 90

o

. B. 120

o

. C. 60

o

. D. 30

o

.

Lời giải

Chọn C



có vectơ pháp tuyến là



1

1; 3n 



.

'

có vectơ pháp tuyến là





2

1; 3n 



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

Khi đó:







 

12

'

12

22

12

1.1 3 3

.

2

1

cos ; cos( ; )

2

4. 4

||.

13.13

nn





     

 

 





.

Vậy góc giữa hai đường thẳng

, '

là

0

60

.

Câu 45: Tính góc tạo bởi giữa hai đường thẳng

1

:2 10 0dxy  và

2

:390.dx y

A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

135 .

Lời giải

Ta có















 

12

;

22

2

1

2

1

22

2.1 1 . 3

1

2

0

2

:2 10 0 2; 1

cos

:39 1;

.1 3

3

1

dd

d

n

xy

dy

n

x









   

























45 .







Chọn B

Câu 46:

Tính góc tạo bởi giữa hai đường thẳng

1

:7 3 6 0dxy

và

2

:2 5 4 0.dxy

A.

4



. B.

3



. C.

2

3



. D.

3

4



.

Lời giải

Ta có







12

11

;

22

14 15

1

.

3

4

49 9.

:7 6 0 7; 3

cos

:2 5 4 0 2; 5

425 2

dd

dnxy

























  











Chọn A

Câu 47:

Tính góc tạo bởi giữa hai đường thẳng

1

:2 2 3 5 0dx y

và

2

:60.dy

A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

90 .

Lời giải

Ta có







12

1

;

1

22

;

3

30 .

6

2

13.0

.

1

:2 2 3 5 0 1 3

cos

:0 0;1

dd

d

y

n

xy

d

















  













Chọn A

Câu 48:

Tính góc tạo bởi giữa hai đường thẳng

1

:30dx y

và

2

.10 0: xd 

A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

90 .

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15







12

1

;

2

1

2

:30 1;3

cos

0

10

1

2

13.1

0:

0

10 1;

dd

d

n

x

xy

n































60 .







Chọn C

Câu 49:

Tính góc tạo bởi giữa hai đường thẳng

1

:6 5 15 0dxy và

2

10 6

:.

15

x

t

d

yt











A.

o

30 .

B.

o

45 .

C.

o

60 .

D.

o

90 .

Lời giải



12

2

;

2

1

2

1

:6 5 15 0 6; 5

10 6

:

1

090.

5; 6

5

dd

dn

nn

n

xy

xt

d

yt





 







 

























Chọn D

Câu 50:

Cho đường thẳng

1

:270dx y và

2

:2 4 9 0dxy. Tính cosin của góc tạo bởi giữa hai

đường thẳng đã cho.

A.

3

5



. B.

2

5

.

C.

3

5

. D.

3

5

.

Lời giải



12

11

2

;

2

:270 1;2

cos

;

.

:2 4 9

1

0

4

3

5

12

14.14

dd

d

x

n

xy

dy

































Chọn C

Câu 51:

Cho đường thẳng

1

220: xyd  và

2

0:dxy. Tính cosin của góc tạo bởi giữa hai

đường thẳng đã cho.

A.

10

. B.

2

3

. C.

3

. D. 3.

Lời giải



12

11

;

22

:1;2

1

.c

220

12

1

01;

14.11 10

os

:

dd

d

xy n























 













Chọn A

Câu 52:

Cho đường thẳng

1

0:10 5 1dxy

và

2

:

1

x

t

d

yt











. Tính cosin của góc tạo bởi giữa hai

đường thẳng đã cho.

A.

310

10

. B.

3

5

. C.

10

. D.

3

10

.

Lời giải







12

11

;

22

:2;

.

1

cos

10 5 1 0

21

3

1; 1

41

2

.1

:

1

11 0

dd

d

x

xy n

n

t

d

yt









































Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

Câu 53:

Cho đường thẳng

1

:3 4 1 0dxy

và

2

15 12

:

15

x

t

d

yt











.

Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho.

A.

56

65

. B.

33

65



. C.

6

65

. D.

33

65

.

Lời giải







12

11

2

;

2

:3 4 1 0 3;4

cos

1

2

.

512

:

15

15 48

33

65

5; 1

9 16. 25 144

dd

d

y

n

xy

xt

d

t









































Chọn D

Dạng 2.2 Viết phương trình đường thẳng liên quan đến góc

Câu 54:

Xác định tất cả các giá trị của a để góc tạo bởi đường thẳng

9

72

x

at

y

t















t  và đường

thẳng

3420xy

bằng 45.

A.

1a 

,

14a 

. B.

2

7

a 

,

14a 

. C.

2a 

,

14a 

. D.

2

7

a 

,

14a 

.

Lời giải

Chọn B

Gọi



là góc giữa hai đường thẳng đã cho.

Đường thẳng

9

72

x

at

y

t















t  có vectơ chỉ phương là





;2ua



.

Đường thẳng

3420xy có vectơ chỉ phương là



4; 3v 



.

Ta có



cos cos ,uv







.

cos 45

.

uv





2

46

1

2

54

a







2

54246aa 

22

25 100 32 96 72aaa

2

796280aa

2

7

14

a















.

Câu 55: Đường thẳng



đi qua giao điểm của hai đường thẳng

1

:2 3 0dxy và

2

:210dx y

đồng thời tạo với đường thẳng

3

:10dy một góc

0

45

có phương trình:

A.

(1 2 ) 0xy 

hoặc

:10xy

. B.

:20xy 

hoặc

:40xy 

.

C.

:0xy

hoặc

:20xy

. D.

:2 1 0x

hoặc

50.y 

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17



1

2

:2 3 0

1

:21 1

1;1 .

0

dxy

x

d

dx y y

dA











 



 



Ta có





33

:10 0;1,dny   



gọi









3

;, ;adbn









. Khi đó

22 2

22

.

1

1: 20

2

1, 1 : 0

1

2

0

o

.

cs

ab ab xy

b

ab b

abab xy

ab



 







      







Chọn C

Câu 56:

Trong mặt phẳng với hệ tọa độ

Oxy

, có bao nhiêu đường thẳng đi qua điểm



2;0A

và tạo với

trục hoành một góc

45 ?

A. Có duy nhất. B.

2

.

C. Vô số. D. Không tồn tại.

Lời giải

Chọn B

Cho đường thẳng

d

và một điểm

.

A

Khi đó.

Có duy nhất một đường thẳng đi qua

A

song song hoặc trùng hoặc vuông góc với

.d

Có đúng hai đường thẳng đi qua

A

và tạo với

d

một góc

.090







Câu 57: Đường thẳng



tạo với đường thẳng

:260dx y

một góc

0

45

. Tìm hệ số góc

k

của

đường thẳng



.

A.

1

3

k 

hoặc

3.k 

B.

1

3

k 

hoặc

3.k 

C.

1

3

k 

hoặc

3.k 

D.

1

3

k 

hoặc

3.k 

Lời giải





:260 1;2,

d

dx y n



gọi



;.

a

ab kn

b







Ta có



22 2 2

22

2

1

cos 45 5 2 8 8

2

.5

ab

ab a abb

ab



 





22

11

3830 .

33

abk

aabb

abk





  











Chọn A

Câu 58:

Biết rằng có đúng hai giá trị của tham số

k

để đường thẳng

:dy kx

tạo với đường thẳng

: yx

một góc

0

60

. Tổng hai giá trị của

k

bằng:

A.

8.

B.

4.

C.

1.

D.

1.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18



12

2

sol

2

:,

22

12

:;1

1

cos 60 1 2 4 2

2

:1;1

1. 2

410 4.

k

d

kk k

dy kx k

k

kkk

yx

n

k

kk kk





 









     











     





Chọn B

Câu 59:

Trong mặt phẳng tọa độ

Ox

y

, cho điểm





1; 1M 

và hai đường thẳng có phương trình

 

12

:10,:250dxy d xy 

. Gọi

A

là giao điểm của hai đường thẳng trên. Biết rằng

có hai đường thẳng



d

đi qua

M

cắt hai đường thẳng trên lần lượt tại hai điểm ,

B

C sao cho

A

BC

là tam giác có

3BC AB

có dạng:

0ax y b

và

0cx y d

, giá trị của

T abcdlà

A. 5T  . B. 6T  . C.

2T 

. D. 0T  .

Lời giải

Chọn C

Tọa độ





2;1A

Gọi



là góc giữa hai đường thẳng





1

d

và



2

d

,

1

cos

10





3

sin

10





Xét tam giác

A

BC

ta có:

1

sin

sin sin

10

AB BC

C

CA



Gọi



là góc giữa hai đường thẳng



d

và



1

d

, suy ra:

13

sin cos

10 10



 



1

Giả sử



d

có vec tơ pháp tuyến là





;nab



Từ



1

ta có:

22

2

33

cos 8 0

10 10

5

ab

aabb

ab





 



7

ab













Với

ab

một vec tơ pháp tuyến





1;1 : 0ndxy



Với

7ab

một vec tơ pháp tuyến





7;1 : 7 6 0ndxy



CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19

Vậy:

10762T  

Câu 60: Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác cân

ABC

có cạnh đáy

:310BC x y

,

cạnh bên

:50AB x y

. Đường thẳng

AC

đi qua

(4;1)M 

. Giả sử toạ độ đỉnh

()

,Cmn

.Tính

Tmn=+

.

A.

5

9

T 

. B.

3T 

. C.

9

5

T 

. D.

9

5

T 

.

Lời giải

Chọn C

Gọi

(;)nab



với

22

(0)ab

là véc tơ pháp tuyến của

AC

,

véctơ

1

(1 ; 3)n 



là véc tơ pháp tuyến của đường thẳng

BC

,

2

(1 ; 1)n 



là

véc tơ pháp tuyến của đường thẳng

AB

.

Ta có:

121

cos cos |cos( , )||cos( , )|BC nn nn 



121

22

121

|, | | , |

|3| |13|

10 . 2

..

10.

nn n n

ab

nn n n

ab



  







22 2 2

22 7 0

7

63babb

ab

aaba

ab





  









+ Với

ab

chọn

1, 1 (1; 1)ab n 



loại vì

//AC AB

+ Với

7

b

a 

chọn

1; 7 : 7 3 0ab ACxy 

. Điểm

81

;

55

CACBC C









Câu 61: Trong mặt phẳng Oxy, cho hai đường thẳng

()

1

:2 5 0dxy-+=

và

()

2

:30dxy+-=

cắt

nhau tại

I

. Phương trình đường thẳng đi qua

()

2;0M -

cắt

()()

12

,dd

tại

A

và

B

sao cho tam

giác

IA B

cân tại

A

có phương trình dạng

20ax by++=

. Tính

5Ta b=-

.

A.

1T =-

. B.

9T =

. C.

9T =-

. D.

11T =

.

Lời giải

Chọn D

Đường thẳng

()()

12

,dd

có véc tơ pháp tuyến lần lượt là

() ()

12

2; 1 , 1;1nn=- =

 

.

Gọi

()

D

là đường thẳng cần tìm có véc tơ pháp tuyến là

()

;nab=



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

Góc giữa 2 đường thẳng

()()

12

,dd

và

()( )

2

, dD

xác định bởi:

()

12

2

222

12

.

2.1 1.1

1

,

10

.

21.11

nn

cos d d

nn

-

== =

+- +

 

.

()

2

2222 22

2

.

,

.

.1 1 2.

nn

ab ab

cos d

nn

ab ab

++

D= = =

++ +



.

Vì

()

D cắt

()()

12

,dd tại

A

và

B

tạo thành tam giác

I

AB

cân tại

A

nên

() ()

22

12 2

22

1

,, 5

10

2.

ab

cos d d cos d a b a b

ab

+

=D =  +=+

+

()

2

22 2 2

2

5250

1

2

ab

ab a b a abb

ab

é

=-

ê

+=+++=ê

ê

=-

ê

ë

.

+

2ab=- : chọn 21ab==-: phương trình đường thẳng là:

(

)

(

)

22 02 40

x

yxy L+-= -+= .

+

1

2

ab=-

: chọn 12ab= =-: phương trình đường thẳng là:

() ()

22 0 2 20 /

x

yxy Tm+- =- += . Do đó

(

)

515211Ta b=- =-- = .

DẠNG 3. KHOẢNG CÁCH

Dạng 3.1 Tính khoảng cách từ 1 điểm đến đường thẳng cho trước

Câu 62:

Khoảng cách từ điểm





1;1A

đến đường thẳng

512 60xy

là

A.

13

. B.

13

. C.

1

. D.

1

.

Lời giải

Chọn D

Khoảng cách từ điểm





1;1A

đến đường thẳng

:5 12 6 0xy

là



2

5.1 12.1 6

,1

512

dA



 



.

Câu 63: Khoảng cách từ điểm

(

)

5; 1M -

đến đường thẳng

32130xy++=

là:

A. 213. B.

28

13

.

C.

26

. D.

13

2

.

Lời giải

Chọn A

Khoảng cách

()

22

3.5 2. 1 13

26

213

13

32

d

+-+

===

+

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

Câu 64:

Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 0xy

là

A.

1

. B.

310

5

. C.

5

2

. D.

210

.

Lời giải

Chọn B

Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 0xy

là



22

3.1 1 4

6310

;.

5

10

31

dM



  



Câu 65:

Trong mặt phẳng

Ox

y

, khoảng cách từ điểm



3; 4M  đến đường thẳng

:3 4 1 0xy

.

A.

8

5

. B.

24

5

. C.

12

5

. D.

24

5



.

Lời giải

Chọn B

Ta có:



2

3.3 4. 4 1

24

,

5

34

dM



 



.

Câu 66: Khoảng cách từ điểm

(3;2)A 

đến đường thẳng

:3 1 0xy

bằng:

A.

10.

B.

11 5

.

5

C.

10 5

.

5

D.

11

.

10

Lời giải

Chọn A

Ta có









2

3. 3 2 1

10

;10.

10

31

dA



  



Câu 67: Trong mặt phẳng

Oxy

, khoảng cách từ gốc tọa độ

O

đến đường thẳng

:4 3 1 0dx y

bằng

A. 3. B.

4

. C.

1

. D.

1

5

.

Lời giải

Chọn D

Ta có



22

4.0 3.0 1

1

,

5

43

dOd







.

Câu 68: Một đường tròn có tâm





3; 2I 

tiếp xúc với đường thẳng

:510.xy 

Hỏi bán kính

đường tròn bằng bao nhiêu?

A.

14

.

26

B.

7

.

13

C. 26. D.

6.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 22

Gọi bán kính của đường tròn là

.

R

Khi đó:









2

35. 2 1

14

,.

26

15

RdI



 



Câu 69: Trong mặt phẳng

Oxy

, khoảng cách từđiểm



0; 4M

đến đường thẳng





:420xcos ysin sin

 



bằng

A.

8

.

B. 4

s

in . C.

4

cos sin 

. D. 8 .

Lời giải

Chọn D

Ta có:







22

0. 4. 4 2

,8

cos sin sin

dM

cos sin

   

 

 

.

Câu 70: Khoảng cách từ

(1; 2)I -

đến đường thẳng

:3 4 26 0xyD--=

bằng

A.

3

. B.

12

. C.

5

. D.

5

3

.

Lời giải

Chọn A

Khoảng cách từ điểm

00

(; )

M

x

y

đến đường thẳng

: 0ax b y cD++=

là:

00

22

(,)

ax by c

dM

ab

++

D=

+

Vậy khoảng cách từ

(1; 2)I - đến đường thẳng :3 4 26 0xyD--= bằng

22

3.1 4.( 2) 26

(, ) 3

3(4)

dI

---

D= =

+-

Câu 71: Khoảng cách từ giao điểm của hai đường thẳng

340xy

và

2310xy

đến đường

thẳng

:3 4 0xy

bằng:

A. 210. B.

310

5

. C.

10

5

. D.

2

.

Lời giải

 

340 1

314

2

1; 1 ; .

2310 1

91 10

xy x

AdA

xy y

 





  



 







Chọn C

Câu 72:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho tam giác

A

BC

có





,1; 2A





0;3B

và





4;0C

.

Chiều cao của tam giác kẻ từ đỉnh

A

bằng:

A.

1

5

. B.

3

. C.

1

25

. D.

3

5

.

Lời giải









3812

1

;.

5

,:34120

91

;

6

1; 2

03 4;0

A

hdABC

BCBC xy







  











Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 23

Câu 73:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho tam giác

A

BC

có



3; 4 ,A 





1; 5B

và





3;1C

. Tính

diện tích tam giác

A

BC

.

A.

10.

B.

5.

C. 26. D. 25.

Lời giải

Cách 1:







3; 4

1; 5 3; 1

2

3; 4

25

5

,

;5

:2 7 0

A

x

A

B

A

BC

hdABC

BC y

C











 

 

 



















1

.2 5. 5 5.

2

ABC

S 

Chọn B

Cách 2:



2

22

1

..

2

ABC

SABAAB AC C







Câu 74:

Khoảng cách từ điểm





0;3M

đến đường thẳng



:cos sin 32sin 0xy

 



bằng:

A. 6. B. 6. C.

3sin .



D.

3

.

cos sin





Lời giải







22

.

32 sin3sin

;6

cos sin

dM













Chọn B

Câu 75:

Khoảng cách từ điểm



2;0M

đến đường thẳng

13

:

24

x

t

yt













bằng:

A.

2.

B.

2

.

5

C.

10

.

5

D.

5

.

2

Lời giải



802

:4 3 2 0 ; 2.

6

13

:

9

4

1

2

xt

yt

xy dM



















 



Chọn A

Câu 76:

Khoảng cách nhỏ nhất từ điểm





15;1M

đến một điểm bất kì thuộc đường thẳng

23

:

x

t

yt













bằng:

A. 10. B.

1

.

10

C.

16

.

5

D. 5.

Lời giải



min

15 3 2

:320 ; 10.:

19

23

N

xy MN dM

xt

yt

























Chọn A

Câu 77:

Tìm tất cả các giá trị của tham số

m

để khoảng cách từ điểm





1; 2A 

đến đường thẳng

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 24

:40mx y m

bằng 25.

A.

2.m 

B.

2

1

2

m











. C.

1

2

m 

. D. Không tồn tại

m

.

Lời giải



22

2

24

;2535.14640

1

mm

dA m m m m

m

 





2

.

1

2

m















Chọn B

Câu 78:

Tìm tất cả các giá trị của tham số

m

để khoảng cách từ giao điểm của hai đường thẳng

1

:

2

x

t

d

yt











và

2

:2 0dx ym đến gốc toạ độ bằng

2

.

A.

4

.

2

m











B.

4

.

2

m











C.

4

.

2

m











D.

4

.

2

m











Lời giải

11

2

::20

4

2

:2 0 2

:2 0

xt

ddxy

x

m

yt

dx ym ym

dx ym























 













12

.4;2Mmm dd

Khi đó:



22

2

24 24 680 .

4

m

OM m m m m

m





      







Chọn C

Câu 79:

Đường tròn





C

có tâm là gốc tọa độ





0;0O

và tiếp xúc với đường thẳng

:8 6 100 0xy

. Bán kính

R

của đường tròn





C

bằng:

A.

4

R



. B.

6R 

. C.

8R 

. D.

10R 

.

Lời giải



100

; 10.

64 36

RdO



 

Chọn D

Câu 80:

Đường tròn





C

có tâm





2; 2I 

và tiếp xúc với đường thẳng

:5 12 10 0xy

. Bán kính

R

của đường tròn





C

bằng:

A.

44

13

R 

. B.

24

13

R 

. C.

44

R



. D.

7

13

R 

.

Lời giải



10 24 10

44

;.

13

25 144

RdI

 

 



Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 25

Câu 81:

Cho đường thẳng

:21 11 10 0.dx y

Trong các điểm





21; 3M 

,



0;4N

,





19;5P 

và



1; 5Q

điểm nào gần đường thẳng

d

nhất?

A.

M

. B.

N

. C.

P

. D.

Q

.

Lời giải



21; 3 464

0; 4 54

;211110 .

19;5 464

1; 5 4 4

fM

fN

fxy x y

fP

fQ

























Chọn D

Câu 82:

Cho đường thẳng

: 7 10 15 0.dx y

Trong các điểm





1; 3M 

,



0;4N

,





19;5P 

và



1; 5Q

điểm nào cách xa đường thẳng

d

nhất?

A.

M

. B.

N

. C.

P

. D.

Q

.

Lời giải













1; 3 38

0; 4 25

; 7 10 15 .

19;5 98

1; 5 4 2

fM

fN

fxy x y

fP

fQ











 













Chọn C

Câu 83:

Khoảng cách giữa hai đường thẳng song song

1

:6 –8 3 0xy và

2

:3 –4 –6 0xy bằng:

A.

1

2

. B.

3

2

. C.

2

. D.

5

2

.

Lời giải







1

2

21

2

|| : 6

2;0

12 3

3

;; .

830

2

100

A

y

ddA

x





 

  













Chọn B

Câu 84:

Tính khoảng cách giữa hai đường thẳng

:7 3 0dxy

và

2

:

27

x

t

yt

 











.

A.

32

2

. B.

15

. C.

9

. D.

9

50

.

Lời giải











2; 2 , 7;1

:7 3 0 7;1

d

An

dxy n











 









14 2 3

3

;; .

50 2

ddd dAd



     

Chọn A

Câu 85:

Khoảng cách giữa hai đường thẳng song song

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 26

1

:6 –8 101 0dxy và

2

:3 –4 0dxy bằng:

A.

10,1

. B.

1, 01

. C.

101

. D.

101

.

Lời giải



2

12

21

4;3

24 24 101

101

;10,1.

10

|| : 6 – 8 101 0

100

Ad

ddd

dd x y







 









Chọn A

Dạng 3.2 Phương trình đường thẳng liên quan đến khoảng cách

Câu 86:

Cho hai điểm









3;1 , 4; 0AB

. Đường thẳng nào sau đây cách đều

A

và

B

?

A. 2230.xy  B. 2230.xy C. 230.xy D. 2230.xy

Lời giải

Chọn D

Gọi

d

là đường thẳng được cho trong các phương án. Khi đó:

+) Phương án

A.





22

2.3 2.1 3 2.4 2.0 3

711

,;, ,,

22 22

dAd dBd dAd dBd

   



 

.

Loại phương án

A.

+) Phương án B.





22

2.3 2.1 3 2.4 2.0 3

15

,;, ,,

22 22

dAd dBd dAd dBd

 

 

 

.

Loại phương án

B.

+) Phương án C.

  

22 22

32.13 42.03

21

,;, ,,

55

12 12

d Ad d Bd d Ad d Bd

 

  



.

Loại phương án

C.

+) Phương án D.

 





22 2

2

2.3 2.1 3 2.4 2.0 3

55

,;, ,,

22 22

22

dAd dBd dAd dBd

 

 





Chọn phương án

D.

Câu 87:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





2;3A

và



1; 4B

. Đường thẳng nào sau

đây cách đều hai điểm

A

và

B

?

A.

20.xy

B.

20.xy

C.

22100.xy

D.

100 0.xy 

Lời giải

Đường thẳng cách đều hai điểm

,

A

B

thì đường thẳng đó hoặc song song với

A

B

, hoặc đi qua

trung điểm

I

của đoạn

A

B

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 27

Ta có:



 

37

;

22

|| : 2 0.

11

2;3

1; 4

;1 1;

AB

A

n

I

AB d x y

B

AB































Chọn A

Câu 88:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho ba điểm



,0;1A



12;5B

và



3; 0 .C 

Đường thẳng

nào sau đây cách đều ba điểm

,

A

B

và

C

.

A.

340xy

. B.

10 0xy  

. C.

0xy

. D.

510xy

.

Lời giải

Dễ thấy ba điểm

,,

A

BC

thẳng hàng nên đường thẳng cách điều

,,

A

BC

khi và chỉ khi chúng

song song hoặc trùng với

A

B

.

Ta có:









.12;4 1; 3 || 3:40

AB

AAB n x yBd 





Chọn A

Câu 89:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





,1;1A





2; 4B 

và đường thẳng

:30mx y

. Tìm tất cả các giá trị của tham số

m

để



cách đều hai điểm

,

A

B

.

A.

1

.

2

m











B.

1

.

2

m











C.

1

.

1

m











D.

2

.

2

m











Lời giải

Gọi

I

là trung điểm đoạn

 

15

;

22

.

3; 3 1;1

AB

I

AB

AB n



















  







Khi đó:









:30;1nmx y m



 



cách đều

,

A

B

5

1

30

.

2

1

2

1

Im

m

































Chọn C

Câu 90:

Đường thẳng



song song với đường thẳng

:3 4 1 0dx y

và cách

d

một khoảng bằng

1

có phương trình:

A.

3460xy

hoặc

3440xy

.

B.

3460xy

hoặc

3440xy

.

C.

3460xy

hoặc

3440xy

.

D.

3460xy

hoặc

3440xy

.

Lời giải



 

:3410 1;1

4

1

1; ; .

6

5

|| : 3 4 0

dx y M d

c

dd dM

c

dxyc

 











   















Chọn A

Câu 91:

Tập hợp các điểm cách đường thẳng

:3 4 2 0xy

một khoảng bằng

2

là hai đường thẳng

có phương trình nào sau đây?

A.

3480xy

hoặc

34120xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 28

B.

3480xy

hoặc

34120xy

.

C.

3480xy

hoặc

34120xy

.

D.

3480xy

hoặc

34120xy

.

Lời giải



34120

342

;; 2 2 .

3480

5

xy

dMxy

xy







   







Chọn B

Câu 92:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

1

:5 3 3 0dxy và

2

:5 3 7 0dxy

song song nhau. Đường thẳng vừa song song và cách đều với

12

, dd

là:

A.

5320.xy

B.

5340.xy

C.

5320.xy

D.

5340.xy

Lời giải



12

533537

;; ;; 5 3 20.

34 34

xy xy

dMxy d dMxy d x y

 



Chọn C

Câu 93:

Trên hệ trục tọa độ

Ox

y

, cho hình vuông

A

BCD

. Điểm

M

thuộc cạnh

CD

sao cho





2

M

CDM

,





0;2019N

là trung điểm của cạnh

B

C

,

K

là giao điểm của hai đường thẳng

A

M

và

B

D

. Biết đường thẳng

A

M

có phương trình

 10 2018 0

x

y

. Khoảng cách từ gốc

tọa độ

O

đến đường thẳng

N

K

bằng

A.

2019

. B.

2019 101

. C.

2018

11

. D.

2019 101

101

.

Lời giải

Chọn D

Gọi cạnh hình vuông bằng

a

. Do 

11

34

MD DK DK

ABK MDK

AB KB DB

.

Ta có

 

  

1

3

AM AD DM AD DC





      

     

313 131

424 244

NK BK BN BD BC BA BC BC BA BC

Từ và suy ra



   

11

...0

44

A

MNK ADBC BADC AM NK

.

Vì



A

MNK

nên NK có phương trình tổng quát:

 10 2019 0

x

y

.

Khoảng cách từ O đến NK là









22

2019

2019 101

,

101

10 1

dONK

.

a

M

K

N

C

A

D

B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 29

Câu 94:

Trong mặt phẳng tọa độ

Ox

y

, gọi

d

là đường thảng đi qua

(4;2)M

và cách điểm

(1; 0)A

khoảng cách

310

10

. Biết rằng phương trình đường thẳng d có dạng

0xbyc

với

,bc

là

hai số nguyên. Tính

.bc

A.

4

. B.

5

. C.

1.-

D.

5-

.

Lời giải

Chọn C

Ta có:

(4;2) 4 2 0 4 2 .

M

dbccb 

(1)

22

2

1

310

( , ) 10(1 ) 9(1 ).

10

1

c

dAd c b

b







(2)

Thay

42cb 

vào PT

(2)

ta được PT:

2

3( )

31 120 81 0

27

()

31

btmdk

bb

bktmdk















3, 2 1.bc bc 

.

Câu 95: Trong mặt phẳng với hệ tọa độ

,Ox

y

cho đường thẳng





:1 0xm ym   (m là tham số

bất kì) và điểm





5;1A . Khoảng cách lớn nhất từ điểm

A

đến



bằng

A.

210

. B.

10

. C.

410

. D.

310

.

Lời giải

Chọn A

 

1

:1 01 0

1

x

xm ym y mxy m

y





   







.

Suy ra

 luôn đi qua điểm cố định





1; 1H 

.

Khi đó, với mọi

M

, ta có





;d A AM AH 

.

Giá trị lớn nhất của





;dA AH

khi





max , 2 10MH dA AH  

.

Câu 96: Chuyên Lê Hồng Phong-Nam Định Đường thẳng

12 5 60xy

tạo với hai trục toạ độ một

tam giác. Tổng độ dài các đường cao của tam giác đó là

A.

60

13

. B.

281

13

. C.

360

17

. D.

20

.

Lời giải

Chọn B

Gọi

A

,

B

lần lượt là giao điểm của đường thẳng đã cho với

Ox

,

O

y

.

Ta có

12 5 60xy 0

512

xy

 

. Do đó





5;0A

,





0;12B

.

Gọi

H

là hình chiếu của

O

lên

A

B

. Khi đó:



22

12.0 5.0 60

60

;

13

12 5

OH d O AB



 



.

Tam giác

OAB

là tam giác vuông tại

O

nên tổng độ dài các đường cao là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 30

OA OB OH

60

512

13

 

281

13



.

Câu 97: Trên mặt phẳng tọa độ

Oxy

, cho các điểm



1; 1A  và



3; 4B . Gọi



d là một đường thẳng bất

kì luôn đi qua

B. Khi khoảng cách từ A đến đường thẳng



d

đạt giá trị lớn nhất, đường

thẳng



d

có phương trình nào dưới đây?

A.

10xy

. B.

34 25xy

. C.

5270xy

. D.

25260xy

.

Lời giải

Chọn D

Gọi

H

là hình chiếu của điểm

A

lên đường thẳng



d

. Khi đó ta có:





22

,314129dAd AH AB . Do đó khoảng cách từ

A

đến đường thẳng



d

đạt giá trị lớn nhất bằng

29

khi

H

B

hay





dAB

tại

B

.

Vì vậy



d đi qua B và nhận





2;5AB 



làm VTPT.

Do đó phương trình của đường thẳng



d

là



2354025260xy xy    

.

DẠNG 4. XÁC ĐNNH ĐIỂM

Câu 98:

Cho đường thẳng

:3 5 15 0dx y

. Trong các điểm sau đây, điểm nào không thuộc đường

thẳng

d

A.





1

5; 0M

. B.





4

5; 6M 

. C.





2

0;3M

. D.



3

5;3M

.

Lời giải

Chọn D

Thay tọa độ các điểm vào phương trình đường thẳng

d

, ta có

142

,,

M

MM d

và

3

M

d

.

Dạng 4.1 Xác định tọa hình chiếu, điểm đối xứng

Câu 99:

Trong mặt phẳng với hệ trục tọa độ

Ox

y

, cho tam giác

A

BC

có





4;3A

,



2;7B

,





3; 8C 

.

Tọa độ chân đường cao kẻ từ đỉnh

A

xuống cạnh

B

C

là:

A.





1; 4

. B.



1; 4

. C.





1; 4

. D.





4;1

.

Lời giải

Chọn C

Phương trình đường thẳng đi qua hai điểm

B

và

C

có dạng:

38

23 78

xy





310xy

.

Đường thẳng đi qua

A

và vuông góc với

B

C

có phương trình:









14330xy 

3130xy  

Tọa độ chân đường cao kẻ từ đỉnh

A

xuống cạnh

B

C

là nghiệm của hệ phương

trình:

310

3130

xy











1

4

x

y













.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 31

Câu 100:

Cho đường thẳng

:3 5 0dxy

và điểm





2;1M 

. Tọa độ hình chiếu vuông góc của

M

trên

d

là

A.

74

;

55









. B.

74

;

55









. C.

74

;

55









. D.

54

;

75









.

Lời giải

Chọn B

Gọi



là đường thẳng đi qua

M

và vuông góc với d .

Ta có phương trình của

 là:

310xy

Tọa độ hình chiếu vuông góc của

M

trên

d

là nghiệm của hệ phương trình:

7

350

5

310 4

5

x

xy

y





























.

Câu 101: Tọa độ hình chiếu vuông góc của điểm





1; 2M

lên đường thẳng

:0xy

là

A.

33

;

22







. B.





1; 1

. C.





2; 2

. D.

33

;

22









.

Lời giải

Chọn A

Đường thẳng



có 1 VTPT là





1; 1n 



nên



có 1 VTCP là





1; 1u 



Gọi H là hình chiếu vuông góc của





1; 2M lên đường thẳng



, tọa độ



;

H

tt

Vì

3

.0 1 20

2

MH MH u MH u t t t

           

  

33

;

22

H







Câu 102:

Trong mặt phẳng tọa độ Oxy , cho tam giác

A

BC

với đỉnh

(

)

2;4A

, trọng tâm

2

2;

3

G

æö

÷

ç

÷

ç

÷

ç

èø

. Biết

rằng đỉnh

B

nằm trên đường thẳng

(

)

d

có phương trình

20xy++=

và đỉnh

C

có hình

chiếu vuông góc trên

(

)

d

là điểm

(

)

2; 4H -

. Giả sử

()

;Bab

, khi đó

3Ta b=-

bằng

A.

4T =

. B.

2T =-

. C.

2T =

. D.

0T =

.

Lời giải

Chọn C

Gọi

M

là trung điểm của cạnh

BC

. Ta có

A

B

C

G

M

H

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 32

()

3

222

2

3

32

2

44

23

M

x

AM AG

y

ì

ï

-= -

ï

=

í

æö

ï

÷

ï

ç

-= -

÷

ï

ç

÷

ç

ï

èø

ï

î

 

, suy ra

(

)

2; 1M - .

(

)

0;3HM =



suy ra

HM

không vuông góc với

(

)

d

nên

B

không trùng với

.

H

()()

;2Bab d b aÎ=--

.

Tam giác

BHC

vuông tại

H

và

CM

là trung tuyến nên ta có

()()

()

22

2

1

219 20

2

a

MB MH a a a a

al

é

=-

ê

=-++=--=

ê

=

ë

Suy ra

(

)

1; 1B --và 32Ta b=- =.

Câu 103:

Trong mặt phẳng tọa độ

Oxy

, cho hình chữ nhật

A

BCD

có điểm

C

thuộc đường thẳng d:

250xy

và điểm

(4;8)A 

. Gọi

M

đối xứng với

B

qua

C

, điểm

(5; 4)N 

là hình chiếu

vuông góc của

B

lên đường thẳng

M

D

. Biết tọa độ

(;)Cmn

, giá trị của

mn

là

A.

6

. B.

6

. C.

8

. D.

7

Lời giải

Chọn C

Gọi

(; 2 5) ( )Ct t d

.

Dễ thấy hai tứ giác

B

CND

và

A

DNB

nội tiếp.

Suy ra



B

NC BDC

B

NA BDA

















o

90

A

NC CN AN.

Do đó

. 0 9(5 ) 12(2 1) 0CN AN t t  

 

1t





1; 7C

.

Vậy

17 8mn

Dạng 4.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc

Câu 104:

Cho hai điểm









3; 1 , 0; 3AB

. Tìm tọa độ điểm

M

thuộc

Ox

sao khoảng cách từ

M

đến

đường thẳng

A

B bằng 1.

A.

7

;0

2

M







và



1; 0M

. B.





13;0M

.

C.



4;0M

. D.



2;0M

.

N

M

B

D

A

C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 33

Lời giải

Chọn A

Gọi



;0

M

x

.

Ta có





3; 4AB 



Phương trình đường thẳng





:4 3 3 0AB x y

4390xy

.



49

;549

5

x

dMAB x





7

2

1

x















Vậy



7

;0 ; 1;0

2

MM







.

Câu 105: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm



1;1A

,





4; 3B 

và đường thẳng

:210dx y

. Tìm điểm

M

thuộc

d

có tọa độ nguyên và thỏa mãn khoảng cách từ

M

đến

đường thẳng

A

B

bằng

6

.

A.





3; 7 .M

B.





7;3 .M

C.



43; 27 .M 

D.

.

27

11

3;M









Lời giải





:210 21;,

.

:4 3 7 0

Mdx y Mm mm

AB x y

  















Khi đó



3

8437

6; 11330 7;3.

27

5

l

11

m

mm

dMAB m M

m





 



  







Chọn B

Câu 106:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho điểm





0;1A

và đường thẳng

2

:

2

3y

d

x

t











. Tìm

điểm

M

thuộc

d

và cách

A

một khoảng bằng

5

, biết

M

có hoành độ âm.

A.



4;4 .M

B.





4; 4

.

24 2

;

55

M



















C.

24 2

;.

55

M









D.





4; 4 .M 



22

223:;

3

xt

M

tt

yt

Md















với

22 0 1.tt

Khi đó







22

2

1

24 2

522225512170 ;;.

17

55

5

tl

AM t t t t M

t









 













Chọn C

Câu 107:

Biết rằng có đúng hai điểm thuộc trục hoành và cách đường thẳng

:2 5 0xy

một

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 34

khoảng bằng 2 5 . Tích hoành độ của hai điểm đó bằng:

A.

75

.

4



B.

25

.

4



C.

225

.

4



D. Đáp số khác.

Lời giải

Gọi





;0Mx Ox

thì hoành độ của hai điểm đó là nghiệm của phương trình:



1

2

5

25

2

;25 25

15

5

2

75

.

4

xx

x

dxxM

xx









  

















Chọn A

Câu 108:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





3; 1A 

và





0;3B

. Tìm điểm

M

thuộc

trục hoành sao cho khoảng cách từ

M

đến đường thẳng

A

B

bằng

1

.

A.



7

;0

2

.

1; 0

M















B.

14

;0

3

.

4

;0

3

M























C.



7

;0

2

.

1; 0

M



















D.

14

;0

3

.

4

;0

3

M



























Lời giải



77

;0

49

22

1; .

5

:4 3 9 0

11;0

xM

Mx

x

dMAB

AB x y

xM

















  



















Chọn A

Câu 109:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho hai điểm





3; 0A

và





0; 4B 

. Tìm điểm

M

thuộc

trục tung sao cho diện tích tam giác

M

AB

bằng

6.

A.







0;0

.

0; 8

M











B.





0; 8 .M 

C.



6;0 .M

D.



0;0

.

0;6

M







Lời giải

Ta có

  



:4 3 12 0

00;0

312

1

56.5..

25

80;8

312

0; ;

5

MAB

M

AB x y

yM

y

AB S

yM

y

My hdMAB





















  









 





Chọn A

Câu 110:

Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

1

:3 2 6 0xy và

2

:3 2 3 0xy

. Tìm điểm

M

thuộc trục hoành sao cho

M

cách đều hai đường thẳng đã

cho.

A.

1

0; .

2

M







B.

1

;0 .

2

M







C.

1

;0 .

2

M









D.





2;0 .M

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 35

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 330

BÀI 21. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ

1. CÁC DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN

1.1.Dạng 1: Phương trình đường tròn





C

có tâm





;

I

ab

bán kính

R

Phương trình có dạng :



22

2



x

aybR

1.2.Dạng 2: Phương trình

22

22 0  x y ax by c

với

22

0abc

là phương trình đường

tròn

tâm



;

I

ab

bán kính

22

Rabc

.

2. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

Cho đường thẳng





:0DAxByC

và đường tròn

   

22

2

:Cxa

y

bR

có tâm





;

I

ab























;;CMN DRDdI  























;CM dDRDI  



















;CdIDRD  

3. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

3.1.Viết phương trình tiếp tuyến





D

với





C

tại điểm





0

M

C



Bước 1: Tìm tọa độ tâm I của





C

.

 Bước 2: Tiếp tuyến





D là đường thẳng đi qua

0

M

và có VTPT là

0

M

I



3.2. Viết phương trình tiếp tuyến





D

với





C

tại điểm





0

M

C



Bước 1: Tìm tọa độ tâm I và bán kính

R

của





C

.

 Bước 2:





D

là đường thẳng đi qua

0

M

nên có dạng









00

0ax x by y 

 Bước 3:





D

tiếp xúc với

















;*CdIDR

. Giải





*

tìm được mối liên hệ

giữa

&ab

. Chọn

&ab

phù hợp để kết luận.

3.3.Viết phương trình tiếp tuyến





D

với





C

biết





D

song song với





1

:0DAxByC



Bước 1: Tìm tọa độ tâm I và bán kính

R

của





C

.

 Bước 2:





D 





1

:0DAxByCnên phương trình có dạng

'0(' )

A

xByC C C 

 Bước 3:





D

tiếp xúc với

















;*CdIDR

. Giải





*

tìm được

'C

so với đk

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 331

để kết luận.

3.4. Viết phương trình tiếp tuyến





D với





C biết





D vuông góc với





1

:0DAxByC



Bước 1: Tìm tọa độ tâm

I

và bán kính

R

của





C .

 Bước 2:





D 





1

:0DAxByC

nên phương trình có dạng

'0Bx Ay C

 Bước 3:





D

tiếp xúc với

















;*CdIDR

. Giải





*

tìm được

'C

so với đk

để kết luận.

4. VN TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

Cho đường tròn





1

C có tâm

1

I

, bán kính

1

R

và đường tròn





2

C có tâm

2

I

, bán kính

2

R

. Giả

sử

12

R

R . Ta có:

 Hai đường tròn tiếp xúc

12 1 2

I

IRR

 Hai đường tròn cắt nhau

1212 12

R

RIIRR 

7.13

Tìm tâm và tính bán kính của đường tròn:

22

(3)(3)36xy.

7.14 Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính

của đường tròn tương ứng.

a)

22

420xyxyx;

b)

22

2450xy xy;

c)

22

6810xy xy.

7.15 Viết phương trình của đường tròn trong mỗi trường hợp sau:

a) Có tâm



2;5I 

và bán kính

7R 

;

b) Có tâm





1; 2I 

và đi qua điểm





2; 2A 

;

c) Có đường kính

A

B

, với









1; 3 , 3; 5AB 

;

d) Có tâm





1; 3I

và tiếp xúc với đường thẳng

230xy

.

7.16

Trong mặt phẳng toạ độ, cho tam giác

A

BC

, với













6; 2, 4;2, 5; 5ABC

. Viết phương trình

đường tròn ngoại tiếp tam giác đó.

7.17 Cho đường tròn



22

:2440Cx y x y

. Viết phương trình tiếp tuyến

d

của





C

tại điểm



0; 2M

.

7.18 Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ.

Theo đó, tại thời điểm





0 180tt

vật thể ở vị trí có tọa độ





2sin;4costt



.

a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.

b) Tìm quỹ đạo chuyển động của vật thể.

BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 332

DẠNG 1: NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN. TÌM TÂM VÀ BÁN KÍNH ĐƯỜNG

TRÒN

Cách 1:

+ Đưa phương trình về dạng:



22

:220 Cx y ax byc  

(1)

+ Xét dấu biểu thức

22

Pa b c

Nếu

0P  thì (1) là phương trình đường tròn





C có tâm





;

I

ab và bán kính

22

Rabc

Nếu

0P 

thì (1) không phải là phương trình đường tròn.

Cách 2:

Đưa phương trình về dạng:

22

()()

x

aybP (2).

Nếu 0P  thì (2) là phương trình đường tròn có tâm





;

I

ab và bán kính RP

Nếu 0P  thì (2) không phải là phương trình đường tròn.

Câu 1:

Trong các phương trình sau, phương trình nào là phương trình đường tròn? Tìm tâm và bán

kính nếu có.

1)

22

2490xy xy (1) 2)

22

64130xy xy (2)

3)

22

226410xyxy (3) 4)

22

22390xy xy (4)

Câu 2: Cho phương trình



22

2426 0xy mx m y m   

(1)

a) Tìm điều kiện của

m

để (1) là phương trình đường tròn.

b) Nếu (1) là phương trình đường tròn hãy tìm toạ độ tâm và bán kính theo m

Câu 3: Cho phương trình đường cong ( )

m

C :









22

2410xy m xm ym  

(2)

a) Chứng minh rằng (2) là phương trình một đường tròn

b) Tìm tập hợp tâm các đường tròn khi m thay đổi

c) Chứng minh rằng khi m thay đổi họ các đường tròn ( )

m

C luôn đi qua hai điểm cố định.

Câu 1:

Phương trình nào sau đây là phương trình của đường tròn?

(I)

22

415120xy x y .

(II)

22

34200xy xy.

(III)

22

224610xyxy

.

A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Chỉ (I) và (III).

Câu 2: Để

22

0(1)x y ax by c là phương trình đường tròn, điều kiện cần và đủ là

A.

22

0abc

. B.

22

0abc

. C.

22

40ab c

. D.

22

40ab c

.

HỆ THỐNG BÀI TẬP.

II

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 333

Câu 3: Phương trình nào sau đây là phương trình đường tròn?

A.

22

90xyxy

. B.

22

0xyx

.

C.

22

210.xy xy  D.

22

2310.xy xy

Câu 4: Phương trình

22

2( 1) 2( 2) 6 7 0xy m x m ym      là phương trình đường tròn khi và chỉ khi

A.

0.m 

B.

1m 

. C.

1m 

. D.

1m 

hoặc

1m 

.

Câu 5:

Cho đường cong





22

:–8100

m

Cxy x ym

. Với giá trị nào của

m

thì





m

C

là đường

tròn có bán kính bằng

7

?

A.

4m  . B. 8m  . C. –8m  . D. =–4m .

Câu 6: Đường tròn

22

33–6990xyxy có bán kính bằng bao nhiêu?

A.

15

2

. B.

5

2

. C. 25 . D.

5

.

Câu 7: Đường tròn

22

22–8410xyxy có tâm là điểm nào sau đây?

A.





8; 4

. B.





2; 1

. C.





8; 4

. D.





2;1

.

Câu 8: Cho hai điểm





2;1A 

,





3; 5B

. Tập hợp điểm





;

M

xy

nhìn

A

B dưới một góc vuông nằm

trên đường tròn có phương trình là

A.

22

610xyxy. B.

22

610xyxy.

C.

22

54110xy xy

. D. Đáp án khác.

Câu 9: Cho hai điểm

(4;2)A 

và

(2; 3)B 

. Tập hợp điểm

(; )

M

xy

thỏa mãn

22

31MA MB

có

phương trình là

A.

22

210xy xy

. B.

22

6510.xy xy

C.

22

26220xy xy. D.

22

26220.xy xy

Câu 10: Cho









1; 0 , 2; 4AB

và





4;1C

. Chứng minh rằng tập hợp các điểm

M

thoả mãn

22 2

32

M

AMB MC

là một đường tròn





.C

Tìm tính bán kính của (C).

A.

107

2

. B.

5

. C.

25

2

. D.

25

4

.

DẠNG 2: VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Cách 1:

+ Tìm toạ độ tâm



;

I

ab

của đường tròn (C)

+ Tìm bán kính R của đường tròn (C)

+ Viết phương trình của (C) theo dạng

222

()()

x

aybR

.

Cách 2: Giả sử phương trình đường tròn (C) là:

22

22 0 xy axbyc  (Hoặc

22

22 0 x y ax by c  ).

+ Từ điều kiện của đề bài thành lập hệ phương trình với ba Nn là a, b, c.

+ Giải hệ để tìm a, b, c từ đó tìm được phương trình đường tròn (C).

Chú ý:

*



A

CIAR

*





C

tiếp xúc với đường thẳng



tại



;

A

IA d I R 

*





C

tiếp xúc với hai đường thẳng

1

 và









212

;;dI dI R    

PHƯƠNG PHÁP.

1

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 334

Câu 1:

Viết phương trình đường tròn trong mỗi trường hợp sau:

a) Có tâm





1; 5I 

và đi qua





0;0 .O

b) N hận

A

B làm đường kính với









1;1 , 7; 5AB

.

c) Đi qua ba điểm:



2; 4 , 5;5 , 6; 2MNP

Câu 2:

Viết phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm





1; 2I 

và tiếp xúc với đường thẳng

:270xy 

b) (C) đi qua





2; 1A 

và tiếp xúc với hai trục toạ độ

Ox

và

Oy

c) (C) có tâm nằm trên đường thẳng

:6100dx y

và tiếp xúc với hai đường thẳng có

phương trình

1

:3 4 5 0dxy và

2

:4 3 5 0dxy

Câu 3: Cho hai điểm





8; 0A

và





0;6B

.

a) Viết phương trình đường tròn ngoại tiếp tam giác

OAB

b) Viết phương trình đường tròn nội tiếp tam giác

OAB

Câu 4: Trong mặt phẳng tọa độ

Oxy

, cho hai đường thẳng

1

:3 0dxy

. và

2

:3 0dxy

. Gọi

(C) là đường tròn tiếp xúc với

1

d tại A, cắt

2

d tại hai điểm B, C sao cho tam giác

A

BC

vuông

tại B.

Viết phương trình của (C), biết tam giác

A

BC

có diện tích bằng

3

2

và điểm A có hoành

độ dương.

Câu 1:

Đường tròn tâm

(3; 1)I 

và bán kính 2

R

 có phương trình là

A.

22

(3)(1)4xy. B.

22

(3)(1)4xy.

C.

22

(3)(1)4xy. D.

22

(3)(1)4xy.

Câu 2: Đường tròn tâm

(1;2)I 

và đi qua điểm

(2;1)M

có phương trình là

A.

22

2450xy xy. B.

22

2430.xy xy

C.

22

2450xy xy. D.

22

2450.xy xy

Câu 3: Cho hai điểm

(5; 1)A 

,

(3;7)B 

. Đường tròn có đường kính

A

B có phương trình là

A.

22

26220xy xy

. B.

22

2 6 22 0.xy xy

C.

22

210xy xy. D.

22

6510.xy xy

Câu 4: Đường tròn

()C

tâm

(4;3)I 

và tiếp xúc với trục tung có phương trình là

A.

22

3049xy xy. B.

22

(4)(3)16xy.

C.

22

(4)(3)16xy. D.

22

8 6 12 0.xy xy

Câu 5: Đường tròn

()C

tâm

(4; 3)I

và tiếp xúc với đườngthẳng

:3 4 5 0xy

có phương trình là

A.

22

(4)(3)1xy. B.

22

(4)(3)1xy.

C.

22

(4)(3)1xy

. D.

22

(4)(3)1xy

Câu 6: Đường tròn





C

đi qua điểm





2; 4A

và tiếp xúc với các trục tọa độ có phương trình là

A.

22

(2)(2)4xy hoặc

22

( 10) ( 10) 100xy

BÀI TẬP TỰ LUẬN.

2

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 335

B.

22

(2)(2)4xy hoặc

22

( 10) ( 10) 100xy

C.

22

(2)(2)4xy hoặc

22

( 10) ( 10) 100xy

D.

22

(2)(2)4xy

hoặc

22

( 10) ( 10) 100xy

Câu 7: Đường tròn

()C

đi qua hai điểm

(1; 3)A

,

(3;1)B

và có tâm nằm trên đường thẳng

:2 7 0dxy

có phương trình là

A.

22

( 7) ( 7) 102xy . B.

22

( 7) ( 7) 164xy .

C.

22

(3)(5)25xy. C.

22

(3)(5)25xy.

Câu 8: Đường tròn

()C

tiếp xúc với trục tung tại điểm

(0; 2)A 

và đi qua điểm

(4; 2)B 

có phương

trình là

A.

22

(2)(2)4xy. B.

22

(2)(2)4xy

C.

22

(3)(2)4xy  D.

22

(3)(2)4xy 

Câu 9: Tâm của đường tròn qua ba điểm





2; 1A

,





2; 5B

,





2; 1C 

thuộc đường thẳng có phương trình

A.

30xy

. B.

30xy

C.

30xy  

D.

30xy

Câu 10: Đường tròn đi qua 3 điểm









0; 2 , 2; 2 , 1; 2()1ABC có phương trình là

A.

22

22 20xy xy 

. B.

22

22 0xy xy .

C.

22

2220xy xy. D.

22

22 20xy xy .

Câu 11: Đường tròn đi qua 3 điểm













11;8 , 13;8 , 14;7ABC

có bán kính

R

bằng

A.

2 . B. 1. C. 5. D.

2

.

DẠNG 3: VN TRÍ TƯƠNG ĐỐI CỦA ĐIỂM; ĐƯỜNG THẲNG; ĐƯỜNG TRÒN VỚI ĐƯỜNG TRÒN

1 Vị trí tương đối của điểm M và đường tròn (C)

Xác định tâm I và bán kính R của đường tròn (C) và tính IM

+ N ếu

IM R

suy ra M nằm trong đường tròn

+ N ếu

IM R suy ra M thuộc đường tròn

+ N ếu

IM R suy ra M nằm ngoài đường tròn

2

Vị trí tương đối giữa đường thẳng  và đường tròn (C)

Xác định tâm I và bán kính R của đường tròn (C) và tính





;dI

+ N ếu





;dI R

suy ra  cắt đường tròn tại hai điểm phân biệt

+ N ếu



; dI R

suy ra  tiếp xúc với đường tròn

+ N ếu





;dI R

suy ra  không cắt đường tròn

Chú ý: Số nghiệm của hệ phương trình tạo bởi phương trình đường thẳng



và đường tròn (C)

bằng số giao điểm của chúng. Tọa độ giao điểm là nghiệm của hệ.

3

Vị trí tương đối giữa đường tròn (C) và đường tròn (C')

Xác định tâm I, bán kính R của đường tròn (C) và tâm I', bán kính R' của đường tròn (C') và

tính

'II ,

', 'RRRR

+ N ếu

''II R R suy ra hai đường tròn không cắt nhau và ở ngoài nhau

+ N ếu

' 'II R R

suy ra hai đường tròn tiếp xúc ngoài với nhau

+ N ếu

' '

I

IRR

suy ra hai đường tròn không cắt nhau và lồng vào nhau

PHƯƠNG PHÁP.

1

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 336

+ N ếu

' '

I

IRR

suy ra hai đường tròn tiếp xúc trong với nhau

+ N ếu

'' 'RR II RR

suy ra hai đường tròn cắt nhau tại hai điểm phân biệt

Chú ý:

Số nghiệm của hệ phương trình tạo bởi phương trình đường thẳng (C) và đường tròn

(C') bằng số giao điểm của chúng. Tọa độ giao điểm là nghiệm của hệ.

Câu 1:

Cho đường thẳng

:10xy

và đường tròn





22

:4240Cx y x y

a) Chứng minh điểm





2;1M

nằm trong đường tròn

b) Xét vị trí tương đối giữa

 và





C

c) Viết phương trình đường thẳng

' vuông góc với  và cắt đường tròn tại hai điểm phân biệt

sao cho khoảng cách của chúng là lớn nhất.

Câu 2: Trong mặt phẳng

Ox

y

, cho hai đường tròn





22

:26150Cx y x y

và



22

': 6 2 3 0Cxy x y

a) Chứng minh rằng hai đường tròn cắt nhau tại hai điểm phân biệt A, B

b) Viết phương trình đường thẳng đi qua A và B

c) Viết phương trình đường tròn đi qua ba điểm A, B và O

Câu 3: Cho đường tròn

22

(): 2 4 4 0Cx y x y có tâm I và đường thẳng

:2 1 2 0xmy

a) Tìm

m

để đường thẳng  cắt đường tròn (C) tại hai điểm phân biệt A, B

b) Tìm m để diện tích tam giác

IAB

là lớn nhất

Câu 1:

Cho đường tròn

22

():( 1) ( 3) 4Cx y  và đường thẳng

:3 4 5 0dx y

. Phương trình của

đường thẳng

d



song song với đường thẳng

d

và chắn trên

()C

một dây cung có độ dài lớn nhất

là

A.

43130xy

. B.

34250xy

. C.

34150xy

. D.

43200xy

.

Câu 2: Tìm tọa độ giao điểm của đường thẳng

:230xy 

và đường tròn

22

(): 2 4 0Cx y x y 

A.





3; 3

và





1;1

. B.





1;1

và





3; 3

. C.





3; 3

và





1; 1

. D.





2;1

và





2; 1

.

Câu 3: Cho đường tròn

22

(): 4 6 5 0Cx y x y. Đường thẳng

d

đi qua

(3;2)A

và cắt

()C

theo

một dây cung ngắn nhất có phương trình là

A.

220xy

. B.

10xy

. C.

10xy

. D.

10xy

.

Câu 4: Cho đường tròn

22

(): 6 2 5 0Cx y x y

và đường thẳng

d

đi qua điểm

(4;2)A 

, cắt

()C

tại hai điểm

,

M

N

sao cho A là trung điểm của

M

N

. Phương trình của đường thẳng

d

là

A.

60xy

. B.

73340xy

. C.

73300xy

. D.

7350xy 

.

BÀI TẬP TỰ LUẬN.

2

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 337

Câu 5: Cho đường tròn

22

(): 4 6 3 0Cx y x y. Mệnh đề nào sau đây đúng?

(I) Điểm

(1;1)A

nằm ngoài

()C

.

(II) Điểm

(0;0)O

nằm trong

()C

.

(III)

()C

cắt trục tung tại hai điểm phân biệt.

A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Cả (I), (II) và (III).

Câu 6: Cho đường tròn

22

(): 2 6 6 0Cx y x y

và đường thẳng

:4 3 5 0dx y

. Đường thẳng

d



song song với đường thẳng

d

và chắn trên

()C

một dây cung có độ dại bằng 23 có

phương trình là

A.

4380xy

. B.

4380xy

hoặc

4318xy

.

C.

4380xy

. D.

4380xy

.

Câu 7: Cho đường tròn

22

(): 6 2 5 0Cx y x y và đường thẳng d đi qua điểm

(4;2)A 

, cắt

()C

tại hai điểm

,

M

N

sao cho A là trung điểm của

M

N

. Phương trình của đường thẳng

d

là

A.

60xy

. B.

73340xy

. C.

73300xy

. D.

7350xy 

.

Câu 8: Đường tròn

22

22230xy xy cắt đường thẳng

20xy

theo một dây cung có độ

dài bằng bao nhiêu?

A.

10

. B.

8

. C.

6

. D.

32

.

Câu 9: Tìm giao điểm 2 đường tròn





22

1

:40Cx y

và





22

2

:4440Cxy xy

A.





2; 2

và (





2; 2

. B.





0; 2 và





0; 2 .

C.





2;0 và





0; 2 . D.





2;0 và





2;0 .

Câu 10: Xác định vị trí tương đối giữa 2 đường tròn





22

1

:4Cx y

và





22

2

: ( 10) ( 16) 1Cx y

.

A.

Cắt nhau. B. Không cắt nhau. C. Tiếp xúc ngoài. D. Tiếp xúc trong.

Câu 11: Với những giá trị nào của

m

thì đường thẳng

:4 3 0xym

tiếp xúc với đường tròn





22

:90Cx y.

A.

3m 

. B.

3m 

và

3m 

. C.

3m 

. D.

15m 

và

15m 

.

Câu 12: Một đường tròn có tâm

(1; 3)I

tiếp xúc với đường thẳng

:3 4 0xy

. Hỏi bán kính đường

tròn bằng bao nhiêu?

A.

3

5

. B.

1

. C. 3. D. 15.

Câu 13: Đường tròn

222

()()

x

aybRcắt đường thẳng

0xyab

theo một dây cung có độ

dài bằng bao nhiêu?

A.

2

R

. B.

2R

. C.

2

R

. D.

R

.

Câu 14:

Xác định vị trí tương đối giữa 2 đường tròn

22

1

(): 4 0Cx y x

và

22

2

(): 8 0Cxy y

.

A.

Tiếp xúc trong. B. Không cắt nhau. C. Cắt nhau. D. Tiếp xúc ngoài.

Câu 15: Đường tròn

()C

có tâm

(1;3)I 

và tiếp xúc với đường thẳng

:3 4 5 0dx y

tại điểm H có

tọa độ là

A.

17

;

55









. B.

17

;

55







. C.

17

;

55









. D.

17

;

55









.

Câu 16: Xác định vị trí tương đối giữa 2 đường tròn





22

1

:4Cx y

và





22

2

:( 3) ( 4) 25Cx y

.

A.

Không cắt nhau. B. Cắt nhau. C. Tiếp xúc ngoài. D. Tiếp xúc trong.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 338

DẠNG 4: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN VỚI ĐƯỜNG TRÒN

Cho đường tròn (C) tâm





;

I

ab

, bán kính R

1. N ếu biết tiếp điểm là





00

;

M

xy

thì tiếp tuyến đó đi qua M và nhận vectơ





00

;IM x a y b



làm vectơ pháp tuyến nên có phương trình là

















000 0

0xaxx ybyy

2. N ếu không biết tiếp điểm thì dùng điều kiện: Đường thẳng  tiếp xúc đường tròn (C) khi và

chỉ khi





;dI R để xác định tiếp tuyến.

Câu 1:

Cho đường tròn (C) có phương trình

22

6260xy xy và điểm hai điểm









1; 1 ; 1; 3AB

a) Chứng minh rằng điểm A thuộc đường tròn, điểm B nằm ngoài đường tròn

b) Viết phương trình tiếp tuyến của (C) tại điểm A

c) Viết phương trình tiếp tuyến của (C) kẻ từ

B.

Câu 2:

Viết phương trình tiếp tuyến  của đường tròn





22

:4410Cx y x y

trong trường

a) Đường thẳng

 vuông góc với đường thẳng

':2 3 4 0xy

b) Đường thẳng

 hợp với trục hoành một góc

0

45

Câu 3: Lập phương trình tiếp tuyến chung của hai đường tròn sau:



22

1

:450Cxy y

và



22

2

:68160Cxy xy

Câu 1:

Cho đường tròn

22

():( 3) ( 1) 10Cx y. Phương trình tiếp tuyến của

()C

tại điểm

(4;4)A

là

A.

350xy

. B.

340xy

. C.

3160xy

. D.

3160xy

.

Câu 2: Cho đường tròn

22

():( 2) ( 2) 9Cx y

. Phương trình tiếp tuyến của

()C

đi qua điểm

(5;1)A 

là

A.

40xy

và

20xy

. B.

5x 

và

1y 

.

C.

230xy

và

3220xy

. D.

3220xy

và

2350xy

.

Câu 3: Cho đường tròn

22

(): 2 6 5 0Cx y x y. Phương trình tiếp tuyến của

()C

song song với

đường thẳng

:2150Dx y

là

A.

20xy

và

2100xy

. B.

20xy

và

2100xy

.

C.

210xy

và

230xy

. D.

210xy

và

230xy

.

Câu 4: Cho đường tròn

22

(): 6 2 5 0Cx y x y và đường thẳng

:2 ( 2) 7 0dxm ym 

.

Với giá trị nào của

m

thì

d

là tiếp tuyến của

()C

?

A.

3m 

. B.

15m 

. C.

13m 

. D.

3m 

hoặc

13m 

.

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 339

Câu 5: Cho đường tròn



22

:28239Cx y x y

và điểm





8; 3M 

. Độ dài đoạn tiếp tuyến của





C

xuất phát từ

M

là:

A.

10

. B.

210

. C.

10

2

. D.

10

.

Câu 6: N ếu đường tròn

   

22

2

:1 3Cx y R 

tiếp xúc với đường thẳng

:5 12 60 0dx y

thì

giá trị của

R

là:

A.

22R 

. B.

19

13

R 

. C. 5R  . D.

2R 

.

Câu 7: Cho đường tròn

   

22

:3 15Cx y

. Phương trình tiếp tuyến của





C

song song với

đường thẳng

:2 7 0dxy

là

A.

20;2100xy xy  

. B.

210;210xy xy 

.

C.

2100;2100xy xy   

. D.

20;2100xy x y   

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 21. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ

1. CÁC DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN

1.1.Dạng 1: Phương trình đường tròn





C có tâm





;

I

ab bán kính

R

Phương trình có dạng :



22

2



x

aybR

1.2.Dạng 2: Phương trình

22

22 0  x y ax by c với

22

0abc

là phương trình đường

tròn

tâm



;

I

ab

bán kính

22

Rabc

.

2. SỰ TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

Cho đường thẳng





:0DAxByC

và đường tròn

   

22

2

:Cxa yb R

có tâm





;

I

ab























;;CMN DRDdI  























;CM dDRDI  



















;CdIDRD  

3. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

3.1.Viết phương trình tiếp tuyến





D

với





C

tại điểm





0

M

C



Bước 1: Tìm tọa độ tâm I của





C

.

 Bước 2: Tiếp tuyến





D

là đường thẳng đi qua

0

M

và có VTPT là

0

M

I



3.2. Viết phương trình tiếp tuyến





D

với





C

tại điểm





0

M

C



Bước 1: Tìm tọa độ tâm I và bán kính

R

của





C

.

 Bước 2:





D

là đường thẳng đi qua

0

M

nên có dạng









00

0ax x by y 

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

 Bước 3:





D

tiếp xúc với

















;*CdIDR

. Giải





*

tìm được mối liên hệ

giữa

&ab

. Chọn

&ab

phù hợp để kết luận.

3.3.Viết phương trình tiếp tuyến





D

với





C

biết





D

song song với





1

:0DAxByC



Bước 1: Tìm tọa độ tâm I và bán kính

R

của





C

.

 Bước 2:





D 





1

:0DAxByC

nên phương trình có dạng

'0(' )

A

xByC C C 

 Bước 3:





D

tiếp xúc với

















;*CdIDR

. Giải





*

tìm được

'C

so với đk

để kết luận.

3.4. Viết phương trình tiếp tuyến





D với





C biết





D vuông góc với





1

:0DAxByC



Bước 1: Tìm tọa độ tâm

I

và bán kính

R

của





C .

 Bước 2:





D 





1

:0DAxByCnên phương trình có dạng

'0Bx Ay C

 Bước 3:





D tiếp xúc với

















;*CdIDR. Giải





* tìm được 'C so với đk

để kết luận.

4. VN TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

Cho đường tròn





1

C

có tâm

1

I , bán kính

1

R

và đường tròn





2

C

có tâm

2

I , bán kính

2

R

. Giả

sử

12

RR

. Ta có:

 Hai đường tròn tiếp xúc

12 1 2

I

IRR

 Hai đường tròn cắt nhau

1212 12

R

RIIRR 

7.13

Tìm tâm và tính bán kính của đường tròn:

22

(3)(3)36xy.

Lời giải

Đường tròn

22

(3)(3)36xy có tâm là điểm



3; 3I 

, có bán kính

6R 

.

7.14 Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính

của đường tròn tương ứng.

a)

22

420xyxyx;

b)

22

2450xy xy;

c)

22

6810xy xy.

Lời giải

a)

22

420xyxyx không phải là phương trình của một đường tròn vì có

xy

.

BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

b)









22

2450 1 2 0xy xy x y 

không phải là phương trình của một đường

tròn vì

0R 

.

c)







2

22

6810 3 4 26xy xy x y   là phương trình của đường tròn tâm



3; 4I 

, bán kính

26R 

.

7.15

Viết phương trình của đường tròn trong mỗi trường hợp sau:

a) Có tâm



2;5I 

và bán kính

7R 

;

b) Có tâm





1; 2I 

và đi qua điểm





2; 2A 

;

c) Có đường kính

A

B

, với









1; 3 , 3; 5AB 

;

d) Có tâm





1; 3I

và tiếp xúc với đường thẳng

230xy

.

Lời giải

a) Phương trình của đường tròn là



22

2549xy

.

b) Ta có





3; 4AI 



, bán kính của đường tròn là



2

345R 

.

Phương trình của đường tròn là









22

1225xy 

.

c) Toạ độ trung điểm

I

của

A

B

là





2;1I 

. Ta có



1; 4AI 



.

Bán kính của đường tròn là



2

14 17R 

.

Phương trình của đường tròn là



22

2117xx

.

d) Có tâm





1; 3I

và tiếp xúc với đường thẳng

230xy

.

Khoảng cách từ tâm

I

đến đường thẳng

230xy

bằng bán kính

|1 2.3 3|

25

5

R



.

Phương trình đường tròn tâm

I

bán kính

R

là

 

22

1320xy 

.

7.16 Trong mặt phẳng toạ độ, cho tam giác

A

BC

, với













6; 2, 4;2, 5; 5ABC

. Viết phương trình

đường tròn ngoại tiếp tam giác đó.

Lời giải

Gọi phương trình đường tròn



C

có dạng

22

22 0.xy axbyc  

Vì đường tròn





C

đi qua ba điểm





6; 2A 

,





4; 2B

,





5; 5C 

nên ta có hệ phương trình

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

 

2

22

2

622.62.2 0

422.42.2 0

552.52.5 0

ab c

abc

ab c



     



  





     





12 4 40 1

84 20 2

10 10 50 20.

abc a

abc b

abc c

 





    





 



Vậy phương trình đường tròn





C

là:

22

24200xy xy.

7.17 Cho đường tròn



22

:2440Cx y x y

. Viết phương trình tiếp tuyến

d

của





C

tại điểm





0; 2M

.

Lời giải

Ta có đường tròn



C

:

22

2440xy xy 









22

121xy 

có tâm là điểm



1; 2I 

.

Do

 

22

01 22 1 

nên điểm

M

thuộc đường tròn (C).

Tiếp tuyến của



C

tại



0; 2M

có vectơ pháp tuyến





1; 0MI 



, nên có phương trình









110 20 10xy x 

.

7.18

Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ.

Theo đó, tại thời điểm





0 180tt

vật thể ở vị trí có tọa độ





2sin;4costt



.

a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.

b) Tìm quỹ đạo chuyển động của vật thể.

Lời giải

a) Vị trí ban đầu của vật thể tại thời điểm 0t  có tọa độ



2;5M

.

Vị trí kết thúc của vật thể tại thời điểm

180t 

có tọa độ





2;3M

.

b) Quỹ đạo chuyển độ của vật thể là các điểm





;

M

xy

thỏa mãn



22

2sin

241

4cos

xt

xy

yt

 



  



 



.

Vậy quỹ đạo chuyển độ của vật thể là đường tròn

    

22

: 2 4 1Cx y

, có tâm



2; 4I

,

bán kính

1

R



.

HỆ THỐNG BÀI TẬP.

II

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

DẠNG 1: NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN. TÌM TÂM VÀ BÁN KÍNH ĐƯỜNG

TRÒN

Cách 1:

+ Đưa phương trình về dạng:



22

:220 Cx y ax byc   (1)

+ Xét dấu biểu thức

22

Pa b c

Nếu

0P 

thì (1) là phương trình đường tròn





C

có tâm





;

I

ab

và bán kính

22

Rabc

Nếu

0P 

thì (1) không phải là phương trình đường tròn.

Cách 2:

Đưa phương trình về dạng:

22

()()

x

aybP (2).

Nếu

0P 

thì (2) là phương trình đường tròn có tâm





;

I

ab

và bán kính

RP

Nếu

0P 

thì (2) không phải là phương trình đường tròn.

Câu 1:

Trong các phương trình sau, phương trình nào là phương trình đường tròn? Tìm tâm và bán

kính nếu có.

1)

22

2490xy xy (1) 2)

22

64130xy xy (2)

3)

22

226410xyxy (3) 4)

22

22390xy xy (4)

Lời giải

1)

Phương trình (1) có dạng

22

22 0 xy axbyc  với

1; 2; 9abc  

Ta có

22

149 0abc

Vậy phương trình (1) không phải là phương trình đường tròn.

2) Ta có:

22

94130abc

Suy ra phương trình (2) không phải là phương trình đường tròn.

3) Ta có:



22

1

3320

2

xy xy

Suy ra:

2

22 2

3115

10

224

Pa b c

  

   

  

  

Vậy phương trình (3) là phương trình đường tròn tâm

3

;1

2

I







bán kính

15

2

R 

4) Phương trình (4) không phải là phương trình đường tròn vì hệ số của

2

x

và

2

y

khác nhau.

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

Câu 2: Cho phương trình



22

2426 0xy mx m y m   

(1)

a) Tìm điều kiện của

m

để (1) là phương trình đường tròn.

b) Nếu (1) là phương trình đường tròn hãy tìm toạ độ tâm và bán kính theo m

Lời giải

a) Phương trình (1) là phương trình đường tròn khi và chỉ khi

22

0abc

Với



;2 2;6amb m c m 

Hay



2

22

2

426 0515100

1

m

mm m mm

m













b) Với điều kiện trên thì đường tròn có tâm









;2 2Im m

và bán kính:

2

51510Rmm

Câu 3: Cho phương trình đường cong ( )

m

C :









22

2410xy m xm ym  

(2)

a) Chứng minh rằng (2) là phương trình một đường tròn

b) Tìm tập hợp tâm các đường tròn khi m thay đổi

c) Chứng minh rằng khi m thay đổi họ các đường tròn

()

m

C

luôn đi qua hai điểm cố định.

Lời giải

a) Ta có





2

22

24

10

22 2

m

mm

abc m





   





Suy ra (2) là phương trình đường tròn với mọi m

b) Đường tròn có tâm I:

2

4

2

I

m

x

m

y





















suy ra 1 0

II

xy

Vậy tập hợp tâm các đường tròn là đường thẳng

:10xy

c) Gọi





00

;

M

xy

là điểm cố định mà họ ()

m

C luôn đi qua.

Khi đó ta có:









22

000

2410,

o

x

ym xm ym m  



22

00 0 0 0

12410,

o

x

ymxyxy m 

00

0

22

0

00 0 0

10

1

0

2410

xy

x

y

xy x y















  





hoặc

0

1

2

x

y











Vậy có hai điểm cố định mà họ ()

m

C luôn đi qua với mọi m là



1

1; 0M 

và



2

1; 2M

.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7

Câu 1: Phương trình nào sau đây là phương trình của đường tròn?

(I)

22

415120xy x y 

.

(II)

22

34200xy xy.

(III)

22

224610xyxy.

A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Chỉ (I) và (III).

Lời giải

Chọn D





I

có:

2

22

15 289

4120

24

abc



  







I

có:

22

34 55

20 0

22 4

abc

 

   

 

 



22

1

23 0

2

III x y x y

, phương trình này có:

2

22

3111

10

224

abc



  





Vậy chỉ





I

và



I

II

là phương trình đường tròn.

Câu 2: Để

22

0(1)x y ax by c là phương trình đường tròn, điều kiện cần và đủ là

A.

22

0abc

. B.

22

0abc

. C.

22

40ab c

. D.

22

40ab c

.

Lời giải

Chọn C

Ta có:





22

0 1

2. . 2. . 0

22 2244

2244

x y ax by c

aa bbab

xx yy c

abab

xy c



 

    

 

 



  





Vậy điều kiện để (1) là phương trình đường tròn:

22

040

44

ab

cabc

Câu 3: Phương trình nào sau đây là phương trình đường tròn?

A.

22

90xyxy. B.

22

0xyx.

C.

22

210.xy xy  D.

22

2310.xy xy

Lời giải

Chọn B

Loại C vì có số hạng

2

x

y

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

Câu A:

22

1

,9 0

2

ab c a b c   

nên không phải phương trình đường tròn.

Câu D: loại vì có

2

y .

Câu B:

22

1

,0,0 0

2

abc abc

nên là phương trình đường tròn.

Câu 4: Phương trình

22

2( 1) 2( 2) 6 7 0xy m x m ym      là phương trình đường tròn khi và chỉ khi

A.

0.m  B. 1m  . C. 1m  . D. 1m  hoặc 1m  .

Lời giải

Chọn D

Ta có:

  

    

  

22

2222

22

2

2 1 2 2 6 7 0 1

21 1 22 2 1 2670

1222

xy m x m ym

xmxm ymym m m m

xm ym m

     

       

    

 

Vậy điều kiện để (1) là phương trình đường tròn:

2

1

220

1

m













Câu 5: Cho đường cong



22

:–8100

m

Cxy x ym

. Với giá trị nào của

m

thì





m

C

là đường

tròn có bán kính bằng

7

?

A.

4m  . B. 8m  . C. –8m  . D. =–4m .

Lời giải

Chọn C

Ta có

22

45 7 8Rmm.

Câu 6: Đường tròn

22

33–6990xyxy có bán kính bằng bao nhiêu?

A.

15

2

. B.

5

2

. C.

25

. D. 5.

Lời giải

Chọn B

22

33–6990xyxy

22

–2 3 3 0xy xy .

Suy ra



2

325

130

24

P



  





. Vậy bán kính là:

5

2

R 

.

Câu 7: Đường tròn

22

22–8410xyxy có tâm là điểm nào sau đây?

A.





8; 4

. B.





2; 1

. C.





8; 4

. D.





2;1

.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9

22

22–8410xyxy

22

1

–4 2 0

2

xy x y 

.

Vậy tâm là:





2; 1I  .

Câu 8: Cho hai điểm





2;1A 

,





3; 5B

. Tập hợp điểm





;

M

xy

nhìn

A

B dưới một góc vuông nằm

trên đường tròn có phương trình là

A.

22

610xyxy. B.

22

610xyxy.

C.

22

54110xy xy

.

D. Đáp án khác.

Lời giải

Chọn A

Tập hợp điểm





;

M

xy nhìn

A

B

dưới một góc vuông nằm trên đường tròn đường kính

A

B

và

tâm là trung điểm của

A

B

.

Tọa độ tâm đường tròn là trung điểm của

A

B

:

1

;3

2

I







.

Bán kính đường tròn:

22

54 41

22 2

AB

R



 

.

Phương trình đường tròn:



2

141

3

24

xy









22

610xyxy.

Câu 9: Cho hai điểm

(4;2)A 

và

(2; 3)B 

. Tập hợp điểm

(; )

M

xy

thỏa mãn

22

31MA MB

có

phương trình là

A.

22

210xy xy. B.

22

6510.xy xy

C.

22

26220xy xy. D.

22

26220.xy xy

Lời giải

Chọn A.

Ta có:

22

31MA MB



2222

22

422331 210xyxy xyxy    

.

Câu 10: Cho









1; 0 , 2; 4AB

và





4;1C

. Chứng minh rằng tập hợp các điểm

M

thoả mãn

22 2

32

M

AMB MC

là một đường tròn





.C

Tìm tính bán kính của (C).

A.

107

2

. B. 5. C.

25

2

. D.

25

4

.

Lời giải

Chọn A

22 2

32

M

AMB MC

    

22222

2

313 2 42421xyxy x y

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

22

11

92 0

2

xy xy

. Bán kính của (C) là:

107

2

R 

.

DẠNG 2: VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Cách 1:

+ Tìm toạ độ tâm



;

I

ab

của đường tròn (C)

+ Tìm bán kính R của đường tròn (C)

+ Viết phương trình của (C) theo dạng

222

()()

x

aybR.

Cách 2: Giả sử phương trình đường tròn (C) là:

22

22 0 xy axbyc  

(Hoặc

22

22 0 x y ax by c  ).

+ Từ điều kiện của đề bài thành lập hệ phương trình với ba Nn là a, b, c.

+ Giải hệ để tìm a, b, c từ đó tìm được phương trình đường tròn (C).

Chú ý:

*



A

CIAR

*





C

tiếp xúc với đường thẳng  tại



;

A

IA d I R 

*





C tiếp xúc với hai đường thẳng

1



và









212

;;dI dI R    

Câu 1:

Viết phương trình đường tròn trong mỗi trường hợp sau:

a) Có tâm





1; 5I  và đi qua





0;0 .O

b) N hận

A

B làm đường kính với









1;1 , 7; 5AB

.

c) Đi qua ba điểm:



2; 4 , 5;5 , 6; 2MNP

Lời giải

a) Đường tròn cần tìm có bán kính là

22

15 26OI 

nên có phương trình là

 

22

1526xy 

b) Gọi I là trung điểm của đoạn

A

B suy ra





4;3I



22

41 31 13AI 

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11

Đường tròn cần tìm có đường kính là

AB

suy ra nó nhận





4;3I

làm tâm và bán kính

13RAI

nên có phương trình là



22

4313xy

c) Gọi phương trình đường tròn (C) có dạng là:

22

22 0 xy axbyc  .

Do đường tròn đi qua ba điểm

,,

M

NP

nên ta có hệ phương trình:

4164 8 0 2

25 25 10 10 0 1

36 4 12 4 0 20

abc a

abc b

abc c

  





   





   



Vậy phương trình đường tròn cần tìm là:

22

42200 xy xy

Nhận xét: Đối với ý c) ta có thể làm theo cách sau

Gọi





;

I

xy và R là tâm và bán kính đường tròn cần tìm

Vì

22

IM IN

IM IN IP

IM IP













nên ta có hệ



2222

2455

2

1

2462

xyxy

x

y

xyxy

























Câu 2: Viết phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm





1; 2I  và tiếp xúc với đường thẳng

:270xy 

b) (C) đi qua





2; 1A 

và tiếp xúc với hai trục toạ độ

Ox

và

Oy

c) (C) có tâm nằm trên đường thẳng

:6100dx y

và tiếp xúc với hai đường thẳng có

phương trình

1

:3 4 5 0dxy và

2

:4 3 5 0dxy

Lời giải

a) Bán kính đường tròn (C) chính là khoẳng cách từ I tới đường thẳng



nên



147

2

;

14 5

RdI

 

 



Vậy phương trình đường tròn (C) là:

 

22

4

12

5

xy 

b) Vì điểm A nằm ở góc phần tư thứ tư và đường tròn tiếp xúc với hai trục toạ độ nên tâm của

đường tròn có dạng





;

I

RR trong đó R là bán kính đường tròn (C).

Ta có:

 

22

22 2 2

1

21 650

5

R

RIA R R R R R

R













Vậy có hai đường tròn thoả mãn đầu bài là:



22

111xy

và



22

5525xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

c) Vì đường tròn cần tìm có tâm K nằm trên đường thẳng d nên gọi





610;

K

aa

Mặt khác đường tròn tiếp xúc với

12

,dd

nên khoảng cách từ tâm I đến hai đường thẳng này

bằng nhau và bằng bán kính R suy ra

3(6 10) 4 5 4(6 10) 3 5

55

aa aa 





0

22 35 21 35

70

43

a

aa

a







 









- Với

0a 

thì





10;0K

và

7R 

suy ra

 

2

:10 49Cx y

- Với

70

43

a





thì

10 70

;

43 43

K









và

7

43

R 

suy ra



222

10 70 7

:

43 43 43

Cx y









Vậy có hai đường tròn thỏa mãn có phương trình là

 

2

:10 49Cx y

và



222

10 70 7

:

43 43 43

Cx y









Câu 3: Cho hai điểm





8; 0A

và





0;6B

.

a) Viết phương trình đường tròn ngoại tiếp tam giác

OAB

b) Viết phương trình đường tròn nội tiếp tam giác

OAB

Lời giải

a) Ta có tam giác

OAB

vuông ở O nên tâm I của đường tròn ngoại tiếp tam giác là trung điểm

của cạnh huyền AB suy ra





4;3I và Bán kính



22

84 03 5RIA   

Vậy phương trình đường tròn ngoại tiếp tam giác OAB là:



22

4325xy

b) Ta có

22

8; 6; 8 6 10OA OB AB

Mặt khác

1

.

2

OA OB pr

(vì cùng bằng diện tích tam giác

A

BC )

Suy ra

.

2

OA OB

r

OA OB AB





Dễ thấy đường tròn cần tìm có tâm thuộc góc phần tư thứ nhất và tiếp xúc với hai trục tọa độ

nên

tâm của đường tròn có tọa độ là





2; 2

Vậy phương trình đường tròn nội tiếp tam giác

OAB

là:



22

224xy

Câu 4: Trong mặt phẳng tọa độ

Oxy

, cho hai đường thẳng

1

:3 0dxy

. và

2

:3 0dxy

. Gọi

(C) là đường tròn tiếp xúc với

1

d tại A, cắt

2

d tại hai điểm B, C sao cho tam giác

A

BC

vuông

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

tại B. Viết phương trình của (C), biết tam giác

A

BC có diện tích bằng

3

2

và điểm A có

hoành độ dương.

Lời giải

Vì

 

12

;3, 0;, ;3, ;3

A

dAa aa BCdBbbCcc   

Suy ra













;3 , ;3

A

Bb a a b ACc a c a 



Tam giác

A

BC vuông tại B do đó AC là đường kính của đường tròn C.

Do đó

1

AC d









1

. 0 1. 3. 3 0 2 0AC u c a a c a c     

 

(1)

2

AB d



2

.01. 3 02 0AB u b a a b b a     



(2)

Mặt khác

 

22

2

23

11 3

;. . 3

222 2

ABC

a

S dAd BC cb cb

21ac b(3)

Từ (1), (2) suy ra



23cb a

thế vào (3) ta được

3

31

3

aa a

Do đó

323

,

63

bc  

323

;1, ;2

33

AC

 



 

 

Suy ra (C) nhận

33

;

62

I









là trung điểm AC làm tâm và bán kính là 1

2

AC

R 

Vậy phương trình đường tròn cần tìm là



2

33

:1

62

Cx x









.

Câu 1:

Đường tròn tâm

(3; 1)I 

và bán kính 2

R

 có phương trình là

A.

22

(3)(1)4xy. B.

22

(3)(1)4xy.

C.

22

(3)(1)4xy

.

D.

22

(3)(1)4xy

.

Lời giải

Chọn C.

d

1

d

2

C

B

A

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

Phương trình đường tròn có tâm





3; 1I  , bán kính 2

R

 là:



22

314xy

Câu 2: Đường tròn tâm

(1;2)I 

và đi qua điểm

(2;1)M

có phương trình là

A.

22

2450xy xy

.

B.

22

2430.xy xy

C.

22

2450xy xy. D.

22

2450.xy xy

Lời giải

Chọn A.

Đường tròn có tâm





1; 2I  và đi qua





2;1M thì có bán kính là:



2

31 10RIM

Khi đó có phương trình là:

 

22

1210 2450xy xyxy 

Câu 3:

Cho hai điểm

(5; 1)A 

,

(3;7)B 

. Đường tròn có đường kính

AB

có phương trình là

A.

22

26220xy xy. B.

22

2 6 22 0.xy xy

C.

22

210xy xy

.

D.

22

6510.xy xy

Lời giải

Chọn A.

Tâm

I

của đường tròn là trung điểm

A

B

nên





1; 3I .

Bán kính



22

11

35 71 42

22

RAB

Vậy phương trình đường tròn là:

 

22

1 3 32 2 6 22 0xy xyxy 

Câu 4:

Đường tròn

()C

tâm

(4;3)I 

và tiếp xúc với trục tung có phương trình là

A.

22

3049xy xy. B.

22

(4)(3)16xy.

C.

22

(4)(3)16xy. D.

22

8 6 12 0.xy xy

Lời giải

Chọn B.





C

tiếp xúc với

'yOy

và có tâm





4; 3I 

nên:

4, 3, 4abRa   

.

Do đó,





C

có phương trình



22

4316xy

.

Câu 5: Đường tròn

()C

tâm

(4; 3)I

và tiếp xúc với đườngthẳng

:3 4 5 0xy

có phương trình là

A.

22

(4)(3)1xy. B.

22

(4)(3)1xy.

C.

22

(4)(3)1xy. D.

22

(4)(3)1xy

Lời giải

Chọn B.





C

có bán kính



2

3.4 4.3 5

,1

34

RdI



 



.

Do đó,





C

có phương trình

22

(4)(3)1xy.

Câu 6: Đường tròn





C

đi qua điểm





2; 4A

và tiếp xúc với các trục tọa độ có phương trình là

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15

A.

22

(2)(2)4xy hoặc

22

( 10) ( 10) 100xy

B.

22

(2)(2)4xy hoặc

22

( 10) ( 10) 100xy

C.

22

(2)(2)4xy

hoặc

22

( 10) ( 10) 100xy

D.

22

(2)(2)4xy hoặc

22

( 10) ( 10) 100xy

Lời giải

Chọn A.

   

22

2

:Cxa yb R

tiếp xúc với các trục tọa độ nên abR và điểm









2; 4

A

C

nằm trong góc phần tư thứ nhất nên





;

I

ab

cũng ở góc phần tư thứ nhất. Suy ra

abR

. Vậy

 

22

2

x

ayaaC

.



22

2 4 12 20 0AC a a a a a



22

224

2

10

10 10 100

xy

a

xy

























Câu 7: Đường tròn

()C

đi qua hai điểm

(1; 3)A

,

(3;1)B

và có tâm nằm trên đường thẳng

:2 7 0dxy

có phương trình là

A.

22

( 7) ( 7) 102xy . B.

22

( 7) ( 7) 164xy.

C.

22

(3)(5)25xy. C.

22

(3)(5)25xy.

Lời giải

Chọn B.





;

I

ab

là tâm của đường tròn





C

, do đó:



22 22

22

13 31AI BI a b a b

Hay:

(1)ab

. Mà



; : 2 7 0 nên 2 7 0 (2)Iab d x y a b   .

Thay (1) vào (2) ta có:

22

7 7 164abRAI     

.

Vậy

   

22

: 7 7 164Cx y

.

Câu 8: Đường tròn

()C

tiếp xúc với trục tung tại điểm

(0; 2)A 

và đi qua điểm

(4; 2)B 

có phương

trình là

A.

22

(2)(2)4xy. B.

22

(2)(2)4xy

C.

22

(3)(2)4xy D.

22

(3)(2)4xy 

Lời giải

Chọn A.

Vì 2 nên '

AB

yy AByOy  và

A

B là đường kính của



C

. Suy ra





2; 2I 

và bán kính

2

R

IA. Vậy

   

22

:2 24Cx y

.

Câu 9: Tâm của đường tròn qua ba điểm





2; 1A

,





2; 5B

,





2; 1C 

thuộc đường thẳng có phương trình

A.

30xy

. B.

30xy

C.

30xy  

D.

30xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

Lời giải

Chọn A.

Phương trình





C

có dạng:

22 22

22 0( 0)x y ax by c a b c   . Tâm





;

I

ab

.













2; 1

414 2 0 0

2; 5 4 25 4 10 0 3 0; 3

414 2 0 1

2; 1

AC

abc a

BC abcbI

abc c

CC



    









 

 

    







Lần lượt thế tọa độ

I vào các phương trình để kiểm tra.

Câu 10: Đường tròn đi qua 3 điểm









0; 2 , 2; 2 , 1; 2()1ABC có phương trình là

A.

22

22 20xy xy 

. B.

22

22 0xy xy .

C.

22

2220xy xy

.

D.

22

22 20xy xy 

.

Lời giải

Chọn B.

Gọi phương trình đường tròn cần tìm có dạng:



22 22

22 0 0x y ax by c a b c   

.

Đường tròn đi qua 3 điểm









0; 2 , 2; 2 , 1; 2()1ABC

nên ta có:



44 0 1

84 4 0 1

0

4222 21 2 0

bc a

abc b

c

abc



 







 









 





Vậy phương trình đường tròn đi qua 3 điểm









0; 2 , 2; 2 , 1; 2()1ABC là

22

22 0xy xy 

Câu 11: Đường tròn đi qua 3 điểm













11;8 , 13;8 , 14;7ABC có bán kính

R

bằng

A.

2

. B.

1

. C.

5

.

D. 2 .

Lời giải

Chọn C.

Gọi phương trình đường tròn cần tìm có dạng:



22 22

22 0 0x y ax by c a b c   

.

Đường tròn đi qua 3 điểm













11;8 , 13;8 , 14;7ABC

nên ta có:

121 64 22 16 0 12

169 64 26 16 0 6

196 49 28 14 0 175

abc a

abc b

abc c

   





   





   



Ta có

22

5Rabc

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17

Vậy phương trình đường tròn đi qua 3 điểm













11;8 , 13;8 , 14;7ABCcó bán kính là 5R 

DẠNG 3: VN TRÍ TƯƠNG ĐỐI CỦA ĐIỂM; ĐƯỜNG THẲNG; ĐƯỜNG TRÒN VỚI ĐƯỜNG TRÒN

1 Vị trí tương đối của điểm M và đường tròn (C)

Xác định tâm I và bán kính R của đường tròn (C) và tính

IM

+ N ếu

IM R suy ra M nằm trong đường tròn

+ N ếu

IM R

suy ra M thuộc đường tròn

+ N ếu

IM R suy ra M nằm ngoài đường tròn

2 Vị trí tương đối giữa đường thẳng



và đường tròn (C)

Xác định tâm I và bán kính R của đường tròn (C) và tính





;dI

+ N ếu





;dI R

suy ra  cắt đường tròn tại hai điểm phân biệt

+ N ếu



; dI R

suy ra  tiếp xúc với đường tròn

+ N ếu





;dI R

suy ra  không cắt đường tròn

Chú ý: Số nghiệm của hệ phương trình tạo bởi phương trình đường thẳng

 và đường tròn (C)

bằng số giao điểm của chúng. Tọa độ giao điểm là nghiệm của hệ.

3 Vị trí tương đối giữa đường tròn (C) và đường tròn (C')

Xác định tâm I, bán kính R của đường tròn (C) và tâm I', bán kính R' của đường tròn (C') và

tính

'II ,

', 'RRRR

+ N ếu

''II R R

suy ra hai đường tròn không cắt nhau và ở ngoài nhau

+ N ếu

' '

I

IRR suy ra hai đường tròn tiếp xúc ngoài với nhau

+ N ếu

' '

I

IRR suy ra hai đường tròn không cắt nhau và lồng vào nhau

+ N ếu

' '

I

IRR

suy ra hai đường tròn tiếp xúc trong với nhau

+ N ếu

'' 'RR II RR

suy ra hai đường tròn cắt nhau tại hai điểm phân biệt

Chú ý: Số nghiệm của hệ phương trình tạo bởi phương trình đường thẳng (C) và đường tròn

(C') bằng số giao điểm của chúng. Tọa độ giao điểm là nghiệm của hệ.

Câu 1:

Cho đường thẳng

:10xy

và đường tròn





22

:4240Cx y x y

a) Chứng minh điểm





2;1M

nằm trong đường tròn

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18

b) Xét vị trí tương đối giữa



và





C

c) Viết phương trình đường thẳng

' vuông góc với  và cắt đường tròn tại hai điểm phân biệt

sao cho khoảng cách của chúng là lớn nhất.

Lời giải

a) Đường tròn (C) có tâm





2; 1I  và bán kính

3R 

.

Ta có



22

22 11 23IM R

do đó M nằm trong đường tròn.

b) Vì



211

;223

11

dI R



   



nên



cắt





C tại hai điểm phân biệt.

c) Vì

'

vuông góc với



và cắt đường tròn tại hai điểm phân biệt sao cho khoảng cách của

chúng là lớn nhất nên

'

vuông góc với



và đi qua tâm I của đường tròn (C).

Do đó

' nhận vectơ



1; 1u







làm vectơ pháp tuyến suy ra









':1 2 1 1 0xy

hay

10xy

Vậy phương trình đường thẳng cần tìm là

': 1 0xy

Câu 2: Trong mặt phẳng

Oxy

, cho hai đường tròn





22

:26150Cx y x y

và



22

': 6 2 3 0Cxy x y

a) Chứng minh rằng hai đường tròn cắt nhau tại hai điểm phân biệt A, B

b) Viết phương trình đường thẳng đi qua A và B

c) Viết phương trình đường tròn đi qua ba điểm A, B và O

Lời giải

a) Cách 1:





C có tâm





1; 3I và bán kính

5R 

,





C có tâm





'3;1I và bán kính 13R 



22

'311322II 

Ta thấy

1212 12

RR II RR 

suy ra hai đường tròn cắt nhau.

Cách 2: Xét hệ phương trình

 

22 22

22

2

26150 26150

6230 30

2

60

3236150

3

xy xy xy xy

xy xy xy

y

yy

yyyy

y

xy

x

y



 





 











 



























Suy ra hai đường tròn cắt nhau tại hai điểm có tọa độ là





1; 2A 

và





6;3B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19

b) Đường thẳng đi qua hai điểm A, B nhận





5;5AB



làm vectơ chỉ phương suy ra phương trình

đường thẳng cần tìm là

15

25

x

t

yt







 



c) Cách 1: Đường tròn cần tìm (C") có dạng

22

22 0x y ax by c  

(C") đi qua ba điểm A, B và O nên ta có hệ

7

2

142 4 0

1

36 9 12 6 0

2

0

a

abc

abc b

c







  







   















Vậy (C"):

22

70xy xy

Cách 2: Vì A, B là giao điểm của hai đường tròn (C) và (C') nên tọa độ đều thỏa mãn phương

trình





22 22

2615 6230xy xy mxy xy 

(*)

Tọa độ điểm O thỏa mãn phương trình (*) khi và chỉ khi



15 . 3 0 5mm 

Khi đó phương trình (*) trở thành

22

70xy xy

Vậy phương trình đường tròn cần tìm là

22

70xy xy

Câu 3: Cho đường tròn

22

(): 2 4 4 0Cx y x y có tâm I và đường thẳng

:2 1 2 0xmy

a) Tìm

m

để đường thẳng  cắt đường tròn (C) tại hai điểm phân biệt A, B

b) Tìm m để diện tích tam giác

IAB là lớn nhất

Lời giải

a) Đường tròn (C) có tâm





1; 2I 

, bán kính

3R 



cắt (C) tại hai điểm phân biệt khi và chỉ khi



2

22 1 2

;3

2

m

dI R

m



  



A

I

B

H

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

2

55170mm

(đúng với mọi m)

b) Ta có

 

199

..sin sin

222

IAB

SIAIBAIB AIB

Suy

9

max

2

IAB

S 

khi và chỉ khi



0

sin 1 90AIB AIB 

Gọi H là hình chiếu của I lên

 khi đó



00

3

45 .cos45

2

AIH IH IA 

Ta có



2

12

3

;81604

2

m

dI IH m m m

m



        



Vậy với

4m  thỏa mãn yêu cầu bài toán.

Câu 1:

Cho đường tròn

22

():( 1) ( 3) 4Cx y  và đường thẳng

:3 4 5 0dx y

. Phương trình của

đường thẳng

d



song song với đường thẳng

d

và chắn trên

()C

một dây cung có độ dài lớn nhất

là

A.

43130xy

. B.

34250xy

. C.

34150xy

. D.

43200xy

.

Lời giải

Chọn C.





C có tâm





1; 3I  và

2. // :3 4 0Rdddxyc





.

Yêu cầu bài toán có nghĩa là

d



qua tâm





1; 3I 

của





C

, tức là :

312 0 1cc    

Vậy

:34150dx y





.

Câu 2: Tìm tọa độ giao điểm của đường thẳng

:230xy 

và đường tròn

22

(): 2 4 0Cx y x y 

A.





3; 3

và





1;1

. B.





1;1

và





3; 3

. C.





3; 3

và





1; 1

. D.





2;1

và





2; 1

.

Lời giải

Chọn A.

Tọa độ giao điểm là nghiệm của hệ phương trình sau

 

2

22

2

23

230

24 0

23 22340

xy

xy xy

yyyy















 

 





2

1

430

1

23

y

yy

x

xy

















hoặc

3

y

x











Vậy tọa độ giao điểm là





3; 3

và





1;1

.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

Câu 3: Cho đường tròn

22

(): 4 6 5 0Cx y x y. Đường thẳng

d

đi qua

(3; 2)A

và cắt

()C

theo

một dây cung ngắn nhất có phương trình là

A.

220xy

. B.

10xy

. C.

10xy

. D.

10xy

.

Lời giải

Chọn C.





22

;465.

(3;2) 9412125 6 0.

fxy x y x y

f



  

Vậy





3; 2A

ở trong





C

.

Dây cung

M

N

ngắn nhất

I

H

lớn nhất

H

A

M

N

có vectơ pháp tuyến là





1; 1IA 



. Vậy

d

có phương trình:

1( 3) 1( 2) 0 1 0xy xy 

.

Câu 4: Cho đường tròn

22

(): 6 2 5 0Cx y x y và đường thẳng d đi qua điểm

(4;2)A 

, cắt

()C

tại hai điểm

,

M

N

sao cho A là trung điểm của

M

N

. Phương trình của đường thẳng

d

là

A.

60xy

. B.

73340xy

. C.

73300xy

. D.

7350xy 

.

Lời giải

Chọn A.





C

có tâm





3; 1 , 5IR. Do đó,

2

I

ARA

ở trong





C

.

A

là trung điểm của



1; 1MN IA MN IA 



là vectơ pháp tuyến của

d

, nên

d

có

phương trình:

1( 4) 1( 2) 0 6 0xy xy 

.

Câu 5: Cho đường tròn

22

(): 4 6 3 0Cx y x y. Mệnh đề nào sau đây đúng?

(I) Điểm

(1;1)A

nằm ngoài

()C

.

(II) Điểm

(0;0)O

nằm trong

()C

.

(III)

()C

cắt trục tung tại hai điểm phân biệt.

A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Cả (I), (II) và (III).

Lời giải

Chọn D.

H

I

M

N

A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 22

Đặt





22

;463

f

xy x y x y



1;1 1 1 4 6 3 1 0

f

A

ở ngoài



C

.

 

0;0 3 0 0; 0fO  

ở trong



C

.

2

0630xyy  . Phương trình này có hai nghiệm, suy ra



C

cắt

'yOy

tại 2 điểm.

Câu 6: Cho đường tròn

22

(): 2 6 6 0Cx y x y

và đường thẳng

:4 3 5 0dx y

. Đường thẳng

d



song song với đường thẳng

d

và chắn trên

()C

một dây cung có độ dại bằng 23 có

phương trình là

A.

4380xy

. B.

4380xy

hoặc

4318xy

.

C.

4380xy

. D.

4380xy

.

Lời giải



C có tâm



1; 3 , 2IR

//dd d





có phương trình



43 0 5xym m .

Vẽ

22 2

3431IH MN HM IH R HM  .



8

4.1 3.( 3)

,1135

18.

16 9

m

dId IH m

m









 









Vậy:

:4 3 8 0

:4 3 18 0

dxy















.

Câu 7: Cho đường tròn

22

(): 6 2 5 0Cx y x y và đường thẳng

d

đi qua điểm

(4;2)A 

, cắt

()C

tại hai điểm

,

M

N

sao cho A là trung điểm của

M

N

. Phương trình của đường thẳng

d

là

A.

60xy

. B.

73340xy

. C.

73300xy

. D.

7350xy 

.

Lời giải

Chọn A.



C

có tâm





3; 1 , 5IR. Do đó,

2

I

ARA

ở trong



C

.

A là trung điểm của



1; 1MN IA MN IA 



là vectơ pháp tuyến của

d

, nên

d

có

phương trình:

1( 4) 1( 2) 0 6 0xy xy 

.

H

I

M

N

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 23

Câu 8: Đường tròn

22

22230xy xy cắt đường thẳng

20xy

theo một dây cung có độ

dài bằng bao nhiêu?

A.

10. B. 8. C. 6 . D. 32.

Lời giải

Chọn A.

Giải hệ PT

22

22230

20

xy xy

xy













2

24230

2

xx

yx













252 252

22

252 252

22

xx

hay

yy





















Độ dài dây cung

10AB  .

Câu 9: Tìm giao điểm 2 đường tròn





22

1

:40Cx y

và





22

2

:4440Cxy xy

A.





2; 2

và (





2; 2

. B.





0; 2 và





0; 2 .

C.





2;0 và





0; 2 . D.





2;0 và





2;0 .

Lời giải

Chọn C.

Giải hệ PT

22

40

4440

xy

xy xy

















22

40

44 4 40

xy













22

40

2

xy















2

240

2

xx

yx



 















2

240

2

xx

yx



 













02

20

xx

hay

yy











.

Vậy giao điểm



0; 2A ,





2;0B .

Câu 10: Xác định vị trí tương đối giữa 2 đường tròn





22

1

:4Cx y

và





22

2

: ( 10) ( 16) 1Cx y

.

A.

Cắt nhau. B. Không cắt nhau. C. Tiếp xúc ngoài. D. Tiếp xúc trong.

Lời giải

Chọn B.



1

C

có tâm và bán kính:





1

0;0I 

,

1

2R  ;





2

C

có tâm và bán kính:



2

10;16I 

,

2

1R  ;

khoảng cách giữa hai tâm

22

12 1 2

10 16 2 89II R R 

.

Vậy





1

C

và





2

C

không có điểm chung.

Câu 11:

Với những giá trị nào của

m

thì đường thẳng

:4 3 0xym

tiếp xúc với đường tròn





22

:90Cx y.

A.

3m 

. B.

3m 

và

3m 

.

C.

3m 

. D.

15m 

và

15m 

.

Lời giải

Chọn D.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 24

Đường tròn



C

có tâm và bán kính là





0;0I  ,

3R 

.



tiếp xúc





C 





,dI R 

3

5

m





15

m











Câu 12: Một đường tròn có tâm

(1; 3)I

tiếp xúc với đường thẳng

:3 4 0xy

. Hỏi bán kính đường

tròn bằng bao nhiêu?

A.

3

5

. B.

1

. C. 3. D. 15.

Lời giải

Chọn C.

22

3.1 3.4

(; ) 3

34

ycbt R d I



  



.

Câu 13: Đường tròn

222

()()

x

aybRcắt đường thẳng

0xyab

theo một dây cung có độ

dài bằng bao nhiêu?

A.

2

R

. B. 2R . C.

2

R

. D.

R

.

Lời giải

Chọn A.

Vì đường tròn có tâm

(;)Iab

, bán kính

R

và tâm

(;)Iab

thuộc đường thẳng

0xyab

.

N ên độ dài của dây cung bằng độ dài đường kính bằng

2

R

.

Câu 14:

Xác định vị trí tương đối giữa 2 đường tròn

22

1

(): 4 0Cx y x

và

22

2

(): 8 0Cxy y

.

A.

Tiếp xúc trong. B. Không cắt nhau. C. Cắt nhau. D. Tiếp xúc ngoài.

Lời giải

Chọn C.

Đường tròn

22

1

(): 4 0Cx y x

có tâm

1

(2;0)I , bán kính

1

2R  .

Đường tròn

22

2

(): 8 0Cxy y có tâm

2

(0; 4)I  , bán kính

2

4R  .

Ta có

2112 21

25RRII RR  

nên hai đường tròn cắt nhau.

Câu 15: Đường tròn

()C

có tâm

(1;3)I 

và tiếp xúc với đường thẳng

:3 4 5 0dx y

tại điểm H có

tọa độ là

A.

17

;

55









. B.

17

;

55







. C.

17

;

55









. D.

17

;

55









.

Lời giải

Chọn B.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 25

:4 3 0IH IH x y cd  

. Đường thẳng

IH

qua





1; 3I 

nên

4( 1) 3.3 0 5cc 

. Vậy

:4 3 5 0IH x y

.

Giải hệ:

1

4350

17

5

;

3450 7

55

5

x

xy

H

xy

y



































.

Câu 16: Xác định vị trí tương đối giữa 2 đường tròn





22

1

:4Cx y

và





22

2

:( 3) ( 4) 25Cx y

.

A.

Không cắt nhau. B. Cắt nhau. C. Tiếp xúc ngoài. D. Tiếp xúc trong.

Hướng dẫn giải

Chọn B.

Ta có: tâm









12

0;0 , 3;4II, bán kính

12

2, 5RR

nên

21 12 21

35 7RR II RR  

nên 2 đường tròn trên cắt nhau.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 26

DẠNG 4: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN VỚI ĐƯỜNG TRÒN

Cho đường tròn (C) tâm





;

I

ab

, bán kính R

1. N ếu biết tiếp điểm là





00

;

M

xy

thì tiếp tuyến đó đi qua M và nhận vectơ





00

;IM x a y b



làm vectơ pháp tuyến nên có phương trình là

















000 0

0xaxx ybyy

2. N ếu không biết tiếp điểm thì dùng điều kiện: Đường thẳng



tiếp xúc đường tròn (C) khi và

chỉ khi





;dI R

để xác định tiếp tuyến.

Câu 1:

Cho đường tròn (C) có phương trình

22

6260xy xy

và điểm hai điểm









1; 1 ; 1; 3AB

a) Chứng minh rằng điểm A thuộc đường tròn, điểm B nằm ngoài đường tròn

b) Viết phương trình tiếp tuyến của (C) tại điểm A

c) Viết phương trình tiếp tuyến của (C) kẻ từ

B.

Lời giải

Đường tròn (C) có tâm





3; 1I  bán kính

2

3162R .

a) Ta có:

2; 25IA R IB R   suy ra điểm A thuộc đường tròn và điểm B nằm ngoài

đường tròn

b) Tiếp tuyến của (C) tại điểm A nhận





2;0IA 



làm vectơ pháp tuyến nên có phương trình là









21010xy 

hay

1

x



b) Phương trình đường thẳng

 đi qua B có dạng:

 

130ax by  

(với

22

0ab

) hay

30ax by a b

Đường thẳng



là tiếp tuyến của đường tròn





;dI R



2

22 2

22

0

33

22 340

34

b

aba b

ab ab b ab

ba

ab

















+ N ếu

0b 

, chọn

1a 

suy ra phương trình tiếp tuyến là

1

x



.

+ N ếu

34ba

, chọn

3, 4ab

suy ra phương trình tiếp tuyến là

34150xy

Vậy qua A kẻ được hai tiếp tuyến với (C) có phương trình là

1

x



và

34150xy

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 27

Câu 2: Viết phương trình tiếp tuyến



của đường tròn





22

:4410Cx y x y

trong trường

a) Đường thẳng

 vuông góc với đường thẳng

':2 3 4 0xy

b) Đường thẳng



hợp với trục hoành một góc

0

45

Lời giải

a) Đường tròn (C) có tâm





2; 2I 

, bán kính

3R 

Vì

'

nên



nhận





3; 2u 



làm VTPT do đó phương trình có dạng

32 0xyc 

Đường thẳng

 là tiếp tuyến với đường tròn (C) khi và chỉ khi



10

;3 3 10313

13

c

dI c



     

Vậy có hai tiếp tuyến là

:3 2 10 313 0xy    

b) Giả sử phương trình đường thẳng

22

:0,0ax by c a b 

Đường thẳng

 là tiếp tuyến với đường tròn (C) khi và chỉ khi

 



2

22

;3 322 9 (*)

abc

dI a b c a b

ab



       



Đường thẳng



hợp với trục hoành một góc

0

45

suy ra



0

22 22

cos ; cos 45

bb

Ox a b

ab ab

   



hoặc

ab

TH1: N ếu

ab

thay vào (*) ta có

22

18 3 2ac c a

, chọn

132ab c

suy ra

:320xy 

TH2: N ếu

ab

thay vào (*) ta có









2

32 4

18 4

32 4

ca

aac

ca











 





Với





32 4ca, chọn



1, 1, 3 2 4 : 3 2 4 0ab c xy  

Với





32 4ca  , chọn





1, 1, 32 4 : 32 4 0ab c xy  

Vậy có bốn đường thẳng thỏa mãn là

1,2 3

:320,:3240xy xy và

4

:3240xy 

Câu 3: Lập phương trình tiếp tuyến chung của hai đường tròn sau:



22

1

:450Cxy y

và



22

2

:68160Cxy xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 28

Lời giải

Đường tròn





1

C có tâm





1

0; 2I bán kính

1

3R 

Đường tròn





2

C có tâm





2

3; 4I  bán kính

2

3R 

Gọi tiếp tuyến chung của hai đường tròn có phương trình

:0ax by c

với

22

0ab



là tiếp tuyến chung của





1

C và





2

C

1

2

(,) 3

dI















22

23 *

34 3

bc a b

abc ab



 







 





Suy ra

2

234

32

2

ab

bc a bc

ab

c







  









TH1: N ếu

2ab

chọn

2, 1ab

thay vào (*) ta được

235c  

nên ta có 2 tiếp tuyến là

22350xy 

TH2: N ếu

32

2

ab

c





thay vào (*) ta được

22

22ba a b  

0a 

hoặc

340ab

+ Với

0acb

, chọn

1bc

ta được

:10y

+ Với

340 3ab cb

, chọn

4, 3, 9ab c

ta được

:4 3 9 0xy

Vậy có 4 tiếp tuyến chung của hai đường tròn là:

22350,10,4390xy y x y    

Câu 1:

Cho đường tròn

22

():( 3) ( 1) 10Cx y. Phương trình tiếp tuyến của

()C

tại điểm

(4;4)A

là

A.

350xy

. B.

340xy

. C.

3160xy

. D.

3160xy

.

Lời giải

Chọn D.





C

có tâm









3; 1 1; 3IIA



là vectơ pháp tuyến của tiếp tuyến

.

D

Suy ra









:1 4 3 4 0 3 16 0Dx y xy  

.

Câu 2:

Cho đường tròn

22

():( 2) ( 2) 9Cx y. Phương trình tiếp tuyến của

()C

đi qua điểm

(5;1)A 

là

A.

40xy

và

20xy

. B.

5x 

và

1y 

.

C.

230xy

và

3220xy

. D.

3220xy

và

2350xy

.

Lời giải

Chọn B.





C

có tâm





2; 2I

và bán kính

3R 

.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 29





;nAB



là vectơ pháp tuyến nên









:5 10DAx By .

D

là tiếp tuyến của





C khi và chỉ khi :











22

25 21

,3.0

AB

dI R AB

AB

 

    



0 chon 0 1

0 chon 0 5

ABy

BAx













.

Câu 3:

Cho đường tròn

22

(): 2 6 5 0Cx y x y. Phương trình tiếp tuyến của

()C

song song với

đường thẳng

:2150Dx y

là

A.

20xy

và

2100xy

. B.

20xy

và

2100xy

.

C.

210xy

và

230xy

. D.

210xy

và

230xy

.

Lời giải

Chọn A.





C

có tâm





1; 3I 

và bán kính

195 5, : 2 0Rdxym 

.

d

là tiếp tuyến của





C khi và chỉ khi:



16

,555

14

m

dId R m

 

   



55 0 :20

5 5 10 : 2 10 0

mmdxy

   







     



.

Câu 4:

Cho đường tròn

22

(): 6 2 5 0Cx y x y và đường thẳng

:2 ( 2) 7 0dxm ym 

.

Với giá trị nào của

m

thì

d

là tiếp tuyến của

()C

?

A.

3m 

. B.

15m 

. C.

13m 

. D.

3m 

hoặc

13m 

.

Lời giải

Chọn D.





C

có tâm





3; 1I 

và bán kính 5R  .

d

là tiếp tuyến của





C

khi va chỉ khi:



2

3

627

,516390.

13

4( 2)

m

mm

dId R m m

m







     









Câu 5: Cho đường tròn



22

:28239Cx y x y

và điểm





8; 3M 

. Độ dài đoạn tiếp tuyến của





C

xuất phát từ

M

là:

A.

10

. B. 210. C.

10

2

. D. 10 .

Lời giải

Chọn D.

Đường tròn



22

:28239Cx y x y

có tâm





1; 4I 

bán kính 40R  .

Độ dài tiếp tuyến là

22

10IM R

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 30

Câu 6: N ếu đường tròn

   

22

2

:1 3Cx y R 

tiếp xúc với đường thẳng

:5 12 60 0dx y

thì

giá trị của

R

là:

A.

22R  . B.

19

13

R 

. C.

5R 

.

D. 2R  .

Lời giải

Chọn B.

Đường tròn

   

22

2

:1 3Cx y R 

có tâm





1; 3I bán kính

R

.

Đường thẳng

:5 12 60 0dx y

tiếp xúc với đường tròn





C khi



33

5.1 12.3 60

19

,

13

512

ddId



 



Câu 7: Cho đường tròn

   

22

:3 15Cx y

. Phương trình tiếp tuyến của





C

song song với

đường thẳng

:2 7 0dxy

là

A.

20;2100xy xy  

. B.

210;210xy xy 

.

C.

2100;2100xy xy   

. D.

20;2100xy x y   

.

Lời giải

Chọn A.

Phương trình tiếp tuyến có dạng

:2 0xym

với

7m 

.

Đường tròn

   

22

:3 15Cx y

có tâm





3; 1I 

và bán kính 5R 

Đường thẳng



tiếp xúc với đường tròn





C

khi



0

2.3 1

;5

10

5

m

dI R

m







   







Vậy

12

:2 0; :2 10 0xy xy

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 340

BÀI 21. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ

DẠNG 1. NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Câu 1: Tìm tất cả các giá trị của tham số

m

để phương trình





22

2241960xy m xmy m    

là phương trình đường tròn.

A.

12.m

B. 2m  hoặc 1m  .

C.

2m 

hoặc

1m 

. D.

1m 

hoặc

2m 

.

Câu 2: Trong mặt phẳng

Oxy

, phương trình nào sau đây là phương trình của đường tròn?

A.

22

24810xyxy. B.

22

4 6 12 0xy xy.

C.

22

28200xy xy. D.

22

410620xy xy .

Câu 3: Phương trình nào sau đây là phương trình của đường tròn?

A.

22

26680xy xy. B.

22

248120xyxy .

C.

22

28180xy xy. D.

22

2246120xyxy.

Câu 4: Phương trình nào sau đây là phương trình của một đường tròn?

A.

22

42830xy xyxy+- ++-=

. B.

22

24510xyxy+-+-=

.

C.

22

14 2 2018 0xy xy+- + + =

. D.

22

4520xy xy+-++=

.

Câu 5:

Cho phương trình





22

2426 0(1)xy mx m y m   

. Điều kiện của

m

để

(1)

là phương

trình của đường tròn.

A.

2m 

. B.

1

2

m











.

C.

12m

. D.

1

2

m











.

DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN KÍNH ĐƯỜNG TRÒN

Câu 6:

Trong mặt phẳng

Oxy

, đường tròn



22

:46120Cx y x y

có tâm là.

A.



2; 3I 

. B.



2;3I

. C.





4;6I

. D.





4; 6I 

.

Câu 7: Đường tròn

22

10 24 0xy y 

có bán kính bằng bao nhiêu?

A.

49

. B.

7

. C. 1. D. 29 .

Câu 8: Xác định tâm và bán kính của đường tròn

   

22

:1 29.Cx y 

A. Tâm





1; 2 ,I 

bán kính

3R 

. B. Tâm





1; 2 ,I 

bán kính

9R 

.

C.

Tâm



1; 2 ,I 

bán kính

3R 

. D. Tâm



1; 2 ,I 

bán kính

9R 

.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

HỆ THỐNG BÀI TẬP. TRẮC NGHIỆM

III

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 341

Câu 9: Tìm tọa độ tâm

I

và bán kính

R

của đường tròn



C

:

22

2410xy xy.

A.





1; 2 ; 4IR. B.





1; 2 ; 2IR. C.





1; 2 ; 5IR

.

D.





1; 2 ; 4IR.

Câu 10: Trong mặt phẳng

Ox

y

, cho đường tròn

   

22

:2 39Cx y

. Đường tròn có tâm và bán

kính là

A.





2;3 , 9IR

. B.





2; 3 , 3IR

. C.





3; 2 , 3IR

. D.





2;3 , 3IR

.

Câu 11: Tìm tọa độ tâm

I

và tính bán kính

R

của đường tròn



22

(): 2 5 9Cx y

.

A.

(2;5), 81.IR

. B.

(2; 5), 9.IR

. C.

(2; 5), 3.IR

. D.

(2;5), 3.IR

Câu 12: Đường tròn





22

:2430Cx y x y

có tâm

I

, bán kính

R

là

A.





1; 2 , 2IR

.

B.





1; 2 , 2 2IR

.

C.





1; 2 , 2IR

.

D.





1; 2 , 2 2IR

.

DẠNG 3. VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Dạng 3.1 Khi biết tâm và bán kính

Câu 13:

Phương trình đường tròn có tâm



1; 2I

và bán kính

5R 

là

A.

22

24200xy xy. B.

22

24200xy xy.

C.

22

24200xy xy. D.

22

24200xy xy.

Câu 14: Đường tròn tâm





1; 2I 

, bán kính

3R 

có phương trình là

A.

22

2440xy xy

. B.

22

2440xy xy

.

C.

22

2440xy xy

. D.

22

2440xy xy

.

Câu 15: Phương trình nào sau đây là phương trình của đường tròn tâm





1; 2I 

, bán kính bằng

3

?

A.

 

22

129xy 

. B.

 

22

129xy 

.

C.

 

22

129xy 

. D.

 

22

129xy 

.

Dạng 3.2 Khi biết các điểm đi qua

Câu 16:

Đường tròn



C đi qua hai điểm



1; 1A ,



5; 3B và có tâm

I

thuộc trục hoành có phương

trình là

A.



2

410xy

. B.



2

410xy

. C.



2

410xy

. D.



2

410xy

.

Câu 17: Trong mặt phẳng với hệ tọa độ

Ox

y

, tìm tọa độ tâm

I

của đường tròn đi qua ba điểm





0; 4A

,





2; 4B

,





2;0C

.

A.





1; 1I

. B.





0;0I

. C.



1; 2I

. D.



1; 0I

.

Câu 18: Cho tam giác

A

BC

có

 

1; 1 , 3; 2 , 5; 5ABC

. Toạ độ tâm đường tròn ngoại tiếp tam giác

A

BC

là

A.

47 13

;

10 10









. B.

47 13

;

10 10







. C.

47 13

;

10 10









. D.

47 13

;

10 10









.

Câu 19: Trong mặt phẳng

Oxy

, đường tròn đi qua ba điểm





1; 2A

,





5; 2B

,



1; 3C 

có phương trình

là.

A.

22

25 19 49 0xy x y  . B.

22

2630xy xy.

C.

22

610xy xy

.

D.

22

610xy xxy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 342

Câu 20: Lập phương trình đường tròn đi qua hai điểm



3; 0 , 0; 2AB

và có tâm thuộc đường thẳng

:0dx y

.

A.

22

1113

222

xy









. B.

22

1113

222

xy









.

C.

22

1113

222

xy









. D.

22

1113

222

xy









.

Câu 21: Cho tam giác

A

BC

biết





3; 2H

,

58

;

33

G







lần lượt là trực tâm và trọng tâm của tam giác,

đường thẳng

B

C

có phương trình

220xy

. Tìm phương trình đường tròn ngoại tiếp tam

giác

A

BC

?

A.



22

1120xy

. B.



22

2420xy

.

C.

 

22

131xy 

. D.

 

22

1325xy 

.

Câu 22: Trong mặt phẳng tọa độ

Ox

y

, cho tam giác

A

BC có trực tâm

H

, trọng tâm





1; 3G  . Gọi

,,

K

MN

lần lượt là trung điểm của

,,

A

HABAC

. Tìm phương trình đường tròn ngoại tiếp tam

giác

A

BC biết đường tròn ngoại tiếp tam giác

K

MN là





22

:44170Cx y x y.

A.

 

22

1 5 100xy 

. B.

 

22

1 5 100xy 

.

C.

 

22

1 5 100xy 

. D.

 

22

1 5 100xy 

.

Câu 23: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

A

BC

có trực tâm

O

. Gọi

M

là trung điểm của

B

C

;

N

,

P

lần lượt là chân đường cao kẻ từ

B

và

C

. Đường tròn đi qua ba điểm

M

,

N

,

P

có phương trình là

 

2

125

:1

24

Tx y



 





. Phương trình đường tròn ngoại tiếp tam giác

A

BC

là:

A.

 

22

1225xy 

. B.



2

125xy 

.

C.



2

150xy 

. D.



22

2125xy

.

Dạng 3.3 Sử dụng điều kiện tiếp xúc

Câu 24:

Trong mặt phẳng tọa độ

Ox

y

, phương trình của đường tròn có tâm là gốc tọa độ

O

và tiếp xúc

với đường thẳng

 :

20xy

là

A.

22

2xy+=

. B.

22

2xy+=

.

C.

(

)

(

)

22

112xy-+-=

. D.

(

)

(

)

22

112xy-+-=

.

Câu 25: Trong mặt phẳng tọa độ





Oxy

, cho đường tròn



S

có tâm I nằm trên đường thẳng

yx

,

bán kính

3R 

và tiếp xúc với các trục tọa độ. Lập phương trình của



S

, biết hoành độ tâm I

là số dương.

A.



22

339xy

. B.



22

339xy

.

C.



22

339xy

. D.



22

339xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 343

Câu 26: Một đường tròn có tâm





3;4I

tiếp xúc với đường thẳng :3 4 10 0xy. Hỏi bán kính

đường tròn bằng bao nhiêu?

A.

5

3

. B.

5

. C.

3

. D.

3

5

.

Câu 27: Trong hệ trục tọa độ

Oxy

, cho điểm





1; 1I

và đường thẳng



:3 4 2 0dxy

. Đường tròn

tâm

I và tiếp xúc với đường thẳng



d

có phương trình

A.



22

115xy

. B.



22

1125xy

.

C.



22

111xy

. D.



22

1

11

5

xy

.

Câu 28: Trên hệ trục tọa độ

Oxy

, cho đường tròn

()C

có tâm





3; 2I 

và một tiếp tuyến của nó có

phương trình là

3490xy

. Viết phương trình của đường tròn

()C

.

A.









22

322xy

. B.









22

322xy 

.

C.









22

324xy 

D.









22

324xy

.

Câu 29: Trên mặt phẳng toạ độ

Ox

y

, cho các điểm





3;0A và





0;4B . Đường tròn nội tiếp tam giác

OAB có phương trình

A.

22

1xy. B.

22

440xy x.

C.

22

2xy. D.



22

111xy

.

Câu 30: Cho hai điểm



3; 0A

,



0;4B

. Đường tròn nội tiếp tam giác

OAB

có phương trình là

A.

22

1xy. B.

22

2210xy xy.

C.

22

68250xy xy. D.

22

2xy.

DẠNG 4. TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

Dạng 4.1. Phương trình tiếp tuyến

Câu 31:

Đường tròn

22

10xy

tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?

A.

3450xy

B.

0xy

C.

3410xy

D.

10xy

Câu 32: Đường tròn nào sau đây tiếp xúc với trục Ox:

A.

22

10 0xy x . B.

22

50xy.

C.

22

10 2 1 0xy xy . D.

22

6590xy xy.

Câu 33: Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn





22

:2430Cx y x y

. Viết

phương trình tiếp tuyến

d

của đường tròn

()C

biết tiếp tuyến đó song song với đường thẳng

:3 4 1 0xy

.

A. 3452110xy ; 3452110xy .

B.

3452110xy 

,

3452110xy 

.

C.

3452110xy 

,

3452110xy 

.

D.

3452110xy 

,

3452110xy 

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 344

Câu 34: Cho đường tròn





22

:2440Cx y x y

và điểm





1; 5A

. Đường thẳng nào trong các

đường thẳng dưới đây là tiếp tuyến của đường tròn





C

tại điểm

A

.

A.

50y 

. B.

50y 

. C.

50xy

. D.

50xy

.

Câu 35: Cho đường tròn





22

:40Cx y

và điểm





1; 2A 

. Đường thẳng nào trong các đường

thẳng dưới đây đi qua

A

và là tiếp tuyến của đường tròn



C

?

A. 43100xy. B. 640xy. C. 34100xy. D. 34110xy.

Câu 36:

Trong mặt phẳng

Ox

y

, cho đường tròn

   

22

:1 44Cx y 

. Phương trình tiếp tuyến với

đường tròn





C song song với đường thẳng

:4 3 2 0xy

là

A.

43180xy

. B.

43180xy

.

C.

43180;4320xy xy 

. D.

43180;4320xy xy 

.

Câu 37: Số tiếp tuyến chung của 2 đường tròn





22

:2410Cx y x y

và





22

': 6 8 20 0Cxy x y

là

A. 1. B. 2 . C. 4 . D.

3

.

Câu 38: Viết phương trình tiếp tuyến của đường tròn

22

():( 2) ( 4) 25Cx y, biết tiếp tuyến vuông

góc với đường thẳng

:3 4 5 0dx y

.

A.

43290xy

. B.

43290xy

hoặc

43210xy

.

C.

4350xy

hoặc

43450xy

D.

4350xy

hoặc

4330xy

.

Câu 39: Trong mặt phẳng tọa độ Oxy, cho đường tròn



C

có phương trình

22

2230xy x y. Từ

điểm



1;1A

kẻ được bao nhiêu tiếp tuyến đến đường tròn





C

A.

1. B. 2. C. vô số. D. 0.

Câu 40: Trong mặt phẳng

Ox

y

, cho đường tròn

   

22

:1 44Cx y 

. Phương trình tiếp tuyến với

đường tròn



C

, biết tiếp tuyến đó song song với đường thẳng

:4 3 2 0xy

là

A.

43180xy

và

4320xy 

. B.

43180xy

và

4320xy

.

C.

43180xy 

và

4320xy

. D.

43180xy 

và

4320xy 

.

Câu 41: Trên mặt phẳng toạ độ

Ox

y

, cho điểm





3; 2P 

và đường tròn

   

22

:3 436Cx y

.

Từ điểm

P kẻ các tiếp tuyến PM và

P

N

tới đường tròn





C

, với

M

,

N

là các tiếp điểm.

Phương trình đường thẳng

M

N

là

A.

10xy

. B.

10xy

. C.

10xy

. D.

10xy

.

Câu 42: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho điểm

(3;1)M 

và đường tròn





22

:2660Cx y x y

. Gọi

1

T ,

2

T là các tiếp điểm của các tiếp tuyến kẻ từ

M

đến. Tính

khoảng cách từ

O

đến đường thẳng

12

.TT

A. 5. B.

5

.

C.

3

5

. D. 22.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 345

Dạng 4.2 Bài toán tương giao

Câu 43:

Trong mặt phẳng với hệ trục tọa độ

Ox

y

, cho hai đường tròn









12

,CC có phương trình lần

lượt là

22 22

(1)( 2)9 và (2)( 2) 4xy x y    

. Khẳng định nào dưới đây là sai?

A. Đường tròn





1

C có tâm





1

1; 2I  và bán kính

1

3R 

.

B.

Đường tròn





2

C có tâm





2

2; 2I và bán kính

2

2R 

.

C. Hai đường tròn









12

,CC

không có điểm chung.

D. Hai đường tròn









12

,CC

tiếp xúc với nhau.

Câu 44: Tìm giao điểm 2 đường tròn

22

1

():x 40Cy

và

22

2

():x 4 4 40.Cyxy

A.





2; 2

và





2; 2

. B.





0; 2

và





0; 2

. C.



2;0

và





2;0

. D.





2;0

và





0; 2 .

Câu 45:

Trong mặt phẳng với hệ trục

Oxy

, cho hai đường tròn

 

2

:1 4Cx y

và



22

:4 316Cx y





cắt nhau tại hai điểm phân biệt

A

và

B

. Lập phương trình đường

thẳng

A

B

A.

20xy

. B.

2. 0xy 

C.

20xy

. D.

20xy

.

Câu 46: Cho đường thẳng

:3 4 19 0xy

và đường tròn

   

22

:1 125Cx y

. Biết đường

thẳng



cắt





C tại hai điểm phân biệt

A

và

B

, khi đó độ dài đọan thẳng

A

B

là

A. 6. B. 3. C. 4. D. 8.

Câu 47: Trong mặt phẳng tọa độ Oxy cho đường tròn





C

có tâm





1; 1I 

bán kính

5R 

. Biết rằng

đường thẳng



:3 4 8 0dxy

cắt đường tròn





C

tại hai điểm phân biệt

,AB

. Tính độ dài

đoạn thẳng

AB

.

A.

8AB 

. B.

4AB 

. C.

3.AB 

. D.

6AB 

.

Câu 48: Trong mặt phẳng với hệ trục tọa độ ,Oxy cho đường tròn





C

có phương trình



22

224xy

và đường thẳng

:3 4 7 0dx y

. Gọi

,

A

B

là các giao điểm của

đường thẳng

d với đường tròn





C . Tính độ dài dây cung

A

B

.

A.

3AB  . B. 25AB  . C. 23AB  . D. 4

A

B  .

Câu 49: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho điểm





3;1A

, đường tròn





22

:2430Cx y x y

. Viết phương trình tổng quát của đường thẳng

d

đi qua

A

và cắt

đường tròn





C

tại hai điểm

B

,

C

sao cho

22BC 

.

A.

:250dx y

. B.

:250dx y

. C.

:250dx y

. D.

:250dx y

.

Câu 50: Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai đường tròn









12

,CC

có phương trình lần

lượt là

22 22

(1)( 2)9 và (2)( 2) 4xy x y    

. Viết phương trình đường thẳng

d

¢

đi

qua gốc tọa độ và tạo với đường thẳng nối tâm của hai đường tròn một góc bằng

45.

A.

:70dx y





hoặc

:7 0dxy





. B.

:70dx y





hoặc

:7 0dxy





.

C.

:70dx y





hoặc

:7 0dxy





. D.

:70dx y





hoặc

:7 0dxy





.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 346

Câu 51:

Trong mặt phẳng tọa độ Oxy

cho điểm





1; 2I

và đường thẳng





:2 5 0.dxy

Biết rằng

có hai điểm

12

,

M

thuộc



d

sao cho

12

10.IM IM

Tổng các hoành độ của

1

M

và

2

M

là

A.

7

.

5

B.

14

.

5

C.

2.

D.

5.

Câu 52: Trong hệ tọa độ

Ox ,y

cho đường tròn





C

có phương trình:

22

42150.

x

yxy I là tâm





C

, đường thẳng

d

đi qua





1; 3M 

cắt





C

tại

,.

A

B

Biết tam giác IAB có diện tích là

8.

Phương trình đường thẳng

d

là:

0.xbyc

Tính

bc

A.

8.

B.

2.

C.

6.

D.

1.

Câu 53: Trong mặt phẳng

Oxy

cho tam giác

A

BC

có đỉnh





5;5A

, trực tâm





1; 13H 

, đường tròn

ngoài tiếp tam giác có phương trình

22

50xy. Biết tọa độ đỉnh





;Cab

, với

0a 

. Tổng

ab bằng

A. 8 . B. 8 . C. 6 . D. 6 .

Câu 54: Trong mặt phẳng

Ox

y

, cho

A

BC nội tiếp đường tròn tâm



2; 2I , điểm

D

là chân đường

phân giác ngoài của góc



B

AC . Đường thẳng

A

D cắt đường tròn ngoại tiếp

A

BC

tại điểm

thứ hai là

M. Biết điểm





2; 2J 

là tâm đường tròn ngoại tiếp

A

CD

và phương trình đường

thẳng

CM là:

20.xy

Tìm tổng hoành độ của các đỉnh

, ,

A

BC

của tam giác

A

BC .

A.

9

5

. B.

12

5

. C.

3

5

. D.

6

5

.

Câu 55: Trong mặt phẳng tọa độ

Ox

y

, cho hai đường thẳng

(

)

:380xyD++=

;

()

:3 4 10 0xy

¢

D-+=

và điểm

()

2;1A -

. Đường tròn có tâm

()

;Iab

thuộc đường thẳng

()

D

,đi qua

A

và tiếp xúc với đường thẳng

()

¢

D

. Tính

ab+

.

A.

4-

. B.

4

. C.

2

. D.

2

.

Câu 56: Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường thẳng

:3 4 1 0dx y

và điểm



1; 2I  . Gọi





C là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có

diện tích bằng 4. Phương trình đường tròn





C

là

A.

 

22

128xy 

. B.

 

22

1220xy 

.

C.

 

22

125xy 

. D.

 

22

1216xy 

.

DẠNG 5. CÂU HỎI MIN-MAX

Câu 57:

Cho đường tròn





22

:2440Cx y x y và điểm





2;1M . Dây cung của





C đi qua

điểm

M có độ dài ngắn nhất là

A.

6

. B.

7

. C.

37

. D. 27.

Câu 58: Trong mặt phẳng tọa độ Oxy, cho hai điểm

(0; 3), (4;1)AB

và điểm M thay đổi thuộc đường

tròn

22

(): ( 1) 4Cx y 

. Gọi

min

P

là giá trị nhỏ nhất của biểu thức

2PMA MB

. Khi đó ta

có

min

P

thuộc khoảng nào dưới đây?

A.





7,7;8,1 .

. B.



7,3;7,7 .

. C.





8,3;8,5 .

. D.





8,1;8, 3 .

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 347

Câu 59: Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường tròn





22

:2430Cx y x y

. Tìm tọa độ

điểm



00

;

M

xy

nằm trên đường tròn



C

sao cho

00

Tx y

đạt giá trị lớn nhất.

A.





2;3M

. B.





0;1M

. C.





2;1M

. D.





0;3M

.

Câu 60: Trong mặt phẳng

Ox

y

, cho điểm

M

nằm trên đường tròn





22

: 86160Cx y x y

. Tính

độ dài nhỏ nhất của

OM

?

A.

3

. B.

1

. C.

5

. D.

2

.

Câu 61:

Gọi I

là tâm của đường tròn





C

:



22

114xy

. Số các giá trị nguyên của

m

để đường

thẳng

0xym 

cắt đường tròn





C

tại hai điểm phân biệt

,

A

B

sao cho tam giác IAB có

diện tích lớn nhất là

A.

1

. B.

3

. C.

2

. D.

0

.

Câu 62: Điểm nằm trên đường tròn





22

:2410Cx y x y

có khoảng cách ngắn nhất đến đường

thẳng

:30dx y

có toạ độ



;

M

ab

. Khẳng định nào sau đây đúng?

A.

2ab

. B.

ab

. C.

2ab

. D.

ab

.

Câu 63: Cho tam giác

A

BC

có trung điểm của

BC

là





3; 2M

, trọng tâm và tâm đường tròn ngoại tiếp

tam giác lần lượt là



22

;,1;2

33

GI









. Tìm tọa độ đỉnh

C

, biết

C

có hoành độ lớn hơn 2 .

A.





9;1C . B.



5;1C . C.



4; 2C . D.



3; 2C  .

Câu 64: Trong mặt phẳng tọa độ

Oxy

, cho đường tròn



22

:24250Cx y x y

và điểm





2;1M

. Dây cung của



C

đi qua

M

có độ dài ngắn nhất là:

A.

27. B.

16 2

. C.

82

. D. 47.

Câu 65: Cho các số thực

,,,abcd

thay đổi, luôn thỏa mãn

 

22

121ab 

và

43d230c 

.

Giá trị nhỏ nhất của biểu thức



22

P

ac bd 

là:

A.

min

28P  . B.

min

3P 

. C.

min

4P 

. D.

min

16P 

.

Câu 66: Trong mặt phẳng tọa độ

,Ox

y

cho đường tròn

   

22

:1 24 Cx y

và các đường thẳng

1

:10, dmxym

2

:10.dxmym Tìm các giá trị của tham số m để mỗi đường

thẳng

12

,dd cắt





C

tại 2 điểm phân biệt sao cho 4 điểm đó lập thành 1 tứ giác có diện tích lớn

nhất. Khi đó tổng của tất cả các giá trị tham số

m là:

A. 0. B. 1. C. 3. D. 2.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 21. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ

DẠNG 1. NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Câu 1: Tìm tất cả các giá trị của tham số

m để phương trình





22

2241960xy m xmy m    

là phương trình đường tròn.

A.

12.m

B.

2m 

hoặc

1m 

.

C.

2m 

hoặc

1m 

. D.

1m 

hoặc

2m 

.

Lời giải

Chọn D

Ta có









22

2241960 1xy m xmy m    

2; 2 ; 19 6.am b mc m   

Phương trình



1

là phương trình đường tròn

22

0abc

2

515100 1mm m

hoặc

2m 

.

Câu 2: Trong mặt phẳng

Oxy

, phương trình nào sau đây là phương trình của đường tròn?

A.

22

24810xyxy. B.

22

4 6 12 0xy xy.

C.

22

28200xy xy. D.

22

410620xy xy .

Lời giải

Chọn B

Để là phương trình đường tròn thì điều kiện cần là hệ số của

2

x

và

2

y

phải bằng nhau nên loại

được đáp án A và

D.

Ta có:

 

22

28200 1 4 30xy xy x y 

vô lý.

Ta có:



22

46120 2 3 25xy xy x y  

là phương trình đường tròn tâm



2; 3I 

, bán kính

5R 

.

Câu 3: Phương trình nào sau đây là phương trình của đường tròn?

A.

22

26680xy xy. B.

22

248120xyxy .

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

HỆ THỐNG BÀI TẬP. TRẮC NGHIỆM

III

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

C.

22

2 8 18 0xy xy. D.

22

2246120xyxy.

Lời giải

Chọn D

Biết rằng

22

22 0x y ax by c   là phương trình của một đường tròn khi và chỉ khi

22

0abc

.

Ta thấy phương trình trong phương án

A và

B

có hệ số của

2

x

,

2

y không bằng nhau nên đây

không phải là phương trình đường tròn.

Với phương án

C có

22

11618 0abc

nên đây không phải là phương trình đường

tròn. Vậy ta chọn đáp án

D

.

Câu 4: Phương trình nào sau đây là phương trình của một đường tròn?

A.

22

42830xy xyxy+- ++-=

. B.

22

24510xyxy+-+-=

.

C.

22

14 2 2018 0xy xy+- + + =

. D.

22

4520xy xy+-++=

.

Lời giải

Chọn D

Phương án A: có tích

x

y

nên không phải là phương trình đường tròn.

Phương án B: có hệ số bậc hai không bằng nhau nên không phải là phương trình đường tròn.

Phương án C: ta có

()()

22

14 2 2018 0 7 1 1968 0xy xy x y+- ++ =- +++ =

không tồn

tại

,

x

y

nên cũng không phải phương trình đường tròn.

Còn lại, Chọn D

Câu 5:

Cho phương trình





22

2426 0(1)xy mx m y m   

. Điều kiện của

m

để

(1)

là phương

trình của đường tròn.

A.

2m 

. B.

1

2

m











.

C.

12m

. D.

1

2

m











.

Lời giải

Chọn B





22

2426 0(1)xy mx m y m   

là phương trình của đường tròn khi và chỉ khi

    

2

1

22 6 0515100

2

m

mm m mm

m





       











.

DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN KÍNH ĐƯỜNG TRÒN

Câu 6:

Trong mặt phẳng

Oxy

, đường tròn



22

:46120Cx y x y

có tâm là.

A.





2; 3I 

. B.



2;3I

. C.





4;6I

. D.





4; 6I 

.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

Ta có phương trình đường tròn là:



22

2325xy

.

Vậy tâm đường tròn là:



2; 3I 

.

Câu 7: Đường tròn

22

10 24 0xy y 

có bán kính bằng bao nhiêu?

A.

49

. B.

7

. C. 1. D. 29 .

Lời giải

Chọn B

Đường tròn

22

10 24 0xy y 

có tâm





0;5I

, bán kính



22

05 24 7R 

.

Câu 8: Xác định tâm và bán kính của đường tròn

   

22

:1 29.Cx y 

A. Tâm



1; 2 ,I  bán kính 3R  . B. Tâm



1; 2 ,I  bán kính 9R  .

C. Tâm



1; 2 ,I  bán kính 3R  . D. Tâm



1; 2 ,I  bán kính 9R  .

Lời giải

Chọn A

Câu 9: Tìm tọa độ tâm

I

và bán kính

R

của đường tròn



C :

22

2410xy xy.

A.





1; 2 ; 4IR

. B.





1; 2 ; 2IR

. C.





1; 2 ; 5IR. D.





1; 2 ; 4IR

.

Lời giải

Chọn B



C

có tâm





1; 2I 

, bán kính



2

1212R 

.

Câu 10: Trong mặt phẳng

Oxy

, cho đường tròn

   

22

:2 39Cx y

. Đường tròn có tâm và bán

kính là

A.





2;3 , 9IR

. B.





2; 3 , 3IR

. C.





3; 2 , 3IR

. D.





2;3 , 3IR

.

Lời giải

Chọn B

Đường tròn



C

có tâm



2; 3I 

và bán kính

3R 

.

Câu 11: Tìm tọa độ tâm

I

và tính bán kính

R

của đường tròn



22

(): 2 5 9Cx y

.

A.

(2;5), 81.IR

. B.

(2; 5), 9.IR

. C.

(2; 5), 3.IR

. D.

(2;5), 3.IR

Lời giải

Chọn D

Theo bài ra ta có tọa độ tâm

(2;5)I 

và bán kính

3R 

.

Câu 12: Đường tròn





22

:2430Cx y x y

có tâm

I

, bán kính

R

là

A.





1; 2 , 2IR

.

B.





1; 2 , 2 2IR

.

C.





1; 2 , 2IR

.

D.





1; 2 , 2 2IR

.

Lời giải

Chọn D

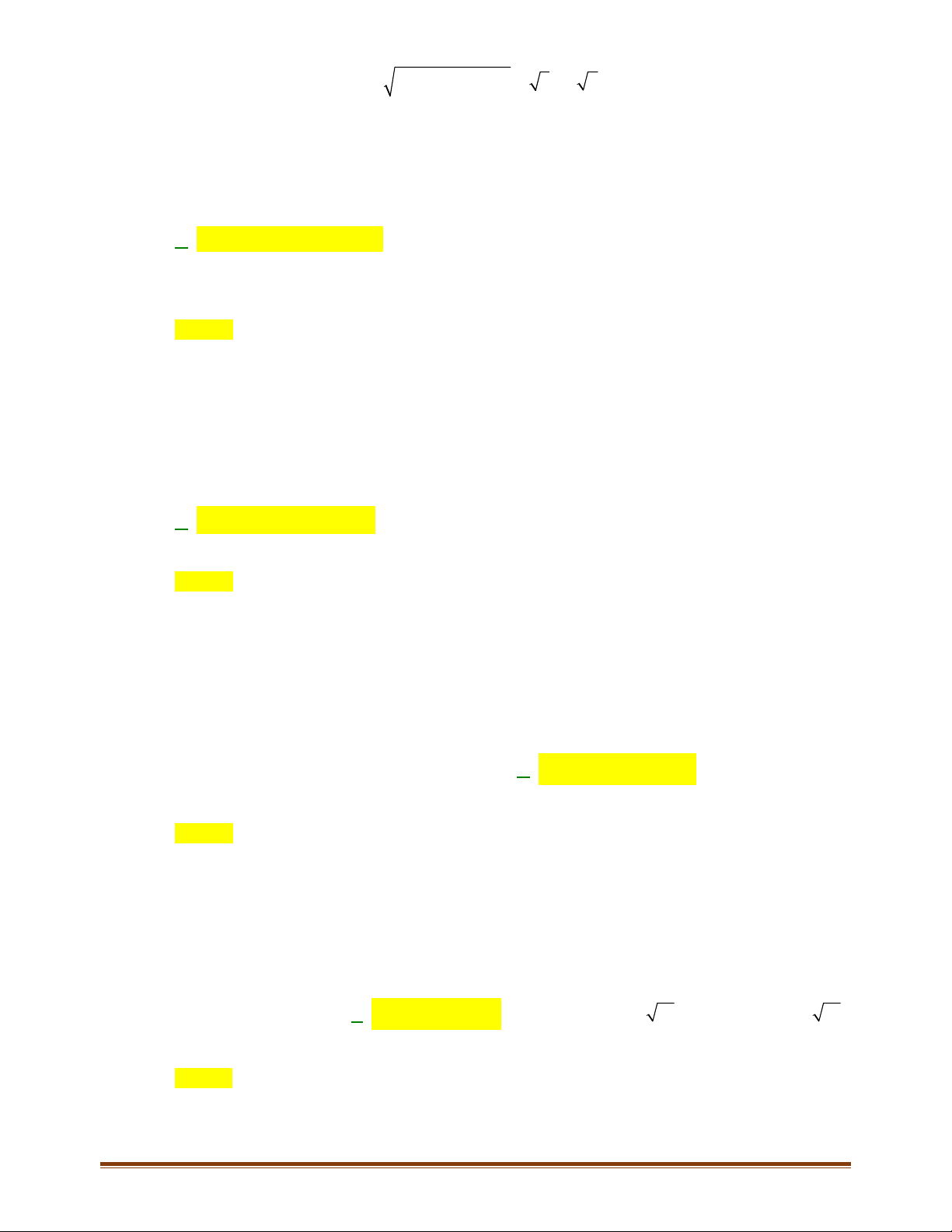
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

Tâm



1; 2I 

, bán kính



2

12 3822R 

.

DẠNG 3. VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Dạng 3.1 Khi biết tâm và bán kính

Câu 13:

Phương trình đường tròn có tâm



1; 2I

và bán kính

5R 

là

A.

22

24200xy xy. B.

22

24200xy xy.

C.

22

24200xy xy. D.

22

24200xy xy.

Lời giải

Chọn A

Phương trình đường tròn có tâm



1; 2I

và bán kính

5R 

là

 

22

2

125xy 

22

21 4 425xx yy

22

24200xy xy.

Câu 14: Đường tròn tâm





1; 2I  , bán kính

3R 

có phương trình là

A.

22

2440xy xy

. B.

22

2440xy xy

.

C.

22

2440xy xy

. D.

22

2440xy xy

.

Lời giải

Chọn C

Đường tròn tâm





1; 2I 

, bán kính

3R 

có phương trình là

 

22

129 2440xy xyxy 

.

Câu 15: Phương trình nào sau đây là phương trình của đường tròn tâm





1; 2I 

, bán kính bằng

3

?

A.

 

22

129xy 

. B.

 

22

129xy 

.

C.

 

22

129xy 

. D.

 

22

129xy 

.

Lời giải

Chọn D

Phương trình đường tròn tâm





1; 2I 

và bán kính

3R 

là:

 

22

129xy 

.

Dạng 3.2 Khi biết các điểm đi qua

Câu 16:

Đường tròn



C

đi qua hai điểm



1; 1A

,



5; 3B

và có tâm I thuộc trục hoành có phương

trình là

A.



2

410xy

. B.



2

410xy

. C.



2

410xy

. D.



2

410xy

.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

Gọi





;0

I

xOx ;

22

IA IB

  

22

115 3xx  

22

211 10259xx x x 

4x

. Vậy tâm đường tròn là





4;0I và bán kính



2

14 1 10RIA  

.

Phương trình đường tròn





C

có dạng



2

410xy

.

Câu 17: Trong mặt phẳng với hệ tọa độ

Ox

y

, tìm tọa độ tâm

I

của đường tròn đi qua ba điểm





0; 4A

,





2; 4B

,





2;0C

.

A.





1; 1I

. B.





0;0I

. C.



1; 2I

. D.



1; 0I

.

Lời giải

Chọn C

Giả sử phương trình đường tròn đi qua 3 điểm ,,

A

BC có dạng





22

:220Cx y ax byc  

Thay tọa độ 3 điểm





0; 4A

,





2; 4B

,





2;0C

ta được:



22

816 1

48 20 2 : 24 0

44 0

bc a

abc b Cxy x y

ac c

 





   





 



.

Vậy





C có tâm



1; 2I và bán kính

5R 

.

Câu 18: Cho tam giác

A

BC có

 

1; 1 , 3; 2 , 5; 5ABC. Toạ độ tâm đường tròn ngoại tiếp tam giác

A

BC là

A.

47 13

;

10 10









. B.

47 13

;

10 10







. C.

47 13

;

10 10









. D.

47 13

;

10 10









.

Lời giải

Chọn A

Gọi





;

I

xy

là tâm đường tròn ngoại tiếp tam giác

A

BC

.

Ta có:

 

22 2 2

22

22 2 2 2 2

47

113 2

4611

10

8 8 48 13

115 5

10

x

xyx y

AI BI x y

xy

AI CI

xyx y

y

















 



  























.

47 13

;

10 10

I











.

Câu 19: Trong mặt phẳng

Oxy

, đường tròn đi qua ba điểm





1; 2A

,





5; 2B

,



1; 3C 

có phương trình

là.

A.

22

25 19 49 0xy x y  . B.

22

2630xy xy.

C.

22

610xy xy. D.

22

610xy xxy.

Lời giải

Chọn C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

Phương trình đường tròn có dạng

22

22 0x y ax by c  . Đường tròn này qua

,,

A

BC

nên

3

142 4 0

1

25 4 10 4 0

2

192 6 0

1

a

abc

abc b

abc

c





  







   





  









.

Vậy phương trình đường tròn cần tìm là

22

610xy xy.

Câu 20: Lập phương trình đường tròn đi qua hai điểm



3; 0 , 0; 2AB

và có tâm thuộc đường thẳng

:0dx y

.

A.

22

1113

222

xy









. B.

22

1113

222

xy









.

C.

22

1113

222

xy









. D.

22

1113

222

xy









.

Lời giải

Chọn A





3; 0A ,



0; 2B ,

:0dx y

.

Gọi

I

là tâm đường tròn vậy





;

I

xx vì

Id

.

22

IA IB

 

22

32

x

xx x 

6944xx   

1

2

x

. Vậy

11

;

22

I









.

22

11 26

3

22 2

IA



 





là bán kính đường tròn.

Phương trình đường tròn cần lập là:

22

1113

222

xy









.

Câu 21: Cho tam giác

A

BC

biết





3; 2H ,

58

;

33

G







lần lượt là trực tâm và trọng tâm của tam giác,

đường thẳng

B

C

có phương trình

220xy

. Tìm phương trình đường tròn ngoại tiếp tam

giác

A

BC

?

A.



22

1120xy

. B.



22

2420xy

.

C.

 

22

131xy 

. D.

 

22

1325xy 

.

Lời giải

Chọn D

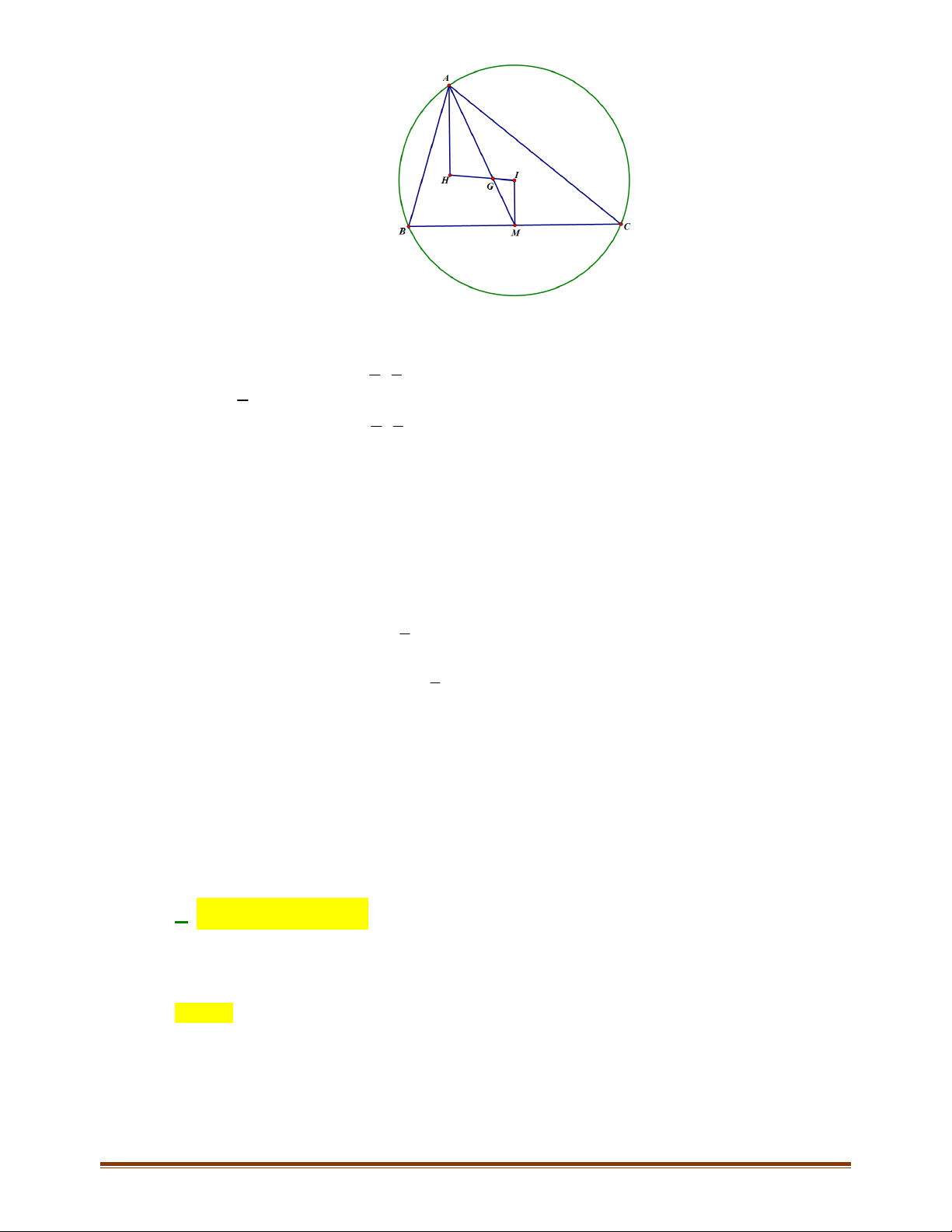
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7

*) Gọi

I

là tâm đường tròn ngoại tiếp tam giác

A

BC

.

3

2

H

IHG

 

35

33

23

38

22

23

I

x

y





 















 









1

3

I

x

y













.

*) Gọi

M

là trung điểm của

B

C

IM BC

:2 1 0IM x y

.

M

IM BC

21

22

xy













0

1

x

y

















0;1M

.

Lại có:

3

M

AMG

 

5

3.

3

8

13. 1

3

A

x

y















 









5

6

A

x

y













.

Suy ra: bán kính đường tròn ngoại tiếp tam giác

A

BC

là

5RIA

.

Vậy phương trình đường tròn ngoại tiếp tam giác

A

BC

là

 

22

1325xy 

.

Câu 22: Trong mặt phẳng tọa độ

Ox

y

, cho tam giác

A

BC

có trực tâm H , trọng tâm





1; 3G 

. Gọi

,,

K

MN

lần lượt là trung điểm của

,,

A

HABAC

. Tìm phương trình đường tròn ngoại tiếp tam

giác

A

BC

biết đường tròn ngoại tiếp tam giác

K

MN

là





22

:44170Cx y x y

.

A.

 

22

15100xy 

. B.

 

22

1 5 100xy 

.

C.

 

22

1 5 100xy 

. D.

 

22

15100xy 

.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

Gọi

E

là trung điểm

BC

,

J

là tâm đường tròn ngoại tiếp

ABC

.

Ta có

MK BH

ME AC

BH AC















MK ME



1

,

KN CH

NE AB

CH AB

















2KN NE

Từ

 

1,2

KMEN

là tứ giác nội tiếp đường tròn đường kính

KE

.

Đường tròn



22

:44170Cx y x y

có tâm



2; 2I 

bán kính

5r  I

là trung điểm

KE

.

KHEJ

là hình bình hành

I

là trung điểm

JH

Ta có:

3IJ IG





2312

2332

J

x

y



 







 





1

5

J

x

y















1; 5J

.

Bán kính đường tròn ngoại tiếp

ABC

là

2210RJA IK r 

.

Phương trình đường tròn ngoại tiếp

ABC

là:

 

22

15100xy 

.

Câu 23: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có trực tâm

O

. Gọi

M

là trung điểm của

BC

;

N

,

P

lần lượt là chân đường cao kẻ từ

B

và

C

. Đường tròn đi qua ba điểm

M

,

N

,

P

có phương trình là

 

2

125

:1

24

Tx y



 





. Phương trình đường tròn ngoại tiếp tam giác

ABC

là:

A.

 

22

1225xy 

. B.



2

125xy 

.

C.



2

150xy 

. D.



22

2125xy

.

Lời giải

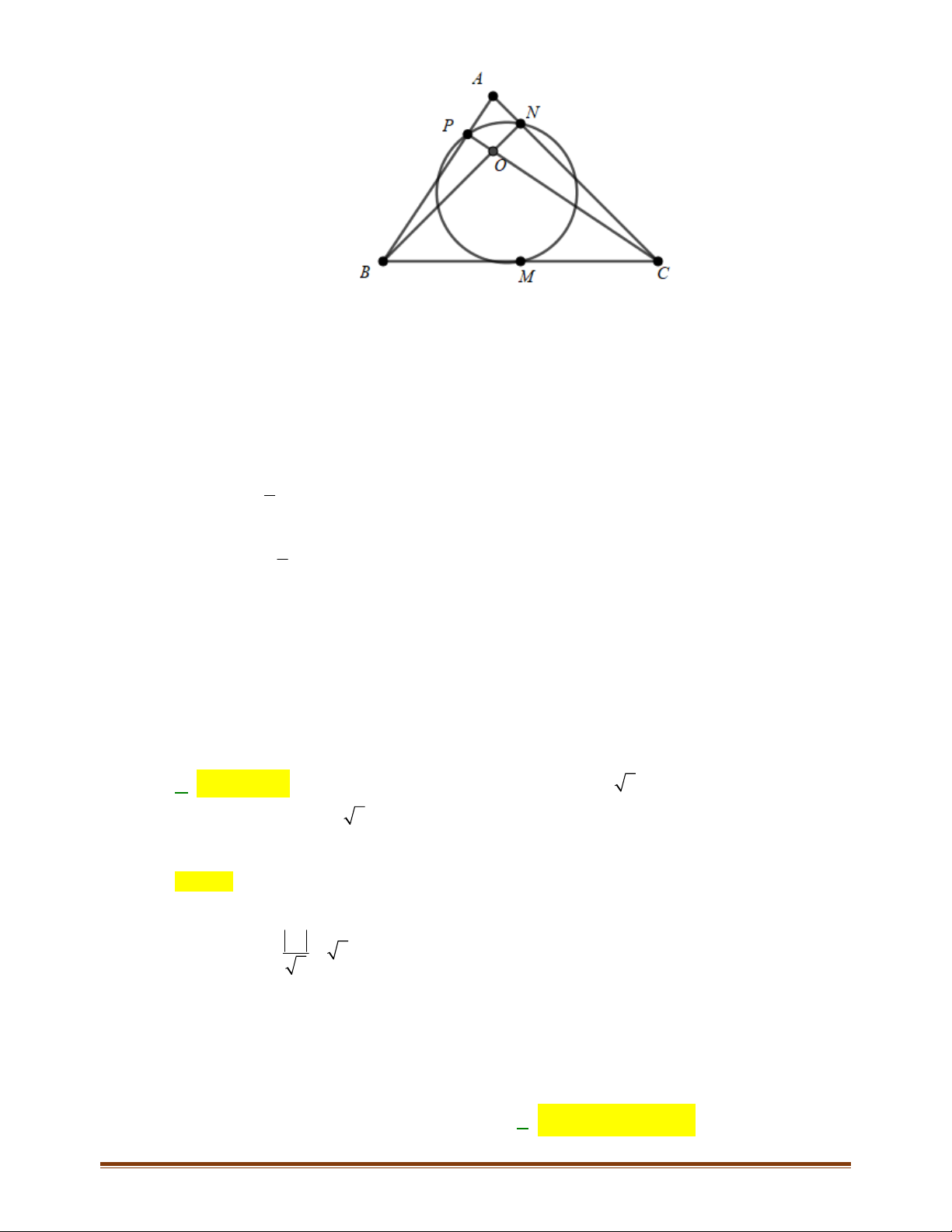
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9

Ta có

M

là trung điểm của

B

C

;

N

,

P

lần lượt là chân đường cao kẻ từ

B

và

C

. Đường tròn

đi qua ba điểm

M

,

N

,

P

là đường tròn Euler. Do đó đường tròn ngoại tiếp tam giác

A

BC

chính là ảnh của đường tròn Euler qua phép vị tự tâm là

O

, tỷ số

2k 

.

Gọi

I

và

I



lần lượt là tâm đường tròn ngoại tiếp tam giác

M

NP

và tam giác

A

BC

.

Gọi

R

và

R



lần lượt là bán kính đường tròn ngoại tiếp tam giác

M

NP

và tam giác

A

BC

.

Ta có

1

1;

2

I









và do đó





22;1OI OI I



 

 

.

Mặt khác

5

2

RR



 

.

Vậy phương trình đường tròn ngoại tiếp tam giác

A

BC

là:



22

2125xy

.

Nhận xét: Đề bài này rất khó đối với học sinh nếu không biết đến đường tròn Euler.

Dạng 3.3 Sử dụng điều kiện tiếp xúc

Câu 24:

Trong mặt phẳng tọa độ

Ox

y

, phương trình của đường tròn có tâm là gốc tọa độ

O

và tiếp xúc

với đường thẳng

 :

20xy

là

A.

22

2xy+=

. B.

22

2xy+=

.

C.

(

)

(

)

22

112xy-+-=

. D.

(

)

(

)

22

112xy-+-=

.

Lời giải

Chọn A

Đường tròn





C

có tâm

O

, bán kính

R

tiếp xúc với  nên có:



2

;2

2

RdO





.

Phương trình đường tròn





C

:

22

2xy+=.

Câu 25: Trong mặt phẳng tọa độ





Oxy

, cho đường tròn



S

có tâm I nằm trên đường thẳng

y

x

,

bán kính

3R 

và tiếp xúc với các trục tọa độ. Lập phương trình của



S

, biết hoành độ tâm

I

là số dương.

A.



22

339xy

. B.



22

339xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

C.



22

339xy

. D.



22

339xy

.

Lời giải

Chọn B

Do tâm

I

nằm trên đường thẳng





;yxIaa   , điều kiện 0a  .

Đường tròn





S có bán kính 3R  và tiếp xúc với các trục tọa độ nên:





















;;333 33;3dIOx dIOy a a n a l I.

Vậy phương trình

   

22

:3 39Sx y

.

Câu 26: Một đường tròn có tâm





3;4I

tiếp xúc với đường thẳng

:3 4 10 0xy

. Hỏi bán kính

đường tròn bằng bao nhiêu?

A.

5

3

. B.

5

. C.

3

. D.

3

5

.

Lời giải

Chọn C

Đường tròn tâm





3;4I

tiếp xúc với đường thẳng

:3 4 10 0xy

nên bán kính đường tròn

chính là khoảng cách từ tâm





3;4I

tới đường thẳng

:3 4 10 0xy

.

Ta có:



32

3.3 4.4 10

15

,3

5

34

RdI



 



.

Câu 27: Trong hệ trục tọa độ

Oxy

, cho điểm





1; 1I

và đường thẳng



:3 4 2 0dxy

. Đường tròn

tâm

I và tiếp xúc với đường thẳng



d

có phương trình

A.



22

115xy

. B.



22

1125xy

.

C.



22

111xy

. D.



22

1

11

5

xy

.

Lời giải

Chọn C

Đường tròn tâm I và tiếp xúc với đường thẳng



d

có bán kính



22

3.1 4.1 2

,1

34

RdId



 



Vậy đường tròn có phương trình là:



22

111xy

.

Câu 28: Trên hệ trục tọa độ

Oxy

, cho đường tròn

()C

có tâm





3; 2I 

và một tiếp tuyến của nó có

phương trình là

3490xy

. Viết phương trình của đường tròn

()C

.

A.









22

322xy

. B.









22

322xy 

.

C.









22

324xy 

D.









22

324xy

.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11

Chọn D

Vì đường tròn

()C

có tâm



3; 2I 

và một tiếp tuyến của nó là đường thẳng



có phương

trình là

3490xy

nên bán kính của đường tròn là

22

3.( 3) 4.2 9

(, ) 2

34

RdI

 

 



Vậy phương trình đường tròn là:



22

324xy

Câu 29: Trên mặt phẳng toạ độ

Oxy

, cho các điểm



3;0A

và



0;4B

. Đường tròn nội tiếp tam giác

OAB

có phương trình

A.

22

1xy. B.

22

440xy x.

C.

22

2xy. D.



22

111xy

.

Lời giải

Chọn D

Vì các điểm



3; 0A

và



0;4B

nằm trong góc phần tư thứ nhất nên tam giác

OAB

cũng nằm

trong góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là



,Iab

thì

0, 0ab

.

Theo đề ra ta có:

 

;;;d I Ox d I Oy d I AB

.

Phương trình theo đoạn chắn của AB là:

1

34

xy



hay

43120xy

.

Do vậy ta có:



0

6

7125

43125

1712 5

ab

al

aa

ab a

aaa



 















 

















.

Vậy phương trình đường tròn cần tìm là:



22

111xy

.

Câu 30: Cho hai điểm



3; 0A

,



0;4B

. Đường tròn nội tiếp tam giác

OAB

có phương trình là

A.

22

1xy

. B.

22

2210xy x y

.

C.

22

68250xy xy. D.

22

2xy.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

Ta có

3, 4, 5.OA OB AB

Gọi

(; )

I

Ix y

là tâm đường tròn nội tiếp tam giác OAB .

Từ hệ thức

...0AB IO OB IA OA IB

    

ta được

...4.3

1

543

(1;1)

.y .y .y 3.4

1

543

OAB

I

OAB

I

AB x OB x OA x

x

AB OB OA

I

AB OB OA

y

AB OB OA









 













 



Mặt khác tam giác

OAB

vuông tại O với r là bán kính đường tròn nội tiếp tam giác thì

1

.

3.4

2

1

345

2

OA OB

S

r

OA OB AB

p

  



(

,Sp

lần lượt là diện tích và nửa chu vi tam giác).

Vậy phương trình đường tròn nội tiếp tam giác

OAB

là

22

(1)(1)1xy

hay

22

2210.xy xy

DẠNG 4. TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

Dạng 4.1. Phương trình tiếp tuyến

Câu 31:

Đường tròn

22

10xy

tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?

A.

3450xy

B.

0xy

C.

3410xy

D.

10xy

Lời giải

Chọn A

22

10xy

có tâm





0;0 , 1OR .

Điều kiện để đường thẳng tiếp xúc với đường tròn là khoảng cách từ tâm tới đường thẳng bằng

bán kính.

Xét đáp án A:



22

|3.0 4.0 5|

:3 4 5 0 , 1

34

xy dO R



  



tiếp xúc với đường tròn.

Câu 32: Đường tròn nào sau đây tiếp xúc với trục Ox:

A.

22

10 0xy x . B.

22

50xy.

C.

22

10 2 1 0xy xy . D.

22

6590xy xy.

Lời giải

Chọn D

Đường tròn





C

tiếp xúc với trục Ox khi



,OxdI R

với I và

R

lần lượt là tâm và bán kính

của đường tròn





C

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

Đường tròn:

22

10 0xy x 

22

(5) 25xy  

có tâm



5; 0I

, bán kính

5R 

,



I,Ox 0d 

. Suy ra:



,OxdI R

. Vậy





C

không tiếp xúc với trục Ox.

không phải là phương trình đường tròn.

.Xét phương trình đường tròn:

22

50xy có





0;0I và

5R 

,



I,Ox 0d  .

Suy ra:



,OxdI R . Vậy





C không tiếp xúc với trục Ox.

Xét phương trình đường tròn:

22

10 2 1 0xy xy 

có





5;1I và 5R  ,





I,Ox 1d  .

Suy ra:



,OxdI R . Vậy





C không tiếp xúc với trục Ox.

Xét phương trình đường tròn:

22

6590xy xy có

5

3;

2

I









và

5

2

R 

,



5

I,Ox

2

d 

. Suy ra:



,OxdI R

. Vậy





C

tiếp xúc với trục Ox

Câu 33: Trong mặt phẳng với hệ tọa độ

Oxy

, cho đường tròn





22

:2430Cx y x y

. Viết

phương trình tiếp tuyến

d

của đường tròn

()C

biết tiếp tuyến đó song song với đường thẳng

:3 4 1 0xy

.

A.

3452110xy 

;

3452110xy 

.

B. 3452110xy , 3452110xy .

C.

3452110xy 

,

3452110xy 

.

D.

3452110xy 

,

3452110xy 

.

Lời giải

Chọn B





22

:2430Cx y x y

 

22

122.xy 

Do đó đường tròn có tâm





1; 2I 

và bán kính

2R 

.

Do

d

song song với đường thẳng



nên

d

có phương trình là 34 0xyk,





1k 

.

Ta có



22

11 52 52 11

11

;21152

34

11 52 52 11

kk

k

dId R k

kk



  



     





  





.

Vậy có hai phương trình tiếp tuyến cần tìm là

3452110xy 

,

3452110xy 

.

Câu 34:

Cho đường tròn





22

:2440Cx y x y

và điểm





1; 5A

. Đường thẳng nào trong các

đường thẳng dưới đây là tiếp tuyến của đường tròn





C

tại điểm

A

.

A.

50y 

. B.

50y 

. C.

50xy

. D.

50xy

.

Lời giải

Chọn A

Đường tròn



C

có tâm





1; 2I





0;3IA



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

Gọi d là tiếp tuyến của



C tại điểm

A

, khi đó d đi qua

A

và nhận vectơ

IA



là một VTPT.

Chọn một VTPT của

d

là





0;1

d

n 



.

Vậy phương trình đường thẳng

d

là

50y 

.

Câu 35: Cho đường tròn





22

:40Cx y

và điểm





1; 2A 

. Đường thẳng nào trong các đường

thẳng dưới đây đi qua

A

và là tiếp tuyến của đường tròn



C

?

A.

43100xy

. B.

640xy

. C.

34100xy

. D.

34110xy

.

Lời giải

Chọn A

Đường tròn





C

có tâm là gốc tọa độ



0;0O

và có bán kính

2

R



.

Họ đường thẳng



qua













1; 2 : 1 2 0Aaxby

, với

22

0ab

.

Điều kiện tiếp xúc





;dO R hay

22

2

ab









2

22

24ab ab  

2

0

34 0

34

a

aab

ab













.

Với

0a 

, chọn

1b 

ta có

1

:20y.

Với

34ab

, chọn

4a 

và

3b 

ta có









2

:4 1 3 2 0 4 3 10 0xy xy

.

Nhận xét: Thực ra bài này khi thay tọa độ điểm





1; 2A 

vào các đường thẳng ở các phương

án thì ta loại

C.

và

D.

Tính khoảng cách từ tâm của đường tròn đến đường thẳng thì chỉ có

phương án

A.

thỏa.

Câu 36: Trong mặt phẳng

Oxy

, cho đường tròn

   

22

:1 44Cx y 

. Phương trình tiếp tuyến với

đường tròn





C

song song với đường thẳng

:4 3 2 0xy

là

A.

43180xy

. B.

43180xy

.

C. 43180;4320xy xy . D.

43180;4320xy xy 

.

Lời giải

Chọn C

Đường tròn

   

22

:1 44Cx y 

có tâm





1; 4I

và bán kính 2

R

 .

Gọi

d là tiếp tuyến của



C .

Vì

//d 

nên đường thẳng



:4 3 0 2dx ym m 

.

d

là tiếp tuyến của





C



2

4.1 3.4

;2

43

m

dI d R



 



CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15

18

810

2

m













Vậy có 2 tiếp tuyến cần tìm :

43180;4320xy xy 

.

Câu 37: Số tiếp tuyến chung của 2 đường tròn





22

:2410Cx y x y và





22

': 6 8 20 0Cxy x y là

A.

1

. B.

2

. C.

4

. D. 3.

Lời giải

Chọn C

Đường tròn





22

:2410Cx y x y có tâm





1; 2I  bán kính 2

R

 .

Đường tròn





22

': 6 8 20 0Cxy x y

có tâm



'3;4I 

bán kính '5R  .

'213II  .

Vậy

''II R R nên 2 đường tròn không có điểm chung suy ra 2 đường tròn có 4 tiếp tuyến

chung.

Câu 38: Viết phương trình tiếp tuyến của đường tròn

22

():( 2) ( 4) 25Cx y, biết tiếp tuyến vuông

góc với đường thẳng

:3 4 5 0dx y.

A.

43290xy

. B.

43290xy

hoặc

43210xy

.

C.

4350xy

hoặc

43450xy

D.

4350xy

hoặc

4330xy

.

Lời giải

Chọn B

Đường tròn

22

():( 2) ( 4) 25Cx y có tâm

(2; 4)I 

, bán kính

5R 

.

Đường thẳng

 vuông góc với đường thẳng

:3 4 5 0dx y

có phương trình dạng:

43 0xyc

 là tiếp tuyến của đường tròn

()C

khi và chỉ khi:

(; )dI R



22

4.2 3.( 4)

5

43

c





425 29

425

425 21

cc

c

cc

 



  



 



. Vậy có hai tiếp tuyến cần tìm là:

43290xy

và

43210xy.

Câu 39: Trong mặt phẳng tọa độ Oxy, cho đường tròn



C có phương trình

22

2230xy x y. Từ

điểm



1;1A

kẻ được bao nhiêu tiếp tuyến đến đường tròn





C

A. 1. B. 2. C. vô số. D. 0.

Lời giải

Chọn D





C

có tâm





1; 1I 

bán kính R=

22

1(1)(3) 5  

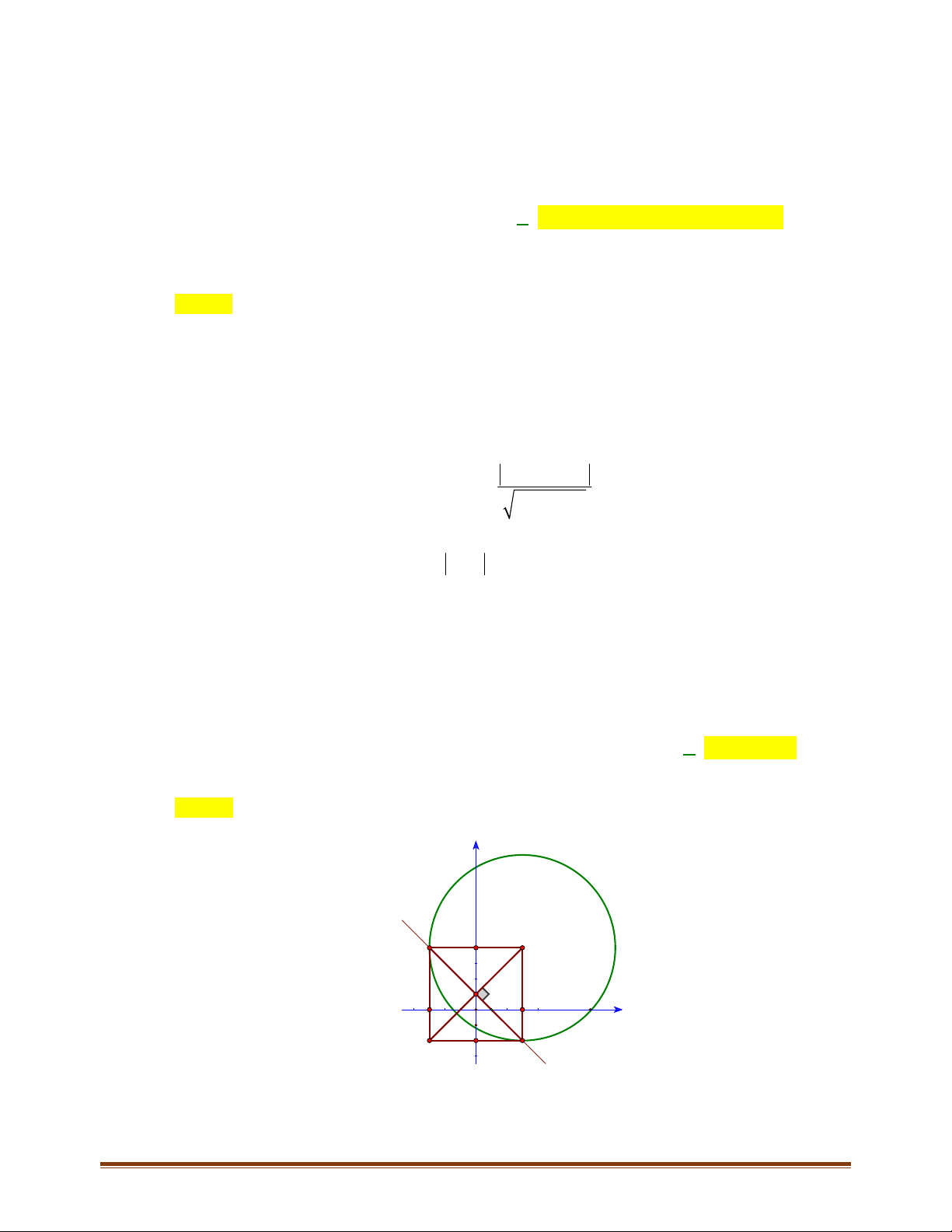
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

Vì

2

I

AR

nên A nằm bên trong





C

.Vì vậy không kẻ được tiếp tuyến nào tới đường tròn





C .

Câu 40: Trong mặt phẳng

Ox

y

, cho đường tròn

   

22

:1 44Cx y 

. Phương trình tiếp tuyến với

đường tròn



C

, biết tiếp tuyến đó song song với đường thẳng

:4 3 2 0xy

là

A.

43180xy

và

4320xy 

. B.

43180xy

và

4320xy

.

C.

43180xy 

và

4320xy

. D.

43180xy 

và

4320xy 

.

Lời giải

Chọn B

Đường tròn

   

22

:1 44Cx y 

có tâm



1; 4I

và bán kính

2

R



.

Gọi

d là tiếp tuyến của



C

.

Vì

//d 

nên đường thẳng



:4 3 0 2dx ym m 

.

d

là tiếp tuyến của



C



2

4.1 3.4

;2

43

m

dI d R



 



18

810

2

m













Vậy có 2 tiếp tuyến cần tìm :

43180;4320xy xy 

.

Câu 41: Trên mặt phẳng toạ độ Oxy , cho điểm





3; 2P 

và đường tròn

   

22

:3 436Cx y

.

Từ điểm

P kẻ các tiếp tuyến PM và

P

N

tới đường tròn





C

, với

M

,

N

là các tiếp điểm.

Phương trình đường thẳng

M

N

là

A.

10xy

. B.

10xy

. C.

10xy

. D.

10xy

.

Lời giải

Chọn D

Gọi

I

là tâm của đường tròn, ta có tọa độ tâm





3; 4I

.

x

y

D

1

-2

4

3

K

N

P

M

I

O

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17

Theo đề ra ta có tứ giác

I

MPN là hình vuông, nên đường thẳng

M

N nhận



6; 6IP  



làm

VTPT, đồng thời đường thẳng

M

N

đi qua trung điểm





0;1K

của

I

P

. Vậy phương trình

đường thẳng MN:



1. 0 1. 1 0xy 

hay

10xy

.

Câu 42: Trong mặt phẳng với hệ tọa độ

Ox

y

, cho điểm

(3;1)M 

và đường tròn



22

:2660Cx y x y. Gọi

1

T

,

2

T

là các tiếp điểm của các tiếp tuyến kẻ từ

M

đến. Tính

khoảng cách từ

O đến đường thẳng

12

.TT

A.

5

. B. 5. C.

3

5

. D.

22

.

Lời giải

Chọn C

+

    

22

:2660134Cx y x y x y 

suy ra có tâm I và R = 2

+ Phương trình đường thẳng

d đi qua

(3;1)M 

có phương trình:









310Ax By .

d là tiếp tuyến với đường tròn khi và chỉ khi





;dId R .

ta có phương trình:

2

22

0

33

23 4 0

34

A

ABAB

AAB

A

B

AB







  









+ Với

0A 

, chọn

1

B



, phương trình tiếp tuyến thứ nhất là





1

:1dy

.

Thế

1y 

vào





22

:2660Cx y x y

, ta được tiếp điểm là





1

1;1T

.

+ Với

34

A

B

, chọn

4; 3AB 

, phương trình tiếp tuyến thứ hai là



2

:4 3 15 0dxy 

Tiếp điểm



2

4

;5

3

x

Tx C









nên



2

43

1534

35

x

xx



  





2

321

;

55

T









.

+ Phương trình đường thẳng









12

:2 1 1 1 0 2 3 0TT x y x y  

.

+ Khoảng cách từ

O

đến đường thẳng

12

TT là:



12

22

3

0;

5

21

dTT







.

Dạng 4.2 Bài toán tương giao

Câu 43:

Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai đường tròn









12

,CC

có phương trình lần

lượt là

22 22

(1)( 2)9 và (2)( 2) 4xy x y    

. Khẳng định nào dưới đây là

sai?

A. Đường tròn





1

C

có tâm





1

1; 2I 

và bán kính

1

3R  .

B.

Đường tròn





2

C có tâm





2

2; 2I và bán kính

2

2R 

.

C. Hai đường tròn









12

,CC

không có điểm chung.

D. Hai đường tròn









12

,CC

tiếp xúc với nhau.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18

Chọn D

Ta thấy đường tròn





1

C có tâm





I1;2 và bán kính

1

3R 

. Đường tròn





2

C có tâm





2

2; 2I và bán kính

2

2R 

.

Khi đó:



22

1212 1

5(21)(22)5

R

RII C   

và





2

C

tiếp xúc nhau.

Câu 44: Tìm giao điểm

2

đường tròn

22

1

():x 40Cy

và

22

2

():x 4 4 40.Cyxy

A.





2; 2 và





2; 2 . B.





0; 2 và





0; 2 . C.



2;0 và



2;0 . D.





2;0 và





0; 2 .

Lời giải

Chọn D

Giao điểm

2

đường tròn là nghiệm của hệ phương trình sau:

22 22 22

22

40 4 4

4440 44 8 2

xy xy xy

xy xy xy xy



  





   





2

22 2

2

0

2

4240

24

22

2

0

y

x

xy y y

yy

xy xy

y

xy

x















 







  

 



 

























Vậy giao điểm 2 đường tròn là:





2;0 và





0; 2 .

Câu 45: Trong mặt phẳng với hệ trục

Oxy

, cho hai đường tròn

 

2

:1 4Cx y

và



22

:4 316Cx y





cắt nhau tại hai điểm phân biệt

A

và

B

. Lập phương trình đường

thẳng

A

B

A. 20xy. B. 2. 0xy  C. 20xy. D. 20xy.

Lời giải

Chọn A

Cách 1: Xét hệ

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19





2

22

14

230

8690

4316

xy

xy x

xy xy

xy



























2

37 17

,

2

22

2610

2230

37 17

,

22

xy

yx

xx

xxx

xy

























 















Suy ra

3717

,

22

A









,

3717

,

22

B









.



C

có tâm



1; 0O

,



C



có tâm





4;3O







3; 3OO







Nên đường thẳng

A

B

qua

A

và nhận





1;1n



là vécto pháp tuyến.

Phương trình:

37 17

11020

22

xy xy











. Chọn

A

.

Cách 2: Giả sử hai đường tròn

 

2

:1 4Cx y

và



22

:4 316Cx y





cắt nhau

tại hai điểm phân biệt

A

và

B

khi đó tọa độ của

A

và thỏa mãn hệ phương trình:





2

22

14

230 (1)

8690(2)

4316

xy

xy x

xy xy

xy

























Lấy

(1)

trừ

(2)

ta được:

66120 20xy xy

là phương trình đường thẳng đi qua 2

điểm

A

và

B

Câu 46: Cho đường thẳng

:3 4 19 0xy

và đường tròn

   

22

:1 125Cx y

. Biết đường

thẳng

 cắt





C

tại hai điểm phân biệt

A

và

B

, khi đó độ dài đọan thẳng

A

B là

A. 6. B. 3. C. 4. D. 8.

Lời giải

Chọn A

Từ



319

:3 4 19 0 1

44

xy y x

.

Thế



1

vào





C

ta được



2

323

125

44

xx



  





2

1

25 85 145

0.

29

16 8 16

5

x

xx

x















+)





141;4.

AA

xy A  

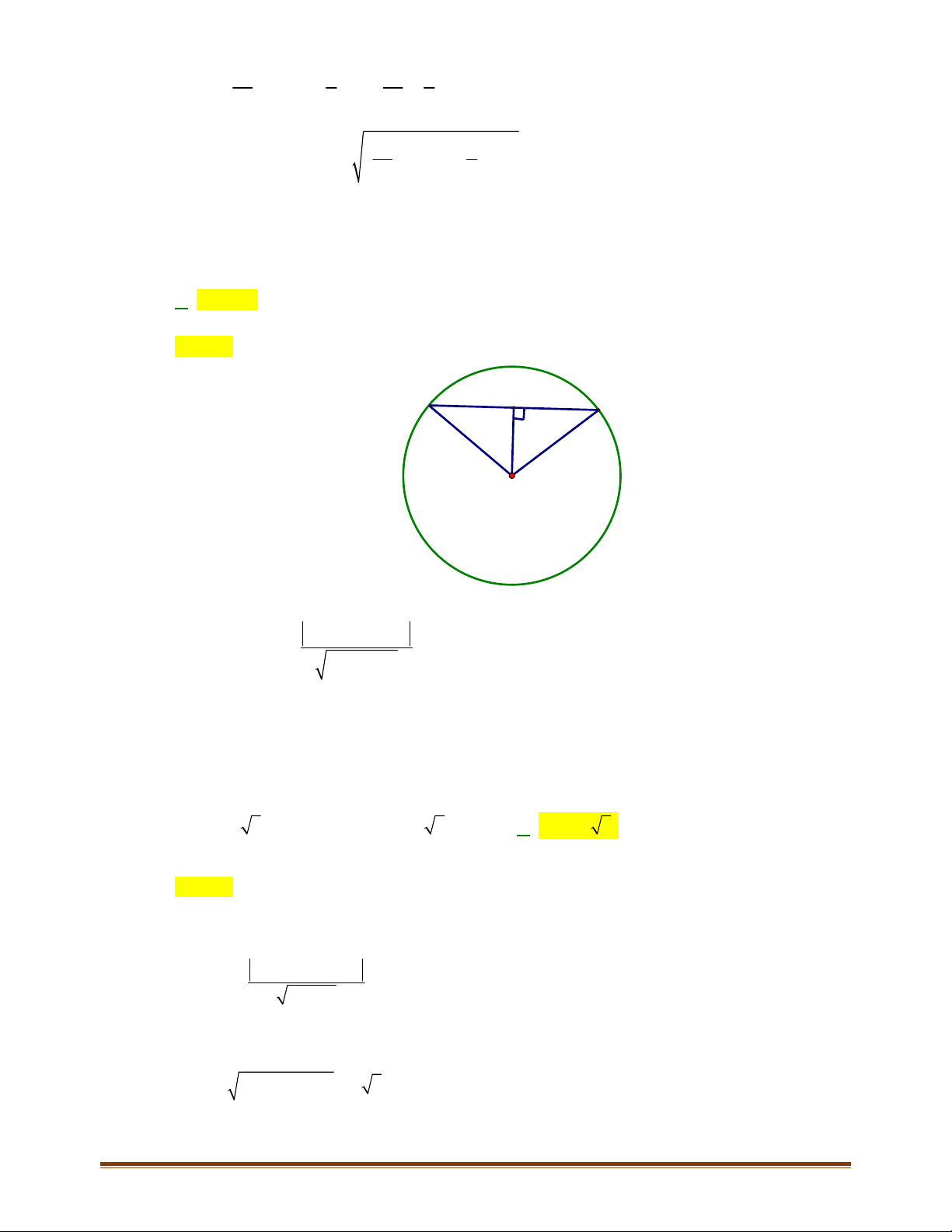
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

+)

29 2 29 2

;.

5555

BB

xyB



 





Độ dài đoạn thẳng

22

29 2

146

55

AB

 



 

 

.

Câu 47: Trong mặt phẳng tọa độ

Oxy

cho đường tròn





C

có tâm





1; 1I 

bán kính

5R 

. Biết rằng

đường thẳng



:3 4 8 0dxy

cắt đường tròn





C

tại hai điểm phân biệt ,AB. Tính độ dài

đoạn thẳng

AB .

A.

8AB 

. B. 4AB  . C.

3.AB 

. D.

6AB 

.

Lời giải

Chọn A

Gọi H là trung điểm của đoạn thẳng AB . Ta có IH AB và









2

3.1 4. 1 8

;3

34

IH d I AB



 



.

Xét tam giác vuông

AHI ta có:

22222

5316HA IA IH 

428HA AB HA 

Câu 48: Trong mặt phẳng với hệ trục tọa độ

,Oxy

cho đường tròn





C

có phương trình



22

224xy

và đường thẳng

:3 4 7 0dx y

. Gọi

,

A

B

là các giao điểm của

đường thẳng

d với đường tròn





C . Tính độ dài dây cung

A

B .

A. 3AB  . B. 25AB  . C. 23AB  . D. 4

A

B  .

Lời giải

Chọn C

Đường tròn





C

có tâm



2; 2I 

bán kính 2

R

 .



22

3.2 4. 2 7

,12

34

dId R







nên

d

cắt



C

tại hai điểm phân biệt.

Gọi

,

A

B

là các giao điểm của đường thẳng

d

với đường tròn





C

.



22

2,23AB R d I d 

.

H

I

A

B

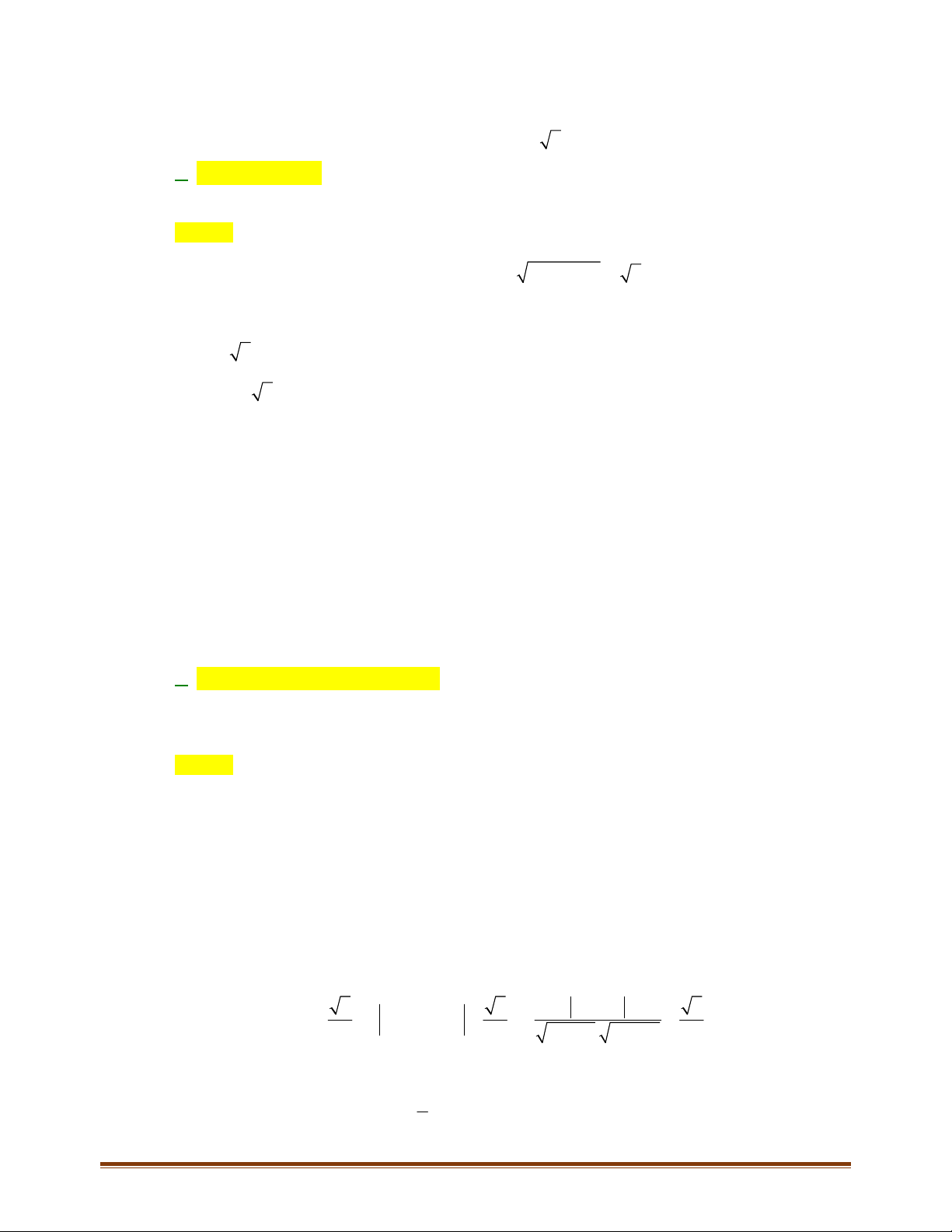
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

Câu 49: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm





3;1A

, đường tròn





22

:2430Cx y x y

. Viết phương trình tổng quát của đường thẳng

d

đi qua A và cắt

đường tròn





C tại hai điểm

B

, C sao cho 22BC  .

A.

:250dx y

. B.

:250dx y

. C.

:250dx y

. D.

:250dx y

.

Lời giải

Chọn A

Đường tròn





C có tâm





1; 2I và bán kính

22

123 2R .

Theo giả thiết đường thẳng

d

đi qua

A

và cắt đường tròn





C

tại hai điểm

B

,

C

sao cho

22BC 

.

Vì

22 2BC R

nên

BC

là đường kính của đường tròn





C

suy ra đường thẳng

d

đi qua

tâm





1; 2I

Ta chọn:



2; 1

d

uIA







1; 2

d

n



.

Vậy đường thẳng

d đi qua





3;1A và có VTPT





1; 2

d

n 



nên phương trình tổng quát của

đường thẳng

d

là:









13210xy 

250xy 

.

Câu 50: Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai đường tròn









12

,CC có phương trình lần

lượt là

22 22

(1)( 2)9 và (2)( 2) 4xy x y    . Viết phương trình đường thẳng

d

¢

đi

qua gốc tọa độ và tạo với đường thẳng nối tâm của hai đường tròn một góc bằng

45

.

A.

:70dx y





hoặc

:7 0dxy





. B.

:70dx y





hoặc

:7 0dxy





.

C.

:70dx y





hoặc

:7 0dxy





. D.

:70dx y





hoặc

:7 0dxy





.

Lời giải

Chọn A

Tọa độ tâm

1

I

của đường tròn





1

C

là:





1

1; 2I 

.

Tọa độ tâm

2

I

của đường tròn





1

C

là:





2

2; 2I

.

Ta có:



12

3; 4II



. Gọi

,dd



lần lượt là đường thẳng nối tâm của hai đường tròn đã cho và

đường thẳng cần lập. Chọn một vectơ pháp tuyến của đường thẳng

d

là:





4; 3

d

n 



. Gọi





;

d

nab





,

22

0ablà một vectơ pháp tuyến của đường thẳng

d



.

Theo đề



2222

43

22 2

cos , ' cos ,

22 2

34.

dd

ab

dd n n

ab





  





.

22

70

74870

1

0

7

ab

aabb

ab







 



 



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 22

Với

1

0

7

ab 

, chọn 71ba   . Phương trình đường thẳng

:70dx y





.

Với

70ab

, chọn 17ba  . Phương trình đường thẳng

:7 0dxy





.

Câu 51:

Trong mặt phẳng tọa độ

Oxy

cho điểm





1; 2I

và đường thẳng





:2 5 0.dxy

Biết rằng

có hai điểm

12

,

M

thuộc



d

sao cho

12

10.IM IM

Tổng các hoành độ của

1

M

và

2

M

là

A.

7

.

5

B.

14

.

5

C. 2. D. 5.

Lời giải

Chọn B



   

22

12

10

, : 1 2 10.

1; 2

IM IM

MM C x y

I















Mặt khác,

1

M

,

2

M

thuộc



:2 5 0dxy

nên ta có tọa độ

1

M

,

2

M

là nghiệm của hệ

  



22

12101

.

250 2

xy



 













225,yx 

thay vào



1

ta có

2

0

5140 .

14

5

x

xx

x















Gọi

12

,

x

x lần lượt là hoành độ của

1

M

và

212

14 14

0.

55

Mxx 

Câu 52: Trong hệ tọa độ

Ox ,

y

cho đường tròn





C có phương trình:

22

42150.

x

yxy I là tâm





C

, đường thẳng

d

đi qua





1; 3M 

cắt





C

tại

,.

A

B

Biết tam giác IAB có diện tích là

8.

Phương trình đường thẳng

d

là:

0.xbyc

Tính

bc

A.

8.

B.

2.

C.

6.

D.

1.

Lời giải

Chọn B





C

có tâm



2; 1 ,I 

bán kính 25.R 

Đặt





,hdIAB

. Ta có:

1

. 8 . 16.

2

IAB

ShABhAB

R

(C)

d

h

M

I

H

B

A

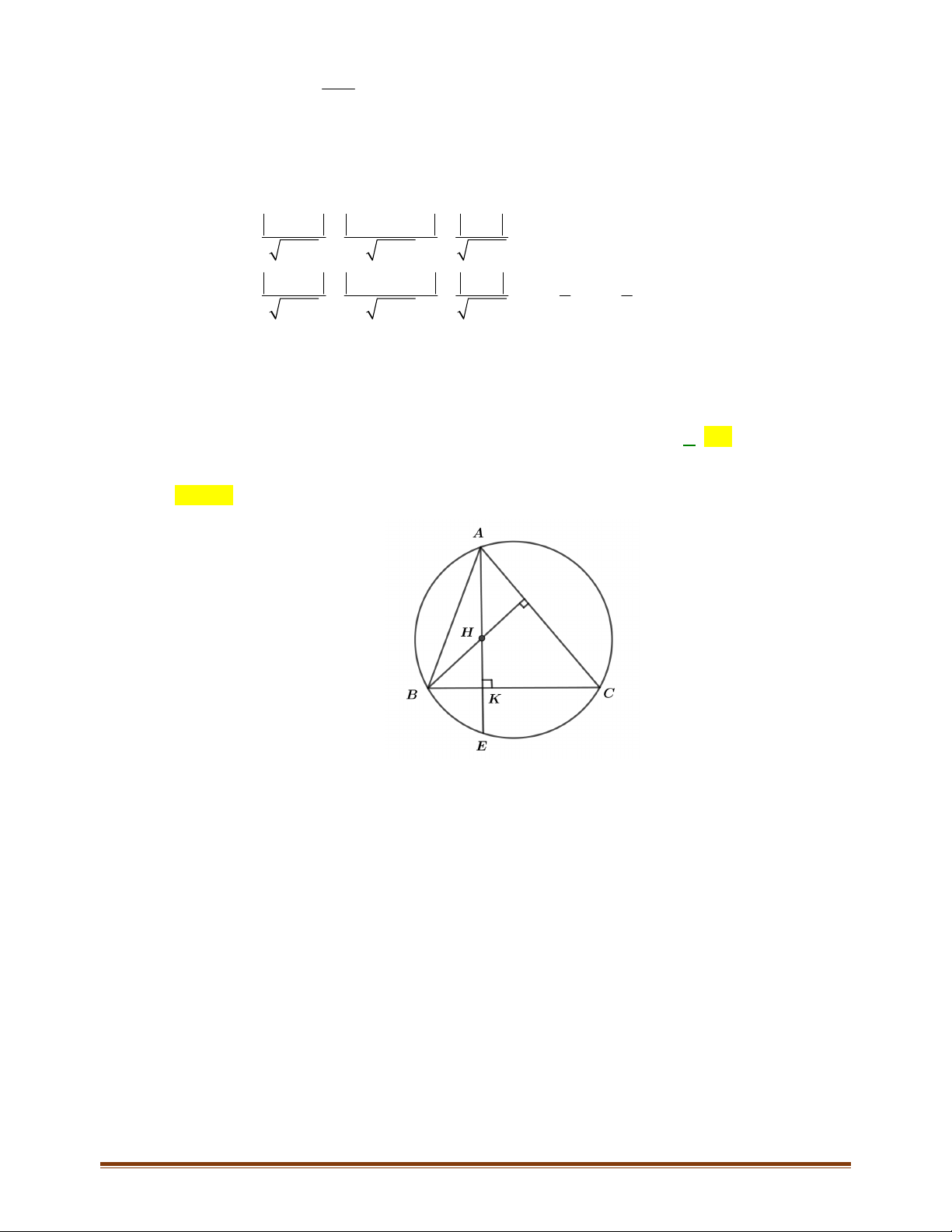
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 23

Mặt khác:

2

22

20

4

AB

Rh 

Suy ra:

42

;

48

hh

AB AB











Vì

d

đi qua



1; 3M 

nên

13 0 3 1 3 1bc bc c b

Với

222

223112

4

111

bc b b b

hb

bbb

   

   



Với

222

223112

35

22.

44

111

bc b b b

hbcbc

bbb

   

    



Câu 53: Trong mặt phẳng

Oxy

cho tam giác

ABC

có đỉnh



5;5A

, trực tâm



1; 13H 

, đường tròn

ngoài tiếp tam giác có phương trình

22

50xy. Biết tọa độ đỉnh



;Cab

, với

0a 

. Tổng

ab

bằng

A.

8

. B.

8

. C.

6

. D.

6

.

Lời giải

Chọn D

Gọi

K

là chân đường cao hạ từ

A

của tam giác

ABC

, gọi

E

là điểm đối xứng với

H

qua

K

suy ra

E

thuộc đường tròn ngoại tiếp tam giác

ABC

.

Ta có



6;8AH 



, chọn



3; 4

AH

u 



.

Phương trình đường thẳng

AH

qua

A

ở dạng tham số

53

54

xt

yt











KAH

suy ra tọa độ điểm

K

có dạng



53;54Ktt

H

và

E

đối xứng nhau qua

K

suy ra tọa độ

E

theo t là



11 6 ; 3 8Ett

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 24









22

2

() 116 38 50

594 0

1

4

5

EC t t

tt

t

 



















 Với

1t  ,





5;5E

 Với

4

5

t





,

31 17

;

55

E







,

13 41

;

55

K







Phương trình đường thẳng

BC có





4;3

BC AH

un

 

và qua điểm

K

có phương trình tham số

13

4

13 41

5

4; 3

41

55

3

5

xt

CBC C t t

yt









   















.



 



22

2

13 41

4350

55

25 70 24 0

2

1; 7

5

12

7;1

5

CC t t

tt

tC KTM

tC



  









  

















Vậy









;7;1 6Cab C a b 

.

Câu 54: Trong mặt phẳng

Oxy

, cho

A

BC

nội tiếp đường tròn tâm



2; 2I

, điểm D là chân đường

phân giác ngoài của góc



BAC . Đường thẳng

A

D cắt đường tròn ngoại tiếp

A

BC

tại điểm

thứ hai là M. Biết điểm





2; 2J 

là tâm đường tròn ngoại tiếp

A

CD

và phương trình đường

thẳng CM là:

20.xy

Tìm tổng hoành độ của các đỉnh

, ,

A

BC

của tam giác

A

BC .

A.

9

5

. B.

12

5

. C.

3

5

. D.

6

5

.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 25

Ta có:



B

CM BAM



1



BAM MAT DAC





2

Từ









1, 2 suy ra



DAC BCM

, mà



,BCM CDA AMC DAC ACM AMC   từ đó suy ra



CDA ACM , do đó

M

C

là tiếp tuyến của đường tròn ngoại tiếp tam giác

A

CD

có tâm

J

nên

JC MC

. Hay

C

là hình chiếu của

J

lên đường thẳng

CM

.

Đường thẳng qua

J

và vuông góc với

CM

có phương trình:



220 40xy xy

Tọa độ điểm

C

là nghiệm của hệ:



21

1; 3

43

xy x

C

xy y

 







 



.

A

C

là đường thẳng qua

C

và vuông góc với



4; 0IJ 



nên có phương trình:

10x 

.

Do đó tọa độ điểm

A

có dạng





1;

A

a

. Ta có



2

22

1

9291

3

a

IA IC a

a













.

Vì

A

C

nên





1; 1A 

.

Tọa độ điểm

M

có dạng



;2

M

mm

. Ta có



2

22 2 2

1

210230

3

m

IM IC m m m m

m













.

Vì

M

C

nên





3; 1M 

.

BC

là đường thẳng qua

C

và vuông góc với





1; 3MI 



nên có phương trình:









13 3 0 3 100xy xy  .

Tọa độ điểm

B

có dạng



310;Bb b

. Ta có



22

3

312 2 10

23

5

b

IB IC b b

b















.

5

4

3

2

1

4 2 2 4

T

D

M

J

B

I

A

C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 26

R

'

I

A

Vì BC nên

19 23

;

55

B







.

Vậy tổng hoành độ của các đỉnh

,,

A

BC

là

19 9

11

55

 

.

Câu 55: Trong mặt phẳng tọa độ

Oxy

, cho hai đường thẳng

(

)

:380xyD++=

;

()

:3 4 10 0xy

¢

D-+=

và điểm

()

2;1A -

. Đường tròn có tâm

()

;Iab

thuộc đường thẳng

()

D

,đi qua

A

và tiếp xúc với đường thẳng

()

¢

D

. Tính

ab+

.

A.

4-

. B.

4

. C.

2

. D. 2 .

Lời giải

Chọn D

.

Vì

()

I ÎD

nên

380 83ab a b++==--

.

Vì đường tròn đi qua

A

và tiếp xúc với đường thẳng

(

)

¢

D

nên:

(

)

;dI IA

¢

D=

()()()

22

3410

211

5

ab

-+

=--+-

.

Thay

83ab=- -

vào

()

1

ta có:

()

()()

22

383 4 10

283 1

5

bb

-- - +

=-++ +-

2

14 13 5 10 34 37bbb- - = + +

()

2

14 13 25 10 34 37bbb- - = + +

2

81 486 729 0bb+ +=

3b=-

.

Với

31ba=-  =

.

2ab+=-

.

Câu 56:

Trong mặt phẳng với hệ tọa độ

Ox

y

, cho đường thẳng

:3 4 1 0dx y

và điểm



1; 2I 

. Gọi





C

là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có

diện tích bằng 4. Phương trình đường tròn





C

là

A.

 

22

128xy 

. B.

 

22

1220xy 

.

C.

 

22

125xy 

. D.

 

22

1216xy 

.

Lời giải

Chọn A

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 27

Ta có:



;2IH d I d

.

212.4

.42

22

IAB

S

SIHABAB AH

IH





.

22 22

22 22RIA AH IH     

.

   

22

:1 28Cx y

.

DẠNG 5. CÂU HỎI MIN-MAX

Câu 57: Cho đường tròn



22

:2440Cx y x y

và điểm



2;1M

. Dây cung của



C

đi qua

điểm M có độ dài ngắn nhất là

A.

6

. B.

7

. C.

37

. D. 27.

Lời giải

Chọn D

Ta có

    

22

:2440:129Cx y x y C x y  

nên có tâm



1; 2 , 3IR

Vì

23IM R

.

Gọi d là đường thẳng đi qua M cắt đường tròn



C

tại các điểm A, B. Gọi

J

là trung điểm

của

AB

. Ta có:

Ta có:

22 2 2

22 2 29227AB AJ R IJ R IM  

.

d

B

A

H

I(1;-2)

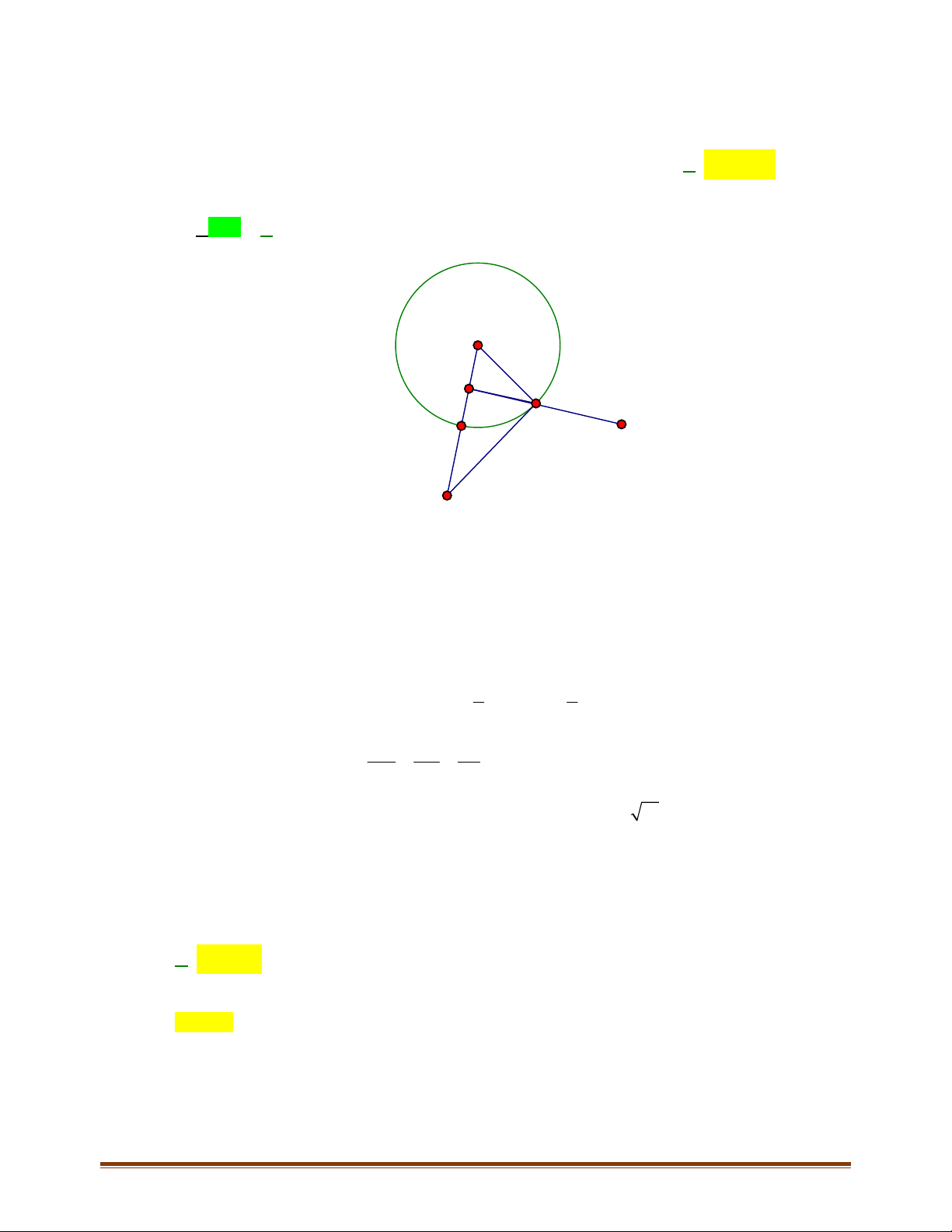
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 28

Câu 58: Trong mặt phẳng tọa độ Oxy, cho hai điểm

(0; 3), (4;1)AB

và điểm M thay đổi thuộc đường

tròn

22

(): ( 1) 4Cx y . Gọi

min

P

là giá trị nhỏ nhất của biểu thức 2PMA MB . Khi đó ta

có

min

P

thuộc khoảng nào dưới đây?

A.





7,7;8,1 .. B.



7,3;7,7 .. C.





8,3;8,5 .. D.





8,1;8, 3 .

Lời giải:

Chọn. D.

Đường tròn

22

(): ( 1) 4Cx y có tâm

I(0;1)

bán kính 2

R

 .

IA IB 4

R



nên ,ABnằm ngoài đường tròn.

Gọi

N

là giao điểm của IA và đường tròn





C

Trên đoạn

IN

lấy điểm P sao cho

11

24

IP IN IP IA P

 

trùng với gốc tọa độ.

Ta có

22

MA IM IN

IAM IMP MA MP

MP IP IP



.

Do đó





min min

2 2 2 2 2 2 17 8,1;8, 3PMAMBMPMBPBP PB P       .

Chọn.

D.

Câu 59:

Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn





22

:2430Cx y x y

. Tìm tọa độ

điểm



00

;

M

xy

nằm trên đường tròn



C

sao cho

00

Tx y

đạt giá trị lớn nhất.

A.





2;3M

. B.





0;1M

. C.





2;1M

. D.





0;3M

.

Lời giải

Chọn A

N

I

M

A

B

P

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 29



22

:2430Cx y x y

,



C

có tâm





1; 2I

,

2R 

.

Suy ra

   

22

:1 220Cx y 

.

Có

00

Tx y









00

123xy

.

Áp dụng bất đẳng thức

B. C. S cho

2

bộ số

















00

1;1 , 1 ; 2xy

.

 

22

00 0 0

1221 2xy x y



     





2 , do









22

00

122xy  

.









00

21 22xy     









00

11 23515xy T     

.

Dấu đẳng thức xảy ra khi











00

22

00

12

122

xy



 





  





.





2

0

11x

0

11

x















00

2, 3 , 5

0, 1, 1

xyT















.

Vậy

maxT 5

khi

00

2, 3xy

.

Câu 60: Trong mặt phẳng

Oxy

, cho điểm

M

nằm trên đường tròn





22

: 86160Cx y x y

. Tính

độ dài nhỏ nhất của

OM

?

A.

3

. B.

1

. C.

5

. D.

2

.

Lời giải 1

Chọn D

Đường tròn



C

có tâm





4;3I 

, bán kính

3R 

.

Ta có



4;3OI 



suy ra phương trình đường thẳng

OI

là

4

3

x

t

yt











.









OI C M

Tọa độ





;

x

y

của

M

là nghiệm hệ

4

2

3

2

1

O

M

I

1

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 30

22 2

82

55

8 6 16 0 25 50 16 0

32 8

44

55

33

24 6

55

tt

xy xy t t

xt xt x x

yt yt

yy









  







      

















Suy ra

12

32 24 8 6

;, ;

55 55

MM









Ta có

22 22

12 min2

32 24 8 6

8, 2 2

55 55

OM OM OM OM

 

       

 

 

.

Cách 2

Đường tròn



C

có tâm





4;3I 

, bán kính

22

43163R 

.

Phương trình đường thẳng

OI

đi qua





0;0O

có vtpt





3; 4n



là:

34 0xy

.

Tọa độ





M

OI C

là nghiệm của hệ:

22

34 0

86160

xy

xy xy











32 8

55

24 6

55

xx

yy



 















Ta có

22

1

32 24

55

OM









8

;

22

2

86

2

55

OM

 



 

 

. Vậy

min

2OM 

.

Câu 61: Gọi I

là tâm của đường tròn





C

:



22

114xy

. Số các giá trị nguyên của

m

để đường

thẳng

0xym 

cắt đường tròn



C

tại hai điểm phân biệt

,

A

B

sao cho tam giác IAB có

diện tích lớn nhất là

A. 1. B.

3

. C. 2 . D.

0

.

Lời giải

Chọn C

Gọi:

:0;dx y m 

tâm của





C

là





1; 1I

, để





dC

tại 2 phân biệt khi đó:

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 31

 

2

0;20 2222 222*

2

m

dId m





Xét

IAB

có:

 

22

111

...sin . .sin .

222

AIB

SIAIBAIBRAIBR





Dấu “=” xảy ra khi:



0

sin 1 90 2 2AIB AIB AB   



0( )

2

;2 2

4( )

2

mTM

m

dId

mTM















.

Câu 62: Điểm nằm trên đường tròn





22

:2410Cx y x y

có khoảng cách ngắn nhất đến đường

thẳng

:30dx y có toạ độ



;

M

ab

. Khẳng định nào sau đây đúng?

A.

2ab

. B.

ab

. C.

2ab

. D.

ab

.

Lời giải

Chọn C

Đường tròn





C

có tâm





1; 2I 

, bán kính 2

R

 .

Gọi

 là đường thẳng qua I và vuông góc với

.d

Khi đó, điểm

M

cần tìm là một trong hai

giao điểm của

 và



C

.

Ta có phương trình

:10xy

.

Xét hệ:

 

22

1

10

2410

124

yx

xy

xy xy

xy

 















 







2

12

1

22

214

12

22

x

yx

y

x

y













 





 

































 









Với







12;22 , 232BdBd  

Với





 

12;22 , 232 ,CdCddBd   

Suy ra

 

12;22 12; 22 212 2

M

ab a     .

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 32

Câu 63: Cho tam giác

A

BC

có trung điểm của

BC

là





3; 2M

, trọng tâm và tâm đường tròn ngoại tiếp

tam giác lần lượt là



22

;,1;2

33

GI









. Tìm tọa độ đỉnh C , biết C có hoành độ lớn hơn

2

.

A.





9;1C . B.



5;1C . C.



4; 2C . D.



3; 2C  .

Lời giải

Chọn B

Vì 2GA GM

 

nên

A

là ảnh của điểm

M

qua phép vị

tự tâm

G , tỉ số

2

, suy ra



4; 2A  .

Đường tròn ngoại tiếp

A

BC có tâm

I

, bán kính

5RIA

có phương trình

 

22

3225xy 

.

Ta có



2; 4IM 



.

Đường thẳng

BC

đi qua

M

và nhận vectơ IM



làm

vectơ pháp tuyến, phương trình

BC

là:









132 20 270xy xy   

.

Điểm

C

là giao điểm của đường thẳng

BC

và đường tròn



;

I

R

nên tọa độ điểm

C

là nghiệm

của hệ phương trình:



22

1, 3

3225

5, 1

270

xy

x

y

xy



























Đối chiếu điều kiện đề bài ta có tọa độ điểm



5;1C .

Câu 64: Trong mặt phẳng tọa độ

Oxy

, cho đường tròn



22

:24250Cx y x y

và điểm





2;1M

. Dây cung của



C

đi qua

M

có độ dài ngắn nhất là:

A. 27. B.

16 2

. C.

82

. D. 47.

Lời giải

Chọn D

+)



C có tâm



1; 2I , bán kính 30R 

+)

AB

là dây cung của





C

đi qua

M

R

K

C

D

B

A

I

M

B

C

A

I

G

M

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 33

+) Ta có

min

A

BABIM

.

Thật vậy, giả sử

CD

là dây cung qua

M

và không vuông góc với IM .

Gọi

K

là hình chiếu của

I

lên

CD

ta có:

22 22

22 2

A

BAM IAIM RIM 

22 22

22 2CD KD ID KD R IK  

Do tam giác

IMK

vuông tại

K

nên

IM IK

.

Vậy

CD AB

.

+) Ta có:



22

21 12 2IM 

22

30 2 28 2 7MA R IM

247AB MA  .

Câu 65: Cho các số thực

,,,abcd

thay đổi, luôn thỏa mãn

 

22

121ab 

và

43d230c 

.

Giá trị nhỏ nhất của biểu thức



22

P

ac bd 

là:

A.

min

28P  . B.

min

3P 

. C.

min

4P 

. D.

min

16P 

.

Lời giải

Chọn D

Xét tập hợp điểm

(;)

M

ab

thỏa mãn

 

22

121ab 

thì M thuộc đường tròn tâm

(1; 2); 1IR

Xét điểm

(; )Ncd

thỏa mãn 43d230c  thì N thuộc đường thẳng có phương trình

43230xy

.

Ta thấy

4623

(; ) 5 1

5

dId R





. Do đó đường thẳng không cắt đường tròn.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 34

Đường thẳng qua I vuông góc với

d

tại L và cắt đường tròn ở

,TK

( K ở giữa T và L )

Vẽ tiếp tuyến tại

K cắt

M

N

tại P .

Có

K

LPNMN

, mà



,

K

LdId R

Do đó

M

N

ngắn nhất khi

M

NKL

Từ đây ta suy ra



22

2

P

ac bd MN  

bé nhất khi và chỉ khi

(; ) 5 1 4MN d I d R

. Vậy giá trị nhỏ nhất

min

16P 

Câu 66: Trong mặt phẳng tọa độ ,Oxy cho đường tròn

   

22

:1 24 Cx y

và các đường thẳng

1

:10, dmxym

2

:10.dxmym Tìm các giá trị của tham số m để mỗi đường

thẳng

12

,dd cắt





C

tại 2 điểm phân biệt sao cho 4 điểm đó lập thành 1 tứ giác có diện tích lớn

nhất. Khi đó tổng của tất cả các giá trị tham số m là:

A. 0. B. 1. C. 3. D. 2.

Lời giải

Chọn A

Ta có

(1; 2)

()

2









I

C

R

Ta dễ thấy đường thẳng

1

d và

2

d cắt nhau tại điểm





1;1M

cố định nằm trong đường tròn





C

và

12

dd. Gọi

,

A

B

là giao điểm của

1

d và





C

,

,CD

là giao điểm của

2

d và





C

.

,HK

lần

lượt là hình chiếu của

I

trên

1

d

và

2

d

Khi đó

 



22

12

22

222

22 2 2

1

.2.2 ,. ,

2

4334

14334

2 4 4 =2 7

11 1 1

 





 

   

  

ABCD

S ABCD AHCK R dId R dId

mm

mmm

mm m m

Do đó max 7



ABCD

S khi

1m

. Khi đó tổng các giá trị của

m

bằng

0.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 340

BÀI 22. BA ĐƯỜNG CONIC

1. ELIP

- Cho hai điểm cố định và phân biệt

1

F

,

2

F

. Đặt

12

20FF c

. Cho số thực a lớn hơn c . Tập

hợp các điểm

M

sao cho

12

2

M

FMF a được gọi là đường elip . Hai điểm

1

F ,

2

F được gọi

là hai tiêu điểm và

12

2FF c được gọi là tiêu cự của elip đó.

- Trong mặt phẳng tọa độ

Oxy

, elip có hai tiêu điểm thuộc trục hoành sao cho

O

là trung điểm

của đọan thẳng nối hai tiêu điểm đó thì có phương trình

22

1

xy

ab



, với 0ab.





2

Ngược lại, mỗi phương trình có dạng





2

đều là phương trình của elip có hai tiêu điểm





22

1

;0Fab

,





22

2

;0Fab

, tiêu cự

22

22cab

và tổng các khoảng cách từ mỗi

điểm thuộc elip đó tới hai tiêu điểm bằng

2a

.

- Phương trình





2

được gọi là phương trình chính tắc của elip tương ứng.

*Tính chất và hình dạng của Elip: Cho elip có phương trình chính tắc

22

1

xy

ab



, với

0ab

.

● Trục đối xứng

Ox

,

Oy

● Tâm đối xứng

O

.

● Tiêu điểm









12

;0 , ;0Fc Fc

.

● Tọa độ các đỉnh

















1212

;0 , ;0 , 0; , 0;

A

aAaB bBb

.

● Độ dài trục lớn

2a

. Độ dài trục bé

2b

.

● Nội tiếp trong hình chữ nhật cơ sở có kích thước là

2a

và

2b

.

● Tâm sai

1

c

e

a



.

● Hai đường chuNn

a

x

e



và

a

x

e



.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 341

●









;

M

xy E

. Khi đó

1

M

Faex

: bán kính qua tiêu điểm trái.

2

M

Faex

: bán kính qua tiêu điểm phải.

2. HYPEBOL

Trên mặt phẳng, nếu hai thiết bị đặt tại các vị trí

1

F ,

2

F nhận được một tín hiệu âm thanh cùng

lúc thì vị trí phát ra tín hiệu cách đều hai điểm

1

F ,

2

F , và do đó, nằm trên đường trung trực của

đoạn thẳng

12

FF .

Cho hai điểm phân biệt cố định

1

F

,

2

F

. Đặt

12

2FF c

. Cho số thực dương

a nhỏ hơn c . Tập

hợp các điểm

M

sao cho

12

2

M

FMF a

được gọi là đường hypebol . Hai điểm

1

F ,

2

F được

gọi là hai

tiêu điểm và

12

2FF c được gọi là tiêu cự của hypebol đó.

Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung

điểm của đoạn thẳng nối hai tiêu điểm đó thì có phương trình

22

1

xy

ab



, với

,0ab

.

N gược lại, mỗi phương trình có dạng





4

đều là phương trình của hypebol có hai tiêu điểm





22

1

;0Fab

,





22

2

;0Fab

, tiêu cự

22

x

ab

và giá trị tuyệt đối của hiệu các

khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng

2a

.

Phương trình được gọi là phương trình chính tắc của hypebol tương ứng.

3. PARABOL

Cho một điểm

F

cố định và một đường thẳng



cố định không đi qua

F

. Tập hợp các điểm

M

cách đều

F

và



được gọi là đường parabol . Điểm

F

được gọi là tiêu điểm,



được gọi

là đường chuNn, khoảng cách từ

F

đến



được gọi là tham số tiêu của parabol đó.

Xét





P

là một parabol với tiêu điểm

F

, đường chuNn



. Gọi

H

là hình chiếu vuông góc của

F

trên



. Khi đó, trong hệ trục tọa độ

Oxy

với gốc

O

là trung điểm của

H

F

, tia

Ox

trùng

với tia

OF

, parabol





P

có phương trình

2

2ypx



5

Phương trình



5

được gọi là phương trình chính tắc của parabol





P

.

N gược lại, mỗi phương trình dạng



5

, với

0p 

, là phương trình chính tắc của parabol có tiêu

điểm

;0

2

p

F







và đường chuNn

:

2

p

x

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 342

4. MỘT SỐ ỨNG DỤNG CỦA BA ĐƯỜNG CONIC. TÍNH CHẤT QUANG HỌC

Tương tự gương cầu lồi thường đặt ở những khúc đường cua, người ta cũng có những gương

elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phản xạ theo một quy tắc được

xác định rõ bằng hình học, chẳng hạn:

 Tia sáng phát ra từ một tiêu điểm của elip, hypebol sau khi gặp elip, hypebol sẽ bị hắt lại theo một

tia nằm trên đường thẳng đi qua tiêu điểm còn lại .

 Tia sáng hướng tới một tiêu điểm của elip, hypebol , khi gặp elip, hypebol sẽ bị hắt lại theo một tia

nằm trên đường thẳng đi qua tiêu điểm còn lại .

 Với gương parabol lõm, tia sáng phát ra từ tiêu điểm khi gặp parabol sẽ bị hắt lại theo một tia

vuông góc với đường chuNn của parabol . N gược lại, nếu tia tới vuông góc với đường chuNn của parabol

thì tia phản xạ sẽ đi qua tiêu điểm của parabol.

Tính chất quang học được đề cập ở trên giúp ta nhận được ánh sáng mạnh hơn khi các tia sáng hội tụ và

giúp ta đổi hướng ánh sáng khi cần. Ta cũng có

điều tương tự đối với tín hiệu âm thanh, tín hiệu truyền

từ vệ tinh.

MỘT SỐ ỨNG DỤNG

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 343

Ba đường conic xuất hiện và có nhiều ứng dụng trong khoa học và trong cuộc sống, chẳng hạn:

 Tia nước bắn ra từ đài phun nước, đường đi bổng của quả bóng là những hình ảnh về đường

parabol;

 Khi nghiêng cốc tròn, mặt nước trong cốc có hình elip. Tương tự, dưới ánh sáng mặt trời, bóng của

một quả bóng, nhìn chung, là một elip;

 Ánh sáng phát ra từ một bóng đèn Led trên trần nhà có thể tạo nên trên tường các nhánh hypebol;

 N hiều công trình kiến trúc có hình elip, parabol hay hypebol.

7.19 Cho elip có phương trình















 1.Tìm tiêu điểm và tiêu cự của elip

7.20 Cho hypebol có phương trình:















 1. Tìm tiêu điểm và tiêu cự của hypebol.

7.21 Cho parabol có phương trình: 𝑦



 8𝑥. Tìm tiêu điểm và đường chuNn của parabol.

7.22 Lập phương trình chính tắc của elip đi qua điềm A và có một tiêu điềm là F

2

.

7.23 Lập phương trình chính tắc của parabol đi qua điểm 𝑀

7.24 Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời

điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch

thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác

định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính t

ắc của hypebol đó theo

đơn vị kilômét.

7.25 Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A điểm cuối là

B, khoảng cách 𝐴𝐵  400𝑚. Đỉnh parabol của khúc cua cách đường thẳng 𝐴𝐵 một khoảng 20

m và cách đều A, B .

a).Lập phương trình chính tắc của , với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 m trên

thực tế.

b). Lập phương trình chính tắc cùa , với 1

đơn vị đo trong mặt phẳng toạ độ tương ứng 1 km

trên thực tế.

BÀI TẬP SÁCH GIÁO KHOA.

HỆ THỐNG BÀI TẬP.

II

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 344

DẠNG 1: XÁC ĐNNH CÁC YẾU TỐ CỦA ELÍP

{ Xác định các đỉnh, độ dài các trục, tiêu cự, tiêu điểm. của elip}

Cho Elip có phương trình chính tắc:



22

:1

xy

E

ab



với

222

bac

.

● Tiêu điểm









12

;0 , ;0

F

cFc

.

● Tọa độ các đỉnh

















1212

;0 , ;0 , 0; , 0;Aa Aa B bB b

.

● Độ dài trục lớn

2a

.

● Độ dài trục bé

2b

.

● Tiêu cự

2c

Câu 1:

Tìm tọa độ các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip:



22

:1

41

xy

E 

.

Câu 2: Tìm tọa độ các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip:





22

:4 25 100Ex y

.

Câu 3: Tìm tọa độ các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip:





22

:4 9 1Ex y

.

Câu 4: Tìm tâm sai của Elíp biết:

a) Mỗi tiêu điểm nhìn trục nhỏ dưới một góc 60

0

.

b) Đỉnh trên trục nhỏ nhìn hai tiêu điểm dưới một góc 60

0

.

c) Khoảng cách giữa hai đỉnh trên hai trục bằng hai lần tiêu cự:

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 345

Câu 1:

Cặp điểm nào là các tiêu điểm của elip



E

:

22

1

54

xy



?

A.





1,2

0; 1F 

. B.





1,2

1; 0F 

. C.





1,2

3; 0F 

. D.





1,2

1; 2F 

.

Câu 2: Cho Elip





22

:4 9 36Ex y

. Mệnh đề nào sai trong các mệnh đề sau:

A.



E

có tỉ số

5

3

c

a



. B.





E

có trục lớn bằng

6.

C.



E

có trục nhỏ bằng

4

. D.





E

có tiêu cự

5

.

Câu 3: Cho elip

22

1

31

xy



. Phát biểu nào sau đây đúng?

A. Tỉ số giữa trục lớn và trục nhỏ bằng

3

. B. Tiêu cự bằng

4

.

C. Tâm sai

2

3

e 

. D. Hai tiêu điểm



1

2;0F 

và



2

2; 0F

.

Câu 4: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip

A.

22

48 32xy. B.

22

1

11

52

xy

. C.

22

1

64 16

xy

.

D.

22

1

84

xy

.

Câu 5: Cho elip

²²

(): 1

94

xy

E 

. Chọn khẳng định sai

A. Điểm

(3;0) ( )

A

E

. B.

()E

có tiêu cự bằng

25

.

C. Trục lớn của

()E

có độ dài bằng

6

. D.

()E

có tâm sai bằng

35

5

.

Câu 6: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip

A.

22

2xy

. B.

22

2xy

. C.

22

22xy. D.

22

2

x

y .

Câu 7: Trong mặt phẳng





Oxy

, cho elip



E

có phương trình

22

1

36 16

xy

. Tìm tiêu cự của



E

.

A.

12

12FF  B.

12

8FF  C.

12

25FF 

D.

12

45FF 

Câu 8: Trong mặt phẳng

Ox

y

, tìm tiêu cự của elip



22

:1

25 16

xy

E .

A.

3

B.

6

C.

4

D.

5

Câu 9: Tìm các tiêu điểm của Elip

22

1

91

xy



A.





1

3; 0 ;F





2

0; 3F 

. B.





1

8;0 ;F





2

0; 8F  .

C.





1

3; 0 ;F 





2

0; 3F 

. D.





1

8;0 ;F 





2

8;0F

.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 346

Câu 10: Elíp có độ dài trục lớn bằng:

A.

25

. B.

50

. C.

10

. D.

5

.

Câu 11: Cho

22

9 25 225xy. Hỏi diện tích hình chữ nhật cơ sở ngoại tiếp





E

là

A.

15

. B.

30

. C.

40

. D.

60

.

Câu 12: Cho





E

có độ dài trục lớn bằng

26

, tâm sai

12

.

13

e 

Độ dài trục nhỏ của





E

bằng

A.

5

. B.

10

. C.

12

D.

24

.

Câu 13: Cho





22

:16 25 100Ex y

và điểm

M

thuộc





E

có hoành độ bằng

2

. Tổng khoảng cách

từ

M

đến

2

tiêu điểm của





E

bằng

A.

5

. B.

22

. C. 43. D. 3.

Câu 14: Cho elip



22

:1

54

xy

E . Tỉ số giữa tiêu cự và độ dài trục lớn bằng

A.

5

4

. B.

5

. C.

35

5

. D.

25

5

.

Câu 15: Phương trình chính tắc của





E

có độ dài trục lớn gấp

2

lần độ dài trục nhỏ và đi qua điểm





2; 2A 

là

A.

22

1

24 16

xy



.

B.

22

1

36 9

xy



.

C.

22

1

16 4

xy



.

D.

22

1

20 5

xy



Câu 16: Phương trình chính tắc của





E nhận điểm





4;3M là một đỉnh của hình chữ nhật cơ sở là

A.

22

1

16 9

xy

. B.

22

1

16 4

xy

. C.

22

1

16 3

xy

. D.

22

1

94

xy



Câu 17: Phương trình chính tắc của





E

có khoảng cách giữa các đường chuNn bằng

50

3

và tiêu cự

bằng

6

là

A.

22

1

64 25

xy

. B.

22

1

89 64

xy

. C.

22

1

25 16

xy

. D.

22

1

16 7

xy



Câu 18: Trong mặt phẳng

Ox

y

, cho đường elip



22

:1

94

xy

E 

có hai tiêu điểm

1

F

,

2

F

.

M

là điểm

thuộc





E

. Tính

12

M

FMF .

A.

5

B.

6

C.

3

D.

2

Câu 19: Trong mặt phẳng Oxy cho elip





22

:36Ex y

. Giá trị nào sau đây là tiêu cự của elip?

A.

2

B.

3

C.

6

D.

4

Câu 20: Trong hệ trục tọa độ





Oxy

, cho elip



22

44

:1

25 9

xy

E . Độ dài tiêu cự của





E

bằng

A.

4

. B.

8

. C.

16

. D.

2

.

22

(): 1

25 9

xy

E 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 347

Câu 21: Cho elip



22

:1

25 9

xy

E 

. Trong các khẳng định sau, khẳng định nào sai?

A.





E có các tiêu điểm





1

4;0F  và





2

4;0F .

B.





E

có tỉ số

4

5

c

a



.

C.



E

có đỉnh





1

5; 0A 

.

D.





E

có độ dài trục nhỏ bằng

3

.

Câu 22: Trong mặt phẳng

Ox

y

cho





E có phương trình:

22

1

94

xy



khẳng định nào sau đây đúng?

A.





E

có tâm sai

5

3

e 

.

B.



12

0; 5 , 0; 5FF

là các tiêu điểm của





E .

C. Độ dài trục lớn là

9

.

D. Các đỉnh nằm trên trục lớn là





1

0;3A và



2

0; 3A  .

Câu 23: Cho Elip có phương trình

2

1

4

x

y. Một tiêu điểm của Elip có tọa độ là:

A.





3;0A . B.





0; 3B . C.





5;0C . D.



0; 5D .

Câu 24: Cho Elip có phương trình

22

41xy. Tiêu cự của Elip là:

A. 5. B. 3. C. 25. D. 23.

Câu 25: Diện tích của tứ giác tạo nên bởi các đỉnh của elip



2

:1

4

x

Ey là

A.

8

. B.

4

. C.

2

. D.

6

.

Câu 26: Trong mặt phẳng

Oxy

cho elip có phương trình



22

:1

25 9

xy

E . Đường thẳng

:4x

cắt

elip





E

tại hai điểm

,

M

N

. Tính độ dài đoạn thẳng

M

N

?

A.

18

25

MN 

. B.

9

25

MN 

. C.

18

5

MN 

. D.

9

5

MN 

.

Câu 27: Trong hệ tọa độ





Ox

y

, cho elip



22

:1

25 16

xy

E 

. Bán kính qua tiêu của





E

đạt giá trị nhỏ

nhất bằng

A.

0

B.

1

C.

3

5

D.

2

Câu 28: Một elip





E

có phương trình

22

1

xy

ab

, trong đó

0ab

. Biết





E

đi qua điểm





2; 2A

và





22;0B

thì





E có độ dài trục bé là

A.

4.

B.

22.

C.

2.

D.

6.

Câu 29: Cho





E

có hai tiêu điểm





1

4;0F 

,





2

4;0F

và điểm

M

thuộc





E

. Biết chu vi tam giác

12

M

FF bằng

18

. Khi đó tâm sai của





E

bằng

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 348

A.

4

18

. B.

4

5

. C.

4

5



. D.

4

9



.

Câu 30: Cho





E có hai tiêu điểm





1

7;0F 

,





2

7;0F

và điểm

9

7;

4

M









thuộc





E . Gọi

N

là

điểm đối xứng với

M

qua gốc tọa độ

.O

Khi đó

A.

12

9

2

NF MF

. B.

21

9

2

NF MF

. C.

21

7

2

NF NF

D.

12

8NF MF.

DẠNG 2: VIẾT PHƯƠNG TRÌNH CHÍNH TẮC CỦA ELIP

{ Phương trình chính tắc của Elip có dạng:



22

:1

xy

E

ab



với

222

bac

; …}

Câu 1:

Lập phương trình chính tắc của Elip, biết:

a) Elip đi qua điểm

5

2;

3

M







và có một tiêu điểm





1

2;0F 

.

b) Elip nhận





2

5; 0F

là một tiêu điểm và có độ dài trục nhỏ bằng 46.

c) Elip có độ dài trục lớn bằng

25 và tiêu cự bằng 2.

d) Elip đi qua hai điểm





2; 2M 

và





6;1N 

.

Câu 2: Lập phương trình chính tắc của Elip, biết:

a) Elip có tổng độ dài hai trục bằng 8 và tâm sai

1

2

e  .

b) Elip có tâm sai

5

3

e 

và hình chữ nhật cơ sở có chu vi bằng 20.

c) Elip có tiêu điểm





1

2;0F 

và hình chữ nhật cơ sở có diện tích bằng 12 5 .

Câu 3: Lập phương trình chính tắc của Elip, biết:

a) Elip đi qua điểm



5;2M  và khoảng cách giữa hai đường chuNn bằng 10.

b) Elip có tâm sai

3

5

e 

và khoảng cách từ tâm đối xứng của nó đến một đường chuNn bằng

25

3

.

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 349

c) Elip có độ dài trục lớn bằng 10 và phương trình một đường chuNn là

25

4

x 

.

d) Khoảng cách giữa các đường chuNn bằng 36 và bán kính qua tiêu điểm của điểm

M

thuộc

Elip là 9 và 15.

Câu 4: Lập phương trình chính tắc của Elip, biết:

a) Elip có hình chữ nhật cơ sở nội tiếp đường tròn



22

:41Cx y

và đi qua điểm





0;5A

.

b) Elip có hình chữ nhật cơ sở nội tiếp đường tròn



22

:21Cx y

và điểm





1; 2M

nhìn hai

tiêu điểm của Elip dưới một góc

0

60

.

c) Một cạnh hình chữ nhật cơ sở của Elip nằm trên

:50dx và độ dài đường chéo hình

chữ nhật bằng 6.

d) Tứ giác

A

BCD

là hình thoi có bốn đỉnh trùng với các đỉnh của Elip. Bán kính của đường

tròn nội tiếp hình thoi bằng

2

và tâm sai của Elip bằng

1

2

.

Câu 5: Lập phương trình chính tắc của Elip, biết

a) Tứ giác

A

BCD là hình thoi có bốn đỉnh trùng với các đỉnh của Elip. Đường tròn tiếp xúc với

các cạnh của hình thoi có phương trình





22

:4Cx y

và

2

A

CBD

,

A

thuộc

Ox

.

b) Elip có độ dài trục lớn bằng 8 và giao điểm của Elip với đường tròn





22

:8Cx y

tạo

thành bốn đỉnh của một hình vuông.

c) Elip có tâm sai

1

3

e 

và giao điểm của Elip với đường tròn





22

:9Cx y

tại bốn điểm

A

,

B

,

C

,

D

sao cho

AB

song song với

Ox

và

3

A

BBC

.

d) Elip có độ dài trục lớn bằng

42

, các đỉnh trên trục nhỏ và các tiêu điểm của Elip cùng nằm

trên một đường tròn.

Câu 6: Lập phương trình chính tắc của Elip, biết

a) Elip có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông có diện tích

bằng 32.

b) Elip có một đỉnh và hai tiêu điểm tạo thành một tam giác đều và chu vi hình chữ nhật cơ sở

của Elip bằng





12 2 3 .

c) Elip đi qua điểm





23;2M và

M

nhìn hai tiêu điểm của Elip dưới một góc vuông.

d) Elip đi qua điểm

3

1;

2

M







và tiêu điểm nhìn trục nhỏ dưới một góc

0

60

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 350

Câu 7: Lập phương trình chính tắc của Elip, biết

a) Elip có một tiêu điểm





1

3;0F 

và đi qua điểm

M

, biết tam giác

12

FMF

có diện tích bằng

1 và vuông tại

M

.

b) Elip đi qua ba đỉnh của tam giác đều

A

BC

. Biết tam giác

A

BC

có trục đối xứng là

O

y

,



0; 2A

và có diện tích bằng

49 3

12

.

c) Khi

M

thay đổi trên Elip thì độ dài nhỏ nhất của

OM

bằng 4 và độ dài lớn nhất của

1

M

F

bằng 8 với

1

F là tiêu điểm có hoành độ âm của Elip.

Câu 1:

Phương trình chính tắc của Elip là

A.

22

1

xy

ab



.

B.

22

1

xy

ab



.

C.



22

10

xy

ab

 . D.

22

1

xy

ab

.

Câu 2: Phương trình chính tắc của elip có tiêu cự bằng

6

và trục lớn bằng

10

.

A.

22

1

25 9

xy

. B.

22

1

100 81

xy

. C.

22

1

25 16

xy

. D.

22

1

25 16

xy

.

Câu 3: Phương trình của Elip





E

có độ dài trục lớn bằng

8

, độ dài trục nhỏ bằng

6

là:

A.

22

9 16 144xy. B.

22

916 1xy. C.

22

1

916

xy

. D.

22

1

64 36

xy

.

Câu 4: Cho





E

có hình chữ nhật cơ sở diện tích bằng

8

, chu vi bằng

6

thì phương trình chính tắc là:

A.

22

1

21

xy

. B.

22

1

41

xy

. C.

22

1

42

xy

. D.

22

1

16 4

xy

.

Câu 5: Cho





E

có tiêu điểm





1

4;0F 

,





2

4;0F

, tâm sai

4

5

e 

thì phương trình là:

A.

22

45 20xy. B.

22

16 25 400xy.

C.

22

9 25 225xy. D.

22

9 16 144xy.

Câu 6: Trong mặt phẳng với hệ trục tọa độ

Ox

y

, cho elip





E có độ dài trục lớn bằng 12 và độ dài

trục bé bằng 6. Phương trình nào sau đây là phương trình của elip





E

A.

22

1

144 36

xy

. B.

22

1

936

xy

. C.

22

1

36 9

xy

. D.

22

0

144 36

xy

.

Câu 7: Tìm phương trình chính tắc của Elip có tâm sai bằng

1

3

và trục lớn bằng

6

.

A.

22

1

93

xy

. B.

22

1

98

xy

. C.

22

1

95

xy

. D.

22

1

65

xy

.

Câu 8: Phương trình Elip có trục lớn bằng 25 và một tiêu điểm





1

1; 0F 

là:

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 351

A.

22

45 20xy. B.

22

4512xy. C.

22

54 20xy D.

22

5412xy.

Câu 9: Phương trình chính tắc của





E

có độ dài trục lớn bằng

8

, trục nhỏ bằng

6

là

A.

22

1

64 36

xy



.

B.

22

1

916

xy



.

C.

22

916 1xy

.

D.

22

1

16 9

xy



.

Câu 10: Phương trình chính tắc của





E có tâm sai

4

5

e 

, độ dài trục nhỏ bằng

12

là

A.

22

1

25 36

xy

. B.

22

1

64 36

xy

. C.

22

1

100 36

xy

. D.

22

1

36 25

xy

.

Câu 11: Phương trình chính tắc của





E

có độ dài trục lớn bằng

6

, tỉ số giữa tiêu cự và độ dài trục lớn

bằng

1

3

là

A.

22

1

93

xy



.

B.

22

1

98

xy



.

C.

22

1

19 5

xy



.

D.

22

1

65

xy



.

Câu 12: Elip có hai đỉnh





3; 0 ;





3; 0 và hai tiêu điểm





1; 0 và





1; 0 có phương trình chính tắc là

A.

22

1

89

xy

. B.

22

1

98

xy

. C.

22

1

94

xy

. D.

22

1

92

xy

.

Câu 13: Phương trình chính tắc của





E

có độ dài trục lớn gấp

2

lần độ dài trục nhỏ và tiêu cự bằng

43 là

A.

22

1

36 9

xy



.

B.

22

1

36 24

xy



.

C.

22

1

24 6

xy



.

D.

22

1

16 4

xy



.

Câu 14: Phương trình chính tắc của





E có đường chuNn

40x 

và tiêu điểm





1; 0F  là

A.

22

1

43

xy

. B.

22

1

16 15

xy

. C.

22

1

16 9

xy

. D.

22

1

98

xy

.

Câu 15: Phương trình chính tắc của





E

có tiêu cự bằng

6

và đi qua điểm





5; 0A

là

A.

22

1

100 81

xy

. B.

22

1

15 16

xy

. C.

22

1

25 9

xy

. D.

22

1

25 16

xy

.

Câu 16: Elip có hai tiêu điểm



1

1; 0F 

;



2

1; 0F

và tâm sai

1

5

e 

có phương trình là

A.

22

1

25 24

xy

. B.

22

1

24 25

xy

. C.

22

1

24 25

xy

. D.

22

1

25 24

xy

.

Câu 17: Trong hệ trục tọa độ

Oxy

, một elip có độ dài trục lớn là

8

, độ dài trục bé là

6

thì có phương

trình chính tắc là.

A.

22

1

916

xy

. B.

22

1

64 36

xy

. C.

22

1

16 9

xy

. D.

22

1

16 7

xy

.

Câu 18: Các đỉnh của Elip





E

có phương trình

22

1

xy

ab

;





0ab

tạo thành hình thoi có một góc

ở đỉnh là

60

, tiêu cự của





E

là

8

, thế thì

22

ab

?

A.

16

. B.

32

. C.

64

. D.

128

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 352

Câu 19: Trong mặt phẳng tọa độ

Oxy

, cho Elip





E

đi qua điểm





0;3M

. Biết khoảng cách lớn nhất

giữa hai điểm bất kì trên





E

bằng

8

. Phương trình chính tắc của Elip là

A.

22

1

916

xy



B.

22

1

16 9

xy



C.

22

1

964

xy



D.

22

1

64 9

xy



Câu 20: Trong mặt phẳng với hệ trục tọa độ

Ox

y

cho đường elip

22

(): 1

16 5

xy

E  và hai điểm









5; 1 , 1;1MN 

. Điểm

K

thay đổi trên elip

()

E

. Diện tích tam giác

M

NK

lớn nhất bằng

A.

95

.

B.

9

2

. C.

9

. D.

18

.

Câu 21: Cho elip



22

:1

16 9

xy

E . Xét các điểm

,

M

N

lần lượt thuộc các tia

,Ox Oy

sao cho đường

thẳng

M

N

tiếp xúc với





E

. Hỏi độ dài ngắn nhất của

M

N

là bao nhiêu?

A.

6

. B.

7

. C.

8

. D.

9

.

DẠNG 3: TÌM ĐIỂM THUỘC ELIP THỎA ĐIỀU KIỆN CHO TRƯỚC

Cho Elip có phương trình chính tắc:



22

:1

xy

E

ab



với

222

bac

.

●



;

M

xy E . Khi đó

1

M

Faex

: bán kính qua tiêu điểm trái.

2

M

Faex : bán kính qua tiêu điểm phải.

Câu 1:

a) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



22

:1

25 16

xy

E . Gọi

1

F ,

2

F là hai tiêu điểm

của Elip;

A

,

B

là hai điểm thuộc





E

sao cho

12

8AF BF. Tính

21

A

FBF .

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

95

xy

E . Gọi

1

F ,

2

F là hai tiêu điểm

của Elip trong đó

1

F có hoành độ âm. Tìm tọa độ điểm

M

thuộc





E

sao cho

12

2

M

FMF .

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

84

xy

E 

. Gọi

1

F ,

2

F là hai tiêu điểm

của Elip trong đó

1

F có hoành độ âm. Tìm tọa độ điểm

M

thuộc



E

sao cho

12

2MF MF.

Câu 2: a) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



22

9

:1

1

xy

E . Tìm những điểm

M

thuộc



E

sao cho nó nhìn hai tiêu điểm của



E

dưới một góc vuông.

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 353

b) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



2

:1

4

x

Ey

với hai tiêu điểm

1

F

,

2

F

.

Tìm tọa độ điểm

M

thuộc





E sao cho góc



0

12

60FMF 

.

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

100 25

xy

E  với hai tiêu điểm

1

F ,

2

F .

Tìm tọa độ điểm

M

thuộc





E sao cho góc



0

12

120FMF 

.

d) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

25 9

xy

E  với hai tiêu điểm

1

F ,

2

F

trong đó

1

F có hoành độ âm. Tìm tọa độ điểm

M

thuộc





E

sao cho góc



0

12

120MF F  .

Câu 3: a) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

41

xy

E  và điểm





2;0C

. Tìm tọa độ

các điểm

A

,

B

thuộc





E

, biết rằng

A

,

B

đối xứng với nhau qua trục hoành và tam giác

A

BC là tam giác đều.

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

41

xy

E . Tìm tọa độ các điểm

A

và

B

thuộc





E

có hoành độ dương sao cho tam giác

OAB

cân tại

O

và có diện tích lớn nhất.

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

91

xy

E 

và điểm





3; 0A . Tìm tọa độ

các điểm

B

, C thuộc





E sao cho tam giác

A

BC vuông cân tại

A

, biết

B

có tung độ dương.

Câu 4: a) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

16 5

xy

E 

và hai điểm





5; 1A 

,

(1;1)B 

. Xác đinh tọa độ điểm

M

thuộc



E

sao cho diện tích tam giác

M

AB

lớn nhất.

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

82

xy

E 

và hai điểm



3; 4A

,

(5;3)B

.

Tìm trên



E

điểm

C

sao cho tam giác

A

BC

có diện tích bằng 4,5.

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

21

xy

E 

. Tìm trên



E

những điểm

sao cho khoảng cách từ điểm đó đến đường thẳng

:2 3 1 0dx y

là lớn nhất.

Câu 5: a) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

94

xy

E 

và các điểm



3; 0A 

,



1; 0I 

. Tìm tọa độ các điểm

B

,

C

thuộc





E

sao cho

I

là tâm đường tròn ngoại tiếp tam

giác

A

BC

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 354

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

25 9

xy

E



có hai tiêu điểm

1

F

,

2

F

. Tìm

tọa độ điểm

M

thuộc





E

sao cho bán kính đường tròn nội tiếp tam giác

12

M

FF

bằng

4

3

.

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

25 9

xy

E 

có hai tiêu điểm

1

F

,

2

F

. Tìm

tọa độ điểm

M

thuộc



E

sao cho đường phân giác trong góc



12

FMF

đi qua điểm

48

;0

25

N









.

Câu 1:

Cho Elip



22

: 1

16 9

xy

E 

. Với

M

là điểm bất kì nằm trên



E

, khẳng định nào sau đây là

khẳng định đúng?

A. 45.OM B. 5.OM  C. 3.OM  D. 34.OM

Câu 2:

Elip đi qua điểm

3

1;

2

M









và có tiêu cự bằng

23

thì có phương trình chính tắc là:

A.

22

1

43

xy



. B.

22

1

41

xy



. C.

22

1

31

xy



. D.

22

1

4

xy



.

Câu 3: Cho Elip



22

:1

169 144

xy

E 

và điểm

M

nằm trên





E

. N ếu điểm

M

có hoành độ bằng

13

thì các khoảng cách từ

M

tới

2

tiêu điểm của



E

bằng:

A.

8; 18

. B.

13 5

. C.

10;16

. D.

13 10

.

Câu 4: Cho Elíp có phương trình

22

16 25y 100x 

. Tính tổng khoảng cách từ điểm thuộc elíp có

hoành độ

2x 

đến hai tiêu điểm.

A.

10

. B.

22

. C.

5

. D.

43

.

Câu 5:

Cho Elip



22

:1

25 9



y

E

x

. Đường thẳng





:4dx

cắt



E

tại hai điểm

,

M

N

. Khi đó:

A.

9

25

MN

. B.

18

25

MN

. C.

18

5

MN

. D.

9

5

MN

.

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 355

Câu 6: Cho Elip có phương trình:

22

1

16 4

xy



.

M

là điểm thuộc



E

sao cho

12

M

FMF

. Khi đó

tọa độ điểm

M

là:

A.









12

0;1 , 0; 1MM

. B.

12

(0;2) , (0; 2)MM

.

C.

12

(4;0), (4;0)MM

. D.

12

(0;4) , (0; 4)MM

.

Câu 7: Dây cung của Elip

 

22

:10

xy

Eba

ab

 

. vuông góc với trục lớn tại tiêu điểm có độ dài

là

A.

2

2c

a

. B.

2

2b

a

. C.

2

2a

c

. D.

2

a

c

.

Câu 8: Cho



E

:

22

1

16 9

xy



và điểm

M

thuộc





E

. Khi đó độ dài

OM

thỏa mãn

A.

3OM 

B.

34OM

. C.

45OM

. D.

5OM 

.

Câu 9: Cho



22

:1.

25 9

xy

E 

Đường thẳng

:4dx

cắt



E

tại hai điểm

M

,

N

. Khi đó, độ dài

đoạn

M

N

bằng

A.

9

5

. B.

9

25

. C.

18

5

. D.

18

25

.

Câu 10: Đường thẳng

ykx

cắt





E

:

22

1

xy

ab



tại hai điểm

M

, N phân biệt. Khi đó

M

, N

A. Đối xứng nhau qua





0;0O

. B. Đối xứng nhau qua

Oy

.

C. Đối xứng nhau qua Ox . D. Đối xứng nhau qua





0;1I

.

Câu 11: Cho elip



22

:1

169 144

xy

E 

và điểm

M

thuộc



E

có hoành độ

13

M

x 

. Khoảng cách từ

M

đến hai tiêu điểm của



E

lần lượt là

A. 10 và 6. B. 8 và 18. C. 13 và

5

. D. 13 và

10

Câu 12: Cho elip

²²

(): 1

25 16

xy

E 

, với tiêu điểm

12

,FF

. Lấy hai điểm

,()

A

BE

sao cho

11

A8.FBF

Khi đó,

22

A?FBF

A.

6

. B.

8

. C.

12

. D.

10

.

Câu 13: Cho elip

²²

(): 1

25 9

xy

E 

. Tìm toạ độ điểm

()

M

E

sao cho M nhìn

12

,FF

dưới một góc

vuông:

A.

(5;0)

. B.

9

4;

5









. C.

(0;4)

. D.

579

;

44







.

Câu 14: Trong mặt phẳng tọa độ

Oxy

cho



22

:1

16 5

xy

E 

và hai điểm









5; 1 , 1;1AB 

. Điểm

M

bất kì thuộc



E

, diện tích lớn nhất của tam giác

M

AB

là:

A.

18

. B.

9

. C.

92

2

. D.

42

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 356

Câu 15: Trong mặt phẳng với hệ tọa độ

Oxy

, cho elip



E

:

22

440xy

. Tìm tất cả những điểm N

trên elip





E

sao cho:



0

12

60FNF 

(

1

F

,

2

F

là hai tiêu điểm của elip



E

)

A.

42 1

;

33

N









hoặc

421

;

33

N









hoặc

42 1

;

33

N









hoặc

421

;

33

N







.

B.

42 1

;

33

N









hoặc

421

;

33

N









hoặc

421

;

33

N







.

C.

421

;

33

N









hoặc

42 1

;

33

N









hoặc

421

;

33

N







.

D.

42 1

;

33

N









hoặc

421

;

33

N







.

Câu 16: Các hành tinh và các sao chổi khi chuyển động xung quanh mặt trời có quỹ đạo là một đường

elip trong đó tâm mặt trời là một tiêu điểm. Điểm gần mặt trời nhất gọi là điểm cận nhật, điểm

xa mặt trời nhất gọi là điểm viễn nhật. Trái đất chuyển động xung quanh mặt trời theo quỹ đạo

là một đường elip có độ dài nửa trụ

c lớn bằng

93.000.000

dặm. Tỉ số khoảng cách giữa điểm

cận nhật và điểm viễn nhật đến mặt trời là

59

.

61

Tính khoảng cách từ trái đất đến mặt trời khi

trái đất ở điểm cận nhật. Lấy giá trị gần đúng.

A. Xấp xỉ

91.455.000

dặm. B. Xấp xỉ

91.000.000

dặm.

C. Xấp xỉ

91.450.000

dặm. D. Xấp xỉ

91.550.000

dặm.

Câu 17: Ông Hoàng có một mảnh vườn hình elip có chiều

dài trục lớn và trục nhỏ lần lượt là

60m

và

30m

.

Ông chia thành hai nửa bằng một đường tròn tiếp

xúc trong với elip để làm mục đích sử dụng khác

nhau. N ửa bên trong đường tròn ông trồng cây lâu

năm, nửa bên ngoài đường tròn ông trồng hoa màu.

Tính tỉ số diện tích T giữa phần trồng cây lâu năm

so với diện tích trồng hoa màu. Biết diện tích elip

được tính theo công thức

Sab





trong đó

,ab

lần

lượt là đọ dài nửa trục lớn và nửa trục bé của elip. Biết độ rộng của đường elip không đáng kể.

A.

2

3

T 

. B.

1T 

. C.

1

2

T 

. D.

3

2

T 

.

Mat troi

Trái dát

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 1

BÀI 22. BA ĐƯỜNG CONIC

1. ELIP

- Cho hai điểm cố định và phân biệt

1

F

,

2

F

. Đặt

12

20FF c

. Cho số thực a lớn hơn c . Tập

hợp các điểm

M

sao cho

12

2

M

FMF a được gọi là đường elip . Hai điểm

1

F ,

2

F được gọi

là hai tiêu điểm và

12

2FF c được gọi là tiêu cự của elip đó.

- Trong mặt phẳng tọa độ

Oxy

, elip có hai tiêu điểm thuộc trục hoành sao cho

O

là trung điểm

của đọan thẳng nối hai tiêu điểm đó thì có phương trình

22

1

xy

ab



, với 0ab.





2

Ngược lại, mỗi phương trình có dạng





2

đều là phương trình của elip có hai tiêu điểm





22

1

;0Fab

,





22

2

;0Fab

, tiêu cự

22

22cab

và tổng các khoảng cách từ mỗi

điểm thuộc elip đó tới hai tiêu điểm bằng

2a

.

- Phương trình





2

được gọi là phương trình chính tắc của elip tương ứng.

*Tính chất và hình dạng của Elip: Cho elip có phương trình chính tắc

22

1

xy

ab



, với

0ab

.

● Trục đối xứng

Ox

,

Oy

● Tâm đối xứng

O

.

● Tiêu điểm









12

;0 , ;0Fc Fc

.

● Tọa độ các đỉnh

















1212

;0 , ;0 , 0; , 0;

A

aAaB bBb

.

● Độ dài trục lớn

2a

. Độ dài trục bé

2b

.

● Nội tiếp trong hình chữ nhật cơ sở có kích thước là

2a

và

2b

.

● Tâm sai

1

c

e

a



.

● Hai đường chuNn

a

x

e



và

a

x

e



.

CHƯƠNG

VII

PHƯƠNG PHÁP TỌA ĐỘ

TRONG MẶT PHẲNG

LÝ THUYẾT.

I

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 2

●









;

M

xy E

. Khi đó

1

M

Faex

: bán kính qua tiêu điểm trái.

2

M

Faex

: bán kính qua tiêu điểm phải.

2. HYPEBOL

Trên mặt phẳng, nếu hai thiết bị đặt tại các vị trí

1

F ,

2

F nhận được một tín hiệu âm thanh cùng

lúc thì vị trí phát ra tín hiệu cách đều hai điểm

1

F ,

2

F , và do đó, nằm trên đường trung trực của

đoạn thẳng

12

FF .

Cho hai điểm phân biệt cố định

1

F

,

2

F

. Đặt

12

2FF c

. Cho số thực dương

a nhỏ hơn c . Tập

hợp các điểm

M

sao cho

12

2

M

FMF a

được gọi là đường hypebol . Hai điểm

1

F ,

2

F được

gọi là hai

tiêu điểm và

12

2FF c được gọi là tiêu cự của hypebol đó.

Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung

điểm của đoạn thẳng nối hai tiêu điểm đó thì có phương trình

22

1

xy

ab



, với

,0ab

.

N gược lại, mỗi phương trình có dạng





4

đều là phương trình của hypebol có hai tiêu điểm





22

1

;0Fab

,





22

2

;0Fab

, tiêu cự

22

x

ab

và giá trị tuyệt đối của hiệu các

khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng

2a

.

Phương trình được gọi là phương trình chính tắc của hypebol tương ứng.

3. PARABOL

Cho một điểm

F

cố định và một đường thẳng



cố định không đi qua

F

. Tập hợp các điểm

M

cách đều

F

và



được gọi là đường parabol . Điểm

F

được gọi là tiêu điểm,



được gọi

là đường chuNn, khoảng cách từ

F

đến



được gọi là tham số tiêu của parabol đó.

Xét





P

là một parabol với tiêu điểm

F

, đường chuNn



. Gọi

H

là hình chiếu vuông góc của

F

trên



. Khi đó, trong hệ trục tọa độ

Oxy

với gốc

O

là trung điểm của

H

F

, tia

Ox

trùng

với tia

OF

, parabol





P

có phương trình

2

2ypx



5

Phương trình



5

được gọi là phương trình chính tắc của parabol





P

.

N gược lại, mỗi phương trình dạng



5

, với

0p 

, là phương trình chính tắc của parabol có tiêu

điểm

;0

2

p

F







và đường chuNn

:

2

p

x

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 3

4. MỘT SỐ ỨNG DỤNG CỦA BA ĐƯỜNG CONIC. TÍNH CHẤT QUANG HỌC

Tương tự gương cầu lồi thường đặt ở những khúc đường cua, người ta cũng có những gương

elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phản xạ theo một quy tắc được

xác định rõ bằng hình học, chẳng hạn:

 Tia sáng phát ra từ một tiêu điểm của elip, hypebol sau khi gặp elip, hypebol sẽ bị hắt lại theo một

tia nằm trên đường thẳng đi qua tiêu điểm còn lại .

 Tia sáng hướng tới một tiêu điểm của elip, hypebol , khi gặp elip, hypebol sẽ bị hắt lại theo một tia

nằm trên đường thẳng đi qua tiêu điểm còn lại .

 Với gương parabol lõm, tia sáng phát ra từ tiêu điểm khi gặp parabol sẽ bị hắt lại theo một tia

vuông góc với đường chuNn của parabol . N gược lại, nếu tia tới vuông góc với đường chuNn của parabol

thì tia phản xạ sẽ đi qua tiêu điểm của parabol.

Tính chất quang học được đề cập ở trên giúp ta nhận được ánh sáng mạnh hơn khi các tia sáng hội tụ và

giúp ta đổi hướng ánh sáng khi cần. Ta cũng có

điều tương tự đối với tín hiệu âm thanh, tín hiệu truyền

từ vệ tinh.

MỘT SỐ ỨNG DỤNG

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 4

Ba đường conic xuất hiện và có nhiều ứng dụng trong khoa học và trong cuộc sống, chẳng hạn:

 Tia nước bắn ra từ đài phun nước, đường đi bổng của quả bóng là những hình ảnh về đường

parabol;

 Khi nghiêng cốc tròn, mặt nước trong cốc có hình elip. Tương tự, dưới ánh sáng mặt trời, bóng của

một quả bóng, nhìn chung, là một elip;

 Ánh sáng phát ra từ một bóng đèn Led trên trần nhà có thể tạo nên trên tường các nhánh hypebol;

 N hiều công trình kiến trúc có hình elip, parabol hay hypebol.

7.19 Cho elip có phương trình















 1.Tìm tiêu điểm và tiêu cự của elip

Lời giải

Ta có:















 1 ⇒

󰇥

𝑎



 36

𝑏



 9

Mặt khác 𝑐



𝑎



𝑏



 36  9  27 ⇒𝑐

√

27.

Vậy ta có hai tiêu điểm 𝐹





√

27;0 và 𝐹





√

27;0,có tiêu cự bằng 2𝑐2

√

27.

7.20 Cho hypebol có phương trình:















 1. Tìm tiêu điểm và tiêu cự của hypebol.

Lời giải

Ta có:















 1 ⇒

󰇥

𝑎



 7

𝑏



 9

Mặt khác 𝑐



𝑎



𝑏



 49  81  130 ⇒𝑐

√

130.

Vậy ta có hai tiêu điểm 𝐹





√

130;0 và 𝐹





√

130;0; có tiêu cự bằng 2𝑐2

√

130.

7.21 Cho parabol có phương trình: 𝑦



 8𝑥. Tìm tiêu điểm và đường chuNn của parabol.

Lời giải

Ta có :

BÀI TẬP SÁCH GIÁO KHOA.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 5

2𝑝8 ⇔𝑝4 nên tiêu điểm của parabol 𝐹

󰇡





;0

󰇢

𝐹 và đường chuNn :𝛥: 𝑥













2

.

7.22 Lập phương trình chính tắc của elip đi qua điềm A và có một tiêu điềm là F

2

.

Lời giải

Ta có:Phương trình elip có dạng:



















 1

Do đi qua

𝐴

󰇛

5; 0

󰇜

nên:















 1 ⇒𝑎



 25

Mặc khác: tiêu điểm

𝐹



󰇛

3; 0

󰇜

nên ⇒𝑐3  𝑐



 9 𝑎



𝑏



Từ và =>

𝑏



 16nên :















 1

7.23 Lập phương trình chính tắc của parabol đi qua điểm 𝑀

Lời giải

Giả sử : 𝑦



 2𝑝𝑥

Vì đi qua 𝑀 nên:16  2𝑝.2  𝑝  4.Vậy 𝑦



 8𝑥

7.24 Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời

điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch

thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác

định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính tắc của hypebol đó theo

đơn vị kilômét.

Lời giải

Ta có:

Do tín hiệu A đến sớm hơn tín hiệu từ B nên tàu thuỷ thuộc đường hepebol nhánh A.

Gọi vị trí tàu thuỷ là điểm M.

Phương trình hyperbol có dạng:

:



















 1

|

𝑀𝐴  𝑀𝐵

|

 2𝑎292000𝑥0,0005  146𝑘𝑚 ⇒ 𝑎  73

𝐴𝐵  300𝑘𝑚  2𝑐⇒𝑐150

Từ đó,

𝑏



𝑐



𝑎



 17171

Vậy phương trình hyperbol

:



















 1

7.25 Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A điểm cuối là

B, khoảng cách

𝐴𝐵  400𝑚. Đỉnh parabol của khúc cua cách đường thẳng 𝐴𝐵 một khoảng 20

m và cách đều A, B .

a).Lập phương trình chính tắc của , với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 m trên

thực tế.

b). Lập phương trình chính tắc cùa , với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 km

trên thực tế.

Lời giải

a) Phương trình chính tắc : 𝑦



 2𝑝𝑥

Theo đề ta có

𝐴, 𝐵, 𝑂

Do đi qua

𝐴 nên suy ra 20



 2𝑝400 ⇒𝑝1

Vậy

: 𝑦



2𝑥

b) Phương trình chính tắc

: 𝑦



 2𝑝𝑥

Theo đề ta có

𝐴, 𝐵, 𝑂

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 6

Do đi qua 𝐴 nên suy ra 0,02



 2𝑝0,4 ⇒𝑝0,001

Vậy

: 𝑦



0,002𝑥

DẠNG 1: XÁC ĐNNH CÁC YẾU TỐ CỦA ELÍP

{ Xác định các đỉnh, độ dài các trục, tiêu cự, tiêu điểm. của elip}

Cho Elip có phương trình chính tắc:



22

:1

xy

E

ab



với

222

bac

.

● Tiêu điểm









12

;0 , ;0Fc Fc

.

● Tọa độ các đỉnh

















1212

;0 , ;0 , 0; , 0;Aa Aa B bB b

.

● Độ dài trục lớn

2a

.

● Độ dài trục bé

2b

.

● Tiêu cự

2c

Câu 1:

Tìm tọa độ các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip:



22

:1

41

xy

E 

.

Lời giải

Từ phương trình của

22

3cab



E

, ta có

2, 1ab

. Suy ra

22

3cab

.

Suy ra tọa độ các đỉnh là

















1212

2; 0 ; 2;0 ; 0; 1 ; 0;1AABB

.

Độ dài trục lớn

12

4AA 

, độ dài trục bé

12

2BB 

.

Tiêu cự

12

223FF c

, tiêu điểm là









12

3;0 ; 3;0FF

.

Tâm sai của

22

3cab

là

3

2

c

e

a



.

Câu 2: Tìm tọa độ các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip:





22

:4 25 100Ex y

.

Lời giải

HỆ THỐNG BÀI TẬP.

II

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 7

Ta có

22

425100 1

25 4

xy

xy

suy ra

5; 2ab

nên

22

21cab

.

Do đó tọa độ các đỉnh là

















1212

5;0; 5;0; 0; 2; 0;2AABB

.

Độ dài trục lớn

12

10AA 

, độ dài trục bé

12

4BB 

.

Tiêu cự

12

2221FF c

, tiêu điểm là









12

21;0 ; 21;0FF

.

Tâm sai của





E

là

21

5

c

e

a



.

Câu 3: Tìm tọa độ các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip:





22

:4 9 1Ex y

.

Lời giải

Ta có

22

491 1

11

49

xy

xy

suy ra

11

;

23

ab

nên

22

5

6

cab

.

Do đó tọa độ các đỉnh là

1212

11 11

;0 ; ;0 ; 0; ; 0;

22 33

AABB









.

Độ dài trục lớn

12

1AA 

, độ dài trục bé

12

2

3

BB 

.

Tiêu cự

12

25

2

6

FF c

, tiêu điểm là

12

55

;0 ; ;0

66

FF









.

Tâm sai của





E

là

5

3

c

e

a



.

Câu 4: Tìm tâm sai của Elíp biết:

a) Mỗi tiêu điểm nhìn trục nhỏ dưới một góc 60

0

.

b) Đỉnh trên trục nhỏ nhìn hai tiêu điểm dưới một góc 60

0

.

c) Khoảng cách giữa hai đỉnh trên hai trục bằng hai lần tiêu cự:

Lời giải

a) Từ giả thiết, ta có:

tan30 .tan30

b

bc

c

   

Suy ra:

c

e

a



22 2

2 2

22222 2 2

1

cos 30

.tan 30 tan 30 1

cc c

e

abcc c

     



F

2

B

1

B

2

O

c

b

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 8

3

cos30

2

e 

b) Từ giả thiết, ta có

cot 30 .cot 30

b

bc

c

   

Suy ra:

c

e

a



22 2

2 2

22222 2 2

1

sin 30

.cot 30 cot 30 1

cc c

e

abcc c

     



1

sin 30

2

e 

c) Từ giả thiết, ta có:

22

4

A

Bc

22 22 2

416ab c ab c

2

222 2 2

15

16

2

c

cbb c b 

.

Suy ra:

c

e

a



22 2

2

222

2

15

17

2

cc c

e

c

abc

c

   



34

2

e

Câu 1:

Cặp điểm nào là các tiêu điểm của elip



E

:

22

1

54

xy



?

A.





1,2

0; 1F 

. B.





1,2

1; 0F 

. C.





1,2

3; 0F 

. D.





1,2

1; 2F 

.

Lời giải

Chọn B.

Ta có:

22 222

5; 4 1ab cab

1c



1,2

1; 0F

.

Câu 2:

Cho Elip





22

:4 9 36Ex y

. Mệnh đề nào sai trong các mệnh đề sau:

A.



E

có tỉ số

5

3

c

a



. B.





E

có trục lớn bằng

6

.

C.



E

có trục nhỏ bằng

4

. D.





E

có tiêu cự

5

.

Lời giải

Chọn D.

BÀI TẬP TRẮC NGHIỆM.

3

b

B

2

O

A

a

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 9



22

:4 9 36 1

94

xy

Ex y

Suy ra:

3, 2, 5abc

Tiêu cự của



E

là

225c 

.

Câu 3: Cho elip

22

1

31

xy



. Phát biểu nào sau đây đúng?

A. Tỉ số giữa trục lớn và trục nhỏ bằng

3

. B. Tiêu cự bằng

4

.

C. Tâm sai

2

3

e 

. D. Hai tiêu điểm



1

2;0F 

và



2

2; 0F

.

Lời giải

Chọn A.

Ta có

2

22

2

222

33

(): 1 1 1

31

22

aa

xy

Ebb

cab c







 











.

Câu 4: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip

A.

4² 8² 32xy

. B.

²²

1

11

52

xy



.

C.

²²

1

64 16

xy



. D.

²²

1

84

xy



.

Lời giải

Chọn A.

Vì

4² 8² 32xy

²²

1

84

xy



.

Câu 5: Cho elip

²²

(): 1

94

xy

E 

. Chọn khẳng định sai

A. Điểm

(3;0) ( )

A

E

. B.

()E

có tiêu cự bằng

25

.

C. Trục lớn của

()E

có độ dài bằng

6

. D.

()E

có tâm sai bằng

35

5

.

Lời giải

Chọn D.

Có

²9 3

²²

(): 1 ² 4 2

94

²²²5 5

aa

xy

Ebb

cab c







 









.

Khi đó

()E

có tâm sai bằng

5

3

c

e

a



.

Câu 6: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip

A.

22

2xy

. B.

22

2xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 10

C.

22

22xy. D.

22

2

x

y .

Lời giải

Chọn C.

Vì

22

22xy

²²

1

21

xy



.

Câu 7: Trong mặt phẳng





Oxy , cho elip



E có phương trình

22

1

36 16

xy



. Tìm tiêu cự của



E .

A.

12

12FF 

B.

12

8FF 

C.

12

25FF  D.

12

45FF 

Lời giải

Chọn D

22

1

36 16

xy



6

4

a

b













222

cab

20

25c

12

45FF.

Câu 8: Trong mặt phẳng

Oxy

, tìm tiêu cự của elip



22

:1

25 16

xy

E .

A.

3

B.

6

C.

4

D.

5

Lời giải

Chọn B

Ta có

2

25

25 16 9 3

16

a

cc

b

















.

Vậy tiêu cự

26c 

.

Câu 9: Tìm các tiêu điểm của Elip

22

1

91

xy



A.





1

3; 0 ;F





2

0; 3F  . B.





1

8;0 ;F





2

0; 8F 

.

C.





1

3; 0 ;F 





2

0; 3F 

. D.





1

8;0 ;F 





2

8;0F .

Lời giải

Chọn D.





E

:

22

1

91

xy

 có

3a 

;

1b 

22

8cab   .

Vậy





E

có các tiêu điểm là:





1

8;0 ;F 





2

8;0F

.

Câu 10: Elíp có độ dài trục lớn bằng:

A.

25

. B.

50

. C.

10

. D.

5

.

Lời giải

Chọn C

22

(): 1

25 9

xy

E 

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 11

Từ phương trình



22

:1

25 9

xy

E 

5a

.

Do đó





E có độ dài trục lớn là

210a 

.

Câu 11: Cho

22

9 25 225xy. Hỏi diện tích hình chữ nhật cơ sở ngoại tiếp





E là

A.

15

. B.

30

. C.

40

. D.

60

.

Lời giải

Chọn D.

Phương trình chính tắc của





E

:

22

1

25 9

xy

.

Ta có

2

25

9

a

b















5

3

a

b













.

Diện tích hình chữ nhật cơ sở ngoại tiếp





E

là

4Sab 60

.

Câu 12: Cho





E

có độ dài trục lớn bằng

26

, tâm sai

12

.

13

e 

Độ dài trục nhỏ của





E

bằng

A.

5

. B.

10

. C.

12

D.

24

.

Lời giải

Chọn B.

Ta có

226 13aa

.

12

13

c

ec

a

 

.

22

169 144 5bac .

Độ dài trục nhỏ là

210b 

.

Câu 13: Cho





22

:16 25 100Ex y và điểm

M

thuộc





E có hoành độ bằng

2

. Tổng khoảng cách

từ

M

đến

2

tiêu điểm của





E bằng

A.

5

. B. 22. C.

43

.

D.

3

.

Lời giải

Chọn A.

Ta có:



22

:1

100 100

16 25

xy

E 

2

100

16

100

25

a

b



















5

2

a

b

















Theo định nghĩa Elip thì với mọi điểm





M

E

ta có:

12

25MF MF a.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 12

Câu 14: Cho elip



22

:1

54

xy

E 

. Tỉ số giữa tiêu cự và độ dài trục lớn bằng

A.

5

4

. B.

5

. C.

35

5

. D.

25

5

.

Lời giải

Chọn B.

Ta có:

2

55aa ;

2

42bb

22

1cab  

.

Vậy tỉ số giữa tiêu cự và độ dài trục lớn bằng

25

c

a



.

Câu 15: Phương trình chính tắc của





E

có độ dài trục lớn gấp

2

lần độ dài trục nhỏ và đi qua điểm





2; 2A 

là

A.

22

1

24 16

xy

. B.

22

1

36 9

xy

. C.

22

1

16 4

xy

. D.

22

1

20 5

xy



Lời giải

Chọn D.

Gọi phương trình elip là



22

:1

xy

E

ab



.

Theo bài ra ta có:

22

4

44

1

ab















22

4

44

1

4

ab

bb

















2

20

5

a

b

















.

Vậy phương trình elip là



22

:1

20 5

xy

E .

Câu 16: Phương trình chính tắc của





E

nhận điểm





4;3M

là một đỉnh của hình chữ nhật cơ sở là

A.

22

1

16 9

xy

. B.

22

1

16 4

xy

. C.

22

1

16 3

xy

. D.

22

1

94

xy



Lời giải

Chọn A.

Gọi phương trình elip là



22

:1

xy

E

ab

.

Vì





4;3M

là một đỉnh của hình chữ nhật cơ sở nên

4a 

,

3b 

.

Vậy phương trình elip là



22

:1

16 9

xy

E .

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 13

Câu 17: Phương trình chính tắc của





E

có khoảng cách giữa các đường chuNn bằng

50

3

và tiêu cự

bằng

6

là

A.

22

1

64 25

xy

. B.

22

1

89 64

xy

. C.

22

1

25 16

xy

. D.

22

1

16 7

xy



Lời giải

Chọn C.

Gọi phương trình elip là

22

1

xy

ab



.

Theo bài ra ta có

2

25

3

26

a

c





















222

16bac

.

Vậy phương trình elip là

22

1

25 16

xy

.

Câu 18: Trong mặt phẳng

Ox

y

, cho đường elip



22

:1

94

xy

E 

có hai tiêu điểm

1

F

,

2

F

.

M

là điểm

thuộc





E

. Tính

12

M

FMF

.

A.

5

B.

6

C.

3

D.

2

Lời giải

Chọn B

Phương trình của



E

có dạng

22

1

xy

ab



(

222

abc

). Suy ra

2

9a 

3a

.

Do

M

thuộc



E

nên

12

2

M

FMF a

6

.

Câu 19: Trong mặt phẳng Oxy cho elip





22

:36Ex y. Giá trị nào sau đây là tiêu cự của elip?

A.

2

B.

3

C.

6

D.

4

Lời giải

Chọn D

Ta có



22

:1,

62

xy

E 

dó đó

6, 2, 2ab c 

. Độ dài tiêu cự là

24.c 

Câu 20: Trong hệ trục tọa độ





Oxy

, cho elip



22

44

:1

25 9

xy

E . Độ dài tiêu cự của





E

bằng

A.

4

. B.

8

. C.

16

. D.

2

.

Lời giải

Chọn A.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 14

Ta có



22

44

:1

25 9

xy

E 

22

1

25 9

44

xy



22

1

53

22

xy



 

 

 

.

Do đó

22

5

2

3

2

a

cab

b







  











. Vậy độ dài tiêu cự là

12

24FF c.

Câu 21: Cho elip



22

:1

25 9

xy

E . Trong các khẳng định sau, khẳng định nào sai?

A.





E

có các tiêu điểm





1

4;0F 

và





2

4;0F

.

B.





E

có tỉ số

4

5

c

a



.

C.





E

có đỉnh





1

5; 0A 

.

D.





E

có độ dài trục nhỏ bằng

3

.

Lời giải

Chọn D

Phương trình elip



22

:1

25 9

xy

E  nên ta có:

5; 3 4ab c

.

N ên các đáp án

A;B;C đúng.

Đáp án

D sai vì độ dài trục nhỏ bằng

26b 

.

Câu 22: Trong mặt phẳng

Ox

y

cho





E

có phương trình:

22

1

94

xy



khẳng định nào sau đây đúng?

A.





E có tâm sai

5

3

e 

.

B.



12

0; 5 , 0; 5FF là các tiêu điểm của





E

.

C. Độ dài trục lớn là

9

.

D. Các đỉnh nằm trên trục lớn là





1

0;3A

và



2

0; 3A 

.

Lời giải

Chọn A

Ta có:

2

93

2

4

aa

b



















Mà

222

945 5cab c

A.





E

có tâm sai

5

3

c

e

a



. Đúng

B. Tiêu điểm của





E

là:



12

5;0 , 5;0FF . Sai

C.

Độ dài trục lớn là :

12

26AA a. Sai

D. Các đỉnh trên trục lớn là :



12

3; 0 , 3; 0AA

. Sai

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 15

Câu 23: Cho Elip có phương trình

2

1

4

x

y

. Một tiêu điểm của Elip có tọa độ là:

A.





3;0A

.

B.





0; 3B

.

C.





5;0C

.

D.



0; 5D

.

Lời giải

Chọn A.

Ta có:

222

413cab

.

N ên tiêu điểm của Elip có tọa độ là:









12

3;0 , 3;0FF

.

Câu 24: Cho Elip có phương trình

22

41xy. Tiêu cự của Elip là:

A. 5. B. 3. C. 25. D. 23.

Lời giải

Chọn B

2

22 2

41 1

1

4

y

xy x.

Ta có :

222

13

1

44

cab

3

2

c

.

Tiêu cự là

23c  .

Câu 25: Diện tích của tứ giác tạo nên bởi các đỉnh của elip



2

:1

4

x

Ey là

A.

8

. B.

4

. C.

2

. D.

6

.

Lời giải

Chọn B.

* Tọa độ các đỉnh của elip



2

:1

4

x

Ey là





1

2;0A 

,



2

2;0A

;





1

0; 1B 

,





2

0;1B

.

* Vì tứ giác

112 2

A

BAB là hình thoi có hai đường chéo

12

4AA  và

12

2BB  .

* Vậy diện tích tứ giác cần tìm là

12 12

1

.4

2

SAABB 

.

Câu 26: Trong mặt phẳng

Ox

y

cho elip có phương trình



22

:1

25 9

xy

E . Đường thẳng

:4x

cắt

elip





E

tại hai điểm

,

M

N

. Tính độ dài đoạn thẳng

M

N

?

A.

18

25

MN 

. B.

9

25

MN 

. C.

18

5

MN 

. D.

9

5

MN 

.

Lời giải

Chọn C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 16

Thế

4x 

vào phương trình elip





E ta được:

2

16

1

25 9

y



9

5

y

.

9

4; ,

5

M









9

4;

5

N









Do đó:

18

5

MN 

.

Câu 27: Trong hệ tọa độ





Oxy , cho elip



22

:1

25 16

xy

E 

. Bán kính qua tiêu của





E đạt giá trị nhỏ

nhất bằng

A.

0

B.

1

C.

3

5

D.

2

Lời giải

Chọn D.

Từ phương trình elip ta có

22

5

3

4

a

cab

b





  







. Bán kính qua tiêu là

1

c

M

Fa x

a



với

axa 

. Suy ra

1

ac MF ac  hay



1

min

532MF a c

.

Câu 28: Một elip





E có phương trình

22

1

xy

ab



, trong đó

0ab

. Biết





E đi qua điểm



2; 2A và





22;0B thì





E

có độ dài trục bé là

A.

4.

B.

22.

C.

2.

D.

6.

Lời giải

Chọn A.





E đi qua



22;0B

nên ta có





2

22

0

1

ab



suy ra 22a  .





E

đi qua



2; 2A nên ta có







2

1

8 b



suy ra

2b 

.

Do đó độ dài trục bé

24b 

.

Câu 29: Cho





E

có hai tiêu điểm





1

4;0F 

,





2

4;0F

và điểm

M

thuộc





E

. Biết chu vi tam giác

12

M

FF bằng

18

. Khi đó tâm sai của





E

bằng

A.

4

18

. B.

4

5

. C.

4

5



. D.

4

9



.

Lời giải

Chọn B.

Ta có

12

8FF  và

4c 

.

12

1212 12

18 10 2 5

MF F

CMFMFFF MFMF aa



 

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 17

Tâm sai của elip:

4

5

c

e

a



.

Câu 30: Cho





E có hai tiêu điểm





1

7;0F 

,





2

7;0F

và điểm

9

7;

4

M









thuộc





E . Gọi

N

là

điểm đối xứng với

M

qua gốc tọa độ

.O

Khi đó

A.

12

9

2

NF MF

. B.

21

9

2

NF MF

. C.

21

7

2

NF NF

D.

12

8NF MF.

Lời giải

Chọn B.

N

đối xứng với

M

qua gốc tọa độ

O

nên

9

7;

4

N









.

Ta có:

12 1 2

923239

;;;

4444

MF MF NF NF  

.

Do đó

21

9

.

2

NF MF

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 18

DẠNG 2: VIẾT PHƯƠNG TRÌNH CHÍNH TẮC CỦA ELIP

{ Phương trình chính tắc của Elip có dạng:



22

:1

xy

E

ab



với

222

bac

; …}

Câu 1:

Lập phương trình chính tắc của Elip, biết:

a) Elip đi qua điểm

5

2;

3

M







và có một tiêu điểm





1

2;0F 

.

b) Elip nhận





2

5; 0F

là một tiêu điểm và có độ dài trục nhỏ bằng

46

.

c) Elip có độ dài trục lớn bằng

25 và tiêu cự bằng 2.

d) Elip đi qua hai điểm





2; 2M  và





6;1N  .

Lời giải

a) Do



E

có một tiêu điểm





1

2;0F 

nên 2c  . Suy ra

2222

4abcb

.

Mặt khác,





E

đi qua điểm

5

2;

3

M







nên

2

22 2 2

5

2425

3

11

49ab b b







 



42 2

9 25 100 0 5bb b 

hoặc

2

20

9

b 

.

Vậy Elip cần tìm có phương trình



22

:1

95

xy

E 

.

b) Do





E

có một tiêu điểm





2

5; 0F

nên 5c  .

Theo giả thiết độ dài trục nhỏ bằng

4 6 nên 246 26bb.

Suy ra





2

2222

526 49abc .

Vậy Elip cần tìm có phương trình



22

:1

49 24

xy

E .

c) Độ dài trực lớn bằng

2 5 nên 225 5aa. Tiêu cự bằng 2 nên

22 1cc

.

Từ hệ thức

222

abc

, suy ra

222

51 4bac

.

Vậy Elip cần tìm có phương trình



22

:1

54

xy

E .

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 19

d) Do





E

đi qua





2; 2M 

và





6;1N 

nên ta có hệ phương trình

2

22 2

2

22 2

42 11

1

8

61 11

4

1

4

a

ab a

b

ab b



 





















 





.

Vậy Elip cần tìm có phương trình



22

:1

84

xy

E 

.

Câu 2: Lập phương trình chính tắc của Elip, biết:

a) Elip có tổng độ dài hai trục bằng 8 và tâm sai

1

2

e  .

b) Elip có tâm sai

5

3

e 

và hình chữ nhật cơ sở có chu vi bằng 20.

c) Elip có tiêu điểm





1

2;0F 

và hình chữ nhật cơ sở có diện tích bằng 12 5 .

Lời giải

a) Tổng độ dài hai trục bằng 8 nên

228ab

.



1

Tâm sai

11

2

22

c

eac

a

 .





2

Từ



1

và





2

, ta có

228

4

24 42

1

2

22

2

ab

cb b c

c

e

ac

ac ac

a











 



 





















.

Thay vào hệ thức

222

abc

, ta được





2

222

242 82160 424ccccc c   .

● Với

42 4c , suy ra

842

442

a

b









 





: không thỏa mãn.

● Với

42 4c 

, suy ra

842

442

a

b









 





. Do đó Elip cần tìm có phương trình





22

:1

842 424

xy

E 



.

b) Elip có tâm sai

553

33

5

c

eac

a

 .



1

Mặt khác, Elip có hình chữ nhật cơ sở có chu vi bằng 20 nên





22 2 20 5 5ab ab b a

.





2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 20

Thay



1

và





2

vào hệ thức

222

abc

, ta được



222

2

222

55

33330

55 250

5555

5

c

cac c cccc

c





  

    



  

  







.

● Với

55c  , suy ra

15

10

a

b











: không thỏa mãn.

● Với

5c 

, suy ra

3

2

a

b











. Do đó Elip cần tìm có phương trình



22

:1

94

xy

E 

.

c) Elip có một tiêu điểm





1

2;0F 

nên 2c  .

Diện tích hình chữ nhật cơ sở

22

2.2 12 5 35 45Sab ab ab.



1

Mặt khác, ta có

2222

4abcb

.





2

Kết hợp



1

và





2

, ta được





22 2 2 4 2 2

45 4 45 4 45 0 5ab b b b b b   

hoặc

2

9b 

.

Với

2

5b 

, suy ra

2

9a 

. Do đó Elip cần tìm có phương trình



22

:1

95

xy

E 

.

Câu 3: Lập phương trình chính tắc của Elip, biết:

a) Elip đi qua điểm



5;2M  và khoảng cách giữa hai đường chuNn bằng 10.

b) Elip có tâm sai

3

5

e 

và khoảng cách từ tâm đối xứng của nó đến một đường chuNn bằng

25

3

.

c) Elip có độ dài trục lớn bằng 10 và phương trình một đường chuNn là

25

4

x 

.

d) Khoảng cách giữa các đường chuNn bằng 36 và bán kính qua tiêu điểm của điểm

M

thuộc

Elip là 9 và 15.

Lời giải

a) Elip đi qua điểm



5;2M  nên

22

54

1

ab



.



1

Khoảng cách giữa hai đường chuNn của Elip bằng 10 nên

2

2. 10 5 5 5

aaa

ac

eec

     .





2

Từ





2

, kết hợp với hệ thức

222

abc

, ta được

222 2

5bac cc

.





3

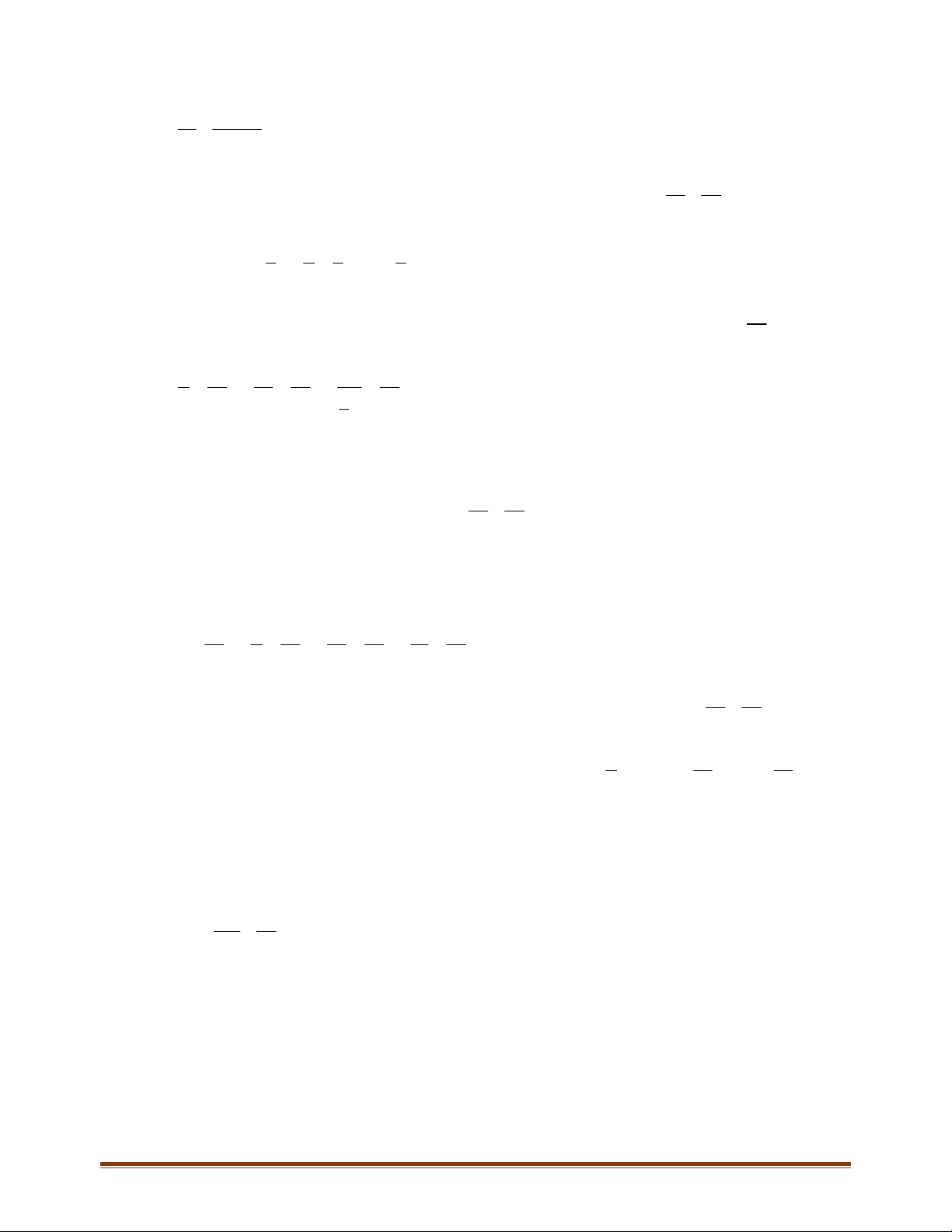
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 21

Thay





2

,





3

vào



1

, ta được

2

54

16903

55

cc c

ccc





.

Với

3c  , suy ra

2

15

6

a

b















. Do đó Elip cần tìm có phương trình



22

:1

15 6

xy

E 

.

b) Ta có

333

555

c

eca

a



.

Elip có khoảng cách từ tâm đối xứng

O đến một đường chuNn một khoảng bằng

25

3

nên

22

25 25 25

5

3

33 3

5

aa a

a

ec

a

 .

Với

5a 

, suy ra

3c 

và

222

16bac

.

Do đó Elip cần tìm có phương trình



22

:1

25 16

xy

E 

.

c) Elip có độ dài trục lớn bằng 10 nên

210 5aa

.

Mặt khác, Elip có phương trình một đường chuNn

22

25 25 25 5 25

4

44 4 4

aa

xc

ec c



.

Suy ra

222

25 16 9bac

. Do đó Elip cần tìm có phương trình



22

:1

25 9

xy

E .

d) Elip có khoảng cách giữa hai đường chuNn bằng 36 nên

22

2. 36 2. 36 18

aaa

ecc

  

.

Mặt khác, ta có

1

2

9

15

MF a ex

 





 



suy ra

224 12aa

.

Với

12a 

, suy ra

8c 

và

222

144 64 80bac 

. Do đó Elip cần tìm có phương trình



22

:1

144 80

xy

E .

Câu 4: Lập phương trình chính tắc của Elip, biết:

a) Elip có hình chữ nhật cơ sở nội tiếp đường tròn



22

:41Cx y

và đi qua điểm





0;5A

.

b) Elip có hình chữ nhật cơ sở nội tiếp đường tròn



22

:21Cx y

và điểm





1; 2M

nhìn hai

tiêu điểm của Elip dưới một góc

0

60

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 22

c) Một cạnh hình chữ nhật cơ sở của Elip nằm trên :50dx và độ dài đường chéo hình

chữ nhật bằng 6.

d) Tứ giác

A

BCD là hình thoi có bốn đỉnh trùng với các đỉnh của Elip. Bán kính của đường

tròn nội tiếp hình thoi bằng

2 và tâm sai của Elip bằng

1

2

.

Lời giải

a) Elip đi qua



0;5AOy

, suy ra

5b 

.

Phương trình các cạnh của hình chữ nhật cơ sở là:

;5xay 

.

Suy ra một đỉnh của hình chữ nhật cơ sở là





;5a

. Theo giả thiết





;5a

thuộc đường tròn





C

22

25 41 16aa

.

Vậy Elip cần tìm có phương trình



22

:1

16 25

xy

E 

.

b) Theo giả thiết bài toán, ta có



0

12

60FMF  suy ra

222 0

12 1 2 1 2

2..cos60F F MF MF MF MF

   

22 22

2

1

41 41 421 4.1 4.

2

cc c c c  

   

22 22

22 2

4 2 10 1 4. 1 4 1 4. 1 4 10 2cc cc cc c  

 



2

22

2

42

10 2 0

05

23 4 19

.

3

14.14102

346750

c

cc c

cc



















 











Phương trình các cạnh của hình chữ nhật cơ sở là:

;

x

a

y

b 

.

Suy ra một đỉnh của hình chữ nhật cơ sở là





;ab

. Theo giả thiết





;ab

thuộc đường tròn





C

nên

22

21ab

.

Lại có

222

abc

, suy ra

22 2

abc

.

● Với

2

23 4 19

3

c





, ta có

22

2

22

2

43 2 19

21

3

23 4 19

20 2 19

3

ab

a

ab

b



































.

Suy ra



22

:1

43 2 19 20 2 19

33

xy

E 



.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 23

● Với

2

23 4 19

3

c





, ta có

22

2

22

2

43 2 19

21

3

23 4 19

20 2 19

3

ab

a

ab

b



































.

Suy ra



22

:1

43 2 19 20 2 19

33

xy

E 



.

Vậy có hai Elip cần tìm thỏa yêu cầu bài toán:



22

:1

43 2 19 20 2 19

33

xy

E 



hoặc



22

:1

43 2 19 20 2 19

33

xy

E 



.

c) Phương trình các cạnh của hình chữ nhật cơ sở là:

;

x

a

y

b 

.

Theo giả thiết, một cạnh hình chữ nhật cơ sở là

:50dx

, suy ra 5a  .

Độ dài đường chéo hình chữ nhật cơ sở bằng 6 nên

22 22 2 2

4 4 64 4 36204 36 4ab ab b b

.

Vậy Elip cần tìm có phương trình



22

:1

54

xy

E .

d) Elip có tâm sai

11

2

22

c

eac

a



.

Elip có các đỉnh

















1212

;0 , ;0 , 0; , 0;Aa Aa B bB b

. Gọi

H

là hình chiếu của

O

lên

22

A

B .

Theo giả thiết suy ra bán kính của đường tròn đã cho bằng

OH

. Ta có

2

222 22 222 22

111111111 111 7

224 2436

c

OH OA OB a b c a c c c

 



.

Suy ra

22

14

4

3

ac

và

222

7

2

bac

.

Vậy Elip cần tìm có phương trình



22

:1

14 7

32

xy

E 

.

Câu 5: Lập phương trình chính tắc của Elip, biết

a) Tứ giác

A

BCD

là hình thoi có bốn đỉnh trùng với các đỉnh của Elip. Đường tròn tiếp xúc với

các cạnh của hình thoi có phương trình





22

:4Cx y

và

2

A

CBD

,

A

thuộc

Ox

.

b) Elip có độ dài trục lớn bằng 8 và giao điểm của Elip với đường tròn





22

:8Cx y

tạo

thành bốn đỉnh của một hình vuông.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 24

c) Elip có tâm sai

1

3

e 

và giao điểm của Elip với đường tròn





22

:9Cx y

tại bốn điểm A

,

B

,

C

, D sao cho

A

B song song với

Ox

và

3

A

BBC

.

d) Elip có độ dài trục lớn bằng

42

, các đỉnh trên trục nhỏ và các tiêu điểm của Elip cùng nằm

trên một đường tròn.

Lời giải

a) Giả sử một đỉnh của hình thoi là





;0Aa

. Suy ra 2

A

Ca và 2BD b .

Theo giả thiết

222.2 2

A

CBD a bab

.

Đường tròn





C

có 2

R

 . Gọi H là hình chiếu của

O

lên

A

B với





0;

B

b

. Khi đó ta có

22 22

11 111

4OA OB OH R

 

2

22 22

111 1 11

5

44 4

b

ab bb

 

.

Suy ra

2

20a 

. Vậy Elip cần tìm có phương trình



22

:1

20 5

xy

E .

b) Elip có độ dài trục lớn bằng 8 nên

28 4aa

.

Do





E

và





C

đều có tâm đối xứng là

O

và hai trục đối xứng là

Ox

và

Oy

nên hình vuông

tạo bởi giữa chúng cũng có tính chất tương tự. Do đó ta giả sử gọi một đỉnh của hình vuông là





;

M

xx

với

0x 

. Vì





M

C

22 2

84xx x

suy ra





22;2xM

.

Ta có



2

22 2

44 44 16

11

16 3

ME b

ab b



.

Vậy Elip cần tìm có phương trình



22

:1

16

3

xy

E .

c) Elip có tâm sai

11

3

33

c

eac

a



.

Đặt

BC x

với

0x 

, suy ra

3

A

Bx

. Giả sử một đỉnh

31

;

22

A

xx







. Ta có



22 2

91 18

9

44 5

AC x x x  

suy ra

310 910310

;

51010

xA









.

Mặt khác,

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 25



2

22 22

22

81 9 81 9 9 9 81

111

10 10 10 80 80

10

10 3

AE c

ab cc

ac

c

      



.

Suy ra

22

729

9

80

ac

và

222

81

10

bac

.

Vậy Elip cần tìm có phương trình



22

:1

729 81

80 10

xy

E .

d) Độ dài trục lớn bằng

42 nên 242 22aa.

Các đỉnh trên trục nhỏ và các tiêu điểm cùng thuộc đường tròn nên

bc .

Từ hệ thức

222 2 2

82 4abc b b 

.

Vậy Elip cần tìm có phương trình



22

:1

84

xy

E .

Câu 6: Lập phương trình chính tắc của Elip, biết

a) Elip có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông có diện tích

bằng 32.

b) Elip có một đỉnh và hai tiêu điểm tạo thành một tam giác đều và chu vi hình chữ nhật cơ sở

của Elip bằng





12 2 3 .

c) Elip đi qua điểm





23;2M và

M

nhìn hai tiêu điểm của Elip dưới một góc vuông.

d) Elip đi qua điểm

3

1;

2

M







và tiêu điểm nhìn trục nhỏ dưới một góc

0

60

.

Lời giải

a) Hai đỉnh trên trục nhỏ và hai tiêu điểm tạo thành một hình vuông nên bc .

Mặt khác, diện tích hình vuông bằng 32 nên

2

2.2 32 8cb b

.

Suy ra

222

16abc

. Vậy Elip cần tìm có phương trình



22

:1

16 8

xy

E .

b) Chu vi hình chữ nhật cơ sở















12 2 3 2 2 2 12 2 3 3 2 3Cabab .



1

Giả sử tam giác

12 2

FFB đều cạnh

12

2FF c mà

212

B

OFF suy ra

212

33

.2 3

22

OB F F b c c

.





2

Từ



1

và





2

, suy ra









32 3 32 3 3ab c.

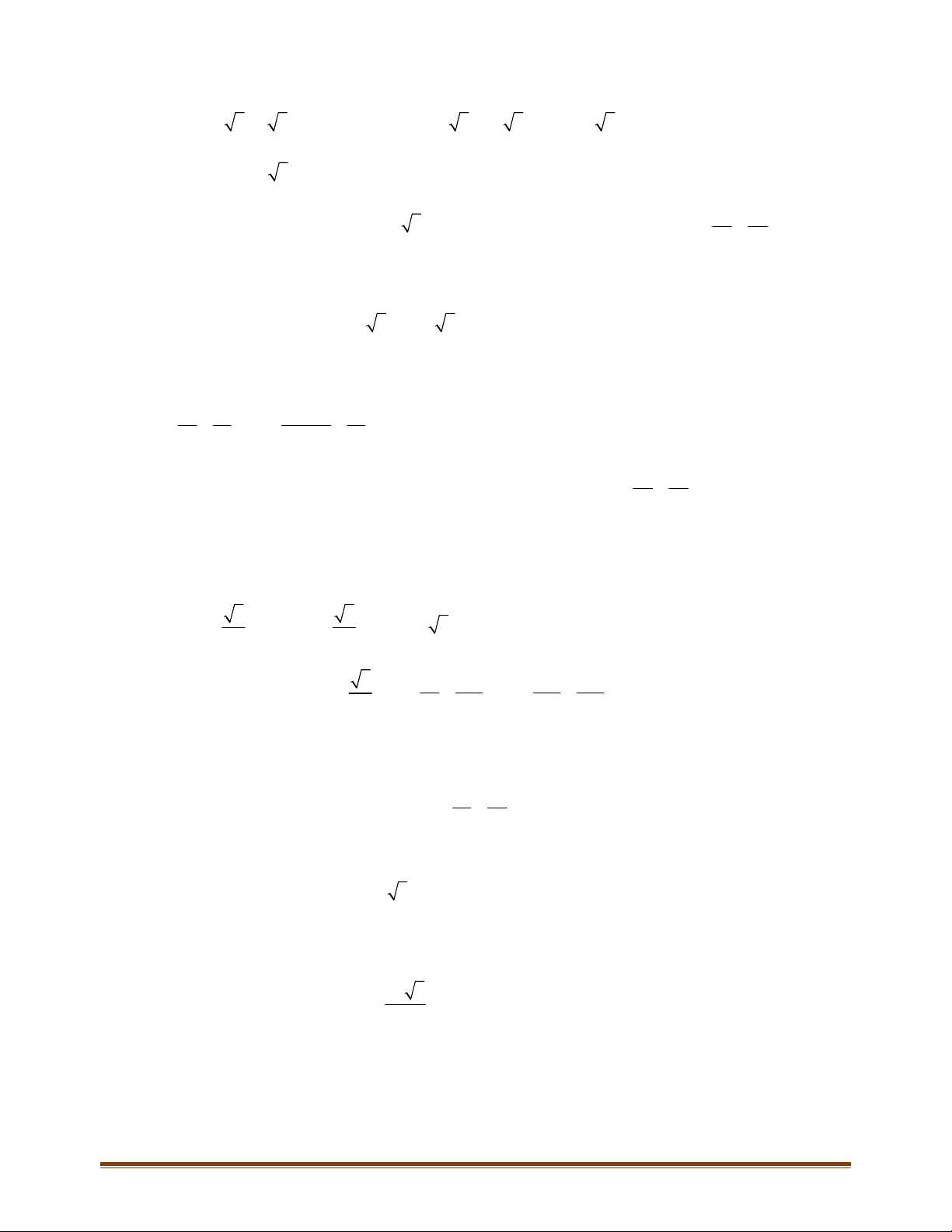
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 26

Thay vào hệ thức

222

abc

, ta được













2

22 2

633 3 3 632 3 633 0 3cccc c c



   



hoặc

12 3 21c   .

Với

3c  , suy ra 6a  và

33b 

. Vậy Elip cần tìm có phương trình



22

:1

36 27

xy

E 

.

c) Từ giả thiết, ta suy ra



0

12

90FMF  hay

12

M

FMF









2

12

. 0 23 23 4 0 16MF MF c c c

 

.

Hơn nữa





E

qua

M

nên

22 4 2 4 2

22 2 2

12 4 12 4

111246416648

16

bb b b b b

ab b b

    



.

Suy ra

222

24abc

. Vậy Elip cần tìm có phương trình



22

:1

24 8

xy

E .

d) Từ giả thiết, ta suy ra



0

11 2

60BFB  mà

11 1 2

FB FB . Suy ra tam giác

112

FBB đều cạnh

12

2BB b

nên

112

33

23

22

FO B B c b c b

.



1

Hơn nưa





E

qua

3

1;

2

M







nên

2

22 22

13 1 3

111

444

b

ab bb



.





2

Từ



1

và





2

, kết hợp với hệ thức

222

abc

, ta được

2

4a 

.

Vậy Elip cần tìm có phương trình



22

:1

41

xy

E .

Câu 7: Lập phương trình chính tắc của Elip, biết

a) Elip có một tiêu điểm





1

3;0F  và đi qua điểm

M

, biết tam giác

12

FMF có diện tích bằng

1 và vuông tại

M

.

b) Elip đi qua ba đỉnh của tam giác đều

A

BC

. Biết tam giác

A

BC

có trục đối xứng là

Oy

,





0; 2A

và có diện tích bằng

49 3

12

.

c) Khi

M

thay đổi trên Elip thì độ dài nhỏ nhất của

OM

bằng 4 và độ dài lớn nhất của

1

M

F

bằng 8 với

1

F

là tiêu điểm có hoành độ âm của Elip.

Lời giải

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 27

a) Elip có tiêu điểm





1

3;0F 

, suy ra

3c  .

Gọi



;

M

xy E

. Theo giả thiết, ta có

12

1

1.1

2

FMF

SMFMF



 



2

222 2 2

2

1

12.2

2

c

aexaex a ex a x

a

  



22

22 2

2

3

.2

3

aa

ax x

a



  .



1

Cũng từ

12

M

FMF

, ta có

















12

.0 0MF MF c x c x y y    



222

3xyc.





2

Từ



1

và





2

, ta có





22

42

22

2

92

33

aa

yx





  

.

Do đó





22 2 4 2

22

2

29 2

;1 1

3

33

xy a a a

Mxy E

ab

a



  











22 422 2

239239 4aa aaa a .

Suy ra

2

1b 

. Vậy Elip cần tìm có phương trình



22

:1

41

xy

E 

.

b) Tam giác

A

BC đều, có điểm



0; 2AOy

và trục đối xứng là

O

y

nên hai điểm

, BC

đối

xứng nhau qua

Oy

.

Giả sử



;

B

xy

với

0, 2xy

, suy ra





;Cxy

. Độ dài cạnh của tam giác là

2

x

.

Theo giả thiết, ta có



2

23

49 3 49 3

12 4 12

ABC

x

S



 , suy ra

7

23

x  .

Đường cao của tam giác đều

23 7 7 3

32

2222

x

hx yy

.

Suy ra

73

;

2

23

B







.

Đến đây bài toán trở thành viết phương trình Elip đi qua hai điểm





0; 2A

và

73

;

2

23

B







.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 28

Vậy Elip cần tìm có phương trình



22

:1

28

4

5

xy

E .

c) Độ dài nhỏ nhất của

OM bằng 4 nên 4b  .

Mặt khác, ta lại có độ dài lớn nhất của

1

M

F bằng

8

nên

8ac

.

Từ đó ta có hệ phương trình

222 2 2

88

16

ac ac

abc a c

 







 



suy ra

5

3

a

c











.

Vậy Elip cần tìm có phương trình



22

:1

25 16

xy

E .

Câu 1:

Phương trình chính tắc của Elip là

A.

22

1

xy

ab

.

B.

22

1

xy

ab

.

C.



22

10

xy

ab

 

.

D.

22

1

xy

ab



.

Lời giải

Chọn C

Câu 2: Phương trình chính tắc của elip có tiêu cự bằng

6

và trục lớn bằng

10

.

A.

22

1

25 9

xy

.

B.

22

1

100 81

xy

.

C.

22

1

25 16

xy

.

D.

22

1

25 16

xy

.

Lời giải

Chọn D

Gọi phương trình elip là

22

1

xy

ab

.

Vì trục lớn bằng

10

nên

210 5aa

.

Elip có tiêu cự bằng

6

nên

22

26 3 3 4cc ab b  

.

Vậy phương trình Elip là:

22

1

25 16

xy



.

Câu 3: Phương trình của Elip





E có độ dài trục lớn bằng

8

, độ dài trục nhỏ bằng

6

là:

A.

22

9 16 144xy. B.

22

916 1xy. C.

22

1

916

xy

.

D.

22

1

64 36

xy

.

Lời giải

Chọn A

Gọi

 

22

:1;

xy

Eab

ab

 

Độ dài trục lớn là:

12

28 4AA a a

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 29

Độ dài trục nhỏ là:

12

26 3BB b b

Vậy phương trình Elip là:



22

: 1 9 16 144

16 9

xy

Exy  

Câu 4: Cho





E có hình chữ nhật cơ sở diện tích bằng

8

, chu vi bằng

6

thì phương trình chính tắc

là:

A.

22

1

21

xy



.

B.

22

1

41

xy



.

C.

22

1

42

xy

.

D.

22

1

16 4

xy

.

Lời giải

Chọn B

Ta có:

22 8

226

ab











2

1

a

b













. Vậy PTCT của





E

là :

22

1

41

xy

.

Câu 5: Cho





E

có tiêu điểm





1

4;0F 

,





2

4;0F

, tâm sai

4

5

e 

thì phương trình là:

A.

22

45 20xy. B.

22

16 25 400xy.

C.

22

9 25 225xy. D.

22

9 16 144xy.

Lời giải

Chọn C

Ta có:



1

4;0

4

5

F

e















4

5

c

a













2

25 16 9b

Vậy PTCT của





E là :

22

1

25 9

xy



22

1

25 9

xy



22

925 225xy .

Câu 6: Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho elip





E

có độ dài trục lớn bằng 12 và độ dài

trục bé bằng 6. Phương trình nào sau đây là phương trình của elip





E

A.

22

1

144 36

xy

. B.

22

1

936

xy

. C.

22

1

36 9

xy

. D.

22

0

144 36

xy

.

Lời giải

Chọn C

Phương trình chính tắc của elip có dạng

 

22

:1 ,0

xy

Eab

ab

 .

Ta có

6a 

,

3b 

, vậy phương trình của Elip là:

22

1

36 9

xy

.

Câu 7: Tìm phương trình chính tắc của Elip có tâm sai bằng

1

3

và trục lớn bằng

6

.

A.

22

1

93

xy



.

B.

22

1

98

xy



.

C.

22

1

95

xy



.

D.

22

1

65

xy



.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 30

Phương trình chính tắc của Elip có dạng



22

10

xy

ab

 

.

Theo giả thiết:

11

33

c

e

a



3ac

và

26 3aa 1c

Khi đó:

222 22

31abc b

2

8b 22b

Vậy phương trình chính tắc của Elip là:

22

1

98

xy



.

Câu 8: Phương trình Elip có trục lớn bằng 25 và một tiêu điểm





1

1; 0F 

là:

A.

22

45 20xy. B.

22

4512xy. C.

22

54 20xy D.

22

5412xy.

Lời giải

Chọn A

Ta có: 225 5aa.

2

222 2

514bac 

.

Vậy phương trình Elip có dạng:

22

14 5 20

54

xy

xy  .

Câu 9:

Phương trình chính tắc của





E

có độ dài trục lớn bằng

8

, trục nhỏ bằng

6

là

A.

22

1

64 36

xy



.

B.

22

1

916

xy



.

C.

22

916 1xy. D.

22

1

16 9

xy



.

Lời giải

Chọn B

Ta có:

28

26

a

b











4

3

a

b













.

Vậy phương trình chính tắc của





E

:

22

1

16 9

xy



Câu 10: Phương trình chính tắc của





E

có tâm sai

4

5

e 

, độ dài trục nhỏ bằng

12

là

A.

22

1

25 36

xy

. B.

22

1

64 36

xy

. C.

22

1

100 36

xy

. D.

22

1

36 25

xy

.

Lời giải

Chọn C

Ta có:

4

5

212

e

b















54

6

ca

b













22

25 16

6

ca

b

















22 2

25 16

6

ab a

b

















10

6

a

b













.

Vậy phương trình của





E

:

22

1

100 36

xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 31

Câu 11: Phương trình chính tắc của





E

có độ dài trục lớn bằng

6

, tỉ số giữa tiêu cự và độ dài trục lớn

bằng

1

3

là

A.

22

1

93

xy



.

B.

22

1

98

xy



.

C.

22

1

19 5

xy



.

D.

22

1

65

xy



.

Lời giải

Chọn B

* Do độ dài trục lớn bằng 6 nên

26a  3.a

* Do tỷ số giữa tiêu cự và độ dài trục lớn bằng

1

3

nên

21

23

cc

aa



3ac 1c

.

* Ta có:

222

918bac



22

:1

98

xy

E

.

Câu 12: Elip có hai đỉnh





3; 0

;





3; 0

và hai tiêu điểm





1; 0

và





1; 0

có phương trình chính tắc là

A.

22

1

89

xy

. B.

22

1

98

xy

. C.

22

1

94

xy

. D.

22

1

92

xy

.

Lời giải

Chọn B

Theo đề bài ta có

222

3

8

1

a

bac

c













.

Vậy phương trình chính tắc của Elip đã cho là

22

1

98

xy



Câu 13: Phương trình chính tắc của





E

có độ dài trục lớn gấp

2

lần độ dài trục nhỏ và tiêu cự bằng

43 là

A.

22

1

36 9

xy

. B.

22

1

36 24

xy

. C.

22

1

24 6

xy

. D.

22

1

16 4

xy

.

Lời giải

Chọn D

* Do độ dài trục lớn gấp

2

lần độ dài trục nhỏ nên

22.2ab 2.ab

* Do tiêu cự bằng

4 3 nên 243c  23c .

* Ta có:

222

bac

22

412bb 

2b 4a



22

:1

16 4

xy

E.

Câu 14: Phương trình chính tắc của





E

có đường chuNn

40x 

và tiêu điểm





1; 0F 

là

A.

22

1

43

xy

. B.

22

1

16 15

xy

. C.

22

1

16 9

xy

. D.

22

1

98

xy

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 32

Lời giải

Chọn A

* Do đường chuNn là

40x  4x

nên

4

a

e



2

4

a

c



2

4ac

.

* Do có tiêu điểm





1; 0F 

nên

1c 

2,a

222

3bac

.

* Phương trình chính tắc của





E là



22

:1

43

xy

E 

.

Câu 15: Phương trình chính tắc của





E

có tiêu cự bằng

6

và đi qua điểm





5; 0A

là

A.

22

1

100 81

xy

. B.

22

1

15 16

xy

. C.

22

1

25 9

xy

. D.

22

1

25 16

xy

.

Lời giải

Chọn D

* Do





E

có tiêu cự bằng

6

nên

26c  3.c

* Do





E

đi qua điểm





5; 0A

nên

5a 

222

25 9 16bac

.

* Phương trình chính tắc của



E

là



22

:1

25 16

xy

E 

.

Câu 16: Elip có hai tiêu điểm



1

1; 0F  ;



2

1; 0F và tâm sai

1

5

e 

có phương trình là

A.

22

1

25 24

xy

. B.

22

1

24 25

xy

. C.

22

1

24 25

xy

. D.

22

1

25 24

xy

.

Lời giải

Chọn A

Phương trình chính tắc của



E

là



22

10

xy

ab

 

Tiêu điểm





1

1; 0 1Fc

Tâm sai

1

5

e 

1

55

5

c

ac

a

 

222

25 1 24bac

.

Vậy



22

:1

25 24

xy

E .

Câu 17: Trong hệ trục tọa độ

Ox

y

, một elip có độ dài trục lớn là

8

, độ dài trục bé là

6

thì có phương

trình chính tắc là.

A.

22

1

916

xy



.

B.

22

1

64 36

xy



.

C.

22

1

16 9

xy



.

D.

22

1

16 7

xy



.

Lời giải

Chọn C

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 33

Độ dài trục lớn là

828 4aa

Độ dài trục nhỏ là

626 3bb

Phương trình chính tắc của elip là

22 22

22

11

16 9

xy xy

ab



.

Câu 18: Các đỉnh của Elip



E

có phương trình

22

1

xy

ab

;





0ab

tạo thành hình thoi có một

góc ở đỉnh là

60

, tiêu cự của



E

là

8

, thế thì

22

ab

?

A.

16

. B.

32

. C.

64

. D.

128

.

Lời giải

Chọn D

Gọi hình thoi là

A

BCD

và



60A .

Tiêu cự là

8



22

64ab



1

.

Mặt khác xét tam giác

A

OB

vuông tại

O

có góc



30BAO  nên

tan 30OB OA.tan30ba 

3

a

thay vào phương trình



1

ta được

2

64

3

a 



2

96a 

2

32b

. Vậy

22

128ab

.

Câu 19: Trong mặt phẳng tọa độ

Oxy

, cho Elip



E

đi qua điểm



0;3M

. Biết khoảng cách lớn nhất

giữa hai điểm bất kì trên



E

bằng

8

. Phương trình chính tắc của Elip là

A.

22

1

916

xy



B.

22

1

16 9

xy



C.

22

1

964

xy



D.

22

1

64 9

xy



Lời giải

Chọn B









0;3

M

E

3b

.

khoảng cách lớn nhất giữa hai điểm bất kì trên



E

bằng

8

4a

.

Phương trình chính tắc của



E

:

22

1

16 9

xy

.

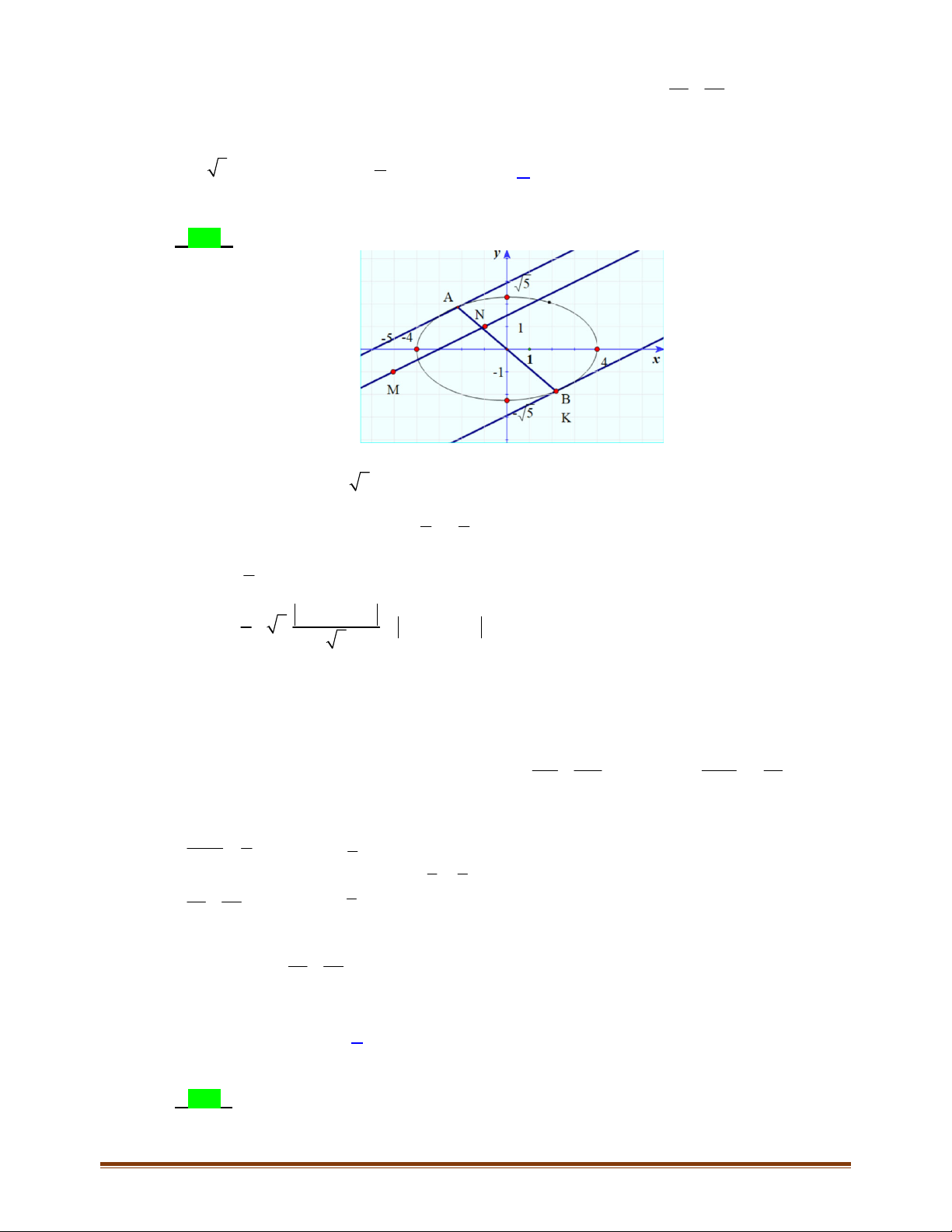
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 34

Câu 20: Trong mặt phẳng với hệ trục tọa độ

Ox

y

cho đường elip

22

(): 1

16 5

xy

E 

và hai điểm









5; 1 , 1;1MN  . Điểm

K

thay đổi trên elip

()

E

. Diện tích tam giác

M

NK

lớn nhất bằng

A. 95. B.

9

2

. C.

9

. D.

18

.

Lời giải

Chọn C

+ Ta có





.4;2 25MN MN



13

.:230hay:

22

MN x y MN y x  



1

...,

2

KMN

SMNdKMN





23

1

.2 5. 2 3

2

5

oo

xy





với





;

oo

K

xy

K

MN

S



 lớn nhất khi





,dKMN

lớn nhất.

+ N hận thấy

()

E

có hai tiếp tuyến song song với

M

N

, gọi

,

A

B

là hai tiếp điểm tương ứng. Khi

đó





,dKMN

lớn nhất khi

K

B

.

+ Mà tiếp tuyến tại





;

oo

K

xy có phương trình là:

5

1

16 5 16

oo o

oo

xx yy x

hay y x

y

  

.

+ Từ đó ta có:

22

5

1

16 2

1

16 5

o

oo

x

y

xy



















5

8

3

oo

o

yx

x



















85

;

33

K









9

KMN

S





Câu 21: Cho elip



22

:1

16 9

xy

E 

. Xét các điểm

,

M

N

lần lượt thuộc các tia

,Ox O

y

sao cho đường

thẳng

M

N

tiếp xúc với



E

. Hỏi độ dài ngắn nhất của

M

N

là bao nhiêu?

A.

6

. B.

7

. C.

8

. D.

9

.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 35

Gọi









;0 , 0;

M

mNn

với

222

,0mn MN m n   . Đường thẳng

:1

xy

MN

mn



.

Cách 1: Dùng điều kiện tiếp tuyến của elip chính tắc

+) Elip chính tắc

22

(): 1

xy

E

ab

 và đường thẳng

:0Ax By C

tiếp xúc với nhau khi và

chỉ khi

22 22 2

aA bB C

.

+) Phương trình tiếp tuyến của elip chính tắc tại

00

(; )

M

xy

là:

00

22

1

xy

x

y

ab



.

M

N

tiếp xúc với

22

16 9

() 1

E

mn



. Ta có

2

22 22

16 9 (4 3)

1

mnmn







22

min

49 7mn MN 

.

Cách 2: Dùng điều kiện tiếp xúc

Đường thẳng

:1

xy n

M

Nyxn

mn m

 

tiếp xúc với elip khi và chỉ khi phương trình

2

1

16 9

n

xn

x

m











có nghiệm kép

222

2

12

10

16 9 9 9

nnn

xx

mm



  





có nghiệm kép

22 2

2

22

19

'0

9 144 6 16

nn m

n

mm

      



.

Khi đó

242 22

22 2

956784(28)

49 49 7.

16 16 16

mmm m

MN m n m

mm m

 

   

 

Nhận xét: Cả 2 cách làm trên hiện tại không có trong chương trình phổ thông, người ra bài

toán này không nắm được chương trình mới.

DẠNG 3: TÌM ĐIỂM THUỘC ELIP THỎA ĐIỀU KIỆN CHO TRƯỚC

Cho Elip có phương trình chính tắc:



22

:1

xy

E

ab

 với

222

bac

.

●



;

M

xy E

. Khi đó

1

M

Faex : bán kính qua tiêu điểm trái.

2

M

Faex : bán kính qua tiêu điểm phải.

Câu 1:

a) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



22

:1

25 16

xy

E . Gọi

1

F ,

2

F là hai tiêu điểm

của Elip;

A

,

B

là hai điểm thuộc





E

sao cho

12

8AF BF. Tính

21

A

FBF .

PHƯƠNG PHÁP.

1

BÀI TẬP TỰ LUẬN.

2

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 36

b) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



22

:1

95

xy

E 

. Gọi

1

F

,

2

F

là hai tiêu điểm

của Elip trong đó

1

F có hoành độ âm. Tìm tọa độ điểm

M

thuộc



E

sao cho

12

2

M

FMF .

c) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



22

:1

84

xy

E 

. Gọi

1

F

,

2

F

là hai tiêu điểm

của Elip trong đó

1

F

có hoành độ âm. Tìm tọa độ điểm

M

thuộc





E

sao cho

12

2MF MF

.

Lời giải

a) Ta có

2

25 5aa

. Do





, AB E

nên

12

210AF AF a và

12

210BF BF a.

Suy ra

1212 21 21

20 8 20 12AF AF BF BF AF BF AF BF

.

b) Ta có

2

93aa

và

2

55bb . Suy ra

222

42cab c

.

Gọi



;

M

xy E

. Ta có



2

12

3

22

332

aa

MF MF a ex a ex x

ec

. Thay vào





E

, ta được

2

91515

1

4.9 5 4 2

y

yy

.

Vậy

315

;

22

M









hoặc

315

;

22

M







.

c) Ta có

2

822aa

và

2

42bb

. Suy ra

222

42cab c

.

Gọi



;

M

xy E

. Ta có



12

122

22 2

2

a

MF MF a ex a ex x

ec

 

.

Thay vào





E

, ta được

2

13 3

84

y

yy.

Vậy





2; 3M 

hoặc





2; 3M

.

Câu 2: a) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



22

9

:1

1

xy

E . Tìm những điểm

M

thuộc





E

sao cho nó nhìn hai tiêu điểm của





E

dưới một góc vuông.

b) Trong mặt phẳng với hệ tọa độ

Ox

y

, cho Elip



2

:1

4

x

Ey với hai tiêu điểm

1

F ,

2

F .

Tìm tọa độ điểm

M

thuộc



E

sao cho góc



0

12

60FMF  .

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

100 25

xy

E  với hai tiêu điểm

1

F ,

2

F .

Tìm tọa độ điểm

M

thuộc



E

sao cho góc



0

12

120FMF  .

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 37

d) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

25 9

xy

E 

với hai tiêu điểm

1

F

,

2

F

trong đó

1

F

có hoành độ âm. Tìm tọa độ điểm

M

thuộc



E sao cho góc



0

12

120MF F 

.

Lời giải

a) Ta có

2

93aa

và

2

11bb 

. Suy ra

222

222cab c

.

Gọi



;

M

xy E . Ta có



0

12

90FMF 

nên

222

12 1 2

FF MF MF



22

2222

22

43222

86337

32 18 2. .

98

22

caex aex aex

xx x

  

 

Thay vào



E

, ta được

2

11

8

22

yy .

Vậy

37 1

;

2222

M







,

37 1

;

22 22

M









,

37 1

;

2222

M









hoặc

37 1

;

22 22

M









.

b) Ta có

2

42aa

và

2

11bb 

. Suy ra

222

33cab c

.

Gọi



;

M

xy E

. Ta có

222 0

12 1 2 1 2

2..cos60F F MF MF MF MF



22

2 222222

2

1

42.1222

2

12 32 4 2

.

39 3

c a ex a ex a ex a ex a e x a e x

a

xx

e

     



  

Thay vào



E

, ta được

22

32 1 1

1

9.4 9 3

yy y

.

Vậy

421

;

33

M







,

42 1

;

33

M









,

421

;

33

M









hoặc

42 1

;

33

M









.

c) Ta có

2

100 10aa

và

2

25 5bb. Suy ra

222

75 5 3cab c .

Gọi



;

M

xy E

. Ta có

222 0

12 1 2 1 2

2 . cos120F F MF MF MF MF



22

2 222222

222 22 2

1

4 2 300 2 2

2

300 3 300 300 0 0.

c a ex a ex a ex a ex a e x a e x

aex ex x x



     





  

Thay vào



E

, ta được

2

0

125 5

100 25

y

yy.

Vậy



0;5M

hoặc





0; 5M 

.

d) Ta có

2

25 5aa

và

2

93bb

. Suy ra

222

16 4cab c

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 38

Gọi



;

M

xy E

. Ta có

222 0

2112 112

2 . cos120MF MF F F MF F F

 

22

2

1

42 2

2

65

44220 .

14

a ex a ex c a ex c

aex c ac ecx x



     







Thay vào



E , ta được

2

243 9 3

196 14

yy

.

Vậy

65 9 3

;

14 14

M









hoặc

65 9 3

;

14 14

M









.

Câu 3: a) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

41

xy

E 

và điểm



2;0C

. Tìm tọa độ

các điểm

A

,

B

thuộc



E

, biết rằng

A

,

B

đối xứng với nhau qua trục hoành và tam giác

A

BC

là tam giác đều.

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

41

xy

E 

. Tìm tọa độ các điểm

A

và

B

thuộc



E có hoành độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

91

xy

E  và điểm





3; 0A

. Tìm tọa độ

các điểm

B

,

C

thuộc



E

sao cho tam giác

A

BC

vuông cân tại

A

, biết

B

có tung độ dương.

Lời giải

a) a có

2

42aa

và

2

11bb 

. Suy ra

222

33cab c .

Giả sử



;

A

xy

suy ra





;Bx y

. Theo giả thiết, tam giác

A

BC

đều

 

22

22 22 2

2423

A

CAB x y y x y

.



1

Hơn nữa



22

144

41

xy

AE x y.





2

Từ



1

và



2

, ta có



2

22

2

23

1

4

0

44

71640

x

xy

y

xy

xx















 















hoặc

2

7

43

7

x

y

















hoặc

2

7

43

7

x

y

















.

Vì

,

A

B

khác

C

nên

243

;

77

A







,

243

;

77

B









hoặc

243

;

77

A









và

243

;

77

B







.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 39

b) Do tam giác

OAB

cân tại

O

và

A

,

B

đều có hoành độ dương nên

A

,

B

đối xứng nhau

qua

Ox

.

Giả sử



;

A

xy

với 0x  , suy ra



;Bx y

. Gọi

H

là hình chiếu của O lên

A

B

. Khi đó ta

có

11

.2

22

OAB

SABOHyxxy





.

Áp dụng bất đẳng thức

Cauchy

, ta có

2

12..

42

xx

y

yxy 

.

Do đó

1

OAB

S





. Dấu

'' ''

xảy ra khi và chỉ khi:

2

4

x

y



.

Thay vào





E

, ta được

22

2

1

4

1

11

12

2

yy

xy

yy

.

Suy ra

2

22xx 

.

Vậy

1

2;

2

A







và

1

2;

2

B









hoặc

1

2;

2

A









và

1

2;

2

B







.

c) Gọi



;Bxy

với 0x  .

Do tam giác

A

BC

vuông cân tại

A

, suy ra

B

và

C

đối xứng nhau qua

Ox

nên



;Cx y

.

Ta có



2

.0 3 0AB AC AB AC x y 



.



1

Hơn nữa,



22

1

91

xy

BE

.



2

Từ



1

và



2

, ta có



2

22

2

30

1

3

9

0

10

1

680

31 0

91

9

x

xy

y

x

xy

y

x

xx

x













 



  







 











hoặc

12

5

3

5

x

y

















.

Vì

,

A

B

khác

C

nên

12 3

;

55

B







,

12 3

;

55

C









.

Câu 4: a) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

16 5

xy

E 

và hai điểm





5; 1A 

,

(1;1)B 

. Xác đinh tọa độ điểm

M

thuộc



E

sao cho diện tích tam giác

M

AB

lớn nhất.

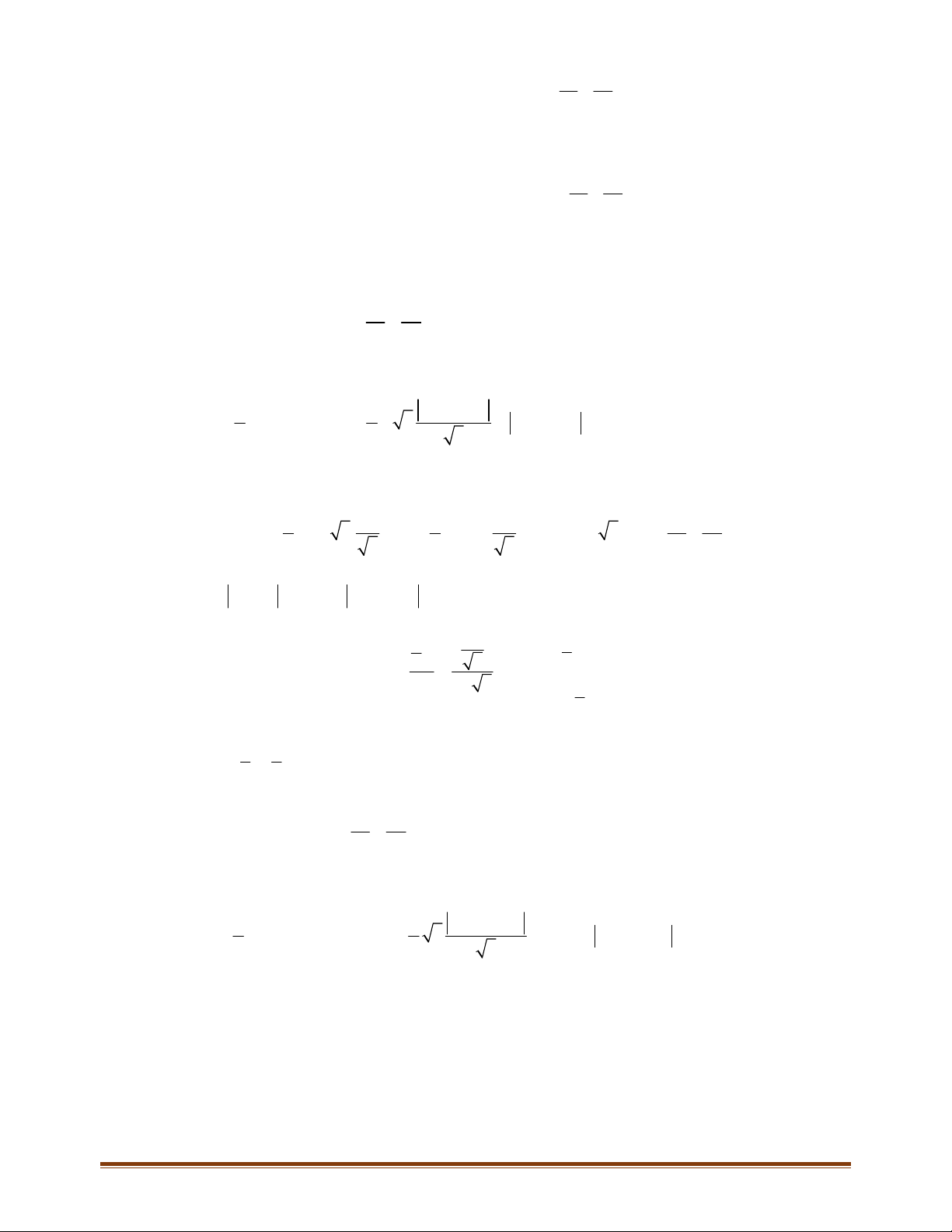
CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 40

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

82

xy

E 

và hai điểm



3; 4A

,

(5;3)B

.

Tìm trên



E

điểm

C

sao cho tam giác

A

BC

có diện tích bằng 4,5.

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

21

xy

E 

. Tìm trên



E

những điểm

sao cho khoảng cách từ điểm đó đến đường thẳng

:2 3 1 0dx y

là lớn nhất.

Lời giải

a) Gọi









;

M

xy E

nên

22

1

16 5

xy



. Phương trình đường thẳng

:230AB x y

.

Ta có



23

11

., .25 23

22

5

MAB

xy

SABdMAB xy





 

.

Áp dụng bất đẳng thức

Bunhiacopxki

, ta được



22

2

22

2

11

2 4. 2 5. 4 2 5 .36 1.36 36

44 165

55

yy xy

xy x x











      





















.

Suy ra

26xy

nên

239xy

.

Dấu

'' ''

xảy ra khi và chỉ khi:

8

1

5

3

4

25

5

239

3

y

x

y

xy























  



.

Vậy

85

;

33

M









thỏa yêu cầu bài toán.

b) Gọi



22

;1

82

xy

Cxy E

.



1

Phương trình đường thẳng

:2110AB x y

. Ta có



211

11

. , 4,5 5 4,5 2 11 9

22

5

ABC

xy

SABdCAB xy





 

2119

xy













.



2

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 41

Từ



1

và



2

, ta có



2

22

2

20 2

2119

20 2

2201000

1

_1

82

xy

y

yy

















 















: vô

nghiệm.

Từ



1

và





3

, ta có



2

22

2

22

2119

13

22

13

1

_1

82

2

xy

x

xy

y











 



 









 



hoặc

13

2

x

y

















.

Vậy

13

13;

2

C











hoặc

13

13;

2

C











.

c) Gọi



22

;122

21

xy

Mxy E x y

. Ta có



231

,

13

xy

dMd





.

Áp dụng bất đẳng thức

Bunhiacopxki

, ta có



2

3917

2 3 2. . 2 2 4 2. 17

22

2

xy x y x y





  









.

Suy ra

23 17xy

nên

231 171xy 

.

Dấu

'' ''

xảy ra khi và chỉ khi:

4

2

3

2

17

2

3

17

23 17

xy

x

y

xy

























.

Vậy





,dMd

lớn nhất bằng

17 1

13



khi

43

;

17 17

M









.

Câu 5: a) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

94

xy

E 

và các điểm



3; 0A 

,



1; 0I 

. Tìm tọa độ các điểm

B

,

C

thuộc





E

sao cho

I

là tâm đường tròn ngoại tiếp tam

giác

A

BC

.

b) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

25 9

xy

E 

có hai tiêu điểm

1

F

,

2

F

. Tìm

tọa độ điểm

M

thuộc





E

sao cho bán kính đường tròn nội tiếp tam giác

12

M

FF

bằng

4

3

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 42

c) Trong mặt phẳng với hệ tọa độ

Oxy

, cho Elip



22

:1

25 9

xy

E 

có hai tiêu điểm

1

F

,

2

F

. Tìm

tọa độ điểm

M

thuộc



E

sao cho đường phân giác trong góc



12

FMF

đi qua điểm

48

;0

25

N









.

Lời giải

a) Phương trình đường tròn ngoại tiếp tam giác

A

BC

có tâm



1; 0I 

, bán kính

2RIA

là:

 

2

:1 4Cx y

.

Theo giả thiết, ta có









,BC E C

nên tọa độ điểm

,BC

là nghiệm của hệ



 

22

22 22

22

2

22

2

49 36 49 36

1

49 36

94

51890

919 36 914 0

14

xy

xy xy

xy

xx

xy xx

xy





 







  



  



   















3

0

x

y













hoặc

3

5

46

5

x

y

















hoặc

3

5

46

5

x

y

















.

Vậy

346

;

55

B









,

346

;

55

C









hoặc

346

;

55

B









,

346

;

55









.

b) Ta có

2

25 5aa

và

2

93bb

. Suy ra

222

16 4cab c

.

Hai tiêu điểm của Elip là:



1

4;0F 

và



2

4; 0F

.

Gọi









;

M

xy E

. Ta có

12

.

MF F

Spr







1212

12 12

1

., .

22

144

.2 . . 4 9. 3 3.

233

MF MF F F

FF d M FF r

cy a c y y y







Thay vào phương trình



E

, ta được

2

9

10

25 9

x

x

.

Vậy



0;3M

hoặc





0; 3M 

.

c) Ta có

2

25 5aa

và

2

93bb

. Suy ra

222

16 4cab c

.

Hai tiêu điểm của Elip là:



1

4;0F 

và



2

4; 0F

.

Gọi









;

M

xy E

. Theo giả thiết

M

N

là phân giác trong của



12

FMF

, suy ra

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 43

11

22

52 4

12 25 0 12.5 25. 0 3

148 5

FN FM a ex

aex x x

FN FM a ex



  



.

Thay vào phương trình



E

, ta được

2

912

1

25 9 5

y

y

.

Vậy

12

3;

5

M









hoặc

12

3;

5

M









.

Câu 1:

Cho Elip



22

: 1

16 9

xy

E 

. Với

M

là điểm bất kì nằm trên



E

, khẳng định nào sau đây là

khẳng định đúng?

A. 45.OM B. 5.OM  C. 3.OM  D. 34.OM

Lời giải

Chọn D.

Từ



22

: 1

16 9

xy

E 

, suy ra

4, 3ab

.

Với một điểm bất kì trên



E

, ta luôn có 34.bOM a OM

Câu 2: Elip đi qua điểm

3

1;

2

M









và có tiêu cự bằng

23

thì có phương trình chính tắc là:

A.

22

1

43

xy



. B.

22

1

41

xy



. C.

22

1

31

xy



. D.

22

1

4

xy



.

Lời giải

Chọn B.

Giả sử



E

có PTCT là:



²²

1 0

²²

xy

ab

 

.

Ta có:



3

1;

2

223

M

E

c





















22

13

1

4

3

ab

















2

4

1

a

b

















Vậy PTCT của



E

là :

22

1

41

xy



Câu 3: Cho Elip



22

:1

169 144

xy

E 

và điểm

M

nằm trên





E

. N ếu điểm

M

có hoành độ bằng

13

thì các khoảng cách từ

M

tới

2

tiêu điểm của



E

bằng:

A.

8; 18

. B.

13 5

. C.

10;16

. D.

13 10

.

Lời giải

Chọn A

Ta có

13a

,

12 5bc

BÀI TẬP TRẮC NGHIỆM.

3

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 44

Vậy

1

8

M

c

MF a x

a

 

2

18

M

c

MF a x

a

 

Câu 4: Cho Elíp có phương trình

22

16 25y 100x 

. Tính tổng khoảng cách từ điểm thuộc elíp có

hoành độ

2x 

đến hai tiêu điểm.

A.

10

. B.

22

. C.

5

. D.

43

.

Lời giải

Chọn C

Phương trình chính tắc của elip có dạng

 

22

:1 ,0

xy

Eab

ab

 

.

Ta có :

5

2

a 

,

2b 

,

6c 

.

Sử dụng công thức bán kính qua tiêu

1

546

25

MF



,

2

546

25

MF



12

5MF MF

.

Cách 2: dễ thấy

12

2a 5MF MF

.

Câu 5: Cho Elip



22

:1

25 9



y

E

x

. Đường thẳng



:4dx

cắt



E

tại hai điểm

,

M

N

. Khi đó:

A.

9

25

MN

. B.

18

25

MN

. C.

18

5

MN

. D.

9

5

MN

.

Lời giải

Chọn C

Theo giả thiết:

4x

nên ta có phương trình:



2

22

4

9

1

25 9 9 25

yy





2

81

25

y

99

4;

55

99

4;

55

yM

yN





 















   









Khi đó:



2

99

55

4

18

4

5



   





MN

.

Câu 6: Cho Elip có phương trình:

22

1

16 4

xy



.

M

là điểm thuộc





E

sao cho

12

M

FMF

. Khi đó

tọa độ điểm

M

là:

A.









12

0;1 , 0; 1MM

. B.

12

(0;2) , (0; 2)MM

.

C.

12

(4;0), (4;0)MM

. D.

12

(0;4) , (0; 4)MM

.

Lời giải

Chọn B

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 45

Phương trình chính tắc của elip có dạng

 

22

:1 ,0

xy

Eab

ab

 

.

N ên

4; 2ab

Vì

12

M

FMF

nên

M

thuộc đường trung trực của

12

FF

chính là trục

Oy

M

là điểm thuộc





E

nên

M

là giao điểm của elip và trục

Oy

Vậy

12

(0;2) , (0; 2)MM

.

Câu 7: Dây cung của Elip

 

22

:10

xy

Eba

ab

 

. vuông góc với trục lớn tại tiêu điểm có độ dài

là

A.

2

2c

a

. B.

2

2b

a

. C.

2

2a

c

. D.

2

a

c

.

Lời giải

Chọn B

Gọi dây cung đó là

12

M

như hình vẽ.

Giả sử

 

1

;0Mcy y

,



22

1

22

1

cy

ME

ab



22 4

22

ac b

yb

aa



 

2

b

y

a



Khi đó,

2

1

;

b

Mc

a







,

2

;

b

Mc

a









2

12

2b

MM

a



.

Câu 8: Cho



E

:

22

1

16 9

xy



và điểm

M

thuộc





E

. Khi đó độ dài

OM

thỏa mãn

A.

3OM 

B.

34OM

. C.

45OM

. D.

5OM 

.

Lời giải

Chọn B

Vì









;

M

xy E

nên

22

1

16 9

xy



và

22

OM x

y



.

Ta có

222222

16 16 16 9 9 9

x

yxyxy



22

1

16 9

OM OM



2

916OM 

34OM 

.

Câu 9: Cho



22

:1.

25 9

xy

E 

Đường thẳng

:4dx

cắt



E

tại hai điểm

M

,

N

. Khi đó, độ dài

đoạn

M

N

bằng

A.

9

5

. B.

9

25

. C.

18

5

. D.

18

25

.

Lời giải

Chọn C

Thay

4x 

vào phương trình đường elip ta được:

2

16 9

1

25 9 5

y



.

Tọa độ hai giao điểm là

99

4; , 4;

55

MN

 



 

 

.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 46

Do đó,

18

5

MN 

.

Câu 10: Đường thẳng

ykx

cắt





E

:

22

1

xy

ab



tại hai điểm

M

, N phân biệt. Khi đó

M

, N

A. Đối xứng nhau qua





0;0O

. B. Đối xứng nhau qua

Oy

.

C. Đối xứng nhau qua

Ox

. D. Đối xứng nhau qua





0;1I

.

Lời giải

Chọn A

Đường thẳng

ykx

đi qua





0;0O

và



E

nhận gốc tọa độ làm tâm đối xứng. Do đó khi

đường thẳng

ykx

cắt



E

tại

M

,

N

phân biệt thì

M

,

N

đối xứng nhau qua





0;0O

.

Câu 11: Cho elip



22

:1

169 144

xy

E 

và điểm

M

thuộc





E

có hoành độ

13

M

x 

. Khoảng cách từ

M

đến hai tiêu điểm của



E

lần lượt là

A.

10

và

6

. B.

8

và

18

. C.

13

và

5

. D.

13

và

10

Lời giải

Chọn B

Ta có



13

013;0

M

x

yM

ME

















.

Ta có

2

169a 

;

2

144b 

2

25 5cc

.

Các tiêu điểm của



E

là



1

5; 0F 

,



2

5; 0F

, suy ra

1

8MF 

,

2

18MF 

.

Câu 12: Cho elip

²²

(): 1

25 16

xy

E 

, với tiêu điểm

12

,FF

. Lấy hai điểm

,()

A

BE

sao cho

11

A8.FBF

Khi đó,

22

A?FBF

A.

6

. B.

8

. C.

12

. D.

10

.

Lời giải

Chọn C

²²

Do ( ) : 1 ² 25 5

25 16

xy

Eaa

.

12

Do ( ) 2 10A E AF AF a 

.

12

Do ( ) 2 10B E BF BF a 

.

11 2 2

()( )20AF BF AF BF 

22 22

8( ) 20 12AF BF AF BF     

.

Câu 13: Cho elip

²²

(): 1

25 9

xy

E 

. Tìm toạ độ điểm

()

M

E

sao cho M nhìn

12

,FF

dưới một góc

vuông:

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 47

A.

(5;0)

. B.

9

4;

5









. C.

(0;4)

. D.

579

;

44







.

Lời giải

Chọn D

(; )

MM

M

xy

nhìn

12

,FF

dưới một góc vuông khi và chỉ khi

1

OM OF

.

Do

22

²²

(): 1 25; 9 ² 25 9 16 4

25 9

xy

Eabc c 

.

Để

22 22

1

416

MM MM

OM OF x y x y 

.

Mặt khác

22

( ) 1 9 25 225

25 9

MM

xy

ME x y  

.

Ta có hệ:

2

22

2

175

57

16

4

81

9

9 25 225

16

4

M

MM

M

x

xy

y



































.

Câu 14: Trong mặt phẳng tọa độ

Oxy

cho



22

:1

16 5

xy

E 

và hai điểm









5; 1 , 1;1AB 

. Điểm

M

bất kì thuộc



E

, diện tích lớn nhất của tam giác

M

AB

là:

A.

18

. B.

9

. C.

92

2

. D.

42

.

Lời giải

Chọn B

Ta có:





4; 2AB 



,

25AB 

.

Phương trình đường thẳng



đi qua

A

,

B

:

230xy

.





 

4cos ; 5sin 0 2ME







.



1

.,

2

MAB

SABdM





. Diện tích lớn nhất khi và chỉ khi



,dM

lớn nhất.

Ta có:



,

4cos 2 5sin 3 4cos 2 5 sin 3

55

M

d

 



  





2

4253

9

,

55

dM

 

 

. Vậy



1

.,9

2

MAB

SABdM





.

Câu 15: Trong mặt phẳng với hệ tọa độ

Oxy

, cho elip



E

:

22

440xy

. Tìm tất cả những điểm

N

trên elip



E

sao cho:



0

12

60FNF 

(

1

F

,

2

F

là hai tiêu điểm của elip



E

)

A.

42 1

;

33

N









hoặc

421

;

33

N









hoặc

42 1

;

33

N









hoặc

421

;

33

N







.

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 48

B.

42 1

;

33

N









hoặc

421

;

33

N









hoặc

421

;

33

N







.

C.

421

;

33

N









hoặc

42 1

;

33

N









hoặc

421

;

33

N







.

D.

42 1

;

33

N









hoặc

421

;

33

N







.

Lời giải

Chọn A



2

1:

4

x

Ey

22

4, 1ab 

2

3c

3c

.

Gọi



22

00

00 1 0

12

44

3

;2

2

23

xy

Nx y E NF x

FF







 









;

20

3

2

NF x

. Xét tam giác

12

FNF theo hệ thức

lượng trong tam giác ta có:



2

22 0

12 1 2 1 2

2os60F F NF NF NF NF c 



22

2

0000

3333

23 2 2 2 2

2222

x

xxx



   





22

00

33

12 8 4

24

x



 





2

0

9

8

4

x

2

0

32

9

x

0

42

3

42

3

x

















2

0

1

9

y

0

1

3

1

3

y

















.

Vậy có tất cả 4 điểm thỏa

42 1

;

33

N









hoặc

421

;

33

N









hoặc

42 1

;

33

N









hoặc

421

;

33

N







.

Câu 16: Các hành tinh và các sao chổi khi chuyển động xung quanh mặt trời có quỹ đạo là một đường

elip trong đó tâm mặt trời là một tiêu điểm. Điểm gần mặt trời nhất gọi là điểm cận nhật, điểm

xa mặt trời nhất gọi là điểm viễn nhật. Trái đất chuyển động xung quanh mặt trời theo quỹ đạo

là một đường elip có độ dài nửa trụ

c lớn bằng 93.000.000 dặm. Tỉ số khoảng cách giữa điểm

cận nhật và điểm viễn nhật đến mặt trời là

59

.

61

Tính khoảng cách từ trái đất đến mặt trời khi

trái đất ở điểm cận nhật. Lấy giá trị gần đúng.

A. Xấp xỉ

91.455.000

dặm. B. Xấp xỉ

91.000.000

dặm.

Mat troi

Trái dát

CHUYÊN ĐỀ VII – TOÁN 10 – CHƯƠNG VII – PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Page 49

C. Xấp xỉ

91.450.000

dặm. D. Xấp xỉ

91.550.000

dặm.

Lời giải

Chọn C

Ta có

93.000.000a 

Và

59 93.000.000

61 61 59 59 1.550.000

61 60 60

ac a

ac acc

ac



     



Suy ra khoảng cách từ trái đất đến mặt trời khi trái đất ở điểm cận nhật là:

91.450.000

Câu 17: Ông Hoàng có một mảnh vườn hình elip có chiều dài trục lớn và trục nhỏ lần lượt là

60m

và

30m

. Ông chia thành hai nửa bằng một đường tròn

tiếp xúc trong với elip để làm mục đích sử dụng

khác nhau. N ửa bên trong đường tròn ông trồng cây

lâu năm, nửa bên ngoài đường tròn ông trồng hoa

màu. Tính tỉ số diện tích T giữa phần trồng cây lâu

năm so với diện tích trồng hoa màu. Biết diện tích

elip được tính theo công thức

Sab





trong đó

,ab

lần lượt là đọ dài nửa trục lớn và nửa trục bé

của elip. Biết độ rộng của đường elip không đáng

kể.

A.

2

3

T 

. B.

1T 

. C.

1

2

T 

. D.

3

2

T 

.

Lời giải

Chọn B

Diện tích hình tròn:

2

.15

T

S





, diện tích elip là .15.30

E

S



 .

Tỉ số diện tích

2

.15 15

1

.15.30 .15 30 15

T

ET

S

T

SS





 



.

Chuyên đề phương pháp tọa độ trong mặt phẳng Toán 10 KNTTvCS

Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT) 78 tài liệu

Toán 10 2.8 K tài liệu

Bình luận

Chuyên đề phương pháp tọa độ trong mặt phẳng Toán 10 KNTTvCS