CHƯƠNG 3: PHÂN SỐ BÀI 5: SO SÁNH PHÂN SỐ Mục tiêu  Kiến thức
+ Nắm vững cách so sánh hai phân số cùng mẫu, hai phân số khác mẫu.
+ Hiểu khái niệm phân số âm và phân số dương.  Kĩ năng
+ Biết so sánh hai phân số.
+ Biết cách sắp xếp dãy các phân số theo thứ tự tăng dần hoặc giảm dần. Trang 1 I. LÍ THUYẾT TRỌNG TÂM
So sánh hai phân số cùng mẫu 4  0 Ví dụ 1:  (vì 4  0 ).
Hai phân số có cùng mẫu dương thì phân số nào 3 3
có tử lớn hơn thì lớn hơn.
Chú ý: Phương pháp bên sử dụng cho hai phân số cùng mẫu dương. 1 2 Ví dụ 2: 
. Ta có thể chuyển các phân số 2  2 
có mẫu âm thành phân số có mẫu dương rồi so sánh.
So sánh hai phân số khác mẫu
Ta viết hai phân số không cùng mẫu thành hai
phân số có cùng mẫu dương rồi so sánh tử số với nhau.
Chú ý: Phân số có tử và mẫu là hai số nguyên cùng
Phân số âm, phân số dương dấu là phân số dương.
Phân số âm: là phân số nhỏ hơn 0.
Phân số có tử và mẫu là các số nguyên khác dấu là
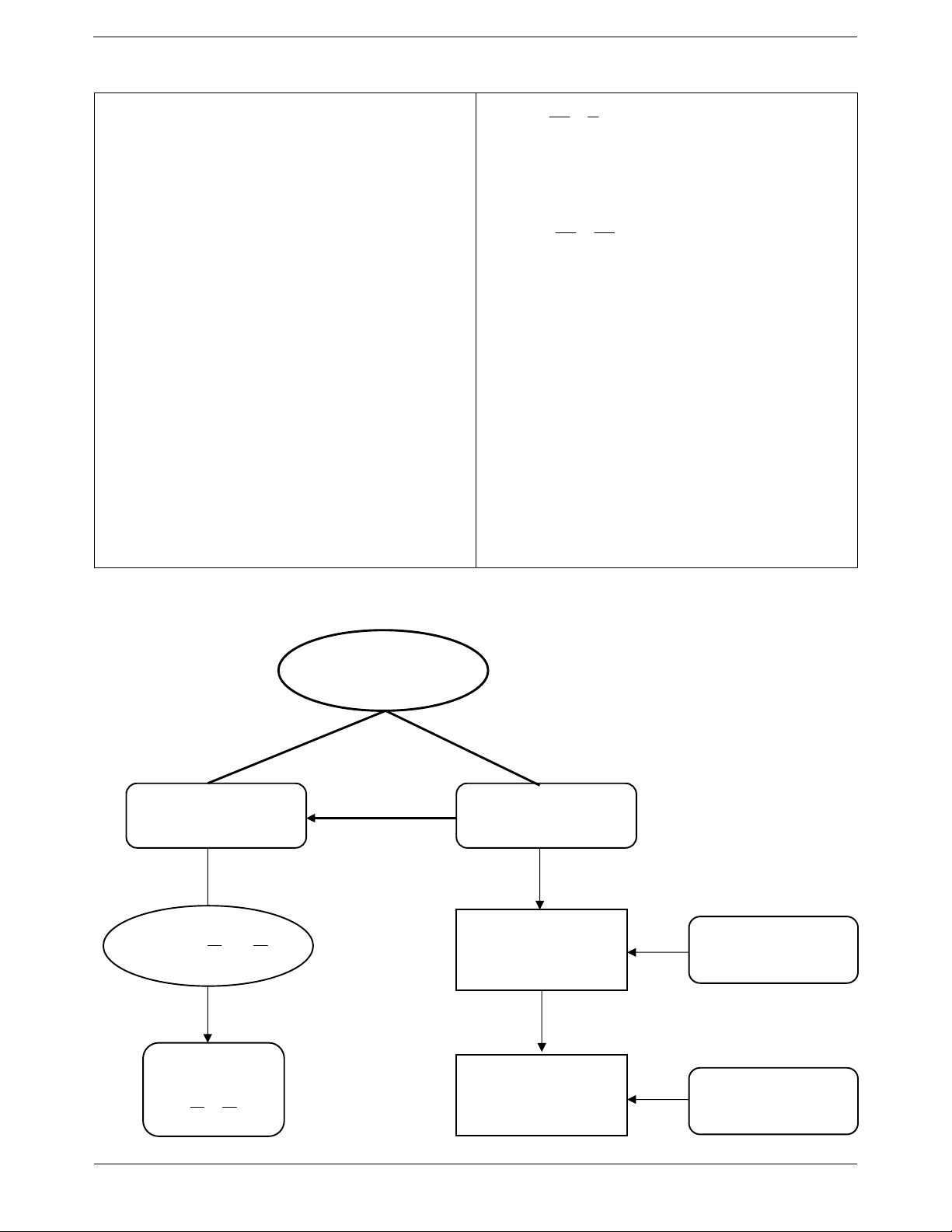
Phân số dương: là phân số lớn hơn 0. phân số âm. HỆ THỐNG SƠ ĐỒ HÓA SO SÁNH HAI PHÂN SỐ So sánh hai phân số Quy đồng mẫu So sánh hai phân số cùng mẫu khác mẫu A C Phân số có tử và So sánh và Phân số lớn hơn 0 mẫu cùng dấu thì B B là phân số dương lớn hơn 0 B>0 Nếu A  C thì Phân số có tử và A C mẫu khác dấu thì Phân số nhỏ hơn 0  là phân số âm B B nhỏ hơn 0 Trang 2 II. CÁC DẠNG BÀI TẬP
Dạng 1: So sánh các phân số cùng mẫu
Bài toán 1. So sánh các phân số Phương pháp giải 2 4 Ví dụ: So sánh và . 5  5  Hướng dẫn giải
Bước 1. Viết phân số có mẫu âm (nếu có) thành 2 2 4 4 Ta có:  ;  . 5  5 5  5 phân số có mẫu dương.  
Bước 2. So sánh tử của các phân số: 2 4 Vì 2  4 nên  . 5 5
Phân số nào có tử lớn hơn thì lớn hơn 2 4 Vậy  . 5  5 Ví dụ mẫu
Ví dụ 1. So sánh các phân số sau: 1 3 3 4 5 3 a) và ; b) và ; c) và . 4  4  7  7  1  1 11 Hướng dẫn giải 1 1  3 3 
a) Viết các phân số dưới dạng mẫu dương:  ;  . 4  4 4  4 1  3 1 3 Vì 1  3  nên  . Vậy  . 4 4 4  4  3 3 4 4
b) Viết các phân số dưới dạng mẫu dương:  ;  . 7  7 7  7 3  4 3 4  Vì 3  4 nên  . Vậy  . 7 7 7  7  Chú ý: 3  4 3  4 Ta có thể nhận xét  0 và  0 nên  . 7 7 7 7 5 3 5 3 c) Ta thấy  0 và  0 nên  . 1  1 11 1  1 11
Bài toán 2. Sắp xếp các phân số Phương pháp giải
Ví dụ: Sắp xếp các phân số sau theo thứ tự tăng 7 24 13 1 43 36 dần: ; ; ; ; ; . 36 36 36 36 36 36 Hướng dẫn giải Trang 3
Vì 1  7  13  24  36  43 nên
Bước 1. So sánh các phân số. 1 7 13 24 36 43      . 36 36 36 36 36 36
Vậy các phân số được sắp xếp theo thứ tự tăng
Bước 2. Sắp xếp các phân số theo thứ tự yêu cầu 1 7 13 24 36 43 dần là: ; ; ; ; ; . của bài toán. 36 36 36 36 36 36 Ví dụ mẫu
Ví dụ 1. Sắp xếp các phân số sau theo thứ tự giảm dần: 5  11 7  13 9 2  7 ; ; ; ; ; . 48 4  8 48 4  8 4  8 48 Hướng dẫn giải
Viết lại các phân số dưới dạng mẫu dương: 11 11    13 13 9 9 ;  ;  . 4  8 48 4  8 48 4  8 48 2  7 13 11 9  7  5  Vì 27  1  3  11  9  7   5 nên      . 48 48 48 48 48 48
Vậy các phân số được sắp xếp theo thứ tự giảm dần là: 5  7  9  1  1 1  3 2  7 ; ; ; ; ; . 48 48 48 48 48 48 9  ... ... ... ... 4
Ví dụ 2. Điền số thích hợp vào chỗ chấm:      . 11 11 11 11 11 11 Hướng dẫn giải 9  8  7 6 5 4       . 11 11 11 11 11 11 Giải thích:
Do các phân số đều có cùng mẫu (dương) nên ta sẽ điền tử số là dãy các số nguyên tăng dần.
Bài tập tự luyện dạng 1
Câu 1: Điền số thích hợp vào ô vuông: 1  3 8 2  2 2  2  2 2  a)      ; b)      ; 18 18 18 18 18 18 9 4 1  1  c)     . 2 24 12 8 3 Câu 2: 1  5 3  6 2  7  7  2 9  7
a) Sắp xếp các phân số sau theo thứ tự tăng dần: ; ; ; ; ; . 24 24 24 24 24 24 71 13 21 12 60 1 8
b) Sắp xếp các phân số sau theo thứ tự giảm dần: ; ; ; ; ; ; . 60 60 60 60 60 60 60 Trang 4
Dạng 2: So sánh các phân số không cùng mẫu Phương pháp giải Cách 1. Quy đồng mẫu. 1  5 5
Ví dụ 1: So sánh các phân số sau: và . 16 8  Hướng dẫn giải
Bước 1. Quy đồng mẫu số các phân số (biến đổi 5 Viết lại phân số
dưới dạng mẫu số dương và 8 
thành các phân số có cùng mẫu dương).    5 5 5.2 10 quy đồng mẫu số:    . 8  8 8.2 16 1  5 1  0
Bước 2. So sánh các phân số có cùng mẫu Vì 15  10 nên  . 16 16 dương. 1  5 5  Vậy . 16 8 4 3
Ví dụ 2: So sánh hai phân số sau: và . 5 7 Hướng dẫn giải Cách 2. Quy đồng tử. Tử số chung là 12. a a 4 4.3 12 3 3.4 12
Nếu a; b; c  0 và b  c thì  . Ta có:   ;   . b c 5 5.3 15 7 7.4 28 12 12 Vì 15  28 nên  . 15 28 4 3 Vậy  . 5 7 7  1
Cách 3. Sử dụng phân số trung gian.
Ví dụ 3: So sánh các phân số sau và . 11 5 a x   Hướng dẫn giải b y  a c    . c x b d 7  1 7  1   Vì  0 và  0 nên  . d y  11 5 11 5 7 21
Ngoài ra, còn một số phương pháp khác để so Ví dụ 4: So sánh các phân số sau: và . 36 108 sánh hai phân số: Hướng đẫn giải Cách 1. Rút gọn • Rút gọn phân số. 21 21: 3 7 Ta có:   . 108 108 : 3 36 7 21 Suy ra  . 36 108
• Sử dụng định nghĩa hai phân số bằng nhau
Cách 2. Sử dụng định nghĩa phân số bằng nhau: Trang 5 Ta có: 7.108  756 ; 36.21  756 . 7 21 Suy ra  . 36 108 Ví dụ mẫu
Ví dụ 1. So sánh các phân số sau bằng hai cách quy đồng tử số và quy đồng mẫu số: 5  4  7  6  a) và ; b) và . 8 7 3 5 Hướng dẫn giải
a) Cách 1 (Quy đồng mẫu số). Mẫu số chung là 56. 5  5.7 3  5 4  4  .8 3  2 Ta có:   ;   . 8 8.7 56 7 7.8 56 3  5 3  2 Vì 35  32 nên  . 56 56 5  4  Vậy  . 8 7
Cách 2 (Quy đồng tử số). 5 4
Ta sẽ so sánh hai phân số vả . 8 7 Tử số chung là 20. 5 5.4 20 4 4.5 20 Ta có:   ;   . 8 8.4 32 7 7.5 35 20 20 Vì 32  35 nên  . 32 35 5 4 5  4  Suy ra  . Vậy  . 8 7 8 7 Chú ý:
Sai lầm thường gặp khi so sánh hai phân số bằng cách quy đồng tử số: 5  5.4 2  0      4 4.5 20 ;   . 8 8.4 32 7 7.5 35 2  0 2  0 Nhận xét 32  35 nên  . 32 35 5  4 Vậy  . 8 7
b) Cách 1 (Quy đồng mẫu số). Mẫu số chung là 15. Trang 6 7  7.5 3  5 6  6.3 18 Ta có:   ;   . 3 3.5 15 5 5.3 15 3  5 1  8 Vì 35  18 nên  . 15 15 7  6  Vậy  . 3 5
Chú ý: Khi so sánh hai phân số âm ta có thể so sánh hai phân số đối của hai phân số đó, từ đó suy ra
kết luận đối với hai phân số ban đầu.
Cách 2 (Quy đồng tử số). 7 6
Ta sẽ so sánh hai phân số và . 3 5 Tử số chung là 42. 7 7.6 42 6 6.7 42 Ta có:   ;   . 3 3.6 18 5 5.7 35 42 42 Vì 18  35 nên  . 18 35 7 6 7  6  Suy ra  . Vậy  . 3 5 3 5
Ví dụ 2. Không quy đồng tử hoặc mẫu, hãy so sánh các phân số sau: 3 5 935 1  0 a) và ; b) và ; 2 6 7  32 9 18 15 c) và . 31 37 Hướng dẫn giải 3 5 3 5
a) Vì  1 (tử lớn hơn mẫu) và  1 (tử nhỏ hơn mẫu) nên  . 2 6 2 6 935 1  0 935 1  0 b) Vì
 0 (tử và mẫu cùng dấu) và
 0 (tử và mẫu trái dấu) nên  . 7  32 9 7  32 9 18 18 15 18 18 15 c) Ta có:  và  . Suy ra  . 31 37 37 37 31 37 Chú ý:
Ta có thể dùng 0 hoặc 1 hoặc một phân số làm số trung gian để so sánh hai phân số.
Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0 (phân số dương). Phân số có tử và mẫu
là hai số nguyên trái dấu thì nhỏ hơn 0 (phân số âm).
Phân số dương có tử lớn hơn mẫu thì phân số đó lớn hơn 1.
Phân số dương có tử nhỏ hơn mẫu thì phân số đó nhỏ hơn 1.
Cách chọn phân số trung gian. Trang 7 a c So sánh ; . b d a c Chọn hoặc . d b
Ví dụ 3. Không quy đồng tử hoặc mẫu, hãy so sánh các phân số sau: 15 13 1  3 1  7 a) và ; b) và . 19 17 20 28 Hướng dẫn giải a) Ta có: 15.17  255; 19.13  247 . 15 13
Suy ra 15.17  19.13 do đó  . 19 17 b) Ta có: 13.28  364 ; 20.17  340 . 13 17
Suy ra 13.28  20.17 do đó  . 20 28 1  3 17 Vậy  . 20 28 Ví dụ 4. a a
a) Cho phân số a,b  ,b  0 . Giả sử  1 và * m   . b b a a  m Chứng minh rằng:  . b b  m 18 17 1 17 17 1
b) Áp dụng kết quả của câu a) để so sánh: A  ; B  . 19 17 1 18 17 1 Hướng dẫn giải a . a b  m . a b  . a m a) Ta có:   b . b b  m 2 b  . b m a  m a  m.b . a b  . m b   b  m b  m 2 .b b  . m b a
Vì  1 nên a  b suy ra . a m  . b m với mọi * m   . b . a b  . a m . a b  . b m Do đó . a b  . a m  . a b  . b m suy ra  . 2 2 b  . b m b  . b m a a  m Vậy  với mọi * m   . b b  m 18 17 1 b) Vì  1 nên 19 17 1 Trang 8
17 1 17 116 17 17 17. 17 18 18 18 17   17 1 17 1 A       B 19 19 19
17 1 17 116 17 17 17. 18 17   18 1 17 1 Vậy A  B .
Bài tập tự luyện dạng 2
Câu 1: So sánh các cặp phân số sau bằng cách quy đồng mẫu số: 2 5 4  3  5  63 3 4 a) và ; b) và ; c) và ; d) và . 3 6 5 7 6 7  0 11 13
Câu 2: So sánh các cặp phân số sau bằng cách quy đồng tử số: 3 6 3  2 4  3  13 39 a) và ; b) và ; c) và ; d) và . 4 7 7 9  9 13 27 47 Câu 3: 2 3
a) Thời gian nào dài hơn: giờ và giờ? 3 4 7 5
b) Đoạn thẳng nào ngắn hơn: m và m? 12 6 7 8
c) Khối lượng nào lớn hơn: kg hay kg? 8 9 4 9
d) Vận tốc nào nhỏ hơn: km/h và km/h? 5 10 2 3 5
Câu 4: Lớp 6A có số học sinh thích bóng chuyền, số học sinh thích cầu lông và số học sinh 5 8 12
thích bóng đá. Hỏi môn thể thao nào được nhiều học sinh lớp 6A yêu thích nhất?
Câu 5: Không quy đồng tử và mẫu, hãy so sánh các phân số sau: 5 13 25 26 1  20 4  5 a) và ; b) và ; c) và . 7 12 3  4 35 133 5  1
Câu 6: Sắp xếp các phân số sau theo thứ tự tăng dần: 13 7 9 2 1 3  7 17 23 7  2  a) ; ; ; ; . b) ; ; ; ; . 20 20 4 5 2 100 5  0 2  5 10 5
Câu 7: Sắp xếp các phân số sau theo thứ tự giảm dần: 13 152 13 5 1  3 2  4 a) ; ; ; . b) ; ; ; . 21 17 17 21 2 4  3 5  Bài tập nâng cao 8  7
Câu 8: Điền số nguyên thích hợp vào ô vuông:   . 15 40 15
Câu 9: Không quy đồng tử và mẫu, hãy so sánh các phân số sau: 23 21 1  7 1  3 9 11 12 19 a) và ; b) và ; c) và ; d) và . 35 37 24 28 16 24 47 77
Câu 10: Tìm các số tự nhiên x sao cho: Trang 9 1 x 1 8 4 5 a)   ; b)   . 5 30 4 5 x 7 1 1
Câu 11: Tìm ba phân số có mẫu khác nhau, các phân số này lớn hơn và nhỏ hơn . 4 3 Câu 12: So sánh: 89 98 1 88 98 1 16 15 1 15 15 1 a) A  và B  . b) C  và D  . 99 98 1 98 98 1 17 15 1 16 15 1 1 1
Câu 13: Tìm hai phân số có mẫu khác nhau, các phân số này lớn hơn nhưng nhỏ hơn . 5 4 Trang 10 ĐÁP ÁN
Dạng 1: So sánh các phân số cùng mẫu Câu 1. 1  3 12 11 10 9 8  a)      . 18 18 18 18 18 18 2 2 2 2 2 2 2  2 2 2  2 2 
b) Ta có      . Suy ra      ; 9 8 7 6 5 4 9 8 7 6 5 4 1  2 2. 3. 8
c) Quy đồng các phân số với mẫu số chung là 24, ta được:     . 24 24 24 24 24 1  2 11 2. 5 3. 3  8 Suy ra     . 24 24 24 24 24 1  1  1 5  3 1  Vậy     . 2 24 12 8 3 Câu 2.
a) Các phân số sắp xếp theo thứ tự tăng dần là: 9  7 7  2 3  6 1  5 7  2  ; ; ; ; ; . 24 24 24 24 24 24
b) Các phân số sắp xếp theo thứ tự giảm dần là: 71 60 21 13 12 8 1 ; ; ; ; ; ; . 60 60 60 60 60 60 60
Dạng 2: So sánh các phân số không cùng mẫu Bài tập cơ bản
Câu 1: So sánh các cặp phân số sau bằng cách quy đồng mẫu số: a) Mẫu số chung là 6. 2 2.2 4 5 Ta có:    . 3 3.2 6 6 2 5 Vậy  . 3 6 b) Mẫu số chung là 35. 4  4  .7 2  8 3  3.5 1  5 Ta có:   ;   . 5 5.7 35 7 7.5 35 2  8 1  5 4  3 Vì  nên  . 35 35 5 7 63 63: 7 9 9 c) Rút gọn phân số    . 7  0 70 : 7 1  0 10 Mẫu số chung là 30. 5  5.5 25 9  9  .3 2  7 Ta có:   ;   . 6 6.5 30 10 10.3 30 Trang 11 2  5 2  7 5  63 Vì  nên  . 30 30 6 7  0
d) Mẫu số chung là 11.13  143 (vì 11 và 13 là hai số nguyên tố cùng nhau). 3 3.13 39 4 4.11 44 Ta có:   ;   . 11 11.13 143 13 13.11 143 39 44 3 4 Vì  nên  . 143 143 11 13 Câu 2. 3 3.2 6 6 3 6 a) Ta có:    . Vậy  . 4 4.2 8 7 4 7 3 2
b) So sánh hai phân số và : 7 9 3 3.2 6 2 2.3 6 Ta có   ;   . 7 7.2 14 9 9.3 27 6 6 3 2 3  2 Vì  nên  . Vậy  . 14 27 7 9 7 9 4 3
c) So sánh hai phân số và : 9 13 4 4.3 12 3 3.4 12 Ta có:   ;   . 9 9.3 27 13 13.4 52 12 12 4 3 4  3 Vì  nên  . Vậy  . 27 52 9 13 9 13 13 13.3 39 39 13 39 d) Ta có    . Vậy  . 27 27.3 81 47 27 47 Câu 3: 2 3 3
a) Vì 2.4  8  3.3  9 nên  . Vậy giờ dài hơn. 3 4 4 5 5.2 10 7 7 b) Ta có:    . Vậy đoạn thẳng m ngắn hơn. 6 6.2 12 12 12 7 7.9 63 8 8.8 64 7 8 c) Ta có:   ;   . Suy ra  . 8 8.9 72 9 9.8 72 8 9 8 Vậy kg lớn hơn. 9 4 4.2 8 9 4 d) Ta có:   
. Vậy vận tốc km/h nhỏ hơn. 5 5.2 10 10 5 Câu 4. 2 3 5
Ta so sánh các phân số: ; và . 5 8 12
Quy đồng tử số của các phân số: 2 2.15 30 3 3.10 30 5 5.6 30   ;   ;   . 5 5.15 75 8 8.10 80 12 12.6 72 Trang 12 30 30 30 5 2 3 Vì   nên   . 72 75 80 12 5 8
Vậy môn bóng đá được nhiều học sinh lớp 6A yêu thích nhất. Câu 5. 5 a) Ta có:
 1 (vì tử nhỏ hơn mẫu); 7
13 1(vì tử lớn hơn mẫu). 12 5 13 Suy ra  . 7 12 25 b) Ta có
 0 (vì tử và mẫu trái dấu); 3  4
26  0 (vì tử và mẫu cùng dấu). 35 25 26 Suy ra  . 3  4 35 1  20 c) Ta có
 0 (vì tử và mẫu trái dấu); 133 4
 5  0 (vì tử và mẫu cùng dấu). 5  1 1  20 4  5 Suy ra  . 133 5  1 Câu 6. 9 9
a) Ta thấy  1 và các phân số còn lại đều nhỏ hơn 1 nên là phân số lớn nhất. 4 4
Quy đồng mẫu số các phân số còn lại với mẫu số chung là 20. 2 2.4 8 1 1.10 10 Ta có:   ;   . 5 5.4 20 2 2.10 20 7 8 10 13 7 2 1 13 Vì    nên    . 20 20 20 20 20 5 2 20
Vậy các phân số được sắp xếp theo thứ tự tăng dần là: 7 2 1 13 9 ; ; ; ; . 20 5 2 20 4
b) Viết lại các phân số dưới dạng mẫu số dương: 17 1  7 23 23  ;  . 5  0 50 2  5 25
Quy đồng mẫu số các phân số với mẫu số chung là 100: 1  7 1  7.2 3  4            23 23.4 92 7 7.10 70 2 2.20 40 ;   ;   ;   . 50 50.2 100 25 25.4 100 10 10.10 100 5 5.20 100 9  2 7  0 40 37 3  4 2  3 7  2  3  7 17 Vì     nên     . 100 100 100 100 100 25 10 5 100 50 Trang 13
Vậy các phân số được sắp xếp theo thứ tự tăng dần là: 2  3 7  2  3  7 1  7 ; ; ; ; . 25 10 5 100 50 Câu 7. 13 152 5 13 a) Ta có:  ;  . 17 17 21 21 13 13 5 13 13 152 Lại có  suy ra    . 21 17 21 21 17 17 152 13 13 5
Vậy các phân số được sắp xếp theo thứ tự giảm dần là: ; ; ; . 17 17 21 21 1 3 2 4
b) Trước hết ta so sánh các phân số ; ; ; . 2 4 3 5 1 1.12 12 3 3.4 12
Quy đồng tử số các phân số:   ;   ; 2 2.12 24 4 4.4 16 2 2.6 12 4 4.3 12   ;   . 3 3.6 18 5 5.3 15 12 12 12 12 1 2 3 4 Vì    nên    . 24 18 16 15 2 3 4 5 1  2  3 4 Suy ra    . 2 3 4  5 1  2  3 4
Vậy các phân số được sắp xếp theo thứ tự giảm dần là: ; ; ; . 2 3 4  5  Bài tập nâng cao Câu 8.
Ta có BCNN 15, 40  120 nên quy đồng mẫu số các phân số, ta được: 8  .8 3. 7  .8 6  4 3. 56   hay   . 15.8 40.3 15.8 120 120 120 Suy ra 64  3.  5
 6 , do đó 3. 63; 6  0;5  7   2  1; 2  0; 1   9 .
Vậy các giá trị thích hợp là –21; –20; –19. Câu 9. 23
a) Chọn phân số trung gian là . 37 23 23 21 23 23 21 Ta có:  ;  . Suy ra  . 35 37 37 37 35 37 17 13 b) Ta so sánh hai phân số và . 24 28 17 Chọn phân số làm phân số trung gian. 28 17 17 13 17 17 13 1  7 1  3 Ta có  ;  . Suy ra  . Do đó  . 24 28 28 28 24 28 24 28 Trang 14 9 11 1 1
c) Ta thấy cả hai phân số và
đều xấp xỉ nên ta dùng phân số làm phân số trung gian. 16 24 2 2 9 8 1 11 12 1 9 11 Ta có:   ;   . Suy ra  . 16 16 2 24 24 2 16 24 12 19 1 1
d) Ta thấy cả hai phân số và
đều xấp xỉ nên ta dùng phân số làm phân số trung gian. 47 77 4 4 12 12 1 19 19 1 12 19 Ta có:   ;   . Suy ra  . 47 48 4 77 76 4 47 77 Câu 10.
a) Quy đồng mẫu số các phân số với mẫu số chung là 60, ta được: 1.12 . x 2 1.15   12 . x 2 15 hay   . 5.12 30.2 4.15 60 60 60 Suy ra 12  . x 2  15 , do đó .
x 2  14 hay x  7 . Vậy x  7 .
b) Quy đồng tử số các phân số với tử số chung là 40, ta được: 8.5 4.10 5.8   40 40 40 hay   . 5.5 . x 10 7.8 25 . x 10 56 Suy ra 25  . x 10  56 , do đó . x 10 30;40;5  0 . Vậy x 3;4;  5 . Câu 11.
Quy đồng các phân số với mẫu số chung là 48, ta được: 1 1.12 12 1 1.16 16   ;   . 4 4.12 48 3 3.16 48 12 13 14 15 16 Ta có:     . 48 48 48 48 48 1 13 7 5 1
Rút gọn các phân số trên ta được:     . 4 48 24 16 3 13 7 5
Vậy ba phân số cần tìm là: ; và . 48 24 16 Câu 12. 89 98 1 a) Ta thấy A 
1 (vì tử nhỏ hơn mẫu) nên: 99 98 1 98 1 98 1 97 98  98 98. 88 89 89 89 98   88 1 98 1 A       B . 99 99 99 98 1 98 1 97 98  98 98. 98 98   98 1 98 1 Vậy A  B . 16 15 1 b) Ta thấy C 
 1 (vì tử nhỏ hơn mẫu) nên: 17 15 1
15 1 15 114 15 15 15. 15 16 16 16 15   15 1 15 1 C       D . 17 17 17
15 1 15 114 15 15 15. 16 15   16 1 15 1 Vậy C  D . Câu 13. Trang 15 1 1
Quy đồng hai phân số và với mẫu số chung là 60, ta được: 5 4 1 1.12 12 1 1.15 15   ;   . 5 5.12 60 4 4.15 60 12 13 14 15 Ta có:    . 60 60 60 60 1 13 7 1
Rút gọn các phân số trên ta được:    . 5 60 30 4 13 7
Vậy hai phân số cần tìm là: và . 60 30 Trang 16