










Preview text:
CHUYÊN ĐỀ ÔN TẬP MỨC ĐỘ 3 CHƯƠNG 2 SÓNG CƠ
1. Đại cương sóng cơ
Câu 1. Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng.
Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li độ dao động của phần tử tại M là
3 cm thì li độ dao động của phần tử tại N là 3
− cm. Biên độ sóng bằng A. 6 cm. B. 2 3 cm. C. 3 cm. D. 3 2 cm.
Câu 2. Một sóng ngang có tần số f = 20Hz truyền trên một sợi dây nằm ngang với tốc độ truyền sóng
bằng 3 m/s. Gọi M, N là hai điểm trên dây cách nhau 20 cm sóng truyền từ M đến N. Tại thời điểm phần
tử N ở vị trí thấp nhất sau đó khoảng thời gian nhỏ nhất bằng bao nhiêu thì phần tử M sẽ đi qua vị trí cân bằng A. 1 s. B. 1 s. C. 1 s. D. 1 s. 60 48 40 30
Câu 3. : Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm
trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t , li độ của ba phần tử A, B, C lần lượt là 1
−4,8 mm; 0 mm; 4,8 mm. Nếu tại thời điểm t , li độ của A và C đều bằng +5,5 mm, thì li độ của phần tử 2 B là mm A. 10,3 mm B. 11,1 mm C. 5,15 mm D. 7,3 mm
Câu 4. Nguồn sóng ở O được truyền theo phương Ox. Trên phương này có hai điểm P và Q cách nhau
PQ = 15 cm. Biết tần số sóng là 10 Hz, tốc độ truyền sóng v = 40 cm/s, biên độ sóng không đổi khi truyền 3
sóng và bằng 3 cm. Nếu tại thời điểm nào đó P có li độ
cm thì li độ tại Q có độ lớn là 2 A. 0 cm. B. 0,75 cm. C. 3 cm. D. 1,5 cm.
Câu 5. Một sóng hình sin lan truyền theo phương Ox với biên độ không đổi A = 4 cm. Hai chất điểm
gần nhất trên cùng một phương truyền sóng mà có cùng li độ là 2 cm, nhưng có vận tốc ngược hướng
nhau thì cách nhau 6 cm. Tỉ số giữa tốc độ dao động cực đại của một phần tử môi trường với tốc độ truyền sóng là: A. s B. s C. 2 s D. 4 s 3 9 9 9
Câu 6. Một nguồn âm có tần số f = 50Hz. Hai điểm gần nhau nhất trên phương truyền sóng cách nhau
2,5cm luôn dao động lệch pha nhau π/4. Vận tốc truyền sóng là: A. 0,5 km/s B. 1km/s C.250m/s D. 750m/s
Câu 7. Sóng truyền dọc theo sợi dây căng ngang và rất dài. Biết phương trình sóng tại O có dạng uo =
3cosπt(cm), vận tốc truyền sóng là v = 20cm/s. Nếu M và N là hai điểm gần nhau nhất dao động vuông
pha với nhau và M cùng pha với O thì khoảng cách từ O đến M và từ O đến N có thể là: A.80cm và 75cm
B. 37,5cm và 12,5cm
C. 80cm và 70cm D. 85,5cmvà 80cm
Câu 8. Một nguồn 0 phát sóng cơ có tần số 10hz truyền theo mặt nước theo đường thẳng với v = 60
cm/s. Gọi M và N là điểm trên phương truyền sóng cách 0 lần lượt 20 cm và 45 cm. Trên đoạn MN có
bao nhiêu điểm dao động lệch pha với nguồn 0 góc + k2 3 A. 2 B. 3 C. 4 D. 5 Trang 1
Câu 9. Một dây đàn hồi dài có đầu A dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng
trên dây là 4m/s. Xét một điểm M trên dây và cách A một đoạn 40cm, người ta thấy M luôn luôn dao
động lệch pha so với A một góc = (k + 0,5) với k là số nguyên. Tính tần số, biết tần số f có giá trị
trong khoảng từ 8 Hz đến 13 Hz. #A. 8,5Hz B. 10Hz C. 12Hz D. 12,5Hz
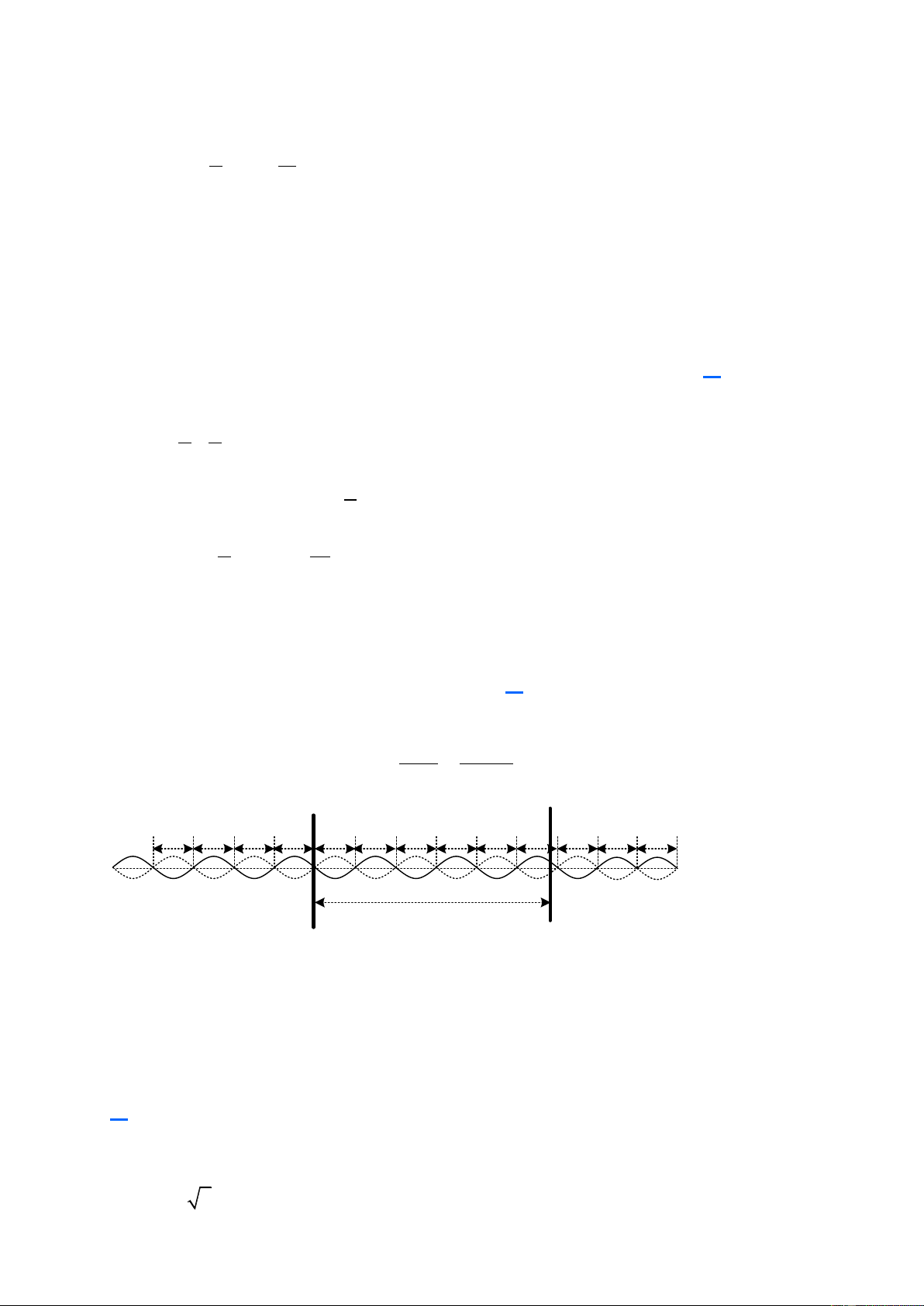
Câu 10. Trên một sợi dây dài đang có sóng ngang hình sin truyền qua
theo chiều dương của trục Ox. Tại thời điểm t một đoạn của sợi dây có 0
dạng như hình bên. Hai phần tử tại M và O dao động lệch pha nhau. 3 2 A. B. C. D. 4 3 4 3
Câu 11. Trên một sợi dây dài đang có sóng ngang hình sin truyền
qua theo chiều dương của trục Ox. Tại thời điểm t u 0, một đoạn của Q
sợi dây có hình dạng như hình bên. Hai phần tử dây tại M và Q
dao động lệch pha nhau: O x A. 2π B. π/3 M C. π/4 D. π
Câu 12. Một sóng hình sin truyền trên một sợ dây dài. Ở thời
điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân
bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng
của sóng này bằng A. 48 cm B. 18 cm C. 36 cm D. 24 cm
Câu 13. Một sóng cơ truyền trên mặt nước theo hướng từ A đến E có B
biên độ 2 cm, tốc độ truyền là 4 m/s. Tại một thời điểm nào đó các
phần tử mặt nước có dạng như hình vẽ. Cho biết khoảng cách A đến C C A
là 20 cm. Phần tử vật chất tại C đang E
A. Đứng yên D
B. Chuyển động đi lên với tốc độ 8 (cm/s)
C. Chuyển động đi xuống với tốc độ 20π (cm/s)
D. Chuyển động đi lên với tốc độ 40π (cm/s)
Câu 14. Một sóng hình sin đang truyền trên một sợi dây, theo
chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây ở
các thời điểm t1 và t = t + 0,3s . Chu kì của sóng là 2 1 A. 0,9 s B. 0,4 s C. 0,6 s D. 0,8 s
Câu 15. Một sóng cơ lan truyền trên một sợi dây dài nằm ngang, với tốc độ 80 cm/s theo chiều dương
trục Ox. Hình dạng của sợi dây tại thời điểm t = 0 được mô tả như hình vẽ. Phương trình sóng truyền trên sợi dây có dạng u(mm) 6 + x 2
#A. u = 6 cos 10 t − −
(u: mm, x: cm, t: s) 8 3 x(cm) O Trang 2 6 − 6 14 3
B. u = 6 cos 5 t − (u: mm, t: s) 4 x 3
C. u = 6 cos 10 t − +
(u: mm, x: cm, t: s) 8 4 x 3
D. u = 6 cos 10 t − − (u: mm, x: cm, t: s) 8 4 2. Giao thoa sóng cơ
Câu 16. Tại hai điểm A và B trên mặt nước cách nhau 10 cm có hai nguồn kết hợp dao động với phương trình: u = u = acos40 t
(cm) , tốc độ truyền sóng trên mặt nước là 30cm / s . Xét đoạn thẳng CD = 4cm 1 2
trên mặt nước có chung đường trung trực với AB. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn
CD chỉ có 5 điểm dao dộng với biên độ cực đại là: A. 5,2 cm. B. 6 cm. C. 4,2 cm. D. 6,8 cm.
Câu 17. Trong thí nghiệm giao thoa sóng nước, hai nguồn kết hợp giống hệt nhau A và B nằm cách
nhau 20 cm tạo ra sóng trên mặt nước với bước sóng 2 cm . Xét điểm dao động với biên độ cực đại nằm
trên mặt nước thuộc đường tròn tâm A bán kính 20 cm , cách đường trung trực của AB một đoạn ngắn nhất bằng A. 0,9 cm B. 2, 0 cm C. 1,0 cm D. 1,9 cm
Câu 18. Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12(cm) đang dao
động vuông góc với mặt nước tạo ra sóng có bước sóng = 1,6cm. C và D là hai điểm khác nhau trên
mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8(cm). Số điểm dao động cùng
pha với nguồn ở trên đoạn CD là A. 3 B. 10 C. 5 D. 6
Câu 19. Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 20 cm dao động theo phương trình u =
acos(ωt) trên mặt nước, coi biên độ không đổi, bước sóng λ = 3 cm. Gọi O là trung điểm của AB. Một
điểm nằm trên đường trung trực AB, dao động cùng pha với các nguồn A và B, cách A hoặc B một đoạn nhỏ nhất là A.12cm B.10cm C.13.5cm D.15cm
Câu 20. Giao thoa sóng nước với hai nguồn giống hệt nhau A, B cách nhau 23 cm có tần số 50Hz. Tốc độ
truyền sóng trên mặt nước là 2 m/s. Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường
tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là A. 26,76 mm B. 29,94mm C. 28,97mm D. 19,34 mm
Câu 21. Trên bề mặt chất lỏng có hai nguồn phát sóng kết hợp A, B dao động cùng pha, cách nhau một
khoảng 30 cm. Trên đường tròn tâm O là trung điểm của AB bán kính 4 cm, có 8 điểm dao động với biên
độ cực đại. Số cực đại trên đoạn AB là A. 9. B. 7. C. 15. D. 13.
Câu 22. Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha,
cùng tần số, cách nhau AB = 12cm tạo ra hai sóng kết hợp có bước sóng λ = 2cm. Trên đường thẳng (Δ)
song song với AB và cách AB một khoảng là 5cm, khoảng cách ngắn nhất từ giao điểm C của (Δ) với
đường trung trực của AB đến điểm M dao động với biên độ cực tiểu là A. 0,47 cm. B. 0,5 cm. C. 0,65 cm. D. 0,68 cm.
Câu 23. Thí nghiệm giao thoa sóng trên mặt nước, hai nguồn kết hợp đặt tại A và B cách nhau 16 cm
dao động cùng pha theo phương thẳng đứng. Sóng truyền ở mặt nước có bước sóng là 3 cm. Ở mặt nước, Trang 3
số điểm trên đường đường thẳng qua A , vuông góc với AB mà phần tử nước ở đó dao động với biên độ cực đại là A. 12. B. 10. C. 5. D. 6.
Câu 24. Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn S1S2 = 9λ phát ra dao động cùng pha
nhau. Trên đoạn S1S2, số điểm có biên độ cực đại cùng pha với nhau và cùng pha với nguồn (không kể hai nguồn) là: A.6 B.10 C.8 D.12
Câu 25. Trên mặt thoáng của chất lỏng có hai nguồn kết hợp A và B giống nhau dao động cùng tần số f =
8Hz tạo ra hai sóng lan truyền với v = 16cm/s. Hai điểm MN nằm trên đường nối AB và cách trung điểm
O của AB các đoạn lần lượt là OM = 3,75 cm, ON = 2,25cm. Số điểm dao động với biên độ cực đại và
cực tiểu trong đoạn MN là:
A. 5 cực đại 6 cực tiểu
B. 6 cực đại, 6 cực tiểu
C. 6 cực đại, 5 cực tiểu D. 5 cực đại, 5 cực tiểu
Câu 26. Trên bề mặt chất lỏng có 2 nguồn phát sóng kết hợp O và O dao động đồng pha, cách nhau 1 2
một khoảng O O bằng 40cm. Biết sóng do mỗi nguồn phát ra có f = 10Hz , vận tốc truyền sóng 1 2 v = 2m / .
s Xét điểm M thuộc mặt nước nằm trên đường thẳng vuông góc với O O tại O . Đoạn O M 1 2 1 1
có giá trị lớn nhất là bao nhiêu để tại M có dao động với biên độ cực đại: A. 20cm B. 50cm C. 40cm D. 30cm
Câu 27. Trên mặt nước, hai nguồn kết hợp A, B cách nhau 40cm luôn dao động cùng pha, có bước sóng
6cm. Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhât, AD=30cm. Số điểm cực đại và
cực tiểu trên đoạn CD lần lượt là : A. 5 và 6 B. 7 và 6 C. 13 và 12 D. 11 và 10
Câu 28. Giao thoa sóng ở mặt nước với hai nguồn kết hợp đặt tại A và B. Hai nguồn dao động điều hòa
theo phương thẳng đứng, cùng pha và cùng tần số 10 Hz. Biết AB = 20 cm, tốc độ truyền sóng ở mặt
nước là 0,3 m/s. Ở mặt nước, O là trung điểm của AB, gọi Ox là đường thẳng hợp với AB một góc 0 60 .
M là điểm trên Ox mà phần tử vật chất tại M dao động với biên độ cực đại (M không trùng với O).
Khoảng cách ngắn nhất từ M đến O là A. 1,72 cm. B. 2,69 cm. C. 3,11 cm. D. 1,49 cm.
Câu 29. Hai nguồn sóng kết hợp giống hệt nhau được đặt cách nhau một khoảng cách x trên đường kính
của một vòng tròn bán kính R (x < R) và đối xứng qua tâm của vòng tròn. Biết rằng mỗi nguồn đều phát
sóng có bước sóng λ và x = 6λ. Số điểm dao động cực đại trên vòng tròn là A. 26 B. 24 C. 22. D.20.
Câu 30. Trong một thí nghiệm giao thoa sóng nước, hai nguồn A và B cách nhau 8 cm, dao động theo
phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80 Hz. Tốc độ truyền sóng trên mặt
nước là 40 cm/s. Ở mặt nước, gọi là đường trung trực của đoạn AB . Trên , điểm M ở cách AB 3
cm; điểm N dao động ngược pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây? A. 0,4 cm. B. 0,8 cm. C. 0,6 cm. D. 1,8 cm. 3. Sóng dừng
Câu 31. Một sợi dây AB dài 40 cm có 2 đầu cố định. Biết rằng khoảng thời gian giữa 5 lần liên tiếp sợi
dây duỗi thẳng là 1 s. Tốc độ truyền sóng trên dây là Tốc độ truyền sóng trên dây là 20 cm/s. Không tính
2 đầu A và B thì trên dây có Trang 4
A. 10 nút và 9 bụng.
B. 9 nút và 9 bụng.
C. 9 nút và 8 bụng.
D. 7 nút và 8 bụng.
Câu 32. Một sợi dây AB dài l đang có sóng dựng với A và B là hai nút sóng. Khoảng cách lớn
nhất giữa hai vị tri cân bằng của hai phần tử dao động có biên độ cực đại là 80 cm .Khoảng cách lớn
nhất giữa hai vị trí của hai phần tử không dao động mà không tính A và B là 70cm. Số bụng sóng trên dây AB là A. 11. B. 8. C. 10. D. 9.
Câu 33. Trên một sợi dây đàn hồi có sóng dừng với bước sóng 1,1 cm. Trên dây có hai điểm A và B cách
nhau 5,4 cm, tại trung điểm của AB là một nút sóng, số nút sóng và bụng sóng trên đoạn dây AB (kể cả A và B) là
A. 9 bụng, 10 nút.
B. 10 bụng, 10 nút.
C. 10 bụng, 9 nút. D. 9 bụng, 9 nút.
Câu 34. Trên một sợi dây đàn hồi chiều dài 1,6 m, hai đầu cố định và đang có sóng dừng với biên độ tại
bụng là#A. Quan sát trên dây thấy có các điểm không phải bụng cách đều nhau những khoảng 20 cm luôn
dao động cùng biên độ A0 (với 0 < A0 < A). Số bụng sóng trên dây là A. 4. B. 8. C. 6. D. 5.
Câu 35. Một sợi dây PQ dài 120 cm, hai đầu cố định, đang có sóng dừng ổn định. Bề rộng của bụng sóng
là 4a. Khoảng cách gần nhất giữa hai điểm dao động cùng pha và cùng biên độ bằng a là 10 cm.Số bụng sóng trên PQ là A. 4 B. 8 C. 6 D. 10
Câu 36. Dây AB dài 90 cm đầu A gắn với nguồn dao động (xem A là nút) và đầu B tự do. Quan sát thấy
trên dây có 8 nút sóng dừng và khoảng thời gian 6 lần liên tiếp sợi dây duỗi thẳng là 0,25 s. Tính tốc độ
truyền sóng trên dây. Tính khoảng cách từ A đến nút thứ 7.
A. 10 m/s và 0,72 m.
B. 0,72 m/s và 2,4 m.
C. 2,4 m/s và 0,72 m. D. 2,4 m/s và 10 cm.
Câu 37. Một sợi dây đàn hồi một đầu cố định, một đàu gắn với âm thoa dao động nhỏ (xem là nút) có tần
số thay đổi được. Khi thay đổi tần số âm thoa thấy với 2 giá trị liên tiếp của tần số là 28 Hz và 42 Hz thì
trên dây có sóng dừng. Hỏi nếu tăng dần giá trị tần số từ 0 Hz đến 50 Hz sẽ có bao nhiêu giá trị của tần số
để trên dây lại có sóng dừng. Coi vận tốc sóng và chiều dài dây là không đổi.
A. 7 giá trị.
B. 6 giá trị.
C. 4 giá trị. D. 3giá trị.
Câu 38. Khảo sát sóng dừng trên một sợi dây đàn hồi dài 0, 5 m có hai đầu cố định, tốc độ truyền sóng
trên dây là 4 m / s . Tần số sóng có giá trị từ 17 Hz đến 25 Hz . Để trung điểm của dây là một nút sóng
thì tần số sóng bằng A. 18 Hz . B. 24 Hz . C. 20 Hz . D. 22 Hz .
Câu 39. Quan sát sóng dừng trên sợi dây AB, đầu A dao động điều hòa theo phương vuông góc với sợi
dây (coi A là nút). Với đầu B tự do và tần số dao động của đầu A là 22 Hz thì trên dây có 6 nút. Nếu đầu
B cố định và coi tốc độ truyền sóng trên dây như cũ, để vẫn có 6 nút thì cần tăng hay giảm tần số bao nhiêu A. giảm 2 Hz. B. tăng 2Hz C. giảm 4. D. không đổi
Câu 40. Một sợi dây đàn hồi một đầu cố định, một đầu tự do. Tần số dao động bé nhất để sợi dây có sóng
dừng là f0. Tăng chiều dài thêm 1 m thì tần số dao động bé nhất để sợi dây có sóng dừng là 6 Hz. Giảm
chiều dài bớt 1 m thì tần số dao động bé nhất để sợi dây có sóng dừng là 20 Hz. Giá trị của f0 là A. 10 Hz. B. 7 Hz. C. 120/13 Hz. D. 8 Hz. Trang 5
Câu 41. Một sợi dây dài 36 cm đang có sóng dừng ngoài hai đầu dây cố định trên dây còn có 2 điểm khác
đứng yên, tần số dao động của sóng trên dây là 50 Hz. Biết trong quá trình dao động tại thời điểm sợi dây
nằm ngang thì tốc độ dao động của điểm bụng khi đó là 8π m/s. Gọi x, y lần lượt là khoảng cách nhỏ nhất
và lớn nhất giữa hai điểm bụng gần nhau nhất trong quá trình dao động. Tỉ số x bằng y A. 0,50 B. 0,60. C. 0,75. D. 0,80
Câu 42. Người ta làm thí nghiệm tạo sóng dừng trên một sợi dây đàn hồi AB có hai đầu cố định. Sợi dây
AB dài 1,2 m. Trên dây xuất hiện sóng dừng với 20 bụng sóng. Xét các điểm N, M, trên dây có vị trí cân
bằng cách A các khoảng lần lượt là 1 cm và 3cm. Biên độ sóng tại M lớn hơn biên độ sóng tại N là 2 cm.
Biên độ của bụng sóng là. A. 4 cm. B. 2 cm.
C. 4 2cm D. 2 2cm
Câu 43. Ba điểm M, N, K trên một sợi dây đàn hồi thỏa mãn MN = 2 cm, MK = 3 cm. Sóng dừng xảy ra
trên dây với bước sóng 10 cm, M là bụng sóng. Khi N có li độ là 2 cm thì K sẽ có li độ là: A. 2 cm. B. -2 cm. C. -3 cm. D. 3 cm
Câu 44. Trên một sợi dây đang có sóng dừng, phần tử tại điểm bụng
dao động điều hoà với biên độ A . Hình bên là hình dạng của một đoạn
dây ở một thời điểm nào đó. Lúc đó li độ của M là 4 mm, còn li độ của
N bằng − A / 2 . Giá trị của A bằng A. 14 mm. B. 7 mm. C. 8 mm. D. 12 mm.
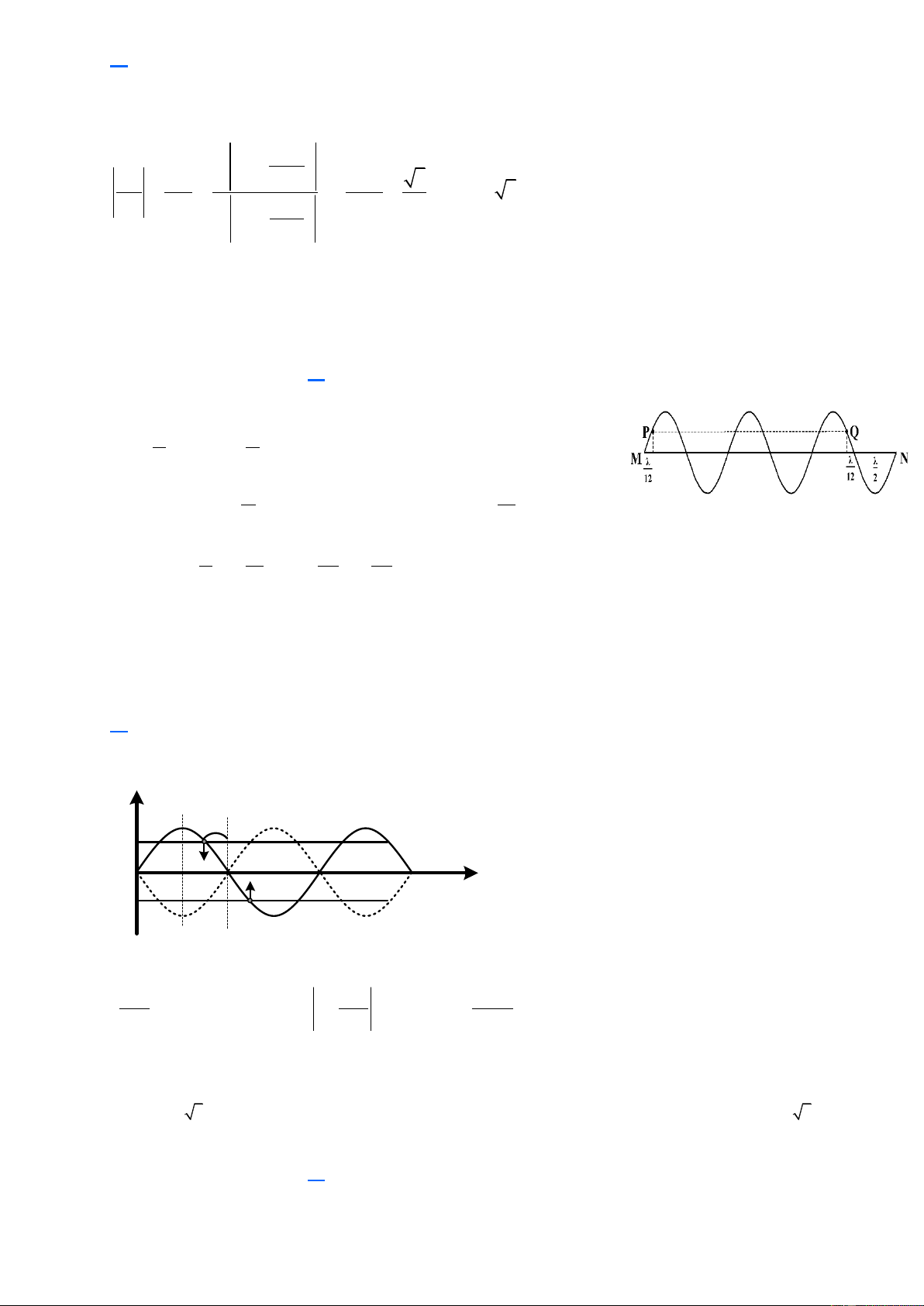
Câu 45. Sóng dừng hình thành trên sợi dây MN dài 72 cm với 7 nút sóng kể cả M và N . Biên độ dao
động tại bụng sóng là 4 cm . P và Q là hai điểm trên sợi dây có cùng biên độ dao động bằng 2 cm và
luôn dao động cùng pha với nhau. Khoảng cách lớn nhất có thể giữa P và Q bằng A. 8 cm
B. 56 cm
C. 60 cm D. 68 cm
Câu 46. Sóng dừng trên một sợi dây có biên độ ở bụng là 5 cm. Giữa hai điểm M, N có biên độ 2,5 cm
cách nhau 20 cm và các điểm nằm trong khoảng MN luôn dao động với biên độ nhỏ hơn 2,5 cm. Tìm bước sóng. A. 120 cm. B. 60 cm. C. 90 cm. D. 108 cm.
Câu 47. Sóng dừng trên một sợi dây có bước sóng 30 cm có biên độ ở bụng là 4 cm. Giữa hai điểm M, N
có biên độ 2 3 cm và các điểm nằm trong khoảng MN luôn dao động với biên độ lớn hon 2 3 cm. Tìm MN. A. 10 cm. B. 5 cm. C. 7,5 cm. D. 8 cm.
Câu 48. Trong hiên tượng sóng dừng hai đầu dây cố định, khoảng cách lớn nhất giữa hai vị trí cân bằng
trên dây có cùng biên độ 4mm là 130cm. Khoảng cách lớn nhất giữa hai vị trí cân bằng trên dây dao động
ngược pha và cùng biên độ 4mm là 110cm. Biên độ sóng dừng tại bụng gần giá trị nào sau đây nhất? A. 6,7mm B. 6,1mm. C. 7,1mm. D. 5,7mm.
Câu 49. Trên một sợi dây có hai đầu cố định, đang có sóng dừng với biên độ dao động của bụng sóng là 4
cm. Khoảng cách giữa hai đầu dây là 60 cm, sóng truyền trên dây có bước sóng là 30 cm. Gọi M và N là
hai điểm trên dây mà phần tử tại đó dao động với biên độ lần lượt là 2 2 cm và 2 3 cm. Khoảng cách
lớn nhất giữa M và N trên phương truyền sóng gần nhất giá trị nào? A. 52 cm B. 50 cm. C. 53 cm. D. 50,5 cm. Trang 6
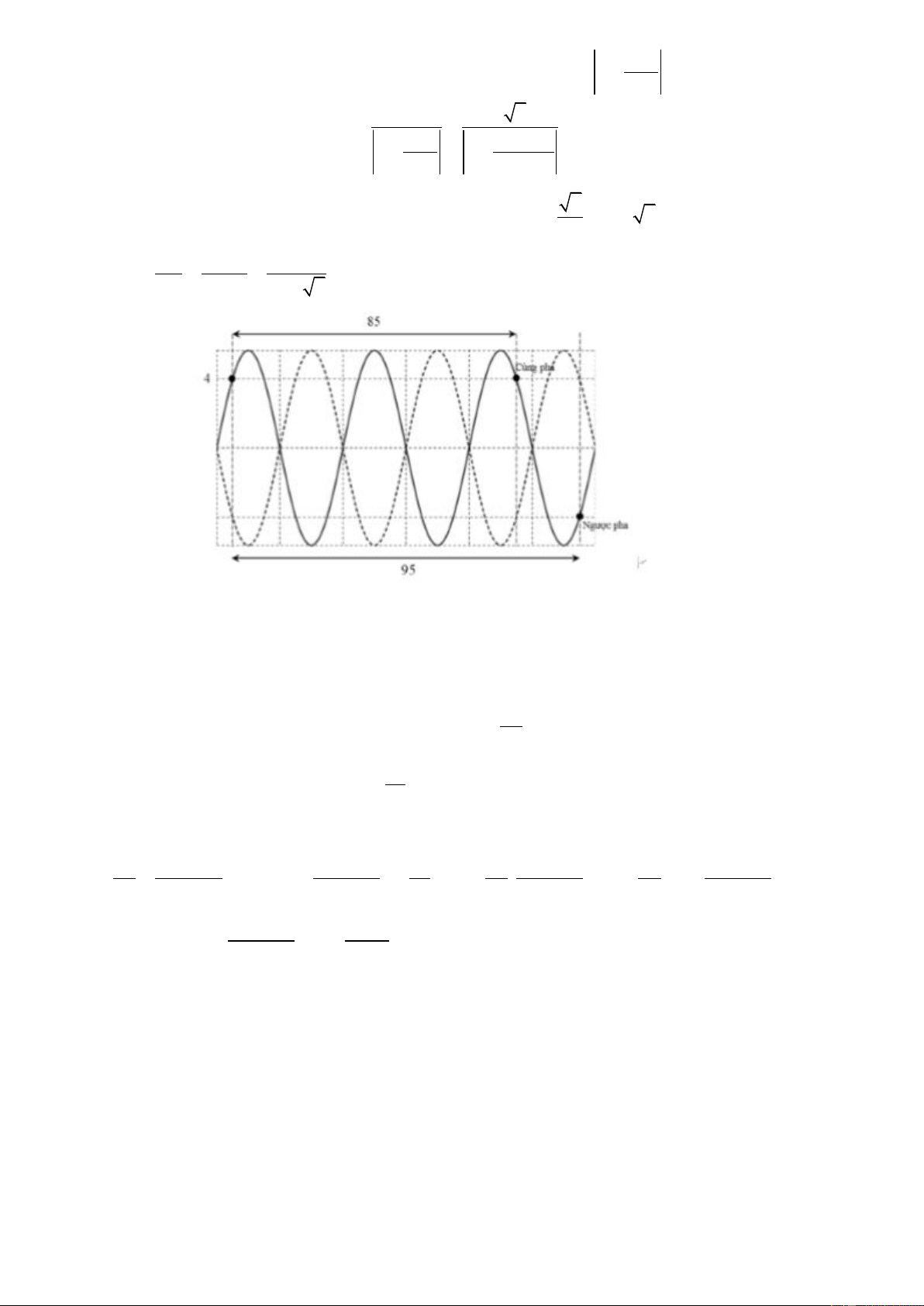
Câu 50. Một sợi dây căng ngang với hai đầu cố định, đang có sóng dừng. Khoảng cách xa nhất giữa hai
phần tử trên dây dao động cùng biên độ 4 2mm là 95 cm, còn khoảng cách xa nhất giữa hai phần tử trên
dây dao động cùng pha với cùng biên độ 4 2mm là 85 cm. Khi sợi dây duỗi thẳng, N là trung điểm giữa
vị trí một nút và vị trí một bụng liền kề. Tỉ số giữa tốc độ truyền sóng trên dây và tốc độ cực đại của phần
tử tại N xấp xỉ là A. 3,98. B. 0,25. C. 0,18. D. 5,63. 4. Sóng âm
Câu 51. Mức cường độ âm do nguồn S gây ra tại M là L, khi cho S tiến lại gần M một đoạn 62m thì mức
cường độ âm thăng thêm 3dB. Khoảng cách từ S đến M là A. 112m B. 210m C. 148m D. 130m
Câu 52. Trên một đường thẳng cố định trong môi trường đẳng hướng, không hấp thụ và phản xạ âm, một
máy thu ở cách nguồn âm một khoảng d thu được âm có mức cường độ âm là L; khi dịch chuyển máy thu
ra xa nguồn âm thêm 9m thì mức cường độ âm thu được là L- 20 dB, Khoảng cách d là A. 1m B. 8m C. 10m D. 9m
Câu 53. Trong một môi trường đẳng hướng và không hấp thụ âm, có ba điểm theo thứ tự A, B, C thẳng
hàng. Một nguồn âm điểm phát âm có công suất P được đặt tại B thì mức cường độ âm tại A là 40 dB, tại
C là 20 dB. Mức cường độ âm tại trung điểm AC có giá trị gần đúng bằng A. 53dB. B. 27dB. C. 34dB. D. 42dB.
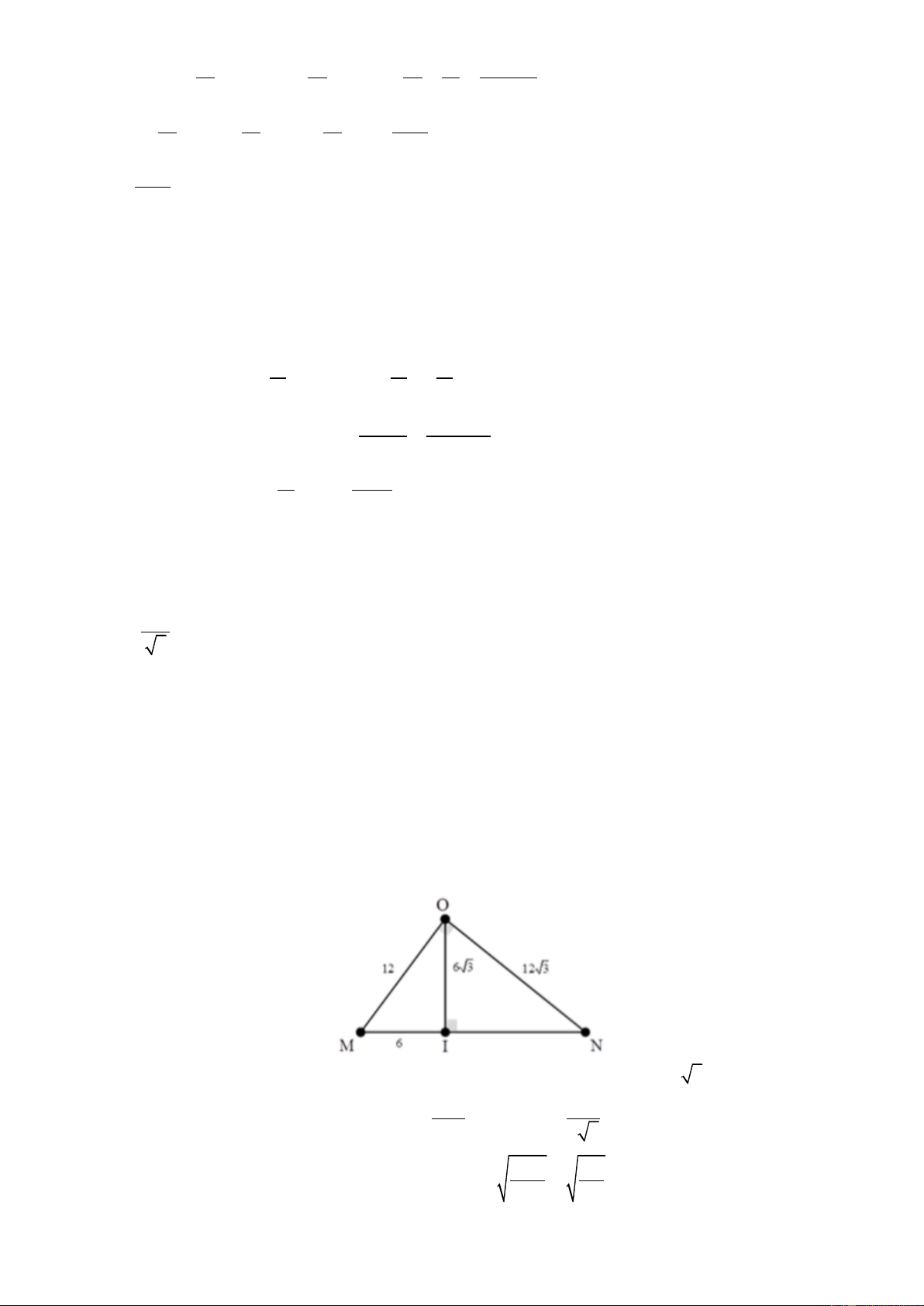
Câu 54. Một thiết bị dùng để xác định mức cường độ âm được phát ra từ một nguồn âm đẳng hướng đặt
tại điểm O, thiết bị bắt đầu chuyển động nhanh dần đều từ điểm M đến điểm N với gia tốc 3 m/s2, biết ON OM =
=12m và ∆OMN vuông tại O. Chọn mốc thời gian kể từ thời điểm máy bắt đầu chuyển động 3
thì mức cường độ âm lớn nhất mà máy đo được khi đi từ M đến N là bao nhiêu và tại thời điểm nào? Biết
mức cường độ âm đo được tại M là 60 dB.
A. 66,02 dB và tại thời điểm 2.
C. 66,02 dB và tại thời điểm 2,6 s.
B. 65,25 dB và tại thời điểm 4 s.
D. 61,25 dB và tại thời điểm 2 s.
Câu 55. Một nguồn âm coi là nguồn âm điểm phát âm đẳng hướng trong không gian. Môi trường không
hấp thụ âm. Mức cường độ âm tại M lúc đầu là 50dB. Nếu tăng công suất của nguồn âm lên 30% thì mức
cường độ âm tại M bằng: A. 61,31dB B. 50,52dB C. 51,14dB D. 50,11dB
Câu 56. Một nguồn âm đặt tại O trong môi trường đẳng hướng. Hai điểm M và N trong môi trường tạo
với O thành một tam giác đều. Mức cường độ âm tại M và N đều bằng 14,75 dB. Mức cường độ âm lớn
nhất mà một máy thu thu được khi đặt tại một điểm trên đoạn MN bằng A. 18 dB. B. 16,8 dB C. 16 dB D. 18,5 dB
Câu 57. Một nguồn âm điểm S phát ra âm đẳng hướng với công suất không đổi trong một môi trường
không hấp thụ và không phản xạ âm. Một người đứng tại A cách nguồn âm 5 m, đo được âm có cường độ
âm I. Khi người này di chuyển theo phương vuông góc với SA một đoạn 5 m thì sẽ đo được âm có cường độ âm là A. I I I . B. C. I D. 2 2 4
Câu 58. Một nguồn âm có công suất không đổi đặt tại A, truyền theo mọi hướng trong một môi trường
không hấp thụ âm. Mức cường độ âm tại hai điểm B và C lần lượt là 50 dB và 48 dB. Biết ba điểm A, B,
C tạo thành tam giác vuông tại B và AB = 8 m. Khoảng cách BC gần giá trị nào sau đây? Trang 7 A. 10 m. B. 4 m. C. 16 m. D. 6 m.
Câu 59. Một vận động viên hàng ngày đạp xe trên đoạn đường thẳng từ điểm A đúng lúc còi báo thức bắt
đầu kêu, khi đến điểm B thì còi vừa dứt. Mức cường độ âm tại A và B lần lượt là 60dB và 54 dB. Còi đặt
tại điểm O phát âm đẳng hướng với công suất không đổi và môi trường không hấp thụ âm; Cho góc AOB
bằng 1200. Do vận động viên này khiếm thính nên chỉ nghe được mức cường độ âm từ 61,94 dB trở lên
và tốc độ đạp xe không đổi. Biết thời gian còi báo thức kêu là 120s. Trên đoạn đường AB vận động viên
nghe thấy tiếng còi báo thức trong khoảng thời gian xấp xỉ bằng A. 42,67s B. 41,71s C. 43,18s D. 44,15s.
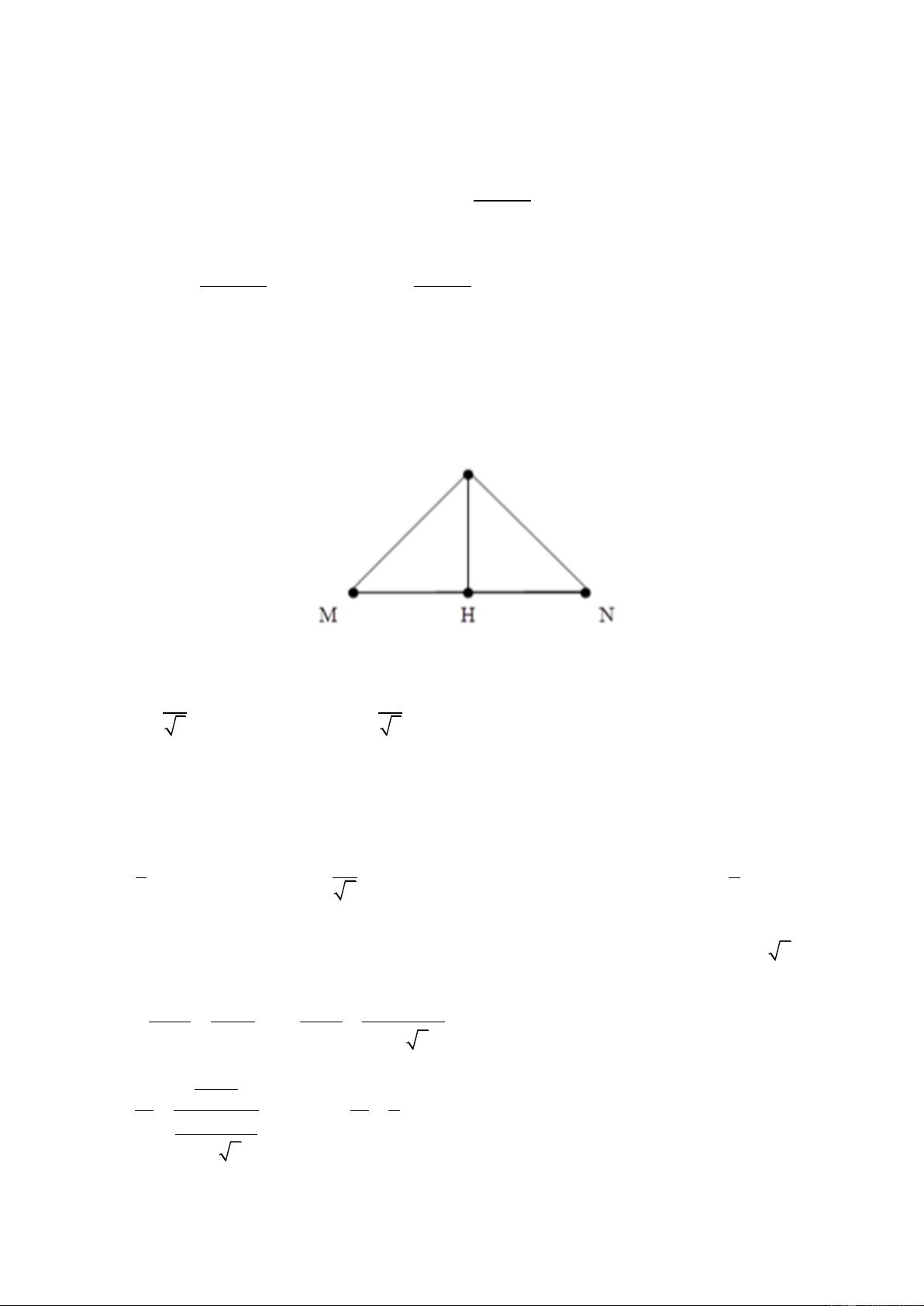
Câu 60. Cho tam giác ABC vuông cân tại A nằm trong một môi trường truyền âm. Một nguồn âm điểm O
có công suất không đổi phát âm đẳng hướng đặt tại B khi đó một người M đứng tại C nghe được âm có
mức cường độ âm là 40dB. Sau đó di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC
sao cho BO = AM. Mức cường độ âm lớn nhất mà người đó nghe được trong quá trình cả hai di chuyển bằng A. 56,6 dB B. 46,0 dB C. 42,0 dB D. 60,2 dB HẾT LỜI GIẢI
1.Đại cương sóng cơ
Câu 1. Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng.
Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li độ dao động của phần tử tại M là
3 cm thì li độ dao động của phần tử tại N là 3
− cm. Biên độ sóng bằng A. 6 cm. B. 2 3 cm. C. 3 cm. D. 3 2 cm. Hướng dẫn: 2 d 2
Độ lệch pha giữa 2 điểm M và N là = = . 3
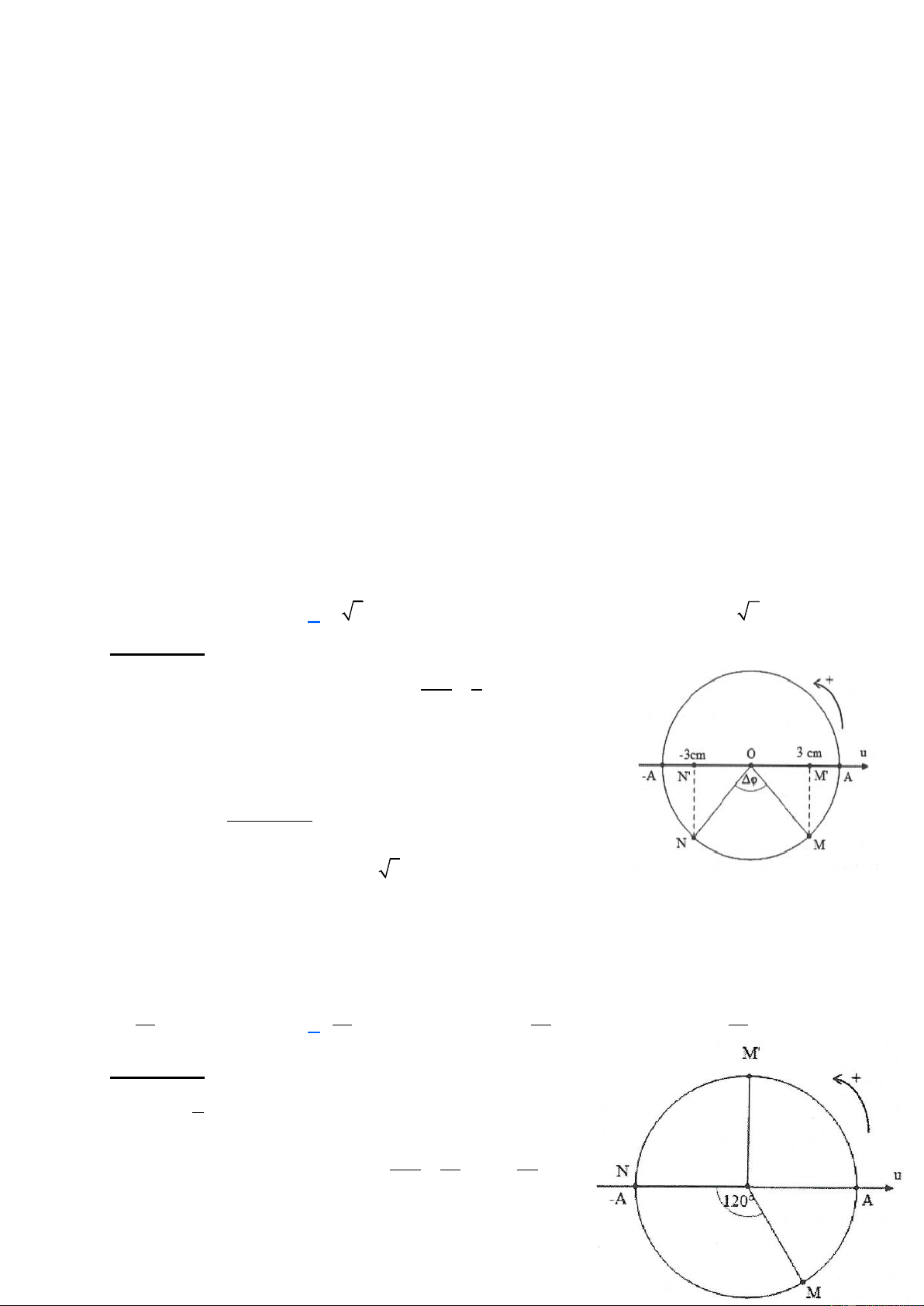
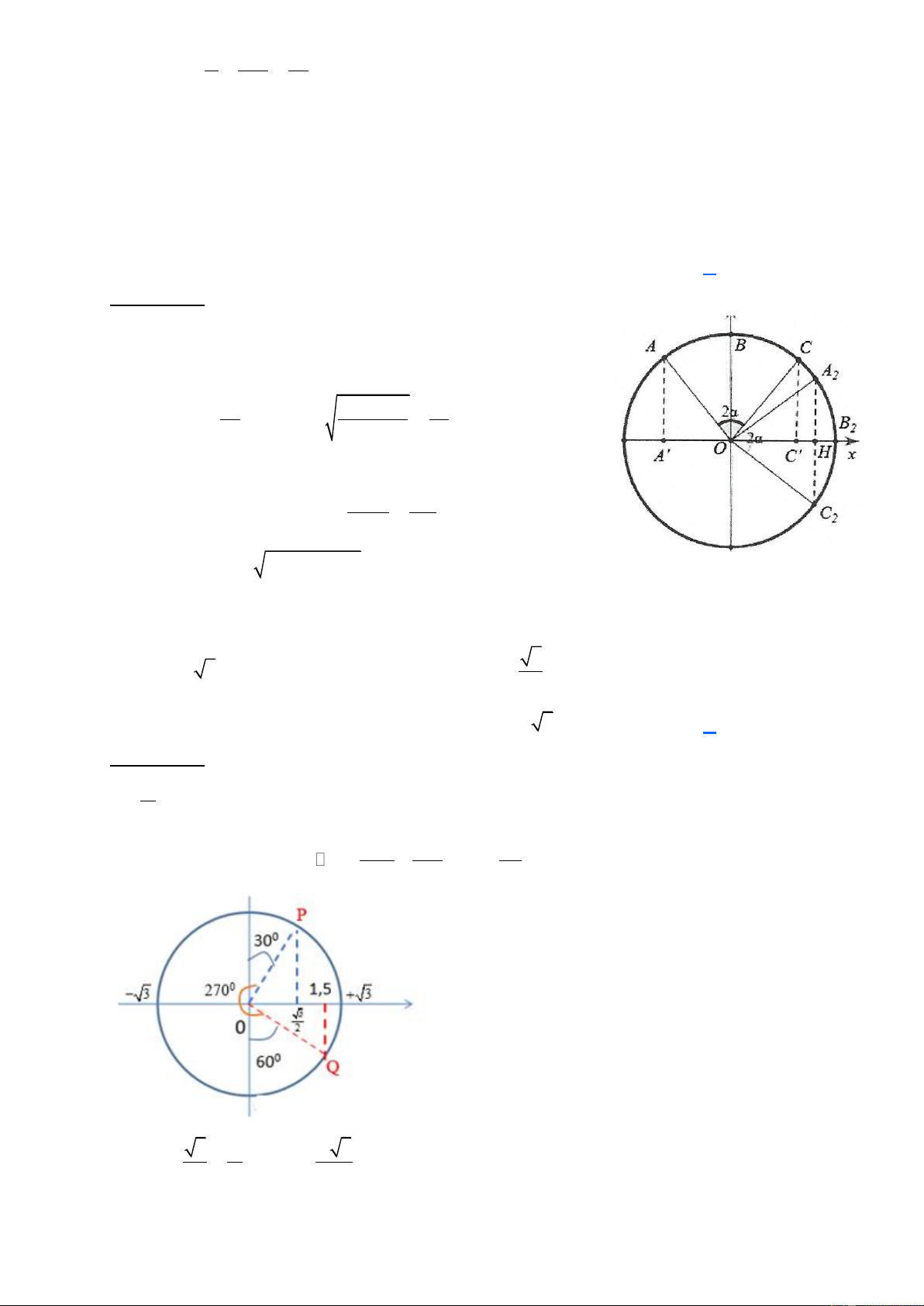
Sóng truyền từ M đến N và tại một thời điểm nào đó phần tử tại M
là 3 cm thì li độ dao động của phần tử tại N là -3cm nên 2 điểm M, N
được biểu diễn trên đường tròn như hình vẽ. 180 −120 Ta có: NON = = 30 . 2
Suy ra ON cos30 = ON ON = 2 3 = A . Đáp án B.
Câu 2. Một sóng ngang có tần số f = 20Hz truyền trên một sợi dây nằm ngang với tốc độ truyền sóng
bằng 3 m/s. Gọi M, N là hai điểm trên dây cách nhau 20 cm sóng truyền từ M đến N. Tại thời điểm phần
tử N ở vị trí thấp nhất sau đó khoảng thời gian nhỏ nhất bằng bao nhiêu thì phần tử M sẽ đi qua vị trí cân bằng A. 1 s. B. 1 s. C. 1 s. D. 1 s. 60 48 40 30 Hướng dẫn: Ta có: v = =15 cm. f
Ta có M nhanh pha hơn N góc: 2 d 8 2 = = = 2 + . 3 3
Để điểm M đến vị trí cân bằng thì nó phải quét được góc 150
trên vòng tròn lượng giác. Trang 8 Khi đó 1 t = = = s. Đáp án B. 2 f 48 Đáp án C.
Câu 3. : Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi, ba điểm A, B và C nằm
trên sợi dây sao cho B là trung điểm của AC. Tại thời điểm t , li độ của ba phần tử A, B, C lần lượt là 1
−4,8 mm; 0 mm; 4,8 mm. Nếu tại thời điểm t , li độ của A và C đều bằng +5,5 mm, thì li độ của phần tử 2 B là mm A. 10,3 mm B. 11,1 mm C. 5,15 mm D. 7,3 mm Hướng dẫn:
Cách 1: Gọi 2 là góc lệch pha giữa B và C
Suy ra Acos(90 − ) = 4,8mm và A cos = 5,5mm Do đó 48 1 55 tan = cos = = A = 7,3 mm 2 55 1+ tan 73
Cách 2: Ta có: AC = 9,6 cm ; OH = 5,5 cm A C AC Do H là trung điểm nên 2 2 A H = = = 4,8 cm 2 2 2 Do đó 2 2
u = OB = OH + A H = 7,3. mm Đáp án D. B 2 2
Câu 4. Nguồn sóng ở O được truyền theo phương Ox. Trên phương này có hai điểm P và Q cách nhau
PQ = 15 cm. Biết tần số sóng là 10 Hz, tốc độ truyền sóng v = 40 cm/s, biên độ sóng không đổi khi truyền 3
sóng và bằng 3 cm. Nếu tại thời điểm nào đó P có li độ
cm thì li độ tại Q có độ lớn là 2 A. 0 cm. B. 0,75 cm. C. 3 cm. D. 1,5 cm. Hướng dẫn: λ = v = 4cm f
Độ lệch pha giữa P và Q là 2 d 15 3 = = = 6 + λ 2 2 Khi 3 A u =
= A thì 3 u =
=1,5cm . Đáp án D P 2 2 Q 2
Câu 5. Một sóng hình sin lan truyền theo phương Ox với biên độ không đổi A = 4 cm. Hai chất điểm
gần nhất trên cùng một phương truyền sóng mà có cùng li độ là 2 cm, nhưng có vận tốc ngược hướng Trang 9
nhau thì cách nhau 6 cm. Tỉ số giữa tốc độ dao động cực đại của một phần tử môi trường với tốc độ truyền sóng là: A. s B. s C. 2 s D. 4 s 3 9 9 9 Hướng dẫn: Đáp án D
Hai điểm gần nhau nhất có cùng li độ 2cm ứng với độ lệch pha 2 d 2 = = → λ = 3d = 3.6 =18cm λ 3
Tỉ số giữa tốc độ dao động cực đại của một phần tử môi trường với tốc độ truyền sóng là:
Câu 6. Một nguồn âm có tần số f = 50Hz. Hai điểm gần nhau nhất trên phương truyền sóng cách nhau
2,5cm luôn dao động lệch pha nhau π/4. Vận tốc truyền sóng là: A. 0,5 km/s B. 1km/s C.250m/s D. 750m/s Hướng dẫn:
Hai điểm gần nhau nhất dao động lệch pha
→ = 2,5 = 20cm 4 8
v = f = 20.50 = 1000cm / s = 1km / s
Câu 7. Sóng truyền dọc theo sợi dây căng ngang và rất dài. Biết phương trình sóng tại O có dạng uo =
3cosπt(cm), vận tốc truyền sóng là v = 20cm/s. Nếu M và N là hai điểm gần nhau nhất dao động vuông
pha với nhau và M cùng pha với O thì khoảng cách từ O đến M và từ O đến N có thể là: A.80cm và 75cm
B. 37,5cm và 12,5cm C. 80cm và 70cm D. 85,5cmvà 80cm Hướng dẫn: 20 =
= 40cm ; M, N gần nhau nhất vuông pha nên MN = =10cm nên OM có thể là 80cm ; ON có 0,5 4 thể là 70cm
Câu 8: Một nguồn 0 phát sóng cơ có tần số 10hz truyền theo mặt nước theo đường thẳng với v = 60
cm/s. Gọi M và N là điểm trên phương truyền sóng cách 0 lần lượt 20 cm và 45 cm. Trên đoạn MN có
bao nhiêu điểm dao động lệch pha với nguồn 0 góc + k2 3 A. 2 B. 3 C. 4 D. 5 Hướng dẫn: MN= 25cm 60 = = 6cm 10 Trang 10
Điểm dao động lệch pha
+ k2 với nguồn ở các khoảng cách: 1cm, 7cm, 13cm, 19cm… 3
Như vậy trên đoạn MN có 4 điểm dao động
Câu 8. Một dây đàn hồi dài có đầu A dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng
trên dây là 4m/s. Xét một điểm M trên dây và cách A một đoạn 40cm, người ta thấy M luôn luôn dao
động lệch pha so với A một góc = (k + 0,5) với k là số nguyên. Tính tần số, biết tần số f có giá trị
trong khoảng từ 8 Hz đến 13 Hz. A. 8,5Hz B. 10Hz C. 12Hz D. 12,5Hz Hướng dẫn: = (k+ 0,5) 2 40. f = (k + 0,5) 400
f = (k + 0,5).5 8 (k + 0,5)5 13
1,1 k 2,1 k = 2 f = 12, 5Hz
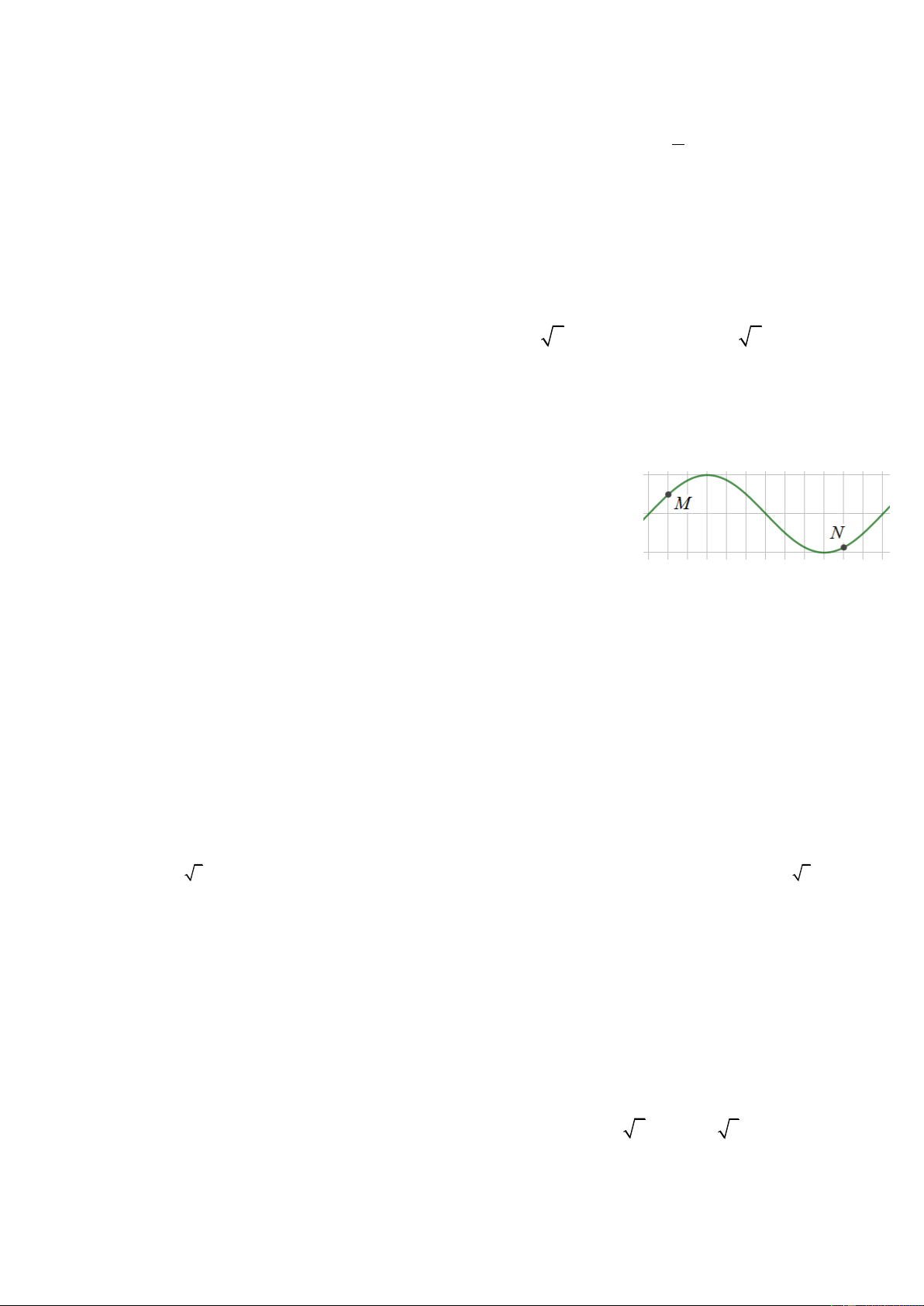
Câu 9. Trên một sợi dây dài đang có sóng ngang hình sin
truyền qua theo chiều dương của trục Ox. Tại thời điểm t một 0
đoạn của sợi dây có dạng như hình bên. Hai phần tử tại M và O
dao động lệch pha nhau. 3 2 A. B. C. D. 4 3 4 3 Lời giải:
Nếu tính 1 ô là một đơn vị thì bước sóng là = 8 . Độ dài OM là OM = 3. Độ 2 .OM 3
lệch pha giữa 2 phần tử tại M và O là = = . Chọn C 4
Câu 10. Trên một sợi dây dài đang có sóng ngang hình sin truyền
qua theo chiều dương của trục Ox. Tại thời điểm t u 0, một đoạn của Q
sợi dây có hình dạng như hình bên. Hai phần tử dây tại M và Q
dao động lệch pha nhau: O x A. 2π B. π/3 M C. π/4 D. π Hướng dẫn: = 6;MQ = 3 2 .3 = = 6 Trang 11
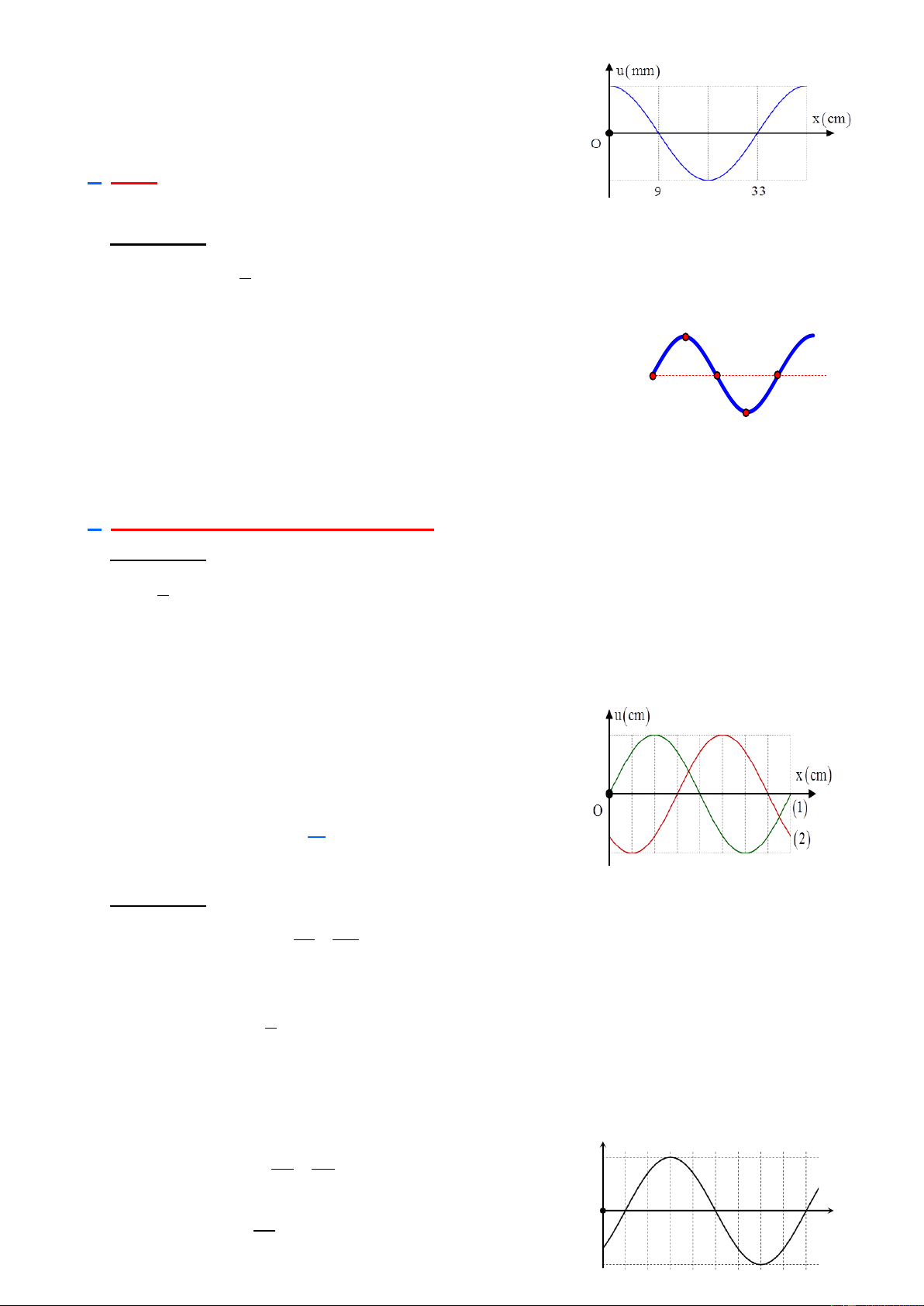
Câu 11. Một sóng hình sin truyền trên một sợ dây dài. Ở thời
điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân
bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng
của sóng này bằng A. 48 cm B. 18 cm C. 36 cm D. 24 cm Hướng dẫn: Từ hình vẽ ta có = 33 − 9 = 48 cm 2
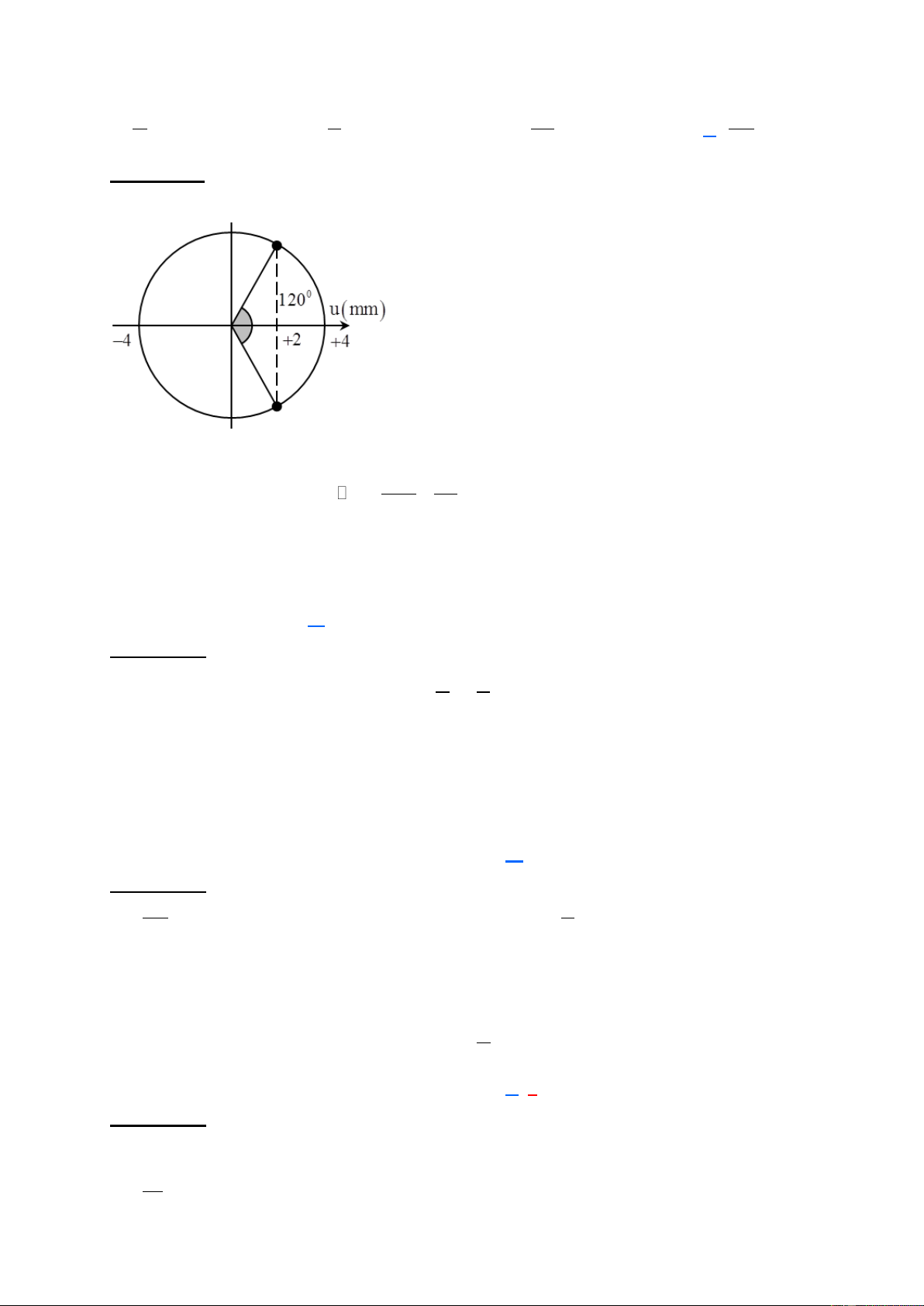
Câu 12. Một sóng cơ truyền trên mặt nước theo hướng từ A đến E có B
biên độ 2 cm, tốc độ truyền là 4 m/s. Tại một thời điểm nào đó các
phần tử mặt nước có dạng như hình vẽ. Cho biết khoảng cách A đến C C A
là 20 cm. Phần tử vật chất tại C đang E
A. Đứng yên D
B. Chuyển động đi lên với tốc độ 8 (cm/s)
C. Chuyển động đi xuống với tốc độ 20π (cm/s)
D. Chuyển động đi lên với tốc độ 40π (cm/s) Hướng dẫn: v + = = 40cm f =10Hz f
+ C đang đi qua VTCB có hướng đi lên vận tốc v = 2 f A = 40 cm / s C ( )
Câu 13. Một sóng hình sin đang truyền trên một sợi dây, theo
chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây ở
các thời điểm t1 và t = t + 0,3s . Chu kì của sóng là 2 1 A. 0,9 s B. 0,4 s C. 0,6 s D. 0,8 s Hướng dẫn: x 3dv Vận tốc truyền sóng v = = =10 dv/s t 0,3
Bước sóng của sóng = 8dv Chu kì của sóng T = = 0,8s v
Câu 14. Một sóng cơ lan truyền trên một sợi dây dài nằm ngang, với tốc độ 80 cm/s theo chiều dương
trục Ox. Hình dạng của sợi dây tại thời điểm t = 0 được mô tả như hình vẽ. Phương trình sóng truyền trên sợi dây có dạng u(mm) x 2 6 +
#A. u = 6 cos 10 t − −
(u: mm, x: cm, t: s) 8 3 x(cm) 3 O
B. u = 6 cos 5 t − (u: mm, t: s) 4 Trang 12 6 − u(mm) 14 x 3
C. u = 6 cos 10 t − +
(u: mm, x: cm, t: s) 8 4 x 3
D. u = 6 cos 10 t − − (u: mm, x: cm, t: s) 8 4 Hướng dẫn:
+ Từ đồ thị ta thấy rằng mỗi độ chia nhỏ nhất của trục Ox tương ứng với 2 cm, bước sóng ứng với 8 độ chia nhỏ nhất → = v 16 cm → 2 = =10 rad/s. t = 0 + Tại
phần tử dây đi qua vị trí 2 u = − theo chiều dương x = 0 2
vì T=16s, thời gian đi từ từ vị trí ban đầu đến vị trí cân bằng mất 2s = T/8, nên vị trí ban đầu 2 u = − 2 → 3 = − 0 4 → x 3
u = 6 cos 10 t − − mm 8 4 2.Giao thoa sóng cơ
Câu 15. Tại hai điểm A và B trên mặt nước cách nhau 10 cm có hai nguồn kết hợp dao động với phương trình: u = u = acos40 t
(cm) , tốc độ truyền sóng trên mặt nước là 30cm / s . Xét đoạn thẳng CD = 4cm 1 2
trên mặt nước có chung đường trung trực với AB. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn
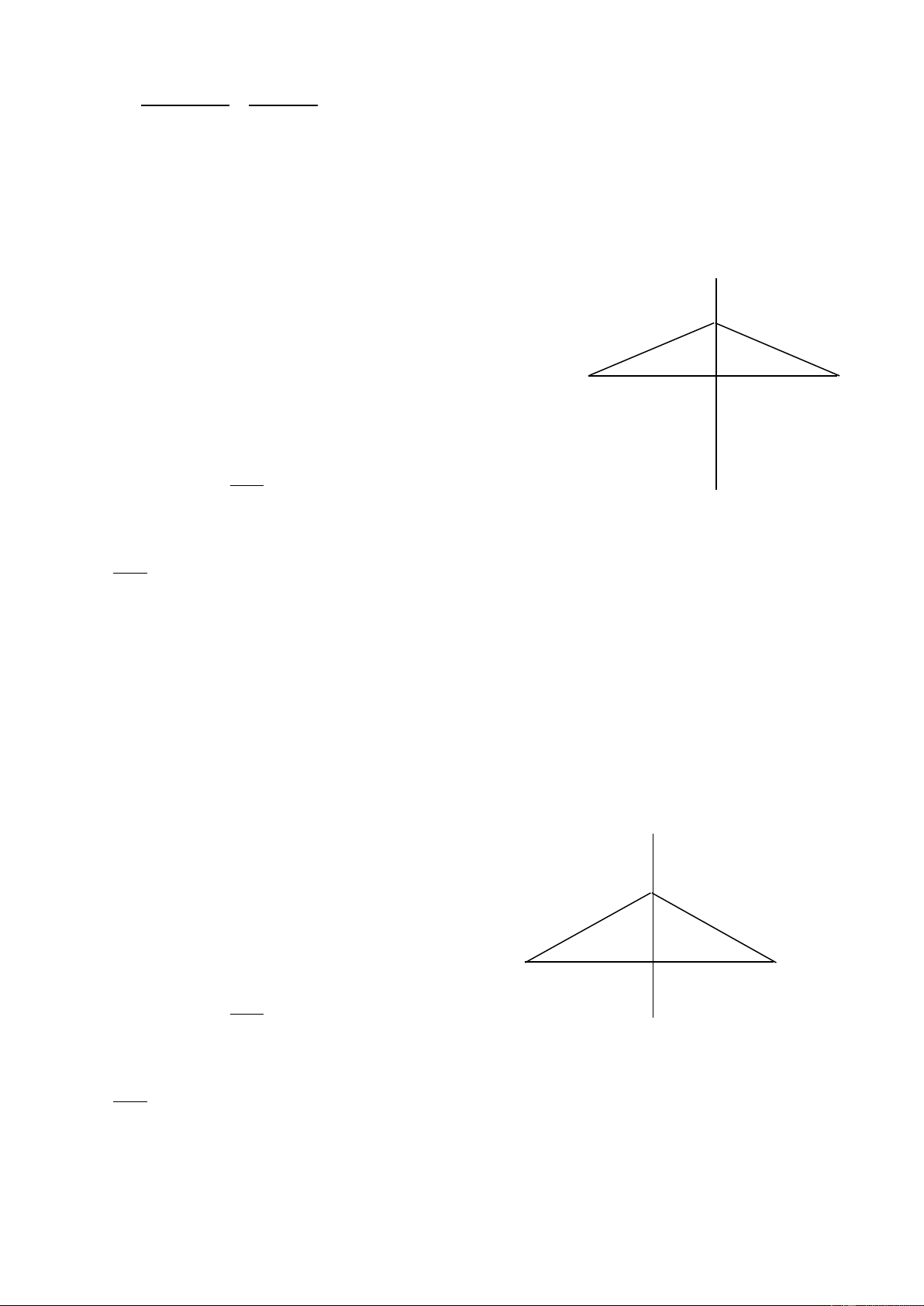
CD chỉ có 5 điểm dao dộng với biên độ cực đại là: A. 5,2 cm. B. 6 cm. C. 4,2 cm. D. 6,8 cm. Giải:
Bước sóng λ = v/f = 30/20 = 1,5 cm
Khoảng cách lớn nhất từ CD đến AB mà trên CD chỉ có 5 điểm
dao đông với biên độ cực đai khi tại C và D thuộc các vân cực đai C D bậc 2 ( k = ± 2). d1 d2 Tại C: d h 2 – d1 = 3 (cm) Khi đó AM = 3cm; BM = 7 cm A B Ta có d 2 M 1 = h2 + 32 d 2 2 = h2 + 72 Do đó d 2 2 2 – d1 = 40
Suy ra d1 = 31/6 cm → h = 4,2 cm. Chọn đáp án C
Câu 16. Trong thí nghiệm giao thoa sóng nước, hai nguồn kết hợp giống hệt nhau A và B nằm cách
nhau 20 cm tạo ra sóng trên mặt nước với bước sóng 2 cm . Xét điểm
dao động với biên độ cực đại nằm trên mặt nước thuộc đường tròn tâm
A bán kính 20 cm , cách đường trung trực của AB một đoạn ngắn nhất bằng A. 0,9 cm B. 2, 0 cm C. 1,0 cm D. 1,9 cm Giải: Trang 13
MA − MB = 20 − MB = 2 MB = 18cm 2 2 2 2 MA − MB 20 −18 x = = =1,9 (cm). Chọn D 2AB 2.20
Câu 17. Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12(cm) đang dao
động vuông góc với mặt nước tạo ra sóng có bước sóng = 1,6cm. C và D là hai điểm khác nhau trên
mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8(cm). Số điểm dao động cùng
pha với nguồn ở trên đoạn CD là A. 3 B. 10 C. 5 D. 6 Giải: C
Biểu thức sóng tại A, B M u = acosωt d
Xét điểm M trên OC: AM = BM = d (cm) A O B
Ta có 6 ≤ d ≤ 10 ( vì OA = 6cm; OC = 8 cm biểu thức sóng tại M u p M = 2acos(ωt- 2 d ). D l
Điểm M dao động cùng pha với nguồn khi
2p d = 2kπ → d = kλ = 1,6k l
6 ≤ d = 1,6k ≤ 10 → 4 ≤ k ≤ 6. Trên OC có 3 điểm dao động cùng pha với nguồn.
Do đó trên CD có 6 điểm dao động cùng pha với nguồn. Chọn đáp án D
Câu 18. Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 20 cm dao động theo phương trình u =
acos(ωt) trên mặt nước, coi biên độ không đổi, bước sóng λ = 3 cm. Gọi O là trung điểm của AB. Một
điểm nằm trên đường trung trực AB, dao động cùng pha với các nguồn A và B, cách A hoặc B một đoạn nhỏ nhất là A.12cm B.10cm C.13.5cm D.15cm Giải:
Biểu thức sóng tại A, B u = acosωt M
Xét điểm M trên trung trực của AB: d AM = BM = d (cm) ≥ 10 cm Biểu thức sóng tại M A B O u p M = 2acos(ωt- 2 d ). l
Điểm M dao động cùng pha với nguồn khi
2p d = 2kπ → d = kλ = 3k ≥ 10 → k ≥ 4 l
d = dmin = 4x3 = 12 cm. Chọn đáp án A
Câu 19. Giao thoa sóng nước với hai nguồn giống hệt nhau A, B cách nhau 23 cm có tần số 50Hz. Tốc độ
truyền sóng trên mặt nước là 2 m/s. Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường
tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là Trang 14 A. 26,76 mm B. 29,94mm C. 28,97mm D. 19,34 mm Giải: M
Bước sóng λ = v/f = 0,04m = 4 cm • d1 d2
Xét điểm N trên AB dao động với biên độ • •
cực đại AN = d’1; BN = d’2 (cm) A B d’1 – d’2 = kλ = 4k d’1 + d’2 = AB = 23 cm d’1 = 10 +1,5k 0≤ d’1 = 11,5 + 2k ≤ 23 → - 5 ≤ k ≤ 5
→ Trên đường tròn có 22 điểm dao động với biên độ cực đại
Điểm gần đường thẳng AB nhất ứng với k = 5
Điểm M thuộc cực đại thứ 5
d1 – d2 = 5λ = 20 cm; d2 = d1 – 20 = 3 cm
Xét tam giác AMB; hạ MH = h vuông góc với AB. Đặt HB = x h2 = d 2
1 – AH2 = 232 – (23 – x)2 h2 = d 2 2 – BH2 = 32 – x2
→ 232 – (23 – x)2 = 32 – x2 → x = 9/46 cm = 90/46 mm
→ h = 29,94 mm. Chọn đáp án B
Câu 20. Trên bề mặt chất lỏng có hai nguồn phát sóng kết hợp A, B dao động cùng pha, cách nhau một
khoảng 30 cm. Trên đường tròn tâm O là trung điểm của AB bán kính 4 cm, có 8 điểm dao động với biên
độ cực đại. Số cực đại trên đoạn AB là A. 9. B. 7. C. 15. D. 13. Giải:
Để trên đường tròn có 8 cực đại thì hai đường cực đại bậc 2 phải tiếp tuyến với đường tròn nên bán
kính đường tròn là R = 2 = = 4cm 2
Số cực đại trên AB là 30 N = 2 +1 =15 4 Chọn đáp án C
Câu 21. Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha,
cùng tần số, cách nhau AB = 12cm tạo ra hai sóng kết hợp có bước sóng λ = 2cm. Trên đường thẳng (Δ)
song song với AB và cách AB một khoảng là 5cm, khoảng cách ngắn nhất từ giao điểm C của (Δ) với
đường trung trực của AB đến điểm M dao động với biên độ cực tiểu là A. 0,47 cm. B. 0,5 cm. C. 0,65 cm. D. 0,68 cm. Giải:
Điểm M dao động với biên độ cực tiểu khi
d1 – d2 = ( k + 0,5) λ; Điểm M gần C nhất khi M là cực tiểu thứ nhất (k = 0) d1 – d2 = 1 (cm), (*) Trang 15 Gọi CM = OH = x d 2 1 = MH2 + AH2 = 52 + (6 + x)2 d 2 C M 2 = MH2 + BH2 = 52 + (6 - x)2 () → d 2 2 • 1 – d2 = 24x (cm) (**) • d1 d2
Từ (*) và (**)→ d1 + d2 = 24x (***) • • • •
Từ (*) và (***)→ d1 = 12x + 0,5 A O H B d 2
1 = 52 + (6 + x)2 = (12x + 0,5)2
→ x = 0,65 (cm) Chọn đáp án C
Câu 22. Thí nghiệm giao thoa sóng trên mặt nước, hai nguồn kết hợp đặt tại A và B cách nhau 16 cm
dao động cùng pha theo phương thẳng đứng. Sóng truyền ở mặt nước có bước sóng là 3 cm. Ở mặt nước,
số điểm trên đường đường thẳng qua A , vuông góc với AB mà phần tử nước ở đó dao động với biên độ cực đại là A. 12. B. 10. C. 5. D. 6. Giải:
+ Số dãy cực đại giao thoa là số giá trị của k thõa mãn bất phương trình AB AB − k . A B → 16 16 − k
↔ −5,3 k 5,3 . 3 3
+ Ta để ý rằng, các dãy cực đại ứng với k = −1, −2...− 5 sẽ cắt đường thẳng đi qua A và vuông góc với
AB tại hai điểm → vậy trên đường thẳng này sẽ có tất cả 10 điểm cực đại giao thoa → Đáp án B
Câu 23. Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn S1S2 = 9λ phát ra dao động cùng pha
nhau. Trên đoạn S1S2, số điểm có biên độ cực đại cùng pha với nhau và cùng pha với nguồn (không kể hai nguồn) là: A.6 B.10 C.8 D.12
Giải: Giả sử pt dao động của hai nguồn u1 = u2 = Acosωt. Xét điểm M trên S1S2 S1M = d1; S2M = d2. u 2p d 2p d 1M = Acos(ωt - 1 ); u2M = Acos(ωt - 2 ). l l u
p (d - d )
p (d + d )
p (d - d ) M = u1M + u2M = 2Acos( 2 1 cos(ωt - 1 2 ) = 2Acos 2 1 cos(ωt -9π) l l l
Để M là điểm dao động với biên độ cực đại, cùng pha với nguồn thì cos p(d - d ) 2 1 = - 1 l
→ p(d - d ) 2 1
= (2k + 1)π → d2 – d1 = (2k + 1)λ và d1 + d2 = 9λ →d1 = (4 - k)λ l
0 < d1 = (4 - k)λ < 9λ → - 5 < k < 4 → Do đó có 8 giá trị của k. Chọn đáp án C
Câu 24. Trên mặt thoáng của chất lỏng có hai nguồn kết hợp A và B giống nhau dao động cùng tần số f =
8Hz tạo ra hai sóng lan truyền với v = 16cm/s. Hai điểm MN nằm trên đường nối AB và cách trung điểm
O của AB các đoạn lần lượt là OM = 3,75 cm, ON = 2,25cm. Số điểm dao động với biên độ cực đại và
cực tiểu trong đoạn MN là:
A. 5 cực đại 6 cực tiểu
B. 6 cực đại, 6 cực tiểu
C. 6 cực đại, 5 cực tiểu D. 5 cực đại, 5 cực tiểu Trang 16 Giải
Giả sử biểu thức sóng của hai nguồn u1 = u2 = a cosωt
Bước sóng λ = v/f = 2 cm., O là trung điểm của AB A M O C N B
Xét điểm C trên MN: OC = d ( 0 < d < AB • • • • • • 2 AB 2p ( + d ) u 2 AB 1M = acos(ωt - ) = acos(ωt - πd - π) l 2 AB 2p ( - d ) u 2 p AB 2M = acos(ωt - ) = acos(ωt + 2 d - 2π) l l 2l = 8cos(ωt + πd AB - π) 2
Điểm M dao động với biên độ cực đại khi uS1M và uS2M cùng pha với nhau
2πd = 2kπ → d = k với -3,75 ≤ k ≤ 2,25 → -3 ≤ k ≤ 2. Có 6 cực đại
Điểm M dao động với biên độ cực đại khi uS1M và uS2M ngược pha với nhau
2πd = (2k + 1)π → d = (2k + 1)/2 = 2k + 0,5 với -3,75 ≤ 2k + 0,5 ≤ 2,25
→ - 4,25 ≤ 2k ≤ 1,755 → - 4 ≤ k ≤ 1 Có 6 cực tiểu
Chọn đáp án B: 6 cực đại, 6 cực tiểu
Câu 25. Trên bề mặt chất lỏng có 2 nguồn phát sóng kết hợp O và O dao động đồng pha, cách nhau 1 2
một khoảng O O bằng 40cm. Biết sóng do mỗi nguồn phát ra có f = 10Hz , vận tốc truyền sóng 1 2 v = 2m / .
s Xét điểm M thuộc mặt nước nằm trên đường thẳng vuông góc với O O tại O . Đoạn O M 1 2 1 1
có giá trị lớn nhất là bao nhiêu để tại M có dao động với biên độ cực đại: A. 20cm B. 50cm C. 40cm D. 30cm Giải: Bước sóng λ = v/f = 20cm O M 1M = d1 (cm); O2M = d2 (cm) Tam giác O d
1O2M là tam giác vuông tại O1 2
Giả sử biểu thức của nguồn sóng: d 1 u = acosωt = acos20πt Sóng truyền từ O O 1; O2 đến M: 2 O1 u 2p d 2p d 1M = acos(20πt - 1 ) u2M = acos(20πt - 2 ) l l u
p (d - d )
p (d + d ) M = 2a cos 1 2 cos[20πt - 1 2 ] l l
M là điểm có biên độ cực đại: cos p(d - d )
p (d - d ) 1 2 = ± 1 → 1 2 = kπ l l d 2 2 2
2 - d1 = kλ, với k nguyên dương. d2 - d1 = 20k (1) d2 – d1 = O1O2 = 1600
→ (d1 + d2)(d2 – d1) =20k(d1 + d2)=1600 → d1 + d2 = 80 = (2) k Trang 17
(2) – (1) Suy ra d1 = 40 - 10k = k nguyên dương k
d1 = d1max khi k = 1 → d1max = 30 cm Chọn đáp án D
Câu 26. Trên mặt nước, hai nguồn kết hợp A, B cách nhau 40cm luôn dao động cùng pha, có bước sóng
6cm. Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhât, AD=30cm. Số điểm cực đại và
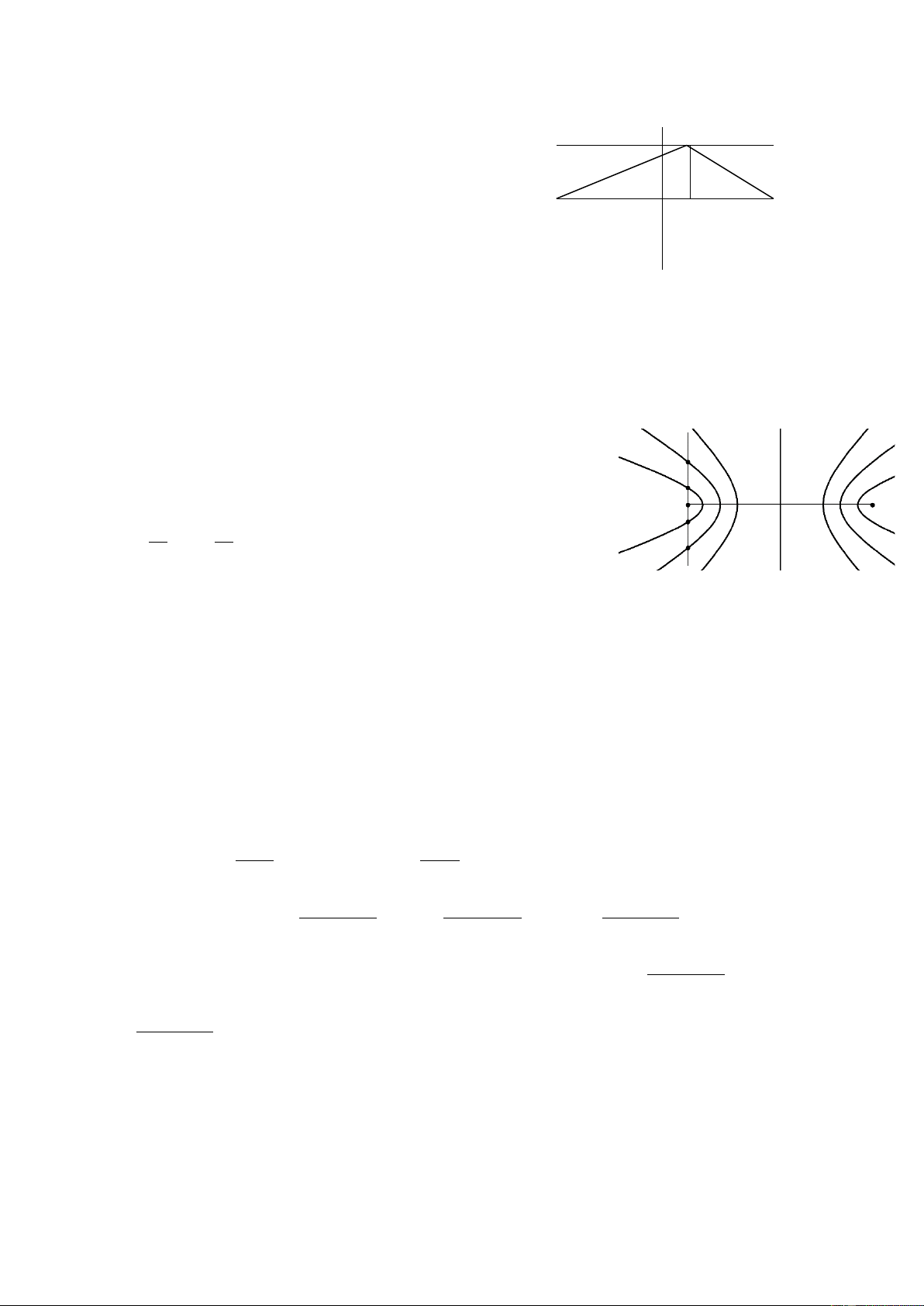
đứng yên trên đoạn CD lần lượt là : A. 5 và 6 B. 7 và 6 C. 13 và 12 D. 11 và 10 Giải
Số điểm cực đại trên đoạn CD thoã mãn : Suy ra : Hay : . Hay :
Giải ra : -3,3Kết luận có 7 điểm cực đại trên CD.
Số điểm cực tiểu trên đoạn CD thoã mãn : Suy ra : Hay : . Thay số : Suy ra :
Vậy : -3,8Kết luận có 6 điểm đứng yên. Đáp án B
Câu 27. Giao thoa sóng ở mặt nước với hai nguồn kết hợp đặt tại A và B. Hai nguồn dao động điều hòa
theo phương thẳng đứng, cùng pha và cùng tần số 10 Hz. Biết AB = 20 cm, tốc độ truyền sóng ở mặt
nước là 0,3 m/s. Ở mặt nước, O là trung điểm của AB, gọi Ox là đường thẳng hợp với AB một góc 0 60 .
M là điểm trên Ox mà phần tử vật chất tại M dao động với biên độ cực đại (M không trùng với O).
Khoảng cách ngắn nhất từ M đến O là A. 1,72 cm. B. 2,69 cm. C. 3,11 cm. D. 1,49 cm. Giải: Ta có: v 0, 3 = = = 3cm. f 10
Để M là cực đại và gần O nhất thì M nằm trên dãy cực đại ứng với k = 1. 2 2 2 0
d = d +10 − 2.10.d.cos60
Áp dụng định lý cos, ta có: 2 2 2 2 0
d = d +10 − 2.10.d.cos120 1
Kết hợp với d − d = = 3cm. 1 2 → 2 2 0 2 2 0
d +10 − 2.10.d.cos120 − d +10 − 2.10.d.cos 60 = 3 cm → d = 3,11 cm. Chọn C Trang 18
Câu 28. Hai nguồn sóng kết hợp giống hệt nhau được đặt cách nhau một khoảng cách x trên đường kính
của một vòng tròn bán kính R (x < R) và đối xứng qua tâm của vòng tròn. Biết rằng mỗi nguồn đều phát
sóng có bước sóng λ và x = 6λ. Số điểm dao động cực đại trên vòng tròn là A. 26 B. 24 C. 22. D.20.
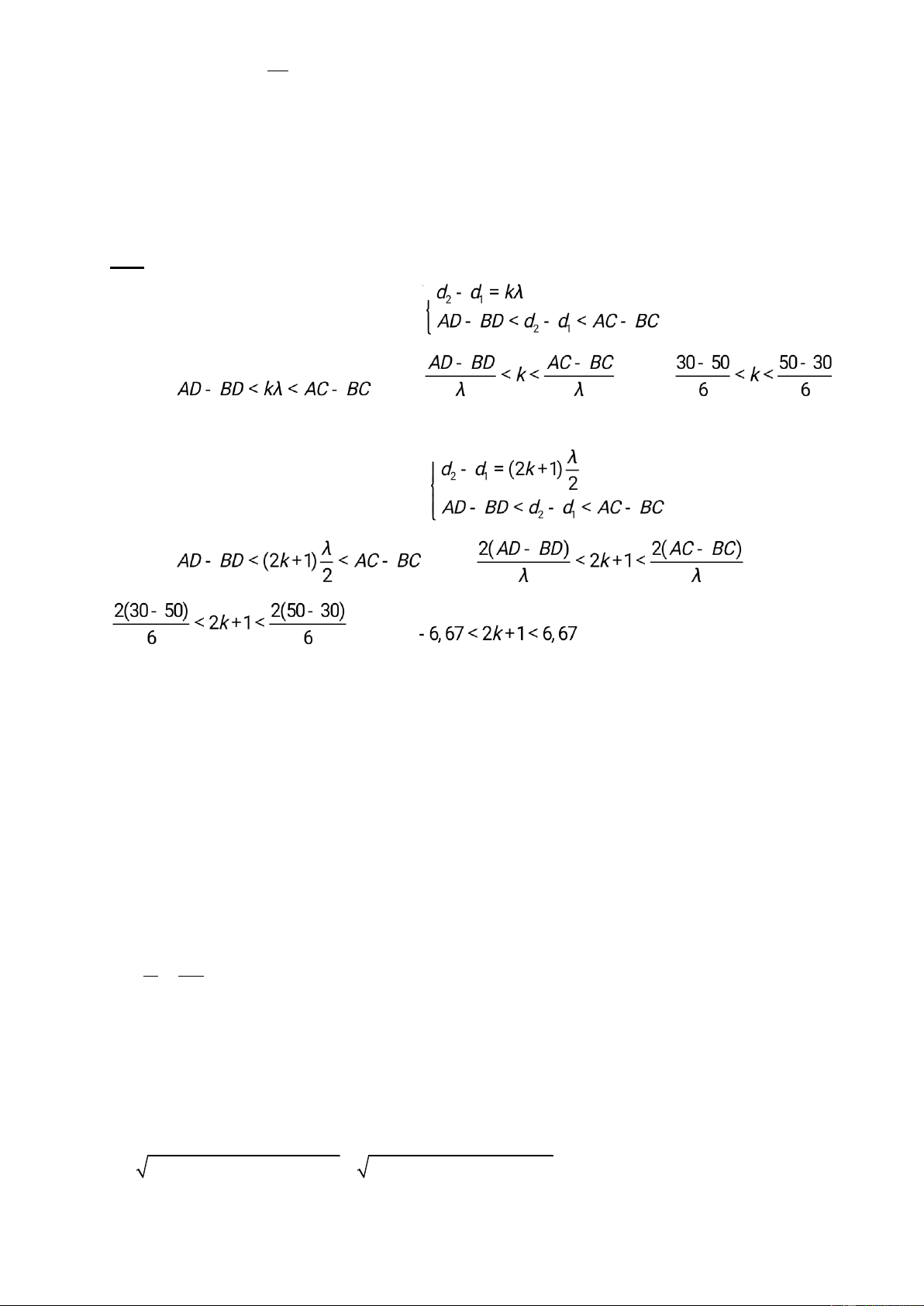
Giải: Xét điểm M trên AB (AB = 2x = 12λ) AM = d1 BM = d2
d1 – d2 = kλ; d1 + d2 = 6λ; → d1 = (3 + 0,5k)λ
0 < d1 = (3 + 0,5k)λ < 6λ → - 6 < k < 6 M
Số điểm dao động cực đại trên AB là 11 điểm A • • B
( không kể hai nguồn A, B). •
Số đường cực đại cắt đường tròn là 11, vì vậy
Số điểm dao động cực đại trên vòng tròn là 22. Chọn đáp án C.
Câu 29. Trong một thí nghiệm giao thoa sóng nước, hai nguồn A và B cách nhau 8 cm, dao động theo
phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80 Hz. Tốc độ truyền sóng trên mặt
nước là 40 cm/s. Ở mặt nước, gọi là đường trung trực của đoạn AB . Trên , điểm M ở cách AB 3
cm; điểm N dao động ngược pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây? A. 0,4 cm. B. 0,8 cm. C. 0,6 cm. D. 1,8 cm. Giải: Chọn A M d +N d −N A B Ta có: v (40) = = = cm. f ( ) 0,5 80 1 d − d = k + . N M 2
→ Để N gần điểm M nhất thì k = 0 hoặc k = −1. + Với 2 2 2 2 k = 0 → 0, 5 d = d + = 5 +
= 5,25 cm → MN = (5,25) −(4) − (5) −(4) = 0,4 cm. N M 2 2 − Với 2 2 2 2 k = −1 → 0, 5 d = d − = 5 −
= 4,75 cm → MN = (5) −(4) − (4,75) −(4) = 0,44 cm. N M 2 2 → MN = 0, 4 cm min 3.Sóng dừng
Câu 30. Một sợi dây AB dài 40 cm có 2 đầu cố định. Biết rằng khoảng thời gian giữa 5 lần liên tiếp sợi
dây duỗi thẳng là 1 s. Tốc độ truyền sóng trên dây là Tốc độ truyền sóng trên dây là 20 cm/s. Không tính
2 đầu A và B thì trên dây có
A. 10 nút và 9 bụng.
B. 9 nút và 9 bụng.
C. 9 nút và 8 bụng.
D. 7 nút và 8 bụng. Trang 19 Hướng dẫn
+ Khoảng thời gian giữa 5 lần liên tiếp là:2T= 1(s) suy ra T= 0,5( s) +Bước sóng: = .
v T = 20.0, 5 = 10(cm) + Ta có 2l l = k k =
= 8 vậy trên dây có 8 bụng vì không kể 2 đầu dây nên trên dây có 7 nút 2 Chọn D
Câu 31. Một sợi dây AB dài l đang có sóng dựng với A và B là hai nút sóng. Khoảng cách lớn
nhất giữa hai vị tri cân bằng của hai phần tử dao động có biên độ cực đại là 80 cm .Khoảng cách lớn
nhất giữa hai vị trí của hai phần tử không dao động mà không tính A và B là 70cm. Số bụng sóng trên dây AB là A. 11. B. 8. C. 10. D. 9. Hướng dẫn + Ta có: + = 80 − 70 =10(c )
m = 20cm 4 4
+ Chiều dài của dây là: l= 80+ = 90cm 2 + Ta có: 20 l = k. 90 = k.
k = 9 Chọn D 2 2
Câu 32. Trên một sợi dây đàn hồi có sóng dừng với bước sóng 1,1 cm. Trên dây có hai điểm A và B cách
nhau 5,4 cm, tại trung điểm của AB là một nút sóng, số nút sóng và bụng sóng trên đoạn dây AB (kể cả A và B) là
A. 9 bụng, 10 nút.
B. 10 bụng, 10 nút.
C. 10 bụng, 9 nút. D. 9 bụng, 9 nút. Hướng dẫn IA 2, 7 s n = 4 +1 = 5
Xét trên đoạn IA (I là trung điểm AB) = = 4,9 0,5 0,5.1,1 s b = 4 +1 = 5 I A / 2 / 2 / 2 / 2 / 2 / 2 / 2 1 2 3 4 5 6 7 8 9 10 2, 7cm sn = 5.2 −1 = 9 Xét trên đoạn AB: Chọn C sb = 5.2 = 10
Câu 33. Trên một sợi dây đàn hồi chiều dài 1,6 m, hai đầu cố định và đang có sóng dừng với biên độ tại
bụng là#A. Quan sát trên dây thấy có các điểm không phải bụng cách đều nhau những khoảng 20 cm luôn
dao động cùng biên độ A0 (với 0 < A0 < A). Số bụng sóng trên dây là A. 4. B. 8. C. 6. D. 5. Hướng dẫn
+ Ta có Các điểm không phải bụng có cùng biên độ A0 mà cách đều nhau một khoảng Δx thì A = A / 2; x = / 4 0 max Trang 20 + Ta có: = ( ) = ( ) AB 1, 6 0, 2 m 0,8 m sb = = = 4 4 0,5 Chọn A 0,5.0,8
Câu 34. Một sợi dây PQ dài 120 cm, hai đầu cố định, đang có sóng dừng ổn định. Bề rộng của bụng sóng
là 4a. Khoảng cách gần nhất giữa hai điểm dao động cùng pha và cùng biên độ bằng a là 10 cm.Số bụng sóng trên PQ là A. 4 B. 8 C. 6 D. 10
Theo bài ra ta có: 2A = 4a A = 2a b b
Khoảng cách gần nhất giữa hai điểm dao động cùng pha và cùng biên độ bằng a = Ab /2 nằm đối xứng
với nhau qua bụng nên ta có:
=10cm = 30cm 3 30
PQ = k 120 = k k = 8 2 2
Câu 35. Dây AB dài 90 cm đầu A gắn với nguồn dao động (xem A là nút) và đầu B tự do. Quan sát thấy
trên dây có 8 nút sóng dừng và khoảng thời gian 6 lần liên tiếp sợi dây duỗi thẳng là 0,25 s. Tính tốc độ
truyền sóng trên dây. Tính khoảng cách từ A đến nút thứ 7.
A. 10 m/s và 0,72 m.
B. 0,72 m/s và 2,4 m.
C. 2,4 m/s và 0,72 m. D. 2,4 m/s và 10 cm. Hướng dẫn
Thay vào công thức Δt = (n − l)T/2 ta được 0,25 = (6 − l)T/2 => T = 0,1 s.
Một đầu nút và một đầu bụng (trên dây có 8 nút nên k = 8): ( = 2k − ) 1 0,9 = (2.8 − ) 1
= 0,24(m) v = = 2,4(m / s) 4 4 T
Khoảng cách từ A đến nút thứ 7: = 7 −1 = 0,72 m Chọn C 7 ( ) ( ) 2
Câu 36. Một sợi dây đàn hồi một đầu cố định, một đàu gắn với âm thoa dao động nhỏ (xem là nút) có tần
số thay đổi được. Khi thay đổi tần số âm thoa thấy với 2 giá trị liên tiếp của tần số là 28 Hz và 42 Hz thì
trên dây có sóng dừng. Hỏi nếu tăng dần giá trị tần số từ 0 Hz đến 50 Hz sẽ có bao nhiêu giá trị của tần số
để trên dây lại có sóng dừng. Coi vận tốc sóng và chiều dài dây là không đổi.
A. 7 giá trị.
B. 6 giá trị.
C. 4 giá trị. D. 3giá trị. Hướng dẫn
Vì sợi dây hai đầu cố định nên f
= f − f = 42 − 28 = 14 Hz f = 14k Hz . min k 1 + k ( ) k ( )
Thay vào điều kiện 0 < f < 50
0 k 3,5 k = 1, 2,3 Chọn D
Câu 37. Khảo sát sóng dừng trên một sợi dây đàn hồi dài 0,5 m có hai đầu cố định, tốc độ truyền sóng
trên dây là 4 m / s . Tần số sóng có giá trị từ 17 Hz đến 25 Hz . Để trung điểm của dây là một nút sóng
thì tần số sóng bằng Trang 21 A. 18 Hz . B. 24 Hz . C. 20 Hz . D. 22 Hz . Hướng dẫn 17 f 25 kv k.4 f l = k. = 0,5 = k =
→ 4,25 k 6,25 2 2 f 2 f 4
Để trung điểm là nút thì k chẵn k = 6 → f = 24Hz . Chọn B
Câu 38. Quan sát sóng dừng trên sợi dây AB, đầu A dao động điều hòa theo phương vuông góc với sợi
dây (coi A là nút). Với đầu B tự do và tần số dao động của đầu A là 22 Hz thì trên dây có 6 nút. Nếu đầu B
cố định và coi tốc độ truyền sóng trên dây như cũ, để vẫn có 6 nút thì cần tăng hay giảm tần số bao nhiêu A. giảm 2 Hz. B. tăng 2Hz C. giảm 4. D. không đổi Hướng dẫn
+ Khi trên dây 1 đầu cố định, 1 đầu tự do ta có: v 11.v l = (2k −1) = (2.6 −1) = (1) 4 4. f 4. f
+ Khi trên dây 2 đầu cố định ta có: v l = k = 5. (2) ' 2 2. f
+ Từ ( 1) và ( 2) suy ra f’ = 20 ( Hz)
+ Cần giảm tần số là 2( Hz) Chọn A
Câu 39. Một sợi dây đàn hồi một đầu cố định, một đầu tự do. Tần số dao động bé nhất để sợi dây có sóng
dừng là f0. Tăng chiều dài thêm 1 m thì tần số dao động bé nhất để sợi dây có sóng dừng là 6 Hz. Giảm
chiều dài bớt 1 m thì tần số dao động bé nhất để sợi dây có sóng dừng là 20 Hz. Giá trị của f0 là A. 10 Hz. B. 7 Hz. C. 120/13 Hz. D. 8 Hz. Hướng dẫn
Vì sợi dây một đầu cố định và một đầu tự do nên điều kiện sóng dừng là ( ) = − = ( − ) v v v 2k 1 2k 1 f = 2k −1 f = k ( ) min 4 4f 4 4 v = 13 6 = 4 ( + ) (m) 1 7
Áp dụng công thức này cho hai trường hợp: v 480 20 = = 4 ( − ) v (m / s) 1 7 480 v 120 7 f = f = = = Hz 0 min ( ) Chọn C 4 13 13 4. 7
Câu 40. Một sợi dây dài 36 cm đang có sóng dừng ngoài hai đầu dây cố định trên dây còn có 2 điểm khác
đứng yên, tần số dao động của sóng trên dây là 50 Hz. Biết trong quá trình dao động tại thời điểm sợi dây
nằm ngang thì tốc độ dao động của điểm bụng khi đó là 8π m/s. Gọi x, y lần lượt là khoảng cách nhỏ nhất
và lớn nhất giữa hai điểm bụng gần nhau nhất trong quá trình dao động. Tỉ số x bằng y A. 0,50 B. 0,60. C. 0,75. D. 0,80 Hướng dẫn
+ Sóng dừng xảy ra trên dây với 4 điểm đúng yên Trang 22 21 2.36 →1 = 3 → = = = 24 . cm 2 3 3
Biên độ dao động của điểm bụng v 800 max A = = = 8c . m 100
+ Khoảng cách giữa hai điểm bụng là nhỏ nhất khi chúng cùng đi qua vị trí cân bằng và lớn nhất khi
chúng cùng đến biên theo hai chiều ngược nhau x 12 → = = 0,6. Chọn B 2 2 y 12 +16
Câu 41. Người ta làm thí nghiệm tạo sóng dừng trên một sợi dây đàn hồi AB có hai đầu cố định. Sợi dây
AB dài 1,2 m. Trên dây xuất hiện sóng dừng với 20 bụng sóng. Xét các điểm N, M, trên dây có vị trí cân
bằng cách A các khoảng lần lượt là 1 cm và 3cm. Biên độ sóng tại M lớn hơn biên độ sóng tại N là 2 cm.
Biên độ của bụng sóng là. A. 4 cm. B. 2 cm.
C. 4 2cm D. 2 2cm Hướng dẫn
+ Khi xảy ra sóng dừng trên dây có 20 bụng sóng → n = 20 → 20 = 120cm → = 12c . m 2
+ Biên độ dao động của các phần tử dây cách nút A một đoạn d được xác định bằng biểu thức: 2 d A = A sin b A = A với M b
A là biên độ của điểm bụng → b A = 0,5A N b
+ Theo giả thuyết của bài toán A − A = 2cm → A = 4c . m Chọn A M N b
Câu 42. Ba điểm M, N, K trên một sợi dây đàn hồi thỏa mãn MN = 2 cm, MK = 3 cm. Sóng dừng xảy ra
trên dây với bước sóng 10 cm, M là bụng sóng. Khi N có li độ là 2 cm thì K sẽ có li độ là: A. 2 cm. B. -2 cm. C. -3 cm. D. 3 cm Hướng dẫn
+ Khoảng cách giữa hai nút là = 5cm 2
+ M là điểm bụng, nên khoảng cách từ nút đến gần M nhất là 2,5cm
+ Vì MN = 2cm, MK = 3cm thì dựa vào hình vẽ có thể thây N và K đối xứng nhau qua nút.
Vậy N và K dao động ngược phan nên khi u N= 2cm thì u K= -2cm Chọn B
Câu 43. Trên một sợi dây đang có sóng dừng, phần tử tại điểm bụng
dao động điều hoà với biên độ A . Hình bên là hình dạng của một
đoạn dây ở một thời điểm nào đó. Lúc đó li độ của M là 4 mm, còn
li độ của N bằng − A / 2 . Giá trị của A bằng Trang 23 A. 14 mm. B. 7 mm. C. 8 mm. D. 12 mm. Hướng dẫn
= 12ô và M cách bụng gần nhất là 2 ô và N cách bụng gần nhất là 1 ô 2π.2 A cos u A M M 12 4 3 = = =
A = 8 3mm 14mm . Chọn A u A π A N N 2 .1 / 2 3 A cos 12
Câu 44. Sóng dừng hình thành trên sợi dây MN dài 72 cm với 7 nút sóng kể cả M và N . Biên độ dao
động tại bụng sóng là 4 cm . P và Q là hai điểm trên sợi dây có cùng biên độ dao động bằng 2 cm và
luôn dao động cùng pha với nhau. Khoảng cách lớn nhất có thể giữa P và Q bằng A. 8 cm
B. 56 cm
C. 60 cm D. 68 cm Hướng dẫn l = k.
72 = 6. = 24cm 2 2 A
A = A = 2cm = P Q 2
P và Q cách nút gần nhất là 12 24 24 PQ = l − − 2. = 72 − − 2. = 56cm max 2 12 2 12 Chọn B
Câu 45. Sóng dừng trên một sợi dây có biên độ ở bụng là 5 cm. Giữa hai điểm M, N có biên độ 2,5 cm
cách nhau 20 cm và các điểm nằm trong khoảng MN luôn dao động với biên độ nhỏ hơn 2,5 cm. Tìm bước sóng. A. 120 cm. B. 60 cm. C. 90 cm. D. 108 cm. Hướng dẫn x A −A
Vì các điểm nằm trong k, nên M và N nằm ở hai bó sóng liền kề và đối xứng nhau qua nút sóng: MN = = ( ) 2 x 2 . 10 x 10 cm A = A sin 2,5 = 5sin = 120 cm max ( ) 2 Chọn A
Câu 46. Sóng dừng trên một sợi dây có bước sóng 30 cm có biên độ ở bụng là 4 cm. Giữa hai điểm M, N
có biên độ 2 3 cm và các điểm nằm trong khoảng MN luôn dao động với biên độ lớn hon 2 3 cm. Tìm MN. A. 10 cm. B. 5 cm. C. 7,5 cm. D. 8 cm. Hướng dẫn Trang 24
Vì các điểm nằm trong khoảng MN luôn dao động với biên độ lớn hơn 2 3 cm nên M và N nằm trên
cùng một bó sóng và đối xứng nhau qua bụng: MN 2 y 2 MN y = A = A cos 2 3 = 4cos
MN = 5 cm Chọn B max ( ) 2 30 2
Câu 47. Trong hiên tượng sóng dừng hai đầu dây cố định, khoảng cách lớn nhất giữa hai vị trí cân bằng
trên dây có cùng biên độ 4mm là 130cm. Khoảng cách lớn nhất giữa hai vị trí cân bằng trên dây dao động
ngược pha và cùng biên độ 4mm là 110cm. Biên độ sóng dừng tại bụng gần giá trị nào sau đây nhất? A. 6,7mm B. 6,1mm. C. 7,1mm. D. 5,7mm. Hướng dẫn
+Hai điểm xa nhau nhất cùng dao động với biên độ 4mm cách nhau 130cm gọi là Mvà P Khoảng cách
lớn nhất giữa hai vị trí cân bằng trên dây dao động ngược pha và cùng biên độ 4mm là 110cm gọi là điểm
M, N. vẽ hình ta có thể thấy N và P là hai điểm dao động ngược pha và cách nhau nửa bước sóng
Vậy bước sóng là = (130 −110).2 = 40cm
Hai điểm M và P cách nhau 130cm, dễ thấy có: 130 = 3.40 + 10cm
Điểm P nằm tại vị trí cách nút sóng 5cm, cách bụng sóng 5cm. Biên độ của bụng là: 2 .5 2 A = 2a cos = 2.4.
= 4 2 = 5,7cm Chọn D 40 2
Câu 48. Trên một sợi dây có hai đầu cố định, đang có sóng dừng với biên độ dao động của bụng sóng là 4
cm. Khoảng cách giữa hai đầu dây là 60 cm, sóng truyền trên dây có bước sóng là 30 cm. Gọi M và N là
hai điểm trên dây mà phần tử tại đó dao động với biên độ lần lượt là 2 2 cm và 2 3 cm. Khoảng cách
lớn nhất giữa M và N trên phương truyền sóng gần nhất giá trị nào? A. 52 cm B. 50 cm. C. 53 cm. D. 50,5 cm. Hướng dẫn Điểm M gần nút A nhất dao động với biên độ là: 2 d 2 d A = A sin M 2 2 = 4 sin M
d = 3,75 cm M b M ( ) 30
Điểm N gần nút B nhất dao động với biên độ là: 2 d 2 d A = A sin N 2 3 = 4 sin N d = 5 cm N b N ( )
Khoảng cách lớn nhất giữa hai điểm M, N trên phương truyền sónglà: d = AB − d − d = 51, 25 cm x M N ( ) Chọn A
Câu 49. Một sợi dây căng ngang với hai đầu cố định, đang có sóng dừng. Khoảng cách xa nhất giữa hai
phần tử trên dây dao động cùng biên độ 4 2mm là 95 cm, còn khoảng cách xa nhất giữa hai phần tử trên
dây dao động cùng pha với cùng biên độ 4 2mm là 85 cm. Khi sợi dây duỗi thẳng, N là trung điểm giữa
vị trí một nút và vị trí một bụng liền kề. Tỉ số giữa tốc độ truyền sóng trên dây và tốc độ cực đại của phần
tử tại N xấp xỉ là A. 3,98. B. 0,25. C. 0,18. D. 5,63. Hướng dẫn
+ Bước sóng của sóng = 2(95 −85) = 20 . cm
+ Với M là điểm dao động với biên độ 4 2cm Trang 25
cách bụng một khoảng d được xác định bởi biểu thức: 2 d A = A cos
với A là biên độ của điểm M B B
bụng và d = 0,5.85 = 42,5cm A 4 2 M → A = = = 8m . m B 2 d 2 .42, 5 cos cos 20
+ N là trung điểm của một nút và một bụng liền kề 2 → A = A = 4 2m . m N 2 b Tỉ số v 200 = = = 5,63. Chọn D A 2 A N 2 .4 2 4.Sóng âm
Câu 50. Mức cường độ âm do nguồn S gây ra tại M là L, khi cho S tiến lại gần M một đoạn 62m thì mức
cường độ âm thăng thêm 3dB. Khoảng cách từ S đến M là A. 112m B. 210m C. 148m D. 130m
Cách giải: Mức cường độ âm tại điểm M: I L = log M M I0
Mức cường độ âm tại N là: I
L = log N = L + 0,3 N M I0 Mặt khác ta có: I (r −62)2 2 2 2 r I I r I r M = I = I . log N = log M . = log M + log 2 N M I r r I I r − − I − N ( 62)2 0 0 ( 62)2 0 (r 62)2 2 r r 0,15 = L + 3 log = = r = m M (r −62) 0,.3 10 210 2 r − 62
Câu 51. Trên một đường thẳng cố định trong môi trường đẳng hướng, không hấp thụ và phản xạ âm, một
máy thu ở cách nguồn âm một khoảng d thu được âm có mức cường độ âm là L; khi dịch chuyển máy thu
ra xa nguồn âm thêm 9m thì mức cường độ âm thu được là L- 20 dB, Khoảng cách d là A. 1m B. 8m C. 10m D. 9m Cách giải: Trang 26 I I I r (r +9)2 2
L = 10 log A ; L = 10 log B = L − 20 A B = = A B A 2 2 I I I r r 0 0 B A I I I r + 9
10 log A = 10 log A −10 log B 20 log = 20 I I I r B 0 0 r + 9 = 10 r = 1m r
Câu 52. Trong một môi trường đẳng hướng và không hấp thụ âm, có ba điểm theo thứ tự A, B, C thẳng
hàng. Một nguồn âm điểm phát âm có công suất P được đặt tại B thì mức cường độ âm tại A là 40 dB, tại
C là 20 dB. Mức cường độ âm tại trung điểm AC có giá trị gần đúng bằng A. 53dB. B. 27dB. C. 34dB. D. 42dB. Cách giải: Ta có r r r
L − L = 20 lg B 20 = 20 lg B B =10 r =10r A B B A r r r A A A + +
C là trung điểm của AB nên r r r 10r A B A A r = = = 5,5r C 2 2 A Suy ra r 5,5r
L − L = 20 lg C = 20 lg
A = 20 lg 5,5 = 14,8 L = 25, 2dB C A C r r A A Chọn B
Câu 53. Một thiết bị dùng để xác định mức cường độ âm được phát ra từ một nguồn âm đẳng hướng đặt
tại điểm O, thiết bị bắt đầu chuyển động nhanh dần đều từ điểm M đến điểm N với gia tốc 3 m/s2, biết ON OM =
=12m và ∆OMN vuông tại O. Chọn mốc thời gian kể từ thời điểm máy bắt đầu chuyển động 3
thì mức cường độ âm lớn nhất mà máy đo được khi đi từ M đến N là bao nhiêu và tại thời điểm nào? Biết
mức cường độ âm đo được tại M là 60 dB.
A. 66,02 dB và tại thời điểm 2.
C. 66,02 dB và tại thời điểm 2,6 s.
B. 65,25 dB và tại thời điểm 4 s.
D. 61,25 dB và tại thời điểm 2 s.
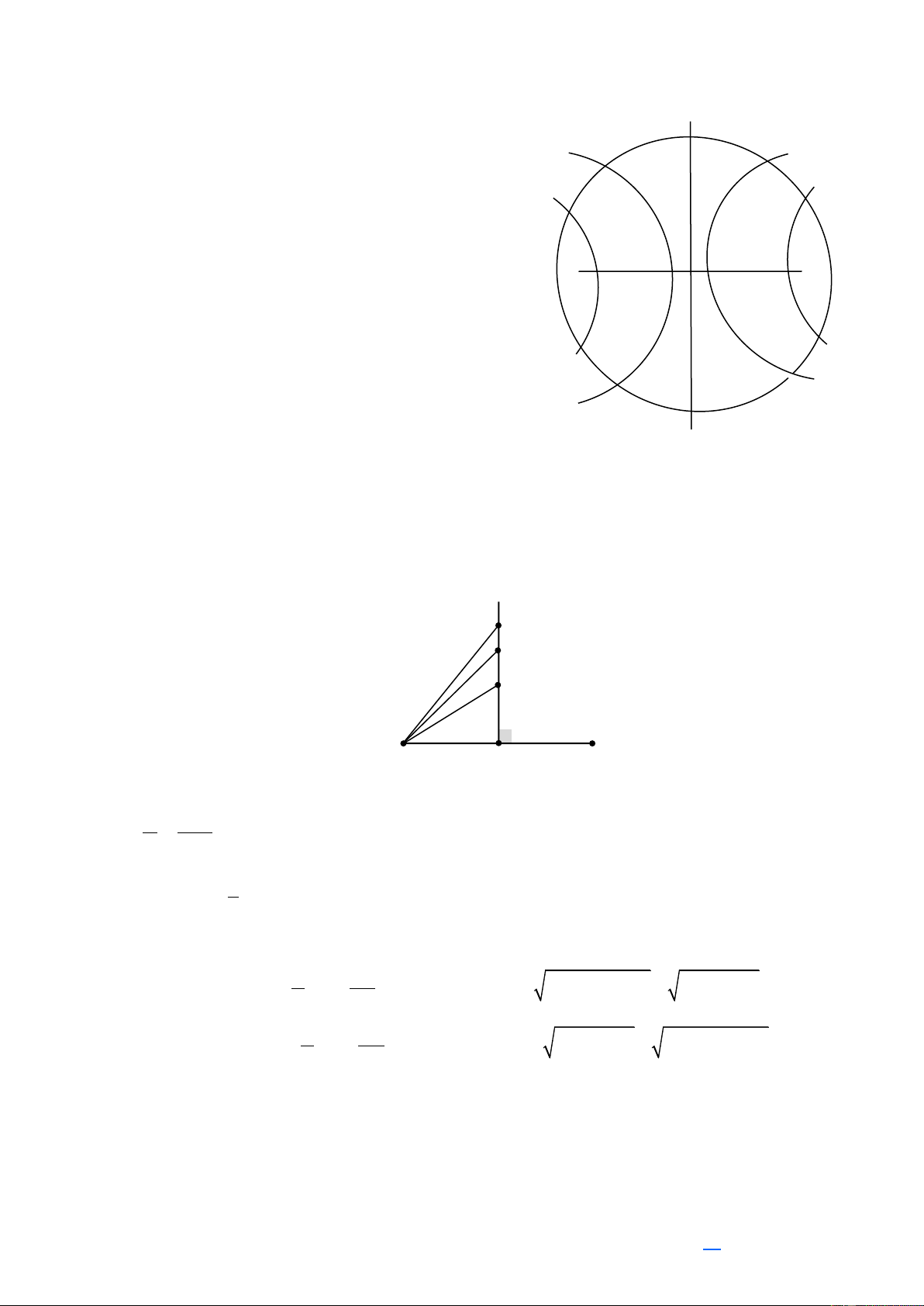
Cách giải: Đáp án D.
+ Khi xác định mức cường độ âm di chuyển từ M đến N thì thu được mức cường độ âm lớn nhất tại I
với I là đường vuông góc hạ từ O xuống MN.
Áp dụng hệ thức lượng trong tam giác vuông ta tìm được MI = 6 cm. OI = 6 3c . m
+ Mức cường độ âm tại I: OM 12 L = L + 20 log = 60 + 20log = 61,25dB I M IM 6 3
+ Thời gian để thiết bị chuyển động từ M đến I: 2MI 2.6 t = = = 2s a 3 Trang 27
Câu 54. Một nguồn âm coi là nguồn âm điểm phát âm đẳng hướng trong không gian. Môi trường không
hấp thụ âm. Mức cường độ âm tại M lúc đầu là 50dB. Nếu tăng công suất của nguồn âm lên 30% thì mức
cường độ âm tại M bằng: A. 61,31dB B. 50,52dB C. 51,14dB D. 50,11dB Cách giải:
+ Lúc đầu, mức cường độ âm tại M: P L = 10 log = 50dB M 2 4 R I0
+ Sau khi tăng công suất của nguồn âm lên 30% P + 0,3P P L = 10 log =10log1,3+10log =1,14 + 50 = 51,14dB M 2 2 4 R I 4 R I 0 0
Câu 55. Một nguồn âm đặt tại O trong môi trường đẳng hướng. Hai điểm M và N trong môi trường tạo
với O thành một tam giác đều. Mức cường độ âm tại M và N đều bằng 14,75 dB. Mức cường độ âm lớn
nhất mà một máy thu thu được khi đặt tại một điểm trên đoạn MN bằng A. 18 dB. B. 16,8 dB C. 16 dB D. 18,5 dB Cách giải:
Tam giác ONM là tam giác vuông cân nên ta dễ dàng chứng minh được 2 OM = OH và 2 L = L + 20 log =16dB H M 3 3
Câu 56. Một nguồn âm điểm S phát ra âm đẳng hướng với công suất không đổi trong một môi trường
không hấp thụ và không phản xạ âm. Một người đứng tại A cách nguồn âm 5 m, đo được âm có cường độ
âm I. Khi người này di chuyển theo phương vuông góc với SA một đoạn 5 m thì sẽ đo được âm có cường độ âm là A. I I I . B. C. I D. 2 2 4
Cách giải: Đáp án A
Do người này di chuyển theo phương vuông góc với SA một đoạn cách A 5 m SB = 5 2m
Cường độ âm tại B được xác định bởi biểu thức P P P P I = = ; I = = A 2 2 B 2 4 d 4 .5 4 d A B 4 .(5 2 )2 P 2 I I I A 4 .5 = = 2 A I = = B I P 2 2 B 4 .(5 2 )2 Trang 28
Câu 57. Một nguồn âm có công suất không đổi đặt tại A, truyền theo mọi hướng trong một môi trường
không hấp thụ âm. Mức cường độ âm tại hai điểm B và C lần lượt là 50 dB và 48 dB. Biết ba điểm A, B,
C tạo thành tam giác vuông tại B và AB = 8 m. Khoảng cách BC gần giá trị nào sau đây? A. 10 m. B. 4 m. C. 16 m. D. 6 m.
Cách giải: Đáp án D L −L 48−50 C B + Ta có: AB 0 − ,1 0 20 20 cos A = =10 =10 =10 37 AC
Ta có BC = ABtan A = 6,11 cm.
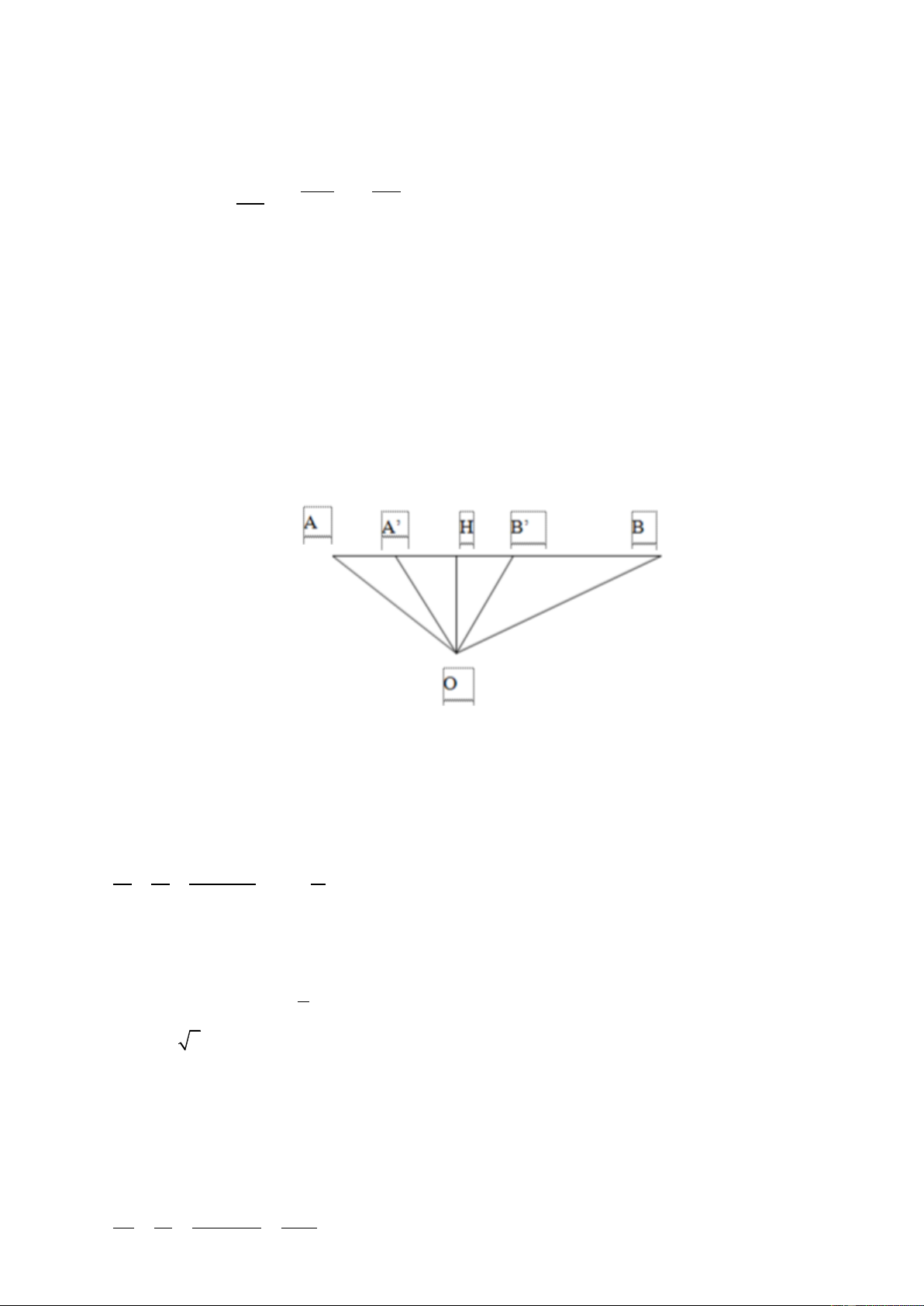
Câu 58. Một vận động viên hàng ngày đạp xe trên đoạn đường thẳng từ điểm A đúng lúc còi báo thức bắt
đầu kêu, khi đến điểm B thì còi vừa dứt. Mức cường độ âm tại A và B lần lượt là 60dB và 54 dB. Còi đặt
tại điểm O phát âm đẳng hướng với công suất không đổi và môi trường không hấp thụ âm; Cho góc AOB
bằng 1200. Do vận động viên này khiếm thính nên chỉ nghe được mức cường độ âm từ 61,94 dB trở lên
và tốc độ đạp xe không đổi. Biết thời gian còi báo thức kêu là 120s. Trên đoạn đường AB vận động viên
nghe thấy tiếng còi báo thức trong khoảng thời gian xấp xỉ bằng A. 42,67s B. 41,71s C. 43,18s D. 44,15s. Cách giải: Ta có hình vẽ sau:
Theo đề bài, mức cường độ âm tại A là 60dB và tại B là 54dB, nên ta có: 6 6 − 2
I = I .10 = 10 W / m A 0 5,4 9 − 2 I = I .10 = 251.10 W / m B 0 2 6 I r 10− r A b = = 4 b 2 2 9 I r 251.10− r B a a
Áp dụng hệ thức lượng trong tam giác OAB ta có: 2 2 2 0
AB = AO + OB − 2 . OA . OB cos120 1 2 2 2 2
AB = r + 4r + 2r .2 r . = 7r a a a a 2 a AB = 7ra
Tai người này chỉ nghe được âm thanh có mức cường độ âm lớn hơn 61,94dB, ta gọi đoạn đường mà
người đó nghe được tiếng còi là từ A’ đến B’. A’ và B’ đối xứng nhau qua H là đường cao của tam giác
OAB. (tại H âm nghe được có mức cường độ âm lớn nhất vì H gần O nhất).
Cường độ âm tại A’ là: 6,194 9 − 2 I = I .10 =156310 W / m A' 0 2 9 I r 156310− 1 A' a = = r = 0,8r 2 6 − a ' I r 10 0, 64 a A a ' Trang 29
Độ dài đoạn OH được xác định thông qua công thức tính diện tích tam giác OAB như sau: 1 1 0 S
= OH.AB = O . A O . B sin120 AOB 2 2 3 0 r .2r . O . A O . B sin120 a a 3 21 2 OH = = = r = r a a AB 7r 21 7 a 2 2
A' H = A'O − OH 0, 46ra
A' B ' = 2A' H 0,92ra
Thời gian mà người đo nghe thấy còi chính là thời gian đi đoạn A’B’: A ' B ' 0, 92r 0, 92r a a t = = = .120 = 41, 71s v AB 7ra 120
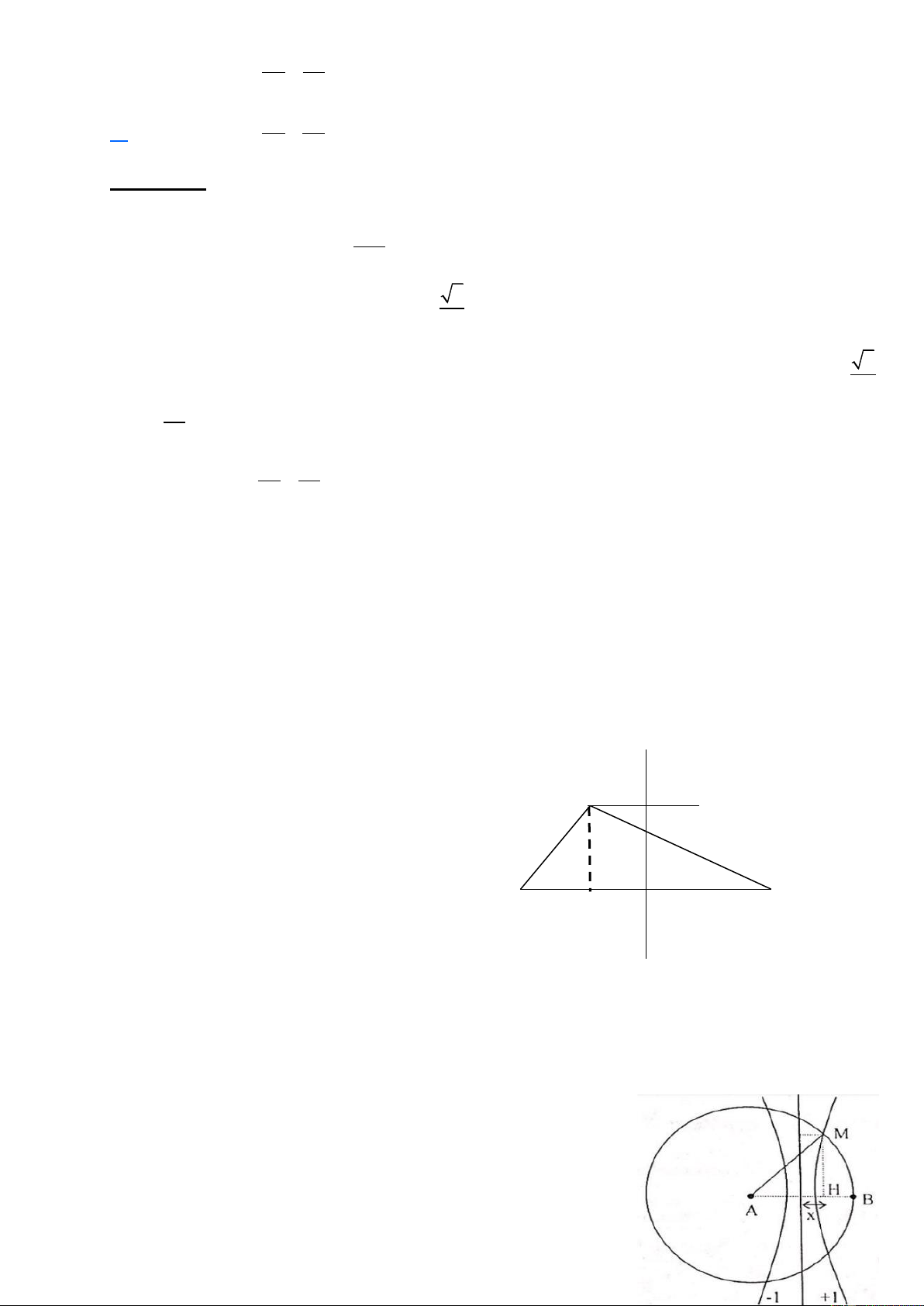
Câu 59. Cho tam giác ABC vuông cân tại A nằm trong một môi trường truyền âm. Một nguồn âm điểm O
có công suất không đổi phát âm đẳng hướng đặt tại B khi đó một người M đứng tại C nghe được âm có
mức cường độ âm là 40dB. Sau đó di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC
sao cho BO = AM. Mức cường độ âm lớn nhất mà người đó nghe được trong quá trình cả hai di chuyển bằng A. 56,6 dB B. 46,0 dB C. 42,0 dB D. 60,2 dB Cách giải:
Khi nguồn âm O đặt tại B, người đứng tại C nghe được âm có mức cường độ âm: P L = 10 log = 40dB C 2 4 BC
Khi di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC sao cho BO = AM thì mức
cường độ âm người nghe được: P L = 10 log M 2 4 OM Ta có: (L OM M ) min max
∆ABC vuông cân tại A có BO = AM => OM
<=> OM là đường trung bình của ∆ABC min BC P 4P OM = L = 10.log = 10.log min ( M )max 2 2 2 BC 4 .BC 4 . 2 ( P P L − L = − = M ) 4 10.log 10.log 10 log 4 max C 2 2 4 .BC 4 .BC (L = L + L = + = dB M ) 10 log 4 C ( M ) 40 10 log 4 46 max max Trang 30




