Chuyên đề thể tích mức vận dụng cao (có lời giải chi tiết)

Chuyên đề thể tích mức vận dụng cao có lời giải chi tiết. Tài liệu được biên soạn dưới dạng file PDF bao gồm 32 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

32 trang 6 tháng trước

Tác giả:

Profile Mỹ Duyên
Trang 1
CHUYÊN ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN MỨC VẬN DỤNG VẬN DỤNG CAO
I. Hệ thông kiến thức liên quan
A.Khoảng cách
1. Khoảng cách từ một điểm tới một đường thẳng.
Cho điểm
M
và một đường thẳng
. Trong
( )
,mp M
gọi
H
là hình chiếu vuông góc của
M
trên
. Khi đó khoảng cách
MH
được gọi là khoảng cách từ điểm
đến
.
( )
,d M MH=
Nhận xét:
,OH OM M
2. Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng
và
'
:
- Nếu
và
'
cắt nhau hoặc trùng nhau thì
( , ') 0d =
.
- Nếu
và
'
song song với nhau thì
( , ') ( , ') ( , )d d M d N = =
3. Khoảng cách từ một điểm tới một mặt phẳng.
Cho mặt phẳng
( )
α
và một điểm
M
, gọi
H
là hình chiếu của điểm
M
trên mặt phẳng
( )
α
. Khi
đó khoảng cách
MH
được gọi là khoảng cách từ điểm
đến mặt phẳng
( )
α
.
( )
( )
,d M MH=
α
4. Khoảng cách từ một đường thẳng tới một mặt phẳng.
'
H
M
K
N
Trang 2
Cho đường thẳng
và mặt phẳng
( )
α
song song với nhau. Khi đó khoảng cách từ một điểm bất kì
trên
đến mặt phẳng
( )
α
được gọi là khoảng cách giữa đường thẳng
và mặt phẳng
( )
α
.
( )
( )
( )
( )
, , ,d d M M =
αα
.
- Nếu
cắt
()
α
hoặc
nằm trong
()
α
thì
( ,( )) 0d =
α
.
5. Khoảng cách giữa hai mặt phẳng.
Cho hai mặt phẳng
( )
α
và
( )
β
song song với nhau, khoảng cách từ một điểm bất kì trên mặt
phẳng này đến mặt phẳng kia được gọi là khoảng cách giữa hai mặt phẳng
( )
α
và
( )
β
.
( ) ( )
( )
( )
( )
( )
( )
, , ,d d M d N==
α β β α
( ) ( )
,,MN
αβ
.
6. Khoảng cách giữa hai đường thẳng chéo nhau.
Cho hai đường thẳng chéo nhau
,ab
. Độ dài đoạn vuông góc chung
MN
của
a
và
b
được gọi là
khoảng cách giữa hai đường thẳng
a
và
b
.
B. Góc trong không gian
1. Góc giữa hai đường thẳng.
a.Định nghĩa:
Góc giữa hai đường thẳng cắt nhau
a
và
b
là góc nhỏ nhất trong bốn
góc mà
a
và
b
cắt nhau tạo nên.
Góc giữa hai đường thẳng cắt nhau
a
và
b
trong không gian là góc giữa
hai đường thẳng
a
và
b
cùng đi qua một điểm và lần lượt song song
(hoặc trùng) với
a
và
b
.
Chú ý: góc giữa hai đường thẳng luôn là góc nhọn ( hoặc vuông ).
b. Phương pháp
Phương pháp 1: Sử dụng định lý hàm số cosin hoặc tỉ số lượng giác.
Phương pháp 2: Sử dụng tích vô hướng: nếu
u
và
v
lần lượt là hai
'
N
M
Trang 3
vecto chỉ phương ( hoặc vecto pháp tuyến ) của hai đường thẳng
a
và
b
thì góc
φ
của hai đường
thẳng này được xác định bởi công thức
( )
.
cos cos , .
.
uv
uv
uv
==
φ
2.Góc giữa đường thẳng và mặt phẳng
Nếu đường thẳng
( )
aP⊥
thì góc giữa đường thẳng
a
và
( )
P
bằng
0
90
.
Nếu đường thẳng
a
không vuông góc với
( )
P
thì góc giữa đường thẳng
a
và
( )
P
là góc giữa
a
và
hình chiếu
a
của
a
trên
( )
P
.
3.Góc giữa hai mặt phẳng
a. Định nghĩa
- Góc giữa hai mặt phẳng
( )
α
và
( )
β
là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt
phẳng đó.
- Nếu hai mặt phẳng đó song song hoặc trùng nhau thì góc giữa chúng bằng
0
.
b. phương pháp tính góc giữa hai mặt phẳng cắt nhau
❖ Phương pháp 1: Dựng hai đường thẳng
a
,
b
lần lượt vuông góc với hai mặt phẳng
( )
α
và
( )
β
. Khi đó, góc giữa hai mặt phẳng
( )
α
và
( )
β
là
( ) ( )
(
)
( )
,,ab=
αβ
. Tính góc
( )
,ab
.
❖ Phương pháp 2:
➢ Xác định giao tuyến
c
của hai mặt phẳng
( )
α
và
( )
β
.
➢ Dựng hai đường thẳng
a
,
b
lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao
tuyến
c
tại một điểm trên
c
. Khi đó:
( ) ( )
(
)
( )
,,ab=
αβ
.
Hay ta xác định mặt phẳng phụ
( )
γ
vuông góc với giao tuyến
c
mà
( ) ( )
a=
αγ
,
( ) ( )
b=
βγ
.
Suy ra
( ) ( )
(
)
( )
,,ab=
αβ
.
P
a'
a
Trang 4
❖ Phương pháp 3: (trường hợp đặc biệt)
➢ Nếu có một đoạn thẳng nối hai điểm
A
,
B
( ) ( )
( )
,AB
αβ
mà
( )
AB ⊥
β
thì qua
A
hoặc
B
ta dựng đường thẳng vuông góc với giao tuyến
c
của hai mặt phẳng tại
H
. Khi đó
( ) ( )
(
)
, AHB=
αβ
.
C. Thể tích khối đa diện
1.Thể tích khối chóp:
d
1
.
3
V h S=
trong đó h là chiều cao và S
d
là diện tích đáy
2.Thể tích khối lăng trụ:
d
.V h S=
trong đó h là chiều cao và S
d
là diện tích đáy
3.Các trường hợp đặc biệt
Định lý Menelaus: Cho tam giác
ABC
đường thẳng
( )
d
cắt các cạnh
,,AB BC CA
lần lượt tại
,,M N P
ta có
. . 1
MA PB NC
MB PC NA
=
Bài toán 1. Cho hình chóp S.ABC. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’. Khi
đó:
/ / /
.
.
' ' '
..
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
Bài toán 2: Cho hình chóp
.S ABCD
có đáy là hình bình hành. Một mặt phẳng
()
α
cắt các cạnh
bên
, , ,SA SB SC SD
của hình chóp lần lượt tại các điểm
/ / / /
, , ,A B C D
. Đặt
/
;
SA
x
SA
=
/
;
SB
y
SB
=
/
;
SC
z
SC
=
/
SD
t
SD
=
. Khi đó
1)
1 1 1 1
x z y t
+ = +
.
2)
/ / / /
.
.
1 1 1 1
()
4
S A B C D
S ABCD
V
xyzt
V x y z t
= + + +
Lời giải
N
A
B
P
M
C
Trang 5
Gọi
O
là giao điểm của
AC
và
BD
;
//
I A C SO=
. Suy ra
//
,,B I D
thẳng hàng.
Kẻ
/ / / /
/ / ; / /AM A C CN A C
. Ta có:
//
11 SA SC
x z SA SC
+ = +
SM SN
SI SI
=+
SM SN
SI
+
=
2SO
SI
=
Chứng minh tương tự ta cũng có:
1 1 2SO
y t SI
+=
, Suy ra điều phải chứng minh.
2)Ta có
/ / / / / / / / /
/
. . .S A B C D S A B C S A D C
V V V=+
/ / /
..
SA B C
SABC
V
x z y
V
=
/ / /
.
1
.
2
S ABCD
SA B C
V xzyV=
.
Chứng minh tương tự ta có
/ / /
.
1
.
2
S ABCD
SA D C
V xztV=
Suy ra
/ / /
/
.
1
()
2
S A B C D
V xz y t=+
(1)
Tương tự ta có
/ / /
/
.
1
()
2
S A B C D
V yt x z=+
(2)
Từ (1) và (2) ta được
/ / /
/
.
4
S A B C D
xyzt x z y t
V
xz yt

++
=+


1 1 1 1
4
xyzt
x y z t

= + + +


.
Bài toán 3: Cho hình lăng trụ tam giác
1 1 1
.ABC A BC
. Trên
1
AA
,
1
BB
,
1
CC
lấy lần lượt các điểm
, , M N P
sao cho
1
AM
a
AA
=
,
1
BN
b
BB
=
,
1
CP
c
CC
=
. Khi đó:
1 1 1
.
.
3
ABC MNP
ABC A B C
V
abc
V
++
=
Lời giải
Trang 6
Không mất tính tổng quát ta giả sử
a c b
.
Khi đó mặt phẳng qua
N
song song với
( )
ABC
cắt
11
, AA CC
lần lượt tại
, DE
.
Mặt phẳng qua
M
song song với
( )
ABC
cắt
11
, BB CC
lần lượt tại
, IH
Ta có
. . .ABC MNP ABC DEN N DEPM
V V V=−
( )
( )
.
1
;.
3
N DEPM DEPM
V d N DEPM S=
( )
( )
( ) ( )
11
; . . ;
32
d N DEPM DM PE d DM PE=+
( )
( )
( )
11
; . 1 . . ;
32
PE
d N DEPM DM d DM PE
DM

=+


( )
( )
11
; . 1 .
32
DEHM
PE
d N DEPM S
DM

=+


.
1
1
2
N DEHM
PE
V
DM

=+


.
12
.1
23
DEN MIH
PE
V
DM

=+


1 1 1
.
1
1
. 1 .
3
ABC A B C
PE DM
V
DM AA

=+


1 1 1
.
11
1
..
3
ABC A B C
DM PE
V
AA AA

=+


.
1 1 1
..
1
ABC DEN ABC A B C
BN
VV
BB
=
Do đó :
1 1 1 1 1 1
. . .
1 1 1
1
..
3
ABC MNP ABC A B C ABC A B C
BN DM PE
V V V
BB AA AA

= − +


1 1 1
.
. 1 1 1 1 1
1
3
ABC MNP
ABC A B C
V
BN BN AM BN CP
V BB BB AA BB CC

= − − + −


1 1 1
.
.
3
ABC MNP
ABC A B C
V
abc
V
++
=
.
Bài toán 4: Cho hình hộp
1 1 1 1
.ABCD A BC D
. Trên các đoạn thẳng
1
AA
,
1
BB
,
1
CC
lấy các điểm
, , M N P
sao cho
1
AM aAA=
,
1
BN bBB=
,
1
CP cCC=
. Mặt phẳng
( )
MNP
cắt
1
DD
tại
Q
. Ta có tỉ
số thể tích:
1 1 1 1
.
.
2
ABCD MNPQ
ABCD A B C D
V
ac
V
+
=
2
bd+
=
.
Lời giải
Dựa vào giả thiết đề cho ta có
1
AM aAA=
,
1
BN bBB=
,
1
CP cCC=
,
1 1 1 1
AA BB CC DD= = =
và
giả sử
1
DQ dDD=
.
Gọi
O
và
I
lần lượt là trung điểm
AC
và
MP
, khi đó
MP
là đường trung bình chung của hình
thang
AMPC
,
BNQD
. Do đó ta có
2AM CP OI+=
và
2BN DQ OI+=
.
Suy ra
AM CP BN DQ+ = +
1 1 1 1
. . . .a AA cCC b BB d DD + = +
.
( ) ( )
1
0a c b d AA + − + =


a c b d + = +
.
Trang 7
Tiếp theo, ta có
( )
1 1 1 1
.
.
2
6
ABCD MNPQ
ABCD A B C D
V
a b d c
V
+ + +
=
1 1 1 1
.
.
22
ABCD MNPQ
ABCD A B C D
V
a c b d
V
++
= =
.
II. Các dạng bài tập thường gặp
Dạng I: Tính thể tích khối chóp
1. Ví dụ minh hoạ
Ví dụ 1. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, các mặt bên
( )
SBC
,
( )
SAD
cùng tạo
với đáy góc
60
, mặt bên
( )
SAB
vuông góc với đáy. Biết khoảng cách từ
A
đến mặt phẳng
( )
SCD
bằng
21
7
, tính thể tích khối chóp
.S ABC
.
A.
3
12
. B.
3
6
. C.
3
8
. D.
3
8
.
Lời giải.
ChọnA
Hạ
,SH AB H AB⊥
, do
( ) ( )
SAB ABCD⊥
nên
( )
SH ABCD⊥
SH BC⊥
Có
ABCD
là hình vuông
AB BC⊥
( )
BC SAB⊥
BC SB⊥
Có
( ) ( )
,SB BC BC AB
SBC ABCD BC
⊥⊥
=
( ) ( )
( )
,ABCD SBC SBH =
(Do
90SAH
)
Chứng minh tương tự
( ) ( )
( )
,ABCD SAD SAH =
Từ giả thiết suy ra:
60SAH SBH = =
mà
H AB
suy ra tam giác
SAB
đều và
H
là trung
điểm của
AB
.
Gọi
M
là trung điểm của
CD
HM CD⊥
Có
( )
SH ABCD SH CD⊥ ⊥
( ) ( )
SHM SCD⊥
. Hạ
HI SM⊥
thì
( )
HI SCD⊥
3
12
HI=
Có
2 2 2
1 1 1
HI SH HM
=+
22
2
1 1 1
21 3
72
BC
AB
= +
1AB=
(Do
AB BC HM==
)
( )
.
1 1 3 1 3
. . .
3 3 2 2 12
S ABC
ABC
V SH S = = =
.
B
A
D
C
S
H
M
I
Trang 8
Ví dụ 2. Cho hình chóp đều S.ABC có góc giữa mặt bên và mặt đáy (ABC) bằng 60
o
. Biết khoảng
cách giữa hai đường thẳng SA và BC bằng
37
14
a
. Tính theo a thể tích V của khối chóp S.ABC
A.
3
3
.
12
a
V =
B.
3
3
.
16
a
V =
C.
3
3
.
18
a
V =
D.
3
3
.
24
a
V =
Giải:
Gọi O là trung điểm AC, x là cạnh của tam giác đều, G là trọng tâm tam giác ABC.
+) Ta có
; SO AC BO AC⊥⊥
; nên góc giữa (SAC) và (ABC) là
60
o
SOB =
.
Vì SABC là chóp đều nên
( )
SG ABC SG GO⊥ ⊥
.
Xét tam giác vuông SAG có
3
.tan60 . 3
62
o
xx
SG OG= = =
+) Từ A kẻ AD / / BC suy ra:
( ) ( )
( )
( )
, , ,(d BC SA d BC SAD d B SAD==
Mặt khác ta có
( )
( )
( )
( )
2
,,
3
d G SAD d B SAD=
Vì
120 , 30 ; 90
o o o
BAD BAG GAD= = =
hay AG ⊥ AD (1)
Lại có SG ⊥AD AD ⊥ (AGS) .
Kẻ
( ) ( )
( )
,GK SA GK AD GK SAD GK d G SAD⊥ ⊥ ⊥ =
Xét tam giác vuông SGA ta có:
22
2 2 2 2
1 1 1 1 1 7 7
7
3
2
3
x
GK
GK GA GS x
x
x
= + = + = =




Suy ra:
7 2 3 7
.
7 3 14
xa
xa= =
Vậy
2
3
;
24
ABC
aa
SG S
==
Trang 9
Thể tích khối chóp S.ABC là:
23
1 1 3 3
. . .
3 3 2 4 24
ABC
a a a
V SG S
= = =
Chọn đáp án D.
Ví dụ 3. Cho hình chóp có tam giác nhọn và nằm trong mặt phẳng vuông góc với mặt
đáy , tam giác vuông tại có . Mặt bên và cùng
tạo với đáy góc bằng nhau và bằng . Thể tích của khối chóp theo là:
A. . B. . C. . D. .
Hướng dẫn giải
Chọn B.
+ Theo đề theo giao tuyến . Dựng .
+ vuông nên .
.
+ Dựng .
.
là hình vuông. Đặt .
vuông nên .
vuông nên .
Từ và : .
Ví dụ 4. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A ,
;AB a=
90
o
SBA SCA==
, góc giữa hai mặt phẳng (SAB) và (SAC) bằng 60
o
. Thể tích của khối đã cho bằng
A.
3
.a
B.
3
.
3
a
C.
3
.
2
a
D.
3
.
6
a
Lời giải
Chọn D
.S ABC
SAB
( )
ABC
ABC
C
, 30= = AC a ABC
( )
SAC
( )
SBC
60
.S ABC
a
3
2(1 5)
a
V =
+
3
3
2(1 3)
a
V =
+
3
2
13
a
V =
+
3
2
2(1 2)
a
V =
+
30
°
Q
A
C
B
S
H
P
( ) ( )
SAB ABC⊥
AB
( )
SH AB SH SAB⊥ ⊥
ABC
tan30 3 = =
AC
BC a
BC
2
13
. (1)
22
ABC
a
S AC BC
==
( ) ( )
( )
( ) ( )
( )
0
, , , 60HP AC HQ BC SPH SQH SAC ABC SBC ABC⊥ ⊥ = = = =
SPH SQH HP HQ = =
HPCQ
,0 3HQ x x a=
3QB a x = −
HQB
3
tan60 3 3
31
= = − = =
+
QB a
x a x x HQ
HQ
SHQ
3
tan60 (2)
31
= =
+
SH a
SH
HQ
(1)
(2)
( )
3
3
2 3 1
a
V =
+
Trang 10
Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA .
Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và
IB IC=
.
( )
, SA IC SA IB SA IBC⊥ ⊥ ⊥
tại I .
. . .
1
.
3
S ABC A IBC S IBC IBC
V V V SAS
= + =
( ) ( )
( )
( )
60
, , 60
120
o
o
BIC
SAB SAC IB IC
BIC
=
= =
=
Ta có
IC IB AB a= =
mà
2BC a=
nên tam giác IBC không thể đều suy ra
120
o
BIC =
.
Trong tam giác IBC đặt
( )
0IB IC x x= =
có:
( )
2
2 2 2 2 2 2
16
2 . .cos120 2 2
23
o
a
BC IB IC IB IC a x x x x

= + − = + − − =


Trong tam giác ABI vuông tại I có:
2
2 2 2
63
33
aa
AI AB IB a

= − = − =



Trong tam giác SAB vuông tại B đường cao BI có:
22
3
3
3
AB a
SA a
IA
a
= = =
Vậy
3
.
1 1 1
. . . 3. . .sin120
3 3 2 6
o
S ABC IBC
a
V SA S a IB IC
= = =
Ví dụ 5. Cho tứ diện
ABCD
và các điểm
M
,
N
,
P
lần lượt thuộc các cạnh
BC
,
BD
,
AC
sao
cho
4BC BM=
,
3AC AP=
,
2BD BN=
. Tính tỉ số thể tích hai phần của khối tứ diện
ABCD
được
phân chia bởi
( )
mp MNP
.
A.
7
13
. B.
7
15
. C.
8
15
. D.
8
13
.
Lời giải
Chọn A.
Trang 11
Gọi
, .I MN DC K AD PI= =
Áp dụng định lý Menelaus cho tam giác
BCD
và
3
điểm
,,M N I
ta có
1
. . 1 .1. 1 3
3
IC ND MB IC IC
ID NB MC ID ID
= = =
Áp dụng định lý Menelaus cho tam giác
ACD
và
3
điểm
,,P K I
ta có
12
. . 1 . .3 1
23
KD PA IC KD KD
KA PC ID KA KA
= = =
2 3 2 1
. . . .1
3 4 4 2
11
(3)
24
V
CP CM CN
CPMN
V CA CB CN
CABN
V V V
CPMN CABN ABCD
= = = =
= =
1 3 1
. . . .1
3 5 5
4 4 4 1 2
(4)
5 5 5 2 5
APKN
ACDN
NCPKD
NCPKD ACDN ABCD ABCD
ACDN
V
AP AK AN
V AC AD AN
V
V V V V
V
= = =
= = = =
( ) ( )
13
3 , 4
20
CMPKDN CPMN NCPKD ABCD
V V V V = + =
7
13
ABMNKP
CMNDK
V
V
=
Ví dụ 6. Cho hình chóp đều
.S ABC
có đáy là tam giác đều cạnh
a
. Gọi
E
,
F
lần lượt là trung
điểm của các cạnh
,SB SC
. Biết mặt phẳng
()AEF
vuông góc với mặt phẳng
()SBC
. Tính thể tích
khối chóp
.S ABC
.
A.
3
5
24
a
. B.
3
5
8
a
. C.
3
3
24
a
. D.
3
6
12
a
.
Lời giải
Chọn A
k
A
B
C
D
I
M
P
N
N
F
E
O
M
A
C
B
S
Trang 12
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
, do
.S ABC
là hình chóp đều nên
( )
SO ABC⊥
.
Gọi
M
,
N
lần lượt là trung điểm của
BC
và
EF
.
Ta có
S
,
M
,
N
thẳng hàng và
SM BC⊥
tại
,
SM EF⊥
tại
N
.
Ta có
( ) ( )
( ) ( )
AEF SBC EF
SM SBC SM AEF MN AN
SM EF
=
⊥ ⊥
⊥
ANM
vuông tại
N
.
Từ đó suy ra
ANM SOM∽
AN AM NM
SO SM OM
= =
..NM SM AM OM=
.
Mà ta có
N
là trung điểm của
SM
(vì
E
,
F
lần lượt là trung điểm của
SB
,
SC
)
1
2
NM SM=
;
ABC
đều cạnh
a
và
O
là tâm đường tròn ngoại tiếp tam giác
ABC
3
2
a
AM=
;
3
6
a
OM =
.
Vậy
2
2
1 3 3
.
2 2 6 4
a a a
SM ==
2
a
SM=
.
Ta có
22
22
15
2 12 6
a a a
SO SM OM= − = − =
;
2
3
4
ABC
a
S =
.
23
.
1 1 15 3 5
. . . .
3 3 6 4 24
S ABC ABC
a a a
V SO S= = =
.
2. Bài tập vận dụng
Câu 1. Cho hình chóp có . Các mặt bên đều
cùng hợp với mặt đáy một góc và hình chiếu của lên nằm khác phía với
đối với đường thẳng . Thể tích khối chóp .
A. . B. . C. . D.
Câu 2. Cho hình chóp , có đáy là tam giác đều cạnh . Các mặt bên , ,
lần lượt tạo với đáy các góc lần lượt là . Tính thể tích của khối chóp
. Biết rằng hình chiếu vuông góc của trên mặt phẳng nằm bên trong tam giác .
A. . B. . C. . D. .
Câu 3. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt đáy
( )
ABCD
và góc giữa
SC
với mặt phẳng
( )
SAB
bằng
30
. Gọi
M
là điểm di động trên cạnh
CD
và
H
là hình chiếu vuông góc của
S
lên đường thẳng
BM
. Khi điểm
di động trên cạnh
CD
thì
thể tích chóp
.S ABH
lớn nhất là
A.
3
2
6
a
V =
. B.
3
2
12
a
V =
. C.
3
2
15
a
V =
. D.
3
2
8
a
V =
.
Câu 4. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy
()ABCD
và
SA a=
. Điểm
M
thuộc cạnh
SA
sao cho
,0 1.
SM
kk
SA
=
Khi đó giá trị của
k
để
mặt phẳng
()BMC
chia khối chóp
.S ABCD
thành hai phần có thể tích bằng nhau là:
A.
15
2
k
−+
=
B.
15
2
k
+
=
. C.
15
4
k
−+
=
. D.
12
2
k
−+
=
.
.S ABC
3, 4, 5AB BC AC= = =
( ) ( ) ( )
,,SAB SAC SBC
( )
ABC
60
H
S
( )
ABC
A
BC
.S ABC
.
63
S ABC
V =
.
12 3
S ABC
V =
.
23
S ABC
V =
.
43
S ABC
V =
.S ABC
ABC
a
( )
SAB
( )
SAC
( )
SBC
000
30 ,45 ,60
V
.S ABC
S
( )
ABC
ABC
( )
3
3
43
a
V =
+
( )
3
3
2 4 3
a
V =
+
( )
3
3
4 4 3
a
V =
+
( )
3
3
8 4 3
a
V =
+
Trang 13
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
2SA a=
. Gọi
', 'BD
là hình chiếu của
A
lần lượt lên
,SB SD
. Mặt phẳng
( )
''AB D
cắt
SC
tại
'C
. Tính thể tích khối chóp
. ' ' 'S AB C D
là:
A.
3
23
9
a
V =
. B.
3
22
9
a
V =
. C.
3
2
9
a
V =
. D.
3
23
3
a
V =
.
Câu 6. Cho hình chóp
.S ABCD
có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm
trên cạnh SC sao cho EC = 2ES. Gọi
( )
α
là mặt phẳng chứa đường thẳng AE và song song với
đường thẳng BD,
( )
α
cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp
S.AMEN.
A.
1
.
6
V
B.
1
.
9
V
C.
1
.
27
V
D.
2
.
3
V
Câu 7. Cho hình chóp
.S ABC
có chân đường cao nằm trong tam giác
ABC
, các mặt bên
( )
SAB
,
( )
SBC
,
( )
SCA
cùng tạo với đáy góc
60
. Biết
3AB =
,
4BC =
,
5CD =
, tính thể tích khối chóp
.S ABC
.
A.
23
. B.
63
. C.
53
. D.
10 3
.
Câu 8. Cho hình chóp
.S ABCD
có
ABCD
là hình chữ nhật tâm
O
với
,3AB a BC a==
. Hình
chiếu vuông góc của
S
lên mặt phẳng
( )
ABCD
là trung điểm
AO
. Biết
( ) ( )
( )
; 60SAC SBC
=
.
Khi đó thể tích của
.S ABCD
là:
A.
3
3
3
a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
6
8
a
.
Câu 9. Để làm một hình chóp tứ giác đều từ một tấm tôn hình vuông có cạnh bằng
13+
, người ta
cắt tấm tôn theo các tam giác cân bằng nhau
, , ,MAN NBP PCQ QDM
sau đó gò các tam giác
, , ,ABN BCP CDQ
DAM
sao cho bốn đỉnh
, , ,M N P Q
trùng nhau(hình vẽ).
Biết rằng, các góc ở đỉnh của mỗi tam giác cân là
0
150
. Tính thể tích
V
của khối chóp đều tạo
thành.
A.
3 6 5 2
24
V
+
=
. B.
2
3
V =
. C.
52 30 3
3
V
+
=
. D.
1
3
V =
Câu 10. Một đống đất được vun thành hình một khối chóp cụt tứ giác đều có cạnh đáy lớn bằng
2m, cạnh đáy nhỏ bằng 1m và chiều cao bằng 2m. Khối lượng (thể tích) đống đất có giá trị gần nhất
với con số
A. 4,55m
3
. B. 4,65m
3
. C. 4,7 m
3
. D. 4,75m
3
.
3. Hướng dẫn giải
Câu 1. Cho hình chóp có . Các mặt bên đều
cùng hợp với mặt đáy một góc và hình chiếu của lên nằm khác phía với
đối với đường thẳng . Thể tích khối chóp .
A. . B. . C. . D.
Hướng dẫn giải
Chọn A.
.S ABC
3, 4, 5AB BC AC= = =
( ) ( ) ( )
,,SAB SAC SBC
( )
ABC
60
H
S
( )
ABC
A
BC
.S ABC
.
63
S ABC
V =
.
12 3
S ABC
V =
.
23
S ABC
V =
.
43
S ABC
V =
Trang 14
.
Gọi là hình chiếu của lên .
Ta có .
Theo bài ra ta có là tâm đường tròn bàng tiếp .
Ta có vuông tại là hình vuông.
Gọi .
.
Ta có là trung điểm của .
.
.
Câu 2. Cho hình chóp , có đáy là tam giác đều cạnh . Các mặt bên , ,
lần lượt tạo với đáy các góc lần lượt là . Tính thể tích của khối chóp
. Biết rằng hình chiếu vuông góc của trên mặt phẳng nằm bên trong tam giác .
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi là hình chiếu vuông góc của trên mặt phẳng
. Kẻ , ,
. Khi đó ta có ,
, . Ta có
suy ra
.
Vậy .
Chọn đáp án D.
Câu 3. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt đáy
( )
ABCD
và góc giữa
SC
với mặt phẳng
( )
SAB
bằng
30
. Gọi
M
là điểm di động trên cạnh
CD
I
P
N
M
C
S
H
B
A
,,M N P
H
,,CB BA AC
SHM SHN SHP HM HN HP = = = =
H
ABC
ABC
B
BMHN
I AH BC=
3 3 3
5 8 2
BI
BI BC
IC
= = =
1
2
BI NH
AB AN
==
B
AN
3HN AB = =
.tan60 3 3SH HN = =
1
.6
2
ABC
S BA BC==
.
1
. 6 3
3
S ABC ABC
V S SH = =
.S ABC
ABC
a
( )
SAB
( )
SAC
( )
SBC
000
30 ,45 ,60
V
.S ABC
S
( )
ABC
ABC
( )
3
3
43
a
V =
+
( )
3
3
2 4 3
a
V =
+
( )
3
3
4 4 3
a
V =
+
( )
3
3
8 4 3
a
V =
+
H
S
( )
ABC
( )
HD AB D AB⊥
( )
HE AC E AC⊥
( )
HF BC E BC⊥
0
3
tan30
SH
HD SH==
0
tan45
SH
HE SH==
0
tan60
3
SH SH
HF ==
2
3
4
ABC
a
S
=
( )
2
1 1 3 3
13
24
3
2 4 3
aa
SH a SH

+ + = =

+

( ) ( )
23
1 3 3 3
..
34
2 4 3 8 4 3
a a a
V ==
++
Trang 15
và
H
là hình chiếu vuông góc của
S
lên đường thẳng
BM
. Khi điểm
di động trên cạnh
CD
thì
thể tích chóp
.S ABH
lớn nhất là
A.
3
2
6
a
V =
. B.
3
2
12
a
V =
. C.
3
2
15
a
V =
. D.
3
2
8
a
V =
.
Lời giải
Chọn B
Lấy điểm
N BC
sao cho
,0BN CM x x a= =
. Gọi
H AN BM=
Xét
ABN
và
BCM
ta có:
BN CM=
,
90ABN BCM= =
và
AB BC=
ABN BCM =
(c.g.c)
BAN CBM=
Mà
90BAN BNA+ =
nên
90CBM BNA+ =
90BHN =
hay
AH BM⊥
Ta có:
( )
BM AH
BM SAH SH BM
BM SA
⊥
⊥ ⊥
⊥
Hình chiếu vuông góc của
S
lên
BM
là
H
.
Do
BHN
đồng dạng với
BCM
nên
BH BN
BC BM
=
22
BH x
a
xa
=
+
22
ax
BH
xa
=
+
Tam giác
ABH
vuông tại
H
nên
2 2 4 2
2 2 2
2 2 2 2
22
a x a a
AH AB BH a
x a x a
xa
= − = − = =
++
+
23
22
2 2 2 2
11
. . . .
2 2 2
ABH
a ax a x
S AH BH
xa
x a x a
= = =
+
++
3 4 3
.
22
1 1 2 2
. . 2. . .
3 3 2 12 12
S ABH ABH
a x a a
V SAS a
x a a
= = =
+
Câu 4. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy
()ABCD
và
SA a=
. Điểm
M
thuộc cạnh
SA
sao cho
,0 1.
SM
kk
SA
=
Khi đó giá trị của
k
để
mặt phẳng
()BMC
chia khối chóp
.S ABCD
thành hai phần có thể tích bằng nhau là:
A.
15
2
k
−+
=
B.
15
2
k
+
=
. C.
15
4
k
−+
=
. D.
12
2
k
−+
=
.
Lời giải
Chọn A.
Phân tích: Bài toán trên chính là bài toán về tỉ số thể tích, vì vậy trước hết phải xác định thiết diện
của hình chóp khi cắt bởi
()BMC
.
Trang 16
Do
()BMC
chứa
BC
song song với
AD
nên
()BMC
cắt
()SAD
theo giao tuyến song song
AD
.
Để tính
.S BCNM
V
nếu xác định đường cao thì phức tạp vì vậy sẽ chia thành hai khối và sử dụng bài
toán tỉ số thể tích.
Kẻ
/ / ;MN AD N SD
khi đó thiết diện của hình chóp
.S ABCD
với
()BMC
là hình thang
BCNM
.
Suy ra
()BMC
chia khối chóp thành hai khối đa diện
SBCNM
và
DABCNM
.
Đặt
1.S BCNM
VV=
;
2 DABCNM
VV=
;
.S ABCD
VV=
.
Để
12
VV=
thì
1
1
2
VV=
.
Ta có
2
.
SNMC
SADC
V
SN SM
k
V SD SA
==
2
1
.
2
SNMC
V k V=
.
Ta có
SMCB
SABC
V
SM
k
V SA
==
1
.
2
SMCB
V kV=
.
Vậy
2
1
1
( ).
2
V k k V=+
.
Khi đó
1
1
2
VV=
2
1kk + =
15
2
15
2
k
k
−−
=
−+
=
.
Do
01k
nên
15
2
k
−+
=
. Vậy chọn đáp án A.
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
2SA a=
. Gọi
', 'BD
là hình chiếu của
A
lần lượt lên
,SB SD
. Mặt phẳng
( )
''AB D
cắt
SC
tại
'C
. Tính thể tích khối chóp
. ' ' 'S AB C D
là:
A.
3
23
9
a
V =
. B.
3
22
9
a
V =
. C.
3
2
9
a
V =
. D.
3
23
3
a
V =
.
Lời giải
Chọn C.
Trang 17
Ta có
2
2
' ' 2 2
33
SB SD a
SB SD a
= = =
nên suy ra
' '/ /B D BD
mà
( )
BD SAC BD SC⊥ ⊥
.
Do đó
''B D SC⊥
(1)
Ta có
( )
'BC SAB BC AB⊥ ⊥
và
'AB SB⊥
suy ra
'AB SC⊥
(2)
Từ (1) và (2) suy ra
( )
' ' 'AB C D SC⊥
nên ta có
'AC SC⊥
2
2
' 2 1
42
SC a
SC a
==
.
Ta có
' ' ' ' ' '
2
' ' 2 1 1
..
2 3 2 3
SA B C D SAB C
SABCD SABC
VV
SB SC
V V SB SC
= = = =
.
Mà
3
2
12
.2
33
SABCD
a
V a a==
.
Vậy
33
' ' '
1 2 2
.
3 3 9
SAB C D
aa
V ==
.
Câu 6. Cho hình chóp
.S ABCD
có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm
trên cạnh SC sao cho EC = 2ES. Gọi
( )
α
là mặt phẳng chứa đường thẳng AE và song song với
đường thẳng BD,
( )
α
cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp
S.AMEN.
A.
1
.
6
V
B.
1
.
9
V
C.
1
.
27
V
D.
2
.
3
V
Lời giải
Chọn A.
Gọi
O AC BD=
và
.I SO AE=
Do
( )
α
đi qua AE và song song với BD nên
( )
α
cắt (SBD)
theo một giao tuyến đi qua I và song song với BD.
Trong (SAC) từ O kẻ một đường thẳng song song với AE giả sử cắt SC tại K, do O là trung điểm
của AC nên K là trung điểm của EC suy ra SE = EK = KC
S
A
D
C
B
D'
C'
B'
K
N
M
O
I
E
D
C
B
A
S
Trang 18
Xét tam giác
SAC
ta có
1
2
SI SE
SO SK
==
Xét tam giác
SBD
ta có
1
2
SM SN SI
SB SD SO
= = =
Do đó
.
.
.
1 1 1 1
..
2 3 6 12
S AME
S AME
S ABC
V
SM SN
VV
V SB SD
= = = =
Tương tự, ta có
.
1
.
12
S ANE
VV=
Vậy
. . .
1 1 1
.
12 12 6
S AMEN S AME S ANE
V V V V V V= + = + =
Phương pháp giải:
Dùng định lí Thalet và phương pháp tỉ số thể tích để tính thể tích khối chóp cần tìm theo V
Chú ý
+) Nếu ba điểm E, A, I thẳng hàng nên áp dụng định lý Menelaus cho tam giác SOC ta có:
1
. . 1 1 .
2
SE CA OI OI SI
EC AO IS SI SO
= = =
Như vậy có thể tính được tỷ số
1
2
SI
SO
=
ngay mà không cần dùng định lý Ta lét
Câu 7. Cho hình chóp
.S ABC
có chân đường cao nằm trong tam giác
ABC
, các mặt bên
( )
SAB
,
( )
SBC
,
( )
SCA
cùng tạo với đáy góc
60
. Biết
3AB =
,
4BC =
,
5CD =
, tính thể tích khối chóp
.S ABC
.
A.
23
. B.
63
. C.
53
. D.
10 3
.
Lời giải
ChọnA
Hạ
( ) ( )
,SH ABC H ABC⊥
,HI AB I AB⊥
;
,HK BC K BC⊥
,
,HG CA G CA⊥
( )
SH ABC SH AB
SI AB
IH AB
⊥ ⊥
⊥
⊥
Có
( ) ( )
,SI AB IH AB
SAB ABC AB
⊥⊥
=
( ) ( )
( )
,ABC SAB HIS =
(Do
90HIS
)
Chứng minh tương tự
( ) ( )
( )
,ABC SBC HKS =
( ) ( )
( )
,ABC SAC SGH =
Từ giả thiết suy ra:
60HIS SKH SGH = = =
3 3 3SH HI HK HG = = =
Mà
H
nằm trong tam giác
ABC
nên
H
và
HI
lần lượt là tâm và bán kính đường tròn nội tiếp của
tam giác
ABC
A
C
B
S
H
K
I
G
Trang 19
Có
2 2 2
AB BC AC+=
nên tam giác
ABC
là tam giác vuông tại
B
.
( )
2
4.3
1
345
ABC
S
HI
AB BC CA
= = =
+ + + +
3SH=
.
( )
.
1 1 3.4
. . 3. 2 3
3 3 2
S ABC
ABC
V SH S = = =
.
Câu 8. Cho hình chóp
.S ABCD
có
ABCD
là hình chữ nhật tâm
O
với
,3AB a BC a==
. Hình
chiếu vuông góc của
S
lên mặt phẳng
( )
ABCD
là trung điểm
AO
. Biết
( ) ( )
( )
; 60SAC SBC
=
.
Khi đó thể tích của
.S ABCD
là:
A.
3
3
3
a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
6
8
a
.
Lời giải
Gọi
I
trung điểm
AO
, suy ra
( )
SI ABCD⊥
.
3
2;
2
a
AC a BI==
.
Vẽ
BE SC⊥
IE SC⊥
.
Vậy
( ) ( )
( )
( )
; ; 60SAC SBC BE IE
==
.
Xét
BIE
vuông tại
I
:
.cot60
2
a
IE BI==
.
Xét
SIC
vuông tại
I
:
2 2 2
1 1 1
IE SI IC
=+
32
8
a
SI=
.
Vậy
3
16
.
38
SABCD ABCD
a
V SI S==
.
Câu 9. Để làm một hình chóp tứ giác đều từ một tấm tôn hình vuông có cạnh bằng
13+
, người ta
cắt tấm tôn theo các tam giác cân bằng nhau
, , ,MAN NBP PCQ QDM
sau đó gò các tam giác
, , ,ABN BCP CDQ
DAM
sao cho bốn đỉnh
, , ,M N P Q
trùng nhau(hình vẽ).
Biết rằng, các góc ở đỉnh của mỗi tam giác cân là
0
150
. Tính thể tích
V
của khối chóp đều tạo
thành.
A.
3 6 5 2
24
V
+
=
. B.
2
3
V =
. C.
52 30 3
3
V
+
=
. D.
1
3
V =
Trang 20
Hướng dẫn giải
Đáp án: B
+
0
15AMN DMQ==
0
60AMD MAD =
đều.
Vì vậy hình chóp tứ giác đều tạo thành có tất cả các cạnh bằng nhau và bằng
MA
.
Trong đó,
( )
0
2 1 3
2
2sin75
62
MN
MA
+
= = =
+
+ Dễ dàng chứng minh được rằng:
“Một khối chóp tứ giác đều có tất cả các cạnh bằng
x
thì có thể tích là
3
2
6
x
V =
”
+ Với
2x =
thì
2
3
V =
Câu 10. Một đống đất được vun thành hình một khối chóp cụt tứ giác đều có cạnh đáy lớn bằng
2m, cạnh đáy nhỏ bằng 1m và chiều cao bằng 2m. Khối lượng (thể tích) đống đất có giá trị gần nhất
với con số
A. 4,55m
3
. B. 4,65m
3
. C. 4,7 m
3
. D. 4,75m
3
.
Hướng dẫn giải
Đáp án: B
Q
P
N
M
D
C
B
A
1+
3
150
0
Q
P
N
M
D
C
B
A
1+
3
150
0
Trang 21
Kéo dài các cạnh bên hình chóp cụt lên phía trên ta được
hình chóp lớn là hình chóp sinh ra hình chóp cụt. Hình
chóp nhỏ và hình chóp lớn đồng dạng theo tỉ số k =
1
2
( là tỉ số giữa độ dài cạnh đáy nhỏ và độ dài cạnh đáy
lớn hình chóp cụt)
Thể tích chóp lớn bằng
2 2 3
1 1 16
. .2 .4
3 3 3
a h m==
Tỉ số giữa thể tích chóp nhỏ và thể tích chóp lớn bằng
3
11
()
28
=
Thể tích chóp cụt bằng
7
8
thể tích chóp lớn và bằng
3
14
3
m
Dạng II. Thể tích khối lăng trụ
1.Ví dụ minh hoạ
Ví dụ 1. Cho hình lập phương . là trung điểm Mặt phẳng chia
khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng.
.
A. . B. . C. . D. .
Hướng dẫn giải
Chọn A.
Coi như khối lập phương có cạnh bằng 1.
Để giải bài toán này, ta phải xác định đúng thiết diện cắt bởi mặt phẳng .
Lấy là trung điểm thì là đường trung bình tam giác nên .
Suy ra bốn điểm cùng thuộc một mặt phẳng .
Thiết diện cắt bởi mặt phẳng là tứ giác .
Phần có thể tích nhỏ hơn là khối đa diện .
Để thuận tiện tính toán ta chia khối trên thành 2 phần là tứ diện và hình chóp .
.
.
Suy ra thể tích khối có thể tích nhỏ hơn là .
.ABCD A B C D
I
.BB
( )
DIC
7
17
1
3
1
2
1
7
( )
DIC
M
AB
IM
ABB
// //IM AB DC

, , ,I M C D
( )
C ID
( )
DIC
C DMI
C IBMDC
IMBD
DIBCC
1 1 1 1 1 1 1
. . . . . . . .1.
3 3 2 6 2 2 24
IMBD BDM
V IB S IB DAMB= = = =
( )
.
1 1 1 1 1 1 1
. . . . . . .1. . 1 .1.
3 3 2 2 2 2 4
D IBCC IBCC
V DC S DC IB CC BC


= = + = +


1 1 7
24 4 24
n IMBD DIBCC
V V V
= + = + =
Trang 22
Thể tích phần lớn hơn là .
Vậy tỉ lệ cần tìm là .
Ví dụ 2. Cho lăng trụ
.ABC A B C
là lăng trụ đứng,
,2AC a BC a==
góc
·
ACB
bằng
120
o
. Góc
giữa đường thẳng
AC
¢
và mặt phẳng
()ABB A
¢¢
bằng
30
o
. Tính thể tích lăng trụ đã cho.
Lời giải
Kẻ
C K A B
¢ ¢ ¢
^
. Vì lăng trụ
.ABC A B C
là lăng trụ đứng nên
C K AA
¢¢
^
. Do đó
()C K ABB A
¢ ¢ ¢
^
.
Góc giữa
AC
¢
và
()ABB A
¢¢
bằng góc
·
C AK
¢
và bằng
30°
(tam giác
C AK
¢
vuông tại
K
nên góc
'C AK
nhọn)
Xét tam giác
ABC
, áp dụng định lý cosin cho cạnh
AB
có:
2 2 2 2 2 2
2. . .cos120 7 7
o
AB AC BC AB AC a A B a
¢¢
= + - = Þ =
.
2
1 1 3
. .sin .2 .sin120
2 2 2
o
ABC
ABC
a
S S CACB ACB a a
¢ ¢ ¢
= = = =
.
Mặt khác
11
. . 7
22
ABC
S C K A B C K a
¢ ¢ ¢
¢ ¢ ¢ ¢
==
Do đó
2
1 3 3
.7
22
7
aa
C K a C K
¢¢
= Û =
Xét tam giác
'AKC
vuông tại
K
nên
3
.cot30 . 3
7
o
a
AK C K C K
¢¢
= = =
Xét tam giác
''A C K
vuông tại
K
nên
2
2 2 2
22
32
7
7
5
7
aa
A K A C KC a
a
AA AK A K
¢ ¢ ¢ ¢
= - = - =
¢¢
Þ = - =
Thể tích của lăng trụ
.ABC A B C
là
23
5 3 105
..
2 14
7
ABC
a a a
V AA S
¢
= = =
.
Ví dụ 3. Cho lăng trụ
.ABC A B C
có đáy là tam giác đều cạnh
a
, đỉnh
A
¢
cách đều
,,A B C
. Biết
khoảng cách giữa đường thẳng
AA
¢
và mặt phẳng
()BCC B
¢¢
bằng
3
4
a
. Tính thể tích khối lăng trụ
.ABC A B C
theo
a
.
Lời giải
.
7 17
1
24 24
l ABCD A B C D n
V V V
= − = − =
: 7:17
nl
VV=
Trang 23
Vì đỉnh
A
¢
cách đều
,,A B C
nên hình chiếu vuông góc của
A
¢
trên
()ABC
là tâm đường tròn ngoại
tiếp tam giác
ABC
. Mà tam giác
ABC
đều nên hình chiếu vuông góc của
A
¢
trên
()ABC
là trọng
tâm
O
của tam giác
ABC
.Gọi
,KI
lần lượt là trung điểm của
BC
¢¢
và
BC
. Từ
'A
kẻ
'A H IK^
.
Ta có
, ' ( ' ) 'BC AI BC A O BC A AI A H BC^ ^ Þ ^ Þ ^
.
Lại có
, ( )A H BC A H IK A H BCC B
¢ ¢ ¢ ¢ ¢
^ ^ Þ ^
( ,( ))
( ,( ' '))
3
4
A BCC B
AA BCC B
a
d d A H
¢ ¢ ¢
¢
¢
Þ = = =
Đặt
'0AA x=>
.
Tam giác
BAC
đều cạnh
a
,
AI
là trung tuyến nên
3 2 3
,
2 3 3
aa
AI AO AI= = =
.
Xét tam giác
A AO
¢
vuông tại
O
:
2 2 2
2 2 2
3
3
3
a x a
A O AA AO x
-
¢¢
= - = - =
.
Diện tích hình bình hành
A KIA
¢
là:
'
22
'
3 3 3
' . . , ' . .
24
3
A KIA
A KIA
x a a a
S A O AI S A H IK x
-
= = = =
22
3 3 3
..
24
3
x a a a
x
-
Þ=
2
'
3
a
x A O aÞ = Þ =
Diện tích tam giác đều
ABC
là
2
3
4
ABC
a
S =
.
Thể tích của lăng trụ đã cho là
23
33
..
44
ABC
aa
V A O S a
¢
= = =
.
Ví dụ 4. Cho hình lăng trụ đứng có đáy là tam giác cân tại , góc
nhọn. Góc giữa và là , khoảng cách giữa và là . Góc giữa hai mặt bên
và là . Thể tích lăng trụ là
A. B. C. D.
Hướng dẫn giải:
Ta có góc giữa hai mặt bên và là
đều.
Vì
Kẻ
ABC.A'B'C'
ABC
A
BAC
AA'
BC'
0
30
AA'
BC'
a
( )
AA'B'B
( )
AA'C'C
0
60
ABC.A'B'C'
3
2a 3
3
3
a3
3
3
a6
6
3
a6
3
( )
AA'B'B
( )
AA'C'C
0
BAC 60=
ABC
(
)
(
)
0
AA'/ /CC' AA'; BC' CC'; BC' BC'C 30 = = =
( )
AI BC AI BB'C'C⊥ ⊥
30
0
60
0
I
A'
B'
C'
C
B
A
Trang 24
Chọn đáp án A.
Ví dụ 5. Cho hình lăng trụ tam giác đều ABC. A’B’C’, có cạnh đáy bằng và cạnh bên bằng .
Lấy M, N lần lượt trên cạnh AB’, A’C sao cho . Tính thể tích V của khối
BMNC’C.
A. B. C. D.
Hướng dẫn giải:
Chọn đáp án B.
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và AA’C’C.
Ta có: (Do G trung điểm AB’).
Xét tam giác ABA’ có AG là trung tuyến và . Suy ra là
trọng tâm tam giác ABA’. Do đó BM đi qua trung điểm I của AA’.
Ta có: (Do K là trung điểm A’C).
Xét tam giác AA’C’ có A’K là trung tuyến và . Suy ra N là trọng tâm của tam giác AA’C’.
Do đó C’N đi qua trung điểm I của AA’.
Từ là trọng tâm tam giác ABA’ và N là trọng tâm của tam giác AA’C’. Suy ra:
.
Gọi lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có:
. Mà . Suy ra .
Hạ AH vuông góc với BC tại H thuộc BC.Ta được AH vuông góc với mặt phẳng (BB’C’C). AA’
song song với mặt phẳng nên khoẳng cách từ I đến mặt phẳng (BB’C’C) bằng khoẳng
cách từ A đến (BB’C’C) và bằng AH. Ta có: .
. Suy ra .
2.Bài tập áp dụng
Câu 1. Cho hình lăng trụ đều
.ABC A B C
có cạnh đáy
a
; biết khoảng cách giữa hai đường thẳng
AB
và
AC
¢
bằng
15
5
a
. Thể tích của khối lăng trụ
.ABC A B C
tính theo
a
bằng:
( ) ( )
( )
= = =
= = = = =
3
ABC.A ' B' C'
0
d AA';BC' d AA'; BB'C'C AI a
2a BC 1 2a 2a 3
BC ,CC' 2a V 2a. .a.
23
tan30
33
a
2a
'1
' ' 3
AM A N
AB A C
==
3
6
108
a
3
26
27
a
3
36
108
a
3
6
27
a
12
' 3 3
AM AM
AB A G
= Þ =
2
3
AM
AG
=
M
' 1 ' 2
' 3 ' 3
A N A N
A C A K
= Þ =
'2
'3
AN
AK
=
M
1
'3
IM IN
IB IC
==
12
;VV
1
2
1
..
'9
V
IM IN IC
V IB IC IC
==
12
V V V+=
2
8
9
VV=
( )
''BB C C
3
2
a
AH =
( )
23
2'
1 1 3 2 6
. ; ' ' . . .
3 3 2 2 12
BCC
a a a
V d I BB C C S
D
éù
= = =
êú
ëû
3
2
8 2 6
9 27
a
VV==
H
K
G
M
N
I
B'
C'
A
C
B
A'
Trang 25
A.
3
33
8
a
. B.
3
3
2
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Câu 2. Cho hình lăng trụ có đáy là tam giác đều cạnh , hình chiếu vuông
góc của lên măt phẳng trùng với tâm của tam giác . Biết khoảng cách giữa
và là . Tính thể tích của khối lăng trụ .
A. B. C. D.
Câu 3. Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác
ABC
vuông cân tại
A
, cạnh
6BC a=
.
Góc giữa mặt phẳng
( )
'AB C
và mặt phẳng
( )
BCC B

bằng
0
60
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
?
A.
3
23
.
3
a
V =
B.
3
3
.
2
a
V =
C.
3
33
.
4
a
V =
D.
3
33
.
2
a
V =
Câu 4. Cho khối hộp
.ABCD A B C D
có đáy là hình chữ nhật với
3AB =
;
7AD =
. Hai mặt
bên
( )
ABB A

và
( )
ADD A

cùng tạo với đáy góc
45
, cạnh bên của hình hộp bằng
1
(hình vẽ).
Thể tích của khối hôp là:
A.
7
. B.
33
. C. 5. D.
77
.
Câu 5. Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông cân đỉnh
A
, mặt bên là
BCC B

hình vuông, khoảng cách giữa
AB
và
CC
bằng
a
. Thể tích khối lăng trụ
.ABC A B C
là
A.
3
2a
. B.
3
2
3
a
. C.
3
a
. D.
3
2
2
a
.
Câu 6. Cho lăng trụ đứng có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa
mặt phẳng và mặt phẳng bằng .Tính thể tích lăng trụ .
A. B. C. D.
Câu 7. Cho hình lập phương có khoảng cách giữa và là 1 cm.
Thể tích khối lập phương là:
A. . B. . C. . D. .
Câu 8. Cho hình hộp ABCDA’B’C’D’. Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng
thời song song với B’D’. Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V
1
, V
2
(
Trong đó V
1
là thể tích khối chứa A). Tính tỉ số .
A. . B. 1. C. . D. .
Câu 9. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ
tâm
O
của tam giác
ABC
đến mặt phẳng
( )
A BC
bằng
6
a
. Thể tích khối lăng trụ bằng
A.
3
32
4
a
. B.
3
32
8
a
. C.
3
32
28
a
. D.
3
32
16
a
Câu 10. Cho lăng trụ đứng
.ABC A B C
. Biết rằng góc giữa hai mặt phẳng
( )
A BC
và
( )
ABC
là
30
, tam giác
A BC
đều và diện tích bằng
3
. Thể tích khối lăng trụ
.ABC A B C
bằng
A.
23
. B.
6
. C.
33
4
. D.
3
4
.
. ' ' 'ABC A B C
ABC
a
'A
( )
ABC
G
ABC
'AA
BC
3
4
a
V
. ' ' 'ABC A B C
3
3
3
a
V =
3
3
6
a
V =
3
3
12
a
V =
3
3
36
a
V =
ABCA B C
()
AB C
()
BB C
0
60
ABCA B C
3
2a
3
2a
3
6a
3
3a
D. ' ' ' 'ABC A B C D
'AC
''CD
D. ' ' ' 'ABC A B C D
3
8 cm
3
22cm
3
33cm
3
27 cm
1
2
=
V
F
V
7
17
17
25
8
17
Trang 26
3. Hướng dẫn giải
Câu 1. Cho hình lăng trụ đều
.ABC A B C
có cạnh đáy
a
; biết khoảng cách giữa hai đường thẳng
AB
và
AC
¢
bằng
15
5
a
. Thể tích của khối lăng trụ
.ABC A B C
tính theo
a
bằng:
A.
3
33
8
a
. B.
3
3
2
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Hướng dẫn giải
Chọn D
Ta có
( )
( )
( )
( )
( )
( )
,
,,
15
/ / / /
5
AB A C
AB A B C B A B C
a
AB A B AB A B C d d d
= = =
Đặt
0AA x
=
.
Tam giác
CA B

cân tại
C
,
22
CA CB a x

= = +
.
Diện tích tam giác
CA B

là
2 2 2
2 2 2 2
1 1 3 4 1
. . . 3 4
2 4 2 2 4
CA B
a a x
S a a x a a a x

+
= + − = = +
Thể tích lăng trụ
( )
2
3
.1
4
a
Vx=
Lại có
( )
( )
22
.
,
1 15 1
3 3. . . . 3 4
3 5 4
B A B C A B C
B A B C
a
V V d S a a x

= = = +
.
Do đó
2
2 2 2 2
3 15 1
. . . 3 4 5 3 15. 3 4 3
4 5 4
aa
x a a x x a x x a= + = + =
.
23
33
.
44
aa
Vx==
.
Câu 2. Cho hình lăng trụ có đáy là tam giác đều cạnh , hình chiếu vuông
góc của lên măt phẳng trùng với tâm của tam giác . Biết khoảng cách giữa
và là . Tính thể tích của khối lăng trụ .
A. B. C. D.
Hướng dẫn giải:
Gọi M là trung điểm B
. ' ' 'ABC A B C
ABC
a
'A
( )
ABC
G
ABC
'AA
BC
3
4
a
V
. ' ' 'ABC A B C
3
3
3
a
V =
3
3
6
a
V =
3
3
12
a
V =
3
3
36
a
V =
( ' )BC A AMÞ^
Trang 27
Gọi H,K lần lượt là hình chiếu vuông góc của G,M trên AA’
Vậy KM là đọan vuông góc chung củaAA’và BC, do đó .
AA’G vuông tại G,HG là đường cao,
Chọn đáp án C.
Câu 3. Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác
ABC
vuông cân tại
A
, cạnh
6BC a=
. Góc giữa mặt phẳng
( )
'AB C
và mặt phẳng
( )
BCC B

bằng
0
60
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
?
A.
3
23
.
3
a
V =
B.
3
3
.
2
a
V =
C.
3
33
.
4
a
V =
D.
3
33
.
2
a
V =
Lời giải
Chọn D
Cách 1.
+ Gọi
M
là trung điểm của
( )
BC AM BCC B

⊥
+ Gọi
,HK
lần lượt là hình chiếu vuông góc của
,MB
trên
BC
+ Khi đó
( ) ( ) ( )
(
)
( )
o
, , 60B C AMH B C AH AB C BB C AH MH AHM
⊥ ⊥ = = =
.
+ Ta có
o
6
2
2
tan60 2
3
a
AM a
MH = = =
22HK MH a = =
.
+ Mặt khác
2 2 2
1 1 1
3B B a
BK BC B B
= + =
.
+ Vậy thể tích của khối lăng trụ
.ABC A B C
là
3
1 3 3
. . .
22
a
V B B AB AC
==
Cách 2.
+ Gọi chiều cao của hình lăng trụ là
h
.
+ Đặt hệ trục tọa độ
Axyz
như hình vẽ. Khi đó
( )
0;0;0A
,
( )
3;0;0Ba
,
( )
0; 3;0Ca
,
( )
3;0;B a h
33
; ;0
22
aa
M




là trung điểm của
BC
.
3
( A',B C)
4
a
d A KM==
3
2
KM
AGH AMH
GH
D D Þ =:
23
36
a
GH KHÞ = =
D
'
3
a
AG=
3
. ' ' '
3
.'
12
ABC A B C ABC
a
V S A G==
M
A
B
C
A'
B'
C'
G
K
H
Trang 28
+ Vì
( )
AM BCC B

⊥
và
33
; ;0
22
aa
AM
=



nên
( )
1;1;0n =
là VTPT của
( )
''BCC B
.
+ Ta có
( ) ( )
2
1
, 3;0; 3 ;0; 3AC AB ah a n h a

= − = −

là VTPT của
( )
'AB C
.
+ Theo giả thiết góc giữa
( )
AB C
và mặt phẳng
( )
BCC B

bằng
60
( )
1
22
1
cos60 cos , 3
2
2. 3
h
n n h a
ha
= = =
+
+ Vậy thể tích của khối lăng trụ
.ABC A B C
là
3
33
.
2
a
V =
Câu 4. Cho khối hộp
.ABCD A B C D
có đáy là hình chữ nhật với
3AB =
;
7AD =
. Hai mặt
bên
( )
ABB A

và
( )
ADD A

cùng tạo với đáy góc
45
, cạnh bên của hình hộp bằng
1
(hình vẽ).
Thể tích của khối hôp là:
A.
7
. B.
33
. C. 5. D.
77
.
Lời giải
Chọn A
Hạ
( ) ( )
,;A H ABCD H ABCD
⊥
,HI AD I AD⊥
;
,HK AB K AB⊥
( )
''
'
A H ABCD A H AD
A I AD
IH AD
⊥ ⊥
⊥
⊥
( ) ( )
( ) ( )
( )
,
,
DD
A I AD IH AD
ABCD ADD A HIA
A A ABCD AD
⊥⊥
=

=
(Do
90HIA
)
Chứng minh tương tự
( ) ( )
( )
,ABCD ABB A HKA
=
Từ giả thiết suy ra:
45HIA HKA

= =
HA HI HK
= =
B'
A'
C'
D'
B
A
H
D
I
C
K
Trang 29
60
0
H
M
I
A
C
B
A'
B'
C'
B'
B
C
M
I
Có
ABCD
là hình chữ nhật,
,HI AD I AD⊥
;
,HK AB K AB⊥
Nên
AIHK
là hình vuông suy ra
22AH HK A H
==
+
( ) ( )
,A H ABCD H ABCD
⊥
AH A H
⊥
2 2 2 2
3AA A H HA A H
= + =
1
3
HA
→=
.
. . 7
ABCD A B C D
V A H AB AD
= =
.
Câu 5. Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông cân đỉnh
A
, mặt bên là
BCC B

hình vuông, khoảng cách giữa
AB
và
CC
bằng
a
. Thể tích khối lăng trụ
.ABC A B C
là
A.
3
2a
. B.
3
2
3
a
. C.
3
a
. D.
3
2
2
a
.
Lời giải
Theo giả thiết, ta có
( ) ( )
( )
( )
( )
; , ,d CC AB d CC ABB A d C ABB A CA a
= = = =
.
Do đó, thể tích khối lăng trụ
.ABC A B C
là
3
2
12
. 2. .
22
ABC
a
V CC S a a
= = =
.
Câu 6. Cho lăng trụ đứng có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa
mặt phẳng và mặt phẳng bằng .Tính thể tích lăng trụ .
A. B. C. D.
Hướng dẫn giải:
Từ A kẻ AI BC I là trung điểm BC
AI (BC ) AI C (1)
Từ I kẻ IM C (2)
Từ (1), (2) C (IAM)
Vậy góc giữa (A C) và ( CB) là
= 60
0
Ta có AI= ; IM=
;
.
Suy ra = ;
ABCA B C
()
AB C
()
BB C
0
60
ABCA B C
3
2a
3
2a
3
6a
3
3a
⊥
⊥

CB
⊥
B
⊥
B
B
⊥
B
B
AMI
1
2
=BC a
0
tan 60
3
=
AI a
2
2
3
==
a
BH IM
2 2 2 2 2 2
1 1 1 3 1 1
' 4 4 2
= − = − =
B B BH BC a a a
BB
2a
2
11
. .2
22
= = =
ABC
S AI BC a a a
Trang 30
Chọn đáp án A.
Câu 7. Cho hình lập phương có khoảng cách giữa và là 1 cm.
Thể tích khối lập phương là:
A. . B. . C. . D. .
Hướng dẫn giải:
Để tìm khoảng cách giữa A’C và C’D’, ta dựng một mặt phẳng chứa A’C và song song với C’D’. Dễ
thấy đó là mặt phẳng (CA’B’).
Gọi a là độ dài cạnh của khối lập phương, lúc này ta có:
Để tính khoảng cách từ điểm D’ đến mặt phẳng (CA’B’), ta xét khối tứ
diện D’CA’B’.
(do tam giác
CA’B’ vuông tại B’)
Suy ra: (cm).
Do đó
Chọn đáp án B.
Câu 8. Cho hình hộp ABCDA’B’C’D’. Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng
thời song song với B’D’. Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V
1
, V
2
(
Trong đó V
1
là thể tích khối chứa A). Tính tỉ số .
A. . B. 1. C. . D. .
Hướng dẫn giải:
*Gọi N là trung điể A’D’. Khi đó (P)BDNM).
Thấy BMDNAA’=I.
Khi đó: V
1
=V(A’MNABD); V
2
=V-V
1
. (Với V là thể tích hình hộp)
* Ta có:
* Mà: nên có:
* Lại có:
*Vậy:
* Do đó: nên . Vậy:
23
2. 2
==
ABC A B C
V a a a
D. ' ' ' 'ABC A B C D
'AC
''CD
D. ' ' ' 'ABC A B C D
3
8 cm
3
22cm
3
33cm
3
27 cm
( ) ( ) ( )
' ', ' ' ', ' ' ', ' '==
d C D A C d C D CA B d D CA B
( )
23
3
' ' ' ' ' '
11
. '. . .
3 3 2 6
= = =
D CA B B A D
aa
V CC S a cm
( )
22
''
1 1 2
S .CB'.B'A' . 2.
2 2 2
= = =
CA B
a a a cm
( ) ( )
3
' ' '
2
''
3
2
2
', ' ' 2
2
2
2
= = = =


D CA B
CA B
a
V
d D CA B a cm a
S
a
33
22==V a cm
1
2
=
V
F
V
7
17
17
25
8
17
( ' ) ( ) 1
( A'B'D') ( ' ' ') 4
==
V IA MN S AMN
V A S A B D
(AA'B'D') 1
6
=
V
V
1
( ' )
24
=V IA MN V
( ' ) '. . 1
( ) . . 8
==
V IA MN IA IM IN
V IABD IA IB ID
1
()
3
=V IABD V
1
1 1 7
3 24 24
= − =V V V V
21
17
24
= − =V V V V
1
2
7
17
=
V
V
C
I
N
M
D
B
C'
A'
B'
D'
A
Trang 31
Chọn đáp án A.
Câu 9. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ
tâm
O
của tam giác
ABC
đến mặt phẳng
( )
A BC
bằng
6
a
. Thể tích khối lăng trụ bằng
A.
3
32
4
a
. B.
3
32
8
a
. C.
3
32
28
a
. D.
3
32
16
a
Lời giải
Gọi
M
là trung điểm của
BC
và
H
là hình chiếu của
A
trên
'AM
.
Ta có
( )
BC AM
BC AA M BC AH
BC AA
⊥
⊥ ⊥
⊥
Mà
( )
2AH A M
⊥
Từ và
( )
( )
,d A A BC AH
=
.
Ta có
( )
( )
( )
( )
,
1
3
,
d O A BC
MO
MA
d A A BC
==
.
( )
( )
( )
( )
, 3 ,
2
a
d A A BC d O A BC

= =
2
a
AH=
.
Xét tam giác vuông
'A AM
:
2 2 2
1 1 1
AH AA AM
=+
2 2 2
1 4 4 3
3
22
a
AA
AA a a
= − =
.
Suy ra thể tích lăng trụ
.'ABC A B C

là:
23
3 3 3 2
..
4 16
22
ABC
a a a
V AA S
= = =
.
Câu 10. Cho lăng trụ đứng
.ABC A B C
. Biết rằng góc giữa hai mặt phẳng
( )
A BC
và
( )
ABC
là
30
, tam giác
A BC
đều và diện tích bằng
3
. Thể tích khối lăng trụ
.ABC A B C
bằng
A.
23
. B.
6
. C.
33
4
. D.
3
4
.
Lời giải
M
C
B
A'
C'
B'
A
H
O
Trang 32
Trong
( )
ABC
vẽ
AH BC⊥
tại
H
.
Dễ thấy
( )
BC A AH BC A H

⊥ ⊥
nên
( ) ( )
( )
( )
, , 30A BC ABC A H AH A HA
= = =
.
Tam giác
A BC
đều có
AH
là đường cao nên đồng thời là đường trung tuyến.
Ta có
.3
tan30
AA
AH A A
==
và
2
sin30
AA
A H A A

==
.
Diện tích
2 2 2
33
3 4 2
44
A BC
S BC BC BC BC
= = = =
.
Mà
3 3 3
3;
2 2 2
BC
A H A A AH

= = = =
.
Thể tích khối lăng trụ
.
1 3 1 3 3 3
. . . . . . .2
2 2 2 2 4
ABC A B C ABC
V A A S A A AH BC


= = = =


.
H
C
B
A
C'
B'
A'
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

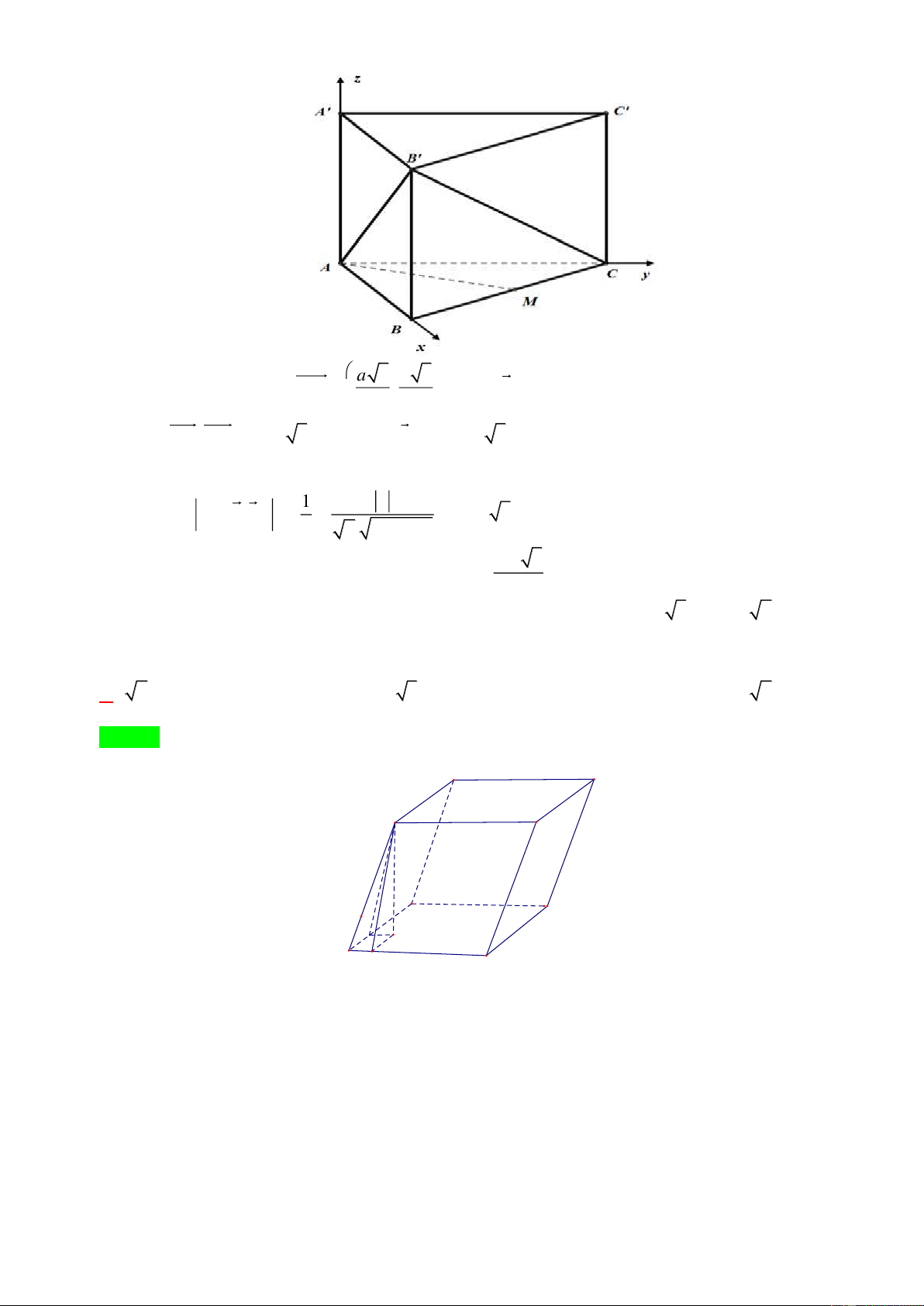
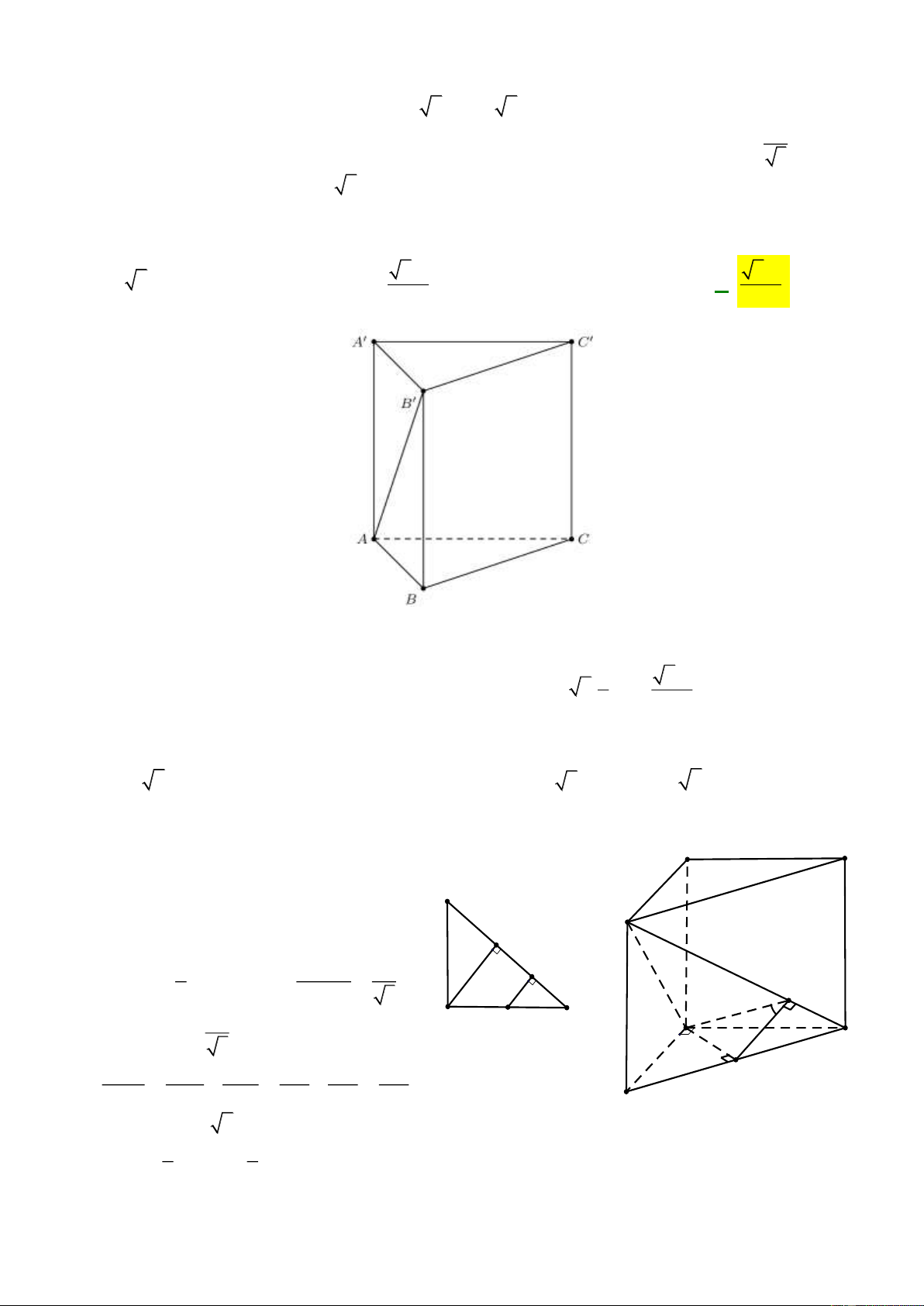
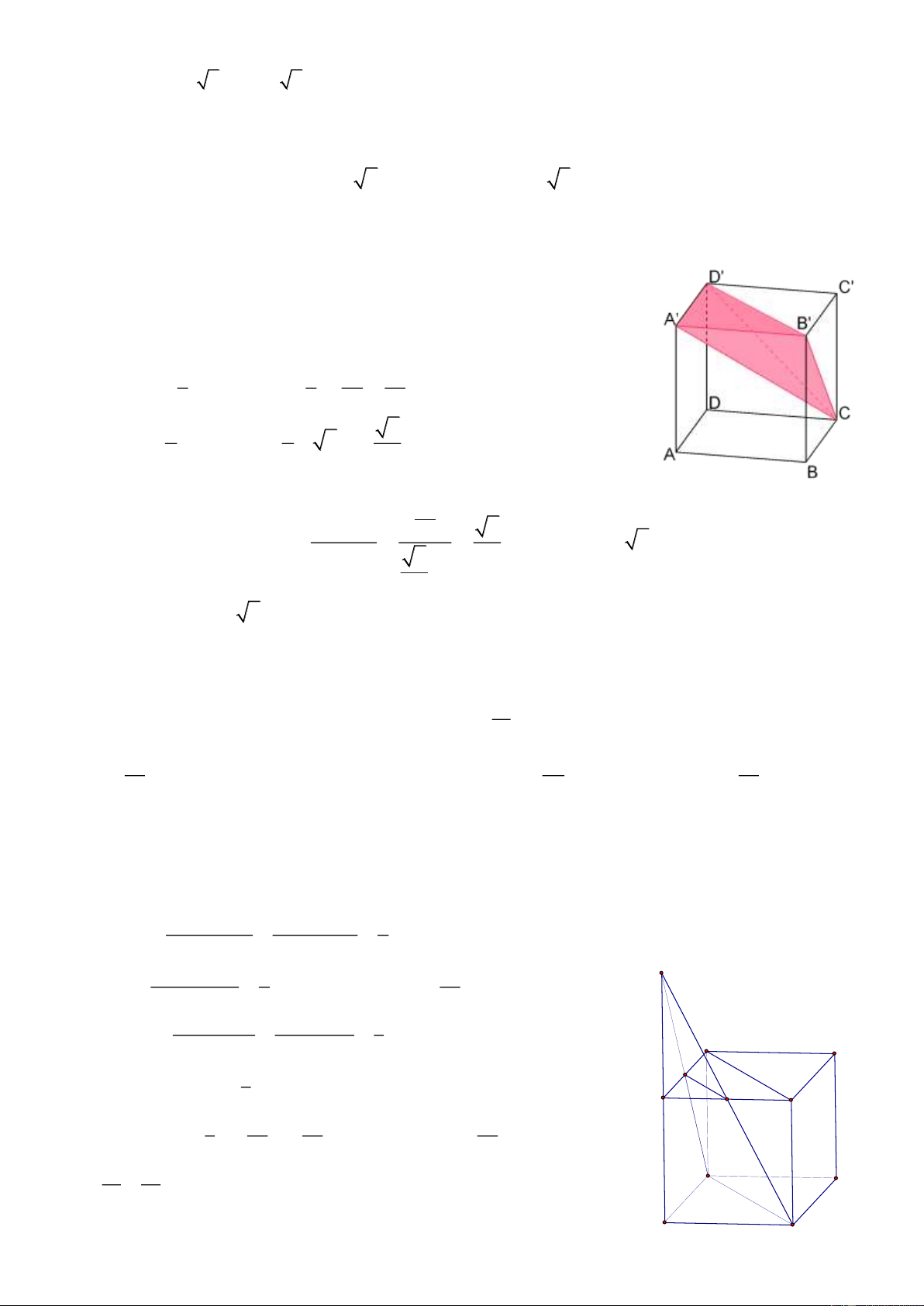
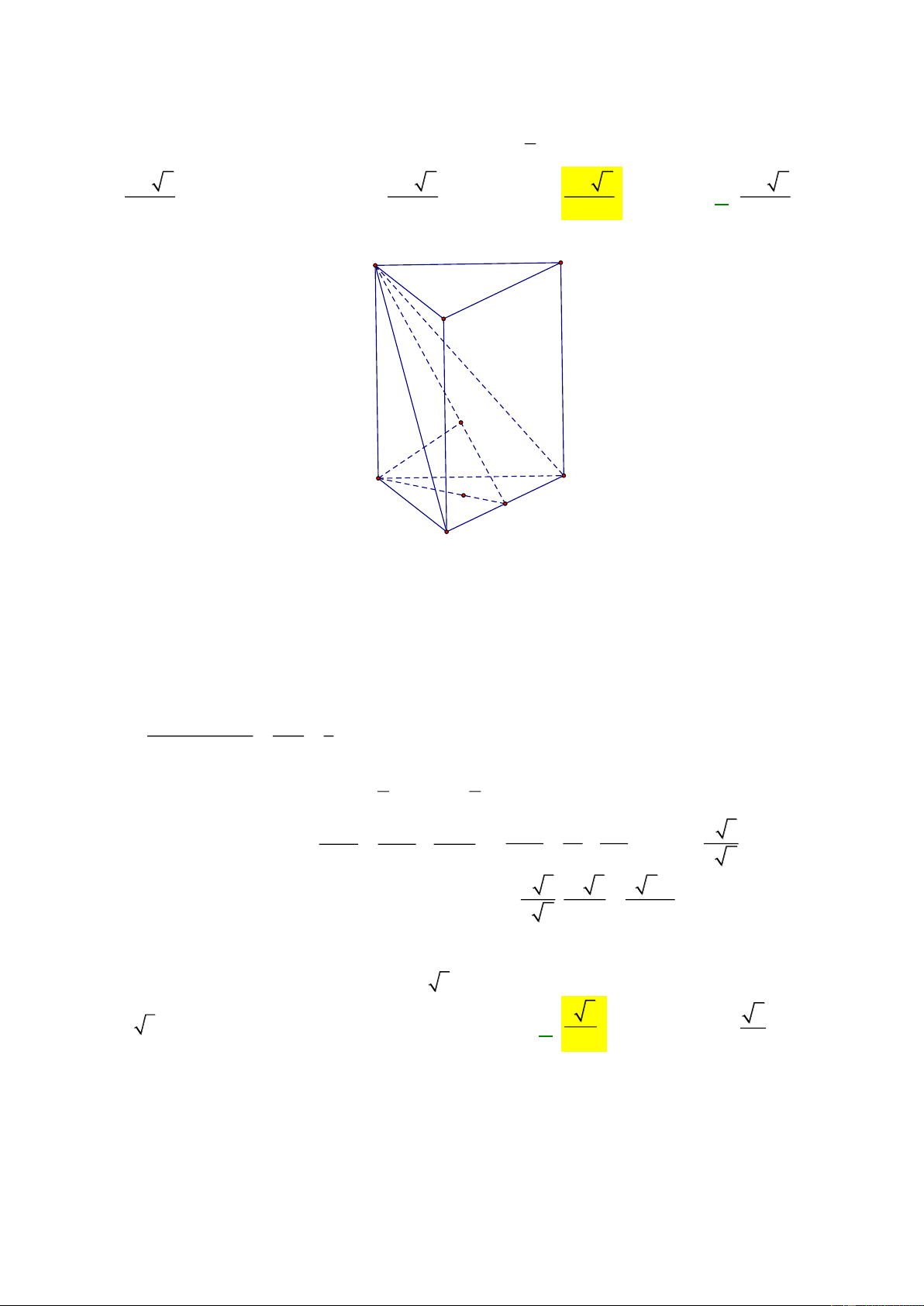
Preview text:

CHUYÊN ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN MỨC VẬN DỤNG VẬN DỤNG CAO
I. Hệ thông kiến thức liên quan A.Khoảng cách
1. Khoảng cách từ một điểm tới một đường thẳng.
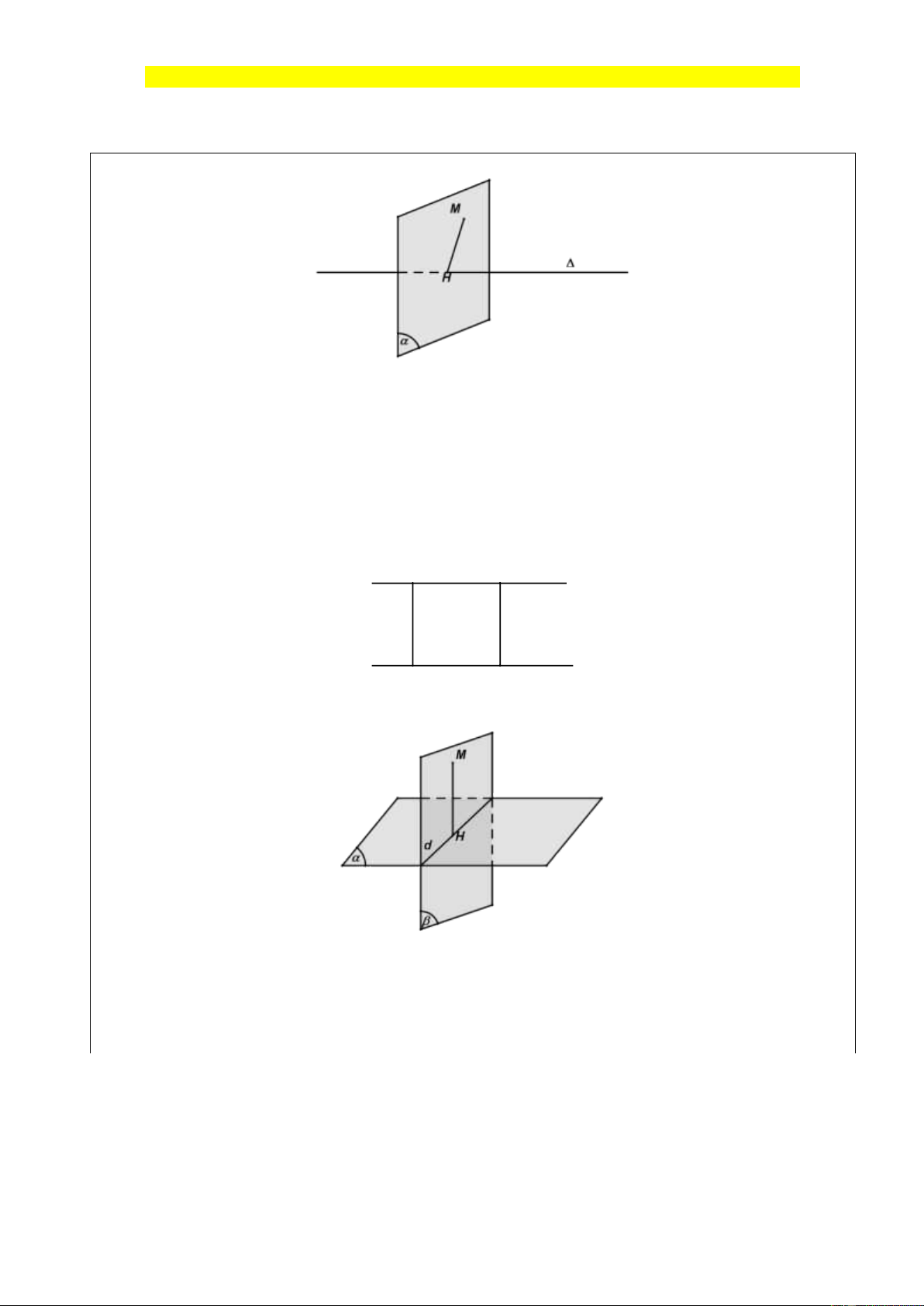
Cho điểm M và một đường thẳng  . Trong mp(M,) gọi H là hình chiếu vuông góc của M
trên  . Khi đó khoảng cách MH được gọi là khoảng cách từ điểm M đến  .
d (M, ) = MH
Nhận xét: OH OM, M  
2. Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng  và ' :
- Nếu  và  ' cắt nhau hoặc trùng nhau thì d( ,  ') = 0 .
- Nếu  và  ' song song với nhau thì d( ,
 ') = d(M,') = d(N, )  M K  ' H N
3. Khoảng cách từ một điểm tới một mặt phẳng.
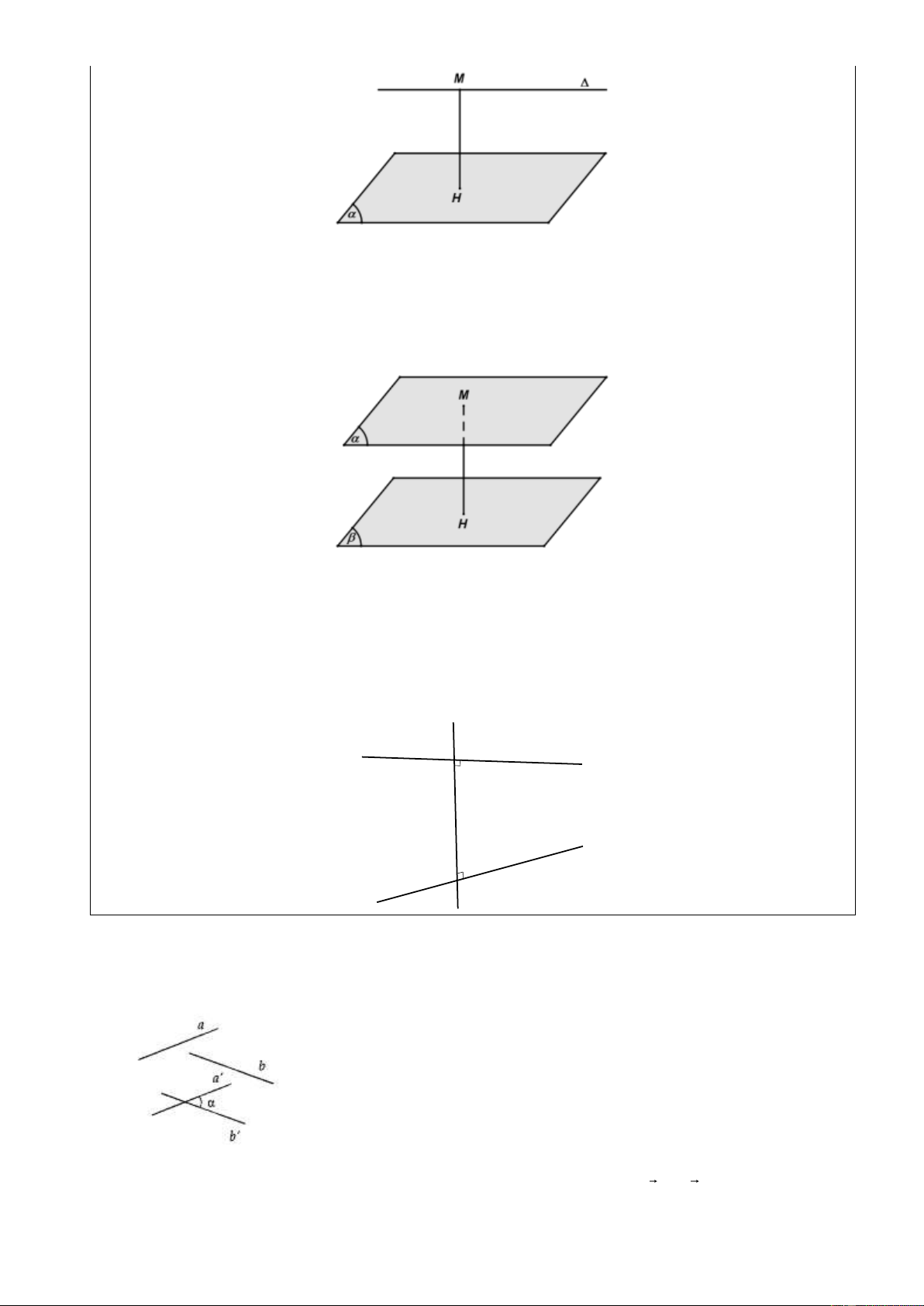
Cho mặt phẳng (α ) và một điểm M , gọi H là hình chiếu của điểm M trên mặt phẳng (α ) . Khi
đó khoảng cách MH được gọi là khoảng cách từ điểm M đến mặt phẳng (α ) .
d (M,(α )) = MH
4. Khoảng cách từ một đường thẳng tới một mặt phẳng. Trang 1
Cho đường thẳng  và mặt phẳng (α ) song song với nhau. Khi đó khoảng cách từ một điểm bất kì
trên  đến mặt phẳng (α ) được gọi là khoảng cách giữa đường thẳng  và mặt phẳng (α ) . d ( ,
 (α )) = d (M,(α )),M  .
- Nếu  cắt (α ) hoặc  nằm trong (α ) thì d( ,  (α)) = 0.
5. Khoảng cách giữa hai mặt phẳng.
Cho hai mặt phẳng (α ) và ( β ) song song với nhau, khoảng cách từ một điểm bất kì trên mặt
phẳng này đến mặt phẳng kia được gọi là khoảng cách giữa hai mặt phẳng (α ) và ( β ) .
d ((α ),( β )) = d (M,( β )) = d (N,(α )) , M (α ), N ( β ) .
6. Khoảng cách giữa hai đường thẳng chéo nhau.
Cho hai đường thẳng chéo nhau a,b . Độ dài đoạn vuông góc chung MN của a và b được gọi là
khoảng cách giữa hai đường thẳng a và b . M  ' N B. Góc trong không gian
1. Góc giữa hai đường thẳng. a.Định nghĩa:
Góc giữa hai đường thẳng cắt nhau a và b là góc nhỏ nhất trong bốn
góc mà a và b cắt nhau tạo nên.
Góc giữa hai đường thẳng cắt nhau a và b trong không gian là góc giữa
hai đường thẳng a và b cùng đi qua một điểm và lần lượt song song
(hoặc trùng) với a và b .
Chú ý: góc giữa hai đường thẳng luôn là góc nhọn ( hoặc vuông ). b. Phương pháp
Phương pháp 1: Sử dụng định lý hàm số cosin hoặc tỉ số lượng giác.
Phương pháp 2: Sử dụng tích vô hướng: nếu u và v lần lượt là hai Trang 2
vecto chỉ phương ( hoặc vecto pháp tuyến ) của hai đường thẳng a vàb thì góc φ của hai đường
thẳng này được xác định bởi công thức φ = (u v) . u v cos cos , = . u . v
2.Góc giữa đường thẳng và mặt phẳng
Nếu đường thẳng a ⊥ (P) thì góc giữa đường thẳng a và (P) bằng 0 90 .
Nếu đường thẳng a không vuông góc với (P) thì góc giữa đường thẳng a và (P) là góc giữa a và
hình chiếu a của a trên (P) . a a' P
3.Góc giữa hai mặt phẳng a. Định nghĩa
- Góc giữa hai mặt phẳng (α ) và ( β ) là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
- Nếu hai mặt phẳng đó song song hoặc trùng nhau thì góc giữa chúng bằng 0 .
b. phương pháp tính góc giữa hai mặt phẳng cắt nhau
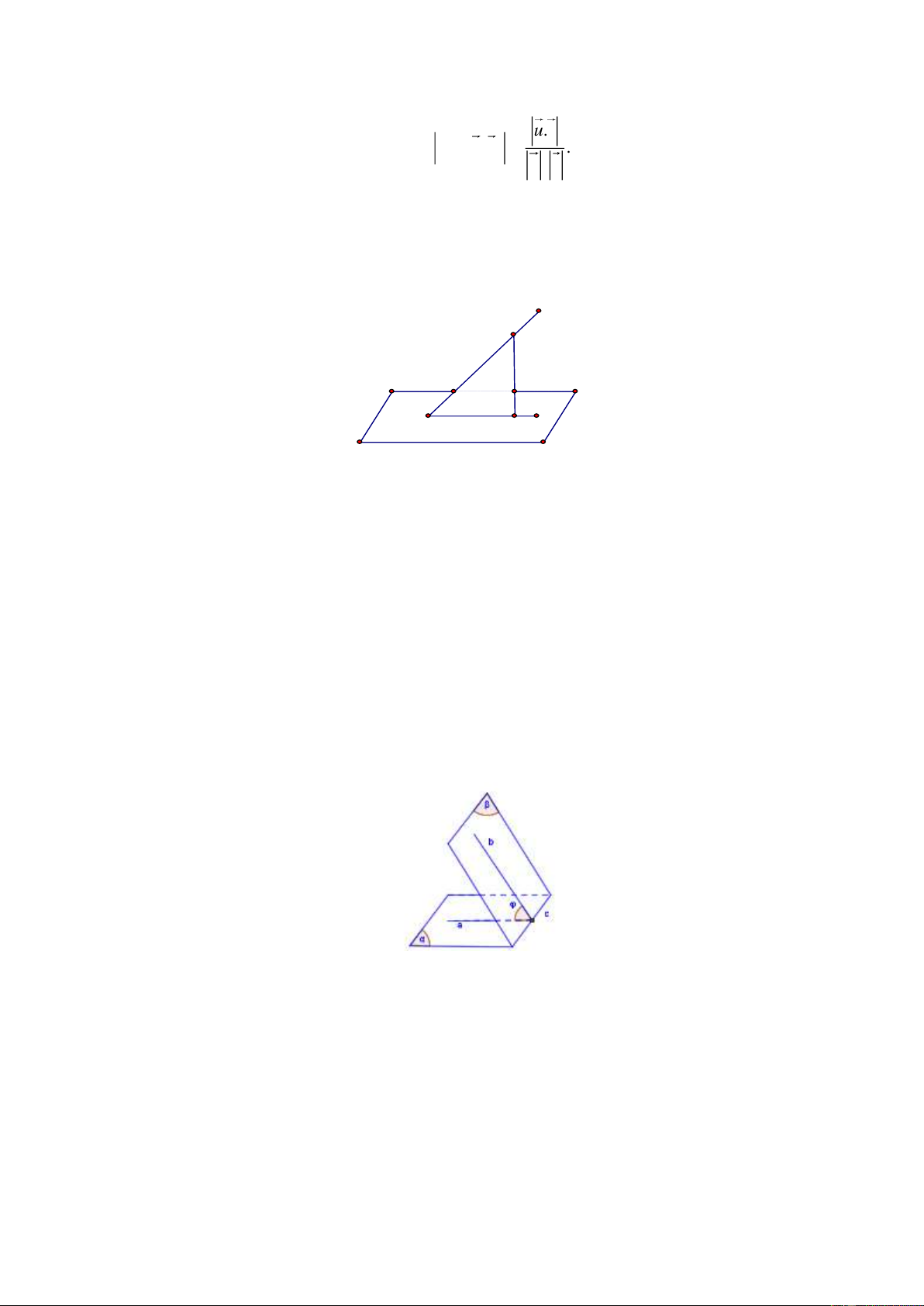
❖ Phương pháp 1: Dựng hai đường thẳng a , b lần lượt vuông góc với hai mặt phẳng (α ) và
(β ). Khi đó, góc giữa hai mặt phẳng (α ) và (β ) là ((α),(β )) =(a,b). Tính góc (a,b).
❖ Phương pháp 2: (α ) (β ) ➢
Xác định giao tuyến c của hai mặt phẳng và . ➢
Dựng hai đường thẳng a , b lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao
tuyến c tại một điểm trên c . Khi đó: ((α ),(β )) = (a,b).
Hay ta xác định mặt phẳng phụ (γ ) vuông góc với giao tuyến c mà (α ) (γ ) = a , ( β ) (γ ) = b .
Suy ra ((α ),(β )) = (a,b). Trang 3
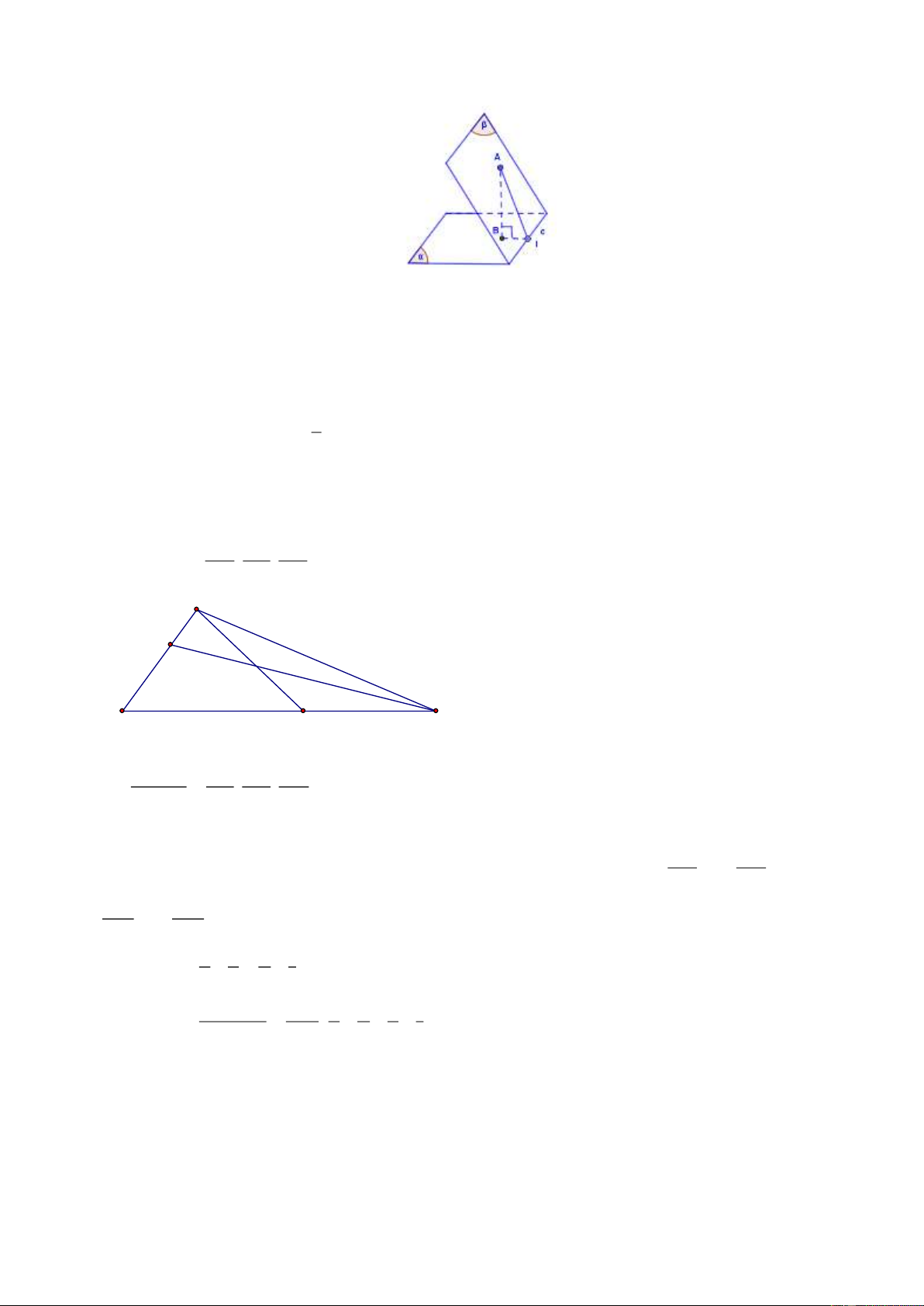
❖ Phương pháp 3: (trường hợp đặc biệt) ➢
Nếu có một đoạn thẳng nối hai điểm A , B ( A(α ), B(β )) mà AB ⊥ ( β ) thì qua A
hoặc B ta dựng đường thẳng vuông góc với giao tuyến c của hai mặt phẳng tại H . Khi đó ((α),(β))= AHB. C.
Thể tích khối đa diện
1.Thể tích khối chóp: 1 V = .
h S trong đó h là chiều cao và Sd là diện tích đáy d 3
2.Thể tích khối lăng trụ: V = .
h S trong đó h là chiều cao và Sd là diện tích đáy d
3.Các trường hợp đặc biệt
Định lý Menelaus: Cho tam giác ABC đường thẳng(d )cắt các cạnh A ,
B BC,CA lần lượt tại MA PB NC
M, N, P ta có . . =1 MB PC NA A M N P B C
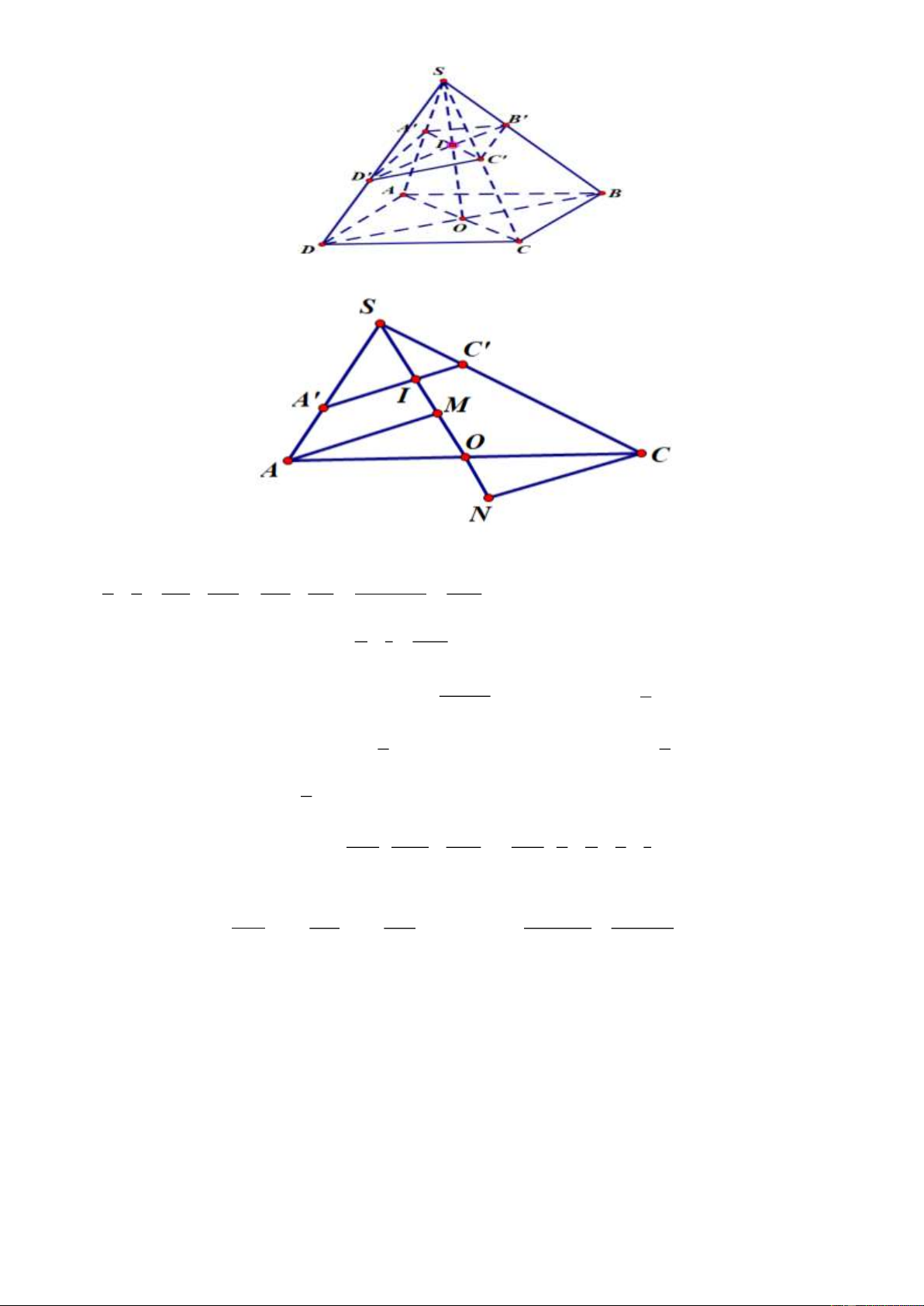
Bài toán 1. Cho hình chóp S.ABC. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’. Khi V đó: / / /
SA ' SB ' SC ' S . A B C = . . V SA SB SC S . ABC
Bài toán 2: Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (α ) cắt các cạnh / / bên SA SB S , A S , B S ,
C SD của hình chóp lần lượt tại các điểm / / / /
A , B , C , D . Đặt = x; = y; SA SB / SC / = SD z; = t . Khi đó SC SD 1) 1 1 1 1 + = + . x z y t V xyzt 1 1 1 1 2) / / / / S . A B C D = ( + + + ) V 4 x y z t S . ABCD Lời giải Trang 4
Gọi O là giao điểm của AC và BD ; / /
I = A C SO . Suy ra / /
B , I , D thẳng hàng. Kẻ / / / /
AM / / A C ;CN / / A C . Ta có: 1 1 SA SC + + = + SM SN = + SM SN = 2SO = / / x z SA SC SI SI SI SI
Chứng minh tương tự ta cũng có: 1 1 2SO + =
, Suy ra điều phải chứng minh. y t SI V 2)Ta có / / / 1 V =V +V SA B C = .
x z.y V = xz . y V . / / / / / / / / / S.A B / / / . / C D S .A B C S .A D C V 2 S ABCD SA B C SABC
Chứng minh tương tự ta có 1 1 V = xzt.V Suy ra V
= xz(y + t) (1) / / / . / / / 2 S ABCD SA D C S . A B / C D 2 Tương tự ta có 1 V
= yt(x + z) (2) / / / S . A B / C D 2  + +    Từ (1) và (2) ta được xyzt x z y t xyzt 1 1 1 1 V = + = + + + . / / /    
S . A B C/ D 4  xz yt  4  x y z t
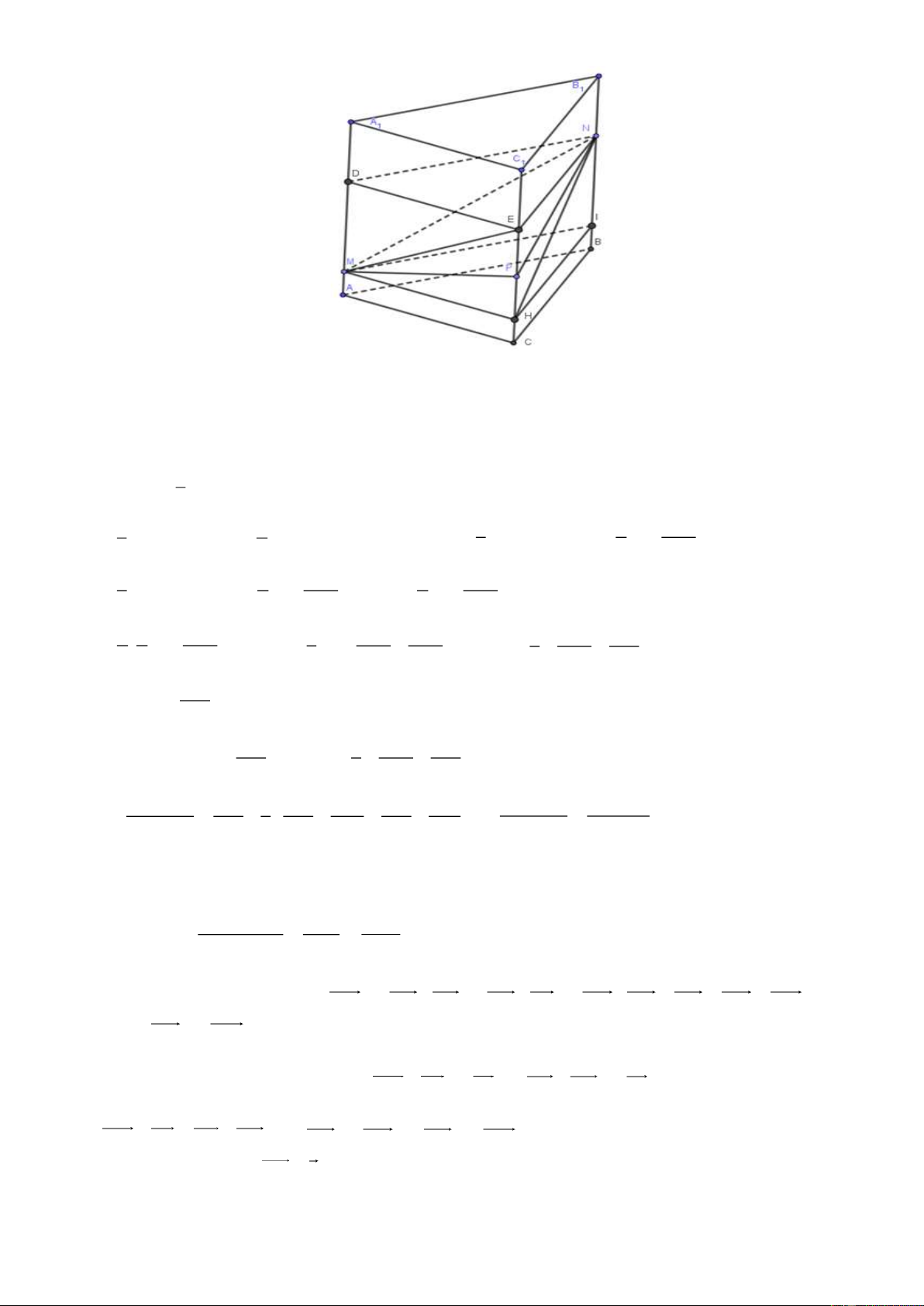
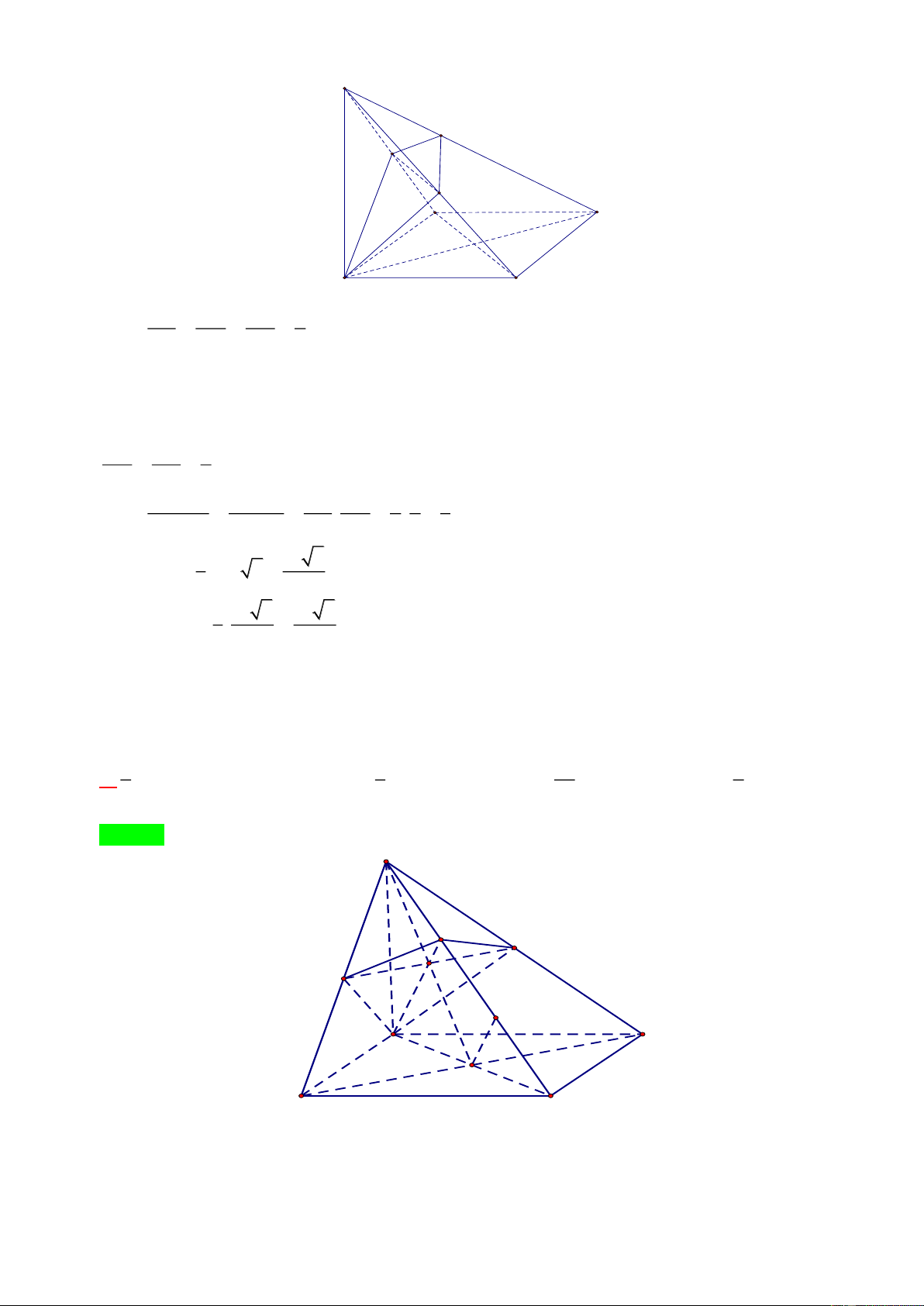
Bài toán 3: Cho hình lăng trụ tam giác ABC.A B C . Trên AA , BB , CC lấy lần lượt các điểm 1 1 1 1 1 1 AM BN CP V a + b + c
M , N, P sao cho = a , = b ,
= c . Khi đó: ABC.MNP = AA BB CC V 3 1 1 1 ABC. 1 A 1 B 1 C Lời giải Trang 5
Không mất tính tổng quát ta giả sử a c b .
Khi đó mặt phẳng qua N song song với ( ABC) cắt AA , CC lần lượt tại , D E . 1 1
Mặt phẳng qua M song song với ( ABC) cắt BB , CC lần lượt tại I, H 1 1 Ta có V = V −V ABC.MNP ABC.DEN N .DEPM 1 V
= d N; DEPM .S N .DEPM ( ( )) 3 DEPM 1 = 1 1  PE
d ( N (DEPM )) 1 ;
. ( DM + PE).d (DM ; PE) = d ( N;(DEPM )). 1+ .DM.d   (DM;PE) 3 2 3 2  DM  1 ( (   = 1  PE DEPM )) 1 PE d N; . 1+ .S   = 1+ V   3 2 DEHMDM  . 2 N DEHMDM  1 2  PE    = 1  PE DM 1 DM PE . 1+ V   = . 1+ . V = . + .V . .   2 3 DEN MIHDM  . 1 1 1 3 ABC A B CDM AA . 1 1 1 3 ABC A B C AA AA 1  1 1  BN V = V ABC.DEN ABC. 1 A 1 B 1 C BB1   Do đó : BN 1 DM PE V = V − . + .V ABC.MNP ABC. 1 A 1 B 1 C ABC. 1 A 1 B 1 BB 3 C AA AA 1  1 1  V BN 1  BN AM BN CP V a + b + c ABC.MNP  = −  − + −  ABC.MNP  = . V BB 3 BB AA BB CC V 3 ABC.   ABC. A B C 1 A 1 B 1 C 1 1 1 1 1 1 1 1
Bài toán 4: Cho hình hộp ABC .
D A B C D . Trên các đoạn thẳng AA , BB , CC lấy các điểm 1 1 1 1 1 1 1
M , N, P sao cho AM = aAA , BN = bBB , CP = cCC . Mặt phẳng (MNP) cắt DD tại Q . Ta có tỉ 1 1 1 1 V + +
số thể tích: ABCD.MNPQ a c = b d = . V 2 2 ABCD. 1 A 1 B 1 C 1 D Lời giải
Dựa vào giả thiết đề cho ta có AM = aAA , BN = bBB , CP = cCC , AA = BB = CC = DD và 1 1 1 1 1 1 1
giả sử DQ = d DD . 1
Gọi O và I lần lượt là trung điểm AC và MP , khi đó MP là đường trung bình chung của hình
thang AMPC , BNQD. Do đó ta có AM + CP = 2OI và BN + DQ = 2OI . Suy ra
AM + CP = BN + DQ  . a AA + . c CC = .
b BB + d.DD . 1 1 1 1
 (a + c) −(b + d ) AA = 0 
a + c = b + d . 1 Trang 6 V
a + 2 b + d + c V + + ABCD.MNPQ ( ) Tiếp theo, ta có = ABCD.MNPQ a c b d  = = . V 6 V 2 2 ABCD. A B C D ABCD. A B C D 1 1 1 1 1 1 1 1
II. Các dạng bài tập thường gặp
Dạng I: Tính thể tích khối chóp 1. Ví dụ minh hoạ
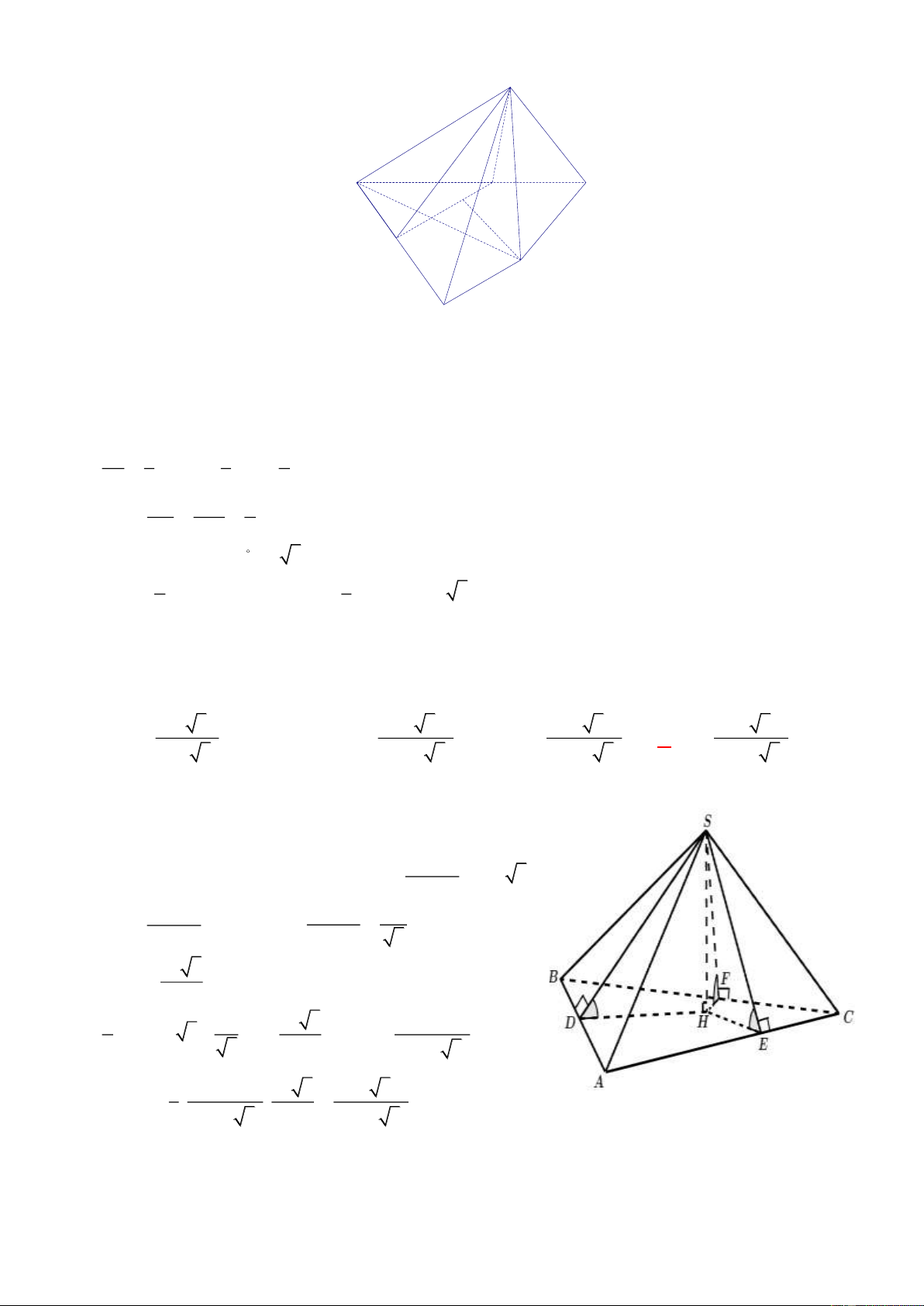
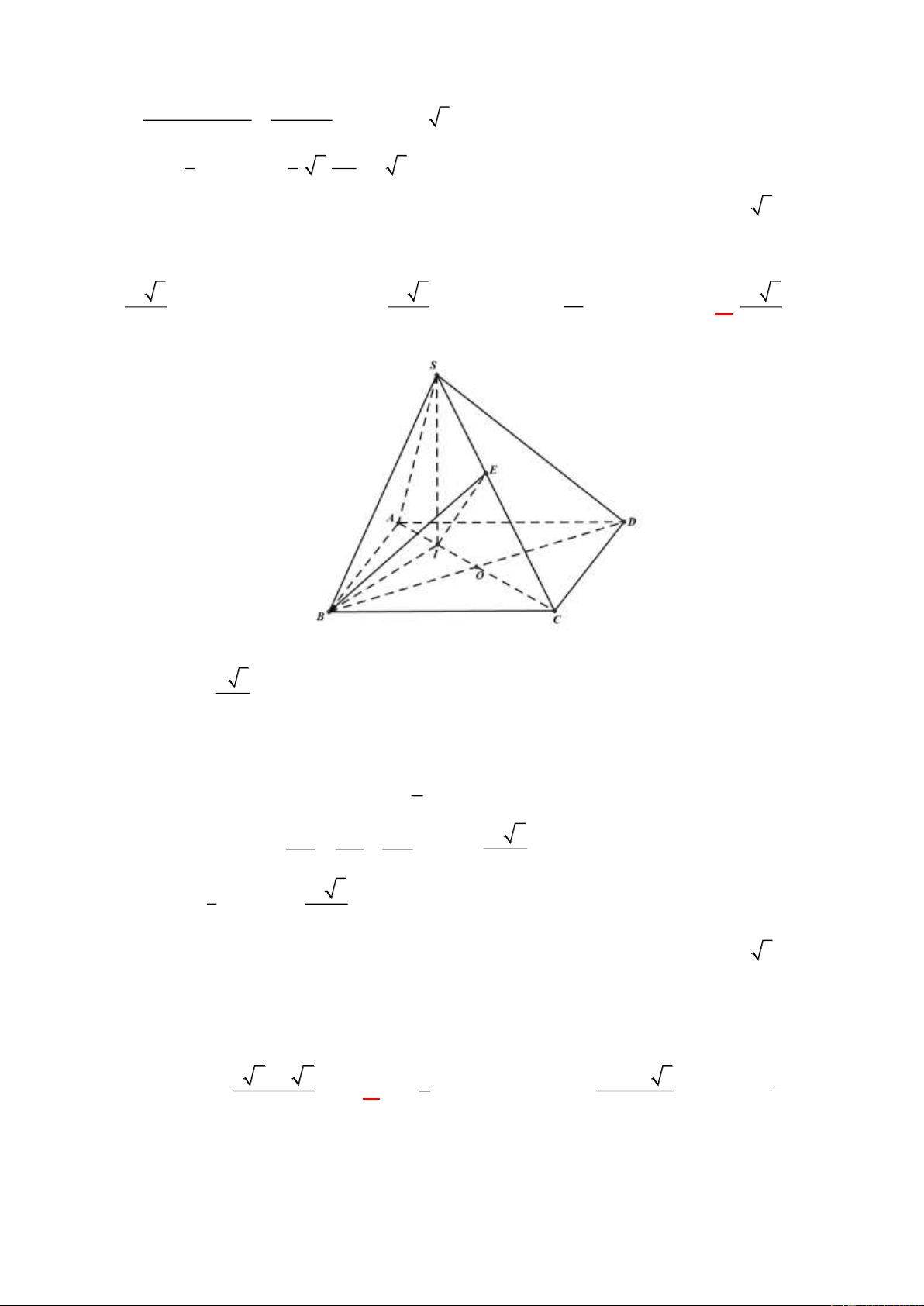
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, các mặt bên (SBC) ,(SAD) cùng tạo
với đáy góc 60, mặt bên (SAB) vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng (SCD)
bằng 21 , tính thể tích khối chóp S.ABC . 7 A. 3 . B. 3 . C. 3 . D. 3 . 12 6 8 8 Lời giải. ChọnA S I C B H M A D Hạ SH ⊥ A ,
B H AB , do (SAB) ⊥ ( ABCD) nên SH ⊥ ( ABCD)  SH ⊥ BC
Có ABCD là hình vuông AB ⊥ BC
BC ⊥ (SAB)  BC ⊥ SB
SB ⊥ BC, BC ⊥ AB  Có(
  (( ABCD),(SBC)) = SBH
SBC )  ( ABCD) = BC  (Do SAH  90 )
Chứng minh tương tự (( ABCD),(SAD)) = SAH
Từ giả thiết suy ra: SAH = S
BH = 60mà H AB suy ra tam giác SAB đều và H là trung điểm của AB .
Gọi M là trung điểm của CD HM ⊥ CD
Có SH ⊥ ( ABCD)  SH ⊥ CD  ( 3
SHM ) ⊥ (SCD) . Hạ HI ⊥ SM thì HI ⊥ (SCD)  HI = 12 Có 1 1 1 = + 1 1 1  = +
AB =1 (Do AB = BC = HM ) 2 2 2 HI SH HM 2 2 2  21   3  BC AB     7 2     1 1 3 1 3 V = SH.S = . . = . S.ABC (ABC) 3 3 2 2 12 Trang 7
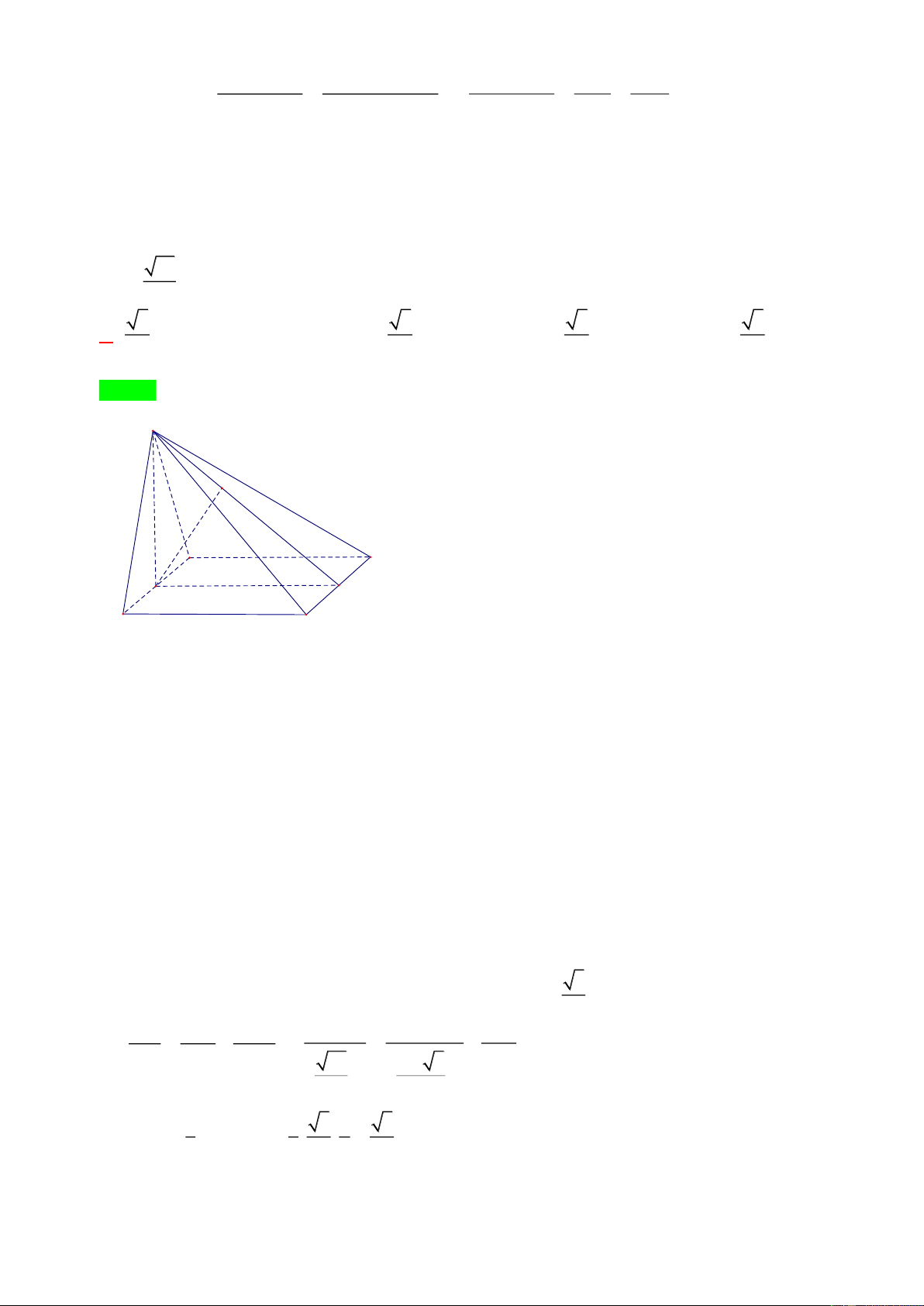
Ví dụ 2. Cho hình chóp đều S.ABC có góc giữa mặt bên và mặt đáy (ABC) bằng 60o . Biết khoảng
cách giữa hai đường thẳng SA và BC bằng 3a 7 . Tính theo a thể tích V của khối chóp S.ABC 14 3 3 3 3 A. a 3 a 3 a 3 a 3 V = . B.V = . C. V = . D.V = . 12 16 18 24 Giải:
Gọi O là trung điểm AC, x là cạnh của tam giác đều, G là trọng tâm tam giác ABC.
+) Ta có SO ⊥ A ;
C BO ⊥ AC ; nên góc giữa (SAC) và (ABC) là 60o SOB = .
Vì SABC là chóp đều nên SG ⊥ ( ABC)  SG ⊥ GO . Xét tam giác vuông SAG có x x o 3 SG = O . G tan 60 = . 3 = 6 2
+) Từ A kẻ AD / / BC suy ra:
d (BC, S )
A = d (BC,(SAD)) = d ( , B (SAD)
Mặt khác ta có d (G (SAD)) 2 ,
= d (B,(SAD)) 3 Vì =120o, = 30o; = 90o BAD BAG GAD
hay AG ⊥ AD (1)
Lại có SG ⊥ADAD ⊥ (AGS) .
Kẻ GK ⊥ SA GK ⊥ AD GK ⊥ (SAD)  GK = d ( , G (SAD))
Xét tam giác vuông SGA ta có: 1 1 1 1 1 7 x 7 = + = + =  GK = 2 2 2 2 2 2 GK GA GS    x x 7 x 3      2 3    Suy ra: x 7 2 3a 7 = .  x = a 7 3 14 2 Vậy a a 3 SG = ; S =  2 ABC 4 Trang 8 2 3
Thể tích khối chóp S.ABC là: 1 1 a a 3 a 3 V = S . G S = . . =  3 ABC 3 2 4 24 Chọn đáp án D.
Ví dụ 3. Cho hình chóp S.ABC có tam giác SAB nhọn và nằm trong mặt phẳng vuông góc với mặt
đáy( ABC) , tam giác ABC vuông tại C có AC = ,
a ABC = 30. Mặt bên (SAC) và (SBC) cùng
tạo với đáy góc bằng nhau và bằng 60 . Thể tích của khối chóp S.ABC theo a là: 3 3 3a 3 3 2a A. a 2a V = . B. V = . C. V = . D. V = . 2(1+ 5) 2(1+ 3) 1+ 3 2(1+ 2)
Hướng dẫn giải Chọn B. S P A C H Q 30° B
+ Theo đề (SAB) ⊥ ( ABC) theo giao tuyến AB . Dựng SH ⊥ AB SH ⊥ (SAB). AC + ABC  vuông nên tan30 =  BC = a 3 . BC 2 1 a 3 S = A . C BC = (1)  . ABC 2 2
+ Dựng HP ⊥ AC HQ ⊥ BC SPH = SQH = ((SAC) ( ABC)) = ((SBC) ( ABC)) 0 , , , = 60 .  SPH = S
QH HP = HQ .
HPCQ là hình vuông. Đặt HQ = x,0  x a 3  QB = a 3 − x . QB a 3 HQB  vuông nên tan 60 =
x 3 = a 3 − x x = = HQ . HQ 3 +1 SH a S  3
HQ vuông nên tan 60 =  SH = (2) . HQ 3 +1 3 3a Từ (1) và (2) : V = . 2 ( 3 + ) 1
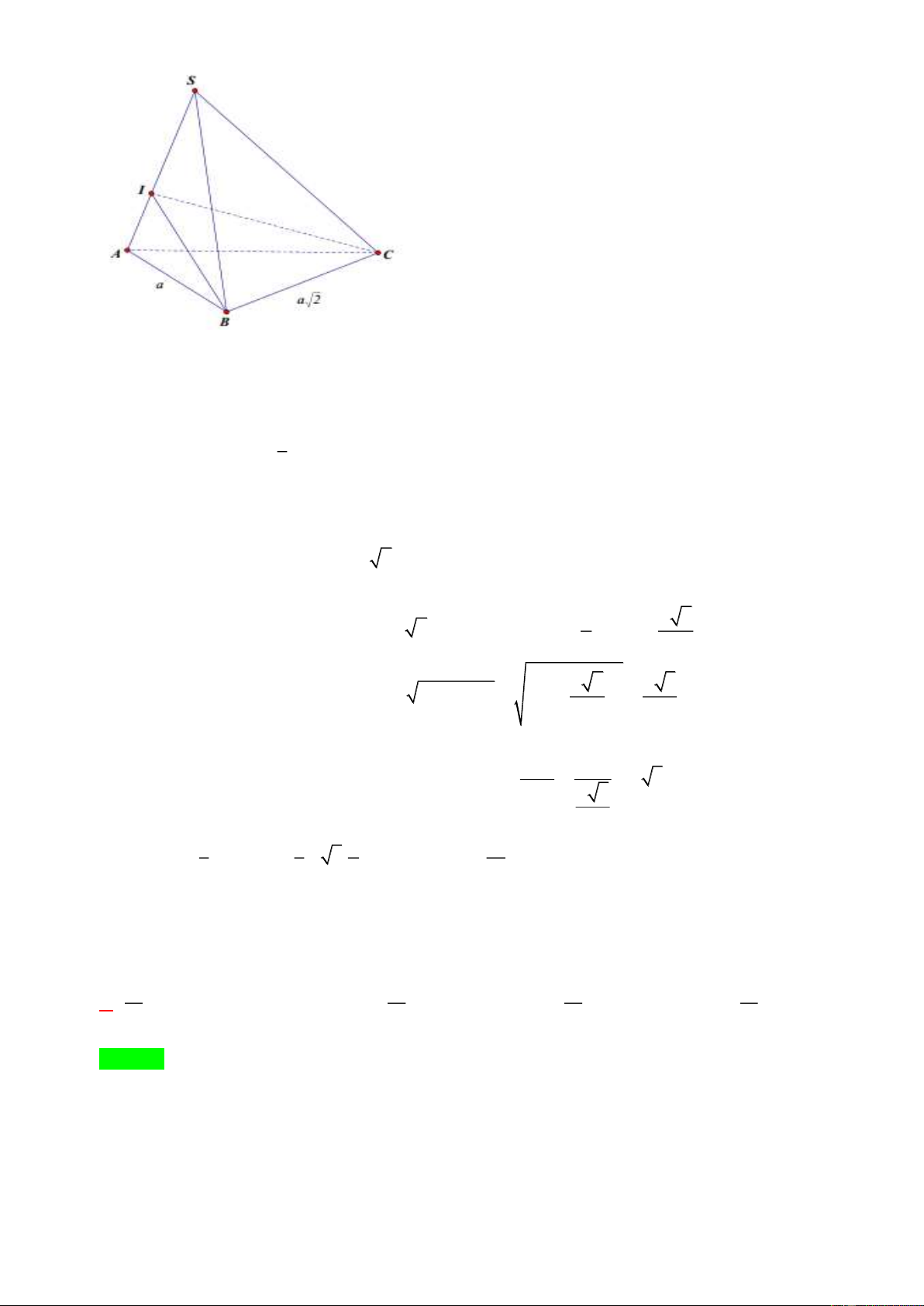
Ví dụ 4. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB = ; a = = 90o SBA SCA
, góc giữa hai mặt phẳng (SAB) và (SAC) bằng 60o . Thể tích của khối đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6 Lời giải Chọn D Trang 9
Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA .
Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và IB = IC .
SA ⊥ IC, SA ⊥ IB SA ⊥ (IBC) tại I . 1 V =V +V = S . A S S.ABC . A IBC S.IBC  3 IBC (  ( =
SAB) (SAC)) = (IB IC) BIC 60 , , = 60o   BIC =120o
Ta có IC = IB AB = a mà BC = a 2 nên tam giác IBC không thể đều suy ra 120o BIC = .
Trong tam giác IBC đặt IB = IC = x ( x  0) có:   a
BC = IB + IC − 2I .
B IC.cos120o  (a 2 )2 1 6 2 2 2 2 2 2
= x + x − 2x −  x =    2  3 2  a 6  a 3
Trong tam giác ABI vuông tại I có: 2 2 2 AI =
AB − IB = a −   =   3 3   2 2 AB a
Trong tam giác SAB vuông tại B đường cao BI có: SA = = = a 3 IA a 3 3 3 Vậy 1 1 1 a V = . . SA S = .a 3. I . B IC.sin120o = S . ABC  3 IBC 3 2 6
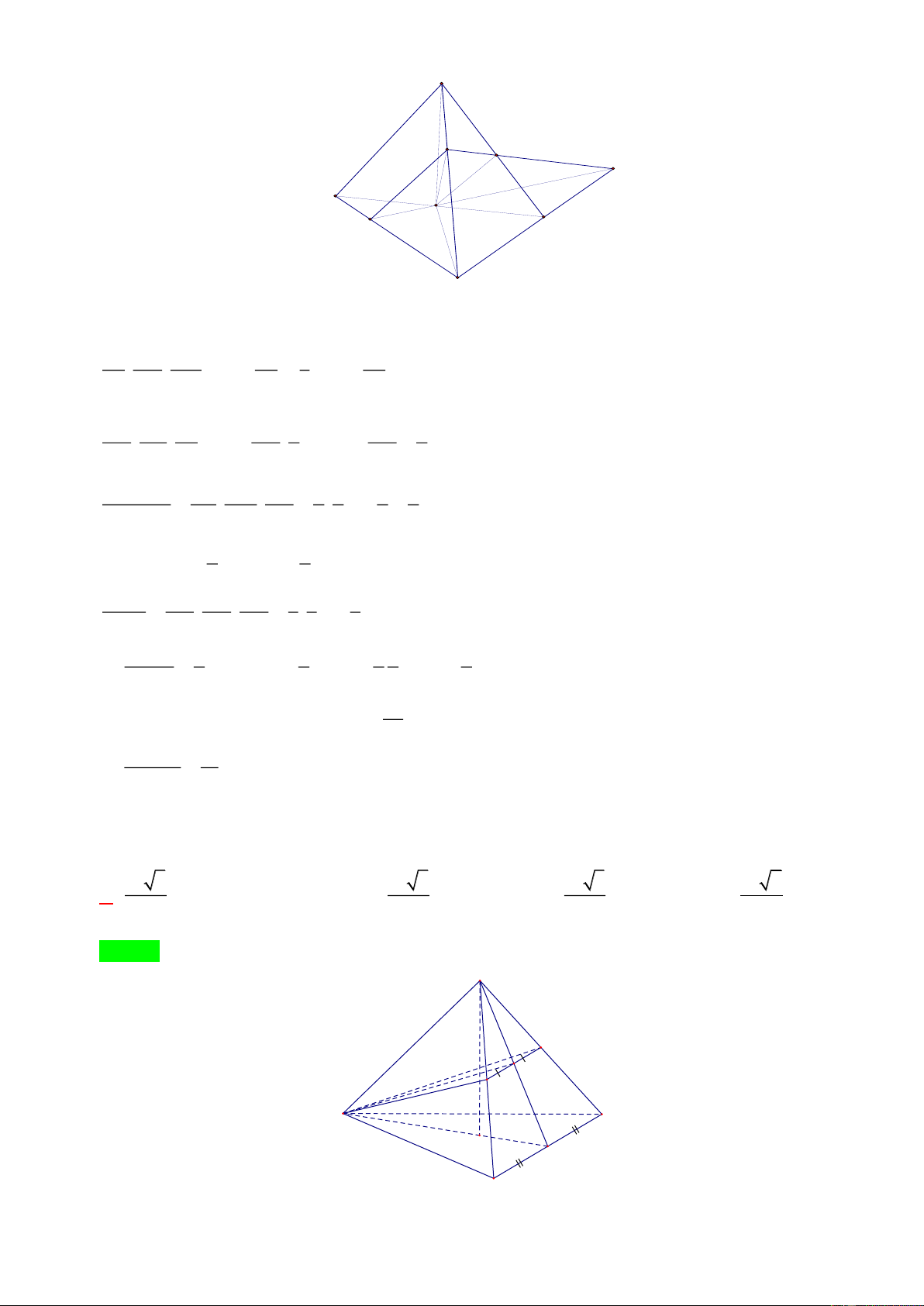
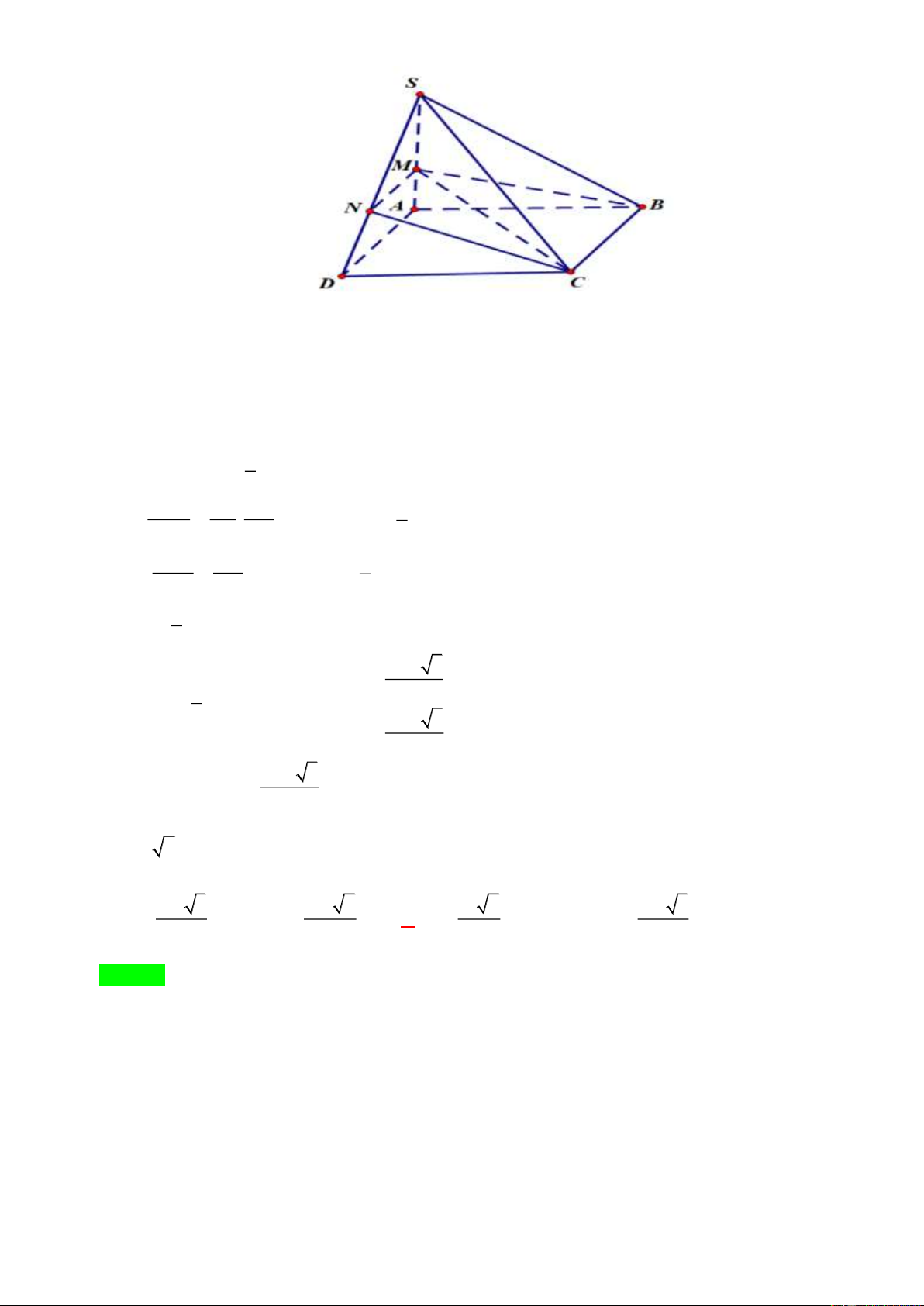
Ví dụ 5. Cho tứ diện ABCD và các điểm M , N , P lần lượt thuộc các cạnh BC , BD , AC sao
cho BC = 4BM , AC = 3AP , BD = 2BN . Tính tỉ số thể tích hai phần của khối tứ diện ABCD được
phân chia bởi mp(MNP) . A. 7 . B. 7 . C. 8 . D. 8 . 13 15 15 13 Lời giải Chọn A. Trang 10 A P k I B N D M C
Gọi I = MN D ,
C K = AD PI.
Áp dụng định lý Menelaus cho tam giác BCD và 3 điểm M, N, I ta có IC ND MB IC 1 IC . . =1  .1. = 1  = 3 ID NB MC ID 3 ID
Áp dụng định lý Menelaus cho tam giác ACD và 3 điểm , P K, I ta có KD PA IC KD 1 KD 2 . . =1  . .3 = 1  = KA PC ID KA 2 KA 3 V CP CM CN 2 3 2 1 CPMN = . . = . .1 = = V CA CB CN 3 4 4 2 CABN 1 1  V = V = V (3) CPMN 2 CABN 4 ABCD V AP AK AN 1 3 1 APKN = . . = . .1 = V AC AD AN 3 5 5 ACDN V 4 4 4 1 2 NCPKD  =  V = V = V = V (4) V 5 NCPKD 5 ACDN 5 2 ABCD 5 ABCD ACDN ( ) ( ) 13 3 , 4  V =V +V = V CMPKDN CPMN NCPKD 20 ABCD V 7 ABMNKP  = V 13 CMNDK
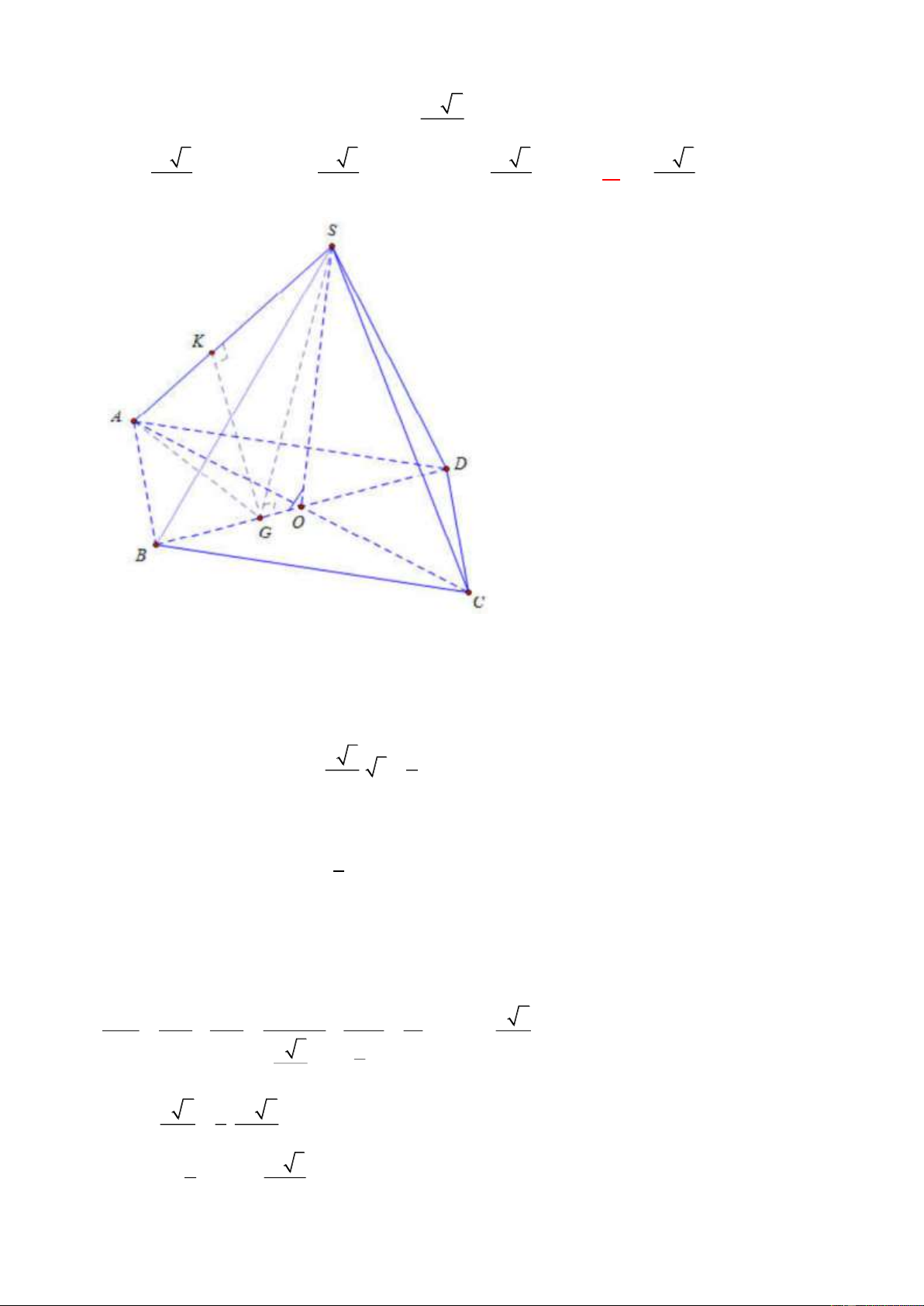
Ví dụ 6. Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a . Gọi E , F lần lượt là trung
điểm của các cạnh S ,
B SC . Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC) . Tính thể tích
khối chóp S.ABC . 3 3 3 3 A. a 5 . a 5 a 3 a 6 B. . C. . D. . 24 8 24 12 Lời giải Chọn A S F N E A C O M B Trang 11
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC , do S.ABC là hình chóp đều nên SO ⊥ ( ABC) .
Gọi M , N lần lượt là trung điểm của BC và EF .
Ta có S , M , N thẳng hàng và SM ⊥ BC tại M , SM ⊥ EF tại N . Ta có
( AEF)(SBC) = EF SM  (SBC )
  SM ⊥ ( AEF )  MN ⊥ AN A
NM vuông tại N .  SM ⊥ EF  Từ đó suy ra ANM ∽ AN AM NM SOM  = =
NM.SM = AM.OM . SO SM OM
Mà ta có N là trung điểm của SM (vì E , F lần lượt là trung điểm của SB , SC ) 1  NM = SM ; 2 a 3 a ABC
đều cạnh a và O là tâm đường tròn ngoại tiếp tam giác ABC AM = ; 3 OM = . 2 6 2 Vậy 1 a 3 a 3 a a 2 SM = . =  SM = . 2 2 6 4 2 2 2 2 Ta có a a a 15 a 3 2 2 SO = SM − OM = − = ; S = . 2 12 6 ABC 4 2 3 1 1 a 15 a 3 a 5 V = .S . O S = . . = . S.ABC 3 ABC 3 6 4 24 2. Bài tập vận dụng
Câu 1. Cho hình chóp S.ABC có AB = 3, BC = 4, AC = 5 . Các mặt bên (SAB),(SAC),(SBC) đều
cùng hợp với mặt đáy ( ABC) một góc 60 và hình chiếu H của S lên ( ABC) nằm khác phía với
A đối với đường thẳng BC . Thể tích khối chóp S.ABC . A. V = 6 3 . B. V =12 3 . C. V = 2 3 . D. V = 4 3 S.ABC S.ABC S.ABC S.ABC
Câu 2. Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Các mặt bên (SAB), (SAC) ,
(SBC) lần lượt tạo với đáy các góc lần lượt là 0 0 0
30 , 45 , 60 . Tính thể tích V của khối chóp S.ABC
. Biết rằng hình chiếu vuông góc của S trên mặt phẳng ( ABC) nằm bên trong tam giác ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . (4+ 3) 2 (4 + 3) 4 (4 + 3) 8(4 + 3)
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt đáy
(ABCD) và góc giữa SC với mặt phẳng (SAB) bằng 30. Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S lên đường thẳng BM . Khi điểm M di động trên cạnh CD thì
thể tích chóp S.ABH lớn nhất là 3 3 3 3 A. a 2 a 2 a 2 a 2 V = . B. V = . C. V = . D. V = . 6 12 15 8
Câu 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy SM (ABC )
D và SA = a . Điểm M thuộc cạnh SA sao cho
= k,0  k 1.Khi đó giá trị của k để SA
mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau là: − + + − + − + A. 1 5 k = B. 1 5 k = . C. 1 5 k = . D. 1 2 k = . 2 2 4 2 Trang 12
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy
SA = a 2 . Gọi B', D' là hình chiếu của A lần lượt lên S ,
B SD . Mặt phẳng ( AB ' D ') cắt SC tại
C ' . Tính thể tích khối chóp S.AB 'C ' D ' là: 3 3 3 3 A. 2a 3 2a 2 a 2 2a 3 V = . B. V = . C. V = . D. V = . 9 9 9 3
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm
trên cạnh SC sao cho EC = 2ES. Gọi (α ) là mặt phẳng chứa đường thẳng AE và song song với
đường thẳng BD, (α ) cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN. A. 1 V . B. 1 V . C. 1 V. D. 2 V . 6 9 27 3
Câu 7. Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC , các mặt bên (SAB) ,
(SBC),(SCA) cùng tạo với đáy góc 60. Biết AB = 3, BC = 4,CD = 5, tính thể tích khối chóp S.ABC . A. 2 3 . B. 6 3 . C. 5 3 . D. 10 3 .
Câu 8. Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm O với AB = a, BC = a 3 . Hình
chiếu vuông góc của S lên mặt phẳng ( 
ABCD) là trung điểm AO . Biết ((SAC);(SBC)) = 60 .
Khi đó thể tích của S.ABCD là: 3 3 3 3 A. a 3 . a 3 a a 6 B. . C. . D. . 3 2 2 8
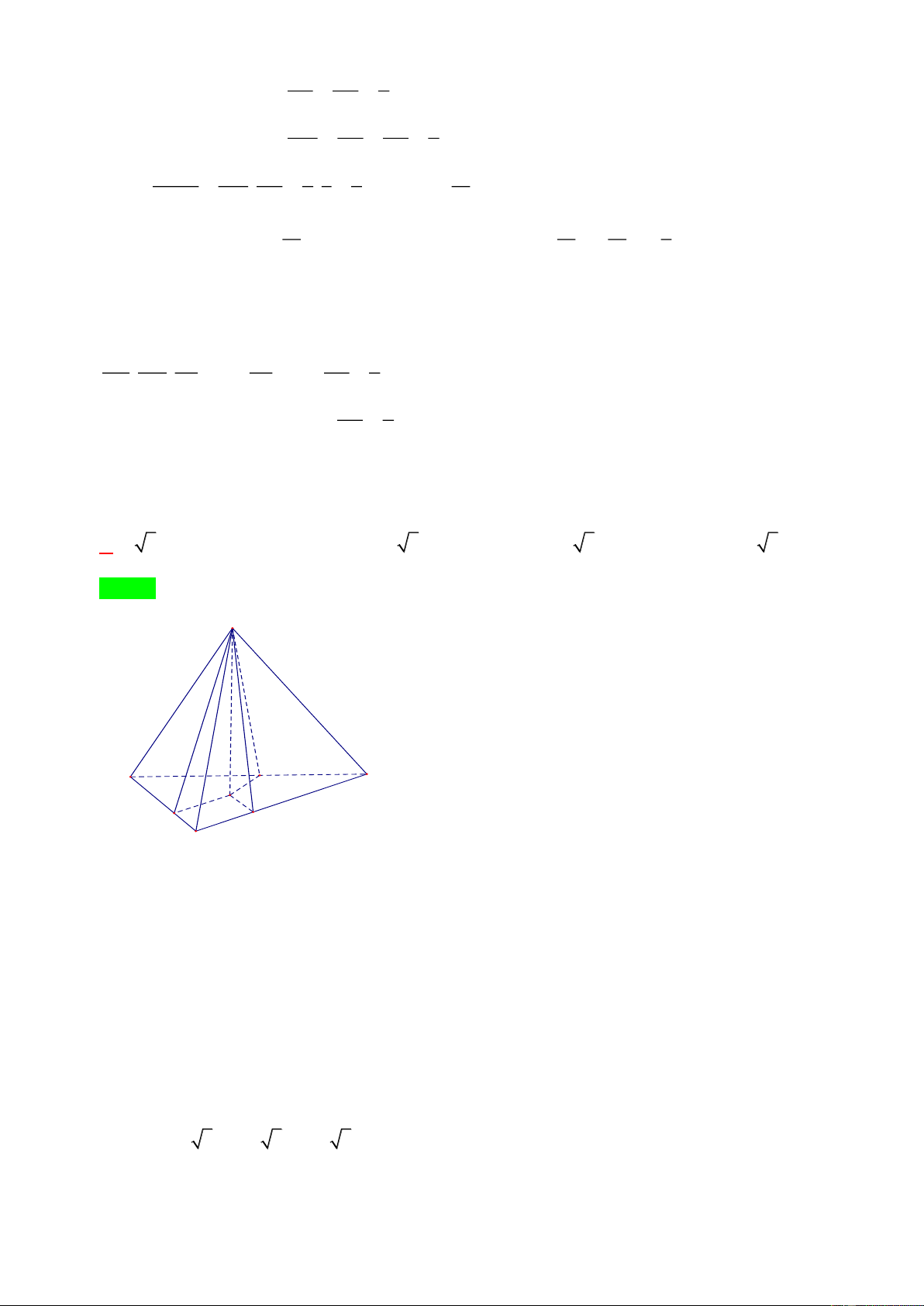
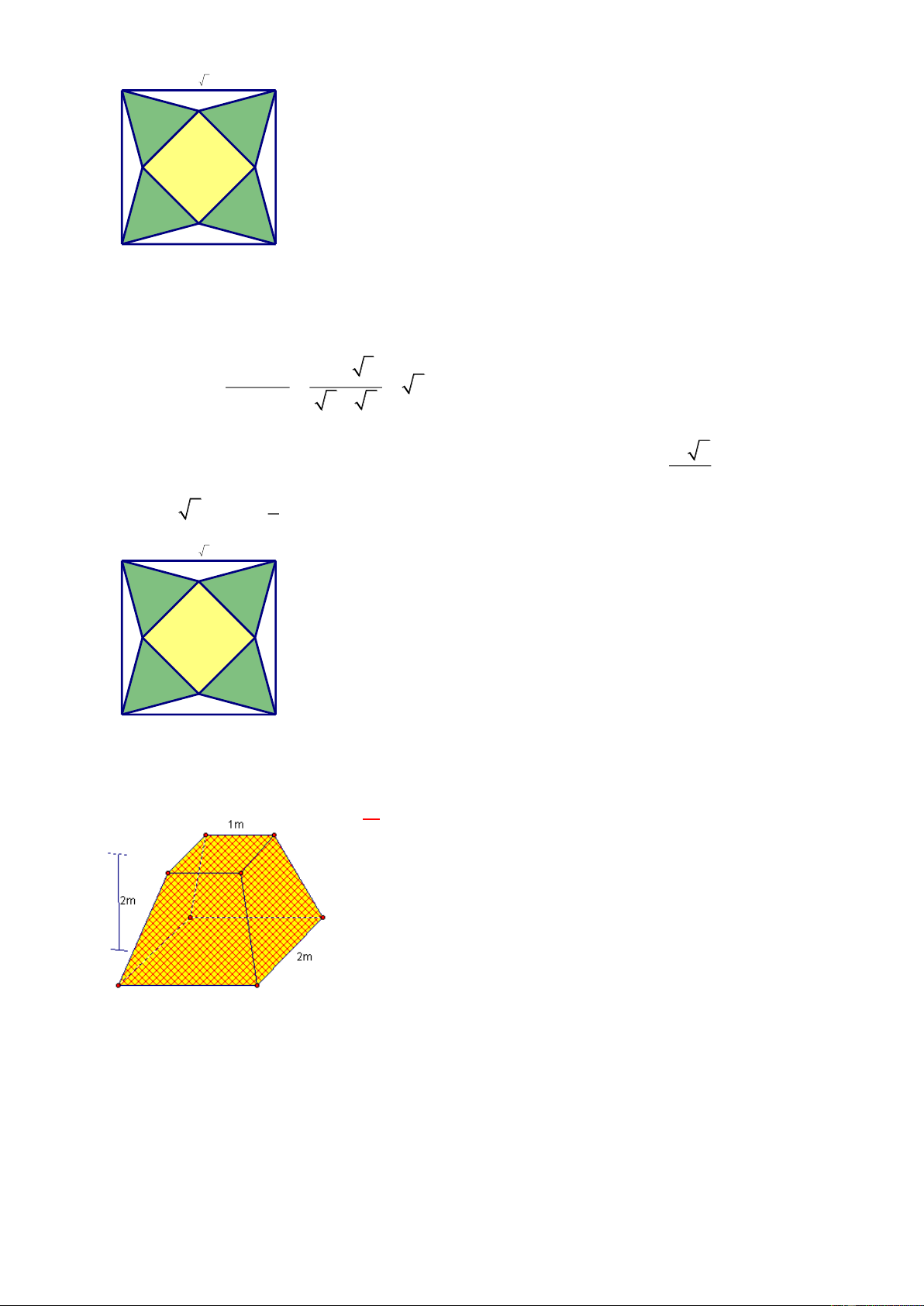
Câu 9. Để làm một hình chóp tứ giác đều từ một tấm tôn hình vuông có cạnh bằng 1+ 3 , người ta
cắt tấm tôn theo các tam giác cân bằng nhau MAN, NB , P PC ,
Q QDM sau đó gò các tam giác ABN, BC , P CD ,
Q DAM sao cho bốn đỉnh M , N, ,
P Q trùng nhau(hình vẽ).
Biết rằng, các góc ở đỉnh của mỗi tam giác cân là 0
150 . Tính thể tích V của khối chóp đều tạo thành. + + A. 3 6 5 2 V = . B. 2 V = . C. 52 30 3 V = . D. 1 V = 24 3 3 3
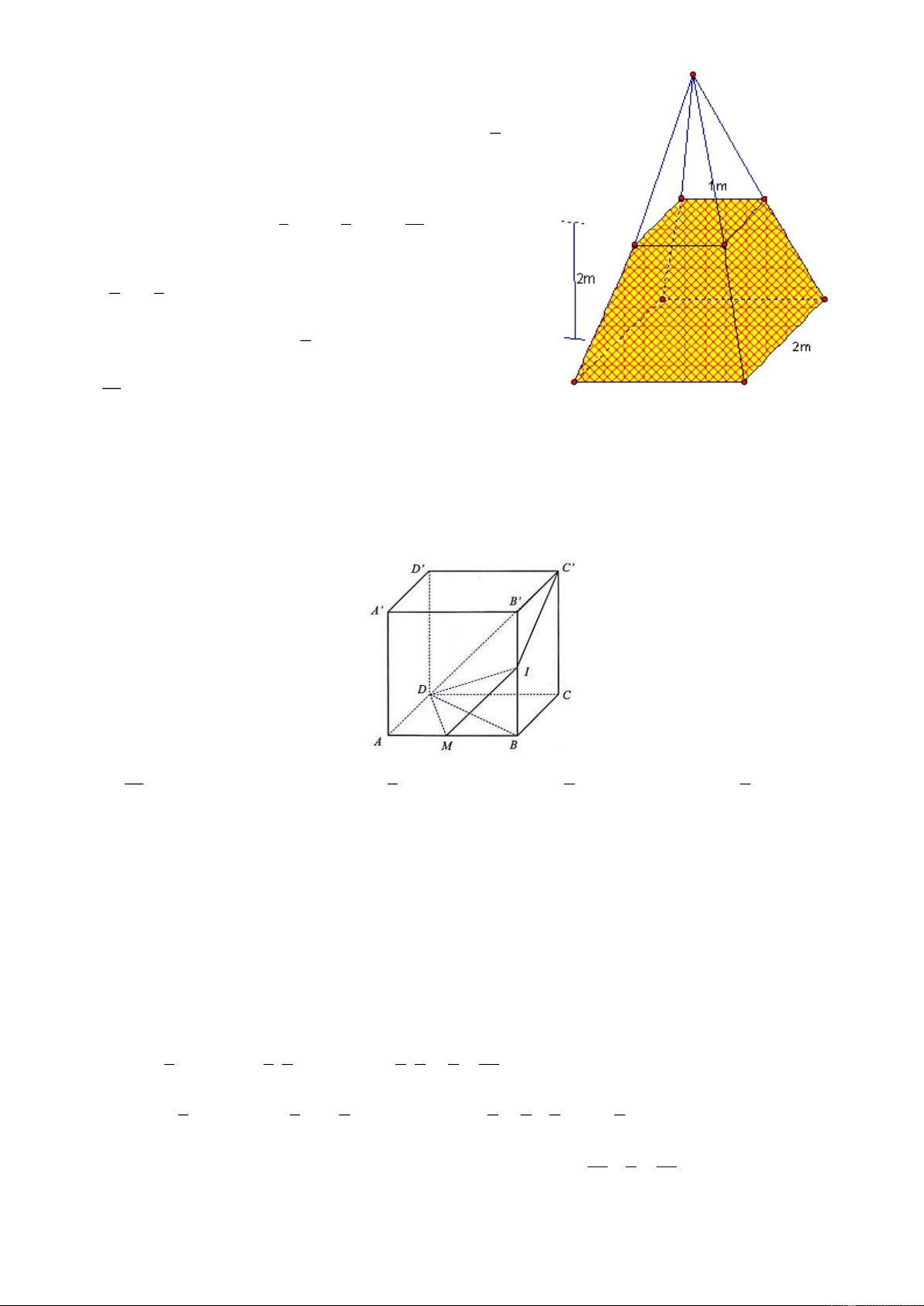
Câu 10. Một đống đất được vun thành hình một khối chóp cụt tứ giác đều có cạnh đáy lớn bằng
2m, cạnh đáy nhỏ bằng 1m và chiều cao bằng 2m. Khối lượng (thể tích) đống đất có giá trị gần nhất với con số A. 4,55m3. B. 4,65m3. C. 4,7 m3. D. 4,75m3. 3. Hướng dẫn giải
Câu 1. Cho hình chóp S.ABC có AB = 3, BC = 4, AC = 5 . Các mặt bên (SAB),(SAC),(SBC) đều
cùng hợp với mặt đáy ( ABC) một góc 60 và hình chiếu H của S lên ( ABC) nằm khác phía với
A đối với đường thẳng BC . Thể tích khối chóp S.ABC . A. V = 6 3 . B. V =12 3 . C. V = 2 3 . D. V = 4 3 S.ABC S.ABC S.ABC S.ABC
Hướng dẫn giải Chọn A. Trang 13 S A M C P I B H N .
Gọi M, N, P là hình chiếu của H lên C , B B , A AC . Ta có SHM = SHN = S
HP HM = HN = HP .
Theo bài ra ta có H là tâm đường tròn bàng tiếp ABC  . Ta có ABC
vuông tại B BMHN là hình vuông.
Gọi I = AH BC . BI 3 3 3
=  BI = BC = . IC 5 8 2 BI NH 1 Ta có =
=  B là trung điểm của AN HN = AB = 3. AB AN 2
SH = HN.tan 60 = 3 3 . 1 1 S = B . A BC = 6  V = S .SH = 6 3 . ABC 2 S .ABC 3 ABC
Câu 2. Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Các mặt bên (SAB), (SAC) ,
(SBC) lần lượt tạo với đáy các góc lần lượt là 0 0 0
30 , 45 , 60 . Tính thể tích V của khối chóp S.ABC
. Biết rằng hình chiếu vuông góc của S trên mặt phẳng ( ABC) nằm bên trong tam giác ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V = . B. V = . C. V = . D. V = . (4+ 3) 2 (4 + 3) 4 (4 + 3) 8(4 + 3) Hướng dẫn giải:
Gọi H là hình chiếu vuông góc của S trên mặt phẳng
( ABC). Kẻ HD ⊥ AB(DAB), HE ⊥ AC(EAC) , SH
HF ⊥ BC (E BC) . Khi đó ta có HD = = SH 3 , 0 tan 30 SH SH SH HE = = SH , HF = = . Ta có 0 tan 45 0 tan 60 3 2 a 3 S = suy ra ABC  4 2 1  1  a 3 3a SH 1+ 3 + a =  SH =   . 2  3  4 2 (4 + 3) 2 3 1 3a a 3 a 3 Vậy V = . . = . 3 2(4 + 3) 4 8(4 + 3) Chọn đáp án D.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt đáy
(ABCD) và góc giữa SC với mặt phẳng (SAB) bằng 30. Gọi M là điểm di động trên cạnh CD Trang 14
và H là hình chiếu vuông góc của S lên đường thẳng BM . Khi điểm M di động trên cạnh CD thì
thể tích chóp S.ABH lớn nhất là 3 3 3 3 A. a 2 a 2 a 2 a 2 V = . B. V = . C. V = . D. V = . 6 12 15 8 Lời giải Chọn B
Lấy điểm N BC sao cho BN = CM = ,
x 0  x a . Gọi H = AN BM Xét ABN  và B
CM ta có: BN = CM , ABN = BCM = 90 và AB = BC ABN = B
CM (c.g.c)  BAN = CBM
Mà BAN + BNA = 90 nên CBM + BNA = 90  BHN = 90 hay AH ⊥ BM BM ⊥ AH Ta có: 
BM ⊥ (SAH )  SH ⊥ BM BM ⊥ SA
 Hình chiếu vuông góc của S lên BM là H . Do BH x ax B
HN đồng dạng với BCM nên BH BN =  =  BH = BC BM 2 2 a x + a 2 2 x + a 2 2 4 2 Tam giác a x a a
ABH vuông tại H nên 2 2 2 AH =
AB − BH = a − = = 2 2 2 2 2 2 x + a x + a x + a 2 3 1 1 a ax a x S = AH.BH = . . = . ABH  2 2 2 2 2 2 2 2 + + 2 x + a x a x a 3 4 3 1 1 a x a 2 a 2 V = S . A S = .a 2. .  = . S.ABH ABH 2 2 3 3 2 x + a 12a 12
Câu 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy SM (ABC )
D và SA = a . Điểm M thuộc cạnh SA sao cho
= k,0  k 1.Khi đó giá trị của k để SA
mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau là: − + + − + − + A. 1 5 k = B. 1 5 k = . C. 1 5 k = . D. 1 2 k = . 2 2 4 2 Lời giải Chọn A.
Phân tích: Bài toán trên chính là bài toán về tỉ số thể tích, vì vậy trước hết phải xác định thiết diện
của hình chóp khi cắt bởi (BMC). Trang 15
Do (BMC)chứa BC song song với AD nên (BMC) cắt (SA )
D theo giao tuyến song song AD . Để tính V
nếu xác định đường cao thì phức tạp vì vậy sẽ chia thành hai khối và sử dụng bài S .BCNM toán tỉ số thể tích. Kẻ MN / / A ;
D N SD khi đó thiết diện của hình chóp S.ABCD với (BMC) là hình thang BCNM .
Suy ra (BMC) chia khối chóp thành hai khối đa diện SBCNM và DABCNM . Đặt V = V ; V = V ; V = V . 1 S .BCNM 2 DABCNM S . ABCD Để 1
V = V thì V = V . 1 2 1 2 V Ta có SN SM 1 SNMC 2 = . = k 2 V = k .V . V SD SA SNMC 2 SADC V Ta có SM SMCB = = 1 k V = k.V . V SA SMCB 2 SABC Vậy 1 2 V =
(k + k).V . 1 2  1 − − 5 k = Khi đó 1 2 V = V 2
k + k =1   . 1 2  1 − + 5 k =  2 − + Do 0  k 1 nên 1 5 k = . Vậy chọn đáp án A. 2
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy
SA = a 2 . Gọi B', D' là hình chiếu của A lần lượt lên S ,
B SD . Mặt phẳng ( AB ' D ') cắt SC tại
C ' . Tính thể tích khối chóp S.AB 'C ' D ' là: 3 3 3 3 A. 2a 3 2a 2 a 2 2a 3 V = . B. V = . C. V = . D. V = . 9 9 9 3 Lời giải Chọn C. Trang 16 S C' D' B' C D A B 2 Ta có SB ' SD ' 2a 2 = =
= nên suy ra B' D'/ /BD mà BD ⊥ (SAC)  BD ⊥ SC . 2 SB SD 3a 3
Do đó B' D' ⊥ SC (1)
Ta có BC ⊥ (SAB)  BC ⊥ AB' và AB' ⊥ SB suy ra AB' ⊥ SC (2)
Từ (1) và (2) suy ra ( AB'C 'D') ⊥ SC nên ta có AC ' ⊥ SC 2 SC ' 2a 1 = = . 2 SC 4a 2 V 2V Ta có SB ' SC ' 2 1 1
SA' B 'C ' D' SAB 'C ' = = . = . = . V 2V SB SC 3 2 3 SABCD SABC 3 Mà 1 a 2 2 V = a .a 2 = . SABCD 3 3 3 3 Vậy 1 a 2 a 2 V = . = .
SAB 'C ' D ' 3 3 9
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm
trên cạnh SC sao cho EC = 2ES. Gọi (α ) là mặt phẳng chứa đường thẳng AE và song song với
đường thẳng BD, (α ) cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN. A. 1 V . B. 1 V . C. 1 V. D. 2 V . 6 9 27 3 Lời giải Chọn A. S E N M I K D A O B C
Gọi O = AC BD và I = SO A .
E Do (α ) đi qua AE và song song với BD nên (α ) cắt (SBD)
theo một giao tuyến đi qua I và song song với BD.
Trong (SAC) từ O kẻ một đường thẳng song song với AE giả sử cắt SC tại K, do O là trung điểm
của AC nên K là trung điểm của EC suy ra SE = EK = KC Trang 17 Xét tam giác SI SE SAC ta có 1 = = SO SK 2 Xét tam giác SM SN SI SBD ta có 1 = = = SB SD SO 2 Do đó V SM SN 1 1 1 1 S.AME = . = . = V = V S. V SB SD 2 3 6 AME 12 S.ABC Tương tự, ta có 1 1 1 1 V = V . Vậy V =V +V = V + V = V . S. ANE 12 S. AMEN S.AME S .ANE 12 12 6 Phương pháp giải:
Dùng định lí Thalet và phương pháp tỉ số thể tích để tính thể tích khối chóp cần tìm theo V Chú ý
+) Nếu ba điểm E, A, I thẳng hàng nên áp dụng định lý Menelaus cho tam giác SOC ta có: SE CA OI OI SI 1 . . =1 =1 = . EC AO IS SI SO 2
Như vậy có thể tính được tỷ số SI 1
= ngay mà không cần dùng định lý Ta lét SO 2
Câu 7. Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC , các mặt bên (SAB) ,
(SBC),(SCA) cùng tạo với đáy góc 60. Biết AB = 3, BC = 4,CD = 5, tính thể tích khối chóp S.ABC . A. 2 3 . B. 6 3 . C. 5 3 . D. 10 3 . Lời giải ChọnA S A C G H I K B
Hạ SH ⊥ ( ABC), H ( ABC) HI ⊥ A ,
B I AB ; HK ⊥ BC, K BC , HG ⊥ C , A G CA
SH ⊥ ( ABC )  SH ⊥ AB SI ⊥ AB IH ⊥ AB 
SI ⊥ AB, IH ⊥ AB  Có(
  (( ABC),(SAB)) = HIS (Do HIS  90 )
SAB)  ( ABC ) = AB
Chứng minh tương tự (( ABC),(SBC)) = HKS
(( ABC),(SAC)) = SGH
Từ giả thiết suy ra: HIS = SKH = SGH = 60
SH = HI 3 = HK 3 = HG 3
Mà H nằm trong tam giác ABC nên H và HI lần lượt là tâm và bán kính đường tròn nội tiếp của tam giác ABC Trang 18 Có 2 2 2
AB + BC = AC nên tam giác ABC là tam giác vuông tại B . 2 ( S ABC) 4.3 HI = = =1  SH = 3 .
AB + BC + CA 3 + 4 + 5 1 1 3.4 V = SH.S = . 3. = 2 3 . S. ABC (ABC) 3 3 2
Câu 8. Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm O với AB = a, BC = a 3 . Hình
chiếu vuông góc của S lên mặt phẳng ( 
ABCD) là trung điểm AO . Biết ((SAC);(SBC)) = 60 .
Khi đó thể tích của S.ABCD là: 3 3 3 3 A. a 3 . a 3 a a 6 B. . C. . D. . 3 2 2 8 Lời giải
Gọi I trung điểm AO , suy ra SI ⊥ ( ABCD) . a 3
AC = 2a; BI = . 2
Vẽ BE ⊥ SC IE ⊥ SC . Vậy (( 
SAC );(SBC)) = (BE; IE) = 60 . Xét a B
IE vuông tại I : IE = BI.cot 60 = . 2 Xét 1 1 1 a S
IC vuông tại I : = + 3 2  SI = . 2 2 2 IE SI IC 8 3 Vậy 1 a 6 V = SI.S = . SABCD ABCD 3 8
Câu 9. Để làm một hình chóp tứ giác đều từ một tấm tôn hình vuông có cạnh bằng 1+ 3 , người ta
cắt tấm tôn theo các tam giác cân bằng nhau MAN, NB , P PC ,
Q QDM sau đó gò các tam giác ABN, BC , P CD ,
Q DAM sao cho bốn đỉnh M , N, ,
P Q trùng nhau(hình vẽ).
Biết rằng, các góc ở đỉnh của mỗi tam giác cân là 0
150 . Tính thể tích V của khối chóp đều tạo thành. + + A. 3 6 5 2 V = . B. 2 V = . C. 52 30 3 V = . D. 1 V = 24 3 3 3 Trang 19 1+ 3 M N 1500 A D B C Q P Hướng dẫn giải Đáp án: B + 0 AMN = DMQ = 15 0
AMD = 60  MAD đều.
Vì vậy hình chóp tứ giác đều tạo thành có tất cả các cạnh bằng nhau và bằng MA . 2 + MN (1 3) Trong đó, MA = = = 2 0 2sin 75 6 + 2
+ Dễ dàng chứng minh được rằng: 3
“Một khối chóp tứ giác đều có tất cả các cạnh bằng x 2
x thì có thể tích là V = ” 6 + Với x = 2 thì 2 V = 3 1+ 3 M N 1500 A D B C Q P
Câu 10. Một đống đất được vun thành hình một khối chóp cụt tứ giác đều có cạnh đáy lớn bằng
2m, cạnh đáy nhỏ bằng 1m và chiều cao bằng 2m. Khối lượng (thể tích) đống đất có giá trị gần nhất với con số A. 4,55m3. B. 4,65m3. C. 4,7 m3. D. 4,75m3. Hướng dẫn giải Đáp án: B Trang 20
Kéo dài các cạnh bên hình chóp cụt lên phía trên ta được
hình chóp lớn là hình chóp sinh ra hình chóp cụt. Hình
chóp nhỏ và hình chóp lớn đồng dạng theo tỉ số k = 1 2
( là tỉ số giữa độ dài cạnh đáy nhỏ và độ dài cạnh đáy lớn hình chóp cụt)
Thể tích chóp lớn bằng 1 1 16 2 2 3 a .h = .2 .4 = m 3 3 3
Tỉ số giữa thể tích chóp nhỏ và thể tích chóp lớn bằng 1 1 3 ( ) = 2 8
 Thể tích chóp cụt bằng 7 thể tích chóp lớn và bằng 8 14 3 m 3
Dạng II. Thể tích khối lăng trụ 1.Ví dụ minh hoạ
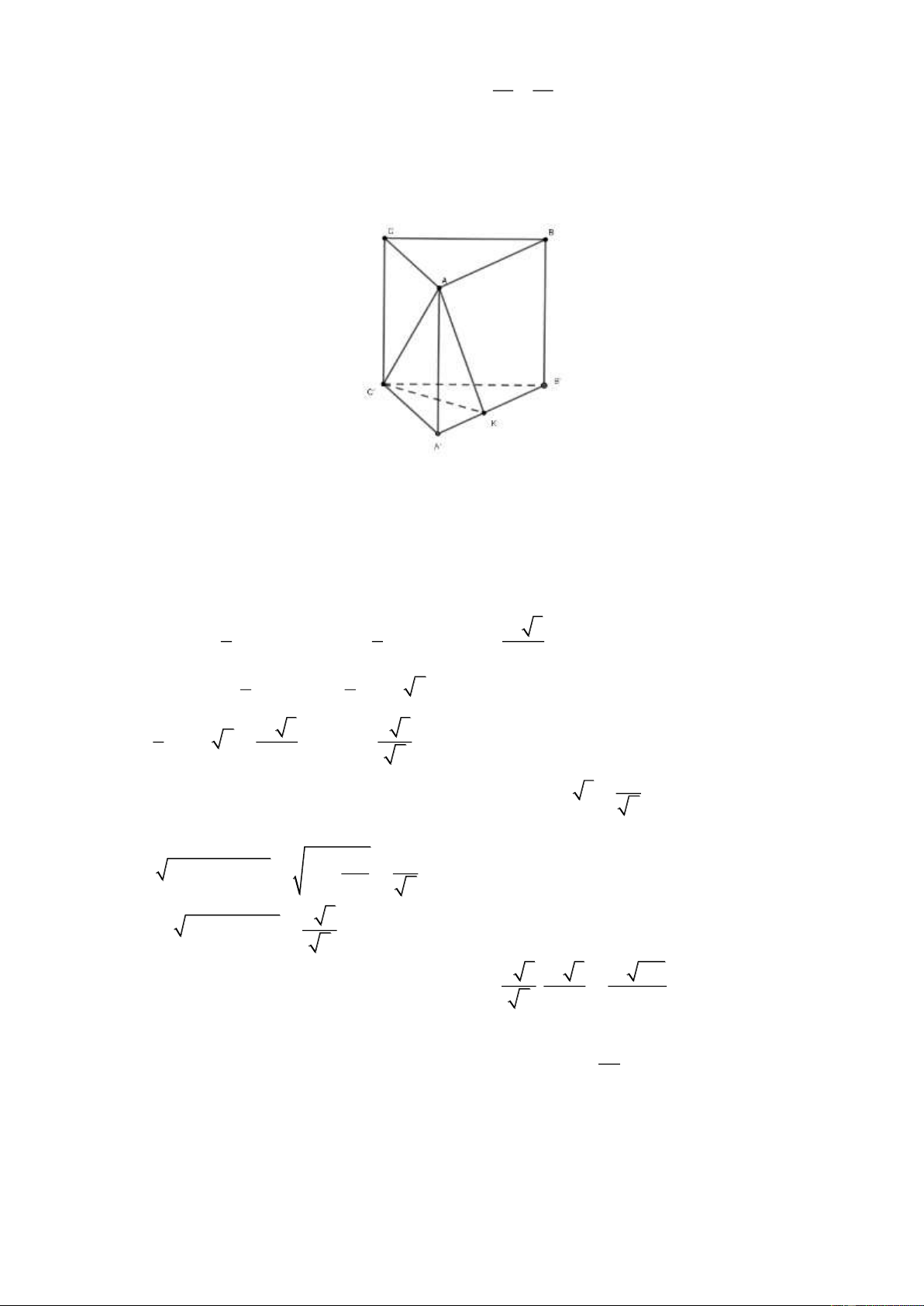
Ví dụ 1. Cho hình lập phương ABC . D A BCD
  . I là trung điểm BB . Mặt phẳng ( DIC) chia
khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng. . 7 1 1 1 A. . B. . C. . D. . 17 3 2 7
Hướng dẫn giải Chọn A.
Coi như khối lập phương có cạnh bằng 1.
Để giải bài toán này, ta phải xác định đúng thiết diện cắt bởi mặt phẳng ( DIC) .
Lấy M là trung điểm AB thì IM là đường trung bình tam giác ABB nên I / M /AB /  /DC.
Suy ra bốn điểm I, M,C , D cùng thuộc một mặt phẳng (C ID) .
Thiết diện cắt bởi mặt phẳng (DIC) là tứ giác C DMI .
Phần có thể tích nhỏ hơn là khối đa diện C IBMDC .
Để thuận tiện tính toán ta chia khối trên thành 2 phần là tứ diện IMBD và hình chóp DIBCC . 1 1 1 1 1 1 1 V = .I . B S = . .I . B D . A MB = . .1. = . IMBD BDM 3 3 2 6 2 2 24 1 1 1 1 1  1  1 V  = .DC.S  =
.DC. . IB + CC .BC = .1. . +1 .1. . D IBCC IBCC ( )   . 3 3 2 2 2  2  4 1 1 7
Suy ra thể tích khối có thể tích nhỏ hơn là V = V +V  = + = . n IMBD DIBCC 24 4 24 Trang 21 7 17
Thể tích phần lớn hơn là V = V
    −V = 1− = . l ABC . D A B C D n 24 24
Vậy tỉ lệ cần tìm là V :V = 7 :17 . n l
Ví dụ 2. Cho lăng trụ AB . C A BC
  là lăng trụ đứng, AC = ,
a BC = 2a góc ·
ACB bằng 120o . Góc
giữa đường thẳng AC¢ và mặt phẳng (ABB A
¢ )¢ bằng 30o . Tính thể tích lăng trụ đã cho. Lời giải Kẻ C K ¢ ^ A B
¢ ¢. Vì lăng trụ AB . C A BC
  là lăng trụ đứng nên C K
¢ ^ AA¢. Do đó C K ¢ ^ (ABB A ¢ )¢ .
Góc giữa AC¢ và (ABB A ¢ )¢ bằng góc · C A
¢ K và bằng 30° (tam giác C A
¢ K vuông tại K nên góc C ' AK nhọn)
Xét tam giác ABC , áp dụng định lý cosin cho cạnh AB có: 2 2 2 o 2 2 2
AB = AC + BC - 2.A . B A .
C cos120 = 7a Þ A B ¢ ¢ = 7a . 2 1 1 a o 3 S S C . A C . B sin ACB . a 2 . a sin120 A B ¢ C ¢ ¢ = = = = . ABC 2 2 2 Mặt khác 1 1 S = C K ¢ .A B ¢ ¢= C K ¢ .a 7 A B ¢ C ¢ ¢ 2 2 2 Do đó 1 a 3 a 3 C K ¢ .a 7 = Û C K ¢ = 2 2 7 Xét tam giác a
AKC ' vuông tại K nên o 3 AK = C K ¢ .cot 30 = C K ¢ . 3 = 7
Xét tam giác A'C ' K vuông tại K nên 2 3a 2a 2 2 2 A K ¢ = A C
¢ ¢ - KC¢ = a - = 7 7 a 5 2 2 Þ AA¢= AK - A K ¢ = 7 2 3 a 5 a 3 a 105
Thể tích của lăng trụ AB . C A BC
  là V = AA .S ¢ = . = . ABC 7 2 14
Ví dụ 3. Cho lăng trụ AB . C A BC
  có đáy là tam giác đều cạnh a , đỉnh A¢ cách đều , A , B C . Biết
khoảng cách giữa đường thẳng a
AA¢ và mặt phẳng (BCC B
¢ )¢ bằng 3 . Tính thể tích khối lăng trụ 4 AB . C A BC   theo a . Lời giải Trang 22
Vì đỉnh A¢ cách đều , A ,
B C nên hình chiếu vuông góc của A¢ trên (ABC) là tâm đường tròn ngoại
tiếp tam giác ABC . Mà tam giác ABC đều nên hình chiếu vuông góc của A¢ trên (ABC) là trọng
tâm O của tam giác ABC .Gọi K, I lần lượt là trung điểm của B C
¢ ¢và BC . Từ A' kẻ A'H ^ IK .
Ta có BC ^ AI, BC ^ A'O Þ BC ^ (A' AI) Þ A' H ^ BC . Lại có A H ¢ ^ BC, A H ¢ ^ IK Þ A H ¢ ^ (BCC B ¢ )¢ 3a Þ d = d = A H ¢ = ( AA ,( ¢ BCC 'B')) ( A , ¢( BCC B ¢ ) ¢ ) 4
Đặt AA' = x > 0. Tam giác a a
BAC đều cạnh a , AI là trung tuyến nên 3 2 3 AI = , AO = AI = . 2 3 3 2 2 2 Xét tam giác a 3x - a A A
¢ O vuông tại O : 2 2 2 A O
¢ = AA¢ - AO = x - = . 3 3
Diện tích hình bình hành A K ¢ IA là: 2 2 3x - a a 3 3a S = A' . O AI = . , S
= A' H.IK = .x A' KIA A' 3 2 KIA 4 2 2 3x - a a 3 3a Þ a . = .x 2 Þ x =
Þ A'O = a 3 2 4 3 2 Diện tích tam giác đều a 3 ABC là S = . ABC 4 2 3
Thể tích của lăng trụ đã cho là a 3 a 3 V = A¢ . O S = . a = . ABC 4 4
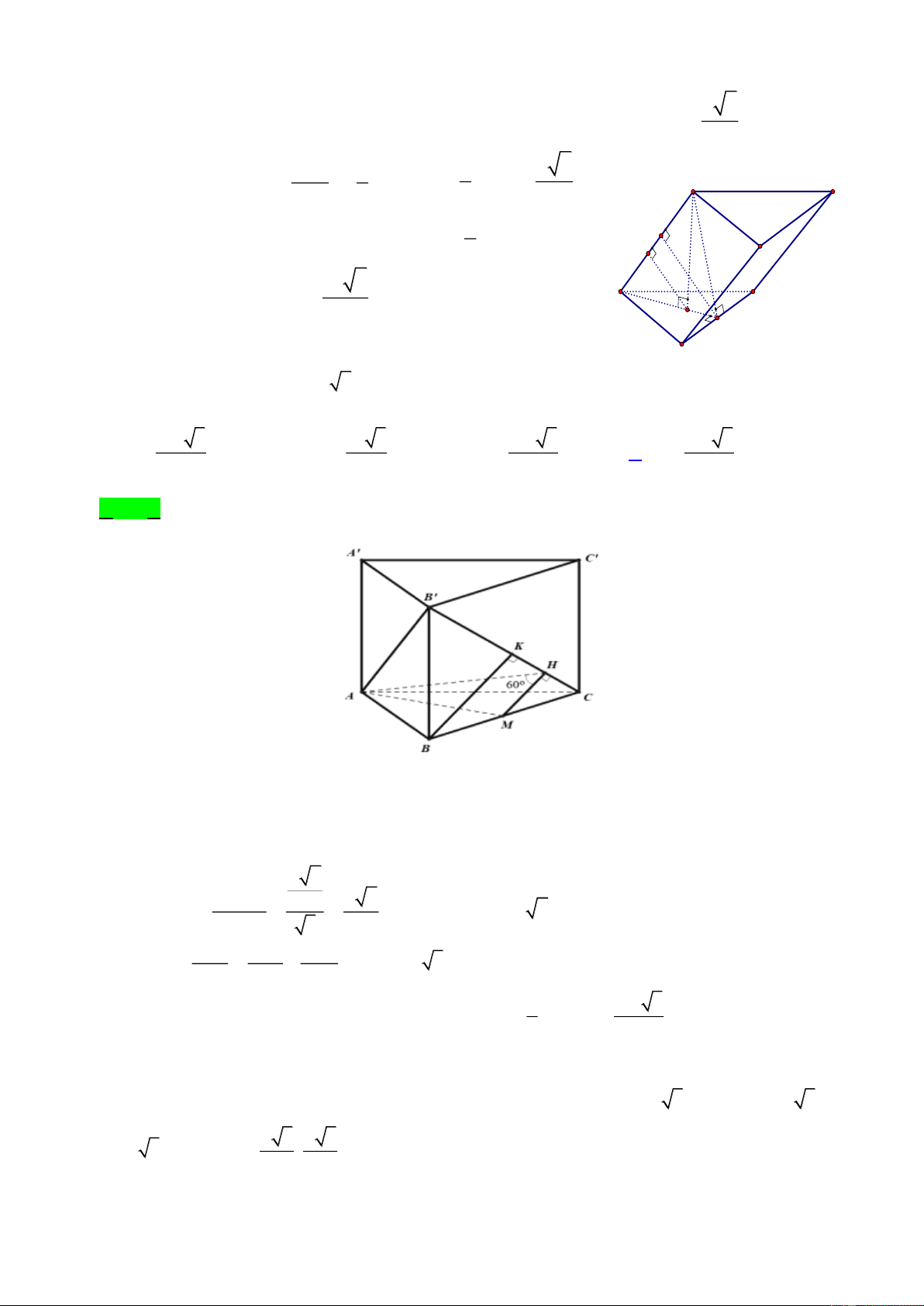
Ví dụ 4. Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A , góc BAC
nhọn. Góc giữa AA' và BC' là 0
30 , khoảng cách giữa AA' và BC' là a . Góc giữa hai mặt bên (AA'B'B) và (AA'C'C) là 0
60 . Thể tích lăng trụ ABC.A' B'C' là 3 2a 3 3 a 3 3 a 6 3 a 6 A. B. C. D. 3 3 6 3 Hướng dẫn giải: A' C'
Ta có góc giữa hai mặt bên (AA'B'B) và (AA'C'C) là 0 BAC = 60  ABC đều. B' 300 Vì  ( )=( ) 0 AA'/ /CC' AA'; BC' CC'; BC' = BC'C = 30
Kẻ AI ⊥ BC  AI ⊥ (BB'C'C) 600 C A I Trang 23 B
d(AA'; BC') = d(AA';(BB'C'C)) = AI = a 3  = 2a = BC =  = 1 2a = 2a 3 BC ,CC' 2a V 2a. .a. 0 ABC.A ' B' C ' 3 tan 30 2 3 3 Chọn đáp án A.
Ví dụ 5. Cho hình lăng trụ tam giác đều ABC. A’B’C’, có cạnh đáy bằng a và cạnh bên bằng a 2 . A M A ' N 1
Lấy M, N lần lượt trên cạnh AB’, A’C sao cho = =
. Tính thể tích V của khối A B ' A 'C 3 BMNC’C. 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27 Hướng dẫn giải: Chọn đáp án B. A' C' N K B' I
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và AA’C’C. G M Ta có: A M 1 A M 2 = Þ = (Do G trung điểm AB’). A B ' 3 A G 3 A C
Xét tam giác ABA’ có AG là trung tuyến và A M 2 = . Suy ra M là A G 3 H
trọng tâm tam giác ABA’. Do đó BM đi qua trung điểm I của AA’. A ' N 1 A ' N 2 Ta có: = Þ =
(Do K là trung điểm A’C). B A 'C 3 A ' K 3 A ' N 2
Xét tam giác AA’C’ có A’K là trung tuyến và =
. Suy ra N là trọng tâm của tam giác AA’C’. A ' K 3
Do đó C’N đi qua trung điểm I của AA’.
Từ M là trọng tâm tam giác ABA’ và N là trọng tâm của tam giác AA’C’. Suy ra: IM IN 1 = = . IB IC ' 3
Gọi V ; V lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có: 1 2 V IM IN IC 1 8 1 = . . =
. Mà V + V = V . Suy ra V = V . V IB IC ' IC 9 1 2 2 9 2
Hạ AH vuông góc với BC tại H thuộc BC.Ta được AH vuông góc với mặt phẳng (BB’C’C). AA’
song song với mặt phẳng (BB 'C 'C ) nên khoẳng cách từ I đến mặt phẳng (BB’C’C) bằng khoẳng
cách từ A đến (BB’C’C) và bằng AH. Ta có: a 3 A H = . 2 2 3 1 1 a 3 a 2 a 6 3 8 2a 6 V .d I
é ; BB 'C 'C .S ù = = . . = V = V = 2 ê ( ) . Suy ra . ë ú DBCC ' 3 û 3 2 2 12 2 9 27 2.Bài tập áp dụng
Câu 1. Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy a ; biết khoảng cách giữa hai đường thẳng a AB và A C ¢ bằng
15 . Thể tích của khối lăng trụ AB . C A BC
  tính theo a bằng: 5 Trang 24 3 3 3 3 A. 3 3a . 3a 3a 3a B. . C. . D. . 8 2 8 4
Câu 2. Cho hình lăng trụ A BC .A ' B 'C ' có đáy A BC là tam giác đều cạnh a , hình chiếu vuông
góc của A ' lên măt phẳng (A BC
) trùng với tâm G của tam giác ABC . Biết khoảng cách giữa a 3
A A ' và BC là
. Tính thể tích V của khối lăng trụ A BC .A ' B 'C ' . 4 3 3 3 3 A. a 3 a 3 a 3 V = B. V = C. a 3 V = D. V = 3 6 12 36
Câu 3. Cho lăng trụ đứng AB . C A BC
  có đáy là tam giác ABC vuông cân tại A , cạnh BC = a 6 .
Góc giữa mặt phẳng ( AB'C) và mặt phẳng (BCC B  ) bằng 0
60 . Tính thể tích V của khối lăng trụ AB . C A BC  ? 3 3 3 3 A. 2a 3 a 3 3a 3 3a 3 V = . B. V = . C. V = . D. V = . 3 2 4 2
Câu 4. Cho khối hộp ABC . D A BCD
  có đáy là hình chữ nhật với AB = 3 ; AD = 7 . Hai mặt bên ( ABB A  ) và ( ADD A
 ) cùng tạo với đáy góc 45, cạnh bên của hình hộp bằng 1 (hình vẽ).
Thể tích của khối hôp là: A. 7 . B. 3 3 . C. 5. D. 7 7 .
Câu 5. Cho hình lăng trụ đứng AB . C A BC
  có đáy là tam giác vuông cân đỉnh A , mặt bên là BCC B
  hình vuông, khoảng cách giữa AB và CC bằng a . Thể tích khối lăng trụ AB . C A BC   là 3 3 A. 3 2a 2a 2a . B. . C. 3 a . D. . 3 2
Câu 6. Cho lăng trụ đứng ABC
A BC có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa mặt phẳng (A
B C) và mặt phẳng (B B C) bằng 0
60 .Tính thể tích lăng trụ ABC A BC . A. 3 a 2 3 B. 3 2a C. 3 a 6 D. 3a
Câu 7. Cho hình lập phương AB D
C .A' B ' C ' D ' có khoảng cách giữa A' C và C ' D ' là 1 cm.
Thể tích khối lập phương AB D
C .A' B ' C ' D ' là: A. 3 8 cm . B. 3 2 2 cm . C. 3 3 3 cm . D. 3 27 cm .
Câu 8. Cho hình hộp ABCDA’B’C’D’. Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng
thời song song với B’D’. Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V1, V2 ( Trong đó V 1
1 là thể tích khối chứa A). Tính tỉ số = V F . V2 7 17 8 A. . B. 1. C. . D. . 17 25 17
Câu 9. Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm a
O của tam giác ABC đến mặt phẳng ( A B
C) bằng . Thể tích khối lăng trụ bằng 6 3 3 3 3 A. 3a 2 . 3a 2 3a 2 3a 2 B. . C. . D. 4 8 28 16
Câu 10. Cho lăng trụ đứng AB . C A BC
 . Biết rằng góc giữa hai mặt phẳng (A B
C) và ( ABC) là 30 , tam giác A B
C đều và diện tích bằng 3 . Thể tích khối lăng trụ AB . C A BC   bằng 3 3 A. 2 3 . B. 6 . C. . D. 3 . 4 4 Trang 25 3. Hướng dẫn giải
Câu 1. Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy a ; biết khoảng cách giữa hai đường thẳng a AB và A C ¢ bằng
15 . Thể tích của khối lăng trụ AB . C A BC
  tính theo a bằng: 5 3 3 3 3 A. 3 3a . 3a 3a 3a B. . C. . D. . 8 2 8 4 Hướng dẫn giải Chọn D Ta có AB A B
   AB ( A BC  ) a 15 / / / /  d( = d = d = AB, A C  )
(AB,(A BC))
(B,(A BC)) 5
Đặt AA = x  0 . Tam giác CA B   cân tại C , 2 2
CA = CB = a + x . 2 2 2 + Diện tích tam giác 1 a 1 3a 4x 1 CA B   là 2 2 2 2 S = + − = = +   . . a a x . a a 3a 4x CA B 2 4 2 2 4 2 Thể tích lăng trụ a 3 V = . x ( )1 4 Lại có 1 a 15 1 2 2 V = 3V = = +   3. d .S .     . . a 3a 4x B.A B C (B,(A B C)) 3 A B C 5 4 2 Do đó a 3 a 15 1 2 2 2 2 . x = . .
a 3a + 4x  5x 3 = 15. 3a + 4x x = a 3 . 4 5 4 2 3 a 3 3a V = . x = . 4 4
Câu 2. Cho hình lăng trụ A BC .A ' B 'C ' có đáy A BC là tam giác đều cạnh a , hình chiếu vuông
góc của A ' lên măt phẳng (A BC
) trùng với tâm G của tam giác ABC . Biết khoảng cách giữa a 3
A A ' và BC là
. Tính thể tích V của khối lăng trụ A BC .A ' B 'C ' . 4 3 3 3 3 A. a 3 a 3 a 3 V = B. V = C. a 3 V = D. V = 3 6 12 36 Hướng dẫn giải:
Gọi M là trung điểm BÞ BC ^ (A ' A M ) Trang 26
Gọi H,K lần lượt là hình chiếu vuông góc của G,M trên AA’ a 3
Vậy KM là đọan vuông góc chung củaAA’và BC, do đó d(A A',BC) = KM = . 4 K M 3 2 a 3 DA GH : DA MH Þ = Þ GH = KH = A' C' GH 2 3 6 a
D AA’G vuông tại G,HG là đường cao,A 'G = K 3 H B' 3 a 3 V = S .A 'G = A C
A BC .A ' B 'C ' A BC 12 G Chọn đáp án C. M
Câu 3. Cho lăng trụ đứng AB . C A BC
  có đáy là tam giác ABC B
vuông cân tại A , cạnh BC = a 6 . Góc giữa mặt phẳng ( AB'C) và mặt phẳng (BCC B  ) bằng 0 60
. Tính thể tích V của khối lăng trụ AB . C A BC  ? 3 3 3 3 A. 2a 3 a 3 3a 3 3a 3 V = . B. V = . C. V = . D. V = . 3 2 4 2 Lời giải Chọn D Cách 1.
+ Gọi M là trung điểm của BC AM ⊥ (BCC B  )
+ Gọi H, K lần lượt là hình chiếu vuông góc của M, B trên B C  + Khi đó B C
 ⊥ ( AMH )  B C
 ⊥ AH  ((AB C  ) (BB C  )) = (AH MH) o , , = AHM = 60 . a 6 AM a 2 + Ta có 2 MH = = =
HK = 2MH = a 2 . o tan 60 3 2 + Mặt khác 1 1 1 = +  B B  = a 3 . 2 2 2 BK BC B B  3
+ Vậy thể tích của khối lăng trụ 1 3a 3 AB . C A BC
  là V = B . B A . B AC = . 2 2 Cách 2.
+ Gọi chiều cao của hình lăng trụ là h .
+ Đặt hệ trục tọa độ Axyz như hình vẽ. Khi đó A(0;0;0) , B(a 3;0;0) , C(0;a 3;0) ,  a a
B(a 3;0;h)  3 3 M  ; ; 0  
 là trung điểm của BC . 2 2   Trang 27   + Vì a a AM ⊥ (BCC B  ) và 3 3 AM =  ; ; 0  
 nên n = (1;1;0) là VTPT của (BCC ' B') . 2 2  
+ Ta có AC, AB =   ( 2 ah 3;0; 3 − a )  = − 1 n
( ;h0; 3a) là VTPT của (AB'C).
+ Theo giả thiết góc giữa ( AB C
 ) và mặt phẳng (BCC B  ) bằng 60   = ( 1 h cos 60 cos , n  =  = 1 n ) h 3a 2 2 2 2. h + 3a 3
+ Vậy thể tích của khối lăng trụ 3a 3 AB . C A BC   là V = . 2
Câu 4. Cho khối hộp ABC . D A BCD
  có đáy là hình chữ nhật với AB = 3 ; AD = 7 . Hai mặt bên ( ABB A  ) và ( ADD A
 ) cùng tạo với đáy góc 45, cạnh bên của hình hộp bằng 1 (hình vẽ).
Thể tích của khối hôp là: A. 7 . B. 3 3 . C. 5. D. 7 7 . Lời giải Chọn A B' C' A' D' B K C H A I D Hạ A H
 ⊥ (ABCD),H (ABCD); HI ⊥ A ,
D I AD ; HK ⊥ A , B K AB
A ' H ⊥ ( ABCD)  A' H ⊥ AD A'I ⊥ AD IH ⊥ AD 
AI ⊥ AD, IH ⊥ AD  (    ABCD ADD A   = HIA (Do HIA  90 ) DD A A  ) ( ABCD) (( ),( )) = AD
Chứng minh tương tự (( ABCD),( ABB A  )) = HKA
Từ giả thiết suy ra: HIA = H
KA = 45  HA = HI = HK Trang 28
Có ABCD là hình chữ nhật, HI ⊥ A ,
D I AD ; HK ⊥ A , B K AB
Nên AIHK là hình vuông suy ra AH = HK 2 = A H  2 + A H
 ⊥ (ABCD),H (ABCD)  AH ⊥ A H  2 2 2 2  AA = A H  + HA = 1 3A H  → HA = 3 V =  =     A H.A . B AD 7 . ABC . D A B C D
Câu 5. Cho hình lăng trụ đứng AB . C A BC
  có đáy là tam giác vuông cân đỉnh A , mặt bên là BCC B
  hình vuông, khoảng cách giữa AB và CC bằng a . Thể tích khối lăng trụ AB . C A BC   là 3 3 A. 3 2a 2a 2a . B. . C. 3 a . D. . 3 2 Lời giải Theo giả thiết, ta có
d (CC ; AB) = d (CC ,( ABB A
 )) = d (C,(ABB A
 )) = CA = a . 3
Do đó, thể tích khối lăng trụ 1 2a AB . C A BC   là 2
V = CC .S = a 2. .a = . ABC  2 2
Câu 6. Cho lăng trụ đứng ABC
A BC có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa mặt phẳng (A
B C) và mặt phẳng (B B C) bằng 0
60 .Tính thể tích lăng trụ ABC A BC . A. 3 a 2 3 B. 3 2a C. 3 a 6 D. 3a Hướng dẫn giải:
Từ A kẻ AI⊥ BC I là trung điểm BCA' ⊥ CB ⊥ BC' AI (BC ) AI C (1)
Từ I kẻ IM⊥ B C (2) B'
Từ (1), (2)  BC ⊥ (IAM) B'
Vậy góc giữa (A BC) và ( BCB) là AMI H = 600 1 AI a M
Ta có AI= BC = a ; IM= = 0 M 2 tan 60 3 B C 600 I 2 A = 2 = a BH IM ; C 3 I 1 1 1 3 1 1 = − = − = . 2 2 2 2 2 2 B ' B BH BC 4a 4a 2a B Suy ra  BB = a 2 ; 1 1 2 S = AI.BC = . a 2a =  a ABC 2 2 Trang 29 2 3 V = a a = a ABC A BC 2. 2 Chọn đáp án A.
Câu 7. Cho hình lập phương AB D
C .A' B ' C ' D ' có khoảng cách giữa A' C và C ' D ' là 1 cm.
Thể tích khối lập phương AB D
C .A' B ' C ' D ' là: A. 3 8 cm . B. 3 2 2 cm . C. 3 3 3 cm . D. 3 27 cm . Hướng dẫn giải:
Để tìm khoảng cách giữa A’C và C’D’, ta dựng một mặt phẳng chứa A’C và song song với C’D’. Dễ
thấy đó là mặt phẳng (CA’B’).
Gọi a là độ dài cạnh của khối lập phương, lúc này ta có:
d (C ' D ', A'C ) = d C ' D ', 
(CA'B') = d D',   (CA'B') 
Để tính khoảng cách từ điểm D’ đến mặt phẳng (CA’B’), ta xét khối tứ diện D’CA’B’. 2 3 1 1 = a a V .CC '.S = . . a = cm D CA B B A D ( 3 ' ' ' ' ' ' ) 3 3 2 6 1 1 2 2 S
= .CB'. B'A' = .a 2.a = a cm CA B ( 2 ' ' ) (do tam giác 2 2 2 CA’B’ vuông tại B’) 3 a 3V 2
Suy ra: d D (CA B ) ' ' ' 2 ', ' '  = = = aD CA B
(cm)  a = 2 (cm). SCA B 2 2 ' ' 2 a 2 Do đó 3 3
V = a = 2 2 cm Chọn đáp án B.
Câu 8. Cho hình hộp ABCDA’B’C’D’. Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng
thời song song với B’D’. Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V1, V2 ( Trong đó V 1
1 là thể tích khối chứa A). Tính tỉ số = V F . V2 7 17 8 A. . B. 1. C. . D. . 17 25 17 Hướng dẫn giải:
*Gọi N là trung điể A’D’. Khi đó (P)BDNM). Thấy BMDNAA’=I.
Khi đó: V1=V(A’MNABD); V2=V-V1. (Với V là thể tích hình hộp)
V (IA ' MN ) S ( AMN ) 1 * Ta có: = = V ( A A 'B'D')
S ( A ' B ' D ') 4 I * Mà: V (AA'B'D') 1 = nên có: 1
V (IA' MN ) = V V 6 24
V (IA ' MN )
IA '.IM .IN 1 * Lại có: = = V (IABD) I . A I . B ID 8 D' C' 1 N
*Vậy: V (IABD) = V M 3 A' B' 1 1 7 17
* Do đó: V = V − V =
V nên V = V −V = V . Vậy: 1 3 24 24 2 1 24 V 7 D 1 = C V 17 2 A B Trang 30 Chọn đáp án A.
Câu 9. Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm a
O của tam giác ABC đến mặt phẳng ( A B
C) bằng . Thể tích khối lăng trụ bằng 6 3 3 3 3 A. 3a 2 . 3a 2 3a 2 3a 2 B. . C. . D. 4 8 28 16 Lời giải A' C' B' H A C O M B
Gọi M là trung điểm của BC và H là hình chiếu của A trên A'M . BC ⊥ AM  Ta có
  BC ⊥ ( AA M
 )  BC ⊥ AH BC ⊥ AA  Mà AH ⊥ A M  (2) Từ và  d ( , A ( A BC)) = AH .
d (O,( ABC )) Ta có MO 1 = = . d ( , A ( A BC )) MA 3  ( a a d , A ( A BC)) = 3d ( , O ( A B
C)) =  AH = . 2 2 Xét tam giác vuông 1 1 1 1 4 4 a 3 A' AM : = +  = −  AA = . 2 2 2 AH AAAM 2 2 2 AAa 3a 2 2 2 3
Suy ra thể tích lăng trụ a 3 a 3 3 2a AB . C A' B C
  là: V = AA .S = . = . ABC  2 2 4 16
Câu 10. Cho lăng trụ đứng AB . C A BC
 . Biết rằng góc giữa hai mặt phẳng (A B
C) và ( ABC) là 30 , tam giác A B
C đều và diện tích bằng 3 . Thể tích khối lăng trụ AB . C A BC   bằng 3 3 A. 2 3 . B. 6 . C. . D. 3 . 4 4 Lời giải Trang 31 C' A' B' C A H B
Trong ( ABC) vẽ AH ⊥ BC tại H .
Dễ thấy BC ⊥ ( A A
H )  BC ⊥ A H  nên (( A B
C),( ABC)) = ( A H  , AH ) = A HA = 30. Tam giác A B
C đều có A H
 là đường cao nên đồng thời là đường trung tuyến.   Ta có A A A A AH = = A . A 3 và A H  = = 2A A  . tan 30 sin 30 Diện tích 3 3 2 2 2 S =  =  =  =  BC BC 3 BC 4 BC 2 . A BC 4 4 Mà BC 3 3 3 A H  = = 3  A A  = ; AH = . 2 2 2  
Thể tích khối lăng trụ 1 3 1 3 3 3 V =  =  = =    A . A S A . A .AH .BC . . .2 . ABC. A B C ABC    2  2 2 2 4 Trang 32