37 trang 27 lượt tải

Chuyên đề thực hiện phép tính bồi dưỡng học sinh giỏi Toán 6 – 7

54

Tài liệu gồm 37 trang, được biên soạn bởi tác giả Ngô Thế Hoàng (giáo viên Toán trường THCS Hợp Đức, tỉnh Bắc Giang), hướng dẫn giải các dạng toán chuyên đề thực hiện phép tính bồi dưỡng học sinh giỏi Toán 6 – 7, giúp các em học sinh khối lớp 6, lớp 7 ôn tập để chuẩn bị cho các kỳ thi chọn HSG.

Chủ đề: Tài liệu chung Toán 6 340 tài liệu

Môn: Toán 6 2.4 K tài liệu

Tác giả:

Profile

Nguyễn Vân

1 năm trước
Danh sách Quiz
/37
1
CHUYÊN ĐỀ : THỰC HIỆN PHÉP TÍNH
DẠNG 1: RÚT GỌN
Bài 1: Thực hiện phép tính:
a,
12 5 6 2 10 3 5 2
2 6 3 9 3
2 .3 4 .9 5 .7 25 .49
(2 .3) (125.7) 5 .14
−−
−
+
b,
18 7 3 15 15
10 15 14 13
2 .18 .3 3 .2
2 .6 3 .15.4
+
+
c,
6 5 9
4 12 11
4 .9 6 .120
8 .3 6
+
−
HD :
a, Ta có:
12 5 6 2 10 3 5 2
2 6 3 9 3
2 .3 4 .9 5 .7 25 .49
(2 .3) (125.7) 5 .14
−−
−
+
( ) ( ) ( ) ( )
( )
6 2 5 2
12 5 2 2 10 3 2 2
3
12 6
3 3 9 3 3
2 .3 2 . 3 5 .7 5 . 7
2 .3
5 .7 5 .2 .7
−−
=−
+
( ) ( )
( )
12 4 10 3
12 5 12 4 10 3 10 4
12 6 9 3 9 3 3 12 6 9 3
2 .3 3 1 5 .7 1 7
2 .3 2 .3 5 .7 5 .7
2 .3 5 .7 5 .2 .7 2 .3 5 .7 1 8
−−
−−
= − = −
++
2
2 5.6 28
3 9 9
−
= − =
b, Ta có:
18 7 14 3 15 15 25 17 15 15
10 15 15 14 28 25 15 15 28
2 .2 .3 .3 3 .2 2 .3 3 .2
2 .2 .3 3 .3.5.2 2 .3 3 .2 .5
++
==
++
( )
( )
( )
15 15 10 2 10 2
10
25 15 3
2 .3 2 .3 1 2 .3 1
2 41
2 .3 1 2 .5
++
==
+
c, Ta có:
6 5 9
4 12 11
4 .9 6 .120
8 .3 6
+
−
=
( ) ( )
( )
65
2 2 9 9 3
12 10 12 10
4
12 12 11 11
3 12 11 11
2 . 3 2 .3 .2 .3.5
2 .3 2 .3 .5
2 .3 2 .3
2 .3 2 .3
+
+
=
−
−
( )
( )
12 10
11 11
2 .3 1 5
2.6 4
2 .3 2.3 1 3.5 5
+
= = =
−
Bài 2: Thực hiện phép tính:
a,
15 9 20 9
9 16 29 6
5.4 .9 4.3 .8
5.2 .9 7.2 .27
−
−
b,
4 2 2
3 3 2
2 .5 .11 .7
2 .5 .7 .11
c,
11 12 11 11
12 11 11 11
5 .7 5 .7
5 .7 9.5 .7
+
+
HD :
a, Ta có:
15 9 20 9
29 16 29 6
5.4 .9 4.3 .8
5.2 .3 7.2 .27
−
−
=
( )
( )
29 18 2
30 18 29 20
29 16 29 18
29 16 2
2 .3 5.2 3
5.2 .3 2 .3
5.2 .3 7.2 .3
2 .3 5 7.3
−
−
=
−
−
=
2
39
58 58
−
=
−
b, Ta có:
4 2 2
3 3 2
2 .5 .11 .7
2 .5 .7 .11
=
2.11 22
5.7 35
=
c, Ta có:
11 12 11 11
12 11 11 11
5 .7 5 .7
5 .7 9.5 .7
+
+
=
( )
( )
11 11
11 11
5 .7 7 1
84
5 .7 5 9 14 7
+
==
+
Bài 3: Thực hiện phép tính:
a,
22 7 15
14 2
11.3 .3 9
(2.3 )
−
b,
10 10 10 9
9 10
2 .3 2 .3
2 .3
−
c,
5 4 9
10 8 8
4 .9 2.6
2 .3 6 .20
−
+
HD :
a, Ta có:
22 7 15
14 2
11.3 .3 9
(2.3 )
−
=
( )
29
29 30
2 28 2 28
3 . 11 3
11.3 3 3.8
6
2 .3 2 .3 4
−
−
= = =
b, Ta có:
10 10 10 9
9 10
2 .3 2 .3
2 .3
−
( )
10 9
9 10
2 .3 3 1
2.2 4
2 .3 3 3
−
= = =
c, Ta có:
5 4 9
10 8 8
4 .9 2.6
2 .3 6 .20
−
+
( )
( )
10 8
10 8 10 9
10 8 10 8 10 8
2 .3 1 3
2 .3 2 .3 2 1
2 .3 2 .3 .5 2 .3 1 5 6 3
−
− − −
= = = =
++
Bài 4: Thực hiện phép tính:
a,
12 5 6 2 10 3 5 2
2 6 4 5 3 9 3
2 .3 4 .9 5 .7 25 .49
(2 .3) 8 .3 (125.7) 5 .14
−−
−
++
b,
15 9 20 9
9 19 29 6
5.4 .9 4.3 .8
5.2 .6 7.2 .27
−
−
c,
5 4 9
10 8 8
4 .9 2.6
2 .3 6 .20
−
+
HD:
2
a, Ta có :
12 5 6 2 10 3 5 2
2 6 4 5 3 9 3
2 .3 4 .9 5 .7 25 .49
(2 .3) 8 .3 (125.7) 5 .14
−−
−
++
=
( )
( )
( )
( )
( )
12 4 10 3
12 5 12 4 10 3 10 4
12 6 12 5 9 3 9 3 3 12 5 9 3
2 .3 3 1 5 .7 1 7 5. 6
2 .3 2 .3 5 .7 5 .7 10
2 .3 2 .3 5 .7 5 .7 .2 2 .3 3 1 5 .7 1 8 9 3
− − −
− − −
− = − = =
+ + + +
b, Ta có :
15 9 20 9
9 19 29 6
5.4 .9 4.3 .8
5.2 .6 7.2 .27
−
−
=
( )
( )
29 18 2
30 18 20 29
28 19 29 18 28 18
2 .3 5.2 3
5.2 .3 3 .2 2
2
5.2 .3 7.2 .3 2 .3 5.3 7.2 1
−
−
= = =
−−
c, Ta có :
5 4 9
10 8 8
4 .9 2.6
2 .3 6 .20
−
+
=
( )
( )
10 8
10 8 10 9
10 8 10 8 10 8
2 .3 1 3
2 .3 2 .3 2 1
2 .3 2 .3 .5 2 .3 1 5 6 3
−
− − −
= = =
++
Bài 5: Thực hiện phép tính:
a,
12 7 15 8
24 14 12 5
15.4 .9 4.3 .8
19.2 .3 6.4 .27
−
−
b,
15 22 16 4
9 7 5 23
3 .2 6 .4
2.9 .8 7.27 .2
+
−
c,
3 10 9
6 12 11
16 .3 120.6
4 .3 6
+
+
HD :
a, Ta có:
12 7 15 8
24 14 12 5
15.4 .9 4.3 .8
19.2 .3 6.4 .27
−
−
=
( )
( )
24 15 2
24 15 26 15
24 14 25 16
24 24 2
2 .3 5 2
5.2 .3 2 .3 3
3
19.2 .3 2 .3 1
2 .3 19 2.3
−
−
= = =
−
−
b, Ta có :
15 22 16 4
9 7 5 23
3 .2 6 .4
2.9 .8 7.27 .2
+
−
=
( )
( )
22 15 2
15 22 24 16
22 18 15 23
22 15 3
2 .3 1 2 .3
3 .2 2 .3 13 13
2 .3 7.3 .2 5 5
2 .3 3 7.2
+
+−
= = =
−−
−
c, Ta có:
( )
( )
( )
( )
( )
( )
3
9
4 10 3
12 10
12 10 12 10
6
12 12 11 11 11 11
11
2 12
2 .3 2 .3.5. 2.3
2 .3 1 5
2 .3 2 .3 .5 2.6 12
2 .3 2 .3 2 .3 2.3 1 3.7 21
2 .3 2.3
+
+
+
= = = =
++
+
Bài 6: Thực hiện phép tính :
a,
( )
( )
12 5 6 2 10 3 5 2
63
93
2 4 5
2 .3 4 .9 5 .7 25 .49
125.7 5 .14
2 .3 8 .3
A
−−
=−
+
+
b,
15 9 20 9
10 12 29 6
5.4 .9 4.3 .8
5.2 .6 7.2 .27
−
−
Bài 7: Thực hiện phép tính:
a,
( )
12 5 6 2
6
2 4 5
2 .3 4 .9
2 .3 8 .3
A
−
=
+
b,
5 4 9
10 8 8
4 .9 2.6
2 .3 6 .20
B
−
=
+
Bài 8: Thực hiện phép tính :
a,
10 10
94
3 .11 3 .5
3 .2
+
b,
10 10
8
2 .13 2 .65
2 .104
+
Bài 9: Thực hiện phép tính:
a,
30 7 13 27
27 7 10 27
2 .5 2 .5
2 .5 2 .5
+
+
b,
( ) ( )
( )
66
53
10
53
3 .15 9 . 15
3 .5 .2
− + −
−
Bài 10: Thực hiện phép tính:
a,
2 11 2 2 6 2
12 4 2 3
5 .6 .16 6 .12 .15
2.6 .10 81 .960
+
−
b,
( )
( )
9
19 3 4
10
9 10
2 .27 .5 15. 4 .9
6 .2 12
A
−−
=
−−
Bài 11: Thực hiện phép tính:
a,
( )
( )
5
15 4 10 20
6
6 3 15
0,8
2 .9 45 .5
:
6 .8 75
0,4

+



b,
( )
15 14
22 21
10 16 15
5 3.7 19.7
2.5 9.5
:
25 7 3.7
A
−
−
=
+
Bài 12: Tính giá trị của biểu thức:
7 3 3
7
77
2 9 3
.5 :
5 4 16
2 .5 512
A
+
=
+
3
Bài 13: Tính biểu thức:
3 3 1
0,6 1 0,875 0,7
14
7 13 6
2 1,21 :
6 6 1
25
1,2 0,25 0,2
7 13 3
B
− − − + −
= − +
− − − +
Bài 14: Tính biêu thức:
( ) ( )
( )
36
3
2
1 1 1 3 .12
84 51. 37 51. 137
3 4 7
27.4
A
−

= − + − + − − − +


Bài 15: Thực hiện phép tính:
a, 1024:
55
(17.2 15.2 )+
b,
3 0 3
5 .2 (23 4 ):2++
c,
5 4 2
(5.3 17.3 ):6+
HD :
a, Ta có: 1024:
55
(17.2 15.2 )+
( )
( )
10 5 10 5 5
2 : 2 17 15 2 : 2 .2 1

= + = =

b, Ta có:
3 0 3
5 .2 (23 4 ):2++
33
5 .2 24:2 250 3 253= + = + =
c, Ta có:
5 4 2
(5.3 17.3 ):6+
( )
( )
45
4 2 2 4 2 2
22
3 .2
3 3.5 17 :3 .2 3 .32 :3 .2 9.8 72
3 .2

+ = = = =

Bài 16: Thực hiện phép tính:
a,
2 2 2 2 2
(10 11 12 ):(13 14 )+ + +
b,
3 4 3 2 2
(2 .9 9 .45):(9 .10 9 )+−
HD :
a, Ta có:
2 2 2 2 2
(10 11 12 ):(13 14 )+ + +
( ) ( )
100 121 144 : 169 196 365:365 1= + + + = =
c Ta có :
3 4 3 2 2
(2 .9 9 .45):(9 .10 9 )+−
=
( ) ( )
( )
83
6
3 8 11 2 2 6
2
3 8 3 .5
3 .143
2 .3 3 .5 : 3 .10 3 13.3
3 .11 11
+
+ + = = =
Bài 17: Thực hiện phép tính:
a,
14 14 16 4
(3 .69 3 .12):3 7 :2

+−

b,
4 4 12 12
24 :3 32 :16−
HD :
a, Ta có:
14 14 16 4
(3 .69 3 .12):3 7 :2

+−

( ) ( )
14 14 2 16 4 15 15 16 4
3 .3.23 3 .3.2 :3 7 :2 3 .23 3 .4 :3 7 :2
= + − = + −
( )
15 16 4 4
3
1
3 .27:3 7 :2 9 7 :2
2

= − = − =

b, Ta có:
4 4 12 12
24 :3 32 :16−
=
( ) ( )
4 12
4 12 12 12
24:3 32:16 8 2 2 2 0− = − = − =
Bài 18: Thực hiện phép tính :
a,
( )
2010 10 8 4 2010 2010
2010 7 :7 3.2 2 :2−−
b,
( ) ( )
100 101 102 97 98 99
2 2 2 : 2 2 2+ + + +
HD :
a, Ta có :
( )
( )
2010 10 8 4 2010 2010 2010
2010 7 :7 3.2 2 :2 2010 49 3.16 1 0− − = − − =
Bài 19: Tính:
5
11
3
4
2
1
3
2
3
5
42
5
53
A
−
−
+
−
=
−
−
−
1
1
4
1
3
13
2
37
B
−
+
=
+−
Bài 20: Thực hiện phép tính :
1
1
1
45 1 1 1
19 2 3 4
−
−
−




− + +







HD :
4
45 1 45 26
1
11
19 19 19
1
2
4
3
= − = − =
+
+
Bài 21: Rút gọn :
3 2 1 3 2 1
:
2 5 10 2 3 12
A
= − + − +
5
DẠNG 2 : TÍNH ĐƠN GIẢN
Bài 1: Thực hiện phép tính:
1 1 1 2 2 2
2003 2004 2005 2002 2003 2004
5 5 5 3 3 3
2003 2004 2005 2002 2003 2004
+ − + −
−
+ − + −
HD:
Ta có :
1 1 1 2 2 2
2003 2004 2005 2002 2003 2004
5 5 5 3 3 3
2003 2004 2005 2002 2003 2004
+ − + −
−
+ − + −
=
1 1 1
1 1 1
2
2002 2003 2004
2003 2004 2005
1 1 1 1 1 1
53
2003 2004 2005 2002 2003 2004

+−
+−


−
+ − + −
1 2 7
5 3 15
−
= − =
Bài 2: Thực hiện phép tính:
33
0,375 0,3
1,5 1 0,75 1890
11 12
: 115
5 5 5
2005
2,5 1.25 0,625 0,5
3 11 12

− + +

+−
++


+ − − + − −

HD:
Ta có :
33
0,375 0,3
1,5 1 0,75 1890
11 12
: 115
5 5 5
2005
2,5 1.25 0,625 0,5
3 11 12

− + +

+−
++


+ − − + − −

=
3 3 3 3 3 3 3
378
2 3 4 8 10 11 12
: 115
5 5 5 5 5 5 5
401
2 3 4 8 10 11 12

+ − − + +

++

−

+ − + − −

=
3 3 378 378
: 115 0: 115 115
5 5 401 401

+ + = + =

−

Bài 3: Thực hiện phép tính:
1 1 1 3 3 3
0,6
9 7 11 25 125 625
4 4 4 4 4 4
0,16
9 7 11 5 125 625
− − − − −
+
− − − − −
HD:
Ta có :
1 1 1 3 3 3
0,6
9 7 11 25 125 625
4 4 4 4 4 4
0,16
9 7 11 5 125 625
− − − − −
+
− − − − −
=
13
1
44
+=
Bài 4: Thực hiện phép tính:
12 12 12 3 3 3
12 3
7 25 71 13 19 101
564. :
4 4 4 5 5 5
45
7 25 71 13 19 101

+ − − + + +



+ − − + + +

HD:
Ta có :
12 12 12 3 3 3
12 3
7 25 71 13 19 101
564. :
4 4 4 5 5 5
45
7 25 71 13 19 101

+ − − + + +



+ − − + + +

=
12 3
564. : 564.5 2820
45

==


Bài 5: Thực hiện phép tính:
6
a,
1 1 1 1
1
2 4 8 16
1 1 1 1
1
2 4 8 16
+ + + +
− + − +
b,
5 5 5
15 15
5
15
3 9 27
11 121
:
8 8 8 16 16
8 16
3 9 27 11 121
− + −
−+
− + − − +
HD:
a, Ta có :
1 1 1 1
1
2 4 8 16
1 1 1 1
1
2 4 8 16
+ + + +
− + − +
=
1 1 1 1
16 1
16 8 4 2 1 31
2 4 8 16
1 1 1 1
16 8 4 2 1 11
16 1
2 4 8 16

+ + + +

+ + + +

==
− + − +

− + − +


b, Ta có :
5 5 5
15 15
5
15
3 9 27
11 121
:
8 8 8 16 16
8 16
3 9 27 11 121
− + −
−+
− + − − +
=
5 15 5 16 2
:.
8 16 8 15 3
==
Bài 6: Thực hiện phép tính:
a,
2 2 2 4 4 4
24
19 43 1943 29 41 2941
:
3 3 3 5 5 5
35
19 43 1943 29 41 2941
− + − − + −
− + − − + −
b,
12 12 12 3 3 3
12 3
7 289 85 13 169 91
:
4 4 4 7 7 7
47
7 289 85 13 169 91
− − − + + +
− − − + + +
HD:
a, Ta có :
2 2 2 4 4 4
24
19 43 1943 29 41 2941
:
3 3 3 5 5 5
35
19 43 1943 29 41 2941
− + − − + −
− + − − + −
=
2 4 2 5 5
:.
3 5 3 4 6
==
b, Ta có :
12 12 12 3 3 3
12 3
7 289 85 13 169 91
:
4 4 4 7 7 7
47
7 289 85 13 169 91
− − − + + +
− − − + + +
=
12 3 7
: 3. 7
4 7 3
==
Bài 7: Thực hiện phép tính:
a,
5 7 9 11 3
(3 )
7 9 11 13 4
10 14 6 22 2
:(2 )
21 27 11 39 3
−

− + − −



+ − + −


b,
3 3 3 3
3
7 11 1001 13
9 9 9 9
9
1001 13 7 11
+ − + −
− + − +
HD:
a, Ta có :
5 7 9 11 3
(3 )
7 9 11 13 4
10 14 6 22 2
:(2 )
21 27 11 39 3
−

− + − −



+ − + −


=
5 7 9 11 9
9
.
9 1 9
7 9 11 13 4
4
:
23
2 5 7 9 11 4
4 2 2
.
:
34
3 7 9 11 13 3

−
− + − +

−−

= = =

+ − +


b, Ta có :
3 3 3 3
3
7 11 1001 13
9 9 9 9
9
1001 13 7 11
+ − + −
− + − +
=
1 1 1 1
31
31
7 11 1001 13
1 1 1 1
93
91
7 11 1001 13

+ − + −


==

+ − + −


Bài 8: Tính nhanh:
4 2 2
50
13 15 17
8 4 4
100
13 15 17
− + −
− + −
HD:
7
Ta có :
4 2 2
50
13 15 17
8 4 4
100
13 15 17
− + −
− + −
=
4 2 2
50
1
13 15 17
4 4 4
2
2 50
13 15 17
− + −
=

− + −


Bài 9: Tính:
a, A=
3 3 3 3
3
24.47 23
7 11 1001 13
.
9 9 9 9
24 47.23
9
1001 13 7 11
+ − + −
−
+
− + − +
b,
2
2 2 5
3.
3 3 6
7 35 35 105 35
:
60 31.37 37.43 43.61 61.67

+−



+ + +


HD:
a, Ta có :
( )
47 23 1 23
24.47 23 47.23 24
1
24 47.23 47.23 24 47.23 24
+−
−+
= = =
+ + +
và
1 1 1 1
31
3 3 1
7 11 1001 13
1 1 1 1
9 9 3
91
7 11 1001 13
A

+ − + −


= = = =

+ − + −


b, Ta có :
2 2 25 8 25 71
3.
3 3 36 3 36 36
TS = + − = − =
7 5.7 5.7 3.5.7 5.7
:
60 31.37 37.43 43.61 61.67
MS

= + + +


7 35 6 6 18 6
:
6 6 31.37 37.43 43.61 61.67


= + + +




7 35 1 1 1 1 1 1 1 1
:
60 6 31 37 37 43 43 61 61 67
MS


= − + − + − + −




7 35 1 1 2077
:
60 6 31 67 1800
MS


= − =




=>
71 2077
:
36 1800
B =
Câu 10: Thực hiện phép tính:
a,
10 5 5 3 3
155 0,9
7 11 23 5 13
26 13 13 7 3
402 0,2
7 11 23 91 10
A
− − + + −
=+
− − + + −
b,
33
0,375 0,3
1,5 1 0,75
11 12
5 5 5
0,625 0,5 2,5 1,25
11 12 3
A
− + +
+−
=+
− + − − + −
8
DẠNG 3 : TÍNH TỔNG TỰ NHIÊN
Bài 1: Tính tổng tự nhiên
a, A=
9 99 999 ... 999...9+ + + +
( 10 số 9) b, B=
1 11 111 ... 111...1+ + + +
(10 số 1)
HD:
a, Ta có:
( )
( ) ( ) ( )
2 3 10
10 1 10 1 10 1 ... 10 1A = − + − + − + + −
( )
2 3 10
10 10 10 ... 10 10 111...10 10 111...100= + + + + − = − =
( 9 số 1)
b, Ta có:
9 9 99 999 .... 9999...99B = + + + +
( 10 số 9). Tính như câu a
Bài 2: Tính tổng tự nhiên
a, C=
4 44 444 ... 444...4+ + + +
(10 số 4) b, D=
2 22 222 ... 222...2+ + + +
(10 số 2)
HD:
a, Ta có:
( )
4 1 11 111 ... 111...11C = + + + +
( 10 số 1)
( )
9 4 9 99 999 ... 999...99C = + + + +
( 10 số 9). Tính như tính ở trên
b, Ta có :
( )
2 1 11 111 ... 111...11D = + + + +
(10 số 1)
( )
9 2 9 99 999 ... 999...99D = + + + +
(10 số 9)
Bài 3 : Tính tổng sau: E=
3 33 333 ... 333...3+ + + +
(10 số 3)
9
DẠNG 4 : TÍNH TỔNG PHÂN SỐ
Bài 1: Tính nhanh tổng sau:
a, A=
1 1 1
...
5.6 6.7 24.25
+ + +
b, B=
2 2 2 2
...
1.3 3.5 5.7 99.101
+ + + +
HD:
a, Ta có :
1 1 1 1 1 1 1 1 4
...
5 6 6 7 24 25 5 25 25
A
= − + − + + − = − =
b, Ta có :
1 1 1 1 1 1 1 1
...
1 3 3 5 5 7 99 101
B
= − + − + − + + −
1 100
1
101 101
= − =
Bài 2: Tính nhanh tổng sau:
a, D=
2 2 2
5 5 5
...
1.6 6.11 26.31
+ + +
b, K=
4 4 4 4
...
11.16 16.21 21.26 61.66
+ + + +
HD :
a, Ta có :
5 5 5 5 1 1 1 1 1 1 1
5 .... 5 1 ...
1.6 6.11 11.16 26.31 6 6 11 11 16 26 31
D
= + + + + = − + − + − + + −
1 30 150
5 1 5.
31 31 31
D

= − = =


b, Ta có:
1 1 1 1 5 5 5 5
4 ... 5 4 ...
11.16 16.21 21.26 61.66 11.16 16.21 21.26 61.66
KK
= + + + + = = + + + +
1 1 1 1 1 1 1 1
5 4 ... 4
11 16 16 21 61 66 11 66
K
= − + − + + − = −
=>
55 4 2
5 4.
11.66 66 33
KK= = = =
Bài 3: Tính nhanh tổng sau:
a, N=
4 4 4 4
...
1.3 3.5 5.7 99.101
+ + + +
b,
1 1 1 1
...
1.1985 2.1986 3.1987 16.2000
F = + + + +
HD :
a, Ta có :
2 2 2 2 1 200
2 ... 2 1
1.3 3.5 5.7 99.101 101 101
N
= + + + + = − =
Bài 4: Tính tổng sau:
5 5 5 5 5
...
3.7 7.11 11.15 81.85 85.89
K = + + + + +
Bài 5: Tính tổng sau:
1 1 1 1
...
25.24 24.23 7.6 6.5
A = + + + +
Bài 6:Tính tổng sau:
5 5 5 5
...
3.6 6.9 9.12 99.102
A = + + + +
Bài 7: Tính giá trị của biểu thức:
3 3 3 3 25 25 25
... ...
1.8 8.15 15.22 106.113 50.55 55.60 95.100
A
= + + + + − + + +
HD:
Ta có :
3 3 3 3
...
1.8 8.15 15.22 106.113
B = + + + +
7 7 7 7
7 3 ...
1.8 8.15 15.22 106.113
B

= = + + + +


1 1 1 1 1 1 1 1 1 112 3.112 48
7 3 ... 3 1 3.
1 8 8 15 15 22 106 113 113 113 7.113 113
BB
= = − + − + − + + − = − = = = =
và
25 25 25 5 5 5
... 5 ...
50.55 55.60 95.100 50.55 55.60 95.100
CC= + + + = = + + +
1 1 1 1
5
50 100 100 500
CC= = − = = =
. Khi đó :
48 1
113 500
A B C= − = −
10
Bài 8: Tính nhanh:
1 9 9 9
...
19 19.29 29.39 1999.2009
+ + + +
HD:
Ta có :
1 9 9 9
...
19 19.29 29.39 1999.2009
+ + + +
=
9 9 9 9
...
9.19 19.29 29.39 1999.2009
A= = + + + +
=>
10 10 10 10 1 1
10 9 ... 9
9.19 19.29 29.39 1999.2009 9 2009
A
= + + + + = −
2000 2000 200
10 9.
9.2009 2009 2009
AA= = = =
Bài 9: Tính tổng sau: C=
2 2 2 2 2
15 35 63 99 143
+ + + +
Bài 10: Tính nhanh tổng sau:
a, E=
1 1 1 1 1 1
7 91 247 475 755 1147
+ + + + +
b, C=
2 2 2 2 2
15 35 63 99 143
+ + + +
HD:
a, Ta có :
1 1 1 1 1 1 1 1 1 1 36
... 1 ... 1
1.7 7.13 13.19 31.37 7 7 13 31 37 37 37
E = + + + + = − + − + + − = − =
b, Ta có :
2 2 2 2 2 1 1 8
3.5 5.7 7.9 9.11 11.13 3 11 33
C = + + + + = − =
Bài 11: Tính nhanh tổng sau
a, F=
2 2 2 2
...
6 66 176 (5 4)(5 1)nn
+ + + +
−+
b, G=
9 9 9 9
1 ...
45 105 189 29997
+ + + + +
HD:
a, Ta có :
( )( ) ( )( )
1 1 1 1 1 1 1 1
2 ... 2
6 66 176 5 4 5 1 1.6 6.11 11.16 5 4 5 1
F
n n n n
= + + + + = + + +
− + − +
( )( )
5 5 5 5
5 2 ...
1.6 6.11 11.16 5 4 5 1
F
nn

= + + + +


−+

15
2 1 2.
5 1 5 1
n
nn

= − =

++

=>
2
51
n
F
n
=
+
b, Ta có :
3 3 3 3 3 3 3 3
1 ... 1 ...
15 35 63 9999 3.5 5.7 7.9 99.101
G = + + + + + = + + + + +
1 1 1 2 2 2
1 3 ... 2 2 3 ...
3.5 5.7 99.101 3.5 5.7 99.101
GG
= + + + + = = + + + +
1 1 98 98 300
2 2 3 2 3. 2
3 101 3.101 101 101
G

= + − = + = + =


150
101
G= =
Bài 12: Tính nhanh tổng sau : M=
1 1 1 6
...
2.15 15.3 3.21 87.90
+ + + +
HD:
Ta có :
6 6 6 6
...
12.15 15.18 18.21 87.90
M = + + + +
3 3 3 1 1 1 1 1 1
2 ... 2 ...
12.15 15.18 87.90 12 15 15 18 87 90
M
= + + + = − + − + + −
=
11
2
12 90

−


Bài 13 : Tính :
50 25 20 10 100 100 1
50 ...
3 3 4 3 6.7 98.99 99
+ + + + + + + +
Bài 14: Tính:
3 3 3 3
1 ...
15 35 63 99.101
+ + + + +
Bài 15: Tính:
1 1 1 1 1 1 1
...
6 12 20 30 42 90 110
A = + + + + + + +
11
Bài 16: Tính:
1 1 1 1 1 1
2 14 35 65 104 152
+ + + + +
Bài 17: Tính tổng:
1 1 1 1 1 1 1 1
10 15 21 28 36 45 55 66
B = + + + + + + +
Bài 18: Tính nhanh tổng sau
a, H=
38 9 11 13 15 17 197 199
...
25 10 15 21 28 36 4851 4950
+ − + − + − + −
b, I=
3 5 7 201
...
1.2 2.3 3.4 100.101
− + − −
HD:
a, Ta có :
38 9 11 13 15 197 199
...
2 50 20 30 42 56 9702 9900
H
= + − + − + + −
38 9 11 13 15 197 199
...
2 50 4.5 5.6 6.7 7.8 98.99 99.100
H
= + − + − + + −
38 1 1 1 1 1 1 1 1 1 1 1 1
...
2 50 4 5 5 6 6 7 7 8 98 99 99 100
H
= + + − + + + − + + + + − +
38 1 1 76 25 1
12
2 50 4 100 100
H
H
+−
= + − = = = =
b, Ta có :
1 1 1 1 1 1 1
1 ...
2 2 3 3 4 100 101
I
= + − + + + − − +
1 100
1
101 101
= − =
Bài 19: Thực hiện phép tính:
1 1 1 1 1
3. 5. 7. ... 15. 17.
1.2 2.3 3.4 7.8 8.9
A = − + − + −
HD:
Ta có :
1 1 1 1 1
3. 5. 7. ... 15. 17.
1.2 2.3 3.4 7.8 8.9
A = − + − + −
=
3 5 7 15 17
...
1.2 2.3 3.4 7.8 8.9
− + − + −
1 1 1 1 1 1 1 1 1 1
...
1 2 2 3 3 4 7 8 8 9
= + − + + + − + + − +
18
1
99
= − =
Bài 20: Không quy đồng, Hãy tính :
5 4 3 1 13
2.1 1.11 11.2 2.15 15.4
B = + + + +
HD:
Ta có :
5 4 3 1 13
2.1 1.11 11.2 2.15 15.4
B = + + + +
=>
5 4 3 1 13
7 2.7 7.11 11.14 14.15 15.28
B
= + + + +
1 1 1 1 1 1 1 1 1 1 1 1 13
7 2 7 7 11 11 14 14 15 15 28 2 28 28
B
= = − + − + − + − + − = − =
=>
7.13 13
28 4
B ==
Bài 21: Tính :
4 6 9 7
7.31 7.41 10.41 10.57
A = + + +
và
7 5 3 11
19.31 19.43 23.43 23.57
B = + + +
HD:
Ta có :
4 6 9 7 1 1 1 1 1 1 1 1 1 1
5 31.35 35.41 41.50 50.57 31 35 35 41 41 50 50 57 31 57
A
= + + + = − + − + − + − = −
7 5 3 11 1 1 1 1 1 1 1 1 1 1
2 31.38 38.43 43.46 46.57 31 38 38 43 43 46 46 57 31 57
B
= + + + = − + − + − + − = −
Khi đó :
5
5 2 2
A B A
B
= = =
Bài 22: Tính nhanh tổng sau: P=
1 1 1 1
...
1.2.3 2.3.4 3.4.5 10.11.12
+ + + +
HD:
Ta có :
2 2 2 2 1 1 1 1 1 1
2 ... ...
1.2.3 2.3.4 3.4.5 10.11.12 1.2 2.3 2.3 3.4 10.11 11.12
P
= + + + + = − + − + + −
12
1 1 65 65
2
1.2 11.12 132 264
PP= − = = =
Bài 23 : Tính :
1 1 1 1 1 1
10 40 88 154 238 340
A = + + + + +
Bài 24 : Tính :
1 1 1 1 1 1
6 35 63 99 143 195
A = − − − − −
Bài 25: Thực hiện phép tính:
1 1 1 1 3 5 ... 49
... .
4.9 9.14 44.49 89
A
− − − −

= + + +


HD:
Đặt :
1 1 1 5 5 5 1 1 45
... 5 ...
4.9 9.14 44.49 4.9 9.14 44.49 4 49 4.49
BB

= + + + = = + + + = − =


=>
9
4.49
B =
và
( )
1 3 5 ... 49
1 3 5 ... 49 1 612 611
89 89 89 89
C
− + + +
− − − − − −
= = = =
Khi đó :
9 611
..
4.49 89
A B C
−
==
Bài 26: Thực hiện phép tính:
1 1 1 1
(1 2 3 ... 100)( )(63.1,2 21.3,6)
2 3 7 9
1 2 3 4 ... 99 100
+ + + + − − − −
− + − + + −
HD:
Ta có:
1 1 1 1
(1 2 3 ... 100)( )(63.1,2 21.3,6)
2 3 7 9
63.1,2 21.3,6 0 0
1 2 3 4 ... 99 100
+ + + + − − − −
− = = =
− + − + + −
Bài 27: Tính tỉ số
A
B
biết :
1 1 1 1
...
1.300 2.301 3.302 101.400
A = + + + +
và
1 1 1 1
...
1.102 2.103 3.104 299.400
B = + + + +
HD:
299 299 299 1 1 1 1 1 1 1 1
299 ... ...
1.300 2.301 101.400 1 300 2 301 3 302 101 400
A
= + + + = − + − + − + + −
1 1 1 1 1 1
299 1 ... ...
2 3 101 300 301 400
A
= = + + + + − + + +
101 101 101 101
101 ...
1.102 2.103 3.104 299.400
B = + + + +
1 1 1 1 1 1 1
1 ...
102 2 103 3 104 299 400
= − + − + − + + −
1 1 1 1 1 1 1 1 1 1 1 1
1 ... ... 1 ... ...
2 3 299 102 103 400 2 3 101 300 301 400
= + + + + − + + + = + + + + − + + +
Khi đó :
101
299 101
299
A
AB
B
= = =
13
DẠNG 5: TÍNH TỔNG TỰ NHIÊN DẠNG TÍCH
Bài 1: Tính nhanh các tổng sau
a, A= 1.2+2.3+3.4+…+98.99 b, B=
1.2 3.4 5.6 ... 99.100+ + + +
HD:
a, Ta có:
( ) ( ) ( ) ( )
3 1.2 3 0 2.3 4 1 3.4 5 2 ... 98.99 100 97A= − + − + − + + −
( ) ( ) ( ) ( )
3 1.2.3 0.1.2 2.3.4 1.2.3 3.4.5 2.3.4 ... 98.99.100 97.98.99A= − + − + − + + −
98.99.100
3 98.99.100
3
AA= = =
b, Ta có:
( ) ( ) ( )
2 2 1 .4 4 1 .6 ... 98 1 .100B = + + + + + + +
( ) ( ) ( )
2 2.4 4 4.6 6 ... 98.100 100B = + + + + + + +
( ) ( )
2.4 4.6 6.8 ... 98.100 2 4 6 ... 100B = + + + + + + + + +
Đặt
2.4 4.6 6.8 ... 98.100M = + + + +
( ) ( ) ( ) ( )
6 2.4 6 0 4.6 8 2 6.8 10 4 ... 98.100 102 96M = − + − + − + + −
( ) ( ) ( ) ( )
6 2.4.6 0.2.4 4.6.8 2.4.6 6.8.10 4.6.8 ... 98.100.102 96.98.100M = − + − + − + + −
98.100.102
6 98.100.102
6
MM= = =
Tính
2 4 6 .... 100N = + + + +
rồi thay vào B
Bài 2: Tính nhanh các tổng sau
a, D= 1.4+2.5+3.6+…+100.103 b, E=
1.3 2.4 3.5 ... 97.99 98.100+ + + + +
HD:
a, Ta có:
( ) ( ) ( ) ( )
1. 1 3 2. 2 3 3 3 3 ... 100. 100 3D = + + + + + + + +
( ) ( ) ( ) ( )
1.1 1.3 2.2 2.3 3.3 3.3 ... 100.100 100.3D = + + + + + + + +
( ) ( )
1.1 2.2 3.3 ... 100.100 3 1 2 3 ... 100D = + + + + + + + + +
Đặt,
1.1 2.2 3.3 ... 100.100A= + + + +
và
1 2 3 4 ... 100B = + + + + +
b, Ta có:
( ) ( ) ( ) ( ) ( )
1 1 2 2 2 2 3 3 2 ... 97 97 2 98 98 2E = + + + + + + + + + +
( ) ( ) ( ) ( ) ( )
1.1 1.2 2.2 2.2 3.3 3.2 ... 97.97 97.2 98.98 98.2E = + + + + + + + + + +
( ) ( )
1.1 2.2 3.3 ... 97.97 98.98 2 1 2 3 4 ... 97 98E = + + + + + + + + + + + +
Đặt
1.1 2.2 3.3 ... 98.98A= + + + +
và
1 2 3 4 ... 97 98B = + + + + + +
Tính rồi thay vào E
Bài 3: Tính nhanh các tổng sau
a, F=
1.3 5.7 9.11 ... 97.101+ + + +
b, G= 1.2.3+2.3.4+3.4.5+…+98.99.100
HD:
a,
( ) ( ) ( ) ( )
1. 1 2 5 5 2 9 9 2 ... 97 97 2F = + + + + + + + +
( ) ( ) ( ) ( )
1.1 1.2 5.5 5.2 9.9 9.2 ... 97.97 97.2F = + + + + + + + +
( ) ( )
1.1 5.5 9.9 ... 97.97 2 1 5 9 ... 97F = + + + + + + + + +
Đặt
1.1 5.5 9.9 ... 97.97, 1 5 9 ... 97AB= + + + + = + + + +
, Tính rồi thay vào F
b,
( ) ( ) ( ) ( )
4 1.2.3 4 0 2.3.4 5 1 3.4.5 6 2 ... 98.99.100 101 97G = − + − + − + + −
( ) ( ) ( ) ( )
4 1.2.3.4 0.1.2.3 2.3.4.5 1.2.3.4 3.4.5.6 2.3.4.5 ... 98.99.100.101 97.98.99.100G = − + − + − + + −
98.99.100.101
4 98.99.100.101
4
GG= = =
14
Bài 4: Tính nhanh các tổng sau
a, H=
1.99 2.98 3.97 ... 50.50+ + + +
b, K=
1.99 3.97 5.95 ... 49.51+ + + +
HD:
a,
( ) ( ) ( )
1.99 2. 99 1 3. 99 2 ... 50 99 49H = + − + − + + −
( ) ( ) ( )
1.99 2.99 1.2 3.99 2.3 ... 50.99 49.50H = + − + − + + −
( ) ( )
1.99 2.99 3.99 ... 50.99 1.2 2.3 3.4 ... 49.50H = + + + + − + + + +
Đặt
( )
99 1 2 3 ... 50 , 1.2 2.3 3.4 ... 49.50AB= + + + + = + + + +
Tính A và B rồi thay vào H
b,
( ) ( ) ( )
1.99 3 99 2 5. 99 4 ... 49 99 48K = + − + − + + −
( ) ( ) ( )
1.99 3.99 2.3 5.99 4.5 ... 49.99 48.49K = + − + − + + −
( ) ( )
1.99 3.99 5.99 ... 49.99 2.3 4.5 ... 48.49K = + + + + − + + +
Đặt
( ) ( )
99 1 3 5 ... 49 , 2.3 4.5 6.7 ... 48.49AB= + + + + = + + + +
Tính A và B rồi thay vào K
Bài 5: Tính nhanh các tổng sau : C=
1.3 3.5 5.7 ... 97.99+ + + +
HD:
( ) ( ) ( ) ( )
1. 1 2 3. 3 2 5 5 2 ... 97. 97 2C = + + + + + + + +
( ) ( ) ( ) ( )
1.1 1.2 3.3 3.2 5.5 5.2 ... 97.97 97.2C = + + + + + + + +
( ) ( )
1.1 3.3 ... 97.97 2 1 3 5 ... 97C = + + + + + + + +
Đặt
1.1 3.3 5.5 ... 97.97, 1 3 5 7 ... 97AB= + + + + = + + + + +
Tính A và B rồi thay vào C
Bài 6: Tính:
1.99 2.98 ... 99.1
1.2 2.3 3.4 ... 99.100
A
+ + +
=
+ + + +
15
DẠNG 6: TÍNH TỔNG CÔNG THỨC
Bài 1: Tính tổng: D =
1 1 1
1 (1 2) (1 2 3) ... (1 2 ... 20)
2 3 20
+ + + + + + + + + +
HD:
Ta có:
1 2.3 1 3.4 1 20.21 3 4 5 21
1 . . ... . 1 ...
2 2 3 2 20 2 2 2 2 2
D = + + + + = + + + + +
( )
11
2 3 4 ... 20 21 .230 115
22
= + + + + + = =
Bài 2: Tính tổng:
1 1 1
1 (1 2) (1 2 3) ... (1 2 ... 2016)
2 3 2016
F = + + + + + + + + + +
HD:
Ta có:
1 2.3 1 3.4 1 2016.2017
1 . . .... .
2 2 3 2 2016 2
F = + + + +
2 1 3 1 4 1 2016 1
1 ...
2 2 2 2
F
+ + + +
= + + + + +
1 1 1 2 3 4 ... 2016
1 ...
2 2 2 2
+ + + +
= + + + + +
1 2018.2015 2015.2019
1 .2015 1
2 2 2
F = + + = +
Bài 3: Tính:
( ) ( ) ( )
1 1 1
1 1 2 1 2 3 ... 1 2 ... 16
2 3 16
+ + + + + + + + + +
HD:
Ta có:
1 2.3 1 3.4 1 16.17
1 . . .... .
2 2 3 2 16 2
F = + + + +
2 1 3 1 4 1 16 1
1 ...
2 2 2 2
F
+ + + +
= + + + + +
1 1 1 2 3 4 ... 16
1 ...
2 2 2 2
+ + + +
= + + + + +
Bài 4: Tính tổng:
1 1 1
1 (1 2) (1 2 3) ... (1 2 ... 100)
2 3 100
G = + + + + + + + + + +
HD:
Ta có:
( ) ( ) ( )
1 2 .2 1 3 .3 1 100 .100
1 1 1
1 . . ... .
2 2 3 2 100 2
G
+ + +
= + + + +
2 1 3 1 4 1 100 1
1 ...
2 2 2 2
G
+ + + +
= + + + + +
1 1 1 2 3 4 ... 100
1 ...
2 2 2 2
+ + + +
= + + + + +
Bài 5: Tính tổng:
1 3.2 1 4.3 1 501.500
1 . . ... .
2 2 3 2 500 2
H = + + + +
HD:
Ta có:
3 4 5 501 3 4 5 ... 501
1 ... 1
2 2 2 2 2
H
+ + + +
= + + + + + = +
Bài 6: Tính:
1 1 1
...
1 2 3 1 2 3 4 1 2 ... 59
+ + +
+ + + + + + + +
HD:
Ta có: =
( ) ( ) ( ) ( )
1 1 1 1
...
1 3 .3 1 4 .4 1 5 .5 1 59 .59
2 2 2 2
+ + + +
+ + + +
2 2 2 2 1 1 1 1
... 2 ...
3.4 4.5 5.6 59.60 3.4 4.5 5.6 59.60

= + + + + = + + + +


1 1 19 19
22
3 60 60 30
= − = =
Bài 7: Tính:
50 25 20 10 100 100 1
50 ...
3 3 4 3 6.7 98.99 99
+ + + + + + + +
16
HD:
Ta có:
50 25 20 10 100 100 100 100
50 ...
3 3 4 3 6.7 7.8 98.99 99.100
A
= + + + + + + + + +
1 1 1 1 1 1 1 1
100 100 ...
1.2 2.3 3.4 4.5 5.6 6.7 7.8 99.100
A
= + + + + + + + +
1 1 1 1 1
100 ... 100. 1 99
1.2 2.3 3.4 99.100 100
A
= + + + + = − =
17
DẠNG 7: TÍNH TÍCH
Bài 1: Tính tích
a, A=
2 2 2 2
2 3 4 20
. . ...
1.3 2.4 3.5 19.21
b, B=
2 2 2 2
1 2 3 10
. . ...
1.2 2.3 3.4 10.11
HD:
a, Ta có:
( )( )
( )( )
2.3.4...20 2.3.4...20
2.2 3.3 4.4 20.20 20.2 40
. . ....
1.3 2.4 3.5 19.21 1.2.3....19 3.4.5...21 21 21
A = = = =
b, Ta có:
( )( )
( )( )
1.2.3....10 1.2.3...10
1.1 2.2 3.3 10.10 1
. . ....
1.2 2.3 3.4 10.11 1.2.3...10 2.3.4...11 11
B = = =
Bài 2: Tính tổng C =
1 1 1 1
1 1 1 ... 1
1 2 1 2 3 1 2 3 4 1 2 3 ... 2016
− − − −
+ + + + + + + + + +
HD:
Ta có:
( ) ( ) ( ) ( )
1 1 1 1
1 . 1 . 1 .... 1
1 2 .2 1 3 .3 1 4 .4 1 2016 .2016
2 2 2 2
C
= − − − −
+ + + +
2 5 9 2017.2016 2 4 10 18 2016.2017 2
. . ..... . . ....
3 6 10 2016.2017 6 12 20 2016.2017
−−
==
1.4 2.5 3.6 2015.2018 1004
. . ....
2.3 3.4 4.5 2016.2017 3009
C ==
Bài 3: Tính: A =
1 1 1 1 1 1 1 1
...
2 3 2 5 2 7 2 99
− − − −
HD:
Ta có:
( )
( )
49 49
1.3.5....97
1 3 5 97 1
. . ....
2.3 2.5 2.7 2.99 2 . 3.5.7...99 2 .99
A = = =
Bài 4: Tính:
1999 1999 1999
1 1 ... 1
1 2 1000
1000 1000 1000
1 1 ... 1
1 2 1999
+ + +
+ + +
HD:
Ta có:
2000 2001 2002 2999 1001 1002 1003 2999
. . ... : . . ....
1 2 3 1000 1 2 3 1999
A
=
2000.2001.2002...2999 1.2.3...1999
.
1.2.3.4...1000 1001.1002....2999
A
=
1001.1002....1999
1
1001.1002...1999
==
Bài 5: Tính:
1 1 1 1
1 1 1 ... 1
4 9 16 400
− − − −
HD:
Ta có:
( )( )
( )( )
1.2.3...19 3.4.5...21
3 8 15 399 1.3 2.4 3.5 19.21
. . .... . . ...
4 9 16 400 2.2 3.3 4.4 20.20 2.3.4...20 2.3.4.5...20
= = =
21 21
20.2 40
==
Bài 6: Tính:
1 1 1
1 1 ... 1
1 2 1 2 3 1 2 3 ... n
− − −
+ + + + + + +
HD:
18
Ta có:
( ) ( ) ( )
1 1 1
1 1 ... 1
1 2 .2 1 3 .3 1 .
2 2 2
A
nn
= − − −
+ + +
( )
2 2 2 2
1 1 1 .... 1
2.3 3.4 4.5 1nn

= − − − −


+

( )
( )
12
4 10 18
. . ....
2.3 3.4 4.5 1
nn
nn
+−
=
+
( )( )
( )
( )( )
( )( )
1 2 1.2.3...(n 1) 4.5....( 2)
1.4 2.5 3.6
. . ...
2.3 3.4 4.5 1 2.3... 3.4.5...( 1)
n n n
n n n n
− + − +
==
++
22
.3 3
nn
nn
++
==
Bài 7: Tính:
a/
1 1 1 1
1 1 1 ... 1
1.3 2.4 3.5 17.19
+ + + +
b/
1 1 1 1
1 1 1 ... 1
21 28 36 1326
− − − −
HD:
a, Ta có:
4 9 16 17.19 1 2.2 3.3 4.4 18.18
. . .... . . ...
1.3 2.4 3.5 17.19 1.3 2.4 3.5 17.19
A
+
==
( )( )
( )( )
2.3.4...18 2.3.4...18
18.2
1.2.3...17 3.4.5...19 19
==
36
19
=
b, Ta có:
20 27 35 1325 40 54 70 2650 5.8 6.9 7.10 50.53
. . .... . . .... . . ...
21 28 36 1326 42 56 72 2652 6.7 7.8 8.9 51.52
B = = =
( )( )
( )( )
5.6.7...50 8.9.10...53
5.53
6.7.8...51 7.8.9...52 51.7
B ==
Bài 8: Tính tích
a, D=
2 2 2 2 2 2 2 2
2 3 4 5 6 7 8 9
. . . . . . .
3 8 15 24 35 48 63 80
b, E=
8 15 24 2499
. . ...
9 16 25 2500
HD:
a,
( )( )
( )( )
2.3.4...8.9 2.3.4...8.9
2.2 3.3 4.4 8.8 9.9 9.2 9
. . .... .
1.3 2.4 3.5 7.9 8.10 1.2.3...7.8 3.4.5...9.10 105
D = = = =
b,
( )( )
( )( )
2.3.4...49 4.5.6...51
2.4 3.5 4.6 49.51 2.51 17
. . ....
3.3 4.4 5.5 50.50 3.4.5...50 3.4.5...50 50.3 25
E = = = =
Bài 9: Tính tích
a, G=
1 1 1 1
1 1 1 ... 1
2 3 4 100
− − − −
b, H=
1 2 3 10
1 1 1 ... 1
7 7 7 7
− − − −
HD:
a, Ta có:
1 2 3 99 1
. . ....
2 3 4 100 100
G ==
b, Ta có:
6 5 4 3 2 1 0 1 2 3
. . . . . . . . . 0
7 7 7 7 7 7 7 7 7 7
H
− − −
==
Bài 10: Tính tích
a, I=
1 1 1 1
1 1 1 ... 1
4 9 16 10000
− − − −
b, J=
1 1 1 1
1 1 1 ... 1
3 6 10 780
− − − −
HD:
a, Ta có:
( )( )
( )( )
1.2.3....99 3.4.5...101
3 8 15 9999 1.3 2.4 3.5 99.101
. . ... . . ....
4 9 16 10000 2.2 3.3 4.4 100.100 2.3.4...100 2.3.4...100
I = = =
101
100.2
=
19
b, Ta có:
2 5 9 779
. . ...
3 6 10 780
J =
4 10 18 1558 1.4 2.5 3.8 38.41
. . .... . . ....
6 12 20 1560 2.3 3.4 4.5 39.40
J ==
( )( )
( )( )
1.2.3...38 4.5.6...40.41
41
2.3.4...39 3.4.5....40 39.3
==
Bài 11: Tính tích
a, K=
1 1 1 1
1 1 1 ... 1
21 28 36 1326
− − − −
b, M=
1 1 1 1
1 1 1 ... 1
2 3 4 999
+ + + +
HD:
a, Ta có:
20 27 35 1325 40 54 70 2650 5.8 6.9 7.10 50.53
. . .... . . .... . . ....
21 28 36 1326 42 56 72 2652 6.7 7.8 8.9 51.52
K = = =
( )( )
( )( )
5.6.7...50 8.9.10....53
5 53
.
6.7.8...51 7.8.9....52 51 7
=
b, Ta có:
3 4 5 1000 1000
. . .... 500
2 3 4 999 2
M = = =
Bài 12: Tính tích
a, F=
2 2 2 2
3 8 15 99
. . ...
2 3 4 10
b, N=
1 1 1 1
1 1 1 ... 1
2 3 4 1000
− − − −
HD:
a,
( )( )
( )( )
1.2.3...9 3.4.5...11
1.3 2.4 3.5 9.11 1.11
. . ....
2.2 3.3 4.4 10.10 2.3.4...10 2.3.4...10 10.2
F = = =
b,
1 2 3 999 1
. . ....
2 3 4 1000 1000
N
− − − −
= = −
Bài 13: Tính tích
a, C=
3 8 15 9999
. . ...
4 9 16 10000
b,
2 2 2 2
2 2 2 2
1 2 1 3 1 4 1 2012
...
2 3 4 2012
A
− − − −
=
HD:
a, Ta có:
( )( )
( )( )
1.2.3...99 3.4.5...101
1.3 2.4 3.5 99.101 1.101
. . ....
2.2 3.3 4.4 100.100 2.3.4...100 2.3.4...100 100.2
C = = =
b, Ta có:
2
3 8 15 1 2012 1.3 2.4 3.5 2011.2013
. . .... . . ....
2.2 3.3 4.4 2012.2012 2.2 3.3 4.4 2012.2012
A
− − − − − − − −
==
( )( )
( )( )
1.2.3...2011 3.4.5...2013
2013
2.3.4....2012 2.3.4...2012 2012.2
= − = −
Bài 14: Tính giá trị của biểu thức:
8 8 8 8
1 1 1 ... 1
10 22 36 8352
C
= + + + +
HD:
Ta có :
8 8 8 8
1 1 1 ... 1
10 22 36 8352
C
= + + + +
=
18 30 44 8360 3.6
. . .... .
10 22 36 8352 2.5
=
Bài 15: Cho
1 1 1
1 1 ... 1
1 2 1 2 3 1 2 3 ...
E
n
= − − −
+ + + + + + +
và
2n
F
n
+
=
, Tính
E
F
HD:
Ta có:
( ) ( ) ( )
1 1 1
1 1 ... 1
1 2 .2 1 3 .3 1 .
2 2 2
E
nn
= − − −
+ + +
20
( )
2 2 2 2
1 1 1 .... 1
2.3 3.4 4.5 1nn

= − − − −


+

( )
( )
12
4 10 18
. . ....
2.3 3.4 4.5 1
nn
nn
+−
=
+
( )( )
( )
( )( )
( )( )
1 2 1.2.3...(n 1) 4.5....( 2)
1.4 2.5 3.6
. . ...
2.3 3.4 4.5 1 2.3... 3.4.5...( 1)
n n n
n n n n
− + − +
==
++
22
.3 3
nn
nn
++
==
Mà
22
3
nn
FE
nn
++
=
Bài 16: Tính:
( )
2
4 4 4 1
1 1 1 ... 1
1 9 25
21
K
n

= − − − −


−

Bài 17: Cho
1024
1 1 1 1
1 1 1 ... 1
2 4 16 2
G
= + + + +
và
2047
1
2
H =
, Tính G + H
Bài 18: Tính:
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
3 5 7 9 11 2 4 6 8 10
A
= − − − − − − − − − −
Bài 19: Tính:
1 1 1 1
1 1 1 ... 1
100 99 98 2
A
= + + + +
Bài 20: Tính nhanh:
6 6 6 6
1 1 1 ... 1
8 18 30 10700
B
= + + + +
Bài 21: Tính nhanh: E=
1 1 1 1 1 1 1 1
1 1 1 ... 1 ...
2 2 3 2 3 4 2 10
+ + + + + + + + +
Bài 22: So sánh :
20
1.3.5....39 1
&
21.22.23...40 2 1
UV==
−
HD:
( )( ) ( ) ( )
10
1.3.5...37.39 1.3.5.7...37.39
21.23.25....39 22.24.26....40 21.23.25....39 2 11.12.13....20
U ==
( )( )( )
10
1.3.5...39
2 21.23....39 11.13...19 12.14.16.18.20
U =
( ) ( )
10 5
1.3.5..39
2 . 11.13...39 2 6.7.8.9.10
=
( ) ( ) ( )
15 15 5
1.3.5..39 1.3.5...39
2 7.9.11....39 . 6.8.10 2 . 7.9...39 .2 .3.5
U ==
=
20 20
1.3.5..39 1
2 .3.5.7...39 2
=
Mà
20 20
11
2 2 1
UV =
−
21
DẠNG 8 : TÍNH TỔNG CÙNG SỐ MŨ
Bài 1: Tổng cùng số mũ:
a, A=
2 2 2 2
1 2 3 ... 98+ + + +
b, B=
2 2 2 2 2 2
1 2 3 4 ... 19 20− + − + − − +
HD:
a, Ta có :
1.1 2.2 3.3 ... 98.98A= + + + +
( ) ( ) ( ) ( )
1 2 1 2 3 1 3 4 1 ... 98 99 1A= = − + − + − + + −
( ) ( )
1.2 2.3 3.4 ... 98.99 1 2 3 ... 98A= = + + + + − + + + +
Đặt
1.2 2.3 3.4 ... 98.99B = + + + +
, Tính tổng B ta được :
( ) ( ) ( ) ( )
3 1.2 3 0 2.3 4 1 3.4 5 2 ... 98.99 100 97B = − + − + − + + −
( ) ( ) ( ) ( )
3 1.2.3 0.1.2 2.3.4 1.2.3 3.4.5 2.3.4 ... 98.99.100 97.98.99B = − + − + − + + −
98.99.100
3 98.99.100 0.1.2 98.99.100
3
BB= − = = =
Thay vào A ta được :
98.99 98.99.100 98.99
2 3 2
AB= + = +
b, Ta có :
2 2 2 2 2 2
1 2 3 4 ... 19 20B = − + − + − − +
2
2 2 2 2 2
(1 2 3 4 ... 19 20 )B= = − − + − + + −
( ) ( )
2 2 2 2 2 2 2 2 2
1 2 3 ... 19 20 2 2 4 6 ... 20B

= − + + + + + − + + + +

( )
2 2 2 2 2
20.21.22 20.21
2.2 1 2 3 ... 10
32
B


= − + − + + + +




( )
10.11.12 10.11
20.22.7 20.7 8 20.7.23 8 10.11.4 5.11
32
B

= − − − + = − − +


Bài 2 : Tổng cùng số mũ :
a, D=
2 2 2 2
1 3 5 ... 99+ + + +
b, E=
2 2 2 2
11 13 15 ... 199+ + + +
HD:
a, Ta có :
( ) ( )
2 2 2 2 2 2 2 2 2 2
1 2 3 4 ... 99 100 2 4 6 ... 100D = + + + + + + − + + + +
( )
2 2 2 2 2
100.101.102 100.101
2 1 2 3 ... 50
32
D

= = + − + + + +


Đặt
2 2 2 2
50.51.52 50.51
1 2 3 ... 50
32
AA= + + + + = = +
, Thay vào D ta được :
( )
100.101.34 50.101 4 50.52.17 25.51D = + − +
b, Ta có :
( )
2 2 2 2 2 2 2 2 2 2
11 12 13 14 15 ... 199 200 12 14 ... 200E = + + + + + + + − + + +
Đặt
2 2 2 2 2 2 2
11 12 13 ... 200 , 12 14 ... 200AB= + + + + = + + +
Tính ta được :
( ) ( ) ( )
11.11 12.12 13.13 ... 200.200 11. 12 1 12. 13 1 ... 200. 201 1A= + + + + = − + − + + −
( ) ( ) ( ) ( )
11.12 11 12.13 12 13.14 13 ... 200.201 200A= = − + − + − + + −
( ) ( )
11.12 12.13 13.14 ... 200.201 11 12 13 ... 200A= + + + + − + + + +
200.201.202 10.11.12 211.190
3 2 2
A
= − −
Và
( )
2 2 2 2 2
100.101.102 5.6.7 106.95
2 6 7 8 ... 100 4
3 2 2
B
= + + + + = − −
Vậy
E A B=−
Bài 3 : Tổng cùng số mũ :
22
a, C=
2 2 2 2
2 4 6 ... 20+ + + +
b, F=
2 2 2 2
1 4 7 ... 100+ + + +
HD:
a, Ta có :
( )
2 2 2 2 2
2 1 2 3 ... 10C = + + + +
Đặt
2 2 2 2
1 2 3 ... 10 1.1 2.2 3.3 ... 10.10A = + + + + = + + + +
( ) ( ) ( ) ( )
1. 2 1 2. 3 1 3. 4 1 ... 10. 11 1A= − + − + − + + −
( ) ( )
1.2 2.3 3.4 ... 10.11 1 2 3 ... 10A = + + + + − + + + +
10.11.12 10.11
32
=−
b, Ta có :
1.1 4.4 7.7 10.10 ... 100.100F = + + + + +
( ) ( ) ( ) ( ) ( )
1 4 3 4 7 3 7 10 3 10 13 3 ... 100 103 3F = − + − + − + − + + −
( ) ( ) ( ) ( ) ( )
1.4 1.3 4.7 3.4 7.10 3.7 10.13 10.3 ... 100.103 100.3F = − + − + − + − + + −
( ) ( )
1.4 4.7 7.10 10.13 ... 100.103 3 1 4 7 10 ... 100F = + + + + + − + + + + +
Đặt
1.4 4.7 7.10 ... 100.103, 1 4 7 10 ... 100AB= + + + + = + + + + +
Tính
( ) ( ) ( ) ( )
9 1.4 9 0 4.7 10 1 7.10 13 4 ... 100.103 106 97A= − + − + − + + −
( ) ( ) ( ) ( )
9 1.4.9 0.1.4 4.7.10 1.4.7 7.10.13 4.7.10 ... 100.103.106 97.100.103A= − + − + − + + −
( )
9 1.4.9 100.103.106 1.4.7A = + −
=>
100.103.106 8
9
A
+
=
Tính B rồi thay vào F ta được :
3F A B=−
Bài 4 : Cho biết :
2 2 2 2
1 2 3 ... 12 650+ + + + =
, Tính nhanh tổng sau :
2 2 2 2
2 4 6 ... 24+ + + +
HD :
Ta có :
( )
2 2 2 2 2 2 2 2
2 4 6 ... 24 2 1 2 ... 12 4.650+ + + + = + + + =
Bài 5 : Tổng cùng số mũ :
a, G=
2 2 2 2
1 3 5 ... 99+ + + +
b, K=
2 2 2 2
1.2 2.3 3.4 ... 99.100+ + + +
HD:
a, Ta có :
1.1 3.3 5.5 7.7 ... 99.99G = + + + + +
( ) ( ) ( ) ( ) ( )
1. 3 2 3. 5 2 5 7 2 7 9 2 ... 99 101 2G = − + − + − + − + + −
( ) ( ) ( ) ( ) ( )
1.3 1.2 3.5 2.3 5.7 2.5 7.9 2.7 ... 99.101 2.99G = − + − + − + − + + −
( ) ( )
1.3 3.5 5.7 7.9 ... 99.101 2 1 3 5 7 ... 99G = + + + + + − + + + + +
Đặt
1.3 3.5 5.7 ... 99.101, 1 3 5 7 ... 99AB= + + + + = + + + + +
Tính
( ) ( ) ( ) ( )
6 1.3 6 0 3.5 7 1 5.7 9 3 ... 99.101 103 97AA= = − + − + − + + −
( ) ( ) ( ) ( )
6 1.3.6 0.1.3 3.5.7 1.3.5 5.7.9 3.5.7 ... 99.101.103 97.99.101A= − + − + − + + −
( )
99.101.103 3
6 1.3.6 99.101.103 1.3.5 99.101.103 3
6
AA
+
= + − = + = =
Tính tổng B rồi thay vào G
b, Ta có :
1.2.2 2.3.3 3.4.4 ... 99.100.100K = + + + +
( ) ( ) ( ) ( )
1.2 3 1 2.3 4 1 3.4 5 1 ... 99.100 101 1K = − + − + − + + −
( ) ( ) ( ) ( )
1.2.3 1.2 2.3.4 2.3 3.4.5 3.4 ... 99.100.101 99.100K = − + − + − + + −
( ) ( )
1.2.3 2.3.4 3.4.5 ... 99.100.101 1.2 2.3 3.4 ... 99.100K = + + + + − + + + +
Đặt
1.2.3 2.3.4 3.4.5 ... 99.100.101, 1.2 2.3 3.4 ... 99.100AB= + + + + = + + + +
Tính
( ) ( ) ( ) ( )
4 1.2.3 4 0 2.3.4 5 1 3.4.5 6 2 ... 99.100.101 102 98AA= = − + − + − + + −
23
( ) ( ) ( ) ( )
4 1.2.3.4 0.1.2.3 2.3.4.5 1.2.3.4 3.4.5.6 2.3.4.5 ... 99.100.101.102 98.99.100.101A= − + − + − + + −
99.100.101.102
4 99.100.101.102
4
AA= = =
Tính B tương tự rồi thay vào K
Bài 6 : Tổng cùng số mũ :
a, H=
2 2 2 2
2 4 6 ... 100+ + + +
b, I=
2 2 2 2
1.3 3.5 5.7 ... 97.99+ + + +
HD:
a, Ta có :
( )
2 2 2 2 2
2 1 2 3 ... 50 4.HA= + + + + =
1.1 2.2 3.3 4.4 ... 50.50A= + + + + +
( ) ( ) ( ) ( ) ( )
1. 2 1 2 3 1 3 4 1 4 5 1 ... 50 51 1A = − + − + − + − + + −
( ) ( ) ( ) ( )
1.2 1 2.3 2 3.4 3 ... 50.51 50A= − + − + − + + −
( ) ( )
1.2 2.3 3.4 ... 50.51 1 2 3 ... 50A= + + + + − + + + +
Tính tổng A ta được :
50.51.51 50.51
32
A =−
, Thay vào H ta được
b, Ta có :
I=
2 2 2 2
1.3 3.5 5.7 ... 97.99+ + + +
=>
1.3.3 3.5.5 5.7.7 ... 97.99.99I = + + + +
( ) ( ) ( ) ( )
1.3 5 2 3.5. 7 2 5.7 9 2 ... 97.99 101 2I = − + − + − + + −
( ) ( ) ( ) ( )
1.3.5 1.3.2 3.5.7 3.5.2 5.7.9 5.7.2 ... 97.99.101 97.99.2I = − + − + − + + −
( ) ( )
1.3.5 3.5.7 5.7.9 ... 97.99.101 2 1.3 3.5 5.7 ... 97.99I = + + + + − + + + +
Đặt
1.3.5 3.5.7 5.7.9 ... 97.99.101, 1.3 3.5 5.7 ... 97.99AB= + + + + = + + + +
Ta có :
( ) ( ) ( )
8 1.3.5.8 3.5.7 9 1 5.7.9 11 3 ... 97.99.101 103 95A= + − + − + + −
( ) ( ) ( )
8 1.3.5.8 3.5.7.9 1.3.5.7 5.7.9.11 3.5.7.9 ... 97.99.101.103 95.97.99.101A= + − + − + + −
8 1.3.5.8 97.99.101.103 1.3.5.7 97.99.101.103 15A= + − = −
=>
97.99.101.103 15
8
A
−
=
Tương tự tính B rồi thay vào I
Bài 7: Tính:
3 3 3 3
1.3 3.5 5.7 ... 49.51A = + + + +
Bài 8: Tính:
2 2 2 2
1.99 2.98 3.97 ... 49.51B = + + + +
Bài 9: Biết :
3 3 3
1 2 ... 10 3025+ + + =
, Tính
3 3 3
2 4 ... 20A = + + +
HD:
( )
3 3 3 3
2 1 2 ... 10A = + + +
Bài 10: Cho biết:
2 2 2 2
1 2 3 ... 12 650+ + + + =
, Tính nhanh tổng sau:
2 2 2 2
2 4 6 ... 24+ + + +
HD:
Ta có:
( )
2 2 2 2 2 2 2 2
2 4 6 ... 24 2 1 2 ... 12 4.650+ + + + = + + + =
24
DẠNG 9: TỔNG CÙNG CƠ SỐ
Bài 1: Tổng cùng cơ số:
a, A=
2 3 2000
1 3 3 3 ... 3+ + + + +
b, B=
3 5 7 2009
2 2 2 2 ... 2+ + + + +
HD:
a, Ta có :
2 3 4 2000 2001
3 3 3 3 3 ... 3 3A = + + + + + +
( )
( ) ( ) ( )
2 2 2000 2000 2001
3 2 3 3 3 3 ... 3 3 3 1A A A= − = = − + − + + − + −
2001
2001
31
2 3 1
2
AA
−
= = − = =
b, Ta có :
2 3 5 7 2009 2011
2 2 2 2 ... 2 2B = + + + + +
( ) ( ) ( ) ( )
3 3 5 5 2009 2009 2011
4 3 2 2 2 2 ... 2 2 2 2B B B= − = = − + − + + − + −
2011
2011
22
3 2 2
3
BB
−
= = − = =
Bài 2: Tổng cùng cơ số:
a, C=
3 5 7 101
5 5 5 5 ... 5+ + + + +
b, D=
2 4 6 100
1 3 3 3 ... 3+ + + + +
HD:
a, Ta có :
2 3 5 7 101 103
5 5 5 5 ... 5 5C = + + + + +
( ) ( ) ( ) ( )
3 3 5 5 101 101 103
25 24 5 5 5 5 ... 5 5 5 5C C C= − = = − + − + + − + −
103
103
55
24 5 5
24
CC
−
= = − = =
b, Ta có :
2 2 4 6 100 102
3 3 3 3 ... 3 3D = + + + + +
( ) ( ) ( ) ( )
2 2 4 4 100 100 102
9 8 3 3 3 3 ... 3 3 3 1D D D= − = = − + − + + − + −
102
102
31
8 3 1
8
DD
−
= = − = =
Bài 3: Tổng cùng cơ số:
a, E=
3 5 99
7 7 7 ... 7+ + + +
b, F=
2 4 6 2016
1 5 5 5 ... 5+ + + + +
HD:
a, Ta có :
2 3 5 7 99 101
7 7 7 7 ... 7 7E = + + + + +
( ) ( ) ( ) ( )
3 3 5 5 99 99 101
49 48 7 7 7 7 ... 7 7 7 7E E E= − = = − + − + + − + −
101
101
77
48 7 7
48
EE
−
= = − = =
b, Ta có :
2 2 4 6 2016 2018
5 5 5 5 ... 5 6F = + + + + +
( ) ( ) ( ) ( )
2 2 4 4 2016 2016 2018
25 24 5 5 5 5 ... 5 5 5 1F F F− = = − + − + + − + −
2018
2018
51
24 5 1
24
FF
−
= − = =
Bài 4: Tổng cùng cơ số: G=
2 4 6 2016
1 2 2 2 ... 2+ + + + +
HD:
Ta có :
2 2 4 6 2016 2018
2 2 2 2 ... 2 2G = + + + + +
( ) ( ) ( ) ( )
2 2 4 4 2016 2016 2018
4 3 2 2 2 2 ... 2 2 2 1G G G− = = − + − + + − + −
=>
2018
2018
21
3 2 1
3
GG
−
= − = =
Bài 5: Tổng cùng cơ số:
a,
50 49 48 2
2 2 2 ... 2 2M = − − − − −
b,
100 99 98 97 2 1
3 3 3 3 ... 3 3 1N = − + − + + − +
HD:
a, Ta có :
( )
50 2 3 48 49
2 2 2 2 ... 2 2M = − + + + + +
25
Đặt
2 3 4 48 49
2 2 2 2 ... 2 2A = + + + + + +
, Tính A ta được :
50
22A =−
, Thay vào M ta được :
( )
50 50 50
2 2 2 2 2MA= − = − − =
b, Ta có :
2 3 98 99 100
1 3 3 3 ... 9 9 3N = − + − + + − +
2 3 4 99 100 101
3 3 3 3 3 ... 3 3 3N= = − + − + + − +
=>
( )
( ) ( ) ( )
2 2 3 3 100 100 101
3 3 3 3 3 3 3 ... 3 3 3 1NN+ = − + − + − + + − + +
101
101
31
4 3 1
4
NN
+
= + = =
Bài 6: Tổng cùng cơ số : I=
2 3 63
1 2 2 ... 2+ + + +
HD:
Ta có :
3 4 64
2 2 2 2 ... 2I = + + + +
( ) ( ) ( ) ( )
3 3 4 4 63 63 64
2 2 2 2 2 ... 2 2 2 2 1II= − = − + − + + − + + −
=>
64
21I =+
Bài 7: Tính giá trị của biểu thức:
2 3 2008
1 2 2 2 ... 2B = − + − + +
HD:
Ta có :
2 3 2008
1 2 2 2 ... 2B = − + − + +
=>
2 3 4 2009
2 2 2 2 2 .... 2B = − + − + +
=>
2009
2009
21
2 3 1 2
3
B B B B
+
+ = = + = =
Bài 8: Tính
( )
9 8 2
2000 2001 2001 ... 2001 2001 1A = + + + + +
HD:
Đặt :
2 3 9
2001 2001 2001 ... 2001B = + + + +
=>
2 3 10
2001 2001 2001 ... 2001B = + + +
10
2001 2000 2001 2001B B B= − = = −
, Khi đó :
10 10
2000 1 2001 2001 1 2001 2000AB= + = − + = −
Bài 9: Cho
2010 2009 2008
2 2 2 ... 2 1H = − − − − −
, Tính
2010
H
HD:
Ta có :
( )
2010 2 3 2008 2009
2 1 2 2 2 ... 2 2H = − + + + + + +
. Đặt :
2 3 2009
1 2 2 2 ... 2A = + + + + +
Tính tổng A ta được :
2010
21A =−
, Thay vào H ta được :
( )
2010 2010
2 2 1 1 2010 2010
H
H = − − = = =
Bài 10: Tính tổng :
( ) ( ) ( ) ( )
0 1 2 2015
3 3 3 ... 3S = − + − + − + + −
Bài 11: Tính:
2 3 4 2007
1 7 7 7 7 ... 7A = + + + + + +
Bài 12: Tính
2 3 100
1 4 4 4 ... 4B = + + + + +
Bài 13: Tổng cùng cơ số : H=
2 3 99
1 2.6 3.6 4.6 ... 100.6+ + + + +
HD :
Ta có :
2 3 4 100
6 6 2.6 3.6 4.6 ... 100.6H = + + + + +
( )
( ) ( ) ( ) ( )
2 2 3 3 99 99 100
6 5 2.6 6 3.6 2.6 4.6 3.6 ... 100.6 99.6 1 100.6H H H− = − = − + − + − + + − + −
( )
2 3 99 100
5 6 6 6 ... 6 1 100.6H− = + + + + + −
Đặt
2 3 99
6 6 6 ... 6A = + + + +
, Tính A ta được :
100
66
5
A
−
=
, Thay vào H ta được :
( )
100
100 100
66
5 1 100.6 1 100.6
5
HA
−
− = + − = + −
100 100 100
6 6 5 500.6 499.6 1
55
− + − +
= = −
26
100
499.6 1
25
H
+
= =
Bài 14: Tính tổng cơ số: A=
2 3 100
1 1 1 1
...
7 7 7 7
+ + + +
HD:
a, Ta có:
2 3 4 100 101
1 1 1 1 1 1
...
7 7 7 7 7 7
A = + + + + +
2 2 3 3 100 100 101
1 1 1 1 1 1 1 1 1
...
7 7 7 7 7 7 7 7 7
AA
− = − + − + + − + −
=>
100 100
101 100
6 7 1 7 1
.
7 7 6.7
AA
−−
= = =
Bài 15: Tính tổng cơ số: B=
2 3 20
1 1 1 1
...
3 3 3 3
+ + + +
HD :
Ta có:
2 3 4 20 21
1 1 1 1 1 1
...
3 3 3 3 3 3
B = + + + + +
2 2 3 3 20 20 21
1 1 1 1 1 1 1 1 1
...
3 3 3 3 3 3 3 3 3
BB
− = − + − + + − + −
20 20
21 20
2 3 1 3 1
.
3 3 2.3
BB
−−
= = = =
Bài 16: Tính tổng cơ số
a, D=
0 1 2 2017
1 1 1 1
...
7 7 7 7
− + − + − + + −
b, E=
2 3 4 50 51
1 1 1 1 1 1
...
3 3 3 3 3 3
− + − + − + −
HD:
a, Ta có:
2 3 2016 2017
1 1 1 1 1
1 ...
7 7 7 7 7
D = − + − + + −
2 3 4 2017 2018
1 1 1 1 1 1 1
...
7 7 7 7 7 7 7
D = − + − + + −
2 2 2017 2017 2018
1 1 1 1 1 1 1 1
... 1
7 7 7 7 7 7 7 7
DD
− − −
+ = + + + + + + + −
2018 2018
2018 2018
8 7 1 7 1
7 7 8.7
DD
−−
= = =
b, Ta có:
2 3 4 51 52
1 1 1 1 1 1
...
3 3 3 3 3 3
E
−
= + − + + −
2 2 3 3 51 51 52
1 1 1 1 1 1 1 1 1
...
3 3 3 3 3 3 3 3 3
EE
− − − − −
+ = + + + + + + + +
=>
51 51
52 51
4 3 1 3 1
3 3 4.3
EE
++
= − = = −
Bài 17: Tính tổng cơ số G=
4 7 100
3 3 3 3
...
5 5 5 5
+ + + +
HD:
Ta có:
4 7 100
3 3 3 3
...
5 5 5 5
G = + + + +
4 7 100
1 1 1 1
3 ...
5 5 5 5
G

= + + + +


Đặt
4 7 100 3 4 7 10 103
1 1 1 1 1 1 1 1 1
... ...
5 5 5 5 5 5 5 5 5
AA= + + + + = = + + + +
4 4 7 7 100 100 103
1 1 1 1 1 1 1 1 1
...
125 5 5 5 5 5 5 5 5
AA
− = − + − + + − + −
102 102
103 103 100
124. 1 1 5 1 5 1
125 5 5 5 5 .124
A
A
−−
= − = = =
Bài 18: Tính tổng cơ số
27
a,
2 2 2
200 3 ...
3 4 100
2
1 2 3 99
...
2 3 4 100
K

− + + + +


==
+ + + +
b, I=
2 3 100
1 1 1 1
1 ...
2 2 2 2
+ + + + +
HD:
a, Ta có:
2 2 2 2
2 2 2 ... 2 1
3 4 5 100
TS
= − + − + − + + − +
4 6 8 198 2
...
3 4 5 100 2
TS = + + + + +
1 2 3 99
2 ... 2.
2 3 4 100
MS

= + + + + =


2
2
TS MS
K
MS MS
= = = =
b, Ta có :
2 3 4 100
1 1 1 1 1
1 ...
2 2 2 2 2
I = + + + + + +
2 3 100 101
1 1 1 1 1 1
...
2 2 2 2 2 2
I= = + + + + +
2 2 3 3 100 100 101
1 1 1 1 1 1 1 1 1 1
... 1
2 2 2 2 2 2 2 2 2 2
II
= − = − + − + − + + − + −
101 101
101 100
1 2 1 2 1
2 2 2
II
−−
= = =
Bài 19: Tính tổng cơ số: C=
3 5 99
1 1 1 1
...
2 2 2 2
+ + + +
HD:
a, Ta có :
2 3 5 7 99 101
1 1 1 1 1 1
...
2 2 2 2 2 2
C = + + + + +
3 3 5 5 98 98 101
1 3 1 1 1 1 1 1 1 1
...
4 4 2 2 2 2 2 2 2 2
C C C
− = = − + − + + − + −
=>
100 100
101 99
3 2 1 2 1
4 2 3.2
CC
−−
= = −
Bài 20: Tính:
a,
100
2 100
1 1 1
4.5 ... 1
5 5 5

+ + + +


b,
1 1 1 1
1 ...
2 4 8 1024
+ + + + +
Bài 21: Tính
2 3 4 50 51
1 1 1 1 1 1
...
3 3 3 3 3 3
A = − + − + − + −
Bài 22: Tính tổng cơ số: H=
2 3 4 2017
1 2 3 4 2017
...
3 3 3 3 3
+ + + + +
HD :
Ta có :
2 3 4 5 2017 2018
1 1 2 3 4 2016 2017
...
3 3 3 3 3 3 3
H = + + + + + +
2 2 3 3 4 4 2017 2017 2018
1 2 1 3 2 4 3 2017 2016 1 2017
...
3 3 3 3 3 3 3 3 3 3 3
HH
− = − + − + − + + − + −
2 3 4 2017 2018
2 1 1 1 1 1 2017
...
3 3 3 3 3 3 3
H = + + + + + −
Đặt
2 3 2017
1 1 1 1
...
3 3 3 3
A = + + + +
, Tính A rồi thay vào H
Bài 23: Tính tổng cơ số: F=
3 4 5 100
3 4 5 100
1 ...
2 2 2 2
+ + + + +
HD:
Ta có:
4 5 6 100 101
1 1 3 4 5 99 100
...
2 2 2 2 2 2 2
F = + + + + + +
4 4 5 5 100 100 3 101
1 4 3 5 4 100 99 3 1 100
... 1
2 2 2 2 2 2 2 2 2 2
FF
− = − + − + + − + + − −
28
4 5 6 100 101
1 1 1 1 1 1 3 100
...
2 2 2 2 2 2 8 2
F

= + + + + + − −


Đặt
4 5 6 100
1 1 1 1
...
2 2 2 2
A = + + + +
. Tính A rồi thay vào F
Bài 24: Tính:
100
2 3 100
1 1 1 1
4.5 ... 1
5 5 5 5
A

= + + + + +


Bài 25: Cho
2 3 2015 2016
3 3 3 ... 3 3A = + + + + +
a, Tính A
b, Tìm chữ số tận cùng của A
c, A có là số chính phương không
HD:
a,
2017
33
2
A
−
=
b,
( ) ( ) ( ) ( )
2 3 4 2013 2014 2015 2016 2 3 2013 2 3
3 3 3 3 ... 3 3 3 3 3 1 3 3 3 ... 3 1 3 3 3A = + + + + + + + + = + + + + + + + +
( )
2013 5 2013
3.40 ... 3 .40 40 3 3 ... 3= + + = + + +
nên A có tận cùng là 0
c, Lập luận được A chia hết cho 3
Lập luận được A không chia hết cho
2
3
Mà 3 là số nguyên tố nên A không là số chính phương
Bài 26: Chứng tỏ rằng :
( )
2017 2016 2
75 4 4 ... 4 4 1 25M = + + + + + +
chia hết cho 100
HD:
Tính tổng
2018
2018
41
75. 25 25.4 100
3
M
−
= + =
29
DẠNG 10: TÍNH ĐƠN GIẢN
Bài 1: Thực hiện phép tính:
a,
1.2.3 2.4.6 4.8.12 7.14.21
1.3.5 2.6.10 4.12.20 7.21.35
+ + +
+ + +
b,
1.7.9 3.21.27 5.35.45 7.49.63
1.3.5 3.9.15 5.15.25 7.21.35
+ + +
+ + +
HD:
a, Ta có :
1.2.3 2.4.6 4.8.12 7.14.21
1.3.5 2.6.10 4.12.20 7.21.35
+ + +
+ + +
=
( )
( )
1.2.3 1 2.2.2 4.4.4 7.7.7
1.2.3 2
1.3.5 1 2.2.2 4.4.4 7.7.7 1.3.5 5
+++
==
+++
b, Ta có :
1.7.9 3.21.27 5.35.45 7.49.63
1.3.5 3.9.15 5.15.25 7.21.35
+ + +
+ + +
=
( )
( )
1.7.9 1 3.3.3 5.5.5 7.7.7
1.7.9 21
1.3.5 1 3.3.3 5.5.5 7.7.7 1.3.5 5
+ + +
==
+ + +
Bài 2: Thực hiện phép tính:
1.2 2.4 3.6 4.8 5.10
3.4 6.8 9.12 12.16 15.20
+ + + +
+ + + +
HD:
Ta có :
1.2 2.4 3.6 4.8 5.10
3.4 6.8 9.12 12.16 15.20
+ + + +
+ + + +
=
( )
( )
1.2 1 2.2 3.3 4.4 5.5
1.2 1
3.4 1 2.2 3.3 4.4 5.5 3.4 6
+ + + +
==
+ + + +
Bài 3: Tính:
a,
1.2 2.4 4.8 7.14
1.3 2.6 4.12 7.21
A
+ + +
=
+ + +
b,
2.3 4.6 6.9 8.12
3.4 6.8 9.12 12.16
B
+ + +
=
+ + +
Bài 4: Tính giá trị của biểu thức sau:
2 5 6 7
5 6 7 2
a b c d
B
b c d a
= + + +
biết
2 5 6 7
5 6 7 2
a b c d
b c d a
= = =
và a, b, c, d # 0
HD:
Đặt
2 5 6 7
5 6 7 2
a b c d
Bk
b c d a
= = = = =
=>
4
2 5 6 7
. . . 1
5 6 7 2
a b c d
kk
b c d a
= = = =
1 =>B=
4
Bài 5: Tính gá trị của biểu thức:
2 3 4 5
3 4 5 2
a b c d
b c d a
+ + +
biết
2 3 4 5
3 4 5 2
a b c d
b c d a
= = =
HD:
Đặt :
4
2 3 4 5 2 3 4 5
. . . 1 1
3 4 5 2 3 4 5 2
a b c d a b c d
k k k
b c d a b c d a
= = = = = = = = =
Khi đó :
2 3 4 5
3 4 5 2
a b c d
b c d a
+ + +
=1 hoặc
2 3 4 5
3 4 5 2
a b c d
b c d a
+ + +
= - 1
Bài 6: Tính gá trị của biểu thức: B=
2 2 2 2
22
a m a n b n b m
ab
− − +
+
HD :
Ta có :
( ) ( )
( )
( )
( )
22
22
22
22
a b m n
a m n b m n
B m n
ab
ab
+−
− + −
= = = −
+
+
Bài 7: Thực hiện phép tính:
( )
( )( ) ( )( )
ab bc cd da abcd
c d a b b c a d
+ + +
+ + + − −
HD:
Ta có :
( )
MS ca cb da bd ab bd ca cd ab bc cd da= + + + + − − + = + + +
Khi đó :
( )
()TS ab bc cd da abcd
abcd
MS ab bc cd da
+ + +
==
+ + +
Bài 8: Tính giá trị của biểu thức:
( )( ) ( )( )
( )
a b x y a y b x
A
abxy xy ay ab bx
+ − − − − −
=
+ + +
HD:
Ta có:
( )
TS ax ay bx by ab ax yb xy ay ab bx xy= − − − − − + + − = − + + +
30
Khi đó:
( )
( )
1
ay ab bx xy
A
abxy ay ab bx xy abxy
− + + +
−
==
+ + +
Bài 9: Tính tổng
a, A=
0 1 2 2004
5 10 2000
2 2 2 ... 2
1 2 2 ... 2
+ + + +
+ + + +
b, B=
2 3 100
2 3 100
1 5 5 5 ... 5
1 4 4 4 ... 4
+ + + + +
+ + + + +
HD:
a, Ta có:
( ) ( ) ( )
2 3 4 5 6 7 8 9 2000 2001 2002 2003 2004
5 10 15 2000
1 2 2 2 2 2 2 2 2 2 ... 2 2 2 2 2
1 2 2 2 ... 2
A
+ + + + + + + + + + + + + + +
=
+ + + + +
( ) ( ) ( )
2 3 4 5 2 3 4 2000 2 3 4
5 10 15 2000
1 2 2 2 2 2 1 2 2 2 2 ... 2 1 2 2 2 2
1 2 2 2 ... 2
A
+ + + + + + + + + + + + + + +
=
+ + + + +
( )( )
( )
( )
2 3 4 5 10 2000
234
5 10 2000
1 2 2 2 2 1 2 2 ... 2
1 2 2 2 2
1 2 2 ... 2
A
+ + + + + + + +
= = + + + +
+ + + +
b, Ta có:
2 3 100
1 5 5 5 ... 5M = + + + + +
2 3 100 101
5 5 5 5 ... 5 5M= = + + + + +
101
101
51
5 4 5 1
4
M M M M
−
= − = = − = =
và
2 3 100
1 4 4 4 ... 4N = + + + + +
101
2 3 4 101 101
41
4 4 4 4 4 ... 4 4 3 4 1
3
N N N N N
−
= = + + + + + = − = = − = =
Khi đó:
M
B
N
=
Bài 10: Thu gọn biểu thức:
95 94 93
31 30 29
... 1
... 1
x x x x
A
x x x x
+ + + + +
=
+ + + + +
Bài 11: Tính tổng: A=
101 100 99 ... 2 1
101 100 99 98 ... 2 1
+ + + + +
− + − + − +
HD:
Ta có:
( )
1 101 .101
101.51 5151
2
TS
+
= = =
( ) ( ) ( )
101 100 99 98 ... 3 2 1 1 1 ... 1 51MS = − + − + + − + = + + + =
. Khi đó:
51.101
101
51
TS
A
MS
= = =
Bài 12: Tính:
1.99 2.98 ... 99.1
1.2 2.3 ... 99.100
+ + +
+ + +
HD:
Ta có:
( ) ( ) ( )
1.99 2. 99 1 3. 99 2 ... 99 99 98TS = + − + − + + −
( ) ( ) ( )
1.99 2.99 1.2 3.99 2.3 ... 99.99 98.99= + − + − + + −
( ) ( )
99 1 2 3 ... 99 1.2 2.3 3.4 ... 98.99= + + + + − + + + +
Đặt
1 2 3 ... 99, 1.2 2.3 3.4 ... 98.99AB= + + + + = + + + +
, Tính A và B rồi thay vào ta được:
Bài 13: Thực hiện phép tính:
a, A=
1 1 1
120 .40.5. .20. 20
2 5 4
1 5 9 ... 33 37 41
−−
+ + + + + +
HD:
a, Ta có:
120 20.5 20 0TS = − − =
, Khi đó
0A =
31
DẠNG 11: TÍNH TỈ SỐ CỦA HAI TỔNG
Bài 1: Thực hiện phép tính:
1 1 1 1
...
2 3 4 2012
2011 2010 2009 1
...
1 2 3 2011
+ + + +
+ + + +
HD:
Mẫu số :
2010 2009 1 2012 2012 2012 2012
1 1 ... 1 1 ...
2 3 2011 2 3 2011 2012
MS
= + + + + + + + = + + + +
1 1 1 1
2012 ... 2012.
2 3 4 2012
MS TS

= + + + + =


Khi đó :
1 1 1 1 1 1 1 1
... ...
1
2 3 4 2012 2 3 4 2012
2011 2010 2009 1
1 1 1
2012
...
2012 ...
1 2 3 2011
2 3 2012
A
+ + + + + + + +
= = =

+ + + +
+ + +


Bài 2: Thực hiện phép tính:
1 1 1 1 1
...
2 3 4 99 100
99 98 97 1
...
1 2 3 99
+ + + + +
+ + + +
HD:
98 97 1 100 100 100 100
1 1 ... 1 1 ...
2 3 99 2 3 99 100
MS
= + + + + + + + = + + + +
1 1 1 1
100 ... 100.
2 3 4 100
MS TS

= + + + + =


Khi đó :
1 1 1 1 1 1 1 1
... ...
1
2 3 4 100 2 3 4 100
99 98 97 1
1 1 1
100
...
100 ...
1 2 3 99
2 3 100
A
+ + + + + + + +
= = =

+ + + +
+ + +


Bài 3: Tính tỉ số
A
B
biết :
1 1 1 1
...
2 3 4 2009
A = + + + +
và
2008 2007 2006 1
...
1 2 3 2008
B = + + + +
HD:
Ta có :
2007 2006 1
1 1 ... 1 1
2 3 2008
B
= + + + + + + + =
2009 2009 2009 2009 2009
...
2 3 4 2008 2009
+ + + + +
1 1 1 1 1
2009 ... 2009.
2 3 4 2008 2009
A

= + + + + + =


Khi đó :
1
2009 2009
AA
BA
==
Bài 4: Tính tỉ số
A
B
biết:
1 1 1 1
...
2 3 4 200
A = + + + +
và
1 2 3 198 199
...
199 198 197 2 1
B = + + + + +
HD:
Ta có :
1 2 3 198 200 200 200 200
1 1 1 ... 1 1 ...
199 198 197 2 199 198 2 200
B
= + + + + + + + + + = + + + +
1 1 1 1
200 ... 200.
199 198 2 200
BA

= + + + + =


=>
1
200
A
B
=
Bài 5: Tính tỉ số
A
B
biết :
1 2 2011 2011
...
2012 2011 2 1
A = + + + +
và
1 1 1 1
...
2 3 4 2013
B = + + + +
HD:
32
Ta có :
1 2 2011 2013 2013 2013 2013
1 1 ... 1 1 ...
2012 2011 2 2012 2011 2 2013
A
= + + + + + + + = + + + +
1 1 1 1
2013 ... 2013. 2013
2 3 4 2013
A
AB
B

= + + + + = = =


Bài 6: Tính tỉ số
A
B
biết :
1 2 3 99
...
99 98 97 1
A = + + + +
và
1 1 1 1
...
2 3 4 100
B = + + + +
HD:
Ta có :
1 2 98 100 100 100 100
1 1 ... 1 1 ...
99 98 2 99 98 2 100
A
= + + + + + + + = + + + +
1 1 1 1
100 ... 100. 100
99 98 2 100
A
AB
B

= + + + + = = =


Bài 7: Cho
2013 2013 2013 2013
...
2 3 4 2013
A = + + + +
và
2013 2012 2011 1
...
1 2 3 2013
B = + + + +
, tính A/B
Bài 8: Thực hiện phép tính:
1 1 1 1
1 ...
3 5 97 99
1 1 1 1
...
1.99 3.97 97.3 99.1
+ + + + +
+ + + +
HD:
Ta có :
1 1 1 1 1 1 1 1
1 ... 100 ...
99 3 97 49 51 1.99 3.97 49.51
TS
= + + + + + + = + + +
1 1 1 1 1 1 1 1 1
... 2 ...
1.99 99.1 3.97 97.3 49.51 51.49 1.99 3.97 49.51
MS
= + + + + + + = + + +
Khi đó :
100
50
2
TS
MS
==
Bài 9: Thực hiện phép tính:
1 1 1 1 1
...
2 4 6 998 1000
1 1 1 1
...
2.1000 4.998 998.4 1000.2
+ + + + +
+ + + +
HD:
Ta có :
1 1 1 1 1 1 1 1 1
... 1002 ...
2 1000 4 998 500 502 2.1000 4.998 500.502
TS
= + + + + + + = + + +
1 1 1 1 1 1
...
2.1000 1000.2 4.998 998.4 500.502 502.500
MS
= + + + + + +
1 1 1
2 ...
2.1000 4.998 500.502
MS

= + + +


Khi đó :
1002
501
2
TS
MS
==
Bài 10: Tính tỉ số
A
B
biết:
1 1 1
1 ...
3 5 999
A = + + + +
và
1 1 1 1
...
1.999 3.997 5.1995 999.1
B = + + + +
HD:
Ta có :
1 1 1 1 1 1000 1000 1000
1 ... ...
999 3 997 499 501 999.1 3.997 499.501
A
= + + + + + + = + + +
1 1 1
1000 ..
999.1 3.997 499.501

= + + +


33
1 1 1 1 1 1 2 2 2
... ...
1.999 999.1 3.997 997.3 499.501 501.499 1.999 3.997 499.501
B
= + + + + + + = + + +
1 1 1
2 ...
1.999 3.997 499.501

= + + +


, Khi đó :
1000
500
2
A
B
==
Bài 11: Thực hiện phép tính:
1 1 1 1
...
51 52 53 100
1 1 1 1
...
1.2 3.4 5.6 99.100
A
+ + + +
=
+ + + +
HD:
Ta có :
1 1 1 1 1 1 1 1 1
... ...
1.2 3.4 99.100 1 2 3 4 99 100
MS = + + + = − + − + + −
=
1 1 1 1 1 1 1 1 1 1
... 2 ...
1 2 3 4 99 100 2 4 6 100
+ + + + + + − + + + +
=
1 1 1 1 1 1 1 1 1 1 1
... ... ...
1 2 3 100 1 2 50 51 52 53 100
TS
+ + + + − + + + = + + + + =
Khi đó :
1
TS
A
MS
==
Bài 12: Tính tỉ số
A
B
biết:
2012 2012 2012 2012
...
51 52 53 100
A = + + + +
và
1 1 1 1
...
1.2 3.4 5.6 99.100
B = + + + +
HD:
Ta có :
1 1 1 1
2012 ...
51 52 53 100
A

= + + + +


1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
... .... 2 ...
1 2 3 4 99 100 1 2 3 99 100 2 4 6 100
B
= − + − + + − = + + + + + − + + + +
1 1 1 1 1 1 1 1 1 1 1 1
... ... ...
1 2 3 100 1 2 3 50 51 52 53 100
B
= + + + + − + + + + = + + + +
Khi đó :
Bài 13: Tính tỉ số
A
B
biết:
1 1 1 1
...
1.2 3.4 5.6 199.200
A = + + + +
và
1 1 1
...
101.200 102.199 200.101
B = + + +
HD:
1 1 1 1 1 1 1 1 1 1 1 1 1
... ... 2 ...
1 2 3 4 199 200 1 2 3 200 2 4 200
A
= − + − + + − = + + + + − + + +
1 1 1 1 1 1 1 1 1 1 1
... ... ...
1 2 3 200 1 2 3 100 101 102 200
A
= + + + + − + + + + = + + +
1 1 1 1 1 1 301 301 301
... ...
101 200 102 199 150 151 101.200 102.199 150.151
A
= + + + + + + = + + +
Và
1 1 1 1 1 1
...
101.200 200.101 102.199 199.102 150.151 151.150
B
= + + + + + +
2 2 2
...
101.200 102.199 150.151
B = + + +
Khi đó :
301
2
A
B
=
34
Bài 14: Tính giá trị
A
B
biết:
1 1 1 1
...
1.2 3.4 5.6 101.102
A = + + + +
và
1 1 1 1 2
...
52.102 53.101 54.100 102.52 77.154
B = + + + + +
HD:
Ta có :
1 1 1 1 1 1 1 1 1 1 1 1
... ...
1 2 3 4 101 102 1 2 3 4 101 102
A
= − + − + + − = − + − + + −
1 1 1 1 1 1 1 1
... 2 ...
1 2 3 101 102 2 4 102
A
= + + + + + − + + +
1 1 1 1 1 1 1 1 1 1 1
... ... ...
1 2 3 102 1 2 51 52 53 101 102
A
= + + + + − + + + = + + + +
1 1 1 1 1 1 1 154 154 154 154
... ...
52 102 53 101 76 78 77 52.102 53.101 76.78 77.154
A
= + + + + + + + = + + + +
và
1 1 1 1 1 1 2
...
52.102 102.52 53.101 101.53 76.78 78.76 77.154
B
= + + + + + + +
2 2 2 2
...
52.102 53.101 76.78 77.154
B = + + + +
=>
154
77
2
A
B
==
Bài 15: Cho
1 1 1 1
...
1.2 3.4 5.6 101.102
A = + + + +
;
1 1 1 1 1
...
52.102 53.101 54.100 101.53 102.52
B = + + + + +
Chứng tỏ rằng
A
B
là số nguyên.
Bài 16: CMR:
1 1 1 1 1 1 1 1 1 1
1 ... ... ...
3 5 99 2 4 6 100 51 52 100
+ + + + − + + + + = + + +
HD:
Ta có :
1 1 1 1 1 1 1 1 1
1 ... 2 ...
2 3 4 99 100 2 4 6 100
VT
= + + + + + + − + + + +
1 1 1 1 1 1 1 1 1 1
1 ... 1 ... ...
2 3 4 100 2 3 50 51 52 100
VT VP
= + + + + + − + + + + = + + + =
Bài 17: Cho
1 1 1 1 1 1
1 ...
2 3 4 2011 2012 2013
S = − + − + + − +
và
1 1 1 1
...
1007 1008 2012 2013
P = + + + +
.
Tính
( )
2013
SP−
HD:
Ta có :
1 1 1 1 1 1
1 .... 2 ...
2 3 2013 2 4 2012
S
= + + + + − + + +
1 1 1 1 1 1 1 1 1 1
1 ... 1 ... ...
2 3 4 2013 2 3 1006 1007 1008 2013
SP
= + + + + + − + + + + = + + + =
Khi đó :
( )
2013
2013
00SP− = =
Bài 18: Chứng minh rằng:
1 1 1 1 2 3 99
100 1 ... ...
2 3 100 2 3 4 100

− + + + + = + + + +


HD:
Ta có :
( )
1 1 1 1 2 3 99
1 1 1 1 ... 1 ...
2 3 100 2 3 4 100
VT
= − + − + − + + − = + + + +
VP=
(đpcm)
35
Bài 19: Tính tỉ số
A
B
biết :
1 2 3 92
92 ...
9 10 11 100
A = − − − − −
và
1 1 1 1
...
45 50 55 500
B = + + + +
HD:
Ta có :
1 2 3 92 8 8 8 1 1 1
1 1 1 ... 1 ... 8 ...
9 10 11 100 9 10 100 9 10 100
A
= − + − + − + + − = + + + = + + +
1 1 1 1
...
5 9 10 100
B

= + + +


. Khi đó :
8
40
1
5
A
B
==
Bài 20: Cho
1 1 1 1 1 1
1 ...
2 3 4 20 16 2017 2018
A = − + − + − + −
và
1 1 1 1 1
...
1010 1011 2016 2017 2018
B = + + + + +
Tính
( )
2018
2017 2017
AB−
36
DẠNG 12: TÍNH GIÁ TRỊ BIỂU THỨC
Bài 1: Cho abc=2015, Tính
2015
2015 2015 2015 1
a b c
A
ab a bc b ac c
= + +
+ + + + + +
HD :
2
2
1
a bc b c
A
ab a bc abc bc b abc ac c
= + +
+ + + + + +
( ) ( )
2
1
1
1 1 1 1
a bc b c ac c
ab ac c b c ac ac c ac c
++
= + + = =
+ + + + + + + +
Bài 2: Cho abc=2, Tính
2
2 1 2 2
a b c
B
ab a bc b ac c
= + +
+ + + + + +
HD :
( ) ( )
22
2
1
1 1 1 1
a b abc a b abc
B
ab a abc bc b ac abc abc a b bc bc b ac bc b
= + + = + + =
+ + + + + + + + + + + +
Bài 3: Cho abc=1, Tính
111
a b c
A
ab a bc b ac c
= + +
+ + + + + +
HD :
( ) ( )
22
2
1
1 1 1 1
a bc b c a bc b c
A
ab a bc abc bc b abc ac c ab ac c b c ac ac c
= + + = + + =
+ + + + + + + + + + + +
Bài 4: Cho
1xyz =
, Tính giá trị của:
1 1 1
x y z
A
xy x yz y xz z
= + +
+ + + + + +
Bài 5: Cho abc= - 2012, Tính
2012
2012 1 2012 2012
a b c
B
ab a bc b ac c
= + −
+ − + + − −
HD :
( ) ( )
22
2
1
1 1 1 1
a b abc a b abc
B
ab a abc bc b ac abc abc a b bc bc b ac bc b
= + + = + + =
+ + + + + + + + + + + +
Bài 6: Chứng minh rằng nếu xyz=1 thì
1 1 1
1
1 1 1x xy y yz z zx
+ + =
+ + + + + +
HD :
( ) ( )
2
11
1
1 1 1 1
xyz xyz xyz xyz
VT VP
xyz x yz xy xyz y yz z zx xy z xz y xz z z zx
= + + = + + = =
+ + + + + + + + + + + +
Bài 7: Cho xyz=2010, CMR:
2010
1
2010 2010 2010 1
x y z
xy x yz y xz z
+ + =
+ + + + + +
HD :
2
2
1
1
x yz y z
VT
xy x yz xyz yz y xyz xz z
= + + =
+ + + + + +
Bài 8: Tính giá trị của biểu thức :
13 19 4 2A a b a b= + + −
với a+b=100
HD:
Ta có :
( ) ( ) ( )
13 4 19 2 17 17 17 17.100 1700A a a b b a b a b= + + − = + = + = =
Bài 9: Tính giá trị của biểu thức:
2
5 6 2xx+−
khi
12x−=
HD:
Ta có : Khi
1 2 3
12
2 2 0
xx
x
xx
− = =

− = = =

− = − =

Khi
2
3 5 6 2 5.9 6.3 2 61x A x x= = = + − = + − =
. Khi
2
0 5 6 2 2x A x x= = = + − = −
Bài 10: Tính giá trị của biểu thức:
53
2 5 4xy−+
, biết
( ) ( )
20 30
1 2 0xy− + + =
37
HD:
Ta có : Vì
( )
( )
( ) ( )
20
20 30
30
10
1 0 1
1 2 0
2 0 2
20
x
xx
xy
yy
y
−
− = =

= − + + = = =
+ = = −

+
, Thay vào ta được :
( )
3
5
2.1 5. 2 4 2 40 4 46A = − − + = + + =
Bài 11: Cho a, b,c khác 0 và đôi 1 khác nhau thỏa mãn :
( ) ( )
22
2013a b c b a c+ = + =
, Tính
2
()A c a b=+
HD:
Ta có :
( ) ( )
22
2013a b c b a c+ = + =
=>
( ) ( )( )
2 2 2 2
00a b a c b a b c ab a b c a b a v+ − − = = − + − + =
( )( )
00a b ab bc ca ab bc ca− + + = = + + =
vì
ab
Khi đó :
( ) ( )
2
0 2013ab bc ca b b a c abc abc+ + = = + = − = − =
tương tự :
( ) ( )
2
0 2013ab bc ca c c a b abc+ + = = + = − =
Bài 12: Cho
1,11 0,19 1,3.2 1 1
:2
2,06 0,54 2 3
A
+−

= − +

+

và
7 1 23
5 2 0,5 :2
8 4 26
B

= − −


a, Rút gọn A và B
b, Tìm x nguyên sao cho:
A x B
HD:
a, Ta có :
1 5 1 5 11
:2
2 6 2 12 12
A
− − −

= − = − =


, Và
25 75 13
:
8 26 12
B ==
b, Ta có :
12 0
11 13 11 12 13
11 12 13
12 12
12 12 12 12 12
x
x
A x B x x
x
=
−−
= = = − =
=
Bài 13: Cho
( )
2 1 5P a a= − − −
a, Rút gọn P
b, Có giá trị nào của a để P=4 không?
HD:
Ta có :
a,
11
2 1 5, 4
22
11
1 2 5, 6 3
22
a a vs a a a
P
a a a a a

− − + +


==

− − + −


b , Để
( )
( )
1
44
0
2
4
2
1
6 3 4
3
2
aa
al
P
al
aa

+ =
=


= = =
=

− =


Vậy không có giá trị nào của a đề P =4

Tài liệu khác của Toán 6

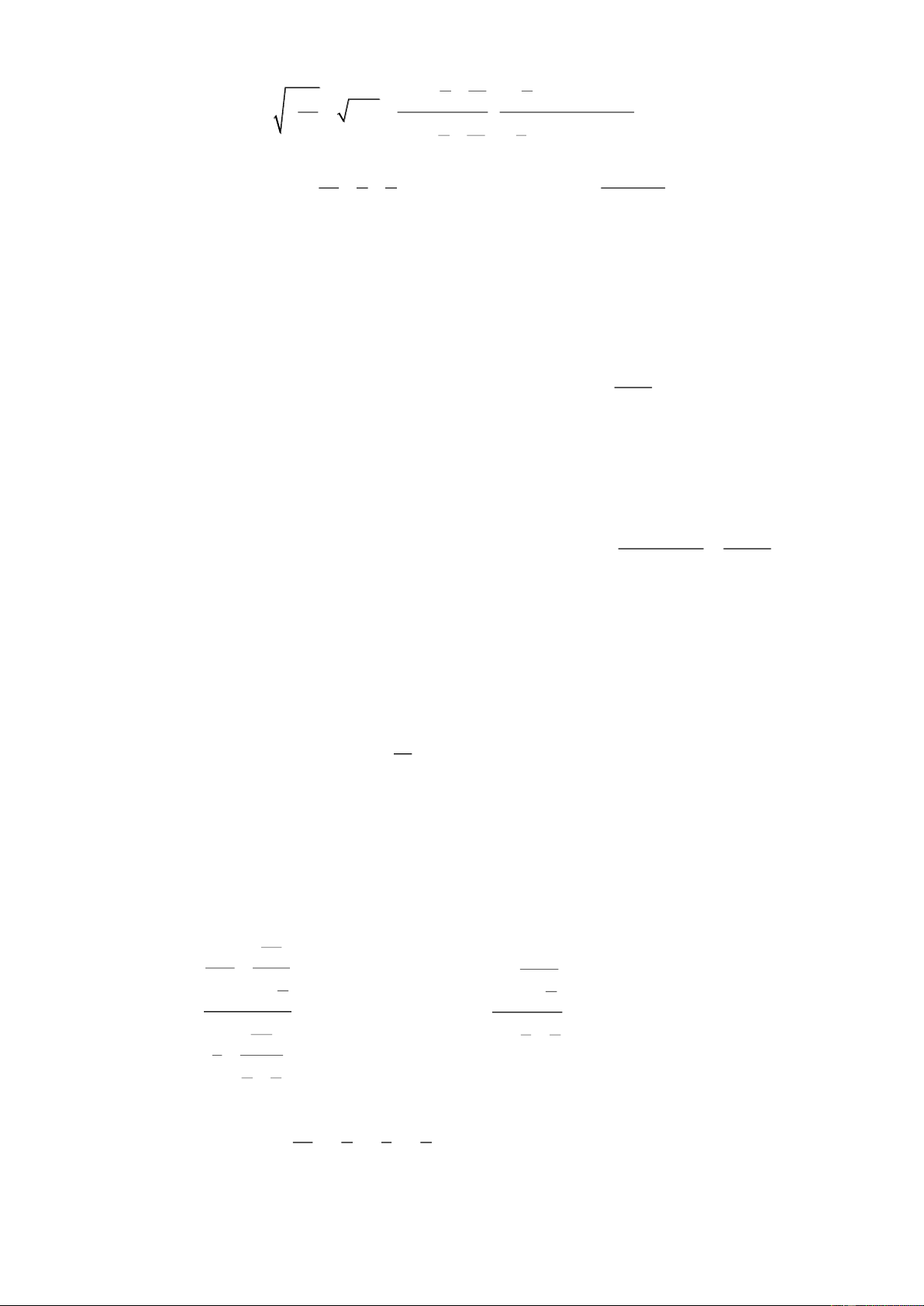
Preview text:

CHUYÊN ĐỀ : THỰC HIỆN PHÉP TÍNH DẠNG 1: RÚT GỌN
Bài 1: Thực hiện phép tính: 12 5 6 2 10 3 5 2 18 7 3 15 15 6 5 9 2 .3 − 4 .9 5 .7 − 25 .49 2 .18 .3 + 3 .2 4 .9 + 6 .120 a, − b, 2 6 3 9 3 (2 .3) (125.7) + 5 .14 10 15 14 13 2 .6 + c, 3 .15.4 4 12 11 8 .3 − 6 HD : 6 2 5 2 12 5 2 2 10 3 2 2 12 5 6 2 10 3 5 2 2 .3 − (2 ) .(3 ) 5 .7 − (5 ) .(7 ) 2 .3 − 4 .9 5 .7 − 25 .49 a, Ta có: − = − 2 6 3 9 3 (2 .3) (125.7) + 5 .14 12 6 2 .3 ( 35)3 3 9 3 3 .7 + 5 .2 .7 12 5 12 4 10 3 10 4 12 4 2 .3 − 2 .3 5 .7 − 5 .7 2 .3 (3 − ) 10 3 1 5 .7 (1− 7) 2 5.6 2 − 8 = − = − = − = 12 6 9 3 9 3 3 12 6 9 3 2 .3 5 .7 + 5 .2 .7 2 .3 5 .7 (1+ 8) 2 3 9 9 18 7 3 15 15 2 .18 .3 + 3 .2 18 7 14 3 15 15 25 17 15 15 2 .2 .3 .3 + 3 .2 2 .3 + 3 .2 b, Ta có: = = 10 15 14 13 2 .6 + 3 .15.4 10 15 15 14 28 25 15 15 28 2 .2 .3 + 3 .3.5.2 2 .3 + 3 .2 .5 15 15 2 .3 ( 10 2 2 .3 + ) 1 ( 10 2 2 .3 + ) 1 = = 25 15 3 10 2 .3 (1+ 2 .5) 2 41 6 5 6 5 9 2 2 9 9 3 4 .9 + 6 .120 (2 ) .(3 ) 12 10 12 10 + 2 .3 .2 .3.5 12 10 2 .3 + 2 .3 .5 2 .3 (1+ 5) 2.6 4 c, Ta có: = = = = 4 12 11 8 .3 − = 6 ( )4 12 12 11 11 11 11 3 12 11 11 2 .3 − 2 .3 2 .3 (2.3 − ) 2 .3 − 2 .3 1 3.5 5
Bài 2: Thực hiện phép tính: 15 9 20 9 5.4 .9 − 4.3 .8 4 2 2 2 .5 .11 .7 11 12 11 11 5 .7 + 5 .7 a, c, 9 16 29 6 5.2 .9 − b, 7.2 .27 3 3 2 2 .5 .7 .11 12 11 11 11 5 .7 + 9.5 .7 HD : 15 9 20 9 29 18 2 5.4 .9 − 4.3 .8 30 18 29 20 − 2 .3 (5.2 − 3 5.2 .3 2 .3 ) 23 9 − a, Ta có: = = = 29 16 29 6 5.2 .3 − = 7.2 .27 29 16 29 18 29 16 5.2 .3 − 7.2 .3 2 .3 ( 2 5 − 7.3 ) 5 − 8 58 4 2 2 2 .5 .11 .7 2.11 22 b, Ta có: = = 3 3 2 2 .5 .7 .11 5.7 35 11 12 11 11 5 .7 + 5 .7 11 11 5 .7 (7 + ) 1 8 4 c, Ta có: = = 12 11 11 11 5 .7 + = 9.5 .7 11 11 5 .7 (5 + 9) 14 7
Bài 3: Thực hiện phép tính: 22 7 15 10 10 10 9 5 4 9 11.3 .3 − 9 2 .3 − 2 .3 4 .9 − 2.6 a, b, c, 14 2 (2.3 ) 9 10 2 .3 10 8 8 2 .3 + 6 .20 HD : 22 7 15 29 30 29 11.3 .3 − 9 11.3 − 3 3 .(11− 3) 3.8 a, Ta có: = = = = 6 14 2 (2.3 ) 2 28 2 28 2 .3 2 .3 4 10 10 10 9 2 .3 − 2 .3 10 9 2 .3 (3 − ) 1 2.2 4 b, Ta có: = = = 9 10 2 .3 9 10 2 .3 3 3 5 4 9 4 .9 − 2.6 10 8 10 9 10 8 2 .3 − 2 .3 2 .3 (1− 3) 2 − 1 − c, Ta có: = = = = 10 8 8 2 .3 + 6 .20 10 8 10 8 10 8 2 .3 + 2 .3 .5 2 .3 (1+ 5) 6 3
Bài 4: Thực hiện phép tính: 12 5 6 2 10 3 5 2 15 9 20 9 5 4 9 2 .3 − 4 .9 5 .7 − 25 .49 5.4 .9 − 4.3 .8 4 .9 − 2.6 a, − 2 6 4 5 3 9 3 b, (2 .3) + 8 .3 (125.7) + 5 .14 9 19 29 6 5.2 .6 − c, 7.2 .27 10 8 8 2 .3 + 6 .20 HD: 1 12 5 6 2 10 3 5 2 2 .3 − 4 .9 5 .7 − 25 .49 a, Ta có : − 2 6 4 5 3 9 3 (2 .3) + 8 .3 (125.7) + 5 .14 12 5 12 4 10 3 10 4 12 4 2 .3 − 2 .3 5 .7 − 5 .7 2 .3 (3 − ) 10 3 1 5 .7 (1− 7) 5.( 6 − ) 1 − 0 = − = − = = 12 6 12 5 9 3 9 3 3 12 5 2 .3 + 2 .3 5 .7 + 5 .7 .2 2 .3 (3 + ) 9 3 1 5 .7 (1+ 8) 9 3 15 9 20 9 29 18 − 2 .3 ( 2 30 18 20 29 5.2 − 3 5.2 .3 3 .2 ) 5.4 .9 − 4.3 .8 2 b, Ta có : = = = 2 9 19 29 6 5.2 .6 − = 7.2 .27 28 19 29 18 28 18 5.2 .3 − 7.2 .3 2 .3 (5.3 − 7.2) 1 5 4 9 4 .9 − 2.6 10 8 10 9 10 8 2 .3 − 2 .3 2 .3 (1− 3) 2 − 1 − c, Ta có : = = = 10 8 8 2 .3 + = 6 .20 10 8 10 8 10 8 2 .3 + 2 .3 .5 2 .3 (1+ 5) 6 3
Bài 5: Thực hiện phép tính: 12 7 15 8 15.4 .9 − 4.3 .8 15 22 16 4 3 .2 + 6 .4 3 10 9 16 .3 +120.6 a, 24 14 12 5 19.2 .3 − b, 6.4 .27 9 7 5 23 2.9 .8 − c, 7.27 .2 6 12 11 4 .3 + 6 HD : 12 7 15 8 24 15 2 15.4 .9 − 4.3 .8 24 15 26 15 − 2 .3 (5 − 2 5.2 .3 2 .3 ) 3 a, Ta có: = = = 3 24 14 12 5 19.2 .3 − = 6.4 .27 24 14 25 16 24 24 19.2 .3 − 2 .3 2 .3 ( 2 19 − 2.3 ) 1 15 22 16 4 22 15 2 3 .2 + 6 .4 15 22 24 16 + 2 .3 (1+ 2 .3 3 .2 2 .3 ) 13 1 − 3 b, Ta có : = = = 9 7 5 23 2.9 .8 − = 7.27 .2 22 18 15 23 22 15 2 .3 − 7.3 .2 2 .3 ( 3 3 − 7.2) 5 − 5 (2 )3.3 +2 .3.5.(2.3)9 4 10 3 12 10 12 10 12 10 2 .3 + 2 .3 .5 2 .3 (1+ 5) 2.6 12 c, Ta có: ( ) = = = = 6 ( ) 12 12 11 11 11 11 11 2 12 2 .3 + 2 .3 2 .3 (2.3 + + ) 1 3.7 21 2 .3 2.3
Bài 6: Thực hiện phép tính : 12 5 6 2 10 3 5 2 2 .3 − 4 .9 5 .7 − 25 .49 15 9 20 9 5.4 .9 − 4.3 .8 a, A = ( − b, 10 12 29 6 2 .3)6 + 8 .3 (125.7)3 9 3 2 4 5 + 5 .14 5.2 .6 − 7.2 .27
Bài 7: Thực hiện phép tính: 12 5 6 2 2 .3 − 4 .9 5 4 9 4 .9 − 2.6 a, A = = ( b, B 10 8 8 2 . )6 2 4 5 3 + 8 .3 2 .3 + 6 .20
Bài 8: Thực hiện phép tính : 10 10 3 .11+ 3 .5 10 10 2 .13 + 2 .65 a, b, 9 4 3 .2 8 2 .104
Bài 9: Thực hiện phép tính: 30 7 13 27 6 6 2 .5 + 2 .5 (− ) 5 3 3 .15 + 9 .( 1 − 5) a, 27 7 10 27 2 .5 + b, 2 .5 (− )10 5 3 3 .5 .2
Bài 10: Thực hiện phép tính: 2 11 2 2 6 2 9 5 .6 .16 + 6 .12 .15 19 3 2 .27 .5 −15.( 4 − ) 4 .9 a, A = 12 4 2 3 2.6 .10 − b, 81 .960 6 .2 − ( 1 − 2)10 9 10
Bài 11: Thực hiện phép tính:  ( − 5( 15 14 22 21 3.7 −19.7 2.5 9.5 ) 0,8)5 15 4 10 20 2 .9  45 .5 a,  + b, A = : 10 16 15 (   0,4) : 6 6 3 15 6 .8 75  25 7 + 3.7 7 3 3  2      7 9 3 .5 + :        5   4  16 
Bài 12: Tính giá trị của biểu thức: A = 7 7 2 .5 + 512 2 3 3 1 0, 6 − − 1 − + 0,875 − 0,7 14 Bài 13: Tính biểu thức: 7 13 6 B = 2 − 1,21 + : 25 6 6 1 1, 2 − − − 0,25 + 0,2 7 13 3 3 6  1 − 1 1  3 .12
Bài 14: Tính biêu thức: A = 8 − 4 + − + 51.( 3 − 7)−51.( 1 − 37)+    3 4 7  (27.4 )3 2
Bài 15: Thực hiện phép tính: a, 1024: 5 5 (17.2 +15.2 ) b, 3 0 3 5 .2 + (23+ 4 ) : 2 c, 5 4 2 (5.3 +17.3 ) : 6 HD : a, Ta có: 1024: 5 5 (17.2 +15.2 ) 10 5 =  ( + ) 10  =   ( 5 5 2 : 2 17 15 2 : 2 .2 ) =1 b, Ta có: 3 0 3 5 .2 + (23+ 4 ) : 2 3 3
= 5 .2 + 24 : 2 = 250 + 3 = 253 3 .2 c, Ta có: 5 4 2 (5.3 +17.3 ) : 6 3  (3.5+17) :3 .2 =   (3 .32) 4 5 4 2 2 4 2 2 : 3 .2 = = 9.8 = 72 2 2 3 .2
Bài 16: Thực hiện phép tính: a, 2 2 2 2 2 (10 +11 +12 ) : (13 +14 ) b, 3 4 3 2 2
(2 .9 + 9 .45) : (9 .10 −9 ) HD : a, Ta có: 2 2 2 2 2 + + +
= 100+121+144 : 169+196 = 365:365 =1 (10 11 12 ) : (13 14 ) ( ) ( ) 8 3 6 3 8 + 3 .5 3 .143 c Ta có : 3 4 3 2 2
(2 .9 + 9 .45) : (9 .10 −9 ) = ( 3 8 11 2 .3 + 3 .5) : ( 2 2 3 .10 + 3 ) ( ) 6 = = =13.3 2 3 .11 11
Bài 17: Thực hiện phép tính: a, 14 14 16 4
(3 .69 + 3 .12) :3 − 7 : 2   b, 4 4 12 12 24 : 3 − 32 :16 HD : a, Ta có: 14 14 16 4
(3 .69 + 3 .12) :3 − 7 : 2   = ( 14 14 2 + ) 16 4 −  =   ( 15 15 + ) 16 4 3 .3.23 3 .3.2 : 3 7 : 2 3 .23 3 .4 : 3 − 7 : 2  1 15 16 4
= 3 .27 :3 − 7 : 2 = (9 − 7) 4 : 2 =   3 2 4 12 b, Ta có: 4 4 12 12 24 : 3 − 32 :16 = ( ) −( ) 4 12 12 12 24 : 3 32 :16 = 8 − 2 = 2 − 2 = 0
Bài 18: Thực hiện phép tính : a, 2010 ( 10 8 4 2010 2010 2010 7 : 7 − 3.2 − 2 : 2 ) b, ( 100 101 102 + + ) ( 97 98 99 2 2 2 : 2 + 2 + 2 ) HD : a, Ta có : 2010 ( 10 8 4 2010 2010 − − ) 2010 2010 7 : 7 3.2 2 : 2 = 2010 (49−3.16− ) 1 = 0 −5 −11 3 + 1 1 − 2 4 4 1 − 1 + Bài 19: Tính: 3 A = 3 − B = 2 1 3 2 + − 3 5 − 3 7 5 4 2 − 5 3 1 − 1 −  1 −  45 1  1 1   
Bài 20: Thực hiện phép tính : −  +  +     19 2  3  4         HD : 3 45 1 45 26 = − = − = 1 19 1 1 19 19 + 2 1 + 4 3  3 2 1   3 2 1 
Bài 21: Rút gọn : A = − + : − +      2 5 10   2 3 12  4
DẠNG 2 : TÍNH ĐƠN GIẢN 1 1 1 2 2 2 + − + −
Bài 1: Thực hiện phép tính: 2003 2004 2005 2002 2003 2004 − 5 5 5 3 3 3 + − + − 2003 2004 2005 2002 2003 2004 HD: 1 1 1 2 2 2 + − + − 2003 2004 2005 2002 2003 2004 Ta có : − 5 5 5 3 3 3 = + − + − 2003 2004 2005 2002 2003 2004 1 1 1  1 1 1  + − 2 + −   2003 2004 2005  2002 2003 2004  − − 1 2 7 = − =  1 1 1   1 1 1  5 3 15 5 + − 3 + −      2003 2004 2005   2002 2003 2004   3 3  0,375 − 0,3 + +  1,5+1−0,75  1890
Bài 2: Thực hiện phép tính: 11 12  +  : +115 5 5 5 2005  2,5+ −1.25 0 − ,625 + 0,5 − −   3 11 12  HD:  3 3  0,375 − 0,3 + +  1,5+1−0,75  1890 11 12 Ta có :  +  : +115 5 5 5 2005  2,5+ −1.25 0 − ,625 + 0,5 − −   3 11 12   3 3 3 3 3 3 3  + − − + +   378 2 3 4 8 10 11 12  3 3  378 378 =  +  : +115 + : +115 = 0: +115 =115   5 5 5 5 − 5 5 5 = 401  + − + − −   5 5 −  401 401  2 3 4 8 10 11 12  1 1 1 3 3 3 − − 0, 6 − − −
Bài 3: Thực hiện phép tính: 9 7 11 25 125 625 + 4 4 4 4 4 4 − − − 0,16 − − 9 7 11 5 125 625 HD: 1 1 1 3 3 3 − − 0, 6 − − − 9 7 11 25 125 625 1 3 Ta có : + + =1 4 4 4 4 4 4 = − − − 4 4 0,16 − − 9 7 11 5 125 625  12 12 12 3 3 3  12 + − − 3 + + +  
Bài 4: Thực hiện phép tính: 7 25 71 13 19 101 564. :  4 4 4 5 5 5  4 + − − 5 + + +   7 25 71 13 19 101  HD:  12 12 12 3 3 3  12 + − − 3 + + +   12 3  Ta có : 7 25 71 13 19 101 564. :  =564. : = 564.5 = 2820   4 4 4 5 5 5   4 5  4 + − − 5 + + +   7 25 71 13 19 101 
Bài 5: Thực hiện phép tính: 5 1 1 1 1 5 5 5 15 15 1+ + + + 5 − + − 15 − + a, 2 4 8 16 b, 3 9 27 11 121 : 1 1 1 1 8 8 8 16 16 1− + − + 8 − + − 16 − + 2 4 8 16 3 9 27 11 121 HD: 1 1 1 1  1 1 1 1  1+ + + + 16 1+ + + +    2 4 8 16  16 + 8 + 4 + 2 +1 31 a, Ta có : 2 4 8 16 = = = 1 1 1 1  1 1 1 1  16 − 8 + 4 − 2 +1 11 1− + − + 16 1− + − +   2 4 8 16  2 4 8 16  5 5 5 15 15 5 − + − 15 − + 5 15 5 16 2 b, Ta có : 3 9 27 11 121 : = : = . = 8 8 8 16 16 8 16 8 15 3 8 − + − 16 − + 3 9 27 11 121
Bài 6: Thực hiện phép tính: 2 2 2 4 4 4 12 12 12 3 3 3 2 − + − 4 − + − 12 − − − 3 + + + a, 19 43 1943 29 41 2941 : b, 7 289 85 13 169 91 : 3 3 3 5 5 5 4 4 4 7 7 7 3 − + − 5 − + − 4 − − − 7 + + + 19 43 1943 29 41 2941 7 289 85 13 169 91 HD: 2 2 2 4 4 4 2 − + − 4 − + − 2 4 2 5 5 a, Ta có : 19 43 1943 29 41 2941 : = : = . = 3 3 3 5 5 5 3 5 3 4 6 3 − + − 5 − + − 19 43 1943 29 41 2941 12 12 12 3 3 3 12 − − − 3 + + + 12 3 7 b, Ta có : 7 289 85 13 169 91 : = : = 3. = 7 4 4 4 7 7 7 4 7 3 4 − − − 7 + + + 7 289 85 13 169 91
Bài 7: Thực hiện phép tính:  5 − 7 9 11  3 − + − (3 − )   3 3 3 3 + − + −  3 7 9 11 13  4 a, 7 11 1001 13  b, 10 14 6 22  2 + − + 9 9 9 9 : (2 − )   − + − + 9  21 27 11 39  3 1001 13 7 11 HD:  5 − 7 9 11  3 − + −  5 7 9 11 9 − (3 − )   9 − + − + .    7 9 11 13  4  7 9 11 13  4 9 − 1 9 − a, Ta có : 4 = = : =  = 10 14 6 22  2 + − + 2  5 7 9 11  4 2 3 4 2 2 : (2 − )   + − + : .    21 27 11 39  3 3  7 9 11 13  3 3 4 3 3 3 3  1 1 1 1  3 + − + − 3 1+ − + −    7 11 1001 13  3 1 b, Ta có : 7 11 1001 13 = = = 9 9 9 9 − + − +  1 1 1 1  9 3 9 9 1+ − + −   1001 13 7 11  7 11 1001 13  4 2 2 50 − + − Bài 8: Tính nhanh: 13 15 17 8 4 4 100 − + − 13 15 17 HD: 6 4 2 2 4 2 2 50 − + − 50 − + − 1 Ta có : 13 15 17 = 13 15 17 = 8 4 4  4 4 4  2 100 − + − 2 50 − + −   13 15 17  13 15 17  Bài 9: Tính: 2 3 3 3 3 2 2  5  3 + − + − + 3. −  24.47 − 23 3 3  6  a, A= 7 11 1001 13 . b, 24 + 47.23 9 9 9 9 − + − + 7  35 35 105 35  9 : + + +   1001 13 7 11
60  31.37 37.43 43.61 61.67  HD: 24.47 − 23 47(23+ ) 1 − 23 47.23 + 24 a, Ta có : = = =1 24 + 47.23 47.23 + 24 47.23+ 24  1 1 1 1  3 1+ − + −    7 11 1001 13  3 3 1 và = = A = =  1 1 1 1  9 9 3 9 1+ − + −    7 11 1001 13  b, Ta có : 2 2 25 8 25 71 TS = + 3. − = − = 3 3 36 3 36 36 7  5.7 5.7 3.5.7 5.7  7 35  6 6 18 6  MS = : + + +   = : + + +   
60  31.37 37.43 43.61 61.67 
6  6  31.37 37.43 43.61 61.67  7 35  1 1 1 1 1 1 1 1  MS = : − + − + − + −   
60  6  31 37 37 43 43 61 61 67  7 35  1 1  2077 71 2077 MS = : − =    => B = : 60  6  31 67  1800 36 1800
Câu 10: Thực hiện phép tính: 10 5 5 3 3 155 − − + + − 0,9 a, 7 11 23 5 13 A = + 26 13 13 7 3 402 − − + + 0,2 − 7 11 23 91 10 3 3 0, 375 − 0, 3 + + 1,5 + 1 − 0, 75 b, 11 12 A = + 5 5 5 0 − ,625 + 0,5 − − 2,5 + −1,25 11 12 3 7
DẠNG 3 : TÍNH TỔNG TỰ NHIÊN
Bài 1: Tính tổng tự nhiên
a, A= 9 + 99 + 999 +... + 999...9 ( 10 số 9)
b, B= 1+11+111+... +111...1 (10 số 1) HD: a, Ta có: A = (
− ) +( 2 − )+( 3 − )+ +( 10 10 1 10 1 10 1 ... 10 − ) 1 = ( 2 3 10
10 +10 +10 + ... +10 ) −10 =111...10 −10 =111...100 ( 9 số 1)
b, Ta có: 9B = 9 + 99 + 999 +....+ 9999...99 ( 10 số 9). Tính như câu a
Bài 2: Tính tổng tự nhiên
a, C= 4 + 44 + 444 +... + 444...4 (10 số 4)
b, D= 2 + 22 + 222 +... + 222...2 (10 số 2) HD:
a, Ta có: C = 4(1+11+111+...+111...1 ) 1 ( 10 số 1)
9C = 4(9 + 99 + 999 +...+ 999...99) ( 10 số 9). Tính như tính ở trên b, Ta có :
D = 2(1+11+111+...+111...1 ) 1 (10 số 1)
9D = 2(9 + 99 + 999 +...+ 999...99) (10 số 9)
Bài 3 : Tính tổng sau: E= 3 + 33 + 333 +... + 333...3 (10 số 3) 8
DẠNG 4 : TÍNH TỔNG PHÂN SỐ
Bài 1: Tính nhanh tổng sau: 1 1 1 2 2 2 2 a, A= + +...+ b, B= + + +...+ 5.6 6.7 24.25 1.3 3.5 5.7 99.101 HD:  1 1   1 1   1 1  1 1 4 a, Ta có : A = − + − +...+ − = − =        5 6   6 7   24 25  5 25 25
1 1   1 1   1 1   1 1  1 100 b, Ta có : B = − + − + − +...+ −         =1− =
1 3   3 5   5 7   99 101 101 101
Bài 2: Tính nhanh tổng sau: 2 2 2 5 5 5 4 4 4 4 a, D= + +...+ b, K= + + +...+ 1.6 6.11 26.31 11.16 16.21 21.26 61.66 HD :  5 5 5 5   1 1 1 1 1 1 1  a, Ta có : D = 5 + + +....+ = 5 1− + − + − +...+ −     1.6 6.11 11.16 26.31  6 6 11 11 16 26 31  1  30 150 D = 5 1− = 5. =    31 31 31  1 1 1 1   5 5 5 5  b, Ta có: K = 4 + + +...+ = 5K = 4 + + +...+     11.16 16.21 21.26 61.66  11.16 16.21 21.26 61.66   1 1 1 1 1 1   1 1  55 4 2 5K = 4 − + − +...+ − = 4 −     => 5K = 4. = K = = 11 16 16 21 61 66  11 66  11.66 66 33
Bài 3: Tính nhanh tổng sau: 4 4 4 4 1 1 1 1 a, N= + + +...+ b, F = + + + ... + 1.3 3.5 5.7 99.101 1.1985 2.1986 3.1987 16.2000 HD :  2 2 2 2   1  200 a, Ta có : N = 2 + + +...+ = 2 1− =     1.3 3.5 5.7 99.101  101 101 5 5 5 5 5
Bài 4: Tính tổng sau: K = + + + ... + + 3.7 7.11 11.15 81.85 85.89 1 1 1 1
Bài 5: Tính tổng sau: A = + + ... + + 25.24 24.23 7.6 6.5 5 5 5 5
Bài 6:Tính tổng sau: A = + + +...+ 3.6 6.9 9.12 99.102
Bài 7: Tính giá trị của biểu thức:  3 3 3 3   25 25 25  A = + + +...+ − + +...+     1.8 8.15 15.22 106.113   50.55 55.60 95.100  HD: 3 3 3 3   Ta có : B = + + +...+ 7 7 7 7 = 7B = 3 + + +...+   1.8 8.15 15.22 106.113 1.8 8.15 15.22 106.113  1 1 1 1 1 1 1 1   1  112 3.112 48 = 7B = 3 − + − + − +...+ − = 3 1− = 3. = B = =     1 8 8 15 15 22 106 113   113  113 7.113 113 25 25 25 5 5 5 và C = + +...+ = 5C = + +...+ 50.55 55.60 95.100 50.55 55.60 95.100 1 1 1 1 48 1 = 5C = − = = C =
. Khi đó : A = B − C = − 50 100 100 500 113 500 9 1 9 9 9 Bài 8: Tính nhanh: + + +...+ 19 19.29 29.39 1999.2009 HD: 1 9 9 9 9 9 9 9 Ta có : + + +...+ = = A = + + +...+ 19 19.29 29.39 1999.2009 9.19 19.29 29.39 1999.2009  10 10 10 10   1 1  => 10A = 9 + + +...+ = 9 −      9.19 19.29 29.39 1999.2009   9 2009  2000 2000 200 10A = 9. = = A = 9.2009 2009 2009 2 2 2 2 2 Bài 9: Tính tổng sau: C= + + + + 15 35 63 99 143
Bài 10: Tính nhanh tổng sau: 1 1 1 1 1 1 2 2 2 2 2 a, E= + + + + + b, C= + + + + 7 91 247 475 755 1147 15 35 63 99 143 HD: 1 1 1 1 1 1 1 1 1 1 36 a, Ta có : E = + + +...+ =1− + − +...+ − = 1− = 1.7 7.13 13.19 31.37 7 7 13 31 37 37 37 2 2 2 2 2 1 1 8 b, Ta có : C = + + + + = − = 3.5 5.7 7.9 9.11 11.13 3 11 33
Bài 11: Tính nhanh tổng sau 2 2 2 2 9 9 9 9 a, F= + + +...+ 1+ + + +...+ 6 66 176 (5n − 4)(5n + b, G= 1) 45 105 189 29997 HD:  1 1 1 1   1 1 1 1  a, Ta có : F = 2 + + +...+ (  =  + + +   n )( n ) 2 6 66 176 5 4 5 1 
1.6 6.11 11.16 (5n 4)(5n )1 − + − +      5 5 5 5   1  5n 2n 5F = 2 + + +...+   = 2 1− = 2.   => F = 1.6 6.11 11.16 (5n 4)(5n )1 − +    5n +1 5n +1 5n + 1 3 3 3 3 3 3 3 3 b, Ta có : G = 1+ + + +...+ =1+ + + +...+ 15 35 63 9999 3.5 5.7 7.9 99.101  1 1 1   2 2 2  G = 1+ 3 + +...+ = 2G = 2 + 3 + +...+      3.5 5.7 99.101  3.5 5.7 99.101  1 1  98 98 300 150 2G = 2 + 3 − = 2 + 3. = 2 + =   = G =  3 101 3.101 101 101 101 1 1 1 6
Bài 12: Tính nhanh tổng sau : M= + + +...+ 2.15 15.3 3.21 87.90 HD: 6 6 6 6 Ta có : M = + + +...+ 12.15 15.18 18.21 87.90  3 3 3   1 1 1 1 1 1   1 1  M = 2 + +...+ = 2 − + − +...+ −     = 2 −   12.15 15.18 87.90  12 15 15 18 87 90  12 90  50 25 20 10 100 100 1 Bài 13 : Tính : 50 + + + + + + ... + + 3 3 4 3 6.7 98.99 99 3 3 3 3 Bài 14: Tính: 1 + + + + ... + 15 35 63 99.101 1 1 1 1 1 1 1 Bài 15: Tính: A = + + + + + ... + + 6 12 20 30 42 90 110 10 1 1 1 1 1 1 Bài 16: Tính: + + + + + 2 14 35 65 104 152 1 1 1 1 1 1 1 1
Bài 17: Tính tổng: B = + + + + + + + 10 15 21 28 36 45 55 66
Bài 18: Tính nhanh tổng sau 38 9 11 13 15 17 197 199 3 5 7 201 a, H= + − + − + −...+ − b, I= − + −...− 25 10 15 21 28 36 4851 4950 1.2 2.3 3.4 100.101 HD: H 38 9 11 13 15 197 199 a, Ta có : = + − + − + ...+ − 2 50 20 30 42 56 9702 9900 H 38 9 11 13 15 197 199 = + − + − +...+ − 2 50 4.5 5.6 6.7 7.8 98.99 99.100 H 38
 1 1   1 1   1 1   1 1   1 1   1 1  = + + − + + + − + +...+ + − +             2 50
 4 5   5 6   6 7   7 8   98 99   99 100  H 38 1 1 76 + 25 −1 = + − = =1 = H = 2 2 50 4 100 100  1   1 1   1 1   1 1  1 100 b, Ta có : I = 1+ − + + + −...− +         =1− =  2   2 3   3 4  100 101 101 101 1 1 1 1 1
Bài 19: Thực hiện phép tính: A = 3. − 5. + 7. −...+15. −17. 1.2 2.3 3.4 7.8 8.9 HD: 1 1 1 1 1 3 5 7 15 17 Ta có : A = 3. − 5. + 7. −...+15. −17. = − + −...+ − 1.2 2.3 3.4 7.8 8.9 1.2 2.3 3.4 7.8 8.9
1 1   1 1   1 1   1 1   1 1  1 8 = + − + + + −...+ + − +           =1− =
1 2   2 3  3 4   7 8   8 9  9 9 5 4 3 1 13
Bài 20: Không quy đồng, Hãy tính : B = + + + + 2.1 1.11 11.2 2.15 15.4 HD: 5 4 3 1 13 B 5 4 3 1 13 Ta có : B = + + + + => = + + + + 2.1 1.11 11.2 2.15 15.4 7 2.7 7.11 11.14 14.15 15.28 B 1 1 1 1 1 1 1 1 1 1 1 1 13 7.13 13 = = − + − + − + − + − = − = => B = = 7 2 7 7 11 11 14 14 15 15 28 2 28 28 28 4 4 6 9 7 7 5 3 11 Bài 21: Tính : A = + + + và B = + + + 7.31 7.41 10.41 10.57 19.31 19.43 23.43 23.57 HD: Ta có : A 4 6 9 7  1 1   1 1   1 1   1 1  1 1 = + + + = − + − + − + − = −         5 31.35 35.41 41.50 50.57
 31 35   35 41  41 50   50 57  31 57 B 7 5 3 11  1 1   1 1   1 1   1 1  1 1 = + + + = − + − + − + − = −         2 31.38 38.43 43.46 46.57
 31 38   38 43   43 46   46 57  31 57 A B A 5 Khi đó : = = = 5 2 B 2 1 1 1 1
Bài 22: Tính nhanh tổng sau: P= + + +...+ 1.2.3 2.3.4 3.4.5 10.11.12 HD: 2 2 2 2  1 1   1 1   1 1  Ta có : 2P = + + +...+ = − + − +...+ −       1.2.3 2.3.4 3.4.5 10.11.12 1.2 2.3   2.3 3.4  10.11 11.12  11 1 1 65 65 2P = − = = P = 1.2 11.12 132 264 1 1 1 1 1 1 Bài 23 : Tính : A = + + + + + 10 40 88 154 238 340 1 1 1 1 1 1 Bài 24 : Tính : A = − − − − − 6 35 63 99 143 195  1 1 1  1−3−5−...− 49
Bài 25: Thực hiện phép tính: A = + +...+ .    4.9 9.14 44.49  89 HD:   Đặ 1 1 1 5 5 5 1 1 45 t : B = + +...+ = 5B = + +...+ = − =   4.9 9.14 44.49 4.9 9.14 44.49  4 49  4.49 9 => B = 4.49 1− 3 − 5 −... − 49 1− (3+ 5 +...+ 49) 1− 612 6 − 11 và C = = = = 89 89 89 89 9 6 − 11 Khi đó : A = . B C = . 4.49 89 1 1 1 1 (1+ 2 + 3 + ... +100)( − − − )(63.1,2 − 21.3,6)
Bài 26: Thực hiện phép tính: 2 3 7 9
1− 2 + 3 − 4 + ... + 99 − 100 HD: 1 1 1 1 (1+ 2 + 3 + ... +100)( − − − )(63.1,2 − 21.3,6) Ta có: 2 3 7 9 63.1, 2 − 21.3, 6 = 0 = = 0
1− 2 + 3 − 4 + ... + 99 − 100 A 1 1 1 1 Bài 27: Tính tỉ số biết : A = + + +...+ và B 1.300 2.301 3.302 101.400 1 1 1 1 B = + + +...+ 1.102 2.103 3.104 299.400 HD: 299 299 299 1 1   1 1   1 1   1 1  299A = + + ... + = − + − + − + ...+ −         1.300 2.301 101.400
1 300   2 301  3 302  101 400   1 1 1   1 1 1 
= 299A = 1+ + + ... + − + + ...+      2 3 101  300 301 400  101 101 101 101 101B = + + + ... + 1.102 2.103 3.104 299.400  1   1 1   1 1   1 1  = 1− + − + − + ...+ −         
102   2 103   3 104   299 400   1 1 1   1 1 1   1 1 1   1 1 1  = 1+ + + ... + − + + ...+ = 1+ + + ...+ − + + ...+          2 3 299  102 103 400   2 3 101  300 301 400  A 101
Khi đó : 299A = 101B = = B 299 12
DẠNG 5: TÍNH TỔNG TỰ NHIÊN DẠNG TÍCH
Bài 1: Tính nhanh các tổng sau a, A= 1.2+2.3+3.4+…+98.99
b, B= 1.2 + 3.4 + 5.6 +...+ 99.100 HD:
a, Ta có: 3A =1.2(3− 0) + 2.3(4 − )
1 + 3.4(5− 2) +...+98.99(100 −97)
3A = (1.2.3− 0.1.2) + (2.3.4 −1.2.3) + (3.4.5 − 2.3.4) +...+ (98.99.100−97.98.99) 98.99.100
3A = 98.99.100 = A = 3
b, Ta có: B = 2 + (2 + ) 1 .4 + (4 + ) 1 .6 +...+ (98+ ) 1 .100
B = 2 + (2.4 + 4) + (4.6 + 6) +...+ (98.100 +100)
B = (2.4 + 4.6 + 6.8+...+ 98.100) + (2 + 4 + 6 +...+100)
Đặt M = 2.4 + 4.6 + 6.8+...+ 98.100
6M = 2.4(6 −0) + 4.6(8− 2) + 6.8(10 − 4) +...+98.100(102 −96)
6M = (2.4.6 − 0.2.4) + (4.6.8− 2.4.6) + (6.8.10 − 4.6.8) +...+ (98.100.102 −96.98.100) 98.100.102
6M = 98.100.102 = M = 6
Tính N = 2 + 4 + 6 +.... +100 rồi thay vào B
Bài 2: Tính nhanh các tổng sau a, D= 1.4+2.5+3.6+…+100.103
b, E= 1.3+ 2.4 + 3.5 +...+ 97.99 + 98.100 HD: a, Ta có: D =1.(1+ ) 3 + 2.(2 + ) 3 + 3(3+ ) 3 +...+100.(100 + ) 3 D = (1.1+1. ) 3 + (2.2 + 2. ) 3 + (3.3+ 3. ) 3 +...+ (100.100+100. ) 3
D = (1.1+ 2.2 + 3.3+...+100.100) +3(1+ 2 +3+...+100)
Đặt, A =1.1+ 2.2 + 3.3+...+100.100 và B =1+ 2 + 3+ 4 +...+100 b, Ta có: E = (
1 1+ 2) + 2(2 + 2) +3(3+ 2) +...+97(97 + 2) +98(98 + 2)
E = (1.1+1.2) + (2.2 + 2.2) + (3.3+ 3.2) +...+ (97.97 + 97.2) + (98.98+ 98.2)
E = (1.1+ 2.2 + 3.3+...+ 97.97 + 98.98) + 2(1+ 2 +3+ 4 +...+97 +98)
Đặt A =1.1+ 2.2 + 3.3+...+ 98.98 và B =1+ 2 + 3+ 4 +...+ 97 + 98 Tính rồi thay vào E
Bài 3: Tính nhanh các tổng sau
a, F= 1.3 + 5.7 + 9.11+...+ 97.101
b, G= 1.2.3+2.3.4+3.4.5+…+98.99.100 HD:
a, F =1.(1+ 2) + 5(5 + 2) + 9(9 + 2) +...+ 97(97 + 2)
F = (1.1+1.2) + (5.5+ 5.2) + (9.9 + 9.2) +...+ (97.97 + 97.2)
F = (1.1+ 5.5+ 9.9 +...+ 97.97) + 2(1+ 5+ 9 +...+ 97)
Đặt A =1.1+ 5.5 + 9.9 +...+ 97.97, B =1+ 5 + 9 +...+ 97 , Tính rồi thay vào F
b, 4G =1.2.3(4 − 0) + 2.3.4(5 − )
1 + 3.4.5(6 − 2) +...+98.99.100(101−97)
4G = (1.2.3.4 −0.1.2. )
3 + (2.3.4.5−1.2.3.4) + (3.4.5.6 − 2.3.4.5) +...+ (98.99.100.101−97.98.99.100) 98.99.100.101
4G = 98.99.100.101 = G = 4 13
Bài 4: Tính nhanh các tổng sau
a, H= 1.99 + 2.98 + 3.97 + ...+ 50.50
b, K= 1.99 + 3.97 + 5.95 +... + 49.51 HD:
a, H =1.99 + 2.(99 − )
1 + 3.(99 − 2) +...+50(99 − 49)
H =1.99 + (2.99 −1.2) + (3.99 − 2. ) 3 +...+ (50.99 − 49.50)
H = (1.99 + 2.99 +3.99 +...+50.99) −(1.2 + 2.3+3.4 +...+ 49.50)
Đặt A = 99(1+ 2+3+...+50), B =1.2 + 2.3+3.4 +...+ 49.50
Tính A và B rồi thay vào H
b, K =1.99 + 3(99 − 2) + 5.(99 − 4) +...+ 49(99 − 48)
K =1.99 + (3.99 − 2. )
3 + (5.99 − 4.5) +...+ (49.99 − 48.49)
K = (1.99 +3.99 +5.99 +...+ 49.99) −(2.3+ 4.5+...+ 48.49)
Đặt A = 99(1+3+5+...+ 49), B = (2.3+ 4.5+ 6.7 +...+ 48.49)
Tính A và B rồi thay vào K
Bài 5: Tính nhanh các tổng sau : C= 1.3+ 3.5 + 5.7 +... + 97.99 HD:
C =1.(1+ 2) +3.(3+ 2) +5(5+ 2) +...+97.(97 + 2)
C = (1.1+1.2) + (3.3+ 3.2) + (5.5+ 5.2) +...+ (97.97 + 97.2)
C = (1.1+ 3.3+...+97.97) + 2(1+3+5+...+97)
Đặt A =1.1+ 3.3+ 5.5 +...+ 97.97, B =1+ 3 + 5 + 7 +...+ 97
Tính A và B rồi thay vào C 1.99 + 2.98 + ... + 99.1
Bài 6: Tính: A = 1.2 + 2.3+ 3.4 +...+ 99.100 14
DẠNG 6: TÍNH TỔNG CÔNG THỨC 1 1 1 Bài 1: Tính tổng: D =1+ (1+ 2) + (1+ 2 + 3) + ... + (1+ 2 + ... + 20) 2 3 20 HD: 1 2.3 1 3.4 1 20.21 3 4 5 21 Ta có: D = 1+ . + . +...+ . =1+ + + +...+ 2 2 3 2 20 2 2 2 2 2 1 1 = (2 + 3+ 4 +...+ 20 + 2 ) 1 = .230 = 115 2 2 1 1 1
Bài 2: Tính tổng: F = 1+ (1+ 2) + (1+ 2 + 3) + ... + (1+ 2 + ... + 2016) 2 3 2016 HD: 1 2.3 1 3.4 1 2016.2017 Ta có: F = 1+ . + . +....+ . 2 2 3 2 2016 2 2 +1 3 +1 4 +1 2016 +1 + + + + F = 1+ + + +...+ 1 1 1 2 3 4 ... 2016 =1+ + +...+ + 2 2 2 2 2 2 2 2 1 2018.2015 2015.2019 F = 1+ .2015 + =1+ 2 2 2 1 1 1 Bài 3: Tính:1+
(1+ 2)+ (1+ 2+3)+...+ (1+ 2+...+16) 2 3 16 HD: 1 2.3 1 3.4 1 16.17 Ta có: F = 1+ . + . +....+ . 2 2 3 2 16 2 2 +1 3 +1 4 +1 16 +1 + + + + F = 1+ + + +...+ 1 1 1 2 3 4 ... 16 =1+ + +...+ + 2 2 2 2 2 2 2 2 1 1 1
Bài 4: Tính tổng: G = 1+ (1+ 2) + (1+ 2 + 3) + ... + (1+ 2 + ... +100) 2 3 100 HD: 1 (1+ 2).2 1 (1+ 3).3 1 (1+100).100 Ta có: G = 1+ . + . +...+ . 2 2 3 2 100 2 2 +1 3 +1 4 +1 100 +1 + + + + G = 1+ + + +...+ 1 1 1 2 3 4 ... 100 =1+ + +...+ + 2 2 2 2 2 2 2 2 1 3.2 1 4.3 1 501.500
Bài 5: Tính tổng: H = 1+ . + . +...+ . 2 2 3 2 500 2 HD: 3 4 5 501 3 + 4 + 5 + ... + 501 Ta có: H = 1+ + + +...+ =1+ 2 2 2 2 2 1 1 1 Bài 6: Tính: + +...+ 1+ 2 + 3 1+ 2 + 3 + 4 1+ 2 + ... + 59 HD: 1 1 1 1
Ta có: = ( + ) + ( + ) + ( + ) +...+ 1 3 .3 1 4 .4 1 5 .5 (1+ 59).59 2 2 2 2 2 2 2 2  1 1 1 1   1 1   19  19 = + + +...+ = 2 + + +...+   = 2 − = 2 =     3.4 4.5 5.6 59.60  3.4 4.5 5.6 59.60   3 60   60  30 50 25 20 10 100 100 1 Bài 7: Tính: 50 + + + + + +...+ + 3 3 4 3 6.7 98.99 99 15 HD:  50 25 20 10  100 100 100 100  Ta có: A = 50 + + + + + + +...+ +      3 3 4 3   6.7 7.8 98.99 99.100   1 1 1 1 1   1 1 1  A = 100 + + + + +100 + +...+     1.2 2.3 3.4 4.5 5.6   6.7 7.8 99.100   1 1 1 1   1  A = 100 + + +...+ =100. 1− = 99     1.2 2.3 3.4 99.100   100  16 DẠNG 7: TÍNH TÍCH Bài 1: Tính tích 2 2 2 2 2 3 4 20 2 2 2 2 1 2 3 10 a, A= . . ... b, B= . . ... 1.3 2.4 3.5 19.21 1.2 2.3 3.4 10.11 HD: 2.2 3.3 4.4 20.20
(2.3.4...20)(2.3.4...20) 20.2 40 a, Ta có: A = . . .... = = = 1.3 2.4 3.5 19.21 (1.2.3....19)(3.4.5...2 ) 1 21 21 1.1 2.2 3.3 10.10 (1.2.3....10)(1.2.3...10) 1 b, Ta có: B = . . .... = = 1.2 2.3 3.4 10.11 (1.2.3...10)(2.3.4...1 ) 1 11  1  1  1   1  Bài 2: Tính tổng C = 1− 1− 1− ... 1−        1+ 2  1+ 2 + 3  1+ 2 + 3 + 4   1+ 2 + 3 +... + 2016  HD:                 1 1 1 1 Ta có: C = 1−  ( + ) .1−   ( + ) .1−   ( + ) ....1−  1 2 .2 1 3 .3 1 4 .4   (1+ 2016).2016           2   2   2   2  2 5 9 2017.2016 − 2 4 10 18 2016.2017 − 2 = . . ..... = . . .... 3 6 10 2016.2017 6 12 20 2016.2017 1.4 2.5 3.6 2015.2018 1004 C = . . .... = 2.3 3.4 4.5 2016.2017 3009
 1 1  1 1  1 1   1 1  Bài 3: Tính: A = − − − ... −      
 2 3  2 5  2 7   2 99  HD: 1 3 5 97 (1.3.5....97) 1 Ta có: A = . . .... = = 49 2.3 2.5 2.7 2.99 2 .(3.5.7...99) 49 2 .99  1999  1999   1999  1+ 1+ ... 1+       1  2   1000  Bài 4: Tính:  1000  1000   1000  1+ 1+ ... 1+       1  2   1999  HD:
 2000 2001 2002 2999  1001 1002 1003 2999  Ta có: A = . . ... : . . ....      1 2 3 1000   1 2 3 1999 
 2000.2001.2002...2999   1.2.3...1999  1001.1002....1999 A = .     = =1  1.2.3.4...1000
 1001.1002....2999  1001.1002...1999  1  1  1   1  Bài 5: Tính: 1− 1− 1− ... 1−        4  9  16   400  HD: 3 8 15 399 1.3 2.4 3.5 19.21 (1.2.3...19)(3.4.5...2 )1 Ta có: = . . .... = . . ... = 21 21 = = 4 9 16 400 2.2 3.3 4.4 20.20
(2.3.4...20)(2.3.4.5...20) 20.2 40  1  1   1  Bài 6: Tính: 1− 1− ... 1−       1+ 2  1+ 2 + 3   1+ 2 + 3 + ... + n  HD: 17           1 1 1 Ta có: A = 1−  ( + ) 1−  ( + ) ...1−  1 2 .2 1 3 .3   (1+ n).n        2  2   2   2  2  2   2  4 10 18 n (n + ) − = 1 2 1− 1− 1− ....     1−  = . . ....  2.3  3.4  4.5   n  (n )1  +  2.3 3.4 4.5 n (n + ) 1 1.4 2.5 3.6
(n− )1(n+ 2) (1.2.3...(n−1))(4.5....(n+ 2)) = n + 2 n + 2 . . ... = = = 2.3 3.4 4.5 n (n + ) 1
(2.3...n)(3.4.5...(n+1)) .3 n 3n Bài 7: Tính:  1  1  1   1   1  1  1   1  a/ 1+ 1+ 1+ ... 1+       b/ 1− 1− 1− ... 1−        1.3  2.4  3.5   17.19   21 28  36   1326  HD: a, Ta có: 4 9 16 17.19 +1 2.2 3.3 4.4 18.18 (2.3.4...18)(2.3.4...18) 18.2 A = . . .... = . . ... = = 36 = 1.3 2.4 3.5 17.19 1.3 2.4 3.5 17.19 (1.2.3...17)(3.4.5...19) 19 19 b, Ta có: 20 27 35 1325 40 54 70 2650 5.8 6.9 7.10 50.53 B = . . .... = . . .... = . . ... 21 28 36 1326 42 56 72 2652 6.7 7.8 8.9 51.52 (5.6.7...50)(8.9.10...53) 5.53 B = ( = 6.7.8...5 ) 1 (7.8.9...52) 51.7 Bài 8: Tính tích 2 2 2 2 2 2 2 2 2 3 4 5 6 7 8 9 8 15 24 2499 a, D= . . . . . . . b, E= . . ... 3 8 15 24 35 48 63 80 9 16 25 2500 HD: 2.2 3.3 4.4 8.8 9.9
(2.3.4...8.9)(2.3.4...8.9) 9.2 9 a, D = . . .... . = = = 1.3 2.4 3.5 7.9 8.10
(1.2.3...7.8)(3.4.5...9.10) 10 5 2.4 3.5 4.6 49.51 (2.3.4...49)(4.5.6...5 ) 1 2.51 17 b, E = . . .... = = = 3.3 4.4 5.5 50.50
(3.4.5...50)(3.4.5...50) 50.3 25 Bài 9: Tính tích  1  1  1   1   1  2  3   10  a, G= 1− 1− 1− ... 1−       b, H= 1− 1− 1− ... 1−        2  3  4   100   7  7  7   7  HD: 1 2 3 99 1 a, Ta có: G = . . .... = 2 3 4 100 100 6 5 4 3 2 1 0 1 − 2 − 3 − b, Ta có: H = . . . . . . . . . = 0 7 7 7 7 7 7 7 7 7 7 Bài 10: Tính tích  1  1  1   1   1  1  1   1  a, I= 1− 1− 1− ... 1−       b, J= 1− 1− 1− ... 1−        4  9  16   10000   3  6  10   780  HD: 3 8 15 9999 1.3 2.4 3.5 99.101 (1.2.3....99)(3.4.5...10 )1 a, Ta có: I = . . ... = . . .... = 101 = 4 9 16 10000 2.2 3.3 4.4 100.100
(2.3.4...100)(2.3.4...100) 100.2 18 2 5 9 779 b, Ta có: J = 4 10 18 1558 1.4 2.5 3.8 38.41 . . ... J = . . .... = . . .... 3 6 10 780 6 12 20 1560 2.3 3.4 4.5 39.40 (1.2.3...38)(4.5.6...40.4 ) 1 41 = ( = 2.3.4...39)(3.4.5....40) 39.3 Bài 11: Tính tích  1  1  1   1   1  1  1   1  a, K= 1− 1− 1− ... 1−       b, M= +1 +1 +1 ... +1        21 28  36   1326   2  3  4   999  HD: 20 27 35 1325 40 54 70 2650 5.8 6.9 7.10 50.53 a, Ta có: K = . . .... = . . .... = . . .... 21 28 36 1326 42 56 72 2652 6.7 7.8 8.9 51.52
(5.6.7...50)(8.9.10....53) 5 53 ( )( ) = . 6.7.8...51 7.8.9....52 51 7 3 4 5 1000 1000 b, Ta có: M = . . .... = = 500 2 3 4 999 2 Bài 12: Tính tích 3 8 15 99  1  1  1   1  a, F= . . ... b, N= −1 −1 −1 ... −1       2 2 2 2 2 3 4 10  2  3  4  1000  HD: 1.3 2.4 3.5 9.11 (1.2.3...9)(3.4.5...1 ) 1 1.11 a, F = . . .... = = 2.2 3.3 4.4 10.10 (2.3.4...10)(2.3.4...10) 10.2 1 − 2 − 3 − 9 − 99 1 b, N = . . .... = − 2 3 4 1000 1000 Bài 13: Tính tích 3 8 15 9999 2 2 2 2
1− 2 1− 3 1− 4  1− 2012  a, C= . . ... b, A =    ...  4 9 16 10000 2 2 2 2
 2  3  4   2012  HD: 1.3 2.4 3.5 99.101 (1.2.3...99)(3.4.5...10 ) 1 1.101 a, Ta có: C = . . .... = = 2.2 3.3 4.4 100.100
(2.3.4...100)(2.3.4...100) 100.2 2 3 − 8 − 1 − 5 1− 2012 1 − .3 2 − .4 3 − .5 2 − 011.2013 b, Ta có: A = . . .... = . . .... 2.2 3.3 4.4 2012.2012 2.2 3.3 4.4 2012.2012 (1.2.3...201 ) 1 (3.4.5...2013) 2013 = − ( = − 2.3.4....2012)(2.3.4...2012) 2012.2  8  8  8   8 
Bài 14: Tính giá trị của biểu thức: C = 1+ 1+ 1+ ... 1+        10  22  36   8352  HD:  8  8  8   8  18 30 44 8360 3.6 Ta có : C = 1+ 1+ 1+ ... 1+       = . . .... = .  10  22  36   8352  10 22 36 8352 2.5  1  1   1  n + 2 E Bài 15: Cho E = 1− 1− ... 1−      và F = , Tính  1+ 2  1+ 2 + 3   1+ 2 + 3 + ... + n n F HD:           1 1 1 Ta có: E = 1−  ( + ) 1−  ( + ) ...1−  1 2 .2 1 3 .3   (1+ n).n        2  2   2  19  2  2  2   2  4 10 18 n (n + ) 1 − 2 = 1− 1− 1− ....     1−  = . . ....  2.3  3.4  4.5   n  (n )1  +  2.3 3.4 4.5 n (n + ) 1 1.4 2.5 3.6
(n− )1(n+ 2) (1.2.3...(n−1))(4.5....(n+ 2)) = n + 2 n + 2 . . ... = = = 2.3 3.4 4.5 n (n + ) 1
(2.3...n)(3.4.5...(n+1)) .3 n 3n n + 2 n + 2 Mà  = F E n 3n 4 4 4  1     
Bài 16: Tính: K = 1 − 1 − 1 − ...     1−  1 9 25  (2n )2 1      −    1  1  1   1  1 Bài 17: Cho G = 1+ 1+ 1+ ... 1+       và H = , Tính G + H 1024  2  4  16   2  2047 2  1  1  1  1  1  1  1  1  1  1 
Bài 18: Tính: A = 1− 1− 1− 1− 1− 1− 1− 1− 1− 1−             3  5  7  9  11 2  4  6  8  10   1  1  1   1  Bài 19: Tính: A = 1+ 1+ 1+ ... 1+        100  99  98   2   6  6  6   6 
Bài 20: Tính nhanh: B = +1 +1 +1 ... +1        8 18  30  10700   1  1 1  1 1 1   1 1  Bài 21: Tính nhanh: E= 1+ 1+ + 1+ + + ... 1+ +...+        2  2 3  2 3 4   2 10  1.3.5....39 1 Bài 22: So sánh : U = &V = 20 21.22.23...40 2 − 1 HD: 1.3.5...37.39 1.3.5.7...37.39 U = ( =
21.23.25....39)(22.24.26....40) (21.23.25....39) 10 2 (11.12.13....20) 1.3.5...39 1.3.5..39 U = = 10
2 (21.23....39)(11.13...19)(12.14.16.18.20) 10 2 .(11.13...39) 5 2 (6.7.8.9.10) 1.3.5..39 1.3.5...39 1.3.5..39 1 U = = = = 15 2 (7.9.11....39).(6.8.10) 15 2 .(7.9...39) 5 .2 .3.5 20 20 2 .3.5.7...39 2 1 1 Mà  = U V 20 20 2 2 − 1 20
DẠNG 8 : TÍNH TỔNG CÙNG SỐ MŨ
Bài 1: Tổng cùng số mũ: a, A= 2 2 2 2 1 + 2 + 3 + ... + 98 b, B= 2 2 2 2 2 2 1
− + 2 − 3 + 4 −...−19 + 20 HD:
a, Ta có : A =1.1+ 2.2 + 3.3 +... + 98.98 = A = ( 1 2 − ) 1 + 2(3− ) 1 + 3(4 − ) 1 +...+ 98(99 − ) 1
= A = (1.2+ 2.3+3.4+...+98.99)−(1+2+3+...+98)
Đặt B =1.2 + 2.3+ 3.4 +...+98.99 , Tính tổng B ta được :
3B =1.2(3− 0) + 2.3(4 − )
1 + 3.4(5− 2) +...+98.99(100 −97)
3B = (1.2.3− 0.1.2) + (2.3.4 −1.2.3) + (3.4.5 − 2.3.4) +...+ (98.99.100−97.98.99) 98.99.100
3B = 98.99.100 − 0.1.2 = 98.99.100 = B = 3 98.99 98.99.100 98.99
Thay vào A ta được : A = B + = + 2 3 2 2 b, Ta có : 2 2 2 2 2 2 B = 1
− + 2 − 3 + 4 −...−19 + 20 2 2 2 2 2 = B = (
− 1 −2 +3 −4 +...+19 −20 ) B = − ( 2 2 2 2 2 + + + + + )− ( 2 2 2 2 1 2 3 ... 19 20
2 2 + 4 + 6 + ... + 20 )  20.21.22 20.21  2 B = − + − 2.2   ( 2 2 2 2 1 + 2 + 3 + ... +10 )  3 2   10.11.12 10.11 B = 2 − 0.22.7 − 20.7 −8 + = 2 − 0.7.23−8   (10.11.4+5.1 ) 1  3 2 
Bài 2 : Tổng cùng số mũ : a, D= 2 2 2 2 1 + 3 + 5 + ... + 99 b, E= 2 2 2 2 11 +13 +15 + ... +199 HD: a, Ta có : D = ( 2 2 2 2 2 2 + + + + + + )−( 2 2 2 2 1 2 3 4 ... 99 100 2 + 4 + 6 + ... +100 ) 100.101.102 100.101 2 = D = + − 2   ( 2 2 2 2 1 + 2 + 3 + ... + 50 )  3 2  50.51.52 50.51 Đặt 2 2 2 2
A = 1 + 2 + 3 + ... + 50 = A = + , Thay vào D ta được : 3 2
D =100.101.34 + 50.101− 4(50.52.17 + 25.5 ) 1 b, Ta có : 2 2 2 2 2 2 2 E = + + + + + + + − ( 2 2 2 11 12 13 14 15 ... 199 200 12 +14 + ... + 200 ) Đặt 2 2 2 2 2 2 2
A =11 +12 +13 +...+ 200 , B =12 +14 +...+ 200 Tính ta được :
A =11.11+12.12 +13.13+...+ 200.200 =11.(12 − ) 1 +12.(13 − ) 1 +... + 200.(201− ) 1 = A = (11.12−1 )
1 + (12.13−12) + (13.14 −13) +...+ (200.201−200)
A = (11.12 +12.13+13.14 +...+ 200.20 ) 1 − (11+12 +13+...+ 200)
 200.201.202 10.11.12   211.190  A = − −      3 2   2 
100.101.102 5.6.7  106.95  Và 2 B = 2 ( 2 2 2 2 6 + 7 + 8 + ... +100 ) = 4 − −      3 2   2 
Vậy E = A − B
Bài 3 : Tổng cùng số mũ : 21 a, C= 2 2 2 2 2 + 4 + 6 + ... + 20 b, F= 2 2 2 2 1 + 4 + 7 + ... +100 HD: a, Ta có : 2 C = ( 2 2 2 2 2 1 + 2 + 3 + ... +10 ) Đặt 2 2 2 2
A = 1 + 2 + 3 + ... +10 = 1.1+ 2.2 + 3.3 + ... +10.10 A =1.(2 − ) 1 + 2.(3− ) 1 + 3.(4 − ) 1 +...+10.(11− ) 1
A = (1.2 + 2.3+ 3.4 +...+10.1 ) 1 − (1+ 2 +3+...+ 10.11.12 10.11 10) = − 3 2
b, Ta có : F =1.1+ 4.4 + 7.7 +10.10 +... +100.100 F = ( 1 4 − ) 3 + 4(7 − ) 3 + 7(10 − )
3 +10(13−3) +...+100(103−3) F = (1.4 −1. )
3 + (4.7 −3.4) + (7.10 −3.7) + (10.13−10. ) 3 +...+ (100.103−100. ) 3
F = (1.4 + 4.7 + 7.10 +10.13+...+100.103) −3(1+ 4 + 7 +10 +...+100)
Đặt A =1.4 + 4.7 + 7.10 +...+100.103, B =1+ 4 + 7 +10 +...+100
Tính 9A =1.4(9 − 0) + 4.7(10 − )
1 + 7.10(13− 4) +...+100.103(106 −97)
9A = (1.4.9 − 0.1.4) + (4.7.10 −1.4.7) + (7.10.13− 4.7.10) +...+ (100.103.106−97.100.10 ) 3 100.103.106 + 8
9A =1.4.9 + (100.103.106 −1.4.7)=> A = 9
Tính B rồi thay vào F ta được : F = A − 3B Bài 4 : Cho biết : 2 2 2 2
1 + 2 + 3 + ... +12 = 650 , Tính nhanh tổng sau : 2 2 2 2 2 + 4 + 6 + ... + 24 HD : Ta có : 2 2 2 2 2 + + + + = ( 2 2 2 2 4 6 ... 24 2 1 + 2 + ... +12 ) = 4.650
Bài 5 : Tổng cùng số mũ : a, G= 2 2 2 2 1 + 3 + 5 + ... + 99 b, K= 2 2 2 2
1.2 + 2.3 + 3.4 + ... + 99.100 HD: a, Ta có :
G =1.1+ 3.3+ 5.5 + 7.7 +...+ 99.99
G =1.(3− 2) + 3.(5− 2) +5(7 − 2) + 7(9 − 2) +...+99(101− 2)
G = (1.3−1.2) + (3.5− 2. )
3 + (5.7 − 2.5) + (7.9 − 2.7) +...+ (99.101− 2.99)
G = (1.3+ 3.5+ 5.7 + 7.9 +...+ 99.10 ) 1 − 2(1+ 3+ 5+ 7 +...+ 99)
Đặt A =1.3+ 3.5 + 5.7 +...+ 99.101, B =1+ 3 + 5 + 7 +...+ 99
A = 6A =1.3(6 − 0) + 3.5(7 − ) 1 + 5.7(9 − ) 3 +...+ 99.10 ( 1 103− 97) Tính 6A = (1.3.6 − 0.1. )
3 + (3.5.7 −1.3.5) + (5.7.9 −3.5.7) +...+ (99.101.103−97.99.10 ) 1 +
6A = 1.3.6 + (99.101.103 −1.3.5) 99.101.103 3
= 99.101.103+ 3 = A = 6
Tính tổng B rồi thay vào G b, Ta có :
K =1.2.2 + 2.3.3+ 3.4.4 +...+ 99.100.100 K =1.2(3− ) 1 + 2.3(4 − ) 1 + 3.4(5− ) 1 +...+ 99.100(101− ) 1
K = (1.2.3−1.2) + (2.3.4 − 2. )
3 + (3.4.5−3.4) +...+ (99.100.101−99.100)
K = (1.2.3+ 2.3.4 +3.4.5+...+99.100.10 )
1 − (1.2 + 2.3+3.4 +...+ 99.100)
Đặt A =1.2.3+ 2.3.4 + 3.4.5 +...+ 99.100.101, B =1.2 + 2.3 + 3.4 +...+ 99.100
A = 4A =1.2.3(4 − 0) + 2.3.4(5− )
1 + 3.4.5(6 − 2) +...+99.100.10 ( 1 102 −98) Tính 22
4A = (1.2.3.4 −0.1.2. )
3 + (2.3.4.5−1.2.3.4) + (3.4.5.6 − 2.3.4.5) +...+ (99.100.101.102 −98.99.100.10 ) 1 99.100.101.102
4A = 99.100.101.102 = A = 4
Tính B tương tự rồi thay vào K
Bài 6 : Tổng cùng số mũ : a, H= 2 2 2 2 2 + 4 + 6 + ... +100 b, I= 2 2 2 2 1.3 + 3.5 + 5.7 + ... + 97.99 HD: a, Ta có : 2 H = ( 2 2 2 2
2 1 + 2 + 3 + ... + 50 ) = 4.A
A =1.1+ 2.2 + 3.3+ 4.4 +...+ 50.50 A =1.(2 − ) 1 + 2(3− ) 1 + 3(4 − ) 1 + 4(5− ) 1 +...+ 50(51− ) 1 A = (1.2 − ) 1 + (2.3− 2) + (3.4 − ) 3 +...+ (50.51−50)
A = (1.2 + 2.3+ 3.4 +...+ 50.5 ) 1 − (1+ 2 + 3+...+ 50) 50.51.51 50.51
Tính tổng A ta được : A = − , Thay vào H ta được 3 2 b, Ta có : I= 2 2 2 2
1.3 + 3.5 + 5.7 + ... + 97.99 => I =1.3.3+ 3.5.5 + 5.7.7 + ...+ 97.99.99
I =1.3(5− 2) + 3.5.(7 − 2) + 5.7(9 − 2) +...+ 97.99(101− 2)
I = (1.3.5−1.3.2) + (3.5.7 −3.5.2) + (5.7.9 −5.7.2) +...+ (97.99.101−97.99.2)
I = (1.3.5+3.5.7 + 5.7.9 +...+ 97.99.10 )
1 − 2(1.3+ 3.5+ 5.7 +...+ 97.99)
Đặt A =1.3.5 + 3.5.7 + 5.7.9 +...+ 97.99.101, B =1.3 + 3.5 + 5.7 +... + 97.99 Ta có :
8A =1.3.5.8 + 3.5.7(9 − ) 1 + 5.7.9(11− ) 3 +... + 97.99.101(103−95)
8A =1.3.5.8 + (3.5.7.9 −1.3.5.7) + (5.7.9.11−3.5.7.9) +...+ (97.99.101.103−95.97.99.10 ) 1 97.99.101.103 −15
8A =1.3.5.8 + 97.99.101.103−1.3.5.7 = 97.99.101.103−15 => A = 8
Tương tự tính B rồi thay vào I Bài 7: Tính: 3 3 3 3
A = 1.3 + 3.5 + 5.7 + ... + 49.51 Bài 8: Tính: 2 2 2 2
B = 1.99 + 2.98 + 3.97 + ... + 49.51 Bài 9: Biết : 3 3 3
1 + 2 + ... +10 = 3025 , Tính 3 3 3 A = 2 + 4 + ... + 20 HD: 3 A = ( 3 3 3 2 1 + 2 + ... +10 ) Bài 10: Cho biết: 2 2 2 2
1 + 2 + 3 + ... +12 = 650 , Tính nhanh tổng sau: 2 2 2 2 2 + 4 + 6 + ... + 24 HD: Ta có: 2 2 2 2 2 + + + + = ( 2 2 2 2 4 6 ... 24 2 1 + 2 + ... +12 ) = 4.650 23
DẠNG 9: TỔNG CÙNG CƠ SỐ
Bài 1: Tổng cùng cơ số: a, A= 2 3 2000 1+ 3 + 3 + 3 + ... + 3 b, B= 3 5 7 2009 2 + 2 + 2 + 2 + ... + 2 HD: a, Ta có : 2 3 4 2000 2001
3A = 3 + 3 + 3 + 3 + ... + 3 + 3
= A− A = A = ( − ) + ( 2 2 − )+ + ( 2000 2000 − )+( 2001 3 2 3 3 3 3 ... 3 3 3 − ) 1 2001 3 −1 2001 = 2A = 3 −1= A = 2 b, Ta có : 2 3 5 7 2009 2011
2 B = 2 + 2 + 2 + ... + 2 + 2
= B − B = B = ( 3 3 − )+( 5 5 − )+ +( 2009 2009 − )+( 2011 4 3 2 2 2 2 ... 2 2 2 − 2) 2011 2 − 2 2011 = 3B = 2 − 2 = B = 3
Bài 2: Tổng cùng cơ số: a, C= 3 5 7 101 5 + 5 + 5 + 5 + ... + 5 b, D= 2 4 6 100 1+ 3 + 3 + 3 + ... + 3 HD: a, Ta có : 2 3 5 7 101 103
5 C = 5 + 5 + 5 + ... + 5 + 5
= C −C = C = ( 3 3 − )+( 5 5 − )+ +( 101 101 − )+( 103 25 24 5 5 5 5 ... 5 5 5 −5) 103 5 −5 103
= 24C = 5 −5 = C = 24 b, Ta có : 2 2 4 6 100 102
3 D = 3 + 3 + 3 + ... + 3 + 3
= D − D = D = ( 2 2 − )+( 4 4 − )+ +( 100 100 − )+( 102 9 8 3 3 3 3 ... 3 3 3 − ) 1 102 3 −1 102
= 8D = 3 −1= D = 8
Bài 3: Tổng cùng cơ số: a, E= 3 5 99 7 + 7 + 7 + ... + 7 b, F= 2 4 6 2016 1+ 5 + 5 + 5 + ... + 5 HD: a, Ta có : 2 3 5 7 99 101
7 E = 7 + 7 + 7 + ... + 7 + 7 = E − E = E = ( 3 3 − )+( 5 5 − )+ +( 99 99 − )+( 101 49 48 7 7 7 7 ... 7 7 7 − 7) 101 7 − 7 101
= 48E = 7 − 7 = E = 48 b, Ta có : 2 2 4 6 2016 2018
5 F = 5 + 5 + 5 + ... + 5 + 6 F − F = F = ( 2 2 − )+( 4 4 − )+ +( 2016 2016 − )+( 2018 25 24 5 5 5 5 ... 5 5 5 − ) 1 2018 5 −1 2018 24F = 5 −1= F = 24
Bài 4: Tổng cùng cơ số: G= 2 4 6 2016 1+ 2 + 2 + 2 + ... + 2 HD: Ta có : 2 2 4 6 2016 2018
2 G = 2 + 2 + 2 + ... + 2 + 2 2018 2 −1
G − G = G = ( 2 2 − )+( 4 4 − )+ +( 2016 2016 − )+( 2018 4 3 2 2 2 2 ... 2 2 2 − ) 1 => 2018 3G = 2 −1= G = 3
Bài 5: Tổng cùng cơ số: a, 50 49 48 2
M = 2 − 2 − 2 − ... − 2 − 2 b, 100 99 98 97 2 1 N = 3
− 3 + 3 − 3 +...+ 3 − 3 +1 HD: a, Ta có : 50 M = −( 2 3 48 49 2 2 + 2 + 2 + ... + 2 + 2 ) 24 Đặt 2 3 4 48 49
A = 2 + 2 + 2 + 2 + ... + 2 + 2 , Tính A ta được : 50
A = 2 − 2 , Thay vào M ta được : 50 50 M = − A = − ( 50 2 2 2 − 2) = 2 b, Ta có : 2 3 98 99 100
N = 1− 3 + 3 − 3 + ... + 9 − 9 + 3 2 3 4 99 100 101
= 3N = 3− 3 + 3 − 3 +...+ 3 − 3 + 3
=> N + N = ( − ) + ( 2 2 − )+( 3 3 − )+ +( 100 100 − ) 101 3 3 3 3 3 3 3 ... 3 3 + 3 +1 101 3 +1 101 4N = 3 +1= N = 4
Bài 6: Tổng cùng cơ số : I= 2 3 63 1+ 2 + 2 + ... + 2 HD: Ta có : 3 4 64
2I = 2 + 2 + 2 + ... + 2
= I − I = ( 3 3 − )+( 4 4 − )+ +( 63 63 − )+( 64 2 2 2 2 2 ... 2 2 2 + 2 − ) 1 => 64 I = 2 +1
Bài 7: Tính giá trị của biểu thức: 2 3 2008
B = 1− 2 + 2 − 2 + ... + 2 HD: Ta có : 2 3 2008
B = 1− 2 + 2 − 2 + ... + 2 => 2 3 4 2009
2B = 2 − 2 + 2 − 2 + .... + 2 2009 2 +1 => 2009
2B + B = 3B = 1+ 2 = B = 3 Bài 8: Tính A = ( 9 8 2
2000 2001 + 2001 + ... + 2001 + 200 ) 1 +1 HD: Đặt : 2 3 9
B = 2001+ 2001 + 2001 + ... + 2001 => 2 3 10
2001B = 2001 + 2001 + ... + 2001 10
= 2001B − B = 2000B = 2001 − 2001, Khi đó : 10 10
A = 2000B +1 = 2001 − 2001+1 = 2001 − 2000 Bài 9: Cho 2010 2009 2008 H = 2 − 2 − 2
−...− 2 −1, Tính 2010H HD: Ta có : 2010 H = −( 2 3 2008 2009 2 1+ 2 + 2 + 2 + ... + 2 + 2 ). Đặt : 2 3 2009
A = 1+ 2 + 2 + 2 + ... + 2 Tính tổng A ta được : 2010 A = 2
−1, Thay vào H ta được : 2010 ( 2010 2 2 )1 1 2010H H = − − = = = 2010 0 1 2 2015
Bài 10: Tính tổng : S = (− ) 3 + (− ) 3 + (− ) 3 + ... + (− ) 3 Bài 11: Tính: 2 3 4 2007
A = 1 + 7 + 7 + 7 + 7 + ... + 7 Bài 12: Tính 2 3 100
B = 1 + 4 + 4 + 4 + ... + 4
Bài 13: Tổng cùng cơ số : H= 2 3 99
1+ 2.6 + 3.6 + 4.6 + ... +100.6 HD : Ta có : 2 3 4 100
6H = 6 + 2.6 + 3.6 + 4.6 + ... +100.6
H − H = − H = ( − ) +( 2 2 − )+( 3 3 − )+ +( 99 99 − )+( 100 6 5 2.6 6 3.6 2.6 4.6 3.6 ... 100.6 99.6 1−100.6 ) 2 3 99 − H = + + + + + ( 100 5 6 6 6 ... 6 1−100.6 ) Đặt 2 3 99
A = 6 + 6 + 6 + ... + 6 , Tính A ta được : 100 6 − 6 A = , Thay vào H ta được : 5 6 −6 100 100 100 6 −6 +5−500.6 499.6 +1 5
− H = A+ (1−100.6 ) 100 100 100 = +1−100.6 = = − 5 5 5 25 100 499.6 +1 = H = 25 1 1 1 1
Bài 14: Tính tổng cơ số: A= + + +...+ 2 3 100 7 7 7 7 HD: 1 1 1 1 1 1 a, Ta có: A = + + +...+ + 2 3 4 100 101 7 7 7 7 7 7 1  1 1   1 1   1 1   1 1  100 100 6 7 −1 7 −1 A − A = − + − +...+ − + −         => .A = = A = 2 2 3 3 100 100 101 7  7 7   7 7   7 7   7 7  101 100 7 7 6.7 1 1 1 1
Bài 15: Tính tổng cơ số: B= + + +...+ 2 3 20 3 3 3 3 HD : 1 1 1 1 1 1 Ta có: B = + + +...+ + 2 3 4 20 21 3 3 3 3 3 3 1  1 1   1 1   1 1   1 1  20 20 2 3 −1 3 −1 B − B = − + − +...+ − + −         = .B = = B = 2 2 3 3 20 20 21 3  3 3   3 3   3 3   3 3  21 20 3 3 2.3
Bài 16: Tính tổng cơ số 0 1 2 2017  1   1   1   1  1 1 1 1 1 1 a, D= − + − + − +...+ −         b, E= − + − + −...+ −  7   7   7   7  2 3 4 50 51 3 3 3 3 3 3 HD: 1 1 1 1 1 a, Ta có: D = 1− + − +...+ − 2 3 2016 2017 7 7 7 7 7 1 1 1 1 1 1 1 D = − + − +...+ − 2 3 4 2017 2018 7 7 7 7 7 7 7 1  1 − 1   1 1 −   1 − 1   1  D + D = + + + +...+ + + 1−         2 2 2017 2017 2018 7  7 7   7 7   7 7   7  2018 2018 8 7 −1 7 −1 D = = D = 2018 2018 7 7 8.7 1 1 − 1 1 1 1 b, Ta có: E = + − +...+ − 2 3 4 51 52 3 3 3 3 3 3 1  1 1 −   1 − 1   1 − 1   1 − 1 −  51 51 4 3 +1 3 +1 E + E = + + + +...+ + + +         => E = − = E = − 2 2 3 3 51 51 52 3  3 3   3 3   3 3   3 3  52 51 3 3 4.3 3 3 3 3
Bài 17: Tính tổng cơ số G= + + +...+ 4 7 100 5 5 5 5 HD: 3 3 3 3  1 1 1 1  Ta có: G = + + + ...+ G = 3 + + +...+   4 7 100 5 5 5 5 4 7 100  5 5 5 5  1 1 1 1 1 1 1 1 1 Đặt A = + + +...+ = A = + + +...+ 4 7 100 3 4 7 10 103 5 5 5 5 5 5 5 5 5 1  1 1   1 1   1 1   1 1  A − A = − + − +...+ − + −         4 4 7 7 100 100 103 125  5 5   5 5   5 5   5 5  102 102 124.A 1 1 5 −1 5 −1 = − = = A = 103 103 100 125 5 5 5 5 .124
Bài 18: Tính tổng cơ số 26  2 2 2  200 − 3 + + +...+    2 3 100 3 4 100  1  1   1   1  a, K = = 2 b, I= 1+ + + +...+       1 2 3 99 + + + 2  2   2   2  ... + 2 3 4 100 HD:  2   2   2   2  a, Ta có: TS = 2 − + 2 − + 2 − +...+ 2 − +1          3   4   5   100  4 6 8 198 2   TS 2MS TS = + + +...+ + 1 2 3 99 = 2 + + +...+ = 2.MS   = K = = = 2 3 4 5 100 2  2 3 4 100  MS MS 1 1 1 1 1 1 1 1 1 1 1 b, Ta có : I = 1+ + + + +...+ = I = + + +...+ + 2 3 4 100 2 2 2 2 2 2 3 100 101 2 2 2 2 2 2 1  1 1   1 1   1 1   1 1   1  = I − I = − + − + − +...+ − + 1−           2 2 3 3 100 100 101 2  2 2   2 2   2 2   2 2   2  101 101 1 2 −1 2 −1 I = = I = 101 100 2 2 2 1 1 1 1
Bài 19: Tính tổng cơ số: C= + + + ...+ 3 5 99 2 2 2 2 HD: 1 1 1 1 1 1 a, Ta có : C = + + +...+ + 2 3 5 7 99 101 2 2 2 2 2 2 1 3  1 1   1 1   1 1   1 1  C − C = C = − + − +...+ − + −         3 3 5 5 98 98 101 4 4  2 2   2 2   2 2   2 2  100 100 3 2 −1 2 −1 => C = = C − 101 99 4 2 3.2 Bài 20: Tính:  1 1 1  1 1 1 1 a, 100 4.5 + +...+ +1   b, 1+ + + +...+ 2 100  5 5 5  2 4 8 1024 1 1 1 1 1 1 Bài 21: Tính A = − + − + − ... + − 2 3 4 50 51 3 3 3 3 3 3 1 2 3 4 2017
Bài 22: Tính tổng cơ số: H= + + + +...+ 2 3 4 2017 3 3 3 3 3 HD : 1 1 2 3 4 2016 2017 Ta có : H = + + + +...+ + 2 3 4 5 2017 2018 3 3 3 3 3 3 3 1  2 1   3 2   4 3 
 2017 2016   1 2017  H − H = − + − + − +...+ − + −           2 2 3 3 4 4 2017 2017 2018 3  3 3   3 3   3 3   3 3   3 3  2 1 1 1 1 1 2017 H = + + +...+ + − 2 3 4 2017 2018 3 3 3 3 3 3 3 1 1 1 1 Đặt A = + + +...+ , Tính A rồi thay vào H 2 3 2017 3 3 3 3 3 4 5 100
Bài 23: Tính tổng cơ số: F= 1+ + + +...+ 3 4 5 100 2 2 2 2 HD: 1 1 3 4 5 99 100 Ta có: F = + + + +...+ + 4 5 6 100 101 2 2 2 2 2 2 2 1  4 3   5 4  100 99   3 1 100  F − F = − + − +...+ − + 1+ − −         4 4 5 5 100 100 3 101 2  2 2   2 2   2 2   2 2 2  27 1 1 1 1 1  1 3 100  F = + + +...+ + − −   4 5 6 100 101 2 2 2 2 2  2 8 2  1 1 1 1 Đặt A = + + +...+ . Tính A rồi thay vào F 4 5 6 100 2 2 2 2  1 1 1 1  Bài 24: Tính: 100 A = 4.5 + + + ... + +1   2 3 100  5 5 5 5  Bài 25: Cho 2 3 2015 2016 A = 3 + 3 + 3 + ... + 3 + 3 a, Tính A
b, Tìm chữ số tận cùng của A
c, A có là số chính phương không HD: 2017 3 − 3 a, A = 2 b, A = ( 2 3 4 + + + ) + + ( 2013 2014 2015 2016 + + + ) = ( 2 3 + + + ) 2013 + + ( 2 3 3 3 3 3 ... 3 3 3 3 3 1 3 3 3 ... 3 1 + 3 + 3 + 3 ) 2013 = + + = ( 5 2013 3.40 ... 3 .40 40 3 + 3 + ... + 3
) nên A có tận cùng là 0
c, Lập luận được A chia hết cho 3
Lập luận được A không chia hết cho 2 3
Mà 3 là số nguyên tố nên A không là số chính phương
Bài 26: Chứng tỏ rằng : M = ( 2017 2016 2 75 4 + 4 + ... + 4 + 4 + ) 1 + 25 chia hết cho 100 HD: 2018 4 −1 Tính tổng 2018 M = 75. + 25 = 25.4 100 3 28
DẠNG 10: TÍNH ĐƠN GIẢN
Bài 1: Thực hiện phép tính:
1.2.3 + 2.4.6 + 4.8.12 + 7.14.21
1.7.9 + 3.21.27 + 5.35.45 + 7.49.63 a, 1.3.5+ 2.6.10+ 4.12.20+ b, 7.21.35 1.3.5 + 3.9.15 + 5.15.25 + 7.21.35 HD:
1.2.3 + 2.4.6 + 4.8.12 + 7.14.21
1.2.3(1+ 2.2.2 + 4.4.4 + 7.7.7) 1.2.3 2 a, Ta có : = = 1.3.5 + 2.6.10 + 4.12.20 + = 7.21.35
1.3.5(1+ 2.2.2 + 4.4.4 + 7.7.7) 1.3.5 5
1.7.9 + 3.21.27 + 5.35.45 + 7.49.63
1.7.9(1+ 3.3.3 + 5.5.5 + 7.7.7) 1.7.9 21 b, Ta có : = = 1.3.5 + 3.9.15 + 5.15.25 + = 7.21.35
1.3.5(1+ 3.3.3 + 5.5.5 + 7.7.7) 1.3.5 5 1.2 + 2.4 + 3.6 + 4.8 + 5.10
Bài 2: Thực hiện phép tính: 3.4+6.8+9.12+12.16+ 15.20 HD: 1.2 + 2.4 + 3.6 + 4.8 + 5.10 1.2(1+ 2.2 + 3.3 + 4.4 + 5.5) 1.2 1 Ta có : = = 3.4 + 6.8 + 9.12 +12.16 + = 15.20 3.4(1+ 2.2 + 3.3 + 4.4 + 5.5) 3.4 6 Bài 3: Tính: 1.2 + 2.4 + 4.8 + 7.14 2.3 + 4.6 + 6.9 + 8.12 a, A = B = 1.3 + 2.6 + 4.12 + b, 7.21 3.4 + 6.8 + 9.12 + 12.16 2a 5b 6c 7d 2a 5b 6c 7d
Bài 4: Tính giá trị của biểu thức sau: B = + + + biết = = = 5b 6c 7d 2a 5b 6c 7d 2a và a, b, c, d # 0 HD: 2a 5b 6c 7d
2a 5b 6c 7d Đặt B = = = = = k => 4 . . .
= k =1 = k =  1 =>B= 4  5b 6c 7d 2a
5b 6c 7d 2a 2a 3b 4c 5d 2a 3b 4c 5d
Bài 5: Tính gá trị của biểu thức: + + + biết = = = 3b 4c 5d 2a 3b 4c 5d 2a HD: 2a 3b 4c 5d
2a 3b 4c 5d Đặt : 4 = = = = k = k = . . . = 1 = k = 1  3b 4c 5d 2a
3b 4c 5d 2a 2a 3b 4c 5d 2a 3b 4c 5d Khi đó : + + + =1 hoặc + + + = - 1 3b 4c 5d 2a 3b 4c 5d 2a 2 2 2 2
a m − a n − b n + b m
Bài 6: Tính gá trị của biểu thức: B= 2 2 a + b HD :
a (m − n) + b (m − n) ( 2 2 2 2
a + b )(m − n) Ta có : B = = = m − n 2 2 a + b ( 2 2 a + b )
(ab+bc +cd + da)abcd
Bài 7: Thực hiện phép tính: (c+d)(a+b)+(b−c)(a− d ) HD:
Ta có : MS = ca + cb + da + bd + ab − bd − ca + cd = (ab + bc + cd + da) TS
(ab + bc + cd + da)abcd Khi đó : = ( + + + ) = abcd MS ab bc cd da
(a +b)(−x − y)−(a − y)(b − x)
Bài 8: Tính giá trị của biểu thức: A =
abxy ( xy + ay + ab + bx) HD: Ta có: TS = a
− x − ay −bx −by − ab + ax + yb − xy = −(ay +ab +bx + xy) 29
−(ay + ab + bx + xy) 1 − Khi đó: A = =
abxy (ay + ab + bx + xy) abxy Bài 9: Tính tổng 0 1 2 2004 2 + 2 + 2 + ... + 2 2 3 100 1+ 5 + 5 + 5 + ... + 5 a, A= 5 10 2000 1+ 2 + 2 + ... + b, B= 2 2 3 100 1+ 4 + 4 + 4 +... + 4 HD: ( 2 3 4 1+ 2 + 2 + 2 + 2 ) + ( 5 6 7 8 9
2 + 2 + 2 + 2 + 2 ) +...+ ( 2000 2001 2002 2003 2004 2 + 2 + 2 + 2 + 2 ) a, Ta có: A = 5 10 15 2000 1+ 2 + 2 + 2 + ... + 2 ( 2 3 4 1+ 2 + 2 + 2 + 2 ) 5 + 2 ( 2 3 4 1+ 2 + 2 + 2 + 2 ) 2000 +...+ 2 ( 2 3 4 1+ 2 + 2 + 2 + 2 ) A = 5 10 15 2000 1+ 2 + 2 + 2 + ... + 2 ( 2 3 4 1+ 2 + 2 + 2 + 2 )( 5 10 2000 1+ 2 + 2 + ... + 2 ) A = ( = + + + + 1+ 2 + 2 + ... + 2 ) ( 2 3 4 1 2 2 2 2 5 10 2000 ) b, Ta có: 2 3 100
M = 1+ 5 + 5 + 5 + ... + 5 101 5 −1 2 3 100 101
= 5M = 5 + 5 + 5 +...+ 5 + 5 101
= 5M − M = 4M = 5 −1= M = 4 và 2 3 100
N = 1+ 4 + 4 + 4 + ... + 4 101 4 −1 2 3 4 101 101
= 4N = 4 + 4 + 4 + 4 +...+ 4 = 4N − N = 3N = 4 −1= N = 3 M Khi đó: B = N 95 94 93
x + x + x + . .+ x +1
Bài 10: Thu gọn biểu thức: A = 31 30 29 x
+ x + x + . .+ x +1 101+100 + 99 + ... + 2 +1
Bài 11: Tính tổng: A= 101−100+99−98+...−2+ 1 HD: (1+10 )1.101 Ta có: TS = =101.51= 5151 2 TS 51.101
MS = (101−100) + (99 −98) +...+ (3− 2) +1=1+1+...+1= 51 . Khi đó: A = = =101 MS 51 1.99 + 2.98 + ... + 99.1 Bài 12: Tính: 1.2+ 2.3+...+ 99.100 HD:
Ta có: TS =1.99 + 2.(99 − )
1 + 3.(99 − 2) +...+ 99(99 −98)
=1.99 +(2.99−1.2)+(3.99−2.3)+...+(99.99−98.99)
= 99(1+ 2+3+...+99)−(1.2+ 2.3+3.4+...+98.99)
Đặt A =1+ 2 + 3+...+ 99, B =1.2 + 2.3+ 3.4 +...+ 98.99 , Tính A và B rồi thay vào ta được:
Bài 13: Thực hiện phép tính: 1 1 1 120 − .40.5. .20. − 20 a, A= 2 5 4 1+ 5 + 9 + ... + 33 + 37 + 41 HD:
a, Ta có: TS =120 − 20.5 − 20 = 0 , Khi đó A = 0 30
DẠNG 11: TÍNH TỈ SỐ CỦA HAI TỔNG 1 1 1 1 + + + ...+
Bài 1: Thực hiện phép tính: 2 3 4 2012 2011 2010 2009 1 + + +...+ 1 2 3 2011 HD:  2010   2009   1  2012 2012 2012 2012 Mẫu số : MS = 1+ + 1+ +...+ 1+ +1= + +...+ +        2   3   2011 2 3 2011 2012  1 1 1 1  MS = 2012 + + +...+ = 2012.TS    2 3 4 2012  1 1 1 1 1 1 1 1 + + +...+ + + +...+ 1 Khi đó : 2 3 4 2012 2 3 4 2012 A = = = 2011 2010 2009 1  1 1 1  2012 + + +...+ 2012 + +...+   1 2 3 2011  2 3 2012  1 1 1 1 1 + + + ...+ +
Bài 2: Thực hiện phép tính: 2 3 4 99 100 99 98 97 1 + + + ...+ 1 2 3 99 HD:  98   97   1  100 100 100 100 MS = 1+ + 1+ +...+ 1+ +1= + +...+ +        2   3   99  2 3 99 100  1 1 1 1  MS = 100 + + +...+ =100.TS    2 3 4 100  1 1 1 1 1 1 1 1 + + +...+ + + +...+ 1 Khi đó : 2 3 4 100 2 3 4 100 A = = = 99 98 97 1  1 1 1  100 + + +...+ 100 + +...+   1 2 3 99  2 3 100  A 1 1 1 1 2008 2007 2006 1 Bài 3: Tính tỉ số biết : A = + + +...+ và B = + + +...+ B 2 3 4 2009 1 2 3 2008 HD:  2007   2006   1  2009 2009 2009 2009 2009 Ta có : B = 1+ + 1+ +...+ 1+ +1=       + + +...+ +  2   3   2008  2 3 4 2008 2009  1 1 1 1 1  = 2009 + + +...+ + = 2009.A    2 3 4 2008 2009  A A 1 Khi đó : = = B 2009 A 2009 A 1 1 1 1 1 2 3 198 199 Bài 4: Tính tỉ số biết: A = + + +...+ và B = + + +...+ + B 2 3 4 200 199 198 197 2 1 HD:  1   2   3   198  200 200 200 200 Ta có : B = 1+ + 1+ + 1+ + ...+ 1+ +1 = + + ...+ +          199   198   197   2  199 198 2 200  1 1 1 1  A 1 B = 200 + + ... + + = 200.A   => = 199 198 2 200  B 200 A 1 2 2011 2011 1 1 1 1 Bài 5: Tính tỉ số biết : A = + +...+ + và B = + + +...+ B 2012 2011 2 1 2 3 4 2013 HD: 31  1   2   2011  2013 2013 2013 2013 Ta có : A = +1 + +1 + ... + +1 +1 = + + ...+ +        2012   2011   2  2012 2011 2 2013  1 1 1 1  A A = 2013 + + + ... + = 2013.B = = 2013    2 3 4 2013  B A 1 2 3 99 1 1 1 1 Bài 6: Tính tỉ số biết : A = + + +...+ và B = + + +...+ B 99 98 97 1 2 3 4 100 HD:  1   2   98  100 100 100 100 Ta có : A = +1 + +1 + ... + +1 +1 = + + ... + +        99   98   2  99 98 2 100  1 1 1 1  A A = 100 + + ... + + = 100.B = = 100    99 98 2 100  B 2013 2013 2013 2013 2013 2012 2011 1 Bài 7: Cho A = + + +...+ và B = + + +...+ , tính A/B 2 3 4 2013 1 2 3 2013 1 1 1 1 1+ + +...+ +
Bài 8: Thực hiện phép tính: 3 5 97 99 1 1 1 1 + +...+ + 1.99 3.97 97.3 99.1 HD:  1   1 1   1 1   1 1 1  Ta có : TS = 1+ + + +...+ + =100 + +...+          99   3 97   49 51 1.99 3.97 49.51  1 1   1 1   1 1   1 1 1  MS = + + + +...+ + = 2 + +...+        
1.99 99.1  3.97 97.3   49.51 51.49  1.99 3.97 49.51 TS 100 Khi đó : = = 50 MS 2 1 1 1 1 1 + + +...+ +
Bài 9: Thực hiện phép tính: 2 4 6 998 1000 1 1 1 1 + +...+ + 2.1000 4.998 998.4 1000.2 HD:  1 1   1 1   1 1   1 1 1  Ta có : TS = + + + +...+ + =1002 + +...+          2 1000   4 998   500 502   2.1000 4.998 500.502   1 1   1 1   1 1  MS = + + + +...+ +      
 2.1000 1000.2   4.998 998.4   500.502 502.500   1 1 1  MS = 2 + +...+    2.1000 4.998 500.502  TS 1002 Khi đó : = = 501 MS 2 A 1 1 1 1 1 1 1 Bài 10: Tính tỉ số biết: A = 1+ + + ...+ và B = + + +...+ B 3 5 999 1.999 3.997 5.1995 999.1 HD:  1   1 1   1 1  1000 1000 1000 Ta có : A = 1+ + + + ... + + = + + ...+        999   3 997   499 501 999.1 3.997 499.501  1 1 1  = 1000 + + .. +    999.1 3.997 499.501 32  1 1   1 1   1 1  2 2 2 B = + + + + ...+ + = + + ...+      
1.999 999.1  3.997 997.3 
 499.501 501.499  1.999 3.997 499.501  1 1 1  A 1000 = 2 + + ... +  , Khi đó : = = 500 1.999 3.997 499.501 B 2 1 1 1 1 + + +...+
Bài 11: Thực hiện phép tính: 51 52 53 100 A = 1 1 1 1 + + + ...+ 1.2 3.4 5.6 99.100 HD: 1 1 1 1 1 1 1 1 1 Ta có : MS = + +...+ = − + − +...+ − 1.2 3.4 99.100 1 2 3 4 99 100 1 1 1 1 1 1   1 1 1 1  = + + + + ... + + − 2 + + + ... +     1 2 3 4 99 100   2 4 6 100  1 1 1 1  1 1 1  1 1 1 1 = + + +...+ − + +...+ = + + +...+ = TS     1 2 3 100  1 2 50  51 52 53 100 TS Khi đó : A = =1 MS A 2012 2012 2012 2012 1 1 1 1 Bài 12: Tính tỉ số biết: A = + + +...+ và B = + + +...+ B 51 52 53 100 1.2 3.4 5.6 99.100 HD:  1 1 1 1  Ta có : A = 2012 + + + ... +    51 52 53 100  1 1 1 1 1 1 1 1 1 1 1   1 1 1 1  B = − + − + ...+ − = + + + ....+ + − 2 + + + ...+     1 2 3 4 99 100 1 2 3 99 100   2 4 6 100  1 1 1 1  1 1 1 1  1 1 1 1 B = + + + ... + − + + + ...+ = + + + ...+     1 2 3 100  1 2 3 50  51 52 53 100 A 2012 Khi đó : = = 2012 B 1 A 1 1 1 1 Bài 13: Tính tỉ số biết: A = + + +...+ B 1.2 3.4 5.6 199.200 1 1 1 và B = + +...+ 101.200 102.199 200.101 HD: 1 1   1 1   1 1  1 1 1 1   1 1 1  A = − + − + ... + − = + + + ...+ − 2 + + ...+           1 2   3 4  199 200  1 2 3 200   2 4 200  1 1 1 1  1 1 1 1  1 1 1 A = + + + ... + − + + + ...+ = + + ...+     1 2 3 200  1 2 3 100  101 102 200  1 1   1 1   1 1  301 301 301 A = + + + + ... + + = + + ... +       101 200  102 199  150 151 101.200 102.199 150.151  1 1   1 1   1 1  Và B = + + + + ... + +      
101.200 200.101 102.199 199.102  150.151 151.150  2 2 2 B = + + ... + 101.200 102.199 150.151 A 301 Khi đó : = B 2 33 A 1 1 1 1 Bài 14: Tính giá trị biết: A = + + +...+ và B 1.2 3.4 5.6 101.102 1 1 1 1 2 B = + + + ... + + 52.102 53.101 54.100 102.52 77.154 HD: 1 1   1 1  1 1 1 1 1 1 1 1  Ta có : A = − + − + ...+ − = − + − + ...+ −       1 2   3 4  101 102 1 2 3 4 101 102  1 1 1 1 1   1 1 1  A = + + + ...+ + − 2 + + ...+     1 2 3 101 102   2 4 102  1 1 1 1  1 1 1  1 1 1 1 A = + + + ...+ − + + ...+ = + + ...+ +     1 2 3 102  1 2 51 52 53 101 102  1 1   1 1   1 1  1 154 154 154 154 A = + + + + ...+ + + = + + ...+ +        52 102   53 101  76 78  77 52.102 53.101 76.78 77.154  1 1   1 1   1 1  2 và B = + + + + ...+ + +      
 52.102 102.52   53.101 101.53   76.78 78.76  77.154 2 2 2 2 A 154 B = + + ... + + => = = 77 52.102 53.101 76.78 77.154 B 2 1 1 1 1 Bài 15: Cho A = + + + ...+ ; 1.2 3.4 5.6 101.102 1 1 1 1 1 B = + + + ...+ + 52.102 53.101 54.100 101.53 102.52 A Chứng tỏ rằng là số nguyên. B  1 1 1   1 1 1 1  1 1 1 Bài 16: CMR: 1+ + +...+ − + + +...+ = + +...+      3 5 99   2 4 6 100  51 52 100 HD:  1 1 1 1 1   1 1 1 1  Ta có : VT = 1+ + + +...+ + − 2 + + +...+      2 3 4 99 100   2 4 6 100   1 1 1 1   1 1 1  1 1 1 VT = 1+ + + +...+ − 1+ + +...+ = + +...+ = VP      2 3 4 100   2 3 50  51 52 100 1 1 1 1 1 1 1 1 1 1 Bài 17: Cho S = 1− + − +...+ − + và P = + +...+ + . 2 3 4 2011 2012 2013 1007 1008 2012 2013 Tính ( − )2013 S P HD:  1 1 1   1 1 1  Ta có : S = 1+ + +....+ − 2 + +...+      2 3 2013   2 4 2012   1 1 1 1   1 1 1  1 1 1 S = 1+ + + +...+ − 1+ + +...+ = + +...+ = P      2 3 4 2013   2 3 1006  1007 1008 2013
Khi đó : (S − P)2013 2013 = 0 = 0  1 1 1  1 2 3 99
Bài 18: Chứng minh rằng: 100 − 1+ + +...+ = + + +...+    2 3 100  2 3 4 100 HD:       Ta có : VT = ( − ) 1 1 1 1 2 3 99 1 1 + 1− + 1− + ...+ 1− = + + + ...+       = VP (đpcm)  2   3   100  2 3 4 100 34 A 1 2 3 92 1 1 1 1 Bài 19: Tính tỉ số biết : A = 92 − − − −...− và B = + + + ...+ B 9 10 11 100 45 50 55 500 HD:  1   2   3   92  8 8 8  1 1 1  Ta có : A = 1− + 1− + 1− + ... + 1− = + + ...+ = 8 + + ...+            9   10   11  100  9 10 100  9 10 100  1  1 1 1  A 8 B = + + ... +   . Khi đó : = = 40 5  9 10 100  B 1 5 1 1 1 1 1 1 1 1 1 1 1 Bài 20: Cho A = 1 − + − + ... − + − B = + + ... + + + 2 3 4 2016 2017 2018 và 1010 1011 2016 2017 2018 Tính ( − )2018 2017 2017 A B 35
DẠNG 12: TÍNH GIÁ TRỊ BIỂU THỨC 2015a b c
Bài 1: Cho abc=2015, Tính A = + +
ab + 2015a + 2015 bc + b + 2015 ac + c + 1 HD : 2 a bc b c A = + + 2
ab + a bc + abc
bc + b + abc ac + c +1 2 a bc b c ac + c +1 = + + = =
ab ( + ac + c) b(c + + ac) 1 1 1 ac + c +1 ac + c + 1 a b 2c
Bài 2: Cho abc=2, Tính B = + + ab + a + 2 bc + b +1 ac + 2c + 2 HD : 2 2 a b abc a b abc B = + + = + + =1 2
ab + a + abc bc + b +1
ac + abc + abc
a (b +1+ bc) bc + b +1 ac (1+ bc + b) a b c
Bài 3: Cho abc=1, Tính A = + + ab + a +1 bc + b +1 ac + c + 1 HD : 2 2 a bc b c a bc b c A = + + = + + =1 2
ab + a bc + abc
bc + b + abc ac + c +1
ab (1+ ac + c) b(c +1+ ac) ac + c + 1 x y z
Bài 4: Cho xyz = 1 , Tính giá trị của: A = + + xy
+ x +1 yz + y +1 xz + z +1 a b 2012c
Bài 5: Cho abc= - 2012, Tính B = + − ab + a − 2012 bc + b +1 ac − 2012c − 2012 HD : 2 2 a b abc a b abc B = + + = + + =1 2
ab + a + abc bc + b +1
ac + abc + abc
a (b +1+ bc) bc + b +1 ac (1+ bc + b) 1 1 1
Bài 6: Chứng minh rằng nếu xyz=1 thì + + =1 1+ x + xy 1+ y + yz 1+ z + zx HD : xyz xyz 1 xyz xyz 1 VT = + + = + + =1= VP 2
xyz + x yz + xy
xyz + y + yz 1+ z + zx
xy ( z + xz + ) 1
y ( xz +1+ z ) 1+ z + zx 2010x y z Bài 7: Cho xyz=2010, CMR: + + =1
xy + 2010x + 2010 yz + y + 2010 xz + z + 1 HD : 2 x yz y z VT = + + =1 2
xy + x yz + xyz
yz + y + xyz xz + z +1
Bài 8: Tính giá trị của biểu thức : A =13a +19b + 4a − 2b với a+b=100 HD:
Ta có : A = (13a + 4a) + (19b − 2b) = 17a +17b = 17(a + b) = 17.100 = 1700
Bài 9: Tính giá trị của biểu thức: 2
5x + 6x − 2 khi x −1 = 2 HD: x −1 = 2 x = 3
Ta có : Khi x −1 = 2 = =   x − 2 = 2 − x = 0 Khi 2
x = 3 = A = 5x + 6x − 2 = 5.9 + 6.3 − 2 = 61. Khi 2
x = 0 = A = 5x + 6x − 2 = 2 − 20 30
Bài 10: Tính giá trị của biểu thức: 5 3
2x − 5y + 4, biết ( x − ) 1 + ( y + 2) = 0 36 HD: (  x −  )20 1  0  − =  = 20 30 x 1 0 x 1 Ta có : Vì  = (x − ) 1 + ( y + 2) = 0 =  =  , Thay vào ta được : (  y +  )30  y + 2 = 0 y = 2 2 0 − A = − (− )3 5 2.1 5. 2 + 4 = 2 + 40 + 4 = 46
Bài 11: Cho a, b,c khác 0 và đôi 1 khác nhau thỏa mãn : 2 a (b + c) 2
= b (a +c) = 2013 , Tính 2
A = c (a + ) b HD: Ta có : 2 a (b + c) 2
= b (a +c) = 2013 => 2 2 2 2
a b + a c − b a − b c = 0 = ab(a − b) + c(a − b)(a + v) = 0
(a −b)(ab+bc +ca) = 0 = ab+bc +ca = 0 vì a b
Khi đó : (ab + bc + ca) 2
b = 0 = b (a + c) = a − bc = a − bc = 2013
tương tự : (ab + bc + ca) 2
c = 0 = c (a + b) = a − bc = 2013
1,11+ 0,19 −1,3.2  1 1   7 1  23 Bài 12: Cho A = − + : 2 
 và B = 5 − 2 − 0,5 : 2   2, 06 + 0,54  2 3   8 4  26 a, Rút gọn A và B
b, Tìm x nguyên sao cho: A x B HD: a, Ta có : 1 −  5  1 − 5 1 − 1 25 75 13 A = − : 2 = − =   , Và B = : = 2  6  2 12 12 8 26 12 b, Ta có : 1 − 1 13 1 − 1 12x 13 1  2x = 0
A x B =  x  =   = 1
− 112x 13 =  12 12 12 12 12 1  2x =12
Bài 13: Cho P = 2a −1 − (a − 5) a, Rút gọn P
b, Có giá trị nào của a để P=4 không? HD: Ta có :   1    1    1 
2a −1 − a + 5, vs a a + 4 a        a + 4 = 4 a     a = 0(l)  2   2   2  = =   a, P =  =  =  b , Để P 4  2 1    1    1   a = (l)
1 − 2a − a + 5, a  6 − 3a a       
6 − 3a = 4 a        3 2    2    2 
Vậy không có giá trị nào của a đề P =4 37

Tài liệu liên quan: