










Preview text:
LỜI CẢM ƠN
Dự án được hoàn thành dưới sự hướng dẫn khoa học của Thầy Hiệu Trưởng Lê
Quốc Trung. Chúng em xin gửi lời tri ân sâu sắc đến thầy vì đã dành sự quan tâm, hỗ
trợ và tạo điều kiện thuận lợi cho chúng em trong quá trình thực hiện dự án "99 bài toán
thực tế lớp 10". Sự chỉ đạo tận tình và những đóng góp quý báu của Thầy đã giúp chúng
em có thêm động lực, định hướng rõ ràng và hoàn thành dự án một cách tốt nhất. Chúng
em vô cùng trân trọng sự giúp đỡ của Thầy và mong rằng sẽ tiếp tục nhận được sự đồng
hành, chia sẻ của Thầy trong những chặng đường học tập và nghiên cứu tiếp theo.
Chúng em xin bày tỏ lòng biết ơn tới Ban Giám hiệu nhà Trường THCS & THPT
Mong Thọ vì đã tạo điều kiện và hỗ trợ chúng em trong suốt quá trình thực hiện thực
tập và thực hiện Dự án về các chuyên đề Toán thực tế lớp 10. Chính sự quan tâm, động
viên và hướng dẫn của quý thầy cô đã giúp chúng em có thêm động lực và tự tin trong
việc thực hiện dự án này.
Chúng em chân thành cảm ơn quý thầy cô đã tận tình hướng dẫn, truyền đạt
những kiến thức và kinh nghiệm quý báu, giúp chúng em nâng cao kỹ năng giảng dạy
cũng như ứng dụng lý thuyết vào thực tế. Đặc biệt, sự chăm chỉ, ham học hỏi của các
bạn học sinh chính là động lực to lớn để chúng em nỗ lực hoàn thành tốt nhiệm vụ của mình.
Chúng em mong rằng dự án này sẽ mang lại nhiều giá trị cho các bạn học sinh
lớp 10, giúp các bạn có thêm cơ hội vận dụng kiến thức toán học vào thực tiễn, từ đó
nuôi dưỡng niềm đam mê và hứng thú với môn học.
Một lần nữa, xin chân thành cảm ơn và kính chúc trường THCS&THPT Mong
Thọ ngày càng phát triển vững mạnh, gặt hái nhiều thành công trong sự nghiệp giáo dục.
Mong Thọ, ngày 16 tháng 02 năm 2025 Nhóm tác giả Triệu Yến Linh Lư Ngọc Cầm Phạm Mỹ Huyền Huỳnh Lê Thuỳ Vương LỜI MỞ ĐẦU
Toán học không chỉ là những con số và công thức trừu tượng, mà còn là công cụ
mạnh mẽ để giải quyết những vấn đề thực tiễn trong cuộc sống. Qua đó, chúng em nhận
ra rằng môn Toán không chỉ tồn tại trong các bài giảng mà còn có thể giải quyết được
những tình huống thực tế hàng ngày. Điều này không chỉ giúp chúng em mở rộng kiến
thức mà còn củng cố niềm đam mê với môn học. Với tinh thần đó, dự án "99 Bài Toán
Thực Tế Toán 10" ra đời nhằm đem lại cho các em học sinh một góc nhìn mới mẻ và
thực tế hơn về toán học.
Chúng em hy vọng rằng những nghiên cứu và kết quả thu được từ dự án này sẽ
góp phần nhỏ vào việc làm phong phú thêm phương pháp giảng dạy môn Toán tại
trường, đồng thời truyền cảm hứng cho các bạn học sinh khác trong việc khám phá, ứng
dụng Toán học vào cuộc sống. Một lần nữa, chúng em xin gửi lời cảm ơn chân thành
tới Ban Giám hiệu, quý thầy cô và các bạn học sinh vì những sự giúp đỡ quý báu trong
suốt quá trình thực hiện dự án.
Dự án Toán thực tế 10 gồm có 8 chuyên đề:
• Chuyên đề 1: Mệnh đề và tập hợp
• Chuyển đề 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
• Chuyên đề 3: Hàm số- Đồ thị và ứng dụng • Chuyên đề 4: Vectơ
• Chuyên đề 5: Đại số tổ hợp
• Chuyên đề 6: Xác suất
• Chuyên đề 7: Hệ thức lượng trong tam giác
• Chuyên đề 8: Phương pháp toạ độ trong mặt phẳng
Ở mỗi chuyên đề tập trung vào một phần kiến thức cơ bản cần nắm vững, kèm
theo các bài toán thực tế liên quan. Các chuyên đề không chỉ giúp củng cố kiến thức mà
còn mang lại cơ hội để các em áp dụng toán học vào các tình huống thực tế, từ đó phát
triển khả năng tư duy logic và sáng tạo. Chúng em hy vọng rằng dự án này sẽ giúp các
em học sinh không chỉ yêu thích môn toán hơn mà còn nhận ra giá trị thực tiễn của toán
học trong cuộc sống hàng ngày.
Dù rất cố gắng nhưng trong quá trình biên soạn không tránh được những sai sót,
nhóm chúng em rất mong nhận được sự góp ý của quý thầy cô, cùng với các bạn giáo
sinh đang công tác tại trường để cho chúng em có cơ hội học hỏi và hoàn thiện dự án lần này. MỤC LỤC
PHẦN NỘI DUNG .................................................................................. 1
Chủ đề 1. MỆNH ĐỀ VÀ TẬP HỢP ................................................... 1
1. Các kiến thức cần nắm ................................................................. 1
2. Các bài toán thực tế ...................................................................... 2
Chủ đề 2. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH
BẬC NHẤT HAI ẨN ................................................................................................. 9
1. Các kiến thức cần nắm ................................................................. 9
2. Các bài toán thực tế .................................................................... 10
Chủ đề 3. HÀM SỐ - ĐỒ THỊ VÀ ỨNG DỤNG .............................. 31
1. Các kiến thức cần nắm ............................................................... 31
2. Các bài toán thực tế .................................................................... 31
Chủ đề 4 . VECTƠ ............................................................................. 48
1. Các kiến thức cần nắm ............................................................... 48
2. Các bài toán thực tế .................................................................... 51
Chủ đề 5. ĐẠI SỐ TỔ HỢP ............................................................... 59
1. Các kiến thức cần nắm ............................................................... 59
2. Các bài toán thực tế .................................................................... 60
Chủ đề 6. XÁC SUẤT ........................................................................ 64
1. Các kiến thức cần nắm ............................................................... 64
2. Các bài toán thực tế .................................................................... 65
Chủ đề 7. HỆ THỨC LƯỢNG TRONG TAM GIÁC ....................... 72
1. Các kiến thức cần nắm ............................................................... 72
Các bài toán thực tế ........................................................................ 73
Chủ đề 8. PHƯƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHẲNG ........ 85
1. Các kiến thức cần nắm ............................................................... 85
2. Các bài toán thực tế .................................................................... 87
KẾT LUẬN ............................................................................................ 98 PHẦN NỘI DUNG
Chủ đề 1. MỆNH ĐỀ VÀ TẬP HỢP
1. Các kiến thức cần nắm
❖ Khái niệm: Mỗi mệnh đề phải đúng hoặc sai. Mỗi mệnh đề không thể vừa đúng, vừa sai.
❖ Mệnh đề kéo theo
Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, và kí hiệu là P Q.
Mệnh đề P Q còn được phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.
Mệnh đề P Q chỉ sai khi P đúng và Q sai.
❖ Mệnh đề tương đương
Mệnh đề Q P được gọi là mệnh đề đảo của mệnh đề P Q
Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
Nếu cả hai mệnh đề P Q và Q P đều đúng ta nói P và Q là hai mệnh đề
tương đương. Khi đó ta có kí hiệu P Q và đọc là tương đương, hoặc là điều kiện
cần và, hoặc khi và chỉ khi. ❖ Tập hợp
• Tập hợp: là một khái niệm cơ bản của toán học, không định nghĩa.
❖ Tập hợp con – Tập hợp bằng nhau • A B ( x
A x B) Các tính chất: + A , A A + , A A + A ,
B B C A B
• A = B (A B và B ) A ( ;
x x A x B)
❖ Một số tập con của tập hợp số thực Khoảng 1
( ;ab) =x | a x b
( ;a+) =x | a x (− ;
b) = x | x b Đoạn
;ab =x | a x b Nửa khoảng
;ab) =x | a x b
( ;ab =x | a x b ;
a +) = x | a x (− ;
b = x | x b
❖ Các phép toán tập hợp
• Giao của hai tập hợp: A B x | x ; A x B
• Hợp của hai tập hợp: A B {x | x A hoặc x } B
• Hiệu của hai tập hợp: A \ B {x | x A và x } B
Phần bù: Cho B \ A thì C B = A \ B . A
2. Các bài toán thực tế
Bài toán thực tế 1
( Đề cương ôn tập học kì I môn Toán, 2024-2025, trường THPT Hoàng Văn
Thụ, Hà Nội): Trong số 50 học sinh của lớp 10A1 có 25 bạn học sinh giỏi môn toán,
20 bạn học sinh giỏi môn văn, 15 bạn vừa là học sinh giỏi toán, vừa là học sinh giỏi
môn Văn. Hỏi lớp 10A1 có bao nhiêu học sinh chưa là học sinh giỏi môn Toán và chưa
là học sinh giỏi môn văn? Lời giải
A={ học sinh giỏi toán } A = 25
B={ học sinh giỏi văn } B = 20
Số học sinh giỏi cả toán và văn: A B = 15.
Ta có: A B = A + B − A B = 30.
Khi đó, số học sinh chưa giỏi toán, cũng chưa giỏi văn là :
50 − A B = 50 − 30 = 20 học sinh.
Bài toán thực tế 2
( Đề cương ôn tập học kì I môn Toán, 2024-2025, trường THPT Hoàng Văn
Thụ, Hà Nội): Điểm trung bình thi học kỳ I môn Toán của một nhóm học sinh lớp 10
là 8,1. Biết rằng tổng điểm môn toán của nhóm này là 72,9. Tìm số học sinh của nhóm. Lời giải
Giả sử nhóm có n học sinh và số điểm của các học sinh là x , x ,..., x . 1 2 n Ta có:
+ Tổng điểm: x , x ...x = 72,9 1 2 n + Điể
x , x ...x m trung bình: 1 2 n = 8,1 n 72,9 Suy ra: n = = 9 học sinh. 8,1
Bài toán thực tế 3
( Đề cương ôn tập học kì I môn Toán, 2024-2025, trường THPT Hoàng Văn
Thụ, Hà Nội): Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm
2018 (đơn vị triệu người) Tỉnh/Thành Dân phố số Hưng Yên 1,19 Thái Bình 1,79 Hà Nam 0,81 Nam Định 1,85 Ninh Bình 0,97 Tỉnh/Thành phố Dân số Hà Nội 7,52 Vĩnh Phúc 1,09 Bắc Ninh 1,25 Quảng Ninh 1,27 Hải Dương 1,81 Hải Phòng 2,01
a) Tìm số trung bình, trung vị của mẫu số liệu trên.
b) Giải thích tại sao số trung bình và trung vị có sự sai khác nhiều?
c) Nên sử dụng trung bình hay trung vị để đại diện cho dân số của các tỉnh Đồng bằng Bắc Bộ? Lời giải a) Số trung bình
7.52 +1.09 +1.25 +1.27 +1.81+ 2.01+1.19 +1.79 + 0.81+1.85 + 0.97 = =1.96 11
Trung vị: Sắp xếp lại mẫu số liệu theo chiều tăng dần của dân số
0.81 0.97 1.09 1.19 1.25 1.27 1.79 1.81 1.85 2.01 7.52
Có tất cả 11 tỉnh thành nên trung vị là 1.27
b) Số trung bình và trung vị có sự sai khác nhiều vì mẫu dữ liệu trên phân phối
lệch ( dân số tập trung đông ở Hà Nội và Hải Phòng) nên số trung bình gần phải , trong
khi đó trung vị là giá trị ở giữa nên ít bị ảnh hưởng.
c) Nên sử dụng trung vị để đại diện cho dân số các tỉnh Đồng bằng Bắc Bộ.
Bài toán thực tế 4
( Đề cương ôn tập học kì I môn Toán, 2024-2025, trường THPT Hoàng Văn
Thụ, Hà Nội): Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt
đầu ném ra được cho bởi công thức h(t) 2 = t
− + 2t + 3 (tính bằng mét), t là thời gian tính
bằng giây ( t 0 ).
a. Tính chiều cao lớn nhất quả bóng đạt được.
b. Hãy tính xem sau bao lâu quả bóng sẽ rơi xuống mặt đất? Lời giải a)
Ta có: h(t) = 2
− t + 2 = 0 t =1.
Khi đó t = 0 thì h(0) = 3 t = 1 thì h( ) 1 = 4
Vậy chiều cao lớn nhất quả bóng đạt được là 4m sau 1s b)
Khi quả bóng rơi xuống đất thì chiều cao bằng 0, nghĩa là: t = 3(n) 2
h(t) = 0 t
− + 2t + 3 = 0 t = 1 − (l) t = 1
− (l) vì t 0
Vậy sau 3s thì quả bóng rơi xuống đất.
Bài toán thực tế 5
( Đề cương ôn tập học kì I môn Toán, 2024-2025, trường THPT Hoàng Văn
Thụ, Hà Nội): Hàng ngày An phải đi đò qua một con sông thẳng chảy về hướng Đông
đến trường. Muốn sang được bến đò đối diện ở bờ Bắc , bác lái đò di chuyển chếch một
góc so với phương vuông góc với bờ. Khi biểu diễn trên mặt phẳng tọa độ Oxy thì vận
tốc của đò so với dòng nước là v = 3
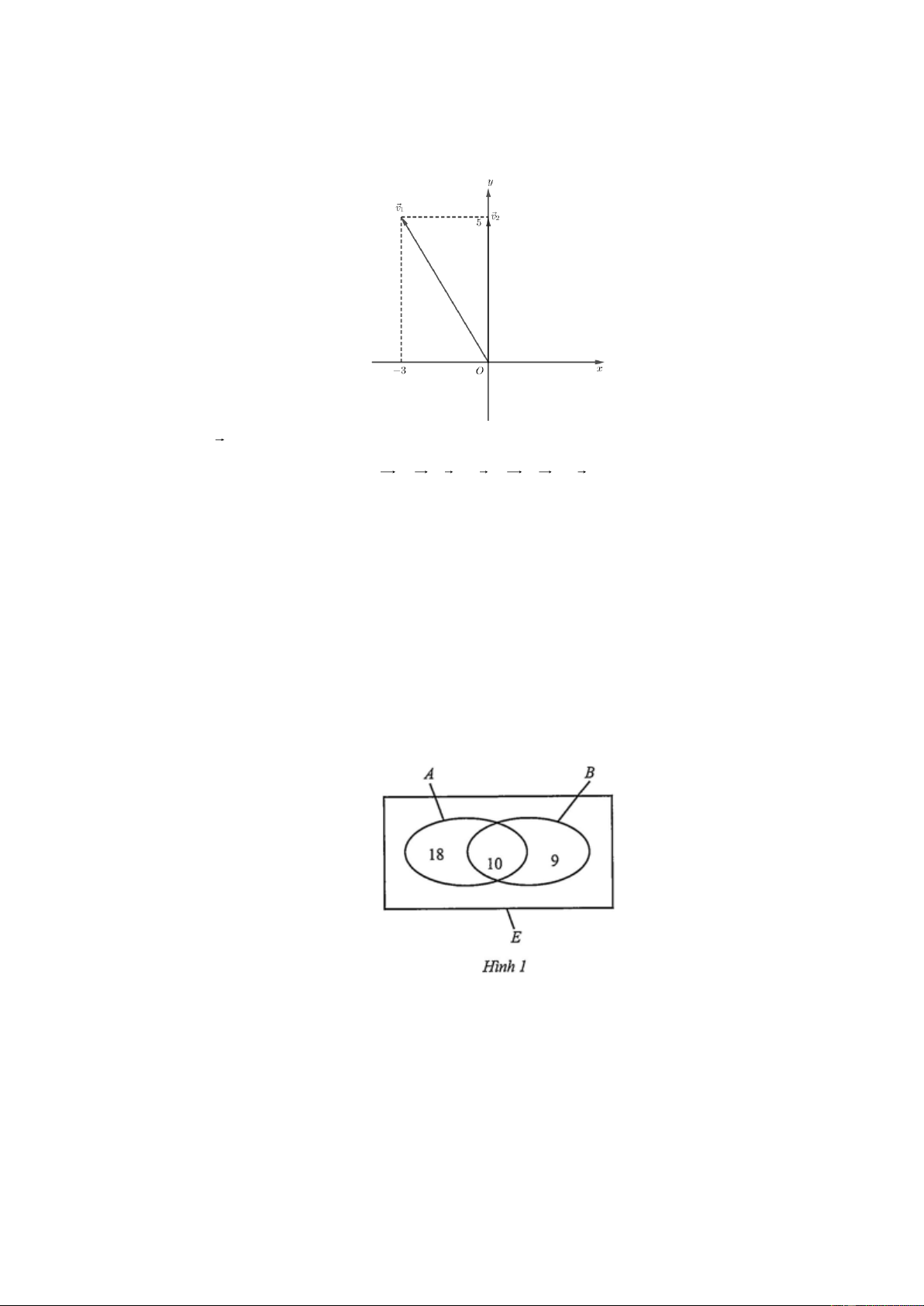
− i + 5 j vận tốc thực của đò so với bờ v = 5 j ( đơn 1 2 vị m / s ). a)
Hãy biểu diễn v ,v trên mặt phẳng tọa độ Oxy . 1 2 b)
Tính tốc độ của dòng nước so với bờ ( tức là độ lớn vận tốc của dòng nước với bờ). Lời giải a)
b) Gọi v là vector vận tốc của dòng nước so với bờ ta có:
v = v + v v = v − v = 3i 2 1 2 1
Suy ra tốc độ của dòng nước so với bờ là : v = 3m / s
Bài toán thực tế 6
Lớp 10B có 28 học sinh tham gia câu lạc bộ thể thao và 19 học sinh tham gia câu
lạc bộ âm nhạc. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên. Có bao nhiêu
học sinh tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?
a) Có bao nhiêu học sinh tham gia ít nhất một trong hai câu lạc bộ trên?
b) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham gia câu lạc bộ
thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ? Lời giải
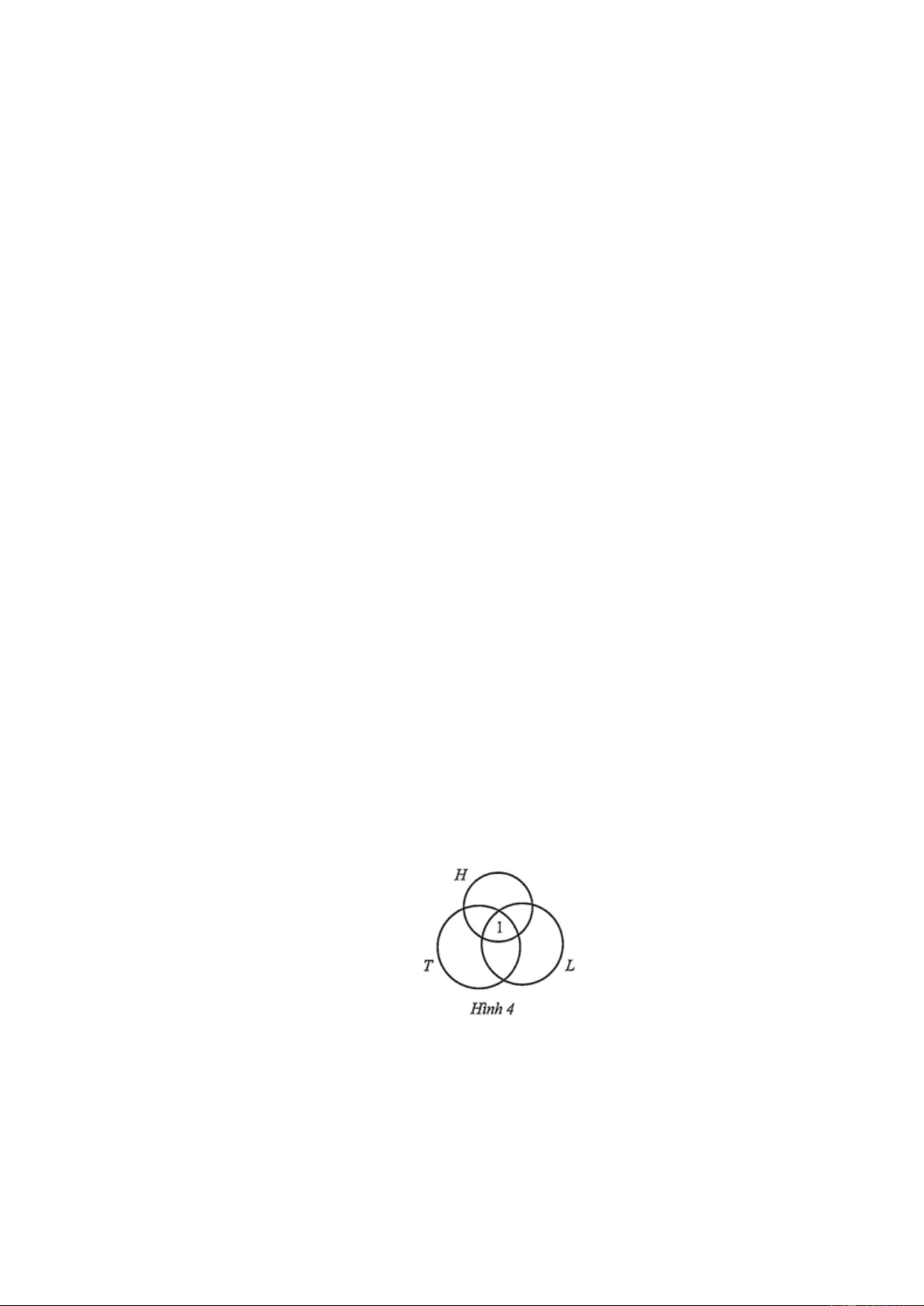
Kí hiệu A là tập hợp học sinh tham gia câu lạc bộ thể thao, B là tập hợp học sinh
tham gia câu lạc bộ âm nhạc, E là tập hợp học sinh của lớp 10 B . Ta có thể biểu diễn
ba tập hợp trên bằng biểu đồ Ven (Hình 1).
a) Khi đó, A B là tập hợp học sinh tham gia cả hai câu lạc bộ trên. Số phần tử của A là 28, số
phần tử của B là 19, số phần tử của tập hợp A B là 10.
Tập hợp các học sinh tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc là
tập hợp A \ B . Số phần tử của A \ B chính là số phần tử của A trừ đi số phần tử của A B .
Vậy số học sinh tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm
nhạc là: 28 −10 =18 (học sinh).
b) Tập hợp các học sinh tham gia ít nhất một trong hai câu lạc bộ trên chính là tập hợp A B .
Do khi đếm số học sinh tham gia câu lạc bộ thể thao là 28, số học sinh tham gia
câu lạc bộ âm nhạc là 19 thì số học sinh tham gia cả hai câu lạc bộ là 10 được tính hai lần.
Vậy số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là: 28 +19 −10 = 37 (học sinh).
c) Số phần tử của E là 40. Tập hợp các học sinh không tham gia câu lạc bộ thể
thao là phần bù của A trong E . Vậy số học sinh không tham gia câu lạc bộ thể thao là: (học sinh).
Tập hợp các học sinh không tham gia cả hai câu lạc bộ là phần bù A B của E.
Vậy số học sinh không tham gia cả hai câu lạc bộ là: 40 − 37 = 3 (học sinh).
Bài toán thực tế 7
Trong kì thi chọn học sinh giỏi các môn văn hoá, lớp 10 A có 7 học sinh đăng kí
thi môn Toán, 5 học sinh đăng kí thi môn Vật lí, 6 học sinh đăng kí thi môn Hoá học;
trong đó có 3 học sinh đăng kí thi cả Toán và Vật lí, 4 học sinh đăng kí thi cả Toán và
Hoá học, 2 học sinh đăng kí thi cả Vật lí và Hoá học, 1 học sinh đăng kí thi cả ba môn.
Hỏi lớp 10A có tất cả bao nhiêu học sinh đăng kí thi học sinh giỏi các môn Toán, Vật lí, Hoá học? Lời giải
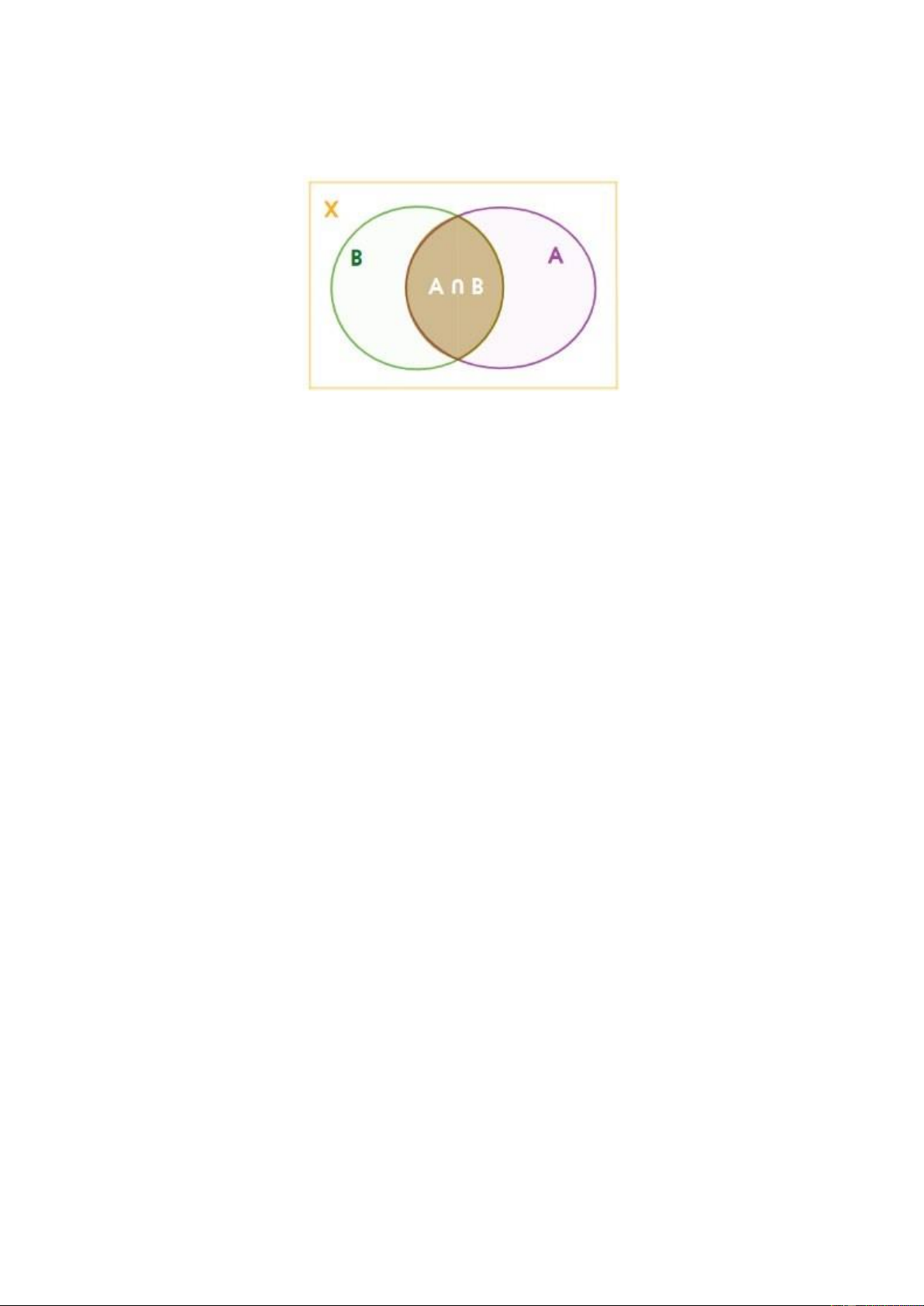
Gọi T là tập hợp các học sinh đăng kí thi môn Toán, L là tập hợp các học sinh
đăng kí thi môn Vật lí, H là tập hợp các học sinh đăng kí thi môn Hoá học. Biểu diễn
cả ba tập hợp bằng biểu đồ Ven (Hình 4).
Dựa vào biểu đồ Ven, ta có số học sinh chỉ đăng kí thi môn Toán là: 7 − 3 − 4 +1 = 1 .
Số học sinh chỉ đăng kí thi môn Vật lí là: 5 − 3 − 2 +1 =1.
Số học sinh đăng kí thi môn Toán và Vật lí mà không đăng kí thi môn Hoá học là: 3 −1 = 2 .
Vậy tổng số học sinh lớp 10A đăng kí thi ba môn trên là: 1+1+ 2 + 6 = 10 (học sinh).
Bài toán thực tế 8
Một cuộc khảo sát về khách du lịch thăm vịnh Hạ Long cho thấy trong 1410
khách du lịch được phỏng vấn có 789 khách du lịch đến thăm động Thiên Cung, 690
khách du lịch đến đảo Titop. Toàn bộ khách được phỏng vấn đã đến ît nhất một trong
hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến thăm động Thiên Cung vừa
đến thăm đảo Titop ở vịnh Hạ Long? Lời giải
Gọi A là tập hợp các khách du lịch đến thăm động Thiên Cung, B là tập hợp các
khách du lịch đến đảo Titop. n( )
A = 789; n(B) = 690; n( A B) =1410 Biểu đồ Ven
Tổng số khách du lịch = Số khách đến động Thiên Cung + Số khách đến đảo Titop
- Số khách du lịch đến cả hai địa điểm. Hay:
n ( A B) = n( A) + n( B) − n( A B)
1410 = 789 + 690 − n( A B)
n( A B) = 69
Vậy có 69 khách du lịch vừa đến thăm động Thiên cung vừa đến thăm đảo Titop ở vịnh Hạ Long.
Bài toán thực tế 9
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích môn Toán, 16 học sinh
thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
Có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
Có bao nhiêu học sinh không thích cả hai môn này? Lời giải
Gọi A, B lần lượt là tập hợp các học sinh thích môn Toán và Tiếng Anh, X là tập hợp học sinh lớp 10H. Theo giả thiết: n( )
A = 20; n(B) =16; n( A B) =12, n( X ) = 35
a) Nhận thấy rằng, nếu tính tổng n( A) + n(B) thì ta được số học sinh thích ít nhất
một trong hai môn Toán và Tiếng Anh, nhựng số học sinh thích cả hai môn Toán và
Tiếng Anh được tính hai lần. Do đó, số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
n( A B) = n( )
A + n(B) − n( A B) = 20 +16 −12 = 24
b) Trong số 35 học sinh lớp 10H, có 24 học sinh thích ít nhất một trong hai môn
Toán và Tiếng Anh, còn lại số học sinh không thích cả hai môn này là: 35 + 24 = 11 (học sinh).
Bài toán thực tế 10
Kí hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á
a) Nêu ít nhất hai phần tử thuộc tập hợp E .
b) Nêu ít nhất hai phần tử không thuộc tập hợp E .
c) Liệt kê các phần tử thuộc tập hợp E. Tập hợp E có bao nhiêu phần tử? Lời giải
a) Việt Nam E ; Thái Lan E ; Lào E .
b) Nhật Bản E ; Hàn Quốc E .
c) E = {Việt Nam; Lào; Campuchia; Thái Lan; Myanmar; Malaysia; Singapore;
Indonesia; Brunei; Philippines; Đông Timor}
Có 11 nước thuộc khu vực Đông Nam Á. Hay tập hợp E có 11 phần tử (n(E) = ) 11 .
Bài toán thực tế 11
Lớp 10 C có 45 học sinh, trong đó có 18 học sinh tham gia cuộc thi vẽ đồ họa
trên máy tính, 24 học sinh tham gia cuộc thi tin học văn phòng cấp trường và 9 học sinh
không tham gia cả hai cuộc thi này. Hỏi có bao nhiêu học sinh của lớp 10C tham gia
đồng thời hai cuộc thi? Lời giải
Gọi X là tập hợp các học sinh của lớp 10C
A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính,
B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.
Theo biểu đồ Ven ta có: n( )
A = 18, n(B) = 24, n( X ) = 45, n( A B) là số học
sinh tham gia ít nhất một trong hai cuộc thi, bằng: 45 − 9 = 36 (học sinh)
Mà n( A B) = n( A) + n(B) − n( A B) (do các học sinh tham gia cả 2 cuộc thi được tính hai lần)
Suy ra số học sinh tham gia cả 2 cuộc thi là:
n( A B) =18 + 24 − 36 = 6
Vậy có 6 học sinh của lớp 10 C tham gia đồng thời hai cuộc thi
Chủ đề 2. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Các kiến thức cần nắm
❖ Bất phương trình bậc nhất hai ẩn x, y , có dạng tổng quát là:
ax + by c ( ) 1
(ax +by ,cax +by ,cax +by c) Trong đó , a ,
b c là các số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
❖ Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn:
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương
trình (1) được gọi là miền nghiệm của nó.
❖ Hệ bất phương trình bậc nhất hai ẩn
Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai
ẩn x,y mà ta phải đi tìm nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi
là nghiệm của hê bất phương trình đã cho.
Cũng giống như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học
tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.
2. Các bài toán thực tế
Bài toán thực tế 12
[ Đề Dự Bị THPT Quốc Gia Năm 2015 ]
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9
lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam
cần 30 g đường, 1 lít nước và 1 g hương liệu; pha chế 1 lít nước táo cần 10 g đường, 1
lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước
táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để
được số điểm thưởng là lớn nhất? Lời giải
Gọi x, y lần lượt là số lít nước cam và táo của mỗi đội pha chế (x, y 0) . Khi đó
số điểm thưởng nhận được của mỗi đội chơi là F = 60x + 80y .
Để pha chế x lít nước cam cần 30x g đường, x lít nước và x( g) hương liệu. Đế
pha chế y lít nước cam cần 10y g đường, y lít nước và 4y( g) hương liệu. Do đó, ta có:
Số gam đường cần dùng là: 30x +10y
Số lít nước cần dùng là: x + y
Số gam hương liệu cần dùng là: x + 4y .
Vi trong cuộc thi pha chễ, mỗi đội chơi sử dụng tối đa 24 g hương liệu, 9 lít nước
và 210 g đường nên x, y thỏa mãn hệ bất phưong trình: 30
x +10y 210 3 x + y 21 x y 9 + x + y 9 x 4y 24 (*) + x + 4y 24 x,y 0 x,y 0
Khi đó bài toán trở thành :
Trong các nghiệm của hệ bất phương trình (*), tìm nghiệm ( x = x ,y = y o o ) sao
cho F = 60x + 80y lớn nhất.
Trong mặt phẳng tọa độ, ta sẽ biểu diễn phần mặt phẳng chứa điểm M(x, y) thỏa
mãn (*). Khi đó miên nghiệm của hệ bất phương trình (*) là ngũ giác OABCD kể cả
miền trong của tam giác ( như hình vẽ) .
Biểu thức F=60x+80y đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác OABCD. Tại các đỉnh ( O 0;0), ( A 7;0), ( B 6;3), ( C 4;5), (
D 0;6). Ta thấy F đạt giá trị lớn nhất
tại x = 4, y = 5 .
Khi đó F = 60.4 + 80.5 = 640 .
Vậy cần pha chế 4 lít nước cam và 5 lít nước táo thì số điểm thưởng lớn nhất là 640 .
Bài toán thực tế 13
[Câu 2 Chuyên đề bài toán thực tế]
Một phân xưởng có hai máy đặc chủng M , M 1
2 sản suất hai loại sản phẩm ký hiệu
là I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu
đồng. Muốn sản suất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M M
2 trong 1 giờ. Muốn sản suất một tấn sản phẩm loại II phải dùng máy 1 trong 1 giờ
và máy M2 trong 1 giờ. Một máy không thể dùng để sản suất đồng thời hai sản phẩm trên. Máy M M
1 làm việc không quá 6 giờ trong một ngày, máy 2 một ngày chi làm việc
không quá 4 giờ. Hãy đặt kế khoạch sản suất sao cho tổng số tiền lãi là lớn nhất? Lời giải
Gọi x, y lần lượt là số tấn sản phẩm loại I , loại II sản suất trong một ngày (x, y 0)
. Khi đó số tiền lãi một ngày là L = 2x +1,6y (triệu đồng) và số giờ làm việc của mỗi ngày của máy M + M + 1 là 3x
y và máy 2 là x y. Vì mỗi ngày máy M M
1 làm việc không quá 6 giờ và máy 2 làm việc không quá 4
giờ nên x, y thỏa mãn hệ bất phưong trình : 3 x + y 6
x + y 4 (*) x,y 0
Khi đó bài toán trở thành:
Trong các nghiệm của hệ bất phương trình (*), tìm nghiệm ( x = x ,y = y 0 0 ) sao
cho L = 2x +1,6y lón nhất.
Trong mặt phẳng tọa độ, ta sẽ biểu diễn phần mặt phẳng chứa điểm M(x, y) thóa
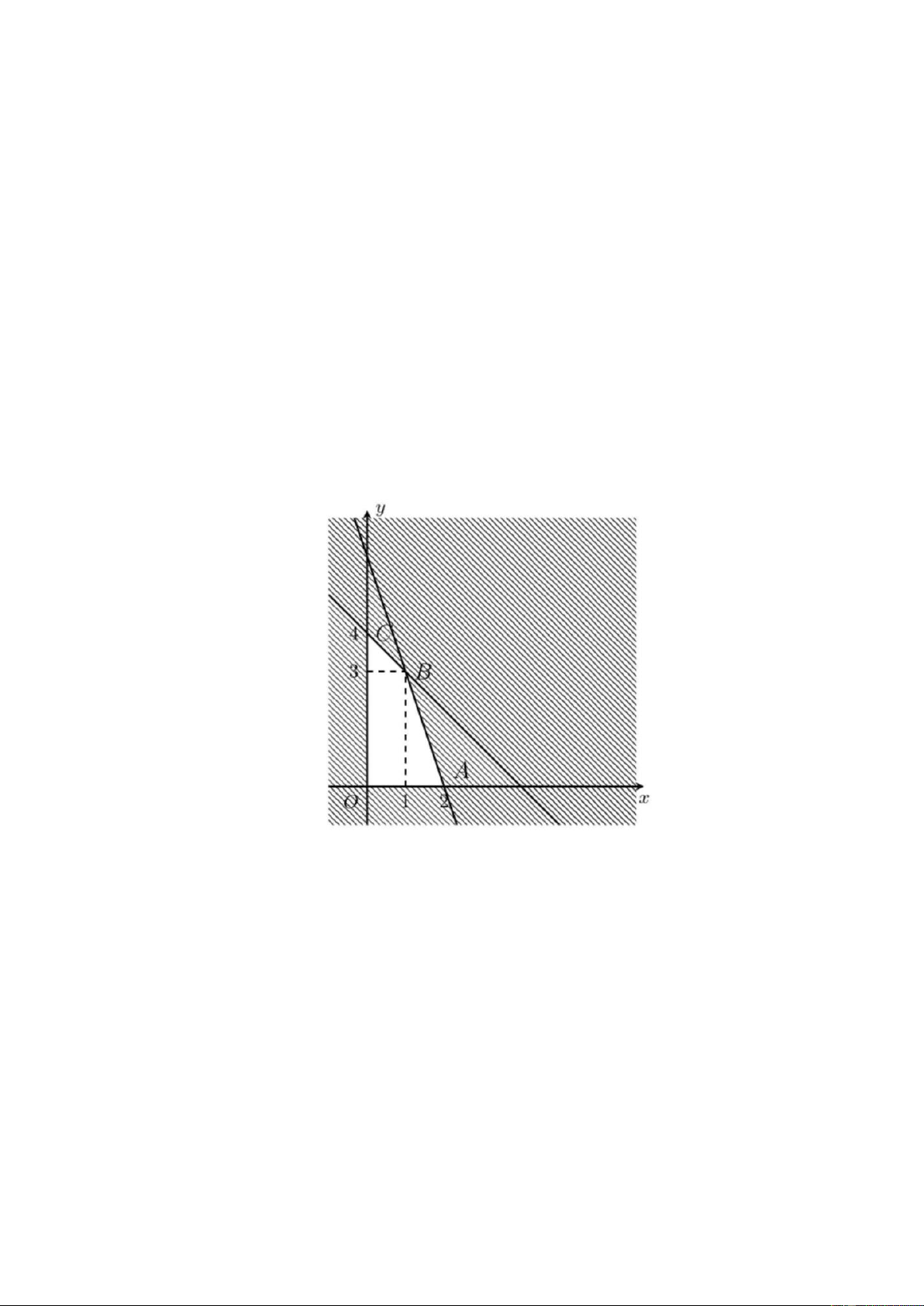
mãn (*). Khi đó miền nghiệm của hệ bất phưong trình (*) là tứ giác OABC kể cả miền
trong của tứ giác ( như hình vẽ) . Biểu thức L=2x+1,6 y đạt giá trị lớn nhất tại một trong
các đỉnh của tứ giác OABC. Tại các đỉnh : ( O 0;0), ( A 0;4), ( B 1;3), ( C 2;0) . Ta thấy
L đạt giá trị lớn nhất tại x =1,y = 3 . Khi đó L = 2.1+1,6.3 = 6,8 .
Vậy để có lãi suất cao nhất, mỗi ngày cần sản suất 1 tấn sản phẩm loại I , và 3 tấn sản phẩm loại II.
Bài toán thực tế 14
[ SGK Đại số & Giải tích 10 nâng cao]
Một gia đình cần ít nhất 900 g chất prôtein và 400 g chất lipit trong thức ăn mỗi
ngày. Biết rằng thịt bò chứa 80% prôtein và 20% lipit. Thịt lợn chứa 60% prôtein và
40% lipit. Biết rằng gia đỉnh này chi mua nhiêu nhất là 1600 g thịt bò và 1100 g thịt
lợn, giá tiền 1 kg thịt bò là 45 nghìn đồng, 1 kg thịt lợn là 35 nghìn đồng. Hỏi gia đình
đó phải muA Bao nhiêu kg thịt mỗi loại để chi phí ít nhất? Lời giải
Giả sử gia đình đó mua x( kg) thịt bò và y ( kg ) thịt lợn (x, y 0) . Khi đó chi
phí mua x( kg) thịt bò và (
y kg) thịt lợn là T = 45x + 35y (nghìn đồng).
Theo giả thuyết, x và y thóa mã đîèu kiện x 1,6; y 1,1.
Khi đó lượng prôtêin có được là 80%x + 60%y và lượng lipit có được là 20%x + 40%y.
Vì gia đînh đó cần ít nhất 0,9 kg chất prôtêin và 0,4 kg chất lipit trong thức ăn
mỗi ngày nên điều kiện turơng úng là 80%x + 60%y 0,9 và 20%x + 40%y 0,4 hay
4x + 3y 4,5 và x + 2y 2 . 0 x 1,6 0 y 1,1
Vậy x, y thỏa mãn hệ bất phương trình: 4x + 3y 4,5
x + 2y 2
Khi đó bài toán trở thành :
Trong các nghiệm của hệ bất phương trình (*), tìm nghiệm ( x = x ,y = y o o ) sao
cho T = 45x + 35y nhỏ nhất.
Trong mặt phẳng tọa độ, ta sẽ biểu diễn phần mặt phẳng chứa điểm M(x, y) thỏa
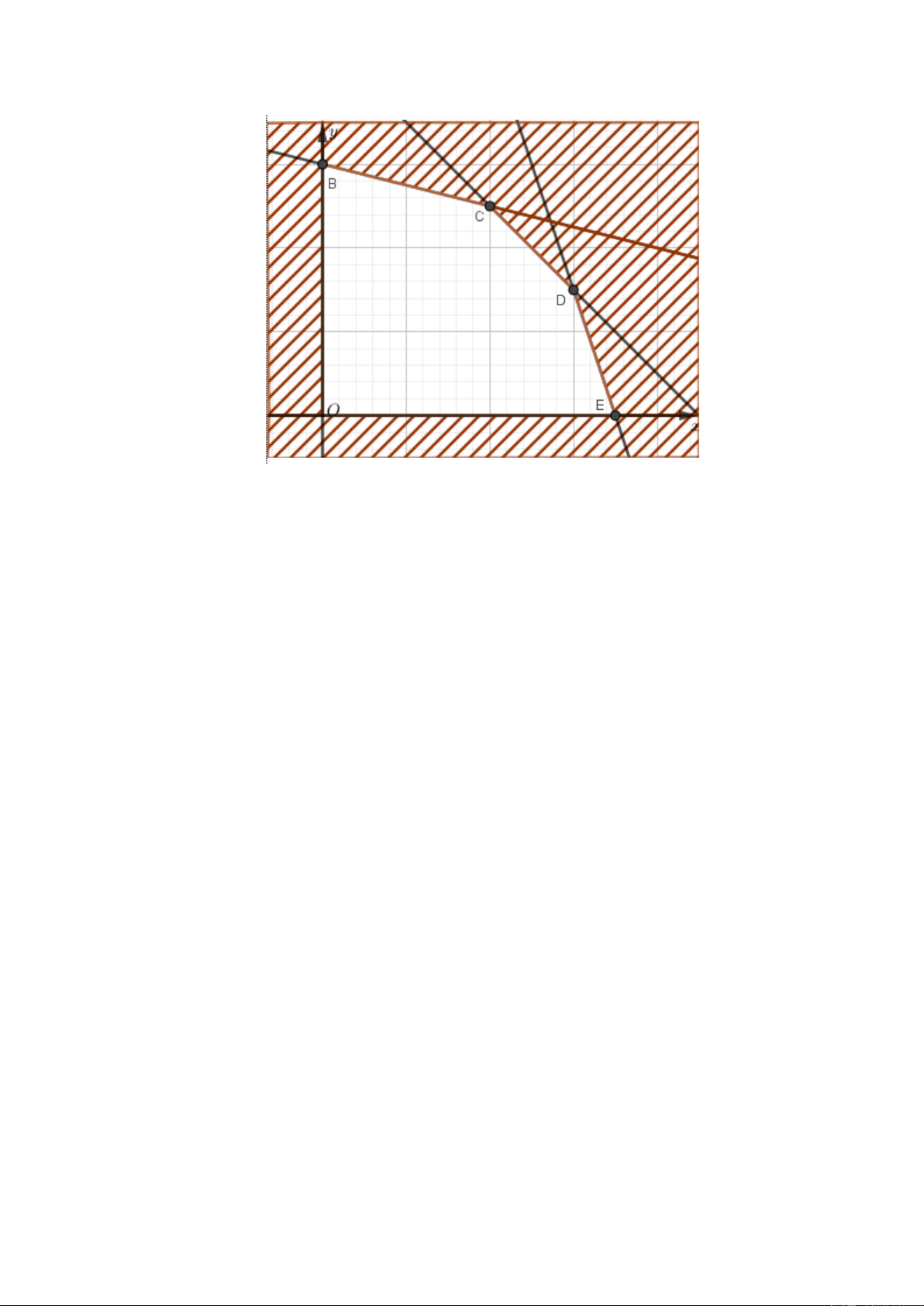
mãn (*). Miền nghiệm của hệ (*) là miền bên trong của tứ giác lồi ABCD và cả biên (
như hình vẽ). T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD. Ta có: ( A 1,6;1,1), ( B 1,6;0,2), ( C 0,6;0,7), ( D 0,3;1)
Kiểm tra được x = 0,6; y = 0,7 thì T = 51,5 (nghìn đồng) là nhỏ nhất.
Vậy gia đình đó mua 0,6 kg thịt bò và 0,7 kg thịt lợn thì chi phí là ít nhất. Cụ thể
là phải chi phí 51,5 nghìn đồng.
Bài toán thực tế 15
[Đề dự Bị THPT Quốc Gia năm 2015 ]
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và
9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg
chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất
được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại
để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể
cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Lời giải
Gọi x tấn nguyên liệu loại I, y tấn nguyên liệu loại II ( ,
x y 0) . Khi đó tổng số
tiền mua nguyên liệu là T = 4x + 3y (đồng)
Vì mỗi tấn nguyên liệu loại I có thể chiết xuất được 20kg chất A và 0,6kg chất B,
mỗi tấn nguyên liệu loại II có thể chiết xuất được 10kg loại A và 1,5kg loại B nên x,y
tấn nguyên liệu loại I và II có thể chiết xuất được 20x +10y kg chất A và 0,6x +1,5y kg chất B.
Khi đó theo giả thuyết ta có: 0 x 9 0 x 9 0 y 10 0 y 10
20x +10 y 140 2x +1y 14
0,6x +1,5y 9
2x +5y 30
Vậy bài toán trở thành:
Trong các nghiệm của hệ phương trình (*), tìm nghiệm ( x = x , y = y sao cho 0 0 )
T = 4x + 3y nhỏ nhất
Trong phương trình mặt phẳng tọa độ, ta biểu diễn phần mặt phẳng chứa điểm M ( ,
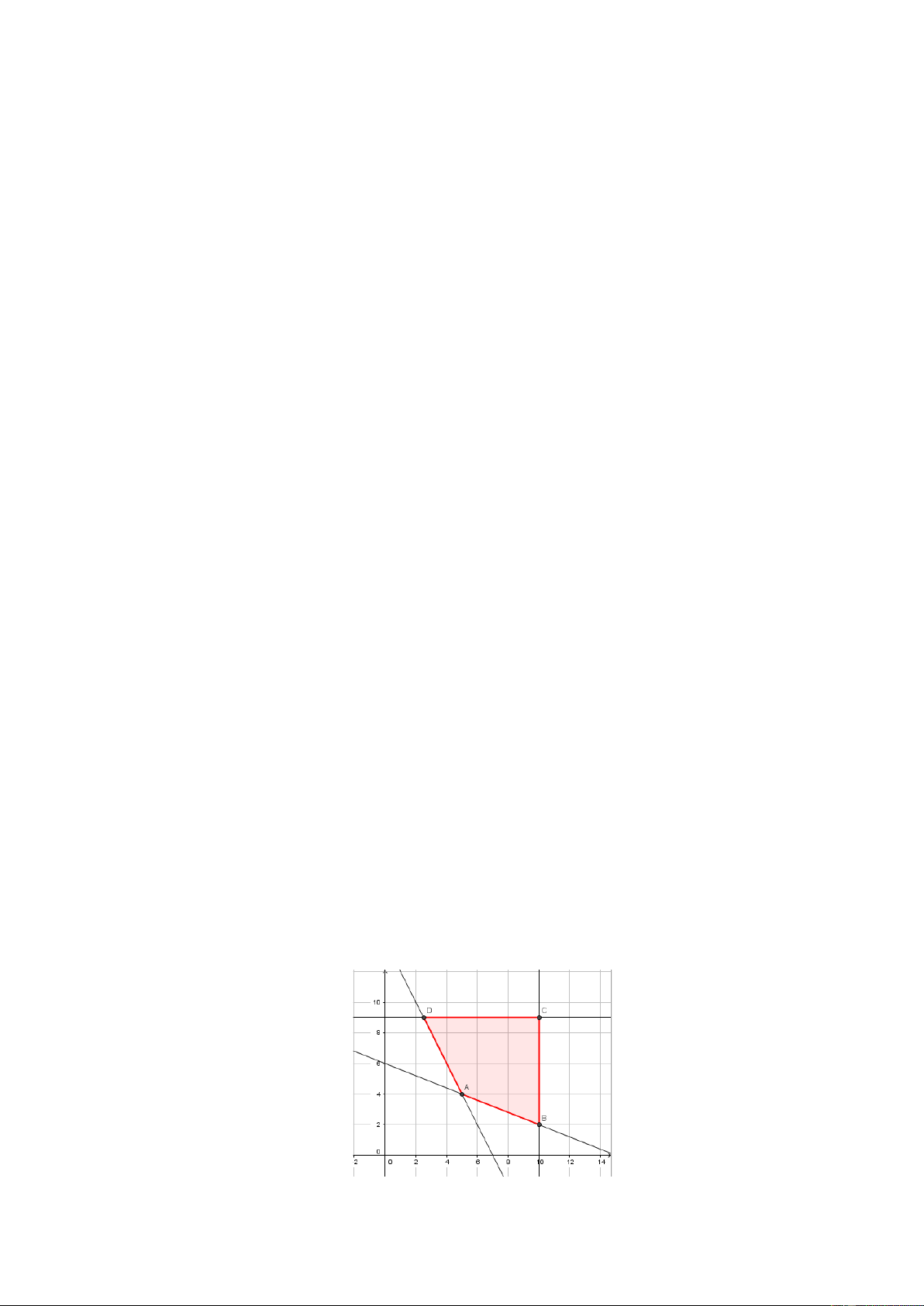
x y) thỏa mãn (*). Khi đó miền nghiệm của hệ bất phương trình (*) là tứ giác D ABC
kể cả miền trong của tứ giác (như hình vẽ). Biểu thức T = 4x + 3y đạt giá trị nhỏ nhất
tại một trong các đỉnh của tứ giác D ABC . Tại các đỉnh: A( ) B( ) C( ) 5 5; 4 , 10; 2 , 10;9 , D ;9
. Ta thấy T đạt giá trị lớn nhất tại x = 5, y = 4 2
Khi đó T = 4.5+3.4 = 32
Vậy để chi phí nhỏ nhất, cần sử dụng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu
loại II. Khi đó, tổng chi phí là 32 triệu đồng.
Bài toán thực tế 16
[Đề dự Bị THPT Quốc Gia năm 2015]
Một hộ nông dân định trồng đậu và cà trên diện tích 8a . Nếu trồng đậu thì cần 20
công và thu 3000000 đồng trên mỗi diện tích a , nếu trồng cà thì cần 30 công và thu
4000000 đồng trên mỗi diện tích a . Hỏi cần trồng mỗi loại cây trên mỗi diện tích bao
nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180? Lời giải
Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị 2
a = 100m ), điều kiện
x 0, y 0, ta có x + y 8 .
Số công cần dùng là 20x + 30y 180 hay 2x + 3y 18
Số tiền thu được là F = 3000000x + 4000000y (đồng) hay F = 3x + 4y (triệu đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình x + y 8 2x + 3y 18 x 0 y 0
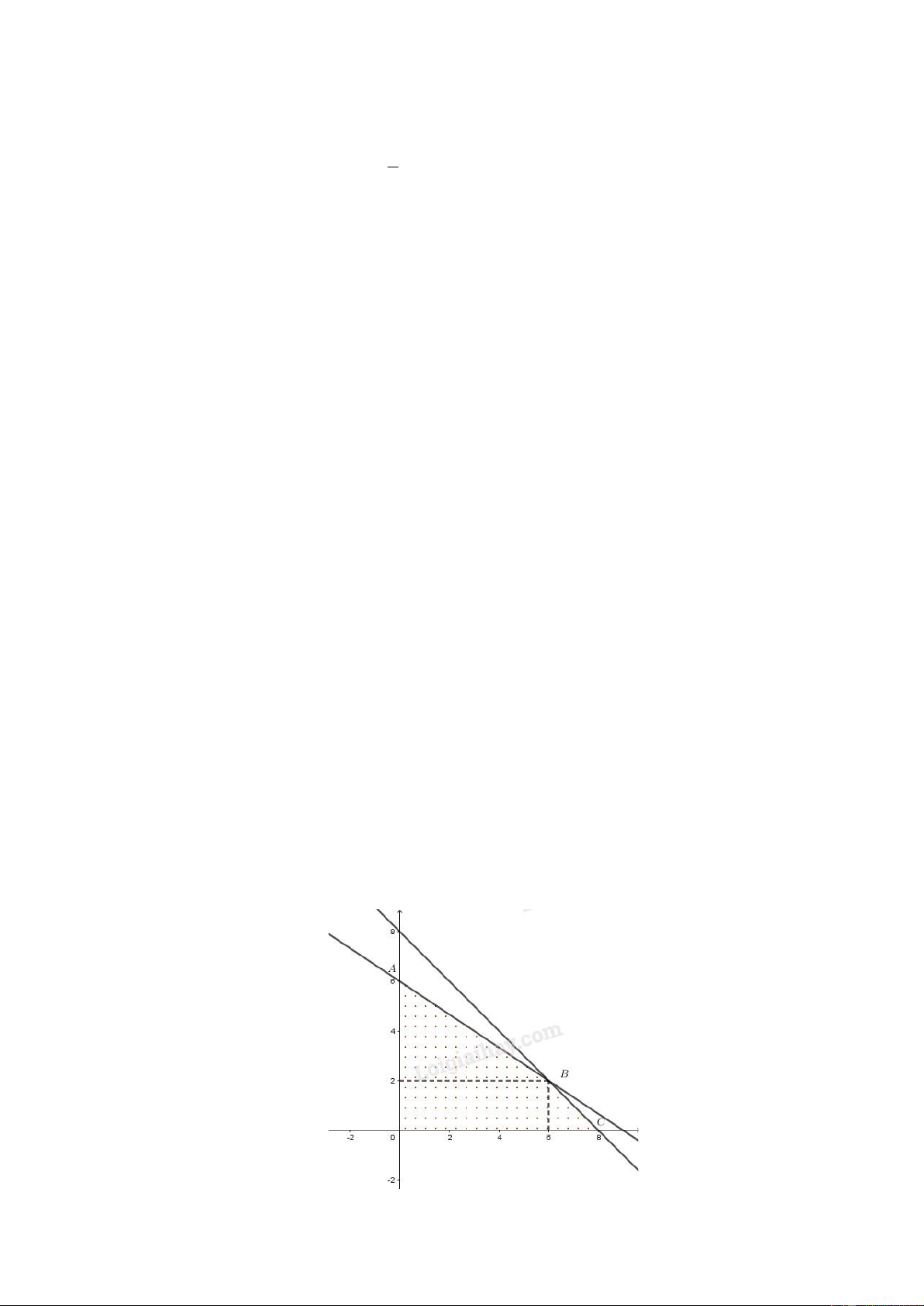
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H ) ta được miền tứ giác OABC với
A(0;6), B(6;2),C (8;0),O(0;0) .
Xét giá trị của F tại các đỉnh , O , A ,
B C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm
B ) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng). Vậy ta cần 2
600m diện tích trồng đậu, 2
200m diện tích trồng cà, thu hoạch được 26000000 (đồng)
Bài toán thực tế 17
[SGK Đại số & Giải tích 10 nâng cao]
Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B
đối với cơ thể con người. Kết quả như sau: Một người mỗi ngày có thể tiếp nhận được
không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B. Một người mỗi
ngày cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B. Do tác động phối hợp của hai loại
vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn 1 số đơn vị vitamin A nhưng 2
không nhiều hơn ba lần số đơn vị vitamin A. Giá của 1 đơn vị vitamin A là 9 đồng, giá
1 đơn vị vitamin B là 7,5 đồng. Tìm phương án dùng 2 loại vitamin A và B thỏa mãn
các điều kiện trên để số tiền phải trả là ít nhất. Lời giải
Gọi x, y lần lượt là số đơn vị vitamin A và B dùng mỗi ngày ( , x y 0).
Vì giá của 1 đơn vị vitamin A là 9 đồng, giá 1 đơn vị vitamin B là 7,5 đồng nên
số tiền cần phải trả là C = 9x + 7,5 . y 0 x 600 0 y 500
Theo giả thuyết ta có: 400 x + y 1000( ) * 1
x y 3x 2
Khi đó bài toán trở thành:
Trong các nghiệm của hệ bất phương trình (*) , tìm nghiệm ( x = x , y = y sao cho 0 0 )
C = 9x + 7,5 nhỏ nhất.
Trong mặt phẳng tọa độ, ta sẽ biểu diễn phần mặt phẳng chứa điểm M ( , x y) thỏa
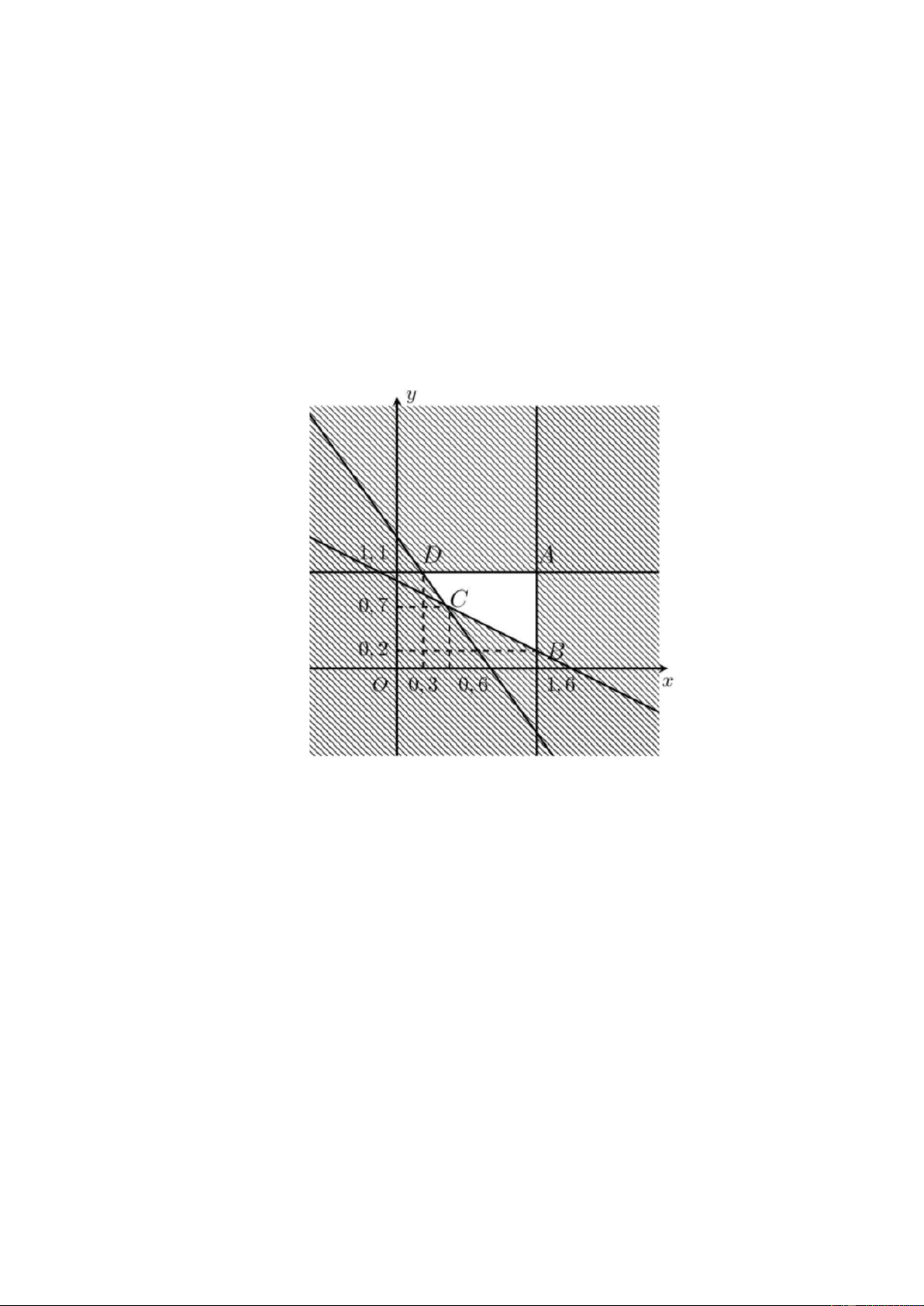
mãn (*) .Khi đó miền nghiệm của hệ bất phương trình (*) là ngũ giác ABCDEF kể cả miền trong của tứ giác nhưng bỏ đi cạnh BC với 800 400 A B C ( ) D( ) E( ) 500 (100;300), ; , 600;300 , 600; 400 , 500;500 , F ;500 . Biểu thức 3 3 3
C = 9x + 7,5y đạt giá trị nhỏ nhất tại một trong các đỉnh A,D,E,F của ngũ giác ABCD.
Khi đó, ta thấy C đạt giá trị lớn nhất x =100, y = 300. Khi đó
C = 9.100 + 7,5.300 = 3150.
Vậy phương án tốt nhất là dùng 100 đơn vị vitamin A và 300 đơn vị B. Chi phí mỗi ngày là 3150 đồng.
Bài toán thực tế 18
[ Chuyên đề bài toán thực tế câu 10]




