











Preview text:
CHUYÊN ĐỀ 12: BỘI VÀ ƯỚC CỦA MỘT SỐ NGUYÊN
I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa Với ,
a b Î Z và b ¹ 0. Nếu có số nguyên q sao cho a = .
bq thì ta ta có phép chia hết a : b = q (trong
đó ta cũng gọi a là số bị chia, b là số chia, q là thương). Khi đó ta nói a chia hết cho b , kí hiệu là a Mb . Khi a Mb ( ,
a b Î Z , b ¹ 0 ) ta còn gọia là bội của b và b là ướccủa a . 2. Nhận xét
- Số 0 là bội của mọi số nguyên khác 0. Số 0 không phải là ước của bất kì số nguyên nào.
- Các số 1 và - 1 là ước của mọi số nguyên. 3. Tính chất
Có tất cả các tính chất như trong tập ¥ .
-Nếu a chia hết cho b và b chia hết cho c thì a cũng chia hết cho c . a M b và bM c Þ a M c
- Nếu a chia hết cho b thì bội của a cũng chia hết cho b . a M b Þ ka M b (k Î ¢ )
- Nếu a , b chia hết cho c thì tổng và hiệu của chúng cũng chia hết cho c . a M, c bM
c Þ a + b M ; c a - b M. c
- Nếu a , b chia cho c cùng số dư thì a – b chia hết cho c . Nhận xét:
- Nếu a chia hết cho b , b chia hết cho a thì a = ± . b
- Nếu a chia hết cho hai số m, n nguyên tố cùng nhau thì a chia hết cho m.n . - Nếu n
a chia hết cho số nguyên tố p thì a chia hết cho p .
- Nếu ab chia hết cho m và ,
b m nguyên tố chung nhau thì a chia hết cho m .
- Trong n số nguyên liên tiếp có đúng một số chia hết cho n . II. CÁC DẠNG BÀI
Dạng 1. Tìm bội và ước của số nguyên
I. Phương pháp giải
-Tập hợp các bội của số nguyên a có vô số phần tử và bằng {k .a | k Î Z }.
- Tập hợp các ước số của số nguyên a (a ¹ 0) luôn là hữu hạn. Cách tìm: Trang 1
Trước hết ta tìm các ước số nguyên dương của phần số tự nhiên a (làm như trong tập số tự nhiên), chẳng hạn là , p ,
q r . Khi đó - , p - ,
q - r cũng là ước số của a. Do đó các ước của a là , p , q r , – , p – , q – r .
Như vậy số các ước nguyên của a gấp đôi số các ước tự nhiên của nó.
- Số ước nguyên dương của số m n t a = x y ….z là (m + ) 1 .(n + ) 1 ( … t + ) 1 II. Bài toán A. TRẮC NGHIỆM
Bài 1.Khi nào ta nói a là bội của b ? A. a b M B. b a M C. a Mb D. b Ma Lời giải Đáp án: A
Bài 2.Hãy nêu cách tìm bội của một số:
A. nhân số đó lần lượt với 1; 2; 3;......
C. chia số đó lần lượt cho 1; 2; 3;......
B. nhân số đó lần lượt với 0;1; 2; 3;......
D. chia số đó lần lượt cho 0;1; 2; 3;...... Lời giải Đáp án: B
Bài 3.Hãy chỉ ra số là ước của tất cả các số: A. 0 B. 2 C.1 D.3 Lời giải Đáp án: C
Bài 4.Số 28 có bao nhiêu ước nguyên? A. 4 B. 6 C. 10 D.12 Lời giải Đáp án: D Giải thích: ta có 2 28 = 2 .7
Số các ước nguyên dương của số 28 là (2 + ) 1 .(1 + ) 1 = 3.2 = 6
Số các ước của 28 là 6.2 = 12
Bài 5. Các số có 2 chữ số là ước của 60 là:
A. 10; 20; 35; 60
C. 10; 12; 15; 20; 30; 60
B. 10; 12; 15; 20; 40; 60 D. 10; 20; 40; 60 Lời giải Đáp án: C
Bài 6. Hãy tìm các số x B(12) và 20 < x < 50 A. x 24; 36; 4 8 B. x 20; 24; 3 6 B. x 24; 36; 5 0 D. x 12; 24; 3 6 Trang 2 Lời giải Đáp án: A B. TỰ LUẬN
Bài 1.Tìm năm bội của: 3 ; -3. Lời giải
Cả 3 và -3 đều có chung các bội dạng 3.m ( m ¢ ), nghĩa là: 0 ; -3 ; 3 ; -6 ; 6 ; -9 ; 9 ;
Chẳng hạn, năm bội của 3 và – 3 là :3 ; 6 ; 9 ; 12 ; 15.
Bài 2. Tìm năm bội của 2 và -2. Lời giải
Muốn tìm một bội của 2, (-2) ta nhân 2, (-2) với một số nguyên nào đó. Chẳng hạn:
Năm bội của 2 là : 2 . 1 = 2; 2 . (− ) 1 = -2; 2 . 2 = 4; 2. ( 2 − ) = - 4; 2 . 3 = 6. Năm bội của -2 là : 2 − ; 2 ; -4 ; 4 ; - 6 .
Tổng quát: Các bội của 2 và -2 có dạng là 2.q với q ¢ : 0 ; -2 ; 2 ; -4 ; 4 ; -6 ; 6 ; -8 ; 8 ;
Bài 3. Tìm các bội của 7 ; − 7. Lời giải
B(7) = 0; 7; 14; 21; 28; B( 7
− ) = 0; 7; 14; 21; 28;
Bài 4. Tìm tất cả các ước của -2, 4, 13, 15, 1 Lời giải
Các ước của -2 là : -1 , 1 ,-2 , 2.
Cấc ước của 4 là : -1 , 1 , -2 , 2 , -4 , 4.
Các ước của 13 là : -1 , 1 , -13 , 13
Các uớc của 15 là : -1 , 1 , -3 , 3 , -5 , 5 , -15 , 15.
Các ước của 1 là : -1 , 1.
Bài 5.Tìm tất cả các ước của - 3 ; 6 ; 11 ; -1. Lời giải
Kí hiệu U(a) là tập hợp các ước của số nguyên a , ta có: U (− ) 3 = 1 − ; 1 ; –3 ;
3 hoặc viết gọn là: U (− ) 3 = 1 ; 3 ;U (6) = 1 ; 2; 3; 6 ; U (1 ) 1 = 1 ; 1 1 ; U ( ) -1 = ± 1
Bài 6.Tìm tất cả các ước của 36. Lời giải
Phân tích 36 ra thừa số nguyên tố: 2 2 36 = 2 .3
Để tìm tất cả các ước của 36 không bị sót, bị trùng, ta có thể làm như sau: Trang 3 thuvienhoclieu.com Ta viết: 2 1 2 2 2 hay 1 2 4 3 1 3 2 3 hay 1 3 9
Các ước nguyên dương của 36 là : 1 2 4 1.3 2.3 4.3 1.9 2.9 4.9
Tất cả có 9 ước nguyên dương là: 1 ; 2 ; 4 ; 3 ; 6 ; 12 ; 9 ; 18 ; 36 .
Tập hợp tất cả các ước nguyên của 36 là :
U (36) = ±1; ± 2; ± 3; ± 4 ; ± 6; ± 9; ± 12; ± 18; ± 3 6
Bài 7. Tìm tất cả các ước của 12 mà lớn hơn – 4. Lời giải Các ước của 12 là: 1
; 2; 3; 4; 6; 12
Các ước của 12 mà lớn hơn – 4 là -3; -2; -1; 1; 2; 3; 4; 6; 12 .
Bài 8.Tìm các số tự nhiên n sao cho: n - 1là ước của 28 Lời giải
Ta có: U (28) = ±1; ± 2; ± 4 ; ± 7; ± 14; ± 2 8 .
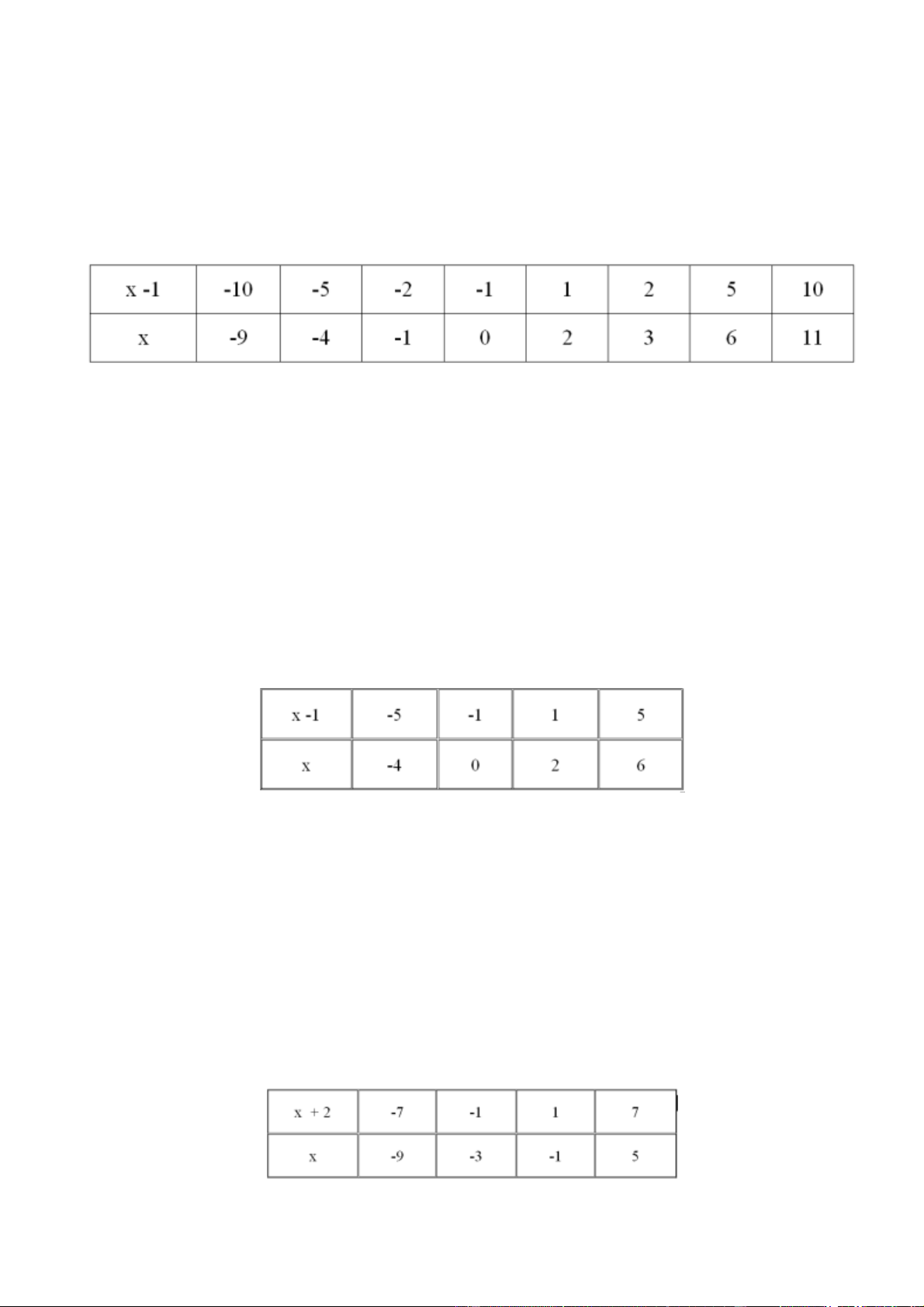
Vì n −1U (28) , ta có bảng sau:
Vì n là số tự nhiên nên n 0; 2; 3; 5; 8; 15; 2 9
Bài 9. Tìm các bội của -13 lớn hơn -40 nhưng nhỏ hơn 40. Lời giải
Các bội của -13 là 0; 13; -13; 26, -26; 39; -39; 52; -52 .
Các bội của -13 lớn hơn -40 nhưng nhỏ hơn 40 x -39;-26;-13;0; 13;26;3 9
Bài 10.Tìm các số tự nhiên x là bội 75 đồng thời là ước của 600 Lời giải
x B(75) (x ¥ ) x 0;75; 150; 300; 600; … x U (600) (x¥ )
x 1; 2; 3; 4; 5; 6; 8; 10;12 ;20; 24; 25; 30; 50; 60; 75; 100;1 20; 150; 200; 300; 60 0 Đáp
án: x 75; 150; 300; 60 0
Bài 11. Chứng tỏ rằng số có dạng aaa là bội của 37 Lời giải
Đáp án: Ta có: aaa= 100a + 10a + a = 111. A = 3. 37.a nên aaa là bội của 37
thuvienhoclieu.com Trang 4 thuvienhoclieu.com
Bài 12. Tìm các chữ số a và b sao cho n = a53b vừa là bội của 5, vừa là bội của 6 Lời giải Ta có n 6 M nên n 2 M
Số n = a53b chia hết cho cả 2 và 5 nên b = 0 n = a530 Ta có n 6 M nên n 3 M (a + 5 + 3 + 0) 3 Mhay (a + 8) 3 M, do đó a 1; 4; 7
Vậy n 1530; 4530; 753
0 cả 3 số này vừa là bội của 5, vừa là bội của 6 Bài 13.
a) Tìm năm bội của: – 5; 5 ;
b) Tìm các bội của – 12 , biết rằng chúng nằm trong khoảng từ – 100 đến 24. Lời giải
a) Các bội số của 5; – 5 đều có dạng 5.k (k Î ¢ ).
Chẳng hạn chọn năm bội số của 5; – 5 là: –15, – 10, – 5, 0, 5 ( ứng với k lần lượt bằng - 3;- 2;- 1; 0; 1; 2 ).
b) Các bội số của –12 có dạng 12.k (k Î ¢ ). Cần tìm k sao cho: –100 < 12k < 24 .
Tức là: –9 < k < 2 , chọn k Î {- 8;- 7;- 6;- 5;- 4;- 3;- 2;- 1;0; } 1 .
Vậy các bội của –12 nằm trong khoảng từ –100 đến 24 là
- 96,- 84,- 72,- 60,- 48,- 36,- 24,- 12, 0,12.
Bài 14. Tìm tất cả các ước của: a) –3 ; b) –25 ; c) 12. Lời giải
a) Các ước tự nhiên của 3 là 1, 3.Do đó các ước của –3 là - 3,- 1, 1, 3.
b) Các ước tự nhiên của 25 là 1, 5, 25.Do đó các ước của 25 là - 25,- 5,- 1, 1, 5, 25.
c) Các ước tự nhiên của 12 là 1, 2, 3, 4, 6, 12.Do đó các ước của 12 là
- 12, - 6, - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, 6, 12. Nhận xét:
Số tự nhiên a phân tích ra thừa số nguyên tố có dạng n . m . k
p q r (p, q, r là số nguyên tố) thì số ước tự
nhiên của a là (n + ) 1 (m + ) 1 (k + )
1 . Khi đó mỗi số nguyên ,
a – a đều có 2(n + ) 1 (m + ) 1 (k + ) 1 ước nguyên.
Số nguyên tố p có 4 ước nguyên là - , p - 1, 1, . p
Bài 15. Tìm số nguyên n để:
a) 5 . n chia hết cho –2 ;
b) 8 chia hết cho n ;
c) 9 chia hết cho n + 1 ;
d) n – 18chia hết cho 17. Lời giải
thuvienhoclieu.com Trang 5 thuvienhoclieu.com
a) 5 . n chia hết cho –2 , nên n là bội của 2 ( vì 5 không chia hết cho 2).
Vậy n = 2k (k là số nguyên tùy ý).
b) 8 chia hết cho n , nên n là ước của 8.
Vậy n Î {- 8;- 4;- 2;- 1; 1; 2; 4; } 8 .
c) 9 chia hết cho n + 1 , nên n + 1 là ước của 9.
Suy ra n + 1 Î {- 9;- 3;- 1; 1; 3; } 9 .
Với n + 1 = - 9 suy ra n = - 9 - 1 hay n = - 10
Với n + 1 = - 3 suy ra n = - 3 - 1 hay n = - 4
Với n + 1 = - 1 suy ra n = - 1 - 1 hay n = - 2
Với n + 1 = 1 suy ra n = 1 - 1 hay n = 0
Với n + 1 = 3 suy ra n = 3 - 1 hay n = 2
Với n + 1 = 9 suy ra n = 9 - 1 hay n = - 8
Vậy n Î {- 10;- 4;- 2; 0; 2; } 8 .
d) n – 18 chia hết cho 17, nên n – 18 là bội của 17. Do đó n – 18 = 17k (k Î ¢ ).
Vậy n = 18 + 17k (k Î ¢ ).
III. Bài tập có hướng dẫn Bài 1.
a) Tìm bốn bội của –9; 9 .
b) Tìm các bội của –24 , biết rằng chúng nằm trong khoảng từ 100 đến 200. HD
a) Chẳng hạn là: –18; –9; 0; 9 b) 120; 144; 168; 192
Bài 2. Tìm tất cả các ước của: a) –17 ; b) 49; c) –100 . HD
a) U (–17) = {–17; – 1; 1; 17} b) U (4 )
9 = {–49; – 7; – 1; 1; 7; 4 } 9 c) U (10 )
0 = {–100; –50; –25; –20; –10; –5; –4; –2; –1; 1; 2; 4; 5; 10; 20; 25; 50; 100} Bài 3.
a) Tìm tập hợp UC (–12; 16);
b) Tìm tập hợp UC (15; –18; –20). HD
thuvienhoclieu.com Trang 6 thuvienhoclieu.com
a) UCLN (12; 16) = 4 suy ra UC (–12; 16) = {–4; –2; –1; 2; 4}
b) UCLN (15; 18; 20) = 1 suy ra UC (15; –18; –20) = {–1; } 1
Bài 4. Tìm số nguyên n để:
a) 7 . n chia hết cho 3;
b) –22 chia hết cho n ;
c) –16 chia hết cho n – 1 ;
d) n + 19 chia hết cho 18. HD
a) 7n M3 mà (7; 3) = 1 nên n M3 do đó n = 3k (k Î ¢ )
b) - 22 Mn nên n Î { - 22; - 11; - 2; - 1; 1; 2; 11; 22}
c) - 16 M(n - 1) nên (n - 1) Î { - 16; - 8; - 4; - 2; - 1; 1; 2; 4; 8; 16}
Vậy n Î { - 15; - 7; - 3; - 1; 0; 2; 3; 5; 9; 17}
d) (n + 19) M18 nên (n + 1) M18 suy ra n = 18k - 1 (k Î ¢ )
Bài 5. Tìm tập hợp BC (15; –12; –3 ) 0 . HD BCNN (15; 20; 30) = 60
Suy ra BC (15; –20; –30) = B (60) = 60k (k Î ¢)
Bài 6. Cho hai tập hợp A = {1; 2; 3; 4; } 5 và B = {- 2;- 4;- } 6 .
a) Viết tập hợp gồm các phần tử có dạng a . b với a Î A, b Î B.
b) Trong các tích trên có bao nhiêu tích chia hết cho 5? HD
a) C = {ab | a Î A; b Î B } = { - 2; - 4; - 6; - 8; - 10; - 12; - 16; - 18; - 20; - 24; - 30}
( Chú ý: Các phần tử trong tập hợp phải khác nhau đôi một)
b) Trong các tích trên có 3 tích chia hết cho 5 ứng với a = 5 và b Î B
Dạng 2. Vận dụng tính chất chia hết của số nguyên
I. Phương pháp giải
Để chứng minh một biểu thức A chia hết cho số nguyên a;
- Nếu A có dạng tích m .n . p thì cần chỉ ra m (hoặc n, hoặc p) chia hết cho a. Hoặc m chia hết cho
a , n chia hết cho a , p chia hết cho a trong đó a = a a a 1 2 3 1 2 3.
- Nếu A có dạng tổng m + n + p thì cần chỉ ra m, n, p cùng chia hết cho a, hoặc tổng các số dư khi
chia m, n, p cho a phải chia hết cho a.
thuvienhoclieu.com Trang 7 thuvienhoclieu.com
- Nếu A có dạng hiệu m – n thì cần chỉ ra m, n chia cho a có cùng số dư. Vận dụng tính chất chia hết
để làm bài toán về tìm điều kiện để một biểu thức thỏa mãn điều kiện cho hết. II. Bài toán
Bài 1. Chứng minh rằng: 2 3 4 5 6 7 8
S = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 chia hết cho - 6 . Lời giải
Nhóm tổng S thành tổng của các bội số của - 6 bằng cách: S = ( 2 + )+ ( 3 4 + )+ ( 5 6 + )+ ( 7 8 2 2 2 2 2 2 2 + 2 ) 2 4 6 = 6 + 2 .6 + 2 .6 + 2 .6
Mỗi số hạng của tổng S đều chia hết cho - 6 , nên S chia hết cho - 6 . Bài 2. Cho số 8 3
a = - 10 + 2 . Hỏi số a có chia hết cho - 9 không? Lời giải 8 3 8
a = - 10 + 2 = - 10 + 1 + 7 = 1 -442 99 4 ..4.3 9 + 7 . goàm 8 chöõ soá 9
Số hạng đầu của a chia hết cho 9, còn 7 không chia hết cho 9 nên a không chia hết cho 9. Do đó a
cũng không chia hết cho - 9. Bài 3. Cho ,
a b là các số nguyên. Chứng minh rằng nếu 6a + 11b chia hết cho 31 thì a + 7b cũng
chia hết cho 31. Điều ngược lại có đúng không? Lời giải
Ta có: 6a + 11b = 6.(a + 7b)- 31 . b (*)
Do đó 31bM31, và 6a + 11bM31, từ (*) suy ra 6(a + 7b)M31,
Mà 6 và 31 nguyên tố cùng nhau, nên suy ra a + 7bM 31.
Ngược lại, nếu a + 7bM31 , mà 31bM31, từ (*) suy ra 6a + 7bM31.
Vậy điều ngược lại cũng đúng.
Ta có thể phát biểu bài toán lại như sau: “Cho ,
a b là các số nguyên. Chứng minh rằng 6a + 11b chia hết cho 31 khi và chỉ khi a + 7b chia hết cho 31”.
Bài 4. Tìm số nguyên x sao cho:
a) 3x + 4 chia hết cho x - 3;
b) x + 1 là ước số của 2 x + 7. Lời giải
a) Nhận thấy 3x + 4 = 3(x - 3)+ 5. Do 3(x - 3) (
Mx - 3), nên (3x + 4) (
Mx - 3) khi và chỉ khi 5 ( Mx - 3).
Suy ra x - 3 Î Ö(5) hay x - 3 Î {- 5;- 1; 1; }
5 . Vậy x Î {- 2; 2; 4; } 8 . b) Nhận thấy 2
x + 7 = x (x + ) 1 - (x + ) 1 + 8.
thuvienhoclieu.com Trang 8 thuvienhoclieu.com Do x (x + ) 1 ( Mx + ) 1 , nên 2 x + 7 ( Mx + ) 1 khi và chỉ khi 8 ( Mx + ) 1 .
Suy ra x + 1 Î {- 8;- 4;- 2;- 1; 1; 2; 4; 8}.
Vậy x Î {- 9; - 5; - 3; - 2; 0; 1; 3; 7}.
III. Bài tập có hướng dẫn
Bài 1. Chứng minh rằng: 2 3 4 5 6 7 8 9
S = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 chia hết cho (- 39). HD 2 3 4 5 6 7 8 9
S = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 2 3 4 5 6 7 8 9
(3 + 3 + 3 ) + (3 + 3 + 3 ) + (3 + 3 + 3 )
= 39 + 33.39 + 36.39 = 39.(1 + 33 + 36)M39 Suy ra S M39 nên M S (- 39)
Bài 2. Cho số a = 11...11 (gồm 20 chữ số 1). Hỏi số a có chia hết cho 111 không? HD Nhận thấy: 17 14 11 8 5 2
a = 111.10 + 111.10 + 111.10 + 111.10 + 111.10 + 111.10 + 11 = 17 14 11 8 5 2 111.(10 + 10 + 10 + 10 + 10 + 10 ) + 11
Suy ra a là tổng của hai số hạng trong đó có 1 số chia hết cho 111, 1 số không chia hết cho 111 nên a
không chia hết cho 111.
Vậy a không chia hết cho 111. Bài 3. Cho ,
a b là các số nguyên. Chứng minh rằng 5a + 2b chia hết cho 17 khi và chỉ khi
9a + 7b chia hết cho 17. HD Xét hiệu 5.(9a + 7 ) b - 9.(5a + 2 ) b = 17b
Nhận thấy 17b M17 nên:
Nếu 9a + 7b M17 thì 9.(5a + 2 )
b M17 , mà (9; 17) = 1 nên 5a + 2b M17
Nếu 5a + 2b M17 thì 5.(9a + 7 )
b M17 , mà (5; 17) = 1 nên (9a + 7 ) b M17
Bài 4. Tìm số nguyên x sao cho:
a) 2x – 5 chia hết cho x – 1;
b) x + 2 là ước số của 2 x + 8. HD
a) 2x - 5 = 2(x - 1) - 3 nên (2x - 5)M (x - 1) Û 3M
(x - 1) do đó (x - 1)Î { - 3;- 1; 1; 3}
Vậy x - 1 Î { - 2; 0; 2; 4}
thuvienhoclieu.com Trang 9 thuvienhoclieu.com b) Do 2
x + 8 = x(x + 2) - 2(x + 2) + 12 nên 2
(x + 8) M(x + 2) Û 12 M(x + 2)
Do đó (x + 2) Î { - 12;- 6;- 4;- 3;- 2;- 1; 1; 2; 3; 4; 6; 12}
Vậy x Î { - 14;- 8;- 6;- 5;- 4;- 3; - 1; 0; 1; 2; 4; 10}
Bài 5. Tìm cặp số nguyên x, y sao cho: a) (x - ) 1 .(y + ) 1 = 5;
b) x.(y + 2) = - 8;
c) xy - 2x - 2y = 0. HD
a) Vì 5 = 5.1 = (- 1).(- 5) nên ta có các trường hợp sau:
1) x - 1 = 1 và y + 1 = 5 Û x = 2 và y = 4
2) x - 1 = 5 và y + 1 = 1 Û x = 6 và y = 0
3) x - 1 = - 1 và y + 1 = - 5 Û x = 0 và y = - 6
4) x - 1 = - 5 và y + 1 = - 1 Û x = - 4 và y = - 2
b) (x;y) = (- 8;- 1); (1;- 10); (8;- 3);(- 1; 6); (- 4; 0); (2;- 6); (4;- 4); (- 2;- 6)
c) xy - 2x - 2y = 0 Û (x - 2).(y - 2) = 4
Do đó tìm được (x;y) = (3; 6);(6; 3);(1;- 2);(- 2; 1);(4; 4);(0; 0) .
Bài 6. Tìm tất cả các cặp số nguyên x, y sao cho 20x + 10y = 2010. HD
Từ điều kiện đề bài suy ra 2x + y = 201
201 là số lẻ và 2x là số chẵn, suy ra y là số lẻ. Khi đó y có dạng:
y = 2k + 1 (k Î ¢ ) Þ x = 100 - k
Chẳng hạn, bốn cặp số nguyên (x; y) thỏa mãn:
(x;y) = (100; 1); (99; 3); (101;- 1); (98; 5)
Bài 7. Tìm số nguyên x sao cho x – 1 là bội của 15 và x + 1 là ước số của 1001. HD U (100 )
1 = {1001; –1001; 143; –143; 91; –91; 77; –77; 13; –13; 11; –11; 7; –7; 1; – } 1
Ta có: x – 1 là bội của 15 nên x – 1 = 15k (k Î ¢ ) suy ra x + 1
= 15k + 2 (k Î ¢ )
Mà x + 1 là ước của 1001 nên kiểm tra thấy x + 1 = 77 hay x = 76 Vậy x = 76
Dạng 3. TÌM SỐ NGUYÊN x THỎA MÃN ĐIỀU KIỆN VỀ CHIA HẾT I. Phương pháp giải.
Áp dụng tính chất: Nếu a + b chia hết cho c và a chia hết cho c thì b chia hết cho c .
thuvienhoclieu.com Trang 10 thuvienhoclieu.com II. Bài toán.
Bài 1.Tìm các số tự nhiên x sao cho 10 ( M x- ) 1 Lời giải Ta có 10 ( M x- ) 1 khi đó ( x- ) 1 là ước của 10
U (10) = ±1; ± 2; ± 5; ± 1 0 . Ta có bảng sau:
Suy ra x 0; 2; 3; 6; 1 1 ( x ¥ )
Bài 2.Tìm x ¢ sao cho :
a) 3x + 2 chia hết cho x – 1; b) 2
x + 2x – 7 chia hết cho x + 2 . Lời giải
a) Ta có: 3x + 2 = 3x – 3 + 5 = 3(x - ) 1 + 5 . Ta có: 3(x – ) 1 chia hết cho x – 1.
Do đó 3x + 2 chia hết cho x – 1 khi 5 chia hết cho x – 1, tức là x – 1 là ước của 5.
Ước của 5 gồm các số ±1, ± 5. Ta có bảng sau: Suy ra x -4; 0 ; 2 ; 6 . b) 2 x + 2x – 7 = x(x + 2) - 7
Ta có: x (x + 2) chia hết cho x + 2
Do đó x(x + 2) - 7 chia hết cho x + 2 khi 7 chia hết cho x + 2
Do đó x + 2 là ước của 7.
Ước của 7 gồm các số ±1, ± 7. Ta có bảng sau:
Suy ra: x -9; -3 ; - 1 ; 5 .
thuvienhoclieu.com Trang 11 thuvienhoclieu.com
Bài 3.Tìm các số nguyên x thoả mãn: a ) (x + 4) (x M + ) 1 ; b ) (4x + ) 3 ( x M – 2) Lời giải a) Ta có x + 4 = (x + ) 1 + 3 nên (x + 4) : (x + ) 1 khi 3:(x + )
1 , tức là x + 1 là ước của 3. Vì U ( ) 3 = - { 1 ; 1 ; 3 - ; } 3 , ta có bảng sau:
ĐS : x = -4 ; -2 ; 0 ; 2.
b) HD: Ta có 4x + 3 = 4(x – 2) + 11 nên (4x + )
3 : (x - 2) khi 11:(x - 2) , tức là (x - 2) là ước của 11.
Đáp số: x -9 ; 1 ; 3 ; 1 3 .
Bài 4.Tìm x ¢ sao cho : a) 2 x + x +1 chia hết cho x + 1
b) 3x - 8 chia hết cho x - 4 . Lời giải a) Ta có: 2 x + x +1= x (x + ) 1 + 1. Ta có: x (x + ) 1 chia hết cho x + 1. Do đó 2
x + x +1 chia hết cho x + 1 khi 1 chia hết cho x + 1, tức là x + 1 là ước của 1.
Ước của 1 gồm các số ±1. Suy ra x 0 ; -2 .
b) Ta có: 3x – 8 = 3(x - 4) + 4
Ta có: 3(x - 4) chia hết cho x - 4 .
Do đó 3x - 8 chia hết cho x - 4 khi 4 chia hết cho x - 4 , tức là x - 4 là ước của 4.
Ước của 4 gồm các số ±1; ±2; ±4. Suy ra x 0 ; 2 ; 3 ; 5 ; 6 ; 8 .
Bài 5.Tìm các số tự nhiên x sao cho x + 20 là bội của x + 2 Lời giải
x + 20 là bội của x + 2 (x + 20) (x M + 2)
x+ 20 = (x+ 2) + 18 (x M +2) mà (x + 2) (x M + 2) Do đó 18 (x M + 2) x + 2Ö(18)
Ö(18) = ±1; ±2; ±3; ±6; ±9; ±1 8
Mà x + 2 2 (x Z) nên x + 2 2; 3; 6; 9; 1 8 x 0; 1; 4; 7; 1 6
thuvienhoclieu.com Trang 12 thuvienhoclieu.com
Bài 6.Tìm số nguyên n biết rằng n + 5 chia hết cho n - 2. Lời giải
Ta có: n + 5 chia hết cho n - 2
n + 5 = (n - 2) + 7 chia hết cho n - 2
Mà n - 2 chia hết cho n - 2 ⇒ 7 chia hết cho n - 2 n - 2thuộc ước của 7
mà U (7) = -7; -1; 1; 7 n - 2 = -7 n = -5 n - 2 = -1 n = 1 n - 2 = 1 n = 3 n - 2 = 7 n = 9 Vậy n -5; 1; 3; 9
Bài 7.Tìm số nguyên dương n sao cho 2n là bội của n -1 . Lời giải
2n là bội của n -1 2n (n M - ) 1 2n = 2(n - ) 1 + 2 ( n M - ) 1 Mà (n - ) 1 (n M - ) 1 . Do đó 2 (n M - ) 1 n - 1 U (2) U (2) = 1 , 2
Mà n - 1 0 nên n - 1 1; 2 n 2; 3
Bài 8. Có hai số nguyên a , b khác nhau mà chia hết cho b và b chia hết cho a không ? Lời giải
a chia hết cho b a = bq (q ¢ ,b 0) 1 1
b chia hết cho a b = aq (q ¢ , a 0) 2 1
a=bq =(aq )q =a(q q ) q q =1 1 2 1 2 1 2 1 q = q =1 hoặc q = q = 1 − 2 1 2 1 Vì a b nên q = q = 1 − . Do đó: a =b(-1)=-b 2 1
Vậy mọi cặp số nguyên đối nhau và khác 0 đều có tính chất a chia hết cho (-a ) và (-a ) chia hết cho
a và chỉ những cặp số đó.
Bài 9. Cho hai tập hợp số: A = 2 ; 3 ; 4 ; 5 ; 6 , B = 21 ; 22 ; 2 3 .
a) Có thể lập được bao nhiêu tổng dạng (a + b) với a A, b B?
b) Trong các tổng trên có bao nhiêu tổng chia hết cho 2 ? Lời giải
thuvienhoclieu.com Trang 13 thuvienhoclieu.com Giải
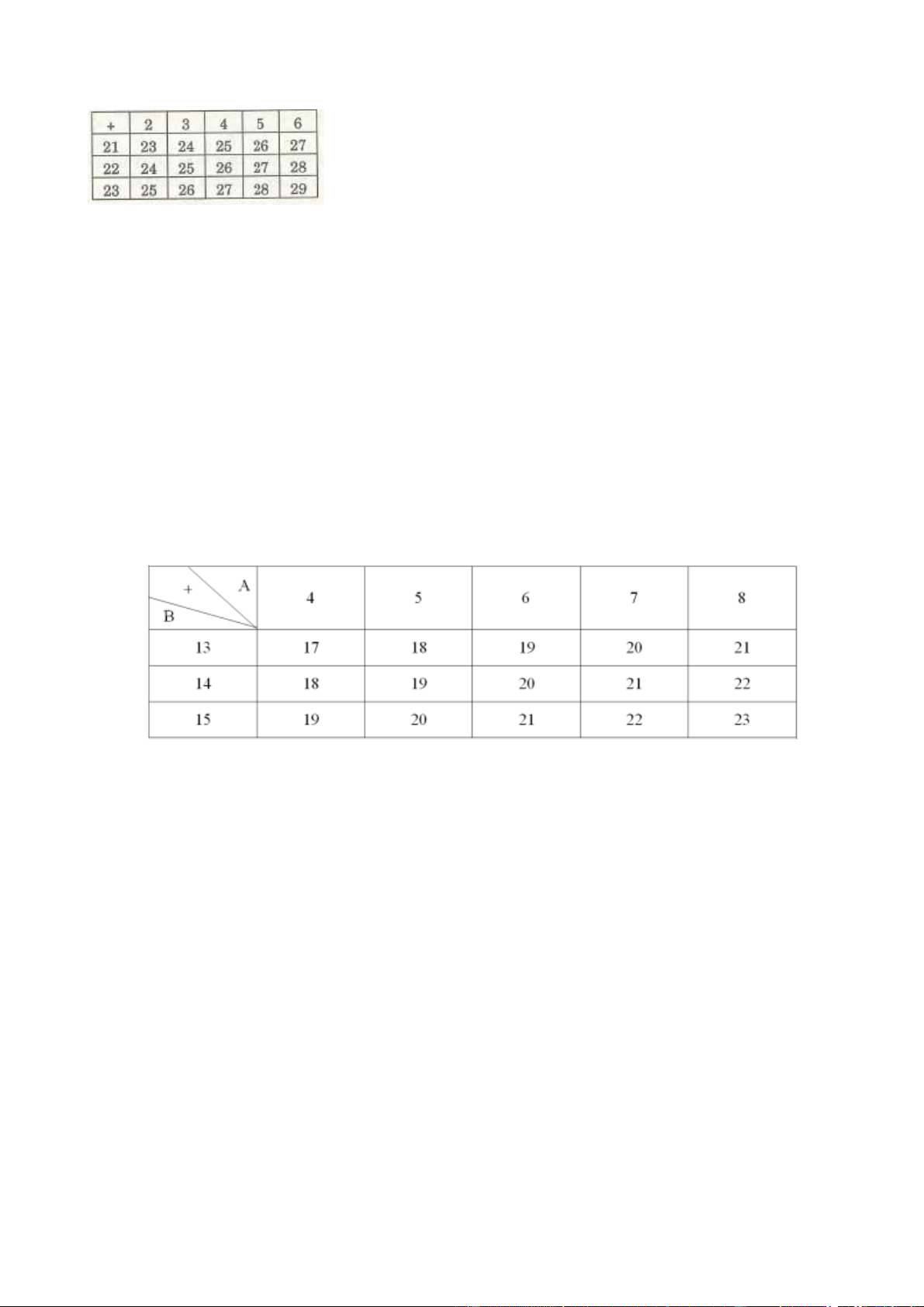
a) Ta lập bảng cộng sau :
Từ bảng trên, ta thấy có 15 tổng được tạo thành, trong đó có 7 tổng khác nhau: 23, 24, 25, 26, 27, 28, 29 .
b) Có 7 tổng chia hết cho 2 là : 24 , 24 , 26 , 26 , 26 , 28 , 28.
(Có 3 tổng khác nhau chia hết cho 2 : 24 , 26 , 28 ).
Bài 10.Cho hai tập hợp số A=4 ; 5 ; 6 ; 7 ; 8 ; B = 13 ; 14 ; 1 5
a) Có thể lập được bao nhiêu tổng dạng (a + b) vớiaA, bB?
b) Trong các tổng trên có bao nhiêu tổng chia hết cho 3? Lời giải Lập bảng ta thấy :
a) Ta lập bảng cộng sau:
Từ bảng trên, ta thấy có 15 tổng được tạo thành, trong đó có 7 tổng khác nhau : 17, 18, 19, 20, 21, 22, 23.
b) Trong đó có 5 tổng chia hết cho 3 là :18, 18, 21, 21, 21.
Như vậy có hai tổng khác nhau chia hết cho 3 là 18 và 21.
thuvienhoclieu.com Trang 14




