Chuyên Đề Xác Suất Có Điều Kiện Ôn Thi Tốt Nghiệp Giải Chi Tiết
Tính xác suất có điều kiện không sử dụng công thức. Tính xác suất có điều kiện sử dụng công thức. Tính xác suất có điều kiện sử dụng sơ đồ hình cây. Sử dụng được công thức xác suất toàn phần, công thức Bayes để tính xác suất có điều kiện. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Tài liệu ôn thi THPTQG môn Toán 278 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
CHUYÊN ĐỀ: XÁC SUẤT CÓ ĐIỀU KIỆN A. ĐẶT VẤN ĐỀ:
Trong Chương trình Giáo dục phổ thông môn Toán 2018, các yêu cầu cần đạt đối với nội
dung Xác suất có điều kiện được phân hóa mức độ rõ ràng từ dễ đến khó. Đầu tiên là để học
sinh “Nhận biết được khái niệm, giải thích được ý nghĩa của Xác suất có điều kiện trong
những tình huống thực tiễn quen thuộc”. Sau đó học sinh phải sử dụng được các kiến thức
liên quan: Sơ đồ cây, công thức Bayes vào việc giải quyết các bài toán ở chương xác suất có
điều kiện. Cuối cùng là “Vận dụng khái niệm để giải quyết một số tình huống thực tiễn”.
Chương xác suất có điều kiện, học sinh đáp ứng được các yêu cầu ở các mức độ: Về lĩnh vực
nhận thức (nhận biết, hiểu, vận dụng), về lĩnh vực tâm lí – vận động (bắt chước, thao tác, chuẩn hóa, phối hợp).
B. HỆ THỐNG CÁC KIẾN THỨC CỦA CHƯƠNG:
Bài 18. XÁC SUẤT CÓ ĐIỀU KIỆN. I. Lý thuyết.
1. Định nghĩa xác suất có điều kiện.
2. Công thức tính xác suất có điều kiện. Công thức nhân xác suất.
II. Các dạng bài tập.
+ Dạng 1. Tính xác suất có điều kiện không sử dụng công thức.
+ Dạng 2. Tính xác suất có điều kiện sử dụng công thức.
+ Dạng 3. Tính xác suất có điều kiện sử dụng sơ đồ hình cây. III. Luyện tập.
1. Câu hỏi – Trả lời trắc nghiệm.
2. Câu hỏi – Trả lời đúng / sai.
3.Câu hỏi – Trả lời ngắn.
Bài 19. CÔNG THỨC XÁC SUẤT TOÀN PHẦN – CÔNG THỨC BAYES. I. Lý thuyết.
1. Công thức xác suất toàn phần. 2. Công thức Bayes.
II. Các dạng bài tập.
+ Dạng 1. Công thức xác suất toàn phần và công thức Bayes.
+ Dạng 2. Các bài toán liên quan đến công thức xác suất toàn phần.
+ Dạng 3. Các bài toán liên quan đến công thức Bayes. III. Luyện tập.
1. Câu hỏi – Trả lời trắc nghiệm.
2. Câu hỏi – Trả lời đúng / sai.
3. Câu hỏi – Trả lời ngắn. Trang 1
C. NỘI DUNG CẦN ÔN TẬP:
I. Mức độ Nhận biết:
Yêu cầu cần đạt: Yêu cầu học sinh nắm rõ và sử dụng thành thạo các kiến thức cơ bản đã
trình bày SGK 12 KNTT theo Chương trình giáo dục 2018 như :
- Nhận biết được khái niệm về xác suất có điều kiện.
- Nhận biết được ý nghĩa của xác suất có điều kiện trong những tình huống đơn giản.
- Nhận biết được công thức xác suất có điều kiện, công thức nhân xác xuất.
- Nhận biết được công thức xác suất toàn phần, công thức Bayes.
Các dạng toán cần ôn tập:
- Thành thạo về khái niệm xác suất có điều kiện,
- Nắm được ý nghĩa của xác suất có điều kiện trong những tình huống đơn giản.
- Thành thạo về công thức xác suất có điều kiện, công thức nhân xác xuất.
- Thành thạo về công thức xác suất toàn phần, công thức Bayes.
Các ví dụ: Dạng câu trắc nghiệm nhiều phương án lựa chọn
Câu 1(NB). Cho A và B là hai biến cố, trong đó PB 0 . Mệnh đề nào sau đây đúng? P A B P A B
A. P A | B .
B. P A | B . P B P B P A B P A B
C. P A | B .
D. P A | B . P A P A
Câu 2(NB). Nếu hai biến cố ,
A B thỏa mãn PB 0,6; P A B 0,2 thì P A | B bằng 3 2 1 4 A. . B. . C. . D. . 25 5 3 5
Câu 3(NB). Cho hai biến cố , A B với 0 ( P )
B 1. Phát biểu nào sau đây là đúng? A. P( )
A P B.P A | B PB.P A | B. B. P( )
A P B.P A | B P B.P A | B. C. P( )
A P B.P A | B PB.P A | B. D. P( )
A P B.P A | B P B.P A | B.
Câu 4(NB). Cho hai biến cố A và B là hai biến cố độc lập, mệnh đề nào sau đây đúng?
A. P A | B P A .
B. P A | B PB .
C. P A | B P AB.
D. P A | B PB | A . Trang 2
II. Mức độ Thông hiểu:
Yêu cầu cần đạt: Học sinh cần nắm vững phần lý thuyết và cách giải bài toán về xác suất có
điều kiện, nắm được ý nghĩa của xác suất có điều kiện trong những tình huống thực tiễn quen thuộc. Cụ thể như:
- Hiểu được khái niệm về xác suất có điều kiện.
- Giải thích được ý nghĩa của xác suất có điều kiện trong những tình huống thực tiễn quen thuộc.
- Sử dụng công thức xác suất có điều kiện, công thức nhân xác xuất để tính xác suất.
- Sử dụng được công thức xác suất toàn phần, công thức Bayes để tính xác suất có điều kiện.
- Sử dụng được sơ đồ hình cây để tính xác suất có điều kiện trong một số bài toán thực tiễn đơn giản.
Các dạng toán cần ôn tập: Thành thạo các dạng toán về xác suất có điều kiện:
- Tính xác suất có điều kiện không sử dụng công thức.
- Tính xác suất có điều kiện sử dụng công thức.
- Tính xác suất có điều kiện sử dụng sơ đồ hình cây.
- Sử dụng được công thức xác suất toàn phần, công thức Bayes để tính xác suất có điều kiện.
- Các bài toán thực tiễn đơn giản liên quan đến công thức xác suất toàn phần.
- Các bài toán thực tiễn đơn giản liên quan đến công thức Bayes. Các ví dụ:
a). Dạng câu trắc nghiệm nhiều phương án lựa chọn Câu 1(TH).
Cho hai biến cố A và B độc lập, biết P A 0,4; PB 0,7. Khi đó P B | A bằng 7 4 7 3 A. . B. . C. . D. . 10 7 25 10 Lời giải
Vì A và B là hai biến cố độc lập nên ta có: P AB P A.PB 0,4.0,7 0,28 P AB 0, 28 3
Ta có: P B | A 1 PB | A 1 . P A 1 0, 4 10
Câu 2(TH). Cho hai biến cố A và B biết P B 0,6; P A | B 0,3; P A| B 0,8 . Tính
P A Trang 3
A. P A 0,3 B. P A 0, 4
C. P A 0,5
D. P A 0,6 Lời giải
Ta có: P B 1 P B 0, 4
P A PB.P A | B PB.P A| B 0,6.0,3 0,4. 0,8 0,5 .
b). Dạng câu trắc nghiệm đúng sai.
Câu 3(TH). Lớp 12A1 có 40 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ Tiếng Anh, 16
học sinh tham gia câu lạc bộ Toán, 12 học sinh vừa tham gia câu lạc bộ tiếng Anh vừa tham gia câu
lạc bộ Toán. Chọn ngẫu nhiên 1 học sinh. Xét các biến cố sau:
A : “Học sinh được chọn tham gia câu lạc bộ Tiếng Anh”;
B : “Học sinh được chọn tham gia câu lạc bộ Toán”. a) ( P ) A 0, 4 . b) ( P ) B 0,625. c) ( P A∣ ) B 0,75 d) ( P B∣ ) A 0, 48 . Lời giải. 25
a) Sai. Xác suất của biến cố A là: P( ) A 0,625 . 40 16
b) Sai. Xác suất của biến cố B là: P(B) 0, 4 . 40
c) Đúng. Số học sinh vừa tham gia câu lạc bộ tiếng Anh vừa tham gia câu lạc bộ Toán là 12, số 12
học sinh tham gia câu lạc bộ Toán là 16 nên P( A∣ B) 0,75 . 16
d) Đúng. Số học sinh vừa tham gia câu lạc bộ tiếng Anh vừa tham gia câu lạc bộ Toán là 12, số 12
học sinh tham gia câu lạc bộ Tiếng Anh là 25 nên P(B∣ ) A 0, 48 . 25
III. Mức độ Vận dụng:
Yêu cầu cần đạt: Học sinh cần nắm vững và sử dụng thành thạo phần lý thuyết và cách giải
bài toán về Xác suất có điều kiện và vận dụng kiến thức đã học vào giải một số bài toán có liên quan
đến thực tiễn. Cụ thể :
- Mô tả được ý nghĩa của xác suất có điều kiện trong những tình huống thực tiễn quen thuộc.
- Mô tả được công thức xác suất toàn phần, công thức Bayes thông qua bảng dữ liệu thống
kê 2x2 và sơ đồ hình cây.
- Sử dụng được sơ đồ hình cây để tính xác suất có điều kiện trong một số bài toán thực tiễn liên quan tới thống kê. Trang 4
- Sử dụng được công thức xác suất toàn phần, công thức Bayes để tính xác suất có điều kiện
và vận dụng vào giải một số bài toán liên quan đến thực tiễn.
Các dạng toán cần ôn tập: Nắm vững và thành thạo các dạng toán về xác suất có điều kiện.
Ứng dụng vào thực tiễn. Cụ thể:
- Tính xác suất có điều kiện không sử dụng công thức.
- Tính xác suất có điều kiện sử dụng công thức.
- Sử dụng được sơ đồ hình cây để tính xác suất có điều kiện trong một số bài toán thực tiễn liên quan tới thống kê.
- Sử dụng được công thức xác suất toàn phần, công thức Bayes để tính xác suất có điều kiện và
vận dụng vào giải một số bài toán liên quan đến thực tiễn. Các ví dụ:
a). Dạng câu trắc nghiệm đúng sai.
Câu 1(VD). Trường THPT Tiểu La có 30% học sinh tham gia câu lạc bộ thể thao. Trong số
những học sinh này, có 70% biết bơi. Ngoài ra, có 20% số học sinh không tham gia câu lạc bộ thể
thao cũng biết bơi. Chọn ngẫu nhiên một học sinh của trường. Xét các biến cố: A : "Chọn được học
sinh thuộc câu lạc bộ thể thao"; B : "Chọn được học sinh biết bơi".
a) Xác suất chọn được học sinh thuộc câu lạc bộ thể thao là P A 0,3 .
b) Xác suất chọn được học sinh biết bơi, biết học sinh đó không thuộc câu lạc bộ thể thao, là
P B∣ A 0,2 .
c) Xác suất chọn được học sinh biết bơi là PB 0,21.
d) Giả sử chọn được học sinh biết bơi. Xác suất chọn được học sinh thuộc câu lạc bộ thể thao là
P A∣ B 0,6 . Lời giải.
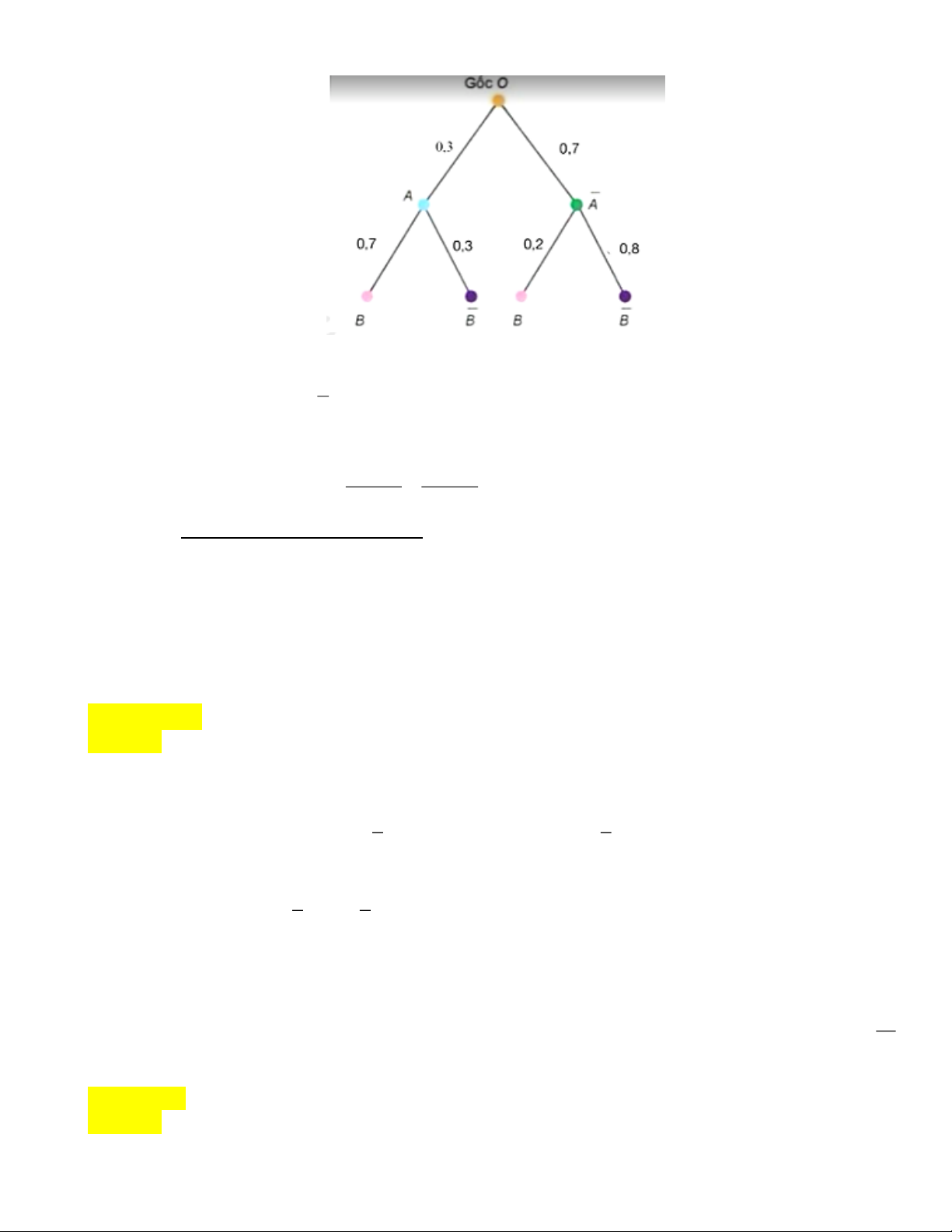
Từ đề bài ta có sơ đồ hình cây như sau: Trang 5
a) Đúng. Vì Trường có 30% học sinh tham gia câu lạc bộ thể thao, do đó P A 30% 0,3 .
b) Đúng. Vì có 20% số học sinh không tham gia câu lạc bổ thể thao cũng biết bơi.
Do đó: P B A ∣ 0,2
c) Sai. Theo sơ đồ, ta có: PB 0,3.0,7 0,7.0,2 0,35 P AB 0, 3.0, 7
d) Đúng. Ta có P A B ∣ . P B 0, 6 0, 35
b). Dạng câu trắc nghiệm trả lời ngắn.
Câu 2(VD). Tất cả các học sinh của trường THPT Tiểu La đều tham gia câu lạc bộ bóng chuyền
hoặc bóng rổ, mỗi học sinh chỉ tham gia đúng một câu lạc bộ. Có 60%học sinh của trường tham gia
câu lạc bộ bóng chuyền và 40%học sinh của trường tham gia câu lạc bộ bóng rổ. Số học sinh nữ
chiếm 65%trong câu lạc bộ bóng chuyền và 25%trong câu lạc bộ bóng rổ. Chọn ngẫu nhiên một
học sinh. Xác suất chọn được học sinh nữ là bao nhiêu? Đáp án: 0, 49 Lời giải:
Xét các biến cố: A: “ Chọn được học sinh thuộc câu lạc bộ bóng chuyền”;
B: “ Chọn được học sinh nữ”.
Theo giả thiết, ta có: P A 0,6;P A 0,4;PB| A 0,65;PB| A 0,25 .
Theo công thức xác suất toàn phần, xác suất chọn được học sinh nữ là:
PB P A.PB| A PA.PB| A 0,6.0,650,4.0,250,49 .
Câu 3(VD). Lớp 12A2 có 16 học sinh nữ, còn lại là học sinh nam. Trong giờ giáo dục thể chất, thầy
giáo khảo sát kết quả rèn luyện thể lực của học sinh bằng cách bốc thăm trong danh sách lớp để 15
chọn hai bạn chạy tiếp sức. Biết xác suất để chọn được hai bạn tham gia khảo sát đều là nữ bằng . 62
Hỏi lớp đó có bao nhiêu học sinh? Đáp án: 32 Lời giải: Trang 6
Gọi A là biến cố: “Lần thứ nhất chọn được bạn nữ”
Gọi B là biến cố: “Lần thứ hai chọn được bạn nữ”
Gọi C là biến cố: “Chọn được hai bạn tham gia khảo sát đều là nữ”
Theo đề bài ta có C AB P C P AB 15 62
Gọi số học sinh của lớp là x, x , x 16 Theo đề 16 15
bài ta có: P A
, P B / A x x 1 15 16 15 x 32
Do P AB P BA P B / A.P A 2 .
x x 992 0 62 x x 1 x 31
Vậy, số học sinh của lớp là 32 học sinh.
D. CÁC KỸ NĂNG HS CẦN NẮM ĐỂ LÀM TOÁN:
1. Xác suất có điều kiện
+ Cho hai biến cố A và B . Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được
gọi là xác suất của A với điều kiện B , kí hiệu P A| B. P A B
n A B
+ Cho hai biến cố A và B bất kì, với PB 0. Khi đó: P A B P B nB
+ Nếu PB 0 thì P .
A B PB.P A | B
2. Công thức nhân xác suất.
+ Nếu A và B là hai biến cố bất kì thì P AB P
A .P B | A PB.P A | B
Chú ý: Cho A và B là hai biến cố, với PB 0. Khi đó,
. P A P A 1
. P A | B P A | B 1
. P AB P AB P A
. P AB P AB PB
. Nếu A và B là hai biến cố độc lập, với 0 P
A 1, 0 PB 1 thì
P A P A | B P A | B
P B P B | A P B | A HS cần biết:
• Xác suất của một biến cố có thể phụ thuộc vào nhiều yếu tố, điều kiện khác nhau nào đó mà
có thể được nói ra hoặc không nói ra (điều kiện hiểu ngầm). Để chỉ ra một cách cụ thể hơn Trang 7
về việc xác suất của một sự kiện A nào đó phụ thuộc vào một điều kiện B nào đó ra sao, ta sử
dụng xác suất có điều kiện.
• Những bài toán xảy ra xác suất điều kiện thường đi kèm với việc sử dụng quy tắc nhân xác
suất, khi gặp bài toán này ta cần lưu ý đến sự độc lập của biến cố để vận dụng công thức đúng.
3. Công thức xác suất toàn phần:
Cho hai biến cố A và B , ta có: P A P B.P A | B P B.P A | B
4. Công thức Bayes:
Cho hai biến cố A và B , với PB 0, ta có:
P B .P A | B
P B .P A | B
P B | A
hoặc P B | A P A
P B.P A | B P B.P A | B HS cần biết:
Công thức xác suất toàn phần và Công thức Bayes được áp dụng trong các trường hợp sự
việc bài toán đề cập đến gồm nhiều giai đoạn có sự liên đới nhau trong quá trình xảy ra. Khi
áp dụng giải toán, biến cố cần tìm xác xuất chi phối bởi hệ đầy đủ biến cố trước đó. Vì vậy ,
để giải toán xác xuất này, ta cần:
• Phân tích kỹ đề bài, linh hoạt liên tưởng vào thực tế.
• Xác định được nhóm biến cố đầy đủ ở giai đoạn đầu của sự việc mà bài toán đã đưa ra.
• Gọi tên biến cố xảy ra ở giai đoạn sau liên quan đến nhóm biến cố đầy đủ được xác định trước đó.
• Xác định xác suất của từng biến cố ở hệ đầy đủ, các xác suất có điều kiện của biến cố ở giai
đoạn sau với từng biến cố trong hệ đầy đủ.
• Áp dụng công thức xác suất toàn phần nếu biến cố cần tìm xác xuất là biến cố xảy ra ở giai đoạn sau.
• Nếu biết biến cố xảy ra trong giai đoạn sau, để xác định xác xuất của một biến cố nào đó ở
giai đoạn trước liên quan đến biến cố ở giai đoạn sau như thế nào ta sử dụng Công thức Bayes.
5. Sơ đồ hình cây:
• Xác suất của các nhánh trong sơ đồ hình cây từ đỉnh thứ hai là xác suất có điều kiện.
• Xác suất xảy ra của mỗi kết quả bằng tích các xác suất trên các nhánh của cây đi đến kết quả đó.
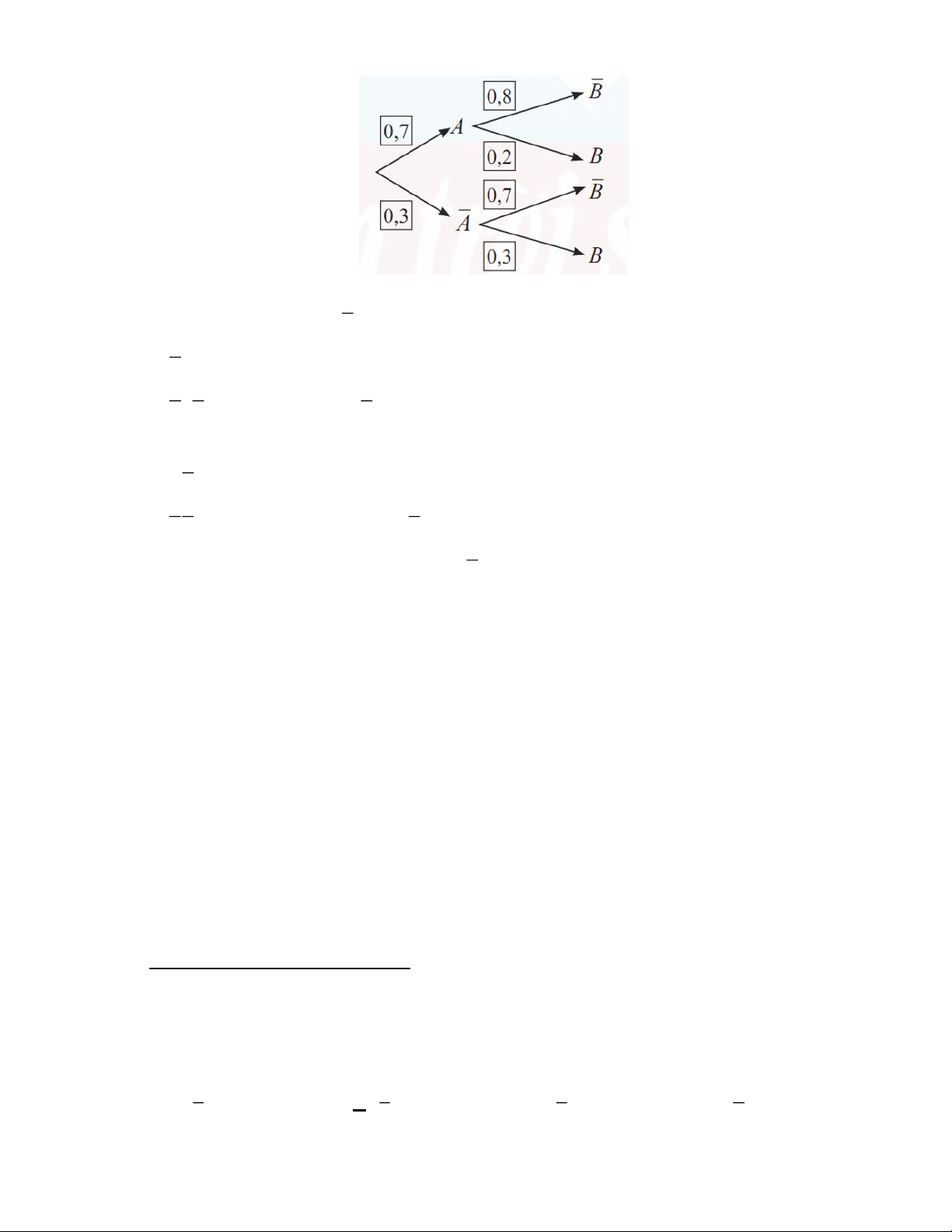
Ví dụ minh họa: Sơ đồ hình cây: Trang 8
* Từ sơ đồ hình cây trên, ta có một số kết quả: + P
A 0,7 ; P A 0,3
+ P B | A 0,8 ; PB | A 0,2
+ P B | A 0,7 ; PB | A 0,3
* Từ đó ta tính được:
+ P AB 0,7.0,8 0,56 ; P AB 0,7.0,2 0,14
+ P AB 0,3.0,7 0,21 ; P AB 0,3.0,3 0,09
+ P B 0,7.0, 2 0,3.0,3 0, 23 ; PB 0,7.0,8 0,3.0,7 0,77 1 PB
Ngoài việc nắm vững kiến thức cơ bản, các em cần “mẹo” học và làm bài thi, từ đó học sinh
dễ dàng định hướng cách giải bài toán cũng như kiểm tra lại đáp án để có thể tối đa hóa điểm số ở
phần xác suất. Các em cũng cần xác định đâu là kiến thức quan trọng để tập trung học chắc và học sâu.
Ngoài ra, máy tính cầm tay là công cụ khá hiệu quả để hỗ trợ học sinh trong quá trình tính
toán. Biết được các kỹ năng sử dụng máy tính cầm tay để tính toán, kiểm tra kết quả, sẽ giúp các em
cải thiện tốc độ làm bài thi. Tuy nhiên, không nên tuyệt đối hóa vai trò của máy tính, vì các câu hỏi
trong đề thi đều có cách hỏi theo xu hướng: Yêu cầu thí sinh phải nắm được bản chất của vấn đề
mới có thể lựa chọn được phương án đúng. Câu nào sử dụng được máy tính cầm tay, các em nên tận
dụng thời gian và dành thời gian cho các câu hỏi khó hơn và những câu hỏi bắt buộc phải giải bằng phương pháp tự luận.
Trong quá trình làm toán, các em cũng cần chú ý kĩ công thức để tránh một số sai sót thường
gặp như: Nhầm lẫn công thức, nhầm lẫn dấu giữa các công thức…
E. ĐỀ TỰ LUYỆN (HS TỰ ÔN):
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Câu 1(NB). Gieo con xúc xắc 1 lần. Gọi A là biến cố xuất hiện mặt 2 chấm. B là biến cố xuất hiện
mặt chẵn. Xác suất P A | B là 1 1 2 1 A. . B. . C. . D. . 2 3 3 6 Trang 9 Đáp án: B
Câu 2(NB). Cho hai biến cố A và B có P( )
A 0, 3; P(B) 0, 6; P(A B) 0, 2. Xác suất P A | B là 1 1 2 1 A. . B. . C. . D. . 2 3 3 6 Đáp án: B
Câu 3(NB). Cho hai biến độc lập ,
A B với P
A 0,8; PB 0,3 . Khi đó, P A B bằng A. 0,8 . B. 0,3 . C. 0, 4 . D. 0, 6 . Đáp án: A
Câu 4(NB). Cho hai biến cố ,
A B với PB 0,7; P AB 0,3 . Tính P A | B 3 1 6 1 A. . B. C. . D. . 7 2 7 7 Đáp án: A
Câu 5(NB). Cho hai biến cố ,
A B với P B 0,8; P A / B 0,5. Tính P AB 3 A. . B. 0, 4 C. 0,8 . D. 0,5 . 7 Đáp án: B
Câu 6(TH). Cho hai biến cố A và B , với P
A 0,8 ; PB 0,65 ; P A B 0,55.
Tính P A B . A. 0, 25 . B. 0,1. C. 0,15 . D. 0,35 . Chọn A
Câu 7(NB). Cho hai biến cố A và B là hai biến cố độc lập, với P
A 0, 2024 , PB 0, 2025.
Tính P A | B . A. 0, 7976 . B. 0, 7975 . C. 0, 2025 . D. 0, 2024 . Chọn D
Câu 8(TH). Cho hai biến cố A và B , với P A 0,8 , PB 0,65, P A B 0,55 . Tính
P A B. A. 0, 25 . B. 0,1 . C. 0,15 . D. 0,35 . Chọn A
Câu 9(TH). Cho hai biến cố A và B , với P A 0,6, PB 0,7 , P A B 0,3 . Tính P B | A . 3 1 6 1 A. . B. . C. . D. . 7 2 7 7 Chọn B
Câu 10(TH). Một lớp có 95 sinh viên, trong đó có 40 nam và 55 nữ. Trong kỳ thi môn Xác suất
thống kê có 23 sinh viên đạt điểm giỏi (trong đó có 12 nam và 11 nữ). Gọi ngẫu nhiên một Trang 10
sinh viên trong danh sách lớp. Tìm xác suất gọi được sinh viên đạt điểm giỏi môn Xác suất
thông kê, biết rằng sinh viên đó là nữ? 1 11 12 11 A. B. C. D. 5 23 23 19 Đáp án: A
Câu 11(TH). Một mảnh đất chia thành hai khu vườn. Khu A có 150 cây ăn quả, khu B có 200 cây
ăn quả. Trong đó, số cây Táo ở khu A và khu B lần lượt là 50 cây và 100 cây. Chọn ngẫu
nhiên 1 cây trong mảnh đất. Xác suất cây được chọn là cây Táo , biết rằng cây đó ở khu B, là : 1 1 1 2 A. . B. . C. . D. . 2 4 3 3 Chọn A
Câu 12(TH). Một hộp chứa 8 bi trắng, 2 bi đỏ. Lần lượt bốc từng bi và không trả lại bi được bốc
vào hộp. Giả sử lần đầu tiên bốc được bi trắng. Xác suất lần thứ 2 bốc được bi đỏ là 2 1 8 2 A. . B. . C. . D. . 9 10 9 5 Chọn A
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1(TH). Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,5 và
dự án 2 là 0,6. Khả năng thắng thầu của 2 dự án là 0,4. Gọi ,
A B lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) A và B là hai biến độc lập.
b) Xác suất công ty thắng thầu đúng 1 dự án là 0,3 .
c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là 0, 4 .
d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là 0,8 . Lời giải Ý a) b) c) d) Kết quả S Đ S S
Câu 2(TH). Khi điều tra sức khỏe nhiều người cao tuổi ở một địa phương, người ta thấy rằng có
40% người cao tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những
người bị bệnh tiểu đường là 70%, trong những người không bị bệnh tiểu đường là 25%. Chọn ngẫu
nhiên một người cao tuổi để kiểm tra sức khỏe.
a) Xác xuất chọn được người bị bệnh tiểu đường là 0,4.
b) Xác xuất chọn được người bị bệnh huyết áp cao, biết người đó bị bệnh tiểu đường là 0,7. Trang 11
c) Xác xuất chọn được người bị bệnh huyết áp cao, biết người đó không bị bệnh tiểu đường là 0,75.
d) Xác xuất chọn được người bị bệnh huyết áp cao là 0,8. Lời giải Ý a) b) c) d) Kết quả Đ Đ S S
Câu 3(TH). Để nghiên cứu sự phát triển của một loại cây, người ta trồng hạt giống của loại cây đó
trên hai lô đất thí nghiệm M, N khác nhau. Xác suất phát triển bình thường của cây đó trên các lô đất
M và N lần lượt là 0,56 và 0,62. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xét các biến cố:
A: “Cây phát triển bình thường trên lô đất M”;
B: “Cây phát triển bình thường trên lô đất N”.
a) Các cặp biến cố A và B, A và B là độc lập.
b) Hai biến cố C A B và D A B không là hai biến cố xung khắc.
c) P( A ) = 0,56; P( B ) = 0,62.
d) Xác suất để cây chỉ phát triển bình thường trên một lô đất là 0,4856. Lời giải Ý a) b) c) d) Kết quả Đ S S Đ
Câu 4(TH). Trong một hộp có 18 quả bóng bàn loại I và 2 quả bóng bàn loại II, các quả bóng bàn
có hình dạng và kích thước như nhau. Một học sinh lấy ngẫu nhiên lần lượt 2 quả bóng bàn
(lấy không hoàn lại) trong hộp. 9
a) Xác suất để lần thứ nhất lấy được quả bóng bàn loại II là . 10
b) Xác suất để lần thứ hai lấy được quả bóng bàn loại II , biết lần thứ nhất lấy được quả bóng bàn 1 loại II, là . 19 9
c) Xác suất để cả hai lần đều lấy được quả bóng bàn loại II là .. 190 189
d) Xác suất để ít nhất 1 lần lấy được quả bóng bàn loại I là . 190 Lời giải Ý a) b) c) d) Kết quả S Đ S Đ Trang 12
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1(VD). Trên kệ sách có 5 quyển sách Toán, 7 quyển sách Vật Lí và 4 quyển sách Hóa (các
quyển sách đều khác nhau). Chọn ngẫu nhiên 3 cuốn sách, tính xác suất để 3 cuốn sách được chọn
không cùng một môn. (kết quả làm tròn đến hàng phần trăm). Đáp án: 0,91
Câu 2(VD). Trong đề kiểm tra thường xuyên môn Toán có 20 câu trắc nghiệm. Mỗi câu trắc nghiệm
có 4 phương án trả lời, trong đó chỉ có một phương án trả lời đúng. Bạn Sơn giải chắc chắn đúng 10
câu, 10 câu còn lại lựa chọn ngẫu nhiên đáp án. Biết rằng mỗi câu trả lời đúng được 0,5 điểm, trả lời
sai không bị trừ điểm. Biết xác suất để Sơn đạt được đúng 8 điểm là p . Khi đó, 100 p bằng bao nhiêu? Đáp án: 1,6
Câu 3(VD). Có hai đội thi đấu môn bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên.
Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II lần lượt là 0, 65 và 0,55. Chọn
ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Xác suất để
vận động viên này thuộc đội I là bao nhiêu ? (làm tròn kết quả đến hàng phần trăm) Đáp án: 0, 46
Câu 4(VD). Điều tra tình hình mắc bệnh ung thư phổi của một vùng thấy tỉ lệ người hút thuốc lá và
mắc bệnh là 15% . Tỉ lệ người hút thuốc lá và không mắc bệnh là 25% , tỉ lệ người không hút thuốc
và không mắc bệnh là 50% và 10% là người không hút thuốc nhưng mắc bệnh. Tỉ lệ mắc bệnh ung
thư phổi giữa người hút thuốc lá và không hút thuốc lá là bao nhiêu? Đáp án: 1,5
Câu 5(VD-Dùng sơ đồ hình cây). Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen,
các chiếc bút có cùng kích thước và khối lượng. Bạn Nam lấy ngẫu nhiên một chiếc bút bi
từ trong hộp, không trả lại. Sau đó bạn Minh lấy ngẫu nhiên một trong 11 chiếc bút còn lại. a a
Xác suất để Nam lấy được bút bi đen và Minh lấy được bút bi xanh bằng , với là phân b b
số tối giản. Giá trị của a b bằng bao nhiêu? Lời giải Trả lời: 167
Câu 6(VD). Một cuộc thi khoa học có 36 bộ câu hỏi, trong đó có 20 bộ câu hỏi về chủ đề tự nhiên
và 16 bộ câu hỏi về chủ đề xã hội. Bạn An lấy ngẫu nhiên 1 bộ câu hỏi (lấy không hoàn
lại), sau đó bạn Bình lấy ngẫu nhiên 1 bộ câu hỏi. Xác suất bạn Bình lấy được bộ câu hỏi a a
về chủ đề xã hội bằng với
là phân số tối giản. Giá trị của a b bằng bao nhiêu? b b Lời giải Trả lời: 50 Trang 13
Với bài báo cáo này, hy vọng các em học sinh sẽ khắc sâu thêm một lượng kiến thức bổ ích trong học tập.
Vì chương này công thức cũng tương đối mới mẽ nên sẽ không tránh khỏi những thiếu sót, rất
mong sự đóng góp của quý thầy cô để nội dung ôn tập được đầy đủ hơn.
Kính chúc quý thầy cô thật nhiều sức khỏe và nhiều thắng lợi. Xin chân thành cảm ơn. Trang 14