


















Preview text:
lOMoAR cPSD| 58137911 TOPIC 1 1)
Describe the basic components of computer architecture according to the John
von Neumann model. Briefly explain the operation of a computer. 2)
Shortly describe and explain the computer abstraction (the hierarchical layers from hardware to software). 3)
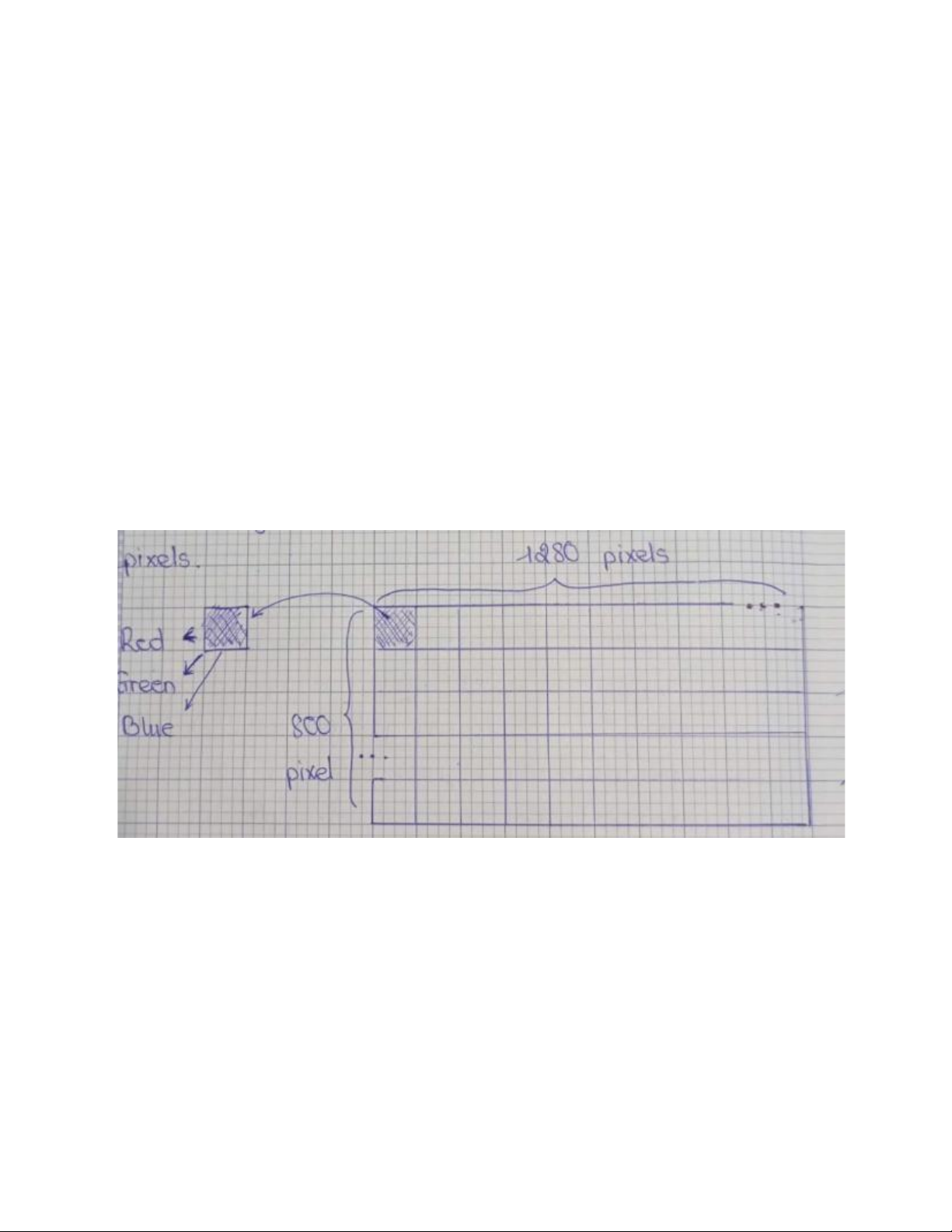
Given a color screen that uses 8 bits to represent a basic color (Red, Green,
Blue) in each pixel, illustrate the minimum capacity of the screen buffer required to
accommodate one image frame with a resolution of 1280x800 pixels? 1.
According to the Computer Model (John von Neumann, 1945), there are five basic components: - Input - Output lOMoAR cPSD| 58137911 - Memory - Datapath - Control
(Datapath and Control are often combined and referred to as the Processor.) Operation of the computer:
- Processor: Receives instructions and data from memory for processing.
- Input: Writes data into memory.
- Output: Reads data from memory.
- Control: Sends control signals to operate the datapath, memory, input, and output. 2.
Software and hardware in a computer are divided into three levels: Application
software, System software, and Hardware. lOMoAR cPSD| 58137911
- The outermost layer (Application software): This is a type of program
that enables the computer to directly perform specific tasks that the user wants to accomplish.
- The middle layer (System software): Acts as a bridge, directly interacting
with the hardware to support the applications. There are many types of system
software, but the two most typical in most modern computer systems are:
+ Operating System (OS): Manages programs and resources on the
computer to support the execution of applications.
+ Compiler: Translates high-level programming language instructions into assembly language.
- The innermost layer (Hardware): Considered the physical structure of the
computer, it is fixed and includes visible and tangible components, such as
electronic devices and hardware parts located inside or outside the machine. 3.
Resolution: 1 280 x 800 (pixels)
Each pixel uses 8 bits per color channels
=> 3 channels x 8 bits = 24 bits/pixel
=> Total screen: 24 x 1 280 x 800 = 24 576 000 bits TOPIC 2 lOMoAR cPSD| 58137911
1) Given 3 processors P1, P2 and P3 execute the same instruction set with clock rate
and CPI as shown in the table below: Processor Clock Rate CPI P1 2 Ghz 1.5 P2 1.5 Ghz 1.0 P3 3 Ghz 2.5 a)
Which processor has the highest performance based on the criteria of number of
instructions executed per second (IPS) and number of millions of instructions executed per second (MIPS). b)
If the processors execute a program for 10 seconds, calculate the total number
of cycles and the total number of instructions, respectively. c)
If we aim to reduce the execution time by 30%, leading to a 20% increase in
CPI (Cycles Per Instruction), what should be the new clock rate for each corresponding processor?
2) Consider two different designs of the same instruction architecture for two
processors P1 and P2. There are 4 instruction classes: A, B, C, and D. The clock
frequency and CPI for each design are given in the table below:
Processor Clock rate CPI Class A CPI Class B CPI Class C CPI Class D P1 1.5 Ghz 1 2 3 4 P2 2 Ghz 2 2 2 3
a) For a program with 10^6 instructions divided into the following classes: 10% Class
A, 20% Class B, 50% Class C, and 20% Class D. Which processor design executes this program faster?
b) Calculate the average CPI for each processor with the given program.
c) Calculate the total number of clock cycles for the program on P1 and P2. 1. a/ IPS lOMoAR cPSD| 58137911 = Clo ck Rat e (in Hz) / CPI
MIPS = Clock Rate (in MHz) / CPI = Clock Rate (in Hz) / (CPI.106) => MIPS = IPS/106 Processor P1: Clock Rate = 2 GHz = 2000 MHz CPI = 1.5
IPSP1 = Clock Rate / CPI = 2.109 / 1.5 ~ 1,333.109 IPS => MIPSP1 = 1,333.103 MIPS Processor P2:
Clock Rate = 1.5 GHz = 1500 MHz CPI = 1.0
IPSP2 = Clock Rate / CPI = 1,5.109 / 1 = 1,5.109 IPS => MIPSP2 = 1,5.103 MIPS Processor P3: Clock Rate = 3 GHz = 3000 MHz CPI = 2.5
IPSP3 = Clock Rate / CPI = 3.109 / 1 = 1,2.109 IPS => MIPSP3 = 1,2.103 MIPS
=> Processor P2 has the highest performance based on IPS and MIPS. b/
Clock Cycle = CPU time x Clock Rate lOMoAR cPSD| 58137911
Instruction = Clock Rate / CPI Processor P1:
Clock Cycle = 10.2.109 = 2.1010
Instructions = 2.109 / 1,5 = 1,333.1010 Processor P2:
Clock Cycle = 10.1,5.109 = 15.109
Instructions = 1,5.109 / 1 = 1,5.109 Processor P3:
Clock Cycle = 10.3.109 = 3.1010
Instructions = 3.1010 / 2,5 = 1,2.1010 c/
CPU time: reduce 30% => New CPU time = 0,7 x Old CPU time
CPI: increases by 20% => New CPI = 1.2 x Old CPI
Clock Rateold = #instruction.CPI / CPU time
Clock Ratenew = #instruction.CPI.1,2 / CPU time.0,7
Clock Ratenew / Clock Rateold = 1,2 / 0,7 = 1,714 Processor P1:
Clock Ratenew = 1,714 x 2 = 3,428 GHz Processor P2:
Clock Ratenew = 1,714 x 1,5 = 2,571 GHz Processor P1:
Clock Ratenew = 1,714 x 3 = 5,142 GHz 2. a/ Total instructions = 106 Distribution: lOMoAR cPSD| 58137911
Class A: 10% = 105 instructions
Class B: 20% = 2.105 instructions
Class C: 50% = 5.105 instructions
Class D: 20% = 2.105 instructions
#Clock Cycle1 = 105 + 2.2.105 + 3.5.105 + 4.2.105 = 2,8.106
#Clock Cycle2 = 2.105 + 2.2.105 + 2.5.105 + 3.2.105 = 2,2.106 b/
CPIP1 = #Clock Cycle / #Instructions = 2,8.106 / 106 = 2,8
CPIP1 = #Clock Cycle / #Instructions = 2,2.106 / 106 = 2,2 c/
CPU timeP1 = #Clock Cycle / Clock Rate = 2,8.106 / 1,5.109 = 1,867.10-3 (s) = 1,867 (ms)
CPU timeP2 = #Clock Cycle / Clock Rate = 2,2.106 / 2.109 = 1,1.10-3 (s) = 1,1 (ms)
=> Processor P2 faster than Processor P1. lOMoAR cPSD| 58137911 TOPIC 3
1) Find the MIPS assembly code equivalent to the C program as follows: a) x = 5 y = x - 2 a = x * 4 b = y * 2 z = (x + a) - (y + b)
Know that the variables x, y, a, b are 32-bit integers b) x = y + a[5]
Suppose each element of array a is a word of 4 bytes.
2) Distinguish the difference between
Big End (Big Endian) and Little End (Little Endian)
Does MIPS use Big End or Little End?
3) Given two numbers x and y, write as follows: x y 4 -6 12 -9 19 -12 60 88
Represent x, y in 8-bit binary with 2's complement and calculate (x + y) in binary 4) List MIPS command formats
Let's represent the command binary: add $t0,$s1,$s2
5) Describe the steps to convert a C program into machine code that can be executed on a computer 6) Given the following code: if (x < 0) h = 0; else. else lOMoAR cPSD| 58137911 h = x; with x, h stored in $s0, $s1
Let's translate the above code into MIPS assembly
7) Procedure implementation steps 8) Procedural structure
9) Write a procedure to calculate: a) 1 + 2 + ... + n b) 1.2.....n
10) Write an assembly language program: a) print "Hello, World!" to the screen,
b) take an integer input n, and perform the calculation: b.1) 1 + 2 + ... + n
b.2) 1.2.....n and then, show the results on the screen 1. a/ $t0 = x $t1 = y $t2 = a $t3 = b $t4 = z li $t0, 5 addi $t1, $t0, -2 sll $t2, $t0, 2 sll $t3, $t1, 1 add $t4, $t0, $t2 sub $t4, $t4, $t1 sub $t4, $t4, $t3 b/ $s0 = x lOMoAR cPSD| 58137911 $s1 = y $s2 = base address of array a lw $t0, 20($s2) add $s0, $s1, $t0 2.
- Big Endian: most significant byte started at the lowest memory address.
- Little Endian: least significant byte started at the lowest memory address.
- MIPS traditionally uses Big Endian, but it can also support Little Endian
depending on the configuration. 3. a/ x = 4ten = 0000 0100two 6ten = 0000 0110two
Invert and 1: 1111 1001 + 1 = 1111 1010 => y = -6ten = 1111 1010
=> x + y = 0000 0100 + 1111 1010 = 1111 1110two = -2ten b/ x = 12ten = 0000 1100two 9ten = 0000 1001two
Invert and 1: 1111 0110 + 1 = 1111 0111 => y = -9ten = 1111 0111
=> x + y = 0000 1100 + 1111 0111 = 1111 0011two = -3ten c/ x = 19ten = 0001 0011two 12ten = 0000 1100two
Invert and 1: 1111 0011+ 1 = 1111 0100 => y = -9ten = 1111 0100 lOMoAR cPSD| 58137911
=> x + y = 0001 0011 + 1111 0100 = 0000 0111two = 7ten d/ x = 60ten = 0011 1100two y = 88ten = 0101 1000two
=> x + y = 0011 1100 + 0101 1000 = 1001 0100two = -108ten (overflow in 8-bit 2’s
complement, since sum = 148 → wraps around)
This is an overflow because the result exceeds the max of +127. 4. MIPS Instruction Types: - R-types: Register - I-types: Immediate - J-types: Jump 5.
Steps to convert a C program to machine code:
- Step 1: Write the C source code
- Step 2: Compile using a compiler into assembly code
- Step 3: Assemble the assembly into machine code (binary) using an assembler
- Step 4: Link with libraries to produce an executable file
- Step 5: Load and execute the binary on the processor via the OS 6. $so = x $s1 = h bltz $s0, set_zero move $s1, $s0 j end set_zero: li $s1, 0 end: lOMoAR cPSD| 58137911 7.
Steps for reducing implementation in MIPS:
- Step 1: Pass argument in $a0 - $a3
- Step 2: Use the stack to save the registers if needed
- Step 3: Perform computation in the procedure body - Step 4: Place result in $v0
- Step 5: Restore saved registers - Step 6: Return using jr $ra 8. Procedural Structure Jal sum … sum: addi $sp, $sp, -8 sw $ra, 4($sp) sw $ra, 0($sp) … lw $ra, 4($sp) lw $ra, 0($sp) addi $sp, $sp, 8 jr $ra 9. a/ sum_n: li $v0, 0 li $t0, 1 sum_loop: bgt $t0, $a0, sum_end add $v0, $v0, $t0 addi $t0, $t0, 1 j sum_loop sum_end: jr $ra lOMoAR cPSD| 58137911 b/ fact_n: li $v0, 1 li $t0, 1 fact_loop: bgt $t0, $a0, fact_end mul $v0, $v0, $t0 addi $t0, $t0, 1 j fact_loop fact_end: jr $ra 10. a/ .data msg: .asciiz "Hello, World!" .text main: li $v0, 4 la $a0, msg syscall b/ .data ask: .asciiz "Enter n: " sum_msg: .asciiz "Sum: "
fact_msg: .asciiz "Factorial: " .text main: li $v0, 4 la $a0, ask syscall li $v0, 5 syscall move $a0, $v0 lOMoAR cPSD| 58137911 jal sum move $t1, $v0 move $a0, $t1 li $v0, 4 la $a0, sum_msg syscall li $v0, 1 move $a0, $t1 syscall move $a0, $v0 li $v0, 4 la $a0, fact_msg syscall move $a0, $v0 li $v0, 1 move $a0, $t2 syscall li $v0, 10 syscall sum: li $v0, 0 move $t0, $a0 li $t2, 1 li $t1, 1 sum_loop: ble $t2, $t0, sum_continue jr $ra sum_continue: add $v0, $v0, $t2 mul $t1, $t1, $t2 addi $t2, $t2, 1 lOMoAR cPSD| 58137911 j sum_loop TOPIC 4
1) Using 8 binary bits to represent decimal integers. Do the calculations: a) 7 + 8 b) 7 – 8 c) 7 x 8 d) 13 : 4 e) -12 x 9 f) -17 : 5
Note, present the steps of the algorithm.
2) Perform calculations on floating point numbers: a) 2.125 + 1.25 b) 1.25 x 2.5 c) 2.5 : 0.25 1. a/ 7ten = 0000 0111two 8ten = 0000 1000two 15ten = 0000 1111two b/
Find the two’s complement of 8.
To subtract 8, we add the two’s complement of 8. Invert the bits of 8
8ten = 0000 1000two => 1111 0111two
Add 1 to get two’s complement: 1111 0111two 0000 0001two 1111 1000two = -8ten lOMoAR cPSD| 58137911 Add 7 and -8: 7ten = 0000 0111two -8ten = 1111 1000two -1ten = 1111 1111two c/ Initilization:
- Multiplicand: 7ten = 0000 0111two
- Mulitiplier: 8ten = 0000 1000two
- Product: 0ten = 0000 0000two
- [Product / Multiplier] [P/M] = 0000 0000.0000 1000 Step Multiplicand [Product / Multiplier] 0 0000 0111 0000 0000.0000 1000 1 0000 0111 0000 0000.0000 100[0] Shift right [P/M] 1 bit 0000 0111 0000 0000.0000 0100 2 0000 0111 0000 0000.0000 010[0] Shift right [P/M] 1 bit 0000 0111 0000 0000.0000 0010 3 0000 0111 0000 0000.0000 001[0] Shift right [P/M] 1 bit 0000 0111 0000 0000.0000 0001 4 0000 0111 0000 0000.0000 000[1] Product = Product + Multiplicand = 0000 0000 + 0000 0111 = 0000 0111 Shift right [P/M] 1 bit 0000 0111 0000 0011.1000 0000 5 0000 0111 0000 0011.1000 000[0] Shift right [P/M] 1 bit 0000 0111 0000 0001.1100 0000 lOMoAR cPSD| 58137911 6 0000 0111 0000 0001.1100 000[0] Shift right [P/M] 1 bit 0000 0111 0000 0000.1110 0000 7 0000 0111 0000 0000.1110 000[0] Shift right [P/M] 1 bit 0000 0111 0000 0000.0111 0000 8 0000 0111 0000 0000.0111 000[0] Shift right [P/M] 1 bit 0000 0111 0000 0000.0011 1000
=> Product = 0000 0000 0011 1000two = 56ten d/ Initilization:
- Divisor: 4ten = 0000 0100two
- Dividend: 13ten = 0000 1101two
- [Remainder / Quotient] [R/Q] = 0000 0000.0000 1101 Step Work Divisor [R/Q] 0 Initilization 0000 0100 0000 0000.0000 1101 1 Shift left [R/Q] 1 bit 0000 0100 0000 0000.0001 1010 R = R – D = 0000 0000 – 0000 0100 R < 0 => Restore R
Assign 0 to the lowest bit of [R/Q] 0000 0000.0001 1010 2 Shift left [R/Q] 1 bit 0000 0100 0000 0000.0011 0100 R = R – D = 0000 0000 – 0000 0100 R < 0 => Restore R
Assign 0 to the lowest bit of [R/Q] 0000 0000.0011 0100 lOMoAR cPSD| 58137911 3 Shift left [R/Q] 1 bit 0000 0100 0000 0000.0110 1000 R = R – D = 0000 0000 – 0000 0100 R < 0 => Restore R
Assign 0 to the lowest bit of [R/Q] 0000 0000.0110 1000 4 Shift left [R/Q] 1 bit 0000 0100 0000 0000.1101 0000 R = R – D = 0000 0000 – 0000 0100 R < 0 => Restore R
Assign 0 to the lowest bit of [R/Q] 0000 0000.1101 0000 5 Shift left [R/Q] 1 bit 0000 0100 0000 0001.1010 0000 R = R – D = 0000 0011 – 0000 0100 R < 0 => Restore R
Assign 0 to the lowest bit of [R/Q] 0000 0001.1010 0000 6 Shift left [R/Q] 1 bit 0000 0100 0000 0011.0100 0000 R = R – D = 0000 0011 – 0000 0100 R < 0 => Restore R
Assign 0 to the lowest bit of [R/Q] 0000 0011.0100 0000 7 Shift left [R/Q] 1 bit 0000 0100 0000 0110.1000 0000 R = R – D = 0000 0110 – 0000 0100 = 0000 0010 > 0
Assign 1 to the lowest bit of [R/Q] 0000 0010.1000 0001 8 Shift left [R/Q] 1 bit 0000 0100 0000 0101.0000 0010 R = R – D = 0000 0101 – 0000 0100 = 0000 0001 > 0
Assign 1 to the lowest bit of [R/Q] 0000 0001.0000 0011
Quotient = 0000 0011two = 3ten lOMoAR cPSD| 58137911
Remainder = 0000 0001two = 1ten e/ 9ten = 0000 1001two 12ten = 0000 1100two Invert 12 and add 1:
1111 0011 + 0000 0001 = 1111 1100two = -12ten
The product is a negative number because the highest bits of 0000 1001 and 1111 1100 are
opposite. We convert operands to positive numbers and do multiplication. Initilization:
- Multiplicand: 12ten = 0000 1100two
- Mulitiplier: 9ten = 0000 1001two
- Product: 0ten = 0000 0000two
- [Product / Multiplier] [P/M] = 0000 0000.0000 1001 Step Multiplicand [Product / Multiplier] 0 0000 1100 0000 0000.0000 1001 1 0000 1100 0000 0000.0000 100[1] Product = Product + Multiplicand = 0000 0001 + 0000 1100 = 0000 1100 Shift right [P/M] 1 bit 0000 1100 0000 0110.0000 0100 2 0000 1100 0000 0110.0000 010[0] Shift right [P/M] 1 bit 0000 1100 0000 0011.0000 0010 3 0000 1100 0000 0011.0000 001[0] Shift right [P/M] 1 bit 0000 1100 0000 0001.1000 0001 lOMoAR cPSD| 58137911 4 0000 1100 0000 0001.1000 000[1] Product = Product + Multiplicand = 0000 0001 + 0000 1100 = 0000 01101 Shift right [P/M] 1 bit 0000 1100 0000 0110.1100 0000 5 0000 1100 0000 0110.1100 000[0] Shift right [P/M] 1 bit 0000 1100 0000 0011.0110 0000 6 0000 1100 0000 0011.0110 000[0] Shift right [P/M] 1 bit 0000 1100 0000 0001.1011 0000 7 0000 1100 0000 0001.1011 000[0] Shift right [P/M] 1 bit 0000 1100 0000 0000.1101 1000 8 0000 1100 0000 0000.1101 100[0] Shift right [P/M] 1 bit 0000 1100 0000 0000.0110 1100
=> Product = 0000 0000 0110 1100two = 108ten Invert 108 and add 1
1111 1111 1001 0011 + 1 = 1111 1111 1001 0100two = -108ten f/ 17ten = 0001 0001 Invert and add 1
1110 1110 + 1 = 1110 1111two = -17ten (Dividend) 5ten = 0000 0101two (Divisor)



