Phân Tích Chi Tiết Bài Tập Chương 2 Môn Kiến trúc máy tính | Đại học Cần Thơ

lOMoAR cPSD| 58137911
Kiến trúc máy tính – CT173 Bài tập chương 2 TS. Lâm Chí Nguyện
(Bài làm có 12 trang)
Họ, tên sinh viên: Phan Văn Đạt Nhóm 02
Mã số sinh viên: B2408782
Bài 1: Trình bày chi tiết biểu diễn số
• -215 bằng phương pháp biểu diễn bù 2 – 9bit
• -25 bằng phương pháp bù K = 127, 8bit Bài giải
Biểu diễn 21510=0110101112
Đổi sang bù 1 của 0110101112 là 1001010002
Đổi sang bù 2 của 1001010002 là 1001010012
Phương pháp bù K = 127 nên 127+(−25)=10210=011001102 Bài tập 2:
Trình bày chi tiết biểu diễn số có dấu chấm động – kết quả biểu diễn hexa code :
• -215.38 bằng chuẩn IEEE-754
• 37.125 bằng chuẩn IEEE-754 Bài giải
-215.38 bằng chuẩn IEEE-754 DEC: -215,38
BIN: ≈−11010111.011000010100100
NORN: −1.1010111011000010100100×27 Signature: 1
Exponent: K+N=127+7=13410=100001102
Fraction: 10101110110000101001000
1 10000110 10101110110000101001000 HEX: C3576148 lOMoAR cPSD| 58137911
37.125 bằng chuẩn IEEE-754 DEC: 37.125 BIN: 100101.001 NORN: 1.00101001×25 Signature: 0
Exponent: K+N=127+5=13210=100001002 Fraction: 00101001000000000000000
01000010000101001000000000000000 HEX: 42148000
Bài tập 3: Trình bày chi tiết trình tự thực hiện giải thuật nhân hai số nguyên • 25 x 19 – 8bit • -11 x 13 - 8bit Bài giải
Trình tự thực hiện giải thuật nhân hai số nguyên 25×19−8bit Iteration Step MP MC Pro 0 Initialization 0001 0011
0000 0000 0001 1001 0000 0000 0000 0000 1 MP[0] = 1, pro = pro + 0001 0011 0000 0000 0001 1001 0000 0000 0001 1001 MC 0000 0000 0011 0010 Shift left MC 0000 1001 Shift right MP 2 MP[0] = 1, pro = pro + 0000 1001 0000 0000 0011 0010 0000 0000 0100 1011 MC 0000 0000 0110 0100 Shift left MC 0000 0100 Shift right MP MP[0] = 0 0000 0100 0000 0000 0110 0100 0000 0000 0100 1011 3 Shift left MC 0000 0000 1100 1000 Shift right MP 0000 0010 MP[0] = 1, pro = pro + 00000010 0000 0000 1100 1000 0000 0000 0100 1011 4 MC 0000 0001 1001 0000 Shift left MC 0000 0001 Shift right MP 5 MP[0] = 1, pro = pro + 0000 0001 0000 0001 1001 0000 0000 0001 1101 1011 MC 0000 0011 0010 0000 Shift left MC 0000 0000 Shift right MP
Trình tự thực hiện giải thuật nhân hai số nguyên −11×13−8bit
Ta thực hiện nhân 2 số 11×13 Iteration Step MP MC Pro 0 Initialization 0000 1101 0000 0000 0000 1011 0000 0000 0000 0000 lOMoAR cPSD| 58137911 1 MP[0] = 1, pro = pro + 0000 1101 0000 0000 0000 1011 0000 0000 0000 1011 MC 0000 0000 0001 0110 Shift left MC 0000 0110 Shift right MP 2 MP[0] = 0 0000 0110 0000 0000 0001 0110 0000 0000 0000 1011 Shift left MC 0000 0000 0010 1100 0000 0000 0010 1100 Shift right MP 0000 0011 3 MP[0] = 1, pro = pro + 0000 0011 0000 0000 0010 1100 0000 0000 0011 0111 MC
0000 0000 0101 1000 0000 0000 0101 1000 Shift left MC 0000 0001 Shift right MP MP[0] = 1, pro = pro + 0000 0001 0000 0000 0101 1000 0000 0000 1000 1111 4 MC 0000 0000 1011 0000 Shift left MC 0000 0000 Shift right MP
Vì −11×13là số âm nên đổi Pro sang bù 2 ta được:
Bù 1: 1111 1111 0111 0000 Bù 2: 1111 1111 0111 0001 Bài tập 4:
Trình bày chi tiết trình tự thực hiện giải thuật nhân cải tiến hai số nguyên • 17 x 19 – 8bit • -13 x 27 – 8bit Bài giải
Trình tự thực hiện giải thuật nhân cải tiến hai số nguyên 17×19−8bit Iteration Step MC Pro 0 Initialization 0001 0011 0000 0000 0001 0001 1 1 1 pro[0] = 1, pro = 0001 0011 0001 0001 pro + MC (left half) 2 2 0000 1001 1000 1000 lOMoAR cPSD| 58137911 shift right pro 2 Pro[0] = 0 0000 1001 1000 1000 Shift right pro 0000 0100 1100 0100 3 pro[0] = 0 0000 0100 1100 0100 shift right pro 0000 0010 0110 0010 4 pro[0] = 0 0000 0010 0110 0010 shift right pro 0000 0001 0011 0001 5 1 1 0001 0100 0011 0001
pro[0] = 1, pro = pro + MC (left half) 0000 1010 0001 1000 2 2 shift right pro 6 pro[0] = 0 0000 1010 0001 1000 shift right pro 0000 0101 0000 1100 7 pro[0] = 0 0000 0101 0000 1100 shift right pro 0000 0010 1000 0110 8 pro[0] = 0 0000 0010 1000 0110 shift right pro 0000 0001 0100 0011
Trình tự thực hiện giải thuật nhân cải tiến hai số nguyên −13×27−8bit
Ta thực hiện nhân 2 số 13×27 Iteration Step MC Pro 0 Initialization 0000 1101 0000 0000 0001 1011 1 1 1 0000 1101 0001 1011
pro[0] = 1, pro = pro + MC (left half) 0000 0110 1000 1101 2 2 shift right pro 2 1 1 pro[0] = 1, pro = 0001 0011 1000 1101 pro + MC (left half) 2 2 0000 1001 1100 0110 Shift right pro 3 pro[0] = 0 0000 1001 1100 0110 shift right pro 0000 0100 1110 0011 4 1 1 0001 0001 1110 0011
pro[0] = 1, pro = pro + MC (left half) 2 2 shift right pro 0000 1000 1111 0001 lOMoAR cPSD| 58137911 5 1 1 0001 0101 1111 0001
pro[0] = 1, pro = pro + MC (left half) 0000 1010 1111 1000 2 2 shift right pro 6 pro[0] = 0 0000 1010 1111 1000 shift right pro 0000 0101 0111 1100 7 pro[0] = 0 0000 0101 0111 1100 shift right pro 0000 0010 1011 1110 8 pro[0] = 0 0000 0010 1011 1110 shift right pro 0000 0001 0101 1111
Vì −13×27 là số âm nên ta đổi pro sang bù 2 Bù 1: 1111 1110 1010 0000 Bù 2: 1111 1110 1010 0001 Bài tập 5:
Trình bày chi tiết giải thuật chia hai số nguyên • 25 : 4 – 6bit • 46 : 13 – 6bit 25 : 4 – 6bit Bài giải Iteration Step DIVD DIVS QUOT REM 0 Initialization 011 001 000 100 000 000 000 000 000 000 011 001 1 REM = REM – DIVS 111 100 011 001 REM < 0, REM = REM + DIVS 000 000 011 001 Shift left QUOT 000 000 Shift right DIVS 000 010 000 000 2 REM = REM – DIVS 111 110 011 001 REM < 0, REM = REM + DIVS 000 000 011 001 Shift left QUOT 000 000 lOMoAR cPSD| 58137911 Shift right DIVS 000 001 000 000 3 REM = REM – DIVS 111 111 011 001 REM < 0, REM = REM + DIVS 000 000 011 001 Shift left QUOT 000 000 Shift right DIVS 000 000 100 000 4 REM = REM – DIVS 111 111 111 001 REM < 0, REM = REM + DIVS 000 000 011 001 Shift left QUOT 000 000 Shift right DIVS 000 000 010 000 5 REM = REM – DIVS 000 000 001 001 REM > 0 shift left QUOT 000 000 QUOT[0] = 1; 000 001 000 000 001 000 Shift right DIVS 6 REM = REM – DIVS 000 000 000 001 REM > 0 shift left QUOT 000 010 QUOT[0] = 1; 000 011 Shift right DIVS 000 000 000 100 7 REM = REM – DIVS 111 111 111 101 REM < 0, REM = REM + DIVS 000 000 000 001 Shift left QUOT 000 110 Shift right DIVS 000 000 000 010 lOMoAR cPSD| 58137911 Iteration Step DIVD DIVS QUOT REM 0 Initialization 101 110 001 101 000 000 000 000 000 000 101 110 1 REM = REM – DIVS 110 011 101 110 REM < 0, REM = REM + DIVS 000 000 101 110 Shift left QUOT 000 000 Shift right DIVS 000 110 100 000 2 REM = REM – DIVS 111 010 001 110 REM < 0, REM = REM + DIVS 000 000 101 110 Shift left QUOT 000 000 Shift right DIVS 000 011 010 000 3 REM = REM – DIVS 111 101 010 000 REM < 0, REM = REM + DIVS 000 000 101 110 Shift left QUOT 000 000 000 001 101 000 Shift right DIVS 000 001 101 000 4 REM = REM – DIVS 111 111 000 110 REM < 0, REM = REM + DIVS 000 000 101 110 Shift left QUOT 000 000 000 000 110 100 Shift right DIVS 000 000 110 100 5 REM = REM – DIVS 111 111 111 010 000 000 101 110 REM < 0, REM = REM + DIVS 000 000 011 010 000 000 Shift left QUOT Shift right DIVS 000 000 011 010 lOMoAR cPSD| 58137911 6 REM = REM – DIVS 000 000 010 100 REM > 0 shift left QUOT 000 000 001 101 46 : 13 – 6bit lOMoAR cPSD| 58137911 QUOT[0] = 1; 000 001 Shift right DIVS 000 000 001 101 7 REM = REM – DIVS 000 010 000 000 000 111 REM > 0 shift left QUOT 000 011 QUOT[0] = 1; Shift right DIVS 000 000 000 110
Bài tập 6: Trình bày chi tiết trình tự thực hiện giải thuật cộng hai số float IEEE 754 • 134.25 + 46.5 • -246.31 + 54.125
Kết quả trình bày dưới dạng Hexa code Bài giải
Cộng hai số float 134.25 + 46.5 theo IEEE
Ta đổi 134.25 và 46,5 ta được
134.25 01000011000001100100000000000000
46,5 01000010001110100000000000000000
So sánh 2 exponent 10000110 và 10000100 số 10000110>10000100
Dịch phải số nhỏ hơn 2 lần: 1.011101→0.01011101
Exponent tăng lên 2: 10000100→10000110
Cộng 2 significant 1.000011001000+0.01011101=1.011010011000
Chuẩn hóa 0100001100110100110000000000000 HEX: 4334C000
Ta đổi -246.31 và 54.125 sang IEEE ta được
-246.31 11000011011101100100111101011100
54.125 01000010010110001000000000000000
So sánh 2 exponent 10000110 và 10000100 10000110>10000100
Dịch phải số nhỏ hơn 2 lần: 1.10110001→0.0110110001
Exponent tăng lên 2: 10000100→10000110 Trừ
2 significant do -246.31 là số âm
1.11101100100111101011100−0.0110110001=¿1. 10000000010111101011100 Chuẩn hóa
11000011010000000010111110101110 HEX: C3402FAE
Bài tập 7: Trình bày chi tiết trình tự thực hiện giải thuật nhân hai số float IEEE 754 lOMoAR cPSD| 58137911 • 24.25 x 37.75 • -24.6 x 14.7 Bài giải Ta
đổi 2 số 24.25 và 37.75 sang IEEE ta được:
24.25 01000001110000100000000000000000
37.75 01000010000101110000000000000000
Cộng 2 số exponent sau đó trừ đi 127
10000011+10000100−01111111=10001000 Nhân 2 significand
1.100001×1.0010111=1.1100100110111 Chuẩn hóa
Kết quả là 01000100011001001101110000000000 HEX: 4464DC00
Ta đổi 2 số -24.6 x 14.7 sang IEEE ta được:
-24.6 1 10000011 10001001100110011001101
14, 7 0 10000010 11010110011001100110011
Cộng 2 số exponent sau đó trừ đi 127 ta được
10000011+10000010−01111111=10000110 Nhân 2 significand
1.1000100110011001100×1.1101011001100110011 ¿10.1101001100111101011100 Chuẩn hóa 1.01101001100111101011100 Exponent = 10000111
Kết quả 11000011101101001100111101011100 HEX: 43B4CF5C Bài tập 8:
Trình bày chi tiết trình tự thực hiện giải thuật chia hai số float IEEE 754 • 635.72 : 46.63
• 34.5 : 3.25 Kết quả trình bày dưới dạng Hexa code Bài giải lOMoAR cPSD| 58137911
Ta đổi 635.72 và 46.63 sang IEEE
635.72 0 10001000 00111101110111000010100
46.63 0 10000100 01110101000010100011111
Trừ 2 exponent rồi cộng cho 127
10001000 – 10000100 + 01111111 = 10000011 Chia 2 significant
1.00111101110111000010100 / 1.01110101000010100011111 = 0.110100111011011001 Chuẩn hóa 1.10100111011011001 Giảm exponent 10000010
Kết quả 0 10000010 10100111011011001000000 HEX 4153B640
Ta đổi 34.5 và 3.25 sang IEEE ta được
34.5 0 10000100 00010100000000000000000
3.25 0 10000000 10100000000000000000000
Ta trừ exponent rồi cộng cho 127 ta được
10000100 – 10000000 + 01111111 = 1000011 Ta chia 2 significant
1.00010100000000000000000 / 1.10100000000000000000000 = 0.101010001111010111 Chuẩn hóa: 1.01010001111010111 Exponent: 10000010
0 10000010 01010001111010111000000 HEX: 4128F5C0 Bài tập 9:
Trình bày so sánh kết quả biểu diễn số -167 dưới các dạng biểu diễn số âm: - Bit dấu - Bù 1 - Bù 2 - Thừa k = 255 Số có 9 bit Bài giải lOMoAR cPSD| 58137911
Đổi 167 sang nhị phân ta được 101001112
Vì -167 là số âm nên bit dấu là 1 do đó -167 = 1101001112
Bù 1 của -167 là 1010110002
Bù 2 của -167 là 1010110012
Thừa số K = 255 nên 255+(−167)=88=0010110002
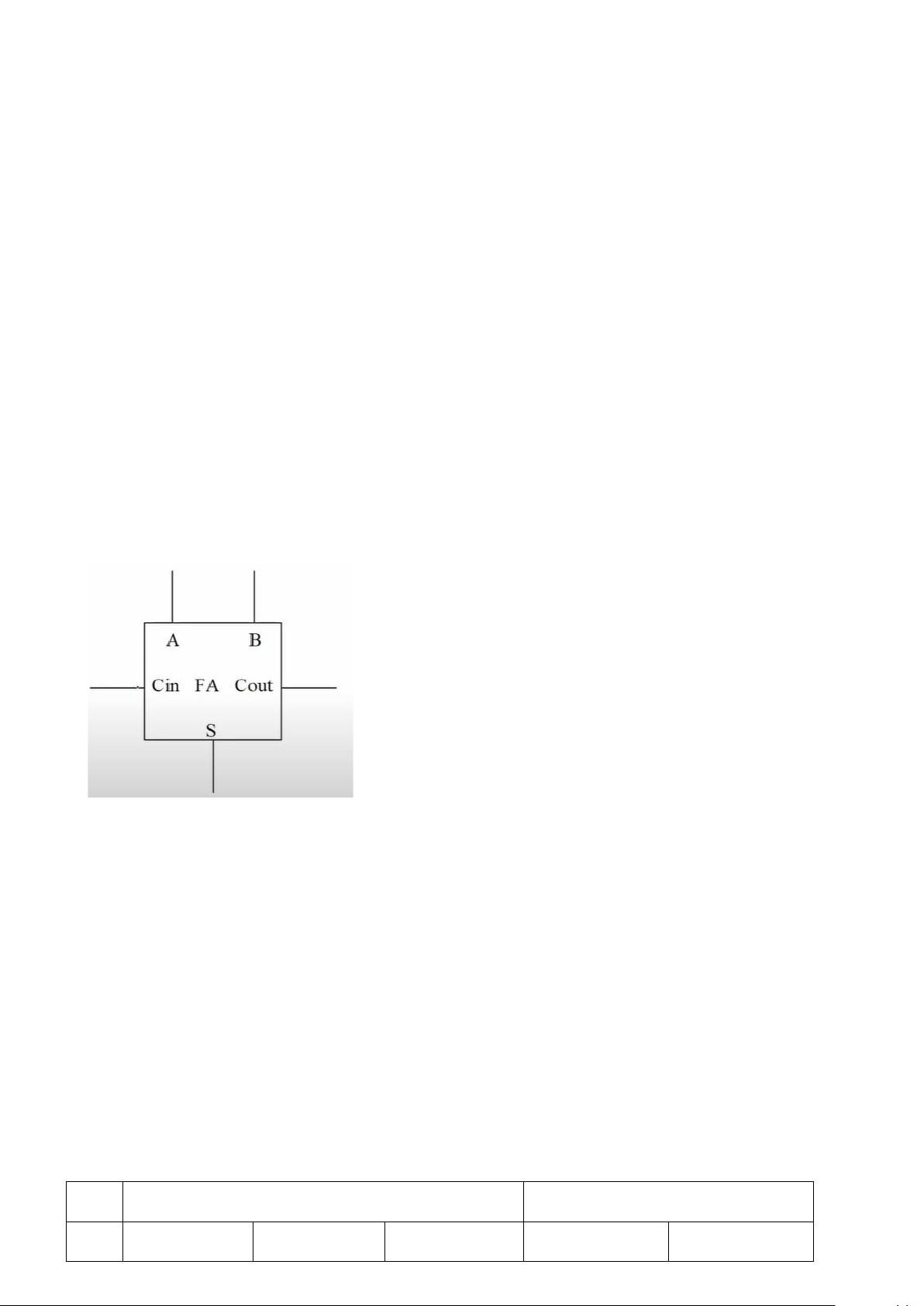
Bài tập 10: Trình bày chi tiết Mạch cộng toàn phần hai số nguyên 5bit Bài giải Trong đó: + Đầu vào:
An là bit thứ i của số thứ nhất.
Bn là bit thứ i của số thứ hai.
Cin là bit nhớ từ phép cộng bit trước đó (n – 1). + Đầu ra:
Sn là kết quả tổng của bit hiện tại.
Cout là bit nhớ sinh ra để truyền cho bit tiếp theo (n + 1 ).
Giả sử A và B có 5 bit: A = 10011 và B = 10101 Ta sẽ có bảng như sau Đầu vào Đầ u ra Bit Cin An Bn Cout S lOMoAR cPSD| 58137911 0 0 1 1 1 0 1 1 1 0 1 0 2 1 0 1 1 0 3 1 0 0 0 1 4 0 1 1 1 0 Ta có sơ đồ mạch sau:
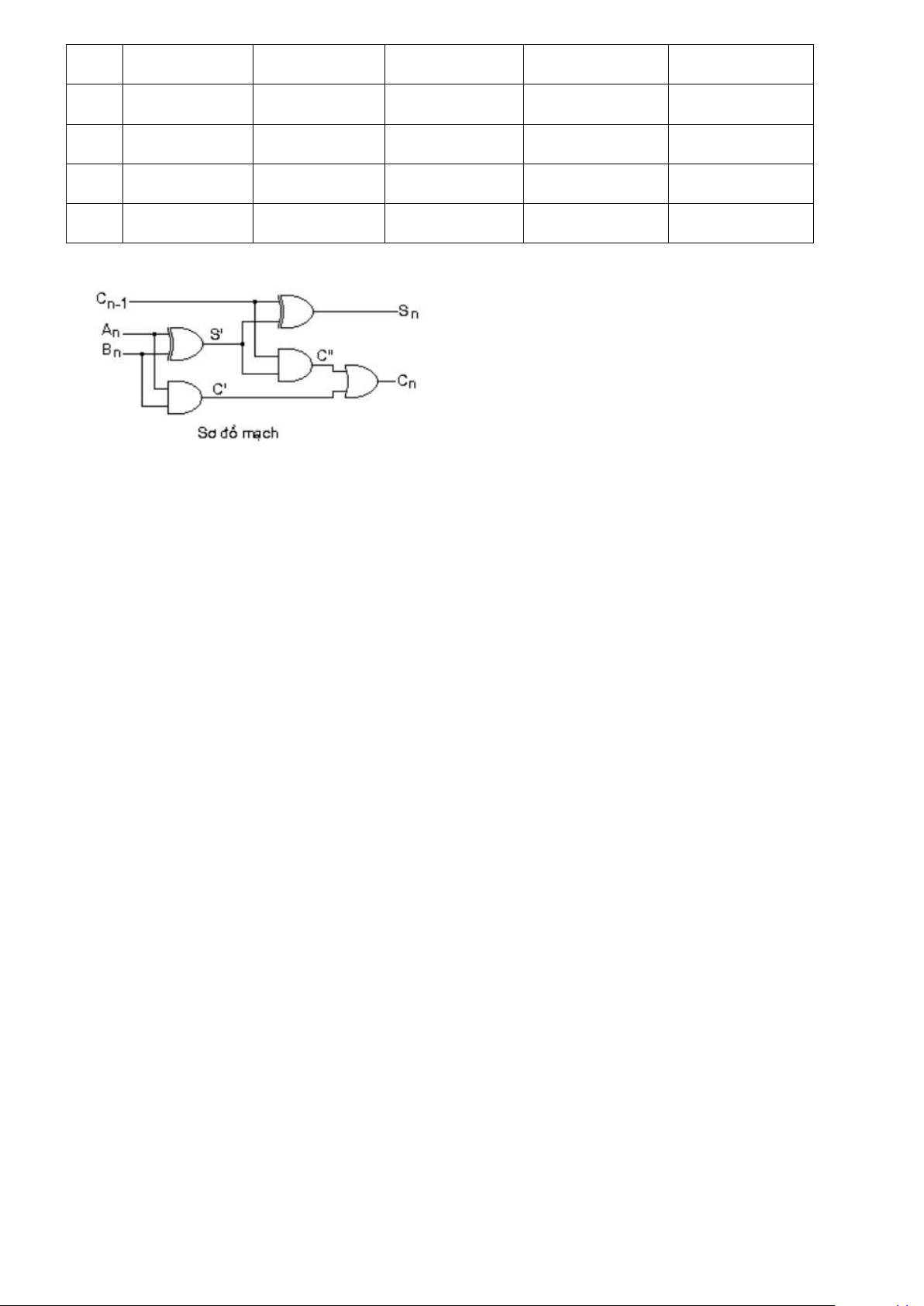
Từ sơ đồ mạch ta có thể tính được:
Sn = XOR(S’, Cn-1) mà S’ = XOR(An, Bn) Cn = OR(C’’, C’) Trong đó C’’ = AND(S’, Cn-1 ) C’ = AND(An, Bn)