Công thức, cách tính tỉ số lượng giác của góc nhọn dễ hiểu nhất

Công thức, cách tính tỉ số lượng giác của góc nhọn dễ hiểu nhất
I. Công thức tính tỉ số lượng giác của góc nhọn
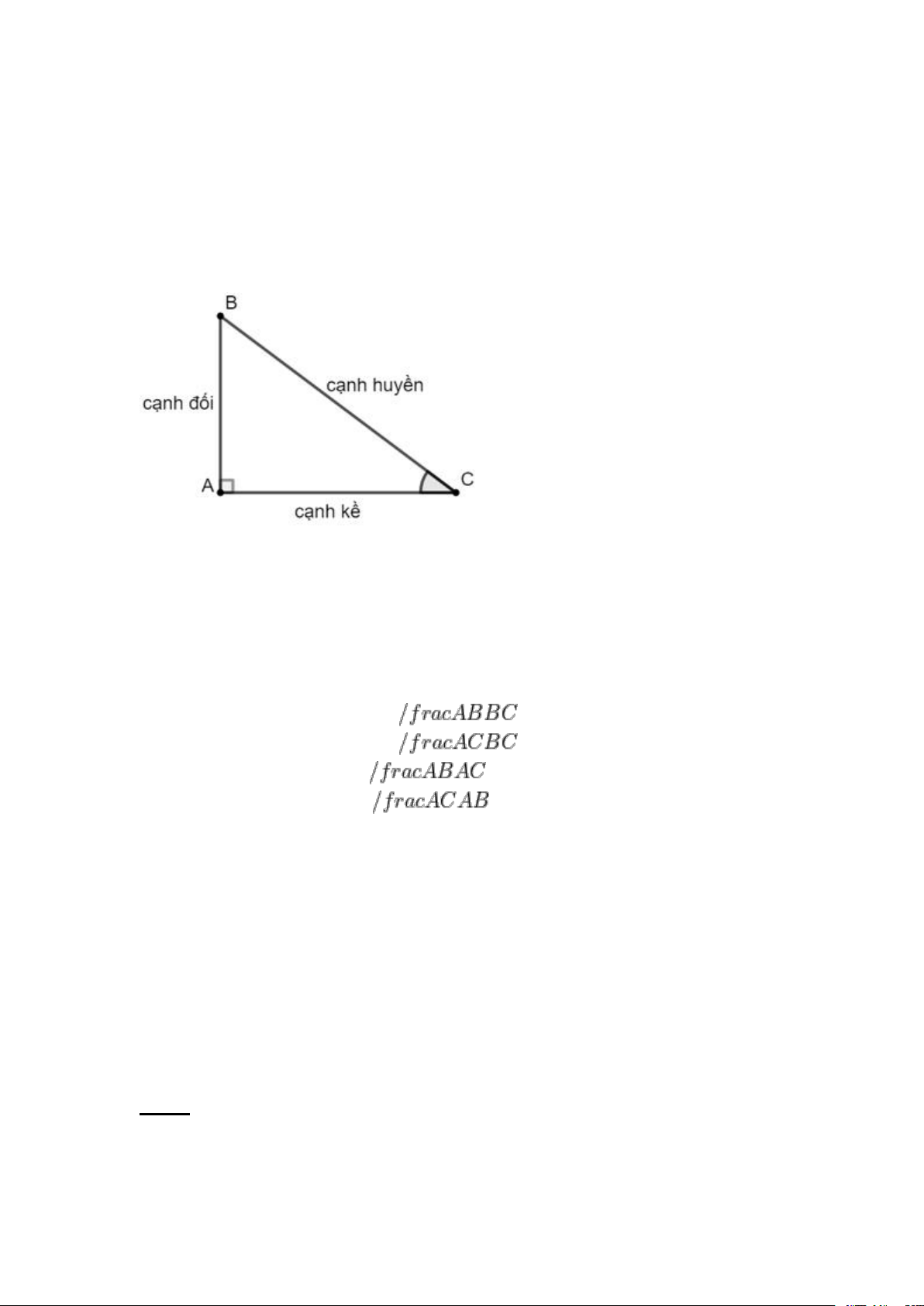
1. Cho góc nhọn α, từ một điểm bất kì trên một cạnh của góc α, kẻ
đường vuông góc với cạnh kia. Khi đo:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của goc α, kí hiệu là sinα.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của goc α, kí hiệu là cosα.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của goc α, kí hiệu là tanα.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của goc α, kí hiệu là cotα.
sinα = cạnh đối : cạnh huyền =
cosα = cạnh kề : cạnh huyền =
tanα = cạnh đối : cạnh kề =
cotα = Cạnh kề : cạnh đối =
2. Nếu hai góc phụ nhau (có tổng số đo bằng 900) thì: sin góc này bằng
cos góc kia, tan góc này bằng cot góc kia
• Xác định cạnh đối, cạnh kề, cạnh huyền, viết tỉ số lượng giác theo định nghĩa
• Tính cạnh còn lại nhờ hệ thức Py – ta – go hoặc hệ thức về cạnh, đường cao
• Tính tỉ số lượng giác còn lại theo định lí tỉ số lượng giác hai goc phụ nhau
B. Bài tâp vân dụng liên quan
Bài 1: Rút gọn và tính biểu thức sau:
A = sin15° – sin60° + cos30° – cos75° + 5 Hướng dẫn giải:
A = sin15° – sin60° + cos30° – cos75° + 5
= (sin15° – cos75°) + (cos30° – sin60°) + 5
Áp dụng tính chất tỉ số lượng giác ta co:
15° + 75° = 90° ⇒ sin15° = cos75°
30° + 60° = 90° ⇒ sin60° = cos30°
⇒ (sin15° – cos75°) + (cos30° – sin60°) + 5 = 0 + 0 + 5 = 5
Bài 2: Rút gọn và tính biểu thức sau: A = + cot24°.cot66° + cos²82° Hướng dẫn giải: A = + cot24°.cot66° + = ( + + cot24°.cot66°
Áp dụng tính chất tỉ số lượng giác goc nhọn ta co: ​ + ° = 1
24° + 66° = 90° ⇒ cot66° = tan24°
⇒ cot24°.cot66° = tan24°.cot24° = 1 ⇒ A = 1 + 1 = 2
Bài 3: Cho tam giác ABC với goc ABC bằng 90 độ. Co AC = 10cm, cosBAC =
1/2. Tính sinBAC và độ dài cạnh AB và BC.
Lời giải chi tiết: + = 1 suy ra = 1 - Suy ra sinBAC = Thay cosBAC = ta co: => sinBAC =
Do sinBAC > 0 vi goc BAC nhọn Ta lại co cosBAC = AB : AC Suy ra AB = AC . cosBAC Thay cosBAC = , AC = 10 cm ta co: AB = 10 . 1/2 = 5 (cm) +) MA sinBAC = BC : AC Suy ra BC = AC . sinBAC Thay số sinBAC = , AC = 10 cm, ta co BC = 10 . = (cm)
Bài 4: Cho tam giác ABC với goc BAC bằng 90 độ . Biết AB = 6cm, AC = 8cm.
Tính sinABC, cos ABC, tan ABC, cotABC Hướng dân giai:
+) Áp dụng định ly Py - ta - go ta co:
Thay số AB = 6cm, AC = 8cm ta co: Suy ra = 100 (cm) => BC = 10 (cm)
Áp dụng tỉ số lương giác của goc nhọn ta co: sinABC = AC : BC = cosABC = AB : BC = tanABC = AC : AB = cotABC = AB : AC =
Bài 4: Cho tam giác ABC vuông tại C, trong đo AC = 0,9m, BC = 1,2 m. Tính
các tỉ số lượng giác của goc B, từ đo suy ra các tỉ số lượng giác của goc A. Lời giai chi tiết:
Theo định ly Py - ta - go ta co: = 2,25 => AB = 1,5
SinB = AC : AB = 0,9 : 1,5 = 0,6
cosB = BC : AB = 1,2 : 1,5 = 0,8
tanB = AC : BC = 0,9 : 1,2 = 0,75 CotB = 1,2 : 0,9 =
Vi goc A và goc B là hai goc phụ nhau, nên ta co sin goc này bằng cos goc
kia, tan goc này bằng cot goc kia: CosA = 0,6 SinA = 0,8 CotA = 0,75 tanA = ​ Bài 5:
Dựng goc nhọn α, biết: a) sin α = 2/3
Vi sin α = đối/huyền nên ta cần vẽ các cạnh đối và cạnh huyền co tỉ lệ là 2/3.
Ta dựng một tam giác vuông co cạnh goc vuông dài 2 cm, cạnh huyền dài 3
cm, goc đối diện với cạnh goc vuông đo là goc α. b) cos α = 0,6
cos α = 0,6 = 3/5 = kề/ huyền nên ta cần vẽ các cạnh kề và cạnh huyền co tỉ lệ là 3/5
Ta dựng một tam giác vuông co cạnh goc vuông dài 3 cm, cạnh huyền dài 5
cm, goc kề với cạnh goc vuông vừa vẽ là goc α. c) tan α = 3/4
tan α = đối/kề nên ta cần vẽ các cạnh đối và kề co tỉ lệ là 3/4.
Ta dựng một tam giác vuông co 1 cạnh goc vuông là 3 cm, 1 cạnh goc vuông
là 4 cm, goc đối diện với cạnh goc vuông dài 3 cm là goc α . d) cot α = 3/2
cot α = kề/đối nên ta cần vẽ các cạnh kề và đối co tỉ lệ 3/2.
Ta dựng một tam giác vuông co 1 cạnh goc vuông là 3 cm, 1 cạnh goc vuông
là 2 cm, goc đối diện với cạnh goc vuông dài 2 cm là goc α .
Bài 6: Cho tam giác ABC co AB = 26 cm, AC = 25 cm, đường cao AH = 24 cm. Tính cạnh BC
Bài 7: Cho tam giác ABC cân(AB = AC) và đường tròn tâm O tiếp xúc với hai
cạnh AB và AC lần lượt ơ B và C. Từ điểm M trên cung nho BC (M khác B và
C) ke MD, ME, MF lần lượt vuông goc với các đường thăng BC, CA, AB
A, Chứng minh các tứ giác MDBF, MBCE nội tiếp
B, Chứng minh các tam giác DBM và ECM đông dangj
C, Cho goc BAC = 60 độ à AB = 2, tinh bán kính đường tròn tâm O
Bài 8: Cho hinh thang ABCD, biết đáy AB = a và CD = 2a; cạnh bên AD = a , goc A = 90 độ a, Chứng minh tanC = 1
B, Tính tỉ số diện tích tam giác DBC và diện tích hinh thang ABCD
C, Tinh tỉ số diện tích tam giác ABC và diện tích tam giác DBC
Bài 9 : Cho tam giác ABC vuông tại A. Biết cos B = 0,8, hãy tính các tỉ số lượng giác của goc C. Hướng dân giai:
Ta nhớ rằng goc B và goc C là hai goc phụ nhau. Vi thế sin C = cos B = 0,8.
Mà theo bài 14, sin² C + cos² C = 1
Vi thế cos² C = 1 – 0,8 ² = 0,36 cos C = 0,6 tan C = sin C/cos C = 4/3 cot C = 1/tan C = 3/4
Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. Hãy tính sin B và sin
C và làm tròn kết qua đến chữ số thập phân thứ tư trong các trường hợp sau: a) AB = 13 cm, BH = 0,5 dm; b) BH = 3 cm, CH = 4 cm
Bài 11: Cho tam giác ABC vuông tại A, goc C = 30º, BC = 10 cm. a) Tính AB, AC
b) Ke từ A các đường thăng AM,AN lần lượt vuông goc với các đường phân
giác trong và ngoài của goc B. Chứng minh rằng MN = AB.
c) Chứng minh các tam giác MAB và ABC đông dạng. Tỉ số đông dạng.
Bài 12: Săp xếp các tỉ số lượng giác sau theo thứ tự tăng dần: A, sin78, cos14, sin47, cos87 B, tg73, cot25, tan62, cot38 Hướng dẫn giải:
a) Ta sẽ đổi tất ca sang 1 loại tỉ số lượng giác: cos 14º = sin 76º ; cos 87º = sin 3º
Vi a tăng từ 0º đến 90º thi sin a tăng, nên ta co:
sin 3º < sin 47º < sin 76º < sin 78º
b) Ta sẽ đổi tất ca sang 1 loại tỉ số lượng giác: cot 25º = tan 65º ; cot 38º = tan 52º
Vi a tăng từ 0º đến 90º thi tan a tăng, nên ta co:
Vi a tăng từ 0º đến 90º thi sin a tăng, nên ta co:
tan 52 º < tan 62 º < tan 65 º < tan 73 º
Document Outline

• Công thức, cách tính tỉ số lượng giác của góc nhọn
  • I. Công thức tính tỉ số lượng giác của góc nhọn
  • B. Bài tập vận dụng liên quan